R语言入门基础教程
《R语言数据分析》课程教案(全)

《R语言数据分析》课程教案(全)第一章:R语言概述1.1 R语言简介介绍R语言的发展历程、特点和应用领域讲解R语言的安装和配置1.2 R语言基本操作熟悉R语言的工作环境学习如何创建、保存和关闭R剧本掌握R语言的基本数据类型(数值型、字符串、逻辑型、复数、数据框等)1.3 R语言的帮助系统学习如何使用帮助文档(help()、?、man()函数)掌握如何搜索和安装R包第二章:R语言数据管理2.1 数据导入与导出学习如何导入CSV、Excel、txt等格式的数据掌握如何将R数据导出为CSV、Excel等格式2.2 数据筛选与排序掌握如何根据条件筛选数据学习如何对数据进行排序2.3 数据合并与分割讲解数据合并(merge、join等函数)的方法和应用场景讲解数据分割(split、apply等函数)的方法和应用场景第三章:R语言统计分析3.1 描述性统计分析掌握R语言中的统计量计算(均值、中位数、标准差等)学习如何绘制统计图表(如直方图、箱线图、饼图等)3.2 假设检验讲解常用的假设检验方法(t检验、卡方检验、ANOVA等)掌握如何使用R语言进行假设检验3.3 回归分析介绍线性回归、逻辑回归等回归分析方法讲解如何使用R语言进行回归分析第四章:R语言绘图4.1 ggplot2绘图系统介绍ggplot2的基本概念和语法学习如何使用ggplot2绘制柱状图、线图、散点图等4.2 基础绘图函数讲解R语言内置的绘图函数(plot、barplot、boxplot等)掌握如何自定义图形和调整图形参数4.3 地图绘制学习如何使用R语言绘制地图讲解如何使用ggplot2绘制地理数据可视化图第五章:R语言编程5.1 R语言编程基础讲解R语言的变量、循环、条件语句等基本语法掌握如何编写R函数和模块化代码5.2 数据框操作学习如何使用数据框进行编程讲解如何使用dplyr等工具包进行数据框操作5.3 面向对象编程介绍R语言的面向对象编程方法掌握如何使用R6和S3编程范式第六章:R语言时间序列分析6.1 时间序列基础介绍时间序列数据的类型和结构学习时间序列数据的导入和预处理6.2 时间序列分解讲解时间序列的分解方法,包括趋势、季节性和随机成分使用R语言进行时间序列分解6.3 时间序列模型介绍自回归模型(AR)、移动平均模型(MA)、自回归移动平均模型(ARMA)和自回归积分滑动平均模型(ARIMA)学习如何使用R语言建立和预测时间序列模型第七章:R语言机器学习7.1 机器学习概述介绍机器学习的基本概念、类型和应用学习机器学习算法选择的标准和评估方法7.2 监督学习算法讲解回归、分类等监督学习算法使用R语言实现监督学习算法7.3 无监督学习算法介绍聚类、降维等无监督学习算法使用R语言实现无监督学习算法第八章:R语言网络分析8.1 网络分析基础介绍网络分析的概念和应用领域学习网络数据的导入和预处理8.2 网络图绘制讲解如何使用R语言绘制网络图学习使用igraph包进行网络分析8.3 网络分析应用介绍网络中心性、网络结构等分析方法使用R语言进行网络分析案例实践第九章:R语言生物信息学应用9.1 生物信息学概述介绍生物信息学的概念和发展趋势学习生物信息学数据类型和常用格式9.2 生物序列分析讲解生物序列数据的导入和处理使用R语言进行生物序列分析9.3 基因表达数据分析介绍基因表达数据的特点和分析方法使用R语言进行基因表达数据分析第十章:R语言项目实战10.1 数据分析项目流程介绍数据分析项目的流程和注意事项10.2 R语言项目实战案例一分析一个真实的统计数据集,实践R语言数据分析方法10.3 R语言项目实战案例二使用R语言解决实际问题,如商业分析、社会研究等10.4 R语言项目实战案例三结合数据库和API接口,进行大规模数据分析和处理重点和难点解析重点环节1:R语言的安装和配置解析:R语言的安装和配置是学习R语言的第一步,对于初学者来说,可能会遇到操作系统兼容性、安装包选择等问题。
R语言入门教程

R语言入门教程R语言是一种功能强大的统计计算和图形化编程语言,广泛应用于数据科学、统计分析、机器学习等领域。
本教程旨在帮助初学者快速入门R语言,并提供基础知识和实际应用示例。
第一章:R语言简介1.1 R语言的起源和发展1.2 R语言的特点和优势1.3 R语言的应用领域和前景第二章:R语言的安装与环境配置2.1 下载和安装R语言2.2 R语言的集成开发环境(RStudio)配置2.3 R语言的包管理器和常用包的安装第三章:基本语法和数据结构3.1 R语言的基本数据类型3.2 变量和赋值操作3.3 基本数学运算和逻辑运算3.4 控制流程语句(if-else, for, while等)3.5 R语言的数据结构:向量、矩阵、数据框和列表第四章:数据导入与导出4.1 从文本文件导入数据4.2 从Excel文件导入数据4.3 从数据库导入数据4.4 将数据输出为文本、Excel或数据库文件第五章:数据处理与清洗5.1 缺失值的处理5.2 异常值的检测和处理5.3 数据转换和重塑5.4 数据合并和拆分第六章:数据可视化6.1 基本图形绘制函数6.2 高级图形包(ggplot2)的使用6.3 图形参数调整和自定义第七章:统计分析和建模7.1 常用统计分析方法的实现7.2 聚类分析和主成分分析7.3 线性回归和逻辑回归模型7.4 机器学习算法(如随机森林、支持向量机)的应用第八章:R语言编程高级技巧8.1 函数的定义和调用8.2 自定义包的创建和使用8.3 面向对象编程(OOP)的实现8.4 并行计算和代码优化技巧第九章:实际案例分析9.1 数据挖掘和预测建模9.2 金融风险管理分析9.3 生物信息学数据处理和分析9.4 社交网络分析和可视化第十章:进阶学习资源推荐10.1 R语言官方文档和在线教程10.2 统计学和数据科学相关书籍推荐10.3 开源R语言项目和社区资源通过本教程的学习,读者将能够掌握R语言的基本语法和数据结构,能够进行数据的导入、处理、可视化和统计分析,在实际应用中能够解决问题和开展研究。
R语言数据科学入门教程

R语言数据科学入门教程第一章:R语言介绍与安装1.1 R语言的历史和发展R语言起源于新西兰奥克兰大学的S语言,经过多年的发展和优化,成为一种功能强大且广泛使用的数据分析和统计编程语言。
1.2 R语言的特点介绍R语言的开源性、跨平台性、扩展性以及丰富的统计分析和数据可视化功能。
1.3 R语言的安装和配置详细介绍如何下载、安装和配置R语言及其相关的集成开发环境(IDE),例如RStudio。
第二章:R语言基础2.1 R语言的基本语法和命令行界面介绍R语言的基本语法规则,解释如何使用R语言的命令行界面进行交互式编程。
2.2 变量和向量介绍R语言中变量的定义和使用方法,以及如何创建和操作向量。
2.3 数据类型和数据结构详细介绍R语言的不同数据类型(如数值型、字符型、逻辑型等),以及常见的数据结构(如数组、矩阵、数据框等)。
2.4 条件语句和循环介绍在R语言中如何使用条件语句(如if-else语句)和循环语句(如for循环和while循环)。
第三章:数据处理与清洗3.1 数据导入与导出介绍如何使用R语言导入和导出各种常见格式的数据文件,包括CSV、Excel、JSON等。
3.2 数据读取和预览介绍如何使用R语言读取和预览数据,包括查看数据的前几行、数据结构和摘要统计信息等。
3.3 缺失值处理介绍如何处理数据中的缺失值,包括删除含有缺失值的观测值或变量、插补缺失值等方法。
3.4 数据变换和重构介绍如何使用R语言对数据进行变换和重构,包括变量转换、数据透视表和合并数据集等操作。
第四章:数据分析与可视化4.1 描述性统计分析介绍如何使用R语言进行常见的描述性统计分析,例如计算均值、中位数、标准差等。
4.2 统计图表绘制详细介绍R语言中的数据可视化功能,包括绘制直方图、散点图、折线图、箱线图等常见图表。
4.3 统计推断和假设检验介绍如何使用R语言进行统计推断和假设检验,包括t检验、方差分析、回归分析等常见的假设检验方法。
aqaqwfdewf3rf4r2t5675j76j''76j-764=y[p42f4ffvf3lfpo2kf-]2-01o-2ed3e41fdede31deqd (2)
![aqaqwfdewf3rf4r2t5675j76j''76j-764=y[p42f4ffvf3lfpo2kf-]2-01o-2ed3e41fdede31deqd (2)](https://img.taocdn.com/s3/m/f30b033df7ec4afe05a1df44.png)
张然
R的获取和安装
1、R可以在CRAN(Comprehensive R Archive Network)上免费下载
2、在https:///下载RStudio
R 的使用
1、R是一种区分大小写的解释型语言,一次交互 式会话期间的所有数据对象都被保存在内存中。
2、示例及帮助函数help.start()
3、输入与输出
R 的工作空间
1、工作空间(workspace)就是当前R的工作环 境,它储存着所有用户定义的对象(向量、矩阵、 函数、数据框、列表) 。在一个R会话结束时, 你可以将当前工作空间保存到一个镜像中,并在 下次启动R时自动载入它。
2、使用函数getwd()来查看当前的工作目录
3、使用函数setwd()设定当前的工作目录
R 的包的
格式组成的集合。计算机上存储包的目录称为库 (library)。library()则可以显示库中有哪些包。 2、从/web/packages下载。 3、使用命令install.packages()即可 4、例如,要使用gclus包,执行命令library(gclus)即可。 5、使用命令update.packages()可以更新已经安装的包。
结束语
本章的学习保证了R语言的正常运行。在下一章 中,我们将着眼于R能够处理的各种数据类型。
R语言入门操作(2)

通过Lasso 来进⾏行行压缩估计和变量量选择2018年年9⽉月24⽇日⽥田甜参数估计与假设检验2019年年4⽉月28⽇日 ⽥田甜CONTENTS01 02 03Rstudio 参数估计假设检验01Rstudio•R,解释器器,IDE的关系R是⼀一种解释型语⾔言,不不需要编译的过程,代码的翻译和执⾏行行是同步的,R不不需要编译器器但需要解释器器图形界⾯面程序(GUI)除了了引⽤用了了解释器器到它主要窗⼝口中外,还实现了了编辑器器,图形展示和快捷按钮等功能,⼀一个GUI程序只需提供对R语⾔言常⽤用功能的图形化包装即可被称R的GUIGUI如果在⼀一个窗⼝口中包括了了解释器器、编辑器器和图形展示等功能则可被称为IDERstudio是⼀一个优秀的R IDE•选择⼀一个适合⾃自⼰己的IDE(Integrated Development Environment)•控制台•⼯工作空间和历史窗⼝口•画图和帮助窗⼝口2.1参数估计-点估计•矩估计因为不不同的分布有不不同的参数,所以在R 的基本包中并没有给出现成的函数,⼀一般要转化为⽅方程组求解:例例:设随机变量量X 服从[ , ]的均匀分布,现有n 个样本, ,估计两个参数解:⽤用样本⼀一阶矩(样本均值)估计总体均值,样本⼆二阶矩(样本⽅方差)估计总体⽅方差,即⽤用rootSolve 包中的函数multiroot()求解⽅方程组install.packages('rootSolve') # 安装rootSolve 程序包library(rootSolve) # 载⼊入包θ2x 1,...,x n θ1E (X )=θ1+θ22=¯x Var (X )=(θ2−θ1)212=1n n ∑i =1(x 1−¯x )2=S 2•输⼊入样本数据,计算样本⼀一阶矩和⼆二阶矩程序运⾏行行结果(采⽤用迭代的⽅方式,因此需要给出初始值)x = c(4, 5, 2, 9, 5, 1, 6, 4, 6, 2)mu = mean(x) # ⼀一阶矩var = sum((x - mean(x)) ^ 2) / 10 # ⼆二阶矩•构建⽅方程组model = function(theta, mu, var){c(F1 = theta[1] + theta[2] - 2 * mu,F2 = (theta[2] - theta[1]) ^ 2 / 12 - var)}•调⽤用函数进⾏行行求解(详细的参数说明可⽤用?multiroot命令来查看)multiroot(f=model,start=c(0,10),mu=mu,var=var)•法⼀一:写出似然函数,求偏导转换为⽅方程组,求解⽅方程组•例例:设X 服从正态分布 ,为来⾃自总体的⼀一组样本,⽤用极⼤大似然估计参数解:似然函数为:求偏导可得:N (μ,σ2)x 1,...,x n L (μ,σ2;x )=n ∏i =1f (x i ;μ,σ2)=(2πσ2)−n /2exp [−12σ2n∑i =1(x i −μ)2]∂lnL (μ,σ2;x )∂μ=−1σ2n ∑i =1(x i −μ)=0∂lnL (μ,σ2;x )∂σ2=−n 2σ2+12σ4n ∑i =1(x i −μ)2=0•输⼊入数据程序运⾏行行结果set.seed(1) # 设置随机种⼦子x = rnorm(10) # ⽣生成10个服从标准正态分布的随机数•构建⽅方程组model = function(e,x){n = length(x)c(F1 = sum(x - e[1]),F2 = - n + sum((x - e[1]) ^ 2) / e[2] ^ 2)}•调⽤用函数进⾏行行求解multiroot(f=model,start=c(0,1),x=x)•法⼆二:写出对数似然函数,调⽤用maxLik 包中的函数maxLik 。
r语言入门教程

r语言入门教程R语言是一种广泛应用于数据分析和统计建模的编程语言。
它具有丰富的数据处理和可视化功能,是许多数据科学家和统计学家的首选工具之一。
R语言的基本语法与其他编程语言有些不同,但学习起来并不困难。
以下是一些入门级别的R语言基础知识,帮助你开始使用R进行数据分析和可视化。
1. 安装R和RStudio:首先,你需要下载并安装R语言。
然后,建议安装RStudio,它是一个集成开发环境,可以更好地管理和组织你的R代码和数据。
2. 使用RStudio:当你打开RStudio时,你会看到几个窗口,包括代码编辑器和R控制台。
在代码编辑器中编写代码,然后按下Ctrl + Enter键或点击"Run"按钮来执行代码。
结果将显示在R控制台中。
3. 变量赋值和基本操作:在R中,你可以使用"="或"<-"符号将值分配给变量。
例如,x <- 10会将值10分配给变量x。
你可以使用实数、整数、字符等数据类型。
4. 向量和矩阵:R中的向量是一系列具有相同数据类型的元素。
你可以使用c()函数创建向量,例如:my_vector <- c(1, 2, 3)。
矩阵是一个二维数据结构,你可以使用matrix()函数创建矩阵。
5. 数据框(Data Frame):数据框是R中最常用的数据结构之一,类似于Excel表格。
你可以使用data.frame()函数创建数据框。
可以使用read.csv()或read.table()函数从外部文件加载数据框。
6. 数据处理和转换:R提供了许多内置函数用于数据处理和转换,例如:subset()、merge()、aggregate()等。
这些函数可以对数据进行过滤、合并、汇总等操作。
7. 统计分析和建模:R拥有强大的统计分析和建模功能,你可以使用内置函数进行描述性统计、假设检验、回归分析等。
例如,mean()用于计算均值、t.test()用于执行t检验。
【R】R语言手册

【R】R语⾔⼿册2018-07-30 21:09:07在R的官⽅教程⾥是这么给R下注解的:⼀个数据分析和图形显⽰的程序设计环境(A system for data analysis and visualization which is built based on S language.)。
R的源起R是S语⾔的⼀种实现。
S语⾔是由 AT&T贝尔实验室开发的⼀种⽤来进⾏数据探索、统计分析、作图的解释型语⾔。
最初S语⾔的实现版本主要是S-PLUS。
S-PLUS是⼀个商业软件,它基于S语⾔,并由MathSoft公司的统计科学部进⼀步完善。
后来Auckland⼤学的Robert Gentleman 和 Ross Ihaka 及其他志愿⼈员开发了⼀个R系统。
R的使⽤与S-PLUS有很多类似之处,两个软件有⼀定的兼容性。
R is freeR是⽤于统计分析、绘图的语⾔和操作环境。
R是属于GNU系统的⼀个⾃由、免费、源代码开放的软件,它是⼀个⽤于统计计算和统计制图的优秀⼯具。
R是⼀套完整的数据处理、计算和制图软件系统。
其功能包括:数据存储和处理系统;数组运算⼯具(其向量、矩阵运算⽅⾯功能尤其强⼤);完整连贯的统计分析⼯具;优秀的统计制图功能;简便⽽强⼤的编程语⾔:可操纵数据的输⼊和输⼊,可实现分⽀、循环,⽤户可⾃定义功能。
R是⼀个免费的⾃由软件,它有UNIX、LINUX、MacOS和WINDOWS版本,都是可以免费下载和使⽤的,在那⼉可以下载到R的安装程序、各种外挂程序和⽂档。
在R的安装程序中只包含了8个基础模块,其他外在模块可以通过CRAN获得。
R的特点(1) 有效的数据处理和保存机制。
(2) 拥有⼀整套数组和矩阵的操作运算符。
(3) ⼀系列连贯⽽⼜完整的数据分析中间⼯具。
(4) 图形统计可以对数据直接进⾏分析和显⽰,可⽤于多种图形设备。
(5) ⼀种相当完善、简洁和⾼效的程序设计语⾔。
它包括条件语句、循环语句、⽤户⾃定义的递归函数以及输⼊输出接⼝。
R语言学习系列17-数据整合Ⅰ—基本操作

16. 数据整合Ⅰ—基本操作目录:一. 数据框创建新变量二、变量的重命名三. 变量的重新编码四. 数据排序五. 数据合并六. 选取数据的子集七. 简单的随机抽样正文:一、数据框创建新变量假设有MyData数据框,其中变量为x1,x2. 现创建名为sumx 和meanx的新变量,分别存储变量x1与x2的加和与均值。
#方法1MyData$sumx<- MyData$x1 + MyData$x2MyData$meanx<- (MyData$x1 + MyData$x2)/2#方法2attach(MyData)MyData$sumx<- x1+x2MyData$meanx<- (x1+x2)/2detach(MyData)#方法3(建议方法)MyData<- transform(MyData,sumx = x1 + x2,meanx = (x1+x2)/2)二、变量的重命名1. 用交互式编辑器若修改数据集x的变量名,键入函数fix(x),即可打开交互式编辑器界面。
score<-data.frame(student=c("A","B","C","D"),gender= c("M","M","F","F"),math=c(90,70,80,60),Eng=c(88,78,69,98), pl=c(66,59,NA,88))fix(score)score.list<-as.list(score)#将score转化为列表fix(score.list)(1)若数据集为矩阵或数据框将打开“数据编辑器”,单击要修改的变量名,在弹出的“变量编辑器”修改即可:(2)若数据集为列表将交互式编辑器为一个记事本,只需修改“.Names”之后对应的变量名即可:2. 用函数rename()reshape包中的函数rename(),用来修改数据库和列表的变量名,但不能修改矩阵的变量名,基本格式为:rename(x, c(oldname="newname",...))其中,oldname为原变量名,newname为新变量名。
R语言入门基础教程

R语言入门基础教程R语言是一种广泛使用的数据分析和统计编程语言,它提供了丰富的函数库和强大的数据处理能力。
本教程将向您介绍R语言的基础知识,包括变量和数据类型、向量和矩阵、条件控制和循环、函数和图形绘制等内容。
1.变量和数据类型在R语言中,可以用来存储数据的基本单元是变量。
变量可以存储不同类型的数据,如整数、浮点数、字符等。
例如,可以使用以下语句将一个整数赋值给变量x:x<-10可以使用print(函数显示变量的值:print(x)R语言支持多种数据类型,常见的有整数(integer)、浮点数(numeric)、字符(character)、逻辑(logical)等。
2.向量和矩阵向量是一种用于存储一维数据序列的数据结构。
可以使用c(函数创建向量,例:vector <- c(1, 2, 3, 4, 5)也可以使用冒号运算符创建数值序列:vector <- 1:5矩阵是一种用于存储二维数据的数据结构。
可以使用matrix(函数创建矩阵,例:matrix <- matrix(c(1, 2, 3, 4, 5, 6), nrow=2, ncol=3)可以使用dim(函数获取矩阵的维度:dim(matrix)3.条件控制和循环R语言提供了if-else语句和for循环等条件控制和循环结构。
如下面的例子所示,该代码将根据条件判断输出不同的结果:x<-10if (x > 0)print("x is positive")} elseprint("x is negative")可以使用for循环来遍历集合或执行重复操作。
如下面的例子所示,该代码将打印出1到5的数字:for (i in 1:5)print(i)4.函数和图形绘制R语言中函数是一组用于执行特定任务的代码块,它可以接受输入参数并返回输出结果。
可以使用function(函数定义一个函数。
R语言(简略版)ppt课件

4)显示变量值:直接输入变量名或使用print()函 数
5)清除:将变量从内存中清除,使用rm() 。
思考题:
下列()表示的是变量。
A.123
B.TRUE
D.abc
下列()不可以作为变量名。
A.1a2b
B.a1b2
D.a.b
下列()可以作为变量名。
8.2 9.1 10.0
三、R语言的数据结构
3、rep(n1,n2) #生成n1重复n2次的向量 > rep(2,3) [1] 2 2 2 > rep(1:5,2) [1] 1 2 3 4 5 1 2 3 4 5 > rep(1:5,1:5) [1] 1 2 2 3 3 3 4 4 4 4 5 5 5 5 5 > rep(1:5,rep(2,5)) [1] 1 1 2 2 3 3 4 4 5 5
R语言
目录
第一章 网络基础知识及R介绍 第二章 R语言基础 第三章 数据的存储与读取 第四章 R的图形功能 第五章 R的程序设计 第六章 综合实例
计算机与R语言
第二章 R语言基础
一、一个简短的R会话 二、R的基本语法 三、R的数据结构
一、一个简短的R会话
• 数据的描述 >?mtcars mtcar:美国Motor Trend杂志收集的32辆汽 车(1973-1974车型)的11项指标。
三、R语言的数据结构
数值型: • 包括整型(integer)、双精度实型(double),对很
大的数据则可用指数形式表示 • 例如:1、0.5、-0.5、2.1e23(指数形式表示的
数值)。 • R可以表示无穷的数值,用Inf和-Inf表示+∞和-
R语言入门经典中文版

R for BeginnersChinese Edition2.0Emmanuel ParadisInstitut des Sciences de l’´EvolutionUniversit´e Montpellier IIF-34095Montpellier c´e dex05FranceE-mail:paradis@isem.univ-montp2.frCo-translated by:XF Wang,YH Xie,JT Li and GH Ding中文版说明“R for beginners”是一本公认的经典手册,非常适合R的初学者。
英文原版初著于2002年,而此稿是基于作者在2005年重新修订的第二版。
Emmanuel Paradis博士为本稿提供了原版所有L A T E X源文件。
翻译工作由四名志愿者共同完成(Chap1–2:王学枫;Chap3:谢益辉;Chap4:李军焘;Chap5–7:丁国徽)。
由华东师范大学汤银才老师负责本文档的编辑校订。
北京大学李东风老师审阅了全稿并提出了大量宝贵意见。
在此一并表示衷心感谢!编译仓促,差错难免,亟盼诸R友襄正。
任何意见请通过pwxf@ 联系我们。
译者2006年4月版权c 2002,2005,Emmanuel ParadisPermission is granted to make and distribute copies,either in part or in full and in any language,of this document on any support provided the above copyright notice is included in all copies.Permission is granted to translate this document,either in part or in full,in any language provided the above copyright notice is included.目录1导言12基本原理与概念32.1基本原理 (3) (5)2.3在线帮助 (7)3R的数据操作93.1对象 (9) (11)3.3存储数据 (14)3.4生成数据 (15)3.4.1规则序列 (15)3.4.2随机序列 (18) (19)3.5.1创建对象 (19)3.5.2对象的类型转换 (24) (26)3.5.4访问一个对象的数值:下标系统 (27)3.5.5访问对象的名称 (30) (32)3.5.7数学运算和一些简单的函数 (32) (34)4R绘图374.1管理绘图 (37)4.1.1打开多个绘图设备 (37)4.1.2图形的分割 (38)4.2绘图函数 (41)4.3低级绘图命令 (42) (44)4.5一个实例 (45)4.6grid和lattice包 (49)5R的统计分析565.1关于方差分析的一个简单例子 (56)5.2公式 (58)5.3泛型函数 (59) (62)6R编程实践656.1循环和向量化 (65)6.2用R写程序 (67) (68)7R相关的文献721导言该手册是关于R的一个入门教材.由于主要针对初学者,我将重点放在了对R的工作原理的解释上。
R 语言入门ppt课件

是否允许同一个对象中有多种类型 否 否 否 否 是 否 是
• 所有的对象都有两个内在的属性:类型和长度,例如:
− > mode(x) − [1] "numeric“
− > length(x) − [1] 1
15
R 语言编程
• 据结构
• 浏览对象的信息,例如:
− > name <- "Carmen"; n1 <- 10; n2 <- 100; m <- 0.5 − > ls( ) − [1] "m" "n1" "n2" "name"
19
R 语言编程
• 数据结构
• 向量的计算
− 向量与一个常数的加、减、乘、除,为向量的每一个元素与该常数的加、 减、乘、除
− 向量的乘方、开方、log, exp, sin, cos, tan等,为每一个元素的相应运算 − 同样长度向量的加、减、乘、除,为位置相同的元素的加、减、乘、除 − 不同长度的向量,长度必须是倍数关系,才能进行相应的运算
4
R 语言的简介
• R 的安装
• 为了显示图形,需要安装libX11-devel相关rpm包 • 创建R的安装目录/usr/R • 从CRAN社区下载最新的R源码R-3.1.3.tar.gz • 将R源码文件R-3.1.3.tar.gz上传到Linux, 例如放在dbadmin用户的home目 录下 • 使用命令tar -zxvf R-3.1.3.tar.gz解压文件 • 进入解压后目录,运行./configure --enable-R-shlib --prefix /usr/R 命令执 行配置 • 在解压目录中,运行make命令执行编译 • 在解压目录中,运行make install命令执行安装
R语言时间序列中文教程

R语言时间序列中文教程2012特别声明:R语言是免费语言,其代码不带任何质量保证,使用R语言所产生的后果由使用者负全责。
前言R语言是一种数据分析语言,它是科学的免费的数据分析语言,是凝聚了众多研究人员心血的成熟的使用范围广泛全面的语言,也是学习者能较快受益的语言。
在R语言出现之前,数据分析的编程语言是SAS。
当时SAS的功能比较有限。
在贝尔实验室里,有一群科学家讨论提到,他们研究过程中需要用到数据分析软件。
SAS的局限也限制了他们的研究。
于是他们想,我们贝尔实验室的研究历史要比SAS长好几倍,技术力量也比SAS强好几倍,且贝尔实验室里并不缺乏训练有素的专业编程人员,那么,我们贝尔实验室为什么不自己编写数据分析语言,来满足我们应用中所需要的特殊要求呢?于是,贝尔实验室研究出了S-PLUS语言。
后来,新西兰奥克兰大学的两位教授非常青睐S-PLUS的广泛性能。
他们决定重新编写与S-PLUS相似的语言,并且使之免费,提供给全世界所有相关研究人员使用。
于是,在这两位教授努力下,一种叫做R的语言在奥克兰大学诞生了。
R基本上是S-PLUS的翻版,但R是免费的语言,所有编程研究人员都可以对R语言做出贡献,且他们已经将大量研究成果写成了R命令或脚本,因而R语言的功能比较强大,比较全面。
研究人员可免费使用R语言,可通过阅读R语言脚本源代码,学习其他人的研究成果。
笔者曾有幸在奥克兰大学受过几年熏陶,曾经向一位统计系的老师提请教过一个数据模拟方面的问题。
那位老师只用一行R语句就解答了。
R语言的强大功能非常令人惊讶。
为了进一步推广R语言,为了方便更多研究人员学习使用R语言,我们收集了R语言时间序列分析实例,以供大家了解和学习使用。
当然,这是非常简单的模仿练习,具体操作是,用复制粘贴把本材料中R代码放入R的编程环境;材料中蓝色背景的内容是相关代码和相应输出结果。
经过反复模仿,学习者便能熟悉和学会。
需要提醒学习者的是:建议学习者安装了R语言编程,再继续阅读本材料;执行R 命令时,请删除命令的中文注解,没使用过在命令中加入中文;如果学习者是初次接触R或者Splus,建议先阅读<<R语言样品比较应用举例>>,如果学习者比较熟悉R语言,还可以阅读优秀时间序列读物Ecomometrics in R,也可以上QuickR 网站。
大一R语言统计学知识点总结

大一R语言统计学知识点总结在大一学习R语言统计学时,我们需要掌握一些基本的知识点。
下面是对这些知识点的总结。
1. R语言的基本语法R语言是一种用于统计计算和绘图的编程语言,具有简洁的语法和丰富的函数库。
在学习R语言之前,我们需要先了解其基本的语法规则,包括对象赋值、变量命名和控制结构等。
2. 数据类型与数据结构R语言支持多种数据类型,包括数值型、字符型、逻辑型等。
此外,R语言还支持多种数据结构,如向量、矩阵、数组、列表和数据框。
学习R语言时,需要熟悉各种数据类型和数据结构的使用方法。
3. 数据的读取与处理在实际的数据分析中,我们需要从外部文件中读取数据,并进行数据的清洗和处理。
R语言提供了多种函数用于读取和处理数据,如read.table()函数用于读取文本文件,str()函数用于查看数据结构,subset()函数用于数据子集的选择等。
4. 描述性统计描述性统计是对数据进行概括和描述的统计方法。
R语言提供了丰富的函数用于计算常用的描述性统计指标,如均值、中位数、标准差和百分位数等。
学习R语言时,需要熟悉这些函数的使用方法。
5. 统计图表绘制统计图表是数据可视化的重要手段,能够直观地展示数据的分布和关系。
R语言提供了多种函数和扩展包用于绘制各种类型的统计图表,如散点图、柱状图、折线图和箱线图等。
学习R语言时,需要熟悉这些函数和扩展包的使用方法。
6. 统计推断统计推断是利用样本数据对总体特征进行推断的方法。
R语言提供了多种函数用于进行统计推断,如假设检验、置信区间估计和回归分析等。
学习R语言时,需要了解这些函数的原理和使用方法。
7. 数据挖掘与机器学习数据挖掘和机器学习是利用计算机算法从数据中发现模式和规律的方法。
R语言提供了多种函数和扩展包用于数据挖掘和机器学习,如聚类分析、分类算法和回归算法等。
学习R语言时,可以通过案例分析和实验来掌握这些方法的应用。
总结:通过学习R语言统计学知识点,我们能够掌握数据分析的基本技能,对数据进行描述和分析。
R语言入门教程

PD
PD
F-
XC
h a n g e Vi e
w
F-
XC
h a n g e Vi e
w
er
er
!
O W
N
y
bu
to
k
lic
C
m
C
lic
k
to
bu
y
N
.c
O W
w
.d o
c u -tr aபைடு நூலகம்c k
!
w
o
.d o
c u -tr a c k
.c
R语言简介
R语言笔记:数据分析与绘图的编程环境
版本1.7
R Development Core Team June 10, 2006
o
m
w
w
w
w
PD
PD
F-
XC
h a n g e Vi e
8 概率分布 28 8.1 R—作为一个统计表的集合 . . . . . . . . . . . . . . . . . . . . . . 28 8.2 检测数据集合的分布 . . . . . . . . . . . . . . . . . . . . . . . . . 29 8.3 单样本和两样本检验 . . . . . . . . . . . . . . . . . . . . . . . . . 32 9 语句组、循环和条件操作 9.1 表达式语句组 . . . . . . . . . . . . 9.2 控制语句 . . . . . . . . . . . . . . 9.2.1 条件执行:if语句 . . . . . . 9.2.2 重复执行:for 循环,repeat 10 编 写自己的函数 10.1 简单示例 . . . . . . 10.2 定义新的二元操作符 10.3 指定的参数和默认值 10.4 参数’...’ . . . . . . . 10.5 函数内的赋值 . . . . 10.6 更多高级示例 . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 和while . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 35 35 35 35 35 37 37 38 38 39 39 39
R语言编程基础-教学大纲

《R语言编程基础》教学大纲
课程名称:R语言编程基础
课程类别:必修
适用专业:大数据技术类相关专业
总学时:48学时(其中理论18学时,实验30学时)
总学分:3.0学分
一、课程的性质
大数据时代已经到来,在商业、经济及其他领域中基于数据和分析去发现问题并做出科学、客观的决策越来越重要。
数据分析技术将帮助企业用户在合理时间内获取、管理、处理以及整理海量数据,为企业经营决策提供积极的帮助。
数据分析作为一门前沿技术,广泛应用于物联网、云计算、移动互联网等战略新兴产业,有实践经验的数据分析人才已经成为了各企业争夺的热门。
为了推动我国大数据,云计算,人工智能行业的发展,满足日益增长的数据分析人才需求,特开设R语言编程基础课程。
二、课程的任务
通过本课程的学习,使学生认识R的编译环境,获取与安装R语言,使用R包,控制流、文件读取、数据可视化及使用可视化工具Rattle进行数据分析等基本操作。
本课程将紧密结合示例操作,及时讲解基础知识、相关函数及可视化操作,为学生今后进行实际编程操作奠定基础,为数据分析可视化提供方法,同时,掌握Rattle工具能更方便的实现数据挖掘相关操作。
三、课程学时分配
四、教学内容及学时安排
1.理论教学
2.实验教学
五、考核方式
突出学生解决实际问题的能力,加强过程性考核。
课程考核的成绩构成= 学习态度(10%)+课堂参与(20%)+期末考核(70%),期末考试建议采用开卷形式,试题应包括基本概念、绘图、分组聚合、数据合并、数据清洗、数据变换、模型构建等部分,题型可采用判断题、选择、简答、应用题等方式。
R语言初步
R语言初步1第一节基本知识一、界面介绍R语言是一种自由软件编程语言与操作环境,主要用于统计分析、绘图、数据挖掘。
R 语言最早由新西兰奥克兰大学的Ross Ihaka和Robert Gentleman开发,所以命名为R语言。
R语言是免费下载的,可以在网站Http:\\/中找到适合自己的镜像网站,下载R语言安装包和其他文件。
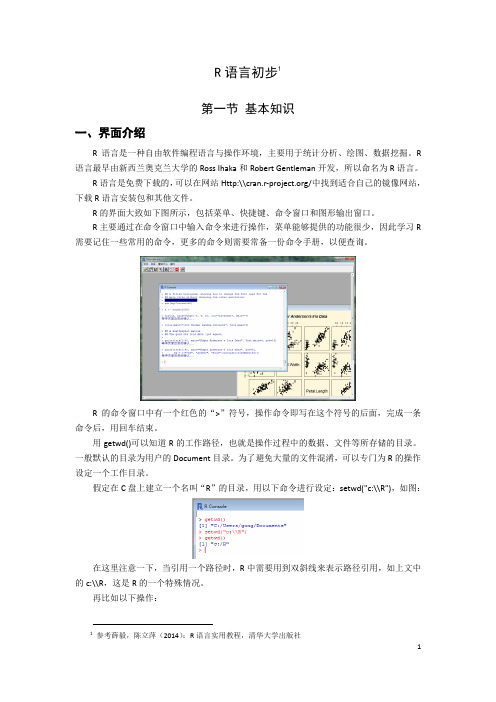
R的界面大致如下图所示,包括菜单、快捷键、命令窗口和图形输出窗口。
R主要通过在命令窗口中输入命令来进行操作,菜单能够提供的功能很少,因此学习R 需要记住一些常用的命令,更多的命令则需要常备一份命令手册,以便查询。
R的命令窗口中有一个红色的“>”符号,操作命令即写在这个符号的后面,完成一条命令后,用回车结束。
用getwd()可以知道R的工作路径,也就是操作过程中的数据、文件等所存储的目录。
一般默认的目录为用户的Document目录。
为了避免大量的文件混淆,可以专门为R的操作设定一个工作目录。
假定在C盘上建立一个名叫“R”的目录,用以下命令进行设定:setwd("c:\\R"),如图:在这里注意一下,当引用一个路径时,R中需要用到双斜线来表示路径引用,如上文中的c:\\R,这是R的一个特殊情况。
再比如以下操作:1参考薛毅,陈立萍(2014):R语言实用教程,清华大学出版社>x1<-c(10,12,14,16,18)>y1<-c(2.5,2.6,3.1,4.6,3.8)>plot(x1,y1)注意几点:(1)式子中的“<-”表示赋值,也就是把右边的数值赋予左边的变量名。
(2)R语言中对于字母的大小写非常敏感,变量名可以用大写也可以用小写,但用大写字母命名的变量如果改用小写来调用,会无法识别。
(3)如果觉得命令窗口上的内容太多,可以用Ctrl-L来清屏幕。
(4)如果要重新调用此前用过的命令,可以用上箭头回溯此前的命令,也可以用history()来查看历史记录。
《R语言入门》课件

VS
详细描述
描述性统计分析包括计算数据的均值、中 位数、众数、标准差等统计指标,以及制 作数据的频数分布表和直方图等可视化图 表,帮助我们了解数据的分布情况和基本 特征。
推断性统计分析
总结词
推断性统计分析是通过样本数据来推断总体特征和规律的方法。
详细描述
推断性统计分析包括参数估计和假设检验等统计方法,通过样本数据来估计总体参数和检验假设,帮 助我们了解总体的情况和规律。
01
数据处理与可视化
数据导入与导
数据导入
R语言支持多种格式的数据导入, 包括CSV、Excel、SQL数据库等 。可以使用`readr`、`tidyverse` 等包来导入数据。
数据导出
R语言可以将处理后的数据导出为 多种格式,如CSV、Excel、PDF 等。可以使用`writexl`、`officer` 等包来实现数据的导出。
01
R语言基础
R语言的安装与配置
总结词
R语言的安装与配置是学习R语言的第一步,需要了解如何下载和安装R语言,以及如何 配置R语言的环境。
详细描述
首先,您需要从CRAN(Comprehensive R Archive Network)上下载适合您操作系 统的R语言安装程序。然后,按照安装向导的指示进行操作,并确保在安装过程中选择 正确的组件和设置。安装完成后,您需要配置环境变量,以便在命令行中运行R语言。
学习如何通过脚本调用外部程序和命令,以及如 何将外部程序的输出作为R的数据源。
3
数据转换和格式化
掌握如何在不同编程语言之间转换和格式化数据 ,以确保数据的一致性和可比较性。
感谢观看
THANKS
THE FIRST LESSON OF THE SCHOOL YEAR
r语言读取本地文件的方法-概述说明以及解释

r语言读取本地文件的方法-概述说明以及解释1.引言1.1 概述概述:本文主要介绍了使用R语言读取本地文件的方法。
在数据分析和处理中,我们常常需要从本地文件中读取数据,并在R语言环境中进行进一步的分析。
了解如何正确读取本地文件是R语言中数据处理的基础操作之一。
本文主要分为三个部分:引言、正文和结论。
在引言部分,我们将概述文章的结构和目的。
在正文部分,将详细介绍R语言读取本地文件的基本方法,并给出了读取文本文件和读取Excel文件的具体例子。
最后,在结论部分,我们将总结R语言读取本地文件的方法,并讨论其应用场景和注意事项,同时展望R语言文件读取的未来发展。
通过本文的阅读,读者将掌握如何使用R语言读取本地文件的基本方法,从而更加熟练地进行数据处理和分析工作。
同时,我们也希望通过本文的介绍,可以为读者展示R语言文件读取技术的潜力和未来发展趋势,从而为读者的研究和实践提供一定的参考和指导。
1.2 文章结构文章结构部分的内容可以如下所示:文章结构:本文共分为引言、正文和结论三个部分。
在引言中,将通过概述、文章结构和目的的方式介绍本文的内容。
接着在正文部分,将详细介绍了R 语言读取本地文件的基本方法,并重点讨论了如何读取文本文件和Excel 文件。
最后,在结论部分将总结R语言读取本地文件的方法,并提供一些应用场景和注意事项的建议。
此外,还将提出对R语言文件读取技术未来发展的展望。
通过这样的文章结构,读者将能够全面了解R语言读取本地文件的方法以及其在实际应用中的一些问题和前景。
1.3 目的本文的目的是介绍在R语言中如何读取本地文件。
通过本文的阐述,读者将能够了解R语言读取本地文件的基本方法,并掌握如何读取文本文件和Excel文件。
同时,本文还将总结R语言读取本地文件的方法,并探讨其应用场景和注意事项。
最后,本文会对R语言文件读取的未来发展进行展望。
通过阅读本文,读者将能够:1. 熟悉R语言读取本地文件的基本方法,了解如何为R程序提供数据源。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
向量(vector)1、seq():产生有规律的数列,间距省略时默认值为1。
例1:seq(10, 20, 0.5)例2:seq(0, by = 0.03, length = 15)2、rep():产生有规律的数列,重复第一个变量若干次。
例1:rep(1:3, 1:3)例2:rep(1:3, rep(2, 3))例3:rep(1:3, length = 10)3、向量运算:一般是对应元素之间的运算,所以两个或多个向量运算时,要求它们包含的元素个素相同(或一个是另一个的整数倍)。
例1:a <- 1:3; b <- 4:6; a * b; b^a例2:a <- 1:3; b <- 4:9; a * b; b^a4、获取向量某一个或多个子集,向量前的负号"-"表示去除相应内容。
例1:x <- c(3, 4, 5, 2, 6); x[1:2]; x[-(1:2)]例2:x <- c(3, 4, 5, 2, 6); x[c(1, 2, 4, 1)]; x[-c(1, 2, 4, 1)]例3:xx <- seq(1, by = 3, length = 10); xx[xx > 13]例4:x <- 1:20; y <--9:11; x[y > (1)] #注意最后一个是"NA"5、主要向量运算函数。
例1:xx <- c(2, 6, 10, 8, 4)sum(xx) #和max(xx) #最大值min(xx) #最小值range(xx) #取值范围mean(xx) #平均值var(xx) #方差sort(xx) #从小到大排序rev(xx) #反排列,所以从大到小排序应该是rev(sort(xx))rank(xx) #单元值大小顺序prod(xx) #乘积,所以阶乘是prod(1:n)例2:x <- seq(1, 15, 2)append(x, 20:30, after = 5) #插入数据append(x, 20:30) #参数after缺省默认从向量的最后插入值replace(x, c(2, 4, 6), -1) #替换函数例3:match(c('Ohio', 'Wyoming'), ) #完全匹配函数pmatch(c('Oh', 'Wy'), ) #部分匹配函数[pmatch(c('Oh', 'Wy'), )]例4:yy <--9:10all(yy > 0) #判断所有all(yy > -10)any(yy == 0) #判断部分any(yy > 0)any(yy < -10)矩阵(matrix)矩阵生成函数matrix():matrix(data, nrow = , ncol = , byrow = F),其中,数据data 是必须的,其他都是选择参数,可以不选。
byrow = F默认为按列来排列数据,如果想要按行排列,令byrow = T。
1、对角矩阵和单位阵。
例1:x <- 1:6; diag(x) #对角矩阵例2:y <- rep(1, 5); diag(y) #单位阵2、矩阵下标例1:xx <- matrix(1:20, 4, 5)xx[2, 2]; xx[2, 3:5]; xx[3:4, 3:4]xx[2, ]; xx[ , 2]3、代数意义下的矩阵乘法"%*%"例1:yy <- matrix(1:6, 3, 2); zz <- matrix(1:6, 2, 3)yy %*% zz; zz %*% yy4、矩阵行和列的维数例1:xx <- matrix(1:20, 4, 5)dim(xx) #行和列的维数nrow(xx); ncol(xx) #行数和列数5、矩阵的主要运算函数例1:x <- 1:6; y <- as.matrix(x) #转换成矩阵is.matrix(x); is.matrix(y) #判断是否矩阵例2:diag() #方阵对角线元素或者生成对角矩阵apply() #对矩阵应用函数eigen() #求特征值和特征向量solve() #求逆矩阵chol() #Choleski分解svd() #奇异值分解qr() #QR分解det() #求行列式dim() #给出行列数t() #矩阵转置6、矩阵合并例1:aa <- matrix(1:6, 3, 2); bb <- matrix(7:12, 3, 2)cbind(aa, bb) #按列合并rbind(aa, bb) #按行合并7、矩阵apply()运算函数:语法是apply(data, dim, function),dim取1表示对行运用函数,取2表示对列运用函数。
例1:xx <- matrix(1:20, 4, 5)colMeans(xx) #列均值colSums(xx) #列和其余大部分都要用到apply()函数例2:xx <- matrix(1:20, 4, 5)apply(xx, 2, mean) #列均值,等同于colMeans(xx)apply(xx, 2, sum) #列和,等同于colMeans(xx),所以矩阵行和列的运算推荐用apply()。
apply(xx, 1, var) #行方差apply(xx, 2, max) #每列最大值apply(xx, 2, rev) #每列的数反排列数组(array)一维数据是向量,二维数据是矩阵,数组是向量和矩阵的直接推广,是由三维或三维以上的数据构成的.数组函数是array(),语法是:array(dadta, dim),其中data必须是同一类型的数据,dim是各维的长度组成的向量。
1、产生一个三维和四维数组。
例1:xx <- array(1:24, c(3, 4, 2)) #一个三维数组例2:yy <- array(1:36, c(2, 3, 3, 2)) #一个四维数组2、dim()函数可将向量转化成数组或矩阵。
例1:xx <- 1:24; dim(xx) <- c(3, 4, 2); xx #效果同array(1:24, c(3, 4, 2))例2:zz <- 1:10; dim(zz) <- c(2, 5); zz #效果同matrix(1:10, 2, 5)列表(list)向量、矩阵和数组的元素必须是同一类型的数据。
一个数据对象需要包含不同的数据类型,它可以采用列表这种形式。
创建列表可用list()函数,语法是:list(name1 = component1, name2 = component2, ...)。
1、创建一个列表例1:xx <- rep(1:2, 3:4)yy <- c('Mr A', 'Mr B', 'Mr C', 'Mr D', 'Mr E', 'Mr D', 'Mr F')zz <- 'discussion group'name.list <- list(group = xx, name = yy, decription = zz) #创建了一个名为"name.list"的列表name.list$n[name.list$g == 2]length(name.list)mode(name.list)names(name.list)因子(factor)和有序因子(ordered factor)因子用来存储类别变量(categorical variables)和有序变量,这类变量不能用来计算而只能用来分类或者计数。
因子表示分类变量,有序因子表示有序变量。
生成因子数据对象的函数是factor(),语法是factor(data, levels, labels, ...),其中data 是数据,levels是因子水平向量,labels是因子的标签向量。
1、创建一个因子。
例1:colour <- c('G', 'G', 'R', 'Y', 'G', 'Y', 'Y', 'R', 'Y')col <- factor(colour)col1 <- factor(colour, levels = c('G', 'R', 'Y'), labels = c('Green', 'Red', 'Yellow')) #labels 的内容替换colour相应位置对应levels的内容col2 <- factor(colour, levels = c('G', 'R', 'Y'), labels = c('1', '2', '3'))col_vec <- as.vector(col2) #转换成字符向量col_num <- as.numeric(col2) #转换成数字向量col3 <- factor(colour, levels = c('G', 'R'))2、创建一个有序因子。
例1:score <- c('A', 'B', 'A', 'C', 'B')score1 <- ordered(score, levels = c('C', 'B', 'A')); score13、用cut()函数将一般的数据转换成因子或有序因子。
例1:exam <- c(98, 97, 52, 88, 85, 75, 97, 92, 77, 74, 70, 63, 97, 71, 98,65, 79, 74, 58, 59, 60, 63, 87, 82, 95, 75, 79, 96, 50, 88)exam1 <- cut(exam, breaks = 3) #切分成3组exam2 <- cut(exam, breaks = c(0, 59, 69, 79, 89, 100)) #切分成自己设置的组attr(exam1, 'levels'); attr(exam2, 'levels'); attr(exam2, 'class')ordered(exam2, labels = c('bad', 'ok', 'average', 'good', 'excellent')) #一个有序因子数据框(data frame)数据框是一种矩阵形式的数据,但数据框中各列可以是不同类型的数据。
