测量不确定度分析评定报告
酸度计不确定度评定报告

2015年度陕西省计量技术机构“酸度量值比对”不确定度评定报告2015年10月,陕西省计量技术机构“酸度量值比对”工作正式开展。
主持此次比对的单位为陕西省质量技术监督局。
参加比对单位是全省9个市级法定技术机构和1个计量授权检定机构。
比对使用的仪器是由上海仪电科学仪器股份有限公司提供的型号为PHS-3E 的数显酸度计,仪器测量范围:0.00~14.00pH ;0~±1999mV ;0~99.9℃。
仪器编号为600710N0015050024,使用E-301F 型复合电极一支。
量值比对仪器的检定方法采用直接比对法。
量值比对仪器的检定依据:JJG119-2005《实验室pH (酸度)计》计量检定规程。
酸度计的测量不确定度分析1.1 酸度计电计pH 示值误差测量的不确定度分析电计示值测量不确定度主要是测量时使用的标准器的不确定度和示值的重复性不确定度或量化误差(最小分辨率)引起的不确定度两项构成。
(1)数学模型电计示值误差服从公式(1):s pH pH d -= (1)式中:d 为示值误差;pH 为被测量电计示值;pH s 为pH 计检定仪示值。
由于pH 与pH s 相互独立,则: 1=∂∂pHd ,1-=∂∂s pH d 故:)()()(22s pH u pH u d u += (2)(2)各分量的标准不确定度a )测量标准器的标准不确定度)(s pH u测量时采用酸度计检定仪,有效期内的检定证书给出的pH 示值误差为+0.009pH 。
考虑为均匀分布,则其pH 值标准不确定度为pH pH pH u s 0026.032009.0)(== b )电计示值测量的重复性标准不确定度)(pH u计算电计示值测量的标准不确定度)(pH u ,实测结果表明:单次测量的标准偏差:00.0)(=pH s ,因而应该考虑量化误差,即分辨力导致的)(量pH u 。
0.01级的pH ,其分辨率力为0.01pH ,考虑为均匀分布,则有pH H pH u pH u 0029.032p 01.0)()(===量 (3)合成不确定度pH pH u pH u d u u s c 0152.00029.00026.0)()()(2222=+=+==(4)扩展不确定度取包含因子2=k ,pH k u U c 0304.020152.0=⨯=⨯=1.2 电计mV 值示值误差测量不确定度分析(1)数学模型电计mV 值示值误差服从以下公式s x V V d -= (3)式中:d 为示值误差:x V 为被测量电计mV 示值;s V 为mV 计检定仪示值。
千分尺不确定度评定

千分尺校准结果的不确定度评定报告1测量任务和目标不确定度1.1测量任务:规程确认的技术要求,测量原理,测量条件,测量方法和测量程序,测量千分尺示值误差1.2测量任务目标不确定度U T根据《测量仪器特性评定技术规范》中5.3.1.4的规定,评定千分尺示值误差的扩展不确定度U(k=2)与其最大允许误差的绝对值MPEV之比,应小于1:3,即由上式可以得到与规程技术要求相对应的目标不确定度U T目标不确定度U T表测量范围(mm)最大允许误差MPE(mm)目标不确定度U T(μm)0-25 ±0.004 1.3325-50 ±0.004 1.3350-75 ±0.005 1.6775-100 ±0.005 1.67100-125 ±0.006 2.00125-150 ±0.006 2.00150-175 ±0.007 2.33175-200 ±0.007 2.332原理、方法。
程序和条件2.1测量原理接触式测量2.2测量方法千分尺示值误差用五等量块进行校准,应在全部测量范围内均匀分布5点以上进行,每个点检测四个位置,取各受检点最大示值误差为该尺的示值误差2.3测量程序校准时,首先将千分尺的测量下限调至正确位置,对于0-25mm的千分尺,用两测量面直接接触调整零位;对其他测量范围的用校对量杆或相应准确度量块调整零位2.4测量条件2.4.1量块经检定符合JJG146-2011《量块》检定规程中四等量块要求2.4.2校准千分尺室内温度对0-100mm为(20±5)℃,对100-200mm为(20±4)℃,校准校对用量块室内温度为(20±2)℃2.4.3校准前受检千分尺在校准实验室内平衡温度时间不少于4h2.4.4操作人员是经过培训的,并且十分熟悉测量过程3数学模型由测量原理得到数学模型如下e=L i-L s+L i·a i·Δl i-L s·a s·Δl s式中L i------为千分尺的读数值(20℃条件下)L s------为量块的实际尺寸(20℃条件下)a i和a s------为千分尺和量块的线膨胀系数Δl i和Δl s------为千分尺和量块偏离参考温度20℃的值4计算标准不确定度分量4.1标准偏差的不确定度分量u1选取一0-25mm千分尺在25mm处重复测量10次,由贝塞尔公式计算得u1=0.60μm4.2由5等量块给出的不确定度分量u2根据JJG146-2011《量块》检定规程规定,四等量块中心长度的测量不确定度估计为正态分布,对应99%置信概率区间的包含因子k=2.567L=25mm时u2=0.25/2.567μm=0.097μmL=50mm时u2=0.30/2.567μm=0.1168μmL=75mm时u2=0.35/2.567μm=0.136μmL=100mm时u2=0.40/2.567μm=0.156μmL=200mm时u2=0.6/2.567μm=0.234μm4.3千分尺对量块的膨胀系数差给出的不确定度分量u3a i和a s在±1×10-6℃-1范围内按三角分布,u3=2×10-6℃-1/=0.82×10-6℃-1L=25mm时,(L·Δt)·u3=25×103μm×1℃×0.58×10-6℃-1=0.02μmL=50mm时,(L·Δt)·u3=50×103μm×1℃×0.58×10-6℃-1=0.04μmL=75mm时,(L·Δt)·u3=75×103μm×1℃×0.58×10-6℃-1=0.06μmL=100mm时,(L·Δt)·u3=100×103μm×1℃×0.58×10-6℃-1=0.08μmL=200mm时,(L·Δt)·u3=200×103μm×1℃×0.58×10-6℃-1=0.16μm4.4千分尺与量块的温度差给出的不确定度分量u4千分尺与量块有一定温差存在,并以等概率落于区间[-0.3,+0.3]℃内取均匀分布,则:u4=0.3℃/=0.17℃,a=11.5×10-6℃-1L=25mm时(L·a)·u4=25×103μm×11.5×10-6℃-1×0.17℃=0.05μmL=50mm时(L·a)·u4=50×103μm×11.5×10-6℃-1×0.17℃=0.10μmL=75mm时(L·a)·u4=75×103μm×11.5×10-6℃-1×0.17℃=0.15μmL=100mm时(L·a)·u4=100×103μm×11.5×10-6℃-1×0.17℃=0.20μmL=200mm时(L·a)·u4=200×103μm×11.5×10-6℃-1×0.17℃=0.39μm5合成标准不确定度u c由于各不确定度分量之间不具有值得考虑的相关性,合成不确定度u c为L=25mm时,L=50mm时,L=75mm时,L=100mm时,L=200mm时,取包含因子k=2,则扩展不确定度:U= L=25mm时,U=0.61μm×2=1.2μmL=50mm时,U=0.62μm×2=1.2μmL=75mm时,U=0.64μm×2=1.3μmL=100mm时,U=0.64μm×2=1.3μm L=200mm时,U=0.77μm×2=1.5μm。
邻苯二甲酸酯测量不确定度评定报告(CPSC-09.4)

邻苯二甲酸酯测量不确定度评定报告1.0 目的:本实验室采用气相色谱-质谱联用仪(GC-MS),对PVC样品中邻苯二甲酸酯含量进行分析检测。
基于JJF1059-1999《测量不确定度评定与表示》的一般要求,分析测试过程中不确定度的主要来源,评估标准不确定度、合成不确定度和扩展不确定度的数值,通过不确定度的分析结果来评定该方法的适用性。
本文主要以测试PVC样品中的邻苯二甲酸二(2-乙基己基)酯(DEHP)为例子,其他邻苯二甲酸酯分析测试过程相同。
2.0 实验原理及步骤2.1 实验原理本实验室依据CPSC-CH-C1001-09.4的标准方法,进行萃取、鉴别和量化 PVC 样品中含有的单体邻苯二甲酸酯。
试样经冷冻粉碎成粉末,在四氢呋喃中将它完全溶解,用正己烷将PVC 聚合物沉淀析出,过滤,然后用正己烷将溶液稀释定容,采用气相色谱-质谱联用仪(GC-MS),鉴别并量化各种邻苯二甲酸酯。
2.2试剂及设备2.2.1 标准物质:邻苯二甲酸二(2-乙基)己酯(DEHP)2.2.2 (BSS224S) 电子天平2.2.3 QP2010Plus气相色谱-质谱联用仪2.2.4 移液管:1mL、5mL2.2.5 容量瓶:50mL 、100mL2.3实验步骤准确称取0.1g(精确至0.1mg)试样。
将试样置于刻度试管中,在试管中加入10mL四氢呋喃超声溶解,之后再加入20ml正己烷沉淀。
实验步骤可见下页图1。
第 1 页共6 页图13.0数学模型Cx =(C-C0)×V/W 式中:Cx = 样品中相应邻苯二甲酸酯计算浓度,mg/kg;C = 样品中相应邻苯二甲酸酯测试浓度,mg/L;C0 = 空白相应溶液浓度,mg/L;V = 样品定容体积,ml;W = 样品质量,g.第 2 页共6 页第 3 页 共 6 页4.0识别各不确定度分量的来源4.1称重引入的不确定度 4.2容积引入的不确定度4.3配制标准溶液引入的不确定度 4.4测量重复性引入的不确定度4.5气相色谱-质谱联用仪引入的不确定度 4.6空白分析引入的不确定度空白分析显示未检出邻苯二甲酸酯,故在使用公式计算时C 0为零,所以不考虑空白分析引入的不确定度。
布氏硬度测量不确定度评定报告范例

布氏硬度测量不确定度评定报告范例一、引言硬度是材料力学性能的重要指标之一,对于各种材料的机械性能评价具有重要意义。
布氏硬度测试是常用的硬度测试方法之一,通过在试样表面施加压力,测量压入的钢珠或钻头的深度来评估材料的硬度。
在布氏硬度测试中,存在着测量不确定度,即测量结果与真实值之间的差异。
评定布氏硬度测量不确定度的目的是为了确定测量结果的可靠性和准确性,并提供合理的测量范围。
二、测量方法与仪器本次实验采用了常见的布氏硬度测试方法,使用了市场上常见的布氏硬度计进行测量。
按照相关标准和规范进行测试,遵循了硬度计的使用说明,并对硬度计进行了合适的校准和调试。
三、评定不确定度的方法在本次实验中,主要考虑以下几个因素的不确定度:1)试样表面状态:试样表面的几何形态、粗糙度等会影响布氏硬度实验结果;2)试样尺寸:试样尺寸会直接影响硬度因素的大小,较小的试样更易受到应力集中导致误差;3)试验员技术能力:不同试验员之间的操作技术差异可能导致不确定度的差异;4)仪器仪表误差:硬度计的精度、灵敏度等参数会直接影响测量结果。
2.实验数据分析在本次实验中,通过对多个试样进行布氏硬度测试,得到了一系列硬度测试值。
通过计算平均值和标准偏差,可以对测量数据进行分析,以确定测量结果的可信度和分散度。
3.不确定度计算根据测量数据的分析,按照不确定度评定公式,计算出不确定度的各个组成部分,包括随机误差、系统误差等。
同时对影响变量的不确定度进行综合,得到最终的测量不确定度。
四、结果和讨论通过对测量数据的分析和计算,得到了本次布氏硬度测量的不确定度评定结果。
结果显示,在所使用的测试方法和仪器条件下,本次测量的不确定度为±0.5HRC。
通过对不确定度评定结果的讨论,可以得出以下结论:1.本次布氏硬度测量结果的不确定度较小,说明所使用的测试方法和仪器条件较为准确和可靠;2.在实际应用中,需要考虑不确定度的影响范围和可接受度,以保证测量结果的准确性和可靠性。
布氏硬度试验测量不确定度评定报告

布氏硬度试验测量不确定度评定报告
一、引言
布氏硬度试验作为常用的金属硬度测试方法,在工程领域有着广泛的应用。
然而,测试结果的准确性和可靠性对于材料的硬度评定和质量控制具有重要意义。
为了评定布氏硬度试验的不确定度,本报告将综合考虑测试设备的精度和稳定性、试样的制备和处理等因素,对布氏硬度试验的不确定度进行评定,并提出相应的控制措施,以保证测试结果的准确性。
二、试验方法与设备
本次试验采用了ASTME10标准规定的布氏硬度试验方法。
试验设备为一台精密布氏硬度计,压头选用对钢材适用的压头。
三、不确定度分析
1.试验设备的不确定度评定
通过多次测量标准样品,计算所得的硬度值的标准偏差为0.1HB。
根据试验设备的技术说明书,设备的精确度为0.2HB。
故设备的不确定度为0.2HB。
3.试样制备与处理的评定
试样制备和处理的不确定度主要包括试样表面的准备、试样尺寸的测量和试样处理的质量等因素。
经过多次试验,试验结果的标准偏差为
0.2HB。
故试样制备与处理的不确定度为0.2HB。
四、不确定度评定与控制
根据进一步的计算分析,可以得到布氏硬度试验的总不确定度为
0.5HB。
为了减小不确定度,以下控制措施可以被采取:
1.定期校准试验设备,确保设备的准确性和稳定性。
3.严格控制试样制备和处理过程,确保试样的质量和尺寸的准确性。
五、结论。
测量不确定度评定报告

*******测量不确定度报告一、概述1.1 测试标准:GB/T1.2 测试环境:温度21℃, 相对湿度65%二、建立数字模型x = xi式中: x ---调湿后织物的断裂强力,Nxi----几个试样的平均断裂强力,N三、不确定度的来源3.1不确定度来源图示如下:强力仪数字修约拉断强力(N)纱线均匀度试样宽度偏差样品间差异试样夹持状态经密度纬密度测试的重复性3.2不确定度在测试过程中主要来源:3.2.1 测试的重复性导致的不确定度分量a. 样品间差异:织物的经密度、纬密度及纱线自身均匀度的差异构成了样品间的差异。
b. 试样宽度偏差:标准规定试样宽度为50mm,如最后一根纱线超过半根则留之,未超过半根则不留,这就导致试样宽度不一致,影响试样的断裂强力。
c. 夹持状态不理想:按要求夹口线应与拉伸线垂直,但在实际操作时,由于织物懂得经纬向分布不平直均匀,难以控制到理想状态,不同人员对同样品作测试的结果也会有差异。
3.2.2 数字修约导致的不确定度分量3.2.3 强力仪导致的不确定度分量由于仪器跟踪应力的灵敏度导致自动显示终端的最大示值误差。
四、不确定度的评定4.1 测试的重复性导致的不确定度分量设计方案如下:取同批样本的六个样品,各裁取经向、纬向各3块,长300mm,宽约60mm,再修正到50mm,如最后一根纱线超过半根则留之。
两个不同方向断裂强力的测试结果见表1。
注:u (x ) 表示试验重复性导致的不确定度分量,其计算方法为:u (x ) =nx u )(=3.68 N ,其中:s(x i ) = 2)x - (x i 1-n 1∑=15.61N 4.2 结果数字修约导致的不确定度分量因结果报告应为计算结果的算术平均值,此值大于10N 且小于1000N 。
那么最大可能值的半宽区间a=1N/2=0.5N ,取矩形分布,按JJF1059-1999中5.6评定引入的不确定度分量为:u (修约)=35.0=0.29N4.3 匀速拉伸试验仪导致的不确定度分量拉伸强力仪经校准后,给出强力机最大示值误差的相对不确定度:u rel (示值)=0.3%,k =2当断裂强力为780N 时,u (示值)= 0.3%/2×780 = 1.17 N五、合成不确定度关于断裂强力不确定度的合成不确定度为:u c (y )=()222((仪器)修约)u u x u ++ = 3.87 N六、扩展不确定度取k =2 ,U = k × u c (y )= 2×3.87N=7.7N七、结果报告按GB/T 3923.1-2013和ASTM D5035-2011对织物进行拉伸强力试验: 经向断裂强力为780N ,U =7.7N ,k =2 同理,纬向断裂强力551N ,U =7.6N ,k =2八、编制审核人信息 编制人:日期:审核人:日期:。
单相标准测量结果不确定度评定报告

电子式单相标准电能表测量结果不确定度评定一、概述1、测量依据:JJG596—1999《电子式电能表检定规程》。
2、环境条件:温度(20±1)℃,相对湿度(60±15)%RH。
3、测量标准:本次使用的测量标准为0.05级三相电能表检定标准,型号为S—6502;检定装置为0.1级三相电能表检定装置,型号为ST—9001D1B。
4、被测对象:单相标准电能表,准确度等级为0.1级,型号为BDJ—1A。
5、测量项目及过程:被检表连接在检定装置上,由输入电压和电流经过有源补偿的电压互感器、电流互感器送入电流一频率变换器转换成信号,由计算机精确地计数和运算,并根据累计电能和预置的参数,计算相对误差。
6、评定结果的使用:符合上述条件的测量结果,一般可直接使用本不确定度的评定方法。
二、数学模型γH=γW0式中:γH—被检标准表的相对误差;γW0—检定装置测得的相对误差。
三、输入量的标准不确定度的评定1、输入量γW0的标准不确定度u c的来源主要有几方面:u1—该不确定度分量主要由被检标准表的重复测量引入的,采用A类方法进行评定;u2—三相电能表检定装置的误差引起的不确定度分项,采用B 类评定方法;2、标准不确定度u1的评定该不确定度分量主要由被检标准表的重复测量引入的,采用A类方法进行评定。
本次测量是在相同环境条件下,相同人员,使用相同仪器,对被检单相标准电能表,220V 5A cosφ=1.0时,重复接线,重复测量10次,得到1组数据,如下表所示。
合并样本标准差:S= ∑=--10102)()1(1iixxnn=0.00072%3、标准不确定度u2的评定该不确定度分量是三相电能表检定装置的误差引起的,采用B 类方法进行评定。
装置准确度等级为0.1级,估计为巨形分布,取a=0.1;包含因子取k=3:u2=a/3=0.1/ 3=0.0577%四、合成标准不确定度的评定1、合成标准不确定度u c的估算标准不确定度u c的计算u c=[ u12+ u22]1/2=[( 0.00072%)2+(0.0577)2]1/2=0.0577%2、合成标准不确定度汇总表五、扩展不确定度的评定取置信概率p=95%,取k=2,得到:扩展不确定度U95为U95=ku c=2×0.0577%=0.1154%六、不确定度报告0.1级BDJ—1A单相标准电能表在220V 5A cosφ=1.0时相对误差测量结果的扩展不确定度为:U95=0.1154% (k=2)2009年6月23日。
游标卡尺不确定度评定

游标卡尺示值误差测量不确定度评定1、概述1.1依据标准:JJG30-2012《通用卡尺检定规程》;JJF1059.1-2012《测量不确定度评定与表示》。
1.2环境条件:温度(20±5)℃,湿度≦80%RH。
1.3测量标准:5等量块,其长度尺寸的不确定度不大于()mL μ55.0+(L—测量长度),包含因子为2.58。
1.4被测对象:测量范围为0~300mm,分度值为0.02mm 的游标卡尺,最大允许示值误差为±0.04mm。
1.5测量过程对于测量范围为0~300mm 的游标卡尺,测量点的分布不少于均匀分布的3点,0~300mm 的游标卡尺,其受测点为101.2、201.5和291.8mm。
被测游标卡尺各点示值误差以该点读数值(示值)与量块尺寸(测量标准)之差确定(量块和卡尺的温度差,以及线膨胀引起的不确定度很小,可以忽略不计)。
1.6评定结果的使用在符合上述条件下的测量结果,一般可直接使用本不确定度的评定结果。
2、数学模型式中:L ∆—游标卡尺的最大允许示值误差;L —游标卡尺的示值;b L —量块的长度尺寸。
bL L L -=∆3、输入量的标准不确定度评定3.1输入L 的不确定度()L u 的评定输入L 的不确定度主要来源于游标卡尺分度值量化误差的不确定度,采用B 类方法进行评定。
游标卡尺的分度值为0.02mm,量化误差为mm ⎪⎭⎫⎝⎛202.0,估计其为均匀分布,包含因子为3,标准不确定度()L u 为()mmm mm L u μ6006.03202.0==⎪⎭⎫⎝⎛=3.2输入量b L 的标准不确定度()b L u 的评定输入量b L 的不确定度主要来源于量块长度尺寸的不确定度,可根据量块证书给出的量块长度尺寸的不确定度来评定,所以采用B 类方法进行评定。
测量用的量块其长度尺寸的不确定度不大于()m L μ55.0+(L—测量长度,单位是m),包含因子为2.58。
当被测尺寸在291.8mm(不确定度可能最大)的情况下,标准不确定度()b L u 为()mm k a L u b μμ75.058.22918.055.0=⨯+==4、合成标准不确定度的评定4.1灵敏系数数学模型bL L L -=∆灵敏系数11=∂∆∂=L Lc 12-=∂∆∂=bL Lc 4.2标准不确定度汇总表输入量的标准不确定度汇总表如下:标准不确定度汇总表标准不确定度分量iu 不确定度来源标准不确定度(m μ)ic ii u c ∙(m μ)()L u 分度值量化误差616()b L U 量块长度尺寸的不确定度0.75-10.754.3合成标准不确定度的计算()6c u L mμ∆=5、扩展不确定度的评定取包含概率为95%,包含因子k 为2.2612U m mμμ=⨯=同理:分辨力为0.02mm 的游标卡尺分度值为0.02mm 的(0~300mm)游标卡尺,最大允许示值误差为±0.04mm,U 小于其半范围的1/3,符合要求。
不确定度分析报告

水表校准系数测量结果的不确定度评定一、 概述1. 测量依据JJG162-2009《冷水水表》 2. 环境条件水温:15℃ 水压:0.2MPa ,水源:稳压状态下的洁净水。
3. 计量标准 水表检定装置 代码12317100 4.比对组件冷水水表,型号为LXH,编号为1108000001,计量等级为C 级。
5.测量过程在测量水表的仪表系数时,将流经水表的水被收集于水表检定装置的工作量器内,比较水表的示值和装置量器中水量的实际值,可得到水表的仪表系数。
二、 数学模型1. 数学模型比对组件的比对参数为其仪表系数V k :标示Q Q V =k式中,示Q —比对组件示值累积量,单位为:L; 标Q —装置测得实际的水的体积值,单位为:L; 2. 灵敏系数)()()k (2222212标示Q u c Q u c u v c +=式中:221,1标示标标示Q Q Q k c Q Q k c v v -=∂∂==∂∂=故:)()(1)k (222222标标示示标Q u Q Q Q u Q u v c ⎪⎪⎭⎫ ⎝⎛-+⎪⎪⎭⎫⎝⎛= 三、输入量的标准不确定度的评定设定用静态容积法水表检定装置对容积式水表在25 L/h 的流量下检定,测得 和 均在10L 左右,则[]222210)()()k (-⨯+=标示Q u Q u u v c 。
1、比对组件示值累积量的标准不确定度)(示Q u a.测量重复性引入的标准不确定度1)(示Q u水表的测量重复性可以通过连续测量得到,采用A 类方法进行评定,按检定规程要求对10L 三个点分别连续测量6次,得到以下值: 9.90 、9.90 、9.91 、9.90、9.89、9.90用贝塞尔公式 1)(12--=∑=n p p s ni i求出标准不确定度:up1=0.006325 L自由度 υp1=n-1=9b.比对组件的分辨力引入的标准不确定度2)(示Q u水表的最小分度值为0.1L ,读数误差一般不会超过1/2分度值,考虑其均匀分布,则有: 028.03211.02=÷⨯=p u L可信度估计为90%,则自由度 502=p ν由于1)(示Q u 和2)(示Q u 不相关,所以)(示Q u 2=1)(示Q u 2+2)(示Q u 2)(示Q u =0.029L2水表检定装置体积值的标准不确定度)(标Q u)(标Q u 由以下几个分量组成:a .水表检定装置引入的标准不确定度1)(标Q u水表检定装置标准量器的准确度等级为0.2级,根据JJG2063—1990《水流量计量器具检定系统》,其容积值的相对扩展不确定度为0.2%,置信度等于95%,服从正态分布,所以u (V 实1)=96.110%2.0⨯=0.010Lb.水位测量引入的标准不确定度2)(标Q u转子流量计的最小分度值为0.01L读数误差一般不会超过1/2分度值,考虑其均匀分布,则有:10L 工作量器的不确定度 003.032101.01=⨯=b u (L )水表检定装置经检定合格,可认为可靠性较高,可信度估计为90%,则其自由度为:501=b νc.介质水温、环境温度引入的标准不确定度3)(标Q u规程规定在介质水温(0~30)℃范围内检定时检定结果不修正。
测量不确定度评定报告
测量不确定度评定报告1、评定目的
2、评定依据
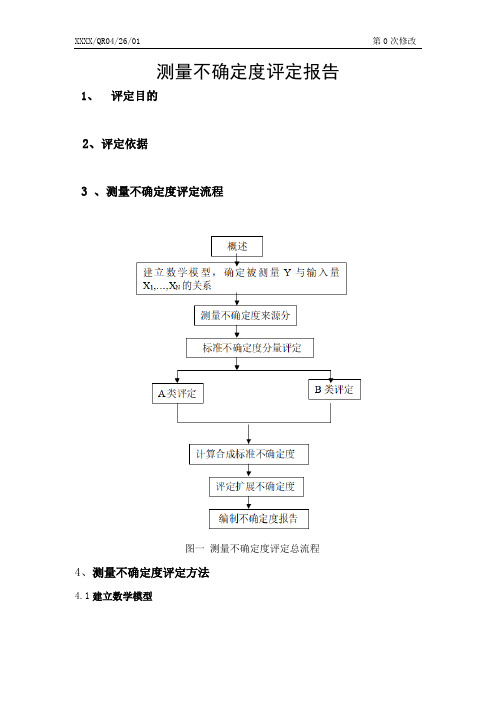
3 、测量不确定度评定流程
图一测量不确定度评定总流程4、测量不确定度评定方法
4.1建立数学模型
4.2不确定度来源分析
测量过程中引起不确定度来源,可能来自于:
a、对被测量的定义不完整;
b、复现被测量定义的方法不理想;
c、取样的代表性不够,即被测量的样本不能完全代表所定义的被测量;
d、对测量过程受环境影响的认识不周全或对环境条件的测量和控制不完善;
e、对模拟式仪器的读数存在人为偏差(偏移);
f、测量仪器的计量性能(如灵敏度、鉴别力阈、分辨力、死区及稳定性等)的
局限性;
g、赋予计量标准的值或标准物质的值不准确;
h、引入的数据和其它参量的不确定度;
i、与测量方法和测量程序有关的近似性和假定性;
j、在表面上完全相同的条件下被测量在重复观测中的变化。
4.3标准不确定度分量评定
4.3.1 A 类评定
4.3.2 标准不确定度的B类评定
4.4合成不确定度U c(y)的计算
4.5扩展不确定度U 的计算
4.6 测量不确定报告
编制人:
批准人:
日期:。
钢直尺测量结果不确定度评定

1 概述 1.1 测量方法: 依据 JJG1—1999《钢直尺检定规程》。 1.2 环境条件:温度(20±2)℃,相对湿度≤85%RH 。 1.3 测量标准:三等金属线纹尺 1.4 测量对象:1000mm 钢直尺最大允许示值误差为±0.20mm。 1.5 测量过程 钢直尺测量时,将放置在检定台上的钢直尺和三等标准金属线纹尺调至平行,并使 两尺的首端(零位)对准,然后在三等标准金属线纹尺上直接读出被测尺的示值误差。 1.6 评定结果的使用 在符合上述条件下的测量结果,一般可参照使用本不确定度的评定方法。 2 数学模型 △L=△е 式中:△L—钢直尺的示值误差; △е—钢直尺在三等金属线纹尺上对应的偏差读数值。 3 输入量△е的标准不确定度分量的评定
u (e3 )
L a 3
0.006mm
第 1 页 共 3 页
单位 mm
测量点
200 0.001
400 0.002
600 0.003
800 0.005
1000 0.006
u (e3 )
3.4 三等金属线纹尺和钢直尺线膨胀系数存在不确定度, 当温度偏离标准温度 20℃引起 的标准不确定度分项 u (e4 ) 的评定(采用 B 类方法进行评定) 由于三 等金属线纹尺和钢直尺的线膨胀系数,钢直尺的线膨胀系数分别在 αs= (16.5±1)×10-6/℃和α=(11.5±1)×10-6/℃范围内分布,两者线膨胀系数中心值差为△α 应在(5±2)×10-6/℃范围内服从三角分布,该三角分布半宽 α为 2×10-6/℃,包含因子 κ 取 6 ,L 以 1000mm 代入,△t 以 2℃代入,得
不确定度来源 校准钢直尺时人眼分辨率 标准金属线纹尺示值误差 温度偏离标准温度 被校准钢直尺和标准金属线纹尺线 膨胀系数的不确定度 被校准钢直尺和标准金属线纹尺两 者温度差
化学成分 测量不确定度评估报告

S=(0.0018±1.1600)% 其中扩展不确定度U=1.1600是由合成标准不确定度 x2得到
Cr=(1.03±1.1604)% 其中扩展不确定度U=1.1600是由合成标准不确定度 x2得到
批准/日期: 审核/日期: 制定/日期:
测量不确定度的评定报告
Mn
P
S
Cr
2.4 仪器的测量精度所引入的B类不确定度,
由仪器的检定证书得到的示值误差分别为: C 0.035% Si 0 Mn 0.03% P 0.001% S 0 Cr 0.028% ,按均匀分布考虑评定其标准不确定度
C = =0.02 % Si = =0 %
Mn = =0.017 % P = =0.00058 %
1.01
1.01
1.04
1.03
1.02
1.03
1.01
1.04
1.04
2.2 计算平均值C %
Si %Mn %
批准/日期: 审核/日期: 制定/日期:
测量不确定度的评定报告
P % S %
Cr %
2.3 单次标准偏差 C
Si Mn
P S
Cr
标准不确定度 C
Si
批准/日期: 审核/日期: 制定/日期:
测量不确定度的评定报告
一、化学成分分析试验概述
试验采用FMX直读光谱仪, 依据GB/T4336-2016 《碳素钢和中低合金钢 多元素含量的测定 火花放电原子发射光谱法(常规法)》,进行化学成分分析。
二、测量不确定度分量
2.1根据定义,可以用标准偏差表示的不确定度称为标准不确定度。通过对试样在重复性条件进行多次测量后得出A类不确定度。设单次化学成分测试用 表示。
压力变送器测量不确定度分析评定报告

压力变送器测量不确定度的评定1 概述 1.1 测量依据JJG882-2004《压力变送器检定规程》。
1.2 环境条件温度(20±2)℃,相对湿度不大于80 %。
1.3 测量标准一等活塞压力计作压力标准器,准确度等级为0.02级。
6位半高性能数字万用表 1.4 被测对象准确度等级为0.1级的压力变送器。
1.5 测量过程根据被检仪器的量程不同,用相应范围的,4位半高性能数字万用表作为被检仪表输出信号检测仪器。
检定前,正确安装连接好后,检定系统应预热不少于十五分钟,并连续对被检器预加测量上限(或下限)压力3次。
对于0.1级的压力变送器,应在测量范围内至少均匀或合理地选取6个检定点(包括零点),连续进行3次循环检定,然后根据检测数据按照规程要求评定被检器的各项误差。
1.6 评定结果的使用符合上述条件的测量结果,一般可直接使用本不确定度的评定结果。
2 数学模型0A A d -=δ (1)式中:δ—变送器的基本误差值(mA );A d —变送器的实际输出值(mA ); A 0—变送器的理论输出值(mA )。
A 0又可分解为:000P P A C A mm•+= (2) 式中: A m —变送器输出量程(mA );P m —变送器输入量程(MPa ); C 0—A 0的起始理论输出值(mA ); P 0—变送器的输入压力值。
此输入压力值P 0包括两项内容,一项是二等活塞压力计产生的标准压力值P 1 ,另一项是变送器取压口与活塞压力计活塞下缘处不是同一水平面产生静压力差P 2。
P 2表达式为:P 2=ρgh (3)式中:ρ—标准压力计用介质液的密度,0.88*103kg/m 3;g —当地重力加速度,9.8m/s 2;h —被检器取压口中心与压力计活塞下端面的高度差。
那么,式(1)可写成:()01C gh P P A A mmd -+-=ρδ (4) 故:()1=∂∂=IuI c ()()MPa mA P A P u P c m m /5.0321611-=-=-=∂∂= ()()1300431.08.9*1088.03216-⋅=⨯⨯-=⋅-=∂∂=m mA g P A h u h c m m ρ 3 分量标准不确定度的分析计算选取一只0.1级(0~32)MPa ,输出电流范围为4~20mA 的压力变送器,选用的活塞压力计为1~60MPa 的0.02级活塞压力计。
测量过程不确定度评定报告

外径千分尺测量阀杆Ø35外径不确定度评定报告1.概述1.1测量依据:按图PFF78-35-02阀杆尺寸进行测量。
1.2环境条件:常温,相对湿度<35%RH 。
1.3测量设备:(25-50)mm 外径千分尺,在其测量范围内最大示值误差为±0.004mm 。
1.4被测对象:外径为025.0087.035--mm 的阀杆。
材料为12Cr13,α1=10.3×10-6/℃。
1.5测量方法:用外径千分尺直接测量。
2. 测量模型:由于对象内径值可以直接在内径千分尺上直接测量 故:L=L S -L S (δα·Δt +αs ·δt)L---被测内孔的测定内径;L S ---内径千分尺对内孔内径的测量值。
δα—被测内孔线膨胀系数与内径千分尺线膨胀系数之差。
Δt — 被测内孔温度对参考温度20℃的偏差,取±10℃。
αs — 内径千分尺线膨胀系数,取11.5×10-6/℃。
δt — 被测内孔温度与内径千分尺温度之差,取±1℃。
3.灵敏系数该数学模型是透明箱模型,必须逐一计算灵敏系数:1 ≈ ∂ ∂)Δ1(=t s t αD S δαδLs f C --= ;t S s αδD s αf C -== ∂ ∂=-35×1㎜℃=-3.5×104µm ℃;δαD f C S t t -=Δ=Δ ∂ ∂=-35×1×10-6㎜/℃=-0.035µm/℃δαf C δα ∂ ∂/==-Ds Δt=-35×10㎜℃=-3.5×105µm ℃ t δf C t δ ∂ ∂/==-Ds αs=-35×11.5×10-6㎜/℃=-0.402µm /℃4.计算各分量标准不确定度4.1外径千分尺示值误差引入的分量u(L S )根据外径千分尺检定规程,在其测量范围内最大示值误差e=±0.004mm在半宽度为区间内,以均匀分布,则u(L S)= 4/1.732 =2.4μm;4.2被测主轴线膨胀系数不准确引入的分量u(αS)由于被测主轴线膨胀系数α1= 10.4×10-6/℃是给定的,是一个常数,故 u(αS)= 0 ,4.3测量环境偏离标准温度20℃引入的分量u(Δt)测量环境偏离标准温度20℃的偏差为±10℃,在半宽为10℃范围内,以等概率分布(均匀分布)。
测量不确定度评定报告

测量不确定度评定报告一、引言二、测量方法和装置本次测量使用的方法是直线测量法,采用直尺和游标卡尺进行测量。
直线测量法是一种简单有效的测量方法,在工程和科学领域得到广泛应用。
1.人为误差测量1:30.2cm测量2:30.1cm测量3:30.3cm根据三次测量结果的平均值,得到被测量值为30.2cm。
通过测量结果的离散程度,可评估人为误差的大小。
2.仪器误差仪器误差是由于测量仪器本身的不准确性而引起的。
在使用直尺和游标卡尺进行测量时,需要考虑到仪器的刻度精度和读数精度。
本次测量中,直尺和游标卡尺的刻度间距分别为0.1cm和0.01cm。
根据仪器的刻度间距,可以评估测量结果在刻度内的不确定度。
例如,如果测量结果位于两个刻度之间,不确定度可以评估为刻度间距的一半。
3.环境影响环境因素如温度、湿度等的变化会对测量结果产生一定的影响。
在本次测量中,环境温度保持相对稳定,湿度变化较小,因此可以忽略环境影响对测量结果的不确定度。
四、测量不确定度评定五、灵敏度分析和建议灵敏度分析用于评估测量结果对误差的敏感程度,从而提供改进测量方法和装置的建议。
1.人为误差的影响2.仪器误差的影响根据前述的仪器误差评估,本次测量结果对仪器误差的敏感程度较高。
为了减小仪器误差对测量结果的影响,可以考虑使用更精密的测量仪器,如数字卡尺等,降低仪器误差。
六、结论本次测量的不确定度评定结果为0.1cm。
测量结果对人为误差的敏感程度较低,对仪器误差的敏感程度较高。
改进测量方法和装置可降低仪器误差对测量结果的影响。
电线电缆测量不确定度分析报告

电线电缆测量不确定度分析一、电线电缆不确定度评定项目有:绝缘厚度、外形尺寸、抗张强度(老化前)、断裂伸长率(老化前)、导体电阻、绝缘电阻。
说明:1、验材料为型号227IEC01(BV)的聚氯乙烯绝缘电线.2、绝缘厚度、外形尺寸的测量为在绝缘层上切取的同一切片,在同一环境条件下测量十次.3、抗张强度、断裂伸长率的测量为在同一根电线上连续截取10段10㎝长的试件.4、体电阻、绝缘电阻测量选用一5m长的试件上测量5次。
二、抗张强度1、建立过程的数学模型:A= F(a)A---绝缘层本身具有的屈服强度a--- WDL-2型微机控制电脑拉力机测量的屈服力值除以测量面积得到的屈服强度设绝缘层本身具有的屈服强度A的测量结果为a=b/S0,A的估计值为a,则可表示为:A= F(a)此式也可认为是数学模型。
b---WDL-2型微机控制电脑拉力机测量的屈服力值S0---绝缘层的原始面积其中,a为10次独立测量的屈服强度平均值,即a=18.8N/mm21、测量不确定度分量主要包括三个部分:1.测量人员在重复性条件下进行重复测量引入的标准不确定度;2.WDL-2型微机控制电脑拉力机测量引入的标准不确定度;3.环境温度误差引起的标准不确定度。
3.1 A类标准不确定度分量评定()()12--=∑n a aa s ii =0.35N/mm 2()()2/11.0mm N na s a s i ==()=a u 10.11N/mm2用相对标准不确定度分量表示为:()%5.01=a U 911=-=n v注:1、试验时,温度为23.1°C ;3.2 B 类不确定度分量评定3.2.1 测量仪制造厂提供的说明书表明,该测量仪的准确度为I 级,意即出厂检定时,最大允许误差在其量程范围内为±1%。
由于没有更多的信息,可估计a 在〔-a --a *1%,-a + -a *1%〕区间内,即在〔18.61N/mm 2,18.99N/mm 2〕范围内都可能出现,且出现的机会在区间内各处均等。
万能试验机测量不确定度评定报告-按照国标

万能试验机示值测量不确定度评定报告1 仪器2 试验方法 ⑴涉及标准JJG139-2014《拉力、压力和万能试验机检定规程》JJF1059.1-2012《测量不确定度评定与表示》GB / T 228.1-2010《金属材料拉伸试验第1部分:室温试验方法》3 测定数据4 测量说明测量试样外径,计算截面积 S 。
将试样固定在高低温拉脱试验机上,然后按照 GB / T 228.1-2010《金属材料拉伸试验第1部分:室温试验方法》的要求进行拉伸试验,以受控速度施加拉力,将试样拉伸至断裂,读取试样拉断过程中最大力 F 。
4.2数学模型SF R m式:m R ﹣抗拉强度 F ﹣最大拉力 S ﹣原始横截面积5 不确定度源分析5.1试验测量的重复误差引入的相对标准不确定度5.2试验机测力系统示值误差带来的相对标准不确定度 5.3标准测力仪的相对标准不确定度。
5.4计算机数据采集系统带来的相对标准不确定度 5.5原始横截面积S 的相对标准不确定度分项6 不确定度组分的评定6.1 A 类不确定度评定以满量程20%测量点为例得单次实验标准偏差及标准不确定度为:平均值a 85.2601MP nmm ni i==∑=用贝塞尔公式计算标准偏差 ()()a 32.011MP n m mm s ni i=--=∑=相对标准偏差 ()%122.0m==m s s 实际测量中,在重复条件下连续测量3次, 以该 3 次测量值的算术平均值作为测量结果,得到标准不确定度故标准不确定度 %07.03%122.0===n s u a6.2 B 类不确定度评定6.2.1 试验机测力系统示值误差带来的相对标准不确定度b1u1.0级的拉力试验机示值误差为土1.0%,按均匀分布考虑 k =。
3,则%577.03%3.0ku b1===α6.2.2 标准测力仪的相对标准不确定度b2u使用0.3级的标准测力仪对试验机进行检定。
重复性 R =0.3%。
可以看成重复性极限,则其相对标准不确定度为:%106.022%3.0u b2==标准不确定度:6.2.3计算机数据采集系统带来的相对标准不确定度b3u计算机数据采集系统所引入的 B 类相对标准不确定度为0.2%。
