体育单招历年数学试卷分类汇编-圆锥曲线
体育专业单招数学试题分类---立体几何

B’DB体育专业单招数学试题----立体几何:1.(2011)13.正三棱锥的底面边长为1。
2.(2011)8. 已知圆锥曲线母线长为5,底面周长为6π,则圆锥的体积是【】(A)6π(B)12π(C)18π(D)36π3.(2012)12. 已知圆锥侧面积是底面积的3倍,高为4cm,则圆锥的体积是cm34.(2012)6. 下面是关于三个不同平面,,αβγ的四个命题1:,pαγβγαβ⊥⊥⇒∥,2:,pαγβγαβ⇒∥∥∥,3:,pαγβγαβ⊥⊥⇒⊥,4:,pαγβγαβ⊥⇒⊥∥,其中的真命题是()A.12,p p B.34,p p C.13,p p D.24,p p(2013)9 若四面体的棱长都相等且它的体积为9a3,则此四面体的棱长为()A.32a B。
a2C。
3a2D。
239a6.(2013)12. 已知圆锥的母线长为13,地面周长为10π,则该圆锥侧面展开图的圆心角的弧度数为-----7.(2014).7.已知A,B为球O的球面上两点,平面AOB截球面所得圆上的劣弧AB的长为10π,且OA OB⊥,则球O的半径等于()A. 40B. 30C. 20D.10.2. (2011)(本题满分18分)如图正方体''''ABCD A B C D-中,P是线段AB上的点,AP=1,PB=3 (I)求异面直线'PB与BD的夹角的余弦值;(II)求二面角'B PC B--的大小;(III)求点B到平面'PCB的距离5.(2012真题)如图,已知正方形ABCD—A1B1C1D1的棱长为1,M是B1D1的中点.(Ⅰ)证明;BM AC⊥(Ⅱ)求异面直线BM与CD1的夹角;ACA1(Ⅲ)求点B 到平面A B 1M 的距离.8. (2013真题)(2014)19.如图,已知长方体ABCD —A B C D 中,AB = 6 ,BC = 4 ,AA = 3, M 为AB 中点。
体育对口单招数学试卷(答案) (4)

体育对口单招数学卷(满分120分,考试时间120分钟)一、选择题:(本题共20小题,每小题6分,共60分)1.复数32ii -+的虚部为()A.i B.-i C.1D.-12.设集合{|2011},{|01}M x x N x x =<=<<,则下列关系中正确的是()A.M N R = B.{|01}M N x x =<< C.N N∈D.M N φ= 3.已知平面向量a,b 满足||1,||2,a b ==a 与b 的夹角为60︒,则“m=1”是“()a mb a -⊥”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件4.从221x y m n -=(其中,{1,2,3}m n ∈-)所表示的圆锥曲线(椭圆、双曲线、抛物线)方程中任取一个,则此方程是焦点在x 轴上的双曲线方程的概率为()A.12B.47C.23D.345、数列{}n a 是递增的整数数列,且13a ,123100n a a a a +++⋯+=,则n 的最大值为()A.9B.10C.11D.126、已知集合A ={}1,3,B ={}2,3,则A B 等于()A.∅B.{}1,2,3C.{}1,2D.{}37.设,“”是“”的()A.充分非必要条件 B.必要充分条件C.充要条件D.既充分又必要条件8.函数)0(tan )(>=ωωx x f 图象的相邻两支截直线4π=y 所得线段长为4π,则)4(πf 的值是()(A)0(B)1(C)-1(D)9.已知n m ,是夹角为o60的单位向量,则n m a +=2和n m b 23+-=的夹角是()(A)o30(B)o60(C)o90(D)o12010.已知锐角ABC ∆的面积为,4,3BC CA ==,则角C 的大小为()A.75°B.60°C.45°D.30°11、“1=x ”是“0122=+-x x ”的()A、充要条件B、充分不必要条件C、必要不充分条件D、既不充分也不必要条件12、“2)1(+=n n a n ”是“0)2(log 21<+x ”的()A、充要条件B、充分不必要条件C、必要不充分条件D、既不充分也不必要条件13、设b a ,为正实数,则“1>>b a ”是“0log log 22>>b a ”的()A、充要条件B、充分不必要条件C、必要不充分条件D、既不充分也不必要条件14.设复数1z bi =+()b R ∈且||2z =,则复数的虚部为()A.i±B.C.1±D.15.若,,,,a b c d R ∈且,a b c d >>,则下列结论正确的是()A.22ac bc>B.ac bd>C.11a b<D.a c b d +>+16、设b a ,是实数,则“0>+b a ”是“0>ab ”的()A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件17、已知x x x f 2)(2+=,则)2(f 与)21(f 的积为()A、5B、3C、10D、818、“ααcos sin =”是“02cos =α”的()A、充分不必要条件B、必要不充分条件C、充要条件D、既不充分也不必要条件19、函数)32(log )(22-+=x x x f 的定义域是()A、[]1,3-B、()1,3-C、(][)+∞-∞-,13, D、()()+∞-∞-,13, 20、设,6.0,6.05.16.0==b a 6.05.1=c ,则c b a ,,的大小关系是()A、c b a <<B、b c a <<C、ca b <<D、ac b <<二、填空题:(本题共5小题,每小题6分,共30分)1、f(x)=+(m-4)x+2为偶函数,那么实数m 的值为____2、f(x)=-+mx 在(一∞,1]上是增函数,么m 的取值范围是___3.计算dxex)1(03-⎰=______4.右图所示的伪代码输出的结果S 为______5.与圆22(4)x y +-=2相切,且在两坐标轴上截距相等的直线共有_______条。
2019-2021年体育单招数学真题考点分类汇编(解析版)

2019-2021年单招数学考点分类汇编§1集合【2019年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第1题】已知集合=>=->=N M x x N x x M 则},1{},1{2( C ) A. }1{->x x B .}11{-<>x x x 或 C. }1{>x x D .}11{<<-x x【2020年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第1题】已知集合}104|{<<=x x A ,},|{2N n n x x B ∈==,则=B A ( C )A .∅B .{3}C .{9}D .{4,9}【2021年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第1题】设集合{}6,3,1=M ,{}5,4,3=N ,则____C =⋂N M {}6,4,1.A {}6,5,4,1.B {}3.C {}6,5,4,3,1.D§2 平面向量【2019年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第2题】已知向量)3,1(),2,1(-==b a ,则=+a 3( A )A 、5B 、4C 、3D 、5【2020年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第12题】已知向量b a ,,2=1=,且a 与b 的夹角为150°,=.【2021年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第14题】若向量b a ,753===,则__215_=⋅b a§3二项式定理【2019年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第11题】(11)7)21(x +的展开式中2x 的系数是___84____;【2020年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第15题】5)3(y x -的展开式中32y x 的系数为___-270___.【2021年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第8题】6221⎪⎭⎫ ⎝⎛-x x 的展开式中的常数项为__B____ 815.-A 1615.B 1615.-C 815.D§4三角函数及解三角形【2019年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第4题】已知)(22Z k k ∈+=ππα,则)(2tan D =α1.-A 22.-B 22.C 1.D【2019年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第10题】函数x x x x f 2cos cos sin )(+=的最大值为( B ) 22.A 221.+B 2.C 21.+D 【2019年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第14题】在ABC ∆中,AC=2,BC=3,AB=4,则=C cos ____41-____;【2019年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第17题】已知ABC ∆的内角C B A ,,成等差数列(1)求B(2)求A A cos 3sin +的最大值解:(1)在ABC ∆中︒=++180C B A 又 C B A ,,成等差数列B C A 2=+∴即︒=60B(2))60sin(2cos 3sin ︒+=+A A A )180,60(60)120,0(︒︒∈︒+∴︒︒∈A A)60sin(︒+∴A 的最大值为1所以 )60sin(2cos 3sin ︒+=+A A A 的最大值为2【2020年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第3题】函数x x x f 2cos sin )(2+=的最小周期是( C )A .π2B .23πC . πD .2π 【2020年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第6题】已知31tan -=x ,则=x 2sin ( D )A .53B .103C .103-D .53-【2020年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第17题】ABC ∆的内角C B A ,,的对边分别是c b a ,,,︒=30B ,1+=c b .(1)若2=c ,求C sin ;(2)若41sin =C ,求ABC ∆的面积. (1)在ABC 中,由1b c =+且2c =,可得3b =, 解:根据正弦定理sin sin b c B C =,可得sin 2sin 301sin 33c B C b ===. (2)由正弦定理可得1sin sin sin 30sin b C b b B C C -===︒, 因为1sin 4C =,可得2,1b c ==, 由余弦定理可得2222cos b a c ac B =+-,可得24121cos30a a =+-⨯⨯⨯,即230a -=,解得a =,所以1sin 2ABC S ab C ==△.【2021年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第4题】若,212cos 2sin=+x x 则x sin =___D___ 41.-A 31.-B 32.-C 43.-D【2021年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第5题】_____198sin 102sin 18cos 168sin C =︒︒-︒︒ 21.-A 0.B 21.C 1.D 【2021年全国普通高等学校运动训练、民族传统体育专业单独统一招生考试数学试卷第17题】记ABC ∆的内角C B A ,,的对边分别为c b a ,,,已知71cos ,8,7===B b a . (1)求c ;(2)求ABC ∆的面积S 。
2005-2024年体育单招历年数学试卷分类汇编 第2章 函数

体育单招历年数学试卷分类汇编目录体育单招历年数学试卷分类汇编第2章函数 (1)2.1 指数运算和指数不等式 (1)2.2 分段函数求值 (1)2.2 对数运算和对数不等式 (1)2.3 二次函数 (1)2.4 函数的定义域 (3)2.5 函数的单调性 (3)2.6 函数的奇偶性 (4)2.7 反函数 (4)2.8 导数 (5)1 第2章 函数2.1 指数运算和指数不等式【例2.1.1】 (2016改编)函数820x−≥的解集为____________.【例2.1.2】 (2019.5)若2x +5>14,则x 的取值范围是( ) A .(-7,+∞) B .(7,+∞) C .(-3,+∞) D .(3,+∞)【例2.1.3】 (2020.10)已知a =0.20.3, b =0.30.3, c =0.2-0.2,则( )A .a <b <cB .b <a <cC .b <c <aD .a <c <b2.2 分段函数求值【例2.1.4】 (2023.2)已知函数23,0()log ,0x x f x x x ⎧≤=⎨>⎩,则1(())3f f =() A.-1 B.1D.32.2 对数运算和对数不等式【例2.1.5】 (2004.03)14lg 23lg5lg 5+−=( ) A .1 B .4 C .18 D .28【例2.1.6】 (2017)=⨯4log 3log 32 .【例2.1.7】 (2005)若63()log f x x =,则(27)f = .【例2.1.8】 (2004)已知函数3log (0)()2(0)x x x f x x >⎧=⎨≤⎩,则1()9f f ⎡⎤⎢⎥⎣⎦的值是 . 【例2.1.9】 (2009)不等式2lg(54)1x x −+<的解集是( )A.(1,6)−B. (1,4)C. (,1)(6,)−∞−+∞ D. (1,1)(4,6)−【例2.1.10】 (2015)若10<<a ,且0)3(log )12(log 2<<+a a a a ,则a 的取值范围是 。
体育单招历年数学试卷分类汇编立体几何,文档

1.〔2021年第9题〕假设四面体的棱长都相等且它的体积为9a3,那么此四面体的棱长是〔〕A.32a B.2aC.32aD.239a2.〔2021年第12题〕4.圆锥的母线长为13,底面周长为10 ,那么该圆锥侧面展开图的圆心角的弧度数为.3.〔2021年第12题〕圆锥的侧面积是底面积的3倍,高为4cm,那么圆锥的体积是 cm3.〔2021年第8题〕圆锥的母线长为5,底面周长为6 ,那么圆锥的体积是〔A.6 B .12 C .18 D .365.〔2021年第13题〕〕正三棱锥的底面边长为1,高为6,那么侧面面积是.66.〔2021年第6题〕一个圆锥的母线长为13cm,高为12cm,那么此圆锥的内切球的外表积Scm3.(轴截面如下列图)7.〔2021年第16题〕外表积为180的球面上有A、B、C三点,AC6,BC8,AB10,那么球心到ABC所在平面的距离为.〔2021年第7题〕关于空间中的平面和直线,有以下四个命题:p1:m l,n l mPn,p2:mP,nP mPn,p1:mPl,l m ,p1:l其中的真命题是〔〕A.p1,p3 B .p2,p4,m与l相交C .p3m.D .p49.〔2021年第6题〕正三棱锥的底面边长为2,体积为3,那么正三棱锥的高是.10.〔2021年第16题〕用平面截球,截得小圆的面积为,假设球心到平面的距离为2,那么球的外表积是.11.〔2004年第14题〕正方体的全面积是a2,它的顶点都在一个球面上,这个球的外表积是.12.〔2004年第6题〕在正方体ABCD A1B1C1D1中,E、F分别是AB、C1D1的中点,那么在正方体的各外表正方形所代表的6个面中,和EF成45A.0个B.2个C.4个角的共有〔D .6个〕〔2021年第6题〕下面是关于三个不同的平面,,的四个命题p1:,P ,p2:P,P P ,p1:,,p1:,P.其中的真命题是〔〕A.p1,p2B.p3,p4 C .p1,p3 D .p2,p414.〔2021年第7题〕下面是关于两条直线m,n和两个平面〔m,n均不在p1:mP,nP mPn,p2:mP , P , 上〕的四个命题:mP ,p3:mP,nP,P mPn,p4:mPn,n,m P .其中的真命题是〔〕A.p1,p3B.p1,p4 C .p2,p3 D .p2,p415.〔2021年第19题18分〕如图,长方体ABCD A1B1C1D1中,AB 6,BC 4,AA13,M为AB中点,求(Ⅰ)二面角M B1C1 A1的大小;(Ⅱ)点D1到平面MB1C1的距离。
浙江十年(2014-2023)单独考试招生文化考试数学真题分类汇编 圆锥曲线含详解

专题06圆锥曲线考点01椭圆1.(2023年浙江)中国刺绣作为一项传统手工技艺,是中国传统文化的重要组成部分.某个椭圆形的刺绣艺术品的尺寸如图所示,则这个椭圆的离心率是()u 53u 56u 52u 552.(2023年浙江)椭圆的标准方程为2+26=1,焦点在x 210,则n=____.3.(2022年浙江)椭圆22221(0)x y a b a b+=>>的焦距为离心率3e =,过点(2,0)-的直线与椭圆交于A ,B 两点,且线段AB 的中点坐标为01,2y ⎛⎫- ⎪⎝⎭.求:(1)椭圆的标准方程;(4分)(2)0y 的值.(6分)4.(2021年浙江)若椭圆2214x y m +=的一个焦点为(0,3)-,则椭圆的离心率为()A.355 B.413 C.313D.313135.(2021年浙江)如图,(4,0)F 为椭圆的右焦点,M 是椭圆上的点,若△OMF是正三角形,则椭圆长轴长为.6.(2020年浙江)若椭圆22221(0)x y a b a b +=>>的焦距为2,离心率为2.斜率为1的直线经过椭圆的左焦点,交椭圆于A ,B 两点.(1)求椭圆的标准方程;(5分)(2)求||AB 的值.(5分)7.(2019年浙江)椭圆标准方程为221244x y t t+=+-,一个焦点为()3,0-,则t 的值为()A.1- B.0C.1D.38.(2019年浙江)已知椭圆中心在原点且对称轴为坐标轴,它与双曲线2213y x -=有且仅有两个公共点,它们的离心率之积为1,则椭圆标准方程为________.9.(2018年浙江)方程+32+2+−32+2=10所表示的曲线为()A.圆B.椭圆C.双曲线D.抛物线10.(2018年浙江)如图所示,椭圆22+22=1的两个焦点坐标为1−2,0,22,0,两个顶点和两个焦点构成一个正方形,求:(1)椭圆的标准方程和离心率;(4分)(2)以点A (a ,0)为顶点,且关于x 轴对称的内接等腰直角三角形的周长.(6分)11.(2017年浙江)已知椭圆方程:224312x y +=,下列说法错误的是()A.焦点为()0,1-,()0,1B.离心率12e =C.长轴在x 轴上D.短轴长为2312.(2016年浙江)椭圆22116x y m +=的离心率34e =,则m 的值为A.7B 7C.7或25D.7或256713.(2015年浙江)若()0,πβ∈,则方程22sin 1x y β+=所表示的曲线是()A .圆B .椭圆C .双曲线D .椭圆或圆14.(2014年浙江)两边靠墙的角落有一个区域,边界线正好是椭圆轨迹的部分,如图所示.现要设计一个长方形花坛,要求其不靠墙的顶点正好落在椭圆的轨迹上.(1)根据所给条件,求出椭圆的标准方程;(3分)(2)求长方形面积S 与边长x 的函数关系式;(3分)(3)求当边长x 为多少时,面积S 有最大值,并求其最大值.(4分)考点02双曲线1.(2023年浙江)如图所示,双曲线的标准方程为22−22=1(>0,>0),1,2为双曲线的两个焦点,实轴长为23,且双曲线经过点(−2,−2);(1)求双曲线的标准方程;(3分)(2)若点M 在双曲线的渐近线上,ΔB 12的面积为122,求点M 的坐标;(4分)(3)点P (m,n )在双曲线右支上,点N 的坐标为(1,n ),求∣B 1∣∣P∣的值.(3分)2.(2022年浙江)己知双曲线221412x y -=的两个焦点为12,F F ,以线段12F F 为直径的圆与双曲线在第一象限的交点为P ,则12F PF △的面积为()A .43B .63C .12D .243.(2021年浙江)已知双曲线的渐近线方程为2y x =±,实轴长为4,则双曲线标准方程是()A.221416x y -= B.221416y x -=或2214x y -=C.2214x y -= D.221416x y -=或2214y x -=4.(2020年浙江)双曲线221x y -=与直线1x y -=交点的个数为()A .0B .1C .2D .45.(2020年浙江)已知双曲线22221x y a b -=的渐近线方程为y =,则该双曲线的离心率为___________.6.(2019年浙江)双曲线22221x y a b-=的实轴长为10,焦距为26,则双曲线的渐近线方程为()A.135y x =±B.125y x =±C.512y x =±D.513y x =±7.(2018年浙江)双曲线216−29=1的焦点坐标为()A.±7,0B.0,±7C.±5,0D.0,±58.(2018年浙江)双曲线22−28=1e =3,则实半轴长9.(2017年浙江)设动点M 到()1F =的距离减去它到)2F 的距离等于4,则动点M 的轨迹方程为()A.22149x y -=(2x ≤-)B.22149x y -=(2x ≥)C.22149x y -=(2y ≥) D.22149x y -=(3x ≥)10.(2017年浙江)双曲线2212516y x -=的两条渐近线方程为______.11.(2016年浙江)已知双曲线22221x y a b -=的离心率52e =,实轴长为4,直线l 过双曲线的左焦点1F 且与双曲线交于,A B 两点,83AB =.(1)求双曲线的方程;(2)求直线l 的方程.12.(2015年浙江)焦点在x 轴上,焦距为8的双曲线,其离心率2e =.则双曲线的标准方程为()A .221412x y -=B .221124x y -=C .221412y x -=D .221124y x -=13.(2014年浙江)双曲线22149x y -=的离心率e =()A .23B .32C .132D .133考点03抛物线1.(2023年浙江)截至2023年2月,被誉为“中国天眼”的500米口径的射电望远镜(FAST),已经发现超740颗脉冲星,为世界各国探索宇宙星空,提供了中国智慧和中国力量.如图所示,这个射电望远镜的轴截面是一个开口向上的抛物线的一部分.当抛物线口径AB 为300米时,抛物线的深度OC 为56.25米,则这个抛物线的标准方程为()A.x 2=400yB.x 2=200yC.y 2=400xD.y 2=200x2.(2022年浙江)己知点(2,2)M 在抛物线22y px =上,则抛物线的焦点坐标为()A .(1,0)-B .(1,0)C .1,02⎛⎫⎪⎝⎭D .1,02⎛⎫-⎪⎝⎭3.(2021年浙江)已知抛物线顶点为原点,准线l :13y =-.(1)求抛物线的标准方程;(4分)(2)过焦点F 的直线与抛物线相交于A ,B 两点,若83AB =,求直线AB 的方程.4.(2020年浙江)若直线y x b =+经过抛物线24x y =的焦点,则b 的值是()A .2-B .1-C .1D .25.(2019年浙江)已知抛物线的顶点在原点,焦点坐标为()3,0F .(1)求抛物线的标准方程;(2)若抛物线上点M 到焦点的距离为4,求点M 的坐标.6.(2018年浙江)抛物线2=12的焦点到其准线的距离是()A.18B.14C.12D.17.(2017年浙江)1992年巴塞罗那奥运会开幕式中,运动员安东尼奥·雷波洛以射箭方式点燃主会场的圣火成为历史经典.如图所示,如果发射点A 离主火炬塔水平距离60m AC =,塔高20m BC =.已知箭的运动轨迹是抛物线,且离火炬塔水平距离20m EC =处达到最高点O .(1)若以O 为原点,水平方向为x 轴,1m 为单位长度建立直角坐标系。
2024年全国普通高等学校运动训练、民族传统体育专业单招考试数学试卷(答案解析)

2024年全国普通高等学校运动训练、民族传统体育专业单招考试数学试卷一、单项选择题1.已知集合{}22|1A x x y =+=,{}2|B y y x ==,则A B = ()A.[]0,1 B.[)0,+∞ C.{}1,1- D.{}0,12.已知复数()()23ai i ++在复平面内对应的点在直线y x =上,则实数a =()A.-2B.-1C.1D.23.若log 0a b <(0a >且1a ≠),221b b ->,则()A.1a >,1b >B.01a <<,1b >C.1a >,01b << D.01a <<,01b <<4.我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是()A.相邻两个节气晷长减少或增加的量为一尺B.春分和秋分两个节气的晷长相同C.立冬的晷长为一丈五寸D.立春的晷长比立秋的晷长短5.有三个筐,一个装着柑子,一个装着苹果,一个装着柑子和苹果,包装封好然后做“柑子”“苹果”“混装”三个标签,分别贴到上述三个筐上,由于马虎,结果全贴错了,则()A.从贴有“柑子”标签的筐里拿出一个水果,就能纠正所有的标签B.从贴有“苹果”标签的筐里拿出一个水果,就能纠正所有的标签C.从贴有“混装”标签的筐里拿出一个水果,就能纠正所有的标签D.从其中一个筐里拿出一个水果,不可能纠正所有的标签6.已知向量OP =,将OP 绕原点O 逆时针旋转45︒到'OP 的位置,则'OP =()A.()1,3B.()3,1-C.()3,1D.()1,3-7.已知函数()f x 对任意,x y R ∈,都有()()()2f x y f x f y +=,且()11f =,则01()ni f i ==∑()A.21n - B.122n -C.112n-D.122n-8.已知正四棱柱1111ABCD A B C D -,设直线1AB 与平面11ACC A 所成的角为α,直线1CD 与直线11A C 所成的角为β,则()A.2βα=B.2αβ= C.αβ= D.2παβ+=二、多项选择题9.随着我国经济结构调整和方式转变,社会对高质量人才的需求越来越大,因此考研现象在我国不断升温.某大学一学院甲、乙两个本科专业,研究生的报考和录取情况如下表,则性别甲专业报考人数乙专业报考人数性别甲专业录取率乙专业录取率男100400男25%45%女300100女30%50%A.甲专业比乙专业的录取率高B.乙专业比甲专业的录取率高C.男生比女生的录取率高D.女生比男生的录取率高10.已知函数()sin()(0,0)f x x ωϕωϕπ=+><<,将()y f x =的图像上所有点向左平移6π个单位,然后纵坐标不变,横坐标缩短为原来的12,得到函数()y g x =的图像.若()g x 为偶函数,且最小正周期为2π,则()A.()y f x =图像关于点(,0)12π-对称B.()f x 在5(0,)12π单调递增C.()()2x f x g =在5(0,)4π有且仅有3个解 D.()g x 在5()124ππ,有且仅有3个极大值点11.已知抛物线()220y px p =>上三点()11,A x y ,()1,2B ,()22,C x y ,F 为抛物线的焦点,则()A.抛物线的准线方程为1x =-B.0FA FB FC ++=,则FA ,FB ,FC 成等差数列C.若A ,F ,C 三点共线,则121y y =-D.若6AC =,则AC 的中点到y 轴距离的最小值为212.已知函数()f x 的定义域为()0,∞+,导函数为()'f x ,()()'ln xf x f x x x -=,且11f e e⎛⎫= ⎪⎝⎭,则()A.1'0f e ⎛⎫= ⎪⎝⎭B.()f x 在1x e=处取得极大值C.()011f << D.()f x 在()0,∞+单调递增三、填空题13.()()52x y x y +-的展开式中24x y 的系数为________.14.已知l 是平面α,β外的直线,给出下列三个论断,①//l α;②αβ⊥;③l β⊥.以其中两个论断为条件,余下的论断为结论,写出一个正确命题:________.(用序号表示)15.已知双曲线()222210,0x y a b a b-=>>过左焦点且垂直于x 轴的直线与双曲线交于P ,Q 两点,以P ,Q ,则双曲线的离心率为________.16.我国的西气东输工程把西部的资源优势变为经济优势,实现了气能源需求与供给的东西部衔接,工程建设也加快了西部及沿线地区的经济发展输气管道工程建设中,某段管道铺设要经过一处峡谷,峡谷内恰好有一处直角拐角,水平横向移动输气管经过此拐角,从宽为27米峡谷拐入宽为8米的峡谷.如图所示,位于峡谷悬崖壁上两点E 、F 的连线恰好经过拐角内侧顶点O (点E 、O 、F 在同一水平面内),设EF 与较宽侧峡谷悬崖壁所成角为θ,则EF 的长为________(用θ表示)米.要使输气管顺利通过拐角,其长度不能低于________米.2024年全国普通高等学校运动训练、民族传统体育专业单招考试数学试卷答案解析一、单项选择题1.已知集合{}22|1A x x y =+=,{}2|B y y x ==,则A B = ()A.[]0,1 B.[)0,+∞ C.{}1,1- D.{}0,1【分析】集合{}22|1A x x y =+=是x 的取值范围,{}2|B y y x ==是函数的值域,分别求出再求交集.【详解】解:2210,11y x x =-≥-≤≤,{}[)2|0,B y y x ===+∞A B = [][)[]1,10,+=0,1=-∞ 故选:A【点睛】考查求等式中变量的范围以及集合的交集运算;基础题.2.已知复数()()23ai i ++在复平面内对应的点在直线y x =上,则实数a =()A.-2B.-1C.1D.2【答案】C 【解析】【分析】化简复数,求出对应点,代入直线方程求解即可.【详解】因为()()236(23)ai i a a i ++=-++,所以对应的点为()6,23a a -+,代入直线y x =可得623a a -=+,解得1a =,故选:C【点睛】本题考查了复数的运算法则、几何意义,直线的方程,考查了推理能力与计算能力,属于基础题.3.若log 0a b <(0a >且1a ≠),221b b ->,则()A.1a >,1b >B.01a <<,1b >C.1a >,01b << D.01a <<,01b <<【分析】先由221b b ->得,20b b ->,又由0b >,可得1b >,而log 0a b <,可得01a <<【详解】解:因为221b b ->,所以20b b ->,因为0b >,所以1b >,因为log 0a b <,1b >,所以01a <<,故选:B【点睛】此题考查的是指数不等式和对数不等式,属于基础题4.我国天文学和数学著作《周髀算经》中记载:一年有二十四个节气,每个节气的晷长损益相同(晷是按照日影测定时刻的仪器,晷长即为所测量影子的长度).二十四节气及晷长变化如图所示,相邻两个节气晷长减少或增加的量相同,周而复始.已知每年冬至的晷长为一丈三尺五寸,夏至的晷长为一尺五寸(一丈等于十尺,一尺等于十寸),则说法不正确的是()A.相邻两个节气晷长减少或增加的量为一尺B.春分和秋分两个节气的晷长相同C.立冬的晷长为一丈五寸D.立春的晷长比立秋的晷长短【答案】D 【解析】【分析】由题意可知夏至到冬至的晷长构成等差数列,其中115a =寸,13135a =寸,公差为d 寸,可求出d ,利用等差数列知识即可判断各选项.【详解】由题意可知夏至到冬至的晷长构成等差数列{}n a ,其中115a =寸,13135a =寸,公差为d 寸,则1351512d =+,解得10d =(寸),同理可知由冬至到夏至的晷长构成等差数列{}n b ,首项1135b =,末项1315b =,公差10d =-(单位都为寸).故选项A 正确;春分的晷长为7b ,7161356075b b d ∴=+=-= 秋分的晷长为7a ,716156075a a d ∴=+=+=,所以B 正确;立冬的晷长为10a ,10191590105a a d ∴=+=+=,即立冬的晷长为一丈五寸,C 正确; 立春的晷长,立秋的晷长分别为4b ,4a ,413153045a a d ∴=+=+=,41313530105b b d =+=-=,44b a ∴>,故D 错误.故选:D【点睛】本题主要考查了等差数列的通项公式,等差数列在实际问题中的应用,数学文化,属于中档题.5.有三个筐,一个装着柑子,一个装着苹果,一个装着柑子和苹果,包装封好然后做“柑子”“苹果”“混装”三个标签,分别贴到上述三个筐上,由于马虎,结果全贴错了,则()A.从贴有“柑子”标签的筐里拿出一个水果,就能纠正所有的标签B.从贴有“苹果”标签的筐里拿出一个水果,就能纠正所有的标签C.从贴有“混装”标签的筐里拿出一个水果,就能纠正所有的标签D.从其中一个筐里拿出一个水果,不可能纠正所有的标签【答案】C 【解析】【分析】若从贴有“柑子”或“苹果”标签的筐内拿出一个水果,无法判定剩余水果是一种还是两种,不能纠正所有标签,若从“混装”标签中取出一个,就能判断其余两个筐内水果.【详解】如果从贴着苹果标签的筐中拿出一个水果,如果拿的是柑子,就无法判断这筐装的全是柑子,还是有苹果和柑子;同理从贴着柑子的筐中取出也无法判断,因此应从贴着苹果和柑子的标签的筐中取出水果.分两种情况:(1)如果取出的是柑子,那说明这筐全是柑子,则贴有柑子的那筐就是苹果,贴有苹果的那筐就是苹果和柑子.(2)如果取出的是苹果,那说明这筐全是苹果,那贴有苹果的那筐就是柑子,贴有柑子的那筐就是苹果和柑子.故选:C【点睛】解决本题的关键在于,其中贴有混装的这筐肯定不是苹果和柑子混在一起,所以能判断不是苹果就是柑子,考查了逻辑推理能力,属于容易题.6.已知向量OP =,将OP 绕原点O 逆时针旋转45︒到'OP 的位置,则'OP =()A.()1,3B.()3,1-C.()3,1D.()1,3-【答案】D 【解析】【分析】设向量OP与x 轴的夹角为α,结合三角函数的定义和两角和与差的正弦、余弦函数公式,求得cos ,sin ,cos(),454si (5n )αααα++︒︒,得到点P '的坐标,进而求得'OP.【详解】由题意,向量OP =,则OP =设向量OP与x 轴的夹角为α,则cos αα==,所以4545sin sin 452210cos()cos cos ααα︒︒-︒=-+=223104545cos s sin()sin co in 452210s ααα︒︒+︒=++=,可得cos()(14510OP α+=-=︒-,45sin()310OP α︒+== 所以'(1,3)OP =-.故选:D.【点睛】本题主要考查了向量的坐标表示,以及三角函数的定义的应用和两角和与差的正弦、余弦函数的综合应用,着重考查推理与运算能力.7.已知函数()f x 对任意,x y R ∈,都有()()()2f x y f x f y +=,且()11f =,则01()ni f i ==∑()A.21n -B.122n -C.112n-D.122n-【答案】B 【解析】【分析】利用赋值法再结合条件,即可得答案;【详解】由所求式子可得(0)0f ≠,令0x y ==可得:(0)(0)(0)(0)22f f f f ⋅=⇒=,令1x y ==可得:(1)(1)1(2)22f f f ⋅==,令1,2x y ==可得:2(1)(2)1(3)22f f f ⋅==,令2x y ==可得:3(2)(2)1(4)22f f f ⋅==,∴11()2n f n -=,∴111011001(12)112222222()122n nni n n i i f i +---==-==++++==--∑∑ ,故选:B.【点睛】本题考查根据抽象函数的性质求函数的解析式,等比数列求和,考查函数与方程思想、转化与化归思想,考查逻辑推理能力、运算求解能力,求解时注意将抽象函数具体化.8.已知正四棱柱1111ABCD A B C D -,设直线1AB 与平面11ACC A 所成的角为α,直线1CD 与直线11A C 所成的角为β,则()A.2βα=B.2αβ= C.αβ= D.2παβ+=【答案】D 【解析】【分析】分别在正四棱柱中找到α和β,将α和β放在同一个平面图形中找关系即可.【详解】作正四棱柱1111ABCD A B C D -如下图:∵在正四棱柱1111ABCD A B C D -中,1AA ⊥平面1111D C B A ,∴111AA B D ⊥∵底面1111D C B A 是正方形∴1111B D AC ⊥又∵1111AA AC A ⋂=∴11BD ⊥平面1111D C B A ∴1B AO ∠是直线1AB 与平面11ACC A 所成的角,即1=B AO α∠∵11CD A B∥∴11BA C ∠是直线1CD 与直线11A C 所成的角,即11=BA C β∠∵11A B B A =,11A O B O =,OA OB =∴11A BO B AO △≌△∴111=BA C AB O β∠∠=∵11B D ⊥平面1111D C B A ∴1B O OA⊥∴11+=+2B AO AB O παβ∠∠=故选:D【点睛】本题主要考查直线与平面和异面直线的夹角,属于中档题.二、多项选择题9.随着我国经济结构调整和方式转变,社会对高质量人才的需求越来越大,因此考研现象在我国不断升温.某大学一学院甲、乙两个本科专业,研究生的报考和录取情况如下表,则性别甲专业报考人数乙专业报考人数性别甲专业录取率乙专业录取率男100400男25%45%女300100女30%50%A.甲专业比乙专业的录取率高B.乙专业比甲专业的录取率高C.男生比女生的录取率高D.女生比男生的录取率高【答案】BC 【解析】【分析】根据数据进行整合,甲专业录取了男生25人,女生90人;乙专业录取了男生180人,女生50人;结合选项可得结果.【详解】由题意可得甲专业录取了男生25人,女生90人;乙专业录取了男生180人,女生50人;甲专业的录取率为259028.75%100300+=+,乙专业的录取率为1805046%400100+=+,所以乙专业比甲专业的录取率高.男生的录取率为2518041%100400+=+,女生的录取率为905035%300100+=+,所以男生比女生的录取率高.故选:BC.【点睛】本题主要考查频数分布表的理解,题目较为简单,明确录取率的计算方式是求解的关键,侧重考查数据分析的核心素养.10.已知函数()sin()(0,0)f x x ωϕωϕπ=+><<,将()y f x =的图像上所有点向左平移6π个单位,然后纵坐标不变,横坐标缩短为原来的12,得到函数()y g x =的图像.若()g x 为偶函数,且最小正周期为2π,则()A.()y f x =图像关于点(,0)12π-对称B.()f x 在5(0,)12π单调递增C.()()2x f x g =在5(0,)4π有且仅有3个解 D.()g x 在5()124ππ,有且仅有3个极大值点【答案】AC 【解析】【分析】根据题意求得2ω=,6π=ϕ,进而求得()cos 4g x x =,()sin(26f x x π=+,然后对选项逐一判断即可.【详解】解:将()y f x =的图像上所有点向左平移6π个单位后变为:sin 6x ωπωϕ⎛⎫++ ⎪⎝⎭,然后纵坐标不变,横坐标缩短为原来的12后变为:sin 26x ωπωϕ⎛⎫++ ⎪⎝⎭,所以()sin 26g x x ωπωϕ⎛⎫=++⎪⎝⎭.因为()g x 的最小正周期为2π,所以222ππω=,解得:2ω=.所以()sin 43g x x πϕ⎛⎫=++ ⎪⎝⎭,又因为()g x 为偶函数,所以,32ππφkπk Z +=+∈,所以6,k k Z πϕπ=+∈.因为0ϕπ<<,所以6π=ϕ.所以()sin 4cos 42g x x x π⎛⎫=+= ⎪⎝⎭,()sin(26f x x π=+.对于选项A ,因为()sin 2()sin 0012126f πππ⎡⎤-=-+==⎢⎥⎣⎦,所以()y f x =图像关于点(,0)12π-对称,故A 正确.对于选项B ,因为x ∈5(0,)12π时,2,66x πππ⎛⎫+∈ ⎪⎝⎭,设26t x π=+,则()sin ,,6f t t t ππ⎛⎫=∈ ⎪⎝⎭,因为()f t 在,6π⎛⎫π⎪⎝⎭不是单调递增,所以()f x 在5(0,)12π不单调递增,故B 错误.对于选项C ,()cos 22x g x =,()sin(2)6f x x π=+,画出(),2x f x g ⎛⎫⎪⎝⎭在5(0,4π图像如图所示:从图中可以看出:(),2x f x g ⎛⎫⎪⎝⎭在5(0,4π图像有三个交点,所以()()2x f x g =在5(0,)4π有且仅有3个解,故C 正确.对于选项D ,()cos 4g x x =在5()124ππ,的图像如图所示:从图中可以看出()g x 在5(124ππ,有且仅有2个极大值点,故D 选项错误.故选:AC .【点睛】本题主要考查正弦型函数、余弦型函数的周期、对称中心、奇偶性、单调性等,考查学生数形结合的能力,计算能力等,属于中档题.11.已知抛物线()220y px p =>上三点()11,A x y ,()1,2B ,()22,C x y ,F 为抛物线的焦点,则()A.抛物线的准线方程为1x =-B.0FA FB FC ++=,则FA ,FB ,FC 成等差数列C.若A ,F ,C 三点共线,则121y y =-D.若6AC =,则AC 的中点到y 轴距离的最小值为2【答案】ABD 【解析】【分析】把点(1,2)B 代入抛物线22y px =即可得到本题答案;根据抛物线的定义,以及0FA FB FC ++=,可得122x x +=,从而可证得2FA FC FB += ;由A ,F ,C 三点共线,得121211y y x x =--,结合22112211,44x y x y ==,化简即可得到本题答案;设AC 的中点为00(,)M x y ,由AF CF AC +≥,结合1201122AF CF x x x +=+++=+,即可得到本题答案.【详解】把点(1,2)B 代入抛物线22y px =,得2p =,所以抛物线的准线方程为1x =-,故A 正确;因为1122(,),(1,2),(,),(1,0)A x y B C x y F ,所以11(1,)FA x y =-,(0,2)FB = ,22(1,)FC x y =- ,又由0FA FB FC ++=,得122x x +=,所以121142FA FC x x FB +=+++== ,即FA ,FB,FC 成等差数列,故B 正确;因为A ,F ,C 三点共线,所以直线斜率AF CF k k =,即121211y y x x =--,所以122212111144y y y y =--,化简得,124y y =-,故C 不正确;设AC 的中点为00(,)M x y ,因为AF CF AC +≥,1201122AF CF x x x +=+++=+,所以0226x +≥,得02x ≥,即AC 的中点到y 轴距离的最小值为2,故D 正确.故选:ABD【点睛】本题主要考查抛物线定义的应用以及抛物线与直线的相关问题,考查学生的分析问题能力和转化能力.12.已知函数()f x 的定义域为()0,∞+,导函数为()'f x ,()()'ln xf x f x x x -=,且11f e e⎛⎫= ⎪⎝⎭,则()A.1'0f e ⎛⎫= ⎪⎝⎭B.()f x 在1x e=处取得极大值C.()011f << D.()f x 在()0,∞+单调递增【答案】ACD 【解析】【分析】根据题意可设()21ln 2f x x x bx =+,根据11f e e⎛⎫= ⎪⎝⎭求b ,再求()f x '判断单调性求极值即可.【详解】∵函数()f x 的定义域为()0,∞+,导函数为()'f x ,()()'ln xf x f x x x -=即满足()()2'ln xf x f x x x x-=∵()()()2'f x xf x f x x x '-⎛⎫=⎪⎝⎭∴()ln f x x x x '⎛⎫=⎪⎝⎭∴可设()21ln 2f x x b x =+(b 为常数)∴()21ln 2f x x x bx=+∵211111ln 2b f e e e e e ⎛⎫=⋅+= ⎪⎝⎭,解得12b =∴()211ln 22f x x x x =+∴()112f =,满足()011f <<∴C 正确∵()()22111ln ln =ln 10222f x x x x '=+++≥,且仅有1'0f e ⎛⎫= ⎪⎝⎭∴B 错误,A、D 正确故选:ACD【点睛】本题主要考查函数的概念和性质,以及利用导数判断函数的单调性和极值点,属于中档题.三、填空题13.()()52x y x y +-的展开式中24x y 的系数为________.【答案】15-【解析】【分析】把5()x y -按照二项式定理展开,可得5(2)()x y x y +-的展开式中24x y 的系数.【详解】()5051423455555233245551(2)()(2)x y x y x y C x C x y C x y C x y C x y C y +-=+⋅⋅⋅+⋅-⋅+⋅-⋅-,故它的展开式中24x y 的系数为5543215C C -=-,故答案为:15-.【点睛】本题主要考查二项式定理的应用,二项展开式的通项公式,二项式系数的性质,属于基础题.14.已知l 是平面α,β外的直线,给出下列三个论断,①//l α;②αβ⊥;③l β⊥.以其中两个论断为条件,余下的论断为结论,写出一个正确命题:________.(用序号表示)【答案】若①③,则②或若②③,则①(填写一个即可);【解析】【分析】利用空间直线与平面的位置关系进行判断,//l α,αβ⊥时,l 与β可能平行或者相交.【详解】因为//l α,αβ⊥时,l 与β可能平行或者相交,所以①②作为条件,不能得出③;因为//l α,所以α内存在一条直线m 与l 平行,又l β⊥,所以m β⊥,所以可得αβ⊥,即①③作为条件,可以得出②;因为αβ⊥,l β⊥,所以//l α或者l α⊂,因为l 是平面α外的直线,所以//l α,即即②③作为条件,可以得出①;故答案为:若①③,则②或若②③,则①(填写一个即可);【点睛】本题主要考查空间位置关系的判断,稍微具有开放性,熟悉空间的相关定理及模型是求解的关键,侧重考查直观想象的核心素养.15.已知双曲线()222210,0x y a b a b-=>>过左焦点且垂直于x 轴的直线与双曲线交于P ,Q 两点,以P ,Q ,则双曲线的离心率为________.【答案】32【解析】【分析】首先求,P Q 两点的坐标,代人圆心到直线的距离,由已知条件建立等式求得2b a =,最后再求双曲线的离心率.【详解】设(),0F c -,当x c =-,代人双曲线方程22221c ya b-=,解得:2b y a =±,设2,b Pc a ⎛⎫- ⎪⎝⎭,2,b Q c a ⎛⎫-- ⎪⎝⎭根据对称性,可设与两圆相切的渐近线是by x a =,则,P Q 两点到渐近线的距离22bc b bc b ---++=,c b > ,上式去掉绝对值为22bc b bc b c c +-+=,即52b a =,那么32c a ==.∴双曲线的离心率32e =.故答案为:32【点睛】本题考查双曲线的离心率,重点考查转化与化归的思想,计算能力,属于基础题型.16.我国的西气东输工程把西部的资源优势变为经济优势,实现了气能源需求与供给的东西部衔接,工程建设也加快了西部及沿线地区的经济发展输气管道工程建设中,某段管道铺设要经过一处峡谷,峡谷内恰好有一处直角拐角,水平横向移动输气管经过此拐角,从宽为27米峡谷拐入宽为8米的峡谷.如图所示,位于峡谷悬崖壁上两点E 、F 的连线恰好经过拐角内侧顶点O (点E 、O 、F 在同一水平面内),设EF 与较宽侧峡谷悬崖壁所成角为θ,则EF 的长为________(用θ表示)米.要使输气管顺利通过拐角,其长度不能低于________米.【答案】(1).278sin cos θθ+(2).【解析】【分析】分别计算出OE 、OF ,相加可得EF 的长;设()2780sin cos 2f πθθθθ⎛⎫=+<< ⎪⎝⎭,利用导数求得()f θ的最小值,即可得解.【详解】如下图所示,过点O 分别作OA AE ⊥,OB BF ⊥,则OEA BOF θ∠=∠=,在Rt OAE △中,27OA =,则27sin sin OA OE θθ==,同理可得8cos OF θ=,所以,278sin cos EF OE OF θθ=+=+.令()2780sin cos 2f πθθθθ⎛⎫=+<< ⎪⎝⎭,则()3333222222278cos tan27cos8sin8sin27cos8 sin cos sin cos sin cosfθθθθθθθθθθθθθ⎛⎫-⎪-⎝⎭=-+='=,令()00fθ'=,得327tan8θ=,得03tan2θ=,由22003tan2sin cos1sin0θθθθ⎧=⎪⎪+=⎨⎪>⎪⎩,解得sin13cos13θθ⎧=⎪⎪⎨⎪=⎪⎩,当00θθ<<时,()0fθ'<;当02πθθ<<时,()0fθ'>.则()()min1313f fθθ===.故答案为:278sin cosθθ+;.【点睛】本题考查导数的实际应用,求得函数的解析式是解题的关键,考查计算能力,属于中等题.。
全国体育单招数学真题分类2011-2015

全国体育单招数学真题分类2011-20151.给定集合M={x|0<x<1},集合N={x|-1<x<1},则M∩N=M。
2.已知集合M={x|x>1},N={x|x≤2},则M∩N=(1,2]。
3.已知集合M={x|-2<x<2},N={x|-3<x<-1},则M∩N=(-2,-1)。
4.设集合A={x|0<x<7,x∈N},则A的元素共有6个。
5.已知集合A={x|x=3n,n∈N},B={x|x=3n+1,n∈N},C={x|x=3n+2,n∈N},其中真命题是①和③。
6.给定函数y=x+5(x≠-5)的反函数为y=x-5(x≠0)。
7.已知函数f(x)=4ax+1/(2x)(a>0)有最小值8,则a=1/2.8.函数y=x/(2x+1)-1的反函数是y=(x+1)/(2-x)(x≠-1/2)。
9.函数f(x)=ln((1-x)/(1+x))的定义域是(-1,1)。
10.下列函数中,减函数的是y=-x+1.一、函数1.函数f(x)=2x-x^2的值域是[A。
+∞),其中A为f(x)的最大值。
2.已知f(x)是奇函数,当x>0时,f(x)=x^2+ln(x+1/x^2),则当x<0时,f(x)=-x^2+ln(-x+1/x^2)。
二、不等式1.不等式|x-1|/x<1的解集是{x|0<x<1}。
2.不等式x+1>x-1的解集是{x|全体实数}。
3.不等式log2(4+3x-x^2)≤log2(4x-2)的解集为{x|-1<x<4}。
4.不等式x^2+x-2<x+5的解集为{x|(-3.-2]∪[1.+∞)}。
5.不等式(1-2x)/(x+3)>0的解集是{x|(-∞。
-3)∪(1/2.+∞)}。
6.若0<a<1,且loga(2a+1)<loga(3a)<1,则a的取值范围是(1/3.1/2)。
体育单招数学圆锥曲线答案

一、选择题(本大题共12小题,每小题5分,共60分)1.椭圆x 29+y 2k 2=1与双曲线x 2k -y 23=1有相同的焦点,则k 应满足的条件是( ) A .k >3B .2<k <3C .k =2D .0<k <2考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 C解析 由9-k 2=k +3,即k 2+k -6=0,解得k =2或-3.又由题意知k 2<9且k >0,所以0<k <3,所以k =2.2.已知双曲线的离心率为2,焦点是(-4,0),(4,0),则双曲线的方程为( )A.x 24-y 212=1 B.x 212-y 24=1 C.x 210-y 26=1 D.x 26-y 210=1 考点 双曲线性质的应用题点 求双曲线的标准方程答案 A解析 依题意得c =4,e =c a =4a=2,a =2,b 2=c 2-a 2=12, 因此所求的双曲线的标准方程为x 24-y 212=1,故选A. 3.若双曲线的顶点为椭圆x 2+y 22=1长轴的端点,且双曲线的离心率与该椭圆的离心率的积为1,则双曲线的方程为( )A .x 2-y 2=1B .y 2-x 2=1C .x 2-y 2=2D .y 2-x 2=2考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 D解析 椭圆x 2+y 22=1的离心率为22,则双曲线的离心率为2,且双曲线的顶点为(0,±2),故选D.4.设圆锥曲线C 的两个焦点分别为F 1,F 2,若曲线C 上存在点P 满足|PF 1|∶|F 1F 2|∶|PF 2|=4∶3∶2,则曲线C 的离心率等于( )A.12或32B.23或2C.12或2 D.23或32考点 圆锥曲线的综合问题题点 圆锥曲线的综合问题答案 A解析 设|PF 1|=4k ,|F 1F 2|=3k ,|PF 2|=2k .若曲线C 为椭圆,则2a =6k,2c =3k ,∴e =c a =2c 2a =12; 若曲线C 为双曲线,则2a =2k,2c =3k ,∴e =c a =2c 2a =32. 5.设双曲线x 2a 2-y 2b 2=1(a >0,b >0)的虚轴长为2,焦距为23,则双曲线的渐近线方程为( ) A .y =±22x B .y =±2x C .y =±12x D .y =±2x 考点 双曲线性质的应用题点 由双曲线的几何性质求方程答案 A解析 ∵2b =2,2c =23,∴b =1,c =3,则a =c 2-b 2=2,∴b a =22. 故双曲线的渐近线方程为y =±b a x =±22x . 6.M 是抛物线y 2=2px (p >0)上一点,F 为抛物线的焦点,以Fx 为始边,FM 为终边的角为α,且α=60°,若|FM |=4,则p 等于( )A .1B .2C .3D .4考点 抛物线的焦点弦问题题点 与焦点弦有关的其他问题答案 B解析 不妨设M 在第一象限,过点M 作MN ⊥x 轴,垂足为N ,计算可得|MN |=23,|FN |=2,所以M 的坐标为⎝⎛⎭⎫p 2+2,23,代入y 2=2px (p >0),得p =2或p =-6(舍).7.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,|AB |=43,则C 的实轴长为( )A. 2 B .2 2 C .4 D .8考点 抛物线的几何性质题点 抛物线与其他曲线结合有关问题 答案 C解析 设双曲线的方程为x 2a 2-y 2a2=1(a >0), 抛物线的准线为x =-4,且|AB |=43,故可得A (-4,23),B (-4,-23),将点A 坐标代入双曲线方程,得a 2=4,故a =2,故实轴长为4.8.已知点A (0,2),B (2,0).若点C 在抛物线x 2=y 的图象上,则使得△ABC 的面积为2的点C 的个数为( )A .4B .3C .2D .1考点 直线与抛物线的位置关系题点 判断交点个数问题答案 A解析 由已知可得|AB |=22,要使S △ABC =2,则点C 到直线AB 的距离必须为2,设C (x ,x 2),而l AB :x +y -2=0, 所以有|x +x 2-2|2=2, 所以x 2+x -2=±2,当x 2+x -2=2时,有两个不同的C 点;当x 2+x -2=-2时,亦有两个不同的C 点.因此满足条件的C 点有4个,故选A.9.已知双曲线y 22-x 23=1的两个焦点分别为F 1,F 2,则满足△PF 1F 2的周长为6+25的动点P 的轨迹方程为( )A.x 24+y 29=1 B.x 24+y 29=1(x ≠0) C.x 29+y 24=1 D.x 29+y 24=1(x ≠0) 考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 B解析 ∵双曲线的方程为y 22-x 23=1, ∴a 2=2,b 2=3,可得c 2=a 2+b 2=5,因此双曲线y 22-x 23=1的两个焦点分别为F 1(0,-5),F 2(0,5). ∵△PF 1F 2的周长为6+25,|F 1F 2|=25,∴|PF 1|+|PF 2|=6>25,∴点P 的轨迹是以F 1,F 2为焦点的椭圆(上、下顶点除外).由椭圆的定义,得椭圆长轴长为6,长半轴长为3,∴该椭圆的短半轴长为2,∴点P 的轨迹方程为x 24+y 29=1(x ≠0). 10.我们把焦点相同,且离心率互为倒数的椭圆和双曲线称为一对“相关曲线”.已知F 1,F 2是一对相关曲线的焦点,P 是它们在第一象限的交点,当∠F 1PF 2=60°时,这一对相关曲线中双曲线的离心率是( )A .2 B. 2 C.233D. 3 考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 D解析 设|F 1P |=m ,|F 2P |=n ,|F 1F 2|=2c ,由余弦定理,得(2c )2=m 2+n 2-2mn cos 60°,即4c 2=m 2+n 2-mn ,设a 1是椭圆的长半轴,a 2是双曲线的实半轴,由椭圆、双曲线定义,得m +n =2a 1,m -n =2a 2,∴m =a 1+a 2,n =a 1-a 2,将它们及离心率互为倒数关系代入前式得3a 22-4c 2+a 21=0,a 1=3a 2,e 1e 2=c a 1·c a 2=⎝⎛⎭⎫c a 223=1, 解得,e 2=3,故选D.11.探照灯反射镜的轴截面是抛物线的一部分,光源位于抛物线的焦点处,已知灯口的直径为60 cm ,灯深40 cm ,则抛物线的标准方程可能是( )A .y 2=254x B .y 2=454x C .x 2=-452y D .x 2=-454y 考点 抛物线的标准方程题点 求抛物线方程答案 C解析 如果设抛物线的方程为y 2=2px (p >0),则抛物线过点(40,30),从而有302=2p ×40,即2p =452, 所以所求抛物线方程为y 2=452x . 虽然选项中没有y 2=452x ,但C 中的2p =452符合题意. 12.已知抛物线y 2=x ,点A ,B 在该抛物线上且位于x 轴的两侧,OA →·OB →=2(其中O 为坐标原点),则△ABO 与△AFO 的面积之和的最小值是( )A .2B .3 C.1728D.10 考点 直线与抛物线的位置关系题点 直线与抛物线相交时的其他问题答案 B解析 如图,可设A (m 2,m ),B (n 2,n ),其中m >0,n <0,则OA →=(m 2,m ),OB →=(n 2,n ),OA →·OB →=m 2n 2+mn =2,解得mn =1(舍)或mn =-2.∴l AB :(m 2-n 2)(y -n )=(m -n )·(x -n 2),即(m +n )(y -n )=x -n 2,令y =0,解得x =-mn =2,∴C (2,0),点C 为直线AB 与x 轴的交点.S △AOB =S △AOC +S △BOC =12×2×m +12×2×(-n )=m -n ,S △AOF =12×14×m =18m ,则S △AOB +S △AOF =m -n +18m =98m -n =98m +2m ≥298m ·2m =3,当且仅当98m =2m ,即m =43时等号成立.故△ABO 与△AFO 的面积之和的最小值为3.二、填空题(本大题共4小题,每小题5分,共20分)13.已知双曲线中心在原点,一个顶点的坐标是(3,0),且焦距与虚轴长之比为5∶4,则双曲线的标准方程为________________.考点 双曲线的标准方程的求法题点 待定系数法求双曲线的标准方程答案 x 29-y 216=1 解析 由题意得双曲线的焦点在x 轴上,且a =3,焦距与虚轴长之比为5∶4,即c ∶b =5∶4, 又c 2=a 2+b 2,所以c =5,b =4,所以双曲线的标准方程为x 29-y 216=1. 14.若椭圆x 2a 2+y 2b2=1过抛物线y 2=8x 的焦点,且与双曲线x 2-y 2=1有相同的焦点,则该椭圆的方程为________________.考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题答案 x 24+y 22=1 解析 抛物线y 2=8x 的焦点坐标为(2,0),双曲线x 2-y 2=1的焦点坐标为(±2,0)由题意得⎩⎪⎨⎪⎧a 2-b 2=2,4a 2=1,∴a 2=4,b 2=2,∴椭圆的方程为x 24+y 22=1. 15.直线x -2y +3=0与椭圆x 2a 2+y 2b 2=1(a >b >0)相交于A ,B 两点,且P (-1,1)恰好为AB 中点,则椭圆的离心率为________.考点 直线与椭圆的位置关系题点 直线与椭圆相交时弦中点问题答案 22 解析 由⎩⎪⎨⎪⎧x -2y +3=0,b 2x 2+a 2y 2=a 2b 2,消去x , 得(4b 2+a 2)y 2-12b 2y +9b 2-a 2b 2=0,Δ=144b 4-4(a 2+4b 2)(9b 2-a 2b 2)>0,即a 2+4b 2>9.设A (x 1,y 1),B (x 2,y 2),则y 1+y 2=12b 2a 2+4b 2, ∵线段AB 的中点为(-1,1),∴12b 2a 2+4b2=2,得a 2=2b 2. 又a 2=b 2+c 2,∴a 2=2c 2,∴e =c a =22. 16.过抛物线C :y 2=4x 的焦点F 作直线l 交抛物线C 于点A ,B ,若|AF |=3|BF |,则l 的斜率是________.考点 直线与抛物线的位置关系题点 直线与抛物线的综合问题答案 ±3解析 ∵抛物线C 的方程为y 2=4x ,∴它的焦点为F (1,0),由题意知,直线l 的斜率存在,∴设直线l 的方程为y =k (x -1),由⎩⎪⎨⎪⎧y =k (x -1),y 2=4x ,消去x 得k 4y 2-y -k =0. 设A (x 1,y 1),B (x 2,y 2),可得y 1+y 2=4k,① y 1y 2=-4,②∵|AF |=3|BF |,∴y 1+3y 2=0,可得y 1=-3y 2,代入①,②得-2y 2=4k,且-3y 22=-4, 消去y 2,得k 2=3,解得k =±3.三、解答题(本大题共6小题,共70分)17.(10分)已知一个椭圆中心在原点,焦点在同一坐标轴上,焦距为213.一双曲线和这个椭圆有公共焦点,且双曲线的实半轴长比椭圆的长半轴长小4,双曲线离心率与椭圆离心率之比为7∶3,求椭圆和双曲线的标准方程.考点 双曲线性质的应用题点 双曲线与椭圆结合的有关问题解 ①若焦点在x 轴上,设椭圆方程为x 2a 2+y 2b 2=1(a >b >0),c =13. 设双曲线方程为x 2m 2-y 2n 2=1,m =a -4. ∵e 双e 椭=73,易得a =7,m =3. ∴b 2=36,n 2=4.∴椭圆的标准方程为x 249+y 236=1,双曲线的标准方程为x 29-y 24=1. ②若焦点在y 轴上,同理可得椭圆的标准方程为x 236+y 249=1,双曲线的标准方程为y 29-x 24=1. 18.(12分)已知双曲线C 1:x 2-y 24=1. (1)求与双曲线C 1有相同焦点,且过点P (4,3)的双曲线C 2的标准方程;(2)直线l :y =x +m 分别与双曲线C 1的两条渐近线相交于A ,B 两点.当OA →·OB →=3时,求实数m 的值.考点 直线与双曲线的位置关系题点 直线与双曲线的位置关系解 (1)∵双曲线C 1:x 2-y 24=1, ∴焦点坐标为(5,0),(-5,0).设双曲线C 2的标准方程为x 2a 2-y 2b 2=1(a >0,b >0), ∵双曲线C 2与双曲线C 1有相同焦点,且过点P (4,3),∴⎩⎪⎨⎪⎧ a 2+b 2=5,16a 2-3b 2=1,解得⎩⎪⎨⎪⎧a =2,b =1, ∴双曲线C 2的标准方程为x 24-y 2=1. (2)双曲线C 1的两条渐近线分别为y =2x ,y =-2x .由⎩⎪⎨⎪⎧ y =2x ,y =x +m ,可得x =m ,y =2m ,∴A (m,2m ). 由⎩⎪⎨⎪⎧y =-2x ,y =x +m ,可得x =-13m ,y =23m , ∴B ⎝⎛⎭⎫-13m ,23m . ∴OA →·OB →=-13m 2+43m 2=m 2. ∵OA →·OB →=3,∴m 2=3,∴m =±3.19.(12分)已知点P (3,4)是椭圆x 2a 2+y 2b 2=1(a >b >0)上的一点,F 1,F 2为椭圆的两焦点,若PF 1⊥PF 2,试求:(1)椭圆的方程;(2)△PF 1F 2的面积.考点 椭圆的几何性质题点 求椭圆的标准方程解 (1)令F 1(-c,0),F 2(c,0),则b 2=a 2-c 2.因为PF 1⊥PF 2,所以kPF 1·kPF 2=-1,即43+c ·43-c=-1, 解得c =5,所以设椭圆方程为x 2a 2+y 2a 2-25=1. 因为点P (3,4)在椭圆上,所以9a 2+16a 2-25=1. 解得a 2=45或a 2=5.又因为a >c ,所以a 2=5舍去.故所求椭圆的方程为x 245+y 220=1. (2)由椭圆定义知|PF 1|+|PF 2|=65,①又|PF 1|2+|PF 2|2=|F 1F 2|2=100,②①2-②,得2|PF 1|·|PF 2|=80,所以12PF F S =12|PF 1|·|PF 2|=20. 20.(12分)已知抛物线y 2=4x 的焦点为F ,直线l 过点M (4,0).(1)若点F 到直线l 的距离为3,求直线l 的斜率;(2)设A ,B 为抛物线上两点,且AB 不与x 轴垂直,若线段AB 的垂直平分线恰过点M ,求证:线段AB 中点的横坐标为定值.考点 直线与抛物线的位置关系题点 直线与抛物线相交时的其他问题(1)解 由已知,x =4不合题意.设直线l 的方程为y =k (x -4),由已知,抛物线C 的焦点坐标为(1,0),因为点F 到直线l 的距离为3, 所以|3k |1+k 2=3,解得k =±22,所以直线l 的斜率为±22. (2)证明 设线段AB 中点的坐标为N (x 0,y 0),A (x 1,y 1),B (x 2,y 2), 因为AB 不垂直于x 轴,则直线MN 的斜率为y 0x 0-4,直线AB 的斜率为4-x 0y 0, 直线AB 的方程为y -y 0=4-x 0y 0(x -x 0), 联立方程⎩⎨⎧ y -y 0=4-x 0y 0(x -x 0),y 2=4x ,消去x ,得⎝⎛⎭⎫1-x 04y 2-y 0y +y 20+x 0(x 0-4)=0, 所以y 1+y 2=4y 04-x 0, 因为N 为AB 的中点,所以y 1+y 22=y 0,即2y 04-x 0=y 0, 所以x 0=2,即线段AB 中点的横坐标为定值2.21.(12分)已知椭圆M :x 2a 2+y 23=1(a >0)的一个焦点为F (-1,0),左、右顶点分别为A ,B ,经过点F 的直线l 与椭圆M 交于C ,D 两点.(1)求椭圆的方程;(2)记△ABD 与△ABC 的面积分别为S 1和S 2,求|S 1-S 2|的最大值. 考点 圆锥曲线的综合问题题点 圆锥曲线的综合问题解 (1)因为F (-1,0)为椭圆的焦点,所以c =1,又b =3,所以a =2,所以椭圆的方程为x 24+y 23=1. (2)当直线l 的斜率不存在时,直线方程为x =-1, 此时可令D ⎝⎛⎭⎫-1,32,C ⎝⎛⎭⎫-1,-32,所以△ABD ,△ABC 的面积相等,|S 1-S 2|=0.当直线l 的斜率存在时,设直线方程为y =k (x +1)(k ≠0),设C (x 1,y 1),D (x 2,y 2),和椭圆方程联立,消去y 得(3+4k 2)x 2+8k 2x +4k 2-12=0,因为焦点在椭圆内部,所以直线l 与椭圆恒有两个交点, 所以x 1+x 2=-8k 23+4k 2,x 1x 2=4k 2-123+4k 2,此时|S 1-S 2|=2||y 1|-|y 2||=2|y 1+y 2|=2|k (x 2+1)+k (x 1+1)|=2|k (x 2+x 1)+2k |=12|k |3+4k 2=123|k |+4|k |≤12212=3⎝⎛⎭⎫k =±32时等号成立,所以|S 1-S 2|的最大值为 3.22.(12分)如图,抛物线C 1:y 2=4x 的准线与x 轴交于点F 1,焦点为F 2.以F 1,F 2为焦点,离心率为12的椭圆记作C 2.(1)求椭圆的标准方程;(2)直线l 经过椭圆C 2的右焦点F 2,与抛物线C 1交于A 1,A 2两点,与椭圆C 2交于B 1,B 2两点,当以B 1B 2为直径的圆经过F 1时,求|A 1A 2|的长.考点 圆锥曲线的综合问题题点 圆锥曲线的综合问题解 (1)设椭圆的标准方程为x 2a 2+y 2b 2=1(a >b >0),依据题意得c =1,c a =12, 则a =2,b 2=a 2-c 2=3,故椭圆的标准方程为x 24+y 23=1. (2)当直线l 与x 轴垂直时,B 1⎝⎛⎭⎫1,-32,B 2⎝⎛⎭⎫1,32, 又F 1(-1,0),此时B 1F 1→·B 2F 1→≠0,所以以B 1B 2为直径的圆不经过F 1,不满足条件. 当直线l 不与x 轴垂直时,设l :y =k (x -1),由⎩⎪⎨⎪⎧ y =k (x -1),x 24+y 23=1,消去y ,得(3+4k 2)x 2-8k 2x +4k 2-12=0. 因为焦点在椭圆内部,所以直线l 与椭圆恒有两个交点. 设B 1(x 1,y 1),B 2(x 2,y 2),则x 1+x 2=8k 23+4k 2,x 1x 2=4k 2-123+4k 2. 因为以B 1B 2为直径的圆经过F 1,所以B 1F 1→·B 2F 1→=0,又F 1(-1,0),所以(-1-x 1)(-1-x 2)+y 1y 2=0,即(1+k 2)x 1x 2+(1-k 2)(x 1+x 2)+1+k 2=0,解得k 2=97. 由⎩⎪⎨⎪⎧y 2=4x ,y =k (x -1),得k 2x 2-(2k 2+4)x +k 2=0. 设A 1(x 3,y 3),A 2(x 4,y 4),则x 3+x 4=2k 2+4k 2=2+4k 2,所以|A1A2|=x3+x4+2=2+4k2+2=649.。
体育单招考试数学卷(答案) (3)

单独招生考试招生文化考试数学试题卷(满分150分,考试时间120分钟)一、选择题:(本题共15小题,每小题3分,共45分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.为了使函数)0(sin >=ωωx y 在区间[0,1]上至少出现50次最大值,则ω的最小值是( ) (A )π98(B )π2197(C )π2199(D )π1002.下列命题中,错误的命题是( )(A )在四边形ABCD 中,若AD AB AC +=,则ABCD 为平行四边形 (B )已知b a b a +,,为非零向量,且b a +平分a 与b 的夹角,则||||b a = (C )已知a 与b 不共线,则b a +与b a -不共线(D )对实数1λ,2λ,3λ,则三向量1λ-a 2λb ,2λ-b 3λc ,3λ-c 1λa不一定在同一平面上3.四个条件:a b >>0;b a >>0;b a >>0;0>>b a 中,能使ba 11<成立的充分条件的个数是( )(A )1 (B )2 (C )3 (D )4 4.点M (2,0),N 是圆221xy +=上任意一点,则线段MN 中点的轨迹是( )(A )椭圆 (B )直线 (C )圆 (D )抛物线5、设集合A ={0,2,a},B ={1,a2},若A ∪B ={0,1,2,5,25},则a 的值为( ) A .6 B .8 C .2 D .5 6.过点(1,2)总可作两条直线与圆2222150xy kx y k ++++-=相切,则实数k 的取值范围是( )(A )2k > (B )32k -<< (C )3k <-或2k > (D )都不对 7.共轭双曲线的离心率分别为1e 和2e ,则1e 和2e 关系为( )(A )1e =2e (B )121e e⋅=(C )12111e e += (D )2212111e e +=8. 已知集合A={-1,0,1},集合B={-3,-1,1,3},则A ∩B=( )A. {-1,1}B. {-2}C. {3}D. ∅9. 不等式x2-4x ≤0的解集为( ) A. [0,4]B. (1,4)C. [-4,0)∪(0,4]D. (-∞,0]∪[4,+∞)10. 已知函数f (x )=ln(x −2)+1x−3的定义域为( )A. (2,+∞)B. [2,+∞)C. (-∞,2]∪[3,+∞)D. (2,3)∪(3,+∞)11. 已知平行四边形ABCD ,则向量AB ⃗⃗⃗⃗⃗ +BC ⃗⃗⃗⃗⃗ =( ) A. BD⃗⃗⃗⃗⃗B. DB⃗⃗⃗⃗⃗C. AC⃗⃗⃗⃗⃗D. CA⃗⃗⃗⃗⃗ 12. 下面函数以π为周期的是( ) A.y =sin (x −π8)B. y =2cos xC. y =sin xD. y =sin 2x13. 本学期学校共开设了20门不同的选修课,学生从中任选2门,则不同选法总数是( ) A. 420B. 200C. 190D. 24014. 已知直线的倾斜角为60°,则此直线的斜率为( ) A. −√33B. −√3C. √3D.√3315. 若sin α>0且tan α<0,则角α终边所在象限是( ) A. 第一象限B. 第二象限C. 第三象限D.第四象限二、填空题:(本题共5小题,每小题6分,共30分.)1.函数f(x)=a “+3的图象一定过定点 P ,则P 点的坐标是_______.2.函数f(x)=x+3x -4的零点是_______.3.曲线y=x+x 在点A(1.2)处的切线方程是____4.{}{},13),(,3),(=+==-=y x y x B y x y x A 那么=B A _____;5、042=-x 是x+2=0的 ____条件.三、解答题:(本题共4小题,每小题10分,共40分.解答应写出文字说明、证明过程或演算步骤.)1、已知椭圆2222:1(0)x y E a b a b +=>>过点(0,2)A -,以四个顶点围成的四边形面积为(1)求椭圆E 的标准方程;(2)过点(0,3)P -的直线l 斜率为k ,交椭圆E 于不同的两点B ,C ,直线AB 、AC 交3y =-于点M 、N ,若||||15PM PN +,求k 的取值范围.2、求经过点),(24-,且与直线033=+-y x 平行的直线方程。
体育对口单招数学试卷(包含答案)

体育对口单招数学卷(满分120分,考试时间120分钟)一、选择题:(本题共10小题,每小题6分,共60分)1.函数()f x =的单调递增区间为()A.[0,1] B.1(,]2-∞ C.1[,1]2D.1[0,]22.已知方程1||+=ax x 有一负根且无正根,则实数的取值范围是()A.1->a B.1=a C.1≥a D.1≤a 3.命题“存在0x ∈R,02x 0”的否定是()A.不存在0x ∈R,02x >0B.存在0x ∈R,02x 0C.对任意的x ∈R,2x 0D.对任意的x ∈R,2x >04.若不等式4)2(2)2(2<-+-x a x a 的解集为,则实数的取值范围是()A )2,2(-B ]2,2(-C ),2()2,(+∞--∞D )2,(-∞5.已知函数()cos cos 2f x x x =-,试判断该函数的奇偶性及最大值()A.奇函数,最大值为2B.偶函数,最大值为2C.奇函数,最大值为98D.偶函数,最大值为986.对24小时内降水在平地上的积水厚度()mm 进行如下定义:0~1010~2525~5050~100小雨中雨大雨暴雨小明用一个圆锥形容器接了24小时的雨水,则这一天的雨水属于哪个等级()A.小雨B.中雨C.大雨D.暴雨7.若tan 2α=,则2sin cos sin 2cos αααα-+的值为()A.0B.34C.1D.548.函数14(cos 22--=πx y 是()A.最小正周期为的奇函数B.最小正周期为的偶函数C.最小正周期为2π的奇函数D.最小正周期为2π的偶函数9.如果函数p x nx y ++=21的图象关于点A (1,2)对称,那么()(A)=p -2,=n 4(B)=p 2,=n -4(C)=p -2,=n -4(D)=p 2,=n 410.已知}{n a 的前n 项和142+-=n nS n ,则||||||1021a a a +++ 的值为()(A)67(B)65(C)61(D)56二、填空题:(共30分.)1、f(x)=+3x-4的零点是____________.2、y=+x 在点A(1,2)处的切线方程是_____.3、等比数列{n a }的公比0q >,已知2a =1,216n n n a a a +++=,则{n a }的前4项和4S =______。
体育对口单招数学卷(含答案) (1)

体育对口单招数学卷(满分120分,考试时间120分钟)一、选择题:(本题共20小题,每小题2.5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.设n S n n 1)1(4321--++-+-= ,则32124++++m m m S S S (∈m N*)的值为()(A )0(B )3(C )4(D )随m 的变化而变化2.已知向量=a (αcos 2,αsin 2),=b (βcos 3,βsin 3),a 与b 的夹角为60o ,则直线021sin cos =+-ααy x 与圆21)sin ()cos (22=++-ββy x 的位置关系是()(A )相切(B )相交(C )相离(D )随βα,的值而定3.已知向量=a (αcos 2,αsin 2),=b (βcos 3,βsin 3),a 与b 的夹角为o 60,则直线021sin cos =+-ααy x 与圆21)sin ()cos (22=++-ββy x 的位置关系是()(A )相切(B )相交(C )相离(D )随βα,的值而定4、0=b 是直线b kx y +=过原点的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件5、方程43)22(log =x 的解为()A.4=x B.2=x C.2=x D.21=x 6.表中数据是我国各种能源消费量占当年能源消费总量的百分率,由表可知,从2011年到2014年,消费量占比增长率最大的能源是()A.天然气 B.核能 C.水利发电 D.再生能源表我国各种能源消费的百分率原油(%)天然气(%)原煤(%)核能(%)水利发电(%)再生能源(%)2011年17.7 4.570.40.7 6.00.72014年17.5 5.666.0 1.08.1 1.87.若角α的终边过点()6,8P -,则角α的终边与圆221x y +=的交点坐标是()A.34,55⎛⎫- ⎪⎝⎭ B.43,55⎛⎫- ⎪⎝⎭ C.34,55⎛⎫- ⎪⎝⎭ D.43,55⎛⎫- ⎪⎝⎭8.关于x,y 的方程y mx n =+和221x y m n +=在同一坐标系中的图象大致是()GD27GD28GD29GD309.已知()2n x -的二项展开式有7项,则展开式中二项式系数最大的项的系数是()A.-280 B.-160 C.160 D.56010.若有7名同学排成一排照相,恰好甲、乙两名同学相邻,并且丙、丁两名同学不相邻的概率是()A.421 B.121 C.114 D.2711、已知定义在R 上的函数12)(-=-m x x f (m 为实数)为偶函数,记)3(log 5.0f a =,)5(log 2f b =,)2(m f c =,则c b a ,,的大小关系为()A 、cb a <<B 、b ac <<C 、bc a <<D 、a b c <<12、不等式152x x ---<的解集是()A 、(,4)-∞B 、(,1)-∞C 、(1,4)D 、(1,5)13、函数x x y 2cos sin =是()A 、偶函数B 、奇函数C 、非奇非偶函数C 、既是奇函数,也是偶函数14、若(12)a +1<(12)4-2a ,则实数a 的取值范围是()A 、(1,+∞)B 、(12,+∞)C 、(-∞,1)D 、(-∞,12)15、化简3a a 的结果是()A 、aB 、12a C 、41a D 、83a 16、下列计算正确的是()A 、(a3)2=a9B 、log36-log32=1C 、12a -·12a =0D 、log3(-4)2=2log3(-4)17、三个数a =0.62,b =log20.3,c =30.2之间的大小关系是()A 、a<c<bB 、a<b<cC 、b<a<cD 、b<c<a18、8log 15.021+-⎪⎭⎫⎝⎛的值为()A 、6B 、72C 、16D 、3719、下列各式成立的是()A 、()52522n m n m +=+B 、(b a)2=12a 12b C 、()()316255-=-D 、31339=20、设2a =5b =m ,且1a +1b=3,则m 等于()A 、310B 、10C 、20D 、100二、填空题:(共20分)1.抛物线的焦点坐标是______. 2.双曲线的渐近线方程是______.3.抛物线x=-的准线方程是________三、解答题:(本题共3小题,共50分.解答应写出文字说明、证明过程或演算步骤.)1.计算:34cos 49()15(4log 2102π+--+.2.设c b a ,,分别是ABC ∆的三个内角A 、B 、C 所对的边,S 是ABC ∆的面积,已知4,5,a b S ===(1)求角C ;(2)求c 边的长度.3.已知函数)1,0()(≠>+=b b b a x f x 的图象过点)4,1(和点)16,2(.(1)求)(x f 的表达式;(2)解不等式23)21()(xx f ->;(3)当]4,3(-∈x 时,求函数6)(log )(22-+=x x f x g 的值域.参考答案:一、选择题1-5题答案:BCCCA 6-10题答案:DADBA 11-15题答案:BABAB;16-20题答案:BBCDA.二、填空题1.答案:2.答案:3x ±2y=03.答案:x=0.125解析:y'=0.5x,抛物线x=-的准线方程是0.125。
体育单招数学圆锥曲线专题复习(含答案)
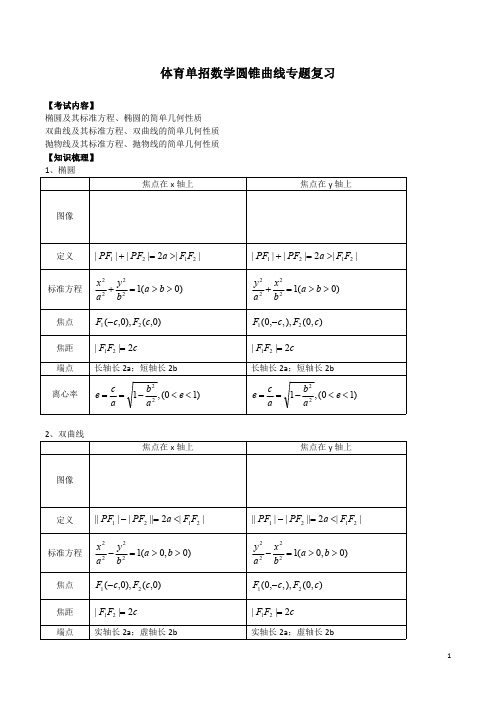
体育单招数学圆锥曲线专题复习【考试内容】椭圆及其标准方程、椭圆的简单几何性质双曲线及其标准方程、双曲线的简单几何性质抛物线及其标准方程、抛物线的简单几何性质【知识梳理】1、椭圆焦点在x 轴上焦点在y 轴上图像定义||2||||2121F F a PF PF >=+||2||||2121F F a PF PF >=+标准方程)0(12222>>=+b a b y a x )0(12222>>=+b a b x a y 焦点)0,(),0,(21c F c F -),0(),,,0(21c F c F -焦距cF F 2||21=cF F 2||21=端点长轴长2a ;短轴长2b长轴长2a ;短轴长2b离心率)10(,122<<-==e a b a c e )10(,122<<-==e ab ac e 2、双曲线焦点在x 轴上焦点在y 轴上图像定义||2||||||2121F F a PF PF <=-||2||||||2121F F a PF PF <=-标准方程)0,0(12222>>=-b a b y a x )0,0(12222>>=-b a b x a y 焦点)0,(),0,(21c F c F -),0(),,,0(21c F c F -焦距cF F 2||21=cF F 2||21=端点实轴长2a ;虚轴长2b实轴长2a ;虚轴长2b离心率)1(,122>+==e a b a c e )1(,122>+==e a b a c e 渐近线x aby ±=x bay ±=3、抛物线焦点在x 轴正半轴焦点在x 轴负半轴焦点在y 轴正半轴焦点在y 轴负半轴图像定义动点到定点的距离等于动点到定直线的距离的点的轨迹标准方程px y 22=px y 22-=py x 22=py x 22-=焦点)0,2(p F )0,2(p F -)2,0(p F )2,0(p F -准线2p x -=2p x =2p y -=2p y =离心率1=e 【题型讲解】题型一、椭圆的定义1.P 是椭圆x 2+4y 2=16上一点,且|PF 1|=7,则|PF 2|=()A .1B .3C .5D .92.已知M 是椭圆C :=1上的一点,则点M 到两焦点的距离之和是()A .6B .9C .14D .103.椭圆+=1上一点P 到它的一个焦点的距离等于3,那么点P 到另一个焦点的距离等于.题型二、椭圆的标准方程4.以(﹣3,0)和(3,0)为焦点,长轴长为8的椭圆方程为()A .B .C .D .5.已知以原点为中心的椭圆C 的左焦点为F (﹣1,0),离心率等于,则C 的方程是()A .B .C .D .6.焦点坐标为(0,﹣4),(0,4),且长半轴长为6的椭圆方程为()A.=1B.=1C.=1D.=1 7.焦点为(﹣2,0),(2,0),离心率为的椭圆的标准方程为()A.=1B.=1C.=1D.=1题型三、椭圆的焦点8.若椭圆+=1的一个焦点为(0,﹣1),则m的值为()A.4B.3C.2D.19.椭圆=1的焦点坐标为()A.(0,﹣4),(0,4)B.(0,),(0,﹣)C.(4,0),(﹣4,0)D.(,0),(﹣,0)10.已知椭圆C:4x2+3y2=12,其焦点坐标为()A.(±1,0)B.(0,±1)C.D.题型四、椭圆的端点11.椭圆的长轴长为()A.16B.8C.D.12.已知椭圆C:=1(a>2)的焦距为2,则C的长轴长为()A.3B.6C.2D.413.已知椭圆的一个焦点为(1,0),则C的短轴的长为()A.B.2C.D.4题型五、椭圆的离心率14.椭圆的离心率为()A.B.C.D.15.直线x﹣2y+2=0经过椭圆的一个焦点和一个顶点,则该椭圆的离心率为()A.B.C.D.16.若椭圆C:(a>b>0)满足2b=a+c,则该椭圆的离心率e=()A.B.C.D.17.已知椭圆的离心率为,则()A.a=2b2B.a=2b C.3a2=4b2D.3a=4b18.已知椭圆C:的一个焦点为(0,2),则C的离心率为()A.B.C.D.题型六、双曲线的定义19.已知点F1(﹣3,0)和F2(3,0),动点P到F1、F2的距离之差为4,则点P的轨迹方程为()A.B.C.D.20.如果方程表示双曲线,则m的取值范围是()A.(2,+∞)B.(﹣2,﹣1)C.(﹣∞,﹣1)D.(1,2)题型七、双曲线的标准方程21.焦距是10,虚轴长是8,经过点(,4)的双曲线的标准方程是()A.B.C.D.22.已知双曲线的中心在原点,焦点在x轴上,焦距为8,离心率为2,则该双曲线的方程为()A.B.C.D.23.已知双曲线的实轴长为2,焦点为(﹣4,0),(4,0),则该双曲线的标准方程为()A.B.C.D.题型八、双曲线的焦点24.双曲线8x2﹣y2=8的焦点坐标是()A.(±3,0)B.(0,±3)C.D.25.双曲线的焦点坐标为()A.B.(±5,0)C.D.(0,±5)题型九、双曲线的离心率26.已知双曲线C:,则C的离心率为()A.B.C.2D.327.已知双曲线的离心率为,则m=()A.2B.4C.8D.12题型十、双曲线的渐近线28.在平面直角坐标系xOy中,双曲线=1的渐近线方程为()A.y=±x B.y=±x C.y=±x D.y=±x29.双曲线﹣y2=﹣4的渐近线方程为()A.y=±2x B.C.y=±4x D.30.双曲线的焦点到C的渐近线的距离为()A.B.C.5D.题型十一、抛物线的标准方程31.已知抛物线的焦点坐标为(﹣,0),则抛物线的方程为()A.x=﹣8y2B.y=﹣8x2C.x=﹣16y2D.y=﹣16x2 32.若抛物线的准线方程为y=2,则该抛物线的标准方程是.题型十二、抛物线的焦点33.抛物线y=ax2(其中a>0)的焦点坐标是()A.B.C.D.34.抛物线x=﹣y2的焦点坐标是()A.(2,0)B.(﹣2,0)C.(0,2)D.(0,﹣2)题型十三、抛物线的准线35.抛物线y2=2x的准线方程是()A.B.C.D.36.抛物线x2=12y的准线方程为()A.y=﹣3B.x=﹣3C.y=﹣6D.x=﹣6 37.抛物线x=4y2的准线方程是()A.B.y=﹣1C.x=﹣D.x=题型十四、解答题38.若椭圆=1(a>b>0)的焦距为2,离心率为.斜率为1的直线经过椭圆的左焦点,交椭圆于A,B两点.(1)求椭圆的标准方程;(2)求|AB|的值.39.已知双曲线的焦点为F1(﹣4,0),F2(4,0),且该双曲线过点P(6,2).(1)求双曲线的标准方程;(2)若双曲线上的点M满足MF1⊥F1F2,求△MF1F2的面积.40.已知抛物线C:y2=2px(p>0)的焦点为F,点A(4,m)在抛物线C.上,且△OAF的面积为(O为坐标原点).(1)求抛物线C的方程;(2)直线l:y=kx+1与抛物线C交于M,N两点,若OM⊥ON,求直线l的方程.【真题再现】1、(2015年)双曲线116922=-y x 的一条渐近线的斜率为3,则它的离心率是()A 、332B 、3C 、2D 、42、(2016年)抛物线px y 22=过点(1,2),则该抛物线的准线方程为()A 、1-=x B 、1=x C 、1-=y D 、1=y 3、(2016年)在一个给定平面内,A ,C 为定点,B 为动点,且|BC |,|AC |,|AB |成等差数列,则点B 的轨迹是()A 、圆B 、椭圆C 、双曲线D 、抛物线4、(2017年)已知抛物线C :y x 42=的焦点为F ,过F 作C 的对称轴的垂线,交C 于A ,B 两点,则|AB |=()A 、8B 、4C 、2D 、15、(2018年)以双曲线C :x 29-y 216=1的中心为顶点,C 的左焦点为焦点的抛物线的方程为()A 、y 2=20xB 、y 2=10xC 、y 2=-10xD 、y 2=-20x6、(2020年)若一个椭圆的两个焦点三等分它的长轴,则该椭圆的离心率为()A 、61B 、31C 、21D 、327、(2020年)双曲线)0,0(12222>>=-b a by a x 的两条渐近线的倾斜角分别为βα,,则=+2cos βα()A 、1B 、23C 、21D 、08、(2017年)直线m x y +=与椭圆1222=+y x 有两个不同的交点,则m 的取值范围是___________9、(2018年)若抛物线px y 22=的准线方程为3-=x ,则P =__________10、(2021年)若椭圆C 的焦点为F 1(-1,0)和F 2(1,0),过F 1的直线交C 于A ,B 两点,且∆ABF 2的周长为12,则C 的方程为______________11、(2021年)双曲线1422=-y x 的离心率是____________12、(2016年)设双曲线1222=-y a x 与椭圆1162522=+y x 有相同的焦点,则该双曲线的渐近线方程是________13、(2015年)若椭圆的焦点为(-3,0),(3,0),离心率为53,则该椭圆的标准方程为___________14、(2015年)已知抛物线C :y x 42=,直线0:=-+m y x l ,(1)证明:C 与l 有两个交点的充分必要条件是1->m ,(2)设1<m ,C 与l 有两个交点A ,B ,线段AB 的垂直平分线交y 轴于点G ,求∆GAB 的面积的取值范围。
历年圆锥曲线单招高考题

历年圆锥曲线单招高考题2011年(解几合计30分,其中圆锥曲线22分)2010年(解几合计34分,其中圆锥曲线18分)2012年(解几合计26分,其中圆锥曲线22分)9.设双曲线22221x y a b-=(0,0)a b >>的虚轴长为2,焦距为的渐近线方程为( )A .y =B .2y x =±C .2y x =± D .12y x =± 17.设斜率为2的直线l 过抛物线22y px = (0)p >的焦点F ,且与y 轴交于点A .若O A F ∆(O 为坐标原点)的面积为4,则此抛物线的方程为 .25.(14分)已知椭圆C :22221x y a b+= (0)a b >>的离心率为23,且该椭圆上的点到右焦点的最大距离为5.(1)求椭圆C 的方程;(2)设椭圆C 的左、右顶点分别为A 、B ,且过点(9,)D m 的直线DA 、DB 与此椭圆的另一个交点分别为M 、N ,其中0m ≠.求证:直线MN 必过x 轴上一定点(其坐标与m 无关).2014年(解几合计22分,其中圆锥曲线14分)23.(14分)已知曲线C 的参数方程为,sin x y θθ⎧=⎪⎨=⎪⎩(θ为参数). (1)求曲线C 的普通方程;(2)设点(,)M x y 是曲线C 2y +的最大值;(3)过点(2,0)N 的直线l 与曲线C 交于,P Q 两点,且满足OP OQ ⊥(O 为坐标原点),求直线l 的方程.2013年(解几合计34分,其中圆锥曲线26分)8.若抛物线px y 22= )0(>p 准线与圆16)3(22=+-y x 相切,则p 的值为( )A .21 B .1 C .2 D .4 12.已知点M 的坐标为)2,3(,F 为抛物线x y 22=的焦点,点P 在抛物线上移动。
当||||PF PM +的值最小时,点P 的坐标为 ( )A .)0,0(B .)1,21( C .)3,29( D .)2,2( 17.设}4,3,2,1{,∈b a ,事件 =A {方程12222=+by a x 表示焦点在x 轴上的椭圆},那么=)(A P 。
14.单招——解三角形及圆锥曲线大题

,求△ABC的面积. 5.(2015•抚顺模拟)设△ABC的内角A,B,C所对应的边长为a,b, c,且(2b﹣ c)cosA= acosC. (1)求角A的大小; (2)若a=1,cosB= ,求△ABC的面积. 6.(2015•济南二模)在△ABC中,角A,B,C的对边分别为a,b, c,且bcosC=(2a﹣c)cosB. (Ⅰ)求角B的大小; (Ⅱ)若a,b,c成等差数列,且b=3,试求△ABC的面积. 7.(2015•永州一模)在锐角△ABC中,角A,B,C的对边分别为a, b,c且sin2A﹣cosA=0. (1)求角A的大小; (2)若b= ,sinB= sinC,求a. 8.(2015•梧州一模)在△ABC中,∠ACB为钝角,AB=2,BC= ,A= ,D为AC延长线上一点,且CD= +1. (1)求∠BCD的大小; (2)求BD的长.
∴sinBcos2A=sinA(2﹣sinAsinB), ∴sinBcos2A+sin2AsinB=2sinA, ∴sinB=2sinA, 由正弦定理可得:b=2a, 与a+b=6联立解得a=2,b=4. (II)∵cosB= , ∴sinB= = , ∴sinA= = cosA= = ; ∴sinC=sin(A+B)=sinAcosB+cosAsinB= + = , ∴S△ABC=
,△ABC的面积是 . (Ⅰ)求b的值; (Ⅱ)求cos2A的值. 【考点】正弦定理;余弦定理. 【专题】解三角形. 【分析】(Ⅰ)由条件利用正弦定理求得a的值,再利用余弦定理求得b 的值. (Ⅱ)由正弦定理求得sinA的值,再利用二倍角的余弦公式求得cos2A 的值. 【解答】解:(Ⅰ)因为△ABC的面积是
9.(2016•福建模拟)已知函数f(x)=2cos2x+ sin2x﹣1. (1)求f( )的值; (2)求函数f(x)的最小正周期和单调递增区间. 10.(2015•惠州模拟)已知向量 =(cosx+sinx,2sinx), =(cosx﹣sinx,﹣cosx),f(x)= • , (1)求f(x)的最小正周期; (2)当x∈[ , ]时,求f(x)的最小值以及取得最小值时x的值. 11.(2015秋•武威校级期末)已知椭圆的中心在坐标原点,焦点在x轴 上,且经过点(2,0)和点(0,1) (1)求椭圆的标准方程; (2)焦点为F1,F2,P为椭圆上的一点,且 • =0,求△F1PF2的面积. 12.(2015秋•九江校级月考)根据已知条件求方程: (1)已知椭圆的两个焦点坐标分别是(﹣1,0),(1,0),并且经
体育对口单招数学试卷(包含答案) (2)

4. (1, 2) ; 5. (3,1) ;
三、问答题:
cosÐ ABC = - 1
3 15
1、参考答案.(1)
4 ;(2) 2
sin B = 12
cosC = 16
2、参考答案.(1) 13 ,A 是锐角;(2)
65
是____________________; 3.已知 f (x) lg(x2 8x 7) 在 (m , m 1) 上是增函数,则 m 的取值范围是________________; 4.已知函数 f (x) sin x 5x ,x (1,1) ,如果 f (1 a) f (1 a2 ) 0 ,则 a 的取值范围是____________;
2. 在△ABC 中,
5,
13 .
(1)求 sinB,并判断 A 是锐角还是钝角;
(2)求 cosC.
参考答案:
一、选择题:
1-5 题答案:DACDD
6-10 题答案:BCBCC
11-15 题答案:CDCCB
16-20 题答案:ABBAA;
21-25 题答案:DCCCB.
二、填空题:
1.答案: 9 2.{1,0,1} ; 3.[1,3] ;
A.{2}
B.{2,3}
C.{3,4,}
D.{2,3,4}
7.已知 z=2-i,则( z(z + i) =( ) A. 6-2i
B. 4-2i
C. 6+2i
D. 4+2i
8.已知圆锥的底面半径为 2 ,其侧面展开图为一个半圆,则该圆锥的母线长为( ) A.2
B.2 2 C.4
D.4 2
9.设二次函数 f (x) ax2 bx c ,如果 f (x1) f (x2)(x1 x2) ,则 f (x1 x2) 等于(
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
圆锥曲线
1.(2013年第15题)
已知椭圆的焦点为、,过斜率为1的直线交椭圆于点、,则的面22
1
32
x y
+=
1
F
2
F
1
F A B
2
F AB
∆
积为 .
2.(2013年第16题)
已知过点的直线与圆相交于、两点,则 .
(1,2)
A-22
(3)(2)1
x y
-++=M N AM AN=
3.(2013年第18题18分)
设、分别为双曲线的左、右焦点,为双曲线右支上一点,且,1
F
2
F
22
1
916
x y
-=M
12
60
F MF
∠=︒
(Ⅰ)求的面积;
12
MF F
∆
(Ⅱ)求点的坐标。
M
4.(2012年第7题)
直线交圆于、两点,为圆心,若的面积是,20(0)
x y m m
-+=>22
20
x x y
-+=A B P PAB
∆
2
5
则()
m=
A B. C D.
12
5.(2012年第16题)
已知曲线的一个焦点与一条渐近线,过焦点作渐近线的垂线,垂足的坐标22
22
1
x y
a b
-=F l F l P
为,则焦点的坐标是 .
4
(,
3
F
6.(2012年第16题)
设是椭圆的右焦点,半圆在点的切线与椭圆交于、两点,F
2
21
2
x
y
+=221(0)
x y x
+=≥Q A B
(Ⅰ)证明:为常数;
AF AQ
+
(Ⅱ)设切线的斜率为1,求的面积(是坐标原点)。
AB OAB
∆O
7.(2011年第12题)
已知椭圆的两个焦点为与,离心率,则椭圆的标准方程是 .
1
(1,0)
F-
2
(1,0)
F
1
3
e=
8.(2011年第19题18分)
设是双曲线的右焦点,过点的直线交双曲线于、两点,是
(,0)(0)F c c >2
2
12
y x -=(,0)F c l P Q O 坐标原点,
(Ⅰ)证明:为常数;
1OP OQ =-
A (Ⅱ)若原点到直线的距离是,求的面积(是坐标原点)。
O l 3
2
OPQ ∆O 9.(2010年第8题)
是椭圆上的一点,点和为椭圆的两个焦点,已知,以为中心,
P 22
12516
x y +=1F 2F 17PF = P 为半径的圆交线段于,则( )
2PF
1PF Q A . B .
1430F Q QP -= 1430F Q QP +=
C .
D .1440F Q QP -= 1340
F Q QP += 10.(2010年第14题)
若双曲线的两条渐近线分别为,,它的一个焦点为,则双曲线的方20x y +=20x y -=(-程是 .
11.(2010年第18题18分)
已知抛物线,为过的焦点且倾斜角为的直线,设与交于、两2:2(0)C y px p =>l C F αl C A B 点,与坐标原点连线交的准线于点。
A C D (Ⅰ)证明:垂直轴;
BD y (Ⅱ)分析分别取什么范围的值时,与的夹角为锐角、直角或钝角。
αOA OB
12.(2009年第13题)
已知双曲线上的一点到双曲线一个焦点的距离为3,则到另一个焦点的距离为
22
1916
x y -=P P 13.(2009年第18题18分)
中心在原点,焦点在轴的椭圆的左、右焦点分别是和,斜率为1的直线过,且到
x C 1F 2F l 2F 1F 的距离等于l (Ⅰ)求的方程;
l (Ⅱ) 与交点、的中点为,已知到轴的距离等于
,求的方程和离心率。
l C A B M M x 3
4
C 14.(2008年第15题)
双曲线的两个焦点是与,离心率,则双曲线的标准方程是 .
1(4,0)F -2(4,0)F 2e =
过点的直线与圆不相交,则直线的斜率的取值范围是 .
(0,2)l 22230x y x +--=l k 16.(2008年第24题)
如图,与是过原点的面积的任意两条互相垂直的直线,分别交的面积于点与点。
1l 2l O 2y x =A B (Ⅰ)证明交轴于固定点;AB x P (Ⅱ) 求的面积的最小值。
OAB ∆17.(2005年第7题)
已知抛物线的顶点在第一象限,且与坐标原点的距离等于5,则(
2213y x px =++Q Q p =)
A .3
B .-3
C .4
D .-4
18.(2005年第8题)
椭圆 的( )
A .离心率是
,焦距是8 B .离心率是,焦距是8 234
9C .离心率是,焦距是4 D .离心率是,焦距是4
234
9
19.(2005年第23题)
已知双曲线的两个焦点分别是与,离心率C (e =(Ⅰ)求双曲线的标准方程;
C (Ⅱ) 证明:若直线与双曲线有两个不同交点和,则与不能相互垂直,其中
l C M N OM ON 是坐标原点。
O 20.(2004年第15题)
将抛物线绕焦点按逆时针方向旋转后,所得抛物线的方程是 .
24y x =90︒21.(2004年第21题)
若椭圆与双曲线有相同的焦点,又椭圆与双曲线交于点,求椭圆22110x y m +=22
1y x b
-=)P y 及双曲线的方程。
22.(2014年第8题)
若双曲线的两条渐近线相互垂直,则双曲线的离心率为( )
22
221(0,0)x y a b a b
-=>>A
B .2 C
23.(2014年第9题)
已知圆与圆外切,则半径为( )222x y r +=222(1)(3)x y r
+++=A B
. 24.(2014年第15题)
抛物线的准线方程是 .
24y x =25.(2014年第18题)
已知椭圆C 中心在原点,焦点在轴上,离心率为,且C 过点x 123
(1,2
-(1)求C 的方程;
(2)如果直线与C 有两个交点,求的取值范围。
:2l y kx =-k 26.(2014年第14题)
过圆与轴正半轴的交点作该圆的切线,切线的方程是 .
22(1)(2)10x y -++=y。
