2019-2020学年北京市朝阳区初三期末地理试卷(附答案)
北京市朝阳区2019~2020学年第一学期初三期末地理试卷逐题精品解析

2020年北京市朝阳区初三期末地理考试试卷逐题解析第一部分(选择题共40分)本部分共40小题,每小题1分,共40分。
在每小题列出的四个选项中,选出最符合题目要求的一项。
2019年10月1日,庆祝中华⼈民共和国成立70周年的游⾏花车备受瞩目。
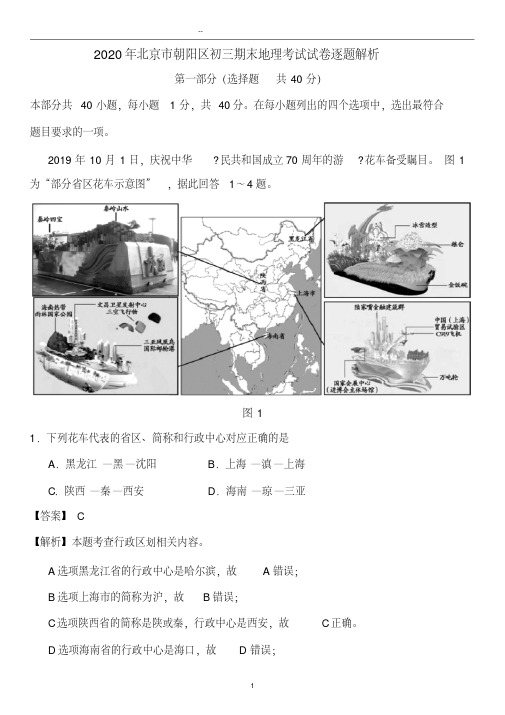
图1为“部分省区花车示意图”,据此回答1~4题。
图11.下列花车代表的省区、简称和行政中心对应正确的是A.黑龙江—黑—沈阳B.上海—滇—上海C.陕西—秦—西安D.海南—琼—三亚【答案】C【解析】本题考查行政区划相关内容。
A选项黑龙江省的行政中心是哈尔滨,故A错误;B选项上海市的简称为沪,故B错误;C选项陕西省的简称是陕或秦,行政中心是西安,故C正确。
D选项海南省的行政中心是海口,故D错误;2.黑龙江省花车中出现了冰雪元素,海南省花车中出现了热带雨林元素,这体现了我国①纬度跨度大②经度跨度大③自然景观差异大④地形类型差异大A.①② B.①③ C.②③ D.②④【答案】B【解析】本题考查中国气候的相关内容。
黑龙江省纬度高,气温低,因此有冰雪元素;海南省纬度低,气温高,因此有热带雨林元素,故南北气温差异大是因为我国南北纬跨度大,故①正确。
冰雪元素、热带雨林元素体现了自然景观差异,故③正确。
综上所述,本题正确答案为B选项。
3.花车反映了该省区最有代表性的自然和人文特征,以下描述正确的是A.横贯陕西省南部的秦岭是我国重要地理分界线B.信息技术产业已经成为上海市的经济支柱C.凭借高新技术,黑龙江省成为我国的粮仓D.海南省四面环海,温带动植物资源丰富【答案】A【解析】本题考查区域特征相关内容。
A选项秦岭位于陕西省南部,是我国重要的地理分界线,故A正确;B选项上海市花车信息未体现信息技术产业,故B错误;C选项黑龙江成为我国粮仓主要因为地广人稀、耕地面积大,余量多,与高新技术产业关系不大,故C选项错误;D选项海南省位于热带,以热带作物为主,故D错误;4.上海建立了“中国(上海)贸易示范区”,其发展贸易的有利社会经济条件有①位于长江与东海的交汇处②居于我国大陆海岸线中枢位置③开发时间早,发展历史悠久④高等院校多,科技实力强A.①② B.①③ C.②③ D.③④【答案】D【解析】本题考查经济发展的相关内容。
北京市朝阳区2019-2020学年中考地理考前模拟卷(3)含解析

北京市朝阳区2019-2020学年中考地理考前模拟卷(3)一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.开发新能源,对于发展绿色、低碳经济具有重要意义,下列属于新能源的是()A.天然气B.煤炭C.太阳能D.石油【答案】C【解析】【分析】【详解】本题考查新能源的分布。
太阳能属于新能源,而天然气、煤炭、石油都属于矿产资源,不属于新能源,故选C。
2.“一带一路”将进一步加强中国与欧洲西部的经济联系,欧洲西部具备的优势是()A.矿产资源丰富,可供大量出口B.人口增长快,劳动力丰富C.工业历史短暂,发展潜力大D.科学技术发达,工业水平高【答案】D【解析】【分析】欧洲西部工农业生产约占世界的33.3%,大多数国家属于经济发达国家,在世界商品贸易中占有重要的地位;对外贸易发达,占世界对外贸易总额的50%以上,其中德国居第一位.【详解】欧洲西部大多数国家属于经济发达国家,科学技术发达,工业水平高。
故选项D符合题意。
故选D。
3.我国从东北到海南岛,自然环境相差很大,人们的生活方式也多种多样。
据此回答下列各题。
1.冬季,东北和海南岛气温差别很大的根本原因是()A.海陆位置不同B.纬度位置不同C.地势高低不同D.昼夜长短不同2.有关我国冬季气温的叙述,正确的是()A.冬季南北气温相差很大B.冬季气温最低的地方在青藏高原C.冬季全国气温普通较低,南北气温相当D.冬季各地气温普遍在10°C以上。
3.从东北到海南岛,下列-些说法正确的是()A.东北农作物成熟的次数多于海南岛B.东北的热量比海南岛充足C.东北进入雨季的时间比海南岛早D.东北河流的结冰期比海南岛长【答案】1.B2.A3.D【解析】【分析】根据我国领土的四至点是:最北端--黑龙江省漠河县北端的黑龙江主航道中心线,53°N附近;最南端--曾母暗沙,4°N附近;最西端--帕米尔高原,73°E附近;最东端--黑龙江与乌苏里江主航道中心线的汇合处,135°E附近;我国地域辽阔,地跨众多的温度带和干湿地区,加上我国地形复杂,地势高低悬殊,更增加了我国气候的复杂多样性。
北京市朝阳区2019-2020学年中考第二次大联考地理试卷含解析
北京市朝阳区2019-2020学年中考第二次大联考地理试卷一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
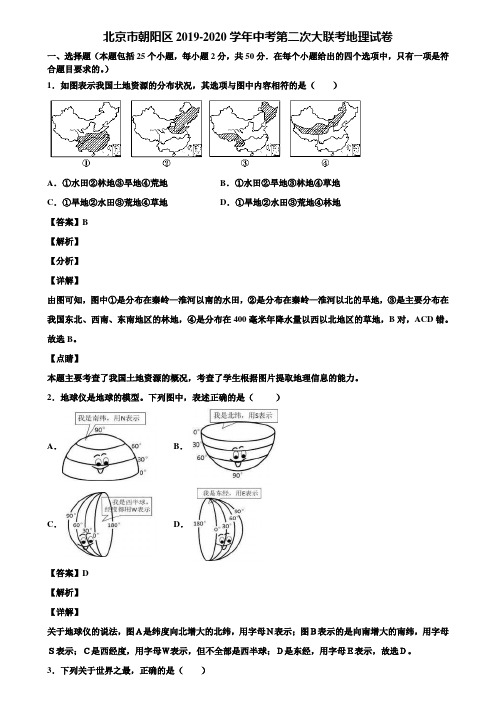
)1.如图表示我国土地资源的分布状况,其选项与图中内容相符的是()A.①水田②林地③旱地④荒地B.①水田②旱地③林地④草地C.①旱地②水田③荒地④草地D.①旱地②水田③荒地④林地【答案】B【解析】【分析】【详解】由图可知,图中①是分布在秦岭—淮河以南的水田,②是分布在秦岭—淮河以北的旱地,③是主要分布在我国东北、西南、东南地区的林地,④是分布在400毫米年降水量以西以北地区的草地,B对,ACD错。
故选B。
【点睛】本题主要考查了我国土地资源的概况,考查了学生根据图片提取地理信息的能力。
2.地球仪是地球的模型。
下列图中,表述正确的是()A.B.C.D.【答案】D【解析】【详解】关于地球仪的说法,图A是纬度向北增大的北纬,用字母N表示;图B表示的是向南增大的南纬,用字母S表示;C是西经度,用字母W表示,但不全部是西半球;D是东经,用字母E表示,故选D。
3.下列关于世界之最,正确的是()A.最深的海沟是马里亚纳海沟B.最大的高原是青藏高原C.世界最大的平原是西欧平原D.世界最大的盆地四川盆地【答案】A【解析】【分析】【详解】世界最深的海沟是马里亚纳海沟,故A正确;世界最大的高原是巴西高原,故B错误;世界最大的平原是亚马孙平原,故C错误;世界最大的盆地是刚果盆地,故D错误。
故选A。
4.我国西北内陆地区气候干燥,同纬度的东部沿海地区气候则比较湿润,造成这种气候差异的主要原因是()A.海陆位置B.纬度位置C.地形影响D.洋流影响【答案】A【解析】【分析】根据影响气候的因素,进行分析解答。
【详解】受海陆因素影响,我国西北地区深居内陆,受海洋影响小,降水稀少,气候干燥,同纬度的东部沿海地区距离海洋较近,夏季能够受到来自太平洋湿润气流的影响。
气候较湿润,故选A。
北京市朝阳区2020届九年级第一学期期末统一检测语文试卷(含答案)

北京市朝阳区2019~2020学年度第一学期期末检测九年级语文试卷(选用) 2020.1学校班级姓名考号考生须知1.本试卷共12页,共五道大题,24道小题,满分100分。
考试时间150分钟。
2.在试卷和草稿纸上准确填写姓名、准考证号、考场号和座位号。
3.试题答案一律填涂或书写在答题卡上,在试卷上作答无效。
4.在答题卡上,选择题用2B铅笔作答,其他试题用黑色字迹签字笔作答。
5.考试结束,将本试卷、答题卡和草稿纸一并交回。
一、基础·运用(共17分)在纪念甲骨文发现120周年之际,学校组织到中国国家博物馆参观“证古泽今——纪念甲骨文发现一百二十周年文化展”。
请你完成下列任务。
1.下面是展览“前言”中的部分文字。
阅读这段文字,完成(1)-(4)题。
(共8分)甲骨文是3000多年前商朝王室用于占.卜记事而在龟甲兽骨上契.①刻的文字。
1899年,王懿荣在无意间发现了一种叫龙骨的药材上刻有图形文字,经推断正是商朝王室使用的文字。
甲骨文得以发现。
这些文字,埋①(藏/葬)在中国人的文化基因中,融化在中国人的血液里,生成了最深沉、持久的力量。
作为我国迄今可见最早成体系的文字,甲骨文不仅仅是一个文明的符号、文化的标志,还印证了包括《史记》在内的一系列文献的真实,把有文字记载的中华文明史向前推进了近5个世纪。
在已知的四大古文字体系中,唯有以殷墟甲骨文为代表的中国古文字体系,一脉相①(成/承),绵延发展,成为今天世界上五分之一的人口仍在使用的文字,并对中国人的价值认同、思维方式、审美观念产生了极其重要的影响。
【甲】。
2017 年,甲骨文成功入选“世界记忆名录”,表明了世界对甲骨文的重要文化价值及其历史意义的高度认可,促进了中国文化在世界的传播。
注:①[契]用刀雕刻。
(1)依次给这段文字中加点的字注音,全都正确的一项是(2分)A.占(zhān)契(qì) B.占(zhān)契(qiè)C.占(zhàn)契(qì)D.占(zhàn)契(qiè)(2)结合语境,在①①处依次填入汉字,全都正确的一项是(2分)A.①藏②成B.①藏②承C.①葬②成D.①葬②承(3)右图是“证古泽今——纪念甲骨文发现一百二十周年文化展”的宣传海报。
2019-2020学年北京市朝阳区九年级上学期期末数学试卷 (解析版)

2019-2020学年北京市朝阳区九年级(上)期末数学试卷一、选择题1.下列事件中,随机事件是()A.通常温度降到0℃以下,纯净的水结冰B.随意翻到一本书的某页,这页的页码是偶数C.明天太阳从东方升起D.三角形的内角和是360°2.抛物线y=(x﹣2)2+1的顶点坐标为()A.(2,1)B.(2,﹣1)C.(﹣2,﹣1)D.(﹣2,1)3.只有1和它本身两个因数且大于1的自然数叫做素数,我国数学家陈景润在有关素数的“哥德巴赫猜想”的研究中取得了世界领先的成果.从5,7,11这3个素数中随机抽取一个,则抽到的数是7的概率是()A.B.C.D.14.把Rt△ABC三边的长度都扩大为原来的3倍,则锐角A的余弦值()A.不变B.缩小为原来的C.扩大为原来的3倍D.扩大为原来的9倍5.如图,△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=1,BD=2,则△ADE 与△ABC的面积之比为()A.1:2B.1:3C.1:4D.1:96.如图,在正方形网格中,△MPN绕某一点旋转某一角度得到△M′P′N′,则旋转中心可能是()A.点A B.点B C.点C D.点D7.已知⊙O1,⊙O2,⊙O3是等圆,△ABP内接于⊙O1,点C,E分别在⊙O2,⊙O3上.如图,①以C为圆心,AP长为半径作弧交⊙O2于点D,连接CD;②以E为圆心,BP长为半径作弧交⊙O3于点F,连接EF;下面有四个结论:①CD+EF=AB②③∠CO2D+∠EO3F=∠AO1B④∠CDO2+∠EFO3=∠P所有正确结论的序号是()A.①②③④B.①②③C.②④D.②③④8.如图,抛物线y=﹣1与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是()A.2B.C.D.3二、填空题(本题共16分,每小题2分)9.点(﹣1,﹣3)关于原点的对称点的坐标为.10.如图,在平面直角坐标系xOy中,射线l的端点为(0,1),l∥x轴,请写出一个图象与射线l有公共点的反比例函数的表达式:.11.如果一个矩形的宽与长的比等于黄金数(约为0.618),就称这个矩形为黄金矩形.如图,矩形ABCD为黄金矩形,宽AD=,则长AB为.12.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=1,∠A=45°,则的长度为.13.如图,在正方形网格中,点A,B,C在⊙O上,并且都是小正方形的顶点,P 是上任意一点,则∠P 的正切值为.14.抛物线y=ax2﹣2ax﹣3与x轴交于两点,分别是(m,0),(n,0),则m+n的值为.15.为了打赢脱贫攻坚战,某村计划将该村的特产柑橘运到A地进行销售.由于受道路条件的限制,需要先将柑橘由公路运到火车站,再由铁路运到A地.村里负责销售的人员从该村运到火车站的所有柑橘中随机抽取若干柑橘,进行了“柑橘完好率”统计,获得的数据记录如下表:柑橘总质量n/kg100150200250300350400450500完好柑橘质量92.40138.45183.80229.50276.30322.70367.20414.45459.50m/kg柑橘完好的频0.9240.9230.9190.9180.9210.9220.9180.9210.919率①估计从该村运到火车站柑橘完好的概率为(结果保留小数点后三位);②若从该村运到A地柑橘完好的概率为0.880,估计从火车站运到A地柑橘完好的概率为.16.如图,分别过第二象限内的点P作x,y轴的平行线,与y,x轴分别交于点A,B,与双曲线分别交于点C,D.下面三个结论,①存在无数个点P使S△AOC=S△BOD;②存在无数个点P使S△POA=S△POB;③存在无数个点P使S四边形OAPB=S△ACD.所有正确结论的序号是.三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题5分,第27,28题,每小题5分)17.计算:sin60°﹣cos30°+tan45°.18.如图,在△ABC中,∠B=30°,tan C=,AD⊥BC于点D.若AB=8,求BC的长.19.如图,△ABC为等边三角形,将BC边绕点B顺时针旋转30°,得到线段BD,连接AD,CD,求∠ADC的度数.20.已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)部分自变量和对应的函数值如下表:x…﹣2﹣1012…y1…01234…y2…0﹣1038…(1)求y2的表达式;(2)关于x的不等式ax2+bx+c>kx+m的解集是.21.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.22.在平面内,O为线段AB的中点,所有到点O的距离等于OA的点组成图形W.取OA 的中点C,过点C作CD⊥AB交图形W于的点D,D在直线AB的上方,连接AD,BD.(1)求∠ABD的度数;(2)若点E在线段CA的延长线上,且∠ADE=∠ABD,求直线DE与图形W的公共点个数.23.阅读下面材料:小军遇到这样一个问题:如图1,在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=45°,AP=1,求BP的长.小军的思路是:根据已知条件可以证明△ACP∽△CBP,进一步推理可得BP的长.请回答:∵AB=AC,∴∠ABC=∠ACB.∵∠PCB=∠PBA,∴∠PCA=.∵∠PAC=∠PCB,∴△ACP∽△CBP.∴.∵∠ACB=45°,∴∠BAC=90°.∴=.∵AP=1,∴PC=.∴PB=.参考小军的思路,解决问题:如图2,在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=30°,求的值;24.点A是反比例函数y=(x>0)的图象l1上一点,直线AB∥x轴,交反比例函数y =(x>0)的图象l2于点B,直线AC∥y轴,交l2于点C,直线CD∥x轴,交l1于点D.(1)若点A(1,1),求线段AB和CD的长度;(2)对于任意的点A(a,b),判断线段AB和CD的大小关系,并证明.25.如图,在矩形ABCD中,E是BA延长线上的定点,M为BC边上的一个动点,连接ME,将射线ME绕点M顺时针旋转76°,交射线CD于点F,连接MD.小东根据学习函数的经验,对线段BM,DF,DM的长度之间的关系进行了探究.下面是小东探究的过程,请补充完整:(1)对于点M在BC上的不同位置,画图、测量,得到了线段BM,DF,DM的长度的几组值,如下表:位置1位置2位置3位置4位置5位置6位置7位置8位置9 BM/cm0.000.53 1.00 1.69 2.17 2.96 3.46 3.79 4.00 DF/cm0.00 1.00 1.74 2.49 2.69 2.21 1.140.00 1.00 DM/cm 4.12 3.61 3.16 2.52 2.09 1.44 1.14 1.02 1.00在BM,DF,DM的长度这三个量中,确定的长度是自变量,的长度和的长度都是这个自变量的函数;(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)结合画出的函数图象,解决问题:当DF=2cm时,DM的长度约为cm.26.在平面直角坐标系xOy中,抛物线y=ax2+bx经过点(3,3).(1)用含a的式子表示b;(2)直线y=x+4a+4与直线y=4交于点B,求点B的坐标(用含a的式子表示);(3)在(2)的条件下,已知点A(1,4),若抛物线与线段AB恰有一个公共点,直接写出a(a<0)的取值范围.27.已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.(1)根据题意补全图1;(2)求证:①∠OAC=∠DCB;②CD=CA(提示:可以在OA上截取OE=OC,连接CE);(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.28.在平面直角坐标系xOy中,已知点A(0,2),点B在x轴上,以AB为直径作⊙C,点P在y轴上,且在点A上方,过点P作⊙C的切线PQ,Q为切点,如果点Q在第一象限,则称Q为点P的离点.例如,图1中的Q为点P的一个离点.(1)已知点P(0,3),Q为P的离点.①如图2,若B(0,0),则圆心C的坐标为,线段PQ的长为;②若B(2,0),求线段PQ的长;(2)已知1≤PA≤2,直线l:y=kx+k+3(k≠0).①当k=1时,若直线l上存在P的离点Q,则点Q纵坐标t的最大值为;②记直线l:y=kx+k+3(k≠0)在﹣1≤x≤1的部分为图形G,如果图形G上存在P的离点,直接写出k的取值范围.参考答案一、选择题(本题共16分,每小题2分)第1-8题均有四个选项,符合题意的选项只有一个.1.下列事件中,随机事件是()A.通常温度降到0℃以下,纯净的水结冰B.随意翻到一本书的某页,这页的页码是偶数C.明天太阳从东方升起D.三角形的内角和是360°【分析】根据随机事件的意义,这个选项进行判断即可.解:“通常温度降到0℃以下,纯净的水结冰”是必然事件;“随意翻到一本书的某页,这页的页码可能是偶数,也可能是奇数”因此选项B符合题意;“明天太阳从东方升起”是必然事件,不符合题意;“三角形的内角和是180°”因此“三角形的内角和是360°”是确定事件中的不可能事件,不符合题意;故选:B.2.抛物线y=(x﹣2)2+1的顶点坐标为()A.(2,1)B.(2,﹣1)C.(﹣2,﹣1)D.(﹣2,1)【分析】抛物线的顶点式为:y=a(x﹣h)2+k,其顶点坐标是(h,k),可以确定抛物线的顶点坐标.解:抛物线y=(x﹣2)2+1是以抛物线的顶点式给出的,其顶点坐标为:(2,1).故选:A.3.只有1和它本身两个因数且大于1的自然数叫做素数,我国数学家陈景润在有关素数的“哥德巴赫猜想”的研究中取得了世界领先的成果.从5,7,11这3个素数中随机抽取一个,则抽到的数是7的概率是()A.B.C.D.1【分析】根据概率=所求情况数与总情况数之比解答即可.解:∵共3个素数,分别是5,7,11,∴抽到的数是7的概率是;故选:C.4.把Rt△ABC三边的长度都扩大为原来的3倍,则锐角A的余弦值()A.不变B.缩小为原来的C.扩大为原来的3倍D.扩大为原来的9倍【分析】根据相似三角形的性质解答.解:三边的长度都扩大为原来的3倍,则所得的三角形与原三角形相似,∴锐角A的大小不变,∴锐角A的余弦值不变,故选:A.5.如图,△ABC中,点D,E分别在AB,AC上,DE∥BC.若AD=1,BD=2,则△ADE 与△ABC的面积之比为()A.1:2B.1:3C.1:4D.1:9【分析】由DE∥BC可得出△ADE∽△ABC,利用相似三角形的性质即可求出△ADE与△ABC的面积之比.解:∵DE∥BC,∴△ADE∽△ABC,∴=()2=()2=.故选:D.6.如图,在正方形网格中,△MPN绕某一点旋转某一角度得到△M′P′N′,则旋转中心可能是()A.点A B.点B C.点C D.点D【分析】连接PP'、NN'、MM',作PP'的垂直平分线,作NN'的垂直平分线,作MM'的垂直平分线,交点为旋转中心.解:如图,∵△MNP绕某点旋转一定的角度,得到△M'N'P',∴连接PP'、NN'、MM',作PP'的垂直平分线,作NN'的垂直平分线,作MM'的垂直平分线,∴三条线段的垂直平分线正好都过B,即旋转中心是B.故选:B.7.已知⊙O1,⊙O2,⊙O3是等圆,△ABP内接于⊙O1,点C,E分别在⊙O2,⊙O3上.如图,①以C为圆心,AP长为半径作弧交⊙O2于点D,连接CD;②以E为圆心,BP长为半径作弧交⊙O3于点F,连接EF;下面有四个结论:①CD+EF=AB②③∠CO2D+∠EO3F=∠AO1B④∠CDO2+∠EFO3=∠P所有正确结论的序号是()A.①②③④B.①②③C.②④D.②③④【分析】根据圆心角、弧、弦的关系,圆周角定理即可得到结论.解:由题意得,AP=CD,BP=EF,∵AP+BP>AB,∴CD+EF>AB;∵⊙O1,⊙O2,⊙O3是等圆,∴=,=,∵+=,∴+=;∴∠CO2D=∠AO1P,∠EO3F=∠BO1P,∵∠AO1P+∠BO1P=∠AO1P,∴∠CO2D+∠EO3F=∠AO1B;∵∠CDO2=∠APO1,∠BPO1=∠EFO3,∵∠P=∠APO1+∠BPO1,∴∠CDO2+∠EFO3=∠P,∴正确结论的序号是②③④,故选:D.8.如图,抛物线y=﹣1与x轴交于A,B两点,D是以点C(0,4)为圆心,1为半径的圆上的动点,E是线段AD的中点,连接OE,BD,则线段OE的最小值是()A.2B.C.D.3【分析】根据抛物线y=﹣1与x轴交于A,B两点,可得A、B两点坐标,D是以点C(0,4)为圆心,根据勾股定理可求BC的长为5,E是线段AD的中点,再根据三角形中位线,BD最小,OE就最小.解:∵抛物线y=﹣1与x轴交于A,B两点,∴A、B两点坐标为(﹣3,0)、(3,0),∵D是以点C(0,4)为圆心,根据勾股定理,得BC=5,∵E是线段AD的中点,O是AB中点,∴OE是三角形ABD的中位线,∴OE=BD,即点B、D、C共线时,BD最小,OE就最小.如图,连接BC交圆于点D′,∴BD′=BC﹣CD′=5﹣1=4,∴OE′=2.所以线段OE的最小值为2.故选:A.二、填空题(本题共16分,每小题2分)9.点(﹣1,﹣3)关于原点的对称点的坐标为(1,3).【分析】直接利用关于原点对称点的性质得出答案.解:点(﹣1,﹣3)关于原点的对称点的坐标为:(1,3).故答案为:(1,3).10.如图,在平面直角坐标系xOy中,射线l的端点为(0,1),l∥x轴,请写出一个图象与射线l有公共点的反比例函数的表达式:答案不唯一,如y=.【分析】直接利用射线的特点得出符合题意的反比例函数解析式.解:∵射线l的端点为(0,1),l∥x轴,∴写出一个图象与射线l有公共点的反比例函数的表达式:答案不唯一,如y=.故答案为:答案不唯一,如y=.11.如果一个矩形的宽与长的比等于黄金数(约为0.618),就称这个矩形为黄金矩形.如图,矩形ABCD为黄金矩形,宽AD=,则长AB为2.【分析】判断黄金矩形的依据是:宽与长之比为0.618,根据已知条件即可得出答案.解:∵矩形ABCD是黄金矩形,且AD=,∴,,∴AB=2,故答案为2.12.如图,线段AB经过⊙O的圆心,AC,BD分别与⊙O相切于点C,D.若AC=BD=1,∠A=45°,则的长度为.【分析】连接OC、OD,根据切线性质和∠A=45°,易证得△AOC和△BOD是等腰直角三角形,进而求得OC=OD=1,∠COD=90°,根据弧长公式求得即可.解:连接OC、OD,∵AC,BD分别与⊙O相切于点C,D.∴OC⊥AC,OD⊥BD,∵∠A=45°,∴∠AOC=45°,∴AC=OC=1,∵AC=BD=1,OC=OD=1,∴OD=BD,∴∠BOD=45°,∴∠COD=180°﹣45°﹣45°=90°,∴的长度为:=π,故答案为:.13.如图,在正方形网格中,点A,B,C在⊙O上,并且都是小正方形的顶点,P是上任意一点,则∠P的正切值为.【分析】:连接OA、OB,作OD⊥AB于D,如图,利用等腰三角形的性质和圆周角定理得到∠AOD=∠APB,再利用正切的性质得到tan∠AOD=,从而得到tan∠P的值.解:连接OA、OB,作OD⊥AB于D,如图,∵OA=OB,OD⊥AB,∴∠AOD=∠AOB,∵∠APB=∠AOB,∴∠AOD=∠APB,在Rt△AOD中,tan∠AOD==,∴tan∠P=.故答案为.14.抛物线y=ax2﹣2ax﹣3与x轴交于两点,分别是(m,0),(n,0),则m+n的值为2.【分析】根据根与系数的关系解答即可.解:∵抛物线y=ax2﹣2ax﹣3与x轴交于两点,分别是(m,0),(n,0),∴m+n=﹣=2.故答案是:2.15.为了打赢脱贫攻坚战,某村计划将该村的特产柑橘运到A地进行销售.由于受道路条件的限制,需要先将柑橘由公路运到火车站,再由铁路运到A地.村里负责销售的人员从该村运到火车站的所有柑橘中随机抽取若干柑橘,进行了“柑橘完好率”统计,获得的数据记录如下表:柑橘总质量n/kg100150200250300350400450500完好柑橘质量92.40138.45183.80229.50276.30322.70367.20414.45459.50m/kg柑橘完好的频0.9240.9230.9190.9180.9210.9220.9180.9210.919率①估计从该村运到火车站柑橘完好的概率为0.920(结果保留小数点后三位);②若从该村运到A地柑橘完好的概率为0.880,估计从火车站运到A地柑橘完好的概率为.【分析】(1)根据表格中频率的变化情况,估计概率即可;(2)根据完好的概率进行列方程求解即可.解:(1)根据抽查的柑橘完好的频率,大约集中在0.920上下波动,因此估计柑橘的完好的概率为0.920,故答案为:0.920;(2)设总质量为m千克,从火车站运到A地柑橘完好的概率为x,由题意得,m×0.920×x=m×0.880,解得,x=,故答案为:.16.如图,分别过第二象限内的点P作x,y轴的平行线,与y,x轴分别交于点A,B,与双曲线分别交于点C,D.下面三个结论,①存在无数个点P使S△AOC=S△BOD;②存在无数个点P使S△POA=S△POB;③存在无数个点P使S四边形OAPB=S△ACD.所有正确结论的序号是①②③.【分析】如图,设C(m,),D(n,),则P(n,),利用反比例函数k的几何意义得到S△AOC=3,S△BOD=3,则可对①进行判断;根据三角形面积公式可对②进行判断;通过计算S四边形OAPB和S△ACD得到m与n的关系可对对③进行判断.解:如图,设C(m,),D(n,),则P(n,),∵S△AOC=3,S△BOD=3,∴S△AOC=S△BOD;所以①正确;∵S△POA=﹣n×=﹣,S△POB=﹣n×=﹣,∴S△POA=S△POB;所以②正确;∵S四边形OAPB=﹣n×=﹣,S△ACD=×m×(﹣)=3﹣,∴当﹣=3﹣,即m2﹣mn﹣2n2=0,所以m=2n(舍去)或m=﹣n,此时P点为无数个,所以③正确.故答案为①②③.三、解答题(本题共68分,第17-22题,每小题5分,第23-26题,每小题5分,第27,28题,每小题5分)17.计算:sin60°﹣cos30°+tan45°.【分析】直接利用特殊角的三角函数值分别代入得出答案.解:原式==1.18.如图,在△ABC中,∠B=30°,tan C=,AD⊥BC于点D.若AB=8,求BC的长.【分析】根据直角三角形中30°角所对的直角边是斜边的一半可以求得AD的长,然后即可求得BD的长,再根据AD的长和tan C=,可以求得CD的长,从而可以求得BC 的长,本题得以解决.解:∵AD⊥BC,∴∠ADB=∠ADC=90°.∵在Rt△ADB中,∠B=30°,AB=8,∴AD=4,BD=,∵在Rt△ADC中,tan C=,AD=4,∴,∴CD=3.∴BC=BD+CD=.19.如图,△ABC为等边三角形,将BC边绕点B顺时针旋转30°,得到线段BD,连接AD,CD,求∠ADC的度数.【分析】首先证明∠ABD=90°,求出∠BDC,∠ADB即可解决问题.解:∵△ABC为等边三角形,∴AB=BC,∠ABC=60°.根据题意可知BD=BC,∠DBC=30°.∴AB=BD.∴∠ABD=90°,∠BDC=75°.∴∠BDA=45°.∴∠ADC=30°.20.已知一次函数y1=kx+m(k≠0)和二次函数y2=ax2+bx+c(a≠0)部分自变量和对应的函数值如下表:x…﹣2﹣1012…y1…01234…y2…0﹣1038…(1)求y2的表达式;(2)关于x的不等式ax2+bx+c>kx+m的解集是x<﹣2或x>1.【分析】(1)根据题意设出y2的表达式,再把(0,0)代入,求出a的值,即可得出y2的表达式;(2)利用表中数据得到直线与抛物线的交点为(﹣2,0)和(1,3),x<﹣2或x>1时,y2>y1,从而得出不等式ax2+bx+c>kx+m的解集.解:(1)根据题意设y2的表达式为:y2=a(x+1)2﹣1,把(0,0)代入得a=1,∴y2=x2+2x;(2)当x=﹣2时,y1=y2=0;当x=1时,y1=y2=3;∴直线与抛物线的交点为(﹣2,0)和(1,3),而x<﹣2或x>1时,y2>y1,∴不等式ax2+bx+c>kx+m的解集是x<﹣2或x>1.故答案为:x<﹣2或x>1.21.筒车是我国古代发明的一种水利灌溉工具,彰显了我国古代劳动人民的智慧,图1,点P表示筒车的一个盛水桶.如图2,当筒车工作时,盛水桶的运行路径是以轴心O为圆心,5m为半径的圆,且圆心在水面上方.若圆被水面截得的弦AB长为8m,求筒车工作时,盛水桶在水面以下的最大深度.【分析】过O点作半径OD⊥AB于E,如图,利用垂径定理得到AE=BE=4,再利用勾股定理计算出OE,然后计算出DE的长即可.解:过O点作半径OD⊥AB于E,如图,∴AE=BE=AB=×8=4,在Rt△AEO中,OE===3,∴ED=OD﹣OE=5﹣3=2,答:筒车工作时,盛水桶在水面以下的最大深度为2m.22.在平面内,O为线段AB的中点,所有到点O的距离等于OA的点组成图形W.取OA 的中点C,过点C作CD⊥AB交图形W于的点D,D在直线AB的上方,连接AD,BD.(1)求∠ABD的度数;(2)若点E在线段CA的延长线上,且∠ADE=∠ABD,求直线DE与图形W的公共点个数.【分析】(1)根据题意,图形W为以O为圆心,OA为直径的圆.如图1,连接OD,根据等边三角形的判定与性质即可求解;(2)根据切线的判定即可求解.解:(1)根据题意,图形W为以O为圆心,OA为直径的圆.如图1,连接OD,∴OA=OD.∵点C为OA的中点,CD⊥AB,∴AD=OD.∴OA=OD=AD.∴△OAD是等边三角形.∴∠AOD=60°.∴∠ABD=30°.(2)如图2,∵∠ADE=∠ABD,∴∠ADE=30°.∵∠ADO=60°.∴∠ODE=90°.∴OD⊥DE.∴DE是⊙O的切线.∴直线DE与图形W的公共点个数为1.23.阅读下面材料:小军遇到这样一个问题:如图1,在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=45°,AP=1,求BP的长.小军的思路是:根据已知条件可以证明△ACP∽△CBP,进一步推理可得BP的长.请回答:∵AB=AC,∴∠ABC=∠ACB.∵∠PCB=∠PBA,∴∠PCA=∠PBC.∵∠PAC=∠PCB,∴△ACP∽△CBP.∴.∵∠ACB=45°,∴∠BAC=90°.∴=.∵AP=1,∴PC=.∴PB=2.参考小军的思路,解决问题:如图2,在△ABC中,AB=AC,P是△ABC内一点,∠PAC=∠PCB=∠PBA.若∠ACB=30°,求的值;【分析】阅读材料:证明△ACP∽△CBP.得出.由等腰直角三角形的性质得出CB=AC得出=.PC=AP=.得出PB=PC=2.解决问题:证明△ACP∽△CBP.得出=,设AP=a,则PC=,得出PB=3a.即可得出.【解答】阅读材料:解:∵AB=AC,∴∠ABC=∠ACB.∵∠PCB=∠PBA,∴∠PCA=∠PBC.∵∠PAC=∠PCB,∴△ACP∽△CBP.∴.∵∠ACB=45°,∴∠BAC=90°.∴CB=AC,∴=.∵AP=1,∴PC=AP=.∴PB=PC=2.故答案为:∠PBC;;2;解决问题:解:作AD⊥BC于D,如图2所示:∵AB=AC,∴∠ABC=∠ACB=30°.BD=CD=BC,∴AD=AC,CD=AD,∴AC=2AD,BC=2CD=2AD,∵∠PCB=∠PBA,∴∠PCA=∠PBC.∵∠PAC=∠PCB,∴△ACP∽△CBP.∴==,设AP=a,则PC=,∴PB=3a.∴.24.点A是反比例函数y=(x>0)的图象l1上一点,直线AB∥x轴,交反比例函数y =(x>0)的图象l2于点B,直线AC∥y轴,交l2于点C,直线CD∥x轴,交l1于点D.(1)若点A(1,1),求线段AB和CD的长度;(2)对于任意的点A(a,b),判断线段AB和CD的大小关系,并证明.【分析】(1)根据题意求得B(3,1),C(1,3),D(,3),即可求得AB和CD 的长度;(2)根据题意得到A(a,),B(3a,).C(a,),D(,),进一步求得AB=2a,CD=.即可求得AB>CD.解:(1)∵AB∥x轴,A(1,1),B在反比例函数的图象上,∴B(3,1).同理可求:C(1,3),D(,3).∴AB=2,CD=.(2)AB>CD.证明:∵A(a,b),A在反比例函数的图象上,∴A(a,).∵AB∥x轴,B在反比例函数的图象上,∴B(3a,).同理可求:C(a,),D(,).∴AB=2a,CD=.∵a>0,∴2a>.∴AB>CD.25.如图,在矩形ABCD中,E是BA延长线上的定点,M为BC边上的一个动点,连接ME,将射线ME绕点M顺时针旋转76°,交射线CD于点F,连接MD.小东根据学习函数的经验,对线段BM,DF,DM的长度之间的关系进行了探究.下面是小东探究的过程,请补充完整:(1)对于点M在BC上的不同位置,画图、测量,得到了线段BM,DF,DM的长度的几组值,如下表:位置1位置2位置3位置4位置5位置6位置7位置8位置9 BM/cm0.000.53 1.00 1.69 2.17 2.96 3.46 3.79 4.00 DF/cm0.00 1.00 1.74 2.49 2.69 2.21 1.140.00 1.00 DM/cm 4.12 3.61 3.16 2.52 2.09 1.44 1.14 1.02 1.00在BM,DF,DM的长度这三个量中,确定BM的长度是自变量,DF的长度和DM的长度都是这个自变量的函数;(2)在同一平面直角坐标系xOy中,画出(1)中所确定的函数的图象;(3)结合画出的函数图象,解决问题:当DF=2cm时,DM的长度约为 2.98和1.35 cm.【分析】(1)由函数的定义可得;(2)描点即可;(3)结合图象,即可求解.解:(1)由函数的定义可得:BM的长度是自变量,DF的长度和DM的长度都是这个自变量的函数,故答案为:BM,DF,DM;(2)如图所示.(3)由图象得到:当DF=2cm时,DM的长度约为2.98cm和1.35cm.26.在平面直角坐标系xOy中,抛物线y=ax2+bx经过点(3,3).(1)用含a的式子表示b;(2)直线y=x+4a+4与直线y=4交于点B,求点B的坐标(用含a的式子表示);(3)在(2)的条件下,已知点A(1,4),若抛物线与线段AB恰有一个公共点,直接写出a(a<0)的取值范围.【分析】(1)将点(3,3)代入解析式即可求得;(2)把y=4代入y=x+4a+4得到关于x的方程,解方程即可求得;(3)根据抛物线与线段AB恰有一个公共点,分两种情况讨论,即可得结论.解:(1)将点(3,3)代入y=ax2+bx,得9a+3b=3.∴b=﹣3a+1.(2)令x+4a+4=4,得x=﹣4a.∴B(﹣4a,4).(3)∵a<0,∴抛物线开口向下,抛物线与线段AB恰有一个公共点,∵A(1,4),B(﹣4a,4)∴点A、B所在的直线为y=4,由(1)得b=1﹣3a,则抛物线可化为:y=ax2+(1﹣3a)x,分两种情况讨论:①当抛物线y=ax2+(1﹣3a)x与直线y=4只有一个公共点时,且抛物线的顶点在点A、B之间,则1≤≤﹣4a或﹣4a≤≤1,方程ax2+(1﹣3a)x=4的根的判别式:△=0,即(1﹣3a)2+16a=0,解得a1=﹣,a2=﹣1,当a1=﹣时,=6(不符合题意),当a2=﹣1时,=2,则1≤≤﹣4a成立.②当抛物线经过点A时,即当x=1,y=4时,a+1﹣3a=4,解得a=﹣;∴a<﹣时,抛物线与线段AB恰有一个公共点,综上:a的取值为:a=﹣1或a<﹣时,抛物线与线段AB恰有一个公共点.27.已知∠MON=120°,点A,B分别在ON,OM边上,且OA=OB,点C在线段OB 上(不与点O,B重合),连接CA.将射线CA绕点C逆时针旋转120°得到射线CA′,将射线BO绕点B逆时针旋转150°与射线CA′交于点D.(1)根据题意补全图1;(2)求证:①∠OAC=∠DCB;②CD=CA(提示:可以在OA上截取OE=OC,连接CE);(3)点H在线段AO的延长线上,当线段OH,OC,OA满足什么等量关系时,对于任意的点C都有∠DCH=2∠DAH,写出你的猜想并证明.【分析】(1)根据题意即可补全图形;(2)①由旋转得∠ACD=120°,由三角形内角和得出∠DCB+∠ACO=60°,∠OAC+∠ACO=60°,即可得出结论;②在OA上截取OE=OC,连接CE,则∠OEC=∠OCE=(180°﹣∠MON)=30°,∠AEC=150°,得出∠AEC=∠CBD,易证AE=BC,由ASA证得△AEC≌△CBD,即可得出结论;(3)猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH,在OH上截取OF=OC,连接CF、CH,则FH=OA,∠COF=180°﹣∠MON=60°,得出△OFC是等边三角形,则CF=OC,∠CFH=∠COA=120°,由SAS证得△CFH≌△COA,得出∠H=∠OAC,由三角形外角性质得出∠BCH=∠COF+∠H=60°+∠H=60°+∠OAC,则∠DCH=60°+∠H+∠DCB=60°+2∠OAC,由CA=CD,∠ACD=120°,得出∠CAD=30°,即可得出∠DCH=2∠DAH.【解答】(1)解:根据题意补全图形,如图1所示:(2)证明:①由旋转得:∠ACD=120°,∴∠DCB+∠ACO=180°﹣120°=60°,∵∠MON=120°,∴∠OAC+∠ACO=180°﹣120°=60°,∴∠OAC=∠DCB;②在OA上截取OE=OC,连接CE,如图2所示:则∠OEC=∠OCE=(180°﹣∠MON)=(180°﹣120°)=30°,∴∠AEC=180°﹣∠OEC=180°﹣30°=150°,由旋转得:∠CBD=150°,∴∠AEC=∠CBD,∵OA=OB,OE=OC,∴AE=BC,在△AEC和△CBD中,,∴△AEC≌△CBD(ASA),∴CD=CA;(3)解:猜想OH﹣OC=OA时,对于任意的点C都有∠DCH=2∠DAH;理由如下:在OH上截取OF=OC,连接CF、CH,如图3所示:则FH=OA,∠COF=180°﹣∠MON=180°﹣120°=60°,∴△OFC是等边三角形,∴CF=OC,∠CFH=∠COA=120°,在△CFH和△COA中,,∴△CFH≌△COA(SAS),∴∠H=∠OAC,∴∠BCH=∠COF+∠H=60°+∠H=60°+∠OAC,∴∠DCH=60°+∠H+∠DCB=60°+2∠OAC,∵CA=CD,∠ACD=120°,∴∠CAD=30°,∴∠DCH=2(∠CAD+∠OAC)=2∠DAH.28.在平面直角坐标系xOy中,已知点A(0,2),点B在x轴上,以AB为直径作⊙C,点P在y轴上,且在点A上方,过点P作⊙C的切线PQ,Q为切点,如果点Q在第一象限,则称Q为点P的离点.例如,图1中的Q为点P的一个离点.(1)已知点P(0,3),Q为P的离点.①如图2,若B(0,0),则圆心C的坐标为(0,1),线段PQ的长为;②若B(2,0),求线段PQ的长;(2)已知1≤PA≤2,直线l:y=kx+k+3(k≠0).①当k=1时,若直线l上存在P的离点Q,则点Q纵坐标t的最大值为6;②记直线l:y=kx+k+3(k≠0)在﹣1≤x≤1的部分为图形G,如果图形G上存在P的离点,直接写出k的取值范围.【分析】(1)①如图可知:C(0,1),在Rt△PQC中,CQ=1,PC=2;②如图,过C作CM⊥y轴于点M,连接CP,CQ,M(0,1).在Rt△ACM中,由勾股定理可得CA=,CQ=.在Rt△PCM中,由勾股定理可得PC=.在Rt△PCQ中,由勾股定理可得PQ==.(2)①当k=1时,y=x+4,Q(t﹣4,t),P的纵坐标为4时,PQ与圆C相切,设B (m,0),则圆心为C(,1),由CQ⊥PQ,可求CQ的解析式为y=﹣x++1,Q 点横坐标为﹣=t﹣4,则C(2t﹣5,1),再由CQ=AC,得到t=6或t=2;②y =kx+k+3经过定点(﹣1,3),PQ是圆的切线,AO是圆的弦,则有PQ2=PA•PO,当k<0时,Q点的在端点(﹣1,3)和(1,2k+3)之间运动,当P(0,4)时,PQ=2,以P为圆心,PQ长为半径的圆与y轴交于点(0,4﹣2),此时k=1﹣2,当P(0,3)时,PQ=,Q(1,2k+3),1+4k2=3,所以1﹣2<k≤﹣;当k >0时,当P(0,4)时,PQ=2,以P为圆心,PQ长为半径的圆与y轴交于点(0,4+2),此时k=1+2,当P(0,3)时,PQ=,Q(1,2k+3),1+4k2=3,所以≤k<1+2.解:(1)①如图可知:C(0,1),在Rt△PQC中,CQ=1,PC=2,∴PQ=,故答案为(0,1);;②如图,过C作CM⊥y轴于点M,连接CP,CQ.∵A(0,2),B(2,0),∴C(1,1).∴M(0,1).在Rt△ACM中,由勾股定理可得CA=.∴CQ=.∵P(0,3),M(0,1),∴PM=2.在Rt△PCM中,由勾股定理可得PC=.在Rt△PCQ中,由勾股定理可得PQ==.(2)①如图1:当k=1时,y=x+4,∴Q(t﹣4,t),∵1≤PA≤2,∴P的纵坐标为4时,PQ与圆C相切,设B(m,0),∴C(,1),∵CQ⊥PQ,∴CQ的解析式为y=﹣x++1,∴Q点横坐标为﹣,∴﹣=t﹣4,∴m=4t﹣10,∴C(2t﹣5,1),∵CQ=AC,∴(2t﹣5)2+1=2(t﹣1)2,∴t=6或t=2,∴t的最大值为6;故答案为6.②∵﹣1≤x≤1,∵y=kx+k+3经过定点(﹣1,3),∵PQ是圆的切线,AO是圆的弦,∴PQ2=PA•PO,当k<0时,Q点的在端点(﹣1,3)和(1,2k+3)之间运动,当P(0,4)时,PQ=2,以P为圆心,PQ长为半径的圆与y轴交于点(0,4﹣2),此时k=1﹣2,当P(0,3)时,PQ=,Q(1,2k+3),∴1+4k2=3,∴k=,∴k=﹣,∴1﹣2<k≤﹣;当k>0时,当P(0,4)时,PQ=2,以P为圆心,PQ长为半径的圆与y轴交于点(0,4+2),此时k=1+2,当P(0,3)时,PQ=,Q(1,2k+3),∴1+4k2=3,∴k=,∴k=,∴≤k<1+2.。
北京市朝阳区2019-2020学年中考第四次模拟地理试题含解析

北京市朝阳区2019-2020学年中考第四次模拟地理试题一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.我国纬度最高和最低的省级行政单位的简称分别是()A.新、琼B.黑、台C.黑、粤D.黑、琼【答案】D【解析】【分析】【详解】从我国省级行政区域图上可以看到,我国纬度最高的省级行政单位是黑龙江省,纬度最低的省级行政单位是海南省。
它们的简称分别是黑和琼。
故本题选D。
【点睛】本题主要考查辽阔的疆域。
2.下列城市与其主要工业部门的连线,正确的是:A.大庆一机械工业B.长春一汽车工业C.鞍山一石油工业D.大连一煤炭工业【答案】B【解析】【分析】【详解】根据所学的知识可知, 大庆石油工业, 长春汽车工业, 鞍山铁矿工业; 大连造船工业;故答案选B.【点睛】该题主要考查的是城市与其主要工业部门的组合,要求学生熟练掌握。
3.南极地区最具代表性的动物是A.B.C.D.【分析】【详解】读图可知,A和C是北极狐和北极熊,生活在北极地区,D是海象,海象是北极地区的特产动物,分布在以北冰洋为中心,也包括大西洋和太平洋最北部一带的海域。
B是企鹅,是南极地区的代表动物。
故选B。
【点睛】该题考查南极地区的动物,记住即可。
4.如果沿南北方向作亚洲的剖面图,下列地形剖面示意图中最合理()A.B.C.D.【答案】B【解析】【分析】【详解】亚洲的地势特点是中间高、四周低,无论东西方向看亚洲地势还是从南北方向看亚洲的地势都是中间高、两边低,与图中B表示的剖面图相符,故选B。
5.撒哈拉以南的非洲气候复杂多样,其中气候分布最广的是。
A.温带大陆性气候B.温带海洋性气候C.热带季风气候D.热带草原气候【答案】D【解析】【详解】非洲主要位于热带地区,有热带大陆之称,撒哈拉以南的非洲气候复杂多样主要是热带雨林气候,热带草原气候,热带沙漠气候,地中海气候,其气候呈对称性分布,其中气候分布最广的是热带草原气候。
朝阳区2020届初三期末地理试题及答案

朝阳区2020届高三第一学期期末地理 2020. 1(考试时间90分钟满分100分)第一部分(选择题共45分)本部分共15小题,每小题3分,共45分。
在每小题列出的四个选项中,选出最符合题目要求的一项。
读图1,回答第1、2题。
1.图示地区A.人口集中区向地势低平地区移动B.环境承载力的直接影响因素是经济发展水平C.未来的人口合理容量有可能提高D.发展要解决的主要问题是扩大绿洲面积2.图中现在城镇相对于古城位置的变化反映了A.该地区生态环境的恶化B.人类对水质的要求越来越高C.人类对水资源的利用率越来越高D.交通条件成为现在城镇选址的首要条件图2为我国某直辖市中心城区公交密度图(数值大小表示公交车站数量)和夜灯指数图(数值大小表示夜间灯光强度)。
读图,回答第3、4题。
3.图中甲乙丙丁所在地A.甲地区位于城郊农业区B.丙地区与其它区域联系较方便C.乙地区为老城住宅区D.丁地区人口密度昼夜差异明显4.该市中心城区A.地形利于基础设施建设B.围绕河流两岸开发新区C.呈现多中心的空间格局D.各区域经济发展较均衡苹果原产于欧洲中部、东南部以及中亚、西亚和中国的新疆地区。
图3为我国苹果产区分布图。
读图,回答第5、6题。
5.据图推测,苹果的生长习性是A.喜高温B.喜湿耐涝C.喜阴D.喜凉爽6.与甲产区相比,阿克苏发展苹果种植的有利区位条件有①热量充足,降水丰富②光照充足,昼夜温差大③土壤深厚肥沃④种植历史悠久⑤靠近市场A.①③B.②④C.②⑤D.③⑤氢气的能量密度比燃油大,氢能被视为未来的理想清洁能源,获取途径主要有化石能源制氢、提纯煤化工等工业废气、电解水制氢。
作为新能源汽车领域的后起之秀,氢能源汽车得到了市场的广泛关注。
回答第7、8题。
7.我国发展氢能产业的主要优势是A.原料丰富B.技术世界领先C.政策支持力度大D.劳动力充足8.与传统汽车相比,氢能源汽车A.制造成本较低B.安全性更可靠C.技术门槛较低D.节能减排效果好图4中阴影示意中国不同类型生态脆弱区分布。
北京市朝阳区2019~2020学年第一学期初三期末地理试卷逐题精品解析
2020年北京市朝阳区初三期末地理考试试卷逐题解析第一部分(选择题共40分)本部分共40小题,每小题1分,共40分。
在每小题列出的四个选项中,选出最符合题目要求的一项。
2019年10月1日,庆祝中华?民共和国成立70周年的游?花车备受瞩目。
图1为“部分省区花车示意图”,据此回答1~4题。
图11.下列花车代表的省区、简称和行政中心对应正确的是A.黑龙江—黑—沈阳B.上海—滇—上海C.陕西—秦—西安D.海南—琼—三亚【答案】C【解析】本题考查行政区划相关内容。
A选项黑龙江省的行政中心是哈尔滨,故A错误;B选项上海市的简称为沪,故B错误;C选项陕西省的简称是陕或秦,行政中心是西安,故C正确。
D选项海南省的行政中心是海口,故D错误;2.黑龙江省花车中出现了冰雪元素,海南省花车中出现了热带雨林元素,这体现了我国①纬度跨度大②经度跨度大③自然景观差异大④地形类型差异大A.①② B.①③ C.②③ D.②④ 【答案】B【解析】本题考查中国气候的相关内容。
黑龙江省纬度高,气温低,因此有冰雪元素;海南省纬度低,气温高,因此有热带雨林元素,故南北气温差异大是因为我国南北纬跨度大,故①正确。
冰雪元素、热带雨林元素体现了自然景观差异,故③正确。
综上所述,本题正确答案为B选项。
3.花车反映了该省区最有代表性的自然和人文特征,以下描述正确的是A.横贯陕西省南部的秦岭是我国重要地理分界线B.信息技术产业已经成为上海市的经济支柱C.凭借高新技术,黑龙江省成为我国的粮仓D.海南省四面环海,温带动植物资源丰富【答案】A【解析】本题考查区域特征相关内容。
A选项秦岭位于陕西省南部,是我国重要的地理分界线,故A正确;B选项上海市花车信息未体现信息技术产业,故B错误;C选项黑龙江成为我国粮仓主要因为地广人稀、耕地面积大,余量多,与高新技术产业关系不大,故C选项错误;D选项海南省位于热带,以热带作物为主,故D错误;4.上海建立了“中国(上海)贸易示范区”,其发展贸易的有利社会经济条件有①位于长江与东海的交汇处②居于我国大陆海岸线中枢位置③开发时间早,发展历史悠久④高等院校多,科技实力强A.①② B.①③ C.②③ D.③④ 【答案】D【解析】本题考查经济发展的相关内容。
北京市朝阳区 2019~2020 学年八年级第一学期期末地理检测答案

北京市朝阳区2019~2020学年度第一学期期末检测八年级地理参考答案及评分标准题号 1 2 3 4 5 6 7 8 9 10 答案 A C D C B D A B D A题号11 12 13 14 15 16 17 18 19 20 答案 B C B D C C A A C B第二部分综合题(共5道题,60分)21.(11分)携手保护森林资源(1)自低纬向高纬逐渐减低 /自高纬向低纬逐渐升高(1分)(2)亚寒带针叶林(1分) -10—0℃(1分) 亚欧(1分) 纬度位置(1分)(3)A、B(2分)(4)全年高温多雨(1分)不容易(1分)干旱(1分) B(1分)22.(12分)“双龙”出征远赴南极(1)秋(1分)(69°S,76°E)(上下浮动2°均可)(2分)(2)错误1:南极洲被四大洋包围(1分)错误2:在中山站可以看到太阳常年在地平线以上(1分)错误3:北极熊在冰面上行走(1分)错误4 :南极科考是为了开发丰富的矿产和淡水资源(1分)任写出3条,即可得分(必须完整的摘抄一句话)(3)(4)合理即可,必须从旅行安全和环境保护两个方面谈(2分)。
23.(13分)香料之路共话联系(1)①大西(1分)②低(1分)③热(1分)④温带海洋性(1分)⑤平原(1分)八年级地理试卷第 1 页(共2 页)⑥湿热/全年高温多雨/气温高,降水多(1分)⑦火山(1分)⑧土壤(1分)⑨畜牧业(1分)⑩ C D(顺序可以调换,各1分)(2)胡椒(C),东南亚/雅加达/马来群岛大部分月份气温在21℃-26℃之间(1分),年降水量约2200毫米(1分),适宜胡椒的生长。
肉蔻(D), 东南亚/雅加达/马来群岛全年气温均在20℃以上(1分),全年高温多雨(1分),水热充足,适宜肉蔻的生长。
24.(14分)沧海孤岛绿色发展(1)岛(1分)南/西(一个即可,1分)惠灵顿(1分)(2)地热(1分)北(1分)较大(大)(1分)多(1分)山地(1分)大(1分)快(1分)(3)选择资料1(选择不给分),形成原因:新西兰地处印度洋板块和太平洋板块交界处(1分),地壳运动活跃/地热资源丰富(1分)资料2:新西兰是个四面环海的岛国(1分),远离其他大陆(1分)(4)A(1分)25.(11分)国际大事,共商未来(1)B(1分)(2)(5分,每空1分)(3)南北对话(1分)(4)人文(1分)地中海(1分)(5)对希腊:提供就业岗位/促进产业升级(1分)对中国:促进中国商品出口,增加经济收入(1分)(其他合理即可,但必须说出对两个国家的分别影响)八年级地理试卷第 2 页(共2 页)。
北京市朝阳区2019-2020学年中考地理第一次调研试卷含解析

北京市朝阳区2019-2020学年中考地理第一次调研试卷一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.高脚屋是为适应什么气候条件而设计的A.全年气候湿热B.全年寒冷干燥C.全来温和多雨D.终年炎热干燥【答案】A【解析】【分析】【详解】许多传统的民居建筑风格往往都与当地的自然环境是相适应的,东南亚气候潮湿闷热,当地居民多建双层的高脚屋,既隔热又便于雨水的排泄。
因此A选项正确,故选A。
2.我国气候主要特征是A.气候复杂多样,多灾害性天气B.气候复杂多样,季风气候显著C.气候复杂多样,海洋性显著D.气候复杂多样,动植物种类丰富【答案】B【解析】【分析】我国是世界上气候类型最多的国家之一。
我国东半部有大范围的季风气候,自南向北有热带季风气候、亚热带季风气候、温带季风气候。
西北地区有温带大陆性气候。
还有高山高原气候。
【详解】气候复杂多样,是我国气候的主要特征之一。
我国地域辽阔,地跨众多的温度带和干湿地区,加上我国地形复杂,地势高低悬殊,更增加了我国气候的复杂多样性。
季风气候显著,是我国气候的主要特征之二,我国东部有热带季风气候、亚热带季风气候和温带季风气候。
故选:B。
【点睛】本题主要考查我国气候的主要特点,牢记即可。
3.亚洲地形的特点是()A.以高原为主,平均海拔最高的洲B.地形复杂多样,地势中部高四周低C.以平原为主,平均海拔最低的洲D.西部是山地,中部是平原,东部是高原【答案】B【解析】【分析】【详解】亚洲是世界七大洲中面积最大的洲,面积辽阔,地形复杂以高原、山地为主,地表起伏大,地势中间高、四周低,高低相差悬殊,使得许多大江大河都发源于亚洲中部,向四周呈放射状奔流入海,故本题选B。
【点睛】本题主要考查我们生活的大洲──亚洲自然环境。
4.吸引农村剩余劳动力进城的原因描述不确切的是()A.教育、医疗条件好B.就业机会多C.生活条件好D.劳动力充足【答案】C【解析】【详解】吸引农村剩余劳动力进成的原因包括城市的教育、医疗条件了,就业机会多、生活条件好,劳动力充足是不正确的,故选D。
北京市朝阳区2019-2020学年中考地理二月模拟试卷含解析

北京市朝阳区2019-2020学年中考地理二月模拟试卷一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.下列有关我国省级行政单位名称、简称和省级行政中心对应正确的是()A.山西-冀-太原B.贵州-黔-遵义C.广东-粤-深圳D.辽宁-辽-沈阳【答案】D【解析】【分析】【详解】山西省的简称是晋,行政中心是太原,故A错误;贵州省的简称是贵或黔,行政中心是贵阳,故B错误;广东省的简称是粤,行政中心是广州,故C错误;辽宁省的简称是辽,行政中心是沈阳,故D正确.故选D.山西省的简称是晋,行政中心是太原,故A错误;贵州省的简称是贵或黔,行政中心是贵阳,故B 错误;广东省的简称是粤,行政中心是广州,故C错误;辽宁省的简称是辽,行政中心是沈阳,故D正确.故选D.2.我国降水量空间分布的总规律是:A.由东南沿海向西北内陆递增B.由东向西递减C.由东南沿海向西北内陆递减D.由南向北递减【答案】C【解析】【详解】我国降水空间分布不均,我国降水量空间分布的总规律是由东南沿海向西北内陆递减,故C符合题意。
【点睛】识记我国降水的分布特点。
3.中东居民通用语言及多数人信仰的宗教分别是A.英语、基督教B.阿拉伯语、伊斯兰教C.英语、伊斯兰教D.阿拉伯语、佛教【答案】B【解析】【详解】中东地区是指亚洲西部除阿富汗外,加上非洲北部国家,这里的居民多属于阿拉伯人,使用的语言是阿拉伯语,多数人信仰伊斯兰教,被称为穆斯林,故选B。
【点睛】本题考查中东地区语言宗教的有关知识,要知道宗教矛盾也是该地区发生冲突的原因。
4.亚洲的河流众多,下列不属于太平洋流域的河流是()A.黄河B.湄公河C.黑龙江D.勒拿河【答案】D【解析】【分析】根据亚洲地面起伏很大,中部高,四周低,地形以高原、山地为主,亚洲是世界上除南极洲外平均海拔高度最高的大洲。
亚洲大河多发源于中部的高原山地,顺地势呈放射状向四周奔流入海,进行分析解答。
北京市朝阳区2019-2020学年中考地理仿真第三次备考试题含解析

北京市朝阳区2019-2020学年中考地理仿真第三次备考试题一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.有关黄土高原水土流失严重的原因的叙述,不正确的是()A.地表光秃裸露,缺少植被的保护B.气候越来越干燥,降水量越来越小C.黄土结构疏松,易溶于水D.降水集中在七八月份,且多暴雨【答案】B【解析】【分析】【详解】关于黄土高原水土流失严重的原因,是由于地表光秃裸露,缺少植被的保护;加上黄土结构疏松,易溶于水和降水集中在七八月份,且多暴雨,并不是因为气候越干燥、降水量越来越小的原因,故选B。
2.欧洲西部多种多样的自然条件和人文风情使其旅游业十分繁荣,下列旅游景点与其所在的国家搭配不正确的是()A.埃菲尔铁塔一法国B.风车一一荷兰C.白金汉宫一英国D.水城威尼斯一德国【答案】D【解析】【详解】埃菲尔铁塔位于法国巴黎,风车是荷兰典型的景观,白金汉宫位于英国伦敦,水城威尼斯位于意大利,不是德国。
故D叙述错误符合题意。
【点睛】本题考查欧洲西部的旅游景点及所属国家。
3.塔里木河的汛期为每年的7~9月,主要原因是()A.夏季风带来了大量降水B.气温高,冰雪融水多C.蒸发量小D.农业灌溉需水量少【答案】B【解析】【分析】【详解】塔里木河地处西北内陆.这里降水稀少,气候干旱,河水主要来自高山冰雪融水.夏季(7﹣9月)气温升高,冰雪融化,内流河水量增多;夏季过后,河流水量逐渐减少,甚至断流.所以,内流河大部分属于季节性河流.故选B.【点睛】本题考查我国内流河的水文特点,要理解记忆.4.暑假里武汉地区酷热难当,小明的父母欲带他去旅游避暑,最理想的避暑地点是下图中的A.B.C.D.【答案】C【解析】【分析】【详解】读图可知,AB两地的夏季最高气温均在20℃以上,气温高,气候炎热,不适宜避暑;D地虽然地处南半球,其7月最低气温仍在20℃以上,不适宜避暑;C地夏季最高气温在20℃以下,气候较为凉爽,适宜避暑。
北京市朝阳区2019-2020学年九年级上学期期末地理试题

北京市朝阳区2019-2020学年九年级上学期期末地理试题一、选择题1. 2019年10月1日,庆祝中华人民共和国成立70周年的游行花车备受瞩目。
下图为“部分省区花车示意图”,据此回答下列问题。
(1)下列花车代表的省区、简称和行政中心对应正确的是A.黑龙江—黑—沈阳B.上海—滇—上海C.陕西—秦—西安D.海南—琼—三亚(2)黑龙江省花车中出现了冰雪元素,海南省花车中出现了热带雨林元素,这体现了我国①纬度跨度大②经度跨度大③自然景观差异大④地形类型差异大A.①②B.①③C.②③D.②④(3)花车反映了该省区最有代表性的自然和人文特征,以下描述正确的是A.横贯陕西省南部的秦岭是我国重要地理分界线B.信息技术产业已经成为上海市的经济支柱C.凭借高新技术,黑龙江省成为我国的粮仓D.海南省四面环海,温带动植物资源丰富(4)上海建立了“中国(上海)贸易示范区”,其发展贸易的有利社会经济条件有①位于长江与东海的交汇处②居于我国大陆海岸线中枢位置③开发时间早,发展历史悠久④高等院校多,科技实力强A.①②B.①③C.②③D.③④2. 新中国成立以来,进行了六次全国人口普查。
下图是六次人口普查的相关数据和反映了我国不同时期的人口问题及制定的相应人口政策图。
读图回答下列问题。
(1)关于六次人口普查的描述,正确的是A.中国人口总数已超过 70 亿B.15~64 岁人口比重持续增长C.65 岁以上人口比重 2010 年最大D.每十年人口大约净增 1 亿以上(2)不同时期的人口问题不同,制定的相应人口政策也不同。
以下描述正确的是A.第一次人口普查后实行了 c 政策B.第三次人口普查后 d 现象严重C.第五次人口普查后 a 问题严重D.第六次人口普查后实行了 b 政策(3)一个国家人口政策的制定与调整说明①人口政策只能解决人口增长问题②人口政策要适应社会的发展需求③人口增长应与资源、环境相协调④人口增长应与社会经济发展相适应A.①②③B.①②④C.①③④D.②③④3. 长江是我国第一大河,是华夏民族的母亲河。
北京市朝阳区2019-2020学年第一学期初三期末语文试题及答案

2020北京朝阳初三(上)期末语文一、基础·运用(共17分)在纪念甲骨文发现120周年之际,学校组织到中国国家博物馆参观“证古泽今——纪念甲骨文发现一百二十周年文化展”。
请你完成下列任务。
1.下面是展览“前言”中的部分文字。
阅读这段文字,完成(1)-(4)题。
(共8分)甲骨文是3000多年前商朝王室用于占.卜记事而在龟甲兽骨上契.①刻的文字。
1899年,王懿荣无意间发现了一种叫龙骨的药材上刻有图形文字,经推断正是商代王室使用的文字。
甲骨文得以发现。
这些文宇,埋①(藏/葬)在中国人的文化基因中,融化在中国人的血液里,生成了最深沉、持久的力量。
作为我国迄今可见最早成体系的文字。
甲骨文不仅仅是一个文明的符号、文化的标志,还印证了包括(史记》在内的一系列文献的真实,把有文字记载的中华文明史向前推进了近5个世纪。
在已知的四大古文字体系中,唯有以殷墟甲骨文为代表的中国古文字体系,一脉相②(成/承),绵延发展,成为今天世界上五分之一的人口仍在使用的文字,并对中国人的价值认同、思维方式、审美观念产生了极其重要的影响。
【甲】。
2017年,甲骨文成功入“世界记忆名录”表明了世界对甲骨文的重要文化价值及其历史意义的高度认可,促进了中国文化在世界的传播。
注:①【契】用刀雕刻。
(1)依次给这段文字中加点的字注音,全都正确的一项是(2分)A.占(zhān)契(qì)B.占(zhān)契(qiè)C.占(zhàn)契(qì)D.占(zhàn)契(qiè)(2)结合语境,在①②处依次填人汉字,全都正确的一项是(2分)A.①藏②成B.①藏②承C.①葬②成D.①葬2承(3)右图是“证古泽今——纪念甲骨文发现一百二十周年文化展”的宣传海报。
结合本次展览“前言”的内容,你认为“证古泽今”在这个情境中具体指的是。
(2分)(4)在【甲】处填入一句承上启下的话,最恰当的一项是(2分)A.甲骨文是全人类共同的精神财富B.甲骨文也是全人类共同的精神财富C.甲骨文是中华民族珍贵的文化遗产D.甲骨文也是中华民族珍贵的文化遗产2.作为此次参观活动的志愿讲解员,小明同学拟写了下面一段讲解词。
北京市朝阳区2019-2020学年中考地理最后模拟卷含解析

北京市朝阳区2019-2020学年中考地理最后模拟卷一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.读图,完成下面小题。
1.与 400mm 年等降水量线大致相同的是A.南方地区与北方地区的分界线B.半湿润与半干旱地区的分界线C.亚热带和暖温带的分界线D.丰水带和多水带的分界线2.对甲、乙、丙、丁四地地理特征的描述,正确的是A.甲地植被属常绿阔叶林B.乙地处于湿润地区C.丙地夏季高温多雨D.丁地河流流量较小【答案】1.B2.C【解析】【分析】综合地理位置、自然地理、人文地理的特点,可以把我国划分为四大地理区域,即北方地区、南方地区、西北地区和青藏地区。
其中,秦岭、淮河一线是北方地区和南方地区的分界线。
大兴安岭-阴山-贺兰山为北方地区和西北地区的分界线。
我国青藏地区和西北地区,北方地区,南方地区的分界线,大致以第一级阶梯和第二级阶梯的分界线。
我国的北方地区和南方地区,在地形、气候、河流流量和植被类型等方面均有明显差异;受自然环境的影响,北方地区和南方地区的人们,在生产方式、生活习惯、文化传统等方面也有很大差异。
1.南方地区与北方地区的分界线、亚热带和暖温带的分界线大致为800mm年等降水量线,丰水带和多水带的分界线是1600mm年等降水量线,半湿润与半干旱地区的分界线是400毫米年等降水量线。
所以ACD错误,B正确。
故选B。
2.图中甲西北地区植被以荒漠、荒漠草原为主;乙地位于内蒙古高原,处于半干旱地区。
丙地位于北方地区,属于温带季风气候,夏季高温多雨,冬季寒冷干燥;丁地位于南方地区,降水丰富,河流流量较大,汛期较长。
所以ABD错误,C正确。
故选:C。
【点睛】2.读亚欧大陆分布图,图中四地气候类型搭配正确的是( )A.A地—乙B.B地—丙C.C地—丁D.D地—甲【答案】A【解析】【分析】亚洲大陆跨寒、温、热三带,气候的主要特征是气候类型复杂多样、季风气候典型和大陆性显著。
北京市朝阳区2019-2020学年中考第二次质量检测地理试题含解析

北京市朝阳区2019-2020学年中考第二次质量检测地理试题一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.我国幅员辽阔,东西相距5000多千米,跨60多度,这就造成了()A.B.C.D.【答案】C【解析】【分析】【详解】同一座山,不同景观是由于受地形影响,水分热量条件发生变化,A选项错误。
同一季节,不同衣着说明我国南北方冬季气温差异大,是纬度差异造成的,B选项错误。
同一时刻,不同景象,帕米尔高原位于我国陆地最西端,地方时晚,处于黑夜;乌苏里江位于我国陆地最东方,地方时早,已经日出,是因为经度差异大,地方时相差大导致的,符合题意;同处平原,不同耕作,南方水田,北方旱地,是由于水分条件决定的,D选项错误。
所以本题选择C选项。
【点睛】本题考查我国的地理位置及特点。
2.下图中表示山脊的是()A.B.C. D.【答案】C【解析】【详解】山脊是山地地形中的一部分,以上四幅地图中,A表示的是山地,B表示的是盆地,C表示的等高线向低①湿润地区与半湿润区的界线②亚热带与暖温带的分界线③400毫米降水量线④一月份0℃等温线⑤南方与北方地区的界线⑥东部和西部地区的界线⑦水田与旱地的界线A.①②③④⑤⑦B.①②④⑤⑦C.①②④⑥⑦D.①④⑤⑥⑦【答案】B【解析】【分析】【详解】秦岭—淮河与1月份0℃等温线和800毫米等降水量线大体一致,是湿润地区与半湿润区的界线,亚热带与暖温带的分界线,南方与北方地区的界线,南方和北方地区的界线,水田与旱地的界线,B对,ACD 错。
故选B。
4.下列省区轮廓与其对应的简称错误的是()A.B.C.D.【答案】C【解析】【详解】根据轮廓可知,A为我国陕西省,简称陕或秦;B为山东省,简称鲁;C为云南省,简称云或滇;D为辽宁省,简称辽。
故选C。
【点睛】本题考查我国的行政区划,要求学生识记掌握。
5.太阳光直射在赤道上的时间是 ( )A.春分日或秋分日B.夏至日C.冬至日D.全年都是【答案】A【解析】【分析】根据当太阳光直射在南回归线上时,这一天称为冬至日,为12月22日,北半球昼短夜长,北极圈以内地区有极夜现象;当太阳光直射在北回归线上时,这一天称为夏至日,为6月22日,北半球昼长夜短,北极圈以内地区有极昼现象;当太阳光第一次直射在赤道上时,这一天称为春分日,为3月21日,全球昼夜平分;第二次直射在赤道上时为秋分日,为9月23日,全球昼夜平分,进行分析解答。
北京市朝阳区(4校联考)2019-2020学年中考模拟地理试题含解析

北京市朝阳区(4校联考)2019-2020学年中考模拟地理试题一、选择题(本题包括25个小题,每小题2分,共50分.在每个小题给出的四个选项中,只有一项是符合题目要求的。
)1.下图中甲表示的地形部位是( )A.山谷B.陡崖C.山峰D.鞍部【答案】C【解析】【分析】【详解】读图可知:甲地的等高线特征是等高线为闭合曲线,数值中间大,四周低,是山峰,故选C。
【点睛】本题考查的是等高线地形图的判读和运用等相关知识,完成本题,需要识别等高线的五种基本类型等,识别等高线的五种基本类型是重点也是难点,需要重点识记。
2.东北地区农作物的熟制主要是()A.一年一熟B.一年两熟C.一年三熟D.两年三熟【答案】A【解析】【详解】东北地区是我国纬度最高的地区,这里由于纬度高、热量不足,地面积雪时间长,农作物的熟制是一年一熟,故选A。
3.我国东北地区与华北地区相同的自然特征是A.1月平均气温均在0℃以下B.河流含沙量都很大C.都位于我国地势的第二级阶梯D.都属于我国的湿润地区【答案】A【解析】【详解】我国东北和华北都位于秦岭-淮河以北,都属于我国北方地区,都属于温带季风气候,1月平均气温均在0℃以下,都位于我国地势第三级阶梯,华北属于我国半湿润地区,东北属于半湿润和湿润地区。
东北的河流含沙量小,华北的河流含沙量大。
故正确的是A。
【点睛】该题考查华北地区和东北地区的地理差异,分析解答即可。
4.日本工业集中分布在太平洋沿岸和濑户内海沿岸的原因,叙述错误的是()A.沿岸城市人口集中,是国内最大的消费地B.工厂靠近码头,有利于废渣、废水的排放C.沿海港口条件优越,巨型船舶可以停靠D.沿海平原集中,填海造陆价格低【答案】B【解析】【详解】日本工业集中分布在太平洋沿岸和濑户内海沿岸,是因为日本工业原料缺乏,沿海港口条件优越,巨型船舶可以停靠;城市人口集中,是国内最大的消费地;沿海平原集中,填海造陆价格低,故选B。
5.读图“中国人口分布图”和“我国某发行邮票图”,完成下面小题。
