苏教版七年级数学有理数整理修订篇
完整版)苏教版七年级上数学知识点总结

完整版)苏教版七年级上数学知识点总结第一章我们与数学同行(略)第二章有理数一、正数和负数1.正数和负数的概念正数是比0大的数,负数是比0小的数。
如果a表示正数,那么-a表示负数;如果a表示负数,那么-a表示正数;如果a表示0,那么-a还是0.需要注意的是,有时候正数在前面会加上"+",但也有时候省略不写。
省略正号的数是正数。
2.具有相反意义的量如果正数表示某种意义的量,那么负数可以表示具有与该正数相反意义的量。
例如,零上8℃表示为+8℃,而零下8℃表示为-8℃。
3.0表示的意义0表示“没有”,例如教室里没有人;它既不是正数也不是负数,而是正数和负数的分界线。
二、有理数1.有理数的概念正整数、负整数、0、正分数和负分数都可以写成分数的形式,这样的数称为有理数。
只有能化成分数的数才是有理数。
有限小数和无限循环小数都可以化成分数,也是有理数。
但是,无限不循环小数(如π)不能写成分数形式,不是有理数。
2.有理数的分类按有理数的意义分类:正整数、负整数、0、正分数和负分数都是有理数。
按正、负来分:正整数、正分数是非负有理数,负整数、负分数是非正有理数。
三、数轴1.数轴的概念数轴是一条向两端无限延伸的直线,规定了原点、正方向和单位长度。
2.数轴上的点与有理数的关系所有的有理数都可以用数轴上的点来表示。
正有理数用原点右边的点表示,负有理数用原点左边的点表示,0用原点表示。
需要注意的是,同一数轴上的单位长度要统一。
所有的有理数都可以用数轴上的点表示,但并非所有数轴上的点都表示有理数,因此有理数与数轴上的点不是一一对应关系。
例如,数轴上的点π不是有理数。
利用数轴可以表示两个数的大小关系。
在数轴上,右边的数总比左边的数大;正数都大于负数;两个负数比较,距离原点远的数比距离原点近的数小。
数轴上有一些特殊的最大(小)数。
最小的自然数是1,无最大的自然数;最小的正整数是1,无最大的正整数;最大的负整数是-1,无最小的负整数。
苏科版七年级上册第二章有理数知识点汇总
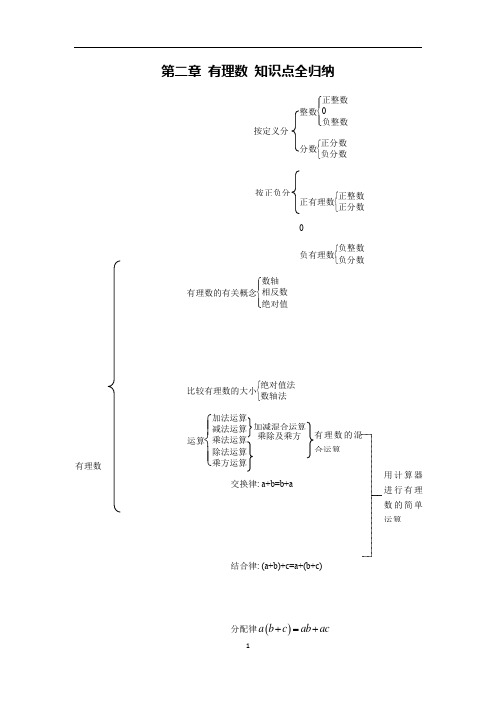
第二章有理数知识点全归纳整数⎩⎪⎨⎪⎧正整数负整数分数⎩⎨⎧正分数负分数正有理数⎩⎨⎧正整数正分数负有理数⎩⎨⎧负整数负分数有理数的有关概念⎩⎪⎨⎪⎧数轴相反数绝对值比较有理数的大小⎩⎨⎧绝对值法数轴法运算⎩⎪⎨⎪⎧加法运算减法运算乘法运算除法运算乘方运算交换律: a+b=b+a结合律: (a+b)+c=a+(b+c)分配律()a b c ab ac+=+有理数按定义分按正负分加减混合运算乘除及乘方混合运算有理数的混合运算用计算器进行有理数的简单运算近似数科学记数法:无理数:无限不循环小数;第1讲 有理数的意义知能解读 (一)正数和负数的意义(1)像3+,l ,8%,3.5这样大于0的数(“+”通常省略不写)叫作正数... (2)像3-, 2.7-%, 4.5-, 1.2-这样在正数前面加上“-”(读负号)的数叫作负数..,负数小于0.注意:(1)0既不是正数也不是负数,它是一个整数,它表示正数和负数的分界.(2)对于正数和负数的概念,不能简单理解为带“+”的数是正数,带“-”的数是负数.如0+是0,0-也是0;当0a <时,a -就是正数.(二)具有相反意义的量正数和负数是根据实际需要而产生的,比如一些具有相反意义的量:收入200元与支出200元,上升7米与下降3米,零上2℃与零下7℃等.虽然它们都表示一定的数量,却意义相反,那么我们如何去表示它们呢?我们把一种意义的量规定为正的(如收入200元规定为200+元),把另一种和它意义相反的量规定为负的(如支出200元规定为200-元),于是就产生了正数和负数.注意:(1)用正数和负数表示具有相反意义的量时,哪种意义的量规定为正,是可以任意选定的(如将上升2米规定为2+米或2-米都可以),一旦选定一种意义的量为正,则另一种意义相反的量就只能为负.(2)具有相反意义的量的特点:①具有相反意义的量是成对出现的,单独一个量不能成为具有相反意义的量;②与一个量意义相反的量不止一个;③具有相反意义的量包含两个要素:一是它们的意义相反,二是它们都具有数量;④具有相反意义的量必须是同类量,如节约3吨油与浪费1吨水不是具有相反意义的量.(三)有理数的分类1.有理数的定义:凡能写成)0p q ,p (pq ≠为整数且形式的数,都是有理数; 正整数、0、负整数统称整数...正分数和负分数统称分数...整数和分数统称有理数.....2.有理数的分类:(1)按定义分类: 整数⎩⎪⎨⎪⎧正整数0负整数分数⎩⎨⎧正分数负分数(有限小数或无限循环小数也是分数) (2)按正负分类:有理数⎩⎪⎨⎪⎧正有理数⎩⎨⎧正整数正分数0(即不是正数也不是负数)负有理数⎩⎨⎧负整数负分数注意:(1)在对有理数进行分类时,要做到不重不漏.(2)在分类时,注意0的地位和意义.(3)正整数,0统称非负整数(也叫自然数);负整数,0统称非正整数.(四)无理数:无限不循环小数角无理数;注:无理数的常见形式:(1)无限不循环小数形式:-2.010010001…(2)含π的形式:⋯-πππ31,, (3)含有根号的:⋯5,3,2(初二上学期学)(五)数轴规定了原点、正方向、单位长度的一条直线叫数轴;它满足以下要求:(1)在直线上任取—个点表示数0,这个0点叫作原点;(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示l ,2,3,…;从原点向左,用类似方法依次表示1-,2-,3-,…(如图所示).点拨:(1)利用数轴,我们可以表示任意一个有理数,还可以表示任意一个无理数.(2)数轴是研究数学的重要工具,也是“数形结合”的重要体现.(3)数轴的定义包含三层含义:①数轴是一条可以向两端无限延伸的直线;②数轴有三要素:原点、单位长度、正方向;③原点的位置、单位长度、正方向都是根据实际需要规定的.65-5-1-2-3-412340有理数 自然数(六)绝对值一般地,数轴上表示数a 的点与原点的距离叫作数a 的绝对值,记作a .正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0,即,00,0,0a a a a a a >⎧⎪==⎨⎪-<⎩点拨:因为有理数的绝对值表示两点之间的距离,距离总是正数或零,所以任意一个有理数的绝对值是非负数,即0a ≥.(七)相反数只有..符号不同,绝对值相等的两个数互为相反数.其中一个数是另一个数的相反数;特别地,0的相反数是0.(1)在数轴上,互为相反数的两个数对应的点与原点的距离相等(几何意义).且在原点两侧;(2)数a 的相反数是a .若a ,b 互为相反数,则0a b +=(或a b =-,或b a =-).(八)有理数大小比较的常用方法(1)数轴比较法:将两数分别表示在数轴上,右边的点表示的数总比左边的点表示的数大.(2)代数比较法:正数大于零,负数小于零,正数大于一切负数;两个负数,绝对值大的反而小.(3)差值比较法:设a ,b 是两个任意数,若0a b ->,则a b >;若0a b -=,则a b =;若0a b -<,则a b <;(4)商值比较法:设a ,b 是两个正数,若1a b >,则a b >;若1a b =,则a b =;若1a b <,则a b <.(初中基本不用,高中用)此外,还有倒数比较法、中间值比较法、平方比较法、换元比较法等.(5)-1,-2,+1,+4,-0.5,以上数据表示与标准质量的差,绝对值越小,越接近标准。
(完整版)苏教版七年级数学-有理数整理、修订篇

苏教版七年级数学《有理数》1.1 正数和负数负数:从前学过的0 之外的数前方加上负号“-”的数叫做负数。
正数:从前学过的0之外的数叫做正数。
0既不是正数也不是负数,0是正数与负数的分界。
在同一个问题中,分别用正数和负数表示的量拥有相反的意义注: -a 不必定是负数, +a 也不必定是正数;1.2.1 有理数:凡能写成q( p,q为整数且 p0) 形式的数,都是有理数。
p(1)正整数、 0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数 .正有理数正整数正整数正分数整数零(2) 有理数的分类 : ①有理数零② 有理数负整数负有理数负整数分数正分数负分数负分数注意:1)0 不是正数,也不是负数;2)不是有理数;无穷不循环小数不是有理数。
无穷循环小数是有理数;3)小数也归为分数。
4)自然数 0 和正整数;5) a>0 a 是正数; a< 0 a 是负数;6) a≥0 a 是正数或 0 a 是非负数;7) a≤ 0 a 是负数或 0 a 是非正数 .1.2.2 数轴:规定了原点、正方向、单位长度的直线叫做数轴。
数轴的作用:全部的有理数都能够用数轴上的点来表达。
注意事项:⑴数轴的原点、正方向、单位长度三因素,缺一不行。
⑵同一根数轴,单位长度不可以改变。
一般地,设 a 是一个正数,则数轴上表示a 的点在原点的右侧,与原点的距离是 a 个单位长度;表示数- a 的点在原点的左侧,与原点的距离是 a 个单位长度。
1.2.3 .相反数:只有符号不一样的两个数叫做相反数。
注意: (1) 一般地, a 和-a 互为相反数,特别地,0 的相反数仍是0;(2) a-b+c 的相反数是-a+b-c ;a-b 的相反数是b-a ;a+b 的相反数是-a-b ;(3)相反数的和为0 a+b=0 a 、b 互为相反数.一般地,设 a 是一个正数,数轴上与原点的距离是 a 的点有两个,它们分别在原点左右,表示 -a 和a,我们说这两点对于原点对称1.2.4. 绝对值:一般地,数轴上表示数 a 的点与原点的距离叫做数 a 的绝对值。
苏教版七年级数学上册 第2章《有理数》考点归纳(含答案)

第2章《有理数》考点归纳知识梳理重难点分类解析考点1相反意义的量【考点解读】中考中对于相反意义的量的考查主要涉及用正负数表示相反意义的量,解此类题的关键是要深刻理解正数、负数的意义.例1一个物体做左右方向的运动,规定向右运动4m记作+4m,那么向左运动4m记作()A.-4mB.4mC.8mD.-8m分析:若向右运动4 m记作+4 m,则向左运动4 m记作-4 m.答案:A【规律·技法】解题时要抓住以下几点:①记住区分相反意义的量;②记住相反意义的量的表示方法.【反馈练习】1.某财务科为保密起见采取新的记账方式,以5万元为1个记数单位,并记100万元为0,少于100万元记为负,多于100万元记为正.例如:95万元记为-1,105万元记为1.依此类推,75万元应记为( )A. -3B. -4C. -5D. -6 点拨:每多5万元记为+1,每少5万元记为-1.2. (2017·苏州期末)一个物体做左右方向的运动,规定向右运动5m 记作+5m ,那么向左运 动5m 记作( )A. -5mB.5mC.10mD. -10 m 点拨:若向右为正,则向左为负. 考点2 数轴【考点解读】中考中对于数轴的考查主要涉及数轴的认识以及数形结合的思想.用数轴上的点来表示有理数,这是运用了数形结合的思想.利用数轴这一工具,加强数形结合的训练可沟通知识间的联系.例2 如图,四个有理数在数轴上的对应点分别为,,,M P N Q ,若点,M N 表示的有理数互 为相反数,则图中表示绝对值最小的数的点是( )A.点MB.点NC.点ND.点Q 分析:因为点,M N 表示的有理数互为相反数,所以原点的位置在线段MN 的中点,所以表示绝对值最小的数的点是点P . 答案:C【规律·技法】解答与数轴有关的问题时要抓住以下几点:①记住数轴上的点与有理数的对应关系;②相反数、点与点之间的距离在数轴上的表示方法;③数轴常常与相反数、距离、绝对值结合考查. 【反馈练习】3.有理数,a b 在数轴上的位置如图所示,则下列各式正确的是( )A. 0a b +<B. 0a b -<C. 0ab >D. 0a b -> 点拨:先判断,a b 的正负和大小关系.4. (2017·苏州期末)有理数,a b 在数轴上的位置如图所示,则下列各式正确的是( )A. 0ab >B. b a <C. 0b a <<D. 0a b +>点拨:先判断,a b的正负和大小关系.考点3绝对值、相反数、倒数【考点解读】中考中对于绝对值、相反数、倒数的考查主要涉及概念的理解,因此掌握基本概念是解题关键.例3(1)(2017·盐城)-2的绝对值是( )A. 2B. -2C. 12D.12-(2)-3的相反数是,-3的绝对值是.(3) 23的倒数是.分析:根据相反数、绝对值、倒数的定义解答.符号不同、绝对值相同的两个数互为相反数,0的相反数是0;正数的绝对值是它本身,负数的绝对值是它的相反数,0的绝对值是0;乘积为1的两个数互为倒数.答案:(1) A (2) 3 3 (3) 3 2【规律·技法】(1)正确理解相反数的概念是关健;(2)数a的绝对值要由字母a本身的取值来确定:①当a是正数时,a的绝对值是它本身;②当a是负数时,a的绝对值是它的相反数-a;③当a是零时,a的绝对值是零;(3)应熟练掌握倒数的定义,需要注意的是负数的倒数还是负数,正数的倒数还是正数,0没有倒数.【反馈练习】5.23-的相反数是( )A.23- B.23C.32- D.32点拨:符号相反、绝对值相同的两个数互为相反数.6.若a与1互为相反数,则1a+等于( )A.-1B. 0C.1D.2点拨:互为相反数的两个数的和为0.考点4有理数大小的比较【考点解读】比较有理数大小的基本方法:①绝对值法:两个正数,绝对值大的正数大;两个负数,绝对值大的负数小;②数轴法:在数轴上表示的两个有理数,右边的点表示的数总比左边的点表示的数大.例4 (1) (2017·扬州)下列各数中,比-2小的数是()A.-3B.-1C. 0D. 1(2)下列各式中,计算结果最大的是( )A. 25 X 132-152B. 16 X 172-182C. 9 X 212-132D. 4X312-122分析:(1)比-2小的数是负数,且绝对值大于2,故只有选项A符合.(2) 25X132-152=(5X13)2-152=4 000 ;16X172-182=(4X17)2-182=4 300;9X212-132=(3X21)2-132=3 800;4X312-122=(2X31)2-122=3700.因为4300>4000>3800>3700,所以计算结果最大的式子是16X172-182. 答案:(1) A (2) B【规律·技法】解答有关有理数大小的比较问题时要抓住以下几点:①比较有理数的大小时,正数大于0,负数小于0,两个负数比较大小,绝对值大的反而小;②比较两个有理数的大小有以下五种情况:正数与正数、正数与负数、0与正数、0与负数、负数与负数的比较. 【反馈练习】7. (2017·扬州期末)在-2,0,1,-4这四个数中,最小的数是()A. -4B. 0C. 1D. -2 点拨:负数小于0,正数大于0;两个负数,绝对值大的负数小.8. (2017·泰州期中)在数轴上把下列各数表示出来,并用“<”号连接各数: 2112.5,1,(2),(1),222----+--.点拨:先把需要化简计算的式子计算出结果,再来画数轴. 考点5 有理数的混合运算 【考点解读】 解答有关有理数运算的问题时要抓住以下几点:(1)符号的判断;(2)运算顺序的选择;(3)运算律的使用.有理数的运算在中考中一般不单独命题,常常与以后学习的实数结合命题考查.例5 (1)计算: 42201721(3)2(1)-÷---⨯-;(2)计算: 1133()33-⨯÷⨯-; (3)若2a ba b a+*=,则(42)(1)**-= . 分析:(1)先算乘方,再算乘除,最后算加减;(2)先将除法运算转化为乘法运算,再根据有理数乘法法则计算;(3)根据新定义计算. 4224224+⨯*==,22(1)(42)(1)2(1)02+⨯-**-=*-==. 解答:(1) 42201721(3)2(1)1682220-÷---⨯-=-÷+=-+=. (2) 111111()33()3()333339-⨯÷⨯-=-⨯⨯⨯-=. (3) 0【规律·技法】有理数混合运算:先算乘方,再算乘除,最后算加减;同级运算,应按从左到右的顺序进行计算;如果有括号,要先算括号内的. 【反馈练习】9. (2017·徐州期末)计算: 2018142(3)-+-+⨯-.点拨:注意运算顺序和符号. 10.计算: 517()(24)8612--+⨯-.点拨:运用乘法分配律计算.考点6 科学记数法【考点解读】 解答有关科学记数法的问题时要抓住以下几点:①对于大于10的数,在科学记数法的表示形式10na ⨯中,110a ≤<,n 为正整数;②小数点移动的位数与指数的关系;③理解近似数的意义. 例6 据报道,2015年全国普通高考报考人数约为9 420 000人,数据9 420 000用科学记数法表示为9.42 X 10n ,则n 的值是( )A. 4B. 5C. 6D. 7 分析:对于大于10的数,科学记数法的表示形式为10na ⨯,其中110a ≤<,n 为正整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.确定10na ⨯(110a ≤<,n 为整数)中n 的值时,由于9 420 000是七位数,所以可以确定n =7-1=6. 答案:C【规律·技法】用科学记数法表示大于10的数时,确定a 与n 的值是关健.其中110a ≤<,n等于原数的整数位数减1. 【反馈练习】11. (2017·庐州)“五一”期间,某市共接待海内外游客约567 000人次,将567 000用科学 记数法表示为( )A. 567 X 103B. 56.7 X 104C. 5.67 X 105D. 0.567 X 106 点拨: 110a ≤<.12. (2017·宁波)2017年2月13日,宁波舟山港45万吨原油码头首次挂靠全球最大油轮— “泰欧”轮,其中45万吨用科学记数法表示为( )A. 0.45 X 106吨B. 4.5 X 105吨C. 45 X 104吨D. 4.5 X 1 04吨 点拨:单位要统一,万吨化为吨. 易错题辨析例1 给出下列各数: ①0.363 663 666 3…(每两个3之间依次多一个6);②2.121 121 112;③355113;④3π-.其中为无理数的是 .(填序号) 错误解答:①③④ 错因分析:把355113化成小数后,误以为是无限不循环小数,其实是循环小数. 正确解答:①④易错辨析:识别无理数时,要抓住其“无限不循环”的定义.本题若忽视无理数是无限小数,就会误认为有限小数2.121 121 112是无理数;若在把分数355113化成小数时,除了几位后,没有继续除下去,会错误的判断它不是循环小数,错误地认为它是无理数.实质上,所有的分数都是有理数,不是无理数. 易错点2 忽视分类讨论例2 在数轴上,点A 表示的数是-3,那么与点A 相距5个单位长度的点表示的数是多少? 它与132-相比较,大小关系如何? 错误解答:与点A 相距5个单位长度的点表不的数是-3+5=2,它与132-的大小关系为1322-<. 错因分析:考虑问题不全面.正确解答:如图,在数轴上,与点A 相距5个单位长度的点有,B C 两个.由点,B C 在数轴上的位置可知它们所表示的数分别为-8,2.在数轴上找到表示132-的点,观察点,B C 与表示132-的点在数轴上的位置,容易发现它们与132-之间的大小关系为13132,822>--<-. 易错辨析:一般地,在数轴上与某点相距一定单位长度的点有两个,分别位于该点的左、右两侧,不要遗漏.易错点3 乘法的分配律对除法不适用例3 计算:11(15)()53-÷- 错误解答:原式=11(15)(15)75453053-÷--÷=-+=-.错因分析:除法没有分配律. 正确解答:原式=215225(15)()(15)()1522-÷-=-⨯-=. 易错辨析:有的同学会错误地认为除法也有分配律,其实除法没有分配律.易错点4 幂的底数识别不清例4 计算:(1) 4(2)-= , 42-= ; (2) 32()3= , 323= .错误解答:(1)-16 -16 (2)827 827错因分析:负数的偶次幂的运算结果是正数,计算分数的幂时,注意分子、分母应分别乘方.在323中,注意是2的3次方,而不是23的3次方.(1) 4(2)-表示4个-2相乘,即它是底数为-2,指数为4的幂,所以4(2)-=16;42-表示42的相反数,即-2不是底数,所以42-=-16.(2)因为32()3表示3个23相乘,即它是底数为23,指数为3的幂,所以322228()333327=⨯⨯=.因为323表示3个2相乘的积与3的商,所以23不是底数,所以322228333⨯⨯==. 正确解答:(1) 16 -16 (2)827 83易错辨析:在进行幂的运算时,首先要区分底数和指数,然后根据幂的意义计算,得出正确结果.易错点5 混合运算顺序不清例5 计算: 23272(2)()83-÷⨯-. 错误解答:原式=2784()4(1)4827÷⨯-=÷-=-. 错因分析:易知328()327-=-,勿将“278”与“827-”结合运算,导致出错.实际上,本题中只有乘、除运算,故应从左往右按步计算. 正确解答:原式=278882564()4()8272727729÷⨯-=⨯⨯-=-. 易错辨析:乘、除是同级运算,应遵循从左往右的计算顺序.【反馈练习】1. (2016·宜昌)给出下列各数:1.414,1.732 050 8…,13-,0,其中为无理数的是( ) A. 1.414 B. 1.732 050 8… C . 13- D. 0 点拨:无理数即为无限不循环小数.2.已知数轴上有,A B 两点,点A 与原点的距离为2, ,A B 两点间的距离为1,则满足条件的 点B 所表示的数为 . 点拨:注意分类讨论.3.计算:(1) 23(2)(1)4-⨯-; (2) 22439-÷;(3) 2225(3)[()](6)439-⨯-+---÷; (4) 2017231(1)[2(1)(3)]6--⨯⨯---;点拨:注意有理数混合运算的顺序. 4.阅读下面的材料,并完成下列问题.计算: 12112()()3031065-÷-+-. 解法一:原式=12111112()()()()3033010306305-÷--÷+-÷-÷-=1111203512-+-+=16.解法二:原式=12112()[()()]3036105-÷+-+=151()()3062-÷-=1330-⨯ 110-.解法三:原式的倒数=21121()()3106530-+-÷- =2112()(30)31065-+-⨯- =203512-+-+ =10-.综上所述,原式=110-(1)上述三种解法得出的结果不同,肯定有错误的解法,解法 是错误的; (2)在正确的解法中,解法 最简便; (3)利用最简便的解法计算: 11322()()4261437-÷-+-.点拨:可以转化为先求原式的倒数. 探究与应用探究1 复杂的有理数混合运算 例1 计算:(1) 86[47(18.751)2]0.461525--÷⨯÷; (2) 32017201723(0.2)(50)(1)()35-⨯-+-⨯-. 点拨:按照有理数的运算法则进行计算即可. 解答:(1)原式=31556100[47(181)]482546--⨯⨯⨯=751556100[47()]482546--⨯⨯=13556100(47)82546-⨯⨯=4610020546⨯=(2)原式=20172017153()(50)()()12535-⨯-+-⨯-=2017253[()()]535+-⨯-=27155+=.规律·提示在有理数的混合运算过程中,要善于观察与思考,在正常运算较繁琐时,要根据算式的特点,灵活选择正确而简洁的解法(如运算律的运用等).对于复杂运算,更要保持不急不躁的态度,切不可跳步,欲速则不达. 【举一反三】 1.计算:(1) 222353()34()8()3532-⨯-÷-⨯+⨯-;(2) 321116(0.5)[2(3)]0.52338---÷⨯-----.探究2 错位相减法巧算例2 求23201712222S =++++⋅⋅⋅+的值.点拨:观察和式,不难发现:后面一个数是它前面一个数的2倍.为此,在和式两边同乘一个常数2后,再与原和式两边分别相减(这里的相减是错位相减),可使计算简便. 解答:因为23201712222S =++++⋅⋅⋅+①, 所以2342018222222S =++++⋅⋅⋅+②,所以②-①,得201821S =-.规律·提示:当一和式乘一个恰当的常数后,得到的新和式与原和式中绝大部分数相同时,应用错位相减法可以简化计算. 【举一反三】2.求23201613333++++⋅⋅⋅+的值.例3 求232017111112222S =++++⋅⋅⋅+的值. 点拨:观察和式,不难发现:后面一个数是它前面一个数的12.那么类似例2,在和式两边同乘一个常数12后,再与原和式两边分别相减(这里的相减是错位相减),可使计算简便. 解答:因为232017111112222S =++++⋅⋅⋅+①,所以2342018111111222222S =++++⋅⋅⋅+②.①-②,得201811122S =-,所以2017122S =-.规律·提示应用错位相减法时,一定要选择一个合适的常数. 【举一反三】 3.计算: 11112481024+++⋅⋅⋅+.探究3 拆项分解法巧算例4 计算: 111112123123100+++⋅⋅⋅+++++++⋅⋅⋅+. 点拨:因为(1)1232n n n ++++⋅⋅⋅+=,所以11222(1)123(1)12n n n n n n n ===-++++⋅⋅⋅+++,所以 111112123123100+++⋅⋅⋅+++++++⋅⋅⋅+可转化为 222222123341001001+-+-+⋅⋅⋅+-+.进一步通过加法的结合律计算,得22121001+-+,至此问题解决. 解答:原式=22222229912123341001001101101+-+-+⋅⋅⋅+-=-=+. 规律·提示(1)12342n n n +++++⋅⋅⋅+=. 这是初中数学计算中的一条重要公式. 再进一步拆分,得1111111,()(1)1()n n n n n n m m n n m=-=-++++.也可以类推三个及三个以上的数的积的拆项. 【举一反三】 4.求111113355720152017+++⋅⋅⋅+⨯⨯⨯⨯的值.探究4 整体换元法巧算例5 计算: 7737121738(172711)(1385)271739172739+-÷+-. 点拨: 73472437761716,2726,1110272717173939===,通过观察可以发现,这3个数分别是第2个括号内3个数的2倍.解答:令1217381385172739A =+-. 因为77373424761727111626102271739271739A +-=+-=, 所以原式=22A A ÷=. 规律·提示把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这种方法叫做换元法.换元法是常用的解题方法,它能化复杂为简单,明确题目的结构特征,丰富解题思路.【举一反三】5.已知33331231514400+++⋅⋅⋅+=,求333324630+++⋅⋅⋅+的值.探究5 配对、分组巧算例6 计算:11212312341235859()()()()23344455556060606060++++++++++⋅⋅⋅++++⋅⋅⋅++. 点拨:观察每个括号内式子的特点,依特征求解;也可用一个符号表示所求的式子,将式子进行整体变形,寻找内在关系,简化运算.解答:解法一:原式=(0.529.5)590.51 1.5229.58852+⨯++++⋅⋅⋅+==. 解法二:原式=0.51 1.5229.5++++⋅⋅⋅+=(0.51 1.5229.5)(1229)++++⋅⋅⋅++++⋅⋅⋅+ (0.529.5)30(129)2988522+⨯+⨯=+= 解法三:设原式之和为S ,对每个括号内的各项都交换位置再相加,显然其和不变, 即121321432159585721()()()()23344455556060606060S =++++++++++⋅⋅⋅++++⋅⋅⋅++. 将原序和倒序相加,其相应两项之和为1,则有 (159)59212345930592S +⨯=++++⋅⋅⋅+==⨯, 所以1559885S =⨯=.规律·提示计算时需要观察规律,本例三种解法分别从三个角度着眼:解法一是配成59个“对子”;解法二是分组计算; 解法三是倒序与正序的综合运用.上述三种解法在计算中的运用都十分广泛.【举一反三】6.计算:(1234)(5678)(9101112)(2013201420152016)+--++--++--+⋅⋅⋅++--.参考答知识梳理负数 分数 不循环 正方向 单位长度 距离 本身 相反数0 绝对值1 异号 相反数 正 负 不等于0 倒数 相同 幂 正整数重难点分类解析【反馈练习】1.C2.A3.B4.C5.B6.B7.A8. 2112 2.5(1)1(2)22-<--<+-<<--9.原式=―310.原式=511.C 12.B易错题辨析1.B2. 3或1或―1或―33. (1) 原式=1;(2) 原式=38-;(3) 原式=―20;(4) 原式= 356-;4.(1)一 (2) 三(3)原式=114-探究与应用【举一反三】1.(1) 原式=7279;(2) 原式=―3.895.2.23201613333++++⋅⋅⋅+= 201713-12(). 3.11112481024+++⋅⋅⋅+= 102310244.111113355720152017+++⋅⋅⋅+⨯⨯⨯⨯= 10082017. 5. 333324630+++⋅⋅⋅+=115200.6. 原式=―2016。
苏教版七年级上册数学[《有理数》全章复习与巩固(基础)知识点整理及重点题型梳理]
![苏教版七年级上册数学[《有理数》全章复习与巩固(基础)知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/f7bb95c3f705cc17552709a3.png)
苏教版七年级上册数学重难点突破知识点梳理及重点题型巩固练习《有理数》全章复习与巩固(基础)【学习目标】1.理解有理数及其运算的意义,发展运算能力;了解无理数的概念,会判断无理数.2.能用数轴上的点表示有理数,会比较有理数的大小;借助数轴理解相反数和绝对值的意义,会求有理数的相反数与绝对值.3.体会转化、归纳等思想;掌握有理数的加、减、乘、除、乘方及混合运算并能解决简单的实际问题.4.会用科学记数法表示较大的数,能对含有较大数字的信息作出合理的解释和推断,发展数感.【知识网络】【要点梳理】要点一、有理数与无理数1.有理数的分类:(1)按定义分类:(2)按性质分类:要点诠释:(1)用正数、负数表示相反意义的量;(2)有理数“0”的作用:作用举例表示数的性质0是自然数、是有理数表示没有3个苹果用+3表示,没有苹果用0表示表示某种状态0C表示冰点表示正数与负数的界点0非正非负,是一个中性数2.无理数:无限不循环小数叫做无理数.要点诠释:(1)无理数的特征:无理数的小数部分位数无限.无理数的小数部分不循环,不能表示成分数的形式.(2)目前常见的无理数有两种形式:①含π类.②看似循环而实质不循环的数,如:1.313113111……(相邻两个3之间1的个数逐渐增加).3.数轴:规定了原点、正方向和单位长度的直线.要点诠释:(1)一切有理数都可以用数轴上的点表示出来,数轴上的点不都表示的是有理数,如π.(2)在数轴上,右边的点所对应的数总比左边的点所对应的数大.4.相反数:只有符号不同的两个数互称为相反数,0的相反数是0.要点诠释:(1)一对相反数在数轴上对应的点位于原点两侧,并且到原点的距离相等,这两点是关于原点对称的.(2)求任意一个数的相反数,只要在这个数的前面添上“-”号即可.(3)多重符号的化简:数字前面“-”号的个数若有偶数个时,化简结果为正,若有奇数个时,化简结果为负.5.绝对值:(1)代数意义:一个正数的绝对值是它本身;一个负数的绝对值是它的相反数;0的绝对值是0.数a的绝对值记作a.(2)几何意义:一个数a的绝对值就是数轴上表示数a的点与原点的距离.要点二、有理数的运算1 .法则:(1)加法法则:①同号两数相加,取相同的符号,并把绝对值相加.②绝对值不相等的异号两数相加,取绝对值较大的加数的符号,并用较大的绝对值减去较小的绝对值.③一个数同0相加,仍得这个数.(2)减法法则:减去一个数,等于加这个数的相反数.即a-b=a+(-b) .(3)乘法法则:①两数相乘,同号得正,异号得负,并把绝对值相乘.②任何数同0相乘,都得0.(4)除法法则:除以一个不等于0的数,等于乘这个数的倒数.即a÷b=a·1b(b≠0) .(5)乘方运算的符号法则:①负数的奇次幂是负数,负数的偶次幂是正数;②正数的任何次幂都是正数,0的任何非零次幂都是0.(6)有理数的混合运算顺序:①先乘方,再乘除,最后加减;②同级运算,从左到右进行; ③如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行.要点诠释:“奇负偶正”口诀的应用:(1)多重负号的化简,这里奇偶指的是“-”号的个数,例如:-[-(-3)]=-3,-[+(-3)]=3.(2)有理数乘法,当多个非零因数相乘时,这里奇偶指的是负因数的个数,正负指结果中积的符号,例如:(-3)×(-2)×(-6)=-36,而(-3)×(-2)×6=36.(3)有理数乘方,这里奇偶指的是指数,当底数为负数时,指数为奇数,则幂为负;指数为偶数,则幂为正,例如: 2(3)9-=, 3(3)27-=-. 2.运算律:(1)交换律: ①加法交换律:a+b=b+a ; ②乘法交换律:ab=ba ;(2)结合律: ①加法结合律:(a+b)+c=a+(b+c); ②乘法结合律:(ab )c=a(bc)(3)分配律:a(b+c)=ab+ac要点三、有理数的大小比较比较大小常用的方法有:(1)数轴比较法;(2)法则比较法:正数大于0,0大于负数,正数大于负数;两个负数,绝对值大的反而小;(3) 作差比较法.(4)作商比较法;(5)倒数比较法.要点四、科学记数法把一个大于10的数表示成10na ⨯的形式(其中110a ≤<,n 是正整数),此种记法叫做科学记数法.例如:200 000=5210⨯.【典型例题】 类型一、有理数与无理数的相关概念1.若一个有理数的:(1)相反数;(2)倒数;(3)绝对值;(4)平方;(5)立方,等于它本身.则这个数分别为(1)________;(2)________;(3)________;(4)________;(5)________.【答案】(1)0; (2)1和-1;(3)正数和0;(4)1和0;(5)-1、0和1【解析】根据定义,把符合条件的有理数写全.【总结升华】要全面正确地理解倒数,绝对值,相反数等概念.举一反三:【有理数专题复习 357133 概念的理解与应用】【变式】(1)321-的倒数是 ;321-的相反数是 ;321-的绝对值是 ; -(-8)的相反数是 ;21-的相反数的倒数是_____. (2)某种食用油的价格随着市场经济的变化涨落,规定上涨记为正,则-5.8元的意义是 _ ;如果这种油的原价是76元,那么现在的卖价是 .(3) 上海浦东磁悬浮铁路全长30km ,单程运行时间约为8min,那么磁悬浮列车的平均速度用科学记数法表示约为 m /min .(4) 若a 、b 互为相反数,c 、d 互为倒数,则=++)(323b a cd ____ . (5)下列各数:2π,0, 0.23,227,0.3000333…,中无理数个数为 个. 【答案】(1)35-; 213; 213;-8;2 (2)降价5.8元,70.2 元;(3)33.7510⨯;(4)3;(5)2.2.(2015春•射洪县月考)如果|x+3|+|y ﹣4|=0,求x+2y 的值.【思路点拨】根据非负数的性质,可求出x 、y 的值,然后将x 、y 的值代入代数式化简计算即可.【答案与解析】解:∵|x+3|+|y ﹣4|=0,∴x+3=0,y ﹣y=0,解得,x=﹣3,y=4,x+2y=﹣3+4×2=5.【总结升华】本题考查了绝对值的性质和非负数的性质,掌握有限个非负数的和为零,那么每一个加数也必为零是解题的关键.3.在下列两数之间填上适当的不等号:20052006________20062007. 【思路点拨】根据“a-b >0,a-b =0,a-b <0分别得到a >b ,a =b ,a <b ”来比较两数的大小.【答案】 <【解析】法一:作差法由于20052006200520072006200610200620072006200720062007⨯-⨯-==-<⨯⨯,所以2005200620062007< 法二:倒数比较法:因为2006112007112005200520062006=+>+= 所以2005200620062007< 【总结升华】比较大小常用的有五种方法,要根据数的特征选择使用. 举一反三:【变式】比较大小:(1)199-________0.001; (2)23-________-0.68 【答案】(1)< (2)>类型二、有理数的运算4.(2016•厦门)计算:.【思路点拨】原式先计算乘方运算,再计算乘除运算,最后算加减运算即可得到结果.【答案与解析】解:原式=10+8×﹣2×5=10+2﹣10=2.【总结升华】有理数的混合运算首先弄清运算顺序,先乘方,再乘除,最后算加减,有括号先算括号里边的,同级运算从左到右依次进行计算,然后利用各种运算法则计算,有时可以利用运算律来简化运算.举一反三:【变式】计算:(1)11(2)(2)22-⨯÷⨯- (2)()20064261031-+--⨯- 【答案】(1)111(2)(2)(1)(2)(1)2(2)4222-⨯÷⨯-=-÷⨯-=-⨯⨯-= (2)()20064261031-+--⨯-=-16+4-3×1 =-15类型三、数学思想在本章中的应用5.(1)数形结合思想:有理数a 在数轴上对应的点如图所示,则a ,-a ,1的大小关系.A .-a <a <1B .1<-a <aC .1<-a <aD .a <1<-a(2)分类讨论思想:已知|x|=5,|y|=3.求x-y 的值.(3)转化思想:计算:3135()147⎛⎫-÷- ⎪⎝⎭ 【答案与解析】(1)将-a 在数轴上标出,如图所示,得到a <1<-a ,所以大小关系为:a <1<-a . 所以正确选项为:D .(2)因为| x|=5,所以x 为-5或5因为|y|=3,所以y 为3或-3.当x =5,y =3时,x-y =5-3=2当x =5,y =-3时,x-y =5-(-3)=8当x =-5,y =3时,x-y =-5-3=-8当x =-5,y =-3时,x-y =-5-(-3)=-2故(x-y )的值为±2或±8(3)原式=33135(7)357724614142⎛⎫--⨯-=⨯+⨯= ⎪⎝⎭【总结升华】在解题中合理利用数学思想,是解决问题的有效手段.数形结合——“以形助数”或“以数解形”使问题简单化,具体化;分类讨论中注意分类的两条原则:分类标准要统一,而且分类要做到不重不漏;转化思想就是把“新知识”转化为“旧知识”,将“未知”转化为“已知”.举一反三:【变式】(2015•宁德)有理数a,b在数轴上对应点的位置如图所示,下列各式正确的是()A.a+b<0 B.a﹣b<0 C.a•b>0 D.>0【答案】B.类型四、规律探索6.将1,12-,13,14-,15,16-,…,按一定规律排列如下:请你写出第20行从左至右第10个数是________.【思路点拨】通过观察题目所给的图形、表格或一段语言叙述,然后归纳总结,寻找规律.【答案】1 200 -【解析】认真观察可知,第1行有1个数,第2行有2个数,第3行有3个数,……,所以第20行有20个数,从第1行到第20行共有1+2+3+…+20=210个数,所以第20行最后一个数的绝对值应是1210;又由表中可知,凡是分母是偶数的分数是负数,故第20行最后一个数是1210-,以此类推向前10个,则得到第20行第10个数是1 200 -.【总结升华】特例助思,探究规律,这类题主要是通过观察分析,从特殊到一般来总结发现规律,并将规律表示出来.。
苏教版七年级上册数学知识点整理

《有理数》知识点总结归纳正数和负数⒈正数和负数的概念负数:比0小的数正数:比0大的数0既不是正数,也不是负数注意:①字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a是正数;当a表示0时,-a仍是0。
(如果出判断题为:带正号的数是正数,带负号的数是负数,这种说法是错误的,例如+a,-a就不能做出简单判断)②正数有时也可以在前面加“+”,有时“+”省略不写。
所以省略“+”的正数的符号是正号。
2.具有相反意义的量若正数表示某种意义的量,则负数可以表示具有与该正数相反意义的量,比如:零上表示为:+;表示为:3.0表示的意义⑴0表示“ 没有”,如教室里有0个人,就是说教室里没有人;⑵0是正数和负数的分界线,0既不是正数,也不是负数。
如:有理数1.有理数的概念⑴正整数、0、负整数统称为整数(0和正整数统称为自然数)⑵正分数和负分数统称为分数⑶正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数。
理解:只有xx分数的数才是有理数。
①π是无限不循环小数,不能写成分数形式,不是有理数。
②有限小数和无限循环小数都可化成分数,都是有理数。
注意:引入负数以后,奇数和偶数的范围也扩大了,像-2,-4,-6,-8…也是偶数,-1,-3,-5…也是奇数。
2.有理数的分类⑴按有理数的意义分类⑵按正、负来分正整数正整数整数 0正有理数负整数正分数有理数有理数0(0不能忽视)正分数负整数分数负有理数负分数负分数总结:①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数数轴⒈数轴的概念规定了原点,正方向,单位xx的直线叫做数轴。
注意:⑴数轴是一条向两端无限延伸的直线;⑵原点、正方向、单位xx 是数轴的三要素,三者缺一不可;⑶同一数轴上的单位xx要统一;⑷数轴的三要素都是根据实际需要规定的。
2.数轴上的点与有理数的关系⑴所有的有理数都可以用数轴上的点来表示,正有理数可用原点右边的点表示,负有理数可用原点左边的点表示,0用原点表示。
七年级数学上册 第二章 有理数 2.6 有理数的乘法与除法 知识点解读 有理数的除法素材 苏科版(

七年级数学上册第二章有理数2.6 有理数的乘法与除法知识点解读有理数的除法素材(新版)苏科版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(七年级数学上册第二章有理数2.6 有理数的乘法与除法知识点解读有理数的除法素材(新版)苏科版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为七年级数学上册第二章有理数2.6有理数的乘法与除法知识点解读有理数的除法素材(新版)苏科版的全部内容。
知识点解读:有理数的除法一、关于有理数的除法知识点一:有理数的除法法则(掌握)有理数的除法法则:(1)法则1:除以一个数等于乘以这个数的倒数.用字母表示为:a ÷b =a ×1b(b ≠0). (2)法则2:两数相除,同号得正,异号得负,并把绝对值相除;0除以任何不等于0的数都得0 .温馨提示:对于除法的两个法则,在计算时可根据具体情况选用,一般在不能整除的情况下选用第二法则较简便;而在能整除的情况下则通常选用第一法则.例1 计算:(1)()()644-÷-; (2)37521446⎛⎫⎛⎫⎛⎫÷-÷-÷- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.析解:两个数的除法运算,应先确定商的符号,然后把被除数和除数的绝对值相除;多个有理数的除法运算,应先转化为乘法运算.解:(1)原式=()644+÷=16;(2)原式=14462375⎛⎫⎛⎫⎛⎫⨯-⨯-⨯- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭=14462375⎛⎫-⨯⨯⨯ ⎪⎝⎭=325-.知识点二:倒数的概念(理解)倒数的概念:与小学学过的互为倒数的概念一样,即乘积为1的两个数互为倒数,如:3和13,5-和15-,56-和65-分别互为倒数.一般的,当0a ≠时,a 与1a互为倒数.对倒数的概念的理解还应注意以下几点:(1)零没有倒数;(2)正数的倒数仍是正数,负数的倒数仍是负数;(3)倒数等于本身的数是1和—1;(4)求分数的倒数,只要把这个分数的分子、分母颠倒位置即可,求一个小数的倒数,要先把小数转化为分数后再求其倒数,求一个带分数的倒数,要先把带分数化为假分数再求.知识点三:有理数的混合运算(拓展)二、关于有理数的混合运算对于乘除混合运算问题,我们可以按从左到右的顺序依次进行计算,也可以直接把除法转化为乘法来计算,若有括号的应先做括号里面的.例2 计算(-81)÷214×49÷(-15).分析:将除法先统一成乘法,再利用约分来简化计算.解:(-81)÷214×49÷(-15)=81×49×49×115=1115.说明:有理数的乘除混合运算必须按从左到右的顺序依次进行计算,像(-81)÷214×49=-81÷94×49=-81,这样计算是错误的.以上就是本文的全部内容,可以编辑修改。
苏科版七年级上册七年级数学上册有理数章节复习与整理

典型例题:
例1:计算:
例2:计算:﹣ - + -( );
易错题型:
1.判断对错
①两个有理数的和为正数时,这两个数都是正数。()
②如果两个有理数的和比其中任何一个加数都大,那么这两个数都是正数。( )
③两个不等的有理数相加,和一定不等于0。()
A.1个B.2个C.3个D.4个
3.如果 都代表有理数,并且 ,那么( )
A. 都是0 B. 两个数至少有一个为0 C. 互为相反数D. 互为倒数
4. 代表有理数,那么 和 的大小关系是( )
A. 大于 B. 小于 C. 大于 或 小于 D. 不一定大于
拓展延伸:
1.如果 互为相反数,那么下面结论中不一定正确的是()
易错题型:
1.下列说法正确的是()
A.有理数就是正有理数和负有理数的统称B.最小的有理数是0
C.有理数都可以在数轴上找到一个表示它的点D.整数不能写成分数形式
2.温度上升 度后,又下降 度实际上就是()
A.上升1度B.上升5度C.下降1度D.下降5度
3.判断对错
①任何正整数都可以看做是由若干个“1”组成的。()
(3) × -(- )× +(- )÷ ;(4)-14-[1-(1-0.5× )×6
2.5有理数的乘法和除法
知识框架:
有理数乘法法则:两数相乘,同号________,异号________,并把________相乘;任何数与0相乘都得________。
多个非零的有理数相乘,积的符号是由________的个数决定的:当________的个数是奇数个时,积为________;当________的个数为偶数个时,积为________。
苏教版初一上册数学知识点整理

《有理数》知识点总结归纳正数和负数⒈正数和负数的概念负数:比0小的数正数:比0大的数0既不是正数,也不是负数注意:①字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a是正数;当a表示0时,-a仍是0。
(如果出判断题为:带正号的数是正数,带负号的数是负数,这种说法是错误的,例如+a,-a就不能做出简单判断)②正数有时也可以在前面加“+”,有时“+”省略不写。
所以省略“+”的正数的符号是正号。
2.具有相反意义的量若正数表示某种意义的量,则负数可以表示具有与该正数相反意义的量,比如:零上8℃表示为:+8℃;零下8℃表示为:-8℃3.0表示的意义⑴0表示“没有”,如教室里有0个人,就是说教室里没有人;⑵0是正数和负数的分界线,0既不是正数,也不是负数。
如:有理数1.有理数的概念⑴正整数、0、负整数统称为整数(0和正整数统称为自然数)⑵正分数和负分数统称为分数⑶正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数。
理解:只有能化成分数的数才是有理数。
①π是无限不循环小数,不能写成分数形式,不是有理数。
②有限小数和无限循环小数都可化成分数,都是有理数。
注意:引入负数以后,奇数和偶数的范围也扩大了,像-2,-4,-6,-8…也是偶数,-1,-3,-5…也是奇数。
2.有理数的分类⑴按有理数的意义分类⑵按正、负来分正整数正整数整数 0 正有理数负整数正分数有理数有理数 0 (0不能忽视)正分数负整数分数负有理数负分数负分数总结:①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数数轴⒈数轴的概念规定了原点,正方向,单位长度的直线叫做数轴。
注意:⑴数轴是一条向两端无限延伸的直线;⑵原点、正方向、单位长度是数轴的三要素,三者缺一不可;⑶同一数轴上的单位长度要统一;⑷数轴的三要素都是根据实际需要规定的。
2.数轴上的点与有理数的关系⑴所有的有理数都可以用数轴上的点来表示,正有理数可用原点右边的点表示,负有理数可用原点左边的点表示,0用原点表示。
苏教版七年级数学上册知识点(详细全面精华)

苏教版七年级数学上册知识点总结第一章有理数1.1 正数和负数⒈正数和负数的概念负数:比0小的数正数:比0大的数0既不是正数,也不是负数注意:①字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a是正数;当a表示0时,-a仍是0。
(如果出判断题为:带正号的数是正数,带负号的数是负数,这种说法是错误的,例如+a,-a就不能做出简单判断)②正数有时也可以在前面加“+”,有时“+”省略不写。
所以省略“+”的正数的符号是正号。
2.具有相反意义的量若正数表示某种意义的量,则负数可以表示具有与该正数相反意义的量,比如:零上8℃表示为:+8℃;零下8℃表示为:-8℃3.0表示的意义⑴0表示“没有”,如教室里有0个人,就是说教室里没有人;⑵0是正数和负数的分界线,0既不是正数,也不是负数。
(3)0表示一个确切的量。
如:0℃以及有些题目中的基准,比如以海平面为基准,则0米就表示海平面。
1.2 有理数1.有理数的概念⑴正整数、0、负整数统称为整数(0和正整数统称为自然数)⑵正分数和负分数统称为分数⑶正整数,0,负整数,正分数,负分数都可以写成分数的形式,这样的数称为有理数。
理解:只有能化成分数的数才是有理数。
①π是无限不循环小数,不能写成分数形式,不是有理数。
②有限小数和无限循环小数都可化成分数,都是有理数。
3,整数也能化成分数,也是有理数注意:引入负数以后,奇数和偶数的范围也扩大了,像-2,-4,-6,-8…也是偶数,-1,-3,-5…也是奇数。
2.有理数的分类⑴按有理数的意义分类⑵按正、负来分正整数正整数整数0 正有理数负整数正分数有理数有理数0(0不能忽视)正分数负整数分数负有理数负分数负分数总结:①正整数、0统称为非负整数(也叫自然数)②负整数、0统称为非正整数③正有理数、0统称为非负有理数④负有理数、0统称为非正有理数3.数轴⒈数轴的概念规定了原点,正方向,单位长度的直线叫做数轴。
注意:⑴数轴是一条向两端无限延伸的直线;⑵原点、正方向、单位长度是数轴的三要素,三者缺一不可;⑶同一数轴上的单位长度要统一;⑷数轴的三要素都是根据实际需要规定的。
苏教版七年级上册数学[有理数与无理数 知识点整理及重点题型梳理]
![苏教版七年级上册数学[有理数与无理数 知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/52e880547e21af45b307a8e9.png)
苏教版七年级上册数学重难点突破知识点梳理及重点题型巩固练习有理数与无理数知识讲解【学习目标】1、理解有理数的意义,知道无理数是客观存在的,了解无理数的概念.2、会判断一个数是有理数还是无理数.【要点梳理】要点一、有理数我们把能够写成分数形式mn(m,n是整数,n≠0)的数叫做有理数.要点诠释:(1)有限小数和循环小数都可以化为分数,他们都是有理数.(2)所有整数都可以写成分母是1的分数,因此可以理解为整数和分数统称为有理数.要点二、无理数1.定义:无限不循环小数叫做无理数.要点诠释:(1)无理数的特征:无理数的小数部分位数无限.无理数的小数部分不循环,不能表示成分数的形式.(2)目前常见的无理数有两种形式:①含π类.②看似循环而实质不循环的数,如:1.313113111…….2.有理数与无理数的区别(1)无理数是无限不循环小数,有理数是有限小数或无限循环小数.(2)任何一个有理数都可以化为分数的形式,而无理数则不能.要点三、循环小数化分数1.定义:如果一个无限小数的各数位上的数字,从小数部分的某一位起,按一定顺序不断重复出现,那么这样的小数叫做无限循环小数,简称循环小数,其中重复出现的一个或几个数字叫做它的一个循环节.2.纯循环小数从小数点后面第一位起就开始循环的小数,叫做纯循环小数.例如:0.666…、0.2..纯循环小数化为分数的方法是:分子是一个循环节的数字组成的数;分母的各位数字都是9,9的个数等于一个循环节的位数.例如310.393==,18970.18999937==.3.混循环小数如果小数点后面的开头几位不循环,到后面的某一位才开始循环,这样的小数叫做混循环小数.例如:0.12、0.3456456….混循环小数化为分数的方法是:分子是不循环部分和一个循环节的数字组成的数减去不循环部分的数字组成的数所得的差,分母就是按一个循环节的位数写几个9,再在后面按不循环部分的位数添写几个0组成的数.例如91891010.918990110-==,2392360.23990025-==,351353535100130.35135999009990037-===.要点诠释:(1)任何一个循环小数都可化为分数.(2)混循环小数化分数也可以先化为纯循环小数,然后再化为分数.【典型例题】类型一、有理数1.下列说法正确的是()A.整数就是正整数和负整数 B.分数包括正分数、负分数C.正有理数和负有理数统称有理数 D.无限小数叫做无理数【答案】B【解析】A选项整数包括正整数、负整数和0;C选项正有理数、负有理数和0统称有理数;D选项无限不循环小数才叫做无理数,所以选B.【总结升华】概念问题同学们往往忽略0的存在而模糊分类的界限,只有对定义达到真正的理解认识才不会出错.举一反三:【变式1】下列说法:①一个有理数不是整数就是分数;②有理数包括正有理数和负有理数;③分数可分为正分数和负分数;④存在最大的负整数;⑤不存在最小的正有理数.其中正确的个数是()A.2个 B.3个 C.4个 D.5个【答案】C【变式2】(2015•杭州模拟)是()A.整数 B.有限小数 C.无限循环小数 D.无限不循环小数【答案】C2.在实数,,0,,,﹣1.414,有理数有()A.1个 B.2个 C.3个 D.4个【思路点拨】根据有理数是有限小数或无限循环小数,可得答案.【答案】D【解析】解:,0,,﹣1.414,是有理数,【总结升华】本题考查了有理数,有理数是有限小数或无限循环小数.类型二、无理数3.(2016•盐城)下列实数中,是无理数的为()A.﹣4 B.0.101001 C. D.【思路点拨】无理数就是无限不循环小数.理解无理数的概念,一定要同时理解有理数的概念,有理数是整数与分数的统称.即有限小数和无限循环小数是有理数,而无限不循环小数是无理数.由此即可判定选择项.【答案】D【解析】解:A、﹣4是整数,是有理数,故本选项不符合题意;B、0.101001是小数,属于分数,故本选项不符合题意;C、是小数,属于分数,故本选项不符合题意;D、是无理数,正确;故选D.【总结升华】此题主要考查了无理数的定义,其中初中范围内学习的无理数有:π,2π等;开方开不尽的数;以及像0.1010010001…,等有这样规律的数.举一反三:【变式】以下各正方形的边长是无理数的是()A.面积为25的正方形;B.面积为16的正方形;C.面积为8的正方形;D.面积为1.44的正方形.【答案】C4.将下列各数填入相应的括号内3π,-2,1-2,3.020020002 0227,-(-2),2012,-0.23整数集合:{}分数集合:{}负有理数集合:{}无理数集合:{}【答案与解析】整数集合:{-2, 0,-(-2),2012}分数集合:{1-2,227,-0.23}负有理数集合:{-2,1-2,-0.23}无理数集合:{3π,3.020020002…,}【总结升华】本题考查了对有理数的有关概念的理解和应用,关键是能区分有关定义,注意:整数包括正整数、0、负整数;有理数包括正有理数、0、负有理数;无理数是指无限不循环小数.类型三、循环小数化分数5.把下列循环小数化分数【思路点拨】按循环小数化分数的规律方法化即可.【答案与解析】(1)(2),所以(3)(4)【总结升华】循环小数化分数时,整数部分不动,在掌握两种化简规律的基础上把小数部分进行相应的化简即可.举一反三:【变式】在6.4040…、3.333、9.505三个数中,是循环小数,把这个数化为分数可以写作.【答案】6.4040…;699。
2022年苏科版七年级上册数学有理数知识点及例题精讲

苏科版七年级上册数学第二章有理数部分知识点及例题精讲知识点:一.有理数:1.有理数旳分类: ① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数注意:①、0既不是正数,也不是负数;-a 不一定是负数,+a 也不一定是正数。
②、之因此所有分数都是有理数,由于所有不能化为整数和有限小数旳分数,都会化为无限循环小数。
③、无理数重要有如下几种体现形式:(1)带根号旳数,前提是不能转化为整数和有限小数;(2)无限不循环小数;(3)含π旳数。
④、自然数⇔ 0和正整数; a >0 ⇔ a 是正数; a <0 ⇔ a 是负数;a ≥0 ⇔ a 是正数或0 ⇔ a 是非负数; a ≤ 0 ⇔ a 是负数或0 ⇔ a 是非正数.2.数轴:数轴是规定了原点、正方向、单位长度旳一条直线。
(三者缺一不可)数轴上旳数是按照从左向右,由小到大旳顺序排列旳。
即:数轴上,右边旳点所示旳数总是不小于左边旳点所示旳数。
3.相反数:(1)只有符号不同旳两个数,我们说其中一种是另一种旳相反数;0旳相反数还是0;(2)注意: a-b+c 旳相反数是-a+b-c ;a-b 旳相反数是b-a ;a+b 旳相反数是-a-b ;(3)相反数旳和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.(4)相反数旳商为-1.(5)相反数旳绝对值相等.4.绝对值:(1)正数旳绝对值等于它自身,0旳绝对值是0,负数旳绝对值等于它旳相反数; 注意:绝对值旳意义是数轴上表达某数旳点离开原点旳距离;(2) 绝对值可表达为:⎪⎩⎪⎨⎧<-=>=)0a (a )0a (0)0a (a a 或 ⎩⎨⎧≤-≥=)0()0(a a a a a ; (3) 0a 1a a>⇔= ; 0a 1a a<⇔-=;(4) |a|是重要旳非负数,即|a|≥0;5.有理数比大小:(1)正数永远比0大,负数永远比0小;(2)正数不小于一切负数;(3)两个负数比较,绝对值大旳反而小;(4)数轴上旳两个数,右边旳数总比左边旳数大;(5)-1,-2,+1,+4,-0.5,以上数据表达与原则质量旳差, 绝对值越小,越接近原则。
2020--2021学年苏科版七年级上册第二章有理数知识点总结

第二章 有理数2.1 正数与负数1、正数概念:大于0的数 表示:可以在正数前面加“+” 负数概念:小于0的数 表示:可以在正数前面加“-”(负号) 0:既不是正数也不是负数,0是正数与负数的分界线。
2、整数与分数正整数、负整数、零统称为整数。
正分数、负分数统称为分数。
2.2 有理数与无理数1、有理数概念:能够写成分数形式m /n(m 、n 是整数,n ≠0)的数。
负整数负分数3、无理数概念:无限不循环小数叫做无理数。
表现形式:①无限不循环小数;②以某种特殊符号出现的数,如:π以及含有π的数;③今后要学到的由开方运算得到的某些数。
例如:面积为2的正方形的边长。
4、数轴概念:在数学中,可以用一条直线上的点表示数,这条直线叫做数轴,它满足以下要求:①在直线上任取一个点表示0这个点叫做原点;②通常规定直线上从原点向右为正方向,从原点向左为负方向;③选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1(向右1个单位长度),2(向右2个单位长度),3(向右3个单位长度),…;从原点向左,用类似方法依次表示-1(向左1个单位长度),-2(向左2个单位长度),-3(向左3个单位长度)…2.3绝对值与相反数1、绝对值几何意义:在数轴上,一个数到原点的距离叫做该数的绝对值。
表示数轴上表示a的点和表示b的点的距离。
|5|指在数轴上5与原点的距离,这个距离是5,所以5的绝对值是5。
同样,|-5|指在数轴上表示-5与原点的距离,这个距离是5,所以-5的绝对值也是5。
|-3+2|指数轴上-3和-2点的距离,这个式子值是1。
|3-2|同样也表示3和2点的距离。
代数意义:非负数(正数和0)的绝对值是它本身,负数的绝对值是它的相反数。
定义:指绝对值相等,正负号相反的两个数互为相反数。
0的相反数是0。
相反数的性质是他们的绝对值相同。
例如:-2与+2互为相反数。
用字母表示a与-a是相反数,0的相反数是0。
苏教版七年级上册数学[《有理数》全章复习与巩固(基础)知识点整理及重点题型梳理]
![苏教版七年级上册数学[《有理数》全章复习与巩固(基础)知识点整理及重点题型梳理]](https://img.taocdn.com/s3/m/127d121ee3bd960590c69ec3d5bbfd0a7956d595.png)
苏教版七年级上册数学[《有理数》全章复习与巩固(基础)知识点整理及重点题型梳理]本文介绍了苏教版七年级上册数学《有理数》全章复与巩固(基础)的研究目标和知识网络。
其中,研究目标包括理解有理数及其运算的意义,了解无理数的概念,掌握有理数的加、减、乘、除、乘方及混合运算并能解决简单的实际问题,以及会用科学记数法表示较大的数,能对含有较大数字的信息作出合理的解释和推断,发展数感。
知识网络包括有理数与无理数、数轴、相反数、绝对值和有理数的运算。
在有理数与无理数方面,本文介绍了有理数的分类和无理数的特征,以及常见的无理数形式。
在数轴方面,本文强调了一切有理数都可以用数轴上的点表示出来,但数轴上的点不都表示的是有理数。
在相反数方面,本文介绍了相反数的定义和性质,并强调了多重符号的化简。
在绝对值方面,本文介绍了代数意义和几何意义,并给出了绝对值的定义和性质。
在有理数的运算方面,本文介绍了有理数的加、减、乘、除、乘方及混合运算的法则,并给出了一些例题进行讲解。
需要注意的是,本文中有一些格式错误,需要进行修改。
同时,文章中存在一些明显有问题的段落,需要进行删除。
加法法则:当两个数同号时,它们相加的结果的符号与它们相同,绝对值为它们绝对值的和。
当两个数异号时,它们相加的结果的符号与绝对值较大的数相同,绝对值为两数绝对值的差。
一个数与0相加等于这个数本身。
减法法则:减去一个数等价于加上它的相反数,即a-b=a+(-b)。
乘法法则:当两个数同号时,它们相乘的结果为正数,绝对值为两数绝对值的积。
当两个数异号时,它们相乘的结果为负数,绝对值为两数绝对值的积。
任何数与0相乘等于0.除法法则:除以一个不等于0的数等价于乘上这个数的倒数,即a÷b=a·(1/b)。
乘方运算的符号法则:负数的奇次幂为负数,偶次幂为正数;正数的任何次幂都为正数,0的任何非零次幂都为0.有理数的混合运算顺序:先进行乘方运算,然后进行乘法和除法,最后进行加法和减法。
苏科版数学七年级上册知识点汇总--有理数

苏科版数学七年级上册知识点汇总
第二章有理数
知识点一、正数和负数
1、正数和负数的概念
正数:比0大的数负数:比0小的数注意:0既不是正数,也不是负数注意:①字母a可以表示任意数,当a表示正数时,-a是负数;当a表示负数时,-a 是正数;当a表示0时-a仍是0。
(如果出判断题为:带正号的数是正数,带负号的数是负数,这种说法是错误的,例如+a,一a就不能作出简单判断。
②正数有时也可以在前面加“+”,有时“+”省略不写。
所以省略“+”的正数的符号是正号。
2、具有相反意义的量
若正数表示某种意义的量,则负数可以表示具有与该正数相反意义的量,比如: 零上8℃表示为:+8℃;零下8℃表示为:-8℃
3、0表示的意义
(1)0表示“没有”,如教室里有0个人,就是说教室里没有人
(2)0是正数和负数的分界线,0既不是正数,也不是负数。
知识点二、整数与分数
注意:有限小数和循环小数可以写成分数的形式,如-4.1=-, -5%=- , 0.1。
=,所有有限小数与循环小数都可以看作分数。
知识点三、有理数
1、有理数:整数和分数统称为有理数。
注意:只有能化成分数的数才是有理数。
①π是无限不循环小数,不能写成分数形式,不是有理数。
②有限小数和无限循环小数都可化成分数,都是有理数。
注意:引入负数以后,奇数和偶数的范围也扩大了,像-2,-4,-6,-8…也是偶数,-1,-3,-5…也是奇数。
2、部分常用数学名词
名称描述名称描述
非负数0和正数非正数0和负数
非正整数0和负整数
非负整数
(自然数)
0 和正整数。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏教版 七年级数学《有理数》正数和负数负数:以前学过的0以外的数前面加上负号“-”的数叫做负数。
正数:以前学过的0以外的数叫做正数。
0既不是正数也不是负数,0是正数与负数的分界。
在同一个问题中,分别用正数和负数表示的量具有相反的意义 注:-a 不一定是负数,+a 也不一定是正数; 有理数:凡能写成)0,(≠p q p pq为整数且形式的数,都是有理数。
(1)正整数、0、负整数统称整数;正分数、负分数统称分数;整数和分数统称有理数.(2)有理数的分类:① ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎩⎨⎧负分数负整数负有理数零正分数正整数正有理数有理数 ② ⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧⎪⎩⎪⎨⎧负分数正分数分数负整数零正整数整数有理数 注意:1) 0不是正数,也不是负数;2) π不是有理数;无限不循环小数不是有理数。
无限循环小数是有理数; 3) 小数也归为分数。
4) 自然数⇔ 0和正整数;5) a >0 ⇔ a 是正数;a <0 ⇔ a 是负数; 6) a ≥0 ⇔ a 是正数或0 ⇔ a 是非负数; 7) a ≤ 0 ⇔ a 是负数或0 ⇔ a 是非正数.数轴:规定了原点、正方向、单位长度的直线叫做数轴。
数轴的作用:所有的有理数都可以用数轴上的点来表达。
注意事项:⑴数轴的原点、正方向、单位长度三要素,缺一不可。
⑵同一根数轴,单位长度不能改变。
一般地,设a 是一个正数,则数轴上表示a 的点在原点的右边,与原点的距离是a 个单位长度;表示数-a 的点在原点的左边,与原点的距离是a 个单位长度。
相反数:只有符号不同的两个数叫做相反数。
注意:(1)一般地,a 和-a 互为相反数,特别地,0的相反数还是0;(2) a-b+c 的相反数是-a+b-c ;a-b 的相反数是b-a ;a+b 的相反数是-a-b ; (3)相反数的和为0 ⇔ a+b=0 ⇔ a 、b 互为相反数.一般地,设a 是一个正数,数轴上与原点的距离是a 的点有两个,它们分别在原点左右,表示-a 和a ,我们说这两点关于原点对称 绝对值:一般地,数轴上表示数a 的点与原点的距离叫做数a 的绝对值。
(1)一个正数的绝对值是它的本身;一个负数的绝对值是它的相反数;0的绝对值是0。
注:绝对值的意义是数轴上表示某数的点到原点的距离。
(2) 绝对值可表示为:⎪⎩⎪⎨⎧<-=>=)0()0(0)0(a a a a a a 或⎩⎨⎧<-≥=)0()0(a a a a a ;(3)绝对值的问题经常分类讨论;01>⇔=a aa ;a 1aa <⇔-=;(4) |a|是重要的非负数,即|a|≥0;注意:|a|·|b|=|a ·b|,baba =. (5)有理数比大小:①正数大于0,0大于负数,正数大于一切负数和0。
②两个负数,绝对值大的反而小。
③正数的绝对值越大,这个数越大; ④大数-小数 > 0,小数-大数 < 0;⑤在数轴上表示有理数,它们从左到右的顺序,就是从小到大的顺序,所以左边的数永远小于右边的数。
即数轴上的两个数,右边的数总比左边的数大补充:倒数:乘积为1的两个数互为倒数; 注(1)0没有倒数;若 a ≠0,那么a 的倒数是a1; (2)倒数是本身的数是±1;(3)若ab=1⇔ a 、b 互为倒数;若ab=-1⇔ a 、b 互为负倒数.有理数加法法则:(1)同号两数相加,取相同的符号,并把绝对值相加;(2)绝对值不相等的饿异号两数相加,取绝对值较大的加数的符号,并用 较大的绝对值减去较小的绝对值。
互为相反数的两个数相加得0。
(3)一个数与0相加,仍得这个数.有理数加法的运算律:(1)加法的交换律:两个数相加,交换加数的位置,和不变。
a+b=b+a(2)加法的结合律:三个数相加,先把前面两个数相加,或者先把后两个数相加,和不变。
(a+b )+c=a+(b+c ).补充:去括号法则:(1)括号前是“+”,把括号和括号前的“+”去掉,括号里各项都不改 变符号。
(2)括号前是“-”,把括号和括号前的“-”去掉,括号里各项都改变符号。
(3)括号外的因数是正数,去括号后式子各项的符号与原括号内式子相应各项的符号相同;括号外的因数是负数,去括号后式子各项的符号与原括号内式子相应各项的符号相反。
有理数减法法则:(有理数的减法可以转化为加法来进行) 减去一个数,等于加上这个数的相反数;即a-b=a+(-b ).有理数乘法法则:(1)两数相乘,同号为正,异号为负,并把绝对值相乘; (2)任何数同零相乘都得零;(3)几个数相乘,有一个因式为零,积为零;几个不是0的数相乘,负因数的个数是偶数时,积是正数;负因数的个数是奇数时,积是负数。
(4)乘积是1的两个数互为倒数。
有理数乘法的运算律:(1)乘法的交换律:两个数相乘,交换因数的位置,积相等。
ab =ba(2)乘法的结合律:三个数相乘,先把前两个数相乘,或者先把后两个数相乘,积相等。
(ab )c =a (bc )(3)乘法的分配律:一个数同两个数的和相乘,等于把这个数分别同这两个数相乘,再把积相加。
a (b +c )=ab +ac 有理数除法法则:除以一个不等于0的数,等于乘这个数的倒数。
a ÷b =a ·b1(b ≠0) 两数相除,同号得正,异号得负,并把绝对值相除。
0除以任何一个不等于0的数,都得0。
因为有理数的除法可以化为乘法,所以可以利用乘法的运算性质简化运算。
乘除混合运算往往 先将除法化成乘法,然后确定积的符号,最后求出结果。
注:零不能做除数,无意义即0a.有理数乘方的法则:求n 个相同因数的积的运算,叫做乘方,乘方的结果叫做幂。
在a n 中,a 叫做底数,叫做指数,当a n 看作a 的n 次方的结果时,也可以读作a 的n 次幂。
(1)负数的奇次幂是负数,负数的偶次幂是正数。
(2)正数的任何次幂都是正数,0的任何正整数次幂都是0。
(3)负数的奇次幂是负数;负数的偶次幂是正数;注意:当n 为正奇数时: (-a)n =-a n 或(a -b)n =-(b-a)n , 当n 为正偶数时: (-a)n =a n 或(a-b)n =(b-a)n .有理数混合运算的运算顺序: ⑴先乘方,再乘除,最后加减; ⑵同极运算,从左到右进行;⑶如有括号,先做括号内的运算,按小括号、中括号、大括号依次进行 (4)a 2是重要的非负数,即a 2≥0;若a 2+|b|=0 ⇔ a=0,b=0;(5)据规律 ⇒⎪⎪⎭⎪⎪⎬⎫⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅===100101101.01.0222底数的小数点移动一位,平方数的小数点移动二位.科学记数法:把一个大于10的数记成a ×10n 的形式,其中a 是整数数位只有一位的数,这种记数法叫科学记数法.注:用科学记数法表示一个n 位整数,其中10的指数是n -1。
近似数和有效数字接近实际数目,但与实际数目还有差别的数叫做近似数。
精确度:一个近似数四舍五入到哪一位,就说精确到哪一位。
从一个数的左边第一个非0 数字起,到末位数字止,所有数字都是这个数的有效数字。
对于用科学记数法表示的数a ×10n ,规定它的有效数字就是a 中的有效数字。
补充:(1)混合运算法则:先乘方,后乘除,最后加减; 注意:怎样算简单,怎样算准确,是数学计算的最重要的原则.(2)特殊值法:是用符合题目要求的数代入,并验证题设成立而进行猜想的一种方法,但不能用于证明.知识点1.负数代表相反意义的量例:(1)下列有正数和负数表示相反意义的量,其中正确的是( ) A. 一天凌晨的气温是—50C ,中午比凌晨上升100C ,所以中午的气温是+100C B. 如果生产成本增加12%,记作+12%,那么—12%表示生产成本降低12% C. 如果+米表示比海平面高米,那么—6米表示比海平面低—6米D. 如果收入增加10元记作+10元,那么—8表示支出减少8元(2)某粮店出售三种品牌的面粉,袋上分别标有质量为(50±)kg 、(50±)kg 、(50±)kg 的字样,从中任意拿出两袋,它们的质量最多相 差 . 知识点2.有理数的定义例:把下列各数填在相应的大括号内-7,,12,,0,3π,+29,…,,… 非负数集合{ }; 整数集合{ }; 负分数集合{ }; 有理数集合{ }。
知识点3.数轴与相反数1.(1)数轴上到-2点的距离是3的点是(2)在数轴上表示数a 的点到原点的距离为3,则._________3=-a 的相反数是 ,3-π的相反数是 与b 互为相反数,c 与d 互为倒数,a+b -cd=4.比较大小45-89- 5.(1) 有理数a 对应点在数轴上的位置如下图所示,则a ,-a ,1的大小关系是。
(2)有理数a 、b 在数轴上的对应的位置如图所示: 则( )A .a + b <0B .a + b >0;C .a -b = 0D .a -b >0 0-11ab知识点4.绝对值1.若∣a ∣=-a ,则a ,若∣a ∣=a ,则a若a 为有理数,且1,a b c a b c ++==1,则a 0,若a ∠0,则1,a b c a b c++== 2. ∣3-π∣=若用A 、B 、C 分别表示有理数a ,b ,c ,O 为原点,如下图所示:化简= 。
3.绝对值为2的数是 ,绝对值小于6的所有整数是4.若∣x ∣=3,∣-y ∣=3,则x+y=5.若∣a ∣=3,∣b ∣=5, 且ab>0,则∣a+b ∣=若|X|=2,则X=______,若|X —3|=0,则X=______,|X —3|=6,则X=______ 若∣a ∣=∣b ∣,则a 与b ,即 。
6. ∣a+2∣+∣b-3∣=0,a+b= 知识点5.加减运算1.加减混合运算:先去括号,再把同号的相加,最后异号两数相加例:38+(-22)+(+62)+(-78) (-8)+(-10)+2+(-1)+(-41)-(-)+21 (+)-(-4)+(-)-(+4)知识点6:有理数乘除运算法则乘法运算法则a :只要有一个因数为0,则积为0。
b:几个不为零的数相乘,积的符号由负数的个数决定,当负数的个数为奇数,则积为负,当负数的个||||||2a c b c b a c ---+++数为偶数,则积为正。
例1、计算:(1)()()3275-⨯-⨯-⨯(2)5411511654⎛⎫⎛⎫⨯-⨯⨯-⎪ ⎪⎝⎭⎝⎭除法是乘法的逆运算1、有理数乘法法则:两数相乘,同号得正,异号得负,并把绝对值相乘.任何数与零相乘都得零。
2、有理数除法法则(1):除以一个不等于0的数等于乘以这个数的倒数;0除以任何一个不等于0的数都等于0 有理数除法法则(2):两数相除,同号得正,异号得负,并把绝对值相除。
