Excel指数平滑法案例分析
实验三 用EXCEL进行指数分析

实验三用EXCEL进行指数分析实验目的:用EXCEL进行指数分析实验步骤:指数分析法是研究社会经济现象数量变动情况的一种统计分析法。
指数有总指数与平均指数之分,在这一节我们介绍如何用Excel进行指数分析与因素分析。
一、用Excel计算总指数【例1】:图中是某企业甲、乙、丙三种产品的生产情况,以基期价格p作为同度量因素,计算生产量指数。
如图1图1用EXCEL计算总指数资料及结果计算步骤:第一步:计算各个p0q0:在G2中输入“=C2*D2”,并用鼠标拖曳将公式复制到G2:G4区域。
第二步:计算各个p0*q1:有H2中输入“=C2*F2”,并用鼠标拖曳将公式复制到H2:H4区域。
第三步:计算Σp0q0和Σp0q1:选定G2:G4区域,单击工具栏上的“Σ”按钮,在G5出现该列的求和值。
选定H2:H4区域,单击工具栏上的“Σ”按钮,在H5出现该列的求和值。
第四步:计算生产量综合指数Iq=Σp0q1/Σp0q0:在C6中输入“=H5/G5”便可得到生产量综合指数注意:在输入公式的时候,不要忘记等号,否则就不会出现数值。
二、用Excel计算平均指数现以生产量平均指数为例,说明加权算术平均法的计算方法。
【例2】:图中的A1:A4区域内是某企业生产情况的统计资料,我们要以基期总成本为同度量因素,计算生产量平均指数。
如图2图2用EXCEL计算平均指数资料及结果计算步骤:第一步:计算个体指数k=q1/q0:在F2中输入“=D2/C2”。
并用鼠标拖曳将公式复制到F2:F4区域。
第二步:计算k*p0q0并求和。
在G2中输入“=F2*E2”并用鼠标拖曳将公式复制到G2:G4区域。
选定G2:G4区域,单击工具栏上的:“Σ”按钮,在G5列出现该列的求和值。
第三步:计算生产量平均指数:在C7中输入“=G5/E5”即得到所求的值。
三、用Excel进行因素分析【例3】:我们还用上面的例子,有关资料如图3图3用EXCEL进行因素分析资料及结果进行因素分析的计算步骤如下:第一步:计算各个p0*q0和∑p0q0:在G2中输入“C2*D2”,并用鼠标拖曳将公式复制到G2:G4区域。
Excel指数平滑法案例分析

Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法设时间序列为,则一次指数平滑公式为:式中为第 t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:由于0<<1,当→∞时,→0,于是上述公式变为:由此可见实际上是的加权平均。
加权系数分别为,,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
用上述平滑值进行预测,就是一次指数平滑法。
其预测模型为:即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法当时间序列没有明显的趋势变动时,使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时,用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此,也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为,则二次指数平滑的计算公式为:若时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直线趋势变化,则与趋势移动平均类似,可用如下的直线趋势模型来预测。
式中t为当前时期数;T为由当前时期数t到预测期的时期数;为第t+T期的预测值;为截距,为斜率,其计算公式为:③三次指数平滑法若时间序列的变动呈现出二次曲线趋势,则需要用三次指数平滑法。
Excel变量与三次指数平滑模拟预测方法

#在 XB 单元格中输入 (1""$: M 4;< ""8$:R4GB<:RKB,&B8 ) # 选 取 XB 单 元 格 # 拖 动 填 充 柄 至 X:@ 单元格 $
则完成了三次指数平滑参数 Y’%-’%T’ 计算公式的输入 ’ ! 下转第 ;:Z 页 "
FGK1
NIJK1 ; !OJKLO ’
! 指标含义是否可比 $ 如国民收入
易与国民总收入混淆 $ 前者是五大物质 生产部门的净产值之和 # 是改革开放前 反映经济总量的主要指标 ’ 后者即过去 所称的国民生产总值 $ 两者指标含义 ( 口 径 ( 及计算方法是完全不同的 $
’ 数据是否经过修正 $ 统计既然是
对社会经济发展变化的一种事后反映# 随着基础数据的不断完善 # 或者计算方 法和分类标准发生了变化 # 就有必要对 一些数据进行修正 # 不仅是当年和上年 数据 # 而且要对历史数据进行调整 # 这是 统计上的国际惯例 $ 如美国季度国内生 产总值及其增长率 # 一般季后 #( 天公布 预 测 数 据 # 季 后 *( 天 公 布 初 步 统 计 数 据 # 季后 E( 天公布初修正统计数据 $ 所 以利用统计资料时 # 必须以最新修正的 数据为准 $ ! 作者单位 : 浙江工商大学统计学院 "
! 在 运 算 表 !44 " 中 # 选 取 ’()’/2 区
域 # 并单击复制 ’
! 作者单位 : 江苏常熟理工学院 "
! 责任编辑 : 亦 民"
!"#
统计与决策
万方数据
Excel变量与三次指数平滑模拟预测方法
作者: 作者单位: 刊名: 英文刊名: 年,卷(期): 引用次数: 丁沧海 江苏常熟理工学院 统计与决策 STATISTICS AND DECISION 2005,(11) 1次
利用Excel进行指数平滑分析

利用Excel进行指数平滑分析与预测(2)【例】连续10年的灌溉面积。
第一步,录入数据(图1)。
图1 原始数据第二步,选项设置。
沿着主菜单的“工具(T)→数据分析(D)”路径打开“数据分析”选项框,选中“指数平滑”(图2)。
图2 数据分析选项框与“指数平滑”的位置确定以后,弹出移动平均对话框(图3),然后按如下步骤进行设置:⒈将光标置入“输入区域”对应的空白栏,然后用鼠标从B1到B11选中全部时间序列连同标志;⒉选中“标志”(位于第一行);⒊在“阻尼系数”对应的空白栏中键入“0.9”,表示指数平滑系数为0.1(即取α=0.1。
注意:指数平滑系数与阻尼系数的关系是“平滑系数+阻尼系数=1”);⒋将光标置入“输出区域”对应的空白栏,选中从C2到C11的单元格,作为计算结果的输出位置;⒌选中“图表输出”和“标准误差”,这样会自动生成移动平均坐标图和标准误差值。
注意:如果“输入区域”对应的空白栏设置为“$B$2:$B$11”,即不包括数据标志项,则不要选中“标志”(图4)。
图3 指数平滑选项框(包括数据标志)图3 指数平滑选项框(不包括数据标志)第三步,输出结果。
完成上述设置以后,确定,即可得到计算结果,包括指数平滑结果及其标准误差(图5),以及指数平滑曲线图(图6)。
图5 移动平均结果:平滑系数为α=0.1图6 阻尼系数为0.9(平滑系数为0.1)的移动平均预测曲线(水红色)如果不借助E x cel 的“数据分析”工具,指数平滑计算也是非常简单的,有关计算方法在“利用Exc el 进行指数平滑分析与预测(1)”中已经详细说明,不赘述,下面只介绍标准误差的计算方法。
与移动平均法的标准误差计算类似,我们有两种途径。
计算方法之一:利用平方根命令sqr t 和计算两个数组相对数值误差的平方和命令sumxm y 2。
指数平滑实训操作过程

第十章综合实训
目标:
1.用EXCEL 表进行一次指数平滑预测。
内容与要求:
1. 按班级每1人为一组,用下列资料,用EXCEL 进行一次指数平滑预测。
平滑系数α=0.5,=∧
1y 8。
ABC 公司销售额资料表
形成过程截图和最终成果截图上交。
成果与检测:
“实训过程考核”(按过程截图)与 “实训结果考核”(按最终成果截图)结合。
(参考答案
1. 将数据输入EXCEL 表,点击工具,并点加载宏,选分析工具库,并点确定(如参考图10-1EXCEL 截图1所示)。
参考图10-1EXCEL截图1
2点击工具,并点击数据分析,选指数平滑(如参考图10-2EXCEL截图2所示)
参考图10-2EXCEL截图2
再确定
3输入区域选B2:B14,阻尼系数选0.5,输出区域选C2:C14,并勾选图表输出(如参考图10-3EXCEL截图3所示)
参考图10-3EXCEL截图3
4点击确定,可得预测值(如参考图10-4EXCEL截图4所示)
参考图10-4EXCEL截图4)。
指数平滑法 实例

指数平滑法实例?
答:指数平滑法是一种常用的时间序列预测方法,可以用于预测未来的销售、需求等。
以下是两个指数平滑法的应用实例:
实例一:某软件公司的销售预测
某软件公司A给出了2000-2005年的历史销售资料。
根据经验判断法,A公司2000-2005年销售额时间序列波动很大,长期趋势变化幅度较大,呈现明显且迅速的上升趋势,宜选择较大的α值,可在0.5-0.8间选值,以使预测模型灵敏度高些。
经过第一次指数平滑后,数列呈现直线趋势,故选用二次指数平滑法即可。
试算结果后,得到了预测模型,可以用于预测2006年的销售额。
实例二:某地财政收入预测
已知某地1983年至1993年的财政收入数据,试用指数平滑法求解趋势直线方程并预测1996年的财政收入。
通过分析工具和计算,得到了趋势线预测模型,从而可以计算出1996年的财政收入预测值。
以上两个实例仅供参考,指数平滑法的应用非常广泛,可以根据不同的数据和需求进行灵活应用。
指数平滑法应用案例

Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法设时间序列为,则一次指数平滑公式为:式中为第 t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:由于0<<1,当→∞时,→0,于是上述公式变为:由此可见实际上是的加权平均。
加权系数分别为,,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
用上述平滑值进行预测,就是一次指数平滑法。
其预测模型为:即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法当时间序列没有明显的趋势变动时,使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时,用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此,也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为,则二次指数平滑的计算公式为:若时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直线趋势变化,则与趋势移动平均类似,可用如下的直线趋势模型来预测。
式中t为当前时期数;T为由当前时期数t到预测期的时期数;为第t+T期的预测值;为截距,为斜率,其计算公式为:③三次指数平滑法若时间序列的变动呈现出二次曲线趋势,则需要用三次指数平滑法。
使用excel计算指数平滑和移动平均
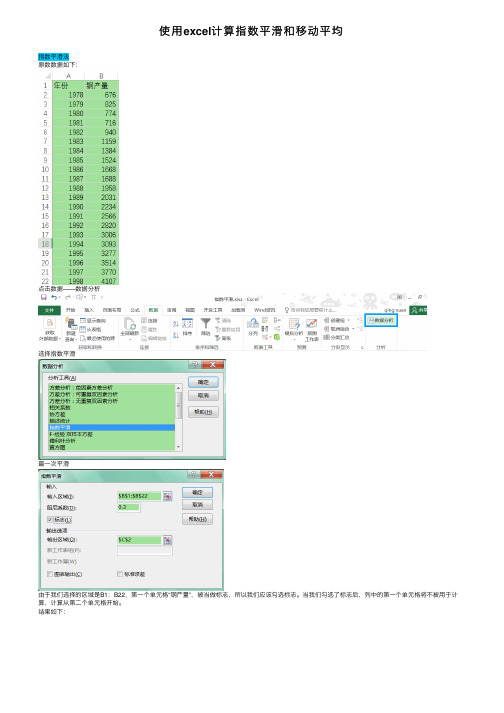
使⽤excel计算指数平滑和移动平均
指数平滑法
原数数据如下:
点击数据——数据分析
选择指数平滑
最⼀次平滑
由于我们选择的区域是B1:B22,第⼀个单元格“钢产量”,被当做标志,所以我们应该勾选标志。
当我们勾选了标志后,列中的第⼀个单元格将不被⽤于计算,计算从第⼆个单元格开始。
结果如下:
做⼆次平滑
这⾥,我们不再采⽤标志,所以数据区间选择在C3:C22
对⽐⼀下
阻尼系数=0.3
阻尼系数=0.05
阻尼系数=0.9
画在⼀张图上对⽐下,可见阻尼系数越⼤,曲线越平。
移动平均(⼀阶和⼆阶)
同理可以使⽤excel计算得到如下表:
相关数据⽂件:附件列表。
EXCEL中数据分析-平滑分析案例

一、平滑分析1・概念:半滑分析也称指数平滑法,是生产预测中常用的一种方法,被称为时间 序列分析预测法,即通过计算指数平滑值,配合一定的时间序列预测模型对现象 的未來进行预测。
2 •案例:EXCEL 表中,有一张表是“某厂近21年的钢产量”,利用EXCEL 平滑分 析来预测第22年的钢产量.步骤一:数据一数据分析一指数平滑步骤二:输入区域(一定要是单行或者单列)步骤三:输入阻尼系数,阻尼系数分四种悄况⑴当时间序列不长,且波动幅度很小,应选较小的Q 值,一般可在0. 05〜0. 20之间取值:(2) 当时间序列不长且有波动,町选稍人的a 值,常在0.1〜0.4之间取值: (3) 当时间序列较长,有波动但仍呈现明显迅速卜.升或卜降趙势,a 应在0. 6〜0. 8间选值;(4)当时间序列数据无波动,而是呈现明显的上升或卜•降趙势时,a 应取O.6~1Z 间。
步骤四:判断“标志”是否需要打勾,即观察选中区域有没有标题 步骤五:选择输出区域步骤六:根据需要勾选“图表输入”利“标准误差”步骤七:根据第一次平滑分析的结果(如下图),代入一次平滑分析的预测公式 來求金额第22年的钢产量。
一次平滑的预测公式:y=报后-年的预测值+ax 最后一年产值和预测值的差额在这里 y = 3665.471 + 0.3 x (4107 - 3665.471) = 3797.93A B1年忙 银1产m 21996 676 #N/A 3199T 825 676 41998 774 780・ 3 5199^ 7丄G 7715. SO G2000 日4。
733. 967 72001 1159 8T8・1901 52QQZ 1354i 107 4:. 75T 92003 1521 1291. 227 1O2004 1 &68 1454. 168 1 12005 1&88 1603・ 85 122006 1958 1662. 755 1320 OT 2031 lSSCj. 427 14, 2OOS3 2234 L£«B2. 328 152OOS 2SB6 21 58. 55B 丄& 20102820 24=43. 76U 173QQ6 Z7OT ・ 13 182012 3093 2&16. 339 192013 327 7 3040. 002 202014 351 4 3205. 901 212015 3770 3421・ 57 22 2016 4=107 3^65. 471. 指数平滑 +买冈I 12 5 4 5 6 7 8 9 101112131415161718192021根据经验判定,该值不太介理(注总,最后一年产值减去预测值可正可负)步骤八:以C3:C22为输入区域,重复上面七个步骤,做第二次平滑分析,结果 如下图步骤九:二次平滑分析后代入二次平滑分析的公式,來求解预测值y=(2X 最后一年1次测值一最后一年2次测值)+亍三x (最后一年1次的预测值-最后一年2次的预测值)3 y = (2 X 3665.471 - 3336.006) +yX (3665.471 一 3336.006) = 4136.1该值比较合理,符合大致规律 A B C D L年尙 枢产壘 21996 676 O/A 31997 825 676 41998 77^ 730. 3 676 51999 716 775. 89 749. 01 62000 940 733. 967 767.826 72001 1159 878. 1901 744.1247 82002 1384 1074. 757 837.9705 92003 1524 1291. 227 1003.721 102004 1668 1454. L68 1204.975 112005 1688 1603. B5 1379. 41 122006 1958 1662. 755 L536.518 132007 2031 1869. 427 1624.884 142008 2234 1982. 528 L79G. 064 152009 2566 2158. 558 1926.589 162010 2820 2443. 768 2088.967 172011 3006 2707. 13 2337.328 182012 3093 2915・ 339 2by6 •傑 192013 3277 3040. 002 2820.294 202014 3514 3205. 901 2974.089 20153770 3421.57 3136.357 22 2016 4107 3665. 471. 3336.00623。
指数平滑法
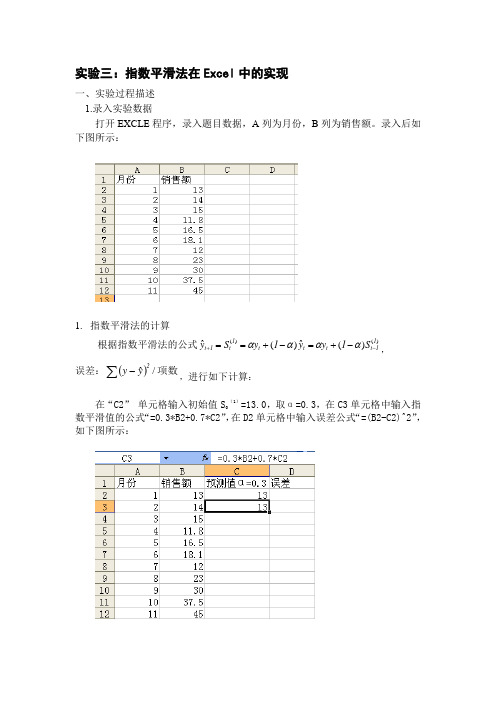
实验三:指数平滑法在Excel 中的实现一、实验过程描述1.录入实验数据打开EXCLE 程序,录入题目数据,A 列为月份,B 列为销售额。
录入后如下图所示:1. 指数平滑法的计算根据指数平滑法的公式)()()(ˆ)(ˆ11t t t t 1t 1t S 1y y 1y S y -+-+=-+==αααα,误差:()项数/ˆ2yy ∑-,进行如下计算:在“C2”单元格输入初始值S 0(1)=13.0,取α=0.3,在C3单元格中输入指数平滑值的公式“=0.3*B2+0.7*C2”,在D2单元格中输入误差公式“=(B2-C2)^2”,如下图所示:将C、D两列向下拉,进行复制,得到如下表格:按照上面的方法,继续求出当α=0.5、α=0.8时的预测值及误差。
其中初始值13.0依次写入E2,G2单元格中。
E列存放α=0.5时的预测值,G列存放α=0.8时的预测值,E2中输入“=0.5*B2+0.5*E2”,G2中输入“=0.8*B2+0.2*G2”,F、H两列存放误差,F1单元格中输入“=(B2-C2)^2”G1中输入“”,并下拉复制各列,结果如下图所示:3.选取合适的α取值在D13、F13、H13单元格中依次计算出不同的α取值情况的平均误差。
在D13中输入“=A VERAGE(D2:D12)”、在F13中输入“=AVERAGE(F2:F12)”、H13中输入“=AVERAGE(H2:H12)”,结果如下图所示,从图中可以看出,当α=0.8时的平均误差最小。
4.绘制图形点击工具菜单中的插入——图表,选择折线图,选择B、C、E、G列作为表的内容,如下所示:单击下一步,以新的工作表插入,得到图形如下:5. 求出十二月的销售额预测值将预测值继续进行向下复制,即可求出第十二各月的预测值,如下图所示:当α=0.3时的预测值为31.39869589、α=0.5时的预测值为37.95097656、α=0.8时的预测值为43.12819702,因为当α=0.8时的平均误差最小,所以选取预测值为43.12819702。
利用Excel进行指数平滑分析与预测

SSE
1500
1400
1300
1200 SSE
1100
1000
900
800
0
0.2
0.4
0.6
0.8
1
图 11 SSE 随平滑系数变化的曲线
MSE
160
150 140
130
MSE
120 110
100
0
0.2
0.4
0.6
0.8
1
图 12 MSE 随平滑系数变化的曲线
第六步�绘制指数平滑曲线。
5
将 α=0.3 时的平滑结果与原数据按顺序排列�图 13��然后利用 Excel 的绘图功能不难绘 制指数平滑曲线图——将原始数据曲线与指数平滑曲线画在统一坐标系�便于比较指数平滑的
6
S t�� � �S t� � (1 � � )S t���1 显然�我们的计算的起点是从 S1’开始的�亦即从 1972 年开始的�否则会有 t-1=-1 的现象�而 我们的时间序号不取负值。
根据习惯方法�取 S0’’=S1’=x1=28.6�平滑系数不妨仍然从 0 开始�以 C3 单元格表示新的 平滑系数 α�0 所在�在 E3 单元格输入 28.6 表示 S0’’�在 E4 单元格中建立公式“= $C$3*D3+ (1-$C$3)*E3”�参见图 15。注意这里是 D3 表示 S1’�E3 表示 S0’’�后面的三次指数平滑要考 虑这个问题��回车�得到 S1’’ =28.6�下拉至 1982 年�给出 α�0 时全部的二次平滑结果� 1971 年对应的年份空着�取 28.6。复制�保存�可以只保存 1971�1980 年间的结果�。
y10�T � 42 .281 � 1.421T
Excel指数平滑法案例分析

Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法设时间序列为,则一次指数平滑公式为:式中为第 t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:由于0<<1,当→∞时,→0,于是上述公式变为:由此可见实际上是的加权平均。
加权系数分别为,,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
用上述平滑值进行预测,就是一次指数平滑法。
其预测模型为:即以第t周期的一次指数平滑值作为第t+1期的预测值.②二次指数平滑法当时间序列没有明显的趋势变动时,使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时,用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此,也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型。
故称为二次指数平滑法.设一次指数平滑为,则二次指数平滑的计算公式为:若时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直线趋势变化,则与趋势移动平均类似,可用如下的直线趋势模型来预测.式中t为当前时期数;T为由当前时期数t到预测期的时期数;为第t+T期的预测值;为截距,为斜率,其计算公式为:③三次指数平滑法若时间序列的变动呈现出二次曲线趋势,则需要用三次指数平滑法。
一次指数平滑法(借鉴内容)

一次指数平滑法一次指数平滑法是指以最后的一个第一次指数平滑。
如果为了使指数平滑值敏感地反映最新观察值的变化,应取较大阿尔法值,如果所求指数平滑值是用来代表该时间序列的长期趋势值,则应取较小阿尔法值。
同时,对于市场预测来说,还应根据中长期趋势变动和季节性变动情况的不同而取不同的阿尔法值,一般来说,应按以下情况处理:1.如果观察值的长期趋势变动接近稳定的常数,应取居中阿尔法值(一般取0.6—0.4)使观察值在指数平滑中具有大小接近的权数;2.如果观察值呈现明显的季节性变动时,则宜取较大的阿尔法值(一般取0.6一0.9),使近期观察在指数平滑值中具有较大作用,从而使近期观察值能迅速反映在未来的预测值中;3.如果观察值的长期趋势变动较缓慢,则宜取较小的e值(一般取0.1—0.4),使远期观察值的特征也能反映在指数平滑值中。
在确定预测值时,还应加以修正,在指数平滑值S,的基础上再加一个趋势值b,因而,原来指数平滑公式也应加一个b。
8.1.2 指数平滑法移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法设时间序列为,则一次指数平滑公式为:式中为第t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:由于0<<1,当→∞时,→0,于是上述公式变为:由此可见实际上是的加权平均。
加权系数分别为,,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
实验6-EXCEL时间序列分析-指数平滑

实验6-EXCEL时间序列分析-指数平滑
EXCEL时间序列分析-指数平滑法
指数平滑法是从移动平均法发展⽽来的,是⼀种改良的加权平均法,在不舍弃历史数据的前提下,对离预测期较近的历史数据给予较⼤的权数,权数由近到远按指数规律递减。
指数平滑法根据本期的实际值和预测值,并借助于平滑系数α进⾏加权平均计算,预测下⼀期的值。
它是对时间序列数据给予加权平滑,从⽽获得其变化规律与趋势。
它是对时间序列数据给予加权平滑,从⽽获得其变化规律与趋势。
我们还是以"企业季度数据"为例,利⽤Excel分析⼯具库---"指数平滑"分析⼯具预测2012年第3季度的销售额会是多少。
【数据】-【分析】-【数据分析】-【指数平滑】
若时间序列数据的波动不⼤,⽐较平稳,则阻尼系数应取⼩⼀些,
如0.1~0.3。
若时间序列数据具有迅速且明显的变动倾向,则阻尼系数应取⼤⼀些,如0.6~0.9 。
图1-1 ⼀次指数平滑结果
跟移动平均法⼀样,公式下拉就可以得到预测结果。
根据这个图,可以知道2012年第3季度的销售额预测值为15581。
现在分别把阻尼系数调整为0.3/0.6及0.9,⽐较不同值下的预测标准误差,看看哪个预测标准误差较⼩。
图1-2 ⼀次指数平滑法
多个阻尼系数的计算结果从上图分析可以得出,在平滑系数=0.9,阻尼系数为0.1时,预测误差最⼩。
Excel在财务预测中的应用

Excel在财务预测中的应用4。
4 利用数据分析工具解决预测问题(1)除了利用前面介绍的几个预测函数进行回归预测分析外,我们还可以使用Excel 的数据分析工具库提供的统计观测分析工具来解决回归预测问题。
Excel的数据分析工具库提供了3种统计观测分析工具,它们是移动平均法、指数平滑法和回归分析法.下面结合实例来说明这3种方法的具体应用。
4.4。
1 移动平均法【例4-5】某企业2000年12个月的销售额如图4-4所示,分别按3期、5期和7期移动平均所做的预测分析如图4-4中的C4︰E13区域所示。
以3期移动平均为例为例,具体计算步骤如下:图4—4 一次移动平均法实例(1)从【工具】菜单中选中【数据分析】命令,则弹出【数据分析】对话框,如图4-5所示。
图4—5 【数据分析】对话框(2)在【数据分析】对话框中的【分析工具】框中选中【移动平均】选项,则弹出【移动平均】对话框,如图4-6所示.图4-6 【移动平均】对话框(3)在【移动平均】对话框中,【输入区域】框中输入“$B$2︰$B$13”,【间隔】框中输入“3”,【输出区域】框中输入“$C$2”,最后选中【图表输出】选项;(4)单击【确定】按钮,则运算结果就显示在单元格区域C4:C13中,如图4-4所示(图中的第13行预测数据即为下月即第13月的预测值),并自动出现输出图表,如图4—7所示。
图4-7 移动期数为3时的输出图表用同样的方法,可以分析当移动期数为5和7时的分析结果,如图4—4所示。
4.4。
2 指数平滑法【例4-6】某企业的有关销售数据如图4—8所示,利用指数平滑法进行预测分析,其步骤如下:图4—8 指数平滑法实例(1)从【工具】菜单中选中【数据分析】命令,则弹出【数据分析】对话框,在【数据分析】对话框中的【分析工具】框中选中【指数平滑】选项,则弹出【指数平滑】对话框,如图4—9所示.图4—9 【指数平滑】对话框(2)在【指数平滑】对话框中,【输入区域】框中输入“$B$2:$B$13”,【阻尼系数】框中输入“0.2",【输出区域】框中输入“$C$3”,最后选中【图表输出】选项。
时间序列预测:Holt双参数指数平滑法excel操作说明
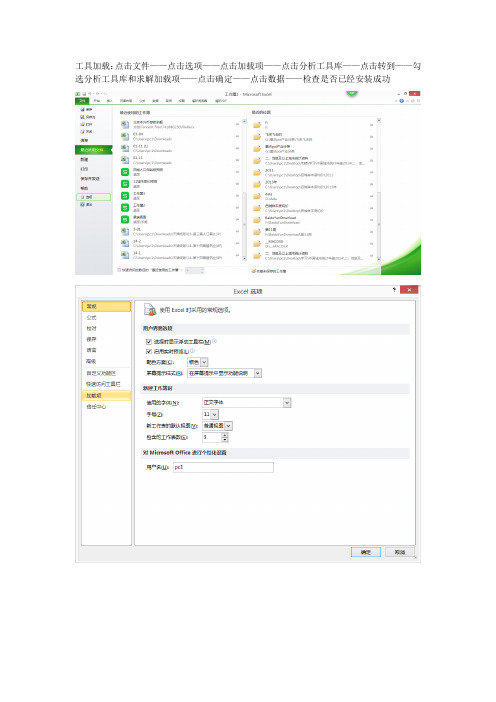
工具加载:点击文件——点击选项——点击加载项——点击分析工具库——点击转到——勾选分析工具库和求解加载项——点击确定——点击数据——检查是否已经安装成功
分析数据:在Y列的左侧插入1列,并填写上数字1-11,代表数据个案1-数据个案11
选取一半的数据做回归分析
点击数据——点击表头右侧的数据分析——点击回归
从回归结果中可以看到,intercept是指常数项,xvariable是指自变量t的系数。
将常数项作为Holt 双参数指数平滑的初始平滑值L0,将自变量t的系数作为Holt双参数指数平滑的趋势值b0(在Holt双参数指数平滑法中的双参数就是指初始平滑值和趋势值)
打开工作簿2——把数据按照以下格式复制到工作簿2
在C5、D5、E5、F5、G5分别输入以下的公式
选取C5-G5单元格,并把鼠标移动到单元格右下角处,但鼠标变为“十”字后,把鼠标下拉到第15行便会呈现出其余空格的数据
在D1中输入以下公式,便会得到总的误差平方和
点击数据——点击规划求解——在规划求解中输入以下单元格和公式——点击求解——选择保留规划求解的解——点击确定
接着会得到在确保总误差最小的情况下,平滑值、趋势值、估计值的最终数值
接着要预测接下来的t=12的Y值=C15+D15(即=1086.495+8.83841)即当t=12时,Y的预测值是1095.334
t=13的Y值=C15+2*D15(即=1086.495+2*8.83841)即当t=13时,Y的预测值是1104.172
如此类推即可得出之后的Y的预测值。
实验二:指数平滑法新

实验二:指数平滑法一、实验目的Part A:一次指数平滑法1根据时间序列数据散点图,熟悉一次指数平滑法适用条件的判断;2熟悉应用一次指数平滑法进行相应预测;3熟悉一次指数平滑法预测精度的分析及其最优平滑系数α的确定;Part B:二次指数平滑法1根据时间序列数据散点图,熟悉二次指数平滑法适用条件的判断;2熟悉应用二次指数平滑法进行相应预测;3熟悉二次指数平滑法预测精度的分析及其最优平滑系数α的确定;二、实验内容及实验过程Part A问题描述某商场在过去1-12周的某冰箱销售量统计数据如表1所示。
(1)试分析统计数据,选择合适的模型来估计下周产品销售量。
(2)平滑系数α=0.2,S0(1)=(X1+X2)/2采用一次指数平滑法进行预测,并分析其预测精度。
(3)何选择合适的平滑系数α,使预测精度较高?实验过程步骤1:绘制过去12周冰箱销售量的“XY散点图”,如图。
从散点图可以看出,冰箱销售量走势基本沿水平方向变化且无季节影响,因而可以使用一次指数平滑法进行预测。
步骤2:计算一次指数平滑预测值。
方法1:公式法取最初2期的观测值作为初始值,即在单元格C2中输入51。
平滑系数取α=0.2,单元格C3中输入一次指数平滑值,即“=0.2*B3+0.8*C2”,如图。
将单元格C3的内容复制到单元格区域C4: C14,得一次指数平滑值,如图在单元格D3输入“=C2”,并将单元格D3的内容复制到单元格区域D14,得一次指数平滑值,如图。
方法2:指数平滑数据分析模块法Excel的数据分析工具也提供了简单方便的指数平滑预测模块。
首先,在单元格B2中输入S0(1)的值“51”,并选择“指数平滑”数据分析。
点击Excel【工具】菜单下的【数据分析】子菜单,打开“数据分析”对话框,从“分析工具”列表中选择“指数平滑”,如图,并点击[确定]按钮。
参数指数平滑设置。
在“指数平滑”对话框中,“输入区域”选择原始数据所在的单元格区域“B2:B14”,“阻尼系数”中输入“0.8”,表示平滑系数a=0.2,“输出区域”选择单元格“C2”,如图,点击[确定]按钮,如图。
利用Excel进行指数平滑分析A

。图线曲测预的均平动移 到得可即�定确。 �9 图� ”图点散线折“择选中”型类表图子“即项子在� ”图点散“的中 ”型类表图“择选中框项选”导向表图“的出弹在�
围范据数的中选 8 图
标图”导向表图“击点�后然
。 �8 图�果结均平动移其及据数部全的 11C 到 1A 从中选�先首
果结滑平数指次三 81 图
置设的滑平数指次二 91 图
值
。 �02 图�91
值测预 值际实
置位的”滑平数指“与框项选析分据数 2 图
。 �2 图� ”滑平数 指“中选�框项选”析分据数“开打径路” �D�析分据数→�T�具工“的单菜主着沿 。置设项选�步二第
据数始原 1 图
。 �1 图�据数入录�步一第 。积面溉灌的年 01 续连】例【
�2�测预与析分滑平数指行进 lecxE 用利
2
1.0=α 为数系滑平�果结均平动移 5 图
5
果结滑平数指的数系尼阻同不于基 21 图
�志标据数括包�项选滑平数指的 8.0 为数系尼阻 11 图
。 �部局为 21 图�果结的有所出算到直�1.0、„、6.0、7.0 为 数系尼阻变改续继。果结到得即立�定确。 �11 图�变不项选他其�11E:2E 为改域区出输将 �2.0=α 数系滑平于应对 �8.0 为改数系尼阻将 � ”框项选滑平数指“ 的示所 3 图开打新重 。算计均平动移复重�步四第
3
2
1 0 01
03 04 05 滑平数指
果结滑平数指次二 61 图
置设的滑平数指次二 51 图
值
值测预 值际实
02
8
。 � ” �1�测预与析分滑平数指行进 lecxE 用利“见参析分细详�择选的数次�步八第 �3.0=α�线曲滑平数指次三 91 图
指数平滑法

指数平滑法应用案例Excel应用案例指数平滑法移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法设时间序列为,则一次指数平滑公式为:式中为第 t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:由于0<<1,当→∞时,→0,于是上述公式变为:由此可见实际上是的加权平均。
加权系数分别为,,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
用上述平滑值进行预测,就是一次指数平滑法。
其预测模型为:即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法当时间序列没有明显的趋势变动时,使用第t周期一次指数平滑就能直接预测第t+1期之值。
但当时间序列的变动出现直线趋势时,用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此,也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为,则二次指数平滑的计算公式为:若时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直线趋势变化,则与趋势移动平均类似,可用如下的直线趋势模型来预测。
式中t为当前时期数;T为由当前时期数t到预测期的时期数;为第t+T期的预测值;为截距,为斜率,其计算公式为:③三次指数平滑法若时间序列的变动呈现出二次曲线趋势,则需要用三次指数平滑法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
Excel应用案例
指数平滑法
移动平均法的预测值实质上是以前观测值的加权和,且对不同时期的数据给予相同的加权。
这往往不符合实际情况。
指数平滑法则对移动平均法进行了改进和发展,其应用较为广泛。
1. 指数平滑法的基本理论
根据平滑次数不同,指数平滑法分为:一次指数平滑法、二次指数平滑法和三次指数平滑法等。
但它们的基本思想都是:预测值是以前观测值的加权和,且对不同的数据给予不同的权,新数据给较大的权,旧数据给较小的权。
①一次指数平滑法
设时间序列为,则一次指数平滑公式为:
式中为第 t周期的一次指数平滑值;为加权系数,0<<1。
为了弄清指数平滑的实质,将上述公式依次展开,可得:
由于0<<1,当→∞时,→0,于是上述公式变为:
由此可见实际上是的加权平均。
加权系数分别为,
,…,是按几何级数衰减的,愈近的数据,权数愈大,愈远的数据,
权数愈小,且权数之和等于1,即。
因为加权系数符合指数规律,且又具有平滑数据的功能,所以称为指数平滑。
用上述平滑值进行预测,就是一次指数平滑法。
其预测模型为:
即以第t周期的一次指数平滑值作为第t+1期的预测值。
②二次指数平滑法
当时间序列没有明显的趋势变动时,使用第t周期一次指数平滑就能直接预测第t+1
期之值。
但当时间序列的变动出现直线趋势时,用一次指数平滑法来预测仍存在着明显的滞后偏差。
因此,也需要进行修正。
修正的方法也是在一次指数平滑的基础上再作二次指数平滑,利用滞后偏差的规律找出曲线的发展方向和发展趋势,然后建立直线趋势预测模型。
故称为二次指数平滑法。
设一次指数平滑为,则二次指数平滑的计算公式为:
若时间序列从某时期开始具有直线趋势,且认为未来时期亦按此直
线趋势变化,则与趋势移动平均类似,可用如下的直线趋势模型来预测。
式中t为当前时期数;T为由当前时期数t到预测期的时期数;为第t+T期的预
测值;为截距,为斜率,其计算公式为:
③三次指数平滑法
若时间序列的变动呈现出二次曲线趋势,则需要用三次指数平滑法。
三次指数平滑是在二次指数平滑的基础上再进行一次平滑,其计算公式为:
三次指数平滑法的预测模型为:
其中:
④加权系数的选择
在指数平滑法中,预测成功的关键是的选择。
的大小规定了在新预测值中新数据和原预测值所占的比例。
值愈大,新数据所占的比重就愈大,原预测值所占比重就愈小,反之亦然。
若把一次指数平滑法的预测公式改写为:
则从上式可以看出,新预测值是根据预测误差对原预测值进行修正得到的。
的大小表明了修正的幅度。
值愈大,修正的幅度愈大,值愈小,修正的幅度愈小。
因此,值既代表了预测模型对时间序列数据变化的反应速度,又体现了预测模型修匀误差的能力。
在实际应用中,值是根据时间序列的变化特性来选取的。
若时间序列的波动不大,比较平稳,则应取小一些,如0.1~0.3;若时间序列具有迅速且明显的变动倾向,则应取大一些,如0.6~0.9。
实质上,是一个经验数据,通过多个值进行试算比较而定,哪个值引起的预测误差小,就采用哪个。
2. 应用举例
已知某厂1978~1998年的钢产量如下表所示,试预测1999年该厂的钢产量。
下面利用
选择工具菜单中的数据分析命令,此时弹出数据分析对话框。
在分析工具列表框中,选择指数平滑工具。
这时将出现指数平滑对话框,如图8-4所示。
图8-4
在输入框中指定输入参数。
在输入区域指定数据所在的单元格区域B1:B22;因指定的输入区域包含标志行,所以选中标志复选框;在阻尼系数指定加权系数0.3。
在输出选项框中指定输出选项。
本例选择输出区域,并指定输出到当前工作表以C2为左上角的单元格区域;选中图表输出复选框。
单击确定按钮。
这时,Excel给出一次指数平滑值,如图8-5所示。
图8-5 从图8-5可以看出,钢产量具有明显的线性增长趋势。
因此需使用二次指数平滑法,即在一次指数平滑
的基础上再进行指数平滑。
所得结果如图8-6所示。
图8-6
利用前面的截距和斜率计算公式可得:
于是,可得钢产量的直线趋势预测模型为:
预测1999年的钢产量为:。
