理论塔板数的计算
理论塔板数的计算

ቤተ መጻሕፍቲ ባይዱ
在一定范围内,增加塔板数可以显著提高分 离度,但超过一定值后,分离度的提高将变
得缓慢。
塔板数与产品纯度的关系
塔板数越多,产品纯度越高。这是因为塔板数越多, 物料在塔内停留的时间越长,越有利于组分的分离。
在实际操作中,为了达到所需的产品纯度,可以通过 增加塔板数来提高分离效果。
理论塔板数计算公式
理论塔板数计算公式是用于计算色谱柱分离效率的重要参数,其计算公式为:$N = 5.54(tR/W1/2)$,其中$N$为理论塔板数, $tR$为峰的保留时间,$W1/2$为半峰宽。
该公式基于色谱理论,通过将色谱峰的保留时间和峰宽等参数代入公式,即可得到理论塔板数。
实际应用中的计算方法
理论塔板数的计算
contents
目录
• 塔板数的定义 • 理论塔板数计算方法 • 塔板数的影响因素 • 塔板数与分离效果的关系 • 塔板数优化方法
01
塔板数的定义
塔板数的概念
01
塔板数是指塔内理论分离层的数 目,用于描述蒸馏塔或吸收塔等 分离设备的分离性能。
02
它反映了塔内各层分离效果的好 坏,是衡量分离设备效率的重要 参数。
在实际应用中,理论塔板数的计算通常需要借助色谱软件或仪器自带软件进行。
这些软件通常会提供自动计算或手动输入参数的功能,用户只需输入保留时间和峰 宽等参数,软件即可自动计算出理论塔板数。
此外,为了获得更准确的计算结果,还需要注意实验条件的标准化和数据的准确性。
计算过程中的注意事项
在计算理论塔板数时,需要注意峰宽的测量方法,因为不同的测量方法 可能会影响计算结果的准确性。
理论塔板数的计算

2、方法: 从塔顶到塔底计算。
精馏段:
xDy1 平 衡 x1操 作 y2 平 衡 x2L xn xq
当xn <xq时,q为加料板,因q点为两点操 作线交点,加料板为提馏段一块板,所以精馏 段理论板数为(n-1)块板。
提馏段:(改用提馏段操作线)
xn x1' (加料板下流液相组成)
例、在一常压连续精馏塔内分离苯-甲苯混合 物,已知进料液流量为80kmol/h,料液中苯含 量40%(摩尔分率,下同),泡点进料,塔顶 流出液含苯90%,要求苯回收率不低于90%, 塔顶为全凝器,泡点回流,回流比取2,在操作 条件下,物系的相对挥发度为2.47。
求:分别用逐板计算法和图解法计算所需的 理论板数。
2)以上理论板数是用泡点进料的情况所得,则 xq=xF,如果不是泡点进料,这时xq≠xF,我们要 把两条操作线交点q坐标求出,当x≤xq,即为加 料板。
3)塔顶采用分凝器:
塔顶分凝器相当于第一块理论板(进一个 气相,出一个气相和一个液相);塔内第一块 板就成为第二块板。
D,yD V, y1
L, xL(2)相平衡方程 Nhomakorabea可写成:
x(y1)y2.47 y1.47 y
解: (1) 根据苯的回收率计算塔顶产品流量:
DFxF0.98 00.43k2m /hol
xD
0.9
由物料恒算计算塔底产品的流量和组成:
W F D 8 0 3 2 4 8 k m o l / h
x W F x F W D x D 8 0 0 .4 4 8 3 2 0 .9 0 .0 6 6 7
其中过q点的梯级为加料板,最后一个梯级 为再沸器。
塔内总共需要(m+n-2)块理论板。
第五节 理论板数的求法
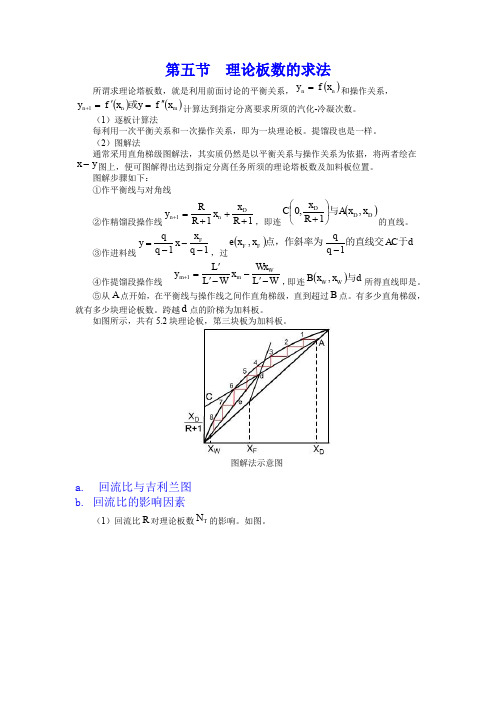
第五节 理论板数的求法所谓求理论塔板数,就是利用前面讨论的平衡关系,()n n x f y =和操作关系,()()m n n x f y x f y ''='=+或1计算达到指定分离要求所须的汽化-冷凝次数。
(1)逐板计算法每利用一次平衡关系和一次操作关系,即为一块理论板。
提馏段也是一样。
(2)图解法通常采用直角梯级图解法,其实质仍然是以平衡关系与操作关系为依据,将两者绘在y x -图上,便可图解得出达到指定分离任务所须的理论塔板数及加料板位置。
图解步骤如下: ①作平衡线与对角线②作精馏段操作线111+++=+R x x R R y D n n ,即连()D D D x x A R x C ,1,0与⎪⎭⎫ ⎝⎛+的直线。
③作进料线11---=q x x q qy F,过()d AC q q x x e F F 于的直线交点,作斜率为1,- ④作提馏段操作线W L Wx x W L L y W m m -'--''=+1,即连()d x x B W W 与,所得直线即是。
⑤从A 点开始,在平衡线与操作线之间作直角梯级,直到超过B 点。
有多少直角梯级,就有多少块理论板数。
跨越d 点的阶梯为加料板。
如图所示,共有5.2块理论板,第三块板为加料板。
图解法示意图a. 回流比与吉利兰图b. 回流比的影响因素(1)回流比R 对理论板数T N 的影响。
如图。
回流比对T N 的影响↑+↓1R x R D ,,操作线靠近平衡线,↑T N 反之,↓+↑1R x R D ,,操作线远离平衡线,↓T N 即 T N 正比于R 1(2)回流比对设备费与操作费的影响 ()D R D L V 1+=+=↑↑V R ,,塔直径↑,冷凝器↑,蒸馏釜↑ 设备费↑↓↑T N R ,,塔高下降,设备费↓↑↑V R ,,冷却水量↑,加热蒸汽量↑, 操作费↑须选一个合适回流比R ,使总费用最省。
5-4 双组分精馏理论塔板数的计算2010

0 x W
xF
xD 1
结果:精馏段操作线下移,操作线与平衡线距离加大, N T ,但热耗 (以热耗为代价换取N T减少)
小 结
一般而言,在热耗不变的条件下,热量尽可能在塔 底输入,冷量尽可能在塔顶输入,即 “ 热在塔底”、 “冷在塔顶 ”,目的使气相回流及液体回流能经过
全塔而发挥作用。
(2)Rmin的求取
1.0 a
xD ye Rmin Rmin 1 xD xe
q
xD Rmin 1
ye
e
Rmin
xD ye ye xe
0 xW
xe
xF
xD 1.0
式中存在求取ye、xe的问题
因挟点为 q 线与相平衡线交点 坐标,联立二方程求解可得:
xf q ye q 1 xe q 1 xe y e 1 ( 1) xe
L D 物料在塔内循环的操作, W F 0,R D (2)全回流时精、提操作线与对角线重合 L D yn+1 xn xD xn V V
yn +1
L W xn xw xn V V
(3)平衡线与操作线间的距离最大,理论板数最少 (4) N Tmin 的求取
QF QB 定值
1
分析:
0 q 1
q0
q 1
q 1
y
若q值愈小,则Q F ,QB , 那么V ,提馏线斜率 , 提馏线向平衡线靠近,N T 。
q0
0
xW
xF
xD 1
工业上有时采用热态甚至气态进料,其目的: 不是为了:减少塔板数 而是为了:减少塔釜的加热量,避免塔釜温度过高, 物料产生聚合或者结焦。
理论塔板数的计算

yW与xW不平衡:
yW xW
V
L
yW
W, xW
xW 图6-37 塔底不平衡蒸发器流程图
6.7.3 图解法
应用逐板计算法求精馏塔所需理论板数的 过程,可以在y-x图上用图解法进行。 一、具体求解步骤如下: 1、相平衡曲线:
x y 1 ( 1) x
(6-10)
在直角坐标系中绘出待分离的双组分物系yx图,如图6-38。
xD R 2 0.9 yn 1 xn xn R 1 R 1 2 1 2 1 0.667 xn 0.3
(1 )
提馏段操作线方程:
L ' L qF L F RD F 2 32 80 144kmol / h
D,yD V, y1
L, xL
D, xD
图6-36 分凝器流程图
因为第一个分凝器实现了一次气液平衡, 理论上相当于一块理论板(进一个气相,出一 个气相和一个液相)。 yD与xL平衡:
y D xD
4)塔底不相当于一块理论板;进入再沸器一个 液相,出一个气相,这在理论上没有实现气-液 平衡,所以不相当于一块理论板。
6.7.
理论塔板数的计算
6.7.1 理论塔板数计算的依据 6.7.2 逐板计算法 6.7.3 图解法 6.7.4 理论板数的简捷计算
本节学习要点: 1、掌握逐板计算法和图解法求理论塔板数。 2、使用逐板计算法和图解法求取理论塔板数, 都要及时更换操作线方程。
6.7.1 理论塔板数计算的依据
F、xF、q、xD、xW、R、(D、W可计算 出来),这些参数是研究理论板的最重要的前 提条件;
D
F xF
xD
0.9 80 0.4 32kmol/ h 0.9
精馏过程工艺参数的确定(理论塔板数计算)

(不包括塔釜) (包括塔釜)
2、图解法 图解法求理论塔板数的基本原
理与逐板计算法相同,所不同的 是用相平衡曲线和操作线分别代 替相平衡方程和操作线方程。用 图解法求理论塔板层数的具体步 骤如下:
(1)绘相平衡曲线 (2)绘操作线 绘出精馏段 操作线和提馏段操作线
(3)绘直角梯级 从(xD,xD)点开始,在精馏段操作线 与平衡线之间绘水平线与垂直线构成直角梯级,当梯级跨 过两段操作线交点d时,则改在提馏段操作线与平衡线之间 作直角梯级,直至梯级的垂线达到或跨过(xW,xW)点为止。 梯级总数即为所需的理论塔板数(包括塔釜)。
职业教育环境监测与治理技术专业教学资源库《化工单元操作》课程
项目八 蒸馏及设备操作
南京科技职业学院
项目八:精馏及设备操作
任务2:精馏过程工艺参数的确定 ---理论塔板数计算 回流比计算
南京科技职业学院 化学工程系
一、理论塔板数计算
(一)理论塔板概念 若汽液两相能在塔板上充分接触,使离
开塔板的汽液两相温度相等,且组成互为平 衡,则称该塔板为理论塔板。
❖ 试用(1)逐板计算法,(2)图解法分别求出所 需的理论板层数及进料板位置。
(三)实际塔板数确定 全塔效率 在指定的分离条件 下,所需的理论塔板 数NT(不包括塔釜) 与实际塔板数N之比 称为全塔效率,用符
号ET表E示T 。N即NT
实际塔板数:
N NT ET
L
泡罩塔塔板效率关系曲线
y3
xn-1
精馏段操作线方程
yn
yn
相平衡方程求
xn≤ xd
直到xn xd(xd为两段操作线交点坐标x数值)时,说明第n 层板为加 料板,该板应属于提馏段。因此精馏段所需理论板数为n -1块。
6.7. 理论塔板数的计算解读

WxW L qF ym1 xm L qF W L qF W
双组分连续精馏塔所需理论板数,可采 用逐板计算法和图解法。
6.7.2 逐板计算法
假设塔顶冷凝器为全凝器,泡点回流,塔 釜为间接蒸汽加热,进料为泡点进料如图6-35 所示。
x1
F, xF
x2 xn xm-1
0.431 0.365<xF 0.301 0.226 0.151 0.089 0.044<xW
精馏塔内理论塔板数为10-1=9块,其中精 馏段4块,第5块为进料板。 (2)图解法计算所需理论板数 在直角坐标系中绘出y-x图(图略)。 根据精馏段操作线方程式(1),找到 a(0.9,0.9),C(0,0.3)点,联接ac即得到精馏段 操作线。 根据式(2)提馏段操作线,通过 b(0.0667,0.0667),以1.5为斜率作直线bq,即为 提馏段操作线。
2、方法:
从塔顶到塔底计算。
精馏段:
x D y1 x1 y2
平衡 操作
x2
平衡
xn xq
当xn <xq时,q为加料板,因q点为两点操 作线交点,加料板为提馏段一块板,所以精馏 段理论板数为(n-1)块板。
提馏段:(改用提馏段操作线)
xn x
' 1 操作
WxW 144 L' 48 0.0667 ym1 xm xm V' V' 96 96 1.5 xm 0.033
(2 )
相平衡方程式可写成:
y x ( 1) y 2.47 1.47 y
y
(3 )
利用操作线方程式(1),式(2)和相平 衡方程式(3),可自上而下逐板计算所需理 论板数。
理论塔板数的计算
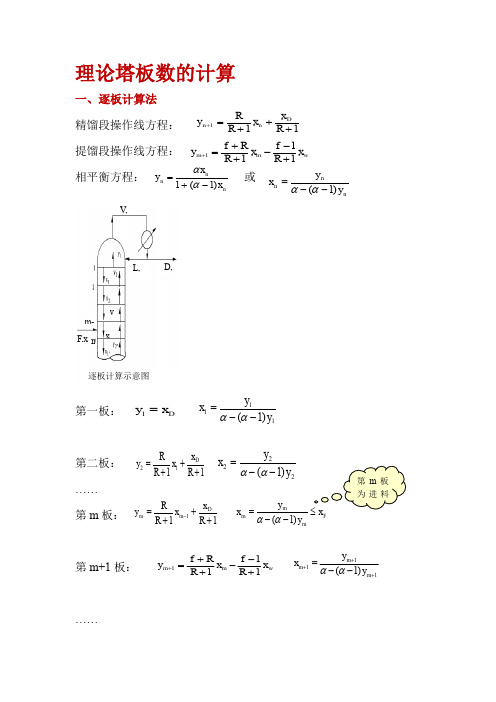
理论塔板数的计算一、逐板计算法精馏段操作线方程: 提馏段操作线方程: 相平衡方程: 或第一板:第二板:…… 第m 板:第m+1板: (1)11+++=+R x x R R y D n n w m m x R f x R R f y 1111+--++=+nn n x x y )1(1-+=ααnn n y y x )1(--=ααD, V, L, xD F,xx y m m-逐板计算示意图 111)1(y y x --=ααDx y =11112+++=R x x R R y D 222)1(y y x --=αα111+++=-R x x R R y D m m F m m m x y y x ≤--=)1(αα第m 板为进料111)1(+++--=m m m y y x ααw m m x R f x R R f y 1111+--++=+第N 板:在计算过程中, 每使用一次平衡关系, 表示需要一层理论板. 由于一般再沸器相当于一层理论板.结果: 塔内共有理论板N 块, 第N 板为再沸器, 其中精馏段m-1块, 提馏段N-m+1块 (包括再沸器), 第m 板为进料板。
二、图解法图解法求理论板层数的基本原理与逐板计算法的完全相同,只不过是用平衡曲线和操作线分别代替平衡方程和操作线方程,用简便的图解法代替繁杂的计算而已。
1、操作线的作法首先根据相平衡数据, 在直角坐标上绘出待分离混合物的x-y 平衡曲线, 并作出对角线.W NN N x y y x ≤--=)1(ααw N N x R f x R R f y 1111+--++=-在x=xD 处作铅垂线, 与对角线交于点a, 再由精馏段操作线的截距xD /(R+1) 值, 在y 轴上定出点b, 联ab. ab为精馏段操作线.在x=xF 处作铅垂线, 与精馏段操作线ab交于点d.在x=xW 处作铅垂线, 与对角线交于点c, 联cd. cd为提留段操作线.2、求N 的步骤自对角线上a点始, 在平衡线与精馏段操作线间绘出水平线及铅垂线组成的梯级.当梯级跨过两操作线交点d 时, 则改在平衡线与提馏操作线间作梯级, 直至某梯级的垂直线达到或小于xw为止.每一个梯级代表一层理论板. 梯级总数即为所需理论板数.3、梯级含义:如第一梯级:由a点作水平线与平衡线交于点1(y1, x1), 相当于用平衡关系由y1求得x1;再自点1作垂线与精馏段操作线相交, 交点坐标为(y2, x1), 即相当于用操作线关系由x1求得y2。
理论塔板数的计算方法

图3 两条操作线与q线
二、理论塔板数的计算方法
3.图解法
(4)在图3中,过a点(xD、xD)在相平 衡线与精馏段操作线之间画梯级;当跨 过d点(q线与精馏段操作线交点)再在 相平衡线与提馏段操作线之间画梯级; 当跨过c点(xW、xW)则终止。每一个 梯级代表一块理论塔板,得到图解法理 论板数求解图,如图4所示。
算。
提馏段操作线方程:
yn1
L L W
xn
W L W
xw
,得到yn+1 。
相平衡方程:yn1
1
(
xn1 1) xn 1
,得到xn+1 。
二、理论塔板数的计算方法
2.逐板计算法
(2)计算步骤
②提馏段计算
第n+2板:
已知条件:xn+1 ,计算yn+2和xn+2 。
提馏段操作线方程:
二、理论塔板数的计算方法
1.计算条件
由于精馏过程是涉及传热与传质的复杂过程,影响因素很多。因此 需要规定一些计算的条件。 (1)精馏塔对外界是绝热的,没有热损失。 (2)回流液由塔顶全凝器提供,其组成与塔顶产品相同。 (3)恒摩尔气流 精馏段各板V相同,提馏段各板V′相同。 (4)恒摩尔溢流 精馏段各板L相同,提馏段各板L′相同。
C. 气液相平衡方程
D. 以上都包括
2. 判断题
(1) 在图解法求解理论塔板数中,步骤是过a点(xD、xD)在相平衡线与 精馏段操作线之间画梯级,在d点(精馏段操作线与q线的交点)之后仍在
相平衡线与精馏段操作线之间作若干个梯级。之后,才转为在相平衡线与
提馏段操作线之间作梯级,直到跨过c点终止。( )
6-2 理论塔板数的计算(简版)

逐 板 法 图 解 法 捷 算 法
23:29:19
6-2 理论塔板数计算 (48)
2
双组分连续精馏塔的计算
理论板 理论板是指离开塔板的蒸汽和液体呈平 衡的塔板,它是人为的理想化的塔板。 理论板可以作为衡量实际塔板分离效果 的一个标准。
23:29:19
6-2 理论塔板数计算 (48)
3
例1 环己烷 80.8℃ 苯 80.1℃ 常压下沸点 糠醛 161.7℃ 苯酚 180℃
环己烷-苯恒沸物 77℃
糠醛能显著降低苯的饱和蒸汽压,而对环己烷影响不明 显,使苯从易挥发组分变为难挥发组分,而且使环己烷-苯的 增大至2以上。
23:29:19
6-2 理论塔板数计算 (48)
22
萃取剂的选择原则:
6-2 理论塔板数计算 (48)
23:29:19
说明: (1)EmV(n)和 EmL(n)不 一定相等, (2)一般情况单板效率 小于 1, 特殊情况它们会 大于 1, 通常出现在塔径 较大的精馏塔中。
16
2.全塔效率E0
又称总板效率,其定义为:
D, xD
理论板数 N E0 实际板数 N e
恒 沸 精 馏 特殊精馏 萃 取 精 馏
23:29:19
6-2 理论塔板数计算 (48)
x
19
1.恒沸精馏
加入的第三组分与原溶液中的一个或者两个组分形成 最低恒沸物,从而形成了“恒沸物-纯组分”的精馏体系, 恒沸物从塔顶蒸出,纯组分从塔底蒸出,这种形式的精馏称 为恒沸精馏,其中所添加的第三组分称为 恒沸剂或者夹带 剂。
ym+1 xm yN-1 xm+1
x N1 1 y N1 2 x N1 2 y N1 3
理论塔板数

理论塔板数1、定义理论塔板数(theoretical plate number)N,色谱的柱效参数之一,用于定量表示色谱柱的分离效率(简称柱效)。
N取决于固定相的种类、性质(粒度、粒径分布等)、填充状况、柱长、流动相的种类和流速及测定柱效所用物质的性质。
如果峰形对称并符合正态分布,N可近似表示为:理论塔板数=5.54(保留时间/半高峰宽)2柱效率用理论塔板数定量地表示:N=16*(t/w )2。
其中,t是溶质从进样到最大洗脱峰出现的时间,w为该溶质的洗脱峰在基线处的宽度。
在一色谱柱中用相同的洗脱条件时候,不同化合物的滞留时间与其洗脱峰宽度之比接近常数。
因此理论塔板数大的色谱柱效率高。
当然,N的大小和柱子长度有密切关系:理论塔板高度H=柱长/N,用H可以衡量单位长度的色谱柱的效率,H越小,则色谱柱效率越高。
N为常量时,W随tR成正比例变化。
在一张多组分色谱图上,如果各组份含量相当,则后洗脱的峰比前面的峰要逐渐加宽,峰高则逐渐降低。
用半峰宽计算理论塔板数比用峰宽计算更为方便和常用,因为半峰宽更容易准确测定,尤其是对稍有拖尾的峰。
N与柱长成正比,柱越长,N越大。
用N表示柱效时应注明柱长,,如果未注明,则表示柱长为1米时的理论塔板数。
(一般HPLC柱的N在1000以上。
)若用调整保留时间(tR′)计算理论塔板数,所得值称为有效理论塔板数(N有效或Neff)=16(tR′/W)2我们知道实际操作过程中,峰会出现拖尾的情况,所以,实用半峰宽比使用峰宽要准确一些,当然这也不是绝对的。
理论塔板高度和理论塔板数都是柱效指标,,由于峰宽或半峰宽是组分分子在色谱柱内离散的度量,总的离散程度是单位柱长内分子离散的累计,其与柱长成正比。
理论塔板数首先应该是和柱子的性能是有关系的,像填料,柱长什么的,和你的流动相,流速,样品分子量大小都是有关系的。
每个峰的理论塔板数肯定是不同的,理论塔板数越高峰形越好。
2、理论塔板数下降后可以考虑色谱柱再生(1)、反相柱分别用甲醇:水=90:10,纯甲醇(HPLC级),异丙醇(HPLC级),二氯甲烷(HPLC级)等溶剂作为流动相,依次冲洗,每种流动相流经色谱柱不少于20倍的色谱柱体积,然后再以相反的次序冲洗。
理论塔板数的计算 (2)

' 1
(加料板下流液相组成)
平衡 ' 2
x y x
' 2
xm xW
提馏段:m块板,提馏段内不包括再沸器,而 xW是再沸器内的浓度,所以m块板中包括再沸 器,再沸器相当一个理论板,所以塔内提馏段 为(m-1)块板。
讨论: 1) 逐板计算法很重要,用计算机编程计算很 快就计算出结果。 2)以上理论板数是用泡点进料的情况所得,则 xq=xF,如果不是泡点进料,这时xq≠xF,我们要 把两条操作线交点q坐标求出,当x≤xq,即为加 料板。 3)塔顶采用分凝器: 塔顶分凝器相当于第一块理论板(进一个 气相,出一个气相和一个液相);塔内第一块 板就成为第二块板。
f
加料过早
e
图6-38 理论板数图解法示意图
2、精馏段操作线:
y n 1
R 1 xn xD R 1 R 1
(6-39)
3、提馏段操作线:
L qF W ym1 xm xW L qF W L qF W
(6-59)
4、画直角梯级: 从a点开始,在精馏段操作线与平衡线之间 作水平线及垂直线,当梯级跨过q点时,则改在 提馏段操作线与平衡线之间作直角梯级,直至 梯级的水平线达到或跨过b点为止。 其中过q点的梯级为加料板,最后一个梯级 为再沸器。 塔内总共需要(m+n-2)块理论板。 作梯级时跨q点换线,用提馏段操作线。
NP
式中:
NT
(5-61)
NP——实际塔板数; NT——理论板数;
η——全塔效率;
根据:
1、平衡关系: ①用某一温度下纯组分的饱和蒸汽压表示; ② t-x-y图; ③ x-y图; ④用相对挥发度表示;
精馏过程工艺参数的确定(理论塔板数计算)最新实用版

(三)实际塔板数确定 全塔效率 在指定的分离条件 下,所需的理论塔板 数NT(不包括塔釜) 与实际塔板数N之比 称为全塔效率,用符
号ET表E示T 。N即NT
实际塔板数:
N NT ET
L
泡罩塔塔板效率关系曲线
❖ 课后思考题
❖ 逐板计算法和图解法求算理论塔板数都是基于恒摩尔流假 定,而假定的主要条件是组分的摩尔汽化潜热相等。对组 分的摩尔汽化潜热相差较大物系,就不能用基于恒摩尔假 定的方法求取理论塔板数。
感谢观看
如此重复计算直至x m xW为止。
理论塔板数与哪些参数有关? 试用(1)逐板计算法,(2)图解法分别求出所需的理论板层数及进料板位置。 理论塔板数常见的确定方法有逐板计算法和图解法 全回流和最少理论塔板数
Rmin
xD yq
yq xq
二、回流比计算
3. 适宜回流比
分析回流比大小对精馏设备费用和操作费用的 影响。以精馏过程的设备费用与操作费用之和最 小为原则来确定适宜回流比。一般取最小回流比 的1.1~2.0倍。
❖ 应该采用什么方法求理论塔板数?请查阅有关书籍。
二、回流比计算
1. 全回流和最少理论塔板数
回流比的最大极限,此时操作过程没有产品, 操作线斜率为1,对应的塔板数为最少,仅用于 精馏开车阶段和科研工作。
二、回流比计算
2. 最小回流比
用图解法求回理论流塔板比层数的最具体小步骤极如下:限,对应的塔板数为无穷多,确
(1)绘相平衡曲线 (2)绘操作线 绘出精馏段 操作线和提馏段操作线
(3)绘直角梯级 从(xD,xD)点开始,在精馏段操作线 与平衡线之间绘水平线与垂直线构成直角梯级,当梯级跨
过两段操作线交点d时,则改在提馏段操作线与平衡线之间
板式吸收塔理论塔板数的计算

板式吸收塔理论塔板数的计算14404806 龙益如通常在吸收操作中,大多采用填料塔。
然而,填料式吸收塔不是在所有情况下均适用,仅在处理量较小,塔径在600毫米以下时(文献得知),采用填料塔比较经济。
当塔径较大时,可能出现严重的壁流和沟流现象,导致吸收效率下降。
故,处理量较大时,采用板式吸收塔。
另外,填料塔不能像板式塔一样设置人孔进行检修和清洗,故此方面依旧板式塔更优。
下面进行板式吸收塔的理论塔板数的计算,主要参照板式精馏塔采用逐级计算法和图解法,另外由查阅文献介绍解析法等其他方法。
方法一:首先,我们假定板式吸收塔中每一块塔板均为理想板,即塔板上的液相组成是均匀的,且离开该板的气液两相处于平衡状态,即所谓理论板。
同时,在气相中采用惰性组分的摩尔比为基准,在液相中采用吸收剂的摩尔比为基准,且满足吸收过程中惰性组分吸收剂的流量均可视为恒定,即各板上升的惰性组分的摩尔流量V均相等,各板下降的吸收剂的摩尔流量L均相等。
基于以上讨论,参照板式精馏塔的处理方式,进行计算:如图所示,在全塔范围内对溶质进行物料衡算得VY b+LX a=VY a+LX b(1-1)V(Y b−Y a)=L(X b−X a)(1-2)在吸收塔的任意两板间(i和i+1)分别与塔顶或者塔底的范围内,对溶质A进行物料衡算得VY i+1+LX a=VY a+LX i移项,得Y i+1=LV X i+(Y a−LVX a)(1-3)即为板式吸收塔的操作线方程。
由以上部分计算对比教材上填料式吸收塔的计算可知,此部分两者的处理方法基本相同。
故,后续部分计算直接采用书上已有公式。
其中,Y a=Y b(1−φA) (1-4)而最小液气比(LV )min=Y b−Y aY bm−X a(1-5)又实际液气比为L V =(1.1~1.2)(LV)min(1-6)图1-1一般情况下,进行吸收操作时,处理量V、进塔气体组成Y b、出塔气体组成Y a以及进塔吸收剂组成X a均为设计时已经确定的量,故式1-2、1-5、1-6可求得出塔吸收液组成X b。
精馏过程工艺参数的确定(理论塔板数计算)讲解

x D = y1
x 根据 x y 根据 y x 根据 x y
相平衡方程求
1
1
精馏段操作线方程
相平衡方程求
2
2
2
精馏段操作线方程
2
3
xn-1
yn
精馏段操作线方程
相平衡方程求
yn
x n≤ x d
直到xn xd(xd为两段操作线交点坐标x数值)时,说明第n 层板为加 料板,该板应属于提馏段。因此精馏段所需理论板数为n -1块。
理论塔板数与哪些参数有关? 与物料量的多少是否有关?
NT f xF , xD , xW , q, R,
与进料位置也有关,提前进料和推迟进料都会使理论塔板数增多
某理想混合液用常压精馏塔进行分离。进料组成含 A81.5%,含B18.5%(摩尔百分数,下同),饱和 液体进料,塔顶为全凝器,塔釜为间接蒸气加热。 要求塔顶产品为含A95%,塔釜为含B95%,此物系 的相对挥发度为2.0,回流比为4.0。 试用(1)逐板计算法,(2)图解法分别求出所需 的理论板层数及进料板位置。
根据 y2 xm-1 ym
相平衡方程求
提馏段操作线方程
相平衡方程求
如此重复计算直至xm xW为止。由于离开塔釜的汽液两相组成达到平 衡,故塔釜相当于一块理论板,提馏段所需的理论塔板数为m-1块。
WxW L y m1 xm L W L W
x A yA 1 ( 1) x A
全塔所需的理论塔板数NT为
N n m 2
T
(不包括塔釜) (包括塔釜)
N n m 1
T
2、图解法 图解法求理论塔板数的基本原 理与逐板计算法相同,所不同的 是用相平衡曲线和操作线分别代 替相平衡方程和操作线方程。用 图解法求理论塔板层数的具体步 骤如下: (1)绘相平衡曲线 (2)绘操作线 绘出精馏段 操作线和提馏段操作线
理论塔板数的计算

塔内总共需要(m+n-2)块理论板。
作梯级时跨q点换线,用提馏段操作线。
讨论:
1、每经过一次平衡需要一块理论板,所以一次 直角梯级仅相当于一块理论板。
2、理论上都会出现非整数板,但理论计算上都 把非整数看作整数板,工程上没有非整数板。
二、最优加料位置的确定
解: (1) 根据苯的回收率计算塔顶产品流量:
D F xF 0.9 80 0.4 32kmol / h
xD
0.9
由物料恒算计算塔底产品的流量和组成:
W F D 80 32 48kmol / h
xW
FxF DxD W
80 0.4 32 0.9 48
0.0667
已知回流比R=2,所以精馏段操作线方程为:
图中横坐标为:
R Rmin R 1
纵坐标为:
N N min N 2
图6-41 吉利兰(Gilliland)关联图
简捷法计算的步骤: 1、先算Rmin; 2、R=(1.1-2)Rmin; 3、Nmin 由芬斯克方程计算;
注意纵坐标中的N和Nmin均为不包括再沸 器的理论塔板数。
简捷算法虽然误差较大,但因简便,所以 特别适用于初步设计计算,可快速地算出理论 塔板数或粗略地寻求塔板数与回流比之间的关 系,供方案比较之用。
D,yD V, y1
L, xL
D, xD
图6-36 分凝器流程图
因为第一个分凝器实现了一次气液平衡,
理论上相当于一块理论板(进一个气相,出一 个气相和一个液相)。
yD与xL平衡:
yD xD
4)塔底不相当于一块理论板;进入再沸器一个 液相,出一个气相,这在理论上没有实现气-液 平衡,所以不相当于一块理论板。
化工原理理论塔板计算

精馏过程的物料衡算和塔板数的计算一、理论塔板连续精馏计算的主要对象是精馏塔的理论塔板数。
所谓的理论塔板是指气液在塔板上充分接触,有足够长的时间进行传热传质,当气体离开塔板上升时与离开塔板下降的液体已达平衡,这样的塔板称为理论塔板。
实际上,由于塔板上气液接触的时间及面积均有限,因而任何形式的塔板上气液两相都难以达到平衡状态,也就是说理论塔板是不存在的,它仅是一种理想的板,是用来衡量实际分离效率的依据和标准。
通常在设计中先求出按生产要求所需的理论塔板数N T然后用塔板效率η予以校正,即可求得精馏设备中的实际塔板数N P二、计算的前提由于精馏过程是涉及传热、传质的复杂过程,影响因素众多。
为处理问题的方便作如下假设,这些就是计算的前提条件。
(1)塔身对外界是绝热的,即没有热损失。
(2)回流液由塔顶全凝器供给,其组成与塔顶产品相同。
(3)塔内上升蒸气由再沸器加热馏残液使之部分气化送入塔内而得到。
(4)恒摩尔气化在精馏操作时,在精馏段内,每层塔板上升的蒸气的摩尔流量都是相等的,提馏段内也是如此,即:精馏段:V1 = V2 = …………=Vn= Vmol/s(下标为塔板序号,下同)提馏段:V′n+1 =V′n+2 =…………=V′m= V′mol/s但Vn不一定与V′m相等,这取决于进料状态。
(5)恒摩尔溢流(或称为恒摩尔冷凝)精馏操作时,在精馏段内每层塔板下降的液体的摩尔流量都是相等的,提馏段也是如此,即:L1 = L2=…………= L n = L mol/sL′n+1= L′n+2=………… = L′m= L′ mol/s但L不一定与L′相等,这也取决于进料的状态。
(6)塔内各塔板均为理论塔板。
三、物料衡算和操作线方程1、全塔物料衡算图4-10 全塔物料衡算示意图如图4-10所示,设入塔进料流量为F,轻组分含量为x F,塔顶产量流量为D,轻组分含量为x D,塔底产品流量为W,轻组分含量为x w,流量单位均为mol/s,含量均为摩尔分率。
理论塔板数求取-61页文档资料
由
Vs
4
D2u
得 D 4V s
u 20
十二、连续精馏装置的热量衡算 (一)全塔的热量衡算
原料液所带入的热量:
QFGF.CF.tF
再沸器所带入的热量:
QGG.R
回流液所带入的热量:
QLGL.CL.tL
21
馏出液所带走的热量: 残液所带走的热量: 热损失:
Q D G D R 1 .IV
简单、造价低、安装维修方便等。
30
二、板式塔结构
板式塔结构如右图所示, 主要由塔体、塔板、裙座、接 口等部分组成。
31
三、板式塔的类型 塔板:有降液管式塔板和无降液管式塔板。
32
(一)泡罩塔
主要元件:升气管及泡罩 泡罩安装在升气管的顶部, 泡罩的下部周边有很多齿 缝,泡罩在塔板上按一定 规律排列。
y x 1( 1)x
代入
得
yq
xq 1(1)xq
Rmi n
xD yq
yq xq
18
(三)适宜回流比的选择
最适宜回流比应通过经济衡算来决定,即按照操作费用与 设备折旧费用之和为最小的原则来确定,它是介于全回流与最 小回流比之间的某个值。通常适宜回流比可取最小回流比的 (1.1-2.0)倍,即
8
2.求N 的步骤 自对角线上a点始, 在平衡线与
精馏段操作线间绘出水平线及铅垂 线组成的梯级. 如右图所示。
当梯级跨过两操作线交点d 时, 则改在平衡线与提馏操作线间作梯 级, 直至某梯级的垂直线达到或小 于xW为止。
每一个梯级代表一层理论板。 梯级总数即为所需理论板数。
9
八、适宜的进料位置
如前所述,图 解过程中当某梯级 跨过两操作线交点 时,应更换操作线。 跨过交点的梯级即 代表适宜的加料板 (逐板计算时也相同), 这是因为对一定的 分离任务而言, 如此 作图所需的理论板 层数为最少。
理论塔板数

理论塔板数定义理论塔板数(theoretical plate number),N色谱的柱效参数之一,用于定量表示色谱柱的分离效率(简称柱效)。
N取决于固定相的种类、性质(粒度、粒径分布等)、填充状况、柱长、流动相的种类和流速及测定柱效所用物质的性质。
如果峰形对称并符合正态分布,N可近似表示为:理论塔板数=5.54(保留时间/半高峰宽)2 (2是平方)柱效率用理论塔板数定量地表示:N=16*(t/w )2。
其中,t是溶质从进样到最大洗脱峰出现的时间,w为该溶质的洗脱峰在基线处的宽度。
在一色谱柱中用相同的洗脱条件时候,不同化合物的滞留时间与其洗脱峰宽度之比接近常数。
因此理论塔板数大的色谱柱效率高。
当然,N的大小和柱子长度有密切关系:理论塔板高度H=柱长/N,用H可以衡量单位长度的色谱柱的效率,H越小,则色谱柱效率越高。
N为常量时,W随tR成正比例变化。
在一张多组分色谱图上,如果各组份含量相当,则后洗脱的峰比前面的峰要逐渐加宽,峰高则逐渐降低。
用半峰宽计算理论塔板数比用峰宽计算更为方便和常用,因为半峰宽更容易准确测定,尤其是对稍有拖尾的峰。
N与柱长成正比,柱越长,N越大。
用N表示柱效时应注明柱长,,如果未注明,则表示柱长为1米时的理论塔板数。
(一般HPLC柱的N在1000以上。
)若用调整保留时间(tR’)计算理论塔板数,所得值称为有效理论塔板数(N有效或Neff)=16(tR’/W)2处理方法理论塔板数下降后可以考虑色谱柱再生1.反相柱分别用甲醇:水=90:10,纯甲醇(HPLC级),异丙醇(HPLC级),二氯甲烷(HPL C级)等溶剂作为流动相,依次冲洗,每种流动相流经色谱柱不少于20倍的色谱柱体积.然后再以相反的次序冲洗.2.正相柱分别用正己烷(HPLC级),异丙醇(HPLC级),二氯甲烷(HPLC级),甲醇(H PLC级)等溶剂做流动相,顺次冲洗,每种流动相流经色谱柱不少于20倍的柱体积(异丙醇粘度大,可降低流速,避免压力过高).注意使用溶剂的次序不要颠倒,用甲醇冲洗完后,再以相反的次序冲洗至正己烷.所有的流动相必须严格脱水.3.离子交换柱长时间在缓冲溶液中使用和进样,将导致色谱柱离子交换能力下降,.用稀酸缓冲溶液冲洗可以使阳离子柱再生,反之,用稀碱缓冲溶液冲洗可以使阴离子柱再生.另外,还可以选择能溶解柱内污染物的溶剂为流动相做正方向和反方向冲洗.但再生后的色谱柱柱效是不可能恢复到新柱的水平的.如果柱子装反了,可以调回来,但可能会造成柱内担体塌陷.在不得已的情况下尽量不要反装色谱柱.梯度洗脱科技名词定义中文名称:梯度洗脱英文名称:gradient elution定义:梯度性地改变洗脱液的组分(成分、离子强度等)或pH,以期将层析柱上不同的组分洗脱出来的方法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
首先要得到相平衡方程和精馏段、提馏段方程,再根据逐板计算求得精馏塔的理论塔板数。
源程序:#include <stdio.h>#include <math.h>#include <string.h>static double R,L,F,W,T0,P,E;static double Xf,Xd,Xw,q,Xe;static double P1,P2;//td和tb的变量static double K1;static double K2;static double X1;static double X2;static double Y1;static double Y2;static double A1;static double B1;static double C1;static double A2;static double B2;static double C2;static double F1;static double F2;double Pressure(double A,double B,double C,double T){double temp1=101325.0/760.0;double temp2=A*1.0-B*1.0/(C+T)*1.0;double temp3=pow(10.0,temp2);double result=temp1*temp3;return result;}double Ftd(double y,double P1,double P2){double temp1=pow(K1,2);double temp2=pow(C1+T0,2);double temp3=pow(K2,2);double temp4=pow(C2+T0,2);double temp5=temp1*P*temp2;double temp6=temp3*P*temp4;double temp7=-1.0*y*P1*B1*log(10);double temp8=-1.0*(1-y)*P2*B2*log(10);double result=temp7/temp5+temp8/temp6;return result;}double Ftb(double x,double P1,double P2) {double temp2=pow(C1+T0,2);double temp4=pow(C2+T0,2);double temp5=P*temp2;double temp6=P*temp4;double temp7=1.0*x*P1*B1*log(10);double temp8=1.0*(1-x)*P2*B2*log(10);double result=temp7/temp5+temp8/temp6;return result;}double Tdm(double y){double Td=T0;double P1;double P2;KTdm:P1=Pressure(A1,B1,C1,Td);P2=Pressure(A2,B2,C2,Td);K1=P1*1.0/P;K2=P2*1.0/P;X1=y*1.0/K1;X2=(1-y)*1.0/K2;F1=X1+X2-1;F2=Ftd(y,P1,P2);if(fabs(F1)>=E){Td=Td-F1*1.0/F2;goto KTdm;}return Td;}double Tbm(double x){double Tb=T0;double P1;double P2;KTbm:P1=Pressure(A1,B1,C1,Tb); P2=Pressure(A2,B2,C2,Tb);K1=P1/P;K2=P2/P;Y1=x*K1;Y2=(1-x)*K2;F1=Y1+Y2-1;F2=Ftb(x,P1,P2);if(fabs(F1)>=E){Tb=Tb-F1*1.0/F2;goto KTbm;}return Tb;}void main(){double Td;double Tb;double x;double y;int n=0;int m=0;int N,M;int Nt;int flag;char end;printf("Please input R\n");scanf("%lf",&R);printf("Please input L\n");scanf("%lf",&L);printf("Please input F\n");scanf("%lf",&F);printf("Please input W\n");scanf("%lf",&W);printf("Please input P\n");scanf("%lf",&P);printf("Please input T0\n");scanf("%lf",&T0);printf("Please input E\n");scanf("%lf",&E);printf("Please input Xf\n");scanf("%lf",&Xf);printf("Please input Xd\n");scanf("%lf",&Xd);printf("Please input Xw\n");scanf("%lf",&Xw);printf("Please input q\n");scanf("%lf",&q);printf("Please input Xe\n");scanf("%lf",&Xe);printf("Please input A1\n");scanf("%lf",&A1);printf("Please input B1\n");scanf("%lf",&B1);printf("Please input C1\n");scanf("%lf",&C1);printf("Please input A2\n");scanf("%lf",&A2);printf("Please input B2\n");scanf("%lf",&B2);printf("Please input C2\n");scanf("%lf",&C2);//-----------------------------------//-----------------------------------y=Xd;flag=1;while(flag){flag=0;//-------------框框--------------x=0.0;Td=Tdm(y);P1=Pressure(A1,B1,C1,Td);P2=Pressure(A2,B2,C2,Td);K1=P1/P;K2=P2/P;Kup:Y1=x*K1;Y2=(1.0-x)*K2;if(fabs(Y1+Y2-1.0)>=E){x=1.0*(x+E);goto Kup;}//-----------------------------n=n+1;if(x>=Xe){flag=1;y=R*x/(R+1.0)+Xd/(R+1.0);}}N=n-1;//-----------------------------------//-----------------------------------x=Xw;flag=1;while(flag){flag=0;//-------------框框--------------y=1;Tb=Tbm(x);P1=Pressure(A1,B1,C1,Tb);P2=Pressure(A2,B2,C2,Tb);K1=P1/P;K2=P2/P;Kdown:X1=y/K1;X2=(1-y)/K2;if(fabs(X1+X2-1)>=E){y=y-E;goto Kdown;}//-----------------------------m=m+1;if(x<Xf){flag=1;x=1.0*(L+q*F)*y/(L+q*F-W)+1.0*W*Xw/(L+q*F-W);}}M=m;//-----------------------------------//-----------------------------------Nt=N+M;printf("\n%d\n",Nt);printf("Print any key to exit!");scanf("%c",&end);scanf("%c",&end);return;}。
