Matlab的基本操作及变量、数组及其答案
matlab期末复习题及答案

matlab期末复习题及答案1. MATLAB基础操作在MATLAB中,如何创建一个名为"myMatrix"的3x3矩阵,其元素分别为1, 2, 3, 4, 5, 6, 7, 8, 9?答案:在MATLAB中,可以通过直接输入矩阵元素来创建矩阵。
例如,要创建一个名为"myMatrix"的3x3矩阵,可以使用以下命令:```matlabmyMatrix = [1 2 3; 4 5 6; 7 8 9];```这样,MATLAB就会创建一个3x3的矩阵,其元素按照行顺序排列。
2. 矩阵运算给定两个矩阵A和B,其中A = [1 2; 3 4],B = [5 6; 7 8],计算矩阵A和B的和。
答案:在MATLAB中,可以使用加号(+)来计算两个矩阵的和。
对于给定的矩阵A和B,可以使用以下命令来计算它们的和:```matlabA = [1 2; 3 4];B = [5 6; 7 8];C = A + B;```执行上述命令后,矩阵C的结果将是:```C = [6 8;10 12];```3. 条件语句编写一个MATLAB脚本,判断一个给定的数n是否为质数,并输出相应的信息。
答案:在MATLAB中,可以使用if-else语句来判断一个数是否为质数。
以下是一个简单的脚本示例:```matlabn = input('请输入一个数:');if mod(n, 2) == 0 && n > 2disp('该数不是质数');elseif n == 1disp('1不是质数');elseisPrime = true;for i = 2:sqrt(n)if mod(n, i) == 0isPrime = false;break;endendif isPrimedisp('该数是质数');elsedisp('该数不是质数');endend```该脚本首先接收用户输入的数n,然后通过一个for循环检查n是否有除了1和它自身以外的因数,从而判断n是否为质数。
MATLAB实验:运算基础,并且附有答案

实验二、MATLAB运算基础一、实验目的掌握MATLAB各种表达式的书写规则及常用函数的使用。
掌握MATLAB中字符串、元胞数组和结构的常用函数的使用。
二、实验内容及步骤1、设有矩阵A和B,A=[1 2 3 4 5;6 7 8 9 10;11 12 13 14 15;16 1718 19 20;21 22 23 24 25],B=[3 0 16;17 -6 9;0 23 -4;9 7 0;4 1311]1)求它们的乘积C >>C=A*B2)将矩阵C的右下角3x2子矩阵赋给D >>I=[3 4 5];J=[2 3];D=C(I,J)也可以用>>D=C([3 4 5],[2 3])D =520 397705 557890 7172、完成下列操作1)求[100,999]之间能被61整除的数及其个数(提示:先利用冒号表达式,再利用find和length函数。
)>> a=100:999;find(rem(a,61)==0)ans =23 84 145 206 267 328 389 450 511572 633 694 755 816 877>> b=a(ans)b =122 183 244 305 366 427 488 549 610 671 732 793 854 915 976>> length(b)ans =152)建立一个字符串向量,删除其中的大写字母(提示:利用find函数和空矩阵。
)a=’I am maying’;a( find(a>’A’&a<’Z’))=[]3、已知A=[23 10 -78 0;41 -45 65 5;32 5 0 32;6 -54 92 14],取出其前3行构成矩阵B,其前两列构成矩阵C,其左下角3x2子矩阵构成矩阵D,B与C的乘积构成矩阵E,分别求E<D、E&D、E|D、~E|~D。
(完整版)MATLAB)课后实验答案[1]
![(完整版)MATLAB)课后实验答案[1]](https://img.taocdn.com/s3/m/f6c08c5902d276a201292ece.png)
1 + e2 (2) z = 1 ln( x + 1 + x 2 ) ,其中 x = ⎡⎢ 2⎣-0.45 ⎦2 2 ⎪t 2 - 2t + 1 2 ≤ t <3 ⎨实验一MATLAB 运算基础1. 先求下列表达式的值,然后显示 MATLAB 工作空间的使用情况并保存全部变量。
(1) z = 2sin 8501221 + 2i ⎤5 ⎥(3) z = e 0.3a - e -0.3asin(a + 0.3) + ln 0.3 + a ,a = -3.0, - 2.9, L , 2.9, 3.03⎧t 2 0 ≤ t < 1 (4) z = ⎪t 2 - 11 ≤ t <2 ,其中 t=0:0.5:2.5 4⎩解:M 文件:z1=2*sin(85*pi/180)/(1+exp(2))x=[2 1+2*i;-.45 5];z2=1/2*log(x+sqrt(1+x^2))a=-3.0:0.1:3.0;3=(exp(0.3.*a)-exp(-0.3.*a))./2.*sin(a+0.3)+log((0.3+a)./2)t=0:0.5:2.5;z4=(t>=0&t<1).*(t.^2)+(t>=1&t<2).*(t.^2-1)+(t>=2&t<3) .*(t.^2-2*t+1)4.完成下列操作:(1)求[100,999]之间能被21整除的数的个数。
(2)建立一个字符串向量,删除其中的大写字母。
解:(1)结果:m=100:999;n=find(mod(m,21)==0);length(n)ans=43(2).建立一个字符串向量例如:ch='ABC123d4e56Fg9';则要求结果是:ch='ABC123d4e56Fg9';k=find(ch>='A'&ch<='Z');ch(k)=[]ch=⎣O2⨯3⎥,其中E、R、O、S分别为单位矩阵、随机矩阵、零矩S⎦阵和对角阵,试通过数值计算验证A=⎢⎥。
MATLAB上机答案

X
1
2
3
4
5
6
7
8
9
10
Y
16
32
70
142 260 436 682 1010 1432 1960
>> x=1:10;y=[16 32 70 142 260 436 682 1010 1432 1960];
>> p1=polyfit(x,y,1)
>>
p1 =
p2=polyfit(x,y,2),y2=polyval(p2,9.5)
0.01
0.005
0
-0.005
-0.01
-0.015
0
1
2
3
4
5
6
7
(3)大气压强 p 随高度 x 变化的理论公式为
,为验证这一公式,
测得某地大气压强随高度变化的一组数据如表所示。试用插值法和拟合法进行计算并绘图,
看那种方法较为合理,且总误差最小。
高度/m
0
300
600
1000
1500
2000
压强/Pa
equally spaced points between X1 and X2. 以 X1 为首元素,X2 为末元素平均生成 100 个元素的行向量。
LINSPACE(X1, X2, N) generates N points between X1 and X2. For N < 2, LINSPACE returns X2.
ans =
pi =
ans =
5
0
3.1416
答:3 次执行的结果不一样。exist()函数是返回变量搜索顺序的一个函数。在第一次
matlab基本操作及答案

1、计算23(85log 4)sin37+⨯-.相应的MATLAB 代码及运算结果如下: >> clear>> format %结果以小数形式输出>> sin((8+5*log2(4))/(abs(3-7))^3) %输入表达式 ans =0.27762、已知634,2,2,ia ib ic eπ=+=-=计算/ab c .相应的MATLAB 代码及运算结果如下: >> clear>> a=3+4*i;b=2-i;c=2*exp(i*pi/6); >> x=a*b/c x =5.5801 - 0.3349i3、求方程3x 5-7x 4+5x 2+2x-18=0的全部根。
相应的MATLAB 代码及运算结果如下: >> clear>> p=[3,-7,0,5,2,-18]; %建立多项式系数向量,向量中的元素不多时可直接赋值 >> x=roots(p) %求根 x =2.1837 1.0000 + 1.0000i 1.0000 - 1.0000i -0.9252 + 0.7197i -0.9252 - 0.7197i4、建一个3*3矩阵,然后将第一行乘1,第二行乘2,第三行乘3。
相应的MATLAB 代码及运算结果如下: >> clear>> A=[1 2 3;2 3 4;3 4 5]; %随机3*3矩阵>> B=diag(1:3); %用diag 函数生成矩阵100020003⎛⎫ ⎪⎪ ⎪⎝⎭,此处如果不会用diag 函数的话,也可以直接把矩阵的值赋给B 矩阵>> C=B*A %用B 左乘A C =1 2 3 4 6 8 9 12 155、求积分 相应的MATLAB 代码及运算结果如下: >> clear >> syms x; %定义符号变量x >> int(x^2+x+3,1,2) %int 函数用于求积分 ans = 41/66、线性方程组的求解相应的MATLAB 代码及运算结果如下: >> clear>> A=[1 1 1;1 2 3;1 3 6];B=[3;1;4];X=A\B X = 10 -12 57、使用plot 函数在同一个坐标系中绘制[0,2π]内的正弦和余弦曲线,要求正弦曲线线型为实线、颜色为红色、数据点型为十字型,余弦曲线线型为双划线、颜色为绿色、数据点型为六角星,图形的X 轴注解为“Input Value ”,Y 轴注解为“Function Value ”,图形标题为“Two Trigonometric Functions ”,图形注解为sin()cos()y x y x ==,要求显示格线。
MATLAB基本使用方法

MATLAB基本使用方法MATLAB是一种用于科学计算和工程设计的高级编程语言和环境。
它提供了强大的数值计算、数据可视化以及矩阵和数组操作的功能。
本文将介绍MATLAB的基本使用方法,包括变量和数据类型、运算符、控制流、函数和脚本等方面。
1.变量和数据类型:在MATLAB中,变量可以存储各种类型的数据,包括数字、字符串和矩阵。
变量的命名遵循一定规则,以字母开头,不能包含空格或特殊字符。
赋值操作使用等号(=)运算符,并可用于创建新的变量。
例如:a=5;%创建变量a并赋值为5b = 'Hello'; % 创建字符串变量b并赋值为"Hello"c=[1,2,3;4,5,6];%创建矩阵变量c2.运算符:MATLAB支持各种算术和逻辑运算符,用于对变量进行操作。
常见的运算符包括加法(+)、减法(-)、乘法(*)、除法(/)、取模(mod)、取整(floor)等。
此外,还有逻辑运算符如与(&)、或(,)、非(~)等。
例如:a=5;b=2;c=a+b;%加法运算d=a>b;%比较运算3.控制流:if语句用于在满足一些条件时执行一些代码,可以包含多个条件。
例如:a=5;b=10;if a < bdisp('a小于b');elseif a == bdisp('a等于b');elsedisp('a大于b');endfor循环用于迭代执行一段代码,可以根据已知的起始值和结束值确定循环次数。
例如:for i = 1:5disp(i);endwhile循环用于在满足一些条件时重复执行一段代码,直到条件不再满足。
例如:i=1;while i <= 5disp(i);i=i+1;end4.函数和脚本:函数的定义格式如下:function [output] = function_name(input)%函数体end例如:function [c] = add_numbers(a, b)c=a+b;end脚本文件可以包含一系列命令,可以按顺序执行。
matlab入门习题答案

matlab入门习题答案Matlab入门习题答案Matlab是一种强大的数值计算和科学编程语言,广泛应用于工程、科学和数学领域。
对于初学者来说,掌握Matlab的基本语法和功能是非常重要的。
在这篇文章中,我将为大家提供一些Matlab入门习题的答案,帮助大家更好地理解和掌握Matlab的使用。
1. 编写一个Matlab程序,计算并输出1到100之间所有偶数的平方。
```matlabfor i = 2:2:100disp(i^2);end```2. 编写一个Matlab程序,计算并输出1到100之间所有奇数的和。
```matlabsum = 0;for i = 1:2:100sum = sum + i;enddisp(sum);```3. 编写一个Matlab程序,计算并输出一个数组中所有元素的平均值。
```matlabarray = [1, 2, 3, 4, 5];mean_value = mean(array);disp(mean_value);```4. 编写一个Matlab程序,将一个字符串反转并输出。
```matlabstr = 'Hello World';reverse_str = fliplr(str);disp(reverse_str);```5. 编写一个Matlab程序,计算并输出斐波那契数列的前20个数。
```matlabfibonacci = zeros(1, 20);fibonacci(1) = 0;fibonacci(2) = 1;for i = 3:20fibonacci(i) = fibonacci(i-1) + fibonacci(i-2);enddisp(fibonacci);```6. 编写一个Matlab程序,生成一个3x3的随机矩阵,并计算其转置矩阵。
```matlabmatrix = rand(3, 3);transpose_matrix = matrix';disp(transpose_matrix);```7. 编写一个Matlab程序,计算并输出一个数组中的最大值和最小值。
matlab第二版习题答案

matlab第二版习题答案Matlab是一种强大的数学软件工具,被广泛应用于科学计算、数据分析和工程设计等领域。
对于学习和掌握Matlab的人来说,习题是不可或缺的一部分。
本文将为大家提供Matlab第二版习题的答案,帮助读者更好地理解和应用Matlab。
第一章:基本操作1.1 Matlab的启动和退出启动Matlab的方法有多种,可以通过桌面图标、命令行或者启动器来打开Matlab。
退出Matlab可以直接关闭窗口或者使用命令"exit"。
1.2 Matlab的基本语法Matlab的基本语法与其他编程语言相似,包括变量的定义、运算符的使用、条件语句和循环语句等。
例如,定义一个变量x并赋值为5可以使用语句"x = 5;"。
1.3 Matlab的数据类型Matlab支持多种数据类型,包括数值型、字符型和逻辑型等。
数值型可以是整数或者浮点数,字符型用单引号或双引号表示,逻辑型只有两个值true和false。
第二章:向量和矩阵操作2.1 向量的定义和运算向量是一维数组,可以通过一对方括号来定义。
Matlab提供了丰富的向量运算函数,如加法、减法、乘法和除法等。
2.2 矩阵的定义和运算矩阵是二维数组,可以通过方括号和分号来定义。
Matlab提供了矩阵的加法、减法、乘法、转置和求逆等运算。
2.3 矩阵的索引和切片可以使用索引和切片来访问矩阵中的元素。
索引从1开始,可以使用冒号表示全部元素。
切片可以用来选择矩阵的一部分。
第三章:函数和脚本文件3.1 函数的定义和调用函数是一段独立的代码块,可以接受输入参数并返回输出结果。
在Matlab中,函数的定义以关键字"function"开头,调用函数使用函数名和参数。
3.2 脚本文件的编写和运行脚本文件是一系列Matlab语句的集合,可以保存为.m文件。
通过运行脚本文件,可以一次性执行多个语句,提高效率。
第四章:图形绘制和数据可视化4.1 图形绘制函数Matlab提供了丰富的图形绘制函数,可以绘制线图、散点图、柱状图等。
MATLAB操作命令大全

MATLAB操作命令大全1.基本操作:- clear: 清除工作区中的所有变量。
- clc: 清除命令窗口的内容。
- close all: 关闭所有图形窗口。
- help function-name: 显示与函数相关的帮助文档。
- who: 显示当前工作区中的所有变量。
- save file-name: 保存当前工作区中的所有变量到指定的文件。
- load file-name: 从文件中加载变量到当前工作区。
2.变量操作:-=:赋值操作符,将右边的值赋给左边的变量。
-+:加法操作符。
--:减法操作符。
-*:乘法操作符。
-/:除法操作符。
-^:幂运算操作符。
- sqrt(x): 计算 x 的平方根。
- abs(x): 计算 x 的绝对值。
- max(x): 返回 x 中的最大值。
- min(x): 返回 x 中的最小值。
- sum(x): 计算 x 中所有元素的和。
3.数组操作:- zeros(m, n): 创建一个 m 行 n 列的全零数组。
- ones(m, n): 创建一个 m 行 n 列的全一数组。
- eye(n): 创建一个 n 行 n 列的单位矩阵。
- size(x): 返回 x 的维度。
- length(x): 返回 x 的长度。
- reshape(x, m, n): 将 x 重新排列为一个 m 行 n 列矩阵。
- transpose(x): 将 x 的行和列互换。
4.控制流程:- if-else: 条件语句,根据条件执行不同的代码块。
- for loop: 循环语句,执行指定次数的代码块。
- while loop: 循环语句,根据条件反复执行代码块。
- break: 在循环中使用,用来跳出当前循环。
- continue: 在循环中使用,用来跳过当前循环的剩余部分。
5.统计分析:- mean(x): 计算 x 的平均值。
- median(x): 计算 x 的中位数。
- std(x): 计算 x 的标准差。
Matlab的基本数据类型和变量操作

Matlab的基本数据类型和变量操作引言Matlab是一款强大的数值计算和科学编程软件,被广泛应用于各个领域的科研、工程和教育中。
要想充分利用Matlab进行编程,了解其基本数据类型和变量操作是至关重要的。
本文将介绍Matlab的基本数据类型和变量操作,帮助读者快速上手并深入理解Matlab编程的基础知识。
一、基本数据类型1. 数值型Matlab中的数值型数据包括整数(integers)和浮点数(floating-point numbers)。
整数可以是有符号的(signed)或者无符号的(unsigned),而浮点数则可以是单精度(single)或者双精度(double)。
在Matlab中,变量的类型由其赋值决定。
例如,可以使用以下方式声明一个整数变量:```matlaba = int8(10); % 有符号8位整数b = uint16(500); % 无符号16位整数```同样,可以使用以下方式声明一个浮点数变量:```matlabc = single(3.14); % 单精度浮点数d = double(2.718); % 双精度浮点数除了基本的整数和浮点数类型,Matlab还支持复数(complex numbers),例如:```matlabz = 2 + 3i; % 复数```2. 字符型字符型数据是指由字符组成的数组,每个字符对应一个整数编码值。
在Matlab 中,可以使用单引号(')或者双引号(")将字符括起来。
```matlabstr1 = 'Hello Matlab'; % 使用单引号定义字符型变量str2 = "Hello World"; % 使用双引号定义字符型变量```可以通过索引访问字符数组中的单个字符:```matlabch = str1(1); % 取得字符数组str1中的第一个字符```3. 逻辑型逻辑型数据只有两个值:真(true)和假(false)。
MATLAB基础知识点

MATLAB基础知识点
1.MATLAB的环境与基本操作
2.数据类型与变量
MATLAB支持多种数据类型,包括数字、字符、逻辑、结构体等。
常
见的变量命名规则为字母开头,后面可以是字母、数字和下划线。
可以使
用等号将值赋给变量,使用clear命令清除变量,使用whos命令查看当
前工作区的所有变量。
3.数组与矩阵
MATLAB中的数组是一种基本的数据结构,可以包含数字、字符等元素。
矩阵是一种特殊的数组,它包含了多行和多列。
可以使用方括号创建
数组,使用分号分隔行,使用逗号或空格分隔列。
可以对数组进行元素级
别的运算,如加减乘除。
4.控制结构
MATLAB提供了各种控制结构来实现程序的流程控制,包括if语句、for循环、while循环等。
if语句用于执行条件判断,for循环用于重复
执行一段代码,while循环用于在满足其中一条件时重复执行一段代码。
5.函数与脚本文件
6.图形绘制与可视化
以上是MATLAB的一些基础知识点的简单介绍,可以帮助初学者快速
了解MATLAB的基本用法和特点。
在实际应用中,还需要深入学习和掌握MATLAB的更多功能和高级技巧,以便更好地应用于科学计算和数据处理。
MATLAB官方提供了详细的文档和教程,可以帮助用户深入学习和使用MATLAB。
matlab第二版课后习题答案

matlab第二版课后习题答案
《MATLAB第二版课后习题答案》
MATLAB是一种强大的数学软件,被广泛应用于工程、科学和金融等领域。
《MATLAB第二版》是一本经典的教材,为了帮助学生更好地掌握MATLAB的使用,书中提供了大量的课后习题。
下面我们将为大家总结一些MATLAB第二版课后习题的答案,希望能对大家的学习有所帮助。
1. 第一章课后习题答案
第一章主要介绍了MATLAB的基本操作,包括变量的定义、矩阵的运算、函数的使用等。
在课后习题中,有一道题目是要求计算一个矩阵的逆矩阵。
答案是使用MATLAB中的inv函数,将原矩阵作为参数传入即可得到逆矩阵。
2. 第二章课后习题答案
第二章介绍了MATLAB中的绘图功能,包括二维和三维图形的绘制。
有一道课后习题是要求绘制一个正弦曲线和余弦曲线,并在同一张图上显示。
答案是使用MATLAB中的plot函数,分别绘制正弦曲线和余弦曲线,并使用legend函数添加图例。
3. 第三章课后习题答案
第三章介绍了MATLAB中的控制流程,包括if语句、for循环和while循环等。
有一道课后习题是要求编写一个程序,计算1到100之间所有偶数的和。
答案是使用for循环遍历1到100之间的所有数,判断是否为偶数并累加。
通过以上几个例子,我们可以看到MATLAB第二版课后习题的答案涵盖了各种基本和高级的操作,对于学习MATLAB是非常有帮助的。
希望大家在学习MATLAB的过程中能够多加练习,掌握更多的技巧和方法。
matlab教材习题答案

matlab教材习题答案Matlab是一种广泛应用于科学与工程领域的计算机编程语言和环境。
它具备强大的数值计算和数据可视化功能,被广泛用于数据分析、信号处理、图像处理、机器学习等领域。
对于初学者而言,掌握Matlab的基本语法和常用函数是非常重要的,而教材习题则是帮助学生巩固所学知识的重要资源。
本文将为大家提供一些Matlab教材习题的参考答案,以帮助读者更好地学习和应用Matlab。
1. 基本语法练习题1.1 计算并输出1到10的平方for i = 1:10fprintf('%d的平方是:%d\n', i, i^2);end1.2 计算并输出1到10的阶乘for i = 1:10fact = 1;for j = 1:ifact = fact * j;endfprintf('%d的阶乘是:%d\n', i, fact);end2. 数值计算练习题2.1 求解一元二次方程的根a = 1;b = -3;c = 2;delta = b^2 - 4*a*c;x1 = (-b + sqrt(delta))/(2*a);x2 = (-b - sqrt(delta))/(2*a);fprintf('一元二次方程的根为:%f, %f\n', x1, x2);2.2 求解线性方程组的解A = [1 2; 3 4];B = [5; 6];X = inv(A) * B;fprintf('线性方程组的解为:%f, %f\n', X(1), X(2));3. 数据处理练习题3.1 统计一个数组中的最大值、最小值和平均值data = [1, 2, 3, 4, 5];max_value = max(data);min_value = min(data);average_value = mean(data);fprintf('最大值:%f\n最小值:%f\n平均值:%f\n', max_value, min_value, average_value);3.2 对一个矩阵进行排序matrix = [4 2 3; 1 5 6; 9 8 7];sorted_matrix = sort(matrix);fprintf('排序后的矩阵为:\n');disp(sorted_matrix);4. 图像处理练习题4.1 读取并显示一张图片image = imread('image.jpg');imshow(image);4.2 对一张图片进行灰度化处理gray_image = rgb2gray(image);imshow(gray_image);5. 信号处理练习题5.1 生成并绘制正弦信号t = 0:0.01:2*pi;x = sin(t);plot(t, x);5.2 对一段音频信号进行傅里叶变换[y, fs] = audioread('audio.wav');Y = fft(y);plot(abs(Y));通过以上几个例子,我们可以看到Matlab的强大功能和灵活性。
Matlab的基本操作及变量、数组及其答案
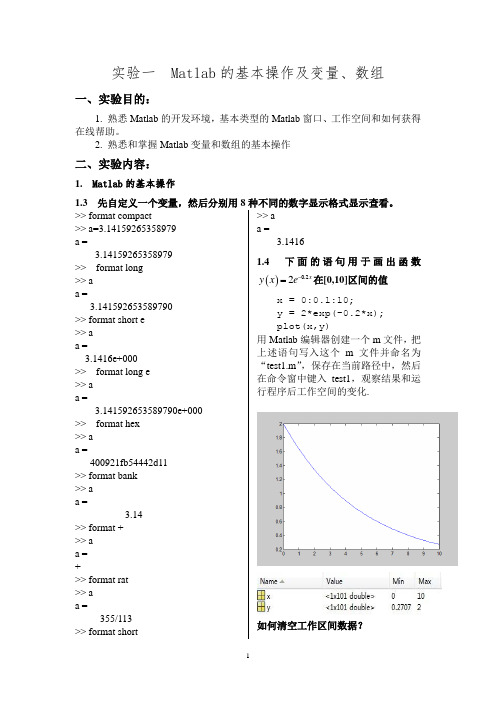
实验一Matlab的基本操作及变量、数组一、实验目的:1. 熟悉Matlab的开发环境,基本类型的Matlab窗口、工作空间和如何获得在线帮助。
2. 熟悉和掌握Matlab变量和数组的基本操作二、实验内容:1. Matlab的基本操作1.3 先自定义一个变量,然后分别用8种不同的数字显示格式显示查看。
>> format compact>> a=3.14159265358979a =3.14159265358979>> format long>> aa =3.141592653589790>> format short e>> aa =3.1416e+000>> format long e>> aa =3.141592653589790e+000 >> format hex>> aa =400921fb54442d11>> format bank>> aa =3.14>> format +>> aa =+>> format rat>> aa =355/113>> format short>> aa =3.14161.4 下面的语句用于画出函数()0.22xy x e-=在[0,10]区间的值x = 0:0.1:10;y = 2*exp(-0.2*x);plot(x,y)用Matlab编辑器创建一个m文件,把上述语句写入这个m文件并命名为“test1.m”,保存在当前路径中,然后在命令窗中键入test1,观察结果和运行程序后工作空间的变化.如何清空工作区间数据? 键入 clear ;如何关闭图像窗口? 键入close ;除了在命令窗输入文件名,还可以怎样运行一个m 文件程序?点击file ,打开m 文件,点击Run 按钮,运行m 文件程序。
试验一:matlab语言的基本使用方法及答案

试验一:matlab语言的基本使用方法及答案【一】实验目的:了解matlab 语言的上机环境,熟悉其主要视窗的使用方法。
熟悉利用Matlab 进行基本的数学运算【二】实验内容1、 Matlab 指令窗的悬停与还原,指令窗中各种标点符号的作用2、历史命令窗口的操作。
历史命令的重新运行,单行命令的运行,不连续多行命令的运行,连续多行命令的运行,历史命令窗口右键快捷菜单各命令的操作。
3、工作空间操作。
工作空间右键快捷方式各种命令的应用4、明确搜索路径对于Matlab 的作用,熟练搜索路径的修改5、使用format 命令查看pi 的各种显示格式6、令A=1.2,B=-4.6,C=8.0,D=3.5, E=-4.0 计算)22arctan(DBC E A T ππ+=并将计算过程保存成M-file 运算 7、令a=5.67,b=7.8 计算)lg(b a e ba ++ 8、已知半径为15的圆,求其直径,周长及面积9、已知三角形三边长分别为a=8.5,b=14.6,c=18.4,求其面积提示area=sqrt (s (s-a )(s-b )(s-c ))S=(a+b+c )/210、计算 y=sin(x)ln(1+x)-x 2其中x=[1 2 3 4 5 ],并画出x ,y 的函数关系11、设 75,24=-=b a ,计算|)tan(||)||sin(|b a b a ++的值。
12、分别画出函数x x y cos 2=和x xz sin =在区间[-6π,6π]上的图形。
实验一:6~~令A=1.2,B=-4.6,C=8.0,D=3.5, E=-4.0 计算)22arctan(DBC E A T ππ+=并将计算过程保存成M-file 运算 >> A=1.2;B=-4.6;C=8.0;D=3.5;E=-4.0;>> T=atan((2*pi*A+E/(2*pi*B*C))/D)T =1.1371>>7~令a=5.67,b=7.8 计算)lg(b a e ba ++ >> a=5.67;b=7.8;>> c=exp(a+b)/log10(a+b)c =6.2677e+005>>10计算 y=sin(x)ln(1+x)-x 2其中x=[1 2 3 4 5 ],并画出x ,y 的函数关系 >> x=[1,2,3,4,5];>> y=sin(x).*log(1+x)-x.*x;>> plot(x,y)>>11设 75,24=-=b a ,计算|)tan(||)||sin(|b a b a ++的值。
matlab试题及答案开卷

matlab试题及答案开卷1. MATLAB基础操作在MATLAB中,如何创建一个名为“myMatrix”的3x3矩阵,其元素从1到9按顺序排列?答案:在MATLAB中,可以使用以下命令创建名为“myMatrix”的3x3矩阵:```matlabmyMatrix = [1 2 3; 4 5 6; 7 8 9];```或者使用内置函数`magic`:```matlabmyMatrix = magic(3);```2. 矩阵运算给定两个矩阵A和B,其中A = [2 3; 4 5],B = [6 7; 8 9],计算A+B的结果。
答案:在MATLAB中,可以使用加号`+`来计算两个矩阵的和:```matlabA = [2 3; 4 5];B = [6 7; 8 9];C = A + B;```计算结果C为:```matlabC = [8 10; 12 14];```3. 向量操作创建一个从0到1的等差数列,步长为0.1。
答案:在MATLAB中,可以使用`linspace`函数或`:`操作符来创建等差数列:```matlabv = 0:0.1:1;```或者使用`linspace`函数:```matlabv = linspace(0, 1, 11);```两种方法都将得到一个包含11个元素的向量,从0开始,到1结束,步长为0.1。
4. 条件语句编写一个MATLAB脚本,判断一个给定的数n是否为素数。
答案:可以通过以下MATLAB脚本来判断一个数n是否为素数:```matlabfunction isPrime = isPrimeNumber(n)if n <= 1isPrime = false;elsefor i = 2:sqrt(n)if mod(n, i) == 0isPrime = false;return;endendisPrime = true;endend```调用此函数时,传入一个数值n,函数将返回一个布尔值,表示n 是否为素数。
第二讲 MATLAB基本操作

三、矩阵及其运算
(四)矩阵的基本数值运算
(1)矩阵与常数的四则运算(同向量与数的四则运算) 矩阵与常数的四则运算(同向量与数的四则运算) 矩阵与常数的四则运算是指矩阵各元素与常 数之间的四则运算。 数之间的四则运算。 例如: 例如 a=[1,2,3;4,5,6;7,8,9]; 求: c=a+2; d=a-2; e=a*2; f=a/2;
(一)矩阵的生成
矩阵的生成有多种方式,通常使用的有四种: 矩阵的生成有多种方式,通常使用的有四种: (1)在命令窗口中直接输入矩阵; 在命令窗口中直接输入矩阵; 把矩阵的元素直接排列到方括号中, 把矩阵的元素直接排列到方括号中,每行 内的元素用空格或逗号相隔, 内的元素用空格或逗号相隔,行于行之间的内 容用分号相隔。 容用分号相隔。 通过语句和函数产生矩阵; (2)通过语句和函数产生矩阵; 文件中建立矩阵; (3)在M文件中建立矩阵; 从外部的数据文件中导入矩阵; (4)从外部的数据文件中导入矩阵; 例如: 例如 a=[1 2 3;4 5 6;7 8 9], b=[2,4,6,8;1,3,5,7;1,2,3,4],
四、数组及其运算
(一)数组的生成
(1)在命令窗口中直接输入向量 格式:a=[a1,a2,a3, …an ] 格式: (2)等差元素向量的生成 生成法: 格式: (i)冒号“:”生成法: 格式:a=a1:m:an )冒号“ (ii)使用线性等分向量函数 )使用线性等分向量函数linspace法: 法 格式: 格式:a=linspace(a1,an,n)
三、矩阵及其运算
(三)矩阵中元素的操作
的第r行 (1)提取矩阵 的第 行:A(r,:) )提取矩阵A的第 ( ,:) 的第r列 (:,r) (2)提取矩阵 的第 列:A(:, ) )提取矩阵A的第 (:, 的每一列, 拉伸为一个列向量: (:) (3)依次提取矩阵 的每一列,将A拉伸为一个列向量:A(:) )依次提取矩阵A的每一列 拉伸为一个列向量 (4)取矩阵 的第 1~i2行、第j1~j2列构成新矩阵 的第i 列构成新矩阵:A(i1:i2, j1:j2) )取矩阵A的第 的第i 构成新矩阵:A(i2:-1:i1,:) (5)以逆序提取矩阵 的第 1~i2行,构成新矩阵 )以逆序提取矩阵A的第 : 的第j 构成新矩阵:A(:, j2:-1:j1 ) (6)以逆序提取矩阵 的第 1~j2列,构成新矩阵 )以逆序提取矩阵A的第 : 的第i 构成新矩阵:A(i1:i2,: ] ,:)=[ (7)删除 的第 1~i2行,构成新矩阵 )删除A的第 的第j 构成新矩阵:A(:, (8)删除 的第 1~j2列,构成新矩阵 :, j1:j2)=[ ] )删除A的第 拼接成新矩阵: (9)将矩阵 和B拼接成新矩阵:[A B];[A;B] )将矩阵A和 拼接成新矩阵 ; ;
matlab基础教程课后答案

matlab基础教程课后答案MATLAB是一种用于数值计算和数据可视化的高级编程语言和环境。
它广泛应用于科学、工程和金融等领域。
下面是MATLAB基础教程的课后答案,希望能帮助你更好地理解和掌握MATLAB的基本概念和操作。
1.MATLAB基础知识 (1) MATLAB是什么?它的特点和优势是什么?答:MATLAB是一种高级的编程语言和环境,用于数值计算和数据可视化。
它的特点和优势包括:•简单易学:MATLAB语法与数学表达式类似,易于理解和使用。
•功能强大:MATLAB提供了丰富的数值计算和数据处理函数,可以方便地进行各种科学计算和数据分析。
•可视化能力强:MATLAB内置了丰富的绘图函数,可以直观地展示数据和结果。
•扩展性好:MATLAB支持用户自定义函数和工具包,可以根据需要扩展功能。
•跨平台:MATLAB可以在Windows、Mac和Linux等操作系统上运行。
(2) 如何定义变量并赋值?答:在MATLAB中,可以使用等号(=)将一个值赋给一个变量。
例如,要将数值3赋给变量x,可以输入x=3。
(3) 如何进行算术运算?答:MATLAB支持常见的算术运算,包括加法、减法、乘法和除法。
可以使用+、-、*和/符号进行运算。
例如,要计算2加上3的结果,可以输入2+3。
(4) 如何进行矩阵运算?答:在MATLAB中,可以使用方括号([])来定义矩阵。
例如,要定义一个2×2的矩阵A,可以输入A=[1 2; 3 4]。
可以使用符号进行矩阵乘法运算。
例如,要计算矩阵A乘以矩阵B的结果,可以输入A B。
2.MATLAB的基本函数和操作 (1) 如何使用help命令查看函数的帮助文档?答:在MATLAB命令窗口中,可以使用help命令查看函数的帮助文档。
例如,要查看sin函数的帮助文档,可以输入help sin。
(2) 如何生成随机数?答:MATLAB提供了rand函数用于生成服从均匀分布的随机数。
MATLAB操作命令大全

MATLAB操作命令大全1.基本操作- help:查看函数的帮助文档。
- save:将变量保存到文件中。
- load:从文件中加载变量。
- clear:清除当前工作空间中的变量。
- who:列出当前工作空间中的变量。
- whos:显示当前工作空间中变量的详细信息。
- quit:退出MATLAB。
2.变量操作-=:赋值操作,将值赋给变量。
- disp:显示变量的值。
- length:返回数组的长度。
- size:返回数组的大小。
- max:返回数组的最大值。
- min:返回数组的最小值。
- sum:返回数组元素的和。
3.数学操作-+:加法操作,将两个数值相加。
--:减法操作,将两个数值相减。
-*:乘法操作,将两个数值相乘。
-/:除法操作,将两个数值相除。
-^:指数操作,将一个数值提高到指定次幂。
- sqrt:返回一个数值的平方根。
- abs:返回一个数值的绝对值。
4.矩阵操作- eye:创建一个单位矩阵。
- zeros:创建一个全0矩阵。
- ones:创建一个全1矩阵。
- rand:创建一个0到1之间的随机矩阵。
- diag:返回对角线元素。
- inv:返回矩阵的逆矩阵。
- det:返回矩阵的行列式。
5.图形操作- plot:绘制二维线图。
- scatter:绘制散点图。
- bar:绘制柱状图。
- hist:绘制直方图。
- surf:绘制三维曲面图。
- contour:绘制等高线图。
- imagesc:绘制矩阵的颜色图。
6.控制流程操作- if:用于条件判断。
- for:用于循环操作。
- while:用于循环操作。
- switch:用于多条件判断。
- break:跳出循环。
- continue:跳过当前循环,并继续执行下一次循环。
7.文件操作- fopen:打开文件。
- fclose:关闭文件。
- fprintf:将数据写入文件。
- fscanf:从文件中读取数据。
- fseek:设置文件指针的位置。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一Matlab的基本操作及变量、数组
一、实验目的:
1. 熟悉Matlab的开发环境,基本类型的Matlab窗口、工作空间和如何获得在线帮助。
2. 熟悉和掌握Matlab变量和数组的基本操作
二、实验内容:
1. Matlab的基本操作
1.3 先自定义一个变量,然后分别用8种不同的数字显示格式显示查看。
>> format compact
>> a=3.14159265358979
a =
3.14159265358979
>> format long
>> a
a =
3.141592653589790
>> format short e
>> a
a =
3.1416e+000
>> format long e
>> a
a =
3.141592653589790e+000 >> format hex
>> a
a =
400921fb54442d11
>> format bank
>> a
a =
3.14
>> format +
>> a
a =
+
>> format rat
>> a
a =
355/113
>> format short
>> a
a =
3.1416
1.4 下面的语句用于画出函数()0.2
2x
y x e-
=在[0,10]区间的值
x = 0:0.1:10;
y = 2*exp(-0.2*x);
plot(x,y)
用Matlab编辑器创建一个m文件,把上述语句写入这个m文件并命名为“test1.m”,保存在当前路径中,然后在命令窗中键入test1,观察结果和运行程序后工作空间的变化.
如何清空工作区间数据? 键入 clear ;
如何关闭图像窗口? 键入close ;
除了在命令窗输入文件名,还可以怎样运行一个m 文件程序?
点击file ,打开m 文件,点击Run 按钮,运行m 文件程序。
如果希望在命令窗中显示x 和y 的所有取值,应对程序做出怎么样的修改?
x = 0:0.1:10;
y = 2*exp(-0.2*x); plot(x,y); x,y
1.5 通过以下两种方式得到关于exp 函数的帮助:
(1) 在命令窗中输入help exp 命令; (2) 运用帮助空间窗口。
思考,用什么指令可以直接打开帮助空间中关于exp 函数的说明?
键入doc exp ;或者点击help ,再点击product help ,键入exp 搜索. 1.6 假设x =3,y = 4,用Matlab 计算下列表达式: (1)
()
23
2
x y x y - (2)
43x
y
(3) 24x x π-
(4) 3
3x
x x y -
>> format compact >> x=3,y=4 x = 3 y = 4
>> x^2*(y^3)/(x-y)^2
ans = 576
>> 4*x/(3*y) ans = 1
>> 4/x*(pi*x^(-2)) ans =
0.4654
>> x^3/(x^3-y^x) ans =
-0.7297
1.7 在当前目录下创建一个m 文件,
键入以下程序并保存,先把文件保存为“2.m ”,运行后观察结果,总结m 文件的文件名(包括Matlab 标识符)命名规则。
对该文件重新命名后运行,保存运行结果。
t = -2*pi:pi/10:2*pi; y = abs(sin(t)); plot(t,y) >> 2 ans = 2
重新命名m 文件后运行的结果:
总结m文件的文件名(包括Matlab标识符)命名规则。
在Matlab中,不能够区别以数字命名的文件是文件名还是数字,不能以单独的数字命名。
变量和常量的标识符最长允许19个字符,函数和文件名则通常不超过8个字符,这些字符包括全部的英文字母,阿拉伯数字和下划线等符号。
标识符中的第一个字符必须是英文字母。
Matlab对大小写敏感。
2. 变量及数组
2.1 在命令窗中输入数组
123
456
789
⎡⎤
⎢⎥
=⎢⎥
⎢⎥
⎣⎦
A,观察输出结果,然后依次实现:
1. 把第4行第2列元素赋值为11
2. 把第五行元素赋值为-13、-14、-15
3. 把第4行第2列元素赋值为第5行第1列元素的绝对值
4. 抽取A的第2行和第5行
5. 把第4
(4+5)/6*2、-7
6. 把A的第1、4行和2、3列相交的元素构成矩阵赋给A1
7. 把A的第1-4行和2-3列相交的元素构成矩阵赋给A2
>> format compact
>> A=[1 2 3;4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> A(4,2)=11
A =
1 2 3
4 5 6
7 8 9
0 11 0
>> A(5, : )=[-13,-14,-15]
A =
1 2 3
4 5 6
7 8 9
0 11 0
-13 -14 -15
>> A(4,2)=abs(A(5,1))
A =
1 2 3
4 5 6 7 8 9
0 13 0
-13 -14 -15
>> A([1,3,4], :)=[]
A =
4 5 6
-13 -14 -15
>> A(4, :)= [sqrt(3),(4+5)/6*2,-7]
A =
4.0000
5.0000
6.0000
-13.0000 -14.0000 -15.0000
0 0 0
1.7321 3.0000 -7.0000 >> A1=A([1,4],[2,3])
A1 =
5 6
3 -7
>> A2=A([1,2,3,4],[2,3])
A2 =
5 6
-14 -15
0 0
3 -7
2.2 在Matlab命令窗口输入:B=[3+4i,1+2i;7+8i,5+6i],观察输出的结果。
1. 试一试还能够用什么形式输出一个矩阵C,结果和上式一样?
2. 求复数2+3i的开方,赋给D
3. 计算D*D
4. 求C的共轭转置矩阵
5. 求C的转置矩阵
6. 求C的共轭矩阵
>> format compact
>> B=[3+4i,1+2i;7+8i,5+6i]
B =
3.0000 +
4.0000i 1.0000 + 2.0000i
7.0000 + 8.0000i 5.0000 + 6.0000i
>> C=[3,1;5,7]+[4,2;8,6]*i
C =
3.0000 +
4.0000i 1.0000 + 2.0000i
5.0000 + 8.0000i 7.0000 +
6.0000i
>> D=sqrt(2+3i)
D =
1.6741 + 0.8960i
>> D*D
ans =
2.0000 +
3.0000i
>> C'
ans =
3.0000 -
4.0000i
5.0000 - 8.0000i
1.0000 -
2.0000i 7.0000 - 6.0000i
>> conj(C)
ans =
3.0000 -
4.0000i 1.0000 - 2.0000i
5.0000 - 8.0000i 7.0000 -
6.0000i
>> conj(C)'
ans =
3.0000 +
4.0000i
5.0000 + 8.0000i
1.0000 +
2.0000i 7.0000 + 6.0000i。
