函数综合练习1
高一数学必修一函数练习题

高一数学必修一函数练习题函数是高中数学中非常重要的概念,它描述了两个集合之间的一种对应关系。
下面为高一学生准备了一系列函数练习题,以帮助学生更好地理解和掌握函数的基本概念和性质。
练习题一:函数的定义域与值域1. 给定函数 \( f(x) = \frac{1}{x - 2} \),求其定义域。
2. 对于函数 \( g(x) = x^2 - 4x + 3 \),找出其值域。
练习题二:函数的单调性1. 判断函数 \( h(x) = x^3 - 3x \) 在 \( x \in (-\infty,\infty) \) 上的单调性。
2. 若函数 \( k(x) = 2x - 1 \) 在 \( x \in [0, 2] \) 上单调递增,求 \( k(x) \) 在 \( x \in [2, 4] \) 上的单调性。
练习题三:函数的奇偶性1. 判断函数 \( f(x) = |x| \) 是否为奇函数或偶函数。
2. 若函数 \( g(x) = x^2 + 1 \) 是偶函数,求证。
练习题四:复合函数1. 已知 \( f(x) = x^2 \) 和 \( g(x) = x + 3 \),求复合函数\( (f \circ g)(x) \)。
2. 若 \( h(x) = \sqrt{x} \) 和 \( k(x) = x - 1 \),求 \( (h \circ k)(x) \)。
练习题五:反函数1. 若 \( f(x) = 2x + 1 \),求其反函数 \( f^{-1}(x) \)。
2. 对于函数 \( g(x) = x^2 \),讨论其反函数的存在性。
练习题六:函数的图像与性质1. 画出函数 \( y = |x - 1| \) 的图像,并标出其顶点坐标。
2. 对于函数 \( y = x^3 \),描述其在 \( x = 0 \) 附近的图像变化趋势。
练习题七:函数的实际应用1. 某工厂生产的产品数量与时间的关系为 \( P(t) = 100t - 5t^2 \),求出生产量达到最大时的时间。
高中数学:函数单调性和奇偶性的综合练习及答案

高中数学:函数单调性和奇偶性的综合练习及答案1.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是()A.y=x3B.y=|x|+1C.y=-x2+1D.y=2-|x|2.f(x)=x2+|x|()A.是偶函数,在(-∞,+∞)上是增函数B.是偶函数,在(-∞,+∞)上是减函数C.不是偶函数,在(-∞,+∞)上是增函数D.是偶函数,且在(0,+∞)是增函数3.已知函数f(x)=3x-(x≠0),则函数()A.是奇函数,且在(0,+∞)上是减函数B.是偶函数,且在(0,+∞)上是减函数C.是奇函数,且在(0,+∞)上是增函数D.是偶函数,且在(0,+∞)上是增函数4.定义在R上偶函数f(x)在[1,2]上是增函数,且具有性质f(1+x)=f(1-x),则函数f(x)()A.在[-1,0]上是增函数B.在[-1,-]上增函数,在(-,0]上是减函数C.在[1,0]上是减函数D.在[-1,-]上是减函数,在(-,0]上是增函数5.f(x)是定义在R上的增函数,则下列结论一定正确的是()A.f(x)+f(-x)是偶函数且是增函数B.f(x)+f(-x)是偶函数且是减函数C.f(x)-f(-x)是奇函数且是增函数D.f(x)-f(-x)是奇函数且是减函数6.已知偶函数f(x)在区间[0,+∞)上的解析式为f(x)=x+1,下列大小关系正确的是()A.f(1)>f(2)B.f(1)>f(-2)C.f(-1)>f(-2)D.f(-1)<f(2)7.已知f(x)是偶函数,对任意的x1,x2∈(-∞,-1],都有(x2-x1)[f(x2)-f(x1)]<0,则下列关系式中成立的是()A.f<f(-1)<f(2)B.f(-1)<f<f(2)C.f(2)<f(-1)<fD.f(2)<f<f(-1)8.定义在区间(-∞,+∞)上的奇函数f(x)为增函数;偶函数g(x)在区间[0,+∞)上的图象与f (x)的图象重合.设a>b>0,给出下列不等式①f(b)-f(-a)>g(a)-g(-b);②f(b)-f(-a)<g(a)-g(-b);③f(a)-f(-b)>g(b)-g(-a);④f(a)-f(-b)<g(b)-g(-a).其中成立的是()A.①与④B.②与③C.①与③D.②与④9.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x2-x1)·[f(x2)-f (x1)]>0,则当n∈N*时,有()A.f(-n)<f(n-1)<f(n+1)B.f(n-1)<f(-n)<f(n+1)C.f(n+1)<f(-n)<f(n-1)D.f(n+1)<f(n-1)<f(-n)10.若函数f(x)是奇函数,且在(-∞,0)上是增函数,又f(-2)=0,则x·f(x)<0的解集是()A.(-2,0)∪(0,2)B.(-∞,-2)∪(0,2)C.(-∞,-2)∪(2,+∞)D.(-2,0)∪(2,+∞)11.已知定义在R上的函数f(x)在(-∞,-2)上是减函数,若g(x)=f(x-2)是奇函数,且g(2)=0,则不等式xf(x)≤0的解集是()A.(-∞,-2]∪[2,+∞)B.[-4,-2]∪[0,+∞)C.(-∞,-4]∪[-2,+∞)D.(-∞,-4]∪[0,+∞)12.设f(x)为奇函数,且在(-∞,0)内是减函数,f(-2)=0,则x·f(x)<0的解集为()A.(-1,0)∪(2,+∞)B.(-∞,-2)∪(0,2)C.(-∞,-2)∪(2,+∞)D.(-2,0)∪(0,2)13.若函数f(x)=ax2+(2+a)x+1是偶函数,则函数f(x)的单调增区间为()A.(-∞,0]B.[0,+∞)C.(-∞,+∞)D.[1,+∞)14.已知函数f(x)=x|x|-2x,则下列结论正确的是________.(填写序号)①f(x)是偶函数,递增区间是(0,+∞);②f(x)是偶函数,递减区间是(-∞,1);③f(x)是奇函数,递减区间是(-1,1);④f(x)是奇函数,递增区间是(-∞,0).15.若f(x)是偶函数,其定义域为(-∞,+∞),且在[0,+∞)上是减函数,设f=m,f=n,则m,n的大小关系是________.16.已知函数f(x)=(k-2)x2+(k-1)x+3是偶函数,则f(x)的单调递增区间是________.17.已知函数y=f(x)的图象关于原点对称,且当x>0时,f(x)=x2-2x+3.(1)试求f(x)在R上的解析式;(2)画出函数的图象,根据图象写出它的单调区间.18.设f(x)是偶函数,g(x)是奇函数,且f(x)+g(x)=x2+2x,求函数f(x),g(x)的解析式.19.已知函数f(x)=-x3+3x.求证:(1)函数f(x)是奇函数;(2)函数f(x)在区间(-1,1)上是增函数.20.已知函数f(x)=ax++c(a,b,c是常数)是奇函数,且满足f(1)=,f(2)=. (1)求a,b,c的值;(2)试判断函数f(x)在区间上的单调性并证明.21.设定义域为R的函数f(x)=(1)在平面直角坐标系内作出函数f(x)的图象,并指出f(x)的单调区间(不需证明);(2)若方程f(x)+2a=0有两个解,求出a的取值范围(只需简单说明,不需严格证明);(3)设定义为R的函数g(x)为奇函数,且当x>0时,g(x)=f(x),求g(x)的解析式.22.已知函数f(x)=ax+(x≠0,常数a∈R).(1)讨论函数f(x)的奇偶性,并说明理由;(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围.答案1.下列函数中,既是偶函数又在(0,+∞)上单调递增的函数是()A.y=x3B.y=|x|+1C.y=-x2+1D.y=2-|x|【答案】B【解析】∵y=x3在定义域R上是奇函数,∴A不对;y=-x2+1在定义域R上是偶函数,但在(0,+∞)上是减函数,故C不对;D中y=2-|x|=|x|虽是偶函数,但在(0,+∞)上是减函数,只有B对.2.f(x)=x2+|x|()A.是偶函数,在(-∞,+∞)上是增函数B.是偶函数,在(-∞,+∞)上是减函数C.不是偶函数,在(-∞,+∞)上是增函数D.是偶函数,且在(0,+∞)是增函数【答案】D3.已知函数f(x)=3x-(x≠0),则函数()A.是奇函数,且在(0,+∞)上是减函数B.是偶函数,且在(0,+∞)上是减函数C.是奇函数,且在(0,+∞)上是增函数D.是偶函数,且在(0,+∞)上是增函数【答案】C【解析】因为f(-x)=-3x+=-(3x-)=-f(x),又因为f(x)在(0,+∞)上是增函数,所以f(x)是奇函数,且在(0,+∞)上是增函数.4.定义在R上偶函数f(x)在[1,2]上是增函数,且具有性质f(1+x)=f(1-x),则函数f(x)()A.在[-1,0]上是增函数B.在[-1,-]上增函数,在(-,0]上是减函数C.在[1,0]上是减函数D.在[-1,-]上是减函数,在(-,0]上是增函数【答案】A【解析】因为f(1+x)=f(1-x),所以函数f(x)的图象关于直线x=1对称,又f(x)为偶函数,且在[1,2]上是增函数,所以f(x)在[-1,0]上是增函数.5.f(x)是定义在R上的增函数,则下列结论一定正确的是()A.f(x)+f(-x)是偶函数且是增函数B.f(x)+f(-x)是偶函数且是减函数C.f(x)-f(-x)是奇函数且是增函数D.f(x)-f(-x)是奇函数且是减函数【答案】C【解析】A错误.设f(x)=x,是增函数,但f(x)+f(-x)=x-x=0是常数函数;同理B错误;C正确.设g(x)=f(x)-f(-x),则g(-x)=f(-x)-f(x)=-[f(x)-f(-x)]=-g(x),函数g(x)是奇函数.任取x1,x2∈R,且x1<x2,则-x1>-x2,g(x1)=f(x1)-f(-x1),g(x2)=f(x2)-f(-x2),因为f(x)是定义在R上的增函数,所以f(x1)<f(x2),f(-x1)>f(-x2),即-f(-x1)<-f(-x2).所以f(x1)-f(-x1)<f(x2)-f(-x2),即g(x1)<g(x2).所以函数g(x)=f(x)-f(-x)是增函数;D错误.故选C.6.已知偶函数f(x)在区间[0,+∞)上的解析式为f(x)=x+1,下列大小关系正确的是()A.f(1)>f(2)B.f(1)>f(-2)C.f(-1)>f(-2)D.f(-1)<f(2)【答案】D【解析】∵当x≥0时,f(x)=x+1是增函数,∴f(1)<f(2),又∵f(x)为偶函数,∴f(1)=f(-1),f(2)=f(-2),7.已知f(x)是偶函数,对任意的x1,x2∈(-∞,-1],都有(x2-x1)[f(x2)-f(x1)]<0,则下列关系式中成立的是()A.f<f(-1)<f(2)B.f(-1)<f<f(2)C.f(2)<f(-1)<fD.f(2)<f<f(-1)【答案】B【解析】∵对任意的x1,x2∈(-∞,-1],都有(x2-x1)[f(x2)-f(x1)]<0,∴函数f(x)在(-∞,-1]上单调递减,∴f(-2)>f>f(-1).又∵f(x)是偶函数,∴f(-2)=f(2).∴f(-1)<f<f(2).8.定义在区间(-∞,+∞)上的奇函数f(x)为增函数;偶函数g(x)在区间[0,+∞)上的图象与f (x)的图象重合.设a>b>0,给出下列不等式()①f(b)-f(-a)>g(a)-g(-b);②f(b)-f(-a)<g(a)-g(-b);③f(a)-f(-b)>g(b)-g(-a);④f(a)-f(-b)<g(b)-g(-a).其中成立的是()A.①与④B.②与③C.①与③D.②与④【答案】C【解析】因为函数f(x)为增函数,偶函数g(x)在区间[0,+∞)的图象与f(x)的图象重合,所以函数g(x)在[0,+∞)上是增函数,在(-∞,0)上是减函数.a>b>0,f(a)>f(b),g(a)>g(b),所以f(a)+g(a)>f(b)+g(b);对于①:f(b)-f(-a)>g(a)-g(-b),即f(b)+f(a)>g(a)-g(b).正确;则②错误;对于③:f(a)-f(-b)>g(b)-g(-a),即f(a)+f(b)>g(b)-g(a).正确;则④错误.9.定义在R上的偶函数f(x)满足:对任意的x1,x2∈(-∞,0](x1≠x2),有(x2-x1)·[f(x2)-f (x1)]>0,则当n∈N*时,有()A.f(-n)<f(n-1)<f(n+1)B.f(n-1)<f(-n)<f(n+1)C.f(n+1)<f(-n)<f(n-1)D.f(n+1)<f(n-1)<f(-n)【答案】C【解析】由(x2-x1)[f(x2)-f(x1)]>0,得f(x)在x∈(-∞,0]上为增函数.又f(x)为偶函数,∴f(x)在x∈[0,+∞)上为减函数.又f(-n)=f(n)且0≤n-1<n<n+1,∴f(n+1)<f(n)<f(n-1),即f(n+1)<f(-n)<f(n-1).10.若函数f(x)是奇函数,且在(-∞,0)上是增函数,又f(-2)=0,则x·f(x)<0的解集是()A.(-2,0)∪(0,2)B.(-∞,-2)∪(0,2)C.(-∞,-2)∪(2,+∞)D.(-2,0)∪(2,+∞)【答案】A【解析】因为函数f(x)是奇函数,且在(-∞,0)上是增函数,又f(-2)=0,所以可画出符合条件的奇函数f(x)的图象,如图所示.因为x·f(x)<0,所以或结合图象,得到答案为A.11.已知定义在R上的函数f(x)在(-∞,-2)上是减函数,若g(x)=f(x-2)是奇函数,且g(2)=0,则不等式xf(x)≤0的解集是()A.(-∞,-2]∪[2,+∞)B.[-4,-2]∪[0,+∞)C.(-∞,-4]∪[-2,+∞)D.(-∞,-4]∪[0,+∞)【答案】C【解析】g(x)=f(x-2)是把函数f(x)向右平移2个单位得到的,且g(2)=f(0),f(-4)=g (-2)=-g(2)=0,f(-2)=g(0)=0,所以函数f(x)的图象关于点(-2,0)对称,所以当x ≤-4或x≥-2时xf(x)≤0成立.12.设f(x)为奇函数,且在(-∞,0)内是减函数,f(-2)=0,则x·f(x)<0的解集为()A.(-1,0)∪(2,+∞)B.(-∞,-2)∪(0,2)C.(-∞,-2)∪(2,+∞)D.(-2,0)∪(0,2)【答案】C【解析】因为函数f(x)为奇函数,且在(-∞,0)内是减函数,f(-2)=0,所以函数f(x)在(0,+∞)内也是减函数,且f(2)=0.则不等式x·f(x)<0可化为或解得x<-2或x>2.13.若函数f(x)=ax2+(2+a)x+1是偶函数,则函数f(x)的单调增区间为()A.(-∞,0]B.[0,+∞)C.(-∞,+∞)D.[1,+∞)【答案】A【解析】因为函数为偶函数,所以a+2=0,a=-2,即该函数为f(x)=-2x2+1,所以函数的单调增区间为(-∞,0].14.已知函数f(x)=x|x|-2x,则下列结论正确的是________.(填写序号)①f(x)是偶函数,递增区间是(0,+∞);②f(x)是偶函数,递减区间是(-∞,1);③f(x)是奇函数,递减区间是(-1,1);④f(x)是奇函数,递增区间是(-∞,0).【答案】③【解析】将函数f(x)=x|x|-2x去掉绝对值得f(x)=画出函数f(x)的图象,如图,观察图象可知,函数f(x)的图象关于原点对称,故函数f(x)为奇函数,且在(-1,1)上单调递减.15.若f(x)是偶函数,其定义域为(-∞,+∞),且在[0,+∞)上是减函数,设f=m,f=n,则m,n的大小关系是________.【答案】m≥n【解析】因为a2+2a+=(a+1)2+≥,又f(x)在[0,+∞)上是减函数,所以f≤f=f.16.已知函数f(x)=(k-2)x2+(k-1)x+3是偶函数,则f(x)的单调递增区间是________.【答案】(-∞,0]【解析】∵f(x)为偶函数,∴图象关于y轴对称,即k=1,此时f(x)=-x2+3,其单调递增区间为(-∞,0].17.已知函数y=f(x)的图象关于原点对称,且当x>0时,f(x)=x2-2x+3.(1)试求f(x)在R上的解析式;(2)画出函数的图象,根据图象写出它的单调区间.【答案】(1)因为函数f(x)的图象关于原点对称,所以f(x)为奇函数,则f(0)=0.设x<0,则-x>0,因为x>0时,f(x)=x2-2x+3.所以f(x)=-f(-x)=-(x2+2x+3)=-x2-2x-3.于是有f(x)=(2)先画出函数在y轴右侧的图象,再根据对称性画出y轴左侧的图象,如图.由图象可知函数f(x)的单调递增区间是(-∞,-1],[1,+∞),单调递减区间是(-1,0),(0,1).18.设f(x)是偶函数,g(x)是奇函数,且f(x)+g(x)=x2+2x,求函数f(x),g(x)的解析式. 【答案】∵f(x)是偶函数,g(x)是奇函数,∴f(-x)=f(x),g(-x)=-g(x),由f(x)+g(x)=2x+x2.①用-x代替x得f(-x)+g(-x)=-2x+(-x)2,∴f(x)-g(x)=-2x+x2,②(①+②)÷2,得f(x)=x2;(①-②)÷2,得g(x)=2x.19.已知函数f(x)=-x3+3x.求证:(1)函数f(x)是奇函数;(2)函数f(x)在区间(-1,1)上是增函数.【答案】(1)显然f(x)的定义域是R.设任意x∈R,因为f(-x)=-(-x)3+3(-x)=-(-x3+3x)=-f(x),所以函数f(x)是奇函数.(2)在区间(-1,1)上任取x1,x2,且x1<x2,则f(x2)-f(x1)=-(x2-x1)(+x2x1+)+3(x2-x1)=(x2-x1)(3--x2x1-).因为-1<x1<x2<1,所以x2-x1>0,(3--x2x1-)>0,所以f(x2)>f(x1).所以函数f(x)=-x3+3x在区间(-1,1)上是增函数.20.已知函数f(x)=ax++c(a,b,c是常数)是奇函数,且满足f(1)=,f(2)=. (1)求a,b,c的值;(2)试判断函数f(x)在区间上的单调性并证明.【答案】(1)∵f(x)为奇函数,∴f(-x)=-f(x),∴-ax-+c=-ax--c,∴c=0,∴f(x)=ax+.又∵f(1)=,f(2)=,∴∴a=2,b=.综上,a=2,b=,c=0.(2)由(1)可知f(x)=2x+.函数f(x)在区间上为减函数.证明如下:任取0<x1<x2<,则f(x1)-f(x2)=2x1+-2x2-=(x1-x2)=(x1-x2).∵0<x1<x2<,∴x1-x2<0,2x1x2>0,4x1x2-1<0.∴f(x1)-f(x2)>0,f(x1)>f(x2).∴f(x)在上为减函数.21.设定义域为R的函数f(x)=(1)在平面直角坐标系内作出函数f(x)的图象,并指出f(x)的单调区间(不需证明);(2)若方程f(x)+2a=0有两个解,求出a的取值范围(只需简单说明,不需严格证明);(3)设定义为R的函数g(x)为奇函数,且当x>0时,g(x)=f(x),求g(x)的解析式.【答案】(1)如图.单调增区间:[-1,0],[1,+∞),单调减区间(-∞,-1],[0,1].(2)在同一坐标系中同时作出y=f(x),y=-2a的图象,由图可知f(x)+2a=0有两个解,须-2a=0或-2a>1,即a=0或a<-.(3)当x<0时,-x>0,所以g(-x)=(-x)2-(-2x)+1=x2+2x+1,因为g(x)为奇函数,所以g(x)=-g(-x)=-x2-2x-1,且g(0)=0,所以g(x)=22.已知函数f(x)=ax+(x≠0,常数a∈R).(1)讨论函数f(x)的奇偶性,并说明理由;(2)若函数f(x)在x∈[3,+∞)上为增函数,求a的取值范围.【答案】(1)定义域(-∞,0)∪(0,+∞),关于原点对称.当a=0时,f(x)=,满足对定义域上任意x,f(-x)=f(x),∴当a=0时,f(x)是偶函数;当a≠0时,f(1)=a+1,f(-1)=1-a,若f(x)为偶函数,则a+1=1-a,a=0矛盾;若f(x)为奇函数,则1-a=-(a+1),1=-1矛盾,∴当a≠0时,f(x)是非奇非偶函数.(2)任取x1>x2≥3,f(x1)-f(x2)=ax1+-ax2-=a(x1-x2)+=(x1-x2)(a-). ∵x1-x2>0,f(x)在[3,+∞)上为增函数,∴a>,即a>+在[3,+∞)上恒成立.∵x1>x2≥3,+<+=,∴a≥.。
二次函数综合练习一(含答案)

2013年-----二次函数综合练习一一.选择题(共17小题)1.(2013•重庆)一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是()2.C D.3.(2013•雅安)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为().C D.2.C D.5.(2013•宿迁)下列三个函数:①y=x+1;②;③y=x 2﹣x+1.其图象既是轴对称图形,又是中心对称图形的个数6.(2013•深圳)已知二次函数y=a (x ﹣1)2﹣c 的图象如图所示,则一次函数y=ax+c 的大致图象可能是( ).CD .7.(2013•齐齐哈尔)数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x 2+1与y=的交点的横8.(2013•攀枝花)二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,则函数y=与y=bx+c 在同一直角坐标系内的大致图象是().CD .9.(2013•聊城)二次函数y=ax 2+bx 的图象如图所示,那么一次函数y=ax+b 的图象大致是( ).CD .10.(2013•呼和浩特)在同一直角坐标系中,函数y=mx+m 和y=﹣mx +2x+2(m 是常数,且m ≠0)的图象可能是.CD .11.(2013•达州)二次函数y=ax 2+bx+c 的图象如图所示,反比例函数与一次函数y=cx+a 在同一平面直角坐标系中的大致图象是( ).CD .12.(2012•西宁)如图,二次函数y=ax 2+bx+c 的图象过(﹣1,1)、(2,﹣1)两点,下列关于这个二次函数的叙述正确的是( )13.(2012•泰安)二次函数y=a (x+m )2+n 的图象如图,则一次函数y=mx+n 的图象经过( )14.(2013•舟山)若一次函数y=ax+b (a ≠0)的图象与x 轴的交点坐标为(﹣2,0),则抛物线y=ax 2+bx 的对称轴216.(2013•泰安)对于抛物线y=﹣(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小,17.(2013•日照)如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有()二.填空题(共10小题)18.(2013•南通)已知x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,且m﹣n+2≠0,则当x=3(m+n+1)时,多项式x2+4x+6的值等于_________.19.(2013•荆州)若根式有意义,则双曲线y=与抛物线y=x2+2x+2﹣2k的交点在第_________象限.20.(2013•营口)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第_________象限.21.(2013•绵阳)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣;④3|a|+|c|<2|b|.其中正确的结论是_________(写出你认为正确的所有结论序号).22.(2013•贺州)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确的是_________.(填正确结论的序号)23.(2013•德阳)已知二次函数的y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c >0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有_________.24.(2013•长春)如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=于点B、C,则BC的长值为_________.25.(2013•本溪)在平面直角坐标系中,把抛物线y=﹣x2+1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是_________.26.(2012•南京)已知下列函数①y=x2;②y=﹣x2;③y=(x﹣1)2+2.其中,图象通过平移可以得到函数y=x2+2x﹣3的图象的有_________(填写所有正确选项的序号).27.(2012•自贡)正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,当BM= _________cm时,四边形ABCN的面积最大,最大面积为_________cm2.三.解答题(共3小题)28.(2013•宁波)已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).(1)求抛物线的解析式和顶点坐标;(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.29.(2013•牡丹江)如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)(1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.30.(2013•牡丹江)如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:(1)求抛物线的解析式.(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣.2013年-----二次函数综合练习一参考答案与试题解析一.选择题(共17小题)1.(2013•重庆)一次函数y=ax+b(a≠0)、二次函数y=ax2+bx和反比例函数y=(k≠0)在同一直角坐标系中的图象如图所示,A点的坐标为(﹣2,0),则下列结论中,正确的是()y=﹣﹣>﹣2.C D.3.(2013•雅安)二次函数y=ax2+bx+c的图象如图所示,则一次函数y=ax+b与反比例函数y=在同一平面直角坐标系中的大致图象为().C D.﹣图象在第一三象限,2.C D.(2013•宿迁)下列三个函数:①y=x+1;②;③y=x2﹣x+1.其图象既是轴对称图形,又是中心对称图形的个数5.y=的函数图象,既是轴对称图形,又是中心对称图形;6.(2013•深圳)已知二次函数y=a(x﹣1)2﹣c的图象如图所示,则一次函数y=ax+c的大致图象可能是().C D.7.(2013•齐齐哈尔)数形结合是数学中常用的思想方法,试运用这一思想方法确定函数y=x2+1与y=的交点的横的图象,即可得解.y=8.(2013•攀枝花)二次函数y=ax 2+bx+c (a ≠0)的图象如图所示,则函数y=与y=bx+c 在同一直角坐标系内的大致图象是( ).CD .,9.(2013•聊城)二次函数y=ax 2+bx 的图象如图所示,那么一次函数y=ax+b 的图象大致是( ).C D.﹣10.(2013•呼和浩特)在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是.C D.,与x=11.(2013•达州)二次函数y=ax2+bx+c的图象如图所示,反比例函数与一次函数y=cx+a在同一平面直角坐标系中的大致图象是().C D.的图象在第一、三象限,12.(2012•西宁)如图,二次函数y=ax2+bx+c的图象过(﹣1,1)、(2,﹣1)两点,下列关于这个二次函数的叙述正确的是()13.(2012•泰安)二次函数y=a(x+m)2+n的图象如图,则一次函数y=mx+n的图象经过()14.(2013•舟山)若一次函数y=ax+b(a≠0)的图象与x轴的交点坐标为(﹣2,0),则抛物线y=ax2+bx的对称轴即可求解.=﹣216.(2013•泰安)对于抛物线y=﹣(x+1)2+3,下列结论:①抛物线的开口向下;②对称轴为直线x=1;③顶点坐标为(﹣1,3);④x>1时,y随x的增大而减小,﹣17.(2013•日照)如图,已知抛物线y1=﹣x2+4x和直线y2=2x.我们约定:当x任取一值时,x对应的函数值分别为y1、y2,若y1≠y2,取y1、y2中的较小值记为M;若y1=y2,记M=y1=y2.下列判断:①当x>2时,M=y2;②当x<0时,x值越大,M值越大;③使得M大于4的x值不存在;④若M=2,则x=1.其中正确的有(),(舍去),二.填空题(共10小题)18.(2013•南通)已知x=2m+n+2和x=m+2n时,多项式x2+4x+6的值相等,且m﹣n+2≠0,则当x=3(m+n+1)时,多项式x2+4x+6的值等于3.x=x==∴19.(2013•荆州)若根式有意义,则双曲线y=与抛物线y=x2+2x+2﹣2k的交点在第二象限.的图象位于第二、四象限,=y=20.(2013•营口)二次函数y=﹣x2+bx+c的图象如图所示,则一次函数y=bx+c的图象不经过第四象限.21.(2013•绵阳)二次函数y=ax2+bx+c的图象如图所示,给出下列结论:①2a+b>0;②b>a>c;③若﹣1<m<n<1,则m+n<﹣;④3|a|+|c|<2|b|.其中正确的结论是①③④(写出你认为正确的所有结论序号).>x﹣轴交点的横坐标分别为﹣b=x﹣>>m+n22.(2013•贺州)已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,给出以下结论:①b2>4ac;②abc>0;③2a﹣b=0;④8a+c<0;⑤9a+3b+c<0,其中结论正确的是①②⑤.(填正确结论的序号)=1=123.(2013•德阳)已知二次函数的y=ax2+bx+c(a≠0)图象如图所示,有下列5个结论:①abc<0;②b<a+c;③4a+2b+c >0;④2c<3b;⑤a+b<m(am+b)(m≠1的实数),其中正确结论的番号有①③④.=1,代入得(﹣24.(2013•长春)如图,在平面直角坐标系中,抛物线y=ax2+3与y轴交于点A,过点A与x轴平行的直线交抛物线y=于点B、C,则BC的长值为6.y=时,25.(2013•本溪)在平面直角坐标系中,把抛物线y=﹣x2+1向上平移3个单位,再向左平移1个单位,则所得抛物线的解析式是y=﹣(x+1)2+4.x﹣(26.(2012•南京)已知下列函数①y=x2;②y=﹣x2;③y=(x﹣1)2+2.其中,图象通过平移可以得到函数y=x2+2x﹣3的图象的有①③(填写所有正确选项的序号).27.(2012•自贡)正方形ABCD的边长为1cm,M、N分别是BC、CD上两个动点,且始终保持AM⊥MN,当BM=cm时,四边形ABCN的面积最大,最大面积为cm2.,即=x×﹣x+,﹣=最大,最大值是﹣×(+×+=cm 故答案是:,三.解答题(共3小题)28.(2013•宁波)已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,﹣3).(1)求抛物线的解析式和顶点坐标;(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=﹣x上,并写出平移后抛物线的解析式.29.(2013•牡丹江)如图,已知二次函数y=x2+bx+c过点A(1,0),C(0,﹣3)(1)求此二次函数的解析式;(2)在抛物线上存在一点P使△ABP的面积为10,请直接写出点P的坐标.∴,∴30.(2013•牡丹江)如图,抛物线y=x2+bx+c过点A(﹣4,﹣3),与y轴交于点B,对称轴是x=﹣3,请解答下列问题:(1)求抛物线的解析式.(2)若和x轴平行的直线与抛物线交于C,D两点,点C在对称轴左侧,且CD=8,求△BCD的面积.注:抛物线y=ax2+bx+c(a≠0)的对称轴是x=﹣.﹣×。
微积分综合练习题及参考答案1

综合练习题1(函数、极限与连续部分)1.填空题 (1)函数)2ln(1)(-=x x f 的定义域是 . 答案:2>x 且3≠x .(2)函数24)2ln(1)(x x x f -++=的定义域是 .答案:]2,1()1,2(-⋃--(3)函数74)2(2++=+x x x f ,则=)(x f. 答案:3)(2+=x x f(4)若函数⎪⎩⎪⎨⎧≥<+=0,0,13sin )(x k x xx x f 在0=x 处连续,则=k .答案:1=k(5)函数x x x f 2)1(2-=-,则=)(x f .答案:1)(2-=x x f(6)函数1322+--=x x x y 的间断点是 .答案:1-=x(7)=∞→xx x 1sinlim .答案:1(8)若2sin 4sin lim 0=→kxxx ,则=k .答案:2=k2.单项选择题(1)设函数2e e xx y +=-,则该函数是( ).A .奇函数B .偶函数C .非奇非偶函数D .既奇又偶函数 答案:B(2)下列函数中为奇函数是().A .x x sinB .2e e xx +- C .)1ln(2x x ++ D .2x x +答案:C(3)函数)5ln(4+++=x x xy 的定义域为( ).A .5->xB .4-≠xC .5->x 且0≠xD .5->x 且4-≠x 答案:D(4)设1)1(2-=+x x f ,则=)(x f ( ) A .)1(+x x B .2x C .)2(-x x D .)1)(2(-+x x 答案:C(5)当=k ( )时,函数⎩⎨⎧=≠+=0,,2)(x k x e x f x 在0=x 处连续.A .0B .1C .2D .3 答案:D(6)当=k ( )时,函数⎩⎨⎧=≠+=0,,1)(2x k x x x f ,在0=x 处连续.A .0B .1C .2D .1- 答案:B(7)函数233)(2+--=x x x x f 的间断点是( ) A .2,1==x xB .3=xC .3,2,1===x x xD .无间断点 答案:A 3.计算题(1)423lim 222-+-→x x x x .解:4121lim )2)(2()1)(2(lim 423lim22222=+-=+---=-+-→→→x x x x x x x x x x x x (2)329lim 223---→x x x x解:234613lim )1)(3()3)(3(lim 329lim 33223==++=+-+-=---→→→x x x x x x x x x x x x (3)4586lim 224+-+-→x x x x x解:3212lim )1)(4()2)(4(lim 4586lim 44224=--=----=+-+-→→→x x x x x x x x x x x x x综合练习题2(导数与微分部分)1.填空题(1)曲线1)(+=x x f 在)2,1(点的切斜率是 . 答案:21(2)曲线x x f e )(=在)1,0(点的切线方程是 . 答案:1+=x y(3)已知x x x f 3)(3+=,则)3(f '= . 答案:3ln 33)(2x x x f +=')3(f '=27()3ln 1+(4)已知x x f ln )(=,则)(x f ''= . 答案:x x f 1)(=',)(x f ''=21x- (5)若x x x f -=e )(,则='')0(f .答案:x x x x f --+-=''e e 2)(='')0(f 2-2.单项选择题(1)若x x f x cos e )(-=,则)0(f '=( ).A. 2B. 1C. -1D. -2 因)(cos e cos )e ()cos e ()('+'='='---x x x x f x x x)sin (cos e sin e cos e x x x x x x x +-=--=---所以)0(f '1)0sin 0(cos e 0-=+-=- 答案:C(2)设y x =lg2,则d y =( ). A .12d x x B .1d x x ln10 C .ln10x x d D .1d xx 答案:B(3)设)(x f y =是可微函数,则=)2(cos d x f ( ). A .x x f d )2(cos 2' B .x x x f d22sin )2(cos ' C .x x x f d 2sin )2(cos 2' D .x x x f d22sin )2(cos '- 答案:D(4)若3sin )(a x x f +=,其中a 是常数,则='')(x f ( ).A .23cos a x +B .a x 6sin +C .x sin -D .x cos 答案:C3.计算题(1)设xx y 12e =,求y '.解: )1(e e 22121xx x y xx -+=')12(e 1-=x x(2)设x x y 3cos 4sin +=,求y '.解:)sin (cos 34cos 42x x x y -+='x x x 2cos sin 34cos 4-=(3)设xy x 2e 1+=+,求y '. 解:2121(21ex x y x -+='+ (4)设x x x y cos ln +=,求y '.解:)sin (cos 12321x x x y -+=' x x tan 2321-= 综合练习题3(导数应用部分)1.填空题(1)函数y x =-312()的单调增加区间是 . 答案:),1(+∞(2)函数1)(2+=ax x f 在区间),0(∞+内单调增加,则a 应满足 .答案:0>a2.单项选择题(1)函数2)1(+=x y 在区间)2,2(-是( ) A .单调增加 B .单调减少 C .先增后减 D .先减后增 答案:D(2)满足方程0)(='x f 的点一定是函数)(x f y =的( ). A .极值点 B .最值点 C .驻点 D . 间断点 答案:C(3)下列结论中( )不正确. A .)(x f 在0x x =处连续,则一定在0x 处可微.B .)(x f 在0x x =处不连续,则一定在0x 处不可导.C .可导函数的极值点一定发生在其驻点上.D .函数的极值点一定发生在不可导点上. 答案: B(4)下列函数在指定区间(,)-∞+∞上单调增加的是( ). A .x sin B .x e C .2x D .x -3答案:B3.应用题(以几何应用为主)(1)欲做一个底为正方形,容积为108m 3的长方体开口容器,怎样做法用料最省?解:设底边的边长为x m ,高为h m ,容器的表面积为y m 2。
高中数学对数与对数函数 综合练习 北师大版 必修1

高中数学对数与对数函数 综合练习 北师大版 必修1一、选择题:(本题共12小题,每小题4分,共48分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、已知32a =,那么33log 82log 6-用a 表示是( )A 、2a -B 、52a -C 、23(1)a a -+D 、 23a a -2、2log (2)log log a a a M N M N -=+,则NM的值为( ) A 、41B 、4C 、1D 、4或1 3、已知221,0,0x y x y +=>>,且1log (1),log ,log 1y a aa x m n x+==-则等于( ) A 、m n + B 、m n - C 、()12m n + D 、()12m n -4、如果方程2lg (lg5lg7)lg lg5lg70x x +++=的两根是,αβ,则αβ的值是( ) A 、lg5lg 7 B 、lg 35 C 、35 D 、351 5、已知732log [log (log )]0x =,那么12x -等于( )A 、13B 23C 22D 336、函数2lg 11y x ⎛⎫=- ⎪+⎝⎭的图像关于( )A 、x 轴对称B 、y 轴对称C 、原点对称D 、直线y x =对称 7、函数(21)log 32x y x -=-的定义域是( )A 、()2,11,3⎛⎫+∞ ⎪⎝⎭B 、()1,11,2⎛⎫+∞⎪⎝⎭C 、2,3⎛⎫+∞ ⎪⎝⎭D 、1,2⎛⎫+∞ ⎪⎝⎭8、函数212log (617)y x x =-+的值域是( )A 、RB 、[)8,+∞C 、(),3-∞-D 、[)3,+∞ 9、若log 9log 90m n <<,那么,m n 满足的条件是( )A 、 1 m n >>B 、1n m >>C 、01n m <<<D 、01m n <<<10、2log 13a <,则a 的取值范围是( )A 、()20,1,3⎛⎫+∞ ⎪⎝⎭B 、2,3⎛⎫+∞⎪⎝⎭ C 、2,13⎛⎫ ⎪⎝⎭ D 、220,,33⎛⎫⎛⎫+∞ ⎪ ⎪⎝⎭⎝⎭11、下列函数中,在()0,2上为增函数的是( ) A 、12log (1)y x =+ B 、22log 1y x =-C 、21log y x = D 、22log (45)y x x =-+ 12、已知()log x+1 (01)a g x a a =>≠且在()10-,上有()0g x >,则1()x f x a +=是( ) A 、在(),0-∞上是增加的 B 、在(),0-∞上是减少的 C 、在(),1-∞-上是增加的 D 、在(),0-∞上是减少的二、填空题:(本题共4小题,每小题4分,共16分,请把答案填写在答题纸上) 13、若2log 2,log 3,m n a a m n a +=== 。
高考数学一轮复习专题2.10函数的综合运用练习(含解析)

第十讲 函数的综合运用考向一新概念题【例1】对于实数a 和b ,定义运算“*”:a *b =⎩⎪⎨⎪⎧a 2-ab ,a ≤b ,b 2-ab ,a >b .设f (x )=(2x -1)*(x -1),且关于x 的方程f (x )=m (m ∈R)恰有三个互不相等的实数根x 1,x 2,x 3,则x 1x 2x 3的取值范围是________.【答案】 ⎝ ⎛⎭⎪⎫1-316,0【解析】 函数f (x )=⎩⎪⎨⎪⎧2x 2-x ,x ≤0,-x 2+x ,x >0的图象如图所示.设y =m 与y =f (x )图象交点的横坐标从小到大分别为x 1,x 2,x 3.由y =-x 2+x =-⎝ ⎛⎭⎪⎫x -122+14,得顶点坐标为⎝ ⎛⎭⎪⎫12,14.当y =14时,代入y =2x 2-x ,得14=2x 2-x ,解得x =1-34(舍去正值),∴x 1∈⎝ ⎛⎭⎪⎫1-34,0.又∵y =-x 2+x 图象的对称轴为x =12,∴x 2+x 3=1,又x 2,x 3>0,∴0<x 2x 3<⎝ ⎛⎭⎪⎫x 2+x 322=14.又∵0<-x 1<3-14,∴0<-x 1x 2x 3<3-116,∴1-316<x 1x 2x 3<0. 【举一反三】1.设f (x )与g (x )是定义在同一区间[a ,b ]上的两个函数,若函数y =f (x )-g (x )在x ∈[a ,b ]上有两个不同的零点,则称f (x )和g (x )在[a ,b ]上是“关联函数”,区间[a ,b ]称为“关联区间”.若f (x )=x 2-3x +4与g (x )=2x +m 在[0,3]上是“关联函数”,则m 的取值范围为( )A .]2,49(--B .[-1,0]C .(-∞,-2]D .),49(+∞-【答案】A【解析】令F (x )=f (x )-g (x )=x 2-3x +4-(2x +m )=x 2-5x +4-m ,则由题意知F (x )=0在[0,3]上有两个不同的实数根,因而2(0)0(3)054(4)0F F m ⎧≥⎪⎪≥⎨⎪∆=-->⎪⎩,即402049m m m -≥⎧⎪--≥⎨⎪>-⎩,解之得-94<m ≤-2,故选A考向二函数性质与零点定理综合运用【例2】已知偶函数 满足 ,当0 时, ,则函数 在区间 内的零点个数为。
一次函数(基础篇)专项练习1 含答案

一次函数(基础篇)专项练习1一、单选题1.下列图象中,表示y 是x 的函数的是()A .B .C .D .2.在函数1y =x 的取值范围是()A .2x >B .2x ≠C .2x <D .2x ≤3.一次函数y =(k ﹣1)x +3的图象经过点(﹣2,1),则k 的值是()A .﹣1B .2C .1D .04.一次函数y=kx+b 的图像经过点(-1,2),则k-b 的值是()A .-1B .2C .1D .-25.一次函数y =12x ﹣m 的图象上有两点A (﹣2,y 1),B (3,y 2),则y 1,y 2的大小关系为()A .y 1>y 2B .y 1=y 2C .y 1<y 2D .无法确定6.如图是一次函数112y x =-的图象,根据图象可直接写出方程1102x -=的解为2x =,这种解题方法体现的数学思想是()A .数形结合思想B .转化思想C .分类讨论思想D .函数思想7.一根蜡烛长30cm ,点燃后每小时燃烧5cm ,燃烧时蜡烛剩余的长度h (cm )和燃烧时间t (小时)之间的函数关系用图像可以表示为中的()A .B .C .D .8.已知一次函数y =﹣2x +4,下列说法错误的是()A .图象经过第一、二、四象限B .图象与x 轴的交点坐标为(4,0)C .y 随x 增大而减小D .该图象可以由y =﹣2x 平移得到9.若关于x 的不等式组2−>0−2≤0有且只有四个整数解,且一次函数y =(k +3)x +k +5的图象不经过第三象限,则符合题意的整数k 有()个.A .4B .3C .2D .110.如图,在平面直角坐标系中,直线1l :152y x =-+与x 轴、y 轴分别交于点A 和点B ,直线2l 经过坐标原点,且21l l ⊥,垂足为C ,则点C 到y 轴的距离为()A .1B .2C .3D .4二、填空题11.已知f (x )=22x x-,那么f (2)=_____.12.如图,在平面直角坐标系中,点A (2,m )在第一象限,若点A 关于x 轴的对称点B 在直线y =﹣x+1上,则m 的值为_____.13.若y=(m ﹣1)x |m|是正比例函数,则m 的值为_____.14.直线2y x b =+(b 为常数)的图象经过第一、三、四象限,则b 的值可以是______(写出一个即可).15.已知正比例函数的图象经过点M (﹣2,1)、A (x 1,y 1)、B (x 2,y 2),如果x 1<x 2,那么y 1_____y 2.(填“>”、“=”、“<”)16.已知一次函数(1)2(1)y m x m m =++-≠-,将该函数图象先向下平移2个单位长度,再向右平移4个单位长度,平移后的函数图象过点(1,2)-,则m 的值为___________.17.已知在正比例函数y =-2mx 中,函数y 的值随x 值的增大而增大,则点P (m ,4)在第______象限.18.若A(x 1,y 1)、B(x 2,y 2)是一次函数2y ax x =+-图像上的不同的两点,记()()1212m x x y y =--,则当m <0时,a 的取值范围是___.19.一次函数y =2x +4的图象与x 轴、y 轴的交点分别为A ,B ,则线段AB 的长为_____________.20.已知一次函数21y x =-+,若21x -≤≤,则y 的最小值为_________________.21.一次函数2y kx k =+的图象如图所示,当0y >时,则x 的取值范围是_______.22.如图,直线y =,点1A 坐标为()1,0,过点1A 作x 轴的垂线交直线于点1B ,以原点O 为圆心,1OB 长为半径画弧交x 轴于点2A ;再过点2A 作x 轴的垂线交直线于点2B ,以原点O 为圆心,2OB 长为半径画弧交x 轴于点3A ,…,按此做法进行下去,点2021B 的坐标为______.三、解答题23.已知一次函数y =kx +b 的图象经过点A (―1,3)和点B (2,―3).(1)求这个一次函数的表达式;(2)求直线AB 与坐标轴围成的三角形的面积.24.有一个容量为8GB(1GB=1024MB)的U盘,U盘中已经存储了1个视频文件,其余空间都用来存储照片.若每张照片占用的内存容量均相同,照片数量x(张)和剩余可用空间y(MB)的部分关系如表:照片数量100150200400800剩余可用空间56005400520044002800(1)求出y与x之间的关系式.(2)若U盘中已经存入1100张照片,那么最多还能存入多少张照片?25.如图,直线l1经过点A(0,2)和C(6,﹣2),点B的坐标为(4,2),点P是线段AB上的动点(点P不与点A重合),直线l2:y=kx+2k(k≠0)经过点P,并与l1交于点M.(1)求l1的函数表达式;(2)若点M坐标为(1,43),求S△APM;(3)无论k取何值,直线l2恒经过点,在P的移动过程中,k的取值范围是.26.某航空公司规定,旅客乘机所携带行李的质量x(kg)与其运费y(元)由如图所示的一次函数图象确定,问:(1)求一次函数解析式(2)旅客可携带的免费行李的最大质量是多少kg?27.直线24y x =-+与x 轴交于点A ,与y 轴交于点B ,直线(y kx b k b =+,是常数,0)k ≠经过点A ,与y 轴交于点C ,且OC OA =.()1求点A 的坐标及k 的值;()2点C 在x 轴的上方,点P 在直线24y x =-+上,若PC PB =,求点P 的坐标.28.如图,已知函数12y x b =-+的图象与x 轴、y 轴分别交于点A ,B ,与函数y =x 的图象交于点M ,点M 的横坐标为2.在x 轴上有一点P (a ,0)(其中a>2),过点P 作x 轴的垂线,分别交函数12y x b =-+和y =x 的图象于点C ,D(1)求点A 的坐标;(2)若OB =CD ,求a 的值.参考答案1.A【分析】根据函数的定义可知,满足对于x 的每一个取值,y 都有唯一确定的值与之对应关系,据此即可确定函数的个数.解:A 、对于x 的每一个取值,y 都有唯一确定的值与之对应,故A 正确;B 、对于x 的每一个取值,y 可能有三个值与之对应,故B 错误;C 、对于x 的每一个取值,y 可能有两个值与之对应,故C 错误;D 、对于x 的每一个取值,y 可能有两个值与之对应,故D 错误;故选:A .【点拨】主要考查了函数的定义,在一个变化过程中有两个变量x ,y ,对于x 的每一个取值,y 都有唯一确定的值与之对应,则y 是x 的函数,x 叫自变量.2.D【分析】根据二次根式的意义,被开方数大于等于0,列不等式求解即可得出结论.解:由题意得:2-x ≥0,解得x ≤2.故选:D .【点拨】本题主要考查了求自变量的取值范围,掌握二次根式的被开方数是非负数是解题的关键.3.B【分析】函数经过点(﹣2,1),把点的坐标代入解析式,即可求得k 的值.解:根据题意得:﹣2(k ﹣1)+3=,解得:k =2.故选B .【点拨】本题主要考查了函数的解析式与图象的关系,满足解析式的点一定在图象上,图象上的点一定满足函数解析式.4.D【分析】根据一次函数的性质即可得.解:由题意,将点(1,2)-代入一次函数的解析式得2k b -+=则2k b -=-故选:D .【点拨】本题考查了一次函数的性质,掌握理解一次函数的性质是解题关键.5.C【分析】直接根据一次函数的增减性判断即可.解:∵一次函数y =12x ﹣m 中,k =12>0,∴y 随x 的增大而增大.∵﹣2<3,∴y 1<y 2.故选:C .【点拨】本题主要考查一次函数的性质,熟练掌握函数性质是解题的关键.6.A【分析】根据图像与x 轴交点可得方程的解,体现的是数形结合的思想.解:由图像可知y =0时,与x 轴交于(2,0)点,故1102x -=的解为2x =,这种解题方法体现的是数形结合的数学思想.【点拨】本题主要考查根据函数图像求方程的解,正确理解函数图像各点的含义是解题关键.7.B【分析】根据蜡烛剩余的长度=总长度-燃烧的长度就可以得出函数的解析式,由题意求出自变量的取值范围就可以得出函数图象.解:由题意,得y=30-5t ,∵y≥0,t≥0,∴30-5t≥0,∴t≤6,∴0≤t≤6,∴y=30-5t 是降函数且图象是一条线段.故选B .【点拨】本题考查一次函数的解析式的运用,一次函数的与实际问题的关系的运用,一次函数的图象的运用,自变量的取值范围的运用,解答时求出函数解析式及自变量的范围是关键.8.B【分析】根据一次函数的解析式中一次项系数20k =-<,40b =>,即可判断经过的象限进而判断A 选项,令0y =即可判断B 选项,根据一次项系数20k =-<,即可判断C 选项,根据一次函数平移的规律可判断D 选项.解:由24y x =-+,20k =-<,40b =>,∴一次函数24y x =-+图象经过第一、二、四象限,故A 选项正确,不符合题意;令0y =,则2x =,∴图象与x 轴的交点坐标为(2,0)故B 选项不正确,符合题意;20k =-<,∴y 随x 增大而减小;故C 选项正确,不符合题意;将一次函数2y x =-图象向上平移4个单位可得24y x =-+,故D 选项正确,不符合题意.故选B【点拨】本题考查了一次函数图象与性质,一次函数图象的平移,一次函数与坐标轴的交点,掌握一次函数的图象与性质是解题的关键.9.D 【解析】试题分析:解不等式组2−>0−2≤0得,2<x≤2,∵不等式组有且只有四个整数解,∴其整数解为:﹣1,0,1,2,∴﹣2≤2<﹣1,即﹣4≤k <﹣2.∵一次函数y=(k+3)x+k+5的图象不经过第三象限,∴+3<0k +5≥0,解得﹣5≤k <﹣3,∴﹣4≤k <﹣3,∴k 的整数解只有﹣4.故选D .【考点】一次函数与一元一次不等式.10.B【分析】先分别求得A ,B 两点坐标,然后利用勾股定理求得AB 的长,结合三角形面积求得OC 的长,再利用勾股定理求得BC ,最后再利用三角形面积求解解:在152y x =-+中,当x =0时,y =5当y =0时,15=02x -+,解得:x =10∴OA =10;OB =5∴在Rt △AOB 中,AB =∵21l l ⊥∴1122AB OC OA OB ⋅=⋅,1151022⨯=⨯⨯,解得:OC =∴在Rt △BOC 中,BC ==过点C 作CD ⊥y 轴∴1122OB CD BC ⋅=⋅,11522CD ⨯=⨯2CD =故选:B【点拨】本题考查一次函数的几何应用及勾股定理解直角三角形,二次根式的乘除运算,利用数形结合思想解题是关键.11.1【分析】把x=2代人f (x )=22x x-,求得答案即可.解:当x =2时,f (2)=2222-=1,故答案为:1.【点拨】考查了函数值的知识,解题的关键是代人后正确的计算,难度不大.12.1【分析】根据关于x 轴的对称点的坐标特点可得B (2,−m ),然后再把B 点坐标代入y =−x +1可得m 的值.解:点A 关于x 轴的对称点B 的坐标为:(2,﹣m ),将点B 的坐标代入直线y =﹣x+1得:﹣m =﹣2+1,解得:m =1,故答案为1.【点拨】此题主要考查了关于x 轴对称点的坐标,以及一次函数图象上点的坐标特点,关键是掌握凡是函数图象经过的点必能使解析式左右相等.13.-1【分析】根据正比例函数的定义,令m-1≠0,|m|=1即可.解:由题意得:m−1≠0,|m|=1,解得:m=−1.故答案为−1.【点拨】本题考查正比例函数的定义.14.-1(答案不唯一,b <0即可)【分析】由一次函数图象经过第一、三、四象限,可知k >0,b <0,在范围内确定b 的值即可.解:因为一次函数2y x b =+(b 为常数)的图象经过第一、三、四象限,所以k >0,b <0,所以b 可以取-1,故答案为:-1(答案不唯一,b <0即可)【点拨】此题考查一次函数图象与系数的关系,根据一次函数图象所经过的象限,可确定一次项系数,常数项的值的符号,从而确定字母k 的取值范围.15.>【分析】根据正比例函数的性质,解答即可.解:设该正比例函数的解析式为y =kx ,则1=﹣2k ,得k =﹣0.5,∴y =﹣0.5x ,∵正比例函数的图象经过点A (x 1,y 1)、B (x 2,y 2),x 1<x 2,∴y 1>y 2,故答案为:>.【点拨】本题考查了正比例函数的性质,掌握性质是解题的关键.16.52-【分析】根据函数图象平移的规律:“上加下减”“左加右减”的原则即可求得.解:由题意得一次函数y=(m+1)(x-4)+m−2-2(m≠−1)经过点(1,-2)∴(m+1)(1-4)+m−2-2=-2,解得:m=-52,故答案为:-52.【点拨】本题考查一次函数的图象与几何变换,熟知平移的原则是解题的关键.17.二【分析】根据正比例函数y 的值随x 值的增大而增大,可知20m ->,求得0m <,即可判断P (m ,4)在第二象限.解:∵函数y 的值随x 值的增大而增大,∴20m ->,解得0m <,∴点P (m ,4)在第二象限.【点拨】本题考查正比例函数,较容易,熟练掌握正比例函数的性质是顺利解题的关键.18.1a <-【分析】根据一次函数的性质知,当k <0时,判断出y 随x 的增大而减小.解:∵A(1x ,1y )、B(2x ,2y )是一次函数()212y ax x a x =+-=+-图象上的不同的两点,()()1212 0m x x y y =--<,∴该函数图象是y 随x 的增大而减小,∴10a +<,解得1a <-.故答案为:1a <-.【点拨】本题考查了一次函数图象上点的坐标特征,要根据函数的增减性进行推理.19.【分析】由一次函数y =2x +4的图象与x 轴、y 轴的交点分别为A ,B ,可求A (-2,0),B (0,4),在Rt △AOB 中,由勾股定理得AB ==.解:∵一次函数y =2x +4的图象与x 轴、y 轴的交点分别为A 、B ,∴当y =0时,240x +=,解得x =-2,∴A (-2,0),∴当x =0时,y=4,∴B (0,4),∵∠AOB =90°,在Rt △AOB 中,OA =2,OB =4,由勾股定理得AB ===.故答案为:【点拨】本题考查直线与两轴的交点坐标,勾股定理,掌握直线与两轴的交点坐标,勾股定理是解题关键.20.-1【分析】由k =-2<0,可得出y 随x 的增大而减小,结合-2≤x ≤1,即可求出y 的最小值.解:∵k =-2<0,∴y 随x 的增大而减小,∴当x =1时,y 取得最小值,此时y =-2×1+1=-1.故答案为:-1.【点拨】本题考查了一次函数的性质,牢记“k >0,y 随x 的增大而增大;k <0,y 随x 的增大而减小”是解题的关键.21.2x >-【分析】根据一次函数2y kx k =+,可以求得0y =时x 的值,然后根据函数图象和一次函数的性质,可以写出当0y >时,x 的取值范围.解:∵()22y kx k k x =+=+,∴当0y =时,2x =-,由图象可知,y 随x 的增大而增大,∴当0y >时,则x 的取值范围是2x >-,故答案为:2x >-.【点拨】本题考查一次函数图象和性质.根据函数图象判断其增减性是解答本题的关键.22.(20202,2【分析】根据题意可以写出A 和B 的前几个点的坐标,从而可以发现各点的变化规律,从而可以写出点A 2021的坐标.解:∵直线y =,点A 1坐标为(1,0),当1x =时,y ==∴点B 1的坐标为(1,在Rt △OA 1B 1中,OA 1=1,A 1B 1∴12OB =,∴点A 2坐标为(2,0),同理,点B 2的坐标为(2,,点A 3坐标为(4,0),点B 3的坐标为(4,,……∴点B n 的坐标为(2n -1,2n ,当n =2021时,点B 2021的坐标为(22020,2,故答案为:(22020,2.【点拨】本题考查一次函数图象上点的坐标特征、规律型,解答本题的关键是明确题意,利用一次函数的性质和数形结合的思想解答.23.(1)一次函数的表达式是y=-2x+1,(2)所围成的三角形面积为14.【分析】把两点坐标分别代入解析式,再解出k,b 即可求出解析式;(2)先根据解析式先求出直线与坐标轴的交点,再利用三角形面积公式求解.解:(1)依题意得323k b k b -+=⎧⎨+=-⎩解得21k b =-⎧⎨=⎩∴所求一次函数的表达式是y=-2x+1,(2)令x =0,由y=-2x+1得,y =1,令y =0,由y=-2x+1,得x =12,∴直线AB 与坐标轴的交点坐标分别是(0,1)和(102)∴所围成的三角形面积为:1111224⨯⨯=.24.(1)y =-4x +6000;(2)400张【分析】(1)运用待定系数法解答即可;(2)根据(1)结果算出当x =0时y 的值,用总内存减去此时y 的值即可得到视频文件占用的内存然后求出每张照片的内存,由此求解即可;解:(1)设y 与x 之间的关系式为y =kx +b ,根据题意得,10056001505400k b k b +=⎧⎨+=⎩,解得46000k b =-⎧⎨=⎩,故y 与x 之间的关系式为y =-4x +6000;(2)当x =0时,y =6000,此时U 盘没有储存照片,只有一个视频文件,8G=8⨯1024MB=8192MB ,8192-6000=2192(MB )∴U 盘中视频文件的占用内存容量为2192MB ;当x =1100时,y =-4×1100+6000=1600,∴此时U 盘有1600MB 内存,当x =100时,y =5600,∴每张照片的内存为(8192-2192-5600)÷100=4MB ,1600÷4=400(张)∴最多还能存入400张照片.答:最多还能存入400张照片.【点拨】本题主要考查了一次函数的应用,熟练掌握待定系数法求函数关系式是解答本题的关键.25.(1)223y x =-+;(2)56APM S ∆=;(3)1(2,0),13k -≤<.【分析】(1)将点A (0,2)和C (6,﹣2)代入y kx b =+,待定系数法求一次函数解析式即可;(2)根据2y kx k +=过点M 4(1,3求出解析式,求出求S △APM ;(3)2(2)y kx k k x +=+=过定点,分别求出P 在AB 、两点的时的k 即可.解:(1)点A (0,2)和C (6,﹣2)代入,y kx b =+得:262b k b =⎧⎨+=-⎩,解得232k b ⎧=-⎪⎨⎪=⎩223y x ∴=-+.(2)2y kx k + =过M 4(1,)3442,39k k k ∴+==4899y x ∴=+ A (0,2),B (4,2),点P 是线段AB 上的动点2y P ∴=直线l 2:y =kx +2k (k ≠0)经过点P4852992x x =+=5(,2)2P ∴52PA =14(2)23APM S PA ∆∴=⨯⨯-154(2223=⨯⨯-56=56APM S ∆∴=.(3)2(2)y kx k k x +=+ =∴过定点(2,0)-当点P 经过A (0,2)时,代入2y kx k=+22k =,解得1k =当点P 经过B (4,2)时,代入2y kx k=+422k k +=,解得13k =当点P 从点A 到点B 的移动过程中,k 的值在不断变小,点P 不与点A 重合.113k ∴≤<.【点拨】本题考查了,待定系数法求一次函数解析式,一次函数围成的三角形面积,过定点的一次函数,通过数形结合,理解题意,正确的解得一次函数解析式是解题的关键.26.(1)y =20x -300;(2)15【分析】(1)根据图象,用待定系数法即可求出函数的解析式;(2)根据解析式取y =0,求出对应的x 即可.解:(1)设y =kx +b ,代入(20,100),(30,300),得:1002030030k b k b =+⎧⎨=+⎩,解得:20300k b =⎧⎨=-⎩,∴y =20x -300;(2)取y =0,则20x -300=0,解得x =15,∴免费行李的最大质量为15kg .【点拨】本题主要考查一次函数的图形,关键是能根据图象用待定系数法求出函数的解析式,然后根据y 的值即可求出x 的值.27.(1) 1k =或1k =-;(2)1 32P ⎛⎫ ⎪⎝⎭,解:分析:(1)令0y =,求得x 的值,即可求得A 的坐标为()20,,由OC OA =得()02C ,或()02-,,然后根据待定系数法即可求得k 的值;(2)由()()0402B C ,,,,根据题意求得P 的纵坐标,代入24y x =-+即可求得横坐标.详解:()1由直线24y x =-+与x 轴交于点A ,与y 轴交于点B ,令0y =,则240x -+=,解得2x =,()20A ∴,,OC OA = ,()02C ,∴或()02-,,直线(y kx b k b =+,是常数,0)k ≠经过点A 和点C ,202k b b +=⎧∴⎨=-⎩或202k b b +=⎧⎨=⎩,解得1k =或1k =-;()()()20402B C ,,,,且PC PB =,P ∴的纵坐标为3,点P 在直线24y x =-+上,把3y =代入24y x =-+解得12x =,132P ⎛⎫∴ ⎪⎝⎭,.点睛:考查了待定系数法求一次函数的解析式以及一次函数的图象与性质.注意待定系数法在求函数解析式中的应用.28.(1)(6,0);(2)4.解:试题分析:(1)先利用直线y=x上的点的坐标特征得到点M的坐标为(2,2),再把M(2,2)代入y=﹣12x+b可计算出b=3,得到一次函数的解析式为y=﹣12x+3,然后根据x轴上点的坐标特征可确定A点坐标为(6,0);(2)先确定B点坐标为(0,3),则OB=CD=3,再表示出C点坐标为(a,﹣12a+3),D点坐标为(a,a),所以a﹣(﹣12a+3)=3,然后解方程即可.试题解析:解:(1)∵点M在直线y=x的图象上,且点M的横坐标为2,∴点M的坐标为(2,2),把M(2,2)代入y=﹣12x+b得﹣1+b=2,解得b=3,∴一次函数的解析式为y=﹣12x+3,把y=0代入y=﹣12x+3得﹣12x+3=0,解得x=6,∴A点坐标为(6,0);(2)把x=0代入y=﹣12x+3得y=3,∴B点坐标为(0,3),∵CD=OB,∴CD=3,∵PC⊥x轴,∴C点坐标为(a,﹣12a+3),D点坐标为(a,a)∴a﹣(﹣12a+3)=3,∴a=4.考点:两条直线相交或平行问题.。
中考数学函数实际应用综合题(解析版)

专题03 函数实际应用综合题1.(2019•常德中考)某生态体验园推出了甲、乙两种消费卡,设入园次数为x时所需费用为y元,选择这两种卡消费时,y与x的函数关系如图所示,解答下列问题:(1)分别求出选择这两种卡消费时,y关于x的函数表达式;(2)请根据入园次数确定选择哪种卡消费比较合算.【解析】(1)设y甲=k1x,根据题意得5k1=100,解得k1=20,∴y甲=20x;设y乙=k2x+100,根据题意得:20k2+100=300,解得k2=10,∴y乙=10x+100.(2)①y甲<y乙,即20x<10x+100,解得x<10,当入园次数小于10次时,选择甲消费卡比较合算;②y甲=y乙,即20x=10x+100,解得x=10,当入园次数等于10次时,选择两种消费卡费用一样;③y甲>y乙,即20x>10x+100,解得x>10,当入园次数大于10次时,选择乙消费卡比较合算.2.(2019•山西中考)某游泳馆推出了两种收费方式.方式一:顾客先购买会员卡,每张会员卡200元,仅限本人一年内使用,凭卡游泳,每次游泳再付费30元.方式二:顾客不购买会员卡,每次游泳付费40元.设小亮在一年内来此游泳馆的次数为x次,选择方式一的总费用为y1(元),选择方式二的总费用为y2(元).(1)请分别写出y1,y2与x之间的函数表达式.(2)小亮一年内在此游泳馆游泳的次数x在什么范围时,选择方式一比方式二省钱.【解析】(1)当游泳次数为x时,方式一费用为:y1=30x+200,方式二的费用为:y2=40x.(2)由y1<y2得:30x+200<40x,解得x>20时,当x>20时,选择方式一比方式二省钱.3.(2019•台州中考)如图1,某商场在一楼到二楼之间设有上、下行自动扶梯和步行楼梯.甲、乙两人从二楼同时下行,甲乘自动扶梯,乙走步行楼梯,甲离一楼地面的高度h (单位:m )与下行时间x (单位:s )之间具有函数关系3610h x =-+,乙离一楼地面的高度y (单位:m )与下行时间x (单位:s )的函数关系如图2所示. (1)求y 关于x 的函数解析式;(2)请通过计算说明甲、乙两人谁先到达一楼地面.【解析】(1)设y 关于x 的函数解析式是y kx b =+,6153b k b =⎧⎨+=⎩,解得,156k b ⎧=-⎪⎨⎪=⎩, 即y 关于x 的函数解析式是165y x =-+. (2)当0h =时,30610x =-+,得20x ,当0y =时,1065x =-+,得30x =, ∵2030<, ∴甲先到达地面.4.(2019•天门中考)某农贸公司销售一批玉米种子,若一次购买不超过5千克,则种子价格为20元/千克,若一次购买超过5千克,则超过5千克部分的种子价格打8折.设一次购买量为x 千克,付款金额为y 元.(1)求y 关于x 的函数解析式;(2)某农户一次购买玉米种子30千克,需付款多少元? 【解析】(1)根据题意,得①当0≤x ≤5时,y =20x ; ②当x >5,y =20×0.8(x -5)+20×5=16x +20. (2)把x =30代入y =16x +20,∴y =16×30+20=500; ∴一次购买玉米种子30千克,需付款500元.5.(2019•天津中考)甲、乙两个批发店销售同一种苹果.在甲批发店,不论一次购买数量是多少,价格均为6元/kg .在乙批发店,一次购买数量不超过元50 kg 时,价格为7元/kg ;一次购买数量超过50kg 时,其中有50kg 的价格仍为7元/kg ,超出50 kg 部分的价格为5元/kg .设小王在同一个批发店一次购买苹果的数量为 kg x (0)x >.(1)根据题意填表:(2)设在甲批发店花费1y 元,在乙批发店花费2y 元,分别求1y ,2y 关于x 的函数解析式; (3)根据题意填空:①若小王在甲批发店和在乙批发店一次购买苹果的数量相同,且花费相同,则他在同一个批发店一次购买苹果的数量为__________kg ;②若小王在同一个批发店一次购买苹果的数量为120 kg ,则他在甲、乙两个批发店中的__________批发店购买花费少;③若小王在同一个批发店一次购买苹果花费了360元,则他在甲、乙两个批发店中的__________批发店购买数量多.【解析】(1)当x =30时,1306180y =⨯=,2307210y =⨯=,当x =150时,11506900y =⨯=,2507515050850y =⨯+-=(), 故答案为:180,900,210,850. (2)16y x =(0)x >. 当050x <≤时,27y x =;当50x >时,27505(50)y x =⨯+-,即25100y x =+. (3)①∵0x >∴6x 7x ≠, ∴当21y y =时,即6x =5x +100,∴x =100, 故答案为:100. ②∵x =12050>,∴16120720y =⨯=;25120100=700y =⨯+, ∴乙批发店购买花费少, 故答案为:乙.③∵当x =50时乙批发店的花费是:350360<, ∵一次购买苹果花费了360元,∴x >50, ∴当1360y =时,6x =360,∴x =60, ∴当2360y =时,5x +100=360,∴x =52, ∴甲批发店购买数量多. 故答案为:甲.6.(2019•湖州中考)某校的甲、乙两位老师同住一小区,该小区与学校相距2400米.甲从小区步行去学校,出发10分钟后乙再出发,乙从小区先骑公共自行车,途经学校义骑行若干米到达还车点后,立即步行走回学校.已知甲步行的速度比乙步行的速度每分钟快5米.设甲步行的时间为x (分),图1中线段OA 和折线B C D --分别表示甲、乙离开小区的路程y (米)与甲步行时间x (分)的函数关系的图象;图2表示甲、乙两人之间的距离s (米)与甲步行时间x (分)的函数关系的图象(不完整).根据图1和图2中所给信息,解答下列问题:(1)求甲步行的速度和乙出发时甲离开小区的路程;(2)求乙骑自行车的速度和乙到达还车点时甲、乙两人之间的距离;(3)在图2中,画出当2530x ≤≤时s 关于x 的函数的大致图象.(温馨提示:请画在答题卷相对应的图上)【解析】(1)由题意,得:甲步行的速度是24003080÷=(米/分), ∴乙出发时甲离开小区的路程是8010800⨯=(米).(2)设直线OA 的解析式为:(0)y kx k =≠, ∵直线OA 过点()30,2400A , ∴302400k =, 解得80k =,∴直线OA 的解析式为:80y x =, ∴当18x =时,80181440y =⨯=,∴乙骑自行车的速度是()14401810180÷-=(米/分). ∵乙骑自行车的时间为251015-=(分), ∴乙骑自行车的路程为180152700⨯=(米).当25x =时,甲走过的路程是8080252000y x ==⨯=(米),∴乙到达还车点时,甲、乙两人之间的距离是27002000700-=(米). (3)乙步行的速度为:80-5=75(米/分),乙到达学校用的时间为:25+(2700-2400)÷75=29(分), 当25≤x ≤30时s 关于x 的函数的大致图象如图所示.7.2019•河南中考)学校计划为“我和我的祖国”演讲比赛购买奖品.已知购买3个A 奖品和2个B 奖品共需120元;购买5个A 奖品和4个B 奖品共需210元. (1)求A ,B 两种奖品的单价;(2)学校准备购买A ,B 两种奖品共30个,且A 奖品的数量不少于B 奖品数量的13.请设计出最省钱的购买方案,并说明理由.【解析】(1)设A 的单价为x 元,B 的单价为y 元,根据题意,得3212054210x y x y +=⎧⎨+=⎩,∴3015x y =⎧⎨=⎩,∴A 的单价30元,B 的单价15元;(2)设购买A 奖品z 个,则购买B 奖品为(30-z )个,购买奖品的花费为W 元, 由题意可知,z ≥13(30-z ), ∴z ≥152, W =30z +15(30-z )=450+15z , ∵15>0,W 随z 的减小而减小 ∴当z =8时,W 有最小值为570元,即购买A 奖品8个,购买B 奖品22个,花费最少.8.(2019•宿迁中考)超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加x 元,每天售出y 件.(1)请写出y 与x 之间的函数表达式;(2)当x 为多少时,超市每天销售这种玩具可获利润2250元?(3)设超市每天销售这种玩具可获利w 元,当x 为多少时w 最大,最大值是多少? 【解析】(1)根据题意得,1502y x =-+. (2)根据题意得,()140(50)22502x x +-+=, 解得:150x =,210x =, ∵每件利润不能超过60元, ∴10x =,答:当x 为10时,超市每天销售这种玩具可获利润2250元. (3)根据题意得,()21140(50)30200022w x x x x =+-+=-++()213024502x =--+, ∵102a =-<, ∴当30x <时,w 随x 的增大而增大,∴当20x时,2400w =增大,答:当x 为20时w 最大,最大值是2400元.9.(2019•潍坊中考)扶贫工作小组对果农进行精准扶贫,帮助果农将一种有机生态水果拓宽了市场.与去年相比,今年这种水果的产量增加了1000千克,每千克的平均批发价比去年降低了1元,批发销售总额比去年增加了20%.(1)已知去年这种水果批发销售总额为10万元,求这种水果今年每千克的平均批发价是多少元? (2)某水果店从果农处直接批发,专营这种水果.调查发现,若每千克的平均销售价为41元,则每天可售出300千克;若每千克的平均销售价每降低3元,每天可多卖出180千克,设水果店一天的利润为w 元,当每千克的平均销售价为多少元时,该水果店一天的利润最大,最大利润是多少?(利润计算时,其它费用忽略不计)【解析】(1)由题意,设这种水果今年每千克的平均批发价是x 元,则去年的批发价为()1x +元, 今年的批发销售总额为()10120%12-=万元, ∴12000010000010001x x -=+, 整理得2191200x x --=,解得24x =或5x =-(不合题意,舍去), 故这种水果今年每千克的平均批发价是24元. (2)设每千克的平均售价为m 元,依题意 由(1)知平均批发价为24元,则有()4124(180300)3mw m -=-⨯+260420066240m m =-+-, 整理得()260357260w m =--+, ∵600a =-<, ∴抛物线开口向下,∴当35m =元时,w 取最大值,即每千克的平均销售价为35元时,该水果店一天的利润最大,最大利润是7260元.10.(2019•南充中考)在“我为祖国点赞”征文活动中,学校计划对获得一、二等奖的学生分别奖励一支钢笔,一本笔记本.已知购买2支钢笔和3个笔记本共38元,购买4支钢笔和5个笔记本共70元. (1)钢笔、笔记本的单价分别为多少元?(2)经与商家协商,购买钢笔超过30支时,每增加一支,单价降低0.1元;超过50支,均按购买50支的单价销售,笔记本一律按原价销售,学校计划奖励一、二等奖学生共计100人,其中一等奖的人数不少于30人,且不超过60人,这次奖励一等学生多少人时,购买奖品金额最少,最少为多少元? 【解析】(1)设钢笔、笔记本的单价分别为x 、y 元,根据题意可得23384570x y x y +=⎧⎨+=⎩, 解得:106x y =⎧⎨=⎩. 答:钢笔、笔记本的单价分别为10元,6元.(2)设钢笔单价为a 元,购买数量为b 支,支付钢笔和笔记本总金额为W 元, ①当30≤b ≤50时,100.1(30)0.113a b b =--=-+,w =b (-0.1b +13)+6(100-b )20.17600b b =-++20.1(35)722.5b =--+, ∵当30b =时,W =720,当b =50时,W =700, ∴当30≤b ≤50时,700≤W ≤722.5. ②当50<b ≤60时, a =8,86(100)2600W b b b =+-=+,∵700720W <≤,∴当30≤b ≤60时,W 的最小值为700元,∴当一等奖人数为50时花费最少,最少为700元.11.(2019•梧州中考)我市某超市销售一种文具,进价为5元/件.售价为6元/件时,当天的销售量为100件.在销售过程中发现:售价每上涨0.5元,当天的销售量就减少5件.设当天销售单价统一为x 元/件(x ≥6,且x 是按0.5元的倍数上涨),当天销售利润为y 元. (1)求y 与x 的函数关系式(不要求写出自变量的取值范围); (2)要使当天销售利润不低于240元,求当天销售单价所在的范围;(3)若每件文具的利润不超过80%,要想当天获得利润最大,每件文具售价为多少元?并求出最大利润.【解析】(1)由题意,y =(x -5)(100-60.5x -×5)=-10x 2+210x -800,故y与x的函数关系式为:y=-10x2+210x-800.(2)要使当天利润不低于240元,则y≥240,∴y=-10x2+210x-800=-10(x-10.5)2+302.5=240,解得,x1=8,x2=13,∵-10<0,抛物线的开口向下,∴当天销售单价所在的范围为8≤x≤13.(3)∵每件文具利润不超过80%,∴50.8xx-≤,得x≤9,∴文具的销售单价为6≤x≤9,由(1)得y=-10x2+210x-800=-10(x-10.5)2+302.5,∵对称轴为x=10.5,∴6≤x≤9在对称轴的左侧,且y随着x的增大而增大,∴当x=9时,取得最大值,此时y=-10(9-10.5)2+302.5=280,即每件文具售价为9元时,最大利润为280元.12.(2019•云南中考)某驻村扶贫小组实施产业扶贫,帮助贫困农户进行西瓜种植和销售.已知西瓜的成本为6元/千克,规定销售单价不低于成本,又不高于成本的两倍.经过市场调查发现,某天西瓜的销售量y(千克)与销售单价x(元/千克)的函数关系如图所示:(1)求y与x的函数解析式(也称关系式);(2)求这一天销售西瓜获得的利润W的最大值.【解析】(1)当6≤x≤10时,设y与x的关系式为y=kx+b(k≠0),根据题意得1000620010k bk b=+⎧⎨=+⎩,解得2002200kb=-⎧⎨=⎩,∴y=-200x+1200,当10<x≤12时,y=200,故y 与x 的函数解析式为:y =2002200(610)200(1012)x x x -+≤≤⎧⎨<≤⎩.(2)由已知得:W =(x -6)y , 当6≤x ≤10时,W =(x -6)(-200x +1200)=-200(x -172)2+1250, ∵-200<0,抛物线的开口向下, ∴x =172时,取最大值, ∴W =1250,当10<x ≤12时,W =(x -6)•200=200x -1200, ∵y 随x 的增大而增大,∴x =12时取得最大值,W =200×12-1200=1200, 综上所述,当销售价格为8.5元时,取得最大利润,最大利润为1250元.13.(2019•成都中考)随着5G 技术的发展,人们对各类5G 产品的使用充满期待,某公司计划在某地区销售一款5G 产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.设该产品在第x (x 为正整数)个销售周期每台的销售价格为y 元,y 与x 之间满足如图所示的一次函数关系. (1)求y 与x 之间的关系式;(2)设该产品在第x 个销售周期的销售数量为p (万台),p 与x 的关系可以用p =12x +12来描述.根据以上信息,试问:哪个销售周期的销售收入最大?此时该产品每台的销售价格是多少元?【解析】(1)设函数的解析式为:y =kx +b (k ≠0),由图象可得,700055000k b k b +=⎧⎨+=⎩,解得5007500kb=-⎧⎨=⎩,∴y与x之间的关系式:y=-500x+7500.(2)设销售收入为w万元,根据题意得,w=yp=(-500x+7500)(12x+12),即w=-250(x-7)2+16000,∴当x=7时,w有最大值为16000,此时y=-500×7+7500=4000(元).答:第7个销售周期的销售收入最大,此时该产品每台的销售价格是4000元.14.(2019•武汉中考)某商店销售一种商品,童威经市场调查发现:该商品的周销售量y(件)是售价x (元/件)的一次函数,其售价、周销售量、周销售利润w(元)的三组对应值如表:售价x(元/件)50 60 80周销售量y(件)100 80 40周销售利润w(元)1000 1600 1600 注:周销售利润=周销售量×(售价-进价)(1)①求y关于x的函数解析式(不要求写出自变量的取值范围);②该商品进价是__________元/件;当售价是__________元/件时,周销售利润最大,最大利润是__________元.(2)由于某种原因,该商品进价提高了m元/件(m>0),物价部门规定该商品售价不得超过65元/件,该商店在今后的销售中,周销售量与售价仍然满足(1)中的函数关系.若周销售最大利润是1400元,求m的值.【解析】(1)①依题意设y=kx+b,则有50100 6080k bk b+=⎧⎨+=⎩,解得2200 kb=-⎧⎨=⎩,所以y关于x的函数解析式为y=-2x+200.②该商品进价是50-1000÷100=40,设每周获得利润w=ax2+bx+c,则有2500501000 3600601600 6400801600a b ca b ca b c++=⎧⎪++=⎨⎪++=⎩,解得22808000 abc=-⎧⎪=⎨⎪=-⎩,∴w=-2x2+280x-8000=-2(x-70)2+1800,∴当售价是70元/件时,周销售利润最大,最大利润是1800元;故答案为:40,70,1800;(2)根据题意得,w=(x-40-m)(-2x+200)=-2x2+(280+2m)x-8000-200m,∵对称轴x=1402m+,∴①当1402m+<65时(舍),②当1402m+≥65时,x=65时,w求最大值1400,解得:m=5.。
高一期末复习1函数练习

期末复习1函数1.若log a 23<1,则a 的取值范围是________. 2.函数f (x )=lg ⎝ ⎛⎭⎪⎫1x 2+1+x 是( ) A .奇函数 B .偶函数 C .既奇又偶函数D .非奇非偶函数3.已知函数f (x )=m ·2x -12x +1为奇函数,则m 的值等于________.4.已知log a 13>log b 13>0,则下列关系正确的是( ) A .0<b <a <1 B .0<a <b <1 C .1<b <aD .1<a <b5.若a =20.2,b =log 4(3.2),c =log 2(0.5),则( ) A .a >b >c B .b >a >c C .c >a >bD .b >c >a6.若f (x )=a ·2x +2a -12x +1为R 上的奇函数,则实数a 的值为________.7.已知函数f (x )=⎩⎪⎨⎪⎧(a -2)x ,x ≥2,⎝ ⎛⎭⎪⎫12x-1,x <2满足对任意的实数x 1≠x 2都有f (x 1)-f (x 2)x 1-x 2<0成立,则实数a 的取值范围为( )A .(-∞,2) B.⎝ ⎛⎦⎥⎤-∞,138 C .(-∞,2] D.⎣⎢⎡⎭⎪⎫138,2 8.已知a =5log 23.4,b =5log 43.6,c =⎝ ⎛⎭⎪⎫15log 30.3,则( )A .a >b >cB .b >a >cC .a >c >bD .c >a >b9.函数f (x )=x 12-⎝ ⎛⎭⎪⎫12x的零点个数为( )A .0B .1C .2D .310.(本小题满分12分)已知函数f (x )=⎩⎨⎧log 2x ,x >0,3x ,x ≤0,且关于x 的方程f (x )+x -a =0有且只有一个实根,求实数a 的取值范围.11.设x 0是方程ln x +x =4的根,且x 0∈(k ,k +1),k ∈Z ,则k =________. 12.用二分法求函数f (x )=2x +3x -7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为( )A .(0,1)B .(0,2)C .(2,3)D .(2,4)13.(2018·全国卷Ⅰ)已知函数f (x )=⎩⎨⎧e x ,x ≤0,ln x ,x >0,g (x )=f (x )+x +a .若g (x )存在2个零点,则a 的取值范围是( )A .[-1,0)B .[0,+∞)C .[-1,+∞)D .[1,+∞)14.已知函数f (x )=a -12x +1(x ∈R ). (1)用定义证明:不论a 为何实数,f (x )在R 上为增函数; (2)若f (x )为奇函数,求a 的值;(3)在(2)的条件下,求f (x )在区间[1,5]上的最小值.1.若log a 23<1,则a 的取值范围是________. [原不等式等价于⎩⎪⎨⎪⎧0<a <1,23>a 或⎩⎪⎨⎪⎧a >1,23<a ,解得0<a <23或a >1,故a 的取值范围为⎝ ⎛⎭⎪⎫0,23∪(1,+∞).]2.函数f (x )=lg ⎝ ⎛⎭⎪⎫1x 2+1+x 是( ) A .奇函数 B .偶函数 C .既奇又偶函数D .非奇非偶函数A [f (x )定义域为R ,f (-x )+f (x )=lg ⎝ ⎛⎭⎪⎫1x 2+1-x +lg ⎝ ⎛⎭⎪⎫1x 2+1+x =lg1(x 2+1)-x 2=lg 1=0,∴f (x )为奇函数,故选A.]3.已知函数f (x )=m ·2x -12x +1为奇函数,则m 的值等于________.1 [由题意可知,f (0)=m ·20-120+1=m -12=0,∴m =1.]4.已知log a 13>log b 13>0,则下列关系正确的是( ) A .0<b <a <1 B .0<a <b <1 C .1<b <aD .1<a <bA [由log a 13>0,log b 13>0,可知a ,b ∈(0,1), 又log a 13>log b 13,作出图象如图所示, 结合图象易知a >b ,∴0<b <a <1.]5.若a =20.2,b =log 4(3.2),c =log 2(0.5),则( ) A .a >b >c B .b >a >c C .c >a >bD .b >c >aA [∵a =20.2>1>b =l o g 4(3.2)>0>c =l o g 2(0.5),∴a >b >c .故选A. 6.若f (x )=a ·2x +2a -12x +1为R 上的奇函数,则实数a 的值为________.13 [因为f (x )=a ·2x +2a -12x +1为R 上的奇函数,所以f (0)=0,即a ·20+2a -120+1=0,所以a =13.]7.已知函数f (x )=⎩⎪⎨⎪⎧(a -2)x ,x ≥2,⎝ ⎛⎭⎪⎫12x-1,x <2满足对任意的实数x 1≠x 2都有f (x 1)-f (x 2)x 1-x 2<0成立,则实数a 的取值范围为( )A .(-∞,2) B.⎝ ⎛⎦⎥⎤-∞,138 C .(-∞,2]D.⎣⎢⎡⎭⎪⎫138,2 B [由题意知函数f (x )是R 上的减函数,于是有⎩⎪⎨⎪⎧a -2<0,(a -2)×2≤⎝ ⎛⎭⎪⎫122-1,由此解得a ≤138,即实数a 的取值范围是⎝ ⎛⎦⎥⎤-∞,138,选B.]8.已知a =5log 23.4,b =5log 43.6,c =⎝ ⎛⎭⎪⎫15log 30.3,则( )A .a >b >cB .b >a >cC .a >c >bD .c >a >bC [c =5log 3103,只需比较log 23.4,log 43.6,log 3103的大小,又0<log 43.6<1,log 23.4>log 33.4>log 3103>1,所以a >c >b .]9.函数f (x )=x 12-⎝ ⎛⎭⎪⎫12x的零点个数为( )A .0B .1C .2D .3B [令f (x )=0,可得x 12=⎝ ⎛⎭⎪⎫12x,在同一平面直角坐标系中分别画出幂函数y=x 12和指数函数y =⎝ ⎛⎭⎪⎫12x的图象,如图所示,可得交点只有一个,所以函数f (x )的零点只有一个.10.(本小题满分12分)已知函数f (x )=⎩⎨⎧log 2x ,x >0,3x ,x ≤0,且关于x 的方程f (x )+x -a =0有且只有一个实根,求实数a 的取值范围.[解]如图,在同一坐标系中分别作出y =f (x )与y =-x +a 的图象,其中a 表示直线在y 轴上的截距,由图可知,当a >1时,直线y =-x +a 与y =log 2x 只有一个交点.所以实数a 的取值范围是(1,+∞).11.设x 0是方程ln x +x =4的根,且x 0∈(k ,k +1),k ∈Z ,则k =________. 2 [令f (x )=ln x +x -4, 且f (x )在(0,+∞)上递增,∵f (2)=ln 2+2-4<0,f (3)=ln 3-1>0, ∴f (x )在(2,3)内有解,∴k =2.]12.用二分法求函数f (x )=2x +3x -7在区间[0,4]上的零点近似值,取区间中点2,则下一个存在零点的区间为( )A .(0,1)B .(0,2)C .(2,3)D .(2,4)B [因为f (0)=20+0-7=-6<0,f (4)=24+12-7>0,f (2)=22+6-7>0,所以f (0)·f (2)<0,所以零点在区间(0,2)内.] 13.已知函数f (x )=a -12x +1(x ∈R ). (1)用定义证明:不论a 为何实数,f (x )在R 上为增函数; (2)若f (x )为奇函数,求a 的值;(3)在(2)的条件下,求f (x )在区间[1,5]上的最小值.[解] (1)证明:∵f (x )的定义域为R ,任取x 1<x 2,则f (x 1)-f (x 2)=a -12x 1+1-a +12x 2+1=2x 1-2x 2(2x 1+1)(2x 2+1). ∵x 1<x 2,∴2x 1-2x 2<0,(1+2x 1)(1+2x 2)>0, ∴f (x 1)-f (x 2)<0,即f (x 1)<f (x 2),∴不论a 为何实数,f (x )在R 上为增函数. (2)∵f (x )在x ∈R 上为奇函数, ∴f (0)=0,即a -120+1=0,解得a =12.(3)由(2)知,f (x )=12-12x +1,由(1)知,f (x )为增函数,∴f (x )在区间[1,5]上的最小值为f (1). ∵f (1)=12-13=16,∴f (x )在区间[1,5]上的最小值为16.14.(2018·全国卷Ⅰ)已知函数f (x )=⎩⎨⎧e x ,x ≤0,ln x ,x >0,g (x )=f (x )+x +a .若g (x )存在2个零点,则a 的取值范围是( )A .[-1,0)B .[0,+∞)C .[-1,+∞)D .[1,+∞)C [函数g (x )=f (x )+x +a 存在2个零点,即关于x 的方程f (x )=-x -a 有2个不同的实根,即函数f(x)的图象与直线y=-x-a有2个交点,作出直线y=-x-a与函数f(x)的图象,如图所示,由图可知,-a≤1,解得a≥-1,故选C.]。
第四章一次函数综合题动点问题练习(1)2021-2022学年 北师大版数学八年级上册

北师大版数学八年级上册第四章一次函数综合题动点问题练习11.如图,直线y=kx+6分别与x轴、y轴交于点E,F,已知点E的坐标为(-8,0),点A的坐标为(-6,0).(1)求k的值;(2)若点P(x,y)是该直线上的一个动点,且在第二象限内运动,试写出△OPA的面积S关于x的函数解析式,并写出自变量x的取值范围;(3)点P是该直线上的一个动点,且在第二象限内运动,探究:当点P运动到什么?并说明理由.位置时,△OPA的面积为2782.如图,已知点A(6,0)、点B(0,2).(1)求直线AB所对应的函数表达式;(2)若C为直线AB上一动点,当△OBC的面积为3时,试求点C的坐标.3.如图,在平面直角坐标系xOy中,直线l1:y=x+3分别交x轴、y轴于点A、B,直线l2:y=-3x与直线l1交于点C,点P为y轴上一动点.(1)求点C的坐标;(2)当PA+PC的值最小时,求此时P点的坐标,并求PA+PC的最小值;(3)在平面直角坐标系中是否存在点M,使以点A、O、C、M为顶点的四边形是平行四边形,若存在,求出点M的坐标;若不存在,请说出理由.4.如图1,已知平行四边形ABCD,AB//x轴,AB=12,点A的坐标为(2,-8),点D的坐标为(-6,8),点B在第四象限,点P是平行四边形ABCD边上的一个动点.(1)若点P在边BC上,PD=CD,求点P的坐标.(2)若点P在边AB,AD上,点P关于坐标轴对称的点Q落在直线y=x-1上,求点P的坐标.(3)若点P在边AB,AD,CD上,点G是AD与y轴的交点,如图2,过点P作y轴的平行线PM,过点G作x轴的平行线GM,它们相交于点M,将△PGM沿直线PG翻折,当点M的对应点落在坐标轴上时,求点P的坐标(直接写出答案).5.直线y=kx-4与x轴、y轴分别交于B,C两点,且OCOB =43.(1)求点B的坐标和k的值.(2)若点A是在第一象限内直线y=kx-4上的一个动点,当它运动到什么位置时,△AOB的面积是12?(3)若点A是直线y=kx-4上的一个动点,设A(x,y),△AOB的面积为s,求s关于x 的函数表达式,并写出x的取值范围.6.已知,直线y=2x-2与x轴交于点A,与y轴交于点B.(1)如图①,点A的坐标为______,点B的坐标为______;(2)如图②,点C是直线AB上不同于点B的点,且CA=AB.①求点C的坐标;②过动点P(m,0)且垂直于x轴的直线与直线AB交于点E,若点E不在线段BC上,则m的取值范围是______;(3)若∠ABN=45°,求直线BN的解析式.7.如图,直线l分别交坐标轴于点A(3,0)、B(0,6).点P(m,n)是直线l上的动点,但不与点A重合,连接OP,设△OAP的面积为S.(1)求直线l所对应的函数表达式;(2)求S与m的函数关系式,并写出自变量m的取值范围;(3)是否存在这样的点P,使S=3?若存在,请求出点P的坐标;若不存在,请说明理由.8.如图,直线y=2x+6交x轴于A,交y轴于B.(1)直接写出A(______,______),B(______,______);x上一点,若以A,B,(2)如图1,点E为直线y=x+2上一点,点F为直线y=12E,F为顶点的四边形是平行四边形,求点E,F的坐标.(3)如图2,点C(m,n)为线段AB上一动点,D(-7m,0)在x轴上,连接CD,点M为CD的中点,求点M的纵坐标y和横坐标x之间的函数关系式,并直接写出在点C移动过程中点M的运动路径长.9.在直角坐标系xOy中,已知点A(3,0),直线l:y=−x+4,在第一象限有一动点P(x,y)在直线l上,直线l与x轴、y轴分别交于点B、C,设ΔOPA的面积为S.(1)分别求出B、C的坐标;(2)求S关于x的函数解析式,并写出x的取值范围;10.已知,直线AB分别交x、y轴于A(4,0)、B两点,C(-4,a)为直线y=-x与AB的公共点.(1)求点B的坐标。
2023年高考数学一轮复习第二章函数1函数的概念及其表示练习含解析

函数的概念及其表示考试要求 1.了解函数的含义,会求简单函数的定义域和值域.2.在实际情景中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.3.了解简单的分段函数,并会简单的应用.知识梳理 1.函数的概念一般地,设A ,B 是非空的实数集,如果对于集合A 中的任意一个数x ,按照某种确定的对应关系f ,在集合B 中都有唯一确定的数y 和它对应,那么就称f :A →B 为从集合A 到集合B 的一个函数,记作y =f (x ),x ∈A . 2.函数的三要素(1)函数的三要素:定义域、对应关系、值域.(2)如果两个函数的定义域相同,并且对应关系完全一致,则这两个函数为同一个函数. 3.函数的表示法表示函数的常用方法有解析法、图象法和列表法. 4.分段函数若函数在其定义域的不同子集上,因对应关系不同而分别用几个不同的式子来表示,这种函数称为分段函数. 常用结论1.直线x =a 与函数y =f (x )的图象至多有1个交点.2.在函数的定义中,非空数集A ,B ,A 即为函数的定义域,值域为B 的子集.3.分段函数虽由几个部分组成,但它表示的是一个函数.分段函数的定义域等于各段函数的定义域的并集,值域等于各段函数的值域的并集. 思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)若两个函数的定义域和值域相同,则这两个函数是同一个函数.( × ) (2)函数y =f (x )的图象可以是一条封闭曲线.( × ) (3)y =x 0与y =1是同一个函数.( × ) (4)函数f (x )=⎩⎪⎨⎪⎧x -1,x ≥0,x 2,x <0的定义域为R .( √ )教材改编题1.下列各曲线表示的y 与x 之间的关系中,y 不是x 的函数的是( )答案 C2.(多选)下列各组函数是同一个函数的是( ) A .f (x )=x 2-2x -1,g (s )=s 2-2s -1B .f (x )=x -1,g (x )=x 2-1x +1C .f (x )=x 2,g (x )=⎩⎪⎨⎪⎧x ,x ≥0,-x ,x <0D .f (x )=-x 3,g (x )=x -x 答案 AC3.(2022·长沙质检)已知函数f (x )=⎩⎪⎨⎪⎧3x,x ≤0,log 3x ,x >0,则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫12等于( )A .-1B .2C.3D.12答案 D解析 ∵f ⎝ ⎛⎭⎪⎫12=log 312<0, ∴f ⎝⎛⎭⎪⎫f⎝ ⎛⎭⎪⎫12=31log 23=12.题型一 函数的定义域例1 (1)(2022·武汉模拟)函数f (x )=1ln x +1+4-x 2的定义域为( ) A .[-2,0)∪(0,2]B .(-1,0)∪(0,2]C .[-2,2]D .(-1,2]答案 B解析 要使函数有意义,则需⎩⎪⎨⎪⎧x +1>0,x +1≠1,4-x 2≥0,解得-1<x ≤2且x ≠0, 所以x ∈(-1,0)∪(0,2].所以函数的定义域为(-1,0)∪(0,2].(2)若函数f (x )的定义域为[0,2],则函数f (x -1)的定义域为________. 答案 [1,3]解析 ∵f (x )的定义域为[0,2], ∴0≤x -1≤2,即1≤x ≤3, ∴函数f (x -1)的定义域为[1,3].延伸探究 将本例(2)改成“若函数f (x +1)的定义域为[0,2]”,则函数f (x -1)的定义域为________. 答案 [2,4]解析 ∵f (x +1)的定义域为[0,2], ∴0≤x ≤2, ∴1≤x +1≤3, ∴1≤x -1≤3, ∴2≤x ≤4,∴f (x -1)的定义域为[2,4]. 教师备选1.(2022·西北师大附中月考)函数y =lg(x 2-4)+x 2+6x 的定义域是( ) A .(-∞,-2)∪[0,+∞) B .(-∞,-6]∪(2,+∞) C .(-∞,-2]∪[0,+∞) D .(-∞,-6)∪[2,+∞) 答案 B解析 由题意,得⎩⎪⎨⎪⎧x 2-4>0,x 2+6x ≥0,解得x >2或x ≤-6.因此函数的定义域为(-∞,-6]∪(2,+∞).2.已知函数f (x )=x1-2x ,则函数f x -1x +1的定义域为( )A .(-∞,1)B .(-∞,-1)C .(-∞,-1)∪(-1,0)D .(-∞,-1)∪(-1,1) 答案 D解析 令1-2x>0, 即2x<1,即x <0.∴f (x )的定义域为(-∞,0).∴函数f x -1x +1中,有⎩⎪⎨⎪⎧x -1<0,x +1≠0,解得x <1且x ≠-1.故函数f x -1x +1的定义域为(-∞,-1)∪(-1,1).思维升华 (1)求给定函数的定义域:由函数解析式列出不等式(组)使解析式有意义. (2)求复合函数的定义域①若f (x )的定义域为[m ,n ],则在f (g (x ))中,由m ≤g (x )≤n 解得x 的范围即为f (g (x ))的定义域.②若f (g (x ))的定义域为[m ,n ],则由m ≤x ≤n 得到g (x )的范围,即为f (x )的定义域. 跟踪训练1 (1)函数f (x )=11-4x2+ln(3x -1)的定义域为( )A.⎝ ⎛⎦⎥⎤13,12B.⎝ ⎛⎭⎪⎫13,12C.⎣⎢⎡⎭⎪⎫-12,14 D.⎣⎢⎡⎦⎥⎤-12,12 答案 B解析 要使函数f (x )=11-4x2+ln(3x -1)有意义,则⎩⎪⎨⎪⎧1-4x 2>0,3x -1>0⇒13<x <12. ∴函数f (x )的定义域为⎝ ⎛⎭⎪⎫13,12. (2)已知函数f (x )的定义域为[-2,2],则函数g (x )=f (2x )+1-2x的定义域为__________. 答案 [-1,0]解析 由条件可知,函数的定义域需满足⎩⎪⎨⎪⎧-2≤2x ≤2,1-2x≥0,解得-1≤x ≤0,所以函数g (x )的定义域是[-1,0]. 题型二 函数的解析式例2 (1)(2022·哈尔滨三中月考)已知f ⎝ ⎛⎭⎪⎫2x+1=lg x ,则f (x )的解析式为________.答案 f (x )=lg2x -1(x >1) 解析 令2x+1=t (t >1),则x =2t -1, 所以f (t )=lg 2t -1(t >1), 所以f (x )=lg2x -1(x >1). (2)已知y =f (x )是二次函数,若方程f (x )=0有两个相等实根,且f ′(x )=2x +2,则f (x )=________. 答案 x 2+2x +1解析 设f (x )=ax 2+bx +c (a ≠0), 则f ′(x )=2ax +b ,∴2ax +b =2x +2, 则a =1,b =2.∴f (x )=x 2+2x +c , 又f (x )=0,即x 2+2x +c =0有两个相等实根. ∴Δ=4-4c =0,则c =1. 故f (x )=x 2+2x +1.(3)已知函数对任意的x 都有f (x )-2f (-x )=2x ,则f (x )=________. 答案 23x解析 ∵f (x )-2f (-x )=2x ,① ∴f (-x )-2f (x )=-2x ,② 由①②得f (x )=23x .教师备选已知f (x )满足f (x )-2f ⎝ ⎛⎭⎪⎫1x =2x ,则f (x )=________.答案 -2x 3-43x解析 ∵f (x )-2f ⎝ ⎛⎭⎪⎫1x =2x ,①以1x代替①中的x ,得f ⎝ ⎛⎭⎪⎫1x -2f (x )=2x,②①+②×2得-3f (x )=2x +4x,∴f (x )=-2x 3-43x.思维升华 函数解析式的求法(1)配凑法;(2)待定系数法;(3)换元法;(4)解方程组法. 跟踪训练2 (1)已知f (1-sin x )=cos 2x ,则f (x )=________. 答案 -x 2+2x ,x ∈[0,2] 解析 令t =1-sin x , ∴t ∈[0,2],sin x =1-t ,∴f (t )=1-sin 2x =1-(1-t )2=-t 2+2t ,t ∈[0,2], ∴f (x )=-x 2+2x ,x ∈[0,2].(2)(2022·黄冈质检)已知f ⎝⎛⎭⎪⎫x 2+1x2=x 4+1x4,则f (x )=__________.答案 x 2-2,x ∈[2,+∞)解析 ∵f ⎝⎛⎭⎪⎫x 2+1x 2=⎝⎛⎭⎪⎫x 2+1x22-2,∴f (x )=x 2-2,x ∈[2,+∞). 题型三 分段函数例3 (1)已知f (x )=⎩⎪⎨⎪⎧cosπx ,x ≤1,f x -1+1,x >1,则f ⎝ ⎛⎭⎪⎫43+f⎝ ⎛⎭⎪⎫-43的值为( ) A.12B .-12C .-1D .1 答案 D解析 f ⎝ ⎛⎭⎪⎫43=f⎝ ⎛⎭⎪⎫43-1+1=f ⎝ ⎛⎭⎪⎫13+1=cosπ3+1=32,f ⎝ ⎛⎭⎪⎫-43=cos ⎝ ⎛⎭⎪⎫-4π3=cos2π3=-12, ∴f ⎝ ⎛⎭⎪⎫43+f ⎝ ⎛⎭⎪⎫-43=32-12=1.(2)已知f (x )=⎩⎪⎨⎪⎧2x+3,x >0,x 2-4,x ≤0,若f (a )=5,则实数a 的值是__________;若f (f (a ))≤5,则实数a 的取值范围是__________. 答案 1或-3 [-5,-1]解析 ①当a >0时,2a+3=5,解得a =1; 当a ≤0时,a 2-4=5, 解得a =-3或a =3(舍). 综上,a =1或-3.②设t =f (a ),由f (t )≤5得-3≤t ≤1. 由-3≤f (a )≤1,解得-5≤a ≤-1. 教师备选1.已知函数f (x )=⎩⎪⎨⎪⎧sin ⎝ ⎛⎭⎪⎫πx +π6,x >1,⎝ ⎛⎭⎪⎫12x,x <1,则f (f (2022))等于( )A .-32B.22C.32D. 2 答案 B解析 f (2022)=sin ⎝ ⎛⎭⎪⎫2022π+π6=sin π6=12,∴f (f (2022))=f ⎝ ⎛⎭⎪⎫12=1212⎛⎫ ⎪⎝⎭=22. 2.(2022·百校联盟联考)已知函数f (x )=⎩⎪⎨⎪⎧x 3,x ≥0,-x 2,x <0,若对于任意的x ∈R ,|f (x )|≥ax ,则a =________. 答案 0解析 当x ≥0时,|f (x )|=x 3≥ax ,即x (x 2-a )≥0恒成立,则有a ≤0; 当x <0时,|f (x )|=x 2≥ax ,即a ≥x 恒成立, 则有a ≥0,所以a =0.思维升华 分段函数求值问题的解题思路(1)求函数值:当出现f (f (a ))的形式时,应从内到外依次求值.(2)求自变量的值:先假设所求的值在分段函数定义区间的各段上,然后求出相应自变量的值,切记要代入检验.跟踪训练3 (1)(2022·河北冀州一中模拟)设f (x )=⎩⎪⎨⎪⎧x +2x-3,x ≥1,x 2+1,x <1.则f (f (-1))=________,f (x )的最小值是________. 答案 0 22-3 解析 ∵f (-1)=2,∴f (f (-1))=f (2)=2+22-3=0,当x ≥1时,f (x )=x +2x-3≥22-3,当且仅当x =2时取等号,f (x )min =22-3, 当x <1时,f (x )=x 2+1≥1,x =0时取等号, ∴f (x )min =1,综上有f (x )的最小值为22-3.(2)(2022·重庆质检)已知函数f (x )=⎩⎪⎨⎪⎧log 2x ,x >1,x 2-1,x ≤1,则f (x )<f (x +1)的解集为________.答案 ⎝ ⎛⎭⎪⎫-12,+∞解析 当x ≤0时,x +1≤1,f (x )<f (x +1), 等价于x 2-1<(x +1)2-1, 解得-12<x ≤0;当0<x ≤1时,x +1>1, 此时f (x )=x 2-1≤0,f (x +1)=log 2(x +1)>0,∴当0<x ≤1时,恒有f (x )<f (x +1);当x >1时,f (x )<f (x +1)⇔log 2x <log 2(x +1)恒成立.综上知,不等式f (x )<f (x +1)的解集为⎝ ⎛⎭⎪⎫-12,+∞.课时精练1.(2022·重庆模拟)函数f (x )=3-xlg x的定义域是( ) A .(0,3) B .(0,1)∪(1,3) C .(0,3] D .(0,1)∪(1,3]答案 D解析 ∵f (x )=3-xlg x,∴⎩⎪⎨⎪⎧3-x ≥0,lg x ≠0,x >0,解得0<x <1或1<x ≤3,故函数的定义域为(0,1)∪(1,3].2.若函数y =f (x )的定义域为M ={x |-2≤x ≤2},值域为N ={y |0≤y ≤2},则函数y =f (x )的图象可能是( )答案 B解析 A 中函数定义域不是[-2,2];C 中图象不表示函数;D 中函数值域不是[0,2]. 3.(2022·安徽江淮十校联考)设函数f (x )=⎩⎪⎨⎪⎧4x -12,x <1,a x ,x ≥1,若f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫78=8,则a 等于( ) A.12 B.34 C .1 D .2答案 D解析 f ⎝ ⎛⎭⎪⎫78=4×78-12=3,则f ⎝ ⎛⎭⎪⎫f ⎝ ⎛⎭⎪⎫78=f (3)=a 3,得a 3=8,解得a =2.4.设函数f ⎝ ⎛⎭⎪⎫1-x 1+x =x ,则f (x )的表达式为( )A.1+x1-x(x ≠-1) B.1+xx -1(x ≠-1) C.1-x1+x(x ≠-1) D.2xx +1(x ≠-1) 答案 C解析 令t =1-x 1+x ,则x =1-t1+t ,∴f (t )=1-t 1+t ,即f (x )=1-x1+x(x ≠-1).5.如图,点P 在边长为1的正方形的边上运动,M 是CD 的中点,当P 沿A -B -C -M 运动时,设点P 经过的路程为x ,△APM 的面积为y ,则函数y =f (x )的图象大致是( )答案 A解析 由题意可得y =f (x )=⎩⎪⎨⎪⎧12x ,0≤x <1,34-x4,1≤x <2,54-12x ,2≤x ≤52.画出函数f (x )的大致图象,故选A.6.(多选)下列函数中,与y =x 是同一个函数的是( ) A .y =3x 3B .y =x 2C .y =lg10xD .y =10lg x答案 AC解析 y =x 的定义域为x ∈R ,值域为y ∈R ,对于A 选项,函数y =3x 3=x 的定义域为x ∈R ,故是同一函数;对于B 选项,函数y =x 2=||x ≥0,与y =x 的解析式、值域均不同,故不是同一函数;对于C 选项,函数y =lg10x=x ,且定义域为R ,故是同一函数;对于D 选项,y =10lg x=x 的定义域为(0,+∞),与函数y =x 的定义域不相同,故不是同一函数.7.(多选)(2022·张家界质检)设函数f (x )=⎩⎪⎨⎪⎧1-x ,x ≤a ,2x,x >a ,若f (1)=2f (0),则实数a可以为( ) A .-1B .0C .1D .2 答案 AB 解析 若a <0,则f (0)=1,f (1)=2,f (1)=2f (0)成立; 若0≤a <1,则f (0)=1,f (1)=2,f (1)=2f (0)成立; 若a ≥1,则f (0)=1,f (1)=0,f (1)=2f (0)不成立. 综上所述,实数a 的取值范围是(-∞,1).8.(多选)具有性质:f ⎝ ⎛⎭⎪⎫1x =-f (x )的函数,我们称为满足“倒负”变换的函数,下列函数满足“倒负”变换的函数的是( ) A .f (x )=x -1xB .f (x )=ln1-x1+xC .f (x )=1ex x-D .f (x )=⎩⎪⎨⎪⎧x ,0<x <1,0,x =1,-1x ,x >1答案 AD解析 对于A ,f (x )=x -1x,f ⎝ ⎛⎭⎪⎫1x =1x-x =-f (x ),满足题意; 对于B ,f (x )=ln1-x1+x,则f ⎝ ⎛⎭⎪⎫1x =ln x -1x +1≠-f (x ),不满足; 对于C ,f ⎝ ⎛⎭⎪⎫1x =111e xx -=ex -1,-f (x )=1ex x--≠f ⎝ ⎛⎭⎪⎫1x ,不满足;对于D ,f ⎝ ⎛⎭⎪⎫1x =⎩⎪⎨⎪⎧1x ,0<1x <1,0,1x =1,-x ,1x >1,即f ⎝ ⎛⎭⎪⎫1x =⎩⎪⎨⎪⎧1x ,x >1,0,x =1,-x ,0<x <1,则f ⎝ ⎛⎭⎪⎫1x =-f (x )满足“倒负”变换,故选AD.9.已知f (x 5)=lg x ,则f (100)=________. 答案 25解析 令x 5=100, 则x =15100=2510, ∴f (100)=25lg 10=25.10.函数f (x )=ln(x -1)+4+3x -x 2的定义域为________. 答案 (1,4]解析 依题意⎩⎪⎨⎪⎧x -1>0,4+3x -x 2≥0,解得1<x ≤4,∴f (x )的定义域为(1,4].11.(2022·广州质检)已知函数f (x )=⎩⎪⎨⎪⎧1-2a x +3a ,x <1,ln x ,x ≥1的值域为R ,则实数a的取值范围是________.答案 ⎣⎢⎡⎭⎪⎫-1,12 解析 ∵当x ≥1时,f (x )=ln x ≥ln1=0, 又f (x )的值域为R ,故当x <1时,f (x )的值域包含(-∞,0).故⎩⎪⎨⎪⎧1-2a >0,1-2a +3a ≥0,解得-1≤a <12.12.设函数f (x )=⎩⎪⎨⎪⎧x ,x <0,1,x >0,则不等式xf (x )+x ≤2的解集是________.答案 [-2,0)∪(0,1] 解析 当x <0时,f (x )=x , 代入xf (x )+x ≤2得x 2+x -2≤0, 解得-2≤x <0; 当x >0时,f (x )=1,代入xf (x )+x ≤2,解得0<x ≤1. 综上有-2≤x <0或0<x ≤1.13.设函数f (x )=⎩⎪⎨⎪⎧2-x,x ≤0,1,x >0,则满足f (x +1)<f (2x )的x 的取值范围是( ) A .(-∞,-1] B .(0,+∞) C .(-1,0) D .(-∞,0)答案 D解析 当x ≤0时,函数f (x )=2-x是减函数,则f (x )≥f (0)=1.作出f (x )的大致图象如图所示,结合图象知,要使f (x +1)<f (2x ),当且仅当⎩⎪⎨⎪⎧x +1<0,2x <0,2x <x +1或⎩⎪⎨⎪⎧x +1≥0,2x <0,解得x <-1或-1≤x <0,即x <0.14.设函数f (x )=⎩⎪⎨⎪⎧-x +λ,x <1λ∈R,2x,x ≥1,若对任意的a ∈R 都有f (f (a ))=2f (a )成立,则λ的取值范围是______. 答案 [2,+∞) 解析 当a ≥1时,2a≥2. ∴f (f (a ))=f (2a)=22a=2f (a )恒成立.当a <1时,f (f (a ))=f (-a +λ)=2f (a )=2λ-a ,∴λ-a ≥1,即λ≥a +1恒成立, 由题意λ≥(a +1)max ,∴λ≥2, 综上,λ的取值范围是[2,+∞).15.(多选)若函数f (x )满足:对定义域内任意的x 1,x 2(x 1≠x 2),有f (x 1)+f (x 2)>2f ⎝ ⎛⎭⎪⎫x 1+x 22,则称函数f (x )具有H 性质.则下列函数中具有H 性质的是( )A .f (x )=⎝ ⎛⎭⎪⎫12xB .f (x )=ln xC .f (x )=x 2(x ≥0) D .f (x )=tan x ⎝ ⎛⎭⎪⎫0≤x <π2 答案 ACD解析 若对定义域内任意的x 1,x 2(x 1≠x 2),有f (x 1)+f (x 2)>2f ⎝ ⎛⎭⎪⎫x 1+x 22,则点(x 1,f (x 1)),(x 2,f (x 2))连线的中点在点⎝⎛⎭⎪⎫x 1+x 22,f ⎝ ⎛⎭⎪⎫x 1+x 22的上方,如图⎝⎛⎭⎪⎫其中a =f⎝ ⎛⎭⎪⎫x 1+x 22,b =f x 1+f x 22.根据函数f (x )=⎝ ⎛⎭⎪⎫12x ,f (x )=ln x ,f (x )=x 2(x ≥0),f (x )=tan x ⎝⎛⎭⎪⎫0≤x <π2的图象可知,函数f (x )=⎝ ⎛⎭⎪⎫12x ,f (x )=x 2(x ≥0),f (x )=tan x ⎝⎛⎭⎪⎫0≤x <π2具有H 性质,函数f (x )=ln x 不具有H 性质.16.设f (x )是定义在R 上的函数,且f (x +2)=2f (x ),f (x )=⎩⎪⎨⎪⎧2x +a ,-1<x <0,b e 2x,0≤x ≤1,其中a ,b 为正实数,e 为自然对数的底数,若f ⎝ ⎛⎭⎪⎫92=f ⎝ ⎛⎭⎪⎫32,则a b 的取值范围为________. 答案 (2e ,+∞)解析 因为f (x +2)=2f (x ),所以f ⎝ ⎛⎭⎪⎫92=f⎝ ⎛⎭⎪⎫12+4=(2)2f ⎝ ⎛⎭⎪⎫12=2e b ,f ⎝ ⎛⎭⎪⎫32=f ⎝ ⎛⎭⎪⎫-12+2=2f ⎝ ⎛⎭⎪⎫-12 =2⎣⎢⎡⎦⎥⎤2×⎝ ⎛⎭⎪⎫-12+a =2(a -1), 因为f ⎝ ⎛⎭⎪⎫92=f ⎝ ⎛⎭⎪⎫32,所以2(a -1)=2e b , 所以a =2e b +1, 因为b 为正实数, 所以a b=2e b +1b=2e +1b∈(2e ,+∞),故a b的取值范围为(2e ,+∞).。
一次函数综合题1

⇔⇔⇔⇔一次函数与几何图形变换直线y 1=k 1x+b 1与直线y 2=k 2x+b 2(k 1≠0,k 2≠0)的位置关系.①k 1≠k 2y1与y2相交;② K 1≠ K 2, b1=b2y1与y2相交于y 轴上同一点(0,b1)或(0,b2);③ K 1 : K 2=b 1 : b 2 k 1≠ k 2y 1与y 2相交于x 轴上同一点(-,0)④ K 1 = K 2, b 1 ≠b 2y 1与y 2互相平行 ⑤ K 1 = K 2 b 1=b 2 y 1与y 2互相重合⑥ K 1 K 2=-1 Y 1与Y 2互相垂直 ⑦ K 1 = - k 2 b 1 = b 2y 1与y 2关于y 轴对称 ⑧ K 1= - k 2 b 1 = -b 2y1与y2关于x 轴对称 ⑨ K 1= k 2 b 1 = - b 2y 1与y 2关于原点对称⑩直线y=kx+b 关于直线y =x 对称直线解析式为直线y=kx+b 关于直线y =-x 对称,直线解析式为〖方法〗:直线的对称问题可通过点的对称解决,所以可在已知直线上取两点,求得对称点的坐标后,再运用待定系数法求其解析式.例填空⑴若直线l 与直线y =2x -1关于x 轴对称,则直线l 的解析式为⑵若直线l 与直线y =2x -1关于y 轴对称,则直线l 的解析式为 ⑶若直线l 与直线y =2x -1关于原点对称,则直线l 的解析式为 __________ . ⑷若直线l 与直线y =2x -1关于直线y =x 对称,则直线l 的解析式为________ . ⑸若直线l 与直线y =2x -1关于直线y =-x 对称,则直线l 的解析式为__________.⑹直线y=k 1x-3与y=k 2x+4相交于x 轴上一点则k 1:k 2=___ ⑺直线y=k 1x-b 1与y=k 2x+4相交于y 轴上一点则b 1=___ ⑻直线y=x+b 1与y=2x+b 2相交于x 轴上一点则b 1:b 2= ⑼函数y 1=x +b 图象与一次函数y 2=kx +4的图象关于y 轴对称,求k 、b 的值⑽函数y 1=x +b 图象与一次函数y 2=kx +4互相垂直则k=------------⑾函数y 1=x +b 图象与一次函数y 2=kx +4互相平行则k= --------- 练习1.已知直线b kx y +=平行于直线y=-3x+4,且与直线y=2x-6的交点在x 轴上,求此一次函数的解析式。
3.1.1 函数的概念 练习(1)(解析版)

3.1.1 函数的概念一、选择题1.(2019·广东高一课时练习)集合A={x|0≤x ≤4},B={y|0≤y ≤2},下列不能表示从A 到B 的函数的是( )A .f :x →y =12x B .f :x →y=2﹣xC .f :x →y =23x D .f :x →y =√x【答案】C【解析】对于C 选项的对应法则是f :x →y=23x ,可得f (4)=83∉B ,不满足映射的定义,故C 的对应法则不能构成映射.故C 的对应f 中不能构成A 到B 的映射.其他选项均符合映射的定义. 故选:C .2.(2019·广东高一课时练习)函数f (x )=√x +1x 的定义域是( )A .{x|x >0}B .{x|x ≥0}C .{x|x ≠0}D .R 【答案】A【解析】要使f(x)有意义,则满足{x ≥0x ≠0 ,得到x>0.故选A.3.(2018·全国高一课时练习)下列每组函数是同一函数的是( ) A .f(x)=x −1,g(x)=(√x −1)2 B .f(x)=x −1,g(x)=√(x −1)2 C .f(x)=x 2−4x−2,g(x)=x +2 D .f(x)=|x|,g(x)=√x 2【答案】D【解析】A ,函数f(x)的定义域为,g (x )的定义域为{x|x ≥1},两个函数的定义域不相同,不是同一函数;B ,函数f (x )和g (x )的值域不相同,不是同一函数;C ,函数f (x )和g (x )的定义域不同,不是同一函数;D ,f (x )=|x |,g (x )=√x 2=|x |,函数f (x )和g (x )的定义域、值域、对应法则都相同,属于同一函数,故选D.4.(2014·全国高一课时练习)变量x 与变量y ,w ,z 的对应关系如下表所示:下列说法正确的是 A .y 是x 的函数 B .w 不是x 的函数 C .z 是x 的函数 D .z 不是x 的函数【答案】C【解析】观察表格可以看出,当x =1时,y =–1,–4,则y 不是x 的函数;根据函数的定义,一个x 只能对应一个y,反之一个y 可以跟多个x 对应,很明显w 是x 的函数,z 是x 的函数. 故选C .5.(2018·全国高三课时练习(文))已知集合{}|A x y ==, {}| B x x a =≥,若A B A ⋂=,则实数a 的取值范围是( )A .(],3-∞-B .(),3-∞-C .(],0-∞D .[)3,+∞ 【答案】A【解析】由已知得[]3,3A =-,由A B A ⋂=,则A B ⊆,又[),B a =+∞,所以3a ≤-.故选A.6.(2017·全国高一课时练习)设()2211x f x x -=+,则()212f f ⎛⎫⎪⎝⎭等于( )A .1B .-1C .35 D .-35【答案】B【解析】()2221413221415f --===++. 221111132********2f ⎛⎫-- ⎪⎛⎫⎝⎭===- ⎪⎝⎭⎛⎫++ ⎪⎝⎭.∴.()2112f f =-⎛⎫ ⎪⎝⎭故选B. 二、填空题7.(2017·全国高一课时练习)已知函数()f x ,()g x 分别由下表给出.(1) ()()1f g =________;(2)若()()g f x =2,则x =________. 【答案】1 1 【解析】由题意得,g (1)=3,则f[g (1)]=f (3)=1 ∵g[f (x )]=2,即f (x )=2,∴x=1. 故答案为:1,1.8.(2017·全国高一课时练习)用区间表示下列数集. (1){x |x ≥2}=________; (2){x |3<x ≤4}=________; (3){x |x >1且x ≠2}=________.【答案】 [2,+∞) (3,4] (1,2)∪(2,+∞) 【解析】由区间表示法知: (1)[2,+∞); (2)(3,4];(3)(1,2)∪(2,+∞).9.(2017·全国高一课时练习)若[a,3a -1]为一确定区间,则a 的取值范围是________. 【答案】1,2⎛⎫+∞⎪⎝⎭【解析】由题意3a -1>a ,得a>12,故填1,.2⎛⎫+∞ ⎪⎝⎭10.(2017·全国高一课时练习)已知f(x)=x 2+x -1,x ∈{0,1,2,3},则f(x)的值域为________. 【答案】{-1,1,5,11}【解析】由已知得f(0)=−1;f(1)=1+1−1=1;f(2)=4+2−1=5;f(3)=9+3−1=11 故答案为{-1,1,5,11}. 三、解答题11.(2018·全国高一课时练习)求下列函数的定义域(1)y =√x +8+√3−x (2)y =√x 2−1+√1−x 2x−1【答案】(1)[−8,3];(2){−1}。
高一数学必修一第三章函数的应用(含幂函数)综合练习题及参考答案

高一数学(必修1)第三章 函数的应用(含幂函数)[综合训练]一、选择题1。
若函数)(x f y =在区间[],a b 上的图象为连续不断的一条曲线,则下列说法正确的是( )A .若0)()(>b f a f ,不存在实数),(b a c ∈使得0)(=c f ;B .若0)()(<b f a f ,存在且只存在一个实数),(b a c ∈使得0)(=c f ;C .若0)()(>b f a f ,有可能存在实数),(b a c ∈使得0)(=c f ;D .若0)()(<b f a f ,有可能不存在实数),(b a c ∈使得0)(=c f ;2.方程0lg =-x x 根的个数为( )A .无穷多错误!未指定书签。
B .3C .1D .03.若1x 是方程lg 3x x +=的解,2x 是310=+x x的解,则21x x +的值为( ) A .23错误!未指定书签。
B .32 C .3 D .31 4.函数2-=x y 在区间]2,21[上的最大值是( ) A .41 B .1- C .4 D .4- 5.设()833-+=x x f x ,用二分法求方程()2,10833∈=-+x x x在 内近似解的过程中得()()(),025.1,05.1,01<><f f f则方程的根落在区间( )A .(1,1.25)B .(1.25,1.5)C .(1.5,2)D .不能确定6.直线3y =与函数26y x x =-的图象的交点个数为( )A .4个B .3个C .2个D .1个7.若方程0x a x a --=有两个实数解,则a 的取值范围是( )A .(1,)+∞B .(0,1)C .(0,2)D .(0,)+∞ 二、填空题1.1992年底世界人口达到54.8亿,若人口的年平均增长率为%x ,2005年底世界人口为y 亿,那么y 与x 的函数关系式为 .2.942--=a a x y 是偶函数,且在),0(+∞是减函数,则整数a 的值是 .3.函数12(0.58)x y -=-的定义域是 .4.已知函数2()1f x x =-,则函数(1)f x -的零点是__________.5.函数2223()(1)mm f x m m x --=--是幂函数,且在(0,)x ∈+∞上是减函数,则实数m =______. 三、解答题1.利用函数图象判断下列方程有没有实数根,有几个实数根:①01272=++x x ;②0)2lg(2=--x x ; ③0133=--x x ; ④0ln 31=--x x 。
一次函数综合测试题及答案 (1)

一、填空 (10×3´=30´)1、已知一个正比例函数的图象经过点(-2,4),则这个正比例函数的表达式是 。
2、若函数y= -2x m+2是正比例函数,则m 的值是 。
3、已知一次函数y=kx+5的图象经过点(-1,2),则k= 。
4、已知y 与x 成正比例,且当x =1时,y =2,则当x=3时,y=____ 。
5、点P (a ,b )在第二象限,则直线y=ax+b 不经过第 象限。
6、已知一次函数y=kx-k+4的图象与y 轴的交点坐标是(0,-2),那么这个一次函数的表达式是______________。
7、已知点A(-1,a), B(2,b)在函数y=-3x+4的象上,则a 与b 的大小关系是____ 。
8、地面气温是20℃,如果每升高1000m,气温下降6℃,则气温t (℃)与高度h (m )的函数关系式是__________。
9、一次函数y=kx+b 与y=2x+1平行,且经过点(-3,4),则表达式为: 。
10、写出同时具备下列两个条件的一次函数表达式(写出一个即可) 。
(1)y 随着x 的增大而减小, (2)图象经过点(1,-3)。
二、选择题 (10×3´=30´)11、下列函数(1)y=πx (2)y=2x-1 (3)y=1x(4)y=2-1-3x 中,是一次函数的有( )(A )4个 (B )3个 (C )2个 (D )1个 12、下面哪个点不在函数32+-=x y 的图像上( ) (A )(-5,13) (B )(0.5,2) (C )(3,0) (D )(1,1)13、直线y=kx+b 在坐标系中的位置如图,则(A)1,12k b =-=- (B )1,12k b =-= (C )1,12k b ==- (D )1,12k b == 14、下列一次函数中,随着增大而减小而的是 ( )(A )x y 3= (B )23-=x y (C )x y 23+= (D )23--=x y15、已知一次函数y=kx+b 的图象如图所示,则k ,b 的符号是( )(A) k>0,b>0 (B) k>0,b<0 (C) k<0,b>0 (D) k<0,b<016、函数y=(m+1)x-(4m-3)的图象在第一、二、四象限,那么m 的取值范围是( ) (A )34m <(B )314m -<< (C )1m <- (D )1m >-17、一支蜡烛长20厘米,点燃后每小时燃烧5厘米,燃烧时剩下的高度h (厘米)与燃烧时间t (时)的函数关系的图象是( )(A) (B) (C ) (D )18、下图中表示一次函数y =mx+n 与正比例函数y =m nx(m ,n 是常数,且mn<0)图像的是( )19.一次函数y =ax +1与y =bx -2的图象交于x 轴上一点,那么a :b 等于A.21B.21C.23D.以上答案都不对20.某公司市场营业员销部的营销人员的个人收入与其每月的销售量成一次函数关系,其图象如图所示.由图中给出的信息可知,营销人员没有销售时的收入是A.310B.300C.290D.280三、计算题 (21、22、25各8分,23、24、26各12分)21、已知一个正比例函数和一个一次函数的图象相交于点A(1,4),且一次函数的图象与x 轴交于点B(3,0) (1)求这两个函数的解析式;(2)画出它们的图象;22、已知y -2与x 成正比,且当x=1时,y= -6(1)求y 与x 之间的函数关系式 (2)若点(a ,2)在这个函数图象上,求a 的值23、已知一次函数y=kx+b 的图象经过点(-1, -5),且与正比例函数y= 12 x 的图象相交于点(2,a),求(1)a 的值(2)k ,b的值(3)这两个函数图象与x 轴所围成的三角形的面积。
三角函数综合练习1

三角函数综合练习题一、选择题1、若sin2α>0,且cos α<0,则角α是 ( )A .第一象限角B .第二象限角C .第三象限角D .第四象限角2、若tan α=2,则2sin α-cos αsin α+2cos α的值为( ) A .0 B.34 C .1 D.543、若△ABC 的内角A 满足sin2A =23,则sin A +cos A = ( ) A.153 B .-153 C.53 D .-534、下列各项中,值为32的是( ) A .2sin15°cos15° B .cos 215°-sin 215° C .2sin 215°-1 D .sin 215°+cos 215°5、已知tan(α+β)=25,tan(β-π4)=14,则tan(α+π4)等于 ( ) A.2318 B.322 C.1322 D.3186、设A 、B 是△ABC 的内角,且cos A =35,sin B =513,则sin(A +B )的值为 ( ) A.6365或-1665 B.1665 C.1665或-6365 D.63657、函数f (x )=sin(π4-x )的一个单调增区间为 ( ) A .(3π4,7π4) B .(-π4,3π4) C .(-π2,π2) D .(-3π4,π4) 8、函数y =sin(2x +π3)的图象的对称轴方程可能是 ( ) A .x =-π6 B .x =-π12 C .x =π6 D .x =π129、将函数y =sin(6x +π4)的图象上各点的横坐标伸长到原来的3倍,再向右平移π8个单位,得到的函数的一个对称中心是 ( )A .(π2,0)B .(π4,0)C .(π9,0)D .(π16,0) 10、若定义在R 上的函数f (x )满足f (π3+x )=-f (x ),且f (-x )=f (x ),则f (x )可以是( ) A .f (x )=2sin 13x B .f (x )=2sin3x C .f (x )=2cos 13x D .f (x )=2cos3x 11、已知函数f (x )=sin(w x +π4)(x ∈R ,w >0)的最小正周期为π.将y =f (x )的图象向左平移|φ|个单位长度,所得图象关于y 轴对称,则φ的一个值是 ( ) A.π2 B.3π8 C.π4 D.π812、函数f (x )=sin 2x +3sin x cos x 在区间[π4,π2]上的最大值是( ) A .1 B.1+32 C.32D .1+ 3 13、若f (x )=2cos 2x +3sin2x +a (a 为实常数)在区间⎣⎡⎦⎤0,π2上的最小值为-4,则a 的值为 ( ) A .-6 B .4 C .-3 D .-414、已知函数f (x )=3sin w x +cos w x (w >0),y =f (x )的图象与直线y =2的两个相邻交点的距离等于π,则f (x )的单调递增区间是 ( )A .[kπ-π12,kπ+5π12],k ∈ZB .[kπ+5π12,kπ+11π12],,k ∈Z C .[kπ-π3,kπ+π6],k ∈Z D .[kπ+π6,kπ+2π3],k ∈Z 15、3-sin70°2-cos 210°=( ) A.12 B.22 C .2 D.32二、填空题1、已知点P (tan α,cos α)在第三象限,则角α的终边在第________象限. 二2、若sin θ=-45,tan θ>0,则cos θ=________.答案:-353、已知点P (sin 34π,cos 34π)落在角θ的终边上,且0≤θ≤2π,则θ=________.答案:7π44、函数f (x )=sin x +2|sin x |,x ∈[0,2π]的图象与直线y =k 有且仅有两个不同的交点,则k 的取值范围是_____答案:1<k <35、给出下列六个命题,其中正确的命题是__________.①存在α满足sin α+cos α=32;②y =sin(52π-2x )是偶函数;③x =π8是y =sin(2x +5π4)的一条对称轴; ④y =e sin2x 是以π为周期的(0,π2)上的增函数;⑤若α、β是第一象限角,且α>β,则tan α>tan β; ⑥函数y =3sin(2x +π3)的图象可由y =3sin2x 的图象向左平移π3个单位得到.答案:②③ 三、解答题1、已知cos2θ=725,π2<θ<π. 求: (1)tan θ的值; (2)2cos 2θ2-sin θ2sin(θ+π4)的值. 解析:(1)由cos2θ=725,得1-2sin 2θ=725,sin 2θ=925. ∵π2<θ<π,∴sin θ=35,cos θ=-45.∴tan θ=sin θcos θ=-34. (2)2cos 2θ2-sin θ2sin(θ+π4)=cos θ+1-sin θsin θ+cos θ=-45+1-3535-45=2. 2、已知3π4<α<π,tan α+cot α=-103. (1)求tan α的值; (2)求5sin 2α2+8sin α2cos α2+11cos 2α2-82sin(α-π4)的值.解析:(1)∵tan α+cot α=-103,∴3tan 2α+10tan α+3=0.解得tan α=-13或tan α=-3. ∵3π4<α<π,∴-1<tan α<0.∴tan α=-13. (2)∵tan α=-13, ∴5sin 2α2+8sin α2cos α2+11cos 2α2-82sin(α-π4)=5(sin 2α2+cos 2α2)+4sin α+6·1+cos α2-8sin α-cos α =5+4sin α+3+3cos α-8sin α-cos α=4sin α+3cos αsin α-cos α=4tan α+3tan α-1=-54. 3、已知sin α=-55,tan β=-13且α、β∈(-π2,0). (1)求α+β的值; (2)求2sin(π4-α)+cos(π4+β)的值. 解析:(1)由sin α=-55及α∈(-π2,0),∴cos α=255.∴tan α=-12,∴tan(α+β)=tan α+tan β1-tan α·tan β=-1. 又∵-π<α+β<0,∴α+β=-π4. (2)由(1)知α+β=-π4, 2sin(π4-α)+cos(π4+β)=2sin(π4-α)+cos(π4-π4-α)=2sin(π4-α)+cos α=2cos α-sin α =2×255+55= 5. 4、已知函数f (x )=cos 2w x +sin w x cos w x -12(w >0)的最小正周期为π. (1)求f (x )在区间[-π2,π8]上的最小值; (2)求函数f (x )的图象上与坐标原点最近的对称中心的坐标.解析:(1)f (x )=cos 2w x +sin w x cos w x -12=12(cos2w x +1)+12sin2w x -12=22sin(2w x +π4). ∵T =2π2w =π,∴w =1,∴f (x )=22sin(2x +π4). ∵当-π2≤x ≤π8时,-3π4≤2x +π4≤π2, ∴当2x +π4=-π2时,f (x )=22sin(2x +π4)取得最小值为-22. (2)令2x +π4=kπ,得x =kπ-π42=kπ2-π8,k ∈Z , 当k =0时,x =-π8,当k =1时,x =3π8, ∴满足要求的对称中心为(-π8,0). 5、设函数f (x )=(sin w x +cos w x )2+2cos 2w x (w >0)的最小正周期为2π3. (1)求w 的值;(2)若函数y =g (x )的图象是由y =f (x )的图象向右平移π2个单位长度得到的.求y =g (x )的单调增区间. 解析:(1)f (x )=sin 2w x +cos 2w x +2sin w x cos w x +1+cos2w x =sin2w x +cos2w x +2=2sin(2w x +π4)+2,依题意得2π2w =2π3,故w =32. (2)依题意得g (x )=2sin[3(x -π2)+π4]+2=2sin(3x -5π4)+2. 由2kπ-π2≤3x -5π4≤2kπ+π2(k ∈Z)解得23kπ+π4≤x ≤23kπ+7π12(k ∈Z). 故g (x )的单调增区间为[23kπ+π4,23kπ+7π12](k ∈Z). 6、设函数f (x )=sin(π4x -π6)-2cos 2π8x +1. (1)求f (x )的最小正周期;(2)若函数y =g (x )与y =f (x )的图象关于直线x =1对称,求当x ∈[0,43]时,y =g (x )的最大值. 解析:(1)由f (x )=sin π4x cos π6-cos π4x sin π6-cos π4x =32sin π4x -32cos π4x =3sin(π4x -π3), 故f (x )的最小正周期为T =2ππ4=8. (2)解法一:在y =g (x )的图象上任取一点(x ,g (x )),它关于x =1的对称点为(2-x ,g (x )).由题设条件,点(2-x ,g (x ))在y =f (x )的图象上,从而g (x )=f (2-x )=3sin[π4(2-x )-π3]=3sin(π2-π4x -π3)=3cos(π4x +π3). 当0≤x ≤43时,π3≤π4x +π3≤2π3,因此 y =g (x )在区间[0,43]上的最大值为g (x )max =3cos π3=32. 解法二:因区间[0,43]关于x =1的对称区间为[23,2],且y =g (x )与y =f (x )的图象关于x =1对称,故y =g (x )在[0,43]上的最大值即为y =f (x )在[23,2]上的最大值. 由(1)知f (x )=3sin(π4x -π3), 当23≤x ≤2时,-π6≤π4x -π3≤π6. 因此y =g (x )在[0,43]上的最大值为g (x )max =3sin π6=32. 7、已知函数f (x )=2cos x cos(π6-x )-3sin 2x +sin x cos x . (1)求f (x )的最小正周期;(2)设x ∈[-π3,π2],求f (x )的值域. 解析:(1)∵f (x )=cos x (3cos x +sin x )-3sin 2x +sin x cos x =3(cos 2x -sin 2x )+2sin x cos x =3cos2x +sin2x=2sin(2x +π3), ∴f (x )的最小正周期为π.(2)∵x ∈[-π3,π2],∴-π3≤2x +π3≤4π3. 又∵f (x )=2sin(2x +π3), ∴f (x )∈[-3,2].∴f (x )的值域为[-3,2].8、已知函数f (x )=3sin ⎝⎛⎭⎫2x -π6+2sin 2⎝⎛⎭⎫x -π12(x ∈R) (1)求函数f (x )的最小正周期;(2)求函数f (x )取得最大值的所有x 组成的集合.解析:(1)f (x )=3sin ⎝⎛⎭⎫2x -π6+1-cos2⎝⎛⎭⎫x -π12 =3sin ⎝⎛⎭⎫2x -π6-cos ⎝⎛⎭⎫2x -π6+1 =2⎣⎡⎦⎤32sin ⎝⎛⎭⎫2x -π6-12cos ⎝⎛⎭⎫2x -π6+1=2sin ⎣⎡⎦⎤⎝⎛⎭⎫2x -π6-π6+1=2sin ⎝⎛⎭⎫2x -π3+1, ∴函数f (x )的最小正周期为T =2π2=π. (2)当f (x )取最大值时,sin ⎝⎛⎭⎫2x -π3=1,此时有2x -π3=2kπ+π2, 即x =kπ+5π12(k ∈Z). ∴所求x 的集合为⎩⎨⎧⎭⎬⎫x |x =kπ+5π12,k ∈Z . 9、已知α∈(0,π2),β∈(π2,π)且sin(α+β)=3365,cos β=-513.求sin α. 解析:∵β∈(π2,π),cos β=-513,∴sin β=1213. 又∵0<α<π2,π2<β<π,∴π2<α+β<3π2,又sin(α+β)=3365,∴π2<α+β<π, cos(α+β)=-1-sin 2(α+β)=-1-(3365)2=-5665,∴sin α=sin[(α+β)-β] =sin(α+β)cos β-cos(α+β)sin β=3365·(-513)-(-5665)·1213=35. 10、已知f (x )=sin 2w x +32sin2w x -12(x ∈R ,w >0),若f (x )的最小正周期为2π. (1)求f (x )的表达式和f (x )的单调递增区间;(2)求f (x )在区间[-π6,5π6]上的最大值和最小值. 解析:(1)由已知f (x )=sin 2w x +32sin2w x -12=12(1-cos2w x )+32sin2w x -12=32sin2w x -12cos2w x =sin(2w x -π6). 又由f (x )的周期为2π,则2π=2π2w ⇒2w =1⇒w =12, ⇒f (x )=sin(x -π6), 2kπ-π2≤x -π6≤2kπ+π2(k ∈Z)⇒2kπ-π3≤x ≤2kπ+2π3(k ∈Z), 即f (x )的单调递增区间为[2kπ-π3,2kπ+2π3](k ∈Z). (2)由x ∈[-π6,5π6]⇒-π6≤x ≤5π6⇒-π6-π6≤x -π6≤5π6-π6⇒-π3≤x -π6≤2π3⇒sin(-π3)≤sin(x -π6)≤sin π2.∴-32≤sin(x -π6)≤1. 故f (x )在区间[-π6,5π6]的最大值和最小值分别为1和-32.11、已知A 、B 、C 三点的坐标分别是A (3,0)、B (0,3),C (cos α,sin α),其中π2<α<3π2. (1)若|AC →|=|BC →|,求角α的值;(2)若AC →·BC →=-1,求2sin 2α+sin2α1+tan α的值. 解析:(1)AC →=(cos α-3,sin α),BC →=(cos α,sin α-3),∵|AC →|=|BC →|,∴|AC →|2=|BC →|2,即(cos α-3)2+sin 2α=cos 2α+(sin α-3)2,化简得sin α=cos α.∵π2<α<3π2,∴α=5π4. (2)-1=AC →·BC →=cos α(cos α-3)+sin α(sin α-3)=1-3(sin α+cos α),∴sin α+cos α=23. 于是2sin α·cos α=(sin α+cos α)2-1=-59, 故2sin 2α+sin2α1+tan α=2sin α(sin α+cos α)cos α+sin αcos α=2sin α·cos α=-59.。
一次函数综合证明题1
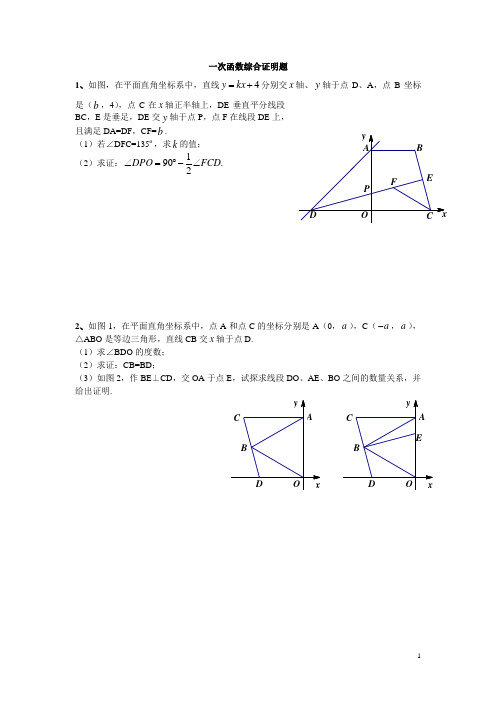
一次函数综合证明题1、如图,在平面直角坐标系中,直线4y kx =+分别交x 轴、y 轴于点D 、A ,点B 坐标是(b ,4),点C 在x 轴正半轴上,DE 垂直平分线段BC ,E 是垂足,DE 交y 轴于点P ,点F 在线段DE 上,且满足DA=DF ,CF=b .(1)若∠DFC=135º,求k 的值; (2)求证:190.2DPO FCD ∠=︒-∠2、如图1,在平面直角坐标系中,点A 和点C 的坐标分别是A (0,a ),C (a -,a ),△ABO 是等边三角形,直线CB 交x 轴于点D. (1)求∠BDO 的度数; (2)求证:CB=BD ;(3)如图2,作BE ⊥CD ,交OA 于点E ,试探求线段DO 、AE 、BO 之间的数量关系,并给出证明.NM PO xy A3、如图,在平面直角坐标系中,A (a ,0),B (0,b ),且a 、b 满足2(2)40a b -+-=.(1)求直线AB 的解析式;(2)若点M 为直线y mx =上一点,且△ABM 是以AB 为底的等腰直角三角形,求m 。
(3)过点A 的直线2y kx k =-交y 轴负半轴于点P ,N 点的横坐标为-1,过N 点的直线22k k y x =-交AP 于点M ,试证明:PM PNAM-的值是定值.4、如图,在平面直角坐标系中,OA=OB=OC=2,点P 从C 点出发,沿y 轴正方向以1个单位/秒的速度向上运动,连结PA ,PB ,D 为AC 的中点 ⑴求直线BC 的解析式;⑵设点P 运动的时间为t 秒,问:当t 为何值时,DP 与DB 垂直且相等。
⑶若PA=AB ,在第一象限内有一动点Q ,连QA ,QB ,QP ,且∠PQA=600,问:当Q 在第一象限内运动时,∠APQ+∠ABQ 的度数和是否会发生改变?若不改变,请说明理由并求这个不变的值 。
MxOy BA5、如图,直线AB :y=-x-b 分别与x 轴y 轴交于A (6,0),B 两点,过点B的直线交x 轴的负半轴于点C ,且OB :OC=3:1 (1) 求直线BC 的解析式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
函数综合练习1班级姓名学号一、选择题:(每题5分,共60分)1、设集合A={1,2,3},集合B={a,b,c},则从集合A到集合B的一一映射共有()A.3个B.6个C.9个D.18个2、设函数)2(log,2)9()1,0(log)(91-=≠>=ffaaxxfa则满足的值是()A.2log3B.22C.2D.23、给出两个命题:p:|x|=x的充要条件是x为正实数;q:存在反函数的函数一定是单调函数,则下列哪个复合命题是真命题()A.p且q B.p或q C.┐p且q D.┐p或q4、对函数baxxxf++=23)(作代换x=g(t),则总不改变f(x)值域的代换是()A.ttg21log)(=B.ttg)21()(=C.g(t)=(t-1)2D.g(t)=cost5、函数axfxxf==)(|,|)(如果方程有且只有一个实根,那么实数a应满足()A.a<0 B.0<a<1 C.a=0 D.a>16、函数)2(loglog2xxyx+=的值域是()A.]1,(--∞B.),3[+∞C.]3,1[-D.),3[]1,(+∞⋃--∞7、方程f(x,y)=0的曲线如图所示,那么方程f(2-x,y)=0的曲线是()8、已知f(x)是定义在在R上的奇函数,且当x<0时,f(x)=2x,则f-1(-41)的值为()A.-21B.21C.-2 D.29、设奇函数]1,1[)(-在xf上是增函数,且,1)1(-=-f若函数12)(2+-≤attxf对所有的]1,1[-∈x 都成立,当]1,1[-∈a 时,则t 的取值范畴是 ( )A .22≤≤-tB .2121≤≤-t C .022=-≤≥t t t 或或 D .02121=-≤≥t t t 或或 10、设a>0为常数,若函数f(x)=x 3-ax 在区间[1,+∞)上是单调函数,则a 的取值范畴是()A .(0,1] B .[1,+∞)C .(0,3]D .[3,+∞)11、关于函数∈-=x xx x f (1)(R 且0≠x ),有下列三个结论: ①)(x f 的值域为R ; ②)(x f 是区间(0,+∞)上的增函数; ③对任意∈x R 且0)()(,0=+-≠x f x f x 有成立.其中全部正确的结论是 ( )A .①②③B .①③C .①②D .②③12、已知)(x f y =是偶函数,当m x f n x xx x f x ≤≤--∈+=>)(,]1,3[,4)(,0时且当时恒成立,则n m -的最小值是 ( )A .31 B .32C .1D .34 二、填空题(本大题共4个小题,每小题5分,共20分) 13. 当0a >且1a ≠时,指数函数2()3x f x a-=-必过定点 .14、函数()lg(2)1f x x x =⋅+-的图象与x 轴的交点个数有15、已知函数)3(log )(221+-=ax x x f 在)1,(-∞上是增函数,则实数a 的范畴是 .16.已知定义在R 上的偶函数)(x f 满足条件:)()1(x f x f -=+,且在[-1,0]上是增函数,给出下面关于)(x f 的命题: ①)(x f 是周期函数; ②)(x f 的图象关于直线1=x 对称; ③)(x f 在[0,1]上是增函数 ④)(x f 在[1,2]上是减函数 ⑤)0()2(f f = 其中正确的命题序号是 .(注:把你认为正确的命题序号都填上) 三、 解答题:共70分,解承诺写出文字说明、证明过程或演算步骤. 17. (本小题满分14分)设函数2()21x f x a =-+, (1) 求证:不论a 为何实数()f x 总为增函数;(2)确定a 的值,使()f x 为奇函数;18、(本小题满分14分) 已知函数)10()1010()(2>+-=x x x x f .(1)求)(x f 的反函数;(2)设102)(1)(1++=-x x f x g ,求函数)(x g y =的最小值及相应的x 的值.19.(本小题满分12分)某厂家拟在2007年举行促销活动,经调查测算,该产品的年销售量(即该厂的年产量)x 万件与年促销费用m 万元(13)0+-=≥m kx m 满足)(k 为常数),假如不搞促销活动,则该产品的年销售量只能是1万件。
已知2004年生产该产品的固定投入为8万元,每生产1万件该产品需要再投入16万元,厂家将每件产品的销售价格定为每件产品年平均成本的1.5倍(产品成本包括固定投入和再投入两部分资金)。
(1)将2007年该产品的利润y 万元表示为年促销费用m 万元的函数; (2)该厂家2007年的促销费用投入多少万元时,厂家的利润最大?20、(本小题满分14分)设函数()f x 在(,)-∞+∞上满足(2)(2)f x f x -=+,(7)(7)f x f x -=+,且在闭区间[0,7]上,只有(1)(3)0f f ==.(Ⅰ)试判定函数()y f x =的奇偶性;(Ⅱ)试求方程()f x =0在闭区间[-2005,2005]上的根的个数,并证明你的结论.21、(本小题16分)函数)(x f y =是偶函数,且是周期为2的周期函数,当x ∈[2,3]时,1)(-=x x f ,在)(x f y =的图象上有两点A 、B ,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C 的坐标为(0,a )(其中a >2),求△ABC 面积的最大值.参考答案一、BCDACD CDCCAC二、13、(2,2)- 14、2 15、42≤≤a 16、①②⑤三、17解析: 由220x->得x <x >而函数的定义域为[,]a b ,∴必有[,]{a b x x ⊆<x >},当b <,22()log (2)y f x x ==-在[,]a b 上单调递减,()f x ∴的值域是[(),()],f b f a2()1()log 14f b f a =⎧∴⎨=⎩ 解得42a b =-⎧⎨=-⎩ ;当a >, 22()log (2)y f x x ==-在[,]a b 上单调递增,()f x ∴的值域为[(),()],f a f b2()1()log 14f a f b =⎧∴⎨=⎩ 解得214a b =⎧⎨=⎩ 综上所述,知42a b =-⎧⎨=-⎩ 或24a b =⎧⎨=⎩. 18、解:(1)由)10()1010(2>+-=x x x y 得,)10(1)1(10<<-+=y yy x . ).10(1)1(10)(1<<-+=∴-x xx x f(2))211(101102)(1)(1+++-=++-=-x xxx x f x g.5222101)121(101132101=⋅≥+++=+++⋅=xx x x x 等号成立的条件为.121xx +=+即21±-=x (舍去21--).223-=∴x . )(,223x g x 时当-=∴有最小值为.5219.解:(1)由题意可知当,123,231),(1,0+-=∴=⇒-=∴==m x k k x m 万件时…2分每件产品的销售价格为)(1685.1元xx+⨯……………………………………4分∴2004年的利润m m m x m x x x x y-+-+=-+=++-+⨯⋅=)123(8484)168(]1685.1[ )0(29)]1(116[≥++++-=m m m ……………………6分(2)8162)1(116,0=≥+++≥m m m 时 ,………………………………9分21,)(31116,21298max ==⇒+=+=+-≤∴y m m m y 时万元当且仅当(万元)…11分答:(略)……………………………………………………………………………12分20、.解:由f(2-x)=f(2+x),f(7-x)=f(7+x)得函数)(x f y =的对称轴为72==x x 和,从而知函数)(x f y =不是奇函数,由)14()4()14()()4()()7()7()2()2(x f x f x f x f x f x f x f x f x f x f -=-⇒⎩⎨⎧-=-=⇒⎩⎨⎧+=-+=-)10()(+=⇒x f x f ,从而知函数)(x f y =的周期为10=T又0)7(,0)0()3(≠==f f f 而,故函数)(x f y =是非奇非偶函数;(II)由)14()4()14()()4()()7()7()2()2(x f x f x f x f x f x f x f x f x f x f -=-⇒⎩⎨⎧-=-=⇒⎩⎨⎧+=-+=-)10()(+=⇒x f x f(II) 又0)9()7()13()11(,0)0()3(=-=-====f f f f f f故f(x)在[0,10]和[-10,0]上均有有两个解,从而可知函数)(x f y =在[0,2005]上有402个解,在[-2005.0]上有400个解,因此函数)(x f y =在[-2005,2005]上有802个解.21、 解:如图,∵f(x)是以2为周期的周期函数,,1)(,]3,2[-=∈x x f x 时∴当x ∈[-1,0]时,;11)()()(+-=+-=-=x x x f x f 当x ∈[1,2]时,f(x)=f(x -2)=-(x -2)+1=-x +3(平移). 设A 、B 的纵坐标为t (1≤t ≤2),并设A 在B 的左边,则A 、B 的横坐标分别为3-t ,t+1,则|AB|=(t+1)-(3-t )=2t -2,△ABC 的面积为.)1())(22(212a t a t t a t S -++-=--=令,0)1(2=++-='a t S t 得.21+=a t 当22123≤+<a ,即2<a ≤3时,S 有最大值;4122+-a a 当221>+a ,即a >3时,0>'t S ,函数单调增,S 有最大值S (2)=a -2.[那个地点可将S 配方;S=)21(412)21(22≤≤+-++--t a a a t 也可直截了当用二次函数理论得出].。
