沪教版(上海)数学高二下册-1两条直线的夹角课件_2
合集下载
沪教版上海数学高二下册-1两条直线的夹角ppt课件[1]
![沪教版上海数学高二下册-1两条直线的夹角ppt课件[1]](https://img.taocdn.com/s3/m/86888beff12d2af90342e65d.png)
1
1
1
1
a1,
b 1
不全为零
l : a x b y c 0 a b2, 2 不全为零
2
2
2
2
例 果1相、交判,断则两求条出直交线点的坐位标置I。m关Na系og,e 如
l1
:
3x
2
y
6
0,
l 2
:
9x
4
y
7
0
练一练:判断下列各组直线的位置关
系,如果相交,则求出交点坐标。
No
(1)
l 1
:
3x
例2、讨论下列各组直线间的位置关系
D a b a b 练一练:判断下列各组直线的位置关系,如果相交,则求出交点坐标。
(1)习题册 P6 11.
1 2 例1、判断两条直线的位置关系,如果相交,则求出交点坐标。
练一练:判断下列各组直线的位置关系,如果相交,则求出交点坐标。
21
例2、讨论下列各组直线间的位置关系
两条直线的位置关系
填表格 几何元素及关系
点A
直线l
代数表示
A(x0, y0)
l : ax by c 0 (a, b不全为0)
填表格 几何元素及关系
点A
直线l
点A在直线l上
代数表示
A(x0, y0)
l : ax by c 0 (a, b不全为0)
填表格 几何元素及关系
点A
直线l
点A在直线l上
代数表示
A(x0, y0)
l : ax by c 0(1) (a, b不全为0)
点A的坐标(x , y )是方程 00
(1)的解
填表格 几何元素及关系
点A
沪教版高中数学高二下册:11.3 两条直线的位置关系-两条直线的夹角 课件

小结
本节课学习了哪些内容?
70.修养的本质如同人的性格,最终还是归结到道德情操这个问题上。——爱默生 65.只要学不死,就往死里学。 74.真正的领导者,其厉害之处不在于能指挥多少君子,而在于能驾驭多少小人。 4.一个真正想成功的人是勤奋与努力的,而不是躺在床上说大话。 100.当我们是大为谦卑的时候,便是我们最近于伟大的时候。——泰戈尔 54.所有的胜利,与征服自己的胜利比起来,都是微不足道。 93.学习这件事,不是缺乏时间,而是缺乏努力。 75.一个人最大的破产是绝望,最大的资产是希望。 28.贫而懒惰乃真穷,贱而无志乃真贱。——罗丹 69.世上最重要的事,不在于我们在何处,而在于我们朝着什么方向走。 30.水不撩不知深浅,人不拼怎知输赢。 52.当一个人用工作去迎接光明,光明很快就会来照耀着他。——冯学峰 34.这个世界不是因为你能做什么,而是你该做什么。 13.你关注什么样的人,决定你将看到什么样的世界。 15.成功是碰到抵触的地方,才把它的活力解放。
11.3 两条直线的夹角
我们已经学习了两直线的位置关系有 平行、重合和相交。当两条直线相交时, 用什么“量”来描述两条直线的相对位置 关系呢?
1、两条直线的夹角的定义
问题
2、求两条直线的夹角
系数确定直线的方程,方程确定直线及其位置, 所以可以利用方程系数来计算夹角。
例1
例2
例3
沪教版高中数学高二下册:11.3 两条直线的位置关系-两条直线的夹角 课件

30. 当你感到悲哀痛苦时,最好是去学些什么东西。学习会使你永远立于不败之地。 12. 成功不是将来才有的,而是从决定去做的那一刻起,持续累积而成。 9、安乐给人予舒适,却又给人予早逝;劳作给人予磨砺,却能给人予长久。 9. 如果寒暄只是打个招呼就了事的话,那与猴子的呼叫声有什幺不同呢?事实上,正确的寒暄必须在短短一句话中明显地表露出你对他的关怀 。
11.3 两条直线的夹角
我们已经学习了两直线的位置关系有 平行、重合和相交。当两条直线相交时, 用什么“量”来描述两条直线的相对位置 关系呢?
1、两条直线的夹角的定义
问题
2、求两条直线的夹角
系数确定直线的方程,方程确定直线及其位置, 所以可以利用方程系数来计算夹角。
例1
例2
例3
23、惜光阴百日犹短,看众志成城拼搏第一;细安排一刻也长,比龙争虎斗谁为争锋 14、生命不是一场赛跑,而是一次旅行。比赛在乎终点,而旅行在乎沿途风景。 21、有一种失败叫做成功之母,有一种爱叫做放手,因此有一种单身叫做宁缺毋滥。 5. 要成功,先发疯,头脑简单向前冲。别再自己摸索,问路才不会迷路。宁愿辛苦一阵子,不要辛苦一辈子。付出才会杰出;为别人创造价值
,别人才愿意和你交往。每天只看目标,别老想障碍。成功需要改变,用新的方法改变过去的结果。成功的秘诀是努力,所以第一名都是练出 来的。
10、高三不再有,劝君珍惜之。一年之经历,终身之财富。 19. 大多数人想要改造这个世界,但却罕有人想改造自己。 4. 取其让性命生锈,不如让性命领光发烧。 3、“少壮不努力,老大徒伤悲。”这是一句熟得令人生厌的话,但是尽管大人们一再提起,多数青少年却并没有懂,甚至于听而不闻,实在可 惜。因为这一条话,不知是多少前人,在试炼多少次失败后,所凝聚的一句真理。
11.3 两条直线的夹角
我们已经学习了两直线的位置关系有 平行、重合和相交。当两条直线相交时, 用什么“量”来描述两条直线的相对位置 关系呢?
1、两条直线的夹角的定义
问题
2、求两条直线的夹角
系数确定直线的方程,方程确定直线及其位置, 所以可以利用方程系数来计算夹角。
例1
例2
例3
23、惜光阴百日犹短,看众志成城拼搏第一;细安排一刻也长,比龙争虎斗谁为争锋 14、生命不是一场赛跑,而是一次旅行。比赛在乎终点,而旅行在乎沿途风景。 21、有一种失败叫做成功之母,有一种爱叫做放手,因此有一种单身叫做宁缺毋滥。 5. 要成功,先发疯,头脑简单向前冲。别再自己摸索,问路才不会迷路。宁愿辛苦一阵子,不要辛苦一辈子。付出才会杰出;为别人创造价值
,别人才愿意和你交往。每天只看目标,别老想障碍。成功需要改变,用新的方法改变过去的结果。成功的秘诀是努力,所以第一名都是练出 来的。
10、高三不再有,劝君珍惜之。一年之经历,终身之财富。 19. 大多数人想要改造这个世界,但却罕有人想改造自己。 4. 取其让性命生锈,不如让性命领光发烧。 3、“少壮不努力,老大徒伤悲。”这是一句熟得令人生厌的话,但是尽管大人们一再提起,多数青少年却并没有懂,甚至于听而不闻,实在可 惜。因为这一条话,不知是多少前人,在试炼多少次失败后,所凝聚的一句真理。
沪教版高中数学高二下册:11.3 两条直线的位置关系-两条直线的夹角 课件(共13张PPT)

?
努力,未来老婆的婚纱都是租的。只有你的笑才能 无尽黑暗中找到光明。我受过的伤都是我的勋章。 而不世故,是最善良的成熟。愿你早日领教过这世 的恶意,然后开启爱他吗谁谁的快意人生。第二名 着你是头号输家——科比·布莱恩特。当你感觉累 你正在走上坡路。如果每个人都理解你,那你得普 么样。赚钱的速度一定要超过父母变老的速度。不 现以前的自己是个傻逼的过程,就是成长。脾气永 大于本事。你那能叫活着么?你那“你如今的气质 着你走过的路,读过的书,和爱过的人。”素质是 问题,和未成年没关系。总会有人是第一,那为什 是我?你可以没钱没颜,但你不可以不努力。如果 取得了成功,一定是昨天我拼上了全部努力。阳光 孩子风雨里做个大人。枯木逢春犹再发,人无两度 世界那么大,我要赚钱带父母去看看人情世故要看
11.3 两条直线的夹角
我们已经学习了两直线的位置关系有 平行、重合和相交。当两条直线相交时, 用什么“量”来描述两条直线的相对位置 关系呢?
1、两条直线的夹角的定义
问题
2、求两条直线的夹角
系数确定直线的方程,方程确定直线及其位置, 所以可以利用方程系数来计算夹角。
例1
例2
例3
努力,未来老婆的婚纱都是租的。只有你的笑才能 无尽黑暗中找到光明。我受过的伤都是我的勋章。 而不世故,是最善良的成熟。愿你早日领教过这世 的恶意,然后开启爱他吗谁谁的快意人生。第二名 着你是头号输家——科比·布莱恩特。当你感觉累 你正在走上坡路。如果每个人都理解你,那你得普 么样。赚钱的速度一定要超过父母变老的速度。不 现以前的自己是个傻逼的过程,就是成长。脾气永 大于本事。你那能叫活着么?你那“你如今的气质 着你走过的路,读过的书,和爱过的人。”素质是 问题,和未成年没关系。总会有人是第一,那为什 是我?你可以没钱没颜,但你不可以不努力。如果 取得了成功,一定是昨天我拼上了全部努力。阳光 孩子风雨里做个大人。枯木逢春犹再发,人无两度 世界那么大,我要赚钱带父母去看看人情世故要看
11.3 两条直线的夹角
我们已经学习了两直线的位置关系有 平行、重合和相交。当两条直线相交时, 用什么“量”来描述两条直线的相对位置 关系呢?
1、两条直线的夹角的定义
问题
2、求两条直线的夹角
系数确定直线的方程,方程确定直线及其位置, 所以可以利用方程系数来计算夹角。
例1
例2
例3
高二数学 两条直线的位置关系——夹角课件
作图、利用倾斜角求解
例2、求过点 ( 3,20 的直线的方程.
y
y=- 3 x+1
o x
( 3 ,-2)
h
7
小结:两个概念、两个公式
注意:1、两个概念的联系与区别; 2、公式的适用范围;
h
8
①若 k1k2 1,则 l1 l2
1
2
2
②若 k1k2 1,则:
y
l 2 1
l1
y l1
l2
1
1
O
2 x
2
O
1
x
121
ta1n tan 2 (1)
1(21)
ta 1 n ta n ( [ 2 1 )]
h
ta n2(1)
4
ta1n ta2 n (1)1tatan2 n1ttaa n n121k 2 k1kk12
l1
到l
2
角公式:
tan1
k2 k1 1k2k1
注意:公式适 用于斜率存在
夹角公式:
tan k2 k1
1 k2k1
且不垂直的两 条相交直线
2、当 l 1 或 l 2 的斜率不存在时
利用直线倾斜角求解
h
y l2 l1
1
2
x
O
5
例1、已知直线 l1:y2x3和
l2
:
y
x
3 2
,
求: l 1 到 l 2 的角 和 l 1 与 l 2 的夹角 .
l2
l1
1
2
4
3
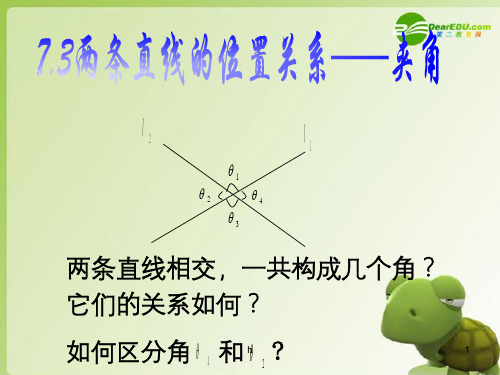
两条直线相交,一共构成几个角? 它们的关系如何?
如何区分角 1 和 h 2 ?
1
新课讲解
定义1:直线 l 1 逆时针方向旋转到与 l 2 重合时 所转过的角叫直线 l 1 到 l 2 的角.
例2、求过点 ( 3,20 的直线的方程.
y
y=- 3 x+1
o x
( 3 ,-2)
h
7
小结:两个概念、两个公式
注意:1、两个概念的联系与区别; 2、公式的适用范围;
h
8
①若 k1k2 1,则 l1 l2
1
2
2
②若 k1k2 1,则:
y
l 2 1
l1
y l1
l2
1
1
O
2 x
2
O
1
x
121
ta1n tan 2 (1)
1(21)
ta 1 n ta n ( [ 2 1 )]
h
ta n2(1)
4
ta1n ta2 n (1)1tatan2 n1ttaa n n121k 2 k1kk12
l1
到l
2
角公式:
tan1
k2 k1 1k2k1
注意:公式适 用于斜率存在
夹角公式:
tan k2 k1
1 k2k1
且不垂直的两 条相交直线
2、当 l 1 或 l 2 的斜率不存在时
利用直线倾斜角求解
h
y l2 l1
1
2
x
O
5
例1、已知直线 l1:y2x3和
l2
:
y
x
3 2
,
求: l 1 到 l 2 的角 和 l 1 与 l 2 的夹角 .
l2
l1
1
2
4
3
两条直线相交,一共构成几个角? 它们的关系如何?
如何区分角 1 和 h 2 ?
1
新课讲解
定义1:直线 l 1 逆时针方向旋转到与 l 2 重合时 所转过的角叫直线 l 1 到 l 2 的角.
高中数学沪教版高二下- 1两条直线的位置关系PPT全文课件

解:对应方程组
kk21xx
y y
3k1 3k2
1 1
0 0
考虑方程组的系数行列式 D k2 k1 , Dx 3(k1 k2 ) , Dy k2 k1 6k1k2
1 当D 0,即k1 k2时,直线l1与l2相交 2 当D=0,即k1=k2时,Dx 6k1, Dy 6k12
所以, 当k1=k2=0时,直线l1与l2重合 当k1=k2 0时,直线l1与l2相交
)有惟一解
x
y
Dx D Dy D
此时直线l1
,l2相交于一点,交点坐标是(
Dx D
,Dy ) D
(2)D 0,即a1b2=a2b1时 :
1 Dx , Dy中至少有一个不为0,方程组()无解
此时直线l1 ,l2没有公共点,即两直线平行
2 Dx =Dy=0,方程组()有无穷多解
此时直线l1 ,l2重合
二元一次方程组
aa21xx
b1x b2 x
c1 c2
0( 0
)
解的情况取决于系数构成的行列式的值
其中,D a1 a2
b1 b2
, Dx
-c1 -c2
b1 b2
, Dy
a1 a2
-c1 -c2
高中数学沪教版高二下- 1两条直线的位置关系PPT全文课件【完 美课件 】
(1)D
0,即a1b2
a2b1时,方程组(
x
(1)相交
(2)平行
O
x
(3)重合
复习:
二元一次方程组的解的判别
aa21xx
b1 b2
y y
c1 c2
(1)D
0,
方程组()有惟一解
x
y
沪教版(上海)数学高二下册-11.3 两直线的夹角 课件

若0 时: 若 为钝角时:
2 于是得:cos cos
d1 y
yd1
d2
d2
l2
o
l1
d
x
2
l2
x
o
l1
1)
2)
向量推导
解:根据l1与l2的方程,取 d1 (b1, a1), d2 (b2, a2 )
为 l1与 l2的方向向量.
由向量的夹角公式得: cos d1 d2
两直线的夹角
复习巩固
平面内两直线的位置关系有哪些?
相交、平行、重合
两相交直线可以用什么量来刻画它们的 相交程度?
新知学习
一、两直线夹角定义及范围
βα
图1
图2
1.两条相交直线的夹角: 两条相交直线所成的锐角或直角.
2.如果两条直线平行或重合,我们
规定它们的夹角为 0
3.平面上两条直线夹角的范围:
0,
2
y
x
o
y
x o
二、两直线夹角公式的探究
已知两直线方程求夹角 已知两条直线:l1 : a1x b1y c1
l2 : a2x b2y c2
求两直线夹角 的大小.
0(a1,b1不同时为0) 0(a2,b2不同时为0)
探究1:
两直线 l1、l2的夹角 与方向向量 d1、d2 的夹角
之间有何关系?
解:(1)根据l1与l2的方程及两直线夹角公式可得:
cos 3 2 1 (1) 2
(1)2 32 12 22 2
因为 0,,所2 以
即直线 l1 和
4
l2 的夹角为
4
练习:求下列各组直线的夹角:
(1)l1 : 3x y 12 0,l2 : x 0; (2)l1 : y 3x 12,l2 : x y 0;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
a1a2 b1b2 0
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
思考:当 k1k2 1时,这两条直线的夹 角是多少呢?
小练习:若直线 6x (a 1) y 8 0
与 (a 4)x (a 6) y 16 0 互相垂直,则实数的值为 _______
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
如何根据两条直线的方程两条直线的夹角?
y
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
O
x
图1
探索1:两条直线的夹角与倾斜角 有怎样的关系?
情况1:
y
1 2
情况2:
(1 2 )
y
=
O
2
1 x
O
2
1
x
l1
l1
图12
图1
l2
l2
tan tan(1 2)
=
tan1 tan2 k1 k2 1 tan1 tan2 1 k1 k2
引例:判断下列各组直线的位置关系。
(1) l1 : 3x y 2 0
l2 : 2x y 3 0
(2) l1 : 3x 4 y 12 0
l2 : x 3
Байду номын сангаас
(3) l1 : 3x 4 y 12 0 l2 : 6x 8y 5 0
思考:前面(1)(2)中,当两条直线相交时, 用什么“量”来描述两条直线的相对位置呢?
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
探索2:两条直线的夹角与方向向 量有怎样的关系?
情况1: y
情况2:
y
O
x
图1
O
x
图2
设 l1 与 l2的一方向向量分别 为d1 与d 2 ,其夹角为,则 不论 还是 均有
.
cos | cos || d1 d2 |
| a1a2 b1b2 |
思考:当 k1k2 1时,这两条直线的夹 角是多少呢?
k1k2 1
是两条直线垂直的充分非必要条件
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
例1: (1)直线 l1 :3x y 2 0
的夹角是————
和 l2 : 2x y 3 0
两条直线的夹角的概念
规定两条相交直线所成的锐角或直角为两 条直线的夹角. 如果两条直线平行或重合,规定它们的夹 角为0.
两条直线的夹角的取值范围是
0,
2
注:两条直线的夹角与倾斜角、两个 向量所成角范围的比较
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
两条直线的夹角公式的推导
设 l1 : a1x b1y c1 0(a1,b1不全为0) l2 : a2x b2 y c2 0(a2,b2不全为0)
| d1 | | d2 |
a12 b12 a2 2 b2 2
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
两条直线的夹角公式
(1)cos =
a1a2 b1b2
a12 b12 a22 b22
(2)tan k1 k2
1 k1k2
注
意: (1)公式使用的条件
(2)两条直线垂直的充要条件是
(2)直线 l1 : 3x 4y 12 0和 l2 : x 3 的夹角是————
(3)直线
l1 :
x 2
y
2 3
的夹角是————
和 l2 : y x 4 0
注意:在使用两条直线的夹角的余弦公式 时,应先将直线方程化成一般式。
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
所在直线 l3 的方程.
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
小结: 1.本节课我们用两种方法推导出两条直 线的夹角公式,采用的都是将未知转化为 已知的思想方法; 2.在运用两条直线的夹角公式时应注意 公式成立的条件. 3.进一步讨论了求直线方程的方法:运 用待定系数法时,可设直线方程为点法向 式、或点斜式方程,而在用点斜式方程时, 需要分类讨论.并注意数形结合 .
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2 沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
谢谢!
例2:已知直线 l 经过 P(2, 3) ,
求且该和直直线线的l0方: x程
3y 2 0 的夹角为
3
,
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
思考:光线沿直线l1 : 2x y 2 0, 照射到 直线 l2 : x 2y 2 0 上后反射 ,求反射线
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
练习:
• 若直线:6x (a 1) y 8 0 与:(a 4)x (a 6)y 16 0 互相垂直,则实数a的值为_______
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
沪教版(上海)数学高二下册-1两条 直线的 夹角课 件_2
