实验一 产生信号波形的仿真实验
北邮通信原理软件实验报告

通信原理软件实验报告学院:信息与通信工程学院班级:一、通信原理Matlab仿真实验实验八一、实验内容假设基带信号为m(t)=sin(2000*pi*t)+2cos(1000*pi*t),载波频率为20kHz,请仿真出AM、DSB-SC、SSB信号,观察已调信号的波形和频谱。
二、实验原理1、具有离散大载波的双边带幅度调制信号AM该幅度调制是由DSB-SC AM信号加上离散的大载波分量得到,其表达式及时间波形图为:应当注意的是,m(t)的绝对值必须小于等于1,否则会出现下图的过调制:AM信号的频谱特性如下图所示:由图可以发现,AM信号的频谱是双边带抑制载波调幅信号的频谱加上离散的大载波分量。
2、双边带抑制载波调幅(DSB—SC AM)信号的产生双边带抑制载波调幅信号s(t)是利用均值为0的模拟基带信号m(t)和正弦载波c(t)相乘得到,如图所示:m(t)和正弦载波s(t)的信号波形如图所示:若调制信号m(t)是确定的,其相应的傅立叶频谱为M(f),载波信号c(t)的傅立叶频谱是C(f),调制信号s(t)的傅立叶频谱S(f)由M(f)和C(f)相卷积得到,因此经过调制之后,基带信号的频谱被搬移到了载频fc处,若模拟基带信号带宽为W,则调制信号带宽为2W,并且频谱中不含有离散的载频分量,只是由于模拟基带信号的频谱成分中不含离散的直流分量。
3、单边带条幅SSB信号双边带抑制载波调幅信号要求信道带宽B=2W, 其中W是模拟基带信号带宽。
从信息论关点开看,此双边带是有剩余度的,因而只要利用双边带中的任一边带来传输,仍能在接收机解调出原基带信号,这样可减少传送已调信号的信道带宽。
单边带条幅SSB AM信号的其表达式:或其频谱图为:三、仿真设计1、流程图:Array2、实验结果&分析讨论实验仿真结果从上至下依次是AM信号、DSB信号、SSB信号。
从仿真结果看,AM调制信号包络清晰,可利用包络检波恢复原信号,接收设备较为简单。
实验一 MATLAB方法实现信号波形和微分方程的建立与求解

实验一 MATLAB方法实现信号波形和微分方程的建立与求解一、实验目的1、熟悉和掌握常用的用于信号与系统时域仿真分析的MA TLAB函数;2、掌握连续时间和离散时间信号的MATLAB产生,掌握用周期延拓的方法将一个非周期信号进行周期信号延拓形成一个周期信号的MA TLAB编程;3、牢固掌握系统的单位冲激响应的概念,掌握LTI系统的卷积表达式及其物理意义,掌握卷积的计算方法、卷积的基本性质;4、掌握利用MA TLAB计算卷积的编程方法,并利用所编写的MA TLAB程序验证卷积的常用基本性质;掌握MATLAB描述LTI系统的常用方法及有关函数,并学会利用MATLAB求解LTI系统响应,绘制相应曲线。
基本要求:掌握用MATLAB描述连续时间信号和离散时间信号的方法,能够编写MA TLAB 程序,实现各种信号的时域变换和运算,并且以图形的方式再现各种信号的波形。
掌握线性时不变连续系统的时域数学模型用MATLAB描述的方法,掌握卷积运算、线性常系数微分方程的求解编程。
二、实验原理信号(Signal)一般都是随某一个或某几个独立变量的变化而变化的,例如,温度、压力、声音,还有股票市场的日收盘指数等,这些信号都是随时间的变化而变化的,还有一些信号,例如在研究地球结构时,地下某处的密度就是随着海拔高度的变化而变化的。
一幅图片中的每一个象素点的位置取决于两个坐标轴,即横轴和纵轴,因此,图像信号具有两个或两个以上的独立变量。
在《信号与系统》课程中,我们只关注这种只有一个独立变量(Independent variable)的信号,并且把这个独立变量统称为时间变量(Time variable),不管这个独立变量是否是时间变量。
在自然界中,大多数信号的时间变量都是连续变化的,因此这种信号被称为连续时间信号(Continuous-Time Signals)或模拟信号(Analog Signals),例如前面提到的温度、压力和声音信号就是连续时间信号的例子。
通信系统的仿真实验资料
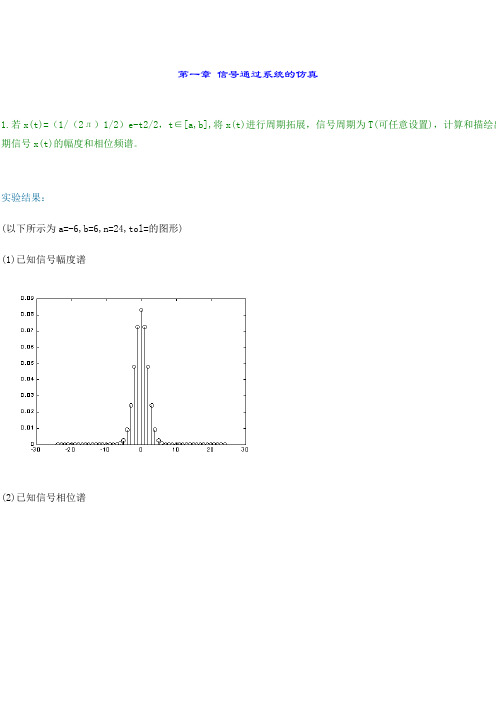
第一章信号通过系统的仿真1.若x(t)=(1/(2л)1/2)e-t2/2,t∈[a,b],将x(t)进行周期拓展,信号周期为T(可任意设置),计算和描绘出期信号x(t)的幅度和相位频谱。
实验结果:(以下所示为a=-6,b=6,n=24,tol=的图形)(1)已知信号幅度谱(2)已知信号相位谱2.信号定义为x(t)= cos(2л*47t)+cos(2л*219t), 0≤t≤100, 其它假设信号以1000抽样/秒进行抽样。
用MATLAB设计一个低通Butterworth滤波器。
确定并绘出输出的功率谱和输入功率谱比较(滤波器的阶数及截频可自行确定)。
实验结果:(以下为阶数=4,截频=100Hz的图形)(1)输入信号功率谱密度(2)输出信号功率谱密度第二章随机过程仿真1.从下式的递归关系中产生一个高斯马尔可夫过程的1000个(等间距)样本的序列Xn=+ωn n=1,2,…1000,式中X0=0,ωn是一个零均值,方差为1,独立的随机变量序列。
绘出序列{ Xn,1≤n≤1000}与时序n的关系及相关函数N-mRx(m)=1/(N-m)ΣXn Xn+m m=0,1,…50 式中N=1000.n-1实验结果:(1)高斯——马尔可夫过程(2)高斯马尔可夫过程的自相关函数2.假设一个具有抽样序列{X(n)}的白噪声过程通过一个脉冲响应如下所示的线性滤波器nh(n)= ,n≥00, n<0求输出过程{Y(n)}的功率谱和自相关函数Ry(τ)。
实验结果:(1)输出的功率谱(2)输出的自相关第三章模拟调制仿真1.用MATLAB软件仿真AM调制。
被调信号为1, (t0/3)>t>0;m(t)=-2, (t0/3)≤t≤(2*t0/3);0, 其它;利用AM 调制方式调制载波。
假设t0=,fc=250hz;调制系数a=。
实验结果:1)调制信号、载波、已调信号的时域波形2)已调信号的频域波形2.被调信号为1, t0/3>t>0;m(t)=-2, t0/3<= t<2*t0/3;0, 其它;采用频率调制方案。
Multisim9电子技术基础仿真实验第三章八-字信号发生器-

3.8.1 面板显示与设置
字信号发生器面板
循环输出 单帧输出 单步输出 字元设置 触发方式选择 输出字元频率
十六进制 十二进制 二进制 ASCII代码 字信号编辑区
chz634187
不改变 载入 保存
清除缓冲 加计数 减计数 右移位 左移位
chz634187
大家应该也有点累了, 稍作休息
大家有疑问的, 可以询问和交流
chz634187
双击自信号发生器图标,将其面板打开。 字信号发生器的面板左侧有4个区:
chz634187
单击Set按钮, 弹出字元设置对话框。。
chz634187
选择Up Counter(加计数)方式。
chz634187
字元设置对话框
确认按钮 取消按钮 十六进制 十二进制 设定缓冲器大小 设定初始值
chz634187
3.6.2 字信号发生器使用举例
提取字信号生器图标。
chz634187
为方便连接, 将其水平翻转。。
chz634187
为便于观察字信号发生器输出的信号波形, 再提取 逻辑分析仪。将字信号发生器的8个输出端接逻辑 分析仪的输入端, 并将连线设定为不同的颜色。。
按Accept按钮确认。
chz634187
打开仿真开关。自信号发生器面板右侧的数字由全是0 逐渐按16进制方式递增。最右边的滑块逐渐下移。面 板最下边的32个小圆圈实时显示各个输出端的信息。
chz634187
过一定时间后, 将仿真开关关闭。。
chz634187
1 实验一 周期信号波形的叠加

实验一 周期信号波形的叠加本实验是用计算机仿真的方法来观察周期信号叠加的原理及过程。
一、实验目的通过观察各次谐波合成某一周期信号波形的过程,比较所合成的波形(方波、锯齿波、三角波)与其理论波形之间存在差异;观察、记录并比较某次谐波的幅值(或相位角)变化对合成波产生的影响,以进一步加深对周期信号频谱结构及其叠加原理的理解与掌握。
二、实验前预习内容1. 课本第一章第二节“周期信号与离散频谱”; 2. 本实验指导书。
三、实验原理根据傅里叶级数的理论,满足狄里赫利条件的周期信号x (t )都可以展开为0001()(cos sin )n n n x t a a n t b n t ωω∞==++∑001sin()n n n a A nw t φ∞==++∑这说明周期信号是由一个或几个,乃至无穷多个不同频率、不同幅值和不同相位的谐波叠加而成的,因此可以用谐波信号叠加合成出复杂的周期信号。
四、实验设备计算机及本实验仿真软件。
五、软件启动及说明:1. 启动计算机并点击执行文件“测试技术实验.exe ”则出现一个封面,随后进入本实验界面;2. 进入界面后就可以在工具栏上的“实验一”上点击即可进入实验,接着请在出现的对话框上选择波形和填写“改阶次”、“振幅比”、“相位差”、“直接显阶”参数,输入数据的时候请从主键盘输入,小键盘已经被锁定;3. 当按完“继续”键后则自动显示出图形,如果要看下一阶的图形,则只需点击工具条上的“向前”按钮(F5);若要返回上一阶图形,则只需点击“返回”(F6);如果要退出图形显示则只需点击“向上一级”按钮(F7);4. 若对程序运行不了解,可以点击“帮助”查阅;5.如果要存储图形只要点击“菜单”中的“另存为(A )…” 即可;当要退出本实验程序时,直接点击“文件”菜单的“退出(X )”即可。
波形显示窗口上的参数说明:TYPE —— 波形代号(1—方波;2—锯齿波;3—三角波) 改阶—— 要改变某谐波的幅值或初相角的阶次,不改则输入零。
通信原理(虚拟仿真实验)

实验五双极性不归零码一、实验目的1.掌握双极性不归零码的基本特征2.掌握双极性不归零码的波形及功率谱的测量方法3.学会用示波器和功率谱分析仪对信号进行分析二、实验仪器1.序列码产生器2.单极性不归零码编码器3.双极性不归零码编码器4.示波器5.功率谱分析仪三、实验原理双极性不归零码是用正电平和负电平分别表示二进制码1和0的码型,它与双极性归零码类似,但双极性非归零码的波形在整个码元持续期间电平保持不变.双极性非归零码的特点是:从统计平均来看,该码型信号在1和0的数目各占一半时无直流分量,并且接收时判决电平为0,容易设置并且稳定,因此抗干扰能力强.此外,可以在电缆等无接地的传输线上传输,因此双极性非归零码应用极广.双极性非归零码常用于低速数字通信.双极性码的主要缺点是:与单极性非归零码一样,不能直接从双极性非归零码中提取同步信号,并且1码和0码不等概时,仍有直流成分。
四、实验步骤1.按照图3.5-1 所示实验框图搭建实验环境。
2.设置参数:设置序列码产生器序列数N=128;观察其波形及功率谱。
3.调节序列数N 分别等于64.256,重复步骤2.图3.5-1 双极性不归零码实验框图实验五步骤2图N=128实验五步骤3图N=64N=256六、实验报告(1)分析双极性不归零码波形及功率谱。
(2)总结双极性不归零码的波形及功率谱的测量方法。
实验六一、实验目的1.掌握双极性归零码的基本特征2.掌握双极性归零码的波形及功率谱的测量方法3.学会用示波器和功率谱分析仪对信号进行分析二、实验仪器1.序列码产生器2.单极性不归零码编码器3.双极性归零码编码器4.示波器5.功率谱分析仪三、实验原理双极性归零码是二进制码0 和1 分别对应于正和负电平的波形的编码,在每个码之间都有间隙产生.这种码既具有双极性特性,又具有归零的特性.双极性归零码的特点是:接收端根据接收波形归于零电平就可以判决1 比特的信息已接收完毕,然后准备下一比特信息的接收,因此发送端不必按一定的周期发送信息.可以认为正负脉冲的前沿起了起动信号的作用,后沿起了终止信号的作用.因此可以经常保持正确的比特同步.即收发之间元需特别的定时,且各符号独立地构成起止方式,此方式也叫做自同步方式.由于这一特性,双极性归零码的应用十分广泛。
数字信号频带传输的仿真设计
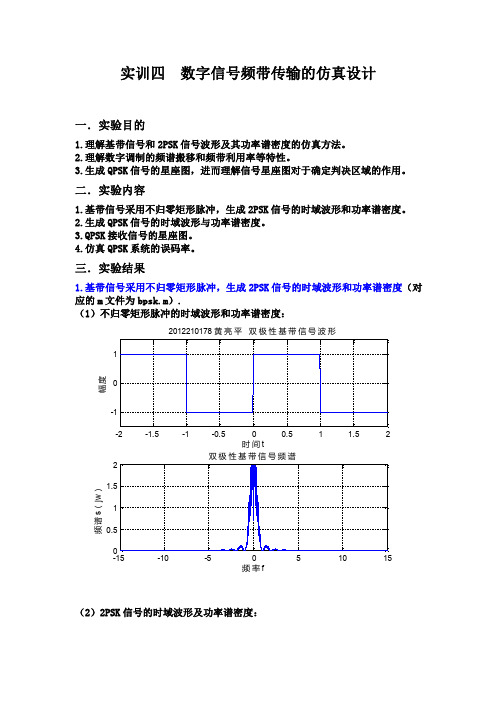
实训四数字信号频带传输的仿真设计一.实验目的1.理解基带信号和2PSK 信号波形及其功率谱密度的仿真方法。
2.理解数字调制的频谱搬移和频带利用率等特性。
3.生成QPSK 信号的星座图,进而理解信号星座图对于确定判决区域的作用。
二.实验内容1.基带信号采用不归零矩形脉冲,生成2PSK 信号的时域波形和功率谱密度。
2.生成QPSK 信号的时域波形与功率谱密度。
3.QPSK 接收信号的星座图。
4.仿真QPSK 系统的误码率。
三.实验结果1.基带信号采用不归零矩形脉冲,生成2PSK 信号的时域波形和功率谱密度(对应的m 文件为bpsk.m).(1)不归零矩形脉冲的时域波形和功率谱密度:-2-1.5-1-0.500.51 1.52-11时间t幅度2012210178 黄亮平 双极性基带信号波形-15-10-505101500.511.52频率f 频谱s (j w )双极性基带信号频谱(2)2PSK 信号的时域波形及功率谱密度:-2-1.5-1-0.500.51 1.52-11时间t幅度2012210178 黄亮平 BPSK 已调信号波形-15-10-505101500.51频率f 频谱s (j w )BPSK 已调信号频谱2.基带信号采用不归零矩形脉冲或滚降系数为1的升余弦谱,生成4PSK 信号的时域波形和功率谱密度(不归零矩形脉冲对应的m 文件为rectqpsk.m,升余弦脉冲对应的m 文件为rcosqpsk.m).(1)不归零矩形脉冲的时域波形和功率谱密度:-2-1.5-1-0.500.51 1.52-11时间t幅度2012210178 黄亮平 双极性基带信号波形-15-10-505101500.511.522.5频率f 频谱s (j w )双极性基带信号频谱(2)QPSK 信号的时域波形与功率谱密度:-2-1.5-1-0.500.51 1.52-11时间t幅度2012210178 黄亮平 QPSK 已调信号波形-15-10-505101500.511.5频率f 频谱s (j w )QPSK 已调信号频谱(3)基带信号为滚降系数为1的升余弦脉冲信号经QPSK 调制得到的已调信号与功率谱密度:02468101214161820-11时间t幅度QPSK 已调信号波形2 2.2 2.4 2.6 2.83 3.2 3.4 3.6 3.8402468频率幅度QPSK 信号频谱3、QPSK 系统的调制和解调原理随机产生10^5个二进制信息数据,串并变换后进行4PSK 调制。
模拟线性调制系统的仿真【实验报告】和【实验指导】

实验一:模拟线性调制系统仿真一、实验目的:1、掌握模拟调制系统的调制和解调原理;2、理解相干解调。
二、实验内容:1、编写AM 、DSB 、SSB 调制,并画出时域波形和频谱图。
2、完成DSB 调制和相干解调。
三、实验步骤1、线性调制1) 假定调制信号为m t ,载波c ()cos 2πm f t =()cos 2πc t f t =,f m =1kHz ,f c =10kHz ; 绘制调制信号和载波的时域波形(保存为图1-1)。
2) 进行DSB 调制,;进行AM 调制,DSB ()()()s t m t c t =⋅[]AM ()1()()s t m t c t =+⋅;绘制DSB 已调信号和AM 已调信号的波形,并与调制信号波形进行对照(保存为图1-2)。
3) 用相移法进行SSB 调制,分别得到上边带和下边带信号,SSB 11ˆ()()()()()22Q s t m t c t m t c t =⋅⋅ ,ˆ()sin 2πm m t f t =,()sin 2πQ c c t f t =。
4) 对载波、调制信号、DSB 已调信号、AM 已调信号和SSB 已调信号进行FFT 变换,得到其频谱,并绘制出幅度谱(保存为图1-3)。
2、DSB 信号的解调1) 用相干解调法对DSB 信号进行解调,解调所需相干载波可直接采用调制载波。
2) 将DSB 已调信号与相干载波相乘。
3) 设计低通滤波器,将乘法器输出中的高频成分滤除,得到解调信号。
4) 绘制低通滤波器的频率响应(保存为图1-4)。
5) 对乘法器输出和滤波器输出进行FFT 变换,得到频谱。
6) 绘制解调输出信号波形;绘制乘法器输出和解调器输出信号幅度谱(保存为图1-5)。
7) 绘制解调载波与发送载波同频但不同相时的解调信号的波形,假定相位偏移分别为ππππ,,,8432(保存为图1-6)。
四、实验思考题1、与调制信号比较,AM 、DSB 和SSB 的时域波形和频谱有何不同?2、低通滤波器设计时应考虑哪些因素?3、采用相干解调时,接收端的本地载波与发送载波同频不同相时,对解调性能有何影响?五、提示:1、Matlab只能处理离散值,所以调制信号、载波、已调信号和解调信号都是用离散序列表示的。
通信原理实验1 FM

kfm=0.2 0.02 0.018 0.016 0.014 0.012 0.01 0.008 0.006 0.004 0.002 0 -3000
-1500
-1000
-500
0
500
1000
1500
2000
-2000
-1000
0
1000
2000
3000
kfm=0.3 0.02 0.018 0.016 0.014 0.012 0.01 0.008 0.006 0.004 0.002 0 -4000
T:
m_t
说明
每秒采 10000 个 点
10000 500 20 0.1 仿真原理
… …
Hz ms [-0.05,0.05]
积分器 Carrier
s_t
R:
m_t
隔直
包络 检波 图 1 FM 系统原理框图
微分器
… …
图1为从通信原理教材中摘录的FM发送以及接收系统的实现框图。从图1 中不难看出,FM的实现架构还是比较简单。由于matlab等数值计算工具完成的 都是离散点的运算, 因此框图中用到的积分器以及微分器实际就是累加器与差分 器。为了方便,后面不对术语作严格的区分。可以调用matlab中提供的函数 cumsum和diff实现上述操作。由于差分后会出现由载波带来的直流成分,因此要 得到原始的消息信号便要滤去直流成分。下面,将从理论上说明图1中系统设计 的可实现性。 根据FM调制信号的特点,其发送信号 s_t =A cos[2 f ct 2 kFM m(t )dt ] 。对 发送信号求导便得:
0.02 0.018 0.016 0.014 0.012 0.01 0.008 0.006 0.004 0.002 0 -5000 -4000 -3000 -2000 -1000
用MatLab仿真通信原理系列实验

用MatLab仿真通信原理系列实验一、引言通信原理是现代通信领域的基础理论,通过对通信原理的研究和仿真实验可以更好地理解通信系统的工作原理和性能特点。
MatLab作为一种强大的数学计算软件,被广泛应用于通信原理的仿真实验中。
本文将以MatLab为工具,介绍通信原理系列实验的仿真步骤和结果。
二、实验一:调制与解调1. 实验目的通过MatLab仿真,了解调制与解调的基本原理,并观察不同调制方式下的信号特征。
2. 实验步骤(1)生成基带信号:使用MatLab生成一个基带信号,可以是正弦波、方波或任意复杂的波形。
(2)调制:选择一种调制方式,如调幅(AM)、调频(FM)或相移键控(PSK),将基带信号调制到载波上。
(3)观察调制后的信号:绘制调制后的信号波形和频谱图,观察信号的频谱特性。
(4)解调:对调制后的信号进行解调,还原出原始的基带信号。
(5)观察解调后的信号:绘制解调后的信号波形和频谱图,与原始基带信号进行对比。
3. 实验结果通过MatLab仿真,可以得到不同调制方式下的信号波形和频谱图,观察到调制后信号的频谱特性和解调后信号的还原效果。
可以进一步分析不同调制方式的优缺点,为通信系统设计提供参考。
三、实验二:信道编码与解码1. 实验目的通过MatLab仿真,了解信道编码和解码的基本原理,并观察不同编码方式下的误码率性能。
2. 实验步骤(1)选择一种信道编码方式,如卷积码、纠错码等。
(2)生成随机比特序列:使用MatLab生成一组随机的比特序列作为输入。
(3)编码:将输入比特序列进行编码,生成编码后的比特序列。
(4)引入信道:模拟信道传输过程,引入噪声和干扰。
(5)解码:对接收到的信号进行解码,还原出原始的比特序列。
(6)计算误码率:比较解码后的比特序列与原始比特序列的差异,计算误码率。
3. 实验结果通过MatLab仿真,可以得到不同编码方式下的误码率曲线,观察不同信道编码方式对信号传输性能的影响。
Simulink仿真 实验报告

集美大学计算机工程学院实验报告一、实验目的:1.熟悉Simulink工作环境及特点2.掌握线性系统仿真常用基本模块的用法3.掌握Simulink的建模与仿真方法。
二、实验内容和步骤1.用信号发生器产生0.2Hz,幅度为1V的正弦波和方波信号,并通过示波器观察波形。
启动simulink->选择Blank Model->点击Library Browser选择输入源模块以及接收端模块选择Sources: Sine Wave作为输入源模块,并设置频率参数为2πf即0.4*pi,接收端选择Scope模块开始仿真选择Sources :Signal Generator: Square作为输入源,设置频率,选择示波器开始仿真问题1.1:请总结一下示波器的使用方法,有哪些主要参数需要设置?示波器的参数设置主要有:Number of input ports 这一项用来设置示波器的输入端口数Layout 这一个操作可以用来设置输出格式,比如同时输出三个不同的波形图Time span 这一项用来设置横坐标的长度Time display offset 用来设置横坐标的起始端点,通常都为0Y-Limits 用来设置纵坐标的最大最小值2.Simulink仿真实际应用1建立一个很小的系统,用示波器观察正弦信号的平方的波形,如图所示系统中所需的模块:正弦波模块、示波器模块。
正弦波仿真电路和参数如下:(在Scope的Parameters里面,把Number of Axes设为3,可以变成有3个输入端的示波器)正弦波1参数:1Hz,幅度为1v;正弦波2参数:1Hz,幅度为2v,通过示波器观察结果,写出数学表达式。
该题目需要将示波器的Number of Input Ports设置为3,并且通过设置Layout来改变示波器的输出格式问题2.1:改变两个正弦波的幅度和频率,观察输出的波形?问题2.2:通过m语言编程实现其波形,给出代码和显示图形。
通信原理仿真实验指导书

通信原理仿真实验指导书XXXXXXXXX 编著XXXXXXXXX通信工程系2011年11月目录实验一AM信号的调制与解调 (2)实验二DSB-SC信号的调制与解调 (6)实验三SSB信号的调制与解调 (9)实验四FM信号的调制与解调 (13)实验五PM信号的调制与解调 (17)实验六PCM的调制与解调实验 (17)实验七数字基带传输实验 (32)实验八基于system view软件的2ASK调制仿真 (40)实验九基于system view软件的2ASK解调仿真 (45)实验十基于system view软件的2FSK调制仿真 (50)实验十一基于system view软件的2FSK解调仿真 (54)实验十二基于system view软件的2PSK调制与解调仿真 (58)实验十三基于system view软件的2DPSK调制与解调仿真 (63)实验一 AM 信号的调制与解调一、实验目的1、掌握AM 信号调制与解调的原理。
2、了解AM 信号调制和解调的时域表达式和频域表达式的推导。
3、知道AM 信号的特点。
二、实验器材装有System View 软件的电脑一台。
三、实验要求1、能够熟练使用System View 软件。
2、会利用软件搭建各种仿真系统。
3、能设计系统中的一些关键参数,以及一些器件的设计。
4、对搭建的系统进行波形仿真。
5、能分析仿真结果,并得出仿真结论。
四、实验原理和内容常规双边带调制就是标准幅度调制,它用调制信号去控制高频载波的振幅,使已调波的振幅按照调制信号的振幅规律线性变化。
对于常规的双边带幅度调制系统,其时域表达式为)cos()]([0c c AM t t f A S θω++=其中0A 为外加的直流分量。
)(t f 为调制信号,可以是已知的确定信号,也可以是随机的信号,但是通常认为其数学期望认为c ω和c θ分别是载波信号的频率和初始相位。
其调制器模型如图所示。
五、 实验步骤x (0c1、根据上面的原理图,可以在System View系统平台中建立普通双边带调制系统模型。
全国大学生电子设计大赛实验报告

瓷片电容
1500PF 2700PF 3000PF
3个
参考文献
[1]余孟尝数字电子技术基础。三版。北京:高等教育出版社,1998
[2]清华大学电子电子教研组杨素行主编。模拟电子技术基础。北京:高等教育出版社。2001
[3]倪叶杰常熟理工学院文摘。江苏:常数大学教育出版社。1997
图2利用基波和3次谐波合成的近似方波
2方案设计
2.1系统分析及整体方案
方波信号由基波成分和若干个谐波成分构成,即 ,本作品根据这一理论原理制作而成。
主要思路上是产生分别产生10K 30K的方波,然后分别通过滤波器提取出它的基波,然后再通过加法器生成方波。
总体设计框图
系统框图如图所示,由电源模块,分频、滤波和移相及正弦波生成模块,正弦波模块和显示模块构成。
关键词:方波信号,滤波器,正弦波信号,滤波,移相,合成
1作品简介
1.1设计目标
设计制作一个电路,能够产生多个不同频率的正弦信号,利用傅里叶原理产生以10KHz为基波,以奇次谐波为辅助谐波的信号,并将这些信号再合成为近似方波和其他信号。电路示意图如图1所示:
图1信号波形合成电路示意图
1.2要求及指标
1.2.1基本要求
材料清单
名称
型号
数量
说明
万能版
1个
集成芯片
NE555P
1个
集成芯片
HD74LSOOP
3个
集成芯片
SN74LS161AN
3个
集成芯片
TL084CN
1个
集成芯片
TL081CP
2个
二极管
1N4148
2个
可控电阻
900Ω1kΩ
2个
信号波形合成实验电路设计

设计报信号波形合成实验电路2016-1-17设计报告信号波形合成实验电路摘要:利用NE555产生10kHz的基准方波信号,用CPLD EPM1270对方波信号进行分频,分别产生10KHZ,30KHz,50KHz 的方波信号,以及500KHz ,1.5MHz的时钟信号(用于巴特沃斯低通滤波器的时钟信号),并完成数据转换控制及LCD显示驱动;用TI的TLC04ID四阶巴特沃斯低通滤波器对10KHz,30KHz方波进行低通滤波,产生相应的正弦波信号,而50KHz的正弦波信号,用二阶有源带通滤波器对50KHz的方波进行处理来获得;采用有源RC网络对正弦波进行移相,调整电阻R可实现对10KHZ,30KHz,50KHz的正弦波信号约101度范围的移相;采用运放求和电路对10KHZ,30KHz,50KHz的正弦波信号进行相加,实现近似方波、三角波的合成。
另外,用AD563将正弦交流电压转换成直流电压,用TI的ADC TLC549进行电压幅度检测,测量误差在5%以内。
完成了该题目的基本要求和发挥部分的全部内容。
共用TI公司五种IC。
关键词:波形合成滤波器移相网络电压测量一、系统方案论证根据题目要求,设计制作一个电路,将产生的频率为6MHz方波信号,经分频滤波后得到10KHz、30KHz、50KHz频率的正弦信号,然后将这些信号再合成为近似方波信号和近似三角波信号,并制作数字显示电表,检测并显示各正弦波信号的幅值。
1. 方波振荡器方案比较方案1: 555电路产生方波信号方案2:运放电路产生方波信号方案3:用门电路及石英晶体产生方波信号。
其中,方案1、2所产生的方波信号频率不高,频率稳定性较差,而方案3产生的方波信号频率稳定度高,也可产生较高频率(MHz以上)信号,故采用方案3产生方波信号。
2. 分频电路方案比较方案1:采用选频电路提取方波的谐波信号,分别得到基波、三次谐波和五次谐波频率信号。
缺点:对选频电路的指标要求高,电路不易实现,得到的谐波信号也不稳定。
通信原理(虚拟仿真实验)

通信原理(虚拟仿真实验)实验五双极性不归零码⼀、实验⽬的1.掌握双极性不归零码的基本特征2.掌握双极性不归零码的波形及功率谱的测量⽅法3.学会⽤⽰波器和功率谱分析仪对信号进⾏分析⼆、实验仪器1.序列码产⽣器2.单极性不归零码编码器3.双极性不归零码编码器4.⽰波器5.功率谱分析仪三、实验原理双极性不归零码是⽤正电平和负电平分别表⽰⼆进制码1和0的码型,它与双极性归零码类似,但双极性⾮归零码的波形在整个码元持续期间电平保持不变.双极性⾮归零码的特点是:从统计平均来看,该码型信号在1和0的数⽬各占⼀半时⽆直流分量,并且接收时判决电平为0,容易设置并且稳定,因此抗⼲扰能⼒强.此外,可以在电缆等⽆接地的传输线上传输,因此双极性⾮归零码应⽤极⼴.双极性⾮归零码常⽤于低速数字通信.双极性码的主要缺点是:与单极性⾮归零码⼀样,不能直接从双极性⾮归零码中提取同步信号,并且1码和0码不等概时,仍有直流成分。
四、实验步骤1.按照图3.5-1 所⽰实验框图搭建实验环境。
2.设置参数:设置序列码产⽣器序列数N=128;观察其波形及功率谱。
3.调节序列数N 分别等于64.256,重复步骤2.图3.5-1 双极性不归零码实验框图实验五步骤2图N=128实验五步骤3图N=64N=256六、实验报告(1)分析双极性不归零码波形及功率谱。
(2)总结双极性不归零码的波形及功率谱的测量⽅法。
实验六⼀、实验⽬的1.掌握双极性归零码的基本特征2.掌握双极性归零码的波形及功率谱的测量⽅法3.学会⽤⽰波器和功率谱分析仪对信号进⾏分析⼆、实验仪器1.序列码产⽣器2.单极性不归零码编码器3.双极性归零码编码器4.⽰波器5.功率谱分析仪三、实验原理双极性归零码是⼆进制码0 和1 分别对应于正和负电平的波形的编码,在每个码之间都有间隙产⽣.这种码既具有双极性特性,⼜具有归零的特性.双极性归零码的特点是:接收端根据接收波形归于零电平就可以判决1 ⽐特的信息已接收完毕,然后准备下⼀⽐特信息的接收,因此发送端不必按⼀定的周期发送信息.可以认为正负脉冲的前沿起了起动信号的作⽤,后沿起了终⽌信号的作⽤.因此可以经常保持正确的⽐特同步.即收发之间元需特别的定时,且各符号独⽴地构成起⽌⽅式,此⽅式也叫做⾃同步⽅式.由于这⼀特性,双极性归零码的应⽤⼗分⼴泛。
Proteus仿真实验-包络检波

Proteus仿真实验:包络检波实验
1.实验目的
(1)进一步了解调幅波的原理,掌握调幅波的解调方法。
(2)掌握二极管峰值包络检波的原理。
(3)掌握包络检波器的主要质量指标和检波效率,观察各种波形的失真现象,分析产生的原因并思考克服的方法。
2.实验内容
(1)完成普通调幅波的解调。
(2)观察普通调幅波解调中的对角切割失真、底部切割失真以及检波器不加高频滤波时的现象。
3.实验原理
二极管包络检波的电路原理。
检波过程是一个解调过程,它与调制过程正好相反。
检波器的作用是从振幅受调制的高频信号中还原出原调制的信号,还原所得的信号,与高频调幅信号的包络变化规律一致,故又称为包络检波器。
当输入信号较大(大于0.5V)时,利用二极管的单向导电特性对振幅调制信号的解调,称为大信号检波。
4.建立仿真实验电路
本实验电路如下图所示,主要由二极管及RC低通滤波器组成,利用二极管的单向导电特性和检波负载RC的充放电过程实现检波,所以RC时间常数的选择很重要。
RC时间常数过大,则会产生对角切割失真,又称惰性失真。
RC常数太小,高频分量会滤不干净。
图1包络检波电路
综合考虑要求应满足下式
式中,ma为调幅系数,max为调制信号的最高角频率。
当检波器的直流负载电阻R与交流音频电阻RΩ不相等,而且调幅度ma又相当大时会产生负峰切割失真(又称底边切割失真),为了保证不产生负峰切割失真,应满足
5. 实验结果。
FSK系统设计几仿真波形

实验题目:移频键控FSK调制与解调系统设计实验一.实验目的1.加深对数字调制中移频键控FSK调制器与解调器工作原理及电路组成的理解与掌握。
2.学会综合地、系统地应用已学到的知识,对移频键控FSK调制与解调系统电路的设计与仿真方法,提高独立分析问题与解决问题的能力。
二.实验任务与要求构建并设计一个数字移频键控FSK传输系统,具体要求是:主载波频率:11800HZ载波1频率:2950HZ(四分频)载波2频率:1475HZ(八分频)数字基带信号NRZ:15位M序列,传输速率约为400波特。
(32分频)FSK调制器可以采用数字门电路构成电子开关电路(或集成模拟开关)与采用集成模拟乘法器,利用键控法实现。
FSK解调器可以采用非相干解调法或过零检测法实现。
传输信道不考虑噪声干扰,采用直接传输。
整个系统用EWB软件仿真完成。
三、2FSK 调制与解调系统原理与电路组成数字频移键控是用载波的频率的变化来传送数字消息的,即用所传送的数字消息控制载波的频率。
实现数字频率调制的方法很多,总括起来有两类。
直接调频法和移频键控法。
注意到相邻两个振荡器波形的相位可能是连续的,也可能是不连续的,因此有相位连续的FSK 及相位不连续的FSK之分。
并分别记作CPFSK及DPFSK。
根据实验任务的要求,本次设计实验采用的是相位连续的FSK调制器与非相干解调器,其电路构成如下图2FSK调制与解调系统电路原理图1)2FSK 调制系统设计本次综合设计实验的调制系统主要由主载波振荡器、分频器、M序列发生器、调制器、相加器构成。
其调制电路的组成框图如图1-2所示由图可以看出,当信码为“1”时,分频链作4分频,即输出频率 图1-2 FSK 调制器电路组成框图为2950Hz 载波,信码为“0”时,分频链作8分频,输出频率为1475Hz 载波。
如此一来,多谐振荡器输出的载波,通过不同次数的分频,就得到了两种不同频率的输出,经相加器后,从而在输出端得到不同频率的已调信号,即FSK 信号,完成了数字基带信号转换为数字频带信号的过程。
EWB仿真实验指导

EWB仿真实验指导时述有主编装备与材料学院实验一基尔霍夫电压定律一、实验目的1、测量串联电阻电路的等效电阻并比较测量值和计算值。
2、确定串联电阻电路中流过每个电阻的电流。
3、确定串联电阻电路中每个电阻两端的电压。
4、根据电路的电流和电压确定串联电阻电路的等效电阻。
5、验证基尔霍夫电压定律。
二、实验器材直流电压源 1个数字万用表 1个电压表 3个电流表 3个电阻 3个三、实验原理及实验电路两个或两个以上的元件首尾依次连在一起称为串联,串联电路中流过每一个元件的电流相等。
若串联的元件是电阻,则总电阻等于各个电阻值和。
因此,在图1—1所示电阻串联电路中R=R1+R2+R3。
图1—1电阻串联电路串联电路的等效电阻确定以后,由欧姆定律,用串联电阻两端的电压U除以等效电阻R,便可求出电流I,即 I=U/R 。
基尔霍夫电压定律指出,在电路中环绕任意闭合路径一周,所有电压降的代数和必须等于所有电压升的代数和。
这就是说,在图1—2所示电路中,串联电阻两端电压降之和必须等于串联电路所加的电源电压之和。
因此,由基尔霍夫电压定律有:U 1=Ubc+Ude+Ufo式中,Ubc=IR1,Ude=IR2,Ufo=IR3。
图1—2基尔霍夫电压定律实验电路四、实验步骤1、建立如图1—1所示的电阻串联实验电路。
2、用鼠标左键单击仿真电源开关,激活实验电路,用数字万用表测量串联电路的等效电阻R,记录测量值,并与计算值比较。
3、建立如图1—2所示的基尔霍夫电压定律实验电路。
4、用鼠标左键单击仿真电源开关,激活实验电路,记录电流Iab 、Icd、Ief及电压Ube 、Ude、Ufo。
5、利用等效电阻R,计算电源电压U1和电流I 。
6、用R1两端的电压计算流过电阻R1的电流IR1。
7、用R2两端的电压计算流过电阻R2的电流IR2。
8、用R3两端的电压计算流过电阻R3的电流IR3。
9、利用电路电流Iab 和电源电压U1计算串联电路的等效电阻R 。
信号检测与估计仿真实验

MATLAB仿真实验(1)单频信号,f=100KHz,T=1ms,采样率fs=500KHz,输入SNR=6dB,脉冲压缩后脉宽,信噪比等参数的变化?(2)线性调频信号,f=90—100KHz,T=20ms,采样率fs=500KHz,输入SNR=6dB,脉冲压缩后脉宽,信噪比等参数的变化?要求:仿真作业需提交MATLAB程序(m文件)和仿真结果分析报告电子版仿真实验(1)1.单频信号脉冲压缩程序clc;clear;close all;f=100e3;%信号频率T=1e-3;%脉宽1msfl=90e3;f2=110e3;B=20e3;%系统带宽fs=500e3;%采样频率m=T*fs;%采样点个数t1=1/fs:1/fs:T;SNR_1=6; %输入信噪比S=sin(2*pi*f*t1);S_max=max(S);%单频信号最大值figure(1); %画出单频信号波形图plot(t1,S);xlabel('t/s');ylabel('单频信号幅度');title('单频信号时域波形图');Noise=randn(1,3*length(S)); %高斯白噪声序列[b,a]=butter(8,[fl,f2]/(fs/2),'bandpass');Noise_filter=filter(b,a,Noise); %白噪声通过滤波器std_Noise=(S_max/sqrt(2))/(10^(SNR_1/20)); %高斯白噪声的标准偏差std_Noise_1=Noise_filter/std(Noise_filter);%通过滤波器后噪声的标准偏差Noise_f_s=std_Noise_1*std_Noise; %满足输入信噪比下的带限白噪声std_Noise_filter_s=std(Noise_f_s);%带限白噪声的标准偏差figure(2);%画出带通滤波后噪声时域图像t2=linspace(0,3*T,1500);%产生时间数组plot(t2,Noise_f_s);xlabel('t/s');ylabel('噪声幅度');title('带通滤波后噪声时域图像');P_Noise=fft(Noise_f_s);%对带限白噪声作快速傅里叶变换figure(3) %画出带通滤波后噪声频域图像t3=linspace(1,500000,1500);plot(t3,abs(P_Noise));xlim([0 200000]);xlabel('f/Hz');ylabel('噪声频谱');title('带通滤波后噪声频域图像');S_send=[zeros(1,500),S,zeros(1,500)];%信号补零,使之处于噪声之中Rec=S_send+Noise_f_s;%接受混有噪声的信号figure(4);%接收信号时域波形t4=linspace(0,3*T,1500);plot(t4,Rec);xlabel('t/s');ylabel('接受信号幅度');title('接受信号');figure(7)P_Rec=fft(Rec);t7=linspace(0,fs,length(P_Rec));plot(t7,abs(P_Rec));xlim([50000 150000]);xlabel('f/Hz');ylabel('接收信号频谱');title('接收信号频谱图像');Rec_x=xcorr(Rec,S_send);figure(5);t5=linspace(0,6*T,length(Rec_x));plot(t5,Rec_x);xlabel('t/s');ylabel('信号幅度');title('脉冲压缩后图像');R_dB=20*log10(abs(hilbert(Rec_x))/max(Rec_x));%归一化并取分贝值figure(6)plot(t5,R_dB);xlabel('t/s');ylabel('信号幅度/dB');title('脉冲压缩后图像');Rec_S=xcorr(S,S);max_Rec_S=max(Rec_S);Rec_max=max(Rec_x);%接收信号最大值Rec_std=std(Rec_x);%接受信号标准值SNR_2=20*log10(Rec_max/Rec_std); %输出信噪比2.仿真结果仿真实验(2)1.线性调频信号脉冲压缩程序clc;clear;close all;T=0.02;%脉宽20msfl=90e3;f2=110e3;B=20e3;%系统带宽f0=100e3;SNR=6;%信噪比6dBfs=500e3;%采样频率m=T*fs;k=B/T;%调频斜率t1=1/fs:1/fs:T;LFM=sin(2*pi*fl*t1+pi*k*t1.^2);%LFM信号figure(1); %画出线性调频信号幅度图像plot(t1,LFM);title('LFM信号时域图像');xlabel('t/s');ylabel('幅度');P_LFM=fft(LFM);%对LFM信号做快速傅里叶变换figure(2);%画出线性调频信号频谱图像t2=linspace(0,fs,length(P_LFM));plot(t2,abs(P_LFM));xlim([50000 150000]);xlabel('f/Hz');ylabel('线性调频信号频谱');title('调频信号频谱图像');Noise=randn(1,3*length(LFM)); %高斯白噪声序列[b,a]=butter(10,[fl,f2]/(fs/2),'bandpass');Noise_f=filter(b,a,Noise); %白噪声通过滤波器std_Noise=(max(LFM)/sqrt(2))/(10^(SNR/20)); %噪声的标准偏差std_Noise_f=Noise_f/std(Noise_f);%通过滤波器后噪声标准偏差Noise_f_s=std_Noise_f*std_Noise; %满足条件的带限白噪声std_Noise_f_s=std(Noise_f_s);%带限白噪声的标准偏差figure(3);%画出瞒住条件的带限噪声信号幅度谱图像t3=linspace(0,3*T,length(Noise_f_s));%产生时间数组plot(t3,Noise_f_s);xlabel('t/s');ylabel('噪声幅度');title('带限噪声信号幅度谱');P_N=fft(Noise_f_s);%对带限噪声做快速傅里叶变换figure(4);%画出带限噪声频谱图像t4=linspace(0,fs,length(P_N));%产生时间数组plot(t4,abs(P_N));xlim([0 200000]);xlabel('f/Hz');ylabel('噪声频谱');title('带限噪声频谱图像');LFM_send=[zeros(1,10000),LFM,zeros(1,10000)];%信号补零,使信号处于噪声中Rec=LFM_send+Noise_f_s;%接收混有噪声的线性调频信号figure(5);%画出接收信号幅度谱图像t5=linspace(0,3*T,length(Rec));%产生时间数组plot(t5,Rec);xlabel('t/s');ylabel('接收信号幅度');title('接受信号幅度谱');Rec_x=xcorr(Rec,LFM_send);%计算自相关函数figure(6); %画出脉冲压缩后幅度谱t6=linspace(0,6*T,length(Rec_x));plot(t6,Rec_x);xlabel('t/s');ylabel('信号幅度');title('脉冲压缩后幅度谱');Max_x_H=max(Rec_x);Rec_x_H=20*log10(abs(hilbert(Rec_x))/max(Rec_x));%取分贝并且归一化figure(7);%画出脉冲压缩后信号级图像t7=linspace(0,6*T,length(Rec_x));%产生时间数组plot(t7,Rec_x_H);xlabel('时间');ylabel('分贝');title('脉冲压缩后信号级图像');Rec_max=max(Rec_x);Rec_std=std(Rec_x);SNR_out=20*log10(Rec_max/Rec_std); %输出信噪比2.仿真结果仿真结果分析:单频信号与线性调频信号脉冲压缩后输出的信噪比都比输入的信噪比高,但对比两种信号的信噪比变大倍数,显然线性调频信号的信噪比变化更大。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验一产生信号波形的仿真实验一、实验目的:熟悉MATLAB软件的使用,并学会信号的表示和以及用MATLAB来产生信号并实现信号的可视化。
二、实验内容:对信号进行时域分析,首先需要将信号随时间变化的规律用二维曲线表示出来。
对于简单信号可以通过手工绘制其波形,但对于复杂的信号,手工绘制信号波形显得十分困难,且难以绘制精确的曲线。
用MATLAB软件的信号处理工具箱(Signal Processing Toolbox)来产生并表示信号。
一种是用向量来表示信号,另一种则是用符合运算的方法来表示信号。
用适当的MATLAB语句表示信号后,可以利用MATLAB的绘图命令绘制出直观的信号波形。
产生以下信号波形3sin(x)、5exp(-x)、sin(x)/x、1-2abs(x)/a、sqrt(a*x)1.向量表示法对于连续时间信号f(t),可以用两个行向量f和t来表示,其中向量t是形如t=t1:p:t2的MATLAB命令定义的时间范围向量,t1为信号起始时间,t2为信号终止时间,p为时间间隔。
向量f为连续信号f(t)在向量t所定义的时间点上的样值。
下面分析连续时间信号f(t)=Sa(t)=sin(t)/t,可用如下的两个变量表示:t= -10:1.5:10f=sin(t)./t命令运行结果为:t =Columns 1 through 8-10.0000 -8.5000 -7.0000 -5.5000 -4.0000 -2.5000 -1.0000 0.5000 Columns 9 through 142.00003.5000 5.0000 6.5000 8.0000 9.5000f =Columns 1 through 8-0.0544 0.0939 0.0939 -0.1283 -0.1892 0.2394 0.8415 0.9589Columns 9 through 140.4546 -0.1002 -0.1918 0.0331 0.1237 -0.0079用上述向量对连续信号进行表示后,就可以用plot命令来绘制出信号的时域波形。
plot命令可将点与点间用直线连接,当点与点间的距离很小时,绘出的波形就成了光滑的曲线。
MATLAB命令如下:plot(t,f);title(‘f(t)=Sa(t)’);xlabel(‘t’);axis([-10,10,-0.4,1.1]);绘出的信号波形如图1所示(左图)。
当把时间间隔p取得更小(例如为0.02)时,就可得到Sa(t)较好的近似波形,如图1所示(右图)。
如图1 Sa(t)的近似波形用以下程序可产生正弦波:t=0:0.001:50;y=sin(2*pi*50*t);plot(t(1:50),y(1:50));用以下程序可产生加入随机噪声的正弦波:t=0:0.001:50;y=sin(2*pi*50*t);s=y+randn(size(t));plot(t(1:50),s(1:50));用以下程序可产生周期方波:t=0:0.001:2.5;y=square(2*pi*30*t);plot(t(1:50),y(1:50));用以下程序可产生周期锯齿波:t=0:0.001:2.5;y=sawtooth(2*pi*30*t);plot(t,y);axis([0 0.2 –1 1]);用以下程序可产生sinc函数:x=linspace(-5,5);y=sinc(x);plot(x,y);用以下程序可产生Dirichlet函数:x=linspace(0,4*pi,300);y1=diric(x,7);y2=diric(x,8);subplot(1,2,1);plot(x,y1);subplot(1,2,2);plot(x,y2);2.符合运算表示法如果信号可以用一个符号表达式来表示它,则我们可用ezplot命令(缺省的区间为[-2*pi,2*pi])绘制出信号的波形,例如对于连续信号f(t)=sin(πt/4),我们可以用符号表达式表示为: f=sym(‘sin(pi/4*t)’);f= sin(pi/4*t);然后用ezplot 命令绘制其波形:ezplot(f,[-16,16]);该命令绘制的信号波形如图2所示,如图2 正弦信号波形图要求:改用其它的信号来练习使用向量表示法和符号运算表示法来绘制信号波形,达到对两种方法的熟练掌握。
实验二 连续时间信号卷积及MATLAB 实现一、实验目的:熟悉使用MATLAB 软件来分析连续时间信号的卷积积分运算并用图形可视化相关结果。
二、实验内容:1.卷积积分卷积积分在信号与线形系统分析中具有非常重要的意义,是信号与系统分析的基本方法之一。
连续时间信号f 1(t)和f 2(t)的卷积积分(简称为卷积)f(t)定义为:由此可得到两个与卷积相关的重要结论,即是:(1) ,即连续信号可分解为一系列幅度由决定的冲激信号及其平移信号之和;1212()()()()d f t f t f f t τττ+∞-∞*=-⎰()()()f t t f t δ*=()f t ()f t ()h t(2)线形时不变连续系统,设其输入信号为 ,单位响应为 ,其零状态响应为 ,则有: 。
可见,连续信号卷积的计算对我们进行连续信号与系统的分析具有重要的意义。
用MATLAB 实现连续信号 与卷积的过程如下: (1)将连续信号 与 以时间间隔Δ进行取样,得到离散序列和; (2)构造与 相对应的时间向量 和 ; (3)调用conv()函数计算卷积积分的近似向量 ; (4)构造对应的时间向量k 。
下面即是利用MATLAB 实现连续时间卷积的通用函数sconv(),该程序在计算出卷积积分的数值近似的同时,还绘出的时域波形图。
需要注意的是,程序中是如何构造 的对应时间向量k 的?另外,程序在绘制波形图时采用的是plot 命令而不是stem 命令。
function [f,k]=sconv(f1,f2,k1,k2,p)%计算连续信号卷积积分f(t)=f1(t)*f2(t)% f: 卷积积分f(t)对应的非零样值向量% k :f(t)的对应时间向量% f1: f1(t)非零样值向量% f2: f2(t)的非零样值向量% k1: f1(t)的对应时间向量% k2: f2(t)的对应时间向量% p :取样时间间隔f=conv(f1,f2); %计算序列f1与f2的卷积和ff=f*p;k0=k1(1)+k2(1); %计算序列f 非零样值的起点位置k3=length(f1)+length(f2)-2; %计算卷积和f 的非零样值的宽度k=k0:p:k3*p; %确定卷积和f 非零样值的时间向量subplot(2,2,1)()y t ()()()y t f t h t =*1()f t 2()f t 1()f k ∆2()f t 1()f t 2()f k ∆1()f k ∆2()f k ∆1k 2k ()f t ()f n ∆()f n ∆()f t ()f t ()f tplot(k1,f1) %在子图1绘f1(t)时域波形图title('f1(t)')xlabel('t')ylabel('f1(t)')subplot(2,2,2)plot(k2,f2) %在子图2绘f2(t)时波形图title('f2(t)')xlabel('t')ylabel('f2(t)')subplot(2,2,3)plot(k,f); %画卷积f(t)的时域波形h=get(gca,'position');h(3)=2.5*h(3);set(gca,'position',h) %将第三个子图的横坐标范围扩为原来的2.5倍title('f(t)=f1(t)*f2(t)')xlabel('t')ylabel('f(t)')三、实验部分:1.已知两连续时间信号如下图所示,试用MATLAB求 f(t)=f1(t)*f2(t),并绘出 f(t) 的时域波形图。
(设定取样时间间隔为p)◆参考程序:p=0.5;k1=0:p:2;f1=0.5*k1;k2=k1;f2=f1;[f,k]=sconv(f1,f2,k1,k2,p)【实验思考】:通过不断改变p的取值并对比所得到的实验效果,观察当取样时间p为多大时,函数sconv()的计算结果就是连续时间卷积f(t)=f1(t)*f2(t) 的较好近似结果?2.已知两连续时间信号如下图所示,试用MATLAB求f(t)=f1(t)*f2(t),并绘出f(t)的时域波形图。
(设定取样时间间隔为p)◆参考程序:p=0.1;k1=-1:p:1f1=2*ones(1,length(k1))k2=-2:p:2f2=ones(1,length(k2))[f,k]=sconv(f1,f2,k1,k2,p)【实验思考】:通过不断改变p的取值并对比所得到的实验效果,观察当取样时间p为多大时,函数sconv()的计算结果就是连续时间卷积f(t)=f1(t)*f2(t)的较好近似结果?实验三系统时域特性的仿真分析实验一、实验目的:通过使用MATLAB 仿真软件对LTI 系统的时域特性进行仿真分析对系统的冲激响应和零状态响应等有更深入的理解和掌握。
二、连续系统的冲激响应、阶跃响应及MATLAB 实现对于LTI 连续系统,求解系统的冲激响应h(t)和阶跃响应g(t)对我们进行连续系统的分析具有非常重要的意义。
MATLAB 为用户提供了专门用于求连续系统冲激响应和阶跃响应并绘制其时域波形的函数impulse ()和step ()。
在调用impulse ()和step ()函数时,我们需要用向量来对连续系统进行分析。
设描述连续系统的微分方程为:()()()()00N Mi ji ji j a y t a x t ===∑∑ 则我们可用向量a 和b 来表示该系统,即:a=[a N ,a N-1,……a 1,a 0]b=[b N ,b N-1,……b 1,b 0]注意,向量a 和b 的元素一定要以微分方程中时间求导的降幂次序来排列,且缺项要用0来补齐。
例如,对微分方程()()()()()'''''32y t y t y t f t f t ++=+,则表示该系统的对应向量应为 a=[1 3 2],b=[1 0 1]。
1. impulse ()函数函数impulse ()将绘出由向量a 和b 表示的连续系统在指定时间范围内的冲激响应h(t)的时域波形图,并能求出指定时间范围内冲激响应的数值解。
