热力学 喷管和扩压管(课堂PPT)
合集下载
【优】喷管PPT资料
（4）补充方程
状态方程： 等熵方程：
p RT
p k
Const
或
dp k d p
故完全气体在喷管中的一维定常等熵流动的控制方程为：
m VA Const
dp VdV 0
H
V2
Const
2
p RT
dp p
k
d
3. 拉瓦尔喷管的理论基础
几何喷管是依靠通道截面积变化使燃气膨胀加速， 以将燃气热能转换为动能。因此，研究燃气在喷管 中的流动特性就是研究在一维定常等熵流动条件下， 通道截面积的变化对燃气流动特性的影响。从而得 到燃气流动参数沿喷管轴线的分布规律。
M<1
M＜1 dA>0
V减小 p增大
M>1 dA>0
V增大 p减小
扩张管道中的流动变化
亚声速区
M<1 M=1
超声速区
M>1
拉瓦尔喷管原理图
（2）喷管截面变化对其他参数的影响
变化方向 参数
条件
收敛管道dA<0
M<1
M>1
扩张管道dA>0
M<1
M>1
dp/p
<0
>0
>0
<0
d/
<0
>0
>0
<0
dT/T
• 目前火箭发动机中最常用的是几何喷管，它是依靠喷管本身特殊的 几何形状来实现以上功能的。
• 本章主要讨论燃气在几何喷管中流动的基本规律，它是研究火箭发 动机性能参数的主要理论基础。
• 1. 流动假设
• 实践证明，燃气在喷管中的流动可简化为理想气体的一维定
喷管(课堂PPT)
在缩－扩形喷管出口建立超音速流的条件有两个, 这就是: 要满足面积比公式 和压力比公式
超音速喷管是一个( )的管道
A、圆柱形 B、扩张形
C、收敛形 D、先缩敛后扩张形
D
超音速缩扩形喷管的工作状态有( )
A、亚音速流动工作状态 B、管内产生激波的工作状态 C、管外产生斜激波的工作状态 D、管外产生膨胀波的工作状态
出口静压等于反压, 而且都等于临界压力是完全膨胀
实际落压比等于可用落压比, 都等于临界压比, 这时, 当来流总压和总温不变时, 通过喷管的质量流量达到 最大值
所以我们定义: 喷管出口反压等于气流的临界压力, 喷 管出口处气流的速度等于音速的工作状态称为临界工 作状态
C、超临界工作状态
当:
π*b
p*4 pb
喷管处于亚临界工作状态喷管内和喷管出口处气流的速度全部为亚音速气流的工作状态称为亚临界工作状态通过喷管的质量流量达到最大值喷管出口处气流的速度等于音速的工作状态称为临界工作状态是不完全膨胀通过喷管的质量流量不随反压的变化而变化喷管出口反压小于气流的临界压力喷管出口处气流的速度等于音速的工作状态称为超临界工作状态
A、排气管和喷口 B、整流锥和喷口 C、中介管和喷口 D、导流器和旋流器
AC
亚音速喷管的喷口位于：
A、排气管之前 C、扩压器之前
B、排气管之后 D、扩压器之后
B
燃气涡轮喷气发动机喷管的实际落压比 是：
A、 喷管进口处的静压与出口处的总压之比 B、喷管进口处的静压与出口处的静压之比 C、喷管进口处的总压与出口处的总压之比 D、喷管进口处的总压与出口处的静压之比
1、亚音速流态: 当p* ＞ pb ≥ pb1时,
缩－扩形喷管内全为亚音速流, 同时Mae＜１。是完全膨胀状态。
超音速喷管是一个( )的管道
A、圆柱形 B、扩张形
C、收敛形 D、先缩敛后扩张形
D
超音速缩扩形喷管的工作状态有( )
A、亚音速流动工作状态 B、管内产生激波的工作状态 C、管外产生斜激波的工作状态 D、管外产生膨胀波的工作状态
出口静压等于反压, 而且都等于临界压力是完全膨胀
实际落压比等于可用落压比, 都等于临界压比, 这时, 当来流总压和总温不变时, 通过喷管的质量流量达到 最大值
所以我们定义: 喷管出口反压等于气流的临界压力, 喷 管出口处气流的速度等于音速的工作状态称为临界工 作状态
C、超临界工作状态
当:
π*b
p*4 pb
喷管处于亚临界工作状态喷管内和喷管出口处气流的速度全部为亚音速气流的工作状态称为亚临界工作状态通过喷管的质量流量达到最大值喷管出口处气流的速度等于音速的工作状态称为临界工作状态是不完全膨胀通过喷管的质量流量不随反压的变化而变化喷管出口反压小于气流的临界压力喷管出口处气流的速度等于音速的工作状态称为超临界工作状态
A、排气管和喷口 B、整流锥和喷口 C、中介管和喷口 D、导流器和旋流器
AC
亚音速喷管的喷口位于：
A、排气管之前 C、扩压器之前
B、排气管之后 D、扩压器之后
B
燃气涡轮喷气发动机喷管的实际落压比 是：
A、 喷管进口处的静压与出口处的总压之比 B、喷管进口处的静压与出口处的静压之比 C、喷管进口处的总压与出口处的总压之比 D、喷管进口处的总压与出口处的静压之比
1、亚音速流态: 当p* ＞ pb ≥ pb1时,
缩－扩形喷管内全为亚音速流, 同时Mae＜１。是完全膨胀状态。
工程热力学课件 (03)
热一律的文字表达式
热力学第一定律用基本文字表达式表示为：
进入系统能量—离开系统能量＝系统储存能量的增加
由基本文字表达式可得到基本能量方程
包括闭口系能量方程和开口系能量方程 热一律在热力学中的应用主要体现在能量方程中
7
第2章 热力学第一定律
2-1 热力学第一定律的实质 2-2 本章涉及的概念 2-3 闭口系统能量方程 2-4 开口系统能量方程
dp<0，工质压力降低，技术功为正，工质对机器 做功，如汽轮机，燃气轮机
dp>0，工质压力增加，技术功为负，机器对工质 做功（消耗外界的功），如压气机、电风扇
23
第2章 热力学第一定律
2-1 热力学第一定律的实质 2-2 本章涉及的概念 2-3 闭口系统能量方程 2-4 开口系统能量方程
2-5 稳定流动能量方程的应用
32
稳定流动开口系能量方程推导
进入系统的能量：
Q
+
m
⎛ ⎜⎝
u1
+
p1v1
+
1 2
cf21
+
gz1
⎞ ⎟⎠
离开系统的能量：
式中u+pv为比焓h
Wi
+
m
⎛ ⎜⎝
u2
+
p2v2
+
1 2
cf22
+
gz2
⎞ ⎟⎠
根据热力学第一定律文字表达式：
⎡⎢⎣Q
+
m
⎛ ⎜⎝
u1
+
p1v1
+
1 2
cf21
+
gz1
⎞⎤ ⎟⎠⎥⎦
工程热力学第7章-气体与蒸汽的流动v3ppt课件
水蒸气 cp / cV
理想气体定比热双原子 cr 0.528
k=1.4
cr f 随工质而变 过热水蒸气k=1.3
cr 0.546
干饱和蒸汽k=1.135 cr 0.577
2） pcr cr p0
可编辑课件PPT
31
3）几何条件
Ma2 1 dcf dA 约束，临界截面只可能
cf A
发生在dA= 0处，考虑到工程实际
第七章 气体与蒸汽的流动
Gas and Steam Flow
7-1 稳定流动的基本方程式 7-2 促使流速改变的条件 7-3 喷管的计算 7-5 有摩阻的绝热流动 7-6 绝热节流
可编辑课件PPT
1
工程热力学的研究内容
1、能量转换的基本定律
2、工质的基本性质与热力过程
3、热功转换设备、工作原理 4、化学热力学基础
p
cf
M a20
d c f d p 异号 cf p
喷管 cf p 扩压管 p cf
即：气体在流动过程中流速增加，则压力下降；
压力升高，则流速必降低。
2）cfdcf vdp
cf
1 2
cf2
的能量来源
是压降，是焓（即技术功）转换成机械能。
h11 2cf21h21 2 可编c辑f22 课 件Ph PT1 2cf2
可编辑课件PPT
27
cf2 2h0h2 普适
cf 2h0 h
2cpT0 T2 理想气体、定比热容
cp 1Rg
2R g1T0T2
pvRgT
分析：
T0 T
p0 p
1
1
2p0v10 1
p2 p0
c f f 1 , p 0 , v 0 , p 2 p 0 , 而 p 0 , v 0 取 决 于 p 1 ， v 1 ， T 1 ， 所 以
理想气体定比热双原子 cr 0.528
k=1.4
cr f 随工质而变 过热水蒸气k=1.3
cr 0.546
干饱和蒸汽k=1.135 cr 0.577
2） pcr cr p0
可编辑课件PPT
31
3）几何条件
Ma2 1 dcf dA 约束，临界截面只可能
cf A
发生在dA= 0处，考虑到工程实际
第七章 气体与蒸汽的流动
Gas and Steam Flow
7-1 稳定流动的基本方程式 7-2 促使流速改变的条件 7-3 喷管的计算 7-5 有摩阻的绝热流动 7-6 绝热节流
可编辑课件PPT
1
工程热力学的研究内容
1、能量转换的基本定律
2、工质的基本性质与热力过程
3、热功转换设备、工作原理 4、化学热力学基础
p
cf
M a20
d c f d p 异号 cf p
喷管 cf p 扩压管 p cf
即：气体在流动过程中流速增加，则压力下降；
压力升高，则流速必降低。
2）cfdcf vdp
cf
1 2
cf2
的能量来源
是压降，是焓（即技术功）转换成机械能。
h11 2cf21h21 2 可编c辑f22 课 件Ph PT1 2cf2
可编辑课件PPT
27
cf2 2h0h2 普适
cf 2h0 h
2cpT0 T2 理想气体、定比热容
cp 1Rg
2R g1T0T2
pvRgT
分析：
T0 T
p0 p
1
1
2p0v10 1
p2 p0
c f f 1 , p 0 , v 0 , p 2 p 0 , 而 p 0 , v 0 取 决 于 p 1 ， v 1 ， T 1 ， 所 以
喷管和扩压管
热工基础
第五章 热工基础的应用
§5-1 喷管和扩压管 §5-2 换热器及其热计算 §5-3 压气机 §5-4 内燃机循环 §5-5 燃气轮机循环 §5-6 蒸汽动力循环 §5-7 制冷循环
1/20
热工基础
第一节 喷管和扩压管
对象：气体和蒸汽在管路设备，如喷管、扩压管、节
流阀内的流动过程。 喷管：用于增加气体或蒸气流速的变截面短管。 主要问题：气体在流经喷管等设备时，气流参数变化与
pcr Tcr vcr 称临界压力、临界温度及临界比体积。
Ｍa < 1
dA = 0
Ｍa = 1
Ｍa > 1
dA < 0
(临界截面)
dA > 0
pcr Tcr ccr = cfcr
12/20
1-3 喷管的计算
热工基础
喷管计算包括设计计算和校核计算。
设计计算：
已知：工质进口参数 (p1, T1, cf1)、背压(出口外环境压力) pb、流量qm 由工作条件(锅炉、发动机)决定
已知条件： p1, T1, cf1, pb, qm 设计原则：符合热力学原理(可逆绝热充分膨胀)。
(1) 外形选择 (2) 尺寸计算
p2 pb
pb pcr cr p1 pb pcr cr p1
渐缩喷管 缩放喷管
A2
qm
v2 cf2
Amin
qm
vcr cf,cr
渐缩喷管 缩放喷管
A2
qm
vdp dh
dh c f dc f 0
c f dc f vdp
流动过程中，欲使工质流速增加，必须有压力降落。
压差是提高工质流动速度的必要条件。
6/20
热工基础
第五章 热工基础的应用
§5-1 喷管和扩压管 §5-2 换热器及其热计算 §5-3 压气机 §5-4 内燃机循环 §5-5 燃气轮机循环 §5-6 蒸汽动力循环 §5-7 制冷循环
1/20
热工基础
第一节 喷管和扩压管
对象：气体和蒸汽在管路设备，如喷管、扩压管、节
流阀内的流动过程。 喷管：用于增加气体或蒸气流速的变截面短管。 主要问题：气体在流经喷管等设备时，气流参数变化与
pcr Tcr vcr 称临界压力、临界温度及临界比体积。
Ｍa < 1
dA = 0
Ｍa = 1
Ｍa > 1
dA < 0
(临界截面)
dA > 0
pcr Tcr ccr = cfcr
12/20
1-3 喷管的计算
热工基础
喷管计算包括设计计算和校核计算。
设计计算：
已知：工质进口参数 (p1, T1, cf1)、背压(出口外环境压力) pb、流量qm 由工作条件(锅炉、发动机)决定
已知条件： p1, T1, cf1, pb, qm 设计原则：符合热力学原理(可逆绝热充分膨胀)。
(1) 外形选择 (2) 尺寸计算
p2 pb
pb pcr cr p1 pb pcr cr p1
渐缩喷管 缩放喷管
A2
qm
v2 cf2
Amin
qm
vcr cf,cr
渐缩喷管 缩放喷管
A2
qm
vdp dh
dh c f dc f 0
c f dc f vdp
流动过程中，欲使工质流速增加，必须有压力降落。
压差是提高工质流动速度的必要条件。
6/20
热工基础
热力学 喷管和扩压管ppt课件
到 M 1 。为使气体流速增加，压力是不断
下降的。气体在喷管内的绝热流动中，压力下 降，温度下降，声速也将不断下降，流速的不 断增加和声速的不断降低使得马赫数总是不断 增加。在渐缩喷管内，马赫数可增加到极限值 1；在渐扩喷管内，马赫数可从1开始增加。
SUCCESS
THANK YOU
2019/6/24
根据过程方程 p
v s
p v有
ca pv RgT
上式说明，气体的声速与气体的热 力状态有关，气体的状态不同，声速也不同。 在气体的流动过程中，气体的热力状态发生 变化，声速也要变化。因此在气体介质中的 声速是当地声速，即某截面处热力状态下的 声速。
马赫数是气体在某截面处的流速与该处声速之比
1 2
c 2
gz
wsh
在喷管和扩压管的流动中，由于流道
较短，工质流速较高，故工质与外界几乎无
热交换。在流动中，工质与外界也无轴功交 换，工质进出口位能差可忽略不计，因此上
式变为
c2 2h
两边微分得
cdc dh
上式说明，工质的流速升高来源于工质 在流动过程中的焓降；工质的流速减小时， 焓将增加。
因而，为使Ｍ从 M 1 连续增加
到 M 1 ，在压差足够大的条件下，应采
用由渐缩喷管和渐扩喷管组合而成的缩放喷 管，又称拉伐尔喷管。在缩放喷管中，最小 截面即喉部截面处的流动是Ｍ＝１的声速流
动。该截面是 M 1的亚声速流动与 M 1
的超声速流动转折点，称为临界截面。临界
截面上的状态参数称为临界参数，用下标cr
种扩压管称为渐扩扩压管。工程上扩压管 比较简单，仅限于Ｍ＜１的情况，故渐扩 两字通常省略。
下降的。气体在喷管内的绝热流动中，压力下 降，温度下降，声速也将不断下降，流速的不 断增加和声速的不断降低使得马赫数总是不断 增加。在渐缩喷管内，马赫数可增加到极限值 1；在渐扩喷管内，马赫数可从1开始增加。
SUCCESS
THANK YOU
2019/6/24
根据过程方程 p
v s
p v有
ca pv RgT
上式说明，气体的声速与气体的热 力状态有关，气体的状态不同，声速也不同。 在气体的流动过程中，气体的热力状态发生 变化，声速也要变化。因此在气体介质中的 声速是当地声速，即某截面处热力状态下的 声速。
马赫数是气体在某截面处的流速与该处声速之比
1 2
c 2
gz
wsh
在喷管和扩压管的流动中，由于流道
较短，工质流速较高，故工质与外界几乎无
热交换。在流动中，工质与外界也无轴功交 换，工质进出口位能差可忽略不计，因此上
式变为
c2 2h
两边微分得
cdc dh
上式说明，工质的流速升高来源于工质 在流动过程中的焓降；工质的流速减小时， 焓将增加。
因而，为使Ｍ从 M 1 连续增加
到 M 1 ，在压差足够大的条件下，应采
用由渐缩喷管和渐扩喷管组合而成的缩放喷 管，又称拉伐尔喷管。在缩放喷管中，最小 截面即喉部截面处的流动是Ｍ＝１的声速流
动。该截面是 M 1的亚声速流动与 M 1
的超声速流动转折点，称为临界截面。临界
截面上的状态参数称为临界参数，用下标cr
种扩压管称为渐扩扩压管。工程上扩压管 比较简单，仅限于Ｍ＜１的情况，故渐扩 两字通常省略。
工程热力学第三章课件
四、焓（ Enthalpy ）及其物理意义
1 2 流动工质传递的总能量为：U mc mgz pV ( J ) 2 1 2 或 u c gz pv （J/kg） 2
焓的定义：h = u + pv H = U + pV
对理想气体：
( J/kg ) (J)
h = u + pv = u + RT＝f(T)
表面张力功、膨胀功和轴功等。 1.膨胀功（容积功）
无论是开口系统还是闭口系统，都有膨胀功；
闭口系统膨胀功通过系统界面传递，开口系统的膨胀 功是技术功的一部分，可通过其它形式（如轴）传递。 系统容积变化是做膨胀功的必要条件，但容积变化不 一定有膨胀功的输出。
2.轴功
系统通过机械轴与外界传递的机械功称为轴功。
第三节 闭口系统能量方程
一、闭口系统能量方程表达式 Q = dU + W (J)
Q = U + W (J)
Q W
q = du + w (J/kg)
q = u + w (J/kg)
对闭口系统而言，系统储存 能中的宏观动能和宏观位能 均不发生变化，因此系统总 储存能的变化就等于系统内 能的变化。即 ΔE= ΔU=U2-U1
p
3 4
2
1
v
对整个循环：∑∆u=0 或
du 0
因而q12 ＋ q23 ＋ q34 ＋ q41 ＝ w12 ＋ w23 ＋ w34 ＋ w41
即
q w
三、理想气体热力学能变化计算
对于定容过程， w = 0，于是能量方程为：
q v = duv=cvdTv
u cV ( )V T
1 2 1 2 Q (h2 c2 gz 2 )m2 (h1 c1 gz1 )m1 Ws dECV 2 2
工程热力学(喷管)
c22 c22 c22
12
N
h1 h2 h1 h2
2
工程热力学 Thermodynamics 二、第二定律分析
s sg 0 I qmT0sg
s
cp
T2 T1
Rg
ln
p2 p1
s2 s1
理想气体 蒸气
T2 c2 2cp T1 T2 c2
s2 h2 , p2查 h2 c2 c2
1、绝热滞止：气体在绝热流动过程中，因受某种物体的阻碍，或 经扩压管后，气体流速降低为零的过程称为绝热滞止过程。
2、滞止参数：气流速度在绝热滞止过程中滞止为0的状态称 为滞止状态，其状态参数称为滞止参数。
h0
h1
c12 2
T0
T1
c12 2cp
p0
工程热力学 Thermodynamics
工程热力学 Thermodynamics
1、比体积 ：比体积就是单位质量的工质所占的体积。即
v V m3 /kg m
2、压力 ：压力即物理学中的压强，单位是Pa。
绝对压力：p
大气压力：pb
pe ：表压力 pv ：真空度
p pb pe p pb pv
工程热力学 Thermodynamics
三、研究步骤
1、*定熵流动的基本规律； 2、有黏性摩阻的流动。
工程热力学 Thermodynamics
第一节 一维稳定流动的基本方程
一、连续性方程
qm1
qm2
A1c1 v1
A2c2 v2qm NhomakorabeaAc v
const
dA dc dv 0 Ac v
工程热力学 Thermodynamics
解：a) 确定出口压力：
喷管 喷管和扩压管(借鉴幻灯)
微分形式 cdc dh （适用于可逆及不可逆过程 ）
说明工质的速度升高来源于流动过程中的焓降。
行业特选
3
引入技术功后：
q (h h ) w
2
1
t
q dh dwt
当q＝0，且可逆时：
q dh wt dh vdp 0
vdp dh
所以有：cdc vdp
说明在流动过程中，工质的流速增加，必须有压力降低。
计算。对于缩放形喷管，还需确定其喉口处的最小截面积。
对于理想气体，出口截面处的速度为：
cf2
k1
2
k
k
1
p*v*
1
p2 p*
k
1
出口处气体的比容为：
1 v2
1 v*
p2 p*
k
气体流量为：
2 k
k 1
qm A
2
k
k 1
p* v*
p2 p*
p2 p*
k
行业特选
13
当喷管出口截面积
根据绝热流动的稳定流动方程为：(c22 c12 ) 2(h2 h1)
喷管出口流速（按滞止焓计算）： c2 2(h* h2)
如采用定值比热，出口速度为： c2 2(h* h2 ) 2cp (T * T2 )
c2
2
k
k
1
Rg
T
*
1
T2 T*
k 1
c2
2
k
k 1
RgT *
1
p2 p*
2
k
k
1
Rg
*T
*
但此值不可能达到，因为压力趋于零，比容就会趋于无穷大，而 截面积是不可能达到无穷大的。
说明工质的速度升高来源于流动过程中的焓降。
行业特选
3
引入技术功后：
q (h h ) w
2
1
t
q dh dwt
当q＝0，且可逆时：
q dh wt dh vdp 0
vdp dh
所以有：cdc vdp
说明在流动过程中，工质的流速增加，必须有压力降低。
计算。对于缩放形喷管，还需确定其喉口处的最小截面积。
对于理想气体，出口截面处的速度为：
cf2
k1
2
k
k
1
p*v*
1
p2 p*
k
1
出口处气体的比容为：
1 v2
1 v*
p2 p*
k
气体流量为：
2 k
k 1
qm A
2
k
k 1
p* v*
p2 p*
p2 p*
k
行业特选
13
当喷管出口截面积
根据绝热流动的稳定流动方程为：(c22 c12 ) 2(h2 h1)
喷管出口流速（按滞止焓计算）： c2 2(h* h2)
如采用定值比热，出口速度为： c2 2(h* h2 ) 2cp (T * T2 )
c2
2
k
k
1
Rg
T
*
1
T2 T*
k 1
c2
2
k
k 1
RgT *
1
p2 p*
2
k
k
1
Rg
*T
*
但此值不可能达到，因为压力趋于零，比容就会趋于无穷大，而 截面积是不可能达到无穷大的。
喷管和扩压管的流动特性及工程实例PPT资料优秀版
当地声速：某点在某一状态下的声速值。
流动特性主要取决于流速是大于还是小于当地声速。
3、马赫数
• 定义：流体中任一确定点的速度与该介质
中的当地声速的比值
• 定义式：
Ma cf c
Ma＜1 亚声速流 Ma=1 声速流 Ma＞1 超声速流
管内流体流速与压力及比体积的关系
• 根据热力学第一定律能量方程，等熵过程
Ma=1 dA=0 临界截面
Ma>1 Ma<1 Ma>1 dA>0 dA<0 dA>0 渐扩 渐缩渐扩
注:扩压管dcf<0,故不同音速下的形状与喷管相反
喷管和扩压管流速变化与截面变化的关系
流动状态
管道种类
喷管 dcf>0 dp<0
扩压管dp>0 dcf<0
Ma<1
1
2
dA 0 A
p1 p2
1
2 dA 0
dh cf dcf 0
渐扩喷管： cf1 ＞c, cf2＞c
通道截面渐扩 管内流体流速度与截面积的关系 节流后做功能力下降，即节流损失。
cf dcf vdp
Ma>1时，超声速流动，dA<0 ，
（1）加速气流dcf>0，dp<0； （2）减速气流dcf<0，dp>0 ；
管内流体流速度与截面积的关系
cf1 ＞c, cf2≥c
通道截面渐扩
节流后做功能力下降，即节流损失。 管内流体流速与压力及比体积的关系
0 dh vdp
渐扩喷管： cf1 ＞c, cf2＞c
水中的c=1400m/s; 空气中的c=340m/s
超声速连续变为亚声速流动，通道截面先缩后扩，在喉部达到声速。
流动特性主要取决于流速是大于还是小于当地声速。
3、马赫数
• 定义：流体中任一确定点的速度与该介质
中的当地声速的比值
• 定义式：
Ma cf c
Ma＜1 亚声速流 Ma=1 声速流 Ma＞1 超声速流
管内流体流速与压力及比体积的关系
• 根据热力学第一定律能量方程，等熵过程
Ma=1 dA=0 临界截面
Ma>1 Ma<1 Ma>1 dA>0 dA<0 dA>0 渐扩 渐缩渐扩
注:扩压管dcf<0,故不同音速下的形状与喷管相反
喷管和扩压管流速变化与截面变化的关系
流动状态
管道种类
喷管 dcf>0 dp<0
扩压管dp>0 dcf<0
Ma<1
1
2
dA 0 A
p1 p2
1
2 dA 0
dh cf dcf 0
渐扩喷管： cf1 ＞c, cf2＞c
通道截面渐扩 管内流体流速度与截面积的关系 节流后做功能力下降，即节流损失。
cf dcf vdp
Ma>1时，超声速流动，dA<0 ，
（1）加速气流dcf>0，dp<0； （2）减速气流dcf<0，dp>0 ；
管内流体流速度与截面积的关系
cf1 ＞c, cf2≥c
通道截面渐扩
节流后做功能力下降，即节流损失。 管内流体流速与压力及比体积的关系
0 dh vdp
渐扩喷管： cf1 ＞c, cf2＞c
水中的c=1400m/s; 空气中的c=340m/s
超声速连续变为亚声速流动，通道截面先缩后扩，在喉部达到声速。
喷管,管内流体热力学
1 v dqout 2 dwact a T p
1 vc p
1 1 v 2 dw f 2 gdz a T p a
理想气体的定常等熵流
• 无轴功定常等熵流的一般特性
• 对无轴功的定常等熵流，忽略高度变化， 伍里斯方程
2 x
2 cy
不连续面
控制面
p
RT
范诺线和瑞利线
• 瑞利线表征流体可逆地流经等截面通 道且与外界有热交换时，参数连续变 化的关系 。
• 范诺线表征流体在等截 面通道内作有摩擦的绝 热流动时参数连续变化 的关系。
范诺线所服从的能量方程
• 能量方程、连续方程、状态方程和热力学 关系分别为
dh cdc 0
• 稳态稳流，且体积力只有重力
Ac 0 Ac 0 x p c 2 4 f z dc g c 0 x 2 D x dx
• 当体积力和摩擦引起的剪切力都可忽略，则 普遍式动量 方程为
p 2 A Ac Ac x x (6-6b)
• 连续方程
T dA dc dv v A c a2 p 2 v v s ds
• 声速方程
dq ds T dA dc dv v A c a2 p 2 v v s
速度系数
对比量与Mk之间的关系
实际工作中的喷管
• 喷管的摩擦损耗 • 喷管效率或速度损失系数估计摩擦影响
喷管效率 速度损失系数 喷管效率和速度损失系数的关系
可逆绝热膨胀和不可逆绝热膨胀
绝热节流
压力比改变时喷管的工作情况-收缩喷管
工程热力学与传热学第7章气体的流动.
第七章 气体的流动(Gas Flow)第一节 气体在喷管和扩压管中的流动主题1：喷管和扩压管的断面变化规律一、稳定流动基本方程气体在喷管和扩压管中的流动过程作可逆绝热过程，气体流动过程所依据的基本方程式有：连续性方程式、能量方程式、及状态方程式。
１、连续性方程连续性方程反映了气体流动时质量守恒的规律。
定值=⋅=vf mg ω写成微分形式ggd v dv f df ωω-=7-1它给出了流速、截面面积和比容之间的关系。
连续性方程从质量守恒原理推得，所以普遍适用于稳定流动过程，即不论流体的性质如何（液体和气体），或过程是否可逆。
２、能量方程能量方程反映了气体流动时能量转换的规律。
由式（3-8），对于喷管和扩压管中的稳定绝热流动过程，212122)(21h h g g -=-ωω 写成微分形式dh d g -=221ω7-2３、过程方程过程方程反映了气体流动时的状态变化规律。
对于绝热过程，在每一截面上，气体基本热力学状态参数之间的关系：定值=k pv写成微分式0=+vdv k p dp 7-3二、音速和马赫数音速是决定于介质的性质及介质状态的一个参数，在理想气体中音速可表示为kRT kpv a ==7-4因为音速的大小与气体的状态有关，所以音速是指某一状态的音速，称为当地音速。
流速与声速的比值称为马赫数：M ag=ω 7-5利用马赫数可将气体流动分类为：m 2g v 222图7-1管道稳定流动示意图亚声速流动：1<M a g <ω超声速流动：1>M a g >ω 临界流动： 1=Ma g =ω三、促使气体流速变化的条件 1、力学条件由式（3-5），对于开口系统可逆稳定流动过程，能量方程⎰-∆=21vdp h q 或 vdp dh q -=δ，式中0=q δ所以 vdp dh = 7-6 联合（7-2）和（7-6）vdp d g g -=ωω7-7由式7-7可见，气体在流动中流速变化与压力变化的符号始终相反，表明气流在流动中因膨胀而压力下降时，流速增加；如气流被压缩而压力升高时，则流速必降低。
喷管内流体热力学
2 c • (6-9)代入 Tds f Tds dp d d gz 2 c2 1 Tdsg dp d d gz 0 2 • 动量方程(6-6a) 1 2 dx c 4 f 2 D dsg (6-12) T
F
x
• 体积力 F Adx F Adx cos z 若体积力只有重力则 F cos g x • 表面力 1）作用在运动方向上的压力
dA p p pA pdA A dx p dx Adx dx x x
• 马赫数 • 某一点的流体流动速度c和同一点的当地声 速a之比 c c
M
• 可压缩流 的分类
M 1 M 1 M 1
a
M
RT
亚声速流 声速流 超声速流
基本概念（3）
• 滞止焓h0
•
c2 h0 h 2 c2 对于理想气体，c p T0 T 2 R cp 1 c M RT
1 2 T0 T 1 M 2 1 2 p0 p 1 M 2
1
（6-3） （6-4）
基本概念（4）
• 激波 如果压力波通过时气体参数发生突然的急 剧变化，这种波称为 激波，垂直于流动方 向的激波称为正激波。
基本定律
• • • • 质量守恒定律 牛顿第二运动定律 热力学第一定律 热力学第二定律
1 v dqout 2 dwact a T p
1 vc p
1 1 v 2 dw f 2 gdz a T p a
理想气体的定常等熵流
• 无轴功定常等熵流的一般特性
• 对无轴功的定常等熵流，忽略高度变化， 伍里斯方程
热工基础(5.1.1)--喷管和扩压管
dv -v
=0
工质流速变化率、截面积变化率、比体积变化率间 关系
4/20
热工基础
1-1 一维稳定流动的基本方程
二、 能量方程
稳定流动：
q
=
h2
-
h1
+
1 2
(cf22
-
c2 f1
)
+
g(z2
-
z1 )
+
wsh
1 cf1
管道流动：
忽略传热：
1
忽 略 势 能 变 化p1, ：v1, T1, A1
wsh = 0 q ﾻ 0 gDz ﾻ 0
渐扩喷管
Ma > 1 dA > 0
缩放喷管(拉伐尔喷管) Ma < 1, Ma = 1, Ma > 1
dA < 0, dA = 0, dA > 0
11/20
热工基础
截面上 Ma=1 、 cf=c ，称临界截面 [ 也称喉部 (throat) 截面 ] ，临界截面上速度达当地声速。
cf = c = k pcrvcr = k RgTcr
�k � �
� � �= �
k
p1v1
� � �ppc1r
k -1
�k � �
16/20
热工基础
2k k
p1v1 -1
� � �1 �
� � �ppc1r
k -1
�k � �
� � �= �
k
p1v1
� � �ppc1r
k -1
�k � �
令 ：n cr
=
pcr p1
( 临界压力比 )
k
2 -
1
喷管内流体热力学
F
x
• 体积力 F Adx F Adx cos z 若体积力只有重力则 F cos g x • 表面力 1）作用在运动方向上的压力
dA p p pA pdA A dx p dx Adx dx x x
dc dA M 1 c A
2
M 1 M 1
dA 0 dc dA 0 dc
截面积变化对流动属性的影响
dA dA 0, 0 dp dc
dA dA 0, 0 dp dc
dc dA 2 M 1 c A
图6-3
cdc
dp
0
亚声速喷管单独使用时成为收缩喷管； 与扩放喷管联合在一起时称为 缩放喷管。
ds 1 dh dh R RT 2(h0 h)
RT a a ( 1)(h0 h)
2 2 0
1 1/ 2 2 1 a0 1 h0 h h0 h 积分 s sx ln 1 1/ 2 R 2 1 h h a 1 h h 0 0 x 0 x
管内气体流动热力学
管内流动
• • • • 管内流动类型： 第一类为喷管和扩压管等管内流动 第二类为输送管内的流动 第三类为换热器 管内的流动和可燃混合气 在管内 燃烧时的流动 等。
p 2 p a RT s s
基本概念（1）
2 c • (6-9)代入 Tds f Tds dp d d gz 2 c2 1 Tdsg dp d d gz 0 2 • 动量方程(6-6a) 1 2 dx c 4 f 2 D dsg (6-12) T
能源第十三章 喷管和扩压管
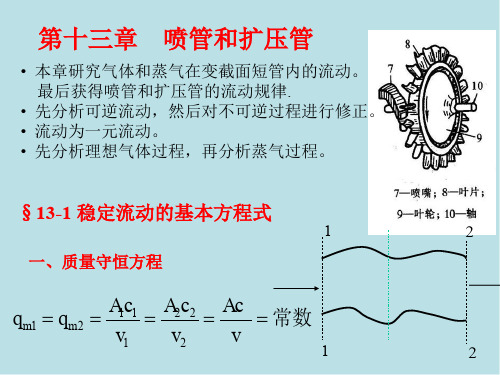
h0
h1
1 2
c12
h2
1 2
c22
对于理想气体
T0
T1
c12 2cp
p0
p1
T0 T1
1
(2)、选择喷管类型, 确定出截面上的压力.
当
pb p0
cr =
pcr p0
时, 即 p2 pb pcr
选择渐缩喷管
当
pb p0
cr =
pcr p0
p2/p0 0 1/4 1/2 3/4 １
在缩放喷管的最小截面, 即临界截面处有
ccr
2
Rg 1
T0
1
p2 p0
1
=
2 p0v0 1
1
pcr p0
1
ca,cr pcrvcr ccr
常数
对于微元过程有
可逆时
dh 1 dc2 0 2
cdc vdp
流动过程中, 当 c = 0 的点称为滞止点，相应的状态称为 滞止状态，参数称为滞止参数。(定熵滞止）
h0
h1
1 2
c12
h2
1 2
c22
h
1 2
c2
对于理想气体有
c pT0
ቤተ መጻሕፍቲ ባይዱ
c pT1
1 2
c12
c pT2
T1
工程热力学课件7气体蒸汽流动解析
2
1
p0v0
2 1 RgT0
当 p2 / p0 = 1时，即进出口没有压差时，流速为零。
27
2、分析
cf2
2
1
p0v0
1
(
p2 p0
1
)
在初态确定的条件下： c f 2 f ( p2 / p0 )
2
1
p0v0
2 1 RgT0
此速度实际上是 达不到的，因为 压力趋于零时比 体积趋于无穷大。
1
临界压力比 cr仅与气体的种类有关，适用于理想气体和
水蒸汽。水蒸汽的κ 值取经验数值。
单原子气体
κ =1.67
cr 0.487
双原子气体 κ =1.40
0.528
三原子气体 κ =1.30
0.546
过热水蒸汽 κ =1.30
0.546
饱和水蒸汽 κ =1.135
0.577
31
cr 物理含义：气流的压力下降多少时，流速恰好等于当
（sonic velocity）
Ma 1 超声速
（supersonic velocity）13
在声速公式中，κ的选取：
水蒸汽、可逆绝热过程 k c p cv
取经验数据
κ=1.3 过热蒸汽 κ=1.135 饱和蒸汽
14
比体积变化率与 流速变化率之比
分析：dA dv dcf ( dv v 1) dcf
Ma≤1
Ma<1
Ma>1
喷管
dA 0 dcf Ma0≥1
Ma>1 喷管截面形状 Ma<1
18
3、 M a＝1 dA＝0
dA A
(M
2 a
1)
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
当喷管进口气体流速较小，可忽略不计时
c2 2(h1h2)
19
由于该式是从能量方程直接推导得到的，
故对于工质和过程是否可逆均无限制。对于
理想气体，由于
c2 2cp(T1，T故2)有
hcpT
对于蒸气， 和 可通过查图、查表
得到。
h1 h 2
20
在定熵条件下，若工质为理想气体，可推得
c2 2 1Rg(T1T2) 2 1RgT11p p1 21
上式说明，在喷管内的气体定熵流动中，
喷管出口的气体流速取决于工质性质、进口参
数和气体出口与进口的压比 p2 / p1。在工质、
气体进口状态都确定的条件下，气体出口流速
仅取决于压比 而增大。当
p2，/ 其p值1 随
p的2 /减p小1
c2 时c，2max
21
p2 / p10
c2max
2 1RgT1
然而，这一最大出口流速是达不到的。因为
9
二、声速和马赫数
由物理学知，声速
ca
p
s
v2p vs
根据过程方程 p
p
有
v s
v
ca pv RgT
10
上式说明，气体的声速与气体的热力状 态有关，气体的状态不同，声速也不同。在 气体的流动过程中，气体的热力状态发生变 化，声速也要变化。因此在气体介质中的声 速是当地声速，即某截面处热力状态下的声 速。
到 M1。为使气体流速增加，压力是不断下
降的。气体在喷管内的绝热流动中，压力下降， 温度下降，声速也将不断下降，流速的不断增 加和声速的不断降低使得马赫数总是不断增加。 在渐缩喷管内，马赫数可增加到极限值1；在 渐扩喷管内，马赫数可从1开始增加。
15
因而，为使Ｍ从 M连1续增加
到 M1，在压差足够大的条件下，应采 用由渐缩喷管和渐扩喷管组合而成的缩放喷 管，又称拉伐尔喷管。在缩放喷管中，最小 截面即喉部截面处的流动是Ｍ＝１的声速流
当 p2 时0， v2 ，此时出口截面积
应趋于无穷大，这显然办不到。事实上，
p2 / p1还受到喷管形状的限制。
22
（二）临界压比
约为0临）界压截力面p上之1 的比气称体为压临力界p压c比r与，进用口（v初c表r 速示
v cr
p cr p1
23
由式
1
ccr
21RgT11
pcr p1
1
ca,cr RgTcr RgT1ppc1r
第九章 喷管和扩压管
本章介绍热工基础理论在喷管和扩压管 中的应用。在叶轮式动力机中，热能向机械 能的转换是在喷管中实现的。喷管就是用于 增加气体或蒸气流速的变截面短管。如图就 是一喷管。气体或蒸气在喷管中绝热膨胀， 压力降低，流速增加。高速流动的气流冲击 叶轮机的叶片，使叶轮机旋转，使气流的动 能转变为叶轮机旋转的机械能。
动。该截面是 M1的亚声速流动与 M1
的超声速流动转折点，称为临界截面。临界
截面上的状态参数称为临界参数，用下标cr
表示。
16
ccrcacr pcrvcr
渐缩喷管的出口流速在极限条件下可
增加到 截面。
c
ca
，此时出口截面也是临界
工程上喷管进口处气流速度一般较低，
Ｍ总是小于1，而进口处Ｍ＞１的渐扩喷管
1
与喷管中的热力过程相反，在工程实际中还 有另一种转换，即高速气流进入变截面短管中 时，气流的流速降低，而压力升高。这种能使 气流压力升高而速度降低的变截面短管称为扩 压管。扩压管在叶轮式压气机中得到应用。
本节讨论比热容为定值的理想气体的可逆过 程，且仅考虑沿流动方向的状态和流速变化， 即认为流动是一维流动；同时假定气体的流动 是稳定流动。
13
故
dA(M2 1)dc
A
c
该式称为管内流动的特征方程
对于喷管而言，增加气体流速是其主要目
的。根据特征方程，当气流的 M1时，要
使 dc0，则必须使 dA0。沿流动方向上
流道截面逐渐减小的喷管称为渐缩喷管，如图
所示。当 M1时，则应 dA0，称为渐扩
喷管，如图所示。
14
工程上许多场合要求气体从 M加1速
几乎不单独使用。
17
对于扩压管，使用的主要目的是为了升 高气流的压力，流动过程中流速降低、压
力升高。当Ｍ＜１时， dA，0 此种
扩压管称为渐扩扩压管。工程上扩压管比 较简单，仅限于Ｍ＜１的情况，故渐扩两 字通常省略。
18
四、喷管的计算
（一）流速计算
由能量方程 c2 2c1 2 2(h 2h 1)
2
一、一维稳定流动的基本方程
（一）连续性方程
根据质量守恒原理，流体稳定流经任一 截面的质量流量保持不变。若任一截面的面 积为A，流体在该截面的流速为c，比体积
为 v，则流量qmFra bibliotekAc v
常数
3
上式称为稳定流动的连续性方程。对其两边微 分得
dA dv dc Av c
4
（二）能量方程
qh1 2c2gzw sh
在喷管和扩压管的流动中，由于流道较 短，工质流速较高，故工质与外界几乎无热 交换。在流动中，工质与外界也无轴功交换， 工质进出口位能差可忽略不计，因此上式变 为
c22h
5
两边微分得
cd cdh
上式说明，工质的流速升高来源于工质 在流动过程中的焓降；工质的流速减小时， 焓将增加。
又 qdhdw t
6
11
马赫数是气体在某截面处的流速与该处声速之比
M c ca
根据M的大小，流动可分为
M1 亚声速流动 M1 声速流动 M1 超声速流动
12
三、气体在喷管和扩压管中的定熵流动
由上面的基本方程可得到马赫数为参 变量的截面积与流速变化的关系式
d v vp pd v vv ca 2dp c ca 2dc c 2 a 2 d c cM 2d cc
当q=0且可逆时 vd p d h
故
cdcvdp
上式说明，在流动过程中欲使工质流速增加， 必须有压力降落。所以压差是提高工质流动速 度的必要条件，也是流速提高的动力。
7
（三）过程方程
在定熵（绝热可逆）流动过程中，工 质的状态参数变化遵循定熵的过程方程
pv 常数
两边微分有
dp dv
p
v
8
上式说明，在定熵流动过程中，若压力下 降，比体积增加。联系能量方程分析知，工 质流速与比体积是同时增加或减少，而压力 变化分别与比体积变化和流速变化相反。
以及 ccr ca,cr 求解得
vcr
pcr p1
211
24
由于绝热指数仅取决于气体热力性质，因 此气体一定，其临界压比一定。对于定值比 热的理想气体
单原子气体 k= 1.67 临界压比为0.487 双原子气体 k=1.4 临界压比为0.528 多原子气体 k=1.3 临界压比为0.546
c2 2(h1h2)
19
由于该式是从能量方程直接推导得到的，
故对于工质和过程是否可逆均无限制。对于
理想气体，由于
c2 2cp(T1，T故2)有
hcpT
对于蒸气， 和 可通过查图、查表
得到。
h1 h 2
20
在定熵条件下，若工质为理想气体，可推得
c2 2 1Rg(T1T2) 2 1RgT11p p1 21
上式说明，在喷管内的气体定熵流动中，
喷管出口的气体流速取决于工质性质、进口参
数和气体出口与进口的压比 p2 / p1。在工质、
气体进口状态都确定的条件下，气体出口流速
仅取决于压比 而增大。当
p2，/ 其p值1 随
p的2 /减p小1
c2 时c，2max
21
p2 / p10
c2max
2 1RgT1
然而，这一最大出口流速是达不到的。因为
9
二、声速和马赫数
由物理学知，声速
ca
p
s
v2p vs
根据过程方程 p
p
有
v s
v
ca pv RgT
10
上式说明，气体的声速与气体的热力状 态有关，气体的状态不同，声速也不同。在 气体的流动过程中，气体的热力状态发生变 化，声速也要变化。因此在气体介质中的声 速是当地声速，即某截面处热力状态下的声 速。
到 M1。为使气体流速增加，压力是不断下
降的。气体在喷管内的绝热流动中，压力下降， 温度下降，声速也将不断下降，流速的不断增 加和声速的不断降低使得马赫数总是不断增加。 在渐缩喷管内，马赫数可增加到极限值1；在 渐扩喷管内，马赫数可从1开始增加。
15
因而，为使Ｍ从 M连1续增加
到 M1，在压差足够大的条件下，应采 用由渐缩喷管和渐扩喷管组合而成的缩放喷 管，又称拉伐尔喷管。在缩放喷管中，最小 截面即喉部截面处的流动是Ｍ＝１的声速流
当 p2 时0， v2 ，此时出口截面积
应趋于无穷大，这显然办不到。事实上，
p2 / p1还受到喷管形状的限制。
22
（二）临界压比
约为0临）界压截力面p上之1 的比气称体为压临力界p压c比r与，进用口（v初c表r 速示
v cr
p cr p1
23
由式
1
ccr
21RgT11
pcr p1
1
ca,cr RgTcr RgT1ppc1r
第九章 喷管和扩压管
本章介绍热工基础理论在喷管和扩压管 中的应用。在叶轮式动力机中，热能向机械 能的转换是在喷管中实现的。喷管就是用于 增加气体或蒸气流速的变截面短管。如图就 是一喷管。气体或蒸气在喷管中绝热膨胀， 压力降低，流速增加。高速流动的气流冲击 叶轮机的叶片，使叶轮机旋转，使气流的动 能转变为叶轮机旋转的机械能。
动。该截面是 M1的亚声速流动与 M1
的超声速流动转折点，称为临界截面。临界
截面上的状态参数称为临界参数，用下标cr
表示。
16
ccrcacr pcrvcr
渐缩喷管的出口流速在极限条件下可
增加到 截面。
c
ca
，此时出口截面也是临界
工程上喷管进口处气流速度一般较低，
Ｍ总是小于1，而进口处Ｍ＞１的渐扩喷管
1
与喷管中的热力过程相反，在工程实际中还 有另一种转换，即高速气流进入变截面短管中 时，气流的流速降低，而压力升高。这种能使 气流压力升高而速度降低的变截面短管称为扩 压管。扩压管在叶轮式压气机中得到应用。
本节讨论比热容为定值的理想气体的可逆过 程，且仅考虑沿流动方向的状态和流速变化， 即认为流动是一维流动；同时假定气体的流动 是稳定流动。
13
故
dA(M2 1)dc
A
c
该式称为管内流动的特征方程
对于喷管而言，增加气体流速是其主要目
的。根据特征方程，当气流的 M1时，要
使 dc0，则必须使 dA0。沿流动方向上
流道截面逐渐减小的喷管称为渐缩喷管，如图
所示。当 M1时，则应 dA0，称为渐扩
喷管，如图所示。
14
工程上许多场合要求气体从 M加1速
几乎不单独使用。
17
对于扩压管，使用的主要目的是为了升 高气流的压力，流动过程中流速降低、压
力升高。当Ｍ＜１时， dA，0 此种
扩压管称为渐扩扩压管。工程上扩压管比 较简单，仅限于Ｍ＜１的情况，故渐扩两 字通常省略。
18
四、喷管的计算
（一）流速计算
由能量方程 c2 2c1 2 2(h 2h 1)
2
一、一维稳定流动的基本方程
（一）连续性方程
根据质量守恒原理，流体稳定流经任一 截面的质量流量保持不变。若任一截面的面 积为A，流体在该截面的流速为c，比体积
为 v，则流量qmFra bibliotekAc v
常数
3
上式称为稳定流动的连续性方程。对其两边微 分得
dA dv dc Av c
4
（二）能量方程
qh1 2c2gzw sh
在喷管和扩压管的流动中，由于流道较 短，工质流速较高，故工质与外界几乎无热 交换。在流动中，工质与外界也无轴功交换， 工质进出口位能差可忽略不计，因此上式变 为
c22h
5
两边微分得
cd cdh
上式说明，工质的流速升高来源于工质 在流动过程中的焓降；工质的流速减小时， 焓将增加。
又 qdhdw t
6
11
马赫数是气体在某截面处的流速与该处声速之比
M c ca
根据M的大小，流动可分为
M1 亚声速流动 M1 声速流动 M1 超声速流动
12
三、气体在喷管和扩压管中的定熵流动
由上面的基本方程可得到马赫数为参 变量的截面积与流速变化的关系式
d v vp pd v vv ca 2dp c ca 2dc c 2 a 2 d c cM 2d cc
当q=0且可逆时 vd p d h
故
cdcvdp
上式说明，在流动过程中欲使工质流速增加， 必须有压力降落。所以压差是提高工质流动速 度的必要条件，也是流速提高的动力。
7
（三）过程方程
在定熵（绝热可逆）流动过程中，工 质的状态参数变化遵循定熵的过程方程
pv 常数
两边微分有
dp dv
p
v
8
上式说明，在定熵流动过程中，若压力下 降，比体积增加。联系能量方程分析知，工 质流速与比体积是同时增加或减少，而压力 变化分别与比体积变化和流速变化相反。
以及 ccr ca,cr 求解得
vcr
pcr p1
211
24
由于绝热指数仅取决于气体热力性质，因 此气体一定，其临界压比一定。对于定值比 热的理想气体
单原子气体 k= 1.67 临界压比为0.487 双原子气体 k=1.4 临界压比为0.528 多原子气体 k=1.3 临界压比为0.546