岭回归ppt
第7章岭回归分析

第7章岭回归分析岭回归分析(Ridge Regression Analysis)是一种线性回归的改进方法,用于解决当自变量之间存在多重共线性(multicollinearity)时,常规最小二乘法(Ordinary Least Squares, OLS)估计的回归系数不稳定的问题。
多重共线性指的是自变量之间存在高度相关性,即两个或多个自变量之间存在线性关系。
在OLS估计中,当出现多重共线性时,回归系数的估计值可能变得非常大,导致模型不可靠。
岭回归通过引入一个惩罚项(penalty term)来解决多重共线性带来的问题。
惩罚项是对回归系数的约束,使得估计值更稳定。
惩罚项的大小由一个称为岭参数(Ridge parameter)的超参数决定,岭参数越大,惩罚项越大。
具体实施岭回归分析的步骤如下:1.收集数据:收集需要进行回归分析的数据,包括自变量(X)和因变量(Y)。
2.数据预处理:对数据进行预处理,包括缺失值处理、异常值处理和标准化处理等。
3.岭回归模型:构建岭回归模型,假设回归方程为:Y=β0+β1X1+β2X2+...+βnXn+ε,其中β0是截距,β1-βn是回归系数,ε是误差项。
4. 岭参数选择:选择适当的岭参数值。
一种常用的方法是交叉验证(cross-validation),通过在训练集上进行模型拟合和验证,选择使得平均误差最小的岭参数。
5.模型拟合:使用选定的岭参数,对模型进行拟合,通过最小化残差平方和(RSS)来估计回归系数的值。
6.结果分析:通过分析回归系数的估计值,评估模型的拟合效果和自变量的影响程度。
岭回归分析的优点是可以解决多重共线性问题,使得回归模型在存在多重共线性时仍然具有较好的稳定性。
同时,通过调节岭参数,还可以控制惩罚项的大小。
然而,岭回归也存在一些限制。
首先,岭回归对于多重共线性问题的处理是通过牺牲模型的拟合度来换取回归系数的稳定性,有时会导致模型的预测能力下降。
其次,选择合适的岭参数值也需要一定的经验和技巧,选择过小的岭参数可能无法很好地解决多重共线性问题,而选择过大的岭参数可能导致模型欠拟合。
岭回归技术的原理和应用

岭回归技术的原理和应用1. 岭回归技术简介岭回归是一种常见的线性回归方法,用于处理特征矩阵存在高度多重共线性的情况。
它通过添加一个正则化项,缩小特征系数的幅度,从而降低过拟合的风险。
本文将介绍岭回归技术的原理和应用。
2. 岭回归的原理岭回归的原理基于以下假设条件: - 原始数据存在线性关系 - 特征矩阵的列之间存在多重共线性岭回归通过对特征矩阵的每一列添加一个正则化项进行优化,可以用以下公式表示:β_ridge = argmin ||y - Xβ||^2 + λ||β||^2其中,β_ridge是岭回归得到的特征系数向量,y是目标变量,X是特征矩阵,λ是正则化参数。
3. 岭回归的应用岭回归在实践中有许多应用场景,下面列举了几个常见的应用:3.1 特征选择岭回归可以通过对特征系数进行优化,选择最重要的特征变量。
通过调整正则化参数λ的值,可以控制特征系数的幅度,从而实现特征选择的目的。
3.2 预测分析岭回归可以用于对数据进行预测分析。
通过使用已有的数据集进行模型训练,得到特征系数向量,然后可以用该向量对新的未知数据进行预测。
3.3 多重共线性处理岭回归的一个主要应用是处理特征矩阵存在多重共线性的情况。
多重共线性指的是特征矩阵中有多个特征变量之间存在高度相关性的情况。
岭回归通过正则化项的引入,可以有效降低多重共线性对模型的影响。
3.4 泛化能力岭回归在具有较小样本量的情况下表现出较好的泛化能力。
通过控制正则化参数λ的值,岭回归可以在一定程度上平衡模型的拟合能力和泛化能力。
4. 总结岭回归技术是一种常见的线性回归方法,通过添加正则化项对特征系数进行优化,从而处理特征矩阵存在多重共线性的情况。
岭回归在特征选择、预测分析、多重共线性处理和提高模型的泛化能力等方面具有广泛的应用。
在实际应用中,需要根据具体问题选择适当的正则化参数λ,以平衡模型的复杂度和拟合能力。
以上是岭回归技术的原理和应用的概述,希望对您有所帮助!。
《森林生态恢复》PPT课件

整理ppt
18
三、林火迹地的恢复策略
3.中度火烧区恢复概况
中度火烧区人工促进天然更新 指采取人工辅助更新措施 , 使幼苗根系扎到土壤中 , 战胜草类 、灌木 , 为森林的自 身繁育创造良好环境条件的更新方式 。人促更新分手工促进和机械促进。与天然更 新相比在开始形成的杨桦林中 , 针叶林所占的比例明显提高 。
整理ppt
19
三、林火迹地的恢复策略
4.重度火烧区恢复概况
重度火烧区天然更新 乔木、灌木和草本基本死亡 , 土壤有机质几乎全部烧掉, 上层林木消失 , 郁闭度降低 ,首先侵入旱生和固氮的草本植被,后喜阴地被物增多。在火前有杨桦的林地上定 量的杨桦等萌生枝条,后形成杨桦为主的阔叶林。最终环境趋向原貌稳定 。
整理ppt
27
四、林火迹地恢复案例
3.火烧区恢复现状
“2016年完成中幼林抚育32万亩,完成计划的100%;完成补植补造生产任务3.5万亩 ,人工造林9000亩。”
——摘自大兴安岭日报/2017年/5月/14日 《扩大森林生态效益 保住职工“金饭碗”十八站林业局筑牢林区生态屏障》
大兴安岭——十八站全景航拍视频(时间:2017年)
整理ppt
12
二、火干扰对森林的影响
2.森林火灾发生的原因及影响
2.2 森林火灾产生的影响
森林火灾带来的危害:
烧毁林木
烧毁林下植物资源
危害野生动物
引起水土流失
引起空气污染
威胁人民生命财产安全
整理ppt
森林有益火的作用: 烧除减少林地可燃物 控制病虫、鼠害 促进森林天然更新 促进灌木生长 改善野生动物栖息环境
2.森林火灾发生的原因及影响
2.1 森林火灾的发生条件
岭回归解决多重共线性

一、引言回归分析是一种比较成熟的预测模型,也是在预测过程中使用较多的模型,在自然科学管理科学和社会经济中有着非常广泛的应用,但是经典的最小二乘估计,必需满足一些假设条件,多重共线性就是其中的一种。
实际上,解释变量间完全不相关的情形是非常少见的,大多数变量都在某种程度上存在着一定的共线性,而存在着共线性会给模型带来许多不确定性的结果。
二、认识多重共线性(一)多重共线性的定义设回归模型01122p p y x x x ββββε=+++⋯++如果矩阵X 的列向量存在一组不全为零的数012,,p k k k k ⋯使得011220i i p i p k k x k x k x +++⋯+=, i =1,2,…n ,则称其存在完全共线性,如果022110≈+⋯+++p i p i i x k x k x k k , i =1,2,…n ,则称其存在近似的多重共线性。
(二)多重共线性的后果 1.理论后果对于多元线性回归来讲,大多数学者都关注其估计精度不高,但是多重共线性不可能完全消除,而是要用一定的方法来减少变量之间的相关程度。
多重共线性其实是由样本容量太小所造成的后果,在理论上称作“微数缺测性”,所以当样本容量n 很小的时候,多重共线性才是非常严重的。
多重共线性的理论后果有以下几点: (1)保持OLS 估计量的BLUE 性质;(2) 戈德伯格提出了近似多重共线性其实是样本观测数刚好超过待估参数个数时出现的情况。
所以多重共线性并不是简单的自变量之间存在的相关性,也包括样本容量的大小问题。
(3)近似的多重共线性中,OLS 估计仍然是无偏估计。
无偏性是一种多维样本或重复抽样的性质;如果X 变量的取值固定情况下,反复对样本进行取样,并对每个样本计算OLS 估计量,随着样本个数的增加,估计量的样本值的均值将收敛于真实值。
(4)多重共线性是由于样本引起的。
即使总体中每一个X 之间都没有线性关系,但在具体取样时仍存在样本间的共线性。
第7章岭回归分析

第7章岭回归分析岭回归分析是一种用于解决多重共线性问题的回归方法。
在多重共线性问题中,自变量之间存在高度相关性,这会导致传统的最小二乘法线性回归产生不稳定的估计结果。
岭回归通过对系数进行约束,来减小估计值的方差,从而提高回归模型的稳定性。
本章将介绍岭回归的原理、步骤和应用。
一、岭回归的原理岭回归是对普通最小二乘法进行修正的一种方法。
其基本思想是通过对最小二乘法中的残差平方和添加一个惩罚项来控制系数的大小,从而减小方差。
岭回归的目标是找到一个最优的系数向量,使得残差平方和和正则化项的加权和最小化。
在岭回归中,通过引入一个正则化参数λ(也称为岭参数),目标函数变为最小二乘法的残差平方和加上λ乘以系数向量的平方和。
正则项的引入使得系数向量的估计值在其中一种程度上受到限制,使回归模型更加稳定。
通过调整正则化参数λ的值,可以控制估计值的偏差和方差之间的权衡。
二、岭回归的步骤岭回归的步骤如下:1.数据准备:将数据集划分为自变量矩阵X和因变量向量y。
2.数据标准化:对X和y进行标准化,使得均值为0,方差为1、这一步骤是为了使得不同变量之间的尺度一致。
3.构建岭回归模型:通过求解最小二乘法,得到系数估计值。
岭回归的系数估计值计算公式为:β^=(X^T*X+λI)^(-1)*X^T*y。
其中,X^T为X的转置矩阵,I为单位矩阵,λ为正则化参数。
4.选择合适的λ:通过交叉验证等方法,选择合适的正则化参数λ。
5.模型评估:使用选择的正则化参数λ对模型进行评估,计算均方误差等指标。
三、岭回归的应用岭回归在实际应用中具有广泛的用途,主要包括以下几个方面:1.多重共线性问题:当自变量之间存在高度相关性时,使用岭回归可以解决多重共线性问题,减小估计值的方差,提高回归模型的稳定性。
2.特征选择:岭回归通过惩罚项的引入,可以压缩系数向量,从而减小不重要的特征对模型的影响,实现特征的选择。
3.数据挖掘:岭回归可以用于数据挖掘任务,如预测、分类等。
岭回归系数

岭回归系数摘要:1.岭回归系数的定义与含义2.岭回归系数的作用与应用3.岭回归系数的计算方法与实例4.岭回归系数在实际问题中的应用5.岭回归系数的发展前景与挑战正文:岭回归系数是一种在统计学和数据分析领域中经常使用的概念,它主要用于岭回归模型的计算和分析。
岭回归模型是一种解决多重共线性问题的方法,它能够通过引入惩罚项来降低回归系数的大小,从而提高模型的稳定性和预测能力。
在这个过程中,岭回归系数扮演着至关重要的角色。
岭回归系数的作用与应用主要体现在以下几个方面:首先,岭回归系数可以用来衡量自变量与因变量之间的相关程度。
在回归分析中,回归系数表示自变量对因变量的影响程度,而岭回归系数则表示在考虑了多重共线性问题的情况下,自变量对因变量的影响程度。
其次,岭回归系数可以用来优化模型的预测效果。
在实际应用中,由于数据之间可能存在较高的相关性,这会导致模型的预测效果受到较大影响。
而岭回归系数可以通过降低相关性较强的自变量的权重,从而提高模型的预测能力。
再次,岭回归系数可以用来检验模型的可靠性。
在岭回归模型中,回归系数的大小受到惩罚项的影响,因此,我们可以通过观察岭回归系数的大小来判断惩罚项是否起到了预期的效果,从而检验模型的可靠性。
最后,虽然岭回归系数在实际问题中的应用已经非常广泛,但是,由于岭回归系数的计算方法较为复杂,需要借助于特殊的算法和工具,因此,对于研究者来说,如何快速准确地计算岭回归系数仍然是一个挑战。
同时,随着数据量的增加和数据分析需求的提高,如何更好地应用岭回归系数来解决实际问题,也是研究者们需要关注的问题。
总的来说,岭回归系数是一种重要的统计学概念,它在解决多重共线性问题,优化模型预测效果,检验模型可靠性等方面有着广泛的应用。
岭回归分析

§7.2 岭回归估计的性质
性质 3 对任意 k>0,‖βˆ ‖≠0 ‖βˆ(k)‖<‖βˆ ‖
这里‖ ‖是向量的模,等于向量各分量的平方和。 这个性质表明βˆ(k)可看成由βˆ 进行某种向原点的压缩,
从βˆ(k)的表达式可以看到,当 k→∞时,βˆ(k)→0, 即βˆ(k)化为零向量。
§7.2 岭回归估计的性质
因此,岭估计βˆ(k)是最小二乘估计βˆ 的一个线性变换, 根据定义式βˆ(k)(XX kI)-1 Xy 知βˆ(k)也是 y
这里需要注意的是,在实际应用中,由于岭参数 k 总是要通过数据来 确定,因而 k 也依赖于y,因此从本质上说βˆ(k)并非βˆ 的线性变换,也不是 y 的线性函数。
§7.2 岭回归估计的性质
性质 2 在认为岭参数 k 是与 y 无关的常数时,βˆ(k)(XX kI)-1 Xy 是最小二乘估计βˆ 的一个线性变换,也是y
因为 βˆ(k)(XX kI)-1 Xy =(XX kI)-1 XX(XX)-1 Xy =(X X kI)-1 XXβˆ
§7.5 用岭回归选择变量
计算X′X的15个特征为: 4.5272,2.7547,2.0545,1.3487,1.2227 0.9605,0.6124, 0.4729,0.3708,0.2163 0.1665,0.1275,0.1142,0.0460,0.0049
注:以上特征根是按照原文献的计算方式,自变量观测阵未包 含代表常数项的第一列1,与用SPSS计算结果有所不同
§7.4 岭参数k的选择
§7.4 岭参数k的选择
二、方差扩大因子法
方差扩大因子 cjj度量了多重共线性的严重程度,计算岭估计 βˆ(k)的协方差阵,得
D(βˆ(k))=cov(βˆ(k),βˆ(k)) =cov((X′X+kI)-1X′y,(X′X+kI)-1X′y) =(X′X+kI)-1X′cov(y,y)X(X′X+kI)-1 =σ 2(X′X+kI)-1X′X(X′X+kI)-1 =σ 2(cij(k))
回归分析法PPT课件

随着大数据时代的到来,回归分析法在各个领域的应用越来越广泛,同 时也面临着新的挑战和机遇。
02
线性回归分析
线性回归模型
线性回归模型
描述因变量与自变量之间线性关 系的数学模型。
模型形式
(Y = beta_0 + beta_1X_1 + beta_2X_2 + cdots + beta_pX_p + epsilon)
解释
非线性回归模型可以用于解释因变量和解释变量之间的关系,通过模型参数和图 形化展示来解释关系。
04
多元回归分析
多元回归模型
01
02
03
多元线性回归模型
描述因变量与多个自变量 之间的关系,通过最小二 乘法估计参数。
非线性回归模型
描述因变量与自变量之间 的非线性关系,通过变换 或使用其他方法实现。
教育研究
在教育学研究中,回归分析法可用于研究教育成果和教育 质量,通过分析学生成绩和教学质量等因素,提高教育水 平。
其他领域的应用案例
市场调研
在市场营销中,回归分析法可用于分析消费者行为和市场趋 势,帮助企业制定更有效的营销策略。
农业研究
在农业研究中,回归分析法可用于研究作物生长和产量影响 因素,提高农业生产效率。
线性回归模型的预测与解释
预测
使用已建立的线性回归模型预测因变量的值。
解释
通过解释模型参数的大小和符号来理解自变量对因变量的影响程度和方向。
03
非线性回归分析
非线性回归模型
线性回归模型的局限性
非线性回归模型的定义
线性回归模型在解释变量与因变量之间的 关系时可能不够准确,无法描述它们之间 的非线性关系。
岭回归

这里需要注意的是,在实际应用中,由于岭参数 k 总是要通过数据来 确定,因而 k 也依赖于y,因此从本质上说βˆ(k)并非βˆ 的线性变换,也不是 y 的线性函数。
在岭回归中,岭迹分析可用来了解各自变量的作用及自变量间的相互 关系。下面由图 7.2 所反映的几种有代表性的情况来说明岭迹分析的作用。
§3
岭迹 分析
§4 岭参数k的选择
一、岭迹法
岭迹法选择k值的一般原则是:
(1 (2)用最小二乘估计时符号不合理的回归系数,其岭估 计的符号变得合理; (3 (4)残差平方和增大不太多。
§1 岭回归估计的定义
我们称 βˆ(k)(XX kI)-1Xy (2)
为β的岭回归估计,其中k称为岭参数。
由于假设X已经标准化,所以X′X就是自变量样本相 关阵,(2)式计算的实际是标准化岭回归估计。
(2)式中因变量观测向量y可以经过标准化也可以 未经标准化。 显然,岭回归做为β的估计应比最小二乘估计稳定, 当k=0时的岭回归估计就是普通的最小二乘估计。
§4 岭参数k的选择
§4 岭参数k的选择
二、方差扩大因子法
方差扩大因子 cjj度量了多重共线性的严重程度,计算岭估计 βˆ(k)的协方差阵,得
D(βˆ(k))=cov(βˆ(k),βˆ(k)) =cov((X′X+kI)-1X′y,(X′X+kI)-1X′y) =(X′X+kI)-1X′cov(y,y)X(X′X+kI)-1 =σ 2(X′X+kI)-1X′X(X′X+kI)-1 =σ 2(cij(k))
岭回归

岭回归一、普通最小二乘估计带来的问题当设计矩阵X 呈病态时,X 的列向量之间有较强的线性相关性,即解释变量间出现严重的多重共线性,在这种情况下,用普通最小二乘法估计模型参数,往往参数估计的方差太大,即jj jj j L C 2)ˆvar(σβ=很大,jβˆ就很不稳定,在具体取值上与真值有较大的偏差,有时会出现与实际经济意义不符的正负号。
下面看一个例子,可以说明这一点。
假设已知1x ,2x 与y 的关系服从线性回归模型:ε+++=213210x x y ,给定1x ,2x 的10个值,如下表1,2行所示:表7.1然后用模拟的方法产生10个正态随机数,作为误差项ε,见表第3行。
然后再由回归模型i i i i x x y ε+++=213210计算出10个i y 值,见表第4行。
现在假设回归系数与误差项是未知的,用普通最小二乘法求回归系数的估计得:0ˆβ=11.292,1ˆβ=11.307,2ˆβ=-6.591,而原模型的参数0β=10,1β=2,2β=3看来相差太大。
计算1x ,2x 的样本相关系数得12r =0.986,表明1x 与2x 之间高度相关。
通过这个例子可以看到解释变量之间高度相关时,普通最小二乘估计明显变坏。
二、岭回归的定义当自变量间存在多重共线性,|X X '|≈0时,设想给X X '加上一个正常数矩阵kI (k>0)那么X X '+kI 接近奇异的程度就会比X X '接近奇异的程度小得多。
考虑到变量的量纲问题,先要对数据标准化,标准化后的设计矩阵仍用X 表示,定义y X kI X X k '+'=-1)()(ˆβ称为β的岭回归估计,其中,k 称为岭参数。
由于假设X 已经标准化,所以X X '就是自变量样本相关阵。
y 可以标准化也可以未标准化,如果y 也经过标准化,那么计算的实际是标准化岭回归估计。
)(ˆk β作为β的估计应比最小二乘估计βˆ稳定,当k=0时的岭回归估计)0(ˆβ就是普通的最小二乘估计。
6、岭回归
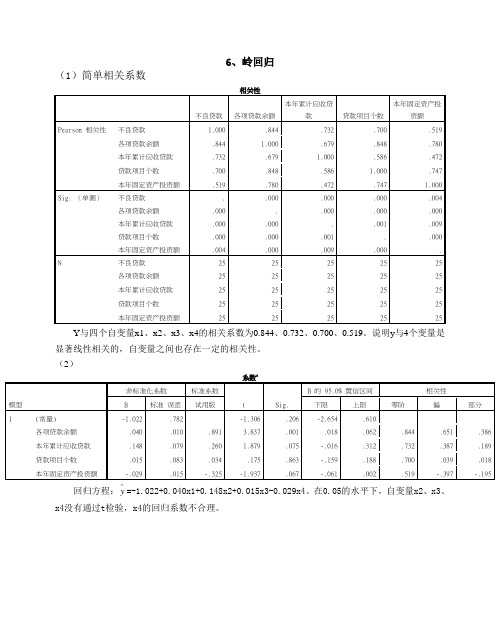
6、岭回归(1)简单相关系数相关性不良贷款各项贷款余额本年累计应收贷款贷款项目个数本年固定资产投资额Pearson 相关性不良贷款 1.000 .844 .732 .700 .519 各项贷款余额.844 1.000 .679 .848 .780本年累计应收贷款.732 .679 1.000 .586 .472贷款项目个数.700 .848 .586 1.000 .747本年固定资产投资额.519 .780 .472 .747 1.000 Sig. (单侧)不良贷款. .000 .000 .000 .004 各项贷款余额.000 . .000 .000 .000本年累计应收贷款.000 .000 . .001 .009贷款项目个数.000 .000 .001 . .000本年固定资产投资额.004 .000 .009 .000 . N 不良贷款25 25 25 25 25 各项贷款余额25 25 25 25 25本年累计应收贷款25 25 25 25 25贷款项目个数25 25 25 25 25本年固定资产投资额25 25 25 25 25 Y与四个自变量x1、x2、x3、x4的相关系数为0.844、0.732、0.700、0.519。
说明y与4个变量是显著线性相关的,自变量之间也存在一定的相关性。
(2)系数a模型非标准化系数标准系数t Sig.B 的 95.0% 置信区间相关性B 标准误差试用版下限上限零阶偏部分1 (常量) -1.022 .782 -1.306 .206 -2.654 .610各项贷款余额.040 .010 .891 3.837 .001 .018 .062 .844 .651 .386 本年累计应收贷款.148 .079 .260 1.879 .075 -.016 .312 .732 .387 .189 贷款项目个数.015 .083 .034 .175 .863 -.159 .188 .700 .039 .018 本年固定资产投资额-.029 .015 -.325 -1.937 .067 -.061 .002 .519 -.397 -.195回归方程:y=-1.022+0.040x1+0.148x2+0.015x3-0.029x4。
第七章 岭回归分析

MSE[
(k
)]
MSE
(
ˆ
)
即
p
E[ j (k) j ]2
p
D(ˆ j )
j 1
j 1
§3 岭迹分析
当岭参数 k 在 (0, ) 内变化时,ˆ j (k)是k 的函数, 在平面坐标系上把函数 ˆ j (k) 描画出来,画出的曲线称
为岭迹。由于尚未找到一种公认的最优选择 k 的方法, 所以在实际应用中,可以根据岭迹曲线的变化形状来确 定适当的 k 值和进行自变量的选择。
用最小二乘法求出回归参数的估计值为
ˆ0 11.292, ˆ1 11.307, ˆ2 6.591,
而原模型的参数为
0 10, 1 2, 3 3,显然相差很大;
计算 X1, X 2 的样本相关系数为 r12 0.986, 表明X1, X 2 之间高度相关.
岭回归的定义
当自变量间存在多重共线性, X X 0 时,设想给 X X 加上一个 正常数矩阵 kI (其中k 0) ,则 X X kI 接近奇异的程度就会比 X X
中 k=0.5 时,岭迹已算平稳,这时 ˆ1(0.5) 2.06已相当接近真值2 , 但此时 ˆ2 (0.5)=1.49与真值3还相差很大 。
岭迹法的缺点是:缺少严格的理论依据; 岭迹法的优点是:发挥了定性分析和定量
分析的有机结合.
方差扩大因子法
记 R 2 j 为自变量 x j 对其余 p 1 个自变量作回 归拟合的复决定系数。这里 R2 j 度量了 x j 与其余 p 1 个变量的线性相关程度。可以证明:
岭迹法
选择k值的一般原则是: 各回归系数的岭估计基本稳定; 用最小二乘估计时符号不合理的回归系数,
其岭估计的符号变得合理; 回归系数没有不合乎经济意义的绝对值; 残差平方和增大不太多.
何晓群:《应用回归分析》第四版-第七章岭回归

然后用模拟的方法产生10个正态随机数,作为误差项1, 2 , ,10 .
见表7.1的第(3)行.
返 回 前一页 后一页
假设已知 x1, x2 与 y 的关系服从线性回归模型
y 10 2x1 3x2
返 回 前一页 后一页
例7.1 我们作回归拟合时,总是希望拟合的经验回归方程与真 实的理论回归方程能够很接近。基于这个想法,这里举一个模 拟的例子。
假设 x1, x2 与 y 的关系服从线性回归模型
y 10 2x1 3x2
(7.1)
给定 x1, x2 的10个值,如表7.1的第(1)(2)行
返 回 前一页 后一页
(4) 在图7.2(d)中, ˆ1(k) 和 ˆ2 (k )都
. 这种情况往往发生在
,但 却 很大的场合, 即
在x1和x2之间存在
的解释某些回归系
数估计的符号不合理的情形, 从实际观点看, ˆ1(k) 和ˆ2 (k ) 不应
有相反符号. 岭回归分析的结果对这一点提供了一种解释.
ˆi (k )
(d)
ˆ1 (k )
O k
ˆ2 (k )
返 回 前一页 后一页
(5) 从全局看,
可用来估计在
, 把所有回归系数的岭迹都描在一张图上, 如果这
些岭迹线的“
”很大, 整个系统呈现比较“乱”的局
面。往往就使人怀疑最小二乘估计是否很好地反映了真实情况,
我们称
ˆ (k) ( X ' X kI )1 X ' y
(7.1)
为回归参数 的岭回归估计. 其中 k 称为岭参数.
回归讲稿_8_12年

第8章 主成分回归与 偏最小二乘
编著: 何晓群 刘文卿 授课: 王振羽
1
§8.1 主成分回归
1
主成分回归 ( princippal components regression, PCR)是对普通最 小二乘估计的一种改进,它的参数估计是一种有偏估计。马西 (W. F. Massy) 于 1965 年根据多元统计分析中的主成分分析提出了主成分回 归,本节首先介绍有关主成分分析的基本思想和性质,然后用实例介 绍主成分回归的应用。
Yp = ap1 X1 + ap2 X2 + ... + app Xp
由于可以任意地对原始变量进行上述线性变换,得到的综合变量 Y 的统计特性也不尽相同。因此,为了取得较好的效果,我们总是希 望 Yi = ai' X 的方差尽可能大,且各 Yi 之间相互独立。
3
§8.1 主成分回归
一、主成分的基本思想
3
3
由于
var(Yi ) = var( ai' X ) = ai' ai
而对于任意常数 c,有
var( cai' X ) = cai' aic = c2ai' ai
因此,对 ai 不加任何时,可使 var(Yi ) 任意增大,问题将变得没能有意义。 我们将线性变换 约束在下面的原则之下: 1. ai'ai = 1, 即 ai12 + ai22 + ... + aip2 = 1 ( i = 1, 2, ..., p ) 2. Yi 与 Yj 不相关 ( i j, i, j = 1, 2, ..., p ) 3. Y1 是 X1, X2, ..., Xp 的所有满足原则 1的线性组合中方差最大者; Y2 是与 Y1 不相关的 X1, X2, ..., Xp 的所有线性组合中方差最大者; .....; Yp 是与 Y1, Y2, ..., Yp–1 不相关的 X1, X2, ..., Xp 的所有线性组合中方差最大者。 基于以上三条原则决定的综合变量Y1, Y2, ..., Yp分别称为第一、第二、 ……、第 p 个主成分。其中,各综合变量在总方差中的比重依次递减。在实 际研究工作中,通常只挑选前几个方差最大的主成分,从而达到简化系统结 构、抓住主要问题实质的目的。
spssau共线性处理方法之岭回归(ridge-regression)

岭回归分析在进行线性回归分析时,很容易出现自变量共线性问题,通常情况下VIF值大于10说明严重共线,VIF大于5则说明有共线性问题。
当出现共线性问题时,可能导致回归系数的符号与实际情况完全相反,本应该显著的自变量不显著,本不显著的自变量却呈现出显著性;共线性问题会导致数据研究出来严重偏差甚至完全相反的结论,因而需要解决此问题。
针对共线性问题的解决方案上,可以考虑使用逐步回归进行分析,直接移除出共线性的自变量X,但此类做法导致自己希望研究的变量无法得到研究。
此时,可以考虑使用更科学的研究方法即岭回归(Ridge regression)。
岭回归是一种改良的最小二乘法,其通过放弃最小二乘法的无偏性,以损失部分信息为代价来寻找效果稍差但回归系数更符合实际情况的模型方程。
针对共线性的病态数据,岭回归的耐受性远强于普通线性最小二乘法回归。
岭回归分析(Ridge Regression)用于解决线性回归分析中自变量共线性的研究算法。
岭回归通过引入k个单位阵,使得回归系数可估计;单位阵引入会导致信息丢失,但同时可换来回归模型的合理估计。
针对岭回归:其研究步骤共为2步,分别是结合岭迹图寻找最佳K值;输入K值进行回归建模。
第一步:岭回归分析前需要结合岭迹图确认K值;K值的选择原则是各个自变量的标准化回归系数趋于稳定时的最小K值。
K值越小则偏差越小,K值为0时则为普通线性OLS回归;SPSSAU提供K值智能建议,也可通过主观识别判断选择K值第二步:对于K值,其越小越好,通常建议小于1;确定好K值后,即可主动输入K 值,得出岭回归模型估计。
SPSSAU操作截图如下:如果输入框中不输入值,此时SPSSAU默认是生成岭迹图,即识别最佳K值(当然SPSSAU 会智能化建议最佳K值);如果输入K值,此时SPSSAU则输出岭回归模型结果。
岭回归分析案例Contents1背景 (3)2理论 (3)3操作 (4)4 SPSSAU输出结果 (5)5文字分析 (6)6剖析 (6)1 背景现测得胎儿身高、头围、体重和胎儿受精周龄数据,希望建立胎儿身高、头围、体重去和胎儿受精周龄间的回归模型。
6、岭回归

6、岭回归(1)简单相关系数相关性不良贷款各项贷款余额本年累计应收贷款贷款项目个数本年固定资产投资额Pearson 相关性不良贷款 1.000 .844 .732 .700 .519 各项贷款余额.844 1.000 .679 .848 .780本年累计应收贷款.732 .679 1.000 .586 .472贷款项目个数.700 .848 .586 1.000 .747本年固定资产投资额.519 .780 .472 .747 1.000 Sig. (单侧)不良贷款. .000 .000 .000 .004 各项贷款余额.000 . .000 .000 .000本年累计应收贷款.000 .000 . .001 .009贷款项目个数.000 .000 .001 . .000本年固定资产投资额.004 .000 .009 .000 . N 不良贷款25 25 25 25 25 各项贷款余额25 25 25 25 25本年累计应收贷款25 25 25 25 25贷款项目个数25 25 25 25 25本年固定资产投资额25 25 25 25 25 Y与四个自变量x1、x2、x3、x4的相关系数为0.844、0.732、0.700、0.519。
说明y与4个变量是显著线性相关的,自变量之间也存在一定的相关性。
(2)系数a模型非标准化系数标准系数t Sig.B 的 95.0% 置信区间相关性B 标准误差试用版下限上限零阶偏部分1 (常量) -1.022 .782 -1.306 .206 -2.654 .610各项贷款余额.040 .010 .891 3.837 .001 .018 .062 .844 .651 .386 本年累计应收贷款.148 .079 .260 1.879 .075 -.016 .312 .732 .387 .189 贷款项目个数.015 .083 .034 .175 .863 -.159 .188 .700 .039 .018 本年固定资产投资额-.029 .015 -.325 -1.937 .067 -.061 .002 .519 -.397 -.195回归方程:y=-1.022+0.040x1+0.148x2+0.015x3-0.029x4。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
二、方差扩大因子法
选择k使得矩阵c(k ) ( X ' X kI ) 1 ( X ' X kI ) 主对角线元素c jj (k ) 10 ˆ(k)的协方差阵为 由于岭估计 ˆ(k) ˆ(k) ˆ(k) D( ) cov( , ) cov((X ' X kI ) 1 x' y, ( X ' X kI ) 1 X ' y ) ( X ' X kI ) 1 cov(y, y )( X ' X kI ) 1 2 ( X ' X kI ) 1 X ' X ( X ' X kI ) 1 2 c(k )
一、INCLUDE'C:\Program Files\SPSS\Ridge regression.sps'.
RIDGEREG DEP=y/ENTER X1 X2 X3 X4 X5. INCLUDE'C:\Program Files\SPSS\Ridge regression.sps'. RIDGEREG DEP=y/ENTER X1 X2 X3 X4 X5 /start=0.0/stop=0.2/inc=0.02. INCLUDE'C:\Program Files\SPSS\Ridge regression.sps'. RIDGEREG DEP=y/ENTER X2 X3 X4 X5 /k=0.08.
P193 图A,系数趋于0,变量不重要 图B.系数由正变负,变化大,对Y有显著影响 图C. 古典模型时系数为正,岭回归时系数为负. 图D. 两个系数不稳定,一个增大时另一个减少, 但其和稳定,可以考虑保留一个变量. 图E. 变量对Y不显著 图F. 变量对Y的影响趋于稳定
岭参数k的选择
一、岭迹法 1、各回归系数基本稳定 2、用最小二乘法时不合理的系数用岭 回归变得合理 3、残差平方和增长不大
第七章 岭回归
主要内容
一、岭回归的引入 二、岭回归参数K的选取,参数粗估计, 参数精估计,确定参数模型 三、岭回归的SPSS程序 四、岭回归模型的应用
一、岭回归的引入
由于解释变量之间的多重共线性,当用普通最小二 乘法时,模型中参数估计的方差较大,使得普通最小二 乘估计的效果不理想.为解决这一问题,统计学家从模 型和数据的角度考虑,采用回归诊断和自变量选择来 克服多重共线性的影响,同时对普通最小二乘法进行 改进,提出了岭回归. 1962年,A.E.Hoerl 首先提出一种改进普通最小二 乘估计的方法,岭回归(Ridge Estimate).
例3.3民航客运量回归模型
year 1987 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 1991 1992 1993
Y 231.00 298.00 343.00 401.00 445.00 391.00 554.00 744.00 997.00 1310.00 1442.00 1283.00 1660.00 2178.00 2886.00 3383.00
j1
ˆ (k ) ] D( ˆ ) E[ j j j
2 j1
p
p
岭回归分析
一、岭迹分析 岭迹 模型系数随参数K变化的曲线 岭迹分析的目的 k的确定与自变量的选择
岭迹图
根据岭迹曲线的变化形状来确定适当的 k值和进行自变量的选择。
X5 180.92 420.39 570.25 776.71 792.43 947.70 1285.22 1783.30 2281.49 2690.23 3169.48 2450.14 2746.20 3335.65 3311.50 4152.70
建立回归模型,共线性诊断 1、VIF,容忍度,条件数, 2、变量X2的系数为负值,经济理论认 为应为正相关。说明共线性造成后果。 解决方案 剔除变量法、主成分回归、岭回归
7.2 岭回归估计的性质 ˆ (k )是回归参数的有偏估计。 性质1
性质2 性质3
ˆ (k ) 在认为岭参数 k与y无关的常数时, ˆ的一个线性变换。 是最小二乘估计 对任意的k 0, 0, 总有 ˆ (k ) ˆ
性质4 使
以MSE表示估计向量的均方误 差,则存在k 0,
X3 81491.00 86389.00 92204.00 95300.00 99922.00 106044.0 110353.0 112110.0 108579.0 112429.0 122645.0 113807.0 95712.00 95081.00 99693.00 105458.0
X4 14.89 16.00 19.53 21.82 23.27 22.91 26.02 27.72 32.43 38.91 37.38 47.19 50.68 55.91 83.66 96.08
X1 3010.00 3350.00 3688.00 3941.00 4258.00 4736.00 5652.00 7020.00 7859.00 9313.00 11738.00 13176.00 14384.00 16557.00 20223.00 24882.00
X2 1888.00 2195.00 2531.00 2799.00 3054.00 3358.00 3905.00 4879.00 5552.00 6386.00 8038.00 9005.00 9663.00 10969.00 12985.00 15949.00
回归系数的有偏估计—岭回归
当 X X 0时,X X kI , k 0接近奇异的程度就小, 首先对数据作标准化, 仍记标准化后的设计矩 阵 为X .定义参数的估计 ˆ (k ) ( X X KI ) 1 X y 称为参数的岭回归估计 。
回归系数的有偏估计—岭回归
K称为岭参数 K=0时为最小二乘估计,0<K<1,选择 一个最合适的K值。 岭回归用于解决模型的自变量共线性问 题。
三、残差平方和法
给定大于1的数c,要求 SSE(k)<cSSE 找使上式成立的最大k值。
岭回归选择变量
ห้องสมุดไป่ตู้
选择变量的标准 1.在岭回归计算中,剔除掉标准化岭回归系 数比较稳定且绝对值很小的自变量。 2. 当k值较小时,标准化岭回归系数并不小, 但不稳定,随k值的增加迅速趋于零.像这样 岭回归系数不稳定、振动趋于零的自变量予 以剔除。 3. 去掉岭回归系数很不稳定的变量。
