2020.06人大附附中考前热身练习
中国人民大学附属中学高三考前热身练习文综地理试题+Word版含答案

中国人民大学附属中学2018届高三考前热身练习文综地理试题注意事项:1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
答题前,考生务必将自己的姓名、考生号填写在答题卡上。
2. 回答第Ⅰ卷时,选出每小题的答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其他答案标号。
写在试卷上无效。
3. 回答第Ⅱ卷时,将答案填写在答题卡上,写在试卷上无效。
4. 考试结束,将本试卷和答题卡一并交回。
第Ⅰ卷本卷共35小题。
每小题4分,共140分。
在每个小题给出的四个选项中,只有一项是符合题目要求的。
天坑是指白于水不断侵蚀固体基岩,使地表发生塌陷形成的一个巨大的深坑。
一队天坑科考人员将于2018年芒种时节从汉中天坑群出发,开始为时一个月世界天抗群的考察。
图1是世界主要的天坑群的分布图,读图1回答第1-3题。
1.图中天坑群所在国家A。
位于低纬、热带地区B。
都处于板块消亡边界C。
沿岸大多有暧流流经D。
人口增长模式都相同2.天坑的形成过程A.②③④⑤①B.①②③④⑤C.⑤④③②①D.⑤①②③④3.考察期间A。
克罗地亚的正午太阳高度逐渐变大B。
中国飞往丞西哥的航向是先东北再东南C。
马来西亚昼长夜短且昼长逐渐加长D。
所到地区都处于雨季,应重点防范滑坡树干液流是植物体内的水分通过植物木质部从根部运输到叶片的过程。
图3为我国某地樟树在同一月份内三种不同天气条件下的液流速率和液流量变化图。
据此回答第4题。
4.依图3中信息推测一年中樟树的液流量和液流速率最大的时期出现在A.春季B.夏季 C。
秋季 D。
冬季据资料表明,热带中东太平洋地区的偏冷海水已基本消失,开始了拉尼娜向厄尔尼诺转换的时期,据50多年我国的气象数据表明,在8个华北春夏极端连早年份中,有7个发生在拉尼娜向卮尔尼诺转换的年份里。
读图4回答第5、6题。
5.当华北出现春夏连旱时A。
大气环流异常,导致①②风力减小B。
⑤运动增强,使副高强度逐渐增大C.③对赤道太平洋东岸地区影响渐弱D.④⑤运动方向形成,强度逐渐变弱6.厄尔尼诺发生时A。
中国人民大学附属中学2020届高三6月高考热身统一练习(三模)英语试题及答案

绝密★启用前中国人民大学附属中学2020届高三毕业班高考考前热身统一练习(三模)英语试题2020年6月28日本试卷共10页。
满分120分。
考试时间100分钟。
将答案填涂、书写在答题纸上、在试卷上作答无效。
第一部分:知识运用(共两节,45分)第一节语法填空(共10小题;每小题1.5分,共15分)阅读下列短文,根据短文内容填空,在未给提示词的空白处仅填写1个适当的单词,在给出提示词的空白处用括号内所给词的正确形式填空。
AA video went viral online that showed a man saving a 2-year-old girl who was stuck in the burglar bars of her apartment in Nanning.On Sunday, the toddler, who was home alone, climbed to the balcony of her home on the fifth floor and became1 (trap) in the burglar bars. Xu Hongwei, a former member of the armed police, climbed up the building's balconies2 (reach) the girl and held her up with hands to keep her from falling for nearly half an hour. He3 (comfort) her by saying, "I am with you. Come on, climb down the balcony." The girl was finally saved4 the help of other neighbors.BMany colleges and universities support gap —year projects by permitting students to delay their admission. Experts say students can grow emotionally and intellectually 5 they work at something they enjoy. The Harvard admissions office has an essay on its web site called "Time Out or Burn Out for the Next Generation."6_ praises the idea of taking time off to step back, think and enjoy gaining life experiences outside the pressure of studies. It also notes that students sometimes 7 (admit) to Harvard or other colleges in part because they did something unusual with that time.C1Our school produces a lot of rubbish every day, such as leftover food, waste paper and plastic bottles, _8 brings a wide range of environmental problems as well as the waste of resources. Therefore, it's time we took immediate action to change the situation.First of all, it is necessary for us to raise 9 (aware) of environmental protection and develop the good habit of garbage sorting. What's more, we should voluntarily differentiate recyclable rubbish from non-recyclables in our daily life.In a word, if everyone does his bit responsibly in garbage sorting, our school 10 (become) better and better.第二节完形填空〔共20小题;每小题1.5分,共30分)阅读下面短文,掌握其大意,从每题所给的A、B、C、D四个选项中,选出最佳选项,并在答题卡上将该项涂黑。
北京市人大附中2020届高三(6月份)高考数学考前热身试题
北京市人大附中2020届高三(6月份)高考数学考前热身试题学校:___________姓名:___________班级:___________考号:___________一、单选题1.已知集合{}|20A x N x =∈-≤,{}|2B x Z x =∈<,则AB =( ) A .{}1B .1,0,1,2C .{}0,1D .()2,2- 2.复数11i z i+=-的模为( )A .1B .2CD 3.若a >0,b >0,则不等式-b <1x<a 等价于( ) A .-1b<x <0或0<x <1a B .-1a <x <1bC .x <-1a 或x >1bD .x <-1b 或x >1a 4.某几何体的主视图和左视图如图所示,则它的俯视图不可能是( )A .B .C .D .5.某公司为激励创新,计划逐年加大研发资金投入.若该公司2021年全年投入研发资金130万元,在此基础上,每年投入的研发资金比上一年增长12%,则该公司全年投入的研发资金开始超过200万元的年份是(参考数据:lg1.12≈0.05,lg1.3≈0.11,lg2≈0.30)( )A .2021年B .2021年C .2022年D .2023年 6.,a b 为非零向量,“||||a b b a =”为“,a b 共线”的() A .充分必要条件B .充分不必要条件C .必要不充分条件D .即不充分也不必要条件 7.已知函数()()2112x x f x x x a e e --+=-++(其中0a >)的最小值为1,则a =( )A .1B .13C .12D .12-8.已知函数21()cos 22x f x x ωω=+-(0)x R ω>∈,,若函数()f x 在区间(,2)ππ内没有零点,则ω的最大值是( )A .512B .56C .1112D .329.已知不过坐标原点O 的直线交抛物线22y px =于A ,B 两点,若直线OA ,AB 的斜率分别为2和6,则直线OB 的斜率为( )A .3B .2C .-2D .-310.2021年“一带一路”沿线64个国家GDP 之和约为12.0万亿美元,占全球GDP 的16.0%;人口总数约为32.1亿,占全球总人口的43.4%;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的21.7%.2021年“一带一路”沿线国家情况关于“一带一路”沿线国家2021年状况,能够从上述资料中推出的是( )A .超过六成人口集中在南亚地区B .东南亚和南亚国家GDP 之和占全球的8%以上C .平均每个南亚国家对外贸易额超过1000亿美元D .平均每个东欧国家的进口额高于平均每个西亚、北非国家的进口额二、填空题11.在()52x -的展开式中,3x 项的系数是__________(用数字作答).12.锐角三角形ABC 中,若2C B ∠=∠,则的范围是 ; 13.已知非零向量m →,n →满足4m →=3n →,cos m →〈,13n →〉=.若n →⊥t m n →→⎛⎫+ ⎪⎝⎭,则实数t 的值为_____________.三、双空题14.双曲线1C :22195x y -=的离心率为______,双曲线2C 与双曲线1C 有共同的渐近线,且2C 过点()3,5M ,则双曲线2C 的方程为______.15.已知函数()2ln ,021,0x x f x x x x ⎧>⎪=⎨+-≤⎪⎩. (1)()f x 的零点是______;(2)若()f x 的图象与直线1y ax =-有且只有三个公共点,则实数a 的取值范围是______.四、解答题16.设函数()sin()sin()62f x x x ππωω=-+-,其中03ω<<.已知()06f π=. (Ⅰ)求ω;(Ⅱ)将函数()y f x =的图象上各点的横坐标伸长为原来的2倍(纵坐标不变),再将得到的图象向左平移4π个单位,得到函数()y g x =的图象,求()g x 在3[,]44ππ-上的最小值.17.为了解学生自主学习期间完成数学套卷的情况,一名教师对某班级的所有学生进行了调查,调查结果如下表.(1)从这班学生中任选一名男生,一名女生,求这两名学生完成套卷数之和为4的概率?(2)若从完成套卷数不少于4套的学生中任选4人,设选到的男学生人数为X ,求随机变量X 的分布列和数学期望;(3)试判断男学生完成套卷数的方差21s 与女学生完成套卷数的方差22s 的大小(只需写出结论).18.平行四边形ABCD 所在的平面与直角梯形ABEF 所在的平面垂直,//BE AF ,112AB BE AF ===,且AB AF ⊥,4CBA π∠=,BC =P 为DF 的中点.(1)求证://PE 平面ABCD ;(2)求证:AC EF ⊥;(3)若直线EF 上存在点H ,使得CF ,BH BH 与平面ADF 所成角的大小.19.已知椭圆C :()222210x y a b a b +=>>的离心率为2,过C 的左焦点做x 轴的垂线交椭圆于P 、Q 两点,且1PQ =.(1)求椭圆C 的标准方程及长轴长;(2)椭圆C 的短轴的上下端点分别为A ,B ,点1,2M m ⎛⎫ ⎪⎝⎭,满足0m ≠,且m ≠若直线AM ,BM 分别与椭圆C 交于E ,F 两点,且BME ∆面积是AMF ∆面积的5倍,求m 的值.20.已知函数()1x x f x e-=. (1)求函数()f x 的单调区间;(2)若对任意[)12,,x x a ∈+∞,都有()()1221ef x f x -≥-成立,求实数a 的最小值. 21.若无穷数列{}n a 满足:1a 是正实数,当2n ≥时,1121max ,,,nn n a a a a a ,则称{}n a 是“Y ﹣数列”. (Ⅰ)若{}n a 是“Y ﹣数列”且11a =,写出4a 的所有可能值;(Ⅱ)设{}n a 是“Y ﹣数列”,证明:{}n a 是等差数列当且仅当{}n a 单调递减;{}n a 是等比数列当且仅当{}n a 单调递增;(Ⅲ)若{}n a 是“Y ﹣数列”且是周期数列(即存在正整数T ,使得对任意正整数n ,都有T n n a a +=),求集合{}112018i i a a ≤≤=的元素个数的所有可能值的个数.参考答案1.B【分析】先求解集合,A B 再求并集即可.【详解】{}{}|200,1,2A x N x =∈-≤=,{}{}|21,0,1B x Z x =∈<=-.故A B =1,0,1,2.故选:B【点睛】本题主要考查了集合的基本运算与绝对值不等式的求解.属于基础题型.2.A【分析】 根据复数的除法运算化简11i z i+=-再求模长即可. 【详解】 ()()()()111111i i i z i i i i +++===--+.模长为1. 故选:A【点睛】本题主要考查了复数的除法与模长的计算.属于基础题型.3.D【解析】试题分析:根据题意分类讨论,当0x >时,只需0{1x ax ><,所以1x a>,当0x <时,只需0{1x bx <->,所以1x b <-,因此1b a x -<<的解是1x b <-或1x a>,故选D . 考点:1、分式不等式;2、分类讨论;3、不等式的恒成立.4.D【分析】直接直观想象举出可能满足条件的几何体即可.【详解】对A,此时该几何体为圆锥,满足.对B,此时该几何体为正四棱锥.满足.对C,此时该几何体为正四棱锥的一半.满足.故选:D【点睛】本题主要考查了直观想象能力与三视图的辨析.属于基础题型.5.B【分析】由题意建立指数型函数模型y =130(1+12%)n ,然后又全年投入的研发资金开始超过200万元,由130(1+12%)n >200求解.【详解】设经过n 年资金开始超过200万元,即130(1+12%)n >200.两边取对数,得n ·lg1.12>lg2-lg1.3, ∴n >lg2lg1.3lg1.12-≈0.300.110.05-=195, ∴n ≥4,∴从2021年开始,该公司投入的研发资金开始超过200万元.故选:B【点睛】本题主要考查指数型函数模型的应用以及指数不等式的解法,属于基础题.6.B【分析】,a b 共线,,a b 方向相同或相反,共线的单位向量不一定相等,结合充分必要条件的判断,即可得出结论.【详解】 ,||||a b b a 分别表示与,a b 同方向的单位向量,||||b a =,则有,a b 共线, 而,a b 共线,则,||||a b b a 是相等向量或相反向量, “||||a b b a =”为“,a b 共线”的充分不必要条件. 故选:B.【点睛】本题考查命题充分不必要条件的判定,考查共线向量和单位向量的间的关系,属于基础题. 7.A【分析】根据题意分析当1x =时()2112,x x y x x y a ee --+=-=+分别取得最小值再求解即可.【详解】由题,因为22y x x =-在1x =时取最小值1-,又()112x x y a e e a a --+=+≥⨯=当且仅当1x =时成立.故当1x =时()()2112x x f x x x a e e --+=-++取最小值121a -+=.解得1a =. 故选:A【点睛】本题主要考查了二次函数与基本不等式求最小值的问题,属于中等题型.8.C 【分析】利用三角恒等变换化简()f x ,结合正弦函数图象,即可求解.【详解】211()cos cos sin()2226xf x x x x x ωπωωωω=+-=+=+, 令()0,(),()66k f x x k k Z x k Z πππωπωω=+=∈=-∈, 函数()f x 在区间(,2)ππ内没有零点,6(1)26k πωωπππωω-≤⎪⎪⎨+⎪-≥⎪⎩解得111()6212k k k Z ω+-≤≤-∈, 50,0,012k ωω>∴=<≤,5111,612k ω=<≤ ω的最大值是1112. 故选:C.【点睛】 本题考查三角函数恒等变换化简,以及三角函数的性质,意在考查直观想象、逻辑推理能力,属于中档题.9.D【解析】 设2,2A A y A y p ⎛⎫ ⎪⎝⎭,2,2B B y B y p ⎛⎫ ⎪⎝⎭,那么22262A B AB A B A B y y p k y y y y p-===-+ ,所以3A B p y y +=,而2222A OA A A y p k y y p=== ,故A y p =,23B y p =-,所以29B x p =,3OB k =-,选D . 10.C【分析】利用表中所给的数据对四个选项逐一判断即可.【详解】A :南亚地区人口总数为174499.0万人,“一带一路”沿线国家人口总数为:321266.1万人,所以174499.0321266.154%≈,故本选项说法不正确的; B :东南亚和南亚国家GDP 之和54948.8亿美元,“一带一路”沿线国家GDP 之和120139.6亿美元,所以54948.8120139.646%≈,所以东南亚和南亚国家GDP 之和占“一带一路”沿线国家GDP 之和的46%,因此东南亚和南亚国家GDP 之和占全球的(46%)(16%)7%⨯≈,故本选项说法是不正确的;C :南亚国家对外贸易额的平均值为:4724.13308.100085.075+=,故本选项说法是正确D :平均每个东欧国家的进口额为:488.775209775.5=,平均每个西亚、北非国家的进口额为:509.24199675.5≈,故本选项说法是不正确的. 故选:C【点睛】本题考查了根据数据对一些说法进行判断,考查了平均数的求法,考查了数学阅读能力. 11.40-【解析】()52x -的展开式的通项为:552()r r r C x --. 令3r =,得5352()40r r r C x x --=-.答案为:-40. 点睛:求二项展开式有关问题的常见类型及解题策略(1)求展开式中的特定项.可依据条件写出第r +1项,再由特定项的特点求出r 值即可.(2)已知展开式的某项,求特定项的系数.可由某项得出参数项,再由通项写出第r +1项,由特定项得出r 值,最后求出其参数.12.(【解析】试题分析:因为2C B ∠=∠,ABC ∆为锐角三角形, 所以2,3,,2264B B C B B ππππ∠∠+∠=∠∴<∠< 根据正弦定理,sin 2sin cos 2cos ,sin sin AB C B B B AC B B===根据余弦函数的图象,可知2cos B <<考点:本小题主要考查正弦定理、二倍角公式以及三角函数图象的性质和应用,考查学生的转化能力和数形结合思想的应用.点评:解决此题时,容易漏掉2B C π∠+∠>,从而产生错误结论,所以解题时一定要严谨.【分析】利用向量的数量积公式、向量垂直的性质直接直解.【详解】非零向量m →,n →满足4m →=3n →,cos m →〈,13n →〉=,n →⊥t m n →→⎛⎫+ ⎪⎝⎭, n →∴⋅22+||||cos ,||t m n t m n n t m n m n n →→→→→→→→→→⎛⎫+=⋅=<>+ ⎪⎝⎭ 223||||034t n n →→=⨯+=, 解得4t =-,故答案为:4-【点睛】本题主要考查了向量的数量积公式、向量垂直的性质等基础知识,考查运算能力,属于中档题.14 2212036y y -= 【分析】(1)根据离心率的定义与,,a b c 的关系求解即可.(2)设2C 的方程为2295x y λ-=,再代入()3,5M 求解即可. 【详解】(1)由题,双曲线229,9514a c ==+=,故离心率3c a ==. (2) 设2C 的方程为2295x y λ-=,代入()3,5M 有2235495λλ-=⇒=-. 故2C 方程222241952036x y y x -=-⇒-=.故答案为:(1). (2). 2212036y y -=本题主要考查了双曲线的基本量求法以及共渐近线的双曲线的求法等.属于基础题型.15.1和 1- ()0,2【分析】(1)分段求解零点即可.(2)数形结合画出()2ln ,021,0x x f x x x x ⎧>=⎨+-≤⎩分析其与直线1y ax =-有三个交点的情况即可.【详解】(1)由()2ln ,021,0x x f x x x x ⎧>=⎨+-≤⎩,当0x >时,ln 01x x =⇒=.当0x ≤时,令2210x x +-=有1x =--(2)画出()2ln ,021,0x x f x x x x ⎧>=⎨+-≤⎩的图象有因为1y ax =-过定点(0,−1),要使()f x 的图象与直线1y ax =-有且只有三个公共点,则0a >,当0x ≤时,2()21f x x x =+-函数的导数'()22f x x =+,函数在点(0,−1)处的切线斜率(0)2k f'==,此时直线和2()21f x x x =+-只有一个交点.当1a =时,因为当0x >时1'()f x x =,1'(1)11f ==,此时直线1y ax =-与()f x 的图象仍有三个交点.由图象知要使()f x 的图象与直线1y ax =-有且只有三个公共点,则满足02a <<,故答案为:(1). 1或1- (2). (0,2)【点睛】本题主要考查了函数零点问题的应用,同时也考查了数形结合求解直线与函数的零点个数问题,需要利用求导求斜率分析直线与曲线的相交情况,属于中等题型.16.(Ⅰ) 2ω=.(Ⅱ) 32-. 【解析】试题分析:(Ⅰ)利用两角和与差的三角函数化简得到()y f x =)3x πω=- 由题设知()06f π=及03ω<<可得.(Ⅱ)由(Ⅰ)得())3f x x π=-从而()))4312g x x x πππ=+-=-. 根据3[,]44x ππ∈-得到2[,]1233x πππ-∈-,进一步求最小值. 试题解析:(Ⅰ)因为()sin()sin()62f x x x ππωω=-+-,所以1()cos cos 2f x x x x ωωω=--3cos 22x x ωω=-13(sin )22x x ωω=-)3x πω=- 由题设知()06f π=, 所以63k ωπππ-=,k Z ∈.故62k ω=+,k Z ∈,又03ω<<,所以2ω=.(Ⅱ)由(Ⅰ)得())3f x x π=-所以()))4312g x x x πππ=+-=-. 因为3[,]44x ππ∈-, 所以2[,]1233x πππ-∈-, 当123x ππ-=-, 即4πx =-时,()g x 取得最小值32-. 【名师点睛】此类题目是三角函数问题中的典型题目,可谓相当经典.解答本题,关键在于能利用三角公式化简函数、进一步讨论函数的性质,本题易错点在于一是图象的变换与解析式的对应,二是忽视设定角的范围.难度不大,能较好的考查考生的基本运算求解能力及复杂式子的变形能力等.17.(1)796(2)详见解析(3)2212s s > 【分析】(1)根据组合的方法求解所有可能的情况与满足条件的情况数再计算概率即可.(2)X 的取值为0,1,2,3,4.再根据超几何分布的方法求分布列与数学期望即可.(3)直接根据数据观察稳定性判断21s 与22s 的大小即可.【详解】解:(1)设事件A :从这个班级的学生中随机选取一名男生,一名女生,这两名学生完成套卷数之和为4,由题意可知,()1341712896P A ⨯+⨯==⨯. (2)完成套卷数不少于4本的学生共8人,其中男学生人数为4人,故X 的取值为0,1,2,3,4.由题意可得()44481070C P X C ===; ()13444816817035C C P X C ====; ()224448361827035C C P X C ====;()31444816837035C C P X C ====; ()44481470C P X C ===. 所以随机变量X 的分布列为随机变量X 的均值116361610123427070707070EX =⨯+⨯+⨯+⨯+⨯=. (3)2212s s >.【点睛】本题主要考查了排列组合解决概率的问题与超几何分布的分布列与均值的求解.属于中等题型.18.(1)证明见解析(2)证明见解析(3)6π 【分析】(1)取AF 的中点Q 或取AD 中点M ,利用证平行四边形的方法再证明//PE 平面ABCD 即可.(2)根据勾股定理与余弦定理证明AB AC ⊥,再根据面面垂直的性质得出AC ⊥平面ABEF 即可证明AC EF ⊥.(3) 以AB 、AF 、AC 所在直线为x 、y 、z 轴建立空间直角坐标系A xyz -.设(),,0EH EF λλλ==-,再利用空间向量求解关于线面角的问题即可.【详解】(1)解法1:取AF 的中点Q ,连结PQ ,PE ,EQ ,在直角梯形ABEF 中,1AQ BE ==,//BE AQ ,所以四边形ABEQ 为平行四边形,所以//AB EQ ,在ADF ∆中PF PD =,QF QA =,所以//PQ AD ,又因为AM AB A =,所以平面//PQE 平面ABCD ,又PE ⊂平面PQE ,所以//PE 平面ABCD .解法2:取AD 中点M ,连结MP ,MB ,在ADF ∆中,PF PD =,MD MA =,所以//MP AF ,且12MP AF =, 又12BE AF =,//BE AF , 所以//MP BE ,MP BE =,所以四边形BEPM 为平行四边形,所以//PE MB ,因为PE ⊄平面ABCD ,BM ⊂平面ABCD ,所以//PE 平面ABCD .(2)在ABC ∆中1AB =,4CBA π∠=,BC =所以2222cos 1AC AB BC AB BC CBA =+-⨯⨯∠=,所以222AC AB BC +=,所以AB AC ⊥,又平面ABCD ⊥平面ABEF ,平面ABCD平面ABEF AB =,AC ⊂平面ABCD ,所以AC ⊥平面ABEF ,因为EF ⊂平面ABEF ,所以AC EF ⊥.(3)由(1)(2)以A 为原点,以AB 、AF 、AC 所在直线为x 、y 、z 轴建立空间直角坐标系A xyz -.所以()1,0,0B ,()0,0,1C ,()1,0,1D -,()1,1,0E ,()0,2,0F , 所以11,1,22P ⎛⎫- ⎪⎝⎭, 所以()0,2,1CF =-,()1,1,0EF =-,()0,1,0BE =,设(),,0EH EF λλλ==-,所以(),1,0BH BE EH λλ=+=-+,所以5BH CFBH CF⋅==, 所以()()2222111λλλ+=++,所以12λ=-, 所以11,,022BH ⎛⎫= ⎪⎝⎭, 设平面ADF 的法向量为(),,n x y z =,所以0000y n AD x z n AF ⎧=⎧⋅=⇒⎨⎨-+=⋅=⎩⎩, 所以令1x =,则()1,0,1n =,如BH 与平面ADF 成的角为θ, 所以1sin 22BH n BH n θ⋅===. 所以6πθ=,即BH 与面ADF 成的角为6π.【点睛】 本题主要考查了线面平行与线线垂直的一般方法,同时也考查了建立空间直角坐标系求解线面角的问题,需要设线段的比例关系,求解关于比例参数的解析式根据线面角大小化简求解.属于难题.19.(1)椭圆C 的标准方程为:2214x y +=,长轴长为4(2)1m =± 【分析】(1)根据通径与椭圆的基本量的关系求解即可.(2)分别设直线AM ,直线BM 的方程,联立椭圆的方程,再利用三角形的面积公式表达出BME ∆面积是AMF ∆面积的5倍,再代入韦达定理求解即可.【详解】解:(1)因为椭圆C 的左焦点横坐标为c -, 由()22221c y a b -+=及222a b c =+,得2b y a =±, 故221b a =,又c a =解得:2241a b ⎧=⎨=⎩, 所以,椭圆C 的标准方程为:2214x y +=,长轴长为4. (2)∵()0,1A ,()0,1B -,1,2M m ⎛⎫ ⎪⎝⎭,且0m ≠, ∴直线AM 的斜率为112k m =-,直线BM 斜率为232k m=, ∴直线AM 的方程为112y x m =-+,直线BM 的方程为312y x m =-, 由2214112x y y x m ⎧+=⎪⎪⎨⎪=-+⎪⎩得()22140m x mx +-=,∴0x =,241m x m =+,∴22241,11m m E m m ⎛⎫- ⎪++⎝⎭, 由2214312x y y x m ⎧+=⎪⎪⎨⎪=-⎪⎩得()229120m x mx +-=,∴0x =,2129m x m =+,∴222129,99m m F m m ⎛⎫- ⎪++⎝⎭; ∵1sin 2AMF S MA MF AMF ∆=∠, 1sin 2BME S MB ME BME ∆=∠, AMF BME ∠=∠,5AMF BME S S ∆∆=, ∴5MA MF MB ME =, 即5MA MBME MF =,又m ≠∴22541219m mm mm m m m =--++, 整理方程得:()22519m m +=+, 解得:1m =±.【点睛】本题主要考查了椭圆中基本量的运算以及直线与椭圆相交求面积的方法等.需要联立方程求解对应的面积表达式,代入韦达定理化简求得参数.属于难题. 20.(1)函数()f x 的单增区间为2,,单减区间为(),2-∞(2)a 的最小值为1【分析】(1)求导后列表分析函数单调性即可.(2)由(1)可知()f x 的最小值为()2f ,再根据恒成立问题的方法分情况分析()()12f x f x -的最小值即可. 【详解】解:(1)由()2'0xx f x e -==解得2x =, 则()'f x 及()f x 的情况如下:所以函数()f x 的单增区间为()2,+∞,单减区间为(),2-∞; (2)法一:当1x >时,()10x xf x e -=<. 当1x <时,()10x xf x e-=>.若1a ≤,由(1)可知()f x 的最小值为()2f ,()f x 的最大值为()f a , 所以“对任意[)12,,x x a ∈+∞,有()()1221ef x f x -≥-恒成立” 等价于“()()212f f a e -≥-”, 即22111a a e e e---≥-, 解得1a ≥.所以a 的最小值为1. 法二:当1x >时,()10x xf x e -=<. 当1x <时,()10x xf x e-=>.且由(1)可知,()f x 的最小值为()212f e =-, 若[)2,a ∈+∞,即2a ≤时, 令12x =,则任取[)2,x a ∈+∞, 有()()()()()122222112e f x f x f f x e f x -=-=--≥-, 所以()20f x ≤对[)2,x a ∈+∞成立,所以必有21x ≥成立,所以[)[),1,a +∞⊆+∞,即1a ≥. 而当1a =时,[)12,1,x x ∀∈+∞,()10f x ≤,()20f x ≤, 所以()()()()1212102f f x e x f x f -≥-≥=-,即1a =满足要求, 而当2a ≥时,求出的a 的值,显然大于1,综上,a 的最小值为1. 【点睛】本题主要考查了根据导数求函数的单调性与利用导数求解恒成立的有关问题,需要求导后分情况讨论函数的最值.属于中等题型.21.(Ⅰ)2,0,2,8;(Ⅱ)证明见解析;(Ⅲ)1009. 【分析】(Ⅰ)利用递推关系,根据分类讨论思想求解即可;(Ⅱ)当{}n a 是等差数列时,利用反证法可证明{}n a 单调递减,根据等比性质可证后者; (Ⅲ)先证1a 是数列{}n a 的最大项,再证明当n 是奇数时,n a 是1a 的奇数倍,当n 是偶数时,n a 是1a 的偶数倍,即可求出. 【详解】(Ⅰ)由题可知2111max a a a a ,则20a =或2,3212max ,a a a a ,∴当20a =时,30max 1,01a ,则31a =或1-, 当22a =时,32max 1,22a ,则30a =或4,43123max ,,a a a a a ,∴当31a =-时,41max 1,0,11a ,则40a =或2-,当30a =时,40max 1,2,02a ,则42a =-或2, 当31a =时,41max 1,0,11a ,则40a =或2, 当34a =时,44max 1,2,44a ,则40a =或8,综上,4a 的所有可能值为2,0,2,8; (Ⅱ)211a a a ,20a ∴=或12a ,当{}n a 是等差数列时,假设212a a =,则321123a a a a =-=, 此时321a a a -=,而{}121max ,2a a a =,矛盾,20a ∴=,于是公差2110d a a a =-=-<,{}n a ∴单调递减,当{}n a 单调递减时,对任意2n ≥,{}1211max ,,,n a a a a -=,又11n n n n a a a a ---=-,11n na a a ,{}n a ∴是等差数列;当{}n a 是等比数列时,20a ≠,212a a ∴=,∴公比21q =>,又10a >,{}n a ∴单调递增,当{}n a 单调递增时,对任意2n ≥,{}1211max ,,,n n a a a a --=,又11n n n n a a a a ---=-,11n nn a a a ,即12n n a a -=,10a ≠,{}n a ∴是等比数列,综上,{}n a 是等差数列当且仅当{}n a 单调递减;{}n a 是等比数列当且仅当{}n a 单调递增; (Ⅲ)先证1a 是数列{}n a 的最大项,事实上,如果i 是第一个大于1a 的项的脚标,则由{}112max ,,,i i i i a a a a a a +-==知,1i a +是i a 的倍数, 假设121,,,i i ik a a a 都是i a 的倍数,则由112111max ,,,max ,,,iki k ik i i ik a a a a a a a a 知,i k a +是i a 的倍数,所以由归纳法知,对任意n i ≥,n a 都是i a 的倍数,但1a 不是i a 的倍数,这与{}n a 是周期数列矛盾,所以1a 是数列{}n a 的最大项,从而当2n ≥时,11n n a a a --=,再证明当n 是奇数时,n a 是1a 的奇数倍;当n 是偶数时,n a 是1a 的偶数倍, 事实上,当1n =时结论成立,假设n k =时成立,当1n k =+时,由11k K a a a 知,结论也成立,所以,当1i a a ,i 的值只能是奇数,所以集合{}112018i i a a ≤≤=的元素个数最多有1009个;下证集合{}112018i i a a ≤≤=的元素个数可以是11009的所有整数, 事实上,对于2019i =,可取数列为:11111,0,,0,,0,,,0,a a a a 个周期即:所有的奇数项均等于1a ,所有的偶数项均等于0,此时,数列为“Y ﹣数列”,且2T =, 对于任意整数11009t ,构造数列的前2018项如下:111111111009,0,,0,,,0,,0,,0,,,0t t a a a a a a 组组共组共组,由于数列是无穷数列,故可取=2018T ,显然满足数列是“Y ﹣数列”, 综上,集合{}112018i i a a ≤≤=的元素个数的所有可能值的个数是1009. 【点睛】本题考查递推关系的综合应用以及反证法证明,属于难题.。
北京市人大附中高考数学前热身练习题 文理 北师大版
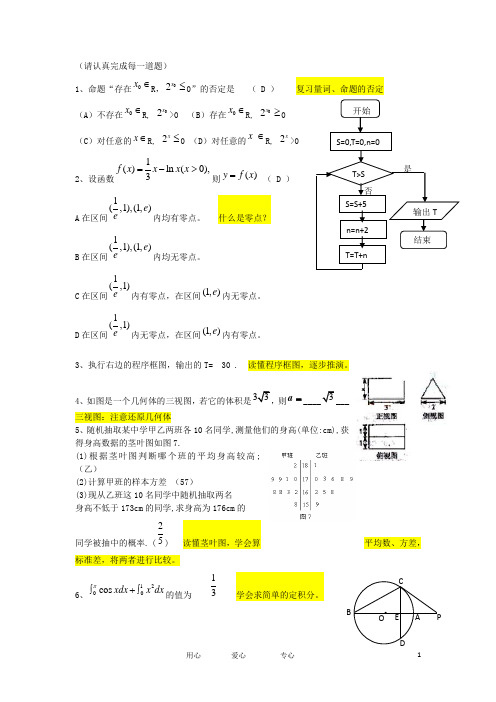
(请认真完成每一道题) 1、命题“存在0x ∈R ,02x ≤0”的否定是 ( D ) 复习量词、命题的否定(A )不存在0x ∈R, 02x >0 (B )存在0x ∈R, 02x ≥0(C )对任意的x ∈R, 2x ≤0 (D )对任意的x ∈R, 2x >02、设函数1()ln (0),3f x x x x =->则()y f x = ( D ) A 在区间1(,1),(1,)e e 内均有零点。
什么是零点? B 在区间1(,1),(1,)e e 内均无零点。
C 在区间1(,1)e 内有零点,在区间(1,)e 内无零点。
D 在区间1(,1)e 内无零点,在区间(1,)e 内有零点。
3、执行右边的程序框图,输出的T= 30 . 读懂程序框图,逐步推演。
4、如图是一个几何体的三视图,若它的体积是33,则=a ____3___ 三视图:注意还原几何体5、随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.(1)根据茎叶图判断哪个班的平均身高较高; (乙)(2)计算甲班的样本方差 (57)(3)现从乙班这10名同学中随机抽取两名 身高不低于173cm 的同学,求身高为176cm 的同学被抽中的概率. (25) 读懂茎叶图,学会算平均数、方差,标准差,将两者进行比较。
6、1200cos xdx x dx π⎰+⎰的值为 13 学会求简单的定积分。
开始S=0,T=0,n=0T>S S=S+5 n=n+2T=T+n输出T 结束是否 · PCBA DEO7、点P (1,0)到曲线⎩⎨⎧==ty t x 22(其中参数t ∈R )上的点的最短距离为 1 参数方程与极坐标相关知识请读教材与笔记8、极坐标方程2cos ρθ=化成直角坐标方__2220x y x +-=_________.9、 如图,PC 切O 于点C ,割线PAB 经过圆心O ,弦CD AB ⊥于点E ,已知O 的半径为3,2PA =,则PC =__4__,OE =___95__. 几何证明:相似、圆的简单问题10、某单位为了了解用电量y (度)与气温x (°C )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:由表中数据得线性回归方程ˆy bx a =+中2b =-,预测当气温为4C -︒时,用电量的度数约为 .68 注意:线性回归方程(读教材)。
2020届北京市人大附中高三(6月份)高考数学考前热身试题(解析版)

A.1B. C. D.
【答案】A
【解析】根据题意分析当 时 分别取得最小值再求解即可.
【详解】
由题,因为 在 时取最小值 ,
又 当且仅当 时成立.
故当 时 取最小值 .解得 .
故选:A
【点睛】
本题主要考查了二次函数与基本不等式求最小值的问题,属于中等题型.
D.平均每个东欧国家的进口额高于平均每个西亚、北非国家的进口额
【答案】C
【解析】利用表中所给的数据区人口总数为174499.0万人,“一带一路”沿线国家人口总数为:321266.1万人,所以 ,故本选项说法不正确的;
B:东南亚和南亚国家GDP之和54948.8亿美元,“一带一路”沿线国家GDP之和120139.6亿美元,所以 ,所以东南亚和南亚国家GDP之和占“一带一路”沿线国家GDP之和的 ,因此东南亚和南亚国家GDP之和占全球的 ,故本选项说法是不正确的;
9.已知不过坐标原点 的直线交抛物线 于 , 两点,若直线 , 的斜率分别为2和6,则直线 的斜率为( )
A.3B.2C.-2D.-3
【答案】D
【解析】设 , ,那么 ,所以 ,而 ,故 , ,所以 , ,选 .
10.2016年“一带一路”沿线64个国家GDP之和约为12.0万亿美元,占全球GDP的 ;人口总数约为32.1亿,占全球总人口的 ;对外贸易总额(进口额+出口额)约为71885.6亿美元,占全球贸易总额的 .
【答案】
【解析】 的展开式的通项为: .
令 ,得 .
答案为:-40.
点睛:求二项展开式有关问题的常见类型及解题策略
(1)求展开式中的特定项.可依据条件写出第r+1项,再由特定项的特点求出r值即可.
2023-2024学年北京市中国人民大学附属中学高三下学期5月热身练习数学试卷(三模)含详解

中国人民大学附属中学高三热身练习数学命题:高三数学组本试卷共7页,150分.考试时长120分钟.考生务必将答案答在答题卡上,在试卷上作答无效.考试结束后,将本试卷和答题卡一并交回.第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}21,{}P x x M a =≤=∣,若P M M = ,则实数a 的取值范围是()A.(,1]-∞- B.[1,1]- C.[)1,+∞ D.][(),11,-∞-⋃+∞2.若||1,||2,( )a b a b a ==-⊥r r r r r,则向量a 与b 的夹角为()A.30︒B.60︒C.120︒D.150︒3.已知nx⎫-⎪⎭的二项式系数之和为64,则其展开式的常数项为()A .240- B.240 C.60D.60-4.已知,R x y ∈,且x y >,则()A.11x y-<0 B.tan tan 0x y ->C.110e e xy⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭D.ln ||ln ||0x y ->5.若双曲线221:142x y C -=与22222:1y x C a b-=具有相同的渐近线,则2C 的离心率为()A.2B.C.D.6.已知函数1,0()1,0x f x x -<⎧=⎨≥⎩,则不等式(1)1xf x -≤的解集为().A.[1,)-+∞ B.(,1]-∞ C.[1,2]D.[1,1]-7.已知(1,0),(1,0)A B -,若点P 满足PA PB ⊥,则点P 到直线:((1)0l m x n y -+-=的距离的最大值为()A.1B.2C.3D.48.在ABC 中,角,,A B C 所对的边分别为,,a b c .则“,,a b c 成等比数列”是sin 2B ≤的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件9.故宫角楼的屋顶是我国十字脊顶的典型代表,如图1,它是由两个完全相同的直三棱柱垂直交叉构成,将其抽象成几何体如图2所示.已知三楼柱ABF CDE -和BDG ACH -是两个完全相同的直三棱柱,侧棱EF 与GH 互相垂直平分,,EF GH 交于点I ,AF BF a ==,AF BF ⊥,则点G 到平面ACEF 的距离是()A.33a B.12a C.2a D.24a 10.2024年1月17日我国自行研制的天舟七号货运飞船在发射3小时后成功对接于空间站天和核心舱后向端口,创造了自动交会对接的记录.某学校的航天科技活动小组为了探索运动物体追踪技术,设计了如下实验:目标P 在地面轨道上做匀速直线运动;在地面上相距7m 的A ,B 两点各放置一个传感器,分别实时记录A ,B 两点与物体P 的距离.科技小组的同学根据传感器的数据,绘制了“距离-时间”函数图像,分别如曲线a ,b 所示.1t 和2t 分别是两个函数的极小值点.曲线a 经过()()0110,,,r t r 和()20,t r ,曲线b 经过()22,t r .已知211212,4m,4s rt r t r t ===,并且从0=t 时刻到2=t t 时刻P 的运动轨迹与线段AB 相交.分析曲线数据可知,P 的运动轨迹与直线AB 所成夹角的正弦值以及P 的速度大小分别为()A.613,m /s 74 B.613,m /s 72 C.235,m /s 74D.235,m /s 72第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.若2i1ia +-是纯虚数,则实数a 的值为__________.12.已知抛物线2:4C y x =的焦点为F ,准线与x 轴的交点为A ,点B 在C 上.若||2FB =,则直线AB 的方程为__________.13.使lg lg lg()a b a b +=+成立的一组a ,b 的值为=a __________,b =__________.14.已知函数()sin(π)(0,0π)f x x ωϕωϕ=+><≤,若()f x 是偶函数,则ϕ=__________;若圆面222x y +≤恰好覆盖()f x 图象的最高点或最低点共3个,则ω的取值范围是__________.15.已知数列{}n a 的前n 项和为1,1n S a =且()2*11,Nn n a S n +=+∈,给出下列四个结论:①长度分别为11,,n n aS +的三条线段可以构成一个直角三角形:②*1N ,2n n n S -∀∈≥;③*21N ,2n n n n a a a ++∀∈+<;④*11πN ,2cos2n n n n a a ++∀∈=.其中所有正确结论的序号是__________.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.如图,四边形ABCD 为菱形,π,23ABC AB ∠==,把ABC 沿着BC 折起,使A 到1A 位置.(1)证明:1BC AA ⊥;(2)若1AA =,求直线1DA 与平面1ABA 所成角的正弦值;(3)在(2)的条件下,求点D 到平面1ABA 的距离.17.已知函数2()cos 2cos ,(0)f x x x x ωωωω=+>的最小正周期为π.(1)求ω的值;(2)在锐角ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .c 为()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值,再从条件①、条件②、条件③这三个条件中选择一个作为已知,求a b -的取值范围.条件①:cos cos 2cos a B b A c C +=;条件②:2sin cos sin 2a A B b A +=;条件③:ABC 的面积为S ,且)2224a b c S +-=.注:如果选择多个条件分别解答,按第一个条件计分.18.某口罩加工厂加工口罩由A ,B ,C 三道工序组成,每道工序之间相互独立,且每道工序加工质量分为高和低两种层次级别,A ,B ,C 三道工序加工的质量层次决定口罩的过滤等级;A ,B ,C 工序加工质量层次均为高时,口罩过滤等级为100等级(表示最低过滤效率为99.97%);C 工序的加工质量层次为高,A ,B 工序至少有一个质量层次为低时,口罩过滤等级为99等级(表示最低过滤效率为99%);其余均为95级(表示最低过滤效率为95%).现从A ,B ,C 三道工序的流水线上分别随机抽取100个口罩进行检测,其中A 工序加工质量层次为高的个数为50个,B 工序加工质量层次高的个数为75个,C 工序加工质量层次为高的个数为80个.表①:表示加工一个口罩的利润.口罩等级100等级99等级95等级利润/元210.5(1)用样本估计总体,估计该厂生产的口罩过滤等级为100等级的概率;(2)X 表示一个口罩的利润,求X 的分布列和数学期望;(3)用频率估计概率,由于工厂中A 工序加工质量层次为高的概率较低,工厂计划通过增加检测环节对A 工序进行升级.在升级过程中,每个口罩检测成本增加了0.2元时,相应的A 工序加工层次为高的概率在原来的基础上增加了b .试问:若工厂升级方案后对一个口罩利润的期望有所提高,写出一个满足条件的b 的值.19.已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,以线段12F F 为直径的圆过C 的上下顶点,点()1,e 在C 上,其中e 为C 的离心率.(1)求椭圆C 的方程和短轴长;(2)点,A B 在C 上,且在x 轴的上方,满足1212//,2AF BF AF BF =,直线2AF 与直线1BF 的交点为P ,求12PF F △的面积.20.已知函数()()e ,()x f x x a x a =--∈R .(1)若曲线()y f x =在(0,(0))f 处的切线为x 轴,求a 的值;(2)在(1)的条件下,判断函数()f x 的单调性;(3)()221()1e 12xg x x ax x x ⎛⎫=-+-++⎪⎝⎭,若1-是()g x 的极大值点,求a 的取值范围.21.给定正整数2n ≥,设数列12,,...,n a a a 是1,2,...,n 的一个排列,对{}1,2,...,i n ∈,i x 表示以i a 为首项的递增子列的最大长度,i y 表示以i a 为首项的递减子列的最大长度.(1)若4n =,11a =,24a =,32a =,43a =,求1x 和2y ;(2)求证:{}1,2,...,1i n ∀∈-,()()22110i i i i x y x y ++-+-≠;(3)求1niii x y=-∑的最小值.中国人民大学附属中学高三热身练习数学第一部分(选择题共40分)一、选择题共10小题,每小题4分,共40分.在每小题列出的四个选项中,选出符合题目要求的一项.1.已知集合{}21,{}P x x M a =≤=∣,若P M M = ,则实数a 的取值范围是()A.(,1]-∞-B.[1,1]- C.[)1,+∞ D.][(),11,-∞-⋃+∞【答案】B【分析】化简集合P ,由P M M = 得出M P ⊆,由子集的定义得出实数a 的取值范围.【详解】 集合{}210{11}[1,1]P x x x x =-≤=-≤≤=-∣∣,{},M a P M M =⋂=,[1,1]M P a ∴⊆∴∈-故选:B【点睛】本题主要考查了根据交集的结果求参数的取值范围,属于基础题.2.若||1,||2,( )a b a b a ==-⊥r r r r r,则向量a 与b 的夹角为()A.30︒B.60︒C.120︒D.150︒【答案】B【分析】根据()a b a -⊥ ,得()0a b a -×=,结合数量积得运算律求出a b ⋅ ,再根据向量夹角公式即可得解.【详解】因为()a b a -⊥ ,所以()0a b a -×= ,即20a a b -⋅= ,所以21a b a ⋅== ,所以1cos ,2a b a b a b ⋅==,又0,180a b ︒︒≤≤ ,所以向量a与b的夹角为60︒.故选:B.3.已知nx⎫-⎪⎭的二项式系数之和为64,则其展开式的常数项为()A.240-B.240C.60D.60-【答案】B【分析】根据二项式系数之和可得6n =,结合二项展开式分析求解.【详解】由题意可知:二项式系数之和为264n =,可得6n =,其展开式的通项为()()63362166C 12C ,0,1,2,,6rr rrr rr r T x xr---+=-=-⋅⋅⋅=⋅⋅⋅,令3302r -=,解得2r =,所以其展开式的常数项为()242612C 240-⋅⋅=.故选:B.4.已知,R x y ∈,且x y >,则()A.11x y-<0 B.tan tan 0x y ->C.110e e xy⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭D.ln ||ln ||0x y ->【答案】C【分析】根据题意,利用不等式的基本性质,正切函数的性质,以及指数函数与对数函数的性质,逐项判定,即可求解.【详解】对于A 中,11y xx y xy--=,其中0y x -<,但xy 的符号不确定,所以A 不正确;对于B 中,例如ππ,4x y ==,此时tan tan 0110x y -=-=-<,所以B 不正确;对于C 中,由函数()1e xf x ⎛⎫= ⎪⎝⎭在R 为单调递减函数,因为x y >,所以11e e xy⎛⎫⎛⎫< ⎪ ⎪⎝⎭⎝⎭,可得110e e xy⎛⎫⎛⎫-< ⎪ ⎪⎝⎭⎝⎭,所以C 正确;对于D 中,例如2,3x y ==-,此时2ln ||ln ||ln 2ln 3ln 03x y -=-=<,所以D 不正确.故选:C.5.若双曲线221:142x y C -=与22222:1y x C a b-=具有相同的渐近线,则2C 的离心率为()A.2B.C.D.【答案】C【分析】先求出两个双曲线的离心率,根据渐近线相等列式,代入离心率求解即可.【详解】双曲线221:142x y C -=的渐近线为2y x =±,22222:1y x C a b -=的渐近线为a y x b =±,由题可知22a b=,所以2C 的离心率c e a ====故选:C.6.已知函数1,0()1,0x f x x -<⎧=⎨≥⎩,则不等式(1)1xf x -≤的解集为().A.[1,)-+∞B.(,1]-∞ C.[1,2]D.[1,1]-【答案】D【分析】由题可得()1,111,1x f x x -<⎧-=⎨≥⎩,然后分类讨论解不等式即得.【详解】∵1,0()1,0x f x x -<⎧=⎨≥⎩,∴1,1(1)1,1x f x x -<⎧-=⎨≥⎩,当1x ≥时,(1)11xf x x -≤⇔≤,∴1x =,当1x <时,(1)111xf x x x -≤⇔-≤⇔≥-,∴1<1x ≤-,综上所述,(1)1xf x -≤的解集为[1,1]-.故选:D .7.已知(1,0),(1,0)A B -,若点P 满足PA PB ⊥,则点P 到直线:((1)0l m x n y -+-=的距离的最大值为()A.1B.2C.3D.4【答案】C【分析】先确定P 的轨迹以及直线l 过的定点,再根据圆的性质特点求最值.【详解】由PA PB ⊥可得点P 的轨迹为以线段AB 为直线的圆,圆心为()0,0,半径为1,又直线:((1)0l m x n y -+-=,其过定点),13+=.故答案为:C8.在ABC 中,角,,A B C 所对的边分别为,,a b c .则“,,a b c 成等比数列”是sin 2B ≤的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分又不必要条件【答案】A【分析】先将2b ac =代入余弦定理,利用基本不等式得到1cos 2B ≥,从而得到3sin 2B ≤,接着根据3sin 2B ≤得到B 可能为钝角,不满足,,a b c 成等比数列,从而得答案.【详解】当,,a b c 成等比数列时,2b ac =,所以22221cos 222a cb ac ac B ac ac +--=≥=,当且仅当a c =时等号成立,又()0,πB ∈,所以π3B ≤,所以3sin 2B ≤,充分性满足;当3sin 2B ≤时,π2π0,,π33B ⎛⎤⎡⎫∈⋃ ⎪⎥⎢⎝⎦⎣⎭,而当2π,π3B ⎡⎫∈⎪⎢⎣⎭时,b 为最长的边,不满足,,a b c 成等比数列,必要性不满足.则“,,a b c 成等比数列”是sin 2B ≤的充分不必要条件.故选:A.9.故宫角楼的屋顶是我国十字脊顶的典型代表,如图1,它是由两个完全相同的直三棱柱垂直交叉构成,将其抽象成几何体如图2所示.已知三楼柱ABF CDE -和BDG ACH -是两个完全相同的直三棱柱,侧棱EF 与GH 互相垂直平分,,EF GH 交于点I ,AF BF a ==,AF BF ⊥,则点G 到平面ACEF 的距离是()A.33a B.12a C.2a D.24a 【答案】B【分析】根据已知条件,结合空间总直线与平面的位置关系,先确定点G 到平面ACEF 的垂线段,在根据已知条件得sin 22KGIGθ==h 即可.【详解】取AC 中点M ,连接MI ,过G 作MI 的垂线交MI 的延长线于点K,取AB 中点N ,连接FN ,由已知,M 、I 分别为AC 、EF 中点,因为ABF CDE -是直三棱柱,所以AF AC ⊥,//EF AC 且EF AC =,所以//FI AM 其=FI AM ,所以四边形AMIF 为平行四边形,又AF AC ⊥,所以AMIF 为矩形,所以EF MK ⊥,又EF GH ⊥,MK ⊂平面KIG ,GH Ì平面KIG ,MK GH I ⋂=,所以EF ⊥平面KIG ,KG ⊂平面KIG ,所以EF KG ⊥,又因为KG MK ⊥,EF ⊂平面ACEF ,MK ⊂平面ACEF ,EF MK I ⋂=,所以KG ⊥平面ACEF ,所以点G 到平面ACEF 的距离等于线段KG 的长度,设为h ;AF BF ⊥,在Rt ABF 中,AF BF a ==,所以AB ==,设角FAB θ∠=,则有2sin 2θ=,因为四边形AMIF 为平行四边形,所以//MI AF ,又因为因为BDG ACH -是直三棱柱,所以//AB HG ,且HG AB a ==,所以KIG FAB θ∠=∠=,22IG =,又因为KG ⊥平面ACEF ,IK ⊂平面ACEF ,所以KG IK ⊥,所以sin 22KGIGθ==2222=,解得2a h =,所以点G 到平面ACEF 的距离是2a ,故选:B.【点睛】关键点点睛:本题关键在于根据空间中点、线、面的位置关系,确定点G 到平面ACEF 的垂线段.10.2024年1月17日我国自行研制的天舟七号货运飞船在发射3小时后成功对接于空间站天和核心舱后向端口,创造了自动交会对接的记录.某学校的航天科技活动小组为了探索运动物体追踪技术,设计了如下实验:目标P 在地面轨道上做匀速直线运动;在地面上相距7m 的A ,B 两点各放置一个传感器,分别实时记录A ,B 两点与物体P 的距离.科技小组的同学根据传感器的数据,绘制了“距离-时间”函数图像,分别如曲线a ,b 所示.1t 和2t 分别是两个函数的极小值点.曲线a 经过()()0110,,,r t r 和()20,t r ,曲线b 经过()22,t r .已知211212,4m,4s rt r t r t ===,并且从0=t 时刻到2=t t 时刻P 的运动轨迹与线段AB 相交.分析曲线数据可知,P 的运动轨迹与直线AB 所成夹角的正弦值以及P 的速度大小分别为()A.613,m /s 74 B.613,m /s 72 C.235,m /s 74D.235,m /s 72【答案】B【分析】建系,设点,作相应的辅助线,分析可知6m,2m AC BC v ==,结合7m AB =分析求解即可.【详解】如图,建立平面直角坐标系,设动点P 的轨迹与y 轴重合,其在120,,t t t =时刻对应的点分别为O (坐标原点),,D E ,P 的速度为m /s,0v v >,因为1122112,4m,2s,4s rt r t r t t ====,可得22m r =,由题意可知:,AD BE 均与y 轴垂直,且4m,2m,2m AD BE OD DE v ====,作BC AD ⊥垂足为C ,则6m,2m AC BC v ==,因为222AC BCAB +=,即236449v +=,解得2v =;又因为BC ∥y 轴,可知P 的运动轨迹与直线AB 所成夹角即为ABC ∠,所以P 的运动轨迹与直线AB 所成夹角的正弦值为6sin 7AC ABC AB∠==.故选:B.【点睛】关键点点睛:建系,设动点P 的轨迹与y 轴重合,以坐标系为依托,把对应的量转化为相应的长度,进而分析求解.第二部分(非选择题共110分)二、填空题共5小题,每小题5分,共25分.11.若2i1ia +-是纯虚数,则实数a 的值为__________.【答案】2【分析】求出复数的代数形式,然后根据纯虚数的定义列方程求解即可.【详解】()()()()()22i 1i 2i 1i 1i 221i1i 1a a a a a a a +++==--+-+++,因为2i1ia +-是纯虚数,所以20210a a -=⎧⎨+≠⎩,得2a =.故答案为:212.已知抛物线2:4C y x =的焦点为F ,准线与x 轴的交点为A ,点B 在C 上.若||2FB =,则直线AB 的方程为__________.【答案】10x y -+=或10x y ++=【分析】先根据焦半径公式求出点B 坐标,进而可得直线方程.【详解】设(),B x y ,则||12FB x =+=,则1x =,此时2y =±,所以()1,2B 或()1,2B -,又由已知()1,0A -,直线AB 的方程为()()20111y x -=+--或()()20111y x --=+--,整理得10x y -+=或10x y ++=.故答案为:10x y -+=或10x y ++=.13.使lg lg lg()a b a b +=+成立的一组a ,b 的值为=a __________,b =__________.【答案】①.2(答案不唯一)②.2(答案不唯一)【分析】根据题意结合对数运算分析可得00ab a b a b =+⎧⎪>⎨⎪>⎩,取特值检验即可.【详解】若lg lg lg()a b a b +=+,则lg lg()ab a b =+,可得00ab a b a b =+⎧⎪>⎨⎪>⎩,例如2a b ==符合上式.故答案为:2;2.(答案不唯一)14.已知函数()sin(π)(0,0π)f x x ωϕωϕ=+><≤,若()f x 是偶函数,则ϕ=__________;若圆面222x y +≤恰好覆盖()f x 图象的最高点或最低点共3个,则ω的取值范围是__________.【答案】①.π2②.[)1,2【分析】根据偶函数的对称性分析可知ππ,Z 2k k ϕ=+∈,即可得结果;结合对称性可知圆面在y 轴右侧仅覆盖1个()f x 图象的最高点或最低点,结合周期性列式求解.【详解】因为()f x 是偶函数,则ππ,Z 2k k ϕ=+∈,且0πϕ<≤,所以π0,2k ϕ==;可得π()sin πcos π2f x x x ωω⎛⎫=+= ⎪⎝⎭,设()f x 的最小正周期为T ,因为()f x 和222x y +≤均关于y 轴对称,可知圆面在y 轴右侧仅覆盖()f x 图象的1个最低点,对于222x y +=,令1y =±,解得1x =(不妨只考虑y 轴右侧,舍负);可得121TT ⎧≤⎪⎨⎪>⎩,解得12T <≤,且0ω>,则2π12πω<≤,解得12ω≤<,所以ω的取值范围是[)1,2,故答案为:π2;[)1,2.15.已知数列{}n a 的前n 项和为1,1n S a =且()2*11,N n n a S n +=+∈,给出下列四个结论:①长度分别为11,,n n aS +的三条线段可以构成一个直角三角形:②*1N ,2n n n S -∀∈≥;③*21N ,2n n n n a a a ++∀∈+<;④*11πN ,2cos 2n n n n a a ++∀∈=.其中所有正确结论的序号是__________.【答案】②【分析】①:先确定11,,n n a S +最大的那个,再根据勾股定理列式判断;②通过放缩得到12n n a a +≥,再进一步通过放缩判断;③④求出123,,a a a ,然后举例排除.【详解】对于①:21110,1n n a S a +=+>=,则11,0n n a S +>>,则221131024n n n n n a S S S S +⎛⎫-=+-=-+> ⎪⎝⎭,即1n n a S +>,假设长度分别为11,,n n a S +的三条线段可以构成一个直角三角形,则1n a +为斜边,所以2211n n a S +=+,所以21111n n a a ++=-+,所以10n a +=或11n a +=,与11n a +>矛盾,故①错误;对于②:21122n n n n a S S a +=+≥≥,当且仅当1n =等号成立,所以12n na a +≥,所以111212422n n n n n a a a a ----≥≥≥≥= ,所以1*2N ,n n n S a n -≥≥∀∈,②正确;对于③:由已知1231,2,10a a a ===,此时1322a a a +>,所以*21N ,2n n n n a a a ++∀∈+<不成立,③错误;对于④:由已知1231,2,10a a a ===,此时323π2cos 2a a ≠,所以*11πN ,2cos 2n nn n a a ++∀∈=不成立,④错误.故答案为:②.【点睛】关键点点睛:对于数列命题正误的判断,我们可以通过求出部分项,然后观察是否成立,从而达到排除的目的.三、解答题共6小题,共85分.解答应写出文字说明,演算步骤或证明过程.16.如图,四边形ABCD 为菱形,π,23ABC AB ∠==,把ABC 沿着BC 折起,使A 到1A 位置.(1)证明:1BC AA ⊥;(2)若16AA =,求直线1DA 与平面1ABA 所成角的正弦值;(3)在(2)的条件下,求点D 到平面1ABA 的距离.【答案】(1)证明见解析;(2)65(3)2155【分析】(1)取线段BC 的中点E ,连接1,AE A E ,通过证明BC ⊥面1A AE 可得结论;(2)先证明出1,,AE A E BC 两两垂直,然后建立空间直角坐标系,利用向量法求线面角;(3)斜线段的长度乘以线面角的正弦可得点到面的距离.【小问1详解】取线段BC 的中点E ,连接1,AE A E ,因为四边形ABCD 为菱形,且π3ABC ∠=,所以ABC ,1A BC 为等边三角形,所以1,BC AE BC A E ⊥⊥,又11,,AE A E E AE A E =⊂ 面1A AE ,所以BC ⊥面1A AE ,又1AA ⊂面1A AE ,所以1BC AA ⊥;【小问2详解】由ABC ,1A BC 为边长为2的等边三角形可得13AE A E ==,所以22211AE A E A A +=,结合BC ⊥面1A AE 可得1,,AE A E BC 两两垂直,如图建立空间直角坐标系,)()()13,2,0,0,0,3,3,0,0,0,1,0DA AB -,(()11,,DA AB A A ===,设面1ABA 的法向量为(),,n x y z =,直线1DA 与平面1ABA 所成角为θ,则10AB n y A A n ⎧⋅=+=⎪⎨⋅=-=⎪⎩ ,取1x =得()n =,116sin 5n DA n DA θ⋅===⋅ ,即直线1DA 与平面1ABA 所成角的正弦值为65;【小问3详解】由(2)得点D 到平面1ABA的距离为16215sin 55DA θ==.17.已知函数2()cos 2cos ,(0)f x x x x ωωωω=+>的最小正周期为π.(1)求ω的值;(2)在锐角ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .c 为()f x 在π0,2⎡⎤⎢⎥⎣⎦上的最大值,再从条件①、条件②、条件③这三个条件中选择一个作为已知,求a b -的取值范围.条件①:cos cos 2cos a B b A c C +=;条件②:2sin cos sin 2a A B b A +=;条件③:ABC 的面积为S,且)2224a b c S +-=.注:如果选择多个条件分别解答,按第一个条件计分.【答案】(1)1(2)(【分析】利用三角恒等变换整理可得π()2sin 216f x x ω⎛⎫=++ ⎪⎝⎭,结合最小正周期分析求解;以π26x +为整体,结合正弦函数最值可得3c =.若选条件①:利用正弦定理结合三角恒等变换可得π3C =,利用正弦定理边化角,结合三角恒等变换可得π3a b A ⎛⎫-=-⎪⎝⎭,结合正弦函数分析求解;若选条件②:利用正弦定理结合三角恒等变换可得π3C =,利用正弦定理边化角,结合三角恒等变换可得π3a b A ⎛⎫-=- ⎪⎝⎭,结合正弦函数分析求解;若选条件③:利用面积公式、余弦定理可得π3C =,利用正弦定理边化角,结合三角恒等变换可得π3a b A ⎛⎫-=- ⎪⎝⎭,结合正弦函数分析求解.【小问1详解】由题意可知:2π()cos 2cos 2cos 212sin 216f x x x x x x x ωωωωωω⎛⎫=+=++=++ ⎪⎝⎭,因为函数()f x 的最小正周期为π,且0ω>,所以2π12πω==.【小问2详解】由(1)可知:π()2sin 216f x x ⎛⎫=++ ⎪⎝⎭,因为π0,2⎡⎤∈⎢⎣⎦x ,则ππ7π2,666x ⎡⎤+∈⎢⎥⎣⎦,可知当ππ262x +=,即π6x =时,()f x 取到最大值3,即3c =.若条件①:因为cos cos 2cos a B b A c C +=,由正弦定理可得sin cos sin cos 2sin cos A B B A C C +=,又因为()sin cos sin cos sin sin A B B A A B C +=+=,可得sin 2sin cos C C C =,且π0,2C ⎛⎫∈ ⎪⎝⎭,则sin 0C ≠,可得1cos 2C =,所以π3C =,由正弦定理可得sin sin sin 32a b c A B C ====,可得,a A b B ==,则π3a b A B A A ⎛⎫-=-=-+⎪⎝⎭1sin cos 22A A A ⎫=-+⎪⎪⎭π3cos 3A A A ⎛⎫=-=- ⎪⎝⎭,因为ABC 锐角三角形,则π022ππ032A A ⎧<<⎪⎪⎨⎪<-<⎪⎩,解得ππ62A <<,可得πππ636A -<-<,则1π1sin 232A ⎛⎫-<-< ⎪⎝⎭,可得b a <-<所以a b -的取值范围为(;若条件②;因为2sin cos sin 2a A B b A +=,由正弦定理可得:22sin cos sin sin 2A B B A A +=,则22sin cos 2sin sin cos A B B A A A +=,因为π0,2A ⎛⎫∈ ⎪⎝⎭,则sin 0A ≠,可得()2sin cos 2sin cos 2sin 2sin A B B A A B C +=+==即3sin 2C =,且π0,2C ⎛⎫∈ ⎪⎝⎭,所以π3C =,由正弦定理可得sin sin sin a b c A B C ====,可得,a A b B ==,则π3a b A B A A ⎛⎫-=-=-+⎪⎝⎭13sin cos 22A A A ⎫=-+⎪⎪⎭π3cos 3A A A ⎛⎫=-=- ⎪⎝⎭,因为ABC 锐角三角形,则π022ππ032A A ⎧<<⎪⎪⎨⎪<-<⎪⎩,解得ππ62A <<,可得πππ636A -<-<,则1π1sin 232A ⎛⎫-<-< ⎪⎝⎭,可得b a <-<所以a b -的取值范围为(;若选③:因为)2224a b c S +-=,则132cos sin 24ab Cab C =,整理得tan C =π0,2C ⎛⎫∈ ⎪⎝⎭,所以π3C =,由正弦定理可得sin sin sin 32a b c A B C ====,可得,a A b B ==,则π3a b A B A A ⎛⎫-=-=-+ ⎪⎝⎭13sin cos 22A A A ⎫=-+⎪⎪⎭π3cos 3A A A ⎛⎫=-=- ⎪⎝⎭,因为ABC 锐角三角形,则π022ππ032A A ⎧<<⎪⎪⎨⎪<-<⎪⎩,解得ππ62A <<,可得πππ636A -<-<,则1π1sin 232A ⎛⎫-<-< ⎪⎝⎭,可得b a <-<所以a b -的取值范围为(.18.某口罩加工厂加工口罩由A ,B ,C 三道工序组成,每道工序之间相互独立,且每道工序加工质量分为高和低两种层次级别,A ,B ,C 三道工序加工的质量层次决定口罩的过滤等级;A ,B ,C 工序加工质量层次均为高时,口罩过滤等级为100等级(表示最低过滤效率为99.97%);C 工序的加工质量层次为高,A ,B 工序至少有一个质量层次为低时,口罩过滤等级为99等级(表示最低过滤效率为99%);其余均为95级(表示最低过滤效率为95%).现从A ,B ,C 三道工序的流水线上分别随机抽取100个口罩进行检测,其中A 工序加工质量层次为高的个数为50个,B 工序加工质量层次高的个数为75个,C 工序加工质量层次为高的个数为80个.表①:表示加工一个口罩的利润.口罩等级100等级99等级95等级利润/元210.5(1)用样本估计总体,估计该厂生产的口罩过滤等级为100等级的概率;(2)X 表示一个口罩的利润,求X 的分布列和数学期望;(3)用频率估计概率,由于工厂中A 工序加工质量层次为高的概率较低,工厂计划通过增加检测环节对A 工序进行升级.在升级过程中,每个口罩检测成本增加了0.2元时,相应的A 工序加工层次为高的概率在原来的基础上增加了b .试问:若工厂升级方案后对一个口罩利润的期望有所提高,写出一个满足条件的b 的值.【答案】(1)0.3(2)分布列见详解;() 1.2E X =元(3)25b =(答案不唯一,满足1132b <≤即可)【分析】(1)根据可得A ,B ,C 三道工序加工的质量层次高的概率,结合独立事件概率乘法公式分析求解;(2)由题意可知:X 的可能取值为2,1,0.5,求相应的概率,进而可得分布列和期望;(3)由题意可知:工厂升级方案后A 道工序加工的质量层次高的概率为[]0.5,0,0.5b b +∈,由题意可知:Y 的可能取值为1.8,0.8,0.3,求相应的概率,进而可得期望,令()()E Y E X >运算求解即可.【小问1详解】设A ,B ,C 三道工序加工的质量层次高的概率分别为123,,p p p ,用频率估计概率可得:1235075800.5,0.75,0.8100100100p p p ======,记“该厂生产的口罩过滤等级为100等级”为事件M ,所以()0.50.750.80.3P M =⨯⨯=.【小问2详解】由题意可知:X 的可能取值为2,1,0.5,则有:()()()()31220.3,110.5P X P M P X p p p =====-=,()()()0.51210.2P X P X P X ==-=-==,所以X 的分布列为X 210.5P0.30.50.2X 的期望()20.310.50.50.2 1.2E X =⨯+⨯+⨯=(元).【小问3详解】由题意可知:工厂升级方案后A 道工序加工的质量层次高的概率为[]0.5,0,0.5b b +∈,设工厂升级方案后一个口罩利润的期望为Y ,由题意可知:Y 的可能取值为1.8,0.8,0.3,则有:()()1.80.50.750.80.60.3P Y b b ==+⨯⨯=+,()()0.80.810.50.750.50.6P Y b b ==-+⨯=-⎡⎤⎣⎦,()()()0.31210.2P Y P Y P Y ==-=-==,所以Y 的期望()()()1.80.60.30.80.50.60.30.20.61E Y b b b =⨯++⨯-+⨯=+(元),令()()E Y E X >,即0.61 1.2b +>,解得1132b <≤,例如25b =符合题意.19.已知椭圆2222:1(0)x y C a b a b+=>>的左右焦点分别为12,F F ,以线段12F F 为直径的圆过C 的上下顶点,点()1,e 在C 上,其中e 为C 的离心率.(1)求椭圆C 的方程和短轴长;(2)点,A B 在C 上,且在x 轴的上方,满足1212//,2AF BF AF BF =,直线2AF 与直线1BF 的交点为P ,求12PF F △的面积.【答案】(1)22:12x C y +=;2(2【分析】(1)线段12F F 为直径的圆过C 的上下顶点,得11OB OF r ==,即b c =,然后计算离心率e ,从而点()1,e 代入C 可得椭圆C 的方程并可求短轴长;(2)由题可知,12PF F △的面积等于1212P F F y ,所以求P y 的值;由1212//,2AF BF AF BF =,得122AF BF =uuu r uuu r ,进而得点,A B 的坐标关系,即1212232x x y y =-⎧⎨=⎩,将点,A B 代入C ,求得2y ,再由12APF F PB △△∽,得12PF BP = ,即223P y y =,从而计算12PF F △的面积即可.【小问1详解】设()()120,,0F c F c -,,上下顶点分别为()()120,,0,B b B b -.由以线段12F F 为直径的圆过C 的上下顶点,得11OB OF r ==,得22b c =,即b c =.因为22222a b c c =+=,即a =,所以22c e a ==,由点2)2在C 上,得22222211a b ⎛⎫ ⎪⎝⎭+=,2211122b b +=,解得1b =,所以2222a b ==,则22:12x C y +=,短轴长1222B B b ==.【小问2详解】根据题意,画出图象如图所示:因为1212//,2AF BF AF BF =,所以122AF BF =uuu r uuu r ,又12APF F PB △△∽,则1122PF AF BP BF ==,即12PF BP =,12PF BP = .设()()()1122,,,,,P P A x y B x y P x y ,()()121,0,1,0F F -由122AF BF =uuu r uuu r 得()12121212x x y y ⎧--=-⎨-=-⎩,即1212232x x y y =-⎧⎨=⎩,因为点()()1122,,,A x y B x y 在椭圆22:12x C y +=上,所以()()222222222322222x y x y ⎧-+⨯=⎪⎨+=⎪⎩,即22222222241287488x x y x y ⎧-+=-⎨+=⎩,两式相减得,21215x =即254x =,2225224y ⎛⎫+= ⎪⎝⎭,又点,A B 在x 轴的上方,所以2148y =.又12PF BP = 得()22P P y y y -=-,即222141433812P y y ==⨯=.于是12121114142221212PF F P S F F y ==⨯⨯= .20.已知函数()()e ,()x f x x a x a =--∈R .(1)若曲线()y f x =在(0,(0))f 处的切线为x 轴,求a 的值;(2)在(1)的条件下,判断函数()f x 的单调性;(3)()221()1e 12x g x x ax x x ⎛⎫=-+-++ ⎪⎝⎭,若1-是()g x 的极大值点,求a 的取值范围.【答案】(1)0(2)(),0∞-上单调递减,()0,∞+上单调递增(3)()e,∞-+【分析】(1)求导,然后根据(0)0f '=列式计算即可;(2)求导,然后通过二次求导确定导函数的正负,进而确定函数的单调性;(3)求导,然后因式分解,确定导函数的零点,讨论零点大小,进而确定极值点.【小问1详解】由已知()(1)e 1x f x x a '=-+-,则0(0)(1)e 1f a a '=-+-=-,由于曲线()y f x =在(0,(0))f 处的切线为x 轴,所以0a -=,所以0a =;【小问2详解】当0a =时,()(1)e 1x f x x '=+-,令()(1)e 1x h x x =+-,则()(2)e x h x x '=+,当<2x -时,()0h x '<,()f x '单调递减,当2x >-时,()0h x '>,()f x '单调递增,又当<2x -时,()0f x '<恒成立,2(2)e 1f -'-=--,0(0)e 10f '=-=,所以当0x <时()0f x '<,0x >时,()0f x '>,所以()f x 在(),0∞-上单调递减,在()0,∞+上单调递增;【小问3详解】由已知()()()2()12e 11(1)e 1x x g x x ax x a x x x a '⎡⎤=-++--+=+-+-⎣⎦,令()(1)e 1x v x x a =-+-,则()(2)e xv x x a '=-+,当2x a <-时,()0v x '<,()v x 单调递减,当2x a >-时,()0v x '>,()v x 单调递增,又当2x a <-时,()0v x <恒成立,且()22e 10a v a --=--<,当x →+∞时,()0v x >,即()v x 在()2,a -+∞上有且只有一个零点,设为0x ,当01x <-,即()11(11)e 10v a --=--+->,解得e a <-,此时若()0g x '<,解得01x x <<-,()g x 在()0,1x -上单调递减,若()0g x '>,解得0x x <或1x >-,()g x 在()()0,,1,x -∞-+∞上单调递增,此时()g x 在=1x -处取极小值,不符合题意,舍去;当01x >-,即()11(11)e 10v a --=--+-<,解得e a >-,此时若()0g x '<,解得01x x -<<,()g x 在()01,x -上单调递减,若()0g x '>,解得1x <-或0x x >,()g x 在()()0,1,,x -∞-+∞上单调递增,此时()g x 在=1x -处取极大值,符合1-是()g x 的极大值点,当01x =-时,即()11(11)e 10v a --=--+-=,解得a e =-,此时()0g x '≥恒成立,()g x 无极值点,综上所述:a 的取值范围为()e,∞-+.【点睛】方法点睛:函数的极值跟导函数的零点有关,当零点不确定的时候,就需要对零点的存在性以及零点的大小进行分类讨论,从而达到确定极值点的目的.21.给定正整数2n ≥,设数列12,,...,n a a a 是1,2,...,n 的一个排列,对{}1,2,...,i n ∈,i x 表示以i a 为首项的递增子列的最大长度,i y 表示以i a 为首项的递减子列的最大长度.(1)若4n =,11a =,24a =,32a =,43a =,求1x 和2y ;(2)求证:{}1,2,...,1i n ∀∈-,()()22110i i i i x y x y ++-+-≠;(3)求1n i i i x y=-∑的最小值.【答案】(1)13x =,22y =(2)证明见解析(3)当n 为偶数时,1n i i i x y =-∑的最小值是2n ;当n 为奇数时,1n i i i x y =-∑的最小值是12n -.【分析】(1)直接根据定义求解;(2)分情况讨论证明11i i i i x y x y ++-≠-,故可推知i i x y -和11i i x y ++-不能同时为零,进而得到结论;(3)对n 的奇偶性分情况讨论,并利用小问2得到的结果即可.【小问1详解】以1a 为首项的最长递增子列是134,,a a a ,以2a 为首项的最长递减子列是23,a a 和24,a a .所以13x =,22y =.【小问2详解】对{}1,2,...,1i n ∈-,由于12,,...,n a a a 是1,2,...,n 的一个排列,故1i i a a +≠.若1i i a a +<,则每个以1i a +为首项的递增子列都可以在前面加一个i a ,得到一个以i a 为首项的更长的递增子列,所以1i i x x +>;而每个以i a 为首项的递减子列都不包含1i a +,且1i i a a +<,故可将i a 替换为1i a +,得到一个长度相同的递减子列,所以1i i y y +≤.这意味着11i i i i x y x y ++->-;若1i i a a +>,同理有1i i y y +>,1i i x x +≤,故11i i i i x y x y ++-<-.总之有11i i i i x y x y ++-≠-,从而i i x y -和11i i x y ++-不能同时为零,故()()22110i i i i x y x y ++-+-≠.【小问3详解】根据小问2的证明过程知i i x y -和11i i x y ++-不能同时为零,故111i i i i x y x y ++-+-≥.情况一:当n 为偶数时,设2n k =,则一方面有()21212211112n k k i i i i i i i i i n x y x y x y k --===-=-+-≥==∑∑∑;另一方面,考虑这样一个数列12,,...,n a a a :2121i i a k i a k i-=-+⎧⎨=+⎩,1,2,...,i k =.则对1,2,...,i k =,有21221i i x k i x k i -=-+⎧⎨=-+⎩,21211i iy k i y k i -=-+⎧⎨=-+⎩.故此时212111112n k k i i i i i i i n x y x y k --===-=-===∑∑∑.结合以上两方面,知1n i i i x y =-∑的最小值是2n .情况二:当n 为奇数时,设21n m =-,则一方面有()11121212211111112n n m m i i i i i i i i i i i i n x y x y x y x y m -----====--≥-=-+-≥=-=∑∑∑∑;另一方面,考虑这样一个数列12,,...,n a a a :1221i i a m a m i a m i +=⎧⎪=+⎨⎪=-⎩,1,2,...,1i m =-.则对1,2,...,1i m =-,有1221i i x m x m i x m i +=⎧⎪=-⎨⎪=-⎩,12211i i y m y m i y m i +=⎧⎪=-+⎨⎪=-⎩.故此时11221111112n m m i i i i i i i n x y x y m --===--=-==-=∑∑∑.结合以上两方面,知1n i i i x y =-∑的最小值是12n -.综上,当n 为偶数时,1n i i i x y =-∑的最小值是2n ;当n 为奇数时,1n i i i x y =-∑的最小值是12n -.【点睛】关键点点睛:求最小(或最大)值的本质在于,先证明所求的表达式一定不小于(或不大于)某个数M ,再说明该表达式在某种情况下能取到M ,就得到了最小(或最大)值是M ,这便是“求最小(或最大)值”的本质.而在这个过程中,“想到M 的具体取值”这个过程并不存在绝对的逻辑性,可以穷尽各种手段,包括直觉、大胆猜测、高观点等,去猜出M 的值,这些内容也无需在证明过程中呈现.只要证明合乎逻辑,“如何想到M 的取值”无需交代,不影响解答的正确性.换言之,所谓“求”,便是“猜出结果,再证明结果正确”,与“算出”、“得出”本就是无关的.在高考范围内,大多数最小值和最大值问题都能够直接化为某个显而易见,容易刻画的模型,然后“直接算出”,但不可将此作为万能法宝,忘记了最小值最大值的原始定义和本质.。
【加15套高考模拟卷】2020届北京市中国人民大学附属中学高三考前热身练习物理试题含解析

2020届北京市中国人民大学附属中学高三考前热身练习物理试题一、单项选择题:本题共6小题,每小题4分,共24分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1、如图所示,一理想变压器,其原副线圈的匝数均可调节,原线圈两端电压为一最大值不变的正弦交流电,为了使变压器输入功率增大,可使A.其他条件不变,原线圈的匝数n1增加B.其他条件不变,副线圈的匝数n2减小C.其他条件不变,负载电阻R的阻值增大D.其他条件不变,负载电阻R的阻值减小2、在如图所示的理想变压器供电线路中,原线圈接在有效值恒定的交流电源上,副线圈接有两个灯泡,电流表、电压表均为理想电表。
开关S原来是断开的,现将开关S闭合,则()A.A1的示数增大,A2的示数增大B.A1的示数不变,A2的示数增大C.V1的示数减小,V2的示数减小。
D.V1的示数不变,V2的示数减小3、下列说法正确的是()A.一个热力学系统吸收热量后,其内能一定增加B.一个热力学系统对外做功后,其内能一定减少C.理想气体的质量一定且体积不变,当温度升高时其压强一定增大D.理想气体的质量一定且体积不变,当温度升高时其压强一定减小4、甲、乙两辆汽车沿同一方向做直线运动,两车在某一时刻刚好经过同一位置,此时甲的速度为5m/s,乙的速度为10m/s,甲车的加速度大小恒为1.2m/s2以此时作为计时起点,它们的速度随时间变化的关系如图所示,根据以上条件可知()A .乙车做加速度先增大后减小的变加速运动B .在前4s 的时间内,甲车运动位移为29.6 mC .在4s t =时,甲车追上乙车D .在10s t =时,乙车又回到起始位置5、在人类太空征服史中,让人类遗憾的是“太空加油站”的缺乏。
当通信卫星轨道校正能源耗尽的时候,它的生命就走到了尽头,有很多成了太空垃圾。
如今“轨道康复者”是救助此类卫星的新型太空航天器,图甲是“轨道康复者”航天器在给太空中“垃圾”卫星补充能源,可简化为图乙所示的模型,让“轨道康复者”N 对已偏离原来正常工作轨道的卫星M 进行校正,则( )A .“轨道康复者”N 从图乙所示轨道上加速,与卫星M 对接补充能源后开动M 上的小发动机向前喷气,能校正卫星M 到较低的轨道运行B .让M 降低到N 所在轨道上,补充能源后再开启卫星M 上的小发动机校正C .在图乙中M 的动能一定小于N 的动能D .在图乙中,M 、N 和地球球心三者不可能处在同一直线上6、某理想自耦变压器接入电路中的示意图如图甲所示,图乙是其输入电压u 的变化规律.已知滑动触头在图示位置时原、副线圈的匝数比为12:10:1n n =,电阻22R =Ω.下列说法正确的是A .通过R 的交流电的频率为100 HzB .电流表A 22C .此时变压器的输入功率为22 WD .将P 沿逆时针方向移动一些,电流表A 1的示数变小二、多项选择题:本题共4小题,每小题5分,共20分。
北京市人大附中2020届高三数学6月考前热身试题(含解析)

【详解】A:南亚地区人口总数为 174499.0 万人,“一带一路”沿线国家人口总数为:
174499.0 54%
321266.1 万人,所以 321266.1
,故本选项说法不正确的;
B:东南亚和南亚国家 GDP 之和 54948.8 亿美元,“一带一路”沿线国家 GDP 之和 120139.6
54948.8 46%
12 , 6
12
11
的最大值是 12 .
故选:C.
【点睛】本题考查三角函数恒等变换化简,以及三角函数的性质,意在考查直观想象、逻辑
推理能力,属于中档题.
9. 已知不过坐标原点 O 的直线交抛物线 y2 2 px 于 A , B 两点,若直线 OA , AB 的斜率
分别为 2 和 6,则直线 OB 的斜率为( )
人口(万人)
GDP(亿美元)
进口额(亿美元) 出口额(亿美元)
蒙古
301.4
116.5
38.7
45.0
东南亚 11 国
63852.5
25802.2
11267.2
11798.6
南亚 8 国
174499.0
29146.6
4724.1
3308.5
中亚 5 国
6946.7
2254.7
422.7
590.7
西亚、北非 19 国 43504.6
A. 3 【答案】D 【解析】
B. 2
C. -2
D. -3
设
A
y
2 A
2p
,
yA
,
B
yB2 2p
,
yB
,那么
k
AB
yA yB yA2 yB2
2020年北京海淀区中国人民大学附属中学高三下学期高考模拟数学试卷(保温练习2)-学生用卷

2020年北京海淀区中国人民大学附属中学高三下学期高考模拟数学试卷(保温练习2)-学生用卷一、选择题(本大题共10小题,每小题4分,共40分)1、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第1题4分2019年北京海淀区高三三模第4题2020年北京海淀区高三三模第4题2018年北京海淀区高三三模第4题2018年北京西城区北京师范大学附属中学高三三模理科第3题5分如果复数z=a2+a−2+(a2−3a+2)i为纯虚数,那么实数的值为().A. 2B. 1C. −2D. 1或−22、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第2题4分2019~2020学年北京东城区北京汇文中学高一上学期期末第4题5分2020年北京海淀区高三三模第9题2015~2016学年北京东城区高三上学期期末理科第4题5分2018年北京海淀区高三三模第9题已知m∈(0,1),令a=log m2,b=m2,c=2m,那么a,b,c之间的大小关系为().A. b<c<aB. b<a<cC. a<b<cD. c<a<b3、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第3题4分下列函数中,满足(1)f(x)+f(−x)=0;(2)在区间(0,1)上对任意x1,x2(x1≠x2)都有[f(x1)−f(x2)](x1−x2)>0的函数是().A. y=−x3B. y=sin(−x)C. y=log2|x|D. y=2x−2−x4、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第4题4分2019~2020学年北京海淀区北京一零一中学高三下学期开学考试第3题2019~2020学年11月北京东城区北京市第五十中学高三上学期月考第2题5分2020年北京西城区北京师范大学第二附属中学高三三模第4题4分2019~2020学年12月北京东城区北京市第五十五中学高三上学期月考第2题5分设a→,b→是向量,则“|a→|=|b→|”是“|a→+b→|=|a→−b→|”的().A. 充分而不必要条件B. 必要而不充分条件C. 充分必要条件D. 既不充分也不必要条件5、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第5题4分2019~2020学年北京海淀区高三上学期期中第6题5分在四边形ABCD中,AB//CD,设AC→=λAB→+μAD→(λ,μ∈R).若λ+μ=32,则|CD|→|AB→|=().A. 13B. 12C. 1D. 26、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第6题4分2017~2018学年北京石景山区北京市第九中学高二上学期期中理科第10题4分2019~2020学年安徽合肥包河区合肥市第一中学高二上学期段考理科(二)第5题5分 2016~2017学年北京海淀区北方交通大学附属中学高二上学期期中理科第4题4分2018年宁夏银川兴庆区银川市第二中学高三二模理科第6题5分在空间直角坐标系O −xyz 中,已知A(2,0,0),B(2,2,0),C(0,2,0),D(1,1,√2),若S 1、S 2、S 3分别是三棱锥D −ABC 在xOy 、yOz 、xOz 坐标平面上的正投影图形的面积,则( ).A. S 1=S 2=S 3B. S 2=S 1且S 2≠S 3C. S 3=S 1且S 3≠S 2D. S 3=S 2且S 3≠S 17、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第7题4分2020年北京房山区高三二模第9题4分把物体放在冷空气中冷却,如果物体原来的温度是θ1°C ,空气的温度是θ0°C ,经过t 分钟后物体的温度θ°C 可由公式θ=θ0+(θ1−θ0)e −kt 求得,其中k 是一个随着物体与空气的接触状况而定的大于0的常数.现有80°C 的物体,放在20°C 的空气中冷却,4分钟以后物体的温度是40°C ,则k 约等于(参考数据:ln3≈1.099)( ).A. 0.6B. 0.5C. 0.4D. 0.38、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第8题4分将函数y =sin(2x −π3)图象上的点P (π4,t)向左平移s (s >0)个单位长度得到点P ′,若P ′位于函数y =sin2x 的图象上,则( ).A. t =12,s 的最小值为π6 B. t =√32,s 的最小值为π6C. t =12,s 的最小值为π3 D. t =√32,s 的最小值为π39、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第9题4分2019~2020学年北京东城区北京市第一七一中学高一上学期期中第10题5分2019~2020学年吉林长春朝阳区长春市第二实验中学高一上学期期中第12题4分2014年高考真题北京卷文科第8题2015~2016学年北京海淀区清华大学附属中学高二下学期期中文科第10题4分加工爆米花时,爆开且不糊的粒数的百分比称为“可食用率”.在特定条件下,可食用率p与加工时间t(单位:分钟)满足的函数关系p=at2+bt+c(a、b、c是常数),下图记录了三次实验的数据.根据上述函数模型和实验数据,可以得到最佳加工时间为().A. 3.50分钟B. 3.75分钟C. 4.00分钟D. 4.25分钟10、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第10题4分2019~2020学年北京海淀区中国人民大学附属中学分校高一下学期期末第10题4分如图,某公园内有一个半圆形湖面,O为圆心,半径为1千米,现规划在半圆弧岸边上取点C,D,E,满足∠AOD=∠DOE=2∠AOC,在扇形AOC和四边形ODEB区域内种植荷花,在扇形COD 区域内修建水上项目,并在湖面上修建栈道DE,EB作为观光路线,则当DE+EB取得最大值时,sin∠AOC=().A. √26B. 14C. √23D. 12二、填空题(本大题共5小题,每小题5分,共25分)11、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第11题5分2018年高考真题北京卷文科第12题5分若双曲线x 2a2−y24=1(a>0)的离心率为√52,则a=.12、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第12题5分2019~2020学年4月北京朝阳区高三下学期月考A卷第11题5分在(√x−2x )5的二项展开式中,x−2的系数为.(用数字作答)13、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第13题5分直线ax+by+c=0,(a2+b2≠0)与圆x2+y2=5交于A,B两点,O为坐标原点,则三角形AOB的面积最大值为,OA→⋅OB→的取值范围是.题5分2019~2020学年4月北京朝阳区高三下学期月考B卷(六校联考)第13题5分2019~2020学年4月北京朝阳区高三下学期月考A卷第13题5分设无穷等比数列{a n}的各项为整数,公比为q,且q≠−1,a1+a3<2a2,写出数列{a n}的一个通项公式.15、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第15题5分2019~2020学年4月北京朝阳区高三下学期月考A卷第15题5分2020~2021学年北京海淀区首都师范大学附属中学高二上学期期中第18题4分关于曲线C:x2−xy+y2=4,给出下列四个结论:①曲线C关于原点对称,但不关于x轴、y轴对称;②曲线C恰好经过4个整点(即横、纵坐标均为整数的点);③曲线C上任意一点都不在圆x2+y2=3的内部;④曲线C上任意一点到原点的距离都不大于2√2.其中,正确结论的序号是.三、解答题(本大题共6小题,共85分)16、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第16题2020年北京房山区高三二模第17题14分已知数列{a n}的前n项和为S n,a1=1,.是否存在正整数k(k>1),使得a1、a k、S k+2成等比数列?若存在,求出k的值;若不存在,说明理由.从①a n+1−2a n=0,②S n=S n−1+n(n⩾2),③S n=n2这三个条件中任选一个,补充在上面问题中并作答.题2019~2020学年4月北京朝阳区高三下学期月考A卷第17题14分2019~2020学年4月北京朝阳区高三下学期月考B卷(六校联考)第17题14分体温是人体健康状况的直接反应,一般认为成年人腋下温度T(单位:°C)平均在36°C∼37°C之间即为正常体温,超过37.1°C即为发热,发热状态下,不同体温可分成以下三种发热类型:低热:37.1⩽T⩽38;高热:38<T⩽40;超高热(有生命危险):T>40.某位患者因患肺炎发热,于12日至26日住院治疗.医生根据病情变化,从14日开始,以3天为一个疗程,分别用三种不同的抗生素为该患者进行消炎退热.住院期间,患者每天上午8:00服药,护士每天下午16:00为患者测量腋下体温记录如下:(1) 请你计算住院期间该患者体温不低于39°C的各天体温平均值.(2) 在19日−23日期间,医生会随机选取3天在测量体温的同时为该患者进行某一特殊项目”α项目”的检查,记X为高热体温下做”α项目”检查的天数,试求X的分布列与数学期望.(3) 抗生素治疗一般在服药后2−8个小时就能出现血液浓度的高峰,开始杀灭细菌,达到消炎退热效果.假设三种抗生素治疗效果相互独立,请依据表中数据,判断哪种抗生素治疗效果最佳,并说明理由.18、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第18题如图,在四棱锥P−ABCD中,PA⊥平面ABCD,AD⊥CD,AD//BC,PA=AD=CD=2,BC=3,E为PD的中点,点F在PC上,且PFPC =13.(1) 求证:CD⊥平面PAD.(2) 求二面角F−AE−P的余弦值.(3) 设面AEF与棱PB交于点G,试求PGPB的值.19、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第19题2020年北京海淀区高三三模第40题2020年北京海淀区北京市中关村中学高三三模第19题14分2016年北京海淀区高三三模第33题2018年北京海淀区高三三模理科第46题已知函数f(x)=(x−a−1)e x.(1) 若函数的最小值为−1,求实数a的值.(2) 若x1>x2,且有x1+x2=2a,求证:f(x1)>f(x2).20、【来源】 2020年北京海淀区中国人民大学附属中学高三下学期高考模拟(保温练习2)第20题2017~2018学年北京西城区北京市回民学校高二上学期期中理科第21题2008年高考真题北京卷理科第19题14分2016~2017学年北京西城区北京市育才学校高二上学期期中第22题14分2016~2017学年广东深圳福田区深圳市福田中学高二上学期期中理科第22题12分已知菱形ABCD的顶点A,C在椭圆x2+3y2=4上,对角线BD所在直线的斜率为1.(1) 当直线BD过点(0,1)时,求直线AC的方程.(2) 当∠ABC=60∘时,求菱形ABCD面积的最大值.21、【来源】 2019~2020学年北京海淀区高三上学期期中第20题14分已知集合M⊆N∗,且M中的元素个数n大于等于5.若集合M中存在四个不同的元素a,b,c,d,使得a+b=c+d,则称集合M是“关联的”,并称集合{a,b,c,d}是集合M的“关联子集”;若集合M不存在“关联子集”,则称集合M是“独立的”.(1) 分别判断集合{2,4,6,8,10}和{1,2,3,5,8}是“关联的”还是“独立的”?若是“关联的”,写出其所有的“关联子集”.(2) 已知集合M={a1,a2,a3,a4,a5}是“关联的”,且任取集合{a i,a j}⊆M,总存在M的“关联子集”A,使得{a i,a j}⊆A.若a1<a2<a3<a4<a5,求证:a1,a2,a3,a4,a5是等差数列.(3) 若集合M是“独立的”,求证:存在x∈M,使得x>n2−n+9.41 、【答案】 C;2 、【答案】 C;3 、【答案】 D;4 、【答案】 D;5 、【答案】 B;6 、【答案】 D;7 、【答案】 D;8 、【答案】 A;9 、【答案】 B;10 、【答案】 B;11 、【答案】4;12 、【答案】−80;13 、【答案】5;[−25,25];214 、【答案】a n=−2n(答案不唯一);15 、【答案】①④;16 、【答案】选择①不存在,证明见解析(或选择②存在,k=6或选择③存在,k=3).;17 、【答案】 (1) 39.55°C.;(2) X的分布列为:E(X)=6.5;(3) ”抗生素B”治疗效果最佳.理由:自使用”抗生素B”开始治疗后,体温才开始稳定下降,且使用”抗生素B”治疗当天共降温0.7°C,是单日降温效果最好的一天,故”抗生素B”治疗效果最佳.;18 、【答案】 (1) 证明见解析.;(2) √3.3;(3) 2.3;19 、【答案】 (1) a=0.;(2) 证明见解析.;20 、【答案】 (1) x+y+2=0.;(2) 4√3.;21 、【答案】 (1) {2,4,6,8,10}是“关联的”,关联子集有{2,4,6,8},{4,6,8,10},{2,4,8,10},{1,2,3,5,8}是“独立的”.;(2) 证明见解析.;(3) 证明见解析.;第11页,共11页。
北京市人大附中高考数学前热身练习题 文理 北师大版

2012高考考前数学热身练习题(请认真完成每一道题) 1、命题“存在0x ∈R ,02x ≤0”的否定是 ( D ) 复习量词、命题的否定(A )不存在0x ∈R, 02x >0 (B )存在0x ∈R, 02x ≥0(C )对任意的x ∈R, 2x ≤0 (D )对任意的x ∈R, 2x >02、设函数1()ln (0),3f x x x x =->则()y f x = ( D )A 在区间1(,1),(1,)e e 内均有零点。
什么是零点? B 在区间1(,1),(1,)e e 内均无零点。
C 在区间1(,1)e 内有零点,在区间(1,)e 内无零点。
D 在区间1(,1)e 内无零点,在区间(1,)e 内有零点。
3、执行右边的程序框图,输出的T= 30 . 读懂程序框图,逐步推演。
4、如图是一个几何体的三视图,若它的体积是则=a三视图:注意还原几何体5、随机抽取某中学甲乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图7.(1)根据茎叶图判断哪个班的平均身高较高; (乙)(2)计算甲班的样本方差 (57)(3)现从乙班这10名同学中随机抽取两名 身高不低于173cm 的同学,求身高为176cm 的同学被抽中的概率. (25) 读懂茎叶图,学会算平均数、方差,标准差,将两者进行比较。
6、12cos xdx x dx π⎰+⎰的值为 13 学会求简单的定积分。
7、点P (1,0)到曲线⎩⎨⎧==ty t x 22(其中参数t ∈R )上的点的最短距离为 1 参数方程与极坐标相关知识请读教材与笔记8、极坐标方程2cos ρθ=化成直角坐标方__2220x y x +-=_________.9、 如图,PC 切O 于点C ,割线PAB 经过圆心O ,弦CD AB ⊥于点E ,已知O 的半径为3,2PA =,则PC =__4__,OE =___95__. 几何证明:相似、圆的简单问题10、某单位为了了解用电量y (度)与气温x (°C )之间的关系,随机统计了某4天的用电量与当天气温,并制作了对照表:由表中数据得线性回归方程ˆy bx a =+中2b =-,预测当气温为4C -︒时,用电量的度数约为 .68 注意:线性回归方程(读教材)。
