各种信号处理方法总结讲解
数字信号处理 名词解释-概述说明以及解释

数字信号处理名词解释-概述说明以及解释1.引言1.1 概述数字信号处理(Digital Signal Processing,简称DSP)是一种广泛应用于信号处理领域的技术,它利用数字化的方式对连续时间信号进行处理和分析。
数字信号处理可以实现信号的滤波、频谱分析、模拟与数字信号的转换、信息编码解码等功能,是现代通信、音视频处理、生物医学领域等各个领域中不可或缺的技术手段。
通过数字信号处理技术,我们可以更加精确和高效地处理各种类型的信号,包括声音、图像、视频等。
数字信号处理可以使信号的处理过程更加稳定可靠,同时也可以方便地与计算机等数字系统进行集成,实现更多复杂功能。
在本篇文章中,我们将深入探讨数字信号处理的定义、应用领域以及基本原理,以期让读者对这一重要领域有更加全面的认识和理解。
1.2 文章结构本文将分为三个主要部分,分别是引言、正文和结论。
在引言部分,我们将对数字信号处理进行简要的概述,并介绍文章的结构和目的。
正文部分将详细讨论数字信号处理的定义、应用领域和基本原理。
最后,在结论部分,我们将总结数字信号处理的重要性,探讨未来数字信号处理的发展趋势,并做出最终的结论。
通过这样的结构安排,读者能够清晰地了解数字信号处理的基本概念、应用以及未来发展方向。
1.3 目的:本文旨在介绍数字信号处理的概念、应用领域和基本原理,旨在帮助读者更深入了解数字信号处理的重要性和作用。
通过对数字信号处理的定义和应用领域的介绍,读者可以了解数字信号处理在各个领域中的广泛应用和重要性。
同时,通过对数字信号处理的基本原理的讲解,读者可以更好地理解数字信号处理的工作原理和技术特点。
通过本文的阐述,希望读者能够全面了解数字信号处理的基本概念和工作原理,进而认识到数字信号处理在现代科学技术中的重要性和必要性。
同时,本文也将展望未来数字信号处理的发展趋势,希望能够启发读者对数字信号处理领域的进一步研究和探索。
最终,通过本文的阐述,读者可以更加深入地理解数字信号处理这一重要的科学技术领域。
数字信号处理复习总结-最终版

绪论:本章介绍数字信号处理课程的基本概念。
0.1信号、系统与信号处理1.信号及其分类信号是信息的载体,以某种函数的形式传递信息。
这个函数可以是时间域、频率域或其它域,但最基础的域是时域。
分类:周期信号/非周期信号确定信号/随机信号能量信号/功率信号连续时间信号/离散时间信号/数字信号按自变量与函数值的取值形式不同分类:2.系统系统定义为处理(或变换)信号的物理设备,或者说,凡是能将信号加以变换以达到人们要求的各种设备都称为系统。
3.信号处理信号处理即是用系统对信号进行某种加工。
包括:滤波、分析、变换、综合、压缩、估计、识别等等。
所谓“数字信号处理”,就是用数值计算的方法,完成对信号的处理。
0.2 数字信号处理系统的基本组成数字信号处理就是用数值计算的方法对信号进行变换和处理。
不仅应用于数字化信号的处理,而且也可应用于模拟信号的处理。
以下讨论模拟信号数字化处理系统框图。
(1)前置滤波器将输入信号x a(t)中高于某一频率(称折叠频率,等于抽样频率的一半)的分量加以滤除。
(2)A/D变换器在A/D变换器中每隔T秒(抽样周期)取出一次x a(t)的幅度,抽样后的信号称为离散信号。
在A/D 变换器中的保持电路中进一步变换为若干位码。
(3)数字信号处理器(DSP)(4)D/A变换器按照预定要求,在处理器中将信号序列x(n)进行加工处理得到输出信号y(n)。
由一个二进制码流产生一个阶梯波形,是形成模拟信号的第一步。
(5)模拟滤波器把阶梯波形平滑成预期的模拟信号;以滤除掉不需要的高频分量,生成所需的模拟信号y a(t)。
0.3 数字信号处理的特点(1)灵活性。
(2)高精度和高稳定性。
(3)便于大规模集成。
(4)对数字信号可以存储、运算、系统可以获得高性能指标。
0.4 数字信号处理基本学科分支数字信号处理(DSP)一般有两层含义,一层是广义的理解,为数字信号处理技术——DigitalSignalProcessing,另一层是狭义的理解,为数字信号处理器——DigitalSignalProcessor。
电路信号处理与分析方法总结

电路信号处理与分析方法总结在电子设备和通信系统中,电路信号处理与分析是非常重要的技术,它涉及信号采集、处理、传输和分析等多个方面。
本文将对电路信号处理与分析的方法进行总结,帮助读者更好地理解和应用这些方法。
一、信号采集与处理方法1. 模拟信号采集与处理模拟信号指的是连续变化的信号,通常通过传感器等转换成电压或电流信号进行采集。
采集后的模拟信号需要进行处理,常见的处理方法包括滤波、放大、采样和保持等。
滤波可以去除杂散干扰,放大可以增加信号的强度,采样和保持可以将连续信号转换为离散信号。
2. 数字信号采集与处理数字信号是离散的信号,常见的数字信号采集设备是模数转换器(ADC)。
数字信号的处理方法包括数字滤波、数字放大、数字化、数据压缩和误差校正等。
数字滤波可以通过计算机算法实现,数字化可以将模拟信号转换为二进制数字,数据压缩可以减少存储和传输的需求,误差校正可以提高数字信号的精度和准确性。
二、信号传输与调制方法1. 信号传输方法信号传输是将采集或处理后的信号传送到其他设备或系统的过程。
常见的信号传输方法包括有线传输和无线传输两种。
有线传输主要通过电缆、光纤等介质进行信号传输,无线传输则利用无线电波或红外线等无线介质进行信号传输。
2. 信号调制方法信号调制是将原始信号按照一定规则转换为适合传输的信号的过程。
常见的信号调制方法有调幅(AM)、调频(FM)和调相(PM)等。
调幅是通过改变信号的振幅来实现信号调制,调频是通过改变信号的频率来实现信号调制,调相是通过改变信号的相位来实现信号调制。
三、信号分析与识别方法1. 时域与频域分析时域分析是将信号在时间轴上进行分析,常见的时域分析方法有时间序列分析和自相关函数分析等。
频域分析是将信号在频率域上进行分析,常见的频域分析方法有傅里叶变换和功率谱分析等。
时域和频域分析可以对信号的幅值、频率和相位等特性进行全面的分析和描述。
2. 数据挖掘与模式识别数据挖掘是通过对大量数据进行分析和挖掘来发现隐藏在数据中的有价值的信息。
阵列信号处理(知识点)

信号子空间:设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑在无噪声条件下,()()()()()12,,,P x t span a a a θθθ∈称()()()()12,,,P span a a a θθθ为信号子空间,是N 维线性空间中的P 维子空间,记为P N S 。
P N S 的正交补空间称为噪声子空间,记为N P N N -。
正交投影设子空间m S R ∈,如果线性变换P 满足,()1),,,2),,,0m mx R Px S x S Px x x R y S x Px y ∀∈∈∀∈=∀∈∀∈-=且则称线性变换P 为正交投影。
导向矢量、阵列流形设N 元阵接收p 个信源,则其信号模型为:()()()()1piiii x t s t a N t θ==+∑,其中矢量()i ia θ称为导向矢量,当改变空间角θ,使其在空间扫描,所形成的矩阵称为阵列流形,用符号A 表示,即(){|(0,2)}a A θθπ=∈波束形成波束形成(空域滤波)技术与时间滤波相类似,是对采样数据作加权求和,以增强特定方向信号的功率,即()()()()HHy t W X t s t W a θ==,通过加权系数W 实现对θ的选择。
最大似然已知一组服从某概率模型()f X θ的样本集12,,,N X X X ,其中θ为参数集合,使条件概率()12,,,N f X X X θ最大的参数θ估计称为最大似然估计。
不同几何形态的阵列的阵列流形矢量计算问题假设有P 个信源,N 元阵列,则先建立阵列的几何模型求第i 个信源的导向矢量()i i a θ 选择阵元中的一个作为第一阵元,其导向矢量()1[1]i a θ=然后根据阵列的几何模型求得其他各阵元与第一阵元之间的波程差n ∆,则确定其导向矢量()2jn i a eπλθ∆=最后形成N 元阵的阵列流形矢量()11221N j j N Pe A e πλπλθ-∆∆⨯⎡⎤⎢⎥⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ 例如各向同性的NxM 元矩形阵,阵元间隔为半个波长,当信源与阵列共面时:首先建立阵列几何模型:对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为(1)sin()(1)cos()mn i i n d m d θθ∆=---故:()1122(sin()cos())22((1)sin()(1)cos())11N j j d j j d N M NM P NM Pe e A e e ππθθλλππθθλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦而当信源与阵列不共面时: 首先将信源投影到阵列平面然后建立阵列模型对于第m 行、第n 列的阵元,其与第1行、第1列阵元之间的波程差为[(1)sin()(1)cos()]sin()mn i i i n d m d θθϕ∆=-+-故:()1122(sin()cos())cos()22((1)sin()(1)cos())cos()11N j j d j j d N M NM P NM Pe e A e e ππθθϕλλππθθϕλλθ-∆-∆---⨯⨯⎡⎤⎡⎤⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦线性约束最小方差准则(LCMV )的自适应波束形成算法: 对于信号模型:()()()0X t s t a J N θ=++, 波束形成输出:()()()()0()H H H yt W X t s t W a W J N θ==++LCMV 准则实际上是使()0HW a θ为一个固定值的条件下,求取使得()HWJ N +方差最小的W 作为最有权值,即:()0min .H X W HW R Ws t W a Fθ⎧⎪⎨⎪=⎩,其中F 为常数利用拉格朗日乘子法可解得:()10X opt W R a μθ-=当取1F =时,则()()11H X a R a μθθ-=,μ的取值不影响SNR 和方向图。
数字信号处理主要知识点整理复习总结

求出对应
的各种可能的序列的表达式。
解: 有两个极点,因为收敛域总是以极点为界,因此收敛域有以下三种情况: 三种收敛域对应三种不同的原序列。
时,
(1)当收敛域
令
,因为c内无极点,x(n)=0;
,C内有极点0,但z=0是一个n阶极点,改为求圆外极点留数,圆外极点有
数字信号处理课程 知识点概要
第1章 数字信号处理概念知识点
1、掌握连续信号、模拟信号、离散时间信号、数字信号的特点及相互关系(时间和幅度的连续性考量) 2、数字信号的产生; 3、典型数字信号处理系统的主要构成。
量化、编码 ——————
采样 ————
模拟信号
离散时间信号
数字信号
5、部分分式法进行逆Z变换 求极点 将X(z)分解成部分分式形式 通过查表,对每个分式分别进行逆Z变换 注:左边序列、右边序列对应不同收敛域 将部分分式逆Z变换结果相加得到完整的x(n)序列 6、Z变换的性质 移位、反向、乘指数序列、卷积
常用序列z变换(可直接使用)
7、DTFT与Z变换的关系
(a) 边界条件 时,是线性的但不是移不变的。
(b) 边界条件 时,是线性移不变的。
令
….
所以:
….
所以:
可见 是移一位的关系, 亦是移一位的关系。因此是移不变系统。
代入差分方程,得:
……..
所以:
因此为线性系统。
3. 判断系统是否是因果稳定系统。
Causal and Noncausal System(因果系统) causal system: (1) 响应不出现于激励之前 (2) h(n)=0, n<0 (线性、时不变系统) Stable System (稳定系统) (1) 有界输入导致有界输出 (2) (线性、时不变系统) (3) H(z)的极点均位于Z平面单位圆内(因果系统)
信号处理的基本知识

传感器类型:根据传感器各构成部分工作方式的不同,可将传感器分成不同的类型;依据接收方式不同,有相对式和绝对式(惯性式)之分;依据机电转换输出量的不同又有发电机型和参数型两种类型。
测量电路可输出不同的关系特性,以适应不同的测试要求。
如位移(间隙)电压特性、速度电压特性、加速度电压特性等等。
所谓相对接收方式,是指以传感器外壳为参考坐标,借助于顶杆或间隙的变化来直接接收机械振动量的一种工作方式。
获得的结果是以外壳为参考坐标的相对振动值。
惯性接收方式通过质量-弹簧单自由度振动系统接收被测振动量,工作时,其外壳固定在振动物体上,整个传感器(包括质量块在内)跟着振动物体一起振动,但其中的机电转换环节---线圈由于是用极为柔软的弹簧片固定在外壳上的,它的自振频率比振动体的振动频率低的多,因而对振动体而言便处于相对静止的状态,换句话说,线圈是固定不动的,是一个绝对参考坐标系统,所以测得的结果是绝对振动值。
惯性接收方式有时也称为地震式。
传感器的性能指标灵敏度:指沿着传感器测量轴方向对单位振动量输入x可获得的电压信号输出值u,即s=u/x。
与灵敏度相关的一个指标是分辨率,这是指输出电压变化量△u可加辨认的最小机械振动输入变化量△x的大小。
为了测量出微小的振动变化,传感器应有较高的灵敏度。
使用频率范围:指灵敏度随频率而变化的量值不超出给定误差的频率区间。
其两端分别为频率下限和上限。
为了测量静态机械量,传感器应具有零频率响应特性。
传感器的使用频率范围,除和传感器本身的频率响应特性有关外,还和传感器安装条件有关(主要影响频率上限)。
动态范围:动态范围即可测量的量程,是指灵敏度随幅值的变化量不超出给定误差限的输入机械量的幅值范围。
在此范围内,输出电压和机械输入量成正比,所以也称为线性范围。
动态范围一般不用绝对量数值表示,而用分贝做单位,这是因为被测振值变化幅度过大的缘故,以分贝级表示使用更方便一些。
相移:指输入简谐振动时,输出同频电压信号相对输入量的相位滞后量。
第四章 阵列信号处理

通常信号的频带B比载波 ω 小很多,即s(t)变化 相对 ω 缓慢,则延时
1 c
r α <<
T
1 B
则可以认为 s (t − r α ) ≈ s (t ) 即信号包络 在各阵元上差异可忽略——窄带信号。
4.2 等距线阵与均匀圆阵
一、等距线阵 M个阵元等距排成一直线,阵元间距为d,到达波 的方向角定义为与阵列法线的夹角 θ ,称为波 达方向(DOA)。 在三维空间中还可以 θ θ 确定信源方位角 ψ
d
5
4
y
ψ
2
1
x
等距线阵(ULA)的方向向量
aULA (θ ) = [1, e = [1, e
−j 2π − j k d sin θ −j
,L, e
2π
− j k ( M −1) d sin θ T
]
λ
d sin θ
,L, e
λ
( M −1) d sin θ
]T
若有多个信源(p个),波达方向分别为 θ i (i − 1, L, p) 方向矩阵为
A = [a(θ1 ), a(θ 2 ),L, a(θ p )] = 1 ⎡ ⎢ e − j 2λπ d sin θ1 =⎢ ⎢ L ⎢ − j 2λπ ( M −1) d sin θ1 ⎣e ⎤ π − j 2λ d sin θ p ⎥ L e ⎥ ⎥ L L π − j 2λ ( M −1) d sin θ p ⎥ L e ⎦ L 1
θ
d sin θ
Vandermonde矩阵
阵列结构不允许其方向向量和空间角之间模糊, 等距线阵阵元间距不能大于 λ ,则可以保证 2 方向矩阵中各个列向量线性独立。 二、等距线阵的阵列响应与方向图 在单个信源情况下,阵列输出为各阵元信号的加 权和(不考虑噪声),
信号预处理 python

信号预处理 python
信号预处理是指对信号进行一系列处理操作,以便为后续的信号处理任务提供更好的输入数据。
在Python中,可以使用一些库和工具来进行信号预处理。
以下是一些常见的信号预处理操作和相应的Python库和工具:
1. 信号滤波:滤波可以去除信号中的噪声和干扰,常用的滤波方法包括移动平均滤波、中值滤波和低通滤波等。
Python中的常用库包括NumPy和SciPy,可以使用这些库中的函数来实现滤波操作。
2. 信号归一化:归一化可以将信号的幅值范围映射到指定的范围内,常用的归一化方法包括最大最小值归一化和Z-score归一化等。
NumPy和SciPy库中的函数可以用于实现归一化操作。
3. 信号降噪:降噪可以去除信号中的噪声成分,常用的降噪方法包括小波去噪和信号平滑等。
Python中的PyWavelets库和SciPy库中的函数可以用于实现降噪操作。
4. 信号分割:分割可以将信号划分为多个部分,以便进行进一步的处理。
常用的分割方法包括基于阈值的分割和基于窗口的分割等。
Python中的NumPy库和SciPy库中的函数可以用于实现分割操作。
5. 信号特征提取:特征提取可以从信号中提取有用的特征,以便进行信号分类和识别等任务。
常用的特征提取方法包括时域特征提取
和频域特征提取等。
Python中的NumPy库和SciPy库中的函数可以用于实现特征提取操作。
以上是一些常见的信号预处理操作和相应的Python库和工具,具体的预处理操作和使用的库可以根据具体的需求进行选择和应用。
数字信号处理知识点

《数字信号处理》辅导一、离散时间信号和系统的时域分析 (一) 离散时间信号(1)基本概念信号:信号传递信息的函数也是独立变量的函数,这个变量可以是时间、空间位置等。
连续信号:在某个时间区间,除有限间断点外所有瞬时均有确定值。
模拟信号:是连续信号的特例。
时间和幅度均连续。
离散信号:时间上不连续,幅度连续。
常见离散信号——序列。
数字信号:幅度量化,时间和幅度均不连续。
(2)基本序列(课本第7——10页)1)单位脉冲序列 1,0()0,0n n n δ=⎧=⎨≠⎩ 2)单位阶跃序列 1,0()0,0n u n n ≥⎧=⎨≤⎩3)矩形序列 1,01()0,0,N n N R n n n N ≤≤-⎧=⎨<≥⎩ 4)实指数序列 ()n a u n5)正弦序列 0()sin()x n A n ωθ=+ 6)复指数序列 ()j n n x n e e ωσ= (3)周期序列1)定义:对于序列()x n ,若存在正整数N 使()(),x n x n N n =+-∞<<∞ 则称()x n 为周期序列,记为()x n ,N 为其周期。
注意正弦周期序列周期性的判定(课本第10页)2)周期序列的表示方法: a.主值区间表示法 b.模N 表示法 3)周期延拓设()x n 为N 点非周期序列,以周期序列L 对作()x n 无限次移位相加,即可得到周期序列()x n ,即()()i x n x n iL ∞=-∞=-∑当L N ≥时,()()()N x n x n R n = 当L N <时,()()()N x n x n R n ≠(4)序列的分解序列共轭对称分解定理:对于任意给定的整数M ,任何序列()x n 都可以分解成关于/2c M =共轭对称的序列()e x n 和共轭反对称的序列()o x n 之和,即()()(),e o x n x n x n n =+-∞<<∞并且1()[()()]2e x n x n x M n *=+- 1()[()()]2o x n x n x M n *=--(4)序列的运算 1)基本运算2)线性卷积:将序列()x n 以y 轴为中心做翻转,然后做m 点移位,最后与()x n 对应点相乘求和——翻转、移位、相乘、求和定义式: 1212()()()()()m y n x m x n m x n x n ∞=-∞=-=*∑线性卷积的计算:A 、图解 B 、解析法C 、不进位乘法(必须掌握)3)单位复指数序列求和(必须掌握)/2/2/2/2/2/21/2/2/2/2/2/2(1)/21()()/(2)1()()/(2)sin(/2)sin(/2)j N j N j N j N j N j N j N N j nj j j j j j j n j N e e e e e e e j ee e e e e e e j N e ωωωωωωωωωωωωωωωωωω------------=-----===---=∑如果2/k N ωπ=,那么根据洛比达法则有sin(/2)(0)(0)(()())sin(/2)N N k N N k N ωδδω===或可以结合作业题3.22进行练习(5)序列的功率和能量能量:2|()|n E x n ∞=-∞=∑功率:21lim |()|21NN n NP x n N →∞=-=+∑ (6)相关函数——与随机信号的定义运算相同(二) 离散时间系统1.系统性质 (1)线性性质定义:设系统的输入分别为1()x n 和2()x n ,输出分别为1()y n 和2()y n ,即1122()[()],()[()]y n T x n y n T x n ==统的输对于任意给定的常数a 、b ,下式成立1212()[()()]()()y n T ax n bx n a y n by n =+=+则该系统服从线性叠加原理,为线性系统,否则为非线性系统。
振动信号处理方法综述_李舜酩

第34卷第8期2013年8月仪器仪表学报Chinese Journal of Scientific InstrumentVol.34No.8Aug.2013收稿日期:2012-11Received Date :2012-11*基金项目:航空基础科学基金(2012ZD52054)资助项目振动信号处理方法综述*李舜酩1,郭海东1,李殿荣2(1.南京航空航天大学能源与动力学院南京210016;2.潍坊小型拖拉机有限公司潍坊261000)摘要:振动信号处理方法一直以来是研究的热点,对设备振动监测和故障诊断都至关重要。
近年来,振动信号的处理方法得到了快速发展,但仍需不断改进和完善。
对近年来的文献进行了分类总结,分别对传统方法中的幅值域分析法、傅里叶变换、相关分析和现代方法中的Wigner-Ville 分布、谱分析、小波分析、盲源分离、Hilbert-Huang 变换及高阶统计量分析的发展、特点以及应用进行了概述和对比分析,最后作出了总结与展望。
关键词:振动信号;处理方法;传统方法;现代方法中图分类号:V231.92文献标识码:A国家标准学科分类代码:590.25Review of vibration signal processing methodsLi Shunming 1,Guo Haidong 1,Li Dianrong 2(1.College of Energy and Power Engineering ,Nanjing University of Aeronautics and Astronautics ,Nanjing 210016,China ;2.Weifang Xiaotuo Tractor Co.,Ltd ,Weifang 261000,China )Abstract :Vibration signal processing method has been an active research topic all the time ,and the equipment vibra-tion monitoring and fault diagnosis are crucial.Though the vibration signal processing methods developed fast in re-cent years ,they still need to be improved and optimized.Some typical approaches referring to recent literatures are classified and summarized in this paper.The developments ,features and applications are presented and discussed for amplitude domain analysis ,Fourier transform ,correlation analysis in traditional methods ,and Wigner-Ville distribu-tion ,spectral analysis ,wavelet analysis ,blind source separation ,Hilbert-Huang transform ,higher order statistics anal-ysis in modern methods.Finally ,we make a conclusion for this paper and an overview is made to guide the future de-velopment in this field.Keywords :vibration signal ;processing method ;traditional method ;modern method1引言信号是信息的载体,为了从实际测量的振动信号中提取各种特征信息,必须采取各种有效的振动信号处理方法进行分析,从而进行参数检测、质量评价、状态监测和故障诊断等,因此振动信号的处理方法已成为科学研究的热点之一[1]。
数字信号处理的常见问题及解决方法总结

数字信号处理的常见问题及解决方法总结数字信号处理在科学、工程领域中的应用越来越广泛。
在实际应用过程中,我们常常会遇到一些问题。
本文总结了一些常见的问题及其解决方法,以帮助读者更好地理解和应用数字信号处理技术。
问题一:信号滤波数字信号往往包含噪声和干扰,需要进行滤波处理以提取有效信息。
常见的信号滤波问题包括滞后滤波器、移动平均滤波器、低通滤波器等。
解决这些问题的方法通常包括设计合适的滤波器参数、选择适当的滤波器类型,并进行滤波器性能评估。
问题二:信号采样率选择在数字信号处理中,采样率的选择对信号重构和频谱分析等方面具有重要影响。
选择过低的采样率会导致信号失真,选择过高的采样率会浪费存储和计算资源。
解决这个问题的方法包括根据信号的带宽和特性选择合适的采样率,并根据需要进行抽取或插值处理。
问题三:频谱分析频谱分析是数字信号处理中的重要步骤,用于研究信号的频域特性。
常见的频谱分析问题包括功率谱密度估计、傅里叶变换等。
解决这些问题的方法包括选择合适的频谱分析方法(如快速傅里叶变换)、处理频谱分辨率问题,并进行频谱分析结果的解释和应用。
问题四:数字滤波器设计数字滤波器的设计是数字信号处理领域的关键问题之一。
常见的数字滤波器设计问题包括低通滤波器设计、高通滤波器设计、带通滤波器设计等。
解决这些问题需要根据滤波器的要求和性能指标,选择适当的设计方法(如窗函数法、频率抽样法),并进行滤波器参数调整和性能评估。
问题五:数字信号压缩数字信号压缩是在保证信号质量的前提下,减少信号数据量的一种技术。
常见的数字信号压缩问题包括有损压缩和无损压缩。
解决这些问题的方法通常包括选择适当的压缩算法(如哈夫曼编码、小波变换压缩),根据压缩效率和信号质量要求进行参数调整。
以上是数字信号处理中常见问题的一些总结及解决方法。
希望能够帮助读者更好地应用数字信号处理技术,解决实际应用中的问题。
常用视频信号接口与处理方法总结
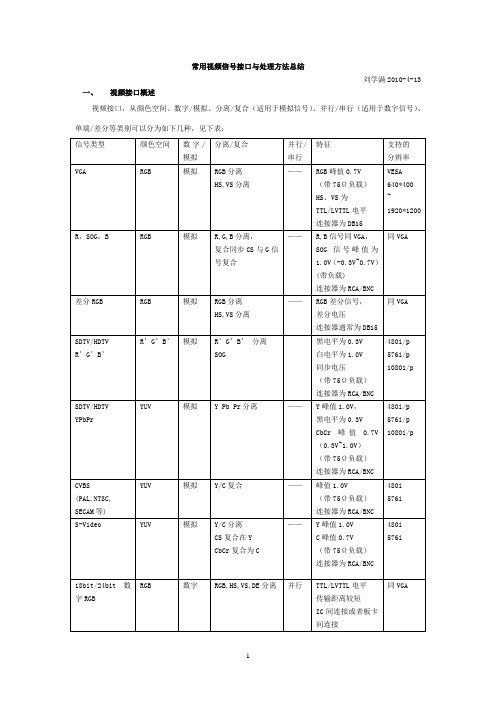
常用视频信号接口与处理方法总结刘学满2010-4-13 一、视频接口概述视频接口,从颜色空间、数字/模拟、分离/复合(适用于模拟信号)、并行/串行(适用于数字信号)、单端/差分等类别可以分为如下几种,见下表:二、模拟视频信号接口1.接口设计模拟信号由于其电压范围很小,如果接口电路设计不当,很可能造成最终的信号质量下降。
因此需要注意以下几个事项:1)阻抗匹配:通常为75Ω,包括发送端,接收端以及传输路径上的阻抗。
2)隔直电容:为了防止不同设备间地电压差对信号造成的影响,此电容不宜过大或者过小。
3)滤波网络:尽可能地消除低频和高频纹波。
4)地平面:根据理论,地平面分隔可以防止数字信号对模拟地干扰,但从实际经验来看,分隔成小的地平面后,实际上会造成环流(AD9883资料中有叙述)。
因此大部分情况下,还是用同一个地。
多层地平面,以及多打过孔,保持地电平的稳定是非常必要的。
5)PCB走线:等长是需要的,而且要确保三个器件经过不同的选择器/缓冲器之后的延时也相差不多,否则很难保证采样相位。
6)ESD保护:如果视频接口经常插拔,就需要加ESD保护二极管。
2.视频ADC完成模拟信号到数字信号的转换,在使用过程中需要注意的主要问题有:1)A/D是否支持交流耦合方式输入2)A/D内部是否有信号增益调整功能3)是否支持差分输入4)A/D内部是否有PLL等器件,采样相位是否可调整5)A/D输出的信号格式(24bit RGB,YCbCr)6)是否支持SOG或者SOY等同步信号输入模拟信号在A/D转换时,通常需要进行一些调整,以达到最佳显示效果:1)调整黑电平位置和最大辐值,通常可以配置A/D芯片有关offset和gain的寄存器,经过此番调整之后,实际上是校准了RGB三色,同时提高了灰度等级。
2)调整PLL锁相环,以达到合适的采样频率,并保证PLL在各种温度条件下均能稳定工作。
3)调整采样起始点和终止点,确保有效信号不丢失。
信号处理中傅里叶变换简介

信号处理中傅里叶变换简介傅里叶变换一、傅里叶变换的表述在数学上,对任意函数f(x),可按某一点进行展开,常见的有泰勒展开和傅里叶展开。
泰勒展开为各阶次幂函数的线性组合形式,本质上自变量未改变,仍为x,而傅里叶展开则为三角函数的线性组合形式,同时将自变量由x变成ω,且由于三角函数处理比较简单,具有良好的性质,故被广泛地应用在信号分析与处理中,可将时域分析变换到频域进行分析。
信号分析与处理中常见的有CFS(连续时间傅里叶级数)、CFT (连续时间傅里叶变换)、DTFT(离散时间傅里叶变换)、DFS(离散傅里叶级数)、DFT(离散傅里叶变换)。
通过对连续非周期信号x c(t)在时域和频域进行各种处理变换,可推导出以上几种变换,同时可得出这些变换之间的关系。
以下将对上述变换进行简述,同时分析它们之间的关系。
1、CFS(连续时间傅里叶级数)在数学中,周期函数f(x)可展开为由此类比,已知连续周期信号x(t),周期为T0,则其傅里叶级数为其中,为了简写,有其中,为了与复数形式联系,先由欧拉公式e j z=cos z+jsin z得故有令则对于D n,有n≤0时同理。
故CFS图示如下:Figure 1理论上,CFS对于周期性信号x(t)在任意处展开都可以做到无误对连续非周期信号x c(t)进行采样,采样间隔为T s,有此时的x s(t)还不是真正的离散信号,它只是在满足t = nT s的时间点上有值,在其它时间点上值为零。
对x s(t)进行进一步处理有规定则其中,x[n]是最终所得的离散信号。
x s(t)自变量为t,其单位为秒s,间隔为T S;x[n]自变量为n,其单位为1,间隔为1。
从频域分析上有其中。
令,定义以上式为DTFT定义式。
DTFT逆变换为DTFT是在时域上对CFT的采样(图示可见Figure 3与Figure 4),在DTFT中,时域信号x[n]为离散的,而对应的频域表示X(e jω)为连续的,且有周期ωs = 2π。
数字信号处理复习总结

数字信号处理复习总结如果系统函数的分母中除a0外,还有其它的ak不为零,则相应的h(n)将是无限长序列,称这种系统为无限长单位脉冲响应(IIR,InfiniteImpulseResponse)系统。
(2)低通、高通、带通、带阻滤波器注意:数字滤波器(DF)与模拟滤波器(AF)的区别数字滤波器的频率响应都是以2π为周期的,滤波器的低通频带处于2π的整数倍处,而高频频带处于π的奇数倍附近。
2.设计指标描述滤波器的指标通常在频域给出。
数字滤波器的频率响应一般为复函数,通常表示为其中,称为幅频响应,称为相频响应。
对IIR数字滤波器,通常用幅频响应来描述设计指标,而对于线性相位特性的滤波器,一般用FIR滤波器设计实现。
IIR低通滤波器指标描述:——通带截止频率,——阻带截止频率,——通带最大衰减,——阻带最小衰减,——3dB通带截止频率3.设计方法(重点)三步:(1)按照实际需要确定滤波器的性能要求。
(2)用一个因果稳定的系统函数去逼近这个性能要求。
(3)用一个有限精度的算法去实现这个系统函数。
IIR滤波器常借助模拟滤波器理论来设计数字滤波器,(重点)设计步骤为:先根据所给的滤波器性能指标设计出相应的模拟滤波器传递函数Ha(s)( butterworth滤波器设计法等,有封闭公式利用),然后由Ha(s)经变换(脉冲响应不变法或者双线性变换法等)得到所需的数字滤波器的系统函数H(z)。
在变换中,一般要求所得到的数字滤波器频率响应应保留原模拟滤波器频率响应的主要特性。
为此要求:(重点)(1)因果稳定的模拟滤波器必须变成因果稳定的数字滤波器;(2)数字滤波器的频响应模仿模拟滤波器的频响。
6.2 脉冲响应不变法、双线性不变法设计IIR数字低通滤波器设计数字滤波器可以按照技术要求先设计一个模拟低通滤波器,得到模拟低通滤波器的传输函数,再按一定的转换关系将转换成数字低通滤波器的系统函数。
其设计流程如图所示6.1所示。
生理信号监测与处理技术评估方法总结

生理信号监测与处理技术评估方法总结概述生理信号监测与处理技术是现代医疗领域中一项关键的技术,可以通过监测人体的各种生理信号,如心电图、脑电图、血压等,来对人体的健康状况进行评估与监测。
然而,不同的监测与处理技术存在一定的差异,并且需要进行科学、准确的评估,以确保其可靠性和有效性。
本文将介绍一些常用的生理信号监测与处理技术评估方法,并总结其优势和局限性。
一、生理信号质量评估方法1. 信号清洗:在进行信号分析之前,需要对原始信号进行预处理,去除噪声和干扰。
常用的信号清洗方法包括滤波、降噪和去伪迹等。
评估方法主要可通过信噪比(SNR)和峰值信噪比(PSNR)来进行,值越高表示信号质量越好。
2. 信号特征提取:信号特征提取是对生理信号进行分析与识别的关键步骤。
评估方法包括频域分析、时域分析和小波分析等。
常用的评估指标包括熵、功率谱密度和相关系数等。
3. 信号分类与识别:通过对提取的特征进行分类与识别,可以实现对生理信号的自动化处理。
评估方法主要通过准确率、灵敏度和特异性进行评估。
二、生理信号传感器评估方法1. 精准度评估:传感器的精准度是评估其测量结果与实际值之间的差异程度。
评估方法主要包括附加误差、线性度和准确性等。
2. 稳定性评估:传感器的稳定性是评估其输出值在相同条件下的长期稳定性。
评估方法包括稳定性系数和漂移等。
3. 响应时间评估:传感器的响应时间是评估其检测值与输入信号变化之间的响应速度。
评估方法主要通过上升时间和下降时间来进行。
三、生理信号处理算法评估方法1. 效率评估:生理信号处理算法的效率主要是评估其运算复杂度和执行速度。
评估方法主要包括计算时间和计算资源消耗。
2. 准确性评估:生理信号处理算法的准确性是评估其处理结果与真实结果之间的差异程度。
评估方法主要通过均方根误差(RMSE)和相关系数来进行评估。
3. 适应性评估:生理信号处理算法的适应性是评估其在不同信号数据和应用场景下的适应能力。
信号处理方法

信号处理方法信号处理是指对信号进行采集、处理、分析和解释的过程。
在现代科技发展中,信号处理方法被广泛应用于通信、图像处理、生物医学工程、雷达、声音处理等领域。
本文将介绍几种常见的信号处理方法,包括滤波、傅里叶变换、小波变换和自适应信号处理。
首先,滤波是一种常见的信号处理方法。
滤波器可以通过增强或者抑制信号的某些频率成分来改变信号的特性。
在通信系统中,滤波器可以用来去除噪声,提高信号的质量;在图像处理中,滤波器可以用来平滑图像、增强图像的边缘等。
常见的滤波器包括低通滤波器、高通滤波器、带通滤波器和带阻滤波器。
其次,傅里叶变换是一种重要的信号处理方法。
傅里叶变换可以将一个时域信号转换为频域信号,从而可以分析信号的频率成分。
傅里叶变换在音频处理、图像处理和通信系统中都有着广泛的应用。
通过傅里叶变换,我们可以得到信号的频谱信息,从而可以进行频域滤波、频域分析等操作。
另外,小波变换是一种近年来备受关注的信号处理方法。
小波变换可以将信号分解为不同尺度的小波函数,从而可以同时获得信号的时域和频域信息。
小波变换在信号压缩、信号去噪、图像处理等领域有着广泛的应用。
与传统的傅里叶变换相比,小波变换可以更好地适应非平稳信号的分析和处理。
最后,自适应信号处理是一种针对信号动态特性的处理方法。
自适应滤波器可以根据信号的实时特性自动调整滤波器的参数,从而可以更好地适应信号的变化。
自适应信号处理在通信系统、雷达系统和生物医学工程中有着重要的应用,可以有效地提高系统的性能和稳定性。
综上所述,滤波、傅里叶变换、小波变换和自适应信号处理是几种常见的信号处理方法。
它们在不同领域有着广泛的应用,可以帮助我们分析和处理各种类型的信号。
随着科技的不断发展,信号处理方法也在不断创新和完善,为我们提供了更多更强大的工具来处理信号,从而推动了科技的进步和应用的拓展。
各种信号处理方法总结

希尔伯特--黄
• (4)优点 • a:HHT能分析非线性非平稳信号。它彻底摆脱了线性和平 稳性束缚,其适用于分析非线性非平稳信号。 • b:HHT具有完全自适应性。HHT能够自适应产生“基”, 即由“筛选”过程产生的IMF。 • c:HHT不受Heisenberg测不准原理制约——适合突变信号。 它可以在时间和频率同时达到很高的精度,这使它非常适 用于分析突变信号。。 • d:HHT的瞬时频率是采用求导得到的。它借助Hilbert变换 求得相位函数,再对相位函数求导产生瞬时频率。这样求 出的瞬时频率是局部性的,而傅立叶变换的频率是全局性 的,小波变换的频率是区域性的。
阶比分析
• 1 、原理:阶比分析的实质是将等时间采样序列 转换成等角度采样序列,从而将时域非稳定信号 转变成角度域稳定信号,以便观察与转速有关的 振动成分。 • 2 、适用信号:非稳定信号 • 3 、优点: • (1)对于转频不断变化的旋转机械振动信号,运 用阶次跟踪分析方法能够避免常规快速傅里叶分 析中出现的“频率模糊”现象。 • (2)由于旋转机械的振动通常与转速有密切联系, 因此阶比分析在旋转机械特征分析的非平稳信号 分析中占有重要地位
倒频谱
• 4 、缺点:进行多段平均的功率谱取对数后,功率谱中与调 制边频带无关的噪声和其他信号也都得到较大的权系数而 放大,降低了信噪比。 • 5 、知识点: • (1)数学上:信号的倒频谱=IFT(log(|FT(信号)|)+j2πm)(m 为实数) • (2)算法:信号 -> 傅立叶变换 -> 取绝对值 -> 取对数 -> 相位展开 -> 逆傅立叶变换 -> 倒频谱 • (3)倒频谱是频谱的频谱。时域信号经过傅立叶积分变换 可转换为频率函数或功率谱密度函数,如果频谱图上呈现 出复杂的周期结构而难以分辨时,对功率谱密度取对数再 进行一次傅立叶积分变换,可以使周期结构呈便于识别的 谱线形式。
常用视频信号接口与处理方法总结

常用视频信号接口与处理方法总结刘学满2010-4-13 一、视频接口概述视频接口,从颜色空间、数字/模拟、分离/复合(适用于模拟信号)、并行/串行(适用于数字信号)、单端/差分等类别可以分为如下几种,见下表:二、模拟视频信号接口1.接口设计模拟信号由于其电压范围很小,如果接口电路设计不当,很可能造成最终的信号质量下降。
因此需要注意以下几个事项:1)阻抗匹配:通常为75Ω,包括发送端,接收端以及传输路径上的阻抗。
2)隔直电容:为了防止不同设备间地电压差对信号造成的影响,此电容不宜过大或者过小。
3)滤波网络:尽可能地消除低频和高频纹波。
4)地平面:根据理论,地平面分隔可以防止数字信号对模拟地干扰,但从实际经验来看,分隔成小的地平面后,实际上会造成环流(AD9883资料中有叙述)。
因此大部分情况下,还是用同一个地。
多层地平面,以及多打过孔,保持地电平的稳定是非常必要的。
5)PCB走线:等长是需要的,而且要确保三个器件经过不同的选择器/缓冲器之后的延时也相差不多,否则很难保证采样相位。
6)ESD保护:如果视频接口经常插拔,就需要加ESD保护二极管。
2.视频ADC完成模拟信号到数字信号的转换,在使用过程中需要注意的主要问题有:1)A/D是否支持交流耦合方式输入2)A/D内部是否有信号增益调整功能3)是否支持差分输入4)A/D内部是否有PLL等器件,采样相位是否可调整5)A/D输出的信号格式(24bit RGB,YCbCr)6)是否支持SOG或者SOY等同步信号输入模拟信号在A/D转换时,通常需要进行一些调整,以达到最佳显示效果:1)调整黑电平位置和最大辐值,通常可以配置A/D芯片有关offset和gain的寄存器,经过此番调整之后,实际上是校准了RGB三色,同时提高了灰度等级。
2)调整PLL锁相环,以达到合适的采样频率,并保证PLL在各种温度条件下均能稳定工作。
3)调整采样起始点和终止点,确保有效信号不丢失。
一些常见的电源地 信号地 数字地和模拟地的处理方式总结

一些常见的电源地信号地数字地和模拟地的处理方式总结一般在我们的AD系统里面,都有非常明确的模拟电源/模拟地和数字电源/数字地,这些的处理相对比较重要。
通常的系统中:1、我们常用10~20欧姆电阻来做模拟电源和数字电源的隔离。
当然,使用分组的隔离电源是最好的选择,但是成本相对较高。
2、处理模拟地和数字地时,最终使用1点接连的办法,这个连接点要选在PCB上的电荷平衡点,以防止出现电压差,这需要良好的PCB和模拟设计基础及经验。
3、使用PSRR较高的LDO,尽量避免使用DCDC 和纹波超过300UV的电源稳压器件。
当然,我们可以通过差分输入来减少来自电源的干扰。
4、良好的屏蔽罩同样可以减少外部空间电磁辐射对AD系统的影响,诸如雷达、手机辐射、紫外线等。
电源地主要是针对电源回路电流所走的路径而言的,一般来说电源地流过的电流较大,而信号地主要是针对两块芯片或者模块之间的通信信号的回流所流过的路径,一般来说信号地流过的电流很小,其实两者都是GND,之所以分开来说,是想让大家明白在布PCB板时要清楚地了解电源及信号回流各自所流过的路径,然后在布板时考虑如何避免电源及信号共用回流路径,如果共用的话,有可能会导致电源地上的大电流在信号地产生一个电压差(可以解释为:导线是有阻抗的,只是阻值很小,但如果所流过的电流较大时,也会在此导线上产生电位差,这也叫共阻抗干扰),使信号地的真实电位高于0V。
信号地的电位较大时,有可能会使本来是高电平的信号被误判为低电平。
当然电源地本来就很不干净,这样做也可以避免由于干扰使信号误判。
所以将电源地和信号地在布线时稍微注意一下,就可以。
一般来说即使在一起也不会产生大的问题,因为数字电路的门限较高。
除了正确进行接地设计、安装,还要正确进行各种不同信号的接地处理。
控制系统中,大致有以下几种地线:(1)数字地:也叫逻辑地,是各种开关量(数字量)信号的零电位。
(2)模拟地:是各种模拟量信号的零电位。
信号分析与处理

信号分析与处理第一章绪论:测试信号分析与处理的主要内容、应用;信号的分类,信号分析与信号处理、测试信号的描述,信号与系统。
测试技术的目的是信息获取、处理和利用。
测试过程是针对被测对象的特点,利用相应传感器,将被测物理量转变为电信号,然后,按一定的目的对信号进行分析和处理,从而探明被测对象内在规律的过程。
信号分析与处理是测试技术的重要研究内容。
信号分析与处理技术可以分成模拟信号分析与处理和数字信号分析与处理技术。
一切物体运动和状态的变化,都是一种信号,传递不同的信息。
信号常常表示为时间的函数,函数表示和图形表示信号。
信号是信息的载体,但信号不是信息,只有对信号进行分析和处理后,才能从信号中提取信息。
信号可以分为确定信号与随机信号;周期信号与非周期信号;连续时间信号与离散时间信号;能量信号与功率信号;奇异信号周期信号无穷的含义,连续信号、模拟信号、量化信号,抽样信号、数字信号在频域里进行信号的频谱分析是信号分析中一种最基本的方法:将频率作为信号的自变量,在频域里进行信号的频谱分析; 信号分析是研究信号本身的特征,信号处理是对信号进行某种运算。
信号处理包括时域处理和频域处理。
时域处理中最典型的是波形分析,滤波是信号分析中的重要研究内容;测试信号是指被测对象的运动或状态信息,表示测试信号可以用数学表达式、图形、图表等进行描述。
常用基本信号(函数)复指数信号、抽样函数、单位阶跃函数单位、冲激函数(抽样特性和偶函数)序列、单位阶跃序列、斜变序列、正弦序列、复指数序列。
离散序列用图形、数列表示,常见序列单位抽样系统是指由一些相互联系、相互制约的事物组成的具有某种功能的整体。
被测系统和测试系统统称为系统。
输入信号和输出信号统称为测试信号。
系统分为连续时间系统和离散时间系统。
系统的主要性质包括线性和非线性,记忆性和无记忆性,因果系统和非因果系统,时不变系统和时变系统,稳定系统和非稳定系统。
第二章连续时间信号分析:周期信号分析(傅立叶级数展开)非周期信号的傅立叶变换、周期信号的傅立叶变换、采样信号分析(从连续开始引入到离散)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
FFT
• 4 、缺点: • (1)Fourier变换是整个时间域内的积分,不能 反映某一局部时间内信号的频谱特性,即在时间 域上没有任何分辨率。(全局变换) • (2)Fourier变换可能会漏掉较短时间内信号的 变化,特别是少数突出点,造成所谓的“谱涂抹” 现象。 • (3)这种方法对于当原始信号为平稳且具有明显 区别的频谱特性时是比较有效的。
STFT
• 4 、缺点: • (1)短时傅里叶变换用来分析分段平稳信号或者 近似平稳信号犹可,但是对于非平稳信号,当信 号变化剧烈时,要求窗函数有较高的时间分辨率; 而波形变化比较平缓的时刻(主要是低频信号), 则要求窗函数有较高的频率分辨率。短时傅里叶 变换不能兼顾频率与时间分辨率的求 。 • (2)短时傅里叶变换使用一个固定的窗函数,窗函 数一旦确定了以后,其形状和大小就不再发生改 变,短时傅里叶变换的分辨率也就确定了。如果 要改变分辨率,则需要重新选择窗函数。
信号处理方法总结
盛媛媛
FFT
• 1 、原理:FFT是离散傅立叶变换的快速算法, 可以将一个信号变换到频域。有些信号在时域上 是很难看出什么特征的,但是如果变换到频域之 后,就很容易看出特征了。 • 2 、适用信号:在分析线性、平稳信号时,傅立叶 变换有优良的性能。 • 3 、优点:利用傅立叶变换把信号映射到频域内, 可以看频域上的频率和相位信息,提取信号的频 谱 ,用信号的频谱特性分析时域内难以看清的问 题。
• 重采样方法:先以恒时间间隔增量Δt , 记录数据, 即对原始数据进行第1次采样,得到时域采样信号。 同时,振动信号和转速信号也在相同的时间间隔被 同步采样,然后根据转速信号来控制采样频率,使 采样频率跟踪转速的变化而变化来进行第2 次采 样即重采样,如果我们要求重采样按每一转速周期 固定采样次数的方式进行,就将等时间间隔的数字 采样转变成等角度间隔的采样, 然后将重采样得 到的信号用角度坐标表达出来, 进行类似于时间 变量的傅氏变换,就可获得在角度坐标上稳定不移 动的基频和其他阶次的分量。这种方法也称为阶 次跟踪分析
小波分析
• 1 、原理:小波分析是一种窗口的大小固定、形 状可变,时间窗和频率窗都可以改变的时频局部 化信号分析方法,即在低频部分具有较高的频率分 辨率和较低的时间分辨率。在高频部分具有较高 的时间分辨率和较低的频率分辨率。 • 2 、适用信号:很适合分析非平稳信号和提取信 号的局部特征。 • 3 、优点: • (1)时域和频域同时具有良好的局部性质,因而 能有效的从信号中提取资讯,能够较准的检测出 信号的奇异性及其出现位置。
希尔伯特变换
• 1 、原理:将信号s(t)与1/(πt)做卷积,以得到s'(t)。 因此,希尔伯特变换结果s'(t)可以被解读为输入是s (t)的线性非时变系统的输出,而此系统的脉冲响 应为1/(πt)。 • 2 、适用信号:窄带信号 • 3 、优点: • (1)通过希尔伯特变换,使得我们对短信号和复杂 信号的瞬时参数的定义及计算成为可能,能够实现 真正意义上的瞬时信号的提取。 • (2)用Hilbert变换就是为了构造解析信号,因为在 分析中用解析信号比较方便,而且该解析信号的谱 是原信号谱的1/2(正半轴的谱)。
阶比分析
(4)知识点: • 阶次分析:阶次就是参考轴(如主轴)每转内发 生的循环振动次数,也即振动频率与轴频之比。 (基准频率(转轴转速)的倍数) O=循环振动次数/r(阶) • 阶次与频率的关系为:f=o*n/60 • 其中,o为阶次,n为参考轴转速(r/min),f为信 号的振动频率。
阶比分析
小波分析
• (2)小波分析具有能够根据分析对象自动调整有 关参数的“自适应性”和能够根据观测对象自动 “调焦”的特性。 • 4 、缺点: • (1)时间窗口与频率窗口的乘积为一个常数。这 就意味着如果要提高时间精度就得牺牲频率精度, 反之亦然,故不能在时间和频率同时达到很高的 精度。 • (2)小波变换通过小波基的伸缩和平移实现信号 的时频分析局部化, 小波基一旦选定,在整个信号 分析过程中只能使用这一个小波基。这将造成信 号能量的泄露,产生虚假谐波。
倒频谱
• 4 、缺点:进行多段平均的功率谱取对数后,功率谱中与调 制边频带无关的噪声和其他信号也都得到较大的权系数而 放大,降低了信噪比。 • 5 、知识点: • (1)数学上:信号的倒频谱=IFT(log(|FT(信号)|)+j2πm)(m 为实数) • (2)算法:信号 -> 傅立叶变换 -> 取绝对值 -> 取对数 -> 相位展开 -> 逆傅立叶变换 -> 倒频谱 • (3)倒频谱是频谱的频谱。时域信号经过傅立叶积分变换 可转换为频率函数或功率谱密度函数,如果频谱图上呈现 出复杂的周期结构而难以分辨时,对功率谱密度取对数再 进行一次傅立叶积分变换,可以使周期结构呈便于识别的 谱线形式。
STFT
• 1 、原理:把信号划分成许多较小的时间间隔,
并且假定信号在短时间间隔内是平稳(伪平稳) 的,用Fourier变换分析每一个时间间隔,以确定 该间隔存在的频率,以达到时频局部化之目的。 • 2适用信号:平稳信号
• 3、 优点:
• (1)比起傅里叶变换更能观察出信号瞬时频率的信 息。 • (2)在一定程度上,克服了傅里叶变换全局变换的 缺点。
阶比分析
• 1 、原理:阶比分析的实质是将等时间采样序列 转换成等角度采样序列,从而将时域非稳定信号 转变成角度域稳定信号,以便观察与转速有关的 振动成分。 • 2 、适用信号:非稳定信号 • 3 、优点: • (1)对于转频不断变化的旋转机械振动信号,运 用阶次跟踪分析方法能够避免常规快速傅里叶分 析中出现的“频率模糊”现象。 • (2)由于旋转机械的振动通常与转速有密切联系, 因此阶比分析在旋转机械特征分析的非平稳信号 分析中占有重要地位
倒频谱
• 1 、原理:倒频谱,就是对功率谱的对数值进行傅立叶逆 变换,将复杂的卷积关系变为简单的线性叠加,从而在其 倒频谱上可以较容易地识别信号的频率组成分量,便于提 取所关心的频率成分较准确地反映故障特性。 • 2 、适用信号:时域信号 • 3 、优点: • (1)该分析方法受传感器的测点位置及传输途径的影响 小,能将原来频谱图上成族的边频带谱线简化为单根谱线, 对于具有同族谐频、异族谐频和多成分边频等复杂信号的 分析甚为有效。 • (2)可以分析复杂频谱图上的周期结构,分离和提取在 密集调频信号中的周期成分,
