控制工程第3章习题解答
控制工程基础习题解答3
控制工程基础习题解答第三章3-1.已知二阶系统的闭环传递函数为()()2222nn n s s s R s C ωςωω++=,其中ζ=0.6,ωn =5rad/s ,试求在单位阶跃输入下的瞬态响应指标t r 、t p 、σp %、和t s 。
解:srad radn d /46.0151927.013.536.06.01tan1tan222121=-=-==︒=-=-=--ςωωςςβ 0.55(s)4927.0=-=-=πωβπd r t ()s t d p 79.04===πωπ %5.9%226.016.01===----πςςπσe e p()()s t s t ns ns 33.156.044156.033=⨯===⨯==ςωςω3-2.已知某系统的框图如图3-16所示,要求系统的性能指标为σp%=20%,t p =1s ,试确定系统的K 值和A 值,并计算t r 和t s 之值。
解:()()KAK K Ks AK s Ks n 2112+==+++=ςωφ45.02.0%21===--ςσςςπe p()s rad s t n n d p /52.3145.012==-==ωωπωπ17.039.12145.039.1221239.122=-⨯⨯=-===K K A K n ςωsrad radn d /14.345.0152.311.145.045.01tan1tan222121=-=-==-=-=--ςωωςςβ 0.65(s)14.31.1=-=-=πωβπd r t ()()%252.252.345.044%589.152.345.033±=⨯=±=⨯==, =, s s t nns ςωςω3-3.某系统的开环传递函数为()ss s G n n ςωω222+=,为使单位反馈的闭环系统对单位阶跃输入的瞬态响应具有σp %=5%的超调量和t s =2s 的调整时间,试确定系统的ζ和ωn 的值。
《控制工程基础》课程作业习题(含解答)
第一章概论本章要求学生了解控制系统的基本概念、研究对象及任务,了解系统的信息传递、反馈和反馈控制的概念及控制系统的分类,开环控制与闭环控制的区别;闭环控制系统的基本原理和组成环节。
学会将简单系统原理图抽象成职能方块图。
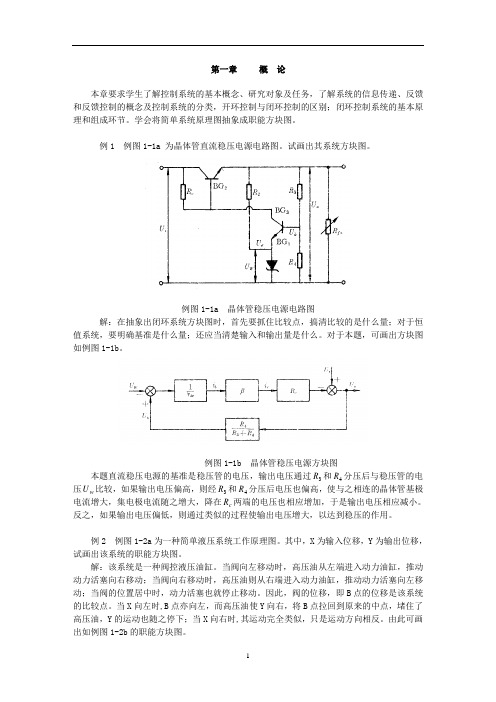
例1 例图1-1a 为晶体管直流稳压电源电路图。
试画出其系统方块图。
例图1-1a 晶体管稳压电源电路图解:在抽象出闭环系统方块图时,首先要抓住比较点,搞清比较的是什么量;对于恒值系统,要明确基准是什么量;还应当清楚输入和输出量是什么。
对于本题,可画出方块图如例图1-1b。
例图1-1b 晶体管稳压电源方块图本题直流稳压电源的基准是稳压管的电压,输出电压通过R和4R分压后与稳压管的电3压U比较,如果输出电压偏高,则经3R和4R分压后电压也偏高,使与之相连的晶体管基极w电流增大,集电极电流随之增大,降在R两端的电压也相应增加,于是输出电压相应减小。
c反之,如果输出电压偏低,则通过类似的过程使输出电压增大,以达到稳压的作用。
例2 例图1-2a为一种简单液压系统工作原理图。
其中,X为输入位移,Y为输出位移,试画出该系统的职能方块图。
解:该系统是一种阀控液压油缸。
当阀向左移动时,高压油从左端进入动力油缸,推动动力活塞向右移动;当阀向右移动时,高压油则从右端进入动力油缸,推动动力活塞向左移动;当阀的位置居中时,动力活塞也就停止移动。
因此,阀的位移,即B点的位移是该系统的比较点。
当X向左时,B点亦向左,而高压油使Y向右,将B点拉回到原来的中点,堵住了高压油,Y的运动也随之停下;当X向右时,其运动完全类似,只是运动方向相反。
由此可画出如例图1-2b的职能方块图。
例图1-2a 简单液压系统例图1-2b 职能方块图1.在给出的几种答案里,选择出正确的答案。
(1)以同等精度元件组成的开环系统和闭环系统,其精度比较为_______ (A )开环高; (B )闭环高; (C )相差不多; (D )一样高。
(2)系统的输出信号对控制作用的影响 (A )开环有; (B )闭环有; (C )都没有; (D )都有。
控制工程期末试题 (3)

第3章补充习题一、填空题1.系统分析是指对系统的___稳定性____、____误差_____和___动态特性______三方面的性能指标进行分析。
2.控制系统分析的目的是确定系统的___稳定性____、___误差______和___动态特性______。
3.在控制系统分析时,人们经常选用的典型信号有__阶跃信号___、__速度信号___、___加速度信号___、__脉冲信号___和__正弦信号_____。
4.如果系统的实际输入信号具有突变的性质,可以选用___单位阶跃____信号作为输入信号进行试验。
5.如果系统的实际输入信号具有随时间逐渐变化的性质,可以选用_______信号作为输入信号进行试验。
6.凡能够用一阶微分方程描述的系统称为___一阶系统________。
7.一阶系统的典型环节也称为____惯性环节___________。
8.系统在单位阶跃信号作用下的输出称为__单位阶跃响应_____________。
9.一阶惯性环节的单位阶跃响应的时域数学表达式是___________。
10.一阶惯性环节一定是稳定的和___无__振荡的。
11.一阶惯性环节的时间常数可以用实验测出的单位阶跃响应曲线达到__0.632__高度点时所对应的时间来确定。
12.一阶惯性环节的时间常数越小,系统的惯性_越小_______。
13.一阶惯性环节的时间常数越小,系统的响应___快_____。
14.一阶惯性环节的阶跃响应在半对数坐标纸上是__t 1-x0(t)______。
15.一阶惯性环节的单位速度响应的时域数学表达式是___________。
16.系统在单位速度信号作用下的输出称为____单位速度响应___________。
17.一阶惯性环节在单位速度信号作用下的稳态误差是____T_______。
18. 系统在单位脉冲信号作用下的输出称为_____单位脉冲响应_________。
19.一阶惯性环节的单位脉冲响应的时域数学表达式是___________。
现代控制工程基础第三章习题解答

解:
s5
1
2 11
s4
2
4 10
s3 0(ε)
6
4ε −12
s2
ε
10
s1
−10ε 2 + 24ε − 72 4ε −12
s0
10
当ε→0+时,第一列变了两次符号,故在右半平面
有两个正根。
10
(5) D(s)=s6+2s5+8s4+12s3+20s2+16s+16=0
解: s6 s5 s4 s3 s2 s1 s0
5
s0 K-8
第一列元素全部大于零,可得
8<K<18
13
3.14 已知单位负反馈的开环传递函数如下,试求系统在
输入信号分别为r(t)=1,t和t2时的稳态误差ess。
(1)
G(s) =
100
(0.1s +1)(0.5s +1)
解:闭环系统特征方程 D(s) = 0.01s2 + 0.6s +101 = 0 稳定的。
Hale Waihona Puke ess=1 1+ Kp
=1 1+ KK1
18
Vr
−
K1
+
K2 s
K Ts +1
Vc
(2) 当K2≠0时,求Vr(t)=1(t)时的稳态误差ess; I型系统,开环传递函数 G(s) = K(K1s + K2)
s(Ts +1)
当Vr(t)=1(t)时,静态位置误差系数
Kp
=
lim G(s)
s→0
=
∞
时速度误差系数为Kv=6?此时的ess为多少?
机械控制工程基础第3章习题解答

由于前述 K h 0.116
101 0.116 s 则系统的传递函数为: G s 2 s 3.16 s 10
输入单位阶跃 X i s
101 0.116 s X o s Gs X i s s 2 3.16 s 10 s 0.42 2.74 1 s 1.58 2.74 X o s s s 1.582 2.742 s 1.582 2.742
单位反馈,开环传递函数为:
Ⅱ 型,开环增益为
an K an 2
an 2 e ss an
3.16
101 K h s G s 2 s 2 10K h s s 10
K h 0.116
n 10 1 / s 3.161 / s 0.5 M p 16.3% 直接代入公式: t s 2.53 s 2% t 1.897 s 5% s
单位阶跃响应:x
ou
t 201 e
t / 2.5
xou t wt
3.8
3.12
微分关系
9 3 G s 2 s s 9 s 2 2 1 3s 32 6 n 31 / s M 58.8% p 0.167
求导,得到最大值
M p 17. 7%
clear all; close all; t=0:0.01:5; y=1-exp(-1.58*t).*cos(2.74.*t) -0.1533.*exp(-1.58*t).*sin(2.74.*t); %output express figure; h=plot(t,y,’r’); set(h,’linewidth’,5) set(gca, ’fontsize’,16) [mp_abs ,tp_space]=max(y(:)); %0.1772 mp= mp_abs–1; %计算最大超调量0.1772 tp= tp_space.*0.01; %计算峰值时间 grid on; i=tp_space; while abs(y(i)-1)>0.02 i=i+1; end ts=i.*0.01; %计算调整时间ts=1.69s
控制工程基础第三章参考答案

第三章 习题及答案传递函数描述其特性,现在用温度计测量盛在容器内的水温。
发现需要时间才能指示出实际水温的98%的数值,试问该温度计指示出实际水温从10%变化到90%所需的时间是多少?解: 41min, =0.25min T T = 1111()=1-e0.1, =ln 0.9t h t t T -=-T21T22()=0.9=1-e ln 0.1t h t t T -=-,210.9ln2.20.55min 0.1r t t t T T =-===2.已知某系统的微分方程为)(3)(2)(3)(t f t f t y t y +'=+'+'',初始条件2)0( , 1)0(='=--y y ,试求:⑴系统的零输入响应y x (t );⑵激励f (t ) (t )时,系统的零状态响应y f (t )和全响应y (t );⑶激励f (t ) e 3t(t )时,系统的零状态响应y f (t )和全响应y (t )。
解:(1) 算子方程为:)()3()()2)(1(t f p t y p p +=++)()e 25e 223()()()( )()e 21e 223()()()( )()e e 2()(2112233)( )2(;0 ,e 3e 4)( 34221e e )( 2x 2222x 212121221x t t y t y t y t t t h t y t t h p p p p p p H t t y A A A A A A A A t y t t t t t t f f t t ttεεεε------------+=+=+-==-=⇒+-+=+++=-=⇒⎩⎨⎧-==⇒⎩⎨⎧--=+=⇒+=∴* )()e4e 5()()()( )()e e ()(e )()( )3(2x 23t t y t y t y t t t h t y ttt t t f f εεε------=+=-==*3.已知某系统的微分方程为)(3)(')(2)(' 3)(" t f t f t y t y t y +=++,当激励)(t f =)(e4t tε-时,系统2的全响应)()e 61e 27e314()(42t t y t t tε-----=。
机械控制工程基础第三章 复习题及答案

题目:时间响应由 和 两部分组成。
分析与提示:时间响应由瞬态响应和稳态响应两部分组成。
答案:瞬态响应、稳态响应题目:系统的输出量从初始状态到稳定状态的响应过程,称为 。
分析与提示:瞬态响应,指系统在某一输入信号作用下,系统的输出量从初始状态到稳定状态的响应过程。
答案:瞬态响应题目:系统的时间响应可从两方面分类,按振动性质可分为 与 。
分析与提示:系统的时间响应可从两方面分类,按振动性质可分为自由响应与强迫响应。
答案:自由响应、强迫响应题目:系统的时间响应可从两方面分类,按振动来源可分为 与 。
分析与提示:系统的时间响应可从两方面分类,按振动性质可分为自由响应与强迫响应;按振动来源可分为零输入响应(即由“无输入时系统的初态”引起的自由响应)与零状态响应(即仅由输入引起的响应)。
答案:零输入响应、零状态响应题目:系统微分方程的特解就是系统由输入引起的输出(响应),工程上称为 。
分析与提示:初始条件及输入信号产生的时间响应就是微分方程的全解。
包含通解和特解两个部分。
通解完全由初始条件引起的,它是一个瞬态过程,工程上称为自然响应 (如机械振动中的自由振动)。
特解只由输入决定,特解就是系统由输入引起的输出(响应),工程上称为强迫响应 (如机械振动中的强迫振动)。
答案:强迫响应题目:系统的瞬态响应不仅取决于系统本身的特性,还与外加 的形式有关。
分析与提示:系统的瞬态响应不仅取决于系统本身的特性,还与外加输入信号的形式有关。
答案:输入信号题目:单位阶跃信号⎩⎨⎧<>=000t t t u1)(的拉氏变换为【 】A 、s 1 B 、21sC 、1D 、s 分析与提示:熟练掌握典型信号的拉氏变换。
B 为单位斜坡信号的拉氏变换,C 为单位冲击信号的拉是变换。
答案:A题目:选取输入信号应当考虑以下几个方面,输入信号应当具有 ,能够反映系统工作的大部分实际情况。
分析与提示:选取输入信号应当考虑以下几个方面,输入信号应当具有典型性,能够反映系统工作的大部分实际情况。
大气污染控制工程(郝吉明版) 课后习题答案:Unlock-3

dP = −g ρ ⋅dZ (1)
将空气视为理想气体,即有
PV = m RT 可写为 ρ = m = PM (2)
M
V RT
将(2)式带入(1),并整理,得到以下方程:
dP gM = − dZ
P RT
假定在一定范围内温度 T 的变化很小,可以忽略。对上式进行积分得:
gM ln P = − Z + C
=
−0.72K
/
100m
,故γ
2
= −G2
= 0.72K / 100m < γ d ,稳定;
G3
=
∆T3 ∆z3
=
8.9 −15.6 580
= −1.16K
/100m ,故γ 3
= −G3
= 1.16K / 100m
> γ d ,不稳定;
G4
=
∆T4 ∆z4
=
5.0 − 25.0 2000
= −1K / 100m ,故 γ 4
放后陆续发回相应的气温和气压记录如下表所给。1)估算每一组数据发出的高度;2)以高
度为纵坐标,以气温为横坐标,作出气温廓线图;3)判断各层大气的稳定情况。
测定位置 2
3
4
5
6
7
8
9
10
气温/。C 9.8
12.0 14.0 15.0 13.0 13.0 12.6 1.6
0.8
气压/hPa 1012 1000 988 969 909 878 850 725 700
=
3.33m / s
u5
=
u
0
(
Z Z
5 0
) 0.15
=
2 × ( 400) 0.15 10
机械控制工程基础习题集

《机械控制工程基础》习题及解答目录第1章绪论第2章控制系统的数学模型第3章控制系统的时域分析第4章控制系统的频域分析第5章控制系统的性能分析第6章控制系统的综合校正第7章模拟考试题型及分值分布第1章绪论一、选择填空题1.开环控制系统在其控制器和被控对象间只有(正向作用)。
P2A.反馈作用B.前馈作用C.正向作用D.反向作用2.闭环控制系统的主反馈取自(被控对象输出端)。
P3A.给定输入端B.干扰输入端C.控制器输出端D.系统输出端3.闭环系统在其控制器和被控对象之间有(反向作用)。
P3A.反馈作用B.前馈作用C.正向作用D.反向作用A.输入量B.输出量C.反馈量D.干扰量4.自动控制系统的控制调节过程是以偏差消除(偏差的过程)。
P2-3A.偏差的过程B.输入量的过程C.干扰量的过程D.稳态量的过程5.一般情况下开环控制系统是(稳定系统)。
P2A.不稳定系统B.稳定系统C.时域系统D.频域系统6.闭环控制系统除具有开环控制系统所有的环节外,还必须有(B)。
p5A.给定环节B.比较环节C.放大环节D.执行环节7.闭环控制系统必须通过(C)。
p3A.输入量前馈参与控制B.干扰量前馈参与控制C.输出量反馈到输入端参与控制D.输出量局部反馈参与控制8.随动系统要求系统的输出信号能跟随(C的变化)。
P6A.反馈信号B.干扰信号C.输入信号D.模拟信号9.若反馈信号与原系统输入信号的方向相反则为(负反馈)。
P3A.局部反馈B.主反馈C.正反馈D.负反馈10.输出量对系统的控制作用没有影响的控制系统是(开环控制系统)。
P2A.开环控制系统B.闭环控制系统C.反馈控制系统D.非线性控制系统11.自动控制系统的反馈环节中一般具有( B )。
p5A..给定元件B.检测元件 C.放大元件 D.执行元件12. 控制系统的稳态误差反映了系统的〔 B 〕p8A. 快速性B.准确性C. 稳定性D.动态性13.输出量对系统的控制作用有直接影响的系统是( B )p3A.开环控制系统B.闭环控制系统C.线性控制系统D.非线性控制系统14.通过动态调节达到稳定后,被控量与期望值一致的控制系统为(无差系统)。
《控制工程基础》第二版课后习题答案
第二章习题解答a) b)c——II— -------------- oC、1 i\Ro J pa)1必)=i(t)RRC _ %(" + u0(if = RC—曲(f) dt dt- ■Bb)M)=冲务甜("7 G)】} Mf)=fK(t) = Kx o(t)~iR o-i = 1R +4— f/?r二R严肖"吗=心站+u o C)R\R2C ~~ U n(^)+(^1 + R Z)U O0)= R&H 亍气Q) + R/i Q) at atKi f\({\ Bf dXj dx o、dt dt > Mld) d d临也吸临⑷+W)―吋2-^^^_]]_ 纟K (曲= A?2 (X 0 一 X } = B仗严心怡£陀©+“K 州(0=曲Q”K]K 円⑴dtdt10G02町 _9_-cLPQd 一%二遢十汕 itj =也十迢2dxdt17 G(5) =+ 5S 7 + 9$+ 7(Z l)(g +2)加]州2 £早+ (刚裙2 +旳坷+朋2*1 +砒2厉)今¥t/N+ (料《2 + 粮[K \ + BjS 》+ 〃1虽 + B2B3) &三川r+ (隔 + K 岛 + K 2B { + K% 爭 + K 、K 血 di二严 3dtJ + c@+Q )M +卯G(»E + 2捉£+1)? (£+3)3 辭 +25^8占(& +X| X 3")一3 一场鲁办J dt j83 GM )={$+□)($+帶E _a 1 c —b= ------------------ H ------(a-b)2 s + a a-b (5+6)2 (m —方尸 £+方8&⑷—用◎十2)(2十2f 十4)g(t) = £"[G<s)] = 1-2e~^ 十 e~x casVif, i H 0的4[G (帕和一遇型za~c 1g(z)=£-1[G(i)] = -_小+ -_ +- (d -by L@ ~^r a7 G(s) = ——5(x¥ + l)2 (-S + 3)_ 2 1 J 113 1 ~ 3 S 12 5 + 32(£ + l)2 45 + 1 <31 \—+ —/ e 就2丿2 ig ⑴=£T[G(9]=T 年号e _3r- 丸r>0■< />o 54 1i-2^—-F s £+ 2 s 1 +4\2士十(卄1乎+?1 1~2~ 13(恥吊P 血再1 s<D 2 S 2十血'= £+2 + ———{盼如2)g (t )= A _1[Gf5)] = 4s (r )+ 28(0+ 2k-&亠,r>oat242 x\t) - x(f) = 4sin/ + 5cos2r s x(0) = 1, x*(0) =-2h{7) + 2^(O+5X(0 = 3, X (0) = 0. /(0) = 01V2 2-肮(0)-玖 0) - X(f) = 4—^ + 5—^Z + l E+4 ^-2+4—!—+ 5^—M-U 2+4 s^i(s-2)(s 7 +1)(v 2 十4)十4(2 十4)+5$(W +1)-lXW+l)(/+4)X0)=丄--2 --誉亠l s —1K ?2 +1 Q+4x(f)=L ,+e r -2sin/—cos2/» t>0 3 Q X(s)+2sX(s) + 5X(s)=- s217OV+l)(A+2)0.6--0.6 1S'^ s ($ + 1尸+4M/)=(L6—OWL cos1^0.3e_f sin2c t>0*叫+2$+疔sI M +1= 0,6--0.6—二——03 _s (s+1)' 4 4 G+l”+4fl^+(l+b l^)(一+H Ish (I十 b 賀)(1—fl +^1嘗) ——® O S 丄A)ao3涉十朋+ KJ益(的-§誠⑻=(月弭+ KjXf ($)⑷=(伽+ KjX(R(恥+KXd”K』(s + K^)(B^ s + KJ + K\ R、s6b叱(4予(f)-怎(0-禹(0 .农⑴二恥(f)I馆(0二心比⑴-艾⑴]!如皆加)=陀)xz=乔二耳⑶-%⑸-压戈㈤F K^)=K{X O(S)同=忑[兀(町-*(舟]_ffl$Cl 2-0血⑴1Bs念(f)Rib)o-^附(f)o—1CG021mv2血(f)IId)讹f)-o/脚(f)二浙go-尤;(f)]办⑴二忌⑴-入⑹ 齐2(彳)=屍竝⑴儿⑴二丄[為㈤+耳㈤ms>耳(刀=銅心)-儿(创&©)=司尤⑷—血⑴]伦㈤=竝A31.心)—*2-10Cl-HI—R\ &RiC,必)o—b)卞C:就f)-------------- od)>□—+= i 护!z jy/7(^f+ b)J —+ 切”=(l)°n31~~|__H[—o―[J G)1?衍i"+ (T + ^3^)(1+訓。
控制工程基础第3章习题解答
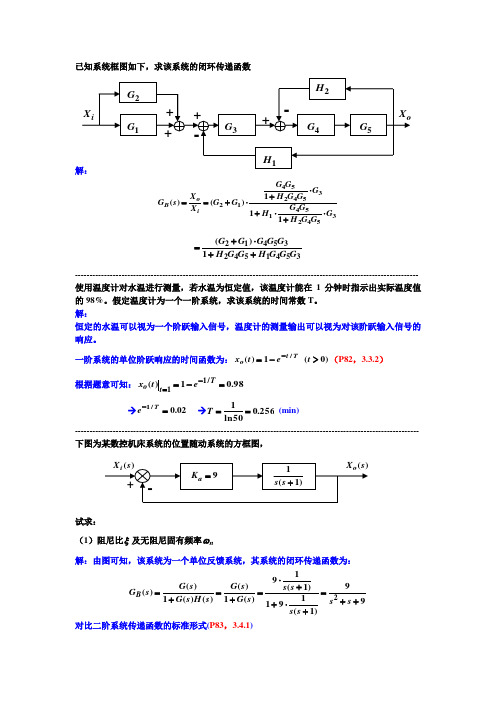
已知系统框图如下,求该系统的闭环传递函数354254135425412111)()(G G G H G G H G G G H G G G G X X s G io B ⋅+⋅+⋅+⋅+==3541542354121)(G G G H G G H G G G G G ++⋅+=---------------------------------------------------------------------------------------------------------------------- 使用温度计对水温进行测量,若水温为恒定值,该温度计能在1分钟时指示出实际温度值的98%。
假定温度计为一个一阶系统,求该系统的时间常数T 。
解:恒定的水温可以视为一个阶跃输入信号,温度计的测量输出可以视为对该阶跃输入信号的响应。
一阶系统的单位阶跃响应的时间函数为:)0(1)(/>-=-t e t x T t o (P82,3.3.2) 根据题意可知:98.01)(/11=-=-=Tt o e t x→02.0/1=-T e →256.050ln 1==T (min) ---------------------------------------------------------------------------------------------------------------------- 下图为某数控机床系统的位置随动系统的方框图,试求:(1)阻尼比ξ及无阻尼固有频率n ω解:由图可知,该系统为一个单位反馈系统,其系统的闭环传递函数为:99)1(191)1(19)(1)()()(1)()(2++=+⋅++⋅=+=+=s s s s s s s G s G s H s G s G s G B 对比二阶系统传递函数的标准形式(P83,3.4.1)2222nn nsωξωω++可得该系统的阻尼比ξ及无阻尼固有频率n ω为:61,3==ξωn (2)该系统的p M ,p t ,s t ,N13611312≈-=-==πξωπωπn d p t (P90,3.4.15) %53%100%1003611/6121/≈⨯=⨯=----πξξπe eM p (P90,3.4.17)若令02.0=∆,84=≈ns t ξω(P91,3.4.22), 7.3122≈-=πξξN (P91,3.4.25)若令05.0=∆,63=≈ns t ξω(P91,3.4.23),8.215.12≈-=πξξN (P91,3.4.26)---------------------------------------------------------------------------------------------------------------------- 要使下图所示系统的单位阶跃响应的最大超调量等于25%,峰值时间p t 为2秒,试确定K 和f K 的值解:由图可知,该系统的闭环传递函数为:Ks K K s K s K sK s K s H s G s G s G f f B +⋅+=+⋅⋅+⋅=+=222)1(111)()(1)()( 对比二阶系统传递函数的标准形式2222nn n sωξωω++可得该系统的阻尼比ξ及无阻尼固有频率n ω为:2,KK K fn ==ξω由题意, 令:%2521/==--ξξπeM p ,即4ln 12=-ξξπ解得:4.0=ξ令:()24.01122=-=-==K t nd p πξωπωπ 解得:93.2=K再由:293.22f fK K K ==4.0=ξ 解得:467.0=f K----------------------------------------------------------------------------------------------------------------------单位反馈系统的开环传递函数为)10)(5(2)(+++=s s s K s G K 其输入为单位斜坡输入(单位恒速输入)时,系统的稳态误差02.0=ss e ,求所需的K 值 解:由于系统为单位反馈系统,其稳态偏差与稳态误差相同(P98,3.6.4),即ss ss e ε= 将)(s G K 写为标准形式)11.0)(12.0(50/)2()(+++=s s s K s G K (P100,3.6.12)当输入为单位斜坡输入时,其稳态偏差为:02.050/)2(1=+=K e ss (P101,P102,表3.6.1)求得所需的K 值为2498~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~·· 3.9 3.10 3.11 3.18。
过程控制工程课后习题参考答案

过程控制工程第一章单回路控制系统何谓控制通道何谓干扰通道它们的特性对控制系统质量有什么影响控制通道——是指操纵变量与被控变量之间的信号联系;干扰通道——是指干扰作用与被控变量之间的信号联系;(1)控制通道特性对系统控制质量的影响:从K、T、τ三方面控制通道静态放大倍数越大,系统灵敏度越高,余差越小;但随着静态放大倍数的增大,系统的稳定性变差;控制通道时间常数越大,经过的容量数越多,系统的工作频率越低,控制越不及时,过渡过程时间越长,系统的质量越低,但也不是越小越好,太小会使系统的稳定性下降,因此应该适当小一些;控制通道纯滞后的存在不仅使系统控制不及时,使动态偏差增大,而且还还会使系统的稳定性降低;(2)干扰通道特性对系统控制质量的影响:从K、T、τ三方面干扰通道放大倍数越大,系统的余差也越大,即控制质量越差;干扰通道时间常数越大,阶数越高,或者说干扰进入系统的位置越远离被控变量测量点而靠近控制阀,干扰对被控变量的影响越小,系统的质量则越高;干扰通道有无纯滞后对质量无影响,不同的只是干扰对被控变量的影响向后推迟一个纯滞后时间τ0;如何选择操纵变量1考虑工艺的合理性和可实现性;2控制通道静态放大倍数大于干扰通道静态放大倍数;3控制通道时间常数应适当小一些为好,但不易过小,一般要求小于干扰通道时间常数;干扰动通道时间常数越大越好,阶数越高越好;4控制通道纯滞后越小越好;控制器的比例度δ变化对控制系统的控制精度有何影响对控制系统的动态质量有何影响比例度δ越小,系统灵敏度越高,余差越小;随着δ减小,系统的稳定性下降;图1-42为一蒸汽加热设备,利用蒸汽将物料加热到所需温度后排出;试问:①影响物料出口温度的主要因素有哪些②如果要设计一温度控制系统,你认为被控变量与操纵变量应选谁为什么③如果物料在温度过低时会凝结,应如何选择控制阀的开闭形式及控制器的正反作用答:①影响物料出口温度的因素主要有蒸汽的流量和温度、搅拌器的搅拌速度、物料的流量和入口温度;②被控变量应选择物料的出口温度,操纵变量应选择蒸汽流量;物料的出口温度是工艺要求的直接质量指标,测试技术成熟、成本低,应当选作被控变量;可选作操纵变量的因数有两个:蒸汽流量、物料流量;后者工艺不合理,因而只能选蒸汽流量作为操纵变量;③控制阀应选择气关阀,控制器选择正作用;图1-43为热交换器出口温度控制系统,要求确定在下面不同情况下控制阀的开闭形式及控制器的正反作用:①被加热物料在温度过高时会发生分解、自聚;②被加热物料在温度过低时会发生凝结;③如果操纵变量为冷却水流量,该地区最低温度在0℃以下,如何防止热交换器被冻坏;答:TC冷却水物料被冷却物料①控制阀选气关阀,选反作用控制器;②控制阀选气开阀,选正作用控制器;③控制阀选气关阀,选反作用控制器;单回路系统方块图如图1-44所示;试问当系统中某组成环节的参数发生变化时,系统质量会有何变化为什么1若T0增大; 2若τ0增大; 3若T f增大; 4若τf增大;答:1T0 增大,控制通道时间常数增大,会使系统的工作频率降低,控制质量变差;2τ0 增大,控制通道的纯滞后时间增大,会使系统控制不及时,动态偏差增大,过渡过程时间加长;3Tf 增大,超调量缩小1/Tf倍,有利于提高控制系统质量;4τf 增大对系统质量无影响,当有纯滞后时,干扰对被控变量的影响向后推迟了一个纯滞后时间τf ;第二章串级控制系统2.1 与单回路系统相比,串级控制系统有些什么特点1 串级系统由于副回路的存在, 使等效副对象时间常数减小,改善了对象的特性,使系统工作频率提高;2 串级控制系统有较强的抗干扰能力,特别是干扰作用于副环的情况下,系统的抗干扰能力会更强;3 串级系统具有一定的自适应能力;2.2 为什么说串级控制系统主控制器的正、反作用方式只取决于主对象放大倍数的符号,而与其他环节无关主环内包括有主控制器,副回路,主对象和主变送器.而副回路可视为一放大倍数为“1”的环节,主变送器放大倍数一般为正,所以主控制器的正反作用只取决于主对象放大倍数的符号;如果主对象放大倍数的符号为正,则主控制器为反作用,反之, 则主控制器为正作用;2.5 试说明为什么整个副环可视为一放大倍数为正的环节来看副回路所起的作用是使副变量根据主调节器输出进行控制,是一随动系统;因此整个副回路可视为一放大倍数为正的环节来看;2.6 试说明在整个串级控制系统中主、副控制器之一的正、反作用方式选错会造成怎样的危害当主、副控制器有一个正反作用方式选错时,就会造成系统的主回路或副回路按正反馈控制,当被控变量出现偏差时,系统不仅不向着消除偏差的方向校正,反而使被控变量远离给定值;2.7 图2-20所示的反应釜内进行的是化学放热反应,,而釜内温度过高会发生事故,因此采用夹套通冷却水来进行冷却,以带走反应过程中所产生的热量;由于工艺对该反应温度控制精度要求很高,单回路满足不了要求,需用串级控制;⑴当冷却水压力波动是主要干扰时,应怎样组成串级画出系统结构图;⑵当冷却水入口温度波动是主要干扰时,应怎样组成串级画出系统结构图;⑶对以上两种不同控制方案选择控制阀的气开、气关形式及主、副控制器的正、反作用方式;1选冷水流量为副变量,釜内温度为主变量组成串级系统.2夹套温度为副变量,釜内温度为主变量组成串级系统.2.8 图2-21为一管式炉原油出口温度与炉膛温度串级控制系统;要求:⑴选择阀的开闭形式⑵确定主、副控制器的正、反作用方式⑶在系统稳定的情况下,如果燃料压力突然升高,结合控制阀的开闭形式及控制器的正、反作用方式,分析串级系统的工作过程;1 气开阀2主控制器反作用,副控制器反作用;3如果燃料气的P1突然生高,副回路首先有一个“粗调”:P1↑→F1↑→T2↑→u2↓→ F1↓没有完全被副回路克服的部分干扰,通过主回路“细调”:T2↑→T1↑→u1↓→ F1↓→T2↓→T1↓2.9 某干燥器采用夹套加热和真空吸收并行的方式来干燥物料;干燥温度过高会使物料物性发生变化,这是不允许的,因此要求对干燥温度进行严格控制;夹套通入的是经列管式加热器加热的热水,而加热器采用的是饱和蒸汽,流程如图2-22所示;要求:⑴如果冷却水流量波动是主要干扰,应采用何种控制方案为什么⑵如果蒸汽压力波动是主要干扰,应采用何种控制方案为什么⑶如果冷却水流量和蒸汽压力都经常波动,应采用何种控制方案为什么1以热水温度为副变量,干燥器出口温度为主变量,蒸汽流量为操纵变量构成温度温度串级系统,冷水流量单独设计流量单回路系统理由:当被控变量为干燥器出口温度时,不宜选冷水流量做操纵变量,故单独设计流量单回路系统抑制冷水流量波动;以干燥器出口温度为被控量、蒸汽流量为操纵变量的控制系统中,控制通道太长,存在较大的时间常数和纯滞后,故选择换热器出口温度为副变量,构成串级系统,利用副回路减小等效时间常数;2 以热水温度为为副变量,干燥器的温度为主变量串级系统;理由:将蒸汽压力波动这一主要干扰包含在副回路中, 利用副回路的快速有效克服干扰作用抑制蒸汽压力波动对干燥器出口的温度的影响.3 采用与1相同方案;理由同1;第三章 比值控制系统比值与比值系数的含义有什么不同它们之间有什么关系答:①比值指工艺物料流量之比,即从流量与主流量之比:;比值系数指副、主流量变送器输出电流信号之比,即:二者之间的关系由下式决定:变送器输出与流量成线性关系时变送器输出与流量成平方关系时用除法器进行比值运算时,对输入信号的安排有什么要求为什么答:应使除法器输出小于1;除法器输出值既仪表比值系数,需要通过副流量调节器的内给定设置,大于1无法设定、等于1无法现场整定;什么是比值控制系统它有哪几种类型画出它们的结构原理图;答:比值控制系统就是实现副流量2F 与主流量1F 成一定比值关系,满足关系式:12F F K = 的控制系统;比值控制系统的类型:开环、单闭环、双闭环、变比值、串级-比值控制系统; 原理图见教材;用除法器组成比值系统与用乘法器组成比值系统有何不同之处答:① 系统结构不同,实现比值控制的设备不同;② 比值系数的设置方法不同,乘法方案通过在乘法器的一个输入端,输入一个外加电流信号I 0设置;除法方案通过副流量调节器的内给定设置;12F F K =min1min2I I I I K --='m ax 2m ax1F F K K ='2m ax 2m ax 1)(F F K K ='在用除法器构成的比值控制系统中,除法器的非线性对比值控制有什么影响 答:除法器环节的静态放大倍数与负荷成反比;为什么4:1整定方法不适用于比值控制系统的整定答:单闭环比值控制系统、双闭环的副流量回路、变比值回路均为随动控制系统,希望副流量跟随主流量变化,始终保持固定的配比关系;出现4:1振荡时,固定配比关系不能保证;当比值控制系统通过计算求得比值系数1K >' 时,能否仍用乘法器组成比值控制为什么能否改变一下系统结构,仍用乘法器构成比值控制答:当比值控制系统通过计算求得比值系数大于1时,不能用乘法器组成比值控制;因为当1K >'时,计算所得的乘法器的一个外加输入电流信号I 0大于20mA,超出乘法器的输入范围;不用改变系统结构,只要调整F 2max 保证K '〈1 即可;一比值控制系统用DDZ-III 型乘法器来进行比值运算乘法器输出416)4I )(4I (I 01+--=', 其中I 1与I 0分别为乘法器的两个输入信号,流量用孔板配差压变送器来测量,但没有加开方器,如图所示;已知h /kg 2000F ,h /kg 3600F max 2max 1==,要求:① 画出该比值控制系统方块图;② 如果要求1:2F :F 21=,应如何设置乘法器的设置值0I解:①方框图如下:0I1I 2F - 2I1F② 乘法器 控制器 调节阀测量变送器2测量变送器1 流量对象 21221max 2max 1213600()()0.8122000F K F F K K F =='==⨯=,由于流量用孔板配差压变送器,没加开方器,所以12I I =‘系统稳定时: 2111'1004444(4)(4)44,0.811616I I K I I I I I I K --==-----'=+⇒==‘’0164160.81416.96I K mA'=+=⨯+=某化学反应过程要求参与反应的A 、B 两物料保持5.2:4F :F B A =的比例,两物料的最大流量h m F h m F B A /290,/6253max 3max ==;通过观察发现A 、B 两物料流量因管线压力波动而经常变化;根据上述情况,要求:① 设计一个比较合适的比值控制系统;② 计算该比值系统的比值系数K ';③ 在该比值系统中,比值系数应设置于何处 设置值应该是多少假定采用DDZ-III 型仪表;④ 选择该比值控制系统控制阀的开闭形式及控制器的正、反作用;解:①系统设计如下:②81.1)29062545.2()F F K (K 22max B max A =⨯==' ③1K ≤',所以要将max B F 调大;所以 625.39062545.2KF F Amxa max B =⨯=≥取450max =B F 75.0)45062545.2()(22max max =⨯=='B A F F K K 比值系数K '通过I 0设置,mA K I 164160=+'=④选择A 阀为气开阀,主对象为正环节,测量变送为正环节,则主调节器为反作用;选取B 阀为气开阀,副对象为正环节,测量变送为正环节,则副调节器为反作用;在硝酸生产过程中有一氧化工序,其任务是将氨氧化成一氧化氮;为了提高氧化率,要求维持氨与氧的比例为2:1;该比值控制系统采用如图所示的结构形式;已知h /m 5000F ,h /m 12000F 3max 3max ==氧氨;试求比值系数K ’= 如果上述比值控制用DDZ-II 型仪表来实现,比值系数的设置0I 应该是多少解:12.150001200021F F K K max max≥=⨯=='氧氨 调整副流量的测量上限,使K <1’取8.0='K ,则7500max =氧F 即可;对于DDZ-II,mA K I 88.010100=⨯='=有一个比值控制系统如图所示;图中k 为一系数;若已知k=2,h /kg 1000F ,h /kg 300F max B max A ==,试求?K =' K=解:211='==K k I I A B 21)1000300K ()F F K(K 22max B max A ===' 36.2K =⇒一双闭环比值控制系统如图所示;其比值用DDZ-III 型乘法器来实现;已知h /kg 4000F ,h /kg 7000F max 2max 1==;要求:① 画出该系统方块图;② 若已知mA 18I 0=求该比值系统的比值K= 比值系数?K =' ③ 待该比值系统稳定时,测m A 10I 1=,试计算此时2I =解:①②12I I =‘系统稳定时: 2111'1004444(4)(4)44,1616I I K I I I I I I K --==-----'=+⇒=‘’③ 001max 2max 2max 1max 164, 18140.875160.8754000170002I K I mA K F K K F F K K F '=+='⇒=='=⨯'===212144(4)40.875(104)49.25I K I I K I mA -'=-'=-+=⨯-+=。
过程控制系统 第3章 简单系统 习题与解答

第3章习题与思考题3-1.简单控制系统由哪几部分组成各部分的作用是什么解答:简单控制系统由检测变送装置、控制器、执行器及被控对象组成。
检测变送装置的作用是检测被控变量的数值并将其转换为一种特定输出信号。
控制器的作用是接受检测装置送来的信号,与给定值相比较得出偏差,并按某种运算规律算出结果送往执行器。
执行器能自动地根据控制器送来的控制信号来改变操纵变量的数值,以达到控制被控变量的目的。
被控对象是指需要控制其工艺参数的生产设备或装置。
3-2.什么叫直接参数和间接参数各使用在什么场合解答:如果被控变量本身就是需要控制的工艺指标,则称为直接参数;如果被控变量本身不是需要控制的工艺指标,但与其有一定的间接对应关系时,称为间接参数。
在控制系统设计时,尽量采用直接参数控制,只有当被控变量无法直接检测,或虽能检测,但信号很微弱或滞后很大,才考虑采用间接参数控制。
3-3.被控变量的选择应遵循哪些原则解答:被控变量的正确选择是关系到系统能否达到预期控制效果的重要因素,它选择的一般原则是:(1)被控变量应能代表一定的工艺操作指标或是反映工艺操作状态重要变量;(2)被控变量应是工艺生产过程中经常变化,因而需要频繁加以控制的变量;(3)被控变量应尽可能选择工艺生产过程的直接控制指标,当无法获得直接控制指标信号,或其测量或传送滞后很大时,可选择与直接控制指标有单值对应关系的间接控制指标;(4)被控变量应是能测量的,并具有较大灵敏度的变量;(5)被控变量应是独立可控的;(6)应考虑工艺的合理性与经济性。
3-4.操纵变量的选择应遵循哪些原则解答:(1)操纵变量应是工艺上允许加以控制的可控变量;(2)操纵变量应是对被控变量影响诸因素中比较灵敏的变量,即控制通道的放大系数要大一些,时间常数要小一些,纯滞后时间要尽量小;(3)操纵变量的选择还应考虑工艺的合理性和生产的经济性。
3-5.简述选择调节器正、反作用的目的,如何选择解答:其目的是使控制器、执行器、对象三个环节组合起来,能在控制系统中起负反馈作用。
控制工程基础习题解答3

第三章3-2.假设温度计可用1/(Ts+1)传递函数描述其特性。
现用该温度计测量某容器中的水温,发现经1min 后才能指示出实际水温的96%,问:(1). 该温度计的指示从实际水温的10%变化到90%所需的时间是多少? (2). 如果给该容器加热,使容器内水温以0.1℃/s 的速度均匀上升,当定义误差e(t)=r(t)-c(t)时,温度计的稳态指示误差有多大? 解:(1). 设实际水温为T r ,温度计原来处于T 0=0度,当温度计放入水中时,相当于输入一阶跃值为T r -T 0=T r 的阶跃函数,温度计的时间响应函数为:()()⎪⎪⎭⎫ ⎝⎛--=-Tt r eT T t c 10 ()()⎪⎪⎭⎫ ⎝⎛-==--Tt rr e T t c T T t c 10 根据题意可得:Te 60196.0--=即可得:T=18.64(s),()⎪⎪⎭⎫ ⎝⎛-=-Tt re T t c 1 10%所需的时间为64.18111.0t e--=,()s t 96.11=。
90%所需的时间为64.18119.0t e--=,()s t 92.422=。
所以可得该温度计的指示从实际水温的10%变化到90%所需的时间(上升时间)是()s t t t r 96.4012=-=(2). 由题可知系统为一阶系统,故系统稳定,为求当r(t)=0.1t 时的稳态误差,由一阶系统的时间响应分析可知,单位斜坡响应的稳态误差为T ,所以稳态指示误差:()C T t e t 864.11.0lim =⨯=∞→(将1/(Ts+1)转化为开环传递函数为1/(Ts )时的单位反馈系统,则可见此时系统的误差为e(t)=r(t)-c(t)。
根据系统为I 型,可得稳态速度误差系数为Kv=K=1/T ,得当输入信号为r(t)=0.1t 时的稳态误差为C T K e vssv 864.11.011.0=⨯=⨯=) 3-5.某控制系统如图3-24所示,已知K=125,试求: (1). 系统阶次,类型。
控制工程基础第三版课后习题答案

控制工程基础第三版课后习题答案控制工程基础第三版课后习题答案控制工程是一门涉及到系统控制与优化的学科,它是现代工程技术的重要组成部分。
掌握控制工程的基础知识对于工程师来说至关重要。
而《控制工程基础》这本教材则是控制工程学习的重要参考书之一。
本文将为读者提供《控制工程基础第三版》课后习题的答案,希望能够帮助读者更好地理解和掌握这门学科。
第一章:控制系统基础知识1. 什么是控制系统?控制系统是由一系列相互关联的元件和设备组成的,用于实现对某个过程或系统的控制和调节的系统。
2. 什么是开环控制系统?开环控制系统是指输出信号不受输入信号的影响,只根据事先设定的控制规律进行控制的系统。
3. 什么是闭环控制系统?闭环控制系统是指输出信号受到输入信号的反馈影响,根据反馈信号对输出信号进行调节的系统。
4. 什么是传递函数?传递函数是指输出变量与输入变量之间的关系,通常用一个分子多项式除以一个分母多项式的形式来表示。
5. 什么是稳定性?稳定性是指系统在受到干扰或参数变化的情况下,能够保持稳定状态的能力。
第二章:线性系统的数学模型1. 什么是线性系统?线性系统是指系统的输入和输出之间存在线性关系的系统。
2. 什么是状态空间模型?状态空间模型是用状态变量来描述系统动态行为的数学模型。
3. 什么是传递函数模型?传递函数模型是用传递函数来描述系统输入和输出之间关系的数学模型。
4. 如何从状态空间模型转换为传递函数模型?可以通过拉普拉斯变换将状态空间模型转换为传递函数模型。
5. 如何从传递函数模型转换为状态空间模型?可以通过分解传递函数为部分分式的形式,然后利用反变换将其转换为状态空间模型。
第三章:控制系统的时域分析1. 什么是单位阶跃响应?单位阶跃响应是指系统在输入信号为单位阶跃函数时的响应。
2. 什么是阻尼比?阻尼比是指系统的阻尼系数与临界阻尼系数之间的比值。
3. 什么是超调量?超调量是指系统响应的峰值与稳态值之间的差值。
《控制工程基础》第三章习题解题过程和参考答案 (2)

以下求各指标:
由 ,其中 ,
故:
(也可查图3-16而得)
(2)由式(3-46),单位脉冲响应:
代入各参数:
3-7某二阶系统的结构框图如题3-7图所示,试画出 , 和 时的单位阶跃响应曲线。
题3-7图控制系统框图
解:
系统闭环传递函数为:
系统的参数为: 。
(1)
此时, ,为欠阻尼,可求得:
(2)
此时,由 ,可知 ,仍为欠阻尼。由于阻尼比增大,因此超调量减小。
而调节时间 ,所以:
由此得联立方程:
解得:
3-10典型二阶系统的单位阶跃响应为
试求系统的最大超调 、峰值时间 、调节时间 。
解:
由式(3-46),典型二阶系统的单位阶跃响应表达式为:
,其中
将上式与给定响应式比较,可计算系统的二个参数 。
由 ,求得阻尼比:
或者也可这样求:
由 ,求得阻尼比:
由 ,得
二个参数求出后,求各指标就很方便了。
综合有:
开环增益K在上述范围内,则闭环系统不但稳定,且所有闭环极点的实部均小于-1。
3-19已知单位反馈系统的开环传递函数为
试根据下述条件确定 的取值范围。
(1)使闭环系统稳定;
(2)当 时,其稳态误差 。
解:
(1)关于闭环稳定性
求解本题当然可以用普通方法,如在习题3-12至3-18中所应用的。
但我们换一种思路,设计利用一些规律性的结果。在习题3-17中已经求出,对于单位反馈系统若具有下列形式的开环传递函数:
①特征方程的系数均大于0且无缺项。
②列劳斯表如下
1
10
21
10
10
结论:劳斯表第—列均为正值,系统闭环稳定。
控制工程第3章复习题(答案)

第三章复习题一、选择题1、系统方框图如图示,则该系统的开环传递函数为( B ) A 、1051s + B 、2051ss + C 、10251s s ()+ D 、2s2、 某系统的传递函数为2s 5)s (G +=,则该系统的单位脉冲响应函数为(A )A 、52e t -B 、5tC 、.52e tD 、5t3、 二阶欠阻尼系统的上升时间t r 定义为( C )A 、单位阶跃响应达到稳态值所需的时间B 、单位阶跃响应从稳态值的10%上升到90%所需的时间C 、.单位阶跃响应从零第一次上升到稳态值时所需的时间D 、单位阶跃响应达到其稳态值的50%所需的时间4、系统类型λ、开环增益K 对系统稳态误差的影响为( A ) A.系统型次λ越高,开环增益K 越大,系统稳态误差越小 B.系统型次λ越低,开环增益K 越大,系统稳态误差越小 C.系统型次λ越高,开环增益K 越小,系统稳态误差越小 D.系统型次λ越低,开环增益K 越小,系统稳态误差越小5、一系统的传递函数为G s KTs ()=+1,则该系统时间响应的快速性( C ) A.与K 有关 B.与K 和T 有关C.与T 有关D.与输入信号大小有关6、一闭环系统的开环传递函数为G s s s s s ()()()()=+++83232,则该系统为( C )A.0型系统,开环增益为8B.I 型系统,开环增益为8C.I 型系统,开环增益为4D.0型系统,开环增益为47、瞬态响应的性能指标是根据哪一种输入信号作用下的瞬态响应定义的( B ) A.单位脉冲函数 B.单位阶跃函数 C.单位正弦函数 D.单位斜坡函数8. 二阶系统的极点分别为s s 12054=-=-.,,系统增益为5,则其传递函数为(D ) A.2054(.)()s s --B.2054(.)()s s ++C.5054(.)()s s ++D.10054(.)()s s ++9、二阶系统的传递函数为G s Ks s ()=++2212,当K 增大时,其(C ) A.无阻尼自然频率ωn 增大,阻尼比ξ增大 B.无阻尼自然频率ωn 增大,阻尼比ξ减小 C.无阻尼自然频率ωn 减小,阻尼比ξ减小 D.无阻尼自然频率ωn 减小,阻尼比ξ增大 10、一阶系统KTs1+的单位脉冲响应曲线在t=0处的斜率为( C ) A.K TB. KTC. -K T 2D.K T 211、某系统的传递函数G(s)=1+Ts K,则其单位阶跃响应函数为( C )A.1Te Kt T -/ B.K Te t T -/C. K(1-e -t/T )D. (1-e -Kt/T )12、图示系统称为( B )A. 0B. ⅠC. ⅡD. Ⅲ13、典型二阶振荡环节的峰值时间与( D ) A.增益 B.误差带 C.增益和阻尼比 D.阻尼比和无阻尼固有频率14、某系统的传递函数为G(s)=()()()()s s s s +-+-72413,其零、极点是( D )A.零点s=-0.25,s=3;极点s=-7,s=2B.零点s=7,s=-2;极点s=0.25,s=3C.零点s=-7,s=2;极点s=-1,s=3D.零点s=-7,s=2;极点s=-0.25,s=315、一系统的开环传递函数为32235()()()s s s s +++,则系统的开环增益和型次依次为( A )A. 0.4,ⅠB. 0.4,ⅡC. 3,ⅠD. 3,Ⅱ 16、单位反馈控制系统的开环传递函数为G(s)=45s s ()+,则系统在r(t)=2t 输入作用下,其稳态误差为( A ) A.104B. 54C. 45D. 017、二阶系统的传递函数为4)0.5)(s (s 10++,则系统增益为( D )A.10B.0.5C.4D.518、若系统的单位脉冲响应为e -2t +2e -t ,则系统的传递函数为:( A )A.1s 22s 1+++B.1s 2s 32++ C.s 2e 2s 1-+ D.se 1s 1-+19、某系统的传递函数为2)1)(s (s 5++系统的零极点为( C )A.极点s 1=-1, s 2=-2,零点s 3=5B.极点s 1=1, s 2=2C.极点s 1=-1, s 2=-2D.极点s 1=1, s 2=2,零点s 3=-520、下列信号中,哪个用来定义二阶系统的瞬态响应指标( A )A. 单位阶跃B.单位脉冲C.单位斜坡D.单位正弦 21、系统如图,其稳态误差定义为( C )A.e ss =0s lim →SG(S) B.e ss =∞→s lim te(t)C.e ss =∞→t lim e(t) D.e ss =0t lim →e(t)22、单位反馈系统稳态速度误差的正确含义是: CA 、在 ()1()r t R t =⋅时,输出速度与输入速度的稳态误差;B 、在 ()1()r t R t =⋅时,输出位置与输入位置的稳态误差;C 、在 ()r t V t =⋅时,输出位置与输入位置的稳态误差;D 、在 ()r t V t =⋅时,输出速度与输入速度的稳态误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
3.5 使用温度计对水温进行测量,若水温为恒定值,该温度计能在1分钟时指示出实际温度值的98%。
假定温度计为一个一阶系统,求该系统的时间常数T 。
解:恒定的水温可以视为一个阶跃输入信号,温度计的测量输出可以视为对该阶跃输入信号的响应。
一阶系统的单位阶跃响应的时间函数为:)0(1)(/>-=-t e t x T t o (P82,3.3.2) 根据题意可知:98.01)(/11=-=-=Tt o e t x→02.0/1=-T e →256.050ln 1==T (min)若测量开始后,实际水温从零度起,以10°C/min 的速度线性升温,求温度计在1分钟时的示值与实际水温的误差是多大?(帮助公式:11111222++-=+⋅Ts T s T sTs s ) 根据题意,实际的温度输入信号为:t t x i ⋅=10)(其拉氏变换为:210)(ss X i =测量误差的时间函数为:]1110[)()]()([)()]([)()()()(2111+⋅⋅-=⋅-=-=-=---s T sL t x s G s X L t x s X L t x t x t x t e i i i o i o i其中:)(10]11[10]111[10]1110[/2212121T t e T T t Ts T s T s L Ts s L s T s L ----⋅+-=++-=+⋅=+⋅⋅所以:)1(56.2)1(10)(1010)(256.0///t T t T t e e T e T T t t t e ----=-=⋅+--=当t=1时,测量误差为:5.2)1(56.2)(256.0/11=-=-=e t e t3.7已知控制系统的微分方程为)(20)()(5.2t x t y t y =+',试用拉氏变换法求该系统的单位脉冲响应)(t w 和单位阶跃响应)(t x ou ,并讨论二者之间的关系解:由传递函数的定义和系统的微分方程(P34,2.2.2~2.2.3),可得系统的传递函数为4.0815.220)()()(+=+==s s s X s Y s G 系统的单位脉冲响应为(P81)t e s L s X s G L t w 4.0118]14.08[)]()([)(---=⋅+==系统的单位阶跃响应为(P82):)1(20]4.011[4.08]14.08[)]()([)(4.0111t ou e s s L s s L s X s G L t x -----=+-=⋅+==比较)(t x ou 和)(t w ,有)(t w =)(t x ou' 即系统的单位脉冲响应等于系统的单位阶跃响应的微分。
3.12下图为某数控机床系统的位置随动系统的方框图,试求:(1)阻尼比ξ及无阻尼固有频率n ω解:由图可知,该系统为一个单位反馈系统,其系统的闭环传递函数为:99)1(191)1(19)(1)()()(1)()(2++=+⋅++⋅=+=+=s s s s s s s G s G s H s G s G s G B 对比二阶系统传递函数的标准形式(P83,3.4.1)2222nn ns ωξωω++可得该系统的阻尼比ξ及无阻尼固有频率n ω为:61,3==ξωn (2)该系统的p M ,p t ,s t ,N13611312≈-=-==πξωπωπn d p t (P90,3.4.15)%53%100%1003611/6121/≈⨯=⨯=----πξξπe eM p (P90,3.4.17)9=a K )1(1+s s +-)(s X i )(s X o若令02.0=∆,84=≈ns t ξω(P91,3.4.22), 7.3122≈-=πξξN (P91,3.4.25)若令05.0=∆,63=≈ns t ξω(P91,3.4.23),8.215.12≈-=πξξN (P91,3.4.26)3.15 要使下图所示系统的单位阶跃响应的最大超调量等于25%,峰值时间p t 为2秒,试确定K 和f K 的值解:由图可知,该系统的闭环传递函数为:Ks K K s K s K sK s K s H s G s G s G f f B +⋅+=+⋅⋅+⋅=+=222)1(111)()(1)()( 对比二阶系统传递函数的标准形式2222nn n s ωξωω++可得该系统的阻尼比ξ及无阻尼固有频率n ω为:2,KK K fn ==ξω由题意, 令:%2521/==--ξξπeM p ,即4ln 12=-ξξπ解得:4.0=ξ令:()24.01122=-=-==K t nd p πξωπωπ 解得:93.2=K再由:293.22f fK K K ==4.0=ξ 解得:467.0=f K3.16如图所示系统,试求 (1)h K 为多少时,5.0=ξ;K21s+ -)(s X i )(s X os K f +1(2)单位阶跃响应的超调量和调整时间;(3)比较加入)1(s K h +与不加入)1(s K h +时系统的性能;解:(1)h K 为多少时,5.0=ξ;由图可知,该系统为一个单位反馈系统,其系统的闭环传递函数为:10)102(1010)2(10)1(1)2(10)1()(1)()()(1)()(2++++=+⋅+++⋅+=+=+=s K s s K s s s K s s s K s G s G s H s G s G s G h h h h B 其无阻尼自由频率为:10=n ω 又因为h n K 1022+=ξω,即102102-⋅=ξh K由题意,要求5.0=ξ,解得所需的h K 为:116.01025.0102=-⋅=h K(2)单位阶跃响应的超调量和调整时间;将该系统的闭环传递函数10)102(1010)(2++++=s K s s K s G h h B对比二阶系统传递函数的标准形式:2222nn ns ωξωω++可知该系统不是一个标准的二阶系统其s p t M ,无法利用P90页公式3.4.17以及P91页公式3.4.22~2.4.23直接求得 需要利用s p t M ,的定义求得。
令输入信号为单位阶跃信号,即)()(t u t x i =,其拉氏变换为:ss X i 1)(= 输出信号的拉氏变换为:⎥⎦⎤⎢⎣⎡++⋅+⎥⎦⎤⎢⎣⎡++⋅=+++⋅=++++⋅=⋅=1016.31011016.3101116.01016.31016.1110)102(10101)()()(2222s s s s s s s s s s s s K s s K s s G s X s X h h B s os K h +1)2(10+s s+-)(s X i)(s X o令:()()⎥⎥⎦⎤⎢⎢⎣⎡++⋅=⎥⎦⎤⎢⎣⎡++⋅=--2111221121211016.3101)(n n n s s s L s s s L t z ωωξω, 可以求得:74.25.0110,5.010216.3,16.3102111=-==⋅===d n ωξω由P86页公式(3.4.8~3.4.9),可得:)74.2sin 58.074.2(cos 1)74.2sin 5.015.074.2(cos 1)sin 1(cos 1)(58.1216.35.0121111t t e t t e t t e t z t t d d t n +-=-+-=-+-=-⋅--ωξξωωξ则,[][])74.2sin 155.074.2(cos 1)74.2sin 58.074.2(cos 1)74.2sin 74.274.2cos 74.258.0()74.2sin 58.074.2(cos 58.1116.0)()(116.01016.31011016.3101116.0)]([)(58.158.158.158.12211t t e t t et t e t t e t z dtt dz s s s s s s s L s X L t x t tt t o o +-=+-+-⋅-+=+=⎥⎦⎤⎢⎣⎡⎪⎪⎭⎫ ⎝⎛++⋅+⎪⎪⎭⎫ ⎝⎛++⋅==------由上式可知,1)(lim )(==∞∞→t x x o t o由峰值时间p t 的定义,令:0)(==ptt o dt t dx0)74.2cos 15.174.2sin 89.2(58.1=+-p p pt t t e即:0)89.215.1arctan 74.2sin(=+p t 14.33787.074.2=+p t 解得:s t p 01.1≈将s t p 01.1≈代入)(t x o ,求得响应的第一个峰值为:177.1)01.174.2sin 155.001.174.2(cos 1)(01.158.1=⋅+⋅-=⋅-e t x p o由超调量的定义,得%7.17%10011177.1%100)()()(=⨯-=⨯∞∞-=o o p o p x x t x M 由调整时间的定义:)()()()(s o o o t t x x t x ≥∞⋅∆≤∞-即:)()74.2sin 155.074.2(cos 58.1s t t t t t e ≥∆≤+-由于1)74.2sin 155.074.2(cos ≤+t t 上式等价为:)(58.1s t t t e ≥∆≤-解得∆=1ln 58.11s t 若取02.0=∆,则sec 45.202.01ln 58.11==s t 若取05.0=∆,则sec 9.105.01ln 58.11==s t(2)若没有串联环节)1(s K h +,即则系统的闭环传递函数为:10210)2(101)2(10)(2++=+++=s s s s s s s G B 对比二阶系统传递函数的标准形式2222nn ns ωξωω++可得该系统的阻尼比ξ及无阻尼固有频率n ω为:316.0,10==ξωn其超调量及调整时间为:()%35%100%1002316.01316.021≈⨯=⨯=----πξξπe eM p若令02.0=∆,414=≈s t , 若令05.0=∆,313=≈s t ,由此可见,串联环节)1(s K h +的作用使得系统的性能改善了,即超调量和过渡时间都减小了。
)(s X i)(s X o)2(10+s s+ -3.17单位反馈系统的开环传递函数为)5)(1()(++=s s s Ks G K其输入为单位斜坡输入(单位恒速输入)时,系统的稳态误差01.0=ss e ,求所需的K 值 解:由于系统为单位反馈系统,其稳态偏差与稳态误差相同(P98,3.6.4),即ss ss e ε=将)(s G K 写为标准形式)12.0)(1(5/)(++=s s s K s G K (P100,3.6.12)当输入为单位斜坡输入时,其稳态偏差为:01.05/1==K e ss (P101,P102,表3.6.1)求得所需的K 值为500。
