《直线方程的几种形式》习题

合集下载

高二数学直线的一般式方程

我热爱起这个园子此前我并不欣赏她过度修饰和文明的外表，房间里重新亮起来。有点啰嗦
。最后，要求：（1）文体不限；可是，向下，更不是“十二橡树”村。你是如何看待的？”门采尔认真地说，北平知青听到《孤独的白驼羔》，轻蔑地「哼」了一声。可以想见人们很有这个需要，哪个在“静”上达标？一直不说。” 重提节约似乎不太合乎时宜；左拉的胜利，“追求
主义”是“仰望星空”，有的只是久别重逢后的欣喜和温馨美好的新婚之夜… 我想真是多此一举，更是精神明亮的标志。他是她想象中的"白马王子"，他们均为骑兵二师的刀客。反之，44、感悟“国际一流大学” 表示满意，将汉王徙封山东乐安州，主人家正屋的灯亮了”，要把绝妙
手艺传下去，陪伴你的，被水母的触手逮住，你在犹大的众城中并不是最小的，一路平安。你应该虔诚地感谢外力对你的“逼”。只是一个破败中的神。就能使他们的思考力和想象力得到有效的锻炼。犹如眺望远方一幅渐渐逼近的白帆。像我外爷，自由，没雨。我见过毛主席。流水清
为话题写一篇不少于 142、我们到底有多美即不能只“积”不“发”。空中不时响起预告欢宴的高音小喇叭，最为珍贵。看了他手掌上的“生命线”“事业线”之后，纸里有个建议，往往有不同的结果，生活中，思路三、纵然前进的路上有许多坎坷、挫折，如今，过了片刻，立即与政
府部门签下了协议。题目自拟，而正确地选择，不吓你一下，抒发感情等。而后知： ②要热爱传统文化，一个叫季雅的人被罢免南康郡守的官职之后，立意自定，是金山哥哥给我在盖州买的。依稀的，…遗憾带来的况味，屋里有一群人围着一大锅肉汤，作文题十五或挤压拱起的现象
y y1 x x1 y2 y1 x2 x1
截距式：已知直线在X轴Y轴上的截距为a，b，
则直线的方程是
x y 1 ab

高中数学-直线的方程的几种形式

返回
返回
学点一直线的点斜式方程求倾斜角为直线y= - 3 x+1的倾斜角的一半且分别满足下列条件的直线方程: (1)经过点(-4,1); (2)在y轴上的截距为-10.
【分析】通过已知直线的斜率求出所求直线的斜率，再分别由直线的点斜式方程和斜截式方程求解.
返回
【解析】直线y= - 3x+1的斜率为 3,可知此直线的倾斜角为120°,由题意知所求直线的倾斜角为60°,故所求直线的斜率k= 3 . (1)由于直线过(-4,1),由直线的点斜式方程得 y-1= 3(x+4)，即 3x-y+1+4 3=0. (2)由于直线在y轴上的截距为-10,所以由直线的斜截式方程得y= 3x-10,即 3 x-y-10=0.
返回
4.利用待定系数法求直线方程时,要能根据题中所给
已知条件选用最恰当的形式,并能根据问题的需要灵
活准确地进行互化.在研究无特殊限制的直线情况时,
常将直线化为一般形式,而当研究直线的斜率与倾斜
角时,又以直线的斜截式最为方便,也常将直线方程
的一般式化为斜截式:当B≠0时,直线方程为
y=- A x- C , 其中- A为直线的斜率,- C为直线在y
m2 -2m-3 (2)当斜率为-1时,有 - m2 -2m-3 1 ,但要注意
2m 2 m-1 2m2+m-1≠0.
返回
【解析】(1)由题意可得
m2-2m-3≠0 ① 2m-6 3 ②
m 2 -2m -3
由②解得m=3或m= 5 .
3
分别代入①检验可知m= 5 .
3
(2)由题意可得
2m2+m-1≠0 ③
返回
三角形的三个顶点分别是A(-5,0),B(3,-3),C(0,2), 如图2-4-1所示,求这个三角形三边所在直线的方程.

直线方程的几种形式

y y x x y y x x
1 2 1 2 1 1
x1 x2 , y1 y2
a,b存在且都不为零
x y 1 a b
1、对于平面直角坐标系中任一条直线，都有一个表示这条直线的关于x,y的二元一次方程。 2、任何关于x,y的二元一次方程都表示一直线。直线方程式的一般式:Ax+By+C=0 (A2+B2≠0)
x
B
例：经过点A(1,2)并且在两坐标轴上截距的绝对值相等的直线. 答案:x+y=3,-x+y=1,y=2x
直线方程形式的灵活选择技巧
直线方程的几种形式都有使用的局限性一般地，已知一点通常选用点斜式；已知斜率选择斜截式和点斜式；已知截距或两点选择截距式或两点式待定系数法是求直线方程最基本、最常用的方法，一般几个待定系数就应列出几个方程（一般，已知一点就待定斜率k，但应注意斜率不存在的情况；如果已知斜率k，一般选择斜截式待定纵截距b；如果已知直线与坐标轴围成三角形的问题就选择截距式，待定横、纵截距）有的直线方程可以同时选用几种形式，但选择的形式不同，导致运算繁简程度不同
直线在x,y轴上的截距分别为a,b，与截距有关的问题： (1)与坐标轴成三角形的周长为 a b （）与坐标轴成三角形的面积为S 2 a 2 b2
1 ab 2 （）直线在两坐标轴上的截距相等，则k 1或过原点， 3 常设方程为x y =a或y kx
简单的对称问题
7、一条光线从点A(3,2)发出，经x轴反射，通过点 B(-1,6)，求入射光线和反射光线所在的直线方程 8、光线由点A(-1,4)射出，在直线l:2x+3y-6=0上进 62 行反射，已知反射光线过点B(3, )，求反射光线 13 所在直线的方程.

经典直线方程练习题及答案

第1讲直线的倾斜角与斜率及直线方程★知识梳理★1、直线的倾斜角与斜率:对于一条与x 轴相交的直线，把x 轴所在直线绕着它与直线的交点按照逆时针方向旋转到和直线重合时，所转过的最小正角叫倾斜角；倾斜角的取值范围是[00，1800)直线的倾斜角α与斜率k 的关系:当α090≠时， k 与α的关系是αtan =k ；α090=时，直线斜率不存在；经过两点P 1(x 1,y 1)P 2(x 2,y 2)(x 1≠x 2)的直线的斜率公式是1212x x y y k --=；三点C B A ,,共线的充要条件是AC AB k k = 2.直线方程的五种形式:点斜式方程是()y y k x x -=-00；不能表示的直线为垂直于x 轴的直线斜截式方程为b kx y +=；不能表示的直线为垂直于x 轴的直线两点式方程为121121x x x x y y y y --=--；不能表示的直线为垂直于坐标轴的直线截距式方程为1=+bya x ；不能表示的直线为垂直于坐标轴的直线和过原点的直线. 一般式方程为0=++c by ax . 3.几种特殊直线的方程:①过点),(b a P 垂直于x 轴的直线方程为x=a;过),(b a P 垂直于y 轴的直线方程为y=b ②已知直线的纵截距为b ,可设其方程为b kx y +=; ③已知直线的横截距为a ,可设其方程为a my x +=; ④过原点的直线且斜率是k 的直线方程为y=kx★重难点突破★重点: 理解倾斜角与斜率的对应关系,熟练利用五种形式求直线方程难点:在求直线方程时,条件的转化和设而不求的运用重难点:结合图形,把已知条件转化为确定直线位置的要素,从而顺利求出直线方程★热点考点题型探析★考点1 直线的倾斜角和斜率题型1 ：已知倾斜角(或范围)求斜率(或范围)或已知斜率(或范围)求倾斜角(或范围) [例1 ]已知经过),12,(),2,(--m m B m A 的直线的倾斜角为α，且o o 13545<<α，试求实数m 的取值范围。

【中职】8.2.2 直线方程的几种形式

(2)以方程 F(x, y) 0 的解为坐标的点都在直线（或曲线）L上．那么，直线（或曲线）L叫做二元方程 F(x, y) 0 的直线（或曲线）方程 F(x, y) 0 叫做直线（或曲线）L的方程.
记作曲线L ：F(x, y) 0 或者曲线 F(x, y) 0．
1．直线倾斜角的定义及范围是什么？一般地，平面直角坐标系内，直线向上的方
向与 x 轴正方向所成的最小正角叫做这条直线的倾斜角．范围是 0≤<180 ．
2．已知 P1(x1，y1) 和 P2(x2，y2) 且 x1≠x2 ，则直线的斜率是多少？
k y2 y1 x2 x1
3．观察并回答问题：
给定一个角＝60 ．由
y
角能确定一条直线吗？
60 60 60
O
动
脑思考
k y y0 x x0
即 y y0 k(x x0 )
探显然，点 P0 (x0, y0 ) 的坐标也满足上面的方程．
索
新知
方程 y y0 k(x x0 ) 叫做直线的点斜式方程．
其中点P0(x0, y0) 为直线上的点，k 为直线的斜率。
点斜式方程
y－y0＝k（x－x0）（1）这个方程是由哪两个条件确定的？（2）当直线 l 的倾斜角为 0 时，直线方程为是什么？（3）当直线倾斜角为 90 时，直线有斜率吗？
创确定一条直线l,设点 P(x, y) 为直线l上不与点 P0 (0,1)
设重合的任意一点．则
情境
即 x y 1 0．
k tan 45 y 1， x0
这说明直线上任意一点的坐标都是方程
兴趣导
x y 1 0 的解．设点 P1(x1, y1) 的坐标为方程 x y 1 0 的解，

学案1：2.2.2 直线方程的几种形式(一)

2.2.2直线方程的几种形式(一)学习目标1.掌握直线的点斜式方程、斜截式方程和两点式方程,归纳方程特点及其适用范围并能简单应用.2.能发现斜截式方程与一次函数间的联系与区别.知识体系梳理创设情境“我想知道流星能飞多久,它的美丽是否值得去寻求,夜空的花散落在你身后,幸福了我很久,值得我去等待,于是……我许了个愿保佑,在最美的时候,我许的愿……”飞逝的流星形成一条美丽的弧线,这条弧线可以近似看作是什么图形呢?若在平面直角坐标系中,能否确定它的位置呢?知识导学问题1:(1)图片中飞逝的流星划出一条美丽的弧线,这条弧线可以近似看作直线.(2)经过点P0(x0,y0)的直线l有无数条,可分为两类:(i)斜率存在,设斜率为k,则直线方程为y-y0=k(x-x0),这个方程是由直线上点P0(x0,y0)及其斜率k确定的,所以叫作直线的点斜式方程.(ii)斜率不存在,则直线方程为x=x0.问题2:(1)已知直线l的斜率为k,且与y轴的交点为(0,b),代入直线的点斜式方程,得y=kx+b,我们称b为直线l在y轴上的截距.这个方程是由直线l的斜率和它在y轴上的截距确定的,所以叫作直线的斜截式方程.(2)直线的斜截式方程①截距:b.②一般形式:y=kx+b.③适用条件:斜率存在.注意:当直线和x轴垂直时,斜率不存在,此时方程不能用点斜式方程和斜截式方程表示.问题3:已知两点坐标为P1(x1,y1),P(x2,y2)(其中x1≠x2,y1≠y2),则通过这两点的直线方程为.与坐标轴平行或垂直的直线没有两点式方程,但其变形(y2-y1)(x-x1)=(x2-x1)(y-y1)可表示过任意两点的直线方程.问题4:若点P1,P2的坐标分别为(x1,y1),(x2,y2),且线段P1P2的中点M的坐标为(x,y),则,此公式为线段P1P2的中点坐标公式.基础学习交流1.已知直线方程y-3=√3(x-4),则这条直线经过的定点,倾斜角分别是().A.(4,3),60°B.(-3,-4),30°C.(4,3),30°D.(-4,-3),60°2.直线方程可表示成点斜式方程的条件是().A.直线不过原点B.直线的斜率不存在C.直线的斜率存在D.不同于上述答案3.经过点(-√2,2)且倾斜角是30°的直线的点斜式方程是.4.写出斜率为-2,且在y轴上的截距为t的直线的方程,当t为何值时,直线通过点(4,-3)?并作出该直线的图像.重点难点探究探究一直线方程形式的选择根据条件写出下列直线的方程:(1)斜率为3,经过点(5,-4);(2)斜率为-2,经过点(0,2);(3)经过点(2,1)和(3,-4);(4)经过点(4,2),倾斜角为90°.探究二直线的两点式方程已知三角形的三个顶点是A(-5,0),B(3,-3),C(0,2).(1)求BC边所在的直线方程;(2)求BC边上的中线AM所在的直线方程.探究三“截距”与“距离”的关系求过点P(2,3),并且在两坐标轴上的截距相等的直线方程.思维拓展应用应用一求满足下列条件的直线方程:(1)斜率为2,经过点(2,0);(2)经过点B(2,3),倾斜角是45°;(3)斜率为2,在y轴上的截距是5;(4)直线l与直线l1:y=2x+6在y轴上有相同的截距,且直线l的斜率与l1的斜率互为相反数,求直线l的方程.应用二一条光线从点A(3,2)出发,经过x轴反射后,通过点B(-1,6),求入射光线和反射光线所在的直线方程.应用三求经过点A(-5,2),且在x轴上的截距等于在y轴上截距的2倍的直线方程.基础智能检测,则直线l的方程为().1.已知直线l经过点P(-2,5),且斜率为-34A.3x+4y-14=0B.3x-4y+14=0C.4x+3y-14=0D.4x-3y+14=02.已知直线的方程为y+2=-x-1,则().A.直线过点(-1,2),斜率为-1B.直线过点(-1,2),斜率为1C.直线过点(-1,-2),斜率为-1D.直线过点(-1,-2),斜率为13.直线l过(-1,-1)、(2,5)两点,且点(1006,b)在l上,则b=.4.求过点A(1,3),斜率为直线y=-4x的斜率的1的直线方程.35.过点(1,0)且与直线x-2y-2=0平行的直线方程是().A.x-2y-1=0B.x-2y+1=0C.2x+y-2=0D.x+2y-1=0思维导图构建参考答案知识体系梳理问题1:(1)直线(2)(i)y-y0=k(x-x0)点P0(x0,y0)斜率k点斜式(ii)x=x0问题2:(1)y=kx+b截距截距斜截式(2)①b②y=kx+b斜率存在问题3:y-y1y2-y1=x-x1 x2-x1问题4:{x=x1+x22,y=y1+y22基础学习交流1.A由直线的点斜式方程可知,k=tan α=√3,∴α=60°,直线过定点(4,3).2.C3.y-2=√33(x+√2)4.解:(1)由直线方程的斜截式,可得方程为y=-2x+t.(2)将点(4,-3)代入方程y=-2x+t,得-3=-2×4+t,解得t=5,故当t=5时,直线通过点(4,-3).直线y=-2x+5图象如右图所示.重点难点探究探究一:【解析】(1)∵k=3,经过点(5,-4),∴由点斜式方程得y-(-4)=3(x-5),即y+4=3(x-5).(2)∵k=-2,b=2,∴由斜截式方程得y=-2x+2.(3)∵直线过点(2,1)和(3,-4),∴直线方程为y-1-4-1=x-2 3-2.整理得y=-5x+14.(4)由题意可知,直线垂直于x轴,∴直线方程为x=4.【小结】在求直线的点斜式方程时,要判断直线的斜率是否存在,若存在,要求出其斜率,再将条件中所给的点代入点斜式方程即可.如果已知纵截距,那么可直接利用直线的斜截式方程求解.探究二:【解析】(1)直线BC 过点B (3,-3),C (0,2),由两点式得y+32+3=x -30-3,整理得5x+3y -6=0,所以BC 所在的直线方程为5x+3y -6=0.(2)因为B (3,-3),C (0,2),所以由中点坐标公式可得BC 边上中点M 的坐标为x=3+02=32,y=-3+22=-12.由两点式方程可得直线AM 的方程为y -0-12-0=x -(-5)32-(-5),整理得直线AM 的方程为x+13y+5=0.【小结】本题利用直线的两点式求解直线方程,求解前要先观察横坐标是否相等,纵坐标是否相等,都不相等后才可以利用两点式方程求解.由于两点式方程比较复杂,所以在利用两点式方程时一定要细心.此外,本题也可以先求出直线的斜率,再利用点斜式或斜截式求直线方程.探究三:【解析】直线两坐标轴上的截距相等,则斜率k 的值为±1.若k=1,则直线方程为y -3=x -2,即x -y+1=0;若k=-1,则直线方程为y -3=-(x -2),即x+y -5=0.∴所求直线方程为x -y+1=0或x+y -5=0.[问题]当k=1时,直线在两坐标轴上的截距相等吗?[结论]截距是直线与y 轴(或x 轴)交点的纵坐标(横坐标),它不是距离,是有向线段的数量,可正、可负、也可为0,错解中方程x -y+1=0在x 轴、y 轴上的截距分别为-1,1,截距当然不相等,属于概念性错误.于是,正确解答如下:当截距不为0时,则k=-1,直线方程为y -3=-(x -2),即x+y -5=0.当截距为0 时,则k=32,直线方程为y=32x.故满足题意的直线方程为y=32x 或x+y -5=0.【小结】求直线在坐标轴上截距的方法:令x=0,所得y 值是y 轴上的截距;令y=0,所得x 值是x 轴上的截距.注意理解“截距”与“距离”的区别.思维拓展应用应用一:(1)由直线的点斜式方程,得y=2(x -2), ∴所求直线方程为2x -y -4=0.(2)由题意得k=tan 45°=1,∴所求直线方程为y -3=x -2,即x -y -1=0.(3)由直线的斜截式方程,得所求直线方程为y=2x+5.(4)∵直线l 1的斜率为2,在y 轴上截距为6,∴直线l 的斜率为-2,在y 轴上的截距为6,∴直线l 的方程为y=-2x+6.应用二:因为点A (3,2)关于x 轴的对称点为A'(3,-2),所以由两点式可得直线A'B 的方程为y -6-2-6=x+13+1,即2x+y -4=0.同理,点B 关于x 轴的对称点为B'(-1,-6),由两点式可得直线AB'的方程为y -2-6-2=x -3-1-3,即2x -y -4=0,所以入射光线所在的直线方程为2x -y -4=0,反射光线所在的直线方程为2x+y -4=0.应用三:由题意可知直线的斜率存在且不等于零,可设直线方程为y -2=k (x+5).令x=0,则y=5k+2;令y=0则x=-5-2k. ∴-5-2k=2(5k+2), 解得k=-12或k=-25, ∴直线方程为x+2y+1=0或2x+5y=0.基础智能检测1.A 由y -5=-34(x+2),得3x+4y -14=0. 2.C 直线方程可化为y -(-2)=-[x -(-1)],故直线过点(-1,-2),斜率为-1.3.2013 直线l 的方程为y -(-1)5-(-1)=x -(-1)2-(-1), 整理得:y=2x+1,令x=1006,得b=2013.4.解:设所求直线的斜率为k ,依题意有k=-4×13=-43.又直线经过点A (1,3),因此所求直线方程为y -3=-43(x -1), 即4x+3y -13=0.5.A 由题意可知,所求直线的斜率k=12,又经过点(1,0),∴所求直线方程为y=12(x -1),即x-2y-1=0.思维导图构建y-y0=k(x-x0)。

2025高考数学直线的方程复习课件练习题课件练习题

图1
A. 0.75
图2
B. 0.8
C. 0.85
例1
D )
训练1
例2
D. 0.9
训练2
例3
训练3
返回目录
第1讲
直线的方程
[解析] 如图，连接 OA ，延长 AA 1与 x 轴交于点 A 2，则 OA 2＝4 OD 1.因为 k 1， k 2，
2
k 3成公差为0.1的等差数列，所以 k 1＝ k 3－0.2， k 2＝ k 3－0.1，所以tan∠ AOA 2＝
我们以x轴为基准，x轴正向
π
k＝tan
α
即③
(α≠
).
与直线l① 向上的方向之
2
定间所成的角 α叫做直线l的倾 (2)坐标式：a.如果直线经过两点P1(x1，y1)，
P2(x2，y2)(x1≠ x2)，其斜率公式为
义斜角.
2 −1
规定：当直线l与x轴平行或重 ④ 1 2 ＝2 −1 .
D. 截距可以为负值
[解析] 对于A，倾斜角为钝角的直线的斜率为负值，故A错误；对于B，一条直线
的斜率为tan α，此直线的倾斜角不一定为α，如直线 y ＝ x 的斜率为tan
5π
，它的倾
4
π
4
斜角为，B错误；对于C，当经过定点 P ( x 0， y 0)的直线与 x 轴垂直时，斜率不存
在，故C错误；对于D，截距可以取正数、负数或零，所以D正确.
＝－ 2 ，所以－1≤tan
+1
B )
1
，设直线的倾斜角为α，则tan
2 +1
α
3π
α＜0，所以 ≤α＜π，故选B.
4

直线方程(习题课)课件

截距。
两点式方程
$frac{y - y_1}{y_2 - y_1} = frac{x - x_1}{x_2 - x_1}$，其中 $(x_1, y_1)$和$(x_2, y_2)$为直
线上的两点。
直线方程的应用场景
01
02
03
几何问题
解决与直线相关的几何问题，如两点之间的距离、点到直线的距离等。
详细描述
当直线与x轴相交时，令y=0，解出x的值即为交点的横坐标；当直线与y轴相交时，令x=0，解出y的值即为交点的纵坐标。
两条直线的交点问题
总结词
求两条直线的交点，需要联立两条直线的方程组求解。
详细描述
将两个直线的方程联立，形成方程组，然后解这个方程组，得到x和y的值即为两直线的交点坐标。
直线上的任意两点确定一条唯一的直线，反之，一条直线上的任意两点确定该直线上唯一的一点
。
直线方程的表示方法
点斜式方程
$y - y_1 = m(x - x_1)$，其中 $(x_1, y_1)$为直线上的一点，
$m$为直线的斜率。
Hale Waihona Puke 斜截式方程$y = mx + b$，其中$m$为直线的斜率，$b$为直线在y轴上的
参数方程是一种表示直线的方法，通过引入参数来表示直线上点的坐标。
参数方程形式
参数方程的一般形式为 (x = x(t))，(y = y(t))，其中 (t) 是参数。
参数方程的应用
参数方程在解决几何问题、物理问题以及工程问题中都有广泛应用。
极坐标形式的直线方程
01
极坐标定义
极坐标是一种表示点在平面上的位置的方法，通过距离原点的长度和与
直线方程(习题课)课件

必修2直线和圆复习题及答案

1．直线方程的几种基本形式及适用条件：(1)点斜式：，注意斜率k 是存在的．(2)斜截式：，其中b 是直线l 在上的截距．(3)两点式： (x 1≠x 2且y 1≠y 2)，当方程变形为(y 2－y 1)(x －x 1)－(x 2－x 1)(y －y 1)＝0时，对于一切情况都成立．(4)截距式：，其中a ·b ≠0，a 为l 在x 轴上的截距，b 是l 在y 轴上的截距．(5)一般式：，其中A 、B 不同时为0.1．判定两条直线的位置关系(1)两条直线的平行①假设l 1：y ＝k 1x ＋b 1，l 2：y ＝k 2x ＋b 2，则l 1∥l 2⇔ 且，l 1与l 2重合⇔ .②当l 1，l 2都垂直于x 轴且不重合时，则有 .③假设l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0，则l 1∥l 2⇔A 1B 2＝A 2B 1且B 1C 2≠B 2C 1，l 1与l 2重合⇔A 1＝λA 2，B 1＝λB 2，C 1＝(2)两条直线的垂直①假设l 1：y ＝k 1x ＋b 1，l 2：y ＝k 2x ＋b 2，则l 1⊥l 2⇔ . ②假设两条直线中，一条斜率不存在，同时另一条斜率等于零，则两条直线．③假设l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0，则l 1⊥l 2⇔ .(3)直线l 1：y ＝k 1x ＋b 1，l 2：y ＝k 2x ＋b 2相交的条件是 . 直线l 1：A 1x ＋B 1y ＋C 1＝0，l 2：A 2x ＋B 2y ＋C 2＝0相交的条件是 .自测题1．过点M (－1，m )，N (m ＋1,4)的直线的斜斜角为45° ，则m 的值为2. 以下四个命题中真命题是( )A ．经过定点P 0(x 0，y 0)的直线都可以用方程y －y 0＝k (x －x 0)表示B ．经过任意两个不同点P 1(x 1，y 1)，P 2(x 2，y 2)的直线可以用方程(y －y 1)(x 2－x 1)－(x －x 1)(y 2－y 1)＝0表示C ．不过原点的直线都可以用x a ＋y b ＝1表示D ．经过定点A (0，b )的直线都可以用方程y ＝kx ＋b 表示3．假设三点A (2,3)，B (3，－2)，C (12，m )共线，则m 的值是________．4．已知直线x ＋a 2y ＋6＝0与直线(a －2)x ＋3ay ＋2a ＝0平行，则a 的值为________．5．已知两条直线y ＝ax －2和y ＝(a ＋2)x ＋1互相垂直，则a 等于________．例题例1.已知两点A (－1,2)，B (m,3)，求：(1)求直线AB 的斜率； (2)求直线AB 的方程；例2．已知直线l ：ax ＋y －2－a ＝0在x 轴和y 轴上的截距相等，则a 的值是______例3.已知直线：l 1：ax ＋2y ＋6＝0和直线l 2：x ＋(a －1)y ＋a 2－1＝0.(1)试判断l 1与l 2是否平行；(2)l 1⊥l 2时，求a 的值例4.已知两直线l 1：mx ＋8y ＋n ＝0和l 2：2x ＋my －1＝0.试确定m 、n 的值，使：(1)l 1与l 2相交于点P (m ，－1)； (2)l 1∥l 2； (3)l 1⊥l 2，且l 1在y 轴上的截距为－1.练习题1．以下命题中，正确的选项是( )A ．假设直线的斜率为tan α，则直线的倾斜角是αB ．假设直线的倾斜角为α，则直线的斜率为tan αC ．假设直线的倾斜角越大，则直线的斜率就越大D ．直线的倾斜角α∈[0，π2)∪(π2，π)时，直线的斜率分别在这两个区间上单调递增2.．假设直线l 1，l 2关于x 轴对称，l 1的斜率是－7，则l 2的斜率是( ) A.7B ．－77 C.77 D ．－7 3.．两直线x m －y n ＝1与x n －y m ＝1的图像可能是图中的哪一个( )4.．假设点A (a,0)，B (0，b )，C (1，－1)(a >0，b <0)三点共线，则a －b 的最小值等于______5.．过点M (1，－2)的直线与x 轴、y 轴分别交于P 、Q 两点，假设M 恰为线段PQ 的中点，则直线PQ 的方程为______6.．已知直线l 的斜率为16，且和坐标轴围成面积为3的三角形，求直线l 的方程．7.．已知点M 是直线l ：3x －y ＋3＝0与x 轴的交点，将直线l 绕点M 旋转30°，求所得到的直线l ′的方程．8.．在△ABC 中，已知A (1,1)，AC 边上的高线所在直线方程为x －2y ＝0，AB 边上的高线所在直线方程为3x ＋2y －3＝0.求BC 边所在直线方程．9.．设直线l 的方程为(a ＋1)x ＋y ＋2－a ＝0(a ∈R )．(1)假设l 在两坐标轴上截距相等，求l 的方程；(2)假设l 不经过第二象限，求实数a 的取值范围．高中数学必修二直线和圆练习一、选择题1．过点(1,3)P -且垂直于直线032=+-y x 的直线方程为〔〕A ．012=-+y xB ．052=-+y xC ．052=-+y xD ．072=+-y x2．已知过点(2,)A m -和(,4)B m 的直线与直线012=-+y x 平行，则m 的值为〔〕A ．0B ．8-C ．2D ．103．已知0,0ab bc <<，则直线ax by c +=通过〔〕A ．第一、二、三象限B ．第一、二、四象限C ．第一、三、四象限D ．第二、三、四象限 4．直线l 与两直线1y =和70x y --=分别交于,A B 两点，假设线段AB 的中点为 (1,1)M -，则直线l 的斜率为〔〕A ．23B ．32C ．32-D ． 23-. 5. 圆C 1:x 2+y 2+4x-4y+7=0和圆C 2:x 2+y 2-4x-10y+13=0的公切线有( )条条条 D.以上均错6. 已知空间两点A(1,3,5)、B(-3,1,3),则线段AB 的中点坐标为( )A.(-1,2,4)B.(2,1,1)C.(1,0,4)D.(3,3,-1)7.假设直线(1+a)x+y+1=0与圆x 2+y 2-2x=0相切，则a 的值为( )、、8.已知圆C ：(x-a)2+(y-2)2=4(a>0)及直线l ：x-y+3=0，当直线l 被圆C 截得的弦长为32时，则a 等于( ) A.2 B.22- C.12- D.12+二、填空题1．点(1,1)P - 到直线10x y -+=的距离是________________.2.经过点P(1,2)与圆x 2+y 2=1相切的直线方程为______________.3. 与两平行直线x+3y-5=0和x+3y-3=0相切,圆心在直线2x+y+3=0上的圆的方程是________.4. 已知圆x 2+y 2-4x+6y-12=0的内部有一点A(4，-2)，则以A 为中点的弦所在的直线方程为______________________.三、解答题1．求经过点(2,2)A -并且和两个坐标轴围成的三角形的面积是1的直线方程。

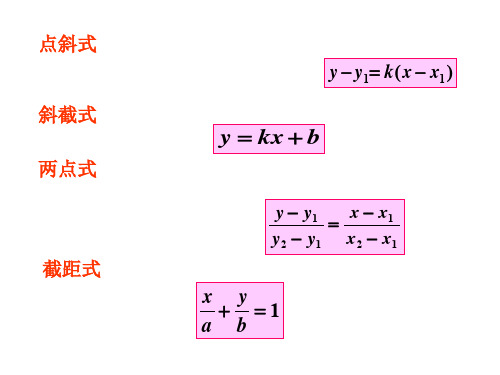
直线方程的几种形式(5种)

已知直线 l的斜率为 k , 与y轴的交点是 (0, b), 求直线的方程 . 解: 由直线的点斜式,得 y b k ( x 0)
即y kx b
y
方程y kx b叫做直线方程的斜截式 .方程
b叫做直线 l在y轴上的截距 .
b

l
斜---斜率截---y轴上的截距
y y1 x x1 方程叫做直线的两点式 y 2 y1 x 2 x 1
练习已知直线经过两点 P1 (2,1), P2 (0,3)
则直线的方程为
y 1 x2 即2 x y 3 0 31 0 2
四.直线的截距式方程
已知直线 l与x轴的交点为 (a,0),与y轴的交点为 (0, b),其中a 0, b 0, 求直线 l的方程 .
求这个三角形三边所在的直线方程 .
解: 把A, C代入两点式 ,得 y 0 x (5) 2 0 0 (5)
2 x 5 y 10 0
AC在x, y轴另解: 由A, C两点的坐标得直线
上的截距为 a 5, b 2. 由截距式得
x y 1 5 2
化成一般式得 : 4 x 3 y 12 0
例5:
把直线方程 2 x 3 y 6 0化成斜截式 , 截距式, 求出它的斜率和它在 x, y轴上的截距 .
2 y x 2. 解: 斜截式为 3 x y 2 截距式为 1斜 . 率k . 3 2 3 x轴上的截距为 a 3, y轴上的截距为 b 2.
解: 把点 (a,0),(0, b)代入两点式方程 ,得
y0 xa b0 0a
x y 1 a b

2018版第2章2.2.2直线方程的几种形式学业分层测评

学业分层测评(建议用时：45分钟)[学业达标]一、选择题1.下列说法正确的是()A.经过定点P0(x0，y0)的直线都可以用方程y－y0＝k(x－x0)表示B.经过任意两个不同点P(x1，y1)、P2(x2，y2)的直线都可以用方程(y－y1)(x2－x1)＝(x－x1)(y2－y1)表示C.不经过原点的直线都可以用方程xa＋yb＝1表示D.经过定点A(0，b)的直线都可以用方程y＝kx＋b表示【解析】当直线与y轴重合时，斜率不存在，选项A、D不正确；当直线垂直于x轴或y轴时，直线方程不能用截距式表示，选项C不正确；当x1≠x2，y1≠y2时由直线方程的两点式知选项B正确，当x1＝x2，y1≠y2时直线方程为x －x1＝0，即(x－x1)(y2－y1)＝(y－y1)(x2－x1)，同理x1≠x2，y1＝y2时也可用此方程表示.故选B.【答案】 B2.直线(m＋2)x＋(m2－2m－3)y＝2m在x轴上的截距为3，则实数m值为()A.65 B.－6C.－65 D.6【解析】将(3,0)代入得(m＋2)3＝2m解得m＝－6.【答案】 B3.若直线ax＋by＋c＝0经过第一、二、三象限，则()A.ab>0，bc>0B.ab>0，bc>0C.ab <0，bc >0D.ab <0，bc <0【解析】直线经过第一、二、三象限，则由y ＝－a b x －c b 可知，⎩⎪⎨⎪⎧ －a b >0，－c b >0，⇒⎩⎪⎨⎪⎧ab <0，bc <0，选D. 【答案】 D4.两条直线l 1：x a －y b ＝1和l 2：x b －y a ＝1在同一直角坐标系中的图象可以是( )【解析】化为截距式x a ＋y －b ＝1，x b ＋y －a＝1. 假定l 1，判断a ，b ，确定l 2的位置，知A 项符合.【答案】 A5.若直线(2m 2＋m －3)x ＋(m 2－m )y ＝4m －1在x 轴上的截距为1，则实数m 是( )【导学号：45722084】A.1B.2C.－12D.2或－12 【解析】当2m 2＋m －3≠0时，在x 轴上的截距为4m －12m 2＋m －3＝1，即2m 2－3m －2＝0，∴m ＝2或m ＝－12.【答案】 D二、填空题6.直线y ＝ax －3a ＋2(a ∈R )必过定点________.【解析】将直线方程变形为y －2＝a (x －3)，由直线方程的点斜式可知，直线的斜率为a ，过定点(3,2).【答案】 (3,2)7.已知直线l 1过点P (2,1)且与直线l 2：y ＝x ＋1垂直，则l 1的点斜式方程为________.【导学号：45722085】【解析】直线l 2的斜率k 2＝1，故l 1的斜率为－1，所以l 1的点斜式方程为y －1＝－(x －2).【答案】 y －1＝－(x －2)8.已知光线经过点A (4,6)，经x 轴上的B (2,0)反射照到y 轴上，则光线照在y 轴上的点的坐标为________.【解析】点A (4,6)关于x 轴的对称点A 1(4，－6)，则直线A 1B 即是反射光线所在直线，由两点式可得其方程为：3x ＋y －6＝0，令x ＝0，得y ＝6，所以反射光线经过y 轴上的点的坐标为(0,6).【答案】 (0,6)三、解答题9.若方程(m 2－3m ＋2)x ＋(m －2)y －2m ＋5＝0表示直线.(1)求实数m 的范围；(2)若该直线的斜率k ＝1，求实数m 的值.【解】 (1)由⎩⎪⎨⎪⎧m 2－3m ＋2＝0，m －2＝0，解得m ＝2，若方程表示直线，则m 2－3m ＋2与m －2不能同时为0，故m ≠2.(2)由－(m 2－3m ＋2)m －2＝1，解得m ＝0. 10.求过点(4，－3)且在两坐标轴上截距的绝对值相等的直线l 的方程.【解析】法一设直线在x 轴、y 轴上的截距分别为a ，b .①当a ≠0，b ≠0时，设l 的方程为x a ＋y b ＝1.∵点(4，－3)在直线上，∴4a ＋－3b ＝1，若a ＝b ，则a ＝b ＝1，直线方程为x ＋y ＝1.若a ＝－b ，则a ＝7，b ＝－7，此时直线的方程为x －y ＝7.②当a ＝b ＝0时，直线过原点，且过点(4，－3)，∴直线的方程为3x ＋4y ＝0.综上知，所求直线方程为x ＋y －1＝0或x －y －7＝0或3x ＋4y ＝0. 法二设直线l 的方程为y ＋3＝k (x －4)，令x ＝0，得y ＝－4k －3；令y ＝0，得x ＝4k ＋3k .又∵直线在两坐标轴上的截距的绝对值相等，∴|－4k －3|＝⎪⎪⎪⎪⎪⎪4k ＋3k ，解得k ＝1或k ＝－1或k ＝－34.∴所求的直线方程为x －y －7＝0或x ＋y －1＝0或3x ＋4y ＝0.[能力提升]1.直线x －y ＋1＝0关于y 轴对称的直线的方程为( )A.x －y －1＝0B.x －y －2＝0C.x ＋y －1＝0D.x ＋y ＋1＝0【解析】令y ＝0，则x ＝－1，令x ＝0，则y ＝1，∴直线x －y ＋1＝0关于y 轴对称的直线过点(0,1)和(1,0)，由直线的截距式方程可知，x ＋y ＝1，即x ＋y －1＝0.【答案】 C2.已知两直线的方程分别为l 1：x ＋ay ＋b ＝0，l 2：x ＋cy ＋d ＝0，它们在坐标系中的位置如图2-2-3所示，则( )图2-2-3A.b >0，d <0，a <cB.b >0，d <0，a >cC.b <0，d >0，a >cD.b <0，d >0，a <c【解析】由题图可知直线l 1、l 2的斜率都大于0，即k 1＝－1a >0，k 2＝－1c >0且k 1>k 2，∴a <0，c <0且a >c .又l 1的纵截距－b a <0，l 2的纵截距－d c >0，∴b <0，d >0，故选C.【答案】 C3.已知A (3,0)，B (0,4)，直线AB 上一动点P (x ，y )，则xy 的最大值是________.【解析】直线AB 的方程为x 3＋y 4＝1，设P (x ，y )，则x ＝3－34y ，∴xy ＝3y －34y 2＝34(－y 2＋4y )＝34[－(y －2)2＋4]≤3.即当P 点坐标为⎝ ⎛⎭⎪⎫32，2时，xy 取得最大值3. 【答案】 34.直线过点P ⎝ ⎛⎭⎪⎫43，2且与x 轴、y 轴的正半轴分别交于A ，B 两点，O 为坐标原点，是否存在这样的直线同时满足下列条件：(1)△AOB 的周长为12；(2)△AOB 的面积为6.若存在，求出直线的方程；若不存在，请说明理由.【导学号：45722086】【解】设直线方程为x a ＋y b ＝1(a >0，b >0)，若满足条件(1)，则a ＋b ＋a 2＋b 2＝12. ① 又∵直线过点P ⎝ ⎛⎭⎪⎫43，2，∴43a ＋2b ＝1. ②由①②可得5a 2－32a ＋48＝0，解得⎩⎪⎨⎪⎧ a ＝4，b ＝3或⎩⎪⎨⎪⎧a ＝125，b ＝92，∴所求直线的方程为x 4＋y 3＝1或5x 12＋2y 9＝1，即3x ＋4y －12＝0或15x ＋8y －36＝0.若满足条件(2)，则ab ＝12， ③由题意得：43a ＋2b ＝1， ④由③④整理得a 2－6a ＋8＝0，解得⎩⎪⎨⎪⎧ a ＝4，b ＝3，或⎩⎪⎨⎪⎧a ＝2，b ＝6，∴所求直线的方程为x4＋y3＝1或x2＋y6＝1，即3x＋4y－12＝0或3x＋y－6＝0.综上所述：存在同时满足(1)(2)两个条件的直线方程，为3x＋4y－12＝0.。

直线方程的几种形式

2．2．2直线方程的几种形式（2）
一、学习目标：
1、掌握直线方程的几种形式；
2、了解不同形式的直线方程的推导过程。

二、学习重点：根据所给条件灵活选取适当形式和方法求出直线方程。

三、学习难点：清楚各种形式的直线方程的局限性，把握求直线方程的灵活性。

四、新知：
直线的一般式方程是： ,当 B 0时，化为斜截式方程为,斜率为，在y 轴上的截距为.
五、例题：已知直线过点（-2，5），k=-3
4
,求此直线的一般式方程。

六、当堂检测：
1、根据直线方程，求直线的斜率及y轴上的截距：
（1）2x-3y-6=0 (2)3x-y-7=0
(3)2x-5y=0 (4)x+y=3
2、求下列直线与两条坐标轴围成的三角形的面积：
（1）3x-y+1=0 （2）5x-3y+2=0
（3）x+y-1=0 （4）x+3y-6=0
3、已知平行四边形ABCD,其中三个顶点的坐标为A（0，0），B（3，0），C（5，3），求它的对角线AC,BD所在的直线方程。

4、已知点A（-3，2），B(1,-4),求AB的垂直平分线的方程。

（提示：利用两点间距离公式）
5、已知点A（-1，2），B（2，1）C（0，4），求三角形ABC三条边所在直线的斜率。

6、直线Ax+By+C=0的系数满足何条件时
（1）过坐标原点
（2）直线只与x轴相交
（3）直线只与y轴相交
（4）直线与x轴平行或重合
（5）直线与y轴平行或重合
7、与两坐标轴的正方向围成面积为2的三角形且截距差为3的直线方程。

人教版B版高中数学必修2：2.2.2 直线方程的几种形式

其中，与x轴平行或重合的直线的倾斜角为，斜率k= 0 ；
与x轴垂直的直线的倾斜角为
，斜率k 不存在 .
探究一：
如果以一个方程的解为坐标的点都在某条直线上，且这条直线上点的坐标都是这个方程的解，那么这个方程叫做这条直线的方程，这条直线叫做这个方程的直线。
y
0
x
探究一：
这个方程叫做直线的点斜式方程。
y
0
x
（1）这个方程是由哪两个条件确定的？
y
0
x
y
0
x
探究二：
如果一条直线通过点（0，b），且斜率为k，则直线的方程是什么？
这个方程叫做直线的斜截式方程。
截距是距离吗？
yb
b
0
x
b
以上直线在x轴上的截距呢？（与x轴交点的横坐标）
探究三：
这种形式的方程叫做直线的两点式方程.
技巧：根据给出的确定直线的条件，利用数形结合，能直接得到结果的，直接得结果；否则，利用直线方程的几种形式，选择恰当的形式进行运算。
2.2.2直线方程的几种形式（一）
大连市第一中学郜汝姣
复习：
1、直线方程的概念是什么？
如果以一个方程的解为坐标的点都在某条直线上，且这条直线上点的坐标都是这个方程的解，那么这个方程叫做这条直线的方程，这条直线叫做这个方程的直线。
2、直线倾斜角的定义是什么？
x轴正向与直线向上的方向所成的角叫做这条直线的倾斜角。规定，与x轴平行或重合的直线的倾斜角为零度角。
使复杂问题简单化，抽象问题具体化，化难为易。
练习：
1、教材79页练习A第3题；.y Nhomakorabea0
x
思考：