一个简单的数学小魔术
有关莫比乌斯带的资料小作文

有关莫比乌斯带的资料小作文好,今天我们来聊聊一个很有趣的数学玩具——莫比乌斯带。
听起来可能有点复杂,但别担心,我会用最简单的方式跟你讲解。
相信我,了解它其实比你想的要简单有趣多了。
首先,大家都知道,数学有时候就像在做魔术。
莫比乌斯带就是这种“魔术”中的一员。
说白了,莫比乌斯带就是一种非常神奇的二维几何形状。
它的特别之处在于,它只有一个面,一个边。
听上去是不是有点不可思议?我也是刚知道的时候瞪大了眼睛。
想象一下,你有一条普通的长纸带,然后你把它扭转一下,再把两个末端粘在一起。
这样,你就做成了一个莫比乌斯带。
这种带子就像是被魔法“变”出来的,因为它的每一面都和另一面连在一起了。
简单来说,如果你在上面画一条线,从头到尾画下去,你会发现这条线最终会回到起点,还是在同一面上。
是不是很神奇?有一次,我和我的小伙伴们在一起玩这个魔术。
小明说:“嘿,咱们来做一个莫比乌斯带吧!”然后他就拿了一条纸带,我们都围在一起,看着他扭来扭去。
我当时有点懵,心想:“这是要搞什么?”小红却兴奋地跳起来说:“我听说这个玩意儿能让你变成数学天才!”纸带做好之后,我们开始在上面画线。
结果,大家都发现了一个有趣的现象:画线画着画着,就变成了一条连续的线,绕了个圈,还回到了原点。
大家都惊呼:“哇,真是太酷了!”那一刻,我们都觉得自己像是在做一些高深的科学实验,尽管其实我们只是玩了个简单的数学游戏。
我记得小刚对这个莫比乌斯带特别感兴趣,他说:“这是不是说明,如果我们在上面爬行的话,我们就永远不会下来?”我笑了笑说:“哈哈,那倒不是,不过你可以在上面走得不停。
”小刚一下子就不说话了,但眼神里却充满了好奇。
然后,我们还发现了另一个有趣的东西。
我们试着把莫比乌斯带剪成两段。
大家都期待着“神奇的效果”。
结果我们剪出来的竟然不是两个分开的带子,而是变成了两个缠绕在一起的环形带子。
真是意想不到!大家又一次笑得前仰后合,小红说:“这简直是数学界的超级魔术!”其实,莫比乌斯带的奇妙之处不仅仅在于它的奇特形状,还在于它能够引发我们对数学和空间的无限想象。
数学魔术:读出你心中的一二三四

数学魔术:读出你心中的一二三四Albert_JIAO2010-12-15 15:23:34魔术师要用四张扑克牌为你表演一个心灵感应魔术。
表演开始了。
魔术师上场后先把准备好的四张扑克牌,红桃 A、红桃 2、红桃 3、红桃 4,从左到右依次摆到桌面上。
接着,魔术师像往常一样在现场找了一位观众,然后对大家说:“今天我要读出你心中的一二三四。
现在我背过身去,然后你在 1、2、3、4 四个数字中选择一个你最喜欢的,把这张数字的牌和红桃 A 互相交换位置。
比如,你选了红桃 2,就要把红桃 2 放到红桃 A 原来的位置上,把红桃 A 放到红桃 2 原来的位置上。
当然,如果你最喜欢的牌正是红桃 A,就什么也不用做了。
”这位观众想了想,选择了红桃 3。
之后,魔术师说:“现在请你把四张牌都翻过去,然后从左到右把四张牌叠在一起,最左面的那张牌自然就被放到了最下面。
”等着这位观众把扑克牌收好之后,魔术师转过身来:“好了,四张扑克牌都在你的手中,我什么也看不到。
为了让你选的那张牌藏得毫无踪迹,下一步就是要把这四张牌洗乱。
那么怎么洗呢?这样,你每次从这叠牌的上面取一张、两张或者三张牌放到牌的最底下,经过十次“翻江倒海”之后,这四张牌的顺序一定就被完全打乱了。
那么,现在就请你开始吧。
”这位观众按照要求把手中的几张牌洗来洗去,结束后交给了魔术师。
“现在我要把这四张扑克牌重新放到桌面上”,他轻轻地用手翻开最上面的一张牌,是红桃 2,然后把它摆在了最左面。
魔术师再把接下来的三张牌依次摆在了后面。
台下的观众看到,四张牌的确已经和开始的时候顺序完全不一样了。
魔术师随后伸出双手,在四张牌的上面挥舞一番,施加起了他的“魔法”。
然后,魔术师神秘兮兮地对这位观众说道,“你选的牌一定不是 2,也不是 A,只剩下了两张牌,3 和 4。
我的第六感觉告诉我,你选的牌一定是——红桃 3。
”随后台下响起一阵热烈的掌声,魔术师成功地答对了这道“四选一”的选择题。
数学魔术

第一部分数学魔术一、简单的小魔术在一张纸上并排画 11 个小方格。
叫你的好朋友背对着你(确保你看不到他在纸上写什么),在前两个方格中随便填两个 1 到 10 之间的数。
从第三个方格开始,在每个方格里填入前两个方格里的数之和。
让你的朋友一直算出第 10 个方格里的数。
假如你的朋友一开始填入方格的数是 7 和 3 ,那么前 10 个方格里的数应该是10 个方格里的数,你只需要在计算器上按几个键,便能说出第 11 个方格里的数应该是多少。
你的朋友会非常惊奇地发现,把第 11 个方格里的数计算出来,所得的结果与你的预测一模一样!这就奇怪了,在不知道头两个数是多少的情况下,只知道第 10 个数的大小,不知道第 9 个数的大小,怎么能猜对第 11 个数的值呢?魔术揭秘:只需要除以 0.618其实,仅凭借第 10 个数来推测第 11 个数的方法非常简单,你需要做的仅仅是把第10 个数除以 0.618,得到的结果四舍五入一下就是第 11 个数了。
在上面的例子中,由于249÷0.618 = 402.913.. ≈ 403,因此你可以胸有成竹地断定,第 11 个数就是 403。
而403。
把头两个方格里的数换一换,结论依然成立:可以看到,第 11 个数应该为 215+348 = 563,而 348 除以 0.618 就等于 563.107..,与实际结果惊人地吻合。
这究竟是怎么回事儿呢?魔术原理:溶液调配的启示不妨假设你的好朋友最初在纸上写下的两个数分别是 a 和 b 。
那么,这 11 个方格里的数分别为:接下来,我们只需要说明,21a+34b 除以 34a+55b 的结果非常接近 0.618 即可。
让我们来考虑另一个看似与此无关的生活小常识:两杯浓度不同的盐水混合在一起,调配出来的盐水浓度一定介于原来两杯盐水的浓度之间。
换句话说,如果其中一杯盐水的浓度是 a/b,另一杯盐水的浓度是 c/d,那么 (a+c)/(b+d) 一定介于 a/b 和 c/d 之间。
4个超有趣的数学小魔术,快来学学看3篇

4个超有趣的数学小魔术,快来学学看第一篇:拆数小魔术材料:一副扑克牌、纸片、笔步骤:1. 将扑克牌洗牌。
2. 请观众从牌组中选取一张牌,并且不要让你知道。
3. 将剩余的牌分为两组,每组都有不同数量的牌。
将每组的牌放在观众的左右两侧。
4. 让观众数出左侧组的牌数,然后让他们反转右侧组的牌数。
5. 让观众将两组牌的数量相加,得到一个数字,并且将结果告诉你。
6. 将这个数字减去1,然后在纸片上写出这个数字对应的扑克牌,例如5就是5号的黑桃牌。
7. 然后请观众拿出他们选的牌,上面的字母就是刚刚写下的扑克牌。
8. 观众一定会很惊奇,不敢相信这个小魔术。
解析:这个小魔术的关键是观众不知道你是如何确定他们选择的扑克牌的。
其实这个魔术基于数学原理,你会得到观众左侧组的牌数和右侧组牌数加起来减去1的数字。
换句话说,你得到的数字就是观众选择的扑克牌在整个牌组中的位置,然后你可以根据对应的顺序写下扑克牌。
很神奇,但就是这么简单!第二篇:数字魔幻材料:一张纸、一支笔步骤:1. 首先让观众想一个三位数(每位的数不相等)。
2. 然后让他们将这个数字的百位数字减去它的个位数字。
(比如531就是5-1=4)3. 让观众记住这个数字。
4. 让他们再把刚刚减掉的那个数字加回去,这个时候数字就变化了。
5. 请观众把数位上的数字按照从大到小的顺序排列,这样就得到了一个新的数字。
6. 然后让他们把新数字减去旧数字,得到的结果一定是9的倍数。
7. 观众一定会对这个结果感到惊奇!解析:这个小魔术的本质是基于数字的规律。
无论观众选择的起始数字是什么,最终得到的结果一定是45或者其倍数。
因为无论如何做,起始数字的百位数字和个位数字一定是会相加,然后中间的数字自然也是出现在结果之中的。
因此,新数字和旧数字只是在重新排列数字顺序这一步有所不同,其他的步骤都是相同的。
这个小魔术看似有些神奇,但其实就是数学规律的运用。
第三篇:魔术算式材料:一副扑克牌、一张纸片、一支笔步骤:1. 把所有的红色牌拿出来,从中选出任意一张牌,并把它放在一边。
借助数学魔术巧学二进制

借助数学魔术巧学二进制二进制是计算机科学中非常重要的一种数据表示方式。
它基于二进制数字,只包括 0 和 1,并且可以更高效地在计算机中处理。
虽然二进制看起来很晦涩难懂,但是我们可以借助一些数学魔术来更容易地理解和学习二进制。
魔术 1:折纸折纸法是一种可以表示二进制的方法。
假设我们有一张纸,在第一个折痕上将其纸张对折,再将其对折。
现在,我们可以把叠在一起的物质形态看作一个 1,还剩下一半的另一半看作一个 0。
如果我们继续折叠纸张,并且建立垂直于前一个对折的轴,我们可以对每一次折叠得到一个新的数字。
当折叠多次后,最后的数字就是使用二进制系统表示的数字。
例如,如果我们折叠了 3 次,就会得到一个以二进制表示为 0111 的数字。
魔术 2:使用锅盖欧洲的某些酒吧,为了让客人更容易地点餐,会在桌子上放置一些锅盖,并在上面用二进制代码表示不同的点菜选项。
每个锅盖可以翻成 0 或 1,表示不同的点菜选项。
当服务员来取餐时,他们只需要简单地读取锅盖的值,并将它们转换为十进制数字即可完成点单。
这种方法使得点单变得更为简单,因为客人只需要翻开需要的锅盖即可点单,而不需要再寻找整个菜单,即便他们不会读取二进制也没有关系。
魔术 3:基于颜色的二进制有一种有趣且有用的二进制表示方式是基于颜色的。
这种方法使用了红、绿、蓝三种颜色,每种颜色代表一个位的值(0 或 1)。
例如,当设置一个颜色,比如 #00ff00,它代表的就是 0001 1111 0000 0000 的 16 位二进制数。
这种方法可以用于制作色码表。
例如,一些设计师使用基于颜色的方法来选择网页上的颜色。
他们只需要将添加的颜色映射到颜色的二进制表示,并选择最小化相邻颜色之间的差异的颜色。
魔术 4:通过图形来学习二进制我们可以通过展示简单的图形并将其转换成二进制来更好地理解二进制。
例如,我们可以展示一个由 1 个球和 3 个立方体组成的图形,我们可以通过一对 0 和 1 表示两种不同的形状。
数学的神奇教二年级学生认识和使用简单的数学魔术

数学的神奇教二年级学生认识和使用简单的数学魔术数学是一门神奇的学科,它可以让我们用逻辑思维解决各种问题。
而数学魔术,则是将数学知识与娱乐巧妙结合的一种表演形式。
今天,我将为大家介绍几个简单的数学魔术,帮助二年级的小朋友们认识和使用数学的魔力。
1. 朋友的年龄我有个小朋友朋友,他的年龄现在是X岁。
通过几个简单的问题,我可以从他回答的内容推算出他的年龄是多少。
首先,我问他现在的年龄加上3岁等于多少,他回答说是Y岁。
接着,我再问他现在的年龄再加上5岁等于多少,他回答说是Z岁。
通过这两个问题的回答,我可以利用一个简单的公式解决这个问题。
首先,我们设朋友现在的年龄为X岁,根据第一个问题的回答,得出X + 3 = Y。
然后,根据第二个问题的回答,得出X + 5 = Z。
接下来,我们将第一个等式乘以2得到2X + 6 = 2Y,然后将第二个等式减去第一个等式得到2 = Z - Y。
最后,我们将第一个等式减去第二个等式得到X = 4。
通过这个简单的数学魔术,我们可以用数学的方式推测出朋友的年龄。
对于二年级的小朋友们来说,这既是一种有趣的游戏,也是练习数学运算的好方法。
2. 手指预测接下来,我要展示一个令人惊叹的数学魔术。
请大家伸出自己的双手,然后说出任意一个数字。
假设某位小朋友说出了数字5。
我会告诉他,将这个数字乘以2,再加上6,再除以2,最后减去他刚才说出的数字。
最后的结果,就是他伸出的手指数目。
让我们来用数学表达式的方式解释一下这个数学魔术。
假设小朋友说的数字是X,按照魔术指导的步骤,我们可以得出表达式:((X × 2 + 6) ÷ 2) - X = Y。
其中,Y代表最后的结果,也就是手指数目。
这个魔术看似神奇,实则是运用了数学运算的原理。
通过对一系列的乘法、加法、除法和减法的操作,我们可以巧妙地将数字和手指数目联系起来。
3. 神奇的九宫格最后,我要给大家介绍一个数学魔术中的经典项目——神奇的九宫格。
数学小魔术猜差(课件)小学数学 有趣的计算通用版

04 注意事项
注意事项: (1)任意写一个三位数,不能让猜差的人知道写的是多少 。 (2)只告诉猜差的人,最后差的个位是几。 (3)猜差的人要故作神秘。 (4)如果差的个位是0,那么差也是0。
感谢聆听
神奇速算法006
数学小魔术 猜差(二)
01 步骤和窍门
数学小魔术——步骤:
(1)任意写一个三位数。
(2)颠倒这个三位数的个位和百位,十位不变。
(3)用较大的三位数减去较小的三位数,得到一个差。
(4)只要告知差的个位。 (5)就能迅速知道差是多少。
窍 门: 差的个位 + 差的百位 = 9
差的十位是9
02 示范猜差(一)
(1)任பைடு நூலகம்写一个三位数——217 (2)颠倒个位和百位——712 (3)较大数减去较小数——712减217 (4)差的个位——5 (5)差的百位——9减5等于4 (6)差的十位是9 (7)差就是495
03 示范猜差(二)
(1)任意写一个三位数——594 (2)颠倒个位和百位——495 (3)较大数减去较小数——594减495 (4)差的个位——9 (5)差的百位——9减9等于0 (6)差的十位是9 (7)差就是99
数学魔术84个神奇的数学小魔术

数学魔术84个神奇的数学小魔术数学魔术是结合数学知识和魔术操作技巧的一种表演形式,可以给观众带来惊喜和兴奋。
以下列举了84个神奇的数学小魔术,让我们一起来畅游于数学的世界吧!1. 把一个正方形剪成两个相等的三角形,再把这两个三角形颠倒位置,竟然可以拼成一个不规则的平行四边形。
2. 把一个正三角形剪成四个相等的小三角形,在摆成一个T字形后,再把T字形整体转90度,就变成了一个长方形。
3. 给定一个心形图形,可以利用一张正方形纸和一支笔完成心形的画法。
4. 以任意一点为圆心割圆,在圆上取三点作为三角形的三个顶点,将其对角线交点用直线连接,竟然可以将三角形划分成6个小三角形。
5. 把一个长方形切成两个相等的小长方形,并把这两个小长方形交错放置,竟然会得到一个看起来比原来长方形宽的“长方形”。
6. 将一个等腰三角形的底边向外翻折,再将其两侧翻转90度,竟然可以得到一个正方形。
7. 在一张正方形纸上做连线,就可以得到一个图案,其元素个数等于所有点对之间的连线个数。
8. 用一个等腰三角形的三边拼成一个小正方形,就可以发现和原来的等腰三角形面积相等。
9. 把一个三角形顺时针旋转120度,再逆时针旋转90度,就可以得到一个正方形。
10. 在一张正方形纸上画四条直线,每条直线都与另外两条直线相交,可以得到一个有6个小正方形的图形。
11. 把一个正方形切成9个相等的小正方形,再将其中4个小正方形取出,可以组成一个大正方形。
12. 在一张纸上画两条平行直线,再在两条直线之间随机用点连线,就可以得到许多个面积相等的小正方形。
13. 把一个五角星剪成10个三角形,再重新拼成一个四边形,竟然可以使四边形的周长比原来的五角星短。
14. 将一个正方形和一个正五边形拼成一个长方形,可以使其周长相等。
15. 在一张纸上画三条相交的直线,可以得到4个小三角形,其中一个小三角形的面积等于其他三个小三角形的面积之和。
16. 把一个长方形剪成两个相等的小长方形,再把这两个小长方形交错放置,竟然会得到一个看起来比原来长方形窄的“长方形”。
六年级数学小故事简短

六年级数学小故事简短在一个幼儿园旁边的小学,有一位充满激情和创意的六年级数学老师,叫做李老师。
她经常用各种小故事和游戏来教授数学知识,让学生们在快乐中学习。
今天,我要跟大家分享几个六年级数学小故事。
故事一:魔术水杯李老师为了教孩子们理解反比例关系,准备了一种特殊的魔术水杯。
杯子里装满的水量和杯子倒立时水的高度成反比例关系。
李老师请一位学生上来演示。
学生小明站在黑板前,手里拿着装满水的杯子,将杯子倒过来放在黑板上。
水开始往外流,同时黑板上出现了一个图表,显示了水的高度随时间的变化。
村民们惊呆了,每个人都聚精会神地观察着水的变化。
水越流越快,杯子里的水减少了,同时黑板上的图表也在变化。
最后,学生小明放下杯子,黑板上的图表显示出了明显的反比例关系。
大家都拍手称赞,李老师满意地微笑着,对学生们说:“大家通过这个魔术水杯的演示,理解了什么是反比例关系,是不是很神奇呢?”故事二:跳绳游戏李老师为了教孩子们理解平方根的概念,设计了一个跳绳游戏。
她要求学生分成几组,每组三个人,其中两个人分别抄起一段绳子,形成一个直角三角形,第三个人则是计时员。
其他同学则是观察员。
计时员开始计时,两个同学不停地跳绳,直到绳子在空中形成一个完美的抛物线。
当绳子回到原位时,计时员停止计时。
然后,同学们交换角色,重复这个过程。
经过几次练习后,李老师让学生们一起观察记录每次跳绳的时间。
他们发现,每次跳绳的时间都不同,但是跳绳次数的平方却和跳绳的时间成正比。
李老师解释道:“通过这个游戏,你们不仅锻炼了身体,还学习到了平方根的概念,真是一举多得。
”故事三:魔术方块李老师想要让学生们理解体积和表面积之间的关系,于是她带来了一个奇特的魔术方块。
这个方块可以根据你的需求自动变化体积和表面积。
学生小华上来挑战,李老师摆出了一个正方体。
小华拿起魔术方块,按下一个按钮,方块立刻变成了一个长方体。
他再按下一个按钮,方块又变成了一个圆柱体。
小华继续按下按钮,方块变成了一个锥体。
神奇的空洞(数学中的小魔术)
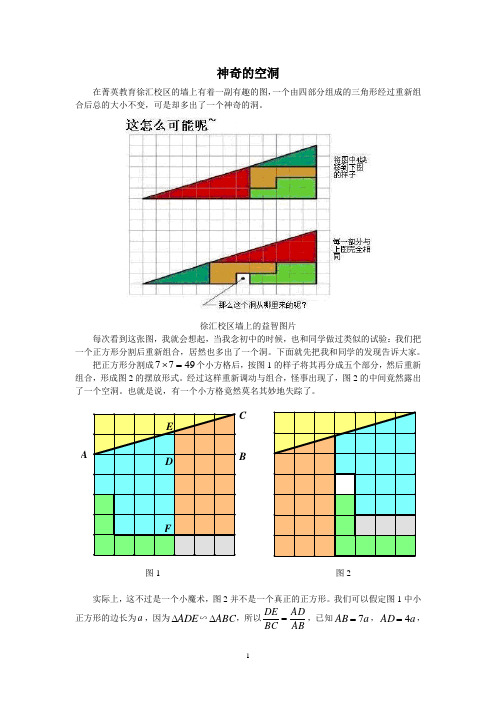
神奇的空洞在菁英教育徐汇校区的墙上有着一副有趣的图,一个由四部分组成的三角形经过重新组合后总的大小不变,可是却多出了一个神奇的洞。
徐汇校区墙上的益智图片每次看到这张图,我就会想起,当我念初中的时候,也和同学做过类似的试验:我们把一个正方形分割后重新组合,居然也多出了一个洞。
下面就先把我和同学的发现告诉大家。
把正方形分割成4977=⨯个小方格后,按图1的样子将其再分成五个部分,然后重新组合,形成图2的摆放形式。
经过这样重新调动与组合,怪事出现了,图2的中间竟然露出了一个空洞。
也就是说,有一个小方格竟然莫名其妙地失踪了。
CBA图1 图2实际上,这不过是一个小魔术,图2并不是一个真正的正方形。
我们可以假定图1中小正方形的边长为a ,因为ADE ∆∽ABC ∆,所以ABAD BC DE =,已知a AB 7=,a AD 4=,a BC 2=,求得a DE 78=,从而a EF 736=,这样一来,图2中右边的总边长就成了a a a 7502736=+,与最一开始的a 7长度并不相符。
但由于只是长了一些,肉眼很难分辨出来而已。
而图2的宽度仍然是a 7,这说明图2其实是个长方形,与图1相差的面积为2777750a a a a a =⨯-⨯,这就是神秘失踪的那个小正方形。
换句话说,图2实际上比图1的面积稍大了一些,减去中间的那个空洞的部分,两者就完全一致了。
现在徐汇校区墙上的那张益智图片你有答案了吗?没错,上方图中的绿色三角形两条直角边的边长之比为2:5,而红色三角形两条直角边的边长之比为3:8,这说明图中的几何形状并不是真正的直角三角形,只是单凭肉眼分辨不出而已。
因此它被重新组合后会出现一个神奇的空缺。
在明白了上述两个欺骗眼睛的游戏后,我再附上一个有趣的图,大家不妨自己动手做做。
请你把图上8个区域的面积算一算,求出它们的总和,但请注意,先别把小洞的面积算进去。
911662222446610101641641129621062121620211=⨯⨯+⨯⨯+⨯⨯⨯+⨯⨯=S ,现在再来算一下这个等腰三角形的面积,4162632212=⨯⨯=S 。
春晚魔术数学解释

春晚魔术数学解释
春晚魔术背后的数学原理主要是“约瑟夫问题”。
这个问题涉及到数学中的序列和循环,通常用在一个固定数量的对象(比如人或物)按照一定的顺序进行排列,然后按照特定的规则逐个淘汰,直到只剩下一个对象。
以刘谦的扑克牌魔术为例,这个魔术首先需要准备四张扑克牌,然后将它们平均撕成两份,叠放在一起。
接着,将牌堆顶数量为“名字字数”的牌移至牌堆底。
最后,将前三张牌放在牌堆中间并取出牌堆顶的牌。
这个魔术中,数学原理的运用使得每张牌被选中的概率都是25%,看起来非常神奇。
另外,硬币进杯和戒指进鸡蛋的魔术则涉及到物理原理。
硬币进杯的魔术中,大杯内部是口大底小的内壁与桌面明显不是垂直的,所以硬币从桌面垂直向上射出后先被大杯壁反弹改变了运动轨迹,再由大杯底反弹就刚好进入小杯。
而戒指进鸡蛋的魔术则是一个典型的“消失和出现”魔术,通过特殊的道具和手法使得看似不可能的事情发生。
总的来说,春晚魔术之所以神奇,背后是各种科学原理的巧妙运用。
这些原理包括数学中的“约瑟夫问题”,以及物理中的运动轨迹和道具手法等。
扑克牌魔术数学规律

扑克牌魔术数学规律稿子一:嘿,亲爱的小伙伴们!今天咱们来聊聊扑克牌魔术里那些超有趣的数学规律。
你知道吗,扑克牌就像是一个藏着好多秘密的小盒子。
比如说,咱们常见的 52 张牌,这里面的数字和花色组合起来,就有很多神奇的地方。
咱们先看看牌的点数,从 1 到 13 ,这数字的排列本身就有点小规律。
每次变魔术的时候,魔术师心里都清楚这些数字之间的关系。
比如说,要是连续抽几张牌,通过简单的加减,就能得出一些让人惊讶的结果。
再说说花色,红桃、黑桃、方块、梅花,它们可不是随便存在的哦。
在某些魔术里,根据抽到的花色就能做出一些巧妙的预测。
还有哦,要是把牌平均分几份,然后做一些交换和重新组合,按照特定的数学公式去操作,展示出来的效果绝对能让你瞪大眼睛。
其实啊,这些数学规律就像是隐藏在扑克牌里的小精灵,只有懂得怎么和它们玩耍的魔术师才能发现它们的秘密,然后给咱们带来精彩的表演。
是不是超级神奇?稿子二:宝子们,今天来和你们讲讲扑克牌魔术的数学规律啦!扑克牌魔术真的太酷啦,每次看到都觉得好神奇,对不对?但其实背后都有数学规律在帮忙呢。
就像每次洗牌,看起来是随意的,但其实魔术师心里有数。
比如说,他们知道在一副牌里,相同点数的牌出现的概率是固定的。
还有哦,如果把牌分成几堆,然后按照一定的顺序和数量拿牌、放牌,这里面就藏着数学的小窍门。
想象一下,魔术师让你随便抽一张牌,然后通过一些巧妙的计算和排列,就能猜出你抽的是哪张。
这可不仅仅是靠运气,全是数学规律在发挥作用。
而且哦,有时候魔术师会利用牌的顺序和数字之间的关系,做出让人意想不到的效果。
比如让某些牌神奇地聚集在一起。
所以说呀,扑克牌魔术可不是纯粹的魔法,而是数学的巧妙运用。
下次再看魔术的时候,咱们可以多想想,说不定能发现其中的小秘密呢!怎么样,是不是觉得扑克牌魔术更有趣啦?。
关于数学的小魔术

关于数学的小魔术数学作为一门学科,常常给人一种枯燥乏味的感觉,但其实数学也可以有趣且富有创意。
在这篇文章中,我将向大家介绍一些有关数学的小魔术,希望能够改变大家对数学的看法,并增加大家对数学的兴趣。
一、数字预测魔术这是一种简单而又令人惊叹的数字预测魔术。
魔术师请观众随意选取一个三位数,并将该数字的各个位上的数字相加。
接着,观众再将得到的数字的各个位上的数字相加,如此重复下去,直到得到一个个位数。
最后,魔术师准确地预测出了观众最终得到的个位数。
这个魔术的秘密在于,无论观众最初选择的是哪个三位数,其最终得到的个位数都只有十个可能性,魔术师只需记住这十个可能性,并在观众进行运算的过程中,根据观众的运算结果,推断出最终的个位数。
二、奇偶魔术这是一种利用数学的奇偶性质进行的魔术。
魔术师请观众选择一个两位数,并将该两位数的数字相加。
接着,将得到的和再次相加,重复这个过程,直到得到一个个位数。
最后,魔术师能够预测出观众最终得到的个位数是奇数还是偶数。
这个魔术的秘密在于,无论观众最初选择的是哪个两位数,其最终得到的个位数只有五个可能性,分别是0、2、4、6、8。
魔术师只需记住这五个可能性,并根据观众的运算过程中出现的奇偶性,推断出最终的个位数是奇数还是偶数。
三、变幻的数字这是一种通过一系列操作让数字变幻的魔术。
魔术师请观众想一个两位数,并且将十位数和个位数的数字交换位置。
接着,将得到的两个数字相减,并将得到的差再加上9。
最后,魔术师能够预测出观众得到的结果是18。
这个魔术的秘密在于,无论观众最初选择的是哪个两位数,经过一系列的操作后得到的结果都是9的倍数。
魔术师只需记住这些9的倍数,并在观众的操作过程中,根据观众得到的结果推断出最终的结果是18。
四、卡片魔术这是一种利用卡片进行的数字魔术。
魔术师准备了一副特殊的卡片,每张卡片上都写着不同的数字。
魔术师请观众随机选择一张卡片,并记住上面的数字。
接着,魔术师将卡片放回牌组,并进行一系列的操作,最后能够准确地猜出观众选择的数字。
春晚节刘谦魔术的数学公式

公式一: ,其中, 为不超过n的2的最大幂;
公式二:
第一步:ABCDABCD
第二步:无论名字有几个字,8个字母依然是4个一循环,例如小唐会得到CDABCDAB,所以不妨仍设为ABCDABCD;
第三步:最上面三张插入中间,注意到留下的五张为DABCD,此时首尾一致。藏起的第一张,必然是D,而最后一张也是D。留下七张XXXXXXD;
第四步:南北方,无所谓,中国人民大团结万岁!因为没有动最后一张;
第五步:男生 扔1留6 XXXD
女生 扔2留5 XXXXD
第六步:见证奇迹的时刻,男生 XXXXDX
女生 XXDXX
第七步:男生 XXXXDXXXD XXD DX DXD
女生 XXDXX XXD XXD DX DXD
数学魔术——猜生日

越
员圆贼
员圆
员圆
原圆垣员圆贼 圆渊员原贼冤
赠越
缘
越 圆贼原 缘
越 圆贼原圆贼员圯贼 越 员原缘贼员
圯赠 越 圆原员圆贼员袁曾 越 怨垣猿员贼员
. All R员i臆g曾h臆t猿s员袁曾R沂e晕s鄢e袁rved愿 . 员
疫
员臆赠臆员圆袁赠沂晕鄢
圯
原 猿员
臆贼员
臆 员圆
圯贼员
越
园
袁
由 贼员 越 园圯曾 越 怨袁赠 越 圆郾 变这个戏法可以很容易猜出某人的生日袁其本质就
圆
圆 圆源
贼沂渊园袁 圆 暂袁从而当 贼 越 圆 时袁栽 越源贼圆 垣圆贼原员 的最大值为 圆 原员援
源
源
圆
渊 收稿日期院圆园员园园源园远冤
是数学中的解不定方程问题援
疑问院这种戏法会不会有两个或多个结果钥 设告诉
的数为 葬
员圆曾垣猿员赠 越 葬袁
同理员
臆曾臆猿员袁曾沂晕鄢
袁假
设
有
两
个
解
为
渊
曾员
袁
赠员
冤
袁
员臆赠臆员圆袁赠沂晕 鄢 袁
渊 曾圆 袁赠圆 冤 袁 员圆曾员 垣猿员赠员 越 葬袁员圆曾圆 垣猿员赠圆 越 葬袁 两式相减得 员圆渊 曾员 原曾圆 冤 垣猿员渊 赠员 原赠圆 冤越 园袁 员圆渊曾员 原曾圆 冤能被 猿员 整除援 又疫 曾员 袁曾圆 沂咱员袁猿员暂 圯曾员 原曾圆 约猿员袁亦 曾员 越 曾圆郾 渊 收稿日期院圆园员园园缘猿园冤
式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式式
渊 上接第 源怨 页冤 五回首摇 边界考虑否
神奇有趣的10个数学小魔术——方法与原理

神奇有趣的10个数学小魔术——方法与原理一、67读心术规则:1、两位数(含)以下的:你心中在0—100间随意想一个数,将这个数乘以67,告诉我结果的后两位,我将你告诉我的数乘以3,得出结果的后两位就是你心中所想之数了。
例如,你心中想83,乘67得5561,用61*3=183,去后两位就是83了。
2、多位数的:让对方心里随便想一个三位数。
让对方将该数乘以667,然后他最开始想的那个数是几位数,就让他告诉你乘积的后几位数。
这时,你用那个后几位数乘以三。
即可得到他最开始想的那个数。
(他最开始想的那个数是几位,就取你算得的乘积的后几位)。
这个算法是可以严格证明其正确性的。
另外,如果把667改成6667,那么对四位数也适用。
(67这个数字会出卖你的灵魂!)证明:当想的数是一位时,不防设为c,第一步:67c,令得到的数的十位以上的数为x,则个位为(67c-10x)第二步:3(67c-100x)=201c-300x=200c-300x+c,显然得到的个位上的数字为c当想的数是两位时,不妨设为bc,第一步:67bc,令得到的数的百位以上的数为y,则十个位为(67bc-100y)第二步:3(67bc-100y)=201bc-300y=200bc-300y+bc,显然得到的数的十个两位是bc当想的数是三位时,不妨设为abc,(三位数时乘以667)第一步:667abc,令得到的数的千位以上的数为z,则百十个位为(667abc-1000z)第二步:3(667abc-1000z)=2001abc-3000z=2000abc-3000z+abc,显然得到的数的百十个位为abc当想的数是四位时,三位数时乘以6667推广:上面我们利用了67*3=201,667*3=2001,6667*3=20001的特性。
我们也可以利用89*9=801,889*9=8001,8889*9=80001的特性设计游戏。
二、魔术与二元一次不定方程规则第一步:让学生在一副数字牌(36张)中随便抽取两张,不让老师看见。
数学魔术

心灵魔术之数字预言术(先在纸上写下了预言数字6760)⑴在纸上写下6760预言数字后折起来请对方保存。
⑵请对方在200—1000之间选择一个数字键入计算器。
⑶加831。
⑷减1000(记住目前的数值)。
⑸将所选的数字减去上面得到的那个数值。
⑹乘以40(即等于预言的数字6760)。
例:对方选345;345+831=1176;1176-1000=176;345-176=169;169×40=6760 心灵魔术之数字预言术(先在纸上写下了预言数字1089)⑴在纸上写下1089预言数字后折起来请对方保存。
⑵请对方在0-9中选三个数字排列成一个三位数,数字要成递减方式,如851、743⑶用该三位数,减去其反向的数字,如851-158=693。
⑷得出的值再加上其反向的数字,即得所预言的数值1089(693+396=1089)心灵魔术之搞笑预言术首先拿出一张白纸跟一只笔,并且告诉观众,你要将你的预言写在这张纸上,请观众猜猜你的预言是否正确。
(观众议论纷纷中.....)接着便在这张纸上写下\"不知道\"三个字,将纸小心折好不要让观众看见内容,折好后放到旁边或者请观众保管。
以上动作完毕后,神秘的问一下观众,你知不知道我刚刚预言了什幺东西呢?(语气缓慢且神秘)观众回答:不知道。
此时请观众自行慢慢的打开刚刚的那张预言,里面写着\"不知道\"三个字,这时候记得要赶快逃,因为已经有观众开始脱鞋子了。
这招蛮适合在表演前当成轻松愉快的开场白,先把观众的心情提升起来,接着再开始接下来您精采的表演。
注意:表演时的营造气氛很重要喔,气氛掌握的好的话,效果觉得超乎你的想象。
我觉得气份很重要,如果表演这魔术搞的观众都很开心的话,也算是一种成功。
心灵魔术之(7张卡片1到127任意想一个数) 这是一种很有趣时髦的魔术哦这是一种很有趣的魔术哦而且有一点时髦的特点。
效应:让观众从1到127任意想一个数。
经典数学魔术及原理

经典数学魔术及原理一、魔术一:猜数字这个魔术可好玩啦。
你让观众在心里想一个1到100之间的数字,然后你通过一些简单的问答就能猜出这个数字哦。
原理其实很简单呢。
你先问观众这个数字是大于50吗?如果观众说是,那你就把范围缩小到51到100;如果说不是,就缩小到1到49。
然后你再把这个新的范围分成两半,继续问类似的问题。
比如在51到100这个范围里,你问是大于75吗。
就这样不断地缩小范围,很快就能猜到那个数字啦。
这就像是我们在做二分查找一样,不断地把可能的答案范围减半。
二、魔术二:消失的硬币这个魔术很神奇哦。
你把一枚硬币放在桌子上,用一个小杯子或者手帕盖住,然后念几句神秘的话,再打开的时候,硬币就消失了。
它的原理是利用了一些小机关或者障眼法。
有时候可能是桌子有个暗格,硬币其实被偷偷地滑到暗格里去了。
还有的时候是利用了视觉错觉,当你快速操作的时候,观众的注意力被分散,其实硬币已经被你用巧妙的手法拿走了,但是观众还以为硬币就在杯子或者手帕下面呢。
三、魔术三:神奇的纸牌预测这个魔术是这样的,你拿出一副纸牌,让观众随便抽一张牌,然后你可以准确地说出观众抽的是哪张牌。
这里面的原理呢,有很多种情况。
一种可能是你用了一些特殊的纸牌,这种纸牌背面有一些很细微的标记,只有你能看出来。
另一种可能是你有一个助手,助手通过一些暗号告诉你观众抽的是哪张牌。
比如说助手在观众抽牌的时候,会根据观众抽牌的位置或者动作给你一些暗示,你就能知道是哪张牌啦。
四、魔术四:会变色的纸牌你拿出两张纸牌,一张红色一张黑色,然后把它们放在一起,再打开的时候,两张牌的颜色居然互换了。
这个魔术的原理是纸牌本身可能是经过特殊处理的。
比如说这两张牌其实是一种特制的双层纸牌,表面的颜色可以通过一些巧妙的手法进行切换,比如利用磁力或者特殊的粘贴技术。
当你操作的时候,就像是变魔术一样,让观众觉得纸牌的颜色神奇地改变了。
五、魔术五:悬浮的物体这个魔术就是让一个小物体,比如一个小钥匙,在空中悬浮起来,看起来超级神奇。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一个简单的数学小魔术
matrix672010-11-19 13:38:51
在一张纸上并排画 11 个小方格。
叫你的好朋友背对着你(确保你看不到他在纸上写什么),在前两个方格中随便填两个 1 到 10 之间的数。
从第三个方格开始,在每个方格里填入前两个方格里的数之和。
让你的朋友一直算出第 10 个方格里的数。
你便能轻易预测出下一个数是多少。
在一张纸上并排画 11 个小方格。
叫你的好朋友背对着你(确保你看不到他在纸上写什么),在前两个方格中随便填两个 1 到 10 之间的数。
从第三个方格开始,在每个方格里填入前两个方格里的数之和。
让你的朋友一直算出第 10 个方格里的数。
假如你的朋友一开始填入方格的数是 7 和 3 ,那么前 10 个方格里的数应该是
7 3 10 13 23 36 59 95 154 249
现在,叫你的朋友报出第 10 个方格里的数,你只需要在计算器上按几个键,便能说出第 11 个方格里的数应该是多少。
你的朋友会非常惊奇地发现,把第 11 个方格里的数计算出来,所得的结果与你的预测一模一样!这就奇怪了,在不知道头两个数是多少的情况下,只知道第 10 个数的大小,不知道第 9 个数的大小,怎么能猜对第 11 个数的值呢?
魔术揭秘:只需要除以 0.618
其实,仅凭借第 10 个数来推测第 11 个数的方法非常简单,你需要做的仅仅是把第 10 个数除以 0.618,得到的结果四舍五入一下就是第 11 个数了。
在上面的例子中,由于249÷0.618 = 402.913.. ≈ 403,因此你可以胸有成竹地断定,第 11 个数就是 403。
而事实上,154 与 249 相加真的就等于 403。
把头两个方格里的数换一换,结论依然成立:
2 9 11 20 31 52 82 13
3 215 348
可以看到,第 11 个数应该为 215+348 = 563,而 348 除以 0.618 就等于 563.107..,与实际结果惊人地吻合。
这究竟是怎么回事儿呢?
不妨假设你的好朋友最初在纸上写下的两个数分别是 a 和 b 。
那么,这 11 个方格里的数分别为:
接下来,我们只需要说明,21a+34b 除以 34a+55b 的结果非常接近 0.618 即可。
让我们来考虑另一个看似与此无关的生活小常识:两杯浓度不同的盐水混合在一起,调配出来的盐水浓度一定介于原来两杯盐水的浓度之间。
换句话说,如果其中一杯盐水的浓度是 a/b,另一杯盐水的浓度是 c/d,那么 (a+c)/(b+d) 一定介于 a/b 和 c/d 之间。
因此,(21a+34b)/(34a+55b) 就一定介于 21a/34a 和 34b/55b 之间。
而21a/34a = 21/34 ≈ 0.6176,34b/55b = 34/55 ≈ 0.6182,可见不管 a 和 b 是多少,(21a+34b)/(34a+55b) 都被夹在了 0.6176 和 0.6182 之间。
如果 a 和 b 都不大,用 21a+34b 的值除以0.618 来推测 34a+55b 是相当靠谱的。
有的读者可能已经发现了,0.618 不是别的数,正是神秘的黄金分割;而上表中出现的系数1, 1, 2, 3, 5, 8, 13, 21, 34, 55, … 正是传说中的斐波那契数列。
算术中最富神秘色彩的两个概念在此交织,看来这个简单小魔术的来头并不简单啊。
