128的二进制有原码反码和补码 (1)
计算机组成原理第2章例题及参考答案
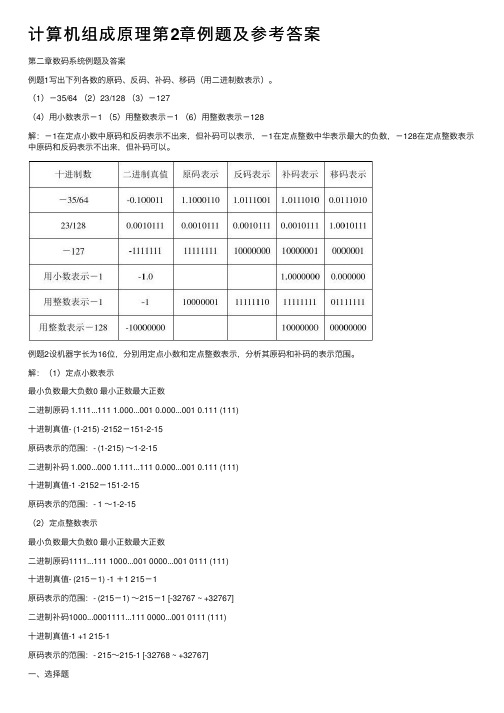
计算机组成原理第2章例题及参考答案第⼆章数码系统例题及答案例题1写出下列各数的原码、反码、补码、移码(⽤⼆进制数表⽰)。
(1)-35/64 (2)23/128 (3)-127(4)⽤⼩数表⽰-1 (5)⽤整数表⽰-1 (6)⽤整数表⽰-128解:-1在定点⼩数中原码和反码表⽰不出来,但补码可以表⽰,-1在定点整数中华表⽰最⼤的负数,-128在定点整数表⽰中原码和反码表⽰不出来,但补码可以。
例题2设机器字长为16位,分别⽤定点⼩数和定点整数表⽰,分析其原码和补码的表⽰范围。
解:(1)定点⼩数表⽰最⼩负数最⼤负数0 最⼩正数最⼤正数⼆进制原码 1.111...111 1.000...001 0.000...001 0.111 (111)⼗进制真值- (1-215) -2152-151-2-15原码表⽰的范围:- (1-215) ~1-2-15⼆进制补码 1.000...000 1.111...111 0.000...001 0.111 (111)⼗进制真值-1 -2152-151-2-15原码表⽰的范围:- 1 ~1-2-15(2)定点整数表⽰最⼩负数最⼤负数0 最⼩正数最⼤正数⼆进制原码1111...111 1000...001 0000...001 0111 (111)⼗进制真值- (215-1) -1 +1 215-1原码表⽰的范围:- (215-1) ~215-1 [-32767 ~ +32767]⼆进制补码1000...0001111...111 0000...001 0111 (111)⼗进制真值-1 +1 215-1原码表⽰的范围:- 215~215-1 [-32768 ~ +32767]⼀、选择题1.下列数中最⼩的数为()。
A.(101001)2B.(52)8C.(101001)BCD D.(233)162.下列数中最⼤的数为()。
A.(10010101)2B.(227)8C.(96)16D.(143)53.在机器数中,()的零的表⽰形式是惟⼀的。
二进制5位数原码、补码、反码表

原码、补码和反码是在计算机中常用的一种数据表示方式。
在这种表示方式中,正数和负数均采用二进制形式表示,通过一定的规则进行转换。
本文将以二进制5位数为例,对原码、补码和反码进行详细介绍和表格展示。
一、二进制5位数原码、补码、反码定义1.1 原码定义原码是最简单的一种表示方式,它的规则是:正数的原码就是其二进制形式,负数的原码是在正数原码的基础上将最高位(符号位)变为1。
+2在5位二进制数中的原码是xxx,-2在5位二进制数中的原码是xxx。
1.2 补码定义补码是计算机中常用的一种表示方式,它的规则是:正数的补码就是其二进制形式,负数的补码是将其绝对值的原码按位取反然后加1。
+2在5位二进制数中的补码是xxx,-2在5位二进制数中的补码是xxx。
1.3 反码定义反码是原码的一种变换形式,它的规则是:正数的反码就是其二进制形式,负数的反码是将其绝对值的原码按位取反。
+2在5位二进制数中的反码是xxx,-2在5位二进制数中的反码是xxx。
二、二进制5位数原码、补码、反码表以下是以二进制5位数为例的原码、补码和反码一览表:原码补码反码xxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxxxxx xxx xxx三、总结通过以上原码、补码和反码的定义和表格展示,我们可以清楚地了解二进制5位数的原码、补码和反码之间的转换规则和关系。
二进制补码规则

二进制补码:定义、计算方法、特点和应用二进制补码是一种用二进制表示有符号整数的方法,它可以使正数和负数的加减法运算更加简单和高效。
本文将介绍二进制补码的定义、计算方法、特点和应用,以及与原码和反码的区别和联系。
一、二进制补码的定义在计算机中,通常用一个固定长度的二进制数来表示一个有符号整数,其中最高位为符号位,0表示正数,1表示负数,其余位为数值位。
例如,用一个8位的二进制数来表示十进制数-5,可以写成10000101,其中第一位1是符号位,表示这是一个负数,后面七位0000101是数值位,表示这个数的绝对值是5。
但是,在计算机中,不同的二进制表示方法会导致不同的运算规则和结果。
为了方便计算机进行有符号整数的加减法运算,人们提出了三种不同的二进制表示方法:原码、反码和补码。
其中,补码是最常用的一种方法,它的定义如下:正数的补码等于其原码,即符号位为0,数值位为其二进制形式。
负数的补码等于其原码除符号位外按位取反再加1,即符号位为1,数值位为其绝对值的二进制形式按位取反再加1。
例如,用一个8位的二进制数来表示十进制数5和-5的补码,可以写成:十进制原码补码50000010100000101-51000010111111011可以看出,正数的补码和原码相同,而负数的补码是在原码的基础上除符号位外按位取反再加1得到的。
例如,-5的原码是10000101,除符号位外按位取反得到11111010,再加1得到11111011。
二、二进制补码的计算方法在计算机中进行有符号整数的加减法运算时,通常先将操作数转换成补码形式,然后按照无符号整数的加减法规则进行运算,最后将结果转换成原码形式输出。
下面介绍如何进行这些步骤。
2.1 将原码转换成补码将原码转换成补码的方法很简单,只需要根据前面给出的定义进行操作即可。
具体步骤如下:如果原码表示的是正数,则直接保留原码作为补码。
如果原码表示的是负数,则除符号位外按位取反再加1得到补码。
原码,反码,补码,和取反运算——适用于二进制底层的概念理解

原码,反码,补码,和取反运算——适⽤于⼆进制底层的概念理解⾸先,看这篇⽂章之前,你需要的是不必纠结,⽐如:为什么正数的原码反码补码就⼀样呢,负数的原码反码补码就各不相同呢?看这篇⽂章之前你只需要记住,这是⼈为规定的。
你可能会想,为什么要这样⼈为规定呢,我现在只能告诉你,这样规定有利于计算机底层对数字进⾏操作,也就是说,这种规定对计算机的底层硬件要求简化了,技术实现起来更简单。
我们⽇常⽤的数字是给我们⼈类⽤的,所以叫真值。
⽽机器(计算机)理解的数字通常是⼆进制所组成的数字,所以称为机器数。
⼆进制在内存中以补码形式在其中存储,计算机计算数字是通过补码的形式进⾏计算的,也就是说不管正数,还是负数在计算机⾥⾯,都要⽤补码来表⽰。
在原码,反码,补码中,最⾼位来表⽰正负,⽤0表是正,1表⽰负;如⼗进制的10表⽰为:+1010--->原码:0 1010;-1010--->原码: 1 1010;笔记⼀:原码,反码,补码*规则:正数中:原码=反码=补码;例⼦拿上⾯的:+1010---> 0 1010;+1010--->原码: 0 1010;(最⾼位0表⽰正号)+1010--->反码: 0 1010;+1010--->补码: 0 1010;+1010--->移码: 1 1010(补码符号位取反)负数中的规则如下:例⼦拿上⾯的:-1010---> 1 1010;-1010--->原码: 1 1010;(最⾼位1表⽰负号)-1010--->反码: 1 0101;(符号位不变,数值位:0变1,1变0)-1010--->补码: 1 0110;(符号位不变,数值位:0变1,1变0。
最后得出来的数字再加1。
简单点总结为:“反码加1”)-1010--->移码: 0 0110(补码符号位取反)最后注释:移码:⽆论正负数,都是补码的符号位取反。
还有这⾥解释⼀下,为什么计算机实际计算数字是⽤补码进⾏运算的,如果你看了我上⾯的例⼦的话,应该清楚了,不管是正数,还是负数,在计算机中,补码最⾼位都是1,意思就是说,补码的作⽤,把正数规定还是正数,⽽负数还是负数,但是正负数进⾏运算的时候转变为加法形式,例如:3-5变成3+(-5).这样⼦,计算机底层很容易实现加法运算。
二进制原码、反码和补码-带符号数的机器码表示方法

原码、反码和补码 —— 带符号数的机器码表示方法1.带符号二进制数的表示方法:2、符号位的表示:最常用的表示方法有原码、反码和补码。
(1)原码表示法一个机器数x 由符号位和有效数值两部分组成,设符号位为x 0,x 真值的绝对值|x|=x 1x 2x 3...x n ,则x 的机器数原码可表示为:[x]原= n x x x x ...210,当x>=0时,x 0=0,当x<0时,x 0=1。
例如:已知:x 1=-1011B ,x 2= +1001B ,则x 1,x 2有原码分别是[x 1] 原=11011B ,[x 2]原=01001B规律:正数的原码是它本身,负数的原码是取绝对值后,在最高位(左端)补“1”。
(2)反码表示法一个负数的原码符号位不变,其余各位按位取反就是机器数的反码表示法。
正数的反码与原码相同。
按位取反的意思是该位上是1的,就变成0,该位上是0的就变成1。
即1=0,0=1例:B x 10111-=,B x 10012+=,求反][1x 和反][2x 。
解:反][1x =B 10100,反][2x =B 01001(3)补码表示法首先分析两个十进制数的运算:78-38=41,79+62=141如果使用两位数的运算器,做79+62时,多余的100因为超出了运算器两位数的范围而自动丢弃,这样在做78-38的减法时,用79+62的加法同样可以得到正确结果。
模是批一个计量系统的测量范围,其大小以计量进位制的基数为底数,位数为指数的幂。
如两位十进制数的测量范围是1——9,溢出量是100,模就是102=100,上述运算称为模运算,可以写作:79+(-38)=79+62 (mod 100)进一步写为 -38=62,此时就说 –38的补法(对模100而言)是62。
计算机是一种有限字长的数字系统,因此它的运算都是有模运算,超出模的运算结果都将溢出。
n 位二进制的模是2n ,一个数的补码记作[x]补,设模是M ,x 是真值,则补码的定义如下:⎩⎨⎧<+≥=)0()0(][][x x M x x x 原补例:设字长n=8位,x=-1011011B ,求[x]补。
计算机基础-二进制原码、反码、补码

二进制原码, 反码, 补码的基础概念和计算方法一. 原码, 反码, 补码的基础概念和计算方法.1. 原码:原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值. 比如如果是8位二进制:[+1]原 = 0000 0001[-1]原= 1000 0001第一位是符号位. 因为第一位是符号位, 所以8位二进制数的取值范围就是:[1111 1111 , 0111 1111]即[-127 , 127]2. 反码反码的表示方法是:正数的反码是其本身负数的反码是在其原码的基础上, 符号位不变,其余各个位取反.[+1] = [00000001]原 = [00000001]反[-1] = [10000001]原 = [11111110]反3. 补码补码的表示方法是:正数的补码就是其本身负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1 (即在反码的基础上+1)[+1] = [00000001]原 = [00000001]反 = [00000001]补[-1] = [10000001]原 = [11111110]反 = [11111111]补二. 为何要使用原码, 反码和补码计算机可以有三种编码方式表示一个数.对于正数因为三种编码方式的结果都相同:[+1] = [00000001]原 = [00000001]反 = [00000001]补但是对于负数:[-1] = [10000001]原 = [11111110]反 = [11111111]补机器可以只有加法而没有减法计算十进制的表达式: 1-1=01.如果用原码表示1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.2.如果用反码表示1 - 1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]反 + [1111 1110]反= [1111 1111]反= [1000 0000]原= -0用反码计算减法, 结果的真值部分是正确的. 而唯一的问题其实就出现在"0"这个特殊的数值上. 虽然人们理解上+0和-0是一样的, 但是0带符号是没有任何意义的.而且会有[0000 0000]原和[1000 0000]原两个编码表示0.3.用补码表示1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原= [0000 0001]补 + [1111 1111]补= [0000 0000]补=[0000 0000]原=0这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:(-1) + (-127) = [1000 0001]原 + [1111 1111]原= [1111 1111]补 + [1000 0001]补= [1000 0000]补=-128注:-1-127的结果应该是-128, 在用补码运算的结果中, [1000 0000]补就是-128. 但是注意因为实际上是使用以前的-0的补码来表示-128, 所以-128并没有原码和反码表示.(对-128的补码表示[1000 0000]补算出来的原码是[0000 0000]原, 这是不正确的)使用补码, 不仅仅修复了0的符号以及存在两个编码的问题, 而且还能够多表示一个最低数. 这就是为什么8位二进制, 使用原码或反码表示的范围为[-127, +127], 而使用补码表示的范围为[-128, 127].(-1) + (-1) = [1000 0001]原 + [1000 0001]原= [1111 1111]补 + [1111 1111]补= [1111 1110]补//负数原码=补码-1,再同位取反,符号位不变=[1000 0010]原=-2因为机器使用补码, 所以对于编程中常用到的32位int类型, 可以表示范围是: [-231, 231-1] 因为第一位表示的是符号位.而使用补码表示时又可以多保存一个最小值.三.总结综上所述,原码、反码和补码是计算机中用于表示有符号二进制数的三种重要方法。
关于-128,+128,-0,+0,-1的反码补码

关于-128,+128,-0,+0,-1的反码补码⼀.反码的范围反码表⽰法规定:正数的反码与其原码相同。
负数的反码是对其原码逐位取反,但符号位除外。
在规定中,8位⼆进制码能表⽰的反码范围是-127~127。
此时(字长为8位), -128没有原码和反码(只有补码)。
那么,为什么规定字长8位时-128没有原码和反码呢?下⾯解释。
⾸先看-0,[-0]原码=1000 000,其中1是符号位,求反操作,算出[-0]反码=1111 1111,再看-128,假如它有原码且[-128]原码=1000 000,假如让-128也有反码,求反操作,则[-128]反码=1111 1111,你会发现,-128的反码和-0的反码相同,所以为了避免⾯混淆,有了-0的原码,便不能有-128的原码补码,这是8位⽐特位位数限制决定的。
⼆.原码反码补码的范围前提:字长是8位⼆进制数。
原码 -127~127 (-128没有原码反码,原因看前⾯解释~)反码 -127~127补码 -128~127对于n位⼆进制数:你会发现,补码⽐其它码多⼀位,这是为什么呢?问题出在0上。
[+0]原码=0000 0000, [-0]原码=1000 0000[+0]反码=0000 0000, [-0]反码=1111 1111[+0]补码=0000 0000, [-0]补码=0000 0000你会发现,+0和-0的补码是⼀样的。
即 0的补码只有⼀种表⽰。
这⾥解释⼀下[-0]补码是怎么得来的。
负数的补码就是反码整体加⼀。
符号位上的进位舍弃。
(所以,舍弃了符号位的补码的第⼀位是数值位,不是符号位,符号位舍弃了)另外解释⼀下原码符号位和补码符号位的关系,补码的符号位不是保持原码的第⼀位不变,⽽是符号位不变,[-0]反码的第⼀个1是符号位,尾数中的7个1是数值位,尾数加⼀后,数值位产⽣了进位,1111 1111+1=1 0000 0000(计算补码的过程中,并不是先保证第⼀位不变,⽽是保证符号位不变,保证补码规则是反码整体加⼀)。
8位原码反码补码表——讲义资料文档
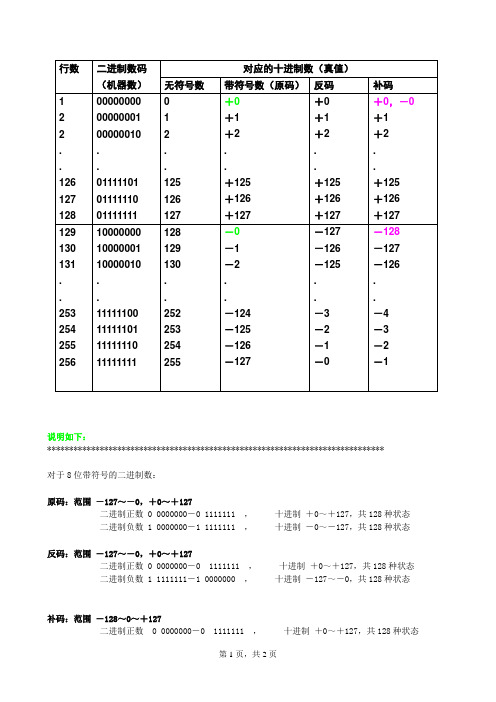
说明如下:*****************************************************************************对于8位带符号的二进制数:原码:范围-127~-0,+0~+127二进制正数 0 0000000-0 1111111 ,十进制+0~+127,共128种状态二进制负数 1 0000000-1 1111111 ,十进制-0~-127,共128种状态反码:范围-127~-0,+0~+127二进制正数 0 0000000-0 1111111 ,十进制+0~+127,共128种状态二进制负数 1 1111111-1 0000000 ,十进制-127~-0,共128种状态补码:范围-128~0~+127二进制正数0 0000000-0 1111111 ,十进制+0~+127,共128种状态二进制负数 1 0000000-1 0000001 ,十进制-128~-1,共128种状态注:[-0]补码=[-0]反码+1=1 11111111+1= 00000000=[+0]补码,即[-0]补码=[+0]补码[-1]补码=[1 0000001]补码=1 1111110+1=1 1111111,即[-1]补码是-127[-127]补码=[1 1111111]补码=1 0000000+1=1 0000001,即[-127]补码是-1[-128]补码=[-127]补码+[-1]补码 = 1 0000001+1 1111111 =1 0000000结论:原码范围:-127~-0,+0~+127,256种状态反码范围:-127~-0,+0~+127,256种状态补码范围:-128~-1,+0~+127,256种状态,因为[-0]补码和[+0]补码相同,在补码中-128代替了-0。
也可认为是一种规定,这样可都是256种状态。
要注意:(-128)没有相对应的原码和反码, (-128) = (10000000)*****************************************************************************。
原码、补码和反码

原码、补码和反码在计算机内,定点数有3种表示法:原码、反码和补码所谓原码就是二进制定点表示法,即最高位为符号位,“0”表示正,“1”表示负,其余位表示数值的大小。
反码表示法规定:正数的反码与其原码相同;负数的反码是对其原码逐位取反,但符号位除外。
补码表示法规定:正数的补码与其原码相同;负数的补码是在其反码的末位加1。
1、原码、反码和补码的表示方法(1)原码:在数值前直接加一符号位的表示法。
例如:符号位数值位[+7]原= 0 0000111 B[ -7]原= 1 0000111 B注意:a. 数0的原码有两种形式:[+0]原=00000000B [-0]原=10000000Bb. 8位二进制原码的表示范围:-127~+127(2)反码:正数:正数的反码与原码相同。
负数:负数的反码,符号位为“1”,数值部分按位取反。
例如:符号位数值位[+7]反= 0 0000111 B[-7]反= 1 1111000 B注意:a. 数0的反码也有两种形式,即[+0]反=00000000B[- 0]反=11111111Bb. 8位二进制反码的表示范围:-127~+127(3)补码的表示方法1)模的概念:把一个计量单位称之为模或模数。
例如,时钟是以12进制进行计数循环的,即以12为模。
在时钟上,时针加上(正拨)12的整数位或减去(反拨)12的整数位,时针的位置不变。
14点钟在舍去模12后,成为(下午)2点钟(14=14-12=2)。
从0点出发逆时针拨10格即减去10小时,也可看成从0点出发顺时针拨2格(加上2小时),即2点(0-10=-10=-10+12=2)。
因此,在模12的前提下,-10可映射为+2。
由此可见,对于一个模数为12的循环系统来说,加2和减10的效果是一样的;因此,在以12为模的系统中,凡是减10的运算都可以用加2来代替,这就把减法问题转化成加法问题了(注:计算机的硬件结构中只有加法器,所以大部分的运算都必须最终转换为加法)。
二进制数的原码、反码及补码表示

(注意:理解的彻底这里)二进制数的原码、反码及补码表示1、机器数与真值机器数:数在机器中的编码表示。
真值:一般书写表示的数。
机器数中,数值和符号完全数字化。
计算机在进行数字运算时,采用把各种符号位和数字位一起编码的方法。
常见的有原码、反码及补码表示法。
2、原码表示法原码表示法是机器数的一种简单表示法。
其符号位用0表示正数,用1表示负数,数值一般用二进制形式表示。
[x]原=符号位+绝对值若x=+1100110 则[x]原=01100110x= -1100110 [x]原=11100110(说明:其实就是把符号+-改为01)所以用8位二进制数来表示整数原码时,其表示范围:最大数:01111111,为(+127)D最小数:11111111,为(-127)D思考:0的原码有两种表示形式!!3、反码表示法机器数的反码可由原码得到。
如果机器数是正数,则机器数的反码与原码一致;若机器数是负数,则机器数的反码是它的原码(符号位除外)的各位取反而得到。
即:正数:[x]反=[x]原负数:[x]反=对[x]原除符号外的各位取反若x=+1100110 则[x]反=01100110x= -1100110 [x]反=100110014、补码表示法机器数的补码也可由原码得到。
如果机器数是正数,则机器数的反码与原码一致;若机器数是负数,则机器数的反码是它的原码(符号位除外)的各位取反,并在末位加1而得到。
即:反码是作为求补码的中间过程。
正数:[x]补=[x]原负数:[x]补=[x]反+1若x=+1100110 则[x]补=01100110x= -1100110 [x]补=10011010注意:补码的0只有一种表示形式![+0]原=00000000 [-0]原=10000000[+0]反=00000000 [-0]反=11111111[+0]补=[-0]补=00000000所以用8位二进制数来表示整数补码时,其表示范围:最大数:01111111,为(+127)D 最小数:10000000,为(-128)D。
二进制原码,反码,补码表示范围

二进制原码,反码,补码表示范围用8位二进制原码表示的范围[一个符号]-127~+127,反码和原码范围一致,且一一对应。
而用其补码表示则是-128~+127---->10000000~01111111。
【解释】数值有正负之分,计算机就用一个数的最高位存放符号(0为正,1为负).这就是机器数的原码了.假设机器能处理的位数为8.即字长为1byte,原码能表示数值的范围为(-127~-0 +0~127)共256个. 根据原码的定义-0和+0值都是0,即两个码对应了一个数值。
有了数值的表示方法就可以对数进行算术运算.但是很快就发现用带符号位的原码进行乘除运算时结果正确,而在加减运算的时候就出现了问题,如下: 假设字长为8bits ( 1 )10- ( 1 )10= ( 1 )10+ ( -1 )10= ( 0 )10用原码计算(00000001)原+ (10000001)原= (10000010)原= ( -2 )显然不正确.因为在两个整数的加法运算中是没有问题的,于是就发现问题出现在带符号位的负数身上,对除符号位外的其余各位逐位取反就产生了反码.反码的取值空间和原码相同且一一对应. 下面是反码的减法运算:( 1 )10- ( 1 )10=( 1 )10+ ( -1 )10= ( 0 )10反码:(00000001)反+ (11111110)反= (11111111)反= ( -0 )10有问题. (你会发现相减结果为正的,反码减法都会比真实值少1个数)( 1 )10- ( 2)10= ( 1 )10+ ( -2 )10= ( -1 )10反码:(00000001)反+ (11111101)反= (11111110)反= ( -1 )正确问题出现在(+0)和(-0)上,在人们的计算概念中零是没有正负之分的.(印度人首先将零作为标记并放入运算之中,包含有零号的印度数学和十进制计数对人类文明的贡献极大).于是就引入了补码概念. 负数的补码就是对反码加一,而正数不变,正数的原码反码补码是一样的.在补码中用(-128)代替了(-0),所以补码的表示范围为:(-128~0~127)共256个.注意:(-128)没有相对应的原码和反码, (-128) = (10000000)。
二进制补码(负数编码)、反码、原码

⼆进制补码(负数编码)、反码、原码补码是对负整数在计算机中存储的⼀种形式;第⼆种形式的负数在计算机中可以使⽤(负号加数字)的形式表⽰⼀个负数;例如(-3 以1000 0011 存储)但是使⽤这种⽅法表⽰的只有(+0,-0),⽽且不可以做算术运算。
讨论⼆进制编码之前,⾸先来了解⼀下什么是计算机数和真值(⼀)计算机数⼀个数在计算机中的⼆进制表⽰形式,叫做这个数的机器数。
机器数数带符号的,由于计算机内部的硬件只能表⽰两种物理状态,在计算机使⽤⼀个数的最⾼位存放符号,正数为 0,负数为 1。
例如:⼗进制中的 +5 和 -5,计算机字长为8位,分别转换为 00000101 和 10000101;这⾥⾯的 00000101 和 10000101 就是机器数机器数的特点:⼀个数值的⼆进制表现形式,就叫做这个数的机器数。
⼆进制的位数是受机器设备的限制的。
机器内部设备⼀次能表⽰的⼆进制位数叫做机器的字长,⼀台机器的字长数固定的。
字长8位的叫做⼀个字节(Byte),机器字长⼀般都是字节的整数倍,如字长 8位、16位、32位、64位。
机器数的分类:根据⼩数点位置固定与否,机器数⼜可以分为定点数和浮点数。
通常使⽤定点数表⽰整数,使⽤浮点数表⽰实数:1、整数:整数没有⼩数部分,⼩数点固定在数的最右边。
整数可以分为(1) ⽆符号整数和 (2) 有符号整数两类。
⽆符号整数的所有⼆进制位全部⽤来表⽰数值的⼤⼩;有符号整数⽤最⾼位表⽰数的正负号,其他位数表⽰数值的⼤⼩。
2、实数:实数的浮点数表⽰⽅法:将⼀个实数的范围和精度分别⽤阶码和位数表⽰。
在计算机中,为了提⾼数据表⽰精度,必须表⽰⼩数点的位置,因此浮点数必须写成规范的形式(位数不为 0 的时候,其绝对值⼤于或等于 0.5 并且⼩于 1(因为是⼆进制位,要求尾数第 1 位必须是 1))。
例如:设机器字长位 16位,尾数为 8位,阶码为 6位,则⼆进制实数 -1101.010 的机内表⽰为 0000100111010100。
计算机原理(原码、反码、补码)

计算机原理- 整数的补码,原码, 反码解释一:对于整数来讲其二进制表示没有符号位.一个字节的表示范围为00000000-11111111,由此可见一个字节的整数表示范围为[0,255=2^8 - 1]。
对于整数来讲,其二进制表示中存在一个符号位.先来看一下下面几个定义:1:在计算机中,负数以其正值的补码形式表达。
正数即在符号位补0.2:原码:一个整数,按照绝对值大小转换成的二进制数,称为原码。
3:反码:将二进制数按位取反,所得的新二进制数称为原二进制数的反码。
4:补码: 反码+1由以上可以得到.计算机储存有符号的整数时,是用该整数的补码进行储存的,0的原码、补码都是0;正数的原码、补码可以特殊理解为相同;负数的补码是它的反码加1。
范围: 正数 [00000000 - 01111111] 即[0, 2^7 - 1]。
负数 [10000000 - 11111111] 。
范围说明. 11111111 - 1 = 11111110,取反=00000001 即是-1. 10000000 -1 = 01111111,取反=10000000, 即是-128. 因此有一个有符号二进制表示范围是从[-128-127].解释二:大家都知道数据在计算机中都是按字节来储存了,1个字节等于8位(1Byte=8bit),而计算机只能识别0和1这两个数,所以根据排列,1个字节能代表256种不同的信息,即2^8(0和1两种可能,8位排列),比如定义一个字节大小的无符号整数(unsigned char),那么它能表示的是0~255(0~2^8 -1)这些数,一共是256个数,因为,前面说了,一个字节只能表示256种不同的信息。
别停下,还是一个字节的无符号整数,我们来进一步剖析它,0是这些数中最小的一个,我们先假设它在计算机内部就用8位二进制表示为00000000(从理论上来说也可以表示成其他不同的二进制码,只要这256个数每个数对应的二进制码都不相同就可以了),再假设1表示为00000001,2表示为00000010,3表示为00000011,依次类推,那么最大的那个数255在8位二进制中就表示为最大的数11111111,然后,我们把这些二进制码换算成十进制看看,会发现刚好和我们假设的数是相同的,而事实上,在计算机中,无符号的整数就是按这个原理来储存的,所以告诉你一个无符号的整数的二进制码,你就可以知道这个数是多少,而且知道在计算机中,这个数本身就是以这个二进制码来储存的。
原码、反码和补码

原码、反码和补码在这篇博⽂中,我希望能从数学的⾓度帮助你理解计算机中的补码世界,并尝试解释以下问题:符号位为什么是最⾼位,为什么1表⽰负,0表⽰正?0表⽰正,1表⽰负,为啥不是0表⽰负,1表⽰正?为什么补码1000 0000表⽰-128 ?为什么补码能够实现减法运算?关于原码、反码、补码的计算这⾥就不赘述了,但是如果你对于原码、反码、补码的计算还是通过⼀个数 -> ⼆进制原码 -> 正数不变,负数保持符号位,其他位取反得反码 -> 反码+1得补码另外也有上⾯的3个疑问的话我强烈建议你忘掉之前关于原码、反码和补码的认知我⾸先抛出三个问题,希望你带着这三个问题去阅读,当你能给出这两个问题的答案的时候,上⾯的3个问题也有答案了1. 同余的定义和意义是什么?2. 在4位系统中,怎么去表⽰负数?3. 在8位系统中,怎么做减法运算?1. 环形系统、模、同余在⼀个环形系统中,能表⽰的数是有限的。
例如在下⾯的表盘中,你能表⽰的数只有0~11,⼤于等于12的数,会被舍弃⼀部分,再在表盘上表⽰出来,在计算机中,我们管这叫「溢出」。
⽐如15点,在钟表上表现的是3。
当表针越过11的时候,⼜从0开始,直到3。
如果在钟表的世界⾥,要表⽰27呢?钟表上⽆法表⽰准确的数字,27在这⾥只能被表⽰为3。
准确地说,在超出这个系统极限值的时候,也就是说溢出了,这个系统只能⽤「余数」来计量在这⾥,所有被12除,余数为3的数,都被归为1类。
在这⾥,还有余数为0、1、2...11的类⽽15和27,称为 15和27关于模12同余,它们的余数就是3在这个系统中,能表⽰的数只有「余数」,表盘上的数字都是被12除后的余数我们可以这样理解这个系统:这个系统将整数分成了12类——被12除余0、1、2、3、4、5、6、7、8、9、10、11的类我们来看看「什么是奇数?什么是偶数?」偶数是被2除余0的整数,奇数是被2除余1的整数。
通过模2我们将整数分成了两类:余0和余1的数,也就是偶数和奇数回到我们的表盘,通过模12,所有的整数也能被分成12类,分别是余0、1、2、3、4、5、6、7、8、9、10、11的类所有的整数对模12做取模运算,按照它们的余数我们可以给它们分类。
什么是原码、反码、补码

[-1] = [10000001]原 = [11111110]反 = [11111111]补
对于负数, 补码表示方式也是人脑无法直观看出其数值的. 通常也需要转换成原码在计算其数值.
三. 为何要使用原码, 反码和补码
在开始深入学习前, 我的学习建议是先"死记硬背"上面的原码, 反码和补码的表示方式以及计算方法.
1-1 = 1 + (-1) = [0000 0001]原 + [1000 0001]原 = [0000 0001]补 + [1111 1111]补 = [0000 0000]补=[0000 0000]原
这样0用[0000 0000]表示, 而以前出现问题的-0则不存在了.而且可以用[1000 0000]表示-128:
于是人们开始探索 将符号位参与运算, 并且只保留加法的方法. 首先来看原码:
计算十进制的表达式: 1-1=0
1 - 1 = 1 + (-1) = [00000001]原 + [10000001]原 = [10000010]原 = -2
如果用原码表示, 让符号位也参与计算, 显然对于减法来说, 结果是不正确的.这也就是为何计算机内部不使用原码表示一个数.
一. 机器数和真值
在学习原码, 反码和补码之前, 需要先了解机器数和真值的概念.
1、机器数
一个数在计算机中的二进制表示形式, 叫做这个数的机器数。机器数是带符号的,在计算机用一个数的最高位存放符号, 正数为0, 负数为1.
比如,十进制中的数 +3 ,计算机字长为8位,转换成二进制就是00000011。如果是 -3 ,就是 10000011 。
x mod y = x - y L x / y J
8位原码反码补码表

***************************************************************************** 对于8位带符号的二进制数:原码:范围-127~-0,+0~+127??????二进制正数00000000-01111111?,??十进制+0~+127,共128种状态??????二进制负数10000000-11111111?,??十进制-0~-127,共128种状态??反码:范围-127~-0,+0~+127??????二进制正数00000000-0?1111111?,??十进制+0~+127,共128种状态??????二进制负数11111111-10000000?,??十进制-127~-0,共128种状态??补码:范围-128~0~+127??????二进制正数?00000000-0?1111111?,??十进制+0~+127,共128种状态??????二进制负数10000000-10000001?,??十进制-128~-1,共128种状态??注:[-0]补码=[-0]反码+1=100000000=[+0]补码,即[-0]补码=[+0]补码[-1]补码=[10000001]补码=11111110+1=11111111,即[-1]补码是-127[-127]补码=[11111111]补码=10000000+1=10000001,即[-127]补码是-1[-128]补码=[-127]补码+[-1]补码=10000001+11111111=10000000结论:原码范围:-127~-0,+0~+127,256种状态反码范围:-127~-0,+0~+127,256种状态补码范围:-128~-1,+0~+127,256种状态,因为[-0]补码和[+0]补码相同,在补码中-128代替了-0。
也可认为是一种规定,这样可都是256种状态。
要注意:(-128)没有相对应的原码和反码,(-128)=*****************************************************************************。
原码、反码、补码之间的相互关系

原码、反码、补码之间的相互关系1、10001的补码是取反后在再加1,也就是11110+1=11111;2、如果是11111变回原码呢?我们可以采取逆过程先减1,11111-1=11110,再取反变为10001;3、如果要是在补码变原码时先去反再加⼀呢?(就是问题中的说法)结果为11111先取反为10000,再加1,10000+1=10001。
这个结果与2是⼀样的,并且也是和1中的原码相吻合。
在取反前减1和在取反后加1的效果是⼀样的。
这就和-3-1=-(3+1)是⼀个道理。
计算机保存最原始的数字,也是没有正和负的数字,叫没符号数字如果我们在内存分配4位(bit)去存放⽆符号数字,是下⾯这样⼦的后来在⽣活中为了表⽰“⽋别⼈钱”这个概念,就从⽆符号数中,划分出了“正数”和“负数”正如上帝⼀挥⼿,从混沌中划分了“⽩天”与“⿊夜”为了表⽰正与负,⼈们发明了"原码",把⽣活应该有的正负概念,原原本本的表⽰出来把左边第⼀位腾出位置,存放符号,正⽤0来表⽰,负⽤1来表⽰但使⽤“原码”储存的⽅式,⽅便了看的⼈类,却苦了计算机我们希望(+1)和(-1)相加是0,但计算机只能算出0001+1001=1010 (-2)这不是我们想要的结果 (╯' - ')╯︵┻━┻另外⼀个问题,这⾥有⼀个(+0)和(-0)为了解决“正负相加等于0”的问题,在“原码”的基础上,⼈们发明了“反码”“反码”表⽰⽅式是⽤来处理负数的,符号位置不变,其余位置相反当“原码”变成“反码”时,完美的解决了“正负相加等于0”的问题过去的(+1)和(-1)相加,变成了0001+1101=1111,刚好反码表⽰⽅式中,1111象征-0⼈们总是进益求精,历史遗留下来的问题—— 有两个零存在,+0 和 -0我们希望只有⼀个0,所以发明了"补码",同样是针对"负数"做处理的"补码"的意思是,从原来"反码"的基础上,补充⼀个新的代码,(+1)我们的⽬标是,没有蛀⽛(-0)有得必有失,在补⼀位1的时候,要丢掉最⾼位我们要处理"反码"中的"-0",当1111再补上⼀个1之后,变成了10000,丢掉最⾼位就是0000,刚好和左边正数的0,完美融合掉了这样就解决了+0和-0同时存在的问题另外"正负数相加等于0"的问题,同样得到满⾜举例,3和(-3)相加,0011 + 1101 =10000,丢掉最⾼位,就是0000(0)同样有失必有得,我们失去了(-0) , 收获了(-8)以上就是"补码"的存在⽅式结论:保存正负数,不断改进⽅案后,选择了最好的"补码"⽅案⼆进制数在内存中以的形式存储。
原码、反码、补码,计算机中负数的表示

原码、反码、补码,计算机中负数的表⽰原码:将⼀个整数,转换成⼆进制,就是其原码。
如单字节的5的原码为:0000 0101;-5的原码为1000 0101。
反码:正数的反码就是其原码;负数的反码是将原码中,除符号位以外,每⼀位取反。
如单字节的5的反码为:0000 0101;-5的反码为1111 1010。
补码:正数的补码就是其原码;负数的反码+1就是补码。
如单字节的5的补码为:0000 0101;-5的补码为1111 1011。
在计算机中,正数是直接⽤原码表⽰的,如单字节5,在计算机中就表⽰为:0000 0101。
负数⽤补码表⽰,如单字节-5,在计算机中表⽰为1111 1011。
这⼉就有⼀个问题,为什么在计算机中,负数⽤补码表⽰呢?为什么不直接⽤原码表⽰?如单字节-5:1000 0101。
我想从软件上考虑,原因有两个 1、表⽰范围 拿单字节整数来说,⽆符号型,其表⽰范围是[0,255],总共表⽰了256个数据。
有符号型,其表⽰范围是[-128,127]。
先看⽆符号,0表⽰为0000 0000,255表⽰为1111 1111,刚好满⾜了要求,可以表⽰256个数据。
再看有符号的,若是⽤原码表⽰,0表⽰为0000 000。
因为咱们有符号,所以应该也有个负0(虽然它还是0):1000 0000。
那我们看看这样还能够满⾜我们的要求,表⽰256个数据么? 正数,没问题,127是0111 1111,1是0000 0001,当然其它的应该也没有问题。
负数呢,-1是1000 0001,那么把负号去掉,最⼤的数是111 1111,也就是127,所以负数中最⼩能表⽰的数据是-127。
这样似乎不太对劲,该如何去表⽰-128?貌似直接⽤原码⽆法表⽰,⽽我们却有两个0。
如果我们把其中的⼀个0指定为-128,不⾏么?这也是⼀个想法,不过有两个问题:⼀是它与-127的跨度过⼤;⼆是在⽤硬件进⾏运算时不⽅便。
所以,计算机中,负数是采⽤补码表⽰。
128的补码

128的补码-128的补码2010-10-24 10:29-128的补码2010年10月23日星期六10:538位定点整数的原码表示范围是-127到127 8位定点整数的补码表示范围是-128到127对上两句说明:用原码表示:01111111 8位有符号最大的数是127 11111111 8位有符号最小的数是-127 用补码表示:01111111 8位有符号最大的数是127 10000001 8位有符号最小的数是-127 但是还有一个更小的就是10000000把这个规定为-128的补码在8位长度下,-128的原码与反码都不存在,因为一个字节的有符号数的原码范围是:-127~+127,既然不存在-128的原码那么就无法求出-128的补码了,怎么办?前几天听汇编老师曲俊华讲过,-128这样的数很特殊,不是取反加一求补码。
-2^n是个特殊数(n为x数值位的长度):它补码的求法应按照公式进行运算: 如:-128"[-2^7]补"=(2^8)+(-2^7)=10000000原来还有更牛x的解释:一般的说法是负数的补码为其原码除符号位外取反然后总体加一,也就是说,要得到一个负数数的补码,要先知道这个负数的原码才行。
那么,问题出现了,在8位长度下,-128的原码与反码都不存在,127~+127,既然不存在-128的原码因为一个字节的有符号数的原码范围是:- 那么就无法求出-128的补码了,怎么办?其实,这个问题的实际意义是,既然说计算机内部的有符号整数都是补码,那么怎么才能有效的实现这一设计呢?潜台词是:根据上面由原码推导出补码的理论,如果是正数,计算机得到其原码,也就是得到了其补码(正数补码等同于原码),如果是负数,先得到其原码,然后再取反加一就可以了。
也就是说按这个思维设计编译器,或计算机电路,就可以了。
但是如果出现开始说的-128的补码问题,这个设计就不能工作了。
其实,在真正的设计中,这种获得负数补码的"取反加一"的方案根本没有实施过~拿现代的计算机举例,输入设备只有键盘,通过编辑器程序把键盘的扫描码变成ascii码存储起来,比如输入'a'就存储0x61,输入'5'就存储0x35,这些都是ascii码。
128的二进制有原码反码和补码

第一次修订 2009-5-6 14:11---------------------1.模的概念(我只讲个例子,具体的可以查数学中的 "同余模")在日常生活中,有许多化减为加的例子。
例如,时钟是逢12进位,12点也可看作0点。
当将时针从10点调整到5点时有以下两种方法:1.将时针逆时针方向拨5格,相当于做减法: 10-5=52.将时针顺时针方向拨7格,相当于做加法:10+(12-5)=12+5=5 (模为 12) 2.模的运用(采用模得到补码)1.补码的得来:是为了让负数变成能够加的正数,so,负数的补码=模-负数的绝对值比如:-1 补码:1111 1111(10000 0000 -1得来)当一个数要减1的时候,可以直接加 1111 11112.原码的得来:(负数的原码,直接把对应正数的最高位改为1)原码能够直观的表示一个负数(能直观的把真值显示出来,如 -1为1000 0001其中最高位表示符号位,不进行算术计算) 3.总结:补码相加,到第9位才舍弃(模10000 0000)原码相加,到第8位舍弃(模1000 0000)反码相加,到第8位舍弃(模1000 0000)3.原码和补码之间转换:1.补码=原码减1,再取反(便于理解)或补码= 反码+1(便于描述和推理)2.演示:补码=原码减1,再取反如-1的原码1000 0001-->1000 0000(减1后)-->1111 1111(取反后)补码3.演示:补码= 反码+1)如-1的原码 1000 0001-->1111 1110(反码)-->1111 1111(加1)补码4.重点:(特别是在有进位的时候)原码和反码的最高位是符号位,不参加算术运算,模为1000 0000(比补码少一个0)而补码所有位都可以相加,模为10000 0000(最高位不是符号位,补码是通过模减去负数绝对值得到的)5.推断-128的原码和补码(用补码= 反码+1)1.关于原码1000 0000,表示的是-0,还是-128呢?(答案是-128而不是-0)1.先看看原码的概念吧:正数的符号位为0,负数的符号位为1,其它位按照一般的方法来表示数的绝对值2.0是负数吗?0既不是正数也不是负数,那么它的符号位到底是0还是1呢?(0的符号位为0,不能为1)3.看看负数补码的公式:负数的补码=10000 0000(模)-数的绝对值比如:-1 1111 1111 =10000 0000-0000 0001-2 1111 1110 =10000 0000-0000 0010现在假设-0为负数,那么-0的补码应该是10000 0000 - 0(这个0,姑且教0的绝对值吧)=0000 0000 反码:1111 1111(0000 0000 -1=0000 0000 +1111 1111=1111 1111)原码:1000 0000现在来推-128-128的补码:10000 0000 - 1000 0000(+128没有符号位)=1000 0000反码:1111 1111(1000 0000 -1=1000 0000+1111 1111=1111 1111)(补码-1)原码:1000 0000(反码取反)从上面看来,一个原码对应了2个补码但是仔细分析:原码的概念,负数的符号位为1,但是0不是负数,所以不能用此公式0也不是正数,但是可以把0定义为原码、反码和补码都一样(即0000 0000)而且据说可以推断出0的补码只有一个(有兴趣的可以去推一下,呵呵)现在原码1000 0000就唯一表示-128了,而不会表示出-0,因为-0不能用这个公式计算现在,补码1000 0000的原码是1000 0000(已证明),那么原码1000 0000的补码是1000 0000吗?原码 1000 0000 (-128,进位被舍去)反码 1111 1111补码 1000 0000(1111 1111(反码) + 1=1000 0000,这里实际上真正相加的是1111 1111后面的7位,第1位是符号位始终不会变,所以,当进到第8位的时候,就表示溢出了,会被舍弃)2.综上所述:1.-128的补码和原码一样都是1000 0000,2.0的原码、反码和补码都一样(即0000 0000)3.如果把-0当做负数,1000 0000就会有歧义(事实上0的补码只有一个0000 0000)第一次的手稿 2009-5-5 22:47-----------------1.使用反码的意义:1.使符号位能与有效值部分一起参加运算,从而简化运算规则。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第一次修订 2009-5-6 14:11
---------------------
1.模的概念(我只讲个例子,具体的可以查数学中的 "同余模")
在日常生活中,有许多化减为加的例子。
例如,时钟是逢12进位,12点也可看作0点。
当将时针从10点调整到5点时有以下两种方法:
1.将时针逆时针方向拨5格,相当于做减法: 10-5=5
2.将时针顺时针方向拨7格,相当于做加法:10+(12-5)=12+5=5 (模为 12) 2.模的运用(采用模得到补码)
1.补码的得来:是为了让负数变成能够加的正数,so,负数的补码=模-负数的绝对值
比如:-1 补码:1111 1111(10000 0000 -1得来)
当一个数要减1的时候,可以直接加 1111 1111
2.原码的得来:(负数的原码,直接把对应正数的最高位改为1)
原码能够直观的表示一个负数(能直观的把真值显示出来,如 -1为1000 0001
其中最高位表示符号位,不进行算术计算) 3.总结:补码相加,到第9位才舍弃(模10000 0000)
原码相加,到第8位舍弃(模1000 0000)
反码相加,到第8位舍弃(模1000 0000)
3.原码和补码之间转换:
1.补码=原码减1,再取反(便于理解)
或补码= 反码+1(便于描述和推理)
2.演示:补码=原码减1,再取反
如-1的原码1000 0001-->1000 0000(减1后)-->1111 1111(取反后)补码
3.演示:补码= 反码+1)
如-1的原码 1000 0001-->1111 1110(反码)-->1111 1111(加1)补码
4.重点:(特别是在有进位的时候)
原码和反码的最高位是符号位,不参加算术运算,模为1000 0000(比补码少一个0)
而补码所有位都可以相加,模为10000 0000(最高位不是符号位,补码是通过模减去负数绝对值得到的)
5.推断-128的原码和补码(用补码= 反码+1)
1.关于原码1000 0000,表示的是-0,还是-128呢?(答案是-128而不是-0)
1.先看看原码的概念吧:正数的符号位为0,负数的符号位为1,其它位按照一般的方法来表示数的绝对值
2.0是负数吗?0既不是正数也不是负数,那么它的符号位到底是0还是1呢?(0的符号位为0,不能为1)
3.看看负数补码的公式:负数的补码=10000 0000(模)-数的绝对值
比如:-1 1111 1111 =10000 0000-0000 0001
-2 1111 1110 =10000 0000-0000 0010
现在假设-0为负数,那么
-0的补码应该是10000 0000 - 0(这个0,姑且教0的绝对值吧)=0000 0000 反码:1111 1111(0000 0000 -1=0000 0000 +1111 1111=1111 1111)
原码:1000 0000
现在来推-128
-128的补码:10000 0000 - 1000 0000(+128没有符号位)=1000 0000
反码:1111 1111(1000 0000 -1=1000 0000+1111 1111=1111 1111)(补码-1)
原码:1000 0000(反码取反)
从上面看来,一个原码对应了2个补码
但是仔细分析:原码的概念,负数的符号位为1,但是0不是负数,所以不能用此公式
0也不是正数,但是可以把0定义为原码、反码和补码都一样(即0000 0000)
而且据说可以推断出0的补码只有一个(有兴趣的可以去推一下,呵呵)
现在原码1000 0000就唯一表示-128了,而不会表示出-0,因为-0不能用这个公式计算
现在,补码1000 0000的原码是1000 0000(已证明),那么原码1000 0000的补码是1000 0000吗?
原码 1000 0000 (-128,进位被舍去)
反码 1111 1111
补码 1000 0000(1111 1111(反码) + 1=1000 0000,这里实际上真正相加的是1111 1111后面的7位,
第1位是符号位始终不会变,所以,当进到第8位的时候,就表示溢出了,会被舍弃)
2.综上所述:1.-128的补码和原码一样都是1000 0000,
2.0的原码、反码和补码都一样(即0000 0000)
3.如果把-0当做负数,1000 0000就会有歧义(事实上0的补码只有一个0000 0000)
第一次的手稿 2009-5-5 22:47
-----------------
1.使用反码的意义:
1.使符号位能与有效值部分一起参加运算,从而简化运算规则。
从而可以简化运算器
的结构,提高运算速度;
(减法运算可以用加法运算表示出来。
)
2.加法运算比减法运算更易于实现。
使减法运算转换为加法运算,进一步简化计算机
中运算器的线路设计。
2.负数的二进制数串表示一般用补码:(如何通过原码推补码,特别是-128的解释)
1.先给出3个原则:
1.因为使用补码可以将符号位和其他位统一处理,同时,减法也可以按加法来处理,
即如果是补码表示的数,
不管是加减法都直接用加法运算即可实现。
2.两个用补码表示的数相加时,如果最高位(符号位)有进位,则进位被舍弃(模的概念,补码的模10000 0000)
比如:1111 1111(-1) +1000 0001(-127)=1000 0000(-128,实际上最高位有3个1,
进位一次后,还保留一个1)
1111 1110(-2) + 0000 0100(4) = 0000 0010(2)
3.模的规则:(自己的推断)
1.补码的模为10000 0000
2.反码的模为1000 0000(从反码的定义也能够知道,即反码的运算不涉及符
号位)
3.模的解释
在日常生活中,有许多化减为加的例子。
例如,时钟是逢12进位,12点也可
看作0点。
当将时针从10点调整到5点时有以下两种方法:
1.时针逆时针方向拨5格,相当于做减法: 10-5=5
2.时针顺时针方向拨7格,相当于做加法:10+(12-5)=12+5=5 (模为 12)
2.原码、反码和补码的定义:(主要讨论负数的)
1.正整数的原码、反码和补码都一样
2.负数:
1.原码就是原来的表示方法
2.反码是原码除符号位(最高位)外取反
3.补码=反码+1
3.举例:以一个单字节来说:(即8位)
-1 原码 1000 0001(通过原码得到真值)
反码 1111 1110
补码 1111 1111(通过补码得到二进制)
-2 原码 1000 0010
反码 1111 1101
补码 1111 1110
**如此类推:原码 1000 0000 (-128)(重点)
反码 1111 1111
补码 1000 0000(1111 1111 + 1=1000 0000,这里实际上真正相加的是1111 1111后面的7位,
第1位是符号位始终不会变,所以,当进到第8位的时候,就表示溢出了,所以会被舍弃,
也就是说反码的模是1000 0000,而补码的模是:10000 0000比反码多一位)
如果用补码反推原码
补码1000 0000
反码1111 1111(1000 0000 -1=1000 0000+1111 1111(相当于2个补码相加,可用模的规则)=1111 1111)
原码1000 0000
4.感慨:很多群人解释不通了,就武断的说-128的二进制为1000 0000,并断定它没有反码和原码,还说是"规定"
而我怎么也没有找到官方的这么个规定(个人觉得这是不严谨的也是不负责任的,呵呵)
5.具体的计算演示:
1+(-1)=0
0000 0001 + 1111 1111=0000 0000
1+(-2)=-1
0000 0001 + 1111 1110=1111 1111(-1)
2+(-1)=1
0000 0010 + 1111 1111=0000 0001
(-128)+1=-127
1000 0000 +0000 0001=1000 0001(补)
1000 0001(补码)
1000 0000(反码=补码-1)
1111 1111(原码 =-127)
3.有一个不正确的解释,貌似还写成书了(个人认为)
采用补码表示还有另外一个原因,那就是为了防止0的机器数有两个编码。
原码和反码表示的0
有两种形式+0和-0,而我们知道,+0和-0是相同的。
这样,8位的原码和反码表示的整数的范围就是-127~+127
(11111111-01111111),而采用补码表示的时候,00000000是+0,即0;10000000不再是-0,而是-128,这样,
补码表示的数的范围就是-128~+127了,不但增加了一个数得表示范围,而且还保证了0编码的唯一性。
我的观点:包括写上面的话的人自己也说过,10000000(补码)没有反码和原码,既然这样,如何得出结论
1000 0000曾经表示的是-0,其实通过上面的分析,1000 0000是有反码(1111 1111)和原码的(1000 0000)
4.一些好的概念:
由于计算机中符号和数字一样,都必须用二进制数串来表示,因此,正负号也必须用0、1来表示。
用最高位0表示正、1表示负, 这种正负号数字化的机内表示形式就称为“机器数”,而相应的机器外部用正负号表示的数称为“真值”,将一个真值表示成二进制字串的机器数的过程就称为编码。
