工程力学(静力学与材料力学)第四版习题答案

合集下载

工程力学材料力学第四版北京科技大学及东北大学习题答案解析

工程力学材料力学第四版北京科技大学及东北大学习题答案解
析
工程力学材料力学 (北京科技大学与东北大学)
第一章轴向拉伸与压缩
1-1:用截面法求下列各杆指定截面的内力
解:
(a):N1=0,N2=N3=P
(b):N1=N2=2kN
(c):N1=P,N2=2P,N3= -P
(d):N1=-2P,N2=P
(e):N1= -50N,N2= -90N
(f):N1=0、896P,N2=-0、732P
注(轴向拉伸为正,压缩为负)
1-2:高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接,连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。

解: σ1=
2
1
1
850
4
P kN
S d
π
=
=35、3Mpa
σ2=
2
2
2
850
4
P kN
S d
π
=
=30、4MPa
∴σmax=35、3Mpa
1-3:试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN,吊杆的尺寸如图b所示。

解:
下端螺孔截面:σ1=1
90
20.065*0.045P S =15、4Mpa 上端单螺孔截面:σ2=2P S =8、72MPa
上端双螺孔截面:σ3=
3P S =9、15Mpa ∴σmax =15、4Mpa。

工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N 1=0,N 2=N 3=P(b):N 1=N 2=2kN(c):N 1=P,N 2=2P,N 3= -P(d):N 1=-2P,N 2=P(e):N 1= -50N,N 2= -90N(f):N 1=0.896P,N 2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC L NL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:Nl l EA l l ε∆=∆=∴N EA ε=62.54*10N EA N ε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

工程力学材料力学第四完整版本习题答案解析

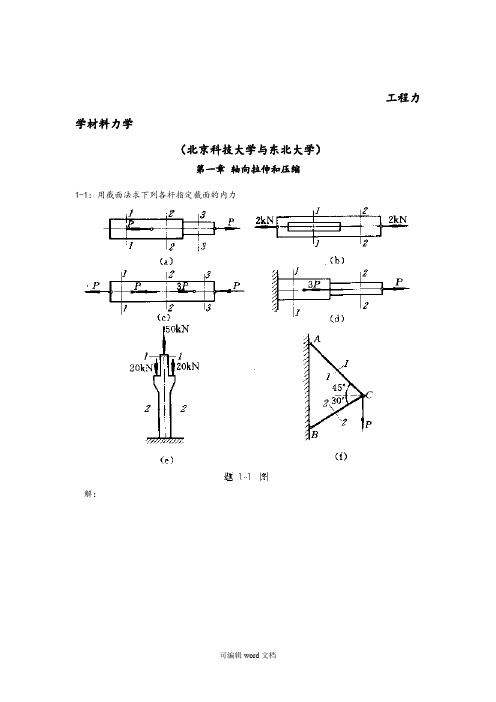
工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC AC LNL EA EA σε===1.59*104,CB CB CB LNL EA EA σε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa. 解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1:用截面法求下列各杆指定截面的内力解：(a):N1=0，N2=N3=P(b）：N1=N2=2kN(c）：N1=P，N2=2P，N3= -P（d)：N1=—2P，N2=P（e）：N1= —50N，N2= -90N（f)：N1=0.896P，N2=—0。

732P注（轴向拉伸为正，压缩为负）1—2：高炉装料器中的大钟拉杆如图a所示,拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示;拉杆上端螺纹的内径d=175mm.以知作用于拉杆上的静拉力P=850kN,试计算大钟拉杆的最大静应力。

解：σ1= =35。

3Mpaσ2= =30。

4MPa∴σmax=35。

3Mpa1—3:试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1= =15。

4Mpa上端单螺孔截面：σ2==8。

72MPa上端双螺孔截面:σ3= =9.15Mpa∴σmax=15。

4Mpa1—4：一桅杆起重机如图所示,起重杆AB为一钢管，其外径D=20mm，内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得:F1＊sin15=F2＊sin45F1*cos15=P+F2＊sin45∴σAB= =-47。

7MPaσBC==103。

5 MPa1—5：图a所示为一斗式提升机.斗与斗之间用链条连接，链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N。

钢链又两层钢板构成，如c所示。

每个链板厚t=4。

5mm，宽h=40mm,H=65mm，钉孔直径d=30mm。

试求链板的最大应力。

解：F=6PS1=h*t=40＊4。

5=180mm2S2=（H-d)＊t=（65-30）＊4。

5=157.5mm2∴σmax==38.1MPa1—6：一长为30cm的钢杆,其受力情况如图所示。

工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析

力，试校核螺栓的强度。
解：
1-11：用绳索吊运一重的重物。设绳索的横截面积，许用应力试问：
（1）当时，绳索强度是否够用？
（2）如改为，再校核绳索的强度。
解：（1）当，强度不够
（2）当，强度够
1-12：图示一板卷夹钳同时吊两个钢卷，已知每个钢卷重100kN,AB与AC两杆夹角为，其横截面为的矩形，
AB段
BC段
比较得最大剪应力发生在BC段，其数值为
(3)最大相对扭转角因轴内各截面扭矩方向都一致，所以最大相对扭转角即为整个轴长的总扭转角。在使用扭转角公式时，注意到该式的使用
条件必须是对应于所算转角的长度段内，、、T为常数。故分别计算两段轴的扭转角，然后相加即得最大相对扭转角。
+ 0.0213弧度=1.22度
解:
1.59*104,
6.36*104
1-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径
d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧
制压力.压头材料的弹性模量E=200Gpa.
最大应力。
解：
1-23两钢杆如图所示，已知截面面积 =1 ， =2 ；材料的弹性模量E=210Gpa，线膨胀系数 =12.5× l C。当
温度升3 C时，试求两杆内的最大应力。
解：
第二章剪切
2-1一螺栓连接如图所示，已知P=200 kN， =2 cm，螺栓材料的许用切应力[τ]=80Mpa，试求螺栓的直径。
解：
1-15悬臂吊车的尺寸和载荷情况如图所示。斜杆BC由两角钢组成，载荷Q=25 kN。设材料的许用应力[] =140 MPa，试选择

工程力学第4版(静力学)答案

工程力学（第四版）--静力学北京科技大学、东北大学
X 0 FAC cos 60 FAB cos30 0 Y 0 FAB sin 30 FAC sin 60 W 0
联立上二式，解得： FAB 0.5W (拉力) FAC 0.866W （压力）
（d）由平衡方程有：
X 0 FAB sin 30 FAC sin 30 0 Y 0 FAB cos30 FAC cos30 W 0
联立上二式，解得： FAB 0.577W (拉力)
工程力学（第四版）--静力学北京科技大学、东北大学
FAC 0.577W (拉力)
2-4 解：（a）受力分析如图所示：
工程力学（第四版）--静力学北京科技大学、东北大学
1-8 结构如图所示，力 P 作用在销钉 C 上，试分别画出 AC，BCE 及 DEH
部分的受力图。
1-1 解：
参考答案
1-2 解：
工程力学（第四版）--静力学北京科技大学、东北大学
工程力学（第四版）--静力学北京科技大学、东北大学
1-3 解：
2-12 解：整体受力交于 O 点，列 O 点平衡
由
x 0 FRA cos FDC P cos30 0
Y 0 FRA sin Psin 30 0
联立上二式得： FRA 2.92KN
FDC 1.33KN （压力）
列 C 点平衡
工程力学（第四版）--静力学北京科技大学、东北大学
3-2 解： P1, P3; P2 , P5; P4 , P6 构成三个力偶
M

P1 (0.3 0.1)
P2
(0.4 0.1) 3 5

工程力学--静力学第4版第五章习题答案.docx

第五章习题5-1 重为W=100N，与水平面间的摩擦因数f=0.3 ，（a）问当水平力P=10N时，物体受多大的摩擦力，（ b）当 P=30N时，物体受多大的摩擦力？（ c）当 P=50N时，物体受多大的摩擦力？5-2 判断下列图中两物体能否平衡?并问这两个物体所受的摩擦力的大小和方向。

已知：（a）物体重Ｗ =1000N，拉力 P=200N，f=0.3 ；（b）物体重Ｗ =200N，拉力 P=500N，f=0.3 。

5-3 重为Ｗ的物体放在倾角为α的斜面上，物体与斜面间的摩擦角为ρ，且α＞ρ。

如在物体上作用一力Ｑ，此力与斜面平行。

试求能使物体保持平衡的力Qde 最大值和最小值。

5-4 在轴上作用一力偶，其力偶矩为 m=-1000N.m，有一半径为 r=25cm 的制动轮装在轴上，制动轮与制动块间的摩擦因数f=0.25 。

试问制动时，制动块对制动轮的压力N至少应为多大？5-5 两物块Ａ和Ｂ重叠放在粗糙的水平面上，在上面的物块Ａ的顶上作用一斜向的力Ｐ。

已知：Ａ重 1000N，B 重 2000N，A 与 B 之间的摩擦因数 f1=0.5 ，B 与地面之间的摩擦因数 f2=0.2 。

问当 P=600N时，是物块 A 相对物块 B 运动呢？还是Ａ、Ｂ物块一起相对地面Ｃ运动？5-6 一夹板锤重 500N，靠两滚轮与锤杆间的摩擦力提起。

已知摩擦因数f=0.4 ，试问当锤匀速上升时，每边应加正应力（或法向反力）为若干？精品文档5-7 尖劈顶重装置如图所示，重块与尖劈间的摩擦因数f（其他有滚珠处表示光滑）。

求：（1）顶住重物所需Ｑ之值（Ｐ、α已知）；（２）使重物不向上滑动所需Ｑ。

注：在地质上按板块理论，太平洋板块向亚洲大陆斜插下去，在计算太平洋板块所需的力时，可取图示模型。

解：取整体∑ F y =0 F NA-P=0∴F NA=P当 F＜ Q1时锲块 A 向右运动，图（ b）力三角形如图（ d）当 F＞ Q2时锲块 A 向左运动，图（ c）力三角形如图（ e）5-8 图示为轧机的两个压辊，其直径均为d=50cm，两棍间的间隙 a=0.5cm，两轧辊转动方向相反，如图上箭头所示。

工程力学-材料力学第4版习题答案

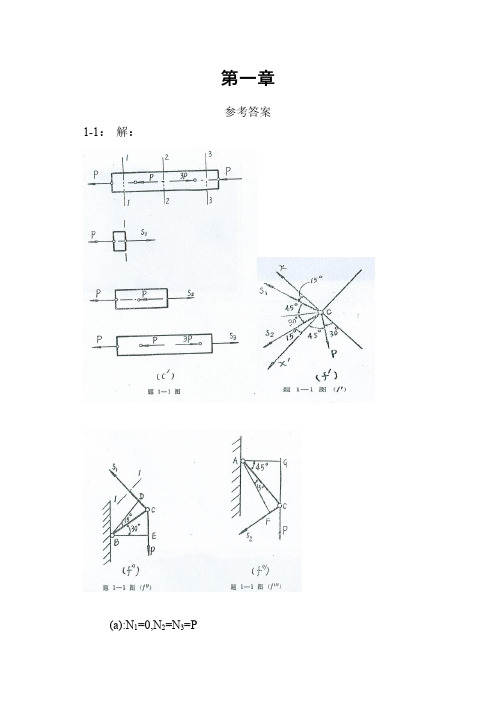
第一章参考答案1-1：解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3=-P(d):N1=-2P,N2=P(e):N1=-50N,N2=-90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2PS =8.72MPa上端双螺孔截面：σ3=3PS =9.15Mpa∴σmax =15.4Mpa1-4：解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5MPa1-5：解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS =38.1MPa1-6:解:(1)σAC =-20MPa,σCD =0,σDB =-20MPa;△l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2)∴AB l ∆=-0.02mm1-7:解:31.8127AC AC CB CB P MPa S P MPa S σσ====AC AC AC L NL EA EA σε===1.59*104,CB CB CB L NL EA EA σε===6.36*1041-8:解: Nll EAl l ε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：解：208,0.317E GPa ν==1-10：解：[][]max59.5MPa σσ=<1-11：解：（1）当45o α=，[]11.2σσ=>强度不够（2）当60o α=，[]9.17σσ=<强度够1-12：解：[]360,200200200*1013.3100*150*10Y p kNS P kNS MPa A σσ-==∴=====<∑1-13：解：[]max 200213MPa MPaσ=<1-14：解： 1.78, 1.26d cm d cm==拉杆链环1-15解：BC F ==70.7kN70.70.505140F S FS σσ=∴=== 查表得：45*45*31-16解：(1)[]2401601.5s s n σσ===MPa [][]24P S P dσσπ≤∴≤24.4D mm∴=(2)2119.51602P P MPa MPaS d σπ===≤⎛⎫ ⎪⎝⎭1-17解：（1）2*250*6154402D F P A N π⎛⎫=== ⎪⎝⎭78.4AC F MPa S σ==300 3.8378.4s n σσ∴===[][]''''60*3.14*15*1542390F SF S Nσσ===='61544014.521542390F n F ===≈1-18解：P=119kN1-19解：::3:4:535()44AB BC AB BC S P S S P S P =∴==拉，[][][]112841123484AB AB S A kN S P kNP kN σ=====同理所以最大载荷84kN1-20解：P=33.3kN1-21解：71,,12123A B C P F F P F P ===1-22解：10MAX MPaσ=-1-23解：A B X R R R=∴==∑t r l l ∆=∆t AB l l tα∆=21211111223533131.3cd R AC DB CD AC CD CD AF CD MAX Rl Rl l l l l EA EA Rl Rl Rl l EA EA EA EA t EA t R l S MPa A ααασ∆=∆+∆+∆=+=+=∴====第二章习题2-1一螺栓连接如图所示，已知P=200kN ，=2cm ，螺栓材料的许用切应力[τ]=80Mpa，试求螺栓的直径。

工程力学第四版课后习题答案

工程力学第四版课后习题答案【篇一：工程力学第 4 版(静力学)答案】题中，凡未标出自重的物体，质量不计。

接触处都不计摩擦。

1-1 试分别画出下列各物体的受力图。

1-2 试分别画出下列各物体系统中的每个物体的受力图。

1-3 试分别画出整个系统以及杆bd ， ad ，ab （带滑轮 c ，重物 e 和一段绳索）的受力图。

1-4 构架如图所示，试分别画出杆1-5 构架如图所示，试分别画出杆hed ，杆bdh ，杆bdc 及杆ab ，销钉aec 的受力图。

a 及整个系统的受力图。

1-6 构架如图所示，试分别画出杆1-7 构架如图所示，试分别画出杆aeb ，销钉aeb ，销钉a 及整个系统的受力图。

c ，销钉 a 及整个系统的受力图。

1-8 结构如图所示，力 p 作用在销钉 c 上，试分别画出 ac ，bce 及 deh 部分的受力图。

参考答案1-1 解：1-2 解：1-3 解：1-4 解：【篇二：工程力学第四版课后答案(张秉荣 )12 章】class=txt>3454 版【篇三：【纯习题答案版】【完整版】工程力学第材料力学 (北科大 ,东北大学 )2-9 章答案】txt> 第二章习题参考答案2-1 解： 2-2 解：2-3 解： 2-4 解：2-5 解： 2-6 解：所以都满足2-7 解： 2-8 解：2-9 解：：第三章习题参考答案3.1 据截面沿指定截面 i-i (i=123) 将杆截为两段，考虑任一段的平衡即可得该指定截面上的扭矩，例如题 b:（1） 1-1 截面由（2） 2-2 截面由（3） 3-3 截面由由以上各扭矩=0 ，=0=0 ，1+2-6+ =0 得=6-2-1=3kn.m ( 方向如图所示，为正扭矩 )=0 ，1+2-=0 得=1+2=3kn.m （方向如图所示，为负扭矩）的计算式可知，轴内任一横截面的扭矩，在数值上就等于该截面一侧规则可迅速求得任一截面的扭矩，而无须将轴截开。

工程力学--材料力学第4版第三章习题答案

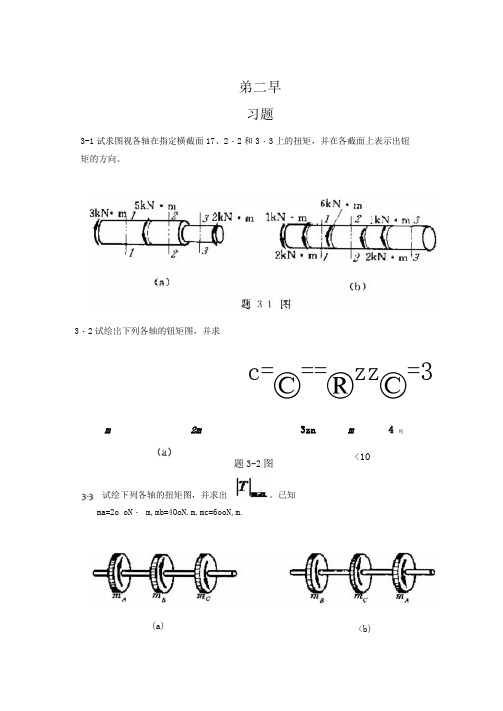
题3-2图试绘下列各轴的扭矩图，并求出。

已知ma=2o oN ・ m,mb=4OoN.m,mc=6ooN,m.<10<b)弟二早习题3-1试求图视各轴在指定横截面17、2・2和3・3上的扭矩，并在各截面上表示出钮矩的方向。

3・2试绘岀下列各轴的钮矩图，并求c=©==®zz ©=3m 2m3znm4 税(a)3-4 一传动轴如图所示，已知 ma=i3oN..cm, mb=3OoN.cm , mc=iooN.cm,md=7oN.cm;^$段轴的直径分别为：Dab=5cm, Dbc=7・5cm, Dcd=5cm （1）画出扭矩图；<2）求1-4、2-2、3-3截面的最大切应力。

3・5图示的空心圆轴，外径D=8cm,内径d二6・巧5,承受扭矩m=ioooN.m・（1）求弘、％（2）绘出横截而上的切应力分布图；（3）求单位长度扭转角，已知G=8ooooMpa・3-6已知变截而钢轴上的外力偶矩^^SooN.m, =i2ooN.m,试求最大切应力和最大相对扭矩。

已知G=8o*l沪Pa.题3-6图3-7 一钢轴的转矩n=24o/min.传递功率丹=44」kN.m.已知L可=4ol\4pa,2」」3,G=8o*l，MPa,试按强度和刚度条件计算轴的直径解：轴的直径由强度条件确泄，3-8图示实心轴通过牙嵌离合器把功率传给空心轴。

传递的功率=7-5kw,轴的转速n=ioor/min,试选择实心轴直径和空心轴外径叫2。

己知％/空2 =0.5，[rlL J=4oMpa・3-9图示AB轴的转速 n=i2or/min,AK B 轮上输入功率丹=4okw,此功率的一半通过锥齿轮传给垂直轴V,另一半功率由水平轴H传走。

已知锥齿轮的节圆直径 a=6oomm：各轴宜径为^=ioomm, ^2=8omm, ^3=6omm, t^=2oMPa.试对各轴进行强度校核。

3-1。

船用推进器的轴，一段是实心的，直径为28omm,列一段是空心的，其内径为外径的一半。

工程力学材料力学第四版[北京科技大学及东北大学]习题答案解析

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a 所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN ，吊杆的尺寸如图b 所示。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS1=h*t=40*4.5=180mm2S2=(H-d)*t=(65-30)*4.5=157.5mm2∴σmax=2FS=38.1MPa1-6:一长为30cm的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1)AC. CD DB 各段的应力和变形.(2)AB杆的总变形.解: (1)σAC=-20MPa,σCD=0,σDB=-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△ l CD =CD LEA σ=0△ L DB =DB LEA σ=-0.01mm (2) ∴ABl ∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变. 解:31.8127AC ACCB CBPMPa S PMPa S σσ====AC AC ACLNL EA EA σε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:NllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

【纯习题答案版】【完整版】工程力学第4版材料力学(北科大,东北大学)2-9章答案

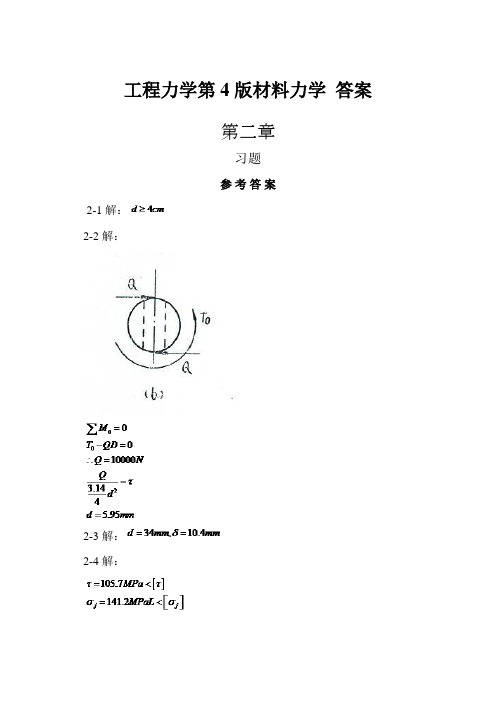
工程力学第4版材料力学答案第二章习题参考答案2-1解：2-2 解：2-3 解：2-4 解：2-5 解：2-6解：所以都满足 2-7 解：2-8 解：：2-9 解：第三章习题参考答案3.1据截面沿指定截面i-i (i=123)将杆截为两段，考虑任一段的平衡即可得该指定截面上的扭矩，例如题b:（1）1-1截面由=0，1+2-=0 得=1+2=3kN.m（方向如图所示，为负扭矩）（2）2-2截面由=0，1+2-6+=0 得=6-2-1=3kN.m (方向如图所示，为正扭矩) （3）3-3截面由=0，=0由以上各扭矩的计算式可知，轴内任一横截面的扭矩，在数值上就等于该截面一侧各外力偶矩值的代数和；而扭矩的方向则与截面任一侧合外力偶的方向规则可迅速求得任一截面的扭矩，而无须将轴截开。

剧此规则可得a各截面的扭矩：=3kN.m，==-2kN.m3-2解：（a）=2，（b）=43-3解：（a）=600N.m ，（b）=400N.m3-4 解：=-130N.m，=170 N.m，=70N.m=5.3 MPa , =2.05 MPa , =2.85MPa3-5 解：3-6 解：（1）各段轴横截面的扭矩：AB段（负扭矩）BC段（为负扭矩）(2) 最大剪应力计算：因两段轴扭矩不同，所以应分别计算每段轴内横截面的最大剪应力值，然后加以比较找到最大减应力值。

AB段BC段比较得最大剪应力发生在BC段，其数值为(3)最大相对扭转角因轴内各截面扭矩方向都一致，所以最大相对扭转角即为整个轴长的总扭转角。

在使用扭转角公式时，注意到该式的使用条件必须是对应于所算转角的长度段内，、、T为常数。

故分别计算两段轴的扭转角，然后相加即得最大相对扭转角。

+0.0213弧度=1.22度3-7解：轴的直径由强度条件确定，。

3-8解：（1）外力偶矩的计算（2）两轴各截面传递的扭矩（3）实心轴所需直径由得选d=45mm.(4) 空心轴的外、内选择由得选所以。

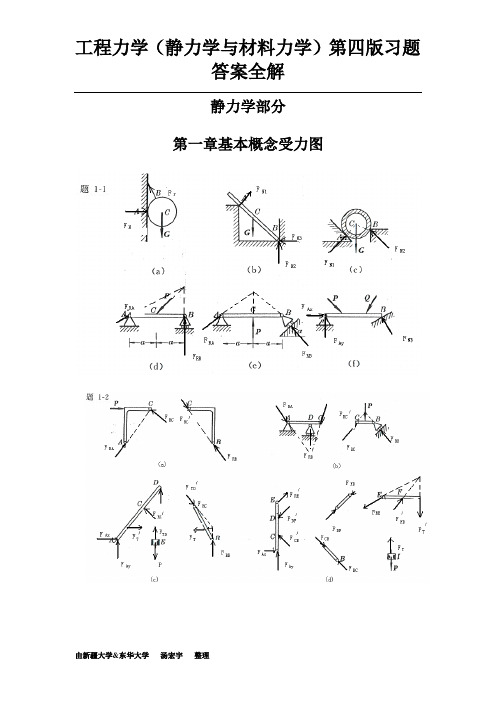
(完整版)工程力学(静力学与材料力学)第四版习题答案

静力学部分第一章基本概念受力图2-1 解：由解析法，23cos 80RX F X P P N θ==+=∑12sin 140RY F Y P P N θ==+=∑故： 22161.2R RX RY F F F N =+=1(,)arccos 2944RY R R F F P F '∠==o v v2-2解：即求此力系的合力，沿OB 建立x 坐标，由解析法，有123cos45cos453RX F X P P P KN ==++=∑o o13sin 45sin 450RY F Y P P ==-=∑o o故： 223R RX RY F F F KN =+= 方向沿OB 。

2-3 解：所有杆件均为二力杆件，受力沿直杆轴线。

（a ）由平衡方程有：0X =∑ sin 300AC AB F F -=o0Y =∑ cos300AC F W -=o0.577AB F W =（拉力） 1.155AC F W =（压力）（b ）由平衡方程有：0X =∑ cos 700AC AB F F -=o0Y =∑ sin 700AB F W -=o1.064AB F W =（拉力）0.364AC F W =（压力）（c ）由平衡方程有：0X =∑ cos 60cos300AC AB F F -=o o0Y =∑ sin 30sin 600AB AC F F W +-=o o0.5AB F W = (拉力)0.866AC F W =（压力）（d ）由平衡方程有：0X =∑ sin 30sin 300AB AC F F -=o o0Y =∑ cos30cos300AB AC F F W +-=o o0.577AB F W = (拉力)0.577AC F W = (拉力)2-4 解：（a ）受力分析如图所示：由0x =∑ 22cos 45042RA F P -=+o15.8RA F KN ∴= 由0Y =∑ 22sin 45042RA RB F F P +-=+o7.1RB F KN ∴=(b)解：受力分析如图所示：由 0x =∑ cos 45cos 45010RA RB F F P --=o o0Y =∑sin 45sin 45010RA RB F F P -=o o联立上二式，得： 22.410RA RB F KNF KN ==2-5解：几何法：系统受力如图所示三力汇交于点D ，其封闭的力三角形如图示所以： 5RA F KN = （压力） 5RB F KN =（与X 轴正向夹150度） 2-6解：受力如图所示：已知，1R F G = ，2AC F G =由0x =∑ cos 0AC r F F α-=12cos G G α∴=由0Y =∑ sin 0AC N F F W α+-=22221sin N F W G W G G α∴=-⋅=--2-7解：受力分析如图所示，取左半部分为研究对象由0x =∑ cos 45cos 450RA CB P F F --=o o0Y =∑sin 45sin 450CB RA F F '-=o o 联立后，解得： 0.707RA F P = 0.707RB F P =由二力平衡定理 0.707RB CB CB F F F P '===2-8解：杆AB ，AC 均为二力杆，取A 点平衡由x =∑cos 60cos300AC AB F F W ⋅--=o o0Y =∑sin 30sin 600AB AC F F W +-=o o联立上二式，解得：7.32AB F KN=-（受压）27.3AC F KN=（受压）2-9解：各处全为柔索约束，故反力全为拉力，以D ，B 点分别列平衡方程（1）取D 点，列平衡方程由x =∑sin cos 0DB T W αα-=DB T Wctg α∴==（2）取B 点列平衡方程：由0Y =∑sin cos 0BDT T αα'-=230BD T T ctg Wctg KN αα'∴===2-10解：取B 为研究对象：由0Y =∑sin 0BC F P α-=sin BC P F α∴=取C 为研究对象：由x =∑cos sin sin 0BCDC CE F F F ααα'--=由0Y =∑ sin cos cos 0BC DC CE F F F ααα--+=联立上二式，且有BCBC F F '= 解得：2cos 12sin cos CE P F ααα⎛⎫=+⎪⎝⎭取E 为研究对象：由0Y =∑ cos 0NH CEF F α'-=CECE F F '=Q 故有：22cos 1cos 2sin cos 2sin NH P PF ααααα⎛⎫=+= ⎪⎝⎭2-11解：取A 点平衡：x =∑sin 75sin 750AB AD F F -=o o0Y =∑cos 75cos 750AB AD F F P +-=o o联立后可得： 2cos 75AD AB PF F ==o取D 点平衡，取如图坐标系：x =∑cos5cos800ADND F F '-=o ocos5cos80NDAD F F '=⋅oo由对称性及ADAD F F '=cos5cos5222166.2cos80cos802cos 75N NDADP F F F KN '∴===⋅=o o o o o2-12解：整体受力交于O 点，列O 点平衡由x =∑cos cos300RA DC F F P α+-=o0Y =∑sin sin 300RA F P α-=o联立上二式得：2.92RA F KN=1.33DC F KN=（压力）列C 点平衡x =∑405DC AC F F -⋅=Y=∑305BC ACF F+⋅=联立上二式得： 1.67ACF KN=（拉力）1.0BCF KN=-（压力）2-13解：（1）取DEH部分，对H点列平衡x=∑05RD REF F'=Y=∑05RDF Q-=联立方程后解得：5RDF Q=2REF Q'=（2）取ABCE 部分，对C 点列平衡x =∑cos 450RE RA F F -=o0Y =∑sin 450RB RA F F P --=o且RE REF F '=联立上面各式得： 22RA F Q =2RB F Q P=+（3）取BCE 部分。

工程力学材料力学第四版习题答案解析

工程力学材料力学（北京科技大学与东北大学）第一章轴向拉伸和压缩1-1：用截面法求下列各杆指定截面的内力解：(a):N1=0,N2=N3=P(b):N1=N2=2kN(c):N1=P,N2=2P,N3= -P(d):N1=-2P,N2=P(e):N1= -50N,N2= -90N(f):N1=0.896P,N2=-0.732P注（轴向拉伸为正，压缩为负）1-2：高炉装料器中的大钟拉杆如图a所示，拉杆下端以连接楔与大钟连接，连接处拉杆的横截面如图b所示；拉杆上端螺纹的内径d=175mm。

以知作用于拉杆上的静拉力P=850kN，试计算大钟拉杆的最大静应力。

解：σ1=2118504P kNS dπ==35.3Mpaσ2=2228504P kNS dπ==30.4MPa∴σmax=35.3Mpa1-3：试计算图a所示钢水包吊杆的最大应力。

以知钢水包及其所盛钢水共重90kN，吊杆的尺寸如图b所示。

解：下端螺孔截面：σ1=19020.065*0.045P S=15.4Mpa上端单螺孔截面：σ2=2P S =8.72MPa 上端双螺孔截面：σ3= 3P S =9.15Mpa∴σmax =15.4Mpa1-4：一桅杆起重机如图所示，起重杆AB为一钢管，其外径D=20mm,内径d=18mm;钢绳CB 的横截面面积为0.1cm2。

已知起重量P=2000N，试计算起重机杆和钢丝绳的应力。

解：受力分析得：F1*sin15=F2*sin45F1*cos15=P+F2*sin45∴σAB=11FS=-47.7MPaσBC=22FS=103.5 MPa1-5：图a所示为一斗式提升机.斗与斗之间用链条连接,链条的计算简图如图b 所示,每个料斗连同物料的总重量P=2000N.钢链又两层钢板构成,如c所示.每个链板厚t=4.5mm,宽h=40mm,H=65mm,钉孔直径d=30mm.试求链板的最大应力.解:F=6PS 1=h*t=40*4.5=180mm 2S2=(H-d)*t=(65-30)*4.5=157.5mm 2∴σmax=2F S =38.1MPa1-6:一长为30cm 的钢杆,其受力情况如图所示.已知杆截面面积A=10cm2,材料的弹性模量E=200Gpa,试求;(1) AC. CD DB 各段的应力和变形.(2) AB 杆的总变形.解: (1)σAC =-20MPa,σCD =0,σDB =-20MPa;△ l AC =NL EA =AC LEA σ=-0.01mm△l CD =CD LEA σ=0△L DB =DB LEA σ=-0.01mm(2) ∴ABl∆=-0.02mm1-7:一圆截面阶梯杆受力如图所示,已知材料的弹性模量E=200Gpa,试求各段的应力和应变.解:31.8127ACACCBCBPMPaSPMPaSσσ====ACACACLNLEA EAσε===1.59*104,CBCBCBLNLEA EAσε===6.36*1041-8:为测定轧钢机的轧制力,在压下螺旋与上轧辊轴承之间装置一测压用的压头.压头是一个钢制的圆筒,其外径D=50mm,内径d=40mm,在压头的外表面上沿纵向贴有测变形的电阻丝片.若测得轧辊两端两个压头的纵向应变均为ε=0.9*10-2,试求轧机的总轧制压力.压头材料的弹性模量E=200Gpa.解:QNllEAllε∆=∆=∴NEAε=62.54*10N EA Nε∴==1-9：用一板状试样进行拉伸试验，在试样表面贴上纵向和横向的电阻丝来测定试样的改变。

工程力学第四版课后习题答案

工程力学第四版课后习题答案工程力学第四版课后习题答案工程力学是一门研究物体静力学和动力学的学科，是工程学的基础课程之一。

通过学习工程力学，可以帮助我们理解和解决各种工程问题。

而课后习题则是巩固和应用所学知识的重要方式。

本文将为读者提供工程力学第四版课后习题的答案，希望能够帮助大家更好地掌握这门学科。

第一章：力的基本概念1. 一个物体的质量是5kg，重力加速度为9.8m/s²，求其重力。

答案：重力 = 质量× 重力加速度= 5kg × 9.8m/s² = 49N2. 一个力的大小为20N，方向与x轴夹角为30°，求其在x轴上的分力。

答案：在x轴上的分力 = 力的大小× cos(夹角) = 20N × cos(30°) ≈ 17.32N第二章：力的作用效果1. 一个物体受到两个力的作用，一个力的大小为10N，方向与x轴正向夹角为30°；另一个力的大小为15N，方向与x轴正向夹角为60°。

求物体所受合力的大小和方向。

答案：合力的x分力= 10N × cos(30°) + 15N × cos(60°) ≈ 17.32N合力的y分力= 10N × sin(30°) + 15N × sin(60°) ≈ 23.09N合力的大小= √(合力的x分力² + 合力的y分力²) ≈ 28.35N合力的方向 = arctan(合力的y分力 / 合力的x分力) ≈ 53.13°第三章：力的分解与合成1. 一个力的大小为30N，方向与x轴夹角为45°，求其在x轴和y轴上的分力。

答案：在x轴上的分力 = 力的大小× cos(夹角) = 30N × cos(45°) ≈ 21.21N在y轴上的分力 = 力的大小× sin(夹角) = 30N × sin(45°) ≈ 21.21N2. 一个物体受到两个力的作用，一个力的大小为20N，方向与x轴正向夹角为60°；另一个力的大小为15N，方向与x轴正向夹角为45°。