导数与函数的极值、最值
导数与函数的极值和最值
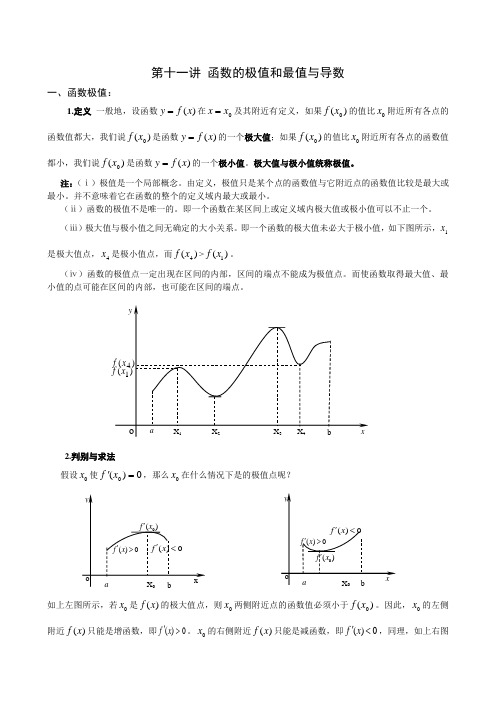
第十一讲函数的极值和最值与导数一、函数极值:1.定义一般地,设函数)(xfy=在xx=及其附近有定义,如果)(xf的值比x附近所有各点的函数值都大,我们说)(xf是函数)(xfy=的一个极大值;如果)(xf的值比x附近所有各点的函数值都小,我们说)(xf是函数)(xfy=的一个极小值。
极大值与极小值统称极值。
注:(ⅰ)极值是一个局部概念。
由定义,极值只是某个点的函数值与它附近点的函数值比较是最大或最小。
并不意味着它在函数的整个的定义域内最大或最小。
(ⅱ)函数的极值不是唯一的。
即一个函数在某区间上或定义域内极大值或极小值可以不止一个。
(ⅲ)极大值与极小值之间无确定的大小关系。
即一个函数的极大值未必大于极小值,如下图所示,1x是极大值点,4x是极小值点,而)(4xf>)(1xf。
(ⅳ)函数的极值点一定出现在区间的内部,区间的端点不能成为极值点。
而使函数取得最大值、最小值的点可能在区间的内部,也可能在区间的端点。
2.判别与求法假设x使0)(='xf,那么x在什么情况下是的极值点呢?如上左图所示,若x是)(xf的极大值点,则x两侧附近点的函数值必须小于)(xf。
因此,x的左侧附近)(xf只能是增函数,即0)(>'xf。
x的右侧附近)(xf只能是减函数,即0)(<'xf,同理,如上右图所示,若0x 是极小值点,则在0x 的左侧附近)(x f 只能是减函数,即0)(<'x f ,在0x 的右侧附近)(x f 只能是增函数,即0)(>'x f ,从而我们得出结论:若0x 满足0)(0='x f ,且在0x 的两侧)(x f 的导数异号,则0x 是)(x f 的极值点,)(0x f 是极值,并且如果)(x f '在0x 两侧满足“左正右负”,则0x 是)(x f 的极大值点,)(0x f 是极大值;如果)(x f '在0x 两侧满足“左负右正”,则0x 是)(x f 的极小值点,)(0x f 是极小值。
《导数与函数的极值、最值》 知识清单

《导数与函数的极值、最值》知识清单一、导数的概念导数是微积分中的重要概念,它描述了函数在某一点处的变化率。
对于函数 y = f(x),其在点 x = x₀处的导数定义为:f'(x₀) = limₕ→₀ f(x₀+ h) f(x₀) / h导数的几何意义是函数曲线在该点处的切线斜率。
如果导数存在,则函数在该点处可导。
二、函数的极值1、极值的定义函数在某区间内的极大值和极小值统称为极值。
极大值是指在该区间内比其附近的函数值都大的函数值;极小值则是指在该区间内比其附近的函数值都小的函数值。
2、极值点的判别方法(1)导数为零的点:若函数 f(x) 在点 x₀处可导,且 f'(x₀) = 0,则 x₀可能是极值点。
(2)导数不存在的点:函数在某些点处导数不存在,但也可能是极值点。
3、第一导数判别法设函数 f(x) 在点 x₀的某个邻域内可导,且 f'(x₀) = 0。
(1)如果当 x < x₀时,f'(x) > 0;当 x > x₀时,f'(x) < 0,则 f(x) 在 x₀处取得极大值。
(2)如果当 x < x₀时,f'(x) < 0;当 x > x₀时,f'(x) > 0,则 f(x) 在 x₀处取得极小值。
4、第二导数判别法设函数 f(x) 在点 x₀处具有二阶导数,且 f'(x₀) = 0,f''(x₀) ≠ 0。
(1)若 f''(x₀) < 0,则函数 f(x) 在 x₀处取得极大值。
(2)若 f''(x₀) > 0,则函数 f(x) 在 x₀处取得极小值。
三、函数的最值1、最值的定义函数在某个区间内的最大值和最小值分别称为函数在该区间内的最值。
2、求最值的步骤(1)求函数在给定区间内的导数。
(2)找出导数为零的点和导数不存在的点。
(3)计算这些点以及区间端点处的函数值。
(4)比较这些函数值,最大的即为最大值,最小的即为最小值。
导数与函数的极值、最值-高考数学复习

1
解:当 a = 时, f ( x )=ln
2
1
x - x ,函数的定义域为
2
1
1
2−
(0,+∞),且f'( x )= - =
,
2Hale Waihona Puke 2令f'( x )=0,得 x =2,
目录
高中总复习·数学
于是当 x 变化时,f'( x ), f ( x )的变化情况如下表:
x
(0,2)
2
(2,+∞)
f'( x )
则函数在(0,+∞)上是增函数,此时函数在定义域上无
极值点;
当 a >0时,若 x ∈
若x∈
1
,+∞
1
0,
,则f'( x )>0,
,则f'( x )<0,
目录
高中总复习·数学
1
故函数在 x = 处有极大值.
综上可知,当 a ≤0时,函数 f ( x )无极值点;
当 a >0时,函数 y = f ( x )有一个极大值点,且为
2. 函数的最值与导数
(1)如果在区间[ a , b ]上函数 y = f ( x )的图象是一条
连续不
断 的曲线,那么它必有最大值和最小值;
(2)若函数 f ( x )在[ a , b ]上单调递增,则 f ( a )为函数
的
最小值 , f ( b )为函数的
最大值 ;若函数 f ( x )
在[ a , b ]上单调递减,则 f ( a )为函数的
导数与函数的极值、最值
1. 借助函数的图象,了解函数在某点取得极值的必要条件和充分条件.
导数与函数的极值、最值。

栏目索引
判断下面结论是否正确(请在括号中打“√”或“×”) (1)函数的极大值不一定比极小值大. (√) (2)对可导函数f(x), f '(x0)=0是x0点为极值点的充要条件. (×) (3)函数的极大值一定是函数的最大值. (×) (4)开区间上的单调连续函数无最值. (√)
栏目索引
又f (2) 40 a, f (0) a, f (2) 8 a
由已知得 40 a 37解得a 3
(2)由(1)知f (x)在2, 2的最大值为3.
反思:本题属于逆向探究题型: 其基本方法最终落脚到比较极值与端点函数值大
小上,从而解决问题,往往伴随恒成立和分类讨论。
栏目索引
2.函数的最值与导数 一般地,求函数y=f(x)在[a,b]上的最大值与最小值的步骤如下: (1)求函数y=f(x)在(a,b)内的⑨ 极值 ; (2)将函数y=f(x)的各极值与⑩ 端点处 的函数值f(a)、 f(b)比较,其中 最大的一个是最大值,最小的一个是最小值. 注:如果在区间[a,b]上,函数y=f(x)的图象是一条连续不断的曲线,那么它 必有最大值和最小值.
栏目索引
导数与函数的极值、最值
栏目索引
1.函数的极值与导数 (1)函数的极小值 若函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值 ① 都小 , f '(a)=0,而且在点x=a附近的左侧② f '(x)<0 ,右侧 ③ f ' (x)>0 ,则点a叫做函数y=f(x)的极小值点, f(a)叫做函数y=f(x)的 极小值. (2)函数的极大值 若函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值 ④ 都大 , f '(b)=0,而且在点x=b附近的左侧⑤ f '(x)>0 ,右侧 ⑥ f ' (x)<0 ,则点b叫做函数y=f(x)的极大值点, f(b)叫做函数y=f(x)的极大值. 注:⑦ 极大值 和⑧ 极小值 统称为极值.
导数与函数的极值、最值

导数与函数的极值、最值一、基础知识1.函数的极值(1)函数的极小值:函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0,则点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.(2)函数的极大值:函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0,则点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.极小值点、极大值点统称为极值点,极大值和极小值统称为极值.①函数f(x)在x0处有极值的必要不充分条件是f′(x0)=0,极值点是f′(x)=0的根,但f′(x)=0的根不都是极值点(例如f(x)=x3,f′(0)=0,但x=0不是极值点).②极值反映了函数在某一点附近的大小情况,刻画的是函数的局部性质.极值点是函数在区间内部的点,不会是端点.2.函数的最值(1)在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值.(2)若函数f(x)在[a,b]上单调递增,则f(a)为函数的最小值,f(b)为函数的最大值;若函数f(x)在[a,b]上单调递减,则f(a)为函数的最大值,f(b)为函数的最小值.二、常用结论(1)若函数f(x)的图象连续不断,则f(x)在[a,b]上一定有最值.(2)若函数f(x)在[a,b]上是单调函数,则f(x)一定在区间端点处取得最值.(3)若函数f(x)在区间(a,b)内只有一个极值点,则相应的极值点一定是函数的最值点.考点一利用导数解决函数的极值问题考法(一)利用导数求函数的极值或极值点[典例](优质试题·天津高考改编)设函数f(x)=(x-t1)·(x-t2)(x-t3),其中t1,t2,t3∈R,且t1,t2,t3是公差为d的等差数列.(1)若t2=0,d=1,求曲线y=f(x)在点(0,f(0))处的切线方程;(2)若d=3,求f(x)的极小值点及极大值.[解](1)由已知,可得f(x)=x(x-1)(x+1)=x3-x,故f′(x)=3x2-1.因此f(0)=0,f′(0)=-1.因此曲线y=f(x)在点(0,f(0))处的切线方程为y-f(0)=f′(0)(x-0),故所求切线方程为x+y=0.(2)由已知可得f(x)=(x-t2+3)(x-t2)(x-t2-3)=(x-t2)3-9(x-t2)=x3-3t2x2+(3t22-9)x-t32+9t2.故f′(x)=3x2-6t2x+3t22-9.令f′(x)=0,解得x=t2-3或x=t2+ 3.当x变化时,f′(x),f(x)的变化情况如下表:所以函数f (x )的极小值点为x =t 2+3,极大值为f (t 2-3)=(-3)3-9×(-3)=6 3.[解题技法] 求函数的极值或极值点的步骤 (1)求导数f ′(x ),不要忘记函数f (x )的定义域; (2)求方程f ′(x )=0的根;(3)检查在方程的根的左右两侧f ′(x )的符号,确定极值点或函数的极值. 考法(二) 已知函数极值点或极值求参数的值或范围[典例] (优质试题·北京高考节选)设函数f (x )=[ax 2-(3a +1)x +3a +2]e x ,若f (x )在x =1处取得极小值,求a 的取值范围.[解] 由f (x )=[ax 2-(3a +1)x +3a +2]e x , 得f ′(x )=[ax 2-(a +1)x +1]e x =(ax -1)(x -1)e x . 若a >1,则当x ∈⎝ ⎛⎭⎪⎫1a ,1时,f ′(x )<0;当x ∈(1,+∞)时,f ′(x )>0. 所以f (x )在x =1处取得极小值.若a ≤1,则当x ∈(0,1)时,ax -1≤x -1<0, 所以f ′(x )>0.所以1不是f (x )的极小值点.综上可知,a 的取值范围是(1,+∞). [解题技法]已知函数极值点或极值求参数的2个要领[专题训练]1.设函数f (x )=2x +ln x ,则( )A .x =12为f (x )的极大值点B .x =12为f (x )的极小值点 C .x =2为f (x )的极大值点D .x =2为f (x )的极小值点解析:选D ∵f (x )=2x +ln x (x >0), ∴f ′(x )=-2x 2+1x ,令f ′(x )=0,则x =2. 当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0. 所以x =2为f (x )的极小值点.2.(优质试题·广州高中综合测试)已知函数f (x )=x 3+ax 2+bx +a 2在x =1处的极值为10,则数对(a ,b )为( )A .(-3,3)B .(-11,4)C .(4,-11)D .(-3,3)或(4,-11)解析:选C f ′(x )=3x 2+2ax +b ,依题意可得⎩⎪⎨⎪⎧f ′(1)=0,f (1)=10,即⎩⎪⎨⎪⎧3+2a +b =0,1+a +b +a 2=10,消去b 可得a 2-a -12=0,解得a =-3或a =4,故⎩⎪⎨⎪⎧ a =-3,b =3或⎩⎪⎨⎪⎧ a =4,b =-11.当⎩⎪⎨⎪⎧a =-3,b =3时,f ′(x )=3x 2-6x +3=3(x -1)2≥0,这时f (x )无极值,不合题意,舍去,故选C.3.设函数f (x )=ax 3-2x 2+x +c (a >0).(1)当a =1,且函数f (x )的图象过点(0,1)时,求函数f (x )的极小值; (2)若f (x )在(-∞,+∞)上无极值点,求a 的取值范围. 解:f ′(x )=3ax 2-4x +1.(1)函数f (x )的图象过点(0,1)时,有f (0)=c =1.当a =1时,f (x )=x 3-2x 2+x +1,f ′(x )=3x 2-4x +1, 由f ′(x )>0,解得x <13或x >1; 由f ′(x )<0,解得13<x <1.所以函数f (x )在⎝ ⎛⎭⎪⎫-∞,13和(1,+∞)上单调递增,在⎝ ⎛⎭⎪⎫13,1上单调递减,所以函数f (x )的极小值是f (1)=13-2×12+1+1=1. (2)若f (x )在(-∞,+∞)上无极值点, 则f (x )在(-∞,+∞)上是单调函数,即f ′(x )=3ax 2-4x +1≥0或f ′(x )=3ax 2-4x +1≤0恒成立. 因为a >0,所以f ′(x )=3ax 2-4x +1≥0在(-∞,+∞)上恒成立, 则有Δ=(-4)2-4×3a ×1≤0,即16-12a ≤0,解得a ≥43. 故a 的取值范围为⎣⎢⎡⎭⎪⎫43,+∞.考点二 利用导数解决函数的最值问题[典例] (优质试题·北京高考)已知函数f (x )=e x cos x -x . (1)求曲线y =f (x )在点(0,f (0))处的切线方程; (2)求函数f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上的最大值和最小值. [解] (1)因为f (x )=e x cos x -x ,所以f ′(x )=e x (cos x -sin x )-1,f ′(0)=0. 又因为f (0)=1,所以曲线y =f (x )在点(0,f (0))处的切线方程为y =1. (2)设h (x )=e x (cos x -sin x )-1,则h ′(x )=e x (cos x -sin x -sin x -cos x )=-2e x sin x .当x ∈⎝ ⎛⎭⎪⎫0,π2时,h ′(x )<0,所以h (x )在区间⎣⎢⎡⎦⎥⎤0,π2上单调递减.所以对任意x ∈⎝ ⎛⎦⎥⎤0,π2,有h (x )<h (0)=0,即f ′(x )<0.所以函数f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上单调递减.因此f (x )在区间⎣⎢⎡⎦⎥⎤0,π2上的最大值为f (0)=1,最小值为f ⎝ ⎛⎭⎪⎫π2=-π2.[解题技法]导数法求给定区间上函数的最值问题的一般步骤(1)求函数f (x )的导数f ′(x );(2)求f (x )在给定区间上的单调性和极值; (3)求f (x )在给定区间上的端点值;(4)将f (x )的各极值与f (x )的端点值进行比较,确定f (x )的最大值与最小值; (5)反思回顾,查看关键点,易错点和解题规范. [专题训练]1.(优质试题·珠海摸底)如图,将一张16 cm ×10 cm 的长方形纸片剪下四个全等的小正方形,使得剩余部分经过折叠能糊成一个无盖的长方体纸盒,则这个纸盒的最大容积是________ cm 3.解析:设剪下的四个小正方形的边长为x cm ,则经过折叠以后,糊成的长方体纸盒是一个底面是长为(16-2x ) cm ,宽为(10-2x ) cm 的长方形,其面积为(16-2x )(10-2x )cm 2,长方体纸盒的高为x cm ,则体积V =(16-2x )(10-2x )×x =4x 3-52x 2+160x (0<x <5)cm 3,所以V ′=12(x -2)·⎝ ⎛⎭⎪⎫x -203,由V ′>0,得0<x <2,则函数V =4x 3-52x 2+160x (0<x <5)在(0,2)上单调递增;由V ′<0,得2<x <5,则函数V =4x 3-52x 2+160x (0<x <5)在(2,5)上单调递减,所以当x =2时,V max =144(cm 3).答案:1442.已知函数f (x )=ln x -ax .(1)若a >0,试判断f (x )在定义域内的单调性; (2)若f (x )在[1,e]上的最小值为32,求实数a 的值.解:(1)由题意得f (x )的定义域是(0,+∞),且f ′(x )=x +ax 2, 因为a >0,所以f ′(x )>0, 故f (x )在(0,+∞)上单调递增. (2)由(1)可得f ′(x )=x +ax 2, 因为x ∈[1,e],①若a ≥-1,则x +a ≥0,即f ′(x )≥0在[1,e]上恒成立, 此时f (x )在[1,e]上单调递增, 所以f (x )min =f (1)=-a =32, 所以a =-32(舍去).②若a ≤-e ,则x +a ≤0,即f ′(x )≤0在[1,e]上恒成立, 此时f (x )在[1,e]上单调递减, 所以f (x )min =f (e)=1-a e =32, 所以a =-e2(舍去).③若-e<a <-1,令f ′(x )=0,得x =-a ,当1<x<-a时,f′(x)<0,所以f(x)在(1,-a)上单调递减;当-a<x<e时,f′(x)>0,所以f(x)在(-a,e)上单调递增,所以f(x)min=f(-a)=ln(-a)+1=32,所以a=- e.综上,a=- e.[课时跟踪检测]A级1.(优质试题·辽宁鞍山一中模拟)已知函数f(x)=x3-3x-1,在区间[-3,2]上的最大值为M,最小值为N,则M-N=()A.20B.18C.3 D.0解析:选A∵f′(x)=3x2-3=3(x-1)(x+1),∴f(x)在(-∞,-1)和(1,+∞)上单调递增,在(-1,1)上单调递减,又∵f(-3)=-19,f(-1)=1,f(1)=-3,f(2)=1,∴M=1,N=-19,M-N=1-(-19)=20.2.(优质试题·梅州期末)函数y=f(x)的导函数的图象如图所示,则下列说法错误的是()A.(-1,3)为函数y=f(x)的单调递增区间B.(3,5)为函数y=f(x)的单调递减区间C.函数y=f(x)在x=0处取得极大值D.函数y=f(x)在x=5处取得极小值解析:选C由函数y=f(x)的导函数的图象可知,当x<-1或3<x<5时,f′(x)<0,y=f(x)单调递减;当x>5或-1<x<3时,f′(x)>0,y=f(x)单调递增.所以函数y=f(x)的单调递减区间为(-∞,-1),(3,5),单调递增区间为(-1,3),(5,+∞).函数y=f(x)在x=-1,5处取得极小值,在x=3处取得极大值,故选项C 错误.3.(优质试题·湖北襄阳四校联考)函数f(x)=12x2+x ln x-3x的极值点一定在区间()A.(0,1)内B.(1,2)内C.(2,3)内D.(3,4)内解析:选B函数的极值点即导函数的零点,f′(x)=x+ln x+1-3=x+ln x -2,则f′(1)=-1<0,f′(2)=ln 2>0,由零点存在性定理得f′(x)的零点在(1,2)内,故选B.4.已知函数f(x)=x3+3x2-9x+1,若f(x)在区间[k,2]上的最大值为28,则实数k的取值范围为()A.[-3,+∞) B.(-3,+∞)C.(-∞,-3) D.(-∞,-3]解析:选D由题意知f′(x)=3x2+6x-9,令f′(x)=0,解得x=1或x=-3,所以f′(x),f(x)随x的变化情况如下表:又f(-3)=28,f(1)=-4,f(2)=3,f(x)在区间[k,2]上的最大值为28,所以k≤-3.5.(优质试题·皖南八校联考)已知函数f (x )=-13x 3+bx 2+cx +bc 在x =1处有极值-43,则b =( )A .-1B .1C .1或-1D .-1或3解析:选A f ′(x )=-x 2+2bx +c ,因为f (x )在x =1处有极值-43,所以⎩⎪⎨⎪⎧f ′(1)=-1+2b +c =0,f (1)=-13+b +c +bc =-43,Δ=4b 2+4c >0,解得⎩⎪⎨⎪⎧b =-1,c =3,故选A.6.设直线x =t 与函数h (x )=x 2,g (x )=ln x 的图象分别交于点M ,N ,则当|MN |最小时t 的值为( )A .1 B.12 C.52D.22解析:选D 由已知条件可得|MN |=t 2-ln t , 设f (t )=t 2-ln t (t >0),则f ′(t )=2t -1t , 令f ′(t )=0,得t =22,当0<t <22时,f ′(t )<0;当t >22时,f ′(t )>0.∴当t =22时,f (t )取得最小值,即|MN |取得最小值时t =22.7.(优质试题·江西阶段性检测)已知函数y =ax -1x 2在x =-1处取得极值,则a =________.解析:因为y ′=a +2x 3,所以当x =-1时,a -2=0,所以a =2,经验证,。
导数与函数极值最值

导数与函数的极值与最值1. 函数的极值⑴.判断 f (x 0)是极值的方法一般地,当函数 y =f (x )在点 x 0 处连续时,①.如果在 x 0 附近的左侧 f ′(x )>0,右侧 f ′(x )<0,那么 f (x 0)是极大值; ②.如果在 x 0 附近的左侧 f ′(x )<0,右侧 f ′(x )>0,那么 f (x 0)是极小值. ⑵.求可导函数极值的步骤:①.求 f ′(x );②.求方程 f ′(x )=0 的根;③.检查 f ′(x )在方程 f ′(x )=0 的根左右值的符号.如果左正右负,那么 y =f (x )在这个根处取得极大值;如果左负右正,那么 y =f (x )在这个根处取得极小值,如果左右两侧符号一样,那么这个根不是极值点.2. 函数的最值⑴.在闭区间[a ,b ]上连续的函数 y =f (x )在[a ,b ]上必有最大值与最小值.⑵.若函数 f (x )在[a ,b ]上单调递增,则 f (a )为函数的最小值,f (b )为函数的最大值;若函数 f (x )在[a ,b ]上单调递减,则 f (a )为函数的最大值,f (b )为函数的最小值.⑶.设函数 f (x )在[a ,b ]上连续,在(a ,b )内可导,求 f (x )在[a ,b ]上的最大值和最小值的步骤如下: ①.求 f (x )在(a ,b )内的极值;②.将 f (x )的各极值与 f (a ),f (b )比较,其中最大的一个是最大值,最小的一个是最小值. 3. 利用极值求参数1. 极值点使得导函数为0,即极值点为导函数的零点.2. 极值点的个数就是导函数变号零点的个数3. 方法:①直接法:直接求方程,得到方程的根,在通过解不等式确定参数取值范围; ②分离参数法:将参数分离,构造新函数转化成求最值或者值域的问题; ③数形结合:先对解析式变形,在坐标系中画出函数图像,通过找交点求解.题型一 求极值【例1】(1)(2019·湖北高二期末)函数()f x 的导函数()f x '的图象如图所示,则( )A .12为()f x 的极大值点 B .2-为()f x 的极大值点 C .2为()f x 的极大值点D .45为()f x 的极小值点 (2)(2019·黑龙江铁人中学高二期中(文))函数()()2312f x x =-+的极值点是( ) A .0x =B .1x =C .1x =-或1D .1x =或0【解析】(1)对于A 选项,当122x -<<时,()0f x '>,当122x <<时,()0f x '<,12为()f x 的极大值点,A 选项正确;对于B 选项,当2x <-时,()0f x '<,当122x -<<时,()0f x '>,2-为()f x 的极小值点,B 错误; 对于C 选项,当122x <<时,()0f x '<,当2x >时,()0f x '>,2为()f x 的极小值点,C 选项错误; 对于D 选项,由于函数()y f x =为可导函数,且405f ⎛⎫'<⎪⎝⎭,45不是()f x 的极值点,D 选项错误.故:A. (2)函数的导数为2233()2(1)(3)6(1)f x x x x x '=-⨯=-, 当()0f x '=得0x =或1x =,当1x >时,()0f x '>,当01x <<时,()0f x '<, 所以1x =是极小值点.当0x <时,()0f x '<,当01x <<时,()0f x '<, 所以0x =不是极值点.故选B .【举一反三】1.(2018·安徽高二期末(理))函数()321313f x x x x =+--的极小值点是( ) A .1B .(1,﹣83)C .3-D .(﹣3,8)【解析】()223f x x x =+-',由2230x x +-=得31x =-或 函数()321313f x x x x =+--在(),3-∞-上为增函数,()3,1-上为减函数, ()1+∞,上为增函数,故()f x 在1x =处有极小值,极小值点为1.选A 2.(2019·安徽高二月考(文))已知函数()2ln f x ax b x =+在点M (1,1)处的切线方程为230x y +-=.(1)求函数()y f x =的解析式;(2)求函数()y f x =的单调区间和极值.【答案】(1)f (x )=x 2-4lnx (2)函数()f x 的单调递增区间是(,单调递减区间是)+∞.极小值为22ln 2-,无极大值 【解析】(1)()2bf x ax x'=+, 因为点M (1,1)处的切线方程为2x +y -3=0,所以()()11122f a f a b ⎧==⎪⎨=+=-'⎪⎩,所以14a b =⎧⎨=-⎩,则f (x )=x 2-4lnx ;(2)定义域为(0,+∞),()24242x f x x x x-'=-=,令()0f x '=,得x =. 列表如下:故函数()f x 的单调递增区间是(,单调递减区间是)+∞.极小值为222ln 2f=-=-,无极大值.题型二 求最值【例2】(2019·黑龙江铁人中学高二期中 )函数32()32f x x x =-+在区间[-1,1]上的最大值是( ) A .4 B .2 C .0 D .-2【答案】B【解析】令()2360f x x x '=-=,解得0x =2x =.()()()()02,22,12,10f f f f ==--=-=,故函数的最大值为2,所以本小题选B.【举一反三】1.(2019·湖南高一月考)已知函数2()4,[0,3],f x x x a x =-++∈若()f x 有最小值2-,则()f x 的最大值为____【解析】二次函数()y f x = 在[]0,2x ∈ 单调递增,当(]2,3x ∈ 单调递减故在x=0时取得最小值,即a=2题型三 利用极值最值求参数【例3】(1)(2019·河北唐山一中高三期中(理))若2x =-是函数21()(1)ex f x x ax -=+-的极值点,则()f x 的极小值为( ).A .1-B .32e --C .35e -D .1(2)(2019·贵州省铜仁第一中学高三(文))若函数()333f x x bx b =-+在()0,1内有极小值,则b 的取值范围为( ) A .01b <<B .1b <C .0b >D .12b <(3)(2019·安徽高二月考(文))若函数f (x )=13x 3+x 2-23在区间(a ,a +5)上存在最小值,则实数a 的取值范围是 A .[-5,0)B .(-5,0)C .[-3,0)D .(-3,0)【答案】(1)A(2)A(3)C 【举一反三】1.已知是函数的极小值点,则的范围是_____2.已知是函数的极小值点,则取值范围________3.已知函数有两个极值点,且,则( )4.(2019·新疆高三月考)已知函数()(ln )f x x x ax =-有两个极值点,则实数a 的取值范围是____.5.若函数在区间内有极值,则取值范围( C )0x =()()()22222f x x a x a x a=-++a ()(),02,-∞⋃+∞1x =()()()2202xk f x x e x kx k =--+>k ()0,e ()221ln f x x x a x =-++12,x x 12x x <D ()212ln 2.4A f x +<-()212ln 2.4B f x -<()212ln 2.4C f x +>-()212ln 2.4D f x ->()()()2122ln 02ax f x a x x a =-++>1,02⎛⎫ ⎪⎝⎭a6. 若函数在上有小于零的极值点,实数的取值范围是( )7. 若函数在区间恰有一个极值点,则实数取值范围______.8. 已知函数在区间上至少有一个极值点,实数取值范围______ 课后训练:1.(2019·江西高三期中(文))若函数()32236f x x mx x =-+在区间()1,+∞上存在极值点,则实数m 的取值范围是( ) A .[)2,+∞ B .(),1-∞ C .(],2-∞ D .()2,+∞【答案】D 【解析】依题意()'2666f x x mx =-+,由于函数()32236f x x mx x =-+在区间()1,+∞上存在极值点,所以()'2666fx x mx =-+在区间()1,+∞上有正有负,由于二次函数()'2666f x x mx =-+开口向上,对称轴为2m x =,2364660m ∆=-⨯⨯>,解得2m <-或2m >.当2m <-时,对称轴12mx =<-,()'060f =>故此时在区间()1,+∞上()'0f x >,函数()f x 单调递增,没有极值点.当2m >时,由于()'16661260f m m =-+=-<,且二次函数()'2666f x x mx =-+开口向上,故()'2666f x x mx =-+区间()1,+∞上必存在零点,也即()f x 在区间()1,+∞上存在极值点. 故选:D.2.(2019·陕西高三(文))函数3()1f x ax x =++有极值的充要条件是 ( ) A .0a > B .0a ≥ C .0a < D .0a ≤【答案】C【解析】因为2()31f x ax '=+,所以221()31030f x ax a x =+=⇒=-<',即0a <,应选答案C 。
导数与函数的极值、最值
知识要点
双基巩固
典型例题
易错辨析
提升训练
【解】 (1)因 f(x)=x3-6x2+3x+1, 所以 f′(x)=3x2-12x+3, ∴f′(x)=3(x-2+ 3)(x-2- 3). 当 f′(x)>0 时,x>2- 3,或 x<2+ 3; 当 f′(x)<0 时,2- 3<x<2+ 3. ∴f(x)的单调增区间是(-∞,2- 3),(2+ 3,+∞),单调减 区间是(2- 3,2+ 3).
解析:f′(x)=x2-4=(x-2)(x+2),令f′(x)=0得,x1=-2,x2=2. 当x<-2时,f′(x)>0,-2<x<2时,f′(x)<0,f(x)在x=-2处取 得极大值.
答案:-2
知识要点
双基巩固
典型例题
易错辨析
提升训练
x2+a 5.若函数 f(x)= 在 x=1 处取极值,则 a=________. x+1 解析:∵f(x)在 x=1 处取极值,∴f′(1)=0.
知识要点
双基巩固
典型例题
易错辨析
提升训练
2.函数f(x)的定义域为(a,b),导函数f′(x)在(a,b)内的图象如图 所示,则函数f(x)在开区间(a,b)内极小值点的个数为( )
A.1
B.2
C.3
D.4
解析:极值点在f′(x)的图象上应是f′(x) 的图象与x轴的交点的横坐标,且极小 值点的左侧图象在x轴下方,右侧图象
知识要点
双基巩固
典型例题
易错辨析
提升训练
∵g(x)在 x=0 和 x=2 点处连续, 又∵g(0)=1,g(1)=2-ln 4,g(2)=3-ln 9, 且 2-ln 4<3-ln 9<1, ∴g(x)的最大值是 1, g(x)的最小值是 2-ln 4. 所以在区间[0,2]上原方程恰有两个相异的实根时实数 a 的 取值范围是: 2-ln 4<a≤3-ln 9.
导数与函数的极值和最值

导数与函数的极值和最值一 函数极值的定义极大值:已知函数()y f x =,设0x 是定义域内任意一点,如果对0x 附近的所有点x ,都有0()()f x f x <,()0f x '=,而且在0x x =附近的左侧()0f x '>,右侧()0f x '<,则称函数()f x 在点0x 处取得极大值,并把0x 称为函数()f x 的一个极大值点.极小值:已知函数()y f x =,设0x 是定义域内任意一点,如果对0x 附近的所有点x ,都有0()()f x f x >,()0f x '=,而且在0x x =附近的左侧()0f x '<,右侧()0f x '>,则称函数()f x 在点0x 处取得极小值,并把0x 称为函数()f x 的一个极小值点.注:可导函数的极值点必须是导数为0的点,但导数为0的点不一定是函数的极值点.二、求函数极值的步骤:(1)确定函数的定义域,求出导函数()f x '.(2)求方程()0f x '=的根.(3)根据极值的定义确定极大值和极小值.例 1求函数31()443f x x x =-+的极值.例2已知函数'()2(1)ln f x f x x =-,则()f x 的极大值为____例3 函数23()(1)2f x x =-+的极值点是____.三、极值与参数范围问题例4. 已知函数3211()32f x x x cx d =-++有极值,则实数c 的取值范围为______.例 5. 若函数21()ln 12f x x x =-+在其定义域内的一个子区间(1,1)a a -+内存在极值,则实数a 的取值范围为_____.例6. 已知函数()(ln )f x x x ax =-有两个极值点,则实数a 的取值范围为______.四、 函数最值(最大值和最小值)如何求函数在[,]a b 上的最值:(1)求函数()y f x =在(,)a b 内的极值和端点值(),()f a f b .(2)将函数()y f x =的各极值与端点处的函数值(),()f a f b 比较,其中最大的一个是最大值,最小值的一个是最小值.例7. 已知函数3()128f x x x =-+在区间[3,3]-上的最大值与最小值分别为,M m ,则M m -=______例8.已知()(ln )f x a x x =-,若函数图像在点(2,(2))f 处切线倾斜角为4π,且32'()[()]2m g x x x f x =++在区间(2,3)上总存在极值,则实数m 的取值范围为_____课后训练题1 .若函数322()f x x ax bx a =--+在1x =处取得极值10,则a =____,b =_____. 2已知函数()(sin cos )x f x e x x =-,若()(sin cos )x f x e x x =-,若02011x π≤≤,则()f x 各极大值和为_____.3.设函数3221()2313f x x ax a x =-+-+,求函数()f x 的极值.3 .已知函数43219()42f x x x x cx =+-+有三个极值点,则实数c 的取值范围为_____.(27,5)-4 .设2()ln(1)f x x a x =++有两个极值点,则实数a 的取值范围为_______1(0,)25.已知()ln f x ax x =+,(1,)x e ∈且()f x 存在极值,则实数a 的取值范围为_____.6.函数()ln f x x x =-在区间(]0,e 上的最大值为____7.已知函数2()(2)x f x x x e =-,[2,)x ∈-+∞,则()f x 的最小值为____.8. 已知()ln f x ax x =-,(]0,x e ∈,当a =____时,()f x 最小值为39. 已知函数3()(3)f x a x ax =--在[]1,1-的最小值为3-,则实数a 的取值范围为_____ 3,122⎡⎤-⎢⎥⎣⎦10. 若函数3212()33f x x x =+-在区间(,5)a a +上存在最小值,则实数a 的取值范围为______11.若函数()ln a f x x x x=++,若()f x 有最值,则实数a 的取值范围为____ ()0,+∞。
一轮复习--导数与函数的极值、最值

其实,世上最温暖的语言,“ 不是我爱你,而是在一起。” 所以懂得才是最美的相遇!只有彼此以诚相待,彼此尊 重,相互包容,相互懂得,才能走的更远。 相遇是缘,相守是爱。缘是多么的妙不可言,而懂得又是多么的难能可贵。否则就会错过一时,错过一世! 择一人深爱,陪一人到老。一路相扶相持,一路心手相牵,一路笑对风雨。在平凡的世界,不求爱的轰轰烈烈;不求誓 言多么美丽;唯愿简单的相处,真心地付出,平淡地相守,才不负最美的人生;不负善良的自己。 人海茫茫,不求人人都能刻骨铭心,但求对人对己问心无愧,无怨无悔足矣。大千世界,与万千人中遇见,只是相识的 开始,只有彼此真心付出,以心交心,以情换情,相知相惜,才能相伴美好的一生,一路同行。 然而,生活不仅是诗和远方,更要面对现实。如果曾经的拥有,不能天长地久,那么就要学会华丽地转身,学会忘记。 忘记该忘记的人,忘记该忘记的事儿,忘记苦乐年华的悲喜交集。 人有悲欢离合,月有阴晴圆ቤተ መጻሕፍቲ ባይዱ。对于离开的人,不必折磨自己脆弱的生命,虚度了美好的朝夕;不必让心灵痛苦不堪, 弄丢了快乐的自己。擦汗眼泪,告诉自己,日子还得继续,谁都不是谁的唯一,相信最美的风景一直在路上。 人生,就是一场修行。你路过我,我忘记你;你有情,他无意。谁都希望在正确的时间遇见对的人,然而事与愿违时, 你越渴望的东西,也许越是无情无义地弃你而去。所以美好的愿望,就会像肥皂泡一样破灭,只能在错误的时间遇到错的人。 岁月匆匆像一阵风,有多少故事留下感动。愿曾经的相遇,无论是锦上添花,还是追悔莫及;无论是青涩年华的懵懂赏 识,还是成长岁月无法躲避的经历……愿曾经的过往,依然如花芬芳四溢,永远无悔岁月赐予的美好相遇。 其实,人生之路的每一段相遇,都是一笔财富,尤其亲情、友情和爱情。在漫长的旅途上,他们都会丰富你的生命,使 你的生命更充实,更真实;丰盈你的内心,使你的内心更慈悲,更善良。所以生活的美好,缘于一颗善良的心,愿我们都能 善待自己和他人。 一路走来,愿相亲相爱的人,相濡以沫,同甘共苦,百年好合。愿有情有意的人,不离不弃,相惜相守,共度人生的每 一个朝夕……直到老得哪也去不了,依然是彼此手心里的宝,感恩一路有你!
导数与函数的极值、最值 解析版

导数与函数的极值、最值【考试提醒】1.借助函数图象,了解函数在某点取得极值的必要和充分条件.2.会用导数求函数的极大值、极小值.3.掌握利用导数研究函数最值的方法.4.会用导数研究生活中的最优化问题.【知识点】1.函数的极值(1)函数的极小值函数y=f(x)在点x=a处的函数值f(a)比它在点x=a附近其他点处的函数值都小,f′(a)=0;而且在点x =a附近的左侧f′(x)<0,右侧f′(x)>0,则a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.(2)函数的极大值函数y=f(x)在点x=b处的函数值f(b)比它在点x=b附近其他点处的函数值都大,f′(b)=0;而且在点x= b附近的左侧f′(x)>0,右侧f′(x)<0,则b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.(3)极小值点、极大值点统称为极值点,极小值和极大值统称为极值.2.函数的最大(小)值(1)函数f(x)在区间[a,b]上有最值的条件:如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.(2)求函数y=f(x)在区间[a,b]上的最大(小)值的步骤:①求函数y=f(x)在区间(a,b)内的极值;②将函数y=f(x)的各极值与端点处的函数值f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.常用结论对于可导函数f(x),“f′(x0)=0”是“函数f(x)在x=x0处有极值”的必要不充分条件【核心题型】题型一 利用导数求解函数的极值问题根据函数的极值(点)求参数的两个要领(1)列式:根据极值点处导数为0和极值这两个条件列方程组,利用待定系数法求解;(2)验证:求解后验证根的合理性.命题点1 根据函数图象判断极值1(2024·四川广安·二模)已知函数f x =ax+1e x,给出下列4个图象:其中,可以作为函数f x 的大致图象的个数为()A.1B.2C.3D.4【答案】D【分析】对a的情况进行分类讨论,借助于导数对函数的单调性进行分析即可判断函数的大致图象.【详解】由题意知,f x 定义域为R,当a=0时,f x =e x,由指数函数的单调性可知函数f x 单调递增,可对应①;当a>0时,f x =ax+a+1e x,令f x =0可得:x=-a+1a<0,所以当x∈-∞,-a+1a时,f x<0,当x∈-a+1a ,+∞时,f x >0,所以,函数f x 先减后增,且当x<-1a时,f x <0,此时可对应②;当a<0时,f x =ax+a+1e x,当f x =0时x=-a+1a,当x∈-∞,-a+1a时,f x >0,当x∈-a+1a ,+∞时,f x <0,所以,函数f x 先增后减,当a<-1时,x=-a+1a<0,且此时0<-1a<1,所以可对应③,当-1<a<0时,x=-a+1a>0,此时-1a>1,所以可对应④.故选:D2(23-24高三上·黑龙江·阶段练习)如图是函数y=f x 的导函数y=f x 的图象,下列结论正确的是()A.y=f x 在x=-1处取得极大值B.x=1是函数y=f x 的极值点C.x=-2是函数y=f x 的极小值点D.函数y=f x 在区间-1,1上单调递减【答案】C【分析】根据导函数的正负即可求解y=f x 的单调性,即可结合选项逐一求解.【详解】由图象可知:当x<-2时,f x <0,f x 单调递减,当x≥-2时,f x ≥0,f x 单调递增,故x=-2是函数y=f x 的极小值点,y=f x 无极大值.故选:C3(2023·河北·模拟预测)函数f(x)=1x4-1x2的大致图象是()A. B.C. D.【答案】D【分析】先判断函数的奇偶性,再利用导数法判断.【详解】解:因为函数f (x )=1x4-1x 2的定义域为:x |x ∈R ,x ≠0 ,且f -x =f x ,所以函数f x 是偶函数,当x >0时,f x =-4x -51-12x 2 ,令fx =0,得x =2,当0<x <2时,f x <0,当x >2时,f x >0,所以当x =2时,f x 取得极小值,故选:D4(2024高三·全国·专题练习)已知函数f (x )的导函数f ′(x )的图象如图所示,则下列结论正确的是()A.曲线y =f (x )在点(1,f (1))处的切线斜率小于零B.函数f (x )在区间(-1,1)上单调递增C.函数f (x )在x =1处取得极大值D.函数f (x )在区间(-3,3)内至多有两个零点【答案】D【详解】解析:由题意,得f ′(1)=0,所以曲线y =f (x )在点(1,f (1))处的切线斜率等于零,故A 错误;当x ∈(-1,1)时,f ′(x )<0,所以f (x )在(-1,1)上单调递减,故B 错误;当-2<x <1时,f ′(x )<0,f (x )单调递减,当x >1,f ′(x )<0,f (x )单调递减,所以x =1不是f (x )的极值点,故C 错误;当x ∈(-3,-2)时,f ′(x )>0,f (x )单调递增,当x ∈(-2,3)时,f ′(x )≤0,f (x )单调递减,所以当f (-2)<0时,f (x )在(-3,3)上没有零点;当f (-2)=0时,f (x )在(-3,3)上只有一个零点;当f (-2)>0时,f (x )在(-3,3)上有两个零点.综上,函数f (x )在区间(-3,3)内至多有两个零点,故选D .命题点2 求已知函数的极值5(2024·宁夏银川·一模)若函数f (x )=x 2-ax -2 e x 在x =-2处取得极大值,则f (x )的极小值为()A.-6e 2B.-4eC.-2e 2D.-e【答案】C【分析】由题意求出a 的值,进而求出f x ,再解出极小值即可.【详解】因为函数f (x )=x 2-ax -2 e x 在x =-2处取得极大值,则f x =x 2+2-a x -2-a ⋅e x ,x ∈R 且f -2 =0,即4-22-a -2-a =0,所以a =2;所以f x =x 2-2x -2 ⋅e x ,f x =x 2-4 ⋅e x =x +2 x -2 e x ,令f x =0,则x =2或x =-2,由x ∈-∞,-2 ,f x >0,x ∈-2,2 ,f x <0,x ∈2,+∞ ,f x >0,所以f x 在-∞,-2 ,2,+∞ 上单调递增,在-2,2 上单调递减.所以函数f x 在x =-2处取得极大值,f 极小=f 2 =-2e 2.故选:C .6(2023·全国·模拟预测)函数f x =2x -tan x -π在区间-π2,π2的极大值、极小值分别为()A.π2+1,-π2+1B.-π2+1,-3π2+1C.3π2-1,-π2+1D.-π2-1,-3π2+1【答案】D【分析】求出f x ,由f (x )<0、f (x )>0可得答案.【详解】由题意,得f(x )=2-sin x cos x =2-1cos 2x =2cos 2x -1cos 2x,当x ∈-π2,-π4 ∪π4,π2 时,2cos 2x -1<0,f (x )<0;当x ∈-π4,π4时,2cos 2x -1>0,f (x )>0.所以f (x )在-π2,-π4 上单调递减,在-π4,π4 上单调递增,在π4,π2上单调递减.当x =-π4时,f (x )取得极小值,为f -π4 =-3π2+1;当x =π4时,f (x )取得极大值,为f π4 =-π2-1.故选:D .7(多选)(2024·全国·模拟预测)已知f (x )=e xx,x >0,-x 2-4x -1,x ≤0, 则方程f 2(x )-(k +3)f (x )+3k =0可能有( )个解.A.3 B.4C.5D.6【答案】BCD【分析】方程f 2(x )-(k +3)f (x )+3k =0得f (x )=3或f (x )=k ,作出函数图象,数形结合判断解的个数.【详解】f (x )=e x x x >0 ,有f(x )=e x x -1 x 2,当0<x <1时f (x )<0,f (x )单调递减;当x >1时f (x )>0,f (x )单调递增,当x =1时,f (x )有极小值f 1 =e.f (x )=-x 2-4x -1x ≤0 ,由二次函数的性质可知,f (x )在-∞,-2 上单调递增,在-2,0 上单调递减,当x =-2时,f (x )有极大值f (-2)=3.由f (x )=e xx,x >0,-x 2-4x -1,x ≤0 的图象如图所示,由f 2(x )-(k +3)f (x )+3k =0得f (x )=3或f (x )=k ,由图象可知f (x )=3有3个解,f (x )=k 可能有1,2,3,4个解,故方程f 2(x )-(k +3)f (x )+3k =0可能有4,5,6,7个解.故选:BCD .【点睛】方法点睛:函数零点的求解与判断方法:(1)直接求零点:令f x =0,如果能求出解,则有几个解就有几个零点.(2)零点存在性定理:利用定理不仅要函数在区间a ,b 上是连续不断的曲线,且f a ⋅f b <0,还必须结合函数的图象与性质(如单调性、奇偶性)才能确定函数有多少个零点.(3)利用图象交点的个数:将函数变形为两个函数的差,画两个函数的图象,看其交点的横坐标有几个不同的值,就有几个不同的零点8(2024·辽宁鞍山·二模)f x =x 2e -x 的极大值为.【答案】4e2【分析】借助导数研究函数的单调性即可得其极大值.【详解】f x =2xe -x +x 2-e -x =2x -x 2 e -x =-x x -2 e -x ,当x ∈-∞,0 ∪2,+∞ 时,f x <0,当x ∈0,2 时,f x >0,故f x 在-∞,0 、2,+∞ 上单调递减,在0,2 上单调递增,故f x 有极大值f 2 =22e -2=4e2.故答案为:4e2命题点3 已知极值(点)求参数9(2024·全国·模拟预测)设x 1,x 2为函数f x =x x -2 x -a (其中a >0)的两个不同的极值点,若不等式f x 1 +f x 2 ≥0成立,则实数a 的取值范围为()A.1,4B.0,4C.0,1D.4,+∞【答案】A【分析】导函数为二次函数,x 1,x 2为对应的一元二次方程的两根,由f x 1 +f x 2 ≥0,代入函数解析式,结合韦达定理化简,可解出实数a 的取值范围.【详解】因为f x =x x -2 x -a ,所以f x =3x 2-22+a x +2a .又函数f x 有两个不同的极值点x 1,x 2,所以Δ=4a 2-2a +4 >0,x 1+x 2=22+a3,x 1x 2=2a 3.解法一:由f x 1 +f x 2 ≥0,得x 31+x 32-a +2 x 21+ x 22 +2a x 1+x 2 ≥0,即x 1+x 2 x 1+x 2 2- 3x 1x 2 -a +2 x 1+x 2 2-2x 1x 2 +2a x 1+ x 2 ≥0∗ .将x 1+x 2,x 1x 2的值代入(*)式,得a 2-5a +4≤0,解得1≤a ≤4,故选:A .解法二:函数y =ax 3+kx a ≠0 为奇函数,图象的对称中心为0,0 ,则函数y =a x -m 3+k x -m +n 图象的对称中心为m ,n 设g x =ax 3+bx 2+cx +d =a x -m 3+k x -m +n ,a x -m 3+k x -m +n =ax 3-3amx 2+3am 2+k x +n -am 3-km ,比较系数,有-3am =b 3am 2+k =c n -am 3-km =d,解得m =-b 3a ,k =c -b 23a ,n =2b 327a2-bc 3a +d =g -b3a 所以函数g x =ax 3+bx 2+cx +d a ≠0 图象的对称中心为-b 3a ,g -b3a,即若f x 存在两个相异的极值点x 1,x 2,则其对称中心为点x 1,f x 1 和点x 2,f x 2 的中点,即f x 1 +f x 2 2=f x 1+x22.由题设得f x 1 +f x 2 ≥0,即f x 1+x 22 ≥0,即f 2+a3≥0,所以a >0,a +23a +23-2 a +23-a ≥0,解得1≤a ≤4.故选:A .10(2024·四川绵阳·三模)若函数f x =12ax 2-x +b ln x a ≠0 有唯一极值点,则下列关系式一定成立的是()A.a >0,b <0B.a <0,b >0C.ab <14D.ab >0【答案】C【分析】求导,构造函数g x =ax 2-x +b a ≠0 ,利用二次函数零点的分布,结合分类讨论以及极值点的定义即可求解.【详解】fx =ax -1+b x =ax 2-x +b x,令g x =ax 2-x +b a ≠0 ,Δ=1-4ab ,若Δ=1-4ab ≤0,则g x =ax 2-x +b ≥0或g x =ax 2-x +b ≤0,此时f x 单调,不存在极值点,故不符合题意,若Δ=1-4ab >0,则方程g x =ax 2-x +b =0有两个实数根,由于f x =12ax 2-x +b ln x a ≠0 有唯一极值点,故g x =ax 2-x +b =0只能有一个正实数根,若另一个实数根为0,此时b =0,显然满足条件,若令一个实数根为负根,则ba <0,故ab <0,结合选项可知,ab <14一定成立,故选:C11(2024·辽宁·一模)已知函数f x =x 3+ax 2+bx +a 2在x =-1处有极值8,则f 1 等于.【答案】-4【分析】求导,即可由f -1 =8且f -1 =0求解a ,b ,进而代入验证是否满足极值点即可.【详解】f x =3x 2+2ax +b ,若函数f x 在x =-1处有极值8,则f -1 =8,f-1 =0,即-1+a -b +a 2=83-2a +b =0,解得:a =3,b =3或a =-2,b =-7,当a =3,b =3时,f x =3x 2+6x +3=3(x +1)2≥0,此时x =-1不是极值点,故舍去;当a =-2,b =-7时,f x =3x 2-4x -7=3x -7 x +1 ,当x >73或x <-1时,f x >0,当-1<x <73,f x <0,故x =-1是极值点,故a =-2,b =-7符合题意,故f x =x 3-2x 2-7x +4,故f 1 =-4.故答案为:-412(2024·全国·模拟预测)已知函数f x =ln x -x 2+ax -2a ∈R .(1)若f x 的极值为-2,求a 的值;(2)若m ,n 是f x 的两个不同的零点,求证:f m +n +m +n <0.【答案】(1)1(2)证明见解析【分析】(1)对函数f x 求导,再根据函数与导数的关系研究函数f x 的性质,即可得解;(2)由题意f m +n +m +n =1m -n m -n m +n -ln m n ,再设m >n >0,t =mn,进而构造函数g t =t -1t +1-ln t t >1 ,利用函数的单调性进行证明即可.【详解】(1)由题知f x 的定义域为0,+∞ ,fx =1x -2x +a =-2x 2+ax +1x.由f x =0可得2x 2-ax -1=0,解得x 1=a -a 2+84(舍去),x 2=a +a 2+84,且ax 2=2x 22-1,∴f x 在0,x 2 上单调递增,在x 2,+∞ 上单调递减,∴f x 有极大值f x 2 =ln x 2-x 22+ax 2-2=ln x 2-x 22+2x 22-1 -2=ln x 2+x 22-3.设h x =ln x +x 2-3,则h x 在0,+∞ 上单调递增,且h 1 =-2,故x 2=1,即a +a 2+84=1,解得a =1.(2)由条件可得f m =ln m -m 2+am -2=0,f n =ln n -n 2+an -2=0,两式相减,可得ln mn -m 2-n 2 +a m -n =0,故a =m +n -ln m nm -n,f m +n +m +n =1m +n-2m +n +a +m +n=1m +n -ln m nm -n =1m -n m -n m +n -ln m n.不妨设m >n >0,t =mn,则t >1,要证f m +n +m +n <0,只需证明m -n m +n -ln mn<0,即证t -1t +1-ln t <0.设g t =t -1t +1-ln t t >1 ,则gt =2t +12-1t =2t t +1 2t t +1 2=-t 2+1t t +1 2<0,∴g t 在1,+∞ 上单调递减,g t <1-11+1-ln1=0,故f m +n +m +n <0.【点睛】方法点睛:(1)研究函数零点、极值时,一般需要求导分析函数、导函数的单调性,并结合特值进行分析判断;(2)证明有关零点的不等式时,需要观察不等式,构造常用函数g t =t -1t +1-ln t t >1 证明即可.题型二 利用导数求函数最值求含有参数的函数的最值,需先求函数的定义域、导函数,通过对参数分类讨论,判断函数的单调性,从而得到函数f (x )的最值.命题点1 不含参函数的最值13(2024·陕西·模拟预测)∀x ∈1,2 ,有a ≥-x 2ln x +x 2恒成立,则实数a 的取值范围为()A.e ,+∞B.1,+∞C.e2,+∞ D.2e ,+∞【答案】C【分析】构造函数μx =-x 2ln x +x 2,x ∈1,2 ,求导可得函数的单调性,即可求解最值μx max =μe =e 2,进而a ≥μx max 即可.【详解】由a ≥-x 2ln x +x 2在x ∈1,2 上恒成立,令μx =-x 2ln x +x 2,x ∈1,2 ,则μ x =-2x ln x -x +2x =-2x ln x +x =x -2ln x +1 .令μ x =0,则x =e ,当x ∈1,e 时,μ x >0,故μ x 在1,e 上单调递增;当x ∈e ,2 时,μ x <0,故μ x 在e ,2 上单调递减;则μx ≤μe =e 2,所以a ≥e2故选:C14(2024·四川·模拟预测)已知f x =x 2-2x +a ln x -x ,若存在x 0∈0,e ,使得f x 0 ≤0成立,则实数a 的取值范围是.【答案】-1,+∞【分析】先用导数证明不等式x -ln x -1≥0,然后对a ≥-1和a <-1分类讨论,即可得出结果.【详解】设g x =x -ln x ,则g x =1-1x =x -1x,从而当0<x <1时g x <0,当x >1时g x >0.所以g x 在0,1 上递减,在1,+∞ 上递增,故对任意x >0有x -ln x =g x ≥g 1 =1,即x -ln x -1≥0.一方面,当a ≥-1时,由于f 1 =1-2-a =-1-a ≤0,故存在x 0=1使得f x 0 ≤0成立;另一方面,当a <-1时,由于对任意x ∈0,e 都有f x =x 2-2x +a ln x -x =x -1 2-1+a ln x -x =x -1 2+-a x -ln x -1=x -1 2+-a x -ln x -1 +-a -1≥0+0+-a -1 (这里用到x -1 2≥0,-a >0,x -ln x -1≥0)=-a -1>0,所以对任意x ∈0,e 都有f x >0.综上,a 的取值范围是-1,+∞ .故答案为:-1,+∞ .【点睛】关键点点睛:对于求取值范围问题,本质上就是要确定一个集合,使得命题成立的充要条件是参数属于该集合. 故本题中我们从两个方面入手,证明了存在x 0∈0,e 使得f x 0 ≤0的充要条件是a ∈-1,+∞ ,即可解决问题15(2024·上海徐汇·二模)如图,两条足够长且互相垂直的轨道l 1,l 2相交于点O ,一根长度为8的直杆AB 的两端点A ,B 分别在l 1,l 2上滑动(A ,B 两点不与O 点重合,轨道与直杆的宽度等因素均可忽略不计),直杆上的点P 满足OP ⊥AB ,则△OAP 面积的取值范围是.【答案】(0,63]【分析】令∠OAB =x 0<x <π2,利用直角三角形边角关系及三角形面积公式求出△OAP 的面积函数,再利用导数求出值域即得.【详解】依题意,设∠OAB =x 0<x <π2,则OA =AB cos x =8cos x ,AP =OA cos x =8cos 2x ,因此△OAP 的面积f (x )=12OA ⋅AP sin x =32sin x cos 3x ,0<x <π2,求导得f (x )=32(cos 4x -3sin 2x cos 2x )=32cos 4x (1-3tan 2x ),当0<x <π6时,f (x )>0,当π6<x <π2时,f (x )<0,即函数f (x )在0,π6 上递增,在π6,π2上递减,因此f (x )max =f π6 =32×32 3×12=63,而f (0)=f π2 =0,则0<f (x )≤63,所以△OAP 面积的取值范围是(0,63].故答案为:(0,63]16(2024·全国·模拟预测)已知函数f x =ln x .(1)求函数g x =f xx的最值.(2)证明:xe x-14x 4-e 2-34x 3-ef x >0(其中e 为自然对数的底数).【答案】(1)最大值为g e =1e,无最小值;(2)证明见解析.【分析】(1)先求出函数的导数,根据导数得出函数的单调区间,从而得出函数的最值.(2)不等式转化为e x-14x3-e2-34x2-e ln xx>0,结合(1)知ln xx≤1e,从而证明:ex-14x3-e2-34x2-1≥0,再结合导数求函数的最小值证得结果.【详解】(1)由题意知g x =ln xx,定义域为0,+∞,从而g x =1-ln x x2.所以当x∈0,e时,g x >0;当x∈e,+∞时,g x <0.所以函数g x 在0,e上单调递增,在e,+∞上单调递减.所以函数g x 的最大值为g e =1e,无最小值.(2)欲证xe x-14x4-e2-34x3-ef x >0,只需证e x-14x3-e2-34x2-e ln xx>0.由(1)知ln xx≤1e,从而e ln xx≤1,当且仅当x=e时取等号.下面证明:e x-14x3-e2-34x2-1≥0.设h x =e x-14x3-e2-34x2-1,x>0,则h x =e x-34x2-e2-32x.设H x =e x-34x2-e2-32x,则H x =e x-32x-e2-32.设F x =e x-32x-e2-32,则Fx =e x-32,故当x∈0,ln 3 2时,F x <0;当x∈ln32,+∞时,F x >0.所以函数F x 在0,ln 3 2上单调递减,在ln32,+∞上单调递增.由于F0 =5-e22<0,F2 =e2-32>0,F ln32=32-32ln32-e2-32<0,故设存在唯一的x0∈ln 3 2 ,2,使F x0 =0,且当x∈0,x0时,F x <0,当x∈x0,+∞时,F x >0.故函数H x 在0,x0上单调递减,在x0,+∞上单调递增.又H0 =1,H1 =e-e22+34=4e+3-2e24<0,H2 =e2-3-e2-3=0,所以存在唯一的x1∈0,1,使H x1=0,故当x∈0,x1∪2,+∞时,H x >0;当x∈x1,2时,H x <0.从而函数h x 在0,x1,2,+∞上分别单调递增,在x1,2上单调递减.因为h0 =e0-0-0-1=0,h2 =e2-2-e2-3-1=0,所以h x ≥0在0,+∞上恒成立,当且仅当x=2时取等号.因为取等条件不相同,所以e x-14x3-e2-34x2-e ln xx>0恒成立,即xe x-14x4-e2-34x3-ef x >0成立.【点睛】本题第(2)问考查的是利用导数证明不等式.证明时有三个关键点:一是不等式的等价变形,由第(1)问的提示可知,需要把所证明的不等式两端同时除以x,使不等式等价转化为e x-14x 3-e 2-34x 2-e ln xx>0;二是放缩法的应用,由(1)知ln x x ≤1e ,从而e ln x x ≤1,此时只需再证明不等式e x-14x 3-e 2-34x 2-1≥0即可;三是构造函数h x =e x-14x 3-e 2-34x 2-1,通过求导研究h x 的单调性,进一步求得h x 的最小值,在研究h x 单调性的过程中,需要注意特殊点、端点,以及隐零点的讨论.命题点2 含参函数的最值17(2024·四川成都·模拟预测)已知函数f (x )=e x -12(a +1)x 2-bx (a ,b ∈R )没有极值点,则ba +1的最大值为()A.e2B.e 2C.eD.e 22【答案】B【分析】转化为f (x )=e x -1a +1x -b ≥0恒成立,构造函数,求导,得到其单调性和最值,从而得到b ≤1a +1+ln a +1 a +1,故b a +1≤ln a +1 +1a +12,换元后,构造函数,求导得到其单调性和最值,求出答案.【详解】函数f x =e x -12a +1x 2-bx 没有极值点,∴f (x )=e x -1a +1x -b ≥0,或f (x )≤0恒成立,由y =e x 指数爆炸的增长性,f (x )不可能恒小于等于0,∴f (x )=e x -1a +1x -b ≥0恒成立.令h x =e x -1a +1x -b ,则h x =e x -1a +1,当a +1<0时,h x >0恒成立,h x 为R 上的增函数,因为e x ∈0,+∞ 是增函数,-1a +1x -b ∈-∞,+∞ 也是增函数,所以,此时h (x )∈-∞,+∞ ,不合题意;②当a +1>0时,h x =e x -1a +1为增函数,由h x =0得x =-ln a +1 ,令h x >0⇔x >-ln a +1 ,h x <0⇔x <-ln a +1 ,∴h x 在-∞,-ln a +1 上单调递减,在-ln a +1 ,+∞ 上单调递增,当x =-ln a +1 时,依题意有h x min =h -ln a +1 =1a +1+ln a +1 a +1-b ≥0,即b ≤1a +1+ln a +1 a +1,∵a +1>0,∴ba +1≤ln a +1 +1a +12,令a +1=x (x >0),u x =ln x +1x2x >0 ,则u x =x -ln x +1 ⋅2x x4=-2ln x +1x 3,令u x >0⇔0<x <1e ,令u x <0,解得x >1e,所以当x =1e 时,u x 取最大值u 1e=e2.故当a +1=1e,b =e 2,即a =e e -1,b =e 2时,b a +1取得最大值e 2.综上,若函数h x 没有极值点,则b a +1的最大值为e2.故选:B .【点睛】关键点睛:将函数没有极值点的问题转化为导函数恒大于等于0,通过构造函数,借助导数研究函数的最小值,从而得解.18(23-24高三下·重庆·阶段练习)若过点a ,b 可以作曲线y =ln x 的两条切线,则()A.b >ln aB.b <ln aC.a <0D.b >e a【答案】A【分析】设切点坐标为(x 0,y 0),由切点坐标求出切线方程,代入坐标(a ,b ),关于x 0的方程有两个不同的实数解,变形后转化为直线与函数图象有两个交点,构造新函数由导数确定函数的图象后可得.【详解】设切点坐标为(x 0,y 0),由于y =1x ,因此切线方程为y -ln x 0=1x 0(x -x 0),又切线过点(a ,b ),则b -ln x 0=a -x 0x 0,b +1=ln x 0+ax 0,设f (x )=ln x +ax,函数定义域是(0,+∞),则直线y =b +1与曲线f (x )=ln x +a x 有两个不同的交点,f (x )=1x -a x 2=x -ax 2,当a ≤0时,f (x )>0恒成立,f (x )在定义域内单调递增,不合题意;当a >0时,0<x <a 时,f (x )<0,f (x )单调递减,x >a 时,f (x )>0,f (x )单调递增,所以f (x )min =f (a )=ln a +1,结合图象可知b +1>ln a +1,即b >ln a .故选:A .19(2024·全国·模拟预测)函数f x =x +2 ln x +1 -ax 只有3个零点x 1,x 2,x 3x 1<x 2<x 3<3 ,则a +x 2的取值范围是.【答案】2,10ln23【分析】由题意对函数求导,为判断导数与零的大小关系,对导数再次求导求其最值,利用分类讨论思想,结合零点存在性定理,建立不等式组,可得答案.【详解】函数f x =x +2 ln x +1 -ax 的定义域为-1,+∞ ,则f x =ln x +1 +x +2x +1-a .设g x =f x ,则g x =1x +1-1x +1 2=xx +1 2,所以当x ∈-1,0 时,g x <0,f x 单调递减,当x ∈0,+∞ 时,g x >0,f x 单调递增,所以f x ≥f 0 =2-a .当2-a ≥0,即a ≤2时,f x ≥0,f x 单调递增,且f 0 =0,此时f x 只有1个零点,不满足题意;当2-a <0,即a >2时,由f1e a -1 =ln 1e a -1+1+1e a-1+21ea -1+1-a =e a +1-2a >0,f e a -1 =ln e a -1+1 +e a-1+2e a-1+1-a =1+1ea >0存在m ∈-1,0 ,n ∈0,+∞ ,使得f m =0,f n =0,当x ∈-1,m ∪n ,+∞ 时,f x >0;当x ∈m ,n 时,f x <0,所以f x 在-1,m 上单调递增,在m ,n 上单调递减,在n ,+∞ 上单调递增,又f 0 =0,易知f m >0,f n <0,由f1ea-1 =1ea-1+2 ln1ea-1+1-a1ea-1=-2ae -a <0,f e a -1 =e a -1+2 ln e a -1+1 -a e a -1 =2a >0,则f x 在-1,m ,n ,+∞ 上各有1个零点,此时满足题意.所以a >2,且x 2=0.由x 3<3,得f 3 =5ln4-3a >0,得a <10ln23.所以a +x 2的取值范围是2,10ln23.故答案为:2,10ln23.【点睛】关键点点睛:本题的关键是对a 分a ≤2和a >2讨论,当a >2时,需要利用零点存在性定理证明其满足题意,再根据x 3<3,则f 3 =5ln4-3a >0,解出即可.4.2024·北京海淀·一模)已知函数f (x )=xe a -12x .(1)求f (x )的单调区间;(2)若函数g (x )=f (x )+e -2a ,x ∈(0,+∞)存在最大值,求a 的取值范围.【答案】(1)f (x )的增区间为-∞,2 ,减区间为(2,+∞)(2)a ≥-1【分析】(1)对函数求导,得到f(x )=ea -12x 1-12x ,再求出f(x )>0和f(x )<0对应的x 取值,即可求出结果;(2)令h (x )=f (x )+e -2a ,对h (x )求导,利用导数与函数单调性间的关系,求出h (x )的单调区间,进而得出h (x )在(0,+∞)上取值范围,从而将问题转化成2e a -1+e -2a ≥e -2a 成立,构造函数m (x )=e x -1+e -2x ,再利用m (x )的单调性,即可求出结果.【详解】(1)易知定义域为R ,因为f (x )=xe a -12x ,所以f(x )=e a -12x -12xe a -12x =e a -12x 1-12x ,由f (x )=0,得到x =2,当x <2时,f (x )>0,当x >2时,f (x )<0,所以,函数f (x )的单调递增区间为-∞,2 ,单调递减区间为2,+∞ .(2)令h (x )=f (x )+e -2a ,则h (x )=f (x ),由(1)知,函数f (x )的单调递增区间为-∞,2 ,单调递减区间为2,+∞ ,所以h (x )在x =2时取得最大值h (2)=2e a -1+e -2a ,所以当x >2时,h (x )=xe a -12x +e -2a >e -2a =h (0),当0<x <2时,h (x )>h (0),即当x ∈(0,+∞)时,h (x )∈h (0),h (2) ,所以函数g (x )=xea -12x +e -2a 在(0,+∞)存在最大值的充要条件是2e a -1+e -2a ≥e -2a ,即2e a -1+e -2a +e -2a 2=e a -1+e -2a ≥0,令m (x )=e x -1+e -2x ,则m (x )=e x -1+e -2>0恒成立,所以m (x )=e x -1+e -2x 是增函数,又因为m (-1)=e -2-e -2=0,所以m (a )=e a -1+e -2a ≥0的充要条件是a ≥-1,所以a 的取值范围为-1,+∞ .【点睛】关键点点晴:本题的关键在于第(2)问,构造函数h (x )=xe a -12x +e -2a ,利用函数单调性得到x ∈(0,+∞)时,h (x )∈h (0),h (2) ,从而将问题转化成2e a -1+e -2a ≥e -2a ,构造函数m (x )=e x -1+e -2x ,再利用m (x )的单调性来解决问题【课后强化】基础保分练一、单选题1(2023·广西·模拟预测)函数f x =x 3+ax 在x =1处取得极小值,则极小值为()A.1B.2C.-2D.-1【答案】C【分析】求出函数f (x )的导数,利用极小值点求出a 值,再借助导数求出极小值作答.【详解】依题意,f x =3x 2+a ,因为函数f (x )在x =1处取得极小值,则f 1 =3+a =0,解得a =-3,此时f x =3x 2-3=3(x +1)(x -1),当x <-1或x >1时,f (x )>0,当-1<x <1,时f (x )<0,因此函数f (x )在-∞,-1 ,1,+∞ 上单调递增,在(-1,1)上单调递减,所以函数f x =x 3-3x 在x =1处取得极小值f (1)=-2.故选:C2(2024·四川凉山·二模)若f x =x sin x +cos x -1,x ∈-π2,π ,则函数f x 的零点个数为()A.0B.1C.2D.3【答案】C【分析】求导,研究函数单调性,极值,画图,根据图象得零点个数.【详解】f x =sin x +x cos x -sin x =x cos x ,当x ∈-π2,0 时,f x <0,f x 单调递减,当x ∈0,π2 时,f x >0,f x 单调递增,当x ∈π2,π 时,f x <0,f x 单调递减,又f -π2 =π2-1>0,f 0 =0,f π2 =π2-1>0,f π =-2<0,则f x =x sin x +cos x -1的草图如下:由图象可得函数f x 的零点个数为2.故选:C .3(2024·黑龙江哈尔滨·一模)在同一平面直角坐标系内,函数y=f x 及其导函数y=f x 的图象如图所示,已知两图象有且仅有一个公共点,其坐标为0,1,则()A.函数y=f x ⋅e x的最大值为1B.函数y=f x ⋅e x的最小值为1C.函数y=f xe x的最大值为1 D.函数y=f xe x的最小值为1【答案】C【分析】AB选项,先判断出虚线部分为y=f x ,实线部分为y=f x ,求导得到y=f x ⋅e x在R上单调递增,AB错误;再求导得到x∈(-∞,0)时,y=f(x)e x单调递增,当x∈(0,+∞)时,y=f(x)e x单调递减,故C正确,D错误.【详解】AB选项,由题意可知,两个函数图像都在x轴上方,任何一个为导函数,则另外一个函数应该单调递增,判断可知,虚线部分为y=f x ,实线部分为y=f x ,故y =f x ⋅e x+f x ⋅e x=f x +f x⋅e x>0恒成立,故y=f x ⋅e x在R上单调递增,则A,B显然错误,对于C,D,y =f (x)e x-f(x)e xe x2=f (x)-f(x)e x,由图像可知x∈(-∞,0),y =f (x)-f(x)e x>0恒成立,故y=f(x)e x单调递增,当x∈(0,+∞),y =f (x)-f(x)e x<0,y=f(x)e x单调递减,所以函数y=f(x)e x在x=0处取得极大值,也为最大值,f0e0=1,C正确,D错误.故选:C4(2024·陕西安康·模拟预测)已知函数f x =ae2x+be x+2x有2个极值点,则()A.0<a<b216B.b>0C.a<4bD.b>2a【答案】A【分析】求出函数的导函数,令t=e x,依题意可得关于t的方程2at2+bt+2=0有两个不相等的正实根t1、t2,则2a≠0Δ>0t1+t2>0t1t2>0,即可判断.【详解】函数f x =ae2x+be x+2x的定义域为R,且f x =2ae2x+be x+2,依题意f x =0有两个不相等实数根,令t=e x,则关于t的方程2at2+bt+2=0有两个不相等的正实根t1、t2,所以2a ≠0Δ=b 2-16a >0t 1+t 2=-b 2a >0t 1t 2=1a >0,所以0<a <b216,b <0.故选:A5(2024·全国·模拟预测)已知函数f x =a sin x +cos xe x+x 在0,π 上恰有两个极值点,则实数a的取值范围是()A.0,22e π4B.-∞,e πC.0,e πD.22e π4,+∞【答案】D【分析】函数f x 在0,π 上恰有两个极值点,fx 在0,π 上有两个变号零点,分离常数得a =e x 2sin x,转化为两函数图象有两个不同的交点,利用数形结合思想进行求解;或直接求函数f x 的单调性,求图象在0,π 上与x 轴有两个交点的条件.【详解】解法一:由题意可得f x =-2a sin xex+1,因为函数f x 在0,π 上恰有两个极值点,所以f x 在0,π 上有两个变号零点.令fx =-2a sin x e x+1=0,可得a =e x 2sin x ,令g x =e x 2sin x ,x ∈0,π ,则直线y =a 与函数y =g x ,x ∈0,π 的图象有两个不同的交点,g x =2e x sin x -cos x 2sin x 2=22e x sin x -π4 2sin x 2,当x ∈π4,π 时,g x >0,所以g x 在π4,π 上单调递增,当x ∈0,π4 时,g x <0,所以g x 在0,π4上单调递减,又g π4 =22e π4,当x 趋近于0时,g x 趋近于+∞,当x 趋近于π时,g x 趋近于+∞,所以可作出g x 的图象如图所示,数形结合可知a >22e π4,即实数a 的取值范围是22e π4,+∞,故选:D .解法二 由题意可得f x =-2a sin xex+1.因为函数f x 在0,π 上恰有两个极值点,所以f x 在0,π 上有两个变号零点.当a ≤0时,f x >0在0,π 上恒成立,不符合题意.当a >0时,令h x =fx =-2a sin x e x +1,则hx=22a sin x -π4 e x,当x ∈π4,π 时,h x >0,h x 单调递增,当x ∈0,π4时,h x <0,h x 单调递减,因为h 0 =h π =1,h π4 =1-2a e π4,所以h π4 =1-2a eπ4<0,则a >22e π4,即实数a 的取值范围是22e π4,+∞,故选:D .【点睛】方法点睛:导函数中常用的两种常用的转化方法:一是利用导数研究含参函数的单调性,常化为不等式恒成立问题.注意分类讨论与数形结合思想的应用;二是函数的零点、不等式证明常转化为函数的单调性、极(最)值问题处理,构造一个适当的函数,利用它的单调性进行解题,是一种常用技巧.二、多选题6(2024·全国·模拟预测)已知函数f x =ae x +bx在定义域内既存在极大值点又存在极小值点,则()A.ab >0B.b a ≤4e2C.4a -be 2>0 D.对于任意非零实数a ,总存在实数b 满足题意【答案】AD【分析】根据给定条件,分类讨论,逐项判断即可.【详解】由题意,得f x =ae x-b x 2=ax 2e x -b x 2.令f x =0,得x 2e x =b a .令g x =x 2e x ,则g x =x x +2 e x .当x ∈-∞,-2 ∪0,+∞ 时,g x >0,此时g x 单调递增;当x ∈-2,0 时,g x <0,此时g x 单调递减.∵g -2 =4e 2,g 0 =0,当x →-∞时,g x →0,∴当0<b a <4e2时,f x 在定义域内既存在极大值点又存在极小值点.故A 正确,B 不正确.当a <0时,由0<b a <4e2知,当b <0时,4a -be 2<0,故C 不正确.对于任意非零实数a ,总存在实数b ,使得0<b a <4e2成立,故D 正确.故选:AD .7(2024·湖北武汉·模拟预测)已知各项都是正数的数列a n 的前n 项和为S n ,且S n =a n 2+12a n,则下列结论正确的是()A.当m >n m ,n ∈N * 时,a m >a nB.S n +S n +2<2S n +1C.数列S 2n 是等差数列D.S n -1S n≥ln n 【答案】BCD【分析】计算数列首项及第二项可判定A ,利用等差数列的定义及S n ,a n 的关系可判定C ,从而求出S n 的通项公式结合基本不等式、函数的单调性可判定B 、D .【详解】对A ,由题意可知a 1=a 12+12a 1⇒a 21=1,所以a 1=1,则a 1+a 2=a 22+12a 2⇒a 22+2a 2-1=0,所以a 2=2-1<a 1,故A 错误;对C ,由S n =a n 2+12a n ⇒S n =S n -S n -12+12S n -S n -1⇒S 2n -S 2n -1=1n ≥2 ,故C 正确;对C ,所以S 2n =1+n -1 =n ⇒S n =n ,则S n +S n +2=n +n +2<2n +n +22=2S n +1,故B 正确;对D ,易知S n -1S n =n -1n,令f x =x -1x -2ln x x ≥1 ,则f x =1+1x2-2x =1x -1 2≥0,则f x 单调递增,所以f x ≥f 1 =0⇒n -1n ≥ln n ,即S n -1S n ≥ln n ,故D 正确.故选:BCD 三、填空题8(2024·上海黄浦·二模)如图是某公园局部的平面示意图,图中的实线部分(它由线段CE ,DF 与分别以OC ,OD 为直径的半圆弧组成)表示一条步道.其中的点C ,D 是线段AB 上的动点,点O 为线段AB ,CD 的中点,点E ,F 在以AB 为直径的半圆弧上,且∠OCE ,∠ODF 均为直角.若AB =1百米,则此步道的最大长度为百米.【答案】π2+42【分析】设半圆步道直径为x 百米,连接AE ,BE ,借助相似三角形性质用x 表示CE ,结合对称性求出步道长度关于x 的函数关系,利用导数求出最大值即得.【详解】设半圆步道直径为x 百米,连接AE ,BE ,显然∠AEB =90°,由点O 为线段AB ,CD 的中点,得两个半圆步道及直道CE ,DF 都关于过点O 垂直于AB 的直线对称,则AC =12-x ,BC =12+x ,又CE ⊥AB ,则Rt △ACE ∽Rt △ECB ,有CE 2=AC ⋅BC ,即有DF =CE =14-x 2,因此步道长f (x )=214-x 2+πx =1-4x 2+πx ,0<x <12,求导得f (x )=-4x 1-4x 2+π,由f(x )=0,得x =π2π2+4,当0<x <π2π2+4时,f (x )>0,函数f (x )递增,当π2π2+4<x <12时,f(x )<0,函数f (x )递减,因此当x =π2π2+4时,f (x )max =1-4π2π2+42+π22π2+4=π2+42,所以步道的最大长度为π2+42百米.故答案为:π2+429(2023·江西赣州·模拟预测)当x =0时,函数f x =ae -x +bx 取得极小值1,则a +b =.【答案】2【分析】求导函数f x =-ae -x +b ,根据f (0)=a =1f (0)=-a +b =0求得a ,b 的值,检验极值点后可得a +b 的值.【详解】函数f x =ae -x +bx ,则f x =-ae -x +b 当x =0时,函数f x =ae -x +bx 取得极小值1,所以f (0)=a =1f (0)=-a +b =0,解得a =1,b =1,所以f x =-e -x+1=e x -1ex ,则函数在x ∈-∞,0 时,f x <0,函数单调递减;在x ∈0,+∞ 时,f x >0,函数单调递增;符合x =0是函数的极值点;故a +b =2.故答案为:2.四、解答题10(2023·河南洛阳·一模)已知函数f x =12x 2+1x +12.(1)求f x 的图像在点2,f 2 处的切线方程;(2)求f x 在12,2上的值域.【答案】(1) 7x -4y -2=0;(2)2,3 .【分析】(1)把点2,f 2 代入函数解析式,得切点坐标,通过求导,得到切线的斜率,根据直线的点斜式方程,求切线方程.(2)解不等式f x >0,得函数增区间,解不等式f x <0,得函数减区间,结合x ∈12,2,确定函数单调性,求得最值,进而得出f x 在12,2上的值域.【详解】(1)因为f x =12x 2+1x +12,所以f x =x -1x2,所以f 2 =3,f 2 =74,故所求切线方程为y -3=74x -2 ,即7x -4y -2=0.(2)由(1)知f x =x 3-1x 2=x -1 x 2+x +1 x 2,x ∈12,2 .令f x >0,得1<x ≤2;令f x <0,得12≤x <1.所以f x 在12,1上单调递减,在1,2 上单调递增,所以f x min =f 1 =2.又f 12 =218,f 2 =3,因为f 2 >f 12,所以2≤f x ≤3,即f x 在12,2上的值域为2,3 .11(2024·上海静安·二模)已知k ∈R ,记f (x )=a x +k ⋅a -x (a >0且a ≠1).(1)当a =e (e 是自然对数的底)时,试讨论函数y =f (x )的单调性和最值;(2)试讨论函数y =f (x )的奇偶性;(3)拓展与探究:① 当k 在什么范围取值时,函数y =f (x )的图象在x 轴上存在对称中心?请说明理由;②请提出函数y =f (x )的一个新性质,并用数学符号语言表达出来.(不必证明)【答案】(1)详见解析;(2)详见解析;(3)①当k <0时,函数y =f (x )有对称中心12log (-k ),0,理由见解析;②答案见解析.【分析】(1)当a =e 时,求得f (x )=e x -k ⋅e -x ,分k ≤0和k >0,两种情况讨论,分别求得函数的单调性,进而求得函数的最值;(2)根据题意,分别结合f (-x )=f (x )和f (-x )=-f (x ),列出方程求得k 的值,即可得到结论;(3)根据题意,得到当k <0时,函数y =f (x )有对称中心12log (-k ),0 ,且k <0时,对于任意的x ∈R ,都有-x ∈R ,并且f (log a (-k )-x )=-f (x ).【详解】(1)解:当a =e 时,函数f (x )=e x +k ⋅e -x ,可得f (x )=e x -k ⋅e -x ,若k ≤0时,f (x )>0,故函数y =f (x )在R 上单调递增,函数y =f (x )在R 上无最值;若k >0时,令f (x )=0,可得x =12ln k ,当x ∈-∞,12ln k 时,f x <0,函数y =f (x )在-∞,12ln k 上为严格减函数;当x ∈12ln k ,+∞ 时,f x >0,函数y =f (x )在12ln k ,+∞ 上为严格增函数,所以,当x =12ln k 时,函数取得最小值,最小值为f 12ln k =2k ,无最大值.综上:当k ≤0时,函数f (x )在R 上无最值;当k >0时,最小值为2k ,无最大值.(2)解:因为“y =f (x )为偶函数”⇔“对于任意的x ∈R ,都有f (-x )=f (x )”即对于任意的x ∈R ,都有-x ∈R ,并且a x +k ⋅a -x =a -x +k ⋅a x ;即对于任意的x ∈R ,(k -1)(a x -a -x )=0,可得k =1,所以k =1是y =f (x )为偶函数的充要条件.因为“y =f (x )为奇函数”⇔“对于任意的x ∈R ,都有f (-x )=-f (x )”,即对于任意的x ∈R ,都有-x ∈R ,并且-a x -k ⋅a -x =a -x +k ⋅a x ,即对于任意的x ∈R ,(k +1)(a x +a -x )=0,可得k =-1,所以k =-1是y =f (x )为奇函数的充要条件,当k ≠±1时,y =f (x )是非奇非偶函数.(3)解:①当k <0时,函数y =f (x )有对称中心12log (-k ),0,当k <0时,对于任意的x ∈R ,都有-x ∈R ,并且f (log a (-k )-x )=-f (x ).证明:当k <0时,令f (x )=0,解得x =12log a (-k )为函数y =f (x )的零点,由f (x )=a x +k ⋅a -x ,。
导数与函数的极值和最值考点及题型

第三节导数与函数的极值、最值❖基础知识1.函数的极值(1)函数的极小值:函数y=f(x)在点x=a的函数值f(a)比它在点x=a附近其他点的函数值都小,f′(a)=0;而且在点x=a附近的左侧f′(x)<0,右侧f′(x)>0,则点a叫做函数y=f(x)的极小值点,f(a)叫做函数y=f(x)的极小值.(2)函数的极大值:函数y=f(x)在点x=b的函数值f(b)比它在点x=b附近其他点的函数值都大,f′(b)=0;而且在点x=b附近的左侧f′(x)>0,右侧f′(x)<0,则点b叫做函数y=f(x)的极大值点,f(b)叫做函数y=f(x)的极大值.极小值点、极大值点统称为极值点,极大值和极小值统称为极值.①函数f(x)在x0处有极值的必要不充分条件是f′(x0)=0,极值点是f′(x)=0的根,但f′(x)=0的根不都是极值点(例如f(x)=x3,f′(0)=0,但x=0不是极值点).②极值反映了函数在某一点附近的大小情况,刻画的是函数的局部性质.极值点是函数在区间内部的点,不会是端点.2.函数的最值(1)在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值.(2)若函数f(x)在[a,b]上单调递增,则f(a)为函数的最小值,f(b)为函数的最大值;若函数f(x)在[a,b]上单调递减,则f(a)为函数的最大值,f(b)为函数的最小值.❖常用结论(1)若函数f(x)的图象连续不断,则f(x)在[a,b]上一定有最值.(2)若函数f(x)在[a,b]上是单调函数,则f(x)一定在区间端点处取得最值.(3)若函数f(x)在区间(a,b)内只有一个极值点,则相应的极值点一定是函数的最值点.考点一利用导数解决函数的极值问题考法(一)利用导数求函数的极值或极值点[典例](2018·天津高考改编)设函数f(x)=(x-t1)·(x-t2)(x-t3),其中t1,t2,t3∈R,且t1,t2,t3是公差为d的等差数列.(1)若t2=0,d=1,求曲线y=f(x)在点(0,f(0))处的切线方程;(2)若d =3,求f (x )的极小值点及极大值.[解] (1)由已知,可得f (x )=x (x -1)(x +1)=x 3-x ,故f ′(x )=3x 2-1.因此f (0)=0,f ′(0)=-1.因此曲线y =f (x )在点(0,f (0))处的切线方程为y -f (0)=f ′(0)(x -0),故所求切线方程为x +y =0. (2)由已知可得f (x )=(x -t 2+3)(x -t 2)(x -t 2-3) =(x -t 2)3-9(x -t 2)=x 3-3t 2x 2+(3t 22-9)x -t 32+9t 2.故f ′(x )=3x 2-6t 2x +3t 22-9.令f ′(x )=0,解得x =t 2-3或x =t 2+ 3. 当x 变化时,f ′(x ),f (x )的变化情况如下表:[解题技法] 求函数的极值或极值点的步骤(1)求导数f ′(x ),不要忘记函数f (x )的定义域; (2)求方程f ′(x )=0的根;(3)检查在方程的根的左右两侧f ′(x )的符号,确定极值点或函数的极值. 考法(二) 已知函数极值点或极值求参数的值或范围[典例] (2018·北京高考节选)设函数f (x )=[ax 2-(3a +1)x +3a +2]e x ,若f (x )在x =1处取得极小值,求a 的取值范围.[解] 由f (x )=[ax 2-(3a +1)x +3a +2]e x ,得f ′(x )=[ax 2-(a +1)x +1]e x =(ax -1)(x -1)e x . 若a >1,则当x ∈⎝⎛⎭⎫1a ,1时,f ′(x )<0; 当x ∈(1,+∞)时,f ′(x )>0. 所以f (x )在x =1处取得极小值.若a ≤1,则当x ∈(0,1)时,ax -1≤x -1<0, 所以f ′(x )>0.所以1不是f (x )的极小值点.综上可知,a 的取值范围是(1,+∞).[解题技法]已知函数极值点或极值求参数的2个要领[题组训练]1.设函数f (x )=2x+ln x ,则( )A .x =12为f (x )的极大值点B .x =12为f (x )的极小值点C .x =2为f (x )的极大值点D .x =2为f (x )的极小值点解析:选D ∵f (x )=2x+ln x (x >0),∴f ′(x )=-2x 2+1x ,令f ′(x )=0,则x =2.当0<x <2时,f ′(x )<0;当x >2时,f ′(x )>0. 所以x =2为f (x )的极小值点.2.(2019·广州高中综合测试)已知函数f (x )=x 3+ax 2+bx +a 2在x =1处的极值为10,则数对(a ,b )为( )A .(-3,3)B .(-11,4)C .(4,-11)D .(-3,3)或(4,-11)解析:选Cf ′(x )=3x 2+2ax +b ,依题意可得⎩⎪⎨⎪⎧f ′(1)=0,f (1)=10,即⎩⎪⎨⎪⎧3+2a +b =0,1+a +b +a 2=10,消去b 可得a 2-a -12=0,解得a =-3或a =4,故⎩⎪⎨⎪⎧a =-3,b =3或⎩⎪⎨⎪⎧a =4,b =-11.当⎩⎪⎨⎪⎧a =-3,b =3时,f ′(x )=3x 2-6x +3=3(x-1)2≥0,这时f (x )无极值,不合题意,舍去,故选C.3.设函数f (x )=ax 3-2x 2+x +c (a >0).(1)当a =1,且函数f (x )的图象过点(0,1)时,求函数f (x )的极小值; (2)若f (x )在(-∞,+∞)上无极值点,求a 的取值范围. 解:f ′(x )=3ax 2-4x +1.(1)函数f (x )的图象过点(0,1)时,有f (0)=c =1.当a =1时,f (x )=x 3-2x 2+x +1,f ′(x )=3x 2-4x +1, 由f ′(x )>0,解得x <13或x >1;由f ′(x )<0,解得13<x <1.所以函数f (x )在⎝⎛⎭⎫-∞,13和(1,+∞)上单调递增,在⎝⎛⎭⎫13,1上单调递减, 所以函数f (x )的极小值是f (1)=13-2×12+1+1=1. (2)若f (x )在(-∞,+∞)上无极值点, 则f (x )在(-∞,+∞)上是单调函数,即f ′(x )=3ax 2-4x +1≥0或f ′(x )=3ax 2-4x +1≤0恒成立. 因为a >0,所以f ′(x )=3ax 2-4x +1≥0在(-∞,+∞)上恒成立, 则有Δ=(-4)2-4×3a ×1≤0,即16-12a ≤0,解得a ≥43.故a 的取值范围为⎣⎡⎭⎫43,+∞. 考点二 利用导数解决函数的最值问题[典例] (2017·北京高考)已知函数f (x )=e x cos x -x .(1)求曲线y =f (x )在点(0,f (0))处的切线方程; (2)求函数f (x )在区间⎣⎡⎦⎤0,π2上的最大值和最小值. [解] (1)因为f (x )=e x cos x -x ,所以f ′(x )=e x (cos x -sin x )-1,f ′(0)=0. 又因为f (0)=1,所以曲线y =f (x )在点(0,f (0))处的切线方程为y =1. (2)设h (x )=e x (cos x -sin x )-1,则h ′(x )=e x (cos x -sin x -sin x -cos x )=-2e x sin x . 当x ∈⎝⎛⎭⎫0,π2时,h ′(x )<0, 所以h (x )在区间⎣⎡⎦⎤0,π2上单调递减. 所以对任意x ∈⎝⎛⎦⎤0,π2,有h (x )<h (0)=0, 即f ′(x )<0.所以函数f (x )在区间⎣⎡⎦⎤0,π2上单调递减. 因此f (x )在区间⎣⎡⎦⎤0,π2上的最大值为f (0)=1, 最小值为f ⎝⎛⎭⎫π2=-π2.[解题技法]导数法求给定区间上函数的最值问题的一般步骤(1)求函数f (x )的导数f ′(x );(2)求f (x )在给定区间上的单调性和极值; (3)求f (x )在给定区间上的端点值;(4)将f (x )的各极值与f (x )的端点值进行比较,确定f (x )的最大值与最小值; (5)反思回顾,查看关键点,易错点和解题规范. [题组训练]1.(2018·珠海摸底)如图,将一张16 cm ×10 cm 的长方形纸片剪下四个全等的小正方形,使得剩余部分经过折叠能糊成一个无盖的长方体纸盒,则这个纸盒的最大容积是________ cm 3.解析:设剪下的四个小正方形的边长为x cm ,则经过折叠以后,糊成的长方体纸盒是一个底面是长为(16-2x ) cm ,宽为(10-2x ) cm 的长方形,其面积为(16-2x )(10-2x )cm 2,长方体纸盒的高为x cm ,则体积V =(16-2x )(10-2x )×x =4x 3-52x 2+160x (0<x <5)cm 3,所以V ′=12(x -2)·⎝⎛⎭⎫x -203,由V ′>0,得0<x <2,则函数V =4x 3-52x 2+160x (0<x <5)在(0,2)上单调递增;由V ′<0,得2<x <5,则函数V =4x 3-52x 2+160x (0<x <5)在(2,5)上单调递减,所以当x =2时,V max =144(cm 3). 答案:1442.已知函数f (x )=ln x -a x.(1)若a >0,试判断f (x )在定义域内的单调性; (2)若f (x )在[1,e]上的最小值为32,求实数a 的值.解:(1)由题意得f (x )的定义域是(0,+∞),且f ′(x )=x +ax 2, 因为a >0,所以f ′(x )>0, 故f (x )在(0,+∞)上单调递增. (2)由(1)可得f ′(x )=x +ax 2,因为x ∈[1,e],①若a ≥-1,则x +a ≥0,即f ′(x )≥0在[1,e]上恒成立, 此时f (x )在[1,e]上单调递增, 所以f (x )min =f (1)=-a =32,所以a =-32(舍去).②若a ≤-e ,则x +a ≤0,即f ′(x )≤0在[1,e]上恒成立, 此时f (x )在[1,e]上单调递减, 所以f (x )min =f (e)=1-a e =32,所以a =-e2(舍去).③若-e<a <-1,令f ′(x )=0,得x =-a , 当1<x <-a 时,f ′(x )<0, 所以f (x )在(1,-a )上单调递减; 当-a <x <e 时,f ′(x )>0, 所以f (x )在(-a ,e)上单调递增,所以f (x )min =f (-a )=ln(-a )+1=32,所以a =- e.综上,a =- e.[课时跟踪检测]A 级1.(2019·辽宁鞍山一中模拟)已知函数f (x )=x 3-3x -1,在区间[-3,2]上的最大值为M ,最小值为N ,则M -N =( )A .20B .18C .3D .0解析:选A ∵f ′(x )=3x 2-3=3(x -1)(x +1),∴f (x )在(-∞,-1)和(1,+∞)上单调递增,在(-1,1)上单调递减,又∵f (-3)=-19,f (-1)=1,f (1)=-3,f (2)=1,∴M =1,N =-19,M -N =1-(-19)=20.2.(2018·梅州期末)函数y =f (x )的导函数的图象如图所示,则下列说法错误的是( )A .(-1,3)为函数y =f (x )的单调递增区间B .(3,5)为函数y =f (x )的单调递减区间C .函数y =f (x )在x =0处取得极大值D .函数y =f (x )在x =5处取得极小值解析:选C 由函数y =f (x )的导函数的图象可知,当x <-1或3<x <5时,f ′(x )<0,y =f (x )单调递减;当x >5或-1<x <3时,f ′(x )>0,y =f (x )单调递增.所以函数y =f (x )的单调递减区间为(-∞,-1),(3,5),单调递增区间为(-1,3),(5,+∞).函数y =f (x )在x =-1,5处取得极小值,在x =3处取得极大值,故选项C 错误.3.(2019·湖北襄阳四校联考)函数f (x )=12x 2+x ln x -3x 的极值点一定在区间( )A .(0,1)内B .(1,2)内C .(2,3)内D .(3,4)内解析:选B 函数的极值点即导函数的零点,f ′(x )=x +ln x +1-3=x +ln x -2,则f ′(1)=-1<0,f ′(2)=ln 2>0,由零点存在性定理得f ′(x )的零点在(1,2)内,故选B.4.已知函数f (x )=x 3+3x 2-9x +1,若f (x )在区间[k,2]上的最大值为28,则实数k 的取值范围为( ) A .[-3,+∞) B .(-3,+∞) C .(-∞,-3)D .(-∞,-3]解析:选D 由题意知f ′(x )=3x 2+6x -9,令f ′(x )=0,解得x =1或x =-3,所以f ′(x ),f (x )随x 的变化情况如下表:5.(2019·皖南八校联考)已知函数f (x )=-13x 3+bx 2+cx +bc 在x =1处有极值-43,则b =( )A .-1B .1C .1或-1D .-1或3解析:选A f ′(x )=-x 2+2bx +c ,因为f (x )在x =1处有极值-43,所以⎩⎪⎨⎪⎧f ′(1)=-1+2b +c =0,f (1)=-13+b +c +bc =-43,Δ=4b 2+4c >0,解得⎩⎪⎨⎪⎧b =-1,c =3,故选A.6.设直线x =t 与函数h (x )=x 2,g (x )=ln x 的图象分别交于点M ,N ,则当|MN |最小时t 的值为( )A .1 B.12C.52D.22解析:选D 由已知条件可得|MN |=t 2-ln t ,设f (t )=t 2-ln t (t >0),则f ′(t )=2t -1t ,令f ′(t )=0,得t =22, 当0<t <22时,f ′(t )<0;当t >22时,f ′(t )>0. ∴当t =22时,f (t )取得最小值,即|MN |取得最小值时t =22. 7.(2019·江西阶段性检测)已知函数y =ax -1x2在x =-1处取得极值,则a =________.解析:因为y ′=a +2x 3,所以当x =-1时,a -2=0,所以a =2,经验证,可得函数y =2x -1x 2在x =-1处取得极值,因此a =2. 答案:28.f (x )=2x +1x 2+2的极小值为________.解析:f ′(x )=2(x 2+2)-2x (2x +1)(x 2+2)2=-2(x +2)(x -1)(x 2+2)2.令f ′(x )<0,得x <-2或x >1; 令f ′(x )>0,得-2<x <1.∴f (x )在(-∞,-2),(1,+∞)上是减函数,在(-2,1)上是增函数, ∴f (x )极小值=f (-2)=-12.答案:-129.若商品的年利润y (万元)与年产量x (百万件)的函数关系式为y =-x 3+27x +123(x >0),则获得最大利润时的年产量为________百万件. 解析:y ′=-3x 2+27=-3(x +3)(x -3),当0<x <3时,y ′>0;当x >3时,y ′<0. 故当x =3时,该商品的年利润最大. 答案:310.已知函数f (x )=x 3+3ax 2+3bx +c 在x =2处有极值,其图象在x =1处的切线平行于直线6x +2y +5=0,则f (x )的极大值与极小值之差为________. 解析:因为f ′(x )=3x 2+6ax +3b ,所以⎩⎪⎨⎪⎧ f ′(2)=3×22+6a ×2+3b =0,f ′(1)=3×12+6a +3b =-3⇒⎩⎪⎨⎪⎧a =-1,b =0.所以y ′=3x 2-6x ,令3x 2-6x =0,得x =0或x =2. 当x <0或x >2时,y ′>0;当0<x <2时,y ′<0.故当x =0时,f (x )取得极大值,当x =2时,f (x )取得极小值, 所以f (x )极大值-f (x )极小值=f (0)-f (2)=4. 答案:411.设函数f (x )=a ln xx+b (a ,b ∈R ),已知曲线y =f (x )在点(1,0)处的切线方程为y =x -1.(1)求实数a ,b 的值; (2)求f (x )的最大值.解:(1)因为f (x )的定义域为(0,+∞),f ′(x )=a (1-ln x )x 2.所以f ′(1)=a ,又因为切线斜率为1,所以a =1. 由曲线y =f (x )过点(1,0),得f (1)=b =0. 故a =1,b =0.(2)由(1)知f (x )=ln xx ,f ′(x )=1-ln x x 2.令f ′(x )=0,得x =e.当0<x <e 时,有f ′(x )>0,得f (x )在(0,e)上是增函数; 当x >e 时,有f ′(x )<0,得f (x )在(e ,+∞)上是减函数. 故f (x )在x =e 处取得最大值f (e)=1e .12.已知函数f (x )=ln x -ax (a ∈R ).(1)当a =12时,求f (x )的极值;(2)讨论函数f (x )在定义域内极值点的个数.解:(1)当a =12时,f (x )=ln x -12x ,函数f (x )的定义域为(0,+∞),f ′(x )=1x -12=2-x2x.令f ′(x )=0,得x =2,于是当x 变化时,f ′(x ),f (x )的变化情况如下表:故f (x )(2)由(1)知,函数f (x )的定义域为(0,+∞),f ′(x )=1x -a =1-ax x(x >0).当a ≤0时,f ′(x )>0在(0,+∞)上恒成立,即函数f (x )在(0,+∞)上单调递增,此时函数f (x )在定义域上无极值点; 当a >0时,令f ′(x )=0,得x =1a .当x ∈⎝⎛⎭⎫0,1a 时,f ′(x )>0, 当x ∈⎝⎛⎭⎫1a ,+∞时,f ′(x )<0, 故函数f (x )在x =1a处有极大值.综上所述,当a ≤0时,函数f (x )无极值点; 当a >0时,函数f (x )有一个极大值点.B 级1.已知函数f (x )=x 3-3ax +b 的单调递减区间为(-1,1),其极小值为2,则f (x )的极大值是________. 解析:因为f (x )的单调递减区间为(-1,1),所以a >0.由f ′(x )=3x 2-3a =3(x -a )(x +a ),可得a =1, 由f (x )=x 3-3x +b 在x =1处取得极小值2, 可得1-3+b =2,故b =4.所以f (x )=x 3-3x +4的极大值为f (-1)=(-1)3-3×(-1)+4=6. 答案:62.(2019·“超级全能生”高考全国卷26省联考)已知函数f (x )=t 3x 3-32x 2+2x +t 在区间(0,+∞)上既有极大值又有极小值,则t 的取值范围是________.解析:f ′(x )=tx 2-3x +2,由题意可得f ′(x )=0在(0,+∞)上有两个不等实根,即tx 2-3x +2=0在(0,+∞)有两个不等实根,所以⎩⎪⎨⎪⎧t ≠0,3t >0,2t >0,Δ=9-8t >0,解得0<t <98.答案:⎝⎛⎭⎫0,98 3.已知函数f (x )=a ln x +1x(a >0).(1)求函数f (x )的单调区间和极值;(2)是否存在实数a ,使得函数f (x )在[1,e]上的最小值为0?若存在,求出a 的值;若不存在,请说明理由.贾老师数学解:由题意,知函数的定义域为(0,+∞),f ′(x )=a x -1x 2=ax -1x 2(a >0). (1)由f ′(x )>0,解得x >1a, 所以函数f (x )的单调递增区间是⎝⎛⎭⎫1a ,+∞; 由f ′(x )<0,解得0<x <1a, 所以函数f (x )的单调递减区间是⎝⎛⎭⎫0,1a . 所以当x =1a 时,函数f (x )有极小值f ⎝⎛⎭⎫1a =a ln 1a+a =a -a ln a ,无极大值. (2)不存在实数a 满足条件.由(1)可知,当x ∈⎝⎛⎭⎫0,1a 时,函数f (x )单调递减; 当x ∈⎝⎛⎭⎫1a ,+∞时,函数f (x )单调递增.①若0<1a≤1,即a ≥1时,函数f (x )在[1,e]上为增函数, 故函数f (x )的最小值为f (1)=a ln 1+1=1,显然1≠0,故不满足条件a ≥1.②若1<1a <e ,即1e<a <1时,函数f (x )在⎣⎡⎭⎫1,1a 上为减函数,在⎝⎛⎦⎤1a ,e 上为增函数, 故函数f (x )的最小值为f (x )的极小值f ⎝⎛⎭⎫1a =a ln 1a+a =a -a ln a =a (1-ln a )=0,即ln a =1,解得a =e ,故不满足条件1e<a <1. ③若1a ≥e ,即0<a ≤1e 时,函数f (x )在[1,e]上为减函数,故函数f (x )的最小值为f (e)=a ln e +1e=a +1e=0, 即a =-1e ,故不满足条件0<a ≤1e. 综上所述,不存在这样的实数a ,使得函数f (x )在[1,e]上的最小值为0.。
导数与函数的极值与最值

导数与函数的极值与最值在微积分中,导数是描述函数局部变化率的工具,而函数的极值和最值则是函数在特定区间内取得的最大值和最小值。
导数与函数的极值与最值密切相关,通过导数的计算可以确定函数的极值和最值点的位置。
本文将探讨导数与函数的极值与最值之间的关系。
一、导数与函数的极值在微积分中,导数反映了函数在某一点的变化率。
对于函数f(x),若存在导数f'(a),则在点a处函数f(x)在该点的变化速率为f'(a)。
导数的正负决定了函数的增减性,即导数大于0表示函数在该点上升,导数小于0表示函数在该点下降。
函数的极值点即为函数在区间内的最值点,包括极大值和极小值。
在导数的帮助下,我们可以通过求解导数为零的点来确定函数的极值点。
根据费马定理,对于可导的函数f(x),如果函数在某一点x=a处取得极值,且f'(a)存在,则f'(a)=0或f'(a)不存在。
为了确定函数的极值点,我们需要进行以下步骤:1. 求函数的导数f'(x);2. 找到导数为零或不存在的点,即f'(x)=0或f'(x)不存在的点;3. 对求得的点进行二阶导数测试,判断其是极大值还是极小值。
二、导数与函数的最值除了极值点外,函数在特定区间内还可能有最大值和最小值。
与极值点不同,最值点可能出现在函数的端点或者函数在区间内的某个点上。
因此,函数的导数对于确定最值点的重要性较小。
对于区间[a, b]上的函数f(x),要确定函数的最大值和最小值,可以按照以下步骤进行:1. 求函数在区间[a, b]内的导数f'(x);2. 找到区间内的所有导数为零或不存在的点,即f'(x)=0或f'(x)不存在的点;3. 将导数为零或不存在的点与区间的端点进行比较,确定最大值和最小值。
需要注意的是,求得的极值和最值点可能存在于导数为0或不存在的点上,也可能出现在区间的端点上。
因此,在寻找最值点时,需要综合考虑这些情况。
考点14 导数与函数的极值、最值

考点十四导数与函数的极值、最值知识梳理1.函数的极值的定义一般地,设函数f(x)在点x0及附近有定义,如果对x0附近的所有的点,都有f(x)<f(x0 ),就说f(x0)是函数的极大值,x0叫做函数的极大值点.如果对x0附近的所有的点,都有f(x)>f(x0 ),就说f(x0)是函数的极小值,x0叫做函数的极小值点.极大值与极小值统称为函数的极值.极大值点与极小值点统称为极值点.注意:可导函数的极值点必须是导数为0的点,但导数为0的点不一定是极值点,即f′(x0)=0是可导函数f(x)在x=x0处取得极值的必要不充分条件.例如函数y=x3在x=0处有y′=0,但x=0不是极值点.2.判断f(x0 )是极大、极小值的方法当函数f(x)在点x0处连续时,若x0满足f′(x0 )=0,且在x0的两侧f(x)的导数值异号,则x0是f(x)的极值点,f(x0 )是极值.如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值;如果在x0附近的左侧f′(x)<0,右侧f′(x)>0,那么f(x0)是极小值.3.求可导函数f(x)的极值的步骤(1)确定函数的定义域,求导数f′(x) ;(2)求方程f′(x) =0的根;(3)检查f′(x)在x0两侧的符号①若f′(x)在x0两侧的符号“左正右负”,则x0为极大值点;②若f′(x)在x0两侧的符号“左负右正”,则x0为极小值点;③若f′(x)在x0两侧的符号相同,则x0不是极值点.4.函数的最值在闭区间[a,b]上连续的函数f(x)在[a,b]上必有最大值与最小值.(1)若函数f(x)在[a,b]上单调递增,则f(a)为函数的最小值,f(b)为函数的最大值;若函数f(x)在[a,b]上单调递减,则f(a)为函数的最大值,f(b)为函数的最小值.(2)设函数f(x)在[a,b]上连续,在(a,b)内可导,求f(x)在[a,b]上的最大值和最小值的步骤如下:①求f(x)在(a,b)内的极值;②将f(x)的各极值与f(a),f(b)进行比较,其中最大的一个是最大值,最小的一个是最小值.5.函数的极值与最值的区别与联系极值是个“局部”概念,而函数最值是个“整体”概念.函数的极值表示函数在某一点附近的情况,是在局部对函数值的比较;函数的最值表示函数在一个区间上的情况,是对函数在整个区间上的函数值的比较.函数的极值不一定是最值,最值也不一定是极值.典例剖析题型一 利用导数求函数的极值例1 已知函数f (x )=x 3-2x 2e x.求f (x )的极大值和极小值.解析 函数f (x )的定义域为R ,f ′(x )=-x (x 2-5x +4)e x =-x (x -1)(x -4)e x ,当x 变化时,f (x )、f ′(x )的符号变化情况如下:∴f (x )的极大值为f (0)=0和f (4)=32e 4,f (x )的极小值为f (1)=-1e.变式训练 设f (x )=e x1+ax 2,其中a 为正实数.(1)当a =43时,求f (x )的极值点;(2)若f (x )为R 上的单调函数,求a 的取值范围.解析 对f (x )求导得f ′(x )=e x·1+ax 2-2ax (1+ax 2)2.①(1)当a =43时,若f ′(x )=0,则4x 2-8x +3=0,解得x 1=32,x 2=12.结合①,可知所以x 1=32是极小值点,x 2=12是极大值点.(2)若f (x )为R 上的单调函数,则f ′(x )在R 上不变号,结合①与条件a >0,知ax 2-2ax +1≥0在R 上恒成立,即Δ=4a 2-4a =4a (a -1)≤0,由此并结合a >0,知0<a ≤1.所以a 的取值范围为{a |0<a ≤1}.题型二 利用极值求参数例2 设f (x )=ln(1+x )-x -ax 2,若f (x )在x =1处取得极值,则a 的值为________. 答案 -14解析 由题意知,f (x )的定义域为(-1,+∞), 且f ′(x )=11+x -2ax -1=-2ax 2-(2a +1)x 1+x,由题意得:f ′(1)=0,则-2a -2a -1=0,得a =-14,又当a =-14时,f ′(x )=12x 2-12x 1+x =12x (x -1)1+x ,当0<x <1时,f ′(x )<0;当x >1时,f ′(x )>0, 所以f (1)是函数f (x )的极小值,所以a =-14.变式训练 已知x =3是函数f (x )=a ln x +x 2-10x 的一个极值点,则实数a =________. 答案 12解析 f ′(x )=a x +2x -10,由f ′(3)=a3+6-10=0,得a =12,经检验满足条件.题型三 利用导数求函数的最值例3 设函数f (x )=x +ax 2+b ln x ,曲线y =f (x )过P (1,0),且在P 点处的切线斜率为2. (1)求a ,b 的值;(2)令g (x )=f (x )-2x +2,求g (x )在定义域上的最值. 答案 (1)a =-1,b =3 (2)最大值为0,无最小值 解析 (1)f ′(x )=1+2ax +bx(x >0),又f (x )过点P (1,0),且在点P 处的切线斜率为2,∴⎩⎪⎨⎪⎧ f (1)=0,f ′(1)=2,即⎩⎪⎨⎪⎧1+a =0,1+2a +b =2.解得a =-1,b =3. (2)由(1)知,f (x )=x -x 2+3ln x ,其定义域为(0,+∞), ∴g (x )=2-x -x 2+3ln x ,x >0.则g ′(x )=-1-2x +3x =-(x -1)(2x +3)x .当0<x <1时,g ′(x )>0;当x >1时,g ′(x )<0.所以g (x )在(0,1)上单调递增,在(1,+∞)上单调递减. ∴g (x )的最大值为g (1)=0,g (x )没有最小值.变式训练 已知函数f (x )=ln x -ax (a ∈R ). (1)求函数f (x )的单调区间;(2)当a >0时,求函数f (x )在[1,2]上的最小值. 解析 (1)f ′(x )=1x-a (x >0),①当a ≤0时,f ′(x )=1x -a >0,即函数f (x )的单调增区间为(0,+∞).②当a >0时,令f ′(x )=1x -a =0,可得x =1a ,当0<x <1a 时,f ′(x )=1-ax x >0;当x >1a 时,f ′(x )=1-ax x<0,故函数f (x )的单调递增区间为⎝⎛⎦⎤0,1a ,单调递减区间为⎣⎡⎭⎫1a ,+∞. (2)①当1a ≤1,即a ≥1时,函数f (x )在区间[1,2]上是减函数,所以f (x )的最小值是f (2)=ln 2-2a .②当1a ≥2,即0<a ≤12时,函数f (x )在区间[1,2]上是增函数,所以f (x )的最小值是f (1)=-a .③当1<1a <2,即12<a <1时,函数f (x )在⎣⎡⎦⎤1,1a 上是增函数,在⎣⎡⎦⎤1a ,2上是减函数.又f (2)-f (1)=ln 2-a ,所以当12<a <ln 2时,最小值是f (1)=-a ;当ln 2≤a <1时,最小值为f (2)=ln 2-2a . 综上可知,当0<a <ln 2时,函数f (x )的最小值是-a ; 当a ≥ln 2时,函数f (x )的最小值是ln 2-2a .解题要点 求函数f (x )在[a ,b ]上的最大值和最小值的步骤: (1)求函数在(a ,b )内的极值;(2)求函数在区间端点处的函数值f (a ),f (b );(3)将函数f (x )的各极值与f (a ),f (b )比较,其中最大的一个为最大值,最小的一个为最小值.当堂练习1.已知函数y =f (x ),其导函数y =f ′(x )的图象如图所示,则y =f (x ) ________.① 在(-∞,0)上为减函数 ② 在x =0处取极小值 ③ 在(4,+∞)上为减函数 ④ 在x =2处取极大值答案 ③解析 由f ′(x )的图象可知,f (x )在(-∞,0)上单调递增,在(0,2)上单调递减,∴f (x )在x =0处取得极大值,同理f (x )在x =2处取得极小值,故①,②,④均不正确 ,由f ′(x )的图象可知f (x )在(4,+∞)上单调递减.2.函数f (x )=(x 2-1)2+2的极值点是________.①x =1 ②x =-1 ③x =1或-1或0 ④x =0 答案 ③解析 ∵f (x )=x 4-2x 2+3,由f ′(x )=4x 3-4x =4x (x +1)(x -1)=0,得x =0或x =1或x =-1.又当x <-1时,f ′(x )<0,当-1<x <0时,f ′(x )>0,当0<x <1时,f ′(x )<0,当x >1时,f ′(x )>0, ∴x =0,1,-1都是f (x )的极值点.3. 若函数y =ax 3+bx 2取得极大值和极小值时的x 的值分别为0和13,则a 与b 的关系是________. 答案 a +2b =0解析 y ′=3ax 2+2bx ,据题意,0,13是方程3ax 2+2bx =0的两根,∴-2b 3a =13,∴a +2b =0.4.函数f (x )=xe x ,x ∈[0,4]的最大值是________.答案 1e5.若函数f (x )=x 2+ax +1在x =1处取极值,则a =________.答案 3解析 f ′(x )=x 2+2x -a(x +1)2,由f (x )在x =1处取得极值知f ′(1)=0,∴a =3.课后作业一、 填空题1.函数f (x )=x 33+x 2-3x -4在[0,2]上的最小值是________.答案 -173解析 f ′(x )=x 2+2x -3,令f ′(x )=0,得x =1(x =-3舍去), 又f (0)=-4,f (1)=-173,f (2)=-103,故f (x )在[0,2]上的最小值是f (1)=-173.2.函数f (x )=x 3-32x 2-6x 的极值点的个数是________.答案 2解析 f ′(x )=3x 2-3x -6=3(x 2-x -2)=3(x -2)(x +1).令f ′(x )=0,得x =-1或x =2.易知x =-1为f (x )的极大值点,x =2为f (x )的极小值点.故f (x )的极值点有2个. 3.函数f (x )=12x -x 3在区间[-3,3]上的最小值是________. 答案 -16解析 由f ′(x )=12-3x 2=0,得x =-2或x =2. 又f (-3)=-9,f (-2)=-16,f (2)=16,f (3)=9, ∴函数f (x )在[-3,3]上的最小值为-16.4.f (x )=e x -x (e 为自然对数的底数)在区间[-1,1]上的最大值是________. 答案 e -1解析 f ′(x )=e x -1,令f ′(x )=0,得x =0.令f ′(x )>0,得x >0,令f ′(x )<0,得x <0,则函数f (x )在(-1,0)上单调递减,在(0,1)上单调递增,f (-1)=e -1+1,f (1)=e -1,f (-1)-f (1)=1e +2-e<12+2-e<0,所以f (1)>f (-1).5.若商品的年利润y (万元)与年产量x (百万件)的函数关系式为y =-x 3+27x +123(x >0),则获得最大利润时的年产量为________. 答案 3百万件解析 依题意得,y ′=-3x 2+27=-3(x -3)(x +3),当0<x <3时,y ′>0;当x >3时,y ′<0.因此,当x =3时,该商品的年利润最大.6.已知函数f (x )=x 3+ax 2+bx -a 2-7a 在x =1处取得极大值10,则ab的值为________.答案 -23解析 由题意知,f ′(x )=3x 2+2ax +b ,f ′(1)=0,f (1)=10,即⎩⎪⎨⎪⎧3+2a +b =01+a +b -a 2-7a =10,解得⎩⎪⎨⎪⎧a =-2b =1或⎩⎪⎨⎪⎧a =-6b =9,经检验⎩⎪⎨⎪⎧a =-6b =9满足题意,故a b =-23. 7.设函数f (x )在R 上可导,其导函数为f ′(x ),且函数y =(1-x )f ′(x )的图象如图所示,则下列结论中一定成立的是________.(填序号)①函数f (x )有极大值f (2)和极小值f (1) ②函数f (x )有极大值f (-2)和极小值f (1) ③函数f (x )有极大值f (2)和极小值f (-2) ④函数f (x )有极大值f (-2)和极小值f (2) 答案 ④解析 由题图可知,当x <-2时,f ′(x )>0;当-2<x <1时,f ′(x )<0;当1<x <2时,f ′(x )<0;当x >2时,f ′(x )>0.由此可以得到函数f (x )在x =-2处取得极大值,在x =2处取得极小值. 8.已知f (x )=2x 3-6x 2+m (m 为常数)在[-2,2]上有最大值3,那么此函数在[-2,2]上的最小值是________. 答案 -37解析 f ′(x )=6x 2-12x =6x (x -2),∴f (x )在(-2,0)上单调递增,在(0,2)上单调递减. ∴x =0为极大值点,也为最大值点. ∴f (0)=m =3,∴m =3. ∴f (-2)=-37,f (2)=-5. ∴最小值是-37.9.函数f (x )=x 3+ x 2-x +2在[0,2]上的最小值是________. 答案4927解析 f ′(x )=3x 3+2x -1,f ′(x )=0,x ∈[0,2],得x =13.比较f (0)=2,f (13)=4927,f (2)=12.可知最小值为4927.10.某商场从生产厂家以每件20元购进一批商品,若该商品零售价为p 元,销量Q (单位:件)与零售价p (单位:元)有如下关系:Q =8 300-170p -p 2,则该商品零售价定为__________ 元时利润最大,利润的最大值为__________. 答案 30 23 000解析 设商场销售该商品所获利润为y 元,则y =(p -20)Q =(p -20)(8 300-170p -p 2)=-p 3-150p 2+11 700p -166 000(p ≥20),∴y ′=-3p 2-300p +11 700. 令y ′=0得p 2+100p -3 900=0,∴p =30或p =-130(舍去),则p ,y ,y ′变化关系如下表:∴当p =30时,y 取极大值为23 000元.又y =-p 3+150p 2+11 700p -166 000在(20,+∞)上只有一个极值,故也是最值. ∴该商品零售价定为每件30元,所获利润最大为23 000元.11.若y =a ln x +bx 2+x 在x =1和x =2处有极值,则a =________,b =________. 答案 -23 -16解析 y ′=ax+2bx +1.由已知⎩⎪⎨⎪⎧a +2b +1=0,a 2+4b +1=0,解得⎩⎨⎧a =-23,b =-16.二、解答题12. (2015北京文节选)设函数f (x )=x 22-k ln x ,k >0.求f (x )的单调区间和极值解析 函数的定义域为(0,+∞).由f (x )=x 22-k ln x (k >0)得f ′(x )=x -k x =x 2-kx.由f ′(x )=0解得x =k (负值舍去).f (x )与f ′(x )在区间(0,+∞)上的变化情况如下表:所以,f (x )f (x )在x =k 处取得极小值f (k )=k (1-ln k )2.13.设函数f (x )=2x 3+3ax 2+3bx +8c 在x =1及x =2时取得极值. (1)求a 、b 的值;(2)若对于任意的x ∈[0,3],都有f (x )<c 2成立,求c 的取值范围. 解析 (1)f ′(x )=6x 2+6ax +3b ,因为函数f (x )在x =1及x =2处取得极值,则有f ′(1)=0,f ′(2)=0,即⎩⎪⎨⎪⎧6+6a +3b =0,24+12a +3b =0.解得a =-3,b =4. (2)由(1)可知,f (x )=2x 3-9x 2+12x +8c ,f ′(x )=6x 2-18x +12=6(x -1)(x -2). 当x ∈(0,1)时,f ′(x )>0;当x ∈(1,2)时,f ′(x )<0;当x ∈(2,3)时,f ′(x )>0. 所以,当x =1时,f (x )取得极大值f (1)=5+8c ,又f (0)=8c ,f (3)=9+8c . 则当x ∈[0,3]时,f (x )的最大值为f (3)=9+8c . 因为对于任意的x ∈[0,3],有f (x )<c 2恒成立, 所以9+8c <c 2,解得c <-1或c >9, 因此c 的取值范围为(-∞,-1)∪(9,+∞).。
导数与函数的极值与最值

导数与函数的极值与最值导数与函数的极值与最值是微积分中的重要概念,它们在实际问题中有着广泛的应用。
本文将介绍导数、函数的极值与最值的基本概念、求解方法及其应用。
一、导数的定义及性质导数是函数的一个基本性质,它描述了函数在某一点上的变化率。
在数学中,导数可以用极限的概念来定义。
当函数f(x)在点x处可导时,它的导数f'(x)的定义如下:f'(x) = lim┬(Δx→0)〖(f(x+Δx)-f(x))/Δx〗导数具有一些重要的性质,包括可导函数的和、差、积、商的导数运算法则。
这些性质为求解函数的极值和最值提供了数学工具。
二、函数的极值与最值函数的极值指的是函数在某一区间内取得的最大值或最小值。
特别地,当函数在某一点上取得最大值或最小值时,称为函数的局部极值。
函数的极大值和极小值统称为极值。
函数的最值是指函数在定义域上取得的最大值或最小值。
与极值不同的是,最值可能发生在函数的端点或无穷远处。
函数的最值是极值的一个特例。
三、求解函数的极值与最值为了求解函数的极值和最值,我们需要利用导数的概念和性质。
下面介绍一些常用的求解方法。
1. 导数为零的点如果在某一点x处,函数的导数f'(x)为零或不存在,那么该点可能是函数的极值点。
然而,这种方法只是提供了一个可能性,我们还需要进行进一步的验证。
2. 导数的符号变化对于连续函数f(x),如果在某一点x处,f'(x)由正数变为负数,或由负数变为正数,那么该点可能是函数的极值点。
3. 极值的判别法通过求解函数的导数f'(x)的零点,可以得到函数的驻点,即可能的极值点。
然后,通过极值的判别法判断哪些点是真正的极值点。
四、导数与函数的极值与最值的应用导数与函数的极值与最值在实际问题中有着广泛的应用。
以下列举几个例子:1. 经济学中的最大收益问题在经济学中,我们常常需要求解某一产品的最大利润。
利用导数与函数的极值与最值的概念,我们可以优化生产过程,使得利润达到最大化。
导数与函数的极值、最值

课 前 ·双 基 落 实
课 堂 ·考 点 突 破
课后· 三维演练
导数与函数的极值、最值 结 束
[小题体验]
1 3 1.(教材习题改编)函数 f(x)= x -4x+4 的极大值为________. 3 28 答案: 3 1 2. 已知函数 f(x)= x-sin x, 则 f(x)在[0, π]上的值域为________. 2
导数与函数的极值、最值 结 束
[题点全练]
角度一:判断函数极值点的个数 1.函数 f(x)=x3+3x2+3x-a 的极值点的个数是________.
解析:f′(x)=3x2+6x+3=3(x+1)2≥0,则 f(x)在 R 上是 增函数,故不存在极值点. 答案:0
课 前 ·双 基 落 实
课 堂 ·考 点 突 破
课 前 ·双 基 落 实
课 堂 ·考 点 突 破
课后· 三维演练
导数与函数的极值、最值 结 束
ex 4.已知函数 f(x)= x . (1)求函数 f(x)的单调区间; (2)设 g(x)=xf(x)-ax+1,若 g(x)在(0,+∞)上存在极 值点,求实数 a 的取值范围.
ex 解:(1)f(x)= x ,x∈(-∞,0)∪(0,+∞), exx-1 所以 f′(x)= . x2 当 f′(x)=0 时,x=1.
1 x∈2,1时,f′(x)<0,故函数 1 f(x)在2,1上单调递减;
当 x∈(1,2]时,f′(x)>0,故函数 f(x)在(1,2]上单调递增,所 以 f(x)min=f(1)=0,所以 a≤0,即 a 的最大值为 0. 答案:0
课 前 ·双 基 落 实 课 堂 ·考 点 突 破 课后· 三维演练
[小题纠偏]
导数与函数极值最值

例5 已知函数f ( x ) (2 x ax 2 )ln(1 x ) 2 x , 若x 0
是f ( x )的极大值点,求a.
小结
1.重视核心概念学习
极值点判断必须经过导数值异号变化,平时
一些易错问题是对定义概念掌握不到位,或者
对条件考虑不周全引起.
2.含参的函数,对参数的讨论做到不重不漏,
导数与函数的极值、最值
高考导航:
理解函数极值的概念及函数在某点取到极值的条
件,会用导数求函数的极大(小)值、会求闭区
间上函数的最大(小)值.
极值的
概念
导数与
极值
极大值
极小值
极大值
极小值
x0 为函数 y=f(x)定义域内一点,如果对 x0 附近所有的 x 都有 f(x)<f(x,0)
严谨规范,注意定义域.
3.含参二次函数,对勾函数等可结合图象判断
单调性.
备用例题
例 6. 函数 f(x)=ax3+(a-1)x2-x+2(0≤x≤1)在 x=1 处取得最
小值,则实数 a 的取值范围是 (
A.a≤0
B.0≤a≤
C.a≤
)
D.a≤1
(1)求f ( x ) ( x 1)ln x在x [ 1 , 2]上的取值范围.
基础信心练
二、高考 联考怎么考(大题模板)
例3 设函数f ( x ) = ( x - a )2 ( x + b )e x,b ∈ R,
x = a 是f(x)的一个极大值点,求的取值范围.
例 4 设函数
f(x)= -k +ln
高中数学知识点总结导数与函数的极值与最值

高中数学知识点总结导数与函数的极值与最值导数与函数的极值与最值是高中数学中的重要知识点,也是数学分析中的基础内容。
导数可以帮助我们分析函数的变化趋势,而极值与最值则能帮助我们找到函数的局部极大值和最大值。
本文将对导数与函数的极值与最值进行总结和介绍。
一、导数的定义与求法1.导数的定义导数表示函数在某一点处的变化率,可以理解为函数图像在该点的斜率。
若函数f(x)在点x处可导,则函数在该点的导数表示为f'(x),可以用极限的形式来定义,即:f'(x) = lim(h→0)[f(x+h)-f(x)]/h2.导数的求法常见函数的导数求法有以下几种方法:(1)利用导数定义进行求解,使用极限的性质来计算;(2)使用基本导数公式,如常数函数导数为0,幂函数导数为幂次减1等;(3)使用导数的基本运算法则,如和差法则、积法则、商法则等;(4)利用复合函数、反函数和参数方程的求导法则;(5)利用隐函数求导法则,将函数的表达式转化为关于x和y的方程,然后进行求导等。
二、函数的极值与最值1.极值的定义函数f(x)在点x=a处的极值,指的是函数在该点的函数值最大或最小。
如果存在f(a) > f(x)(或f(a) < f(x))对于x在a的某个邻域内成立,则称f(a)是函数的极大值(或极小值)。
2.函数极值的判定条件对于函数f(x),有以下判定条件可以帮助我们确定其极值:(1)一阶导数的零点:若f'(x) = 0,则该点可能为函数的极值点;(2)二阶导数的符号:若f''(x) > 0,则该点为函数的极小值点;若f''(x) < 0,则该点为函数的极大值点;(3)导数的单调性:若f'(x)在某个区间上始终保持正(或负)号,则该区间上的极值点为极小值(或极大值)点;(4)端点:函数在区间的端点上也可能存在极值。
3.最值的定义与求法函数f(x)在区间[a, b]上的最大值与最小值称为最值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
导数与函数的极值、最值最新考纲了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(其中多项式函数不超过三次);会求闭区间上函数的最大值、最小值(其中多项式函数不超过三次).知识梳理1.函数的极值与导数(1)判断f(x0)是极值的方法一般地,当函数f(x)在点x0处连续且f′(x0)=0,①如果在x0附近的左侧f′(x)>0,右侧f′(x)<0,那么f(x0)是极大值;②如果在x0附近的左侧f′(x)≤0,右侧f′(x)≥0,那么f(x0)是极小值.(2)求可导函数极值的步骤:①求f′(x);②求方程f′(x)=0的根;③检查f′(x)在方程f′(x)=0的根的左右两侧的符号.如果左正右负,那么f(x)在这个根处取得极大值;如果左负右正,那么f(x)在这个根处取得极小值.2.函数的最值与导数(1)函数f(x)在[a,b]上有最值的条件如果在区间[a,b]上函数y=f(x)的图象是连续不断的曲线,那么它必有最大值和最小值.(2)设函数f(x)在[a,b]上连续且在(a,b)内可导,求f(x)在[a,b]上的最大值和最小值的步骤如下:①求f(x)在(a,b)内的极值;②将f(x)的各极值与f(a),f(b)比较,其中最大的一个是最大值,最小的一个是最小值.诊断自测1.判断正误(在括号内打“√”或“×”)精彩PPT展示(1)函数在某区间上或定义域内极大值是唯一的.(×)(2)函数的极大值不一定比极小值大.(√)(3)对可导函数f(x),f′(x0)=0是x0点为极值点的充要条件.(×)(4)函数的最大值不一定是极大值,函数的最小值也不一定是极小值.(√)2.函数f(x)=-x3+3x+1有()A.极小值-1,极大值1B.极小值-2,极大值3C.极小值-2,极大值2D.极小值-1,极大值3解析因为f(x)=-x3+3x+1,故有y′=-3x2+3,令y′=-3x2+3=0,解得x =±1,于是,当x变化时,f′(x),f(x)的变化情况如下表:f(x)极大值极小值所以f(x)的极小值为f(-1)=-1,f(x)的极大值为f(1)=3.答案 D3.设函数f(x)在R上可导,其导函数为f′(x),且函数y=(1-x)f′(x)的图象如图所示,则下列结论中一定成立的是()A.函数f(x)有极大值f(2)和极小值f(1)B.函数f(x)有极大值f(-2)和极小值f(1)C.函数f(x)有极大值f(2)和极小值f(-2)D.函数f(x)有极大值f(-2)和极小值f(2)解析由题图可知,当x<-2时,f′(x)>0;当-2<x<1时,f′(x)<0;当1<x <2时,f′(x)<0;当x>2时,f′(x)>0.由此可以得到函数f(x)在x=-2处取得极大值,在x=2处取得极小值.答案 D4.(2015·陕西卷)函数y=x e x在其极值点处的切线方程为________.解析由y=x e x可得y′=e x+x e x=e x(x+1),从而可得y=x e x在(-∞,-1)上递减,在(-1,+∞)上递增,所以当x=-1时,y=x e x取得极小值-e-1,因为y′|x=-1=0,故切线方程为y=-e-1,即y=-1e.答案y=-1 e5.(人教A选修1-1P97例5改编)函数f(x)=13x3-4x+4在[0,3]上的最大值与最小值分别为________.解析由f(x)=13x3-4x+4,得f′(x)=x2-4=(x-2)(x+2),令f′(x)>0,得x>2或x<-2;令f′(x)<0,得-2<x<2.所以f(x)在(-∞,-2),(2,+∞)上单调递增;在(-2,2)上单调递减,而f(2)=-43,f(0)=4,f(3)=1,故f(x)在[0,3]上的最大值是4,最小值是-43.答案 4,-43考点一 利用导数研究函数的极值问题 [微题型1] 求不含参函数的极值【例1-1】 已知函数f (x )=x 4+a x -ln x -32,其中a ∈R ,且曲线y =f (x )在点(1,f (1))处的切线垂直于直线y =12x . (1)求a 的值; (2)求函数f (x )的极值.解 (1)对f (x )求导得f ′(x )=14-a x 2-1x ,由f (x )在点(1,f (1))处的切线垂直于直线y =12x , 知f ′(1)=-34-a =-2,解得a =54.(2)由(1)知f (x )=x 4+54x -ln x -32,则f ′(x )=x 2-4x -54x 2. 令f ′(x )=0,解得x =-1或x =5.因为x =-1不在f (x )的定义域(0,+∞)内,故舍去. 当x ∈(0,5)时,f ′(x )<0,故f (x )在(0,5)上为减函数; 当x ∈(5,+∞)时,f ′(x )>0,故f (x )在(5,+∞)上为增函数. 由此知函数f (x )在x =5时取得极小值f (5)=-ln 5,f (x )无极大值.[微题型2] 求含参函数的极值【例1-2】 (2015·银川一中一模)求函数f (x )=ln x -ax ,a ∈R 的极值. 解 函数f (x )的定义域为(0,+∞). 求导数,得f ′(x )=1x -a =1-ax x .(1)若a ≤0,则f ′(x )>0,f (x )是(0,+∞)上的增函数,无极值; (2)若a >0,令f ′(x )=0,得x =1a .当x ∈⎝ ⎛⎭⎪⎫0,1a 时,f ′(x )>0,f (x )在⎝ ⎛⎭⎪⎫0,1a 上是增函数; 当x ∈⎝ ⎛⎭⎪⎫1a ,+∞时,f ′(x )<0,f (x )在⎝ ⎛⎭⎪⎫1a ,+∞上是减函数.∴当x =1a 时,f (x )有极大值,极大值为f ⎝ ⎛⎭⎪⎫1a =ln 1a -1=-ln a -1.综上所述,当a ≤0时,f (x )无极值;当a >0时,f (x )极大值为-ln a -1,无极小值. 规律方法 运用导数求可导函数y =f (x )的极值的步骤:(1)先求函数y =f (x )的定义域,再求函数y =f (x )的导数f ′(x );(2)求方程f ′(x )=0的根;(3)检查导数f ′(x )在方程根左右的值的符号. [微题型3] 已知极值求参数【例1-3】 已知关于x 的函数f (x )=-13x 3+bx 2+cx +bc 在x =1处有极值-43,试求b ,c 的值.解 ∵f ′(x )=-x 2+2bx +c ,由f (x )在x =1处有极值-43, 可得⎩⎪⎨⎪⎧f ′(1)=-1+2b +c =0,f (1)=-13+b +c +bc =-43.解得⎩⎨⎧b =1,c =-1或⎩⎨⎧b =-1,c =3. 若b =1,c =-1,则f ′(x )=-x 2+2x -1=-(x -1)2≤0,此时f (x )没有极值; 若b =-1,c =3,则f ′(x )=-x 2-2x +3=-(x +3)(x -1). 当x 变化时,f (x ),f ′(x )的变化情况如下表:∴当x =1时,f (x )有极大值-43,故b =-1,c =3即为所求.规律方法 已知函数的极值求参数时,通常利用函数的导数在极值点处的取值等于零来建立关于参数的方程.需注意的是,可导函数在某点处的导数值等于零只是函数在该点处取得极值的必要条件,所以必须对求出的参数值进行检验,看是否符合函数取得极值的条件.【训练1】 设函数f (x )=ax 3-2x 2+x +c (a >0). (1)当a =1,且函数图象过(0,1)时,求函数的极小值; (2)若f (x )在R 上无极值点,求a 的取值范围. 解 由题意得f ′(x )=3ax 2-4x +1. (1)函数图象过(0,1)时,有f (0)=c =1. 当a =1时,f ′(x )=3x 2-4x +1.令f ′(x )>0,解得x <13或x >1;令f ′(x )<0,解得13<x <1.所以函数在⎝ ⎛⎭⎪⎫-∞,13和(1,+∞)上单调递增;在⎣⎢⎡⎦⎥⎤13,1上单调递减, 故函数f (x )的极小值是f (1)=13-2×12+1+1=1.(2)若f (x )在R 上无极值点,则f (x )在R 上是单调函数,即f ′(x )≥0或f ′(x )≤0恒成立.当a =0时,f ′(x )=-4x +1,显然不满足条件;当a ≠0时,f ′(x )≥0或f ′(x )≤0恒成立的充要条件是Δ=(-4)2-4×3a ×1≤0,即16-12a ≤0,解得a ≥43. 综上,a 的取值范围是⎣⎢⎡⎭⎪⎫43,+∞.考点二 利用导数解决函数的最值问题【例2】(2015·德阳模拟)已知函数f(x)=13x3-ax+1.(1)当x=1时,f(x)取得极值,求a的值;(2)求f(x)在[0,1]上的最小值.解因为f′(x)=x2-a,(1)当x=1时,f(x)取得极值,所以f′(1)=1-a=0,a=1,又当x∈(-1,1)时,f′(x)<0;x∈(1,+∞)时,f′(x)>0,所以f(x)在x=1处取得极小值,即a=1时符合题意.(2)①当a≤0时,f′(x)>0对x∈(0,1)恒成立,所以f(x)在(0,1)上单调递增,f(x)在x=0处取得最小值f(0)=1.②当a>0时,令f′(x)=x2-a=0,解得x=-a或a.ⅰ.当0<a<1时,a<1,当x∈(0,a)时,f′(x)<0,f(x)单调递减;当x∈(a,1)时,f′(x)>0,f(x)单调递增,所以f(x)在x=a处取得最小值f(a)=1-2a a 3.ⅱ.当a≥1时,a≥1.x∈(0,1)时,f′(x)<0,f(x)单调递减,所以f(x)在x=1处取得最小值f(1)=43-a.综上所述,当a≤0时,f(x)在x=0处取得最小值f(0)=1,当0<a<1时,f(x)在x=a处取得最小值f(a)=1-2a a3,当a≥1时,f(x)在x=1处取得最小值f(1)=43-a.规律方法(1)如果在区间[a,b]上函数y=f(x)的图象是一条连续不断的曲线,那么它必有最大值和最小值.(2)求闭区间上可导函数的最值时,对函数的极值是极大值还是极小值可不作判断,直接与端点的函数值比较即可.(3)当连续函数的极值点只有一个时,相应的极值必为函数的最值.【训练2】 (2014·江西卷)已知函数f (x )=(4x 2+4ax +a 2)x ,其中a <0. (1)当a =-4时,求f (x )的单调递增区间; (2)若f (x )在区间[1,4]上的最小值为8,求a 的值. 解 (1)当a =-4时,由f ′(x )=2(5x -2)(x -2)x=0得x =25或x =2,由f ′(x )>0得x ∈⎝ ⎛⎭⎪⎫0,25或x ∈(2,+∞),故函数f (x )的单调递增区间为⎝ ⎛⎭⎪⎫0,25和(2,+∞). (2)f ′(x )=(10x +a )(2x +a )2x,a <0,由f ′(x )=0得x =-a 10或x =-a2. 当x ∈⎝ ⎛⎭⎪⎫0,-a 10时,f (x )单调递增; 当x ∈⎝ ⎛⎭⎪⎫-a10,-a 2时,f (x )单调递减;当x ∈⎝ ⎛⎭⎪⎫-a 2,+∞时,f (x )单调递增.易知f (x )=(2x +a )2x ≥0,且f ⎝ ⎛⎭⎪⎫-a 2=0.①当-a2≤1,即-2≤a <0时, f (x )在[1,4]上的最小值为f (1), 由f (1)=4+4a +a 2=8, 得a =±22-2,均不符合题意.②当1<-a2≤4,即-8≤a <-2时,f (x )在[1,4]上的最小值为f ⎝ ⎛⎭⎪⎫-a 2=0,不符合题意.③当-a2>4,即a <-8时,f (x )在[1,4]上的最小值可能在x =1或x =4处取得,而f (1)≠8,由f (4)=2(64+16a +a 2)=8得a =-10或a =-6(舍去),当a =-10时,f (x )在(1,4)上单调递减,f (x )在[1,4]上的最小值为f (4)=8,符合题意. 综上,a =-10.考点三利用导数研究生活中的优化问题【例3】某村庄拟修建一个无盖的圆柱形蓄水池(不计厚度).设该蓄水池的底面半径为r米,高为h米,体积为V立方米.假设建造成本仅与表面积有关,侧面的建造成本为100元/平方米,底面的建造成本为160元/平方米,该蓄水池的总建造成本为12 000π元(π为圆周率).(1)将V表示成r的函数V(r),并求该函数的定义域;(2)讨论函数V(r)的单调性,并确定r和h为何值时该蓄水池的体积最大.解(1)因为蓄水池侧面的总成本为100·2πrh=200πrh元,底面的总成本为160πr2元.所以蓄水池的总成本为(200πrh+160πr2)元.又根据题意得200πrh+160πr2=12 000π,所以h=15r(300-4r2),从而V(r)=πr2h=π5(300r-4r3).因r>0,又由h>0可得0<r<53,故函数V(r)的定义域为(0,53).(2)因V(r)=π5(300r-4r3)(0<r<53),故V′(r)=π5(300-12r2),令V′(r)=0,解得r=5或-5(因r=-5不在定义域内,舍去).当r∈(0,5)时,V′(r)>0,故V(r)在(0,5)上为增函数;当r∈(5,53)时,V′(r)<0,故V(r)在(5,53)上为减函数.由此可知,V(r)在r=5处取得最大值,此时h=8.即当r=5,h=8时,该蓄水池的体积最大.规律方法求实际问题中的最大值或最小值时,一般是先设自变量、因变量,建立函数关系式,并确定其定义域,利用求函数的最值的方法求解,注意结果应与实际情况相结合.用导数求解实际问题中的最大(小)值时,如果函数在开区间内只有一个极值点,那么依据实际意义,该极值点也就是最值点.【训练3】某商场销售某种商品的经验表明,该商品每日的销售量y(单位:千克)与销售价格x(单位:元/千克)满足关系式y=ax-3+10(x-6)2,其中3<x<6,a为常数,已知销售价格为5元/千克时,每日可售出该商品11千克.(1)求a的值;(2)若该商品的成本为3元千克,试确定销售价格x的值,使商场每日销售该商品所获得的利润最大.解(1)因为x=5时,y=11,所以a2+10=11,a=2.(2)由(1)知,该商品每日的销售量y=2x-3+10(x-6)2.所以商场每日销售该商品所获得的利润f(x)=(x-3)[2x-3+10(x-6)2]=2+10(x-3)(x-6)2,3<x<6.从而,f′(x)=10[(x-6)2+2(x-3)(x-6)]=30(x-4)(x-6).于是,当x变化时,f′(x),f(x)的变化情况如下表:x (3,4)4(4,6)f′(x)+0-f(x)单调递增极大值42单调递减由上表可得,x=4是函数f(x)在区间(3,6)内的极大值点,也是最大值点. 所以,当x=4时,函数f(x)取得最大值,且最大值等于42.答当销售价格为4元千克时,商场每日销售该商品所获得的利润最大.[思想方法]1.利用导数研究函数的单调性、极值、最值可列表观察函数的变化情况,直观而且条理,减少失分.2.求极值、最值时,要求步骤规范、表格齐全;含参数时,要讨论参数的大小.3.可导函数y=f(x)在点x0处取得极值的充要条件是f′(x0)=0,且在x0左侧与右侧f′(x)的符号不同.4.若函数y=f(x)在区间(a,b)内有极值,那么y=f(x)在(a,b)内绝不是单调函数,即在某区间上单调函数没有极值.[易错防范]1.求函数单调区间与函数极值时要养成列表的习惯,可使问题直观且有条理,减少失分的可能.2.求函数最值时,不可想当然地认为极值点就是最值点,要通过认真比较才能下结论.。
