人教版必修四数学《任意角》PPT课件
合集下载
07【数学】1.1.1《任意角》课件(新人教A版必修4)

B o
A
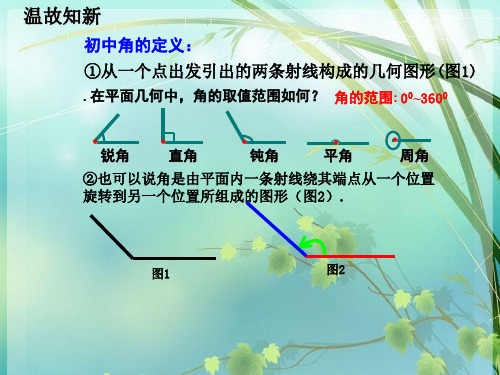
知识探究(一):角的概念的推广
思考1:对于角的图形特点有如下两种认 识:①角是由平面内一点引出的两条射 线所组成的图形(如图1);②角是由平 面内一条射线绕其端点从一个位置旋转 到另一个位置所组成的图形(如图2). 你认为哪种认识更科学、合理?
图1
图2
思考2:如图,一条射线的端点是O,它
知识学习:终边在坐标轴上角的取值
900 +Kx3600 y
1800 +Kx3600
x 00 +Kx3600
o 或3600+KX3600
2700 +Kx3600
例2 写出终边落在y轴上的角的集合。
• 解:在0°~360°范围内,在终边在y轴上的角有两个,90°,270°
∴与90°角终边相同的角构成的集合 {偶数}∪{奇数}
S1={β| β=900+K∙3600,K∈Z}
∴与270°角终边相同的角构成的集合
={整数}
S2={β| β=2700+K∙3600,K∈Z} ={β| β=900+1800+2K∙1800,K∈Z}
900+K∙3600 Y
所以 终边落在y轴上的角的集合为
X O
S=S1∪S2 ={β| β=900+2K∙1800,K∈Z} ∪{β| β=900+(2K+1)1800 ,K∈Z} 2700+k∙3600
就说这个角是第几象限的角;如果角的
终边在坐标轴上,就认为这个角不属于
如何象限,或称这个角为轴线角.那么下
列各角:-50°,405°,210°,
-200°,-450°分别是第几象限的角?
y
y
人教版必修四年级数学《任意角》PPT教学课件

S={β|β=90°+2k·180°,k∈Z}∪{β|β=90°+180°+2k·180°, k∈Z} = {β|β = 90°+ 2k·180°, k∈Z}∪{β|β = 90°+ (2k + 1)·180°,k∈Z}={β|β=90°+n·180°,n∈Z}.
·新课讲授·
思考 2:
终边在x轴、y轴上的角的集合分别如何表示?
知识迁移 1:
终边在射线上的角如何表示?
S | k 360 , k Z
·新课讲授·
思考 2:
终边在x轴、y轴上的角的集合分别如何表示?
解 S={α|α=k·360°,k∈Z}∪{α|α=k·360°+180°,k∈Z} ={α |α =2k ·180°,k ∈Z}∪{α |α =(2k +1)·180°,k ∈Z} ={α |α =n ·180°,n ∈Z}.
《任意角》
·人教版必修四数学PPT课件·
优品老师
目 录
一 学习目标 二 新课导入 三 新课讲授
四 课堂检测 五 课堂总结
一 学习目标
·学习目标·
(1)推广角的概念、引入大于角和负角; (2)理解并掌握正角、负角、零角的定义; (3)理解任意角以及象限角的概念; (4)掌握所有与角终边相同的角(包括角)的表示方法; (5)树立运动变化观点,深刻理解推广后的角的概念;
一般地,所有与角α 终边相同的角,连同角α 在内,可构成一个集合S={β|β=α +k·360°, k∈Z},即任一与角α 终边相同的角,都可以表示成角α 与整数个周角的和.
注意: (1)α 为任意角. (2)k·360°与α 之间是“+”号,k·360°-α 可理解为k·360°+(-α ). (3)相等的角终边一定相同;终边相同的角不一定相等,终边相同的角有无数多个,它们相差360°的整数倍. (4)k∈Z这一条件不能少.
·新课讲授·
思考 2:
终边在x轴、y轴上的角的集合分别如何表示?
知识迁移 1:
终边在射线上的角如何表示?
S | k 360 , k Z
·新课讲授·
思考 2:
终边在x轴、y轴上的角的集合分别如何表示?
解 S={α|α=k·360°,k∈Z}∪{α|α=k·360°+180°,k∈Z} ={α |α =2k ·180°,k ∈Z}∪{α |α =(2k +1)·180°,k ∈Z} ={α |α =n ·180°,n ∈Z}.
《任意角》
·人教版必修四数学PPT课件·
优品老师
目 录
一 学习目标 二 新课导入 三 新课讲授
四 课堂检测 五 课堂总结
一 学习目标
·学习目标·
(1)推广角的概念、引入大于角和负角; (2)理解并掌握正角、负角、零角的定义; (3)理解任意角以及象限角的概念; (4)掌握所有与角终边相同的角(包括角)的表示方法; (5)树立运动变化观点,深刻理解推广后的角的概念;
一般地,所有与角α 终边相同的角,连同角α 在内,可构成一个集合S={β|β=α +k·360°, k∈Z},即任一与角α 终边相同的角,都可以表示成角α 与整数个周角的和.
注意: (1)α 为任意角. (2)k·360°与α 之间是“+”号,k·360°-α 可理解为k·360°+(-α ). (3)相等的角终边一定相同;终边相同的角不一定相等,终边相同的角有无数多个,它们相差360°的整数倍. (4)k∈Z这一条件不能少.
1.1.1《任意角》课件(人教A版必修4)

5.与1 991°终边相同的最小正角是_____. 【解析】∵与1 991°终边相同的角β=1 991°+ k²360°,(k∈Z),∴0°<1 991°+k²360°≤360°
191 <k≤ 191 又k∈Z, 即 -5 -4 , 360 360 ∴k=-5,∴与1 991°终边相同的最小正角是
)
(B)钝角是第二象限角
(C)终边相同的角一定相等 (D)不相等的角,它们的终边必不相同 【解析】选B.因为钝角α满足90°<α<180°,所以角α的 终边一定在第二象限.
3.若α 是第四象限角,则180°+α 一定是( (A)第一象限角 (B)第二象限角
)
(C)第三象限角
(D)第四象限角
【解析】选B.方法一:∵α是第四象限角 ∴-90°+k²360°<α<k²360° ∴90°+k²360°<180°+α<180°+k²360°(k∈Z) 方法二:由角的运算知,角α与角180°+α关于原点对称,即
∴θ=120°或240°.
7.在0°~360°范围内,找出与下列各角终边相同的角,并 判断它们是第几象限角: (1)918°;(2)-624°18′. 【解析】(1)∵918°=2〓360°+198°,
而198°∈(180°,270°),
∴918°与198°的终边相同,是第三象限角. (2)∵-624°18′=-2〓360°+95°42′, 又95°42′∈(90°,180°), ∴-624°18′与95°42′的终边相同,是第二象限角.
n²360°,
∴ 是第三象限角. 3 答案:一、三、四
4.(15分)若集合A={α |k²180°+30°<α <k²180°+90°, k∈Z},集合B={β |k²360°-45°<β <k²360°+45°, k∈Z},求A∩B.
高中数学人教版必修四课件:1.1.1任意角 (共20张PPT)

定义 : 所有与角 终边相同的角,连同角 在内,
可构成一个集合:S { | k 360 ,k Z}. 即任一与角 终边相同的角,都可以表示成角
与整数个周角的和。
注意:终边落在坐标轴上的角,不属于任何象限,
称为轴线角.
y
(1)终边在x轴上的角的集合:
{ | n 180 ,n Z}.
解 (1)因为-150°=-360°+210°,所以在 0°~360°范围 内,与-150°角终边相同的角是 210°角,它是第三象限角. (2)因为 650°=360°+290°,所以在 0°~360°范围内,与 650° 角终边相同的角是 290°角,它是第四象限角. (3)因为-950°15′=-3×360°+129°45′,所以在 0°~ 360°范围内,与-950°15′角终边相同的角是 129°45′角, 它是第二象限角. 小结 解答本题可先利用终边相同的角的关系:β=α+ k·360°,k∈Z,把所给的角化归到 0°~360°范围内,然后利 用 0°~360°范围内的角分析该角是第几象限角.
故
2
是第三象限的角 .
2
综上可知: 是第一或第三象限的角 .
2
0°
360° x
又 k 120 k 120 30 ,k Z .
3
y
90°
当 k 3n(n Z)时,
n 360 n 360 30 ,k Z , 180°
故
3 是第一象限的角 .
O
当
3
k
3n 1(n Z)时,
跟踪训练 1 判断下列角的终边落在第几象限内: (1)1 400°; (2)-2 010°.
解 (1)1 400°=3×360°+320°,∵320°是第四象限角, ∴1 400°也是第四象限角.
可构成一个集合:S { | k 360 ,k Z}. 即任一与角 终边相同的角,都可以表示成角
与整数个周角的和。
注意:终边落在坐标轴上的角,不属于任何象限,
称为轴线角.
y
(1)终边在x轴上的角的集合:
{ | n 180 ,n Z}.
解 (1)因为-150°=-360°+210°,所以在 0°~360°范围 内,与-150°角终边相同的角是 210°角,它是第三象限角. (2)因为 650°=360°+290°,所以在 0°~360°范围内,与 650° 角终边相同的角是 290°角,它是第四象限角. (3)因为-950°15′=-3×360°+129°45′,所以在 0°~ 360°范围内,与-950°15′角终边相同的角是 129°45′角, 它是第二象限角. 小结 解答本题可先利用终边相同的角的关系:β=α+ k·360°,k∈Z,把所给的角化归到 0°~360°范围内,然后利 用 0°~360°范围内的角分析该角是第几象限角.
故
2
是第三象限的角 .
2
综上可知: 是第一或第三象限的角 .
2
0°
360° x
又 k 120 k 120 30 ,k Z .
3
y
90°
当 k 3n(n Z)时,
n 360 n 360 30 ,k Z , 180°
故
3 是第一象限的角 .
O
当
3
k
3n 1(n Z)时,
跟踪训练 1 判断下列角的终边落在第几象限内: (1)1 400°; (2)-2 010°.
解 (1)1 400°=3×360°+320°,∵320°是第四象限角, ∴1 400°也是第四象限角.
人教A版课标版高中数学必修4第一章1.1.1 任意角(共17张PPT)

例1.在0º~ 360º范围内,找出与下列各角
终边相同的角,并判断它是哪个象限的角.
(1) -120º;
(2) 3410º
例2.写出与下列各角终边相同的角的集合 S,并把 S 中在-360º~720º间的角写出 来:
(1) 60º;
(2) -21º
课堂小结
1.角的概念推广后,角的大小可以任意取值. 把角放在直角坐标系中进行研究,对于一个 给定的角,都有唯一的一条终边与之对应, 并使得角具有代数和几何双重意义. 2.终边相同的角有无数个,在0°~360°范 围内与已知角β 终边相同的角有且只有一个.
作业 :
1、课本第5页练习:第2、3题 2、课本第9页习题1.1:第1、2、3题
顺时针旋转 30
0
30
0
(2)家中的钟表快了1小时5分钟,如何 校准?校准后分针旋转了多少度?
逆时针旋转 3900
390
0
两个形 状大小相同 的齿轮,互 相咬合。当 黄色齿轮按 逆时针方向 旋转整2周时 尝试分别写 出两个齿轮 此时旋转的 角度。
作终边
α
O 顶点
始边 A
(一)角的概念的推广
正角: 按逆时针方向旋转形成的角.
负角: 按顺时针方向旋转形成的角.
零角: 一条射线没有作任何旋转,称形成零角.
① 角有正负之分;
② 角可以任意大;
③ 还有零角。
问题回顾(请用任意角的概念回答)
(1)家中的钟表慢了5分钟,如何校准? 校准后分针旋转了多少度?
0 0
0
(二)象限角
象限角:在直角坐标系内,角的顶点与原点重 合,始边与x轴的非负半轴重合,那么角的终边 在第几象限,我们就说这个角是第几象限角.
人教A版高中数学必修四第一章 1.1.1任意角公开课教学课件 (共21张PPT)

列各角终边相同的角,并判定它们是第 几象限角.
(1) 120 ;(2) 6600 ;
(1) 120 ; (2)6600 ;
解:∵ 120 240 (1) 360
∴与 120 角终边相同的角是 240 角,
它是第三象限的角;
(2)ቤተ መጻሕፍቲ ባይዱ 660 300 1 360
∴与660 角终边相同的角是300角,
3、下列说法中,正确的是( )
A.第一象限的角是锐角
B.锐角是第一象限的角
C.小于90°的角是锐角
D.终边相同的角一定相
等
4、把-1485°转化为α+k·360°(0°≤α<360°, k∈Z)
的形式是( )
A.45°-4×360°
B.-45°-4×360°
C.-45°-5×360° D.315°-5×360°
的元素是
363 14 2 360 356 46,
363 14 1 360 3 14,
363 14 0 360 363 14.
变式训练:
写出下列各角终边相同的角的集合, 并把集合中适合不等式 - 720 0 360 0 的元素 写出来: (1)1303018′(2)- 2250
小结:
四、终边相同的角及其表示方法
注:所有与角 终边相同的角,连同角
在内,可以构成一个集合
{ | k 360 0, k Z}
即任一与角 终边相同的角,都可以表示
成角 与整数个周角的和。
说明:终边相同 的角不一定相 等,相等的角终
边一定相同
五、例题分析:
【例1】在 0 ~ 360 间,找出与下
y -3300
3900
300
x
o
300 =300+0x3600
(1) 120 ;(2) 6600 ;
(1) 120 ; (2)6600 ;
解:∵ 120 240 (1) 360
∴与 120 角终边相同的角是 240 角,
它是第三象限的角;
(2)ቤተ መጻሕፍቲ ባይዱ 660 300 1 360
∴与660 角终边相同的角是300角,
3、下列说法中,正确的是( )
A.第一象限的角是锐角
B.锐角是第一象限的角
C.小于90°的角是锐角
D.终边相同的角一定相
等
4、把-1485°转化为α+k·360°(0°≤α<360°, k∈Z)
的形式是( )
A.45°-4×360°
B.-45°-4×360°
C.-45°-5×360° D.315°-5×360°
的元素是
363 14 2 360 356 46,
363 14 1 360 3 14,
363 14 0 360 363 14.
变式训练:
写出下列各角终边相同的角的集合, 并把集合中适合不等式 - 720 0 360 0 的元素 写出来: (1)1303018′(2)- 2250
小结:
四、终边相同的角及其表示方法
注:所有与角 终边相同的角,连同角
在内,可以构成一个集合
{ | k 360 0, k Z}
即任一与角 终边相同的角,都可以表示
成角 与整数个周角的和。
说明:终边相同 的角不一定相 等,相等的角终
边一定相同
五、例题分析:
【例1】在 0 ~ 360 间,找出与下
y -3300
3900
300
x
o
300 =300+0x3600
高中数学必修四:1.1.1《任意角》 PPT课件 图文
精讲领学
例题1 写出与下列各角终边相同的角的集合S,并把S中在 360~720范围的角写出来.
( 1 ) 6 0 ;( 2 ) 2 1 ;( 3 ) 3 6 3 1 4
解: ( 1 ) S {| k 3 6 0 6 0 , k Z }300,60,420
( 2 ) S {| k 3 6 0 2 1 , k Z }21,339,699
2、下列角中终边与330°相同的角是( ) A.30° B.-30° C.630° D.-630°
3、把-1485°转化为α+k·360° (0°≤α<360°, k∈Z)的形式是( ) A.45°-4×360° B.-45°-4×360° C.-45°-5×360° D.315°-5×360°
反馈固学
1.1.1 任意角
第一课时
(1)推广角的概念;理解并掌握正角、负角、零角的定义; (2)理解任意角以及象限角的概念; (3)掌握所有与角终边相同的角(包括角)的表示方法; (4)树立运动变化观点,深刻理解推广后的角的概念;
思考:那么工人在拧紧或拧松螺丝时,转动的角度 如何表示才比较合适?
逆时 针
4、下列结论中正确的是( ) A.小于90°的角是锐角 B.第二象限的角是钝角 C.相等的角终边一定相同 D.终边相同的角一定相等
5:任意两个角的数量大小可以相加、相减.
例如50°+80°=130°, 50°-80°=-30°, 你能解释一下这两个式子的几何意义吗?
130°是以50°角的终边为始边,逆时针旋转80°所成的角. -30°是以50°角的终边为始边,顺时针旋转80°所成的角.
注3:(1) 为任意角 (2) k Z这一条件必不可少;
(3) 终边相同的角不一定相等, 终边相等的角有无数多个,它们相差3600的整数倍.
人教A版高中数学必修4-.1任意角精品PPT课件

{偶数}∪{奇数} ={整数}
终边落在y轴非正半轴上的角的集合为
900+K∙3600
S2={β| β=2700+K∙3600,K∈Z}
Y
={β| β=900+1800+2K∙1800,K∈Z} ={β| β=900+(2K+1)1800 ,K∈Z}
={β| β=900+1800 的奇数倍}
X O
所以 终边落在y轴上的角的集合为
P5练习:5
人教A版高中数学必修4:.1任意角课 件-精品 课件pp t(实用 版)
人教A版高中数学必修4:.1任意角课 件-精品 课件pp t(实用 版)
• 小结:
正角:射线按逆时针方向旋转形成的角
1.任意角的概念 负角:射线按顺时针方向旋转形成的角
零角:射线不作旋转形成的角
1)置角的顶点于原点 2.象限角 2)始边重合于X轴的正半轴
不唯一
y
o
x
那么终边相同的角在大小上有什么关系?
320,3280, 3920
320
3280
3 9 2 0
320 3600
3 2 0 3 6 0 0
320 03600
320 13600
3 2 0( - 1 ) 3 6 0 0
320 2 3600 320 ( -2) 3600
……
……
与 - 3 2 0 终 边 相 同 的 角 可 表 示 为 :
7200的元素 写出来
解:终边在直线y=x上的角的集合:
S{ 4 5 0 K1 8 0 0,KZ }
当K=-2,-1,0,1,2,3时符合条件
S 中 适 合 3 6 0 0 7 2 0 0 的 元 素 是 :
高中数学人教版必修4课件:.1任意角

00+7200<x<900+7200
…,
…,
{x|k·3600<x<900+3600·k, k ∈ Z}
终边在第三象限的角的集合:
{x| 1800+k·3600<x<2700+k·3600, k ∈Z}
退出
§1.1 任意角
温故
知新1
知新2
知新3 知识应用 小结
作业
例4 写出终边落在y轴正半轴上的角的集合。
温故
知新1
知新2 同知终新边3角 知识应用 小结
作业
y
o
x
y
o
x
退出
§1.1 任意角
温故
知新1
知新2
知新3 知识应用 小结
作业
例1、在0 到360 范围内,找出与下列角终边 相同的角,并判定它们是第几象限角.
120 640 950 12
解 : ∵-950°12′= 129048′-3×3600,
∴在0°~360°范围内, 与-950°12′角终 边相同的角是129°48′, 它是第二象限角.
若k为奇数,则2 是第四象限角.
综上,
2
是第二或第四象限角.
2
退出
利温故用上述知新方1 法判知断新2,可§1得.1知任新如3意下角结知识论应用:y 小结
作业
若 是第(数字)象限角,
3 2
则 是(区域)象限的角?
2
4
1
o 1
4
x
23
当在第一象限时, 在第一或第三象限.
当第二象限时,
2 在第一或第三象限.
(2) 把集合 |k120 k 120 30 , k Z 表示的角的
高中数学人教A版必修4--1.1.1任意角 精品课件

4,再循环一遍,直到填满为止,则
有标号n的就是α为第n象限时,
α 2
所
在象限数.
一般地,要确定
θ n
所在的象限,可以把各个象限都n等
分,从x轴的正半轴起,按逆时针方向把这4n个区域依次循环
标上号码1、2、3、4,则标号是几的区域,就是θ为第几象限
的角时,θn终边落在的区域,θn所在的象限就可直观地看出.
{α|α=k·180°+90°,k∈Z}
终边落在x轴上
{α|α=k·180°,k∈Z}
终边落在坐标轴上
{α|α=k·90°,k∈Z}
α是第二象限角,180°-α是第几象限角( ) A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
[答案] A
[解析] 方法1:特例淘汰法:α=120°,180°-α=, 否定B、C、D,故选A.
负角
按顺时针方向旋转形成的角
零角 一条射线没有作任何 旋转 形成的角
(3)记法:用一个希腊字母表示,如α,β,γ,…;也可用 3个大写的英文字母表示(字母前面要写“∠”),其中中间字 母表示角的顶点,如∠AOB,∠DEF,….
[破疑点](1)确定任意角的大小要明确其旋转方向和旋转 量;(2)零角的始边和终边重合,但始边和终边重合的角不一 定是零角,如周角等;(3)角的范围由0°~360°推广到任意角 后,角的加减运算类似于实数的加减运算.(4)画图表示角 时,应注意箭头的方向不可丢掉,箭头方向代表角的正负.
-30°是( ) A.第一象限角 C.第三象限角
B.第二象限角 D.第四象限角
[答案] D
3.终边相同的角 (1)研究终边相同的角的前提条件是:角的顶点与原点重 合,角的始边与x轴的非负半轴重合. (2)终边相同的角的集合:所有与角α终边相同的角,连同 角α在内,可构成一个集合S={β|β= α+k·360°,k∈Z},即任 一与角α终边相同的角,都可以表示成角α与整数个周角的 和.
人教版高中数学课件:必修四 1.1任意角 (共41张PPT)

={β|β=90°+n·180°,n∈Z }
思考1:终边在x轴正半轴、负半轴,y轴正半轴、负半轴、 x
轴、y轴、坐标轴上的角分别如何表示? x轴正半轴:α= k·360°,k∈Z ; x轴负半轴:α= 180°+k·360°,k∈Z ; y轴正半轴:α= 90°+k·360°,k∈Z ; y轴负半轴:α= 270°+k·360°,k∈Z ; x轴:α= k·180°,k∈Z ; y轴:α= 90°+k·180°,k∈Z ;
o
90°
x
例题分析
于是,终边在y轴上的角的集合
S=S1∪S2 ={β|β=90°+k·360°,k∈Z}∪{β|β=270°+k·360°,k∈Z} ={β|β=90°+2k·180°,k∈Z }∪{β|β=90°+180°+2k·180°,k∈Z }
={β|β=90°+2k·180°,k∈Z } ∪{β|β=90°+(2k+1)180°,k∈Z }
欢迎同仁指导
执教者:卢连伟
请欣赏周华健的一首歌——《花心》片段
花的心藏在蕊中 空把花期都错过 你的心忘了季节 从不轻易让人懂 为何不牵我的手 共听日月唱首歌 黑夜又白昼黑夜又白昼 人生为欢有几何 春去春会来 花谢花会再开 只要你愿意只要你愿意 让梦划向你的心海 春去春会来 花谢花会再开 只要你愿意只要你愿意 让梦划向你的心海 花瓣泪飘落风中 虽有悲意也从容 你的泪晶莹剔透 心中一定还有梦 为何不牵我的手 同看海天成一色 潮起又潮落潮起又潮落 送走人间许多愁
0 4. 终边相同的角的表示法: S | k 360 , k Z
质疑再探
你对以上的内容还有什么问题或不明白的 地方,请提出来,大家一起交流.
高中数学 1.1.1 任意角课件 新人教A版必修4

2.象限角的表示 (1)终边在第一象限内的角为{α|α=k·360°+β,0°<β< 90° , k∈Z} , 即 将 不 等 式 0° < β < 90° 的 两 边 同 时 加 上 k·360°,可得终边在第一象限的角的表示为{α |k·360°<α< k·360°+90°,k∈Z}. (2)终边在第二象限的角的表示为 {α|k·360°+90°<α<k·360°+180°,k∈Z}.
【纠错提升】1.对角的概念的推广的认识 对角的认识不能仅仅局限于正角的范围,还有负角和零 角.
2.明确角的分类
按照角的旋转方向分为正角,负角和零角; 按照角的终边位置分为象限角和终边在坐标轴上的角.
【即时演练】 下列说法中正确的是( B.第一象限角必是锐角 C.不相等的角终边一定不相同 D.若β=α+k·360°(k∈Z),则α和β终边相同 ) A.三角形的内角必是第一、二象限角
提示: 不唯一.如:终边落在 y 轴的非正半轴上的角的集
合也可以表示为{α|α=k·360°-90°,k∈Z}.
1.解读任意角的概念
(1)用运动的观点来定义角,就可以把角的概念推广到任意 角,包括任意大小的正角、负角和零角. (2)对角的概念的认识关键是抓住“旋转”二字: ①要明确旋转方向; ②要明确旋转的大小; ③要明确射线未作任何旋转时的位置.
(4)终边相同的角不一定相等,终边相同的角有无数个,它
们相差周角的整数倍.相等的角终边一定相同.
象限角的判定
已知角的顶点与坐标原点重合,始边落在x轴的非 负半轴上,作出下列各角,并指出它们是第几象限的角.
(1)-75°;(2)855°;(3)-510°.
思路点拨: 画平面直角坐标系 → 作出相应角 → 判断象限角
第一章Biblioteka 三角函数1.1 任意角和弧度制
高中数学人教版必修4精品PPT课件-.1任意角-【完整版】

终边
y 终边
x 0
始边
是第一象限角 是第二象限角 是第三象限角
终边
终边 是第四象限角
1 . 指出下列各角是第几象限角
(1) 30° (2)120 °
第一象限角 第二象限角
(3)-60 ° (4) 225°
第四象限角 第三象限角
合作探究
在坐标系中画出角30o,390o,-330o并找
y
出它们终边的关系? -3300
[0º, 360º]
现实生活中还有其他的角
1.在体操运动中, “转体720º”、 “转体1080º”等动 作名称的含义
现实生活中还有其他的角
2.钟表的指针旋转
现实生活中还有其他的角
3.自行车车轮的转动 一根辐条
现实生活中还有其他的角
4.主从动轮的转动等.
思考:这些旋转形成图形是?
自主学习(一)
终边相同的角,并判断它是哪个象限的角 (1)-120°(2)640°(3) -230o12'
解(1)与-120°角终边相同的角是β=-120º+k·360º,k∈Z k=1, β=-120°+360°=240°,是第三象限角。
(2)280°角,它是第四象限角。
(3)129o48 ’ 角,它是第二象限角。
解:β=k·360º+60º,k∈Z. 所以 =k·120º+20º, k∈Z.
3
当k=0时,得角为20º,
当k=1时,得角为140º, 当k=2时,得角为260º.
高中数学人教版必修4课件:.1任意角 -精品 课件ppt (实用 版)
2、写出终边在坐标系四个象限角分线上 的角的集合。
高中数学人教版必修4课件:.1任意角 -精品 课件ppt (实用 版)
