全国高考模拟文科数学分类汇编三角函数和解三角形
三角函数、解三角形——2024届高考数学试题分类汇编(解析版)

2024高考复习·真题分类系列2024高考试题分类集萃·三角函数、解三角形
微专题总述:三角函数的图像与性质
【扎马步】2023高考三角函数的图像与性质方面主要考察“卡根法”的运用,是最为基础的表现
【雕龙头】在稳中求新的过程中,2023高考试题也透露出了新的风向,加强图像考察与其他知识点如几何、函数的结合,对称思想的隐含
微专题总述:正弦定理与余弦定理的应用
【扎马步】2023高考解三角形小题部分紧抓“教考衔接”基础不放,充分考察正余弦定理的运用
【雕龙头】在稳中求新的过程中,2023高考试题也透露出了新的风向,在考察正余弦定理时与角平分线定理结合(初中未涉及此定理)
微专题总述:解三角形综合问题
【扎马步】2023高考解三角形大题部分仍然与前几年保持一直模式,结构不良题型日益增多,但方向不变,均是化为“一角一函数”模式是达到的最终目的,考察考生基本计算与化简能力
【雕龙头】在稳中求新的过程中,2023高考试题也透露出了新的风向,如新高考卷中出现的数形结合可加快解题速度,利用初中平面几何方法快速求出对应参量在近几年高考题中频繁出现,可见初高中结合的紧密 2023年新课标全国Ⅰ卷数学
16.已知在ABC 中,
()3,2sin sin A B C A C B +=−=. (1)求sin A ;
(2)设5AB =,求AB 边上的高.
2023高考试题分类集萃·三角函数、解三角形参考答案
2。
2022全国二卷文科数学真题文科数学2022-2022高考真题分类训练专题四三角函数与解三角形第十一

2022全国二卷文科数学真题文科数学2022-2022高考真题分类训练专题四三角函数与解三角形第十一讲三角函数的综合应用—后附解析答案专题四三角函数与解三角形第十一讲三角函数的综合应用一、选择题1.(2022年天津)已知函数,.若在区间内没有零点,则的取值范围是A.B.C.D.2.(2022全国II卷)函数的最大值为A.4B.5C.6D.73.(2022年陕西高考)如图,港口一天6时到18时的水深变化曲线近似满足函数,据此函数可知,这段时间水深(单位:m)的最大值为A.5B.6C.8D.104.(2022浙江)存在函数满足,对任意都有A.B.C.D.5.(2022新课标2)如图,长方形ABCD的边AB=2,BC=1,O是AB的中点,点P沿着边BC,CD与DA运动,∠BOP=.将动点P到A,B两点距离之和表示为的函数,则的图像大致为ABCD6.(2022新课标1)如图,圆O的半径为1,A是圆上的定点,P是圆上的动点,角的始边为射线,终边为射线,过点作直线的垂线,垂足为,将点到直线的距离表示为的函数,则=在[0,]上的图像大致为A.B.C.D.二、填空题7.(2022浙江)我国古代数学家刘徽创立的“割圆术”可以估算圆周率,理论上能把的值计算到任意精度。
祖冲之继承并发展了“割圆术”,将的值精确到小数点后七位,其结果领先世界一千多年,“割圆术”的第一步是计算单位圆内接正六边形的面积,=.8.(2022浙江)已知向量,满足,则的最小值是,最大值是.9.(2022年浙江)已知,则______.10.(2022陕西)设,向量,若,则____.三、解答题11.(2022江苏)农场有一块农田,如图所示,它的边界由圆的一段圆弧(为此圆弧的中点)和线段构成.已知圆的半径为40米,点到的距离为50米.现规划在此农田上修建两个温室大棚,大棚Ⅰ内的地块形状为矩形,大棚Ⅱ内的地块形状为,要求均在线段上,均在圆弧上.设与所成的角为.(1)用分别表示矩形和的面积,并确定的取值范围;(2)若大棚Ⅰ内种植甲种蔬菜,大棚Ⅱ内种植乙种蔬菜,且甲、乙两种蔬菜的单位面积年产值之比为.求当为何值时,能使甲、乙两种蔬菜的年总产值最大.12.(2022江苏)如图,水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为32cm,容器Ⅰ的底面对角线的长为10cm,容器Ⅱ的两底面对角线,的长分别为14cm和62cm.分别在容器Ⅰ和容器Ⅱ中注入水,水深均为12cm.现有一根玻璃棒,其长度为40cm.(容器厚度、玻璃棒粗细均忽略不计)(1)将放在容器Ⅰ中,的一端置于点处,另一端置于侧棱上,求没入水中部分的长度;(2)将放在容器Ⅱ中,的一端置于点处,另一端置于侧棱上,求没入水中部分的长度.13.(2022山东)设.(Ⅰ)求的单调区间;(Ⅱ)在锐角△中,角,的对边分别为,若,求△面积的最大值.14.(2022湖北)实验室一天的温度(单位:℃)随时间t(单位:h)的变化近似满足函数关系:,。
2011年—2018年新课标全国卷(1卷、2卷、3卷)文科数学试题分类汇编—8

2011年—2018年新课标全国卷(1卷、2卷、3卷)文科数学试题分类汇编—8.三角函数、解三角形2011年—2018年新课标全国卷Ⅰ文科数学分类汇编7.三角函数、解三角形一、选择题2018年新课标Ⅰ文8题:已知函数$f(x)=2\cos x-\sin x+2$,则$f(x)$的最小正周期为$\pi$,最大值为3.2018年新课标Ⅰ文11题:已知角$\alpha$的顶点为坐标原点,始边与$x$轴的非负半轴重合,终边上有两点$A(1,0)$,$B(2,b)$,且$\cos2\alpha=\frac{1}{5}$,则$a-b=\frac{1}{5}$。
2018年新课标Ⅱ文7题:在$\triangle ABC$中,$\cos C=\frac{5}{\sqrt{26}}$,$BC=1$,$AC=5$,则$AB=5\sqrt{2}$。
2018年新课标Ⅱ文10题:若$f(x)=\cos x-\sin x$在$[0,a]$是减函数,则$a$的最大值是$\frac{3\pi}{4}$。
2018年新课标Ⅲ文4题:若$\sin \alpha=\frac{1}{\sqrt{8}}$,则$\cos 2\alpha=-\frac{7}{8}$。
2018年新课标Ⅲ文6题:函数$f(x)=\frac{\tan x}{1+\tan^2 x}$的最小正周期为$\pi$。
2018年新课标Ⅲ文11题:triangle ABC$的内角$A$,$B$,$C$的对边分别为$a$,$b$,$c$。
若$\triangle ABC$的面积为$4$,则$\cosC=\frac{3}{4}$。
2017年新课标Ⅰ文11题:triangle ABC$的内角$A$、$B$、$C$的对边分别为$a$、$b$、$c$。
已知$\sin B+\sin A(\sin C-\cos C)=\frac{3}{2}$,$a=2$,$c=2$,则$C=\frac{\pi}{3}$。
2024年上海市高考数学一模考试题分类(三角与三角函数 )汇编(附答案)

1一、三角定义、常用三角公式1.(2024 高三一模闵行 2)若sin 3α=,则()sin πα-=______.2.(2024高三一模青浦3)已知α满足cos m α=,则πsin 2α⎛⎫+=⎪⎝⎭.(结果用含有m 的式子表示).3.(2024高三一模杨浦3)若3sin 5α=,则cos 2α=______.4.(2024高三一模嘉定4)已知tan 2α=,则tan 2πα⎛⎫+= ⎪⎝⎭______.5.(2024高三一模金山5)已知角α、β的终边关于原点O 对称,则()cos αβ-=______.6.(2024高三一模松江5)已知3sin ,0,52πθθ⎛⎫=∈ ⎪⎝⎭,则tan 4πθ⎛⎫- ⎪⎝⎭的值为______.7.(2024高三一模虹口6)已知1cos 3x =-,且x 为第三象限的角,则tan 2x =______.8.(2024高三一模静安14)设α是第一象限的角,则2α所在的象限为()A.第一象限B.第三象限C.第一象限或第三象限D.第二象限或第四象限9.(2024高三一模长宁15)设点P 是以原点为圆心的单位圆上的动点,它从初始位置()01,0P 出发,沿单位圆按逆时针方向转动角02παα⎛⎫<< ⎪⎝⎭后达点1P ,然后继续沿单位圆按逆时针方向转动角4π到2P .若点2P 的横坐标为35-,则点1P 的纵坐标为()A.210B.25 C.325D.7210二、解三角形1.(2024 高三一模黄浦 8)在 ∆ABC 中,三个内角 A , B ,C 的对边长分别为a ,b ,c ,若5a 2 −5b 2 +6bc −5c 2 =0,则sin 2A 的值为______.2.(2024 高三一模松江 9)在 ∆ABC 中,设角 A , B ,C 所对边的边长分别为a ,b ,c ,若a =3,c =5, B =2A ,则边长b =______.2024年上海市高考数学一模考试题分类(三角与三角函数 )汇编3.(2024高三一模普陀14)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c ,若a =20c b C -+=,则该三角形外接圆的半径为()A.1B.C.2D.4.(2024高三一模虹口17)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若()sin sin sin ,sin m A B C A =+- ,(),n c b c a =+- ,且m //n .(1)求角B 的大小;(2)若△ABC 为锐角三角形,求sin sin y A C =+的取值范围.5.(2024高三一模奉贤17)在ABC ∆中,设角A 、B 及C 所对边的边长分别为a 、b 及c .cos sin A a B=+(1)求角B 的大小;(2)当a =b =c 和ABC ∆的面积S .6.(2024高三一模嘉定17)已知三角形ABC ,1CA CB ⋅=- ,三角形的面积12S =,(1)求角C 的值;(2)若3sin cos 4A A =,2a =,求c .7.(2024高三一模宝山18)在ABC ∆中,角C B A 、、的对边分别为c b a 、、.(1)若2sin a B =,求角A 的大小;(2)若BC 边上的高等于2a ,求cbb c +的最大值.8.(2024高三一模崇明18)在ABC ∆中,5a =,6b =.(1)若4cos 5B =-,求A 和ABC ∆外接圆半径R 的值;(2)若ABC ∆的面积4S =,求c 的值.9.(2024高三一模闵行18)在ABC △中,角A B C 、、所对边的边长分别为a b c 、、,且2cos a c B c -=.(1)若1cos 3B =,3c =,求b 的值;(2)若ABC △为锐角三角形,求sin C 的取值范围.10.(2024高三一模青浦18)在△ABC 中,角,,A B C 所对的边分别为a ,b ,c ,且满足2220a c b ac -++=.(1)求角B 的大小;(2)若23b =,求△ABC 的周长的最大值.三、三角函数及其性质1.(2024 高三一模嘉定 3)函数y =sin πx 的最小正周期为______.2.(2024高三一模普陀6)若函数tan 3y x =在区间,6m π⎛⎫⎪⎝⎭上是严格增函数,则实数m 的取值范围为______.3.(2024高三一模闵行7)若将函数()()sin 20y x ϕϕπ=+<<的图像向右平移3π个单位,得到的图像所对应的函数为奇函数,则ϕ=______.4.(2024高三一模虹口8)已知函数()()cos 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图像如右图所示,则()f x =______.(第8题图)5.(2024高三一模青浦8)若函数cos()y x ϕ=+是奇函数,则该函数的所有零点是.6.(2024高三一模奉贤9)设函数()sin 0y x ωω=>在区间()0,2π上恰有三个极值点,则ω的取值范围为______.7.(2024高三一模金山9)已知()()sin 0y x ωω=>在区间[]0,π上是严格增函数,且其图像关于()4,0π对称,则ω的值为______.8.(2024高三一模黄浦10)若ϕ是一个三角形的内角,且函数()3sin 2y x ϕ=+在区间,46ππ⎡⎤-⎢⎥⎣⎦上是单调函数,则ϕ的取值范围是______.9.(2024高三一模杨浦10)函数()()cos f x x ωϕ=+,()0,2ϕπ∈,在x ∈R 上是单调增函数,且函数关于原点对称,则满足条件的数对(),ωϕ=______.10.(2024高三一模普陀10)设函数()sin 2y x ϕ=+02πϕ⎛<<⎫⎪⎝⎭的图像与直线y t =相交的连续的三个公共点从左到右依次记为A ,B ,C ,若2BC AB =,则正实数t 的值为______.11.(2024高三一模浦东新区10)如图,已知函数()sin 0,0,02y A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭的图像与y 轴的交点为()0,1,并已知其在y 轴右侧的第一个最高点和第一个最低点的坐标分别为()0,2x 和()02,2x π+-.记()y f x =,则3f π⎛⎫= ⎪⎝⎭______.12.(2024高三一模长宁11)若函数()sin cos x a x f x =+在27,36ππ⎛⎫⎪⎝⎭上是严格单调函数,则实数a 的取值范围为______.13.(2024高三一模静安17)记)(cos sin 32cos sin )(22R ∈++-=x x x x x x f λ,其中λ为实常数.(1)求函数)(x f y =的最小正周期;(2)若函数)(x f y =的图像经过点⎪⎭⎫ ⎝⎛0,2π,求该函数在区间⎥⎦⎤⎢⎣⎡π32,0上的最大值和最小值.四、三角应用题1.(2024 高三一模奉贤 10)某林场为了及时发现火情,设立了两个观测点A 和B . 某日两个观测点的林场人员都观测到C 处出现火情. 在 A 处观测到火情发生在北偏西40方向,而在B 观测到火情在北偏西60方向. 已知B 在A 的正东方向10km 处(如图所示),则BC AC -=______km.(精确到0.1km )2.(2024高三一模徐汇10)某建筑物内一个水平直角型过道如图所示,两过道的宽度均为3米,有一个水平截面为矩形的设备需要水平通过直角型过道.若该设备水平截面矩形的宽BC 为1米,则该设备能水平通过直角型过道的长AB 不超过______米.3.(2024高三一模长宁19)汽车转弯时遵循阿克曼转向几何原理,即转向时所有车轮中垂线交于一点,该点称为转向中心.如图1,某汽车四轮中心分别为A、B、C、D,向左转向,左前轮转向角为α,右前轮转向角为β,转向中心为O.设该汽车左右轮距AB为w米,前后轴距AD为l米.(1)试用w、l和α表示tanβ;(2)如图2,有一直角弯道,M为内直角顶点,EF为上路边,路宽均为3.5米,汽车行驶其中,左轮A、D与路边FS相距2米.试依据如下假设,对问题*做出判断,并说明理由.假设:①转向过程中,左前轮转向角α的值始终为30︒;②设转向中心O到路边EF的距离为d,若OB d<且OM ODw=,<,则汽车可以通过,否则不能通过;③ 1.570l=.2.680问题*:可否选择恰当转向位置,使得汽车通过这一弯道?图1图24.(2024高三一模杨浦19)某数学建模小组研究挡雨棚(图1),将它抽象为柱体(图2),底面ABC 与111A B C 全等且所在平面平行,ABC △与111A B C △各边表示挡雨棚支架,支架1AA 、1BB 、1CC 垂直于平面ABC .雨滴下落方向与外墙(所在平面)所成角为π6(即π6AOB ∠=),挡雨棚有效遮挡的区域为矩形11AA O O (O 、1O 分别在CA 、11C A 延长线上).(1)挡雨板(曲面11BB C C )的面积可以视为曲线段BC 与线段1BB 长的乘积.已知1.5OA =米,0.3AC =米,12AA =米,小组成员对曲线段BC 有两种假设,分别为:①其为直线段且π3ACB ∠=;②其为以O 为圆心的圆弧.请分别计算这两种假设下挡雨板的面积(精确到0.1平方米);(2)小组拟自制ABC △部分的支架用于测试(图3),其中0.6AC =米,π2ABC ∠=,CAB θ∠=,其中ππ62θ<<,求有效遮挡区域高OA 的最大值.图15.(2024高三一模浦东新区19)某街道规划建一座口袋公园.如图所示,公园由扇形AOC 区域和三角形COD 区域组成.其中A O D 、、三点共线,扇形半径OA 为30米.规划口袋公园建成后,扇形AOC 区域将作为花草展示区,三角形COD 区域作为亲水平台区,两个区域的所有边界修建休闲步道.(1)若π3AOC ∠=,2OD OA =,求休闲步道总长(精确到米);(2)若π6ODC ∠=,在前期民意调查时发现,绝大部分街道居民对亲水平台区更感兴趣.请你根据民意调查情况,从该区域面积最大或周长最长的视角出发,选择其中一个方案,设计三角形COD 的形状.6.(2024高三一模黄浦19)某公园的一个角形区域AOB 如图所示,其中23AOB π∠=.现拟用长度为100米的隔离档板(折线DCE )与部分围墙(折线DOE )围成一个花卉育苗区ODCE ,要求满足OD OC OE ==.(1)设333DOC πππαα⎛⎫∠=+-<< ⎪⎝⎭,试用α表示OD ;(2)为使花卉育苗区的面积最大,应如何设计?请说明理由.7.(2024高三一模金山19)网络购物行业日益发达,各销售平台通常会配备送货上门服务.小金正在配送客户购买的电冰箱,并获得了客户所在小区门户以及建筑转角处的平面设计示意图.图1图2第19题图(1)为避免冰箱内部制冷液逆流,要求运送过程中发生倾斜时,外包装的底面与地面的倾斜角α不能超过4π,且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形ABCD ,0.8m AD =, 2.4m AB =,而客户家门高度为2.3米,其他过道高度足够.若以倾斜角4πα=的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.(2)由于客户选择以旧换新服务,小金需要将客户长方体形状的旧冰箱进行回收.为了省力,小金选择将冰箱水平推运(冰箱背面水平放置于带滚轮的平板车上,平板车长宽均小于冰箱背面).推运过程中遇到一处直角过道,如图2所示,过道宽为1.8米.记此冰箱水平截面为矩形EFGH , 1.2m EH =.设PHG β∠=,当冰箱被卡住时(即点H 、G 分别在射线PR 、PQ 上,点O 在线段EF 上),尝试用β表示冰箱高度EF 的长,并求出EF 的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其高度的最大值是多少?(结果精确到0.1m )8.(2024高三一模徐汇19)2023年杭州亚运会首次启用机器狗搬运赛场上的运动装备.如图所示,在某项运动赛事扇形场地OAB 中,2AOB π∠=,500OA =米,点Q 是弧AB 的中点,P 为线段OQ 上一点(不与点O ,Q 重合).为方便机器狗运输装备,现需在场地中铺设三条轨道PO ,PA ,PB .记APQ θ∠=,三条轨道的总长度为y 米.(1)将y 表示成θ的函数,并写出θ的取值范围;(2)当三条轨道的总长度最小时,求轨道PO 的长.参考答案1一、三角定义、常用三角公式1. (2024 高三一模闵行 2)若sin 3α=,则()sin πα-=______.【答案】13【解析】诱导公式,()1sin sin 3παα-==.2.(2024高三一模青浦3)已知α满足cos m α=,则πsin 2α⎛⎫+=⎪⎝⎭.(结果用含有m 的式子表示).【答案】m【解析】由诱导公式πsin 2α⎛⎫+= ⎪⎝⎭cos α,所以答案为m .3.(2024高三一模杨浦3)若3sin 5α=,则cos 2α=______.【答案】725【解析】27cos 212sin 25αα=-=.4.(2024高三一模嘉定4)已知tan 2α=,则tan 2πα⎛⎫+= ⎪⎝⎭______.【答案】12-【解析】11tan cot 2tan 2πααα⎛⎫+=-=-=- ⎪⎝⎭.5.(2024高三一模金山5)已知角α、β的终边关于原点O 对称,则()cos αβ-=______.【答案】1-【解析】角α、β的终边关于原点O 对称,所以()21,k k αβπ-=+∈Z ,所以()cos 1αβ-=-.6.(2024高三一模松江5)已知3sin ,0,52πθθ⎛⎫=∈ ⎪⎝⎭,则tan 4πθ⎛⎫- ⎪⎝⎭的值为______.【答案】17-【解析】343sin ,0,,cos ,tan 5254πθθθθ⎛⎫=∈∴== ⎪⎝⎭,3tan tan1144tan 3471tan tan 144πθπθπθ--⎛⎫∴-===- ⎪⎝⎭++.7.(2024高三一模虹口6)已知1cos 3x =-,且x 为第三象限的角,则tan 2x =______.【答案】427-【解析】1cos 3x =-,且x 为第三象限的角,则sin 3x =-,tan x ∴=,()222tan 22242tan 21tan 71x x x ⨯∴===---.8.(2024高三一模静安14)设α是第一象限的角,则2α所在的象限为()A.第一象限B.第三象限C.第一象限或第三象限D.第二象限或第四象限【答案】C【解析】由题意,222k k ππαπ<<+,k ∈Z ,则24k k απππ<<+,k ∈Z ,当k 为奇数时,2α在第三象限,当k 为偶数时,2α在第一象限,故选C.8.(2024高三一模长宁15)设点P 是以原点为圆心的单位圆上的动点,它从初始位置()01,0P 出发,沿单位圆按逆时针方向转动角02παα⎛⎫<< ⎪⎝⎭后达点1P ,然后继续沿单位圆按逆时针方向转动角4π到2P .若点2P 的横坐标为35-,则点1P 的纵坐标为()A.10B.5C.5D.10【答案】D【解析】由题意可知3cos 45πα⎛⎫+=- ⎪⎝⎭,因为3444πππα<+<,所以4sin 45πα⎛⎫+=⎪⎝⎭24372sin sin sin cos cos sin 44444425510ππππππαααα⎡⎤⎛⎫⎛⎫⎛⎫⎫=+-=+-+=+=⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦故选D.二、解三角形1.(2024 高三一模黄浦 8)在 ∆ABC 中,三个内角 A , B ,C 的对边长分别为a ,b ,c ,若5a 2 −5b 2 +6bc −5c 2 =0,则sin 2A 的值为______.【答案】2425【解析】222222655650,5bca b bc c b c a -+-=∴+-=,222635cos 225bcb c a A bc bc +-∴===,4sin 5A ∴=,4324sin 22sin cos 25525A A A ∴==⨯⨯=.2.(2024高三一模松江9)在ABC ∆中,设角,,A B C 所对边的边长分别为,,a b c ,若3,5,2a c B A ===,则边长b =______.【答案】【解析】由正弦定理sin sin sin 22sin cos a b b b A B A A A ===得cos 2bA a=①,由余弦定理可得222cos 2b c a A bc+-=②,则2222225322625b bc a b b b a bc b +-+-=⇒=⇒=⨯.3.(2024高三一模普陀14)在ABC ∆中,角A ,B ,C 所对的边分别为a ,b ,c,若a =20c b C -+=,则该三角形外接圆的半径为()A.1B.C.2D.【答案】A【解析】20c b C -+=,因为a =22cos 0c b a C -+=,由正弦定理可得sin 2sin 2sin cos 0C B A C -+=,即()sin 2sin 2sin cos 0C A C A C -++=,化简可得1cos 2A =,所以sin 2A =,由正弦定理可得2sin aR A=(R 为外接圆半径),解得1R =.故选A.4.(2024高三一模虹口17)设△ABC 的内角A ,B ,C 所对的边分别为a ,b ,c ,若()sin sin sin ,sin m A B C A =+- ,(),n c b c a =+- ,且m //n.(1)求角B 的大小;(2)若△ABC 为锐角三角形,求sin sin y A C =+的取值范围.【答案】(1)3B π=;(2)32,⎛ ⎝【解析】(1)因为m //n,所以()()sin sin sin sin A B C b c a c A +-⋅+-=⋅,由正弦定理,可得()()a b c b c a ac +-⋅+-=,即222ac a c b =+-.于是,由余弦定理得2221cos 22a c b B ac+-==,又()0,B π∈,所以3B π=.(2)由(1)可知2,3A C π+=所以2sin sin sin sin()3y A C A A π=+=+-3sin cos )226A A A π=+=+……11分由△ABC 为锐角△,得20,0,232A A πππ<<<-<且所以,62A ππ<<从而362.3A πππ<+<所以sin sin )6y A C A π=+=+的取值范围为32,.⎛ ⎝5.(2024高三一模奉贤17)在ABC ∆中,设角A 、B 及C 所对边的边长分别为a 、b 及c .cos sin A a B=+(1)求角B 的大小;(2)当a =b =时,求边长c 和ABC ∆的面积S .【答案】(1)3π=B ;(2)3+【解析】(1)由正弦定理得B A A B C sin sin cos sin 3sin 3⋅+⋅=由于()B A C +-=π,得()BA AB B A sin sin cos sin 3sin 3⋅+⋅=+展开得B A A B B A B A sin sin cos sin 3sin cos 3cos sin 3⋅+⋅=⋅+⋅化简得B B sin cos 3=,则3tan =B ,所以3π=B (2)由正弦定理,得2322sin sin sin3π==cA C Cc A sin sin 2260sin 32==,22sin =A ,因为<a b ,所以A 是锐角,即4π=A 因为32π=+C A ,所以,5,sin 12sin 3π===C c C所以115sin sin32212ABC S ab C π∆==⨯=+6.(2024高三一模嘉定17)已知三角形ABC ,1CA CB ⋅=- ,三角形的面积12S =,(1)求角C 的值;(2)若3sin cos 4A A =,2a =,求c .【答案】(1)34π;(2)c =【解析】(1)1cos 1CA CB ab C ⋅=⇒=-,1sin 12S ab C =⇒=,两式相除得:tan 1C =-,所以3π4C =.(2)sin cos sin 242A A A =⇒=,所以π6A =或π3(舍),所以π6A =,所以π12B =,sin 4B =由正弦定理得,sin sin a c C A =,sin sin b c C B=,所以22sin sin sin abc C A B=,由(1)ab =所以22c=+即c =7.(2024高三一模宝山18)在ABC ∆中,角C B A 、、的对边分别为c b a 、、.(1)若2sin a B =,求角A 的大小;(2)若BC 边上的高等于2a,求c b b c +的最大值.【答案】(1)323ππ或=A ;(2)22【解析】(1)根据正弦定理得2sin sin A B B =,所以23sin =A ,所以323ππ或=A .(2)由三角形面积公式得A bc a a sin 212121=⋅,即A bc a sin 22=,又由余弦定理A bc c b a cos 2222-+=,得A bc c b A bc cos 2sin 222-+=,解得()A A bc c b cos sin 222+=+,从而()⎪⎭⎫ ⎝⎛+=+=+4sin 22cos sin 222πA A A bc c b .当24ππ=+A 即4π=A 时bc c b 22+有最大值22,即cbb c +的最大值为22.8.(2024高三一模崇明18)在ABC ∆中,5a =,6b =.(1)若4cos 5B =-,求A 和ABC ∆外接圆半径R 的值;(2)若ABC ∆的面积4S =,求c 的值.【答案】(1)6A π=,5R =;(2)4c =或c =【解析】(1)因为4cos 5B =-,()0,B π∈,所以3sin 5B ==,由正弦定理,得2sin sin a bR A B==,即5623sin 5R A ==,所以1sin 2A =,5R =,因为a b <,所以0,2A π⎛⎫∈ ⎪⎝⎭,因此6A π=,5R =(2)由1sin 2ABC S ab C =△得224sin 564ABC S C ab ===⨯△,于是3cos 4C ==±,当3cos 4C =时,由余弦定理,得222356256164c =+-⨯⨯⨯=当3cos 4C =-时,由余弦定理,得2223562561064c ⎛⎫=+-⨯⨯⨯-= ⎪⎝⎭.所以,4c =或c =.9.(2024高三一模闵行18)在ABC △中,角A B C 、、所对边的边长分别为a b c 、、,且2cos a c B c -=.(1)若1cos 3B =,3c =,求b 的值;(2)若ABC △为锐角三角形,求sin C 的取值范围.【答案】(1)b =;(2)1sin (,)22C ∈【解析】(1)将1cos 3B =,3c =带入条件中可得5a =,由余弦定理2222cos b a c ac B =+-可得b =;(2)2cos a c B c -= ,由正弦定理可得sin 2sin cos sin A C B C -=,sin sin()sin cos cos sin A B C B C B C =+=+ ,sin cos sin cos sin B C C B C ∴-=,sin()sin B C C -=,(,),(0,)222B C C πππ-∈-∈ ,所以B C C -=,即2B C =,又因为ABC △为锐角三角形,(,)64C ππ∴∈,1sin (,22C ∈10.(2024高三一模青浦18)在△ABC 中,角,,A B C 所对的边分别为a ,b ,c ,且满足2220a c b ac -++=.(1)求角B 的大小;(2)若b =ABC 的周长的最大值.【答案】(1)120B ∠=︒;(2)4+【解析】(1)因为222a cb ac +-=-,由余弦定理得2221cos 22a c b B ac+-∠==-,120B ∠=︒.(2)由正弦定理得,a =4sin A ,c =4sin (600 −A ),所以,∆ABC 的周长为a +b +c =4sin A +4sin (600−A +)=4sin (A +600 +)200 <A <600当 A =300 时,∆ABC 的周长的最大值为4 +.三、三角函数及其性质1.(2024 高三一模嘉定 3)函数y =sin πx 的最小正周期为______.【答案】2【解析】22T ππ==.2.(2024高三一模普陀6)若函数tan 3y x =在区间,6m π⎛⎫⎪⎝⎭上是严格增函数,则实数m 的取值范围为______.【答案】,66ππ⎛⎫-⎪⎝⎭【解析】由题意,32666m m m ππππ⎧>-⎪⎪⇒-<<⎨⎪<⎪⎩.3.(2024高三一模闵行7)若将函数()()sin 20y x ϕϕπ=+<<的图像向右平移3π个单位,得到的图像所对应的函数为奇函数,则ϕ=______.【答案】23π【解析】函数向右平移3π个单位可以得到2sin 23y x πϕ⎛⎫=-+ ⎪⎝⎭,此时函数为奇函数,则有2sin 003πϕ⎛⎫-+= ⎪⎝⎭,则2,3k k πϕπ-=∈Z ,因为0ϕπ<<,所以23πϕ=.4.(2024高三一模虹口8)已知函数()()cos 0,2f x x πωϕωϕ⎛⎫=+>< ⎪⎝⎭的部分图像如右图所示,则()f x =______.(第8题图)【答案】cos 26x π⎛⎫- ⎪⎝⎭【解析】由题意知12243124T T πππππωω=-=⇒==⇒=,将,112π⎛⎫⎪⎝⎭代入,解得cos 21126ππϕϕ⎛⎫⨯+=⇒=- ⎪⎝⎭,则()cos 26f x x π⎛⎫=-⎪⎝⎭.5.(2024高三一模青浦8)若函数cos()y x ϕ=+是奇函数,则该函数的所有零点是.【答案】π,x k k =∈Z【解析】函数cos()y x ϕ=+是奇函数,则,2k k Z πϕπ=+∈,cos()sin y x x ϕ=+=±,所以函数零点为π,x k k =∈Z .6.(2024高三一模奉贤9)设函数()sin 0y x ωω=>在区间()0,2π上恰有三个极值点,则ω的取值范围为______.【答案】5744⎛⎤ ⎥⎝⎦,【解析】cos y x ωω'=,令0y '=,即cos 0x ω=,即,2x k k πωπ=+∈Z ,因为函数在区间()0,2π上恰有三个极值点,则2257244232ππωπωππωπ⎧>+⎪⎪⇒<≤⎨⎪≤+⎪⎩.7.(2024高三一模金山9)已知()()sin 0y x ωω=>在区间[]0,π上是严格增函数,且其图像关于()4,0π对称,则ω的值为______.【答案】14或12【解析】因为函数在区间[]0,π上是严格增函数,所以2πωπ≤,所以12ω≤,又图像关于()4,0π对称,所以4,k k πωπ=∈Z ,即,4k k ω=∈Z ,所以14k =或12.8.(2024高三一模黄浦10)若ϕ是一个三角形的内角,且函数()3sin 2y x ϕ=+在区间,46ππ⎡⎤-⎢⎥⎣⎦上是单调函数,则ϕ的取值范围是______.【答案】0,6π⎛⎤⎥⎝⎦【解析】由题意知()0,ϕπ∈,因为函数()3sin 2y x ϕ=+在区间,46ππ⎡⎤-⎢⎥⎣⎦上是单调函数,则2,23x ππϕϕϕ⎡⎤+∈-++⎢⎥⎣⎦,则220,632ππϕπϕππϕ⎧-+≥-⎪⎪⎡⎤⇒∈⎨⎢⎥⎣⎦⎪+≤⎪⎩,0,6πϕ⎛⎤∴∈ ⎥⎝⎦.9.(2024高三一模杨浦10)函数()()cos f x x ωϕ=+,()0,2ϕπ∈,在x ∈R 上是单调增函数,且函数关于原点对称,则满足条件的数对(),ωϕ=______.【答案】0,2π⎛⎫ ⎪⎝⎭或30,2π⎛⎫ ⎪⎝⎭【解析】当0ω≠时,函数在x ∈R 上显然不具备单调性,故0ω=,又函数关于原点对称,所以函数值为0,所以cos 0ϕ=,又()0,2ϕπ∈,所以2πϕ=或32π,因此满足条件的数对为0,2π⎛⎫ ⎪⎝⎭或30,2π⎛⎫ ⎪⎝⎭.10.(2024高三一模普陀10)设函数()sin 2y x ϕ=+02πϕ⎛<<⎫⎪⎝⎭的图像与直线y t =相交的连续的三个公共点从左到右依次记为A ,B ,C ,若2BC AB =,则正实数t 的值为______.【答案】12【解析】由题意可得T π=,函数与y t =()0t >相交图像如图所示,可知C A x x π-=,又2BC AB =,所以3B A x x π=+,()sin 2A t x ϕ=+,()2cos 21A x t ϕ+=-则()()2sin 2sin 2sin 23A B A x x x πϕϕϕ⎛⎫+=+=++⎪⎝⎭()()22sin 2coscos 2sin 33A A x x ππϕϕ=+++,即12t t =-+12t =或12t =-(舍),所以12t =.11.(2024高三一模浦东新区10)如图,已知函数()sin 0,0,02y A x A πωϕωϕ⎛⎫=+>><< ⎪⎝⎭的图像与y 轴的交点为()0,1,并已知其在y 轴右侧的第一个最高点和第一个最低点的坐标分别为()0,2x 和()02,2x π+-.记()y f x =,则3f π⎛⎫= ⎪⎝⎭______.【解析】由题意2A =,()00222T x x ππ=+-=,所以2142T ππωω==⇒=,()02sin 16f πϕϕ==⇒=,所以()12sin 26f x x π⎛⎫=+ ⎪⎝⎭,所以2sin 366f πππ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭.12.(2024高三一模长宁11)若函数()sin cos x a x f x =+在27,36ππ⎛⎫⎪⎝⎭上是严格单调函数,则实数a 的取值范围为______.【答案】3⎡-⎢⎣【解析】()cos sin x x a x f '=-,因为函数()sin cos x a x f x =+在27,36ππ⎛⎫⎪⎝⎭上是严格单调函数,所以()0f x '≥或()0f x '≤,当x π=时,()1f π'=-,则()0f x '≥不符合题意,由()0f x '≤,得sin cos a x x ≥,当2,3x ππ⎛⎫∈⎪⎝⎭时,sin 0x >,所以1tan a x ≥在2,3x ππ⎛⎫∈ ⎪⎝⎭上恒成立,即求max 1tan a x ⎛⎫≥ ⎪⎝⎭,因为2,3x ππ⎛⎫∈ ⎪⎝⎭,所以()tan x ∈,1,tan 3x ⎛∈-∞- ⎝⎭,所以33a ≥-;当7,6x ππ⎛⎫∈ ⎪⎝⎭时,sin 0x <,所以1tan a x ≤在7,6x ππ⎛⎫∈ ⎪⎝⎭上恒成立,即求min 1tan a x ⎛⎫≤ ⎪⎝⎭,因为7,6x ππ⎛⎫∈ ⎪⎝⎭,所以3tan 0,3x ⎛⎫∈ ⎪ ⎪⎝⎭,)1tan x ∈+∞,所以a ≤;综上,33a ⎡-⎢⎣∈.13.(2024高三一模静安17)记)(cos sin 32cos sin )(22R ∈++-=x x x x x x f λ,其中λ为实常数.(1)求函数)(x f y =的最小正周期;(2)若函数)(x f y =的图像经过点⎪⎭⎫ ⎝⎛0,2π,求该函数在区间⎥⎦⎤⎢⎣⎡π32,0上的最大值和最小值.【答案】(1)π;(2)最大值1,最小值2-【解析】(1)()cos 22f x x x =-+π2sin 26x ⎛⎫=- ⎪⎝⎭λ+.所以,函数)(x f y =的最小正周期π.(2) π102f λ⎛⎫=+=⎪⎝⎭,∴1λ=-.∴π()2sin 216f x x ⎛⎫=-- ⎪⎝⎭.令π26x t -=,则π7π,66t ⎡⎤∈-⎢⎥⎣⎦.当ππ266x -=-或7π6,即0x =或2π3时,min 2f =-.当ππ262x -=,即π3x =时,max 1f =.四、三角应用题1.(2024 高三一模奉贤 10)某林场为了及时发现火情,设立了两个观测点A 和B . 某日两个观测点的林场人员都观测到C 处出现火情. 在 A 处观测到火情发生在北偏西40方向,而在B 观测到火情在北偏西60方向. 已知B 在A 的正东方向10km 处(如图所示),则BC AC -=______km.(精确到0.1km )【答案】7.8【解析】由图可知130CAB ∠=,30ABC ∠=,20ACB ∠=2.(2024高三一模徐汇10)某建筑物内一个水平直角型过道如图所示,两过道的宽度均为3米,有一个水平截面为矩形的设备需要水平通过直角型过道.若该设备水平截面矩形的宽BC 为1米,则该设备能水平通过直角型过道的长AB 不超过______米.【答案】22-【解析】分别以,OB OA 所在直线为x ,y 轴建立平面直角坐标系如图所示,则()3,3M ,令()0,A b ,(),0B a ,()0,0a b >>,则直线AB 的方程为1x ya b+=,则点M 直线上方,且到AB 的距离为1,即22331331111a b a b a b ⎧+>⎪+-=⎛⎫⎛⎫+ ⎪ ⎪⎝⎭⎝⎭,则2233111a b a b ⎛⎫⎛⎫+-=+ ⎪ ⎪⎝⎭⎝⎭,整理可得223()a b a b ab +=+-,设AB r =,0,0,2OAB r πθθ⎛⎫⎡⎤∠=>∈ ⎪⎢⎥⎣⎦⎝⎭,则sin a r θ=,cos b r θ=,223()a b a b ab +=+-可化为23(sin cos )sin cos r r r θθθθ=+-,令sin cos 0,2t πθθθ⎛⎫⎡⎤=+∈ ⎪⎢⎥⎣⎦⎝⎭,则224t πθ⎛⎫⎡=+∈ ⎪⎣⎝⎭,则223(sin cos )131121281sin cos (31)(31)999231t r t t t t θθθθ+--===⨯--+---188(31)231t t =--+-,由1,2t ⎡⎤∈⎣⎦,得312,321t⎡⎤-∈-⎣⎦,所以889(31)2321231321321t t --+≤--+=---,所以()1823218(31)231t t ≥---+-,当且仅当2t =时等号成立,该设备能水平通过直角型过道的长AB 不超过622-米.3.(2024高三一模长宁19)汽车转弯时遵循阿克曼转向几何原理,即转向时所有车轮中垂线交于一点,该点称为转向中心.如图1,某汽车四轮中心分别为A 、B 、C 、D ,向左转向,左前轮转向角为α,右前轮转向角为β,转向中心为O.设该汽车左右轮距AB 为w 米,前后轴距AD 为l 米.(1)试用w 、l 和α表示tan β;(2)如图2,有一直角弯道,M 为内直角顶点,EF 为上路边,路宽均为3.5米,汽车行驶其中,左轮A 、D 与路边FS 相距2米.试依据如下假设,对问题*做出判断,并说明理由.假设:①转向过程中,左前轮转向角α的值始终为30︒;②设转向中心O 到路边EF 的距离为d ,若OB d <且OM OD <,则汽车可以通过,否则不能通过;③ 1.570w =,2.680l =.问题*:可否选择恰当转向位置,使得汽车通过这一弯道?图1图2【答案】(1)tan tan llw βα=+;(2)选择恰当转向位置,汽车可以通过弯道【解析】(1)由已知AOD α∠=,tan BOC β∠=,所以tan l OD α=,tan lOC w α=+,进而tan tan llw βα=+.(2)以EF 和FS 分别为x 轴和y 轴建立坐标系,则()3.5, 3.5M --.3 4.642tan lOD l α===,()223 6.766OB l l w=++=,设(),O a b ()0,0a b <<,32 6.642a l =--=-,d b =-,()()()2223.5 3.59.872 3.5OM a b b =+++=++,由OM OD <,得()29.872 3.521.548b ++<,进而 6.9170.83b -<<-,由OB d <,得 6.766b <-,所以当 6.917 6.765b -<<时,OB d <且OM OD <,此时汽车可以通过弯道.答:选择恰当转向位置,汽车可以通过弯道.4.(2024高三一模杨浦19)某数学建模小组研究挡雨棚(图1),将它抽象为柱体(图2),底面ABC 与111A B C 全等且所在平面平行,ABC △与111A B C △各边表示挡雨棚支架,支架1AA 、1BB 、1CC 垂直于平面ABC .雨滴下落方向与外墙(所在平面)所成角为π6(即π6AOB ∠=),挡雨棚有效遮挡的区域为矩形11AA O O (O 、1O 分别在CA 、11C A 延长线上).(1)挡雨板(曲面11BB C C )的面积可以视为曲线段BC 与线段1BB 长的乘积.已知1.5OA =米,0.3AC =米,12AA =米,小组成员对曲线段BC 有两种假设,分别为:①其为直线段且π3ACB ∠=;②其为以O 为圆心的圆弧.请分别计算这两种假设下挡雨板的面积(精确到0.1平方米);(2)小组拟自制ABC △部分的支架用于测试(图3),其中0.6AC =米,π2ABC ∠=,CAB θ∠=,其中ππ62θ<<,求有效遮挡区域高OA 的最大值.【答案】(1)若选择①,挡雨板材料的面积为1.8平方米;若选择②,挡雨板材料的面积为图13π5平方米,约为1.9平方米;(2)OA 的最大值为0.3米【解析】(1)若选择①,结合π6AOB ∠=,得OBC △是直角三角形,10.92BC OC ==米,挡雨板材料的面积为1.8平方米.若选择②,则COB 是一个圆心角为π6的扇形,BC 弧长为π3π1.8610⨯=,挡雨板材料的面积为3π5平方米,约为1.9平方米.(2)在直角ABC △中,由cos AB AC θ=;在ABO △中,由正弦定理,ππsinsin 66AO ABθ=⎛⎫- ⎪⎝⎭,即π6π2sin sin cos 656AO AB θθθ⎛⎫⎛⎫=-=- ⎪ ⎪⎝⎭⎝⎭2631sin cos cos 522θθθ⎛⎫=⋅-⋅ ⎪⎝⎭3311sin 2cos25222θθ⎛⎫=⋅-⋅- ⎪⎝⎭3π3sin 25610θ⎛⎫=-- ⎪⎝⎭,其中ππ62θ<<.当ππ262θ-=,即π3θ=时,AO 取得最大值310.综上所述,有效遮挡区域高OA 的最大值为0.3米.5.(2024高三一模浦东新区19)某街道规划建一座口袋公园.如图所示,公园由扇形AOC 区域和三角形COD 区域组成.其中A O D 、、三点共线,扇形半径OA 为30米.规划口袋公园建成后,扇形AOC 区域将作为花草展示区,三角形COD 区域作为亲水平台区,两个区域的所有边界修建休闲步道.(1)若π3AOC ∠=,2OD OA =,求休闲步道总长(精确到米);(2)若π6ODC ∠=,在前期民意调查时发现,绝大部分街道居民对亲水平台区更感兴趣.请你根据民意调查情况,从该区域面积最大或周长最长的视角出发,选择其中一个方案,设计三角形COD 的形状.【答案】(1)231米;(2)见解析【解析】(1)休闲步道总长为 2AC OA OD CD+++π301203=⨯++10π120=++231≈米.所以休闲步道总长为231米.(2)方案一:设5π,0,6COD θθ⎛⎫∠=∈ ⎪⎝⎭COD ∆中,由正弦定理得π5πsin sin sin 66OCOD CD θθ==⎛⎫- ⎪⎝⎭,得5π5π60sin ,60sin ,0,66OD CD θθθ⎛⎫⎛⎫=-=∈⎪ ⎪⎝⎭⎝⎭故COD ∆的面积15π5π3060sin sin 900sin sin 266S θθθθ⎛⎫⎛⎫=⨯⨯-⋅=-⋅ ⎪ ⎪⎝⎭⎝⎭π450sin 23θ⎛⎫=-+ ⎪⎝⎭因为5π0,6θ⎛⎫∈ ⎪⎝⎭,所以ππ4π2333θ⎛⎫-∈- ⎪⎝⎭,当ππ232θ-=,即5π12θ=时有max S 450=+平方米因此,当亲水平台区的面积最大时,COD ∆是以OC 为底边的等腰三角形.方案二:设5π,0,6COD θθ⎛⎫∠=∈ ⎪⎝⎭COD ∆中,由正弦定理得π5πsin sin sin 66OCOD CD θθ==⎛⎫- ⎪⎝⎭,得5π5π60sin ,60sin ,0,66OD CD θθθ⎛⎫⎛⎫=-=∈⎪ ⎪⎝⎭⎝⎭故COD ∆的周长5π60sin 60sin 306L θθ⎛⎫=+-+ ⎪⎝⎭(60sin 30cos 30θθ=+++π233012θ⎛⎫=+++ ⎪⎝⎭因为5π0,6θ⎛⎫∈ ⎪⎝⎭,所以ππ11π121212θ⎛⎫+∈ ⎪⎝⎭,当ππ122θ+=,即5π12θ=时有max L 60233030630230=+=+米因此,当亲水平台区的周长最长时,COD ∆是以OC 为底边的等腰三角形.(本题也可用余弦定理、均值不等式解决)6.(2024高三一模黄浦19)某公园的一个角形区域AOB 如图所示,其中23AOB π∠=.现拟用长度为100米的隔离档板(折线DCE )与部分围墙(折线DOE )围成一个花卉育苗区ODCE ,要求满足OD OC OE ==.(1)设333DOC πππαα⎛⎫∠=+-<< ⎪⎝⎭,试用α表示OD ;(2)为使花卉育苗区的面积最大,应如何设计?请说明理由.【答案】(1)50cos2OD α=;(2)当0α=时,花卉育苗区的面积最大,为12503平方米【解析】(1)由πππ()333DOC αα∠=+-<<,2π3AOB ∠=,可知π3COE α∠=-,作OF CD ⊥,垂足为F ,由OD OC =,可知CF DF =且1π262DOF DOC α∠=∠=+,在直角DOF △中,πsin()62DF OD α=+,故π2sin(62CD OD α=+,同理可得ππ2sin(2sin()6262EC OC OD αα=-=-,所以π2sin()62OD α++π2sin()10062OD α-=,可得OD =5050ππsin()sin()cos62622ααα=++-(米).(2)设花卉育苗区的面积为S 平方米,则221π1πsin()sin()2323S OD OD αα=++-22150ππ[sin()sin()]233cos 2ααα=++-.501]1cos1cos2Sα=α==-+α+α.当且仅当cos1α=且ππ33α-<<,即0α=时,S取最大值,此时50OD=米.故使π3DOC∠=,且50OD=米,可使花卉育苗区的面积最大.7.(2024高三一模金山19)网络购物行业日益发达,各销售平台通常会配备送货上门服务.小金正在配送客户购买的电冰箱,并获得了客户所在小区门户以及建筑转角处的平面设计示意图.图1图2第19题图(1)为避免冰箱内部制冷液逆流,要求运送过程中发生倾斜时,外包装的底面与地面的倾斜角α不能超过4π,且底面至少有两个顶点与地面接触.外包装看作长方体,如图1所示,记长方体的纵截面为矩形ABCD,0.8mAD=, 2.4mAB=,而客户家门高度为2.3米,其他过道高度足够.若以倾斜角4πα=的方式进客户家门,小金能否将冰箱运送入客户家中?计算并说明理由.(2)由于客户选择以旧换新服务,小金需要将客户长方体形状的旧冰箱进行回收.为了省力,小金选择将冰箱水平推运(冰箱背面水平放置于带滚轮的平板车上,平板车长宽均小于冰箱背面).推运过程中遇到一处直角过道,如图2所示,过道宽为1.8米.记此冰箱水平截面为矩形EFGH, 1.2mEH=.设PHGβ∠=,当冰箱被卡住时(即点H、G分别在射线PR、PQ上,点O在线段EF上),尝试用β表示冰箱高度EF的长,并求出EF的最小值,最后请帮助小金得出结论:按此种方式推运的旧冰箱,其高度的最大值是多少?(结果精确到0.1m)【答案】(1)能;(2)2.6m【解析】(1)当倾斜角π4α=时,冰箱倾斜后实际高度(即冰箱最高点到地面的距离)ππ820.8sin 2.4cos 2.3445h=+=<,故冰箱能够按要求运送入客户家中.(2)延长EF与直角走廊的边相交于M、N,则 1.8 1.8+sin cos MN OM ON =+=ββ, 1.2tan EM β=, 1.2tan FN β=,又EF MN ME NF =--,设()EF f β=,π0,2β⎛⎫∈ ⎪⎝⎭,则 1.8 1.81() 1.2(tan )sin cos tan f =+-+βββββ1.8(sin cos ) 1.2sin cos ββββ+-=,π0,2β⎛⎫∈ ⎪⎝⎭.2222332222221.8(cos sin )(sin cos )(1.8(sin cos ) 1.2)(cos s in )()sin cos 1.8(cos sin ) 1.2(cos sin ) 1.8(sin cos )(cos 1)(sin 1)sin cos sin cos f βββββββββββββββββββββββ--+--'=⋅--+----==⋅⋅求得驻点π4β=,作表格得βπ(0,)4π4ππ(,)42()f β'-0+()f β严格减极小值严格增所以()f β最小值π18212() 2.6945f -=≈.由实际意义需向下取整,此情况下能顺利通过过道的冰箱高度的最大值为2.6米.8.(2024高三一模徐汇19)2023年杭州亚运会首次启用机器狗搬运赛场上的运动装备.如图所示,在某项运动赛事扇形场地OAB 中,2AOB π∠=,500OA =米,点Q 是弧AB 的中点,P 为线段OQ 上一点(不与点O ,Q 重合).为方便机器狗运输装备,现需在场地中铺设三条轨道PO ,PA ,PB .记APQ θ∠=,三条轨道的总长度为y 米.(1)将y 表示成θ的函数,并写出θ的取值范围;(2)当三条轨道的总长度最小时,求轨道PO 的长.【答案】(1)2sin cos 52502,,sin 48y θθππθθ+-⎛⎫=⋅∈ ⎪⎝⎭;(2)()2503263PO =-【解析】(1)因为点Q 是弧AB 的中点,由对称性,知PA PB =,4AOP BOP π∠=∠=,又APO πθ∠=-,4OAP πθ∠=-,500OA =由正弦定理,得()sin sinsin 44APOAOPπππθθ==-⎛⎫- ⎪⎝⎭,所以500sin 25024,sin sin AP OP πθθθ⎛⎫- ⎪⎝⎭==.所以500sin 42sin y AP BP OP AP OP πθθ⎛⎫+- ⎪⎝⎭=++=+=2sin cos sin θθθ+-=,因为APQ AOP ∠>∠,所以4πθ>,13248AQO OAQ πππ⎛⎫∠=∠=-=⎪⎝⎭,所以5,48ππθ⎛⎫∈⎪⎝⎭.(2)法一:由(1)得:2cos sin y θθ-=,5,48ππθ⎛⎫∈ ⎪⎝⎭.记2cos sin t θθ-=,则sin cos 2t θθ+=,由辅助角公式可得:)2sin()1θϕθϕ+=⇒+=,解得tt 5sin()1,6348ππππθθ⎛⎫+=⇒=∈ ⎪⎝⎭,等号可以取得.故当3πθ=时,三条轨道的总长度最小,此时(2503OP =.法二:由(1)得:2cos sin y θθ-=+,5,48ππθ⎛⎫∈ ⎪⎝⎭.记2cos sin t θθ-=,tan tan ,tan 2816x θππ5⎛⎫=∈ ⎪⎝⎭,则由万能置换公式可得:2222123111132221x x x t x x x x x --+⎛⎫+===+≥= ⎪⎝⎭+,当且仅当33x =即3πθ=时等号成立.故当3πθ=,三条轨道的总长度最小,此时(2503OP =.法三:令()2sin cos sin f θθθθ+-=,5,48ππθ⎛⎫∈ ⎪⎝⎭.由()212cos '0sin f θθθ-==,解得3πθ=,则有θ43ππθ<<3πθ=538ππθ<<()'f θ0<0=0>()f θ严格减极小值严格增所以当3πθ=,即(2503OP =米时,()f θ有唯一的极小值,即是最小值,则()min 1f θ=+,三条轨道的最小值为+.故当3πθ=时,三条轨道的总长度最小,此时(2503OP =.。
2021-2021 高考全国卷三角函数解三角形真题汇编(文科)

2021-2021 高考全国卷三角函数、解三角形真题汇编(文科)2021-2021 高考全国卷三角函数、解三角形真题汇编(文科)学校:姓名:班级:考号:评卷人得分一、选择题1. [2021・全国新课标卷I(文)]函数y=的部分图象大致为 ( ) -A. B. C.D.2. [2021・全国新课标卷I(文)]△ABC的内角A,B,C的对边分别为a,b,c.已知sinB+sin A(sin C-cos C)=0,a=2,c= ,则C= ( )A. B. C. D.3. [2021・全国新课标卷II(文)]函数f(x)=sin 的最小正周期为( ) A. 4πB. 2πC. πD.4. [2021・全国新课标卷III (文)]已知sin α-cos α=,则sin 2α= ( ) A. -B. -C.D.5. [2021・全国新课标卷III (文)]函数f(x)=sin +cos - 的最大值为 ( )A. B. 1 C. D. 6. [2021・全国新课标卷III (文)]函数y=1+x+的部分图象大致为( )第1页共4页A. B.C.D.7. [2021・高考全国新课标卷Ⅰ(文),4]△ABC的内角A,B,C的对边分别为a,b,c.已知a= ,c=2,cos A=,则b= ( )A. B. C. 2 D. 38. [2021・高考全国新课标卷Ⅰ(文),6]将函数y=2sin 的图象向右平移个周期后,所得图象对应的函数为 ( )A. y=2sinB. y=2sinC. y=2sin -D.y=2sin -9. [2021・高考全国新课标卷Ⅰ(文),12]若函数f(x)=x-sin 2x+asin x在(-∞,+∞)单调递增,则a的取值范围是 ( )A. [-1,1]B. -C. -D. - -10. [2021・高考全国新课标卷Ⅱ(文),3]函数y=Asin(ωx+φ)的部分图象如图所示,则 ( )A. y=2sin -B. y=2sin -C. y=2sinD. y=2sin11. [2021・高考全国新课标卷Ⅱ(文),11]函数f(x)=cos2x+6cos - 的最大值为( )A. 4B. 5C. 6D. 712. [2021・高考全国新课标卷Ⅲ(文),6]若tan θ=-,则cos 2θ= ( )第2页共4页A. -B. -C.D.13. [2021・高考全国新课标卷Ⅲ(文),9]在△ABC中,B=,BC边上的高等于BC,则sin A= ( ) A. B. C. D.14. [2021・高考全国新课标卷Ⅰ(文),8]函数f(x)=cos(ωx+φ)的部分图象如图所示,则f(x)的单调递减区间为( )A. - ,k∈ZB. - ,k∈ZC. - ,k∈ZD. - ,k∈Z15. [2021�q高考全国新课标卷Ⅰ(文),7]在函数①y=cos|2x|,②y=|cos x|,③y=cos(2x+),④y=tan(2x-)中,最小正周期为π的所有函数为( )A. ②④B. ①③④C. ①②③D. ①③16. [2021・高考全国新课标卷I(文),9]函数f(x)=(1-cosx)sinx在[-π,π]的图象大致为( )A. B.C. D.17. [2021・高考全国新课标卷I(文),10]已知锐角△ABC的内角A,B,C的对边分别为2a,b,c,23cosA+cos2A=0,a=7,c=6,则b=( ) A. 10 B. 9 C.8 D. 5第3页共4页18. [2021・高考全国新课标卷II(文),4]△ABC的内角A,B,C的对边分别为a,b,c,已知b=2,B=,C=,则△ABC的面积为( )A. 2 +2B. +1C. 2 -2D. -119. [2021・高考全国新课标卷II(文),6]已知sin2α=,则cos(α+)=( ) A.B. C. D. 评卷人得分二、填空题220. [2021・全国新课标卷I(文)]已知α∈ ,tan α=2,则cos - = . 21. [2021・全国新课标卷II(文)]函数f(x)=2cos x+sin x的最大值为 . 22. [2021・全国新课标卷II(文)]△ABC的内角A,B,C的对边分别为a,b,c,若2bcos B=acos C+ccos A,则B= .23. [2021・全国新课标卷III (文)]△ABC的内角A,B,C的对边分别为a,b,c.已知C=60°,b= ,c=3,则A= .24. [2021・高考全国新课标卷Ⅰ(文),14]已知θ是第四象限角,且sin ,则tan - = .25. [2021・高考全国新课标卷Ⅱ(文),15]△ABC的内角A,B,C的对边分别为a,b,c,若cos A=,cos C=,a=1,则b= .26. [2021・高考全国新课标卷Ⅲ(文),14]函数y=sin x- cos x的图象可由函数y=2sin x的图象至少向右平移个单位长度得到.27. [2021�q高考全国新课标卷Ⅰ(文),16]如图,为测量山高MN,选择A和另一座山的山顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知山高BC=100 m,则山高MN=________m.28. [2021�q高考全国新课标Ⅱ(文),14]函数f(x)=sin(x+φ)-2sin φcos x的最大值为________. 29. [2021・高考全国新课标卷I(文),16]设当x=θ时,函数f(x)=sinx-2cosx取得最大值,则cosθ= .30. [2021・高考全国新课标卷II(文),16]函数y=cos(2x+φ)(-π≤φ函数y=sin(2x+)的图象重合,则φ= .第4页共4页感谢您的阅读,祝您生活愉快。
(word完整版)三角函数与解三角形高考模拟考试题(卷)精选(含详细答案解析)(2021年整理)

(word完整版)三角函数与解三角形高考模拟考试题(卷)精选(含详细答案解析)(word版可编辑修改)编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望((word完整版)三角函数与解三角形高考模拟考试题(卷)精选(含详细答案解析)(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为(word完整版)三角函数与解三角形高考模拟考试题(卷)精选(含详细答案解析)(word版可编辑修改)的全部内容。
三角函数与解三角形高考试题精选一.解答题(共31小题)1.在△ABC中,角A,B,C的对边分别为a,b,c,已知2(tanA+tanB)=+.(Ⅰ)证明:a+b=2c;(Ⅱ)求cosC的最小值.2.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asinA=4bsinB,ac=(a2﹣b2﹣c2).(Ⅰ)求cosA的值;(Ⅱ)求sin(2B﹣A)的值.3.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.(Ⅰ)求C;(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.4.在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=,sinB=C.(1)求tanC的值;(2)若a=,求△ABC的面积.5.在△ABC中,角A,B,C所对的边分别是a,b,c,且+=.(Ⅰ)证明:sinAsinB=sinC;(Ⅱ)若b2+c2﹣a2=bc,求tanB.6.在△ABC中,已知AB=2,AC=3,A=60°.(1)求BC的长;(2)求sin2C的值.7.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3,b﹣c=2,cosA=﹣.(Ⅰ)求a和sinC的值;(Ⅱ)求cos(2A+)的值.8.△ABC的内角A,B,C所对的边分别为a,b,c.向量=(a,b)与=(cosA,sinB)平行.(Ⅰ)求A;(Ⅱ)若a=,b=2,求△ABC的面积.9.设△ABC的内角A,B,C所对边的长分别为a,b,c,且b=3,c=1,△ABC的面积为,求cosA与a的值.10.如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=,EA=2,∠ADC=,∠BEC=.(Ⅰ)求sin∠CED的值;(Ⅱ)求BE的长.11.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.(Ⅰ)证明:A=2B;(Ⅱ)若△ABC的面积S=,求角A的大小.12.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A=,b2﹣a2=c2.(1)求tanC的值;(2)若△ABC的面积为3,求b的值.13.在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8.(Ⅰ)若a=2,b=,求cosC的值;(Ⅱ)若sinAcos2+sinBcos2=2sinC,且△ABC的面积S=sinC,求a和b的值.14.△ABC的内角A,B,C所对应的边分别为a,b,c.(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);(Ⅱ)若a,b,c成等比数列,求cosB的最小值.15.△ABC的内角A、B、C所对的边分别为a,b,c.(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值.16.四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.(1)求C和BD;(2)求四边形ABCD的面积.17.△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2.(1)求cosB;(2)若a+c=6,△ABC的面积为2,求b.18.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.(1)证明:A=2B;(2)若cosB=,求cosC的值.19.设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.20.△ABC中,角A,B,C所对的边分别为a,b,c,已知cosB=,sin(A+B)=,ac=2,求sinA和c的值.21.设△ABC的内角A,B,C的对边分别为a,b,c,a=btanA.(Ⅰ)证明:sinB=cosA;(Ⅱ)若sinC﹣sinAcosB=,且B为钝角,求A,B,C.22.△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC面积的2倍.(1)求;(2)若AD=1,DC=,求BD和AC的长.23.已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.(Ⅰ)若a=b,求cosB;(Ⅱ)设B=90°,且a=,求△ABC的面积.24.△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC(Ⅰ)求.(Ⅱ)若∠BA C=60°,求∠B.25.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a﹣c=b,sinB=sinC,(Ⅰ)求cosA的值;(Ⅱ)求cos(2A﹣)的值.26.△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cosA=,B=A+.(Ⅰ)求b的值;(Ⅱ)求△ABC的面积.27.在△ABC中,角A,B,C的对边分别是a,b,c.(1)若sin(A+)=2cosA,求A的值.(2)若cosA=,b=3c,求sinC的值.28.在△ABC中,角A,B,C的对边是a,b,c,已知3acosA=ccosB+bcosC(1)求cosA的值(2)若a=1,cosB+cosC=,求边c的值.29.在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=a•cosB.(1)求角B的大小;(2)若b=3,sinC=2sinA,分别求a和c的值.30.在△ABC中,a=3,b=2,∠B=2∠A.(Ⅰ)求cosA的值;(Ⅱ)求c的值.三角函数与解三角形高考试题精选参考答案与试题解析一.解答题(共31小题)1.在△ABC中,角A,B,C的对边分别为a,b,c,已知2(tanA+tanB)=+.(Ⅰ)证明:a+b=2c;(Ⅱ)求cosC的最小值.【解答】解:(Ⅰ)证明:由得:;∴两边同乘以cosAcosB得,2(sinAcosB+cosAsinB)=sinA+sinB;∴2sin(A+B)=sinA+sinB;即sinA+sinB=2sinC(1);根据正弦定理,;∴,带入(1)得:;∴a+b=2c;(Ⅱ)a+b=2c;∴(a+b)2=a2+b2+2ab=4c2;∴a2+b2=4c2﹣2ab,且4c2≥4ab,当且仅当a=b时取等号;又a,b>0;∴;∴由余弦定理,=;∴cosC的最小值为.2.在△ABC中,内角A,B,C所对的边分别为a,b,c.已知asinA=4bsinB,ac=(a2﹣b2﹣c2).(Ⅰ)求cosA的值;(Ⅱ)求sin(2B﹣A)的值.【解答】(Ⅰ)解:由,得asinB=bsinA,又asinA=4bsinB,得4bsinB=asinA,两式作比得:,∴a=2b.由,得,由余弦定理,得;(Ⅱ)解:由(Ⅰ),可得,代入asinA=4bsinB,得.由(Ⅰ)知,A为钝角,则B为锐角,∴.于是,,故.3.△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.(Ⅰ)求C;(Ⅱ)若c=,△ABC的面积为,求△ABC的周长.【解答】解:(Ⅰ)∵在△ABC中,0<C<π,∴sinC≠0已知等式利用正弦定理化简得:2cosC(sinAcosB+sinBcosA)=sinC,整理得:2cosCsin(A+B)=sinC,即2cosCsin(π﹣(A+B))=sinC2cosCsinC=sinC∴cosC=,∴C=;(Ⅱ)由余弦定理得7=a2+b2﹣2ab•,∴(a+b)2﹣3ab=7,∵S=absinC=ab=,∴ab=6,∴(a+b)2﹣18=7,∴a+b=5,∴△ABC的周长为5+.4.在△ABC中,内角A,B,C的对边分别为a,b,c.已知cosA=,sinB=C.(1)求tanC的值;(2)若a=,求△ABC的面积.【解答】解:(1)∵A为三角形的内角,cosA=,∴sinA==,又cosC=sinB=sin(A+C)=sinAcosC+cosAsinC=cosC+sinC,整理得:cosC=sinC,则tanC=;(2)由tanC=得:cosC====,∴sinC==,∴sinB=cosC=,∵a=,∴由正弦定理=得:c===,则S△ABC=acsinB=×××=.5.在△ABC中,角A,B,C所对的边分别是a,b,c,且+=.(Ⅰ)证明:sinAsinB=sinC;(Ⅱ)若b2+c2﹣a2=bc,求tanB.【解答】(Ⅰ)证明:在△ABC中,∵+=,∴由正弦定理得:,∴=,∵sin(A+B)=sinC.∴整理可得:sinAsinB=sinC,(Ⅱ)解:b2+c2﹣a2=bc,由余弦定理可得cosA=.sinA=,=+==1,=,tanB=4.6.在△ABC中,已知AB=2,AC=3,A=60°.(1)求BC的长;(2)求sin2C的值.【解答】解:(1)由余弦定理可得:BC2=AB2+AC2﹣2AB•ACcosA=4+9﹣2×2×3×=7,所以BC=.(2)由正弦定理可得:,则sinC===,∵AB<BC,BC=,AB=2,角A=60°,在三角形ABC中,大角对大边,大边对大角,>2,∴角C<角A,角C为锐角.sinC>0,cosC>0则cosC===.因此sin2C=2sinCcosC=2×=.7.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知△ABC的面积为3,b﹣c=2,cosA=﹣.(Ⅰ)求a和sinC的值;(Ⅱ)求cos(2A+)的值.【解答】解:(Ⅰ)在三角形ABC中,由cosA=﹣,可得sinA=,△ABC的面积为3,可得:,可得bc=24,又b﹣c=2,解得b=6,c=4,由a2=b2+c2﹣2bccosA,可得a=8,,解得sinC=;(Ⅱ)cos(2A+)=cos2Acos﹣sin2Asin==.8.△ABC的内角A,B,C所对的边分别为a,b,c.向量=(a,b)与=(cosA,sinB)平行.(Ⅰ)求A;(Ⅱ)若a=,b=2,求△ABC的面积.【解答】解:(Ⅰ)因为向量=(a,b)与=(cosA,sinB)平行,所以asinB﹣=0,由正弦定理可知:sinAsinB﹣sinBcosA=0,因为sinB≠0,所以tanA=,可得A=;(Ⅱ)a=,b=2,由余弦定理可得:a2=b2+c2﹣2bccosA,可得7=4+c2﹣2c,解得c=3,△ABC的面积为:=.9.设△ABC的内角A,B,C所对边的长分别为a,b,c,且b=3,c=1,△ABC的面积为,求cosA与a的值.【解答】解:∵b=3,c=1,△ABC的面积为,∴=,∴sinA=,又∵sin2A+cos2A=1∴cosA=±,由余弦定理可得a==2或2.10.如图,在平面四边形ABCD中,DA⊥AB,DE=1,EC=,EA=2,∠ADC=,∠BEC=.(Ⅰ)求sin∠CED的值;(Ⅱ)求BE的长.【解答】解:(Ⅰ)设α=∠CED,在△CDE中,由余弦定理得EC2=CD2+ED2﹣2CD•DEcos∠CDE,即7=CD2+1+CD,则CD2+CD﹣6=0,解得CD=2或CD=﹣3,(舍去),在△CDE中,由正弦定理得,则sinα=,即sin∠CED=.(Ⅱ)由题设知0<α<,由(Ⅰ)知cosα=,而∠AEB=,∴cos∠AEB=cos()=cos cosα+sin sinα=,在Rt△EAB中,cos∠AEB=,故BE=.11.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.(Ⅰ)证明:A=2B;(Ⅱ)若△ABC的面积S=,求角A的大小.【解答】(Ⅰ)证明:∵b+c=2acosB,∴sinB+sinC=2sinAcosB,∴sinB+sin(A+B)=2sinAcosB∴sinB+sinAcosB+cosAsinB=2sinAcosB∴sinB=sinAcosB﹣cosAsinB=sin(A﹣B)∵A,B是三角形中的角,∴B=A﹣B,∴A=2B;(Ⅱ)解:∵△ABC的面积S=,∴bcsinA=,∴2bcsinA=a2,∴2sinBsinC=sinA=sin2B,∴sinC=cosB,∴B+C=90°,或C=B+90°,∴A=90°或A=45°.12.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知A=,b2﹣a2=c2.(1)求tanC的值;(2)若△ABC的面积为3,求b的值.【解答】解:(1)∵A=,∴由余弦定理可得:,∴b2﹣a2=bc﹣c2,又b2﹣a2=c2.∴bc﹣c2=c2.∴b=c.可得,∴a2=b2﹣=,即a=.∴cosC===.∵C∈(0,π),∴sinC==.∴tanC==2.或由A=,b2﹣a2=c2.可得:sin2B﹣sin2A=sin2C,∴sin2B﹣=sin2C,∴﹣cos2B=sin2C,∴﹣sin=sin2C,∴﹣sin=sin2C,∴sin2C=sin2C,∴tanC=2.(2)∵=×=3,解得c=2.∴=3.13.在△ABC中,内角A、B、C所对的边分别是a、b、c,且a+b+c=8.(Ⅰ)若a=2,b=,求cosC的值;(Ⅱ)若sinAcos2+sinBcos2=2sinC,且△ABC的面积S=sinC,求a和b的值.【解答】解:(Ⅰ)∵a=2,b=,且a+b+c=8,∴c=8﹣(a+b)=,∴由余弦定理得:cosC===﹣;(Ⅱ)由sinAcos2+sinBcos2=2sinC可得:sinA•+sinB•=2sinC,整理得:sinA+sinAcosB+sinB+sinBcosA=4sinC,∵sinAcosB+cosAsinB=sin(A+B)=sinC,∴sinA+sinB=3sinC,利用正弦定理化简得:a+b=3c,∵a+b+c=8,∴a+b=6①,∵S=absinC=sinC,∴ab=9②,联立①②解得:a=b=3.14.△ABC的内角A,B,C所对应的边分别为a,b,c.(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);(Ⅱ)若a,b,c成等比数列,求cosB的最小值.【解答】解:(Ⅰ)∵a,b,c成等差数列,∴2b=a+c,利用正弦定理化简得:2sinB=sinA+sinC,∵sinB=sin[π﹣(A+C)]=sin(A+C),∴sinA+sinC=2sinB=2sin(A+C);(Ⅱ)∵a,b,c成等比数列,∴b2=ac,∴cosB==≥=,当且仅当a=c时等号成立,∴cosB的最小值为.15.△ABC的内角A、B、C所对的边分别为a,b,c.(Ⅰ)若a,b,c成等差数列,证明:sinA+sinC=2sin(A+C);(Ⅱ)若a,b,c成等比数列,且c=2a,求cosB的值.【解答】解:(Ⅰ)∵a,b,c成等差数列,∴a+c=2b,由正弦定理得:sinA+sinC=2sinB,∵sinB=sin[π﹣(A+C)]=sin(A+C),则sinA+sinC=2sin(A+C);(Ⅱ)∵a,b,c成等比数列,∴b2=ac,将c=2a代入得:b2=2a2,即b=a,∴由余弦定理得:cosB===.16.四边形ABCD的内角A与C互补,AB=1,BC=3,CD=DA=2.(1)求C和BD;(2)求四边形ABCD的面积.【解答】解:(1)在△BCD中,BC=3,CD=2,由余弦定理得:BD2=BC2+CD2﹣2BC•CDcosC=13﹣12cosC①,在△ABD中,AB=1,DA=2,A+C=π,由余弦定理得:BD2=AB2+AD2﹣2AB•ADcosA=5﹣4cosA=5+4cosC②,由①②得:cosC=,则C=60°,BD=;(2)∵cosC=,cosA=﹣,∴sinC=sinA=,则S=AB•DAsinA+BC•CDsinC=×1×2×+×3×2×=2.17.△ABC的内角A,B,C的对边分别为a,b,c,已知sin(A+C)=8sin2.(1)求cosB;(2)若a+c=6,△ABC的面积为2,求b.【解答】解:(1)sin(A+C)=8sin2,∴sinB=4(1﹣cosB),∵sin2B+cos2B=1,∴16(1﹣cosB)2+cos2B=1,∴16(1﹣cosB)2+cos2B﹣1=0,∴16(cosB﹣1)2+(cosB﹣1)(cosB+1)=0,∴(17cosB﹣15)(cosB﹣1)=0,∴cosB=;(2)由(1)可知sinB=,∵S△ABC=ac•sinB=2,∴ac=,∴b2=a2+c2﹣2accosB=a2+c2﹣2××=a2+c2﹣15=(a+c)2﹣2ac﹣15=36﹣17﹣15=4,∴b=2.18.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知b+c=2acosB.(1)证明:A=2B;(2)若cosB=,求cosC的值.【解答】(1)证明:∵b+c=2acosB,∴sinB+sinC=2sinAcosB,∵sinC=sin(A+B)=sinAcosB+cosAsinB,∴sinB=sinAcosB﹣cosAsinB=sin(A﹣B),由A,B∈(0,π),∴0<A﹣B<π,∴B=A﹣B,或B=π﹣(A﹣B),化为A=2B,或A=π(舍去).∴A=2B.(II)解:cosB=,∴sinB==.cosA=cos2B=2cos2B﹣1=,sinA==.∴cosC=﹣cos(A+B)=﹣cosAcosB+sinAsinB=+×=.19.设△ABC的内角A、B、C的对边分别为a、b、c,a=btanA,且B为钝角.(Ⅰ)证明:B﹣A=;(Ⅱ)求sinA+sinC的取值范围.【解答】解:(Ⅰ)由a=btanA和正弦定理可得==,∴sinB=cosA,即sinB=sin(+A)又B为钝角,∴+A∈(,π),∴B=+A,∴B﹣A=;(Ⅱ)由(Ⅰ)知C=π﹣(A+B)=π﹣(A++A)=﹣2A>0,∴A∈(0,),∴sinA+sinC=sinA+sin(﹣2A)=sinA+cos2A=sinA+1﹣2sin2A=﹣2(sinA﹣)2+,∵A∈(0,),∴0<sinA<,∴由二次函数可知<﹣2(sinA﹣)2+≤∴sinA+sinC的取值范围为(,]20.△ABC中,角A,B,C所对的边分别为a,b,c,已知cosB=,sin(A+B)=,ac=2,求sinA和c的值.【解答】解:①因为△ABC中,角A,B,C所对的边分别为a,b,c已知cosB=,sin(A+B)=,ac=2,所以sinB=,sinAcosB+cosAsinB=,所以sinA+cosA=①,结合平方关系sin2A+cos2A=1②,由①②解得27sin2A﹣6sinA﹣16=0,解得sinA=或者sinA=﹣(舍去);②由正弦定理,由①可知sin(A+B)=sinC=,sinA=,所以a=2c,又ac=2,所以c=1.21.设△ABC的内角A,B,C的对边分别为a,b,c,a=btanA.(Ⅰ)证明:sinB=cosA;(Ⅱ)若sinC﹣sinAcosB=,且B为钝角,求A,B,C.【解答】解:(Ⅰ)证明:∵a=btanA.∴=tanA,∵由正弦定理:,又tanA=,∴=,∵sinA≠0,∴sinB=cosA.得证.(Ⅱ)∵sinC=sin[π﹣(A+B)]=sin(A+B)=sinAcosB+cosAsinB,∴sinC﹣sinAcosB=cosAsinB=,由(1)sinB=cosA,∴sin2B=,∵0<B<π,∴sinB=,∵B为钝角,∴B=,又∵cosA=sinB=,∴A=,∴C=π﹣A﹣B=,综上,A=C=,B=.22.△ABC中,D是BC上的点,AD平分∠BAC,△ABD面积是△ADC面积的2倍.(1)求;(2)若AD=1,DC=,求BD和AC的长.【解答】解:(1)如图,过A作AE⊥BC于E,∵==2∴BD=2DC,∵AD平分∠BAC∴∠BAD=∠DAC在△ABD中,=,∴sin∠B=在△ADC中,=,∴sin∠C=;∴==.…6分(2)由(1)知,BD=2DC=2×=.过D作DM⊥AB于M,作DN⊥AC于N,∵AD平分∠BAC,∴DM=DN,∴==2,∴AB=2AC,令AC=x,则AB=2x,∵∠BAD=∠DAC,∴cos∠BAD=cos∠DAC,∴由余弦定理可得:=,∴x=1,∴AC=1,∴BD的长为,AC的长为1.23.已知a,b,c分别是△ABC内角A,B,C的对边,sin2B=2sinAsinC.(Ⅰ)若a=b,求cosB;(Ⅱ)设B=90°,且a=,求△ABC的面积.【解答】解:(I)∵sin2B=2sinAsinC,由正弦定理可得:>0,代入可得(bk)2=2ak•ck,∴b2=2ac,∵a=b,∴a=2c,由余弦定理可得:cosB===.(II)由(I)可得:b2=2ac,∵B=90°,且a=,∴a2+c2=b2=2ac,解得a=c=.∴S△ABC==1.24.△ABC中,D是BC上的点,AD平分∠BAC,BD=2DC(Ⅰ)求.(Ⅱ)若∠BAC=60°,求∠B.【解答】解:(Ⅰ)如图,由正弦定理得:,∵AD平分∠BAC,BD=2DC,∴;(Ⅱ)∵∠C=180°﹣(∠BAC+∠B),∠BAC=60°,∴,由(Ⅰ)知2sin∠B=sin∠C,∴tan∠B=,即∠B=30°.25.在△ABC中,内角A,B,C所对的边分别为a,b,c,已知a﹣c=b,sinB=sinC,(Ⅰ)求cosA的值;(Ⅱ)求cos(2A﹣)的值.【解答】解:(Ⅰ)将sinB=sinC,利用正弦定理化简得:b=c,代入a﹣c=b,得:a﹣c=c,即a=2c,∴cosA===;(Ⅱ)∵cosA=,A为三角形内角,∴sinA==,∴cos2A=2cos2A﹣1=﹣,sin2A=2sinAcosA=,则cos(2A﹣)=cos2Acos+sin2Asin=﹣×+×=.26.△ABC中,角A,B,C所对的边分别为a,b,c.已知a=3,cosA=,B=A+.(Ⅰ)求b的值;(Ⅱ)求△ABC的面积.【解答】解:(Ⅰ)∵cosA=,∴sinA==,∵B=A+.∴sinB=sin(A+)=cosA=,由正弦定理知=,∴b=•sinB=×=3.(Ⅱ)∵sinB=,B=A+>∴cosB=﹣=﹣,sinC=sin(π﹣A﹣B)=sin(A+B)=sinAcosB+cosAsinB=×(﹣)+×=,∴S=a•b•sinC=×3×3×=.27.在△ABC中,角A,B,C的对边分别是a,b,c.(1)若sin(A+)=2cosA,求A的值.(2)若cosA=,b=3c,求sinC的值.【解答】解:(1)因为,所以sinA=,所以tanA=,所以A=60°(2)由及a2=b2+c2﹣2bccosA得a2=b2﹣c2故△ABC是直角三角形且B=所以sinC=cosA=28.在△ABC中,角A,B,C的对边是a,b,c,已知3acosA=ccosB+bcosC (1)求cosA的值(2)若a=1,cosB+cosC=,求边c的值.【解答】解:(1)由余弦定理可知2accosB=a2+c2﹣b2;2abcosc=a2+b2﹣c2;代入3acosA=ccosB+bcosC;得cosA=;(2)∵cosA=∴sinA=cosB=﹣cos(A+C)=﹣cosAcosC+sinAsinC=﹣cosC+sinC ③又已知 cosB+cosC=代入③cosC+sinC=,与cos2C+sin2C=1联立解得 sinC=已知 a=1正弦定理:c===29.在△ABC中,内角A,B,C的对边分别为a,b,c,且bsinA=a•cosB.(1)求角B的大小;(2)若b=3,sinC=2sinA,分别求a和c的值.【解答】解:(1)∵bsinA=a•cosB,由正弦定理可得:sinBsinA=sinAcosB,∵sinA≠0,∴sinB=cosB,B∈(0,π),可知:cosB≠0,否则矛盾.∴tanB=,∴B=.(2)∵sinC=2sinA,∴c=2a,由余弦定理可得:b2=a2+c2﹣2accosB,∴9=a2+c2﹣ac,把c=2a代入上式化为:a2=3,解得a=,∴.30.在△ABC中,a=3,b=2,∠B=2∠A.(Ⅰ)求cosA的值;(Ⅱ)求c的值.【解答】解:(Ⅰ)由条件在△ABC中,a=3,,∠B=2∠A,利用正弦定理可得,即=.解得cosA=.(Ⅱ)由余弦定理可得 a2=b2+c2﹣2bc•cosA,即 9=+c2﹣2×2×c×,即 c2﹣8c+15=0.解方程求得 c=5,或 c=3.当c=3时,此时a=c=3,根据∠B=2∠A,可得B=90°,A=C=45°,△ABC是等腰直角三角形,但此时不满足a2+c2=b2,故舍去.当c=5时,求得cosB==,cosA==,∴cos2A=2cos2A﹣1==cosB,∴B=2A,满足条件.综上,c=5.。
2011—2017年高考全国卷Ⅰ文科数学三角函数、解三角形汇编

新课标全国卷Ⅰ文科数学汇编三角函数、解三角形一、选择题【2017,11】△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .已知sin sin (sin cos )0B A C C +-=,a=2,2,则C=( ) A .π12B .π6C .π4D .π3【2016,4】ABC △的内角A B C ,,的对边分别为a b c ,,.已知5a =2c =,2cos 3A =,则b =( ) A .2 B3 C .2 D .3【2016,6】若将函数π2sin 26y x ⎛⎫=+⎪⎝⎭的图像向右平移14个周期后,所得图像对应的函数为( ). A .π2sin 24y x ⎛⎫=+⎪⎝⎭ B .π2sin 23y x ⎛⎫=+ ⎪⎝⎭ C .π2sin 24y x ⎛⎫=- ⎪⎝⎭D .π2sin 23y x ⎛⎫=- ⎪⎝⎭【2015,8】函数f (x )=cos(ωx +φ)的部分图像如图所示,则f (x )的单调递减区间为( ) A .13(,),44k k k Z ππ-+∈ B .13(2,2),44k k k Z ππ-+∈ C .13(,),44k k k Z -+∈ D .13(2,2),44k k k Z -+∈ 【2014,7】在函数① y=cos|2x|,②y=|cos x |,③)62cos(π+=x y ,④)42tan(π-=x y 中,最小正周期为π的所有函数为( )A .①②③B .①③④C .②④D .①③【2014,2】若tan 0α>,则( )A . sin 0α>B . cos 0α>C . sin 20α>D . cos20α>【2013,10】已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c,23cos 2A +cos 2A =0,a =7,c =6,则b =( )A .10B .9C .8D .5 【2012,9】9.已知0ω>,0ϕπ<<,直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=( ) A .4π B .3π C .2πD .34π 【2011,7】已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos2θ=( ).A .45-B .35-C .35D .45【2011,11】设函数ππ()sin 2cos 244f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则 ( ) A .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递增,其图象关于直线π4x =对称 B .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递增,其图象关于直线π2x =对称 C .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递减,其图象关于直线π4x =对称 D .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递减,其图象关于直线π2x =对称 二、填空题【2017,15】已知0,2πα⎛⎫∈ ⎪⎝⎭,tan 2α=,则cos 4πα⎛⎫-= ⎪⎝⎭________. 【2016,】14.已知θ是第四象限角,且π3sin 45θ⎛⎫+= ⎪⎝⎭,则πtan 4θ⎛⎫-= ⎪⎝⎭. 【2013,16】设当x =θ时,函数f (x )=sin x -2cos x 取得最大值,则cos θ=______.【2014,16】如图所示,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角60MAN ∠=︒,C 点的仰角 45CAB ∠=︒以及75MAC ∠=︒;从C 点测得60MCA ∠=︒. 已知山高100BC m =,则山高MN = m . 【2011,15】ABC △中,120B =,7AC =,5AB =,则ABC △的面积为 . 三、解答题【2015,17】已知,,a b c 分别为ABC △内角,,A B C 的对边,2sin 2sin sin B A C =.(1)若a b =,求cos B ;(2)设90B ∠=,且2a =ABC △的面积.【2012,17】已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,3sin cos c a C c A =-.(1)求A ;(2)若2a =,△ABC 3,求b ,c .解 析一、选择题【2017,11】△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .已知sin sin (sin cos )0B A C C +-=,a=2,2,则C=( ) A .π12B .π6C .π4D .π3【答案】B【解法】解法一:因为sin sin (sin cos )0B A C C +-=,sin sin()B A C =+,所以sin (sin cos )0C A A +=,又sin 0C >,所以sin cos A A =-,tan 1A =-,又0A π<<,所以34A π=,又a =2,c 222=即1sin 2C =.又02C π<<,所以6C π=,故选B .解法二:由解法一知sin cos 0A A +=2)04A π+=,又0A π<<,所以34A π=.下同解法一.【2016,4】ABC △的内角A B C ,,的对边分别为a b c ,,.已知5a =2c =,2cos 3A =,则b =( ) A .2 B3 C .2 D .3解析:选D .由余弦定理得222cos 2b c a A bc +-=,即245243b b +-=, 整理得()28113033b b b b ⎛⎫--=-+= ⎪⎝⎭,解得3b =.故选D . 【2016,6】若将函数π2sin 26y x ⎛⎫=+⎪⎝⎭的图像向右平移14个周期后,所得图像对应的函数为( ). A .π2sin 24y x ⎛⎫=+⎪⎝⎭ B .π2sin 23y x ⎛⎫=+ ⎪⎝⎭ C .π2sin 24y x ⎛⎫=- ⎪⎝⎭ D .π2sin 23y x ⎛⎫=- ⎪⎝⎭解析:选D .将函数π2sin 26y x ⎛⎫=+⎪⎝⎭的图像向右平移14个周期,即向右平移π4个单位, 故所得图像对应的函数为ππ2sin 246y x ⎡⎤⎛⎫=-+ ⎪⎢⎥⎝⎭⎣⎦π2sin 23x ⎛⎫=- ⎪⎝⎭.故选D . 【2015,8】函数f (x )=cos(ωx +φ)的部分图像如图所示,则f (x )的单调递减区间为( ) A .13(,),44k k k Z ππ-+∈ B .13(2,2),44k k k Z ππ-+∈C .13(,),44k k k Z -+∈ D .13(2,2),44k k k Z -+∈ 解:选D .依图,153++4242ππωϕωϕ==且,解得ω=π,=4πϕ, ()cos()4f x x ππ∴=+, 224k x k πππππ<+<+由,,解得132244k x k -<<+,故选D . 【2014,7】在函数① y=cos|2x|,②y=|cos x |,③)62cos(π+=x y ,④)42tan(π-=x y 中,最小正周期为π的所有函数为( )A .①②③B .①③④C .②④D .①③解:选A .由cos y x =是偶函数可知①y=cos|2x|=cos2x ,最小正周期为π;②y=|cos x |的最小正周期也是π;③中函数最小正周期也是π;正确答案为①②③,故选A【2014,2】若tan 0α>,则( )A . sin 0α>B . cos 0α>C . sin 20α>D . cos20α>解:选C .tan α>0,α在一或三象限,所以sin α与cos α同号,故选C【2013,10】已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c,23cos 2A +cos 2A =0,a =7,c =6,则b =( ).A .10B .9C .8D .5解析:选D .由23cos 2A +cos 2A =0,得cos 2A =125.∵A ∈π0,2⎛⎫⎪⎝⎭,∴cos A =15.∵cos A =2364926b b +-⨯,∴b =5或135b =-(舍).【2012,9】9.已知0ω>,0ϕπ<<,直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,则ϕ=( )A .4π B .3π C .2πD .34π【解析】选A .由直线4x π=和54x π=是函数()sin()f x x ωϕ=+图像的两条相邻的对称轴,得()sin()f x x ωϕ=+的最小正周期52()244T πππ=-=,从而1ω=.由此()sin()f x x ϕ=+,由已知4x π=处()sin()f x x ϕ=+取得最值,所以sin()14πϕ+=±,结合选项,知ϕ=4π,故选择A .【2011,7】已知角θ的顶点与原点重合,始边与x 轴的正半轴重合,终边在直线2y x =上,则cos2θ=( ).A .45-B .35-C .35D .45【解析】设(,2)(0)P t t t ≠为角θ终边上任意一点,则cosθ=当0t >时,cos θ=0t <时,cos θ=.因此223cos 22cos 1155θθ=-=-=-.故选B .【2011,11】设函数ππ()sin 2cos 244f x x x ⎛⎫⎛⎫=+++ ⎪ ⎪⎝⎭⎝⎭,则 ( ) A .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递增,其图象关于直线π4x =对称 B .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递增,其图象关于直线π2x =对称 C .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递减,其图象关于直线π4x =对称 D .()f x 在π0,2⎛⎫ ⎪⎝⎭单调递减,其图象关于直线π2x =对称【解析】因为ππππ()sin 2cos 2224444f x x x x x ⎛⎫⎛⎫⎛⎫=+++=++= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,当π02x <<时,02πx <<,故()f x x =在π0,2⎛⎫⎪⎝⎭单调递减.又当π2x =π22⎛⎫⨯= ⎪⎝⎭π2x =是()y f x =的一条对称轴.故选D .二、填空题【2017,15】已知0,2πα⎛⎫∈ ⎪⎝⎭,tan 2α=,则cos 4πα⎛⎫-= ⎪⎝⎭________.【解析】10.0,2πα⎛⎫∈ ⎪⎝⎭,sin tan 22sin 2cos cos ααααα=⇒=⇒=,又22sin cos 1αα+=,解得sin α=,cos α=,cos sin )4210πααα⎛⎫∴-=+= ⎪⎝⎭.【基本解法2】0,2πα⎛⎫∈ ⎪⎝⎭,tan 2α=,∴角α的终边过(1,2)P ,故sin y r α==,cos 5x r α==,其中r ==cos (cos sin )4210πααα⎛⎫∴-=+= ⎪⎝⎭.【2016,】14.已知θ是第四象限角,且π3sin 45θ⎛⎫+= ⎪⎝⎭,则πtan 4θ⎛⎫-= ⎪⎝⎭. 解析:43-.由题意sin sin 442θθπππ⎡⎤⎛⎫⎛⎫+=-+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦3cos 45θπ⎛⎫=-= ⎪⎝⎭.因为2222k k θ3ππ+<<π+π()k ∈Z ,所以722444k k θ5ππππ+<-<π+()k ∈Z , 从而4sin 45θπ⎛⎫-=- ⎪⎝⎭,因此4tan 43θπ⎛⎫-=- ⎪⎝⎭.故填43-. 方法2:还可利用ππtan tan 144θθ⎛⎫⎛⎫-+=- ⎪ ⎪⎝⎭⎝⎭来进行处理,或者直接进行推演,即由题意4cos 45θπ⎛⎫+= ⎪⎝⎭,故3tan 44θπ⎛⎫+= ⎪⎝⎭,所以tan 4θπ⎛⎫-= ⎪⎝⎭143tan 4θ-=-π⎛⎫+ ⎪⎝⎭. 【2013,16】设当x =θ时,函数f (x )=sin x -2cos x 取得最大值,则cos θ=______.答案:解析:25. ∵f (x )=sin x -2cos x 5sin(x -φ),其中sin φ25cos φ5当x -φ=2k π+π2(k ∈Z)时,f (x )取最大值.即θ-φ=2k π+π2(k ∈Z),θ=2k π+π2+φ(k ∈Z).∴cos θ=πcos 2ϕ⎛⎫+ ⎪⎝⎭=-sin φ=255-.【2014,16】16.如图所示,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M点的仰角60MAN ∠=︒,C 点的仰角45CAB ∠=︒以及 75MAC ∠=︒;从C 点测得60MCA ∠=︒.已知山高100BC m =,则山高MN = m .解:在RtΔABC 中,由条件可得1002AC =,在ΔMAC 中,∠MAC=45°;由正弦定理可得sin60sin 45AM AC =︒︒,故310032AM AC =RtΔMAN 中,MN=AM sin60°=150.【2011,15】ABC △中,120B =,7AC =,5AB =,则ABC △的面积为 .【解析】由余弦定理知2222cos120AC AB BC AB BC =+-⋅,即249255BC BC =++,解得3BC =.故113153sin120532224ABC S AB BC =⋅=⨯⨯⨯=△.故答案为1534.三、解答题【2015,17】已知,,a b c 分别为ABC △内角,,A B C 的对边,2sin 2sin sin B A C =.(1)若a b =,求cos B ;(2)设90B ∠=,且a =ABC △的面积.解析:(1)由正弦定理得,22b ac =.又a b =,所以22a ac =,即2a c =.则22222212cos 2422a a a a cb B a ac a ⎛⎫+- ⎪+-⎝⎭===⋅.(2)解法一:因为90B ∠=,所以()2sin 12sin sin 2sin sin 90B A C A A ===-, 即2sin cos 1A A =,亦即sin 21A =.又因为在ABC △中,90B ∠=,所以090A <∠<, 则290A ∠=,得45A ∠=.所以ABC △为等腰直角三角形,得a c ==112ABC S ==△. 解法二:由(1)可知22b ac =,① 因为90B ∠=,所以222a c b +=,② 将②代入①得()20a c -=,则a c ==,所以112ABC S ==△. 解:(Ⅰ) 因为sin 2B =2sin A sin C . 由正弦定理可得b 2=2ac .又a =b ,可得a=2c , b=2c ,由余弦定理可得2221cos 24a cb Bac. (Ⅱ)由(Ⅰ)知b 2=2ac . 因为B=90°,所以a 2+c 2=b 2=2ac . 解得a =. 所以ΔABC 的面积为1.【2012,17】已知a ,b ,c 分别为△ABC三个内角A ,B ,C 的对边,sin cos c C c A =-.(1)求A ;(2)若2a =,△ABC ,求b ,c . 【解析】(1)根据正弦定理2sin sin a cR A C==,得A R a sin 2=, C Rc sin 2=, 因为sin cos c C c A =-,所以2sin sin )sin 2sin cos R C R A C R C A =-⋅, 化简得C C A C A sin sin cos sin sin 3=-, 因为0sin ≠C ,所以1cos sin 3=-A A ,即21)6sin(=-πA , 而π<<A 0,6566πππ<-<-A ,从而66ππ=-A ,解得3π=A . (2)若2a =,△ABC1)得3π=A ,则⎪⎪⎩⎪⎪⎨⎧==-+=43cos 233sin 21222a bc c b bc ππ,化简得⎩⎨⎧=+=8422c b bc , 从而解得2=b ,2=c .。
2022高考数学真题分类汇编07 三角函数与解三角形【含答案】

2022高考数学真题分类汇编五、三角函数与解三角形一、单选题1.(2022·全国甲(文)T5)将函数的图像向左平移个单位π()sin (0)3f x x ωω⎛⎫=+> ⎪⎝⎭π2长度后得到曲线C ,若C 关于y 轴对称,则的最小值是()ωA. B. C. D. 16141312【答案】C 【解析】【分析】先由平移求出曲线的解析式,再结合对称性得,即可C ,232k k ωππππ+=+∈Z求出的最小值.ω【详解】由题意知:曲线为,又关于C sin sin(2323y x x ππωππωω⎡⎤⎛⎫=++=++ ⎪⎢⎥⎝⎭⎣⎦C 轴对称,则,y ,232k k ωππππ+=+∈Z解得,又,故当时,的最小值为.12,3k k ω=+∈Z0>ω0k =ω13故选:C.2.(2022·全国甲(理)T11)设函数在区间恰有三个极值点、π()sin 3f x x ω⎛⎫=+ ⎪⎝⎭(0,π)两个零点,则的取值范围是( )ωA. B. C. D.513,36⎫⎡⎪⎢⎣⎭519,36⎡⎫⎪⎢⎣⎭138,63⎛⎤⎥⎝⎦1319,66⎛⎤ ⎥⎝⎦【答案】C 【解析】【分析】由的取值范围得到的取值范围,再结合正弦函数的性质得到不等式组,x 3x πω+解得即可.【详解】解:依题意可得,因为,所以,0>ω()0,x π∈,333x πππωωπ⎛⎫+∈+ ⎪⎝⎭要使函数在区间恰有三个极值点、两个零点,又,的图象如()0,πsin y x =,33x ππ⎛⎫∈ ⎪⎝⎭下所示:则,解得,即.5323ππωππ<+≤13863ω<≤138,63ω⎛⎤∈ ⎥⎝⎦故选:C .3.(2022·全国乙(文)T11) 函数在区间的最小值、()()cos 1sin 1f x x x x =+++[]0,2π最大值分别为()A. B. C. D.ππ22-,3ππ22-,ππ222-+,3ππ222-+,【答案】D 【解析】【分析】利用导数求得的单调区间,从而判断出在区间上的最小值和()f x ()f x []0,2π最大值.【详解】,()()()sin sin 1cos 1cos f x x x x x x x'=-+++=+所以在区间和上,即单调递增;()f x π0,2⎛⎫ ⎪⎝⎭3π,2π2⎛⎫⎪⎝⎭()0f x '>()f x 在区间上,即单调递减,π3π,22⎛⎫⎪⎝⎭()0f x '<()f x 又,,,()()02π2f f ==ππ222f ⎛⎫=+ ⎪⎝⎭3π3π3π11222f ⎛⎫⎛⎫=-++=-⎪ ⎪⎝⎭⎝⎭所以在区间上的最小值为,最大值为.()f x []0,2π3π2-π22+故选:D4.(2022·新高考Ⅰ卷T6) 记函数的最小正周期为T .若()sin (0)4f x x b πωω⎛⎫=++> ⎪⎝⎭,且的图象关于点中心对称,则( )23T ππ<<()y f x =3,22π⎛⎫ ⎪⎝⎭2f π⎛⎫=⎪⎝⎭A. 1 B. C. D. 33252【答案】A 【解析】【分析】由三角函数的图象与性质可求得参数,进而可得函数解析式,代入即可得解.【详解】由函数的最小正周期T 满足,得,解得,23T ππ<<223πππω<<23ω<<又因为函数图象关于点对称,所以,且,3,22π⎛⎫ ⎪⎝⎭3,24k k Z ππωπ+=∈2b =所以,所以,,12,63k k Z ω=-+∈52ω=5()sin 224f x x π⎛⎫=++ ⎪⎝⎭所以.5sin 21244f πππ⎛⎫⎛⎫=++= ⎪ ⎪⎝⎭⎝⎭故选:A5.(2022·北京卷T5) 已知函数,则( )22()cos sin f x x x =-A. 在上单调递减B. 在上单调递增()f x ,26ππ⎛⎫-- ⎪⎝⎭()f x ,412ππ⎛⎫- ⎪⎝⎭C. 在上单调递减D. 在上单调递增()f x 0,3π⎛⎫⎪⎝⎭()f x 7,412ππ⎛⎫⎪⎝⎭【答案】C 【解析】【分析】化简得出,利用余弦型函数的单调性逐项判断可得出合适的选项.()cos 2f x x=【详解】因为.()22cos sin cos 2f x x x x=-=对于A 选项,当时,,则在上单调递增,26x ππ-<<-23x ππ-<<-()f x ,26ππ⎛⎫-- ⎪⎝⎭A 错;对于B 选项,当时,,则在上不单调,B 错;412x ππ-<<226x ππ-<<()f x ,412ππ⎛⎫- ⎪⎝⎭对于C 选项,当时,,则在上单调递减,C 对;03x π<<2023x π<<()f x 0,3π⎛⎫ ⎪⎝⎭对于D 选项,当时,,则在上不单调,D 错.7412x ππ<<7226x ππ<<()f x 7,412ππ⎛⎫⎪⎝⎭故选:C.6.(2022·北京卷T10) 在中,.P 为所在平面ABC 3,4,90AC BC C ==∠=︒ABC 内的动点,且,则的取值范围是( )1PC =PA PB ⋅A. B. C. D. [5,3]-[3,5]-[6,4]-[4,6]-【答案】D 【解析】【分析】依题意建立平面直角坐标系,设,表示出,,根据数量积()cos ,sin P θθPA PB的坐标表示、辅助角公式及正弦函数的性质计算可得;【详解】解:依题意如图建立平面直角坐标系,则,,,()0,0C ()3,0A ()0,4B因为,所以在以为圆心,为半径的圆上运动,1PC =P C 1设,,()cos ,sin P θθ[]0,2θπ∈所以,,()3cos ,sin PA θθ=--()cos ,4sin PB θθ=--所以()()()()cos 3cos 4sin sin PA PB θθθθ⋅=-⨯-+-⨯-22cos 3cos 4sin sin θθθθ=--+13cos 4sin θθ=--,其中,,()15sin θϕ=-+3sin 5ϕ=4cos 5ϕ=因为,所以,即;()1sin 1θϕ-≤+≤()415sin 6θϕ-≤-+≤[]4,6PA PB ⋅∈-故选:D7.(2022·浙江卷T6) 为了得到函数的图象,只要把函数2sin 3y x =图象上所有的点( )π2sin 35y x ⎛⎫=+ ⎪⎝⎭A. 向左平移个单位长度B. 向右平移个单位长度π5π5C .向左平移个单位长度D. 向右平移个单位长度π15π15【答案】D 【解析】【分析】根据三角函数图象的变换法则即可求出.【详解】因为,所以把函数图象ππ2sin 32sin 3155y x x ⎡⎤⎛⎫==-+ ⎪⎢⎥⎝⎭⎣⎦π2sin 35y x ⎛⎫=+ ⎪⎝⎭上的所有点向右平移个单位长度即可得到函数的图象.π152sin 3y x =故选:D.二、填空题1.(2022·全国甲(文)T16). 已知中,点D 在边BC 上,ABC .当取得最小值时,________.120,2,2ADB AD CDBD ∠=︒==ACAB BD =##1--【解析】【分析】设,利用余弦定理表示出后,结合基本不等式即可得220CD BD m ==>22AC AB 解.【详解】设,220CD BD m ==>则在中,,ABD △22222cos 42AB BD AD BD AD ADB m m =+-⋅∠=++在中,,ACD △22222cos 444AC CD AD CD AD ADC m m =+-⋅∠=+-所以()()()2222224421214441243424211m m m AC m m AB m m m mm m ++-++-===-+++++++,44≥=-当且仅当即时,等号成立,11m m +=+1m =-所以当取最小值时,.ACAB 1m =.12.(2022·全国甲(理)T16)已知中,点D 在边BC 上,ABC .当取得最小值时,________.120,2,2ADB AD CDBD ∠=︒==ACAB BD =##1--【解析】【分析】设,利用余弦定理表示出后,结合基本不等式即可得220CD BD m ==>22AC AB 解.【详解】设,220CD BD m ==>则在中,,ABD △22222cos 42AB BD AD BD AD ADB m m =+-⋅∠=++在中,,ACD △22222cos 444AC CD AD CD AD ADC m m =+-⋅∠=+-所以()()()2222224421214441243424211m m m AC m m AB m m m mm m ++-++-===-+++++++,44≥=-当且仅当即时,等号成立,11m m +=+1m =-所以当取最小值时,.ACAB 1m =.13.(2022·全国乙(理)T15) 记函数的最小正周()()cos (0,0π)f x x ωϕωϕ=+><<期为T ,若为的零点,则的最小值为____________.()f T =9x π=()f x ω【答案】3【解析】【分析】首先表示出,根据求出,再根据为函数的零点,即可求出T ()f T =ϕπ9x =的取值,从而得解;ω【详解】解: 因为,(,)()()cos f x x ωϕ=+0>ω0πϕ<<所以最小正周期,因为,2πT ω=()()2πcos cos 2πcos f T ωϕϕϕω⎛⎫=⋅+=+== ⎪⎝⎭又,所以,即,0πϕ<<π6ϕ=()πcos 6f x x ω⎛⎫=+ ⎪⎝⎭又为的零点,所以,解得,π9x =()f x ππππ,Z962k k ω+=+∈39,Z k k ω=+∈因为,所以当时;0>ω0k =min3ω=故答案为:34.(2022·新高考Ⅱ卷T6) 角满足,αβ,则()sin()cos()sin 4παβαβαβ⎛⎫+++=+ ⎪⎝⎭A. B. tan()1αβ+=tan()1αβ+=-C. D. tan()1αβ-=tan()1αβ-=-【答案】D 【解析】【分析】由两角和差的正余弦公式化简,结合同角三角函数的商数关系即可得解.【详解】由已知得:,()sin cos cos sin cos cos sin sin 2cos sin sin αβαβαβαβααβ++-=-即:,sin cos cos sin cos cos sin sin 0αβαβαβαβ-++=即:,()()sin cos 0αβαβ-+-=所以,()tan 1αβ-=-故选:D5.(2022·新高考Ⅱ卷T9)函数的图象以中心对称,()sin(2)(0π)f x x ϕϕ=+<<2π,03⎛⎫⎪⎝⎭则()A. 在单调递减y =()f x 5π0,12⎛⎫⎪⎝⎭B. 在有2个极值点y =()f x π11π,1212⎛⎫- ⎪⎝⎭C. 直线是一条对称轴7π6x =D. 直线是一条切线y x =-【答案】AD 【解析】【分析】根据三角函数的性质逐个判断各选项,即可解出.【详解】由题意得:,所以,,2π4πsin 033f ϕ⎛⎫⎛⎫=+= ⎪ ⎪⎝⎭⎝⎭4ππ3k ϕ+=k ∈Z 即,4ππ,3k k ϕ=-+∈Z 又,所以时,,故.0πϕ<<2k =2π3ϕ=2π()sin 23f x x ⎛⎫=+ ⎪⎝⎭对A ,当时,,由正弦函数图象知在5π0,12x ⎛⎫∈ ⎪⎝⎭2π2π3π2,332x ⎛⎫+∈ ⎪⎝⎭sin y u =()y f x =上是单调递减;5π0,12⎛⎫⎪⎝⎭对B ,当时,,由正弦函数图象知π11π,1212x ⎛⎫∈- ⎪⎝⎭2ππ5π2,322x ⎛⎫+∈ ⎪⎝⎭sin y u =只有1个极值点,由,解得,即为函数的唯一极值点;()y f x =2π3π232x +=5π12x =5π12x =对C ,当时,,,直线不是对称轴;7π6x =2π23π3x +=7π()06f =7π6x =对D ,由得:,2π2cos 213y x ⎛⎫'=+=- ⎪⎝⎭2π1cos 232x ⎛⎫+=- ⎪⎝⎭解得或,2π2π22π33x k +=+2π4π22π,33x k k +=+∈Z 从而得:或,πx k =ππ,3x k k =+∈Z 所以函数在点处的切线斜率为,()y f x =⎛⎝02π2cos 13x ky =='==-切线方程为:即.(0)y x =--y x =-故选:AD .6.(2022·北京卷T13) 若函数的一个零点为,则()sin f x A x x =-3π________;________.A =12f π⎛⎫=⎪⎝⎭【答案】 ①. 1②. 【解析】【分析】先代入零点,求得A 的值,再将函数化简为,代入自变量π()2sin()3f x x =-,计算即可.π12x =【详解】∵,∴π()03f A =-=1A =∴π()sin2sin(3f x x x x ==-ππππ()2sin()2sin121234f =-=-=故答案为:1,7.(2022·浙江卷T11) 我国南宋著名数学家秦九韶,发现了从三角形三边求面积的公式,他把这种方法称为“三斜求积”,它填补了我国传统数学的一个空白.如果把这个方法写成公式,就是,其中a ,b ,c 是三角形的三边,S 是三角S=形的面积.设某三角形的三边,则该三角形的面积2a b c ===___________.S =【解析】【分析】根据题中所给的公式代值解出.【详解】因为,所以S =.S ==8.(2022·浙江卷T13)若,则__________,3sin sin 2παβαβ-=+=sin α=_________.cos 2β=【答案】 ①②. 45【解析】【分析】先通过诱导公式变形,得到的同角等式关系,再利用辅助角公式化简成正弦型α函数方程,可求出,接下来再求.αβ【详解】,∴,即2παβ+=sin cos βα=3sin cos αα-=即,令,αα⎫=⎪⎪⎭sin θ=cos θ=,∴,即,()αθ-=22k k Zπαθπ-=+∈,22k παθπ=++∴,sinsin 2cos 2k παθπθ⎛⎫=++==⎪⎝⎭则.224cos 22cos 12sin 15ββα=-=-=;.45三、解答题1.(2022·全国乙(文)T17)记的内角A ,B ,C 的对边分别为a ,b ,c ﹐已知ABC.()()sin sin sin sin C A B B C A -=-(1)若,求C ;2A B =(2)证明:2222a b c =+【答案】(1);5π8(2)证明见解析.【解析】【分析】(1)根据题意可得,,再结合三角形内角和定理即可解出;()sin sin C C A =-(2)由题意利用两角差的正弦公式展开得,再根据正弦定理,余()()sin sin cos cos sin sin sin cos cos sin C A B A B B C A C A -=-弦定理化简即可证出.【小问1详解】由,可得,,2A B =()()sin sin sin sin C A B B C A -=-()sin sin sin sin C B B C A =-而,所以,即有,而π02B <<()sin 0,1B ∈()sin sin 0C C A =->,显然,所以,,而,0π,0πC C A <<<-<C C A ≠-πC C A +-=2A B =,所以.πA B C ++=5π8C =【小问2详解】由可得,()()sin sin sin sin C A B B C A -=-,再由正弦定理可得,()()sin sin cos cos sin sin sin cos cos sin C A B A B B C A C A -=-,然后根据余弦定理可知,cos cos cos cos ac B bc A bc A ab C -=-,化简得:()()()()22222222222211112222a c b b c a b c a a b c +--+-=+--+-,故原等式成立.2222a b c =+2.(2022·全国乙(理)T17)记的内角的对边分别为,已知ABC ,,A B C ,,a b c .sin sin()sin sin()C A B B C A -=-(1)证明:;2222a b c =+(2)若,求的周长.255,cos 31a A ==ABC 【答案】(1)见解析 (2)14【解析】【分析】(1)利用两角差的正弦公式化简,再根据正弦定理和余弦定理化角为边,从而即可得证;(2)根据(1)的结论结合余弦定理求出,从而可求得,即可得解.bc b c +【小问1详解】证明:因为,()()sin sin sin sin C A B B C A -=-所以,sin sin cos sin sin cos sin sin cos sin sin cos C A B C B A B C A B A C -=-所以,2222222222222a c b b c a a b c ac bc ab ac bc ab +-+-+-⋅-⋅=-⋅即,()22222222222a c b a b c b c a +-+--+-=-所以;2222a b c =+【小问2详解】解:因为,255,cos 31a A ==由(1)得,2250b c +=由余弦定理可得,2222cos a b c bc A =+-则,50502531bc -=所以,312bc =故,()2222503181b c b c bc +=++=+=所以,9b c +=所以的周长为.ABC 14a b c ++=3.(2022·新高考Ⅰ卷T18)记的内角A ,B ,C 的对边分别为a ,b ,c ,已知ABC .cos sin 21sin 1cos2A BA B =++(1)若,求B ;23C π=(2)求的最小值.222a b c +【答案】(1);π6(2).5【解析】【分析】(1)根据二倍角公式以及两角差的余弦公式可将化成cos sin 21sin 1cos2A BA B =++,再结合,即可求出;()cos sin A B B+=π02B <<(2)由(1)知,,,再利用正弦定理以及二倍角公式将π2C B =+π22A B =-化成,然后利用基本不等式即可解出.222a b c +2224cos 5cos B B +-【小问1详解】因为,即2cos sin 22sin cos sin 1sin 1cos 22cos cos A B B B BA BB B ===++,()1sin cos cos sin sin cos cos 2B A B A B A B C =-=+=-=而,所以;π02B <<π6B =【小问2详解】由(1)知,,所以,sin cos 0B C =->πππ,022C B <<<<而,πsin cos sin 2B C C ⎛⎫=-=- ⎪⎝⎭所以,即有.π2C B =+π22A B =-所以222222222sin sin cos 21cos sin cos a b A B B B cC B +++-==.()2222222cos 11cos 24cos 555cos cos B BB BB -+-==+-≥-=-当且仅当的最小值为.2cos B =222a b c +5-4.(2022·新高考Ⅱ卷T18) 记的三个内角分别为A ,B ,C ,其对边分别为ABC a ,b ,c ,分别以a ,b ,c为边长的三个正三角形的面积依次为,已知123,,S S S .12313S S S B -+==(1)求的面积;ABC (2)若,求b .sinsin A C =【答案】(1(2)12【解析】【分析】(1)先表示出,再由求得,结合余123,,S S S 123S S S -+=2222a c b +-=弦定理及平方关系求得,再由面积公式求解即可;ac (2)由正弦定理得,即可求解.22sin sin sin b acB AC =【小问1详解】由题意得,则22221231,,2S a S S =⋅===,222123S S S -+==即,由余弦定理得,整理得,则2222a c b +-=222cos 2a c b B ac +-=cos 1ac B =,又,cos 0B >1sin 3B =则,cos B ==1cos ac B ==1sin 2ABC S ac B== 【小问2详解】由正弦定理得:,则sin sin sin b a c B A C ==,则,.229sin sin sin sin sin 4b ac ac B A C A C =⋅===3sin 2b B =31sin 22bB ==5.(2022·北京卷T16)在中,.ABC sin2C C =(1)求;C ∠(2)若,且的面积为的周长.6b =ABC ABC 【答案】(1)6π(2)6+【解析】【分析】(1)利用二倍角的正弦公式化简可得的值,结合角的取值范围可求得角cos C C 的值;C (2)利用三角形的面积公式可求得的值,由余弦定理可求得的值,即可求得的a c ABC周长.【小问1详解】解:因为,则,()0,C π∈sin 0C >2sin cos C C C =可得,因此,.cos C =6C π=【小问2详解】解:由三角形的面积公式可得,解得.13sin22ABC S ab C a ===a =由余弦定理可得,2222cos 48362612c a b abC =+-=+-⨯=c ∴=所以,的周长为.ABC 6a b c ++=+6.(2022·浙江卷T18) 在中,角A ,B,C 所对的边分别为a ,b ,c .已知ABC .34,cos 5a C ==(1)求的值;sin A (2)若,求的面积.11b =ABC 【答案】(1;(2).22【解析】【分析】(1)先由平方关系求出,再根据正弦定理即可解出;sin C (2)根据余弦定理的推论以及可解出,即可由三角形面222cos 2a b c C ab +-=4a =a 积公式求出面积.in 12s S ab C =【小问1详解】由于, ,则.因为,3cos 5C =0πC <<4sin 5C=4a =由正弦定理知,则4sin A C =sin A C ==【小问2详解】因为,由余弦定理,得,4a =2222221612111355cos 22225a a a a b c C ab a a +--+-====即,解得,而,,26550a a +-=5a =4sin 5C =11b =所以的面积.ABC 114sin 51122225S ab C ==⨯⨯⨯=。
2024年高考数学真题分类汇编05:三角函数与解三角形

解法二:令 h x f (x) g x , x 1,1 ,可知 h x 为偶函数,根据偶函数的对称性可
知 h x 的零点只能为 0,即可得 a 2 ,并代入检验即可. 【解析】解法一:令 f (x) g x ,即 a(x 1)2 1 cos x 2ax ,可得 ax2 a 1 cos x , 令 F x ax2 a 1,G x cos x ,
三角函数与解三角形
一、单选题
1.(2024·全国)已知 cos( ) m, tan tan 2 ,则 cos( ) ( )
A. 3m
B. m 3
C.
m 3
D. 3m
2.(2024·全国)当
xÎ
[0, 2 ] 时,曲线
y
sin
x
与
y
2
sin
3x
6
的交点个数为(
)
A.3
B.4
C.6
的最小正周期为
π
.则函数在
π 12
,
π 6
的最小值是( )
A. 3
2
B. 3 2
C.0
D. 3 2
9.(2024·上海)下列函数 f x 的最小正周期是 2π 的是( )
A. sinx cosx C. sin2x cos2x
B. sinxcosx D. sin2x cos2x
二、多选题
y
f
x 在 0,1 处的切线与两坐标轴围
成的三角形的面积为( )
A. 1 6
B.
1 3
C.
1 2
D.
2 3
7.(2024·北京)已知fxFra biblioteksinx
高考全国卷三角函数、解三角形真题汇编(文科)
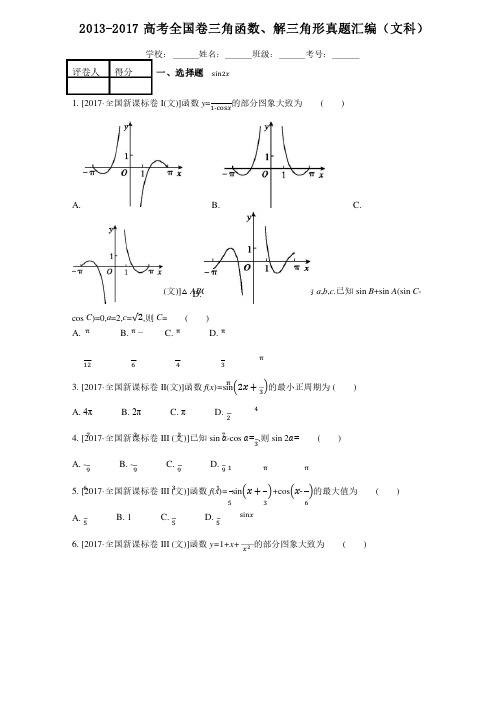
2013-2017 高考全国卷三角函数、解三角形真题汇编(文科)学校: 姓名: 班级: 考号:评卷人评卷人 得分得分一、选择题 1. [2017·全国新课标卷I(文)]函数y =sin2x 1-cosx 的部分图象大致为的部分图象大致为( ) A. B. C.D. 2. [2017·全国新课标卷I(文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.已知sin B +sin A (sin C -cos C )=0,a =2,c =√2,则C = ( )A. π12B. π6C. π4D. π3 3. [2017·全国新课标卷II(文)]函数f (x )=sin (2x +π3)的最小正周期为 ( ) A. 4π B. 2π C. π D. π24. [2017·全国新课标卷III (文)]已知sin α-cos α=43,则sin 2α= ( )A. -79B. -29C. 29D. 79 5. [2017·全国新课标卷III (文)]函数f (x )=15sin (x +π3)+cos (x (x--π6)的最大值为的最大值为 ( ) A. 65 B. 1 C. 35 D. 15 6. [2017·全国新课标卷III (文)]函数y=1+x+sinx x 2的部分图象大致为的部分图象大致为 ( )A. B.C. D.7. [2016·高考全国新课标卷Ⅰ(文),4]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知a =√5,c =2,cos A =23,则b = ( ) A. √2 B. √3C. 2D. 3 8. [2016·高考全国新课标卷Ⅰ(文),6]将函数y =2sin (2x +π6)的图象向右平移14个周期后,所得图象对应的函数为象对应的函数为 ( ) A. y =2sin (2x +π4) B. y =2sin (2x +π3) C. y =2sin (2x (2x--π4) D. y =2sin (2x (2x--π3) 9. [2016·高考全国新课标卷Ⅰ(文),12]若函数f (x )=x -13sin 2x +a sin x 在(-∞,+∞)单调递增,则a 的取值范围是的取值范围是 ( ) A. [-1,1] B. [-1,13] C. [-13,13] D. [-1,1,--13] 10. [2016·高考全国新课标卷Ⅱ(文),3]函数y =A sin(ωx +φ)的部分图象如图所示,则 ( ) A. y =2sin (2x (2x--π6) B. y =2sin (2x (2x--π3) C. y =2sin (x +π6) D. y =2sin (x +π3)11. [2016·高考全国新课标卷Ⅱ(文),11]函数f (x )=cos2x +6cos (π2-x)的最大值为( ) A. 4 B. 5 C. 6 D. 7 12. [2016·高考全国新课标卷Ⅲ(文),6]若tan θ=-13,则cos 2θ= ( )A. -45B. -15C. 15 D. 45 13. [2016·高考全国新课标卷Ⅲ(文),9]在△ABC 中,B =π4,BC 边上的高等于13BC ,则sin A = ( ) A. 310 B. √1010 C. √55 D. 3√101014. [2015·高考全国新课标卷Ⅰ(文),8]函数f (x )=cos(ωx+φ)的部分图象如图所示,则f (x )的单调递减区间为( )A. (kπ(kπ--14,kπ+34),k ∈Z B. (2kπ(2kπ--14,2kπ+34),k ∈Z C. (k (k--14,k +34),k ∈Z D. (2k (2k--14,2k +34),k ∈Z 15. [2014﹒高考全国新课标卷Ⅰ(文),7]在函数①y =cos|2x |,②y =|cos x |,③y =cos(2x +π6),④y =tan(2x -π4)中,最小正周期为π的所有函数为( )A. ②④B. ①③④C. ①②③D. ①③16. [2013·高考全国新课标卷I(文),9]函数f (x )=(1-cos x )sin x 在[-π,π]的图象大致为( )A. B.C. D. 17. [2013·高考全国新课标卷I(文),10]已知锐角△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,23cos 2A+cos2A=0,a=7,c=6,则b=( )A. 10B. 9C. 8D. 518. [2013·高考全国新课标卷II(文),4]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知b=2,B=π6,C=π4,则△ABC 的面积为( )A. 2√3+2B. √3+1C. 2√3-2D. √3-1 19. [2013·高考全国新课标卷II(文),6]已知sin2α=23,则cos 2(α+π4)=( ) A. 16 B. 13 C. 12 D. 23 评卷人评卷人 得分得分 二、填空题20. [2017·全国新课标卷I(文)]已知α∈(0,π2),tan α=2,则cos (α(α--π4)= . 21. [2017·全国新课标卷II(文)]函数f (x )=2cos x+sin x 的最大值为 .22. [2017·全国新课标卷II(文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若2b cos B=a cos C+c cos A ,则B= .23. [2017·全国新课标卷III (文)]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c.已知C=60°60°,,b=√6,c=3,则A= .24.[2016·高考全国新课标卷Ⅰ(文),14]已知θ是第四象限角,且sin (θ+π4)=35,则tan (θ(θ--π4)= 25. [2016·高考全国新课标卷Ⅱ(文),15]△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,若cos A =45,cos C =513,a =1,则b = . 26. [2016·高考全国新课标卷Ⅲ(文),14]函数y =sin x -√3cos x 的图象可由函数y =2sin x 的图象至少向右平移 个单位长度得到.27. [2014﹒高考全国新课标卷Ⅰ(文),16]如图,为测量山高MN ,选择A 和另一座山的山顶C 为测量观测点.从A 点测得M 点的仰角∠MAN =60°60°,,C 点的仰角∠CAB =45°以及∠MAC =75°;从C 点测得∠MCA =60°60°..已知山高BC =100 m,则山高MN =________m.28. [2014﹒高考全国新课标Ⅱ(文),14]函数f (x )=sin(x +φ)-2sin φcos x 的最大值为________. 29. [2013·高考全国新课标卷I(文),16]设当x=θ时,函数f (x )=sin x-2cos x 取得最大值,则cos θ= .30. [2013·高考全国新课标卷II(文),16]函数y=cos(2x+φ)(-π≤φ<π)的图象向右平移π2个单位后,与函数y=sin(2x+π3)的图象重合,则φ= .。
历年(2020-2024)全国高考数学真题分类(解三角形大题)汇编(附答案)

历年(2020-2024)全国高考数学真题分类(解三角形大题)汇编考点01 求面积的值及范围或最值1.(2024∙北京∙高考真题)在ABC 中,内角,,A B C 的对边分别为,,a b c ,A ∠为钝角,7a =,sin 2cos B B =.(1)求A ∠;(2)从条件①、条件②、条件③这三个条件中选择一个作为已知,使得ABC 存在,求ABC 的面积.条件①:7b =;条件②:13cos 14B =;条件③:sin c A =注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.2.(2023∙全国甲卷∙高考真题)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知2222cos b c aA+-=.(1)求bc ; (2)若cos cos 1cos cos a B b A ba Bb A c--=+,求ABC 面积.3.(2023∙全国乙卷∙高考真题)在ABC 中,已知120BAC ∠=︒,2AB =,1AC =. (1)求sin ABC ∠;(2)若D 为BC 上一点,且90BAD ∠=︒,求ADC △的面积.4.(2022∙浙江∙高考真题)在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .已知34,cos 5a C ==. (1)求sin A 的值;(2)若11b =,求ABC 的面积.考点02 求边长、周长的值及范围或最值1.(2024∙全国新Ⅱ卷∙高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin 2A A =. (1)求A .(2)若2a =sin sin 2C c B =,求ABC 的周长.2.(2024∙全国新Ⅰ卷∙高考真题)记ABC 的内角A 、B 、C 的对边分别为a ,b ,c ,已知sin C B =,222a b c +-=(1)求B ;(2)若ABC 的面积为3c .3.(2023∙全国新Ⅱ卷∙高考真题)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知ABCD 为BC 中点,且1AD =.(1)若π3ADC ∠=,求tan B ; (2)若228b c +=,求,b c .4.(2022∙全国新Ⅱ卷∙高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,分别以a ,b ,c 为边长的三个正三角形的面积依次为123,,S S S ,已知123123S S S B -+==. (1)求ABC 的面积;(2)若sin sin 3A C =,求b . 5.(2022∙全国乙卷∙高考真题)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知sin sin()sin sin()C A B B C A -=-.(1)证明:2222a b c =+; (2)若255,cos 31a A ==,求ABC 的周长.6.(2022∙北京∙高考真题)在ABC 中,sin 2C C =. (1)求C ∠;(2)若6b =,且ABC 的面积为ABC 的周长.7.(2022∙全国新Ⅰ卷∙高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos sin 21sin 1cos2A BA B=++.(1)若23C π=,求B ; (2)求222a b c +的最小值.8.(2020∙全国∙高考真题)ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.(1)若a,b ,求ABC 的面积;(2)若sin AC C . 9.(2020∙全国∙高考真题)ABC 中,sin 2A -sin 2B -sin 2C =sin B sin .C(1)求A ;(2)若BC =3,求ABC 周长的最大值.考点03 求角和三角函数的值及范围或最值1.(2024∙天津∙高考真题)在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知92cos 5163a Bbc ===,,. (1)求a ; (2)求sin A ;(3)求()cos 2B A -的值.2.(2023∙天津∙高考真题)在ABC 中,角,,A B C 所对的边分别是,,a b c .已知2,120a b A ==∠= . (1)求sin B 的值; (2)求c 的值; (3)求()sin B C -的值.3.(2022∙天津∙高考真题)在ABC 中,角A 、B 、C 的对边分别为a ,b ,c.已知12,cos 4a b c A ===-.(1)求c 的值; (2)求sin B 的值; (3)求sin(2)A B -的值.4.(2021∙天津∙高考真题)在ABC ,角 ,,A B C 所对的边分别为,,a b c ,已知sin :sin :sin 2A B C =b =. (I )求a 的值; (II )求cos C 的值;(III )求sin 26C π⎛⎫- ⎪⎝⎭的值.5.(2021∙全国新Ⅰ卷∙高考真题)记ABC 是内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=. (1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠.6.(2020∙天津∙高考真题)在ABC 中,角,,A B C 所对的边分别为,,a b c .已知 5,a b c === (Ⅰ)求角C 的大小; (Ⅱ)求sin A 的值;(Ⅲ)求sin 24A π⎛⎫+ ⎪⎝⎭的值.7.(2020∙浙江∙高考真题)在锐角△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且2sin 0b A =. (I )求角B 的大小;(II )求cos A +cos B +cos C 的取值范围.8.(2020∙江苏∙高考真题)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知3,45a c B ==︒.(1)求sin C 的值;(2)在边BC 上取一点D ,使得4cos 5ADC ∠=-,求tan DAC ∠的值.考点04 求三角形的高、中线、角平分线及其他线段长1.(2023∙全国新Ⅰ卷∙高考真题)已知在ABC 中,()3,2sin sin A B C A C B +=-=. (1)求sin A ;(2)设5AB =,求AB 边上的高.考点05 三角形中的证明问题1.(2022∙全国乙卷∙高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ﹐已知()()sin sin sin sin C A B B C A -=-.(1)若2A B =,求C ; (2)证明:2222a b c =+2.(2021∙全国新Ⅰ卷∙高考真题)记ABC 是内角A ,B ,C 的对边分别为a ,b ,c .已知2b ac =,点D 在边AC 上,sin sin BD ABC a C ∠=. (1)证明:BD b =;(2)若2AD DC =,求cos ABC ∠.参考答案考点01 求面积的值及范围或最值1.(2024∙北京∙高考真题)在ABC 中,内角,,A B C 的对边分别为,,a b c ,A ∠为钝角,7a =,sin 2cos B B =.(1)求A ∠;(2)从条件①、条件②、条件③这三个条件中选择一个作为已知,使得ABC 存在,求ABC 的面积. 条件①:7b =;条件②:13cos 14B =;条件③:sin c A =注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分. 【答案】(1)2π3A =; (2)选择①无解;选择②和③△ABC【详细分析】(1)利用正弦定理即可求出答案; (2)选择①,利用正弦定理得3B π=,结合(1)问答案即可排除;选择②,首先求出sin 14B =,再代入式子得3b =,再利用两角和的正弦公式即可求出sin C ,最后利用三角形面积公式即可;选择③,首先得到5c =,再利用正弦定理得到sin 14C =,再利用两角和的正弦公式即可求出sin B ,最后利用三角形面积公式即可;【答案详解】(1)由题意得2sin cos cos B B B =,因为A 为钝角, 则cos 0B ≠,则2sin 7B b =,则7sin sin sin b a BA A ===,解得sin 2A =, 因为A 为钝角,则2π3A =. (2)选择①7b =,则sin 7B ===2π3A =,则B 为锐角,则3B π=, 此时πA B +=,不合题意,舍弃;选择②13cos 14B =,因为B为三角形内角,则sin 14B ==,则代入2sin 7B =得2147⨯=,解得3b =,()2π2π2πsin sin sin sin cos cos sin 333C A B B B B ⎛⎫=+=+=+ ⎪⎝⎭131********⎛⎫=+-⨯= ⎪⎝⎭,则11sin 7322ABC S ab C ==⨯⨯=选择③sin c A =2c ⨯=5c =,则由正弦定理得sin sin a c A C =5sin C ,解得sin C =,因为C 为三角形内角,则11cos 14C ==, 则()2π2π2πsin sin sin sin cos cos sin 333B A C C C C ⎛⎫=+=+=+⎪⎝⎭11121421414⎛⎫=+-⨯= ⎪⎝⎭,则11sin 7522144ABC S ac B ==⨯⨯⨯=△ 2.(2023∙全国甲卷∙高考真题)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知2222cos b c a A+-=.(1)求bc ; (2)若cos cos 1cos cos a B b A ba Bb A c--=+,求ABC 面积.【答案】(1)1(2)4【详细分析】(1)根据余弦定理即可解出;(2)由(1)可知,只需求出sin A 即可得到三角形面积,对等式恒等变换,即可解出.【答案详解】(1)因为2222cos a b c bc A =+-,所以2222cos 22cos cos b c a bc Abc A A+-===,解得:1bc =.(2)由正弦定理可得cos cos sin cos sin cos sin cos cos sin cos sin cos sin a B b A b A B B A Ba Bb Ac A B B A C---=-++()()()()()sin sin sin sin 1sin sin sin A B A B B BA B A B A B ---=-==+++,变形可得:()()sin sin sin A B A B B --+=,即2cos sin sin A B B -=,而0sin 1B <≤,所以1cos 2A =-,又0πA <<,所以sin 2A =,故ABC的面积为11sin 122ABC S bc A ==⨯△.3.(2023∙全国乙卷∙高考真题)在ABC 中,已知120BAC ∠=︒,2AB =,1AC =. (1)求sin ABC ∠;(2)若D 为BC 上一点,且90BAD ∠=︒,求ADC △的面积. 【答案】(1)14;【详细分析】(1)首先由余弦定理求得边长BC的值为BCcos 14B =,最后由同角三角函数基本关系可得sin 14B =; (2)由题意可得4ABDACD S S =△△,则15ACD ABC S S =△△,据此即可求得ADC △的面积. 【答案详解】(1)由余弦定理可得:22222cos BC a b c bc A ==+-41221cos1207=+-⨯⨯⨯= ,则BC =222cos 214a c b B ac +-===,sin ABC ∠==(2)由三角形面积公式可得1sin 90241sin 302ABD ACDAB AD S S AC AD ⨯⨯⨯==⨯⨯⨯ △△,则11121sin12055210ACD ABC S S ⎛⎫==⨯⨯⨯⨯=⎪⎝⎭△△. 4.(2022∙浙江∙高考真题)在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c.已知34,cos 5a C ==. (1)求sin A 的值;(2)若11b =,求ABC 的面积. 【答案】;(2)22.【详细分析】(1)先由平方关系求出sin C ,再根据正弦定理即可解出;(2)根据余弦定理的推论222cos 2a b c C ab +-=以及4a =可解出a ,即可由三角形面积公式in 12s S ab C =求出面积.【答案详解】(1)由于3cos 5C =, 0πC <<,则4sin 5C =.因为4a =,由正弦定理知4sin A C =,则sin 45A C ==. (2)因为4a ,由余弦定理,得2222221612111355cos 22225a a aa b c C ab a a +--+-====, 即26550a a +-=,解得5a =,而4sin 5C =,11b =, 所以ABC 的面积114sin 51122225S ab C ==⨯⨯⨯=.5.(2019∙全国∙高考真题)ABC ∆的内角,,A B C 的对边分别为,,a b c ,已知sin sin 2A Ca b A +=. (1)求B ;(2)若ABC ∆为锐角三角形,且1c =,求ABC ∆面积的取值范围. 【答案】(1) 3B π=;(2). 【详细分析】(1)利用正弦定理化简题中等式,得到关于B 的三角方程,最后根据A,B,C 均为三角形内角解得3B π=.(2)根据三角形面积公式1sin 2ABC S ac B =⋅ ,又根据正弦定理和1c =得到ABC S 关于C 的函数,由于ABC 是锐角三角形,所以利用三个内角都小于2π来计算C 的定义域,最后求解()ABC S C 的值域.【答案详解】(1)[方法一]【最优解:利用三角形内角和为π结合正弦定理求角度】 由三角形的内角和定理得222A C Bπ+=-, 此时sinsin 2A C a b A +=就变为sin sin 22B a b A π⎛⎫-= ⎪⎝⎭. 由诱导公式得sin cos 222B B π⎛⎫-= ⎪⎝⎭,所以cos sin 2B a b A =.在ABC 中,由正弦定理知2sin ,2sin a R A b R B ==, 此时就有sin cossin sin 2BA AB =,即cos sin 2B B =,再由二倍角的正弦公式得cos2sin cos 222B B B=,解得3B π=. [方法二]【利用正弦定理解方程求得cos B 的值可得B ∠的值】 由解法1得sin sin 2A CB +=, 两边平方得22sinsin 2A CB +=,即21cos()sin 2A CB -+=. 又180A BC ++=︒,即cos()cos A C B +=-,所以21cos 2sin B B +=, 进一步整理得22cos cos 10B B +-=, 解得1cos 2B =,因此3B π=. [方法三]【利用正弦定理结合三角形内角和为π求得,,A BC 的比例关系】 根据题意sinsin 2A Ca b A +=,由正弦定理得sin sin sin sin 2A C A B A +=, 因为0A π<<,故sin 0A >, 消去sin A 得sin sin 2A CB +=. 0<B π<,02A C π+<<,因为故2A C B +=或者2A CB π++=, 而根据题意A BC π++=,故2A C B π++=不成立,所以2A CB +=, 又因为A BC π++=,代入得3B π=,所以3B π=.(2)[方法一]【最优解:利用锐角三角形求得C 的范围,然后由面积函数求面积的取值范围】 因为ABC 是锐角三角形,又3B π=,所以,6262A C ππππ<<<<, 则1sin 2ABCS ac B ==V 22sin 1sin 3sin 24sin 4sin C a A c B c C Cπ⎛⎫- ⎪⎝⎭⋅⋅=⋅=⋅=22sincos cos sin 333sin 8tan C CC C ππ-=. 因为,62C ππ⎛⎫∈ ⎪⎝⎭,所以tan C ⎫∈+∞⎪⎪⎝⎭,则1tan C ∈,从而ABC S ⎝⎭∈ ,故ABC面积的取值范围是82⎫⎪⎪⎝⎭. [方法二]【由题意求得边a 的取值范围,然后结合面积公式求面积的取值范围】 由题设及(1)知ABC的面积4ABC S a =△. 因为ABC 为锐角三角形,且1,3c B π==,所以22221cos 0,21cos 0,2b a A bb a C ab ⎧+-=>⎪⎪⎨+-⎪=>⎪⎩即22221010.b a b a ⎧+->⎨+->⎩, 又由余弦定理得221b a a =+-,所以220,20,a a a ->⎧⎨->⎩即122a <<,所以82ABC S << ,故ABC面积的取值范围是⎝⎭. [方法三]【数形结合,利用极限的思想求解三角形面积的取值范围】如图,在ABC 中,过点A 作1AC BC ⊥,垂足为1C ,作2AC AB ⊥与BC 交于点2C . 由题设及(1)知ABC的面积ABC S =△,因为ABC 为锐角三角形,且1,3c B π==,所以点C 位于在线段12C C 上且不含端点,从而cos cos cc B a B⋅<<, 即1cos3cos 3a ππ<<,即122a <<,所以82ABC S << , 故ABC面积的取值范围是82⎛⎫⎪ ⎪⎝⎭.【整体点评】(1)方法一:正弦定理是解三角形的核心定理,与三角形内角和相结合是常用的方法; 方法二:方程思想是解题的关键,解三角形的问题可以利用余弦值确定角度值; 方法三:由正弦定理结合角度关系可得内角的比例关系,从而确定角的大小. (2)方法一:由题意结合角度的范围求解面积的范围是常规的做法;方法二:将面积问题转化为边长的问题,然后求解边长的范围可得面积的范围;方法三:极限思想和数形结合体现了思维的灵活性,要求学生对几何有深刻的认识和灵活的应用.6.(2017∙全国∙高考真题)ABC ∆的内角,,A B C 的对边分别为,,,a b c已知sin 0,2A A a b +===.(1)求角A 和边长c ;(2)设D 为BC 边上一点,且AD AC ⊥,求ABD ∆的面积. 【答案】(1)23π,4;(2【答案详解】试题详细分析:(1)先根据同角的三角函数的关系求出tan A = 从而可得A 的值,再根据余弦定理列方程即可求出边长c 的值;(2)先根据余弦定理求出cos C ,求出CD 的长,可得12CD BC =,从而得到12ABD ABC S S ∆∆=,进而可得结果. 试题解析:(1)sin 0,tan A A A =∴= 20,3A A ππ<<∴=,由余弦定理可得2222cos a b c bc A =+-,即21284222c c ⎛⎫=+-⨯⨯- ⎪⎝⎭,即22240c c +-=,解得6c =-(舍去)或4c =,故4c =. (2)2222cos c b a ab C =+-Q,1628422cos C ∴=+-⨯⨯,2cos 2cos AC C CD C ∴=∴===12CD BC ∴=,1142222ABC S AB AC sin BAC ∆∴=⋅⋅∠=⨯⨯⨯=12ABD ABC S S ∆∆∴==7.(2016∙全国∙高考真题)ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知2cos (cos cos )C a B b A c +=. (1)求角C ;(2)若c =2ABC S ∆=,求ABC ∆的周长. 【答案】(1)3C π=(2)5【答案详解】试题详细分析:(1)根据正弦定理把2cos (cos cos )C a B b A c +=化成2cos (sin cos sin cos )sin C A B B A C +=,利用和角公式可得1cos ,2C =从而求得角C ;(2)根据三角形的面积和角C 的值求得6ab =,由余弦定理求得边a 得到ABC ∆的周长. 试题解析:(1)由已知可得2cos (sin cos sin cos )sin C A B B A C += 12cos sin()sin cos 23π∴+=⇒=⇒=C A B C C C (2)11sin 6222∆=⇒=⇒=ABC S ab C ab ab又2222cos +-= a b ab C c2213a b ∴+=,2()255∴+=⇒+=a b a bABC ∆∴的周长为5考点:正余弦定理解三角形.8.(2015∙浙江∙高考真题)在ABC ∆中,内角A ,B ,C 所对的边分别为,,a b c .已知tan()24A π+=.(1)求2sin 2sin 2cos AA A+的值;(2)若,34B a π==,求ABC ∆的面积. 【答案】(1)25;(2)9 【答案详解】(1)利用两角和与差的正切公式,得到1tan 3A =,利用同角三角函数基本函数关系式得到结论;(2)利用正弦定理得到边b 的值,根据三角形,两边一夹角的面积公式计算得到三角形的面积.试题解析:(1)由tan()24A π+=,得1tan 3A =,所以22sin 22sin cos 2tan 2sin 2cos 2sin cos cos 2tan 15A A A A A A A A A A ===+++.(2)由1tan 3A =可得,sin A A ==3,4a B π==,由正弦定理知:b =又sin sin()sin cos cos sin 5C A B A B A B =+=+=,所以11sin 3922ABC S ab C ∆==⨯⨯=. 考点:1.同角三角函数基本关系式;2.正弦定理;3.三角形面积公式.9.(2015∙全国∙高考真题)已知,,a b c 分别是ABC ∆内角,,A B C 的对边, 2sin 2sin sin B A C =. (1)若a b =,求cos ;B(2)若90B = ,且a =求ABC ∆的面积. 【答案】(1)14;(2)1 【答案详解】试题详细分析:(1)由2sin 2sin sin B A C =,结合正弦定理可得:22b ac =,再利用余弦定理即可得出cos ;B(2)利用(1)及勾股定理可得c ,再利用三角形面积计算公式即可得出 试题解析:(1)由题设及正弦定理可得22b ac = 又a b =,可得2,2b c a c ==由余弦定理可得2221cos 24a c b B ac +-==(2)由(1)知22b ac =因为90B = ,由勾股定理得222a c b += 故222a c ac +=,得c a == 所以的面积为1考点:正弦定理,余弦定理解三角形10.(2015∙山东∙高考真题)设()2sin cos cos 4f x x x x π⎛⎫=-+ ⎪⎝⎭.(Ⅰ)求()f x 的单调区间;(Ⅱ)在锐角ABC ∆中,角,,A B C 的对边分别为,,a b c ,若0,12A f a ⎛⎫== ⎪⎝⎭,求ABC ∆面积的最大值.【答案】(Ⅰ)单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦(Ⅱ)ABC ∆【答案详解】试题详细分析:(Ⅰ)首先利用二倍角公式化简函数()f x 的解析式,再利用正弦函数的单调性求其单调区间;(Ⅱ)首先由02A f ⎛⎫= ⎪⎝⎭结合(Ⅰ)的结果,确定角A 的值,然后结合余弦定理求出三角形ABC ∆面积的最大值. 试题解析:解:(Ⅰ)由题意知()1cos 2sin 2222x x f x π⎛⎫++ ⎪⎝⎭=-sin 21sin 21sin 2222x x x -=-=- 由222,22k x k k Z ππππ-+≤≤+∈ 可得,44k x k k Z ππππ-+≤≤+∈由3222,22k x k k Z ππππ+≤≤+∈ 可得3,44k x k k Z ππππ+≤≤+∈所以函数()f x 的单调递增区间是(),44k k k Z ππππ⎡⎤-++∈⎢⎥⎣⎦;单调递减区间是()3,44k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦ (Ⅱ)由1sin 0,22A f A ⎛⎫=-= ⎪⎝⎭得1sin 2A =由题意知A 为锐角,所以cos 2A =由余弦定理:2222cos a b c bc A =+-可得:2212b c bc =+≥即:2bc ≤ 当且仅当b c =时等号成立.因此1sin 2bc A ≤所以ABC ∆面积的最大值为24考点:1、诱导公式;2、三角函数的二倍角公式;3、余弦定理;4、基本不等式.考点02 求边长、周长的值及范围或最值1.(2024∙全国新Ⅱ卷∙高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin 2A A =. (1)求A .(2)若2a =sin sin 2C c B =,求ABC 的周长. 【答案】(1)π6A =(2)2+【详细分析】(1)根据辅助角公式对条件sin 2A A =进行化简处理即可求解,常规方法还可利用同角三角函数的关系解方程组,亦可利用导数,向量数量积公式,万能公式解决; (2)先根据正弦定理边角互化算出B ,然后根据正弦定理算出,b c 即可得出周长. 【答案详解】(1)方法一:常规方法(辅助角公式)由sin 2A A =可得1sin 12A A =,即sin()1π3A +=,由于ππ4π(0,π)(,333A A ∈⇒+∈,故ππ32A +=,解得π6A = 方法二:常规方法(同角三角函数的基本关系)由sin 2A A =,又22sin cos 1A A +=,消去sin A 得到:224cos 30(2cos 0A A A -+=⇔=,解得cos A = 又(0,π)A ∈,故π6A =方法三:利用极值点求解设()sin (0π)f x x x x =<<,则π()2sin (0π)3f x x x ⎛⎫=+<< ⎪⎝⎭,显然π6x =时,max ()2f x =,注意到π()sin 22sin(3f A A A A =+==+,max ()()f x f A =,在开区间(0,π)上取到最大值,于是x A =必定是极值点,即()0cos f A A A '==,即tan A = 又(0,π)A ∈,故π6A =方法四:利用向量数量积公式(柯西不等式)设(sin ,cos )a b A A == ,由题意,sin 2a b A A ⋅==,根据向量的数量积公式,cos ,2cos ,a b a b a b a b ⋅==, 则2cos ,2cos ,1a b a b =⇔= ,此时,0a b =,即,a b 同向共线,根据向量共线条件,1cos sin tan 3A A A ⋅=⇔=, 又(0,π)A ∈,故π6A =方法五:利用万能公式求解设tan 2A t =,根据万能公式,22sin 21t A A t ==+整理可得,2222(2(20((2t t t -+==-,解得tan22A t ==22tan 13t A t ==-, 又(0,π)A ∈,故π6A =(2)由题设条件和正弦定理sin sin 2sin 2sin sin cos C c B B C C B B =⇔=,又,(0,π)B C ∈,则sin sin 0B C ≠,进而cos B =π4B =,于是7ππ12C A B =--=,sin sin(π)sin()sin cos sin cos 4C A B A B A B B A =--=+=+=, 由正弦定理可得,sin sin sin a b cA B C ==,即2ππ7πsin sin sin6412b c==,解得b c == 故ABC的周长为2+2.(2024∙全国新Ⅰ卷∙高考真题)记ABC 的内角A 、B 、C 的对边分别为a ,b ,c,已知sin C B =,222a b c +-=(1)求B ;(2)若ABC的面积为3c . 【答案】(1)π3B =(2)【详细分析】(1)由余弦定理、平方关系依次求出cos ,sin C C,最后结合已知sin C B =得cos B 的值即可;(2)首先求出,,A B C ,然后由正弦定理可将,a b 均用含有c 的式子表示,结合三角形面积公式即可列方程求解.【答案详解】(1)由余弦定理有2222cos a b c ab C +-=,对比已知222a b c +-=,可得222cos 222a b c C ab ab +-===, 因为()0,πC ∈,所以sin 0C >,从而sin 2C ===,又因为sin C B =,即1cos 2B =, 注意到()0,πB ∈, 所以π3B =. (2)由(1)可得π3B =,cos 2C =,()0,πC ∈,从而π4C =,ππ5ππ3412A =--=,而5πππ1sin sin sin 124622224A ⎛⎫⎛⎫==+=+= ⎪ ⎪⎝⎭⎝⎭,由正弦定理有5πππsin sin sin 1234a b c==,从而1,4222a cbc +====, 由三角形面积公式可知,ABC 的面积可表示为21113sin 222228ABC S ab C c c ==⋅⋅= , 由已知ABC的面积为323=所以c =3.(2023∙全国新Ⅱ卷∙高考真题)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知ABCD 为BC 中点,且1AD =. (1)若π3ADC ∠=,求tan B ; (2)若228b c +=,求,b c . 【答案】(2)2b c ==.【详细分析】(1)方法1,利用三角形面积公式求出a ,再利用余弦定理求解作答;方法2,利用三角形面积公式求出a ,作出BC 边上的高,利用直角三角形求解作答.(2)方法1,利用余弦定理求出a ,再利用三角形面积公式求出ADC ∠即可求解作答;方法2,利用向量运算律建立关系求出a ,再利用三角形面积公式求出ADC ∠即可求解作答. 【答案详解】(1)方法1:在ABC 中,因为D 为BC 中点,π3ADC ∠=,1AD =,则1111sin 12222ADC ABC S AD DC ADC a S =⋅∠=⨯⨯===,解得4a =, 在ABD △中,2π3ADB ∠=,由余弦定理得2222cos c BD AD BD AD ADB =+-⋅∠, 即2141221()72c =+-⨯⨯⨯-=,解得c =cos 14B ==,sin B ===,所以sin tan cos 5B B B ==. 方法2:在ABC 中,因为D 为BC 中点,π3ADC ∠=,1AD =,则1111sin 12222ADC ABC S AD DC ADC a S =⋅∠=⨯⨯===,解得4a =, 在ACD 中,由余弦定理得2222cos b CD AD CD AD ADC =+-⋅∠,即214122132b =+-⨯⨯⨯=,解得b =,有2224AC AD CD +==,则π2CAD ∠=,π6C =,过A 作AE BC ⊥于E,于是3cos ,sin 2CE AC C AE AC C ====,52BE =,所以tan 5AE B BE ==. (2)方法1:在ABD △与ACD 中,由余弦定理得222211121cos(π)4211121cos 42c a a ADC b a a ADC ⎧=+-⨯⨯⨯-∠⎪⎪⎨⎪=+-⨯⨯⨯∠⎪⎩,整理得222122a b c +=+,而228b c +=,则a =,又11sin 22ADC S ADC =⨯∠=,解得sin 1ADC ∠=,而0πADC <∠<,于是π2ADC ∠=,所以2b c ===.方法2:在ABC 中,因为D 为BC 中点,则2AD AB AC =+ ,又CB AB AC =-,于是2222224()()2()16AD CB AB AC AB AC b c +=++-=+= ,即2416a +=,解得a =,又11sin 2ADC S ADC =⨯∠ sin 1ADC ∠=,而0πADC <∠<,于是π2ADC ∠=,所以2b c ===.4.(2022∙全国新Ⅱ卷∙高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,分别以a ,b ,c 为边长的三个正三角形的面积依次为123,,S S S,已知123123S S S B -+==. (1)求ABC 的面积; (2)若sin sin 3A C =,求b . 【答案】(2)12【详细分析】(1)先表示出123,,S S S,再由1232S S S -+=求得2222a c b +-=,结合余弦定理及平方关系求得ac ,再由面积公式求解即可;(2)由正弦定理得22sin sin sin b acB AC =,即可求解.【答案详解】(1)由题意得22221231,,22444S a a S b S c =⋅⋅===,则222123S S S -+==, 即2222a c b +-=,由余弦定理得222cos 2a c b B ac +-=,整理得cos 1ac B =,则cos 0B >,又1sin 3B =,则cos 3B ==,1cos 4ac B ==,则1sin 28ABC S ac B == ; (2)由正弦定理得:sin sin sin b a c B A C ==,则229sin sin sin sin sin 43b ac ac B A C A C =⋅==,则3sin 2b B =,31sin 22b B ==. 5.(2022∙全国乙卷∙高考真题)记ABC 的内角,,A B C 的对边分别为,,a b c ,已知sin sin()sin sin()C A B B C A -=-.(1)证明:2222a b c =+; (2)若255,cos 31a A ==,求ABC 的周长. 【答案】(1)见解析 (2)14【详细分析】(1)利用两角差的正弦公式化简,再根据正弦定理和余弦定理化角为边,从而即可得证; (2)根据(1)的结论结合余弦定理求出bc ,从而可求得b c +,即可得解. 【答案详解】(1)证明:因为()()sin sin sin sin C A B B C A -=-, 所以sin sin cos sin sin cos sin sin cos sin sin cos C A B C B A B C A B A C -=-,所以2222222222222a c b b c a a b c ac bc ab ac bc ab +-+-+-⋅-⋅=-⋅, 即()22222222222a cb a bc b c a +-+--+-=-, 所以2222a b c =+;(2)解:因为255,cos 31a A ==, 由(1)得2250bc +=,由余弦定理可得2222cos a b c bc A =+-, 则50502531bc -=, 所以312bc =, 故()2222503181b c b c bc +=++=+=, 所以9b c +=,所以ABC 的周长为14a b c ++=.6.(2022∙北京∙高考真题)在ABC 中,sin 2C C =. (1)求C ∠;(2)若6b =,且ABC 的面积为ABC 的周长. 【答案】(1)6π(2)6+【详细分析】(1)利用二倍角的正弦公式化简可得cos C 的值,结合角C 的取值范围可求得角C 的值; (2)利用三角形的面积公式可求得a 的值,由余弦定理可求得c 的值,即可求得ABC 的周长.【答案详解】(1)解:因为()0,C π∈,则sin 0C >2sin cos C C C =,可得cos 2C =,因此,6C π=.(2)解:由三角形的面积公式可得13sin 22ABC S ab C a === ,解得a =.由余弦定理可得2222cos 48362612c a b ab C =+-=+-⨯=,c ∴=所以,ABC 的周长为6a b c ++=.7.(2022∙全国新Ⅰ卷∙高考真题)记ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知cos sin 21sin 1cos2A BA B=++.(1)若23C π=,求B ; (2)求222a b c +的最小值.【答案】(1)π6;(2)5.【详细分析】(1)根据二倍角公式以及两角差的余弦公式可将cos sin 21sin 1cos2A BA B=++化成()cos sin A B B +=,再结合π02B <<,即可求出; (2)由(1)知,π2C B =+,π22A B =-,再利用正弦定理以及二倍角公式将222a b c +化成2224cos 5cos B B +-,然后利用基本不等式即可解出. 【答案详解】(1)因为2cos sin 22sin cos sin 1sin 1cos 22cos cos A B B B BA B B B===++,即()1sin cos cos sin sin cos cos 2B A B A B A BC =-=+=-=, 而π02B <<,所以π6B =;(2)由(1)知,sin cos 0B C =->,所以πππ,022C B <<<<, 而πsin cos sin 2B C C ⎛⎫=-=- ⎪⎝⎭,所以π2C B =+,即有π22A B =-,所以30,,,424B C πππ⎛⎫⎛⎫∈∈ ⎪ ⎪⎝⎭⎝⎭所以222222222sin sin cos 21cos sin cos a b A B B Bc C B +++-==()2222222cos 11cos 24cos 555cos cos B BB BB-+-==+-≥=.当且仅当2cos B =222a b c +的最小值为5. 8.(2020∙全国∙高考真题)ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知B =150°.(1)若a,b ,求ABC 的面积;(2)若sin AC =2,求C . 【答案】(1(2)15︒.【详细分析】(1)已知角B 和b 边,结合,a c 关系,由余弦定理建立c 的方程,求解得出,a c ,利用面积公式,即可得出结论;(2)方法一 :将30A C =︒-代入已知等式,由两角差的正弦和辅助角公式,化简得出有关C 角的三角函数值,结合C 的范围,即可求解.【答案详解】(1)由余弦定理可得2222282cos1507b a c ac c ==+-⋅︒=,2,c a ABC ∴==∴△的面积1sin 2S ac B == (2)[方法一]:多角换一角 30A C +=︒ ,sin sin(30)A C C C ∴=︒-1cos sin(30)22C C C ==+︒=, 030,303060C C ︒<<︒∴︒<+︒<︒ ,3045,15C C ∴+︒=︒∴=︒. [方法二]:正弦角化边由正弦定理及150B =︒得22sin sin sin ====a c bR b A C B.故sin ,sin 22==a c A C b b .由sin 2A C =,得a +=.又由余弦定理得22222cos =+-⋅=+b a c ac B a 2+c ,所以()222()2=++a a c ,解得a c =.所以15=︒C .【整体点评】本题考查余弦定理、三角恒等变换解三角形,熟记公式是解题的关键,考查计算求解能力,属于基础题.其中第二问法一主要考查三角恒等变换解三角形,法二则是通过余弦定理找到三边的关系,进而求角.9.(2020∙全国∙高考真题)ABC 中,sin 2A -sin 2B -sin 2C =sin B sin .C(1)求A ;(2)若BC =3,求ABC 周长的最大值.【答案】(1)23π;(2)3+【详细分析】(1)利用正弦定理角化边,配凑出cos A 的形式,进而求得A ;(2)方法一:利用余弦定理可得到()29AC AB AC AB +-⋅=,利用基本不等式可求得AC AB +的最大值,进而得到结果.【答案详解】(1)由正弦定理可得:222BC AC AB AC AB --=⋅,2221cos 22AC AB BC A AC AB +-∴==-⋅,()0,A π∈ ,23A π∴=. (2)[方法一]【最优解】:余弦+不等式由余弦定理得:2222cos BC AC AB AC AB A =+-⋅229AC AB AC AB =++⋅=, 即()29AC AB AC AB +-⋅=.22AC AB AC AB +⎛⎫⋅≤ ⎪⎝⎭(当且仅当AC AB =时取等号), ()()()22223924AC AB AC AB AC AB AC AB AC AB +⎛⎫∴=+-⋅≥+-=+ ⎪⎝⎭,解得:AC AB +≤AC AB =时取等号),ABC ∴周长3L AC AB BC =++≤+ABC ∴周长的最大值为3+[方法二]:正弦化角(通性通法)设,66ππαα=+=-B C ,则66ππα-<<,根据正弦定理可知sin sin sin a b cA B C===,所以sin )b c B C +=+sin sin 66ππαα⎤⎛⎫⎛⎫=++- ⎪ ⎪⎥⎝⎭⎝⎭⎦α=≤,当且仅当0α=,即6B C π==时,等号成立.此时ABC周长的最大值为3+ [方法三]:余弦与三角换元结合在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c .由余弦定理得229b c bc =++,即2213924⎛⎫++= ⎪⎝⎭b c c .令13sin ,20,2b c c θπθθ⎧+=⎪⎛⎫∈⎨ ⎪⎝⎭⎪=⎩,得3sin b c θθ+=6πθ⎛⎫+≤ ⎪⎝⎭,易知当6C π=时,max ()b c +=所以ABC周长的最大值为3+【整体点评】本题考查解三角形的相关知识,涉及到正弦定理角化边的应用、余弦定理的应用、三角形周长最大值的求解问题;方法一:求解周长最大值的关键是能够在余弦定理构造的等式中,结合基本不等式构造不等关系求得最值. 方法二采用正弦定理边化角,利用三角函数的范围进行求解最值,如果三角形是锐角三角形或有限制条件的,则采用此法解决.方法三巧妙利用三角换元,实现边化角,进而转化为正弦函数求最值问题.10.(2018∙全国∙高考真题)在平面四边形ABCD 中,90ADC ∠= ,45A ∠= ,2AB =,5BD =.(1)求cos ADB ∠; (2)若DC =,求BC . 【答案】(1)5;(2)5. 【详细分析】(1)方法一:根据正弦定理得到sin sin BD AB A ADB =∠∠,求得sin 5ADB ∠=,结合角的范围,利用同角三角函数关系式,求得cos 5ADB ∠==;(2)方法一:根据第一问的结论可以求得cos sin 5BDC ADB ∠=∠=,在BCD △中,根据余弦定理即可求出.【答案详解】(1)[方法1]:正弦定理+平方关系在ABD △中,由正弦定理得sin sin BD AB A ADB =∠∠,代入数值并解得sin 5ADB ∠=.又因为BD AB >,所以A ADB ∠>∠,即ADB ∠为锐角,所以cos 5ADB ∠=. [方法2]:余弦定理在ABD △中,2222cos 45BD AB AD AB AD =+-⋅ ,即2254222AD AD =+-⨯⨯⨯,解得:AD =所以,2254cos5ADB +-∠==. [方法3]:【最优解】利用平面几何知识如图,过B 点作BE AD ⊥,垂足为E ,BF CD ⊥,垂足为F .在Rt AEB 中,因为45A ∠=︒,=2AB ,所以AE BE ==.在Rt BED △中,因为5BD =,则DE ===.所以cos ADB ∠=[方法4]:坐标法以D 为坐标原点,DC 为x 轴,DA为y 轴正方向,建立平面直角坐标系(图略).设BDC α∠=,则(5cos ,5sin )B αα.因为45A ∠=︒,所以(0,5sin A α.从而2AB ==,又α是锐角,所以cos 5α=,cos sin ADB α∠===(2)[方法1]:【通性通法】余弦定理在BCD △,由(1)得,cos 5ADB ∠=,()2222cos 90BC BD DC BD DC ADB︒=+-⋅-∠2252525ADB =+-⨯⨯∠=,所以=5BC .[方法2]:【最优解】利用平面几何知识作BF DC ⊥,垂足为F ,易求,BF =FC =,由勾股定理得=5BC .【整体点评】(1)方法一:根据题目条件已知两边和一边对角,利用正弦定理和平方关系解三角形,属于通性通法;方法二:根据题目条件已知两边和一边对角,利用余弦定理解三角形,也属于通性通法; 方法三:根据题意利用几何知识,解直角三角形,简单易算.方法四:建立坐标系,通过两点间的距离公式,将几何问题转化为代数问题,这是解析思想的体现. (2)方法一:已知两边及夹角,利用余弦定理解三角形,是通性通法. 方法二:利用几何知识,解直角三角形,简单易算.11.(2017∙全国∙高考真题)△ABC 的内角、、A B C 的对边分别为a b c 、、,已知△ABC 的面积为23sin a A(1)求sin sin B C ;(2)若6cos cos 1,3,B C a ==求△ABC 的周长.【答案】(1)2sin sin 3B C =(2) 3【答案详解】试题详细分析:(1)由三角形面积公式建立等式21sin 23sin a ac B A=,再利用正弦定理将边化成角,从而得出sin sin B C 的值;(2)由1cos cos 6B C =和2sin sin 3B C =计算出1cos()2B C +=-,从而求出角A ,根据题设和余弦定理可以求出bc 和b c +的值,从而求出ABC 的周长为3+试题解析:(1)由题设得21sin 23sin a ac B A=,即1sin 23sin a c B A =.由正弦定理得1sin sin sin 23sin A C B A =. 故2sin sin 3B C =. (2)由题设及(1)得1cos cos sin sin ,2B C B C -=-,即()1cos 2B C +=-.所以23B C π+=,故3A π=. 由题设得21sin 23sin a bc A A=,即8bc =.由余弦定理得229b c bc +-=,即()239b c bc +-=,得b c +故ABC 的周长为3+点睛:在处理解三角形问题时,要注意抓住题目所给的条件,当题设中给定三角形的面积,可以使用面积公式建立等式,再将所有边的关系转化为角的关系,有时需将角的关系转化为边的关系;解三角形问题常见的一种考题是“已知一条边的长度和它所对的角,求面积或周长的取值范围”或者“已知一条边的长度和它所对的角,再有另外一个条件,求面积或周长的值”,这类问题的通法思路是:全部转化为角的关系,建立函数关系式,如sin()y A x b ωϕ=++,从而求出范围,或利用余弦定理以及基本不等式求范围;求具体的值直接利用余弦定理和给定条件即可.12.(2017∙山东∙高考真题)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,已知b =3,6AB AC ⋅=-,S △ABC =3,求A 和a .【答案】34A π=,a =【答案详解】试题详细分析:先由数量积公式及三角形面积公式得3cos 613sin 32c A c A =-⎧⎪⎨⨯=⎪⎩,由此求A ,再利用余弦定理求a .试题解析:因为6AB AC ⋅=-, 所以cos 6bc A =-, 又3ABC S =△, 所以sin 6bc A =,因此tan 1A =-,又0πA <<, 所以3π4A =, 又3b =,所以c =由余弦定理2222cos a b c bc A =+-,得29823(a =+-⨯⨯,所以a = 【考点】解三角形【名师点评】正、余弦定理是应用极为广泛的两个定理,它将三角形的边和角有机地联系起来,从而使三角与几何产生联系,为求与三角形有关的量(如面积、外接圆、内切圆半径和面积等)提供了理论依据,也是判断三角形形状、证明三角形中有关等式的重要依据.其主要方法有:化角法,化边法,面积法,运用初等几何法.注意体会其中蕴涵的函数与方程思想、等价转化思想及分类讨论思想.13.(2017∙全国∙高考真题)△ABC 的内角,,A B C 的对边分别为,,a b c ,已知2sin()8sin2B AC +=.(1)求cos B ;(2)若6a c +=,△ABC 的面积为2,求b . 【答案】(1)1517;(2)2. 【答案详解】试题详细分析:(1)利用三角形的内角和定理可知A C B π+=-,再利用诱导公式化简()sin A C +,利用降幂公式化简28sin 2B,结合22sin cos 1B B +=,求出cos B ;(2)由(1)可知8sin 17B =,利用三角形面积公式求出ac ,再利用余弦定理即可求出b . 试题解析:(1)()2sin 8sin2BA C +=,∴()sin 41cosB B =-,∵22sin cos 1B B +=, ∴()22161cos cos 1B B -+=,∴()()17cos 15cos 10B B --=,∴15cos 17B =; (2)由(1)可知8sin 17B =, ∵1sin 22ABC S ac B =⋅=,∴172ac =, ∴()2222222217152cos 2152153617154217b ac ac B a c a c a c ac =+-=+-⨯⨯=+-=+--=--=, ∴2b =.14.(2016∙全国∙高考真题)ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知2cos (cos cos )C a B b A c +=.(1)求角C ;(2)若c =ABC S ∆=ABC ∆的周长.【答案】(1)3C π=(2)5【答案详解】试题详细分析:(1)根据正弦定理把2cos (cos cos )C a B b A c +=化成2cos (sin cos sin cos )sin C A B B A C +=,利用和角公式可得1cos ,2C =从而求得角C ;(2)根据三角形的面积和角C 的值求得6ab =,由余弦定理求得边a 得到ABC ∆的周长. 试题解析:(1)由已知可得2cos (sin cos sin cos )sin C A B B A C += 12cos sin()sin cos 23π∴+=⇒=⇒=C A B C C C(2)11sin 622∆=⇒=⇒=ABC S ab C ab ab 又2222cos +-= a b ab C c2213a b ∴+=,2()255∴+=⇒+=a b a bABC ∆∴的周长为5考点:正余弦定理解三角形.15.(2015∙浙江∙高考真题)在ABC ∆中,内角 A ,B , C 所对的边分别为a , b ,c ,已知 4A π=,22b a -=122c .(1)求tan C 的值;(2)若ABC ∆的面积为3,求 b 的值. 【答案】(1)2;(2)3b =.【答案详解】(1)根据正弦定理可将条件中的边之间的关系转化为角之间满足的关系,再将式 子作三角恒等变形即可求解;(2)根据条件首先求得sin B 的值,再结合正弦定理以及三角 形面积的计算公式即可求解.试题解析:(1)由22212b a c -=及正弦定理得2211sin sin 22B C -=, ∴2cos 2sin B C -=,又由4A π=,即34B C π+=,得cos 2sin 22sin cos B C C C -==,解得tan 2C =;(2)由tan 2C =,(0,)C π∈得sin 5C =,cos 5C =,又∵sin sin()sin()4B A C C π=+=+,∴sin B =3c b =,又∵4A π=,1sin 32bc A =,∴bc =3b =. 考点:1.三角恒等变形;2.正弦定理.16.(2015∙山东∙高考真题)ABC 中,角A B C ,,所对的边分别为,,a b c .已知cos ()39B A B ac =+==求sin A 和c 的值.【答案】,1.3【详细分析】由条件先求得sin sin C A ,,再由正弦定理即可求解.【答案详解】在ABC 中,由cos 3B =,得sin 3B =.因为A B C π++=,所以sin sin()9C A B =+=,因为sin sin C B <,所以C B <,C 为锐角,cos 9C =,因此sin sin()sin cos cos sin A B C B C B C =+=+39393=⨯+⨯=.由sin sin a c A C =,可得sin sin 9cc A a C ===,又ac =1c =.考点03 求角和三角函数的值及范围或最值1.(2024∙天津∙高考真题)在ABC 中,角,,A B C 所对的边分别为,,a b c ,已知92cos 5163a Bbc ===,,. (1)求a ; (2)求sin A ;(3)求()cos 2B A -的值.【答案】(1)4(2)4 (3)5764【详细分析】(1)2,3a t c t ==,利用余弦定理即可得到方程,解出即可;(2)法一:求出sin B ,再利用正弦定理即可;法二:利用余弦定理求出cos A ,则得到sin A ;(3)法一:根据大边对大角确定A 为锐角,则得到cos A ,再利用二倍角公式和两角差的余弦公式即可;法二:直接利用二倍角公式和两角差的余弦公式即可.【答案详解】(1)设2,3a t c t ==,0t >,则根据余弦定理得2222cos b a c ac B =+-,即229254922316t t t t =+-⨯⨯⨯,解得2t =(负舍); 则4,6a c ==.(2)法一:因为B为三角形内角,所以sin B ===再根据正弦定理得sin sin a b A B =,即4sin A =sin A =法二:由余弦定理得2222225643cos 22564b c a A bc +-+-===⨯⨯,因为()0,πA ∈,则sin A ==(3)法一:因为9cos 016B =>,且()0,πB ∈,所以π0,2B ⎛⎫∈ ⎪⎝⎭, 由(2)法一知sin 16B =,。
三角函数--2023高考真题分类汇编完整版

三角函数--高考真题汇编第一节三角函数概念、同角三角函数关系式和诱导公式1.(2023全国甲卷理科7)“22sin sin 1αβ+=”是“sin cos 0αβ+=”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件【分析】根据充分条件、必要条件概念及同角三角函数的基本关系得解.【解析】当2απ=,0β=时,有22sin sin 1αβ+=,但sin cos 0αβ+≠,即22sin sin 1αβ+=推不出sin cos 0αβ+=;当sin cos 0αβ+=时,()2222sin sin cos sin 1αβββ+=-+=,即sin cos 0αβ+=能推出22sin sin 1αβ+=.综上可知,22sin sin 1αβ+=是sin cos 0αβ+=成立的必要不充分条件.故选B.2.(2023北京卷13)已知命题:p 若,αβ为第一象限角,且αβ>,则tan tan αβ>.能说明p 为假命题的一组,αβ的值为α=;β=.【分析】根据正切函数单调性以及任意角的定义分析求解.【解析】因为()tan f x x =在π0,2⎛⎫⎪⎝⎭上单调递增,若00π02αβ<<<,则00tan tan αβ<,取1020122π,2π,,k k k k ααββ=+=+∈Z ,则()()100200tan tan 2πtan ,tan tan 2πtan k k αααβββ=+==+=,即tan tan αβ<,令12k k >,则()()()()102012002π2π2πk k k k αβαβαβ-=+-+=-+-,因为()1200π2π2π,02k k αβ-≥-<-<,则()()12003π2π02k k αβαβ-=-+->>,即12k k >,则αβ>.不妨取1200ππ1,0,,43k k αβ====,即9ππ,43αβ==满足题意.故答案为:9ππ;43.第二节三角恒等变换1.(2023新高考I 卷6)过点()0,2-与圆22410x y x +--=相切的两条直线的夹角为α,则sin α=()A.1B.154C.104D.64【解析】()222241025x y x x y +--=⇒-+=,所以圆心为()2,0B ,记()0,2A -,设切点为,M N ,如图所示.因为AB =,BM =,故AM =cos cos2AM MAB AB α=∠==,sin 2α=,15sin 2sincos 2224ααα==⨯.故选B.2.(2023新高考I 卷8)已知()1sin 3αβ-=,1cos sin 6αβ=,则()cos 22αβ+=()A.79B.19 C.19-D.79-【解析】()1sin sin cos cos sin 3αβαβαβ-=-=,1cos sin 6αβ=,所以1sin cos 2αβ=,所以()112sin sin cos cos sin 263αβαβαβ+=+=+=,()()()2221cos 22cos 212sin 1239αβαβαβ⎛⎫+=+=-+=-⨯= ⎪⎝⎭.故选B.3.(2023新高考II 卷7)已知α为锐角,1cos 4α+=,则sin 2α=()A.38- B.18-+ C.34- D.14-+【解析】21cos 12sin 24αα+=-=,所以2231sin 284α⎫-==⎪⎪⎝⎭,则1sin24α-=或1sin 24α=.因为α为锐角,所以sin02α>,15sin24α-=舍去,得51sin 24α-=.故选D.第三节三角函数的图像与性质1.(2023新高考II 卷16)已知函数()()sin f x x ωϕ=+,如图所示,A ,B 是直线12y =与曲线()y f x =的两个交点,若π=6AB ,则()πf =_______.【解析】sin y x =的图象与直线12y =两个相邻交点的最近距离为2π3,占周期2π的13,所以12ππ36ω⋅=,解得4ω=,所以()()sin 4f x x ϕ=+.再将2π,03⎛⎫⎪⎝⎭代入()()sin 4f x x ϕ=+得ϕ的一个值为2π3-,即()2πsin 43f x x ⎛⎫=- ⎪⎝⎭.所以()2π3πsin 4π32f ⎛⎫=-=- ⎪⎝⎭.2.(2023全国甲卷理科10,文科12)已知()f x 为函数cos 26y x π⎛⎫=+ ⎪⎝⎭向左平移6π个单位所得函数,则()y f x =与1122y x =-交点个数为()A.1B.2C.3D.4【解析】因为函数πcos 26y x ⎛⎫=+ ⎪⎝⎭向左平移π6个单位可得()sin 2.f x x =-而1122y x =-过10,2⎛⎫- ⎪⎝⎭与()1,0两点,分别作出()f x 与1122y x =-的图像如图所示,考虑3π3π7π2,2,2222x x x =-==,即3π3π7π,,444x x x =-==处()f x 与1122y x =-的大小关系,结合图像可知有3个交点.故选C.3.(2023全国乙卷理科6,文科10)已知函数()()sin f x x ωϕ=+在区间2,63ππ⎛⎫⎪⎝⎭单调递增,直线6x π=和23x π=为函数()y f x =的图像的两条对称轴,则512f π⎛⎫-= ⎪⎝⎭()A. B.12-C.12【解析】2222362T T ωωππππ=-=⇒=π=⇒=,所以()()sin 2.f x x ϕ=+又222,32k k ϕππ⋅+=+π∈Z ,则52,6k k ϕπ=-+π∈Z .所以5555sin 22sin 121263f k π⎡ππ⎤π⎛⎫⎛⎫⎛⎫-=⋅--+π=-= ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦故选D.【评注】本题考查了三角函数图像与性质,当然此题也可以通过画图快速来做,读者可以自行体会.4.(2023全国乙卷理科10)已知等差数列{}n a 的公差为23π,集合{}*cos n S a n =∈N ,若{},S a b =,则ab =()A.1- B.12-C.0D.12【解析】解法一(利用三角函数图像与性质)因为公差为23π,所以只考虑123,,a a a ,即一个周期内的情形即可.依题意,{}{}cos ,n S a a b ==,即S 中只有2个元素,则123cos ,cos ,cos a a a 中必有且仅有2个相等.如图所示,设横坐标为123,,a a a 的点对应图像中123,,A A A 点.①当12cos cos a a =时,且2123a a π-=,所以图像上点的位置必为如图1所示,12,A A 关于x =π对称,且1223A A π=,则1233a ππ=π-=,2433a ππ=π+=,32a =π.所以11122ab ⎛⎫=-⨯=- ⎪⎝⎭.②当13cos cos a a =时,3143a a π-=,所以图像上点的位置必为如图2所示,13,A A 关于x =π对称,且1343A A π=,则133a 2ππ=π-=,3533a 2ππ=π+=,2a =π.所以()11122ab =⨯-=-.综上所述,12ab =-.故选B.解法二(代数法)()()11113n a a n d a n 2π=+-=+-,21cos cos 3a a 2π⎛⎫=+ ⎪⎝⎭,31cos cos 3a a 4π⎛⎫=+ ⎪⎝⎭,由于{}{}*cos ,n S a n a b =∈=N ,故123cos ,cos ,cos a a a 中必有2个相等.①若121111cos cos cos cos 322a a a a a 2π⎛⎫==+=-- ⎪⎝⎭,即113cos 22a a =-,解得11cos 2a =或11cos 2a =-.若11cos 2a =,则1sin a =,3111113cos cos cos 132244a a a a 4π⎛⎫=+=-+=--=- ⎪⎝⎭,若11cos 2a =-,则1sin a =,3111113cos cos cos 13244a a a a 4π⎛⎫=+=-=+= ⎪⎝⎭,故131cos cos 2a a ab ==-.②若131111cos cos cos cos sin 322a a a a a 4π⎛⎫==+=-+ ⎪⎝⎭,得113cos 2a a =,解得11cos 2a =或11cos 2a =-.当11cos 2a =时,1sin a =,21111313cos cos cos 132244a a a a 2π⎛⎫=+=--=--=- ⎪⎝⎭,当11cos 2a =-时,1sin a =213cos 144a =+=,故121cos cos 2a a ab ==-.③若23cos cos a a =,与①类似有121cos cos 2a a ab ==-.综上,故选B.5.(2023北京卷17)已知函数()sin cos cos sin ,0,2f x x x ωϕωϕωϕπ=+><.(1)若()0f =,求ϕ的值;(2)若()f x 在区间2,33ππ⎡⎤-⎢⎥⎣⎦上单调递增,且213f π⎛⎫= ⎪⎝⎭,再从条件①、条件②、条件③这三个条件中选择一个作为已知,使函数()f x 存在,求,ωϕ的值.条件①:3f π⎛⎫= ⎪⎝⎭;条件②:13f π⎛⎫-=- ⎪⎝⎭;条件③:()f x 在,23ππ⎡⎤--⎢⎥⎣⎦上单调递减.注:如果选择的条件不符合要求,第(2)问得0分;如果选择多个符合要求的条件分别解答,按第一个解答计分.【分析】(1)把0x =代入()f x 的解析式求出sin ϕ,再由π||2ϕ<即可求出ϕ的值;(2)若选条件①不合题意;若选条件②,先把()f x 的解析式化简,根据() f x 在π2π,33⎡⎤⎢⎥⎣⎦-上的单调性及函数的最值可求出T ,从而求出ω的值;把ω的值代入()f x 的解析式,由π13f ⎛⎫-=- ⎪⎝⎭和π||2ϕ<即可求出ϕ的值;若选条件③:由() f x 的单调性可知() f x 在π3x =-处取得最小值1-,则与条件②所给的条件一样,解法与条件②相同.【解析】(1)因为π()sin cos cos sin ,0,||2f x x x ωϕωϕωϕ=+><所以()()3(0)sin 0cos cos 0sin sin 2f ωϕωϕϕ=⋅+⋅==-,因为π||2ϕ<,所以π3ϕ=-.(2)因为π()sin cos cos sin ,0,||2f x x x ωϕωϕωϕ=+><,所以()π()sin ,0,||2f x x ωϕωϕ=+><,所以() f x 的最大值为1,最小值为1-.若选条件①:因为()()sin f x x ωϕ=+的最大值为1,最小值为1-,所以π3f ⎛⎫= ⎪⎝⎭无解,故条件①不能使函数()f x 存在;若选条件②:因为() f x 在π2π,33⎡⎤⎢⎥⎣⎦-上单调递增,且2π13f ⎛⎫= ⎪⎝⎭,π13f ⎛⎫-=- ⎪⎝⎭,所以2πππ233T ⎛⎫=--= ⎪⎝⎭,所以2πT =,2π1Tω==,所以()()sin f x x ϕ=+,又因为π13f ⎛⎫-=- ⎪⎝⎭,所以πsin 13ϕ⎛⎫-+=- ⎪⎝⎭,所以ππ2π,32k k ϕ-+=-+∈Z ,所以π2π,6k k ϕ=-+∈Z ,因为||2ϕπ<,所以π6ϕ=-.所以1ω=,π6ϕ=-;若选条件③:因为() f x 在π2π,33⎡⎤⎢⎥⎣⎦-上单调递增,在ππ,23⎡⎤--⎢⎥⎣⎦上单调递减,所以() f x 在π3x =-处取得最小值1-,即π13f ⎛⎫-=- ⎪⎝⎭.以下与条件②相同.第四节解三角形1.(2023全国甲卷理科16)在ABC △中,2AB =,60BAC ∠=︒,BC =D 为BC 上一点,AD 平分BAC ∠,则AD =.【解析】如图所示,记,,,AB c AC b BC a ===由余弦定理可得22222cos606b b +-⨯⨯⨯︒=,解得1b =(负值舍去).由ABC ABD ACD S S S =+△△△可得,1112sin602sin30sin30222b AD AD b ⨯⨯⨯︒=⨯⨯⨯︒+⨯⨯⨯︒,解得1212bAD b +===+.2.(2023全国甲卷文科17)记ABC △的内角,,A B C 的对边分别为,,a b c ,已知2222cos b c a A+-=.(1)求bc .(2)若cos cos 1cos cos a B b A ba Bb A c--=,求ABC △面积.3.(2023全国乙卷理科18)在ABC △中,120BAC ∠=︒,2AB =,1AC =.(1)求sin ABC ∠;(2)若D 为BC 上一点,且90BAD ∠=︒,求ADC △的面积.【解析】(1)利用余弦定理可得2222cos 14212cos120527BC AC AB AC AB BAC =+-⋅∠=+-⨯⨯⨯︒=+=.故BC =.又由正弦定理可知sin sin BC ACBAC ABC=∠∠.故sin sin14AC BAC ABC BC ⋅∠∠====.(2)由(1)可知tan ABC ∠=在Rt BAD △中,tan 2AD AB ABC =⋅∠=⨯=故1122255ABD S AB AD =⨯⨯=⨯⨯=△,又11sin 21sin120222ABC S AB AC BAC =⨯⨯⨯∠=⨯⨯⨯︒=△,所以2510ADC ABC ABD S S S =-=-=△△△.5.(2023新高考I 卷17)已知在ABC △中,3A B C +=,()2sin sin A C B -=.(1)求sin A ;(2)设=5AB ,求AB 边上的高.【解析】(1)解法一因为3A B C +=,所以4A B C C ++==π,所以4C π=,2sin()sin()A C A C -=+2sin cos 2cos sin sin cos cos sin A C A C A C A C⇒-=+sin cos 3cos sin A C A C ⇒=tan 3tan 3sin A C A ⇒==⇒=解法二因为3A B C +=,所以4A B C C ++==π,所以4C π=,所以4A B 3π+=,所以4B A 3π=-,故2sin()sin()4AC A 3π-=-,即2sin cos 2cos sin sin cos cos sin 4444A A A A ππ3π3π-=-,得sin 3cos A A =.又22sin cos 1A A +=,()0,A ∈π,得310sin 10A =.(2)若||5AB =.如图所示,设AC 边上的高为BG ,AB 边上的高为CH ,||CH h =,由(1)可得10cos 10A =,||||cos ||102AG AB A AB =⋅==,||||2BG CG ===,所以||AC =,||||2||6||5AC BG CH AB ===.6.(2023新高考II 卷17)记ABC △的内角,,A B C 的对边分别为,,a b c ,已知ABC △的面,D 为BC 的中点,且1AD =.(1)若π3ADC ∠=,求tan B ;(2)若228b c +=,求,b c .【解析】(1)依题意,122ADC ABC S S ==△△,133sin 242ADC S AD DC ADC =⋅⋅∠==△,解得2DC =,2BD =.如图所示,过点A 作AE BC ⊥于点E .因为60ADC ∠= ,所以12DE =,32AE =,则15222BE =+=,所以3tan 5AE B BE ==.(2)设AB = c ,AC = b ,由极化恒等式得2214AB AC AD BC ⋅- =,即2114⋅--b c =b c ,化简得()22244⋅-+=-b c =b c ,即cos cos 2BAC bc BAC ⋅⋅∠=∠=-b c =b c ①,又1sin 2ABC S bc BAC =∠=△,即sin bc BAC ∠=.②①得tan BAC ∠=0πBAC <∠<得2π3BAC ∠=,代入①得4bc =,与228b c +=联立可得2b c ==.7.(2023北京卷7)在ABC △中,()()()sin sin sin sin a c A C b A B +-=-,则C ∠=()A.6π B.3π C.32π D.65π【分析】利用正弦定理的边角变换与余弦定理即可得解.【解析】因为()(sin sin )(sin sin )a c A C b A B +-=-,所以由正弦定理得()()()a c a c b a b +-=-,即222a c ab b -=-,则222a b c ab +-=,故2221cos 222a b c ab C ab ab +-===,又0πC <<,所以π3C =.故选B.。
高考数学模拟试卷复习试题三角函数和解三角形正弦定理和余弦定理的应用

高考数学模拟试卷复习试题三角函数和解三角形正弦定理和余弦定理的应用一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选择中,只有一个是符合题目要求的。
)1.一船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75°距塔68海里的M 处,下午2时到达这座灯塔的东南方向的N 处,则这只船的航行速度为()A.1762海里/小时B .346海里/小时C.1722海里/小时 D .342海里/小时2.一船向正北航行,看见正西方向有相距10海里的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这艘船的速度是每小时()A .5海里B .53海里C .10海里D .103海里3.某人在C 点测得某塔在南偏西80°,塔顶仰角为45°,此人沿南偏东40°方向前进10米到D ,测得塔顶A 的仰角为30°,则塔高为()A .15米B .5米C .10米D .12米4.如图所示,要测量河对岸A ,B 两点间的距离,今沿河对岸选取相距40米的C ,D 两点,测得∠ACB =60°,∠BCD =45°,∠ADB =60°,∠ADC =30°,则AB 的距离是() A .402米B .202米C .203米D .206米5.已知两座灯塔A 和B 与海洋观察站C 的距离都等于a km ,灯塔A 在观察站C 的北偏东20°,灯塔B 在观察站C 的南偏东40°,则灯塔A 与B 的距离为()A .a kmB .3a km C.2a km D .2a km6.两座灯塔A 和B 与海岸观察站C 的距离相等,灯塔A 在观察站北偏东40°,灯塔B 在观察站的南偏东60°,则灯塔A 在灯塔B 的()A .北偏东10°B .北偏西10°C .南偏东10°D .南偏西10°7.如图所示,设A 、B 两点在河的两岸,一测量者在A 所在的河岸边选定一点C ,测出AC 的距离为50m ,∠ACB =45°,∠CAB =105°后,就可以计算A 、B 两点的距离为 ()A .502mB .503mC .252m D.2522m8.已知A 、B 两地间的距离为10km ,B 、C 两地间的距离为20km ,现测得∠ABC =120°,则A 、C 两地间的距离为()A .10km B.3km C .105kmD .107km9.一船向正北航行,看见正西方向有相距10n mile 的两个灯塔恰好与它在一条直线上,继续航行半小时后,看见一灯塔在船的南偏西60°,另一灯塔在船的南偏西75°,则这只船的速度是每小时()A .5n mileB .53n mileC .10n mileD .103n mile10.为测量某塔AB 的高度,在一幢与塔AB 相距20m 的楼顶D 处测得塔顶A 的仰角为30°,测得塔基B 的俯角为45°,那么塔AB 的高度是()A .20⎝⎛⎭⎫1+33m B .20⎝⎛⎭⎫1+32mC .20(1+3)m D .30m11.已知A 船在灯塔C 北偏东80°处,且A 到C 距离为2km ,B 船在灯塔C 北偏西40°,A B 两船距离为3km ,则B 到C 的距离为()A.19km B .(6-1)km C .(6+1)kmD.7km12.一船自西向东匀速航行,上午10时到达一座灯塔P 的南偏西75°距塔68n mile 的M 处,下午2时到达这座灯塔的东南方向的N 处,则这只船的航行速度为()A.1762n mile/hB .346n mile/h C.1722n mile/hD .342n mile/h二、填空题(本大题共4小题,每小题5分,共20分。
2018全国高考模拟文科数学分类汇编__三角函数及解三角形

2018年全国高考模拟文科数学分类汇编——三角函数和解三角形一、选择题1. 10.(5分)已知定义在R 上的函数f (x )满足:(1)f (x )+f (2﹣x )=0,(2)f (x ﹣2)=f (﹣x ),(3)在[﹣1,1]上表达式为f (x )=,则函数f (x )与函数g (x )=的图象区间[﹣3,3]上的交点个数为( )A .5B .6C .7D .82. 11.(5分)已知函数f (x )=sin (ωx +φ)(ω>0,|φ|<)的最小正周期是π,若将其图象向右平移个单位后得到的图象关于原点对称,则函数f (x )的图象( ) A .关于直线x=对称 B .关于直线x=对称 C .关于点(,0)对称 D .关于点(,0)对称3. 4.若tanθ+=4,则sin2θ=( )A .B .C .D .4. 7.将函数()2sin 13f x x π⎛⎫=-- ⎪⎝⎭的图象向右平移3π个单位,再把所有的点的横坐标缩短到原来的12倍(纵坐标不变),得到函数()y g x =的图象,则图象()y g x =的一个对称中心为 A .,03π⎛⎫⎪⎝⎭ B .,012π⎛⎫ ⎪⎝⎭ C.,13π⎛⎫- ⎪⎝⎭ D .,112π⎛⎫- ⎪⎝⎭5. 7.(5分)若将函数f (x )=sin (2x +)图象上的每一个点都向左平移个单位,得到g (x )的图象,则函数g (x )的单调递增区间为( ) A .[kπ﹣,kπ+](k ∈Z ) B .[kπ+,kπ+](k ∈Z )C .[kπ﹣,kπ﹣](k ∈Z )D .[kπ﹣,kπ+](k ∈Z )6. 11.函数()[]()cos ,x f x xe x ππ=∈-的图象大致是7. 8. 已知函数,则下列结论中正确的是A. 函数的最小正周期为B. 函数的图象关于点对称C. 由函数的图象向右平移个单位长度可以得到函数的图象D. 函数在区间上单调递增8. 9. 函数,则函数的导数的图象是( )A. B. C. . D.9. 8.(5分)已知函数y=Asin (ωx +φ)(ω>0,|φ|<,x ∈R )的图象如图所示,则该函数的单调减区间是( )A .[2+16k ,10+16k ](k ∈Z )B .[6+16k ,14+16k ](k ∈Z )C .[﹣2+16k ,6+16k ](k ∈Z )D .[﹣6+16k ,2+16k ](k ∈Z )10. 8.已知曲线1215:sin ,:cos 26C y x C y x π⎛⎫==-⎪⎝⎭,则下列说法正确的是 A .把1C 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB .把1C 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线2C C.把曲线1C 向右平移3π个单位长度,再把得到的曲线上各点横坐标缩短到原来的12,纵坐标不变,得到曲线2C D .把曲线1C 向右平移6π个单位长度,再把得到的曲线上各点横坐标缩短到原来的12,纵坐标不变,得到曲线2C 11. 10.函数()21cos 1xf x x e ⎛⎫=-⎪+⎝⎭(其中e 为自然对数的底数)图象的大致形状是12. 9.已知曲线12:2cos ,:2cos2C y x C y x x ==-,则下面结论正确的是 A .把1C 各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线C 2B .把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移至3π个单位长度,得到曲线C 2C .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线C 2D .把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线C 213. 11.现有四个函数①sin y x x =⋅ ②cos y x x =⋅ ③cos y x x =⋅ ④2xy x =⋅的部分图象如下,但顺序被打乱,则按照从左到右将图象对应的函数序号排列正确的一组是A .①④②③B .①④③②C .④①②③D .③④②①14. 6.已知函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为4π,则 A .函数()f x 的图象关于原点对称 B .函数()f x 的图象关于直线3x π=对称C .函数()f x 图象上的所有点向右平移3π个单位长度后,所得的图象关于原点对称 D .函数()f x 在区间()0,π上单调递增 15. 7.函数()()1cos 0f x x x x x x ππ⎛⎫=--≤≤≠ ⎪⎝⎭且的图象可能为16. 11.已知函数2()2ln ||f x x x =-与()sin()g x x ωϕ=+有两个公共点,则在下列函数中满足条件的周期最大的函数()g x =( )A .πsin π2x ⎛⎫- ⎪⎝⎭B .πsin π2x ⎛⎫+ ⎪⎝⎭C .πsin 2x ⎛⎫+π ⎪⎝⎭D .πsin 2π2x ⎛⎫+ ⎪⎝⎭17. 3.已知1sin()3απ+=-,则tan 2απ⎛⎫- ⎪⎝⎭值为( )A .B .-C D .±18. 5.为了得到函数2sin(3)4y x π=+的图象,只需把函数2sin 3y x =的图象上所有的点( ) A. 向左平移4π个单位 B. 向左平移12π个单位C. 向右平移4π个单位 D. 向右平移12π个单位 19. 6.已知函数)2,0,0)(sin()(πϕωϕω<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式是( ) A. ()sin(3)3f x x π=+ B. ()sin(2)3f x x π=+C. ()sin()3f x x π=+ D. ()sin(2)6f x x π=+ 二、填空题1. 14.(5分)已知函数f (x )=2sin (ϖx +φ)对任意x 都有f (+x )=f (﹣x ),则|f ()|= .2. 15.设△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若a=4,A=,B=,则△ABC 的面积S= .三、解答题1. 17.(10分)已知点,Q (cosx ,sinx ),O 为坐标原点,函数.(1)求函数f (x )的最小值及此时x 的值;(2)若A 为△ABC 的内角,f (A )=4,BC=3,求△ABC 的周长的最大值.2. 17.(本小题满分12分)在ABC ∆中,角A ,B ,C 的对边分别为,,,sin sin a b c a B C ==,且.(I)求角A 的大小;(Ⅱ)若a =B 的平分线交AC 于点D ,求线段BD 的长度.3. 17.(12分)在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c ,且2ccosB=2a +b .(1)求角C ;(2)若△ABC 的面积为,求ab 的最小值.4. 17. 在△中,分别为内角的对边,.(Ⅰ) 求的大小;(Ⅱ) 若,, 求△的面积.5. 17.(12分)已知△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,bsin (B +C )+acosA=0,且c=2,sinC=. (1)求证:A=+B ;(2)求△ABC 的面积.6. 17.(12分)在ABC ∆中,角A ,B ,C 的对边分别为,,,2sin .a b c b c B A ==,且 (1)求cos B 的值;(2)若2a ABC =∆,求的面积.7. 17.(本小题满分10分)在平面直角坐标系中,O 为原点,()221,0,2cos ,sin ,2cos ,22OA OB OC βαα⎛⎫⎛=== ⎪ ⎝⎭⎝)sin ,0ββαπ<<<.(I)若,AB AC BC ⊥求;(Ⅱ)设()1,1,OD AB AC AD αβ=+=若求,的值.8. 17.(12分)在ABC V 中,角A ,B ,C 的对边分别为a ,b ,c .(1)若223cos cos20A A +=,且ABC V 为锐角三角形,7a =,6c =,求b 的值;(2)若a =,3A π=,求b c +的取值范围.答案一、选择题1. 10.(5分)已知定义在R上的函数f(x)满足:(1)f(x)+f(2﹣x)=0,(2)f(x﹣2)=f(﹣x),(3)在[﹣1,1]上表达式为f(x)=,则函数f(x)与函数g(x)=的图象区间[﹣3,3]上的交点个数为()A.5 B.6 C.7 D.8【分析】由题意可得函数f(x)的图象关于点M(1,0)对称,又关于直线x=﹣1对称;再结合g(x)的解析式画出这2个函数区间[﹣3,3]上的图象,数形结合可得它们的图象区间[﹣3,3]上的交点个数.【解答】解:由f(x)+f(2﹣x)=0,可得函数f(x)的图象关于点M(1,0)对称.由f(x﹣2)=f(﹣x),可得函数f(x)的图象关于直线x=﹣1对称.又f(x)在[﹣1,1]上表达式为f(x)=,可得函数f(x)在[﹣3,3]上的图象以及函数g(x)=在[﹣3,3]上的图象,数形结合可得函数f(x)的图象与函数g(x)的图象区间[﹣3,3]上的交点个数为6,故选:B.【点评】本题主要考查函数的图象的对称性,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.2. 11.(5分)已知函数f (x )=sin (ωx +φ)(ω>0,|φ|<)的最小正周期是π,若将其图象向右平移个单位后得到的图象关于原点对称,则函数f (x )的图象( ) A .关于直线x=对称 B .关于直线x=对称 C .关于点(,0)对称 D .关于点(,0)对称【分析】根据三角函数的性质求出函数的解析式进行求解即可. 【解答】解:∵函数f (x )=sin (ωx +φ)(ω>0,|φ|<)的最小正周期是π,∴T==π,解得ω=2,即f (x )=sin (2x +φ),将其图象向右平移个单位后得到y=sin [2(x ﹣)+φ]=sin (2x +φ﹣),若此时函数关于原点对称,则φ﹣=kπ,即φ=+kπ,k ∈Z ,∵|φ|<,∴当k=﹣1时,φ=.即f (x )=sin (2x ).由2x =,解得x=+,k ∈Z ,故当k=0时,函数的对称轴为x=,故选:B【点评】本题主要考查三角函数解析式的求解以及三角函数的性质的应用,根据条件求出函数的解析式是解决本题的关键.3. 4.若tanθ+=4,则sin2θ=( )A .B .C .D .【考点】二倍角的正弦;同角三角函数间的基本关系.【分析】先利用正弦的二倍角公式变形,然后除以1,将1用同角三角函数关系代换,利用齐次式的方法化简,可求出所求. 【解答】解:sin2θ=2sinθcosθ=====。
高考数学真题+高考数学模拟题(文科)专项汇编专题06三角函数及解三角形Word版含解析

专题06 三角函数及解三角形1.【2019年高考全国Ⅰ卷文数】函数f (x )=2sin cos ++x xx x在[,]-ππ的图像大致为 A .B .C .D .【答案】D【解析】由22sin()()sin ()()cos()()cos x x x xf x f x x x x x-+----===--+-+,得()f x 是奇函数,其图象关于原点对称,排除A .又22π1π42π2()1,π2π()2f ++==>2π(π)01πf =>-+,排除B ,C ,故选D .【名师点睛】本题考查函数的性质与图象,渗透了逻辑推理、直观想象和数学运算素养,采取性质法或赋值法,利用数形结合思想解题.解答本题时,先判断函数的奇偶性,得()f x 是奇函数,排除A ,再注意到选项的区别,利用特殊值得正确答案.2.【2019年高考全国Ⅰ卷文数】tan255°=A .−2B .−C .2D .【答案】D【解析】tan 255tan(18075)tan 75tan(4530)︒=︒+︒=︒=︒+︒=tan 45tan 301tan 45tan 30︒+︒-︒︒12+==+故选D. 【名师点睛】本题主要考查三角函数的诱导公式、两角和与差的三角函数、特殊角的三角函数值、运算求解能力.首先应用诱导公式,将问题转化成锐角三角函数的计算,进一步应用两角和的正切公式计算求解.题目较易,注重了基础知识、基本计算能力的考查.3.【2019年高考全国Ⅰ卷文数】△ABC 的内角A ,B ,C 的对边分别为a ,b ,c ,已知a sin A −b sin B =4c sin C ,cos A =−14,则b c=A .6B .5C .4D .3【答案】A【解析】由已知及正弦定理可得2224a b c -=,由余弦定理推论可得2222214131cos ,,,422424b c a c c c A bc bc b +---==∴=-∴=3462b c ∴=⨯=,故选A . 【名师点睛】本题考查正弦定理及余弦定理推论的应用.先利用余弦定理推论得出a ,b ,c 关系,再结合正弦定理边角互换列出方程,解出结果. 4.【2019年高考全国Ⅱ卷文数】若x 1=4π,x 2=43π是函数f (x )=sin x ω(ω>0)两个相邻的极值点,则ω= A .2 B .32 C .1D .12【答案】A【解析】由题意知,()sin f x x ω=的周期232()44T ωπππ==-=π,解得2ω=.故选A .【名师点睛】本题考查三角函数的极值和周期,渗透了直观想象、逻辑推理和数学运算素养.利用周期公式,通过方程思想解题. 5.【2019年高考全国Ⅱ卷文数】已知a ∈(0,π2),2sin2α=cos2α+1,则sin α=A .15BCD 【答案】B【解析】2sin 2cos21αα=+,24sin cos 2cos .0,,cos 02αααααπ⎛⎫∴⋅=∈∴> ⎪⎝⎭,sin 0,α>2sin cos αα∴=,又22sin cos 1αα+=,2215sin 1,sin 5αα∴==,又s i n 0α>,sin α∴=B . 【名师点睛】本题是对三角函数中二倍角公式、同角三角函数基本关系式的考查,中等难度,判断正余弦的正负,运算准确性是关键,题目不难,需细心,解决三角函数问题,研究角的范围后得出三角函数值的正负很关键,切记不能凭感觉.解答本题时,先利用二倍角公式得到正余弦关系,再利用角范围及正余弦平方和为1关系得出答案. 6.【2019年高考全国Ⅲ卷文数】函数()2sin sin2f x x x =-在[0,2π]的零点个数为 A .2 B .3 C .4D .5【答案】B【解析】由()2sin sin 22sin 2sin cos 2sin (1cos )0f x x x x x x x x =-=-=-=, 得sin 0x =或cos 1x =,[]0,2πx ∈,0π2πx ∴=、或.()f x ∴在[]0,2π的零点个数是3,故选B .【名师点睛】本题考查在一定范围内的函数的零点个数,渗透了直观想象和数学运算素养.令()0f x =,得sin 0x =或cos 1x =,再根据x 的取值范围可求得零点.7.【2019年高考北京卷文数】设函数f (x )=cos x +b sin x (b 为常数),则“b =0”是“f (x )为偶函数”的A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】C【解析】0b =时,()cos sin cos f x x b x x =+=,()f x 为偶函数; ()f x 为偶函数时,()=()f x f x -对任意的x 恒成立,即()cos()sin()cos sin f x x b x x b x -=-+-=-,cos sin cos sin x b x x b x +=-,得sin 0b x =对任意的x 恒成立,从而0b =.从而“0b =”是“()f x 为偶函数”的充分必要条件,故选C.【名师点睛】本题较易,注重基础知识、逻辑推理能力的考查.根据定义域为R 的函数()f x 为偶函数等价于()=()f x f x -恒成立进行判断.8.【2019年高考北京卷文数】如图,A ,B 是半径为2的圆周上的定点,P 为圆周上的动点,APB ∠是锐角,大小为β.图中阴影区域的面积的最大值为A .4β+4cos βB .4β+4sin βC .2β+2cos βD .2β+2sin β【答案】B【解析】设圆心为O ,如图1,连接OA ,OB ,AB ,OP ,则22AOB APB ∠=∠=β,所以22242OABS ⨯==扇形ββ,因为ABP AOB OAB S S S S =+-△△阴影扇形,且AOB OAB S S △扇形,都已确定, 所以当ABP S △最大时,阴影部分面积最大.观察图象可知,当P 为弧AB 的中点时(如图2),阴影部分的面积S 取最大值,此时∠BOP =∠AOP =π−β,面积S 的最大值为ABP AOB OAB S S S S =+-△△阴影扇形=4β+S △POB + S △POA =4β+12|OP ||OB |sin (π−β)+12|OP ||OA |sin (π−β)=4β+2sin β+2sin β=4β+4 sin β,故选B. 【名师点睛】本题主要考查阅读理解能力、数学应用意识、数形结合思想及数学式子变形和运算求解能力,有一定的难度.关键是观察分析区域面积最大时的状态,并将面积用边角等表示.9.【2019年高考天津卷文数】已知函数()sin()(0,0,||π)f x A x A ωϕωϕ=+>><是奇函数,且()f x 的最小正周期为π,将()y f x =的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),所得图象对应的函数为()g x .若π4g ⎛⎫= ⎪⎝⎭3π8f ⎛⎫= ⎪⎝⎭A .−2B .C D .2【答案】C【解析】∵()f x 为奇函数,∴(0)sin 0,=π,,0,f A k k k ϕϕ==∴∈∴=Z 0ϕ=; ∵()f x 的最小正周期为π,2ππ,T ∴==ω∴2ω=,∴1()sin sin ,2g x A x A x ==ω又π()4g =2A =,∴()2sin 2f x x =,3π()8f = 故选C.【名师点睛】本题主要考查函数的性质和函数的求值问题,解题关键是求出函数()g x ,结合函数性质逐步得出,,A ωϕ的值即可.10.【2019年高考全国Ⅰ卷文数】函数3π()s i n (2)3c o s 2f x xx =+-的最小值为___________. 【答案】4-【解析】23π()sin(2)3cos cos 23cos 2cos 3cos 12f x x x x x x x =+-=--=--+ 23172(cos )48x =-++,1cos 1x -≤≤,∴当cos 1x =时,min ()4f x =-,故函数()f x 的最小值为4-.【名师点睛】本题首先应用诱导公式,转化得到二倍角的余弦,进一步应用二倍角的余弦公式,得到关于cos x 的二次函数,从而得解.注意解答本题的过程中,部分考生易忽视1cos 1x -≤≤的限制,而简单应用二次函数的性质,出现运算错误.11.【2019年高考全国Ⅱ卷文数】ABC △的内角A ,B ,C 的对边分别为a ,b ,c .已知b sin A +a cos B =0,则B =___________. 【答案】3π4【解析】由正弦定理,得sin sin sin cos 0B A A B +=.(0,),(0,)A B ∈π∈π,sin 0,A ∴≠∴sin cos 0B B +=,即tan 1B =-,3.4B π∴=【名师点睛】本题考查利用正弦定理转化三角恒等式,渗透了逻辑推理和数学运算素养.采取定理法,利用转化与化归思想解题.本题容易忽视三角形内角的范围致误,三角形内角均在(0,π)范围内,化边为角,结合三角函数的恒等变化求角.12.【2019年高考江苏卷】已知tan 2π3tan 4αα=-⎛⎫+ ⎪⎝⎭,则πsin 24α⎛⎫+ ⎪⎝⎭的值是 ▲ .【答案】10【解析】由()t a n 1t ant a n t a n 2t a n 1πt a n 13t a n 1t a n 4αααααααα-===-++⎛⎫+ ⎪-⎝⎭,得23t a n 5t an2αα--=, 解得tan 2α=,或1tan 3α=-. πππsin 2sin 2cos cos 2sin 444ααα⎛⎫+=+ ⎪⎝⎭)22222sin cos cos sin sin 2cos 2sin cos αααααααα⎫+-=+⎪+⎝⎭222tan 1tan =2tan 1ααα⎛⎫+- ⎪+⎝⎭, 当tan 2α=时,上式222212==22110⎛⎫⨯+- ⎪+⎝⎭ 当1tan 3α=-时,上式=22112()1()33[]=1210()13⨯-+---+综上,πsin 2410α⎛⎫+= ⎪⎝⎭ 【名师点睛】本题考查三角函数的化简求值,渗透了逻辑推理和数学运算素养.采取转化法,利用分类讨论和转化与化归思想解题.由题意首先求得tan α的值,然后利用两角和的正弦公式和二倍角公式将原问题转化为齐次式求值的问题,最后切化弦求得三角函数式的值即可.13.【2019年高考浙江卷】在ABC △中,90ABC ∠=︒,4AB =,3BC =,点D 在线段AC 上,若45BDC ∠=︒,则BD =___________,cos ABD ∠=___________.,10【解析】如图,在ABD △中,由正弦定理有:s i n s i n A B B DA DB B A C=∠∠,而3π4,4AB ADB =∠=, 5AC ,34sin ,cos 55BC AB BAC BAC AC AC ∠==∠==,所以5BD =ππcos cos()cos cos sin sin 4410ABD BDC BAC BAC BAC ∠=∠-∠=∠+∠=.【名师点睛】本题主要考查解三角形问题,即正弦定理、三角恒等变换、数形结合思想及函数方程思想.在ABD △中应用正弦定理,建立方程,进而得解.解答解三角形问题,要注意充分利用图形特征.14.【2019年高考全国Ⅲ卷文数】ABC △的内角A 、B 、C 的对边分别为a 、b 、c .已知sinsin 2A Ca b A +=. (1)求B ;(2)若△ABC 为锐角三角形,且c =1,求△ABC 面积的取值范围. 【答案】(1)B =60°;(2)(,82. 【解析】(1)由题设及正弦定理得sin sinsin sin 2A CA B A +=. 因为sin A ≠0,所以sinsin 2A CB +=. 由180A BC ︒++=,可得sincos 22A C B +=,故cos 2sin cos 222B B B=. 因为cos02B ≠,故1sin 22B =,因此B =60°. (2)由题设及(1)知△ABC的面积4ABC S a =△. 由正弦定理得()sin 120sin 1sin sin 2C c A a C C ︒-===.由于△ABC 为锐角三角形,故0°<A <90°,0°<C <90°,由(1)知A +C =120°,所以30°<C <90°,故122a <<ABC S <<△.因此,△ABC 面积的取值范围是⎝⎭.【名师点睛】这道题考查了三角函数的基础知识,以及正弦定理的使用(此题也可以用余弦定理求解),最后考查V ABC 是锐角三角形这个条件的利用,考查的很全面,是一道很好的考题.15.【2019年高考北京卷文数】在△ABC 中,a =3,–2b c =,cos B =12-. (1)求b ,c 的值; (2)求sin (B +C )的值.【答案】(1)7b =,5c =;(2)14. 【解析】(1)由余弦定理2222cos b a c ac B =+-,得2221323()2b c c =+-⨯⨯⨯-.因为2b c =+,所以2221(2)323()2c c c +=+-⨯⨯⨯-. 解得5c =. 所以7b =.(2)由1cos 2B =-得sin 2B =.由正弦定理得sin sin 14a A Bb ==. 在ABC △中,B C A +=π-.所以sin()sin B C A +==【名师点睛】本题主要考查余弦定理、正弦定理的应用,两角差的正弦公式的应用等知识,意在考查学生的转化能力和计算求解能力.16.【2019年高考天津卷文数】在ABC △中,内角,,A B C 所对的边分别为,,a b c .已知2b c a +=,3sin 4sin c B a C =.(1)求cos B 的值;(2)求sin 26πB ⎛⎫+ ⎪⎝⎭的值.【答案】(1)14-;(2). 【解析】(1)在ABC △中,由正弦定理sin sin b cB C=,得sin sin b C c B =, 又由3sin 4sin c B a C =,得3sin 4sin b C a C =,即34b a =.又因为2b c a +=,得到43b a =,23c a =. 由余弦定理可得222222416199cos 22423a a a a cb B ac a a +-+-===-⋅⋅. (2)由(1)可得sin B ==,从而sin 22sin cos B B B ==227cos 2cos sin 8B B B =-=-,故71sin 2sin 2cos cos 2sin 66682B B B πππ⎛⎫+=+=⨯= ⎪⎝⎭. 【名师点睛】本小题主要考查同角三角函数的基本关系,两角和的正弦公式,二倍角的正弦与余弦公式,以及正弦定理、余弦定理等基础知识.考查运算求解能力. 17.【2019年高考江苏卷】在△ABC 中,角A ,B ,C 的对边分别为a ,b ,c .(1)若a =3c ,bcos B =23,求c 的值; (2)若sin cos 2A B a b =,求sin()2B π+的值. 【答案】(1)3c =(2)5. 【解析】(1)因为23,3a cb B ===, 由余弦定理222cos 2a c b B ac +-=,得2222(3)323c c c c+-=⨯⨯,即213c =.所以c =(2)因为sin cos 2A Ba b =, 由正弦定理sin sin a b A B =,得cos sin 2B Bb b=,所以cos 2sin B B =. 从而22cos (2sin )B B =,即()22cos 41cos B B =-,故24cos 5B =.因为sin 0B >,所以cos 2sin 0B B =>,从而cos 5B =.因此πsin cos 25B B ⎛⎫+== ⎪⎝⎭. 【名师点睛】本小题主要考查正弦定理、余弦定理、同角三角函数关系、诱导公式等基础知识,考查运算求解能力.18.【2019年高考江苏卷】如图,一个湖的边界是圆心为O 的圆,湖的一侧有一条直线型公路l ,湖上有桥AB (AB 是圆O 的直径).规划在公路l 上选两个点P 、Q ,并修建两段直线型道路PB 、QA .规划要求:线段PB 、QA 上的所有点到点O 的距离均不小于圆....O 的半径.已知点A 、B 到直线l 的距离分别为AC 和BD (C 、D 为垂足),测得AB =10,AC =6,BD =12(单位:百米).(1)若道路PB 与桥AB 垂直,求道路PB 的长;(2)在规划要求下,P 和Q 中能否有一个点选在D 处?并说明理由;(3)在规划要求下,若道路PB 和QA 的长度均为d (单位:百米).求当d 最小时,P 、Q 两点间的距离.【答案】(1)15(百米);(2)见解析;(3)17+. 【解析】解法一:(1)过A 作AE BD ⊥,垂足为E .由已知条件得,四边形ACDE 为矩形,6, 8DE BE AC AE CD =====.' 因为PB ⊥AB ,所以84cos sin 105PBD ABE ∠=∠==. 所以12154cos 5BD PB PBD ===∠. 因此道路PB 的长为15(百米).(2)①若P 在D 处,由(1)可得E 在圆上,则线段BE 上的点(除B ,E )到点O 的距离均小于圆O 的半径,所以P 选在D 处不满足规划要求. ②若Q 在D 处,连结AD ,由(1)知10AD ==,从而2227cos 0225AD AB BD BAD AD AB +-∠==>⋅,所以∠BAD 为锐角.所以线段AD 上存在点到点O 的距离小于圆O 的半径. 因此,Q 选在D 处也不满足规划要求. 综上,P 和Q 均不能选在D 处. (3)先讨论点P 的位置.当∠OBP <90°时,线段PB 上存在点到点O 的距离小于圆O 的半径,点P 不符合规划要求; 当∠OBP ≥90°时,对线段PB 上任意一点F ,OF ≥OB ,即线段PB 上所有点到点O 的距离均不小于圆O 的半径,点P 符合规划要求.设1P 为l 上一点,且1PB AB ⊥,由(1)知,1P B =15, 此时11113sin cos 1595PD PB PBD PB EBA =∠=∠=⨯=; 当∠OBP >90°时,在1PPB △中,115PB PB >=. 由上可知,d ≥15. 再讨论点Q 的位置.由(2)知,要使得QA ≥15,点Q 只有位于点C 的右侧,才能符合规划要求.当QA =15时,CQ ===此时,线段QA 上所有点到点O 的距离均不小于圆O的半径.综上,当PB⊥AB,点Q位于点C右侧,且CQ=d最小,此时P,Q两点间的距离PQ=PD+CD+CQ=17+因此,d最小时,P,Q两点间的距离为17+.解法二:(1)如图,过O作OH⊥l,垂足为H.以O为坐标原点,直线OH为y轴,建立平面直角坐标系.因为BD=12,AC=6,所以OH=9,直线l的方程为y=9,点A,B的纵坐标分别为3,−3.因为AB为圆O的直径,AB=10,所以圆O的方程为x2+y2=25.从而A(4,3),B(−4,−3),直线AB的斜率为3 4 .因为PB⊥AB,所以直线PB的斜率为43 -,直线PB的方程为42533 y x=--.所以P(−13,9),15PB==.因此道路PB的长为15(百米).(2)①若P在D处,取线段BD上一点E(−4,0),则EO=4<5,所以P选在D处不满足规划要求.②若Q在D处,连结AD,由(1)知D(−4,9),又A(4,3),所以线段AD:36(44)4y x x=-+-剟.在线段AD上取点M(3,154),因为5OM==,所以线段AD上存在点到点O的距离小于圆O的半径. 因此Q选在D处也不满足规划要求.综上,P 和Q 均不能选在D 处. (3)先讨论点P 的位置.当∠OBP <90°时,线段PB 上存在点到点O 的距离小于圆O 的半径,点P 不符合规划要求; 当∠OBP ≥90°时,对线段PB 上任意一点F ,OF ≥OB ,即线段PB 上所有点到点O 的距离均不小于圆O 的半径,点P 符合规划要求.设1P 为l 上一点,且1PB AB ⊥,由(1)知,1P B =15,此时1P (−13,9); 当∠OBP >90°时,在1PPB △中,115PB PB >=. 由上可知,d ≥15. 再讨论点Q 的位置.由(2)知,要使得QA≥15,点Q 只有位于点C 的右侧,才能符合规划要求.当QA =15时,设Q (a ,9),由15(4)AQ a ==>,得a =4+,所以Q(4+9),此时,线段QA 上所有点到点O 的距离均不小于圆O 的半径.综上,当P (−13,9),Q (4+9)时,d 最小,此时P ,Q 两点间的距离4(13)17PQ =+-=+.因此,d 最小时,P ,Q 两点间的距离为17+.【名师点睛】本小题主要考查三角函数的应用、解方程、直线与圆等基础知识,考查直观想象和数学建模及运用数学知识分析和解决实际问题的能力. 19.【2019年高考浙江卷】设函数()sin ,f x x x =∈R .(1)已知[0,2),θ∈π函数()f x θ+是偶函数,求θ的值; (2)求函数22[()][()]124y f x f x ππ=+++的值域.【答案】(1)π2θ=或3π2;(2)[1+. 【解析】(1)因为()si n()f x x θθ+=+是偶函数,所以,对任意实数x 都有s i n ()s i n ()x x θθ+=-+,即sin cos cos sin sin cos cos sin x x x x θθθθ+=-+, 故2sin cos 0x θ=,所以cos 0θ=. 又[0,2π)θ∈,因此π2θ=或3π2. (2)2222ππππsin sin 124124y fx f x x x ⎡⎤⎡⎤⎛⎫⎛⎫⎛⎫⎛⎫=+++=+++ ⎪ ⎪ ⎪ ⎪⎢⎥⎢⎥⎝⎭⎝⎭⎝⎭⎝⎭⎣⎦⎣⎦ππ1cos 21cos 2136212sin 22222x x x x ⎛⎫⎛⎫-+-+ ⎪ ⎪⎫⎝⎭⎝⎭=+=--⎪⎪⎝⎭π123x ⎛⎫=-+ ⎪⎝⎭.因此,函数的值域是[1+. 【名师点睛】本题主要考查三角函数及其恒等变换等基础知识,同时考查运算求解能力. 20.【重庆西南大学附属中学校2019届高三第十次月考数学试题】已知角α的顶点在坐标原点,始边与x轴正半轴重合,终边经过点(1)P ,则cos2=αAB .13 C .13-D. 【答案】B【解析】因为角α的顶点在坐标原点,始边与x 轴正半轴重合,终边经过点(1)P ,所以cos 3==-α, 因此21cos 22cos 13=-=αα.故选B. 【名师点睛】本题主要考查三角函数的定义,以及二倍角公式,熟记三角函数的定义与二倍角公式即可,属于常考题型.解答本题时,先由角α的终边过点(1)P ,求出cos α,再由二倍角公式,即可得出结果.21.【四川省宜宾市2019届高三第三次诊断性考试数学试题】已知4cos 5=-α,()π,0∈-α,则πtan 4⎛⎫-= ⎪⎝⎭αA .17B .7C .17-D .7-【答案】C 【解析】()4cos ,π,05a =-∈-α,∴ππ,2⎛⎫∈-- ⎪⎝⎭α,33sin ,tan 54∴=-=αα,则πtan 1tan 41tan -⎛⎫-=⎪+⎝⎭ααα31143714-==-+.故选C . 【名师点睛】本题主要考查了同角三角函数关系式及两角差的正切公式的简单应用,属于基础题.解答本题时,根据已知cos α的值,结合同角三角函数关系式可求tan α,然后根据两角差的正切公式即可求解.22.【广东省韶关市2019届高考模拟测试(4月)数学文试题】已知函数π()sin()6f x x =+ω(0)>ω的相邻对称轴之间的距离为π2,将函数图象向左平移π6个单位得到函数()g x 的图象,则()g x = A .πsin()3x + B .πsin(2)3x +C .cos2xD .πcos(2)3x +【答案】C【解析】由函数π()sin()(0)6f x x =+>ωω的相邻对称轴之间的距离为π2,得π22T =,即πT =,所以2ππ=ω,解得2=ω,将函数π()sin(2)6f x x =+的图象向左平移π6个单位, 得到ππππ()sin[2()]sin 2cos 26636g x x x x ⎛⎫=++=++= ⎪⎝⎭的图象,故选C . 【名师点睛】本题考查的知识要点:三角函数关系式的平移变换和伸缩变换的应用,正弦型函数性质的应用,主要考查学生的运算能力和转换能力,属于基础题型.解答本题时,首先利用函数的图象求出函数的关系式,进一步利用图象的平移变换的应用求出结果.23.【河南省郑州市2019届高三第三次质量检测数学试题】已知函数()()sin f x A x =+ωϕ,π0,0,2A >><ωϕ的部分图象如图所示,则使()()0f a x f a x +--=成立的a 的最小正值为A .π12B .π6 C .π4D .π3【答案】B【解析】由图象易知,2A =,(0)1f =,即2sin 1=ϕ,且π2<ϕ,即6π=ϕ, 由图可知,11π()0,12f =所以11ππ11ππsin()0,π,126126k k ⋅+=∴⋅+=∈Z ωω,即122,11k k -=∈Z ω, 又由图可知,周期11π2π11π24,121211T >⇒>∴<ωω,且0>ω, 所以由五点作图法可知2,2k ==ω, 所以函数π()2sin(2)6f x x =+,因为()()0f a x f a x +--=,所以函数()f x 关于x a =对称,即有ππ2π,62a k k +=+∈Z ,所以可得ππ,26k a k =+∈Z , 所以a 的最小正值为π6.故选B.【名师点睛】本题考查了三角函数的图象和性质,熟练运用三角函数的图象和周期对称性是解题的关键,属于中档题.解答本题时,先由图象,求出,,A ϕω,可得函数()f x 的解析式,再由()()0f a x f a x +--=易知()f x 的图象关于x a =对称,即可求得a 的值.24.【山东省实验中学等四校2019届高三联合考试数学试题】在ABC △中,a ,b ,c 分别为角A ,B ,C 的对边,若ABC △的面积为S ,且()22a b c =+-,则πsin 4C ⎛⎫+= ⎪⎝⎭A .1B .2C D 【答案】D【解析】由()22a b c =+-,得2221sin 22ab C a b c ab =+-+,∵2222cos a b c ab C +-=,∴sin 2cos 2C ab C ab =+,cos 1C C -=,即π2sin 16C ⎛⎫-= ⎪⎝⎭,则π1sin 62C ⎛⎫-= ⎪⎝⎭, ∵0πC <<,∴ππ5π666C -<-<,∴ππ66C -=,即π3C =, 则πππππππsin sin sin cos cos sin 4343434C ⎛⎫⎛⎫+=+=+=⎪ ⎪⎝⎭⎝⎭122224+⨯=, 故选D .【名师点睛】本题主要考查解三角形的应用,结合三角形的面积公式以及余弦定理求出C 的值以及利用两角和差的正弦公式进行计算是解决本题的关键.解答本题时,根据三角形的面积公式以及余弦定理进行化简求出C 的值,然后利用两角和的正弦公式进行求解即可.25.【山东省烟台市2019届高三3月诊断性测试(一模)数学试题】在ABC △中,角A ,B ,C 的对边分别为a ,b ,c ,若1a =cos )cos 0A C C b A ++=,则角A =A .2π3B .π3 C .π6D .5π6【答案】D【解析】∵1a =cos )cos 0A C C b A ++=,cos cos cos A C C A b A =-,)cos A C B b A +==-,sin cos B b A =-,sin sin cos A B B A =-,∵sin 0B >cos A A =-,即tan 3A =-, ∵(0,π)A ∈,∴5π6A =.故选D . 【名师点睛】本题主要考查解三角形,熟记正弦定理,两角和的正弦公式即可,属于基cos )cos 0A C C b A ++=,可得sin cos B b A =-,再由正弦定理得到tan 3A =-,结合(0,π)A ∈,即可求得A 的值.26.【广东省韶关市2019届高考模拟测试(4月)数学试题】在ABC △中,a 、b 、c 分别是内角A 、B 、C cos sin (cos cos )A A a C c A =+. (1)求角A 的大小;(2)若a =ABC △,求ABC △的周长.【答案】(1)π3A =;(2).【解析】(1cos sin (cos cos )A A a C c A =+, ∴由正弦定理可得:cos sin (sin cos sin cos )B A A A C C A =+sin sin()sin sin A A C A B =+=,cos B A sin sin A B =, ∵sin 0B ≠,∴tan A = ∵(0,π)A ∈, ∴π3A =.(2)∵π3A =,a =ABC △,1sin 2bc A ∴==, ∴5bc =,∴由余弦定理可得:2222cos a b c bc A =+-,即222212()3()15b c bc b c bc b c =+-=+-=+-,解得:b c +=∴ABC △的周长为a b c ++==.【名师点睛】本题主要考查了正弦定理,两角和的正弦函数公式,三角形的面积公式,余弦定理在解三角形中的综合应用,考查了计算能力和转化思想,属于基础题. (1)由正弦定理,两角和的正弦函数公式化简已知等式可得cos sin sin B A A B =,由sin 0B ≠,可求tan A =(0,π)A ∈,可求π3A =.(2)利用三角形的面积公式可求5bc =,进而根据余弦定理可得b c +=即可计算ABC △的周长的值.27.【北京市昌平区2019届高三5月综合练习(二模)数学试题】已知函数1(=cos cos )+2f x x x x -).(1)求π()3f 的值;(2)当π[0,]2x ∈时,不等式()2c f x c <<+恒成立,求实数c 的取值范围.【答案】(1)1;(2)1(1,)2--. 【解析】(1)21(cos cos +2f x x x x -1=2cos 222x x - π=sin(2)6x -, 所以π()13f =. (2)因为π02x ≤≤, 所以ππ5π2666x -≤-≤, 所以1sin 226x π-≤-≤()1. 由不等式()2c f x c <<+恒成立,得1221c c ⎧<-⎪⎨⎪+>⎩,解得112c -<<-. 所以实数c 的取值范围为1(1,)2--.【名师点睛】本题主要考查三角函数的性质及其应用,恒成立问题的处理方法等知识,意在考查学生的转化能力和计算求解能力.(1)首先整理函数的解析式,然后结合函数的解析式求解函数值即可;(2)首先求得函数()f x 在区间π0,2⎡⎤⎢⎥⎣⎦上的值域,然后结合恒成立的结论得到关于c 的不等式组,求解不等式组可得c 的取值范围.。
(3)三角函数与解三角形——2024年高考数学真题模拟试题专项汇编

(3)三角函数与解三角形——2024年高考数学真题模拟试题专项汇编一、选择题1.[2024年新课标Ⅰ卷高考真题]已知cos()m αβ+=,tan tan 2αβ=,则cos()αβ-=()A.3m- B.3m -C.3m D.3m2.[2024年新课标Ⅱ卷高考真题]设函数2()(1)1f x a x =+-,()cos 2g x x ax =+,当(1,1)x ∈-时,曲线()y f x =和()y g x =恰有一个交点.则a =()A.-1B.12C.1D.23.[2024年新课标Ⅰ卷高考真题]当[0,2π]x ∈时,曲线sin y x =与π2sin(36y x =-的交点个数为()A.3B.4C.6D.84.[2024届·黑龙江齐齐哈尔·一模]已知π1cos 64α⎛⎫+= ⎪⎝⎭,则sin 26πα⎛⎫-= ⎪⎝⎭()A.78B.78-C.38D.38-5.[2024届·山西长治·一模校考]已知函数()sin()(0f x A x A ωϕ=+>,0ω>,π||)2ϕ<的部分图象如图所示,若方程()f x m =在π[,0]2-上有两个不相等的实数根,则实数m 的取值范围是()A.[2,--B.(2,-C.(2,1]--D.[2,1]--6.[2024届·江西·模拟考试]在ABC △中,若sin 2cos cos A B C =,则22cos cos B C +的取值范围为()A.61,5⎡⎫⎪⎢⎣⎭B.11,2⎡⎤+⎢⎥⎣⎦C.6,25⎛⎫⎪⎝⎭D.1,22⎫+⎪⎪⎣⎭7.[2024届·湖北·模拟考试联考]在ABC △中,若2225AC BC AB +=,则tan tan tan tan C CA B+=()A.23B.12C.2D.28.[2024届·湖南师大附中·模拟考试]若锐角α,β满足3cos()cos cos αβαβ+=,则tan()αβ+的最小值为()A. B. C. D.二、多项选择题9.[2024年新课标Ⅱ卷高考真题]对于函数()sin 2f x x =和π()sin 24g x x ⎛⎫=- ⎪⎝⎭,下列说法中正确的有()A.()f x 与()g x 有相同的零点B.()f x 与()g x 有相同的最大值C.()f x 与()g x 有相同的最小正周期D.()f x 与()g x 的图像有相同的对称轴10.[2024届·河北衡水·二模联考]如图,点A ,B ,C 是函数()()sin (0)f x x ωϕω=+>的图象与直线2y =相邻的三个交点,且π3BC AB -=,π012f ⎛⎫-= ⎪⎝⎭,则()A.4ω=B.9π182f ⎛⎫=⎪⎝⎭C.函数()f x 在ππ,32⎛⎫⎪⎝⎭上单调递减D.若将函数()f x 的图象沿x 轴平移θ个单位,得到一个偶函数的图像,则θ的最小值为π24三、填空题11.[2024年新课标Ⅱ卷高考真题]已知α为第一象限角,β为第三象限角,tan tan 4αβ+=,tan tan 1αβ=+,则sin()αβ+=__________.12.[2024届·山东威海·二模]在ABC △中,角A ,B ,C 所对的边分别为a ,b ,c ,已知a =4b c +=,cos 66C =-.则sin A =________.13.[2024届·长沙市第一中学·模拟考试]已知函数()ππsin (01)33f x x x x ωωωω⎛⎫⎛⎫=++-+<< ⎪ ⎪⎝⎭⎝⎭的图象的一条对称轴为直线π4x =,则ω=__________.四、解答题14.[2024年新课标Ⅰ卷高考真题]记ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin C B =,222a b c +-=.(1)求B ;(2)若ABC △的面积为3+,求c .15.[2024年新课标Ⅱ卷高考真题]记ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知sin 2A A =.(1)求A ;(2)若2a =sin sin 2C c B =,求ABC △的周长.参考答案1.答案:A解析:由cos()m αβ+=得cos cos sin sin m αβαβ-=①.由tan tan 2αβ=得sin sin 2cos cos αβαβ=②,由①②得cos cos sin sin 2mm αβαβ=-⎧⎨=-⎩,所以cos()cos cos sin sin 3m αβαβαβ-=+=-,故选A.2.答案:D解析:由题意知()()f x g x =,则2(1)1cos 2a x x ax +-=+,即()2cos 11x a x =+-.令()2()cos 11h x x a x =-++.易知()h x 为偶函数,由题意知()h x 在(1,1)-上有唯一零点,所以(0)0h =,即cos 0(01)10a -++=,得2a =,故选D.3.答案:C解析:因为函数π2sin 36y x ⎛⎫=- ⎪⎝⎭的最小正周期2π3T =,所以函数π2sin 36y x ⎛⎫=- ⎪⎝⎭在[0,2π]上的图象恰好是三个周期的图象,所以作出函数π2sin 36y x ⎛⎫=- ⎪⎝⎭与sin y x =在[0,2π]上的图象如图所示,由图可知,这两个图象共有6个交点,故选C.4.答案:A 解析:设π6t α+=,则π6t α=-,1cos 4t =,ππππsin 2sin 2sin 26662t t α⎡⎤⎛⎫⎛⎫⎛⎫-=--=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦()2217cos22cos 12148t t ⎡⎤⎛⎫=-=--=-⨯-=⎢⎥ ⎪⎝⎭⎢⎥⎣⎦.故选:A.5.答案:B解析:观察图象知,2A =,函数()f x 的周期4π2π[()]π3123T =--=,2π2Tω==,由π(212f =,得ππ22π122k ϕ⨯+=+,k ∈Z ,而π||2ϕ<,则π3ϕ=,于是π()2sin(23f x x =+,当π[,0]2x ∈-时,π2ππ2[,]333x +∈-,当π2ππ2[,332x +∈--,即π5π[,]212x ∈--,函数()f x单调递减,函数值从减小到2-,当πππ2[,]323x +∈-,即5π[,0]12x ∈-时,函数()f x 单调递增,函数值从2-,显然函数()f x 的ππ[,]23--上的图象关于直线5π12x =-对称,方程()f x m =在π[,0]2-上有两个不相等的实数根,即直线y m =与函数()y f x =在π[,0]2-上的图象有两个公共点,所以实数m的取值范围是(2,-.故选:B.6.答案:B解析:由sin 2cos cos A B C =得sin cos cos sin 2cos cos B C B C B C +=,所以tan tan 2B C +=,又2cos cos 0B C >,所以B ,C 均为锐角,即tan 0B >,tan 0C >.22222cos cos cos sin cos BB C B B+=++()()222222222222222cos 112tan tan tan tan 2sin cos 1tan 1tan tan tan tan tan 11tan 1tan C B C B C C C B C B C B C B C ++++=+==++++++++.因为()222tan tan tan tan 2tan tan 42tan tan B C B C B C B C +=+-=-,所以22cos cos B C +=2262tan tan tan tan 2tan tan 5B CB C B C --+,设3tan tan B C m -=,则()()2222cos cos 3235m B C m m +=---+2228484m m m m m==-++-,因为2tan tan tan tan 12B C B C +⎛⎫≤= ⎪⎝⎭,当且仅当π4A B ==时等号成立,所以[)2,3m ∈,8m m ⎡⎤+∈⎣⎦,221cos cos 1,2B C ⎡⎤+∈⎢⎥⎣⎦.故选B .7.答案:B解析:设AC b =,BC a =,AB c =,由2225AC BC AB +=,则2225b a c +=,tan tan cos cos tan tan tan sin sin C C A B C A B A B ⎛⎫+=+ ⎪⎝⎭sin sin()cos sin sin C A B C A B +=⋅2sin sin sin cos C A B C=22222c a b cab ab=+-⨯12=,故选:B.8.答案:D解析:23cos()cos cos 3cos cos 3sin sin cos cos tan tan 3αβαβαβαβαβαβ+=⇒-=⇒=.于是tan tan tan()3(tan tan )621tan tan αβαβαβαβ++==+≥-.选D.9.答案:BC解析:对于A ,令()0f x =,则π2k x =,k ∈Z ,又π02k g ⎛⎫≠ ⎪⎝⎭,故A 错误;对于B ,()f x 与()g x 的最大值都为1,故B 正确;对于C ,()f x 与()g x 的最小正周期都为π,故C 正确;对于D ,()f x 图象的对称轴方程为π2π2x k =+,k ∈Z ,即ππ42k x =+,k ∈Z ,()g x 图象的对称轴方程为ππ2π42x k -=+,k ∈Z ,即3ππ82k x =+,k ∈Z ,故()f x 与()g x 的图象的对称轴不相同,故D 错误.故选BC.10.答案:ACD解析:令()()3sin 2f x x ωϕ=+=得,π2π3x k ωϕ+=+或2π2π3x k ωϕ+=+,k ∈Z ,由图可知:π2π3A x k ωϕ+=+,π2π+2π3C x k ωϕ+=+,2π2π3B x k ωϕ+=+,所以1π2π3C B BC x x ω⎛⎫=-=-+ ⎪⎝⎭,1π3B A AB x x ω=-=⋅,所以π12π2π33BC AB ω⎛⎫=-=-+ ⎪⎝⎭,所以4ω=,故A 选项正确,所以()()sin 4f x x ϕ=+,由π012f ⎛⎫-= ⎪⎝⎭且π12x =-处在减区间,得πsin 03ϕ⎛⎫-+= ⎪⎝⎭,所以ππ2π3k ϕ-+=+,k ∈Z ,所以4π2π3k ϕ=+,k ∈Z ,所以()44sin 42sin 4sin 4333f x x k x x πππ⎛⎫⎛⎫⎛⎫=++π=+=-+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,991sin 8232f πππ⎛⎫⎛⎫=-+=- ⎪ ⎪⎝⎭⎝⎭,故B 错误.当ππ,32x ⎛⎫∈ ⎪⎝⎭时,π5ππ4,2π333x ⎛⎫+∈+ ⎪⎝⎭,因为sin y t =-在5ππ,2π33t ⎛⎫∈+ ⎪⎝⎭为减函数,故()f x 在ππ,32⎛⎫⎪⎝⎭上单调递减,故C 正确;将函数()f x 的图象沿x 轴平移θ个单位得()πsin 443g x x θ⎛⎫=-++ ⎪⎝⎭,(0θ<时向右平移,0θ>时向左平移),()g x 为偶函数得ππ4π32k θ+=+,k ∈Z ,所以ππ244k θ=+,k ∈Z ,则θ的最小值为π24,故D 正确.故选:ACD.11.答案:223-解析:由题知tan tan tan()1tan tan αβαβαβ++==--⋅,即sin())αβαβ+=-+,又22sin ()cos ()1αβαβ+++=,可得22sin()3αβ+=±.由π2π2π2k k α<<+,k ∈Z ,3π2ππ2π2m m β+<<+,m ∈Z ,得2()ππ2()π2πk m k m αβ++<+<++,k m +∈Z .又tan()0αβ+<,所以αβ+是第四象限角,故22sin()3αβ+=-.12.答案:3解析:在ABC △中,由余弦定理可得2222cos c a b ab C =+-,所以226(6c b -=-⨯-,所以()()62c b c b b -+=+,因为4c b +=,所以4()62c b b -=+,所以466c b -=解得1b =,3c =,由cos 66C =-,可得30sin 6C =,在ABC △中,由正弦定理可得sin sin c aC A=,所以30sin 6sin 33a CA c===.故答案为:53.13.答案:23解析:ππππ()sin coscos sin cos sin 3333f x x x x x x ωωωωω=+++π2sin 4sin 3x x x ωωω⎛⎫=+=+ ⎪⎝⎭,由于()f x 的图象的一条对称轴为直线π4x =,所以ππππ()432k k ω+=+∈Z ,解得24()3k k ω=+∈Z .又因为0||1ω<<,所以23ω=.故答案为:23.14.答案:(1)π3B =(2)c =解析:(1)由余弦定理得2222cos 22a b c C ab +-==,又0πC <<,π4C ∴=.2sin 2B C ==,1cos 2B ∴=,又0πB <<,π3B ∴=.(2)由(1)得5ππ12A B C =--=,由正弦定理sin sin a cA C =22=,132a c +∴=.ABC ∴△的面积211sin 3242S ac B c +==⨯=+,得c =15.答案:(1)π6A =(2)2+解析:(1)解法一:由sin 2A A =,得13sin cos 122A A +=,所以πsin 13A ⎛⎫+= ⎪⎝⎭.因为0πA <<,所以ππ4π333A <+<,所以ππ32A +=,故π6A =.解法二:由sin 2A A =2sin A A =-,两边同时平方,得223cos 44sin sin A A A =-+,则()2231sin 44sin sin A A A -=-+,整理,得214sin 4sin 0A A -+=,所以2(12sin )0A -=,则1sin 2A =.因为0πA <<,所以π6A =或5π6A =.当π6A =时,sin 2A A +=成立,符合条件;当5π6A =时,sin 2A A +=不成立,不符合条件.故π6A =.解法三:由sin 2A A =,得sin 2A A =,两边同时平方,得22sin 43cos A A A =-+,则221cos 43cos A A A -=-+,整理,得234cos 0A A -+=,所以22cos )0A -=,则3cos 2A =.因为0πA <<,所以π6A =.(2sin sin 2C c B =sin 2sin cos C c B B =,2cos cb B =,所以cos 2B =,因为0πB <<,所以π4B =.7ππ()12C A B =-+=,所以7πππππππsin sinsin sin cos cos sin 12343434C ⎛⎫==+=+ ⎪⎝⎭32126222224+=⨯+⨯=.解法一:由正弦定理sin sin sin a b c A B C ==,得π2sinsin 4πsin sin 6a Bb A ===7π2sin sin 12πsin sin 6a C c A ===所以ABC △的周长为2a b c ++=+解法二:由正弦定理sin sin sin a b c A B C ==,得24πsin sin sin sin sin 6a abc A A B C ++===++,所以14(sin sin sin )42224a b c A B C ⎛⎫++=++=⨯++=+ ⎪ ⎪⎝⎭所以ABC △的周长为2++。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2018年全国高考模拟文科数学分类汇编——三角函数和解三角形一、选择题1. 10.(5分)已知定义在R 上的函数f(x)满足:(1)f (x)+f(2﹣x )=0,(2)f(x ﹣2)=f (﹣x),(3)在[﹣1,1]上表达式为f (x)=,则函数f(x)与函数g (x)=的图象区间[﹣3,3]上的交点个数为( )A.5 B .6ﻩC .7ﻩD.82. 11.(5分)已知函数f(x)=s in(ωx +φ)(ω>0,|φ|<)的最小正周期是π,若将其图象向右平移个单位后得到的图象关于原点对称,则函数f(x)的图象( )A.关于直线x=对称ﻩB.关于直线x=对称 C.关于点(,0)对称 D .关于点(,0)对称3. 4.若tanθ+=4,则sin2θ=( )A.ﻩB .ﻩC.ﻩD .4. 7.将函数()2sin 13f x x π⎛⎫=-- ⎪⎝⎭的图象向右平移3π个单位,再把所有的点的横坐标缩短到原来的12倍(纵坐标不变),得到函数()y g x =的图象,则图象()y g x =的一个对称中心为 A.,03π⎛⎫⎪⎝⎭ B.,012π⎛⎫ ⎪⎝⎭ C .,13π⎛⎫- ⎪⎝⎭ D .,112π⎛⎫- ⎪⎝⎭5. 7.(5分)若将函数f (x)=sin (2x+)图象上的每一个点都向左平移个单位,得到g(x )的图象,则函数g(x)的单调递增区间为( ) A .[kπ﹣,kπ+](k∈Z)B.[kπ+,kπ+](k ∈Z)C.[kπ﹣,kπ﹣](k∈Z)ﻩD.[kπ﹣,kπ+](k ∈Z)6. 11.函数()[]()cos ,x f x xe x ππ=∈-的图象大致是7. 8. 已知函数,则下列结论中正确的是A . 函数的最小正周期为B . 函数的图象关于点对称C . 由函数的图象向右平移个单位长度可以得到函数的图象D. 函数在区间上单调递增8. 9. 函数,则函数的导数的图象是( )A .B . C. . D.9. 8.(5分)已知函数y =Asin (ωx +φ)(ω>0,|φ|<,x ∈R )的图象如图所示,则该函数的单调减区间是( )A.[2+16k,10+16k ](k ∈Z)B.[6+16k,14+16k ](k∈Z ) C.[﹣2+16k ,6+16k](k ∈Z)ﻩD .[﹣6+16k,2+16k ](k∈Z)10. 8.已知曲线1215:sin ,:cos 26C y x C y x π⎛⎫==-⎪⎝⎭,则下列说法正确的是 A .把1C 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线2CB.把1C 上各点横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线2C C.把曲线1C 向右平移3π个单位长度,再把得到的曲线上各点横坐标缩短到原来的12,纵坐标不变,得到曲线2C D.把曲线1C 向右平移6π个单位长度,再把得到的曲线上各点横坐标缩短到原来的12,纵坐标不变,得到曲线2C 11. 10.函数()21cos 1xf x x e ⎛⎫=-⎪+⎝⎭(其中e 为自然对数的底数)图象的大致形状是12. 9.已知曲线12:2cos ,:2cos2C y x C y x x ==-,则下面结论正确的是 A.把1C 各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线C 2B.把1C 上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移至3π个单位长度,得到曲线C 2C.把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移23π个单位长度,得到曲线C 2D.把1C 上各点的横坐标缩短到原来的12倍,纵坐标不变,再把得到的曲线向右平移3π个单位长度,得到曲线C 213. 11.现有四个函数①sin y x x =⋅ ②cos y x x =⋅ ③cos y x x =⋅ ④2x y x =⋅的部分图象如下,但顺序被打乱,则按照从左到右将图象对应的函数序号排列正确的一组是A.①④②③ ﻩB.①④③② C.④①②③ﻩ D.③④②①14. 6.已知函数()()sin 06f x x πωω⎛⎫=+> ⎪⎝⎭的最小正周期为4π,则 A .函数()f x 的图象关于原点对称 B.函数()f x 的图象关于直线3x π=对称C.函数()f x 图象上的所有点向右平移3π个单位长度后,所得的图象关于原点对称 D.函数()f x 在区间()0,π上单调递增 15. 7.函数()()1cos 0f x x x x x x ππ⎛⎫=--≤≤≠ ⎪⎝⎭且的图象可能为16. 11.已知函数2()2ln ||f x x x =-与()sin()g x x ωϕ=+有两个公共点,则在下列函数中满足条件的周期最大的函数()g x =( )A .πsin π2x ⎛⎫- ⎪⎝⎭ B.πsin π2x ⎛⎫+ ⎪⎝⎭C.πsin 2x ⎛⎫+π ⎪⎝⎭D .πsin 2π2x ⎛⎫+ ⎪⎝⎭17. 3.已知1sin()3απ+=-,则tan 2απ⎛⎫- ⎪⎝⎭值为( )A.ﻩ B .-C.4ﻩ ﻩ D.±18. 5.为了得到函数2sin(3)4y x π=+的图象,只需把函数2sin3y x =的图象上所有的点( )A. 向左平移4π个单位 B. 向左平移12π个单位 C . 向右平移4π个单位 D. 向右平移12π个单位19. 6.已知函数)2,0,0)(sin()(πϕωϕω<>>+=A x A x f 的部分图象如图所示,则)(x f 的解析式是( ) A. ()sin(3)3f x x π=+ B . ()sin(2)3f x x π=+C. ()sin()3f x x π=+ D. ()sin(2)6f x x π=+ 二、填空题1. 14.(5分)已知函数f(x )=2sin (ϖx +φ)对任意x 都有f(+x )=f(﹣x),则|f ()|= .2. 15.设△ABC 中,角A,B,C 所对的边分别为a,b,c ,若a=4,A=,B =,则△A BC 的面积S = .三、解答题1. 17.(10分)已知点,Q(cos x,sinx ),O 为坐标原点,函数.(1)求函数f (x)的最小值及此时x 的值;(2)若A 为△AB C的内角,f(A )=4,BC=3,求△ABC 的周长的最大值.2. 17.(本小题满分12分)在ABC ∆中,角A ,B,C的对边分别为,,,3sin sin a b c a b B C ==,且.(I)求角A 的大小;(Ⅱ)若23a =,角B 的平分线交AC 于点D,求线段BD 的长度.3. 17.(12分)在△ABC 中,角A ,B,C的对边分别为a ,b,c ,且2cco sB=2a +b.(1)求角C;(2)若△ABC 的面积为,求ab 的最小值.4. 17. 在△中,分别为内角的对边,.(Ⅰ) 求的大小; (Ⅱ) 若,, 求△的面积.5. 17.(12分)已知△ABC 中,角A ,B,C 所对的边分别为a,b ,c ,bsin(B +C)+acos A=0,且c =2,sinC=. (1)求证:A =+B;(2)求△ABC 的面积.6. 17.(12分)在ABC ∆中,角A,B,C的对边分别为,,,2sin 3.a b c b c B A ==,且 (1)求cos B 的值;(2)若2a ABC =∆,求的面积.7. 17.(本小题满分10分)在平面直角坐标系中,O 为原点,()221,0,2cos,sin ,2cos ,22OA OB OC βαα⎛⎫⎛=== ⎪ ⎝⎭⎝)sin ,0ββαπ<<<.(I)若,AB AC BC ⊥求;(Ⅱ)设()1,1,OD AB AC AD αβ=+=若求,的值.8. 17.(12分)在ABC 中,角A ,B ,C 的对边分别为a ,b ,c .(1)若223cos cos20A A +=,且ABC 为锐角三角形,7a =,6c =,求b 的值;(2)若a =,3A π=,求b c +的取值范围.答案一、选择题1.10.(5分)已知定义在R上的函数f(x)满足:(1)f(x)+f(2﹣x)=0,(2)f(x ﹣2)=f(﹣x),(3)在[﹣1,1]上表达式为f(x)=,则函数f(x)与函数g(x)=的图象区间[﹣3,3]上的交点个数为()A.5B.6ﻩC.7D.8【分析】由题意可得函数f(x)的图象关于点M(1,0)对称,又关于直线x=﹣1对称;再结合g(x)的解析式画出这2个函数区间[﹣3,3]上的图象,数形结合可得它们的图象区间[﹣3,3]上的交点个数.【解答】解:由f(x)+f(2﹣x)=0,可得函数f(x)的图象关于点M(1,0)对称.由f(x﹣2)=f(﹣x),可得函数f(x)的图象关于直线x=﹣1对称.又f(x)在[﹣1,1]上表达式为f(x)=,可得函数f(x)在[﹣3,3]上的图象以及函数g(x)=在[﹣3,3]上的图象,数形结合可得函数f(x)的图象与函数g(x)的图象区间[﹣3,3]上的交点个数为6,故选:B.【点评】本题主要考查函数的图象的对称性,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.2. 11.(5分)已知函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期是π,若将其图象向右平移个单位后得到的图象关于原点对称,则函数f(x)的图象()A.关于直线x=对称ﻩB.关于直线x=对称C.关于点(,0)对称D.关于点(,0)对称【分析】根据三角函数的性质求出函数的解析式进行求解即可.【解答】解:∵函数f(x)=sin(ωx+φ)(ω>0,|φ|<)的最小正周期是π,∴T==π,解得ω=2,即f(x)=sin(2x+φ),将其图象向右平移个单位后得到y=sin[2(x﹣)+φ]=sin(2x+φ﹣),若此时函数关于原点对称,则φ﹣=kπ,即φ=+kπ,k∈Z,∵|φ|<,∴当k=﹣1时,φ=.即f(x)=sin(2x).由2x=,解得x=+,k∈Z,故当k=0时,函数的对称轴为x=,故选:B【点评】本题主要考查三角函数解析式的求解以及三角函数的性质的应用,根据条件求出函数的解析式是解决本题的关键.3. 4.若tanθ+=4,则sin2θ=()A.B.ﻩC.ﻩD.【考点】二倍角的正弦;同角三角函数间的基本关系.【分析】先利用正弦的二倍角公式变形,然后除以1,将1用同角三角函数关系代换,利用齐次式的方法化简,可求出所求.【解答】解:sin2θ=2sinθcosθ=====。
