土木工程毕业设计第六章竖向荷载(恒载+活载)作用下框架内力计算
竖向荷载作用下框架结构的内力计算

竖向荷载作用下框架结构的内力计算竖向荷载作用下框架结构的内力计算4.5竖向荷载作用下框架结构的内力计算取⑧轴线横向框架进行计算,由于房间内布置有次梁,结合计算简图得大多都是单向板. 故屋面和楼面荷载通过次梁和纵向框架梁以集中力的形式传给横向框架使用于各节点上。
由于纵向框架梁的中心线与柱的中心线不重合,因此在框架节点上还作用有集中力矩。
(1) 屋面框架节点集中荷载标准值边柱纵自重: 5.17×8.4=43.428 kN1.1m 女儿墙自重:5.76×8. 4=48.384 kN屋面板传来自重:1/2×8.4×2.5×6.09=63.945kN顶层边节点A 集中荷载: 155.757 kN次梁自重:4.755×8. 4=39.924 kN屋面板传来自重:8.4×(1.25+1.5) ×6.09=140.679 kN 顶层1节点集中荷载:180.603 kN2节点集中荷载: 180.603 kN3节点集中荷载: 193.392 kN4节点集中荷载: 193.392 kN中柱纵梁自重: 5.17×8.4=43.428 kN屋面板传来自重:8.4×2.75×6.09=140.679 kN顶层中节点B 点集中荷载: 184.107 kN边柱纵梁自重: 5.17×8.4=43.428 kN1.1m 女儿墙自重:5.76×8. 4=48.384 kN屋面板传来自重:1/2×8.4×3×6.09=76.728kN 顶层边节点C 集中荷载: 168.54 kN(2) 楼面框架节点集中荷载标准值边柱纵梁自重: 43.428 kN窗加墙自重: 3.933×8.4=33.037 kN框架柱自重:9.408×4. 2=39.514 kN纵梁传来楼面自重:8.4×1. 25×3. 83=40.215kN 中间层边跨节点A 集中荷载:156.194 kN次梁自重: 39.924 kN屋面板传来自重:8.4 ×(1. 25+1.5)×3. 83=88.473kN 中间层1节点集中荷载:128.397kN2节点集中荷载: 128.397kN3节点集中荷载:136.44kN4节点集中荷载:136.44kNB 轴节点集中荷载标准值中柱纵梁自重: 43.428kN框架柱自重: 39.514kN楼面板传来自重:8.4×2.75×3. 83=88.473 kN 中间层中跨节点B 集中荷载:123.157KNC 轴节点集中荷载标准值边柱纵梁自重: 43.428kN框架柱自重: 39.514kN窗加墙自重: 3.933×8.4=33.037 kN纵梁传来楼面自重:8.4×1. 5×3. 83=48.258kN 点C 集中荷载: 120.809KN2)活荷载标准值的计算屋面活荷载标准值取2.0kN/ m2雪荷载标准值为0.4 kN/ m2,两者不应同时考虑,取两者较大值2.0 kN/ m2楼面活荷载标准值3.5 kN/ m2集中荷载标准值:P A =8.4×1. 25×2.0=21 KNP 1=8. 4×2. 75×2=46.2KNP 2=8. 4×2. 75×2=46.2KNP 3=8. 4×3.00×2=50.4KNP 4=8. 4×3.00×2=50.4KNP B =8.4×2. 75×2=46.2KN P C =8. 4×1.5×2.0=25.2KN 中间层:P A =8.4×1. 25×3.5=36.75 KN P 1=8. 4×2. 75×3.5=80.85KN P 2=8. 4×2. 75×3.5=80.85KN P3=8. 4×3.00×3.5=88.2KN P 4=8. 4×3.00×3.5=88.2KN P B =8.4×2.75×3.5=80.85KN P C =8. 4×1.5×3.5=44.1KN。
框架结构在竖向荷载作用下的内力计算

框架结构在竖向荷载作用下的内力计算
框架结构在竖向荷载作用下的内力计算可近似地采用分层法.
在进行竖向荷载作用下的内力分析时,可假定:(1)作用在某一层框架梁上的竖向荷载对其他楼层的框架梁的影响不计,而仅在本楼层的框架梁以及与本层框架梁相连的框架柱产生弯矩和剪力.(2)在竖向荷载作用下,不考虑框架的侧移.
计算过程可如下:
(1)分层:分层框架柱子的上下端均假定为固定端支承,
(2)计算各个独立刚架单元:用弯矩分配法或迭代法进行计算各个独立刚架单元.而分层计算所得的各层梁的内力,即为原框架结构中相应层次的梁的内力.
(3)叠加:在求得各独立刚架中的结构内力以后,则可将相邻两个独立刚架中同层同柱号的柱内力叠加,作为原框架结构中柱的内力.
叠加后为原框架的近似弯距图,由于框架柱节点处的弯矩为柱上下两层之和因此叠加后的弯距图,在框架节点处常常不平衡.这是由于分层计算单元与实际结构不符所带来的误差.若欲提高精度,可对节点,特别是边节点不平衡弯矩再作一次分配,予以修正.。
土木工程毕业设计 第六章 竖向荷载(恒载 活载)作用下框架内力计算讲解
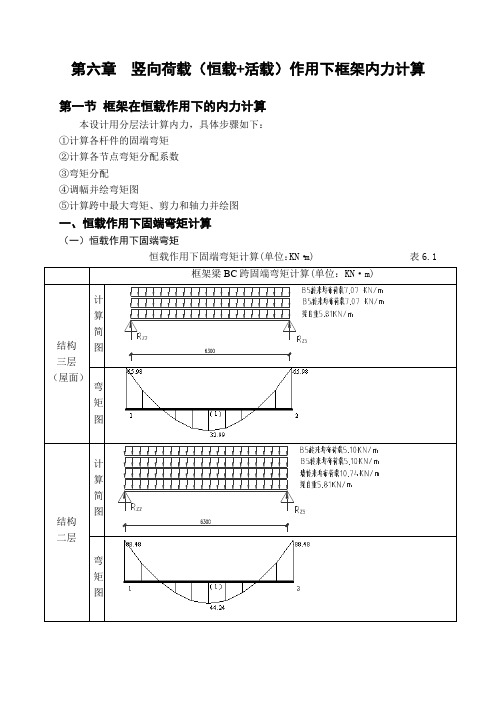
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表6.1弯矩图恒载作用下梁固端弯矩计算统计表6.2(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以0.9修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=1.5Ir两边有楼板:I=2.0Ir④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图6.1 修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=5.37÷(5.37+1.18)=0.820①梁μB3C3μ=5.37÷(5.37+3.52+1.18)=0.533C3B3=3.52÷(5.37+3.52+1.18)=0.350μC3D3=3.52÷(3.52+1.18)=0.749μD3C3=1.18÷(5.37+1.18)=0.180②柱μB3B2=1.18÷(5.37+3.52+1.18)=0.117μC3C2=1.18÷(3.52+1.18)=0.251μD3D2结构二层①梁μ=5.37÷(1.18+1.18+5.37)=0.695B2C2=5.37÷(1.18+1.18+5.37+3.52)=0.477μC2B2μ=3.52÷(1.18+1.18+5.37+3.52)=0.313 C2D2=3.52÷(1.18+1.18+3.52)=0.5986 μD2C2=1.18÷(1.18+1.18+5.37)=0.1525②柱μB2B3μ=1.18÷(1.18+1.18+5.37)=0.1525B2B1=1.18÷(1.18+1.18+5.37+3.52)=0.105 μC2C3μ=1.18÷(1.18+1.18+5.37+3.52)=0.105 C2C1=1.18÷(1.18+1.18+3.52)=0.2007 μD2D3μ=1.18÷(1.18+1.18+3.52)=0.2007D2D1结构一层=5.37÷(1.18+1+5.37)=0.711①梁μB1C1=5.37÷(1.18+1+5.37+3.52)=0.485 μC1B1=3.52÷(1.18+1+5.37+3.52)=0.318 μC1D1=3.52÷(1.18+1+3.52)=0.618μD1C1=1.18÷(1.18+1+5.37)=0.156②柱μB1B2=1÷(1.18+1+5.37)=0.133μB1B0=1.18÷(1.18+1+5.37+3.52)=0.107μC1C2=1÷(1.18+1+5.37+3.52)=0.090μC1C0μ=1.18÷(1.18+1+3.52)=0.207D1D2μ=1÷(1.18+1+3.52)=0.175D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表6.3B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配14.650 -13.883 226.915 20.861 -251.346 84.509 -112.810 二次分配14.512 -14.512 228.818 21.278 -250.096 105.707 -105.707恒载作用下结构二层弯矩分配表6.40.768 12.717 -28.301↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配 6.931 4.431 -4.607 308.811 46.295 47.232 -385.113 169.804 -113.072 -92.837二次分配 5.901 3.401 -9.302 300.595 44.486 45.423 -390.504 191.416 -105.826 -85.591恒载作用下结构一层弯矩分配表6.52.127 9.081 -7.935↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次7.030 5.338 -12.368 267.469 35.352 22.097 -324.919 357.349 -46.247 -15.172 -295.930图6.2 弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
竖向荷载下的框架内力计算
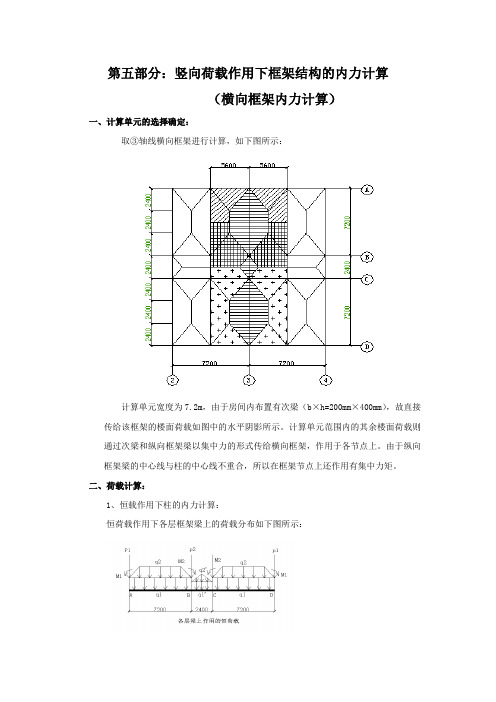
第五部分:竖向荷载作用下框架结构的内力计算(横向框架内力计算)一、计算单元的选择确定:取③轴线横向框架进行计算,如下图所示:计算单元宽度为7.2m,由于房间内布置有次梁(b×h=200mm×400mm),故直接传给该框架的楼面荷载如图中的水平阴影所示。
计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
由于纵向框架梁的中心线与柱的中心线不重合,所以在框架节点上还作用有集中力矩。
二、荷载计算:1、恒载作用下柱的内力计算:恒荷载作用下各层框架梁上的荷载分布如下图所示:(1)、对于第6层,q1、q1,代表横梁自重,为均布荷载形式。
q1=0.3×0.6×25=4.5 KN/mq1,=0.25×0.4×25=2.5KN/mq2、和q2,分别为屋面板和走道板传给横梁的梯形荷载和三角形荷载。
q2=5.35×3.6=19.26 KN/mq2,=5.35×1.8=9.63 KN/mP1、P2分别由边纵梁、中纵梁直接传给柱的恒载,它包括主梁自重、次梁自重、楼板重等重力荷载,计算如下:P1=[(3.6×2.4/2)×2+(2.4+7.2)×1.8/2] ×5.35+4.5×7.2+0.2×0.4×25×7.2=132.95 KNP2=[(3.6×2.4/2)×2+(2.4+7.2)×1.8/2+(2.7+3.6)×2×1.2 /2] ×5.35+4.5×7.2+0.2×0.4×25×7.2=173.39 KN集中力矩M1=P1e1=132.95×(0.65-0.3)/2=23.27 KN·mM2=P2e2=173.39×(0.65-0.3)/2=30.34 KN·m(2)、对于2-5层,包括梁自重和其上横墙自重,为均布荷载,其它荷载的计算方法同第6层。
土木工程专业毕业设计常见答辩问题(附答案)

土木工程专业毕业设计常见答辩问题很多同学在做完设计后虽然对自己的设计很有把握,但是还在担心着答辩这一关,那么多老师,那么多同学在台下看这自己,内向点的肯定心慌了,呵呵,在答辩前作好答辩的充分准备,没有什么可怕的!1。
介绍你设计的内容有哪些?2. 框架体系的优点是什么?说明它的应用范围.答:框架结构体系的优点是:整体性和抗震性均好于混合结构,平面布置灵活,可提供较大的使用空间,也可形成丰富多变的立面造型。
适用范围:工业厂房及公共建筑中广泛使用。
3.框架结构的设计步骤是什么?答:(1)、结构平面布置;(2)、柱网和层高的确定;(3)、承重方案的确定(4)、荷载计算;(5)、内力、位移计算;(6)、配筋计算;(7)、钢筋选择;(8)、绘制结构施工图。
4. 怎样确定柱网尺寸?答:框架结构柱网应满足房屋使用要求,同时构件的规格、类型要少,柱网间距一般不宜小于3。
6m,也不宜大于6。
0m,柱网跨度根据使用要求不同,有2。
4m、2。
7m、3。
0m、5。
8m、7.5m、8。
0m、12.0m等。
5. 怎样确定框架梁、柱截面尺寸?答:框架梁的截面尺寸,(1)应满足刚度要求;(2)满足构造要求;(3)满足承载力要求。
框架柱的截面尺寸,(1)应满足稳定性要求;(2)满足构造要求;(3)满足承载力要求。
6. 怎样计算水平荷载作用下框架的内力和侧移?答:水平荷载作用下框架内力的计算方法用反弯点法和D值法。
具体计算步骤是:反弯点位置的确定;柱的侧移刚度的确定;各柱剪力的分配;柱端弯矩的计算;梁端弯矩的计算;梁的剪力的计算.水平荷载作用下的侧移的计算:可认为是由梁柱弯曲变形引起的侧移和柱轴向变形的叠加.7. 修正反弯点法(D值法)计算要点是什么?答:修正反弯点法(D值法)的计算要点是:1)修正柱的抗侧移刚度;2)修正反弯点刚度;3)柱的剪力分配;4)柱端弯矩计算;5)梁端弯矩的计算;6)梁的剪力的计算。
8. 怎样计算在重力荷载下的框架内力?答:重力荷载作用下框架内力计算:重力荷载属于竖向荷载,将多层框架分层,以每层梁与上下柱组成的当成框架作为计算单元,按无侧移框架计算,一般采用弯矩分配法或迭代法。
(整理)10竖向荷载作用下内力计算.

第六章竖向荷载作用下横向框架结构的内力计算6.1 计算单元取H轴线横向框架进行计算,计算单元宽度为6m,荷载传递方式如图中阴影部分所示。
“荷载时以构件的刚度来分配的”,刚度大的分配的多些,因此板上的竖向荷载总是以最短距离传递到支撑上的。
于是就可理解到当双向板承受竖向荷载是,直角相交的相邻支撑梁总是按45°线来划分负荷范围的,故沿短跨方向的支撑承受梁承受板面传来的三角形分布荷载;沿长跨方向的支撑梁承受板传来的梯形分布荷载,见图5.1:精品文档精品文档6.2 荷载计算6.2.1 恒载计算图5.2 各层梁上作用的荷载在图5,2中,1q 、1q '代表横梁自重,为均布荷载形式,1、对于第五层,m kN q 0764.41= m kN q 2.2'1=2q 为梯形荷载,2q '为三角形荷载。
由图示几何关系可得, m kN q 18.30603.52=⨯=m kN q 07.124.203.5'2=⨯=节点集中荷载1P :边纵梁传来:(a) 屋面自重: 5.03⨯6⨯3=90.54kN (b) 边纵梁自重: 4.0764⨯6=24.45kN女儿墙自重: 4.320⨯6=25.93kN 次梁传递重量: 2.2⨯6=13.2kN 上半柱重: 6.794⨯1.5=10.191kN 墙重以及窗户:0.24⨯6⨯2.4⨯18-1.5⨯1.8⨯18⨯2⨯0.24+0.4⨯1.5⨯ 1.8⨯0.24⨯2)⨯0.5=25.53kN 合计: 1P =189.84kN 节点集中荷载2P :精品文档屋面自重: 5.03⨯6⨯(3+1.2)=126.76kN 中纵梁自重: 24.45kN次梁传递重量: 2.2⨯(3+1.2)⨯2=18.48kN 上半柱重: 10.19kN 墙重以及门重:(0.24⨯6⨯2.4⨯11.8-0.9⨯2.1⨯11.8⨯2⨯0.24+ 0.2⨯0.9⨯2.1⨯0.24⨯2)⨯0.5=15.13kN合计: 2P = 195.01kN 2、对于1~4层,计算的方法基本与第五层相同,计算过程如下:m kN q 0764.41= m kN q 2.2'1=m kN q 98.22683.32=⨯= m kN q 192.94.283.3'2=⨯= 节点集中荷载1P :屋面自重: 68.94kN 纵梁自重: 24.45kN 墙重以及窗户: 25.53kN次梁传递重量: 13.2kN 下半柱重: 10.19kN 合计: kN P 31.1421= 节点集中荷载2P :纵梁自重: 24.45kN 内墙以及门自重: 15.13kN 楼面自重: 96.52kN次梁传递重量: 18.48kN精品文档合计: kN P 58.1542=6.2.2 活荷载计算活荷载作用下各层框架梁上的荷载分布如图5.3:图5.3各层梁上作用的活载1、对于第五层,m kN q 365.02=⨯= m kN q 2.14.25.0,2=⨯= 节点集中荷载1P :屋面活载: 95.063=⨯⨯kN合计: kN P 91=节点集中荷载2P :屋面活载:0.5⨯(3+1.2)⨯6=12.6kN合计: kN P 6.122=2、对于1~4层,m kN q 1260.22=⨯= m kN q 0.64.25.2'2=⨯= 节点集中荷载1P :楼面活载: 36263=⨯⨯kN精品文档合计: kN P 361= 中节点集中荷载2P :楼面以及走道活载: 2⨯6⨯3+1.2⨯6⨯2.5=54kN合计: kN P 542=6.2.3 屋面雪荷载计算同理,在屋面雪荷载作用下m kN q 7.2645.02=⨯= m kN q 08.14.245.0'2=⨯= 节点集中荷载1P :屋面雪载: 0.45⨯(3⨯6)=8.1kN合计: kN P 1.81= 中节点集中荷载2P :屋面雪载: 0.45⨯(3+1.2)⨯6=11.34kN合计: kN P 34.112=6.3 内力计算6.3.1 计算分配系数按照弹性理论设计计算梁的支座弯矩时,可按支座弯矩等效的原则。
毕业设计--框架竖向荷载作用下内力计算0415

2018/3/21
30
2018/3/21
5
第三部分 框架结构 竖向荷载作用下的内力计算
上下柱尺 寸变,形 心偏心距e
2018/3/21
第三部分 框架结构 竖向荷载作用下的内力计算
上柱下端轴力N
2018/3/21
第三部分 框架结构 竖向荷载作用下的内力计算
梁中至柱中距≦相 应柱边长/4,节点 附加弯矩忽略
节点附加弯矩M=N*e 参于节点不平衡弯矩
节点附加弯矩 M=N*e 参于节点不平 衡弯矩
2018/3/21
第三部分 框架结构 竖向荷载作用下的内力计算
一、 弯矩二次分配法计算过程 1、确定梁柱弯矩分配系数 2、求出荷载作用下梁端弯矩 3、求出节点不平衡弯矩(含纵向框架传来弯矩) 4、第一次分配 5、同时向远端传递 6、 第二次分配 7、叠加得最终弯矩
第三部分 框架结构 竖向荷载作用下的内力计算
2018/3/21
第三部分 框架结构 竖向荷载作用下的内力计算
2018/3/21
第三部分 框架结构 竖向荷载作用下的内力计算
2018/3/21
第三部分 框架结构 竖向荷载作用下的内力计算
四、固端弯矩计算 TSSD、材料力学均可 五、梁端剪力计算
TSSD、材料力学均可
求分配系数 第三部分 框架结构 竖向荷载作用下的内力计算 求固端弯矩 先对各节点的不平衡弯 矩进行第一次分配
向远端传递(传递系数为 1/2);
再将传递弯矩产生的新 的不平衡弯矩进行第二次 分配
最终弯矩
第三部分 框架结构 竖向荷载作用下的内力计算
二、梁端的弯矩调幅
由于钢筋混凝土结构具有塑性内力重分布性能,在竖向荷 载作用下可以考虑适当降低梁端弯矩,即进行弯矩调幅。调 幅系数β如下: (1)现浇框架结构: β=0.8-0.9 (2)装配整体式框架: β=0.7-0.8
土木工程毕业设计 第六章 竖向荷载作用下框架内力计算

第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表恒载作用下梁固端弯矩计算统计表(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=两边有楼板:I=④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层=÷+=①梁μB3C3μ=÷++=C3B3=÷++=μC3D3μ=÷+=D3C3=÷+=②柱μB3B2μ=÷++=C3C2μ=÷+=D3D2结构二层=÷++=①梁μB2C2μ=÷+++=C2B2=÷+++=μC2D2μ=÷++=D2C2②柱μ=÷++=B2B3=÷++=μB2B1=÷+++=μC2C3=÷+++=μC2C1=÷++=μD2D3μ=÷++=D2D1结构一层=÷+1+=①梁μB1C1=÷+1++=μC1B1=÷+1++=μC1D1=÷+1+=μD1C1=÷+1+=②柱μB1B2=1÷+1+=μB1B0=÷+1++=μC1C2=1÷+1++=μC1C0μ=÷+1+=D1D2μ=1÷+1+=D1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配二次分配恒载作用下结构二层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配二次分配恒载作用下结构一层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次二次图弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
第六章-框架在竖向荷载作用下的内力分析
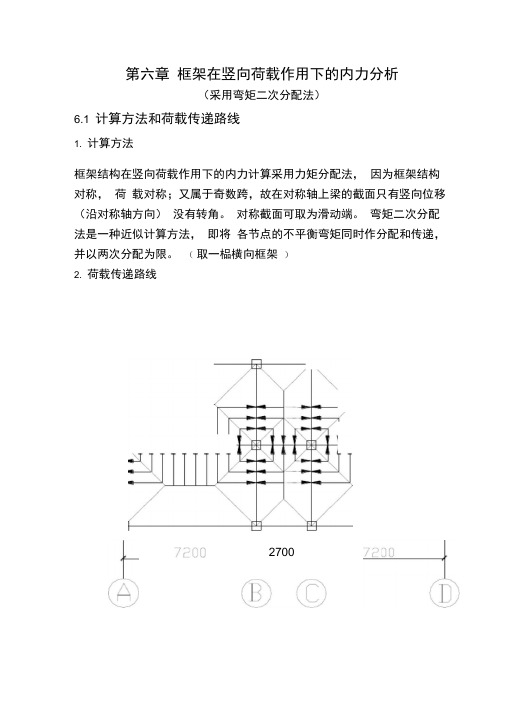
第六章框架在竖向荷载作用下的内力分析(采用弯矩二次分配法)6.1 计算方法和荷载传递路线1. 计算方法框架结构在竖向荷载作用下的内力计算采用力矩分配法,因为框架结构对称,荷载对称;又属于奇数跨,故在对称轴上梁的截面只有竖向位移(沿对称轴方向)没有转角。
对称截面可取为滑动端。
弯矩二次分配法是一种近似计算方法,即将各节点的不平衡弯矩同时作分配和传递,并以两次分配为限。
(取一榀横向框架)2. 荷载传递路线2700对于边跨板,为7.2 m×4.5m,由于7.2/4.5<3.0 所以按双向板计算对于中跨板,为 4.5m×2. 7m,由于 4.5/2.7 〈3.0 所以按双向板计算6.2 竖向荷载计算5.2.1 A-B(C-D) 轴间框架梁板传至梁上的三角形或梯形荷载等效为均布荷载。
1. 屋面板传载恒载: 5.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=18.85kN/m活载:0.5 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=1.89kN/m2. 楼面板传荷载恒载: 3.99 ×4.5/2 ×(1-2 × 0.31 2+0.31 3) ×2=15.08kN/m活载: 2.0 ×4.5/2 ×(1-2 ×0.312+0.313) ×2=7.56kN/m3. 梁自重: 5.46 kN/mA-B(C-D) 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=5.46 kN/m+18.85 kN/m=24.31 kN/m 活载=板传荷载=1.89 kN/m楼面梁:恒载=梁自重+板传荷载=5.46 kN/m+15.08 kN/m=20.54 kN/m 活载=板传荷载=7.56 kN/m5.2.2 B-C 轴间框架梁1. 屋面板传载恒载: 5.0 ×2.4/2 ×5/8 ×2=8.44kN/m活载:0.5 ×2.7/2 ×5/8 ×2=0.84kN/m2. 楼面板传荷载恒载: 3.99 ×2.7/2 ×5/8 ×2=6.73kN/m活载: 2.0 ×2.7/2 ×5/8 ×2=4.22kN/m3. 梁自重: 3.9kN/mB-C 轴间框架梁均布荷载为:屋面梁:恒载=梁自重+板传荷载=3.9 kN/m+8.44kN/m=12.34kN/m 活载=板传荷载=0.84kN/m楼面梁:恒载=梁自重+板传荷载=3.9 kN/m+6.73kN/m=10.63kN/m 活载=板传荷载=4.22kN/m6.3 框架计算简图g=24.31KN/m g=12.34KN/m g=24.31KN/m(q=1.89KN/m)2700框架计算简图6.4. 梁固端弯矩梁端弯矩以绕杆端顺时针为正,反之为负。
土木工程毕业设计ZH03横向框架内力计算d.竖向活载内力计算
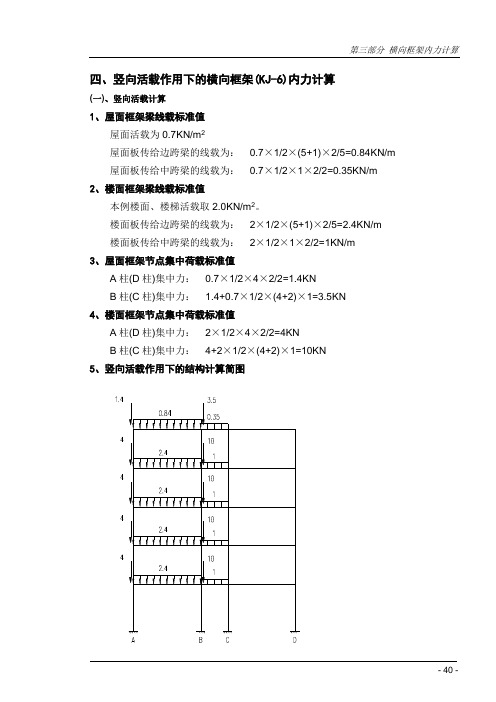
四、竖向活载作用下的横向框架(KJ-6)内力计算(一)、竖向活载计算1、屋面框架梁线载标准值屋面活载为0.7KN/m2屋面板传给边跨梁的线载为:0.7×1/2×(5+1)×2/5=0.84KN/m 屋面板传给中跨梁的线载为:0.7×1/2×1×2/2=0.35KN/m2、楼面框架梁线载标准值本例楼面、楼梯活载取2.0KN/m2。
楼面板传给边跨梁的线载为:2×1/2×(5+1)×2/5=2.4KN/m楼面板传给中跨梁的线载为:2×1/2×1×2/2=1KN/m3、屋面框架节点集中荷载标准值A柱(D柱)集中力:0.7×1/2×4×2/2=1.4KNB柱(C柱)集中力: 1.4+0.7×1/2×(4+2)×1=3.5KN4、楼面框架节点集中荷载标准值A柱(D柱)集中力:2×1/2×4×2/2=4KNB柱(C柱)集中力:4+2×1/2×(4+2)×1=10KN5、竖向活载作用下的结构计算简图(二)、竖向荷载作用下横向框架(KJ-6)内力计算 1、求各梁端的固端弯矩第五层 M AB = -M BA = M CD = -M DC =-121ql 2= -121×0.84×52= -1.75KNm M BC = -M CB =-121ql 2= -121×0.35×22= -0.12KNm 第一~四层 M AB = -M BA = M CD = -M DC = -121ql 2= -121×2.4×52= -5KNm M BC = -M CB =-121ql 2= -121×1×22 =-0.33KNm 2、计算各梁和柱的分配系数各梁柱的线刚度及相对线刚度如下图所示:梁柱的分配系数如下表所示:注:在计算分配系数时,除底层柱外的其余各层柱,其线刚度均应乘以折减系数0.9。
竖向荷载作用下框架内力计算
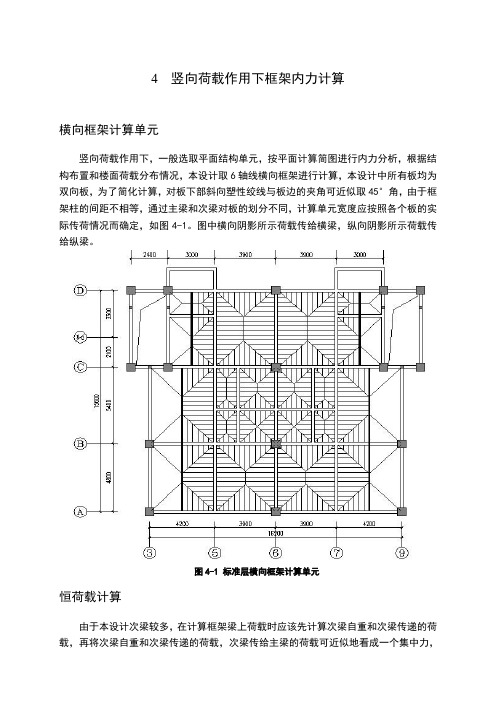
4 竖向荷载作用下框架内力计算横向框架计算单元竖向荷载作用下,一般选取平面结构单元,按平面计算简图进行内力分析,根据结构布置和楼面荷载分布情况,本设计取6轴线横向框架进行计算,本设计中所有板均为双向板,为了简化计算,对板下部斜向塑性绞线与板边的夹角可近似取45°角,由于框架柱的间距不相等,通过主梁和次梁对板的划分不同,计算单元宽度应按照各个板的实际传荷情况而确定,如图4-1。
图中横向阴影所示荷载传给横梁,纵向阴影所示荷载传给纵梁。
图4-1 标准层横向框架计算单元恒荷载计算由于本设计次梁较多,在计算框架梁上荷载时应该先计算次梁自重和次梁传递的荷载,再将次梁自重和次梁传递的荷载,次梁传给主梁的荷载可近似地看成一个集中力,因此在框架节点处还应作用有集中力矩。
标准层次梁恒荷载计算1、5或7轴线次梁上线荷载1)AB 跨的次梁上的荷载分布如图4-2所示。
图4-1 AB 跨的次梁上的荷载分布次梁自重:m kN m m m kN q /13.350.025.0/253=⨯⨯=次;根据《实用建筑结构静力计算手册》(第二版),对于双向板楼面荷载传递按45°塑性绞线方向分为三角形荷载和梯形荷载,三角形荷载和梯形荷载均折算成等效均布面荷载。
三角形荷载:q 85,梯形荷载:()q αα⋅+-3221,其中,0l a α=。
对于BC 跨中有三角形荷载和梯形荷载同时在同一跨中出现,按理应该按照结构力学的方法进行求解,但为了简化计算,本设计中的三角形荷载和梯形荷载按上述方法计算,且按上述方法计算的荷载也能满足工程精度要求。
44.04800/21001==mm mm α;()()223231211/18.3/54.444.044.02121m kN m kN q ααq =⨯+⨯-=⋅+-='; m kN m m kN l q q /68.61.2/18.32011=⨯=⋅'=; m kN m kN m kN q q q AB /49.162/68.6/13.31=⨯+=+=次;2)BC 跨的次梁上的荷载分布如图4-2所示。
第六章-竖向荷载作用下的内力计算
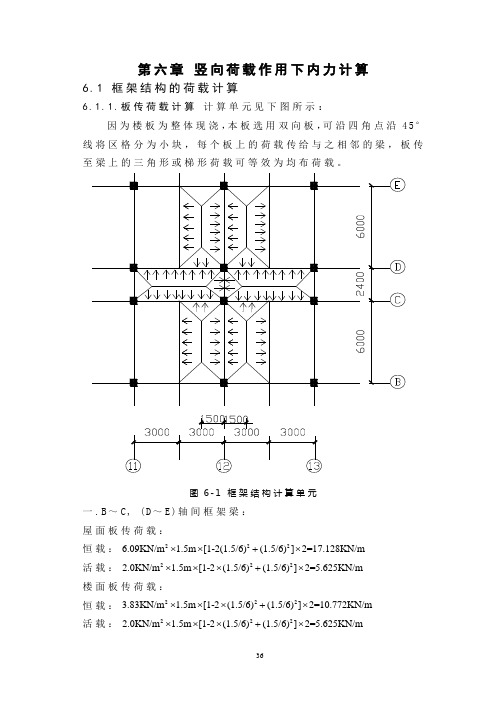
第六章竖向荷载作用下内力计算6.1 框架结构的荷载计算6.1.1.板传荷载计算计算单元见下图所示:因为楼板为整体现浇,本板选用双向板,可沿四角点沿45°线将区格分为小块,每个板上的荷载传给与之相邻的梁,板传图6-1框架结构计算单元一.B~C,(D~E)轴间框架梁:屋面板传荷载:恒载:222⨯⨯+⨯N/m6.09K N/m 1.5m[1-2(1.5/6)(1.5/6)]2=17.128K 活载:222⨯⨯⨯+⨯2.0K N/m 1.5m[1-2(1.5/6)(1.5/6)]2=5.625K N/m楼面板传荷载:恒载:222⨯⨯⨯+⨯N/m3.83K N/m 1.5m[1-2(1.5/6)(1.5/6)]2=10.772K 活载:222⨯⨯⨯+⨯m2.0K N/m 1.5m[1-2(1.5/6)(1.5/6)]2=5.625K N/梁自重:3.95K N /mB ~C , (D ~E )轴间框架梁均布荷载为:屋 面 梁:恒载=梁自重+板传荷载=17.128 K N /m +3.95 K N /m =21.103 K N /m活载=板传荷载=5.625 K N /m楼面板传荷载:恒载=梁自重+板传荷载=3.95 K N /m +10.772 K N /m =14.747 K N /m活载=板传荷载=5.625 K N /m图6-2 框架结构计算单元等效荷载二. C ~D 轴间框架梁:屋面板传荷载:恒载:26.09K N /m 1.2m 5/82=9.135K N /m ⨯⨯⨯ 活载:22.0K N /m 1.5m 5/82=3K N /m⨯⨯⨯ 楼面板传荷载:恒载:23.83K N /m 1.25/82=5.745K N /m⨯⨯⨯ 活载:22.0K N /m 1.2m 5/82=3.75K N /m ⨯⨯⨯ 梁自重:3.95K N /mC ~D 轴间框架梁均布荷载为:屋 面 梁:恒载=梁自重+板传荷载=2.349 K N /m +9.135 K N /m =11.484 K N /m活载=板传荷载=3 K N /m楼面板传荷载:恒载=梁自重+板传荷载=2.349 K N /m +5.745K N /m =8.09K N /m活载=板传荷载=3.75 K N /m三.B 轴柱纵向集中荷载计算:顶层柱:女儿墙自重:(做法:墙高900㎜,100㎜的混凝土压顶)330.240.918/25/0.10.24m m kn m KN m m m ⨯⨯+⨯⨯+()1.220.240.5 5.806/m m m KN m ⨯+⨯=顶层柱恒载=女儿墙+梁自重+板传荷载=5.806/6 3.975/(60.6)KN m KN m m m ⨯+⨯-⨯()()2212 1.5/6 1.5/66/42 6.09/ 1.55/832123.247KN m m KN ⎡⎤-⨯+⨯⨯+⨯⨯⨯⨯=⎣⎦顶层柱活载=板传荷载=()()222.0/ 1.512 1.5/6 1.5/66/42KN m m ⎡⎤⨯⨯-⨯+⨯⨯+⎣⎦2.0/ 1.55/83219.688KN m m KN ⨯⨯⨯⨯=标准层柱恒载=墙自重+梁自重+板荷载=7.794/(60.6) 3.975/(60.6) 3.83/ 1.55/832KN m KN m KN m m ⨯-+⨯-+⨯⨯⨯⨯ (2.332311.52)61/42 2.3325/61/42KN m ++⨯⨯⨯+⨯⨯⨯+()()223.83 1.512 1.5/6 1.5/66/42124.172m m KN ⎡⎤⨯⨯-⨯+⨯⨯=⎣⎦标准层柱活载=板传荷载=()()222.0 1.512 1.5/6 1.5/63 2.0 1.55/83219.688m m m m KN ⎡⎤⨯⨯-⨯+⨯+⨯⨯⨯⨯=⎣⎦基础顶面荷载=底层外纵墙自重+基础自重=9.738/(60.6) 2.5/(60.6)16.085KN m m m KN m m m KN ⨯-+⨯-=四.C 柱纵向集中力计算:顶层柱荷载=梁自重+板传梁荷载=3.975/(90.9) 2.349/(1.20.3) 6.09/ 1.55/832KN m m KN m m KN m m ⨯-+⨯-+⨯⨯⨯⨯6.09/ 1.25/8 1.22(2.3323/11.52/)61/42KN m m KN m KN m m +⨯⨯⨯⨯++⨯⨯⨯ 154.318KN =顶层柱活载=板传荷载=()()222.0 1.512 1.5/6 1.5/63m m ⎡⎤⨯⨯-⨯+⨯+⎣⎦()()222.0 1.212 1.2/6 1.2/63 2.0 1.2m m m m ⎡⎤⨯⨯-⨯+⨯+⨯⎣⎦5/8 1.22 2.0 1.55/83239.272m m KN ⨯⨯⨯+⨯⨯⨯⨯=标准柱恒载=墙+梁自重+板传荷载=11.52/(30.6)15.12/(30.6)15.12/(30.6)KN m m KN m m KN m m ⨯-+⨯-+⨯-+2.349/(1.20.3)3.975/(60.6) 6.09/ 1.55/832KN m m KN m m KN m m ⨯-+⨯-+⨯⨯⨯⨯+26.09/61/21/2 2.67/ 2.4/26 3.83/36200.173KN m m KN m m KN m m m KN ⨯⨯⨯+⨯⨯+⨯⨯=标准层活载=板传荷载=222.0/36 2.5/ 1.2654KN m m m KN m m m KN ⨯⨯+⨯⨯=基础顶面恒载=底层外纵墙自重+基础自重9.738/(60.6) 2.5/(60.6)66.085KN m m m KN m m m KN ⨯-+⨯-=(3).框架柱自重:柱自重:底层:1.2×0.6m ×0.6m ×253/KN m ×4.55m =49.14K N其余柱:1.2×0.6m ×0.6m ×253/K N m ×3.6m =38.88K N6.2恒荷载作用下框架的内力6.2.1.恒荷载作用下框架的弯矩计算一.恒荷载作用下框架可按下面公式求得:21/12ab M ql =- (61)- 21/12ba M ql = (62)- 故:2771/1221.03663.09.B C M KN m =-⨯⨯=-7763.09.C B M KN m =2771/1211.4846 5.512.C D M KN m =-⨯⨯=-77 5.512.C D M KN m =2661/1214.747644.241.B C M KN m =-⨯⨯=-6644.241.C B M KN m =2661/128.096 3.883.C D M KN m =-⨯⨯=-66 3.883.D C M KN m =恒荷载作用下框架的受荷简图如图6-3所示:图6-3竖向受荷总图:注:1.图中各值的单位为K N2.图中数值均为标准值3.图中括号数值为活荷载图6-4:恒载作用下的受荷简图(2).根据梁,柱相对线刚度,算出各节点的弯矩分配系数ij μ:/()ij c b i i i μ=∑+∑ (63)-分配系数如图6-5 , 图6-6所示:图6-5 B 柱弯矩各层分配系数简图B 柱:底层:0.801/(0.8010.609 1.0i ++=下柱= 1.0/(0.8010.609 1.0)0.415i ++=上柱=0.609/(0.8010.609 1.0)0.253i ++=左梁=标准层: 1.0/(0.609 1.0 1.0)i ++=上柱= 1.0/(0.609 1.0 1.0)0.383i ++=下柱=0.609/(0.609 1.0 1.0)0.234i ++=左梁=顶层: 1.0/(0.609 1.0)0.6i +=下柱= 0.609/(0.609 1.0)0.622i +=左梁=图6-6 C 柱弯矩各层分配系数简图C 柱: 0.609/(0.609 1.00.2110.801)0i +++=右梁= 1.0/(0.609 1.00.2110.801)0.382i +++=上柱= 0.801/(0.609 1.00.2110.801)0i +++=下柱=0.211/(0.609 1.00.2110.801)0.081i +++=左梁=标准层: 1.0/(0.609 1.00.2110.8i +++=下柱= 1.0/(0.609 1.00.2110.801)0.355i +++=上柱=0.609/(0.609 1.00.2110.801)0.216i +++=右梁=0.211/(0.609 1.00.2110.801)0.074i +++=左梁=顶层: 1.0/(0.609 1.00.211)0.i ++=下柱= 0.211/(0.609 1.00.211)0.116i ++=左梁=0.609/(0.609 1.00.211)0.335i ++=右梁=三.恒荷载作用下的弯矩剪力计算,根据简图(6-4)梁:A M 0∑= 21/2.0A B B M M ql Q l ---=/1/2B A B Q M M l ql =--B M 0∑= 21/2.0A B A M M ql Q l -+-=/1/2A A B Q M M l ql =-+ (6-4) 柱:C M 0∑= .0C D D M M Q h ---=()/D C D Q M M h =-+D M 0∑= .0C D C M M Q h ---=()/C C D Q M M h =-+ (6-5)四.恒荷载作用下的边跨框架的轴力计算,包括连梁传来的荷载及柱自重.7123.24721.1036/2186.556N KN=+⨯=67124.17214.7476/238.88393.849N N KN =++⨯+=56124.17214.7476/238.88601.142N N KN =++⨯+=45124.17214.7476/238.88808.435N N KN =++⨯+=34124.17214.7476/238.881015.728N N KN =++⨯+=23124.17214.7476/238.881223.021N N KN =++⨯+=12124.17214.7476/238.881382.487N N KN =++⨯+=图6-5 恒荷载作用下的计算简图恒荷载作用下的中跨框架的轴力计算:7154.31811.484 2.4/2168.099N KN=+⨯= 67200.1738.09 2.4/238.88416.88N N KN =++⨯+=56200.1738.09 2.4/238.88665.621N N KN =++⨯+=45200.1738.09 2.4/238.88808.435N N KN =++⨯+=34200.1738.09 2.4/238.881015.728N N KN =++⨯+=23200.1738.09 2.4/238.881223.021N N KN =++⨯+=12200.1738.09 2.4/238.881382.487N N KN =++⨯+=五.弯矩分配及传递弯矩二次分配法比分层法作了更进一步的简化。
竖向荷载作用下框架结构的内力计算计算书3:正文6-11章

第6章竖向荷载作用下框架结构的内力计算6.1计算单元的确定取7轴线横向框架进行计算,计算单元宽度为2.75m,如图6.1所示。
传给该框架的楼面荷载如图中的水平阴影线所示,计算单元范围内的其余楼面荷载则通过次梁和纵向框架梁以集中力的形式传给横向框架,作用于各节点上。
由于纵向框架的中心线与柱的中心线不重合,因此在框架节点上还作用有集中力矩。
图6.1 计算单元6.2 竖向荷载计算6.2.1恒荷计算1.1-5层荷载计算:梁自重:梁AB=2.1kN/m梁BD=2.1kN/m梁DE=2.1kN/m挑梁=0.525kN/m板传递给梁的梯形及三角形荷载:板AB(左)=3.742kN/m×1.35m=5.05kN/m板AB(右)=3.742kN/m×1.5m=5.61kN/m板BD(左)=3.742kN/m×1.95m=7.29kN/m板BD(右)=3.742kN/m×2.1m=7.85kN/m板DE(左)=3.742kN/m×1.35m=5.05kN/m板DE(右)=3.742kN/m×1.4m=5.24kN/m悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零墙自重:墙AB =2.12×2.4=5.09kN/m墙BD =2.12×2.4=5.09kN/m墙DE =2.12×2.4=5.09kN/m墙悬挑=2.12×2.6=5.51kN/m恒载:梁自重+板传荷载+墙自重挑梁=梁自重+墙自重柱的集中力:A 3.740.50.5 2.71.350.531.5 2.850.525 2.375 2.6 2.8526.78kNP=⨯⨯⨯⨯+⨯⨯⨯⨯⨯=()++B 3.740.50.5 2.7 1.350.53 1.5 2.850.5250.5 3.743.150.750.50.5 1.95 1.950.5 2.1 3.9 2.12 2.6 2.8538.31k NP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯=()++() D 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.743.150.750.50.5 1.951.950.5 2.1 3.5 2.12 2.6 2.7536.31kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯+⨯⨯=()++() E 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.740.65 5.52.375 2.6 2.8532.8kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯+⨯⨯=()++E 0.5 3.740.65 5.5 2.750.525 2.375110.5kN P -=⨯⨯⨯⨯+⨯=+柱所受集中力产生的弯矩:A 26.78(0.450.2)/2 3.35kN m M =⨯-=⋅B 0kN m M =⋅D 36.31(0.450.2)/2 4.45kN m M =⨯-=⋅E 32.8(0.450.2)/2 4.1kN m M =⨯-=⋅ 2.6层荷载计算:梁自重:梁AB=2.1kN/m梁BD=2.1 kN/m 梁DE=2.1kN/m挑梁=0.525 kN/m板传递给梁的梯形及三角形荷载: 板AB (左)=3.742kN/m ×1.35m=5.05kN/m 板AB (右)=3.742kN/m ×1.5m=5.61kN/m 板BD (左)=3.742kN/m ×1.95m=7.29kN/m 板BD (右)=3.742kN/m ×2.1m=7.85kN/m 板DE (左)=3.742kN/m ×1.35m=5.05kN/m 板DE (右)=3.742kN/m ×1.4m=5.24kN/m 悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零 墙自重: 墙AB =2.12×1.925=4.081kN/m墙BD =2.12×3.36=7.12kN/m 墙DE =2.12×1.725=3.657kN/m恒载:梁自重+板传荷载+墙自重挑梁=梁自重 柱的集中力 A 3.740.50.5 2.71.350.531.5 2.850.525 2.3750.6 2.8513.17kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯=()++ B 3.740.50.5 2.71.350.531.5 2.850.5250.5 3.74 3.150.750.50.51.951.950.5 2.1 3.922.6kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() D 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.74 3.150.750.50.51.951.950.5 2.1 3.521.15kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() E 3.740.50.5 2.71.350.5 2.81.4 2.750.5250.5 3.740.65 5.5 2.375 0.6 2.8519.26 kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯+⨯⨯=()++-E 0.5 3.740.65 5.5 2.750.5258.13kN P =⨯⨯⨯⨯=+柱所受集中力产生的弯矩:A 13.17(0.450.2)/2 1.65kN m M =⨯-=⋅B 0kN m M =⋅D 21.15(0.450.2)/2 2.64kN m M =⨯-=⋅E 19.26(0.450.2)/2 2.41kN m M =⨯-=⋅ 3.顶层荷载计算:梁自重:梁AB=2.35 kN/m 梁BD=2.35 kN/m 梁DE=2.35 kN/m板传递给梁的梯形及三角形荷载: 板AB (左)=5.192kN/m ×1.35m=7.01kN/m 板AB (右)=5.192kN/m ×1.5m=7.79kN/m 板BD (左)= 5.192kN/m ×1.95m=7.29kN/m 板BD (右)= 5.192kN/m ×2.1m=10.9kN/m 板DE (左)= 5.192kN/m ×1.35m=7.01kN/m 板DE (右)= 5.192kN/m ×1.4m=7.27kN/m 悬挑部分的板为单向板,所以直接传递给梁的恒荷载为零柱的集中力: A 5.190.50.5 2.71.350.531.5 2.850.5251.1212.24kN P =⨯⨯⨯⨯+⨯⨯⨯⨯=()+ B 5.190.50.5 2.7 1.350.53 1.5 2.850.525 1.120.55.19 3.15 0.750.50.51.951.950.5 2.1 3.915.83kN P =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() D 5.190.50.5 2.71.350.5 2.81.4 2.750.5251.120.5 5.19 3.150.750.50.51.951.950.5 2.1 3.528.97kNP =⨯⨯⨯⨯+⨯⨯⨯⨯⨯⨯⨯⨯+⨯⨯+⨯⨯=()++() E 5.190.50.5 2.7 1.350.5 2.8 1.49.82k NP =⨯⨯⨯⨯+⨯⨯=()柱所受集中力产生的弯矩:A 12.24(0.450.2)/2 1.53kN m M =⨯-=⋅B 0kN m M =⋅ D 28.97(0.450.2)/2 3.62kN m M =⨯-=⋅ E 9.82(0.450.2)/2 1.23kN m M =⨯-=⋅6.2.2 活荷载计算活荷载作用下各层框架梁上活载为板传递给梁的荷载。
毕业设计框架竖向荷载作用下内力计算

毕业设计框架竖向荷载作用下内力计算随着工程设计技术的进步和使用材料的不断发展,对结构设计的要求也日益增加。
在工程结构设计中,内力计算是必不可少的步骤之一,它对结构的合理设计和安全性评估起着至关重要的作用。
本文将以毕业设计框架竖向荷载作用下内力计算为研究对象,详细介绍内力计算的相关内容。
一、绪论1.1研究背景随着现代城市建设的不断推进,各种桥梁、建筑、道路等工程结构被广泛使用,其中设计的合理性和结构的安全性成为工程结构设计中不可忽视的问题。
而内力计算作为结构设计的基本内容,对于结构的合理设计和安全性评估起着重要的作用。
1.2研究目的本文旨在通过研究毕业设计框架竖向荷载作用下内力计算的方法和步骤,探讨结构的安全性评估及设计中的关键问题,为工程结构设计提供一定的参考和指导。
二、内力计算方法与步骤分析2.1内力计算方法内力计算方法主要包括静力学方法、动力学方法和有限元分析法等。
在这些方法中,静力学是最常用也是最基本的方法。
静力学方法主要是通过平衡方程和力和力矩的平衡条件来计算结构的内力。
2.2内力计算步骤内力计算的步骤包括:确定结构的边界条件、建立结构的模型、计算荷载的作用、分析和计算结构的内力等。
其中,确定结构的边界条件是内力计算的前提条件,建立结构的模型是内力计算的基础,计算荷载的作用是内力计算的关键步骤,分析和计算结构的内力是内力计算的最终目的。
三、毕业设计框架竖向荷载作用下内力计算实例分析在本实例中,我们以栋大楼的毕业设计框架为对象,研究竖向荷载作用下内力计算的方法和步骤。
3.1确定边界条件首先,需要确定建筑结构的边界条件,包括支座类型、结构的几何形状、结构材料等。
这些参数将对内力计算产生重要影响。
3.2建立结构模型建立结构模型是内力计算的基础,可以使用计算机辅助设计软件进行模型的三维建立。
建模时需要注意建筑结构的几何形状和材料属性的准确反映。
3.3计算荷载的作用在竖向荷载作用下,首先需要将楼层的荷载施加到结构模型上。
土木工程毕业设计手算步骤

框架结构计算步骤1、主梁截面高度按梁跨度的1/12—1/8估算,次梁按跨度的1/18—1/12估算。
依据轴压比限值估算柱子截面2、框架侧移刚度的计算:先计算梁、柱的线刚度,然后计算各层横向框架侧移刚度(D值法),判断是否为规则框架(位移角是否满足规范要求)。
3、集中于各楼层标高处的重力荷载代表值计算:计算重力荷载代表值的公式为:G〔= G恒+ 0.5G活,形成“糖葫芦串”。
4、横向水平荷载(地震作用)作用下框架结构的内力和侧移计算(D值法),主要是各层柱端弯矩及剪力计算;梁端弯矩、剪力及柱轴力计算。
5、竖向荷载作用下框架结构的内力计算,采用分层法及弯矩分配法计算恒载作用下的梁端、柱端弯矩,另,梁端剪力可根据梁上竖向荷载引起的剪力与梁端弯矩引起的剪力相叠加而得。
柱轴力可由梁端剪力和节点集中力叠加得到。
6、横向框架内力组合,包括框架梁内力组合、框架柱内力组合:首先计算跨间最大弯矩并进行弯矩调幅(梁柱节点在理论计算中一般看作是绝对刚接,但实际的钢筋混凝土梁柱节点做不到完全刚接,更接近于刚接和铰接之间。
尤其是混凝土梁端开裂后,刚接的假定更是不太成立。
竖向荷载作用下,如果按照假定为刚接的理论计算值去设计,而实际做不到完全刚接,那么实质上是低估了跨中截面的实际弯矩值。
因此,可以考虑用梁端塑性调幅的方法来体现这一影响。
还有一个方面的考虑,梁端负弯矩钢筋都在梁顶部布置,如果数量过多,很难布置,混凝土也很难浇捣,施工质量没有保障。
适当的塑性调幅,相当于减少梁端负弯矩钢筋,增加梁跨中正弯矩钢筋,方便施工,保证质量。
弯矩调幅与抗震设计中的强柱弱梁无关,且只对竖向荷载作用下的内力进行调幅。
),然后进行框架梁的内力组合,最后进行梁端剪力的调整。
框架柱内力组合,取每层柱顶和柱底两个控制截面进行组合,组合后进行柱端弯矩调整。
7、框架结构抗震设计时候需要:“强剪弱弯”=调整梁端剪力和柱端剪力;“强柱弱梁”=调整柱端弯矩。
8、在算框架梁配筋计算中截面的弯矩设计值之前,是先要调幅,再把调幅后的M,V值进行内力组合,然后再把各种内力组合中的最大值提出来,进行截面设计,也就是你要问的“在框架梁配筋计算中截面的弯矩设计值”。
竖向荷载作用下的内力计算

竖向荷载作用下的内力计算4.1竖向荷载作用下荷载计算由于二至六楼的楼面的完全采用一种做法,为了计算方便,我们只选取了二楼楼面进行计算,导荷方式如图所示:标准层屋面荷载计算(1)对2层楼板B1进行计算(7.8/4.2=1.86为双向板):传至纵向框架梁(KL 250×500)D轴、梁(KL 250×500)F轴上的荷载为三角形荷载。
恒载:3.99X4.2/2=8.379KN/m 活载:3.5X4.2/2=7.35KN/m若化为均布荷载:恒载:8.379X5/8=5.24KN/m 活载:7.35X5/8=4.59KN/m传至框架梁(KL 250×700)3轴上的荷载为梯形荷载。
恒载:3.99X4.2/2=8.379KN/m 活载:3.5X4.2/2=7.35KN/m若化为均布荷载.06.625.4=⨯=a 4.2/2x7.8=0.27恒载:(1-2X 227.0+327.0)X8.379=7.33KN/m活载:(1-2X 227.0+327.0)X4.2=3.671KN/m对2层楼板B2进行计算(4.2/3=1.4为双向板):传至纵向框架梁(KL 250×400)3轴上的荷载为三角形荷载。
恒载:3.99X3/2=5.985KN/m 活载2.5X3/2=3.75KN/m 若化为均布荷载:恒载:5.985X5/8=3.741KN/m 活载:3.75X5/8=2.34KN/m传至框架梁(KL 250×500)C 轴、梁(KL 250×500)D 轴上的荷载为梯形荷载。
恒载:3.99X3/2=5.985KN/m 活载:2.5X3/2=3.75KN/m若化为均布荷载.06.625.4=⨯=a 3/2x4.2=0.357恒载:(1-2X 2357.0+3357.0)X5.985=4.74KN/m活载:(1-2X 2357.0+3357.0)X3.75=2.97KN/m(2)梁(KL 250×500)传给边柱(KZ-1)的集中荷载为:恒载=梁自重 + 墙自重+ B1传荷载⨯2()()KN G G 30.56225.498.425.45.476.4772.21114=⨯÷⨯++⨯+==(2.64+2.8)X (4.2+4.2)/2+5.24x4.2x2/2=44.86KN 活载=B1传荷载×2Q Q 65.12225.481.21411=⨯÷⨯== 4.59x4.2x2/2=19.28KN由于梁的形心与柱的形心不一致,因此梁传给柱的集中荷载可向柱形心简化为一个集中荷载与一个力矩恒荷载作用下()m KN G M M G G ∙=⨯=-⨯==04.7125.030.56125.025.0111411(0.25-0.125)=44.86x0.125=5.61KN/m活荷载作用下()m KN Q M M Q Q ∙=⨯=-⨯==58.1125.065.12125.025.0111411(0.25-0.125)=19.28x0.125=2.41KN/m梁(KL 250×500)传给中柱(KZ-1)的集中荷载为:恒载=梁自重 + 墙自重 + B1传荷载×2 + B2传荷载×2)KNG G 07.72225.4723.3225.498.425.45.4254.590.4272.21312=⨯÷⨯+⨯÷⨯++⨯⎪⎭⎫ ⎝⎛++==(2.64+5.72)x(4.2x4.2)/2+5.24x4.2x2/2+4.732x4.2x2/2=77.03KN 活载=B1传荷载×2+ B2传荷载×2Q Q 5.24225.4634.2225.481.21312=⨯÷⨯+⨯÷⨯== 4.59x4.2x2/2+2.97x4.2x2/2=31.75KN 由于梁的形心与柱的形心不一致,因此梁传给柱的集中荷载可向柱形心简化为一个集中荷载与一个力矩恒荷载作用下()m KN G M M G G ∙=⨯=-⨯==81.10150.007.72100.025.0121312(0.25-0.125)=77.03x0.125=9.63KN.M 活荷载作用下()m KN G M M Q Q ∙=⨯=-⨯==68.3150.05.24100.025.0121312(0.25-0.125)=31.75x0.125=3.97KN.M屋面板传荷载:(1)对屋面板B1进行计算(7.8/4.2=1.86为双向板):传至纵向框架梁(KL 250×500)D 轴、梁(KL 250×500)F 轴上的荷载为三角形荷载。
框架在竖向荷载作用下内力计算共28页文档

51、没有哪个社会可以制订一部永远 适用的 宪法, 甚至一 条永远 适用的 法律。 ——杰 斐逊 52、法律源于人的自卫本能。——英 格索尔
53、人们通常会发现,法律就是这样 一种的 网,触 犯法律 的人, 小的可 以穿网 而过, 大的可 以破网 而出, 只有中 等的才 会坠入 网中。 ——申 斯通 54、法律就是法律它是一座雄伟的大 夏,庇 护着我 们大家 ;它的 每一块 砖石都 垒在另 一块砖 石上。 ——高 尔斯华 绥 55、今天的法律未必明天仍是法律。 ——罗·伯顿
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
25、学习是劳动,是充满思想的劳动。——乌申斯基
竖向荷载作用下的内力计算

竖向荷载作用下的内力计算4.1竖向荷载作用下荷载计算由于二至六楼的楼面的完全采用一种做法,为了计算方便,我们只选取了二楼楼面进行计算,导荷方式如图所示:标准层屋面荷载计算(1)对2层楼板B1进行计算(7.8/4.2=1.86为双向板):传至纵向框架梁(KL 250×500)D轴、梁(KL 250×500)F轴上的荷载为三角形荷载。
恒载:3.99X4.2/2=8.379KN/m 活载:3.5X4.2/2=7.35KN/m若化为均布荷载:恒载:8.379X5/8=5.24KN/m 活载:7.35X5/8=4.59KN/m传至框架梁(KL 250×700)3轴上的荷载为梯形荷载。
恒载:3.99X4.2/2=8.379KN/m 活载:3.5X4.2/2=7.35KN/m若化为均布荷载.06.625.4=⨯=a 4.2/2x7.8=0.27恒载:(1-2X 227.0+327.0)X8.379=7.33KN/m活载:(1-2X 227.0+327.0)X4.2=3.671KN/m对2层楼板B2进行计算(4.2/3=1.4为双向板):传至纵向框架梁(KL 250×400)3轴上的荷载为三角形荷载。
恒载:3.99X3/2=5.985KN/m 活载2.5X3/2=3.75KN/m 若化为均布荷载:恒载:5.985X5/8=3.741KN/m 活载:3.75X5/8=2.34KN/m传至框架梁(KL 250×500)C 轴、梁(KL 250×500)D 轴上的荷载为梯形荷载。
恒载:3.99X3/2=5.985KN/m 活载:2.5X3/2=3.75KN/m若化为均布荷载.06.625.4=⨯=a 3/2x4.2=0.357恒载:(1-2X 2357.0+3357.0)X5.985=4.74KN/m活载:(1-2X 2357.0+3357.0)X3.75=2.97KN/m(2)梁(KL 250×500)传给边柱(KZ-1)的集中荷载为:恒载=梁自重 + 墙自重+ B1传荷载⨯2()()KN G G 30.56225.498.425.45.476.4772.21114=⨯÷⨯++⨯+==(2.64+2.8)X (4.2+4.2)/2+5.24x4.2x2/2=44.86KN 活载=B1传荷载×2Q Q 65.12225.481.21411=⨯÷⨯== 4.59x4.2x2/2=19.28KN由于梁的形心与柱的形心不一致,因此梁传给柱的集中荷载可向柱形心简化为一个集中荷载与一个力矩恒荷载作用下()m KN G M M G G ∙=⨯=-⨯==04.7125.030.56125.025.0111411(0.25-0.125)=44.86x0.125=5.61KN/m活荷载作用下()m KN Q M M Q Q ∙=⨯=-⨯==58.1125.065.12125.025.0111411(0.25-0.125)=19.28x0.125=2.41KN/m梁(KL 250×500)传给中柱(KZ-1)的集中荷载为:恒载=梁自重 + 墙自重 + B1传荷载×2 + B2传荷载×2)KNG G 07.72225.4723.3225.498.425.45.4254.590.4272.21312=⨯÷⨯+⨯÷⨯++⨯⎪⎭⎫ ⎝⎛++==(2.64+5.72)x(4.2x4.2)/2+5.24x4.2x2/2+4.732x4.2x2/2=77.03KN 活载=B1传荷载×2+ B2传荷载×2Q Q 5.24225.4634.2225.481.21312=⨯÷⨯+⨯÷⨯== 4.59x4.2x2/2+2.97x4.2x2/2=31.75KN 由于梁的形心与柱的形心不一致,因此梁传给柱的集中荷载可向柱形心简化为一个集中荷载与一个力矩恒荷载作用下()m KN G M M G G ∙=⨯=-⨯==81.10150.007.72100.025.0121312(0.25-0.125)=77.03x0.125=9.63KN.M 活荷载作用下()m KN G M M Q Q ∙=⨯=-⨯==68.3150.05.24100.025.0121312(0.25-0.125)=31.75x0.125=3.97KN.M屋面板传荷载:(1)对屋面板B1进行计算(7.8/4.2=1.86为双向板):传至纵向框架梁(KL 250×500)D 轴、梁(KL 250×500)F 轴上的荷载为三角形荷载。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第六章竖向荷载(恒载+活载)作用下框架内力计算第一节框架在恒载作用下的内力计算本设计用分层法计算内力,具体步骤如下:①计算各杆件的固端弯矩②计算各节点弯矩分配系数③弯矩分配④调幅并绘弯矩图⑤计算跨中最大弯矩、剪力和轴力并绘图一、恒载作用下固端弯矩计算(一)恒载作用下固端弯矩恒载作用下固端弯矩计算(单位:KN·m) 表框架梁BC跨固端弯矩计算(单位:KN·m)结构三层(屋面)计算简图弯矩图结构二层计算简图弯矩图结构一层计算简图弯矩图楼层框架梁CD跨固端弯矩计算(单位:KN·m)结构三层(屋面)计算简图弯矩图节点3弯矩为·m3单元最大负弯矩为 KN·m结构二层计算简图弯矩图结构一层计算简图弯矩图楼层框架梁D-1/D悬挑梁固端弯矩计算(单位:KN·m)结构一层计算简图弯矩图恒载作用下梁固端弯矩计算统计表结构层MBC(KN·m)MCB(KN·m)MCD(KN·m)MDC(KN·m)MD-1/D(KN·m)三层0(二)计算各节点弯矩分配系数用分层法计算竖向荷载,假定结构无侧移,计算时采用力矩分配法,其计算要点是:①计算各层梁上竖向荷载值和梁的固端弯矩。
②将框架分层,各层梁跨度及柱高与原结构相同,柱端假定为固端。
③计算梁、柱线刚度。
对于柱,假定分层后中间各层柱柱端固定与实际不符,因而,除底层外,上层柱各层线刚度均乘以修正。
有现浇楼面的梁,宜考虑楼板的作用。
每侧可取板厚的6倍作为楼板的有效作用宽度。
设计中,可近似按下式计算梁的截面惯性矩:一边有楼板:I=两边有楼板:I=④计算和确定梁、柱弯矩分配系数和传递系数。
按修正后的刚度计算各结点周围杆件的杆端分配系数。
所有上层柱的传递系数取1/3,底层柱的传递系数取1/2。
⑤按力矩分配法计算单层梁、柱弯矩。
⑥将分层计算得到的、但属于同一层柱的柱端弯矩叠加得到柱的弯矩。
(1)计算梁、柱相对线刚度图修正后梁柱相对线刚度(2)计算弯矩分配系数结构三层①梁μ=÷+=B3C3=÷++=μC3B3=÷++=μC3D3=÷+=μD3C3=÷+=②柱μB3B2=÷++=μC3C2=÷+=μD3D2结构二层①梁μ=÷++=B2C2=÷+++=μC2B2μ=÷+++=C2D2=÷++=μD2C2②柱μ=÷++=B2B3=÷++=μB2B1μ=÷+++=C2C3μ=÷+++=C2C1μ=÷++=D2D3=÷++=μD2D1结构一层=÷+1+=①梁μB1C1μ=÷+1++=C1B1=÷+1++=μC1D1=÷+1+=μD1C1=÷+1+=②柱μB1B2μ=1÷+1+=B1B0=÷+1++=μC1C2μ=1÷+1++=C1C0=÷+1+=μD1D2=1÷+1+=μD1D0(三)分层法算恒载作用下弯矩恒载作用下结构三层弯矩分配表B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计一次分配二次分配恒载作用下结构二层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递←→分配传递→←合计↓一次分配二次分配恒载作用下结构一层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递→←分配传递←→分配传递→←分配传递←→分配传递→←分配传递←→分配传递→←合计一次二次图弯矩再分配后恒载作用下弯矩图(KN·m)(四)框架梁弯矩塑性调幅为了减少钢筋混凝土框架梁支座处的配筋数量,在竖向荷载作用下可以考虑竖向内力重分布,主要是降低支座负弯矩,以减小支座处的配筋,跨中则应相应增大弯矩。
《高层建筑混凝土结构技术规程》(JGJ3-2010)5.2.3条:在竖向荷载作用下,可考虑框架梁端塑性变形内力重分布对梁端负弯矩乘以调幅系数进行调幅,并应符合下列规定:①装配整体式框架梁端负弯矩调幅系数可取为~,现浇框架梁端负弯矩调幅系数可取为~;②框架梁端负弯矩调幅后,梁跨中弯矩应按平衡条件相应增大;③应先对竖向荷载作用下框架梁的弯矩进行调幅,再与水平作用产生的框架梁弯矩进行组合;④截面设计时,框架梁跨中截面正弯矩设计值不应小于竖向荷载作用下按简支梁计算的跨中弯矩设计值的50%。
本设计取梁端支座负弯矩调幅系数可取为。
='(计算过程从略)M.0M85图调幅后恒载作用下弯矩图(KN·m)(五)恒载作用下梁跨内最大弯矩、梁端剪力和柱轴力计算1.恒载作用下梁跨内最大弯矩计算本设计计算梁跨内最大弯矩时,采用按简支计算时的梁跨内最大弯矩与计算得的调幅后的梁端弯矩进行叠加得到。
计算过程计算如下:简支条件下恒载作用下固端弯矩计算表弯矩图调幅后弯矩图结构二层计算简图弯矩图调幅后弯矩图结构一层计算简图弯矩图调幅后弯矩图楼层框架梁CD跨固端弯矩计算(单位:KN·m)结构一层计算简图弯矩图节点3弯矩大小为·m,单元(3)跨内最大弯矩为 KN·m 调幅后弯矩图结构二层计算简图弯矩图调幅后弯矩图结构一层计算简图弯矩图调幅后弯矩图楼层框架梁D-1/D悬挑梁固端弯矩计算(单位:KN·m)结构一层计算简图弯矩图调幅后弯矩图(1)对于BC跨结构三层(屋面层)在简支条件下叠加调幅后弯矩剪力图如下剪力为0处距离B点距离:ml70.1)81.507.707.7(93.33=++÷=剪力为0处弯矩:m KN M •-=+⨯++⨯+⨯-=52.16335.1270.1)81.507.707.7(2170.193.332结构二层剪力为0处距离B 点距离:m l 68.1)81.574.1001.501.5(96.44=+++÷= 剪力为0处弯矩:m KN M •-=+⨯++⨯⨯+⨯-=26.24907.768.1)81.574.10210.5(2168.194.442 结构一层剪力为0处距离B 点距离:m l 71.1)81.574.1001.501.5(37.45=+++÷= 剪力为0处弯矩:m KN M •-=+⨯++⨯⨯+⨯-=96.27513.1071.1)81.574.10210.5(2171.137.452 (2)对于CD 跨 结构三层(屋面层)在简支条件下叠加调幅后弯矩剪力图如下剪力为0处距离C 点距离:m l 04.43)81.5207.7()96.9907.73212381.537.159(=++⨯÷-⨯⨯⨯-⨯-=剪力为0处距离D 点距离:m l 56.504.46.9=-= 剪力为0处弯矩:m KN M •-=+⨯+⨯⨯+⨯-=39.218851.8956.5)81.5207.7(2156.590.1102结构二层剪力为0处距离C 点距离:m l 53.33)74.1081.5210.5()18910.53212381.587.235(=+++⨯÷-⨯⨯⨯-⨯-=剪力为0处距离D 点距离:m l 07.653.36.9=-= 剪力为0处弯矩:m KN M •-=+⨯++⨯⨯+⨯-=32.330704.16207.6)74.1081.5210.5(2107.641.1622 结构一层在节点3处,剪力有突变,由突变为KN V 36.618910.53212381.537.215-=-⨯⨯⨯-⨯-=故剪力为0处距离C 点距离:m l 3= 剪力为0处距离D 点距离:m l .636.9=-= 剪力为0处弯矩:m KN M •-=+⨯++⨯⨯+⨯-=21.312747.3036)74.1081.5210.5(21691.1822 本设计取调幅后的梁跨内弯矩最大值和简支时梁跨内弯矩最大值的50%中的较大者,比较如下表:梁跨内弯矩最大值取值 表说明:m ax M —调幅后的梁跨内弯矩最大值;m ax M —简支时梁跨内弯矩最大值。
依据上表绘制恒载作用下B ~D 轴×○3轴框架弯矩图如下图 恒载作用下B ~D 轴×○3轴框架弯矩图(KN ·m )3.恒载作用下梁、柱端剪力计算梁端剪力计算计算方法为取隔离体进行计算,具体计算如下: 屋顶层BC 跨对B取矩=0BMVC×+=+(×2+)××,故VC=对C取矩∑=0CMVB×+=+(×2+)××,故VB=屋顶层CD跨对C取矩∑=0CMVD×+=+××+×3×+××+×3,故VD=对D取矩∑=0DMVC×+=+××+×3×+××+×, 故VC=其他剪力计算类似,因此计算过程省略,以下汇总剪力:梁截面剪力(单位:表V B3=VB2=综上,其他柱计算类似。
V上=V下=(M上+M下)÷h,下面汇总柱剪力恒载作用下柱剪力(KN)表图恒载作用下B~D轴×○3轴框架剪力图(KN)4.恒载作用下柱端轴力计算根据节点平衡法可求得柱轴力,规定柱受压为正,受拉为负:B 3轴力=B3集中力+梁B3C3剪力NB3=+=其它柱计算类似,计算过程省略。
图柱截面表示图恒载作用下柱轴力(单位KN)表图恒载作用下柱轴力(KN)二、框架在活载作用下的内力计算(一)活载作用下固端弯矩计算活载作用下固端弯矩表楼层框架梁BC跨固端弯矩计算(单位:KN·m)结构三层(屋面)计算简图弯矩图结构二层算简图弯矩图结构一层计算简图弯矩图楼层框架梁CD跨固端弯矩计算(单位:KN·m)结构三层(屋面)计算简图弯矩图结构二层算简图弯矩图结构一层计算简图弯矩图楼层框架梁D-1/D悬挑梁固端弯矩计算(单位:KN·m)结构一层计算简图弯矩图活载作用下梁固端弯矩计算统计表(二)各节点弯矩分配系数节点弯矩分配系数同恒载,计算略。
(三)分层法算活载作用下弯矩活载作用下结构三层弯矩分配表B C D上柱偏心弯矩分配系数0固端弯矩分配传递分配传递分配传递分配传递分配传递分配传递分配传递合计往下传一次二次分配活载作用下结构二层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递分配传递分配传递分配传递分配传递→←分配传递←→分配传递→←合计↓一次二次分配活载作用下结构一层弯矩分配表↑↑↑B C D偏心弯矩分配系数固端弯矩分配传递→←分配传递←→分配传递→←分配传递←→分配传递→←分配传递←→分配传递→←合计一次二次图弯矩再分配后活载作用下弯矩(KN·m)(四)框架梁弯矩塑性调幅图调幅后活载作用下弯矩图(KN·m)(五)活载作用下梁跨内最大弯矩、梁端剪力和柱轴力1.活载作用下梁跨内最大弯矩本设计计算梁跨内最大弯矩时,采用按简支计算时的梁跨内最大弯矩与计算得的调幅后的梁端弯矩进行叠加得到。
