北京工业大学 信号处理与matlab(自学)大作业
数字信号处理及matlab实现部分作业详解

1、把序列⎪⎩⎪⎨⎧== ,01 ,20 ,1)(其他=n n n x 表示为单位阶跃之和的形式。
解:)2(2)1()( )]2()1([2)1()()1(2)()(---+=---+--=-+=n u n u n u n u n u n u n u n n n x δδ2、判断下列系统线性性、因果性、稳定性。
(a))()(n nx n y =;(b)b n ax n y +=)()(,其中a ,b 为常数;解:(a)线性性:对于两个输入序列)(1n x 和)(2n x ,相应的输出分别为)(1)(1n nx n y =)(2)(2n nx n y =这两个输出的线性组合为)(2)(1)](2)(1)(3n bnx n anx n by n ay n y +=+=这两个输入信号的线性组合产生的输出为)(2)(1)](2)(1[)](2)(1[)(4n bnx n anx n bx n ax n n bx n ax T n y +=+=+=现在)(4)(3n y n y =,所以系统为线性系统;因果性:因为系统只与当前输入有关,所以系统是因果的;稳定性:若)(n x 有界,即∞<≤M n x |)(|,则nM n x n n nx n y ≤≤=|)(||)(||)(|,当∞→n 时,∞→)(n y ,所以不稳定。
(b)线性性:对于两个输入序列)(1n x 和)(2n x ,相应的输出分别为b n ax n y +=)(1)(1bn ax n y +=)(2)(2这两个输出的线性组合为dbn dax cb n cax n dy n cy n y +++=+=)(2)(1)](2)(1)(3这两个输入信号的线性组合产生的输出为b n dax n cax b n dx n cx a n dx n cx T n y ++=++=+=)(2)(1)](2)(1[)](2)(1[)(4现在)(4)(3n y n y ≠,所以系统为非线性系统;因果性:因为系统只与当前输入有关,所以系统是因果的;稳定性:若)(n x 有界,即∞<≤M n x |)(|,则|||||||)(||)(||)(|b M a b n ax b n ax n y +≤+≤+=,即|)(|n y 有界,所以稳定。
数字信号处理课后习题Matlab作业

数字信号处理MATLAB习题数字信号处理MATLAB 习题M1-1 已知1()cos(6)g t t π=,2()cos(14)g t t π=,3()cos(26)g t t π=,以抽样频率10sam f Hz =对上述三个信号进行抽样。
在同一张图上画出1()g t ,2()g t 和3()g t 及抽样点,对所得结果进行讨论。
解:从以上两幅图中均可看出,三个余弦函数的周期虽然不同,但它们抽样后相应抽样点所对应的值都相同。
那么这样还原回原先的函数就变成相同的,实际上是不一样的。
这是抽样频率太小的原因,我们应该增大抽样频率才能真实还原。
如下图:f=50Hz程序代码f=10;t=-0.2:0.001:0.2;g1=cos(6.*pi.*t);g2=cos(14.*pi.*t);g3=cos(26.*pi.*t);k=-0.2:1/f:0.2;h1=cos(6.*pi.*k);h2=cos(14.*pi.*k);h3=cos(26.*pi.*k);% subplot(3,1,1);% plot(k,h1,'r.',t,g1,'r');% xlabel('t');% ylabel('g1(t)');% subplot(3,1,2);% plot(k,h2,'g.',t,g2,'g');% xlabel('t');% ylabel('g2(t)');% subplot(3,1,3);% plot(k,h3,'b.',t,g3,'b');% xlabel('t');% ylabel('g3(t)');plot(t,g1,'r',t,g2,'g',t,g3,'b',k,h1,'r.',k,h2,'g.',k,h3,'b.')xlabel('t');ylabel('g(t)');legend('g1(t)','g2(t)','g3(t)');M2-1 利用DFT的性质,编写一MATLAB程序,计算下列序列的循环卷积。
数字信号处理习题答案及matlab实验详解.pdf

阶跃响应为: y[n] x[n] h[n] x[m]h[n m] h(n m), n m, m 0
m
m0
即 y(0) 0, y(1) 0.25, y(2) 0.5, y(3) 0.75,其余y(n) 1, (n 3)
利用函数 h=impz(b,a,N)和 y=filter(b,a,x)分别绘出冲激和阶跃响应 b=[0,0.25,0.25,0.25,0.25]; a=1; x=ones(1,100); h=impz(b,a,100);y=filter(b,a,x) figure(1) subplot(2,1,1); stem(h,’.’); subplot(2,1,2); plot(y,’.’);
4
解:(1)系统的转移函数是是其单位抽样响应的 Z 变换,因此
H (z)
1 1 z1
1 1 0.3z1
1 1 0.6z1
(1
3 3.8z1 1.08z2 z1)(1 0.3z1)(1 0.6z1)
1
3 1.9
3.8z1 1.08z2 z1 1.08z2 0.18z
3
Z 1
系统的零极点图如下图所示: B=[3,-3.8,1.08]; A=[1,-1.9,1.08,-0.18]; [Z,P,K]=tf2zp(B,A); Zplane(B,A)
5
单位抽样响应:
h(n)
1 2
n1
u
(n
1)
(n)
1
y(n) x(n) * h(n)
2 m1
1 2
m1
e
j (n m)
e
jn
e
jn
e j
1 2 1
2
n
u(n1)
matlab课程设计大作业

matlab课程设计大作业一、教学目标本课程的教学目标是使学生掌握MATLAB基本语法、编程技巧以及MATLAB 在工程计算和数据分析中的应用。
通过本课程的学习,学生将能够熟练使用MATLAB进行简单数学计算、线性方程组求解、函数图像绘制等。
1.掌握MATLAB基本语法和编程结构。
2.了解MATLAB在工程计算和数据分析中的应用。
3.熟悉MATLAB的函数库和工具箱。
4.能够使用MATLAB进行简单数学计算。
5.能够使用MATLAB求解线性方程组。
6.能够使用MATLAB绘制函数图像。
7.能够利用MATLAB进行数据分析和处理。
情感态度价值观目标:1.培养学生对计算机辅助设计的兴趣和认识。
2.培养学生团队合作和自主学习的能力。
二、教学内容本课程的教学内容主要包括MATLAB基本语法、编程技巧以及MATLAB在工程计算和数据分析中的应用。
1.MATLAB基本语法:介绍MATLAB的工作环境、基本数据类型、运算符、编程结构等。
2.MATLAB编程技巧:讲解MATLAB的函数调用、脚本编写、函数文件编写等编程技巧。
3.MATLAB在工程计算中的应用:介绍MATLAB在数值计算、线性方程组求解、图像处理等方面的应用。
4.MATLAB在数据分析中的应用:讲解MATLAB在数据采集、数据分析、数据可视化等方面的应用。
三、教学方法本课程采用讲授法、案例分析法、实验法等多种教学方法相结合的方式进行教学。
1.讲授法:通过讲解MATLAB的基本语法、编程技巧以及应用案例,使学生掌握MATLAB的基本知识和技能。
2.案例分析法:通过分析实际工程案例,使学生了解MATLAB在工程计算和数据分析中的应用。
3.实验法:安排上机实验,使学生在实际操作中巩固所学知识,提高实际编程能力。
四、教学资源本课程的教学资源包括教材、实验设备、多媒体资料等。
1.教材:选用《MATLAB教程》作为主要教材,辅助以相关参考书籍。
2.实验设备:为学生提供计算机实验室,配备有MATLAB软件的计算机。
MATLAB大作业

M A T L A B大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
90问题五:利用MATLAB软件绘制一朵鲜花,实现一定的仿真效果。
提示:二维/三维绘图,对花瓣、花蕊、叶片、花杆等的形状和颜色进行详细设置。
第二类:插值与拟合。
(B级)问题一:有人对汽车进行了一次实验,具体过程是,在行驶过程中先加速,然后再保持匀速行驶一段时间,接着再加速,然后再保持匀速,如此交替。
注意,整个实验过程中从未减速。
在一组时间段50个时间点的速度。
(2)绘制插值图形并标注样本点。
问题二:估算矩形平板各个位置的温度。
已知平板长为5m,宽为3m,平板上3×5栅格点上的温度值为44,25,20,24,30;42,21,20,23,38;25,23,19,27,40。
(1)分别使用最近点插值、线性插值和三次样条插值进行计算。
(2)用杆图标注样本点。
(3)绘制平板温度分布图。
对a,b,c,d的值。
提示:曲线拟合并绘图分析第三类:定积分问题。
(B级)问题一:地球密度随着离中心(r=0)距离的变化而变化,不同半径处的密度如表所示,试估问题二:河道平均流量Q(m3/s)可使用速度和深度的乘积的积分来计算(河道横截面不规则),公式如下。
其中V(x)是离岸x(m)距离处的水速(m/s),H(x)是离岸x距离处的水深(m)。
根据收集到过5(1(2(3(Q,单位是m(1(2(1(2(3)将节点1的力改为方向向上,计算这种改变对H2和V2的影响。
(4)将节点1的力撤销,而在节点1和2处施加1500N的水平外力,求节点3处垂直反作用力(V3)。
(完整版)信号与系统Matlab实验作业

(完整版)信号与系统Matlab实验作业实验一典型连续时间信号和离散时间信号一、实验目的掌握利用Matlab 画图函数和符号函数显示典型连续时间信号波形、典型时间离散信号、连续时间信号在时域中的自变量变换。
二、实验内容1、典型连续信号的波形表示(单边指数信号、复指数信号、抽样信号、单位阶跃信号、单位冲击信号)1)画出教材P28习题1-1(3) ()[(63)(63)]t f t e u t u t =----的波形图。
function y=u(t) y=t>=0; t=-3:0.01:3;f='exp(t)*(u(6-3*t)-u(-6-3*t))'; ezplot(f,t); grid on;2)画出复指数信号()()j t f t e σω+=当0.4, 8σω==(0<t<10)时的实部和虚部的< p="">波形图。
t=0:0.01:10;f1='exp(0.4*t)*cos(8*t)'; f2='exp(0.4*t)*sin(8*t)'; figure(1) ezplot(f1,t); grid on; figure(2) ezplot(f2,t); grid on;t=-10:0.01:10; f='sin(t)/t'; ezplot(f,t); grid on;t=0:0.01:10;f='(sign(t-3)+1)/2'; ezplot(f,t);grid on;5)单位冲击信号可看作是宽度为?,幅度为1/?的矩形脉冲,即t=t 1处的冲击信号为11111()()0 t t t x t t t otherδ??<<+?=-=画出0.2?=, t 1=1的单位冲击信号。
t=0:0.01:2;f='5*(u(t-1)-u(t-1.2))'; ezplot(f,t); grid on;axis([0 2 -1 6]);2、典型离散信号的表示(单位样值序列、单位阶跃序列、实指数序列、正弦序列、复指数序列)编写函数产生下列序列:1)单位脉冲序列,起点n0,终点n f,在n s处有一单位脉冲。
MATLAB大作业题目备选

MATLAB大作业题目备选matlab大作业备选题目1.基于MATLAB的含噪语音信号处理本课题要求基于matlab对有噪音语音信号进行处理,综合运用数字信号处理的理论知识对加噪语音信号进行时域、频域分析和滤波,利用matlab作为工具进行计算机实现。
在设计实现的过程中,要求使用双线性变换法设计iir数字滤波器,对模拟加噪语音信号进行低通滤波、高通滤波及带通滤波,并利用matlab作为辅助工具完成设计中的计算与图形的绘制。
2.基于MATLAB的学生平均学分和分数计算软件设计学分与绩点,是每位大学生所关心的重要指标之一,很多同学辛苦学习,早出晚归,不断的奔波于教室、图书馆、食堂、寝室之间,为的就是能够考个好成绩,取得好的绩点。
然而在平时我们计算学分与绩点的时候,大都只能用计算器一个一个数据的输入,其过程繁琐麻烦,又容易出错。
因此,本课题要求利用MATLAB知识实现平均学分和分数的计算,并开发相应的人机界面。
3、基于matlab的试卷分析管理系统本设计要求采用基于MATLAB图形用户界面的编程方法,并涉及相关数据库知识。
要求通过一个简单的用户交互界面,实现试卷的录入、查询、修改和整体分析功能。
目的是学习使用matlab编程,尤其是掌握matlab中的GUI,加深对matlab的理解,并学会使用matlab实现实际应用。
4、基于matlab的图像处理软件设计学习Matlab GUI程序设计,使用Matlab图像处理工具箱设计并实现一个简单的图像处理软件,实现以下功能:1)图像读取和保存。
2)设计一个图形用户界面,使用户可以任意调整图像的亮度和对比度,并显示和比较变换前后的图像。
3)设计一个图形用户界面,让用户可以用鼠标选择图像的感兴趣区域,显示并保存所选区域。
4)编写一个程序,通过最近邻插值和双线性插值等算法,将用户选择的图像区域放大缩小整数倍,保存并比较几种插值的效果。
5)对于图像直方图统计和直方图均衡化,需要显示直方图统计并比较直方图均衡化的效果。
MATLAB大作业

MATLAB在数字信号处理中的应用1、计算系统的频率响应已知系统的差分方程y(n)-y(n-1)+y(n-2)=x(n)+2x(n-1),试画出系统的幅度响应曲线和相位响应曲线。
程序:b=[1,2];a=[1,-1,1];N=128;%设定点数[H,w] = freqz(b,a,N,'whole');%计算频率响应magH = abs(H(1:N));%计算幅度phaH = angle(H(1:N));%计算相位w = w(1:N);subplot(2,1,1);plot(w/pi,magH);%画幅度响应曲线grid;ylabel('Magnitude');title('Magnitude Response');subplot(2,1,2);plot(w/pi,phaH);%画相位响应曲线grid;xlabel('Frequency Unit:pi');ylabel('Phase'); title('Phase Response');运行结果:2、实现周期序列傅里叶级数设3{)(≤≤=nnnx其他,将x(n)以N=5为周期进行周期延拓,得到周期为5的周期序列)~(nx,求)~(nx的离散傅里叶级数。
程序:xn=[0,1,2,3,0];%设定序列N=5;%设定周期n=[0:1:N-1];%设定nk=[0:1:N-1];WN=exp(-j*2*pi/N);%设定WN因子nk=n'*k;WNnk=WN.^nk;%计算W矩阵Xk=xn*WNnk;%计算DFS的系数Xkdisp(xn);disp(Xk);运行结果:0 1 2 3 06.0000 -3.7361 - 0.3633i 0.7361 - 1.5388i 0.7361 + 1.5388i -3.7361 + 0.3633i3、用DFT计算线性卷积x(n)=R4(n),求:(1)用conv函数求x(n)与x(n)的线性卷积y(n),并绘出图形;(2)用FFT求x(n)与x(n)的4点循环卷积y1(n);并绘出图形;程序:N=4;n= 0:1:N-1;x=[1,1,1,1];subplot(2,2,1);stem(n,x);title('序列x(n)');subplot(2,2,2);stem(0:1:length(y1)-1,y1),grid on;title('x(n)与x(n)的线性卷积');X2=fft(x);Y2=X2.*X2;y2=ifft(Y2);subplot(2,2,3);stem(n,y2);title('x(n)与x(n)的4点循环卷积');运行结果:。
北工大matlab作业实验报告

北工大MATLAB实验报告完成日期:2018.12目录实验一用FFT进行谱分析 (3)一、实验内容 (3)二、实验过程 (3)三、实验代码 (4)四、实验结果及分析 (5)五、实验心得 (5)实验二噪声数据的抑制 (6)一、实验内容 (6)二、实验过程 (7)三、实验结果分析 (14)四、实验心得 (15)参考文献 (15)实验一用FFT进行谱分析一、实验内容FFT的用途之一是找出隐藏或淹没在噪声时域信号中信号的频率成分。
本题要求用FFT 对试验数据进行谱分析,指出数据包含的频率成份。
提示:首先建立试验数据。
过程推荐如下:生成一个包含两个频率成分的试验信号,对这个信号加入随机噪声,形成一个加噪信号y。
(试验数据参数推荐为:数据采样频率为1000Hz,时间区间从t=0到t=0.25,步长0.001秒,噪声的标准偏差为2,两个频率成分的试验信号可取50Hz和120Hz)。
(1)绘制加噪信号y它的波形。
(2)求出含噪声信号y的离散傅立叶变换(取它的FFT),(FFT试验参数推荐为:256点)。
(3)求出信号的功率谱密度(它是不同频率所含能量的度量),并绘制功率谱图,标记出两个频谱峰值对应的频率分量。
二、实验过程1.打开matlab软件,根据实验要求,用已知条件求出重要参数:N=256;n=0:N-1;t=n/fs;2.绘制加入了噪声信号的y图象:y=sin(2*pi*50*t)+sin(2*pi*120*t)+2*randn(size(t));subplot(2,2,1);plot(y);title('y的波形');3.对y求付里叶变换:Y=fft(y,N);4.绘制Y的幅值图象:fudu=abs(Y);f=n*fs/N;subplot(2,2,2)plot(f,fudu);5.抽取256点进行绘图:subplot(2,2,3)plot(f(1:N/2),fudu(1:N/2));6.利用y的自相关函数求出y的功率谱,并绘图:y2=xcorr(y,'unbiased');y2p=fft(y2,N);yk=abs(y2p);subplot(2,2,4)plot(f(1:N/2),yk(1:N/2));title('功率谱')三、实验代码N=256;n=0:N-1;t=n/fs;y=sin(2*pi*50*t)+sin(2*pi*120*t)+2*randn(size(t)); subplot(2,2,1);plot(y);title('y的波形');Y=fft(y,N);fudu=abs(Y);f=n*fs/N;subplot(2,2,2)plot(f,fudu)subplot(2,2,3)plot(f(1:N/2),fudu(1:N/2));y2=xcorr(y,'unbiased');y2p=fft(y2,N);yk=abs(y2p);subplot(2,2,4)plot(f(1:N/2),yk(1:N/2));title('功率谱')四、实验结果及分析结果分析:功率谱的两个峰值对应的频率分别为:f=50Hz和120Hz五、实验心得学习了一个学期的MATLAB,现在终于能够进行一次实践了。
数字信处理课后习题matlab作业

数字信号处理MATLAB习题数字信号处理MATLAB 习题M1-1 已知1()cos(6)g t t π=,2()cos(14)g t t π=,3()cos(26)g t t π=,以抽样频率10sam f Hz =对上述三个信号进行抽样。
在同一张图上画出1()g t ,2()g t 和3()g t 及抽样点,对所得结果进行讨论。
解:从以上两幅图中均可看出,三个余弦函数的周期虽然不同,但它们抽样后相应抽样点所对应的值都相同。
那么这样还原回原先的函数就变成相同的,实际上是不一样的。
这是抽样频率太小的原因,我们应该增大抽样频率才能真实还原。
如下图:f=50Hz程序代码f=10;t=-0.2:0.001:0.2;g1=cos(6.*pi.*t);g2=cos(14.*pi.*t);g3=cos(26.*pi.*t);k=-0.2:1/f:0.2;h1=cos(6.*pi.*k);h2=cos(14.*pi.*k);h3=cos(26.*pi.*k);% subplot(3,1,1);% plot(k,h1,'r.',t,g1,'r');% xlabel('t');% ylabel('g1(t)');% subplot(3,1,2);% plot(k,h2,'g.',t,g2,'g');% xlabel('t');% ylabel('g2(t)');% subplot(3,1,3);% plot(k,h3,'b.',t,g3,'b');% xlabel('t');% ylabel('g3(t)');plot(t,g1,'r',t,g2,'g',t,g3,'b',k,h1,'r.',k,h2,'g.',k,h3,'b.')xlabel('t');ylabel('g(t)');legend('g1(t)','g2(t)','g3(t)');M2-1 利用DFT的性质,编写一MATLAB程序,计算下列序列的循环卷积。
matlab综合大作业(附详细答案)

m a t l a b综合大作业(附详细答案)-标准化文件发布号:(9456-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《MATLAB语言及应用》期末大作业报告1.数组的创建和访问(20分,每小题2分):1)利用randn函数生成均值为1,方差为4的5*5矩阵A;实验程序:A=1+sqrt(4)*randn(5)实验结果:A =0.1349 3.3818 0.6266 1.2279 1.5888-2.3312 3.3783 2.4516 3.1335 -1.67241.2507 0.9247 -0.1766 1.11862.42861.5754 1.6546 5.3664 0.8087 4.2471-1.2929 1.3493 0.7272 -0.6647 -0.38362)将矩阵A按列拉长得到矩阵B;实验程序:B=A(:)实验结果:B =0.1349-2.33121.25071.5754-1.29293.38183.37830.92471.65461.34930.62662.4516-0.17665.36640.72721.22793.13351.11860.8087-0.66471.5888-1.67242.42864.2471-0.38363)提取矩阵A的第2行、第3行、第2列和第4列元素组成2*2的矩阵C;实验程序:C=[A(2,2),A(2,4);A(3,2),A(3,4)]实验结果:C =3.3783 3.13350.9247 1.11864)寻找矩阵A中大于0的元素;]实验程序:G=A(find(A>0))实验结果:G =0.13491.25071.57543.38183.37830.92471.65461.34930.62662.45165.36640.72721.22793.13351.11860.80871.58882.42864.24715)求矩阵A的转置矩阵D;实验程序:D=A'实验结果:D =0.1349 -2.3312 1.2507 1.5754 -1.29293.3818 3.3783 0.9247 1.6546 1.34930.6266 2.4516 -0.1766 5.3664 0.72721.2279 3.1335 1.1186 0.8087 -0.66471.5888 -1.67242.4286 4.2471 -0.38366)对矩阵A进行上下对称交换后进行左右对称交换得到矩阵E;实验程序:E=flipud(fliplr(A))实验结果:E =-0.3836 -0.6647 0.7272 1.3493 -1.29294.2471 0.80875.3664 1.6546 1.57542.4286 1.1186 -0.1766 0.9247 1.2507-1.6724 3.1335 2.4516 3.3783 -2.33121.5888 1.2279 0.6266 3.3818 0.13497)删除矩阵A的第2列和第4列得到矩阵F;实验程序:F=A;F(:,[2,4])=[]实验结果:F =0.1349 0.6266 1.5888-2.3312 2.4516 -1.67241.2507 -0.17662.42861.5754 5.3664 4.2471-1.2929 0.7272 -0.38368)求矩阵A的特征值和特征向量;实验程序:[Av,Ad]=eig(A)实验结果:特征向量Av =-0.4777 0.1090 + 0.3829i 0.1090 - 0.3829i -0.7900 -0.2579 -0.5651 -0.5944 -0.5944 -0.3439 -0.1272-0.2862 0.2779 + 0.0196i 0.2779 - 0.0196i -0.0612 -0.5682 -0.6087 0.5042 - 0.2283i 0.5042 + 0.2283i 0.0343 0.6786 0.0080 -0.1028 + 0.3059i -0.1028 - 0.3059i 0.5026 0.3660 特征值Ad =6.0481 0 0 0 00 -0.2877 + 3.4850i 0 0 00 0 -0.2877 - 3.4850i 0 00 0 0 0.5915 00 0 0 0 -2.30249)求矩阵A的每一列的和值;实验程序:lieSUM=sum(A)实验结果:lieSUM =-0.6632 10.6888 8.9951 5.6240 6.208710)求矩阵A的每一列的平均值;实验程序:average=mean(A)实验结果:average =-0.1326 2.1378 1.7990 1.1248 1.24172.符号计算(10分,每小题5分):1)求方程组20,0++=++=关于,y z的解;uy vz w y z w实验程序:S = solve('u*y^2 + v*z+w=0', 'y+z+w=0','y,z');y= S. y, z=S. z实验结果:y =[ -1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))-w] [ -1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))-w] z =[ 1/2/u*(-2*u*w-v+(4*u*w*v+v^2-4*u*w)^(1/2))] [ 1/2/u*(-2*u*w-v-(4*u*w*v+v^2-4*u*w)^(1/2))]2)利用dsolve 求解偏微分方程,dx dyy x dt dt==-的解; 实验程序:[x,y]=dsolve('Dx=y','Dy=-x')实验结果:x =-C1*cos(t)+C2*sin(t)y = C1*sin(t)+C2*cos(t)3.数据和函数的可视化(20分,每小题5分):1)二维图形绘制:绘制方程2222125x y a a +=-表示的一组椭圆,其中0.5:0.5:4.5a =;实验程序:t=0:0.01*pi:2*pi; for a=0.5:0.5:4.5; x=a*cos(t); y=sqrt(25-a^2)*sin(t); plot(x,y) hold on end实验结果:2) 利用plotyy 指令在同一张图上绘制sin y x =和10x y =在[0,4]x ∈上的曲线;实验程序:x=0:0.1:4; y1=sin(x); y2=10.^x;[ax,h1,h2]=plotyy(x,y1,x,y2); set(h1,'LineStyle','.','color','r'); set(h2,'LineStyle','-','color','g'); legend([h1,h2],{'y=sinx';'y=10^x'});实验结果:3)用曲面图表示函数22z x y =+;实验程序:x=-3:0.1:3; y=-3:0.1:3; [X,Y]=meshgrid(x,y); Z=X.^2+Y.^2; surf(X,Y,Z)实验结果:4)用stem 函数绘制对函数cos 4y t π=的采样序列;实验程序:t=-8:0.1:8;y=cos(pi.*t/4); stem(y)实验结果:4. 设采样频率为Fs = 1000 Hz ,已知原始信号为)150π2sin(2)80π2sin(t t x ⨯+⨯=,由于某一原因,原始信号被白噪声污染,实际获得的信号为))((ˆt size randn x x+=,要求设计出一个FIR 滤波器恢复出原始信号。
信号与系统matlab作业
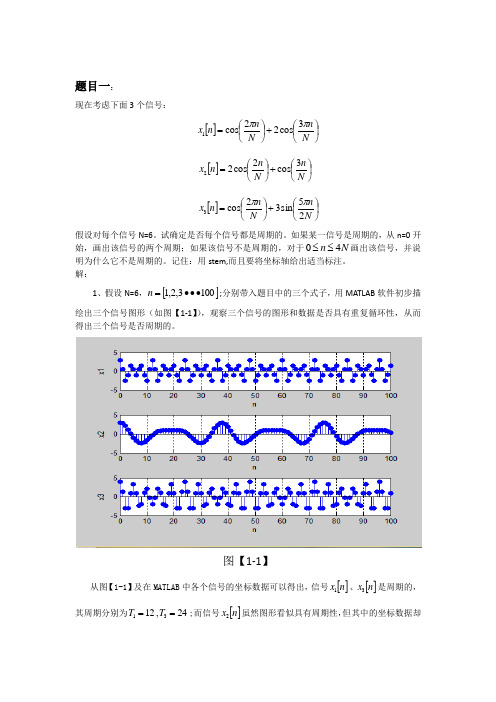
题目一:现在考虑下面3个信号:[]⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=N n N n n x ππ3cos 22cos 1 []⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=N n N n n x 3cos 2cos 22 []⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=N n N n n x 25sin 32cos 3ππ 假设对每个信号N=6。
试确定是否每个信号都是周期的。
如果某一信号是周期的,从n=0开始,画出该信号的两个周期;如果该信号不是周期的,对于N n 40≤≤画出该信号,并说明为什么它不是周期的。
记住:用stem,而且要将坐标轴给出适当标注。
解:1、假设N=6,[]1003,2,1•••=n ;分别带入题目中的三个式子,用MATLAB 软件初步描绘出三个信号图形(如图【1-1】),观察三个信号的图形和数据是否具有重复循环性,从而得出三个信号是否周期的。
图【1-1】从图【1-1】及在MATLAB 中各个信号的坐标数据可以得出,信号[]n x 1、[]n x 3是周期的,其周期分别为24,1231==T T ;而信号[]n x 2虽然图形看似具有周期性,但其中的坐标数据却不是循环重复的,即该信号[]n x 2不是周期的。
图【1-1】的MATLAB 程序:Clc ,clearN=6;for n=0:100x1(n+1)=cos(2*pi*n./N)+2*cos(3*pi*n./N);x2(n+1)=2*cos(2*n./N)+cos(3*n./N);x3(n+1)=cos(2*pi*n./N)+3*cos(5*pi*n./(2*N));endn=0:100;subplot(3,1,1)stem(n,x1,'fill')grid;xlabel('n')ylabel('x1')subplot(3,1,2)stem(n,x2,'fill')grid;xlabel('n')ylabel('x2')subplot(3,1,3)stem(n,x3,'fill')grid;xlabel('n')ylabel('x3')2、上面得出了各个信号是否具有周期性,即按照要求用MATLAB 对各个信号进行图像处理:(1)对信号[][]n x n x 21, 得出各自两个周期的波形图像,如图【1-2】:图【1-2】图【1-2】的MATLAB 程序:clc,clearN=6;for n1=0:24x1(n1+1)=cos(2*pi*n1./N)+2*cos(3*pi*n1./N);endn1=0:24;for n3=0:48x3(n3+1)=cos(2*pi*n3./N)+3*cos(5*pi*n3./(2*N));endn3=0:48;subplot(2,1,1)stem(n1,x1,'fill')grid;xlabel('n')ylabel('x1')subplot(2,1,2)stem(n3,x3,'fill')grid;xlabel('n')ylabel('x3')(2)对信号[]n x 2,当N n 40≤≤时用MATLAB 画出该信号的波形图像,如图【1-3】:图【1-3】图【1-3】的MATLAB 程序:clc,clearN=6;for n2=0:1:4*Nx2(n2+1)=2*cos(2*n2./N)+cos(3*n2./N);endn2=0:1:4*N;stem(n2,x2,'fill')grid;xlabel('n')ylabel('X2')因为一个周期信号在形状上的每一个特点都必须周期性地重现;而在图【1-3】上来说,离散信号[]n x 2在对N n 40≤≤中,并没有满足周期信号的条件:[]N n x n x +=][(其中N 指周期)所以,离散信号[]n x 2不是周期信号。
matlab数字信号处理作业

Matlab 数字信号处理实验第1次作业院系:理学院2010级电子信息科学与技术学号:2010142112姓名:李家宁1、 阅读例子程序,观察输出波形,理解每条语句的含义。
程序1:clear all;close all;clc;%清除原所有变量,关闭窗口,对命令窗口请屏n=0:9;x=(0.8).^n;%设定函数nx 8.0X=fft(x,4096);%将信号做FFT 运算Xk1=DFT(n,x,10);Xk2=DFT(n,x,20);%分别将学x(n)做 DTT 运算subplot(211),plot((0:4095)/4095*10,abs(X));%画图排列hold on;%前轴及图形保持而不被刷新stem(0:9,abs(Xk1),'LineWidth',2);%画火柴柱形legend('x(n)的幅频特性','x(n)的10点DFT 的幅度');%画Xk1的频谱、幅度谱 xlabel('k');axis([-1 11 -1 5]);grid;%横坐标的位置subplot(212),plot((0:4095)/4095*20,abs(X));hold on; 画图排列stem(0:19,abs(Xk2),'LineWidth',2); %画火柴柱形legend('x(n)的幅频特性','x(n)的20点DFT 的幅度'); %画Xk1的频谱、幅度谱 xlabel('k');axis([-1 21 -1 5]);grid; %横坐标的位置set(gcf,'color','w');%颜色设定程序2:xn=[0,1,2,3,4,5,6,7];%设定n 的取值N=length(xn);%将N 设定为n 取值总长度n=0:N-1;k=0:N-1;%设定n 的变化范围Xk=xn*exp(-j*2*pi/N).^(n'*k); %离散傅里叶变换x=(Xk*exp(j*2*pi/N).^(n'*k))/N; %离散傅里叶逆变换subplot(2,2,1),stem(n,xn,'k');%画x(n)的频谱图形title('x(n)');axis([-1,N,1.1*min(xn),1.1*max(xn)]);%设定标题和横坐标的取值subplot(2,2,2),stem(n,abs(x),'k'); %显示逆变换结果title('IDFT|X(k)|');%将幅度谱命名axis([-1,N,1.1*min(x),1.1*max(x)]);%设定横坐标的范围subplot(2,2,3),stem(k,abs(Xk),'k'); %显示序列的幅度谱title('|X(k)|'); %将幅度谱命名axis([-1,N,1.1*min(abs(Xk)),1.1*max(abs(Xk))]); 设定纵坐标的范围subplot(2,2,4),stem(k,angle(Xk),'k');%显示序列的相位谱title('arg|X(k)|'); 将相位谱命名axis([-1,N,1.1*min(angle(Xk)),1.1*max(angle(Xk))]); 将相位谱横坐标范围程序3:xn=[0,1,2,3,4,5,6,7]; %设定n的取值N=length(xn); %将N设定为n取值总长度n=0:4*N-1;k=0:4*N-1; %设定n的变化范围xn1=xn(mod(n,N)+1);%xn1=[xn,xn,xn,xn];Xk=xn1*exp(-j*2*pi/N).^(n'*k); %离散傅里叶变换subplot(2,2,1),stem(xn,'k'); %显示序列主值title('原主值信号x(n)'); %将原信号命名subplot(2,2,2),stem(n,xn1,'k'); %显示周期序列title('周期序列信号'); %将周期号命名axis([-1,4*N,1.1*min(xn1),1.1*max(xn1)]);设定横坐标的范围subplot(2,2,3),stem(k,abs(Xk),'k'); %显示序列的幅度谱title('|X(k)|'); %将幅度谱命名axis([-1,4*N,1.1*min(abs(Xk)),1.1*max(abs(Xk))]);设定纵坐标的范围subplot(2,2,4),stem(k,angle(Xk),'k');%显示序列的相位谱title('arg|X(k)|'); %将相位谱命名axis([-1,4*N,1.1*min(angle(Xk)),1.1*max(angle(Xk))]);设定纵坐标的范围程序4:xn=[0,1,2,3,4,5,6,7]; %设定n的取值N=length(xn); %将N设定为n取值总长度n=0:N-1; %设定n的变化范围w=linspace(-2*pi,2*pi,500);%将[-2π,2π]区间分割为500份X=xn*exp(-j*n'*w); %离散时间傅里叶变换subplot(3,1,1),stem(n,xn,'k'); %画图排列ylabel('x(n)');%将纵轴命名subplot(3,1,2),plot(w,abs(X),'k'); %显示序列的幅度谱axis([-2*pi,2*pi,1.1*min(abs(X)),1.1*max(abs(X))]);设定纵坐标的范围ylabel('幅度谱');subplot(3,1,3),plot(w,angle(X),'k');%显示序列的相位谱axis([-2*pi,2*pi,1.1*min(angle(X)),1.1*max(angle(X))]);设定纵坐标的范围ylabel('相位谱');程序5:N=100;%设置周期xn=[0,1,2,3,4,5,6,7,zeros(1,N-8)];%设置信号n=0:N-1;k=0:N-1; %设定n的变化范围Xk=xn*exp(-j*2*pi/N).^(n'*k); %离散傅里叶变换x=(Xk*exp(j*2*pi/N).^(n'*k))/N; %离散傅里叶逆变换subplot(2,2,1),stem(n,xn,'k'); %画图排列title('x(n)');axis([0,N,1.1*min(xn),1.1*max(xn)]);设定纵坐标的范围subplot(2,2,2),stem(n,abs(x),'k'); %显示逆变换结果title('IDFT|X(k)|'); %将逆变换命名axis([0,N,1.1*min(x),1.1*max(x)]);设定纵坐标的范围subplot(2,2,3),stem(k,abs(Xk),'k'); %显示序列的幅度谱title('|X(k)|');axis([0,N,1.1*min(abs(Xk)),1.1*max(abs(Xk))]);subplot(2,2,4),stem(k,angle(Xk),'k');%显示序列的相位谱title('arg[X(k)]');axis([0,N,1.1*min(angle(Xk)),1.1*max(angle(Xk))]);2、已知有限长序列x(n)=[7,6,5,4,3,2],求DFT和IDFT,要求:画出序列傅立叶变换对应的幅度谱和相位谱;画出原信号与傅立叶逆变换IDFT[X(k)]的图形进行比较。
matlab大作业Matlab在数字信号处理及图像处理中的应用
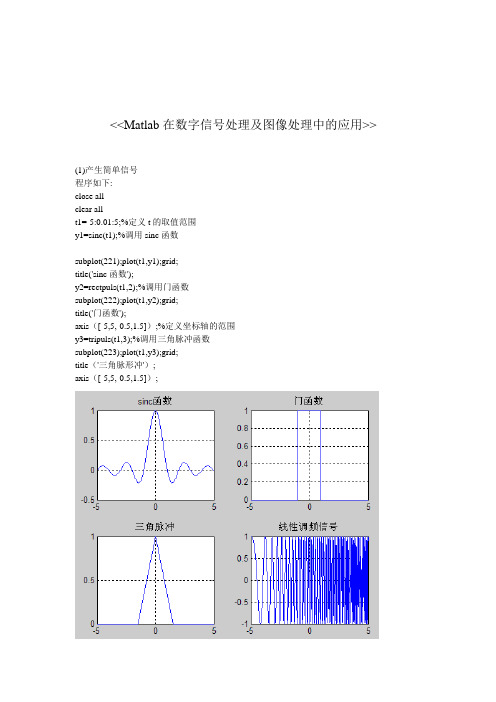
<<Matlab在数字信号处理及图像处理中的应用>>(1)产生简单信号程序如下:close allclear allt1=-5:0.01:5;%定义t的取值范围y1=sinc(t1);%调用sinc函数subplot(221);plot(t1,y1);grid;title('sinc函数');y2=rectpuls(t1,2);%调用门函数subplot(222);plot(t1,y2);grid;title('门函数');axis([-5,5,-0.5,1.5]);%定义坐标轴的范围y3=tripuls(t1,3);%调用三角脉冲函数subplot(223);plot(t1,y3);grid;title('三角脉形冲');axis([-5,5,-0.5,1.5]);(2)求模型的零输入响应⎥⎥⎦⎤⎢⎢⎣⎡∙∙21x x =⎥⎦⎤⎢⎣⎡--7814.005572.07814.0⎦⎤⎢⎣⎡12x x +⎥⎦⎤⎢⎣⎡-0210⎥⎦⎤⎢⎣⎡12u u Y=[1.9691 6.4493]⎥⎦⎤⎢⎣⎡12x x ,初始条件为x(0)=⎥⎦⎤⎢⎣⎡01程序如下a=[-0.5572 -0.7814;0.7814 0];c=[1.969 6.4493];x0=[1 ; 0]%初始状态x0 =1sys=ss(a,[],c,[]);%状态方程initial(sys,x0)(3)滤波器设计1.设计一个butterworth 数字低通滤波器,抽样频率为1000HZ ,滤波器的3db 截至频率为40HZ ,阻带截止频率为150HZ ,阻带最小衰减为60db.绘制该滤波器的频率响应曲线。
程序如下:Wp=40/500;%通带截止频率Ws=150/500;%阻带截止频率[n,Wn]=buttord(Wp,Ws,3,60)%求butterworth滤波器的阶数和3db带宽的截止频率[b,a]=butter(n,Wn);%调用butter函数设计模拟滤波器freqz(b,a,512,1000);%画频率响应图title('巴特沃斯滤波器')2.设计一个chebysheI数字低通滤波器,抽样频率为1000HZ,滤波器的3db截至频率为40HZ,阻带截止频率为150HZ,阻带最小衰减为60db.绘制该滤波器的频率响应曲线。
数字信号处理matlab作业

fs=10;ts=1/fs;n=-2:ts:2;f=cos(6*pi*n);subplot(3,1,1),stem(n,f,'filled'); g=cos(14*pi*n);subplot(3,1,2),stem(n,g,'filled'); h=cos(26*pi*n);subplot(3,1,3),stem(n,h,'filled');fs=10;ts=1/fs;n=-2:ts:2;f=cos(1*pi*n);subplot(3,1,1),stem(n,f,'filled'); g=cos(14*pi*n);subplot(3,1,2),stem(n,g,'filled'); h=cos(2600000*pi*n); subplot(3,1,3),stem(n,h,'filled');(1) x=[1 -3 4 2 0 -2 ];h=[3 0 1 -1 2 1]; L=length(x)+length(h)-1;XE=fft(x,L);HE=fft(h,L);y1=ifft(XE.*HE);y=[1 0 -1 0 1 0];g=[1 3 9 27 81 243] M=length(y)+length(g)-1;YE=fft(y,M);GE=fft(g,M);y2=ifft(YE.*GE);a=0:L-1;subplot(2,1,1);stem(a,real(y1));b=0:M-1;subplot(2,1,2);stem(b,real(y2));M2-2N=10;k=0:N-1;f=cos(pi*k/20);F=fft(f);plot(k/10,abs(F),'o');hold onset(gca,'xtick',[0,0.25,0.5,0.75,1]); set(gca,'ytick',[0,2,4,6,8]);grid onhold offM2-3N=input('lenth of signal:N=');M=input('points of DFT:M=');k = 0:N-1;f = cos(2*pi*100*k/600)+cos(2*pi*150*k/600); %0.15* w=hamming(length(f));f=f*w; %加hamming窗F= fft(f, M);L = 0:(M-1);plot(L/M,abs(F))grid on;xlabel('Normalized frequency');ylabel('Magnitude');M2-4M=4;N=64;n=-(N-1)/2:(N-1)/2;x=cos(2*pi*n/15)+0.75*cos(2.3*pi*n/15);X=fft(x,N);subplot(2,1,1);stem(n,fftshift(x));ylabel('x[n]');xlabel('Time n');subplot(2,1,2);stem(omega,real(fftshift(X)));ylabel('X[k]');xlabel('Frequency(rad)');hold;M2-5w=linspace(0,10,1024);plot(w,2./(w.^2+1));% sampling points and frequency(rad/s)N=input('抽样点数=');Ws=input('抽样角频率=');Ts=2*pi/Ws;%compute the sampling pointsk=0:N/2;t=k*Ts;f1=exp(-3*t);f1(N/2+1)=2*f1(N/2+1);f2=f1(2:N/2);f=[f1 fliplr(f2)];F=Ts*real(fft(f));w=k*Ws/N;w1=linspace(0,Ws/2,512);plot(w1,2./(w1.^2+1),w,F(1:N/2+1),'r');axis([0 10 0 2.2]);xlabel('频率(秒/弧度)');ylabel('幅度');z=['N=' num2str(N) ' Ws=' num2str(Ws) '的结果']; legend('理论值',z);title('exp(-|t|)的谱');M4-1wp=10;ws=2;Ap=1;As=40;[N,Wc]=cheb1ord(wp,ws,Ap,As,'s'); [num,den]=cheby1(N,Ap,Wc,'s'); disp('LP 分子多项式');fprintf('%.4e\n',num);disp('LP 分母多项式');fprintf('%.4e\n',den);[numt,dent]=lp2hp(num,den,1);disp('HP 分子多项式');fprintf('%.4e\n',numt);disp('LP 分母多项式');fprintf('%.4e\n',dent);M4-2wp=1;ws=3.3182;Ap=1;As=32;w0=sqrt(48);B=2;[N,Wc]=buttord(wp,ws,Ap,As,'s'); [num,den]=butter(N,Wc,'s'); [numt,dent]=lp2bp(num,den,w0,B); w=linspace(2,12,1000);h=freqs(numt,dent,w);plot(w,20*log10(abs(h)));grid;xlabel('Frequency in rad/s'); ylabel('Gain in dB');M4-3wp=1;ws=3.3182;Ap=1;As=32;w0=sqrt(48);B=2;[N,Wc]=ellipord(wp,ws,Ap,As,'s'); [num,den]=ellip(N,Ap,As,Wc,'s'); [numt,dent]=lp2bp(num,den,w0,B); w=linspace(2,12,1000);h=freqs(numt,dent,w);plot(w,20*log10(abs(h)));grid; xlabel('Frequency in rad/s'); ylabel('Gain in dB');M4-4Ap=1;As=10;wp1=6;wp2=13;ws1=9;ws2=11;B=ws2-ws1;w0=sqrt(ws1*ws2);wLp1=B*wp1/(w0*w0-wp1*wp1);wLp2=B*wp2/(w0*w0-wp2*wp2);wLp=max(abs(wLp1),abs(wLp2));[N,wc]=ellipord(wp,ws,Ap,As,'s'); [num,den]=ellip(N,Ap,As,Wc,'s');[numt,dent]=lp2bs(num,den,w0,B);w=linspace(5,35,1000);h=freqs(numt,dent,w);plot(w,20*log10(abs(h)));w=[wp1 ws1 ws2 wp2];set(gca,'xtick',w);grid;h=freqs(numt,dent,w);grid;h=freqs(numt,dent,w);A=-20*log10(abs(h))M4-5Wp=0.1*pi;Ws=0.4*pi;Ap=1;As=25;Fs=1;wp=Wp*Fs;ws=Ws*Fs;N=cheb2ord(wp,ws,Ap,As,'s');wc=wp/(10^(0.1*Ap)-1)^(1/2/N);[numa,dena]=cheby2(N,As,wc,'s');[numd,dend]=impinvar(numa,dena,Fs);w=linspace(0,pi,512);h=freqz(numd,dend,w);norm=max(abs(h));numd=numd/norm;plot(w*pi,20*log10(abs(h)/norm))w=[Wp Ws]h=freqz(numd,dend,w);fprintf('Ap=%.4f\n',-20*log10(abs(h(1))));fprintf('Ap=%.4f\n',-20*log10(abs(h(2))));M4-6M4-7Wp=0.2*pi;Ws=0.4*pi;Ap=1;As=15;Fs=1;wp=Wp*Fs;ws=Ws*Fs;N=cheb1ord(wp,ws,Ap,As,'s');wc=wp/(10^(0.1*Ap)-1)^(1/2/N);[numa,dena]=cheby1(N,Ap,wc,'s');[numd,dend]=impinvar(numa,dena,Fs);w=linspace(0,pi,512);h=freqz(numd,dend,w);norm=max(abs(h));numd=numd/norm;plot(w*pi,20*log10(abs(h)/norm))w=[Wp Ws]h=freqz(numd,dend,w);fprintf('Ap=%.4f\n',-20*log10(abs(h(1))));fprintf('Ap=%.4f\n',-20*log10(abs(h(2))));M4-8Wp=4*pi/44.1;Ws=20*pi/44.1;Ap=0.5;As=50; Fs=44100;wp=Wp*Fs;ws=Ws*Fs;N=buttord(wp,ws,Ap,As,'s');wc=wp/(10^(0.1*Ap)-1)^(1/N/2);[numa,dena]=butter(N,wc,'s');[numd,dend]=impinvar(numa,dena,Fs);w=linspace(0,pi,1024);h=freqz(numd,dend,w);norm=max(abs(h));numd=numd/norm;plot(w/pi,20*log10(abs(h/norm)));xlabel('f');ylabel('Gain');w=[Wp Ws];h=freqz(numd,dend,w);fprintf('Ap=%.4f\n',-20*log10(abs(h(1))));fprintf('As=%.4f\n',-20*log10(abs(h(2))));Wp=4*pi/44.1;Ws=20*pi/44.1;Ap=0.5;As=50;T=2;Fs=1/T;wp=2*tan(Wp/2)/T;ws=2*tan(Ws/2)/T;[N,wc]=buttord(wp,ws,Ap,As,'s');wc=wp/(10^(0.1*Ap)-1)^(1/N/2);[numa,dena]=butter(N,wc,'s');[numd,dend]=bilinear(numa,dena,Fs);w=linspace(0,pi,1024);h=freqz(numd,dend,w);plot(w/pi,20*log10(abs(h)));axis([0 1 -50 0]);xlabel('f');ylabel('Gain');w=[Wp Ws];h=freqz(numd,dend,w);fprintf('Ap=%.4f\n',-20*log10(abs(h(1))));fprintf('As=%.4f\n',-20*log10(abs(h(2))));M4-9Wp=0.8*pi;Ws=0.6*pi;Ap=0.5;As=30;T=2;Fs=1/T;wp=2*tan(Wp/2)/T;ws=2*tan(Ws/2)/T;[N,wc]=buttord(wp,ws,Ap,As,'s');wc=wp/(10^(0.1*Ap)-1)^(1/N/2);[numa,dena]=butter(N,wc,'s');[numt,dent]=lp2hp(numa,dena,1);[numd,dend]=bilinear(numt,dent,Fs);w=linspace(0,pi,1024);h=freqz(numd,dend,w);plot(w/pi,20*log10(abs(h)));axis([0 1 -50 0]);xlabel('f');ylabel('Gain');w=[Wp Ws];h=freqz(numd,dend,w);fprintf('Ap=%.4f\n',-20*log10(abs(h(1)))); fprintf('As=%.4f\n',-20*log10(abs(h(2))));M5-1function FIR_LPclearclcwp=0.2*pi;ws=0.3*pi;tr_width=ws-wp;N=ceil(6.6*pi/tr_width)+1;n=[0:1:N-1];wc=(ws+wp)/2;%理想LPF截止频hd=ideal_lp(wc,N);%理想低通滤波器计算,hd=0-(N-1)之间的理想脉冲响应,wc=截止频率(弧度),N=理想滤波器的长度wd1=hanning(N)';b1=hd.*wd1;wd2=hamming(N)';b2=hd.*wd2;wd3=blackman(N)';b3=hd.*wd3;wd4=kaiser(N)';b4=hd.*wd4;[db1,mag1,pha1,w]=freqz_m(b1,1);%汉宁窗delta_w=2*pi/1000;rp1=-(min(db1(1:1:wp/delta_w+1)));%实际带通波动rp1as1=-round(max(db1(ws/delta_w+1:1:501)));%最小带阻衰减as1[db2,mag2,pha2,w]=freqz_m(b2,1);%海明窗delta_w=2*pi/1000;rp2=-(min(db2(1:1:wp/delta_w+1)));%实际带通波动rp2as2=-round(max(db2(ws/delta_w+1:1:501)));%最小带阻衰减as2[db3,mag3,pha3,w]=freqz_m(b3,1);%blackmandelta_w=2*pi/1000;rp3=-(min(db3(1:1:wp/delta_w+1)));%实际带通波动rp3as3=-round(max(db3(ws/delta_w+1:1:501)));%最小带阻衰减as3[db4,mag4,pha4,w]=freqz_m(b4,1);%kaiserdelta_w=2*pi/1000;rp4=-(min(db4(1:1:wp/delta_w+1)));%实际带通波动rp4as4=-round(max(db4(ws/delta_w+1:1:501)));%最小带阻衰减as4figure(1)stem(n,hd);title('理想脉冲响应')axis([0 N-1 -0.1 0.3]);xlabel('n');ylabel('hd(n)');figure(2)subplot(2,2,1)plot(w,mag1,':b')legend('汉宁窗低通滤波器')subplot(2,2,2)plot(w,mag2,'-.g')legend('海明窗低通滤波器')subplot(2,2,3)plot(w,mag3,'--r')legend('布来克曼窗低通滤波器')subplot(2,2,4)plot(w,mag4,'-c')legend('凯泽窗低通滤波器')figure(3)plot(w,mag1,':b',w,mag2,'-.g',w,mag3,'--r',w,mag4,'-c')legend('汉宁窗低通滤波器','海明窗低通滤波器','布来克曼窗低通滤波器','凯泽窗低通滤波器')figure(4)plot(w/pi,20*log10(mag1),':b',w/pi,20*log10(mag2),'-.g',w/pi,20*log10(mag3),'--r',w/pi,20*log10 (mag4),'-c')legend('汉宁窗幅度响应(dB)','海明窗幅度响应(dB)','布来克曼窗幅度响应(dB)','凯泽窗幅度响应(dB)')figure(5)plot(n,b1,':b',n,b2,'-.g',n,b3,'--r',n,b4,'-c')legend('汉宁窗h(n)','海明窗h(n)','布来克曼窗h(n)','凯泽窗h(n)')M5-2Wp=0.6*pi;Ws=0.4*pi;Ap=1;As=45;N=ceil(7*pi/(Wp-Ws));N=mod(N+1,2)+N;M=N-1;w=hamming(N)';Wc=(Wp+Ws)/2;k=0:M;hd=-(Wc/pi)*sinc(Wc*(k-0.5*M)/pi);hd(0.5*M+1)=hd(0.5*M+1)+1;h=hd.*w;omega=linspace(0,pi,512);mag=freqz(h,[1],omega);plot(omega/pi,20*log10(abs(mag)));M5-4N=40;alfa=(40-1)/2;k=0:N-1;w1=(2*pi/N)*k;T1=0.109021; T2=0.59417456;hrs=[zeros(1,5),T1,T2,ones(1,7),T2,T1,zeros(1,9),T1,T2,ones(1,7),T2,T1,zeros(1,4)]; hdr=[0,0,1,1,0,0]; wd1=[0,0.2,0.35,0.65,0.8,1];k1=0:floor((N-1)/2); k2=floor((N-1)/2)+1:N-1;angH=[-alfa*(2*pi)/N*k1,alfa*(2*pi/N*(N-k2))];H=hrs.*exp(j*angH);h=real(ifft(H));[db,mag,pha,grd,w] = freqz_m(h,1);[Hr,ww,a,L] =Hr_Type2(h);figure(1)subplot(2,2,1)plot(w1(1:21)/pi,hrs(1:21),'o',wd1,hdr)axis([0,1,-0.1,1.1]);title('带通:N=40,T1=0.109021,T2=0.59417456')ylabel('Hr(k)');set(gca,'XTickMode','manual','XTick',[0,0.2,0.35,0.65,0.8,1])set(gca,'YTickMode','manual','YTick',[0,0.059,0.109,1]);grid %绘制带网格的图像subplot(2,2,2);stem(k,h);axis([-1,N,-0.4,0.4])title('脉冲响应'); ylabel('h(n)'); text(N+1,-0.4,'n')subplot(2,2,3); plot(ww/pi,Hr,w1(1:21)/pi,hrs(1:21),'o');axis([0,1,-0.1,1.1]);title('振幅响应')xlabel('频率(单位:pi)'); ylabel('Hr(w)')set(gca,'XTickMode','manual','XTick',[0,0.2,0.35,0.65,0.8,1]);set(gca,'YTickMode','manual','YTick',[0,0.059,0.109,1]);gridsubplot(2,2,4); plot(w/pi,db); axis([0,1,-100,10]);gridtitle('幅度响应');xlabel('频率(单位:pi)'); ylabel('分贝')set(gca,'XTickMode','manual','XTick',[0,0.2,0.35,0.65,0.8,1])set(gca,'YTickMode','manual','YTick',[-60;0]);set(gca,'YTickLabelMode','manual','YTickLabels',[60;0]);[s,fs,nbits]=wavread('sj.wav');%信号de 取样频率为44100HZx=s(:,1);sound(x,fs);L=length(x);f=fs*(0:L-1)/L;t=0:1/fs:(L-1)/fs; %将所加噪声信号的点数调整到与原始信号相同%Au=1d=0.03*abs(max(x))*[cos(2*pi*22000*t)]'; %噪声为500和3300Hz的余弦信号%dz=cos(0.5*pi*fs*t)';%载波dz=[cos(2*pi*11025*t)]';xd=x.*dz;xz=xd+d;sound(xz,fs); %播放加噪声后的语音信号X=fft(x); %求信号的频谱XD=fft(xd); %信号调制后的频谱XZ=fft(xz);figure(2)subplot(3,1,1);plot(t,x)title('未加噪的信号'); xlabel('time s');ylabel('幅度');subplot(3,1,2);plot(t,xd)title('调制后的信号'); xlabel('time s');ylabel('幅度');subplot(3,1,3);plot(t,xz)title('调制加噪后的信号'); xlabel('time n');ylabel('fuzhi n');figure(3)subplot(3,1,1);plot(f,abs(X));title('原始语音信号频谱');xlabel('频率(单位:Hz)');ylabel('幅度');subplot(3,1,2);plot(f,abs(XD));title('调制后的信号频谱');xlabel('频率(单位:Hz)');ylabel('幅度');subplot(3,1,3);plot(f,abs(XZ));title('加噪后的信号频谱');xlabel('频率(单位:Hz)');ylabel('幅度');y = fftfilt(h,xd);Y=fft(y);sound(3*y,fs);figure(4)subplot(2,1,1);plot(t,3*y)title('滤波后的信号'); xlabel('time s');ylabel('幅度');subplot(2,1,2);plot(f,abs(Y));title('滤波后的信号频谱'); xlabel('频率(单位:Hz)');ylabel('幅度');xj=y.*d;M5-5Wp=0.55*pi; Ws=0.45*pi; Ap=1; As=25;N=ceil(7*pi/(Wp-Ws));N=mod(N+1,2)+N;M=N-1;w=hamming(N);Wc=(Wp+Ws)/2;k=0:M;hd=-(Wc/pi)*sinc(Wc*(k-0.5*M)/pi);h=hd'.*w;omega=linspace(0,pi,512);mag=freqz(h,[1],omega);magdb=abs(mag);plot(omega/pi,magdb);grid;W=Ws-Wp;M1=8;k2=-M1:M1;Wc=(Wp+Ws)/2;hd=sinc(W*k2/2).*(sin(Wc*k2)./(k2.*pi)); hd(M1+1)=Wc/pi;omega2=linspace(0,pi,512);mag2=freqz(hd,[1],omega2);magdb2=abs(mag2);hold on;plot(omega2/pi,magdb2,'r');title('À¶ÏßΪµÚÒ»·½°¸£¬ºìÏßΪµÚ¶þ·½°¸');。
matlab大作业

Matlab大作业大作业要求:1 以下matlab编程和simulink题目各选做一个,大作业总共两道题。
2如果不做给定的题目,自己选题,提前qq(244731524)上和我说下,根据题目的难易,可以考虑多给些时间。
3 第十周前由各班学委统一将纸质版交给我,写上班级,学号,姓名。
4 请勿抄袭。
Matlab编程1、使用m文件对周期信号频域进行分析(1)用matlab求周期矩形脉冲的傅里叶级数,并绘制出周期矩形脉冲信号及其频谱图(2),用matlab求改变周期、脉冲宽度后的周期矩形脉冲的傅里叶级数和频谱,并分析周期,脉宽对周期信号频谱的影响。
2、使用m文件对非周期信号频域进行分析(1)用matlab对矩形脉冲信号的频谱进行分析(2)利用matalb函数绘制给定信号的幅度谱和相位谱。
Simulink1、使用Simulink的积分模块求解二阶微分方程:x’’+0.2x’+0.4x =0.2u(t) ,u (t) 是单位阶跃函数a、用积分模块创建求解微分方程的模型思路:利用连续系统模块库中的积分器Integrator,解微分方程。
建模仿真:阶跃信号Step ,求和sum,常数增益gain,积分器,示波器scopeb、用传递函数求微分方程思路:对微分方程作laplace变换,移项整理后求得传递函数,利用连续系统模块库中的传递函数模块Transfer Fcn ,解微分方程。
建模仿真:阶跃信号Step ,示波器scope,传递函数模块Transfer Fcn等2、使用simupower system模块求解电路。
电路如图所示,参数如下:R1=2,R2=4,R3=12,R4=4,R5=12,R6=4,R7=2,Us=10V。
求i3,U4,U7;。
数字信号处理matlab作业

Matlab 作业M2-1:(1)t=-2: 0.02: 4;x=rectpuls(t-1,2);plot(t,x);(2)t=-2:0.001:5;ft=(t>=0);plot(t,ft);(3)t=0:0.002:5;xt=10*exp(-1*t)-5*exp(-2*t);plot(t,xt);(4)t=-2:0.002:5;xt=t.*(t>=0) ;plot(t,xt);(5)t=-2*pi:0.002:2*pi;xt=2*abs(sin(10*pi*t+pi/3)); plot(t,xt) ;axis([-0.5,0.5,0,2])(6)t=-2*pi:0.002:2*pi;xt=cos(t)+sin(2*pi*t);plot(t,xt)(7)t=-2*pi:0.002:2*pi;xt=4*exp(-0.5*t).*cos(2*pi*t); plot(t,xt)(8)t=-2:0.001:5;xt=sinc(t).*cos(30*t);plot(t,xt)M2-3t=-2:0.001:6;y=t.*(t>=0&t<=2)+2.*(t>2&t<3)+(-1).*(t>3&t<5); subplot(3,1,1) plot(t,y) title('x(t)')xlabel('t'),ylabel('x(t)') axis([-2,6,-1.5,2.5]) subplot(3,1,2) plot(2*t,y) title('x(0.5t)')xlabel('t'),ylabel('x(t)') axis([-2,6,-1.5,2.5]) subplot(3,1,3) plot(2*(2+t),y) title('x(2-0.5t)')xlabel('t'),ylabel('x(t)') axis([-2,6,-1.5,2.5])x(t)t x (t )x(0.5t)t x (t )x(2-0.5t)tx (t )M3-1 (1)ts=0;te=5;dt=0.01; sys=tf([2 1],[1 3 2]); t=ts:dt:te;x=exp(-3*t).*(t>=0); y=lsim(sys,x,t); plot(t,y);M3-4k=-2:3;x=[0.85,0.53,0.21,0.67,0.84,0.12]; m=-1:3;y=[0.68,0.37,0.83,0.52,0.71];z=conv(x,y);N=length(z);stem(0:N-1,z);M3-8k=0:30;a=[1 0.7 -0.45 -0.6];b=[0.8 -0.44 0.36 0.02];h=impz(b,a,k);stem(k,h)M4-1(1)N=20;n1= -N:-1; %计算n=-N 到-1的Fourier 系数 c1= sinc(n1/2).*exp(-1*j*n1*pi/2)/2;c0=sinc(0).*exp(-1*j*0*pi/2)/2-1/2;%计算n=0时的Fourier 系数 n2=1:N; %计算n=1到N 的Fourier 系数 c2=sinc(n2/2).*exp(-1*j*n2*pi/2)/2; cn=[c1 c0 c2]; n= -N:N;subplot(2,1,1);stem(n,abs(cn),'filled');ylabel('Cn 的幅度'); subplot(2,1,2);stem(n,angle(cn),'filled');ylabel('Cn 的相位');xlabel('\omega/\omega0');C n 的幅度C n 的相位ω/ω0(2) N=8; n1= -N:-1;c1= -2*j*sin(n1*pi/2)/pi^2./n1.^2.*exp(-j*n1*1/2); c0=-2*j*sin(0*pi/2)/pi^2./0.^2.*exp(-j*0*1/2)+2*pi; n2=1:N;c2= -2*j*sin(n2*pi/2)/pi^2./n2.^2.*exp(-j*n2*1/2); cn=[c1 c0 c2]; n= -N:N;subplot(2,1,1);stem(n,abs(cn));ylabel(' Cn 的幅度'); subplot(2,1,2); stem(n,angle(cn));ylabel(' Cn 的相位');xlabel('\omega/\omega0');C n 的幅度-8-6-4-202468C n 的相位ω/ω0M4-6 (4) k=0:5 x=[1,2,3,0,0] X=fft(x) m=0:4subplot(2,1,1) stem(m,real(X)) title('X[m] 的实部') xlabel('m') subplot(2,1,2) stem(m,imag(X)) title('X[m] 的虚部') xlabel('m') subplot(2,1,2)00.51 1.52 2.53 3.54mX[m]的虚部00.51 1.52 2.53 3.54mM4-7(3) k=0:10a=0.5xk=a.^kX=fft(xk)m=0:10stem(m,real(X))title('X[m]的实部')xlabel('m')figurestem(m,imag(X))title(‘X[m]的虚部’)xlabel('m')xr=ifft(X)figurestem(m,real(xr))xlabel('k')title('重建的x[k]')246810X[m]的实部m0246810X[m]的虚部m重建的x[k]kM5-2(1)t=0:0.05:2.5x1t=1.*(t>=0&t<=1)subplot(3,1,1)plot(t,x1t)xlabel('t')ylabel('x1t')axis([0,2.5,-2,2])x2t=t.*(t>=0&t<=1)+(2-t).*(t>1&t<=2)subplot(3,1,2)plot(t,x2t)xlabel('t')ylabel('x2t')x3t=x1t+x2t.*cos(50*t)subplot(3,1,3)plot(t,x3t)xlabel('t')ylabel('x3t')00.511.522.5-22tx 1t00.511.522.50.51tx 2t0.511.522.5-1012tx 3t(2)w=linspace(0,2*pi,200) b=[10000]a=[1,26.131,341.42,2613.1,10000] H=freqs(b,a,w) subplot(2,1,1) plot(w,abs(H)) xlabel('\omega')ylabel('abs(H(j\omega))') subplot(2,1,2) plot(w,angle(H)) xlabel('\omega')ylabel('\phi(H(j\omega))')012345670.9850.990.99511.005ωa b s (H (j ω))01234567-2-1.5-1-0.50ωφ(H (j ω))(3)t=0:0.05:2.5 x1t=1.*(t>=0&t<=1)x2t=t.*(t>=0&t<=1)+(2-t).*(t>1&t<=2) xt=x1t+x2t.*cos(50*t)H=tf([10000],[1,26.131,341.42,2613.1,10000]) yt=lsim(H,x3t,t) subplot(2,1,1) plot(yt,t) xlabel('t') ylabel('y1(t)')x4t=x3t.*cos(50*t) y2t=lsim(H,x4t,t) subplot(2,1,2) plot(y2t,t) xlabel('t') ylabel('y2(t)')-0.200.20.40.60.81 1.2ty 1(t )-0.10.10.20.30.40.50.6ty 2(t )M6-1(1)num=[41.6667]den=[1,3.7444,25.7604,41.6667] [r,p,k]=residue(num,den)[angle,mag]=cart2pol(real(r),imag(r)) 运行结果: r =-0.9361 - 0.1895i -0.9361 + 0.1895i 1.8722 p =-0.9361 + 4.6237i -0.9361 - 4.6237i -1.8722 k =[]angle =-2.9418 2.9418 0mag =0.9551 0.95511.8722 由此可得: X(s)= 4.6237i - 0.9361s 0.1895i - 0.9361-+ + 4.6237i+ 0.9361s 0.1895i+ 0.9361-+-1(2)num=[16,0,0]den=[1,5.6569,816,2262.7,160000] [r,p,k]=residue(num,den)[angle,mag]=cart2pol(real(r),imag(r)) 运行结果: r =0.0992 - 1.5147i 0.0992 + 1.5147i -0.0992 + 1.3137i -0.0992 - 1.3137i p =-1.5145 +21.4145i -1.5145 -21.4145i -1.3140 +18.5860i -1.3140 -18.5860i k =[]angle =-1.50541.50541.6462-1.6462mag =1.51801.51801.31751.3175(3)num=[1,0,0,0]den=conv([1,5],[1,5,25])[r,p,k]=residue(num,den) [angle,mag]=cart2pol(real(r),imag(r)) 运行结果:r =-2.5000 - 1.4434i-2.5000 + 1.4434i-5.0000p =-2.5000 + 4.3301i-2.5000 - 4.3301i-5.0000k =1angle =-2.61802.61803.1416mag =2.88682.88685.0000(4)num=[833.3025]den=conv([1,4.1123,28.867],[1,9.9279,28.867]) [r,p,k]=residue(num,den)[angle,mag]=cart2pol(real(r),imag(r))运行结果:r =2.4819 - 5.9928i2.4819 + 5.9928i-2.4819 + 1.0281i-2.4819 - 1.0281ip =-4.9640 + 2.0558i-4.9640 - 2.0558i-2.0562 + 4.9638i-2.0562 - 4.9638ik =[]angle =-1.17821.17822.7489-2.7489mag =6.48646.48642.68642.6864M6-2t=0:0.001:10sys=tf([2,1],[1,4,3])x=1.*(t>=0)yzs=lsim(sys,x,t)subplot(2,1,1)plot(t,yzs)xlabel('t')ylabel('yzs(t)')eq='D2y+4*Dy+3*y=0'; cond='y(0)=1,Dy(0)=2';yzi=simplify(dsolve(eq,cond))t=0:0.001:10sys=tf([2,1],[1,4,3])x=1.*(t>=0)yzs=lsim(sys,x,t)subplot(2,1,1)plot(t,yzs)xlabel('t')ylabel('yzs(t)')yzi=5/2.*exp(-t)-3/2.*exp(-3*t) subplot(2,1,2)plot(t,yzi)xlabel('t')ylabel('yzi(t)')0123456789100.20.40.60.8ty z s (t )1234567891000.511.5ty z i (t )M6-5num=[1,2] den=[1,2,2,1] sys=tf(num,den) subplot(4,1,1) pzmap(sys) t=0:0.02:10 w=0:0.02:5h=impulse(num,den,t) subplot(4,1,2) plot(t,h) xlabel('t') ylabel('h(t)')y=step(num,den,t) subplot(4,1,3) plot(t,y) xlabel('t')ylabel('阶跃响应') H=freqs(num,den,w) subplot(4,1,4) plot(w,abs(H)) xlabel('\omega') ylabel('幅度响应')-2-1.8-1.6-1.4-1.2-1-0.8-0.6-0.4-0.2P ole-Zero MapI m a g i n a r y A x i s12345678910-101th (t )12345678910024t阶跃响应0.511.522.533.544.55024ω幅度响应M7-1(1)num=[2,16,44,56,32] den=[3,3,-15,18,-12][r,p,k]=residuez(num,den) 运行结果: r =-0.0177 9.4914 -3.0702 + 2.3398i -3.0702 - 2.3398i p =-3.2361 1.2361 0.5000 + 0.8660i 0.5000 - 0.8660i k =-2.6667X[k]= -2.6667+1-3.2361z 10.0177-++12361.119.4914--z +1-0.866i)z (0.5-1 2.3398i + 3.0702-++1-0.866i)z(0.5-1 2.3398i- 3.0702-+(2)num=[4,-8.68,-17.98,26.74,-8.04] den=[1,-2,10,6,65][r,p,k]=residuez(num,den) 运行结果: r =1.0971 + 1.3572i 1.0971 - 1.3572i0.9648 - 1.2511i0.9648 + 1.2511i p =2.0000 +3.0000i 2.0000 - 3.0000i -1.0000 + 2.0000i -1.0000 - 2.0000i k =-0.1237X[k]= -0.1237+1-3i)z (2-1 1.3572i + 1.0971++1)32(1 1.3572i - 1.0971---z i +1-2i)z (-1-1 1.2511i - 0.9648++1-2i)z-(-1-1 1.2511i+ 0.9648 M7-2num=[12 -3 -1.5] den=[2 -4 1.5] k=0:10k1=length(k) y01=[1 3] x01=[0 0]x1=zeros(1,k1)z1=filtic(num,den,y01,x01) yi=filter(num,den,x1,z1) subplot(3,1,1) stem(k,yi)title('零输入响应') y02=[0 0] x02=[0 0] x2=0.5.^kz2=filtic(num,den,y02,x02) yz=filter(num,den,x2,z2) subplot(3,1,2) stem(k,yz)title('零状态响应')y03=[1 3]x03=[0 0]x3=0.5.^kz3=filtic(num,den,y03,x03)y=filter(num,den,x1,z3)subplot(3,1,3)stem(k,y)title('全响应')零输入响应012345678910零状态响应全响应012345678910M7-3(1)num=[2,16,44,56,32]den=[3,3,-15,18,-12][z,p,k]=tf2zp(num,den)zplane(num,den)-4-3.5-3-2.5-2-1.5-1-0.500.51-2-1.5-1-0.500.511.52Real Part I m a g i n a r y P a r t系统不稳定(2)num=[4,-8.68,-17.98,26.74,-8.04] den=[1,-2,10,6,65][z,p,k]=tf2zp(num,den)zplane(num,den)-3-2-101234-3-2-1123Real Part I m a g i n a r y P a r t系统不稳定。
matlab的大作业

华东交通大学matlab 大作业(matlab在信号与系统中的应用)班级:姓名:学号:前言此次的大作业内容是matlab在信号与系统中的应用。
在信号与系统中有各种各样的信号还有系统要分析,而matlab特别适用与信号通过系统的分析。
而且本人对于matlab在信号与系统中的运用蛮感兴趣的,况且当初学习时对于其在信号与系统中的运用不是很了解,故借此机会,也顺便再系统地学习和掌握matlab在信号与系统的运用。
这次设计的程序主要是围绕用matlab求解信号与系统中一些信号描述、零输入响应的求解、冲激响应的求解、卷积的计算、零状态响应的求解、傅里叶的分析(包括方波分解为正弦波之和非周期信号的频谱分析,以及用傅里叶变换计算滤波器的响应和输出)。
接下来就描述一下设计的程序。
一、程序描述Chengxu1是对于信号与系统中的一些信号的描述。
包括单位冲激函数、单位阶跃函数、复数指数信号。
程序中,t0,tf,dt,分别指的是t的起点、终点、间隔。
t1指的是在冲激函数在t1处冲激,在t1处是阶跃函数的转折点。
用matlab来描述这些信号,是根据这些信号的特点来一一描述的。
而且此次的画图用的是stairs而不是plot。
是因为要描述的是连续信号中的不连续点,故用stairs,若要波形光滑些,则用plot效果更好一些。
就如冲激函数和阶跃函数的波形对比如下(此处所取的是t0=0,tf=5,dt=0.05,t1=1):用plot所画用stairs所画此外,复数指数信号可以分解为余弦和正弦信号,他们分别是复数信号的是实部和虚部,即相位差为90度。
图如下(此处alpha=-0.5,w=10):Chengxu2是求解LTI 系统的零输入,题型为:描述n 阶线性时不变连续系统的微分方程为已知y 及其各阶导数的初始值为 求系统的零输入响应。
可以根据具体的函数求解其零输入。
Chengxu3是求解阶LTI 系统的冲激响应,是求解系统函数为: 的冲激响应。
MATLAB大作业

M A T L A B大作业(总15页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--MATLAB大作业作业要求:(1)编写程序并上机实现,提交作业文档,包括打印稿(不含源程序)和电子稿(包含源程序),以班为单位交,作业提交截止时间6月24日。
(2)作业文档内容:问题描述、问题求解算法(方案)、MATLAB程序、结果分析、本课程学习体会、列出主要的参考文献。
打印稿不要求MATLAB程序,但电子稿要包含MATLAB程序。
(3)作业文档字数不限,但要求写实,写出自己的理解、收获和体会,有话则长,无话则短。
不要抄袭复制,可以参考网上、文献资料的内容,但要理解,要变成自己的语言,按自己的思路组织内容。
(4)从给出的问题中至少选择一题(多做不限,但必须独立完成,严禁抄袭)。
(5)大作业占过程考核的20%,从完成情况、工作量、作业文档方面评分。
第一类:绘制图形。
(B级)问题一:斐波那契(Fibonacci)螺旋线,也称黄金螺旋线(Golden spiral),是根据斐波那契数列画出来的螺旋曲线,自然界中存在许多斐波那契螺旋线的图案,是自然界最完美的经典黄金比例。
斐波那契螺旋线,以斐波那契数为边的正方形拼成的长方形,然后在正方形里面画一个90度的扇形,连起来的弧线就是斐波那契螺旋线,如图所示。
问题二:绘制谢尔宾斯基三角形(Sierpinskitriangle)是一种分形,由波兰数学家谢尔宾斯基在1915年提出,它是一种典型的自相似集。
其生成过程为:取一个实心的三角形(通常使用等边三角形),沿三边中点的连线,将它分成四个小三角形,然后去掉中间的那一个小三角形。
接下来对其余三个小三角形重复上述操作,如图所示。
问题三:其他分形曲线或图形。
分形曲线还有很多,教材介绍了科赫曲线,其他还有皮亚诺曲线、分形树、康托(G. Cantor)三分集、Julia集、曼德布罗集合(Mandelbrot set),等等。
matlab与信号处理作业7

周治国
2018.10
作业7
基于MATLAB的数字滤波器的设计
要求
1.每人都需要做,形式为PPT+支撑材料(如论文原文,相 关背景文档,程序代码等) 2.自行分组,建议6人一组;每组准备一份PPT ,用于课 堂讲解(演示),时间15分钟左右; PPT内容可以选择作 业题目的一条或几条,范围可以有所扩展,但要把握思路 主线,展开详细论述 3.做好的两份PPT发到邮箱3220180517@,个人 PPT命名 '班号-学号-姓名',小组PPT里面要写上'组员姓 名学号'
作业7
GUI界面 IIR滤波器设计
• 设置参数 • 设
在线论文发表网站 整理教材+课件 基于印象笔记的合作“共建型”教学系统
OBE:知识成果可积累
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
freq = (1:n/2)/(n/2)*nyquist;%%求频率
plot(freq,power)%%作出功率与频率的关系曲线
xlabel('cycles/year')%%标注横坐标
title('Periodogram')
(2)对功率和频率的前100个分量作它的周期图,方便观察。
Y=fft(wolfer); %%对全部数据做FFT
Y(1)=[ ]; %%舍弃第一个点,因为Y(1)为所有FFT数值之和
plot(Y,'ro') %%在复平面作图,且为空心点
>> figure%%作图
plot(year(1:100),wolfer(1:100),'b.-');%%取年份1700-1800
xlabel('Years');ylabel(' Sunspot Data ');%%标注横纵坐标
title('At the first 100 years ')
分析:由上图可以更加清楚地看到周期大约为10到12年之间。
[2]孙燕. 用数字信号处理方法分析太阳黑子活动的周期性[J]. 青海师范大学学报(自然科学版), 2006, (4): 1-3
[3]唐洁. 功率谱分析方法在周期分析中的应用[J]. 陕西理工学院学报, 2013, 29(5): 1-5
七、MATLAB程序源代码
>> load sunspotyear.csv %%装载太阳黑子的数据
用pwd命令来查找当前工作路径。
>>pwd
ans=
C:\Program Files\MATLAB\R2012b\bin
下面的分析选择1700年到2013年期间,共313年的数据。首先用如下程序语句装载太阳黑子的年度数据:
>> load sunspotyear.csv%%装载太阳黑子的数据
2.以横坐标表示年份,纵坐标表示黑子出现的数量,绘制Wolfer图。
(1)由1700年到2013年期间Wolfer图。
>> year=sunspotyear(:,1);%%读取年份信息
wolfer=sunspotyear(:,2);%%读取太阳黑子活动数据
plot(year,wolfer);%%作以year为横坐标,wolfer为纵坐标的图象
xlabel('Years');ylabel(' Sunspot Data ')%%标注横坐标为年份,纵坐标为黑子数量
title('Sunspot Data')
分析:由上图可见,太阳黑子数据具有周期性,但是仅根据上图周期的准确值难以确定。不过可以确定上图中任意两个峰值之间的年份之差,从而获得一个周期的估计值。比如第3个峰值出现在1728年,第4个峰值出现在1739年,因此周期的近似值是11年。
(2)由1700到1800年期间Wolfer图。
>>figure
plot(freq(1:100),power(1:100))
xlabel('cycles/year')
pause
分析:图象中出现的其它尖峰可能是因为太阳黑子数据中的噪声引起的;或者是因为泄露产生的。
(3)确定太阳黑子活动周期
确定出太阳黑子的活动周期。为清楚起见,画出功率与周期(频率的倒数)的关系曲线图。在功率与周期关系曲线图中标出功率的最高点.
程序如下:
figure
period=1./freq;%%求周期
plot(period,power);%%作功率与周期的关系
axis([0 50 0 2e+7]);%%确定横纵坐标的范围
ylabel('Power');%%标注纵坐标为功率
xlabel('Period (Years/Cycle)');%%标注横坐标为周期
text(period(index)+2,power(index),['Period = ',mainPeriodStr]); %%文字标注该点
holdoff;
由上图可以近似得出太阳黑子活动周期为11年。
四、结论及优缺点改进
实验得出的太阳黑子的活动周期为11.0385年,与沃尔夫得出的11年的周期规律一致,
pause
index=find(power==max(power)); %%找到频率最大点,该点横坐标即为太阳黑子周期
mainPeriodStr=num2str(period(index));
plot(period(index),power(index),'r.', 'MarkerSize',25); %%用实心点指出该点
22年模型:美国天文学家乔治•海尔【George Ellery Hale(1868 - 1938)】发现在每一个施瓦贝周期,太阳的磁场都会扭转,因此磁极要两次扭转之后才会回到相同磁极的状态,他因此发现了22年周期。
其他曾经发现的模型:87年模型、210年模型、哈尔斯塔周期等。
在太空运行的人造卫星、飞行器、宇宙飞船和高空飞行的飞机,受到来自太阳的高能带电粒子的袭击,会造成有些零部件损坏导致整个设备系统不能正常工作。乘坐在飞机和飞行器上的飞行员和宇航员的身体也会受到来自太阳的高能带电粒子伤害。受太阳活动影响的还有长距离的高压输电系统和输油管道
则可将DFT化为
利用系数 的可约性,即 ,上式可表示成
(3)功率谱密度: ,
则
3.流程图
三、实验过程及分析
1.下载太阳黑子的数据monthssv.dat,下载数据的时间段从1700年1月到2013年12月,共314年。这个数据文件的第1列是年和月,第2列是该月太阳黑子的平均数,sunspotyear.csv同时保存到matlab工作路径。
根据DFT的频域单位K与DTFT的频域单位w的关系表达式 以及W与f对应
关系 ( 为采样频率),可以看出K与f成线性关系 。又因为前 个数据已经包含了Wolfer数的全部信息,只取前 个数据分析功率-频率图时,对应的横坐标应取 。
2.函数名称
(1)离散时间傅里叶正变换:
离散时间傅里叶逆变换:
(2)按时间抽选的FFT算法:将N= 的序列 先按n的奇偶分成两组:
xlabel('Real Axis');%%标注横坐标为实轴
ylabel('Imaginary Axis&#模的平方被定义为功率,功率与频率的关系曲线则被定义为周期图)。
(1)绘制周期图
>> n=length(Y);
power= abs(Y(1:n/2)).^2;%%求功率
我们利用Matlab强大的数据处理与仿真功能,对Wolfer数进行功率谱密度分析从而可以得到对太阳黑子活动周期的结论。
二、分析方法
1.实验原理
在对太阳黑子活动周期的分析中,对Wolfer数序列作FFT变换后得到Y(长度为n),只
取前 个数据的功率谱密度的估计值 。原因是时序为离散的实序列的傅里叶变换对应于具有周期性且偶对称的频域特性,因此Y的前 个数据已经包含了Wolfer数的全部信息。
year=sunspotyear(:,1); %%读取年份信息
wolfer=sunspotyear(:,2); %%读取太阳黑子活动数据
plot(year,wolfer); %%作以year为横坐标,wolfer为纵坐标的图象
xlabel('Years');ylabel(' Sunspot Data ') %%标注横坐标为年份,纵坐标为黑子数量
作业1太阳黑子活动周期的分析
一、问题描述
太阳黑子的活动是周期的,大约每11年达到一个爆发高峰。
太阳周期是太阳行为上的循环变化,人们已经构建了许多可能的太阳黑子活动模型,
但在观测上只有11年和22年的周期容易被清除地观察到。
11年模型:1843年,塞瑟尔•海因里希•施瓦布【Samuel HeinrichSchwabe(1789–1875)】发现了太阳活动周期。从1826年到1843年,施瓦贝每天仔细观察看太阳表面,记录太阳上的黑子数,经过17年间的长期艰辛观测,他整理了观测资料,于1843年发表了一篇题为《1843年间的太阳观测》的论文,文章指出:“太阳的年平均黑子数具有周期性的变化,变化的周期约十年”。伯尔尼天文台台长的鲁道夫沃尔夫在搜集整理太阳黑子数观测资料的过程中,为使不同观测台站以及不同人的太阳黑子观测资料具有可比性,于1848年提出了太阳黑子相对数的概念。沃尔夫经过几年的仔细观测和精心的资料整理,返现太阳黑子数变化周期平均为11.1年。观测到的最短黑子周期为9年,最长黑子周期为14年。不同周期之间和字数的变化也非常明显。到1852年他还发现地磁活动和极光与太阳活动有关。沃尔夫提出将太阳黑子数从一个极小到另一个极小之间的事件定为一个周期,并将1755年之1766年的周期定为第一个太阳活动周。根据连续的观测记录推算下来,2008是第24个太阳活动周。
title('Sunspot Data')
figure %%作图
plot(year(1:100),wolfer(1:100),'b.-'); %%取年份1700-1800
xlabel('Years');ylabel(' Sunspot Data '); %%标注横纵坐标
title('At the first 100 years ')
总体而言,这次实验虽只是对信号的简单处理,但是在程序设计中遇到很多问题,这些都是在平时学习中所不曾注意到的,面对这些问题我通过查阅资料、网络、与同组同学的探讨,得到很大程度的解决。
