2021年沪教版六年级数学下册《画角的和差倍》优质公开课课件.ppt

合集下载

沪教小学数学六年级下册《7.5画角的和、差、倍》word精品教案 (2)

7.5(2) 画角的和、差、倍（第二课时）教学目标1. 理解角平分线的概念，掌握用量角器画角平分线的方法，体验类比的数学思想.2. 初步体会角平分线的几何符号表示方法，感知几何符号语言的简洁性，初步感知因果关系形式的几何说理方法.3．会用尺规作出已知角的平分线，探究用尺规法作出45度、90度等特殊角的方法，初步会用几何作图的基本语言写出作法.教学重点1. 理解角平分线的概念，掌握角平分线的画法，.2. 会用尺规作出已知角的平分线以及正确完整地写出作法.教学难点：1．完整规范地写出用尺规方法作出角平分线的作法.2．探究用尺规画出30度、45度、60度等特殊角的方法.教学设计流程教学过程一．情景引入：思考：问题1. 什么是线段的中点？问题2：如果C 是线段AB 的中点，那么AB=__AC ，BC=___AB课堂小结创设情景提出问题引发思考角平分线的定义及几何表示方法实践操作观察归纳实践操作画角平分线实验操作：用纸片作材料任意剪一个角，折叠这张纸片，使角的两边叠合在一起，再展开摊平.思考：中间的折痕我们把它称作什么？如果把角的两边无限延伸，那么这条折痕是直线、线段还是射线？如何给角平分线下定义？二．学习新课.1．角平分线：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.（教师板书）2．角平分线的几何表示：如果OC是∠AOB的平分线，那么也可以说成1∠AOB 或∠是OC平分∠AOB，就有下列等式：∠AOC=∠BOC=2AOB=2∠AOC=2∠BOC. D C三．例题分析：例题1：如图，∠AOD=80°， B∠COD=30°，OB是∠AOC的平分线，那么∠AOC=（）°，O A∠AOB=（）°.说明：此题让学生应用角平分线的性质解决一些简单的角的度数计算问题，可以让学生模仿说理几何的要求，简单写出解题过程，体验几何学习的重点是说清理由，而不是只要一个结果.3：用量角器画已知角的平分线：例题：如图，已知∠ABC，画出它的角平分线.说明：教师与学生一起回忆线段中点的画法，此例题让学生自己思考，教师在学生讨论、交流的基础上，与学生一起归纳出完整、规范的画法.重点指出画图过程的先后顺序，画什么，写什么，特别提出在∠ABC的内部画射线BM，否则在∠ABC的外部也可以画出∠ABM=24度，反复让学生体验数学学习中应该具有严谨的学习态度.4．角平分线的尺规画法：已知∠ABC，求作的平分线.5．思考并操作：如何用尺规作出90度直角以及45度角？说明：教师可以安排学生先进行思考，提出解决问题的方法；一般学生难以想出解决问题的方法，教师可以先作出角平分线，然后可以再请学生比较与线段中点作法的异同.同时在书写作法时，截取线段时要明确在什么已知射线（或直线、线段）上，还可以回忆截取线段就是以顶点为圆心，以适当长度为半径作弧，与角的两边交于两点，体验同圆半径相等的性质；作弧必须要交待以什么点为圆心，半径长是多大，强调两弧在角的内部相交，让学生体验几何作图的严谨性.最后教师还可以通过把∠ABC转换成一个平角，学生容易看出作线段中点的过程，其实也作出了平角的平分线；在此基础上学生不难想出作45度交的方法.6．操作与理解：如图，（1）分别作出∠A、∠B的平分线，并作出它们的交点O；（2）如果∠A的平分线与BD相交于E点，通过测量，判断△ABE 的形状.A CB D说明：本题着重让学生熟练角平分线的尺规作法，以及尝试作法的书写，在学生相互交流的基础上归纳出较为规范的作法.另外此图形中，故意假定AC与BD平行，是在练习7.4第4题的基础上增加了一个问题，教师可以将AC饶A点进行旋转，让学生观察△ABE形状的变化，为今后学习平行线、等腰三角形、轴对称等数学知识留下一些印象.四．课堂小结：今天我们学习到了什么？你感兴趣的是什么？五．布置作业：习题7.5说明：本节课中通过与线段中点学习过程的比较，相类比地进行新知识的学习，能够让学生比较地学习数学，进而体验类比思想经常用于数学学习过程中，有利于学生对新旧知识的理解与掌握.另外，本节课要重视学生的动手操作，让学生能够得到充分的体验，进而加深对作法的理解，为今后尺规作图打下扎实的基础.。

上海市松江区六年级数学下册7.2画线段的和、差、倍精选教学PPT课件沪教版五四制

D是
已知线段a，那么2a、3a…na 表示什么含义呢？
分别表示a的的2倍、3倍…及a的n倍例题2：已知线段a、b，作一条线段，
使它等于2a－b．
a
①画射线OP；
b
②在射线OP上顺次截取
OA=AB=a；
③在线段BO上截取BC=b．
练一练：书91/3
线段OC就是所要画的线段
填空
OC
OC
OA
AB
OA
OD
DB
你有什么办法，能在AB上找一点C，使点C把线段AB分成
相等的两条线段？
A
C
B
1、度量法；
2、折叠法；
3、尺规法．
将一条线段分成两条相等线段的点叫做这条线段的中点．
已知线段AB，画出它的中点C．解： ①用刻度尺量出AB＝6cm；
②在线段AB上截取AC＝3cm;
CB 1 AB 2
AB=2CB．
已知：如图,点C是线段AB的中点， D是线段BC的中点, 则
A
C DB
AC=(CB)=
1 2
( AB
)
CD=(DB
)=
1(
2
CB)
= 1(
4
AB
)
练一练：书90/2
AB=2( AC ) =2( CB) =4( CD) =4(DB )
AD=(
3
)BD=(
1
1 2
敞开一直紧握的手掌，爱情，翻一翻身，化成了一只鸟儿，立在自己的肩头，向着雨后的阳光，向着草地的那一头，向着逐渐靠近的彩虹，啁啾而歌。温暖，是一种贴心的感觉，渐渐的弥漫。微笑，是一种明亮的色彩，慢慢的展开。兴奋，是一种揪心的疼爱，缓缓的溢出。激动，是一种苦苦的等待，盈盈的走来。

2021年沪教版六年级数学下册《画角的和差倍》优质公开课课件

B C
解 ∵∠AOB=∠1+∠2，
∠1=(3x-2)°,∠2=(x+8)°，
2
∠AOB=62°
1
∴(3x-2)＋(x+8)=62
O
小结
A
解得 x =14
∠1=40°,∠2=22°
本题是将几何问题转化为用代数方程来解决.
自主小结
1．角平分线
从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.
解 ⑴∵ ∠AOC =∠1＋∠2， ∠1=m°，∠2=n°
∴∠AOC =m° ＋n° ，同理 ∠BOD = m°＋n°.
⑵∵∠AOC = m°＋n° ，
∠BOD = m°＋n° ， ∴∠AOC=∠BOD．
练一练
已知：如图,已知∠AOB=62°, ∠1=(3x-2)°,∠2=(x+8)°. 求：∠1、∠2的度数.
例1 如图，已知∠AOB，画出它的角平分线．
B
方法二
尺规作法
E
O
D
C
解 ⑴以∠AOB的顶点为圆心，以取
定的长a为半径，作弧分别交∠AOB
A 的两边于点D、E；
1
⑵ 的同分别一以长点度D为、半点径E作为弧圆，心两，弧以交大于于∠2DAEOB
的内的一点C；
⑶作射线OC．射线OC就是所求作的∠AOB的平分线．
二、新授画角的和、差、倍
例题１：如图，已知∠α、∠β，画一个角，使它（1）等于∠α+∠β．
β α
二、新授画角的和、差、倍
例题１：如图，已知∠α、∠β，画一个角，使它（1）等于∠α+∠β．
解：①用量角器画出∠ABC＝ ∠α;

上海市松江区六年级数学下册7.2画线段的和、差、倍ppt课件沪教版五四制

如图所示，A、B、C三点在同一条直线上， 3 线段，它们分别是 1、图中有___ 6 条射线．线段 AB、BC和AC ______________ ；有____ 2、试着填：
AC AB＋BC=____; BC ；AC－BC＝＿＿． AB AC－AB=____
A
B
C
两条线段可以相加(减)，它们的和 (差)也是一条线段，它们的长度等于两条线段长度的和(差)．
AC=CB 1 AC AB, 2 AB=2AC,
1 CB AB 2
AB=2CB．
已知：如图,点C是线段AB的中点， D是线段BC的中点, 则
1 练一练： AC=(CB )= ( AB ) 2 书90/2 1 1 CD=(DB )= ( CB) = ( AB ) 4 2
A
C
D
B
AB=2( AC ) =2( CB) =4( CD) =4( DB )
1 3 AD=( 3 )BD=( 1 )BC=( )AB． 2 4
1、不要做刺猬，能不与人结仇就不与人结仇，谁也不跟谁一辈子，有些事情没必要记在心上。 2、相遇总是猝不及防，而离别多是蓄谋已久，总有一些人会慢慢淡出你的生活，你要学会接受而不是怀念。 3、其实每个人都很清楚自己想要什么，但并不是谁都有勇气表达出来。渐渐才知道，心口如一，是一种何等的强大! 4、有些路看起来很近，可是走下去却很远的，缺少耐心的人永远走不到头。人生，一半是现实，一半是梦想。 5、没什么好抱怨的，今天的每一步，都是在为之前的每一次选择买单。每做一件事，都要想一想，日后打脸的时候疼不疼。 6、过去的事情就让它过去，一定要放下。学会狠心，学会独立，学会微笑，学会丢弃不值得的感情。 7、成功不是让周围的人都羡慕你，称赞你，而是让周围的人都需要你，离不开你。 8、生活本来很不易，不必事事渴求别人的理解和认同，静静的过自己的生活。心若不动，风又奈何。你若不伤，岁月无恙。 9、与其等着别人来爱你，不如自己努力爱自己，对自己好点，因为一辈子不长，对身边的人好点，因为下辈子不一定能够遇见。 10、你迷茫的原因往往只有一个，那就是在本该拼命去努力的年纪，想得太多，做得太少。 11、有一些人的出现，就是来给我们开眼的。所以，你一定要禁得起假话，受得住敷衍，忍得住欺骗，忘得了承诺，放得下一切。 12、不要像个落难者，告诉别人你的不幸。逢人只说三分话，不可全抛一片心。 13、人生的路，靠的是自己一步步去走，真正能保护你的，是你自己的选择。而真正能伤害你的，也是一样，自己的选择。 14、不要那么敏感，也不要那么心软，太敏感和太心软的人，肯定过得不快乐，别人随便的一句话，你都要胡思乱想一整天。 15、不要轻易去依赖一个人，它会成为你的习惯，当分别来临，你失去的不是某个人，而是你精神的支柱;无论何时何地，都要学会独立行走，它会让你走得更坦然些。 16、在不违背原则的情况下，对别人要宽容，能帮就帮，千万不要把人逼绝了，给人留条后路，懂得从内心欣赏别人，虽然这很多时候很难。 17、要使整个人生都过得舒适、愉快，这是不可能的，因为人类必须具备一种能应付逆境的态度。——卢梭 18、不要太高估自己在集体中的力量，因为当你选择离开时，就会发现即使没有你，太阳照常升起。 19、时间不仅让你看透别人，也让你认清自己。很多时候，就是在跌跌拌拌中，我们学会了生活。 20、命运要你成长的时候，总会安排一些让你不顺心的人或事刺激你。 21、你的假装努力，欺骗的只有你自己，永远不要用战术上的勤奋，来掩饰战略上的懒惰。 22、成长是一场和自己的比赛，不要担心别人会做得比你好，你只需要每天都做得比前一天好就可以了。 23、你没那么多观众，别那么累。做一个简单的人，踏实而务实。不沉溺幻想，更不庸人自扰。 24、奋斗的路上，时间总是过得很快，目前的困难和麻烦是很多，但是只要不忘初心，脚踏实地一步一步的朝着目标前进，最后的结局交给时间来定夺。 25、你心里最崇拜谁，不必变成那个人，而是用那个人的精神和方法，去变成你自己。 26、运气是努力的附属品。没有经过实力的原始积累，给你运气你也抓不住。上天给予每个人的都一样，但每个人的准备却不一样。不要羡慕那些总能撞大运的人，你必须很努力，才能遇上好运气。 27、时间只是过客，自己才是主人，人生的路无需苛求，只要你迈步，路就在你的脚下延伸，只要你扬帆，便会有八面来风，启程了，人的生命才真正开始。 28、每个人身上都有惰性和消极情绪，成功的人都是懂得管理自己的情绪和克服自己的惰性，并像太阳一样照亮身边的人，激励身边的人。

2021年沪教版六年级数学下册《角的概念与表示》优质课课件

N地
P地
7.3 角的概念与表示 9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。
2021/2/62021/2/6Saturday, February 06, 2021 10、人的志向通常和他们的能力成正比例。2021/2/62021/2/62021/2/62/6/2021 1:37:47 AM 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/2/62021/2/62021/2/6Feb-216-Feb-21 12、越是无能的人，越喜欢挑剔别人的错儿。2021/2/62021/2/62021/2/6Saturday, February 06, 2021 13、志不立，天下无可成之事。2021/2/62021/2/62021/2/62021/2/62/6/2021
北A
D
30°
西 30°
东
48°O 45°
B C南
OA方向为北偏东30°
OB方向为南偏东45° 东南方向
OC方向为南偏西42° OD方向为北偏西60°
东北方向西北方向西南方向
北偏东45° 北偏西45°
南偏西45°
例3、在某一张地图上有M、N、P三地，但地图被墨迹污染，M地的具体位置看不清楚。现在知道M地在N地的南偏西40°，在P地的北偏东70°，请在地图上确定M地的位置。
定义1、角是具有公共端点的两条射线组成的图形。
终止位置的那条射线
角的顶点角的边
边
终边
顶点边
始边
初始位置的那条射线
定义2、角是由一条射线绕着它的端点旋转到另一个位置所成的图形。
角的始边转动到角的终边所经过的平面部分，叫做角的内部，简称角内。通常角的内部用不带箭头或带箭头的弧线表示。

沪教版六年级下7.5_画角的和、差、倍(1)教案

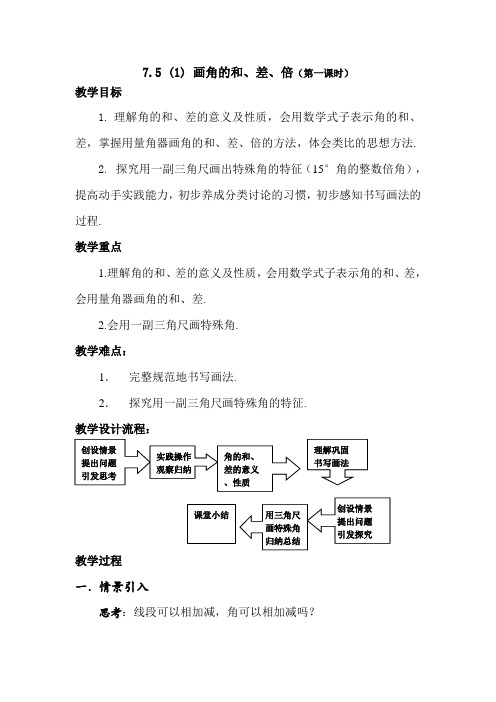
7.5 (1) 画角的和、差、倍（第一课时）教学目标1.理解角的和、差的意义及性质，会用数学式子表示角的和、差，掌握用量角器画角的和、差、倍的方法，体会类比的思想方法.2.探究用一副三角尺画出特殊角的特征（15°角的整数倍角），提高动手实践能力，初步养成分类讨论的习惯，初步感知书写画法的过程.教学重点1.理解角的和、差的意义及性质，会用数学式子表示角的和、差，会用量角器画角的和、差.2.会用一副三角尺画特殊角.教学难点：1．完整规范地书写画法.2．探究用一副三角尺画特殊角的特征.教学设计流程：教学过程一．情景引入思考：线段可以相加减，角可以相加减吗？操作：如何用圆规（作为角的模型）来演示一下，怎样表示两个角相加及相减？说明：在学生操作基础上引出角的(和差)的意义及性质.这样设计，主要让学生体验数学知识中存在许多的类比性，知识之间有着极为相似的地方，有利于学生理解新知识，同时也适当复习旧知识.另外让学生合作操作，既让每个学生动能够得到实践体会，也能够增强他们的协作意识.二．学习新课：角的和、差的意义和性质.（板书）两个角可以相加（或相减），它们的和（或差）也是一个角，它的度数等于这两个角的度数的和（或差）.例题1：如图，图中共有多少个角？ A B它们之间有什么等量关系？ O C此题由学生思考回答，并上黑板写出三个等量关系式. 例题2：如图，已知∠α、∠β，用量角器画一个角，使它（1）等于∠α+∠β；（2）等于2∠α- 说明：然后每个学生自己再画出两个大小不相等的角，用量角器画出它们的和及差；学生一般会有两种方法，一种用量角器量出∠α、∠β的度数，计算出它们度数的和、差，再用量角器画出等于它们度数和、差的角；另一种用量角器在∠β外画出∠α，再请学生讨论如何书写画图的过程.教师在学生描述的基础上逐渐进行补充，特别在画出一个角后，要重点强调3个要素不能少一个，即以B 为顶点，以射线BC为一边，在∠ABC的外部画出∠CBD=∠β，最后要回答哪个角就是所要画的角.强调数学解题的完整性、严密性、规范性，体验学习数学需要有严谨的科学态度.而2∠α-∠β则让学生独立完成.三．练习与巩固1.如图，已知∠AOB=62°， B∠1=(3x-2)°，∠2=(x+8)°求∠1、∠2的度数说明：此题在理解角的和、差的意义上，通过建立方程来求出最后的结果，让学生体验方程法是解决实际问题的一种常用的数学方法.2.如图，已知∠AOB=∠COD=m°， D C∠BOC=n°（1）用m、n的代数式分别表示∠AOC、∠BOD的大小； B（2）比较∠AOC和∠BOD的大小. O A四．应用与探究思考：用一幅（两块）三角尺可以画出怎样的特殊角？这些角具有什么特殊性？说明：教师要敢于放手，让学生自己去尝试解决问题的方法，也培养他们的动手操作的能力，让每个同学在纸上画出所有能够画出的特殊角，然后进行相互交流，探讨，然后请学生在投影仪上展示他们的画图（从角的个数少的逐渐到个数多的），让学生说出为什么少画了，当时有没有按规律进行两个角相加或相减（学生往往是杂乱无章的把两个角相加或相减，这里指出学生思考问题缺乏规律性、系统性的结症所在），最后让学生总结这些角的特殊性，提高他们的探究规律和概括归纳的能力.例题3：小明从点A出发向南偏东30°方向走了3m到点B，小林从点A出发向北偏东20°方向走了6m到点C．那么∠BAC等于多少度？并画出相应的图形，确定出A、B、C三点的位置(用1cm表示3m)．并从图上求出B点到C点的实际距离．说明：此例题同样由学生先独立思考，再画出图形，并得出结论.这样可以帮助学生将本章的知识贯穿起来，完善知识结构的，又会用新知识解决一些简单的实际问题，让学生体验数学与生活紧密相关.四．课堂小结今天我们学习到了什么知识？你感受最深的是什么？五．布置作业：习题 7.57.5(2) 画角的和、差、倍（第二课时）教学目标1.理解角平分线的概念，掌握用量角器画角平分线的方法，体验类比的数学思想.2.初步体会角平分线的几何符号表示方法，感知几何符号语言的简洁性，初步感知因果关系形式的几何说理方法.3．会用尺规作出已知角的平分线，探究用尺规法作出45度、90度等特殊角的方法，初步会用几何作图的基本语言写出作法.教学重点1. 理解角平分线的概念，掌握角平分线的画法，.2. 会用尺规作出已知角的平分线以及正确完整地写出作法. 教学难点：1．完整规范地写出用尺规方法作出角平分线的作法.2．探究用尺规画出30度、45度、60度等特殊角的方法. 教学设计流程教学过程一．情景引入：思考：问题1. 什么是线段的中点？问题2：如果C 是线段AB 的中点，那么AB=__AC ，BC=___AB实验操作：用纸片作材料任意剪一个角，折叠这张纸片，使角的两边叠合在一起，再展开摊平.思考：中间的折痕我们把它称作什么？如果把角的两边无限延伸，那么这条折痕是直线、线段还是射线？如何给角平分线下定义？二．学习新课.1．角平分线：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.（教师板书）2．角平分线的几何表示：如果OC是∠AOB的平分线，那么也可以1∠AOB 说成是OC平分∠AOB，就有下列等式：∠AOC=∠BOC=2或∠AOB=2∠AOC=2∠BOC. D C三．例题分析：例题1：如图，∠AOD=80°， B∠COD=30°，OB是∠AOC的平分线，那么∠AOC=（）°，O A∠AOB=（）°.说明：此题让学生应用角平分线的性质解决一些简单的角的度数计算问题，可以让学生模仿说理几何的要求，简单写出解题过程，体验几何学习的重点是说清理由，而不是只要一个结果.3：用量角器画已知角的平分线：例题：如图，已知∠ABC，画出它的角平分线.说明：教师与学生一起回忆线段中点的画法，此例题让学生自己思考，教师在学生讨论、交流的基础上，与学生一起归纳出完整、规范的画法.重点指出画图过程的先后顺序，画什么，写什么，特别提出在∠ABC的内部画射线BM，否则在∠ABC的外部也可以画出∠ABM=24度，反复让学生体验数学学习中应该具有严谨的学习态度.4．角平分线的尺规画法：已知∠ABC，求作的平分线.5．思考并操作：如何用尺规作出90度直角以及45度角？说明：教师可以安排学生先进行思考，提出解决问题的方法；一般学生难以想出解决问题的方法，教师可以先作出角平分线，然后可以再请学生比较与线段中点作法的异同.同时在书写作法时，截取线段时要明确在什么已知射线（或直线、线段）上，还可以回忆截取线段就是以顶点为圆心，以适当长度为半径作弧，与角的两边交于两点，体验同圆半径相等的性质；作弧必须要交待以什么点为圆心，半径长是多大，强调两弧在角的内部相交，让学生体验几何作图的严谨性.最后教师还可以通过把∠ABC转换成一个平角，学生容易看出作线段中点的过程，其实也作出了平角的平分线；在此基础上学生不难想出作45度交的方法.6．操作与理解：如图，（1）分别作出∠A、∠B的平分线，并作出它们的交点O；（2）如果∠A的平分线与BD相交于E点，通过测量，判断△ABE的形状.A CB D说明：本题着重让学生熟练角平分线的尺规作法，以及尝试作法的书写，在学生相互交流的基础上归纳出较为规范的作法.另外此图形中，故意假定AC与BD平行，是在练习7.4第4题的基础上增加了一个问题，教师可以将AC饶A点进行旋转，让学生观察△ABE形状的变化，为今后学习平行线、等腰三角形、轴对称等数学知识留下一些印象.四．课堂小结：今天我们学习到了什么？你感兴趣的是什么？五．布置作业：习题7.5说明：本节课中通过与线段中点学习过程的比较，相类比地进行新知识的学习，能够让学生比较地学习数学，进而体验类比思想经常用于数学学习过程中，有利于学生对新旧知识的理解与掌握.另外，本节课要重视学生的动手操作，让学生能够得到充分的体验，进而加深对作法的理解，为今后尺规作图打下扎实的基础.。

【新】沪教版六年级数学下册《画角的和、差、倍》优质课课件 (2).ppt

B
方法二
尺规作法
E
O
D
C
解 ⑴以∠AOB的顶点为圆心，以取
定的长a为半径，作弧分别交∠AOB
A 的两边于点D、E；
1
⑵ 的同分别一以长点度D为、半点径E作为弧圆，心两，弧以交大于于∠2DAEOB
的内的一点C；
⑶作射线OC．射线OC就是所求作的∠AOB的平分线．
例2 如图，已知∠1=∠3=m°，∠2=n°．（1）用含m、n的式子分别表示∠AOC、∠BOD的大小；（2）比较∠AOC和∠BOD的大小．
2
O
A
=
1
×
50°
2
=25°
思考怎样画出一个角的角平分线呢？
例1 如图，已知∠AOB，画出它的角平分线．
B
方法一
用量角器画
M
解 ⑴用量角器量得∠AOB =48°；
O
A
⑵在∠AOB的内部画射线
OM，使∠AOM =24°．
射线OM就是所要画的∠AOB的平分线．
思考怎样画出一个角的角平分线呢？
例1 如图，已知∠AOB，画出它的角平分线．
。2020年12月15日星期二2020/12/152020/12/152020/12/15
▪ 15、会当凌绝顶，一览众山小。2020年12月2020/12/152020/12/152020/12/1512/15/2020
▪ 16、如果一个人不知道他要驶向哪头，那么任何风都不是顺风。2020/12/152020/12/15December 15, 2020
B C
解 ∵∠AOB=∠1+∠2，
∠1=(3x-2)°,∠2=(x+8)°，
2
∠AOB=62°

沪教小学数学六年级下册《7.5画角的和、差、倍》word精品教案 (1)

2020--2021学年沪教版(上海)数学六年级第二学期7.5画角的和、差、倍教案

《7.5 画角的和、差、倍》在学习本单元之前，学生已经对线段和角有了初步的认识，能区分线段、射线和直线，掌握了角的分类。

本单元就是进一步探究有关线段和角的知识，能比较线段的大小及画线段的和、差、倍，能比较角的大小，掌握角的和、差、倍的画法，并认识余角和补角。

本课的教学内容是使学生掌握角的和、差、倍的意义，会用数学等式表示角的和、差、倍的关系，并会画角的和、差、倍。

【知识与能力目标】1．理解角的和、差、倍的意义，会用数学等式表示角的和、差、倍的关系2．会画角的和、差、倍3．理解角平分线的意义，会作已知角的角平分线。

【过程与方法目标】在探究角平分线的画法的过程中，培养学生初步的空间观念和空间想象能力。

【情感态度价值观目标】使学生初步建立空间观念，培养学生用数学进行交流、合作探究和创新的意识，感受数学与现实生活的密切联系，激发学生学习数学的兴趣。

【教学重点】用尺规作图法准确作角的和、差、倍以及角平分线。

【教学难点】用尺规作图法准确作角的和、差、倍以及角平分线。

多媒体课件。

◆教材分析◆教学目标◆教学重难点◆◆课前准备◆一、探究新知问题：线段可以相加减，角可以相加减吗？问题：射线OC在∠AOB的内部，图中有几个角？它们之间有什么等量关系？答：图中有∠AOC、∠COB、∠AOB共3个角，它们有如下的等量关系：∠AOC+∠COB=∠AOB，∠AOB-∠AOC=∠COB，∠AOB-∠COB=∠AOC。

结论：两个角可以相加（或相减），它们的和（或差）也是一个角，且它的度数等于这两个角的度数的和（或差）。

教师播放课件，探究例1.例1 如图，已知∠1、∠2，画一个角，使它等于∠1+∠2。

解：（1）用量角器画出∠ABC=∠1；（2）以点B为顶点，射线BC为一边，在∠ABC的外部用量角器画∠CBD=∠2.∠ABD就是所要画的角。

小结：作已知两个角的和（差）的步骤：（1）作一个角等于∠1；（2）以∠1的一边为始边，∠1的顶点为顶点，在∠1的外（内）部作一个角等于∠2。

【新】沪教版六年级数学下册《角的概念与表示》优质课课件.ppt

谈一谈：本节课你有何收获？
1. 角的两种定义； 2. 角的三种表示方法； 3. 方位角；
作业布置：作业本，课本作业题
再见
▪ 9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。 2021/1/112021/1/11Monday, January 11, 2021
角用“∠”表示，读做“角”。角
的表示方法有下面几种：
A
(1) 用三个大写字母表示：B
C
如：∠ABC（顶点字母写在中间）
(2) 用角的顶点字母表示：如：∠B（只有一个角时）B
A D
C
这里能用∠ B表示角吗？
A
(3) 用一个数字表示：
D
2
如：∠1、∠2
B1 C
(4)也可用一个希腊字母表示： A
如：∠a、∠ β
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
7.3 角的概念与表示
角的定义： B
终边
边
顶点
O边
顶点
始边
A
1、角是由两条有公共端点的射线所组成的图形。

2022年沪教版六年级数学下册《画角的和、差、倍》优课件

谢谢观赏
You made my day!
我们，还在路上……
经过折叠，折痕所在的射线将一个角分成了两个相等的角．角平分线
学习新知
角平分线：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.
B
因为 OC是∠AOB的平分线，
C
(也可以说OC平分∠AOB )
所以 ∠AOC=∠BOC，
O
A
∠AOC= 1∠AOB 2
1 ∠BOC= 2∠AOB
∠AOB=2∠AOC， ∠AOB=2∠BOC.
练一练
如图，∠AOD=80°，∠COD=30°， OB是∠AOC的平分线, 那么∠AOC=（ 50）°， ∠AOB=（ 25 ）°.
分析 ∠AOC= ∠AOD—∠COD
D C
= 80°— 30° = 50°
B 因为OB是∠AOC的平分线,
所以∠AOB= 1 ∠AOC
B
因为 OC是∠AOB的平分线，
C
1
所以∠AOC=∠BOC= ∠AOB，
O
A
2
或∠AOB=2∠AOC=2∠BOC.
2．作已知角的平分线
3．用数学语言来表述简单的几何说理．
4．感受化归和方程的数学思想．
▪1、书籍是朋友,虽然没有热情,但是非常忠实。2022年2月14日星期一2022/2/142022/2/142022/2/14 ▪2、科学的灵感，决不是坐等可以等来的。如果说，科学上的发现有什么偶然的机遇的话，那么这种‘偶然的机遇’只能给那些学有素养的人，给那些善于独立思考的人，给那些具有锲而不舍的人。2022年2月2022/2/142022/2/142022/2/142/14/2022 ▪3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/2/142022/2/14February 14, 2022 ▪4、享受阅读快乐，提高生活质量。2022/2/142022/2/142022/2/142022/2/14

2022年沪教版六年级数学下册《画角的和、差、倍》优质课课件

B
方法二
尺规作法
E
O
D
C
解 ⑴以∠AOB的顶点为圆心，以取
定的长a为半径，作弧分别交∠AOB
A 的两边于点D、E；
1
⑵ 的同分别一以长点度D为、半点径E作为弧圆，心两，弧以交大于于∠2DAEOB
的内的一点C；
⑶作射线OC．射线OC就是所求作的∠AOB的平分线．
例2 如图，已知∠1=∠3=m°，∠2=n°．（1）用含m、n的式子分别表示∠AOC、∠BOD的大小；（2）比较∠AOC和∠BOD的大小．
∠AOB=2∠AOC， ∠AOB=2∠BOC.
练一练
如图，∠AOD=80°，∠COD=30°， OB是∠AOC的平分线, 那么∠AOC=（ 50）°， ∠AOB=（ 25 ）°.
分析 ∠AOC= ∠AOD—∠COD
D C
= 80°— 30° = 50°
B 因为OB是∠AOC的平分线,
所以∠AOB= 1 ∠AOC
B C
解 ∵∠AOB=∠1பைடு நூலகம்∠2，
∠1=(3x-2)°,∠2=(x+8)°，
2
∠AOB=62°
1
∴(3x-2)＋(x+8)=62
O
小结
A
解得 x =14
∠1=40°,∠2=22°
本题是将几何问题转化为用代数方程来解决.
自主小结
1．角平分线
从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.
解 ⑴∵ ∠AOC =∠1＋∠2， ∠1=m°，∠2=n°
∴∠AOC =m° ＋n° ，同理 ∠BOD = m°＋n°.
⑵∵∠AOC = m°＋n° ，

六年级数学下册7.5《画角的和、差、倍》教案沪教版五

7。

5 画角的和、差、倍一、教学目标1．理解角的和、差、倍的意义，会用数学等式表示角的和、差、倍的关系2．会画角的和、差、倍3．理解角平分线的意义，会作已知角的角平分线二、教学重、难点用尺规作图法准确作角的和、差、倍以及角平分线三、教学过程1、预习反馈：提问预导中不会的2、新课引入:（1）思考:线段可以相加减,角可以相加减吗?得出结论：两个角和（或差）也是一个角，且其度数等于两个角的度数的和（或差）(2）操作：用一副(两块）三角尺可以画出哪些度数的角？(展示7种不同的拼法,并引导学生观察出作角的和差倍时都是以一角的顶点为顶点,一边为始边不同的是，作角的差时在已知角内部作终边，和和倍时在外部作）3、例题讲解:例1:如图，已知∠1、 ∠2，画一个角,使它等于∠1+∠2归纳：作已知两个角的和（差）的步骤：（1）作一个角等于∠1；（2）以∠1的一边为始边， ∠1的顶点为顶点，在∠1的外（内）部作一个角等于∠2 作角的倍数参考角的和作法4、操作探究：用纸片作材料任意剪一个角,折叠这张纸片，使角的两边叠合在一起，再展开摊平，可以看到什么？()A O E A O B ∠=∠+()A O C A O D ∠=∠-角平分线定义:从一个角的顶点引出一条射线，把这个角分成两个相等的角,这条射线叫做这个角的平分线。

5、例题讲解：例2 如图，已知∠AOB，画出它的角平分线6、练习巩固：例3 如图，已知∠1=∠3=m°,∠2=n°．（1)用含m、n的式子分别表示∠AOC、∠BOD的大小;（2)比较∠AOC和∠BOD的大小7、课堂小结：（1）理解角和、差、倍的意义，会作角的和、差、倍（2）理解角平分线的意义，会作角平分线8、当堂测验：αβ。

7-5(1)画角的和、差、倍21—22学年沪教版(上海)六年级第二学期

操作: 用纸片作材料任意剪一个角，折叠这张纸片，使角的两边叠合在一起，再展开摊平，可以看到什么？
经过折叠，折痕所在的射线将一个角分成了两个相等的角．角平分线
学习新知
角平分线：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.
B
因为 OC是∠AOB的平分线，
15度；
二、新授画角的和、差、倍
例题１：如图，已知∠α、∠β，画一个角，使它等于∠α+∠β．
α β
二、新授画角的和、差、倍
例题１：如图，已知∠α、∠β，画一个角，使它等于∠α+∠β．
D
C
β
α
B
A
解：①用量角器画出∠ABC＝ ∠α;
②以点B为顶点，射线BC为一边，在∠ ABC的外部用量角器画∠CBD ＝ ∠β 。
∠ABD就是所要画的角.
二、新授画角的和、差、倍
例题2：如图，已知∠α、∠β，画一个角，使它等于∠α-∠β
D
C
β
α
B
A
C
β α
B
解：①用量角器画出∠ABC＝ ∠α; ②以点B为顶点，射线BC为一边，在∠ ABC的外内部部用量角器画 ∠CBD＝ ∠β 。
∠ABD就是所要画的角. D
A
试一试：如果要画一个角等于2∠α-∠β呢？
2．作已知角的平分线
3．用数学语言来表述简单的几何说理．
C
(也可以说OC平分∠AOB )
所以 ∠AOC=∠BOC，
O
A ∠AOC= ∠AOB ∠BOC= ∠AOB
∠AOB=2∠AOC， ∠AOB=2∠BOC.
练一练
如图，∠AOD=80°，∠COD=30°，

2021年沪教版六年级数学下册《角的概念与表示》.ppt课件

7.3角的概念与表示
房顶的角
吊扇扇叶的夹角
剪刀的角
画一画:画一个角说一说:角是由什么图形组成？
具有公共端点的两条射线组成的图形叫做角。角的顶点角的边
边顶点
试一试：
1、判断下列哪些图形是角？
（）（）（× ）（ × ）（）（×）
角是由一条射线绕着它的端点旋转到另一个位置Байду номын сангаас 成的图形。
O
角可以用表示顶点的字母表示。 B
记作：∠O。
D
C
如果以点O为顶点的角有多个，那
B 么其中任何一个角必须用三个大
写英文字母表示，而不能记作∠O。
O
A
观察有几个以点O为顶点的角？
D
C
在角的内部标上一个小写的
希腊字母，如α、β、γ；
B
O
记作：∠α、∠β、∠γ、
A
D
C
在角的内部标上一个数字，
32 1
O
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
▪ 10、人的志向通常和他们的能力成正比例。2021/2/62021/2/62021/2/62/6/2021 1:35:54 AM ▪ 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/2/62021/2/62021/2/6Feb-216-Feb-21 ▪ 12、越是无能的人，越喜欢挑剔别人的错儿。2021/2/62021/2/62021/2/6Saturday, February 06, 2021 ▪ 13、志不立，天下无可成之事。2021/2/62021/2/62021/2/62021/2/62/6/2021

2021年沪教版六年级数学下册《角的大小比较》优质课课件

（3）看角的另一边落在量角器的什么刻度线上. （读数）
书P98
1、角的大小比较
1、目测法
2、度量法（对中、对边、读数）
3、叠合法（两“合”一“同”）
例如：已知∠AOB，移动∠DEF,
D
A (D)
（1）使顶点O与顶点E重合，
（2）使边EF与边OB叠合， E
（3）使ED与OA在OB的同侧.
F O(E) B(F)
▪ 10、人的志向通常和他们的能力成正比例。2021/2/62021/2/62021/2/62/6/2021 1:36:06 AM ▪ 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/2/62021/2/62021/2/6Feb-216-Feb-21 ▪ 12、越是无能的人，越喜欢挑剔别人的错儿。2021/2/62021/2/62021/2/6Saturday, February 06, 2021 ▪ 13、志不立，天下无可成之事。2021/2/62021/2/62021/2/62021/2/62/6/2021
这时ED对于∠AOB而言，有几种可能的位置关系？（请填写课本P96—表格）
2、画一个角等于已知角
1.度量法
例题1 已知∠α，用量角器画∠AOB，使∠AOB=∠α.
解
（1）量出∠α=??°；
（2）画出 ∠AOB=??°.
A
O
47练习：用量角器画40°的角
B
∠AOB就是所要画的角.
2、画一个角等于已知角
2、画一个角等于已知角
练习2 已知∠ABC，用直尺和圆规画∠COD=∠ABC .
A
C
E
F
解 1、作射线OC；
2、以∠B的顶点为圆心，以B 任意长a为半径

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

B C
解 ∵∠AOB=∠1+∠2，
∠1=(3x-2)°,∠2=(x+8)°，
2
∠AOB=62°
1
∴(3x-2)＋(x+8)=62
O
小结
A
解得 x =14
∠1=40°,∠2=22°
本题是将几何问题转化为用代数方程来解决.
自主小结
1．角平分线
从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.
二、新授画角的和、差、倍
例题１：如图，已知∠α、∠β，画一个角，使它（1）等于∠α+∠β．
β α
二、新授画角的和、差、倍
例题１：如图，已知∠α、∠β，画一个角，使它（1）等于∠α+∠β．
解：①用量角器画出∠ABC＝ ∠α;
②以点B为顶点，射线BC为一边，
DBβCA
在∠ ABC的外部用量角器画∠CBD ＝ ∠β 。
B
因为 OC是∠AOB的平分线，
C
1
所以∠AOC=∠BOC= ∠AOB，
O
A
2
或∠AOB=2∠AOC=2∠BOC.
2．作已知角的平分线
3．用数学语言来表述简单的几何说理．
4．感受化归和方程的数学思想．
▪ 9、春去春又回，新桃换旧符。在那桃花盛开的地方，在这醉人芬芳的季节，愿你生活像春天一样阳光，心情像桃花一样美丽，日子像桃子一样甜蜜。 2021/1/92021/1/9Saturday, January 09, 2021
回顾 A
M
线段中点将这条线段分成相等的
两部分．
B
已知点M是线段AB的1中点，那么AM=__M__B__=___2__AB， AB=__2__AM=__2_MB．
思考
角是否也有将其分成相等两部分的图形呢？
操作: 用纸片作材料任意剪一个角，折叠这张纸片，使角的两边叠合在一起，再展开摊平，可以看到什么？
经过折叠，折痕所在的射线将一个角分成了两个相等的角．角平分线
学习新知
角平分线：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的平分线.
B
因为 OC是∠AOB的平分线，
C
(也可以说OC平分∠AOB )
所以 ∠AOC=∠BOC，
O
A
∠AOC= 1∠AOB 2
1 ∠BOC= 2∠AOB
α
∠ABD就是所要画的角.
二、新授画角的和、差、倍
例题１：如图，已知∠α、∠β，画一个角，使它（1）等于∠α+∠β．（2）等于∠α-∠β
DBβCA
α
C
β α
B
解：①用量角器画出∠ABC＝ ∠α; ②以点B为顶点，射线BC为一边，在∠ ABC的外内部部用量角器画 ∠CBD＝ ∠β 。
∠ABD就是所要画的角. D
练一练
如图，∠AOD=80°，∠COD=30°， OB是∠AOC的平分线, 那么∠AOC=（ 50）°， ∠AOB=（ 25 ）°.
分析 ∠AOC= ∠AOD—∠COD
D C
= 80°— 30° = 50°
B 因为OB是∠AOC的平分线,
所以∠AOB= 1 ∠AOC
2
O
A
=
1
×
50°
2
=25°
例2 如图，已知∠1=∠3=m°，∠2=n°．（1）用含m、n的式子分别表示∠AOC、∠BOD的大小；（2）比较∠AOC和∠BOD的大小．
▪ 10、人的志向通常和他们的能力成正比例。2021/1/92021/1/92021/1/91/9/2021 8:25:04 PM ▪ 11、夫学须志也，才须学也，非学无以广才，非志无以成学。2021/1/92021/1/92021/1/9Jan-219-Jan-21 ▪ 12、越是无能的人，越喜欢挑剔别人的错儿。2021/1/92021/1/92021/1/9Saturday, January 09, 2021 ▪ 13、志不立，天下无可成之事。2021/1/92021/1/92021/1/92021/1/91/9/2021
7.5 画角的和、差、倍
一、回顾线段和差倍的画法和意义
两条线段的和（或差）也是一条线段;
其长度等于这两条线段的长度的和（或差）。
a
b
c
o
A
B
p
线段OB就是所要画的线段a+b 画2a-b+c
B
A
p
线段OB就是所要画的线段a-b
二、新授画角的和、差、倍
用一副（两块）三角尺可以画出哪些度数的角？
45度，30度，60度，90度； 75度，105度，135度，120度，150度； 15度；
A
试一试：如果要画一个角等于2∠α-∠β呢？
练习：
如图，已知∠1、 ∠2， ∠3 ，画一个角，使它等于2∠1- ∠2 + ∠3 ．
2
3

1
三、角的和、差、倍意义的简单应用
根据图形，填空。
(1)∠ABC= ＋ (2)∠ADC－∠ADB=_______ (3)∠BDE＋ =∠BDC
B
A D
E
C
问题引入
∠AOB=2∠AOC， ∠AOB=2∠BOC.
思考怎样画出一个角的角平分线呢？
例1 如图，已知∠AOB，画出它的角平分线．
B
方法一
用量角器画
M
解 ⑴用量角器量得∠AOB =48°；
O
A
⑵在∠AOB的内部画射线
OM，使∠AOM =24°．
射线OM就是所要画的∠AOB的平分线．
思考怎样画出一个角的角平分线呢？
解 ⑴∵ ∠AOC =∠1＋∠2， ∠1=m°，∠2=n°
∴∠AOC =m° ＋n° ，同理 ∠BOD = m°＋n°.
⑵∵∠AOC = m°＋n° ，
∠BOD = m°＋n° ， ∴∠AOC=∠BOD．
练一练
已知：如图,已知∠AOB=62°, ∠1=(3x-2)°,∠2=(x+8)°. 求：∠1、∠2的度数.
• 14、Thank you very much for taking me with you on that splendid outing to London. It was the first time that I had seen the Tower or any of the other famous sights. If I'd gone alone, I couldn't have seen nearly as much, because I wouldn't have known my way about.
例1 如图，已知∠AOB，画出它的角平分线．
B
方法二
尺规作法
E
O
D
C
解 ⑴以∠AOB的顶点为圆心，以取
定的长a为半径，作弧分别交∠AOB
A 的两边于点D、E；
1
⑵ 的同分别一以长点度D为、半点径E作为弧圆，心两，弧以交大于于∠2DAEOB
的内的一点C；
⑶作射线OC．射线OC就是所求作的∠AOB的平分线．