正弦函数余弦函数的图像
合集下载
正弦函数和余弦函数的图像与性质
例2.求下列函数的最大值与最小值，及取到最值 时的自变量 x 的值. (2) y 3sin x cos x (1) y sin(2 x )
4 解:(1)视为 y sin u , u 2 x 4
8 3 当 u 2k ，即 x k , k Z 时， 2 8 ymin 1 2
二、正弦函数与余弦函数的周期
对于任意 x R 都有
sin( x 2k ) sin x, k Z cos( x 2k ) cos x, k Z
正弦函数是周期函数， k , k Z , k 0 都是它的 2
周期，最小正周期是 2 余弦函数是周期函数， k , k Z , k 0 都是它的 2 周期，最小正周期是 2
注：一般三角函数的周期都是指最小正周期
1 (1) f ( x) cos 2 x (2) f ( x) sin( x ) 2 6 解: (1)设 f ( x)的周期为 T f ( x T ) f ( x)
即 cos[2( x T )] cos 2 x 即 cos(2 x 2T ) cos 2 x 即 对任意 u 都成立：cos(u 2T ) cos u 因此 2T 2 ，从而 T 解毕
第六章 三角函数
5.6.4 正弦定理、余弦定理和解斜三角形
6.1.1 正弦函数和余弦函数的图像与性质
一、正弦函数和余弦函数的概念 实数集与角的集合可以建立一一对应的关系， 每一个确定的角都对应唯一的正弦(余弦)值. 因此，任意给定一个实数 x ，有唯一确定的值
sin x(cos x) 与之对应.
函数 y sin x 叫做正弦函数 函数 y cos x 叫做余弦函数 正弦函数和余弦函数的定义域是 R 正弦函数和余弦函数的值域是[1,1]
正弦函数、余弦函数的图像(完整)
(
3 2
,1)
(1) 列表(列出对图象形状起关键作用的五点坐标)
(2) 描点(定出五个关键点)
(3) 连y线(用光滑的曲线顺次连结五个点)
图象的最高点
1-
-
(0,1) (2 ,1)
与x轴的交点
-
-1
o
6
2
3
2 3
5
7
6
6
4 3
3 5
2
3
11 6
2
x
(
2
,0)
(
3 2
,0)
-1 -
图象的最低点 ( ,1)
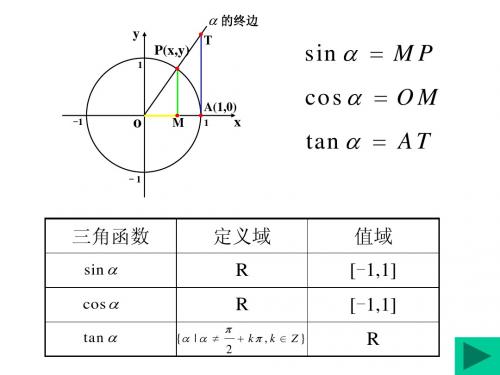
三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦函数的图象
问题：如何作出正弦函数的图象？
途径：利用单位圆中正弦线来解决。
描图：用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
4
5 6 x
正弦、余弦函数的图象
如何由正弦函数图像得y 到余弦函数图像？
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象
y=cosx=sin(x+ ), xR
2
余弦函数的图象
y
1
正弦曲 线
形状完全一样 只是位置不同
余弦曲 线
-4 -3
-2
- o
-1
正弦函数和余弦函数的图像与性质.ppt
, 0), (2 ,1)
2
2
并注意-4 曲线的“凹凸”变化.
课堂练习
1.作函数 y sin x 与 y sin x 1在 [0, 2 ]
上的大致图像. 2.指出1.中各图像与正弦函数图像的位置关系.
3.作函数 y cos x, x [ , ]的大致图像.
4.利用3.解不等式：cos x sin x, x [ , ]
-2
五个关键点：(0, 0), ( ,1), ( , 0), (3 , 1), (2 , 0)
2
2
利用五个关-4键点作简图的方法称为“五点法”
10
三、余弦函数的图像
根据诱导公式
cos
8
x
sin(
x) 可知余弦函数
y
cos
6
x的图像可由
y
2 sin
x
的图像向左平移
2
4
个单位得到.
1
2
2
-10
3-5
0
2
1
-2
余弦函数的值域是[1,1] -4
当且仅当 x 2k , k Z 时， -6
余弦函数取得最大值1；-8
5
2
35
x10
2
yP
OM x
当且仅当 x 2k , k-10 Z 时，
余弦函数取得最小值-1-1.2例1.求下列函数的源自大值与最小值，及取到最值6
课堂练习答案
12
1. y sin x, x [0, 2 ] y4
10
x
0
2
3 2
2
2 8
5
-10
1.4.1正弦、余弦函数的图象
y=sinx是一个函数，称为正弦函数；同 样y=cosx也是一个函数，称为余弦函数， 这两个函数的定义域是什么？
正弦函数的图象
y=sinx ( x∈[0,2] )
2 y
5
6
3
2
31
6
● ●
●
7
6 4
2
●
0
11
3 5 6 -1
632
3 23
●
7 4 3 5 11
●
6 3 2 3 6 2
2 5 ●
（2）用五点作图法画正弦、余弦函数的简图
作业：1.课本P46. 1题，《导学案》1题
2.预习1.4.2
函数y=sinx, x[0,2]
y
1
. 函数y=sinx, x[0,2]的图象
.
.
.
o /2 3/2 2
xห้องสมุดไป่ตู้
-1
.
关键点：
(0,0)、(
2
,1)、(
,
0)、(
3
2
,-1)、(
2
,
0)
y=sinx的图象与y=cosx的图象之间的关系
y=cosx=sin(x + ), xR
2
y y = sin x, x∈R 1
x
0
sinx 0
2
3
2
2
1 0 -1 0
1+sinx 1
21 0 1
y
2
y=1+sinx，x[0, 2]
1
o
2
-1●
● 2
●
y=sinx，x[0, 2]
3
2
x
2
●
正弦函数的图象
y=sinx ( x∈[0,2] )
2 y
5
6
3
2
31
6
● ●
●
7
6 4
2
●
0
11
3 5 6 -1
632
3 23
●
7 4 3 5 11
●
6 3 2 3 6 2
2 5 ●
（2）用五点作图法画正弦、余弦函数的简图
作业：1.课本P46. 1题，《导学案》1题
2.预习1.4.2
函数y=sinx, x[0,2]
y
1
. 函数y=sinx, x[0,2]的图象
.
.
.
o /2 3/2 2
xห้องสมุดไป่ตู้
-1
.
关键点：
(0,0)、(
2
,1)、(
,
0)、(
3
2
,-1)、(
2
,
0)
y=sinx的图象与y=cosx的图象之间的关系
y=cosx=sin(x + ), xR
2
y y = sin x, x∈R 1
x
0
sinx 0
2
3
2
2
1 0 -1 0
1+sinx 1
21 0 1
y
2
y=1+sinx，x[0, 2]
1
o
2
-1●
● 2
●
y=sinx，x[0, 2]
3
2
x
2
●
正弦函数、余弦函数的图像(基础知识+基本题型)(含解析)
5.4.1 正弦函数、余弦函数的图像（基础知识+基本题型）知识点一 正弦函数的图象 1.正弦曲线的几何作法正弦函数sin ,y x x R 的图象如图，我们把正弦函数的图象叫做正弦曲线.如图，在直角坐标系的x 轴上取一点1O ，以1O 为圆心，单位长为半径作圆，从圆1O 与x 轴的交点A 起，把圆1O 分成12等份（份数越多，画出的图象越精确）.过圆1O 上各分点作x 轴的垂线，得到对应于0,,,,,2632等角的正弦线，相应地，再把x 轴上从0到2这一段分成12等份，把角x 的正弦线向右平移，使它的起点与x 轴上的点x 重合，再把这些正弦线的终点用光滑曲线连接起来，即得sin ,[0,2]y x x 的图象.2.用“五点法”作sin ,[0,2]y x x 的简图在函数sin ,[0,2]y x x 的图象上，起关键作用的点有五个：(0,0)，(,1)2，(,0)，3(,1)2，(2,0). 一般地，在精确度要求不高时，我们常常先找出这五个关键点，再用光滑的曲线将它们连接起来，就得到正弦函数在[0,2]上的简图.这种方法叫“五点法”.【提示】（1）“五点法”作三角函数图象的实质是分别找到函数图象的最高点、最低点及三个平衡点，这五个点大致确定了函数图象的位置与形状.（2）用“五点法”作sin ,[0,2]y x x 的图象后，将其向左右平移(每次2个单位长度)，可得出sin ,y x x R 的图象.知识点二 余弦函数的图象 1.利用图象变换作余弦函数的图象 由诱导公式六，有cos sin()2y x x .因此，将正弦函数sin ,y x x R 的图象向右平移2个单位长度，就得到函数sin()cos ,2y x x x R 的图象. 我们把余弦函数cos ,y x x R 的图象叫做余弦曲线，如图所示.2.用“五点法”作cos ,[0,2]y x x 的简图在函数cos ,[0,2]y x x 的图象上，起关键作用的点是它与x 轴的交点、函数图象的最高点和最低点，它们的坐标依次为：(0,1)，(,0)2，(,1)，3(,0)2，(2,1).用光滑的曲线将它们连接起来，就得到余弦函数在[0,2]上的简图.【提示】（1）作余弦函数图象时，可通过正弦函数的图象平移得到，但要注意平移的单位长度. （2）作x R 的余弦函数图象，可由cos ,[0,2]y x x 的图象左右平移得到，也可由 sin ,y x x R 的图象向左平移2个单位长度得到.考点一 通过图象变换作函数的图象 【例1】作函数32sin y x π⎛⎫=+⎪⎝⎭的图象. 解：3sin |cos |2y x x π⎛⎫=+= ⎪⎝⎭cos 22,Z 22,3cos 22,Z .22x k x k k x k x k k ππππππππ⎧⎛⎫-+≤≤+∈ ⎪⎪⎪⎝⎭=⎨⎛⎫⎪-+<<+∈ ⎪⎪⎝⎭⎩故|cos |y x =的图象实际就是cos y x =的图象在x 轴下方的部分翻折到x 轴上方后得到的图象，如图由于余弦函数的图象是利用诱导公式依据图象变换画出的，故掌握利用诱导公式化简三角函数式也是画三角函数图象的切入点。
正余弦函数的图象
将函数图像沿y轴方向折叠，得到关于 x轴对称的新函数图像。
水平翻折
将函数图像沿x轴方向折叠，得到关于 y轴对称的新函数图像。
05
三角函数图象的应用
在物理学中的应用
01
描述周期性运动
正余弦函数可以用来描述许多周 期性运动，如简谐振动、交流电 等。
02
03
电磁波传播
波动现象
电磁波的传播可以用正余弦函数 来描述，例如在研究无线电波、 光波等传播规律时。
正余弦函数的图象
目录
• 正弦函数的图象 • 余弦函数的图象 • 正余弦函数图象的对比 • 正余弦函数图象的变换 • 三角函数图象的应用
01
正弦函数的图象
正弦函数的定义
总结词
正弦函数是三角函数的一种，它描述 了直角三角形中锐角对应的对边与斜 边的比值。
详细描述
正弦函数定义为 $sin x = frac{y}{r}$， 其中 $x$ 是角度，$y$ 是直角三角形中 锐角的对边长度，$r$ 是斜边长度。
正弦函数的周期性
总结词
正弦函数具有周期性，这意味着函数 值会重复出现。
详细描述
正弦函数的周期为 $360^circ$ 或 $2pi$ 弧度。这意味着在角度增加 $360^circ$ 或 $2pi$ 的过程中，函 数值会重复。
正弦函数的奇偶性
总结词
正弦函数是奇函数，因为对于任何角度 $x$，都有 $sin(-x) = sin x$。
VS
形状
正弦函数的图像在y轴两侧是对称的，而 余弦函数的图像在y轴两侧是不对称的。
正余弦函数在实际问题中的应用
01
02
03
振动与波动
正余弦函数在描述振动和 波动现象中有着广泛的应 用，如机械振动、电磁波 等。
正弦函数、余弦函数的图像 课件
五点描出后，余弦函数y＝cos x，x∈[0，2π]的图像的形状也
就基本上确定了．
2．利用三角函数图像解三角不等式的步骤： (1)作出相应的正弦函数或余弦函数的图像； (2)写出在[0，2π]上适合不等式的解集； (3)根据公式一写出定义域内的解集．
②描点：
③连线：用光滑的曲线依次连接各点，即得 所求的图像．
(2)画法：①列表：
x
0
sin x
0
－sin x
0
π 2
π
3π 2
2π
1 0 －1 0
－1 0 1 0
②描点： ③连线：用平滑曲线依次连接各点，即可得到所求图像．
[一点通] 作形如 y＝asin x＋b(或 y＝acos x＋b)，x∈[0，2π] π
1．正弦曲线 正弦函数y＝sin x，x∈R的图像叫正弦曲线．
2．正弦函数图像的画法
(1)几何法： ①利用 正弦线 画出y＝sin x，x∈[0，2π]上的图像； ②将图像向左、向右 平行移动(每次2π个单位)．
(2)五点法：
画出正弦曲线在[0，2π]上的图像的五个关键点 (0，0)，
(
π
2 ，1)，
集合为{x|π6 ＋2kπ≤x≤56π＋2kπ，k∈Z}．
(12分)
法二：(利用单位圆中三角函数线)
如图(2)，在0≤x＜2π中，满足sin
x≥
1 2
的角x的集合为
{x|π6 ≤x≤5π6 }．
(10分)
因此当x∈R时，
集合为{x|π6 ＋2kπ≤x≤56π＋2kπ，k∈Z}．
(12分)
[一点通] 正、余弦函数图像的作用主要有：解三角不 等式，确定交点个数及求定义域等，具体地确定范围时，应 先确定出[0，2π]上的范围，再向左向右扩展，即得整个实 数集上的范围．求交点个数时图像务必准确．
正弦,余弦函数的图像PPT教学课件
y= sinx，x[0, 2]
和
y=
cosx，x[
2
,
3 2
]的简图：
x
0 2
20
csionsx
10
01
3
3
2
2
22
-01
0-1
10
向左y平移 个单位长度 22
1
o
2
-1
3
2
2
y= cosx，x[ , 3 ]
22
y=sinx，x[0, 2]
2
x
正弦、余弦函数的图象
几何画法
小 1. 正弦曲线、余弦曲线 五点法 结
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
正弦曲 线
形状完全一样 只是位置不同
余弦函数的图象
y
余弦曲
-4 -3
-2
(0,11)
正弦、余弦函数的图象
X
正弦、余弦函数的图象
三角函数
三角函数线
正弦函数 余弦函数 正切函数
-1
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
O
M A(1,0) x
注意：三角 函数线是有 向线段！
正弦、余弦函数的图象
问题：如何作出正弦、余弦函数的图象？
途径：利用单位圆中正弦、余弦线来解决。
必修4正弦,余弦函数图像
y
y = cos x
π
x ∈ [0, 2π ]
-
1-
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
7π 6
4π 3
3π 2
5π 3
π 11 6
2π
x
在函数 y = cos x, x ∈ [0, 2π ] 的图象上，起关键作用的点有： 的图象上，起关键作用的点有： 最高点： 最高点： (0,1) (2π ,1) 最低点： 最低点：
9π −4π − 7π −3π 2 2
5π−2π 3π − 2 2
x∈R
−π
−
π 2
y
1
−
−
-1
π 2
π
3π 2π 5π 2 2
3π
7π 4π 9π 2 2
5π x
y 余弦曲线： 余弦曲线： = cos x
−
9π −4π 7π −3π 5π −2π 3π − − − 2 2 2 2
x∈R
−π
−
π 2
y
1
-1
π 2
π
3π 2π 5π 2 2
3π
7π 2
4π 9π 2
5π x
y
1-
y = sin x
x ∈ [0, 2π ]
-
-1
o
-1 -
π
6
π
3
π
2
2π 3
5π 6
π
7π 6
4π 3
3π 2
5π 3
11 π 6
2π
x
在函数 y = sin x, x ∈ [0, 2π ] 的图象上，起关键作用的点有： 的图象上，起关键作用的点有： 最高点： 最高点： (
正弦,余弦函数的图像PPT课件
途径：利用单位圆中正弦、余弦线来解决。
描图：用光滑曲线
y
B
1
将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
3
3
3
3
-1
y=sinx
终边相同角的三角函数值相等 即： sin(x+2k)=sinx, kZ
x[0,2]
f(x2k)f(x)利用图象平移
y=sinx xR
正弦、余弦函数的图象
y 1
o
2
2
-1
y=sinx x[0,2]
y
y=sinx xR
1
-4 -3
-2
- o
-1
3
2
x
2
正弦曲 线
2
3
4
5 6 x
正弦、余弦函数的图象
如何作出正弦函数的图象（在精确度要求不太高时）？
y
五点画图法
1
(2
,1)
( 2 ,1)
( ,0)
( 2 ,0)
五点法——
2
(
(0,0)o
(0,0)
2
(0,0)
-1
(0,0)
汇报人：XXX 汇报日期：20XX年10月10日
2 ,0) x
2 ,0)
( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0) ( 2 ,0)
正弦、余弦函数的图象
y
1
-4 -3
-2
- o
-1
2
3
4
5 6 x
正弦函数的图象 y=cosx=sin(x+ ), xR
2
《正余弦函数图像》课件
余弦函数基本概念介绍
定义与特点
余弦函数是周期性变化的函数，描述了单位圆上一个点的横坐标随角度变化而变化的规律。
公式
余弦函数公式为y = A * cos(B * (x - C)) + D，其中A、B、C、D分别影响振幅、周期、相位 和纵坐标偏移。
图像特征
余弦函数图像呈现周期性的波浪曲线，对称于x轴和y轴，振幅与A值相关。
《正余弦函数图像》PPT 课件
本课程将介绍正弦函数和余弦函数的基本概念，探索它们的图像及性质，比 较分析两者的图像，并以小测验来巩固所学知识。最后给出结论和参考资料。
正弦函数基本概念介绍
1 定义与特点
正弦函数是周期性变化的函数，描述了单位圆上一个点的纵坐标随角度变化而变化的规 律。
2 公式
正弦函数公式为y = A * sin(B * (x - C)) + D，其中A、B、C、D分别影响振幅、周期、相 位和纵坐标偏移。
相似性
正弦函数和余弦函数都是周 期性的函数，呈现波动或波 浪形状的图像。
差异性
相位差：正弦函数和余弦函 数的图像相位差90度。
振幅：正弦函数图像纵向的 上下震动幅度，而余弦函数 图像横向的左右震动幅度。
应用
正弦函数常用于描述周期性 变化的现象，如音波、电流 等；余弦函数通常用于描述 旋转变化的现象，如天体运 动等。
余弦函数图像及性质
1
调节振幅
2
余弦函数图像的振幅可以通过改变A
的值来调节，振幅表示纵向的上下震
动幅度。
3
波动与震动
余弦函数图像呈现连续的波动曲线， 每个周期具有相同的形状，与正弦函 数的图像相位差90度。
平移与初始位置
改变C的值可以使整个图像左右平移， 影响图像的起始位置。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
632 3 6 6323 6
0 2 5 7 4 3 5 1 1 2 63236 63236
sina ,coas,tana 的几何意义是什么
?
正弦线MP
y
T
sin=MP
1P
A
oM 1 x
余弦线OM cos=OM
正切线AT
tan=AT
既然作与单位圆有关的三角函数线可得相应的角的
三角函数值,那么通过描点(x,sinx),连线即可得到函数
别说出它们y的坐标 。
五点法
1
(2
,1)
( 2 ,1)
( ,0)
( 2
五个关键点— 2
(0,0o
) (0,0 ) (0,0
2
-1 )
(0,0,()0,00,0
)
(
2 ,1)
(
( 2 ,1)
(2
,1)
( 2 ,1)
( 2 ,1)
( 2 ,1)
( 2 ,1)
,0) 3 ( ,0) 2
ysix,n x 0 ,2 的图象
问题：如何作出正弦、余弦函数的图象？
途径：利用单位圆中正弦、余弦线来解决。
y
B
1
描图：用光滑曲线 将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
3
3
3
3
-1
y=sinx ( x [0, 2 ] )
5
我们在作正弦函数y=sinx x∈[0,2 π]的图象时，描
出了12个点，但其中起关键作用的点是哪些？分
正弦、余弦函数的图象
几何画法
小 1. 正弦曲线、余弦曲线 五点法 结
2.注意与诱导公式、三角函数线等知识的联系
y
1
y=cosx，x[0, 2]
o
2
2
-1
3
2
x
2
y=sinx，x[0, 2]
14
个人观点供参考，欢迎讨论
1
yc o s,x[ 0 , 2 π ]
O
-1
π π 3π2π x
2
2
ycos,xx[0,2π]
练习：在同一坐标系内，用五点法分别画出函数
y= sinx，x[0, 2] 和 y= cosx，x[ , 3 ]的简图：
22
02
20
10
01
2
3
2
23
2
-01
0-1
10
向左y平移 个单位长度 22
,0)( 2
2,0)
( 2
(
((,0((,()0,0)),0,,(1003))2))(3 2,(1(-33)22,(13(12,,)3-1()23,)21(1,(13-3))2,)21,),--
,0) ( 2
,0)( 2 ,0)( 2 (,02)
( 2,0) ( 2,0)
,0)
x
0
2
0
1
3 2
0
-1
1.4.1正弦函数、余弦函数的图像
物理中把简谐运动的图像叫做“正弦曲线”或“余弦曲 线”
沙漏单摆实验
知识探究：正弦函数y=sinx的图象
思考1：作函数图象最原始的方法是什么？
答：列表、描点、连线
思考2：用描点法作正弦函数y=sinx在[0， 2π]内的图象，可取哪些点？
让 x取 0,,,,2,5,,7,4,3,5,11 ,2等值
1
- o
-1
2
正弦函数的图象
y=cosx=sin(x+ ), xR
2
余弦函数的图象
y
-4 -3
-2
(0,11
3
( 2
-
)
(-o12 ,0)
( 2 ,0) ,1)
2
( ,-
1)
3
4
5 6 x
正弦曲 线
形状完全一样 只是位置不同
余弦曲 线
3
4
5 6 x
8
像作二次函数图象那样为了快速用描点法 作出正弦曲线与余弦曲线。下面我们通过观察 函数图象寻找图象上起关键作用的点：
1
y=sinx，x[0, 2]
o
3
2
2
2
-1
y= cosx，x[ , 3 ]
22
2
x
12
思考：如何画出函数 ysinx,xR的简图
解：按关键点列表
2
3 2
2
y sinx
描点并将它们用光滑曲线连 接起来
y ysinx,xR 1
2 3
2
2
o
3
2
2
-1
y=sinx，x[0, 2]
2 x
13
2
0
6
y=sinx
终边相同角的三y角函数值相等 x[0,2] 即： sin(x+2k)=sinx, kZ
f(x2k)f(x)利用图象平移
y=sinx xR
1
-4π -3π -2π
-
o /2 3/2 2π
3π 4π
x
-1
函数y=sinx, xR的图象 正弦曲线
正弦、余弦函数的图象
y
-4 -3
-2
sinx
2
π
3π 2
π
1sinx
2y . 1.
y1s i nx x[,0 , 2 π
.
.
o
π
.
3π
-1
2
2
2
x
ysinxx[,0,2 π ]
（2）画出y=-cosx , x∈[0，2]的简图
x0
π π3 π 2 π
2
2
c o 1s 0 x - 1 0 1
- co - 1 s 0x 1 0- 1
y
图象的最高点(
2
,1)
ysix,n x 0 ,2 图象与x轴的交点(0,0) ( ,0) (2,0)
图象的最低点(
3
2,
1)
图象的最高点(0,1) (2,1)
y co x ,x s0 ,2
图象与x轴的交点(
2
,0)(
3 2
,0)
图象的最低点(,1)
9
例1：（1）画出y=1+sinx , x∈[0，2 ]的简图
0 2 5 7 4 3 5 1 1 2 63236 63236
sina ,coas,tana 的几何意义是什么
?
正弦线MP
y
T
sin=MP
1P
A
oM 1 x
余弦线OM cos=OM
正切线AT
tan=AT
既然作与单位圆有关的三角函数线可得相应的角的
三角函数值,那么通过描点(x,sinx),连线即可得到函数
别说出它们y的坐标 。
五点法
1
(2
,1)
( 2 ,1)
( ,0)
( 2
五个关键点— 2
(0,0o
) (0,0 ) (0,0
2
-1 )
(0,0,()0,00,0
)
(
2 ,1)
(
( 2 ,1)
(2
,1)
( 2 ,1)
( 2 ,1)
( 2 ,1)
( 2 ,1)
,0) 3 ( ,0) 2
ysix,n x 0 ,2 的图象
问题：如何作出正弦、余弦函数的图象？
途径：利用单位圆中正弦、余弦线来解决。
y
B
1
描图：用光滑曲线 将这些正弦线的 终点连结起来
A
O1
O
2
4
5
2
x
3
3
3
3
-1
y=sinx ( x [0, 2 ] )
5
我们在作正弦函数y=sinx x∈[0,2 π]的图象时，描
出了12个点，但其中起关键作用的点是哪些？分
正弦、余弦函数的图象
几何画法
小 1. 正弦曲线、余弦曲线 五点法 结
2.注意与诱导公式、三角函数线等知识的联系
y
1
y=cosx，x[0, 2]
o
2
2
-1
3
2
x
2
y=sinx，x[0, 2]
14
个人观点供参考，欢迎讨论
1
yc o s,x[ 0 , 2 π ]
O
-1
π π 3π2π x
2
2
ycos,xx[0,2π]
练习：在同一坐标系内，用五点法分别画出函数
y= sinx，x[0, 2] 和 y= cosx，x[ , 3 ]的简图：
22
02
20
10
01
2
3
2
23
2
-01
0-1
10
向左y平移 个单位长度 22
,0)( 2
2,0)
( 2
(
((,0((,()0,0)),0,,(1003))2))(3 2,(1(-33)22,(13(12,,)3-1()23,)21(1,(13-3))2,)21,),--
,0) ( 2
,0)( 2 ,0)( 2 (,02)
( 2,0) ( 2,0)
,0)
x
0
2
0
1
3 2
0
-1
1.4.1正弦函数、余弦函数的图像
物理中把简谐运动的图像叫做“正弦曲线”或“余弦曲 线”
沙漏单摆实验
知识探究：正弦函数y=sinx的图象
思考1：作函数图象最原始的方法是什么？
答：列表、描点、连线
思考2：用描点法作正弦函数y=sinx在[0， 2π]内的图象，可取哪些点？
让 x取 0,,,,2,5,,7,4,3,5,11 ,2等值
1
- o
-1
2
正弦函数的图象
y=cosx=sin(x+ ), xR
2
余弦函数的图象
y
-4 -3
-2
(0,11
3
( 2
-
)
(-o12 ,0)
( 2 ,0) ,1)
2
( ,-
1)
3
4
5 6 x
正弦曲 线
形状完全一样 只是位置不同
余弦曲 线
3
4
5 6 x
8
像作二次函数图象那样为了快速用描点法 作出正弦曲线与余弦曲线。下面我们通过观察 函数图象寻找图象上起关键作用的点：
1
y=sinx，x[0, 2]
o
3
2
2
2
-1
y= cosx，x[ , 3 ]
22
2
x
12
思考：如何画出函数 ysinx,xR的简图
解：按关键点列表
2
3 2
2
y sinx
描点并将它们用光滑曲线连 接起来
y ysinx,xR 1
2 3
2
2
o
3
2
2
-1
y=sinx，x[0, 2]
2 x
13
2
0
6
y=sinx
终边相同角的三y角函数值相等 x[0,2] 即： sin(x+2k)=sinx, kZ
f(x2k)f(x)利用图象平移
y=sinx xR
1
-4π -3π -2π
-
o /2 3/2 2π
3π 4π
x
-1
函数y=sinx, xR的图象 正弦曲线
正弦、余弦函数的图象
y
-4 -3
-2
sinx
2
π
3π 2
π
1sinx
2y . 1.
y1s i nx x[,0 , 2 π
.
.
o
π
.
3π
-1
2
2
2
x
ysinxx[,0,2 π ]
（2）画出y=-cosx , x∈[0，2]的简图
x0
π π3 π 2 π
2
2
c o 1s 0 x - 1 0 1
- co - 1 s 0x 1 0- 1
y
图象的最高点(
2
,1)
ysix,n x 0 ,2 图象与x轴的交点(0,0) ( ,0) (2,0)
图象的最低点(
3
2,
1)
图象的最高点(0,1) (2,1)
y co x ,x s0 ,2
图象与x轴的交点(
2
,0)(
3 2
,0)
图象的最低点(,1)
9
例1：（1）画出y=1+sinx , x∈[0，2 ]的简图