实验四控制系统的稳定性分析样本
仿真实验线性系统稳定性分析报告.doc

实验四 Stability analysis of linear systems线性系统稳定性分析一、实验目的1.通过响应曲线观测特征参量ζ和n ω对二阶系统性能的影响。
2.熟练掌握系统的稳定性的判断方法。
二、基础知识及MATLAB 函数注意:routh ()和hurwitz ()不是MATLAB 中自带的功能函数,(在共享文件夹里有劳斯判据和赫尔维茨判据的m 文件,把其中的routh.m 和hurwitz .m 放到MATLAB 文件夹下的work 文件夹中才能运行)。
1)直接求根判稳roots()控制系统稳定的充要条件是其特征方程的根均具有负实部。
因此,为了判别系统的稳定性,就要求出系统特征方程的根,并检验它们是否都具有负实部。
MATLAB 中对多项式求根的函数为roots()函数。
若求以下多项式的根24503510234++++s s s s ,则所用的MATLAB 指令为: >> roots([1,10,35,50,24])ans =-4.0000 -3.0000 -2.0000 -1.0000特征方程的根都具有负实部,因而系统为稳定的。
2)劳斯稳定判据routh ()劳斯判据的调用格式为:[r, info]=routh(den)该函数的功能是构造系统的劳斯表。
其中,den 为系统的分母多项式系数向量,r 为返回的routh 表矩阵,info 为返回的routh 表的附加信息。
以上述多项式为例,由routh 判据判定系统的稳定性。
>> syms EPS den=[1,10,35,50,24]; ra=routh(den,EPS) r=1 35 24 10 50 0 30 24 0 42 0 0 24 0 0 info=[ ]由系统返回的routh 表可以看出,其第一列没有符号的变化,系统是稳定的。
3)赫尔维茨判据hurwitz ()赫尔维茨的调用格式为:H=hurwitz (den )。
实验四三阶系统的瞬态响应及稳定性分析

实验四三阶系统的瞬态响应及稳定性分析引言:实际工程中经常遇到三阶系统,对三阶系统的瞬态响应及稳定性进行分析能够帮助我们更好地设计和优化控制系统。
本实验旨在通过实验,研究三阶系统的瞬态响应及稳定性,并加深对其理论知识的理解和掌握。
实验一:三阶系统的瞬态响应1.实验目的:通过三阶系统的瞬态响应实验,观察系统的输出响应情况,了解系统的动态特性。
2.实验仪器:示波器、波形发生器、三阶系统实验箱3.实验原理:三阶系统的瞬态响应是指系统在初始状态发生突变时,输出的响应情况。
三阶系统的瞬态响应主要涉及到系统阶跃响应、系统脉冲响应。
4.实验步骤:a.将波形发生器的正弦波信号输入三阶系统实验箱。
b.设置示波器的观测通道,将示波器的探头连接到三阶系统实验箱的输出端口。
c.调节波形发生器的频率和幅度,观察示波器上得到的输出响应波形。
5.数据处理:a.根据示波器上输出的响应波形,可以观察到系统的超调量、调整时间等指标,根据公式可以计算得到这些指标的具体数值。
b.将实验得到的数据记录下来,进行分析和比较。
1.实验目的:通过三阶系统的稳定性分析实验,了解系统的稳定性及稳定性判据。
2.实验仪器:示波器、三阶系统实验箱3.实验原理:三阶系统的稳定性是指系统在初始状态发生突变或受到外部扰动时,系统是否能够回到稳定状态。
常见的稳定性分析方法包括极点判据、频率响应法等。
4.实验步骤:a.将示波器的探头连接到三阶系统实验箱的输出端口。
b.调节系统的输入信号,观察示波器上得到的系统输出响应波形。
c.根据观察到的输出波形,分析系统的稳定性。
5.数据处理:a.根据实验得到的数据和观察到的波形,可以从输入输出关系中提取出系统的稳定性信息,比如振荡频率、稳定的输出值等。
b.根据提取出的信息,判断系统的稳定性。
实验三:实验结果和分析1.通过实验一,我们可以观察到三阶系统的瞬态响应,并根据输出波形,计算得到系统的超调量、调整时间等指标。
通过对比不同输入频率和幅度下的响应波形,可以分析系统的动态特性。
控制系统的稳定性分析实验总结

控制系统的稳定性分析实验总结:控制系统稳定性实验分析提高控制系统稳定性最小相位系统对控制系统的基本要求篇一:实验三、控制系统稳定性分析实验三、控制系统稳定性分析注意:进入实验室前的要求学习教材108-182和402-405页内容;电动机传递函数Gm KT(KT --转矩系数La –电感Ra –电阻)Las?Ra机械系统传递函数d2?d?J2?B?K??T (J—质量B—阻尼K—刚度)dtdt对其求拉斯变换,得到所要传函。
1.试验目的1) 学习并掌握Matlab控制系统的简单使用方法2) 掌握控制系统稳定性分析方法3) 掌握放大环节(如比例调节器)、延迟环节对控制系统稳定性的影响2.验仪器系统安装有matlab软件的计算机实验系统3.实验内容用Bode图分析下面系统中,调节器kc及延迟环节对系统稳定性的影响。
(分析调节器kc时,延迟常数=0; 分析延迟常数时,调节器kc=10)其中Gc(s)为调节器,Gc(s)=k;Gp(s)为功率放大器,Gp(s)=500;Gm(s)为电动机,其电阻r=10欧,电感L=0.1亨,电磁转矩系数Kt =0.01,反电势系数Ke=0.1;H(s)为检测传感器,H(s)=0.1伏/弧度/s;G(s)为被驱动机械对象,可以看成质量-刚度-阻尼系统,J=0.5; -TsK=1;C=0.1; e为系统中的延迟,主要有材料等引起。
(以上参数取值及结构,实验指导老师可是情况变动)4.实验步骤1)写出系统开环传递函数;2)打开matlab 3)建立***.m文件4)编制程序(主要指令: tf、bode、nyquist、margin、pade ; 注释用“%”开头,如: )5)运行所编制程序6)运行结果记录7)存储所编制程序 6. 结果分析和实验报告K=4; %K=8,12,20,100,200,500,1000 s1=tf([K],[1]); s2=tf([500],[1]); s3=tf([0.01],[0.1,10]);s4=tf([1,0],[0.5,0.1,1]); s5=tf([1],[1,0]); s6=tf([0.1],[1]); s7=tf([0.1],[1]); s8=s3*s4; s9=feedback(s8,0.1,-1); s10=s1*s2*s9*s5*s7 nyquist(s10) bode(s10)K=4时伯德图:Magntude (dB)Phase (deg)Frequency (rad/sec)K=4时传递函数:2 s--------------------------------------0.05 s + 5.01 s + 1.101 s + 10 s实验结果分析:实验程序:T=0.1; %T=0.1,0.8,1,2,4,8,10,11 s1=tf([100],[1]) s2=tf([500],[1]) s3=tf([0.01],[0.1,10]) s4=tf([1,0],[0.5,0.1,1])s5=tf([1],[1,0]) s6=tf([0.1],[1]) s7=tf([0.1],[1]) [num,den]=pade(7 - 4.541e014 s+ 6.054e016 s - 5.881e018 s + 3.97e020 s - 1.676e022 s+ 3.352e023 s-----------------------------------------------------------------------------------0.05 s+ 60.01 s+ 3.521e004 s+ 1.327e007 s+ 3.555e009 s+ 7.07e011 s + 1.061e014 s + 1.196e016 s + 9.877e017 s+ 5.668e019 s + 2.025e021 s + 3.404e022 s + 1.073e022 s实验结果分析:思考题:1. 开环传递函数中的比例对系统稳定性有何影响?答:系统稳定性变得不好。
系统响应及系统稳定性实验报告

系统响应及系统稳定性实验报告系统响应及系统稳定性实验报告引言:系统响应和系统稳定性是控制论中重要的概念。
在工程和科学领域中,我们经常需要对系统的响应和稳定性进行评估和分析,以便设计和优化控制系统。
本实验旨在通过实际测量和数据分析,探讨系统响应和系统稳定性的相关概念。
一、实验背景控制系统是由输入、输出和系统本身组成的。
系统响应是指系统对输入信号的反应。
而系统稳定性则是指系统在长时间运行中是否趋于稳定状态。
了解系统的响应和稳定性对于设计和优化控制系统至关重要。
二、实验目的1. 了解系统响应和系统稳定性的概念和定义。
2. 掌握测量系统响应和稳定性的方法和技巧。
3. 分析实验数据,评估系统的响应和稳定性。
三、实验装置和方法本实验使用了一个简单的电路系统作为示例。
实验装置包括一个信号发生器、一个电路板和一个示波器。
实验步骤如下:1. 将信号发生器连接到电路板的输入端,设置合适的频率和振幅。
2. 将示波器连接到电路板的输出端,用于测量输出信号。
3. 通过改变信号发生器的输入信号,观察并记录系统的响应。
四、实验结果与数据分析在实验中,我们通过改变信号发生器的输入信号频率和振幅,记录了系统的输出信号。
根据实验数据,我们可以绘制出系统的频率响应曲线和幅频特性曲线。
1. 频率响应曲线频率响应曲线是描述系统对不同频率输入信号的响应的曲线。
通过绘制频率响应曲线,我们可以观察到系统对于不同频率信号的增益和相位变化。
从实验数据中绘制的频率响应曲线中,我们可以观察到系统在低频时具有较高的增益,而在高频时增益逐渐降低。
2. 幅频特性曲线幅频特性曲线是描述系统对不同幅度输入信号的响应的曲线。
通过绘制幅频特性曲线,我们可以观察到系统对于不同幅度信号的增益变化。
从实验数据中绘制的幅频特性曲线中,我们可以观察到系统在低幅度信号时具有较高的增益,而在高幅度信号时增益逐渐饱和。
五、系统稳定性分析系统稳定性是指系统在长时间运行中是否趋于稳定状态。
自控实验报告四离散系统的稳定性分析

实验四离散系统的稳定性分析一、实验目的1.掌握香农定理,了解信号的采样保持与采样周期的关系。
2.掌握采样周期对采样系统的稳定性影响。
二、实验设备PC 机一台,TD-ACC+(或TD-ACS)教学实验系统一套。
三、实验原理及内容本实验采用“采样-保持器”LF398 芯片,它具有将连续信号离散后以零阶保持器输出信号的功能。
其管脚连接图如 5.1-1 所示,采样周期 T 等于输入至 LF398 第 8 脚 (PU) 的脉冲信号周期,此脉冲由多谐振器 (由 MC1555 和阻容元件构成) 发生的方波经单稳电路 (由 MC14538 和阻容元件构成) 产生,改变多谐振荡器的周期,即改变采样周期。
图 5.1-2 是 LF398 采样-保持器功能的原理方块图。
1.信号的采样保持:电路如图 5.1-3 所示。
连续信号 x(t) 经采样器采样后变为离散信号 x*(t),香农 (Shannon) 采样定理指出,离散信号 x*(t)可以完满地复原为连续信号条件为:2.闭环采样控制系统(1) 原理方块图图 5.1-4 所示闭环采样系统的开环脉冲传递函数为:从式(5.1-4) 知道,特征方程式的根与采样周期T有关,若特征根的模均小于1,则系统稳定,若有一个特征根的模大于1,则系统不稳定,因此系统的稳定性与采样周期T的大小有关。
四、实验步骤1.准备:将信号源单元的“ST”的插针和“+5V”插针用“短路块”短接。
2.信号的采样保持实验步骤(1) 按图 5.1-3 接线。
检查无误后开启设备电源。
(2) 将正弦波单元的正弦信号 (将频率调为 2.5HZ) 接至 LF398 的输入端“IN1”。
(3) 调节信号源单元的信号频率使“S”端的方波周期为 20ms 即采样周期 T = 20ms。
(4) 用示波器同时观测 LF398 的 OUT1 输出和IN1 输入,此时输出波形和输入波形一致。
(5) 改变采样周期,直到 200ms,观测输出波形。
系统稳定性分析实验报告

一、实验目的1. 理解系统稳定性的基本概念和稳定性判据。
2. 掌握控制系统稳定性分析的方法和步骤。
3. 分析系统开环增益和时间常数对系统稳定性的影响。
4. 通过实验验证稳定性分析方法的有效性。
二、实验原理系统稳定性分析是自动控制理论中的一个重要内容,主要研究系统在受到扰动后能否恢复到原来的稳定状态。
根据系统传递函数的极点分布,可以将系统分为稳定系统和不稳定系统。
稳定系统在受到扰动后,其输出会逐渐恢复到原来的平衡状态;而不稳定系统在受到扰动后,其输出会发散,无法恢复到原来的平衡状态。
三、实验仪器1. 自动控制系统实验箱一台2. 计算机一台3. 数据采集卡一台四、实验内容1. 系统模拟电路搭建根据实验要求,搭建一个典型的控制系统模拟电路,如图1所示。
电路中包含一个比例积分(PI)控制器和一个被控对象。
被控对象可以用一个一阶环节表示,传递函数为G(s) = K / (Ts + 1),其中K为开环增益,T为时间常数。
图1 系统模拟电路图2. 系统稳定性分析(1)观察系统的不稳定现象在实验箱上设置不同的K和T值,观察系统在受到扰动后的响应情况。
当K值较大或T值较小时,系统容易产生增幅振荡,表现为不稳定现象。
(2)研究系统开环增益和时间常数对稳定性的影响通过改变K和T的值,观察系统稳定性的变化。
分析以下情况:1)当K值增加时,系统稳定性降低,容易出现增幅振荡;2)当T值减小时,系统稳定性降低,容易出现增幅振荡;3)当K和T同时改变时,系统稳定性受到双重影响。
(3)验证稳定性分析方法的有效性使用劳斯-赫尔维茨稳定性判据,分析系统传递函数的极点分布,判断系统是否稳定。
将实验得到的K和T值代入传递函数,计算特征方程的根,判断系统稳定性。
五、实验步骤1. 搭建系统模拟电路,连接实验箱和计算机。
2. 设置实验箱参数,调整K和T的值。
3. 观察系统在受到扰动后的响应情况,记录数据。
4. 使用劳斯-赫尔维茨稳定性判据,分析系统稳定性。
控制系统的稳定性分析实验报告范文

控制系统的稳定性分析实验报告范文下载提示:该文档是本店铺精心编制而成的,希望大家下载后,能够帮助大家解决实际问题。
文档下载后可定制修改,请根据实际需要进行调整和使用,谢谢!本店铺为大家提供各种类型的实用资料,如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等,想了解不同资料格式和写法,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!控制系统的稳定性分析实验报告1. 引言控制系统的稳定性分析是控制工程领域的重要研究方向之一。
自动控制原理实验四-线性定常控制系统的稳定分析

实验四线性定常控制系统的稳定分析
一、实验目的
(1)深刻理解反馈对系统稳定性的作用和影响;
(2)深刻理解系统类型对系统稳定性的影响的规律;
(3)深刻理解零点对系统稳定性无影响;
(4)理解系统参数对系统稳定性的影响。
二、实验原理及内容:
1.单位反馈对系统稳定性的影响
(1) 已知开环系统结构图如图4-1所示。
R (S
其中W(S)分别为:(a )1()0.11W s s =+和(b )1()0.2
W s s =- (2)闭环系统单位负反馈形式为:
图4-2 闭环系统
其中W(S)同(1)。
通过观察两组W (S )在开环和闭环两种形式下系统的零、极点分布和单位阶跃响应曲。
控制系统的稳定性分析实验报告

控制系统的稳定性分析实验报告引言控制系统的稳定性是指系统在扰动作用下,能否保持稳定运行的能力。
在实际应用中,对于控制系统的稳定性分析具有重要的意义。
本实验旨在通过实际实验,分析控制系统的稳定性,并对结果进行报告。
实验设备和方法设备本实验使用的设备如下:1.一台控制系统稳定性分析实验设备2.一台电脑方法1.将实验设备接通电源,等待设备启动完毕。
2.打开电脑,运行实验软件。
3.在实验软件中设置实验参数,包括控制系统的传递函数、采样时间等。
4.开始实验,并记录实验过程中的数据。
5.分析实验结果,得出控制系统的稳定性结论。
6.撰写实验报告。
实验结果与分析在本次实验中,我们选择了一个二阶惯性系统作为被控对象,传递函数为$G(s)=\\frac{1}{(s+1)(s+2)}$。
我们使用了PID控制器进行控制,并设置了合适的参数。
实验过程中,我们输入了一个单位阶跃信号,观察系统的响应。
通过记录实验数据并进行分析,我们得到了以下实验结果:1.系统的超调量为5%;2.系统的稳态误差为0.1;3.系统的调节时间为2秒。
根据实验结果,我们可以得出以下结论:1.系统的超调量很小,说明系统具有较好的动态性能;2.系统的稳态误差较小,说明系统具有较好的稳定性;3.系统的调节时间较短,说明系统的响应速度较快。
综上所述,实验结果表明控制系统具有较好的稳定性。
结论通过本次实验,我们通过实际实验和数据分析,得出了控制系统的稳定性结论。
实验结果表明控制系统具有较好的稳定性。
控制系统的稳定性是保证系统正常运行的重要指标,对于工程应用具有重要的意义。
参考文献无。
自动控制原理实验报告--控制系统的稳定性和稳态误差

本科实验报告课程名称:自动控制原理实验项目:控制系统的稳定性和稳态误差实验地点:多学科楼机房专业班级:学号:学生姓名:指导教师:2012 年5 月15 日一、实验目的和要求:1.学会利用MATLAB 对控制系统的稳定性进行分析; 2.学会利用MATLAB 计算系统的稳态误差。
二、实验内容和原理:1.利用MATLAB 描述系统数学模型如果系统的的数学模型可用如下的传递函数表示nn n m m m a s a s b s b s b s U s Y s G ++++++==-- 11110)()()( 则在MATLAB 下,传递函数可以方便的由其分子和分母多项式系数所构成的两个向量惟一确定出来。
即num=[b 0,b 1 ,…, b m ]; den=[1,a 1,a 2 ,…,a n ]例2-1 若系统的传递函数为5234)(23+++=s s s s G 试利用MA TLAB 表示。
当传递函数的分子或分母由若干个多项式乘积表示时,它可由MA TLAB 提供的多项式乘法运算函数conv( )来处理,以获得分子和分母多项式向量,此函数的调用格式为 p=conv(p1,p2)其中,p1和p2分别为由两个多项式系数构成的向量,而p 为p1和p2多项式的乘积多项式系数向量。
conv( )函数的调用是允许多级嵌套的。
例2-2 若系统的传递函数为)523)(1()66(4)(232++++++=s s s s s s s s G试利用MA TLAB 求出其用分子和分母多项式表示的传递函数。
2.利用MATLAB 分析系统的稳定性在分析控制系统时,首先遇到的问题就是系统的稳定性。
判断一个线性系统稳定性的一种最有效的方法是直接求出系统所有的极点,然后根据极点的分布情况来确定系统的稳定性。
对线性系统来说,如果一个连续系统的所有极点都位于左半s 平面,则该系统是稳定的。
MATLAB 中根据特征多项式求特征根的函数为roots( ),其调用格式为r=roots(p) 其中,p 为特征多项式的系数向量;r 为特征多项式的根。
控制系统的稳定性分析实验报告
控制系统的稳固性分析一、实验目的1.视察系统的不稳固现象。
2.研究系统开环增益和时间常数对稳固性的影响。
二、实验仪器1.自动控制系统实验箱一台2.运算机一台三、实验内容系统模拟电路图如图系统模拟电路图其开环传递函数为:G(s)=10K/s(0.1s+1)(Ts+1)式中 K1=R3/R2,R2=100KΩ,R3=0~500K;T=RC,R=100KΩ,C=1μf或C=0.1μf 两种情形。
四、实验步骤1.连接被测量典型环节的模拟电路。
电路的输入U1接A/D、D/A卡的DA1输出,电路的输出U2接A/D、D/A卡的AD1输入,将纯积分电容两端连在模拟开关上。
检查无误后接通电源。
2.启动运算机,在桌面双击图标 [自动控制实验系统] 运行软件。
3.在实验项目的下拉列表中挑选实验三[控制系统的稳固性分析]5.取R3的值为50KΩ,100KΩ,200KΩ,此时相应的K=10,K1=5,10,20。
视察不同R3值时显示区内的输出波形(既U2的波形),找到系统输生产生增幅振荡时相应的R3及K值。
再把电阻R3由大至小变化,即R3=200kΩ,100kΩ,50kΩ,视察不同R3值时显示区内的输出波形, 找出系统输生产生等幅振荡变化的R3及K值,并视察U2的输出波形。
五、实验数据1模拟电路图2.画出系统增幅或减幅振荡的波形图。
C=1uf时:R3=50K K=5:R3=100K K=10R3=200K K=20:等幅振荡:R3=220k:增幅振荡:R3=220k:R3=260k:C=0.1uf时:R3=50k:R3=100K:R3=200K:。
控制系统的稳定性分析实验报告

控制系统的稳定性分析实验报告一、实验目的1.了解控制系统的稳定性分析方法。
2.通过实验,掌握系统稳态误差、系统阻尼比、系统根轨迹等稳态分析方法。
3.掌握控制系统的稳定性分析实验步骤。
二、实验原理1.系统稳态误差分析系统稳态误差是指系统在达到稳态时,输出与输入之间的偏差。
对于稳态误差的分析,可以采用开环传递函数和闭环传递函数进行分析。
开环传递函数:G(s)闭环传递函数:G(s)/(1+G(s)H(s))其中,H(s)为系统的反馈环节,G(s)为系统的前向传递函数。
稳态误差可以分为静态误差和动态误差。
静态误差是指系统在达到稳态时,输出与输入之间的偏差;动态误差是指系统在达到稳态时,输出与输入之间的波动。
2.系统阻尼比分析系统阻尼比是指系统在达到稳态时,振荡的阻尼程度。
阻尼比越大,系统越稳定;阻尼比越小,系统越不稳定。
系统阻尼比的计算公式为:ζ=1/(2ξ)其中,ξ为系统的阻尼比,ζ为系统的阻尼比。
3.系统根轨迹分析系统根轨迹是指系统的极点随着控制参数变化而在复平面上的轨迹。
根轨迹分析可以用来判断系统的稳定性和性能。
系统的根轨迹可以通过以下步骤进行绘制:(1)确定系统的传递函数G(s)(2)将G(s)写成标准形式(3)计算系统的极点和零点(4)绘制系统的根轨迹三、实验步骤1.系统稳态误差分析实验(1)将系统的开环传递函数和闭环传递函数写出。
(2)通过实验,测量系统的静态误差和动态误差。
(3)根据静态误差和动态误差的测量结果,计算系统的稳态误差。
2.系统阻尼比分析实验(1)通过实验,测量系统的振荡频率和衰减周期。
(2)根据振荡频率和衰减周期的测量结果,计算系统的阻尼比。
3.系统根轨迹分析实验(1)将系统的传递函数写成标准形式。
(2)计算系统的极点和零点。
(3)绘制系统的根轨迹,并根据根轨迹的形状,判断系统的稳定性和性能。
四、实验结果分析通过实验,我们可以得到系统的稳态误差、阻尼比和根轨迹等数据。
根据这些数据,我们可以分析系统的稳定性和性能,并对系统进行优化。
控制系统的稳定性分析实验报告范文

控制系统的稳定性分析实验报告范文摘要:本文在回顾顾客满意度理论和系统理论的基础上,创新性地运用系统理论的新视角研究顾客满意度。
顾客满意度系统是由企业/产品形象、顾客期望、顾客感知价值、顾客感知质量、顾客感知价值等因素组成复杂社会系统,探索运用控制系统论的理论和方法研究顾客满意度系统,推导出顾客满意度系统稳定运行的系统检验系数,形成了独特的顾客满意度系统稳定性检验理论。
传统衡量顾客满意度的高低是以顾客满意度指数的大小为依据,本文认为:顾客满意度的高低不仅取决于顾客满意度指数的大小,也取决于顾客满意度系统稳定性的优劣。
通过中油运输服务企业实证研究,验证了顾客满意度系统稳定性检验理论,得出了顾客满意度系统检验系数是系统稳定性的判据,也是企业运行质量晴雨表的重要结论。
关键词:控制系统论顾客满意度系统稳定性理论研究一、引言进入20世纪80年代以来,以顾客为中心、追求顾客满意和顾客忠诚的经营理念已在发达国家逐步形成和发展,并逐步向其他国家蔓延和渗透。
自从Oliver(1980)首先提出了前人满意决策认知模型以来,世界很多国家纷纷建立了各自的顾客满意度指数(CSI)模型。
瑞典于1989年建立了世界上第一个顾客满意度指数结构模型以来,美国、欧洲、中国等许多国家也建立了各自国家的顾客满意度模型,其应用涉及到营销、教育、医疗、宾馆、电子商务等诸多领域。
随着我国社会主义市场经济的建立和发展,人们的质量意识逐步增强,质量作为产品和服务的重要衡量尺度已深入人心。
然而,由于质量在人们心目中的概念是模糊的,没有一个相对准确的衡量指标,而且各种产品和服务的质量没有可比性,而顾客满意度则是从客观角度衡量质量的综合指标,它是企业、行业乃至国家衡量经济发展质量与水平的晴雨表。
从企业角度讲,以顾客为中心,满足顾客需求的经营理念是企业质量竞争的重要前提,ClaeFornell,刘金兰(2006)对顾客满意定义为:顾客在使用某种产品或享受某项服务以后,形成的满意和不满意的态度,包括某种特定交易的顾客满意和积累的顾客满意。
实验四 控制系统的稳定性分析

西京学院实验教学教案实验课程:现代控制理论基础课序: 4 教室:工程舫0B-14实验日期:2013-6-3、4、6 教师:万少松一、实验名称:系统的稳定性及极点配置二、实验目的1.巩固控制系统稳定性等基础知识;2.掌握利用系统特征根判断系统稳定性的方法;3.掌握利用李雅普诺夫第二法判断系统的稳定性的方法;4. 掌握利用状态反馈完成系统的极点配置;5.通过Matlab编程,上机调试,掌握和验证所学控制系统的基本理论。
三、实验所需设备及应用软件型号备注序号1计算机2Matlab软件四、实验内容1.利用特征根判断稳定性;2.利用李雅普诺夫第二法判断系统的稳定性;3.状态反馈的极点配置;五、实验方法及步骤1.打开计算机,运行MATLAB软件。
2.将实验内容写入程序编辑窗口并运行。
3.分析结果,写出实验报告。
一、利用特征根判断稳定性用matlab 求取一个系统的特征根,可以有许多方法,如,,,()eig ()pzmap 2ss zp ,等。
下面举例说明。
2tf zp roots 【例题1】已知一个系统传递函数为,试不同的方法分析闭环系统的稳定性。
()G s 2(3)()(5)(6)(22)s G s s s s s +=++++解:num=[1,3]den=conv([1,2,2],conv([1,6],[1,5]))sys=tf(num,den)(1)()eig p=eig(sys)显示如下:p = -6.0000 -5.0000 -1.0000 + 1.0000i -1.0000 - 1.0000i 所有的根都具有负的实部,所以系统稳定。
(2) ()pzmap pzmap(sys) 从绘出的零极点图可看见,系统的零极点都位于左半平面,系统稳定。
(3)2()tf zp [z,p,k]=tf2zp(num,den)(4)()roots roots(den)【例题2】已知线性定常连续系统的状态方程为122122xx x x x ==- 试用特征值判据判断系统的稳定性。
机电控制工程基础实验报告(4实验)参考模板
西华大学实验报告(理工类)开课学院及实验室:电气信息专业实验中心 6a-201 实验时间 :2016年 5 月 日一、实验目的1、 通过模拟实验,定性和定量地分析二阶系统的两个参数T 和ζ对二阶系统动态性能的影响。
2、 通过模拟实验,定性和定量地分析系统开环增益K 对系统稳定性的影响。
二、实验原理1.典型的二阶系统稳定性分析结构框图如下图所示。
图1-1系统开环传递函数为:先算出临界阻尼、欠阻尼、过阻尼时电阻R 的理论值,再将理论值应用于模拟电路中,观察二阶系统的动态性能及稳定性,应与理论分析基本吻合。
在此实验中(图1-2),系统闭环传递函数为:其中自然振荡角频率:阻尼比:对应的模拟电路图:如图1-2所示。
(其中R 取10 K Ω,50 K Ω,160 K Ω,200 K Ω)图1-2三、实验设备、仪器及材料TDN-AC/ACS 教学实验系统、导线四、实验步骤(按照实际操作过程)1. 典型二阶系统瞬态性能指标的测试(1) 按模拟电路图1-2接线,将阶跃信号接至输入端,取R = 10K 。
(2) 用示波器观察系统响应曲线C(t),测量并记录超调M P 、峰值时间t p 和调节时间t S 。
(3) 分别按R = 50K ;160K ;200K ;改变系统开环增益,观察响应曲线C(t),测量并记录性能指标M P 、t p 和t S ,及系统的稳定性。
并将测量值和计算值(实验前必须按公式计算出)进行比较。
将实验结果填入表1-1中。
五、实验过程记录(数据、图表、计算等) 参数项目RKΩKl/sωnl/sC(t p) C(∞)pM tp t s阶跃响应曲线计算值测量值计算值测量值计算值测量值0<ζ<1欠阻尼1050ζ=1临界阻尼160ζ>1过阻尼200表1-1六、实验结果分析及问题讨论西华大学实验报告(理工类)开课学院及实验室:电气信息专业实验中心 6a-201 实验时间:2016年5 月日一、实验目的掌握波特图的绘制方法及由波特图来确定系统开环传函。
控制系统的稳定性分析

…
控制系统的稳定性分析
例 已知一调速系统的特征方程式为
S 3 + 41.5S 2 + 517 S + 2.3 × 104 = 0 试用劳斯判据判别系统的稳定性。 试用劳斯判据判别系统的稳定性。
解:列劳斯表
S3 S2 S1 S0
1 41.5 − 38.5 2.3× 4 10
517 2.3×104
0 0
控制系统的稳定性分析
系统的特征方程为: 2s 4 + s3 + 3s 2 + 5s + 10 = 0 例 系统的特征方程为: 试用胡尔维茨判据判别系统的稳定性。 试用胡尔维茨判据判别系统的稳定性。 解:由特征方程知:1) ai=0 由特征方程知: 1 2 2) ∆n = 0 0 5 3 1 2 0 10 5 3 0 0 0 10
控制系统的稳定性分析
s n a0 a2 a4 a6 L 表中 s n −1 a1 a3 a5 a7 L b1 = a1a2 − a0 a3 , b2 = a1a4 − a0 a5 , b3 = a1a6 − a0 a7 ⋅⋅⋅ a1 a1 a1 n−2 s b1 b2 b3 b4 L ba −ab ba −ab ba −ab n −3 c1 = 1 3 1 2 , c2 = 1 5 1 3 , c3 = 1 7 1 4 ⋅⋅⋅ s c1 c2 c3 L b1 b1 b1 M s 2 d1 d 2 d3 ed −d e f1 = 1 2 1 2 s1 e1 e2 e1 0 s f1 考察劳斯阵列表中第一列各数的符号,如果第一列中各数a0 a1、 a0、 3)考察劳斯阵列表中第一列各数的符号,如果第一列中各数a0、a1、 b1、c1、 的符号相同, b1、c1、……的符号相同,则表示系统具有正实部特征根的个数等 的符号相同 于零,系统稳定;如果符号不同,系统不稳定, 于零,系统稳定;如果符号不同,系统不稳定,且符号改变的次数等 于系统具有的正实部特征根的个数。 于系统具有的正实部特征根的个数。
控制系统仿真实验四

实验四:控制系统的时域分析一,实验目的1、使用MATLAB 分析系统的稳定性及稳态性能。
2、分析系统的暂态性能并会计算暂态性能指标。
二、实验内容1、已知系统的闭环传递函数为:38440014020200)(234++++=S S G S S S ,分析系统的稳定性,并求该系统的单位阶跃响应曲线。
>> num=[200];>> den=[1 20 140 400 384];>> [z,p]=tf2zp(num ,den);>> ii=find(real(p)>0);n1=length(ii);>> if(n1>0)disp('The Unstable Poles are:');disp(p(ii));else disp('System is Stable');endSystem is Stable>>step(num,den)2、已知离散系统5.08.06.1)(22+--=Z Z Z Z Z φ,求该系统的单位阶跃响应曲线。
>> num=[1.6 -1 0];>> den=[1 -0.8 0.5];>> dstep(num,den);3、控制系统的状态空间模型为:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡.3.2.1x x x =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--17120100010⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡x x x 321+u ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡100 []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=x x x y 321132,求该系统在[0,3]区间上的单位脉冲响应曲线。
>> A=[0 1 0;0 0 1;0 -12 -17];B=[0;0;1];C=[2 3 1];D=0;>> impulse(A,B,C,D)4、已知控制系统模型为:u x x x x ⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡10961021.2.1,[]⎥⎦⎤⎢⎣⎡=x x y 2111,求系统在y=sint 时的响应。
实验四 随动系统的静态和稳定性试验
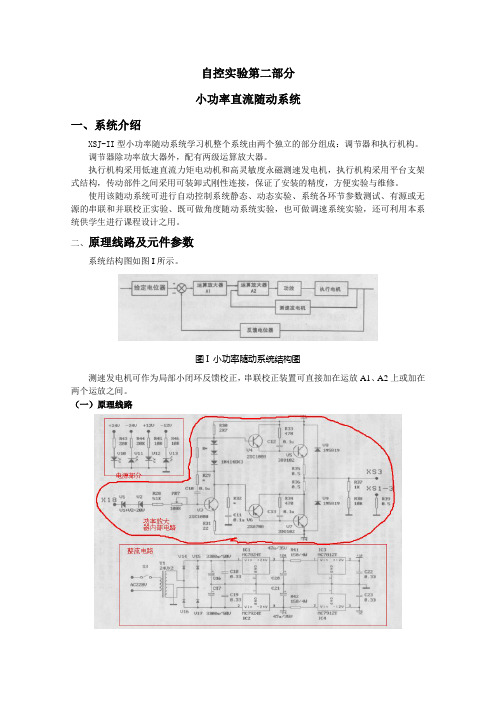
自控实验第二部分小功率直流随动系统一、系统介绍XSJ-II型小功率随动系统学习机整个系统由两个独立的部分组成:调节器和执行机构。
调节器除功率放大器外,配有两级运算放大器。
执行机构采用低速直流力矩电动机和高灵敏度永磁测速发电机,执行机构采用平台支架式结构,传动部件之间采用可装卸式刚性连接,保证了安装的精度,方便实验与维修。
使用该随动系统可进行自动控制系统静态、动态实验、系统各环节参数测试、有源或无源的串联和并联校正实验、既可做角度随动系统实验,也可做调速系统实验,还可利用本系统供学生进行课程设计之用。
二、原理线路及元件参数系统结构图如图I所示。
图I 小功率随动系统结构图测速发电机可作为局部小闭环反馈校正,串联校正装置可直接加在运放A1、A2上或加在两个运放之间。
(一)原理线路图II 面板内部电路图III 面板电路图IV 小功率随动系统接线示意图(二)元器件参数:1.测量电位器a)导电塑料电位器WDD65S-2b)阻值1KΩ,功率2W,电气角度340c)机械转动角度360无止档d)线性度0.5%2.直流力矩电机:型号SYL-1.5a)转子绕组绝缘电阻不小于100MΩb)转子绕组经受耐压500V/1minc)静摩擦力矩≤0.0294 N.md)空载启动电流0.18Ae)转子直流电阻27Ω±10%f)连续堵转力矩0.147 N.m -5%g)连续堵转电流≤0.9Ah)连续堵转电压约20Vi)空载转速约800转/minj)转向火花≤1.5级3.测速电机:型号70CDY-1a)灵敏度1伏/弧度/秒b)纹波电压1%c)每转纹波频率33周/转d)线性度1%e)不对称度1%f)最大运行速度400转/分g)直流电阻230KΩh)最小负载电子23KΩi)静摩擦力矩300g.cm三、性能指标1.开环增益可调范围80db2.系统灵敏度可达1mV,跟踪角度不小于±1603.加校正后,系统过渡过程时间可在30ms以下(空载)4.调速范围300转/分~1/5转/分5.功放最大输出功率不小于30W6.电源AC220V ±10%DC ±24V四、使用警示1.执行机构上的反馈电位器是360无止档,可任意转动不会损坏,但连续转动容易影响电位器的精度和寿命。
实验四控制系统的稳定性分析

实验四 控制系统的稳定性分析班级:电信171:远 **:1700506163一、 实验目的1、 了解系统的开环增益和时间常数对系统稳定性的影响;2、 研究系统在不同输入下的稳态误差的变化;二、 实验容 系统开环传递函数为:)1)(11.0(10)(++=Ts s s K s G 1、 分析开环增益K 和时间常数T 对系统稳定性及稳态误差的影响。
(1) 取T=0.1,令K=1,2,3,4,5,绘制相应的阶跃响应曲线,分析开环增益K 的变化对系统阶跃响应和稳定性的影响。
(2) 在K=1〔系统稳定〕和K=2〔系统临界稳定〕两种情况下,分别绘制T=0.1和T=0.01时系统的阶跃响应,分析时间常数T 的变化对系统阶跃响应和稳定性的影响。
提示:由开环传递函数转换为闭环传递函数可以使用反应连接函数feedback ,举例如下:Gopen=tf 〔num ,den 〕 %建立开环传递函数Gclose=feedback 〔Gopen ,1,-1〕 %建立闭环传递函数2、 分析系统在不同输入时的稳态误差。
取K=1,T=0.01,改变系统输入r ,使r 分别为单位阶跃函数、单位斜坡函数和单位加速度函数,观察系统在不同输入下的响应曲线及相应的稳态误差。
提示:lsim 函数可用来绘制系统在任意自定义输入下的响应曲线,用法如下:lsim 〔sys ,input ,t 〕 %其中sys 是待求的系统,input 是自定义的输入信号,t 是时间。
例如:G1=tf 〔num ,den 〕t=0:0.01:5u1=t ;lsim 〔G1, u1,t 〕三、 实验结果:〔1〕取T=0.1,令K=1,2,3,4,5,绘制相应的阶跃响应曲线。
MATLAB 代码:K=1时系统的阶跃响应曲线:K=2时系统的阶跃响应曲线:K=3时系统的阶跃响应曲线:K=4时系统的阶跃响应曲线:K=5时系统的阶跃响应曲线:分析:随着增益系数的K的增加,系统将趋于不稳定,其中K=2是临界状态〔2〕在K=1〔系统稳定〕和K=2〔系统临界稳定〕两种情况下,分别绘制T=0.1和T=0.01时系统的阶跃响应MATLAB代码K=1〔系统稳定〕时系统的阶跃响应曲线:(绿色是T=0.1,红色是T=0.01)K=2〔系统临界稳定〕时系统的阶跃响应曲线:(黄色是T=0.1,蓝色是T=0.01)分析:时间常数T减小时,系统的动态性能得到改善。
控制系统的稳定性研究
实验:控制系统的稳定性研究
实验台:日期:系别:
班级:学号:姓名:
一、实验目的
1.观察系统的不稳定现象。
2.研究系统开环增益和时间常数对稳定性的影响。
二、实验电路
图1典型三阶系统的模拟电路
三、实验步骤
1.按图1所示模拟电路接线,输入端r(t)接阶跃信号,并与数字示波器OSC的CH1
连接,CH2接输出端C(t) 。
注:用连续阶跃信号输入时放电短路子接“AUTO”,用手动阶跃信号输入时放电短路子接“HDC”。
2.打开实验箱电源。
3.启动计算机,运行“SAC-ZJT-A1”,进入网络实验系统。
4.选择串口( 如不选择,则默认COM1为通讯口)。
5.选择“自控实验”,点击“控制系统的稳定性研究”。
6.点击“启动显示”,打开实验界面。
7.点击“运行”,观察并调整输入阶跃为1V。
8.调整电位器R2,观察并记录输出波形,找出系统输出产生等幅振荡时相应的R2值,
填入表1中。
9.在等幅振荡情况,电容C由1μF变成5μF,观察并记录系统稳定性的变化。
10.调整电位器R2,记录系统输出增幅振荡,减幅和无振荡时相应的R2值,填入表2,3,4中。
四、实验记录
表1
表2
表3
表4
五、实验设备
1、SAC-ZJⅡ网络智能自控计控实验装置。
2、SAC-ZJT-A1软件(包括与之相适应的并已经安装该软件的计算机)。
3、与实验台板上相配套的导线若干。
4、万用表.
六、实验分析及结论。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
西京学院实验教学教案
实验课程: 现代控制理论基础课序: 4 教室: 工程舫0B-14
实验日期: -6-3、 4、 6 教师: 万少松
一、实验名称: 系统的稳定性及极点配置
二、实验目的
1.巩固控制系统稳定性等基础知识;
2.掌握利用系统特征根判断系统稳定性的方法;
3.掌握利用李雅普诺夫第二法判断系统的稳定性的方法;
4. 掌握利用状态反馈完成系统的极点配置;
5.经过Matlab编程, 上机调试, 掌握和验证所学控制系统的基本理论。
三、实验所需设备及应用软件
四、实验内容
1.利用特征根判断稳定性;
2.利用李雅普诺夫第二法判断系统的稳定性;
3.状态反馈的极点配置;
五、实验方法及步骤
1.打开计算机, 运行MATLAB软件。
2.将实验内容写入程序编辑窗口并运行。
3.分析结果, 写出实验报告。
一、 利用特征根判断稳定性
用matlab 求取一个系统的特征根, 能够有许多方法, 如()eig , ()pzmap , 2ss zp , 2tf zp , roots 等。
下面举例说明。
【例题1】已知一个系统传递函数为()G s , 试不同的方法分析闭环系统的稳定性。
2(3)()(5)(6)(22)
s G s s s s s +=++++ 解:
num=[1,3]
den=conv([1,2,2],conv([1,6],[1,5]))
sys=tf(num,den)
(1)()eig
p=eig(sys)
显示如下:
p =
-6.0000
-5.0000
-1.0000 + 1.0000i
-1.0000 - 1.0000i
所有的根都具有负的实部, 因此系统稳定。
(2) ()pzmap
pzmap(sys)
从绘出的零极点图可看见, 系统的零极点都位于左半平面, 系统稳定。
( 3) 2()tf zp
[z,p,k]=tf2zp(num,den)
( 4) ()roots
roots(den)
【例题2】已知线性定常连续系统的状态方程为
12
2122x x x x x ==-
试用特征值判据判断系统的稳定性。
解:
A=[0,1;2,-1]
eig(A)
显示ans =
1
-2
有一个正根, 因此系统不稳定。
二、 利用李雅普诺夫第二法判断系统的稳定性
1、 李雅普诺夫判据: 线性定常连续系统
x Ax =
在平衡状态0e x =处, 渐进稳定的充要条件是: 对任意给定的一个正定对称矩阵Q , 如下形式的李雅普诺夫矩阵方程
T A P PA Q +=-
存在唯一正定对称矩阵解P 。
2、 推论: 如果Q 矩阵取为半正定, 且1/2(,)A Q 为完全能观测, 则0e x =为渐进稳定的充分必要条件是上述李雅普诺夫矩阵方程有唯一正定对称解P 。
3、 标量函数()T v x x Px =是这个系统的一个二次型形式的李雅普诺夫函数。
4、 Matlab 实现
matlab 提供了李雅普诺夫方程的求解函数()lyap , 其调用格式为
(,)P lyap A Q =。
要判定系统是否稳定,需要做以下工作:
① 求出P, 并验证P 是正定的;
② 求出V(x), 并判验证V(x) 是正定的;
③ 结论: 系统是稳定的。
【例题3】已知单位负反馈系统的前向通道分别是三个环节串联而成, 这三个环节分别是两个惯性环节和一个积分环节:
15()1G s s =+、 21()2G s s =+、 31()G s s
= 试分析系统的李雅普诺夫稳定性。
解: 研究系统的稳定性时, 能够令给定输入()0u t =。
( 1) 、 求出闭环系统的传递函数
G1=tf(5,[1,1])
G2=tf(1,[1,2])
G3=tf(1,[1,0])
Gtf=feedback(G1*G2*G3,1)
%运行结果如下:
%Transfer function:
% 5
%---------------------
%s^3 + 3 s^2 + 2 s – 5
%下面建立ss 模型
num=5
den=[1,3,2,-5]
[A,B,C,D]=tf2ss(num,den) %也能够
这样: [A,B,C,D]=tf2ss(Gtf.num{1},Gtf.den{1})
%选择半正定矩阵000000001Q ⎡⎤
⎢⎥=⎢⎥
⎢⎥⎣⎦
, 且1/2(,)A Q 为完全能观测
%能观测性验证:
Q=[0,0,0;0,0,0;0,0,1]
Q1=Q^(1/2)
rank(ctrb(A,Q1))
%运行结果:
%ans = 3
%因此1/2(,)A Q 为完全能观测
%计算李雅普诺夫函数的解, 并判断是否正定
P=lyap(A,Q)
det1=det(P(1,1))
det2=det(P(2,2))
detp=det(P)
%程序运行结果:
%P =
% 12.5000 0.0000 -7.5000
% 0.0000 7.5000 -0.5000
% -7.5000 -0.5000 4.7000。
