全国高中数学联赛模拟试题(十)
高中数学竞赛模拟试题(含详细答案)

高中数学竞赛试题(模拟)一、选择题:(本大题共10个小题;每小题5分,共50分,在每小题给出的四个选项中, 有且只有一项是符合题目要求的)1.已知函数f(x)是R 上的奇函数,g(x)是R 上的偶函数,若129)()(2++=-x x x g x f ,则=+)()(x g x f ( )A .1292-+-x x B .1292-+x xC .1292+--x xD . 1292+-x x2.有四个函数:① y=sinx+cosx ② y= sinx-cosx ③ y=x x cos sin ⋅ ④ xxy cos sin = 其中在)2,0(π上为单调增函数的是 ( )A .①B .②C .①和③D .②和④3.方程x xx x x x ππ)1(12122-+=-+-的解集为A(其中π为无理数,π=3.141…,x 为实数),则A 中所有元素的平方和等于 ( ) A .0 B .1C .2D .44.已知点P(x,y)满足)(4)sin 4()cos 4(22R y x ∈=-+-θθθ,则点P(x,y)所在区域的面积为 A .36π B .32π C .20π D .16π ( )5.将10个相同的小球装入3个编号为1、2、3的盒子(每次要把10个球装完),要求每个盒子里球的个数不少于盒子的编号数,这样的装法种数为 ( ) A .9 B .12 C .15 D .186.已知数列{n a }为等差数列,且S 5=28,S 10=36,则S 15等于 ( ) A .80B .40C .24D .-487.已知曲线C :x x y 22--=与直线0:=-+m y x l 有两个交点,则m 的取值范围是 ( )A .)2,12(--B .)12,2(--C .)12,0[-D .)12,0(-8.过正方体ABCD-A 1B 1C 1D 1的对角线BD 1的截面面积为S ,S max 和S min 分别为S 的最大值和最小值,则minmaxS S 的值为 ( ) A .23 B .26 C .332 D .362 9.设7log ,1sin ,82.035.0===z y x ,则x 、y 、z 的大小关系为 ( )A .x<y<zB .y<z<xC .z<x<yD . z<y<x10.如果一元二次方程09)3(222=+---b x a x 中,a 、b 分别是投掷骰子所得的数字,则该二次方程有两个正根的概率P= ( )A .181 B .91 C .61 D .1813 二、填空题(本大题共4个小题,每小题8分,共32分)11.设P 是椭圆191622=+y x 上异于长轴端点的任意一点,F 1、F 2分别是其左、右焦点,O 为中心,则=+⋅221||||||OP PF PF ___________.12.已知△ABC 中,==,,试用、的向量运算式子表示△ABC 的面积,即S △ABC = ____________________.13.从3名男生和n 名女生中,任选3人参加比赛,已知3人中至少有1名女生的概率为3534,则n=__________.14.有10名乒乓球选手进行单循环赛,比赛结果显示,没有和局,且任意5人中既有1人胜其余4人,又有1人负其余4人,则恰好胜了两场的人数为____________个.三、解答题(本大题共5个小题,15-17题每小题12分,18题、19题每小题16分,共68分) 15.对于函数f(x),若f(x)=x,则称x 为f(x)的“不动点”,若x x f f =))((,则称x 为f(x)的“稳定点”,函数f(x)的“不动点”和“稳定点”的集合分别记为A 和B ,即x x f x A ==)(|{}})]([|{x x f f x B ==.(1). 求证:A ⊆B(2).若),(1)(2R x R a ax x f ∈∈-=,且φ≠=B A ,求实数a 的取值范围.16.某制衣车间有A 、B 、C 、D 共4个组,各组每天生产上衣或裤子的能力如下表,现在上衣及裤子要配套生产(一件上衣及一条裤子为一套),问在7天内,这4个组最多能生产多少套?17.设数列}{n a 满足条件:2,121==a a ,且 ,3,2,1(12=+=++n a a a n n n ) 求证:对于任何正整数n ,都有 nnn n a a 111+≥+18.在周长为定值的△ABC 中,已知|AB|=6,且当顶点C 位于定点P 时,cosC 有最小值为257. (1).建立适当的坐标系,求顶点C 的轨迹方程.(2).过点A 作直线与(1)中的曲线交于M 、N 两点,求||||BN BM ⋅的最小值的集合.19.已知三棱锥O-ABC 的三条侧棱OA 、OB 、OC 两两垂直,P 是底面△ABC 内的任一点,OP 与三侧面所成的角分别为α、β、γ. 求证:33arcsin32≤++<γβαπ参考答案一、选择题: ADCBC CCCBA 二、填空题:11. 25 12.13. 4 14. 1 三、解答题:15.证明(1).若A=φ,则A ⊆B 显然成立;若A ≠φ,设t ∈A ,则f(t)=t,f(f(t))=f(t)=t,即t ∈B,从而 A ⊆B. 解 (2):A 中元素是方程f(x)=x 即x ax =-12的实根.由 A ≠φ,知 a=0 或 ⎩⎨⎧≥+=∆≠0410a a 即 41-≥aB 中元素是方程 x ax a =--1)1(22 即 0122243=-+--a x x a x a 的实根 由A ⊆B ,知上方程左边含有一个因式12--x ax ,即方程可化为 0)1)(1(222=+-+--a ax x a x ax因此,要A=B ,即要方程 0122=+-+a ax x a ① 要么没有实根,要么实根是方程 012=--x ax ② 的根. 若①没有实根,则0)1(4222<--=∆a a a ,由此解得 43<a 若①有实根且①的实根是②的实根,则由②有 a ax x a +=22,代入①有 2ax+1=0.由此解得 a x 21-=,再代入②得,012141=-+a a 由此解得 43=a . 故 a 的取值范围是 ]43,41[-16.解:A 、B 、C 、D 四个组每天生产上衣与裤子的数量比分别是:76,117,129,108,且11712910876>>> ① 只能让每天生产上衣效率最高的组做上衣,生产裤子效率最高的组做裤子,才能使做的套数最多.由①知D 组做上衣效率最高,C 组做裤子效率最高,于是,设A 组做x 天上衣,其余(7-x)天做裤子;B 组做y 天上衣,其余(7-y)天做裤子;D 组做7天上衣,C 组做7天裤子.则四个组7天共生产上衣 6×7+8x+9y (件);生产裤子11×7+10(7-x)+12(7-y) (条)依题意,有 42+8x+9y=77+10(7-x)+12(7-y),即 769x y -=. 令 μ= 42+8x+9y=42+8x+9(769x -)=123+x 72 因为 0≤x ≤7,所以,当x=7时,此时y=3, μ取得最大值,即μmax =125.因此,安排A 、D 组都做7天上衣,C 组做7天裤子,B 组做3天上衣,4天裤子,这样做的套数最多,为125套.17.证明:令 10=a ,则有 11-++=k k k a a a ,且 ),2,1(1111 =+=+-+k a aa a k k k k 于是 ∑∑=+-=++=nk k k nk k k a aa a n 11111由算术-几何平均值不等式,可得nn n a a a a a a 132211+⋅⋅⋅≥ +n n n a aa a a a 113120+-⋅⋅⋅ 注意到 110==a a ,可知nn n nn a a a 11111+++≥,即 nnn n a a 111+≥+18.解:(1) 以AB 所在直线为x 轴,线段AB 的中垂线为y 轴建立直角坐标系,设 |CA|+|CB|=2a(a>3)为定值,所以C 点的轨迹是以A 、B 为焦点的椭圆,所以焦距 2c=|AB|=6.因为 1||||182||||236||||2|)||(|||||26||||cos 22222--=--+=-+=CB CA a CB CA CB CA CB CA CB CA CB CA C又 22)22(||||a a CB CA =≤⋅,所以 2181cos a C -≥,由题意得 25,25718122==-a a. 此时,|PA|=|PB|,P 点坐标为 P(0,±4).所以C 点的轨迹方程为)0(1162522≠=+y y x (2) 不妨设A 点坐标为A(-3,0),M(x 1,y 1),N(x 2,y 2).当直线MN 的倾斜角不为900时,设其方程为y=k(x+3) 代入椭圆方程化简,得 0)1169(83)16251(2222=-+++k x k x k 显然有 △≥0, 所以 222122212516400225,2516150k k x x k k x x +-=+-=+而由椭圆第二定义可得25165311442553125251614453125251614481251645025259)(325)535)(535(||||22222222212121+-⋅+=+-+=+-+++=++-=--=⋅k k kk k k k k x x x x x x BN BM只要考虑251653114422+-k k 的最小值,即考虑2516531144251612++-k 取最小值,显然. 当k=0时,||||⋅取最小值16.当直线MN 的倾斜角为900时,x 1=x 2=-3,得 16)534(||||2>=⋅BN BM 但)0(1162522≠=+y y x ,故0≠k ,这样的M 、N 不存在,即||||⋅的最小值的集合为空集.19.证明:由 题意可得 1sin sin sin 222=++γβα,且α、β、 )2,0(πγ∈所以 )cos()cos()2cos 2(cos 21sin sin 1sin 222γβγβγβγβα-+=+=--= 因为 )cos()cos(γβγβ+>-,所以 )](2[sin )(cos sin 222γβπγβα+-=+>当2πγβ≥+时,2πγβα>++.当2πγβ<+时,)(2γβπα+->,同样有 2πγβα>++故 2πγβα>++另一方面,不妨设 γβα≥≥,则 33sin ,33sin ≤≥γα 令 βγα2211sin )33(1sin ,33sin --==, 则 1sin sin sin12212=++γβα)cos()cos()cos()cos(sin 11112γαγαγαγαβ-+=-+=因为 γαγα-≤-11,所以 )cos()cos(11γαγα-≥- 所以 )cos()cos(11γαγα+≥+ 所以 11γαγα+≤+如果运用调整法,只要α、β、γ不全相等,总可通过调整,使111γβα++增大. 所以,当α=β=γ=33arcsin时,α+β+γ取最大值 333arcsin . 综上可知,33arcsin32≤++<γβαπ。
全国高中数学联赛模拟试题及参考答案

全国高中数学联赛训练题(1)第一试一、填空题1.函数3()2731x x f x +=-+在区间[0,3]上的最小值为_____.2.在数列{}n a 中,11a =且21n n n a a a ++=-.若20002000a =,则2010a =_____.3.若集合{|61,}A x x n n N ==-∈,{|83,}B x x n n N ==+∈,则A B 中小于2010的元素个数为_____.4.若方程sin (1)cos 2n x n x n ++=+在π<<x 0上有两个不等实根,则正整数n 的最小值为_____.5.若c b a >>,0=++c b a ,且21,x x 为02=++c bx ax 的两实根,则||2221x x -的取值范围为_____.6.有n 个中心在坐标原点,以坐标轴为对称轴的椭圆的准线都是1x =.若第k (1,2,,)k n = 个椭圆的离心率2k k e -=,则这n 个椭圆的长轴之和为_____.7.在四面体-O ABC 中,若点O 处的三条棱两两垂直,则在四面体表面上与点A 距离为2的点所形成的曲线长度之和为_____.8.由ABC ∆内的2007个点122007,,,P P P 及顶点,,A B C 共2010个点所构成的所有三角形,将ABC ∆分 割成互不重叠的三角形个数最多为_____.二、解答题9.设抛物线22y px =(0)p >的焦点为F ,点A 在x 轴上F 的右侧,以FA 为直径的圆与抛物线在x 轴上方交于不同的两点,M N ,求证:FM FN FA +=.10.是否存在(0,)2πθ∈,使得sin ,cos ,tan ,cot θθθθ的某一排列成等差数列?并说明理由.11.已知实数123123,,,,,a a a b b b 满足:123123a a a b b b ++=++,122331122331a a a a a a bb b b b b ++=++,且123min{,,}a a a 123min{,,}b b b ≤,求证:123max{,,}a a a 123max{,,}b b b ≤.第二试一、设圆的内接四边形ABCD 的顶点D 在直线,,AB BC CA 上的射影分别为,,P Q R ,且ABC ∠与ADC ∠的平分线交于点E ,求证:点E 在AC 上的充要条件是PR QR =.二、已知周长为1的i i i ABC ∆(1,2)i =的三条边的长分别为,,i i i a b c ,并记2224i i i i i i i p a b c a bc =+++(1,2)i =,求证:121||54p p -<.三、是否存在互不相同的素数,,,p q r s ,使得它们的和为640,且2p qs +和2p qr +都是完全平方数?若存在,求,,,p q r s 的值;若不存在,说明理由.四、对n 个互不相等的正整数,其中任意六个数中都至少存在两个数,使得其中一个能整除另一个.求n 的最小值,使得在这n 个数中一定存在六个数,其中一个能被另外五个整除.全国高中数学联赛训练题(1)参考答案:令3xt =,[0,3]x ∈则3()()271f x g t t t ==-+,[1,27]t ∈,而'()3(3)(3)g t t t =-+.故当[1,3]t ∈时,'()0g t <,()g t 单调递减,当[3,27]t ∈时,'()0g t >,()g t 单调递增.所以当3t =,()g t 取得最小值min ()(3)53g t g ==-,即当1x =时,()f x 取得最小值53-.:设2a t =,则由21n n n a a a ++=-依次写出数列{}n a 的前8项为:1,,1,1,,1,1,t t t t t - - - - .于是易知:该数列是以周期6T =的一个周期数列,故由20002000a =可得20006333222000a a a t ⨯+====,从而2010335661120001999a aa t ⨯===-=-=-,即20101999a =-. :由题意若x A ∈,则5(mod 6)x ≡ ,若x B ∈,则3(mod 8)x ≡ ,故若x AB ∈ ,则11(mod 24)x ≡ ,即若x A B ∈ ,则2411x k =+,于是可得满足题意的元素共有84个.:由已知得11sin 12cos x n x --=---,而1sin 2cos xx---表示上半个单位圆(不包括端点)上的动点(cos ,sin )P x x 与定点(2,1)Q -的斜率k ,要满足题意就要直线PQ 与上半个单位圆(不包括端点)有两个不同的交点,此时4(,1)3k ∈--,从而可得11(0,)3n ∈,故3n >,即正整数n 的最小值为4.:由0=++c b a 知方程02=++c bx ax 有一个实数根为1,不妨设11x =,则由韦达定理可知2c x a=.而c b a >>,0=++c b a ,故0,0a c ><,且a a c c >-->,则122c a -<<-,故2221()44c x a<=<,从而可得2212||[0,3)x x -∈.:设第k 个椭圆的长半轴为k a ,焦半径为k c ,则由题意有21k ka c =,2k k k k ce a -==,故可得2k k a -=,于是可得121222212n n n a a a ----+++=+++=- ,故这n 个椭圆的长轴之和为12(12)22n n---=-.:如图,点,M N 分别在棱,AB AC 上,且2AM AN ==,点,E F 分别在棱,OB OC 上,且1OE OF ==,则2AE AF ==,因此,符合题意的点形成的曲线有:①在面OBC 内,以O 为圆心,1为半径的弧EF ,其长度为2π;②在面AOB 内,以A 为圆心,2为半径的弧EM ,其长度为6π;③在面AOC 内,以A 为圆心,2为半径的弧FN ,其长度为6π;④在面ABC 内,以A 为圆心,2为半径的弧MN ,其长度为23π.所以,所求的曲线长度之和为2326632πππππ+++=.:设三角形最多有n 个,则根据角度相等可得20072n πππ⨯+=⨯,故2200714015n =⨯+=.: 令1122(,),(,)M x y N x y ,设点(,0)A a ,则由(,0)2p F 得12FA a p =-,故以FA 为直径的圆为22222()()44a p a p x y +--+=,则可知12,x x 是方程2222()2()44a p a p x px +--+=的两个实根,即是说12,x x 是方程22(23)0x a p x ap --+=,由韦达定理得1223322a p x x a p -+==-. 故121131()()()2222FM FN x p x p a p p a p FA +=+++=-+=-=,即FM FN FA +=.:当(0,)2πθ∈时,函数s i n y x =与cos y x =的图像关于直线4x π=对称,函数t a n y x =与cot y x =的图像也关于直线4x π=对称,且当4πθ=时,sin ,cos ,tan ,cot θθθθ的任一排列均不可能成等差数列.故只需考虑是否存在(0,)4πθ∈使得sin ,cos ,tan ,cot θθθθ的某一排列成等差数列即可.假设存在(0,)4πθ∈符合题意,则由sin cos tan cot θθθθ<<<可知cot tan cos sin θθθθ-=-,从而有s i n c o s s i n c o s θθθθ+=⋅,故2(sin cos )12sin cos 1sin 2θθθθθ⋅=+⋅=+.而2(sin cos )1θθ⋅<,且1sin 21θ+>,故假设不成立.即,不存在这样的θ,使得sin ,cos ,tan ,cot θθθθ的某一排列成等差数列.:设123123a a a b b b p ++=++=,122331122331a a a a a a bb b b b b q ++=++=,且123a a a r =,123'b b b r =, 则123,,a a a 是函数32()f x x px qx r =-+-的零点,123,,b b b 是函数32()'g x x px qx r =-+-的零点.不妨设123123,a a a b b b ≤≤ ≤≤,则由123min{,,}a a a 123min{,,}b b b ≤知11a b ≤. 而1()0f a =,1111213()()()()0g a a b a b a b =---≤,故11()()g a f a ≤,即3232111111'a pa qa r a pa qa r -+-≤-+-,故3232333333'a pa qa r a pa qa r -+-≤-+-, 即33()()g a f a ≤,也即是33132333()()()()()0g a a b a b a b f a =---≤=.若33a b >,则313233()()()0a b a b a b --->,这与33132333()()()()()0g a a b a b a b f a =---≤=矛盾! 所以有123max{,,}a a a 123max{,,}b b b ≤.:由西姆松定理知,,P Q R 共线.由题意易知,,,C Q D R 四点共圆,则有DCA DQR DQP ∠=∠=∠,同样有,,,A P R D 四点共圆,则有DAC DPR DPQ ∠=∠=∠.故DAC ∆∽DPQ ∆,同理可得:DAB ∆∽DRQ ∆,DBC ∆∽DPR ∆,因此有:PRDB DA DP PR BA BC DC DQ QR BCDB BA⋅===⋅⋅.从而PR QR =的充要条件是DA BABC =.又由角平分线的性质得,ABC ADC ∠∠的平分线分AC 的比分别为,BA DABC DC.故命题成立. :由题意知1i i i a b c ++=,且不妨设i i i a b c ≤≤,则由于三角形的三边关系可得102i i i a b c <≤≤<,即可得312121210(12)(12)(12)()327i i i i i i a b c a b c -+-+-<---≤=.2222222(12)(12)(12)12()4()814()812[()()]812(4)12i i i i i i i i i i i i i i ii i i i i i i i i i i i i i i i i i i i i i i i ia b c a b c a b b c c a a b c a b b c c a a b c a b c a b c a b c a b c a b c p ---=-+++++-=-+++-=-+++-++-=-+++=- 从而可得131272i p ≤<,所以121||54p p -<. :由640p q r s +++=,及,,,p q r s 是不同的素数知,,,p q r s 都是奇数.设2222p qs m p qr n ⎧+=⎪⎨+= ⎪⎩ ①②, 并不妨设s r <,则m n <.由①,②可得()()()()m p m p qsn p n p qr-+=⎧⎨-+=⎩.若1m p ->,则由m p n p n p -<-<+可得m p q n p +==-,故2q m n =+,,s m p r n p =-=+,从而2s r m n q +=+=,故23640p q r s p q q p q +++=++=+=.又由23s m p q p =-=-≥,故可得90p ≤,逐一令p 为不大于90的素数加以验证便知此时无解.若1m p -=,则21qs m p p =+=+,故12qs p -=.而q m p n p <+<+,故,2q n p r n p p q =-=+=+. 故332(1)26402p q r s p q s qs q s +++=++=-++=,即有(32)(34)3857719q s ++==⨯⨯于是得3419,3272s q +=+=⨯,故5,67s q ==,从而167,401p r ==.综上可得167,67,401,5p q r s ====或167,67,5,401p q r s ====. :所求的最小正整数26n =.我们分两步来证明,第一步说明25n ≤不行,我们构造如下的25个正整数:543215432154321543215432122222;33333;55555;7,7777;1111111111,,,,,,,,,,,,,,,,,,,①②③④⑤.如上,我们把这25个正整数分成5组,则任意选取六个数都一定会有两个数在同一组,显然在同一组中的这两个数中的一个能整除另一个;另一方面,由于每一组数只有5个,因此所选的六个数必然至少选自两组数,即是说在所选的六个数中不存在其中一个能被另五个整除的数.所以,当25n =时是不行的.对于25n <,也可类似地证明.第二步说明26n =是可以的.我们首先定义“好数组”.如果一数组中的数都在所给定的26个正整数中,其中最大的一个记为a ,除a 外的25个数中没有a 的倍数,且这25个数中所有a 的约数都在这组数中,那么我们称这个数组为“好数组”.(一个“好数组”中的数可以只有一个).现证这样的“好数组”至多有五个.否则,必存在六个“好数组”,我们考虑这六个“好数组”中的最大数,分别记为,,,,,a b c d e f ,由题知六个数,,,,,a b c d e f 中必然存在一个能整除另一个,不妨记为|b a ,即是说a 的约数b 不在a 所在的“好数组”中,这与“好数组”的定义不符,故“好数组”至多有五个.由于“好数组”至多有五个,而所给的正整数有26个,因此至少存在一个“好数组”中有六个数,考虑这个“好数组”中的最大数,由“好数组”的定义知这个数组中至少另有五个数都能整除该数.综上可得,所求的最小正整数26n =.陕西师范大学附中 王全 710061 wangquan1978@。
高考数学高三模拟试卷试题压轴押题全国高中数学联赛吉林赛区预赛高中数学联赛试题及参考答案

高考数学高三模拟试卷试题压轴押题全国高中数学联赛(吉林赛区)预赛高中数学联赛试题及参考答案一、选择题(每小题6分,共30分)1.已知函数⎪⎩⎪⎨⎧>+=<=01000)(x x x x x f π,则)]}1([{-f f f 的值为( ) A .1+π B .0 C .1 D .π2.在ABC ∆中,120=A ,5=AB ,7=BC ,则CBsin sin 的值为( ) A .58B . 85 C .35D .533.下列函数既是奇函数,又在区间[]1,1-上单调递减的是( ) A .()sin f x x =B .()1f x x =-+ C .2()ln2x f x x -=+D .()1()2x x f x a a -=+4.某地举行一次民歌大奖赛,六个省各有一对歌手参加决赛,现要选出4名优胜者.则选出的4名中恰只有两个人是同一省份的歌手的概率为( ) A .3316B .12833C .3332D .1145.若五项的数列:}{n a 12345,,,,a a a a a 满足123450a a a a a ≤<<<<,且对任意的,(15)i j i j ≤≤≤,均有i j a a -在该数列中.①10a =; ②524a a =; ③{}n a 为等差数列;④ 集合{|15}i j A a a i j =+≤≤≤含9个元素.则上述论断正确的有( )个.A .1B .2C .3D .4二、填空题(每小题6分,共30分)6.函数y=f(x)是定义在R 上的周期为3的函数,右图中表示的是该函数在区间[−2, 1]上的图像,则(2014)(5)(15)ff f⨯的值等于.7.在ABC∆中,AB3=,BC1=,cos cosAC B BC A=,则AC AB⋅=8.下图是一个几何体的三视图,则该几何体的体积为_______________.9.给定平面上四点,,,O A B C,满足4,3,2,3OA OB OC OB OC===⋅=,则ABC∆面积的最大值为_________.10.方程组⎪⎪⎩⎪⎪⎨⎧==+++-=+++++-=+++3432abcdabcabdacdbcdcdbdbcadacabdcba的一个实数解为⎪⎪⎩⎪⎪⎨⎧====____________________________________dcba三、解答题(第12题15分,第13,14,15每小题25分,共90分)11.设集合}023|{2≤++=xxxA,}0|{2≤++=baxxxB,(1) 若RBACxxBACRR=≤<-=)(},21|{)(,求ba,的值;(2)若1=b,且ABA=,求实数a的取值范围.12.函数xxxxf3cossin)1cos2(2)(2++=,Rx∈.求函数)(xf的最大值.13.直线m的方程为1y kx=+,,A B为直线m上的两点,其横坐标恰为关于x的一元二次方程22(1)220k x kx---=的两个不同的负实数根.直线l过点(2,0)P-和线段AB的中点,CD是y轴上的一条动线段,考虑一切可能的直线l,当l和线段CD无公共点时,CD长的最大值是否存在?如果存在,求出最大值;如果不存在,说明理由.14.若存在集合,A B满足:A B=∅,且A B+=N,则称(,)A B为+N的一个二分划.(Ⅰ)设{|3,},{|31,},A x x k k B x x k k ==∈==±∈++N N 判断(,)A B 是否为+N 的一个二分划,说明理由; (Ⅱ)是否能找到+N 的一个二分划(,)A B 满足: ①A 中不存在三个成等比数列的数; ②B 中不存在无穷的等比数列. 说明理由.一、选择题(每小题5分,共30分)1.已知函数⎪⎩⎪⎨⎧>+=<=01000)(x x x x x f π,则)]}1([{-f f f 的值为( ) A .1+π B .0 C .1 D .π 解:{[(1)]}((0))()1f f f f f f ππ-===+. 答案: A .2.在ABC ∆中,120=A ,5=AB ,7=BC ,则CBsin sin 的值为( ) A .58B . 85 C .35D .53解:由正弦定理,得5sin sin 7c C A a ===,于是cot C =.所以sin sin()sin cos cos sin sin cot cos sin sin sin B A C A C A CA C A C C C++===+1325=-=. 答案: D .3.下列函数既是奇函数,又在区间[]1,1-上单调递减的是( ) A .()sin f x x =B .()1f x x =-+C .2()ln 2x f x x -=+D .()1()2x x f x a a -=+ 解:设2()ln 2x f x x-=+,则22()ln ln ()22x xf x f x x x +--==-=--+因此,2()ln 2xf x x-=+是奇函数.又24122x t x x-==-+++为区间[]1,1-上的单调递减函数,ln y t =为区间(0,)+∞上的单调递增函数,而2()ln 2x f x x-=+为ln y t =与22x t x -=+的复合函数,因此函数2()ln 2xf x x-=+在区间[]1,1-上单调递减. 答案: C .4.某地举行一次民歌大奖赛,六个省各有一对歌手参加决赛,现要选出4名优胜者.则选出的4名中恰只有两个人是同一省份的歌手的概率为( )A .3316B .12833C .3332D .114 解:选出的4名选手中恰有且只有两个人是同一省份的歌手的概率1265412221633C C P C ⨯⨯==. 答案: A .5.若五项的数列:}{n a 12345,,,,a a a a a 满足123450a a a a a ≤<<<<,且对任意的,(15)i j i j ≤≤≤,均有i j a a -在该数列中.①10a =; ②524a a =; ③{}n a 为等差数列;④ 集合{|15}i j A a a i j =+≤≤≤含9个元素. 则上述论断正确的有( )个.A .1B .2C .3D .4 解:论断正确的有①②③④.因为∈=-011a a {}n a ,所以10a =; 因为132425250a a a a a a a a =<-<-<-< 且324252,,a a a a a a ---}{n a ∈所以 322423524,,a a a a a a a a a -=-=-= 于是 21324354a a a a a a a a -=-=-=-所以{}n a 为等差数列,且{}:0,,2,3,4n a d d d d , 因此524a a =;集合{|15}i j A a a i j =+≤≤≤含9个元素.答案: D .二、填空题(每小题5分,共30分)6.函数y=f(x)是定义在R 上的周期为3的函数,右图中表示的是该函数在区间[−2, 1]上的图像,则(2014)(5)(15)f f f ⨯的值等于.解:(2014)(1)22(5)(15)(1)(0)(1)1f f f f f f ===-⨯-⨯-⨯.7.在ABC ∆中,AB 3=,BC 1=,cos cos AC B BC A =,则AC AB ⋅=解:由已知得3,1,cos cos c a b B a A ===,于是sin cos sin cos B B A A =,即sin2sin2B A =.所以B A =或90B A +=︒.情形1:B A =,此时1,3,30b a c A ====︒,所以33cos 13;2AC AB bc A ⋅==⨯⨯= 情形2:90B A +=︒,此时22,3,cos 3b c A ===, 所以2cos 2323AC AB bc A ⋅==⨯⨯=.8.下图是一个几何体的三视图,则该几何体的体积为_______________.解:由三视图判断该几何体为三棱锥P ABC -(如图),由俯视图知平面PAB 丄平面ABC ,,2,1AC BC OC OA OB ====;再根据左视图得出OP AB ⊥,进而OP 丄平面ABC ,且OC AB ⊥,又从主视图中得出2OP OC ==.所以346131=⋅⋅=⋅=∆-OP OC AB OP S V ABC ABC P . 9.给定平面上四点,,,O A B C ,满足4,3,2,3OA OB OC OB OC ===⋅=,则ABC ∆面积的最大值为_________.解:由题可知,2227BC OB OC OB OC =+-⋅=,且OB 与OC 的夹角为60︒.O A B P C考虑以原点O 为圆心,半径分别为2,3,4的三个圆123,,O O O ,则可以将,C B 固定在圆12,O O 上,将A 在圆3O 上运动.作OD BC ⊥于D ,则当且仅当,,D O A 三点共线且DO 与DA 方向相同时,ABC ∆面积取得最大值最大.此时由sin BC OD OC OB BOC ⋅=⋅⋅∠,得OD =max (OA OD)BC 1(42272ABC S ∆+⋅==+=.10.方程组⎪⎪⎩⎪⎪⎨⎧==+++-=+++++-=+++ 3432abcd abc abd acd bcd cd bd bc ad ac ab d c b a 的一个实数解为⎪⎪⎩⎪⎪⎨⎧====____________________________________d c b a解:d c b a ,,,恰为方程03432234=+--+x x x x 的四个实根. 方程03432234=+--+x x x x 可变形为08)1(6)1(222=+++-++x x x x .于是212=++x x 或412=++x x所以方程组的四个实数解为:251+-,251--,2131+-,2131--的排列. (答出四个数的任意一个排列即可).三、解答题(第12题15分,第13,14,15每小题25分,共90分) 11.设集合}023|{2≤++=x x x A ,}0|{2≤++=b ax x x B , (1) 若R B A C x x B A C R R =≤<-= )(},21|{)(,求b a ,的值; (2)若1=b ,且A B A = ,求实数a 的取值范围.解:]1,2[--=A ,),1()2,(+∞---∞= A C R ,设b ax x x f ++=2)(. (1) 由R B A C x x B A C R R =≤<-= )(},21|{)(可得]2,2[-=B ,∴0,4.a b =⎧⎨=-⎩(2)∵A B A = ,A B ⊂∴.∴当Φ=B 时,由0<∆得22<<-a .当Φ≠B 时,若0=∆,则2±=a ,当2a =-时,{1}B =,不合题意;当2a =时,{1}B =-,符合题意.若0>∆,则0,(1)0,.(2)0,12 1.f a f a ∆>⎧⎪-≥⎪⎪⇒∈Φ-≥⎨⎪⎪-≤-≤-⎪⎩综上,22≤<-a .12.函数x x x x f 3cos sin )1cos 2(2)(2++=,R x ∈.求函数)(x f 的最大值. 解:x x x x f 3cos sin )1cos 2(2)(2++=)2cos(sin 2sin 2sin 22x x x x x +++=x x x x x x x sin 2sin cos 2cos sin 2sin 2sin 22-++= x x x x x 2sin 2cos 2cos sin 2sin ++=x x x 2sin 2)2cos(+-=x x cos sin 22+=2cos cos 22++-=x x817)41(cos 22+--=x 817≤.当41cos =x 时,函数)(x f 取最大值817. 13.直线m 的方程为1y kx =+,,A B 为直线m 上的两点,其横坐标恰为关于x 的一元二次方程22(1)220k x kx ---=的两个不同的负实数根.直线l 过点(2,0)P -和线段AB 的中点,CD 是y 轴上的一条动线段,考虑一切可能的直线l ,当l 和线段CD 无公共点时,CD 长的最大值是否存在?如果存在,求出最大值;如果不存在,说明理由.解:设1122(,),(,)A x y B x y ,则12221kx x k +=- 记线段AB 的中点为M ,则12221,1211M M Mx x k x y kx k k +===+=--. 设直线l 交y 轴于(0,)Q b ,根据(2,0)P -、(0,)Q b 、221(,)11k M k k --三点共线得: 2210010(2)(2)1b k k k---=-----,于是2112b k k =-++. 又12,x x 为关于x 的一元二次方程22(1)220k x kx ---=的两个不同的负实数根,知1221222220, 120, 148(1)0.k x x k x x k k k ⎧+=<⎪-⎪-⎪=>⎨-⎪∆=+->⎪⎪⎩解得1k <<.于是21(,(2(2,)12b k k =∈-∞-+∞-++.所以线段CD 长的最大值存在,且24||max +=CD . 14.若存在集合,A B 满足:A B =∅,且AB +=N ,则称(,)A B 为+N 的一个二分划.(Ⅰ)设{|3,},{|31,},A x x k k B x x k k ==∈==±∈++N N 判断(,)A B 是否为+N 的一个二分划,说明理由; (Ⅱ)是否能找到+N 的一个二分划(,)A B 满足: ①A 中不存在三个成等比数列的数; ②B 中不存在无穷的等比数列. 说明理由.(Ⅰ)1,1A B ∉∉, A B +∴≠N ,故(,)A B 不是+N 的一个二分划.(Ⅱ)能找到.+N 中形成的等比数列可以唯一地用一个正整数数对(,)a q 来表示,其中a 为数列的首项,q 为数列的公比,反之每一对(,)a q 也唯一地表示一个无穷的等比数列.正整数数对(,)a q 可以排序如下(1,2),(1,3),(2,2),(1,4),(2,3),(3,2),.将这些数对所对应的无穷等比数列依次记为12,,,,.k s s s先在1s 中任取一个数1a ,在2s 中取数2a ,使得21a a >;在3s 中取数3a ,使得2231a a a >;在4s 中取数4a ,使得2341a a a >;;一般的,在k s 中取数k a ,使得211kk a a a ->;.如此得到正整数12,,,,k a a a ,由这些数组成集合A ,并令B A =+N ,可以证明上述构造的A 和B 满足题设①和②.首先+N 中每一个无穷等比数列中至少有一项在A 中,所以B 中不存在无穷等比数列.再证A 中不存在三数成等比数列.任取,,m n r a a a A ∈,不妨设m n r <<,则m n r a a a <<,但由A 的取法知222111n n r r ma a a a a a a ->≥≥,故2,r m na a a >即,,m n r a a a 不成等比数列,所以A 中不存在三个成等比数列的数.高考理科数学试卷普通高等学校招生全国统一考试注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至5页. 2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成,答在本试题上无效. 4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷(2) 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合{1,}A =2,3,{|(1)(2)0,}B x x x x =+-<∈Z ,则AB =(A ){1}(B ){12},(C ){0123},,,(D ){10123}-,,,, (2)已知(3)(1)i z m m =++-在复平面内对应的点在第四象限,则实数m 的取值范围是(A )(31)-,(B )(13)-,(C )(1,)∞+(D )(3)∞--,(3)已知向量(1,)(3,2)m =-,=a b ,且()⊥a +b b ,则m= (A )-8(B )-6 (C )6 (D )8(4)圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a= (A )43-(B )34-(C )3(D )2(5)如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为(A )24 (B )18 (C )12 (D )9(6)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为(A )20π(B )24π(C )28π(D )32π(7)若将函数y=2sin 2x 的图像向左平移π12个单位长度,则评议后图象的对称轴为(A )x=kπ2–π6 (k ∈Z) (B )x=kπ2+π6 (k ∈Z) (C )x=kπ2–π12 (k ∈Z) (D )x=kπ2+π12(k ∈Z)(8)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图, 若输入的x=2,n=2,依次输入的a 为2,2,5,则输出的s=(A )7 (B )12 (C )17 (D )34 (9)若cos(π4–α)=35,则sin 2α=(A )725(B )15(C )–15(D )–725(10)从区间[]0,1随机抽取2n 个数1x ,2x ,…,nx ,1y ,2y ,…,ny ,构成n 个数对()11,x y ,()22,x y ,…,(),n n x y ,其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为(A )4n m (B )2n m (C )4m n (D )2m n(11)已知F1,F2是双曲线E 22221x y a b-=的左,右焦点,点M 在E 上,M F1与x 轴垂直,sin 2113MF F ∠=,则E 的离心率为(AB )32(CD )2 (12)已知函数学.科网()()f x x ∈R 满足()2()f x f x -=-,若函数1x y x+=与()y f x =图像的交点为1122(,),(,),,(,),m m x y x y x y ⋅⋅⋅则1()mi i i x y =+=∑(A )0 (B )m (C )2m (D )4m第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答.二、填空题:本大题共3小题,每小题5分(13)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若cos A=45,cos C=513,a=1,则b=. (14)α、β是两个平面,m 、n 是两条直线,有下列四个命题:(1)如果m ⊥n ,m ⊥α,n ∥β,那么α⊥β. (2)如果m ⊥α,n ∥α,那么m ⊥n.(3)如果α∥β,m ⊂α,那么m ∥β. (4)如果m ∥n ,α∥β,那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号)(15)有三张卡片,分别写有1和2,1和3,2和3。
全国高中数学联赛省级预赛模拟题

全国高中数学联赛省级初赛模拟试题 第Ⅰ卷(选择题 共60分)参照公式1.三角函数的积化和差公式1 sin α ?cos β=[sin(α +β )+sin(-β )],α 21α -+sin(β)-αβ )],cos α ?sin β=[sin(21α +β )+cos(-β )],αcos α ?cos β=[cos(21 α +-cos(β)α-β )].sin α ?sin β=[cos(22.球的体积公式V 球 = 4π R3( R 为球的半径) 。
3一、选择题(每题5 分,共 60 分)1.设在 xOy 平面上, 0<y ≤ x2,0 ≤ x 所≤1围成图形的面积为1。
则会集3M={(x,y)|x ≤ |y|}, N={(x,y)|x≥ y2|的交集 M ∩N 所表示的图形面积为21C . 11A .B .D .3362.在周围体 ABCD 中,设 AB=1 ,CD=3 ,直线 AB 与直线 CD 的距离为 2,夹角为 。
3则周围体 ABCD 的体积等于 矚慫润厲钐瘗睞枥庑赖賃軔。
A .311D .3B .C .32 3 23.有 10 个不相同的球,其中, 2 个红球、 5 个黄球、 3 个白球。
若取到一个红球得 5 分,取到一个白球得 2 分,取到一个黄球得 1 分,那么,从中取出5 个球,使得总分大于 10 分且小于 15 分的取法种数为 聞創沟燴鐺險爱氇谴净祸測。
A .90B . 100C . 110D .1204.在 ABC 中,若 (sinA+sinB)(cosA+cosB)=2sinC ,则 A . ABC 是等腰三角形,但不用然是直角三角形 B . ABC 是直角三角形,但不用然是等腰三角形 C . ABC 既不是等腰三角形,也不是直角三角形 D .ABC 既是等腰三角形,也是直角三角形5.已知 f(x)=3x2-x+4, f(g(x))=3x4+18x3+50x2+69x+48. 那么,整系数多项式函数 g(x) 的各项系数和为 残骛楼諍锩瀨濟溆塹籟婭骒。
全国高中数学联赛模拟试卷试题.doc

全国高中数学竞赛模拟试题一、选择题(每题 6 分共 36 分)1. 由 0,1,2,3,4,5六个数字能组成数字不重复且百位数字不是5 的偶数有 [ ] 个A.360B.252C.720D.2402. 已知数列 { a n }(n ≥ 1) 满足 a n 2 = a n 1 - a n ,且 a 2 =1, 若数列的前2020 项之和为 2020,则前2020 项的和等于 [ ] A.2020B.2020C.2020D.20203. 有一个四棱锥,底面是一个等腰梯形,并且腰长和较短的底长都是1,有一个底角是 60 0,又侧棱与底面所成的角都是450 ,则这个棱锥的体积是[ ]A.1B. 3C.3 D.3424. 若 ( 2x 4)2 naa x ax2a+则 a 2 a 4 a 2 n 被 3 除的余数2 2 n x 2n (n ∈ N ),0 1是 [ ] A.0 B.1C.2D.不能确定5. 已知 x, y(2, 2 ) ,且 xy 1 ,则24 的最小值是[ ]2422 xyA 、20B 、12C 、 16 4 2D 、 16 4 277776. 在边长为 12 的正三角形中有 n 个点,用一个半径为 3 的圆形硬币总可以盖住其中的2 个点,则 n 的最小值是 [ ]A.17B.16C.11D.10二、填空题(每题 9 分共 54 分)7. 在锐角三角形 ABC 中,设 tanA,tanB,tanC 成等差数列且函数 f(x) 满足f(cos2C)=cos(B+C-A) ,则 f(x) 的解析是为100 8.[(10i 1)(10i 3)(10i 7)(10i 9)] 的末三位数是 _______i 19. 集合 A 中的元素均为正整数,具有性质:若a A ,则 12- aA ,这样的集合共有 个 .10. 抛物线的顶点在原点,焦点在 x 轴的正半轴上,直线 x+y-1=0 与抛物线相交于 A 、 B 两点,且 |AB|= 86. 在抛物线上是否存在一点 C ,使△ ABC 为正三角形,若存在, C 点的11坐标是.11. 在数列 { a n } 中, a 1 = 2, a nan 11(n N * ) ,设 S n 为数列 { a n } 的前 n 项和,则S 2007 2S 2006S 2005 的值为12. 函数f ( x) 3 1 x x,其中0. 函数 f ( x)在[ 0, ) 上是减函数;的取范是 _____________________. 三、解答题(每题20 分共 60 分)13. 已知点 A 5,0和曲 x2 y 21 2x2 5,y上的点P、P、P n。
(完整word版)20.2012年全国高中数学联赛模拟卷(十)答案

2012年全国高中数学联赛模拟卷(十)第一试(考试时间:80分钟 满分:120分)姓名:_____________考试号:______________得分:____________一、填空题(共8题,每题8分,64分)1.用区间表示函数1()ln(1)3xf x x -=-+的定义域为 。
( 3.1)-- 2.在△ABC 中。
若1sin cos 3A A +=-,则cos2A =。
93.在数列{}n a 中,1*112,22()n n n a a a n N ++=-=∈,则使10n a >成立的最小正整数n 的值是 。
提示:3,*1112,1()22n n n n a a a n N ++=-=∈ 4.已知()f x 是R 上的奇函数,对任意x R ∈,均有(2)()f x f x +=,且(0,1)x ∈时,2()f x x =,则3()(1)2f f -+= 。
提示:14,(12)(1),(1)0f f f -+=-=5.如图,在四棱锥P ABCD -中,底面ABCD 为正方形,△PAB 为等 边三角形,O 为AB 边的中点,且PO ⊥平面ABCD ,则二面角P AC D --的余弦值为。
6.若正整数m 使得对任意一组满足12341a a a a =的正数1234,,,a a a a 都有123412341111m m m m a a a a a a a a +++≥+++成立,则正整数m 的最小值为 。
提示:3,用排序不等式,右边=234134124123a a a a a a a a a a a a +++不妨设1234a a a a ≥≥≥,列出三组必定成立 7.函数22*()sin cos ,()kk f x x x k N =+∈的最小值为 。
提示:112k -,观察,归纳,证明。
8.将方程33[]40x x -⨯-=([]x 表示不超过x 的最大整数)的实数解从小到大排列成12,,,k x x x L ,则33312k x x x +++=L 。
2023年全国高中数学联赛江西省预赛数学试题及参考答案

.
解:由边长为1正六面体被一个平面所截的面积最大的平面是边长为
6⋅ ⋅
√
⋅
√
=
√
的正六边形,故最大面积为
.
6、若锐角, , 满足 + + = 2,则
是
√
.
1 / 5
+
+的最小值解:由111
+
+
填空题(每小题 7 分,共 56 分)
一、
1、用 12 种不同的动物图案制作成一些动物卡片,使得每张卡片上都有其中的 4 种不同的动物图案,
且制作过程中要求任取的两张卡片有且仅有一种动物是相同的,则最多能制作的卡片数量为
.
解:将 12 种不同的动物图案编号为 1,2,…,12,如果考虑相同的一种动物是 1 号,最多有 3 种,
2023 年全国高中数学联赛江西省预赛试题
一、
(考试时间:2023 年 5 月 21 日上午 9 : 30 12 : 00 )
填空题(每小题 7 分,共 56 分)
1 、用 12 种不同的动物图案制作成一些动物卡片,使得每张卡片上都有其中的 4 种不同的动物图案,
且制作过程中要求任取的两张卡片有且仅有一种动物是相同的,则最多能制作的卡片数量为
2
2
4
4
sin A cos B sin B cos C sin C cos 4 A
2
.
7 、设 A, B 为双曲线 W :
x2 y2
1 与实轴的交点, P (0,1) 为双曲线外一点, PA, PB 分别交双曲线于另
全国高中数学联赛模拟训练题.docx

的交点为交、C.现有以A为焦点,过B、C且开口向左的抛物线,抛物线的顶点坐标当椭圆的离心率e满足|<^2<1,求实数秫的取值范围.四、(20分)。
、b、c均为实数,奸b, b?c, c^a.证明:2/M.2C|+"-M|+|C3-24<2.2 \a - b\ + \b - c\ + \c - a\五、(20分)已知fi^x^ax^+b^+cx^+dx,满足(i)。
、》、c、d均大于0; (ii)对于任一个{-2, -1,0,1,2},/3)为整数;(iii,/(5)=70.试说明,对于每个整数X, Rr)是否为整数.弟—试—、(50分)设K为、AB C的内心,点G、瓦分别为边A3、AC的中点,直线AC与GK交于点B2,直线AB于BiK交于点C2.若△AB2C2于△ABC的面积相等,试求ZCAB.二、(50 分) 设w = cosy + isin,/(.V)=(.V-M')(A'-VV3)(.V-VV7)(A'-M'9).求证:/U)为一整系数多项式,且Rx)不能分解为两个至少为一次的整系数多项式之积.三、(50分)在圆上有21个点.求在以这些点为端点组成的所有的弧中,不超过120°的弧的条数的最小值.参旁答案第一试(3 ,目、三、1,兰士 .四、证略.五、是.第二试一、60°;二、证略.三、100.I 4 J金国高甲够样联赛模拟试茎(^)ZvZv 、_41弟一试一、选择题:(每小题6分,共36分)1、设log力是一个整数,且log a - > log a4b > \og b a2,给出下列四个结论b®— > 4b > a2;②logaZ?+log*=0;③OV Q V^VI;④沥一1=0.b 」」其中正确结论的个数是(A) 1 (B) 2 (C) 3 (D) 4金国高中够样联赛模拟试茎(^)ZvZv 、_41弟一试一、选择题:(每小题6分,共36分)1、a、0是异面直线,直线c与a所成的角等于c与。
高考数学高三模拟考试试卷压轴题全国高中数学联赛预赛试卷含答案

高考数学高三模拟考试试卷压轴题全国高中数学联赛预赛试卷(含答案)一、填空题(10小题,每小题6分,共60分)1.在数列{}n a 中,11a =,23a =,且21n n n a a a ++=-(*∈N n ),则=2014a .【答案】1.2.如图所示的程序框图中输出的结果为a ,若二项式24mx ((m>0)的展开式中含3x 的项的系数为2a,则常数m=_________.【答案】123.已知对任意1,32m ⎡⎤∈⎢⎥⎣⎦,不等式x2+mx +4>2m +4x 恒成立,则x 的取值范围是_____________.【答案】x>2或x<-1 4.已知2a ≥-,且{}2A x x a =-≤≤,{}23,B y y x x A ==+∈,{}Ax x z z C ∈==,2,若C B ⊆,则实数a 的取值范围是.【答案】1,32⎡⎤⎢⎥⎣⎦.5.AFS 国际文化交流组织(AFSInterculturalPrograms )拟将18个中学生交流项目的名额分配给4所学校, 要求每校至少有一个名额且各校分配的名额互不相等, 则不同的分配方法种数为:______________. 【答案】3606.设m>1,在约束条件,,1.y x y mx x y ≥⎧⎪≤⎨⎪+≤⎩下,目标函数z =x +my 的最大值小于2,则m 的取值范围为__________. 【答案】(1,1+2)7.圆锥的轴截面SAB 是边长为2的等边三角形,O 为底面中心,M 为SO 的中点,动点P 在圆锥底面内(包括圆周).若AM ⊥MP ,则P 点形成的轨迹的长度为. 【答案】27. 8.直角梯形ABCD 中,AD ⊥AB, AB//DC , AB=4,AD=DC=2,设点N 是DC 边的中点,点M 是梯形ABCD 内或边界上的一个动点,则AM AN ⋅的最大值是______________.【答案】69.设实数1a <-,变量x 满足2x ax x +≤-,且2x ax +的最小值为12-,则a =. 【答案】32-10.已知焦点在x 轴上的双曲线的渐近线过椭圆221416x y +=和椭圆221164ax y +=(0<1a ≤)的交点,则双曲线的离心率的取值范围是. 【答案】)321,2[ 二、解答题(4小题,共60分)11.(本小题满分14分)在数列{}n a 中,11a =,122n n a a n +=-+,n ∈*N .求数列{}n a 的前n 项和n S .解:由122n n a a n +=-+得12((1))n n a n a n +-=--,n ∈*N .所以数列{}(1)n a n --是首项为1,且公比为2的等比数列.∴121n n a n -=+-.…………10分所以数列{}n a 的前n 项和(1)212nn n n S -=-+.…………14分 12.(本小题满分14分)已知△ABC 的角A ,B ,C 的对边依次为a ,b ,c ,若满足3tan tan tan 3A B A B ⋅--=(Ⅰ)求∠C 大小;(Ⅱ)若c=2,且△ABC 为锐角三角形,求a2+b2取值范围. 解:(I 3tan tan tan 3A B A B ⋅--=tan tan 3(tan tan 1)A B A B +=⋅-∴tan tan 31tan tan A BA B+=--⋅tan()3A B +=-,∴tan 3C =3C π=…………6分(II )2262sin sin sin 23A a b c B A A B C A B πππππ⎧<⎪⎪⎪<⇒<<==⎨⎪⎪+=⎪⎩,由正弦定理,2222162[sin sin ()]33168sin(2)336512sin(2)1,6266626a b A A A A A A ππππππππ+=+-=+-<<∴<-<∴<-≤,,22208.3a b <+≤即…………14分13.(本小题满分16分)已知双曲线C :22221x y a b-=(0a >,0b >)的离心率为2,过点(0)P m ,(0m >)斜率为1的直线l 交双曲线C 于A 、B 两点,且3AP PB =,3OA OB ⋅=.(1)求双曲线方程;(2)设Q 为双曲线C 右支上动点,F 为双曲线C 的右焦点,在x 轴负半轴上是否存在定点M 使得2QFM QMF ∠=∠?若存在,求出点M 的坐标;若不存在,请说明理由.解:(1)由双曲线离心率为2知,2c a =,b =,所以双曲线方程可化为222213x y a a-=.又直线l 方程为y x m =+.由222213x y a a y x m ⎧-=⎪⎨⎪=+⎩,得2222230x mx m a ---=.①设11()A x y ,,22()B x y ,,则12x x m +=,221232m a x x --=.因为3AP PB =,所以1122()3()x m y x y m --=-,,,故123x x =-. 结合12x x m +=,解得132x m =,212x m =-. 代入221232m a x x --=,得2223342m a m ---=,化简得226m a =.又1212121222221212()()2()33OA OB x x y y x x x m x m x x m x xm m a a ⋅=+=+++=+++=-=,因为已知3OA OB ⋅=. 所以21a =.此时,m =2290x --=,显然该方程有两个不同的实根.21a =符合要求.故双曲线C 的方程为2213y x -=.…………8分(2)假设点M 存在,设(0)M t ,.由(1)知,双曲线右焦点为(20)F ,.设00()Q x y ,(01x ≥)为双曲线C 右支上一点.当02x ≠时,00tan 2Q F y QFM k x ∠=-=--,00tan Q M y QMF k x t∠==-,因为2QFM QMF ∠=∠,所以0002000221()y y x ty x x t⨯--=---. 将220033y x =-代入,并整理得,22200002(42)4223x t x t x tx t -++-=--++.于是242243t t t t +=-⎧⎨-=+⎩,解得1t =-. 当02x =时,090QFM ∠=,而1t =-时,045QMF ∠=,符合2QFM QMF ∠=∠. 所以1t =-符合要求.满足条件的点M 存在,其坐标为(10)-,.…………16分 14.(本小题满分16分)已知函数()ln(1)1axf x x x =+++()a ∈R . (Ⅰ)当2a =时,求函数()x f y =的图象在0x =处的切线方程; (Ⅱ)判断函数()f x 的单调性;(Ⅲ)求证:2111ln 1n n n⎛⎫+>- ⎪⎝⎭(*n N ∈).解:(Ⅰ)当2a =时,2()ln(1)1xf x x x =+++, ∴22123()1(1)(1)x f x x x x +'=+=+++, ∴(0)3f '=,所以所求的切线的斜率为3. 又∵()00f =,所以切点为()0,0. 故所求的切线方程为:3y x =. …………4分 (Ⅱ)∵()ln(1)1axf x x x =+++(1)x >-, ∴221(1)1()1(1)(1)a x ax x a f x x x x +-++'=+=+++. ①当0a ≥时,∵1x >-,∴()0f x '>;②当0a <时,由()01f x x '<⎧⎨>-⎩,得11x a -<<--;由()01f x x '>⎧⎨>-⎩,得1x a >--;综上,当0a ≥时,函数()f x 在(1,)-+∞单调递增;当0a <时,函数()f x 在(1,1)a ---单调递减,在(1,)a --+∞上单调递增.…………10分 (Ⅲ)方法一:由(Ⅱ)可知,当1a =-时, ()()ln 11xf x x x =+-+在()0,+∞上单调递增. ∴ 当0x >时,()()00f x f >=,即()ln 11xx x +>+. 令1x n =(*n ∈N ),则111ln 1111n n n n ⎛⎫+>= ⎪+⎝⎭+.另一方面,∵()2111n n n <+,即21111n n n-<+,∴21111n n n>-+. ∴2111ln 1n n n⎛⎫+>- ⎪⎝⎭(*n ∈N ).…………16分方法二:构造函数2()ln(1)F x x x x =+-+,(01)x ≤≤ ∴1(21)'()1211x x F x x x x +=-+=++, ∴当01x <≤时,'()0F x >; ∴函数()F x 在(0,1]单调递增. ∴函数()(0)F x F >,即()0F x >∴(0,1]x ∀∈,2ln(1)0x x x +-+>,即2ln(1)x x x +>- 令1x n =(*n ∈N ),则有2111ln 1n n n⎛⎫+>- ⎪⎝⎭.…………16分 方法三:数学归纳法 酌情给分高考理科数学试卷普通高等学校招生全国统一考试注意事项: 1.本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.第Ⅰ卷1至3页,第Ⅱ卷3至5页. 2.答题前,考生务必将自己的姓名、准考证号填写在本试题相应的位置. 3.全部答案在答题卡上完成,答在本试题上无效. 4.考试结束后,将本试题和答题卡一并交回.第Ⅰ卷一. 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.(1)已知集合{1,}A =2,3,{|(1)(2)0,}B x x x x =+-<∈Z ,则AB =(A ){1}(B ){12},(C ){0123},,,(D ){10123}-,,,, (2)已知(3)(1)i z m m =++-在复平面内对应的点在第四象限,则实数m 的取值范围是(A )(31)-,(B )(13)-,(C )(1,)∞+(D )(3)∞--, (3)已知向量(1,)(3,2)m =-,=a b ,且()⊥a +b b ,则m= (A )-8(B )-6 (C )6 (D )8(4)圆2228130x y x y +--+=的圆心到直线10ax y +-=的距离为1,则a= (A )43-(B )34-(C )3(D )2(5)如图,小明从街道的E 处出发,先到F 处与小红会合,再一起到位于G 处的老年公寓参加志愿者活动,则小明到老年公寓可以选择的最短路径条数为(A )24 (B )18 (C )12 (D )9(6)右图是由圆柱与圆锥组合而成的几何体的三视图,则该几何体的表面积为 (A )20π(B )24π(C )28π(D )32π(7)若将函数y=2sin 2x 的图像向左平移π12个单位长度,则评议后图象的对称轴为(A )x=kπ2–π6 (k ∈Z) (B )x=kπ2+π6 (k ∈Z) (C )x=kπ2–π12 (k ∈Z) (D )x=kπ2+π12 (k ∈Z)(8)中国古代有计算多项式值的秦九韶算法,右图是实现该算法的程序框图.执行该程序框图,若输入的x=2,n=2,依次输入的a 为2,2,5,则输出的s= (A )7 (B )12 (C )17 (D )34 (9)若cos(π4–α)=35,则sin 2α=(A )725(B )15(C )–15(D )–725(10)从区间[]0,1随机抽取2n 个数1x ,2x ,…,nx ,1y ,2y ,…,ny ,构成n 个数对()11,x y ,()22,x y ,…,(),n n x y ,其中两数的平方和小于1的数对共有m 个,则用随机模拟的方法得到的圆周率π的近似值为(A )4n m (B )2n m (C )4m n (D )2m n(11)已知F1,F2是双曲线E 22221x y a b-=的左,右焦点,点M 在E 上,M F1与x 轴垂直,sin 2113MF F ∠=,则E 的离心率为 (AB )32(CD )2(12)已知函数学.科网()()f x x ∈R 满足()2()f x f x -=-,若函数1x y x+=与()y f x =图像的交点为1122(,),(,),,(,),m m x y x y x y ⋅⋅⋅则1()mi i i x y =+=∑(A )0 (B )m (C )2m (D )4m第II 卷本卷包括必考题和选考题两部分.第(13)题~第(21)题为必考题,每个试题考生都必须作答.第(22)题~第(24)题为选考题,考生根据要求作答.二、填空题:本大题共3小题,每小题5分(13)△ABC 的内角A 、B 、C 的对边分别为a 、b 、c ,若cos A=45,cos C=513,a=1,则b=. (14)α、β是两个平面,m 、n 是两条直线,有下列四个命题:(1)如果m ⊥n ,m ⊥α,n ∥β,那么α⊥β. (2)如果m ⊥α,n ∥α,那么m ⊥n.(3)如果α∥β,m ⊂α,那么m ∥β. (4)如果m ∥n ,α∥β,那么m 与α所成的角和n 与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号)(15)有三张卡片,分别写有1和2,1和3,2和3。
2024年全国高中数学联赛一试模拟试卷试题含答案

2024年全国高中数学联赛一试模拟试卷试题含答案一、选择题(本题共15小题,每小题5分,满分75分)1. 设集合A={x|3x-7<2x+5},B={x|x²-5x+6<0},则A∩B的取值范围是()A. (-∞, 2)B. (-∞, 3)C. (2, 3)D. (3, +∞)答案:B2. 若a、b为实数,且a≠b,则方程ax²-(a+b)x+b=0有实根的充要条件是()A. a+b=0B. a-b=0C. a²+b²=0D. ab=1答案:A3. 已知函数f(x)=x²-2x+3的最小值为m,则实数m的取值范围是()A. m>0B. m≥3C. m<3D. m≤0答案:B4. 若等差数列{an}的前n项和为Sn,且S5=10,S10=30,则S15的值为()A. 50B. 60C. 70D. 80答案:C5. 设函数f(x)=x²+2x+1,若f(x+1)=16,则x的值为()A. 2B. 3C. 4D. 5答案:D6. 若函数g(x)=x²+2x+k在x=1处取得最小值,则实数k的取值范围是()A. k≥-3B. k≤-3C. k≥3D. k≤3答案:A7. 已知函数f(x)=2x³-3x²+x+1,求f(-1)的值。
A. 0B. 1C. -1D. -3答案:D8. 若a、b、c成等比数列,且a+b+c=12,abc=27,则a、b、c的值分别为()A. 1, 3, 9B. 3, 3, 3C. 1, 9, 3D. 9, 3, 1答案:A9. 设等差数列{an}的公差为d,若a3+a5+a7=12,则a1+a6+a9的值为()A. 9B. 12C. 15D. 18答案:B10. 若a、b、c为等差数列,且a+b+c=12,abc=27,则a²+b²+c²的最小值为()A. 18B. 24C. 30D. 36答案:C二、填空题(本题共5小题,每小题15分,满分75分)11. 已知函数f(x)=x²+2x+1,求f(x+2)的值。
2023年全国高中数学联赛山东省预赛试题(含答案)

2023全国数学联赛山东省预赛试题一、填空题(每小题8分,共80分)1、已知},33811|{1Z x x A x ∈≤<=-,},032|{N x x x x B ∈<-+=,则集合},,|{B y A x xy m m C ∈∈==的元素个数是.2、已知:3tan sin 41=-αα2,0((πα∈,则α是.3、已知关于x 的方程023=+++c bx ax x 的三个非零实数根成等比数列,则33b c a -的值是.4、正方体1111D C B A ABCD -的底面1111D C B A 内有一个动点M ,且C AD BM 1//平面,则MD D 1tan ∠的最大值是.5、数列}{n a 中,11=a ,),2,1(211 =+=+n a a n n ,那么=n a .6、已知0,,>z y x ,则z y x x z z y y x f 539164222222+++++++=的最小值是.7、设ABC ∆的内心为I ,而且满足0652=++IC IB IA ,则B ∠cos 的值是.8、已知双曲线H :221x y -=上第一象限内一点M ,过M 的作H 的切线l ,与双曲线H 切于M ,交H的渐近线于P ,Q 两点(P 在第一象限),R 与Q 在同一渐近线上.则RP RQ ⋅ 的最小值为.9、小张参加一次十道选择题的测试,做对一道得一分,做错一道扣一分,不做得零分.他的目标是至少得7分,7分及格.小张现在确定他前六道题的答案是正确的,而剩下的每道题做对的概率为21,小张应该做______多少道题,及格的概率最大.10、设实数y x ,使得y x -,22y x -,33y x -均为素数,则y x -的值是.二、解答题(共70分)11、(本题15分)已知:O 是ABC ∆的外心,E D ,分别是边AB AC ,上的点.线段CE BD DE ,,的中点分别为R Q P ,,.DE OH ⊥垂足为H .求证:P ,Q ,R ,H 四点共圆.12、(本题15分)在区间)2,2(32n n 中任取1212+-n 个奇数.求证:在所取出的数中,必有两个数,其中一个数的平方不能被另一个数整除.13、(本题20分)已知:c b a ,,为正实数.证明:)(9)2)(2)(2(222ca bc ab c b a ++≥+++.14、(本题20分)1010⨯的表格上填入1到100,第i 行第j 列填入j i +-)1(10.每次操作如下:取一个格子,或者将此格2023全国数学联赛山东省预赛试题解析一、填空题(每小题8分,共80分)1、答案:72、答案:18π 3、答案:0 4、答案:25、答案:),2,1(1)2(32 =--+=n a n n6、答案:55 7、答案:85 8、答案:21- 9、答案:7或910、答案:3二、解答题(共70分)11、 证明:设ADE ∆的三个内角分别为E D A ,,,ABC ∆的外接圆半径为R由AC RP AB QP //,//知E QPH sin sin =∠,A QPR sin sin =∠,D HPR sin sin =∠ 又2,2CD PR BE PQ ==, 故 H R Q P ,,,四点共圆⇔QPR PH QPH PR RPH PQ ∠=∠-∠sin sin sin ⇔A PH E CD D BE sin sin 2sin 2=- ⇔DE PH AD CD AE BE ⋅=⋅-⋅2 ⇔)()()()(2222EH DH EH DH OD R DE R +⋅-=---⇔2222EH DH OE OD -=-⇔DE OH ⊥ 得证12、13、 证明:由抽屉原理,c b a ,,中必有两个数同时不大于1,或同时比小于1,设为b a , 则由0)1)(1(22≥--b a 得22221b a b a +≥+所以)2)(422()2)(2)(2(22222222++++=+++c b a b a c b a)11)(1(3222c b a ++++≥2)(3c b a ++≥)(9ca bc ab ++≥14、 证明:设一开始填数字k 的格子为k a ,令∑==1001i i ia A则A 在操作中是不变量,始终为33835010012=∑=i i又因此数为表格中1到100所能得到的最大值,故等号成立,所以顺序不变.。
(整理)全国高中数学联赛模拟试题目

全国高中数学联赛模拟试题(一)(命题人:吴伟朝)第一试一、 选择题:(每小题6分,共36分)1、方程6×(5a 2+b 2)=5c 2满足c ≤20的正整数解(a ,b ,c )的个数是(A )1 (B )3 (C )4 (D )52、函数12-=x x y (x ∈R ,x ≠1)的递增区间是(A )x ≥2 (B )x ≤0或x ≥2 (C )x ≤0(D )x ≤21-或x ≥23、过定点P (2,1)作直线l 分别交x 轴正向和y 轴正向于A 、B ,使△AOB (O为原点)的面积最小,则l 的方程为 (A )x +y -3=0 (B )x +3y -5=0 (C )2x +y -5=0 (D )x +2y -4=04、若方程cos2x +3sin2x =a +1在⎥⎦⎤⎢⎣⎡2,0π上有两个不同的实数解x ,则参数a 的取值范围是 (A )0≤a <1 (B )-3≤a <1 (C )a <1 (D )0<a <1 5、数列1,2,2,3,3,3,4,4,4,4,5,5,5,5,5,6,…的第1000项是(A )42 (B )45 (C )48 (D )516、在1,2,3,4,5的排列a 1,a 2,a 3,a 4,a 5中,满足条件a 1<a 2,a 2>a 3,a 3<a 4,a 4>a 5的排列的个数是 (A )8 (B )10 (C )14 (D )16二、 填空题:(每小题9分,共54分)1、[x ]表示不大于x 的最大整数,则方程21×[x 2+x ]=19x +99的实数解x 是 .2、设a 1=1,a n +1=2a n +n 2,则通项公式a n = .3、数799被2550除所得的余数是 .4、在△ABC 中,∠A =3π,sin B =135,则cos C = .5、设k 、θ是实数,使得关于x 的方程x 2-(2k +1)x +k 2-1=0的两个根为sin θ和cos θ,则θ的取值范围是 . 6、数()n2245+(n ∈N )的个位数字是 .三、 (20分)已知x 、y 、z 都是非负实数,且x +y +z =1.求证:x (1-2x )(1-3x )+y (1-2y )(1-3y )+z (1-2z )(1-3z )≥0,并确定等号成立的条件.四、 (20分)(1) 求出所有的实数a ,使得关于x 的方程x 2+(a +2002)x +a =0的两根皆为整数.(2) 试求出所有的实数a ,使得关于x 的方程x 3+(-a 2+2a +2)x -2a 2-2a =0有三个整数根.五、 (20分)试求正数r 的最大值,使得点集T ={(x ,y )|x 、y ∈R ,且x 2+(y -7)2≤r 2}一定被包含于另一个点集S ={(x ,y )|x 、y ∈R ,且对任何θ∈R ,都有cos2θ+x cos θ+y ≥0}之中.第一试一、选择题:题号 1 23 4 5 6 答案 C CDABD二、填空题:1、38181-或381587;2、7×2n -1-n 2-2n -3;3、343;4、261235-; 5、{θ|θ=2n π+π或2n π-2π,n ∈Z } ;6、1(n 为偶数);7(n 为奇数).三、证略,等号成立的条件是31===z y x 或⎪⎩⎪⎨⎧===021z y x 或⎪⎩⎪⎨⎧===021y z x 或⎪⎩⎪⎨⎧===021z z y .四、(1)a 的可能取值有0,-1336,-1936,-1960,-2664,-4000,-2040;(2)a 的可能取值有-3,11,-1,9.五、r max =24.第二试一、(50分)设a、b、c∈R,b≠ac,a≠-c,z是复数,且z2-(a-c)z-b=0.求证:()12=-+-+baczcaba的充分必要条件是(a-c)2+4b≤0.二、(50分)如图,在△ABC中,∠ABC和∠ACB均是锐角,D是BC边上的内点,且AD平分∠BAC,过点D 分别向两条直线AB、AC作垂线DP、DQ,其垂足是P、Q,两条直线CP与BQ相交与点K.求证:(1)AK⊥BC;AC B DQKP(2) BCS AQ AP AK ABC△2<=<,其中ABC S △表示△ABC 的面积.三、(50分)给定一个正整数n ,设n 个实数a 1,a 2,…,a n 满足下列n 个方程:∑==+=+ni i n j j ji a 1),,3,2,1(124.确定和式∑=+=ni ii a S 112的值(写成关于n 的最简式子).参考答案第一试一、选择题:题号1 23456答案 CC D A B D二、填空题:1、38181-或381587;2、7×2n -1-n 2-2n -3;3、343;4、261235-; 5、{θ|θ=2n π+π或2n π-2π,n ∈Z } ;6、1(n 为偶数);7(n 为奇数).三、证略,等号成立的条件是31===z y x 或⎪⎩⎪⎨⎧===021z y x 或⎪⎩⎪⎨⎧===021y z x 或⎪⎩⎪⎨⎧===021z z y .四、(1)a 的可能取值有0,-1336,-1936,-1960,-2664,-4000,-2040;(2)a 的可能取值有-3,11,-1,9.五、r max =24.第二试一、证略(提示:直接解出()2i42⋅---±-=b c a c a z ,通过变形即得充分性成立,然后利用反证法证明必要性).二、证略(提示:用同一法,作出BC 边上的高AR ,利用塞瓦定理证明AR 、BQ 、CP 三线共点,从而AK ⊥BC ;记AR 与PQ 交于点T ,则BCS ABC△2=AR >AT >AQ =AP ,对于AK <AP ,可证∠APK <∠AKP ).三、()11212++-=n S .。
2012年全国高中数学联赛模拟卷(10)(一试+二试,附详细解答)

2012年全国高中数学联赛模拟卷(10)第一试(考试时间:80分钟 满分:120分)姓名:_____________考试号:______________得分:____________一、填空题(本大题共8小题,每小题8分,共64分)1、设a , b 是两个正整数, 它们的最小公倍数是24·33·72·11, 那么这样的有序正整数对(a , b )有 _ 组.2、方程16sin πx cos πx =16x +1x的解集合为3、三棱锥S ABC -是三条侧棱两两垂直的三棱锥,O 是底面ABC ∆内的一点, 那么tan tan tan W OSA OSB OSC =∠⋅∠⋅∠的最小值是______________4、对任意,x y R ∈,代数式M =________5、计算:232010sinsinsin sin 2011201120112011ππππ= _______________ 6、篮球场上有5个人在练球,其战术是由甲开始发球(第一次传球),经过六次传球跑动后(中途每人的传球机会均等)回到甲,由甲投3分球,其中不同的传球方式为___________种. 7、对,x y R ∀∈,函数(,)f x y 都满足:①(0,)1f y y =+;②(1,0)(,1)f x f x +=; ③(1,1)(,(1,))f x y f x f x y ++=+;则(3,2011)f =__________________8、设2n 个实数122,,,n a a a 满足条件21211()1n i i i aa -+=-=∑则12212()()n n n n a a a a a a μ++=+++-+++ 的最大值为________________二、解答题(本大题共3小题,第9题16分,第10、11题20分,共56分)9.设由不超过1000的两个正整数组成的数对(,)m n满足条件:11m m n n+<<+. 试求所有这样的数对(,)m n 的个数.10. P 是椭圆x 2a 2+y 2b 2=1(a >b >0)上任意一点,12,F F 是椭圆的焦点,12,PF PF 分别交椭圆与,A B 两点,求证:1212||||||||PF PF F A F B +是定值.11. 给定大于2011的正整数n ,将21,2,3,,n 分别填入n n ⨯的棋盘的方格中,使每个方格恰有一个数,如果一个方格中填的数大于它所在行至少2011个方格内所填的数,且大于它所在列至少2011个方格内所填的数,则称这个方格为“优格”,求棋盘中“优格”个数的最大值.(考试时间:150分钟 满分:180分)姓名:_____________考试号:______________得分:____________一、(本题满分40分)设D 为ABC ∆内的一点,作DP ⊥BC 于P ,DQ ⊥AC 于Q ,DR ⊥AB 于R求证:QR PQ =是DCDABC BA =的充要条件。
全国高中数学联赛模拟试题(十)

全国高中数学联赛模拟试题(十)第一试一、多项选择题:(每个子题6分,共36分)1、设集合m={-2,0,1},n={1,2,3,4,5},映射f:m→n使对任意的x∈m,都有x+f(x)+xf(x)是奇数,则这样的映射f的个数是(a) 45(b)27(c)15(d)112、已知sin2q=a,cos2q=b,0<q<,给出值的五个答案:①; ②; ③; ④;⑤.正确的答案是:(a)①②⑤(b)②③④(c)①④⑤(d)③④⑤3.将多个边长为2、3和5的长方体在同一方向上组装成边长为90的立方体,然后计算通过立方体对角线的小长方体的数量(a)64(b)66(c)68(d)704.递增顺序1,3,4,9,10,12,13,。
由一些正整数组成,它们要么是3的幂,要么是几个3的幂的和,那么这个序列的第100项是(a)729(b)972(c)243(d)9815.(其中[x]表示不超过x的最大整数)为(a)(b)(c)(d)6、一个五位的自然数称为“凸”数,当且仅当它满足a<b<c,c>d>e(如12430,13531等),则在所有的五位数中“凸”数的个数是(a) 8568(b)2142(c)2139(d)1134二、填空题:(每小题9分,共54分)1.通过椭圆上的任意点P,使椭圆的右引导线的垂直线pH(H为垂直底脚),并将pH延伸至Q,使HQ=LPH(L≥ 1)当P点在椭圆上移动时,q点轨迹的偏心范围为2、已知异面直线a、b所成的角为60°,过空间一点p作与a、b都成角a(0<a<90°)的直线l,则这样的直线l的条数是f(a)=.3.不等式的解集为4、设复数z满足条件|z-i|=1,且z≠0,z≠2i,又复数w使得为实数,则复数w-2的辐角主值的取值范围是.5.让A1,A2,。
,A2002是正实数,然后是A1A2的最小值。
A2002是6、在一个由十进制数字组成的数码中,如果它含有偶数个数字8,则称它为“优选”数码(如12883,787480889等),否则称它为“非优选”数码(如2348756,958288等),则长度不超过n(n为自然数)的所有“优选”数码的个数之和为.三、(20分)已知数列{an}是首项为2,公比为的等比数列,且前n项和为sn.(1)用Sn表示Sn+1;(2)是否存在自然数c和k,使得>2成立.四、(20分)设异面直线a、b成60°角,它们的公垂线段为ef,且|ef|=2,线段ab的长为4,两端点a、b分别在a、b上移动.求线段ab中点p的轨迹方程.五、(20分)已知定义在r+上的函数f(x)满足(i)对于任何a,B∈ R+,f(AB)=f(a)+f(b);(ii)当x>1时,f(x)<0;(iii)f(3)=-1。
2019年全国高中数学联赛模拟试题(十)
x
1
15.(1)(2 分)先化简,再求值: x-
÷ 1+
,其中 x= 3-1.
x+1
x2-1
1
x-1
(2) 解分式方程:(2 分)解方程:
+3=
.
x-2
2-x
(3).(2
分)解不等式组
x-2 3
+3<x-1
�
1-3(x+1) 6-x
�
16、(6 分)如图,梯形 ABCD 中,AD∥BC,点 M 是 BC 的中点,且 MA=MD. 求证:四边形 ABCD 是等腰梯形.
x
AO
点作 y 轴, x 轴的垂线,垂足为 E,F,连接 CF,DE.
Fx
有下列四个结论:
C
E
①△CEF 与△DEF 的面积相等; ②△AOB∽△FOE;
③△DCE≌△CDF;
④ AC BD .
(第 16 题)
其中正确的结论是
.(把你认为正确结论的序号都填上)
三、解答题(本大题共 4 个小题,满分 28 分)
2019 年全国高中数学联赛模拟试题(十)
一、选择题(每题 3 分,共 27 分) 1.下列各式运算中,正确的是( )
A. (a b)2 a2 b2
B. (3)2 3
C. a3 a4 a12
D. ( 3)2 a
6 a2
(a
0)
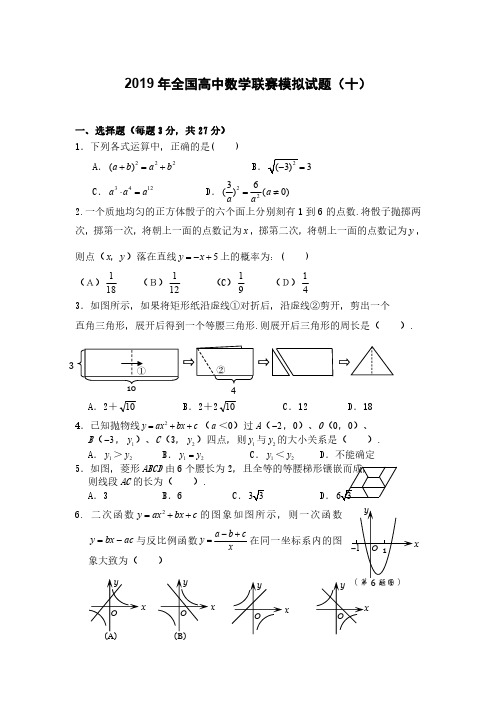
2.一个质地均匀的正方体骰子的六个面上分别刻有 1 到 6 的点数.将骰子抛掷两
y C
A O
l
P
NB
M
x
别以
A
AB、AC 为直径作半圆,则图中阴影部分的面积是
()
A. 64 12 7 C.16 24 7
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
全国高中数学联赛模拟试题(十)
姓名______ 学校______ 得分_______
第一试
一、选择题:(每小题6分,共36分)
1、 设集合M ={-2,0,1},N ={1,2,3,4,5},映射f :M →N 使对任意的x ∈M ,都有
x +f (x )+xf (x )是奇数,则这样的映射f 的个数是
(A )45 (B )27 (C )15 (D )11
2、 已知sin2=a ,cos2=b ,0<<
4π,给出⎪⎭⎫ ⎝
⎛
+4tan πθ值的五个答案:
①
a b
-1; ②
b a
-1; ③
a
b
+1; ④
b
a
+1; ⑤1
1
-++-b a b a .
其中正确的是:
(A )①②⑤ (B )②③④ (C )①④⑤ (D )③④⑤
3、 若干个棱长为2、3、5的长方体,依相同方向拼成棱长为90的正方体,则正方体
的一条对角线贯穿的小长方体的个数是
(A )64 (B )66 (C )68 (D )70
4、 递增数列1,3,4,9,10,12,13,…,由一些正整数组成,它们或者是3的幂,或者是
若干个3的幂之和,则此数列的第100项为 (A )729 (B )972 (C )243 (D )981
5、 1
4951C C C C +++++m n n n n Λ(其中⎥⎦
⎤
⎢⎣⎡-=41n m ,[x ]表示不超过x 的最大整数)的值为 (A )4
cos
2π
n n
(B )4
sin
2πn n
(C )
⎪⎭
⎫ ⎝⎛+-4cos 22211πn n
n (D )
⎪⎭
⎫ ⎝⎛+-4sin 22211πn n
n 6、 一个五位的自然数abcde 称为“凸”数,当且仅当它满足a <b <c ,c >d >e (如
12430,13531等),则在所有的五位数中“凸”数的个数是
(A )8568 (B )2142 (C )2139 (D )1134
二、填空题:(每小题9分,共54分)
1、 过椭圆12
32
2=+y x 上任意一点P ,作椭圆的右准线的垂线PH (H 为垂足),并延长PH 到Q ,使得HQ =PH (≥1).当点P 在椭圆上运动时,点Q 的轨迹的离心率的
取值范围是
.
2、 已知异面直线a 、b 所成的角为60°,过空间一点P 作与a 、b 都成角(0<<
90°)的直线l ,则这样的直线l 的条数是f ()= . 3、 不等式
()
9221142
2+<+-
x x
x 的解集为 .
4、 设复数z 满足条件|z -i|=1,且z ≠0,z ≠2i ,又复数使得
i
2i 2-⋅
-z z
ωω为实数,则复数-2的辐角主值的取值范围是 . 5、 设a 1,a 2,…,a 2002均为正实数,且
2
1
212121200221=++++++a a a Λ,则a 1a 2…a 2002
的最小值是 .
6、 在一个由十进制数字组成的数码中,如果它含有偶数个数字8,则称它为“优选”
数码(如12883,787480889等),否则称它为“非优选”数码(如2348756,958288等),则长度不超过n (n 为自然数)的所有“优选”数码的个数之和为 . 三、(20分)
已知数列{a n }是首项为2,公比为2
1
的等比数列,且前n 项和为S n . (1) 用S n 表示S n +1;
(2) 是否存在自然数c 和k ,使得
c
S c
S k k --+1>2成立.
四、(20分)
设异面直线a 、b 成60°角,它们的公垂线段为EF ,且|EF |=2,线段AB 的长为4,两端点A 、B 分别在a 、b 上移动.求线段AB 中点P 的轨迹方程.
五、(20分)
已知定义在R +
上的函数f (x )满足
(i )对于任意a 、b ∈R +
,有f (ab )=f (a )+f (b ); (ii )当x >1时,f (x )<0; (iii )f (3)=-1.
现有两个集合A 、B ,其中集合A ={(p ,q )|f (p 2+1)-f (5q )-2>0,p 、q ∈R +
},
集合B ={(p ,q )|f (q p )+2
1=0,p 、q ∈R +
}.试问是否存在p 、q ,使∅≠B A I ,说明理由.
第二试
一、(50分)
如图,AM 、AN 是⊙O 的切线,M 、N 是切点,L 是劣弧MN 上异于M 、N 的点,过
点A 平行于MN 的直线分别交ML 、NL 于点Q 、P .若POQ O S S △⊙3
2π=
,求证:∠
POQ =60°.
二、(50分)
已知数列a 1=20,a 2=30,a n +2=3a n +1-a n (n ≥1).求所有的正整数n ,使得1+5a n a n +1
是完全平方数.
三、(50分)
设M 为坐标平面上坐标为(p ·2002,7p ·2002)的点,其中p 为素数.求满足下列条件的直角三角形的个数:
(1) 三角形的三个顶点都是整点,而且M 是直角顶点; (2) 三角形的内心是坐标原点.
P
Q
参考答案 第一试
二、填空题:
1、⎪⎪⎭
⎫⎢⎣⎡1,33;
2、()⎪⎪⎪⎩⎪
⎪⎪⎨⎧︒
<<︒︒=︒<<︒︒=︒
<<︒=900,460,36030,230,1300,0ααααααf ;
3、⎪⎭
⎫
⎝⎛⎪⎭⎫⎢⎣⎡-
845,00,21Y ;
4、⎪⎭
⎫⎢⎣⎡
-ππ,34arctan
; 5、40022002
;
6、⎪⎪⎭
⎫
⎝⎛-+++63142789102111n n .
三、(1)22
1
1+=+n n S S ; (2)不存在.
四、19
22
=+y x .
五、不存在.
第二试
一、证略;
二、n =3.
三、 p ≠2,7,11,13时,324个;p =2时,162个;p =7,11,13时,180个.。
