2021届东北三省三校高三第一次模拟考试数学(文)试题Word版含答案

合集下载

东北三省三校-2025届高三第二次模拟考试文科综合试题-Word版含答案

东北三省三校 2024届高三其次次模拟考试文科综合试题一、选择题：本题共35小题，每小题4分，共I40分。

在每小题给出的四个选项中．只有一项是符合题目要求的。

2024年l0月，重厌交通高校依据土壤的属性，独创了将沙子和水搅拌形成土壤的黏合剂，并在内蒙古乌兰布和沙漠进行试验，成功地把4000余亩沙漠变成了绿洲，成为世界治沙史上的奇迹。

据此完成1-2题．1．该治沙技术大面积运用的限制性因素是A．技术 B．土壤 C．交通 D．水源2．该技术可以给当地带来的干脆影响有A．变更大气环流，增加夏季的降水量 B．可以保水防渗，增加土壤抗风蚀实力C．促进产业结构调整，加快二、三产业发展 D．协调区域联系，促进矿产资源的开发当一股低温的海流在厄加勒新浅滩向北流淌的时候，南非拟沙丁直便追随其向北迁徙产卵。

图l为南非拟沙丁鱼迁徙路途示意图，据此完成3～4题。

3南非拟沙丁鱼向北迁徙至产卵地时，可能出现的现象是A．德班旁边草木繁茂B．开普敦旁边海疆一帆风顺C．莺歌海盐场相宜晒盐D．华北地区红叶满山4．海中浮游生物生存多依靠养分盐，该海区养分盐的来源是A．低温海流携带至海表的养分盐 B．盛行风吹送至此的养分盐C．暖流携带至海表的养分盐 D．低温海流与南下暖流相遇养分盐上泛一段时期内，我国东部某区域受某天气系统影响，出现多日睛好天气，该系统中，心位于图3中B地。

图2为摄影爱好者在该地一公园内所拍摄的景观照片。

椐此完成5~6题．5．若受此系统持续影响，则该地区可能A．空气质量越来越差 B．风力明显增大C．昼夜温差减小 D．阴雨连绵6．若A、C两地也在废天气系统限制之下，与C相比A地天气相对A．湿冷 B．干冷 C．暖干 D．暖湿区位熵是用来衡量某一区域要素的空间分布指标，值越大说明地位和作用越高。

图4为2024年圣彼得堡城市土地利用区位熵值空间分布图。

据此完成7~8题。

7．圣彼得堡从市中心到郊区空间分布上差异最明显的用地类型是A．工业用地 B．商业用地 C．居住用地 D．交通用地8关于圣彼得堡城市发展，下列说法正确的是A．环状交通线缓解了市中心呵郊区的交通压力B．商业区的发展带动了城市居住地的快速发展C．条带状城市形态的形成与工业用地联系紧密D．该市城市化水平已完全进入了逆城市化阶段相邻的两条河流，在发育的过程中，低位河若具有较强的侵蚀力，河谷上源不断加长，致与高住河相遇，进而袭夺其河水的现象称为河流袭夺。

2021年高考数学真题模拟试题专项汇编之立体几何(文)(Word版,含解析)

（8）立体几何（文）——2021年高考数学真题模拟试题专项汇编1.【2021年新高考Ⅰ卷，3】已知圆锥的底面半径为2，其侧面展开图为一个半圆，则该圆锥的母线长为( ) A.2B.22C.4D.422.【2021年新高考Ⅱ卷，4】卫星导航系统中，地球静止同步轨道卫星的轨道位于地球赤道所在平面，轨道高度为36000km （轨道高度指卫星到地球表面的最短距离）.把地球看成一个球心为O ，半径为6400km 的球，其上点A 的纬度是指OA 与赤道所在平面所成角的度数，地球表面能直接观测到的一颗地球静止同步轨道卫星的点的纬度的最大值记为α.该卫星信号覆盖的地球表面面积22π(1cos )S r α=-（单位：2km ），则S 占地球表面积的百分比为( ) A.26%B.34%C.42%D.50%3.【2021年北京卷，4】某四面体的三视图如图所示，该四面体的表面积为( )33+ B.1213+3 4.【2021年浙江卷，4】某几何体的三视图如图所示(单位：cm )，则该几何体的体积(单位：3cm )是( )A.32B.3C.322D.325.【2021年新高考Ⅱ卷，5】正四棱台的上、下底面的边长分别为2，4，侧棱长为2，则四棱台的体积为( ) A.5623B.562C.282D.28236.【2021年浙江卷，6】如图，已知正方体1111ABCD A B C D -，,M N 分别是1A D ，1D B 的中点，则( )A.直线1A D 与直线1D B 垂直，直线//MN 平面ABCDB.直线1A D 与直线1D B 平行，直线MN ⊥平面11BDD BC.直线1A D 与直线1D B 相交，直线//MN 平面ABCDD.直线1A D 与直线1D B 异面，直线MN ⊥平面11BDD B7.【2021年北京卷，8】定义：24小时内降水在平地上积水厚度（mm ）来判断降雨程度.其中小雨（10<mm ），中雨（10mm —25mm ），大雨（25mm —50mm ），暴雨（50mm —100mm ），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级( )A.小雨B.中雨C.大雨D.暴雨8.【2021年全国乙卷(文)，10】在正方体1111ABCD A B C D -中，P 为11B D 的中点，则直线PB 与1AD 所成的角为( ) A.π2B.π3C.π4D.π69.【2021年全国甲卷(文)，14】已知一个圆锥的底面半径为6，其体积为30π，则该圆锥的侧面积为__________.10.【2021年上海卷，9】已知圆柱的底面半径为1，高为2，AB 为上底面圆的一条直径，点C 为下底底面圆周上的一个动点，点C 绕着下底底面旋转一周，则ABC △面积的取值范围为____________.11.【2021年全国乙卷(文)，16】以图①为正视图，在图②③④③中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为___________（写出符合要求的一组答案即可）.12.【2021年全国乙卷(文)，18】如图，四棱锥P ABCD -的底面是矩形，PD ⊥底面ABCD ，M 为BC 的中点，且PB AM ⊥.（1）证明：平面PAM ⊥平面PBD ；（2）若1PD DC ==，求四棱锥P ABCD -的体积.13.【2021年安徽怀宁模拟，18】如图，在三棱柱111ABC A B C -中，侧面11AAC C ⊥底面11,2,ABC AA AC AC AB BC ====，且AB BC ⊥，O 为AC 的中点.（1）求证：平面11A B O ⊥平面1BCA ；（2）若点E 在1BC 上，且//OE 平面1A AB ，求三棱锥1E A BC -的体积.14.【2021年广西桂林模拟(文)，18】如图所示，在三棱锥A BCD -中，侧棱AB ⊥平面BCD ，F 为线段BD 中点，Q 为线段AB 中点，2π3BCD ∠=，3AB =，2BC CD ==.证明：（1）CF ⊥平面ABD ；（2）求点D 到平面QCF 的距离.15.【2021年全国甲卷(文)，19】已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形.2AB BC ==，E ，F 分别为AC 和1CC 的中点，11BF A B ⊥，（1）求三棱锥F EBC -的体积；（2）已知D 为棱11A B 上的点，证明：BF DE ⊥.答案以及解析1.答案：B解析：本题考查圆锥的侧面展开图.设圆锥的底面半径为r ，母线长为l .由题意可得2ππr l =，所以222l r ==. 2.答案：C解析：由题意可知，6400cos 0.1536000640036000r r α==≈++，所以从同步卫星上可望见的地球的表面积222π(1cos )2π(10.15)S r r α=-≈-，此面积与地球表面积之比约为222π(10.15)100%42%4πr r -⨯≈.3.答案：A解析：画正方体，删点，剩下的4个点就是三棱锥的顶点，如图：1333311(11)2S +=⨯⨯⨯+=表. 4.答案：A解析：本题考查几何体的三视图.该几何体是高为1的四棱柱，其底面为三个全等的直角边为1的等腰直角三角形拼成的梯形，面积为32，故其体积是32. 5.答案：D解析：本题考查棱台的体积.将正四棱台1111A B C D ABCD -补成四棱锥P ABCD -，作PO ⊥底面ABCD 于点O ，交平面1111A B C D 于点1O ，则棱台1111A B C D ABCD -的体积1111P ABCD P A B C D V V V --=-.由题意，11112142PA PO A B PA PO AB ====，易知，4PA =，22AO =22224(22)22PO PA AO --=，所以12PO =，则1322(44)223P ABCD V -=⨯⨯⨯，1111142(22)23P A B C D V -=⨯⨯，所以棱台1111A B C D ABCD -的体积111132242282P ABCD P A B C D V V V --=-==.6.答案：A解析：本题考查空间的线线关系与线面关系.易知1A D ⊥平面1ABD ，故11A D D B ⊥，排除B ，C 项；连接1AD ，可知//MN AB ，所以//MN 平面ABCD ，A 项正确；因为AB 不垂直于平面11BDD B ，//MN AB ，所以直线MN 不垂直于平面11BDD B ，D 项错误.7.答案：B解析：由相似的性质可得，小圆锥的底面半径2002502r ==，故231π5015050π3V =⨯⨯⨯=⋅小圆锥，积水厚度3250π12.5π100V h S ⋅===⋅大小圆锥圆，属于中雨，故选B. 8.答案：D解析：本题考查立体几何中的线面关系及解三角形的应用.如图，记正方体的棱长为a ，则1111112AD C B A C B D a ====，所以1122B P PC a ==，221162BP B P B B a =+=.在1BC P 中，由余弦定理得22211113cos 22PB C B PC PBC PB C B +-∠==⋅，所以1π6PBC ∠=.又因为11//AD BC ，所以1PBC ∠即为直线PB 与1AD 所成的角，所以直线PB 与1AD 所成的角为π6.9.答案：39π解析：本题考查圆锥的体积与侧面积.由题可得圆锥的体积21π12π30π3V r h h ===，可得52h =，故圆锥的母线22132l r h +，所以圆锥的侧面积π39πS rl ==. 10.答案：5]解析：本题主要考查空间几何体.上顶面圆心记为O ，下底面圆心记为O '，连接OC ，过点C 作CM AB ⊥，垂足为点M ，则12ABCSAB CM =⨯⨯，根据题意，AB 为定值2，所以ABCS 的大小随着CM 长短的变化而变化.当点M 与点O 重合时，22125CM OC ==+=，取得最大值，此时12552ABCS =⨯⨯=.当点M 与点B 重合时，CM 取最小值2，此时12222ABCS=⨯⨯=.综上所述，ABCS 的取值范围为[2,5].11.答案：②⑤或③④解析：本题考查几何体的三视图.由高度可知，侧视图只能为②或③.当侧视图为②时，则该三棱锥的直观图如图1，平面PAC ⊥平面ABC ，2PA PC ==，5BA BC =2AC =，此时俯视图为⑤；当侧视图为③时，则该三棱锥的直观图如图2，PA ⊥平面ABC ，1PA =，5AC AB ==2BC =，此时俯视图为④.12.答案：（1）因为PD ⊥底面ABCD ，AM ⊂底面ABCD ，所以PD AM ⊥.又因为PB AM ⊥，PD PB P ⋂=，PB ，PD ⊂平面PBD ，所以AM ⊥平面PBD .因为AM ⊂平面PAM ，所以平面PAM ⊥平面PBD .（2）由PD ⊥底面ABCD ，所以PD 即为四棱锥P ABCD -的高，DPB 是直角三角形. 由题可知底面ABCD 是矩形，1PD DC ==，M 为BC 的中点，且PB AM ⊥.设2AD BC a ==，取CD 的中点为E ，CP 的中点为F ，连接MF ，AF ， EF ，AE ，可得//MF PB ，//EF DP ，那么AM M F ⊥，AM F 为直角三角形，且12EF =，2144AE a =+，21AM a =+，222142AF EF AE a =++因为DPB 是直角三角形，所以根据勾股定理得224BP a =+，则2242a MF +=.由AM F 是直角三角形，可得222AM MF AF +=，解得22a =，所以底面ABCD 的面积22S a ==，则四棱锥P ABCD -的体积11221333V S h =⋅⋅=⨯⨯-.13.答案：（1）1111,//,AB BC AB A B BC A B ⊥∴⊥，在1A AC 中，112AA AC AC ===，O 是AC 的中点，1AO AC ∴⊥，又平面11AAC C ⊥平面ABC ，平面11AAC C平面ABC AC =，1A O ∴⊥平面ABC .BC ⊂平面1,ABC AO BC ∴⊥. 111,A B AO ⊂平面111111,A B O A B AO A =，BC ∴⊥平面11A B O ，又BC ⊂平面1BCA ，∴平面1BCA ⊥平面11A B O .（2）如图，连接1B C ，设1B C 与1BC 交于点E ，连接1,OE AB ，易得1//OE AB ，1AB ⊂平面11,ABB A OE ⊄平面11ABB A ，//OE ∴平面11ABB A ，∴满足条件的E 为1BC 的中点.11111 1122E A BCC A BC B A CC V V V ---==三棱锥三棱锥三棱锥21133212346=⨯⨯⨯⨯=，故三棱锥1E A BC -的体积为36.14.答案：（1）AB ⊥平面BCD ，CF ，BD ⊂平面BCD ，AB CF ∴⊥，AB BD ⊥.2BC CD ==，F 为BD 中点，CF BD ∴⊥.又CF AB ⊥，AB BD B =，AB ，BD ⊂平面ABD ，CF ∴⊥平面ABD .（2）在三棱锥Q DCF -中，设D 到平面QFC 距离为d . Q DCF D QCF V V --=，1133DCFQCFQB Sd S ∴⋅⋅=⋅⋅，DCFQCFQB S d S ⋅∴=.1112π322sin 2223DCFDCBSS ==⨯⨯⨯⨯=，2π44222cos 233BD =+-⨯⨯⨯.AB BD ⊥，3AB =，Q ，F 分别为AB ，BD 的中点.22912212ADAB BD QF ++∴====.QCF 中，π2cos 13CF ==，235422CQ ⎛⎫=+ ⎪⎝⎭，21QF =. 25211244cos 55212QCF +-∴∠==⨯⨯，21sin QCF ∴∠=. 152121122QCFS∴=⨯⨯=. 33372221d ∴==.15.答案：（1）如图，取BC 的中点为M ，连接EM .由已知易得//EM AB ，2AB BC ==，1CF =，112EM AB ==，11//AB A B ，由11BF A B ⊥得EM BF ⊥，又易得EM CF ⊥，BF CF F ⋂=，所以EM ⊥平面BCF ，故1111121132323F EBC E FBC V V BC CF EM --==⨯⨯⨯=⨯⨯⨯⨯=三棱锥三棱锥.（2）连接1A E ，1B M ，由（1）知11//EM A B ，所以ED 在平面11EMB A 内.在正方形11CC B B 中，由于F ，M 分别是1CC ，BC 的中点，所以1tan 2CF CBF BC ∠==，111tan 2BM BB M BB ∠==，且这两个角都是锐角，所以1CBF BB M ∠=∠，所以111190BHB BMB CBF BMB BB M ∠=∠+∠=∠+∠=︒，所以1BF B M ⊥，又11BF A B ⊥，1111B M A B B ⋂=，所以BF ⊥平面11EMB A ，又DE ⊂平面11EMB A ，所以BF DE ⊥.。

2021年高三上学期联考数学(文)试题含答案

2021年高三上学期联考数学（文）试题含答案一、选择题（5×10=50分）1. 若数列｛a n｝的前n项和为S n＝kq n－k(k≠0)，则这个数列的特征是( )(A)等比数列(B)等差数列(C)等比或等差数列 (D)非等差数列2. 已知，则的值为(A) (B) (C) (D)3. 数在点处的切线方程为（）(A) (B) (C) (D)4. 设是等差数列的前项和，若，则＝( )(A)1 (B)－1 (C)2 D.5.若变量满足约束条件，则的最大值为(A) (B) (C) (D)6. 在A B C中，a，B，c分别是角A，B，C的对边，若，B=A．45°或135° (B)45° (C)135°(D) 以上答案都不对7. 已知等比数列的前三项依次为，，，则（）(A) (B) (C) (D)8. 设是正实数，以下不等式恒成立的序号为（）① ，② ，③ ，④(A) ②③ (B) ①④(C) ②④ (D) ①③9. 若曲线处的切线与两坐标轴围成的三角形的面积为9，则a=(A)16 (B)8 (C)32 (D)6410. 已知向量()()ABC,cos30120cos的形状为,120,sin45sin︒∆=︒,=则︒︒(A)直角三角形(B)等腰三角形 (C)钝角三角形 (D)锐角三角形二、填空题（5×5=25分）11. 在等比数列中，为其前项和，已知，，则此数列的公比为.12. 若数列满足，，则它的通项．到．其中正确命题的序号是_______(把你认为正确的都填上)15. 设G 是△ABC 的重心，若∠A =120°，,则的最小值= ．三、解答题（4×12+13+14=75分）16. 中，分别为内角的对边且，2sin (2)sin (2)sin a A b c B c b C =+++（1）求的大小；（2）若，试判断的形状．17. （12分）在中，已知．（1）求证：tanB=3tanA （2）若求A 的值．18．（12分）已知,)sin ,cos sin (),cos 32,cos sin (x x x b x x x a ωωωωωω+-=--=设函数f (x )=的图像关于对称,其中，为常数,且∈ （1）求函数f (x )的最小正周期T ；（2）函数过求函数在上取值范围。

河北省大名县第一中学2022届高三(实验班)上学期第一次月考数学(文)试题 Word版含答案

高三文科数学月考试题学校：姓名：班级：考号：评卷人得分一、选择题1. [2021·吉大附中高三四模(文)]已知集合A={x|x2+x-2≤0},B={y|y=2x,x∈R},则A∩B等于()A. (0,1]B. [1,+∞)C.(0,2] D.2. [2021·哈三中一模(文)]已知f(x)是定义在R上的偶函数,周期为2,则“f(x)为[0,1]上的增函数”是“f(x)为[3,4]上的减函数”的()A. 既不充分也不必要条件B. 充分不必要条件C. 必要不充分条件D. 充要条件3. [2021·哈三中一模]下列结论中正确的个数是()①“x=”是“”的充分不必要条件;②若a>b,则am2>bm2;③命题“∀x∈R,sin x≤1”的否定是“∀x∈R,sin x>1”;④函数f(x )=-cos x在[0,+∞)内有且仅有两个零点.A. 1B. 2C. 3D. 44. [2021·吉林长春普高高三二模]下列函数中,既是奇函数又在(0,+∞)上单调递增的函数是() A. y=e x+e-x B. y=ln(|x|+1) C.y= D. y=x-5. [2021·吉大附中高三四模(文)]设函数f(x)=ln(1+x2)-,则使得f(x)>f(2x-1)成立的x的取值范围是()A. B. C.D.6. [2021·吉林市普高高三第三次调研]若直角坐标平面内的两点P,Q满足条件:①P,Q都在函数y=f(x)的图象上;②P,Q关于原点对称,则称点对(P,Q)是函数y=f(x)的一对“友好点对”(点对(P,Q)与(Q,P)看作同一对“友好点对”).已知函数f(x)=则此函数的“友好点对”有()A. 3对B. 2对C. 1对 D. 0对7. [2021·河北唐山高三摸底月考]设函数,“是偶函数”是“的图象关于原点对称”的( )A. 充分不必要条件B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件8. [2021·吉林长春高三二模(文)]关于函数y=2sin+1,下列叙述有误．．的是()A. 其图象关于直线x=-对称B. 其图象可由y=2sin+1图象上全部点的横坐标变为原来的倍得到C. 其图象关于点对称D. 其值域为[-1,3]9. [2022·甘肃省高考诊断(二)(文)]已知△ABC的外接圆半径为1,圆心为O,且=0,则△ABC 的面积为()A. 1+B.C.1+ D.10. [2022·哈尔滨市第六中学高三一模(文)]已知向量a=(cosθ,-sinθ),b=(-cos2θ,sin2θ)(θ∈(π,2π)),若向量a,b的夹角为φ,则有()A. φ=θB. φ=π-θC.φ=θ-π D. φ=θ-2π11. [2021·河北武邑中学高二入学考试]已知数列,都是公差为1的等差数列，是正整数，若，则( )A. 81B. 99C. 108D. 11712. [2021·河南南阳一中高三第三次月考]已知函数,关于的方程R)有四个相异的实数根,则的取值范围是( )A. B. C.D.评卷人得分二、填空题13. [2021·河北五个一名校联盟高三一模(文)]设△的内角,,所对的边长分别为,若,则的值为.14. [2021·河南南阳方城一中高二开学考试]设△ABC的内角A，B，C所对边的长分别为a，b，c，若b+c=2a，3sin A=5sin B，则角C= . 15. [2021·河南许昌五校高二第一次联考]已知在中，，，，，，则的值为.16. [2010·高考辽宁卷，16]已知数列{a n}满足a1=33，a n+1-a n=2n，则的最小值为.评卷人得分三、解答题17. [2021·吉林市普高高三第三次调研]已知函数f(x)=cos 2x+2sin2x+2sin x.(1)将函数f(2x)的图象向右平移个单位得到函数g(x)的图象,若x∈,求函数g(x)的值域;(2)已知a,b,c分别为△ABC中角A,B,C的对边,且满足f(A)=+1,A∈,a=2,b=2,求△ABC的面积.18. [2021·吉林长春高三二模(文)]已知数列{a n}满足a1=,a n+1=3a n-1(n∈N*).(1)若数列{b n}满足b n=a n-,求证:{b n}是等比数列;(2)求数列{a n}的前n项和S n.19. [2021·河南八市重点高中高二第一次月考(文)]正项数列满足.(1)求数列的通项公式；(2)令，求数列的前项和为.20. [2021·吉林长春高三二模(文)]已知三棱锥A-BCD中,△ABC是等腰直角三角形,且AC⊥BC,BC=2,AD⊥平面BCD,AD=1.(1)求证:平面ABC⊥平面ACD;(2)若E为AB中点,求点A到平面CED的距离.21. [2021·湖南长沙长郡中学高三入学考试]已知椭圆的两个焦点分别为,以椭圆短轴为直径的圆经过点.(1)求椭圆的方程;(2)过点的直线与椭圆相交于两点,设点,直线的斜率分别为,问是否为定值?并证明你的结论.22. [2021·广东省仲元中学、中山一中等七校高三联考(一)]在中,角所对的边分别为,且.(1)求的大小;(2)设的平分线交于,求的值.参考答案1. 【答案】A【解析】本题考查集合的基本运算、解一元二次不等式及求指数函数的值域,属于基础题.由于x2+x-2≤0,所以-2≤x≤1,依据指数函数的性质知y=2x>0,所以集合A =,B =,则A∩B =,故选A.2. 【答案】D【解析】本题考查充分条件与必要条件,函数的奇偶性与周期性,属于中档题.函数在上递增,利用偶函数得函数在上递减,利用周期得函数在上递减,故充分性成立;函数在上递减,利用周期得函数在上递减,利用偶函数得函数在上递增,必要性成立,综上,充分性与必要性均成立,故选D.3. 【答案】A【解析】本题考查充分必要条件、不等式性质、命题的否定及命题真假的判定,属于中档题.对于①,当x=时,sin ,充分性成立;当sin 时,x ++2kπ或x ++2kπ,k∈Z,得x=-+2kπ或x=+2kπ,k∈Z,故必要性不成立,故①正确;对于②,当m=0时,若a>b,am2>bm2不成立,故②不正确;对于③,命题“∀x∈R,sin x≤1”的否定是“∃x0∈R,sin x0>1”,故③不正确;对于④,函数y =与y=cos x的图象有且只有一个交点,故函数f(x )=-cos x 在内有且仅有一个零点,故④不正确.综上,正确的只有一个,故选A.4. 【答案】D【解析】本题考查函数的单调性与奇偶性学问,属于基础题.A,B选项中的函数为偶函数,排解,C选项中的函数是奇函数,但在(0,+∞)上不是单调递增函数.故选D.5. 【答案】A【解析】本题考查函数的奇偶性及导数在争辩函数中的应用,解一元二次不等式、确定值不等式,属于难题.∵f(-x )= ln =ln =f(x),∴函数f(x)为偶函数.当x≥0时,f(x)=ln (1+x2),求导得f'(x )=恒为正,即函数f(x)在单调递增,∵f(x)是偶函数,∴f(x)在(-∞,0)上单调递减,则f(x)>f(2x-1)等价于f(|x|)>f(|2x-1|),即|x|>|2x-1|,平方得3x2-4x+1<0,解得<x<1,故选A.6. 【答案】C【解析】本题考查新概念和函数的图象与性质,考查了数形结合的数学思想,属于中档题.设f(x )=(x>0)图象上任一点为A(x,y)(x>0,y>0),点A关于原点的对称点A'(-x,-y)在y=x+1上,所以-y=-x+1,即y=x-1,得“友好点对”的个数就是方程组的根的个数,而y=x-1(x>0)的图象与y的图象有且只有一个交点,∴“友好点对”共1对,故选C.7. 【答案】B【解析】本题考查函数的奇偶性,考查图象的对称性.若是偶函数,而不肯定是奇函数,故的图象不肯定关于原点对称;当的图象关于原点对称时,函数是奇函数,则是偶函数,因此“是偶函数”是“的图象关于原点对称”的必要不充分条件.故选B.8. 【答案】C【解析】本题考查三角函数的性质、图象变换,属于中档题.关于函数y =2sin+1,令x=-,求得y=-1,为函数的最小值,故A正确;由y =2sin+1图象上全部点的横坐标变为原来的倍,可得y =2sin+1的图象,故B正确;令x =π,求得y=1,可得函数的图象关于点对称,故C错误;函数的值域为[-1,3],故D正确.故选C.9. 【答案】D【解析】本题考查向量的运算.由=0得=-,两边平方可得·=0,则∠AOB =90°;由=0得=-,两边平方可得·=,则∠AOC=135°;同理可得∠BOC=135°,则△ABC的面积为S△AOB+S△BOC+S△AOC =,故选D.10. 【答案】C【解析】本题考查向量的夹角、向量的坐标运算、二倍角、同角三角函数的基本关系、诱导公式.由题意知cosφ==- () =-cosθ=cos(θ-π).由于θ∈(π,2π),所以θ-π∈(0,π),而φ∈[0,π],所以φ=θ-π,故选C.11. 【答案】D【解析】本题考查等差数列的通项公式与数列求和，考查计算力量.,.故选D. 12. 【答案】A【解析】本题考查分段函数导函数的应用，函数与方程的关系.=,当时时,单调递减，时,单调递增,且当,当, 当时，恒成立，时,单调递增且,方程R)有四个相异的实数根.令=则,,即.13. 【答案】4【解析】本题考查正弦定理与余弦定理、两角和与差公式,考查计算力量.由正弦定理可得=,又由于==,所以=,即, 所以.14. 【答案】【解析】本题考查正弦定理及余弦定理.由正弦定理得, 5b=3a,又b+c=2a,则，由余弦定理得，，又，所以.15. 【答案】【解析】本题主要考查平面对量的线性运算及平面对量数量积.在中，，建立直角坐标系,,,,依题意有D,E(2,0)得，得，故填. 16. 【答案】【解析】由已知可得a n-a n-1=2(n-1),a n-1-a n-2=2(n-2),…,a3-a2=2×2,a2-a1=2×1,左右两边分别相加可得a n-a1=2(1+2+3+…+(n-1)]=n(n-1),∴a n=n2-n+33.=n+-1,令F(n)=n+-1,n≤5时为减函数,n≥6时为增函数且F(5)>F(6),∴F(n)≥F(6)=,故的最小值为.17.(1) 【答案】f(x)=cos 2x+2sin2x+2sin x=cos2x-sin2x+2sin2x+2sin x=cos2x+sin2x+2sin x=1+2sin x,所以f(2x)=1+2sin2x.由于函数f(2x)的图象向右平移个单位得到函数g(x)的图象,所以g(x )=2sin+1,即g(x )=2sin+1.由于x ∈,所以2x ∈所以sin ∈,所以g(x)∈[0,3],所以函数g(x)的值域为[0,3].(2) 【答案】由于f(A )=+1,所以sin A =,由于A ∈,所以cos A=.又cos A =,a =2,b=2,所以c=4.所以△ABC面积S△ABC=bc sin A =2.18.(1) 【答案】由题可知a n+1=3(n∈N*),从而有b n+1=3b n,b1=a1-=1,所以{b n}是以1为首项,3为公比的等比数列.(2) 【答案】由第1问知b n=3n-1,从而a n=3n-1+,有S n=30++3++…＋3n-1+=30+31+32+…+3n-1+×n =.19.(1) 【答案】由，得，由于数列是正项数列，所以.(2) 【答案】由第1问得,，所以.20.(1) 【答案】由于AD⊥平面BCD,BC⊂平面BCD,所以AD⊥BC,又由于AC⊥BC,AC∩AD=A, 所以BC⊥平面ACD,BC⊂平面ABC,所以平面ABC⊥平面ACD.(2) 【答案】由已知可得CD =,取CD中点为F,连接EF,由于ED=EC=AB =,所以△ECD为等腰三角形,从而EF =,S△ECD =,由第1问知BC⊥平面ACD,所以E到平面ACD的距离为1,S△ACD =,令A到平面CED的距离为d,由V A-ECD=·S△ECD·d=V E-ACD=·S△ACD·1,解得d =.所以点A到平面CED 的距离为21.(1) 【答案】由题意得,,, 解得,所以椭圆的方程为.(2) 【答案】①当直线的斜率不存在时,由, 解得,设,则.②当直线的斜率存在时,设直线的方程为,代入整理化简,得,依题意,直线与椭圆必相交于两点,设,则, 又,所以====.综上所述,为定值2.(说明:若假设直线为,按相应步骤给分)22.(1) 【答案】,,,,.(2) 【答案】在中,由正弦定理:,得,,.。

2021届江西省临川第一中学暨临川一中实验学校高三第一次月考数学(文)试题(解析版)

2021届江西省临川第一中学暨临川一中实验学校高三第一次月考数学（文）试题一、单选题1．若集合{P x N x =∈≤，a = ）A ．aP B ．{}a P ∈C ．{}a P ⊆D ．a P ∉【答案】D【解析】由a N =，结合元素与集合、集合与集合的关系即可得解. 【详解】因为a N =，集合{P x N x =∈≤，所以a P ∉，{}a P ⊆/. 故选：D. 【点睛】本题考查了元素与集合、集合与集合关系的判断，属于基础题.2．设x ∈R ，则“38x >”是“2x ” 的A ．充分而不必要条件B ．必要而不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】分析：求解三次不等式和绝对值不等式，据此即可确定两条件的充分性和必要性是否成立即可.详解：求解不等式38x >可得2x >，求解绝对值不等式2x可得2x >或2x <-，据此可知：“38x >”是“||2x >” 的充分而不必要条件. 本题选择A 选项.点睛：本题主要考查绝对值不等式的解法，充分不必要条件的判断等知识，意在考查学生的转化能力和计算求解能力. 3．已知1275a -⎛⎫= ⎪⎝⎭，1357b ⎛⎫= ⎪⎝⎭，25log 7c =，则a 、b 、c 的大小关系是（）． A ．b a c << B ．c b a <<C ．c a b <<D ．b c a <<【答案】C【解析】先与0比较，c 小于0，再a 与b 比较，即可判断大小. 【详解】12125757a -⎛⎫=⎛⎫= ⎝⎭⎪⎭⎪⎝<135()7b =，因此c a b << 故选：C. 【点睛】本题考查比较大小、指数函数单调性、对数函数单调性，考查基本分析判断能力，属基础题.4．已知集合{}0M x x a =-=，{}10N x ax =-=，若M N N =，则实数a 的值是（） A ．1 B ．1-C ．1或1-D ．以上答案都不对【答案】D 【解析】由M N N =，转化为N M ，分N =∅和 N ≠∅两种情况讨论求解.【详解】已知集合{}{}0M x x a a =-==，{}10N x ax =-=，因为MN N =，所以N M ，当N =∅时，0a =，符合题意；当N ≠∅时，{}110N x ax a ⎧⎫=-==⎨⎬⎩⎭，则1a a=，解得1a =±，综上：实数a 的值是0或1或-1 故选：D 【点睛】本题主要考查集合的基本运算和集合的基本关系的应用，还考查了转化求解问题的能力，属于基础题.5．若函数()f x 是定义在R 上的奇函数，且()()2f x f x -=-，则()6f -=（） A ．0B ．1-C ．1D ．2【答案】A【解析】本题先根据题意判断函数是周期为4的周期函数，再根据奇函数求解即可. 【详解】解：∵()f x 是R 上的奇函数，∴()00f =， ∵()()2f x f x -=-，∴()()(4)(2)22(())()f x f x f x f x f x -=--=--=--=， ∴函数()f x 的周期为4， ∴()()()6200f f f -=-=-=．故选：A ．【点睛】本题考查函数的奇偶性与函数的周期性，是基础题.6．平面向量a 与b 的夹角为60︒，()2,0,1a b ==，则2+a b 等于( ) A ．22 B ．23C ．12D ．10【答案】B【解析】因为||2,||1a b ==，a 与b 的夹角为60︒，故||||cos 601a b a b ⋅=⋅=，则244423a b +=++=，应选答案B ．7．高为H ，满缸水量为V 的鱼缸的轴截面如图所示，若鱼缸水深为h 时水的体积为v ，则函数()v f h =的大致图像是（）A ．B ．C ．D ．【答案】B【解析】由函数的自变量为水深h ，函数值为水的体积，得到水深h 越大，水的体积v 就越大，而且增的速度先慢后快再慢的，即可求解. 【详解】由图可知水深h 越大，水的体积v 就越大，故函数()v f h =是个增函数，故排除A ，C 项，由鱼缸形状可知，下面细中间粗，上面较细，所以随着水深的增加，体积的变化的速度是先慢后快再慢的，所以B 正确. 故选：B 【点睛】本题主要考查了函数的应用问题，重点考查分析问题和解决问题的能力.8．已知直线l 过点(0,2)-，当直线l 与圆222x y y +=相交时，其斜率k 的取值范围是（） A．(-B．(,)-∞-⋃+∞C．44⎛- ⎝⎭D．,44⎛⎛⎫-∞-⋃+∞⎪⎝⎭⎝⎭【答案】B【解析】由圆的方程可得圆的圆心和半径，再由直线与圆相交的性质即可得1d =<，即可得解.【详解】圆222x y y +=的方程可变为()2211x y +-=，圆心为()0,1，半径为1，因为直线l 过点(0,2)-，且斜率为k ，所以直线l 的方程为2y kx +=即20kx y --=，若要使直线l 与圆相交，则圆心到直线l的距离1d =<，解得((),k ∈-∞-⋃+∞. 故选：B. 【点睛】本题考查了直线与圆位置关系的应用，考查了运算求解能力，属于基础题.9．已知函数25(1)()(1)x ax x f x a x x⎧---⎪=⎨>⎪⎩，，是R 上的增函数，则a 的取值范围是（）A ．30a -<B ．32a --C ．2a -D ．以上答案都不对【答案】B【解析】设2()5(1)g x x ax x =---，()(1)ah x x x =>，由25(1)()(1)x ax x f x a x x⎧---⎪=⎨>⎪⎩，，在R 上是增函数，则()g x 在1x ≤时单调递增，()h x 在()1,+∞上递增，且()(1)1g h ≤，从而可求. 【详解】函数25,(1)(),(1)x ax x f x a x x⎧---⎪=⎨>⎪⎩是R 上的增函数，设2()5(1)g x x ax x =---，，()(1)ah x x x=>，，由分段函数的性质可知，函数2()5g x x ax =---在(],1-∞单调递增，函数()a h x x=在(1,)+∞单调递增，且()(1)1g h ≤，∴1206a a a a⎧-⎪⎪<⎨⎪--⎪⎩，∴203a a a -⎧⎪<⎨⎪-⎩解得32a -- 故选：B. 【点睛】考查分段函数在R 上的单调性，既需要分段考虑，又需要整体考虑，基础题. 10．定义在R 上的函数()y f x =，恒有()(2)f x f x =-成立，且()(1)0f x x '⋅->，对任意的12x x <，则()()12f x f x <成立的充要条件是（）． A ．211x x >≥ B ．122x x +>C ．122x x +≤D ．2112x x >≥【答案】B【解析】根据题中条件，先得到()f x 关于1x =对称；判定函数单调性，分别讨论11x ≥，11<x 两种情况，结合充分条件和必要条件的概念，即可得出结果.【详解】由()(2)f x f x =-，得函数()f x 关于1x =对称，由()(1)0f x x '⋅->得，当1x >时，()0f x '>，此时函数()f x 为增函数，当1x <时，()0f x '<，此时函数()f x 为减函数，因为12x x <，若11x ≥时，函数()f x 在1x >上为增函数，满足对任意的12x x <，()()12f x f x <，此时122x x +>；若11<x ，∵函数()f x 关于1x =对称，则()()112f x f x =-，则121x ->，由()()12f x f x <得()()()1212f x f x f x =-<，此时122x x -<，即122x x +>；即对任意的12x x <，()()12f x f x <得122x x +>；反之也成立，所以对任意的12x x <，则()()12f x f x <成立的充要条件为“122x x +>”. 故选：B. 【点睛】本题主要考查充分条件和必要条件的判断，根据条件判断函数的对称性和单调性之间的关系，利用条件进行转化是解决本题的关键，属于常考题型.11的直线l 与椭圆22221x y a b +=（0a b >>）交于不同的两点，且这两个交点在x 轴上的射影恰好是椭圆的两个焦点，则该椭圆的离心率为（） A．3B ．12C．2D ．13【答案】A【解析】由题意，2b ac =，得)22ac a c =-，20e +=，所以2e =，故选C ．点睛：由椭圆的对称性可知，两个焦点关于原点对称，则直线l 是过原点的直线，且其交点投影恰好是椭圆焦点，由垂径的交点坐标为2,b c a ⎛⎫⎪⎝⎭，则有22b ac =，整理后同除以2a20e +=，求出离心率．12．函数2()(0)f x ax bx c a =++≠的图象关于直线2bx a=-对称.据此可推测，对任意的非零实数,,,,,a b c m n p ，关于x 的方程2[()]()0m f x nf x p ++=的解集都不可能是（） A ．{1,6}- B ．{2,4} C ．{2,5,4,7} D ．{1,4,8,16}【答案】D【解析】方程()()20mf x nf x p ++=不同的解的个数可为0,1,2,3,4.若有4个不同解，则可根据二次函数的图像的对称性知道4个不同的解中，有两个的解的和与余下两个解的和相等，故可得正确的选项. 【详解】设关于()f x 的方程()()20mfx nf x p ++=有两根，即()1f x t =或()2f x t =.而()2f x ax bx c =++的图象关于2bx a=-对称，因而()1f x t =或()2f x t =的两根也关于2bx a =-对称．而选项D 中4811622++≠. 故选：D. 【点睛】对于形如()0f g x =⎡⎤⎣⎦的方程（常称为复合方程），通过的解法是令()t x g =，从而得到方程组()()0f tg x t ⎧=⎪⎨=⎪⎩，考虑这个方程组的解即可得到原方程的解，注意原方程的解的特征取决于两个函数的图像特征. 二、填空题13．函数y =________．【答案】[0,3]【解析】. 【详解】因为20x ≥，所以299x -≤，又要使根式有意义，则290x -≥，所以2099x ≤-≤，所以03≤≤，故函数y =[0,3]. 故答案为：[0,3]. 【点睛】本题考查了具体函数值域的求解，属于基础题.14．已知()f x 为奇函数，当0x <时，()ln()3f x x x =-+，则()y f x =的解析式为______.【答案】()ln()3,00,0ln 3,0x x x f x x x x x -+<⎧⎪==⎨⎪-+>⎩【解析】由()f x 为奇函数，可得()f x 的定义域关于原点对称，且()()f x f x =--，且当0x >时，0x -＜，将x -代入()()f x f x =--可得答案. 【详解】解：由()f x 为奇函数，可得()f x 的定义域关于原点对称，且()00f =，()()f x f x =--，当0x >时，0x -＜，故()(ln 3()3])[ln x f x f x x x x =--=--=++-，∴()ln()3,00,0ln 3,0x x x f x x x x x -+<⎧⎪==⎨⎪-+>⎩.故答案为：()ln()3,00,0ln 3,0x x x f x x x x x -+<⎧⎪==⎨⎪-+>⎩. 【点睛】本题主要考查利用函数的奇偶性求函数解析式，相对简单. 15．若函数()2cos()f x x m ωθ=++对任意的实数f()()99t t f t ππ+=-都有且()3,9f π=-则m =_______ .【答案】1- 或5-【解析】对任意的实数f()99t t f t 都有ππ⎛⎫+=- ⎪⎝⎭,说明函数图像的一条对称轴为9x π=，()39f π=-，则23m ±+=- ，1m =- 或5m =-.16．如图，在长方体1111ABCD A B C D －中，16,3,8AA AB AD ===，点M 是棱AD 的中点，N 在棱1AA 上，且满足12AN NA ＝，P 是侧面四边形11ADD A 内一动点(含边界)，若1C P ∥平面CMN ，则线段1C P 长度最小值是________.【解析】取11A D 的中点Q ,过点Q 在面11ADD A 作MN 的平行线交1DD 于E则易知面1//C QE 面CMN ,在1C QE ∆中作1C P QE ⊥,则1C P .三、解答题17．在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ．（1）若223cos cos 20A A +=，且ABC 为锐角三角形，7a =，6c =，求b 的值；（2）若a =3A π=，求b c +的取值范围．【答案】（1）b ＝5（2）b c +∈【解析】（1）运用二倍角的余弦公式，化简整理可得cos A ，再由余弦定理，解方程可得b ；（2）运用正弦定理和两角和差的正弦公式，以及正弦函数的图象和性质，即可得到所求范围；【详解】解：（1）22223cos cos223cos 2cos 10A A A A +=+-=，∴21cos 25A =，又A 为锐角，1cos 5A =，而2222cos a b c bc A =+-，即2121305b b --=，解得5b =或135b =-（舍去），5b ∴=；（2）由正弦定理可得22(sin sin )2sin sin 36b c B C B B B ππ⎡⎤⎛⎫⎛⎫+=+=+-=+ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦，203B π<<， ∴5666B πππ<+<， ∴1sin 126B π⎛⎫<+ ⎪⎝⎭，∴b c+∈．【点睛】本题考查三角函数的恒等变换，三角形的正弦定理和余弦定理的运用，以及运算能力，属于中档题．18．某中学高三年级有学生500人，其中男生300人，女生200人.为了研究学生的数学成绩是否与性别有关，采用分层抽样的方法，从中抽取了100名学生，统计了他们期中考试的数学分数，然后按照性别分为男、女两组，将两组的分数分成5组：[100,110),[110,120)，[120,130),[130,140)，[]140,150分别加以统计，得到如图所示的频率分布直方图.（1）从样本分数小于110分的学生中随机抽取2人，求两恰为一男一女的概率；（2）若规定分数不小于130分的学生为“数学尖子生”，请你根据已知条件完成22⨯列联表，并判断是否有90%的把握认为“数学尖子生与性别有关”？附：随机变量22()()()()()n ad bcKa b c d a c b d-=++++.【答案】（1）5；（2）列联表见解析，没有90%的把握认为“数学尖子生与性别有关”.【解析】（1）由分层抽样的概念可得抽取的100名学生中，男女生的人数，进而可得样本中分数小于110分的学生中，男女生的人数，根据列举法可得所有的基本事件数及符合要求的基本事件数，再由古典概型的概率公式即可得解；（2）由频率分布直方图可得分数不小于130分的学生中，男女生的人数，即可完成列联表，计算出2K后，与2.706比较即可得解.【详解】（1）由题意，抽取的100名学生中，男生10030060500⨯=人，女生10020040500⨯=人，所以分数小于110分的学生中，男生有600.005103⨯⨯=人，记为A，B，C，女生有400.005102⨯⨯=人，记为D ，E ，则从样本分数小于110分的学生中随机抽取2人，有基本事件为：(),A B ，(),A C ，(),A D ，(),A E ，(),B C ，(),B D ，(),B E ，(),C D ，(),C E ，(),D E ，共10种；其中恰为一男一女的基本事件为：(),A D ，(),A E ，(),B D ，(),B E ，(),C D ，(),C E ，共6种；故所求概率63105P ==；（2）分数不小于130分的学生中，男生有()0.020.005160150+⨯⨯=人，女生有()400.03250.0051015⨯+⨯=人，所以可得22⨯列联表如下：所以22100(15254515)251.7862.7066040307014K ⨯⨯-⨯==≈<⨯⨯⨯，所以没有90%的把握认为“数学尖子生与性别有关”. 【点睛】本题考查了频率分布直方图的应用及古典概型概率的求解，考查了独立性检验的应用，属于中档题.19．如图，四棱锥P ABC -中，PA ⊥平面ABCD ，AD BC ∥，3AB AD AC ===，4PA BC ，M 为线段AD 上一点，2AM MD =，N 为PC 的中点．（I ）证明MN ∥平面PAB ；（II ）求四面体N BCM -的体积.【答案】【解析】试题分析：（Ⅰ）取PB 的中点T ，然后结合条件中的数据证明四边形AMNT 为平行四边形，从而得到MNAT ，由此结合线面平行的判断定理可证；（Ⅱ）由条件可知四面体N-BCM 的高，即点N 到底面的距离为棱PA 的一半，由此可顺利求得结果．试题解析：（Ⅰ）由已知得，取的中点T ，连接，由N 为中点知，.又，故平行且等于，四边形AMNT 为平行四边形，于是.因为平面，平面，所以平面.（Ⅱ）因为平面，N 为的中点，所以N 到平面的距离为.取的中点，连结.由得，.由得到的距离为，故145252BCMS=⨯⨯=. 所以四面体的体积14532N BCM BCMPA V S -=⨯⨯=. 【考点】直线与平面间的平行与垂直关系、三棱锥的体积【技巧点拨】（1）证明立体几何中的平行关系，常常是通过线线平行来实现，而线线平行常常利用三角形的中位线、平行四边形与梯形的平行关系来推证；（2）求三棱锥的体积关键是确定其高，而高的确定关键又找出顶点在底面上的射影位置，当然有时也采取割补法、体积转换法求解．20．已知椭圆()2222:10x y C a b a b +=>>过点31,2⎛⎫ ⎪ ⎪⎝⎭3 （1）求椭圆C 的标准方程；（2）若点P 与点Q 均在椭圆C 上，且,P Q 关于原点对称，问：椭圆上是否存在点M （点M 在一象限），使得PQM ∆为等边三角形？若存在，求出点M 的坐标；若不存在，请说明理由．【答案】（1）2214x y +=；（2）存在，2165215M ⎝⎭．【解析】试题分析：（1）根据已知条件，列出不等式组，求解2,1a b ==，即可求解椭圆的椭圆的方程；（2）设直线OM 的斜率为k ，则直线:OM y kx =，代入椭圆的方程，解得M 点的坐标，同理可得直线PQ 的方程，代入求解所以2165215M M x y ==，即可求解点M 的坐标．试题解析：（1）由题意222221314{a bc a a b c +===+，解得2,1a b ==，所以椭圆C 的标准方程为2214x y +=．（2）由题意知直线PQ 经过坐标原点O ，假设存在符合条件的点M ，则直线OM 的斜率存在且大于零，,OM PQ OM ⊥= ① 设直线OM 的斜率为k ，则直线:OM y kx =，联立方程组22{14y kxx y =+=，得M M x y ==所以OM =②同理可得直线PQ的方程为1,y x OP k =-=③ 将②③代入①式得= 化简得21110k-=，所以11k=所以M M x y ==，综上所述，存在符合条件的点1515M ⎛ ⎝⎭【考点】椭圆的标准方程；直线与椭圆的位置关系．【方法点晴】本题主要考查了椭圆的标准方程及直线与椭圆的位置关系的应用，其中解答中涉及到椭圆的几何性质的应用、函数与方程思想等知识点的综合考查，着重考查了学生的推理与运算能力以及转化与化归思想的应用，此类问题的解答中把直线的方程与圆锥曲线的方程联立，转化为方程的根与系数的关系、判别式和韦达定理的应用是解答的关键，试题运算量大，有一定的难度，属于难题．21．已知函数2()x f x e a =-，()x g x e b =-，且()f x 与()g x 的图象有一个斜率为1的公切线（e 为自然对数的底数）. （1）求b a -；（2）设函数ln 21()()()22h x f x g x mx =--+-，讨论函数()h x 的零点个数. 【答案】（1）1ln 222b a -=-（2）见解析【解析】（1）由()f x 与()g x 的图象有一个斜率为1的公切线，分别对()f x 与()g x 求导并求出切线方程，列出等量关系可得b a -；（2）利用换元将2()2x xh x e e m '=--转化为二次函数，分类讨论对其单调性，对图像特点进行分析，分情况讨论出函数()h x 的零点个数. 【详解】（1）2()2=1xf x e '=，可得ln 2ln 21,()222x f a =--=-. ()f x 在ln 21(,)22a --处的切线方程为1ln 2()22y a x --=+，即ln 2122y x a =++-. ()1x g x e '==，0,(0)1x g b ==-. ()g x 在(0,1)b -处的切线方程为(1)y b x --=，1y x b =+-，故ln 21122a b +-=-，可得1ln 222b a -=-. （2）由（1）可得22ln 21()()22xx x x h x ea eb mx e e mx =----+-=--， 2()2x x h x e e m '=--，令x t e =，则22y t t m =--，=1+8m ∆，1m 时，220t t m --=有两根，12,t t 且120t t <<，12()2()()0x x h x e t e t '=--=，得：2ln x t =，在2(ln ),t -∞上，()0h x '<，在2(ln ,)t +∞上，()0h x '>，此时，2(ln )(0)0h t h <=.又x →-∞时，(),h x x →+∞→+∞时，()h x →+∞. 故在2(ln ),t -∞和2(ln ,)t +∞上，()h x 各有1个零点.1m =时，1()2()(1)2x x h x e e '=+-()h x 最小值为(0)0h =，故()h x 仅有1个零点.01m <<时，12()2()()x x h x e t e t '=--.其中120t t <<，同1m ，()h x 在2(ln ),t -∞与2(ln ,)t +∞上， ()h x 各有1个零点，0m =时，2()x x h x e e =-，仅在(0)0h =有1个零点， 108m -<<时，对方程220,180t t m m --=∆=+>. 方程有两个正根12,t t ，12()2()()x xh x e t e t '=--.在1(,ln )t -∞上，()0h x '>，在12(ln ,ln )t t 上，()0h x '<，在2(ln ,)t +∞，()0h x '>.由1212120t t t t ⎧+=⎪⎨⎪<<⎩，可得1211042t t <<<<，故22ln 0,(ln )(0)0t h t h <<=.11110,120,ln 0t t t -<-><，故1(ln )0h t <.故在1(,ln )t -∞上，1()(ln )0h x h t <<，在12(ln ,ln )t t 上，()0h x <，在2(ln ,)t +∞上，()h x 有1个零点：0x =.18m ≤-时，2()20x x h x e e m '=--≥恒成立，()h x 为增函数，()h x 仅有1个零点：0x =.综上，0m ≤或1m =时，()h x 有1个零点，01m <<或1m 时，()h x 有2个零点.【点睛】本题考查导数的应用，利用导数求切线是常考点，利用导数讨论零点个数是难点，通常结合分类讨论思想进行分析解决，属于难题.22．在平面直角坐标系xOy 中，曲线1C 的参数方程为1cos sin x y αα=+⎧⎨=⎩（α为参数）；在以原点O 为极点，x 轴的正半轴为极轴的极坐标系中，曲线2C 的极坐标方程为2cos sin ρθθ=.（1）求曲线1C 的极坐标方程和曲线2C 的直角坐标方程；（2）若射线(0)l y kx x ≥：＝与曲线1C ，2C 的交点分别为A B ，（A B ，异于原点），当斜率(k ∈时，求·OA OB 的取值范围. 【答案】（1）1C 的极坐标方程为2cos ρθ=；2C 的直角坐标方程为2x y =；（2）(2,.【解析】（1）由1cos sin x y αα=+⎧⎨=⎩，利用平方关系可得1C 的普通方程，再将cos sin x y ρθρθ=⎧⎨=⎩代入普通方程中化简求得极坐标方程；曲线2C 的极坐标方程2cos sin ρθθ=可化为22cos sin ρθρθ=，将cos sin x y ρθρθ=⎧⎨=⎩代入上式即可得解；（2）分别联立射线(0)l y kx x ≥：＝与曲线1C ，2C 的极坐标方程，求出A B ，两点的极坐标，进而得出·OA OB 的取值范围．【详解】（1）曲线1C 的直角坐标方程为22(1)1x y -+=，即2220x x y -+=，将cos sin x y ρθρθ=⎧⎨=⎩代入并化简得曲线1C 的极坐标方程为2cos ρθ=，由2cos sin ρθθ=两边同时乘ρ，得22cos sin ρθρθ=，结合cos sin x y ρθρθ=⎧⎨=⎩得曲线2C 的直角坐标方程为2x y =；（2）设射线(0)l y kx x ≥：＝的倾斜角为ϕ，则射线的极坐标方程为θϕ=，且(k tan ϕ=∈.联立2cos ρθθϕ=⎧⎨=⎩得2A OA cos ρϕ== ，联立2cos sin ρθθθϕ⎧=⎨=⎩得2sin cos B OB ϕρϕ==，所以(2sin ·222cos 2,A B OA OB cos tan k ϕρρϕϕϕ⋅==∈=⋅=，即·OA OB 的取值范围是(2,. 【点睛】本题考查三种方程间的互化，考查极坐标方程的应用，考查逻辑思维能力和转化能力，属于中档题.23．设命题p ：实数x 满足()()30x a x a --<，其中0a >，命题q ：实数x 满足302x x -≤-．（1）若1a =，且p q ∧为真，求实数x 的取值范围；（2）若p ⌝是q ⌝的充分不必要条件，求实数a 的取值范围．【答案】（1）()2,3；（2）12a <≤．【解析】（1）若1a =，分别求出p ，q 成立的等价条件，利用且p q ∧为真，求实数x 的取值范围；（2）利用p ⌝是q ⌝的充分不必要条件，即q 是p 的充分不必要条件，求实数a 的取值范围．【详解】解：由()()30x a x a --<，其中0a >，得3a x a <<，0a >，则p ：3a x a <<，0a >．由302x x -≤-解得23x <≤．即q ：23x <≤．（1）若1a =，则p ：13x <<，若p q ∧为真，则p ，q 同时为真，即2313x x <≤⎧⎨<<⎩，解得23x <<，∴实数x 的取值范围()2,3．（2）若p ⌝是q ⌝的充分不必要条件，即q 是p 的充分不必要条件， ∴332a a >⎧⎨≤⎩，即12a a >⎧⎨⎩，解得12a <≤．【点睛】本题主要考查复合命题与简单命题之间的关系，利用逆否命题的等价性将p ⌝是q ⌝的充分不必要条件，转化为q 是p 的充分不必要条件是解决本题的关键，属于基础题.。

【名师解析】陕西省西安市第一中学2021届高三大练习(一)(一模)数学(文科)试题 Word版含解析

2021年陕西省西安一中高考数学一模试卷（文科）一、选择题：（每小题5分，共50分）1．（5分）（2022•齐齐哈尔三模）若复数（x∈R）为纯虚数，则x等于（）A．0 B． 1 C．﹣1 D．0或1【考点】：复数代数形式的乘除运算；复数的基本概念．【专题】：计算题．【分析】：利用两个复数代数形式的除法法则化简z为（x2﹣x）﹣xi，再由z 为纯虚数，可得，由此求得x的值．【解答】：解：∵===（x2﹣x）﹣xi，又z为纯虚数，则有，故x=1，故选B．【点评】：本题主要考查复数的基本概念，两个复数代数形式的除法，属于基础题．2．（5分）（2007•广东）已知函数的定义域为M，g（x）=ln（1+x）的定义域为N，则M∩N=（）A．{x|x＞﹣1} B．{x|x＜1} C．{x|﹣1＜x＜1} D．∅【考点】：交集及其运算；函数的定义域及其求法．【分析】：依据题目中使函数有意义的x的值求得函数的定义域M和N，再求它们的交集即可．【解答】：解：∵函数的定义域是指使函数式有意义的自变量x的取值范围，∴由1﹣x＞0求得函数的定义域M={x|x＜1}，和由1+x＞0 得，N=[x|x＞﹣1}，∴它们的交集M∩N={x|﹣1＜x＜1}．故选C．【点评】：本题属于以函数的定义为平台，求集合的交集的基础题，也是高考常会考的题型．3．（5分）（2011•福建模拟）在各项均为正数的等比数列{a n}中，a3a5=4，则数列{log2a n}的前7项和等于（）A．7 B．8 C．27 D．28【考点】：等差数列的前n项和；等比数列的性质．【专题】：计算题．【分析】：依据等比数列的性质，由已知的等式求出a4的值，然后利用对数的运算性质化简数列{log2a n}的前7项和，把a4的值代入即可求出数列{log2a n}的前7项和．【解答】：解：由a3a5=a42=4，又等比数列{a n}的各项均为正数，∴a4=2，则数列{log2a n}的前7项和S7=++…+====7．故选A【点评】：此题考查同学机敏运用等比数列的性质化简求值，把握对数的运算性质，是一道基础题．4．（5分）在△ABC中，a，b，c是角A，B的对边，若a，b，c成等比数列，A=60°，=（）A．B． 1 C．D．【考点】：正弦定理；等比数列的性质．【专题】：计算题．【分析】：a，b，c成等比数列可得，b2=ac，由正弦定理可得sin2B=sinAsinC=【解答】：解：∵a，b，c成等比数列∴b2=ac由正弦定理可得sin2B=sinAsinC==故选D【点评】：本题主要考查了利用正弦定理进行解三角形，属于基础试题，难度不大．5．（5分）（2011•湘西州一模）如图为一个几何体的三视图，尺寸如图所示，则该几可体的表面积为（）（不考虑接触点）A．B．C．D．32+π【考点】：由三视图求面积、体积．【专题】：计算题．【分析】：由三视图可以看出，此几何体由一个半径为1的球体与一底面连长为2的直三棱柱所组成，故其表面积为球体的表面积加上直三棱柱的表面积．【解答】：解：由三视图知，此组合体上部是一个半径为的球体，故其表面积为π下部为始终三棱柱，其高为3，底面为一边长为2的正三角形，且题中已给出此三角形的高为故三棱柱的侧面积为3×（2+2+2）=18，由于不考虑接触点，故只求上底面的面积即可，上底面的面积为×2×=故组合体的表面积为故选C【点评】：本题考点是由三视图求几何体的面积、体积，考查对三视图的理解与应用，主要考查对三视图与实物图之间的关系，用三视图中的数据还原出实物图的数据，再依据相关的公式求表面积与体积，本题求的是表面积．三视图的投影规章是主视、俯视长对正；主视、左视高平齐，左视、俯视宽相等．6．（5分）已知图象不间断函数f（x）是区间[a，b]上的单调函数，且在区间（a，b）上存在零点．上图是用二分法求方程f（x）=0近似解的程序框图，推断框内可以填写的内容有如下四个选择：①f（a）f（m）＜0，②f（a）f（m）＞0，③f（b）f（m）＜0，④f（b）f（m）＞0，其中能够正确求出近似解的是（）A．①④ B．②③ C．①③ D．②④【考点】：程序框图．【专题】：函数的性质及应用；算法和程序框图．【分析】：由零点的判定定理知，推断框可以填写f（a）f（m）＜0或f（m）f（b）＞0，由此可得答案．【解答】：解：由二分法求方程f（x）=0近似解的流程知：当满足f（a）f（m）＜0时，令b=m；否则令a=m；故①正确，②错误；当满足f（m）f（b）＞0时，令a=m；否则令b=m；故④正确，③错误．故选：A．【点评】：本题考查了程序框图的应用问题，解题时应模拟程序框图的运行过程，以便得出正确的结论，是基础题．7．（5分）（2010•宁夏）如图，质点P在半径为2的圆周上逆时针运动，其初始位置为P0（，﹣），角速度为1，那么点P到x轴距离d关于时间t的函数图象大致为（）A．B．C．D．【考点】：函数的图象．【分析】：本题的求解可以利用排解法，依据某具体时刻点P的位置到到x轴距离来确定答案．【解答】：解：通过分析可知当t=0时，点P到x轴距离d 为，于是可以排解答案A，D，再依据当时，可知点P在x轴上此时点P到x轴距离d为0，排解答案B，故应选C．【点评】：本题主要考查了函数的图象，以及排解法的应用和数形结合的思想，属于基础题．8．（5分）已知函数f（x）=若f（2﹣x2）＞f（x），则实数x的取值范围是（）A．（﹣∞，﹣1）∪（2，+∞）B．（﹣∞，﹣2）∪（1，+∞）C．（﹣1，2）D．（﹣2，1）【考点】：函数单调性的性质．【专题】：计算题；函数的性质及应用．【分析】：由x=0时分段函数两个表达式对应的函数值相等，可得函数图象是一条连续的曲线．结合对数函数和幂函数f（x）=x3的单调性，可得函数f（x）是定义在R上的增函数，由此将原不等式化简为2﹣x2＞x，不难解出实数x的取值范围．【解答】：解：∵当x=0时，两个表达式对应的函数值都为零∴函数的图象是一条连续的曲线∵当x≤0时，函数f（x）=x3为增函数；当x＞0时，f（x）=ln（x+1）也是增函数∴函数f（x）是定义在R上的增函数因此，不等式f（2﹣x2）＞f（x）等价于2﹣x2＞x，即x2+x﹣2＜0，解之得﹣2＜x＜1，故选D【点评】：本题给出含有对数函数的分段函数，求不等式的解集．着重考查了对数函数、幂函数的单调性和函数的图象与性质等学问，属于基础题．9．（5分）已知双曲线方程为=1，过其右焦点F的直线（斜率存在）交双曲线于P、Q两点，PQ的垂直平分线交x轴于点M ，则的值为（）A．B．C．D．【考点】：双曲线的简洁性质．【专题】：计算题．【分析】：依题意，不妨设过其右焦点F的直线的斜率为1，利用双曲线的其次定义可求得可求得|PQ|，继而可求得PQ的垂直平分线方程，令x=0可求得点M的横坐标，从而使问题解决．【解答】：解：∵双曲线的方程为﹣=1，∴其右焦点F（5，0），不妨设过其右焦点F的直线的斜率为1，依题意，直线PQ的方程为：y=x﹣5．由得：7x2+90x﹣369=0，设P（x1，y1），Q（x2，y2），则x1，x2为方程7x2+90x﹣369=0的两根，∴x1+x2=﹣，y1+y2=（x1﹣5）+（x2﹣5）=x1+x2﹣10=﹣，∴线段PQ的中点N （﹣，﹣），∴PQ的垂直平分线方程为y+=﹣（x+），令y=0得：x=﹣．又右焦点F（5，0），∴|MF|=5+=．①设点P在其准线上的射影为P′，点Q在其准线上的射影为Q′，∵双曲线的一条渐近线为y=x，其斜率k=，直线PQ的方程为：y=x﹣5，其斜率k′=1，∵k′＜k，∴直线PQ与双曲线的两个交点一个在左支上，另一个在右支上，不妨设点P在左支，点Q在右支，则由双曲线的其次定义得：==e==，∴|PF|=x1﹣×=x1﹣3，同理可得|QF|=3﹣x2；∴|PQ|=|QF|﹣|PF|=3﹣x2﹣（x1﹣3）=6﹣（x1+x2）=6﹣×（﹣）=．②∴==．故选B．【点评】：本题考查双曲线的其次定义的应用，考查直线与圆锥曲线的相交问题，考查韦达定理的应用与直线方程的求法，综合性强，难度大，属于难题．10．（5分）（2021•肇庆一模）在实数集R中定义一种运算“⊕”，具有性质：①对任意a，b∈R，a⊕b=b⊕a；②对任意a∈R，a⊕0=a；③对任意a，b，c∈R，（a⊕b）⊕c=c⊕（ab）+（a⊕c）+（b⊕c）﹣2c．函数f（x）=x ⊕（x＞0）的最小值为（）A．4 B． 3 C．2D． 1【考点】：进行简洁的合情推理；函数的值域．【专题】：计算题；新定义．【分析】：依据题中给出的对应法则，可得f（x）=（x ⊕）⊕0=1+x+，利用基本不等式求最值可得x+≥2，当且仅当x=1时等号成立，由此可得函数f（x）的最小值为f（1）=3．【解答】：解：依据题意，得f（x）=x ⊕=（x ⊕）⊕0=0⊕（x •）+（x⊕0）+（⊕0 ）﹣2×0=1+x+。

2021-2022学年吉林省长春市东北师大附中高三(上)第一次摸底数学试卷(文科)(解析版)

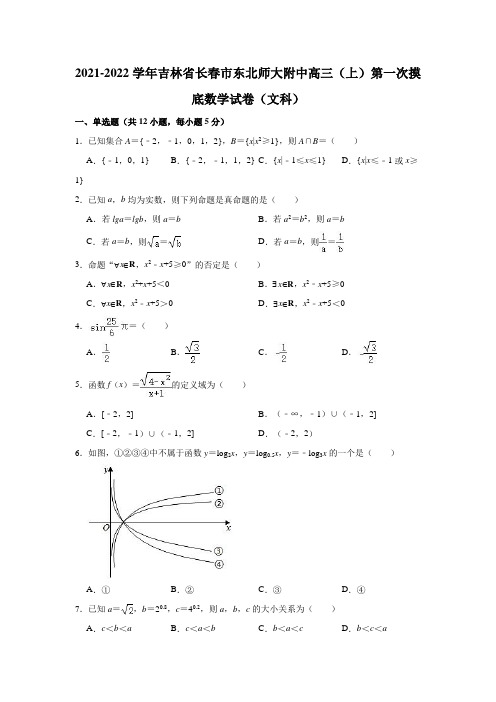
2021-2022学年吉林省长春市东北师大附中高三（上）第一次摸底数学试卷（文科）一、单选题（共12小题，每小题5分）1．已知集合A＝{﹣2，﹣1，0，1，2}，B＝{x|x2≥1}，则A∩B＝（）A．{﹣1，0，1}B．{﹣2，﹣1，1，2}C．{x|﹣1≤x≤1}D．{x|x≤﹣1或x≥1}2．已知a，b均为实数，则下列命题是真命题的是（）A．若lga＝lgb，则a＝b B．若a2＝b2，则a＝bC．若a＝b，则＝D．若a＝b，则＝3．命题“∀x∈R，x2﹣x+5≥0”的否定是（）A．∀x∈R，x2+x+5＜0B．∃x∈R，x2﹣x+5≥0C．∀x∈R，x2﹣x+5＞0D．∃x∈R，x2﹣x+5＜04．＝（）A．B．C．D．5．函数f（x）＝的定义域为（）A．[﹣2，2]B．（﹣∞，﹣1）∪（﹣1，2]C．[﹣2，﹣1）∪（﹣1，2]D．（﹣2，2）6．如图，①②③④中不属于函数y＝log2x，y＝log0.5x，y＝﹣log3x的一个是（）A．①B．②C．③D．④7．已知a＝，b＝20.8，c＝40.2，则a，b，c的大小关系为（）A．c＜b＜a B．c＜a＜b C．b＜a＜c D．b＜c＜a8．已知，则sin2α+cos2α等于（）A．B．C．D．9．“a＝1”是“函数f（x）＝+为偶函数”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件10．已知函数f（x）＝A sin（ωx+φ）（x∈R，A＞0，ω＞0，|φ|＜）的图象（部分）如图所示，则f（x）的解析式是（）A．f（x）＝2sin（πx+）B．f（x）＝2sin（2πx+）C．f（x）＝2sin（πx+）D．f（x）＝2sin（2πx+）11．定义域为R的函数f（x）满足f（﹣x）＝f（x）且f（2﹣x）＝f（x），当x∈[0，1]时，f（x）＝x3，函数g（x）＝log4|x|，则函数h（x）＝g（x）﹣f（x）零点的个数为（）A．3B．4C．5D．612．若a＝2021ln2019，b＝2020ln2020，c＝2019ln2021，则（）A．a＞c＞b B．c＞b＞a C．a＞b＞c D．b＞a＞c二、填空题（本大题共4小题。

河北省邯郸市2021届高三数学摸底考试试题文（含解析）

邯郸市2021届高三年级摸底考试文科数学【试卷综评】本试卷试题要紧注重大体知识、大体能力、大体方式等当面的考察，覆盖面广，注重数学思想方式的简单应用，试题有新意，符合课改和教改方向，能有效地测评学生，有利于学生自我评判，有利于指导学生的学习，既重视双基能力培育，偏重学生自主探讨能力，分析问题和解决问题的能力，突出应用，同时对观看与猜想、阅读与试探等方面的考查。

一.选择题【题文】1.已知集合{}{}1,2,3,14M N x Z x ==∈<<，那么A.N M ⊆B.N M =C.}3,2{=N MD.)4,1(=N M 【知识点】交集的运算.A1 【答案解析】C 解析：因为{}{}142,3N x Z x =∈<<=，因此{2,3}M N =，应选C.【思路点拨】先化简集合N ，再进行判定即可.【题文】2.复数+1i z i =（为虚数单位）在复平面内所对应的点在A ．第一象限B ．第二象限C ．第三象限D ．第四象限【知识点】复数的代数表示法及其几何意义．L4【答案解析】D 解析：∵()()()1+11•i i i z i i i i ，+-===--∴复数+1i z i =（为虚数单位）在复平面内对应的点位于第四象限．应选：D ．【思路点拨】利用复数的代数运算将原式转化，即可判定它在复平面内的位置．【题文】3.某校数学教研组为了解学生学习数学的情形，采纳分层抽样的方式从高一600人、高二780人、高三n 人中，抽取35人进行问卷调查，已知高二被抽取的人数为13人，那么n 等于 A 、660 B 、720 C 、780 D 、800 【知识点】分层抽样方式．I1【答案解析】B 解析：：∵高一600人、高二780人、高三n 人中，抽取35人进行问卷调查，已知高二被抽取的人数为13人，∴1378035600780n ＝++，解得n=720，应选：B ．【思路点拨】依照分层抽样的概念，成立条件关系即可取得结论．【题文】4.设2log 3a =，4log 6b =，8log 9c =，那么以下关系中正确的选项是A ．a b c >>B ．a c b >>C ．c b a >>D ．c a b >> 【知识点】对数函数的性质；比较大小.B7【答案解析】A解析：因为242221log 6log 6log 6log 2b ====82log 9log c ==，又因为2log y x =是概念域内的增函数，且2>> a b c >>，应选A 。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2021届东北三省三校高三第一次模拟考试数学（文）试题第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.集合{}*2,A x x x N =≤∈，{}2,B y y x x R ==∈，则A B =( ) A.{}0x x ≥B.{}1x x ≥C.{}1,2D.{}0,1,22.已知复数z 满足()12i z i +=，i 为虚数单位，则z 等于( ) A.1i -B.1i +C.1122i - D.1122i + 3.在下列向量中，可以把向量()3,1a =-表示出来的是( ) A.()10,0e =，()23,2e =B.()11,2e =-，()23,2e =C.()13,5e =，()26,10e =D.()13,5e =-，()23,5e =-4.在区间()0,3上任取一个实数x ，则22x <的概率是( ) A.23B.12C.13D.145.抛物线24y x =的焦点到准线的距离为( ) A.2B.1C.14D.186.已知,a b 都是实数，p ：直线0x y +=与圆()()222x a y b -+-=相切；q ：2a b +=，则p 是q 的( ) A.充分不必要条件 B.必要不充分条件 C.充要条件D.既不充分也不必要条件7.如图所示的程序框图的算法思路来源于我国古代数学名著《九章算术》，执行该程序框图若输出的4a =，则输入的,a b 不可能为( )A.4，8B.4，4C.12，16D.15，188.已知函数()sin 3f x x π⎛⎫=+ ⎪⎝⎭，则下列说法不正确的是( )A.()f x 的一个周期为2πB.()f x 向左平移3π个单位长度后图象关于原点对称 C.()f x 在7,66ππ⎡⎤⎢⎥⎣⎦上单调递减D.()f x 的图象关于56x π=-对称9.函数()af x x x=+(其中a R ∈)的图象不可能是( )ABCD10.如图所示是一个三棱锥的三视图，则此三棱锥的外接球的体积为( )A.43π3556π11.设双曲线()222210,0x y a b a b -=>>的两条渐近线与直线2a x c =分别交于,A B 两点，F 为该双曲线的右焦点，若6090AFB <<∠°°，则该双曲线离心率e 的取值范围是( ) A.(2B.23⎫+∞⎪⎪⎝⎭C.)2,2D.232⎝12.已知函数()()()21221221x x x x f x x --⎧-+-≤⎪=⎨->⎪⎩，()()1cos g x a x x R =-∈，若对任意的12,x x R ∈，都有()()12f x g x ≤，则实数a 的取值范围为( )A.[]0,2B.RC.[]2,0-D.(][),20,-∞-+∞二、填空题（每题5分，满分20分，将答案填在答题纸上）13.若直线l ⊥平面β，平面α⊥平面β，则直线l 与平面α的位置关系为_____________. 14.若实数,x y 满足不等式组01030x x y x y ≥⎧⎪-+≤⎨⎪+-≤⎩，则32y x +-的取值范围是_____________.15.甲、乙、丙三人中只有一人做了好事，他们各自都说了一句话，而且其中只有一句真话。

甲说：是乙做的。

乙说：不是我做的。

丙说：不是我做的。

则做好事的是_____________.(填甲、乙、丙中的一个)16.ABC △中，2BC =，AB =，则ABC △面积的最大值为_____________.三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17.已知数列{}n a 的前n 项和为()()31*1227n n S n N +=-∈. (1)求数列{}n a 的通项公式； (2)设2log n n b a =，求12231111n n b b b b b b ++++…. 18.中国政府实施“互联网+”战略以来，手机作为客户端越来越为人们所青睐，通过手机实现衣食住行消费已经成为一种主要的消费方式，“一机在手，走遍天下”的时代已经到来。

在某著名的夜市，随机调查了100名顾客购物时使用手机支付的情况，得到如下的22⨯列联表，已知其中从使用手机支付的人群中随机抽取1人，抽到青年的概率为710. (1)根据已知条件完成22⨯列联表，并根据此资料判断是否有99.5%的把握认为“市场购物用手机支付与年龄有关”？(2)现采用分层抽样从这100名顾客中按照“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本，设事件A 为“从这个样本中任选2人，这2人中至少有1人是不使用手机支付的”，求事件A 发生的概率？0k3.841 5.024 6.635 7.87922⨯列联表青年中老年合计使用手机支付 60 不使用手机支付 24 合计100附：()()()()()22n ad bc K a b c d a c b d -=++++19.已知圆锥SO ，2SO =，AB 为底面圆的直径，2AB =，点C 在底面圆周上，且OC AB ⊥，E 在母线SC 上，且4SE CE =，F 为SB 中点，M 为弦AC 中点.(1)求证：AC ⊥平面SOM ； (2)求四棱锥O EFBC -的体积.20.已知椭圆()2222:10x y C a b a b+=>>的离心率为22，()1,0F c -，()2,0F c 为椭圆C 的左、右焦点，M 为椭圆C 上的任意一点，12MF F △的面积的最大值为1，A 、B 为椭圆C 上任意两个关于x 轴对称的点，直线2a x c =与x 轴的交点为P ，直线PB 交椭圆C 于另一点E . (1)求椭圆C 的标准方程； (2)求证：直线AE 过定点.21.已知函数()34f x x ax =-+，x R ∈.(1)讨论函数()f x 的单调性；(2)若函数()f x 在[]1,1-上的最大值为1，求实数a 的取值集合.22.已知在极坐标系中曲线1C 的极坐标方程为：4cos ρθ=，以极点为坐标原点，以极轴为x 轴的正半轴建立直角坐标系，曲线2C的参数方程为：132x t y ⎧=-⎪⎪⎨⎪=⎪⎩(t 为参数)，点()3,0A .(1)求出曲线1C 的直角坐标方程和曲线2C 的普通方程； (2)设曲线1C 与曲线2C 相交于,P Q 两点，求AP AQ ⋅的值. 23.已知函数()2521f x x x =-++. (1)求不等式()1f x x >-的解集；(2)若()1f x a >-对于x R ∈恒成立，求实数a 的范围.2021届东北三省三校高三第一次模拟考试数学（文）试题参考答案一、选择题（本大题共12小题，每小题5分，共60分）1.C2.A3.B4.C5.D6.B7.D8.B9.C 10.C 11.C 12.A 二、填空题（本大题共4小题，每小题5分，共20分）13． //l α或l α⊂ 14． []5,2-- 15．丙 16．三、解答题（本大题共70分） 17.（本小题满分12分）解：（Ⅰ）当2≥n 时，3+13232111(22)(22)277n n n n n n a S S ---=-=---= 当1=n 时，112a S ==312=2⨯-，符合上式所以32*2()n n a n -=∈N . （Ⅱ）由（Ⅰ）得322log 2=32n n b n -=-, 所以=+-++⨯+⨯=++++)13)(23(174141111113221n n b b b b b b n n 13)1311(31)]131231()7141()411[(31+=+-=+--++-+-n n n n n ． 18.（本小题满分12分）解：(Ⅰ)从使用手机支付的人群中随机抽取1人，抽到青年的概率为710∴使用手机支付的人群中的青年的人数为7604210⨯=人，则使用手机支付的人群中的中老年的人数为604218-=人，所以22⨯列联表为:2K 的观测值2100(42241816)1800=8.86758426040203k ⨯-⨯=≈⨯⨯⨯ 28.8677.879(7.879)0.005P K >≥=，，故有99.5%的把握认为“市场购物用手机支付与年龄有关”.(Ⅱ) 这100名顾客中采用分层抽样从“使用手机支付”和“不使用手机支付”中抽取得到一个容量为5的样本中：使用手机支付的人有6053100⨯=人，记编号为1,2,3 不使用手机支付的人有2人，记编号为a,b ，则从这个样本中任选2人有(1,2)(1,3)(1,a)(1,b)(2,3)(2,a)(2,b)(3,a)(3,b)(a,b)共10种其中至少有1人是不使用手机支付的(1,a)(1,b) (2,a)(2,b)(3,a)(3,b)(a,b)共7种，故7()10P A =. 19.（本小题满分12分）（Ⅰ）证明：∵SO ⊥平面ABC ，∴SO AC ⊥，又∵点M 是圆O 内弦AC 的中点，AC MO ∴⊥，又SO MO O =AC ∴⊥平面SOM（Ⅱ）∵SO ⊥平面ABC ，SO 为三棱锥S OCB -的高，111112323S OCB O SCB V V --∴==⨯⨯⨯⨯=而O EFBC V -与O SCB V -等高，1sin 2215sin 2ESF SCBSE SF ESF S S SC SB CSB ∆∆⨯⨯∠==⨯⨯∠， ∴35SCB EFBC S S ∆=四边形因此，33115535O EFBC O SCB V V --==⨯=20.（本小题满分12分）解：（Ⅰ）2c e a ==，当M 为椭圆C 的短轴端点时，12MF F ∆的面积的最大值为112112c b bc ∴⨯⨯=∴=，而222a b c =+1a b ∴==故椭圆C 标准方程为：2212x y += （Ⅱ）设112211(,),,),(,)B x y Ex y A x y -（，且12x x ≠， 2=2a x c=，(2,0)P ∴由题意知BP 的斜率必存在，设BP ：(2)y k x =-，代入2212x y +=得 2222(21)8820k x k x k +-+-=0∆>得212k <22121222882,2121k k x x x x k k -+=⋅=++12x x ≠∴AE 斜率必存在，AE ：121121()y y y y x x x x ++=--由对称性易知直线AE 过的定点必在x 轴上，则当0y =时，得121122112211121212()(2)(2)()4y x x y x y x k x x k x x x x y y y y k x x k-+-+-=+==+++-2222121221228282222()2121=184421k k x x x x k k k x x k -⋅-⋅-+++==+--+ 即在212k <的条件下，直线AE 过定点（1，0）.21. （本小题满分12分）解：（Ⅰ）2()12f x x a '=-+.当0a =时，3()4f x x =-在R 上单调递减；当0a <时，2()120f x x a '=-+<，即3()4f x x ax =-+在R 上单调递减；当0a >时，2()12f x x a '=-+.(,x ∈-∞时，()0f x '<，()f x在(,-∞上递减；(66x ∈-时，()0f x '>，()f x在(,66-上递增；)6x ∈+∞时，()0f x '<，()f x在)6+∞上递减；综上，当0a ≤时，()f x 在R 上单调递减；当0a >时，()f x 在(,)6-∞-上递减；在(上递增；)+∞上递减. （Ⅱ）∵函数()f x 在[1,1]-上的最大值为1. 即对任意[1,1]x ∈-，()1f x ≤恒成立。