【授课】第二章知识点复习
数学必修2第二章复习总结知识点PPT课件

简记为:线线垂直,则线面垂直。
3.直线与平面垂直的另一种判定方法
两条平行直线中的一条垂直一个平面,则另
一202条1/7/2直4 线也垂直这个平面.
11
直线和平面垂直的判定与性质
4.直线与平面所成的角 定义:平面的一条斜线和它在平面上的射影所 成的锐角,叫做这条直线和这个平面所成的角. 直线与平面所成的角的范围α: 00≤α ≤900
若两个平面平行,则一个平面内的所有
直2021线/7/24都平行于另一个平面.
10
直线和平面垂直的判定与性质
1.直线与平面垂直的概念
如果直线 l 与平面内的任意一条直线都 垂直,我们说直线 l 与平面 互相垂直,
2.直线与平面垂直的判定定理
一条直线与一个平面内的两条相交直线都垂直, 则该直线与此平面垂直.
2021/7/24
18
简记为:线面平行,则线线平行。
2021/7/24
9
平面和平面平行的判定与性质
1.判定定理:一个平面内的两条相交直线与 另一个平面平行,则这两个平面平行.
简记为:线面平行,则面面平行.
2.性质定理:如果两个平行平面同时和 第三个平面相交,那么它们的交线平行.
简记为:面面平行,则线线平行.
3.两个平面平行的一个性质:
6.平面与平面垂直的性质定理
定理:两个平面垂直,则一个平面内垂直于交线 的直线与另一个平面垂直.
简记为:面面垂直,则线面垂直
7.另一个性质:两个平面垂直,过一个平面的一点
作202另1/7/2一4 个平面的垂线,必在第一个平面内.
14
一些常用结论 1.三条两两相交的直线可确定1个或3个平面. 2.不共面的四点可确定4个平面. 3.三个平面两两相交,交线有1条或3条. 4.正方体各面所在平面将空间分成27个部分.
浙教版九年级上册数学第二章本章复习课(解析版)

浙教版九年级上册数学第二章本章复习课(解析版)本章复习课_类型之一随机事件1.[2019·长沙]下列说法正确的是(D)A.检测某批次灯泡的使用寿命,适宜用全面调查B.可能性是1%的事件在一次试验中一定不会发生C.数据3,5,4,1,-2的中位数是4D.“367中有2人同月同日出生”为必然事件【解析】A.检测某批次灯泡的使用寿命,调查具有破坏性,应采用抽样调查,此选项错误;B.可能性是1%的事件在一次试验中可能发生,,5,4,1,-2的中位数是3,此选项错误;D.“367中有2人同月同日出生”为必然事件,此选项正确.类型之二概率的意义与计算2.[2019·贺州]从分别标有数-3,-2,-1,0,1,2,3的七张没有明显差别的卡片中,随机抽取一张,所抽卡片上的数的绝对值不小于2的概率是(D)A.17 B.27 C.37 D.473.[2019·杭州]已知一包糖果共有5种颜色(糖果只有颜色差别),如图2-1是这包糖果颜色分布百分比的统计图,在这包糖果中任意取一粒,则取出糖果的颜色为绿色或棕色的概率是__12__.图2-1【解析】棕色所占的百分比为1-20%-15%-30%-15%=1-80%=20%,∴P(绿色或棕色)=30%+20%=50%=1 2.类型之三用树状图或列表法求概率4.[2019·株洲]三名九年级学生坐在仅有的三个座位上,起身后重新就坐,恰好有两名同学没有坐回原座位的概率为(D)A.19 B.16 C.14 D.12【解析】列表(用A,B,C表示三位同学,用a,b,c表示他们原来的座位)共有6种等可能的结果数,其中恰好有两名同学没有坐回原座位的结果数为3,所以恰好有两名同学没有坐回原座位的概率=36=12.5.[2019·泰州]在学校组织的朗诵比赛中,甲、乙两名学生以抽签的方式从3篇不同的文章中抽取一篇参加比赛,抽签规则是:在3个相同的标签上分别标注字母A,B,C,各代表1篇文章,一名学生随机抽取一个标签后放回,另一名学生再随机抽取.用画树状图或列表的方法列出所有等可能的结果,并求甲、乙抽中同一篇文章的概率.解:画树状图如答图,第5题答图所有等可能的结果有9种,甲、乙抽中同一篇文章的情况有3种,概率为39=13.6.[2019·衡阳]有四张背面完全相同的纸牌A,B,C,D,其中正面分别画有四个不同的几何图形(如图2-2),小华将这四张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A,B,C,D 表示);(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.图2-2解:(1)画树状图如答图,第6题答图则共有16种等可能的结果;(2)∵既是中心对称又是轴对称图形的只有B,C,∴既是轴对称图形又是中心对称图形的有4种情况,∴既是轴对称图形又是中心对称图形的概率为416=14.类型之四用频率估计概率7.[2019·眉山]一个口袋中放有290个涂有红、黑、白三种颜色的质地相同的小球.若红球个数是黑球个数的2倍多40个.从袋中任取一个球是白球的概率是1 29.(1)求袋中红球的个数;(2)求从袋中任取一个球是黑球的概率.解:(1)290×129=10(个),290-10=280(个),(280-40)÷(2+1)=80(个),280-80=200(个).故袋中红球的个数是200个;(2)80÷290=8 29.答:从袋中任取一个球是黑球的概率是8 29.类型之五概率在实际生活中的应用8.[2019·枣庄]为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法,学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如图2-3的两幅不完整的统计图,请结合图中所给信息解答下列问题:图2-3(1)本次调查的学生共有__50__人,在扇形统计图中,m的值是__30%__;(2)将条形统计图补充完整;(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.解:(1)20÷40%=50(人),15÷50=30%;(2)50×20%=10(人),50×10%=5(人),补全条形统计图如答图;第8题答图(3)∵5-2=3(名),∴选修书法的5名同学中,有3名男同学,2名女同学,列表如下:男1男2男3女1女2 男1——男2男1男3男1女1男1女2男1男2男1男2——男3男2女1男2女2男2男3男1男3男2男3——女1男3女2男3女1男1,女1男2女1男3女1——女2女1女2男1女2男2女2男3女2女1女2——所有等可能的情况有20种,其中抽取的2名同学恰好是1名男同学和1名女同学的情况有12种, 则P (一男一女)=1220=35. 类型之六 概率与方程(组)、几何、统计等知识的综合运用9.从3,0,-1,-2,-3这5个数中,随机抽取1个数,作为函数y =(5-m 2)x 和关于x 的方程(m +1)x 2+mx +1=0中m 的值,恰好使所得函数的图象经过第一、三象限,且方程有实数根的概率为__25__.【解析】 ∵所得函数的图象经过第一、三象限, ∴5-m 2>0,∴m 2<5,∴3,0,-1,-2,-3中,3和-3均不符合题意. 将m =0代入(m +1)x 2+mx +1=0,得x 2+1=0, b 2-4ac =-4<0,无实数根;将m =-1代入(m +1)x 2+mx +1=0,得-x +1=0,解得x =1,有实数根; 将m =-2代入(m +1)x 2+mx +1=0,得x 2+2x -1=0,b 2-4ac =4+4=8>0,有实数根. ∴所求的概率为25.10.一个不透明的袋子里装有编号分别为1,2,3的球(除编号以外,其余都相同),其中1号球1个,3号球3个,从中随机摸出1个球是2号球的概率为13.(1)求袋子里2号球的个数;(2)甲、乙两人分别从袋中摸出1个球(不放回),甲摸出球的编号记为x ,乙摸出球的编号记为y ,用列表法求点A (x ,y )在直线y =x 下方的概率. 解:(1)设袋子里2号球的个数为x , 则x 1+x +3=13,解得x =2,经检验,x =2为所列方程的解, ∴袋子里2号球的个数为2; (2)列表:x (x ,y )122333y1(2,1)(2,1)(3,1)(3,1)(3,1) 2(1,2)(2,2)(3,2)(3,2)(3,2) 2(1,2)(2,2)(3,2)(3,2)(3,2) 3(1,3)(2,3)(2,3)(3,3)(3,3) 3(1,3)(2,3)(2,3)(3,3)(3,3) 3(1,3)(2,3)(2,3)(3,3)(3,3)∴共有30种等可能的结果,其中点在直线y=x下方的有(2,1),(2,1),(3,1),(3,1),(3,1),(3,2),(3,2),(3,2),(3,2),(3,2),(3,2),共11种,∴点A(x,y)在直线y=x下方的概率P=11 30.。
苏教版七年级上册数学 第二章 小结与复习 教学课件

例2:一个四边形的周长是48cm,已知第 一条边长是acm,第二条边比第一条边的 2倍长3cm,第三条边长等于第一、二条 变长的和
(1)写出表示第四条边长的式子; (2)当a=3cm或7cm时,还能得到四边 形吗?这时的图形是什么形状?
(1)第四条边长为: 48-a-(2a+3)-(a+2a+3)
么这两个数字可以表示为 10a+b ;交换这个两位数的十位数字
和个位数字,得到的新两位数是 10b+a
;这两个两位数的
和是 10a+b+(10b+a)=11a+11b ,他能被 11 整除。如果把
这两个两位数相减,你得到的规律是 9a-9b能被9整除。
变式练习:x表示一个两位数,y表示一个 三位数,若把x放在y的左边组成一个五位 数M,把y放在x的左边组成一个五位数N试 说明M-N是9的倍数
=48-a-2a-3-3a-3 =42-6a(cm)
(2)当a=3cm时,四边形的四条边分别为 3cm,9cm,12cm,24cm因为3+9+12=24.所 以这时的图形不是四边形是一条线段。
当a=7cm时,四边形的四条边分别为cm, 17cm,24cm,0cm显然这时的图形不是四边 形。仍然是一条线段。
类项,即把它们的系数相加作为新的系数,而 字母部分不变.
[注意] (1)同类项不考虑字母的排列顺序,如-7xy与yx是同类 项;
(2)只有同类项才能合并,如x2+x3不能合并.
3、去括号法则
法则1.括号前面是“+”号,把括号和它前面的“+”号去掉, 括号里各项都不改变符号; 法则2.括号前面是“—”号,把括号和它前面的“—”号去掉, 括号里各项都要改变符号
高中数学必修课件第二章章末复习

学会运用数学语言描述实际问题和解决实际问题 。
3
应用问题的解决方法
掌握应用问题的基本解决方法,如建立数学模型 、运用数学工具进行计算和求解等。
05 跨学科知识融合 与应用
数学与物理相结合问题
运动学中的数学应 用
理解速度、加速度等物理概念,运用数学公式进行计算。
力学中的数学应用
掌握力的合成与分解,运用三角函数、向量等数学知识解 决问题。
仔细审题
明确题目要求,注意关键词和限定条 件。
验证答案
将所选答案代入题目进行验证,确保 答案正确。
分析选项
比较各选项的异同,运用排除法缩小 选择范围。
填空题答题技巧
审清题意
明确填空的内容和要求, 注意单位、符号等细节。
寻找线索
根据题目中的已知条件和 公式,寻找与填空相关的 线索。
验证答案
将所得答案代入原题进行 验证,确保答案的准确性 和合理性。
本单元测试卷主要考察了第二章 中的基础知识点,包括函数的概 念、性质、图像以及基本初等函
数等。
重点难点分析
在测试中发现,学生对于函数的 概念和性质理解较为深入,但在 应用方面存在一定困难,尤其是 在解决复合函数和分段函数的问
题时容易出现错误。
学生表现评估
大部分学生能够掌握本章的基础 知识,但在解题思路和技巧方面 还需加强训练。对于表现不佳的 学生,需要针对其薄弱环节进行
等问题,我将采取更加严谨的学习态度,加强练习和反思,争取在后续
的学习中取得更好的成绩。
下一步学习计划
复习巩固计划
针对本章学习中存在的薄弱环节,我将制定详细的复习计 划,加强对重点难点知识的巩固和练习。
拓展提升计划
人教版高中数学必修2第二章知识点汇总

人教版高中数学必修二第二章知识点汇总第二章 直线与平面的位置关系2.1空间点、直线、平面之间的位置关系2.1.11 平面含义:平面是无限延展的2 平面的画法及表示(1)平面的画法:水平放置的平面通常画成一个平行四边形,锐角画成450,且横边画成邻边的2倍长(如图)(2)平面通常用希腊字母α、β、γ等表示,如平面α、平面β等,也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示,如平面AC 、平面ABCD 等。
3 三个公理:(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内符号表示为A∈LB∈L => L α A∈α B∈αLA· α DCBAα公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面。
符号表示为:A 、B 、C 三点不共线 => 有且只有一个平面α, 使A∈α、B∈α、C∈α。
公理2作用:确定一个平面的依据。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线。
符号表示为:P∈α∩β =>α∩β=L,且P∈L 公理3作用:判定两个平面是否相交的依据 2.1.2空间中直线与直线之间的位置关系 1 空间的两条直线有如下三种关系:相交直线:同一平面内,有且只有一个公共点;平行直线:同一平面内,没有公共点;异面直线: 不同在任何一个平面内,没有公共点。
2 公理4:平行于同一条直线的两条直线互相平行。
符号表示为:设a 、b 、c 是三条直线a∥bC·B ·A· α P·αLβ共面直线 =>a ∥cc∥b强调:公理4实质上是说平行具有传递性,在平面、空间这个性质都适用。
公理4作用:判断空间两条直线平行的依据。
3 等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补4 注意点:① a'与b'所成的角的大小只由a 、b 的相互位置来确定,与O 的选择无关,为简便,点O 一般取在两直线中的一条上;② 两条异面直线所成的角∈(0, );③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a⊥b; ④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;⑤ 计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角。
八年级上册数学-第二章-知识点复习总结
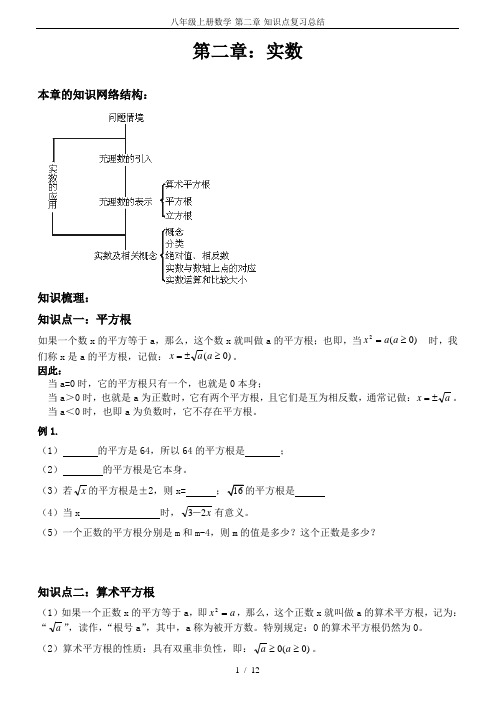
第二章:实数本章的知识网络结构:知识梳理: 知识点一:平方根如果一个数x 的平方等于a ,那么,这个数x 就叫做a 的平方根;也即,当)0(2≥=a a x 时,我们称x 是a 的平方根,记做:)0(≥±=a a x 。
因此:当a=0时,它的平方根只有一个,也就是0本身;当a >0时,也就是a 为正数时,它有两个平方根,且它们是互为相反数,通常记做:a x ±=。
当a <0时,也即a 为负数时,它不存在平方根。
例1.(1) 的平方是64,所以64的平方根是 ; (2) 的平方根是它本身。
(3)若x 的平方根是±2,则x= ;16的平方根是 (4)当x 时,x 23-有意义。
(5)一个正数的平方根分别是m 和m-4,则m 的值是多少?这个正数是多少?知识点二:算术平方根(1)如果一个正数x 的平方等于a ,即a x =2,那么,这个正数x 就叫做a 的算术平方根,记为:“a ”,读作,“根号a ”,其中,a 称为被开方数。
特别规定:0的算术平方根仍然为0。
(2)算术平方根的性质:具有双重非负性,即:)0(0≥≥a a 。
(3) 算术平方根与平方根的关系:算术平方根是平方根中正的一个值,它与它的相反数共同构成了平方根。
因此,算术平方根只有一个值,并且是非负数,它只表示为:a ;而平方根具有两个互为相反数的值,表示为:a ±。
例2.(1)下列说法正确的是 ( )A .1的立方根是1±;B .24±=; C.81的平方根是3±; D.0没有平方根; (2)下列各式正确的是 ( )A 、981±=B 、14.314.3-=-ππC 、3927-=-D 、235=- (3)2)3(-的算术平方根是 。
(4)若x x -+有意义,则=+1x ___________。
(5)已知△ABC 的三边分别是,,,c b a 且b a ,满足0)4(32=-+-b a ,求c 的取值范围。
【授课】第二章知识点复习

1)在酸性条件下 不能大量共存的有OH-、HCO3-、 HS-、S2-、SO32-、HSO3- 、 CO322)在强碱性条件下 不能大量共存的有H+、NH4+、Mg2+、 Al3+、Ca2+、Fe3+、Cu2+、Fe2+、 HCO3-、HSO3-
氧化还原反应常见问题
问题一: 判断依据及本质 问题二: 四种基本反应类型与氧化还原反应的关系 问题三: 双线桥法表示氧化还原反应 1. 步骤 2.得失电子数的判断 问题四: 单线桥法表示氧化还原反应 问题五: 氧化性与还原性强弱判断
<1 nm
体
能否通 能否通 过半透 过滤纸 膜
胶体:分散质微粒的直径大小在1~100 nm 之间的分散系 浊液、溶液、胶体三种分散系的区别
主要 特征
举例
溶液
均一 透明 稳定
透明 介稳性
能
能
NaCl溶液
胶体 浊液
1~100 nm 多数均一
不能
能
豆浆、牛奶 墨水、血液
泥浆水
>100 nm 不透明
不稳定
不均一
2 2
3. Zn+H2SO4 = ZnSO4+H2
√
×
4. 2KClO3
△
KCl +O2
离子反应发生的条件: 复 1.生成难溶物(沉淀) 分 如:硝酸银溶液和氯化钠溶液 解 型 2.难电离物质(弱酸、弱碱、H2O等) 离 子 如:盐酸和氢氧化钠溶液 反 应 3.生成气体 如:碳酸钙和稀盐酸
4. 发生了氧化还原反应 如: 氯化铁溶液和铁粉
实验:分别用激光照射盛硫酸铜溶液和氢氧 化铁胶体的烧杯,在光束垂直的方向观察现 象。并完成下列表格:
北师大版九年级上册数学 第二章复习第二章复习教案1

第二章 一元二次方程教学目标1、灵活运用直接开平方法、配方法、公式法、因式分解法解一元二次方程,运用一元二次方程解决简单的实际问题.2、发展学生的独立思考能力和创新精神.3、本节主要是对一元二次方程进行系统复习,巩固所学知识,提升应用能力.重点难点重点:运用知识、技能解决问题;难点:解题分析能力的提高.教学过程一、知识网络图表 一元二次方程解法 直接开平方法 配方法 公式法 因式分解法 判别式 应用 列方程或方程组解应用题二、知识要点归纳(一)一元二次方程1、一元二次方程定义:含有一个未知数,并且未知数的最高次数是2的整式方程叫做一元二次方程。
2、一元二次方程的一般形式: )0(02≠=++a c bx ax 。
它的特征是:等式左边是一个关于未知数x 的二次多项式,等式右边是零; 其中2ax 叫做二次项,a 叫做二次项系数;bx 叫做一次项,b 叫做一次项系数;c 叫做常数项。
二、一元二次方程的解法 :1、直接开平方法利用平方根的定义直接开平方求一元二次方程的解的方法叫做直接开平方法。
直接开平方法适用于解形如b a x =+2)(的一元二次方程。
根据平方根的定义可知, a x +是b 的平方根,当0≥b 时,b a x ±=+,b a x ±-=,当b<0时,方程没有实数根。
既:左边是一个完全平方式,右边是一个大于等于0的数例1: 降次—直接开平方法(将被开放式看作一个整体)212:(21)521=55125151,22x x x x x +=+±±-=---==例解:2、配方法配方法是一种重要的数学方法,它不仅在解一元二次方程上有所应用,而且在数学的其他领域也有着广泛的应用。
配方法的理论根据是完全平方公式:222)(2b a b ab a +=+±,把公式中的a 看做未知数x ,并用x 代替,则有222)(2b x b bx x ±=+±。
数学第二章知识点

数学第二章知识点数学第二章知识点在日常过程学习中,是不是听到知识点,就立刻清醒了?知识点也不一定都是文字,数学的知识点除了定义,同样重要的公式也可以理解为知识点。
为了帮助大家掌握重要知识点,下面是店铺帮大家整理的数学第二章知识点,仅供参考,欢迎大家阅读。
数学第二章知识点1数轴的三要素:原点、正方向、单位长度(三者缺一不可)。
任何一个有理数,都可以用数轴上的一个点来表示。
(反过来,不能说数轴上所有的点都表示有理数)如果两个数只有符号不同,那么我们称其中一个数为另一个数的相反数,也称这两个数互为相反数。
(0的相反数是0)在数轴上,表示互为相反数的两个点,位于原点的侧,且到原点的距离相等。
数轴上两点表示的数,右边的总比左边的大。
正数在原点的右边,负数在原点的左边。
绝对值的定义:一个数a的绝对值就是数轴上表示数a的点与原点的距离。
数a的绝对值记作|a|。
正数的绝对值是它本身;负数的绝对值是它的数;0的绝对值是0。
或绝对值的性质:除0外,绝对值为一正数的数有两个,它们互为相反数;互为相反数的两数(除0外)的绝对值相等;任何数的绝对值总是非负数,即|a|0比较两个负数的大小,绝对值大的反而小。
比较两个负数的大小的步骤如下:①先求出两个数负数的绝对值;②比较两个绝对值的大小;③根据两个负数,绝对值大的反而小做出正确的判断。
绝对值的性质:①对任何有理数a,都有|a|0②若|a|=0,则|a|=0,反之亦然③若|a|=b,则a=b④对任何有理数a,都有|a|=|-a|有理数加法法则:①同号两数相加,取相同符号,并把绝对值相加。
②异号两数相加,绝对值相等时和为0;绝对值不等时取绝对值较大的数的符号,并用较大数的绝对值减去较小数的绝对值。
③一个数同0相加,仍得这个数。
加法的交换律、结合律在有理数运算中同样适用。
灵活运用运算律,使用运算简化,通常有下列规律:①互为相反的两个数,可以先相加;②符号相同的数,可以先相加;③分母相同的数,可以先相加;④几个数相加能得到整数,可以先相加。
教资科目二第二章必背知识点

教资科目二第二章必背知识点一、知识概述《教育的基本规律》①基本定义:教育的基本规律就是教育内部、教育与其他事物之间一些本质性的关系。
比如教育与人的发展规律,就是说教育如何影响人成长、发展的一些内在关系;教育与社会发展规律,则是阐述教育和社会中的政治、经济、文化等方面存在什么样的相互作用关系。
②重要程度:这部分是教资科目二第二章的核心内容,就相当于一栋房子的地基。
如果不掌握教育的基本规律,后面关于教学、德育等内容的理解都会受到影响,因为这些都要遵循这些基本规律。
③前置知识:需要了解一些基本的教育概念,像教育是什么、教育的目的之类的基础知识。
例如,知道教育是有目的地培养人的社会活动,这样有助于理解教育规律中教育与人的关系。
④应用价值:在实际教学过程中,依据教育与社会发展规律,可以知道根据社会的不同需求调整教学内容和方式。
比如现在社会强调创新能力,那教育就应该增加培养创新能力的课程和活动。
根据教育与人的发展规律,教师能根据学生的年龄特点和身心发展阶段进行因材施教。
二、知识体系①知识图谱:教育的基本规律是整个第二章知识体系的基干部分,其他章节像教学、德育等知识都是在遵循这些规律的基础上展开的。
②关联知识:和教育学中的教学原则、德育原则等知识联系紧密。
例如,教学原则中的因材施教原则就是根据教育与人的发展规律制定的,要根据学生的个体差异来教学。
③重难点分析:- 掌握难度:难。
因为这些规律比较抽象,需要深入理解社会、教育、人的复杂关系。
- 关键点:抓住教育与人、教育与社会的相互影响和作用的关键点。
比如教育是如何促进社会文化传承的,又是怎样受社会经济制约的。
④考点分析:- 在考试中的重要性:非常重要。
一般会以选择题、简答题,甚至辨析题的形式考查。
- 考查方式:选择题可能会出一个实例让选择体现了哪种教育规律;简答题就可能直接让阐述教育与社会发展的关系有哪些。
三、详细讲解(以理论概念类为例)①概念辨析:- 教育与人的发展规律:主要谈教育对人的影响以及人的发展规律对教育的要求。
初二上册第二章讲义

初二上册第二章讲义————————————————————————————————作者:————————————————————————————————日期:ﻩ第二章 实数——认识无理数一、 知识要点1.无理数定义: 无限不循环 小数。
如:圆周率有理数:任何有限小数或无限循环小数,若可以用有限小数或无限循环小数表示的也是有理数。
2.在理解无理数时,要抓住“无限不循环”这一时之,归纳起来有四类:(1)开方开不尽的数,如32,7等;(2)有特定意义的数,如圆周率π,或化简后含有π的数,如3π+8等; (3)有特定结构的数,如0.1010010001…等;(4)某些三角函数值,如si n60o 等。
二、课堂大练兵1.下列说法正确的是( )A .()0是无理数ﻩB.是有理数 C.是无理数 D.是有理数2.下列各数中,是无理数的是( )A .0ﻩB .﹣2ﻩC .ﻩD .3.下列实数中,是无理数的为( )A .0ﻩB. C .3.14ﻩD.4.下列实数中是无理数的是( )A .ﻩB. C. D.3.145.在3.14,,π和这四个实数中,无理数是( )A .3.14和ﻩB.π和 C.和 D.π和第二节 平方根一、知识要点认识平方根、算术平方根1、算术平方根:一般地,如果一个正数x 的平方等于a ,即x2=a,那么这个正数x 就叫做a 的算术平方根。
特别地,0的算术平方根是0。
表示方法:记作“a ”,读作根号a 。
性质:正数和零的算术平方根都只有一个,零的算术平方根是零。
2、平方根:一般地,如果一个数x 的平方等于a,即x2=a ,那么这个数x 就叫做a 的平方根(或二次方根)。
表示方法:正数a的平方根记做“a ±”,读作“正、负根号a ”。
性质:一个正数有两个平方根,它们互为相反数;零的平方根只有零;负数没有平方根。
开平方:求一个数a 的平方根的运算,叫做开平方。
0≥a注意a 的双重非负性:a ≥0二、 课堂大练兵1.在式子()()()230,2,12,20,3,1,2x x y y x x x x y +=--++中,二次根式有( )A . 2个 B. 3个 C. 4个 D. 5个2.下列各式一定是二次根式的是( )A. 7- B. 32m C. 21a + D. a b3.若()424A a=+,则A =( ) A. 24a + B . 22a + C . ()222a + D. ()224a + 4.下列计算正确的是( ) ①69494=-⋅-=--))((;②69494=⋅=--))((; ③145454522=-⋅+=-;④145452222=-=-;A.1个 B .2个 C.3个 D.4个5.9的值等于 ( )A.3 ﻩ B.-3ﻩ C.±3ﻩD. 36.估计的值( ) ﻩA.在2到3之间ﻩB.在3到4之间ﻩC.在4到5之间ﻩD.在5到6之间7.计算 ⑴))((36163--⋅- ⑵63312⋅⋅;⑶)(102132531-⋅⋅ ⑷z y x 10010101⋅⋅-.8.有一个数值转换器,原理如下:当输入的x=64时,输出的y 等于( )A.2 B.8 C. D .9. 25的算术平方根是( )A .5ﻩB.﹣5 C.±5ﻩD. 10.已知:2420-=x ,求221xx +的值.第三节 立方根一、知识要点一般地,如果一个数x的立方等于a ,即x 3=a 那么这个数x 就叫做a 的立方根(或三次方根)。
高中数学-人教A版-必修2-第二章知识点总结

年级高一学科数学版本人教新课标A版课程标题必修2 第二章第1节空间点、直线、平面之间的位置关系编稿老师一校二校审核一、学习目标:1. 掌握平面的表示法及水平放置的直观图;掌握平面的基本性质、作用及公理1-3;2. 了解空间中两条直线的位置关系;理解异面直线的概念、画法,理解并掌握公理4;理解并掌握等角定理;异面直线所成角的定义、范围及应用.3. 了解空间中直线与平面的位置关系;了解空间中平面与平面的位置关系。
二、重点、难点:重点:平面的概念及表示;平面的基本性质,公理1-3中的图形语言及符号语言;异面直线的概念;公理4及等角定理;空间直线与平面、平面与平面之间的位置关系.难点:平面基本性质的掌握与运用;异面直线所成角的计算;用图形表达直线与平面、平面与平面的位置关系.三、考点分析:考纲对这部分知识的要求是:理解空间点、直线和平面的位置关系,掌握平面的基本特性,直线与直线、直线与平面、平面与平面的位置关系。
在考试中对点、线、面位置关系的考查经常出现在选择题中,求异面直线所成的角经常出现在选择题和解答题中。
1. 平面的含义、画法及表示2. 点和面的位置关系点A在平面α内,记作:A∈α点B在平面α外,记作:B α3. 公理1—3(1)公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内符号语言表示为:A lB l l A B ααα∈⎫⎪∈⎪⇒⊂⎬∈⎪⎪∈⎭lαBA公理1作用:判断直线是否在平面内(2)公理2:过不在一条直线上的三点,有且只有一个平面.符号语言表示为:A 、B 、C 三点不共线⇒有且只有一个平面α,使A ∈α、B ∈α、C ∈α.公理2作用:确定一个平面的依据.推论1:过一条直线和直线外一点,有且只有一个平面。
推论2:过两条相交直线,有且只有一个平面。
推论3:过两条平行直线,有且只有一个平面。
(3)公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.符号语言表示为:P ∈α∩β⇒α∩β=l 且P ∈l 公理3作用:判定两个平面是否相交的依据 4. 空间中的两条直线的位置关系异面直线:不同在任何一个平面内,没有公共点. 5. 公理4:平行于同一条直线的两条直线互相平行. 符号表示为:设a 、b 、c 是三条直线c ab c b a //////⇒⎭⎬⎫公理4作用:判断空间两条直线平行的依据. 6. 异面直线所成的角(1)已知异面直线a 、b ,经过空间中任一点O 作直线a'∥a 、b'∥b ,我们把a'与b'所成的锐角(或直角)叫异面直线a 与b 所成的角(夹角).(2)注意:① a'与b'所成的角的大小只由a 、b 的相互位置关系来确定,与O 点的选择无关,为了简便,点O 一般取在两直线中的一条上;② 两条异面直线所成的角θ∈(0,2π]③ 当两条异面直线所成的角是直角时,我们就说这两条异面直线互相垂直,记作a ⊥b ; ④ 两条直线互相垂直,有共面垂直与异面垂直两种情形;⑤ 计算中,通常把两条异面直线所成的角转化为两条相交直线所成的角. 7. 直线与平面的位置关系(1)直线在平面内 —— 有无数个公共点 (2)直线与平面相交 —— 有且只有一个公共点 (3)直线与平面平行 —— 没有公共点直线与平面相交或平行的情况统称为直线在平面外,可用α⊄a 来表示a α⊂ a∩α=A a ∥α8. 两个平面的位置关系(1)两个平面平行——没有公共点(2)两个平面相交——有且只有一条公共直线用类比的方法,可使学生快速地理解与掌握新内容,这两种位置关系用图形语言表示为βααβlα∥β α∩β=l知识点一:确定平面例1. 空间四点可以确定几个平面?三条直线两两相交可确定几个平面?空间四条平行直线可以确定几个平面?一条直线和直线外不在同一条直线上的三点可确定多少个平面?思路分析:利用公理2可以解决确定平面的问题 解答过程:1. 空间四点可以确定0个、1个、4个平面。
【授课】第二章光现象知识点

第二章光现象知识点第一节光的传播一、光源能够发光的物体叫光源。
光源有好多种;按形成原因分,可分为自然光源和人造光源;按发光原理分,可分为热光源和冷光源。
自然光源:太阳、萤火虫、灯笼鱼、斧头鱼、乌贼、水母等。
人造光源:手电筒、火把、油灯、蜡烛、白炽灯、日光灯、霓虹灯以及钠灯、汞灯、氖灯等。
热光源:太阳、手电筒、火把、油灯、蜡烛、电灯等。
冷光源:萤火虫、灯笼鱼、斧头鱼、乌贼、水母等。
【注意】月亮不是光源,月亮本身不发光,只是反射太阳的光。
二、光的直线传播光在真空中或均匀介质中是沿直线传播的。
常见的均匀介质如:空气、水、玻璃等。
【注意】光在不均匀介质中如不均匀的空气、不同介质的界面处,传播方向发生改变。
三、光的速度与光年真空中的光速是宇宙最快的速度,c=3×108m/s。
空气中的光速略小于真空中的光速,约为3×108m/s;光在水中的速度约为真空中光速的3/4;玻璃中的光速约为真空中光速的2/3。
光年是光在一年里传播的距离,因此,光年是距离的单位。
1光年=9.4608×1015m。
第二节光的反射一、光的反射光遇到水面、玻璃以及其他任何物体的表面都会发生反射。
我们看到不发光物体,都是由于它的表面能反射,反射光进入人的眼睛,人就看到了物体。
反射定义:光从一种介质射向另一种介质表面时,有部分光返回原介质的传播现象叫做光的反射。
二、光的反射规律1、垂直于镜面的直线ON叫做法线;如图所示,入射光线于法线的夹角i叫做入射角;反射光线与法线的夹角r叫做反射角。
2、光的反射规律在发射现象中,反射角等于入射角,在反射现象中,光路是可逆的。
3、漫反射和镜面反射(1)凹凸不平的表面把光线向着四面八方反射,这种反射叫做漫反射。
(2)阳光射到镜子上,迎着反射光的方向可以看到刺眼的光,这是因为射到镜子上的平行光线反射后仍然是平行的。
光滑镜面的反射叫做镜面反射。
(3)漫反射和镜面反射都遵守光的反射规律。
八年级数学上册第二章实数复习点整理

八年级数学上册第二章实数复习点整理八年级数学上册第二章实数复习点整理一实数的组成实数又可分为正实数,零,负实数2.数轴:数轴的三要素——原点、正方向和单位长度。
数轴上的点与实数一一对应二相反数、绝对值、倒数1.相反数:只有符号不同的两个数称为相反数。
数a的相反数是-a。
正数的相反数是负数,负数的相反数是正数,零的相反数是零.性质:互为相反数的两个数之和为0。
2.绝对值:表示点到原点的距离,数a的绝对值为3.倒数:乘积为1的两个数互为倒数。
非0实数a的倒数为.0没有倒数。
4.相反数是它本身的数只有0,;绝对值是它本身的数是非负数(0和正数);倒数是它本身的数是±1.三、平方根与立方根1.平方根:如果一个数的平方等于a,这个数叫做a的平方根。
数a的平方根记作(a≥0)特性:一个正数有两个平方根,它们互为相反数,零的平方根还是零。
负数没有平方根。
正数a的正的平方根也叫做a的.算术平方根,零的算术平方根还是零。
开平方:求一个数的平方根的运算,叫做开平方。
2.立方根:如果一个数的立方等于a,则称这个数为a立方根。
数a的立方根用表示。
任何数都有立方根,一个正数有一个正的立方根;一个负数有一个负的立方根,零的立方根是零。
开立方:求一个数的立方根(三次方根)的运算,叫做开立方。
四实数的运算1.有理数的加法法则:a)同号两数相加,取相同的符号,并把绝对值相加;b)异号两数相加。
绝对值相等时和为0;绝对值不相等时,取绝对值较大的数的符号,并用较大的绝对值减去较小的绝对值.任何数与零相加等于原数。
2.有理数的减法法则:减去一个数等于加上这个数的相反数。
3.乘法法则:a)两数相乘,同号得正,异号得负,并把绝对值相乘;零乘以任何数都得零.b)几个不为0的有理数相乘,积的符号由负因数的个数决定,当负因数的个数为奇数时,积为负,为偶数,积为正c)几个数相乘,只要有一个因数为0,积就为04.有理数除法法则:a)两个有理数相除(除数不为0)同号得正,异号得负,并把绝对值相除。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
电离时生成金属阳离子(或铵根离子)和酸
? 根离子的化合物叫做盐。 NaHCO3= 正盐 Na2SO4=2Na+ + SO42-
盐 酸式盐 NaHSO4=Na+ + H+ + SO42-
碱式盐 Cu2(OH)2CO3= 2Cu2+ +2OH- +CO32-
强电解质和弱电解质
电解质:在水溶液或熔融状态下 能导电的化合物。
如:H2SO4、 NaOH、 CuSO4、CaO
酸 、碱、盐、活泼金属氧化物
非电解质:在水溶液和熔融状态下 都不导电的化合物。
如:酒精、蔗糖、CO2 、SO3 、 NH3
非金属氧化物和大部分有机物
思考:为什么电解质在水溶液 或熔融状态下能导电?
因为电解质在水溶液或熔融状态 下自身发生了电离,产生了能够 自由移动的离子。
Fe(OH)3(胶体)+3HCl
胶体的光学性质----丁达尔效应
(2)溶液和胶体的区别
实验:分别用激光照射盛硫酸铜溶液和氢氧
化铁胶体的烧杯,在光束垂直的方向观察现
象。并完成下列表格:
硫酸铜溶液
光束氢照氧化射铁胶时体 的现象
Fe(OH)3胶体
有光亮通路
CuSO4溶液
无光亮通路
产生的原因----光的散射
纯净物
单质
金属单质 非金属单质
Cu
O2
化合物
酸
碱
盐 氧化物
Ba(OH)2 KNO3 CO2
复习
树状分类法:是对同类物质按照属性进一
步细分的方法;
树状分类图的分类原则:同一层次的物质 类别间一般是相互独立,没有交叉的。
交叉分类法:按照事物表现的不同属性,将 一种事物按多种标准进行分类的方法.
Na2CO3
胶体聚沉后可能形成沉淀,也可能形成凝胶态物质
常见胶体及其应用
胶体的应用 (1)静电除尘 (2)土壤的保肥 (3)石膏或卤水点豆腐、制造果冻和皮冻 (4)明矾净水原理 (5)江河入海处形成沙洲 (6)使用蓝色墨水的钢笔抽黑色墨水容易堵塞 (7)喝豆浆放糖不放盐
……
胶体及其应用
思考与交流
向 氢氧化铁胶体中滴加稀硫酸溶液,随着 硫酸量的增多会出现什么现象?说出你的 道理?
一元酸
H2SO4 = 2H+ + SO42-
二元酸
电离时生成的阳离子全部是氢离子 (H+)的化合物叫做酸。
硫酸氢钠的电离方程式如下:
NaHSO4=Na+ + H+ + SO42-
请问:硫酸氢钠是酸吗?为什么?
请写出NaOH、Ca(OH)2电离方程式并从电 离的角度概括出碱的本质。
NaOH = Na+ + OH-
NaCl固体溶于水 熔融盐导电性实验
NaCl=Na+ + Cl-
电离 (1)定义:
电解质溶解于水或受热熔化时,离解 成自由移动的离子的过程。
(2)电离方程式 用离子符号表示电解质电离的式子
电离方程式书写原则: a.遵守质量守恒和电荷守恒 b.原子团不能拆开
请写出HCl、H2SO4的电离方程式:
HCl = H+ + Cl-
100 nm
多数均一 透明
不能
介稳性
能
豆浆、牛奶 墨水、血液
浊液
>100 nm
不均一 不透明
不稳定
不能 不能
泥浆水
思考
胶体为什么具有介稳性?
原因一 胶体粒子可通过吸附离子而带 有相同电性的电荷。
原因二 胶体粒子在不停的做无规则的 运动——布朗运动。
由于胶体粒子带有电荷,如果给胶 体通直流电,胶体粒子向电极作定 向移动,这种现象叫做电泳。
纯净物
物
化合物 溶液 胶体 浊液 混合物
质
一元酸: HCl HNO3
根据电离 的H+数目
二元酸: H2SO4
三元酸: H3PO4
酸
根据是否 含有氧元 素
含氧酸:HNO3 H2SO4 无氧酸:HCl
学习与思考
练习一 按照物质的组成和性质,对纯净物进行分 类,作出树状分类图。然后选择下列合适的物质填在 物质类别上。(O2 Cu Ba(OH)2 KNO3 CO2 空气)
云、雾 烟、灰尘
泡沫
牛奶、酒精的水溶液 油漆
泡沫塑料 珍珠(包藏着水的碳酸钙)
有色玻璃、合金
科学探究
(1)氢氧化铁胶体的制备:
取一个小烧杯,加入25 mL蒸馏水, 加热至沸腾,然后向沸水中滴加5~6滴 FeCl3饱和溶液。继续煮沸至溶液呈红褐 色后,停止加热,即制得Fe(OH)3胶体。
FeCl3+3H2O
化学反应分类
化合反应(A+B=AB)
四种基本反应类型
分解反应(AB=A+B) 置换反应(A+BC=AC+B)
复分解反应(AB+CD=AD+BC)
ቤተ መጻሕፍቲ ባይዱ
氧化还原反应 根据反应中是否有得失氧 非氧化还原反应
离子反应
根据反应中是否有离子参加
非离子反应
树状分类法
金属单质 非金属单质 氧化物
酸
碱
盐
单质
按 物 质 的 组 成
Ca(OH)2 = Ca2+ + 2OH-
电离时生成的阴离子全部是氢氧根 (OH-)的化合物叫做碱。
铜绿的电离方程式如下:
Cu2(OH)2CO3=2Cu2++2OH- +CO32-
请问:铜绿是碱吗?为什么?
请写出NaCl、NH4NO3的电离方程式并概 括出盐的本质:
NaCl = Na+ + Cl-
钠盐
Na2CO3
碳酸盐
二 分散系及其分类
分散系:把一种(或)多种物质分 散在另一种(或多种)物质中得到 的体系。 分散质:被分散的物质; 分散剂:容纳分散质的物质。
分散质+分散剂=分散系
九种组合方式实例分析
分散质 气 液 固 气 液 固 气 液 固
分散剂 气 气 气 液 液 液 固 固 固
实
例
空气
强电解质:在水溶液中全部电离成离子 的电解质(强酸强碱及大多数的盐) 特征: 全部电离 如:NaCl、AgNO3 弱电解质:在水溶液中部分电离成离子的 电解质(弱酸弱碱及少数盐,水) 特征: 部分电离 如:CH3COOH 一些常见的弱电解质:
生活中的丁达尔现象
光线透过树叶间的缝隙射入密林 灯光射入暗室形成的光柱
胶体
胶体:分散质微粒的直径大小在1~100 nm 之间的分散系
浊液、溶液、胶体三种分散系的区别
分散系 分散质 主要 粒子大 特征 小
能否通 能否通 过半透 过滤纸
膜
举例
均一
溶液 <1 nm 透明
能
稳定
能 NaCl溶液
~ 胶体
1
参看P28 图2-8
静电除尘
Fe(OH)3胶体粒 子向阴极移动,
说明胶体粒子带
正电。
使胶体粒子聚集成为较大的颗粒, 从而形成沉淀从分散剂里析出的过 程叫做聚沉。
思考:
1、石膏点豆腐 2、江河在入海口 处形成沙洲
向胶体中加入电解质为什么能使胶体聚沉?
使胶体聚沉的方法:
(1)加入少量电解质溶液 (2)加入带相反电荷胶粒的胶体 (3)加热
