人工智能知识表示与推理博弈树搜索复习课程
人工智能复习题(答案)12768

一:单选题1.人工智能的目的是让机器能够(D),以实现某些脑力劳动的机械化。
A.具有完全的智能B.和人脑一样考虑问题C.完全代替人D.模拟、延伸和扩展人的智能2.下列关于人工智能的叙述不正确的有(C)。
A.人工智能技术它与其他科学技术相结合极大地提高了应用技术的智能化水平。
B.人工智能是科学技术发展的趋势。
C.因为人工智能的系统研究是从上世纪五十年代才开始的,非常新,所以十分重要D.人工智能有力地促进了社会的发展。
3.自然语言理解是人工智能的重要应用领域,下面列举中的(C)不是它要实现的目标。
A.理解别人讲的话。
B.对自然语言表示的信息进行分析概括或编辑。
C.欣赏音乐。
D.机器翻译。
4.下列不是知识表示法的是(A)。
A.计算机表示法B.谓词表示法C.框架表示法D.产生式规则表示法5.关于“与/或”图表示知识的叙述,错误的有(D)。
A.用“与/或”图表示知识方便使用程序设计语言表达,也便于计算机存储处理。
B.“与/或”图表示知识时一定同时有“与结点”和“或结点”。
C.“与/或”图能方便地表示陈述性知识和过程性知识。
D.能用“与/或”图表示的知识不适宜用其他方法表示。
6.一般来讲,下列语言属于人工智能语言的是(D)。
A.VJB.C#C.FoxproD.LISP7.专家系统是一个复杂的智能软件,它处理的对象是用符号表示的知识,处理的过程是(C)的过程。
A.思考B.回溯C.推理D.递归8.确定性知识是指(A)知识。
A.可以精确表示的B.正确的C.在大学中学到的知识D.能够解决问题的9.下列关于不精确推理过程的叙述错误的是(B)。
A.不精确推理过程是从不确定的事实出发B.不精确推理过程最终能够推出确定的结论C.不精确推理过程是运用不确定的知识D.不精确推理过程最终推出不确定性的结论10.我国学者吴文俊院士在人工智能的(A)领域作出了贡献。
A.机器证明B.模式识别C.人工神经网络D.智能代理11.1997年5月12日,轰动全球的人机大战中,“更深的蓝”战胜了国际象棋之子卡斯帕罗夫,这是(C)。
人工智能中的知识表示与推理

人工智能中的知识表示与推理人工智能(Artificial Intelligence,AI)已经成为当今科技领域的热门话题,它迅速改变着我们的生活方式和工作方式。
而在AI的核心技术中,知识表示与推理是至关重要的一环。
本文将探讨人工智能中的知识表示与推理,以及它们在实际应用中的意义和挑战。
一、知识表示知识表示是指将知识以适合计算机理解和处理的形式进行表达。
在人工智能中,常用的知识表示方式有以下几种。
1.符号逻辑表示符号逻辑是指用逻辑符号和规则来表示和处理知识的方法。
它将事物和关系抽象成逻辑符号,通过逻辑推理来达成目的。
例如,利用一阶谓词逻辑可以表示“所有猫都喜欢鱼”,然后通过推理得出“Tom是猫,所以Tom喜欢鱼”。
2.网络表示网络表示使用图结构来表示和处理知识。
图的节点代表事物,边代表事物之间的关系。
例如,使用有向图可以表示“Tom是Jerry的朋友”,节点Tom指向节点Jerry,表示Tom是Jerry的朋友。
3.语义网络表示语义网络是一种特殊的网络表示方法,它将知识以概念和关系的形式进行表达。
概念节点代表事物,关系边代表事物之间的关系。
例如,利用语义网络可以表示“猫是哺乳动物”,节点猫和节点哺乳动物通过关系边连接。
二、推理推理是指根据已知的事实和规则,通过逻辑推导得出新的结论或解决问题的过程。
在人工智能中,常用的推理方法有以下几种。
1.前向推理前向推理是从已知的事实出发,应用规则和逻辑推理,逐步推导得出结论的过程。
它从已知事实出发,逐级扩展,直到无法再得到新结论为止。
2.后向推理后向推理是从目标出发,逐步向前推导,找出能够满足目标的事实和规则。
它逆向推理,直到得到满足目标的结论或无法再向前推导。
3.不确定推理不确定推理是指在处理不完全或不准确的信息时,通过概率推断得到结论的方法。
它可以用于处理模糊、不确定的情况,通过概率模型计算出结论的概率。
三、知识表示与推理的应用知识表示与推理在人工智能的各个领域都有广泛的应用,下面以几个典型的应用为例进行介绍。
人工智能 第3章(确定性推理3-与或树搜索)

包括基于距离的启发式函数、基于成本的启发式函数、基于规则的启发式函数等。
节点排序和选择策略
节点排序的目的和意义
节点排序是为了在扩展节点时,按照一定的顺序选择下一个要扩展的节点,以优化搜索过程。
常用节点排序策略
包括最佳优先搜索、广度优先搜索、深度优先搜索等。最佳优先搜索根据启发式函数的值来选择最优节点; 广度优先搜索按照节点的层次顺序进行扩展;深度优先搜索则尽可能深地扩展节点。
盲目搜索方法比较与选择
• 宽度优先搜索、深度优先搜索和迭代加深搜索都是盲目搜索方法,它们在不同的场景下有不同的应用。 • 宽度优先搜索适用于问题空间较大、解存在于较浅层次的情况,因为它可以逐层遍历整个问题空间,找到最短
路径。 • 深度优先搜索适用于问题空间较小、解存在于较深层次的情况,因为它可以尽可能深地搜索树的分支,找到更
启发式信息获取途径
01
02
03
问题自身的特性
通过分析问题的性质、结 构、约束条件等,提取出 对搜索过程有指导意义的 启发式信息。
领域知识
利用领域内的经验、规则、 常识等,为搜索过程提供 有价值的启发式信息。
搜索过程中的信息
在搜索过程中,通过评估 当前状态、已搜索路径、 未搜索路径等,动态地获 取启发式信息。
04 与或树搜索优化技术
剪枝策略
01
剪枝的定义和目的
剪枝是在搜索过程中,通过某些评估标准,提前终止对某些无意义或低
效的节点的扩展,以减少搜索空间,提高搜索效率。
02 03
常用剪枝策略
包括限界剪枝、启发式剪枝、概率剪枝等。限界剪枝通过设置上下界来 限制搜索范围;启发式剪枝利用启发式函数来评估节点的重要性;概率 剪枝则根据节点的概率分布来进行剪枝。
人工智能--确定性推理 ppt课件

ppt课件
21
流程图
ppt课件
22
注意几点:
①搜索过程产生的节点和指针构成一棵隐式定义的 状态空间树的子树,称之为搜索树
ppt课件
23
② 宽度优先搜索方法能够保证在搜索树中找到 一条通向目标节点的最短途径(所用操作符 最少)
ppt课件
24
例:八数码问题
初始状态
283
1
4
765
目标状态
123
8
初始节点
目标状态
目标节点
操作符
有向弧
ppt课件
7
解的含义:
在状态空间中,解是从初始状态到目标状态的 操作符序列
在图中,解是从初始节点到目标节点的一条路 径
ppt课件
8
必须记住哪下从些一目 点步标走还返过可回了以的走路哪径 些点
状态:(城市名) 算子:常德→益阳
益阳→常德 益阳汨罗 益阳宁乡 益阳娄底 …
是否会认为老师的教学方法需要改进? • 你所经历的课堂,是讲座式还是讨论式? • 教师的教鞭 • “不怕太阳晒,也不怕那风雨狂,只怕先生骂我
笨,没有学问无颜见爹娘 ……” • “太阳当空照,花儿对我笑,小鸟说早早早……”
解决实际问题的两个关键之处:
①问题的表达 状态空间法 问题归约法 谓词逻辑法
②问题的求解 搜索技术
P-1
P
P+1
P+3
ppt课件
27
空格移动规则
顺序 规则
1
左移
2
上移
3
下移
4
右移
前提条件
应用结果
P≠1,4,7 P 位置与 P-1 位置上的元素互换
P≠1,2,3
《人工智能》课程简介

《人工智能》课程简介
课程目标:
人工智能是研究如何利用计算机来模拟人脑所从事的感知、推理、学习、思考、规划等人类智能活动,来解决需要用人类智能才能解决的问题,以延伸人们智能的科学。
掌握人工智能的基本概念、基本原理、知识的表示、推理机制和求解技术,以及机器学习的技术方法. 掌握人工智能的一个问题和三大技术,即通用问题求解和知识表示技术、搜索技术、推理技术。
课程主要内容:
1.搜索技术
✧图搜索技术
✧盲目搜索算法(宽度优先搜索、深度优先搜索、均一代价搜索)
✧启发式搜索算法(登山法、分支界限法、动态规划法、A算法、A*算法)
✧与或图搜索(AO*搜索)
✧博弈树搜索(极大极小法,剪枝的?-?剪枝法)
✧高级搜索技术(遗传算法)
2. 归结推理方法
✧谓词逻辑表达式
✧谓词逻辑归结原理
✧Herbrand定理。
3.知识表示方法
✧产生式规则表示法
✧语义网络表示法
✧框架表示法
✧脚本方法
✧过程表示
✧直接表示
4.机器学习
✧实例学习
✧解释的学习
✧决策树学习
✧神经网络学习(人工神经网络的结构、模型,解BP算法)。
人工智能复习题(答案)

一:单选题1. 人工智能的目的是让机器能够(D),以实现某些脑力劳动的机械化。
A. 具有完全的智能B. 和人脑一样考虑问题C. 完全代替人D. 模拟、延伸和扩展人的智能2. 下列关于人工智能的叙述不正确的有(C)。
A. 人工智能技术它与其他科学技术相结合极大地提高了应用技术的智能化水平。
B. 人工智能是科学技术发展的趋势。
C. 因为人工智能的系统研究是从上世纪五十年代才开始的,非常新,所以十分重要。
D. 人工智能有力地促进了社会的发展。
3. 自然语言理解是人工智能的重要应用领域,下面列举中的(C)不是它要实现的目标。
A. 理解别人讲的话。
B. 对自然语言表示的信息进行分析概括或编辑。
C. 欣赏音乐。
D. 机器翻译。
4. 下列不是知识表示法的是(A)。
A. 计算机表示法B. 谓词表示法C. 框架表示法D. 产生式规则表示法5. 关于“与/或”图表示知识的叙述,错误的有(D)。
A. 用“与/或”图表示知识方便使用程序设计语言表达,也便于计算机存储处理。
B. “与/或”图表示知识时一定同时有“与结点”和“或结点”。
C. “与/或”图能方便地表示陈述性知识和过程性知识。
D. 能用“与/或”图表示的知识不适宜用其他方法表示。
6. 一般来讲,下列语言属于人工智能语言的是(D)。
A. VJB. C#C. FoxproD. LISP7. 专家系统是一个复杂的智能软件,它处理的对象是用符号表示的知识,处理的过程是(C)的过程。
A. 思考B. 回溯C. 推理D. 递归8. 确定性知识是指(A)知识。
A. 可以精确表示的B. 正确的C. 在大学中学到的知识D. 能够解决问题的9. 下列关于不精确推理过程的叙述错误的是(B)。
A. 不精确推理过程是从不确定的事实出发B. 不精确推理过程最终能够推出确定的结论C. 不精确推理过程是运用不确定的知识D. 不精确推理过程最终推出不确定性的结论10. 我国学者吴文俊院士在人工智能的(A)领域作出了贡献。
《人工智能》课程教学大纲
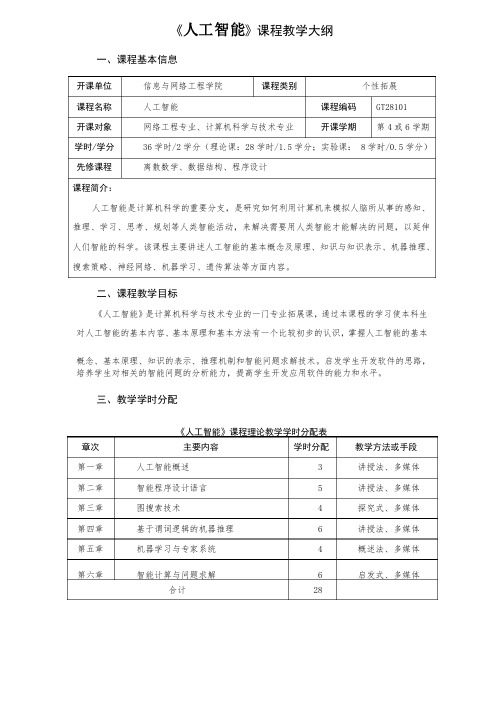
《人工智能》课程教学大纲一、课程基本信息开课单位 信息与网络工程学院 课程类别 个性拓展课程名称 人工智能课程编码 GT28101 开课对象 网络工程专业、计算机科学与技术专业开课学期第4或6学期学时学时//学分 36学时学时/2/2学分(理论课:学分(理论课:2828学时学时/1.5/1.5学分;实验课:学分;实验课: 8 8学时学时/0.5/0.5学分) 先修课程 离散数学、数据结构、程序设计课程简介:人工智能是计算机科学的重要分支,是研究如何利用计算机来模拟人脑所从事的感知、推理、学习、思考、规划等人类智能活动,来解决需要用人类智能才能解决的问题,以延伸人们智能的科学。
该课程主要讲述人工智能的基本概念及原理、知识与知识表示、机器推理、搜索策略、神经网络、机器学习、遗传算法等方面内容。
二、课程教学目标《人工智能》是计算机科学与技术专业的一门专业拓展课,通过本课程的学习使本科生对人工智能的基本内容、基本原理和基本方法有一个比较初步的认识,掌握人工智能的基本概念、基本原理、知识的表示、推理机制和智能问题求解技术。
启发学生开发软件的思路,培养学生对相关的智能问题的分析能力,提高学生开发应用软件的能力和水平。
三、教学学时分配《人工智能》课程理论教学学时分配表章次 主要内容学时分配教学方法或手段 第一章 人工智能概述 3 讲授法、多媒体 第二章 智能程序设计语言 5 讲授法、多媒体 第三章 图搜索技术4 探究式、多媒体 第四章 基于谓词逻辑的机器推理 6 讲授法、多媒体 第五章 机器学习与专家系统 4 概述法、多媒体 第六章智能计算与问题求解6 启发式、多媒体合计28《人工智能》课程实验内容设置与教学要求一览表序号实验项目名称实验内容教学要求学时分配实验类别实验类型每组人数实实验一 一分支与循环程序设计1) Prolog 运行环境; 2)2)利用利用PROLOG 进行事实库、规则库的编写; 3)3)分支程序设计;分支程序设计;4)4)循环程序设计;循环程序设计;5)5)输入出程序设计。
人工智能中的知识表示与推理技术

人工智能中的知识表示与推理技术人工智能中的知识表示和推理技术是人工智能领域中的两个重要方面。
知识表示是指将事物、概念、关系等抽象的信息以某种形式进行表达和存储的过程。
推理技术是指利用已有的知识进行逻辑上的推理和演绎,从而得出新的结论或解决问题的过程。
本文将介绍人工智能中常用的知识表示与推理技术,并探讨其在人工智能应用中的重要性和应用场景。
一、知识表示技术1.逻辑表示逻辑表示是一种使用逻辑语言描述知识的方法。
其中,一阶逻辑是最常用的逻辑表示形式,它使用谓词逻辑描述事实、规则和约束等知识。
二阶逻辑和高阶逻辑则更为复杂,可以用于表示更复杂的知识和关系。
2.语义网络语义网络是使用图结构表示知识的一种方式,其中节点表示概念或实体,边表示概念或实体之间的关系。
语义网络可以用于表示结构化的知识,并且方便进行关系的推理和查询。
3.本体论本体论是一种用于描述和组织领域知识的方式,它定义了一种公共的、精确的术语和概念的语义结构。
本体论可以用于知识的共享和交流,同时也能够支持知识的推理和查询。
4.语义表达语义表达是一种使用语义标记和符号描述知识的方法。
常见的语义表达方法包括基于XML的标记语言、RDF和OWL等语义描述语言。
语义表达可以使计算机理解和处理知识,从而支持知识的推理和应用。
二、推理技术1.基于规则的推理基于规则的推理是最常见的推理方法之一,它使用一组规则来描述知识和推理过程。
推理引擎根据这些规则对已有的知识进行逻辑推理和演绎,从而得出新的结论或解决问题。
2.神经网络推理神经网络推理是利用神经网络模型进行推理和决策的方法。
神经网络通过学习和迭代更新权重,可以对输入数据进行分类、预测和推理。
神经网络推理在图像、语音和自然语言处理等领域有广泛应用。
3.不确定推理不确定推理是一种处理不完全或不确定信息的推理方法,它考虑到知识的不完整性、不确定性和不一致性。
常用的不确定推理方法包括贝叶斯网络、模糊逻辑和模糊推理等。
人工智能复习总结讲解

➢ 综合数据库,用于存放求解过程中各种当前信息的数据结构,如问题是的初始状态、
事实或证据、中间推理结论和最后结果等。
➢ 规则库,用于存放与求解问题有关的某个领域知识的规则之集合及其交换规则。
➢
其基本形式为
•
IF 前提 THEN 结论
➢ 控制策略的作用是说明下一步应该选用什么规则。
2.2.4 语义网络法
3.3 启发式搜索 ➢ 盲目搜索的不足:效率低,耗费过多的计算空间与时间。 ➢ 宽度优先、深度优先搜索,或代价树搜索算法,其主要的差别是 OPEN 表中待扩展节 点的顺序问题。人们就试图找到一种方法用于排列待扩展节点的顺序,即选择最有 希望的节点加以扩展,那么,搜索效率将会大为提高。 ➢ 启发信息:进行搜索技术一般需要某些有关具体问题领域的特性的信息。 ➢ 把利用启发信息的搜索方法叫做启发式搜索方法。 ➢ 启发式搜索策略 ➢ 启发信息用于决定要扩展的下一个节点, ➢ 这种搜索总是选择“最有希望”的节点作为下一个被扩展的节点。
(4)喜欢读《三国演义》的人必读《水浒》。
定义谓词:
MAN(x):x 是人。
LIKE(x,y):x 喜欢读 y。
(x)(MAN(x)∧LIKE(x, 《SANGUOYANYI》)
→LIKE(x, 《SHUIHU》))
(5)有的人喜欢梅花,有的人喜欢菊花,有的人既喜欢梅花又喜欢菊花。
定义谓词:
MAN(x):x 是人。
例: 一个用来描述硕士生有关情况的框架 Frame <硕士生>
姓名: 单位(姓,名) 性别:范围(男,女)
默认:男 年龄:单位(岁)
条件:岁>16 学习专业:单位(专业名)
研究方向:单位(方向名) 导师姓名:单位(姓,名) 参加课题:范围(国家级,省部级,其他)
人工智能培训课件(ppt 51页)

• 定义6 人工智能是用计算模型研究智力行为 (Charniak和McDermott,1985)。
• 定义7 人工智能是研究那些使理解、推理和行为成为 可能的计算(Winston,1992)。
– 专家系统
– 知识工程
– 知识工程席卷全球
– 各国发展计划:
• 美国星球大战计划
• 英国ALVEY计划
• 法国UNIKA 计划
• 例子2:能够进行深海探测的潜水机器人。
• 例子3:在星际探险中的移动机器人,如美国研制的
火星探测车。
9
1.1.1 人工智能的定义
• 定义2 人工智能(学科) 人工智能(学科)是计算机科学中涉及研究、设计
和应用智能机器的一个分支。它的近期主要目标在于 研究用机器来模仿和执行人脑的某些智力功能,并开 发相关理论和技术。 • 定义3 人工智能(能力)
Artificial Intelligence 人计工算智机科能学与应用专业
计算机科学与技术专业
1
课程简介
1. 本课程较系统地介绍人工智能的基本概念、原理和 方法,为学生研究或应用人工智能技术打下基础。
2. 掌握人工智能基本原理,包括人工智能的两大支柱: 搜索技术(盲目搜索、启发式搜索)和知识表示 (知识表示和推理方法:一阶谓词逻辑,即命题演 算和谓词演算)及其计算机实现。
人工智能(能力)是智能机器所执行的通常与人类 智能有关的智能行为,如判断、推理、证明、识别、 感知、理解、通信、设计、思考、规划、学习和问题 求解等思维活动。
10
其它几种关于人工智能的定义
• 定义4 人工智能是一种使计算机能够思维,使机器具 有智力的激动人心的新尝试(Haugeland,1985)。
研究生第2章知识表示与推理6-与或树搜索

2024/2/20
2.3.1 与或树盲目搜索技术
问题归约法
与或图
原始问题
起始节点
中间问题
中间节点
本原问题集
终叶节点
操作符
2024/2/20
生成“与”、“ 或” 后继节点的有向弧
可解节点的定义是(递归地):
2024/2/20
(4)、 扩 展 节 点 n , 生 成 其 全 部 后 继 节 点 , 送 OPEN表末端,并设置指向 n 的指针
说明:此时可能出现三种情况 ➢节点 n 无后继节点 ➢节点 n 有后继节点、并有叶节点 ➢节点 n 有后继节点、但无叶节点
2024/2/20
(5)、若 n 无后继节点,标志 n 为不可解,并转(9) ((10)、(11));若后继节点中有叶节点,则标 志这些叶节点为可解节点,并继续((6)、(7)、 (8));否则转(3)
2024/2/20
第五大循环((3)、(4)、(5)步): (3)、从OPEN表中取出节点5,并送到CLOSED表 (4)、扩展节点5,生成后继节点B、C,并送到
OPEN表的末端 (5)、无叶节点,转到(3)步
OPEN= { 6, 7, 8, 9, B, C } CLOSED= { 1 , 2, 3, 4, 5 }
说明: 先扩展的节点画在左边
√
1
√
2
3
X
√
5
6
7
t
1
X
t
t
2
3
√√
√
1
√
2
√
3
X
√
人工智能.ppt

图的搜索技术: ➢盲目搜索技术 ➢启发式搜索技术
差别: ✓选取待扩展节点的规则不同
2020/10/23
盲目搜索技术
宽度优先:先扩展出来的节点优先(OPEN 为队 列)
深度优先:后者扩展出来的节点优先(OPEN 为 堆栈) ,有深度限制
代价优先:到起始节点代价小的节点优先 ( OPEN 为线性表)
定理证明的过程、编写简单的Prolog程序
2020/10/23
本课程的三大部分:
➢问题求解 ➢谓词逻辑 ➢计算智能
2020/10/23
2020/10/23
消解原理的应用: ➢定理的证明(前提结论) ➢回答问题
Visual Prolog语言
2020/10/23
要求掌握的算法: ✓ 图的宽度优先、深度优先、代价优先、有序搜
索算法 ✓ 与或树的宽度优先、深度优先搜索算法 ✓ 博弈树的极大极小过程 ✓ 谓词公式化成子句集、合一算法、消解原理、
用倒推的方法(自己下的棋取大者,对手下 的棋取小者)计算出其余各层节点的静态估 计函数值,最后决定走哪一步棋
2020/10/23
-剪枝过程:用深度优先策略来扩展节点,同 时进行函数值的倒推,省去某些比当前结果更差 的棋局
2020/10/23
4 谓词逻辑法与消解原理 ➢谓词公式化成子句集(九步) ➢合一算法求出最一般的合一者(mgu) ➢消解原理
2020/10/23
启发式搜索技术 有序算法:估价函数值小的节点优先 A*算法:估价函数值小的节点优先,启发函
数以最佳启发函数为上界,即 h(n) ≤ h*(n)
2020/10/23
2 问题归约法,与或树和与或图搜索技术 问题归约法表示问题的关键:原始问题、本原问题、
《人工智能》课程教学大纲(本科)
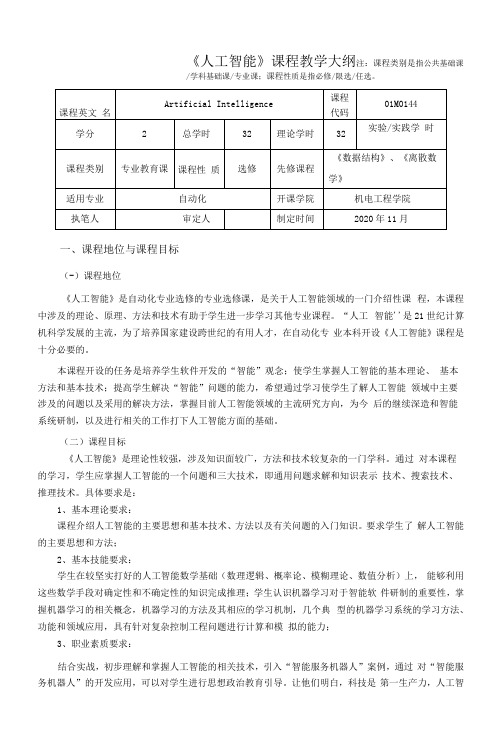
《人工智能》课程教学大纲注:课程类别是指公共基础课/学科基础课/专业课;课程性质是指必修/限选/任选。
一、课程地位与课程目标(-)课程地位《人工智能》是自动化专业选修的专业选修课,是关于人工智能领域的一门介绍性课程,本课程中涉及的理论、原理、方法和技术有助于学生进一步学习其他专业课程。
“人工智能''是21世纪计算机科学发展的主流,为了培养国家建设跨世纪的有用人才,在自动化专业本科开设《人工智能》课程是十分必要的。
本课程开设的任务是培养学生软件开发的“智能”观念;使学生掌握人工智能的基本理论、基本方法和基本技术;提高学生解决“智能”问题的能力,希望通过学习使学生了解人工智能领域中主要涉及的问题以及采用的解决方法,掌握目前人工智能领域的主流研究方向,为今后的继续深造和智能系统研制,以及进行相关的工作打下人工智能方面的基础。
(二)课程目标《人工智能》是理论性较强,涉及知识面较广,方法和技术较复杂的一门学科。
通过对本课程的学习,学生应掌握人工智能的一个问题和三大技术,即通用问题求解和知识表示技术、搜索技术、推理技术。
具体要求是:1、基本理论要求:课程介绍人工智能的主要思想和基本技术、方法以及有关问题的入门知识。
要求学生了解人工智能的主要思想和方法;2、基本技能要求:学生在较坚实打好的人工智能数学基础(数理逻辑、概率论、模糊理论、数值分析)上,能够利用这些数学手段对确定性和不确定性的知识完成推理;学生认识机器学习对于智能软件研制的重要性,掌握机器学习的相关概念,机器学习的方法及其相应的学习机制,几个典型的机器学习系统的学习方法、功能和领域应用,具有针对复杂控制工程问题进行计算和模拟的能力;3、职业素质要求:结合实战,初步理解和掌握人工智能的相关技术,引入“智能服务机器人”案例,通过对“智能服务机器人”的开发应用,可以对学生进行思想政治教育引导。
让他们明白,科技是第一生产力,人工智能作为一个关键技术,会影响一个国家的格局和国际竞争力。
AI实验4-博弈树搜索

4实验四博弈树搜索(一)实验名称:博弈树搜索(二)目的:熟悉和掌握博弈树搜索算法过程,包括极小极大分析法和α-β剪枝方法,理解求解流程。
(三)原理:极小极大分析法实际是先生成一棵博弈树,然后再计算其倒推值。
但是极小极大分析法效率较低,于是在其基础上提出了α-β剪枝技术。
α-β剪枝技术的基本思想或算法是,边生成博弈树边计算评估各节点的倒推值,并且根据评估出的倒推值范围,及时停止扩展那些已无必要再扩展的子节点,即相当于剪去了博弈树上的一些分枝,从而节约了机器开销,提高了搜索效率。
(四)步骤:极大极小过程的基本思路:①对于每一格局(棋局)给出(定义或者倒推)一个静态估价函数值。
值越大对MAX越有利,反之越不利②对于给定的格局,MAX给出可能的走法,然后MIN对应地给出相应的走法,这样重复若干次,得到一组端节点(必须由MIN走后得到的,由MAX下的棋局)。
这一过程相当于节点扩展③对于每一个端节点,计算出它们的静态估价函数,然后自下而上地逐层计算倒推值,直到MAX开始的格局。
在MIN下的格局中取估值的最小值,在MAX下的格局中取估值的最大值④取估值最大的格局作为MAX要走的一招棋符号:✓OPEN:存放待扩展的节点,此时为队列,即以宽度优先的策略扩展节点✓CLOSED:存放已扩展的节点,此时为堆栈,即后扩展的节点先计算静态估价函数值算法分成两个阶段:第一阶段:用宽度优先算法生成规定深度k的全部博弈树,然后对其所有端节点计算e(P) 第二阶段:自下而上逐级求节点的倒推估价值,直至求出初始节点的e(S) 为止,再由e(S) 选得相对较好的走法,过程结束12(五)实验结果与分析:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
0 e(P)0
0
MAX占优,MIN不利 势均力敌
MAX不利,MIN占优
2020/6/3
符号:
✓ OPEN:存放待扩展的节点,此时为队列, 即以宽度优先的策略扩展节点
✓ CLOSED:存放已扩展的节点,此时为堆栈, 即后扩展的节点先计算静态估价函数值
2020/6/3
极大极小搜索过程为: 1、将初始节点 S 放入 OPEN 表中,开始时搜索
对于比较复杂的博弈问题,只能模拟人的思维 “向前看几步”,然后作出决策,选择最有利自 己的一步。即只能给出几层走法,然后按照一定 的估算办法,决定走一好招
2020/6/3
2.4.2 极大极小过程 对于复杂的博弈问题,要规定搜索深度与时间, 以便于博弈搜索能顺利进行
假设由MAX来选择走一步棋,问题是: MAX如何来选择一步好棋?
但是,从MAX的角度出发,所有使MAX获胜的 状态格局都是本原问题,是可解节点,而使MIN 获胜的状态格局是不可解节点
2020/6/3
例 Grundy博弈:分配物品的问题
如果有一堆数目为N的钱币,由两位选手轮流进 行分配,要求每个选手每次把其中某一堆分成数 目不等的两小堆,直至有一选手不能将钱币分成 不等的两堆为止,则判定这位选手为输家
2020/6/3
6、若 np 属于MAX层,且对于它的属于MIN层
的子节点 nci 的 e ( nci )有值,则: e ( np ) =max { nci }
某一个节点属于MAX的含义 是该节点等待MAX来扩展
2020/6/3
(续) 若 np 属于MIN层,且对于它的属于MAX层的子 节点 nci 的 e ( nci )有值,则:
双人博弈:即两位选手对垒,轮流依次走步,
其中任何一方都完全知道对方过去已经走过的 棋步和今后可能的走步,其结果是一方赢(而另 一方则输),或双方和局
2020/6/3
博弈的例子: ➢ 一字棋 ➢ 跳棋 ➢ 中国象棋 ➢ 围棋 ➢ 五子棋
2020/6/3
人工智能中研究的博弈问题:
如何根据当前的棋局,选择对自己最有利的 一步棋 ?!
人工智能
Artificial Intelligence (AI)
曲维光 wgqu@ 南京师范大学计算机学院
2020/6/3
ቤተ መጻሕፍቲ ባይዱ
2.4 博弈问题的搜索技术 2.4.1 博弈问题的表达 2.4.2 极大极小搜索过程 2.4.3 - 剪枝法
2020/6/3
2.4.1 博弈问题的表达
博弈是一类具有竞争性的智能活动
2020/6/3
极大极小过程的基本思路:
① 对于每一格局(棋局)给出(定义或者倒推) 一个静态估价函数值。值越大对MAX越有利,反 之越不利
2020/6/3
② 对于给定的格局,MAX给出可能的走法,然 后MIN对应地给出相应的走法,这样重复若干次, 得 到 一 组 端 节 点 ( 必 须 由 MIN 走 后 得 到 的 , 由 MAX下的棋局)。这一过程相当于节点扩展 注:博弈树深度或层数一定是偶数
2020/6/3
博弈问题的表示:
用博弈树来表示,它是一种特殊的与或图。节点 代表博弈的格局(即棋局),相当于状态空间中 的状态,反映了博弈的信息。 与节点、或节点 隔层交替出现
2020/6/3
为什么与节点、或节点隔层交替出现?
假设博弈双方为:MAX和MIN 在博弈过程中,规则是双方轮流走步。在博弈 树中,相当于博弈双方轮流扩展其所属节点
2020/6/3
(续) 此时,若搜索深度d{ ni }小于预先设定的深度 k, 则将{ ni }放入OPEN表的末端,转2;否则,ni 达到深度k,计算e ( ni ),并转2
2020/6/3
步2
Open为空,即已经扩展完节点
5、若CLOSED表 为空 ,则转8;否则取出
CLOSED表中的第一个节点,记为 np
树 T 由初始节点 S 构成
2、若 OPEN 表为空,则转5
3 、 将 OPEN 表 中 第 一 个 节 点 n 移 出 放 入
CLOSED 表的前端
2020/6/3
4、若 n 可直接判定为赢、输、或平局,则令对
应的 e(n)=∞,-∞或 0,并转2;否则扩展 n, 产生 n 的后继节点集 { ni },将{ ni }放入搜索树 T中
2020/6/3
用数字序列加上一个说明来表示一个状态: (3, 2, 1, 1, MAX)
数字序列:表示不同堆中钱币的个数 说明:表示下一步由谁来分,即取MAX或MIN
2020/6/3
现在取N=7的简单情况,并由MIN先分
(7,MIN)
所有可能的分法
(6,1,MAX)
(5,2,MAX)
(4,3,MAX)
理由:
因为扩展MAX方节点时,MAX方可选择扩展最 有利于自己的节点,只要可扩展的子节点中有 一个对已有利, 则该节点就对已有利
2020/6/3
总之 从MAX方来说,与节点、或节点交替出现;反之, 从MIN方的角度来看,情况正好相反
2020/6/3
在博弈树中,先行一方的初始状态对应着树的根 节点,而任何一方获胜的最终格局为目标状态, 对应于树的终叶节点(可解节点或本原问题)
2020/6/3
从MAX方的角度来看:
MIN
所有MIN方节点都是与节点
好招
理由:
因为MIN方必定选择最不利于MAX方的方式来 扩展节点,只要MIN方节点的子节点中有一个 对MAX方不利,则该节点就对MAX方不利,故 为“与节点”
2020/6/3
MAX
从MAX方的角度来看:
所有属于MAX方的节点都是“或节点” 好招
2020/6/3
③ 对于每一个端节点,计算出它们的静态估价函 数,然后自下而上地逐层计算倒推值,直到MAX 开始的格局。在MIN下的格局中取估值的最小值, 在MAX下格局中取估值的最大值 ④ 取估值最大的格局作为MAX要走的一招棋
2020/6/3
例:向前看一步的两层博弈树
2020/6/3
定义静态函数e(P)的一般原则:
(5,1,1,MIN)
(4,2,1,MIN)
(3,2,2,MIN)
(3,3,1,MIN)
(4,1,1,1,MAX) (3,1,1,1,1,MIN)
(3,2,1,1,MAX)
(2,2,2,1,MAX)
(2,2,1,1,1,MIN)
(2,1,1,1,1,1,MAX)
注:2020如/6/3 果MAX走红箭头的分法,必定获胜
