2019年哈尔滨市中考数学试题及答案
2019年黑龙江省哈尔滨市中考数学试卷(含答案)

考点: 一元二次方程的解. 专题: 计算题.
分析: 根据 x=﹣1 是已知方程的解,将 x=﹣1 代入方程即可求出 m 的值.
解答: 解:将 x=﹣1 代入方程得:1﹣3+m+1=0, 解得:m=1.
黑龙江省哈尔滨市 2019 年中考数学试卷
一、选择题(共 10 小题,每小题 3 分,满分 30 分)
1.(3 分)(2019 年黑龙江哈尔滨)哈市某天的最高气温为 28℃,最低气温为 21℃,则这一天的最高气温与
最低气温的差为( )
A.5℃
B.6℃
C.7℃
D.8℃
分析: 根据有理数的减法,减去一个数等于加上这个数的相反数,可得答案.
A.6
B.4
C.3
D.3
考点: 旋转的性质. 分析: 利用直角三角形的性质得出 AB=4,再利用旋转的性质以及三角形外角的性质得出 AB′=2,进而 得出答案. 解答: 解:∵在 Rt△ABC 中,∠ACB=90°,∠B=60°,BC=2, ∴∠CAB=30°,故 AB=4, ∵△A′B′C 可以由△ABC 绕点 C 顺时针旋转得到,其中点 A′与点 A 是对应点,点 B′与点 B 是对应点,连接 AB′,且 A、B′、A′在同一条直线上, ∴AB=A′B′=4,AC=A′C, ∴∠CAA′=∠A′=30°, ∴∠ACB′=∠B′AC=30°, ∴AB′=B′C=2, ∴AA′=2+4=6. 故选:A. 点评: 此题主要考查了旋转的性质以及直角三角形的性质等知识,得出 AB′=B′C=2 是解题关键. 10.(3 分)(2019 年黑龙江哈尔滨)早晨,小刚沿着通往学校唯一的一条路(直路)上学,途中发现忘带饭 盒,停下往家里打电话,妈妈接到电话后带上饭盒马上赶往学校,同时小刚返回,两人相遇后,小刚立即 赶往学校,妈妈回家,15 分钟妈妈到家,再经过 3 分钟小刚到达学校,小刚始终以 100 米/分的速度步行, 小刚和妈妈的距离 y(单位:米)与小刚打完电话后的步行时间 t(单位:分)之间的函数关系如图,下列 四种说法: ①打电话时,小刚和妈妈的距离为 1250 米;
【数学】2019年黑龙江省哈尔滨市中考真题(解析版)

黑龙江省哈尔滨市2019年中考试卷试卷第I 卷选择题(共30分)一、选择题(每小题3分,共计30分) 1.-9的相反数是( ) (A )-9 (B )-91(C )9 (D )91 【答案】C【解析】﹣9的相反数是9,故选:C . 2.下列运算一定正确的是( ). (A )2222a a a =+ (B )632a a a =• (C )6326)2(a a =(D )22))((b a b a b a -=-+【答案】D【解析】2a +2a =4a ,A 错误;a 2•a 3=a 5,B 错误;(2a 2)3=8a 6,C 错误;故选:D . 3.下列图形中既是轴对称图形又是中心对称图形的是( ).【答案】B【解析】A .是轴对称图形,但不是中心对称图形,故此选项错误; B .是中心对称图形,也是轴对称图形,故此选项正确; C .是轴对称图形,不是中心对称图形,故此选项错误;D .是轴对称图形,不是中心对称图形,故此选项错误.故选:B . 4.七个大小相同的正方体搭成的几何体如图所示,其左视图是( ).【答案】B【解析】这个立体图形的左视图有2列,从左到右分别是2,1个正方形, 故选:B .5.如图,P A ,PB 分别与⊙O 相切于A ,B 两点,点C 为⊙O 上一点,连接AC ,BC ,若∠P =50°,则∠ACB 的度数为( )(A )60° (B )75°(C )70°(D )65°【答案】D【解析】连接OA ,OB ,∵P A ,PB 分别与⊙O 相切于A ,B 两点, ∴OA ⊥P A ,OB ⊥PB , ∴∠OAP =∠OBP =90°,∴∠AOB =180°﹣∠P =180°﹣50°=130°, ∴∠ACB =∠AOB =×130°=65°. 故选:D .6.将抛物线22x y =向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( )(A )3)2(22++=x y (B )3)2(22+-=x y (C )3)2(22--=x y(D )3)2(22-+=x y【答案】B【解析】将抛物线y =2x 2向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式为y =2(x ﹣2)2+3,故选:B .7.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ). (A )20% (B )40% (C )18%(D )36%【答案】A【解析】设降价的百分率为x 根据题意可列方程为25(1﹣x )2=16 解方程得,(舍)∴每次降价得百分率为20% 故选:A .8.方程x x 3132=-的解为( ) (A )x =113 (B )x =311(C )x =73(D )x =37 【答案】C 【解析】xx 3132=-,∴2x =9x ﹣3, ∴x =73; 将检验x =73是方程的根, ∴方程的解为x =73;故选:C .9.点(-1,4)在反比例函数 的图象上,则下列各点在此函数图象上的是( )【答案】A【解析】将点(﹣1,4)代入y =, ∴k =﹣4, ∴y =,∴点(4,﹣1)在函数图象上, 故选:A .10.如图,在平行四边形ABCD 中,点E 在对角线BD 上,EM ∥AD ,交AB 于点M ,EN ∥AB ,交AD 于点N ,则下列式子一定正确的是( )(A )DE NEBM AM =(B )AD ANAB AM =(C )BDBE ME BC =(D )EMBC BE BD =【答案】D【解析】∵在▱ABCD 中,EM ∥AD ∴易证四边形AMEN 为平行四边形 ∴易证△BEM ∽△BAD ∽△END ∴==,A 项错误=,B 项错误 ==,C 项错误 ==,D 项正确故选:D .第Ⅱ卷非选择题(共90分)二、填空题(每小题3分,共计30分)11.将数6 260 000科学记数法表示为_______________. 【答案】6.26×106【解析】6260000用科学记数法可表示为6.26×106,故答案为:6.26×106. 12.在函数323-=x xy 中,自变量x 的取值范围是_______________. 【答案】x ≠ 【解析】函数323-=x xy 中分母2x ﹣3≠0,∴x ≠; 故答案为x ≠.13.分解因式:22396ab b a a +-=_______________. 【答案】a (a ﹣3b )2 【解析】a 3﹣6a 2b +9ab 2=a (a 2﹣6ab +9b 2) =a (a ﹣3b )2. 故答案为:a (a ﹣3b )2.14.不等式组⎪⎩⎪⎨⎧≥+≤-123023x x的解集是________________.【答案】x ≥3 【解析】解不等式≤0,得:x ≥3,解不等式3x +2≥1,得:x ≥﹣, ∴不等式组的解集为x ≥3, 故答案为:x ≥3.15.二次函数8)6(2+--=x y 的最大值是_______________. 【答案】8【解析】∵a =﹣1<0, ∴y 有最大值,当x =6时,y 有最大值8. 故答案为8.16.如图将△ABC 绕点C 逆时针旋转得到△A ′B ′C ,其中点A ′与A 是对应点,点B ′与B 是对应点,点B ′落在边AC 上,连接A ′B ,若∠ACB =45°,AC =3,BC =2,则A ′B 的长为____.【答案】【解析】∵将△ABC 绕点C 逆时针旋转得到△A ′B ′C , ∴AC =A 'C =3,∠ACB =∠ACA '=45° ∴∠A 'CB =90° ∴A 'B ==故答案为17.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是_____________度.【答案】110【解析】根据l===11π,解得:n=110,故答案为:110.18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为_______________度.【答案】60°或10【解析】分两种情况:①如图1,当∠ADC=90°时,∵∠B=30°,∴∠BCD=90°﹣30°=60°;②如图2,当∠ACD=90°时,∵∠A=50°,∠B=30°,∴∠ACB=180°﹣30°﹣50°=100°,∴∠BCD=100°﹣90°=10°,综上,则∠BCD的度数为60°或10°;故答案为:60°或10.19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为_______________.【答案】【解析】列表得:(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)(1,5)(2,5)(3,5)(4,5)(5,5)(6,5)(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)(1,1)(2,1)(3,1)(4,1)(5,1)(6,1)由表可知一共有36种情况,两枚骰子点数相同的有6种,所以两枚骰子点数相同的概率为=,故答案为:.20.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接B(D)CE,CE 与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为_______________.【答案】2【解析】如图,连接AC交BD于点O,∵AB=AD,BC=DC,∠A=60°,∴AC垂直平分BD,△ABD是等边三角形,∴∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,∵CE∥AB,∴∠BAO=∠ACE=30°,∠CED=∠BAD=60°,∴∠DAO=∠ACE=30°,∴AE=CE=6,∴DE=AD﹣AE=2,∵∠CED=∠ADB=60°,∴△EDF是等边三角形,∴DE=EF=DF=2,∴CF =CE ﹣EF =4,OF =OD ﹣DF =2, ∴OC ==2,∴BC ==2.三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分) 21.先化简再求值:24)44422(2--÷+----+x x x x x x x ,其中x =4tan45°+2cos30°. 解:原式=[﹣]÷=(﹣)•=•=, 当x =4tan 45°+2cos 30°=4×1+2×=4+时,原式===.22.图1.2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC 的两个端点均在小正方形的顶点上;(1)在图1中画出以AC 为底边的等腰直角△ABC ,点B 在小正方形顶点上;(2)在图2中画出以AC 为腰的等腰△ACD ,点D 在小正方形的顶点上,且△ACD 的面积为8.解:(1)作AC 的垂直平分线,作以AC 为直径的圆,垂直平分线与圆的交点即为点B ; (2)以C 为圆心,AC 为半径作圆,格点即为点D ;23.建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动,为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育.科技.国防.农业.工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图,请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名解:(1)根据题意得:18÷30%=60(名),答:在这次调查中,一共抽取了60名学生;(2)60﹣(18+9+12+6)=15(名),则本次调查中,选取国防类书籍的学生有15名,补全条形统计图,如图所示:(3)根据题意得:1500×=225(名),答:该校最想读科技类书籍的学生有225名.24.已知:在矩形ABCD 中,BD 是对角线,AE ⊥BD 于点E ,CF ⊥BD 于点F ;(1)如图1,求证:AE =CF ;(2)如图2,当∠ADB =30°时,连接AF .CE ,在不添加任何辅助线的情况下,请直 接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积的81.(1)证明:∵四边形ABCD 是矩形,∴AB =CD ,AB ∥CD ,AD ∥BC ,∴∠ABE =∠DF , ∵AE ⊥BD 于点E ,CF ⊥BD 于点F , ∴∠AEB =∠CFD =90°, 在△ABE 和△CDF 中,,∴△ABE ≌△CDF (AAS ),∴AE =CF .(2)解:△ABE 的面积=△CDF 的面积=△BCE 的面积=△ADF 的面积=矩形ABCD 面积的81.理由如下: ∵AD ∥BC ,∴∠CBD =∠ADB =30°, ∵∠ABC =90°,∴∠ABE =60°,∵AE ⊥BD ,∴∠BAE =30°,∴BE =AB ,AE =AD , ∴△ABE 的面积=BE ×AE =×AB ×AD =81AB ×AD =81矩形ABCD 的面积, ∵△ABE ≌△CDF ,∴△CDF 的面积═81矩形ABCD 的面积; 作EG ⊥BC 于G ,如图所示: ∵∠CBD =30°,∴EG =BE =×AB =AB ,∴△BCE 的面积=BC ×EG =BC ×AB =81BC ×AB =81矩形ABCD 的面积, 同理:△ADF 的面积=81矩形ABCD 的面积.25.寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用,若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?解:(1)设每副围棋x元,每副中国象棋y元,根据题意得:,∴,∴每副围棋16元,每副中国象棋10元;(2)设购买围棋z副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,∴z≤25,∴最多可以购买25副围棋;26.已知:MN为⊙O的直径,OE为⊙O的半径,A(B)CH是⊙O的两条弦,AB⊥OE于点D,CH ⊥MN于点K,连接HN.HE,HE与MN交于点P;(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;图1(2)如图2,连接ME,OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;图2(3)如图3,在(2)的条件下,连接O(C)B(C)AH,OC与EH交于点G,AH与MN交于点R,连接RG,若HK:ME=2:3,BC=2,求RG的长.图3解:(1)如图1,∵AB⊥OE于点D,CH⊥MN于点K,∴∠ODB=∠OKC=90°,∵∠ODB+∠DFK+∠OKC+∠EON=360°,∴∠DFK+∠EON=180°,∵∠DFK+∠HFB=180°,∴∠HFB=∠EON,∵∠EON=2∠EHN,∴∠HFB=2∠EHN.(2)如图2,连接OB,∵OA⊥ME,∴∠AOM=∠AOE,∵AB⊥OE,∴∠AOE=∠BOE,∴∠AOM+∠AOE=∠AOE+∠BOE,即:∠MOE=∠AOB,∴ME=AB,∵∠EON=4∠CHN,∠EON=2∠EHN,∴∠EHN=2∠CHN,∴∠EHC=∠CHN,∵CH⊥MN,∴∠HPN=∠HNM,∵∠HPN=∠EPM,∠HNM=HEM,∴∠EPM=∠HEM,∴MP=ME,∴MP=AB.(3)如图3,连接BC,过点A作AF⊥BC于F,过点A作AL⊥MN于L,连接AM,AC,由(2)知:∠EHC=∠CHN,∠AOM=∠AOE,∴∠EOC=∠CON,∵∠EOC+∠CON+∠AOM+∠AOE=180°,∴∠AOE+∠EOC=90°,∠AOM+∠CON=90°,∵OA⊥ME,CH⊥MN,∴∠OQM=∠OKC=90°,CK=HK,ME=2MQ,∴∠AOM+∠OMQ=90°,∴∠CON=∠OMQ,∵OC=OA,∴△OCK≌△MOQ(AAS),∴CK=OQ=HK,∵HK:ME=2:3,即:OQ:2MQ=2:3,∴OQ:MQ=4:3,∴设OQ=4k,MQ=3k,则OM===5k,AB=ME=6k,在Rt△OAC中,AC===5k,∵四边形ABCH内接于⊙O,∠AHC=∠AOC=×90°=45°,∴∠ABC=180°﹣∠AHC=180°﹣45°=135°,∴∠ABF=180°﹣∠ABC=180°﹣135°=45°,∴AF =BF =AB •cos ∠ABF =6k •cos45°=3k , 在Rt △ACF 中,AF 2+CF 2=AC 2,即:,解得:k 1=1,(不符合题意,舍去), ∴OQ =HK =4,MQ =OK =3,OM =ON =5,∴KN =KP =2,OP =ON ﹣KN ﹣KP =5﹣2﹣2=1,在△HKR 中,∠HKR =90°,∠RHK =45°,∴=tan ∠RHK =tan45°=1,∴RK =HK =4,∴OR =RN ﹣ON =4+2﹣5=1,∵∠CON =∠OMQ ,∴OC ∥ME ,∴∠PGO =∠HEM ,∵∠EPM =∠HEM ,∴∠PGO =∠EPM ,∴OG =OP =OR =1,∴∠PGR =90°,在Rt △HPK 中,PH ===2,∵∠POG =∠PHN ,∠OPG =∠HPN ,∴△POG ∽△PHN ,∴,即,PG =, ∴RG ===.27.如图,在平面直角坐标系中,点0为坐标原点,直线y =34x +4与x 轴交于点A ,与y 轴交 于点B ,直线BC 与x 轴交于点C ,且点C 与点A 关于y 轴对称;(1)求直线BC 的解析式;(2)点P 为线段AB 上一点,点Q 为线段BC 上一点,BQ =AP ,连接PQ ,设点P 的横坐标为t , △PBQ 的面积为S (S ≠0),求S 与t 之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E 在线段OA 上,点R 在线段BC 的延长线上,且点R 的纵坐标为-52, 连接PE .BE .AQ ,AQ 与BE 交于点F ,∠APE =∠CBE ,连接PF ,PF 的延长线与y 轴的负半轴交 于点M ,连接QM .MR ,若tan ∠QMR =2324,求直线PM 的解析式.解:(1)∵y =34x +4,∴A (﹣3,0)B (0,4), ∵点C 与点A 关于y 轴对称,∴C (3,0),设直线BC 的解析式为y =kx +b ,将B (0,4),C (3,0)代入,, 解得k =34,b =4,∴直线BC 的解析式; (2)如图1,过点A 作AD ⊥BC 于点点D ,过点P 作PN ⊥BC 于N ,PG ⊥OB 于点G .∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠P AE=∠ACB,AT∥BC,∴∠TAE=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMPQ为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R作RH⊥MQ于点H,。
哈市中考19年试题答案

哈市中考19年试题答案哈尔滨市中考数学试题答案解析一、选择题1. 答案:C解析:根据题目所给的方程,我们可以将其化简为2x + 3y = 6的形式,通过解方程组可以得到x = 1, y = 2,因此选项C为正确答案。
2. 答案:B解析:本题考查的是平面直角坐标系中点的坐标特点。
根据题目描述,点A(2,3)向右平移3个单位,再向上平移4个单位,新的坐标为(5,7)。
因此,选项B正确。
3. 答案:A解析:根据题目所给的三角形ABC,我们可以利用勾股定理计算出直角边的长度。
设直角边为a和b,斜边为c,则有a^2 + b^2 = c^2。
根据题目数据,我们可以得出a = 3, b = 4, c = 5,所以直角边长为3和4,选项A正确。
4. 答案:D解析:本题考查的是比例的性质。
根据题目中的比例关系,我们可以得出3:x = 5:12,通过交叉相乘得到3 * 12 = 5x,解得x = 7.2。
因此,选项D是正确答案。
5. 答案:B解析:本题考查的是数据的平均数计算。
将题目中给出的数据相加得到总和,然后除以数据的个数,即(2 + 4 + 6 + 8 + 10) ÷ 5 = 6。
所以平均数为6,选项B正确。
二、填空题1. 答案:-2解析:根据题目所给的多项式,我们可以先进行合并同类项,得到-x^2 + 3x - 2。
接下来,我们需要将其分解为两个一次因式的乘积,即(-x + 2)(x + 1)。
因此,答案为-2。
2. 答案:π解析:本题考查的是圆周率的概念。
圆周率π是一个无理数,其值约为 3.14159,用于计算圆的周长与直径的比值。
所以,答案为π。
3. 答案:4:9解析:根据题目所给的图形,我们可以发现这是一个等腰直角三角形,其中直角边的比例为1:√2。
根据相似三角形的性质,我们可以得出两个三角形的面积比为边长平方的比,即1^2 : (√2)^2 = 1 : 2。
所以,答案为4:9。
三、解答题1. 解:首先,我们需要解方程组:\begin{cases}2x + y = 5 \\x - 3y = 1\end{cases}通过消元法或代入法,我们可以得到x = 2,y = 1。
2019年黑龙江省哈尔滨市中考数学试卷附分析答案
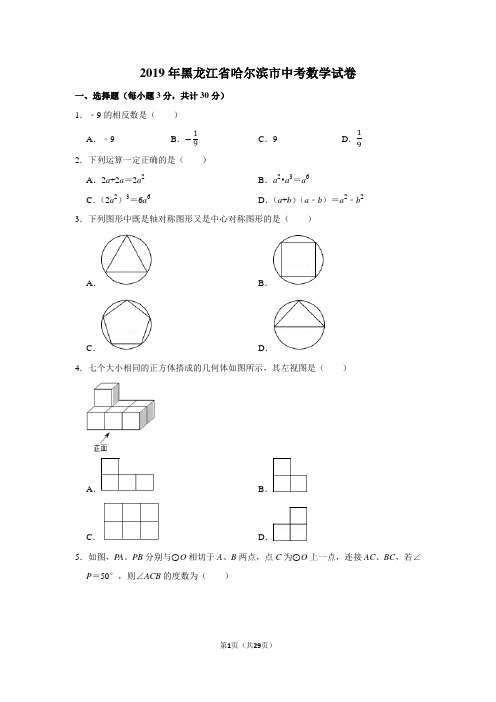
=a(a2﹣6ab+9b2)
=a(a﹣3b)2.
故答案为:a(a﹣3b)2.
t 14.(3 分)不等式组
的解集是 x≥3 .
t
t
【解答】解:解不等式
0,得:x≥3,
解不等式 3x+2≥1,得:x ,
∴不等式组的解集为 x≥3,
故答案为:x≥3. 15.(3 分)二次函数 y=﹣(x﹣6)2+8 的最大值是 8 .
故答案为:6.26×106.
12.(3 分)在函数 y
t t
中,自变量 x 的取值范围是
x
.
【解答】解:函数 y
t t
中分母 2x﹣3≠0,
∴x ;
第 10页(共 26页)
故答案为 x ;
13.(3 分)把多项式 a3﹣6a2b+9ab2 分解因式的结果是 a(a﹣3b)2 .
【解答】解:a3﹣6a2b+9ab2
第 7页(共 26页)
A.
B.
C.
D.
【解答】解:这个立体图形的左视图有 2 列,从左到右分别是 2,1 个正方形,
故选:B.
5.(3 分)如图,PA、PB 分别与⊙O 相切于 A、B 两点,点 C 为⊙O 上一点,连接 AC、BC,
若∠P=50°,则∠ACB 的度数为( )
A.60°
B.75°
C.70°
=2,则 A′B 的长为
.
17.(3 分)一个扇形的弧长是 11πcm,半径是 18cm,则此扇形的圆心角是
度.
18.(3 分)在△ABC 中,∠A=50°,∠B=30°,点 D 在 AB 边上,连接 CD,若△ACD
为直角三角形,则∠BCD 的度数为
2019年黑龙江省哈尔滨市中考数学试卷及答案

*!+,$"%&$ ! ’#-) !" ’$
//! *0%*"/1*! /%! 2! ! ! /!! 3"34!5#%! %
/(! 2"!!
/)! -!
/*! #/! ! /+! //"! /-6 /" ! *"!
/.6
/ *
!
%"6 %# + 6
.!/0$"12 #$%&& $3 ’ ’#&!%&( $4 ) ’#&*%&’ $4 $+ ’#-) ," ’$
6 B0
,#1?0-@-&,-%
)
.
#5) 7.#’}u *-.0 8#*-(*0#-.(0.#**(95"#& 6 % *0 }0@&# ! >5 ."
op -0$.6#.6 k -0 <=& B# .6+*-#q *-(!#.6(9#1 -. -r%
"
."/0%&12 !"#!! %3 $ )*!%#!& %3 ’ )*!(#!$ %3 ") )*+, *) Βιβλιοθήκη -7 6!."
-. 76
( -6 -0
!0"
-0 -6
( -. 76
-
!!" #$%&’( !" )*
. ! ,5 ."
!"#$%&’(% $ )*+, $5 )-
++) D,9 #95 555 EFGH,IJK%
2019年中考数学试题-2019年黑龙江省哈尔滨市中考试题带答案详解

黑龙江省哈尔滨市2019年中考试卷试卷
第I 卷选择题(共
30分)一、选择题(每小题
3分,共计30分)1.-9的相反数是(
)(A )-9
(B )-91(C )9 (D )91【答案】C
【解析】﹣9的相反数是9,故选:C .
2.下列运算一定正确的是(
). (A )2222a a a
(B )632a a a (C )6326)
2(a a (D )2
2))((b a b a b a 【答案】D 【解析】2a+2a =4a ,A 错误;a 2?a 3=a 5,B 错误;(2a 2)3=8a 6
,C 错误;故选:D .
3.下列图形中既是轴对称图形又是中心对称图形的是(). 【答案】B
【解析】A.是轴对称图形,但不是中心对称图形,故此选项错误;
B.是中心对称图形,也是轴对称图形,故此选项正确;
C.是轴对称图形,不是中心对称图形,故此选项错误;
D.是轴对称图形,不是中心对称图形,故此选项错误.故选:
B .4.七个大小相同的正方体搭成的几何体如图所示,其左视图是().
【答案】B
【解析】这个立体图形的左视图有
2列,从左到右分别是2,1个正方形,故选:B .
5.如图,P A,PB 分别与⊙O 相切于A,B 两点,点C 为⊙O 上一点,连接AC,BC,若∠P=50°,则。
2019年哈尔滨中考数学试卷

2019年哈尔滨中考数学试卷一、选择题(每小题3分,共计30分)1.-9的相反数是().A.-9B.−19C.9D.1 92.下列运算一定正确的是()A.2a+2a=2a2 B.a2·a3=a6C.(2a2)3=6a6 D.(a+b)(a-b)=a2-b23.下列图形中既是轴对称图形又是中心对称图形的是().A.B.C.D.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是().A.B.C.D.5.如图,PA,PB分别与⊙O相切于A,B两点,点C为⊙O上一点,连接AC,BC,若⊙P=50°,则⊙ACB的度数为().A.60°B.75°C.70°D.65°6.将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为().A.y=2(x+2)2+3B.y=2(x-2)2+3C.y=2(x-2)2-3D.y=2(x+2)2-37.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为().A.20%B.40%C.18%D.36%8.方程23x−1= 3x的解为().A.x= 311B.x= 113C.x= 37D.x= 739.点(-1,4)在反比例函数y= k x的图象上,则下列各点在此函数图象上的是().A.(4,-1)B.(−14,1)C.(-4,-1)D.(14,2)10.如图,在▱ABCD中,点E在对角线BD上,EM⊙AD,交AB于点M,EN⊙AB,交AD于点N,则下列式子一定正确的是().A.AMBM=NEDE B.AMAB=ANAD C.BCME=BEBD D.BDBE=BCME二、填空题(每小题3分,共计30分)11.将数6260000用科学记数法表示为。
12.在函数y= 3x2x−3中,自变量x的取值范围是。
13.把多项式a3-6a2b+9ab2分解因式的结果是。
【2019年中考真题系列】黑龙江省哈尔滨市2019年中考数学真题试卷含答案(解析版)

2019年中考真题系列,精心整理,含答案
2019年黑龙江省哈尔滨市中考数学试卷
一、选择题(每小题3分,共计30分)
1.(3分)﹣9的相反数是()
A .﹣9
B .﹣
C .9
D .【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.
【解答】解:﹣9的相反数是9,
故选:C .
【点评】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.
2.(3分)下列运算一定正确的是(
)A .2a+2a =2a
2B .a 2?a 3=a 6C .(2a 2)3=6a 6D .(a+b )(a ﹣b )=a 2﹣b
2【分析】利用同底数幂的乘法,幂的乘方与积的乘法法则,平方差公式解题即可;
【解答】解:2a+2a =4a ,A 错误;
a 2?a 3=a 5
,B 错误;
(2a 2)3=8a 6,C 错误;
故选:D .
【点评】本题考查整式的运算;熟练掌握同底数幂的乘法,幂的乘方与积的乘法法则,平方差公式是解题的关键.
3.(3分)下列图形中既是轴对称图形又是中心对称图形的是()A .B .
C .
D .
【分析】根据轴对称及中心对称图形的定义对各选项进行逐一分析即可.
【解答】解:A 、是轴对称图形,但不是中心对称图形,故此选项错误;
B 、是中心对称图形,也是轴对称图形,故此选项正确;。
2019年黑龙江省哈尔滨市中考数学试卷及答案解析
2019年黑龙江省哈尔滨市中考数学试卷一、选择题(每小题3分,共计30分)1.﹣9的相反数是()A.﹣9B.−19C.9D.192.下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b23.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.5.如图,P A、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A .60°B .75°C .70°D .65°6.将抛物线y =2x 2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为( )A .y =2(x +2)2+3B .y =2(x ﹣2)2+3C .y =2(x ﹣2)2﹣3D .y =2(x +2)2﹣37.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为( ) A .20% B .40%C .18%D .36%8.方程23x−1=3x的解为( )A .x =311 B .x =113C .x =37D .x =739.点(﹣1,4)在反比例函数y =k x 的图象上,则下列各点在此函数图象上的是( ) A .(4,﹣1)B .(−14,1)C .(﹣4,﹣1)D .(14,2)10.如图,在▱ABCD 中,点E 在对角线BD 上,EM ∥AD ,交AB 于点M ,EN ∥AB ,交AD 于点N ,则下列式子一定正确的是( )A .AM BM=NE DEB .AM AB=AN ADC .BCME=BE BDD .BD BE=BC EM二、填空题(每小题3分,共计30分) 11.将数6260000用科学记数法表示为 . 12.在函数y =3x2x−3中,自变量x 的取值范围是 . 13.把多项式a 3﹣6a 2b +9ab 2分解因式的结果是 .14.不等式组{3−x2≤03x +2≥1的解集是 .15.二次函数y =﹣(x ﹣6)2+8的最大值是 .16.如图,将△ABC 绕点C 逆时针旋转得到△A ′B ′C ,其中点A ′与A 是对应点,点B ′与B 是对应点,点B ′落在边AC 上,连接A ′B ,若∠ACB =45°,AC =3,BC =2,则A ′B 的长为 .17.一个扇形的弧长是11πcm ,半径是18cm ,则此扇形的圆心角是 度.18.在△ABC 中,∠A =50°,∠B =30°,点D 在AB 边上,连接CD ,若△ACD 为直角三角形,则∠BCD 的度数为 度.19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为 .20.如图,在四边形ABCD 中,AB =AD ,BC =DC ,∠A =60°,点E 为AD 边上一点,连接BD 、CE ,CE 与BD 交于点F ,且CE ∥AB ,若AB =8,CE =6,则BC 的长为 .三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分) 21.(7分)先化简再求值:(x+2x−2−x 2−2x x 2−4x+4)÷x−4x−2,其中x =4tan45°+2cos30°.22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD 的面积为8.23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.24.(8分)已知:在矩形ABCD 中,BD 是对角线,AE ⊥BD 于点E ,CF ⊥BD 于点F . (1)如图1,求证:AE =CF ;(2)如图2,当∠ADB =30°时,连接AF 、CE ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积的18.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?26.(10分)已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB ⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN 交于点R,连接RG,若HK:ME=2:3,BC=√2,求RG的长.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=43x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为−25,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=2423,求直线PM的解析式.2019年黑龙江省哈尔滨市中考数学试卷参考答案与试题解析一、选择题(每小题3分,共计30分)1.﹣9的相反数是()A.﹣9B.−19C.9D.19【解答】解:﹣9的相反数是9,故选:C.2.下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b2【解答】解:2a+2a=4a,A错误;a2•a3=a5,B错误;(2a2)3=8a6,C错误;故选:D.3.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.【解答】解:A、是轴对称图形,但不是中心对称图形,故此选项错误;B、是中心对称图形,也是轴对称图形,故此选项正确;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,不是中心对称图形,故此选项错误.故选:B.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.【解答】解:这个立体图形的左视图有2列,从左到右分别是2,1个正方形,故选:B.5.如图,P A、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°【解答】解:连接OA、OB,∵P A、PB分别与⊙O相切于A、B两点,∴OA⊥P A,OB⊥PB,∴∠OAP=∠OBP=90°,∴∠AOB=180°﹣∠P=180°﹣50°=130°,∴∠ACB=12∠AOB=12×130°=65°.故选:D.6.将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3D.y=2(x+2)2﹣3【解答】解:将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式为y=2(x﹣2)2+3,故选:B.7.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20%B.40%C.18%D.36%【解答】解:设降价的百分率为x根据题意可列方程为25(1﹣x)2=16解方程得x1=15,x2=95(舍)∴每次降价得百分率为20%故选:A.8.方程23x−1=3x的解为()A.x=311B.x=113C.x=37D.x=73【解答】解:去分母得:2x=9x﹣3,解得:x=3 7,经检验x=37是分式方程的解,故选:C.9.点(﹣1,4)在反比例函数y=kx的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(−14,1)C.(﹣4,﹣1)D.(14,2)【解答】解:将点(﹣1,4)代入y=k x,∴k=﹣4,∴y=−4 x,∴点(4,﹣1)在函数图象上,故选:A.10.如图,在▱ABCD 中,点E 在对角线BD 上,EM ∥AD ,交AB 于点M ,EN ∥AB ,交AD 于点N ,则下列式子一定正确的是( )A .AM BM=NE DEB .AM AB=AN ADC .BCME=BE BDD .BD BE=BC EM【解答】解:∵在▱ABCD 中,EM ∥AD ∴易证四边形AMEN 为平行四边形 ∴易证△BEM ∽△BAD ∽△END ∴AM BM=NE BM=DE BE,A 项错误AM AB =ND AD ,B 项错误 BC ME =ADME =BD BE ,C 项错误 BD BE=AD ME=BC ME,D 项正确故选:D .二、填空题(每小题3分,共计30分)11.将数6260000用科学记数法表示为 6.26×106 . 【解答】解:6260000用科学记数法可表示为6.26×106, 故答案为:6.26×106.12.在函数y =3x 2x−3中,自变量x 的取值范围是 x ≠32 . 【解答】解:函数y =3x2x−3中分母2x ﹣3≠0, ∴x ≠32; 故答案为x ≠32;13.把多项式a 3﹣6a 2b +9ab 2分解因式的结果是 a (a ﹣3b )2 . 【解答】解:a 3﹣6a 2b +9ab 2 =a (a 2﹣6ab +9b 2)=a (a ﹣3b )2. 故答案为:a (a ﹣3b )2.14.不等式组{3−x2≤03x +2≥1的解集是 x ≥3 .【解答】解:解不等式3−x 2≤0,得:x ≥3,解不等式3x +2≥1,得:x ≥−13, ∴不等式组的解集为x ≥3, 故答案为:x ≥3.15.二次函数y =﹣(x ﹣6)2+8的最大值是 8 . 【解答】解:∵a =﹣1<0, ∴y 有最大值,当x =6时,y 有最大值8. 故答案为8.16.如图,将△ABC 绕点C 逆时针旋转得到△A ′B ′C ,其中点A ′与A 是对应点,点B ′与B 是对应点,点B ′落在边AC 上,连接A ′B ,若∠ACB =45°,AC =3,BC =2,则A ′B 的长为 √13 .【解答】解:∵将△ABC 绕点C 逆时针旋转得到△A ′B ′C , ∴AC =A 'C =3,∠ACB =∠ACA '=45° ∴∠A 'CB =90° ∴A 'B =√BC 2+A′C2=√13故答案为√1317.一个扇形的弧长是11πcm ,半径是18cm ,则此扇形的圆心角是 110 度. 【解答】解:根据l =nπr 180=nπ⋅18180=11π, 解得:n =110, 故答案为:110.18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为60°或10度.【解答】解:分两种情况:①如图1,当∠ADC=90°时,∵∠B=30°,∴∠BCD=90°﹣30°=60°;②如图2,当∠ACD=90°时,∵∠A=50°,∠B=30°,∴∠ACB=180°﹣30°﹣50°=100°,∴∠BCD=100°﹣90°=10°,综上,则∠BCD的度数为60°或10°;故答案为:60°或10;19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为16.【解答】解:列表得:(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)(1,5)(2,5)(3,5)(4,5)(5,5)(6,5)(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)(1,2) (2,2) (3,2) (4,2) (5,2) (6,2) (1,1)(2,1)(3,1)(4,1)(5,1)(6,1)由表可知一共有36种情况,两枚骰子点数相同的有6种, 所以两枚骰子点数相同的概率为636=16,故答案为:16.20.如图,在四边形ABCD 中,AB =AD ,BC =DC ,∠A =60°,点E 为AD 边上一点,连接BD 、CE ,CE 与BD 交于点F ,且CE ∥AB ,若AB =8,CE =6,则BC 的长为 2√7 .【解答】解:如图,连接AC 交BD 于点O∵AB =AD ,BC =DC ,∠A =60°, ∴AC 垂直平分BD ,△ABD 是等边三角形 ∴∠BAO =∠DAO =30°,AB =AD =BD =8, BO =OD =4 ∵CE ∥AB∴∠BAO =∠ACE =30°,∠CED =∠BAD =60° ∴∠DAO =∠ACE =30°∴AE =CE =6 ∴DE =AD ﹣AE =2 ∵∠CED =∠ADB =60° ∴△EDF 是等边三角形 ∴DE =EF =DF =2∴CF =CE ﹣EF =4,OF =OD ﹣DF =2 ∴OC =√CF 2−OF 2=2√3 ∴BC =2+OC2=2√7三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分) 21.(7分)先化简再求值:(x+2x−2−x 2−2xx 2−4x+4)÷x−4x−2,其中x =4tan45°+2cos30°. 【解答】解:原式=[x+2x−2−x(x−2)(x−2)2]÷x−4x−2=(x+2x−2−x x−2)•x−2x−4=2x−2•x−2x−4 =2x−4, 当x =4tan45°+2cos30°=4×1+2×√32=4+√3时,原式=4+3−4=3 =2√33. 22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC 的两个端点均在小正方形的顶点上.(1)在图1中画出以AC 为底边的等腰直角三角形ABC ,点B 在小正方形顶点上; (2)在图2中画出以AC 为腰的等腰三角形ACD ,点D 在小正方形的顶点上,且△ACD 的面积为8.【解答】解;(1)作AC的垂直平分线,作以AC为直径的圆,垂直平分线与圆的交点即为点B;(2)以C为圆心,AC为半径作圆,格点即为点D;23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.【解答】解:(1)根据题意得:18÷30%=60(名), 答:在这次调查中,一共抽取了60名学生; (2)60﹣(18+9+12+6)=15(名),则本次调查中,选取国防类书籍的学生有15名, 补全条形统计图,如图所示:(3)根据题意得:1500×960=225(名), 答:该校最想读科技类书籍的学生有225名.24.(8分)已知:在矩形ABCD 中,BD 是对角线,AE ⊥BD 于点E ,CF ⊥BD 于点F . (1)如图1,求证:AE =CF ;(2)如图2,当∠ADB =30°时,连接AF 、CE ,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积的18.【解答】(1)证明:∵四边形ABCD 是矩形, ∴AB =CD ,AB ∥CD ,AD ∥BC , ∴∠ABE =∠CDF ,∵AE ⊥BD 于点E ,CF ⊥BD 于点F , ∴∠AEB =∠CFD =90°,在△ABE 和△CDF 中,{∠ABE =∠CDF ∠AEB =∠CFDAB =CD ,∴△ABE ≌△CDF (AAS ), ∴AE =CF ;(2)解:△ABE 的面积=△CDF 的面积=△BCE 的面积=△ADF 的面积=矩形ABCD 面积的18.理由如下:∵AD ∥BC ,∴∠CBD =∠ADB =30°, ∵∠ABC =90°, ∴∠ABE =60°, ∵AE ⊥BD , ∴∠BAE =30°, ∴BE =12AB ,AE =12AD ,∴△ABE 的面积=12BE ×AE =12×12AB ×12AD =18AB ×AD =18矩形ABCD 的面积, ∵△ABE ≌△CDF ,∴△CDF 的面积═18矩形ABCD 的面积;作EG ⊥BC 于G ,如图所示: ∵∠CBD =30°,∴EG =12BE =12×12AB =14AB , ∴△BCE 的面积=12BC ×EG =12BC ×14AB =18BC ×AB =18矩形ABCD 的面积,同理:△ADF 的面积=18矩形ABCD 的面积.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?【解答】解:(1)设每副围棋x 元,每副中国象棋y 元,根据题意得:{3x +5y =988x +3y =158, ∴{x =16y =10, ∴每副围棋16元,每副中国象棋10元;(2)设购买围棋z 副,则购买象棋(40﹣z )副,根据题意得:16z +10(40﹣z )≤550,∴z ≤25,∴最多可以购买25副围棋;26.(10分)已知:MN 为⊙O 的直径,OE 为⊙O 的半径,AB 、CH 是⊙O 的两条弦,AB⊥OE 于点D ,CH ⊥MN 于点K ,连接HN 、HE ,HE 与MN 交于点P .(1)如图1,若AB 与CH 交于点F ,求证:∠HFB =2∠EHN ;(2)如图2,连接ME 、OA ,OA 与ME 交于点Q ,若OA ⊥ME ,∠EON =4∠CHN ,求证:MP =AB ;(3)如图3,在(2)的条件下,连接OC 、BC 、AH ,OC 与EH 交于点G ,AH 与MN交于点R,连接RG,若HK:ME=2:3,BC=√2,求RG的长.【解答】解:(1)如图1,∵AB⊥OE于点D,CH⊥MN于点K∴∠ODB=∠OKC=90°∵∠ODB+∠DFK+∠OKC+∠EON=360°∴∠DFK+∠EON=180°∵∠DFK+∠HFB=180°∴∠HFB=∠EON∵∠EON=2∠EHN∴∠HFB=2∠EHN(2)如图2,连接OB,∵OA⊥ME,∴∠AOM=∠AOE∵AB⊥OE∴∠AOE=∠BOE∴∠AOM+∠AOE=∠AOE+∠BOE,即:∠MOE=∠AOB∴ME=AB∵∠EON=4∠CHN,∠EON=2∠EHN∴∠EHN=2∠CHN∴∠EHC=∠CHN∵CH⊥MN∴∠HPN=∠HNM∵∠HPN=∠EPM,∠HNM=HEM∴∠EPM=∠HEM∴MP=ME∴MP=AB(3)如图3,连接BC,过点A作AF⊥BC于F,过点A作AL⊥MN于L,连接AM,AC,由(2)知:∠EHC=∠CHN,∠AOM=∠AOE∴∠EOC=∠CON∵∠EOC+∠CON+∠AOM+∠AOE=180°∴∠AOE+∠EOC=90°,∠AOM+∠CON=90°∵OA⊥ME,CH⊥MN∴∠OQM=∠OKC=90°,CK=HK,ME=2MQ,∴∠AOM+∠OMQ=90°∴∠CON=∠OMQ∵OC=OA∴△OCK≌△MOQ(AAS)∴CK=OQ=HK∵HK:ME=2:3,即:OQ:2MQ=2:3∴OQ:MQ=4:3∴设OQ=4k,MQ=3k,则OM=√OQ2+MQ2=√(4k)2+(3k)2=5k,AB=ME=6k在Rt△OAC中,AC=√OA2+OC2=√(5k)2+(5k)2=5√2k∵四边形ABCH内接于⊙O,∠AHC=12∠AOC=12×90°=45°,∴∠ABC=180°﹣∠AHC=180°﹣45°=135°,∴∠ABF=180°﹣∠ABC=180°﹣135°=45°∴AF=BF=AB•cos∠ABF=6k•cos45°=3√2k在Rt△ACF中,AF2+CF2=AC2即:(3√2k)2+(3√2k+√2)2=(5√2k)2,解得:k1=1,k2=−17(不符合题意,舍去)∴OQ=HK=4,MQ=OK=3,OM=ON=5∴KN=KP=2,OP=ON﹣KN﹣KP=5﹣2﹣2=1,在△HKR中,∠HKR=90°,∠RHK=45°,∴RKHK=tan∠RHK=tan45°=1∴RK=HK=4∴OR=RN﹣ON=4+2﹣5=1∵∠CON=∠OMQ∴OC∥ME∴∠PGO=∠HEM∵∠EPM=∠HEM∴∠PGO=∠EPM∴OG=OP=OR=1∴∠PGR=90°在Rt△HPK中,PH=2+PK2=√42+22=2√5∵∠POG=∠PHN,∠OPG=∠HPN∴△POG∽△PHN∴PGPO =PNPH,即PG1=2√5,PG=2√55∴RG=√RP2−PG2=22−(255)2=4√55.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=43x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为−25,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=2423,求直线PM的解析式.【解答】解:(1)∵y=43x+4,∴A(﹣3,0),B(0,4),∵点C与点A关于y轴对称,∴C(3,0),设直线BC 的解析式为y =kx +b ,将B (0,4),C (3,0)代入,{3k +b =0b =4, 解得k =−43,b =4,∴直线BC 的解析式y =−43x +4;(2)如图1,过点A 作AD ⊥BC 于点D ,过点P 作PN ⊥BC 于N ,PG ⊥OB 于点G .∵OA =OC =3,OB =4,∴AC =6,AB =BC =5,∴sin ∠ACD =AD AC =OB BC , 即AD 6=45, ∴AD =245,∵点P 为直线y =43x +4上,∴设P (t ,43t +4), ∴PG =﹣t ,cos ∠BPG =cos ∠BAO ,即PG PB =OA AB=35, ∴PB =−53t ,∵sin ∠ABC =PN PB =AD AB =2455=2425, ∴PN =2425PB =2425×(−53t)=−85t ,∵AP=BQ,∴BQ=5+53 t,∴S=12BQ⋅PN=12(5+53t)⋅(−85t),即S=−43t2−4t;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM,PT交OA于点S.∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠P AE=∠ACB,AT∥BC,∴∠TAF=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMQP为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R作RH⊥MQ于点H,∵sin∠ABC=sin∠MQR=RHRQ=2425,设QR=25a,HR=24a,则QH=7a,∵tan∠QMR=24 23,∴MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.∵点R的纵坐标为−2 5,∴RK=2 5,∵sin∠BCO=BOBC=sin∠KCR=KRCR=45,∴CR=12,BR=112,∴55a=112,a=110,∴BQ=30a=3,∴5+53t=3,t=−65,∴P(−65,125),∴PS=12 5,∵BM=PT=2PS=245,BO=4,∴OM=4 5,∴M(0,−4 5),设直线PM的解析式为y=mx+n,∴{−65m+n=125n=−45,解得{m =−83n =−45, ∴直线PM 的解析式为y =−83x −45.。
2019年黑龙江省哈尔滨市中考数学试题及标准答案
@def+&/fg‘/bc,
’% hi/j#kl #( mn>?*ohi/j#kl $%) pqrstuvwtn<="tx
yz&nu{|,
)% }~BDz"& &"Mkl?&C&f,
.%- /0123 &" 452675
!"#$%&’() & *+,- &$ *.
;%& .#4<=8>)5/%.?=@"
%
%
#$$ >! $ 2ABC %& 9D6.EFGHI
H% %’&"= ’ >)5/%.?=@%
#!$ >! ! 2ABC %& 9F.EFIH% %&(" = ( >)5/%.?=@"J!%&( .KL9 )" !*+ !"# " $%
& !$
+ï !! b!$
*!+,$"%&$ ! ’#-) !" ’$
//! *0%*"/1*! /%! 2! ! ! /!! 3"34!5#%! %
/(! 2"!!
/)! -!
/*! #/! ! /+! //"! /-6 /" ! *"!
/.6
/ *
!
%"6 %# + 6
.!/0$"12 #$%&& $3 ’ ’#&!%&( $4 ) ’#&*%&’ $4 $+ ’#-) ," ’$
2019年黑龙江省哈尔滨市中考数学试卷答案解析版
17. 一个扇形的弧长是 11πcm,半径是 18cm,则此扇形的圆心角是______度. 18. 在△ABC 中,∠A=50°,∠B=30°,点 D 在 AB 边上,连接 CD,若△ACD 为直角三角
形,则∠BCD 的度数为______度. 19. 同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有 1 到 6 的点数,则这两
B.
������������ ������������
������������ = ������������
C.
������������ ������������
������������ = ������������
D.
������������ ������������
������������ = ������������
21.
先化简再求值:(������ + 2- ������2−2������ )÷������−4,其中 x=4tan45°+2cos30°.
������−2 ������2−4������ + 4 ������−2
第 3 页,共 23 页
22. 图 1、2 是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为 1,线段 AC 的两个端点均在小正方形的顶点上. (1)在图 1 中画出以 AC 为底边的等腰直角三角形 ABC,点 B 在小正方形顶点上; (2)在图 2 中画出以 AC 为腰的等腰三角形 ACD,点 D 在小正方形的顶点上,且 △ACD 的面积为 8.
线为( )
A. ������ = 2(������ + 2)2 +3
B. ������ = 2(������−2)2 +3 C. ������ = 2(������−2)2−3
2019年黑龙江省哈尔滨市中考数学试卷附解答
2019 年黑龙江省哈尔滨市中考数学试卷一、选择题(每小题3 分,共计30 分)1.(3 分)﹣9 的相反数是()A.﹣9 C.9 D.2.(3 分)下列运算一定正确的是()A.2a+2a=2a2 B.a2•a3=a6C.(2a2)3=6a6 D.(a+b)(a﹣b)=a2﹣b23.(3 分)下列图形中既是轴对称图形又是中心对称图形的是()A. B.C. D.4.(3 分)七个大小相同的正方体搭成的几何体如图所示,其左视图是()A. B.C.5.(3 分)如图,PA、PB 分别与⊙O 相切于A、B 两点,点C 为⊙O 上一点,连接AC、BC,若∠P=50°,则∠ACB 的度数为()A.60°B.75°C.70°D.65°6.(3 分)将抛物线y=2x2 向上平移3 个单位长度,再向右平移2 个单位长度,所得到的抛物线为()A.y=2(x+2)2+3 B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3 D.y=2(x+2)2﹣3 7.(3 分)某商品经过连续两次降价,售价由原来的每件25 元降到每件16 元,则平均每次降价的百分率为()A.20% B.40% C.18% D.36%8.(3 分)方程=的解为()A.x= B.x=C.x= D.x=9.(3 分)点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)10.(3 分)如图,在▱ABCD 中,点E 在对角线BD 上,EM∥AD,交AB 于点M,EN∥AB,交AD 于点N,则下列式子一定正确的是()A.==C.==二、填空题(每小题3 分,共计30 分)11.(3 分)将数6260000 用科学记数法表示为.12.(3 分)在函数y=中,自变量x 的取值范围是.13.(3 分)把多项式a3﹣6a2b+9ab2 分解因式的结果是.14.(3 分)不等式组的解集是.15.(3 分)二次函数y=﹣(x﹣6)2+8 的最大值是.16.(3 分)如图,将△ABC 绕点C 逆时针旋转得到△A′B′C,其中点A′与A 是对应点,点B′与B 是对应点,点B′落在边AC 上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B 的长为.17.(3 分)一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.18.(3 分)在△ABC 中,∠A=50°,∠B=30°,点D 在AB 边上,连接CD,若△ACD 为直角三角形,则∠BCD 的度数为度.19.(3 分)同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1 到6 的点数,则这两枚骰子向上的一面出现的点数相同的概率为.20.(3 分)如图,在四边形ABCD 中,AB=AD,BC=DC,∠A=60°,点E 为AD 边上一点,连接BD、CE,CE 与BD 交于点F,且CE∥AB,若AB=8,CE=6,则BC 的长为.三、解答题(其中21~22 题各7 分,23-24 题各8 分,25~27 题各10 分,共计60 分)21.(7 分)先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.22.(7 分)图1、2 是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC 的两个端点均在小正方形的顶点上.(1)在图1 中画出以AC 为底边的等腰直角三角形ABC,点B 在小正方形顶点上;(2)在图2 中画出以AC 为腰的等腰三角形ACD,点D 在小正方形的顶点上,且△ACD 的面积为8.23.(8 分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500 名学生,请你估计该校最想读科技类书籍的学生有多少名.24.(8 分)已知:在矩形ABCD 中,BD 是对角线,AE⊥BD 于点E,CF⊥BD 于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2 中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积.25.(10 分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3 副围棋和5 副中国象棋需用98 元;若购买8 副围棋和3 副中国象棋需用158 元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40 副,总费用不超过550 元,那么寒梅中学最多可以购买多少副围棋?26.(10 分)已知:MN 为⊙O 的直径,OE 为⊙O 的半径,AB、CH 是⊙O 的两条弦,AB⊥OE 于点D,CH⊥MN 于点K,连接HN、HE,HE 与MN 交于点P.(1)如图1,若AB 与CH 交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA 与ME 交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC 与EH 交于点G,AH 与MN 交于点R,连接RG,若,求RG 的长.27.(10 分)如图,在平面直角坐标系中,点O 为坐标原点,直线y=x+4 与x 轴交于点A,与y 轴交于点B,直线BC 与x 轴交于点C,且点C 与点A 关于y 轴对称;(1)求直线BC 的解析式;(2)点P 为线段AB 上一点,点Q 为线段BC 上一点,BQ=AP,连接PQ,设点P 的横坐标为t,△PBQ 的面积为S(S≠0),求S 与t 之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点 E 在线段OA 上,点R 在线段BC 的延长线上,且点R 的纵坐标为,连接PE、BE、AQ,AQ 与BE 交于点F,∠APE=∠CBE,连接PF,PF 的延长线与y 轴的负半轴交于点M,连接QM、MR,若,求直线PM 的解析式.2019 年黑龙江省哈尔滨市中考数学试卷参考答案与试题解析一、选择题(每小题3 分,共计30 分)1.(3 分)﹣9 的相反数是()A.﹣9 C.9 D.【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.【解答】解:﹣9 的相反数是9,故选:C.【点评】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.2.(3 分)下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b2【分析】利用同底数幂的乘法,幂的乘方与积的乘法法则,平方差公式解题即可;【解答】解:2a+2a=4a,A 错误;a2•a3=a5,B 错误;(2a2)3=8a6,C 错误;故选:D.【点评】本题考查整式的运算;熟练掌握同底数幂的乘法,幂的乘方与积的乘法法则,平方差公式是解题的关键.3.(3 分)下列图形中既是轴对称图形又是中心对称图形的是()A. B.C. D.【分析】根据轴对称及中心对称图形的定义对各选项进行逐一分析即可.【解答】解:A、是轴对称图形,但不是中心对称图形,故此选项错误;B、是中心对称图形,也是轴对称图形,故此选项正确;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,不是中心对称图形,故此选项错误.故选:B.【点评】本题考查的是中心对称图形,熟知把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形是解答此题的关键.4.(3 分)七个大小相同的正方体搭成的几何体如图所示,其左视图是()A. B.C.【分析】左视图有 2 列,从左到右分别是2,1 个正方形.【解答】解:这个立体图形的左视图有2 列,从左到右分别是2,1 个正方形,故选:B.【点评】此题主要考查了三视图的画法,正确掌握三视图观察的角度是解题关键.5.(3 分)如图,PA、PB 分别与⊙O 相切于A、B 两点,点C 为⊙O 上一点,连接AC、BC,若∠P=50°,则∠ACB 的度数为()A.60°B.75°C.70°D.65°【分析】先利用切线的性质得∠OAP=∠OBP=90°,再利用四边形的内角和计算出∠AOB 的度数,然后根据圆周角定理计算∠ACB 的度数.【解答】解:连接OA、OB,∵PA、PB 分别与⊙O 相切于A、B 两点,∴OA⊥PA,OB⊥PB,∴∠OAP=∠OBP=90°,∴∠AOB=180°﹣∠P=180°﹣50°=130°,∴∠ACB=∠AOB=×130°=65°.故选:D.【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.6.(3 分)将抛物线y=2x2 向上平移3 个单位长度,再向右平移2 个单位长度,所得到的抛物线为()A.y=2(x+2)2+3 B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3 D.y=2(x+2)2﹣3【分析】根据“上加下减、左加右减”的原则进行解答即可.【解答】解:将抛物线y=2x2 向上平移3 个单位长度,再向右平移2 个单位长度,得到的抛物线的解析式为y=2(x﹣2)2+3,故选:B.【点评】本题考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.7.(3 分)某商品经过连续两次降价,售价由原来的每件25 元降到每件16 元,则平均每次降价的百分率为()A.20% B.40% C.18% D.36%【分析】设降价得百分率为x,根据降低率的公式a(1﹣x)2=b 建立方程,求解即可.【解答】解:设降价的百分率为x根据题意可列方程为25(1﹣x)2=16解方程,(舍)∴每次降价得百分率为20%故选:A.【点评】本题考查了一元二次方程实际应用问题关于增长率的类型问题,按照公式a(1﹣x)2=b 对照参数位置代入值即可,公式的记忆与运用是本题的解题关键.8.(3 分)方程=的解为()A.x= B.x=C.x= D.x=【分析】将分式方程化,即可求解;同时要进行验根即可求解;【解答】解=,,∴2x=9x﹣3,∴x=;将检验是方程的根,∴方程的解为;故选:C.【点评】本题考查解分式方程;熟练掌握分式方程的解法及验根是解题的关键.9.(3 分)点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)【分析】将点(﹣1,4)代入,求出函数解析式即可解题;【解答】解:将点(﹣1,4)代入,∴k=﹣4,∴y=,∴点(4,﹣1)在函数图象上,故选:A.【点评】本题考查反比例函数的图象及性质;熟练掌握待定系数法求函数解析式的方法是解题的关键.10.(3 分)如图,在▱ABCD 中,点E 在对角线BD 上,EM∥AD,交AB 于点M,EN∥AB,交AD 于点N,则下列式子一定正确的是()A.==C.==【分析】根据平行四边形的性质以及相似三角形的性质.【解答】解:∵在▱ABCD 中,EM∥AD∴易证四边形AMEN 为平行四边形∴易证△BEM∽△BAD∽△END∴==,A 项错误=,B 项错误==,C 项错误==,D 项正确故选:D.【点评】此题主要考查相似三角形的性质及平行四边形的性质,本题关键是要懂得找相似三角形,利用相似三角形的性质求解.二、填空题(每小题3 分,共计30 分)11.(3 分)将数6260000 用科学记数法表示为 6.26×106 .【分析】科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1 时,n 是正数;当原数的绝对值<1 时,n 是负数.【解答】解:6260000 用科学记数法可表示为6.26×106,故答案为:6.26×106.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n 的形式,其中1≤|a|<10,n 为整数,表示时关键要正确确定a 的值以及n 的值.12.(3 分)在函数y=中,自变量x 的取值范围是 x≠.【分析】函数中分母不为零是函数有意义的条件,因此2x﹣3≠0 即可;【解答】解:函数中分母2x﹣3≠0,∴x≠;故答案为;【点评】本题考查函数自变量的取值范围;熟练掌握函数中自变量的取值范围的求法是解题的关键.13.(3 分)把多项式a3﹣6a2b+9ab2 分解因式的结果是a(a﹣3b)2 .【分析】原式提取公因式,再利用完全平方公式分解即可.【解答】解:a3﹣6a2b+9ab2=a(a2﹣6ab+9b2)=a(a﹣3b)2.故答案为:a(a﹣3b)2.【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.14.(3 分)不等式组的解集是 x≥3 .【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等≤0,得:x≥3,解不等式3x+2≥1,得,∴不等式组的解集为x≥3,故答案为:x≥3.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.15.(3 分)二次函数y=﹣(x﹣6)2+8 的最大值是 8 .【分析】利用二次函数的性质解决问题.【解答】解:∵a=﹣1<0,∴y 有最大值,当x=6 时,y 有最大值8.故答案为8.【点评】本题主要考查二次函数的最值,熟练掌握二次函数的图象和性质是解题的关键.16.(3 分)如图,将△ABC 绕点C 逆时针旋转得到△A′B′C,其中点A′与A 是对应点,点B′与B 是对应点,点B′落在边AC 上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B 的长为.【分析】由旋转的性质可得AC=A'C=3,∠ACB=∠ACA'=45°,可得∠A'CB=90°,由勾股定理可求解.【解答】解:∵将△ABC 绕点C 逆时针旋转得到△A′B′C,∴AC=A'C=3,∠ACB=∠ACA'=45°∴∠A'CB=90°∴A'B==故答案为【点评】本题考查了旋转的性质,勾股定理,熟练掌握旋转的性质是本题的关键.17.(3 分)一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是 110 度.【分析】直接利用弧长公式即可求出n 的值,计算即可.【解答】解:根据==11π,解得:n=110,故答案为:110.【点评】本题考查了扇形弧长公式计算,注意公式的灵活运用是解题关键.18.(3 分)在△ABC 中,∠A=50°,∠B=30°,点D 在AB 边上,连接CD,若△ACD 为直角三角形,则∠BCD 的度数为60°或10 度.【分析】当△ACD 为直角三角形时,存在两种情况:∠ADC=90°或∠ACD=90°,根据三角形的内角和定理可得结论.【解答】解:分两种情况:①如图1,当∠ADC=90°时,∵∠B=30°,∴∠BCD=90°﹣30°=60°;②如图2,当∠ACD=90°时,∵∠A=50°,∠B=30°,∴∠ACB=180°﹣30°﹣50°=100°,∴∠BCD=100°﹣90°=10°,综上,则∠BCD 的度数为60°或10°;故答案为:60°或10;【点评】本题考查了三角形的内角和定理和三角形外角的性质,分情况讨论是本题的关键.19.(3 分)同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1 到6 的点数,则这两枚骰子向上的一面出现的点数相同的概率为.【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两枚骰子点数相同的情况,再利用概率公式即可求得答案.【解答】解:列表得:由表可知一共有36 种情况,两枚骰子点数相同的有6 种,所以两枚骰子点数相同的概率=,故答案为.【点评】本题考查了列表法与树状图法求随机事件的概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;解题时还要注意是放回试验还是不放回试验.用到的知识点为:概率=所求情况数与总情况数之比.20.(3 分)如图,在四边形ABCD 中,AB=AD,BC=DC,∠A=60°,点E 为AD 边上一点,连接BD、CE,CE 与BD 交于点F,且CE∥AB,若AB=8,CE=6,则BC 的长为 2 .【分析】连接AC 交BD 于点O,由题意可证AC 垂直平分BD,△ABD 是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF 是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC ,BC 的长.【解答】解:如图,连接AC 交BD 于点O∵AB=AD,BC=DC,∠A=60°,∴AC 垂直平分BD,△ABD 是等边三角形∴∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4∵CE∥AB∴∠BAO=∠ACE=30°,∠CED=∠BAD=60°∴∠DAO=∠ACE=30°∴AE=CE=6∴DE=AD﹣AE=2∵∠CED=∠ADB=60°∴△EDF 是等边三角形∴DE=EF=DF=2∴CF=CE﹣EF=4,OF=OD﹣DF=2∴OC==2∴BC==2【点评】本题考查了等边三角形的性质和判定,勾股定理,熟练运用等边三角形的判定是本题的关键.三、解答题(其中21~22 题各7 分,23-24 题各8 分,25~27 题各10 分,共计60 分)21.(7 分)先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.【分析】先根据分式的混合运算顺序和运算法则化简原式,再依据特殊锐角三角函数值求得 x 的值,代入计算可得. 【解答】解:原式﹣]÷=(﹣)•=• =, 当=4+时,【点评】本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则.22.(7 分)图 1、2 是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为 1,线段 AC 的两个端点均在小正方形的顶点上.(1)在图 1 中画出以 AC 为底边的等腰直角三角形 ABC ,点 B 在小正方形顶点上;(2)在图 2 中画出以 AC 为腰的等腰三角形 ACD ,点 D 在小正方形的顶点上,且△ACD 的面积为 8.【分析】(1)作 AC 的垂直平分线,作以 AC 为直径的圆,垂直平分线与圆的交点即为点B ;(2)以 C 为圆心,AC 为半径作圆,格点即为点 D ;【解答】解;(1)作 AC 的垂直平分线,作以 AC 为直径的圆,垂直平分线与圆的交点即为点 B ;(2)以 C 为圆心,AC 为半径作圆,格点即为点 D ;原式= = =.【点评】本题考查尺规作图,等腰三角形的性质;熟练掌握等腰三角形和直角三角形的尺规作图方法是解题的关键.23.(8 分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500 名学生,请你估计该校最想读科技类书籍的学生有多少名.【分析】(1)由最想读教育类书籍的学生数除以占的百分比求出总人数即可;(2)确定出最想读国防类书籍的学生数,补全条形统计图即可;(2)求出最想读科技类书籍的学生占的百分比,乘以1500 即可得到结果.【解答】解:(1)根据题意得:18÷30%=60(名),答:在这次调查中,一共抽取了60 名学生;(2)60﹣(18+9+12+6)=15(名),则本次调查中,选取国防类书籍的学生有15 名,补全条形统计图,如图所示:(3)根据题意得:1500×=225(名),答:该校最想读科技类书籍的学生有225 名.【点评】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.24.(8 分)已知:在矩形ABCD 中,BD 是对角线,AE⊥BD 于点E,CF⊥BD 于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2 中四个三角形,使写出的每个三角形的面积都等于矩形ABCD 面积.【分析】(1)由AAS 证明△ABE≌△CDF,即可得出结论;(2)由平行线的性质得出∠CBD=∠ADB=30°,由直角三角形的性质得出AB,AE =AD,得出△ABE 的面积=AB×AD=矩形ABCD 的面积,由全等三角形的性质得出△CDF 的面积矩形ABCD 的面积;作EG⊥BC 于G,由直角三角形的性质得出EG=BE=×AB=AB,得出△BCE 的面积=矩形ABCD 的面积,同理:△ADF 的面积矩形ABCD 的面积.【解答】(1)证明:∵四边形ABCD 是矩形,∴AB=CD,AB∥CD,AD∥BC,∴∠ABE=∠DF,∵AE⊥BD 于点E,CF⊥BD 于点F,∴∠AEB=∠CFD=90°,在△ABE 和△CDF 中,,∴△ABE≌△CDF(AAS),∴AE=CF;(2)解:△ABE 的面积=△CDF 的面积=△BCE 的面积=△ADF 的面积=矩形ABCD 面积.理由如下:∵AD∥BC,∴∠CBD=∠ADB=30°,∵∠ABC=90°,∴∠ABE=60°,∵AE⊥BD,∴∠BAE=30°,∴BE=AB,AE=AD,∴△ABE 的面积BE×AE=×AB×AD=AB×AD=矩形ABCD 的面积,∵△ABE≌△CDF,∴△CDF 的面积矩形ABCD 的面积;作EG⊥BC 于G,如图所示:∵∠CBD=30°,∴EG=BE=× AB=AB,∴△BCE 的面积BC×EG=BC×AB=BC×AB=矩形ABCD 的面积,同理:△ADF 的面积矩形ABCD 的面积.【点评】本题考查了矩形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质、平行线的性质、三角形面积公式等知识;熟练掌握矩形的性质和含30°角的直角三角形的性质,证明三角形全等是解题的关键.25.(10 分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3 副围棋和5 副中国象棋需用98 元;若购买8 副围棋和3 副中国象棋需用158 元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40 副,总费用不超过550 元,那么寒梅中学最多可以购买多少副围棋?【分析】(1)设每副围棋x 元,每副中国象棋y 元,根据题意得,求解即可;(2)设购买围棋z 副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,即可求解;【解答】解:(1)设每副围棋x 元,每副中国象棋y 元,根据题意得:,∴,∴每副围棋16 元,每副中国象棋10 元;(2)设购买围棋z 副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,∴z≤25,∴最多可以购买25 副围棋;【点评】本题考查二元一次方程组,一元一次不等式的应用;能够通过已知条件列出准确的方程组和不等式是解题的关键.26.(10 分)已知:MN 为⊙O 的直径,OE 为⊙O 的半径,AB、CH 是⊙O 的两条弦,AB⊥OE 于点D,CH⊥MN 于点K,连接HN、HE,HE 与MN 交于点P.(1)如图1,若AB 与CH 交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA 与ME 交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC 与EH 交于点G,AH 与MN 交于点R,连接RG,若,求RG 的长.【分析】(1)利用“四边形内角和为360°”、“同弧所对的圆周角是圆心角的一半”即可;(2)根据同圆中,相等的圆心角所对的弦相等,先证AB=MB,再根据“等角对等边”,证明MP=ME;(3)由全等三角形性质和垂径定理可将HK:ME=2:3 转化为OQ:MQ=4:3;可设Rt △OMQ 两直角边为:OQ=4k,MQ=3k,再构造直角三角形利用,求出k 的值;求得OP=OR=OG,得△PGR 为直角三角形,应用勾股定理求RG.【解答】解:(1)如图1,∵AB⊥OE 于点D,CH⊥MN 于点K∴∠ODB=∠OKC=90°∵∠ODB+∠DFK+∠OKC+∠EON=360°∴∠DFK+∠EON=180°∵∠DFK+∠HFB=180°∴∠HFB=∠EON∵∠EON=2∠EHN∴∠HFB=2∠EHN(2)如图2,连接OB,∵OA⊥ME,∴∠AOM=∠AOE∵AB⊥OE∴∠AOE=∠BOE∴∠AOM+∠AOE=∠AOE+∠BOE,即:∠MOE=∠AOB∴ME=AB∵∠EON=4∠CHN,∠EON=2∠EHN∴∠EHN=2∠CHN∴∠EHC=∠CHN∵CH⊥MN∴∠HPN=∠HNM∵∠HPN=∠EPM,∠HNM=HEM∴∠EPM=∠HEM∴MP=ME∴MP=AB(3)如图3,连接BC,过点A 作AF⊥BC 于F,过点A 作AL⊥MN 于L,连接AM,AC,由(2)知:∠EHC=∠CHN,∠AOM=∠AOE∴∠EOC=∠CON∵∠EOC+∠CON+∠AOM+∠AOE=180°∴∠AOE+∠EOC=90°,∠AOM+∠CON=90°∵OA⊥ME,CH⊥MN∴∠OQM=∠OKC=90°,CK=HK,ME=2MQ,∴∠AOM+∠OMQ=90°∴∠CON=∠OMQ∵OC=OA∴△OCK≌△MOQ(AAS)∴CK=OQ=HK∵HK:ME=2:3,即:OQ:2MQ=2:3∴OQ:MQ=4:3∴设OQ=4k,MQ=3k,则==5k,AB=ME=6k在Rt△OAC 中==5k∵四边形ABCH 内接于∠AOC=×90°=45°,∴∠ABC=180°﹣∠AHC=180°﹣45°=135°,∴∠ABF=180°﹣∠ABC=180°﹣135°=45°∴AF=BF=AB•cos∠ABF=6k•cos45°=3k在Rt△ACF 中,AF2+CF2=AC2即:,解得:k1=1,(不符合题意,舍去)∴OQ=HK=4,MQ=OK=3,OM=ON=5∴KN=KP=2,OP=ON﹣KN﹣KP=5﹣2﹣2=1,在△HKR 中,∠HKR=90°,∠RHK=45°,∴=tan∠RHK=tan45°=1∴RK=HK=4∴OR=RN﹣ON=4+2﹣5=1∵∠CON=∠OMQ∴OC∥ME∴∠PGO=∠HEM∵∠EPM=∠HEM∴∠PGO=∠EPM∴OG=OP=OR=1∴∠PGR=90°在Rt△HPK 中==2∵∠POG=∠PHN,∠OPG=∠HPN,PG = = ∴△POG ∽△PHN∴,即 ∴RG = = .【点评】本题是有关圆的几何综合题,难度较大,综合性很强;主要考查了垂径定理, 圆周角与圆心角,同圆中圆心角、弧、弦的关系,圆内接四边形性质,全等三角形性质, 勾股定理及解直角三角形等.27.(10 分)如图,在平面直角坐标系中,点 O 为坐标原点,直线 y =x +4 与 x 轴交于点 A ,与 y 轴交于点 B ,直线 BC 与 x 轴交于点 C ,且点 C 与点 A 关于 y 轴对称;(1)求直线 BC 的解析式;(2)点P 为线段AB 上一点,点Q 为线段BC 上一点,BQ=AP,连接PQ,设点P 的横坐标为t,△PBQ 的面积为S(S≠0),求S 与t 之间的函数关系式(不要求写出自变量t的取值范围);(3)在(2)的条件下,点E 在线段OA 上,点R 在线段BC 的延长线上,且点R 的纵坐标为,连接PE、BE、AQ,AQ 与BE 交于点F,∠APE=∠CBE,连接PF,PF的延长线与y 轴的负半轴交于点M,连接QM、MR,若,求直线PM 的解析式.【分析】(1)由y=x+4,求出A(﹣3,0)B(0,4),所以C(3,0),设直线BC 的解析式为y=kx+b,将B(0,4),C(3,0)代入,解得k=,b=4,所以直线BC 的解析;(2)过点A 作AD⊥BC 于点点D,过点P 作PN⊥BC 于N,PG⊥OB 于点G.由sin∠ACD =,即,求出AD=,设P(t,t+4),由cos∠BPG=cos∠BAO,即,求出,由,求得PN==,BQ =,所以S =,即S =;(3)如图,延长BE 至T 使ET=EP,连接AT、PT、AM、PT 交OA 于点S,易证AT∥BC,所以∠TAE=∠FQB,△ATF≌△QBF,于是AF=QF,TF=BF,再证明△MBF≌△PTF,所以MF=PF,BM=PT,于是四边形AMPQ 为平行四边形,由sin∠ABC=sin∠MQR =,设QR=25a,HR=24a,则QH=7a,tan∠QMR=,所以MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R 作RK⊥x 轴于点K.求得M(0,),设直线PM 的解析式为y=mx+n,解得,因此直线PM 的解析式为y=.【解答】解x+4,∴A(﹣3,0)B(0,4),∵点C 与点A 关于y 轴对称,∴C(3,0),设直线BC 的解析式为y=kx+b,将B(0,4),C(3,0)代入,,解得,b=4,∴直线BC 的解析;(2)如图1,过点A 作AD⊥BC 于点点D,过点P 作PN⊥BC 于N,PG⊥OB 于点G.∵OA=OC=3,OB=4,∴AC=6,AB=BC=5,∴sin∠ACD=,即,∴AD=,∵点P 为直线x+4 上,∴设P(t,t+4),∴PG=﹣t,cos∠BPG=cos∠BAO,即,∴,∵sin∠ABC=,∴PN==,∵AP=BQ,∴BQ=5+,∴S=,即S=;(3)如图,延长BE 至T 使ET=EP,连接AT、PT、AM、PT 交OA 于点S.∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠PAE=∠ACB,AT∥BC,∴∠TAE=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMPQ 为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R 作RH⊥MQ 于点H,∵sin∠ABC=sin∠MQR=,设QR=25a,HR=24a,则QH=7a,∵tan∠QMR=,∴MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R 作RK⊥x 轴于点K.∵点R 的纵坐标为,∴RK=,∵sin∠BCO=,∴CR=,BR=,∴,a=,∴BQ=30a=3,∴5+=3,t=,∴P(),∴,∵BM=PT=2PS=,BO=4,∴OM=,∴M(0,),设直线PM 的解析式为y=mx+n,∴,解得,∴直线PM 的解析式为y=.【点评】本题考查了一次函数,熟练运用待定系数法、三角形全等以及三角函数是解题的关键.。
2019年黑龙江省哈尔滨市中考数学试卷(含答案解析)
2019年黑龙江省哈尔滨市中考数学试卷(含答案解析)一、选择题(每小题3分,共计30分)1.(3分)﹣9的相反数是()A.﹣9B.﹣C.9D.2.(3分)下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b23.(3分)下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.4.(3分)七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.5.(3分)如图,P A、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°6.(3分)将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3D.y=2(x+2)2﹣37.(3分)某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20%B.40%C.18%D.36%8.(3分)方程=的解为()A.x=B.x=C.x=D.x=9.(3分)点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)10.(3分)如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是()A.=B.=C.=D.=二、填空题(每小题3分,共计30分)11.(3分)将数6260000用科学记数法表示为.12.(3分)在函数y=中,自变量x的取值范围是.13.(3分)把多项式a3﹣6a2b+9ab2分解因式的结果是.14.(3分)不等式组的解集是.15.(3分)二次函数y=﹣(x﹣6)2+8的最大值是.16.(3分)如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC =2,则A′B的长为.17.(3分)一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.18.(3分)在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD 为直角三角形,则∠BCD的度数为度.19.(3分)同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为.20.(3分)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为.三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分)21.(7分)先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD 的面积为8.23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.24.(8分)已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?26.(10分)已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB ⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN 交于点R,连接RG,若HK:ME=2:3,BC=,求RG的长.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为﹣,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF 的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=,求直线PM的解析式.2019年黑龙江省哈尔滨市中考数学试卷参考答案与试题解析一、选择题(每小题3分,共计30分)1.(3分)﹣9的相反数是()A.﹣9B.﹣C.9D.【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.【解答】解:﹣9的相反数是9,故选:C.【点评】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.2.(3分)下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b2【分析】利用同底数幂的乘法,幂的乘方与积的乘法法则,平方差公式解题即可;【解答】解:2a+2a=4a,A错误;a2•a3=a5,B错误;(2a2)3=8a6,C错误;故选:D.【点评】本题考查整式的运算;熟练掌握同底数幂的乘法,幂的乘方与积的乘法法则,平方差公式是解题的关键.3.(3分)下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据轴对称及中心对称图形的定义对各选项进行逐一分析即可.【解答】解:A、是轴对称图形,但不是中心对称图形,故此选项错误;B、是中心对称图形,也是轴对称图形,故此选项正确;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,不是中心对称图形,故此选项错误.故选:B.【点评】本题考查的是中心对称图形,熟知把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形是解答此题的关键.4.(3分)七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.【分析】左视图有2列,从左到右分别是2,1个正方形.【解答】解:这个立体图形的左视图有2列,从左到右分别是2,1个正方形,故选:B.【点评】此题主要考查了三视图的画法,正确掌握三视图观察的角度是解题关键.5.(3分)如图,P A、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°【分析】先利用切线的性质得∠OAP=∠OBP=90°,再利用四边形的内角和计算出∠AOB的度数,然后根据圆周角定理计算∠ACB的度数.【解答】解:连接OA、OB,∵P A、PB分别与⊙O相切于A、B两点,∴OA⊥P A,OB⊥PB,∴∠OAP=∠OBP=90°,∴∠AOB=180°﹣∠P=180°﹣50°=130°,∴∠ACB=∠AOB=×130°=65°.故选:D.【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.6.(3分)将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3D.y=2(x+2)2﹣3【分析】根据“上加下减、左加右减”的原则进行解答即可.【解答】解:将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式为y=2(x﹣2)2+3,故选:B.【点评】本题考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.7.(3分)某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20%B.40%C.18%D.36%【分析】设降价得百分率为x,根据降低率的公式a(1﹣x)2=b建立方程,求解即可.【解答】解:设降价的百分率为x根据题意可列方程为25(1﹣x)2=16解方程得,(舍)∴每次降价得百分率为20%故选:A.【点评】本题考查了一元二次方程实际应用问题关于增长率的类型问题,按照公式a(1﹣x)2=b对照参数位置代入值即可,公式的记忆与运用是本题的解题关键.8.(3分)方程=的解为()A.x=B.x=C.x=D.x=【分析】将分式方程化为,即可求解x=;同时要进行验根即可求解;【解答】解:=,,∴2x=9x﹣3,∴x=;将检验x=是方程的根,∴方程的解为x=;故选:C.【点评】本题考查解分式方程;熟练掌握分式方程的解法及验根是解题的关键.9.(3分)点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)【分析】将点(﹣1,4)代入y=,求出函数解析式即可解题;【解答】解:将点(﹣1,4)代入y=,∴k=﹣4,∴y=,∴点(4,﹣1)在函数图象上,故选:A.【点评】本题考查反比例函数的图象及性质;熟练掌握待定系数法求函数解析式的方法是解题的关键.10.(3分)如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD于点N,则下列式子一定正确的是()A.=B.=C.=D.=【分析】根据平行四边形的性质以及相似三角形的性质.【解答】解:∵在▱ABCD中,EM∥AD∴易证四边形AMEN为平行四边形∴易证△BEM∽△BAD∽△END∴==,A项错误=,B项错误==,C项错误==,D项正确故选:D.【点评】此题主要考查相似三角形的性质及平行四边形的性质,本题关键是要懂得找相似三角形,利用相似三角形的性质求解.二、填空题(每小题3分,共计30分)11.(3分)将数6260000用科学记数法表示为 6.26×106.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:6260000用科学记数法可表示为6.26×106,故答案为:6.26×106.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.(3分)在函数y=中,自变量x的取值范围是x≠.【分析】函数中分母不为零是函数y=有意义的条件,因此2x﹣3≠0即可;【解答】解:函数y=中分母2x﹣3≠0,∴x≠;故答案为x≠;【点评】本题考查函数自变量的取值范围;熟练掌握函数中自变量的取值范围的求法是解题的关键.13.(3分)把多项式a3﹣6a2b+9ab2分解因式的结果是a(a﹣3b)2.【分析】原式提取公因式,再利用完全平方公式分解即可.【解答】解:a3﹣6a2b+9ab2=a(a2﹣6ab+9b2)=a(a﹣3b)2.故答案为:a(a﹣3b)2.【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.14.(3分)不等式组的解集是x≥3.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式≤0,得:x≥3,解不等式3x+2≥1,得:x≥﹣,∴不等式组的解集为x≥3,故答案为:x≥3.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.15.(3分)二次函数y=﹣(x﹣6)2+8的最大值是8.【分析】利用二次函数的性质解决问题.【解答】解:∵a=﹣1<0,∴y有最大值,当x=6时,y有最大值8.故答案为8.【点评】本题主要考查二次函数的最值,熟练掌握二次函数的图象和性质是解题的关键.16.(3分)如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC =2,则A′B的长为.【分析】由旋转的性质可得AC=A'C=3,∠ACB=∠ACA'=45°,可得∠A'CB=90°,由勾股定理可求解.【解答】解:∵将△ABC绕点C逆时针旋转得到△A′B′C,∴AC=A'C=3,∠ACB=∠ACA'=45°∴∠A'CB=90°∴A'B==故答案为【点评】本题考查了旋转的性质,勾股定理,熟练掌握旋转的性质是本题的关键.17.(3分)一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是110度.【分析】直接利用弧长公式l=即可求出n的值,计算即可.【解答】解:根据l===11π,解得:n=110,故答案为:110.【点评】本题考查了扇形弧长公式计算,注意公式的灵活运用是解题关键.18.(3分)在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为60°或10度.【分析】当△ACD为直角三角形时,存在两种情况:∠ADC=90°或∠ACD=90°,根据三角形的内角和定理可得结论.【解答】解:分两种情况:①如图1,当∠ADC=90°时,∵∠B=30°,∴∠BCD=90°﹣30°=60°;②如图2,当∠ACD=90°时,∵∠A=50°,∠B=30°,∴∠ACB=180°﹣30°﹣50°=100°,∴∠BCD=100°﹣90°=10°,综上,则∠BCD的度数为60°或10°;故答案为:60°或10;【点评】本题考查了三角形的内角和定理和三角形外角的性质,分情况讨论是本题的关键.19.(3分)同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为.【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两枚骰子点数相同的情况,再利用概率公式即可求得答案.【解答】解:列表得:(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)(1,5)(2,5)(3,5)(4,5)(5,5)(6,5)(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)(1,1)(2,1)(3,1)(4,1)(5,1)(6,1)由表可知一共有36种情况,两枚骰子点数相同的有6种,所以两枚骰子点数相同的概率为=,故答案为:.【点评】本题考查了列表法与树状图法求随机事件的概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;解题时还要注意是放回试验还是不放回试验.用到的知识点为:概率=所求情况数与总情况数之比.20.(3分)如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为2.【分析】连接AC交BD于点O,由题意可证AC垂直平分BD,△ABD是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC,BC的长.【解答】解:如图,连接AC交BD于点O∵AB=AD,BC=DC,∠A=60°,∴AC垂直平分BD,△ABD是等边三角形∴∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4∵CE∥AB∴∠BAO=∠ACE=30°,∠CED=∠BAD=60°∴∠DAO=∠ACE=30°∴AE=CE=6∴DE=AD﹣AE=2∵∠CED=∠ADB=60°∴△EDF是等边三角形∴DE=EF=DF=2∴CF=CE﹣EF=4,OF=OD﹣DF=2∴OC==2∴BC==2【点评】本题考查了等边三角形的性质和判定,勾股定理,熟练运用等边三角形的判定是本题的关键.三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分)21.(7分)先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.【分析】先根据分式的混合运算顺序和运算法则化简原式,再依据特殊锐角三角函数值求得x的值,代入计算可得.【解答】解:原式=[﹣]÷=(﹣)•=•=,当x=4tan45°+2cos30°=4×1+2×=4+时,原式===.【点评】本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则.22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD 的面积为8.【分析】(1)作AC的垂直平分线,作以AC为直径的圆,垂直平分线与圆的交点即为点B;(2)以C为圆心,AC为半径作圆,格点即为点D;【解答】解;(1)作AC的垂直平分线,作以AC为直径的圆,垂直平分线与圆的交点即为点B;(2)以C为圆心,AC为半径作圆,格点即为点D;【点评】本题考查尺规作图,等腰三角形的性质;熟练掌握等腰三角形和直角三角形的尺规作图方法是解题的关键.23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.【分析】(1)由最想读教育类书籍的学生数除以占的百分比求出总人数即可;(2)确定出最想读国防类书籍的学生数,补全条形统计图即可;(2)求出最想读科技类书籍的学生占的百分比,乘以1500即可得到结果.【解答】解:(1)根据题意得:18÷30%=60(名),答:在这次调查中,一共抽取了60名学生;(2)60﹣(18+9+12+6)=15(名),则本次调查中,选取国防类书籍的学生有15名,补全条形统计图,如图所示:(3)根据题意得:1500×=225(名),答:该校最想读科技类书籍的学生有225名.【点评】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.24.(8分)已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.【分析】(1)由AAS证明△ABE≌△CDF,即可得出结论;(2)由平行线的性质得出∠CBD=∠ADB=30°,由直角三角形的性质得出BE=AB,AE=AD,得出△ABE的面积=AB×AD=矩形ABCD的面积,由全等三角形的性质得出△CDF的面积═矩形ABCD的面积;作EG⊥BC于G,由直角三角形的性质得出EG=BE=×AB=AB,得出△BCE的面积=矩形ABCD的面积,同理:△ADF的面积=矩形ABCD的面积.【解答】(1)证明:∵四边形ABCD是矩形,∴AB=CD,AB∥CD,AD∥BC,∴∠ABE=∠DF,∵AE⊥BD于点E,CF⊥BD于点F,∴∠AEB=∠CFD=90°,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AE=CF;(2)解:△ABE的面积=△CDF的面积=△BCE的面积=△ADF的面积=矩形ABCD 面积的.理由如下:∵AD∥BC,∴∠CBD=∠ADB=30°,∵∠ABC=90°,∴∠ABE=60°,∵AE⊥BD,∴∠BAE=30°,∴BE=AB,AE=AD,∴△ABE的面积=BE×AE=×AB×AD=AB×AD=矩形ABCD的面积,∵△ABE≌△CDF,∴△CDF的面积═矩形ABCD的面积;作EG⊥BC于G,如图所示:∵∠CBD=30°,∴EG=BE=×AB=AB,∴△BCE的面积=BC×EG=BC×AB=BC×AB=矩形ABCD的面积,同理:△ADF的面积=矩形ABCD的面积.【点评】本题考查了矩形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质、平行线的性质、三角形面积公式等知识;熟练掌握矩形的性质和含30°角的直角三角形的性质,证明三角形全等是解题的关键.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?【分析】(1)设每副围棋x元,每副中国象棋y元,根据题意得:,求解即可;(2)设购买围棋z副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,即可求解;【解答】解:(1)设每副围棋x元,每副中国象棋y元,根据题意得:,∴,∴每副围棋16元,每副中国象棋10元;(2)设购买围棋z副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,∴z≤25,∴最多可以购买25副围棋;【点评】本题考查二元一次方程组,一元一次不等式的应用;能够通过已知条件列出准确的方程组和不等式是解题的关键.26.(10分)已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB ⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN 交于点R,连接RG,若HK:ME=2:3,BC=,求RG的长.【分析】(1)利用“四边形内角和为360°”、“同弧所对的圆周角是圆心角的一半”即可;(2)根据同圆中,相等的圆心角所对的弦相等,先证AB=MB,再根据“等角对等边”,证明MP=ME;(3)由全等三角形性质和垂径定理可将HK:ME=2:3转化为OQ:MQ=4:3;可设Rt△OMQ两直角边为:OQ=4k,MQ=3k,再构造直角三角形利用BC=,求出k的值;求得OP=OR=OG,得△PGR为直角三角形,应用勾股定理求RG.【解答】解:(1)如图1,∵AB⊥OE于点D,CH⊥MN于点K∴∠ODB=∠OKC=90°∵∠ODB+∠DFK+∠OKC+∠EON=360°∴∠DFK+∠EON=180°∵∠DFK+∠HFB=180°∴∠HFB=∠EON∵∠EON=2∠EHN∴∠HFB=2∠EHN(2)如图2,连接OB,∵OA⊥ME,∴∠AOM=∠AOE∵AB⊥OE∴∠AOE=∠BOE∴∠AOM+∠AOE=∠AOE+∠BOE,即:∠MOE=∠AOB∴ME=AB∵∠EON=4∠CHN,∠EON=2∠EHN∴∠EHN=2∠CHN∴∠EHC=∠CHN∵CH⊥MN∴∠HPN=∠HNM∵∠HPN=∠EPM,∠HNM=HEM∴∠EPM=∠HEM∴MP=ME∴MP=AB(3)如图3,连接BC,过点A作AF⊥BC于F,过点A作AL⊥MN于L,连接AM,AC,由(2)知:∠EHC=∠CHN,∠AOM=∠AOE∴∠EOC=∠CON∵∠EOC+∠CON+∠AOM+∠AOE=180°∴∠AOE+∠EOC=90°,∠AOM+∠CON=90°∵OA⊥ME,CH⊥MN∴∠OQM=∠OKC=90°,CK=HK,ME=2MQ,∴∠AOM+∠OMQ=90°∴∠CON=∠OMQ∵OC=OA∴△OCK≌△MOQ(AAS)∴CK=OQ=HK∵HK:ME=2:3,即:OQ:2MQ=2:3∴OQ:MQ=4:3∴设OQ=4k,MQ=3k,则OM===5k,AB=ME=6k在Rt△OAC中,AC===5k∵四边形ABCH内接于⊙O,∠AHC=∠AOC=×90°=45°,∴∠ABC=180°﹣∠AHC=180°﹣45°=135°,∴∠ABF=180°﹣∠ABC=180°﹣135°=45°∴AF=BF=AB•cos∠ABF=6k•cos45°=3k在Rt△ACF中,AF2+CF2=AC2即:,解得:k1=1,(不符合题意,舍去)∴OQ=HK=4,MQ=OK=3,OM=ON=5∴KN=KP=2,OP=ON﹣KN﹣KP=5﹣2﹣2=1,在△HKR中,∠HKR=90°,∠RHK=45°,∴=tan∠RHK=tan45°=1∴RK=HK=4∴OR=RN﹣ON=4+2﹣5=1∵∠CON=∠OMQ∴OC∥ME∴∠PGO=∠HEM∵∠EPM=∠HEM∴∠PGO=∠EPM∴OG=OP=OR=1∴∠PGR=90°在Rt△HPK中,PH===2∵∠POG=∠PHN,∠OPG=∠HPN∴△POG∽△PHN∴,即,PG=∴RG===.【点评】本题是有关圆的几何综合题,难度较大,综合性很强;主要考查了垂径定理,圆周角与圆心角,同圆中圆心角、弧、弦的关系,圆内接四边形性质,全等三角形性质,勾股定理及解直角三角形等.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为﹣,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF 的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=,求直线PM的解析式.【分析】(1)由y=x+4,求出A(﹣3,0)B(0,4),所以C(3,0),设直线BC的解析式为y=kx+b,将B(0,4),C(3,0)代入,解得k=﹣,b=4,所以直线BC 的解析式y=﹣;(2)过点A作AD⊥BC于点点D,过点P作PN⊥BC于N,PG⊥OB于点G.由sin∠ACD=,即,求出AD=,设P(t,t+4),由cos∠BPG=cos∠BAO,即,求出,由sin∠ABC=,求得PN==,BQ=5+,所以S=,即S=;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM、PT交OA于点S,易证AT ∥BC,所以∠TAE=∠FQB,△ATF≌△QBF,于是AF=QF,TF=BF,再证明△MBF ≌△PTF,所以MF=PF,BM=PT,于是四边形AMQP为平行四边形,由sin∠ABC=sin∠MQR=,设QR=25a,HR=24a,则QH=7a,tan∠QMR=,所以MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.求得M(0,),设直线PM的解析式为y=mx+n,解得,因此直线PM的解析式为y=.【解答】解:(1)∵y=x+4,∴A(﹣3,0)B(0,4),∵点C与点A关于y轴对称,∴C(3,0),设直线BC的解析式为y=kx+b,将B(0,4),C(3,0)代入,,解得k=﹣,b=4,∴直线BC的解析式y=﹣;(2)如图1,过点A作AD⊥BC于点点D,过点P作PN⊥BC于N,PG⊥OB于点G.∵OA=OC=3,OB=4,∴AC=6,AB=BC=5,∴sin∠ACD=,即,∴AD=,∵点P为直线y=x+4上,∴设P(t,t+4),∴PG=﹣t,cos∠BPG=cos∠BAO,即,∴,∵sin∠ABC=,∴PN==,∵AP=BQ,∴BQ=5+,∴S=,即S=;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM、PT交OA于点S.∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠P AE=∠ACB,AT∥BC,∴∠TAE=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMQP为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R作RH⊥MQ于点H,∵sin∠ABC=sin∠MQR=,设QR=25a,HR=24a,则QH=7a,∵tan∠QMR=,∴MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.∵点R的纵坐标为﹣,∴RK=,∵sin∠BCO=,∴CR=,BR=,∴,a=,∴BQ=30a=3,∴5+=3,t=,∴P(),∴,∵BM=PT=2PS=,BO=4,∴OM=,∴M(0,),设直线PM的解析式为y=mx+n,∴,解得,∴直线PM的解析式为y=.【点评】本题考查了一次函数,熟练运用待定系数法、三角形全等以及三角函数是解题的关键.。
2019年黑龙江省哈尔滨市中考数学试卷及答案

2019年黑龙江省哈尔滨市中考数学试卷一、选择题(每小题3分,共计30分)1.﹣9的相反数是()A.﹣9B.﹣C.9D.2.下列运算一定正确的是()A.2a+2a=2a2 B.a2•a3=a6 C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b23.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.5.如图,P A、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°6.将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3D.y=2(x+2)2﹣37.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20%B.40%C.18%D.36%8.方程=的解为()A.x=B.x=C.x=D.x=9.点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)10.如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD 于点N,则下列式子一定正确的是()A.=B.=C.=D.=二、填空题(每小题3分,共计30分)11.将数6260000用科学记数法表示为.12.在函数y=中,自变量x的取值范围是.13.把多项式a3﹣6a2b+9ab2分解因式的结果是.14.不等式组的解集是.15.二次函数y=﹣(x﹣6)2+8的最大值是.16.如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为.17.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为度.19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为.20.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为.三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分)21.(7分)先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD 的面积为8.23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.24.(8分)已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?26.(10分)已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB ⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN 交于点R,连接RG,若HK:ME=2:3,BC=,求RG的长.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为﹣,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=,求直线PM的解析式.2019年黑龙江省哈尔滨市中考数学试卷参考答案与试题解析一、选择题(每小题3分,共计30分)1.﹣9的相反数是()A.﹣9B.﹣C.9D.【分析】根据只有符号不同的两个数互为相反数,可得一个数的相反数.【解答】解:﹣9的相反数是9,故选:C.【点评】本题考查了相反数,在一个数的前面加上负号就是这个数的相反数.2.下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b2【分析】利用同底数幂的乘法,幂的乘方与积的乘法法则,平方差公式解题即可;【解答】解:2a+2a=4a,A错误;a2•a3=a5,B错误;(2a2)3=8a6,C错误;故选:D.【点评】本题考查整式的运算;熟练掌握同底数幂的乘法,幂的乘方与积的乘法法则,平方差公式是解题的关键.3.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.【分析】根据轴对称及中心对称图形的定义对各选项进行逐一分析即可.【解答】解:A、是轴对称图形,但不是中心对称图形,故此选项错误;B、是中心对称图形,也是轴对称图形,故此选项正确;C、是轴对称图形,不是中心对称图形,故此选项错误;D、是轴对称图形,不是中心对称图形,故此选项错误.故选:B.【点评】本题考查的是中心对称图形,熟知把一个图形绕某一点旋转180°,如果旋转后的图形能够与原来的图形重合,那么这个图形就叫做中心对称图形是解答此题的关键.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.【分析】左视图有2列,从左到右分别是2,1个正方形.【解答】解:这个立体图形的左视图有2列,从左到右分别是2,1个正方形,故选:B.【点评】此题主要考查了三视图的画法,正确掌握三视图观察的角度是解题关键.5.如图,P A、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°【分析】先利用切线的性质得∠OAP=∠OBP=90°,再利用四边形的内角和计算出∠AOB的度数,然后根据圆周角定理计算∠ACB的度数.【解答】解:连接OA、OB,∵P A、PB分别与⊙O相切于A、B两点,∴OA⊥P A,OB⊥PB,∴∠OAP=∠OBP=90°,∴∠AOB=180°﹣∠P=180°﹣50°=130°,∴∠ACB=∠AOB=×130°=65°.故选:D.【点评】本题考查了切线的性质:圆的切线垂直于经过切点的半径.也考查了圆周角定理.6.将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3D.y=2(x+2)2﹣3【分析】根据“上加下减、左加右减”的原则进行解答即可.【解答】解:将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,得到的抛物线的解析式为y=2(x﹣2)2+3,故选:B.【点评】本题考查的是二次函数的图象与几何变换,要求熟练掌握平移的规律:左加右减,上加下减.7.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20%B.40%C.18%D.36%【分析】设降价得百分率为x,根据降低率的公式a(1﹣x)2=b建立方程,求解即可.【解答】解:设降价的百分率为x根据题意可列方程为25(1﹣x)2=16解方程得,(舍)∴每次降价得百分率为20%故选:A.【点评】本题考查了一元二次方程实际应用问题关于增长率的类型问题,按照公式a(1﹣x)2=b对照参数位置代入值即可,公式的记忆与运用是本题的解题关键.8.方程=的解为()A.x=B.x=C.x=D.x=【分析】将分式方程化为,即可求解x=;同时要进行验根即可求解;【解答】解:=,,∴2x=9x﹣3,∴x=;将检验x=是方程的根,∴方程的解为x=;故选:C.【点评】本题考查解分式方程;熟练掌握分式方程的解法及验根是解题的关键.9.点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)【分析】将点(﹣1,4)代入y=,求出函数解析式即可解题;【解答】解:将点(﹣1,4)代入y=,∴k=﹣4,∴y=,∴点(4,﹣1)在函数图象上,故选:A.【点评】本题考查反比例函数的图象及性质;熟练掌握待定系数法求函数解析式的方法是解题的关键.10.如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD 于点N,则下列式子一定正确的是()A.=B.=C.=D.=【分析】根据平行四边形的性质以及相似三角形的性质.【解答】解:∵在▱ABCD中,EM∥AD∴易证四边形AMEN为平行四边形∴易证△BEM∽△BAD∽△END∴==,A项错误=,B项错误==,C项错误==,D项正确故选:D.【点评】此题主要考查相似三角形的性质及平行四边形的性质,本题关键是要懂得找相似三角形,利用相似三角形的性质求解.二、填空题(每小题3分,共计30分)11.将数6260000用科学记数法表示为 6.26×106.【分析】科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数.确定n 的值时,要看把原数变成a时,小数点移动了多少位,n的绝对值与小数点移动的位数相同.当原数绝对值>1时,n是正数;当原数的绝对值<1时,n是负数.【解答】解:6260000用科学记数法可表示为6.26×106,故答案为:6.26×106.【点评】此题考查科学记数法的表示方法.科学记数法的表示形式为a×10n的形式,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.12.在函数y=中,自变量x的取值范围是x≠.【分析】函数中分母不为零是函数y=有意义的条件,因此2x﹣3≠0即可;【解答】解:函数y=中分母2x﹣3≠0,∴x≠;故答案为x≠;【点评】本题考查函数自变量的取值范围;熟练掌握函数中自变量的取值范围的求法是解题的关键.13.把多项式a3﹣6a2b+9ab2分解因式的结果是a(a﹣3b)2.【分析】原式提取公因式,再利用完全平方公式分解即可.【解答】解:a3﹣6a2b+9ab2=a(a2﹣6ab+9b2)=a(a﹣3b)2.故答案为:a(a﹣3b)2.【点评】此题考查了提公因式法与公式法的综合运用,熟练掌握因式分解的方法是解本题的关键.14.不等式组的解集是x≥3.【分析】分别求出每一个不等式的解集,根据口诀:同大取大、同小取小、大小小大中间找、大大小小无解了确定不等式组的解集.【解答】解:解不等式≤0,得:x≥3,解不等式3x+2≥1,得:x≥﹣,∴不等式组的解集为x≥3,故答案为:x≥3.【点评】本题考查的是解一元一次不等式组,正确求出每一个不等式解集是基础,熟知“同大取大;同小取小;大小小大中间找;大大小小找不到”的原则是解答此题的关键.15.二次函数y=﹣(x﹣6)2+8的最大值是8.【分析】利用二次函数的性质解决问题.【解答】解:∵a=﹣1<0,∴y有最大值,当x=6时,y有最大值8.故答案为8.【点评】本题主要考查二次函数的最值,熟练掌握二次函数的图象和性质是解题的关键.16.如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC=2,则A′B的长为.【分析】由旋转的性质可得AC=A'C=3,∠ACB=∠ACA'=45°,可得∠A'CB=90°,由勾股定理可求解.【解答】解:∵将△ABC绕点C逆时针旋转得到△A′B′C,∴AC=A'C=3,∠ACB=∠ACA'=45°∴∠A'CB=90°∴A'B==故答案为【点评】本题考查了旋转的性质,勾股定理,熟练掌握旋转的性质是本题的关键.17.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是110度.【分析】直接利用弧长公式l=即可求出n的值,计算即可.【解答】解:根据l===11π,解得:n=110,故答案为:110.【点评】本题考查了扇形弧长公式计算,注意公式的灵活运用是解题关键.18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为60°或10度.【分析】当△ACD为直角三角形时,存在两种情况:∠ADC=90°或∠ACD=90°,根据三角形的内角和定理可得结论.【解答】解:分两种情况:①如图1,当∠ADC=90°时,∵∠B=30°,∴∠BCD=90°﹣30°=60°;②如图2,当∠ACD=90°时,∵∠A=50°,∠B=30°,∴∠ACB=180°﹣30°﹣50°=100°,∴∠BCD=100°﹣90°=10°,综上,则∠BCD的度数为60°或10°;故答案为:60°或10;【点评】本题考查了三角形的内角和定理和三角形外角的性质,分情况讨论是本题的关键.19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为.【分析】首先根据题意列出表格,然后由表格即可求得所有等可能的结果与两枚骰子点数相同的情况,再利用概率公式即可求得答案.【解答】解:列表得:(1,6)(2,6)(3,6)(4,6)(5,6)(6,6)(1,5)(2,5)(3,5)(4,5)(5,5)(6,5)(1,4)(2,4)(3,4)(4,4)(5,4)(6,4)(1,3)(2,3)(3,3)(4,3)(5,3)(6,3)(1,2)(2,2)(3,2)(4,2)(5,2)(6,2)(1,1)(2,1)(3,1)(4,1)(5,1)(6,1)由表可知一共有36种情况,两枚骰子点数相同的有6种,所以两枚骰子点数相同的概率为=,故答案为:.【点评】本题考查了列表法与树状图法求随机事件的概率,列表法可以不重复不遗漏的列出所有可能的结果,适合于两步完成的事件;解题时还要注意是放回试验还是不放回试验.用到的知识点为:概率=所求情况数与总情况数之比.20.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为2.【分析】连接AC交BD于点O,由题意可证AC垂直平分BD,△ABD是等边三角形,可得∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4,通过证明△EDF是等边三角形,可得DE=EF=DF=2,由勾股定理可求OC,BC的长.【解答】解:如图,连接AC交BD于点O∵AB=AD,BC=DC,∠A=60°,∴AC垂直平分BD,△ABD是等边三角形∴∠BAO=∠DAO=30°,AB=AD=BD=8,BO=OD=4∵CE∥AB∴∠BAO=∠ACE=30°,∠CED=∠BAD=60°∴∠DAO=∠ACE=30°∴AE=CE=6∴DE=AD﹣AE=2∵∠CED=∠ADB=60°∴△EDF是等边三角形∴DE=EF=DF=2∴CF=CE﹣EF=4,OF=OD﹣DF=2∴OC==2∴BC==2【点评】本题考查了等边三角形的性质和判定,勾股定理,熟练运用等边三角形的判定是本题的关键.三、解答题(其中21~22题各7分,23-24题各8分,25~27题各10分,共计60分)21.(7分)先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.【分析】先根据分式的混合运算顺序和运算法则化简原式,再依据特殊锐角三角函数值求得x的值,代入计算可得.【解答】解:原式=[﹣]÷=(﹣)•=•=,当x=4tan45°+2cos30°=4×1+2×=4+时,原式===.【点评】本题主要考查分式的化简求值,解题的关键是掌握分式的混合运算顺序和运算法则.22.(7分)图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD 的面积为8.【分析】(1)作AC的垂直平分线,作以AC为直径的圆,垂直平分线与圆的交点即为点B;(2)以C为圆心,AC为半径作圆,格点即为点D;【解答】解;(1)作AC的垂直平分线,作以AC为直径的圆,垂直平分线与圆的交点即为点B;(2)以C为圆心,AC为半径作圆,格点即为点D;【点评】本题考查尺规作图,等腰三角形的性质;熟练掌握等腰三角形和直角三角形的尺规作图方法是解题的关键.23.(8分)建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.【分析】(1)由最想读教育类书籍的学生数除以占的百分比求出总人数即可;(2)确定出最想读国防类书籍的学生数,补全条形统计图即可;(2)求出最想读科技类书籍的学生占的百分比,乘以1500即可得到结果.【解答】解:(1)根据题意得:18÷30%=60(名),答:在这次调查中,一共抽取了60名学生;(2)60﹣(18+9+12+6)=15(名),则本次调查中,选取国防类书籍的学生有15名,补全条形统计图,如图所示:(3)根据题意得:1500×=225(名),答:该校最想读科技类书籍的学生有225名.【点评】此题考查了条形统计图,扇形统计图,以及用样本估计总体,弄清题意是解本题的关键.24.(8分)已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.【分析】(1)由AAS证明△ABE≌△CDF,即可得出结论;(2)由平行线的性质得出∠CBD=∠ADB=30°,由直角三角形的性质得出BE=AB,AE=AD,得出△ABE的面积=AB×AD=矩形ABCD的面积,由全等三角形的性质得出△CDF的面积═矩形ABCD的面积;作EG⊥BC于G,由直角三角形的性质得出EG=BE=×AB=AB,得出△BCE的面积=矩形ABCD的面积,同理:△ADF的面积=矩形ABCD的面积.【解答】(1)证明:∵四边形ABCD是矩形,∴AB=CD,AB∥CD,AD∥BC,∴∠ABE=∠DF,∵AE⊥BD于点E,CF⊥BD于点F,∴∠AEB=∠CFD=90°,在△ABE和△CDF中,,∴△ABE≌△CDF(AAS),∴AE=CF;(2)解:△ABE的面积=△CDF的面积=△BCE的面积=△ADF的面积=矩形ABCD 面积的.理由如下:∵AD∥BC,∴∠CBD=∠ADB=30°,∵∠ABC=90°,∴∠ABE=60°,∵AE⊥BD,∴∠BAE=30°,∴BE=AB,AE=AD,∴△ABE的面积=BE×AE=×AB×AD=AB×AD=矩形ABCD的面积,∵△ABE≌△CDF,∴△CDF的面积═矩形ABCD的面积;作EG⊥BC于G,如图所示:∵∠CBD=30°,∴EG=BE=×AB=AB,∴△BCE的面积=BC×EG=BC×AB=BC×AB=矩形ABCD的面积,同理:△ADF的面积=矩形ABCD的面积.【点评】本题考查了矩形的性质、全等三角形的判定与性质、含30°角的直角三角形的性质、平行线的性质、三角形面积公式等知识;熟练掌握矩形的性质和含30°角的直角三角形的性质,证明三角形全等是解题的关键.25.(10分)寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?【分析】(1)设每副围棋x元,每副中国象棋y元,根据题意得:,求解即可;(2)设购买围棋z副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,即可求解;【解答】解:(1)设每副围棋x元,每副中国象棋y元,根据题意得:,∴,∴每副围棋16元,每副中国象棋10元;(2)设购买围棋z副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,∴z≤25,∴最多可以购买25副围棋;【点评】本题考查二元一次方程组,一元一次不等式的应用;能够通过已知条件列出准确的方程组和不等式是解题的关键.26.(10分)已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB ⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN 交于点R,连接RG,若HK:ME=2:3,BC=,求RG的长.【分析】(1)利用“四边形内角和为360°”、“同弧所对的圆周角是圆心角的一半”即可;(2)根据同圆中,相等的圆心角所对的弦相等,先证AB=MB,再根据“等角对等边”,证明MP=ME;(3)由全等三角形性质和垂径定理可将HK:ME=2:3转化为OQ:MQ=4:3;可设Rt△OMQ两直角边为:OQ=4k,MQ=3k,再构造直角三角形利用BC=,求出k的值;求得OP=OR=OG,得△PGR为直角三角形,应用勾股定理求RG.【解答】解:(1)如图1,∵AB⊥OE于点D,CH⊥MN于点K∴∠ODB=∠OKC=90°∵∠ODB+∠DFK+∠OKC+∠EON=360°∴∠DFK+∠EON=180°∵∠DFK+∠HFB=180°∴∠HFB=∠EON∵∠EON=2∠EHN∴∠HFB=2∠EHN(2)如图2,连接OB,∵OA⊥ME,∴∠AOM=∠AOE∵AB⊥OE∴∠AOE=∠BOE∴∠AOM+∠AOE=∠AOE+∠BOE,即:∠MOE=∠AOB∴ME=AB∵∠EON=4∠CHN,∠EON=2∠EHN∴∠EHN=2∠CHN∴∠EHC=∠CHN∵CH⊥MN∴∠HPN=∠HNM∵∠HPN=∠EPM,∠HNM=HEM∴∠EPM=∠HEM∴MP=ME∴MP=AB(3)如图3,连接BC,过点A作AF⊥BC于F,过点A作AL⊥MN于L,连接AM,AC,由(2)知:∠EHC=∠CHN,∠AOM=∠AOE∴∠EOC=∠CON∵∠EOC+∠CON+∠AOM+∠AOE=180°∴∠AOE+∠EOC=90°,∠AOM+∠CON=90°∵OA⊥ME,CH⊥MN∴∠OQM=∠OKC=90°,CK=HK,ME=2MQ,∴∠AOM+∠OMQ=90°∴∠CON=∠OMQ∵OC=OA∴△OCK≌△MOQ(AAS)∴CK=OQ=HK∵HK:ME=2:3,即:OQ:2MQ=2:3∴OQ:MQ=4:3∴设OQ=4k,MQ=3k,则OM===5k,AB=ME=6k在Rt△OAC中,AC===5k∵四边形ABCH内接于⊙O,∠AHC=∠AOC=×90°=45°,∴∠ABC=180°﹣∠AHC=180°﹣45°=135°,∴∠ABF=180°﹣∠ABC=180°﹣135°=45°∴AF=BF=AB•cos∠ABF=6k•cos45°=3k在Rt△ACF中,AF2+CF2=AC2即:,解得:k1=1,(不符合题意,舍去)∴OQ=HK=4,MQ=OK=3,OM=ON=5∴KN=KP=2,OP=ON﹣KN﹣KP=5﹣2﹣2=1,在△HKR中,∠HKR=90°,∠RHK=45°,∴=tan∠RHK=tan45°=1∴RK=HK=4∴OR=RN﹣ON=4+2﹣5=1∵∠CON=∠OMQ∴OC∥ME∴∠PGO=∠HEM∵∠EPM=∠HEM∴∠PGO=∠EPM∴OG=OP=OR=1∴∠PGR=90°在Rt△HPK中,PH===2∵∠POG=∠PHN,∠OPG=∠HPN∴△POG∽△PHN∴,即,PG=∴RG===.【点评】本题是有关圆的几何综合题,难度较大,综合性很强;主要考查了垂径定理,圆周角与圆心角,同圆中圆心角、弧、弦的关系,圆内接四边形性质,全等三角形性质,勾股定理及解直角三角形等.27.(10分)如图,在平面直角坐标系中,点O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t 的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为﹣,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=,求直线PM的解析式.【分析】(1)由y=x+4,求出A(﹣3,0)B(0,4),所以C(3,0),设直线BC的解析式为y=kx+b,将B(0,4),C(3,0)代入,解得k=,b=4,所以直线BC的解析式;(2)过点A作AD⊥BC于点点D,过点P作PN⊥BC于N,PG⊥OB于点G.由sin∠ACD=,即,求出AD=,设P(t,t+4),由cos∠BPG=cos∠BAO,即,求出,由sin∠ABC=,求得PN==,BQ=5+,所以S=,即S=;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM、PT交OA于点S,易证AT ∥BC,所以∠TAE=∠FQB,△ATF≌△QBF,于是AF=QF,TF=BF,再证明△MBF ≌△PTF,所以MF=PF,BM=PT,于是四边形AMPQ为平行四边形,由sin∠ABC=sin∠MQR=,设QR=25a,HR=24a,则QH=7a,tan∠QMR=,所以MH =23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.求得M(0,),设直线PM的解析式为y=mx+n,解得,因此直线PM的解析式为y=.【解答】解:(1)∵y=x+4,∴A(﹣3,0)B(0,4),∵点C与点A关于y轴对称,∴C(3,0),设直线BC的解析式为y=kx+b,将B(0,4),C(3,0)代入,,解得k=,b=4,∴直线BC的解析式;(2)如图1,过点A作AD⊥BC于点点D,过点P作PN⊥BC于N,PG⊥OB于点G.∵OA=OC=3,OB=4,∴AC=6,AB=BC=5,∴sin∠ACD=,即,∴AD=,∵点P为直线y=x+4上,∴设P(t,t+4),∴PG=﹣t,cos∠BPG=cos∠BAO,即,∴,∵sin∠ABC=,∴PN==,∵AP=BQ,∴BQ=5+,∴S=,即S=;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM、PT交OA于点S.∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠P AE=∠ACB,AT∥BC,∴∠TAE=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMPQ为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R作RH⊥MQ于点H,∵sin∠ABC=sin∠MQR=,设QR=25a,HR=24a,则QH=7a,∵tan∠QMR=,∴MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.∵点R的纵坐标为﹣,∴RK=,∵sin∠BCO=,∴CR=,BR=,∴,a=,∴BQ=30a=3,∴5+=3,t=,∴P(),∴,∵BM=PT=2PS=,BO=4,∴OM=,∴M(0,),设直线PM的解析式为y=mx+n,∴,解得,∴直线PM的解析式为y=.【点评】本题考查了一次函数,熟练运用待定系数法、三角形全等以及三角函数是解题的关键.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2019年哈尔滨中考数学试卷一.选择题(共10小题)1.﹣9的相反数是()A.﹣9 B.﹣C.9 D.2.下列运算一定正确的是()A.2a+2a=2a2B.a2•a3=a6C.(2a2)3=6a6D.(a+b)(a﹣b)=a2﹣b23.下列图形中既是轴对称图形又是中心对称图形的是()A.B.C.D.4.七个大小相同的正方体搭成的几何体如图所示,其左视图是()A.B.C.D.5.如图,PA、PB分别与⊙O相切于A、B两点,点C为⊙O上一点,连接AC、BC,若∠P=50°,则∠ACB的度数为()A.60°B.75°C.70°D.65°6.将抛物线y=2x2向上平移3个单位长度,再向右平移2个单位长度,所得到的抛物线为()A.y=2(x+2)2+3 B.y=2(x﹣2)2+3C.y=2(x﹣2)2﹣3 D.y=2(x+2)2﹣37.某商品经过连续两次降价,售价由原来的每件25元降到每件16元,则平均每次降价的百分率为()A.20% B.40% C.18% D.36%8.方程=的解为()A.x=B.x=C.x=D.x=9.点(﹣1,4)在反比例函数y=的图象上,则下列各点在此函数图象上的是()A.(4,﹣1)B.(﹣,1)C.(﹣4,﹣1)D.(,2)10.如图,在▱ABCD中,点E在对角线BD上,EM∥AD,交AB于点M,EN∥AB,交AD 于点N,则下列式子一定正确的是()A.=B.=C.=D.=二.填空题(共10小题)11.将数6260000用科学记数法表示为.12.在函数y=中,自变量x的取值范围是.13.把多项式a3﹣6a2b+9ab2分解因式的结果是.14.不等式组的解集是.15.二次函数y=﹣(x﹣6)2+8的最大值是.16.如图,将△ABC绕点C逆时针旋转得到△A′B′C,其中点A′与A是对应点,点B′与B是对应点,点B′落在边AC上,连接A′B,若∠ACB=45°,AC=3,BC =2,则A′B的长为.17.一个扇形的弧长是11πcm,半径是18cm,则此扇形的圆心角是度.18.在△ABC中,∠A=50°,∠B=30°,点D在AB边上,连接CD,若△ACD为直角三角形,则∠BCD的度数为度.19.同时掷两枚质地均匀的骰子,每枚骰子的六个面上分别刻有1到6的点数,则这两枚骰子向上的一面出现的点数相同的概率为.20.如图,在四边形ABCD中,AB=AD,BC=DC,∠A=60°,点E为AD边上一点,连接BD、CE,CE与BD交于点F,且CE∥AB,若AB=8,CE=6,则BC的长为.三.解答题(共7小题)21.先化简再求值:(﹣)÷,其中x=4tan45°+2cos30°.22.图1、2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上.(1)在图1中画出以AC为底边的等腰直角三角形ABC,点B在小正方形顶点上;(2)在图2中画出以AC为腰的等腰三角形ACD,点D在小正方形的顶点上,且△ACD的面积为8.23.建国七十周年到来之际,海庆中学决定举办以“祖国在我心中”为主题的读书活动.为了使活动更具有针对性,学校在全校范围内随机抽取部分学生进行问卷调查,要求学生在“教育、科技、国防、农业、工业”五类书籍中,选取自己最想读的一种(必选且只选一种),学校将收集到的调查结果适当整理后,绘制成如图所示的不完整的统计图.请根据图中所给的信息解答下列问题:(1)在这次调查中,一共抽取了多少名学生?(2)请通过计算补全条形统计图;(3)如果海庆中学共有1500名学生,请你估计该校最想读科技类书籍的学生有多少名.24.已知:在矩形ABCD中,BD是对角线,AE⊥BD于点E,CF⊥BD于点F.(1)如图1,求证:AE=CF;(2)如图2,当∠ADB=30°时,连接AF、CE,在不添加任何辅助线的情况下,请直接写出图2中四个三角形,使写出的每个三角形的面积都等于矩形ABCD面积的.25.寒梅中学为了丰富学生的课余生活,计划购买围棋和中国象棋供棋类兴趣小组活动使用.若购买3副围棋和5副中国象棋需用98元;若购买8副围棋和3副中国象棋需用158元;(1)求每副围棋和每副中国象棋各多少元;(2)寒梅中学决定购买围棋和中国象棋共40副,总费用不超过550元,那么寒梅中学最多可以购买多少副围棋?26.已知:MN为⊙O的直径,OE为⊙O的半径,AB、CH是⊙O的两条弦,AB⊥OE于点D,CH⊥MN于点K,连接HN、HE,HE与MN交于点P.(1)如图1,若AB与CH交于点F,求证:∠HFB=2∠EHN;(2)如图2,连接ME、OA,OA与ME交于点Q,若OA⊥ME,∠EON=4∠CHN,求证:MP=AB;(3)如图3,在(2)的条件下,连接OC、BC、AH,OC与EH交于点G,AH与MN 交于点R,连接RG,若HK:ME=2:3,BC=,求RG的长.27.如图,在平面直角坐标系中,点O为坐标原点,直线y=x+4与x轴交于点A,与y轴交于点B,直线BC与x轴交于点C,且点C与点A关于y轴对称;(1)求直线BC的解析式;(2)点P为线段AB上一点,点Q为线段BC上一点,BQ=AP,连接PQ,设点P的横坐标为t,△PBQ的面积为S(S≠0),求S与t之间的函数关系式(不要求写出自变量t的取值范围);(3)在(2)的条件下,点E在线段OA上,点R在线段BC的延长线上,且点R的纵坐标为﹣,连接PE、BE、AQ,AQ与BE交于点F,∠APE=∠CBE,连接PF,PF 的延长线与y轴的负半轴交于点M,连接QM、MR,若tan∠QMR=,求直线PM 的解析式.答案:1.C.2.D.3.B.4.B.5.D.6.B.7.A.8.C.9.A.10.D.11.6.26×106.12.x≠.13.a(a﹣3b)2.14.x≥3.15.8.16..17.110.8.60°或10.19..20.2.21.解:原式=[﹣]÷=(﹣)•=•=,当x=4tan45°+2cos30°=4×1+2×=4+时,原式===.22.解:23.解:(1)根据题意得:18÷30%=60(名),答:在这次调查中,一共抽取了60名学生;(2)60﹣(18+9+12+6)=15(名),则本次调查中,选取国防类书籍的学生有15名,补全条形统计图,如图所示:(3)根据题意得:1500×=225(名),答:该校最想读科技类书籍的学生有225名.24.解:(1)∵四边形ABCD为矩形∴AB∥CD且AB=CD∴∠ABE=∠CDF∵AE⊥BD ∴∠AEB=90°∵CE⊥BD∴∠CFD=90°∴△ABE≌△CDF(AAS)∴AE=CF.(2)△AFD,△ABE,△BEC,△FDC.25.解:(1)设每副围棋x元,每副中国象棋y元,根据题意得:,∴,答:每副围棋16元,每副中国象棋10元;(2)设购买围棋z副,则购买象棋(40﹣z)副,根据题意得:16z+10(40﹣z)≤550,∴z≤25,答:最多可以购买25副围棋;26.解:(1)如图1,∵AB⊥OE于点D,CH⊥MN于点K ∴∠ODB=∠OKC=90°∵∠ODB+∠DFK+∠OKC+∠EON=360°∴∠DFK+∠EON=180°∵∠DFK+∠HFB=180°∴∠HFB=∠EON∵∠EON=2∠EHN∴∠HFB=2∠EHN(2)如图2,连接OB,∵OA⊥ME,∴∠AOM=∠AOE∵AB⊥OE∴∠AOE=∠BOE∴∠AOM+∠AOE=∠AOE+∠BOE,即:∠MOE=∠AOB∴ME=AB∵∠EON=4∠CHN,∠EON=2∠EHN∴∠EHN=2∠CHN∴∠EHC=∠CHN∵CH⊥MN∴∠HPN=∠HNM∵∠HPN=∠EPM,∠HNM=HEM∴∠EPM=∠HEM∴MP=ME∴MP=AB(3)如图3,连接BC,过点A作AF⊥BC于F,过点A作AL⊥MN于L,连接AM,AC,由(2)知:∠EHC=∠CHN,∠AOM=∠AOE∴∠EOC=∠CON∵∠EOC+∠CON+∠AOM+∠AOE=180°∴∠AOE+∠EOC=90°,∠AOM+∠CON=90°∵OA⊥ME,CH⊥MN∴∠OQM=∠OKC=90°,CK=HK,ME=2MQ,∴∠AOM+∠OMQ=90°∴∠CON=∠OMQ∵OC=OA∴△OCK≌△MOQ(AAS)∴CK=OQ=HK∵HK:ME=2:3,即:OQ:2MQ=2:3∴OQ:MQ=4:3∴设OQ=4k,MQ=3k,则OM===5k,AB=ME=6k在Rt△OAC中,AC===5k∵四边形ABCH内接于⊙O,∠AHC=∠AOC=×90°=45°,∴∠ABC=180°﹣∠AHC=180°﹣45°=135°,∴∠ABF=180°﹣∠ABC=180°﹣135°=45°∴AF=BF=AB•cos∠ABF=6k•cos45°=3k在Rt△ACF中,AF2+CF2=AC2即:,解得:k1=1,(不符合题意,舍去)∴OQ=HK=4,MQ=OK=3,OM=ON=5∴KN=KP=2,OP=ON﹣KN﹣KP=5﹣2﹣2=1,在△HKR中,∠HKR=90°,∠RHK=45°,∴=tan∠RHK=tan45°=1∴RK=HK=4∴OR=RN﹣ON=4+2﹣5=1∵∠CON=∠OMQ∴OC∥ME∴∠PGO=∠HEM∵∠EPM=∠HEM∴∠PGO=∠EPM∴OG=OP=OR=1∴∠PGR=90°在Rt△HPK中,PH===2∵∠POG=∠PHN,∠OPG=∠HPN∴△POG∽△PHN∴,即,PG=∴RG===.27.解:(1)∵y=x+4,∴A(﹣3,0)B(0,4),∵点C与点A关于y轴对称,∴C(3,0),设直线BC的解析式为y=kx+b,将B(0,4),C(3,0)代入,,解得k=,b=4,∴直线BC的解析式;(2)如图1,过点A作AD⊥BC于点点D,过点P作PN⊥BC于N,PG⊥OB于点G.∵OA=OC=3,OB=4,∴AC=6,AB=BC=5,∴sin∠ACD=,即,∴AD=,∵点P为直线y=x+4上,∴设P(t,t+4),∴PG=﹣t,cos∠BPG=cos∠BAO,即,∴,∵sin∠ABC=,∴PN==,∵AP=BQ,∴BQ=5+,∴S=,即S=;(3)如图,延长BE至T使ET=EP,连接AT、PT、AM、PT交OA于点S.∵∠APE=∠EBC,∠BAC=∠BCA,∴180°﹣∠APE﹣∠BAC=180°﹣∠EBC﹣∠ACB,∴∠PEA=∠BEC=∠AET,∴PT⊥AE,PS=ST,∴AP=AT,∠TAE=∠PAE=∠ACB,AT∥BC,∴∠TAE=∠FQB,∵∠AFT=∠BFQ,AT=AP=BQ,∴△ATF≌△QBF,∴AF=QF,TF=BF,∵∠PSA=∠BOA=90°,∴PT∥BM,∴∠TBM=∠PTB,∵∠BFM=∠PFT,∴△MBF≌△PTF,∴MF=PF,BM=PT,∴四边形AMPQ为平行四边形,∴AP∥MQ,MQ=AP=BQ,∴∠MQR=∠ABC,过点R作RH⊥MQ于点H,∵sin∠ABC=sin∠MQR=,设QR=25a,HR=24a,则QH=7a,∵tan∠QMR=,∴MH=23a,BQ=MQ=23a+7a=30a,BR=BQ+QR=55a,过点R作RK⊥x轴于点K.∵点R的纵坐标为﹣,∴RK=,∵sin∠BCO=,∴CR=,BR=,∴,a=,∴BQ=30a=3,∴5+=3,t=,∴P(),∴,∵BM=PT=2PS=,BO=4,∴OM=,∴M (0,),设直线PM 的解析式为y =mx +n ,∴,解得,∴直线PM 的解析式为y =.选择填空解析:一、选择题(每小题3分,共计30分)1、-9的相反数是( )。
