异步电动机直接转矩控制基本原理
浅析异步电动机直接转矩控制系统

- 79 -工 业 技 术0 前言基于交流调速具有显著的优越性,以电力电子器件及计算机技术的不断发展为支撑,20世纪90年代以来,异步电动机变频调速技术得到了快速发展。
目前广泛研究应用的调速技术有恒压频比控制方式、矢量控制、直接转矩控制等。
相比于其他变频调速技术,直接转矩控制具有系统结构简单、动态性能更好、鲁棒性强等优势。
该文就异步电动机的直流转矩控制做了简要分析。
1 直接转矩控制技术的应用背景及发展现状直接转矩控制技术是20世纪80年代中期诞生的,美国学者A.B.Plunkett 1977年在IEEE 杂志上首次提出,德国鲁尔大学的德彭伯罗克教授于1985年第一次进行实际应用。
该技术的提出较大程度地解决了矢量控制等技术存在的问题,如计算量较大、控制系统结构复杂等。
但是传统的直接转矩控制也存在低速范围内转矩脉动大等缺陷,随着技术的发展,新型直接转矩控制技术不断出现,传统技术存在的问题得以不断改善。
当前,日、美、德等国家都致力于该技术的开发,其趋势不断向最优的全数字化发展。
如直接转矩控制中引入DSP 芯片,加强了数据处理的实时性、快速性以及数字控制功能,实现了数据监视、诊断和保护等。
再如,将现代控制理论的多种控制策略如非线性控制、模糊控制、神经网络控制等应用到直接转矩控制中,弥补其固有的一些缺陷,提高系统的动态和鲁棒性能等。
目前,主要的新型直接转矩控制技术有3种。
1)直接转矩无差拍控制。
该技术是一种离散化的直接转矩控制系统。
依据异步电动机的数学模型,得出转矩偏差与电动机各物理量间的数学关系,可消除定子磁链模值以及电磁转矩动、静态误差。
从技术上,该系统逆变器的开关频率得以提高并保持稳定,无滞环比较器,电压谐波减少,电机的低速性能提高,缺点是该技术依赖电机参数,计算量较大,算法实现难度高[1]。
2)直接解耦控制(DDC)。
有2种方法,一种含有PI 调节器即PI-DDC,该法消除转矩脉动能力强,动、静态特性较好,纵使转速极低(5rad/sec),转矩脉动也很小,主要问题是计算量比较大,因为该法需同时估计定子磁链和转子磁链;另一种就是预测直接解耦控制即P-DDC。
异步电动机直接转矩控制基本原理

异步电动机直接转矩控制基本原理从1985年德国鲁尔大学德彭布洛克(Depenbrock )教授首次提出直接转矩控制理论以来,短短十几年时间,直接转矩控制理论以它简明的系统结构,优良的静、动态性能得到迅猛发展和应用。
1 异步电动机的数学模型异步电机数学模型是一个高阶、强耦合、多变量、非线性系统。
理想状态下(一般这样假设)电机三相(定、转子)均对称,定、转子表面光滑,无齿槽效应,电机气隙磁势在空间正弦分布,铁心涡流、饱和及磁滞损耗不计。
在固定坐标系下(α,β,0),用异步电机转子的量来表示异步电机数学模型(则有r u α=r u β=0)。
基本方程如下:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--+++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡r r s s r r rmm r r r mm m ss m s s s s i i i i L R L L LL L R L L L L R L L R u u βαβαβαωωωω........000000 (1) )()(r s r s m p s s s s p e i i i i L n i i n T βααβαββαψψ-=-= (2)pe p n F TL T dt n Jd ωω--= (3) s R 、s L :定子电阻和自感r R 、r L :转子电阻和自感 m L :定子互感ω:电机转子角速度,即机械角速度s u α 、s u β:定子电压(α、β)分量 s i α 、s i β:定子电流(α、β)分量r u α、r u β:转子电压(α、β)分量 r i α、r i β:转子电压(α、β)分量J ,F 分别为机械转动惯量和机械磨擦系数本文均采用空间矢量分析方法,图1是异步电机的空间矢量等效图,在正交定子坐标系(βα-各个物理量定义如下:)(t u s —定子电压空间矢量)(t i s —定子电流空间矢量)(t i r —转子电流空间矢量)(t s ψ—定子磁链空间矢量 ω —电角速度依图1以下表达式表示异步电机在定子坐标系下的方程:s s s s i R U ψ+= (4) 0 =r r i R -r ψ+j ωr ψ (5)s ψ=L u i (6)r ψ =s ψ-r i L σ (7) 定子旋转磁场输出功率为(下式s ω表示定子旋转磁场的频率):P=d s T ω=*}{23s s i RE ψ=)(23ββααψψs s s s i i + (8) 并且有 s .ψ=)(βαωs s s ji i L j + (9)把表达式(9)分解到(βα-)坐标下得:ββαψωωψs s s s s Li -=-=.(10) ααβψωωψs s s s s Li -=-=.(11) 把式(10)和式(11)代入式(8)得转矩表达式:)(23αββαψψs s s s d i i T -=(12) 从图1可得:r u s i i i +=,结合式(6)、式(7)得:)(231βααβσψψψr s r s d i L T -=(13) 上式也可以表示成(θ为磁通角,即定子磁链与转子磁链之间的夹角):θψψσsin 231r s d L T =(14) 定子磁链的幅值根据式(4)由定子电压积分来计算的,而转子磁链幅值由负载决定的,它根据式(5)由转子电流决定,而稳态转矩据式(14)则通过计算磁通角来实现。
异步电动机直接转矩控制原理与展望

异步电动机直接转矩控制原理与展望一、引言电动机调速是各行各业中电动机应用系统的必需环节。
直流电动机因其磁链与转矩电流各自独立,不存在耦合关系,能够获得很好的调速范围和调速精度,静、动态特性均比较好而获得广泛应用。
交流(异步)电动机结构简单却因其磁链与电流强耦合,而且是多变量非线性系统,调速难度大,长期以来在调速系统的应用受到限制。
直到近三十年来,一系列新型的传动调速技术的出现才开始了交流传动的新篇章。
1.交流传动的发展简述首先是变压变频调速系统(VVVF),后来出现了矢量控制(FOC)和直接转矩控制(DTC)调速系统。
由于VVVF系统只是维持电动机内的磁链恒定,并没有解决磁链和电流强耦合的问题,其调速范围窄,调速性能也不佳。
矢量控制是以转子磁场定向,采用矢量变换的方法,通过两次旋转坐标变换,实现异步电动机的转速和磁链控制的完全解耦。
但实际上由于转子磁链很难准确观测,系统特性受电机参数的影响较大,且计算也比较复杂。
1985年,德国的M.Depenbrock和日本的I.Takahashi先后提出直接转矩控制理论。
直接转矩控制在定子坐标系下,避开旋转坐标变换,直接控制转子磁链,采用转矩和磁链的bang-bang控制,不受转子参数随转速变化而变化的影响,简化了控制结构,动态响应快,对参数鲁棒性好,因而得到广泛的深入研究和应用。
2.矢量控制(FOC)和直接转矩控制(DTC)的简略对比(1)控制原理:FOC是在转子磁通坐标系中,通过分别控制q轴和d轴定子电流分量,实现转速和磁链的解耦控制。
其实质是通过坐标变换重建的电动机数学模型等效为直流电动机,从而象直流电动机那样进行快速的转矩和磁通控制。
DTC是在定子坐标系下通过检测电动机定子电压和电流,采用空间矢量理论计算电动机的转矩和磁链,并根据与给定值比较所得差值,实现转矩和磁链的直接控制。
(2)控制性能:FOC的调速范围较宽(1:20~200),调速精度较高,低速特性连续,响应速度较快,但受参数变化影响较大,且计算复杂,控制相对繁琐。
第三十八讲%20异步电动机直接转矩控制

✓“+”:定子磁链矢量正向 旋转,转差率增大,电磁转 矩加大;
✓“-”:定子磁链矢量反向
旋转,产生制动转矩; ✓“0”:定子磁链矢量停在 原地,转差率为负,电磁转 矩减小 。
定子电压的控制作用
2.直接转矩控制系统
➢ 直接转矩控制系统原理结构图
直接转矩控制系统
Control)系统,是继矢量控制系统之后发展起 来的另一种高动态性能的交流电动机变压变 频调速系统。 ➢ 在转速环内,利用转矩反馈直接控制电动机 的电磁转矩,因而得名。
直接转矩控制
➢ 直接转矩控制利用转矩偏差和定子磁链 幅值偏差的符号,根据当前定子磁链矢 量所在的位置,直接选取合适的定子电 压矢量,减小定子磁链幅值的偏差和电 磁转矩的偏差,实施电磁转矩和定子磁 链的控制。
✓ 选择定子磁链作为被控量,计算磁链的模型 可以不受转子参数变化的影响,提高了控制 系统的鲁棒性。
直接转矩控制系统的特点
➢ 直接转矩控制系统的特点:
✓ 采用了直接转矩控制,在加减速或负载变化 的动态过程中,可以获得快速的转矩响应, 但必须注意限制过大的冲击电流,以免损坏 功率开关器件,因此实际的转矩响应也是有 限的。
✓ 电磁转矩偏差ΔTe<0,Sgn(ΔTe)=0, 采用定子磁场停止转动,使电磁转矩减小 。
直接转矩控制系统
➢ 当期望的电磁转矩为负时,P/N=0
✓ 电磁转矩偏差ΔTe<0,Sgn(ΔTe)=0 ,应使定子磁场反向旋转,使实际转矩 反向增大。
✓ 电磁转矩偏差ΔTe>0,Sgn(ΔTe)=1 ,采用定子磁场停止转动,使反向电磁 转矩减小。
➢ AΨR和ATR分别为定子磁链调节器和转矩调 节器,两者均采用带有滞环的双位式控制器。
直接转矩控制的原理框图
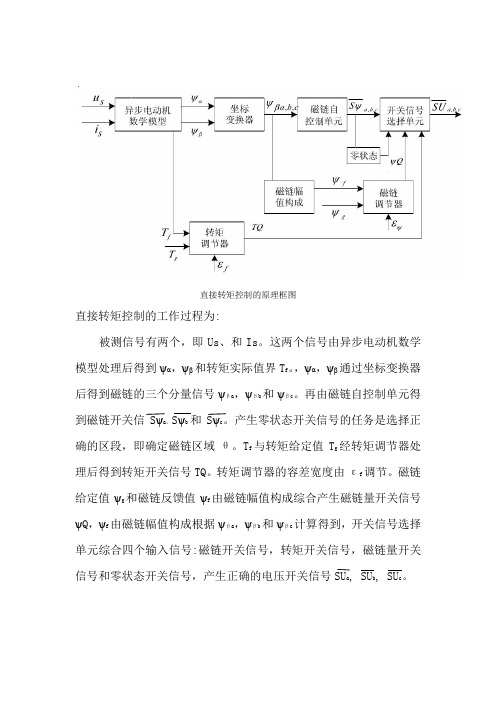
直接转矩控制的原理框图
直接转矩控制的工作过程为:
被测信号有两个,即Us、和Is。
这两个信号由异步电动机数学模型处理后得到ѱα,ѱβ和转矩实际值界T f。
,ѱα,ѱβ通过坐标变换器
后得到磁链的三个分量信号ѱ
βa,ѱβb和ѱβc。
再由磁链自控制单元得到磁链开关信a,Sѱb和c
确的区段,即确定磁链区域θ。
T f与转矩给定值T g经转矩调节器处理后得到转矩开关信号TQ。
转矩调节器的容差宽度由εf调节。
磁链给定值ѱg和磁链反馈值ѱf由磁链幅值构成综合产生磁链量开关信号ѱQ,ѱf由磁链幅值构成根据ѱβa,ѱβb和ѱβc计算得到,开关信号选择单元综合四个输入信号:磁链开关信号,转矩开关信号,磁链量开关信号和零状态开关信号,产生正确的电压开关信号a b, SU c。
异步电机直接转矩控制

05
仿真与实验验证
仿真模型建立与参数设置
电机模型
选择合适的异步电机模型,如感 应电机模型,并设置电机参数, 如定子电阻、转子电阻、互感等 。
控制器模型
设计直接转矩控制器模型,包括 转矩和磁链观测器、开关表、滞 环比较器等部分,并设置相应的 参数。
开关表选择
根据电机的运行状态和误差信号,选择合适的开关表,实现对电机 的高效控制。
现代直接转矩控制策略
空间矢量调制技术
通过空间矢量调制技术,实现对 电机转矩和磁链的连续控制,提
高电机的运行性能。
无差拍控制
采用无差拍控制技术,实现对电 机转矩的快速响应和无超调控制
,提高系统的动态性能。
预测控制
基于电机的数学模型和实时运行 状态,采用预测控制技术对电机 的未来行为进行预测和控制,提
异步电机直接转矩控制
汇报人:XX
目录
• 引言 • 异步电机数学模型与特性分析 • 直接转矩控制策略与方法 • 异步电机直接转矩控制系统设计 • 仿真与实验验证 • 总结与展望
01
引言
异步电机概述
异步电机的基本结构
异步电机的分类
包括定子、转子、端盖、轴承等部分 ,其中定子和转子是电机的核心部分 。
性。
负载特性
研究异步电机在不同负载下的电压 、电流、功率因数和转速等特性变 化。
调速特性
探讨异步电机在不同转速下的电压 、电流、功率因数和转矩等特性变 化。
异步电机运行状态与转矩关系
电动状态
01
异步电机作为电动机运行时,电磁转矩与转速方向相同,驱动
负载转动。
8第八讲异步电动机的直接转矩控制系统-吴学智

2εΨ
s* s
定子磁链的控制
圆形轨迹控制原理
从A点到B点的路径有无 数条。
从A点出发沿顺时针方向 前进的矢量可以选择V4、 V2、V6
从保证电压矢量控制效果 考虑选择V2、V6
要有效地控制磁链轨迹,必须解决三个问题: 选择电压矢量;确定各电压矢量的作用时间;确定各电 压矢量的作用次序。
运动轨迹的关系
定子磁链的控制
电压型逆变器的输出电压矢量
三相电压型逆变器输出的8种 电压空间矢量。
6个有效矢量,2个零矢量;
改变逆变器输出状态可改变
U 3 (010)
输出电压矢量。
U 4 (011)
U 5 (001)
b
U 2 (110)
U 1 (100)
U0 (000)
a
U 7 (111)
直接转矩控制采用空间矢量的分析方法,直接在定 子坐标系下计算控制交流电机的转矩,采用定子磁 场定向,借助了离散两点式调节(Bang-Bang控制)产生 PWM信号,直接对逆变器开关状态进行最优控制, 以获得转矩的高动态性能。
直接转矩控制系统的原理
空间电压矢量 如果三相交流电压是正弦波,相电压为:
U s
U C0 c
直接转矩控制系统的原理
逆变器供电的空间电压矢量
三相电压型逆变器,有 六个功率开关,有8种可 能的开关组合。
规定a、b、c三相负载的 某一相与直流母线正极 接通时,该相开关状态 为“ 1 ”态,反之,与 负极接通时为“ 0 ”态, 则八种开关模式得出的 八种电压空间矢量
sa sb sc
电动机的定子磁链和转子磁链: 电流模型法计算 定子磁链,精度不受转速降低的影响,
异步电动机的直接转矩控制系统

异步电动机直接转矩控制系统1直接转矩控制简介直接转矩控制( Direct Torque Control — DTC ),国外的原文有的也称为 Direct self-control — DSC,直译为直接自控制,这类“直接自控制”的思想以转矩为中心来进行综合控制,不单控制转矩,也用于磁链量的控制和磁链自控制。
直接转矩控制与矢量控制的差别是,它不是经过控制电流、磁链等量间接控制转矩,而是把转矩直接作为被控量控制,其实质是用空间矢量的剖析方法,以定子磁场定向方式,对定子磁链和电磁转矩进行直接控制的。
这类方法不需要复杂的坐标变换,而是直接在电机定子坐标上计算磁链的模和转矩的大小,并经过磁链和转矩的直接追踪实现 PWM 脉宽调制和系统的高动向性能。
直接转矩控制系统的主要特色有:(1)直接转矩控制是直接在定子坐标系下剖析沟通电动机的数学模型,控制电动机的磁链和转矩。
(2)直接转矩控制的磁场定向采纳的是定子磁链轴,只需知道定子电阻就能够把它观测出来。
(3)直接转矩控制采纳空间矢量的观点来剖析三相沟通电动机的数学模型和控制各物理量,使问题变得简单了然。
(4)直接转矩控制重申的是转矩的直接控制成效。
直接转矩控制技术用空间矢量的剖析方法,直接在定子坐标系下计算与控制电动机的转矩,采纳定子磁场定向,借助于失散的两点式调理( Band-Band )产生 PWM 波信号,直接对逆变器的开关状态进行最正确控制,以获取转矩的高动向性能。
它省去了复杂的矢量变换与电动机的数学模型简化办理,没有往常的 PWM 信号发生器。
它的控制思想新奇,控制结构简单,控制手段直接,信号办理的物理观点明确。
为了让读者更好的理解直接转矩控制,在正式介绍三相异步电机的直接转矩控制系统前,先从直接转矩控制的基本物理观点讲起。
2 直接转矩控制的基本物理观点2.1 直接转矩控制中磁通和转矩的丈量在几种用于控制感觉电机的方法中,直接转矩控制(DTC )据有很重要的地位。
异步电机直接转矩控制

1.2.1
1985年,德国人M.Depenbrock提出了直接转矩控制理论,在实现磁链的同时也实现了对直接转矩的控制。直接转矩控制技术一诞生,就以自己新颖的控制思想,简洁明了的系统结构,优良的静态性能受到了普遍的注意和得到了迅速的发展。
根据M.Depenbrock所提出的直接转矩控制理论所实现的系统中,其磁链的轨迹是按正六边形运动,其六边分别有相应的六个非零电压矢量与之对应,可简单的切换六个工作状态直接由六个非零电压矢量完成六边形磁链轨迹,磁环控制简单。
(4)于数字化。因此实现数字化的直接转矩控制的交流调速系统具有很大的经济价值和世纪意义。但是如何解决实时性是个问题,高速DSP价格昂贵,普通单片机运行较慢,如何找到一个折中的方法是需要考虑的问题。
1.3
本文工作主要在于介绍了直接转矩控制系统的基本结构和原理,并利用MATLAB/SIMULINK软件根据异步电动机的数学模型建立仿真模型。然后在SIMNLINK环境下使用该模型组建异步电动机直接转矩控制系统。通过改变控制系统中直接影响电动机性能的转矩滞环调节器和磁链滞环调节器的参数,通过仿真得到仿真图,对仿真进行分析,验证直接转矩控制方法的有效性和可靠性。
日本东芝公司的Takahashi教授于1986年提出了磁链轨迹的园形方案,即让磁链矢量基本上沿园形轨迹运动。这是一种磁链的实时控制,通过比较实时计算所得的实际磁链幅值与给定值相比较,并同时考虑此时磁链所处的位置来选择电压矢量及持续时间的长短。
T.G.Haberler提出了一种预前控制法,即依据当前状态的转矩、磁链误差和反电势,在一固定的开关周期条件下选择和计算下一个状态所需要的空间电压矢量。实现恒逆变开关频率控制。
2.2
控制系统利用异步电机空间矢量的等效电路进行分析。该效电路等效电路是在正交定子坐标系上描述异步电动机的,下图为异步电动机空间矢量等电效电路。
异步电动机直接转矩控制基本原理

从式(14)可知,异步电机的转矩由定、转子磁链的幅值、磁通角 决定的。而转子磁链幅值由负载决定的。为了充分利用电机铁芯,保持定子磁链为恒量。改变转矩可以通过磁通角来实现,即通过改变电压空间矢量 来控制定子磁链旋转速度,使其走走停停,以达到改变定子磁链的平均速度 ,从而实现改变磁通角 ,最后达到控制转矩的目的。这个过程可以用图9来解释。 时刻定子与转子磁链分别为 、
把逆变器的输出电压用空间矢量来表示,电压空间顺序见图4。 表示电压矢量,则7有个离散的电压空间矢
量。每个工作电压空间矢量在空间位置
相差60°,矢量以逆时针顺序旋转,即顺序为 → → → → → 。其中六边形的中心是零电压矢量。
对异步电机三相分析,将三维矢
量转化为二维矢量,在这用Park
变换。将异步电机三相定子坐标
直接转矩控制是根据定子磁链 ,转矩 的要求,从1~7状态中选出一个最佳控制矢量使电机运行在特定的状态。
3磁链控制
磁链控制的任务是识别磁链的运动轨迹的区段或位置,给出正确的磁链开关信号,以产生相应的电压空间矢量,控制六边形轨迹或圆形轨迹正确地旋转。
3.1 磁链轨迹的控制
由式(4)可得:
(17)
如果忽略 则式(17)可表示成
系的 轴与Park矢量复平面的实
轴 重合,则三相物理量 、
、 的Park矢量 为:
= [ + + ](15)
其中 = 。
由图 2的接法,其输出电压空间矢量 的Park矢量变换表达式为:
= [ + + ] (16)
、 、 分别是a、b、c三相定子负载绕组的相电压。依图3给出的 、 、 并代入式(16)可以计算出从1~6各个状态输出的电压空间矢量 。
各个物理量定义如下:
第8讲 异步电动机的直接转矩控制系统

4
ω *r
T*e ωr
2、直接转矩控 制系统的原理
Ψ *s Ψs
Te
和VC系统一样,直接转矩控制控制系统分别控制异步电动 机的转矩(转速)和磁链,转速调节器ASR的输出作为电磁转矩 的给定信号T*e,在T*e后面设置转矩控制环,它可以抑制磁链 变化对转速的影响,从而使转速和磁链系统近似解耦。因此, 从总体控制结构上看,直接转矩控制系统(DTC)和矢量控制系 5 统(VC)是一致的,都能获得较高的静、动态性能。
3
鉴于电气机车等具有大惯量负载的运动系统在起、制动时 需要快速瞬态转矩响应,1985年德国鲁尔大学的Depenbrock 教授研制了直接自控制系统(DSR),并提出了直接转矩控制理 论,该理论采用转矩模型和电压型磁链模型,以及电压空间 矢量控制PWM逆变器,实现转速和磁链的砰-砰控制(BangBang Control) 。这在很大程度上解决了矢量控制中计算控 制复杂、特性易受电动机参数影响的问题。
a
U 5 ( 001)
U 6 (101) 14
图8-1 电压空间矢量
二、电压空间矢量对定子磁链和转矩的控制作用
1、定子磁链与定子电压的关系 d s u s Rs is (8 12) dt d s 忽略定子电阻的影响: s u (8 13) dt s u s t (8 14) 通过改变定子电压矢量的大小、方向及所作用的时间就 能对定子磁链矢量进行调节。
8
综前所述,直接转矩控制,采用电压空间矢量的分析方法, 直接在定子坐标系下计算控制交流电机的转矩,采用定子磁 场定向,借助了离散滞环调节(Bang-Bang控制)产生PWM信号, 直接对逆变器开关状态进行最优控制,以获得转矩的高动态 性能。
第八章 异步电机直接转矩控制系统

第八章异步电机直接转矩控制系统主讲人:宋文胜讲师,博士Email: songwsh@西南交通大学电气工程学院列车控制与牵引传动研究室《电力牵引交流传动控制系统 8.1 直接转矩控制基本原理8.2 直接转矩控制系统的实现8.3 直接转矩控制在电力牵引中的应用低速时圆形磁链轨迹控制高速时六边形磁链轨迹控制弱磁升速恒功率控制8.4 矢量控制与直接转矩控制的比较主要内容3《电力牵引交流传动控制系统》8.1 直接转矩控制基本原理8.1 直接转矩控制基本原理 基本思想直接转矩控制系统简称DTC ( Direct Torque Control) 系统,是继矢量控制系统之后发展起来的另一种高动态性能的交流电动机变压变频调速系统。
在它的转速环里面,利用转矩反馈直接控制电机的电磁转矩,因而得名。
《电力牵引交流传动控制系统直接转矩控制技术简介直接转矩控制是继矢量控制之后,1985年由德国鲁尔大学M.Depenbrock 和日本的I.Takahashi 教授分别提出的直接自控制(Direct Self Control)和直接转矩控制(Direct Torque Control )发展而来的一项新型的交流电机控制技术,其中前者的方法是基于六边形磁链轨迹进行控制的,主要应用了大功率调速系统;后者的方法是基于圆形磁链轨迹来进行控制的,主要用中小功率的场合。
在直接转矩控制中不需要对转矩和磁链进行解耦,因此没有复杂的坐标变换;其以磁链和转矩为控制对象,因此可以获得很好的动态性能。
5《电力牵引交流传动控制系统》电磁转矩控制原理电机转矩:电磁转矩决定于定子磁链矢量和转子磁链矢量的矢量积,即决定于两者幅值和其间的空间电角度s m s rs r s L i L L L ψψ=−′′K K K ''33sin 22m m p r s p s r srr s r sL L T n n L L L L ψψψψδ=×=K K K K e 32p s sT n i ψ=×K K rms sL L L L 2−=′《电力牵引交流传动控制系统8.2 传统直接转矩控制原理8.2 传统直接转矩控制原理33()sin 22m m e ps r p s r sr s r s rL L T n j n L L L L ψψψψδδδ=•=K KK K7《电力牵引交流传动控制系统》8.2 直接转矩控制系统实现8.2 直接转矩控制系统实现 系统组成图8-1 按定子磁链控制的直接转矩控制系统《电力牵引交流传动控制系统1、结构特点1、结构特点 转速双闭环:z ASR 的输出作为电磁转矩的给定信号;z 设置转矩控制内环,它可以抑制磁链变化对转速子系统的影响,从而使转速和磁链子系统实现了近似的解耦。
异步电机直接转矩

基于Matlab/Simulink异步电机矢量控制系统仿真XXX(江南大学物联网工程学院无锡·中国 214122)摘要:针对异步电机交流调速系统的特点,采用了直接转矩控制(DTC)交流变频调速方案。
直接对电机定子磁链和电磁转矩进行控制,避免了矢量控制中复杂的变换和参数运算,使控制结构变得十分简单。
应用MATLAB/Simulink对直接转矩控制的定子磁链近似圆形控制的方法进行了仿真,从理论上证明了这种方法的可行性,并且对仿真波形进行分析,验证系统的正确性.关键词:直接转矩;MATLAB/Simulink;异步电动机中图分类号:TM30 文献标识码:AAbstract:In view of the characteristics of storage Asynchronous motor drive system using an advanced AC frequency converter program: Direct Torque Control (DTC), which directly to control the motor stator flux and torque, the method of DTC avoid the computational complexity of the transformation parameters, which control structure is very simple.The simulation models of approximate circle flux control system are presented based on the application of MATLAB/Simulink by the author. The feasibility and correctness of this method are testified in theory and the correlative waveforms which can explain the advantage of system are captured.Key words:DTC, MATLAB/Simulink, Asynchronous motor1 引言德国鲁尔大学MDepenbrock教授于1985年首次提出了直接转矩控制(DTC)理论。
异步电机直接转矩控制

直接转矩控制系统主要特点
在具体控制方法上,DTC系统和VC系统有所不同, ⑴ 转矩和磁链的控制采用Bang—Bang控制器,并在PWM逆变
器中直接用这两个控制信号产生电压的SVPWM波形,从而 避开了将定子电流分解成转矩和磁链分量,省去了矢量旋 转变换和电流控制,简化了控制器的结构; ⑵ 选择定子磁链作为被控量,而不像VC系统那样选择转子 磁链,计算磁链的电压模型不受转子参数变化的影响,提 高了控制系统的鲁棒性。
•电压空间矢量 Vs V jV
•a-b-c系 系坐标变换(3 / 2)
Vs 23[Vab+Vbcej23 Vcaej43 ]
(1)
•按3 / 2变换关系,可定出逆变器输出8个电压空间矢量的
空间位置
幅值大小
转向
以
开
关
状
态
(
S
a
S
b
S
)
c
=1
0
0为
例
据
图
2
有
:
Va
=
b
+
Vbc=0
E
Vca= - E
S0 不变-Te
0
Te
说明实际转矩 Te
瞬时值在
T
e
Te
间变化
平均值 Te= Te
3、转矩与定、转子磁链 s ,r的关系
•
Te
KT Lm
s
r
KT Lm
s
r s in
s , r
s ,
大
r
小
恒
定
时
,
T e s in
直接转矩控制原理与机理

第二章直接转矩控制的基本原理和结构2.1异步电动机的数学模型2. 1. 1电动机变量的空间矢量二相变量的空间矢量对十异步电动机的分析和控制是十分方便的,在直接转矩控制中,常用的矢量有电压空间矢量、电流矢量、磁通矢量等。
这里对它们的基本概念作简要介绍。
1)电压空间矢量为方便分析,这里针对一个理想的电压型逆变器进行讨论。
如图2.1所示,它由二组、六个开关(Sp, Sp, Sb, Sb, S}, S})组成。
上下两个按180。
导通模式,即一个导通(状态为1),另一个断开(状态为0)。
二组开关有8种开关组合,对应8种电压状态,如表2. 1所示。
其中状态1-6对应的输出电压各不相同,称为工作状态,7和8对应上小桥全开和全关的状态,没有电压输出,称为零状态对于电压型逆变器,在六种工作状态电压作用下,逆变器输出的相电压波形、幅值及其与电压状态的对应关系如图2.2所示。
如果把逆变器的输出电压用电压空间矢量来表示,则逆变器的各种电压状态就有了空间的概念。
在此,引入Park变换,Park矢量将二个表2.1逆变器开关状态与电压状态对照表┌────┬─────────────────┬─────┐│状态│工作状态│零状态││├──┬──┬──┬──┬──┬──┼──┬──┤││1 │2 │3 │4 │5 │6 │7 │8 │├────┼──┼──┼──┼──┼──┼──┼──┼──┤│Sa │0 │0 │1 │1 │1 │0 │0 │1 │├────┼──┼──┼──┼──┼──┼──┼──┼──┤│Sb │1 │0 │0 │0 │1 │1 │0 │1 │├────┼──┼──┼──┼──┼──┼──┼──┼──┤│Sc │1 │1 │1 │0 │0 │0 │0 │1 │├────┼──┼──┼──┼──┼──┼──┼──┼──┤│电压状态│U51 │Usz │U53 │U54 │U 55│Use │Uso │Use │└────┴──┴──┴──┴──┴──┴──┴──┴──┘标量(二维)变换为一个矢量(二维)。
第六章 异步电动机矢量控制与直接转矩控制

Lr Lm Lr Lm
[∫ (u
αs
− Rdqs iαs )dt − σLs iαs − Rdqs i βs )dt − σLs i βs
] ]
(6-13)
[∫ (u
βs
根据式(6-13),可以画出计算转子磁链的电压模型, 如图6-4所示。
σL s
iαs uαs Rdqs
+
∫
+
--
Lr Lm
Ψαr
6.1 矢量控制(VC:vector control)的基本思路 6.1.1 模仿直流电动机 粗略地讲,矢量控制是模仿他励直流电动 机的控制。忽略磁饱和及电枢反应的影响,直 流电动机的转矩方程为 Te=CT´IaIf
这里 If—励磁电流,产生Ψf ; Ia—电枢电流,产生Ψa。
如果把它们看作是空间矢量,它们互相垂 直、解耦。这意味着,当我们用Ia去控制转矩的 时候,磁链Ψf不受影响,如果磁链是额定磁链, 将得到快速的动态响应和最大的转矩安培比。 反过来,用If去控制磁链Ψf时,Ψa也不受影响。
一起构成矢量控制基本方程。
6.2.2 转子磁链模型 为了实现转子磁链定向矢量控制,关键是获 得实际转子磁链Ψr的幅值和相位角,坐标变换需 要磁链相位角(φ),转矩计算、转差计算等需 要磁链的幅值。但是转子磁链是电机内部的物理 量,直接测量在技术上困难很多。因此在实际应 用系统中,多采用间接计算(或观测)的方法。 通过容易检测得到的电动机运行时的物理量,如 电压、电流、转速等,根据电机的动态数学模型, 实时推算出转子磁链的瞬时值,包括幅值和相位 角。 在磁链计算模型中,根据所用实测信号的不 同,可以分为电压模型和电流模型两种。
励磁分量 转矩分量 图6-1 (a)他励直流电动机 (b)矢量控制异步电动机
模糊控制在异步电动机直接转矩控制中的应用

h s o tet dt nDTC. to f1 a io e l r i
K y o L: u z ot l D CDi c ru n o) e w N  ̄F zycn o T ( r toq e o t 1 r e t c r
S mu a in i lt o 一
直接转 矩控制是在定子坐标系下对电机 进
Zh z o R lcrcCo , d u h uCS E e ti .Lt
摘
要: 针对 传统 直 接转 矩 控制 的缺 点 , 以异 步 电
1 直接转矩控 制的基本原理及Maaa / t lb
Smu i k i ln  ̄真 ,
1 基本原理 . 1 直接转矩控制的基本原理是【 】充分利用 : ,
逆 变 器 的 开关 特 点 , 过不 断 切 换 电压 状 态 , 通 使 定 子 磁 链 轨 迹 逼 近 圆 形 ; 通 过 零 电压 矢 量 的 并
动 机 和逆 变 器 的数 学 模 型为 基 础 , 模 糊控 制理 论 应 将
用 到直接 转矩 控制 系统 。 使用M aaa 软件 中的 电力系 t lb 统 模 块 库 , 立了模 糊 直 接 转 矩 控 制 系统 模 型 。 于 建 基 Maa bSm l k t a/i ui 仿真平台, l n 对此 控制 系统 进行了仿真 , 并对仿 真结果 进行了对 比分析 。 结果 表 明模 糊 直接转 矩
模 糊控制是将专家的知识及现 场操作人员
的经验作为 知识库 。 然后通过特 定的模 糊规 则
和 模 糊 法 则 转 换 为推 理 运 算 。模 糊 控 制 系统 将
理 图。
Ab i a l Ag  ̄ t e s o t o n so e ta iin l sr e : mn h h rc mi g ft r d t a h o DTC. h u z o to e r s a p i d i t e DT t e f z y c n r lt o y wa p le n o t C h h b s d u o e ma e t  ̄ mo e fb t h y c r n u a e p n t t ma h h d l o l t es n h o o s o I mo o n n e t e . e mod lo uz z t e a d i v r o r Th e f f z y DTC wa s e t b ih d b a ft e p we yse b o h o e sa ls e y me nso o r s t m l c ft h h M a h a o t r . e c n r ls se s smu a e n t l b s f wa e Th o t o y t m wa i l t d o t e p af r o a h a / u i k a d t e s u a e e u t h lto m fM t l b i ln n i l t d r s l m h m s s o d t a h u z h we tt e f z y DTC h d b te c u a y q i k r h a e t ra c r c . u c e r s O n m l e u t a i n o e ma n tc l a em a e p s a d s l rf c u t ft g e i i g n e a l o h k
异步电机直接转矩控制策略

汇报人:日期:CATALOGUE 目录•异步电机概述•直接转矩控制(DTC)策略简介•异步电机DTC策略的实现方法•异步电机DTC策略的性能优化•异步电机DTC策略的应用案例与未来展望01异步电机概述异步电机的定义和工作原理定义异步电机,又称感应电机,是一种基于电磁感应原理工作的电动机。
与同步电机不同,异步电机的转子速度与定子磁场旋转速度存在一定的转速差。
工作原理当定子绕组通入三相交流电时,会在气隙中产生旋转磁场。
这个旋转磁场与转子导体产生相对运动,从而在转子导体中产生感应电动势和感应电流。
根据电磁感应原理,这个感应电流会与旋转磁场相互作用,产生电磁力,驱动转子转动。
发电机的励磁异步电机可以作为发电机的励磁机,通过控制励磁电流来调节发电机的输出电压和频率。
电力系统的调峰填谷异步电机可以作为电力系统的调峰填谷手段,通过控制其运行状态来调节电力系统的有功功率和无功功率。
拖动各种生产机械异步电机具有结构简单、运行可靠、维护方便等优点,因此被广泛应用于拖动各种生产机械,如风机、水泵、压缩机等。
异步电机在电力系统中的应用异步电机控制的重要性提高运行效率01通过采用先进的控制策略,可以提高异步电机的运行效率,降低能耗,实现节能减排。
改善电能质量02异步电机的运行状态直接影响到电力系统的电能质量。
通过有效控制异步电机,可以减少谐波、降低电压波动和闪变,提高电能质量。
增强系统稳定性03异步电机作为电力系统的重要组成部分,其稳定性对于整个系统的稳定运行至关重要。
采用适当的控制策略,可以提高异步电机的稳定性,增强整个电力系统的稳定性。
02直接转矩控制(DTC)策略简介电压矢量选择DTC策略中,根据电机的当前状态和期望的转矩,选择合适的电压矢量来驱动电机。
这种选择通常基于查找表或者优化的算法。
原理概述DTC策略基于电机的电磁转矩方程,通过直接调节电机的电压矢量来控制转矩,从而实现对电机速度和位置的精确控制。
转矩和磁链观测为了实时调节电机的转矩,DTC 策略需要实时观测电机的转矩和磁链。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
异步电动机直接转矩控制基本原理从1985年德国鲁尔大学德彭布洛克(Depenbrock )教授首次提出直接转矩控制理论以来,短短十几年时间,直接转矩控制理论以它简明的系统结构,优良的静、动态性能得到迅猛发展和应用。
1 异步电动机的数学模型异步电机数学模型是一个高阶、强耦合、多变量、非线性系统。
理想状态下(一般这样假设)电机三相(定、转子)均对称,定、转子表面光滑,无齿槽效应,电机气隙磁势在空间正弦分布,铁心涡流、饱和及磁滞损耗不计。
在固定坐标系下(α,β,0),用异步电机转子的量来表示异步电机数学模型(则有r u α=r u β=0)。
基本方程如下:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡+--+++=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡r r s s r r rmm r r r mm m ss m s s s s i i i i L R L L LL L R L L L L R L L R u u βαβαβαωωωω........000000 (1) )()(r s r s m p s s s s p e i i i i L n i i n T βααβαββαψψ-=-= (2)pe p n F TL T dt n Jd ωω--= (3) s R 、s L :定子电阻和自感r R 、r L :转子电阻和自感 m L :定子互感ω:电机转子角速度,即机械角速度s u α 、s u β:定子电压(α、β)分量 s i α 、s i β:定子电流(α、β)分量r u α、r u β:转子电压(α、β)分量 r i α、r i β:转子电压(α、β)分量J ,F 分别为机械转动惯量和机械磨擦系数本文均采用空间矢量分析方法,图1是异步电机的空间矢量等效图,在正交定子坐标系(βα-各个物理量定义如下:)(t u s —定子电压空间矢量)(t i s —定子电流空间矢量)(t i r —转子电流空间矢量)(t s ψ—定子磁链空间矢量 ω —电角速度依图1以下表达式表示异步电机在定子坐标系下的方程:s s s s i R U ψ&+= (4)0 =r r i R -r ψ&+j ωr ψ(5)s ψ=L u i (6)r ψ =s ψ-r i L σ (7) 定子旋转磁场输出功率为(下式s ω表示定子旋转磁场的频率):P=d s T ω=*}{23s s i RE ψ&=)(23ββααψψs s s s i i &&+ (8) 并且有 s .ψ=)(βαωs s s ji i L j + (9)把表达式(9)分解到(βα-)坐标下得:ββαψωωψs s s s s Li -=-=.(10) ααβψωωψs s s s s Li -=-=.(11) 把式(10)和式(11)代入式(8)得转矩表达式:)(23αββαψψs s s s d i i T -=(12) 从图1可得:r u s i i i +=,结合式(6)、式(7)得:)(231βααβσψψψr s r s d i L T -=(13) 上式也可以表示成(θ为磁通角,即定子磁链与转子磁链之间的夹角):θψψσsin 231r s d L T =(14) 定子磁链的幅值根据式(4)由定子电压积分来计算的,而转子磁链幅值由负载决定的,它根据式(5)由转子电流决定,而稳态转矩据式(14)则通过计算磁通角来实现。
2 电压型逆变器的模型逆变器是直接转矩伺服驱动器中的重要部分,本系统采用的是电压型逆变器。
如图2,每个桥臂各有上、下两个开关管(a S 、b S 、c S 、-a S 、-b S 、-c S ),一个闭合。
其中a S与-a S ,b S 与-b Sc S 与-c S 均互为反向,也即一个导通而另一个断开。
a 、b 、c 表示异 步电机的三相。
逆变器总共有8种开关状态,如表1:表1 逆变器8种开关状态从表1可以看出,开关状态0、7属于同一状态,其相当于把电机三相A 、B 、C 同时接到同一电位上,这两种状态称为零状态;而另外状态1~6则称为工作状态。
所以实际上电压逆变器共有7种不同状态。
由图2可知,当电压型逆变器在没有零电平输出时它的六种工作状态的电压波形、电压幅度和开关状态的对应关系如图3,图中1s u 、2s u 、3s u 、4s u 、5s u 、6s u 分别对应状态(011)、(001)、(101)、(100)、(110)、(010)。
a u bu cuS (t u s 图2-3 工作状态三相电压波形把逆变器的输出电压用空间矢量来表示,电压空间顺序见图4。
)(t u t 表示电压矢量,则7有个离散的电压空间矢 量。
每个工作电压空间矢量在空间位置 相差60°,矢量以逆时针顺序旋转,即顺序为1s u →2s u →3s u →4s u →5s u →6s u 。
其中六边形的中心是零电压矢量。
对异步电机三相分析,将三维矢 量转化为二维矢量,在这用Park 变换。
将异步电机三相定子坐标 系的α轴与Park 矢量复平面的实 轴α重合,则三相物理量)(t X a 、)(t X b 、)(t X c 的Park 矢量)(t X 为:)(t X =32[)(t X a +ρ)(t X b +2ρ)(t X c ] (15)其中ρ=︒120j e。
由图 2的接法,其输出电压空间矢量)(t u s 的Park 矢量变换表达式为:)(t u s =32[a u +3/2πj b e u +3/4πj c e u ] (16)a u 、b u 、c u 分别是a 、b 、c 三相定子负载绕组的相电压。
依图3给出的a u 、b u 、c u 并代入式(16)可以计算出从1~6各个状态输出的电压空间矢量)(t u s 。
直接转矩控制是根据定子磁链s ψ,转矩e T 的要求,从1~7状态中选出一个最佳控制矢量使电机运行在特定的状态。
3磁链控制磁链控制的任务是识别磁链的运动轨迹的区段或位置,给出正确的磁链开关信号,以产生相应的电压空间矢量,控制六边形轨迹或圆形轨迹正确地旋转。
1s 2s )1013s 010(6s u 图2-4 六边形电压空间矢量3.1 磁链轨迹的控制由式(4)可得:⎰-=dt R t i t u t s s s s ))()(()(ψ (17)如果忽略s R 则式(17)可表示成dt t u t s s )()(⎰≈ψ (18)由式(18)可以看出电机定子磁链s ψ的运动方向是依)(t u s 方向进行的。
当电压逆变器开关状态不发生变化时,定子电压矢量不变,此时电机采用非零空间电压矢量,则s ψ的运行方向与幅值将发生变化;但当采用零电压矢量时s ψ的运行将受到抑制。
按照状态1s u →5s u →4s u →6s u →2s u →3s u 顺序运行一周后,将形成一个六边形磁链轨迹,如图4。
而合适地施加非零矢量顺序和合理的作用时间比例,可以形成一个多边形磁链轨迹,以致近似圆形轨迹。
把(βα-)复平面分成6个区域,如图5,6)12()(6)32(πφπ-<≤-N N N N =1,2,3,4,5,6 (19) 假设测得的定子磁链为s ψ,给定磁链为sref ψ, 将s ψ与sref ψ之间的偏差进行滞后比较,当误差 不在所允许的范围之内时就进行电压切换,以 减小误差。
实现这种功能的环节称为磁链调节器,实际上它是一个施密特触发器。
图6为磁链 调节器的功能图。
图中ψY 为磁链调节器的输出,ψσ为磁链误差带宽。
当 sref ψ-s ψ≥2ψσ 时,磁链调节器输 出ψY =1,即选择电压矢量使s ψ增加。
当 2ψσψψ<-s sref 时,磁链调节器输出ψY 不变。
当sref ψ-s ψ≤-2ψσ 时,磁链调节器输出ψY =0,即选择电压矢量使s ψ减少。
根据以上的控制方法可以使磁链幅值在给定的范围内变化,s ψ轨迹接近圆形。
3.2 磁链轨迹区段的确定在直接转矩控制中,为了能够选取合适的电压空间矢量,必须确定磁链所在区段的具体位置。
只有这样才能结合磁链与转矩开关信号给出当前所需要接通的电压矢量。
1. 六边形磁链轨迹区段的确定2.3.1节指出电机定子磁链s ψ的运动方向是依)(t u s 方向进行,六种工作状态电压形成磁链轨迹六个边。
将定子磁链分解成三相(如图7):定子磁链三相分量为a βψ、b βψ、c βψ。
a βψ、b βψ、c βψ通过施密特触发器得磁链开关信号a S ψ、b S ψ、c S ψ,这三个磁链信号与电压开关信号关系为: a S ψ=c SU ;b S ψ=a SU ;c S ψ=b SU ,其中a SU 、b SU 、c SU 是开关信号a SU 、α图8 (βα-)坐标下 圆形磁链轨迹区域图αbβb SU 、c SU 的反相。
定子磁链与六边形区段对应关系如表2:表2 定子磁链与六边形区段对应关系表2. 圆形磁链轨迹区段的确定圆形磁链轨迹磁链幅为:22βαψψψs s += ,αψs ,βψs 为定子磁链在(坐标βα-)下的投影。
如图8将圆形轨迹分成六个区域,根据αψs ,βψs 的正负值可以确定磁链轨迹在哪个区域中。
;例如在第一象限,θ=30°,在ab 弧θ≤30°,而在bc 弧段θ≥30°。
通过这种方式可以确定磁链在圆形轨迹的任何一个区域。
4转矩控制从式(14)可知,异步电机的转矩由定、转子磁链的幅值、磁通角θ决定的。
而转子磁链幅值由负载决定的。
为了充分利用电机铁芯,保持定子磁链为恒量。
改变转矩可以通过磁通角来实现,即通过改变电压空间矢量)(t u s 来控制定子磁链旋转速度,使其走走停停,以达到改变定子磁链的平均速度s ϖ,从而实现改变磁通角θ,最后达到控制转矩的目的。
这个过程可以用图9来解释。
1t 时刻定子与转子磁链分别为)(1t s ψ、)(1t r ψ,磁通角为)(1t θ,从1t 运 行到2t 时刻,此时对定子所加的 电压空间矢量)(t u s 为)101(3s u , 定子磁链从位置)(1t s ψ到位置)(2t s ψ所运行的轨迹为s ψ∆, 轨迹方向与)101(3s u 所指的方向一致,而且沿着3S 。
由式子:0=r R直接跟随超前于它的定子磁链,实际上在此运行期间转子磁链变化位置受到定子平均频率s ω的影响。
综上所述,在1t 时刻到2t 时刻期间,定子磁链旋转速度大于转子旋转速度;磁通角)(t θ(即磁通角由)(1t θ到)(2t θ的夹角)增大,相应地,根据式(14)转矩也增大。
而如果在2t 时刻引入零电压空间矢量,此时定子磁链)(2t s ψ则保持在2t 时刻位置不动,而转子磁链空间矢量则继续以s ω速度向前运行,必然的,磁通角减小,即转矩减小。
