人教版PPT()高一物理必修二第七章第二节万有引力定律PPT
合集下载
人教版高中物理必修2第7章第2节万有引力定律课件(共30张PPT)

=2.4012×10-7N
此力不到一粒芝麻重的几千分之一所以根本感觉不到它的存在。
新知讲解
计算:太阳的质量为M=2.0×1030kg,地球质量为m=6.0×1024kg, 日地之间的距离为R=1.5×1011m请计算:太阳与地球之间的万有引力 又是多大呢?
解:通F常=情G况M r下2 m,=万6—.有6—7引×—1力0(—-非111.—常×5×小—21.00,—×11只)1—0有230—质×—6量.0—巨×1大—02的—4 星=球3.5间×或10天22体(N与)
下面我们根据牛顿运动定律及开普勒行星运动定律来讨论太阳与行 星间的引力。
新知讲解
二、行星与太阳间的引力 1、简化模型:行星轨道按照“圆”来处理;
行星做匀速圆周运动时,受到一 个指向圆心(太阳)的引力提供 了向心力,太阳与行星间引力的 方向沿着二者的连线。
v F’ F
太阳
行星
新知讲解
2、太阳和行星之间的引力
新知讲解
科学漫步
牛顿的科学生涯
阅读回答下面问题: 1、简述牛顿的科学生涯。 2、说一说牛顿在前人的基础上形成了比较全面的科学方法 是什么? 3、在科学研究方面我们应该学习牛顿的哪些品质?
课堂练习
1.火星轨道半径是地球轨道半径的a倍,火星质量约为地球质量的b倍,
b
那么火星与太阳之间的引力约为地球与太阳之间引力的__a_2 ___倍。
2.在牛顿发现太阳与行星间的引力过程中,得出太阳对行星的引力表
达式后推出行星对太阳的引力表达式,是一个很关键的论证步骤,
这一步骤采用的论证方法是( D )
A.研究对象的选取 B.理想化过程
C.控制变量法
D.等效法
课堂练习
3、一名宇航员来到一个星球上,如果该星球的质量是地球质量的一 半,它的直径也是地球直径的一半,那么这名宇航员在该星球上 所受的万有引力大小是他在地球上所受万有引力大小C的( )
此力不到一粒芝麻重的几千分之一所以根本感觉不到它的存在。
新知讲解
计算:太阳的质量为M=2.0×1030kg,地球质量为m=6.0×1024kg, 日地之间的距离为R=1.5×1011m请计算:太阳与地球之间的万有引力 又是多大呢?
解:通F常=情G况M r下2 m,=万6—.有6—7引×—1力0(—-非111.—常×5×小—21.00,—×11只)1—0有230—质×—6量.0—巨×1大—02的—4 星=球3.5间×或10天22体(N与)
下面我们根据牛顿运动定律及开普勒行星运动定律来讨论太阳与行 星间的引力。
新知讲解
二、行星与太阳间的引力 1、简化模型:行星轨道按照“圆”来处理;
行星做匀速圆周运动时,受到一 个指向圆心(太阳)的引力提供 了向心力,太阳与行星间引力的 方向沿着二者的连线。
v F’ F
太阳
行星
新知讲解
2、太阳和行星之间的引力
新知讲解
科学漫步
牛顿的科学生涯
阅读回答下面问题: 1、简述牛顿的科学生涯。 2、说一说牛顿在前人的基础上形成了比较全面的科学方法 是什么? 3、在科学研究方面我们应该学习牛顿的哪些品质?
课堂练习
1.火星轨道半径是地球轨道半径的a倍,火星质量约为地球质量的b倍,
b
那么火星与太阳之间的引力约为地球与太阳之间引力的__a_2 ___倍。
2.在牛顿发现太阳与行星间的引力过程中,得出太阳对行星的引力表
达式后推出行星对太阳的引力表达式,是一个很关键的论证步骤,
这一步骤采用的论证方法是( D )
A.研究对象的选取 B.理想化过程
C.控制变量法
D.等效法
课堂练习
3、一名宇航员来到一个星球上,如果该星球的质量是地球质量的一 半,它的直径也是地球直径的一半,那么这名宇航员在该星球上 所受的万有引力大小是他在地球上所受万有引力大小C的( )
人教版高一物理必修第二册7.2万有引力定律课件(共42张PPT)

为F= G r ,若它们间的距离缩短为 2 r,其中一个质点 C2..两P、个Q质做量圆均周匀运的动球的体线2 相速距度为大r小,相它等们之间的万有引力为1×10-8N,若它们的质量、距离都增加为原来的2倍,则它们之间的万有引力
为【的(拓展例质)题】量考查内变容:为万有原引力与来抛体的运动2综倍合问题,则它们之间的万有引力为8F,
二 万有引力与重力的关系
任务1 万有引力与重力的关系
1.万有引力和重力的关系:如图所示,设地球的质量为
M,半径为R,A处物体的质量为m,则物体受到地球的吸
引力为F,方向指向地心O,由万有引力公式得F=G
Mm R2
。
引力F可分解为F1、F2两个分力,其中F1为物体随地球自
转做圆周运动的向心力Fn,F2就是物体的重力mg。
A.P、Q做圆周运动的向心力大小相等 P、Q两质点距离地心的距离相等,根据F=
2.万有引力定律的适用条件:
知,两质点受到的地球引力大小相等,故B正确、D错误;
P、Q两点的角速度相同,做圆周运动的半径不同,根据F向=mrω2可知向心力大小不相等,A错误;
公式F=G 适用于两质点间的相互作用,当两物体相距很近时,两物体不能看成质点,所以选项B错误。
B.使两物体间的距离和两物体的质量都减为原来的
1 4
C.使两物体间的距离增为原来的2倍,质量不变
D.使其中一个物体的质量减小到原来的
1 4
,距离不变
【解析】选B。使两物体的质量各减小一半,距离不变,
根据万有引力定律F=
G
Mm r2
可知,万有引力变为原来的
1 4
,
故A可以采用;使两物体间的距离和两物体的质量都减为
万有引力定律
为【的(拓展例质)题】量考查内变容:为万有原引力与来抛体的运动2综倍合问题,则它们之间的万有引力为8F,
二 万有引力与重力的关系
任务1 万有引力与重力的关系
1.万有引力和重力的关系:如图所示,设地球的质量为
M,半径为R,A处物体的质量为m,则物体受到地球的吸
引力为F,方向指向地心O,由万有引力公式得F=G
Mm R2
。
引力F可分解为F1、F2两个分力,其中F1为物体随地球自
转做圆周运动的向心力Fn,F2就是物体的重力mg。
A.P、Q做圆周运动的向心力大小相等 P、Q两质点距离地心的距离相等,根据F=
2.万有引力定律的适用条件:
知,两质点受到的地球引力大小相等,故B正确、D错误;
P、Q两点的角速度相同,做圆周运动的半径不同,根据F向=mrω2可知向心力大小不相等,A错误;
公式F=G 适用于两质点间的相互作用,当两物体相距很近时,两物体不能看成质点,所以选项B错误。
B.使两物体间的距离和两物体的质量都减为原来的
1 4
C.使两物体间的距离增为原来的2倍,质量不变
D.使其中一个物体的质量减小到原来的
1 4
,距离不变
【解析】选B。使两物体的质量各减小一半,距离不变,
根据万有引力定律F=
G
Mm r2
可知,万有引力变为原来的
1 4
,
故A可以采用;使两物体间的距离和两物体的质量都减为
万有引力定律
6.3《万有引力定律》—人教版高中物理必修二课件(共22张PPT)

6.3《万有引力定律》
知识回顾
太阳对行星的引力与行星的质量成正比,与行 星和太阳距离的二次方成反比。
m F r2
行星对太阳的引力与太阳的质量M成正比,与行 星、太阳距离的二次方成反比。
F'
M r2
太阳与行星间的引力与太阳的质量、行星 的质量成正比,与两者距离的二次方成反比。
F
Mm r2
F
G
Mm r2
根据上述公式对月—地系统和地面上物体的 分别可用公式得:
G
M地m月 r地月2
m月a月
;
GMr地 地m 2物m物a物m物g
两式相比,得月球对地球运动得向心加速度:
a月
(
r地 )2 r地月
g
因为地球和月球之间的距离
半径r地 的60倍,所以
r地月
约为地球
a月 4T22r地 月2.7103ms2
数据表明所算的结果与实 际相符,这证明引力公式 是可靠的。
间万有引力为 6.67×10-11 N
卡文迪许扭称实验的意义: (1) 证明了万有引力的存在,使万有引力定
律进入了真正实用的时代; (2) 开创了微小量测量的先河,使科学放大
思想得到了推广。
思考:既然任意两个物体之间都有万有引力,
那为什么我们感觉不到旁边同学的引力呢?
下面我们粗略地来计算一下两 个质量为50kg,相距0.5m的
刻度尺
扭秤实验的物理思想和科学方法
1、扭秤装置把微小力转变成力 矩来反映;
2、扭秤装置把扭转角度又通过 光标的移动体现出来。
放大的思想方法
扭秤实验测定结果和意义
实验结果:G = 6.67259×10-11 N m2/kg2 通常取:G = 6.67×10-11 N m2/kg2
知识回顾
太阳对行星的引力与行星的质量成正比,与行 星和太阳距离的二次方成反比。
m F r2
行星对太阳的引力与太阳的质量M成正比,与行 星、太阳距离的二次方成反比。
F'
M r2
太阳与行星间的引力与太阳的质量、行星 的质量成正比,与两者距离的二次方成反比。
F
Mm r2
F
G
Mm r2
根据上述公式对月—地系统和地面上物体的 分别可用公式得:
G
M地m月 r地月2
m月a月
;
GMr地 地m 2物m物a物m物g
两式相比,得月球对地球运动得向心加速度:
a月
(
r地 )2 r地月
g
因为地球和月球之间的距离
半径r地 的60倍,所以
r地月
约为地球
a月 4T22r地 月2.7103ms2
数据表明所算的结果与实 际相符,这证明引力公式 是可靠的。
间万有引力为 6.67×10-11 N
卡文迪许扭称实验的意义: (1) 证明了万有引力的存在,使万有引力定
律进入了真正实用的时代; (2) 开创了微小量测量的先河,使科学放大
思想得到了推广。
思考:既然任意两个物体之间都有万有引力,
那为什么我们感觉不到旁边同学的引力呢?
下面我们粗略地来计算一下两 个质量为50kg,相距0.5m的
刻度尺
扭秤实验的物理思想和科学方法
1、扭秤装置把微小力转变成力 矩来反映;
2、扭秤装置把扭转角度又通过 光标的移动体现出来。
放大的思想方法
扭秤实验测定结果和意义
实验结果:G = 6.67259×10-11 N m2/kg2 通常取:G = 6.67×10-11 N m2/kg2
人教版高一物理必修第二册7.2万有引力定律课件(36张PPT)

质点.( √ )
4.月球绕地球做匀速圆周运动是因为月球受力平衡.( × )
5.月球做圆周运动的向心力是由地球对它的引力产生的.( √ )
6.地球对月球的引力与地面上的物体所受的地球的引力是两种不
同性质的力.( × )
课堂互动探究
要点一 对太阳与行星间引力的理解
1.两个理想化模型
在公式F=G
Mm r2
一种力,同样遵从“ 平方反比 ”的规律.
(2)推理: G
M 地m月 r地月2
m月a月,G
M 地m物 r地2
m物g
a月 g
r地 r地月
2
物体在月球轨道上运动时的加速度大约是它在地面附近下 1
落时的加速度的 602 .
(3)结论:月球所受地球的引力,地球表面物体所受地球的引
力,与太阳、行星间的引力遵从 完全相同 的规律.
对行星的引力提供了行星做匀速圆周运动的向心力,故A选项正
确;由太阳与行星间引力的表达式F=G
Mm r2
可知,太阳对行星
的引力大小与太阳的质量成正比,与行星的质量成正比,与行
星到太阳的距离的平方成反比,B选项正确,C选项错误;由牛
顿第三定律知,太阳对行星的引力与行星对太阳的引力是一对
作用力和反作用力,其大小相等、方向相反,D选项错误.
2.F=Gmr1m2 2的适用条件 (1)万有引力定律的公式适用于计算质点间的相互作用,当 两个物体间的距离比物体本身大得多时,可用此公式近似计算 两物体间的万有引力. (2)质量分布均匀的球体间的相互作用,可用此公式计算, 式中r是两个球体球心间的距离. (3)一个均匀球体与球外一个质点的万有引力也可用此公式 计算,式中的r是球体球心到质点的距离.
万有引力定律—人教版高中物理必修第二册教学课件

万有引力定律—人教版高中物理必修 第二册 课件
2.万有引力定律
万有引力定律—人教版高中物理必修 第二册 课件
知识导图
核心素养 物理观念:太阳与行星间的引力、万有引力定律、引力常量 科学思维:(1)模型建构——把行星绕太阳运转简化为匀速 圆周运动; (2)类比法——天体运动与地面物体运动遵循相同的力学定 律. 科学探究:“猜想、假设与验证”探究方法的应用 科学态度与责任:(1)了解和体会科学研究方法对人们认识 自然规律的重要性. (2)在实验探究合作中既能坚持观点,又能修正错误
(2)假设地球对苹果的吸引力也是 同一种力,同理可知,苹
果的自由落体加速度 a 苹=mF苹=GmR地2 (式中 m 地是地球质量,R 是
地球中 由心 以与 上苹 两果 式间 可的 得距 a月离 =)R.r22 a苹
.由于月球与地球中心的距离
r
约为
地球半径
R
的
60
倍,所以a月= a苹
1 602
.
(3)结论:地面物体所受地球的引力、月球所受地球的引力,
提示:(1)由于行星轨道的半长轴和半短轴大小差不多,中 学里就把行星的椭圆运动简化为圆周运动处理.进行处理后,半 长轴就变为了半径.
(2)行星做圆周运动需要向心力,行星与太阳间有相互作用 力,太阳对行星的引力提供行星运动的向心力.
(3)由 F=mvr2或 F=mω2r 可知,向心力与做圆周运动物体的 质量、线速度、角速度、周期、轨道半径等有关系.行星既然做 圆周运动,它的向心力也应该与这些有关系,自然跟它的质量有 关.行星的向心力是太阳对行星的引力,它与行星对太阳的引力 是一对相互作用力,这个引力既然与行星的质量有关,也应该与 太阳的质量有关.
知识点一 行星与太阳间的引力
2.万有引力定律
万有引力定律—人教版高中物理必修 第二册 课件
知识导图
核心素养 物理观念:太阳与行星间的引力、万有引力定律、引力常量 科学思维:(1)模型建构——把行星绕太阳运转简化为匀速 圆周运动; (2)类比法——天体运动与地面物体运动遵循相同的力学定 律. 科学探究:“猜想、假设与验证”探究方法的应用 科学态度与责任:(1)了解和体会科学研究方法对人们认识 自然规律的重要性. (2)在实验探究合作中既能坚持观点,又能修正错误
(2)假设地球对苹果的吸引力也是 同一种力,同理可知,苹
果的自由落体加速度 a 苹=mF苹=GmR地2 (式中 m 地是地球质量,R 是
地球中 由心 以与 上苹 两果 式间 可的 得距 a月离 =)R.r22 a苹
.由于月球与地球中心的距离
r
约为
地球半径
R
的
60
倍,所以a月= a苹
1 602
.
(3)结论:地面物体所受地球的引力、月球所受地球的引力,
提示:(1)由于行星轨道的半长轴和半短轴大小差不多,中 学里就把行星的椭圆运动简化为圆周运动处理.进行处理后,半 长轴就变为了半径.
(2)行星做圆周运动需要向心力,行星与太阳间有相互作用 力,太阳对行星的引力提供行星运动的向心力.
(3)由 F=mvr2或 F=mω2r 可知,向心力与做圆周运动物体的 质量、线速度、角速度、周期、轨道半径等有关系.行星既然做 圆周运动,它的向心力也应该与这些有关系,自然跟它的质量有 关.行星的向心力是太阳对行星的引力,它与行星对太阳的引力 是一对相互作用力,这个引力既然与行星的质量有关,也应该与 太阳的质量有关.
知识点一 行星与太阳间的引力
人教版(新教材)高中物理必修2:第2节 万有引力定律ppt课件

【例3】 (2020·江苏连云港市锦屏高级中学高一期中)我国成功发射了第11颗北斗导 航卫星,标志着北斗卫星导航系统建设又迈出了坚实一步。若卫星质量为m、离 地球表面的高度为h,地球质量为M、半径为R,G为引力常量,则地球对卫星万 有引力的大小为( )
A.GMh m
B.GRM+mh
GMm C. h2
A.2倍
B.3倍
C.4倍
D.0.5倍
解析 设此时火箭离地球表面高度为h。 由牛顿第二定律得FN-mg′=ma,① 在地球表面处 mg=GMRm2 ② 由①可得g′=0.625 m/s2。③
又因 h 处 mg′=G(RM+mh)2,④
由②④得gg′=(R+R2h)2。 代入数据解得h=3R,故选项B正确。 答案 B
上述公式中 m 地为地球质量,m 月为月球质量,r 为地球中心与月球中心的距离,R
是地球中心与苹果间的距离。由以上两式可得aa月 苹=Rr22。由于月球与地球中心的距离 r 约为地球半径 R 的 60 倍,所以aa月 苹=__6_10_2__。
2.结论:月球绕地球运动的向心加速度与我们的预期符合得很好。这表明:地面物 体所受地球的引力、月球所受地球的引力,与太阳、行星间的引力遵从_相__同___的 规律。
■归纳拓展 1.物体在地球表面上所受引力与重力的关系:除两极以外,地面上其他点的物体,
都围绕地轴做圆周运动,这就需要一个垂直于地轴的向心力。地球对物体引力的 一个分力F′提供向心力,另一个分力为重力G,如图所示。
(1)当物体在两极时:G=F 引,重力达到最大值 Gmax=GMRm2 。
(2)当物体在赤道上时 F′=mω2R 最大,此时重力最小 Gmin=GMRm2 -mω2R (3)从赤道到两极:随着纬度增加,向心力 F′=mω2R′减小,F′与 F 引夹角增大,所 以重力 G 在增大,重力加速度增大。 因为 F′、F 引、G 不在一条直线上,重力 G 与万有引力 F 引方向有偏差,重力大小 mg<GMRm2 。
物理人教版(2019)必修第二册7.2万有引力定律(共25张ppt)

观察与思考
利用已知行星与太阳间引力公式推导月球加速度
1.已知月心到地心的距离约为地球半径的60倍,则月球绕地球做圆周运
动的加速度与物体在地面附近下落时的加速度比值是多少?
月球受地球引力为: =
地月
2
地
月 =
= 2
月
苹果受地球引力为: =
地 苹
2
地
苹 =
= 2
观察与思考
思考1:生活中的匀速圆周运动遵从怎样的动力学规律?
合力提供向心力,即合 =
2
4π2
= 2 =2
思考2:行星绕太阳可看做匀速圆周运动,什么力提供
向心力?
太阳对行星的引力提供行星做圆周运动的向心力
观察与思考
思考3:太阳对行星的引力提供向心力,那么这
3
由开普勒三定律: 2
6.67×10-11 m2/kg2。
卡文迪什
4.对万有引力定律的理解
普遍性 宇宙间任何两个有质量的物体之间都存在着相互吸引的力
相互性 两个有质量的物体之间的万有引力是一对作用力和反作用力
宏观性
地面上的一般物体之间的万有引力比较小,与其他力比较可忽略不计,但在
质量巨大的天体之间或天体与其附近的物体之间,万有引力起着决定性作用
m太m
(2)太阳与行星间的引力公式 F=G 2 中,G与太阳、行星都没有关
r
系。( √ )
(3)太阳对行星的引力大小等于行星对太阳的引力大小。(
√)
(4)太阳对行星的引力与行星的质量成正比,与太阳质量无关。
(
×)
月—地检验
观察与思考
如图甲所示秋天苹果成熟后会从树上落下来;如图乙所示为月球绕着地
物理人教版(2019)必修第二册7.2万有引力定律(共24张ppt)
)
A、
G
m1m2 r2
C、
G
m1m2 (r1 r2 )2
B、
Байду номын сангаас
G
m 1 m2 r12
D 、G (r
m1m2 r1 r2 )2
r1
r2
r
3、如图所示,在距一个质量为M,半径为R,密度均匀的球体 表面R处,有一个质量为m的质点。此时M对m的万有引力为F1。 当从M中挖去如图所示半径为R/2的球体时,剩下部分对m的万 有引力为F2,则F1与F2的比为多少?
思考:两个物体距离越近,相互之间的引力就越大,对吗?
适用条件: 1、严格来讲,公式只适用于两个质点。 2、两个质量分布均匀的球体 3、质量分布均匀的球体与质点
m1
m2 r
四.引力常量G
卡文迪什也因此被称为“能称出地球质量的人”
亨利·卡文迪什
卡文迪什扭秤实验的测量方法 放大法
1.扭秤装置把微小力通过杠杆旋转 明显反映出来(一次放大);
2.扭转角度(微小形变)通过光标 的移动来反映(二次放大),从而 确定物体间的万有引力。 实验数据:G=6.67×10-11 N·m2/kg2 实验意义:
①引力常量的普适性成了万有引力定 律正确性的有力证据;
②开创了微小量测量的先河,使科学 放大思想得到推广;
巩固练习
例1.计算两个质量都为50kg,相距0.5m的同学之间的万有引力 (两个同学可以看成质点)
地表处万有引力和重力的关系
赤道:F G m2r
两极:F=G
思考:为什么随着纬 度的增加,重力加速 度增大?
高空处万有引力和重力的关系
重力就是万有引力
mg GMm (R h)2
思考:为什么随着高 度的增加,重力加速 度减小?
人教版(新)高中物理必修第二册万有引力定律(16页)-PPT优秀课件

F = G m1m2 r2
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
2、适用条件:
⑴万有引力只适用于质点间引力大小的计算,当两物体间的距离 远远大于每个物体的尺寸时,物体可看成质点,直接使用万有 引力计算。
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
至此,牛顿一直是在已有的观测结果和理论引导下 进行推测和分析,观测结果仅对“行星绕太阳运动” 成立,这还不是万有引力定律。 牛顿是怎样把天体间的引力与地球对地面附近物体 的引力统一起来证明它们遵循相同的规律进而得到 万有引力的?
胡克
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
当年牛顿在前人研究的基础 上,并凭借其超凡的数学能力 和坚定的信念,深入研究,最 终发现了万有引力定律。
牛顿 (1643—1727) 英国著名的物理学家
牛顿在1676年给友人的信中写道:
如果说我看的比别人更远,那 是因为我站在巨人的肩膀上。
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
伽利略 笛卡尔
一切物体都有合并的趋势。
行星的运动是受到了来自太阳的类 似于磁力的作用 ,与距离成反比。
在行星的周围有旋转的物质(以太)作 用在行星上,使得行星绕太阳运动。
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
2、适用条件:
⑴万有引力只适用于质点间引力大小的计算,当两物体间的距离 远远大于每个物体的尺寸时,物体可看成质点,直接使用万有 引力计算。
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
至此,牛顿一直是在已有的观测结果和理论引导下 进行推测和分析,观测结果仅对“行星绕太阳运动” 成立,这还不是万有引力定律。 牛顿是怎样把天体间的引力与地球对地面附近物体 的引力统一起来证明它们遵循相同的规律进而得到 万有引力的?
胡克
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
当年牛顿在前人研究的基础 上,并凭借其超凡的数学能力 和坚定的信念,深入研究,最 终发现了万有引力定律。
牛顿 (1643—1727) 英国著名的物理学家
牛顿在1676年给友人的信中写道:
如果说我看的比别人更远,那 是因为我站在巨人的肩膀上。
人 教 版 ( 20 19)高 中物理 必修第 二册 7 . 2 万有 引力定 律(共 16张P PT)
伽利略 笛卡尔
一切物体都有合并的趋势。
行星的运动是受到了来自太阳的类 似于磁力的作用 ,与距离成反比。
在行星的周围有旋转的物质(以太)作 用在行星上,使得行星绕太阳运动。
【最新】人教版高一物理必修二教学课件 6.3 万有引力定律 (共36张PPT)

F
1m
F
1kg
G引力常量最早由卡文迪许测出G=6.67×10-11N·m2/kg2
万有引力定律的意义
17世纪自然科学最伟大的成果之一,第一次揭示 了自然界中的一种基本相互作用的规律,在人类认 识自然的历史上树立了一座里程碑。
在文化发展史上的重大意义:统一了地面物体运 动规律和天体运动规律,使人们建立了有能力理解 天地间的各种事物的信心,解放了人们的思想,在 科学文化的发展史上起了积极的推动作用。
卡文迪许扭秤实验
光杠杆“放大”
卡文迪许(英国)
力矩“放大” Kθ =2 F L=2 L (Gmm’/r2)
原理:力矩平衡
“能称出地球质量的人” 知:g、R、G求M 重力近似等于万有引力 G M m/R2=m g M =gR2/G 地球密度ρ =M/V=(R2g/G)÷(4π R3/3 )=3g/(4π GR)
2、测中心天体的质量M和密度ρ
4 2 r 3 M GT 2 3 r GT 2 R3
3
中心天体 太阳 太阳 地球 地球 其他行星
环绕天体 地球 其他行星 月球 人造卫星 卫星
环绕m
中心M R
r
已知地球绕太阳公转的轨道半径是1.50×1011m,公转 周期是3.16×107s,求太阳质量M?
R2 g 2 g0 r
1 9.8 g g0 2.7 103 m / s 2 3600 3600
r
月球圆周运动向心加速度
4 2 r 4 2 60 6400 103 a 2 T (27.3 24 3600)2 =2.7 10-3m / s 2
两者相等说明了地球对苹果的引力和地球对月球的引力 是同一性质的力,都是万有引力。
7.2 万有引力定律课件-2023学年高一下学期物理人教版(2019)必修第二册

相距约3.8×108 m,由此可计算出加速度a=0.002 7 m/s2;
(2)地球表面的重力加速度为9.8 m/s2,月球的向心加速度与地球表面重力
加速度之比为1∶3 630,而地球半径(6.4×106 m)和月球与地球间距离的比为
1∶60。这个比的平方1∶3 600与上面的加速度之比非常接近。
以上结果说明( A )
月球周期 T = 27.3天 ≈ 2.36×106 s
月地距离 r ≈ 60R=3.84×108m
月 Байду номын сангаас
苹 =
苹果做自由落体运动:
苹 = g = 9.8m/s2
月球做匀速圆周运动:
月 =
≈ . × − /
≈
三、月-地检验
178
2 2
2
(3.9 10 )
F2 mr1
五、练习与应用
教材第54页
4. 木星有4颗卫星是伽利略发现的,称为伽利略卫星,其中三颗卫星的周期之比为
1∶2∶4。小华同学打算根据万有引力的知识计算木卫二绕木星运动的周期,她收集到
了如下一些数据。
8
木卫二的数据:质量4.8×10 22 kg、绕木星做匀速圆周运动的轨道半径6.7×10 m。木
F
D.
4
练3
如图所示,操场两边放着半径分别为r1、r2,质量分别为m1、m2的篮
球和足球,二者的间距为r。两球间的万有引力大小为( D )
m1m2
A.G 2
r
m1m2
B.G 2
r1
m1m2
C.G
(r1+r2)2
(2)地球表面的重力加速度为9.8 m/s2,月球的向心加速度与地球表面重力
加速度之比为1∶3 630,而地球半径(6.4×106 m)和月球与地球间距离的比为
1∶60。这个比的平方1∶3 600与上面的加速度之比非常接近。
以上结果说明( A )
月球周期 T = 27.3天 ≈ 2.36×106 s
月地距离 r ≈ 60R=3.84×108m
月 Байду номын сангаас
苹 =
苹果做自由落体运动:
苹 = g = 9.8m/s2
月球做匀速圆周运动:
月 =
≈ . × − /
≈
三、月-地检验
178
2 2
2
(3.9 10 )
F2 mr1
五、练习与应用
教材第54页
4. 木星有4颗卫星是伽利略发现的,称为伽利略卫星,其中三颗卫星的周期之比为
1∶2∶4。小华同学打算根据万有引力的知识计算木卫二绕木星运动的周期,她收集到
了如下一些数据。
8
木卫二的数据:质量4.8×10 22 kg、绕木星做匀速圆周运动的轨道半径6.7×10 m。木
F
D.
4
练3
如图所示,操场两边放着半径分别为r1、r2,质量分别为m1、m2的篮
球和足球,二者的间距为r。两球间的万有引力大小为( D )
m1m2
A.G 2
r
m1m2
B.G 2
r1
m1m2
C.G
(r1+r2)2
新人教版高中物理必修二课件:6.3《万有引力定律》 (共10张PPT)

• 11、夫学须志也,才须学也,非学无以广才,非志无以成学。2021/3/72021/3/72021/3/7Mar-217-Mar-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。2021/3/72021/3/72021/3/7Sunday, March 07, 2021 • 13、志不立,天下无可成之事。2021/3/72021/3/72021/3/72021/3/73/7/2021
F引 ∝ Mm/r2
写成等式:F引= GMm/r2
行星绕太阳运动遵守这个规律,那么 在其他物体之间是否适用这个规律呢??
牛顿还研究了月球绕地球的运动,发现它们间的 引力跟太阳与行星间的引力遵循同样规律。
牛顿在研究了许多物体间遵循规律的引力之后, 进一步把这个规律推广到自然界中任何两个物体之间, 于1687年正式发表了万有引力定律:
思考与讨论
◆ 我们人与人之间也一样存在万有引力,可是为 什么我们感受不到呢?
假设质量均为60千克的两位同学,相距1米, 他们之间的相互作用的万有引力多大?
F=Gm1m2/r2 =6.67×10-11×60×60/12 =2.4×10-7(N)
2.4×10-7N是一粒芝麻重的几千分之一, 这么小的力人根本无法察觉到。
17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。2021/3/72021/3/72021/3/72021/3/7
谢谢观看
◆ 那么太阳与地球之间的万有引力又是多大呢?
已知:太阳的质量为M=2.0×1030kg,地球 质量为m=5.8×1025kg,日地之间的距离为 R=1.5×1011km
F=GMm/R2 =6.67×10-11×2.0×1030×6.0×1024/(1.5×1011)2 =3.5×1022(N)
新版物理必修2人教版 6.3万有引力定律 (共18张PPT)学习PPT

C.万 3倍有引力定律是由D牛.顿4发倍现的,而引力常量是由胡克测定的 4变、式设、想宇把航一员质在量某为星m球的表物面体以放初在速地度球v的0竖中直心向,问上物抛体出受一到个地物球体对,它物的体万上有升引的力最为大多高少度?为h。
有引力大小为( ) 离1、地为面什高么度我们感处觉为不4到m旁g 边同学的引力呢?
2
.
公
式
:
F
=
G
m1m2 r2
,
其
中
G = 6.67×10 - 11
N·m2/kg2,它是在牛顿发现万有引力定律一百年
后由英国物理学家卡文迪许利用实验测出的.
1、为什么我们感觉不到旁边同学的引力呢?
下面我们粗略地来计算一下两个质量为50kg,相距 0.5m的人之间的引力?(为什么说是粗略?)
F=GMm/R2=6.67×10-7N
2、那么太阳与地球之间的万有引力又是多大?
已知:太阳的质量为M=2.0×1030kg,地球质量为 m=5.9×1024kg,日地之间的距离为R=1.5×1011m
F=GMm/R2=3.5×1023N 说明:引力在天体与天体间,天体与物体间比较 显著,但通常物体间的引力可忽略不计.
3、 由
F=G
m1m2 r2
m m 1m、1、为m什2么受我到们的感引觉力不总到是旁大边小同相学等的、引方力向呢相?反,是一对平衡力
1 2 mm 离公地式面 中高的度F应理解处为为m41m、gm2所受引力之和
A. G 2 大于 1 2 随例着2:半地径球为自R转,质加量快为,地M面的上均的匀物球体体会,在不其会内飞部起挖来去?一个半径为R/2的小球,在距离大球圆心为L处有一个质量为为m的小球,求此两个球体之
新人教版高中物理必修二(课件)6.3 万有引力定律 (共18张PPT)

A、G m1m2 r2
C、
G
m1m2 (r1 r2 ) 2
B、G m1 m2
答案:D
r12
ห้องสมุดไป่ตู้
D、
G
(r
m1m2 r1 r2
)2
r1
r2
r
三、引力常量的测量——扭秤实验 (1)实验原理: 科学方法——放大法
卡文迪许实验室
卡文迪许
(2)实验数据
G值为6.67×10-11 Nm2/kg2 G值的物理含义: 两个质量为1kg的物体相距1m时,它们之 间万有引力为6.67×10-11 N
•
T H E E N D 17、一个人如果不到最高峰,他就没有片刻的安宁,他也就不会感到生命的恬静和光荣。上午11时5分57秒上午11时5分11:05:5721.3.18
谢谢观看
例题2 估算两个质量50kg的同学相距0.5m 时之间的万有引力约有多大?
答案:6.67×10-7牛
(3)卡文迪许扭称实验的意义 ①证明了万有引力的存在,使万有引力定律 进入了真正实用的时代; ②开创了微小量测量的先河,使科学放大思 想得到推广;
四、学习思考
纵观万有引力定律的发现历程,你觉得科学发现的一 般过程是什么?你能概括一下吗?
• 9、春去春又回,新桃换旧符。在那桃花盛开的地方,在这醉人芬芳的季节,愿你生活像春天一样阳光,心情像桃花一样美丽,日子像桃子一样甜蜜。2 1.3.1821.3.18Thursday, March 18, 2021
• 10、人的志向通常和他们的能力成正比例。11:05:5711:05:5711:053/18/2021 11:05:57 AM • 11、夫学须志也,才须学也,非学无以广才,非志无以成学。21.3.1811:05:5711:05Mar-2118-Mar-21 • 12、越是无能的人,越喜欢挑剔别人的错儿。11:05:5711:05:5711:05Thursday, March 18, 2021 • 13、志不立,天下无可成之事。21.3.1821.3.1811:05:5711:05:57March 18, 2021
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
月地检验
地表重力加速度:g = 9.8 m/s2
地球半径:R=6400×103m
月球周期:T =27.3天≈2.36×106 s
月球轨道半径:r≈60R=3.84×108m
求:月球绕地球的向心加速度 ?
即证明
即a月
1 602
g
r
R
“月——地”检验示意图
月地检验
根据向心加速度公式,有:a月
r 2
r
二、月-地检验 牛顿的思考
<1>地球和月球之间的吸引力会
不会与地球吸引苹果的力是同一
种力呢?
<2>地球表面的重力能否延伸到很 远的地方,会不会作用到月球上?
<3>拉住月球使它绕地球运动的力, 与拉着苹果使它下落的力,以及众行 星与太阳之间的作用力也许真的是同 一种力,遵循相同的规律?
牛顿的猜想
这些力是同一种性质 的力,并且都遵从与距离 的平方成反比的规律。
m F r2
科 探究1: 太阳对行星的引力F
学 探 究
F
m r2
请太用阳中对文行描星述的这引力跟受力
m 关星 星个系体、关式的太系中质阳式量距!是成离受正的力比二,次与方行 成
天反体比还. 是施力天体 的质量?
既然太阳对行
星有引力,那
么行星对太阳
有 有引 怎力 样吗定?量它的星 行
关系呢?
F F′
的作用 ,与距离成反比。
开普勒
在行星的周围有旋转的物质(以太)作用在行星上, 使得行星绕太阳运动。
笛卡尔
行星的运动是太阳吸引的缘故,并且力的大小与
到太阳距离的平方成反比。
胡克
科
学
当年牛顿在前人研究的基础上,
足
也经过类似同学这样的思考,并凭借
迹
其超凡的数学能力和坚定的信念,深
入研究,最终发现了万有引力定律。
建 立
探究1: 太阳对行星的引力F
模
型
V
r
行星
太阳
m
F
M
思考:
太阳对行星的引力提供向 心力,那么这个力大小有 什么样定量关系?
科
学 探
F mv2 r
究
v 2 r
T
v 行星运行速度 容易观测吗?怎么办?
v 消去 F 4 2mr
T2
T 消去
4 2km
F
r3 =k
r2
讨论
T2
为什么能从上式得到下式?
知 识
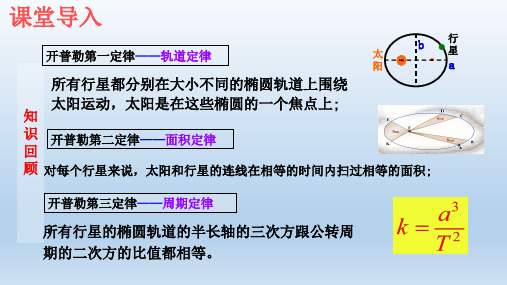
开普勒三定律
回 开普勒第一定律——轨道定律 顾 所有行星都分别在大小不同的椭圆轨道上围绕
太阳运动,太阳是在这些椭圆的一个焦点上;
开普勒第二定律——面积定律
对每个行星来说,太阳和行星的连线在相 等的时间扫过相等的面积;
开普勒第三定律——周期定律
所有行星的轨道的半长轴的三次方跟公转 周期的二次方的比值都相等.
F
m r2
G为比例系数,
与太阳、行星无关。
F 和F ′是一对作用力和反作用
类 比 法
牛 三
牛三 力,那么可以得出F大小跟太
Mm Mm 阳质量M、行星质量m的关系 F r 式有什2么关系?F=G r2
F'
M r2
方向:沿着太阳与
行星间的连线 。
根据牛顿第三定律,行星对太阳的力与太阳对行星的力是一对相
b
太阳
行星
a
v=
一、行星与太阳之间的引力 二、月-地检验 三、万有引力定律
一、行星与太阳之间的引力 行星的运动
“太阳坐在它的皇位上,管理 着围绕它的一切星球”
——哥白尼
行星为什么绕太阳做如此和谐而 又有规律地椭圆运动?
科
学 足
一切物体都有合并的趋势。
迹 伽利略 行星的运动是受到了来自太阳的类似于磁力
4 2
T2
即:a月
4 3.142 2.36 106
2 3.84108
=2.72×10-3m/s2
1 602
g
r
R
“月——地”检验示意图
三、万有引力定律
1、内容:自然界中任何两个物体都是互相吸引的,引力的大小 跟这两个物体的质量的乘积成正比,跟它们的距离的二次方成反比.
2、表达式:由
F
G
Mm( r2
m1m 2 r2
G
Fr 2 m1m 2
可知
G 的单位:
N m 2 / kg 2
100多年后,由英国物理学家卡文迪许测出
G值的测量:卡文迪许扭秤实验
第一个能称出 地球质量的人
金属丝
扭
秤
T形架
装
置
平面镜
光源
刻度尺
扭秤实验的测量结果
万有引力常量
卡文迪许扭秤实验的意义:
(1)证明了万有引力的存在,并测得引力常 量G,使万有引力定律进入了真正实用的时 代;
(2)开创了微小量测量的先河,使科学放大 思想得到了推广.
牛顿 (1643—1727) 英国著名的物理学家
牛顿在1676年给友人的信中写道:
如果说我看的比别人更远, 那是因为我站在巨人的肩膀上。
建
立
行星
思考:行星的实际运动是
模
太阳
椭圆运动,但我们还不了
型
a
解椭圆运动规律,那应该
怎么办?能把阳 r
把行星绕太阳的运动简化为 匀速圆周运动
太 阳
科 学
探究2: 行星对太阳的引力F′
探 究
F
m r2
太阳对行星的引力跟受力 星体的质量成正比,与行 星、太阳距离的二次方成 反比.
类 比 法
牛 三
F'
M r2
行星对太阳的引力F′跟太
阳的质量成正比,与行星、
太阳距离的二次方成反比.
星行
太 F F′ 阳
科 探究3: 太阳与行星间的引力F
学 探 究
互作用的性质相同的力,据此推知行星对太阳(受力物体)的力F′
有怎样的关系?
答案
与太阳的质量M成正比
即
F∝
M
r2
由上述2、3结论,结合F=F′可猜测太阳与行星间的引力满足什
么关系式?
答案
F∝
M
r2
F∝
M
r2
若这两个力相等,F=F′∝Mr2m
古人观点
牛顿思考
理论演算 建模
总结规律
类比
理想化
随堂练习
1、下列关于行星对太阳的引力的说法中正确的是( ) A.行星对太阳的引力与太阳对行星的引力是同一性质的力 B.行星对太阳的引力与太阳的质量成正比,与行星的质量无关 C.太阳对行星的引力大于行星对太阳的引力 D.行星对太阳的引力大小与太阳的质量成正比,与行星距太阳的 距离成反比
当然这仅仅是猜想, 还需要事实来检验!
月地检验
检验目的:地球和月球之间的吸引力是否
与地球吸引苹果的力为同一种力.
检验原理:
且r 60R
故 F月轨道
1 60 2
F地表
根据牛顿第二定律,知:F月轨道 ma月轨道, F地表 mg
即 a月
1 60 2
g
ma 月轨道
1 mg 60 2
r
R
“月——地”检验示意图
M
:太阳质量
, m : 行星质量)
得出:
F
G
m1m r2
2(
m
:物体
1
1的质量
, m 2 : 物体 2的质量)
F
G
m1m2 r2
G: 引力常量 6.67×10-11N·m2/kg2
(1)引力常量适用于任何两个物体; (2)意义:在数值上等于两个质量都是1kg的物体
相距1m时的相互作用力。
3、由
F
G
