(完整word版)计量经济学(第四版)习题及参考答案详细版
计量经济学(第四版)第三章练习题及答案
第三章练习题及参考解答3.1进入21世纪后,中国的家用汽车增长很快。
家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素,都会影响中国汽车拥有量。
为了研究一些主要因素与家用汽车拥有量的数量关系,选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量,2016年全国各省市区的有关数据如表3.5。
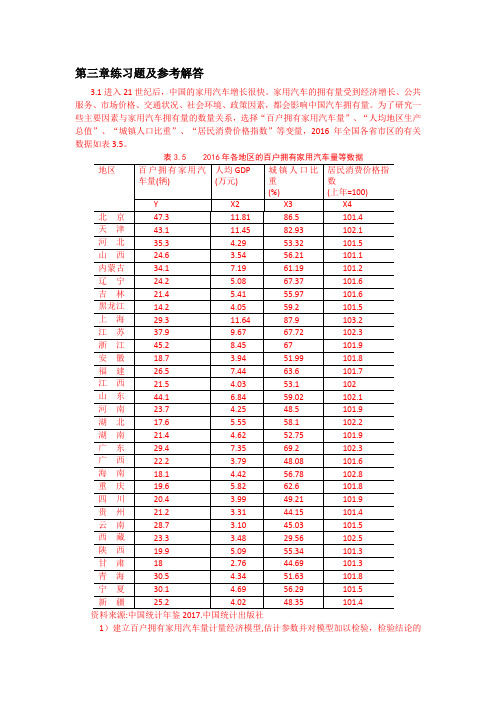
表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1)建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验,检验结论的依据是什么?。
2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】:1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007,可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。
解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=,表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。
2)X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。
由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。
汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。
计量经济学精要第四版课后习题答案.doc
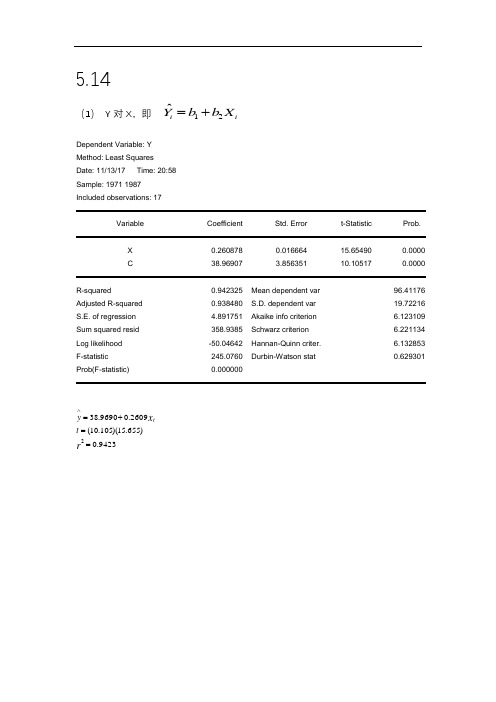
5.14(1) Y 对X ,即12ˆi iY b b X =+Dependent Variable: Y Method: Least Squares Date: 11/13/17 Time: 20:58 Sample: 1971 1987 Included observations: 17VariableCoefficient Std. Error t-Statistic Prob.X 0.260878 0.016664 15.65490 0.0000 C38.969073.85635110.10517 0.0000R-squared0.942325 Mean dependent var 96.41176 Adjusted R-squared 0.938480 S.D. dependent var 19.72216 S.E. of regression 4.891751 Akaike info criterion 6.123109 Sum squared resid 358.9385 Schwarz criterion 6.221134 Log likelihood -50.04642 Hannan-Quinn criter. 6.132853 F-statistic 245.0760 Durbin-Watson stat 0.629301Prob(F-statistic) 0.0000009423.0)655.15)(105.10(2609.09690.382==+=∧r x t y t(2)InY 对InX ,即 12ˆi iInY b b InX =+9642.0)090.20)(954.8(ln 5890.04041.1ln 2==+=∧r x t y tDependent Variable: LNY Method: Least Squares Date: 11/13/17 Time: 21:40 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C 1.404051 0.156813 8.953649 0.0000 LNX0.5889650.02931720.08981 0.0000R-squared0.964166 Mean dependent var 4.547848 Adjusted R-squared 0.961777 S.D. dependent var 0.213165 S.E. of regression 0.041675 Akaike info criterion -3.407698 Sum squared resid 0.026052 Schwarz criterion -3.309673 Log likelihood 30.96543 Hannan-Quinn criter. -3.397954 F-statistic 403.6007 Durbin-Watson stat 0.734161Prob(F-statistic)0.000000(3)InY 对X ,即 12ˆi iInY b b X =+Dependent Variable: LNY Method: Least Squares Date: 11/13/17 Time: 21:42 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C 3.931578 0.046430 84.67764 0.0000 X0.0027990.00020113.94972 0.0000R-squared0.928433 Mean dependent var 4.547848 Adjusted R-squared 0.923662 S.D. dependent var 0.213165 S.E. of regression 0.058896 Akaike info criterion -2.715956 Sum squared resid 0.052031 Schwarz criterion -2.617930 Log likelihood 25.08562 Hannan-Quinn criter. -2.706212 F-statistic 194.5946 Durbin-Watson stat 0.529132Prob(F-statistic) 0.0000009284.0)950.13)(678.84(0028.09316.3ln 2==+=∧r X t y t(4)Y 对InX ,即 12ˆi iY b b InX =+Dependent Variable: Y Method: Least Squares Date: 11/13/17 Time: 21:43 Sample: 1971 1987 Included observations: 17Variable Coefficient Std. Error t-Statistic Prob.C -192.9661 16.38000 -11.78059 0.0000 LNX54.212573.06227817.70335 0.0000R-squared0.954325 Mean dependent var 96.41176 Adjusted R-squared 0.951280 S.D. dependent var 19.72216 S.E. of regression 4.353186 Akaike info criterion 5.889824 Sum squared resid 284.2535 Schwarz criterion 5.987849 Log likelihood -48.06350 Hannan-Quinn criter. 5.899568 F-statistic 313.4086 Durbin-Watson stat 0.610822Prob(F-statistic) 0.0000009542.0)703.17)(781.11(ln 2126.549661.1922=-=+-=∧r X t Y t解:1.XY∆∆=1ˆβ斜率说明X 每变动一个单位,Y 的绝对变动量;2. E XX Y Y =∆∆=//ˆ1β斜率便是弹性系数; 3. XY Y ∆∆=/ˆ1β斜率表示X 每变动一个单位,Y 的均值的瞬时增长率; 4,. XX Y/ˆ1∆∆=β斜率表示X 的相对变化对Y 的绝对量的影响。
计量经济学精要习题参考答案(第四版)

计量经济学(第四版)习题参考答案第一章 绪论1.1 一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析1.2 我们在计量经济模型中列出了影响因变量的解释变量,但它(它们)仅是影响因变量的主要因素,还有很多对因变量有影响的因素,它们相对而言不那么重要,因而未被包括在模型中。
为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4 估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y 就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2 NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即此样本不是取自一个均值为120元、标准差为10元的正态总体。
伍德里奇-计量经济学(第4版)答案

伍德里奇-计量经济学(第4版)答案计量经济学答案第二章2.4 (1)在实验的准备过程中,我们要随机安排小时数,这样小时数(hours )可以独立于其它影响SAT 成绩的因素。
然后,我们收集实验中每个学生SAT 成绩的相关信息,产生一个数据集{}n i hours sat i i ,...2,1:),(=,n 是实验中学生的数量。
从式(2.7)中,我们应尽量获得较多可行的i hours 变量。
(2)因素:与生俱来的能力(天赋)、家庭收入、考试当天的健康状况①如果我们认为天赋高的学生不需要准备SAT 考试,那天赋(ability )与小时数(hours )之间是负相关。
②家庭收入与小时数之间可能是正相关,因为收入水平高的家庭更容易支付起备考课程的费用。
③排除慢性健康问题,考试当天的健康问题与SAT 备考课程上的小时数(hours )大致不相关。
(3)如果备考课程有效,1β应该是正的:其他因素不变情况下,增加备考课程时间会提高SAT 成绩。
(4)0β在这个例子中有一个很有用的解释:因为E (u )=0,0β是那些在备考课程上花费小时数为0的学生的SAT平均成绩。
2.7(1)是的。
如果住房离垃圾焚化炉很近会压低房屋的价格,如果住房离垃圾焚化炉距离远则房屋的价格会高。
(2)如果城市选择将垃圾焚化炉放置在距离昂贵的街区较远的地方,那么log(dist)与房屋价格就是正相关的。
也就是说方程中u包含的因素(例如焚化炉的地理位置等)和距离(dist)相关,则E(u︱log(dist))≠0。
这就违背SLR4(零条件均值假设),而且最小二乘法估计可能有偏。
(3)房屋面积,浴室的数量,地段大小,屋龄,社区的质量(包括学校的质量)等因素,正如第(2)问所提到的,这些因素都与距离焚化炉的远近(dist,log(dist))相关2.11(1)当cigs(孕妇每天抽烟根数)=0时,预计婴儿出生体重=110.77盎司;当cigs(孕妇每天抽烟根数)=20时,预计婴儿出生体重(bwght)=109.49盎司。
第四章练习题及参考解答(第四版)计量经济学

第四章练习题及参考解答4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,有人建议你分别进行如下回归:1221i i i Y X u αα=++ 1332i i i Y X u γγ=++(1) 是否存在3322ˆˆˆˆβγβα==且?为什么? (2) 1ˆβ会等于1ˆα或1ˆγ或者两者的某个线性组合吗? (3) 是否有()()22ˆˆVar Var βα=且()()33ˆˆVar Var βγ=?【练习题4.1参考解答】(1) 存在2233ˆˆˆˆαβγβ==且 。
因为 ()()()()()()()2233232ˆi iii ii iy x x y x x x-∑∑∑∑资料来源:《中国统计年鉴2017》考虑建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?(3)进行以下回归:121ln ln t t i Y A A GDP v =++ 122ln ln t t i Y B B CPI v =++ 123ln ln t t i GDP C C CPI v =++ 根据这些回归你能对多重共线性的性质有什么认识?(4)假设经检验数据有多重共线性,但模型中32ˆˆββ和在5%水平上显著,并且F 检验也显著,你对此模型的应用有何建议?【练习题4.2参考解答】建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?其中居民消费价格指数CPI 对商品进口额影响为负,与预期不符合,可能存在多重共线性。
(3)分别进行以下回归:1)作回归121ln ln t t i Y A A GDP v =++说明GDP 的确对商品进口额有正的影响,是重要变量。
计量经济学(第四版)习题及参考答案详细版知识讲解

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学第四版习题及参考答案解析

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学(第四版)第三章练习题及答案

第三章练习题及参考解答3.1进入21世纪后,中国的家用汽车增长很快。
家用汽车的拥有量受到经济增长、公共服务、市场价格、交通状况、社会环境、政策因素,都会影响中国汽车拥有量。
为了研究一些主要因素与家用汽车拥有量的数量关系,选择“百户拥有家用汽车量”、“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量,2016年全国各省市区的有关数据如表3.5。
表3.5 2016年各地区的百户拥有家用汽车量等数据资料来源:中国统计年鉴2017.中国统计出版社1)建立百户拥有家用汽车量计量经济模型,估计参数并对模型加以检验,检验结论的依据是什么?。
2)分析模型参数估计结果的经济意义,你如何解读模型估计检验的结果? 3) 你认为模型还可以如何改进?【练习题3.1 参考解答】:1)建立线性回归模型: 1223344t t t t t Y X X X u ββββ=++++ 回归结果如下:由F 统计量为14.69998, P 值为0.000007,可判断模型整体上显著, “人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”等变量联合起来对百户拥有家用汽车量有显著影响。
解释变量参数的t 统计量的绝对值均大于临界值0.025(27) 2.052t =,或P 值均明显小于0.05α=,表明在其他变量不变的情况下,“人均地区生产总值”、“城镇人口比重”、“居民消费价格指数”分别对百户拥有家用汽车量都有显著影响。
2)X2的参数估计值为4.8117,表明随着经济的增长,人均地区生产总值每增加1万元,平均说来百户拥有家用汽车量将增加近5辆。
由于城镇公共交通的大力发展,有减少家用汽车的必要性,X3的参数估计值为-0.4449,表明随着城镇化的推进,“城镇人口比重”每增加1%,平均说来百户拥有家用汽车量将减少0.4449辆。
汽车价格和使用费用的提高将抑制家用汽车的使用, X4的参数估计值为-5.7685,表明随着家用汽车使用成本的提高, “居民消费价格指数”每增加1个百分点,平均说来百户拥有家用汽车量将减少5.7685辆。
第四章练习题及参考解答(第四版)计量经济学

第四章练习题及参考解答4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,有人建议你分别进行如下回归:1221i i i Y X u αα=++ 1332i i i Y X u γγ=++(1) 是否存在3322ˆˆˆˆβγβα==且?为什么? (2) 1ˆβ会等于1ˆα或1ˆγ或者两者的某个线性组合吗? (3) 是否有()()22ˆˆVar Var βα=且()()33ˆˆVar Var βγ=?【练习题4.1参考解答】(1) 存在2233ˆˆˆˆαβγβ==且 。
因为 ()()()()()()()22332322222323ˆi iii ii iiii iy x x y x x x x x x x β-=-∑∑∑∑∑∑∑当23X X 与 之间的相关系数为零时,离差形式的230i ix x =∑有 ()()()()223222222223ˆˆi i ii i iiiy x x y x xx x βα===∑∑∑∑∑∑ 同理有: 33ˆˆγβ= (2)会的。
(3) 存在 ()()()()2233ˆˆˆˆvar var var var βαβγ==且 因为 ()()2222223ˆvar 1ix r σβ=-∑当 230r = 时, ()()()22222222223ˆˆvar var 1iix x r σσβα===-∑∑ 同理,有 ()()33ˆˆvar var βγ=4.2 表4.4给出了1995—2016年中国商品进口额Y 、国生产总值GDP 、居民消费价格指数CPI 的数据。
表4.4 中国商品进口额、国生产总值、居民消费价格指数资料来源:《中国统计年鉴2017》考虑建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?(3)进行以下回归:121ln ln t t i Y A A GDP v =++ 122ln ln t t i Y B B CPI v =++ 123ln ln t t i GDP C C CPI v =++ 根据这些回归你能对多重共线性的性质有什么认识?(4)假设经检验数据有多重共线性,但模型中32ˆˆββ和在5%水平上显著,并且F 检验也显著,你对此模型的应用有何建议?【练习题4.2参考解答】建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
第七章练习题及参考解答(第四版)计量经济学

第七章练习题及参考解答7.1 表7.4中给出了1981-2015年中国城镇居民人均年消费支出(PCE)和城镇居民人均可支配收入(PDI)数据。
表7.4 1981-2015年中国城镇居民消费支出(PCE)和可支配收入(PDI)数据 (单位:元)估计下列模型:tt t t tt t PCE B PDI B B PCE PDI A A PCE υμ+++=++=-132121(1) 解释这两个回归模型的结果。
(2) 短期和长期边际消费倾向(MPC )是多少?分析该地区消费同收入的关系。
(3) 建立适当的分布滞后模型,用库伊克变换转换为库伊克模型后进行估计,并对估计结果进行分析判断。
【练习题7.1参考解答】(1) 解释这两个回归模型的结果。
Dependent Variable: PCE Method: Least Squares Date: 03/10/18 Time: 09:12 Sample: 1981 2005Variable Coefficient Std. Error t-Statistic Prob.C 149.0975 24.56734 6.068933 0.0000R-squared 0.998965 Mean dependent var 2983.768Adjusted R-squared 0.998920 S.D. dependent var 2364.412S.E. of regression 77.70773 Akaike info criterion 11.62040Sum squared resid 138885.3 Schwarz criterion 11.71791Log likelihood -143.2551 F-statistic 22196.24Durbin-Watson stat 0.531721 Prob(F-statistic) 0.000000收入跟消费间有显著关系。
(完整版)伍德里奇计量经济学(第4版)答案

2.7(1)是的。如果住房离垃圾焚化炉很近会压低房屋的价格,如果住房离垃圾焚化炉距离远则房屋的价格会高。
(2)如果城市选择将垃圾焚化炉放置在距离昂贵的街区较远的地方,那么log(dist)与房屋价格就是正相关的。也就是说方程中u包含的因素(例如焚化炉的地理位置等)和距离(dist)相关,则E(u︱log(dist))≠0。这就违背SLR4(零条件均值假设),而且最小二乘法估计可能有偏。
(3)如果在方程中加入paredc作为一个独立变量引入,交叉项系数是负的。Educ*pareduc的t统计量大约是-1.33.在10%的显著性水平上,在双侧对立假设上,t统计量是不显著的。注意到,pareduc的系数在5%的显著性水平上,在双侧对立假设下是显著的。这表明省略一个效应水平会如何导致交互效应的有偏估计。
3.4(1)如果成年人为工作而放弃睡眠,工作多意味着睡眠会减少。所以 >0.
(2)一般说来, 和 的的符号并不确定。虽然有人认为受过较高教育的人想要得到更完美的生活,所以他们的睡觉时间很少( <0)。睡眠时间与年龄之间的关系要比模型中给的复杂多,经济学家也并未对此作出更好的解释。
(3)因为工作时间以分钟为单位,我们把5小时化为分钟,则总工作时间为300分钟。睡眠时间预计会减少0.148*300=44.4分钟。从一周来看,少睡45分钟并不算是很大的舍弃。
(4)零假设检验: : = –1.T统计量=[–0.951– (–1)]/0.37= (1–0.951)/0.37 0.132;这个数字很小,我们不能拒绝单侧或双侧假设。即sales/employ提高1%将伴随以废品率下降1%。
经济计量学精要第四版课后练习题含答案

经济计量学精要第四版课后练习题含答案前言经济计量学是运用数学和统计方法研究经济现象及其规律的一门学科。
经济计量学精要第四版是经济计量学的入门教材,本文将为各位读者提供该教材课后练习题及答案,帮助读者更好地掌握该门学科。
第一章经济计量学基础选择题1.什么是偏差?A.衡量回归直线的直角离散程度B.已知均值估计总体标准差C.样本中的观测值与其相应总体值之差D.对称分布的方差答案:C2.在经济计量分析中,线性关系是基本关系之一。
下列哪个假设是错误的?A.线性关系是基本关系之一B.线性关系是在整个取值区间内成立的C.在一些情况下线性关系只在某一特定范围内成立D.线性方程存在可比较的斜率答案:B填空题1.在经验研究中,一般采用______________式估计总体参数。
答案:样本2.如果增加自变量个数,再加上满足一定条件,使得求出的参数估计仍有标准正态分布的概率较大,这就是多元_____________中的问题。
答案:线性回归第二章单一线性回归模型选择题1.在单一线性回归中,为使OLS估计量无偏,必须假定误差项都等于____。
A.正态分布B.泊松分布C.自变量D.零答案:D2.投资量与利息率之间可能存在一种哪种关系?A.负向线性关系B.正向线性关系C.非线性关系D.都不正确答案:B填空题1.在单一线性回归模型中,因变量和自变量之间需要满足线性关系,使散点图大致呈现出一个______________。
答案:直线趋势2.单一线性回归模型的OLS估计量被定义为将所有预测误差的平方之和最小化得来的样本_______________。
答案:回归方程第三章多元线性回归模型选择题1.当模型自变量与因变量的简单相关系数大于0.7时,发生的问题是什么?A.多重共线性B.异方差性C.自相关D.标准误增大答案:A2.关于多解释变量线性回归模型,下列哪个描述是错误的?A.利用OLS估计法估计各个参数的估计值B.OLS含有多个系数,这些系数代表因变量特定解释变量的影响。
练习题及参考解答第四版计量经济学

第七章练习题及参考解答表中给出了1981-2015年中国城镇居民人均年消费支出(PCE)和城镇居民人均可支配收入(PDI)数据。
表 1981-2015年中国城镇居民消费支出(PCE)和可支配收入(PDI)数据(单位:元)估计下列模型:(1) 解释这两个回归模型的结果。
(2) 短期和长期边际消费倾向(MPC)是多少分析该地区消费同收入的关系。
(3) 建立适当的分布滞后模型,用库伊克变换转换为库伊克模型后进行估计,并对估计结果进行分析判断。
【练习题参考解答】(1) 解释这两个回归模型的结果。
Dependent Variable: PCEMethod: Least SquaresDate: 03/10/18 Time: 09:12Sample: 1981 2005Included observations: 25Variable CoefficientStd.Errort-StatisticProb.CPDIR-squared Mean dependentvarAdjusted R-squared . dependent var. of regression Akaike infocriterionSum squared resid Schwarz criterionLog likelihood F-statisticDurbin-Watsonstat Prob(F-statistic)收入跟消费间有显着关系。
收入每增加1元,消费增加元。
Dependent Variable: PCEMethod: Least SquaresDate: 03/10/18 Time: 09:13Sample(adjusted): 1982 2005Included observations: 24 after adjusting endpointsVariable CoefficientStd.Errort-StatisticProb.C PDIPCE(-1)R-squared Mean dependentvarAdjusted R-squared . dependent var. of regression Akaike infocriterionSum squared resid Schwarz criterionLog likelihood F-statisticDurbin-Watsonstat Prob(F-statistic)(2) 短期和长期边际消费倾向(MPC)是多少分析该地区消费同收入的关系。
(完整版)伍德里奇计量经济学(第4版)答案

计量经济学答案第二章2.4 (1)在实验的准备过程中,我们要随机安排小时数,这样小时数(hours )可以独立于其它影响SAT 成绩的因素。
然后,我们收集实验中每个学生SAT 成绩的相关信息,产生一个数据集{}n i hours sat i i ,...2,1:),(=,n 是实验中学生的数量。
从式(2.7)中,我们应尽量获得较多可行的i hours 变量。
(2)因素:与生俱来的能力(天赋)、家庭收入、考试当天的健康状况①如果我们认为天赋高的学生不需要准备SAT 考试,那天赋(ability )与小时数(hours )之间是负相关。
②家庭收入与小时数之间可能是正相关,因为收入水平高的家庭更容易支付起备考课程的费用。
③排除慢性健康问题,考试当天的健康问题与SAT 备考课程上的小时数(hours )大致不相关。
(3)如果备考课程有效,1β应该是正的:其他因素不变情况下,增加备考课程时间会提高SAT 成绩。
(4)0β在这个例子中有一个很有用的解释:因为E (u )=0,0β是那些在备考课程上花费小时数为0的学生的SAT 平均成绩。
2.7(1)是的。
如果住房离垃圾焚化炉很近会压低房屋的价格,如果住房离垃圾焚化炉距离远则房屋的价格会高。
(2)如果城市选择将垃圾焚化炉放置在距离昂贵的街区较远的地方,那么log(dist)与房屋价格就是正相关的。
也就是说方程中u 包含的因素(例如焚化炉的地理位置等)和距离(dist)相关,则E (u ︱log(dist))≠0。
这就违背SLR4(零条件均值假设),而且最小二乘法估计可能有偏。
(3)房屋面积,浴室的数量,地段大小,屋龄,社区的质量(包括学校的质量)等因素,正如第(2)问所提到的,这些因素都与距离焚化炉的远近(dist,log(dist))相关2.11(1)当cigs (孕妇每天抽烟根数)=0时,预计婴儿出生体重=110.77盎司;当cigs (孕妇每天抽烟根数)=20时,预计婴儿出生体重(bwght )=109.49盎司。
第四章练习题及参考解答(第四版)计量经济学

第四章练习题及参考解答4.1 假设在模型i i i i u X X Y +++=33221βββ中,32X X 与之间的相关系数为零,有人建议你分别进行如下回归:1221i i i Y X u αα=++ 1332i i i Y X u γγ=++(1) 是否存在3322ˆˆˆˆβγβα==且?为什么? (2) 1ˆβ会等于1ˆα或1ˆγ或者两者的某个线性组合吗? (3) 是否有()()22ˆˆVar Var βα=且()()33ˆˆVar Var βγ=?【练习题4.1参考解答】(1) 存在2233ˆˆˆˆαβγβ==且 。
因为 ()()()()()()()22332322222323ˆi iii ii iiii iy x x y x x xx x x x β-=-∑∑∑∑∑∑∑当23X X 与 之间的相关系数为零时,离差形式的230i ixx =∑有 ()()()()223222222223ˆˆi i i i i iiiy x x y x xx x βα===∑∑∑∑∑∑ 同理有: 33ˆˆγβ= (2)会的。
(3) 存在 ()()()()2233ˆˆˆˆvar var var var βαβγ==且 因为 ()()2222223ˆvar 1ix r σβ=-∑当 230r = 时, ()()()22222222223ˆˆvar var 1iix x r σσβα===-∑∑ 同理,有 ()()33ˆˆvar var βγ=4.2 表4.4给出了1995—2016年中国商品进口额Y 、国内生产总值GDP 、居民消费价格指数CPI 的数据。
表4.4 中国商品进口额、国内生产总值、居民消费价格指数资料来源:《中国统计年鉴2017》考虑建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
(2)你认为数据中有多重共线性吗?(3)进行以下回归:121ln ln t t i Y A A GDP v =++ 122ln ln t t i Y B B CPI v =++ 123ln ln t t i GDP C C CPI v =++ 根据这些回归你能对多重共线性的性质有什么认识?(4)假设经检验数据有多重共线性,但模型中32ˆˆββ和在5%水平上显著,并且F 检验也显著,你对此模型的应用有何建议?【练习题4.2参考解答】建立模型: i t t t u CPI GDP Y ++=ln ln ln 321βββ+ (1)利用表中数据估计此模型的参数。
第七章练习题及参考解答(第四版)计量经济学

第七章练习题及参考解答7.1表 7.4 中给出了 1981-2015 年中国城镇居民人均年消费支出 (PCE)和城镇居民人均可支配收入 (PDI) 数据。
表7.4 1981-2015 年中国城镇居民消费支出(PCE) 和可支配收入(PDI) 数据(单位:元)估计下列模型:PCE t A1 A2PDI t tPCE t B1 B2PDI t B3PCE t 1 t(1)解释这两个回归模型的结果。
(2)短期和长期边际消费倾向( MPC )是多少?分析该地区消费同收入的关系。
(3)建立适当的分布滞后模型,用库伊克变换转换为库伊克模型后进行估计,并对估计结果进行分析判断。
【练习题7.1 参考解答】(1)解释这两个回归模型的结果。
Dependent Variable: PCEMethod: Least SquaresDate: 03/10/18 Time: 09:12Sample: 1981 2005Included observations: 25Variable Coefficient Std. Error t-Statistic Prob.C 149.0975 24.56734 6.068933 0.0000PDI 0.757527 0.005085 148.9840 0.0000R-squared 0.998965 Mean dependent var 2983.768Adjusted R-squared 0.998920 S.D. dependent var 2364.412S.E. of regression 77.70773 Akaike info criterion 11.62040Sum squared resid 138885.3 Schwarz criterion 11.71791Log likelihood -143.2551 F-statistic 22196.24Durbin-Watson stat 0.531721 Prob(F-statistic) 0.000000收入跟消费间有显著关系。
计量经济学(第四版)习题及参考问题详解详细版

计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NS S x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
计量经济学第四版李子奈课后答案

计量经济学第四版李子奈课后答案第一章:简介1.什么是计量经济学?它与其他学科有什么区别?计量经济学是经济学的一个重要分支,主要研究经济现象的数理模型、计量方法以及经济政策的评估方法。
它与其他学科的区别在于,计量经济学着重于将经济理论转化为具体的计量模型,并利用统计分析方法对经济数据进行验证和评估,以获得对经济问题的深入理解和预测能力。
2.请简要介绍计量经济学的基本步骤。
计量经济学的基本步骤包括以下几个方面:•确定经济理论模型:根据研究的经济问题和理论基础,构建适当的经济理论模型。
•收集数据:收集所需的经济数据,包括自变量和因变量的观测值。
•数据处理:对数据进行处理和清洗,包括缺失数据的处理、异常值的检测和处理等。
•模型估计:利用统计方法对经济模型的参数进行估计,获得合适的模型参数估计值。
•模型检验:利用统计检验方法对模型的合理性进行检验,包括参数的显著性检验、模型拟合优度的检验等。
•模型应用和预测:根据模型估计结果,应用模型进行实际问题的分析和预测。
第二章:线性回归模型1.请解释简单线性回归模型的含义。
简单线性回归模型是一种描述两个变量之间线性关系的模型。
它假设因变量(被解释变量)可以通过一个线性函数来解释,该线性函数包含一个自变量(解释变量)。
形式化地表示为:$y_i = \\beta_0 + \\beta_1x_i + u_i$,其中y i表示因变量的观测值,x i表示自变量的观测值,$\\beta_0$和$\\beta_1$表示模型的参数,u i表示误差项。
2.如何进行线性回归模型的估计和检验?线性回归模型的参数可以通过最小二乘法进行估计。
最小二乘法通过最小化观测值和模型估计值之间的差异,来获取最优的模型参数估计。
具体的估计方法可以通过计算样本数据的一阶矩和二阶矩来获得。
线性回归模型的检验可以通过对模型参数的显著性进行检验来进行。
通常使用t检验或F检验来判断模型参数的显著性。
t检验用于检验单个参数的显著性,而F检验用于检验多个参数的显著性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
计量经济学(第四版)习题参考答案潘省初第一章 绪论1.1 试列出计量经济分析的主要步骤。
一般说来,计量经济分析按照以下步骤进行:(1)陈述理论(或假说) (2)建立计量经济模型 (3)收集数据 (4)估计参数 (5)假设检验 (6)预测和政策分析 1.2 计量经济模型中为何要包括扰动项?为了使模型更现实,我们有必要在模型中引进扰动项u 来代表所有影响因变量的其它因素,这些因素包括相对而言不重要因而未被引入模型的变量,以及纯粹的随机因素。
1.3什么是时间序列和横截面数据? 试举例说明二者的区别。
时间序列数据是按时间周期(即按固定的时间间隔)收集的数据,如年度或季度的国民生产总值、就业、货币供给、财政赤字或某人一生中每年的收入都是时间序列的例子。
横截面数据是在同一时点收集的不同个体(如个人、公司、国家等)的数据。
如人口普查数据、世界各国2000年国民生产总值、全班学生计量经济学成绩等都是横截面数据的例子。
1.4估计量和估计值有何区别?估计量是指一个公式或方法,它告诉人们怎样用手中样本所提供的信息去估计总体参数。
在一项应用中,依据估计量算出的一个具体的数值,称为估计值。
如Y就是一个估计量,1nii YY n==∑。
现有一样本,共4个数,100,104,96,130,则根据这个样本的数据运用均值估计量得出的均值估计值为5.107413096104100=+++。
第二章 计量经济分析的统计学基础2.1 略,参考教材。
2.2请用例2.2中的数据求北京男生平均身高的99%置信区间NSS x ==45=1.25 用α=0.05,N-1=15个自由度查表得005.0t =2.947,故99%置信限为 x S t X 005.0± =174±2.947×1.25=174±3.684也就是说,根据样本,我们有99%的把握说,北京男高中生的平均身高在170.316至177.684厘米之间。
2.3 25个雇员的随机样本的平均周薪为130元,试问此样本是否取自一个均值为120元、标准差为10元的正态总体? 原假设 120:0=μH备择假设 120:1≠μH 检验统计量()10/25XX μσ-Z ====查表96.1025.0=Z 因为Z= 5 >96.1025.0=Z ,故拒绝原假设, 即 此样本不是取自一个均值为120元、标准差为10元的正态总体。
2.4 某月对零售商店的调查结果表明,市郊食品店的月平均销售额为2500元,在下一个月份中,取出16个这种食品店的一个样本,其月平均销售额为2600元,销售额的标准差为480元。
试问能否得出结论,从上次调查以来,平均月销售额已经发生了变化? 原假设 : 2500:0=μH备择假设 : 2500:1≠μH()00)100/120.83ˆX X t μσ-==== 查表得 131.2)116(025.0=-t 因为t = 0.83 < 131.2=c t , 故接受原假 设,即从上次调查以来,平均月销售额没有发生变化。
第三章 双变量线性回归模型3.1 判断题(说明对错;如果错误,则予以更正) (1)OLS 法是使残差平方和最小化的估计方法。
对(2)计算OLS 估计值无需古典线性回归模型的基本假定。
对(3)若线性回归模型满足假设条件(1)~(4),但扰动项不服从正态分布,则尽管OLS 估计量不再是BLUE ,但仍为无偏估计量。
错只要线性回归模型满足假设条件(1)~(4),OLS 估计量就是BLUE 。
(4)最小二乘斜率系数的假设检验所依据的是t 分布,要求βˆ的抽样分布是正态分布。
对(5)R 2=TSS/ESS 。
错R 2 =ESS/TSS 。
(6)若回归模型中无截距项,则0≠∑t e 。
对(7)若原假设未被拒绝,则它为真。
错。
我们可以说的是,手头的数据不允许我们拒绝原假设。
(8)在双变量回归中,2σ的值越大,斜率系数的方差越大。
错。
因为∑=22)ˆ(tx V ar σβ,只有当∑2t x 保持恒定时,上述说法才正确。
3.2设YX βˆ和XYβˆ分别表示Y 对X 和X 对Y 的OLS 回归中的斜率,证明 YX βˆXYβˆ=2r r 为X 和Y 的相关系数。
证明:22222222ˆˆ()ˆˆi ii ii i YXXYiiii i YX XYi i x y y x x yxyyx y x yr x y ββββ===⎛⎫⋅===∑∑∑∑∑∑∑∑∑3.3证明:(1)Y 的真实值与OLS 拟合值有共同的均值,即Y nY nY ==∑∑ˆ;(2)OLS 残差与拟合值不相关,即 0ˆ=∑tt eY 。
(1),得两边除以,=n ˆ0ˆ)ˆ(ˆ∑∑∑∑∑∑∑∑=∴+=⇒+=⇒+=tt t tt t t tt t t t YY e e Y Y e YY e Y YY nY nY ==∑∑ˆ,即Y 的真实值和拟合值有共同的均值。
(2)的拟合值与残差无关。
,=,即因此,(教材中已证明),由于Y 0ˆˆ),ˆ(0ˆ0,0e ˆˆ)ˆˆ(ˆ22t∑∑∑∑∑∑∑∑∑∑====+=+=tttt tttt tt tt ttttt eY e Y e Y Cov e Ye X eX e e X e Y βαβα 3.4证明本章中(3.18)和(3.19)两式:(1)∑∑=222)ˆ(tt x n X Var σα(2)∑-=22)ˆ,ˆ(txX Cov σβα(1)222222222221112222222ˆˆ,ˆˆ()ˆˆˆ2u()()ˆ()2()()()()ˆ2()()ˆ2()iit tti n n n t ii j i ii j i ji j i jtY X Y X u u X u X X u u x uX X nn xu u u x u x u X X nn x uu u x ux x u u X nn x αβαβααββααββββββββββ≠≠=+=++-=---=--+-=-⋅⋅+-++=-⋅+-+++=-⋅+-∑∑∑∑∑∑∑∑∑∑∑()2X2222222222222222()ˆˆ2E()1(()2())()2i i j i i i j i j i j i j t i i j i j i i j i j i i i j i j i jt u u u x u x x u u E E XE X n n x u u u E E u E u u n n n nx u x x u u XE n x ααββσσ≠≠≠≠≠⎛⎫⎡⎤+++ ⎪⎢⎥-=-⎪⎢⎥ ⎪⎢⎥⎝⎭⎣⎦⎛⎫+ ⎪=+==⎪⎪⎝⎭++∑∑∑∑∑∑∑∑∑∑∑∑两边取期望值,有:()-+等式右端三项分别推导如下:22222222222222222222212(()()())200ˆE()()ˆ[]0ii i i j i j ii jt t t t tt tt x Xx E u x x E u u Xx n x n x X X x x nX X X E n x n x n x σσββσσσσαα≠⎛⎫ ⎪ ⎪⎪⎝⎭=++==-=+-=-+==∑∑∑∑∑∑∑∑∑∑∑∑∑(=)因此()∑∑=222)ˆ(tt x n X Var σα即(2)2222ˆˆ,ˆˆ()ˆˆˆˆˆˆ(,)[()][(())()]ˆˆ[(()][()]ˆ0()01ˆ()t Y X Y X u u X Cov E E u X E u XE XE XVar X x αβαβααββαβααβββββββββββββσ=+=++-=--=--=---=---=--=-=-∑()(第一项为的证明见本题())3.5考虑下列双变量模型: 模型1:i i i u X Y ++=21ββ模型2:i i i u X X Y +-+=)(21αα(1)β1和α1的OLS 估计量相同吗?它们的方差相等吗? (2)β2和α2的OLS 估计量相同吗?它们的方差相等吗?(1)X Y 21ˆˆββ-=,注意到 nx n x x x n x Var x n X Var Y x Y x x X X x ii i i ii i i i 22222221222121)()ˆ()ˆ(ˆˆ,0,0,σσσασβαα==-==-==-=∑∑∑∑∑∑∑==则我们有从而由上述结果,可以看到,无论是两个截距的估计量还是它们的方差都不相同。
(2)∑∑∑∑∑∑∑==---==222222222)ˆ()ˆ()())((ˆ,ˆiiiiiiiiii xVar Var xyx x x Y Y x x xy x σαβαβ=容易验证,这表明,两个斜率的估计量和方差都相同。
3.6有人使用1980-1994年度数据,研究汇率和相对价格的关系,得到如下结果:)333.1()22.1(:528.0318.4682.6ˆ2Se R X Yt t =-=其中,Y =马克对美元的汇率X =美、德两国消费者价格指数(CPI )之比,代表两国的相对价格 (1)请解释回归系数的含义; (2)X t 的系数为负值有经济意义吗?(3)如果我们重新定义X 为德国CPI 与美国CPI 之比,X 的符号会变化吗?为什么?(1)斜率的值 -4.318表明,在1980-1994期间,相对价格每上升一个单位,(GM/$)汇率下降约4.32个单位。
也就是说,美元贬值。
截距项6.682的含义是,如果相对价格为0,1美元可兑换6.682马克。
当然,这一解释没有经济意义。
(2)斜率系数为负符合经济理论和常识,因为如果美国价格上升快于德国,则美国消费者将倾向于买德国货,这就增大了对马克的需求,导致马克的升值。
(3)在这种情况下,斜率系数被预期为正数,因为,德国CPI 相对于美国CPI 越高,德国相对的通货膨胀就越高,这将导致美元对马克升值。
3.7随机调查200位男性的身高和体重,并用体重对身高进行回归,结果如下:)31.0()15.2(:81.031.126.76ˆ2Se R Height eight W =+-=其中Weight 的单位是磅(lb ),Height 的单位是厘米(cm )。
(1)当身高分别为177.67cm 、164.98cm 、187.82cm 时,对应的体重的拟合值为多少?(2)假设在一年中某人身高增高了3.81cm ,此人体重增加了多少? (1)78.16982.187*31.126.76ˆ86.13998.164*31.126.76ˆ49.15667.177*31.126.76ˆ=+-==+-==+-=eight Weight Weight W(2)99.481.3*31.1*31.1ˆ==∆=∆height eight W3.8设有10名工人的数据如下: X 10 710 5886 7910Y11 10 12 6 10 7 910 11 10其中 X=劳动工时, Y=产量(1)试估计Y=α+βX + u (要求列出计算表格); (2)提供回归结果(按标准格式)并适当说明; (3)检验原假设β=1.0。
