双曲线焦点三角形性质练习题
双曲线焦点三角形内心的性质与应用

设 犉1犇 = 犉1犎 =犿, 犉2犇 = 犉2犈 =狀, 犘犈 = 犘犎 =狆,内切圆的半径为狉,结合双曲线的 定 义 及 圆 的 切 线 长 性 质,可 得 犘犉1 - 犘犉2 =
犉1犇 - 犉2犇 =犿 -狀=2犪. 而 犉1犉2 = 犉1犇 + 犉2犇 =犿 +狀=2犮,可求
得 犿 =犮+犪,狀=犮-犪.
教学
2020年2月 解法探究
参谋
双曲线焦点三角形内心的性质与应用
? 福建省平和第一中学 赖平民
众所周知,圆锥曲线一直是高中数学中的重点和 难点之一,备受关注.圆锥曲线中,往往交汇着代数与 几何,既有“数”又有“形”,既有“动”又有“静”,是各方 面知识融合与交汇的场所,要求有较强的综合能力与 应变能力,是 考 查 数 学 能 力,体 现 选 拔 功 能 的 主 阵 地 之一.下面结合一个双曲线焦点三角形内心的两个性 质加以展现、证明,并结合实际加以巧妙应用.
犉1、犉2 分别为双曲线犆 的左、右焦点,△犘犉1犉2 的内 切圆的圆心为犐,设直线犐犉1,犐犉2 的斜率分别为犽1,
犽2,则犽犽1 2 =
.
分析:结合题目条件中给出的双曲线 犆 的离心
率,直接根据性质2中双曲线的焦点三角形内心的性
一、性质展现
【性质1】已知犘
为双曲线犆:狓犪22
狔2 -犫2
=1(犪
>0,
犫>0)上的任意一点,犉1、犉2 分别为双曲线犆 的左、右
焦点,△犘犉1犉2 的内切圆的圆心为犐,则点犐必在直线
狓=±犪 上.
图1
证明:根据对称性,不失一般性,假定犘 为双曲线 犆 右支上的任意一点,如图1所示,设 △犘犉1犉2 的内切 圆的圆心犐 在对应三边上的投影分别为犇、犈、犎 .
双曲线中的焦点三角形性质整理

双曲线中的焦点三角形江苏省盱眙中学 赵福余1.设双曲线19422=-y x ,1F 、2F 是其两个焦点,点P 在双曲线上,若︒=∠6021PF F ,则21PF F ∆的面积为 .设双曲线为()0,012222>>=-b a by a x ,1F 、2F 是其两个焦点,点P 在双曲线上, 性质1 :若θ=∠21PF F ,则21PF F ∆的面积为 .性质2:通过以上求解过程,若θ=∠21PF F ,则=21PF PF ;21PF PF 的最小值是 .(1)设双曲线14422=-y x ,1F 、2F 是其两个焦点,点P 在双曲线上,︒=∠9021PF F ,则21PF F ∆的周长为 .(2)若1F 、2F 分别是双曲线191622=-y x 的左、右焦点,AB 是双曲线左支上过点1F 的弦,且6=AB ,则2ABF ∆的周长是 .2.双曲线焦点三角形21PF F ∆的内切圆与21F F 相切于点A ,则=21.AF AF . 性质3:切点A 的位置为 .3.设双曲线()0,012222>>=-b a by a x ,1F 、2F 是其两个焦点,点P 在双曲线上,O 是中心,则OP PF PF t 21+=的范围是 .性质4:21.PF PF 与OP 的等式关系为 .4.设双曲线()0,012222>>=-b a by a x ,1F 、2F 是其两个焦点,点P 在双曲线右支上一点若离心率2=e ,则=2tan2tanβα .性质5:=2tan2tanβα .(用离心率e 表示) 5.双曲线离心率为e ,其焦点三角形21F PF ∆的旁心为A ,线段PA 的延长线交21F F 的延长线于点B ,若4=BA ,2=AP ,则离心率=e .性质6:=e .(用BA ,AP 表示)Welcome !!! 欢迎您的下载,资料仅供参考!。
双曲线知识点总结及经典练习题

双曲线知识点总结及经典练习题圆锥曲线(三)------双曲线知识点一:双曲线定义平面内与两个定点F i , F2的距离之差的绝对值等于常数(小于|F I F2| )的点的轨迹称为双曲线•即:||MF1 | |MF2 || 2a,(2a | F1 F2 |)。
这两个定点称为双曲线的焦点,两焦点的距离称为双曲线的焦距.1.双曲线的定义中,常数2a应当满足的约束条件:『囲-f耳卜力兰區禺|,这可以借助于三角形中边的相关性质两边之差小于第三边”来理解;2.若去掉定义中的绝对值”常数□满足约束条件:1纠卜戸场1“—1瓦码1^ - ■),则动点轨迹仅表示双曲线中靠焦点F2的一支;若|^|-|^| = 2^<|^|严>0 ),贝劇点轨迹仅表示双曲线中靠焦点Fi的一支;3•若常数a 满足约束条件:||珂T輕卜加=|垃也则动点轨迹是以F i、F2为端点的两条射线(包括端点);若常数a满足约束条件:||〃1卜『码|| =加二・冈珂|,则动点轨迹不存在;5 •若常数a 0,贝劇点轨迹为线段F i F2的垂直平分线。
知识点二:双曲线的标准方程1•当焦点在工‘轴上时,双曲线的标准方程,其中/二F十沪.2•当焦点在,轴上时,双曲线的标准方程:—L -………V ,其中r a—沖+护注意:1 •只有当双曲线的中心为坐标原点,对称轴为坐标轴建立直角坐标系时,才能得到双曲线的标准方程;2•在双曲线的两种标准方程中,都有''-;3•双曲线的焦点总在实轴上,即系数为正的项所对应的坐标轴上.当匕的系数为正时,焦点在工轴上,双曲线的焦点坐标为■;当厂的系数为正时,焦点在T轴上,双曲线的焦点坐标为,.知识点三:双曲线性质1、双曲线, 下(a> 0,b> 0)的简单几何性质一 f y(1)对称性:对于双曲线标准方程r 丁(a>0, b>0),把x换成一x,或把y换成一y,或把x、y同时换成一X、一y,方程都不变,所以双曲线一-- (a> 0, b> 0)是以x轴、y轴为对称轴的轴对称图形,且是以原点为对称中心的中心对称图形,这个对称中心称为双曲线的中心。
双曲线性质总结及经典例题

双曲线性质总结及经典例题双曲线知识点总结1. 双曲线的第一定义:⑴①双曲线标准方程:.一般方程:.⑵①i. 焦点在x轴上:顶点:焦点:准线方程渐近线方程:或ii. 焦点在轴上:顶点:. 焦点:. 准线方程:. 渐近线方程:或②轴为对称轴,实轴长为2a, 虚轴长为2b,焦距2c. ③离心率. ④准线距(两准线的距离). ⑤参数关系. ⑥焦点半径公式:对于双曲线方程(分别为双曲线的左、右焦点或分别为双曲线的上下焦点)例题分析定义类1,已知12(5,0),(5,0)F F -,一曲线上的动点P 到21,F F 距离之差为6,则双曲线的方程为点拨:一要注意是否满足122||a F F <,二要注意是一支还是两支12||||610PF PF -=< ,P 的轨迹是双曲线的右支.其方程为)0(116922>=-x y x2双曲线的渐近线为x y 23±=,则离心率为 点拨:当焦点在x 轴上时,23=a b ,213=e ;当焦点在y轴上时,23=b a ,313=e4 设P 为双曲线11222=-y x 上的一点F 1、F 2是该双曲线的两个焦点,若|PF 1|:|PF 2|=3:2,则△PF 1F 2的面积为 ( )A .36B .12C .312D .24 解析:2:3||:||,13,12,121====PF PF c b a 由 ①又,22||||21==-a PF PF ②由①、②解得.4||,6||21==PF PF,52||,52||||2212221==+F F PF PF为21F PF ∴直角三角形,.124621||||212121=⨯⨯=⋅=∴∆PF PF S F PF 故选B 。
1已知双曲线C 与双曲线162x -42y =1有公共焦点,且过点(32,2).求双曲线C 的方程.【解题思路】运用方程思想,列关于c b a ,,的方程组 [解析] 解法一:设双曲线方程为22a x -22b y =1.由题意易求c =25.又双曲线过点(32,2),∴22)23(a -24b =1.又∵a 2+b 2=(25)2,∴a 2=12,b 2=8.故所求双曲线的方程为122x-82y =1.解法二:设双曲线方程为kx -162-ky +42=1,将点(32,2)代入得k =4,所以双曲线方程为122x -82y =1.2.已知双曲线的渐近线方程是2xy ±=,焦点在坐标轴上且焦距是10,则此双曲线的方程为 ; [解析]设双曲线方程为λ=-224y x ,当0>λ时,化为1422=-λλy x ,2010452=∴=∴λλ, 当0<λ时,化为1422=---λλy y ,2010452-=∴=-∴λλ,综上,双曲线方程为221205x y -=或120522=-x y3.以抛物线x y 382=的焦点F 为右焦点,且两条渐近线是03=±y x 的双曲线方程为___________________.[解析] 抛物线x y 382=的焦点F 为)0,32(,设双曲线方程为λ=-223y x ,9)32(342=∴=∴λλ,双曲线方程为13922=-y x【例1】若椭圆()0122 n m ny m x =+与双曲线221x y a b-=)0( b a 有相同的焦点F 1,F 2,P 是两条曲线的一个交点,则|PF 1|·|PF 2|的值是 ( )A. a m -B. ()a m -21 C. 22a m -D.am -()1221m PF PF m∴+=,()1222a PF PF a∴-=±,()()()2212121244PF PF m a PF PF m a-⋅=-⇒⋅=-:,故选A.【评注】严格区分椭圆与双曲线的第一定义,是破解本题的关键. 【例2】已知双曲线127922=-y x 与点M(5,3),F 为右焦点,若双曲线上有一点P ,使PMPF 21+最小,则P 点的坐标为XY O F(6,0)M(5,3)P N P ′N ′X=32【分析】待求式中的12是什么?是双曲线离心率的倒数.由此可知,解本题须用双曲线的第二定义.【解析】双曲线的右焦点F (6,0),离心率2e =, 右准线为32l x =:.作MN l ⊥于N ,交双曲线右支于P , 连FP ,则122PF e PN PN PN PF ==⇒=.此时 PM 1375225PF PM PN MN +=+==-=为最小. 在127922=-y x 中,令3y =,得2122 3.xx x =⇒=±∴0,取23x =所求P 点的坐标为23(,).【例3】过点(1,3)且渐近线为x y 21±=的双曲线方程是【解析】设所求双曲线为()2214x y k -=点(1,3)代入:135944k =-=-.代入(1): 22223541443535x y x y -=-⇒-=即为所求.【评注】在双曲线22221x y a b -=中,令222200x y x y a b a b-=⇒±=即为其渐近线.根据这一点,可以简洁地设待求双曲线为2222x y k a b-=,而无须考虑其实、虚轴的位置.【例7】直线l 过双曲线12222=-by a x 的右焦点,斜率k =2.若l 与双曲线的两个交点分别在左右两支上,则双曲线的离心率e 的范围是 ( ) A .e >2 B.1<e <3 C.1<e <5 D.e >5【解析】如图设直线l 的倾斜角为α,双曲线渐近线m的倾斜角为β.显然。
双曲线知识点及例题

双曲线知识点一:双曲线的定义: 在平面内,到两个定点、的距离之差的绝对值等于常数(大于0且)的动点的轨迹叫作双曲线的轨迹叫作双曲线..这两个定点、叫双曲线的焦点,两焦点的距离叫作双曲线的焦距两焦点的距离叫作双曲线的焦距. . 注意:注意:1. 1. 双曲线的定义中,常数双曲线的定义中,常数应当满足的约束条件:,这可以借助于三角形中边的相关性质“两边之差小于第三边”来理解; 2. 2. 若去掉定义中的“绝对值”,常数若去掉定义中的“绝对值”,常数满足约束条件:(),则动点轨迹仅表示双曲线中靠焦点的一支;若(),则动点轨迹仅表示双曲线中靠焦点的一支;的一支;3. 3. 若常数若常数满足约束条件:,则动点轨迹是以F 1、F 2为端点的两条射线(包括端点);端点的两条射线(包括端点); 4.若常数满足约束条件:,则动点轨迹不存在;,则动点轨迹不存在;5.若常数,则动点轨迹为线段F 1F 2的垂直平分线。
的垂直平分线。
知识点二:双曲线与的简单几何性质标准方程图形性质焦点, ,焦距范围,,对称性 关于x 轴、y 轴和原点对称顶点 轴长 实轴长=,虚轴长=离心率 渐近线方程1.通径:过焦点且垂直于实轴的弦,其长ab 222.2.等轴双曲线等轴双曲线等轴双曲线 : : :当双曲线的实轴长与虚轴长相等即当双曲线的实轴长与虚轴长相等即2a=2b 时,我们称这样的双曲线为等轴双曲线。
其离心率,两条渐近线互相垂直为,等轴双曲线可设为3.3.与双曲线与双曲线有公共渐近线的双曲线方程可设为(,焦点在轴上,,焦点在y 轴上)轴上)4.4.焦点三角形的面积焦点三角形的面积2cot221qb SF PF =D ,其中21PF F Ð=q 5.5.双曲线的焦点到渐近线的距离为双曲线的焦点到渐近线的距离为b.6.在不能确定焦点位置的情况下可设双曲线方程为:)0(122<=+mn ny mx 7.7.椭圆、双曲线的区别和联系:椭圆、双曲线的区别和联系:椭圆、双曲线的区别和联系:椭圆双曲线根据|MF 1|+|MF 2|=2a根据|MF 1|-|MF 2|=|=±±2aa >c >0, a 22-c 22=b 22(b >0)0<a <c , c 22-a 22=b 22(b >0), ,(a>b>0)(a>0,b>0,a不一定大于b)典型例题1、已知双曲线:()的离心率为,则的渐近线方程为()D.A.B.C.试题分析:由题意可知,因为渐近线方程为 所以渐近线的方程为 2、已知分别是双曲线的左右焦点,过做垂直于轴的直线交双曲线于两点,若为钝角三角形,则双曲线的离心率的范围是A.B.C.D.试题分析:由题意为钝角三角形,则,所以,又,,所以,所以,所以.考点:双曲线离心率.3、已知双曲线(a>0,b>0)的一条渐近线为,则它的离心率为()A.B.C.D.试题分析:由已知得,又在双曲线中有,所以得到;故选A.4、若双曲线的两准线间的距离是焦距的,则双曲线的离心率为_________. 试题分析:双曲线的两准线的距离为:,两焦点间的距离为:,根据题意可由:化简为:解得:,所以答案为:. 5、双曲线的离心率 .试题分析:双曲线即为,其中6、如图,、是双曲线的左、右焦点,过的直线与双曲线的左右两支分别交于点、.若为等边三角形,则双曲线的离心率为( )A.4B.C.D.试题分析:因为为等边三角形,不妨设,为双曲线上一点,,为双曲线上一点,则,,由,则,在中应用余弦定理得:,得,则7、设双曲线的一条渐近线与抛物线只有一个公共点,则双曲线的离心率为()A.B.C.D.试题分析:的一条渐近线方程与抛物线只有一个公共点,把代入中,得,由,,则8、过双曲线的右焦点F2的一条弦PQ,|PQ|=7,F1是左焦点,那么△F1PQ的周长为()A.18B.C.D.试题分析:可化为;由双曲线的定义,得的周长为.9、双曲线的顶点到其渐近线的距离等于_________.试题分析:双曲线的顶点为,渐近线方程为,即;则顶点到其渐近线的距离为. 10、双曲线的离心率,则的取值范围是()A.B.C.D.试题分析:由题意知,又,∴,∴. 11、双曲线的实轴长是()A.2B.2C.4D.4试题分析:双曲线方程可变形为,所以. 12、双曲线:的渐近线方程是()A.B.C.D.试题分析:由双曲线的渐近线方程的公式可知的渐近线方程是.13、斜率为的直线过双曲线的右焦点,且与双曲线的左右两支都相交,则双曲线的离心率的取值范围是()A.B.C.D.试题分析:如图,要使斜率为的直线过双曲线的右焦点,且与双曲线的左右两支都相交,必须且只需即可,从而有所以有离心率,故选D. 14、过原点的直线与双曲线有两个交点,则直线的斜率的取值范围为()A.B.C.D.试题分析:双曲线的焦点在y轴上,通过双曲线的图象与性质可知当直线与双曲线有两交点时直线的斜率k>1或k<-1,因此答案选B。
双曲线中的焦点三角形性质整理.pdf

双曲线中的焦点三角形江苏省盱眙中学 赵福余1.设双曲线19422=−y x ,1F 、2F 是其两个焦点,点P 在双曲线上,若︒=∠6021PF F ,则21PF F ∆的面积为 .设双曲线为()0,012222>>=−b a by a x ,1F 、2F 是其两个焦点,点P 在双曲线上, 性质1 :若θ=∠21PF F ,则21PF F ∆的面积为 .性质2:通过以上求解过程,若θ=∠21PF F ,则=21PF PF ;21PF PF 的最小值是 .(1)设双曲线14422=−y x ,1F 、2F 是其两个焦点,点P 在双曲线上,︒=∠9021PF F ,则21PF F ∆的周长为 .(2)若1F 、2F 分别是双曲线191622=−y x 的左、右焦点,AB 是双曲线左支上过点1F 的弦,且6=AB ,则2ABF ∆的周长是 .2.双曲线焦点三角形21PF F ∆的内切圆与21F F 相切于点A ,则=21.AF AF . 性质3:切点A 的位置为 .3.设双曲线()0,012222>>=−b a by a x ,1F 、2F 是其两个焦点,点P 在双曲线上,O 是中心,则OP PF PF t 21+=的范围是 .性质4:21.PF PF 与OP 的等式关系为 .4.设双曲线()0,012222>>=−b a by a x ,1F 、2F 是其两个焦点,点P 在双曲线右支上一点若离心率2=e ,则=2tan2tanβα .性质5:=2tan2tanβα .(用离心率e 表示) 5.双曲线离心率为e ,其焦点三角形21F PF ∆的旁心为A ,线段PA 的延长线交21F F 的延长线于点B ,若4=BA ,2=AP ,则离心率=e . 性质6:=e .(用BA ,AP 表示)。
专题11 双曲线及其性质(知识梳理+专题过关)(原卷版)
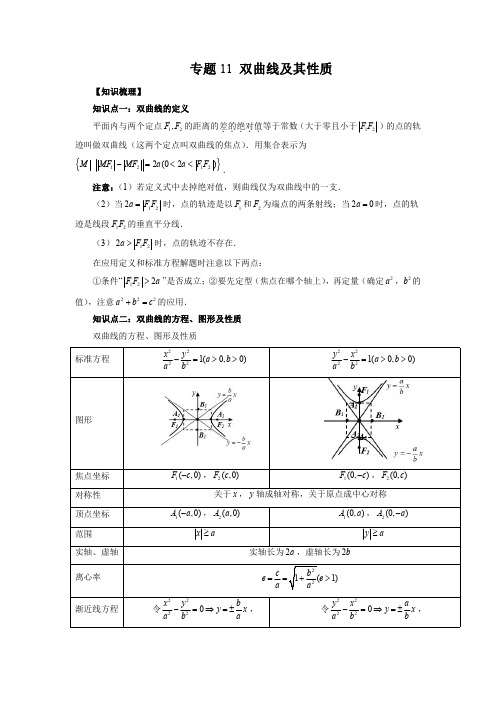
专题11双曲线及其性质【知识梳理】知识点一:双曲线的定义平面内与两个定点12,F F 的距离的差的绝对值.....等于常数(大于零且小于12F F )的点的轨迹叫做双曲线(这两个定点叫双曲线的焦点).用集合表示为{}12122(02)MMF MF a a F F -=<<.注意:(1)若定义式中去掉绝对值,则曲线仅为双曲线中的一支.(2)当122a F F =时,点的轨迹是以1F 和2F 为端点的两条射线;当20a =时,点的轨迹是线段12F F 的垂直平分线.(3)122a F F >时,点的轨迹不存在.在应用定义和标准方程解题时注意以下两点:①条件“122F F a >”是否成立;②要先定型(焦点在哪个轴上),再定量(确定2a ,2b 的值),注意222a b c +=的应用.知识点二:双曲线的方程、图形及性质双曲线的方程、图形及性质A 222121sinsin21cos tanFr r bθθθ==⋅=-考点2:双曲线方程的充要条件考点3:双曲线中焦点三角形的周长与面积及其他问题考点4:双曲线上两点距离的最值问题考点5:双曲线上两线段的和差最值问题考点6:离心率的值及取值范围考点7:双曲线的简单几何性质问题考点8:利用第一定义求解轨迹考点9:双曲线的渐近线考点10:共焦点的椭圆与双曲线【典型例题】考点1:双曲线的定义与标准方程1.(2022·江西科技学院附属中学高二期中(理))已知O为坐标原点,设F1,F2分别是双曲线x2-y2=1的左、右焦点,P为双曲线左支上任意一点,过点F1作∠F1PF2的平分线的垂线,垂足为H,则|OH|=()A.1B.2C .4D .122.(2022·黑龙江·铁人中学高二期中)双曲线222112x y a -=(0a >)的左、右两个焦点分别是1F 与2F ,焦距为8;M 是双曲线左支上的一点,且15MF =,则2MF 的值为()A .1B .9C .1或9D .9或133.(2022·天津·耀华中学高二期中)与椭圆22:11612y x C +=共焦点且过点(的双曲线的标准方程为()A .2213y x -=B .2221yx -=C .22122y x -=D .2213y x -=4.(2022·河北·高二期中)已知双曲线22221x y a b-=的左、右焦点分别为1F ,2F ,O 为坐标原点,1210F F =,点M 是双曲线左支上的一点,若OM =1243MF MF =,则双曲线的标准方程是()A .224121x y -=B .221214x y -=C .22124y x -=D .22124x y -=5.(2022·北京工业大学附属中学高二期中)已知双曲线的上、下焦点分别为()10,3F ,()20,3F -,P 是双曲线上一点且124PF PF -=,则双曲线的标准方程为()A .22145x y -=B .22154x y -=C .22145y x -=D .22154y x -=6.(2022·广西·钦州一中高二期中(文))已知平面内两定点()13,0F -,()23,0F ,下列条件中满足动点P 的轨迹为双曲线的是()A .127PF PF -=±B .126PF PF -=±C .124PF PF -=±D .22126PF PF -=±7.(2022·福建·南靖县第一中学高二期中)(1)求以(-4,0),(4,0)为焦点,且过点的椭圆的标准方程.(2)已知双曲线焦点在y 轴上,焦距为10,双曲线的渐近线方程为20x y ±=,求双曲线的方程.8.(2022·黑龙江·大兴安岭实验中学高二期中)求满足下列条件的双曲线的标准方程:(1)焦点分别为(0,6)-,(0,6),且经过点(5,6)A -;(2)经过点,(4,--;考点2:双曲线方程的充要条件9.(多选题)(2022·全国·高二期中)已知曲线22:1C mx ny +=.则()A .若m >n >0,则C 是椭圆B .若m =n >0,则C 是圆C .若mn <0,则C 是双曲线D .若m =0,n >0,则C 是两条直线10.(2022·河南·高二期中(文))已知k ∈R ,则“23k <<”是“方程22162x y k k -=--表示双曲线”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件11.(2022·吉林·辽源市田家炳高级中学校高二期中(理))“0mn <”是“方程221x y m n+=表示的曲线为双曲线”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件考点3:双曲线中焦点三角形的周长与面积及其他问题12.(2022·安徽·淮北师范大学附属实验中学高二期中)已知1F 、2F 是等轴双曲线22:1C x y -=的左、右焦点,点P 在C 上,1260F PF ∠=,则12PF PF ⋅等于___________.13.(2022·上海金山·高二期中)已知1F 、2F 分别为双曲线22221(0,0)x y a b a b -=>>的左、右焦点,若点2F 到该双曲线的渐近线的距离为2,点P 在双曲线上,且1260F PF ∠=︒,则三角形12F PF 的面积为___________.14.(多选题)(2022·湖南省汨罗市第二中学高二期中)已知点P 是双曲线E :221169x y -=的右支上一点,1F ,2F 为双曲线E 的左、右焦点,12PF F △的面积为20,则下列说法正确的是()A .点P 的横坐标为203B .12PF F △的周长为803C .12F PF ∠小于3πD .12PF F △的内切圆半径为3415.(2022·四川·阆中中学高二期中(文))已知12F F ,为双曲线C :221164x y-=的两个焦点,P ,Q 为C 上关于坐标原点对称的两点,且12PQ F F =,则四边形12PFQF 的面积为________.16.(2022·广东·江门市第二中学高二期中)双曲线2216416y x -=上一点P 与它的一个焦点的距离等于1,那么点P 与另一个焦点的距离等于___________.17.(2022·新疆维吾尔自治区喀什第二中学高二期中(理))已知双曲线22145x y -=的左、右焦点分别为1F ,2F ,点P 是双曲线左支上一点且128PF PF +=,则1221sin sin PF F PF F ∠=∠______.18.(2022·天津市咸水沽第二中学高二期中)已知1F ,2F 分别是双曲线221916x y -=的左、右焦点,AB 是过点1F 的一条弦(A ,B 均在双曲线的左支上),若2ABF 的周长为30,则||AB =___________.19.(2022·吉林·白城一中高二期中)双曲线221916x y -=的两个焦点为12,F F ,点P 在双曲线上,若1PF ·2PF =0,则点P 到x 轴的距离为________.20.(2022·上海市崇明中学高二期中)已知双曲线221169x y -=的两个焦点分别为1F 、2F ,P 为双曲线上一点,且122F PF π∠=,则12F PF △的面积为_________.21.(2022·江苏·高二专题练习)双曲线()222210,0x y a b a b-=>>过焦点1F 的弦AB ,A 、B 两点在同一支上且长为m ,另一焦点为2F ,则2ABF 的周长为().A .4aB .4a -mC .4a +2mD .4a -2m22.(2022·新疆·乌鲁木齐101中学高二期中(文))设1F ,2F 是双曲线22146x y-=的左、右焦点,P 为双曲线上一点,且213PF PF =,则12PF F △的面积等于()A .6B .12C.D.23.(2022·辽宁大连·高二期中)已知1F ,2F 分别是双曲线221916x y -=的左、右焦点,若P 是双曲线左支上的点,且1232PF PF ⋅=.则12F PF △的面积为()A .8B.C .16D.考点4:双曲线上两点距离的最值问题24.(2022·上海中学东校高二期末)过椭圆221(9)9x y m m m +=>-右焦点F 的圆与圆22:4O x y +=外切,该圆直径FQ 的端点Q 的轨迹记为曲线C ,若P 为曲线C 上的一动点,则FP 长度最小值为()A .0B .12C .1D .225.(2022·安徽省宣城市第二中学高二阶段练习(理))已知12,F F 分别是双曲线2214xy -=的左、右焦点,P 为双曲线右支上异于顶点的任意一点,若12PF F △内切圆圆心为I ,则圆心I 到圆22(1)1y x +-=上任意一点的距离最小值为()A .2B1C .1D226.(2022·101中学高二期末)双曲线22142x y C -=:的右焦点为F ,点P 在椭圆C 的一条渐近线上.O 为坐标原点,则下列说法错误的是()A2B .双曲线22142-=y x 与双曲线C 的渐近线相同C .若PO PF ⊥,则PFO △D .PF27.(2022·北京八中高二期中)已知定点A 、B ,且|AB |=4,动点P 满足||PA |﹣|PB ||=3,则|PA |的最小值是()A .12B .32C .72D .5考点5:双曲线上两线段的和差最值问题28.(2022·湖南·长沙市南雅中学高二期中)设双曲线C :22124y x -=的左焦点和右焦点分别是1F ,2F ,点A 是C 右支上的一点,则128AF AF +的最小值为___________.29.(2022·黑龙江·鸡西市第一中学校高二期中)P 是双曲线22145x y -=的右支上一点,M 、N 分别是圆()2232x y ++=和()2231x y -+=上的点,则|PM |-|PN |的最大值为_________.30.(2022·黑龙江·哈九中高二期中)已知双曲线的方程为2214y x -=,如图所示,点()A ,B是圆(221x y +=上的点,点C 为其圆心,点M 在双曲线的右支上,则MA MB +的最小值为______31.(2022·北京·高二期中)已知点()2,0A -,()2,0B ,(11C ,动点M 到A 的距离比到B 的距离多2,则动点M 到B ,C 两点的距离之和的最小值为___________.32.(2022·湖南·嘉禾县第一中学高二阶段练习)过双曲线2218y x -=的右支上的一点P 分别向圆221:(3)4C x y ++=和圆222:(3)1C x y -+=作切线,切点分别为M ,N ,则22||||PM PN -的最小值为()A .8B .9C .10D .1133.(2022·四川省江油市第一中学高二期中(文))已知12F F ,为双曲线222:1(0)16x yC a a -=>的左、右焦点,点A 在双曲线的右支上,点(72)P ,是平面内一定点.若对任意实数m ,直线430x y m ++=与双曲线C 的渐近线平行,则2AP AF +的最小值为()A .2376B .1035-C .837D .25234.(2022·吉林市田家炳高级中学高二期中)设F 是双曲线221412x y -=的左焦点,()1,4A ,P 是双曲线右支上的动点,则PF PA +的最小值为()A .5B .543+C .7D .935.(2022·江西南昌·高二期中(理))设(),P x y 是双曲线22154x y -=的右支上的点,则代数22222169x y y x y x +-++-+)A 10B .2510C 105D 563考点6:离心率的值及取值范围36.(2022·广东·汕头市潮南区陈店实验学校高二阶段练习)已知0a b >>,1F ,2F ,是双曲线22122:1x y C a b-=的两个焦点,若点Р为椭圆22222:1x y C a b +=上的动点,当P 为椭圆的短轴端点时,12F PF ∠取最小值,则椭圆2C 离心率的取值范围为()A .⎛ ⎝⎦B .⎫⎪⎪⎣⎭C .⎛ ⎝⎦D .23⎫⎪⎢⎪⎣⎭37.(2022·四川省仁寿县文宫中学高二阶段练习(文))已知1F ,2F 是双曲线22221x y a b-=(0a >,0b >)的左、右焦点,点1F 关于渐近线的对称点恰好落在以2F 为圆心,2OF 为半径的圆上,则该双曲线的离心率为()ABC .2D 138.(2022·福建·泉州市城东中学高二期中)已知双曲线2222:1(0,0)x y C a b a b-=>>的右顶点为A ,若以点A 为圆心,以b 为半径的圆与C 的一条渐近线交于M ,N 两点,且2OM ON =,则C 的离心率为()A .43B C D .239.(2022·江西省万载中学高二阶段练习(理))已知双曲线两条渐近线的夹角为60°,则该双曲线的离心率为()A .2B C .2D .1240.(2022·福建·厦门外国语学校高二期末)如图所示,1F ,2F 是双曲线C :22221()00a x y a bb >-=>,的左、右焦点,过1F 的直线与C 的左、右两支分别交于A ,B 两点.若22345AB BF AF =∶∶∶∶,则双曲线的离心率为()A .2BCD41.(2022·广东汕头·高二期末)已知双曲线22221x y a b-=(a 、b 均为正数)的两条渐近线与直线1x =-)ABC .D .242.(2022·湖北·鄂州市教学研究室高二期末)已知1F ,2F 分别是双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点,以12F F 为直径的圆与双曲线C 有一个交点P ,设12PF F △的面积为S ,若()21212PF PF S +=,则双曲线C 的离心率为()A .2B .2C D .43.(2022·安徽省临泉第一中学高二期末)已知双曲线()2222:10,0x y C a b a b-=>>的两个焦点分别为()1,0F c -,()2,0F c ,M 是双曲线C 上一点,若120MF MF ⋅=,2212OM OF c ⋅=,则双曲线C 的离心率为()AB 1C D 144.(2022·江西上饶·高二期末(文))已知双曲线2222:1(0,0)x y C a b a b -=>>的焦距为122,,c F F 为其左右两个焦点,直线l 经过点(0,)b 且与渐近线平行,若l 上存在第一象限的点P 满足122PF PF b -=,则双曲线C 离心率的取值范围为()A .B .C .D .)+∞考点7:双曲线的简单几何性质问题45.(多选题)(2022·河北·衡水市第二中学高二期中)已知曲线C :221mx ny +=,则()A .若0m n =>,则曲线CB .若0m n >>,则曲线C 是椭圆,其焦点在y 轴上C .若曲线C 过点(,⎛⎫⎪ ⎪⎝⎭,则C 是双曲线D .若0mn =,则曲线C 不表示任何图形46.(多选题)(2022·江苏连云港·高二期中)关于,x y 的方程2222126x y m m+=+-(其中26m ≠)表示的曲线可能是()A .焦点在y 轴上的双曲线B .圆心为坐标原点的圆C .焦点在x轴上的双曲线D .长轴长为47.(多选题)(2022·河北省曲阳县第一高级中学高二期中)若方程22131x y t t +=--所表示的曲线为C ,则下面四个选项中正确的是()A .若13t <<,则曲线C 为椭圆B .若曲线C 为椭圆,且长轴在y 轴上,则23t <<C .若曲线C 为双曲线,则3t >或1t <D .曲线C 可能是圆.48.(多选题)(2022·云南·罗平县第一中学高二开学考试)已知曲线22:124x y C m m+=+-,则()A .当2m =时,则C 的焦点是)1F ,()2F B .当6m =时,则C 的渐近线方程为12y x =±C .当C 表示双曲线时,则m 的取值范围为2m <-D .存在m ,使C 表示圆49.(多选题)(2022·江苏江苏·高二期中)已知双曲线C :2213x y -=,则()A .双曲线C 的焦距为4B .双曲线C 的两条渐近线方程为:3y =±C .双曲线CD .双曲线C 有且仅有两条过点()1,0Q 的切线50.(多选题)(2022·黑龙江·哈师大附中高二开学考试)双曲线的标准方程为2213y x -=,则下列说法正确的是()A .该曲线两顶点的距离为B .该曲线与双曲线2213x y -=有相同的渐近线C .该曲线上的点到右焦点的距离的最小值为1D .该曲线与直线l :)2y x =-,有且仅有一个公共点51.(2022·上海市新场中学高二期中)当0ab <时,方程22ax ay b -=所表示的曲线是()A .焦点在x 轴的椭圆B .焦点在x 轴的双曲线C .焦点在y 轴的椭圆D .焦点在y 轴的双曲线考点8:利用第一定义求解轨迹52.(2022·河南·濮阳一高高二期中(理))若双曲线C 的方程为22145x y -=,记双曲线C 的左、右顶点为A ,B .弦PQ ⊥x 轴,记直线PA 与直线QB 交点为M ,其轨迹为曲线T ,则曲线T 的离心率为________.53.(2022·吉林·白城一中高二期中)已知ABC 的两个顶点A B ,分别为椭圆2255x y +=的左焦点和右焦点,且三个内角A B C ,,满足关系式1sin sin sin 2B AC -=.(1)求线段AB 的长度;(2)求顶点C 的轨迹方程.54.(2022·全国·高二专题练习)如图所示,已知定圆1F :()2251x y ++=,定圆2F :()22516x y -+=,动圆M 与定圆1F ,2F 都外切,求动圆圆心M 的轨迹方程.55.(2022·福建·厦门一中高二期中)已知动圆M 与圆221:(4)4C x y ++=外切与圆222:(4)4C x y -+=内切,则动圆圆心M 的轨迹C 的方程为___________.56.(2022·上海市新场中学高二期中)已知两点()(),3,03,0A B -,若4PA PB -=±,那么P 点的轨迹方程是______.57.(2022·吉林一中高二期中)若动圆过定点A ()3,0-且和定圆C :()2234x y -+=外切,则动圆圆心P 的轨迹方程是_________.58.(2022·广东·深圳市宝安中学(集团)高二期中)已知点(3,0),(3,0),(1,0)M N B -,动圆C 与直线MN 相切于点B ,过M ,N 与圆C 相切的两直线相交于点P ,则点P 的轨迹方程为()A .221(1)8y x x -=>B .221(1)8y x x -=<-C .221(0)8y x x +=>D .221(1)10y x x -=>59.(2022·江苏省镇江中学高二期中)动圆M 与圆1C :()2241x y ++=,圆2C :22870x y x +-+=,都外切,则动圆圆心M 的轨迹方程为()A .22115x y +=B .22115y x -=C .()221115y x x -=≥D .()221115y x x -=≤-60.(2022·新疆·博尔塔拉蒙古自治州蒙古中学高二期中)动点P 到点(1,0)M 及点(3,0)N 的距离之差为2,则点P 的轨迹是()A .双曲线B .双曲线的一支C .两条射线D .一条射线61.(2022·江西·景德镇一中高二期中(理))已知定圆221:10240F x y x +++=,定圆222:100F x y x +-=,动圆圆M 与定圆12F F 、都内切,则动圆M 的圆心的轨迹方程为()A .221(0)421x y x -=>B .221(0)421x y x -=<C .221(0)421x y y -=≠D .224121x y -=62.(2022·浙江·效实中学高二期中)与圆()2222x y ++=外切,且与圆2240x y x +-=内切的圆的圆心在()A .抛物线上B .圆上C .双曲线的一支上D .椭圆上63.(2022·天津河西·高二期中)与圆221x y +=及圆228120x y x +-+=都外切的圆的圆心在()A .椭圆上B .双曲线的一支上C .线段上D .圆上考点9:双曲线的渐近线64.(2022·全国·高二期中)以双曲2214x y -=的右焦点为圆心,且与其渐近线相切的圆的方程为______.65.(2022·陕西汉中·高二期末(理))已知双曲线2221(0)x y a a -=>的渐近线与圆22(2)1x y +-=相切,则a =()A .13B .3C .3D 66.(2022·湖南·高二期末)若双曲线()2222:10,0x y C a b a b-=>>则直线b x a=与两条渐近线围成的三角形的面积为()A .B .4C .D 67.(2022·北京市十一学校高二期末)椭圆1C :22143x y +=与双曲线2C :22221x ya b-=的离心率之积为1,则双曲线2C 的两条渐近线的倾斜角分别为()A .π6,π6-B .π3,π3-C .π6,5π6D .π3,2π368.(2022·河南·新蔡县第一高级中学高二阶段练习(理))已知双曲线()222210,0x y a b a b-=>>的左,右焦点分别为1F ,2F ,若双曲线的左支上存在一点P ,使得2PF 与双曲线的一条渐近线垂直于点Q ,且223PF F Q =,则双曲线的渐近线方程为()A .34y x=±B .43y x =±C .23y x=±D .32y x=±69.(2022·河南·封丘一中高二期末(文))已知点()F 是双曲线()2222:10,0x y C a b a b-=>>的右焦点,过F 作双曲线C 的一条渐近线的垂线,垂足为M ,若△OMF (点O 为坐标原点)的面积为8,则C 的实轴长为()A .8B .C .6D .70.(2022·福建三明·高二期中)双曲线2214y x -=的右顶点到渐近线的距离为()A B C .1D .2考点10:共焦点的椭圆与双曲线71.(2022·全国·高二期末)已知椭圆2222x y a b +=1(a >b >0)与双曲线2222x y m n-=1(m >0,n >0)具有相同焦点F 1、F 2,P 是它们的一个交点,且∠F 1PF 23π=,记椭圆与双曲线的离心率分别为e 1、e 2,则3e 12+e 22的最小值是()A .2B .3C .4D .572.(2022·全国·高二课时练习)已知椭圆()221112211:10,0x y C a b a b +=>>与双曲线()222222222:10,0x y C a b a b -=>>有相同的焦点12F F 、,P 点是曲线1C 与2C 的一个公共点,12,e e 分别是1C 和2C 的离心率,若12PF PF ⊥,则22124e e +的最小值为()A .35B .92C .112D .13273.(2022·江苏·南通市海门实验学校高二期中)已知双曲线2222:1(0,0)x y C a b a b-=>>满足b a =,且与椭圆221123x y +=有公共焦点,则双曲线C 的方程为()A .22145x y -=B .221810x y -=C .22154x y -=D .22143x y -=74.(2022·吉林·延边二中高二期中(理))若椭圆2212516x y +=和双曲线22145x y -=的共同焦点为1F ,2F ,P 是两曲线的一个交点,则12cos F PF ∠的值为__________.。
【高中数学】秒杀秘诀MS05双曲线的焦点三角形问题

双曲线的焦点三角形问题秒杀秘籍:双曲线的焦点三角形长度问题定理一:双曲线12222=-by a x (0>a ,0>b )的两个焦点为1F 、2F ,弦AB 过左焦点1F (A 、B 都在左支上),l AB =,则2ABF ∆的周长为l a 24+(如图1)图1例1:已知双曲线221169x y -=的左、右焦点分别为1F ,2F ,过2F 的直线与该双曲线的右支交于A 、B 两点,若5=AB ,则1ABF ∆的周长为_________.解:5=AB ,1ABF ∆的周长为26101624=+=+l a 双曲线焦长公式已知双曲线的对称轴为坐标轴(或平行于坐标轴),焦点为F ,设倾斜角为α的直线l 经过F 1,且与圆锥曲线交于A 、B 两点,则(1)当AB 交双曲线于一支时,α2222cos 2||c a ab AB -=,ααcos 110cos 222<<⇒>-e c a (图2);(2)当AB 交双曲线于两支时,2222cos 2||ac ab AB -=α,ααcos 10cos 222>⇒<-e c a (图3)。
证明:如图2直线与双曲线的两个交点A 、B 在同一支上,连,设,由双曲线定义可得,由余弦定理可得整理可得,同理,则可求得弦长。
如图3,直线l 与双曲线交点A、B 在两支上,连,设,则,,由余弦定理可得,整理可得,则例2:过双曲线1322=-y x 的左焦点F 1作倾斜角为6π的直线l 交双曲线于A 、B 两点,则||AB =_________.解:024341cos 222<-=⨯-=-αc a ,故直线l 交双曲线于两支;3136cos 2||2222=-=-=a c ab AB α。
1.过双曲线22143x y -=左焦点F 1的直线交双曲线的左支于M 、N 两点,F 2为其右焦点,则|MF 2|+|NF 2|-|MN |的值为()A .6B .8C .10D .162.如果12,F F 分别是双曲线191622=-y x 的左、右焦点,AB 是双曲线左支上过点F 1的弦,且||6AB =,则2ABF ∆的周长是________.3.过双曲线x 2-4y 2=4的焦点F 1且在双曲线一支上的弦AB 的长度为5,F 2为另一焦点,则△ABF 2的周长为_______.4.1F 、2F 是双曲线19222=-my x 的左、右焦点,A 、B 都在左支上,且AB 过1F ,若2AFB ∆的周长为30,则弦AB 的长为_________.5..斜率为2的直线l 过双曲线12222=-b y a x (0,0>>b a )的右焦点,且与双曲线的左右两支分别相交,则双曲线的离心率e 的取值范围是()A.e <2B.1<e <3C.1<e <5D.e >56.已知双曲线12222=-by a x 的右焦点为F,若过点F 且倾斜角为︒60的直线与双曲线的右支有且仅有一个交点,则此双曲线离心率的范围是() A.(]2,1 B.()2,1 C.[)+∞,2 D.()+∞,27.过双曲线116922=-y x 的左焦点F 1作倾斜角为4πα=的直线与双曲线交于A ,B 两点,求|AB|.8.经过双曲线1322=-y x 的右焦点F 2作倾斜角为300的弦AB ,求:(1)|AB|;(2)∆F 1AB 的周长(F 1是双曲线的左焦点)。
双曲线的焦点三角形问题知多少

ʏ河北省张家口市第一中学 郝荩华双曲线的焦点三角形问题,既能考查同学们对双曲线定义的理解和灵活运用,又能考查大家的解三角形技能和数学运算素养,因此备受命题者青睐㊂那么这类问题主要有哪些呢?下面举例说明㊂1.焦点三角形的面积问题例1 已知双曲线C :y2m -x 28=1m >0 的上㊁下焦点分别为F 1㊁F 2,P 为双曲线C 上一点,且满足øF 1P F 2=120ʎ,则әP F 1F 2的面积为( )㊂A.833B .83C .3m3D .3m 分析:记|P F 1|=r 1,|P F 2|=r 2,øF 1P F 2=θ,根据双曲线定义结合余弦定理可得r 1r 2=2b21-c o s θ,再利用三角形面积公式可推得S әF 1P F2=b2t a nθ2,即可求得答案㊂解:记|P F 1|=r 1,|P F 2|=r 2,øF 1P F 2=θ㊂因为|r 1-r 2|=2a ,所以(r 1-r 2)2=4a 2㊂在әF 1P F 2中,由余弦定理得r 21+r 22-2r 1r 2c o s θ=(2c )2,配方得(r 1-r 2)2+2r 1r 2-2r 1r 2c o s θ=4c 2,即4a 2+2r 1r 2(1-c o s θ)=4c 2㊂所以r 1r 2=2(c 2-a 2)1-c o s θ=2b21-c o s θ㊂由面积公式得S әF1P F2=12r 1r 2s i n θ=b 2s i n θ1-c o s θ=b 22s i n θ2c o s θ22s i n 2θ2=b 2t a nθ2㊂所以S әF1P F2=b2t a nθ2,本题中b 2=8㊂又因为θ=120ʎ,所以S әP F 1F 2=8t a n 60ʎ=833㊂本题选A ㊂2.焦点三角形的周长问题例2 已知双曲线C :x 2-y 23=1的右焦点为F ,P 是双曲线C 的左支上一点,M (0,2),则әP F M 的周长的最小值为( )㊂A.2+42 B .4+22C .32D .26+3分析:设双曲线C 的左焦点为F 1,则|P F |-|P F 1|=2a ㊂由题意可得әP F M 的周长为|M F |+|M P |+|P F |=22+2+|M P |+|P F 1|,当M ,P ,F 1三点共线时,|M P |+|P F 1|的值最小,从而可得答案㊂解:设双曲线C 的左焦点为F 1,则|P F |-|P F 1|=2a ㊂由题可知a =1,c =2㊂所以|P F |=2+|P F 1|,F 1(-2,0),F (2,0)㊂易得|M F |=22㊂әP F M 的周长为|M F |+|M P |+|P F |=22+2+|M P |+|P F 1|㊂因为当M ,P ,F 1三点共线时,|M P |+|P F 1|的值最小,最小值为|M F 1|=22,所53解题篇 经典题突破方法 高二数学 2022年11月Copyright ©博看网. All Rights Reserved.以әP F M 周长的最小值为2+42㊂故本题选A ㊂3.焦点三角形的内角问题例3 在平面直角坐标系x O y 中,曲线C :x 2a 2-y2b 2=1(a >0,b >0)的左㊁右焦点分别为F 1㊁F 2,点A 是以线段F 1F 2为直径的圆与双曲线C 在第一象限内的交点,过点A 且与直线A O 垂直的直线与x 轴相交于点B ,若øB A F 2=15ʎ,则双曲线C 的离心率为( )㊂A.2 B .3 C .2 D .5分析:根据圆的性质㊁同角的余角相等,结合双曲线的定义㊁双曲线离心率公式㊁辅助角公式进行求解即可㊂图1解:如图1,设双曲线C的焦距为2c ㊂因为øF 1A F 2=90ʎ,øO A B =90ʎ,所以øO A F 2+øO A F 1=øO A F 2+øB A F 2=90ʎ,可得øO A F 1=øB A F 2=15ʎ㊂又由|O A |=|O F 1|,可得øA F 1O =15ʎ㊂在R t әA F 1F 2中,|A F 1|=2c c o s 15ʎ,|A F 2|=2c s i n 15ʎ㊂由双曲线的定义得2a =|A F 1|-|A F 2|,也即2a =2c (c o s 15ʎ-s i n 15ʎ),解得a =2c c o s 60ʎ,则e =2㊂故选A ㊂4.焦点三角形的内切圆问题例4 已知点F 1(-3,0)㊁F 2(3,0)分别是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左㊁右焦点,M 是双曲线C 右支上的一点,M F 1与y 轴交于点P ,әM P F 2的内切圆在边P F 2上的切点为Q ,若|P Q |=2,则双曲线C 的离心率为㊂分析:设әM P F 2的内切圆与M F 1,M F 2的切点分别为A ,B ,然后根据切线长定理结合双曲线的定义列方程可求出a ,从而求出离心率㊂解:设әM P F 2的内切圆与M F 1,M F 2的切点分别为A ,B ㊂由切线长定理可知|M A |=|M B |,|P A |=|P Q |,|B F 2|=|Q F 2|㊂又|P F 1|=|P F 2|,所以|M F 1|-|M F 2|=|M A |+|A P |+|P F 1|-(|M B |+|B F 2|)=|P Q |+|P F 2|-|Q F 2|=2|P Q |㊂由双曲线的定义可知|M F 1|-|M F 2|=2a ,所以|P Q |=a =2㊂又因为c =3,所以双曲线的离心率e =c a =32㊂故答案为32㊂5.焦点三角形的综合应用例5 已知F 1㊁F 2分别是双曲线C :x 2a 2-y2b2=1(a >0,b >0)的左㊁右焦点,点B 为双曲线C 的左顶点,动点A 在双曲线C 上,当A F 2ʅB F 2时,|A F 2|=|B F 2|,且|A F 1|-|A F 2|=2,则双曲线C 的方程为( )㊂A.x 23-y 2=1 B .x 2-y 24=1C .x 24-y 2=1 D .x 2-y 23=1分析:先根据双曲线的定义求出a ,再根据直角三角形中|A F 1|2=|A F 2|2+|F 1F 2|2建立方程求出c ,根据双曲线的系数关系即可求得方程㊂解:因为|A F 1|-|A F 2|=2a =2,所以a =1㊂所以|A F 2|=|B F 2|=|O B |+|O F 2|=a +c =1+c ㊂又因为|A F 1|-|A F 2|=2,所以|A F 1|=|A F 2|+2=3+c ㊂因为A F 2ʅB F 2,所以在R tәA F 1F 2中,由勾股定理得|A F 1|2=|A F 2|2+|F 1F 2|2,于是4c 2+(1+c )2=(3+c )2,即c 2-c -2=0㊂解得c =-1(舍去)或c =2㊂由a 2+b 2=c 2,得b 2=3,故双曲线C 的方程为x 2-y 23=1,选D ㊂(责任编辑 徐利杰)63 解题篇 经典题突破方法 高二数学 2022年11月Copyright ©博看网. All Rights Reserved.。
双曲线中焦点三角形的探索

双曲线中焦点三角形的探索 基本条件:1:该三角形一边长为焦距2c ,另两边的差的约对值为定值2a 。
2:该三角形中由余弦定理得||||2||||||cos 21221222121PF PF F F PF PF PF F ⋅-+=∠结合定义,有 性质一、设若双曲线方程为2222x y 1a b -=(a >0,b>0),F1,F2分别为它的左右焦点,P 为双曲线上任意一点,则有:若12F PF ,∠=θ则122F PF S b cot 2θ=;特别地,当12F PF 90∠=时,有122F PF S b =。
证明:记2211||,||r PF r PF ==,由双曲线的定义得在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ 配方得:.4cos 22)(22121221c r r r r r r =-+-θ 即.4)cos 1(242212c r r a =-+θ 由任意三角形的面积公式得:2cot 2sin 22cos 2sin 2cos 1sin sin 2122222121θθθθθθθ⋅=⋅=-⋅==∆b b b r r S PF F . 特别地,当θ=︒90时,2cot θ=1,所以122F PF S b =同理可证,在双曲线12222=-b x a y (a >0,b >0)中,公式仍然成立.例4 若P 是双曲线1366422=-y x 上的一点,1F 、2F 是其焦点,且︒=∠6021PF F ,求△21PF F 的面积.解法一:在双曲线1366422=-y x 中,,10,6,8===c b a 而.60︒=θ记.||,||2211r PF r PF ==点P 在双曲线上,∴由双曲线定义得:.16221==-a r r 在△21PF F 中,由余弦定理得:.)2(cos 22212221c r r r r =-+θ 配方,得:=+-21221)(r r r r 400 .25640021=-∴r r 从而.14421=r r解法二:在双曲线1366422=-y x 中,362=b ,而.60︒=θ考题欣赏(2010全国卷1理)(9)已知1F 、2F 为双曲线C:221x y -=的左、右焦点,点P 在C 上,∠1F P 2F =060,则P 到x 轴的距离为(A)2(B)2【答案】 B(2010全国卷1文)(8)已知1F 、2F 为双曲线C:221x y -=的左、右焦点,点P 在C 上,∠1F P 2F =060,则12||||PF PF =(A)2 (B)4 (C) 6 (D) 8【答案】B 【解析1】.由余弦定理得cos ∠1F P 2F =222121212||||||2||||PF PF F F PF PF +- 12||||PF PF =4 【解析2】由焦点三角形面积公式得:12||||PF PF =4性质一推论:在双曲线12222=-b y a x (a >0,b >0)中,左右焦点分别为1F 、2F ,当点P 是双曲线左支上任意一点,若θ=∠21F PF ,则θθcos sin 221c a c b S PF F +=∆.特别地,当︒=∠9021F PF 时,有a c b S PF F 221=∆。
双曲线焦点三角形内心的性质及其应用

! #&
Copyright©博看网. All Rights Reserved.
复习
!"!!年!月 上半月!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!解法探究
备考
E 分别为 2(4#4!!2'4#4! 的内心!则 2D4!E 的
形状为)!!*!
C!锐角三角形 !!!! D!直角三角形
质!转化坐标关系式为半径关系式通过例!的结论
的应用并 结 合 直 线 与 渐 近 线 的 关 系 建 立 不 等 式综
合双曲线的离心率取值范围来确定即可!
解析设 2(4#4!!2'4#4! 的内切圆半径分别 为N#!N!!根据双曲线焦点三角形内心的性质#和性质 !!结合 %D $, %E 可知N# $,N!!由例!可知!直线
$ !
!
在
2=4!D
中!<:6 3=4!D
$
) * <:6%"G"$!
N# $ =4!
&在 2=4!E 中!<:63=4!E
$<:6$! $
N! =4!
!结合N#FN! $,F#!可得N# $,N!!
) * 则有,<:6$! $<:6%"G"$!
# $<:6$!
!解得<:6$!
$
!<:6$ 槡,,!所以直线.的斜率为<:6$$#"<:6!! $! $槡,!故选
并结合二倍角的正切公式来分析与求解! 解析设 点 D!E 分 别 为
2(4#4!!2'4#4! 的 内 心! 如图! 所 示!根 据 双 曲 线 焦 点 三角形的内心性质#和性质!! 可得 DE 1& 轴!且 3D4!E 为直角!设直线. 的倾斜角为
双曲线微专题二 焦点三角形问题

双曲线微专题二:双曲线中焦点三角形问题题型一 焦点三角形的周长问题12PF F ∆由两焦点和双曲线上一点形成,我们把这种三角形叫焦点三角形. 求焦点三角形的周长时,通常会利用双曲线的第一定义.例1:椭圆y 249+x 224=1与双曲线y 2-x 224=1有公共点P ,则P 与双曲线两焦点连线构成三角形的周长为( )解:由已知得椭圆与双曲线具有共同的焦点F 1(0,5)和F 2(0,-5),又由椭圆的定义可得1214PF PF +=又1210F F =因此P 与双曲线两焦点连线构成三角形的周长为24。
整理:已知双曲线x 2a 2-y 2b 2=1(a >0,b >0),其焦点为F 1、F 2,过F 1作直线交双曲线同一支于A 、B 两点,且|AB |=m ,则△ABF 2的周长是4a +2m简要证明:由双曲线的定义知,|AF 2|-|AF 1|=2a ,(1)|BF 2|-|BF 1|=2a ,(2) 又|AF 1|+|BF 1|=|AB |=m ,(3)∴由(1),(2),(3)得|AF 2|+|BF 2|=4 a+m . 故△ABF 2的周长为|AF 2|+|BF 2|+|AB |=4 a+2m .例2:已知双曲线的左、右焦点分别为F 1,F 2,在左支上过F 1的弦AB 的长为5,若2a =8,那么△ABF2的周长是( ) A .16B .18C .21D .26解:如图所示,由双曲线的定义知,|AF 2|-|AF 1|=8,(1)|BF 2|-|BF 1|=8,(2)又|AF 1|+|BF 1|=|AB |=5,(3)∴由(1),(2),(3)得|AF 2|+|BF 2|=21.故△ABF 2的周长为|AF 2|+|BF 2|+|AB |=26.答案 D练习:1.如果12,F F 分别是双曲线191622=−y x 的左、右焦点,AB 是双曲线左支上过点1F 的弦,且||6AB =,则2ABF ∆的周长是 .(28)2.若12,F F 分别是双曲线22x y 1m 7−=的左、右焦点,AB 是双曲线左支上过点1F 的弦,且||4=AB ,2ABF ∆的周长是20,则m= 答案:题型二 焦点三角形的面积问题求焦点三角形的面积时,通常会利用双曲线的定义、正弦定理、余弦定理等,焦点三角形的面积主要有两种求法:1212121211sin =2c |y |22PF F PF F P S r r F PF S =∠ 和。
秒杀题型 焦点三角形(椭圆与双曲线)

2020年高考数学试题调研之秒杀圆锥曲线压轴题之秒杀题型三:椭圆、双曲线焦点三角形椭圆的焦点三角形:椭圆上任意一点P 与两焦点1F 、2F 构成的三角形:12PF F ∆。
秒杀题型一:性质:1.周长为定值:2()a c +。
2.12,F PF θ∠=当点P 靠近短轴端点时θ增大,当点P 靠近长轴端点时θ减小;与短轴端点重合时θ最大。
类比:(注:椭圆中端点三角形(长轴两端点与椭圆上一点构成)当P 在短轴端点时顶角最大。
)。
1.(2017年新课标全国卷I 文12)设A 、B 是椭圆C 1323=+m y x 长轴的两个端点,若C 上存在点M 满足︒=∠120AMB ,则m 的取值范围是()A.(][)+∞,91,0 B.(][)+∞,93,0 C.(][)+∞,41,0 D.(][)+∞,43,0【解析】:当03m <<时,椭圆的焦点在x 轴上,要使C 上存在点M 满足120AMB ∠=,则tan 60ab≥= ,即≥.得01m <≤;当3m >时,椭圆的焦点在y 轴上,要使C 上存在点M 满足120AMB ∠= ,则tan 60ab ≥= ,≥,得9m ≥,故m 的取值范围为(][)+∞,91,0 ,选A.秒杀题型二:3.三角形面积:212tan 22S c y c y b θ=⨯⨯=⨯=,max ,S bc =即P 与短轴端点重合时面积最大。
1.(高考题)已知1F ,2F 是椭圆1:2222=+by a x C )0(>>b a 的两个焦点,P 为椭圆C 上一点,21PF PF ⊥.若21F PF ∆的面积为9,则b =.【解析】:由椭圆焦点三角形面积公式得:94tanb 22==b π,3=∴b 。
〖母题1〗已知12,F F 是椭圆22195x y +=的焦点,点P 在椭圆上且123F PF π∠=,求12F PF ∆的面积.【解析】:由椭圆定义及余弦定理得:533。
双曲线练习题带答案,知识点总结(基础版)
双曲线重难点复习一.知识点总结双曲线:平面内与两个定点1F 、2F 的距离的差的绝对值等于常数2a (其中122a F F <)1 a 半实轴长;b 半虚轴长;c 半焦距;a 、b 、c 之间满足c a b =+. e 叫做椭圆的离心率,ce a=且1e >.e 越大,双曲线的张口就越大.2.实轴和虚轴等长的双曲线叫做等轴双曲线,其离心率e =渐近线方程为y x =±3.y y=0b ax x y x a b±=±焦点在轴上和在轴上的渐近线方程分别为和,容所以常把双曲线标准方程右边的常数写成,分解因式即得渐近易记错,线方程。
4.双曲线的焦点到渐近线的距离为b.122ta 5n2.PF F S b θ= 焦点三角形的面积22222222222222226.1010x y x y a b a b x y x y b a b aλλλλ-=-=≠-=-=≠与双曲线有共同渐近线的双曲线方程可以表示为();与双曲线有共同渐近线的双曲线方程可以表示为().1.已知F 为双曲线C :116922=-y x 的左焦点,P ,Q 为C 上的点.若PQ 的长等于虚轴长的2倍,点A (5,0)在线段PQ 上,则△PQF 的周长为________. 442.已知双曲线22221(0)x y a b a b-=>>的焦距为20x y +=垂直,则双曲线的方程为A. 2214x y -=B. 2214y x -= C. 22331205x y -= D. 22331520x y -= 【答案】A【解析】由题可知2c =,则c =.渐近线方程为12y x =,则12b a =.又222c a b =+可得,224,1a b ==.所以双曲线的方程为2214x y -=;故本题答案选A .视频3.已知O 为坐标原点,设F 1,F 2分别是双曲线x 2−y 2=1的左、右焦点,点P 为双曲线左支上任一点,自点F 1作∠F 1PF 2的平分线的垂线,垂足为H ,则|OH |=( ) A. 1 B. 2 C. 4 D. 12【答案】A【解析】延长F 1H 交PF 2于点Q ,由角分线性质可知|PF 1|=|PQ |,根据双曲线的定义,||PF 1|−|PF 2||=2,从而|QF 2|=2,在ΔF 1QF 2中,OH 为其中位线,故|OH |=1.故选A.点睛:对于圆锥曲线问题,善用利用定义求解,注意数形结合,画出合理草图,巧妙转化.4.等轴双曲线C 的中心在原点,焦点在x 轴上,C 与抛物线y 2=16x 的准线交于A ,B 两点,||43AB =,则C 的实轴长为( ) A ..4 D .85.设双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别为12F F A 、,是双曲线渐近线上的一点,212AF F F ⊥,原点O 到直线1AF 的距离为113OF ,则渐近线的斜率为(A (B (C )1或1-(D )2或2- D6.已知双曲线x 2-23y =1的左顶点为A 1,右焦点为F 2,P 为双曲线右支上一点,则1PA ·2PF的最小值为________.-27.已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为M (-12,-15),则E 的方程为( )A.x 23-y 26=1B.x 24-y 25=1C.x 26-y 23=1D.x 25-y 24=1 答案 B解析 由已知易得l 的斜率为k =k FM =1.设双曲线方程为x 2a 2-y 2b2=1(a >0,b >0),A (x 1,y 1),B (x 2,y 2),则有⎩⎨⎧x 21a 2-y 21b 2=1,x 22a 2-y 22b2=1,两式相减并结合x 1+x 2=-24,y 1+y 2=-30,得y 1-y 2x 1-x 2=4b 25a 2,从而4b 25a2=1,即4b 2=5a 2.又a 2+b 2=9,解得a 2=4,b 2=5,故选B. 8与双曲线622=-y x的左支交于不同的两点,()A .()11-, C【答案】C试题分析:联立方程2226y kx x y =+⎧⎨-=⎩得()2214100k x kx ---=…① 若直线y=kx+2与双曲线622=-y x 的左支交于不同的两点,则方程①有两个不等的负根k 9.经过双曲线4−y 2=1右焦点的直线与双曲线交于A ,B 两点,若 AB =4,则这样的直线的条数为( )A. 4条B. 3条C. 2条D. 1条 【答案】B【解析】由双曲线x 24−y 2=1,可得a =2,b =1,若AB 只与双曲线右支相交时,AB 的最小值距离是通径长度为2b 2a=1,∵AB =4>1,∴此时有两条直线符合条件;若AB 只与双曲线两支相交时,此时AB 的最小距离是实轴两顶点的即距离长度为2a =4,距离无最大值;∵AB =4,∴此时有1条直线符合条件;综上可得,共有3条直线符合条件,故选B.10.P 是双曲线C :x 2−y 2=2左支上一点,直线l 是双曲线C 的一条渐近线,P 在l 上的射影为Q ,F 2是双曲线C 的右焦点,则 PF 2 + PQ 的最小值为( ) A.22B. 2C. 3 2D. 2+22【答案】C【解析】由题知|PF 2|−|PF 1|=2a =2 2,则|PF 2|+|PQ |=|PF 1|+|PQ |+2 2,由对称性,当F 1,P ,Q 在同一直线上时|PF 1|+|PQ |最小,由渐近线方程y =x ,|F 1O |=2知|F 1Q |= 2 则|PF 2|+|PQ |的最小值为3 2.故本题答案选C .11.点P 是双曲线22221(0,0)x y a b a b -=>>上的点,12,F F 是其焦点,双曲线的离心率是54,且12•0PF PF = ,若12F PF ∆的面积是9,则a b +的值等于() A. 4 B. 7 C. 6 D. 5 【答案】B【解析】双曲线的离心率是5344c b a a ==⇒=,120PF PF ⋅=1212,PF PF PFF ∴⊥∴ 的面积121219182S PF PF PF PF =⋅=∴⋅=,. 在12PF F 中,由勾股定理可得222222*********||2?4369c PF PF PF PF PF PF a a b a =+=-+=+∴+=+(),,34b a ∴=∴=,,7a b ∴+=,故选 C .12.若双曲线C :x 2a2−y 2b 2=1(a >0,b >0)的一条渐近线被圆 x −2 2+y 2=4所截得的弦长为2,则C 的离心率为( ) A. 2 B. C. D. 2 33【答案】A【解析】由几何关系可得,双曲线x 2a 2−y 2b 2=1 a >0,b >0 的渐近线方程为bx ±ay =0,圆心 2,0 到渐近线距离为d = 2−12= 3,则点 2,0 到直线bx +ay =0的距离为d =22=2b c= 3,即4(c 2−a 2)c =3,整理可得c 2=4a 2,双曲线的离心率e = c 2a = 4=2.故选A .13.右焦点分别为12,F F ,过1F 作倾斜角为030的直线与y 轴和双曲线右支分别交于两点,若点A 平分1F B ,则该双曲线的离心率是()C. 2D.【答案】A14.右焦点分别为12,F F ,焦距为2(0)c c >,且120AOB ∠= ,其中O 为原点,则双曲线的离心率为()A. 2B. 【答案】C 【解析】如下图:,(0a >,0b >),过其左焦点F 作x 轴的垂线,交双曲两点,若双曲线的右顶点在以AB 为直径的圆内,则双曲线离心率的取值范围是()B. ()1,2C.D. ()2,+∞ 【答案】D【解析】AB 是双曲线通径,即2222a a cbc a +<=-,2220c ac a -->,即,故选D .16.设1F ,2F 分别为椭圆1C :221122111(0)x y a b a b +=>>与双曲线2C :222222221(0,0)x y a b a b -=>>的公共焦点,它们在第一象限内交于点M ,1290F MF ∠=︒,若椭圆的离心率134e =,则双曲线2C 的离心率2e 的值为()A. 92B. 2C. 32D. 54【答案】B【解析】设12,m MF n MF ==,所以1122122{{ 2m n a m a am n a n a a+==+∴-==-,由1290F MF ∠= 得()()()()222222212121222c m n a a a a a a =+=++-=+,222222212121222222121122a a a a c a a c c c e e +∴=+∴==+=+,1234e e =∴= 17.已知双曲线C :x 2a −y 2b =1(a >0,b >0),F 1,F 2分别为其左、右焦点,过F 1的直线l 与双曲线C 的左、右两支分别交于A ,B 两点,若|AB |:|BF 2|:|AF 2|=3:4:5,则双曲线C 的离心率为( )A. 2B. 4C. 13D. 15 【答案】A 【解析】∵|AB|:|BF 2|:|AF 2|=3:4:5,不妨令 AB =3, BF 2 =4,|AF 2|=5, ∵|AB |2+|BF 2|2=|AF 2|2 ,∴∠ABF 2=90∘又由双曲线的定义得:|BF 1|−|BF 2|=2a ,|AF 2|−|AF 1|=2a ∴|AF 1|+3−4=5−|AF 1|,∴|AF 1|=3 ,|BF 1|−|BF 2|=3+3−4=2a ,∴a =1在RtΔBF 1F 2 中,|F 1F 2|2=|BF 1|2+|BF 2|2=62+42=52, 又|F 1F 2|2=4c 2,∴4c 2=52,∴c = 13 所以双曲线的离心率e =c = 13 ,故选C.18.已知12,F F 是双曲线的左右焦点,过2F 作双曲线一条渐近线的垂线,垂足为点A ,交另一条渐近线于点B ,且则该双曲线的离心率为B. D. 2【答案】A则A. 19.已知F 为双曲线的左焦点,定点A 为双曲线虚轴的一个端点,过,F A 两点的直线与双曲线的一条渐近线在y 轴右侧的交点为B ,若3A B F A = ,则此双曲线的离心率为__________.【解析】F 为双曲线的左焦点,定点A 为双曲线虚轴的一个端点,。
双曲线(经典导学案及练习答案详解)

§8.7双曲线学习目标1.了解双曲线的定义、几何图形和标准方程.2.掌握双曲线的几何性质(范围、对称性、顶点、离心率、渐近线).3.了解双曲线的简单应用.知识梳理1.双曲线的定义把平面内与两个定点F1,F2的距离的差的绝对值等于非零常数(小于|F 1F2|)的点的轨迹叫做双曲线.两个定点F1,F2叫做双曲线的焦点,两焦点间的距离叫做双曲线的焦距.2.双曲线的标准方程和简单几何性质标准方程x2a2-y2b2=1(a>0,b>0)y2a2-x2b2=1(a>0,b>0)图形性质焦点F1(-c,0),F2(c,0)F1(0,-c),F2(0,c)焦距|F1F2|=2c范围x≤-a或x≥a,y∈R y≤-a或y≥a,x∈R对称性对称轴:坐标轴;对称中心:原点顶点A1(-a,0),A2(a,0)A1(0,-a),A2(0,a)轴实轴:线段A1A2,长:2a;虚轴:线段B1B2,长:2b,实半轴长:a,虚半轴长:b离心率e=ca∈(1,+∞)渐近线y=±ba x y=±ab xa,b,c的关系c2=a2+b2 (c>a>0,c>b>0)常用结论(1)双曲线的焦点到其渐近线的距离为b.(2)若P是双曲线右支上一点,F1,F2分别为双曲线的左、右焦点,则|PF1|min=a+c,|PF2|min=c -a .(3)同支的焦点弦中最短的为通径(过焦点且垂直于实轴的弦),其长为2b 2a.(4)若P 是双曲线上不同于实轴两端点的任意一点,F 1,F 2分别为双曲线的左、右焦点,则12PF F S △=b 2tan θ2,其中θ为∠F 1PF 2.(5)与双曲线x 2a 2-y 2b 2=1(a >0,b >0)有共同渐近线的方程可表示为x 2a 2-y 2b 2=t (t ≠0).思考辨析判断下列结论是否正确(请在括号中打“√”或“×”)(1)到两定点的距离差的绝对值等于常数的点的轨迹是双曲线.( × ) (2)方程x 2m -y 2n =1(mn >0)表示焦点在x 轴上的双曲线.( × )(3)双曲线x 2m 2-y 2n 2=1(m >0,n >0)的渐近线方程是x m ±yn =0.( √ )(4)等轴双曲线的渐近线互相垂直,离心率等于 2.( √ ) 教材改编题1.若双曲线x 2a 2-y 2b 2=1(a >0,b >0)的焦点到其渐近线的距离等于实轴长,则该双曲线的离心率为( )A. 5 B .5 C. 2 D .2 答案 A解析 由题意知焦点到其渐近线的距离等于实轴长,即b =2a , 又a 2+b 2=c 2,∴5a 2=c 2. ∴e 2=c 2a 2=5,∴e = 5. 2.设P 是双曲线x 216-y 220=1上一点,F 1,F 2分别是双曲线的左、右焦点,若|PF 1|=9,则|PF 2|等于( )A .1B .17C .1或17D .以上均不对 答案 B解析 根据双曲线的定义得||PF 1|-|PF 2||=8⇒|PF 2|等于1或17.又|PF 2|≥c -a =2,故|PF 2|=17. 3.(2022·汕头模拟)写一个焦点在y 轴上且离心率为3的双曲线方程________. 答案y 2-x 22=1(答案不唯一,符合要求就可以) 解析 取c =3,则e =ca=3,可得a =1,∴b =c 2-a 2=2, 因此,符合条件的双曲线方程为y 2-x 22=1(答案不唯一,符合要求就可以).题型一 双曲线的定义及应用例1 (1)已知定点F 1(-2,0),F 2(2,0),N 是圆O :x 2+y 2=1上任意一点,点F 1关于点N 的对称点为M ,线段F 1M 的中垂线与直线F 2M 相交于点P ,则点P 的轨迹是( ) A .椭圆 B .双曲线 C .抛物线 D .圆答案 B解析 如图,连接ON ,由题意可得|ON |=1,且N 为MF 1的中点,又O 为F 1F 2的中点,所以|MF 2|=2.因为点F 1关于点N 的对称点为M ,线段F 1M 的中垂线与直线F 2M 相交于点P ,由垂直平分线的性质可得|PM |=|PF 1|, 所以||PF 2|-|PF 1||=||PF 2|-|PM || =|MF 2|=2<|F 1F 2|,所以由双曲线的定义可得,点P 的轨迹是以F 1,F 2为焦点的双曲线.(2)已知F 1,F 2为双曲线C :x 2-y 2=2的左、右焦点,点P 在C 上,∠F 1PF 2=60°,则△F 1PF 2的面积为______. 答案 2 3解析 不妨设点P 在双曲线的右支上, 则|PF 1|-|PF 2|=2a =22, 在△F 1PF 2中,由余弦定理,得 cos ∠F 1PF 2=|PF 1|2+|PF 2|2-|F 1F 2|22|PF 1|·|PF 2|=12, ∴|PF 1|·|PF 2|=8,∴12F PF S △=12|PF 1|·|PF 2|·sin 60°=2 3.延伸探究 在本例(2)中,若将“∠F 1PF 2=60°”改为“PF 1―→·PF 2―→=0”,则△F 1PF 2的面积为_____.答案 2解析 不妨设点P 在双曲线的右支上, 则|PF 1|-|PF 2|=2a =22, ∵PF 1―→·PF 2―→=0,∴PF 1―→⊥PF 2―→,∴在△F 1PF 2中,有|PF 1|2+|PF 2|2=|F 1F 2|2, 即|PF 1|2+|PF 2|2=16, ∴|PF 1|·|PF 2|=4,∴12F PF S △=12|PF 1|·|PF 2|=2.教师备选1.已知圆C 1:(x +3)2+y 2=1,C 2:(x -3)2+y 2=9,动圆M 同时与圆C 1和圆C 2相外切,则动圆圆心M 的轨迹方程为( ) A .x 2-y 28=1B.x 28-y 2=1 C .x 2-y 28=1(x ≤-1) D .x 2-y 28=1(x ≥1) 答案 C解析 设圆M 的半径为r ,由动圆M 同时与圆C 1和圆C 2相外切, 得|MC 1|=1+r ,|MC 2|=3+r , |MC 2|-|MC 1|=2<6,所以点M 的轨迹是以点C 1(-3,0)和C 2(3,0)为焦点的双曲线的左支, 且2a =2,a =1,又c =3, 则b 2=c 2-a 2=8, 所以点M 的轨迹方程为x 2-y 28=1(x ≤-1). 2.(2022·长春模拟)双曲线C 的渐近线方程为y =±233x ,一个焦点为F (0,-7),点A (2,0),点P 为双曲线第一象限内的点,则当点P 的位置变化时,△P AF 周长的最小值为( ) A .8 B .10 C .4+37 D .3+317答案 B解析 由已知得双曲线方程为y 24-x 23=1,设双曲线的另一个焦点为F ′,则|PF |=|PF ′|+4,△P AF 的周长为|PF |+|P A |+|AF |=|PF ′|+4+|P A |+3,当F ′,P ,A 三点共线时, |PF ′|+|P A |有最小值,为|AF ′|=3, 故△P AF 的周长的最小值为10.思维升华 在“焦点三角形”中,常利用正弦定理、余弦定理,结合||PF 1|-|PF 2||=2a ,运用平方的方法,建立与|PF 1|·|PF 2|的联系.跟踪训练1 (1)(2022·扬州、盐城、南通联考)已知双曲线C 的离心率为3,F 1,F 2是C 的两个焦点,P 为C 上一点,|PF 1|=3|PF 2|,若△PF 1F 2的面积为2,则双曲线C 的实轴长为( ) A .1 B .2 C .3 D .6 答案 B解析 由题意知,|PF 1|-|PF 2|=2a , 所以|PF 2|=a ,|PF 1|=3a , 又离心率e =ca =3,|F 1F 2|=2c =23a ,所以cos ∠F 1PF 2=9a 2+a 2-12a 22·3a ·a=-2a 26a 2=-13, sin ∠F 1PF 2=223,所以12PF F S △=12·a ·3a ·223=2a 2=2,所以a =1,实轴长2a =2.(2)已知F 是双曲线x 24-y 212=1的左焦点,A (1,4),P 是双曲线右支上的动点,则|PF |+|P A |的最小值为________. 答案 9解析 设双曲线的右焦点为F 1,则由双曲线的定义,可知|PF |=4+|PF 1|, 所以当|PF 1|+|P A |最小时满足|PF |+|P A |最小. 由双曲线的图象,可知当点A ,P ,F 1共线时, 满足|PF 1|+|P A |最小,|AF 1|+4即|PF |+|P A |的最小值. 又|AF 1|=5,故所求的最小值为9. 题型二 双曲线的标准方程例2 (1)(2021·北京)双曲线C :x 2a 2-y 2b 2=1过点(2,3),且离心率为2,则该双曲线的标准方程为( )A .x 2-y 23=1B.x 23-y 2=1 C .x 2-3y 23=1D.3x 23-y 2=1答案 A解析 ∵e =ca=2,则c =2a ,b =c 2-a 2=3a , 则双曲线的方程为x 2a 2-y 23a2=1,将点(2,3)的坐标代入双曲线的方程可得2a 2-33a 2=1a 2=1,解得a =1,故b =3,因此,双曲线的方程为x 2-y 23=1. (2)若双曲线经过点(3,2),且渐近线方程是y =±13x ,则双曲线的标准方程是________.答案y 2-x 29=1 解析 设双曲线的方程是y 2-x 29=λ(λ≠0). 因为双曲线过点(3,2), 所以λ=2-99=1,故双曲线的标准方程为y 2-x 29=1. 教师备选1.过双曲线C :x 2a 2-y 2b 2=1(a >b >0)的右顶点作x 轴的垂线,与C 的一条渐近线相交于点A .若以C 的右焦点F 为圆心、半径为4的圆经过A ,O 两点(O 为坐标原点),则双曲线C 的标准方程为( ) A.x 24-y 212=1 B.x 27-y 29=1 C.x 28-y 28=1 D.x 212-y 24=1 答案 A解析 因为渐近线y =ba x 与直线x =a 交于点A (a ,b ),c =4且(4-a )2+b 2=4,解得a 2=4,b 2=12,因此双曲线的标准方程为x 24-y 212=1. 2.经过点P (3,27),Q (-62,7)的双曲线的标准方程为________.答案 y 225-x 275=1解析 设双曲线方程为mx 2-ny 2=1(mn >0).∴⎩⎪⎨⎪⎧9m -28n =1,72m -49n =1, 解得⎩⎨⎧m =-175,n =-125.∴双曲线的标准方程为y 225-x 275=1.思维升华 求双曲线的标准方程的方法(1)定义法:由题目条件判断出动点轨迹是双曲线,确定2a ,2b 或2c ,从而求出a 2,b 2. (2)待定系数法:“先定型,再定量”,如果焦点位置不好确定,可将双曲线方程设为x 2m 2-y 2n 2=λ(λ≠0),再根据条件求λ的值.跟踪训练2 (1)已知双曲线过点(2,3),渐近线方程为y =±3x ,则该双曲线的标准方程是( ) A.7x 216-y 212=1 B.y 23-x 22=1 C .x 2-y 23=1 D.3y 223-x 223=1 答案 C解析 因为双曲线的渐近线方程为y =±3x ,所以可设双曲线的方程为x 2-y 23=λ(λ≠0),将点(2,3)代入其中,得λ=1,所以该双曲线的标准方程为x 2-y 23=1. (2)(2022·佛山调研)已知F 1,F 2分别为双曲线x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,P 为双曲线上一点,PF 2与x 轴垂直,∠PF 1F 2=30°,且虚轴长为22,则双曲线的标准方程为( ) A.x 24-y 22=1 B.x 23-y 22=1 C.x 24-y 28=1 D .x 2-y 22=1 答案 D解析 由题意可知|PF 1|=43c3, |PF 2|=23c3, 2b =22,由双曲线的定义可得43c 3-23c3=2a ,即c =3a .又b =2,c 2=a 2+b 2,∴a =1,∴双曲线的标准方程为x 2-y 22=1.题型三 双曲线的几何性质 命题点1 渐近线例3 (1)由伦敦著名建筑事务所Steyn Studio 设计的南非双曲线大教堂惊艳世界,该建筑是数学与建筑完美结合造就的艺术品.若将如图所示的大教堂外形弧线的一段近似看成双曲线y 2a 2-x 2b 2=1(a >0,b >0)下支的一部分,且此双曲线的下焦点到渐近线的距离为2,离心率为2,则该双曲线的方程为( )A.y 212-x 24=1 B.3y 24-x 24=1 C.x 24-y 24=1 D.y 216-x 24=1 答案 B解析 由题意知,b =2, 又因为e =ca =1+⎝⎛⎭⎫b a 2=2,解得a 2=43,所以双曲线的方程为3y 24-x 24=1.(2)设O 为坐标原点,直线x =a 与双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的两条渐近线分别交于D ,E 两点,若△ODE 的面积为8,则C 的焦距的最小值为( ) A .4 B .8 C .16 D .32 答案 B解析 由题意知双曲线的渐近线方程为y =±bax .因为D ,E 分别为直线x =a 与双曲线C 的两条渐近线的交点, 所以不妨设D (a ,b ),E (a ,-b ),所以S △ODE =12×a ×|DE |=12×a ×2b =ab =8,所以c 2=a 2+b 2≥2ab =16(当且仅当a =b 时等号成立), 所以c ≥4,所以2c ≥8, 所以C 的焦距的最小值为8.思维升华 (1)渐近线的求法:求双曲线x 2a 2-y 2b 2=1(a >0,b >0)的渐近线的方法是令x 2a 2-y 2b 2=0,即得两渐近线方程x a ±yb =0⎝⎛⎭⎫y =±b a x . (2)在双曲线的几何性质中重点是渐近线方程和离心率,在双曲线x 2a 2-y 2b 2=1(a >0,b >0)中,离心率e 与双曲线的渐近线的斜率k =±ba ,满足关系式e 2=1+k 2.命题点2 离心率例4 (1)(2021·全国甲卷)已知F 1,F 2是双曲线C 的两个焦点,P 为C 上一点,且∠F 1PF 2=60°,|PF 1|=3|PF 2|,则C 的离心率为( ) A.72 B.132C.7D.13 答案 A解析 设|PF 2|=m ,则|PF 1|=3m , 在△F 1PF 2中,|F 1F 2|=m 2+9m 2-2×3m ×m ×cos 60° =7m ,所以C 的离心率e =c a =2c 2a =|F 1F 2||PF 1|-|PF 2|=7m 2m =72. 高考改编已知双曲线E :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,点A 在双曲线E 的左支上,且∠F 1AF 2=120°,|AF 2|=2|AF 1|,则双曲线E 的离心率为( ) A. 3 B. 5 C.7 D .7答案 C解析 点A 在双曲线E 的左支上,左、右焦点分别为F 1,F 2, 设|AF 1|=m ,由|AF 2|=2|AF 1|知|AF 2|=2m ,由双曲线定义得|AF 2|-|AF 1|=2m -m =m =2a , 在△AF 1F 2中,|AF 1|=2a ,|AF 2|=4a ,∠F 1AF 2=120°, 由余弦定理知,|F 1F 2|2=|AF 1|2+|AF 2|2-2|AF 1||AF 2|cos 120° =4a 2+16a 2+8a 2=28a 2, ∴|F 1F 2|=27a , 又|F 1F 2|=2c ,∴27a =2c ,e =ca=7.(2)(2022·滨州模拟)已知F 1,F 2分别是双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点,点P是双曲线C 上在第一象限内的一点,若sin ∠PF 2F 1=3sin ∠PF 1F 2,则双曲线C 的离心率的取值范围为( ) A .(1,2) B .(1,3) C .(3,+∞) D .(2,3)答案 A解析 在△PF 1F 2中, sin ∠PF 2F 1=3sin ∠PF 1F 2, 由正弦定理得,|PF 1|=3|PF 2|,又点P 是双曲线C 上在第一象限内的一点, 所以|PF 1|-|PF 2|=2a , 所以|PF 1|=3a ,|PF 2|=a ,在△PF 1F 2中,由|PF 1|+|PF 2|>|F 1F 2|, 得3a +a >2c ,即2a >c , 所以e =ca <2,又e >1,所以1<e <2. 教师备选1.(2022·济南模拟)已知双曲线x 2m +1-y 2m =1(m >0)的渐近线方程为x ±3y =0,则m 等于( )A.12B.3-1C.3+12D .2答案 A解析 由渐近线方程y =±b a x =±33x , 所以b a =33, 则b 2a 2=13, 即m m +1=13,m =12. 2.设F 为双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的右焦点,O 为坐标原点,以OF 为直径的圆与圆x 2+y 2=a 2交于P ,Q 两点.若|PQ |=|OF |,则C 的离心率为( )A. 2B. 3 C .2D. 5答案 A解析 令双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的右焦点F 的坐标为(c ,0),则c =a 2+b 2. 如图所示,由圆的对称性及条件|PQ |=|OF |可知,PQ 是以OF 为直径的圆的直径,且PQ ⊥OF .设垂足为M ,连接OP ,则|OP |=a ,|OM |=|MP |=c 2, 由|OM |2+|MP |2=|OP |2,得⎝⎛⎭⎫c 22+⎝⎛⎭⎫c 22=a 2,∴c a=2,即离心率e = 2. 思维升华 求双曲线的离心率时,将提供的双曲线的几何关系转化为关于双曲线基本量a ,b ,c 的方程或不等式,利用c 2=a 2+b 2和e =c a转化为关于e 的方程(或不等式),通过解方程(或不等式)求得离心率的值(或范围).跟踪训练3 (1)(多选)已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的离心率e =2,C 上的点到其焦点的最短距离为1,则( )A .双曲线C 的焦点坐标为(0,±2)B .双曲线C 的渐近线方程为y =±3xC .点(2,3)在双曲线C 上D .直线mx -y -m =0(m ∈R )与双曲线C 恒有两个交点答案 BC解析 双曲线C 上的点到其焦点的最短距离为c -a =1,离心率e =c a =2,所以a =1,c =2,所以b 2=3,所以双曲线C 的方程为x 2-y 23=1,所以C 的焦点坐标为(±2,0),A 错误; 双曲线C 的渐近线方程为y =±b ax =±3x ,B 正确; 因为22-323=1,所以点(2,3)在双曲线C 上,C 正确; 直线mx -y -m =0即y =m (x -1),恒过点(1,0),当m =±3时,直线与双曲线C 的一条渐近线平行,此时直线与双曲线只有一个交点,D 错误.(2)(2022·威海模拟)若双曲线C 1:y 24-x 29=1与双曲线C 2:x 2a 2-y 2b2=1(a >0,b >0)有公共点,则双曲线C 2的离心率的取值范围是( )A.⎝⎛⎭⎫1,132B.⎝⎛⎭⎫1,133 C.⎝⎛⎭⎫132,+∞ D.⎝⎛⎭⎫133,+∞ 答案 D解析 因为双曲线C 1:y 24-x 29=1的渐近线方程为y =±23x , 双曲线C 2:x 2a 2-y 2b 2=1(a >0,b >0)的渐近线方程为y =±b ax , 为使双曲线C 1:y 24-x 29=1与双曲线C 2:x 2a 2-y 2b2=1(a >0,b >0)有公共点, 只需b a >23, 则离心率为e =c a =a 2+b 2a 2=1+⎝⎛⎭⎫b a 2>1+49=133. 课时精练1.双曲线9x 2-16y 2=1的焦点坐标为( )A.⎝⎛⎭⎫±512,0 B.⎝⎛⎭⎫0,±512 C .(±5,0) D .(0,±5)答案 A解析 将双曲线的方程化为标准形式为x 219-y 2116=1, 所以c 2=19+116=25144, 所以c =512, 所以焦点坐标为⎝⎛⎭⎫±512,0. 2.已知双曲线x 2m -y 2m +6=1(m >0)的虚轴长是实轴长的2倍,则双曲线的标准方程为( ) A.x 22-y 24=1 B.x 24-y 28=1 C .x 2-y 28=1 D.x 22-y 28=1 答案 D解析 由题意,得2m =m +6,解得m =2,所以双曲线的标准方程为x 22-y 28=1. 3.若双曲线E :x 29-y 216=1的左、右焦点分别为F 1,F 2,点P 在双曲线E 上,且|PF 1|=3,则|PF 2|等于( )A .11B .9C .5D .3答案 B解析 方法一 依题意知,点P 在双曲线的左支上,根据双曲线的定义,得|PF 2|-|PF 1|=2×3=6,所以|PF 2|=6+3=9.方法二 根据双曲线的定义,得||PF 2|-|PF 1||=2×3=6,所以||PF 2|-3|=6,所以|PF 2|=9或|PF 2|=-3(舍去).4.(2022·大连模拟)若双曲线C :x 29-y 2b 2=1的右焦点到它的一条渐近线的距离是33,则C 的离心率为( )A .2 B. 3 C.43 D.233答案 A解析 双曲线C :x 29-y 2b 2=1的右焦点坐标为(9+b 2,0),渐近线方程为y =±b 3x ,即bx ±3y =0, ∵双曲线C :x 29-y 2b 2=1的右焦点到它的一条渐近线的距离是33, ∴b 9+b 2b 2+9=33, 解得b =33,∴c =9+b 2=9+(33)2=6,∴离心率e =c a =63=2. 5.(多选)已知双曲线C 的方程为x 216-y 29=1,则下列说法正确的是( ) A .双曲线C 的实轴长为8B .双曲线C 的渐近线方程为y =±34x C .双曲线C 的焦点到渐近线的距离为3D .双曲线C 上的点到焦点距离的最小值为94答案 ABC解析 因为a 2=16,所以a =4,2a =8,故A 正确;因为a =4,b =3,所以双曲线C 的渐近线方程为y =±b a x =±34x ,故B 正确; 因为c =a 2+b 2=16+9=5,所以焦点坐标为(-5,0),(5,0),焦点(5,0)到渐近线3x -4y =0的距离为|15|32+(-4)2=3,故C 正确;双曲线C 上的点到焦点距离的最小值为c -a =1,故D 错误. 6.(多选)(2022·潍坊模拟)已知双曲线C :x 2a 2-y 29=1(a >0)的左、右焦点分别为F 1,F 2,一条渐近线方程为y =34x ,P 为C 上一点,则以下说法正确的是( ) A .C 的实轴长为8B .C 的离心率为53 C .|PF 1|-|PF 2|=8D .C 的焦距为10 答案 AD解析 由双曲线方程知,渐近线方程为y =±3a x ,而一条渐近线方程为y =34x , ∴a =4,故C :x 216-y 29=1, ∴双曲线实轴长为2a =8,离心率e =c a =16+94=54, 由于P 可能在C 不同分支上,则有||PF 1|-|PF 2||=8,焦距为2c =2a 2+b 2=10.∴A ,D 正确,B ,C 错误.7.(2021·新高考全国Ⅱ)已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的离心率e =2,则该双曲线C 的渐近线方程为________.答案 y =±3x解析 因为双曲线x 2a 2-y 2b2=1(a >0,b >0)的离心率为2, 所以e =c 2a 2=a 2+b 2a 2=2,所以b 2a2=3, 所以该双曲线的渐近线方程为y =±b ax =±3x . 8.设双曲线x 29-y 216=1的右顶点为A ,右焦点为F .过点F 且平行于双曲线的一条渐近线的直线与双曲线交于点B ,则△AFB 的面积为________.答案 3215解析 因为a 2=9,b 2=16,所以c =5.所以A (3,0),F (5,0),不妨设直线BF 的方程为y =43(x -5), 代入双曲线方程解得B ⎝⎛⎭⎫175,-3215. 所以S △AFB =12|AF |·|y B |=12×2×3215=3215. 9.已知双曲线x 216-y 24=1的左、右焦点分别为F 1,F 2. (1)若点M 在双曲线上,且MF 1-→·MF 2-→=0,求M 点到x 轴的距离;(2)若双曲线C 与已知双曲线有相同的焦点,且过点(32,2),求双曲线C 的方程. 解 (1)不妨设M 在双曲线的右支上,M 点到x 轴的距离为h ,∵MF 1-→·MF 2-→=0,∴MF 1⊥MF 2.设|MF 1|=m ,|MF 2|=n ,由双曲线的定义知m -n =2a =8.①在Rt △F 1MF 2中,由勾股定理得m 2+n 2=(2c )2=80,②由①②得m ·n =8.∵12MF F S △=12mn =4=12×2ch , ∴h =255. 即M 点到x 轴的距离为255. (2)设双曲线C 的方程为x 216-λ-y 24+λ=1(-4<λ<16). ∵双曲线C 过点(32,2),∴1816-λ-44+λ=1, 解得λ=4或λ=-14(舍去),∴双曲线C 的方程为x 212-y 28=1. 10.已知双曲线C :x 2a 2-y 2b 2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,渐近线方程是y =±255x ,点A (0,b ),且△AF 1F 2的面积为6.(1)求双曲线C 的标准方程;(2)直线l :y =kx +m (k ≠0,m ≠0)与双曲线C 交于不同的两点P ,Q ,若|AP |=|AQ |,求实数m 的取值范围. 解 (1)由题意得b a =255,① 12AF F S △=12×2c ·b =6,②a 2+b 2=c 2,③由①②③可得a 2=5,b 2=4,∴双曲线C 的标准方程是x 25-y 24=1. (2)由题意知直线l 不过点A .设P (x 1,y 1),Q (x 2,y 2),线段PQ 的中点为D (x 0,y 0),连接AD (图略).将y =kx +m 与x 25-y 24=1联立,消去y , 整理得(4-5k 2)x 2-10kmx -5m 2-20=0,由4-5k 2≠0且Δ>0,得⎩⎪⎨⎪⎧4-5k 2≠0,80(m 2-5k 2+4)>0,④ ∴x 1+x 2=10km 4-5k 2,x 1x 2=-5m 2+204-5k 2, ∴x 0=x 1+x 22=5km 4-5k 2, y 0=kx 0+m =4m 4-5k 2. 由|AP |=|AQ |知,AD ⊥PQ ,又A (0,2),∴k AD =y 0-2x 0=4m 4-5k 2-25km 4-5k 2=-1k, 化简得10k 2=8-9m ,⑤由④⑤,得m <-92或m >0. 由10k 2=8-9m >0,得m <89. 综上,实数m 的取值范围是m <-92或0<m <89.11.(多选)双曲线C :x 24-y 22=1的右焦点为F ,点P 在双曲线C 的一条渐近线上,O 为坐标原点,则下列说法正确的是( )A .双曲线C 的离心率为62B .双曲线y 24-x 28=1与双曲线C 的渐近线相同 C .若PO ⊥PF ,则△PFO 的面积为 2D .|PF |的最小值为2答案 ABC解析 因为a =2,b =2,所以c =a 2+b 2=6,所以e =c a =62, 故A 正确;双曲线y 24-x 28=1的渐近线方程为y =±22x ,双曲线C 的渐近线方程为y =±22x ,故B 正确; 因为PO ⊥PF ,点F (6,0)到渐近线2x -2y =0的距离d =|2×6|6=2, 所以|PF |=2,所以|PO |=(6)2-(2)2=2,所以△PFO 的面积为12×2×2=2, 故C 正确;|PF |的最小值即为点F 到渐近线的距离,即|PF |=2,故D 不正确.12.(2022·湖南师大附中模拟)已知双曲线C: x 24-y 2b2=1(b >0),以C 的焦点为圆心,3为半径的圆与C 的渐近线相交,则双曲线C 的离心率的取值范围是( )A.⎝⎛⎭⎫1,32 B.⎝⎛⎭⎫1,132 C.⎝⎛⎭⎫ 32,132 D .(1,13) 答案 B解析 由题意可知双曲线的其中一条渐近线为y =b 2x ,即bx -2y =0, 又该圆的圆心为(c ,0),故圆心到渐近线的距离为bc b 2+4, 则由题意可得bc b 2+4<3,即b 2c 2<9(b 2+4), 又b 2=c 2-a 2=c 2-4,则(c 2-4)c 2<9c 2,解得c 2<13,即c <13,则e =c a =c 2<132,又e >1, 故离心率的取值范围是⎝⎛⎭⎫1,132. 13.已知双曲线x 2a 2-y 2b2=1(a >0,b >0)的一条渐近线方程为x -2y =0,双曲线的左焦点在直线x +y +5=0上,A ,B 分别是双曲线的左、右顶点,点P 为双曲线右支上位于第一象限的动点,直线P A ,PB 的斜率分别为k 1,k 2,则k 1+k 2的取值范围为( )A .(1,+∞)B .(2,+∞)C .(2,+∞)D .[2,+∞)答案 A 解析 由双曲线x 2a 2-y 2b 2=1(a >0,b >0)的一条渐近线方程为x -2y =0,可得a =2b ,由双曲线的左焦点在直线x +y +5=0上,可得c =5,则由a 2+b 2=c 2,得a =2,b =1,双曲线的方程为x 24-y 2=1, 由题意可得A (-2,0),B (2,0),设P (m ,n )(m >2,n >0),则m 24-n 2=1,即n 2m 2-4=14, k 1k 2=n m +2·n m -2=n 2m 2-4=14, 易知k 1,k 2>0,则k 1+k 2≥2k 1k 2=1,由A ,B 分别为双曲线的左、右顶点,可得k 1≠k 2,则k 1+k 2>1.14.已知双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点分别为F 1,F 2,O 为原点,若以F 1F 2为直径的圆与C 的渐近线的一个交点为P ,且|F 1P |=3|OP |,则C 的渐近线方程为________. 答案 y =±3x解析 根据双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左、右焦点为F 1,F 2,O 为原点,以F 1F 2为直径的圆与C 的渐近线的一个交点为P ,如图所示,则|F 1O |=|OP |=c ,|F 1P |=3|OP |=3c ,所以在△POF 1中,由余弦定理可得cos ∠POF 1=|OP |2+|OF 1|2-|PF 1|22|OP |·|OF 1|=c 2+c 2-()3c 22×c ×c=-12. 所以∠POF 1=2π3,则∠POF 2=π3,所以tan ∠POF 2=tan π3=3, 则渐近线方程为y =±3x .15.(多选)双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的焦点在圆O :x 2+y 2=13上,圆O 与双曲线C 的渐近线在第一、二象限分别交于点M ,N ,点E (0,a )满足EO →+EM →+EN →=0(其中O 为坐标原点),则( )A .双曲线C 的一条渐近线方程为3x -2y =0B .双曲线C 的离心率为132C .|OE →|=1D .△OMN 的面积为6答案 ABD解析 如图,设双曲线C 的焦距为2c =213,MN 与y 轴交于点P ,由题意可知|OM |=c =13,则P (0,b ),由EO →+EM →+EN →=0得点E 为△OMN 的重心,可得|OE |=23|OP |, 即a =23b ,b 2a 2=c 2-a 2a 2=94, 所以a =2,b =3,e =132. 双曲线C 的渐近线方程为3x ±2y =0,|OE →|=2,M 的坐标为(2,3),S △OMN =6.16.双曲线C :x 2a 2-y 2b2=1(a >0,b >0)的左顶点为A ,右焦点为F ,动点B 在C 上.当BF ⊥AF 时,|AF |=|BF |.(1)求C 的离心率;(2)若B 在第一象限,证明:∠BF A =2∠BAF .(1)解 设双曲线的半焦距为c ,则F (c ,0),B ⎝⎛⎭⎫c ,±b 2a , 因为|AF |=|BF |,所以b 2a=a +c , 所以c 2-a 2a=a +c , 所以c -a =a ,即c =2a ,所以e =2.(2)证明 设B (x 0,y 0),其中x 0>a ,y 0>0. 因为e =2,故c =2a ,b =3a , 故双曲线的渐近线方程为y =±3x ,所以∠BAF ∈⎝⎛⎭⎫0,π3,∠BF A ∈⎝⎛⎭⎫0,2π3. 当∠BF A =π2时, 由题意易得∠BAF =π4, 此时∠BF A =2∠BAF .当∠BF A ≠π2时, 因为tan ∠BF A =-y 0x 0-c =-y 0x 0-2a, tan ∠BAF =y 0x 0+a, 所以tan 2∠BAF =2y 0x 0+a 1-⎝⎛⎭⎫y 0x 0+a 2=2y 0(x 0+a )(x 0+a )2-y 20 =2y 0(x 0+a )(x 0+a )2-b 2⎝⎛⎭⎫x 20a 2-1 =2y 0(x 0+a )(x 0+a )2-3a 2⎝⎛⎭⎫x 20a 2-1 =2y 0(x 0+a )(x 0+a )2-3(x 20-a 2) =2y 0(x 0+a )-3(x 0-a ) =-y 0x 0-2a=tan ∠BF A ,因为2∠BAF ∈⎝⎛⎭⎫0,2π3,故∠BF A =2∠BAF . 综上,∠BF A =2∠BAF .。
双曲线焦点三角形的内切圆问题

(变式2)
已知双曲线
x2 a2
y2 b2
1(a
0, b
0)的左,右焦点分别为F1,F2 , 过F2 的直线交双曲线的右支
于A,B两点,AF1B 90 ,AF1B的内切圆圆心的纵坐标为
7a 2
. 则双曲线的离心率为
.
解:正方形F1EID中,对角线F1I =2 2a
勾股定理得:(2
解:如图作辅助线,则切线长相等:F1D F1E (1)AF1 AF2 F1D GF2 F1E GF2 2a
(2)BF1 BF2 BF1 (BG GF2 ) F1E GF2 2a GF2 0,即G与F2重合,
IF2 AB
SABF1
=
1 2
( AF2
F2 B
BA)
R
1 2
(4a
2AB)
R
( AB
2a)
R
SABF1
=
1 2
2c
yA yB
c AB sin
AB 2aR c sin R
1
2ep e2 cos2
a2
2ab2 c2 cos2
R
c sin
R
a2
b2
2a)2 (c a2 )2 ( c
7a 2
)2
求离心率 e = c 令a 1,则e c 1 a
(c
1)2 c
8
7 4
25 4
双曲线中常考的十六条焦点性质及其证明

点的轨迹是以实轴为直径的圆,除去实轴的两个端点(四)双曲线焦三角形中,以焦半径为直径的圆必与以双曲线实轴为直径的圆相外切(或内切).证明:以焦半径MF 2为直径的圆的半径为r 1,圆心为O 1;以MF 1为直径的圆的半径为r 2,圆心为O 2,由双曲线定义知12||||||MF MF AB =+∴112111||||(||||)22OO F M M F AB r a ==+=+,∴圆O 1与圆O 外切又12||||||MF AB MF -=∴221211||||(||||)22OO F M M F AB r a ==-=-,∴圆O 2与圆O 内切(五)双曲线22221(0,0)x y a b a b-=>>的两个顶点为1(,0)A a -,2(,0)A a ,与y 轴平行的直线交双曲线于P 1、P 2时A 1P 1与A 2P 2交点的轨迹方程是22221x y a b +=.证明:设交点0012(,),(,),(,)S x y P m n P m n -∵111P A A SK K =,222P A P S K K =,∴0220000222200000y n m a x ay y y n n n y m a m a x a x a a m x a n m a x a ⎧=⎪++-⎪⇒⋅=⋅⇒=⎨+-+----⎪=⎪--⎩又222222222222211m n n m n b a b b a a m a-=⇒=-⇒=--,∴22220002222201y x y b x a a a b =-⇒+=-即22221x y a b+=(六)若000(,)P x y 在双曲线22221(0,0)x y a b a b-=>>上,则过0P 的双曲线的切线方程是00221x x y ya b-=.证明:求导可得:202220220'x b x y y y a b y a '⋅-=⇒=,切线方程2000002220()1x b x x y yy y x x y a a b-=-⇒-=(七)若000(,)P x y 在双曲线22221(0,0)x y a b a b-=>>外,则过P 0作双曲线的两条切线切点为P 1、P 2,则切点弦P 1P 2的直线方程是00221x x y ya b-=.证明:设111222(,),(,)P x y P x y ,则过12P P 切线分别为11122:1x x y yl a b -=,22222:1x x y yl a b-=∵0P 在12l l 、上∴1010221x x y y a b +=,2020221x x y y a b+=∴过12P P 方程00221x x y y a b-=(八)AB 是双曲线22221(0,0)x y a b a b-=>>的不平行于对称轴且不过原点的弦,M 为AB 的中点,则22OM AB b k k a⋅=.证明:设(,),(,)A A B B A x y B x y ,则()22A B A Bx x y y M ++⋅,2222A B A B A B OM ABA B A B A By y y y y y K K x x x x x x +--=⋅=+--又22222222222222A b A AB B A Bx x x y x y y y a b a b a b ---=-⇒=,∴22OM ABb K K a=(九)若000(,)P x y 在双曲线22221(0,0)x y a b a b-=>>内,则过P 0的弦中点的轨迹方程是22002222x x y yx y a b a b-=-.证明:设弦与双曲线交于111222(,),(,)P x y P x y ,中点(,)S m n 122222220112212222222012()()P P POS n y x y x y x x b mb K K m x a b a b y y a na -+-=-⇒====-+22222200m b mb x n a na y ⇒-=-22002222x m y ym n a b a b⇒+=-,即22002222x x y yx y a b a b-=-。
《焦点三角形的应用》练习题

焦点三角形的应用一.焦点三角形的周长问题1.设F 1、F 2分别是椭圆E :22221(0)y x a b a b+=>>的左、右焦点,过F 1斜率为1的直线l 与E 相交于A 、B 两点,且|AF 2|、|AB|、|BF 2|成等差数列,求E 22.已知F 1、F 2为椭圆221259y x +=的两个焦点,过F 1的直线交椭圆于A 、B 两点,若|F 2A|+|F 2B|=12,则|AB|=8 3.已知ABC 的顶点B 、C 在椭圆2213x y +=上,顶点A 是椭圆的一个焦点,且椭圆另外一个焦点在BC 边上,则ΔABC 的周长是(C )A. B.6 C. D.124.在平面直角坐标系xOy 中,椭圆C 的中心为原点,焦点F 1、F 2在x ,过点F 1的直线l 交C 于A 、B 两点,且ΔABF 2的周长为16,那么C 的方程为221168y x += 5.过双曲线22143y x -=左焦点F 1的直线交曲线的左支于M 、N 两点,F 2为其右焦点,则|MF 2|+|NF 2|-|MN|的值为8 二.焦点三角形的面积1.已知椭圆221169y x +=的左、右焦点为F 1、F 2,P 在椭圆上,若P 、F 1、F 2是一个直角三角形的三个顶点,则点P 到x 轴的距离为(D )A.95C.3D.94 2.已知双曲线2212y x -=的焦点为F 1、F 2,点M 在双曲线上,且120MF MF ⋅=,则点M 到x 轴的距离为(C )A.43B.533.已知F 1、F 2为双曲线C :221x y -=的左、右焦点,点P 在C 上,且∠F 1PF 2=600,则点P 到x 轴的距离为(B )4.已知F 1、F 2为椭圆C :22221(0)y x a b a b+=>>的两个焦点,P 为椭圆C 上一点,且PF 1⊥PF 2,若ΔPF 1F 2的面积为9,则b =35.已知F 1、F 2为双曲线C :221x y -=的左、右焦点,点P 在C 上,且∠F 1PF 2=600,则|PF 1|⋅|PF 2|=(B )A.2B.4C.6D.86.设P 为双曲线22112y x -=上的一点,F 1、F 2是该双曲线的两个焦点,若|PF 1|:|PF 2|=3:2,则ΔPF 1F 2的面积为(B )A. B.12 C. D.247.已知双曲线22163y x -=的焦点为F 1、F 2,点M 在双曲线上且MF 1⊥x 轴,则点F 1到直线F 2M 的距离为(C )三.焦点三角形的角平分线1.已知F 1、F 2为椭圆2211612y x +=的左、右焦点,点A (2,3)在椭圆上,求∠F 1AF 2的角平分线所在直线l 的方程 012=--y x2.已知F 1、F 2为双曲线C :221927y x -=的左、右焦点,A 为C 上一点,点M 的坐标为(-2,0),AM 为∠F 1AF 2的角平分线,则|AF 2|=123.P 是椭圆C :2214x y +=上除长轴端点外的任一点,连接PF 1、PF 2,设∠F 1PF 2的角平分线PM 交C 的长轴于点M (),0m ,求m 的取值范围33,22⎛⎫- ⎪⎝⎭四.焦点三角形的内切圆1.设P 是椭圆22221(0)y x a b a b+=>>上的动点,F 1、F 2是椭圆的两个焦点,ΔPF 1F 2的内切圆半径为r ,求证:12()PF F S r a c ∆=+2.已知椭圆22221(0)y x a b a b+=>>的左、右焦点分别为F 1、F 2,O 为椭圆的中心,P 是椭圆上的点,ΔPF 1F 2的内切圆的圆心为I ,延长直线PI 交x 轴于点B ,若e 为椭圆的离心率,则||||PI IB =(C ) A.e B.1 C.1e D.不确定 3.已知P 是椭圆22143y x +=上的一点,F 1、F 2是椭圆的左、右焦点,ΔPF 1F 2的内切圆的半径为12,则12PF PF ⋅的值为(C ) A.32 B.94- C.94D.04.已知P (12,,点F 1、F 2是双曲线221169y x -=的左、右焦点,点I 是ΔPF 1F 2的内心,且2112IPF IPF IF F S S S λ∆∆∆=-,则λ=(A ) A.45 B.45- C.35D.35- 5.已知双曲线22221(0,0)y x a b a b-=>>的左、右焦点分别为F 1、F 2,O 为双曲线的中心,P 是双曲线右支上的点,ΔPF 1F 2的内切圆的圆心为I ,且圆I 与x 轴相切于点A ,若e 为双曲线的离心率,则|OA|=(B )A.bB.aC.cD.不确定6.已知双曲线22221(0,0)y x a b a b-=>>的左、右焦点分别为F 1、F 2,O 为双曲线的中心,P 是双曲线右支上的点,ΔPF 1F 2的内切圆的圆心为I ,且圆I 与x 轴相切于点A ,过F 2作直线PI 的垂线,垂足为B ,若e 为双曲线的离心率,则(C )A.|OB|=e |OA|B. |OA|=e |OB|C. |OB|=|OA|D.|OB|与|OA|的关系不确定五.焦点三角形的中位线1.已知椭圆的左焦点为F 1,若椭圆上存在一点P ,满足以椭圆短轴为直径的圆与线段PF 1相切于线段PF 1的中点E ,则椭圆的离心率为(A )2.F 1、F 2是双曲线22221(0,0)y x a b a b-=>>的左、右焦点,过点F 1作斜率为k 的直线交双曲线右支于点P ,且∠F 1PF 2为锐角,M 为线段F 1P 的中点,过坐标原点O 作OT ⊥F 1P 于点T ,且|OM|-|TM|=b a -,则k =(B ) A.ba B.ab 3.从双曲线22221(0,0)y x a b a b-=>>的左焦点F 引圆222x y a +=的切线l ,切点为T ,且l 交双曲线的右支于点P ,若点M 是线段FP 的中点,O 为坐标原点,则|OM|-|TM|=(B ) A.2b a - B.b a - C.2a b + D.2b a + 4.过双曲线22221(0,0)y x a b a b-=>>的左焦点F 1(),0c -作圆222x y a +=的切线,切点为E ,延长F 1E 交抛物线24y cx =于点P ,若E 是线段F 1P 的中点,则双曲线的离心率是(A )5.已知椭圆C :14922=+y x ,点M 与C 的焦点不重合,若M 关于C 的焦点的对称点分别为A 、B ,线段MN 的中点在C 上,则|AN|+|BN|=126.已知点M 是双曲线22221(0,0)y x a b a b-=>>右支上的任意一点,F 2是它的右焦点,则以MF 2为直径的圆与圆O :222x y a +=的位置关系是(B )A.内切B.外切C.外切或内切D.无公共点或相交7.已知点A 是椭圆22221(0)y x a b a b+=>>上的任意一点,F 2是椭圆的右焦点,则以AF 2为直径的圆与圆O :222x y a +=的位置关系是(A )A.内切B.外切C.外切或内切D.无公共点或相交8.过椭圆左焦点作弦AB ,以AB 为直径的圆与椭圆左准线( C )A.相切B.相交C.相离D.位置关系不确定9.过双曲线C :22221(0,0)y x a b a b-=>>的右焦点F 2的直线l 与双曲线的右支交于A 、B 两点,以线段AB 为直径的圆被双曲线C 的右准线截得的劣弧的弧度数为3π,那么双曲线的离心率e 为(B )1 D.2 10.F 1、F 2是椭圆22221(0)y x a b a b+=>>的左、右焦点,P 是椭圆上任意一点,从右焦点F 2引∠F 1PF 2外角的角平分线的垂线,则垂足Q 的轨迹为(A )A.圆B.椭圆C.双曲线D.抛物线11.已知点P 是椭圆22221(0,0)y x a b xy a b+=>>≠上的动点,F 1(),0c -,F 2(),0c 为椭圆的左、右焦点,O 为坐标原点,若M 是∠F 1PF 2的角平分线上的一点,且F 1M ⊥MP ,则|OM|的取值范围是(A )A.()0,cB.()0,aC.(),b aD.(),c a。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
双曲线焦点三角形性质练习题
【例7】已知1F 、2F 是椭圆)0(122
22>>=+b a b
y a x 的两个焦点,
椭圆上一点P 使︒=∠9021PF F ,求椭圆离心率e 的取值范围.
【例8】已知椭圆19
42
2=+y x 的两个焦点分别为12,F F ,点P 在椭圆上,若P 、F 1、F 2是一
个直角三角形的三个项点,21PF PF >,则
2
1PF PF 的值是 .
【例9】已知P 是双曲线
2
214x y 上的一点,1F 、2F 是两焦点,且021=⋅PF PF ,则2
1F PF ∆的面积为( ) A .6
B .4
C .2
D .1
【例10】设P 是双曲线
2
2
1412
x y 右支上的一个动点,1F 、2F 为左右两个焦点,在∆PF 1F 2
中,令α=∠21F PF ,β=∠12F PF ,则2
tan
2
tan
β
α
÷的值为( )
A .31
B .223-
C .3
D .与P 的位置有关
【例11】设1F 、2F 分别是双曲线22
221x y a b -=的左、右焦点,若双曲线上存在点A ,使
∠F 1AF 2=90º,且|AF 1|=3|AF 2|,则双曲线离心率为( )
A
B C D
【例12】双曲线18
22
=-y x 的焦点为1F 、2F ,点P 为双曲线上的动点,当21·
0PF PF <时,点P 的横坐标的取值范围是( ) A .(354-,3
54) B .(354-,22-]∠[22,354) C .(7354-,7
35
4) D .(7354-
,22-]∠[22,7
35
4)
【例13】已知椭圆22162x y +
=与双曲线2
213x y -=共焦点,两个公共焦点分别为1F 、2F ,点P 为两曲线的一个交点,那么12cos F PF ∠= ;12PF PF ⋅= .
【例14】已知1F ,2F 是椭圆和双曲线的公共焦点,P 是它们的一个公共点.且1230F PF ∠=︒,则椭圆和双曲线的离心率的平方和的最小值为( ) A .2 B .1
C .3
2 D .43
【例15】若双曲线()0,012
22
2>>=-b a b y a x 的焦点到渐近线的距离等于实轴长,则双曲线的
离心率为 .。
