同济大学钢结构基本原理(沈祖炎)课后习题答案完全版

(完整版)钢结构基本原理课后习题与答案完全版

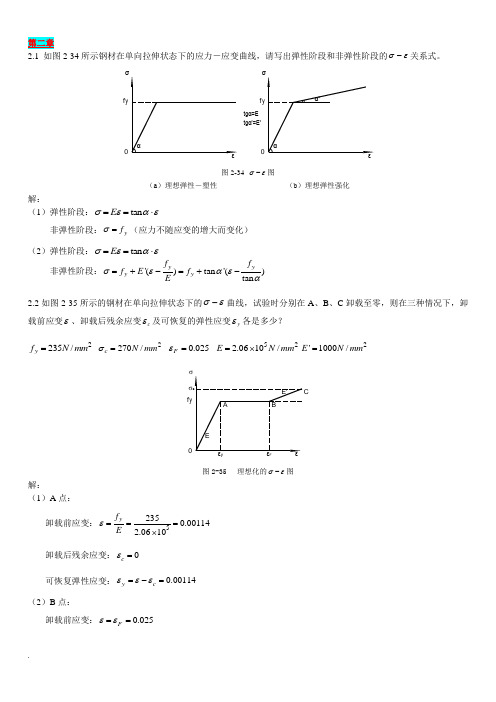
2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε==卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

钢结构基本原理(沈祖炎)课后习题答案完全版之欧阳治创编

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅ 非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386yc f E εε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+= 卸载后残余应变：0.05869c c Eσεε=-= 可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

钢结构基本原理课后习题答案解析完全版

2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线,请写出弹性阶段和非弹性阶段的σε-关系式.图2-34 σε-图〔a 〕理想弹性－塑性〔b 〕理想弹性强化解：〔1〕弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=〔应力不随应变的增大而变化〕〔2〕弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？图2-35 理想化的σε-图解：〔1〕A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=〔2〕B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=〔3〕C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下,钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系. 答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时,即材料处于弹性阶段时,反复应力作用下钢材材性无变化,不存在残余变形,钢材σε-曲线基本无变化；当y f σ>时,即材料处于弹塑性阶段,反复应力会引起残余变形,但若加载－卸载连续进行,钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低〔时效现象〕.钢材σε-曲线会相对更高而更短.另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材σε-曲线也会更高而更短.钢材疲劳强度与反复力大小和作用时间关系：反复应力大小对钢材疲劳强度的影响以应力比或应力幅〔焊接结构〕来量度.一般来说,应力比或应力幅越大,疲劳强度越低；而作用时间越长〔指次数多〕,疲劳强度也越低.2.4试述导致钢材发生脆性破坏的各种原因. 答：〔1〕钢材的化学成分,如碳、硫、磷等有害元素成分过多；〔2〕钢材生成过程中造成的缺陷,如夹层、偏析等；〔3〕钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响；〔4〕钢材工作温度影响,可能会引起蓝脆或冷脆；〔5〕不合理的结构细部设计影响,如应力集中等；〔6〕结构或构件受力性质,如双向或三向同号应力场；〔7〕结构或构件所受荷载性质,如受反复动力荷载作用. 2.5 解释以下名词：〔1〕延性破坏延性破坏,也叫塑性破坏,破坏前有明显变形,并有较长持续时间,应力超过屈服点fy 、并达到抗拉极限强度fu 的破坏.〔2〕损伤累积破坏指随时间增长,由荷载与温度变化,化学和环境作用以及灾害因素等使结构或构件产生损伤并不断积累而导致的破坏.〔3〕脆性破坏脆性破坏,也叫脆性断裂,指破坏前无明显变形、无预兆,而平均应力较小〔一般小于屈服点fy 〕的破坏. 〔4〕疲劳破坏指钢材在连续反复荷载作用下,应力水平低于极限强度,甚至低于屈服点的突然破坏. 〔5〕应力腐蚀破坏应力腐蚀破坏,也叫延迟断裂,在腐蚀性介质中,裂纹尖端应力低于正常脆性断裂应力临界值的情况下所造成的破坏.〔6〕疲劳寿命指结构或构件中在一定恢复荷载作用下所能承受的应力循环次数. 2.6 一两跨连续梁,在外荷载作用下,截面上A 点正应力为21120/N mm σ=,2280/N mm σ=-,B 点的正应力2120/N mm σ=-,22120/N mm σ=-,求梁A 点与B 点的应力比和应力幅是多少？解：〔1〕A 点：应力比：21800.667120σρσ==-=- 应力幅：2max min 12080200/N mm σσσ=-=+= 〔2〕B 点：应力比：12200.167120σρσ=== 应力幅：2max min 20120100/N mm σσσ=-=-+= 2.7指出以下符号意义： <1>Q235AF <2>Q345D <3>Q390E<4>Q235D答：〔1〕Q235AF ：屈服强度2235/y f N mm =、质量等级A 〔无冲击功要求〕的沸腾钢〔碳素结构钢〕〔2〕Q345D ：屈服强度2345/y f N mm =、质量等级D 〔要求提供-200C 时纵向冲击功34k A J =〕的特殊镇静钢〔低合金钢〕〔3〕Q390E ：屈服强度2390/y f N mm =、质量等级E 〔要求提供-400C 时纵向冲击功27k A J =〕的特殊镇静钢〔低合金钢〕〔4〕Q235D ：屈服强度2235/y f N mm =、质量等级D 〔要求提供-200C 时纵向冲击功27k A J =〕的特殊镇静钢〔碳素结构钢〕2.8根据钢材下选择原则,请选择以下结构中的钢材牌号：〔1〕在北方严寒地区建造厂房露天仓库使用非焊接吊车梁,承受起重量Q>500KN 的中级工作制吊车,应选用何种规格钢材品种？〔2〕一厂房采用焊接钢结构,室内温度为-100C,问选用何种钢材？答：〔1〕要求钢材具有良好的低温冲击韧性性能、能在低温条件下承受动力荷载作用,可选Q235D 、Q345D 等；〔2〕要求满足低温可焊性条件,可选用Q235BZ 等.2.9钢材有哪几项主要机械指标？各项指标可用来衡量钢材哪些方面的性能？答：主要机械性能指标：屈服强度y f 、极限强度u f 以及伸长率5δ或10δ,其中,屈服强度y f 、极限强度u f 是强度指标,而伸长率5δ或10δ是塑性指标.2.10影响钢材发生冷脆的化学元素是哪些？使钢材发生热脆的化学元素是哪些？答：影响钢材发生冷脆的化学元素主要有氮和磷,而使钢材发生热脆的化学元素主要是氧和硫. 第四章第五章5.1 影响轴心受压稳定极限承载力的初始缺陷有哪些?在钢结构设计中应如何考虑? 5.2 某车间工作平台柱高2.6m,轴心受压,两端铰接.材料用I16,Q235钢,钢材的强度设计值2215/d f N mm =.求轴心受压稳定系数ϕ及其稳定临界荷载. 如改用Q345钢2310/d f N mm =,则各为多少?解答:查P335附表3-6,知I16截面特性,26.57, 1.89,26.11x y i cm i cm A cm ===柱子两端较接,1.0x y μμ==故柱子长细比为1.0260039.665.7x x xli μλ⨯===,2600 1.0137.618.9y y y l i μλ⨯===因为x yλλ<,故对于Q235钢相对长细比为137.61.48λπ===钢柱轧制,/0.8b h ≤.对y 轴查P106表5-4<a>知为不b 类截面. 故由式5-34b 得<或计算137.6λ=,再由附表4-4查得0.354ϕ=>故得到稳定临界荷载为20.35426.1110215198.7crd d N Af kNϕ==⨯⨯⨯=当改用Q365钢时,同理可求得 1.792λ=.由式5-34b 计算得0.257ϕ= <或由166.7λ=,查表得0.257ϕ=>故稳定临界荷载为20.25726.1110310208.0crd d N Af kNϕ==⨯⨯⨯=5.3 图5-25所示为一轴心受压构件,两端铰接,截面形式为十字形.设在弹塑性范围内/E G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为Q235.5.4 截面由钢板组成的轴心受压构件,其局部稳定计算公式是按什么准则进行推导得出的.5.5 两端铰接的轴心受压柱,高10m,截面为三块钢板焊接而成,翼缘为剪切边,材料为Q235,强度设计值2205/d f N mm =,承受轴心压力设计值3000kN <包括自重>.如采用图5-26所示的两种截面,计算两种情况下柱是否安全.图5-26 题5.5 解答:截面特性计算: 对a>截面: 对b>截面:整体稳定系数的计算: 钢柱两端铰接,计算长度10000ox oy l l mm==对a>截面:1000040.88244.6ox x x l i λ===1000075.87131.8ox yy l i λ===对b>截面:1000050.08199.7kx x x l i λ===1000094.88105.4ox y yl i λ===根据题意,查P106表5-4<a>,知钢柱对x 轴为b 类截面,对y 轴为c 类截面. 对a>截面: 对x 轴:<或计算40.88λ=,再由附表4-4查得0.896xϕ>对y 轴:<或计算75.87λ=,再由附表4-5查得0.604yϕ>故取该柱的整体稳定系数为0.604ϕ= 对b>截面,同理可求得0.852x ϕ=,0.489y ϕ=,故取该柱截面整体稳定系数为0.489ϕ=整体稳定验算: 对a>截面 0.604240002052971.68 3000 crd d N Af kN kN ϕ==⨯⨯=<不满足.对b>截面0.489240002052405.88 3000 crd N kN kN =⨯⨯=<不满足.5.6 一轴心受压实腹柱,截面见图5-27.求轴心压力设计值.计算长度08x l m =,04y l m =<x轴为强轴>.截面采用焊接组合工字形,翼缘采用I28a 型钢.钢材为Q345,强度设计值2310/d f N mm =.5.7 一轴心受压缀条柱,柱肢采用工字型钢,如图5-28所示.求轴心压力设计值.计算长度030x l m =,015y l m =<x轴为虚轴>,材料为Q235,2205/d f N mm =.图5-28 题5.7 解答:截面及构件几何性质计算截面面积:2286.07172.14A cm =⨯= I40a 单肢惯性矩:41659.9I cm =绕虚轴惯性矩:241102[659.986.07()]522043.32x I cm =⨯+⨯=绕实轴惯性矩:422171443428y I cm =⨯=回转半径:55.07x i cm===15.88y i cm =长细比:300054.4855.07ox x x l i λ===150094.4615.88oy y y l i λ===缀条用L75⨯6,前后两平面缀条总面积2128.79717.594x A cm =⨯=由P111表5-5得：56.85ox λ===构件相对长细比,因ox yλλ<,只需计算yλ:查P106表5-4<a>可知应采用b 类截面：<或计算94.46λ=,再由附表4-4查得0.591ϕ=>故轴的压力设计值为20.591172.14102052085.6crd d N Af kNϕ==⨯⨯⨯=5.8 验算一轴心受压缀板柱.柱肢采用工字型钢,如图5-29所示.已知轴心压力设计值2000N kN =<包括自重>,计算长度020x l m =,010y l m =<x轴为虚轴>,材料为Q235, 2205/d f N mm =,2125/vd f N mm =.图5-29 题5.8 解答:一、整体稳定验算截面及构件几何性质计算:截面面积:2286.07172.14A cm =⨯= I40a 单肢惯性矩:41659.9I cm =绕虚轴惯性矩:241102[659.986.07()]522043.32x I cm =⨯+⨯=绕实轴惯性矩:422171443428y I cm =⨯=回转半径:55.07x i cm===15.88y i cm =长细比:200036.3255.07ox x x l i λ===100062.9715.88oy yy l i λ===缀板采用303001100mm ⨯⨯. 计算知1/6b K K >,由P111表5-5得46.40ox λ===<其中18028.882.77λ==>构件相对长细比: 因ox yλλ<,只需计算yλ:查P106表5-4<a>可知应采用b 类截面<或计算62.97λ=,再由附表4-4查得0.791ϕ=>故20.791172.14102052791.34crd d N Af kNϕ==⨯⨯⨯=,满足.二、局部稳定验算:1>单肢截面板件的局部稳定单肢采用型钢,板件不会发生局部失稳. 2>受压构件单肢自身稳定单肢回转半径1 2.77i cm=长细比满足：01max 18028.880.50.562.9731.492.77a i λλ===<=⨯=,且满足140λ<故单肢自身稳定满足要求.3>缀板的稳定轴心受压构件的最大剪力:2max172.14102054151685V N ⨯⨯===缀板剪力:14151611002075821100a T V N c ==⨯=缀板弯矩:71415161100 1.14210222a M V N mm ==⨯=⨯缀板厚度满足:11003027.5 40b t mm =≥=,故只作强度验算:故由以上整体稳定验算和局部稳定验算可知,该缀板柱满足要求.5.9 有一拔杆,采用Q235钢,2215/d f N mm =,如图5-30所示,缀条采用斜杆式体系.设考虑起吊物时的动力作用等,应将起重量乘以1.25,并设平面内、外计算长度相等.问60θ=︒时,拔杆最大起重量设计值为多少? 第六章6.1 工字形焊接组合截面简支梁,其上密铺刚性板可以阻止弯曲平面外变形.梁上均布荷载〔包括梁自重〕4/q kN m =,跨中已有一集中荷载090F kN =,现需在距右端4m 处设一集中荷载1F .问根据边缘屈服准则,1F 最大可达多少.设各集中荷载的作用位置距梁顶面为120mm,分布长度为120mm.钢材的设计强度取为2300/N mm .另在所有的已知荷载和所有未知荷载中,都已包含有关荷载的分项系数.图6-34 题6.1解：〔1〕计算截面特性〔2〕计算0F 、1F 两集中力对应截面弯矩令10M M >,则当1147F kN >,使弯矩最大值出现在1F 作用截面. 〔3〕梁截面能承受的最大弯矩令0M M =得：1313.35F kN =；令1M M =得：1271.76F kN = 故可假定在1F 作用截面处达到最大弯矩. 〔4〕a ．弯曲正应力61max 68(244)1033003.22910x x F M W σ+⨯==≤⨯① b.剪应力1F 作用截面处的剪力1111122412449053()2233V F F kN ⎛⎫=⨯⨯-⨯+⨯+=+ ⎪⎝⎭311max925310185800031.33108m x F V S I t τ⎛⎫+⨯⨯ ⎪⎝⎭==≤⨯⨯② c.局部承压应力在右侧支座处：()312244510330081205122120c F σ⎛⎫++⨯⎪⎝⎭=≤⨯+⨯+⨯③ 1F 集中力作用处：()311030081205122120c F σ⨯=≤⨯+⨯+⨯④d.折算应力1F 作用截面右侧处存在很大的弯矩,剪力和局部承压应力,计算腹板与翼缘交界处的分享应力与折算应力.正应力：1400412x x M W σ=⋅剪应力：31111925310121800031.33108x F V S I t τ⎛⎫+⨯⨯ ⎪⎝⎭==⨯⨯局部承压应力：()311081205122120c F σ⨯=⨯+⨯+⨯联立①-⑤解得：1271.76F kN ≤故可知1max 271.76F kN =,并且在1F 作用截面处的弯矩达到最大值.6.2 同上题,仅梁的截面为如图6-35所示.6.3 一卷边Z 形冷弯薄壁型钢,截面规格1606020 2.5⨯⨯⨯,用于屋面檩条,跨度6m.作用于其上的均布荷载垂直于地面, 1.4/q kN m =.设檩条在给定荷载下不会发生整体失稳,按边缘屈服准则作强度计算.所给荷载条件中已包含分项系数.钢材强度设计值取为2210/N mm .6.4 一双轴对称工字形截面构件,一端固定,一端外挑4.0m,沿构件长度无侧向支承,悬挑端部下挂一重载F .若不计构件自重,F 最大值为多少.钢材强度设计值取为2215/N mm .图6-37 题6.4解：〔1〕截面特性计算〔2〕计算弯曲整体稳定系数按《钢结构设计规范》附录B 公式B.1-1计算梁的整体稳定系数查表B.4,由于荷载作用在形心处,按表格上下翼缘的平均值取值：截面为双轴对称截面,0b η=则24320235]b b b x y y Ah W f ϕβηλ=⋅⋅ 取0.282' 1.070.9853.333b ϕ=-= 〔3〕F 最大值计算由,,400022x xb b h h M F f I I ϕϕ⋅⨯⨯=≤,解得30.02F kN =. 6.5 一双轴对称工字形截面构件,两端简支,除两端外无侧向支承,跨中作用一集中荷载480F kN =,如以保证构件的整体稳定为控制条件,构件的最大长度l 的上限是多少.设钢材的屈服点为2235/N mm 〔计算本题时不考虑各种分项系数〕.图6-38 题6.5解：依题意,当1113.0l b <时,整体稳定不控制设计,故长度需满足13.04005200 5.2l mm m ≥⨯==.〔1〕截面特性计算〔2〕整体稳定计算按《钢结构设计规范》附录B 公式B.5-1近似计算梁的整体稳定系数：21.0744000235y yb f λϕ=-⋅①又有 y yl i λ=② 由整体稳定有2b x hM f I ϕ⋅≤⋅,即142b x h Fl I f ϕ⋅≤③ 联立①-③解得：12283l mm ≤ 故可取max 12.28l m =.〔注：严格应假定长度l ,再按《钢结构设计规范》附录B 公式B.1-1计算梁的整体稳定系数,然后验算③式,通过不断迭代,最终求得的长度为所求〕第七章压弯构件7.1 一压弯构件长15m,两端在截面两主轴方向均为铰接,承受轴心压力1000N kN =,中央截面有集中力150F kN =.构件三分点处有两个平面外支承点〔图7-21〕.钢材强度设计值为2310/N mm .按所给荷载,试设计截面尺寸〔按工字形截面考虑〕.解：选定截面如下图示：图1 工字形截面尺寸下面进行截面验算：〔1〕截面特性计算〔2〕截面强度验算36226100010562.510172.3/310/20540 4.4810x M N N mm f N mm A W σ⨯⨯=+=+=<=⨯ 满足.〔3〕弯矩作用平面内稳定验算长细比1500056.3266.2x λ== 按b 类构件查附表4-4,56.368.2==,查得0.761x ϕ=. 弯矩作用平面内无端弯矩但有一个跨中集中荷载作用：371000101.00.2 1.00.20.981.2010 1.1mxEX N N β⨯=-⨯=-⨯=⨯⨯, 取截面塑性发展系数 1.05x γ= 22189.54/310/N mm f N mm =<= ,满足.〔4〕弯矩作用平面外稳定验算长细比500075.566.2y λ==,按b 类构件查附表4-4, 75.591.5=,查得0.611x ϕ=. 弯矩作用平面外侧向支撑区段,构件段有端弯矩,也有横向荷载作用,且端弯矩产生同向曲率,取 1.0tx β=.弯矩整体稳定系数近似取2275.53451.07 1.070.884400023544000235yyb f λϕ=-⋅=-⨯=,取截面影响系数 1.0η=. 满足.〔5〕局部稳定 a.翼缘：15077.1510.720b t -==<=〔考虑有限塑性发展〕,满足要求. b.腹板腹板最大压应力：3620max6100010562.510610166.6/205406504.4810x h N M N mm A W h σ⨯⨯=+⋅=+⨯=⨯ 腹板最小压应力：3620min6100010562.51061069.2/205406504.4810x h N M N mm A W h σ⨯⨯=-⋅=-⨯=-⨯ 系数max min 0max 166.669.2 1.42166.6σσασ-+===[[061043.6160.52516 1.420.556.32562.614w w h t αλ==<++⨯+⨯+,满足. 由以上验算可知,该截面能满足要求.7.2 在上题的条件中,将横向力F 改为作用在高度10m 处,沿构件轴线方向,且有750mm 偏心距,图7-22,试设计截面尺寸.7.3 一压弯构件的受力支承及截面如图7-23所示〔平面内为两端铰支支承〕.设材料为Q235〔2235/y f N mm =〕,计算其截面强度和弯矩作用平面内的稳定性. 解：〔1〕截面特性计算〔2〕截面强度验算362268001012010148.9/215/10960 1.5810x M N N mm f N mm A W σ⨯⨯=+=+=<=⨯,满足. 〔3〕弯矩作用平面外的稳定验算长细比1200070.8169.6x λ==,按b 类构件查附表4-4,70.870.8=,查得0.746x ϕ=. 弯矩作用平面内构件段有有横向荷载作用,也有端弯矩作用且端弯矩产生反向曲率,取：取截面塑性发展系数 1.05x γ=,22133.6/215/N mm f N mm =<=,满足.故可知,该截面强度和平面内稳定均得到满足.7.4 某压弯缀条式格构构件,截面如图7-24所示,构件平面内外计算长度029.3x l m =,018.2y l m =.已知轴压力〔含自重〕2500N kN =,问可以承受的最大偏心弯矩x M 为多少.设钢材牌号为Q235,N 与x M 均为设计值,钢材强度设计值取2205/N mm . 解：〔1〕截面特性计算63I a ：215459A mm =849.4010x I mm =⨯,741.7010y I mm =⨯,264.6x i mm =,33.2y i mm = 12510L ⨯：2243.73A mm =,最小回转半径min 24.6i mm =格构截面：由于截面无削弱,失稳破坏一般先于强度破坏,故这里不考虑强度破坏的问题. 〔2〕平面内整体稳定虚轴方向长细比2930032.5901.0ox x x l i λ===换算长细比52.6ox λ== 按b 类构件查附表4-4,查得0.845x ϕ=,取弯矩等效系数 1.0mx β=. 根据平面内整体稳定计算公式有：11'mx xx x x EX M Nf AN W N βϕϕ+≤⎛⎫- ⎪⎝⎭①〔3〕单肢稳定单肢最大压力：max 21800xM N N =+② 最大受压分肢弯矩平面内长细比：1180054.233.2x λ== 最大受压分肢弯矩平面外长细比：11820073.8246.6y λ==11y x λλ>,按轴心受压构件查附表4-4得稳定系数10.728y ϕ=根据轴心受压构件稳定计算公式：max1y N f Aϕ≤③ <4>缀条稳定由缀条稳定计算公式看出,斜缀条的受力与所求x M 无关,这里不作考虑因此,由①计算得2741x M kN m ≤⋅,由②③计算得1902x M kN m ≤⋅,取1902x M kN m =⋅.第八章连接的构造与计算 8.1、下图中I32a 牛腿用对接焊缝与柱连接.钢材为Q235钢,焊条为E43型,手工焊,用II 级焊缝的检验质量标准.对接焊缝的抗压强度设计值2215/w f f N mm =,抗剪强度设计值2125/w v f N mm =.已知：I32a 的截面面积267.12A cm =；截面模量3692.2x W cm =,腹板截面面积225.4w A cm =.试求连接部位能承受的外力F 的最大值〔施焊时加引弧板〕.图牛腿连接示意图解：T V 707.0=,T N 707.0=<1>221125104.25707.0mm N T A V w =⨯==τ<或：2211251095.032707.0mm N T A V w =⨯⨯==τ<2>2222154.141707.0mm NWT A T =+=σ <3> 折算应力〔在顶部中点亦可〕得：)(1.4263KN T ≤ 〔KNT f T 3wf 33.484 1.10.000488≤≤或〕由T 1、T 2、T 3中取最小值,得T ＝426.1〔KN 〕8.3、有一支托角钢,两边用角焊缝与柱连接〔如图〕.400N KN =,钢材为Q345钢,焊条为E50型,手工焊,2200/w f f N mm =.试确定焊缝厚度.图支托连接示意图解：200=w l22.1=f β,f ff f h h A V 6.14282801045=⨯==τmmh f 4.7≥,取mmh f 8=.8.5、如图所示的牛腿用角焊缝与柱连接.钢材为Q235钢,焊条用E43型,手工焊,角焊缝强度设计值2160/w f f N mm =.350T kN=,验算焊缝的受力.图牛腿角焊缝示意图解：焊缝所受内力为：247.45N kN =,247.45V kN =,49.49M kN m =⋅焊缝有效厚度：上翼缘最外侧焊缝：上翼缘与腹板交界处：折算应力：牛腿角焊缝满足要求.8.6、计算如图所示的工字形截面焊接梁在距支座5m 拼接处的角焊缝.钢材为Q345钢,焊条为E50型,2200/w f f N mm =,200F kN =.问：〔1〕腹板拼接处是否满足要求？〔2〕确定翼缘2．强度计算：(1) 翼缘强度计算：由232007.0)22.14002240(46.1105.1683mm N h fm mN ≤⨯⨯⨯+⨯⨯⨯⋅设mmh f 10=即2007.1701≤fh ,得：mmf h 5.8≥,取mmf h 10=(2) 腹板连接强度也可直接略去中间段竖焊缝,按下面方法计算：由WM 引起的：29634.2410535.124.137109.543mm N M f y=⨯⨯⨯⨯=σ<两侧有板> 由V 引起：2332.2290051020087.0)4802162(210200mm Nh l V e w Vf y=⨯=⨯⨯+⨯⨯⨯==τ22222003.1212.115)22.13.242.22(mm N mm N <=++,满足强度要求. 8.7、验算如图所示桁架节点焊缝"A"是否满足要求,确定焊缝"B"、"C"的长度.已知焊缝A 的角焊缝10f h mm=,焊缝B 、C 的角焊缝6f h mm=.钢材为Q235B 钢.焊条用E43型,手工焊,2160/w f f N mm =.在不利组合下杆件力为1150N kN =,2489.41N kN =,3230N kN =,414.1N kN =,5250N kN=.图桁架受力示意图解：〔1〕焊缝A 的受力：〔2〕确定焊缝"B"、"C"的长度：等边角钢双面焊.焊缝B ：肢背7.0=μ,mm3132********.0102307.0＝＋＝背⨯⨯⨯⨯⨯B l 肢尖3.0=μ,mm36412216067.0102303.0＝＋＝尖⨯⨯⨯⨯⨯B l 焊缝C ：肢背,mm3C 14312216067.0102507.0＝＋＝背⨯⨯⨯⨯⨯l 肢尖,mm3C 6812216067.0102503.0＝＋＝尖⨯⨯⨯⨯⨯l8.9、下图所示为一梁柱连接,100M kN m =⋅,600V kN =.钢材为Q235C 钢.剪力V 由支托承受,焊条用E43型,角焊缝的强度设计值2160/w f f N mm =,端板厚14mm,支托厚20mm.〔1〕求角焊缝"A"的fh .〔2〕弯矩M 由螺栓承受,4.8级螺栓M24,验算螺栓强度.2170/b t f N mm =.图梁柱连接示意图解：<1>Nh f 510621602807.0⨯=⨯⨯⨯⨯mmf h 57.921602807.01065=⨯⨯⨯⨯=,取10mm<2>2622222max 1002)3625941(600101002)600500300200100(600⨯⨯++++⨯⨯=⨯++++⨯=M N螺栓强度满足要求.8.10、确定如图所示A 级螺栓连接中的力F 值.螺栓M20,250N kN =,钢板采用Q235B,厚度为t=10mm,螺栓材料为45号钢〔8.8级〕,2320/b v f N mm =,2405/b c f N mm =.图螺栓连接示意图解：(1) 抗剪： <2> 承压：<3> 净截面：NF F 33003102.668];21510)5.203200[(1210⨯=⨯⨯⨯-=〔后线〕 NF 3'3109.55621510)5.202300(⨯=⨯⨯⨯-= 〔前线〕NF 3''3104.31621510)55.204414.130240(⨯=⨯⨯⨯-⨯⨯+⨯=〔折线〕最终取KN F 9.556≤8.12、如图所示的螺栓连接采用45号钢,A 级8.8级螺栓,直径16d mm =,2320/b v f N mm =,2405/b c f N mm =.钢板为Q235钢,钢板厚度12mm,抗拉强度设计值2215/f N mm =.求此连接能承受的max F 值.图螺栓连接示意图解：<1> 抗剪：23110132320261210F Nπ=⨯⨯⨯=⨯<2> 承压：32202013405210610F N=⨯⨯⨯=⨯<3> 净截面：NF 3310111220)5.61320(215⨯=⨯-⨯=选用KNF 1112max =若用M16替M20,则：选用1163KN. 8.13、8.14、下图梁的拼接用高强度螺栓承压型连接,F=200kN,构造如下图所示,高强度螺栓的钢材为10.9级,梁的钢板用Q235B,螺栓M20,梁连接处的接触面采用喷砂处理,螺栓的强度设计值2310/b v f N mm =,2470/b c f N mm =.〔1〕确定翼缘接头处螺栓数目和连接板尺寸；〔2〕验算腹板拼接螺栓是否满足要求. 图梁拼接示意图解：KN A V 200=,mKN A M ⋅=2200腹板mKN W M ⋅=5.516,翼缘mKN f M ⋅=5.1683(1) 计算翼缘连接：KNm y N 115346.15.1683==取M20,P n N f b v μ⨯=9.045.0=μKNP 155= 〔查表〕i 〕摩擦型：NN b v 3310775.621015545.09.0⨯=⨯⨯⨯=承压型：KNNb vbvf d N 39.9797389310420422==⨯⨯==ππ〔注：新规范取此值,但荷载性质同普通螺栓〕按KNb v N 6.81775.623.1(3.1＝摩擦）＝⨯, 取KNb v N 6.81=单面连接：5.151.11.146.811.111531.1=⨯=⨯=⨯=bv y f N N n ,取M20,16个,布置情况如下图所示：ii 〕净截面：〔注：按平列166=σ；按错列第一排7.153=σ〕(2) 抗剪〔腹板〕连接：KN A V 200=,mKN m KN W M ⋅=⨯+=5.53409.02005.516KN 6.81<,满足.8.15、下图所示为屋架与柱的连接节点.钢材为Q235B,焊条用E43型,手工焊.C 级普通螺栓用Q235BF 钢.已知：2160/w f f N mm =,2170/b t f N mm =.〔1〕验算角焊缝A 的强度,确定角焊缝B 、C 、D 的最小长度,焊缝厚度10f h mm=.〔2〕验算连接于钢柱的普通螺栓强度,假定螺栓不受剪力〔即连接处竖向力由支托承受〕.螺栓直径为24mm. 图屋架节点示意图解：<1> 验算承托两侧焊缝：KN KNV 15.318707.0450=⨯=1606.2067.01021103181502=>=⨯⨯⨯=wf f f mm N τ 不满足.用三面围焊,承托宽度为150mm .221608.1227.010)1502110(318150mm N f mm N w f f =<=⨯⨯+⨯=τ,满足.<2> 斜杆肢背焊缝验算,焊缝C 〔肢尖焊缝不必计算〕注：此处按构造焊缝厚度不得大于mm mm6.982.1=⨯,略超出.(3) 水平杆肢背,焊缝D(4) 焊缝A ： (5) 螺栓验算：先设拉力和M 作用下螺栓全部受拉,绕螺栓群形心转动.说明螺栓不是全部受拉,另行假设绕顶排螺栓转动：查表得：所以max bt N N <,满足强度要求.。

钢结构基本原理-同济第二版沈祖炎重点习题课后答案

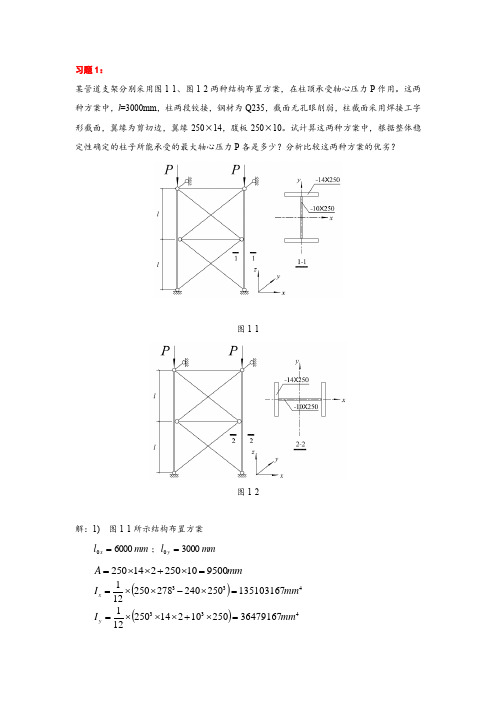
习题1：某管道支架分别采用图1-1、图1-2两种结构布置方案，在柱顶承受轴心压力P 作用。

这两种方案中，l =3000mm ，柱两段铰接，钢材为Q235，截面无孔眼削弱，柱截面采用焊接工字形截面，翼缘为剪切边，翼缘-250×14，腹板-250×10。

试计算这两种方案中，根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少？分析比较这两种方案的优劣？图1-1图1-2解：1) 图1-1所示结构布置方案mm l x 60000=；mm l y 30000=mm A 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=mm A I i x x 3.1199500135103167===；mm AI i y y 0.62950036479167===3.503.11960000===x x x i l λ；4.480.6230000===y y y i l λ此截面对x 轴为b 类，对y 轴为c 类，查表得855.0=x ϕ(附表4-4)；785.0=y ϕ(附表4-5)应根据y ϕ确定柱子整体稳定的承载力kN Af P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案mm l x 60000=；mm l y 30000=mm A 9500=；mm i x 0.62=；mm i y 3.119= 8.960.6260000===x x x i l λ；1.253.11930000===y y y i l λ此截面对x 轴为c 类，对y 轴为b 类，查表得478.0=x ϕ(附表4-5)；953.0=y ϕ(附表4-4)应根据x ϕ确定柱子整体稳定的承载力kN Af P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同，但是图1-1所示方案（为下文表述的方便，以后简称方案A ）的承载力为1603kN ，而图1-2所示方案（为下文表述的方便，以后简称方案B ）的承载力仅为976kN 。

同济大学钢结构基本原理课后习题答案完全版

第二章如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？ 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε= 可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f E εε=-= 可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变：0.05869c c E σεε=-= 可恢复弹性应变：0.00131y c εεε=-=试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

(完整版)钢结构基本原理课后习题与答案完全版

2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε==卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

2023大学_钢结构基本原理第二版(沈祖炎著)课后答案下载

2023钢结构基本原理第二版（沈祖炎著）课后答
案下载
2023钢结构基本原理第二版（沈祖炎著）课后答案下载
前言
第一章绪论.
第一节钢结构的特点和应用
第二节钢结构设计要求与设计方法
第三节钢结构的发展方向
第四节本课程的主要内容、特点和学习方法
思考题
第二章钢结构的材料
第一节钢结构对材料的要求
第二节钢材的塑性破坏和脆性破坏
第三节钢材的主要性能
第四节影响钢材性能的因素
第五节钢材的疲劳
第六节钢材的种类和规格
思考题
钢结构基本原理第二版（沈祖炎著）：内容简介
点击此处下载钢结构基本原理第二版（沈祖炎著）课后答案
钢结构基本原理第二版（沈祖炎著）：图书目录
本书主要依据国家标准《钢结构设计规范》(GB 50017--)编写。

全书共分七章，基本内容包括绪论、钢结构的材料、钢结构的'连接、轴心受力构件、受弯构件设计、拉弯压弯构件和钢结构最新技术。

(完整版)钢结构基本原理同济第二版沈祖炎重点习题课后答案

习题1：某管道支架分别采用图1-1、图1-2两种结构布置方案，在柱顶承受轴心压力P 作用。

这两种方案中，l =3000mm ，柱两段铰接，钢材为Q235，截面无孔眼削弱，柱截面采用焊接工字形截面，翼缘为剪切边，翼缘-250×14，腹板-250×10。

试计算这两种方案中，根据整体稳定性确定的柱子所能承受的最大轴心压力P 各是多少？分析比较这两种方案的优劣？图1-1图1-2解：1) 图1-1所示结构布置方案；mm l x 60000=mml y 30000=mmA 950010250214250=⨯+⨯⨯=()433135103167250240278250121mm I x =⨯-⨯⨯=()4333647916725010214250121mm I y =⨯+⨯⨯⨯=；mm A I i x x 3.1199500135103167===mmAI i y y 0.62950036479167===；3.503.11960000===x x x i l λ4.480.6230000===y y y i l λ此截面对x 轴为b 类，对y 轴为c 类，查表得(附表4-4)；(附表4-5)855.0=x ϕ785.0=y ϕ应根据确定柱子整体稳定的承载力y ϕkNAf P d y 16032159500785.0max =⨯⨯==ϕ2) 图1-2所示结构布置方案；mm l x 60000=mml y 30000=；；mm A 9500=mm i x 0.62=mmi y 3.119=；8.960.6260000===x x x i l λ1.253.11930000===y y y i l λ此截面对x 轴为c 类，对y 轴为b 类，查表得(附表4-5)；(附表4-4)478.0=x ϕ953.0=y ϕ应根据确定柱子整体稳定的承载力x ϕkNAf P d x 9762159500478.0max =⨯⨯==ϕ3) 分析比较两种结构布置方案所使用的材料完全相同，但是图1-1所示方案（为下文表述的方便，以后简称方案A ）的承载力为1603kN ，而图1-2所示方案（为下文表述的方便，以后简称方案B ）的承载力仅为976kN 。

同济大学钢结构基本原理课后习题答案完全

第二章如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？ 2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε= 可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f E εε=-= 可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c y F f E σεε-=-=+= 卸载后残余应变：0.05869c c E σεε=-= 可恢复弹性应变：0.00131y c εεε=-=试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版 (1)

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσF图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

钢结构基本原理(沈祖炎)课后习题答案完全版

第二章2。

1 如图2－３4所示钢材在单向拉伸状态下的应力-应变曲线,请写出弹性时期和非弹性时期的关系式、图２－34 图(a)理想弹性－塑性ﻩﻩ (ｂ)理想弹性强化解:(1)弹性时期:非弹性时期:(应力不随应变的增大而变化)(2)弹性时期:非弹性时期:2。

2如图2—35所示的钢材在单向拉伸状态下的曲线,试验时分别在A 、B 、C 卸载至零,则在三种情况下,卸载前应变、卸载后残余应变及可恢复的弹性应变各是多少？图2—35ﻩ理想化的图解:(1)A 点:卸载前应变:卸载后残余应变:ﻩ可恢复弹性应变:(２)B 点:ﻩ卸载前应变:卸载后残余应变:ﻩ可恢复弹性应变:(3)C 点:ﻩ卸载前应变:卸载后残余应变:ﻩ可恢复弹性应变:２、3试述钢材在单轴反复应力作用下,钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答:钢材曲线与反复应力大小和作用时间关系:当构件反复力时,即材料处于弹性时期时,反复应力作用下钢材材性无变化,不存在残余变形,钢材曲线基本无变化;当时,即材料处于弹塑性时期,反复应力会引起残余变形,但若加载—卸载连续进行,钢材曲线也基本无变化;若加载－卸载具有一定时间间隔,会使钢材屈服点、极限强度提高,而塑性韧性降低(时效现象)。

钢材tgα'=E'f y0f y 0tgα=E曲线会相对更高而更短。

另外,载一定作用力下,作用时间越快,钢材强度会提高、而变形能力减弱,钢材曲线也会更高而更短。

钢材疲劳强度与反复力大小和作用时间关系:反复应力大小对钢材疲劳强度的影响以应力比或应力幅(焊接结构)来量度。

一般来说,应力比或应力幅越大,疲劳强度越低;而作用时间越长(指次数多),疲劳强度也越低、2。

4试述导致钢材发生脆性破坏的各种原因。

答:(1)钢材的化学成分,如碳、硫、磷等有害元素成分过多;(2)钢材生成过程中造成的缺陷,如夹层、偏析等;(３)钢材在加工、使用过程中的各种影响,如时效、冷作硬化以及焊接应力等影响;(4)钢材工作温度影响,估计会引起蓝脆或冷脆;(5)不合理的结构细部设计影响,如应力集中等;(6)结构或构件受力性质,如双向或三向同号应力场;(7)结构或构件所受荷载性质,如受反复动力荷载作用。

钢结构基本原理(沈祖炎)课后习题答案完全版之欧阳音创编

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅非弹性阶段：'()tan '()tan yyy y f f f E f E σεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610yf E ε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε== 卸载后残余应变：0.02386yc f E εε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+= 卸载后残余应变：0.05869c c Eσεε=-= 可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

(完整版)钢结构基本原理课后习题与答案完全版

2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε==卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

(完整版)钢结构基本原理课后习题与答案完全版

2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f y 0f y 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f yσ图2-35 理想化的σε-图解：（1）A 点：卸载前应变：52350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=（2）B 点：卸载前应变：0.025F εε==卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版

第二章2.1 如图2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的σε-关系式。

tgα'=E'f 0f 0tgα=E 图2-34 σε-图（a ）理想弹性－塑性（b ）理想弹性强化解：（1）弹性阶段：tan E σεαε==⋅非弹性阶段：y f σ=（应力不随应变的增大而变化）（2）弹性阶段：tan E σεαε==⋅ 非弹性阶段：'()tan '()tan y y y y f f f E f Eσεαεα=+-=+-2.2如图2-35所示的钢材在单向拉伸状态下的σε-曲线，试验时分别在A 、B 、C 卸载至零，则在三种情况下，卸载前应变ε、卸载后残余应变c ε及可恢复的弹性应变y ε各是多少？2235/y f N mm = 2270/c N mm σ= 0.025F ε= 522.0610/E N mm =⨯2'1000/E N mm =f 0σF图2-35 理想化的σε-图解：（1）A 点：卸载前应变：2350.001142.0610y f Eε===⨯卸载后残余应变：0c ε=可恢复弹性应变：0.00114y c εεε=-=卸载前应变：0.025F εε== 卸载后残余应变：0.02386y c f Eεε=-=可恢复弹性应变：0.00114y c εεε=-=（3）C 点：卸载前应变：0.0250.0350.06'c yF f E σεε-=-=+=卸载后残余应变：0.05869cc Eσεε=-=可恢复弹性应变：0.00131y c εεε=-=2.3试述钢材在单轴反复应力作用下，钢材的σε-曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材σε-曲线与反复应力大小和作用时间关系：当构件反复力y f σ≤时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材σε-曲线基本无变化；当y f σ>时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材σε-曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

同济钢结构基本原理课后习题答案完全版

y
fy 235
166.7
,查表得 0.257 )
Ncrd Af d 0.257 26.11102 310 208.0kN
5.3 图 5-25 所示为一轴心受压构件 ,两端铰接 ,截面形式为十字形.设在弹塑性范围内 E / G 值保持常数,问在什么条件下,扭转屈曲临界力低于弯曲屈曲临界力,钢材为 Q235. 5.4 截面由钢板组成的轴心受压构件 ,其局部稳定计算公式是按什么准则进行推导得出的. 5.5 两端铰接的轴心受压柱,高 10m,截面为三块钢板焊接而成,翼缘为剪切边 ,材料为 Q235,强度设计值
1 1 I x 2 ( 500 203 20 500 2602 ) 8 5003 1.436 109 mm4 12 12 1 1 I y 2 20 5003 500 83 4.167 108 mm4 12 12
A 2 500 20 500 8 24000mm2
fy E
0.02386
可恢复弹性应变： y c 0.00114 （3） C 点：卸载前应变： F
c f y
E'
0.025 0.035 0.06
卸载后残余应变： c
c
E
0.05869
可恢复弹性应变： y c 0.00131 2.3 试述钢材在单轴反复应力作用下，钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。答：钢材曲线与反复应力大小和作用时间关系：当构件反复力 f y 时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材曲线基本无变化；当 f y 时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。钢材曲线会相对更高而更短。另外，载一定作用力下，作用时间越快，钢材强度会提高、而变形能力减弱，钢材曲线也会更高而更短。钢材疲劳强度与反复力大小和作用时间关系：反复应力大小对钢材疲劳强度的影响以应力比或应力幅（焊接结构）来量度。一般来说，应力比或应力幅越大，疲劳强度越低；而作用时间越长（指次数多），疲劳强度也越低。 2.4 试述导致钢材发生脆性破坏的各种原因。答：（ 1）钢材的化学成分，如碳、硫、磷等有害元素成分过多；（ 2）钢材生成过程中造成的缺陷，如夹层、偏析等；（3）钢材在加工、使用过程中的各种影响，如时效、冷作硬化以及焊接应力等影响；（ 4）钢材工作温度影响，可能会引起蓝脆或冷脆；（ 5）不合理的结构细部设计影响，如应力集中等；（ 6）结构或构件受力性质，如双向或三向同号应力场；（7）结构或构件所受荷载性质，如受反复动力荷载作用。 2.5 解释下列名词：（1）延性破坏延性破坏，也叫塑性破坏，破坏前有明显变形，并有较长持续时间，应力超过屈服点 fy、并达到抗拉极限强度 fu 的破坏。（2）损伤累积破坏指随时间增长，由荷载与温度变化，化学和环境作用以及灾害因素等使结构或构件产生损伤并不断积累而导致的破坏。

同济大学钢结构基本原理(沈祖炎)课后习题答案完全版

第二章2.1如图2-34所示钢材在单向拉伸状态下的应力一应变曲线，请写出弹性阶段和非弹性阶段的关系式。

解：（1）弹性阶段：E tan非弹性阶段：f y （应力不随应变的增大而变化）（2）弹性阶段：E tanf yf y 非弹性阶段：f y E'（丄）f y tan '（匚）Etan卸载后残余应变： c 0可恢复弹性应变:(2) B 点:（b ）理想弹性强化2.2如图2-35所示的钢材在单向拉伸状态下的曲线，试验时分别在 A 、B 、C 卸载至零,则在三种情况下，卸载前应变、卸载后残余应变 c 及可恢复的弹性应变y 各是多少?2f y 235N/mm 22c270 N / mm 2F 0.025 E 2.06 105N/mm 2 E' 1000N/mm 2解：（1）A 点：卸载前应f yE235 2.06 1050.001140.00114图图2-35 理想化的图卸载前应变：F0.025卸载后残余应变：c0.02386E可恢复弹性应变：y c0.00114(3) C点：c fy卸载前应变：F0.025 0.035 0.06 E'卸载后残余应变：c c0.05869 E可恢复弹性应变：y c0.001312.3试述钢材在单轴反复应力作用下，钢材的曲线、钢材疲劳强度与反复应力大小和作用时间之间的关系。

答：钢材曲线与反复应力大小和作用时间关系：当构件反复力| | fy时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材曲线基本无变化；当I I fy时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载-卸载连续进行，钢材曲线也基本无变化；若加载-卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。

钢材曲线会相对更高而更短。

另外，载一定作用力下，作用时间越快，钢材强度会提高、而变形能力减弱，钢材曲线也会更高而更短。

钢结构基本原理课后习题答案

钢结构基本原理课后习题答案【篇一：钢结构基本原理(沈祖炎)课后习题答案完全版】2-34所示钢材在单向拉伸状态下的应力－应变曲线，请写出弹性阶段和非弹性阶段的???关系式。

00图2-34 ???图（a）理想弹性－塑性（b）理想弹性强化解：（1）弹性阶段：??e??tan???非弹性阶段：??fy（应力不随应变的增大而变化）（2）弹性阶段：??e??tan???非弹性阶段：??fy?e(??fye)?fy?tan?(??fytan?)2.2如图2-35所示的钢材在单向拉伸状态下的???曲线，试验时分别在a、b、c卸载至零，则在三种情况下，卸载前应变?、卸载后残余应变?c及可恢复的弹性应变?y各是多少？fy?235n/mm2 ?c?270n/mm2 ?f?0.025e?2.06?105n/mm2e?1000n/mm20f图2-35 理想化的???图解：（1）a点：卸载前应变：??fye?235卸载后残余应变：?c?0 可恢复弹性应变：?y????c?0.00114卸载前应变：???f?0.025 卸载后残余应变：?c???fye?0.02386 可恢复弹性应变：?y????c?0.00114（3）c点：卸载前应变：???f??c?fye?0.025?0.035?0.06 ?卸载后残余应变：?c???c?0.05869 e可恢复弹性应变：?y????c?0.001312.3试述钢材在单轴反复应力作用下，钢材的?作用时间之间的关系。

??曲线、钢材疲劳强度与反复应力大小和答：钢材???曲线与反复应力大小和作用时间关系：当构件反复力??fy时，即材料处于弹性阶段时，反复应力作用下钢材材性无变化，不存在残余变形，钢材???曲线基本无变化；当??fy时，即材料处于弹塑性阶段，反复应力会引起残余变形，但若加载－卸载连续进行，钢材???曲线也基本无变化；若加载－卸载具有一定时间间隔，会使钢材屈服点、极限强度提高，而塑性韧性降低（时效现象）。