机器学习决策树 ID3算法的源代码

合集下载

决策树之ID3算法

决策树之ID3算法⼀、决策树之ID3算法简述 1976年-1986年，J.R.Quinlan给出ID3算法原型并进⾏了总结，确定了决策树学习的理论。

这可以看做是决策树算法的起点。

1993，Quinlan将ID3算法改进成C4.5算法，称为机器学习的⼗⼤算法之⼀。

ID3算法的另⼀个分⽀是CART(Classification adn Regression Tree, 分类回归决策树)，⽤于预测。

这样，决策树理论完全覆盖了机器学习中的分类和回归两个领域。

本⽂只做了ID3算法的回顾，所选数据的字段全部是有序多分类的分类变量。

C4.5和CART有时间另花篇幅进⾏学习总结。

本⽂需要有⼀定的pandas基础、了解递归函数。

1、ID3算法研究的核⼼思想是if-then，本质上是对数据进⾏分组操作。

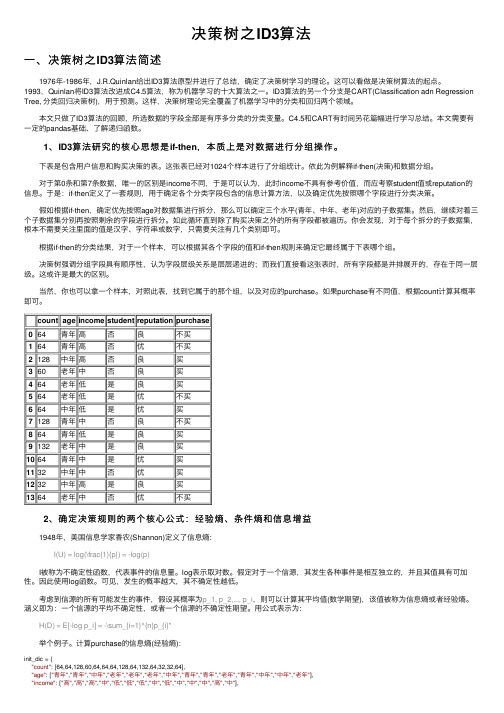
下表是包含⽤户信息和购买决策的表。

这张表已经对1024个样本进⾏了分组统计。

依此为例解释if-then(决策)和数据分组。

对于第0条和第7条数据，唯⼀的区别是income不同，于是可以认为，此时income不具有参考价值，⽽应考察student值或reputation的信息。

于是：if-then定义了⼀套规则，⽤于确定各个分类字段包含的信息计算⽅法，以及确定优先按照哪个字段进⾏分类决策。

假如根据if-then，确定优先按照age对数据集进⾏拆分，那么可以确定三个⽔平(青年、中年、⽼年)对应的⼦数据集。

然后，继续对着三个⼦数据集分别再按照剩余的字段进⾏拆分。

如此循环直到除了购买决策之外的所有字段都被遍历。

你会发现，对于每个拆分的⼦数据集，根本不需要关注⾥⾯的值是汉字、字符串或数字，只需要关注有⼏个类别即可。

根据if-then的分类结果，对于⼀个样本，可以根据其各个字段的值和if-then规则来确定它最终属于下表哪个组。

决策树强调分组字段具有顺序性，认为字段层级关系是层层递进的；⽽我们直接看这张表时，所有字段都是并排展开的，存在于同⼀层级。

id3决策树算法python程序

id3决策树算法python程序关于ID3决策树算法的Python程序。

第一步：了解ID3决策树算法ID3决策树算法是一种常用的机器学习算法，用于解决分类问题。

它基于信息论的概念，通过选择最佳的特征来构建决策树模型。

ID3算法的核心是计算信息增益，即通过选择最能区分不同类别的特征来构建决策树。

第二步：导入需要的Python库和数据集在编写ID3决策树算法的Python程序之前，我们需要导入一些必要的Python库和准备好相关的数据集。

在本例中，我们将使用pandas库来处理数据集，并使用sklearn库的train_test_split函数来将数据集拆分为训练集和测试集。

pythonimport pandas as pdfrom sklearn.model_selection import train_test_split# 读取数据集data = pd.read_csv('dataset.csv')# 将数据集拆分为特征和标签X = data.drop('Class', axis=1)y = data['Class']# 将数据集拆分为训练集和测试集X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2) 第三步：实现ID3决策树算法的Python函数在此步骤中，我们将编写一个名为ID3DecisionTree的Python函数来实现ID3决策树算法。

该函数将递归地构建决策树，直到满足停止条件。

在每个递归步骤中，它将计算信息增益，并选择最佳特征作为当前节点的分裂依据。

pythonfrom math import log2from collections import Counterclass ID3DecisionTree:def __init__(self):self.tree = {}def calc_entropy(self, labels):label_counts = Counter(labels)entropy = 0for count in label_counts.values():p = count / len(labels)entropy -= p * log2(p)return entropydef calc_info_gain(self, data, labels, feature):feature_values = data[feature].unique()feature_entropy = 0for value in feature_values:subset_labels = labels[data[feature] == value]feature_entropy += len(subset_labels) / len(labels) * self.calc_entropy(subset_labels)return self.calc_entropy(labels) - feature_entropydef choose_best_feature(self, data, labels):best_info_gain = 0best_feature = Nonefor feature in data.columns:info_gain = self.calc_info_gain(data, labels, feature)if info_gain > best_info_gain:best_info_gain = info_gainbest_feature = featurereturn best_featuredef build_tree(self, data, labels):if len(set(labels)) == 1:return labels[0]elif len(data.columns) == 0:return Counter(labels).most_common(1)[0][0] else:best_feature = self.choose_best_feature(data, labels)sub_data = {}for value in data[best_feature].unique():subset = data[data[best_feature] == value].drop(best_feature, axis=1)sub_labels = labels[data[best_feature] == value]sub_data[value] = (subset, sub_labels)tree = {best_feature: {}}for value, (subset, sub_labels) in sub_data.items():tree[best_feature][value] = self.build_tree(subset, sub_labels)return treedef fit(self, data, labels):self.tree = self.build_tree(data, labels)def predict(self, data):predictions = []for _, row in data.iterrows():node = self.treewhile isinstance(node, dict):feature = list(node.keys())[0]value = row[feature]node = node[feature][value]predictions.append(node)return predictions第四步：使用ID3决策树模型进行训练和预测最后一步是使用我们实现的ID3DecisionTree类进行训练和预测。

id3算法代码

id3算法代码ID3算法简介ID3算法是一种常用的决策树算法，它通过对数据集的属性进行分析，选择最优属性作为节点，生成决策树模型。

ID3算法是基于信息熵的思想，通过计算每个属性对样本集合的信息增益来选择最优划分属性。

ID3算法步骤1. 计算数据集的熵首先需要计算数据集的熵，熵越大表示样本集合越混乱。

假设有n个类别，则数据集D的熵可以表示为：$$ Ent(D) = -\sum_{i=1}^{n}p_i\log_2p_i $$其中$p_i$表示第i个类别在数据集D中出现的概率。

2. 计算每个属性对样本集合的信息增益接下来需要计算每个属性对样本集合的信息增益。

假设有m个属性，则第j个属性$A_j$对数据集D的信息增益可以表示为：$$ Gain(D, A_j) = Ent(D) - \sum_{i=1}^{v}\frac{|D_i|}{|D|}Ent(D_i) $$其中$v$表示第j个属性可能取值的数量，$D_i$表示在第j个属性上取值为$i$时所包含的样本子集。

3. 选择最优划分属性从所有可用属性中选择最优划分属性作为当前节点。

选择最优划分属性的方法是计算所有属性的信息增益，选择信息增益最大的属性作为当前节点。

4. 递归生成决策树使用选择的最优划分属性将数据集划分成若干子集，对每个子集递归生成子树。

ID3算法代码实现下面是Python语言实现ID3算法的代码：```pythonimport mathimport pandas as pd# 计算熵def calc_entropy(data):n = len(data)label_counts = {}for row in data:label = row[-1]if label not in label_counts:label_counts[label] = 0label_counts[label] += 1entropy = 0.0for key in label_counts:prob = float(label_counts[key]) / n entropy -= prob * math.log(prob, 2) return entropy# 划分数据集def split_data(data, axis, value):sub_data = []for row in data:if row[axis] == value:sub_row = row[:axis]sub_row.extend(row[axis+1:])sub_data.append(sub_row)return sub_data# 计算信息增益def calc_info_gain(data, base_entropy, axis):values = set([row[axis] for row in data])new_entropy = 0.0for value in values:sub_data = split_data(data, axis, value)prob = len(sub_data) / float(len(data))new_entropy += prob * calc_entropy(sub_data) info_gain = base_entropy - new_entropyreturn info_gain# 选择最优划分属性def choose_best_feature(data):num_features = len(data[0]) - 1base_entropy = calc_entropy(data)best_info_gain = 0.0best_feature = -1for i in range(num_features):info_gain = calc_info_gain(data, base_entropy, i)if info_gain > best_info_gain:best_info_gain = info_gainbest_feature = ireturn best_feature# 多数表决函数，用于确定叶子节点的类别def majority_vote(class_list):class_count = {}for vote in class_list:if vote not in class_count:class_count[vote] = 0class_count[vote] += 1sorted_class_count = sorted(class_count.items(), key=lambda x:x[1], reverse=True)return sorted_class_count[0][0]# 创建决策树def create_tree(data, labels):class_list = [row[-1] for row in data]if class_list.count(class_list[0]) == len(class_list):return class_list[0]if len(data[0]) == 1:return majority_vote(class_list)best_feature_idx = choose_best_feature(data)best_feature_label = labels[best_feature_idx]tree_node = {best_feature_label: {}}del(labels[best_feature_idx])feature_values = [row[best_feature_idx] for row in data] unique_values = set(feature_values)for value in unique_values:sub_labels = labels[:]sub_data = split_data(data, best_feature_idx, value) tree_node[best_feature_label][value] =create_tree(sub_data, sub_labels)return tree_node# 预测函数def predict(tree, labels, data):first_str = list(tree.keys())[0]second_dict = tree[first_str]feat_index = labels.index(first_str)key = data[feat_index]value_of_feat = second_dict[key]if isinstance(value_of_feat, dict):class_label = predict(value_of_feat, labels, data) else:class_label = value_of_featreturn class_label# 测试函数def test():# 读取数据集df = pd.read_csv('iris.csv')data = df.values.tolist()# 划分训练集和测试集train_data = []test_data = []for i in range(len(data)):if i % 5 == 0:test_data.append(data[i])else:train_data.append(data[i])# 创建决策树labels = df.columns.tolist()[:-1]tree = create_tree(train_data, labels)# 测试决策树模型的准确率correct_count = 0for row in test_data:true_label = row[-1]pred_label = predict(tree, labels, row[:-1])if true_label == pred_label:correct_count += 1accuracy = float(correct_count) / len(test_data)if __name__ == '__main__':test()```代码解释以上代码实现了ID3算法的主要功能。

matlab实现的ID3 分类决策树算法

function D = ID3(train_features, train_targets, params, region)% Classify using Quinlan's ID3 algorithm% Inputs:% features - Train features% targets - Train targets% params - [Number of bins for the data, Percentage of incorrectly assigned samples at a node]% region - Decision region vector: [-x x -y y number_of_points]%% Outputs% D - Decision sufrace[Ni, M] =size(train_features); %·µ»ØÐÐÊýNiºÍÁÐÊýM%Get parameters[Nbins, inc_node] = process_params(params);inc_node = inc_node*M/100;%For the decision regionN = region(5);mx = ones(N,1) * linspace(region(1),region(2),N); %linspace(ÆðÊ¼Öµ£¬ÖÕÖ¹Öµ£¬ÔªËØ¸öÊý)my = linspace (region(3),region(4),N)' * ones(1,N);flatxy = [mx(:), my(:)]';%Preprocessing[f, t, UW, m] = PCA(train_features,train_targets, Ni, region);train_features = UW * (train_features -m*ones(1,M));flatxy = UW * (flatxy - m*ones(1,N^2));%First, bin the data and the decision region data [H, binned_features]=high_histogram(train_features, Nbins, region); [H, binned_xy] = high_histogram(flatxy, Nbins, region);%Build the tree recursivelydisp('Building tree')tree = make_tree(binned_features,train_targets, inc_node, Nbins);%Make the decision region according to the tree disp('Building decision surface using the tree') targets = use_tree(binned_xy, 1:N^2, tree, Nbins, unique(train_targets));D = reshape(targets,N,N);%ENDfunction targets = use_tree(features, indices, tree, Nbins, Uc)%Classify recursively using a treetargets = zeros(1,size(features,2)); %size(features,2)·µ»Øfeatu resµÄÁÐÊýif (size(features,1) == 1),%Only one dimension left, so work on itfor i = 1:Nbins,in = indices(find(features(indices) == i));if ~isempty(in),if isfinite(tree.child(i)),targets(in) = tree.child(i);else%No data was found in the training set for this bin, so choose it randomallyn = 1 +floor(rand(1)*length(Uc));targets(in) = Uc(n);endendendbreakend%This is not the last level of the tree, so:%First, find the dimension we are to work ondim = tree.split_dim;dims= find(~ismember(1:size(features,1), dim)); %And classify according to itfor i = 1:Nbins,in = indices(find(features(dim, indices) == i));targets = targets + use_tree(features(dims, :), in, tree.child(i), Nbins, Uc);end%END use_treefunction tree = make_tree(features, targets,inc_node, Nbins)%Build a tree recursively[Ni, L] = size(features);Uc = unique(targets);%When to stop: If the dimension is one or the number of examples is smallif ((Ni == 1) | (inc_node > L)),%Compute the children non-recursivelyfor i = 1:Nbins,tree.split_dim = 0;indices = find(features == i);if ~isempty(indices),if(length(unique(targets(indices))) == 1),tree.child(i) =targets(indices(1));elseH =hist(targets(indices), Uc);[m, T] = max(H);tree.child(i) = Uc(T);endelsetree.child(i) = inf;endendbreakend%Compute the node's Ifor i = 1:Ni,Pnode(i) = length(find(targets == Uc(i))) / L; endInode = -sum(Pnode.*log(Pnode)/log(2));%For each dimension, compute the gain ratio impurity delta_Ib = zeros(1, Ni);P = zeros(length(Uc), Nbins);for i = 1:Ni,for j = 1:length(Uc),for k = 1:Nbins,indices = find((targets == Uc(j)) & (features(i,:) == k));P(j,k) = length(indices);endendPk = sum(P);P = P/L;Pk = Pk/sum(Pk);info = sum(-P.*log(eps+P)/log(2));delta_Ib(i) =(Inode-sum(Pk.*info))/-sum(Pk.*log(eps+Pk)/log( 2));end%Find the dimension minimizing delta_Ib[m, dim] = max(delta_Ib);%Split along the 'dim' dimensiontree.split_dim = dim;dims = find(~ismember(1:Ni, dim));for i = 1:Nbins,indices = find(features(dim, :) == i); tree.child(i) = make_tree(features(dims, indices), targets(indices), inc_node, Nbins); end。

【机器学习笔记】ID3构建决策树

【机器学习笔记】ID3构建决策树好多算法之类的，看理论描述，让⼈似懂⾮懂，代码⾛⼀⾛，现象就了然了。

引：from sklearn import treenames = ['size', 'scale', 'fruit', 'butt']labels = [1,1,1,1,1,0,0,0]p1 = [2,1,0,1]p2 = [1,1,0,1]p3 = [1,1,0,0]p4 = [1,1,0,0]n1 = [0,0,0,0]n2 = [1,0,0,0]n3 = [0,0,1,0]n4 = [1,1,0,0]data = [p1, p2, p3, p4, n1, n2, n3, n4]def pred(test):dtre = tree.DecisionTreeClassifier()dtre = dtre.fit(data, labels)print(dtre.predict([test]))with open('treeDemo.dot', 'w') as f:f = tree.export_graphviz(dtre, out_file = f, feature_names = names)pred([1,1,0,1]) 画出的树如下：关于这个树是怎么来的，如果很粗暴地看列的数据浮动情况：或者说是⽅差，⽅差最⼩该是第三列，fruit，然后是butt，scale（⽅差3.0），size（⽅差3.2857）。

再⼀看树节点的分叉情况，fruit，butt，size，scale，两相⽐较，好像发现了什么？衡量数据⽆序度：划分数据集的⼤原则是：将⽆序的数据变得更加有序。

那么如何评价数据有序程度？⽐较直观地，可以直接看数据间的差距，差距越⼤，⽆序度越⾼。

但这显然还不够聪明。

组织⽆序数据的⼀种⽅法是使⽤信息论度量信息。

机器学习-ID3决策树算法（附matlaboctave代码）

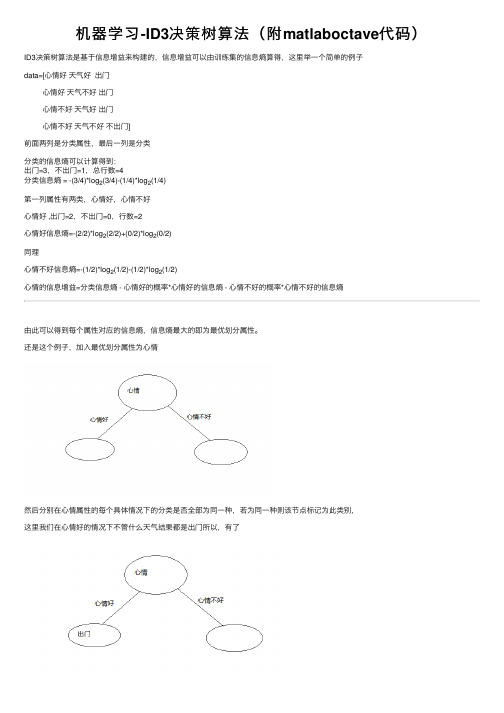
机器学习-ID3决策树算法（附matlaboctave代码）ID3决策树算法是基于信息增益来构建的，信息增益可以由训练集的信息熵算得，这⾥举⼀个简单的例⼦data=[⼼情好天⽓好出门⼼情好天⽓不好出门⼼情不好天⽓好出门⼼情不好天⽓不好不出门]前⾯两列是分类属性，最后⼀列是分类分类的信息熵可以计算得到：出门=3，不出门=1，总⾏数=4分类信息熵 = -(3/4)*log2(3/4)-(1/4)*log2(1/4)第⼀列属性有两类，⼼情好，⼼情不好⼼情好 ,出门=2，不出门=0，⾏数=2⼼情好信息熵=-(2/2)*log2(2/2)+(0/2)*log2(0/2)同理⼼情不好信息熵=-(1/2)*log2(1/2)-(1/2)*log2(1/2)⼼情的信息增益=分类信息熵 - ⼼情好的概率*⼼情好的信息熵 - ⼼情不好的概率*⼼情不好的信息熵由此可以得到每个属性对应的信息熵，信息熵最⼤的即为最优划分属性。

还是这个例⼦，加⼊最优划分属性为⼼情然后分别在⼼情属性的每个具体情况下的分类是否全部为同⼀种，若为同⼀种则该节点标记为此类别，这⾥我们在⼼情好的情况下不管什么天⽓结果都是出门所以，有了⼼情不好的情况下有不同的分类结果，继续计算在⼼情不好的情况下，其它属性的信息增益，把信息增益最⼤的属性作为这个分⽀节点，这个我们只有天⽓这个属性，那么这个节点就是天⽓了，天⽓属性有两种情况，如下图在⼼情不好并且天⽓好的情况下，若分类全为同⼀种，则改节点标记为此类别有训练集可以，⼼情不好并且天⽓好为出门，⼼情不好并且天⽓不好为不出门，结果⼊下图对于分⽀节点下的属性很有可能没有数据，⽐如，我们假设训练集变成data=[⼼情好晴天出门⼼情好阴天出门⼼情好⾬天出门⼼情好雾天出门⼼情不好晴天出门⼼情不好⾬天不出门⼼情不好阴天不出门]如下图：在⼼情不好的情况下，天⽓中并没有雾天，我们如何判断雾天到底是否出门呢？我们可以采⽤该样本最多的分类作为该分类，这⾥天⽓不好的情况下，我们出门=1，不出门=2，那么这⾥将不出门，作为雾天的分类结果在此我们所有属性都划分了，结束递归，我们得到了⼀颗⾮常简单的决策树。

机器学习决策树算法ID3

机器学习决策树算法ID3决策树是一种重要的机器学习算法，它能够处理分类和回归的问题，并且易于理解和解释。

其中，ID3（Iterative Dichotomiser 3）算法是决策树学习中最简单和最流行的一种算法，本文将介绍ID3算法的基本原理和实现过程。

什么是决策树决策树是一种树形结构，其中每个内部节点表示一个属性上的判断，每个叶子节点表示一种分类结果。

决策树的生成分为两个步骤：构建和剪枝。

构建过程是将数据集通过分裂形成一颗完整的决策树；剪枝过程是通过去除不必要的分支来提高模型的泛化能力。

ID3算法的基本原理ID3算法是一种贪心算法，也就是说，在每一次分裂时，它都会选择当前最优的特征进行分裂。

其基本思想是：通过计算某个特征的信息增益来确定每个节点的最优分割策略。

信息增益是指在选择某个特征进行分割后，熵的减少量。

熵的计算公式如下：$$ H(D) = -\\sum_{k=1}^{|y|}p_klog_2p_k $$其中，|y|表示类别的数量，p k表示第k个类别在所有样本中出现的概率。

信息增益的计算公式如下：$$ Gain(D,F) = H(D) - \\sum_{v\\in V(F)}\\frac{|D_v|}{|D|}H(D_v) $$其中，F表示属性，V(F)表示属性F的取值集合。

D v表示选择属性F取值为v时的样本集。

在计算信息增益时，需要选择具有最大信息增益的属性作为分裂属性。

ID3算法的实现过程ID3算法的实现过程可以分为以下几个步骤：1.选择分裂属性：选择信息增益最大的属性作为分裂属性；2.构建节点：将节点标记为分裂属性；3.分裂样本：按照分裂属性将样本集分裂为若干子集；4.递归继续分裂：对于每个子集，递归地执行步骤1到步骤3，直到构建完整个决策树。

具体实现时，可以使用递归函数来实现决策树的构建。

代码如下所示：```python def create_tree(dataset, labels):。

广工ID3决策树算法实验报告

三、实验代码及数据记录1.代码#ID3算法实现代码import pandas as pdimport numpy as npimport timeimport treePlotter as treeplotterdef getData():testdata =pd.read_csv('C:/Users/asus/PycharmProjects/ID3/car_evalution-databases.csv',encoding = "utf-8")# 获取测试数据集特征feature = np.array(testdata.keys())feature = np.array(feature[1:feature.size])# 将测试数据转换成数组S = np.array(testdata)S = np.array(S[:, 1:S.shape[1]])return S,feature#统计某一特征的各个取值的概率def Probability(x):value = np.unique(np.array(x)) #统计某列特征取值类型valueCount = np.zeros(value.shape[0]).reshape(1,value.shape[0])for i in range(0, value.shape[0]):q = np.matrix(x[np.where(x[:,0] == value[i])[0]])valueCount[:,i] = q.shape[0]p = valueCount/valueCount.sum()return p#计算Entropy#S为矩阵类型#返回entropydef Entropy(S):P = Probability(S[:,S.shape[1]-1])logP = np.log(P)entropy = -np.dot(P,np.transpose(logP))[0][0]return entropy#计算EntropyA#S为数组类型#返回最小的信息熵的特征的索引值#返回最小的信息熵值def getMinEntropyA(S):entropy = np.zeros(S.shape[1]-1)for i in range(0, S.shape[1]-1):value = np.unique(np.array(S[:,i]))valueEntropy = np.zeros(value.shape[0]).reshape(1,value.shape[0]) for j in range(0,value.shape[0]):q = np.matrix(S[np.where(S[:,i] == value[j])[0]])valueEntropy[:,j] = Entropy(q)proportion = Probability(np.matrix(S[:, i]).transpose())entropy[i] = np.dot(proportion, valueEntropy.transpose())[0][0] minEntropyA = entropy.min()positionMinEntropA = entropy.transpose().argmin()return positionMinEntropA, minEntropyA#计算Gain#S为数组类型#返回最大信息增益的特征的索引值def getMaxGain(S):entropyS = Entropy(np.matrix(S))positionMinEntropyA, entropyA = getMinEntropyA(S)if(entropyS - entropyA > 0):return positionMinEntropyA#ID3算法#返回ID3决策树def id3Tree(S,features):if(Entropy(np.matrix(S)) == 0):return S[0][S.shape[1] - 1]elif features.size == 1:typeValues = np.unique(S[:, S.shape[1]-1])max = 0maxValue = S[0][S.shape[1] - 1]for value in typeValues:Stemp = np.array(S[np.where(S[:, S.shape[1]-1] == value)[0]]) if max < Stemp.shape[0]:max = Stemp.shape[0]maxValue = valuereturn maxValueelse:bestFeatureIndex = getMaxGain(S)bestFeature = features[bestFeatureIndex]bestFeatureValues = np.unique(S[:, bestFeatureIndex])# 划分S，featurefeatures = delArrary(features, bestFeatureIndex)id3tree = {bestFeature:{}}for value in bestFeatureValues:Stemp = np.array(S[np.where(S[:, bestFeatureIndex] == value)[0]]) Stemp = delArrary(Stemp, bestFeatureIndex)id3tree[bestFeature][value] = id3Tree(Stemp,features)return id3tree#删除数组中的某一列,维数小于2def delArrary(arrary,index):if(arrary.shape[0] == arrary.size):x = np.array(arrary[0:index])y = np.array(arrary[index+1:arrary.shape[0]])return np.array(np.append(x,y))else:x = np.array(arrary[:,0:index])y = np.array(arrary[:,index+1:arrary.shape[1]])return np.array(np.hstack((x,y)))def Classify(tree, feature, S):firstStr = list(tree.keys())[0]secondDict = tree[firstStr]index = list(feature).index(firstStr)for key in secondDict.keys():if S[index] == key:if type(secondDict[key]) != type(1):classlabel = Classify(secondDict[key],feature,S)else:classlabel = secondDict[key]return classlabeltic = time.process_time()S, feature = getData()S2 = np.array(S[30:S.shape[0]])S1 = np.array(S[0:29])a = np.zeros(S1.shape[0],int)b = np.array(S[0:29:,S.shape[1]-1])#生成决策树tree = id3Tree(S, feature)#print(tree)treeplotter.createPlot(tree)print('决策树生成至C:/Users/asus/PycharmProjects/ID3/决策树.png')#生成ID3决策树代码import matplotlib.pyplot as plt"""绘决策树的函数"""decisionNode = dict(boxstyle="round4", color="yellow",fc="1.0") # 定义分支点的样式leafNode = dict(boxstyle="round4", color="green",fc="1.0") # 定义叶节点的样式arrow_args = dict(arrowstyle="<-") # 定义箭头标识样式# 计算树的叶子节点数量def getNumLeafs(myTree):numLeafs = 0firstStr = list(myTree.keys())[0]secondDict = myTree[firstStr]for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':numLeafs += getNumLeafs(secondDict[key])else:numLeafs += 1return numLeafs# 计算树的最大深度def getTreeDepth(myTree):maxDepth = 0firstStr = list(myTree.keys())[0]secondDict = myTree[firstStr]for key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':thisDepth = 1 + getTreeDepth(secondDict[key])else:thisDepth = 1if thisDepth > maxDepth:maxDepth = thisDepthreturn maxDepth# 画出节点def plotNode(nodeTxt, centerPt, parentPt, nodeType):createPlot.ax1.annotate(nodeTxt, xy=parentPt, xycoords='axes fraction', \xytext=centerPt, textcoords='axes fraction', va="center", ha="center",\bbox=nodeType, arrowprops=arrow_args)# 标箭头上的文字def plotMidText(cntrPt, parentPt, txtString):lens = len(txtString)xMid = (parentPt[0] + cntrPt[0]) / 2.0yMid = (parentPt[1] + cntrPt[1]) / 2.0createPlot.ax1.text(xMid, yMid, txtString)def plotTree(myTree, parentPt, nodeTxt):numLeafs = getNumLeafs(myTree)depth = getTreeDepth(myTree)firstStr = list(myTree.keys())[0]cntrPt = (plotTree.x0ff + \(1.0 + float(numLeafs)) / 2.0 / plotTree.totalW, plotTree.y0ff) plotMidText(cntrPt, parentPt, nodeTxt)plotNode(firstStr, cntrPt, parentPt, decisionNode)secondDict = myTree[firstStr]plotTree.y0ff = plotTree.y0ff - 1.0 / plotTree.totalDfor key in secondDict.keys():if type(secondDict[key]).__name__ == 'dict':plotTree(secondDict[key], cntrPt, str(key))else:plotTree.x0ff = plotTree.x0ff + 1.0 / plotTree.totalWplotNode(secondDict[key], \(plotTree.x0ff, plotTree.y0ff), cntrPt, leafNode)plotMidText((plotTree.x0ff, plotTree.y0ff) \, cntrPt, str(key))plotTree.y0ff = plotTree.y0ff + 1.0 / plotTree.totalDdef createPlot(inTree):fig = plt.figure(figsize=(300,15))fig.clf()axprops = dict(xticks=[], yticks=[])createPlot.ax1 = plt.subplot(111, frameon=False, **axprops)plotTree.totalW = float(getNumLeafs(inTree))plotTree.totalD = float(getTreeDepth(inTree))plotTree.x0ff = -0.5 / plotTree.totalWplotTree.y0ff = 1.0plotTree(inTree, (0.5, 1.0), '')plt.savefig(""C:/Users/asus/PycharmProjects/ID3/决策树.png") #plt.show()2.结果截图决策树截图：。

day-7sklearn库实现ID3决策树算法

day-7sklearn库实现ID3决策树算法本⽂介绍如何利⽤决策树/判定树（decision tree）中决策树归纳算法（ID3）解决机器学习中的回归问题。

⽂中介绍基于有监督的学习⽅式，如何利⽤年龄、收⼊、⾝份、收⼊、信⽤等级等特征值来判定⽤户是否购买电脑的⾏为，最后利⽤python和sklearn库实现了该应⽤。

1、决策树归纳算法（ID3）实例介绍 2、如何利⽤python实现决策树归纳算法（ID3）1、决策树归纳算法（ID3）实例介绍⾸先介绍下算法基本概念，判定树是⼀个类似于流程图的树结构：其中，每个内部结点表⽰在⼀个属性上的测试，每个分⽀代表⼀个属性输出，⽽每个树叶结点代表类或类分布。

树的最顶层是根结点。

决策树的优点：直观，便于理解，⼩规模数据集有效决策树的缺点：处理连续变量不好，类别较多时，错误增加的⽐较快，可规模性⼀般以如下测试数据为例：我们有⼀组已知训练集数据，显⽰⽤户购买电脑⾏为与各个特征值的关系，我们可以绘制出如下决策树图像（绘制⽅法后⾯介绍）此时，输⼊⼀个新的测试数据，就能根据该决策树很容易判定出⽤户是否购买电脑的⾏为。

有两个关键点需要考虑：1、如何决定分⽀终⽌；2如何决定各个节点的位置，例如根节点如何确定。

1、如何决定分⽀终⽌如果某个节点所有标签均为同⼀类，我们将不再继续绘制分⽀，直接标记结果。

或者分⽀过深，可以基于少数服从多数的算法，终⽌该分⽀直接绘制结果。

例如，通过年龄划分，所有middle_aged对象，对应的标签都为yes，尽管还有其它特征值，例如收⼊、⾝份、信⽤等级等，但由于标签所有都为⼀类，所以该分⽀直接标注结果为yes，不再往下细分。

2、如何决定各个节点的位置，例如根节点如何确定。

在说明这个问题之前，我们先讨论⼀个熵的概，信息和抽象，如何度量？1948年，⾹农提出了 “信息熵(entropy)”的概念，⼀条信息的信息量⼤⼩和它的不确定性有直接的关系，要搞清楚⼀件⾮常⾮常不确定的事情，或者是我们⼀⽆所知的事情，需要了解⼤量信息==>信息量的度量就等于不确定性的多少例⼦：猜世界杯冠军，假如⼀⽆所知，猜多少次？每个队夺冠的⼏率不是相等的，也就说明该信息熵较⼤。

机器学习决策树ID3算法的源代码

机器学习决策树ID3算法的源代码决策树算法（ID3）是一种机器学习算法，利用决策树的方式来学习和预测数据。

它是一种递归算法，可以根据现有的数据对分类功能进行估计。

ID3算法一般包括以下几个步骤：1、首先从所有的可能的特征中选择一个最好的分类特征，这个特征会从样本中提取出最有区分度的分类特征；2、接着把训练数据集按照这个特征的取值，划分成若干个小数据集；3、然后，从小数据集中，继续选择一个具有最大信息增益的特征作为子节点分裂依据；4、将节点分裂后，立即分类节点，叶子节点的样本类型应经过多数投票法，确定这个节点所属的分类；5、再把上述过程应用到每一个子节点上，一直迭代直到每一个节点只包含单一类别的样本；6、最后，根据决策树规则，得到一个分类模型，用于预测新的样本属于哪一类；下面是实现ID3算法的源代码：# -*- coding: utf-8 -*-import pandas as pdimport numpy as npfrom math import log2"""计算基尼不纯度parameters:dfData - 训练数据class_col - 分类的列returns:giniIndex - 基尼不纯度"""def giniIndex(dfData, class_col):giniIndex = 1class_count = dfData[class_col].value_counts( #计算每个类别出现的次数sum_count = dfData.shape[0] #数据的总条数for k in class_count:giniIndex -= (k / sum_count)**2 #基尼不纯度公式return giniIndex"""计算信息增益parameters:。

数据挖掘-决策树ID3分类算法的C++实现

数据挖掘-决策树ID3分类算法的C++实现数据挖掘课上⾯⽼师介绍了下决策树ID3算法，我抽空余时间把这个算法⽤C++实现了⼀遍。

决策树算法是⾮常常⽤的分类算法，是逼近离散⽬标函数的⽅法，学习得到的函数以决策树的形式表⽰。

其基本思路是不断选取产⽣信息增益最⼤的属性来划分样例集和，构造决策树。

信息增益定义为结点与其⼦结点的信息熵之差。

信息熵是⾹农提出的，⽤于描述信息不纯度(不稳定性)，其计算公式是Pi为⼦集合中不同性(⽽⼆元分类即正样例和负样例)的样例的⽐例。

这样信息收益可以定义为样本按照某属性划分时造成熵减少的期望，可以区分训练样本中正负样本的能⼒，其计算公司是我实现该算法针对的样例集合如下该表记录了在不同⽓候条件下是否去打球的情况，要求根据该表⽤程序输出决策树C++代码如下，程序中有详细注释#include <iostream>#include <string>#include <vector>#include <map>#include <algorithm>#include <cmath>using namespace std;#define MAXLEN 6//输⼊每⾏的数据个数//多叉树的实现//1 ⼴义表//2 ⽗指针表⽰法，适于经常找⽗结点的应⽤//3 ⼦⼥链表⽰法，适于经常找⼦结点的应⽤//4 左长⼦，右兄弟表⽰法,实现⽐较⿇烦//5 每个结点的所有孩⼦⽤vector保存//教训:数据结构的设计很重要，本算法采⽤5⽐较合适，同时//注意维护剩余样例和剩余属性信息，建树时横向遍历考循环属性的值，//纵向遍历靠递归调⽤vector <vector <string> > state;//实例集vector <string> item(MAXLEN);//对应⼀⾏实例集vector <string> attribute_row;//保存⾸⾏即属性⾏数据string end("end");//输⼊结束string yes("yes");string no("no");string blank("");map<string,vector < string > > map_attribute_values;//存储属性对应的所有的值int tree_size = 0;struct Node{//决策树节点string attribute;//属性值string arrived_value;//到达的属性值vector<Node *> childs;//所有的孩⼦Node(){attribute = blank;arrived_value = blank;}};Node * root;//根据数据实例计算属性与值组成的mapvoid ComputeMapFrom2DVector(){unsigned int i,j,k;bool exited = false;vector<string> values;for(i = 1; i < MAXLEN-1; i++){//按照列遍历for (j = 1; j < state.size(); j++){for (k = 0; k < values.size(); k++){if(!values[k].compare(state[j][i])) exited = true;}if(!exited){values.push_back(state[j][i]);//注意Vector的插⼊都是从前⾯插⼊的，注意更新it，始终指向vector头}exited = false;}map_attribute_values[state[0][i]] = values;values.erase(values.begin(), values.end());}}//根据具体属性和值来计算熵double ComputeEntropy(vector <vector <string> > remain_state, string attribute, string value,bool ifparent){ vector<int> count (2,0);unsigned int i,j;bool done_flag = false;//哨兵值for(j = 1; j < MAXLEN; j++){if(done_flag) break;if(!attribute_row[j].compare(attribute)){for(i = 1; i < remain_state.size(); i++){if((!ifparent&&!remain_state[i][j].compare(value)) || ifparent){//ifparent记录是否算⽗节点if(!remain_state[i][MAXLEN - 1].compare(yes)){count[0]++;}else count[1]++;}}done_flag = true;}}if(count[0] == 0 || count[1] == 0 ) return 0;//全部是正实例或者负实例//具体计算熵根据[+count[0],-count[1]],log2为底通过换底公式换成⾃然数底数double sum = count[0] + count[1];double entropy = -count[0]/sum*log(count[0]/sum)/log(2.0) - count[1]/sum*log(count[1]/sum)/log(2.0);return entropy;}//计算按照属性attribute划分当前剩余实例的信息增益double ComputeGain(vector <vector <string> > remain_state, string attribute){unsigned int j,k,m;//⾸先求不做划分时的熵double parent_entropy = ComputeEntropy(remain_state, attribute, blank, true);double children_entropy = 0;//然后求做划分后各个值的熵vector<string> values = map_attribute_values[attribute];vector<double> ratio;vector<int> count_values;int tempint;for(m = 0; m < values.size(); m++){tempint = 0;for(k = 1; k < MAXLEN - 1; k++){if(!attribute_row[k].compare(attribute)){for(j = 1; j < remain_state.size(); j++){if(!remain_state[j][k].compare(values[m])){tempint++;}}}}count_values.push_back(tempint);}for(j = 0; j < values.size(); j++){ratio.push_back((double)count_values[j] / (double)(remain_state.size()-1));}double temp_entropy;for(j = 0; j < values.size(); j++){temp_entropy = ComputeEntropy(remain_state, attribute, values[j], false);children_entropy += ratio[j] * temp_entropy;}return (parent_entropy - children_entropy);}int FindAttriNumByName(string attri){for(int i = 0; i < MAXLEN; i++){if(!state[0][i].compare(attri)) return i;}cerr<<"can't find the numth of attribute"<<endl;return 0;}//找出样例中占多数的正/负性string MostCommonLabel(vector <vector <string> > remain_state){int p = 0, n = 0;for(unsigned i = 0; i < remain_state.size(); i++){if(!remain_state[i][MAXLEN-1].compare(yes)) p++;else n++;}if(p >= n) return yes;else return no;}//判断样例是否正负性都为labelbool AllTheSameLabel(vector <vector <string> > remain_state, string label){int count = 0;for(unsigned int i = 0; i < remain_state.size(); i++){if(!remain_state[i][MAXLEN-1].compare(label)) count++;}if(count == remain_state.size()-1) return true;else return false;}//计算信息增益，DFS构建决策树//current_node为当前的节点//remain_state为剩余待分类的样例//remian_attribute为剩余还没有考虑的属性//返回根结点指针Node * BulidDecisionTreeDFS(Node * p, vector <vector <string> > remain_state, vector <string> remain_attribute){ //if(remain_state.size() > 0){//printv(remain_state);//}if (p == NULL)p = new Node();//先看搜索到树叶的情况if (AllTheSameLabel(remain_state, yes)){p->attribute = yes;return p;}if (AllTheSameLabel(remain_state, no)){p->attribute = no;return p;}if(remain_attribute.size() == 0){//所有的属性均已经考虑完了,还没有分尽string label = MostCommonLabel(remain_state);p->attribute = label;return p;}double max_gain = 0, temp_gain;vector <string>::iterator max_it = remain_attribute.begin();vector <string>::iterator it1;for(it1 = remain_attribute.begin(); it1 < remain_attribute.end(); it1++){temp_gain = ComputeGain(remain_state, (*it1));if(temp_gain > max_gain) {max_gain = temp_gain;max_it = it1;}}//下⾯根据max_it指向的属性来划分当前样例，更新样例集和属性集vector <string> new_attribute;vector <vector <string> > new_state;for(vector <string>::iterator it2 = remain_attribute.begin(); it2 < remain_attribute.end(); it2++){if((*it2).compare(*max_it)) new_attribute.push_back(*it2);}//确定了最佳划分属性，注意保存p->attribute = *max_it;vector <string> values = map_attribute_values[*max_it];int attribue_num = FindAttriNumByName(*max_it);new_state.push_back(attribute_row);for(vector <string>::iterator it3 = values.begin(); it3 < values.end(); it3++){for(unsigned int i = 1; i < remain_state.size(); i++){if(!remain_state[i][attribue_num].compare(*it3)){new_state.push_back(remain_state[i]);}}Node * new_node = new Node();new_node->arrived_value = *it3;if(new_state.size() == 0){//表⽰当前没有这个分⽀的样例，当前的new_node为叶⼦节点new_node->attribute = MostCommonLabel(remain_state);}elseBulidDecisionTreeDFS(new_node, new_state, new_attribute);//递归函数返回时即回溯时需要1 将新结点加⼊⽗节点孩⼦容器 2清除new_state容器p->childs.push_back(new_node);new_state.erase(new_state.begin()+1,new_state.end());//注意先清空new_state中的前⼀个取值的样例，准备遍历下⼀个取值样例 }return p;}void Input(){string s;while(cin>>s,pare(end) != 0){//-1为输⼊结束item[0] = s;for(int i = 1;i < MAXLEN; i++){cin>>item[i];}state.push_back(item);//注意⾸⾏信息也输⼊进去，即属性}for(int j = 0; j < MAXLEN; j++){attribute_row.push_back(state[0][j]);}}void PrintTree(Node *p, int depth){for (int i = 0; i < depth; i++) cout << '\t';//按照树的深度先输出tabif(!p->arrived_value.empty()){cout<<p->arrived_value<<endl;for (int i = 0; i < depth+1; i++) cout << '\t';//按照树的深度先输出tab}cout<<p->attribute<<endl;for (vector<Node*>::iterator it = p->childs.begin(); it != p->childs.end(); it++){PrintTree(*it, depth + 1);PrintTree(*it, depth + 1);}}void FreeTree(Node *p){if (p == NULL)return;for (vector<Node*>::iterator it = p->childs.begin(); it != p->childs.end(); it++){ FreeTree(*it);}delete p;tree_size++;}int main(){Input();vector <string> remain_attribute;string outlook("Outlook");string Temperature("Temperature");string Humidity("Humidity");string Wind("Wind");remain_attribute.push_back(outlook);remain_attribute.push_back(Temperature);remain_attribute.push_back(Humidity);remain_attribute.push_back(Wind);vector <vector <string> > remain_state;for(unsigned int i = 0; i < state.size(); i++){remain_state.push_back(state[i]);}ComputeMapFrom2DVector();root = BulidDecisionTreeDFS(root,remain_state,remain_attribute);cout<<"the decision tree is :"<<endl;PrintTree(root,0);FreeTree(root);cout<<endl;cout<<"tree_size:"<<tree_size<<endl;return 0;}输⼊的训练数据如下Day Outlook Temperature Humidity Wind PlayTennis1 Sunny Hot High Weak no2 Sunny Hot High Strong no3 Overcast Hot High Weak yes4 Rainy Mild High Weak yes5 Rainy Cool Normal Weak yes6 Rainy Cool Normal Strong no7 Overcast Cool Normal Strong yes8 Sunny Mild High Weak no9 Sunny Cool Normal Weak yes10 Rainy Mild Normal Weak yes11 Sunny Mild Normal Strong yes12 Overcast Mild High Strong yes13 Overcast Hot Normal Weak yes14 Rainy Mild High Strong noend程序输出决策树如下可以⽤图形表⽰为有了决策树后，就可以根据⽓候条件做预测了例如如果⽓候数据是{S unny,Cool,Normal,Strong} ,根据决策树到左侧的yes叶节点，可以判定会去游泳。

机器学习之决策树一-ID3原理与代码实现

机器学习之决策树⼀-ID3原理与代码实现决策树之系列⼀ID3原理与代码实现本⽂系作者原创，转载请注明出处:应⽤实例：你是否玩过⼆⼗个问题的游戏，游戏的规则很简单：参与游戏的⼀⽅在脑海⾥想某个事物，其他参与者向他提问题，只允许提20个问题，问题的答案也只能⽤对或错回答。

问问题的⼈通过推断分解，逐步缩⼩待猜测事物的范围。

决策树的⼯作原理与20个问题类似，⽤户输⼈⼀系列数据，然后给出游戏的答案。

如下表假如我告诉你，我有⼀个海洋⽣物，它不浮出⽔⾯可以⽣存，并且没有脚蹼，你来判断⼀下是否属于鱼类？通过决策树，你就可以快速给出答案不是鱼类。

决策树的⽬的就是在⼀⼤堆⽆序的数据特征中找出有序的规则，并建⽴决策树（模型）。

决策树⽐较⽂绉绉的介绍决策树学习是⼀种逼近离散值⽬标函数的⽅法。

通过将⼀组数据中学习的函数表⽰为决策树，从⽽将⼤量数据有⽬的的分类，从⽽找到潜在有价值的信息。

决策树分类通常分为两步---⽣成树和剪枝；树的⽣成 --- ⾃上⽽下的递归分治法；剪枝 --- 剪去那些可能增⼤错误预测率的分枝。

决策树的⽅法起源于概念学习系统CLS（Concept Learning System）, 然后发展最具有代表性的ID3（以信息熵作为⽬标评价函数）算法，最后⼜演化为C4.5, C5.0,CART可以处理连续属性。

这篇⽂章主要介绍ID3算法原理与代码实现（属于分类算法）分类与回归的区别回归问题和分类问题的本质⼀样，都是针对⼀个输⼊做出⼀个输出预测，其区别在于输出变量的类型。

分类问题是指，给定⼀个新的模式，根据训练集推断它所对应的类别（如：+1，-1），是⼀种定性输出，也叫离散变量预测；回归问题是指，给定⼀个新的模式，根据训练集推断它所对应的输出值（实数）是多少，是⼀种定量输出，也叫连续变量预测。

举个例⼦：预测明天的⽓温是多少度，这是⼀个回归任务；预测明天是阴、晴还是⾬，就是⼀个分类任务。

分类模型可将回归模型的输出离散化，回归模型也可将分类模型的输出连续化。

python实现ID3决策树算法

python实现ID3决策树算法决策树之ID3算法及其Python实现，具体内容如下主要内容决策树背景知识决策树⼀般构建过程ID3算法分裂属性的选择ID3算法流程及其优缺点分析ID3算法Python代码实现1. 决策树背景知识决策树是数据挖掘中最重要且最常⽤的⽅法之⼀，主要应⽤于数据挖掘中的分类和预测。

决策树是知识的⼀种呈现⽅式，决策树中从顶点到每个结点的路径都是⼀条分类规则。

决策树算法最先基于信息论发展起来，经过⼏⼗年发展，⽬前常⽤的算法有：ID3、C4.5、CART算法等。

2. 决策树⼀般构建过程构建决策树是⼀个⾃顶向下的过程。

树的⽣长过程是⼀个不断把数据进⾏切分细分的过程，每⼀次切分都会产⽣⼀个数据⼦集对应的节点。

从包含所有数据的根节点开始，根据选取分裂属性的属性值把训练集划分成不同的数据⼦集，⽣成由每个训练数据⼦集对应新的⾮叶⼦节点。

对⽣成的⾮叶⼦节点再重复以上过程，直到满⾜特定的终⽌条件，停⽌对数据⼦集划分，⽣成数据⼦集对应的叶⼦节点，即所需类别。

测试集在决策树构建完成后检验其性能。

如果性能不达标，我们需要对决策树算法进⾏改善，直到达到预期的性能指标。

注：分裂属性的选取是决策树⽣产过程中的关键，它决定了⽣成的决策树的性能、结构。

分裂属性选择的评判标准是决策树算法之间的根本区别。

3. ID3算法分裂属性的选择——信息增益属性的选择是决策树算法中的核⼼。

是对决策树的结构、性能起到决定性的作⽤。

ID3算法基于信息增益的分裂属性选择。

基于信息增益的属性选择是指以信息熵的下降速度作为选择属性的⽅法。

它以的信息论为基础，选择具有最⾼信息增益的属性作为当前节点的分裂属性。

选择该属性作为分裂属性后，使得分裂后的样本的信息量最⼤，不确定性最⼩，即熵最⼩。

信息增益的定义为变化前后熵的差值，⽽熵的定义为信息的期望值，因此在了解熵和信息增益之前，我们需要了解信息的定义。

信息：分类标签xi 在样本集 S 中出现的频率记为 p(xi)，则 xi 的信息定义为：−log2p(xi) 。

id3决策树算法代码

id3决策树算法代码ID3决策树算法是一种常用的机器学习算法，它可以根据给定的训练数据集构建决策树模型，用于分类和预测任务。

下面我们将详细介绍ID3决策树算法的实现过程。

决策树是一种树结构模型，它由节点和有向边组成。

在决策树中，每个内部节点表示一个特征或属性，每条边表示一个特征取值，叶节点表示一个类别。

决策树的构建过程是一个递归的过程，通过选择最优的特征来划分数据集，使得每个子节点上的样本尽可能属于同一类别。

在ID3算法中，选择最优的特征是通过计算信息增益来实现的。

信息增益表示在特征F的条件下，样本集D的不确定性减少的程度。

具体计算公式如下：信息增益(Gain) = Entropy(D) - ∑(|Dv|/|D|) * Entropy(Dv)其中，Entropy(D)表示样本集D的信息熵，Entropy(Dv)表示在特征F的取值为v时，样本集Dv的信息熵，|Dv|表示样本集Dv的样本个数，|D|表示样本集D的样本个数。

信息熵表示样本集的不确定性，熵越大表示样本集的不确定性越高。

ID3算法的实现步骤如下：1. 若样本集D中的所有样本属于同一类别C，则将该节点标记为C，并返回。

2. 若特征集A为空集，或者样本集D中的所有样本在特征集A上取值相同，则将该节点标记为D中样本数最多的类别，并返回。

3. 计算特征集A中每个特征的信息增益，选择信息增益最大的特征F。

4. 将节点标记为特征F，并根据特征F的取值将样本集D划分为多个子集Dv。

5. 对于每个子集Dv，递归调用ID3算法，构建子节点。

6. 返回决策树模型。

ID3算法的实现过程比较简单，但也存在一些问题。

首先，ID3算法倾向于选择具有较多取值的特征，导致决策树过于复杂。

其次，ID3算法不能处理连续型特征，需要将其离散化。

此外，ID3算法容易产生过拟合问题，可以通过剪枝来解决。

为了避免决策树过于复杂，可以使用剪枝技术对决策树进行优化。

剪枝分为预剪枝和后剪枝两种方式。

决策树算法（1）含java源代码

决策树算法（1）含java源代码信息熵：变量的不确定性越⼤，熵越⼤。

熵可⽤下⾯的公式描述：-（p1*logp1+p2*logp2+...+pn*logpn)pi表⽰事件i发⽣的概率ID3：GAIN(A)=INFO(D)-INFO_A(D)节点A的信息增益为不加节点A时的信息量INFO(D)-加上A后的信息量INFO_A(D)算法步骤：1、树以代表训练样本的某个结点开始2、如果样本都在同⼀类，则将该节点设置为叶⼦，并使⽤该类标号3、否则，算法使⽤熵度量每个样本的分类结点，选择可以获得最⼤信息的节点4、所有的属性都是分类的，连续值必须离散化停⽌条件：该节点上所有的样本都属于⼀个类没有剩余的属性没有属性时，⽐如已经分到第三个属性，但是没有第四个属性，这时将样本分到最多的那类C4.5与ID3区别在于属性度量⽅式的不同优点：直观、便于理解、⼩规模数据有效缺点：处理连续变量不好类别较多时，错误增加⽐较快可规模性⼀般package dTree;import java.util.ArrayList;import java.util.HashMap;import java.util.Iterator;import java.util.List;import java.util.Map;import java.util.Set;public class dataClass {public static void main(String[] args) {double [][]exerciseData = {{1,1,0,0},{1,3,1,1},{3,2,1,1},{2,2,1,1},{3,2,1,1},{2,3,0,1},{2,1,0,0},{3,2,0,1},{2,1,0,1},{1,1,1,0}};//每⼀列表⽰⼀个属性值，最后⼀列表⽰决策层int[] index = gainResult(exerciseData);//输出的结果表⽰按照决策树规则所对应的属性参考顺序for(int i = 0;i<index.length;i++){System.out.print(" "+(index[i]+1));}}private static int[] gainResult(double[][] exerciseData) {int dataQuantity = exerciseData.length;int attributeQuantity = exerciseData[0].length-1;int []attribute = new int[attributeQuantity];int []newAttribute = new int [attributeQuantity];double [][]newExerciseData = exerciseData ;double [][]maxgainIndexData = new double[dataQuantity][attributeQuantity];for(int i = 0;i<attributeQuantity;i++){attribute[i] = MaxgainIndex(newExerciseData);for(int j = 0;j<maxgainIndexData.length;j++){maxgainIndexData[j][i] = newExerciseData[j][attribute[i]];}newExerciseData = NewData(newExerciseData,attribute[i]);}boolean flag =true;for(int i = 0;i<maxgainIndexData[0].length;i++){//寻找第i列所对应的exerciseDatafor(int k = 0;k<exerciseData[0].length-1;k++){flag = true;for(int j = 0;j<exerciseData.length;j++){if(maxgainIndexData[j][i]!=exerciseData[j][k]){flag = false;break;}}if(flag==true){newAttribute[i] = k;}}}return newAttribute;}//矩阵转置private static double[][] Transpose(double[][] exerciseData){int rows = exerciseData.length;int columns = exerciseData[0].length;double [][]newData = new double [columns][rows];for(int i = 0;i<columns;i++){for(int j= 0;j<rows;j++){newData[i][j] = exerciseData[j][i];}}return newData;}private static double[][] NewData(double[][] exerciseData,int maxIndex) {//删除exerciseData中maxindex列的数据，产⽣新数据double [][]newExerciseData = new double[exerciseData.length][];for(int i = 0;i<exerciseData.length;i++){newExerciseData[i] = new double[exerciseData[i].length-1];for(int j = 0;j<newExerciseData[i].length;j++){if(j>=maxIndex){newExerciseData[i][j] = exerciseData[i][j+1];}else{newExerciseData[i][j] = exerciseData[i][j];}}}return newExerciseData;}private static int MaxgainIndex(double[][] exerciseData) {//获取exerciseData最⼤增益率所对应的⼀列double []gainRatio = gainAll(exerciseData);double maxGain = gainRatio[0];//最⼤增益率int maxIndex = 0;//最⼤增益率所对应的索引值for(int i=1;i<gainRatio.length-1;i++){if(maxGain<gainRatio[i]){maxGain = gainRatio[i];maxIndex = i;}}return maxIndex;}public static double[] gainAll(double [][]Data){//得到Data中每⼀列的增益值int col = Data.length;//数据个数int vol = Data[0].length;//属性个数double [][]count = new double[vol][];double []info = new double[vol];double Lcount[][] = new double[vol][];//第i个属性的第j个分类的⽐率double Mcount[][] = new double[vol][];List <List<Map1>>listM = new ArrayList<List<Map1>>();List <List<Map1>>listM2 = new ArrayList<List<Map1>>();double []gain;//矩阵的属性统计for (int i = 0;i<vol;i++){//属性i的不重复的分类集（mapList加⼊了属性i以及对应的决策层的值）List<Map> mapList = new ArrayList<Map>();for(int j = 0;j<col;j++){Map y = new HashMap();y.put(Data[j][i],Data[j][vol-1]);if(!mapList.contains(y)){mapList.add(y);}}//属性i全部分类集（重复，listM2加⼊了i值以及决策层的值）List<Map> AllmapList = new ArrayList<Map>();for(int j = 0;j<col;j++){Map y = new HashMap();y.put(Data[j][i],Data[j][vol-1]);AllmapList.add(y);}count[i] = new double[mapList.size()];double sum = 0;double num = 0;List<Map1>LM = new ArrayList<Map1>();for(int j=0;j<mapList.size();j++){Iterator it =((Map)(mapList.get(j))).keySet().iterator(); num = (Double) it.next();for(int k = 0;k<AllmapList.size();k++){if(mapList.get(j).equals(AllmapList.get(k))){count[i][j] = count[i][j]+1;}}Map1 p = new Map1();p.setKey(count[i][j]);p.setValue(num);LM.add(p);}listM2.add(LM);}for( int k = 0;k<vol;k++){List <Double>list = new ArrayList<Double>();for(int i = 0;i<col;i++){if(!list.contains(Data[i][k])){list.add(Data[i][k]);}}Lcount[k] = new double[list.size()];Mcount[k] = new double[list.size()];for(int j = 0;j<col;j++){int index = list.indexOf(Data[j][k]);Lcount[k][index] = Lcount[k][index]+1;Mcount[k][index] = Mcount[k][index]+1;}double LastSum = 0;for(int i = 0;i<Lcount[k].length;i++){LastSum = LastSum+Lcount[k][i];}for(int j = 0;j<Lcount[k].length;j++){Lcount[k][j] = Lcount[k][j]/LastSum;}List<Map1> LM = new ArrayList<Map1>();for(int i = 0;i<Lcount[k].length;i++){Map1 p = new Map1();p.setKey(Mcount[k][i]);p.setValue(list.get(i));LM.add(p);}listM.add(LM);}gain = new double[listM2.size()];for(int i = 0; i<listM2.size()-1;i++){List listi = new ArrayList();listi = listM.get(i);double sum = 0;for(int j=0;j<listi.size();j++){Map1 p = (Map1) listi.get(j);double key = p.getKey();double value = p.getValue();for(int k = 0;k<listM2.get(i).size();k++){Map1 p1 = (Map1) listM2.get(i).get(k);if(p1.value==value){sum = sum+xlog2(p1.key/p.key);}//System.out.println(sum);}gain[i]+=sum*Lcount[i][j];sum = 0;}}for(int i = 0;i<Lcount[Lcount.length-1].length;i++){gain[listM2.size()-1] += -xlog2(Lcount[Lcount.length-1][i]); }for(int j = 0;j<gain.length-1;j++){gain[j] = gain[gain.length-1]+gain[j];}double[]Scount = new double [Lcount.length-1];for(int j= 0;j<Lcount.length-1;j++){double sum = 0;for(int k = 0;k<Lcount[j].length;k++){sum += xlog2(Lcount[j][k]);}Scount[j] = -sum;}for(int j= 0;j<Scount.length;j++){gain[j] = gain[j]/Scount[j];}return gain;}public static boolean contain(Map mapList,double key,double value){ if(value==Double.parseDouble(mapList.get(key).toString())){return true;}else{return false;}}public static double xlog2(double x){return x*(Math.log(x)/Math.log((double)2));}}。

【IT专家】决策树ID3算法python实现

本文由我司收集整编，推荐下载，如有疑问，请与我司联系决策树ID3算法python实现1 from math import log2 import numpy as np3 import matplotlib.pyplot as plt4 import operator56 #计算给定数据集的香农熵7 def calcShannonEnt(dataSet):8 numEntries = len(dataSet)9 labelCounts = {}10 for featVec in dataSet: #|11 currentLabel = featVec[-1] #|12 if currentLabel not in labelCounts.keys(): #|获取标签类别取值空间(key)及出现的次数(value)13 labelCounts[currentLabel] = 0 #|14 labelCounts[currentLabel] += 1 #|15 shannonEnt = 0.016 for key in labelCounts: #|17 prob = float(labelCounts[key])/numEntries #|计算香农熵18 shannonEnt -= prob * log(prob, 2) #|19 return shannonEnt20 21 #创建数据集22 def createDataSet():23 dataSet = [[1,1,’yes’],24 [1,1,’yes’],25 [1,0,’no’],26 [0,1,’no’],27 [0,1,’no’]]28 labels = [‘no surfacing’, ‘flippers’]29 return dataSet, labels30 31 #按照给定特征划分数据集32 def splitDataSet(dataSet, axis, value):33 retDataSet = []34 for featVec in dataSet: #|35 if featVec[axis] == value: #|36 reducedFeatVec = featVec[:axis] #|抽取出符合特征的数据37 reducedFeatVec.extend(featVec[axis+1:]) #|38 retDataSet.append(reducedFeatVec) #|39 return retDataSet40 41 #选择最好的数据集划分方式42 def chooseBestFeatureToSplit(dataSet):43 numFeatures = len(dataSet[0]) - 144 basicEntropy = calcShannonEnt(dataSet)45 bestInfoGain = 0.0; bestFeature = -146 for i in range(numFeatures): #计算每一个特征的熵增益47 featlist = [example[i] for example in dataSet]48 uniqueVals = set(featlist)49 newEntropy = 0.050 for value in uniqueVals: #计算每一个特征的不同取值的熵增益51 subDataSet = splitDataSet(dataSet, i, value)52 prob = len(subDataSet)/float(len(dataSet))53 newEntropy += prob * calcShannonEnt(subDataSet) #不同取值的熵增加起来就是整个特征的熵增益54 infoGain = basicEntropy - newEntropy55 if (infoGain bestInfoGain): #选择最高的熵增益作为划分方式56 bestInfoGain = infoGain57 bestFeature = i58 return bestFeature59 #挑选出现次数最多的类别60 def majorityCnt(classList):61 classCount={}62 for vote in classList:63 if vote not in classCount.keys():64 classCount[vote] = 065 classCount[vote]。

决策树ID3算法--python实现

决策树ID3算法--python实现参考：有完整程序对进⾏了详细的介绍特别理论1#coding:utf-82# ID3算法，建⽴决策树3import numpy as np4import math5import uniout6'''7#创建数据集8def creatDataSet():9 dataSet = np.array([[1,1,'yes'],10 [1,1,'yes'],11 [1,0,'no'],12 [0,1,'no'],13 [0,1,'no']])14 features = ['no surfaceing', 'fippers']15 return dataSet, features16'''1718#创建数据集19def createDataSet():20 dataSet = np.array([['青年', '否', '否', '否'],21 ['青年', '否', '否', '否'],22 ['青年', '是', '否', '是'],23 ['青年', '是', '是', '是'],24 ['青年', '否', '否', '否'],25 ['中年', '否', '否', '否'],26 ['中年', '否', '否', '否'],27 ['中年', '是', '是', '是'],28 ['中年', '否', '是', '是'],29 ['中年', '否', '是', '是'],30 ['⽼年', '否', '是', '是'],31 ['⽼年', '否', '是', '是'],32 ['⽼年', '是', '否', '是'],33 ['⽼年', '是', '否', '是'],34 ['⽼年', '否', '否', '否']])35 features = ['年龄', '有⼯作', '有⾃⼰房⼦']36return dataSet, features3738#计算数据集的熵39def calcEntropy(dataSet):40#先算概率41 labels = list(dataSet[:,-1])42 prob = {}43 entropy = 0.044for label in labels:45 prob[label] = (labels.count(label) / float(len(labels)))46for v in prob.values():47 entropy = entropy + (-v * math.log(v,2))48return entropy4950#划分数据集51def splitDataSet(dataSet, i, fc):52 subDataSet = []53for j in range(len(dataSet)):54if dataSet[j, i] == str(fc):55 sbs = []56 sbs.append(dataSet[j, :])57 subDataSet.extend(sbs)58 subDataSet = np.array(subDataSet)59return np.delete(subDataSet,[i],1)6061#计算信息增益，选择最好的特征划分数据集，即返回最佳特征下标62def chooseBestFeatureToSplit(dataSet):63 labels = list(dataSet[:, -1])64 bestInfoGain = 0.0 #最⼤的信息增益值65 bestFeature = -1 #*******66#摘出特征列和label列67for i in range(dataSet.shape[1]-1): #列68#计算列中，各个分类的概率69 prob = {}70 featureCoulmnL = list(dataSet[:,i])71for fcl in featureCoulmnL:72 prob[fcl] = featureCoulmnL.count(fcl) / float(len(featureCoulmnL))73#计算列中，各个分类的熵74 new_entrony = {} #各个分类的熵75 condi_entropy = 0.0 #特征列的条件熵76 featureCoulmn = set(dataSet[:,i]) #特征列77for fc in featureCoulmn:78 subDataSet = splitDataSet(dataSet, i, fc)79 prob_fc = len(subDataSet) / float(len(dataSet))80 new_entrony[fc] = calcEntropy(subDataSet) #各个分类的熵81 condi_entropy = condi_entropy + prob[fc] * new_entrony[fc] #特征列的条件熵82 infoGain = calcEntropy(dataSet) - condi_entropy #计算信息增益83if infoGain > bestInfoGain:84 bestInfoGain = infoGain85 bestFeature = i86return bestFeature8788#若特征集features为空，则T为单节点，并将数据集D中实例树最⼤的类label作为该节点的类标记，返回T89def majorityLabelCount(labels):90 labelCount = {}91for label in labels:92if label not in labelCount.keys():93 labelCount[label] = 094 labelCount[label] += 195return max(labelCount)9697#建⽴决策树T98def createDecisionTree(dataSet, features):99 labels = list(dataSet[:,-1])100#如果数据集中的所有实例都属于同⼀类label，则T为单节点树，并将类label作为该结点的类标记，返回T101if len(set(labels)) == 1:102return labels[0]103#若特征集features为空，则T为单节点，并将数据集D中实例树最⼤的类label作为该节点的类标记，返回T104if len(dataSet[0]) == 1:105return majorityLabelCount(labels)106#否则，按ID3算法就计算特征集中各特征对数据集D的信息增益，选择信息增益最⼤的特征beatFeature107 bestFeatureI = chooseBestFeatureToSplit(dataSet) #最佳特征的下标108 bestFeature = features[bestFeatureI] #最佳特征109 decisionTree = {bestFeature:{}} #构建树，以信息增益最⼤的特征beatFeature为⼦节点110del(features[bestFeatureI]) #该特征已最为⼦节点使⽤，则删除，以便接下来继续构建⼦树111 bestFeatureColumn = set(dataSet[:,bestFeatureI])112for bfc in bestFeatureColumn:113 subFeatures = features[:]114 decisionTree[bestFeature][bfc] = createDecisionTree(splitDataSet(dataSet, bestFeatureI, bfc), subFeatures)115return decisionTree116117#对测试数据进⾏分类118def classify(testData, features, decisionTree):119for key in decisionTree:120 index = features.index(key)121 testData_value = testData[index]122 subTree = decisionTree[key][testData_value]123if type(subTree) == dict:124 result = classify(testData,features,subTree)125return result126else:127return subTree128129130if__name__ == '__main__':131 dataSet, features = createDataSet() #创建数据集132 decisionTree = createDecisionTree(dataSet, features) #建⽴决策树133print'decisonTree：',decisionTree134135 dataSet, features = createDataSet()136 testData = ['⽼年', '是', '否']137 result = classify(testData, features, decisionTree) #对测试数据进⾏分类138print'是否给',testData,'贷款：',result相关理论：决策树概念原理决策树是⼀种⾮参数的监督学习⽅法，它主要⽤于分类和回归。

机器学习决策树_ID3算法的源代码

机器学习决策树ID3算法的源代码（VC6.0）#include<iostream.h>#include<fst ream.h>#include<string.h>#include<stdlib.h>#include<math.h>#include<iomanip.h>#define N 500 //N定义为给定训练数据的估计个数#define M 6 //M定义为候选属性的个数#define c 2 //定义c=2个不同类#define s_max 5 //定义s_max为每个候选属性所划分的含有最大的子集数int av[M]={3,3,2,3,4,2};int s[N][M+2],a[N][M+2]; //数组s[j]用来记录第i个训练样本的第j个属性值int path_a[N][M+1],path_b[N][M+1]; //用path_a[N][M+1],path_b[N][M+1]记录每一片叶子的路径int count_list=M; //count_list用于记录候选属性个数int count=-1; //用count+1记录训练样本数int attribute_t est_list1[M];int leaves=1;//用数组ss[k][j]表示第k个候选属性划分的子集S j中类Ci的样本数，数组的具体大小可根据给定训练数据调整int ss[M][c][s_max];//第k个候选属性划分的子集Sj中样本属于类Ci的概率double p[M][c][s_max];//count_s[j]用来记录第i个候选属性的第j个子集中样本个数int count_s[M][s_max];//分别定义E[M]，Gain[M]表示熵和熵的期望压缩double E[M];double Gain[M];//变量max_Gain用来存储最大的信息增益double max_Gain;int Trip=-1; //用Trip记录每一个叶子递归次数int most;void main(void){int i,j=-1,k,t emp,l,count_t est,t rue_class=0,count_train;char trainname[256],t estname[256];int t est[N][8];cout<<"请输入训练集文件名:";cin>>trainname;ifstream trainfile;trainfile.open(trainname,ios::in|ios::nocreat e);if(!trainfile){cout<<"无法使用训练集，请重试!"<<'\n';exit(1);}//读取训练集while(t rainfile>>temp){j=j+1;k=j%(M+2);if(k==0||j==0) count+=1;//count为训练集的第几个,k代表室第几个属性switch(k){case 0:s[count][0]=temp;break;case 1:s[count][1]=temp;break;case 2:s[count][2]=temp;break;case 3:s[count][3]=temp;break;case 4:s[count][4]=temp;break;case 5:s[count][5]=temp;break;case 6:s[count][6]=temp;break;case 7:s[count][7]=temp;break;}}trainfile.close();//输出训练集for(i=0;i<=count;i++){if(i%2==0) cout<<'\n';for(j=0;j<M+2;j++)cout<<setw(4)<<s[j];}//most记录训练集中哪类样本数比较多，以用于确定递归终止时不确定的类别for(i=0,j=0,k=0;i<=count;i++){if(s[0]==0) j+=1;else k+=1;}if(j>k) most=0;else most=1;//count_train记录训练集的样本数count_t rain=count+1;//训练的属性for(i=0;i<M;i++)attribut e_test_list1=i+1;//首次调用递归函数，即是生成根结点的分支Generat e_decision_tree(s,count+1,attribut e_test_list1,count_list,0,0);cout<<'\n'<<"叶子结点的个数为:"<<leaves<<'\n'; cout<<"请输入测试集文件名:";cin>>t estname;ifstream testfile;testfile.open(testname,ios::in|ios::nocreat e);if(!t estfile){cout<<"无法使用训练集，请重试!"<<'\n';exit(1);}count_t est=0;j=-1;//读取测试集数据while(t estfile>>temp){j=j+1;k=j%(M+2);if(k==0) count_test+=1;switch(k){case 0:test[count_test][7]=temp;break;case 1:test[count_test][1]=temp;break;case 2:test[count_test][2]=temp;break;case 3:test[count_test][3]=temp;break;case 4:test[count_test][4]=temp;break;case 5:test[count_test][5]=temp;break;case 6:test[count_test][6]=temp;break;}}testfile.close();for(i=1;i<=count_test;i++)test[0]=0; //以确保评估分类准确率cout<<"count_test="<<count_test<<'\n';cout<<"count_train="<<count_t rain<<'\n';//用测试集来评估分类准确率for(i=1;i<=count_test;i++){l=0;for(j=1;j<=leaves;j++)if(t est[path_b[j][1]]==path_a[j][1]&&test[path_b[j][2]]==path_a[j][2]&&t est[path_b[j][3] ]==path_a[j][3]&&t est[path_b[j][4]]==path_a[j][4]&&test[path_b[j][5]]==path_a[j][5]&&t est[path _b[j][6]]==path_a[j][6]){l=1;if(test[7]==path_a[j][0]) true_class+=1;break;}if(t est[7]==most && l==0) true_class+=1;}cout<<"测试集与训练集的比例为:"<<float(count_train)/count_test<<'\n';cout<<"分类准确率为:"<<float(true_class)/count_test<<'\n';}void Gener ate_decis ion_tree(int b[][M+2],int bn,int attribute_te s t_lis t[],int s n,int ai,int aj){//定义数组a记录目前待分的训练样本集，定义数组b记录目前要分结点中所含的训练样本集//s am e_clas s用来记数，判别s amples是否都属于同一个类Trip+=1;//用Trip记录每一个叶子递归次数path_a[leav es][Trip]=ai;//用p ath_a[N][M+1],path_b[N][M+1]记录每一片叶子的路径path_b[leaves][Trip]=aj;int s ame_class,i,j,k,l,ll,lll;if(bn==0){//待分结点的样本集为空时，加上一个树叶，标记为训练集中最普通的类//记录路径与前一路径相同的部分for(i=1;i<Trip;i++)if(path_a[leaves][i]==0){p ath_a[leaves][i]=path_a[l eaves-1][i];p ath_b[leaves][i]=path_b[leaves-1][i];}c out<<'\n'<<"I F ";for(i=1;i<=Trip;i++)if(i==1) c out<<"a["<<p ath_b[leaves][i]<<"]="<<p ath_a[leaves][i];els e cout<<"^a["<<path_b[leaves][i]<<"]="<<path_a[leaves][i];c out<<" THEN class="<<mos t;path_a[leaves][0]=m os t;//修改树的深度if(path_a[leaves][Trip]==av[p ath_b[leaves][Trip]-1])for(i=Trip;i>1;i--)if(path_a[leaves][i]==av[path_b[leaves][i]-1]) Trip-=1;els ebreak;Trip-=1;leaves+=1;}els e{s ame_clas s=1;for(i=0;i<bn-1;i++)if(b[i][0]==b[i+1][0])s ame_clas s+=1;if(s ame_class==bn){//待分样本集属于同一类时以该类标记//记录路径与前一路径相同的部分for(i=1;i<Trip;i++)if(path_a[leaves][i]==0){p ath_a[leaves][i]=path_a[l eaves-1][i];p ath_b[leaves][i]=path_b[leaves-1][i];}c out<<'\n'<<"I F ";for(i=1;i<=Trip;i++)if(i==1)cout<<"a["<<path_b[leaves][i]<<"]="<<path_a[leav es][i];els ecout<<"^a["<<path_b[leaves][i]<<"]="<<path_a[l eaves][i];c out<<" THEN class="<<b[0][0];path_a[leaves][0]=b[0][0];//修改树的深度if(path_a[leaves][Trip]==av[p ath_b[leaves][Trip]-1])for(i=Trip;i>1;i--)if(path_a[leaves][i]==av[path_b[leaves][i]-1])Trip-=1;els ebreak;Trip-=1;leaves+=1;//未分类的样本集减少for(i=0,l=-1;i<=c ount;i++){for(j=0,lll=0;j<bn;j++)if(s[i][M+1]==b[j][M+1])lll++;if(lll==0){l+=1;for(ll=0;ll<M+2;ll++)a[l][ll]=s[i][ll];}}for(i=0,k=-1;i<l;i++){k++;for(ll=0;ll<M+2;ll++)s[k][ll]=a[i][ll];}c ount=count-bn;}els e{if(s n==0){//候选属性集为空时，标记为训练集中最普通的类//记录路径与前一路径相同的部分for(i=1;i<Trip;i++)if(path_a[leaves][i]==0){p ath_a[leaves][i]=path_a[l eaves-1][i];p ath_b[leaves][i]=path_b[leaves-1][i];}c out<<'\n'<<"I F ";for(i=1;i<=Trip;i++)if(i==1) c out<<"a["<<p ath_b[leaves][i]<<"]="<<p ath_a[leaves][i];els e cout<<"^a["<<path_b[leaves][i]<<"]="<<path_a[leaves][i];//判断类别for(i=0,ll=0,lll=0;i<bn;i++){if(b[i][0]==0) ll+=1;els e lll+=1;}if(ll>lll) {cout<<" THEN clas s=0";path_a[leav es][0]=0;}els e{cout<<" THEN clas s=1";path_a[leav es][0]=1;}//修改树的深度if(path_a[leaves][Trip]==av[p ath_b[leaves][Trip]-1])for(i=Trip;i>1;i--)if(path_a[leaves][i]==av[path_b[leaves][i]-1]) Trip-=1;els ebreak;Trip-=1;leaves+=1;//未分类的样本集减少for(i=0,l=-1;i<=c ount;i++){for(j=0,lll=0;j<bn;j++)if(s[i][M+1]==b[j][M+1]) lll++;if(lll==0){l+=1;for(ll=0;ll<M+2;ll++)a[l][ll]=s[i][ll];}}for(i=0,k=-1;i<l;i++){k++;for(ll=0;ll<M+2;ll++)s[k][ll]=a[i][ll];}c ount=count-bn;}els e//待分结点的样本集不为空时{//定义c ount_Pos itive记录属于正例的样本数int count_Pos itive=0;//p1,p2分别定义为正负例的比例double p1,p2;double Entropy_Es; //Entropy_Es表示熵for(i=0;i<=c ount;i++)if(s[i][0]==1)c ount_Pos itive+=1;p1=d ouble(count_Pos itive)/(count+1);p2=1-p1;Entropy_Es=-p1*log10(p1)/log10(2)-p2*log10(p2)/log10(2);cout<<p1<<'\t'<<p2<<'\t'<<Entropy_Es<<'\n';//初始化for(i=0;i<s n;i++)//当前的属性包含的个数for(j=0;j<c;j++)//类别for(k=0;k<av[i];k++)//以当前属性分成的小类(每个属性包含的种类数)s s[attribute_te s t_lis t[i]-1][j][k]=0;//用数组s s[k][i][j]表示第k个候选属性划分的子集Sj中类Ci的样本数，数组的具体大小可根据给定训练数据调整 for(i=0;i<s n;i++)for(j=0;j<av[i];j++)c ount_s[attribute_test_lis t[i]-1][j]=0;//初始化某个属性的某个具体值的全部个数for(i=0;i<count+1;i++)for(j=1;j<=s n;j++)if(s[i][0]==0){//找出每个属性具体某个值属于反例的个数s s[attribute_test_lis t[j-1]-1][0][s[i][j]-1]+=1;c ount_s[attribute_test_list[j-1]-1][s[i][j]-1]+=1;}els e{s s[attribute_te s t_lis t[j-1]-1][1][s[i][j]-1]+=1;count_s[attribute_te s t_lis t[j-1]-1][s[i][j]-1]+=1;}//计算分别以各个候选属性划分样本后，各个子集Sj中的样本属于类Ci的概率for(i=0;i<s n;i++)for(j=0;j<c;j++)for(k=0;k<av[i];k++)if(count_s[attribute_test_lis t[i]-1][k]!=0)p[attribute_test_lis t[i]-1][j][k]=double(s s[attribute_test_lis t[i]-1][j][k])/count_s[attribute_te s t_list[i]-1][k];for(i=0;i<s n;i++)E[attribute_test_lis t[i]-1]=0.0;//计算熵for(i=0;i<s n;i++)for(j=0;j<av[attribute_tes t_list[i]-1];j++){//if语句处理0*l og10(0)=0if(p[attribute_test_lis t[i]-1][0][j]==0||p[attribute_tes t_list[i]-1][1][j]==0) {p[attribute_tes t_list[i]-1][0][j]=1;p[attribute_tes t_list[i]-1][1][j]=1;}E[attribute_test_lis t[i]-1]+=(s s[attribute_test_lis t[i]-1][0][j]+ss[attribute_test_lis t[i]-1][1][j])*(-(p[ attribute_test_lis t[i]-1][0][j]*log10(p[attribute_tes t_list[i]-1][0][j])/log10(2)+p[attribute_tes t_list[i]-1][1][j]*log10 (p[attribute_tes t_list[i]-1][1][j])/log10(2)))/(c ount+1);}//计算熵的信息增益for(i=0;i<s n;i++)Gain[attribute_tes t_list[i]-1]=Entropy_Es-E[attribute_te s t_lis t[i]-1];//找出信息增益的最大值,用j记录哪个候选属性的信息增益最大m ax_Gain=Gain[0];j=attribute_tes t_lis t[0]-1;for(i=0;i<s n;i++)//找出最大的信息增益if(max_Gain<Gain[attribute_tes t_list[i]-1]) {m ax_Gain=Gain[attribute_tes t_lis t[i]-1];j=attribute_te s t_lis t[i]-1;}//利用得到的具有最大信息增益的属性来划分待分的样本集b[bn][8]int temp[s_max];int b1[N][M+2];int temp1=-1;int temp_b[s_max][N][M+2];for(i=1;i<=av[j];i++){temp[i]=-1;for(k=0;k<bn;k++)//样本的个数if(b[k][j+1]==i){temp[i]+=1;for(l=0;l<M+2;l++)temp_b[i][t emp[i]][l]=b[k][l];}}//对于每一个分支使用递归函数重复生成树for(i=1;i<=av[j];i++){for(k=0;k<=temp[i];k++)for(l=0;l<M+2;l++)b1[k][l]=t emp_b[i][k][l];if(i==1){for(ll=0,l=0;ll<s n;ll++)if(attribute_tes t_list[ll]-1!=j) attribute_te s t_lis t[l++]=attribute_tes t_lis t[ll]; Gener ate_d ecision_tree(b1,k,attribute_te s t_lis t,l,i,j+1);s n-=1;}els e{Gener ate_decis ion_tree(b1,k,attribute_tes t_lis t,s n,i,j+1);if(i==av[j]) attribute_test_list[s n]=j+1;}}}}}}。

ID3决策树算法实现（Python版）

ID3决策树算法实现（Python版） 1# -*- coding:utf-8 -*-23from numpy import *4import numpy as np5import pandas as pd6from math import log7import operator89#计算数据集的⾹农熵10def calcShannonEnt(dataSet):11 numEntries=len(dataSet)12 labelCounts={}13#给所有可能分类创建字典14for featVec in dataSet:15 currentLabel=featVec[-1]16if currentLabel not in labelCounts.keys():17 labelCounts[currentLabel]=018 labelCounts[currentLabel]+=119 shannonEnt=0.020#以2为底数计算⾹农熵21for key in labelCounts:22 prob = float(labelCounts[key])/numEntries23 shannonEnt-=prob*log(prob,2)24return shannonEnt252627#对离散变量划分数据集，取出该特征取值为value的所有样本28def splitDataSet(dataSet,axis,value):29 retDataSet=[]30for featVec in dataSet:31if featVec[axis]==value:32 reducedFeatVec=featVec[:axis]33 reducedFeatVec.extend(featVec[axis+1:])34 retDataSet.append(reducedFeatVec)35return retDataSet3637#对连续变量划分数据集，direction规定划分的⽅向，38#决定是划分出⼩于value的数据样本还是⼤于value的数据样本集39def splitContinuousDataSet(dataSet,axis,value,direction):40 retDataSet=[]41for featVec in dataSet:42if direction==0:43if featVec[axis]>value:44 reducedFeatVec=featVec[:axis]45 reducedFeatVec.extend(featVec[axis+1:])46 retDataSet.append(reducedFeatVec)47else:48if featVec[axis]<=value:49 reducedFeatVec=featVec[:axis]50 reducedFeatVec.extend(featVec[axis+1:])51 retDataSet.append(reducedFeatVec)52return retDataSet5354#选择最好的数据集划分⽅式55def chooseBestFeatureToSplit(dataSet,labels):56 numFeatures=len(dataSet[0])-157 baseEntropy=calcShannonEnt(dataSet)58 bestInfoGain=0.059 bestFeature=-160 bestSplitDict={}61for i in range(numFeatures):62 featList=[example[i] for example in dataSet]63#对连续型特征进⾏处理64if type(featList[0]).__name__=='float'or type(featList[0]).__name__=='int':65#产⽣n-1个候选划分点66 sortfeatList=sorted(featList)67 splitList=[]68for j in range(len(sortfeatList)-1):69 splitList.append((sortfeatList[j]+sortfeatList[j+1])/2.0)7071 bestSplitEntropy=1000072 slen=len(splitList)73#求⽤第j个候选划分点划分时，得到的信息熵，并记录最佳划分点74for j in range(slen):75 value=splitList[j]76 newEntropy=0.077 subDataSet0=splitContinuousDataSet(dataSet,i,value,0)78 subDataSet1=splitContinuousDataSet(dataSet,i,value,1)79 prob0=len(subDataSet0)/float(len(dataSet))80 newEntropy+=prob0*calcShannonEnt(subDataSet0)81 prob1=len(subDataSet1)/float(len(dataSet))82 newEntropy+=prob1*calcShannonEnt(subDataSet1)83if newEntropy<bestSplitEntropy:84 bestSplitEntropy=newEntropy85 bestSplit=j86#⽤字典记录当前特征的最佳划分点87 bestSplitDict[labels[i]]=splitList[bestSplit]88 infoGain=baseEntropy-bestSplitEntropy89#对离散型特征进⾏处理90else:91 uniqueVals=set(featList)92 newEntropy=0.093#计算该特征下每种划分的信息熵94for value in uniqueVals:95 subDataSet=splitDataSet(dataSet,i,value)96 prob=len(subDataSet)/float(len(dataSet))97 newEntropy+=prob*calcShannonEnt(subDataSet)98 infoGain=baseEntropy-newEntropy99if infoGain>bestInfoGain:100 bestInfoGain=infoGain101 bestFeature=i102#若当前节点的最佳划分特征为连续特征，则将其以之前记录的划分点为界进⾏⼆值化处理103#即是否⼩于等于bestSplitValue104if type(dataSet[0][bestFeature]).__name__=='float'or type(dataSet[0][bestFeature]).__name__=='int': 105 bestSplitValue=bestSplitDict[labels[bestFeature]]106 labels[bestFeature]=labels[bestFeature]+'<='+str(bestSplitValue)107for i in range(shape(dataSet)[0]):108if dataSet[i][bestFeature]<=bestSplitValue:109 dataSet[i][bestFeature]=1110else:111 dataSet[i][bestFeature]=0112return bestFeature113114#特征若已经划分完，节点下的样本还没有统⼀取值，则需要进⾏投票115def majorityCnt(classList):116 classCount={}117for vote in classList:118if vote not in classCount.keys():119 classCount[vote]=0120 classCount[vote]+=1121return max(classCount)122123#主程序，递归产⽣决策树124def createTree(dataSet,labels,data_full,labels_full):125 classList=[example[-1] for example in dataSet]126if classList.count(classList[0])==len(classList):127return classList[0]128if len(dataSet[0])==1:129return majorityCnt(classList)130 bestFeat=chooseBestFeatureToSplit(dataSet,labels)131 bestFeatLabel=labels[bestFeat]132 myTree={bestFeatLabel:{}}133 featValues=[example[bestFeat] for example in dataSet]134 uniqueVals=set(featValues)135if type(dataSet[0][bestFeat]).__name__=='str':136 currentlabel=labels_full.index(labels[bestFeat])137 featValuesFull=[example[currentlabel] for example in data_full]138 uniqueValsFull=set(featValuesFull)139del(labels[bestFeat])140#针对bestFeat的每个取值，划分出⼀个⼦树。