极限学习机的回归拟合及分类
机器学习中的回归算法解析

机器学习中的回归算法解析引言:机器学习是一门研究如何利用计算机模拟、实现并自动更新某一类问题的学习方法和技术。
而回归算法则是机器学习中重要的一类算法,用于预测和建立变量之间的关系模型。
本文将对机器学习中的回归算法进行解析,并介绍其中的几个常用方法。
一、线性回归算法 (Linear Regression)线性回归是最简单、最常用的回归算法之一。
它假设自变量和因变量之间存在线性关系,并通过最小化残差平方和来确定模型的参数。
在给定训练数据集后,线性回归算法可以通过求解最优参数来拟合出一个线性模型,从而进行预测。
二、多项式回归算法 (Polynomial Regression)多项式回归是在线性回归的基础上进行拓展的一种方法。
它通过添加高次特征变量来增加模型的复杂度,以更好地适应非线性关系。
多项式回归可以通过增加特征的次数来灵活地调整模型的拟合度,从而更准确地预测结果。
三、岭回归算法 (Ridge Regression)岭回归是一种用于解决特征间存在共线性问题的回归算法。
在特征矩阵存在多重共线性的情况下,最小二乘法无法求解唯一解。
岭回归通过添加一个L2正则项来调整模型的复杂度,从而降低特征的相关性,得到更稳定的参数估计。
四、Lasso回归算法 (Lasso Regression)Lasso回归是一种通过添加L1正则项来选择特征的回归算法。
与岭回归不同,Lasso回归可以使部分系数为零,从而实现特征的自动选择。
通过增加L1正则化项,Lasso回归可以将一些不重要的特征对应的系数缩减至零,达到特征选择和降维的效果。
五、弹性网回归算法 (Elastic Net Regression)弹性网回归是线性回归和Lasso回归的结合,综合了两者的优点。
它通过同时添加L1和L2正则化项,既能够进行特征选择,又能够处理特征间的相关性。
弹性网回归在应对高维数据和共线性问题时表现较好。
结语:回归算法在机器学习中有着重要的地位,它们能够通过建立合适的模型对因变量进行预测。
机器学习中的回归与分类算法

机器学习中的回归与分类算法随着人工智能技术的不断发展,机器学习成为近年来受到广泛关注的领域之一。
在机器学习中,回归和分类算法是最为基础且常用的两种算法。
它们是将输入数据映射到输出结果的关键步骤。
一、回归算法回归算法广泛应用于预测数值型输出数据。
在回归过程中,我们需要使用一组重要的输入变量来预测输出变量。
例如,根据房屋的大小、位置和其他特征,我们可以预测房屋的价格。
在回归算法中,关键是找到一个最佳拟合曲线来表示输入与输出之间的关系。
最常用的回归算法之一是线性回归,它利用一条直线来拟合输入和输出的关系。
如果数据集呈现出曲线或波动形式,即非线性关系,我们可以使用非线性回归算法,如多项式回归或径向基函数(RBF)核回归。
二、分类算法分类算法是机器学习中引人注目的主题之一。
分类是指通过将输入数据映射到不同类别的输出,实现将数据集分为不同组的过程。
例如,我们可以通过分类算法将电子邮件分为垃圾邮件和非垃圾邮件。
分类算法可以分为监督和无监督模型。
在监督学习中,模型在训练过程中使用有标签的样本,以便在测试阶段中进行预测。
常用的监督分类算法包括朴素贝叶斯分类和决策树分类。
相比之下,无监督模型不需要有标签的输入数据,而是依靠模型自身从数据中找到隐藏的模式来实现分类。
常用的无监督分类算法包括聚类和维度缩减。
三、回归算法与分类算法的区别回归算法和分类算法之间的主要区别在于输出类型。
回归算法的输出是数值型数据,它们用于预测连续值。
而分类算法的输出是离散型数据,它们用于将数据集分为不同类别。
此外,两种算法的训练过程也有所不同。
在回归算法中,我们通过损失函数和优化算法来确定模型参数。
而在分类算法中,我们通常使用交叉熵损失函数和梯度下降方法来训练模型。
四、结论回归算法和分类算法是机器学习中最常用的两种算法,它们为许多数据科学问题提供了基础解决方案。
无论是在生物学、金融领域还是社交媒体数据分析方面,二者都有着广泛的应用。
当然,不同的问题需要不同的算法和技术工具,因此选择正确的机器学习算法变得异常重要。
回归拟合的方法

回归拟合的方法
回归拟合是一种常用的统计分析方法,用于描述自变量和因变量之间的关系。
回归分析可以帮助我们预测未来的趋势,找出变量之间的关联性,并进行数据的拟合和预测。
回归拟合的方法有很多种,包括线性回归、多项式回归、对数回归等等。
线性回归是最简单的一种回归拟合方法,它假设自变量和因变量之间存在线性关系。
通过最小二乘法来求解模型参数,从而得到最佳拟合直线。
多项式回归则是对非线性数据进行拟合的一种方法,通过增加自变量的高次项来拟合数据,可以更好地适应复杂的数据分布。
对数回归则是适用于因变量呈现对数分布的情况,通过对因变量进行对数变换,再进行线性回归拟合来得到结果。
回归拟合的方法可以应用于各种领域,比如经济学、金融、医学、生态学等等。
在经济学中,我们可以利用回归拟合来分析GDP与人均收入之间的关系;在医学中,可以利用回归拟合来预测疾病的发生率和死亡率;在生态学中,可以利用回归拟合来研究物种数量和环境因素之间的关系。
回归分析的结果可以帮助我们理解数据之间的关系,进行未来的预测和规划。
但是在进行回归拟合时,也需要注意一些问题,比如过拟合和欠拟合的情况,需要通过交叉验证等方法来解决。
此外,还需要考虑自变量的选择和模型的合理性,以及对结果的解释和验证。
总之,回归拟合是一种非常有用的统计分析方法,可以帮助我们理解和预测数据之间的关系。
通过选择合适的回归模型和方法,我们可以得到准确的拟合结果,并为未来的决策和规划提供有力的支持。
回归模型的拟合方法

回归模型的拟合方法嘿,咱今儿就来唠唠回归模型的拟合方法!这玩意儿啊,就好比是给模型这个大宝贝儿穿上合身的衣服。
你想啊,要是这衣服不合身,那多别扭呀!回归模型也是一样,拟合方法要是不对,那得出的结果能靠谱吗?肯定不行啊!咱常见的拟合方法呢,就像是各种不同款式的衣服。
有那种简单直接的,一下子就能把模型给包裹得差不多;也有精细复杂的,一点点地去调整,让模型变得更加完美。
比如说最小二乘法,这可是个经典的方法呢!它就好像是一件基础款的衣服,虽然不花哨,但实用啊!能在很多情况下发挥大作用,让模型稳稳当当的。
还有其他一些方法呢,就像是各种时尚的设计,各有各的特点和优势。
它们能根据不同的数据情况和需求,给模型打造出最适合它的样子。
你看啊,要是数据就像一群调皮的小孩子,到处乱跑,那咱就得用合适的拟合方法把它们给收服住,让它们乖乖听话,给咱呈现出有意义的结果。
这拟合方法选得好啊,那模型就能像个武林高手一样,威力大增!能准确地预测、分析各种情况。
可要是选得不好呢,那就像是让高手穿着不合适的鞋子去打架,那能发挥出实力吗?所以啊,咱可得好好琢磨琢磨这些拟合方法,就像咱挑衣服一样,得用心,得仔细。
别随便抓一个就用,那可不行!咱得根据实际情况,选出最适合咱模型的那个拟合方法。
你想想,要是随便乱用拟合方法,那不就跟乱穿衣服一样,不仅不好看,还可能出问题呢!咱得让回归模型漂漂亮亮、利利索索地发挥作用呀!总之呢,回归模型的拟合方法可不是随便玩玩的,那是得认真对待的。
咱得像个聪明的裁缝一样,给咱的模型量体裁衣,让它焕发出最耀眼的光芒!这样咱才能在数据分析的道路上走得稳稳当当,收获满满的成果呀!这可不是开玩笑的哟!。
机器学习中的分类算法与极限学习机

机器学习中的分类算法与极限学习机机器学习一直是计算机科学领域中备受关注和研究的一项技术。
其中,分类算法是机器学习领域最为重要的算法之一。
分类算法主要是根据已知数据集中的特征和属性信息对新数据进行自动分类和预测,广泛应用于社交网络分析、智能推荐系统、数据挖掘和图像处理等领域。
本文将详细讨论机器学习中的分类算法与极限学习机,并探讨其原理、特点以及应用场景。
一、机器学习中的分类算法1.朴素贝叶斯分类器朴素贝叶斯分类器是基于贝叶斯定理的一种分类算法,主要用于解决文本分类、垃圾邮件过滤和情感分析等问题。
该算法将数据集中的各个特征间视为相互独立且相同分布的,从而计算出新数据与不同类别之间的概率,并将概率最大的类别作为分类结果。
朴素贝叶斯分类器具有分类速度快、准确率高的优点,但是对于数据集中出现的特殊特征,其分类效果比较差。
2.支持向量机分类器支持向量机分类器是一种常用的分类算法,主要是通过将不同类别之间的分界线尽可能地放置于最大间隔区域来进行分类。
该算法适用于小数据集和高维数据集中的分类问题,并且可以使用核函数对不规则的数据集进行处理。
支持向量机分类器具有分类效果好、可解释性强的优点,但是对于大数据集和特征较多的数据集来说,其训练时间比较长。
3.决策树分类器决策树分类器是一种基于树状结构进行决策的分类算法,主要用于解决分类问题和回归问题。
该算法通过对数据集中各个特征进行分析和选择,创建一颗决策树来判断新数据的类别。
决策树分类器具有分类效果好、容易实现的优点,但是对于数据集中存在噪声和缺失值的情况,其分类效果比较差。
4.K近邻分类器K近邻分类器是一种基于距离度量进行分类的算法,主要是通过计算新数据与已知数据集中每个样本之间的距离来进行分类。
K近邻分类器具有分类效果好、预处理简单的优点,但是对于特征维度较高的数据集以及没有明显规律的数据集,其分类效果比较差。
二、极限学习机极限学习机,也称为极限随机网络,是一种基于人工神经网络的分类算法,主要用于解决分类和回归问题。
回归模型介绍

回归模型介绍回归模型是统计学和机器学习中常用的一种建模方法,用于研究自变量(或特征)与因变量之间的关系。
回归分析旨在预测或解释因变量的值,以及评估自变量与因变量之间的相关性。
以下是回归模型的介绍:•线性回归(Linear Regression): 线性回归是最简单的回归模型之一,用于建立自变量和因变量之间的线性关系。
简单线性回归涉及到一个自变量和一个因变量,而多元线性回归包含多个自变量。
线性回归模型的目标是找到一条最佳拟合直线或超平面,使得预测值与实际观测值的误差最小。
模型的形式可以表示为:Y=b0+b1X1+b2X2+⋯+b p X p+ε其中,Y是因变量, X1,X2,…X p 是自变量,b0,b1,…,b p 是回归系数,ε是误差项。
•逻辑回归(Logistic Regression): 逻辑回归是用于处理分类问题的回归模型,它基于逻辑函数(也称为S形函数)将线性组合的值映射到概率范围内。
逻辑回归常用于二元分类问题,例如预测是否发生某个事件(0或1)。
模型的输出是一个概率值,通常用于判断一个样本属于某一类的概率。
逻辑回归的模型形式为:P(Y=1)=11+e b0+b1X1+b2X2+⋯+b p X p其中P(Y=1)是事件发生的概率,b0,b1,…,b p是回归系数,X1,X2,…X p是自变量。
•多项式回归(Polynomial Regression): 多项式回归是线性回归的扩展,允许模型包括自变量的高次项,以适应非线性关系。
通过引入多项式特征,可以更灵活地拟合数据,但也可能导致过拟合问题。
模型形式可以表示为:Y=b0+b1X+b2X2+⋯+b p X p+ε其中,X是自变量,X2,X3,…,X p是其高次项。
•岭回归(Ridge Regression)和Lasso回归(Lasso Regression): 岭回归和Lasso 回归是用于解决多重共线性问题的回归技术。
这些方法引入了正则化项,以减小回归系数的大小,防止模型过度拟合。
机器学习公式详解

机器学习公式详解
机器学习公式指的是应用于机器学习的函数、模型和算法的数学表达式,用于解决机器学习问题。
它们可以使机器学习项目从理论到实践顺利运行。
以下是机器学习中常用的几个公式:
1.线性回归:y=wx+b
线性回归用于预测连续值问题。
其中W和b分别代表系数和偏移量,即权重和偏置,它们可以通过调整参数让拟合线更好。
2.Logistic回归:sigmoid(wx+b)
Logistic回归也称之为逻辑斯蒂回归,用于解决分类问题。
sigmoid函数用于将任意实数转换为0~1之间的概率值,即把线性回归的输出(wx+b)映射为0~1之间的概率值,用于代表某一个特征属于某一特定类别的可能性。
3.Softmax回归: softmax(WX+B)
softmax回归是多分类问题中常用的模型,用于将线性回归模型的输出转换成每一类的概率。
它的公式与sigmoid函数非常类似,但是它的输出的结果满足概率的加和性质。
4.朴素贝叶斯: P(c|x) = P(c) * P(x|c) / P(x)
朴素贝叶斯模型用于进行分类问题,它是基于贝叶斯定理以及特殊情形下独立性假设。
其中P(c|x)表示特征x属于类别c的概率,P(c)表示类别c的先验概率,P(x|c)表示特征x在类别c的条件下的概率,P(x)表示特征x的概率。
当计算出特征x属于不同类别的概率时,可以比较各自的概率大小,从而预测其最可能的类别。
以上就是机器学习公式的几个典型范例,机器学习也有很多不同的公式,可以根据实际情况来找到最合适的模型和公式。
Lasso极限最小学习机

o p t i m i s a t i o n o f i t e r a t i o n e x p r e s s i o n L a s s o( L a s s o — E L M) , i t h a s t h e f o l l o w i n g a d v a n t a g e s :( a )i t c a n s i g n i i f c a n t l y d e c r e a s e t h e n u m b e r o f t h e n o d e s i n h i d d e n l a y e r o f n e u r a l n e t w o r k s ; ( b )i t h a s b e t t e r g e n e r a l i s a t i o n c a p a b i l i t y o f n e u r a l n e t w o r k s . E x p e r i m e n t s s h o w, t h e c o mp r e h e n s i v e
网络节 点的参数结合最小二乘法达到 了减少训练 时间的 目的, 但 它需要产 生大量 的神经 网络节点协助运 算。提 出一种利 用迭代 式 L a s s o回归优化 的极限最小学 习机( L a s s o . E L M) , 它具有 以下优势 : ( 1 )能大幅减少 神经 网络隐藏层 节点的数量 ; ( 2 )具 有更好 的神 经 网络泛化 能力 。实验表 明 L a s s o - E L M 的综合性能优于 E L M、 B P与 S V M。
p e f r o r ma n c e o f L a s s o — E L M o u t p e f r o r ms t h e EL M ,B P a n d S VM . Ke y wo r d s E x t r e me l e a r n i n g ma c h i n e L a s s o Ne u r a l n e t wo r k
35种原点回归模式

35种原点回归模式详解在数据分析与机器学习的领域中,回归分析是一种重要的统计方法,用于研究因变量与自变量之间的关系。
以下是35种常见的回归分析方法,包括线性回归、多项式回归、逻辑回归等。
1.线性回归(Linear Regression):最简单且最常用的回归分析方法,适用于因变量与自变量之间存在线性关系的情况。
2.多项式回归(Polynomial Regression):通过引入多项式函数来扩展线性回归模型,以适应非线性关系。
3.逻辑回归(Logistic Regression):用于二元分类问题的回归分析方法,其因变量是二元的逻辑函数。
4.岭回归(Ridge Regression):通过增加一个正则化项来防止过拟合,有助于提高模型的泛化能力。
5.主成分回归(Principal Component Regression):利用主成分分析降维后进行线性回归,减少数据的复杂性。
6.套索回归(Lasso Regression):通过引入L1正则化,强制某些系数为零,从而实现特征选择。
7.弹性网回归(ElasticNet Regression):结合了L1和L2正则化,以同时实现特征选择和防止过拟合。
8.多任务学习回归(Multi-task Learning Regression):将多个任务共享部分特征,以提高预测性能和泛化能力。
9.时间序列回归(Time Series Regression):专门针对时间序列数据设计的回归模型,考虑了时间依赖性和滞后效应。
10.支持向量回归(Support Vector Regression):利用支持向量机技术构建的回归模型,适用于小样本数据集。
11.K均值聚类回归(K-means Clustering Regression):将聚类算法与回归分析相结合,通过对数据进行聚类后再进行回归预测。
12.高斯过程回归(Gaussian Process Regression):基于高斯过程的非参数贝叶斯方法,适用于解决非线性回归问题。
极限学习机在车身前纵梁装配中误差预测应用

10.16638/ki.1671-7988.2020.20.052极限学习机在车身前纵梁装配中误差预测应用张鑫,王立影,陈樟(上汽通用汽车有限公司,上海201206)摘要:在智能制造推动下,制造业对大数据的收集与特征分析愈加重视,数据分析技术更是大数据应用的关键技术,总结现有基于数据驱动的装配偏差控制方法,提出基于极限学习机建模的车身装配偏差预测控制方法,通过对检测数据的拟合建模,实现车身产品装配质量预测,并应用于制造生产线指导。
文章应用极限学习机(Extreme Learning Machine,ELM)基于采集的车身前纵梁制造装配数据预测装配过程中的关键特征质量误差状态,从结果分析角度说明ELM准确预测误差状态。
关键词:极限学习机;数据处理;回归拟合;质量预测中图分类号:U462 文献标识码:A 文章编号:1671-7988(2020)20-161-04The application of extreme learning machine to the prediction of error statein front side rail assemblyZhang Xin, Wang Liying, Chen Zhang( Saic General Motors Co. Ltd, Shanghai 201206 )Abstract: In intelligent manufacturing, manufacturing characteristics of big data collection and analysis of more and more attention, the data analysis technology is the key technology of big data applications, summarizes the existing problem of assembling deviation control method based on data driven, modeling was proposed based on extreme learning machine body assembling deviation predictive control method, through the fitting modeling of test data, the assembly quality prediction of body products can be realized, and applied to the manufacturing line. This paper applied Extreme Learning Machine (ELM) to predict the mass error state in the assembly process based on the collected manufacturing assembly data, and illustrate the accurate prediction error state of ELM from the perspective of result analysis.Keywords: ELM; Data processing; Regression fitting; Quality predictionCLC NO.: U462 Document Code: A Article ID: 1671-7988(2020)20-161-04前言汽车制造业海量的数据源为大数据挖掘分析提供了良好的应用基础,基于“数据驱动质量”(Data-driven)的思想,车身制造过程中偏差源的及时发现、故障预警和快速诊断是汽车质量控制中的关键环节,开展汽车制造过程中多源数据融合与质量诊断预测控制成为智能制造下研究的热点。
极限学习机原理介绍

T n
ti [ti1 , ti 2 ,..., tim ] R m ,给定任意小误差 0 ,和一个任意区间无限可微的
激活函数 g : R R,则总存在一个含有 K ( K Q ) 个隐含层神经元的 SLFN,在 任意赋值 wi R 和 bi
n
R 的情况下,有 || H N M M m T ' ||
其中, wi
(5)
[ wi1 , wi 2 ,..., win ] ; x j x1 j , x2 j ,..., xnj
T
式(5)可表示为
H T '
'
(6)
其中,T 为矩阵 T 的转置; H 称为神经网络的隐含层输出矩阵,具体形式如下:
H ( w1 , w2 ,..., wl , b1 , b2 ,..., bl , x1 , x2 ,...xQ ) g ( w1 x1 b1 ) g ( w2 x1 b2 ) g ( w x b ) g ( w x b ) 1 2 1 2 2 2 ... ... g ( w1 xQ b1 ) g ( w2 xQ b2 ) ... g ( wl x1 bl ) ... g ( wl x2 bl ) ... ... ... g ( wl xQ bl )
机器学习中的回归算法介绍

机器学习中的回归算法介绍一、引言机器学习(Machine Learning)是人工智能(AI)领域中的一个重要分支,它的主要任务是通过有限的训练数据来学习数据背后的模式和规律,然后将这些模式和规律应用到新的数据中,以达到更好的预测和决策效果。
在机器学习中,回归(Regression)是一种广泛应用的算法。
回归是一种机器学习的方法,通常用于预测唯一的因变量(响应变量),其结果可以是任何一种数字形式的输出结果,例如实数、整数等。
回归算法的主要目标是建立一个方程,根据独立变量(输入特征)来预测响应变量(输出结果)。
本文将介绍机器学习中常用的回归算法。
二、线性回归算法线性回归(Linear Regression)是一种最常用的回归算法,它主要基于最小二乘法(Least Squares Method)来预测因变量的值。
最小二乘法是一种优化方法,通过寻找使误差平方和最小的参数来确定线性回归的系数。
线性回归可以用于单一特征和多特征的预测任务。
三、岭回归算法岭回归(Ridge Regression)是一种形式的线性回归算法,它主要用于处理多重共线性数据。
多重共线性是指存在两个或多个独立变量之间的高度相关性的情况。
当多重共线性存在时,传统的线性回归算法会导致模型过度拟合,从而导致预测性能下降。
岭回归通过对模型中的参数进行平方化惩罚项调整,缓解因多重共线性而导致的过度拟合问题。
四、Lasso回归算法Lasso回归(Least Absolute Shrinkage and Selection Operator Regression)是另一种形式的线性回归算法,与岭回归不同的是,Lasso回归会通过对模型中的参数进行L1正则化惩罚来调整模型的系数,从而实现特征选择和模型简化的目的。
Lasso回归通常用于具有大量数据方式的特征选择问题。
五、决策树回归算法决策树回归(Decision Tree Regression)是一种非常有用的回归算法,它可以处理非线性数据,并且不需要任何数据分布的假设。
机器学习之拟合和过拟合问题

机器学习之拟合和过拟合问题
过拟合:当某个模型过度的学习训练数据中的细节和噪⾳,以⾄于模型在新的数据上表现很差,我们称过拟合发⽣了,通俗点就是:模型在训练集中测试的准确度远远⾼于在测试集中的准确度。
过拟合问题通常发⽣在变量特征过多的时候。
这种情况下训练出的⽅程总是能很好的拟合训练数据,也就是说,我们的代价函数可能⾮常接近于0或者就为0,使其拟合只局限于训练样本中,⽆法很好预测其他新的样本。
⽋拟合:在训练数据和未知数据上表现都很差
解决过拟合问题的⽅法主要有:
1. 减少特征数量,通过⼈⼯或者算法选择哪些特征有⽤保留,哪些特征没⽤删除,但会丢失信息。
2. 正则化,保留特征,但减少特征对应参数的⼤⼩,让每个特征都对预测产⽣⼀点影响。
解决⽋拟合问题的⽅法主要有:
1.减少正则化:正则化可以避免过拟合的发⽣,因此在出现过拟合的情况时,可以通过减少正则化的损失函数来防⽌过拟合的发⽣。
2.添加数据量和特征维度:由于模型可⽤于学习的数据规模可能不⾜够⼤,导致模型训练的不够充分,模型复杂度不够。
还有如果统计的数据信息中,各个维度数量收集的不够或者维度信息中⼤部分不具有区分样本的特质。
⾯对这种问题主要⽅法是收集更多的特质维度,或者增加采样信息等⽅式来扩充数据。
3.增加算法模型的复杂度:例如很多训练样本不是线性可分的,如果单⽤线性⽅法来拟合可能⽆法达到⼀个理想的拟合⽅法,这时候引⼊⾮线性⽅法,如核函数等⽅法或者更复杂的深度学习等⽅法来增加模型的复杂度。
机器学习中的线性回归模型解析与性能优化方法总结

机器学习中的线性回归模型解析与性能优化方法总结机器学习中的线性回归模型是一种简单但广泛使用的预测模型。
它通过拟合输入特征和输出标签之间的线性关系,来预测未知数据的输出。
本文将对线性回归模型进行详细解析,并总结一些性能优化方法。
1. 线性回归模型概述线性回归模型是一种监督学习算法,适用于回归问题。
它通过构建一个线性拟合函数,来描述输入特征和输出标签之间的关系。
线性回归的公式可以表示为:y= w0 + w1 * x1 + w2 * x2 + ... + wn * xn,其中y是输出,x1, x2, ..., xn 是输入特征,w0, w1, w2, ..., wn 是模型参数。
2. 最小二乘法最小二乘法是一种用于估计线性回归模型参数的常见方法。
它通过最小化预测值与真实值之间的平方误差,来求解最优参数。
最小二乘法的解析解可以通过求解矩阵方程 (X^T*X)^-1 * X^T * y 获得,其中X是输入特征矩阵,y是输出标签向量。
3. 梯度下降法梯度下降法是一种迭代优化算法,用于求解无解析解的问题。
对于线性回归模型,梯度下降法通过计算损失函数关于参数的梯度,并沿着负梯度方向更新参数,直到收敛到最优解。
梯度下降的更新规则可以表示为:w = w - α * ∇J(w),其中α是学习率,∇J(w)是损失函数关于参数的梯度。
4. 特征缩放和标准化特征缩放和标准化是一种常见的性能优化方法,用于将输入特征的值缩放到相似的范围。
这可以使模型更好地学习特征之间的权重,并提高模型的稳定性和收敛速度。
常见的特征缩放方法包括最小-最大缩放和标准化。
5. 特征选择和特征工程特征选择和特征工程是另一种性能优化方法,用于选择最相关的特征和构造新的特征。
通过选择最相关的特征,可以降低模型复杂度和提高模型的泛化能力。
通过构造新的特征,可以提取更高层次的特征表示,从而提高模型的表达能力。
6. 正则化方法正则化是一种常用的性能优化方法,用于控制模型的复杂度并避免过拟合。
机器学习中的分类与回归模型

机器学习中的分类与回归模型在机器学习中,分类和回归是两种重要的问题类型。
分类通常用于将数据划分为不同的集合,而回归则用于预测数值数据。
在这篇文章中,我们将介绍如何使用分类和回归模型,并且会讨论一些最流行的算法,如支持向量机,决策树和神经网络。
分类模型分类问题是指将数据划分为不同的集合。
例如,对于一组猫和狗的图片,我们需要训练一个模型,以便对新的图片进行分类。
这可以用于许多不同的应用程序,如面部识别、文本分类和智能风格推荐。
支持向量机是一个流行的分类算法,它基于将数据映射到高维空间,并通过最大化类之间的间隔来找到分界线。
它可以很好地处理非线性分类问题,但需要调整一些超参数。
另一种分类算法是决策树。
该模型通过一系列的二元分支来将数据分割成互不重叠且尽可能均匀的类别。
这种模型的优点是易于理解和解释,但可能会过度拟合数据。
神经网络是一种具有许多隐藏层的多层感知器,它可以通过反向传播算法来进行训练。
这个模型在许多应用中都有很好的表现,但是需要处理大量的超参数,并且可能过度拟合数据。
回归模型回归问题是指预测数值数据。
例如,对于一组商品的历史销售数据,我们可能会希望预测未来的销售量。
这类问题常见于金融预测、风险评估和房价预测。
线性回归是一个常见的回归算法,它试图通过一个线性方程来拟合数据,最小化残差平方和。
这种模型可以很好地处理线性关系,但是可能会过度拟合复杂的数据。
另一种回归算法是决策树回归,它与分类树一样,但是输出的是数值而不是类别。
这可以用于处理非线性结构的数据。
神经网络在回归问题上也很好用,可以通过单个输出神经元来拟合数据并最小化误差。
这种模型适用于广泛的应用领域,但是需要大量的超参数优化。
结论分类和回归模型是机器学习领域中最基本、最重要的类别。
选择不同的算法和模型取决于特定问题的性质和数据类型。
在实际应用中,我们需要考虑数据的质量、量和误差等因素,并尝试优化模型以达到最好的表现。
简单易学的机器学习算法 极限学习机(ELM)
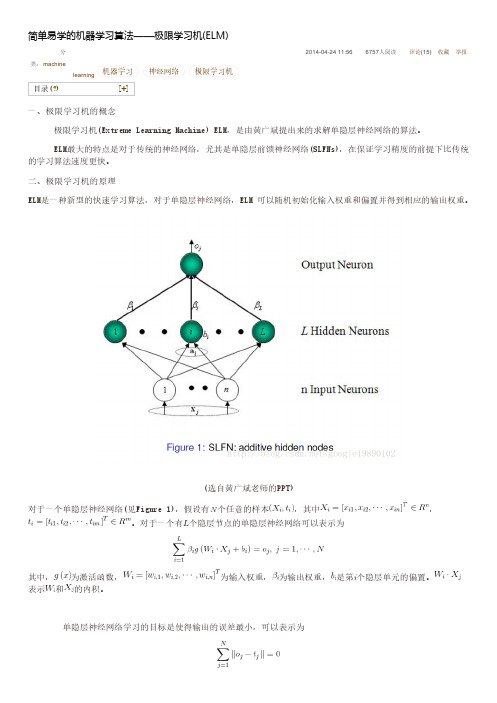
(选自黄广斌老师的PPT)对于一个单隐层神经网络(见Figure 1),假设有个任意的样本,其中,。
对于一个有个隐层节点的单隐层神经网络可以表示为其中,为激活函数,为输入权重,为输出权重,是第个隐层单元的偏置。
表示和的内积。
即存在,和,使得可以矩阵表示为其中,是隐层节点的输出,为输出权重,为期望输出。
,为了能够训练单隐层神经网络,我们希望得到,和,使得其中,,这等价于最小化损失函数传统的一些基于梯度下降法的算法,可以用来求解这样的问题,但是基本的基于梯度的学习算法需要在迭代的过程中调整所有参数。
而在ELM算法中, 一旦输入权重和隐层的偏置被随机确定,隐层的输出矩阵就被唯一确定。
训练单隐层神经网络可以转化为求解一个线性系统。
并且输出权重可以被确定其中,是矩阵的Moore-Penrose广义逆。
且可证明求得的解的范数是最小的并且唯一。
三、实验我们使用《简单易学的机器学习算法——Logistic回归》中的实验数据。
原始数据集我们采用统计错误率的方式来评价实验的效果,其中错误率公式为:对于这样一个简单的问题,。
MATLAB代码主程序[plain]01. %% 主函数,二分类问题02.03. %导入数据集04. A = load('testSet.txt');05.06. data = A(:,1:2);%特征07. label = A(:,3);%标签08.09. [N,n] = size(data);10.11. L = 100;%隐层节点个数12. m = 2;%要分的类别数13.14. %‐‐初始化权重和偏置矩阵15. W = rand(n,L)*2‐1;16. b_1 = rand(1,L);17. ind = ones(N,1);18. b = b_1(ind,:);%扩充成N*L的矩阵19.20. tempH = data*W+b;21. H = g(tempH);%得到H22.23. %对输出做处理24. temp_T=zeros(N,m);25. for i = 1:N26. if label(i,:) == 027. temp_T(i,1) = 1;28. else29. temp_T(i,2) = 1;30. end31. end32. T = temp_T*2‐1;33.34. outputWeight = pinv(H)*T;35.36. %‐‐画出图形37. x_1 = data(:,1);38. x_2 = data(:,2);39. hold on40. for i = 1 : N41. if label(i,:) == 042. plot(x_1(i,:),x_2(i,:),'.g');43. else44. plot(x_1(i,:),x_2(i,:),'.r');45. end46. end47.48. output = H * outputWeight;49. %‐‐‐计算错误率50. tempCorrect=0;51. for i = 1:N52. [maxNum,index] = max(output(i,:));53. index = index‐1;54. if index == label(i,:);55. tempCorrect = tempCorrect+1;56. end57. end58.59. errorRate = 1‐tempCorrect./N;激活函数[plain]01. function [ H ] = g( X )02. H = 1 ./ (1 + exp(‐X));03. end黄老师提供的极限学习机的代码:点击打开链接。
MATLAB-智能算法30个案例分析-终极版(带目录)

MATLAB 智能算法30个案例分析(终极版)1 基于遗传算法的TSP算法(王辉)2 基于遗传算法和非线性规划的函数寻优算法(史峰)3 基于遗传算法的BP神经网络优化算法(王辉)4 设菲尔德大学的MATLAB遗传算法工具箱(王辉)5 基于遗传算法的LQR控制优化算法(胡斐)6 遗传算法工具箱详解及应用(胡斐)7 多种群遗传算法的函数优化算法(王辉)8 基于量子遗传算法的函数寻优算法(王辉)9 多目标Pareto最优解搜索算法(胡斐)10 基于多目标Pareto的二维背包搜索算法(史峰)11 基于免疫算法的柔性车间调度算法(史峰)12 基于免疫算法的运输中心规划算法(史峰)13 基于粒子群算法的函数寻优算法(史峰)14 基于粒子群算法的PID控制优化算法(史峰)15 基于混合粒子群算法的TSP寻优算法(史峰)16 基于动态粒子群算法的动态环境寻优算法(史峰)17 粒子群算法工具箱(史峰)18 基于鱼群算法的函数寻优算法(王辉)19 基于模拟退火算法的TSP算法(王辉)20 基于遗传模拟退火算法的聚类算法(王辉)21 基于模拟退火算法的HEV能量管理策略参数优化(胡斐)22 蚁群算法的优化计算——旅行商问题(TSP)优化(郁磊)23 基于蚁群算法的二维路径规划算法(史峰)24 基于蚁群算法的三维路径规划算法(史峰)25 有导师学习神经网络的回归拟合——基于近红外光谱的汽油辛烷值预测(郁磊)26 有导师学习神经网络的分类——鸢尾花种类识别(郁磊)27 无导师学习神经网络的分类——矿井突水水源判别(郁磊)28 支持向量机的分类——基于乳腺组织电阻抗特性的乳腺癌诊断(郁磊)29 支持向量机的回归拟合——混凝土抗压强度预测(郁磊)30 极限学习机的回归拟合及分类——对比实验研究(郁磊)智能算法是我们在学习中经常遇到的算法,主要包括遗传算法,免疫算法,粒子群算法,神经网络等,智能算法对于很多人来说,既爱又恨,爱是因为熟练的掌握几种智能算法,能够很方便的解决我们的论坛问题,恨是因为智能算法感觉比较“玄乎”,很难理解,更难用它来解决问题。
基于极限学习机的蚜虫刺吸电位波形的分类识别

基于极限学习机的蚜虫刺吸电位波形的分类识别吴莉莉; 邢玉清; 林爱英; 郑宝周; 潘建斌; 闫凤鸣【期刊名称】《《传感技术学报》》【年(卷),期】2019(032)010【总页数】6页(P1535-1540)【关键词】极限学习机; 小波变换; 刺吸电位波形; 特征提取; 分类【作者】吴莉莉; 邢玉清; 林爱英; 郑宝周; 潘建斌; 闫凤鸣【作者单位】河南农业大学理学院郑州450002; 河南农业大学植物保护学院郑州450002【正文语种】中文【中图分类】TP391; TN911.72蚜虫是一类体型很小的植食性刺吸式昆虫,大多数是重要的农林害虫,如棉蚜、桃蚜、大豆蚜、禾谷缢管蚜等,是世界上最具破坏性的害虫类别之一;蚜虫还是植物病毒最主要的传毒介体类别之一。
昆虫刺吸电位仪(Electrical Penetration Graph,EPG)作为进行昆虫取食行为、昆虫传毒机制、作物抗虫机制等方面研究的有力工具[1-2],可以为包括蚜虫在内的刺吸式昆虫的防控方法研究及其所传播植物病毒的机理研究提供技术支撑,目前已成功应用于蚜虫、粉虱、飞虱、叶蝉、蓟马、蝽等50多种昆虫的相关研究。
但EPG波形的识别和分析一直是靠人工进行,费时费力,很大程度上限制了EPG技术的应用和作用的发挥,因此迫切需要EPG波形的自动识别。
EPG技术最早应用于蚜虫取食行为的研究,现阶段国内外对蚜虫的EPG波形研究也最深入和广泛。
蚜虫EPG波形典型且稳定,不同蚜虫种类的EPG波形差异很小,是进行其他类别昆虫EPG波形识别的重要参考。
结合透射电镜、同位素示踪、口针切割等技术,已明确了蚜虫的7种基本波形及其生物学意义,见表1。
这7种波形分别为np波(非刺探波,此时蚜虫口针未刺入植物表皮内,波形几近直线)、C波(路径波,包含A波和B波,在判读中一般将一些不能明确区分的波也归入C 波)、pd波(口针穿刺波)、E1波(韧皮部分泌唾液波)、E2波(韧皮部取食波)、G波(木质部取食波)和F波(机械障碍波)[2]。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
极限学习机的回归拟合及分类
单隐含层前馈神经网络(single-hidden layer feedforward neural network)以其良好的学习能力在许多领域中得到了广泛的应用。
然而,传统的学习方法(如BP算法等)固有的一些缺点,成为制约其发展的主要瓶颈。
前馈神经网络大多采用梯度下降方法,该方法主要存在以下几方面的缺点:
(1)训练速度慢。
由于梯度下降法需要多次迭代以达到修正权值和阈值的目的,因此训练过程耗时较长。
(2)容易陷入局部极小点,无法达到全局最小。
(3)学习率η的选择敏感。
学习率η对神经网络的性能影响较大,必须选择合适的η,才能获得较为理想的网络。
若η太小,则算法收敛速度很慢,训练过程耗时长;
反之,若η太大,则训练过程可能不稳定(收敛)。
因此,探索一种训练速度快,获得全局最优解,且具有良好的泛化性能的训练算法是提升前馈神经网络性能的主要目标,也是近年来的研究热点和难点。
本文将介绍一个针对SLFN的新算法——极限学习机(extreme learning machine,ELM),该算法随即产生输入层和隐含层的连接权值及隐含层神经元的阈值,且在训练过程中无需调整,只需要在设置隐含层神经元的个数便可以获得唯一的最优解。
与传统的训练方法相比,该方法具有学习速度快、泛化性能好等优点。
1.1ELM的基本思想
典型的单隐含层前馈神经网络结构如图1所示,该网络由输入层、隐含层和输出层组成,输入层与隐含层、隐含层与输出层神经元间全连接。
其中,输入层有n个神经元,对应n个输入变量;隐含层有l个神经元;输出层有m个神经元,对应m个输入变量。
图1
不是一般性,设输入层与隐含层的连接权值W为
1112121
22
212
n n l l ln l n
W ωωωωωωωωω⨯⎡⎤⎢⎥⎢⎥
=⎢⎥⎢
⎥⎣⎦
其中,ji ω表示输入层第i 个神经元与隐含层第j 个神经元间的连接权值。
设隐含层与输出层的连接权值β为
1112121
2221
2
m m l l lm l m
ββββββββββ⨯⎡⎤⎢⎥⎢⎥
=⎢⎥⎢⎥⎣⎦
其中,jk β表示隐含层第j 个神经元与输出层第k 个神经元间的连接权值。
设隐含层神经元的阈值b 为
121
l l b b b b ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦
设具有Q 个样本的训练集输入矩阵X 和输出矩阵Y 分别为
1112
121
2221
2
Q Q n n nQ n Q x x x x x x X x x x ⨯⎡⎤⎢⎥⎢
⎥=⎢⎥⎢⎥⎢⎥⎣⎦ ,11
12
121
2121
2
Q Q m m mQ m Q
y y y y y y Y y y y ⨯⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎢⎥⎣⎦ ,1,2,3,,j Q =
其中,12[,,,]i i i in W ωωω= ,'12[,,,]i j j nj X x x x = 。
上式可表示为
'H T β=
其中,'
T 为矩阵T 的转置;H 称为神经网络的隐含层输出矩阵,具体形式为
12121211121211122221122(,,,,,,,,,,,)()()()()()()()()()l l Q l l l l Q Q l Q l Q l
H b b b x x x g x b g x b g x b g x b g x b g x b g x b g x b g x b ωωωωωωωωωωωω⨯=
+++⎡⎤
⎢⎥
+++⎢
⎥⎢⎥⎢⎥+++⎢⎥⎣⎦。
