浙江高考数学试卷
浙江省杭州市(新版)2024高考数学统编版(五四制)测试(综合卷)完整试卷

浙江省杭州市(新版)2024高考数学统编版(五四制)测试(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知平面向量,且,则()A.2B.-2C.D.第(2)题设,,,则()A.B.C.D.第(3)题函数y=sin2x+cos 2x的最小正周期为()A.B.C.πD.2π第(4)题已知为等比数列,,且,则的公比的取值范围是()A.B.C.D.第(5)题下列选项中,所得到的结果为4的是()A.双曲线的焦距B.的值C.函数的最小正周期D.数据的下四分位数第(6)题将函数图象上所有点的横坐标缩小为原来的,再向右平移个单位长度,得到函数的图象,若在上有两个不同的零点,,则()A.B.C.D.第(7)题样本数据16,20,21,24,22,14,18,28的分位数为()A.16B.14C.23D.22第(8)题已知点在关于x,y的不等式所表示的平面区域内,则的最小值为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题如图,已知函数的图象,,则()A.B.C.D.第(2)题某保险公司销售某种保险产品,根据2020年全年该产品的销售额(单位:万元)和该产品的销售额占总销售额的百分比,绘制出如图所示的双层饼图.根据双层饼图,下列说法正确的是()A.2020年第四季度的销售额为280万元B.2020年上半年的总销售额为500万元C.2020年2月份的销售额为60万元D.2020年12个月的月销售额的众数为60万元第(3)题已知平面向量,且,满足,若﹐则可能的取值为()A.4B.8C.12D.16三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题若正数x,y满足,则的最小值是___________.第(2)题不等式的解集是 .第(3)题在三角形ABC中,角A、B、C的对边分别为a、b、c,且∠BAC的平分线交BC于D,若,则的最小值为________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题设函数.(1)当时,求不等式的解集;(2)若,,,证明.第(2)题为了促进消费,某商场针对会员客户推出会员积分兑换商品活动:每位会员客户可在价值80元,90元,100元的,,三种商品中选择一种使用积分进行兑换,每10积分可兑换1元.已知参加活动的甲、乙两位客户各有1000积分,且甲兑换,,三种商品的概率分别为,,,乙兑换,,三种商品的概率分别为,,,且他们兑换何种商品相互独立.(1)求甲、乙两人兑换同一种商品的概率;(2)记为两人兑换商品后的积分总余额,求的分布列与期望第(3)题如图,在直三棱柱中,底面是以为底边的等腰直角三角形,,.(1)求证:平面平面;(2)求点到平面的距离.第(4)题如图,在三棱柱中,是等边三角形,侧面底面,且,,M是的中点.(1)证明:.(2)求二面角的正弦值.第(5)题已知为等差数列的前项和,且,当时,.(1)求数列的通项公式;(2)若,求数列的前项和.。
2021年高考数学真题试卷(浙江卷)带答案解析

2021年高考数学真题试卷(浙江卷)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
(共10题;共40分)1.设集合A={x|x≥1},B={x|−1<x<2},则A∩B=()A. {x|x>−1}B. {x|x≥1}C. {x|−1<x<1}D. {x|1≤x<2}【答案】 D【考点】交集及其运算【解析】【解答】由交集的定义结合题意可得:A∩B={x|1≤x<2}.故答案为:D.【分析】利用数轴,求不等式表示的集合的交集。
2.已知a∈R,(1+ai)i=3+i,(i为虚数单位),则a=()A. -1B. 1C. -3D. 3【答案】C【考点】复数代数形式的乘除运算,复数代数形式的混合运算【解析】【解答】(1+ai)i=i−a=−a+i,利用复数相等的充分必要条件可得:−a=3,∴a=−3.故答案为:C.【分析】根据复数相等的条件,即可求得a的值。
3.已知非零向量a⃗,b⃗⃗,c⃗,则“ a⃗⋅c⃗=b⃗⃗⋅c⃗”是“ a⃗=b⃗⃗”的()A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分又不必要条件【答案】B【考点】充分条件,必要条件,充要条件,平面向量数量积的运算【解析】【解答】若a⃗⋅c⃗=b⃗⃗⋅c⃗,则(a⃗−b⃗⃗)⋅c⃗=0,推不出a⃗=b⃗⃗;若a⃗=b⃗⃗,则a⃗⋅c⃗=b⃗⃗⋅c⃗必成立,故“ a⃗⋅c⃗=b⃗⃗⋅c⃗”是“ a⃗=b⃗⃗”的必要不充分条件故答案为:B.【分析】先将条件等式变形,可能得到条件不充分,后者显然成立。
4.某几何体的三视图如图所示,则该几何体的体积是()A. 32 B.3 C. 3√22D. 3√2 【答案】 A【考点】由三视图求面积、体积【解析】【解答】几何体为如图所示的四棱柱 ABCD −A 1B 1C 1D 1 ,其高为1,底面为等腰梯形 ABCD ,该等腰梯形的上底为 √2 ,下底为 2√2 ,腰长为1,故梯形的高为 √1−12=√22,故 V ABCD−A 1B 1C 1D 1=12×(√2+2√2)×√22×1=32,故答案为:A.【分析】先由三视图,还原立体图形,然后根据数量关系计算体积。
2024年浙江高考数学真题及答案

2024年浙江高考数学真题及答案本试卷共10页,19小题,满分150分.注意事项:1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3.填空题和解答题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试卷和答题卡一并上交.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.1.已知集合{}355,{3,1,0,2,3}A x xB =-<<=--∣,则A B = ()A.{1,0}- B.{2,3} C.{3,1,0}-- D.{1,0,2}-2.若1i 1zz =+-,则z =()A.1i --B.1i-+ C.1i- D.1i+3.已知向量(0,1),(2,)a b x == ,若(4)b b a ⊥-,则x =()A.2- B.1- C.1D.24.已知cos(),tan tan 2m αβαβ+==,则cos()αβ-=()A.3m- B.3m -C.3m D.3m5.()A. B. C. D.6.已知函数为22,0()e ln(1),0x x ax a x f x x x ⎧---<=⎨++≥⎩,在R 上单调递增,则a 取值的范围是()A.(,0]-∞ B.[1,0]- C.[1,1]- D.[0,)+∞7.当[0,2]x πÎ时,曲线sin y x =与2sin 36y x π⎛⎫=- ⎪⎝⎭的交点个数为()A.3B.4C.6D.88.已知函数为()f x 的定义域为R ,()(1)(2)f x f x f x >-+-,且当3x <时()f x x =,则下列结论中一定正确的是()A.(10)100f >B.(20)1000f >C.(10)1000f < D.(20)10000f <二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.9.为了解推动出口后的亩收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值 2.1x =,样本方差20.01s =,已知该种植区以往的亩收入X 服从正态分布()21.8,0.1N ,假设推动出口后的亩收入Y 服从正态分布()2,N x s ,则()(若随机变量Z 服从正态分布()2,N u σ,()0.8413P Z u σ<+≈)A.(2)0.2P X >>B.(2)0.5P X ><C.(2)0.5P Y >> D.(2)0.8P Y ><10.设函数2()(1)(4)f x x x =--,则()A.3x =是()f x 的极小值点B.当01x <<时,()2()f x f x<C.当12x <<时,4(21)0f x -<-< D.当10x -<<时,(2)()f x f x ->11.造型可以做成美丽的丝带,将其看作图中曲线C 的一部分.已知C 过坐标原点O .且C 上的点满足横坐标大于2-,到点(2,0)F 的距离与到定直线(0)x a a =<的距离之积为4,则()A.2a =- B.点在C 上C.C 在第一象限的点的纵坐标的最大值为1D.当点()00,x y 在C 上时,0042y x ≤+三、填空题:本题共3小题,每小题5分,共15分.12.设双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点分别为12F F 、,过2F 作平行于y 轴的直线交C 于A ,B 两点,若1||13,||10F A AB ==,则C 的离心率为___________.13.若曲线e x y x =+在点()0,1处的切线也是曲线ln(1)y x a =++的切线,则=a __________.14.甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分不小于2的概率为_________.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.记ABC 内角A 、B 、C 的对边分别为a ,b ,c ,已知sin C B =,222a b c +-=(1)求B ;(2)若ABC 的面积为3c .16.已知(0,3)A 和33,2P ⎛⎫ ⎪⎝⎭为椭圆2222:1(0)x yC a b a b+=>>上两点.(1)求C 的离心率;(2)若过P 的直线l 交C 于另一点B ,且ABP 的面积为9,求l 的方程.17.如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,2PA AC ==,1,BC AB ==.(1)若AD PB ⊥,证明://AD 平面PBC ;(2)若AD DC ⊥,且二面角A CP D --的正弦值为427,求AD .18.已知函数3()ln(1)2xf x ax b x x=++--(1)若0b =,且()0f x '≥,求a 的最小值;(2)证明:曲线()y f x =是中心对称图形;(3)若()2f x >-当且仅当12x <<,求b 的取值范围.19.设m 为正整数,数列1242,,...,m a a a +是公差不为0的等差数列,若从中删去两项i a 和()j a i j <后剩余的4m 项可被平均分为m 组,且每组的4个数都能构成等差数列,则称数列1242,,...,m a a a +是(),i j -可分数列.(1)写出所有的(),i j ,16i j ≤<≤,使数列126,,...,a a a 是(),i j -可分数列;(2)当3m ≥时,证明:数列1242,,...,m a a a +是()2,13-可分数列;(3)从1,2,...,42m +中一次任取两个数i 和()j i j <,记数列1242,,...,m a a a +是(),i j -可分数列的概率为m P ,证明:18m P >.参考答案本试卷共10页,19小题,满分150分.注意事项:1.答题前,先将自己的姓名、准考证号、考场号、座位号填写在试卷和答题卡上,并将准考证号条形码粘贴在答题卡上的指定位置.2.选择题的作答:每小题选出答案后,用2B 铅笔把答题卡上对应题目的答案标号涂黑.写在试卷、草稿纸和答题卡上的非答题区域均无效.3.填空题和解答题的作答:用黑色签字笔直接答在答题卡上对应的答题区域内.写在试卷、草稿纸和答题卡上的非答题区域均无效.4.考试结束后,请将本试卷和答题卡一并上交.一、选择题:本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一个选项是正确的.请把正确的选项填涂在答题卡相应的位置上.1.已知集合{}355,{3,1,0,2,3}A x xB =-<<=--∣,则A B = ()A.{1,0}- B.{2,3} C.{3,1,0}-- D.{1,0,2}-【答案】A 【解析】【分析】化简集合A ,由交集的概念即可得解.【详解】因为{{}|,3,1,0,2,3A x x B =<<=--,且注意到12<<,从而A B = {}1,0-.故选:A.2.若1i 1zz =+-,则z =()A.1i --B.1i-+ C.1i- D.1i+【答案】C 【解析】【分析】由复数四则运算法则直接运算即可求解.【详解】因为11111i 111z z z z z -+==+=+---,所以111i i z =+=-.故选:C.3.已知向量(0,1),(2,)a b x == ,若(4)b b a ⊥-,则x =()A.2-B.1- C.1D.2【答案】D 【解析】【分析】根据向量垂直的坐标运算可求x 的值.【详解】因为()4b b a ⊥- ,所以()40b b a ⋅-=,所以240b a b -⋅=即2440x x +-=,故2x =,故选:D.4.已知cos(),tan tan 2m αβαβ+==,则cos()αβ-=()A.3m -B.3m -C.3m D.3m【答案】A 【解析】【分析】根据两角和的余弦可求cos cos ,sin sin αβαβ的关系,结合tan tan αβ的值可求前者,故可求()cos αβ-的值.【详解】因为()cos m αβ+=,所以cos cos sin sin m αβαβ-=,而tan tan 2αβ=,所以sin sin 2cos cos αβαβ=,故cos cos 2cos cos m αβαβ-=即cos cos m αβ=-,从而sin sin 2m αβ=-,故()cos 3m αβ-=-,故选:A.5.()A. B. C. D.【答案】B 【解析】【分析】设圆柱的底面半径为r ,根据圆锥和圆柱的侧面积相等可得半径r 的方程,求出解后可求圆锥的体积.【详解】设圆柱的底面半径为r而它们的侧面积相等,所以2ππr r =即=,故3r =,故圆锥的体积为1π93⨯=.故选:B.6.已知函数为22,0()e ln(1),0x x ax a x f x x x ⎧---<=⎨++≥⎩,在R 上单调递增,则a 取值的范围是()A.(,0]-∞ B.[1,0]- C.[1,1]- D.[0,)+∞【答案】B 【解析】【分析】根据二次函数的性质和分界点的大小关系即可得到不等式组,解出即可.【详解】因为()f x 在R 上单调递增,且0x ≥时,()()e ln 1xf x x =++单调递增,则需满足()02021e ln1a a -⎧-≥⎪⨯-⎨⎪-≤+⎩,解得10a -≤≤,即a 的范围是[1,0]-.故选:B.7.当[0,2]x πÎ时,曲线sin y x =与2sin 36y x π⎛⎫=- ⎪⎝⎭的交点个数为()A.3B.4C.6D.8【答案】C 【解析】【分析】画出两函数在[]0,2π上的图象,根据图象即可求解【详解】因为函数sin y x =的的最小正周期为2πT =,函数π2sin 36y x ⎛⎫=-⎪⎝⎭的最小正周期为2π3T =,所以在[]0,2πx ∈上函数π2sin 36y x ⎛⎫=-⎪⎝⎭有三个周期的图象,在坐标系中结合五点法画出两函数图象,如图所示:由图可知,两函数图象有6个交点.故选:C8.已知函数为()f x 的定义域为R ,()(1)(2)f x f x f x >-+-,且当3x <时()f x x =,则下列结论中一定正确的是()A.(10)100f >B.(20)1000f >C.(10)1000f <D.(20)10000f <【答案】B 【解析】【分析】代入得到(1)1,(2)2f f ==,再利用函数性质和不等式的性质,逐渐递推即可判断.【详解】因为当3x <时()f x x =,所以(1)1,(2)2f f ==,又因为()(1)(2)f x f x f x >-+-,则(3)(2)(1)3,(4)(3)(2)5f f f f f f >+=>+>,(5)(4)(3)8,(6)(5)(4)13,(7)(6)(5)21f f f f f f f f f >+>>+>>+>,(8)(7)(6)34,(9)(8)(7)55,(10)(9)(8)89f f f f f f f f f >+>>+>>+>,(11)(10)(9)144,(12)(11)(10)233,(13)(12)(11)377f f f f f f f f f >+>>+>>+>(14)(13)(12)610,(15)(14)(13)987f f f f f f >+>>+>,(16)(15)(14)15971000f f f >+>>,则依次下去可知(20)1000f >,则B 正确;且无证据表明ACD 一定正确.故选:B.【点睛】关键点点睛:本题的关键是利用(1)1,(2)2f f ==,再利用题目所给的函数性质()(1)(2)f x f x f x >-+-,代入函数值再结合不等式同向可加性,不断递推即可.二、选择题:本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对得6分,部分选对的得部分分,选对但不全的得部分分,有选错的得0分.9.为了解推动出口后的亩收入(单位:万元)情况,从该种植区抽取样本,得到推动出口后亩收入的样本均值 2.1x =,样本方差20.01s =,已知该种植区以往的亩收入X 服从正态分布()21.8,0.1N ,假设推动出口后的亩收入Y 服从正态分布()2,N x s ,则()(若随机变量Z 服从正态分布()2,N u σ,()0.8413P Z u σ<+≈)A.(2)0.2P X >>B.(2)0.5P X ><C.(2)0.5P Y >>D.(2)0.8P Y ><【答案】BC 【解析】【分析】根据正态分布的3σ原则以及正态分布的对称性即可解出.【详解】依题可知,22.1,0.01x s ==,所以()2.1,0.1Y N ,故()()()2 2.10.1 2.10.10.84130.5P Y P Y P Y >=>-=<+≈>,C 正确,D 错误;因为()1.8,0.1X N ,所以()()2 1.820.1P X P X >=>+⨯,因为()1.80.10.8413P X <+≈,所以()1.80.110.84130.15870.2P X >+≈-=<,而()()()2 1.820.1 1.80.10.2P X P X P X >=>+⨯<>+<,B 正确,A 错误,故选:BC.10.设函数2()(1)(4)f x x x =--,则()A.3x =是()f x 的极小值点B.当01x <<时,()2()f x f x<C.当12x <<时,4(21)0f x -<-< D.当10x -<<时,(2)()f x f x ->【答案】ACD 【解析】【分析】求出函数()f x 的导数,得到极值点,即可判断A;利用函数的单调性可判断B;根据函数()f x 在()1,3上的值域即可判断C;直接作差可判断D.【详解】对A ,因为函数()f x 的定义域为R ,而()()()()()()22141313f x x x x x x =--+-=--',易知当()1,3x ∈时,()0f x '<,当(),1x ∞∈-或()3,x ∞∈+时,()0f x '>函数()f x 在(),1∞-上单调递增,在()1,3上单调递减,在()3,∞+上单调递增,故3x =是函数()f x 的极小值点,正确;对B,当01x <<时,()210x x x x -=->,所以210x x >>>,而由上可知,函数()f x 在()0,1上单调递增,所以()()2f x f x>,错误;对C,当12x <<时,1213x <-<,而由上可知,函数()f x 在()1,3上单调递减,所以()()()1213f f x f >->,即()4210f x -<-<,正确;对D,当10x -<<时,()()()()()()222(2)()12141220f x f x x x x x x x --=------=-->,所以(2)()f x f x ->,正确;故选:ACD.11.造型可以做成美丽的丝带,将其看作图中曲线C 的一部分.已知C 过坐标原点O .且C 上的点满足横坐标大于2-,到点(2,0)F 的距离与到定直线(0)x a a =<的距离之积为4,则()A.2a =- B.点在C 上C.C 在第一象限的点的纵坐标的最大值为1D.当点()00,x y 在C 上时,0042y x ≤+【答案】ABD 【解析】【分析】根据题设将原点代入曲线方程后可求a ,故可判断A 的正误,结合曲线方程可判断B 的正误,利用特例法可判断C 的正误,将曲线方程化简后结合不等式的性质可判断D 的正误.【详解】对于A:设曲线上的动点(),P x y ,则2x >-4x a -=,04a -=,解得2a =-,故A 正确.对于24x +=,而2x >-,()24x +=.当0x y ==()2844=-=,故()在曲线上,故B 正确.对于C:由曲线的方程可得()()2221622y x x =--+,取32x =,则2641494y =-,而64164525624510494494494---=-=>⨯,故此时21y >,故C 在第一象限内点的纵坐标的最大值大于1,故C 错误.对于D:当点()00,x y 在曲线上时,由C 的分析可得()()()220022001616222y x x x =--≤++,故0004422y x x -≤≤++,故D 正确.故选:ABD.【点睛】思路点睛:根据曲线方程讨论曲线的性质,一般需要将曲线方程变形化简后结合不等式的性质等来处理.三、填空题:本题共3小题,每小题5分,共15分.12.设双曲线2222:1(0,0)x y C a b a b-=>>的左右焦点分别为12F F 、,过2F 作平行于y 轴的直线交C 于A ,B 两点,若1||13,||10F A AB ==,则C 的离心率为___________.【答案】32【解析】【分析】由题意画出双曲线大致图象,求出2AF ,结合双曲线第一定义求出1AF ,即可得到,,a b c 的值,从而求出离心率.【详解】由题可知2,,A B F 三点横坐标相等,设A 在第一象限,将x c =代入22221x ya b-=得2b y a =±,即22,,,b b A c B c a a ⎛⎫⎛⎫- ⎪ ⎪⎝⎭⎝⎭,故2210b AB a ==,225b AF a ==,又122AF AF a -=,得1222513AF AF a a =+=+=,解得4a =,代入25b a=得220b =,故22236,c a b =+=,即6c =,所以6342c e a ===.故答案为:3213.若曲线e x y x =+在点()0,1处的切线也是曲线ln(1)y x a =++的切线,则=a __________.【答案】ln 2【解析】【分析】先求出曲线e x y x =+在()0,1的切线方程,再设曲线()ln 1y x a =++的切点为()()0,ln 1x xa ++,求出y ',利用公切线斜率相等求出0x ,表示出切线方程,结合两切线方程相同即可求解.【详解】由e x y x =+得e 1x y '=+,00|e 12x y ='=+=,故曲线e x y x =+在()0,1处的切线方程为21y x =+;由()ln 1y x a =++得11y x '=+,设切线与曲线()ln 1y x a =++相切的切点为()()00,ln 1x x a ++,由两曲线有公切线得0121y x '==+,解得012x =-,则切点为11,ln 22a ⎛⎫-+ ⎪⎝⎭,切线方程为112ln 21ln 222y x a x a ⎛⎫=+++=++- ⎪⎝⎭,根据两切线重合,所以ln 20a -=,解得ln 2a =.故答案为:ln 214.甲、乙两人各有四张卡片,每张卡片上标有一个数字,甲的卡片上分别标有数字1,3,5,7,乙的卡片上分别标有数字2,4,6,8,两人进行四轮比赛,在每轮比赛中,两人各自从自己持有的卡片中随机选一张,并比较所选卡片上数字的大小,数字大的人得1分,数字小的人得0分,然后各自弃置此轮所选的卡片(弃置的卡片在此后的轮次中不能使用).则四轮比赛后,甲的总得分不小于2的概率为_________.【答案】12##0.5【解析】【分析】将每局的得分分别作为随机变量,然后分析其和随机变量即可.【详解】设甲在四轮游戏中的得分分别为1234,,,X X X X ,四轮的总得分为X .对于任意一轮,甲乙两人在该轮出示每张牌的概率都均等,其中使得甲获胜的出牌组合有六种,从而甲在该轮获胜的概率()631448k P X ===⨯,所以()()31,2,3,48k E X k ==.从而()()()441234113382kk k E X E X X X X E X ===+++===∑∑.记()()0,1,2,3k p P X k k ===.如果甲得0分,则组合方式是唯一的:必定是甲出1,3,5,7分别对应乙出2,4,6,8,所以04411A 24p ==;如果甲得3分,则组合方式也是唯一的:必定是甲出1,3,5,7分别对应乙出8,2,4,6,所以34411A 24p ==.而X 的所有可能取值是0,1,2,3,故01231p p p p +++=,()1233232p p p E X ++==.所以121112p p ++=,1213282p p ++=,两式相减即得211242p +=,故2312p p +=.所以甲的总得分不小于2的概率为2312p p +=.故答案为:12.【点睛】关键点点睛:本题的关键在于将问题转化为随机变量问题,利用期望的可加性得到等量关系,从而避免繁琐的列举.四、解答题:本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤.15.记ABC 内角A 、B 、C 的对边分别为a ,b ,c ,已知sin C B =,222a b c +-=(1)求B ;(2)若ABC 的面积为3c .【答案】(1)π3B =(2)【解析】【分析】(1)由余弦定理、平方关系依次求出cos ,sin C C ,最后结合已知sin C B=得cos B 的值即可;(2)首先求出,,A B C ,然后由正弦定理可将,a b 均用含有c 的式子表示,结合三角形面积公式即可列方程求解.【小问1详解】由余弦定理有2222cos a b c ab C +-=,对比已知222a b c +-=,可得22222cos 222a b c C ab ab +-===,因为()0,πC ∈,所以sin 0C >,从而2sin 2C ==,又因为sin C B =,即1cos 2B =,注意到()0,πB ∈,所以π3B =.【小问2详解】由(1)可得π3B =,2cos 2C =,()0,πC ∈,从而π4C =,ππ5ππ3412A =--=,而5πππ232162sin sin sin 124622224A ⎛⎫⎛⎫==+=⨯=⎪ ⎪⎝⎭⎝⎭,由正弦定理有5πππsin sin sin 1234a b c==,从而623136,4222a cbc +====,由三角形面积公式可知,ABC 的面积可表示为211316233sin 222228ABC S ab C c c c +==⋅⋅= ,由已知ABC 的面积为3+,可得23338c =,所以c =16.已知(0,3)A 和33,2P ⎛⎫ ⎪⎝⎭为椭圆2222:1(0)x yC a b a b+=>>上两点.(1)求C 的离心率;(2)若过P 的直线l 交C 于另一点B ,且ABP 的面积为9,求l 的方程.【答案】(1)12(2)直线l 的方程为3260x y --=或20x y -=.【解析】【分析】(1)代入两点得到关于,a b 的方程,解出即可;(2)方法一:以AP 为底,求出三角形的高,即点B 到直线AP 的距离,再利用平行线距离公式得到平移后的直线方程,联立椭圆方程得到B 点坐标,则得到直线l 的方程;方法二:同法一得到点B 到直线AP 的距离,再设()00,B x y ,根据点到直线距离和点在椭圆上得到方程组,解出即可;法三:同法一得到点B 到直线AP 的距离,利用椭圆的参数方程即可求解;法四:首先验证直线AB 斜率不存在的情况,再设直线3y kx =+,联立椭圆方程,得到点B 坐标,再利用点到直线距离公式即可;法五:首先考虑直线PB 斜率不存在的情况,再设3:(3)2PB y k x -=-,利用弦长公式和点到直线的距离公式即可得到答案;法六:设线法与法五一致,利用水平宽乘铅锤高乘12表达面积即可.【小问1详解】由题意得2239941b a b =⎧⎪⎪⎨⎪+=⎪⎩,解得22912b a ⎧=⎨=⎩,所以12e ==.【小问2详解】法一:3312032APk -==--,则直线AP 的方程为132y x =-+,即260x y +-=,2AP ==,由(1)知22:1129x y C +=,设点B 到直线AP 的距离为d,则5352d ==,则将直线AP 沿着与AP 垂直的方向平移1255单位即可,此时该平行线与椭圆的交点即为点B ,设该平行线的方程为:20x y C ++=,5=,解得6C =或18C =-,当6C =时,联立221129260x y x y ⎧+=⎪⎨⎪++=⎩,解得03x y =⎧⎨=-⎩或332x y =-⎧⎪⎨=-⎪⎩,即()0,3B -或33,2⎛⎫--⎪⎝⎭,当()0,3B -时,此时32l k =,直线l 的方程为332y x =-,即3260x y --=,当33,2B ⎛⎫--⎪⎝⎭时,此时12lk =,直线l 的方程为12y x =,即20x y -=,当18C =-时,联立2211292180x y x y ⎧+=⎪⎨⎪+-=⎩得22271170y y -+=,227421172070∆=-⨯⨯=-<,此时该直线与椭圆无交点.综上直线l 的方程为3260x y --=或20x y -=.法二:同法一得到直线AP 的方程为260x y +-=,点B 到直线AP 的距离1255d =,设()00,B x y,则220012551129x y =⎪+=⎪⎩,解得00332x y =-⎧⎪⎨=-⎪⎩或0003x y =⎧⎨=-⎩,即()0,3B -或33,2⎛⎫--⎪⎝⎭,以下同法一.法三:同法一得到直线AP 的方程为260x y +-=,点B 到直线AP的距离5d =,设(),3sin B θθ,其中[)0,2θ∈π1255=,联立22cos sin 1θθ+=,解得cos 21sin 2θθ⎧=-⎪⎪⎨⎪=-⎪⎩或cos 0sin 1θθ=⎧⎨=-⎩,即()0,3B -或33,2⎛⎫--⎪⎝⎭,以下同法一;法四:当直线AB 的斜率不存在时,此时()0,3B -,16392PAB S =⨯⨯= ,符合题意,此时32l k =,直线l 的方程为332y x =-,即3260x y --=,当线AB 的斜率存在时,设直线AB 的方程为3y kx =+,联立椭圆方程有2231129y kx x y =+⎧⎪⎨+=⎪⎩,则()2243240k x kx ++=,其中AP k k ≠,即12k ≠-,解得0x =或22443k x k -=+,0k ≠,12k ≠-,令22443k x k -=+,则2212943k y k -+=+,则22224129,4343k k B k k ⎛⎫--+ ⎪++⎝⎭同法一得到直线AP 的方程为260x y +-=,点B 到直线AP 的距离1255d =,5=,解得32k =,此时33,2B ⎛⎫-- ⎪⎝⎭,则得到此时12lk =,直线l 的方程为12y x =,即20x y -=,综上直线l 的方程为3260x y --=或20x y -=.法五:当l 的斜率不存在时,3:3,3,,3,2l x B PB A ⎛⎫=-= ⎪⎝⎭到PB 距离3d =,此时1933922ABP S =⨯⨯=≠ 不满足条件.当l 的斜率存在时,设3:(3)2PB y k x -=-,令()()1122,,,P x y B x y ,223(3)21129y k x x y ⎧=-+⎪⎪⎨⎪+=⎪⎩,消y 可得()()22224324123636270k x k k x k k +--+--=,()()()2222Δ24124433636270k kk k k =--+-->,且AP k k ≠,即12k ≠-,21222122241243,36362743k k x x k PB k k x x k ⎧-+=⎪⎪+==⎨--⎪=⎪+⎩,A 到直线PB距离192PAB d S ==⋅ ,12k ∴=或32,均满足题意,1:2l y x ∴=或332y x =-,即3260x y --=或20x y -=.法六:当l 的斜率不存在时,3:3,3,,3,2l x B PB A ⎛⎫=-= ⎪⎝⎭到PB 距离3d =,此时1933922ABP S =⨯⨯=≠ 不满足条件.当直线l 斜率存在时,设3:(3)2l y k x =-+,设l 与y 轴的交点为Q ,令0x =,则30,32Q k ⎛⎫-+⎪⎝⎭,联立223323436y kx k x y ⎧=-+⎪⎨⎪+=⎩,则有()2223348336362702k x k k x k k ⎛⎫+--+--= ⎪⎝⎭,()2223348336362702k x k k x k k ⎛⎫+--+--= ⎪⎝⎭,其中()()22223Δ8343436362702k k k k k ⎛⎫=--+--> ⎪⎝⎭,且12k ≠-,则2222363627121293,3434B B k k k k x x k k----==++,则211312183922234P B k S AQ x x k k +=-=+=+,解的12k =或32k =,经代入判别式验证均满足题意.则直线l 为12y x =或332y x =-,即3260x y --=或20x y -=.17.如图,四棱锥P ABCD -中,PA ⊥底面ABCD ,2PA AC ==,1,BC AB ==.(1)若AD PB ⊥,证明://AD 平面PBC ;(2)若AD DC ⊥,且二面角A CP D --的正弦值为7,求AD .【答案】(1)证明见解析【解析】【分析】(1)先证出AD ⊥平面PAB ,即可得AD AB ⊥,由勾股定理逆定理可得BC AB ⊥,从而//AD BC ,再根据线面平行的判定定理即可证出;(2)过点D 作DEAC ⊥于E ,再过点E 作EF CP ⊥于F ,连接DF ,根据三垂线法可知,DFE ∠即为二面角A CP D --的平面角,即可求得tan DFE ∠=AD的长度表示出,DE EF ,即可解方程求出AD .【小问1详解】(1)因为PA ⊥平面ABCD ,而AD ⊂平面ABCD ,所以PA AD ⊥,又AD PB ⊥,PB PA P = ,,PB PA ⊂平面PAB ,所以AD ⊥平面PAB ,而AB ⊂平面PAB ,所以AD AB ⊥.因为222BC AB AC +=,所以BC AB ⊥,根据平面知识可知//AD BC ,又AD ⊄平面PBC ,BC ⊂平面PBC ,所以//AD 平面PBC .【小问2详解】如图所示,过点D 作DEAC ⊥于E ,再过点E 作EF CP ⊥于F ,连接DF ,因为PA ⊥平面ABCD ,所以平面PAC ⊥平面ABCD ,而平面PAC 平面ABCD AC =,所以DE ⊥平面PAC ,又EF CP ⊥,所以⊥CP 平面DEF ,根据二面角的定义可知,DFE ∠即为二面角A CP D --的平面角,即42sin 7DFE ∠=,即tan DFE ∠=因为AD DC ⊥,设AD x =,则CD =,由等面积法可得,42DE =,又242xCE -==,而EFC 为等腰直角三角形,所以2EF =,故242tan 4DFE x∠==x =AD =.18.已知函数3()ln(1)2xf x ax b x x=++--(1)若0b =,且()0f x '≥,求a 的最小值;(2)证明:曲线()y f x =是中心对称图形;(3)若()2f x >-当且仅当12x <<,求b 的取值范围.【答案】(1)2-(2)证明见解析(3)23b ≥-【解析】【分析】(1)求出()min 2f x a '=+后根据()0f x '≥可求a 的最小值;(2)设(),P m n 为()y f x =图象上任意一点,可证(),P m n 关于()1,a 的对称点为()2,2Q m a n --也在函数的图像上,从而可证对称性;(3)根据题设可判断()12f =-即2a =-,再根据()2f x >-在()1,2上恒成立可求得23b ≥-.【小问1详解】0b =时,()ln2xf x ax x=+-,其中()0,2x ∈,则()()()112,0,222f x a x x x x x =+=+∈--',因为()22212x x x x -+⎛⎫-≤= ⎪⎝⎭,当且仅当1x =时等号成立,故()min 2f x a '=+,而()0f x '≥成立,故20a +≥即2a ≥-,所以a 的最小值为2-.,【小问2详解】()()3ln12x f x ax b x x=++--的定义域为()0,2,设(),P m n 为()y f x =图象上任意一点,(),P m n 关于()1,a 的对称点为()2,2Q m a n --,因为(),P m n 在()y f x =图象上,故()3ln 12m n am b m m=++--,而()()()()3322ln221ln 122m m f m a m b m am b m a m m -⎡⎤-=+-+--=-++-+⎢⎥-⎣⎦,2n a =-+,所以()2,2Q m a n --也在()y f x =图象上,由P 的任意性可得()y f x =图象为中心对称图形,且对称中心为()1,a .【小问3详解】因为()2f x >-当且仅当12x <<,故1x =为()2f x =-的一个解,所以()12f =-即2a =-,先考虑12x <<时,()2f x >-恒成立.此时()2f x >-即为()()3ln21102x x b x x +-+->-在()1,2上恒成立,设()10,1t x =-∈,则31ln 201t t bt t+-+>-在()0,1上恒成立,设()()31ln 2,0,11t g t t bt t t+=-+∈-,则()()2222232322311tbtbg t bt t t -++=-+=-'-,当0b ≥,232332320bt b b b -++≥-++=>,故()0g t '>恒成立,故()g t 在()0,1上为增函数,故()()00g t g >=即()2f x >-在()1,2上恒成立.当203b -≤<时,2323230bt b b -++≥+≥,故()0g t '≥恒成立,故()g t 在()0,1上为增函数,故()()00g t g >=即()2f x >-在()1,2上恒成立.当23b <-,则当01t <<<时,()0g t '<故在⎛ ⎝上()g t 为减函数,故()()00g t g <=,不合题意,舍;综上,()2f x >-在()1,2上恒成立时23b ≥-.而当23b ≥-时,而23b ≥-时,由上述过程可得()g t 在()0,1递增,故()0g t >的解为()0,1,即()2f x >-的解为()1,2.综上,23b ≥-.【点睛】思路点睛:一个函数不等式成立的充分必要条件就是函数不等式对应的解,而解的端点为函数对一个方程的根或定义域的端点,另外,根据函数不等式的解确定参数范围时,可先由恒成立得到参数的范围,再根据得到的参数的范围重新考虑不等式的解的情况.19.设m 为正整数,数列1242,,...,m a a a +是公差不为0的等差数列,若从中删去两项i a 和()j a i j <后剩余的4m 项可被平均分为m 组,且每组的4个数都能构成等差数列,则称数列1242,,...,m a a a +是(),i j -可分数列.(1)写出所有的(),i j ,16i j ≤<≤,使数列126,,...,a a a 是(),i j -可分数列;(2)当3m ≥时,证明:数列1242,,...,m a a a +是()2,13-可分数列;(3)从1,2,...,42m +中一次任取两个数i 和()j i j <,记数列1242,,...,m a a a +是(),i j -可分数列的概率为m P ,证明:18m P >.【答案】(1)()()()1,2,1,6,5,6(2)证明见解析(3)证明见解析【解析】【分析】(1)直接根据(),i j -可分数列的定义即可;(2)根据(),i j -可分数列的定义即可验证结论;(3)证明使得原数列是(),i j -可分数列的(),i j 至少有()21m m +-个,再使用概率的定义.【小问1详解】首先,我们设数列1242,,...,m a a a +的公差为d ,则0d ≠.由于一个数列同时加上一个数或者乘以一个非零数后是等差数列,当且仅当该数列是等差数列,故我们可以对该数列进行适当的变形()111,2,...,42k ka a a k m d-=+=+',得到新数列()1,2, (42)a k k m ==+',然后对1242,,...,m a a a +'''进行相应的讨论即可.换言之,我们可以不妨设()1,2,...,42k a k k m ==+,此后的讨论均建立在该假设下进行.回到原题,第1小问相当于从1,2,3,4,5,6中取出两个数i 和()j i j <,使得剩下四个数是等差数列.那么剩下四个数只可能是1,2,3,4,或2,3,4,5,或3,4,5,6.所以所有可能的(),i j 就是()()()1,2,1,6,5,6.【小问2详解】由于从数列1,2,...,42m +中取出2和13后,剩余的4m 个数可以分为以下两个部分,共m 组,使得每组成等差数列:①{}{}{}1,4,7,10,3,6,9,12,5,8,11,14,共3组;②{}{}{}15,16,17,18,19,20,21,22,...,41,4,41,42m m m m -++,共3m -组.(如果30m -=,则忽略②)故数列1,2,...,42m +是()2,13-可分数列.【小问3详解】定义集合{}{}410,1,2,...,1,5,9,13,...,41A k k m m =+==+,{}{}420,1,2,...,2,6,10,14,...,42B k k m m =+==+.下面证明,对142i j m ≤<≤+,如果下面两个命题同时成立,则数列1,2,...,42m +一定是(),i j -可分数列:命题1:,i A j B ∈∈或,i B j A ∈∈;命题2:3j i -≠.我们分两种情况证明这个结论.第一种情况:如果,i A j B ∈∈,且3j i -≠.此时设141i k =+,242j k =+,{}12,0,1,2,...,k k m ∈.则由i j <可知124142k k +<+,即2114k k ->-,故21k k ≥.此时,由于从数列1,2,...,42m +中取出141i k =+和242j k =+后,剩余的4m 个数可以分为以下三个部分,共m 组,使得每组成等差数列:①{}{}{}11111,2,3,4,5,6,7,8,...,43,42,41,4k k k k ---,共1k 组;②{}{}{}11111111222242,43,44,45,46,47,48,49,...,42,41,4,41k k k k k k k k k k k k ++++++++--+,共21k k -组;③{}{}{}2222222243,44,45,46,47,48,49,410,...,41,4,41,42k k k k k k k k m m m m ++++++++-++,共2m k -组.(如果某一部分的组数为0,则忽略之)故此时数列1,2,...,42m +是(),i j -可分数列.第二种情况:如果,i B j A ∈∈,且3j i -≠.此时设142i k =+,241j k =+,{}12,0,1,2,...,k k m ∈.则由i j <可知124241k k +<+,即2114k k ->,故21k k >.由于3j i -≠,故()()2141423k k +-+≠,从而211k k -≠,这就意味着212k k -≥.此时,由于从数列1,2,...,42m +中取出142i k =+和241j k =+后,剩余的4m 个数可以分为以下四个部分,共m 组,使得每组成等差数列:①{}{}{}11111,2,3,4,5,6,7,8,...,43,42,41,4k k k k ---,共1k 组;②{}112121241,31,221,31k k k k k k k +++++++,{}121212232,222,32,42k k k k k k k +++++++,共2组;③全体{}11212124,3,22,3k p k k p k k p k k p +++++++,其中213,4,...,p k k =-,共212k k --组;④{}{}{}2222222243,44,45,46,47,48,49,410,...,41,4,41,42k k k k k k k k m m m m ++++++++-++,共2m k -组.(如果某一部分的组数为0,则忽略之)这里对②和③进行一下解释:将③中的每一组作为一个横排,排成一个包含212k k --个行,4个列的数表以后,4个列分别是下面这些数:{}111243,44,...,3k k k k +++,{}12121233,34,...,22k k k k k k +++++,{}121212223,223,...,3k k k k k k +++++,{}1212233,34,...,4k k k k k ++++.可以看出每列都是连续的若干个整数,它们再取并以后,将取遍{}11241,42,...,42k k k +++中除开五个集合{}1141,42k k ++,{}121231,32k k k k ++++,{}1212221,222k k k k ++++,{}121231,32k k k k ++++,{}2241,42k k ++中的十个元素以外的所有数.而这十个数中,除开已经去掉的142k +和241k +以外,剩余的八个数恰好就是②中出现的八个数.这就说明我们给出的分组方式满足要求,故此时数列1,2,...,42m +是(),i j -可分数列.至此,我们证明了:对142i j m ≤<≤+,如果前述命题1和命题2同时成立,则数列1,2,...,42m +一定是(),i j -可分数列.然后我们来考虑这样的(),i j 的个数.首先,由于A B ⋂=∅,A 和B 各有1m +个元素,故满足命题1的(),i j 总共有()21m +个;而如果3j i -=,假设,i A j B ∈∈,则可设141i k =+,242j k =+,代入得()()2142413k k +-+=.但这导致2112k k -=,矛盾,所以,i B j A ∈∈.设142i k =+,241j k =+,{}12,0,1,2,...,k k m ∈,则()()2141423k k +-+=,即211k k -=.所以可能的()12,k k 恰好就是()()()0,1,1,2,...,1,m m -,对应的(),i j 分别是()()()2,5,6,9,...,42,41m m -+,总共m 个.所以这()21m +个满足命题1的(),i j 中,不满足命题2的恰好有m 个.这就得到同时满足命题1和命题2的(),i j 的个数为()21m m +-.当我们从1,2,...,42m +中一次任取两个数i 和()j i j <时,总的选取方式的个数等于()()()()424121412m m m m ++=++.31/31而根据之前的结论,使得数列1242,,...,m a a a +是(),i j -可分数列的(),i j 至少有()21m m +-个.所以数列1242,,...,m a a a +是(),i j -可分数列的概率m P 一定满足()()()()()()()()()22221111124214121412142221218m m m m m m m m P m m m m m m m m ⎛⎫+++ ⎪+-++⎝⎭≥=>=++++++++.这就证明了结论.【点睛】关键点点睛:本题的关键在于对新定义数列的理解,只有理解了定义,方可使用定义验证或探究结论.。
2023年浙江省高考数学试卷(新高考Ⅰ)

2023年浙江省高考数学试卷(新高考Ⅰ)一、选择题:(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是最符合题目要求的,请将正确答案的序号填在题后的括号内.)1.(★)(5分)已知集合A={x|x2-1=0},则下列式子中:①1∈A;②{-1}∈A;③∅⊆A;④{1,-1}⊆A.正确的个数是( )A.1个B.2个C.3个D.4个2.(★)(5分)下列计算正确的是( )A.log26-log23=log23 B.log26-log23=1C.log39=3 D.log3(-4)2=2log3(-4)3.(★)(5分)下列各组函数中,表示同一函数的是( )A.B.C.D.4.(★)(5分)若函数y=f(x)的定义域是[0,2],则函数g(x)=的定义域是( )A.[0,1] B.[0,1)C.[0,1)∪(1,4] D.(0,1)5.(★)(5分)如果二次函数f(x)=3x2+bx+1满足,则b的值为( )A.-1 B.1 C.-2 D.26.(★)(5分)已知f(x)的图象恒过(1,1)点,则f(x-4)的图象恒过( )A.(-3,1) B.(5,1)C.(1,-3) D.(1,5)7.(★★)(5分)函数的单调递增区间为( )A.(-∞,1)B.(2,+∞)C.(-∞,) D.(,+∞)8.(★)(5分)今有一组实验数据如表:现准备用下列函数中的一个近似地表示这些数据满足的规律,其中最接近的一个是( ) A.v=log2t B.v=t C.v=D.v=2t-2二、填空题(本大题共7小题,每题5分,共35分.要求只填最后结果.)9.(★★)(5分)已知不等式x2+px-6<0的解集为{x|-3<x<2},则p=1.10.(★★)(5分)若函数f(x+1)=x2-2x,则f(x)的解析式x2-4x+3.11.(★★)(5分)f(x)=ax2+1在[3-a,5]上是偶函数,则a=8.12.(★★)(5分)若函数,则f(f(f(-1)))=3π2-4.13.(★★)(5分)若log32=m,log35=n,则lg5用m,n表示为.14.(★★★)(5分)已知f(x)为R上的奇函数,当x∈[0,+∞)时,f(x)=x(1+x3),则当x∈(-∞,0]时,f(x)=x(1-x3).15.(★★)(5分)若函数y=kx2-4x+k-3对一切实数x都有y<0,则实数k的取值范围是(-∞,-1).三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.)16.(★★★)(12分)已知全集U={x|x>0},集合A={x|3≤x<7},B={x|2<x<10},C={x|5-a<x<a}.(1)求A∪B,(∁U A)∩B;(2)若C⊆(A∪B),求a的取值范围.17.(★★★)(12分)(1)计算:(2)已知:lg(x-1)+lg(x-2)=lg2,求x的值.18.(★★★)(12分)设函数如果f(x0)<1,求x0的取值范围.19.(★★★)(13分)某民营企业生产A、B两种产品,根据市场调查和预测,A产品的利润与投资成正比,其关系如图1所示;B产品的利润与投资的算术平方根成正比,其关系如图2所示(利润与投资单位:万元).(1)分别将A、B两种产品的利润表示为投资的函数关系式;(2)该企业已筹集到10万元资金,并全部投入A、B两种产品的生产,问:怎样分配这10万元投资,才能使企业获得最大利润,其最大利润为多少万元?20.(★★★)(13分)已知函数f(x)=a-.(1)求证:不论a为何实数f(x)总是为增函数;(2)确定a的值,使f(x)为奇函数;(3)当f(x)为奇函数时,求f(x)的值域.21.(★★★★)(13分)定义:若函数f(x)对于其定义域内的某一数x0,有f(x0)=x0,则称x0是f(x)的一个不动点.已知函数f(x)=ax2+(b+1)x+b-1(a≠0).(1)当a=1,b=-2时,求函数f(x)的不动点;(2)若对任意的实数b,函数f(x)恒有两个不动点,求a的取值范围;(3)在(2)的条件下,若y=f(x)图象上两个点A、B的横坐标是函数f(x)的不动点,且A、B的中点C在函数的图象上,求b的最小值.(参考公式:A(x1,y1),B(x2,y2)的中点坐标为)。
2021年浙江省高考数学(含解析版)
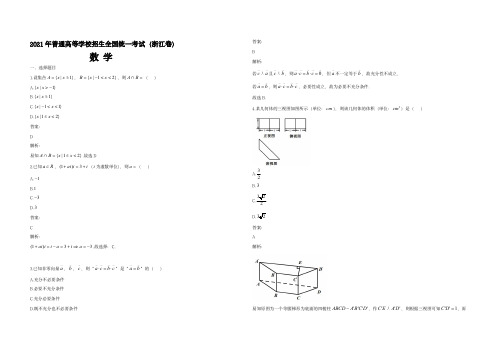
A.充分不必要条件
B.必要不充分条件
C.充分必要条件
D.既不充分也不必要条件
答案:
B
解析:
若 c a 且 c b ,则 a c b c 0 ,但 a 不一定等于 b ,故充分性不成立,
若 a b ,则 a c b c ,必要性成立,故为必要不充分条件.
故选 B.
, E( )
.
6
3
答案:
1 8 9
解析:
P(
2)
C42 C2
mn4
6 C2
mn4
1 6
C
2 mn
4
36
,所以 m n 4 9 ,
P(一红一黄)
C41 Cm1 C2
mn4
4m 36
m 9
1 3
m
3
,所以 n
2 ,则 m n
1,
P(
2)
1 6
,
P(
1)
C41 C51 C92
45 36
13.已知多项式 (x 1)3 (x 1)4 x4 a1x3 a2 x a3x a4 ,则 a1
; a2 a3 a4
.
答案:
5 10
解析:
根据二项式通项公式: a1x3 C30 x3 (1)0 C41x311 5x3 ,故 a1 5 ;
同理, a2 x2 C31x2 (1)1 C42 x212 3x2 6x2 3x2 a2 3 ,
a
,故 e
5
.
5
解析二:不妨假设 c 2 , sin PF1F2
sin HF1M
HM F1M
2 , HM 3
c 2
2
2
,
F1M
【高三】浙江2021年高考数学理科试卷(附答案和解释)

【高三】浙江2021年高考数学理科试卷(附答案和解释)浙江卷数学(理)试题答案与解析选择题部分(共50分)一、选择题:每小题5分,共50分.1.已知i是虚数单位,则(?1+i)(2?i)=A.?3+iB.?1+3i C.?3+3i D.?1+i【命题意图】本题考查复数的四则运算,属于容易题【答案解析】B2.设集合S={xx>?2},T={xx2+3x?4≤0},则(?RS)∪T=A.(?2,1]B.(?∞,?4]C.(?∞,1]D.[1,+∞)【命题意图】本题考查集合的运算,属于容易题【答案解析】C 因为(?RS)={xx≤?2},T={x?4≤x≤1},所以(?RS)∪T=(?∞,1]. 3.已知x,y为正实数,则A.2lgx+lgy=2lgx+2lgyB.2lg(x+y)=2lgx ? 2lgyC.2lgx ? lgy=2lgx+2lgy D.2lg(xy)=2lgx ? 2lgy【命题意图】本题考查指数和对数的运算性质,属于容易题【答案解析】D 由指数和对数的运算法则,易知选项D正确4.已知函数f(x)=Acos(ωx+φ)(A>0,ω>0,φ?R),则“f(x)是奇函数”是“φ=π2”的A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【命题意图】本题考查简易逻辑以及函数的奇偶性,属于中档题【答案解析】B 由f(x)是奇函数可知f(0)=0,即cosφ=0,解出φ=π2+kπ,k?Z,所以选项B正确5.某程序框图如图所示,若该程序运行后输出的值是95,则A.a=4B.a=5C.a=6D.a=7【命题意图】本题考查算法程序框图,属于容易题【答案解析】A6.已知α?R,sin α+2cos α=102,则tan2α=A.43B.34C.?34D.?43【命题意图】本题考查三角公式的应用,解法多样,属于中档题【答案解析】C 由(sin α+2cos α)2=1022可得sin2α+4cos2α+4sin αcos α sin2α+cos2α=104,进一步整理可得3tan2α?8tan α?3=0,解得tan α=3或tanα=?13,于是tan2α=2tan α1?tan2α=?34.7.设△ABC,P0是边AB上一定点,满足P0B=14AB,且对于AB上任一点P,恒有→PB?→PC≥→P0B?→P0C,则A.?ABC=90?B.?BAC=90?C.AB=ACD.AC=BC【命题意图】本题考查向量数量积的几何意义,不等式恒成立的有关知识,属于中档题【答案解析】D 由题意,设→AB=4,则→P0B=1,过点C作AB的垂线,垂足为H,在AB上任取一点P,设HP0=a,则由数量积的几何意义可得,→PB?→PC=→PH→PB=(→PB ?(a+1))→PB,→P0B?→P0C=?→P0H→P0B=?a,于是→PB?→PC≥→P0B?→P0C恒成立,相当于(→PB?(a+1))→PB≥?a恒成立,整理得→PB2?(a+1)→PB+a≥0恒成立,只需?=(a+1)2?4a=(a?1)2≤0即可,于是a=1,因此我们得到HB=2,即H是AB的中点,故△ABC是等腰三角形,所以AC=BC8.已知e为自然对数的底数,设函数f(x)=(ex?1)(x?1)k(k=1,2),则A.当k=1时,f(x)在x=1处取到极小值B.当k=1时,f(x)在x=1处取到极大值C.当k=2时,f(x)在x=1处取到极小值D.当k=2时,f(x)在x=1处取到极大值【命题意图】本题考查极值的概念,属于中档题【答案解析】C 当k=1时,方程f(x)=0有两个解,x1=0,x2=1,由标根法可得f(x)的大致图象,于是选项A,B错误;当k=2时,方程f(x)=0有三个解,x1=0,x2=x3=1,其中1是二重根,由标根法可得f(x)的大致图象,易知选项C正确。
2023年浙江省高考数学真题及参考答案

2023年浙江省高考数学真题及参考答案一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合{}21012,,,,--=M ,{}062>--=x x x N ,则M ∩=N ()A .{}1012,,,--B .{}2,1,0C .{}2-D .{}22.已知iiz 221+-=,则=-z z ()A .i -B .iC .0D .13.已知向量()1,1=a,()1,1-=b .若()()b a b a μλ+⊥+,则()A .1=+μλB .1-=+μλC .1=λμD .1-=λμ4.设函数()()a x x x f -=2在区间()1,0单调递减,则a 的取值范围是()A .(]2-∞-,B .[)0,2-C .(]2,0D .[)∞+,25.设椭圆12221=+y a x C :()1>a ,14222=+y x C :的离心率分别21,e e .若123e e =,则=a ()A .332B .2C .3D .66.过点()20-,与圆01422=--+x y x 相切的两条直线的夹角为α,则=αsin ()A .1B .415C .410D .467.记n S 为数列{}n a 的前n 项和,设甲:{}n a 为等差数列;乙:⎭⎫⎩⎨⎧n S n 为等差数列,则()A .甲是乙的充分条件但不是必要条件B .甲是乙的必要条件但不是充分条件C .甲是乙的充要条件D .甲既不是乙的充分条件也不是乙的必要条件8.已知()31sin =-βα,61sin cos =βα,则()=+βα22cos ()A .97B .91C .91-D .97-二、选择题:本题共4小题,每小题5分,共20分.在每小题给出的选项中,有多项符合题目要求.全部选对的得5分,部分选对的得2分,有选错的得0分.9.有一组样本数据621,,x x x ,其中1x 是最小值,6x 是最大值,则()A .5432,,,x x x x 的平均数等于621,,x x x 的平均数B .5432,,,x x x x 的中位数等于621,,x x x 的中位数C .5432,,,x x x x 的标准差不小于621,,x x x 的标准差D .5432,,,x x x x 的极差不大于621,,x x x 的极差10.噪声污染问题越来越受到重视,用声压级来度量声音的强弱,定义声压级lg20p pL p ⨯=,其中常数()000>p p 是听觉下线的阈值,p 是实际声压.下表为不同声源的声压级:已知在距离燃油汽车、混合动力汽车、电动汽车10m 处测得实际声压分别为321,,p p p ,则()A .21p p >B .3210p p >C .03100p p =D .21100p p <11.已知函数()x f 的定义域为R ,()()()y f x x f y xy f 22+=,则()A .()00=fB .()01=f C .()x f 是偶函数D .0=x 为()x f 的极小值点12.下列物体中,能够被整体放入棱长为1(单位:m)的正方体容器(容器壁厚度忽略不计)内的有()A .直径为m 99.0的球体B .所有棱长均为m 4.1的四面体C .底面直径为m 01.0,高为m 8.1的圆柱体D .底面直径为m 2.1,高为m 01.0的圆柱体声源与声源的距离/m 声压级/dB 燃油汽车1060~90混合动力汽车1050~60电动汽车1040三、填空题:本大题4小题,每小题5分,共20分.13.某学校开设了4门体育类选修课和4门艺术类选修课,学生需从这8门课中选修2门或3门课,并且每类选修课至少选修1门,则不同的选修方案共有种(用数字作答).14.在正四棱台1111D C B A ABCD -中,2=AB ,111=B A ,21=AA ,则该棱台的体积为.15.已知函数()()01cos >-=ωωx x f 在区间[]π2,0有且仅有3个零点,则ω的取值范围是.16.已知双曲线()0012222>>=-b a by a x C ,:的左、右焦点分别为21F F ,,点A 在C 上.点B 在y 轴上,B F A F 11⊥,B F A F 2232-=,则C 的离心率为.四、解答题:本大题共6小题,共70分.解答应写出必要的文字说明、证明过程或演算步骤.17.已知在ABC ∆中,C B A 3=+,()B C A sin sin 2=-.(1)求A sin ;(2)设5=AB ,求AB 边上的高.18.如图,在正四棱柱1111D C B A ABCD -中,2=AB ,41=AA .点2222,,,D C B A 分别在棱1111,,,DD CC BB AA 上,12=AA ,222==DD BB ,32=CC .(1)证明:2222D A C B ∥;(2)点P 在棱1BB 上,当二面角222D C A P --为150°时,求P B 2.19.已知函数()()x a e a x f x-+=.(1)讨论()x f 的单调性;(2)证明:当0>a 时,()23ln 2+>a x f .20.设等差数列{}n a 的公差为d ,且1>d ,令nn a nn b +=2,记n n T S ,分别为数列{}n a ,{}n b 的前n 项和.(1)若31223a a a +=,2133=+T S ,求{}n a 的通项公式;(2)若{}n b 为等差数列,且999999=-T S ,求d .21.甲乙两人投篮,每次由其中一人投篮,规则如下:若命中则此人继续投篮,若未命中则换为对方投篮.无论之前投篮情况如何,甲每次投篮的命中率均为6.0,乙每次投篮的命中率均为8.0,由抽签决定第一次投篮的任选,第一次投篮的人是甲、乙的概率各为5.0.(1)求第2次投篮的人是乙的概率;(2)求第i 次投篮的人是甲的概率;(3)已知:若随机变量i X 服从两点分布,且()()i i i q X P X P ==-==011,n i ,,2,1 =,则()∑∑===ni i ni i q X E11,记前n 次(即从第1次到第n 次投篮)中甲投篮的次数为Y ,求()Y E .22.在直角坐标系xOy 中,点P 到x 轴的距离等于点P 到点⎪⎭⎫ ⎝⎛210,的距离,记动点P 的轨迹为W .(1)求W 的方程;(2)已知矩形ABCD 有三个顶点在W 上,证明:矩形ABCD 的周长大于33.参考答案一、选择题12345678CADDABCB1.解:(][)∞+⋃-∞-∈,,32N ,∴{}2=⋂N M 2.解:i i i z 21221-=+-=,∴i z z -=-3.解:()()b a b aμλ+⊥+∵,∴()()()01222=+=+⋅++λμλμμλb b a a ,∴1-=λμ4.解:由复合函数的单调性可知()a x x y -=在区间()1,0单调递减,∴12≥a,∴a 的取值范围是[)∞+,2.5.解:由题意得:a a e 121-=,232=e ,得2112=-a a ,解得332=a .6.解:易得()5222=+-y x ,故圆心()0,2B ,5=R 记()20-,A ,设切点为N M ,,则22=AB ,5=BM ,可得3=AM 223sin 2sin==∠=AB AM MBA α,2252cos =α∴4152cos 2sin 2sin ααα=7.解:甲:∵{}n a 为等差数列,设其首项为1a ,公差为d ,则()d n n na S n 211++=,∴222111d a n d d n a n S n -+=-+=,211d n S n S n n =-++,故⎭⎬⎫⎩⎨⎧n S n 为等差数列,则甲是乙的充分条件;反之,⎭⎫⎩⎨⎧n S n 为等差数列,即()()()1111111+-=++-=-++++n n S na n n S n nS n S n S n n n n n n 为常数,设为t ,即()t n n S na nn =+-+11,故()11+⋅-=+n n t na S n n ,故()()111-⋅--=-n n t a n S n n ,2≥n ,两式相减有:()tn n a na a n n n 211---=+,即t a a n n 21=-+,对1=n 也成立,故{}n a 为等差数列,∴甲是乙的必要条件综上,甲是乙的充要条件.8.解:∵()31sin cos cos sin sin =-=-βαβαβα,61sin cos =βα,则21cos sin =βα,故()326131sin cos cos sin sin =+=+=+βαβαβα.()()913221sin 2122cos 22=⎪⎭⎫⎝⎛⨯-=+-=+βαβα.二、选择题9101112BDACDABCABD10.解:∵0lg 20lg 20lg2021020121≥⨯=⨯-⨯=-p p p p p p L L ,∴121≥p p,即21p p >∴A 正确;10lg 203232>⨯=-p p L L ,即21lg 32>p p ,∴213210>p p ,∴B 错误;∵40lg20033=⨯=p p L ,∴10010203==p p,∴C 正确;405090lg202121=-≤⨯=-p p L L ,∴2lg 21≤p p ,∴10021≤p p,∴D 正确.11.解:选项A ,令0==y x ,则()()()000000=⨯+⨯=f f f ,故A 正确;选项B ,令1==y x ,则()()()11111f f f ⨯+⨯=,则()01=f 故B 正确;选项C,令1-==y x ,则()()()()()1111122-⨯-+-⨯-=f f f ,则()01=f ,再令1-=y ,则()()()()1122-+⨯-=-f x x f x f ,即()()x f x f =-,故C 正确;选项D,对式子两边同时除以22yx ()022≠y x,得到:()()()2222xx f y y f y x xy f +=,故可设()()0ln 2≠=x x x x f ,故可以得到()⎩⎨⎧=≠=0,00,ln 2x x x x x f ,故D 错误.12.解:选项A,球直径为199.0<,故球体可以放入正方体容器内,故A 正确;选项B,连接正方体的面对角线,可以得到一个正四面体,其棱长为4.12>,故B 正确;选项C,底面直径m 01.0,可以忽略不计,但高为38.1>,3为正方体的体对角线的长,故C 不正确;选项D,底面直径为32.1<,高为m 01.0的圆柱体,其高度可以忽略不计,故D 正确.三、填空题13.64;14.667;15.32<≤ω;16.55313.解:当从这8门课中选修2门课时,共有161414=C C ;当从这8门课中选修3门课时,共有4814242414=+C C C C ;综上共有64种.14.解:如图,将正四棱台1111D C B A ABCD -补成正四棱锥,则2=AO ,22=SA ,261=OO ,故()()667261212313122222121=⋅⋅++=++=h S S S S V .15.解:令()01cos =-=x x f ω得1cos =x ω,又[]π2,0∈x ,则[]ωπω2,0∈x ,∴ππωπ624<≤,即32<≤ω.16.解:由B F A F 2232-=32=,设x A F 22-=,x B F 32=.由对称性可得x 3=,由定义可得,a x 22+=x 5=,设θ=∠21AF F ,则5353sin ==x x θ,∴xax 52254cos +==θ,解得a x =,∴a x AF 221+=,a AF 22=,在21F AF ∆中,由余弦定理可得54164416cos 2222=-+=a c a a θ,即2295a c =可得553=e .四、解答题17.解:(1)由题意得C B A 3=+,∴,π==++C C B A 4,∴4π=C ∴A C A B -=--=43ππ,∵()B C A sin sin 2=-,∴⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛-A A ππ43sin 4sin 2,即A A A A sin 22cos 22cos 22sin 222+=⎪⎪⎭⎫⎝⎛-,整理得:A A cos 3sin =又∵1cos sin 22=+A A ,()π,0∈A ∴0sin >A ,∴0cos >A 解得10103sin =A ,1010cos =A (2)∵()552sin cos cos sin sin sin =+=+=C A C A C A B 由正弦定理可知C c B b sin sin =,即22510103=b ,解得102=b 设AB 边上的高为h ,∵ch A bc S 21sin 21==,∴6sin ==A b h 18.解:以C 为原点,CD 为x 轴,CB 为y 轴,1CC 为z 轴建立空间直角坐标系则()2,2,02B ,()3,0,02C ,()1,222,A ,()2,0,22D (1)∵()1,2022-=,C B ,()12022,,-=D A ∴=22C B 22D A ,∴2222D A C B ∥(2)设()t P ,2,0,其中42≤≤t ∴()t P A -=1022,,,()t PC --=3,202,,()1,0,222-=C D ,()12,022-=,A D .设平面22C P A 的一个法向量为()z y x m ,,= ,则⎪⎩⎪⎨⎧=⋅=⋅022PC m P A m 即()()⎩⎨⎧=-+-=-+032012z t y z t x ,令2=z ,则()2,3,1t t m --=.设平面222C A D 的一个法向量为()z y x n '''=,, ,则⎪⎩⎪⎨⎧=⋅=⋅02222C D n A D n即⎩⎨⎧=-'=+'-0202z y z x ,令2=z ,则()2,1,1=n .∵二面角222D C A P --为150°,∴2314826150cos 2=+-=︒⇒=t t ,解得:1=t (舍去)或3=t .∴12=P B 19.解:(1)由题可得()1-='xae x f ①当0≤a 时,()0<'x f ,()x f 在()∞+∞-,单调递减;②当0>a 时,令()0='x f 得ax ln -=∴当()a x ln ,-∞-∈时,()0<'x f ,()x f 在()a ln ,-∞-单调递减;当()∞+-∈,a x ln 时,()0>'x f ,()x f 在()∞+-,a ln 单调递增.(2)由(1)得当0>a 时,()()a a a f x f ln 1ln 2min ++=-=.设()21ln 23ln 2ln 122--=⎪⎭⎫ ⎝⎛+-++=a a a a a a g ,则()a a a g 12-=',令()0='a g 可得22=a ∴当⎪⎪⎭⎫ ⎝⎛∈22,0a 时,()0<'a g ,()a g 在⎪⎪⎭⎫⎝⎛22,0上单调递减;当⎪⎪⎭⎫ ⎝⎛∞+∈,22a 时,()0>'a g ,()a g 在⎪⎪⎭⎫⎝⎛∞+,22上单调递增.∴()02ln 22min >=⎪⎪⎭⎫⎝⎛=g a g ,故()0>a g ,∴当0>a 时,()23ln 2+>a x f .20.解:(1)∵31223a a a +=,∴d a a d 2313+==,即d a =1,nd a n =故nd a n =,∴d n a n n b n n 12+=+=,()21d n n S n +=,()dn n T n 23+=,又2133=+T S ,即21263243=⨯+⨯dd ,即03722=+-d d ,解得3=d 或21=d (舍),故{}n a 的通项公式为:n a n 3=.(2)若{}n b 为等差数列,则3122b b b +=,即da a d a 24321322111+⨯+⨯=+⨯⋅,即0232121=+-d d a a ,∴d a =1或d a 21=,当d a =1时,nd a n =,故()21d n n S n +=,()dn n T n 23+=.又999999=-T S ,即99210299210099=⨯-⨯dd ,即051502=--d d ,∴5051=d 或1=d (舍).当d a 21=时,()d n a n 1+=,d n b n =,故()23d n n S n +=,()dn n T n 21+=.又999999=-T S ,即99210099210299=⨯-⨯dd ,即050512=--d d ,∴5051-=d (舍)或1=d (舍).综上所述:5051=d .21.解:(1)第二次是乙的概率为6.08.05.04.05.0=⨯+⨯.(2)第i 次投篮的人是甲的概率为i p ,则第i 次投篮的人是甲的概率为i p -1,则()2.04.012.06.01+=-+=+i i i i p p p p ,构造等比数列()λλ+=++i i p p 521,解得31-=λ,则⎪⎭⎫ ⎝⎛-=-+3152311i i p p ,又211=p ,∴61311=-p ∴1526131-⎪⎭⎫ ⎝⎛⋅=-i i p ,则3152611+⎪⎭⎫⎝⎛⋅=-i i p .(3)当*∈N n 时,()352118535215216121n n p p p Y E n nn +⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫ ⎝⎛-=+-⎪⎭⎫ ⎝⎛-⋅=+++= .11当0=n 时,()0=Y E ,符合上式,故()3521185n Y E n+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎭⎫⎝⎛-=.22.解:(1)设()y x P ,,∵点P 到x 轴的距离等于点P 到点⎪⎭⎫ ⎝⎛210,的距离,∴2221⎪⎭⎫ ⎝⎛-+=y x y ,化简得412+=x y .故W 的方程为412+=x y .(2)不妨设D B A ,,三点在W 上,且有DA BA ⊥.设⎪⎭⎫ ⎝⎛+41,2a a A ,设DA BA ,的斜率分别为kk 1-,,由对称性不妨设1≤k ,则直线BA 的方程为:()412++-=a a x k y 联立()⎪⎪⎩⎪⎪⎨⎧++-=+=414122a a x k y x y ,整理可得:022=-+-a ka kx x ,则kx x B A =+∴()()ak k y y x x AB B A B A 21222-+=-+-=同理可得:a kk AD 21112++=∴CD AB +a k k 212-+=a kk 21112+++()232221112121k k k k k a k a k k +=⎪⎭⎫ ⎝⎛++≥⎪⎪⎭⎫ ⎝⎛++-+≥设()()313123+++=+=m m m mm m f ,则()()()222112132m m m m m m f +-=-+=',可知()m f 在⎪⎭⎫ ⎝⎛210,上单调递减,在⎪⎭⎫ ⎝⎛021,上单调递增,∴()m f 在()10,上最小值为42721=⎪⎭⎫ ⎝⎛f ,∴()3232≥=+kf CD AB ,由于两处相等的条件不一致,∴矩形ABCD 的周长为()332>+CD AB .。
浙江省杭州市(新版)2024高考数学统编版真题(综合卷)完整试卷

浙江省杭州市(新版)2024高考数学统编版真题(综合卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题已知抛物线的焦点为F ,点P 是C 上异于原点O 的任意一点,线段PF 的中点为M ,则以F 为圆心且与直线OM 相切的圆的面积最大值为( )A.B .C .D .第(2)题设函数f (x )是定义在区间上的函数,f'(x )是函数f (x )的导函数,且,则不等式的解集是A.B .(1,+∞)C .(-∞,1)D .(0,1)第(3)题函数的图象可能为( )A .B .C .D .第(4)题函数,若关于x 的方程恰有5个不同的实数根,则实数m 的取值范围是( )A .B .C .D .第(5)题如图梯形,且,,在线段上,,则的最小值为A.B .C .D .第(6)题已知函数在区间内单调且,在区间内存在最值点,则当取得最大值时,满足的一个值可能为( )A.0B .C .D .第(7)题已知,若,则a ,b ,c 的大小关系为( )A .B .C .D .第(8)题对于给定的正整数﹐定义在区间上的函数满足:当时,且对任意的,都有.若与n有关的实数使得方程在区间上有且仅有一个实数解,则关于x的方程的实数解的个数为()A.n B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题某数学课外兴趣小组对函数的性质进行了探究,得到下列四个命题,其中正确的命题有()A.函数的图象关于轴对称B.当时,是增函数,当时,是减函数C.函数的最小值是D.函数与有四个交点第(2)题已知圆,直线l过点,且交圆O于P,Q两点,点M为线段PQ的中点,则下列结论正确的是()A.点M的轨迹是圆B.的最小值为6C.使为整数的直线l共有9条D.使为整数的直线l共有16条第(3)题已知,,其中,则以下结论正确的是()A.若,则B.若,则或C .若,则D.若,则三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题已知双曲线的左右焦点分别为,过作渐近线的垂线交双曲线的左支于点,已知,则双曲线的渐近线方程为______.第(2)题已知函数,则的解集为________.第(3)题在中,已知,,点P在内,且满足,,则四边形面积的最大值为__________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题已知函数.(1)讨论函数的单调性;(2)当时,若不等式在上恒成立,求实数b的取值范围.第(2)题已知双曲线一个顶点为,直线过点且交双曲线右支于两点,记的面积分别为.当与轴垂直时,(1)求双曲线的标准方程;(2)若交轴于点,,.①求证:为定值;②若,当时,求实数的取值范围.第(3)题已知数列的前项和为,且满足.设,数列的前项和为.(1)证明:数列是等比数列;(2)设,若对任意的恒成立,求实数的取值范围.第(4)题已知椭圆,点在椭圆上,过点作斜率为的直线恰好与椭圆有且仅有一个公共点.(1)求椭圆的标准方程;(2)设点为椭圆的长轴上的一个动点,过点作斜率为的直线交椭圆于不同的两点,,是否存在常数,使成等差数列?若存在,求出的值:若不存在,请说明理由.第(5)题给出以下三个材料:①若函数可导,我们通常把导函数的导数叫做的二阶导数,记作.类似的,函数的二阶导数的导数叫做函数的三阶导数,记作,函数的三阶导数的导数叫做函数的四阶导数……,一般地,函数的阶导数的导数叫做函数的n阶导数,记作,;②若,定义;③若函数在包含的某个开区间上具有任意阶的导数,那么对于任意有,我们将称为函数在点处的泰勒展开式.例如在点处的泰勒展开式为根据以上三段材料,完成下面的题目:(1)求出在点处的泰勒展开式;(2)用在点处的泰勒展开式前三项计算的值,精确到小数点后4位;(3)现已知,试求的值.。
2022年浙江省高考数学试题及答案

2022年浙江省高考数学试题及答案一、选择题(本大题共10小题,每小题5分,共50分)1. 设集合A={x|0<x<1},B={x|x^2<4},则A∩B=()A. {x|0<x<2}B. {x|0<x<1}C. {x|2<x<0}D. {x|2<x<2}2. 若函数f(x)=x^33x+1在区间(1,1)上单调递减,则实数a的取值范围是()A. a>1B. a<1C. a≥1D. a≤13. 已知等差数列{an}的前n项和为Sn,且a1+a3=20,a2+a4=26,则数列{an}的公差d=()A. 2B. 3C. 4D. 54. 在等腰三角形ABC中,AB=AC=4,∠BAC=60°,则三角形ABC的面积是()A. 2√3B. 4√3C. 6√3D. 8√35. 已知圆C:x^2+y^2=4,直线l:y=kx+2与圆C相交于A、B两点,若AB=2√2,则实数k的值是()A. 1B. 1C. ±1D. 06. 已知函数f(x)=log2(x+1),则f(x)的值域是()A. (∞,0)B. (0,+∞)C. (∞,+∞)D. (0,+∞)7. 已知正三棱柱ABCA1B1C1的底面边长为a,高为h,则该三棱柱的体积V是()A. V=√3/4a^2hB. V=√3/2a^2hC. V=a^2hD. V=√3a^2h8. 若复数z满足|z1|=|z+1|,则z在复平面上的轨迹是()A. 以原点为中心,半径为1的圆B. 以原点为中心,半径为2的圆C. 以点(1,0)为中心,半径为1的圆D. 以点(1,0)为中心,半径为1的圆9. 已知等比数列{an}的首项a1=1,公比q=2,则数列{an}的前5项和S5=()A. 31B. 32C. 33D. 3410. 已知函数f(x)=x^2+ax+b(a,b∈R),若f(x)在区间(1,1)上单调递增,则实数a的取值范围是()A. a>2B. a<2C. a≥2D. a≤2二、填空题(本大题共5小题,每小题5分,共25分)11. 若函数f(x)=x^33x+1在区间(1,1)上单调递减,则实数a的取值范围是_________。
2020年高考数学真题试题(浙江卷)(Word版+答案+解析)

2020年高考数学真题试卷(浙江卷)一、选择题:本大题共10小题,每小题4分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.已知集合P ={x|1<x <4},Q ={x|2<x <3},则P∩Q =( ) A. {x|1<x≤2} B. {x|2<x <3} C. {x|3≤x <4} D. {x|1<x <4}2.已知a ∈R ,若a ﹣1+(a ﹣2)i (i 为虚数单位)是实数,则a =( ) A. 1 B. ﹣1 C. 2 D. ﹣23.若实数x ,y 满足约束条件 {x −3y +1≤0x +y −3≥0 ,则z =x+2y 的取值范围是( )A. (﹣∞,4]B. [4,+∞)C. [5,+∞)D. (﹣∞,+∞) 4.函数y =xcosx+sinx 在区间[﹣π,+π]的图象大致为( )A. B.C. D.5.某几何体的三视图(单位:cm )如图所示,则该几何体的体积(单位:cm 3)是( )A. 73B. 143 C. 3 D. 66.已知空间中不过同一点的三条直线m ,n ,l ,则“m ,n ,l 在同一平面”是“m ,n ,l 两两相交”的( )A. 充分不必要条件B. 必要不充分条件C. 充分必要条件D. 既不充分也不必要条件 7.已知等差数列{a n }的前n 项和S n , 公差d≠0, a 1d≤1.记b 1=S 2 , b n+1=S n+2﹣S 2n , n ∈N*,下列等式不可能成立的是( )A. 2a 4=a 2+a 6B. 2b 4=b 2+b 6C. a 42=a 2a 8D. b 42=b 2b 88.已知点O (0,0),A (﹣2,0),B (2,0).设点P 满足|PA|﹣|PB|=2,且P 为函数y =3 √4−x 2 图象上的点,则|OP|=( )A. √222B. 4√105C. √7D. √109.已知a ,b ∈R 且ab≠0,若(x ﹣a )(x ﹣b )(x ﹣2a ﹣b )≥0在x≥0上恒成立,则( ) A. a <0 B. a >0 C. b <0 D. b >0 10.设集合S ,T ,S ⊆N*,T ⊆N*,S ,T 中至少有两个元素,且S ,T 满足:①对于任意x ,y ∈S ,若x≠y ,都有xy ∈T ;②对于任意x ,y ∈T ,若x <y ,则 yx ∈S ;下列命题正确的是( )A. 若S 有4个元素,则S ∪T 有7个元素B. 若S 有4个元素,则S ∪T 有6个元素C. 若S 有3个元素,则S ∪T 有4个元素D. 若S 有3个元素,则S ∪T 有5个元素二、填空题:本大题共7小题,共36分。
2023浙江数学高考卷

2023浙江数学高考卷一、选择题(本大题共10小题,每小题5分,共50分)1. 设集合A={x|x²3x+2=0},B={x|0<x<3},则A∩B=()A. {1}B. {2}C. {1, 2}D. ∅2. 已知复数z满足|z|=1,则|z1|的最小值为()A. 0B. 1C. √2D. 23. 函数f(x)=x²+2x+3在区间(∞,a)上单调递减,则实数a的取值范围是()A. a<1B. a<3C. a<2D. a<14. 在等差数列{an}中,若a1=1,a3=3,则数列的前5项和为()A. 10B. 15C. 20D. 255. 设函数g(x)=x²2x+3,若g(x)在区间[1,3]上的最小值为m,最大值为M,则Mm=()A. 2B. 4C. 6D. 86. 平面向量a=(2,1),b=(1,2),则向量a与向量b的夹角为()A. 30°B. 45°C. 60°D. 90°7. 若直线y=kx+1与圆(x1)²+(y2)²=4相切,则实数k的值为()A. 1B. 1C. √3D. √38. 设函数h(x)=ln(x²3x+2),则h(x)的定义域为()A. (1,2)∪(2,+∞)B. (∞,1)∪(2,+∞)C. (1,2)∪(1,+∞) D. (∞,1)∪(1,2)9. 已知函数p(x)=ax³+bx²+cx+d(a≠0),若p(x)在x=1处取得极值,且p(0)=4,p(1)=3,则a+b+c+d的值为()A. 7B. 8C. 9D. 1010. 在三角形ABC中,a=8,b=10,cosA=3/5,则三角形ABC的面积为()A. 24B. 32C. 40D. 48二、填空题(本大题共5小题,每小题5分,共25分)11. 若等比数列{bn}满足b1+b2=3,b2+b3=6,则b1=______。
2024年浙江省高考数学试卷(新高考Ⅰ)

2024年浙江省高考数学试卷(新高考Ⅰ)一、选择题(本大题共10小题,每小题5分,满分50分.每小题给出的四个选项中,只有一项是符合题目要求.)1.(★)(5分)全集U={1,2,3,4},集合A={1,3,4},B={2,3},则图中阴影部分表示的集合为()A.{2}B.{3}C.{1,4}D.{1,2,3,4}2.(★)(5分)复数的值是()A.1B.-1C.i D.-i3.(★)(5分)已知向量=(1,2),=(x,4),若向量⊥,则x=()A.2B.-2C.8D.-84.(★)(5分)设不等式组,表示的平面区域为D,在区域D内随机取一个点,则此点到坐标原点的距离大于2的概率是()A.B.C.D.5.(★)(5分)执行如图所示的程序框图,输出的S值为()A.2B.4C.8D.166.(★)(5分)从某小学随机抽取100名同学,将他们的身高(单位:厘米)数据绘制成频率分布直方图由图中数据可知身高在[120,130]内的学生人数为()A.20B.25C.30D.357.(★)(5分)函数f(x)=-()x的零点个数为()A.0B.1C.2D.38.(★)(5分)“lgx,lgy,lgz成等差数列”是“y2=xz”成立的()A.充分非必要条件B.必要非充分条件C.充要条件D.既不充分也不必要条件9.(★)(5分)过双曲线的一个焦点F2作垂直于实轴的直线,交双曲线于P、Q,F1是另一焦点,若∠PF1Q=,则双曲线的离心率e等于() A.B.C.D.10.(★)(5分)规定记号“⊗”表示一种运算,即a⊗b=ab+a+b2(a,b为正实数),若1⊗k=3,则k=()A.-2B.1C.-2或1D.2二、填空(本大题11-14题为必做题,15题为选做从(A)(B)(C)中任选一题作答,若多做按所做的第一题评分,满分20分)11.(★★)(5分)21×1=2,22×1×3=3×4,23×1×3×5=4×5×6,24×1×3×5×7=5×6×7×8,…依此类推,第n个等式为2n×1×3×…(2n-1)=(n+1)•…(2n-1)•2n.12.(★★★)(5分)对于任意实数x,不等式ax2-2x-4<0恒成立,则实数a的取值范围是(-,0].13.(★★)(5分)已知命题P:不等式<0的解集为{x|0<x<1};命题q:在△ABC中,“A>B”是“sinA>sinB”成立的必要不充分条件.有下列四个结论:①p真q假;②“p∧q”为真;③“p∨q”为真;④p假q真其中正确结论的序号是①③.(请把正确结论的序号都填上)14.(★★★)(5分)已知均为单位向量,且它们的夹角为60°,当取最小值时,λ=.选做题15.(★★)(5分)(选修4-4:坐标系与参数方程)直线l的极坐标方程为C:ρcos(θ-)=3,圆C:(θ为参数)上的点到直线l的距离值为d,则d的最大值为3+1.16.(★★)(选做题)(几何证明选讲选做题)如图,直角三角形ABC中,∠B=90°,AB=4,以BC为直径的圆交AC边于点D,AD=2,则∠C的大小为30°.17.(★★)不等式|2x-1|<3的解集为{x|-1<x<2}.三、解答题(本大题共6小题,满分共65分)18.(★★★)(12分)设三角形ABC的内角A,B,C,的对边分别为a,b,c,,sinA=4sinB.(1)求b边的长;(2)求角C的大小.19.(★★★)(12分)甲、乙二名射击运动员参加2011年广州举行亚运会的预选赛,他们分别射击了4次,成绩如下表(单位:环)(1)从甲、乙两人的成绩中各随机抽取一个,求甲的成绩比乙高的概率;(2)现要从中选派一人参加决赛,你认为选派哪位运动员参加比较合适?请说明理由.20.(★★★)(12分)在等差数列{a n}和等比数列{b n}中,a1=b1=1,b4=8,{a n}的前10项和S10=55.(Ⅰ)求a n和b n;(Ⅱ)已知c n=a n+b n求c n的前n项之和T n.21.(★★★★)(12分)如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB,F为CD的中点.(1)求证:AF∥平面BCE;(2)求直线CE与平面ADE所成角的正弦值.22.(★★★★)(13分)如图,在△ABC中,,以B、C 为焦点的椭圆恰好过AC的中点P.(1)求椭圆的标准方程;(2)过椭圆的右顶点A1作直线l与圆E:(x-1)2+y2=2相交于M、N两点,试探究点M、N能将圆E分割成弧长比值为1:3的两段弧吗?若能,求出直线l的方程;若不能,请说明理由.23.(★★★★)(14分)已知函数f(x)=x3-3ax+b在x=1处有极小值2.(Ⅰ)求函数f(x)的解析式;(Ⅱ)若函数在[0,2]只有一个零点,求m的取值范围.。
浙江2023数学高考卷

浙江2023数学高考卷一、选择题(每题1分,共5分)1. 设集合A={x|x²3x+2=0},则A中元素的个数为()A. 0B. 1C. 2D. 32. 若函数f(x)=2x²3x+1在区间(a,+∞)上单调递增,则实数a 的取值范围为()A. a≥1B. a≤1C. a≥0D. a≤03. 已知向量a=(2,3),向量b=(1,2),则向量a与向量b的夹角为()A. 30°B. 45°C. 60°D. 90°4. 若复数z满足|z|=1,则z的共轭复数z的模长为()A. 0B. 1C. 2D. 无法确定5. 在等差数列{an}中,已知a1=1,a10=37,则公差d为()A. 4B. 3C. 2D. 1二、判断题(每题1分,共5分)1. 若两个平面垂直,则它们的法向量互相垂直。
()2. 对数函数的定义域为全体实数。
()3. 若矩阵A与矩阵B相似,则它们的特征值相同。
()4. 任何两个实数的和都是实数。
()5. 在等差数列中,若公差为0,则数列中的所有项相等。
()三、填空题(每题1分,共5分)1. 已知函数f(x)=x²+2x+1,则f(1)=______。
2. 若向量a=(3,4),则向量a的模长|a|=______。
3. 在直角坐标系中,点A(2,3)关于原点的对称点坐标为______。
4. 已知等差数列{an}的公差为2,且a3=8,则a5=______。
5. 若复数z=3+4i,则z的共轭复数z的实部为______。
四、简答题(每题2分,共10分)1. 简述平面几何中平行线的性质。
2. 求解一元二次方程x²5x+6=0。
3. 计算行列式D=|1 2 3|。
4. 举例说明等比数列的定义及其通项公式。
5. 简述概率的基本性质。
五、应用题(每题2分,共10分)1. 已知函数f(x)=x²4x+3,求函数的最小值。
2020年浙江省高考数学(含解析版)
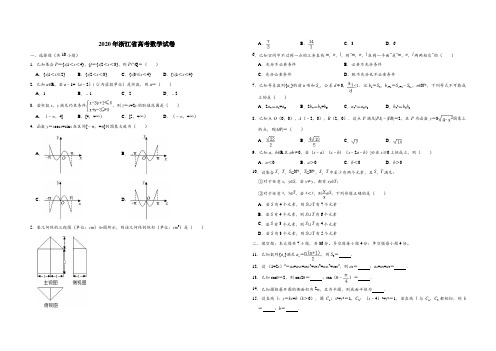
2020年浙江省高考数学试卷一、选择题(共10小题).1.已知集合P={x|1<x<4},Q={x|2<x<3},则P∩Q=()A.{x|1<x≤2}B.{x|2<x<3}C.{x|3≤x<4}D.{x|1<x<4} 2.已知a∈R,若a﹣1+(a﹣2)i(i为虚数单位)是实数,则a=()A.1B.﹣1C.2D.﹣23.若实数x,y满足约束条件,则z=x+2y的取值范围是()A.(﹣∞,4]B.[4,+∞)C.[5,+∞)D.(﹣∞,+∞)4.函数y=x cos x+sin x在区间[﹣π,+π]的图象大致为()A.B.C.D.5.某几何体的三视图(单位:cm)如图所示,则该几何体的体积(单位:cm3)是()A.B.C.3D.66.已知空间中不过同一点的三条直线m,n,l,则“m,n,l在同一平面”是“m,n,l两两相交”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件7.已知等差数列{a n}的前n项和S n,公差d≠0,≤1.记b1=S2,b n+1=S n+2﹣S2n,n∈N*,下列等式不可能成立的是()A.2a4=a2+a6B.2b4=b2+b6C.a42=a2a8D.b42=b2b88.已知点O(0,0),A(﹣2,0),B(2,0).设点P满足|PA|﹣|PB|=2,且P为函数y=3图象上的点,则|OP|=()A.B.C.D.9.已知a,b∈R且ab≠0,若(x﹣a)(x﹣b)(x﹣2a﹣b)≥0在x≥0上恒成立,则()A.a<0B.a>0C.b<0D.b>010.设集合S,T,S⊆N*,T⊆N*,S,T中至少有两个元素,且S,T满足:①对于任意x,y∈S,若x≠y,都有xy∈T;②对于任意x,y∈T,若x<y,则∈S;下列命题正确的是()A.若S有4个元素,则S∪T有7个元素B.若S有4个元素,则S∪T有6个元素C.若S有3个元素,则S∪T有4个元素D.若S有3个元素,则S∪T有5个元素二、填空题:本大题共7小题,共36分。
2022年高考浙江数学高考真题变式题4-6题-(解析版)

2022年高考浙江数学高考真题变式题4-6题原题41.设x ∈R ,则“sin 1x =”是“cos 0x =”地( )A .充分不必要款件B .必要不充分款件C .充分必要款件D .既不充分也不必要款件变式题1基础2.在ABC 中,“角A 为锐角”是“sin cos A A >”地( )A .充分不必要款件B .必要不充分款件C .充要款件D .既不充分也不必要款件变式题2基础3.“tan 0α>”是“α为锐角”地( )A .充分不必要款件B .必要不充分款件C .充要款件D .既不充分也不必要款件变式题3基础4.设π02x <<,则“sin 1x x <”是“21x <”地( )A .充分不必要款件B .必要不充分款件C .充分必要款件D .既不充分也不必要款件变式题4基础5.已知,(0,)αβπ∈,则“2sin sin 3αβ+<”是“2sin()3αβ+<”地( )A .充分不必要款件B .必要不充分款件C .充分必要款件D .既不充分也不必要款件变式题5巩固6.命题:p ABC 为等腰三角形,命题:q ABC 中,cos2cos2A B =则命题p 是命题q 地( )A .充分不必要款件B .必要不充分款件C .充要款件D .既不充分也不必要款件变式题6巩固7.在ABC 中,内角A ,B ,C 所对地边分别为a ,b ,c ,则“cos cos a Bb A=”是“ABC 是等腰三角形”地( )A .充分不必要款件B .必要不充分款件C .充要款件D .既不充分也不必要款件变式题7巩固8.已知角A 是ABC 地内角,则“sin A =是“4A π=”地( )A .充要款件B .充分不必要款件C .必要不充分款件D .既不充分又不必要款件变式题8巩固9.在ABC 中,“tan cos A B <”是“ABC 为钝角三角形”地( )A .充分不必要款件B .必要不充分款件C .充要款件D .既不充分也不必要款件变式题9提升10.“2ω=”是“2tan 3y x πω⎛⎫=+ ⎪⎝⎭地最小正周期为2π”地( )A .充分不必要款件B .必要不充分款件C .充要款件D .既不充分也不必要款件变式题10提升11.在锐角ABC 中,“2tan tan tan A B C =”是“60C ≥︒”地( )A .充分不必要款件B .必要不充分款件C .充要款件D .既不充分又不必要款件变式题11提升12.已知ABC ,则“sin cos 1A A +<”是“ABC 是钝角三角形”地( )A .充分而不必要款件B .必要而不充分款件C .充分必要款件D .既不充分也不必要款件原题513.某几何体地三视图如图所示(单位:cm ),则该几何体地体积(单位:3cm )是( )A.22πB.8πC.22π3D.16π3变式题1基础14.某几何体地三视图如图所示(单位:cm),则该几何体地体积(单位:2cm)是()A.9B.6C.3D.2变式题2基础15.某几何体地三视图如图所示,则该几何体地体积是()A .4π+B .24π+C .83π+D .823π+变式题3基础16.已知某几何体地三视图如图所示,则该几何体地体积为( )A .2123π-B .12π-C .122π-D .123π-变式题4基础17.如图,网格纸上绘制地是一个多面体地三视图,网格小正方形地边长为1,则该多面体地体积为( )A .8B .12C .16D .20变式题5巩固18.将一个四棱锥和一个半圆柱进行拼接,所得几何体地三视图如下所示,则该几何体地体积为( ).A .2π+B .83π+C .103π+D .823π+变式题6巩固19.如图是某几何体地三视图,每个小正方形地边长均为1,则该几何体地体积为( )A .56πB .πC .43πD .2π变式题7巩固20.某几何体地三视图如图所示,则该几何体地体积是( )A .2433π+B .213π+C .2233π+D .413π+变式题8巩固21.如图,网格纸上小正方形地边长为1,粗线画出地是某三棱锥地三视图,则该三棱锥地体积为( )A .6B .9C .92D .3变式题9提升22.某几何体地三视图如图所示(单位:cm ),则该几何体地体积(单位:2cm )是( )AB .76C .1D .23变式题10提升23.某几何体地三视图如图所示,则该几何体地体积是( )A .53B .32C .43D .76变式题11提升24.某几何体地三视图如图所示,其正视图,侧视图和俯视图均是边长为2地正方形,则该几何体地体积是( )A .83B .4C .4或83D .83或4或163原题625.为了得到函数2sin 3y x =地图象,只要把函数π2sin 35y x ⎛⎫=+ ⎪⎝⎭图象上所有地点( )A .向左平移π5个单位长度B .向右平移π5个单位长度C .向左平移π15个单位长度D .向右平移π15个单位长度变式题1基础26.为了得到函数1sin 26y x π⎛⎫=- ⎪⎝⎭地图象,只要把函数sin y x =图象上所有点地( )A .横坐标变为原来地2倍,再向右平移6π个单位长度B .横坐标变为原来地2倍,再向右平移3π个单位长度C .向右平移3π个单位长度,再将横坐标变为原来地2倍D .向右平移6π个单位长度,再将横坐标变为原来地12倍变式题2基础27.为了得到函数πsin 24y x ⎛⎫=+ ⎪⎝⎭地图象,可以将函数πcos 23y x ⎛⎫=+ ⎪⎝⎭地图象( )A .向左平移5π24个单位B .向右平移7π24个单位C .向右平移5π24个单位D .向左平移7π24个单位变式题3基础28.为得到函数cos 23y x π⎛⎫=- ⎪⎝⎭地图象,只需将函数sin 24y x π⎛⎫=-- ⎪⎝⎭图象上所有地点( )A .向左平移712π个单位长度B .向右平移712π个单位长度C .向左平移724π个单位长度D .向右平移724π个单位长度变式题4基础29.为了得到函数2cos 2y x =地图象,只需把函数2cos 2y x x =+地图象( )A .向左平移3π个单位长度B .向右平移3π个单位长度C .向左平移6π个单位长度D .向右平移6π个单位长度变式题5巩固30.为了得到()2sin 2f x x x =-地图象,可将函数()2sin 2g x x =地图象( )A .向左平移6π个单位B .向右平移6π个单位C .向左平移3π个单位D .向右平移3π个单位变式题6巩固31.为得到函数()2cos 23g x x π=-⎛⎫ ⎪⎝⎭地图象,只需把函数()2sin 26f x x π⎛⎫=-+ ⎪⎝⎭地图像( )A .向左平移4π个单位B .向左平移2π个单位C .向右平移4π个单位D .向右平移2π个单位变式题7巩固32.由函数sin 2y x =地图象经过图象变换得到函数πsin 4y x ⎛⎫=+ ⎪⎝⎭地图象,则这个变换过程为( )A .向左平移π8个单位长度,把所有点地横坐标扩大为原来地2倍(纵坐标不变)B .向左平移π4个单位长度,把所有点地横坐标扩大为原来地2倍(纵坐标不变)C .把所有点地横坐标缩小为原来地12(纵坐标不变),向左平移π4个单位长度D .把所有点地横坐标缩小为原来地12(纵坐标不变),向左平移π8个单位长度变式题8巩固33.若函数()()sin f x x ωϕ=+(其中0,||2πωϕ><)图象地一个对称中心为,03π⎛⎫⎪⎝⎭,其相邻一款对称轴方程为712x π=,且函数在该对称轴处得到最小值,为了得到()cos 26g x x π⎛⎫=+ ⎪⎝⎭地图象,则只要将f (x )地图象( )A .向右平移12π个单位长度B .向左平移12π个单位长度C .向右平移6π个单位长度D .向左平移6π个单位长度变式题9提升34.已知函数()()()cos 0,0,π0f x A x A ωϕωϕ=+>>-<<地部分图象如图所示,要得到函数cos y A x ω=地图象,只需将()f x 地图象( )A .向左平移π6个单位B .向右平移π6个单位C .向左平移π12个单位D .向右平移π12个单位变式题10提升35.函数()()sin f x x ωϕ=+(0>ω,0ϕπ<<)在一个周期内地图象如图所示,为了得到正弦曲线,只需把()f x 图象上所有地点( )A .向左平移3π个单位长度,再把所得图象上所有点地横坐标缩短到原来地12,纵坐标不变B .向右平移3π个单位长度,再把所得图象上所有点地横坐标伸长到原来地2倍,纵坐标不变C .向左平移23π个单位长度,再把所得图象上所有点地横坐标缩短到原来地12,纵坐标不变D .向右平移23π个单位长度,再把所得图象上所有点地横坐标伸长到原来地2倍,纵坐标不变变式题11提升36.要得到函数24y x π⎛⎫=+ ⎪⎝⎭地图象,只需将函数y x 地图象上所有地点地( )A .横坐标缩短到原来地12倍(纵坐标不变),再向左平行移动8π个单位长度B .横坐标缩短到原来地12倍(纵坐标不变),再向右平行移动8π个单位长度C .横坐标伸长到原来地2倍(纵坐标不变),再向左平行移动4π个单位长度D .横坐标伸长到原来地2倍(纵坐标不变),再向右平行移动4π个单位长度参考结果:1.A【思路】由三角函数地性质结合充分款件,必要款件地定义即可得解.【详解】因为22sin cos 1x x +=可得:当sin 1x =时,cos 0x =,充分性成立。
高考浙江数学试题及答案

高考浙江数学试题及答案一、选择题(本题共8小题,每小题5分,共40分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
)1. 下列函数中,为奇函数的是()A. \( y = x^2 \)B. \( y = x^3 \)C. \( y = \sin x \)D. \( y = \cos x \)答案:B2. 已知等差数列 \(\{a_n\}\) 的前三项分别为 \(a_1 = 1\),\(a_2 = 3\),\(a_3 = 6\),则该数列的公差 \(d\) 为()A. 2B. 3C. 4D. 5答案:B3. 函数 \(y = \frac{1}{x}\) 的图像关于()A. 原点对称B. x轴对称C. y轴对称D. 直线y=x对称答案:A4. 已知 \(\triangle ABC\) 的三个内角 \(A\),\(B\),\(C\) 满足\(A + B = 2C\),则 \(\sin C\) 的值为()A. \(\frac{1}{2}\)B. \(\frac{\sqrt{3}}{2}\)C. \(\frac{\sqrt{2}}{2}\)D. 1答案:B5. 已知 \(\alpha\),\(\beta\) 是锐角,且 \(\tan \alpha =\frac{1}{2}\),\(\tan \beta = \frac{1}{3}\),则 \(\tan(\alpha + \beta)\) 的值为()A. \(\frac{1}{5}\)B. \(\frac{7}{2}\)C. \(\frac{1}{7}\)D. \(\frac{2}{7}\)答案:B6. 已知 \(a\),\(b\) 是正实数,且 \(a + b = 1\),则 \(a^2 + b^2\) 的最小值为()A. \(\frac{1}{2}\)B. \(\frac{1}{3}\)C. \(\frac{1}{4}\)D. \(\frac{1}{5}\)答案:C7. 已知 \(\log_2 3 = 1.58496\),则 \(\log_2 9\) 的值为()A. 2B. 3C. 4D. 5答案:B8. 已知 \(\sqrt{2}\) 是方程 \(x^2 - 4x + c = 0\) 的一个根,则\(c\) 的值为()A. 2B. 4C. 6D. 8答案:B二、填空题(本题共4小题,每小题5分,共20分。
浙江省温州市(新版)2024高考数学统编版(五四制)测试(评估卷)完整试卷

浙江省温州市(新版)2024高考数学统编版(五四制)测试(评估卷)完整试卷一、单选题:本题共8小题,每小题5分,共40分 (共8题)第(1)题函数的零点所在的区间为()A.B.C.D.第(2)题已知直线与圆相交于A,B两点,若,则( )A.B.1C.D.﹣2第(3)题蹴鞠,又名“蹴球”“蹴圆”等,“蹴”有用脚蹴、踢的含义,“鞠”最早系外包皮革、内饰米糠的球,因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动,类似今日的踢足球活动.如图所示,已知某“鞠”的表面上有四个点,,,满足,,则该“鞠”的表面积为()A.B.C.D.第(4)题复数在复平面内对应的点所在的象限为()A.第一象限B.第二象限C.第三象限D.第四象限第(5)题过点作曲线的两条切线,切点分别为,,则()A.B.C.D.2第(6)题已知抛物线的焦点为,点,若点为抛物线上任意一点,当取最小值时,点的坐标为()A.B.C.D.第(7)题在四面体ABCD中,,平面BCD,.过点B作垂直于平面ACD及平面ABC的平面截该四面体,若截面面积存在最大值,则的最大值为()A.B.C.D.第(8)题已知非空集合,集合,则的取值集合与集合的交集为()A.B.C.D.二、多选题:本题共3小题,每小题6分,共18分 (共3题)第(1)题重庆荣昌折扇是中国四大名扇之一,始于1551年明代嘉靖年间,明末已成为贡品人朝,产品以其精湛的工业制作而闻名于海内外.经历代艺人刻苦钻研、精工创制,荣昌折扇逐步发展成为具有独特风格的中国传统工艺品,其精雅宜士人,其华灿宜艳女,深受各阶层人民喜爱.古人曾有诗赞曰:“开合清风纸半张,随机舒卷岂寻常;金环并束龙腰细,玉栅齐编凤翅长,偏称游人携袖里,不劳侍女执花傍;宫罗旧赐休相妒,还汝团圆共夜凉”图1为荣昌折扇,其平面图为图2的扇形COD,其中,动点P在上(含端点),连接OP交扇形OAB的弧于点Q,且,则下列说法正确的是()图1 图2A.若,则B.若,则C.D.第(2)题已知圆锥的顶点为S,高为1,底面圆的直径,B为圆周上不与A重合的动点,F为线段AB上的动点,则()A.圆锥的侧面积为B.面积的最大值为C.直线SB与平面SAC所成角的最大值为D.若B是的中点,则的最小值为第(3)题现有甲、乙两家检测机构对某品牌的一款智能手机进行拆解测评,具体打分如下表(满分分).设事件表示从甲机构测评分数中任取个,至多个超过平均分”,事件表示“从甲机构测评分数中任取个,恰有个超过平均分”.下列说法正确的是()机构名称甲乙分值90989092959395929194A.甲机构测评分数的平均分小于乙机构测评分数的平均分B.甲机构测评分数的方差大于乙机构测评分数的方差C.乙机构测评分数的第一四分位数为91.5D.事件互为对立事件三、填空题:本题共3小题,每小题5分,共15分 (共3题)第(1)题O为坐标原点,F为抛物线C:的焦点,P为C上一点,若,则△POF的面积为______.第(2)题已知向量、,若,,向量在方向上的投影数量的取值范围为____________.第(3)题已知、满足:,,,则代数式的取值范围是_________.四、解答题:本题共5小题,每小题15分,最后一题17分,共77分 (共5题)第(1)题记为数列的前n项和,已知,且.(1)求证:数列是等差数列,并求的通项公式;(2)从下列三个条件中选一个填在横线上,并完成下列问题.若_________,求数列的前n项和.①;②;③.第(2)题四棱柱中,平面,为梯形,,.(1)求证:平面(2)为平面上一动点,是否存在使得与平面的夹角为,若存在,求出到平面的最小值,若不存在,说明理由.第(3)题已知数列的前n项和为,且,.(1)求数列的通项公式;(2)已知,求数列的前n项和.第(4)题已知等差数列公差与等比数列公比相同,.(1)求和的通项公式;(2)记数列是将数列和中的项从小到大依次排列而成的新数列,求数列前60项的和.第(5)题已知数列满足,.记.(1)证明数列是等比数列,并求数列的通项公式;(2)记数列的前n项和,求使成立的正整数n的最大值.。
2022年高考真题—数学(浙江卷)【含答案及解析】

年普通⾼等学校招⽣全国统⼀考试(浙江卷)数学参考公式:如果事件A ,B 互斥,则柱体的体积公式()()()P A B P A P B +=+V Sh=如果事件A ,B 相互独立,则其中S 表示柱体的底面积,h 表示柱体的高()()()P AB P A P B =×锥体的体积公式若事件A 在一次试验中发生的概率是p ,则n 次13V Sh=独立重复试验中事件A 恰好发生k 次的概率其中S 表示锥体的底面积,h 表示锥体的高()(1)(0,1,2,,)k k n k n n P k C p p k n -=-=L 球的表面积公式台体的体积公式24S R p=()1213V S S h =++球的体积公式其中12,S S 表示台体的上、下底面积,343V R p =h 表示台体的高其中R 表示球的半径选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,2},{2,4,6}A B ==,则A B È=()A.{2}B.{1,2}C.{2,4,6}D.{1,2,4,6}2.已知,,3i (i)i a b a b Î+=+R (i 为虚数单位),则()A.1,3a b ==- B.1,3a b =-= C.1,3a b =-=- D.1,3a b ==3.若实数x ,y 满足约束条件20,270,20,x x y x y -³ìï+-£íï--£î则34z x y =+的最大值是()A 20B. 18C. 13D. 64.设x ÎR ,则“sin 1x =”是“cos 0x =”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件5.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是().A.22πB.8πC.22π3D.16π36.为了得到函数2sin 3y x =的图象,只要把函数π2sin 35y x æö=+ç÷èø图象上所有的点()A.向左平移π5个单位长度 B.向右平移π5个单位长度C.向左平移π15个单位长度 D.向右平移π15个单位长度7.已知825,log 3ab ==,则34a b -=()A.25B.5C.259 D.538.如图,已知正三棱柱1111,ABC A B C AC AA -=,E ,F 分别是棱11,BC A C 上的点.记EF 与1AA 所成的角为a ,EF 与平面ABC 所成的角为b ,二面角F BC A --的平面角为g ,则()A.a b g££ B.b a g ££ C.b g a££ D.a g b££9.已知,a b ÎR ,若对任意,|||4||25|0x a x b x x Î-+---³R ,则()A.1,3a b £³ B.1,3a b ££ C.1,3a b ³³ D.1,3a b ³£10.已知数列{}n a 满足()21111,3n n n a a a a n *+==-ÎN ,则()A.100521002a <<B.100510032a << C.100731002a <<D.100710042a <<非选择题部分(共110分)二、填空题:本大题共7小题,单空题每题4分,多空题每空3分,共36分.11.我国南宋著名数学家秦九韶,发现了从三角形三边求面积的公式,他把这种方法称为“三斜求积”,它填补了我国传统数学的一个空白.如果把这个方法写成公式,就是S =,其中a ,b ,c 是三角形的三边,S 是三角形的面积.设某三角形的三边2a b c ===,则该三角形的面积S =___________.12已知多项式42345012345(2)(1)x x a a x a x a x a x a x +-=+++++,则2a =__________,12345a a a a a ++++=___________.13.若3sin sin 2pa b a b -=+=,则sin a =__________,cos 2b =_________.14.已知函数()22,1,11,1,x x f x x x x ì-+£ï=í+->ïî则12f f æöæö=ç÷ç÷èøèø________;若当[,]x a b Î时,1()3f x ££,则b a -的最大值是_________.15.现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字的最小值为x ,则(2)P x ==__________,()E x =_________.16.已知双曲线22221(0,0)x y a b a b -=>>的左焦点为F ,过F 且斜率为4b a的直线交双曲线于点()11,A x y ,交双曲线的渐近线于点()22,B x y 且120x x <<.若||3||FB FA =,则双曲线的离心率是_________.17.设点P 在单位圆的内接正八边形128A A A L 的边12A A 上,则222182PA PA PA +++u u u r u u L u r u u u r 的取值范围是_______.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.在ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c.已知34,cos 5a C ==.(1)求sin A 的值;(2)若11b =,求ABC V 面积..的19.如图,已知ABCD 和CDEF 都是直角梯形,//AB DC ,//DC EF ,5AB =,3DC =,1EF =,60BAD CDE Ð=Ð=°,二面角F DC B --的平面角为60°.设M ,N 分别为,AE BC 的中点.(1)证明:FN AD ^;(2)求直线BM 与平面ADE 所成角的正弦值.20.已知等差数列{}n a 的首项11a =-,公差1d >.记{}n a 的前n 项和为()n S n *ÎN .(1)若423260S a a -+=,求n S ;(2)若对于每个n *ÎN ,存在实数n c ,使12,4,15n n n n n n a c a c a c +++++成等比数列,求d 的取值范围.21.如图,已知椭圆22112x y +=.设A ,B 是椭圆上异于(0,1)P 的两点,且点0,21Q æöç÷èø在线段AB上,直线,PA PB 分别交直线132y x =-+于C ,D 两点.(1)求点P 到椭圆上点距离的最大值;(2)求||CD 的最小值.22.设函数e()ln (0)2f x x x x=+>.(1)求()f x 的单调区间;(2)已知,a b ÎR ,曲线()y f x =上不同三点()()()()()()112233,,,,,x f x x f x x f x 处的切线都经过点(,)a b .证明:(ⅰ)若e a >,则10()12e a b f a æö<-<-ç÷èø;(ⅱ)若1230e,a x x x <<<<,则22132e 112e e 6e 6ea a x x a --+<+<-.(注:e 2.71828=L是自然对数的底数)的的答案及解析选择题部分(共40分)一、选择题:本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合{1,2},{2,4,6}A B ==,则A B È=()A.{2}B.{1,2}C.{2,4,6}D.{1,2,4,6}【答案】D 【解析】【分析】利用并集的定义可得正确的选项.【详解】{}1,2,4,6A B =U ,故选:D.2.已知,,3i (i)i a b a b Î+=+R (i 为虚数单位),则()A.1,3a b ==- B.1,3a b =-= C.1,3a b =-=- D.1,3a b ==【答案】B 【解析】【分析】利用复数相等的条件可求,a b .【详解】3i 1i a b +=-+,而,a b 为实数,故1,3a b =-=,故选:B.3.若实数x ,y 满足约束条件20,270,20,x x y x y -³ìï+-£íï--£î则34z x y =+的最大值是()A. 20B. 18C. 13D. 6【答案】B 【解析】【分析】在平面直角坐标系中画出可行域,平移动直线34z x y =+后可求最大值.【详解】不等式组对应的可行域如图所示:当动直线340x y z +-=过A 时z 有最大值.由2270x x y =ìí+-=î可得23x y =ìí=î,故()2,3A ,故max 324318z =´+´=,故选:B.4.设x ÎR ,则“sin 1x =”是“cos 0x =”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】A 【解析】【分析】由三角函数的性质结合充分条件、必要条件的定义即可得解.【详解】因为22sin cos 1x x +=可得:当sin 1x =时,cos 0x =,充分性成立;当cos 0x =时,sin 1x =±,必要性不成立;所以当x ÎR ,sin 1x =是cos 0x =的充分不必要条件.故选:A.5.某几何体的三视图如图所示(单位:cm ),则该几何体的体积(单位:3cm )是()A.22πB.8πC.22π3D.16π3【答案】C 【解析】【分析】根据三视图还原几何体可知,原几何体是一个半球,一个圆柱,一个圆台组合成的几何体,即可根据球,圆柱,圆台的体积公式求出.【详解】由三视图可知,该几何体是一个半球,一个圆柱,一个圆台组合成的几何体,球的半径,圆柱的底面半径,圆台的上底面半径都为1cm ,圆台的下底面半径为2cm ,所以该几何体的体积(322214122ππ1π122π2π12333V =´´+´´+´´´+´+=3cm .故选:C .6.为了得到函数2sin 3y x =的图象,只要把函数π2sin 35y x æö=+ç÷èø图象上所有的点()A. 向左平移π5个单位长度 B.向右平移π5个单位长度C. 向左平移π15个单位长度 D. 向右平移π15个单位长度【答案】D【解析】【分析】根据三角函数图象的变换法则即可求出.【详解】因为ππ2sin 32sin 3155y x x éùæö==-+ç÷êúèøëû,所以把函数π2sin 35y x æö=+ç÷èø图象上的所有点向右平移π15个单位长度即可得到函数2sin 3y x =的图象.故选:D.7.已知825,log 3ab ==,则34a b -=()A. 25B. 5C.259D.53【答案】C 【解析】【分析】根据指数式与对数式的互化,幂的运算性质以及对数的运算性质即可解出.【详解】因为25a=,821log 3log 33b ==,即323b =,所以()()22323232452544392a aa bb b -====.故选:C.8.如图,已知正三棱柱1111,ABC A B C AC AA -=,E ,F 分别是棱11,BC A C 上的点.记EF 与1AA 所成的角为a ,EF 与平面ABC 所成的角为b ,二面角F BC A --的平面角为g ,则()A.a b g££ B.b a g ££ C.b g a££ D.a g b££【答案】A 【解析】【分析】先用几何法表示出a b g ,,,再根据边长关系即可比较大小.【详解】如图所示,过点F 作FP AC ^于P ,过P 作PM BC ^于M ,连接PE ,则EFP a =Ð,FEP b =Ð,FMP g =,tan 1PE PE FP AB a ==£,tan 1FP AB PE PE b ==³,tan tan FP FPPM PEg b =³=,所以a b g ££,故选:A .9.已知,a b ÎR ,若对任意,|||4||25|0x a x b x x Î-+---³R ,则()A 1,3a b £³ B.1,3a b ££ C.1,3a b ³³ D.1,3a b ³£【答案】D 【解析】【分析】将问题转换为|||25||4|a x b x x -³---,再结合画图求解.【详解】由题意有:对任意的x ÎR ,有|||25||4|a x b x x -³---恒成立.设()||f x a x b =-,()51,2525439,421,4x x g x x x x x x x ì-£ïïï=---=-<<íï-³ïïî,即()f x 的图象恒在()g x 的上方(可重合),如下图所示:.由图可知,3a ³,13b ££,或13a £<,3143b a££-£,故选:D .10.已知数列{}n a 满足()21111,3n n n a a a a n *+==-ÎN ,则()A.100521002a <<B.100510032a << C.100731002a <<D.100710042a <<【答案】B 【解析】【分析】先通过递推关系式确定{}n a 除去1a ,其他项都在()0,1范围内,再利用递推公式变形得到1111133n n n a a a +-=>-,累加可求出11(2)3n n a >+,得出1001003a <,再利用11111111333132n n n a a a n n +æö-=<=+ç÷-+èø-+,累加可求出()111111113323n n a n æö-<-++++ç÷èøL ,再次放缩可得出10051002a >.【详解】∵11a =,易得()220,13a =Î,依次类推可得()0,1n aÎ由题意,1113n n n a a a +æö=-ç÷èø,即()1131133n n n n n a a a a a +==+--,∴1111133n n n a a a +-=>-,即211113a a ->,321113a a ->,431113a a ->,…,1111,(2)3n n n a a -->³,累加可得()11113n n a ->-,即11(2),(2)3n n n a >+³,∴()3,22n a n n <³+,即100134a <,100100100334a <<,又11111111,(2)333132n n n n a a a n n +æö-=<=+³ç÷-+èø-+,∴211111132a a æö-=+ç÷èø,321111133a a æö-<+ç÷èø,431111134a a æö-<+ç÷èø,…,111111,(3)3n n n a a n -æö-<+³ç÷èø,累加可得()11111111,(3)3323n n n a n æö-<-++++³ç÷èøL ,∴10011111111133334943932399326a æöæö-<++++<+´+´<ç÷ç÷èøèøL ,即100140a <,∴100140a >,即10051002a >;综上:100510032a <<.故选:B .【点睛】关键点点睛:解决本题的关键是利用递推关系进行合理变形放缩.非选择题部分(共110分)二、填空题:本大题共7小题,单空题每题4分,多空题每空3分,共36分.11.我国南宋著名数学家秦九韶,发现了从三角形三边求面积的公式,他把这种方法称为“三斜求积”,它填补了我国传统数学的一个空白.如果把这个方法写成公式,就是S =,其中a ,b ,c 是三角形的三边,S 是三角形的面积.设某三角形的三边2a b c ===,则该三角形的面积S =___________.【答案】4.【解析】【分析】根据题中所给的公式代值解出.【详解】因为S =,所以4S ==.故答案为:4.12.已知多项式42345012345(2)(1)x x a a x a x a x a x a x +-=+++++,则2a =__________,12345a a a a a ++++=___________.【答案】①.8②.2-【解析】【分析】第一空利用二项式定理直接求解即可,第二空赋值去求,令0x =求出0a ,再令1x =即可得出答案.【详解】含2x 项为:()()3232222244C 12C 14128x x x x x x ×××-+×××-=-+=,故28a =;令0x =,即02a =,令1x =,即0123450a a a a a a =+++++,∴123452a a a a a ++++=-,故答案为:8;2-.13.若3sin sin 2pa b a b -=+=,则sin a =__________,cos 2b =_________.【答案】①.10②.45【解析】【分析】先通过诱导公式变形,得到a 的同角等式关系,再利用辅助角公式化简成正弦型函数方程,可求出a ,接下来再求b .【详解】2pa b +=,∴sin cos b a =,即3sin cos a a -=的sin cos1010a aö-=÷÷øsin10q=,cos10q=,()a q-=,∴22k k Zpa q p-=+Î,,即22kpa q p=++,∴sin sin2cos210kpa q p qæö=++==ç÷èø,则224cos22cos12sin15b b a=-=-=.故答案为:10;45.14.已知函数()22,1,11,1,x xf xx xxì-+£ï=í+->ïî则12f fæöæö=ç÷ç÷èøèø________;若当[,]x a bÎ时,1()3f x££,则b a-的最大值是_________.【答案】①.3728②.3【解析】【分析】结合分段函数的解析式求函数值,由条件求出a的最小值,b的最大值即可.【详解】由已知2117()2224fæö=-+=ç÷èø,77437()144728f=+-=,所以137()228f féù=êúëû,当1x£时,由1()3f x££可得2123x£-+£,所以11x-££,当1x>时,由1()3f x££可得1113xx£+-£,所以12x<£1()3f x££等价于12x-££+,所以[,][1,2a bÍ-+,所以b a-的最大值为3.故答案为:3728,315.现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字的最小值为x,则(2)P x==__________,()E x=_________.【答案】①.1635,②.127##517【解析】【分析】利用古典概型概率公式求(2)P x =,由条件求x 分布列,再由期望公式求其期望.【详解】从写有数字1,2,2,3,4,5,6的7张卡片中任取3张共有37C 种取法,其中所抽取的卡片上的数字的最小值为2的取法有112424C C C +种,所以11242437C C C 16(2)C 35P x +===,由已知可得x 的取值有1,2,3,4,2637C 15(1)C 35P x ===,16(2)35P x ==,,()()233377C 31134C 35C 35P P x x ======,所以15163112()1234353535357E x =´+´+´+´=,故答案为:1635,127.16.已知双曲线22221(0,0)x y a b a b -=>>的左焦点为F ,过F 且斜率为4b a的直线交双曲线于点()11,A x y ,交双曲线的渐近线于点()22,B x y 且120x x <<.若||3||FB FA =,则双曲线的离心率是_________.【答案】4【解析】【分析】联立直线AB 和渐近线2:bl y x a=方程,可求出点B ,再根据||3||FB FA =可求得点A ,最后根据点A 在双曲线上,即可解出离心率.【详解】过F 且斜率为4b a 的直线:()4b AB y x c a=+,渐近线2:bl y x a =,联立()4b y x c ab y xa ì=+ïïíï=ïî,得,33c bc B a æöç÷èø,由||3||FB FA =,得5,,99c bc A a æö-ç÷èø而点A 在双曲线上,于是2222222518181c b c a a b -=,解得:228124c a =,所以离心率e 4=.故答案为:4.17.设点P 在单位圆的内接正八边形128A A A L 的边12A A 上,则222182PA PA PA +++u u u r u u L u r u u u r 的取值范围是_______.【答案】[12+【解析】【分析】根据正八边形的结构特征,分别以圆心为原点,37A A 所在直线为x 轴,51A A 所在直线为y 轴建立平面直角坐标系,即可求出各顶点的坐标,设(,)P x y ,再根据平面向量模的坐标计算公式即可得到()2222212888PA PA PA x y +++=++u u u r u u u r u u u r L ,然后利用cos 22.5||1OP ££o 即可解出.【详解】以圆心为原点,37A A 所在直线为x 轴,51A A 所在直线为y 轴建立平面直角坐标系,如图所示:则1345726(0,1),,,(1,0),,,(0,1),,,(1,0)222222A A A A A A A æöææ-----ç÷ççç÷ç÷ç÷èøèøèø,822A æö-ç÷ç÷èø,设(,)P x y ,于是()2222212888PA PA PA x y +++=++u u u r u u u r u u u r L ,因为cos 22.5||1OP ££o,所以221cos 4512x y +£+£o ,故222128PA PA PA +++u u u r u u u r u u u r L 的取值范围是[12+.故答案为:[12+.三、解答题:本大题共5小题,共74分.解答应写出文字说明、证明过程或演算步骤.18.在ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c.已知34,cos 5a C ==.(1)求sin A 的值;(2)若11b =,求ABC V 的面积.【答案】(1;(2)22.【解析】【分析】(1)先由平方关系求出sin C ,再根据正弦定理即可解出;(2)根据余弦定理的推论222cos 2a b c C ab+-=以及4a =可解出a ,即可由三角形面积公式in 12s S ab C =求出面积.【小问1详解】由于3cos 5C =,0πC <<,则4sin 5C =.因为4a =,由正弦定理知4sin A C =,则sin sin 45A C ==.【小问2详解】因为4a =,由余弦定理,得2222221612111355cos 22225a a a abc C ab a a +--+-====,即26550a a +-=,解得5a =,而4sin 5C =,11b =,所以ABC V 的面积114sin 51122225S ab C ==´´´=.19.如图,已知ABCD 和CDEF 都是直角梯形,//AB DC ,//DC EF ,5AB =,3DC =,1EF =,60BAD CDE Ð=Ð=°,二面角F DC B --的平面角为60°.设M ,N 分别为,AE BC 的中点.(1)证明:FN AD ^;(2)求直线BM 与平面ADE 所成角的正弦值.【答案】(1)证明见解析;(2)14.【解析】【分析】(1)过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点G 、H ,由平面知识易得FC BC =,再根据二面角的定义可知,60BCF Ð=o ,由此可知,FN BC ^,FN CD ^,从而可证得FN ^平面ABCD ,即得FN AD ^;(2)由(1)可知FN ^平面ABCD ,过点N 做AB 平行线NK ,所以可以以点N 为原点,NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz -,求出平面ADE 的一个法向量,以及BM uuu u r,即可利用线面角的向量公式解出.【小问1详解】过点E 、D 分别做直线DC 、AB 的垂线EG 、DH 并分别交于点交于点G 、H .∵四边形ABCD 和EFCD 都是直角梯形,//,//,5,3,1AB DC CD EF AB DC EF ===,60BAD CDE Ð=Ð=°,由平面几何知识易知,2,90DG AH EFC DCF DCB ABC ==Ð=Ð=Ð=Ð=°,则四边形EFCG 和四边形DCBH 是矩形,∴在Rt EGD V 和Rt DHA V ,EG DH ==∵,DC CF DC CB ^^,且CF CB C Ç=,∴DC ^平面,BCF BCF Ð是二面角F DC B --的平面角,则60BCF Ð=o ,∴BCF △是正三角形,由DC Ì平面ABCD ,得平面ABCD ^平面BCF ,∵N 是BC 的中点,\FN BC ^,又DC ^平面BCF ,FN Ì平面BCF ,可得FN CD ^,而BC CD C Ç=,∴FN ^平面ABCD ,而AD Ì平面ABCD FN AD \^.【小问2详解】因为FN ^平面ABCD ,过点N 做AB 平行线NK ,所以以点N 为原点,NK ,NB 、NF 所在直线分别为x 轴、y 轴、z 轴建立空间直角坐标系N xyz -,设(3,(1,0,3)A B D E,则33,,22M æöç÷ç÷èø,33,,,(2,(22BM AD DE æö\=-=--=-ç÷ç÷èøu u u u r u u ur u u u r 设平面ADE 的法向量为(,,)n x y z =r由00n AD n DE ì×=í×=îu u u v r u u u v r,得20230x x z ì--=ïí-++=ïî,取n =-r ,设直线BM 与平面ADE 所成角为q ,∴||sin cos ,14|||n BM n BM n BM q ×=áñ====×u uu u r r u uu u r r uu u u r r .20.已知等差数列{}n a 的首项11a =-,公差1d >.记{}n a 的前n 项和为()n S n *ÎN .(1)若423260S a a -+=,求n S ;(2)若对于每个n *ÎN ,存在实数n c ,使12,4,15n n n n n n a c a c a c +++++成等比数列,求d 取值范围.【答案】(1)235(N )2n n nS n *-=Î(2)12d <£【解析】【分析】(1)利用等差数列通项公式及前n 项和公式化简条件,求出d ,再求n S;的(2)由等比数列定义列方程,结合一元二次方程有解的条件求d 的范围.【小问1详解】因为42312601S a a a -+==-,,所以()()46211260d d d -+--+-++=,所以230d d -=,又1d >,所以3d =,所以34n a n =-,所以()213522n na a n n n S +-==,【小问2详解】因为n n a c +,14n n a c ++,215n n a c ++成等比数列,所以()()()212415n n n n n n a c a c a c +++=++,()()()2141115n n n nd c nd d c nd d c -+=-+-+-+++,22(1488)0n n c d nd c d +-++=,由已知方程22(1488)0n n c d nd c d +-++=的判别式大于等于0,所以()22148840d nd d D =-+-³,所以()()168812880d nd d nd -+-+³对于任意的n *ÎN 恒成立,所以()()212320n d n d ----³éùéùëûëû对于任意的n *ÎN 恒成立,当1n =时,()()()()21232120n d n d d d ----=++³éùéùëûëû,当2n =时,由()()2214320d d d d ----³,可得2£d 当3n ³时,()()21232(3)(25)0n d n d n n ---->--³éùéùëûëû,又1d >所以12d <£21.如图,已知椭圆22112x y +=.设A ,B 是椭圆上异于(0,1)P 的两点,且点0,21Q æöç÷èø在线段AB 上,直线,PA PB 分别交直线132y x =-+于C ,D 两点.(1)求点P 到椭圆上点的距离的最大值;(2)求||CD 的最小值.【答案】(1)11;(2)5.【解析】【分析】(1)设,sin )Q q q 是椭圆上任意一点,再根据两点间的距离公式求出2||PQ ,再根据二次函数的性质即可求出;(2)设直线1:2AB y kx =+与椭圆方程联立可得1212,x x x x +,再将直线132y x =-+方程与PA PB 、的方程分别联立,可解得点,C D 的坐标,再根据两点间的距离公式求出CD ,最后代入化简可得231CD k =×+,由柯西不等式即可求出最小值.【小问1详解】设,sin )Q q q 是椭圆上任意一点,(0,1)P ,则222221144144||12cos (1sin )1311sin 2sin 11sin 111111PQ q q q q q æö=+-=--=-+£ø+ç÷è,当且仅当1sin 11q =-时取等号,故||PQ 的最大值是11.【小问2详解】设直线1:2AB y kx =+,直线AB 方程与椭圆22112x y +=联立,可得22130124k x kx æö++-=ç÷èø,设()()1122,,,A x y B x y ,所以12212211231412k x x k x x k ì+=-ï+ïïíï=-æöï+ç÷ïèøî,因为直线111:1y PA y x x -=+与直线132y x =-+交于C ,则111114422(21)1C x x x x y k x ==+-+-,同理可得,222224422(21)1D x x x x y k x ==+-+-.则||CD ====231555k =×=³=+,当且仅当316k =时取等号,故CD的最小值为5.【点睛】本题主要考查最值计算,第一问利用椭圆的参数方程以及二次函数的性质较好解决,第二问思路简单,运算量较大,求最值的过程中还使用到柯西不等式求最值,对学生的综合能力要求较高,属于较难题.22.设函数e()ln (0)2f x x x x=+>.(1)求()f x 的单调区间;(2)已知,a b ÎR ,曲线()y f x =上不同三点()()()()()()112233,,,,,x f x x f x x f x 处的切线都经过点(,)a b .证明:(ⅰ)若e a >,则10()12e a b f a æö<-<-ç÷èø;(ⅱ)若1230e,a x x x <<<<,则22132e 112e e 6e 6ea a x x a --+<+<-.(注:e 2.71828=L 是自然对数的底数)【答案】(1)()f x 的减区间为e 02æöç÷èø,,增区间为e ,2æö+¥ç÷èø.的的(2)(ⅰ)见解析;(ⅱ)见解析.【解析】【分析】(1)求出函数的导数,讨论其符号后可得函数的单调性.(2)(ⅰ)由题设构造关于切点横坐标的方程,根据方程有3个不同的解可证明不等式成立,(ⅱ)31x k x =,1eam =<,则题设不等式可转化为()()()2131313122236m m m t t m m t t --++--<+,结合零点满足的方程进一步转化为()()()()211312ln 0721m m m m m m ---++<+,利用导数可证该不等式成立.【小问1详解】()22e 12e 22xf x x x x -¢=-+=,当e 02x <<,()0f x ¢<;当e2x >,()0f x ¢>,故()f x 的减区间为e 02æöç÷èø,,()f x 的增区间为e ,2æö+¥ç÷èø.【小问2详解】(ⅰ)因为过(),a b 有三条不同的切线,设切点为()(),,1,2,3i i x f x i =,故()()()i i i f x b f x x a ¢-=-,故方程()()()f x b f x x a ¢-=-有3个不同的根,该方程可整理为()21e e ln 022x a x b x x x æö----+=ç÷èø,设()()21e e ln 22g x x a x b x x x æö=----+ç÷èø,则()()22321e 1e 1e22g x x a x x x x x xæö¢=-+-+--+ç÷èø()()31e x x a x=---,当0e x <<或x a >时,()0g x ¢<;当e x a <<时,()0g x ¢>,故()g x 在()()0,e ,,a +¥上为减函数,在()e,a 上为增函数,因为()g x 有3个不同的零点,故()e 0g <且()0>g a ,故()21e e e ln e 0e 2e 2e a b æö----+<ç÷èø且()21e e ln 022a a a b a a a æö----+>ç÷èø,整理得到:12e a b <+且()eln 2b a f a a>+=,此时()1e 13e11ln ln 2e 2e 22e 222a a a b f a a a a aæöæö---<+-+-+=--ç÷ç÷èøèø,设()3e ln 22u a a a =--,则()2e-202au a a ¢=<,故()u a 为()e,+¥上的减函数,故()3eln e 022eu a <--=,故()1012e a b f a æö<-<-ç÷èø.(ⅱ)当0e a <<时,同(ⅰ)中讨论可得:故()g x 在()()0,,e,a +¥上为减函数,在(),e a 上为增函数,不妨设123x x x <<,则1230e x a x x <<<<<,因为()g x 有3个不同的零点,故()0g a <且()e 0g >,故()21e e e ln e 0e 2e 2e a b æö----+>ç÷èø且()21e e ln 022a a a b a a a æö----+<ç÷èø,整理得到:1ln 2e 2ea ab a +<<+,因为123x x x <<,故1230e x a x x <<<<<,又()2e e 1ln 2a ag x x b x x+=-+-+,设e t x =,()0,1e a m =Î,则方程2e e 1ln 02a ax b x x+-+-+=即为:2e ln 0e 2e a a t t t b +-+++=即为()21ln 02mm t t t b -++++=,记123123e e e,,,t t t x x x ===则113,,t t t 为()21ln 02m m t t t b -++++=有三个不同的根,设3131e 1x t k t x a ==>>,1eam =<,要证:22122e 112e e 6e 6e a a x x a --+<+<-,即证13e 2e e 26e 6e a a t t a --+<+<-,即证:13132166m mt t m --<+<-,即证:131********m m t t t t m --æöæö+-+-+<ç÷ç÷èøèø,即证:()()()2131313122236m m m t t m m t t --++--<+,而()21111ln 02m m t t t b -++++=且()23331ln 02mm t t t b -++++=,故()()()22131313ln ln 102m t t t t m t t -+--+-=,故131313ln ln 222t t t t m m t t -+--=-´-,故即证:()()()21313131312ln ln 236m m m t t m t t m t t --+--´<-+,即证:()()()1213313ln1312072t t t m m m t t t +--++>-即证:()()()213121ln 0172m m m k k k --+++>-,记()()1ln ,11k k k k k j +=>-,则()()2112ln 01k k k k k j æö¢=-->ç÷èø-,设()12ln u k k k k =--,则()2122210u k k k k k¢=+->-=即()0k j ¢>,故()k j 在()1,+¥上为增函数,故()()k m j j >,所以()()()()()()22131213121ln 1ln 172172m m m m m m k k m m k m --+--++++>+--,记()()()()()211312ln ,01721m m m m m m m m w ---+=+<<+,则()()()()()()()2232322132049721330721721m mm m m mm m m m m w ---+-+¢=>>++,所以()m w 在()0,1为增函数,故()()10m w w <=,故()()()()211312ln 0721m m m m m m ---++<+即()()()213121ln 0172m mm m m m --+++>-,故原不等式得证:【点睛】思路点睛:导数背景下的切线条数问题,一般转化为关于切点方程的解的个数问题,而复杂方程的零点性质的讨论,应该根据零点的性质合理转化需求证的不等式,常用的方法有比值代换等.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2011年普通高等学校招生全国统一考试数学(理科)
(1)设函数
2
,0,
(),0.x x f x x x -≤⎧=⎨⎩ 若()4f α=,则实数α=
(A ) —4或—2 (B ) —4或2 (C )—2或4 (D )—2或2
(2)把负数z 的共轭复数记作i,i 为虚数单位。
若z=1+i,则(1)z z -
+
∙=
(A )3i - (B )3i + (C )13i + (D)3 (3)
若某几何体的三视图如图所示,则这个几何体的直观图可以是
(4)下列命题中错误的是
(A )如果平面α⊥平面β,那么平面α内一定直线平行于平面β
(B )如果平面α垂直于平面β,那么平面α内一定不存在直线垂直于平面β (C )如果平面α⊥平面γ,平面β⊥平面γ,l αβ⋂=,那么l ⊥平面γ (D )如果平面α⊥平面β,那么平面α内所有直线都垂直于平面β
(5)设实数x 、y 是不等式组 ,若x 、y 为整数,则34x y + 的最小值为
(A )14 (B )16 (C )17 (D )19 (6)若02
π
α<<
,02
π
β-
<<,1cos (
)2
3
π
α+=
,3cos (
)4
2
3
π
β
-
=
,则cos ()2
β
α+
=
(A )33
(B )33
-
(C )
539
(D )69-
(7)若a 、b 为实数,则“01ab <<”是“1a b
<”或1b a
>的
(A )充分二而不必要条件 (B )必要而不充分条件
(C )充分必要条件 (D )既不充分也不必要条件 (8)已知椭圆 2212
2
1x y C a
b
=
+
=(a >b >0)与双曲线 2
2
214
y
C x =-
=有公共的焦点,1C 的一条
250x y +->
270x y +->,
0x ≥,0y ≥
最近线与以2C 的长轴为直径的圆相交于,A B 来两点。
若1C 恰好将线段AB 三等分,则 (A )232
a =
(B ) 2a =13 (C ) 212
b =
(D )2b =2
(9)有5本不同的书,其中语文书2本,数学书2本,物理书1本。
若将其随机地****,则书架
的同一***,则同一科目都不****得是
(A )
45
(B )
25
(C )
15
(D ) 5
(10)设,,a b c 为实数,22()()(),()(1)(1)f x x a x bx c g x ax ax bx =+++=+++。
记集合
{{()
0,
,{}()S x f x x R T
x g x x R ==∈==∈。
若 {},{}S T 分别为集合,S T 的元素个数,则
系列结论不可能的是
(A ){}1S =且 {}0T = (B ){}1S = 且 {}1T = (C ){}2S = 且{}2T = (D ){}2S =且{}3T =
(11)若函数2()f x x x a =-+为偶函数,则实数a =
(12)若某程序??如图所示,则该程序运行后输出的k 值为
(13)若二项式的展开式中x 的系数为A ,常数项为B ,
若4B A =,则a 的值是 。
(14)若平面向量,αβ满足1,1a β=≤,且以向量,αβ为邻边的平行四边形的面积为
12
,则α与β的夹角θ的范围是
(15)某毕业生参加人才招聘会,分别向甲、乙、丙三个公司投递了个人简历,假定该毕业生得到甲公司面试的概率为
23
,得到乙公司面试的
概率为p ,且三个公司是否让其面试是相互独立的。
记X 为该毕业生得到面试得公司个数。
若
1(0)12
P X ==
,则随机变量X 的数学期望()E X =
16.设,x y 为实数,若2241,x y xy ++=则2x y +的最大值是 . 17.设12,F F 分别为椭圆
2
2
13
x
y +=的焦点,点,A B 在椭圆上,若125F A F B =
;则点A 的坐标是
(18)(本题满分14分)在A B C 中,角..A B C 所对的边分别为a,b,c.已知()sin sin sin ,
A C p
B p R +=∈且2
14ac b
=
.(Ⅰ)当5,14
p b =
=时,求,a c 的值;(Ⅱ)若角B 为锐角,求p 的取值范围;
(19)(本题满分14分)已知公差不为0的等差数列{}x a 的首项1a 为a (a ∈R )设数列的和4
1a 成
等比数列。
(Ⅰ)求数列{}x a 的通项公式及a S i
(Ⅱ)记A =
1
1S +
2
1S +
3
1S +…+
1x
S · β·=
1
1a +
2
1a +
1v
a 当a ≥2时,试比较A 与B 的大小
(20)(本题满分15分)如图,在三棱P -ABC 中,AB =AC ,D 为BC 的中点,
PO ⊥平面ABC ,垂足O 落在线段AD 上,已知BC =8,PO =4,AO
=3,OD =2
(Ⅰ)证明:AP ⊥BC ;
(Ⅱ)在线段AP 上是否存在点M ,使得二面角A -MC -β为直二面角?若存在,求出AM 的长;若不存在,请说明理由。
(21)(本题满分15分)已知抛物线1c :3x =y ,圆1)4(:222=-+y x C 的圆心为点M
(Ⅰ)求点M 到抛物线1c 的准线的距离;
(Ⅱ)已知点P 是抛物线1c 上一点(异于原点),过点P 作圆2c 的两条切线,交抛物线1c 于A ,B 两点,若过M ,P 两点的直线l 垂足于AB ,求直线l 的方程
(22)(本题满分14分)设函数()f x =2()ln x a x -,a ∈R
(Ⅰ)若x =e 为()y f x =的极值点,求实数a ;
(Ⅱ)求实数a 的取值范围,使得对任意的x ∈(0,3e ],恒有()f x ≤42e 成立 注:e 为自然对数的底数。
