信号与系统MATLAB作业
信号与系统matlab实验及答案
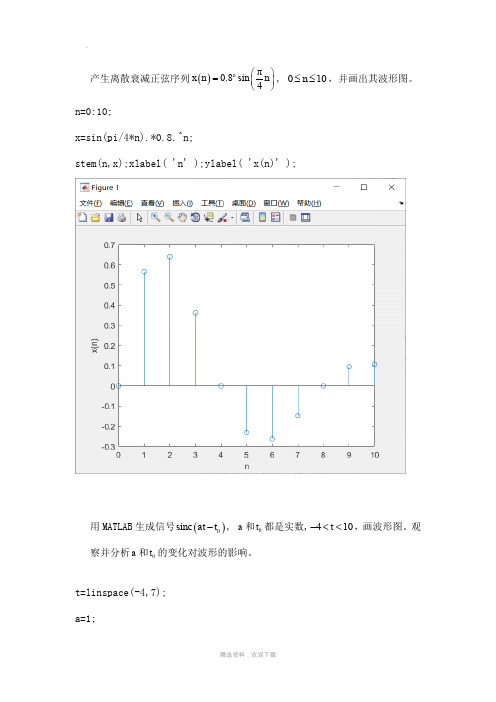
产生离散衰减正弦序列()π0.8sin 4n x n n ⎛⎫= ⎪⎝⎭, 010n ≤≤,并画出其波形图。
n=0:10;x=sin(pi/4*n).*0.8.^n;stem(n,x);xlabel( 'n' );ylabel( 'x(n)' );用MATLAB 生成信号()0sinc at t -, a 和0t 都是实数,410t -<<,画波形图。
观察并分析a 和0t 的变化对波形的影响。
t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=2;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);三组对比可得a 越大最大值越小,t0越大图像对称轴越往右移某频率为f 的正弦波可表示为()()cos 2πa x t ft =,对其进行等间隔抽样,得到的离散样值序列可表示为()()a t nT x n x t ==,其中T 称为抽样间隔,代表相邻样值间的时间间隔,1s f T=表示抽样频率,即单位时间内抽取样值的个数。
抽样频率取40 Hz s f =,信号频率f 分别取5Hz, 10Hz, 20Hz 和30Hz 。
请在同一张图中同时画出连续信号()a x t t 和序列()x n nT 的波形图,并观察和对比分析样值序列的变化。
可能用到的函数为plot, stem, hold on 。
fs = 40;t = 0 : 1/fs : 1 ;% ƵÂÊ·Ö±ðΪ5Hz,10Hz,20Hz,30Hz f1=5;xa = cos(2*pi*f1*t) ; subplot(1, 2, 1) ;plot(t, xa) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('t(s)') ;ylabel('Xa(t)') ;line([0, max(t)],[0,0]) ; subplot(1, 2, 2) ;stem(t, xa, '.') ;line([0, max(t)], [0, 0]) ;axis([0, max(t), min(xa), max(xa)]) ;xlabel('n') ;ylabel('X(n)') ;频率越高,图像更加密集。
信号与系统matlab实验试题

、已知某连续系统的系统函数s 4,试用 Matlab 画出该系统的零极点1H ( s)1)3(s图,并分析系统的稳定性。
clc,clear;num=[1 -4];den=[-2 3 -1];zs=roots(num);ps=roots(den);figure(1);plot(real(zs),imag(zs),'o',real(ps),imag(ps),'kx','markersize',12);axis([0 4 -1 1]);grid on;sys=tf(num,den);figure(2);pzmap(sys);axis([0 4 -1 1]);系统不稳定2、已知序列 h(n)= [1, 3,2,0,5]-1f(n) = [1 , 2, 3, 1]2求:y(n) = h(n) *f(n) ,并画出 h( n)、f(n)以及 y( n)的图形(要求在一个大图上画 3 个从上到下排列的子图)。
n1=-1:3;h=[1 3 2 0 5];n2=2:5;f=[1 2 3 1];figure(1);subplot(3,1,1)stem(n1,h)grid on;xlabel(' 输入序列h(n)')subplot(3,1,2)stem(n2,f)grid on;xlabel(' 单位序列响应f(n)')y=conv(h,f)n=n1(1)+n2(1):n1(length(n1))+n2(length(n2))subplot(3,1,3)stem(n,y)grid on;xlabel(' 输出响应y(n)')、已经离散信号z2并写3 f (n) 的z变换为 F ( z),求其单边逆 z 变换 f ( n)z 2z2出其表达式。
F1=sym('(z^2)/(z^2-z-2)');f1=iztrans(F1)f1=simple(f1)表达式: f1 =1/3*(-1)^n+2/3*2^n4、已知序列 f (n)2n e 3n u( n) ,求序列 f(n) 的单边 z 变换 F(z),并写出 F(z)的表达式。
信号与系统MATLAB实验课后习题答案

读书破万卷下笔如有神 ........ ........ ........ .3-1 a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure; subplot(2,2,1); step(sys);subplot(2,2,2); x_step=zeros(size(t));x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t);subplot(2,2,3); impulse(sys,t); title('Impulse Resp on se'); xlabel('Time(sec)'); ylabel('Amplitude');subplot(2,2,4); x_delta=zeros(size(t));x_delta(t==O)=1OO; [y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2); title('Impulse Resp on se'); xlabel('Time(sec)'); ylabel('Amplitude');\\\• \Step Resp on seL in ear Simulati onResults11eedduuttiillppmm 0.50.5AA0001005510 Time (sec)Time (sec) Impulse Response1 Impulse Response1 「Lo.5ed 0.5 u ed ti u lp til m pOm A°A- 0.5-0.51050 0510Time(sec) Time(sec) (sec) 读书破万卷下笔如有神_______________________________3-2函数inti如下:fun ctio n [F,tF]=i nt1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf));tF=zeros(size(tf));tF=tf;for n=1:le ngth(tf)-1;F(n+1)=F( n)+T*f( n);end验证如下:t=[-1:0.01:4];e=zeros(size(t));e=(t>-1/2&t<1);[z,zz]=i nt1(e,t,-1);figure;plot(zz,z);读书破万卷下笔如有神_______________________________ 4-1T1=1;N1=10000;t1=li nspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=li nspace(-OMG/2,OMG/2-OMG/K1,K1)';X1= T1/N1*exp(-j*kro n(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kro n( t1,omg.'))*X1;T2=5;N2=10000;t2=li nspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kro n(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kro n(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Freque ncy'),ylabel('Amplitude')ti tle(' 单个锯齿周期幅频特性曲线 ');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Fu ncti on after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Freque ncy'),ylabel('Amplitude')ti tle(' 五个锯齿周期幅频特性曲线 ');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Fu ncti on after recovered')title('Fu ncti on after recovered');读书破万卷 下笔如有神 ______________________________0.50.6eedduutt00.4iillppmmAA -0.50.2 -1000.5 -500-10050仃imeFrequencyFunction after recovered 个五锯齿周期幅频特曲线性 - ---■/if || -A 片 1] L 1 Pi 1 Lf P L I ¥ 1 I 『1 A「 r F 单个锯齿周期幅频特性曲线 Function after recovered10.8|l J\ '' 1erev11.5oceedru rtOleiltpfam nAo -10.5itcnuF -20024650 -50-1000TimeFrequency 4-2fsana函数如下:fun cti on F=fsa na(t,f,N)omg1=2*pi/(max(t)-mi n( t));k=[-N:N]';F=1/le ngth(t)*exp(-j*kro n( k*omg1,t.'))*f;fssyn函数如下:fun cti on f=fss yn( F,t)omg1=2*pi/(max(t)-mi n( t));N=floor(le ngth(F)/2);k=[-N:N];f=exp(j*kro n(t,k*omg1))*F;验证如下:clcclearclose allT1=1;N1=256;t=li nspace(0,T1-T1/N1,N1)';f=1-2*t;subplot(3,1,1);plot(t,f);title(' 验证原函数')N=25;读书破万卷下笔如有神 ........ ........ ........ .F1=fsa na(t,f,N);subplot(3,1,2);stem(abs(F1),'s');title(' 前N项傅立叶级数系数幅度曲线')f2=fssyn(F1,t);subplot(3,1,3);plot(t,f2);xlabel('time[s]'),ylabel('Amplitude');ti tle(' 傅立叶逆变换后时域函数');验证原函数10-100.10.20.30.40.50.60.70.80.91 前N项傅立叶级数系数幅度曲线0.4■—7一一. ■” g______ jfj r-------- J。
长江大学信号与系统matlab实验答案

实验1 信号变换与系统非时变性质的波形绘制●用MA TLAB画出习题1-8的波形。
●用MA TLAB画出习题1-10的波形。
Eg 1.8代码如下:function [y]=zdyt(t) %定义函数zdyty=-2/3*(t-3).*(heaviside(-t+3)-heaviside(-t));endt0=-10;t1=4;dt=0.02;t=t0:dt:t1;f=zdyt(t);y=zdyt(t+3);x=zdyt(2*t-2);g=zdyt(2-2*t);h=zdyt(-0.5*t-1);fe=0.5*(zdyt(t)+zdyt(-t));fo=0.5*(zdyt(t)-zdyt(-t));subplot(7,1,1),plot(t,f);title('信号波形的变化')ylabel('f(t)')grid;line([t0 t1],[0 0]);subplot(7,1,2),plot(t,y);ylabel('y(t)')grid;line([t0 t1],[0 0]);subplot(7,1,3),plot(t,x);ylabel('x(t)')grid;line([t0 t1],[0 0]);subplot(7,1,4),plot(t,g);ylabel('g(t)')grid;line([t0 t1],[0 0]);subplot(7,1,5),plot(t,h);ylabel('h(t)')grid;line([t0 t1],[0 0]);subplot(7,1,6),plot(t,fe);ylabel('fe(t)')grid;line([t0 t1],[0 0]);subplot(7,1,7),plot(t,fo);ylabel('fo(t)')grid;line([t0 t1],[0 0]);xlabel('Time(sec)')结果:Eg1.10代码如下:function [u]=f(t) %定义函数f(t) u= heaviside(t)-heaviside(t-2); endfunction [u] =y(t) %定义函数y(t)u=2*(t.*heaviside(t)-2*(t-1).*heaviside(t-1)+(t-2).*heaviside(t-2)); endt0=-2;t1=5;dt=0.01; t=t0:dt:t1; f1=f(t); y1=y(t); f2=f(t)-f(t-2); y2=y(t)-y(t-2); f3=f(t)-f(t+1); y3=y(t)-y(t+1);subplot(3,2,1),plot(t,f1); title('激励——响应波形图') ylabel('f1(t)')grid;line([t0 t1],[0 0]);-10-8-6-4-2024012信号波形的变化f (t)-10-8-6-4-2024012y (t)-10-8-6-4-2024012x (t)-10-8-6-4-2024012g (t)-10-8-6-4-2024012h (t)-10-8-6-4-202400.51f e (t)-10-8-6-4-2024-101f o (t)Time(sec)subplot(3,2,2),plot(t,y1); ylabel('y1(t)')grid;line([t0 t1],[0 0]); subplot(3,2,3),plot(t,f2); ylabel('f2(t)')grid;line([t0 t1],[0 0]); subplot(3,2,4),plot(t,y2); ylabel('y2(t)')grid;line([t0 t1],[0 0]); subplot(3,2,5),plot(t,f3); ylabel('f3(t)')grid;line([t0 t1],[0 0]); subplot(3,2,6),plot(t,y3); ylabel('y3(t)')grid;line([t0 t1],[0 0]); xlabel('Time(sec)')结果:实验2 微分方程的符号计算和波形绘制上机内容用MA TLAB 计算习题2-1,并画出系统响应的波形。
东南大学信号与系统MATLAB实践第二次作业

东南大学信号与系统MATLAB实践第二次作业. . . . 练习二实验六一.用MATLAB语言描述下列系统,并求出极零点、1.>> Ns=[1];Ds=[1,1];sys1=tf(Ns,Ds)实验结果:sys1 =1-----s + 1>> [z,p,k]=tf2zp([1],[1,1])z =Empty matrix: 0-by-1p =. . . .-1k =12.>>Ns=[10]Ds=[1,-5,0]sys2=tf(Ns,Ds)实验结果:Ns =10Ds =sys2 =10---------s^2 - 5 s>>[z,p,k]=tf2zp([10],[1,-5,0]) z =Empty matrix: 0-by-1p =5k =10二.已知系统的系统函数如下,用MATLAB描述下列系统。
1.>> z=[0];p=[-1,-4];k=1;sys1=zpk(z,p,k)实验结果:sys1 =s-----------(s+1) (s+4)Continuous-time zero/pole/gain model.2.>> Ns=[1,1]Ds=[1,0,-1]sys2=tf(Ns,Ds)实验结果:Ns =1 1Ds =sys2 =s + 1-------s^2 - 1Continuous-time transfer function.3.>> Ns=[1,6,6,0];Ds=[1,6,8];sys3=tf(Ns,Ds)实验结果:Ns =1 6 6 0Ds =1 6 8sys3 =s^3 + 6 s^2 + 6 s-----------------s^2 + 6 s + 8Continuous-time transfer function.六.已知下列H(s)或H(z),请分别画出其直角坐标系下的频率特性曲线。
1.>> clear;for n = 1:400w(n) = (n-1)*0.05;H(n) = (1j*w(n))/(1j*w(n)+1); endmag = abs(H);phase = angle(H);subplot(2,1,1)plot(w,mag);title('幅频特性') subplot(2,1,2)plot(w,phase);title('相频特性')实验结果:2.>> clear;for n = 1:400w(n) = (n-1)*0.05;H(n) = (2*j*w(n))/((1j*w(n))^2+sqrt(2)*j*w(n)+1); end mag = abs(H);phase = angle(H);subplot(2,1,1)plot(w,mag);title('幅频特性')subplot(2,1,2)plot(w,phase);title('相频特性')实验结果:3.>>clear;for n = 1:400w(n) = (n-1)*0.05;H(n) = (1j*w(n)+1)^2/((1j*w(n))^2+0.61); end mag = abs(H);phase = angle(H);subplot(2,1,1)plot(w,mag);title('幅频特性')subplot(2,1,2)plot(w,phase);title('相频特性')实验结果:4.>>clear;for n = 1:400w(n) = (n-1)*0.05;H(n) =3*(1j*w(n)-1)*(1j*w(n)-2)/(1j*w(n)+1)*(1j*w(n)+2); end mag = abs(H);phase = angle(H);subplot(2,1,1)plot(w,mag);title('幅频特性')subplot(2,1,2)plot(w,phase);title('相频特性') 实验结果:实验七三.已知下列传递函数H(s)或H(z),求其极零点,并画出极零图。
信号与系统matlab课后作业-北京交通大学

信号与系统MATLAB平时作业学院:电子信息工程学院班级::学号:教师:钱满义MATLAB 习题M3-1 一个连续时间LTI系统满足的微分方程为y ’’(t)+3y ’(t)+2y(t)=2x ’(t)+x(t)(1)已知x(t)=e -3t u(t),试求该系统的零状态响应y zs (t); (2)用lism 求出该系统的零状态响应的数值解。
利用(1)所求得的结果,比较不同的抽样间隔对数值解精度的影响。
解:(1) 由于''()3'()2()2'()(),0h t h t h t t t t δδ++=+≥则2()()()t t h t Ae Be u t --=+ 将()h t 带入原方程式化简得(2)()()'()2'()()A B t A B t t t δδδδ+++=+所以1,3A B =-=2()(3)()t t h t e e u t --=-+又因为3t ()()x t e u t -= 则该系统的零状态响应3t 23t 2t ()()()()(3)()0.5(6+5)()zs t t t y t x t h t e u t e e u t e e e u t ----=*=*-+=-- (2)程序代码 1、ts=0;te=5;dt=0.1;sys=tf([2 1],[1 3 2]);t=ts:dt:te;x=exp(-3*t).*(t>=0);y=lsim(sys,x,t)2、ts=0;te=5;dt=1;sys=tf([2 1],[1 3 2]);t=ts:dt:te;x=exp(-3*t).*(t>=0);y1=-0.5*exp(-3*t).*(exp(2*t)-6*exp(t)+5).*[t>=0];y2=lsim(sys,x,t)plot(t,y1,'r-',t,y2,'b--')xlabel('Time(sec)')legend('实际值','数值解')用lism求出的该系统的零状态响应的数值解在不同的抽样间隔时与(1)中求出的实际值进行比较将两种结果画在同一幅图中有图表 1 抽样间隔为1图表 2 抽样间隔为0.1图表 3 抽样间隔为0.01当抽样间隔dt减小时,数值解的精度越来越高,从图像上也可以看出数值解曲线越来越逼近实际值曲线,直至几乎重合。
信号与系统课程作业
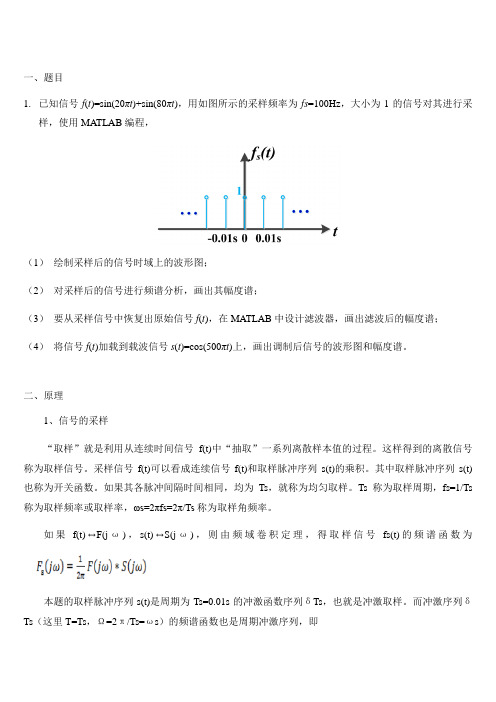
一、题目1.已知信号f(t)=sin(20πt)+sin(80πt),用如图所示的采样频率为fs=100Hz,大小为1的信号对其进行采样,使用MATLAB编程,(1)绘制采样后的信号时域上的波形图;(2)对采样后的信号进行频谱分析,画出其幅度谱;(3)要从采样信号中恢复出原始信号f(t),在MATLAB中设计滤波器,画出滤波后的幅度谱;(4)将信号f(t)加载到载波信号s(t)=cos(500πt)上,画出调制后信号的波形图和幅度谱。
二、原理1、信号的采样“取样”就是利用从连续时间信号f(t)中“抽取”一系列离散样本值的过程。
这样得到的离散信号称为取样信号。
采样信号f(t)可以看成连续信号f(t)和取样脉冲序列s(t)的乘积。
其中取样脉冲序列s(t)也称为开关函数。
如果其各脉冲间隔时间相同,均为Ts,就称为均匀取样。
Ts称为取样周期,fs=1/Ts 称为取样频率或取样率,ωs=2πfs=2π/Ts称为取样角频率。
如果f(t)↔F(jω),s(t)↔S(jω),则由频域卷积定理,得取样信号fs(t)的频谱函数为本题的取样脉冲序列s(t)是周期为Ts=0.01s的冲激函数序列δTs,也就是冲激取样。
而冲激序列δTs(这里T=Ts,Ω=2π/Ts=ωs)的频谱函数也是周期冲激序列,即2、采样定理所谓模拟信号的数字处理方法就是将待处理模拟信号经过采样、量化和编码形成数字信号,再利用数字信号处理技术对采样得到的数字信号进行处理。
一个频带限制在(0,fc)Hz的模拟信号m(t),若以采样频率fs≥2fc对模拟信号m(t)进行采样,得到最终的采样值,则可无混叠失真地恢复原始模拟信号m(t)。
其中,无混叠失真地恢复原始模拟信号m(t)是指被恢复信号与原始模拟信号在频谱上无混叠失真,并不是说被恢复信号与原始信号在时域上完全一样。
由于采样和恢复器件的精度限制以及量化误差等存在,两者实际是存在一定误差或失真的。
奈奎斯特频率:通常把最低允许的采样频率fs=2fc称为奈奎斯特频率。
(完整版)信号与系统Matlab实验作业

(完整版)信号与系统Matlab实验作业实验一典型连续时间信号和离散时间信号一、实验目的掌握利用Matlab 画图函数和符号函数显示典型连续时间信号波形、典型时间离散信号、连续时间信号在时域中的自变量变换。
二、实验内容1、典型连续信号的波形表示(单边指数信号、复指数信号、抽样信号、单位阶跃信号、单位冲击信号)1)画出教材P28习题1-1(3) ()[(63)(63)]t f t e u t u t =----的波形图。
function y=u(t) y=t>=0; t=-3:0.01:3;f='exp(t)*(u(6-3*t)-u(-6-3*t))'; ezplot(f,t); grid on;2)画出复指数信号()()j t f t e σω+=当0.4, 8σω==(0<t<10)时的实部和虚部的< p="">波形图。
t=0:0.01:10;f1='exp(0.4*t)*cos(8*t)'; f2='exp(0.4*t)*sin(8*t)'; figure(1) ezplot(f1,t); grid on; figure(2) ezplot(f2,t); grid on;t=-10:0.01:10; f='sin(t)/t'; ezplot(f,t); grid on;t=0:0.01:10;f='(sign(t-3)+1)/2'; ezplot(f,t);grid on;5)单位冲击信号可看作是宽度为?,幅度为1/?的矩形脉冲,即t=t 1处的冲击信号为11111()()0 t t t x t t t otherδ??<<+?=-=画出0.2?=, t 1=1的单位冲击信号。
t=0:0.01:2;f='5*(u(t-1)-u(t-1.2))'; ezplot(f,t); grid on;axis([0 2 -1 6]);2、典型离散信号的表示(单位样值序列、单位阶跃序列、实指数序列、正弦序列、复指数序列)编写函数产生下列序列:1)单位脉冲序列,起点n0,终点n f,在n s处有一单位脉冲。
利用matlab设计仿真信号与系统作业

Q1-2:以Q1_2为文件名存盘,产生实门信号)(2t g 和信号t t g t f π10cos )()(2=。
要求在图形中加上网格线,并使用函数axis()控制图形的时间范围在-2~2秒之间。
然后执行该程序,保存所的图形。
syms t;gt=sym(heaviside(t+1)-heaviside(t-1));ft=gt*cos(10*pi*t);ezplot(ft,[-2,2]);grid on;axis([-2,2,-2,2]);title('ft=gt*cos(10*pi*t),gt=u(t+2)-u(t-2)');xlabel('t');Q1-4:根据示例程序的编程方法,编写一个MATLAB 程序,以Q1_5为文件名存盘,由给定信号x(t) = e -0.5t u(t)求信号y(t) = x(1.5t+3),并绘制出x(t) 和y(t)的图形。
编写的程序Q1_5如下:syms txt=exp((-0.5*t))*heaviside(t);yt=xt*(1.5*t+3);subplot(1,2,1),ezplot(xt,[-2,6]),title(' xt=exp((-0.5*t))*u(t)')subplot(1,2,2),ezplot(yt,[-2,6]),title(' yt=xt*(1.5*t+3)')信号x(t)的波形图 和 信号y(t) = x(1.5t+3) 的波形Q1-6编写程序Q1_8,用Matlab 的方法计算并绘制由如下微分方程表示系统的冲激响应和阶跃响应,并分为上下两个子图绘制在一个图中。
)()(5.0)(2)(3)('22t f t f t y dt t dy dtt y d +=++num=[0.5,1];den=[1,3,2];t=0:0.01:8;subplot(2,1,1) ,impulse(num,den,8) subplot(2,1,2) ,step(num,den,8)Q1-7:做如下总结:1、信号与系统分析,就是基于信号的分解,在时域中,信号主要分解成:连续时间信号和离散时间信号2、写出卷积的运算步骤,并谈谈你对卷积的一些基本性质的理解。
北京交通大学《信号与系统》 课后matlab作业
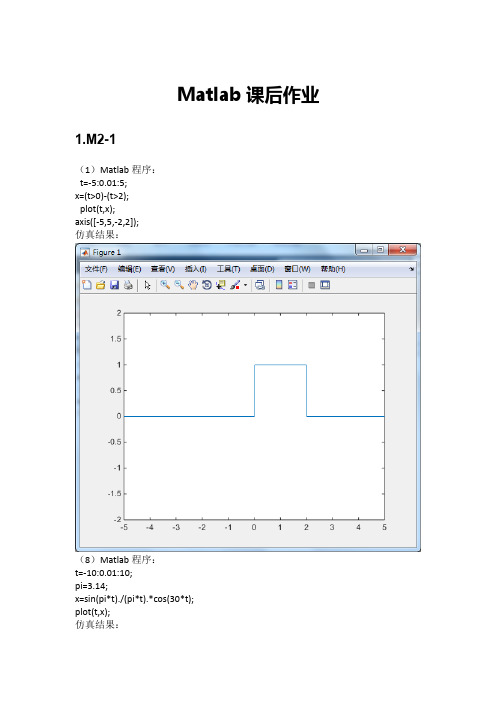
Matlab课后作业1.M2-1(1)Matlab程序:t=-5:0.01:5;x=(t>0)-(t>2);plot(t,x);axis([-5,5,-2,2]);仿真结果:(8)Matlab程序:t=-10:0.01:10;pi=3.14;x=sin(pi*t)./(pi*t).*cos(30*t);plot(t,x);仿真结果:M2-2Matlab程序:t=-2:0.001:2;x=(t>-1)-(t>0)+2*tripuls(t-0.5,1,0); plot(t,x);axis([-2,2,-2,2]);仿真结果:M3-3(1)function yt=f(t)yt=t.*(t>0)-t.*(t>=2)+2*(t>=2)-3*(t>3)+(t>5); (2)Matlab程序:t=-10:0.01:11;subplot(3,1,1);plot(t,f(t));title('x(t)');axis([-1,6,-2,3]);subplot(3,1,2);plot(t,f(0.5*t));axis([-1,11,-2,3]);title('x(0.5t)');subplot(3,1,3);plot(t,f(2-0.5*t));title('x(2-0.5t)');axis([-9,5,-2,3]);仿真结果:M2-9(1)Matlab程序:k=-4:7;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; stem(k,x);仿真结果:(2)Matlab程序:k=-12:21;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; N=length(x);y=zeros(1,3*N-2);y(1:3:end)=x;stem(k,y);仿真结果:Matlab程序:k=-1:3;x=[0,0,-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; x1=x(1:3:end);stem(k-1,x1);仿真结果:(3)Matlab程序:k=-6:5;x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; stem(k,x);仿真结果:程序>> k=-2:9;>> x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; >> stem(k,x);结果程序>> k=-4:7;>> x=[-3,-2,3,1,-2,-3,-4,2,-1,4,1,-1]; >> xk=fliplr(x);>> k1=-fliplr(k);>> stem(k1,xk);结果M3-1(1)程序>> ts=0;te=5;dt=0.01; >> sys=tf([2 1],[1 3 2]); >> t=ts:dt:te;>> x=exp(-3*t).*(t>=0); >> y=lsim(sys,x,t);>> plot(t,y);>> xlabel('Time(sec)') >> ylabel('y(t)')结果(2)程序>> ts=0;te=5;dt=0.0001; >>sys=tf([2 1],[1 3 2]); >>t=sys:dt:te;>>x=exp(-3*t).*(t>=0); >>y=lsim(sys,x,t);>>plot(t,y);>>xlabel('Time(sec)') >>ylabel('y(t)')结果M3-4>> x=[0.85,0.53,0.21,0.67,0.84,0.12]; >> k1=-2:3;>> h=[0.68,0.37,0.83,0.52,0.71];>> k2=-1:3;>> y=conv(x,h);>> k=(k1(1)+k2(1)):(k1(end)+k2(end)); >> stem(k,y)结果M6-1(1)>> num=[16 0 0];>> den=[1 5.6569 816 2262.7 160000]; >> [r,p,k]=residue(num,den)得r =0.0992 - 1.5147i0.0992 + 1.5147i-0.0992 + 1.3137i-0.0992 - 1.3137ip =-1.5145 +21.4145i-1.5145 -21.4145i-1.3140 +18.5860i-1.3140 -18.5860ik =[]所以可得 X(s)=j s j j s j j s j 5860.183140.13137.10992.05860.183140.13137.10992.04145.215145.15147.10992.021.4145j -1.5145s j 5147.1-0992.0++--+-++-++++++x(t)=3.0108e-1.5145tcos(21.4145t-1.5054)u(t)+2.635e-1.314tcos(18.586t+1.6462)u(t ) (2)X(s)=)2552^)(5(2^+++s s s s解:>> num=[1 0 0 0];den=conv([1 5],[1 5 25]);[r,p,k]=residue(num,den)[angle,mag]=cart2pol(real(r),imag(r))得r =-5.0000 + 0.0000i-2.5000 - 1.4434i-2.5000 + 1.4434ip =-5.0000 + 0.0000i-2.5000 + 4.3301i-2.5000 - 4.3301ik =1angle =3.1416-2.61802.6180mag =5.00002.88682.8868所以X(s)=3301.45.24434.15.23301.45.24434.15.25s 5.0-1j s j j s j +++-+-+--+++x(t)=δ(t)+5e-5tu(t)+5.7736e-2.5tcos(4.3301t-2.618)u(t)M6-2程序>> t=0:0.1:10;>> y1=(2.5*exp(-t)-1.5*exp(-3*t)).*(t>=0);>> y2=((1/3)+2*exp(-t)-(5/6)*exp(-3*t)).*(t>=0);>> y=((1/3)+(9/2)*exp(-t)-(7/3)*exp(-3*t)).*(t>=0);>> plot(t,y1,'r-',t,y2,'g--',t,y,'b-')>> xlabel('Time');>> legend('零输入响应','零状态响应','完全响应')结果M6-5>> num=[1 2];>> den=[1 2 2 1];>> sys=tf(num,den);>> pzmap(sys)>> num=[1 2];den=[1 2 2 1];[r,p,k]=residue(num,den) [angle,mag]=cart2pol(real(r),imag(r))1.0000 + 0.0000i-0.5000 - 0.8660i-0.5000 + 0.8660ip =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660ik =[]angle =-2.09442.0944mag =1.00001.00001.0000所以H(s)=866.05.0866.05.0866.05.0866.05.01s 1j s j j s j +++-+-+--++系统冲激响应h(t)=e-tu(t)+2e-0.5tcos(0.866t-2.0944)u(t)>> num=[1 2];>> den=conv([1 0],[1 2 2 1]);>> [r,p,k]=residue(num,den)r =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660i2.0000 + 0.0000ip =-1.0000 + 0.0000i-0.5000 + 0.8660i-0.5000 - 0.8660i0.0000 + 0.0000ik =[][angle,mag]=cart2pol(real(r),imag(r))angle =3.14162.0944-2.0944mag =1.00001.00001.00002.0000所以Y(s)=s j s j j s j 2866.05.0866.05.0866.05.0866.05.0-1s 1-+++--+-++++ 系统阶跃响应y(t)=e-tu(t)+2e-0.5tcos(0.866t+2.0944)u(t)因为系统的冲激响应h(t)=e-tu(t)-1.00001e-0.5tcos(0.866t)u(t)+1.73205e-0.5tsin(0.866t)u(t) 所以系统的频率响应H(j ω)=5.0)866.0(866.05.0)866.0(866.05.0)866.0(5.05.0)886.0(5.01j 1j j j j ++--+--++-+++++ωωωωω。
信号与系统matlab作业2:对任意两段声音的卷积
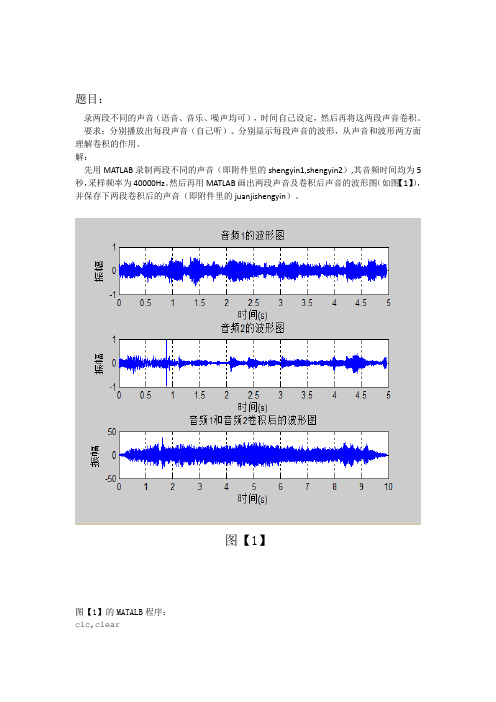
题目:录两段不同的声音(语音、音乐、噪声均可),时间自己设定,然后再将这两段声音卷积。
要求:分别播放出每段声音(自己听)、分别显示每段声音的波形,从声音和波形两方面理解卷积的作用。
解:先用MATLAB录制两段不同的声音(即附件里的shengyin1,shengyin2),其音频时间均为5秒,采样频率为40000Hz。
然后再用MATLAB画出两段声音及卷积后声音的波形图(如图【1】),并保存下两段卷积后的声音(即附件里的juanjishengyin)。
图【1】图【1】的MATALB程序:clc,clear[Y1,fs1]=audioread('shengyin1.wav');%获取音频1文件,并返回采样数据到向量y 中,fs表示采样频率[Y2,fs2]=audioread('shengyin2.wav');%获取音频1文件,并返回采样数据到向量y 中,fs表示采样频率ft1 = Y1(:,1);sigLength1 = length(ft1); %获取声音长度t1=(0:sigLength1-1)/fs1; %求出音频1对应的时间坐标subplot(3,1,1);plot(t1,ft1);%画出音频1的波形图title('音频1的波形图');xlabel('时间(s)');ylabel('振幅');grid;ft2 = Y2(:,1);sigLength2 = length(ft2); %获取声音长度t2=(0:sigLength2-1)/fs2; %求出音频2对应的时间坐标subplot(3,1,2);plot(t2, ft2);%画出音频2的波形图title('音频2的波形图');xlabel('时间(s)');ylabel('振幅');grid;ft=conv(ft1,ft2); %将两段音频进行卷积sigLength = length(ft); %获取声音长度t=(0:sigLength-1)/fs1;subplot(3,1,3);plot(t,ft);%画出卷积后的波形图title('音频1和音频2卷积后的波形图');xlabel('时间(s)');ylabel('振幅');grid;wavwrite(ft,40000,16,'juanjishengyin');%保存卷积后的声音总结:通过这次MATALB作业,观察三个不同的波形图(如图【1】)可知,卷积的作用就是一个信号函数在另一个信号函数上的加权叠加,通俗的说,它就是在输入信号的每个位置,叠加一个单位响应,就得到了输出信号。
信号与系统_MATLAB_实验_课后习题答案
第三章练习题 1、a=[1,1,1]; b=[1,1]; sys=tf(b,a); t=[0:0.01:10]; figure;subplot(2,2,1); step(sys);subplot(2,2,2);x_step=zeros(size(t)); x_step(t>0)=1; x_step(t==0)=1/2; lsim(sys,x_step,t); subplot(2,2,3); impulse(sys,t);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude'); subplot(2,2,4);x_delta=zeros(size(t)); x_delta(t==0)=100;[y1,t]=lsim(sys,x_delta,t); y2=y1;plot(t,y2);title('Impulse Response'); xlabel('Time(sec)'); ylabel('Amplitude');00.511.5Step ResponseTime (sec)A m p l i t u d eLinear Simulation ResultsTime (sec)A m p l i t u d e-0.500.51Impulse ResponseTime(sec) (sec)A m p l i t u d eImpulse ResponseTime(sec)A m p l i t u d e2、函数int1如下:function [F,tF]=int1(f,tf,a)T=tf(2)-tf(1);F=zeros(size(tf)); tF=zeros(size(tf));tF=tf;for n=1:length(tf)-1;F(n+1)=F(n)+T*f(n);end验证如下:t=[-1:0.01:4];e=zeros(size(t));e=(t>-1/2&t<1);[z,zz]=intl(e,t,-1);figure;plot(zz,z);第四章练习题1、T1=1;N1=10000; t1=linspace(0,T1-T1/N1,N1)';f1=1-2*t1;OMG=32*pi;K1=100;omg=linspace(-OMG/2,OMG/2-OMG/K1,K1)';X1=T1/N1*exp(-j*kron(omg,t1.'))*f1;fs1=OMG/2/pi/K1*exp(j*kron(t1,omg.'))*X1;T2=5;N2=10000;t2=linspace(0,T2-T2/N2,N2)';fs2=0*t2;f2=sawtooth(t2*2*pi,0);X2=T2/N2*exp(-j*kron(omg,t2.'))*f2;fs2=fs2+OMG/2/pi/K1*exp(j*kron(t2,omg.'))*X2;figure;subplot(2,2,1);plot(omg,abs(X1),'r');xlabel('Frequency'),ylabel('Amplitude')title('单个锯齿周期幅频特性曲线');subplot(2,2,2);plot(t1,fs1,'r');xlabel('Time'),ylabel('Amplitude')title('Function after recovered');subplot(2,2,3);plot(omg,abs(X2),'r');xlabel('Frequency'),ylabel('Amplitude')title('五个锯齿周期幅频特性曲线');subplot(2,2,4);plot(t2,fs2,'r');xlabel('Time'),ylabel('Function after recovered')title('Function after recovered');-100-5005000.20.40.60.8FrequencyA m p l i t u d e单个锯齿周期幅频特性曲线00.51-1-0.500.51TimeA m p l i t u d eFunction after recovered-100-5005000.511.52FrequencyA m p l i t u d e五个锯齿周期幅频特性曲线246-2-1012TimeF u n c t i o n a f t e r r e c o v e r e dFunction after recovered2、fsana 函数如下:function F=fsana(t,f,N); omg1=2*pi/(max(t)-min(t)); k=[-N:N]';F=1/length(t)*exp(-j*kron(k*omg1,t.'))*f; fssyn 函数如下:function f=fssyn(F,t)omg1=2*pi/(max(t)-min(t)); N=floor(length(F)/2); k=[-N:N];f=exp(j*kron(t,k*omg1))*F; 验证如下: clc clearclose allT1=1;N1=256; t=linspace(0,T1-T1/N1,N1)'; f=1-2*t;subplot(3,1,1); plot(t,f);title('验证原函数') N=25;F1=fsana(t,f,N); subplot(3,1,2); stem(abs(F1),'s');title('前N 项傅立叶级数系数幅度曲线') f2=fssyn(F1,t) ;subplot(3,1,3); plot(t,f2);xlabel('time[s]'),ylabel('Amplitude'); title('傅立叶逆变换后时域函数');00.10.20.30.40.50.60.70.80.91-101验证原函数00.20.4前N 项傅立叶级数系数幅度曲线00.10.20.30.40.50.60.70.80.91-202time[s]A m p l i t u d e傅立叶逆变换后时域函数第五章练习题1、(a) Residue计算a1=[1,5,6];b1=[4,5];[r1,p1,k1]=residue(b1,a1); t=[0:0.01:10];e1=zeros(size(t));for n=1:size(r1);e1=e1+r1(n)*exp(p1(n)*t); end;figure;subplot(1,2,1);plot(t,e1);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([4,5],[1,5,6]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h1=lsim(sys1,delta,t); subplot(1,2,2);plot(t,h1);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同(b)Residue计算t=[0,0.01,10];delta=zeros(size(t));delta(t==0)=100;e2=sin(t);figure;subplot(2,1,1);plot(t,e2);title('residue计算');xlabel('t/s');ylabel('u/v');lism仿真sys1=tf([1,0,2],[1,0,1]);t=[0:0.01:10];delta=zeros(size(t));delta(t==0)=100;h2=lism(sys1,delta,t); subplot(2,1,2);plot(h,t2);axis([0,10,-1,1]);title('lism仿真');xlabel('t/s');ylabel('u/v');Residue计算和lism仿真结果相同2、S=isstable(sys)函数:Function s=isstable(sys);X=ploe(sys);S=1;For n=1:Size(x)If x(n)>0S=0;break;End;End;稳定系统:Sys=tf(1,[1,2]);S=isstable(sys);S=1不稳定系统:Sys=tf(1,[1,-2]);S=isstable(sys);S=第七章练习题1、a=[1,0.5,-0.2,-0.1]; b=[1,-0.3];n=[0:10]';[hi,t]=impz(b,a,n); subplot(1,2,1);stem(n,hi);u=(n>=0);hn=filter(b,a,u); subplot(1,2,2);stem(n,hn);2、n1=[0:9]';n2=[10:19]';x1=(n1>=0);x2=-(n2>=10);a1=[1,-0.2,-0.1];a2=[1,-0.2,0.5];b=[1,0.01];[y1,wf1]=filter(b,a1,x1,[0,1]); [y2,wf2]=filter(b,a2,x2,wf1); stem(n1,y1);hold on;stem(n2,y2);。
信号与系统matlab作业
题目一:现在考虑下面3个信号:[]⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=N n N n n x ππ3cos 22cos 1 []⎪⎭⎫ ⎝⎛+⎪⎭⎫⎝⎛=N n N n n x 3cos 2cos 22 []⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=N n N n n x 25sin 32cos 3ππ 假设对每个信号N=6。
试确定是否每个信号都是周期的。
如果某一信号是周期的,从n=0开始,画出该信号的两个周期;如果该信号不是周期的,对于N n 40≤≤画出该信号,并说明为什么它不是周期的。
记住:用stem,而且要将坐标轴给出适当标注。
解:1、假设N=6,[]1003,2,1•••=n ;分别带入题目中的三个式子,用MATLAB 软件初步描绘出三个信号图形(如图【1-1】),观察三个信号的图形和数据是否具有重复循环性,从而得出三个信号是否周期的。
图【1-1】从图【1-1】及在MATLAB 中各个信号的坐标数据可以得出,信号[]n x 1、[]n x 3是周期的,其周期分别为24,1231==T T ;而信号[]n x 2虽然图形看似具有周期性,但其中的坐标数据却不是循环重复的,即该信号[]n x 2不是周期的。
图【1-1】的MATLAB 程序:Clc ,clearN=6;for n=0:100x1(n+1)=cos(2*pi*n./N)+2*cos(3*pi*n./N);x2(n+1)=2*cos(2*n./N)+cos(3*n./N);x3(n+1)=cos(2*pi*n./N)+3*cos(5*pi*n./(2*N));endn=0:100;subplot(3,1,1)stem(n,x1,'fill')grid;xlabel('n')ylabel('x1')subplot(3,1,2)stem(n,x2,'fill')grid;xlabel('n')ylabel('x2')subplot(3,1,3)stem(n,x3,'fill')grid;xlabel('n')ylabel('x3')2、上面得出了各个信号是否具有周期性,即按照要求用MATLAB 对各个信号进行图像处理:(1)对信号[][]n x n x 21, 得出各自两个周期的波形图像,如图【1-2】:图【1-2】图【1-2】的MATLAB 程序:clc,clearN=6;for n1=0:24x1(n1+1)=cos(2*pi*n1./N)+2*cos(3*pi*n1./N);endn1=0:24;for n3=0:48x3(n3+1)=cos(2*pi*n3./N)+3*cos(5*pi*n3./(2*N));endn3=0:48;subplot(2,1,1)stem(n1,x1,'fill')grid;xlabel('n')ylabel('x1')subplot(2,1,2)stem(n3,x3,'fill')grid;xlabel('n')ylabel('x3')(2)对信号[]n x 2,当N n 40≤≤时用MATLAB 画出该信号的波形图像,如图【1-3】:图【1-3】图【1-3】的MATLAB 程序:clc,clearN=6;for n2=0:1:4*Nx2(n2+1)=2*cos(2*n2./N)+cos(3*n2./N);endn2=0:1:4*N;stem(n2,x2,'fill')grid;xlabel('n')ylabel('X2')因为一个周期信号在形状上的每一个特点都必须周期性地重现;而在图【1-3】上来说,离散信号[]n x 2在对N n 40≤≤中,并没有满足周期信号的条件:[]N n x n x +=][(其中N 指周期)所以,离散信号[]n x 2不是周期信号。
信号与系统matlab实验与答案

产生离散衰减正弦序列xn 0.8nsin πn, 0 n 10,并画出其波形图。
4n=0:10;x=sin(pi/4*n).*0.8.^n;stem(n,x);xlabel( 'n' );ylabel( 'x(n)' );用MATLAB生成信号sincat t0,a和t0都是实数,4 t 10,画波形图。
观察并分析a和t0的变化对波形的影响。
t=linspace(-4,7);a=1;t0=2;y=sinc(a*t-t0);plot(t,y);t=linspace(-4,7); a=2;t0=2;y=sinc(a*t-t0); plot(t,y);t=linspace(-4,7); a=1;t0=2;y=sinc(a*t-t0); plot(t,y);三组对比可得a越大最大值越小,t0越大图像对称轴越往右移某频率为f的正弦波可表示为x a t cos2π,对其进行等间隔抽样,得到ft的离散样值序列可表示为xnx a t ,其中T称为抽样间隔,代表相邻tnT样值间的时间间隔,f s1表示抽样频率,即单位时间内抽取样值的个数。
T抽样频率取f s40Hz,信号频率f分别取5Hz,10Hz,20Hz和30Hz。
请在同一张图中同时画出连续信号x a t t和序列xn nT的波形图,并观察和对比分析样值序列的变化。
可能用到的函数为plot,stem,holdon。
fs=40;t=0:1/fs:1;%?μ?ê·?±e?a5Hz,10Hz,20Hz,30Hzf1=5;xa=cos(2*pi*f1*t);subplot(1,2,1);plot(t,xa);axis([0,max(t),min(xa),max(xa)]);xlabel( 't(s)' );ylabel('Xa(t)');line([0,max(t)],[0,0]);subplot(1,2,2);stem(t,xa, '.' );line([0,max(t)],[0,0]);axis([0,max(t),min(xa),max(xa)]);xlabel( 'n' );ylabel( 'X(n)' );频率越高,图像更加密集。
MATLAB在信号与系统中的应用(习题)

实验四MATLAB在信号与系统中的应用第一部分连续时间信号与系统(习题)2、编写程序,完成下列连续信号波形1)F(t)=u(t-2)+u(t-4) (-2≤t≤6)2)F(t)=e-t cos(4πt) (0≤t≤3)3)F(t)=3e(0.2+j0.5π)t (0≤t≤4π)1)方法一>> cleart0=-2;tf=6;dt=0.05;t1=2;t2=4;t=[t0:dt:tf];st=length(t);n1=floor((t1-t0)/dt);x1=[zeros(1,n1),ones(1,st-n1)];n2=floor((t2-t0)/dt);x2=[zeros(1,n2),ones(1,st-n2)];x=x1+x2;stairs(t,x),grid onaxis([0,5,0,3])方法二>> cleart0=-2;tf=6;dt=0.05;t1=2;t2=4;t=[t0:dt:tf];st=length(t);x1=(t>=t1);x2=(t>=t2);x=x1+x2;stairs(t,x),grid on2)cleart0=0;tf=3;dt=0.05;t1=4*pi;t=[t0:dt:tf];st=length(t);alpha=-1;w=0;x1=exp((alpha+j*w).*t);x2=cos(t1.*t);x=x1.*x2;subplot(1,1,1),plot(t,x),grid on3)cleart0=0;tf=4*pi;dt=0.05;t=[t0:dt:tf];st=length(t);alpha=0.2;w=0.5*pi;x=3*exp((alpha+j*w).*t);subplot(2,1,1),plot(t,real(x)),gridon, title ' real x'subplot(2,1,2),plot(t,imag(x)),gridon, title ' imag x'3、已知某连续时间系统的微分方程为:()2()()()2()r t r t r t e t e t ''''++=+,求当输入信号为2()()t e t e t ε-=,该系统的零状态响应r(t)。
(完整版)信号与系统matlab实验3

一、实现下述周期信号的傅立叶级数分解与合成(a )首先,推导出求解0a ,n a ,nb 的公式,计算出前10次系数; (b )利用MATLAB 求解0a ,n a ,n b 的值,其中n a ,nb 求解前10次系数,并给出利用这些系数合成的信号波形。
解:(a)110220[sign(t) - sign(t - 1)]0.25Ta dt ==⎰ 112202[sign(t) - sign(t - 1)][cos()]Tn n t a dt Tπ=⋅⎰ 112202[sign(t) - sign(t - 1)][sin()]T n n t b dt T π=⋅⎰ 程序:function [A_sym,B_sym]=CTFShchsymsyms t n k xT=4;if nargin<4;Nf=10;endif nargin<5;Nn=32;endx=time_fun_x(t);A0=int(x,t,0,1)/T;As=int(2*x*cos(2*pi*n*t/T)/T,t,0,1);Bs=int(2*x*sin(2*pi*n*t/T)/T,t,0,1);A_sym(1)=double(vpa(A0,Nn));for k=1:NfA_sym(k+1)=double(vpa(subs(As,n,k),Nn));B_sym(k+1)=double(vpa(subs(Bs,n,k),Nn));endif nargout==0c=A_sym;disp(c);d=B_sym;disp(d);t=-8:0.01:9;f1=c(1)+c(2).*cos(2*pi*1*t/T)+d(2).*sin(2*pi*1*t/T); f2=c(3).*cos(2*pi*2*t/T)+d(3).*sin(2*pi*2*t/T); f3=c(4).*cos(2*pi*3*t/T)+d(4).*sin(2*pi*3*t/T); f4=c(5).*cos(2*pi*4*t/T)+d(5).*sin(2*pi*4*t/T); f5=c(6).*cos(2*pi*5*t/T)+d(6).*sin(2*pi*5*t/T);f6=c(7).*cos(2*pi*6*t/T)+d(7).*sin(2*pi*6*t/T);f7=c(8).*cos(2*pi*7*t/T)+d(8).*sin(2*pi*7*t/T);f8=c(9).*cos(2*pi*8*t/T)+d(9).*sin(2*pi*8*t/T);f9=c(10).*cos(2*pi*9*t/T)+d(10).*sin(2*pi*9*t/T);f10=c(11).*cos(2*pi*10*t/T)+d(11).*sin(2*pi*10*t/T);ff1=f1+f2+f3+f4+f5+f6+f7+f8+f9+f10;ff2=f1+f2+f3+f4+f5+f6+f7;ff3=ff2+f8;ff4=ff3+f9;subplot(2,2,1)plot(t,ff1),hold ony=time_fun_e(t) %µ÷ÓÃÁ¬Ðøʱ¼äº¯Êý-ÖÜÆÚ¾ØÐÎÂö³å plot(t,y,'r:')title('ÖÜÆÚ¾ØÐ⨵ÄÐγɡª1+2+3+4+5+6+7+8+9+10´Îг²¨')axis([-4,4.5,-0.5,1.5])grid onsubplot(2,2,2)grid onplot(t,ff2),hold ony=time_fun_e(t)plot(t,y,'r:')title('ÖÜÆÚ¾ØÐ⨵ÄÐγɡª1+2+3+4+5+6+7´Îг²¨')axis([-4,4.5,-0.5,1.5])grid onsubplot(2,2,3)plot(t,ff3),hold ony=time_fun_e(t)plot(t,y,'r:')title('1+2+3+4+5+6+7+8´Îг²¨')axis([-4,4.5,-0.5,1.5])grid onsubplot(2,2,4)plot(t,ff4),hold ony=time_fun_e(t)plot(t,y,'r:')title('1+2+3+4+5+6+7+8+9´Îг²¨')axis([-4,4.5,-0.5,1.5])grid onendfunction x=time_fun_x(t)h=1;x1=sym('0.5+0.5*sign(t)')*h;x=x1-sym('(0.5+0.5*sign(t-1))')*h;%-------------------------------------------function y=time_fun_e(t)a=0.5;T=5;h=1;t=-8:0.01:9;e1=(1/2+1/2.*sign(t))-(1/2+1/2.*sign(t-1));e2=(1/2+1/2.*sign(t-4))-(1/2+1/2.*sign(t-5));e3=(1/2+1/2.*sign(t+4))-(1/2+1/2.*sign(t+3));y=e1+e2+e3;结果如下:A_sym =0.2500 0.3183 0.0000 -0.1061 -0.0000 0.0637 0.0000 -0.0455 -0.0000 0.0354 0.0000B_sym =0 0.3183 0.3183 0.1061 0.0000 0.0637 0.1061 0.0455 0.0000 0.0354 0.0637二、知周期为T=4的三角波,在第一周期(-2<t<2)内表示成:)(,试用MATLAB求该信号的傅立叶级数,并绘制它的频谱图。
信号与系统——Matlab部分习题

课程设计(论文)课程名称:信号与系统课程论文题目:信号与系统——MATLAB课程设计姓名:系:专业:物理学(电子信息工程方向)年级:大学二年级学号:指导教师:职称:2017年 5 月22日目录摘要---------------------------------------------------------------------- 1关键词-------------------------------------------------------------------- 1一、M2-7 --------------------------------------------------------------- 21、问题重述--------------------------------------------------------------- 22、问题分析--------------------------------------------------------------- 23、仿真程序与仿真结果----------------------------------------------------- 2(1)仿真程序---------------------------------------------------------------------------------------------------------- 2频率为262Hz的正弦信号声音波形 ------------------------------------------------------------------------------- 2频率为294Hz的正弦信号声音波形 ------------------------------------------------------------------------------- 3频率为330Hz的正弦信号声音波形 ------------------------------------------------------------------------------- 3频率为349Hz的正弦信号声音波形 ------------------------------------------------------------------------------- 4频率为392Hz的正弦信号声音波形 ------------------------------------------------------------------------------- 4频率为440Hz的正弦信号声音波形 ------------------------------------------------------------------------------- 5频率为494Hz的正弦信号声音波形 ------------------------------------------------------------------------------- 5频率为524Hz的正弦信号声音波形 ------------------------------------------------------------------------------- 6结果分析:--------------------------------------------------------------------------------------------------------------- 6(2)仿真程序:------------------------------------------------------------------------------------------------------- 6仿真结果:--------------------------------------------------------------------------------------------------------------- 7结果分析:--------------------------------------------------------------------------------------------------------------- 7(3)仿真程序:------------------------------------------------------------------------------------------------------- 7仿真结果:--------------------------------------------------------------------------------------------------------------- 7结果分析:--------------------------------------------------------------------------------------------------------------- 8二、M3-3 ------------------------------------------------------------------ 81、问题重述--------------------------------------------------------------- 82、问题分析--------------------------------------------------------------- 83、仿真程序与仿真结果----------------------------------------------------- 8(1)仿真程序:------------------------------------------------------------------------------------------------------- 8仿真结果:--------------------------------------------------------------------------------------------------------------- 8结果分析:--------------------------------------------------------------------------------------------------------------- 9(2)仿真程序:------------------------------------------------------------------------------------------------------- 9仿真结果:--------------------------------------------------------------------------------------------------------------- 9结果分析:--------------------------------------------------------------------------------------------------------------- 9三、M4-3 ----------------------------------------------------------------- 101、问题重述:------------------------------------------------------------ 102、问题分析-------------------------------------------------------------- 103、仿真程序与仿真结果---------------------------------------------------- 10(1)仿真程序:----------------------------------------------------------------------------------------------------- 10仿真结果:------------------------------------------------------------------------------------------------------------- 10结果分析:------------------------------------------------------------------------------------------------------------- 10(2)仿真程序:----------------------------------------------------------------------------------------------------- 11仿真结果:------------------------------------------------------------------------------------------------------------- 11结果分析:------------------------------------------------------------------------------------------------------------- 12(3)女声变男声:-------------------------------------------------------------------------------------------------- 12仿真程序:------------------------------------------------------------------------------------------------------------- 12仿真结果:------------------------------------------------------------------------------------------------------------- 12结果分析:------------------------------------------------------------------------------------------------------------- 124、自主学习内容---------------------------------------------------------- 125、阅读文献-------------------------------------------------------------- 126、发现问题-------------------------------------------------------------- 127、问题探究-------------------------------------------------------------- 13信号与系统——MATLAB课程设计摘要:1.(1)掌握信号的建模,了解基本信号及其特点;(2)掌握基本信号的叠加及播放;(3)掌握MA TLAB对语音信号的读取与播放及其时域波形分析。
信号与系统-Matlab上机实验报告

江南大学物联网工程学院信号与系统—Matlab
上机实验报告
班级:物联网工程1302班
姓名:明坤
学号:1030613221
实验任务:
1.画出f(t) = 2sin200πt·cos20πt·e-2t + cos50πt·sin70πt的频谱。
2.画出f(t) = 2sin200πt·cos20πt·e-2t * cos50πt·sin70πt的波形和频谱。
源码:
%信号与系统Matlab作业
t=0:1e-3:100;%选择分析的时域范围离散化ft
%为方便计算把ft分成两部分
f1 = 2*sin( 200*pi*t ) .* cos( 20*pi*t ).*exp( -2*t ) ;
f2 = cos( 50*pi*t ) .* sin( 70*pi*t ) ;
ft_1=f1+f2;%第一题ft
y=fft(ft_1);%快速傅里叶变换
subplot(3,1,1);%分割绘图区域
plot(abs(y));%求出Fourier变换后的振幅
grid on;title('第一题频谱图');
ft_2=conv(f1,f2);%第二题ft 利用卷积函数
subplot(3,1,2);plot(ft_2);grid on;title('第二题时域波形');
axis([0 600 -5 5]);%为时域图选择一个合适的绘图范围
y=fft(ft_2);
subplot(3,1,3);plot(abs(y));grid on;title('第二题频谱图');
图形结果:。
《信号与系统》matlab仿真实验

《信号与系统》matlab仿真实验综合实验一《信号与系统》的MATLAB仿真实验一.实验目的1.熟悉MA TLAB软件平台、工具箱、高效的数值计算及符号计算功能。
2.熟悉MATLAB软件的信号处理编程方法和结果的可视化3.了解数字信号处理的计算机仿真方法4.进一步加深对信号与系统的基本原理、方法及应用的理解。
二.实验软件MATLAB 6.5 界面三.实验内容1.基本信号的表示及可视化2.连续信号的时域运算与时域变换3.线性系统的时域分析及Matlab实现4.连续时间信号的频域分析及Matlab实现四.实验原理方法及相关MATLAB函数1.基本信号的表示及可视化1.1 连续时间信号(1)表示出连续信号f(t)=Sa(t)=sin(t)/tMatlab命令如下:t=-10:1.5:10;%向量t时间范围t=t1:p:t2,p为时间间隔f=sin(t)./t;plot(t,f); %显示该信号的时域波形title(‘f(t)=Sa(t)’);xlabel(‘t’)axis([-10,10,-0.4,1.1])注:改变p可使信号波形更平滑,同学们可以试一试。
(2)单位阶跃信号定义阶跃函数function f=Heaviside(t)f=(t>0)调用阶跃函数t=-1:0.01:3;f=Heaviside(t)plot(t,f);axis([-1,3,-0.2,1.2]);(2)单位冲击信号 (t)定义冲击函数functionchongji(t1,t2,t0)dt=0.01;t=t1:dt:t2;n=length(t);x=zeros(1,n);x(1,(-t0-t1)/dt+1)=1/dt;stairs(t,x);axis([t1,t2,0,1.2/dt])title('单位冲击信号δ(t)')调用的是chongji(-1,5,0);可以试着给别的t1,t2,t0.1.2离散时间信号(1)单位阶跃序列ε(k)定义阶跃序列function jyxulie(k1,k2,k0)k=k1:-k0-1;kk=-k0:k2;n=length(k);nn=length(kk);u=zeros(1,n); %k0前信号赋值为零uu=ones(1,nn);%k0后信号赋值为一stem(kk,uu,’filled’)hold onstem(k,u,’filled’)holdofftitle(‘单位阶跃序列’)axis([k1 k20 1.5])调用阶跃序列函数jyxulie(-2,6,0)(3)单位序列δ(k)定义单位序列函数functiondwxulie(k1,k2,k0)k=k1:k2;n=length(k);f=zeros(1,n);f(1,-k0-k1+1)=1;stem(k,f,’filled’)axis([k1,k2,0,1.5])title(‘单位序列δ(k)’)调用单位序列函数dwxulie(-3,5,0)2.连续信号的时域运算与时域变换运算、变换的符号运算方法:相加、相乘、移位、反折、尺度变换、倒相已知信号)]2()2([)21()(--+⨯+=ttttfεε,用matlab求f(t+2),f(t-2),f(-t),f(2t),-f(t),并绘出时域波形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例2: 在一个图形窗口中以子图形式同时绘制正弦、 余弦、正切、余切曲线。
sin(x) cos(x) 1 0.5 1 0.5
x=linspace(0,2*pi,60); y=sin(x);z=cos(x); t=sin(x)./(cos(x)+eps); ct=cos(x)./(sin(x)+eps); subplot(2,2,1);plot(x,y); title('sin(x)');axis ([0,2*pi,-1,1]); subplot(2,2,2);plot(x,z); title('cos(x)');axis ([0,2*pi,-1,1]); subplot(2,2,3);plot(x,t); title('tangent(x)');axis ([0,2*pi,-40,40]); subplot(2,2,4);plot(x,ct); title('cotangent(x)');axis ([0,2*pi,-40,40]);
MATLAB的应用(信号与系统)
例5:已知系统函数为
H (s) 1 s 3 2s 2 2s 1
试画出零极点分布图,并求系统的冲激响应 h(t)和频率响应H(jw),并判断系统是否稳定。 解:已知系统函数H(s),求系统的冲激响应h(t) 和频率响应H(jw),可调用impulse函数和freqs函数。
-1.0000
-0.5000 + 0.8660i -0.5000 - 0.8660i
由系统的零极点分布图知,系统函数的极点位于 s左半平面,故系统稳定。
MATLAB的应用(信号与系统)
系统的冲激响应
系统的频率响应
MATLAB的应用(信号与系统)
例6:已知系统函数为
试画出零极点分布图。
A=[1 2 -3 2 1];
H ( s) 1 s 2 5s 6 ,试画出零极点分布图,
MATLAB的应用(信号与系统)
(1) f (t ) 5e t 5e 3t , t 0 ~ 5 (2) f (t ) sin(t ) sin(8t ), t 0 ~ 10 (3) f (t ) sin(t ) sin(8t ), t 0 ~ 10 (4)
f (t ) 5 sin(100 t ) , t 0 ~ 0.2
axis([-3.5,2.5,-1,1]);grid on
MATLAB的应用(信号与系统)
>> p =
-3.1300
q=
0.7247 - 0.6890i 0.7247 + 0.6890i -0.3195
2.0000 -2.0000
MATLAB的应用(信号与系统)
作业: 1、在同一个窗口,不同的区域描绘下列各函数 的波形(其中对于连续信号可取时间间隔为0.001).
MATLAB的应用(信号与系统)
用部分分式展开法求F(s)的反变换
s2 F (s) 4 s 3s 3 3s 2 s
%ex1205031.m
>> r = 2.0000
num=[1 -2]; den=[1 3 3 1 0]; [r,p]=residue(num,den)
2.0000
3.0000 -2.0000
MATLAB的应用(信号与系统)
2.求
F ( s)
4 拉氏反变换. ( s 1)( s 2)3
2 s 2 3s 3 3. 求 F ( s ) 3 拉氏反变换. 2 s 6 s 11s 6
4.已知系统函数为 并求系统的冲激响应h(t)和频率响应H(jw),并判断系统是否 稳定。
1.绘制二维曲线的基本函数 (1)plot函数的基本调用格式为: plot(x,y) 其中x和y为长度相同的向量,分别用于存储x坐标 和y坐标数据。 (2)含多个输入参数的plot函数 含多个输入参数的plot函数调用格式为: plot(x1,y1,x2,y2,…,xn,yn) (3)含选项的plot函数 含选项的plot函数调用格式为: plot(x1,y1,选项1,x2,y2,选2,…,xn,yn,选项n)
0.8701 - 1.7048i
-0.8701 + 0.7796i -0.8701 - 0.7796i MATLAB的应用(信号与系统)
绘制系统的零极点分布图时,直接应用pzmap函数, 调用形式为: pzmap(sys) 表示画出sys所描述系统的零极点图。 LTI系统模型sys借助tf函数获得,其调用方式为 sys=tf(b,a) 式中b和a分别为系统函数H(s)分子多项式和分母 多项式的系数向量。
p=
-1.0000 -1.0000
-1.0000
0
MATLAB的应用(信号与系统)
2 2 3 2 F ( s) 2 3 ( s 1) ( s 1) ( s 1) s
故原函数为:
f (t ) (2et 2tet 1.5t 2et 2)u(t )
MATLAB的应用(信号与系统)
s2 4 H ( s) 4 s 2s 3 3s 2 2s 1
%ex1206042.m
B=[1 0 -4];
p=roots(A);p=p' q=roots(B);q=q' plot(real(p),imag(p),'x');hold on plot(real(q),imag(q),'o');
3、H(s)的零极点与系统特性的MATLAB计算 系统函数H(s)通常是一个有理分式,其分子 和分母均为多项式。计算的零极点可以应用MATLAB 中的roots函数,求出分子和分母多项式的根即可。 例4:多项式 N (s) s 4 2s 2 4s 5 的根。
>> N=[1 0 2 4 5]; >> r=roots(N) r= 0.8701 + 1.7048i
n
故
h(t ) rk e pk t
k 1
n
MATLAB的应用(信号与系统)
MATLAB实现部分分式展开式 用MATLAB函数residue实现部分分式展开式 调用形式为:
[r,p,k]=residue(num,den)
式中,num和den分别为F(s)的分子多项式 和分母多项式的系数,r为部分分式的系数,p为 极点,k为多项式的系数,若F(s)为真分式,则 k=0。
0 0 -0.5 -0.5 -1 0 2 4 6 -1 0 tangent(x) 40 20 0 40 20 0 -20 -40 -20 -40 0 2 4 6 0
2
4
6
cotangent(x)
2
4
6
MATLAB的应用(信号与系统)
2、n阶LTI系统的冲激响应 例3:n阶微分方程所示,其系统函数为
MATLAB的应用(信号与系统)
选项’color_linestyle_marker’
色彩(c) 说明 时标(m) 说明 加号 线型(l) 说明 实线
线 型 、 点 型 和 颜 色
r
红色
+
g
b c m y k w
绿色
蓝色 青色 洋红 黄色 黑色 白色
o
* . x s d ^ v > < p h
圆圈
星号 点 十字 矩形 菱形 上三角 下三角 右三角 左三角 五边形 六边形
Y (s) b1s m b2 s m1 ... bm s bm1 H ( s) U (s) a1s n a2 s n1 ... an s an1
求系统的冲激响应。 解:设系统函数的分母多项式没有重根,则
rk H ( s) k 1 s pk
-: -.
虚线
点线 点划线
MATLAB的应用(信号与系统)
例1: 用图形保持功能在同一坐标内绘制曲线 y=2e-0.5xsin(2πx)及其包络线。 x=(0:pi/100:2*pi)'; y1=2*exp(-0.5*x)*[1,-1]; y2=2*exp(-0.5*x).*sin(2*pi*x); plot(x,y1,'b:'); axis([0,2*pi,-2,2]); %设置坐标 hold on; %设置图形保持状态 plot(x,y2,'k'); legend('包络线','包络线','曲线y'); %加图例 hold off; %关闭图形保持 grid %网格线控制
MATLAB的应用(信号与系统)
%ex1206041.m
num=[1];
t=0:0.02:10;
h=impulse(num,den,t); figure(2);plot(t,h) title('Impulse Respone') [H,w]=freqs(num,den);
den=[1 2 2 1];
sys=tf(numቤተ መጻሕፍቲ ባይዱden); poles=roots(den) figure(1);pzmap(sys);
figure(3);plot(w,abs(H))
xlabel('\omega') title('Magnitude Respone')
MATLAB的应用(信号与系统)
>> poles =
系统的零极点分布图
