2021-2022年高中数学课时作业31.3三视图北师大版
高考数学课时作业31 文(含解析)北师大版

高考数学课时作业31 文(含解析)北师大版一、选择题1.已知平面向量a =(1,-3),b =(4,-2),若λa -b 与a 垂直,则实数λ= A .-1 B .1 C .-2D .2解析:λa -b =(λ-4,-3λ+2),则(λ-4)+(-3λ+2)(-3)=0,解得λ=1. 答案:B2.(2012年济南二模)平面向量a 与b 的夹角为2π3,a =(3,0),|b |=2,则|a +2b |=( )A .7 B.37 C.13 D .3解析:|a +2b |=a +2b2=|a |2+4|b |2+4|a ||b |cos 2π3=13.答案:C3.已知正方形ABCD 的边长为2,令AB →=a ,BC →=b ,AC →=c ,则|a +b +c |= A .0 B. 2 C .2D .4解析:|a +b +c |2=|a |2+|b |2+|c |2+2a ·b +2b ·c +2a ·c =2+2+4+4·22cos 45°=16,∴|a +b +c |=4. 答案:D4.函数y =tan(π4x -π2)的部分图象如图所示,则(OA →+OB →)·AB →=( )A .6B .4C .-4D .-6解析:如图,A (2,0),B (3,1),(OA →+OB →)·AB →=-(OA →+OB →)·(OA →-OB →)=OB →2-OA →2=10-4=6,选A.答案:A5.(2012年江西九校联考)向量a ,b 均为单位向量,且a ·b =12,向量a -c 与向量b-c 的夹角为π6,则向量a -c 的模长的最大值为( )A.32 B .1C.232D .2解析:由题意画图:令OA →=a ,OB →=b ,OC →=c ;向量a 和向量b 的夹角为60°,又向量a -c 和向量b -c 的夹角为30°,故点A 、B 、C 三点在同一个单位圆上.当A 、O 、C 三点共线时,|a -c |取到最大值,其最大值恰为单位圆的直径长2.故选D.答案:D6.关于平面向量a ,b ,c ,有下列命题: ①(a ·b )c -(c ·a )b =0; ②|a |-|b |<|a -b |;③(b ·c )a -(c ·a )b 不与c 垂直;④非零向量a 和b 满足|a |=|b |=|a -b |,则a 与a +b 的夹角为30°. 其中真命题的个数为( )A .1B .2C .3D .4解析:①(a ·b )c -(c ·a )b =0不正确,向量的数量积不满足乘法运算的结合律故上述结论不一定成立.②|a |-|b |<|a -b |不正确,也有取等号的可能.③(b ·c )a -(c ·a )b 不与c 垂直不正确,因为前后两个向量的数量积恰好为0,故两向量始终是垂直的.④非零向量a 和b 满足|a |=|b |=|a -b |,则a 与a +b 的夹角为30°.是正确的,因为上述三个向量恰好构成一个等边三角形,a +b 恰好是三角形的角平分线,故a 与a +b 的夹角为30°.所以选A.答案:A二、填空题7.(2012年佛山质检)已知向量a =(1,1),2a +b =(4,2),则向量a ,b 的夹角为________. 解析:由a =(1,1),2a +b =(4,2),得b =(4,2)-2(1,1)=(2,0). 设向量a ,b 的夹角为θ,则cos θ=a ·b |a ||b |=222=22,θ=π4.答案:π48.(2012年安徽)若平面向量a ,b 满足:|2a -b |≤3,则a ·b 的最小值是________. 解析:|2a -b |≤3⇔4a 2+b 2≤9+4a ·b , 4a 2+b 2≥4|a ||b |≥-4a ·b ⇒9+4a ·b ≥-4a ·b ⇔a ·b ≥-98.答案:-989.在正三角形ABC 中,D 是BC 上的点,若AB =3,BD =1,则AB →·AD →=________.解析:在△ABD 中,由余弦定理,得|AD →|=7,则cos θ=9+7-12×3×7=527.故AB →·AD →=|AB →|·|AD →|·co s θ=152.答案:152三、解答题10.设向量a =(4cos α,sin α),b =(sin β,4cos β),c =(cos β,-4sin β). (1)若a 与b -2c 垂直,求tan(α+β)的值; (2)求|b +c |的最大值;(3)若tan αtan β=16,求证:a ∥b . 解:(1)因为a 与b -2c 垂直,所以a ·(b -2c )=4cos αsin β-8cos αcos β+4sin αcos β+8sin αsin β=4sin (α+β)-8cos (α+β)=0,因此tan(α+β)=2.(2)由b +c =(sin β+cos β,4cos β-4sin β),得|b +c |=sin β+cos β2+4cos β-4sin β2=17-15sin 2β≤4 2.又当β=k π-π4(k ∈Z )时,等号成立,所以|b +c |的最大值为4 2.(3)由tan αtan β=16得4cos αsin β=sin α4cos β,即16cos βcos α=sin αsin β, 所以a ∥b .11.在△ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,设向量m =(sin A ,cos B ),n =(cos A ,sin B ).(1)若m ∥n ,求角C ;(2)若m ⊥n ,B =15°,a =6+2,求边c 的大小.解:(1)由m ∥n ⇒sin A sin B -cos A cos B =0⇒cos (A +B )=0, 因为0°<A +B <180°,所以A +B =90°,C =180°-(A +B )=90°.(2)由m ⊥n ⇒sin A cos A +sin B cos B =0⇒sin 2A +sin 2B =0,已知B =15°,所以sin 2A +sin 30°=0,sin 2A =-12,因为0<2A <360°-2B =330°,所以2A =210°,A =105°,C =180°-15°-105°=60°.根据正弦定理a sin A =c sin C ⇒6+2sin 105°=csin 60°⇒c =6+2sin 60°sin 105°,因为sin 105°=sin (45°+60°)=6+24, 所以c =6+2×326+24=2 3.12.设△ABC 的三个内角A 、B 、C 所对的边分别为a 、b 、c ,且满足(2a +c )BC →·BA →+cCA →·CB →=0.(1)求角B 的大小;(2)若b =23,试求AB →·CB →的最小值.解:(1)因为(2a +c )BC →·BA →+cCA →·CB →=0, 所以(2a +c )ac cos B +cab cos C =0, 即(2a +c )cos B +b cos C =0,则(2sin A +sin C )cos B +sin B cos C =0, 所以2sin A cos B +sin (C +B )=0, 即cos B =-12,所以B =2π3.(2)因为b 2=a 2+c 2-2ac cos 2π3,所以12=a 2+c 2+ac ≥3ac ,即ac ≤4. 当且仅当a =c 时取等号,此时ac 最大值为4. 所以AB →·CB →=ac cos 2π3=-12ac ≥-2,即AB →·CB →的最小值为-2. [热点预测]13.设向量a =(cos α,sin α),b =(cos β,sin β),其中0<α<β<π,若|2a +b |=|a -2b |,则β-α=( )A.π2 B .-π2C.π4D .-π4解析:由|2a +b |=|a -2b |两边平方整理得3|a |2-3|b |2+8a ·b =0. ∵|a |=|b |=1,故a ·b =0,∴cos αcos β+sin αsin β=0, 即cos (α-β)=0,由于0<α<β<π, 故-π<α-β<0,∴α-β=-π2,即β-α=π2.答案:A14.已知a =(2,-1),b =(λ,3),若a 与b 的夹角为钝角,则λ的取值范围是________. 解析:由a ·b <0,即2λ-3<0,解得λ<32,由a ∥b 得:6=-λ,即λ=-6.因此λ<32,且λ≠-6.答案:(-∞,-6)∪⎝⎛⎭⎪⎫-6,32 15.若△ABC 的面积是30,cos A =1213,则AB →·AC →的值为________.解析:由cos A =1213,得sin A =1-⎝ ⎛⎭⎪⎫12132=513. 又12bc sin A =30,∴bc =156. ∴AB →·AC →=bc cos A =156×1213=144.答案:144。
北师大高中数学必修二课时跟踪检测:第一章 立体几何初步 §3 31 32 含解析

第一章立体几何初步§3三视图3.1简单组合体的三视图3.2由三视图还原成实物图课时跟踪检测一、选择题1.以下说法正确的是()A.任何物体的三视图都与物体摆放位置有关B.任何物体的三视图都与物体摆放位置无关C.有的物体的三视图与物体的摆放位置无关D.正方体的三视图一定是三个全等的正方形解析:大部分物体三视图与物体摆放位置有关,但球的三视图与摆放位置无关.答案:C2.如图(1)、(2)、(3)为三个几何体的三视图,根据三视图可以判断这三个几何体依次分别为()A.三棱台、三棱柱、圆锥B.三棱台、三棱锥、圆锥C.三棱柱、正四棱锥、圆锥D.三棱柱、三棱台、圆锥解析:由三视图知,(1)是横放的三棱柱,(2)是正四棱锥,(3)是圆锥.答案:C3.在一个几何体的三视图中,主视图和俯视图如右图所示,则相应的左视图可以为()解析:此几何体为半个圆锥与三棱锥构成的组合体,左视图为三角形,且左视图中有看到的棱,所以选D.答案:D4.(2018·天津卷)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是()解析:观察图形图可知,俯视图为,故答案为A.答案:A5.已知几何体的三视图如图,则这个几何体自上而下依次为()A.四棱台圆台B.四棱台四棱台C.四棱柱四棱柱D.不能判断解析:由主视图与左视图可判断为上、下都为台体,由俯视图可确定为棱台.答案:B6.(2018·北京卷)某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为()A.1 B.2C.3 D.4解析:由三视图可得四棱锥P-ABCD,在四棱锥P-ABCD中,PD=2,AD=2,CD=2,AB=1,由勾股定理可知,P A=22,PC=22,PB=3,BC=5,则在四棱锥中,直角三角形有:△P AD,△PCD,△P AB共三个,故选C.答案:C二、填空题7.根据下列物体的三视图,可知该几何体的名称为________.解析:由主视图和左视图可判断为柱体,由俯视图知为棱柱.答案:三棱柱8.一个几何体的主视图为一个三角形,则这个几何体可能是下列几何体中的________.①三棱锥②四棱锥③三棱柱④四棱柱⑤圆锥⑥圆柱解析:三棱锥、四棱锥和圆锥的主视图都是三角形,当三棱柱的一个侧面平行于水平面,底面对着观察者时其主视图是三角形,其余的主视图均不是三角形.答案:①②③⑤9.一个正三棱柱的侧棱长和底面边长均等于43,它的三视图中的俯视图如图所示,左视图是一个矩形,则该矩形的面积为________.解析:俯视图与左视图均可体现三棱柱的宽,即左视图宽为43×32=6,左视图的高为43,∴面积为6×43=24 3.答案:24 3三、解答题10.画出如下图所示几何体的三视图(阴影部分为主视方向).解:(1)(2)11.如图所示,是一个零件的直观图,画出这个几何体的三视图.解:12.已知一个几何体的三视图如图,试根据三视图想象物体的原形,并试着画出实物草图.解:由三视图知,该物体下部为长方体、上部为一个与长方体等高的圆柱,且圆柱的底面相切于长方体的上底面,由此可画出实物草图如图.13.如图所示是由几个小立方体所搭的几何体的俯视图,小正方形中的数字表示在该位置小立方体的个数,请画出这个几何体的主视图和左视图.解:由俯视图画主视图和左视图,方法有二:一是先摆出几何体,再画主视图和左视图;二是先由俯视图确定主视图,左视图的列数及每列上小正方体的个数:①主视图与俯视图列数相同,其每列小正方体数是俯视图中该列中的最大数字;②左视图的列数与俯视图中的行数相同,其每列的小正方体数是俯视图中该行中的最大数字,该几何体的主视图和左视图如下:。
《红对勾》2021届高三数学第一轮复习北师大版 课时作业31 Word版含解析

课时作业31 数列求和一、选择题(每小题5分,共40分)1.(2022·西安调研)等比数列{a n }的前n 项和为S n ,若a 1=1,且4a 1,2a 2,a 3成等差数列,则S 4=( )A .7B .8C .15D .16解析:设数列{a n }的公比为q ,则4a 2=4a 1+a 3,∴4a 1q =4a 1+a 1q 2,即q 2-4q +4=0,∴q =2.∴S 4=1-241-2=15.答案:C2.数列1×12,2×14,3×18,4×116,…的前n 项和为( ) A .2-12n -n2n +1B .2-12n -1-n2nC.12(n 2+n +2)-12nD.12n (n +1)+1-12n -1解析:S =1×12+2×14+3×18+4×116+…+n ×12n =1×121+2×122+3×123+…+n ×12n ,①则12S =1×122+2×123+3×124+…+(n -1)×12n +n ×12n +1,②①-②得12S =12+122+123+…+12n -n ×12n +1=12⎝ ⎛⎭⎪⎫1-12n 1-12-n 2n +1=1-12n -n2n +1. ∴S =2-12n -1-n 2n .答案:B3.(2022·日照模拟)已知数列{a n }的通项公式为a n =log 2n +1n +2(n ∈N +),设其前n 项和为S n ,则使S n <-5成立的自然数n ( )A .有最大值63B .有最小值63C .有最大值32D .有最小值32解析:S n =a 1+a 2+a 3+…+a n =log 223+log 234+log 245+…+log 2n +1n +2=log 2⎝ ⎛⎭⎪⎫23×34×45×…×n +1n +2=log 22n +2<-5,∴2n +2<132, ∴64<n +2, ∴n >62, ∴n min =63. 答案:B4.(2022·临沂模拟)在数列{a n }中,a n =1n (n +1),若{a n }的前n 项和为2 0132 014,则项数n 为( )A .2 011B .2 012C .2 013D .2 014解析:∵a n =1n (n +1)=1n -1n +1,∴S n =1-1n +1=n n +1=2 0132 014,解得n =2 013.答案:C5.(2022·新课标全国)数列{a n }满足a n +1+(-1)n a n =2n -1,则{a n }的前60项和为( )A .3 690B .3 660C .1 845D .1 830解析:当n =2k 时,a 2k +1+a 2k =4k -1, 当n =2k -1时,a 2k -a 2k -1=4k -3, ∴a 2k +1+a 2k -1=2, ∴a 2k +1+a 2k +3=2, ∴a 2k -1=a 2k +3, ∴a 1=a 5=…=a 61.∴a 1+a 2+a 3+…+a 60=(a 2+a 3)+(a 4+a 5)+…+(a 60+a 61)=3+7+11+…+(4×30-1)=30×(3+119)2=30×61=1 830. 答案:D6.(2022·山东日照一模,10)已知数列{a n }的前n 项和S n =n 2-6n ,则{|a n |}的前n 项和T n =( )A .6n -n 2B .n 2-6n +18C.⎩⎪⎨⎪⎧6n -n 2 (1≤n ≤3)n 2-6n +18 (n >3) D.⎩⎪⎨⎪⎧6n -n 2 (1≤n ≤3)n 2-6n (n >3) 解析:由S n =n 2-6n 得{a n }是等差数列,且首项为-5,公差为2. ∴a n =-5+(n -1)×2=2n -7, ∴n ≤3时,a n <0;n >3时,a n >0,∴T n =⎩⎨⎧6n -n 2 (1≤n ≤3),n 2-6n +18 (n >3).答案:C7.已知数列{a n }满足a n +1=12+a n -a 2n ,且a 1=12,则该数列的前2 012项的和等于( )A.3 0152 B .3 015 C .1 509D .2 010解析:由于a 1=12,又a n +1=12+a n -a 2n ,所以a 2=1,从而a 3=12,a 4=1,即得a n =⎩⎪⎨⎪⎧12,n =2k -1(k ∈N *),1,n =2k (k ∈N *),故数列的前2 012项的和等于S 2 012=1 006×(1+12)=1 509.答案:C。
高中数学课时跟踪检测(三)三视图北师大版必修2
高中数学课时跟踪检测(三)三视图北师大版必修2课时跟踪检测(三)三视图一、基本能力达标1.若一个几何体的主视图和左视图都是等腰三角形,俯视图是带圆心的圆,则这个几何体可能是( )A.圆柱B.三棱柱C.圆锥D.球体解析:选C 主视图和左视图都是等腰三角形,俯视图是带圆心的圆说明此几何体是圆锥.2.已知一个几何体的三视图如图所示,则此几何体的组成为( )A.上面为棱台,下面为棱柱B.上面为圆台,下面为棱柱C.上面为圆台,下面为圆柱D.上面为棱台,下面为圆柱解析:选C 结合三视图,易知该几何体上面为圆台,下面为圆柱.3.(2018·全国卷Ⅲ)中国古建筑借助榫卯将木构件连接起来.构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是( )解析:选A 由题意可知带卯眼的木构件的直观图如图所示,由直观图可知其俯视图应选A.4.如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱解析:选B 将三视图还原为几何体即可.如图,几何体为三棱柱.5.如图所示,四面体ABCD的四个顶点是长方体的四个顶点(长方体是虚拟图形,起辅助作用),则四面体ABCD的主视图、左视图、俯视图依次是( )A.①②⑥B.①②③C.④⑤⑥D.③④⑤解析:选B 四面体ABCD的主视图是边长分别为3,4的矩形,对角线左上至右下为虚线,左下至右上为实线,为①;左视图是边长分别为4,5的矩形,对角线左上至右下为实线,左下至右上为虚线,为②;俯视图是边长分别为3,5的矩形,对角线左上至右下为实线,左下至右上为虚线,为③,故选B.6.如图所示的几何体中,主视图与左视图都是长方形的是________.解析:②的左视图是三角形,⑤的主视图和左视图都是等腰梯形,其余的都符合条件.答案:①③④7.如图所示,在正方体ABCDA1B1C1D1中,点P是上底面A1B1C1D1内一动点,则三棱锥PABC的主视图与左视图的面积的比值为________.解析:三棱锥PABC的主视图与左视图为底边和高均相等的三角形,故它们的面积相等,面积比值为1.答案:18.如图,E,F分别是正方体ABCDA1B1C1D1的面ADD1A1和面BCC1B1的中心,则四边形BFD1E 在该正方体的面上的正投影可能是________(把所有可能图形的序号都填上).解析:图②是在平面DCC1D1或平面ABCD上的正投影;图③是在平面BCC1B1上的正投影.图①④均不符合.答案:②③9.画出图中几何体的三视图.解:该几何体的三视图如图所示.10.根据如图所示的三视图,画出几何体.解:由主视图、左视图可知,该几何体为简单几何体的组合体,结合俯视图为大正方形里有一个小正方形,可知该组合体上面为一个正方体,下面为一个下底面是正方形的倒置的四棱台.如图所示.二、综合能力提升1.直角边分别为1和3的三角形,绕一条直角边所在直线旋转,形成的圆锥的俯视图是半径为1的圆,则它的主视图是( )A.等腰直角三角形B.边长为3的等边三角形C.边长为2的等边三角形D.不能确定解析:选C 由俯视图知长为3的边在轴上.因此主视图为边长为2的等边三角形.2.在一个几何体的三视图中,主视图和左视图是两个完全相同的图形,如图所示,则相应的俯视图可以为( )A.①②B.②③C.③④D.②④解析:选D 若俯视图为图①,则该几何体的主视图的上方三角形应该没有高线,故俯视图不可能为图①,排除选项A;若俯视图为图③,则该几何体的左视图的上方应该没有左边小三角形,故俯视图不可能为图③,排除选项B、C;若俯视图为图②,则该几何体是由上面是正四棱锥,下面是正方体组合而成的简单组合体;若俯视图为图④,则该几何体是由上面是正四棱锥,下面是圆柱组合而成的简单组合体.故选D.3.底面水平放置的正三棱柱的所有棱长均为2,当其主视图有最大面积时,其左视图的面积为( )A.2 3 B.3C. 3 D.4解析:选A 当主视图的面积最大时,可知其正三棱柱某个侧面的面积,可以按如图所示放置,此时S左=2 3.4.一四面体的三视图如图所示,则该四面体四个面中最大的面积是( )A .2B .2 2 C. 3D .2 3解析:选D 由四面体的三视图知其直观图为如图所示的正方体中的四面体A BCD ,由三视图知正方体的棱长为2.所以S △ABD =12×2×22=22,S △ADC =12×22×22×32=23, S △ABC =12×2×22=22, S △BCD =12×2×2=2.所以所求的最大面积为2 3.故选D.5.若一个正三棱柱(底面为正三角形,侧面为矩形的棱柱)的三视图如图所示,则这个正三棱柱的侧棱长和底面边长分别为________、________.解析:左视图中尺寸2为正三棱柱的侧棱长,尺寸23为俯视图正三角形的高,所以正三棱柱的底面边长为4.答案:2 46.由小正方体木块搭成的几何体的三视图如图所示,则该几何体由________块小正方体木块搭成.解析:小木块的排列方式如图所示.由图知,几何体由7块小正方体木块搭成.答案:77.如图所示的几何体是由一个长方体木块锯成的.(1)判断该几何是否为棱柱; (2)画出它的三视图.解:(1)是棱柱.因为该几何体的前、后两个面互相平行,其余各面都是矩形,而且相邻矩形的公共边都互相平行.(2)该几何体的三视图如图所示.探究应用题8.如图,在正四棱柱ABCD A 1B 1C 1D 1中,AB =1,AA 1=2,点P 是平面A 1B 1C 1D 1内的一个动点,求三棱锥P ABC 的主视图与俯视图的面积的比值的最大值.解:点P 是平面A 1B 1C 1D 1内的一个动点,则三棱锥P ABC 的主视图始终是一个底为1,高为2的三角形,其面积S 1=12×1×2=1.当点P 在底面ABCD 内的投影点在△ABC 的内部或边界上时,其俯视图的面积最小,最小面积S 2=12×1×1=12,所以三棱锥P ABC 的主视图与俯视图的面积的比值的最大值为S 1S 2=2.。
北师大版必修二 空间几何体的三视图、表面积与体积 课时作业

空间几何体的三视图表面积与体积课时作业一、选择题1.下列结论正确的是(D)(A)各个面都是三角形的几何体是三棱锥(B)一平面截一棱锥得到一个棱锥和一个棱台(C)棱锥的侧棱长与底面多边形的边长相等,则该棱锥可能是正六棱锥(D)圆锥的顶点与底面圆周上的任意一点的连线都是母线解析:如图所示,由两个结构相同的三棱锥叠放在一起构成的几何体,各面都是三角形,但它不是棱锥,故A错误;一平行于底面的平面截一棱锥才能得到一个棱锥和一个棱台,因此B错误;若六棱锥的所有棱长都相等,则底面多边形是正六边形.由过底面中心和顶点的截面知,若以正六边形为底面,侧棱长必然要大于底面边长,故C错误;根据圆锥母线的定义知,D正确.故选D.2.下列几何体中为棱柱的是(A)解析:A中几何体有两个面互相平行,其余各个面都是平行四边形,是棱柱.故选A.3.(2018·嘉兴模拟)某几何体的三视图如图(单位: m),则该几何体的体积是(A)(A)m3 (B)m3 (C)2 m3 (D)4 m3解析:由三视图可得:该几何体是一个以俯视图为底面的三棱锥,底面的底边长为2 m,底面的高,即为三视图的宽1 m,故底面面积S=×2×1=1 m2,棱锥的高即为三视图的高,故h=2 m,故棱锥的体积V=×1×2=m3,故选A.4.(2018·台州4月调研考试)某几何体的三视图如图所示,其中俯视图是半径为1的圆,则该几何体的体积是(A)(A)π(B)(C)(D)解析:该几何体下部是一个底面半径为1,高为2的圆锥,上部是半径为1的四分之一球体,所以体积V=×π×12×2+××π×13=+=π.故选A.5.长方体ABCD-A1B1C1D1的八个顶点落在球O的表面上,已AB=3,AD=4,BB1=5,那么球O的表面积为(D)(A)25π(B)200π (C)100π (D)50π解析:因为长方体ABCD-A1B1C1D1的八个顶点都在球面上,所以长方体的体对角线为外接球的直径,设半径为r,则长方体的体对角线长为=5,则2r=5,则r=,所以外接球的表面积为4πr2=50π.故选D.6.母线长为1的圆锥的侧面展开图的圆心角等于120°,则该圆锥的体积为(A)(A)π(B)π(C)π(D)π解析:因为母线长为1的圆锥的侧面展开图的圆心角等于120°,120°=,所以侧面展开图的弧长为1×=,弧长=底面周长=2πr,所以r=,所以圆锥的高h==,所以圆锥体积V=×π×r2×h=π.故选A.7.(2018·浙江卷)某几何体的三视图如图所示(单位:cm),则该几何体的体积(单位:cm3)是(C)(A)2 (B)4 (C)6 (D)8解析:由几何体的三视图可知,该几何体是一个底面为直角梯形,高为2的直四棱柱,所以V=2×[×(2+1)×2]=6.故选C.8.已知三棱锥O ABC的顶点A,B,C都在半径为3的球面上,O是球心,∠AOB=150°,当△AOC与△BOC的面积之和最大时,三棱锥O-ABC的体积为(D)(A)(B)(C)(D)解析:设球O的半径为R,由S△AOC+S△BOC=R2(sin∠AOC+sin∠BOC)知,当sin∠AOC=sin∠BOC=90°时,S△AOC+S△BOC取得最大值,此时OA⊥OC,OB⊥OC,所以OC⊥平面AOB,==R3sin∠AOB=.故选D.二、填空题9.已知一个几何体的三视图如图所示,则此几何体的表面积是,体积是.解析:三视图的直观图如图所示.由题知正方体的棱长为2,点M为棱A′D′的中点,所以AM=B′M=,AB′=2,在等腰三角形AB′M中,底边AB′边上的高为,该几何体的表面积S=2(S正方形ABCD+S△ABB′+S△ADM+S△AB′M)=2×(2×2+×2×2+×2×2+×2×)=16+2,体积V=-2=2×2×2-2×××1×2×2=8-=.答案:16+210. 如图所示,四边形ABCD的直观图四边形A′B′C′D′是一个底角为45°,腰和上底均为1的等腰梯形,那么原平面图形的面积是.解析:根据斜二测画法可知,原图形为直角梯形,其中上底AD=1,高AB=2A′B′=2,下底为BC=1+,所以×2=2+.即原平面图形的面积是+2.答案:+211.(2018·湖州、衢州、丽水三市高三联考)某几何体的三视图如图所示(单位:cm),则此几何体的体积是cm3,表面积是cm2.解析:由三视图可得直观图如图,体积V=×1=3(cm3),表面积S=2×1+(2+1)×2××2+1×1+1×2+1×=2+6+1+2+=(11+)cm2.答案:311+12.已知一个正三棱柱的侧面积为18,且侧棱长为底面边长的2倍,则该正三棱柱的体积为.解析:设底面边长为a,则高为2a,侧面积为S侧=3×(a×2a)=6a2=18,所以a=,该三棱柱的体积为V=Sh=(×××sin 60°)×2=.答案:13.体积为8的正方体的顶点都在同一个球面上,则该球的体积为.解析:由题意得球的直径等于正方体的体对角线长,设正方体的边长为a,球的半径为R,即2R=a,而a3=8,所以R=.该球的体积为πR3=π()3=4π.答案:4π14.(2018·杭州二模)一个几何体的三视图如图所示,则该几何体的体积是,表面积是.解析:由三视图知,该几何体是由四分之一球与半个圆锥组合而成,则该组合体的体积为V=·π·23+·π×22·3=π,表面积为S=·4π·22+·π·22+·4·3+··2π·2·=6+(6+)π,从而问题可得解.答案:π6+(6+)π15.(2018·天津卷) 已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为.解析:依题意,易知四棱锥M EFGH是一个正四棱锥,且底面边长为,高为.故=×()2×=.答案:16. 三棱锥P-ABC满足:AB⊥AC,AB⊥AP,AB=2,AP+AC=4,则该三棱锥的体积V的取值范围是.解析:由于AB⊥AP,AB⊥AC,AC∩AP=A,所以AB⊥平面APC,V=S△APC·AB=S△APC,在△APC中,AP+AC=4,要使△APC面积最大,只需AP=AC,∠PAC=90°,AP·AC≤()2=4,所以S△APC的最大值为×4=2,V的最大值为,该三棱锥的体积V的取值范围是(0,].答案:(0,]三、解答题17. 一个多面体的直观图和三视图如下:(其中M,N分别是AF,BC中点)(1)求证:MN∥平面CDEF;(2)求多面体A-CDEF的体积.(1)证明:由三视图知,该多面体是底面为直角三角形的直三棱柱,且AB=BC=BF=2,DE=CF=2,所以∠CBF=90°.取BF中点G,连MG,NG,由M,N分别是AF,BC中点,可得:NG∥CF,MG∥EF,所以平面MNG∥平面CDEF,所以MN∥平面CDEF.(2)解:作AH⊥DE于H,由于三棱柱ADE BCF为直三棱柱,所以AH⊥平面CDEF,且AH=,所以=SCDEF·AH=×2×2×=.巩固提高B一、选择题1. 水平放置的△ABC,用斜二测画法作出的直观图是如图所示的△A′B′C′,其中O′A′=O′B′=2,O′C′=,则△ABC绕AB所在直线旋转一周后形成的几何体的表面积为(B)(A)8π(B)16π(C)(8+3)π (D)(16+12)π解析:根据斜二测画法可知,AB=4,OC=2,可知△ABC为等边三角形.△ABC绕AB所在直线旋转一周后形成的几何体是两个对着底的圆锥,其两个侧面积就是这个几何体的表面积,表面积为S=2×π×2×4=16π.故选B.2.(2018·全国Ⅲ卷) 中国古建筑借助榫卯将木构件连接起来,构件的凸出部分叫榫头,凹进部分叫卯眼,图中木构件右边的小长方体是榫头.若如图摆放的木构件与某一带卯眼的木构件咬合成长方体,则咬合时带卯眼的木构件的俯视图可以是(A)解析:由题意可知带卯眼的木构件的直观图如图所示,由直观图可知其俯视图应选A.3.三棱锥P-ABC三条侧棱两两垂直,三个侧面面积分别为,,,则该三棱锥的外接球的表面积为(B)(A)4π(B)6π(C)8π(D)10π解析:三棱锥P-ABC的三条侧棱PA,PB,PC两两互相垂直,它的外接球就是它扩展为长方体的外接球,设PA=a,PB=b,PC=c,则ab=,bc=,ca=,所以①×②×③÷②2得=,即a2=2,所以a=,同理b=1,c=.则长方体的体对角线的长为=.所以球的直径是,半径长R=,则球的表面积S=4πR2=6π.故选B.4.《九章算术》中,将底面是直角三角形的直三棱柱称之为“堑堵”,已知某“堑堵”的三视图如图所示,俯视图中虚线平分矩形的面积,则该“堑堵”的侧面积为(C)(A)2 (B)4+2(C)4+4(D)4+6解析:由三视图知几何体为一三棱柱,底面为一等腰直角三角形,高为1,则底面三角形腰长为,底边长为2,三棱柱高为2,所以侧面积为2×2+2××2=4+4.故选C.5.如图是一个底面半径为1的圆柱被平面截开所得的几何体,截面与底面所成的角为45°,过圆柱的轴的平面截该几何体所得的四边形ABB′A′为矩形,若沿AA′将其侧面剪开,其侧面展开图形状大致为(A)解析:截面方程为x2+=1,截面在轴截面A′ABB′上的投影为圆x2+y2=1,沿AA′剪开,其展开图不可能是B,C,D.故选A.6.正方体ABCD-A1B1C1D1的棱长为1,点E,F分别是棱D1C1,B1C1的中点,过E,F作一平面α,使得平面α∥平面AB1D1,则平面α截正方体的表面所得平面图形为(D)(A)三角形(B)四边形(C)五边形(D)六边形解析:由题意,在正方体ABCD-A1B1C1D1中,E,F分别为棱D1C1,B1C1的中点,取BB1,AB,AD,DD1的中点G,H,M,N,可得正六边形EFGHMN,此时平面AB1D1∥平面EFGHMN.故选D.7.祖暅是南北朝时期的伟大科学家,5世纪末提出体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等.现有以下四个几何体:图①是从圆柱中挖出一个圆锥所得的几何体;图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为(D)(A)①②(B)①③(C)②④(D)①④解析:设截面与底面的距离为h,则①中截面内圆半径为h,则截面圆环的面积为π(R2-h2);②中截面圆的半径为R-h,则截面圆的面积为π(R-h)2;③中截面圆的半径为R-,则截面圆的面积为π(R-)2;④中截面圆的半径为,则截面圆的面积为π(R2-h2),所以①④中截面的面积相等.故选D.8.(2018·宁波5月模拟)已知x,y均为非负实数,且x+y≤1,则4x2+4y2+(1-x-y)2的取值范围为(A)(A) [,4](B)[1,4] (C)[2,4] (D)[2,9]解析:因为x,y≥0,所以≤x2+y2≤(x+y)2.令t=x+y,则0≤t≤1.4x2+4y2+(1-x-y)2≤4t2+(1-t)2=5t2-2t+1≤4.当xy=0且t=1,即x=0,y=1或x=1,y=0时取等号;另一方面,4x2+4y2+(1-x-y)2≥2t2+(1-t)2=3t2-2t+1≥.当x=y=时取等号.所以4x2+4y2+(1-x-y)2∈[,4].故选A.二、填空题9.(2018·温州模拟)如图,一个简单几何体三视图的正视图与侧视图,都是边长为1的正三角形,其俯视图的轮廓为正方形,则该几何体的体积是,表面积是.解析:由正视图和侧视图为等边三角形可得此几何体为锥体,由俯视图为四边形可得此几何体为四棱锥,因为正视图为边长为1的正三角形,所以正三角形的高,也就是棱锥的高为,俯视图的边长为1,所以正四棱锥的体积为V=×1×1×=,表面积为S=1+4××1×1=3.答案: 310.在四面体P-ABC中,PA=PB=PC=BC=1,则该四面体体积的最大值为.解析:由于平面PBC是边长为1的正三角形,=,底面面积固定,要使体积最大,只需高最大,故当PA⊥平面PBC时体积最大,V=××12×1=.答案:11.已知圆锥的母线长为5 cm,侧面积为15πcm2,则此圆锥的体积为cm3.解析:已知圆锥的母线长为5 cm,侧面积为15πcm2,所以圆锥的底面周长为6πcm,底面半径是3 cm,圆锥的高是4 cm,此圆锥的体积为×9π×4=12π(cm3). 答案:12π12.(2018·全国Ⅱ卷)已知圆锥的顶点为S,母线SA,SB所成角的余弦值为,SA与圆锥底面所成角为45°,若△SAB的面积为5,则该圆锥的侧面积为.解析:如图,因为SA与底面成45°角,所以△SAO为等腰直角三角形.设OA=r,则SO=r,SA=SB=r.在△SAB中,cos∠ASB=,所以sin∠ASB=,所以S△SAB=SA·SB·sin∠ASB=(r)2·=5,解得r=2,所以SA=r=4,即母线长l=4,所以S圆锥侧=πr·l=π×2×4=40π.答案:40π13.有三个球,第一个球内切于正方体,第二个球与这个正方体的各条棱相切,第三个球过这个正方体的各个顶点.则这三个球的半径之比为.解析:设正方体的棱长为a,则正方体的内切球直径为a,则半径为.第二个球与正方体的各条棱相切,由截面知球直径为a,则半径为 a.正方体的外接球,过正方体的各个顶点,其直径为a,则半径为 a.可得三个球的半径之比为1∶∶.答案:1∶∶14.若圆锥的底面直径和高都与一个球的直径相等,圆锥、球的表面积分别记为S1,S2,则的值是. 解析:设球的直径为2R,由题意可知,S1=πR2+πR×=(+1)πR2,S2=4πR2,据此可得=.答案:15. 如图,在棱长为1的正方体ABCD A1B1C1D1中,点P是线段BD1上的动点.当△PAC在平面DC1,BC1,AC上的正投影都为三角形时,将它们的面积分别记为S1,S2,S3.(1)S1S2(填“>”“=”或“<”);(2)S1+S2+S3的最大值为.解析:如图,因=,=,故PO=QN,同理可得RM=PO,所以RM=QN,则S1=S2,特别地当点P与点D1重合时,三个投影面的面积都最大,都是,所以S1+S2+S3=,即最大值是.答案:=三、解答题16. 如图四棱锥P-ABCD中,底面ABCD是平行四边形,∠ACB=90°,PA⊥平面ABCD,PA=BC=1,AB=,F是BC的中点.(1)求证:DA⊥平面PAC;(2)点G为线段PD的中点,证明CG∥平面PAF;(3)求三棱锥A-CDG的体积.(1)证明:因为四边形ABCD是平行四边形,∠ACB=∠DAC=90°,因为PA⊥平面ABCD,所以PA⊥DA,又AC⊥DA,AC∩PA=A,所以DA⊥平面PAC.(2)证明:PD的中点为G,在平面PAD内作GH⊥PA于H,则GH平行且等于AD,连接FH,则四边形FCGH为平行四边形,所以GC∥FH,因为FH⊂平面PAF,CG⊄平面PAF,所以CG∥平面PAF.(3)解:设S为AD的中点,连结GS,则GS平行且等于PA=,因为PA⊥平面ABCD,所以GS⊥平面ABCD,所以==S△ACDGS=.。
2021年高中数学课时作业31.3三视图北师大版必修
2021年高中数学课时作业31.3三视图北师大版必修|基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )解析:本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C,都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.答案:D2.如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的几何体分别为( )①长方体;②圆锥;③三棱锥;④圆柱.A.④③②B.①③②C.①②③ D.④②③解析:由于甲中的俯视图是圆,则甲对应的几何体是旋转体,又主视图和左视图均是矩形,所以该几何体是圆柱;易知乙对应的几何体是三棱锥;由丙中的俯视图,可知丙对应的几何体是旋转体,又主视图和左视图均是三角形,所以该几何体是圆锥.答案:A3.(xx·河北名师俱乐部3月模拟)某几何体的三视图如图所示,记A为此几何体所有棱的长度构成的集合,则( )A.3∈A B.5∈AC.26∈A D.43∈A解析:由三视图可得,该几何体的直观图如图所示,其中底面是边长为4的正方形,AF⊥平面ABCD,AF∥DE,AF=2,DE=4,可求得BE的长为43,BF的长为25,EF的长为25,EC的长为42,故选D.答案:D4.如图为某组合体的三视图,则俯视图中的长和宽分别为( )A.10,4 B.10,8C.8,4 D.10,5解析:根据三视图中的“主、俯视图长对正,主、左视图高平齐,俯、左视图宽相等”,可知俯视图的长和主视图的长相等,为2+6+2=10,俯视图的宽与左视图的宽相等,为1+2+1=4,所以选A.答案:A5.(xx·东北四市联考(二))如图,在正方体ABCD-A1B1C1D1中,P是线段CD的中点,则三棱锥P-A1B1A的侧视图为( )解析:如图,画出原正方体的侧视图,显然对于三棱锥P-A1B1A,B(C)点均消失了,其余各点均在,从而其侧视图为D.答案:D二、填空题(每小题5分,共15分)6.桌上放着一个半球,如图所示,则在它的三视图及右面看到的图形中,有三个图相同,这个不同的图应该是________.解析:俯视图为圆,主视图与左视图均为半圆.答案:俯视图7.如图,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为________.解析:由三视图的画法可知,该几何体的左视图是一个矩形,其底面边长为2sin60°=3,高为3,∴面积S=3 3.答案:3 38.(xx·山东安丘市高二上期末)一个几何体的三视图如图所示,其中正视图是边长为2的正三角形,俯视图是正方形,那么该几何体的侧视图的面积是________.解析:根据三视图可知该几何体是一个四棱锥,其底面是正方形,侧棱相等,所以这是一个正四棱锥.其侧视图与正视图是完全一样的正三角形.故其面积为34×22= 3.答案: 3三、解答题(每小题10分,共20分)9.试画出如图所示的正四棱台的三视图.解析:如图.10.根据图中的三视图想象物体原形,并画出物体的实物草图.解析:由俯视图并结合其他两个视图可以看出,这个物体是由上面一个正四棱台和下面一个正方体组合而成的,它的实物草图如图所示.|能力提升|(20分钟,40分)11.(xx·广东省台山市华侨中学高二上期末)定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱.将正三棱柱截去一个角(如图1所示,M,N分别是AB,BC的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图为( )解析:N的投影是C,M的投影是AC的中点.对照各图.选D.答案:D12.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.解析:三棱锥、四棱锥和圆锥的正视图都是三角形,当三棱柱的一个侧面平行于水平面,底面对着观测者时其正视图是三角形,四棱柱、圆柱无论怎样放置,其正视图都不可能是三角形.答案:①②③⑤13.如图所示,是一个长方体截去一个角所得多面体的直观图和它的主视图和左视图(单位:cm).请在正视图下面,按照画三视图的要求画出该多面体的俯视图.解析:依据三视图的绘图原则,可作出该几何体的俯视图如图.14.某建筑由相同的若干房间组成,该楼房的三视图如图所示,问:(1)该楼房有几层?从前往后最多要经过几个房间?(2)最高一层的房间在什么位置?请画出此楼房的大致形状.解析:(1)由主视图和左视图可以知道,该楼房有3层;由俯视图知道,从前往后最多要经过3个房间;(2)从主视图和左视图可以知道,最高一层的房间在左侧的最后一排的房间.楼房大致形状如图所示.。
2021年高考数学 第七章 第一节 空间几何体的结构特征及三视图和直观图课时提升作业 文 北师大版
2021年高考数学第七章第一节空间几何体的结构特征及三视图和直观图课时提升作业文北师大版一、选择题1.以下四个命题:①正棱锥的所有侧棱相等;②直棱柱的侧面都是全等的矩形;③圆柱的母线垂直于底面;④用经过旋转轴的平面截圆锥,所得的截面一定是全等的等腰三角形.其中,真命题的个数为( )(A)4 (B)3 (C)2 (D)12.下列几何体各自的三视图中,有且仅有两个视图相同的是( )(A)①②(B)①③(C)①④(D)②④3.(xx安康模拟)一个锥体的主视图和左视图如图所示,下面选项中,不可能是该锥体的俯视图的是( )4.如图,△ABC为正三角形,AA′∥BB′∥CC′,CC′⊥平面ABC且3AA′=BB′=CC′=AB,则多面体ABC-A′B′C′的主视图是( )5.(xx·铜川模拟)一个水平放置的平面图形的斜二测直观图是直角梯形(如图所示),∠ABC=45°,AB=AD=1,DC⊥BC,则这个平面图形的面积为( )(A)+ (B)2+(C)+ (D)+6.(能力挑战题)一个正方体截去两个角后所得几何体的主视图、左视图如图所示,则其俯视图为( )7.(xx·西安模拟)一只蚂蚁从正方体ABCD-A1B1C1D1的顶点A处出发,经正方体的表面,按最短路线爬行到达顶点C1位置,则下列图形中可以表示正方体及蚂蚁最短爬行路线的主视图是( )(A)①②(B)①③(C)②④(D)③④二、填空题8.等腰梯形ABCD,上底CD=1,腰AD=CB=,下底AB=3,以下底所在直线为x轴,则由斜二测画法画出的直观图A′B′C′D′的面积为.9.(xx·德州模拟)一个正三棱柱的侧棱长和底面边长相等,体积为2,它的三视图中的俯视图如图所示,左视图是一个矩形,则这个矩形的面积是.10.(xx·宝鸡模拟)一个三棱锥的主视图和左视图及其尺寸如图所示,则该三棱锥的俯视图的面积为.三、解答题11.(能力挑战题)某几何体的一条棱长为,在该几何体的主视图中,这条棱的投影是长为的线段,在该几何体的左视图与俯视图中,这条棱的投影分别是长为a和b的线段,求a+b的最大值.答案解析1.【解析】选B.由正棱锥的定义可知所有侧棱相等,故①正确;由于直棱柱的底面的各边不一定相等,故侧面矩形不一定全等,因此②不正确;由圆柱母线的定义可知③正确;结合圆锥轴截面的作法可知④正确.综上,正确的命题有3个.2.【解析】选D.在各自的三视图中,①正方体的三个视图都相同;②圆锥的两个视图相同;③三棱台的三个视图都不同;④正四棱锥的两个视图相同,故选D.【变式备选】正三棱柱(底面为正三角形的直棱柱)ABC-A 1B1C1如图所示,以四边形ABB1A1为水平面,四边形BCC1B1的前面为正前方画出的三视图正确的是( )【解析】选A.矩形BCC1B1的前面为正前方,故主视图为矩形,左侧为△ABC,所以左视图为三角形.俯视图为两个有公共边的矩形,公共边为CC1在面ABB1A1内的投影,故选A.3.【解析】选C.当俯视图为A,B时表示底面为等腰直角三角形,且过直角顶点的棱与底面垂直的三棱锥.当俯视图为D时,表示底面为正方形,且有一条侧棱与底面垂直的四棱锥.故选C.【方法技巧】由直观图画三视图的技巧(1)可以想象将一几何体放在自己面前,然后从正前方,左侧及上面观察该几何体,进而得到主视图、左视图和俯视图.(2)在画三视图时,要注意看得见的轮廓线画成实线,看不见的轮廓线画成虚线.4.【解析】选D.由AA′∥BB′∥CC′及CC′⊥平面ABC,知AA′⊥平面ABC,BB′⊥平面ABC.又CC′=BB′=3AA′,且△ABC为正三角形,故主视图应为D中的图形.5.【解析】选B.如图将直观图ABCD还原后为直角梯形A′BCD′,其中A′B=2AB=2,BC=1+,A′D′=AD=1,∴S=×(1+1+)×2=2+.6.【解析】选C.依题意可知该几何体的直观图如图所示,故其俯视图应为C.7.【解析】选C.依题意得,题中提供的选项中,图②④可以表示正方体及蚂蚁最短爬行路线的主视图,选C.8.【解析】如图所示,∵OE==1,∴O′E′=,E′F′=,∴直观图A′B′C′D′的面积为S′=×(1+3)×=.答案:9.【解析】设正三棱柱的底面边长为a,利用体积为2,很容易求出这个正三棱柱的底面边长和侧棱长都是2,所以底面正三角形的高为,故所求矩形的面积为2.答案:210.【解析】由题意可知,该三棱锥的俯视图是一个底边长为2,高为1的三角形,则其面积为1.答案:111.【思路点拨】可将该几何体放在长方体中,且已知长为的棱为长方体的体对角线来解决.【解析】如图,把几何体放到长方体中,使得长方体的体对角线刚好为几何体的已知棱,则长方体的体对角线A1C=,则它的主视图投影长为A1B=,左视图投影长为A1D=a,俯视图投影长为A1C1=b,则a2+b2+()2=2×()2,即a2+b2=8,又≤,当且仅当“a=b=2”时等号成立.∴a+b≤4,即a+b的最大值为4.26183 6647 晇 36537 8EB9 躹32518 7F06 缆la037876 93F4 鏴"26798 68AE 梮Z22333 573D 圽35644 8B3C 謼`I。
2021高中数学第一章 课时作业北师大版必修2
课时作业1 简单几何体|基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.下面的几何体中是棱柱的有()A.3个B.4个C.5个D.6个解析:棱柱有三个特征:(1)有两个面相互平行;(2)其余各面是四边形;(3)侧棱相互平行.本题所给几何体中⑥⑦不符合棱柱的三个特征,而①②③④⑤符合,故选C.答案:C2.下面图形中,为棱锥的是()A.①③B.①③④C.①②④D.①②解析:根据棱锥的定义和结构特征可以判断,①②是棱锥,③不是棱锥,④是棱锥.故选C.答案:C3.下列图形中,是棱台的是()解析:由棱台的定义知,A、D的侧棱延长线不交于一点,所以不是棱台;B中两个面不平行,不是棱台,只有C符合棱台的定义,故选C.答案:C4.给出下列说法:①以直角三角形的一边所在直线为旋转轴,旋转一周而得的旋转体是圆锥;②以直角梯形的一边所在直线为旋转轴,旋转一周而得的旋转体是圆台;③圆锥、圆台的底面都是圆面;④分别以矩形长和宽(长和宽不相等)所在直线为旋转轴,旋转一周而得的两个圆柱是两个不同的圆柱.其中正确说法的个数是()A.1 B.2C.3 D.4解析:以直角三角形的一条直角边所在直线为旋转轴,旋转一周所得的旋转体才是圆锥,若以斜边所在直线为旋转轴,旋转一周所得的旋转体是由两个圆锥组成的组合体,故①错误;以直角梯形中垂直于底边的腰所在直线为旋转轴,旋转一周而得的旋转体是圆台,以其他的边所在直线为旋转轴,旋转一周而得的旋转体不是圆台,②错误;③④是正确的.答案:B5.一个正方体内有一个内切球,作正方体的对角面,所得截面图形是下图中的()解析:由组合体的结构特征知,球只与正方体的上、下底面相切,而与两侧棱相离.故正确答案为B.答案:B二、填空题(每小题5分,共15分)6.以等腰梯形的对称轴为轴旋转一周,所形成的旋转体是________.解析:等腰梯形的对称轴为两底中点的连线,此线把等腰梯形分成两个全等的直角梯形,旋转后形成圆台.答案:圆台7.已知正四棱锥V-ABCD,底面面积为16,一条侧棱长为211,则它的斜高为________.解析:由S底=16,知底面边长为4,又侧棱长为211,故斜高h′=(211)2-22=210.答案:2108.下列说法正确的有________个.①有一个面是多边形,其余各面都是三角形的几何体是棱锥.②正棱锥的侧面是等边三角形.③底面是等边三角形,侧面都是等腰三角形的三棱锥是正三棱锥.解析:①不正确.棱锥的定义是:有一个面是多边形,其余各面都是有一个公共顶点的三角形,由这些面所围成的多面体叫做棱锥.而“其余各面都是三角形”并不等价于“其余各面都是有一个公共顶点的三角形”,故此说法是错误的.如图所示的几何体满足此说法,但它不是棱锥,理由是△ADE和△BCF无公共顶点.②错误.正棱锥的侧面都是等腰三角形,不一定是等边三角形.③错误.由已知条件知,此三棱锥的三个侧面未必全等,所以不一定是正三棱锥.如图所示的三棱锥中有AB=AD=BD=BC=CD.满足底面△BCD为等边三角形.三个侧面△ABD,△ABC,△ACD都是等腰三角形,但AC长度不一定,三个侧面不一定全等.答案:0三、解答题(每小题10分,共20分)9.一个有30°角的直角三角板绕其各条边所在直线旋转一周所得几何体是圆锥吗?如果以斜边上的高所在的直线为轴旋转180°得到什么图形?解析:图(1)、(2)旋转一周得到的几何体是圆锥;图(3)旋转一周所得几何体是两个圆锥拼接而成的几何体.图(4)旋转180°是两个半圆锥的组合体.10.如图所示为长方体ABCD-A′B′C′D′,当用平面BCFE把这个长方体分成两部分后,各部分形成的多面体还是棱柱吗?如果不是,请说明理由;如果是,指出底面及侧棱.解析:截面BCFE上方部分是棱柱BB′E-CC′F,其中平面BB′E和平面CC′F 是其底面,BC,B′C′,EF是其侧棱.截面BCFE下方部分是棱柱ABEA′-DCFD′,其中平面ABEA′和平面DCFD′是其底面,AD,BC,EF,A′D′是其侧棱.|能力提升|(20分钟,40分)11.有下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线;②圆锥顶点与底面圆周上任意一点的连线是圆锥的母线;③在圆台上、下底面圆周上各取一点,则这两点的连线是圆台的母线;④圆柱的任意两条母线所在的直线是互相平行的.其中正确的是()A.①②B.②③C.①③D.②④解析:对于①③两点的连线不一定在圆柱、圆台的曲面上,当然有可能不是母线了,②④由母线的定义知正确.答案:D12.如图,这是一个正方体的表面展开图,若把它再折回成正方体后,有下列命题:①点H与点C重合;②点D与点M与点R重合;③点B与点Q重合;④点A与点S重合.其中正确命题的序号是________.(注:把你认为正确的命题的序号都填上)解析:还原成正方体考虑.答案:②④13.如图所示是一个三棱台ABC-A′B′C′,试用两个平面把这个三棱台分成三部分,使每一部分都是一个三棱锥.解析:过A′,B,C三点作一个平面,再过A′,B,C′作一个平面,就把三棱台ABC-A′B′C′分成三部分,形成的三个三棱锥分别是A′-ABC,B-A′B′C′,A′-BCC′.(答案不唯一)14.如图所示的直角梯形ABCD,AB⊥BC,绕着CD所在直线l旋转一周形成一个几何体,试说明该几何体的结构特征.解析:如图所示,过A,B分别作AO1⊥l,BO2⊥l,垂足分别为O1,O2,则Rt△CO2B绕l旋转一周所形成的几何体是圆锥,直角梯形O1ABO2绕l旋转一周所形成的几何体是圆台,Rt△DO1A绕l旋转一周所形成的几何体是圆锥.综上,可知所求几何体下面是一个圆锥,上面是一个圆台挖去了一个以圆台上底面为底面的圆锥.课时作业2 直观图|基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.关于直观图画法的说法中,不正确的是()A.原图形中平行于x轴的线段,其对应线段仍平行于x′轴,其长度不变B.原图形中平行于y轴的线段,其对应线段仍平行于y′轴,其长度不变C.画与坐标系xOy对应的坐标系x′O′y′时,∠x′O′y′可画成135°D.作直观图时,由于选轴不同,所画直观图可能不同解析:根据斜二测画法的规则可知B不正确.答案:B2.用斜二测画法得到的一个水平放置的平面图形的直观图为如图所示的一个正方形,则原来的图形是()解析:直观图中的多边形为正方形,对角线的长为2,所以原图形为平行四边形,位于y 轴上的对角线的长为2 2.答案:A 3.(2017·太原高一期末)如图所示的用斜二测法画的直观图,其平面图形的面积为( )A .3 B.322C .6D .3 2解析:该直观图的原图为直角三角形,两条直角边分别为4和3,所以平面图形的面积为12×3×4=6.答案:C4.已知一条边在x 轴上的正方形的直观图是一个平行四边形,此平行四边形中有一边长为4,则原正方形的面积是( )A .16B .64C .16或64D .以上都不对解析:根据直观图的画法,平行于x 轴的线段长度不变,平行于y 轴的线段变为原来的一半,于是直观图中长为4的边如果平行于x ′轴,则正方形的边长为4,面积为16;长为4的边如果平行于y ′轴,则正方形的边长为8,面积为64.答案:C 5.若用斜二测画法把一个高为10 cm 的圆柱的底面画在x ′O ′y ′平面上,则该圆柱的高应画成( )A .平行于z ′轴且长度为10 cmB .平行于z ′轴且长度为5 cmC .与z ′轴成45°且长度为10 cmD .与z ′轴成45°且长度为5 cm解析:平行于z 轴的线段,在直观图中平行性和长度都不变,故选A. 答案:A二、填空题(每小题5分,共15分)6.已知正三角形ABC 的边长为2,那么△ABC 的直观图△A ′B ′C ′的面积为________.解析:如图,图①,图②所示的分别是实际图形和直观图. 从图②可知,A ′B ′=AB =2,O ′C ′=12OC =32,C ′D ′=O ′C ′sin45°=32×22=64. 所以S △A ′B ′C ′=12A ′B ′·C ′D ′=12×2×64=64.答案:647.一个水平放置的平面图形的直观图是直角梯形ABCD ,如图所示,∠ABC =45°,AB =AD =1,DC ⊥BC ,则这个平面图形的面积为________.解析:由直观图,可知原图形为直角梯形,且上底为1,下底为22+1,高为2,故面积为12×⎝⎛⎭⎫1+22+1×2=2+22.答案:4+228.一条边在x 轴上的正方形的面积是4,按斜二测画法所得的直观图是一个平行四边形,则这个平行四边形的面积是________.解析:正方形的面积为4,则边长为2,由斜二测画法的规则,知平行四边形的底为2,高为22,故面积为 2.答案: 2三、解答题(每小题10分,共20分)9.将图中所给水平放置的直观图绘出原形.解析:10.画棱长为2 cm 的正方体的直观图. 解析:(1)作水平放置的正方形的直观图ABCD ,使∠BAD =45°,AB =2 cm ,AD =1 cm. (2)过点A 作z ′轴,使∠BAz ′=90°,分别过点A ,B ,C ,D ,沿z ′轴的正方向取AA 1=BB 1=CC 1=DD 1=2 cm.(3)连接A 1B 1,B 1C 1,C 1D 1,D 1A 1如下图①,擦去辅助线,把被遮住的线改为虚线,得到的图形如下图②就是所求的正方体的直观图.|能力提升|(20分钟,40分)11.如图所示是水平放置三角形的直观图,点D 是△ABC 的BC 边中点,AB ,BC 分别与y ′轴、x ′轴平行,则三条线段AB ,AD ,AC 中( )A .最长的是AB ,最短的是AC B .最长的是AC ,最短的是AB C .最长的是AB ,最短的是AD D .最长的是AC ,最短的是AD解析:由条件知,原平面图形中AB ⊥BC ,从而AB <AD <AC . 答案:B12.如图为△ABO 水平放置的直观图△A ′B ′O ′,由图判断△ABO 中,AB ,BO ,BD ,OD 由小到大的顺序是______________________.解析:由题图可知,△ABO 中,OD =2,BD =4,AB =17,BO =2 5. 答案:OD <BD <AB <BO 13.用斜二测画法画出图中水平放置的△OAB 的直观图.解析:(1)在已知图中,以O 为坐标原点,以OB 所在的直线及垂直于OB 的直线分别为x 轴与y 轴建立平面直角坐标系,过点A 作AM 垂直x 轴于点M ,如图1.另选一平面画直观图,任取一点O ′,画出相应的x ′轴、y ′轴,使∠x ′O ′y ′=45°.(2)在x ′轴上取点B ′,M ′,使O ′B ′=OB ,O ′M ′=OM ,过点M ′作M ′A ′∥y ′轴,取M ′A ′=12MA .连接O ′A ′,B ′A ′,如图2.(3)擦去辅助线,则△O′A′B′为水平放置的△OAB的直观图.14.画正六棱柱的直观图.解析:画法如下:(1)画轴:画x′轴、y′轴、z′轴,使∠x′O′y′=45°,∠x′O′z′=90°;(2)画底面:画正六边形的直观图ABCDEF(O′为正六边形的中心);(3)画侧棱:过A,B,C,D,E,F各点分别作z′轴的平行线,在这些平行线上分别截取AA′,BB′,CC′,DD′,EE′,FF′,使AA′=BB′=CC′=DD′=EE′=FF′;(4)连线成图:连接A′B′,B′C′,C′D′,D′E′,E′F′,F′A′,并加以整理(去掉辅助线,将被遮挡的部分改为虚线),就得到正六棱柱ABCDEF-A′B′C′D′E′F′,如图所示.课时作业3 三视图|基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是()解析:本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C,都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.答案:D2.如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的几何体分别为()①长方体;②圆锥;③三棱锥;④圆柱.A.④③②B.①③②C.①②③D.④②③解析:由于甲中的俯视图是圆,则甲对应的几何体是旋转体,又主视图和左视图均是矩形,所以该几何体是圆柱;易知乙对应的几何体是三棱锥;由丙中的俯视图,可知丙对应的几何体是旋转体,又主视图和左视图均是三角形,所以该几何体是圆锥.答案:A3.(2016·河北名师俱乐部3月模拟)某几何体的三视图如图所示,记A为此几何体所有棱的长度构成的集合,则()A.3∈A B.5∈AC.26∈A D.43∈A解析:由三视图可得,该几何体的直观图如图所示,其中底面是边长为4的正方形,AF⊥平面ABCD,AF∥DE,AF=2,DE=4,可求得BE的长为43,BF的长为25,EF 的长为25,EC的长为42,故选D.答案:D4.如图为某组合体的三视图,则俯视图中的长和宽分别为()A.10,4 B.10,8C.8,4 D.10,5解析:根据三视图中的“主、俯视图长对正,主、左视图高平齐,俯、左视图宽相等”,可知俯视图的长和主视图的长相等,为2+6+2=10,俯视图的宽与左视图的宽相等,为1+2+1=4,所以选A.答案:A5.(2016·东北四市联考(二))如图,在正方体ABCD-A1B1C1D1中,P是线段CD的中点,则三棱锥P-A1B1A的侧视图为()解析:如图,画出原正方体的侧视图,显然对于三棱锥P-A1B1A,B(C)点均消失了,其余各点均在,从而其侧视图为D.答案:D二、填空题(每小题5分,共15分)6.桌上放着一个半球,如图所示,则在它的三视图及右面看到的图形中,有三个图相同,这个不同的图应该是________.解析:俯视图为圆,主视图与左视图均为半圆.答案:俯视图7.如图,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为________.解析:由三视图的画法可知,该几何体的左视图是一个矩形,其底面边长为2sin60°=3,高为3,∴面积S=3 3.答案:3 38.(2016·山东安丘市高二上期末)一个几何体的三视图如图所示,其中正视图是边长为2的正三角形,俯视图是正方形,那么该几何体的侧视图的面积是________.解析:根据三视图可知该几何体是一个四棱锥,其底面是正方形,侧棱相等,所以这是一个正四棱锥.其侧视图与正视图是完全一样的正三角形.故其面积为34×22= 3.答案: 3三、解答题(每小题10分,共20分)9.试画出如图所示的正四棱台的三视图.解析:如图.10.根据图中的三视图想象物体原形,并画出物体的实物草图.解析:由俯视图并结合其他两个视图可以看出,这个物体是由上面一个正四棱台和下面一个正方体组合而成的,它的实物草图如图所示.|能力提升|(20分钟,40分)11.(2016·广东省台山市华侨中学高二上期末)定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱.将正三棱柱截去一个角(如图1所示,M,N分别是AB,BC的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图为()解析:N的投影是C,M的投影是AC的中点.对照各图.选D.答案:D12.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.解析:三棱锥、四棱锥和圆锥的正视图都是三角形,当三棱柱的一个侧面平行于水平面,底面对着观测者时其正视图是三角形,四棱柱、圆柱无论怎样放置,其正视图都不可能是三角形.答案:①②③⑤13.如图所示,是一个长方体截去一个角所得多面体的直观图和它的主视图和左视图(单位:cm).请在正视图下面,按照画三视图的要求画出该多面体的俯视图.解析:依据三视图的绘图原则,可作出该几何体的俯视图如图.14.某建筑由相同的若干房间组成,该楼房的三视图如图所示,问:(1)该楼房有几层?从前往后最多要经过几个房间?(2)最高一层的房间在什么位置?请画出此楼房的大致形状.解析:(1)由主视图和左视图可以知道,该楼房有3层;由俯视图知道,从前往后最多要经过3个房间;(2)从主视图和左视图可以知道,最高一层的房间在左侧的最后一排的房间.楼房大致形状如图所示.课时作业4 公理1、公理2、公理3及应用|基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.点P在直线l上,而直线l在平面α内,用符号表示为()A.P⊂l⊂αB.P∈l∈αC.P⊂l∈αD.P∈l⊂α解析:直线和平面可看作点的集合,点是基本元素.故选D.答案:D2.已知a、b是异面直线,直线c∥直线a,那么c与b()A.一定是异面直线B.一定是相交直线C.不可能是平行直线D.不可能是相交直线解析:若b∥c,∵a∥c,∴a∥b,这与a、b异面矛盾,其余情况均有可能.答案:C3.(2017·安庆市石化一中高二上期中)若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a成90°角解析:因为直线a平行于平面α,所以a与平面α内的直线平行或异面,故A错误;α内有无数条直线与a平行,故B正确;直线a上的点到平面α的距离相等,故C正确;α内存在无数条直线与a成90°角,故D正确.故选A.答案:A4.一条直线与两条异面直线中的一条相交,则它与另一条的位置关系是()A.异面B.平行C.相交D.可能相交、平行、也可能异面解析:一条直线与两条异面直线中的一条相交,它与另一条的位置关系有三种:平行、相交、异面,如下图所示.答案:D5.(2015·广东卷)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是()A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交解析:由直线l1和l2是异面直线可知l1与l2不平行,故l1,l2中至少有一条与l相交.答案:D二、填空题(每小题5分,共15分)6.设平面α与平面β相交于直线l,直线a⊂α,直线b⊂β,a∩b=M,则点M与l 的位置关系为________.解析:因为a∩b=M,aα,bβ,所以M∈α,M∈β.又平面α与平面β相交于直线l,所以点M在直线l上,即M∈l.答案:M∈l7.给出以下命题:①和一条直线都相交的两条直线在同一平面内;②三条两两相交的直线在同一平面内;③有三个不同公共点的两个平面重合;④两两平行的三条直线确定三个平面.其中正确命题的个数是________.解析:空间中和一条直线都相交的两条直线不一定在同一平面内,故①错;若三条直线相交于一点时,不一定在同一平面内,如长方体一角的三条线,故②错;若两平面相交时,也可有三个不同的公共点,故③错;若三条直线两两平行且在同一平面内,则只有一个平面,故④错.答案:08.如图,在正方体ABCD-A1B1C1D1中,M,N分别为棱C1D1,C1C的中点,有以下四个结论:①直线AM与CC1是相交直线;②直线AM与BN是平行直线;③直线BN与MB1是异面直线;④直线AM与DD1是异面直线.其中正确的结论为________.(注:把你认为正确的结论的序号都填上)解析:直线AM与CC1是异面直线,直线AM与BN也是异面直线,所以①②错误.点B,B1,N在平面BB1C1C中,点M在此平面外,所以BN,MB1是异面直线.同理AM,DD1也是异面直线.答案:③④三、解答题(每小题10分,共20分)9.完成下列各题:(1)将下列文字语言转换为符号语言.①点A在平面α内,但不在平面β内;②直线a经过平面α外一点M;③直线l在平面α内,又在平面β内(即平面α和平面β相交于直线l).(2)将下列符号语言转换为图形语言.①a⊂α,b∩α=A,A∉a;②α∩β=c,a⊂α,b⊂β,a∥c,b∩c=P.解析:(1)①A∈α,A∉β.②M∈a,M∉α.③α∩β=l.(2)①②10.如图所示,正方体ABCD-A1B1C1D1中,M、N分别是A1B1、B1C1的中点,问:(1)AM和CN是否是异面直线?说明理由;(2)D1B和CC1是否是异面直线?说明理由.解析:(1)不是异面直线,理由:连结MN,A1C1、AC,如图,因为M、N分别是A1B1、B1C1的中点,所以MN∥A1C1.又因为A1A綊D1D,D1D綊C1C,所以A1A綊C1C,四边形A1ACC1为平行四边形,所以A1C1∥AC,故MN∥A1C1∥AC,所以A、M、N、C在同一个平面内,故AM和CN不是异面直线.(2)是异面直线,证明如下:假设D1B与CC1在同一个平面CC1D1内,则B∈平面CC1D1,C∈平面CC1D1,所以BC⊂平面CC1D1,这显然是不正确的,所以假设不成立,故D1B与CC1是异面直线.|能力提升|(20分钟,40分)11.下列说法中正确的个数是()①平面α与平面β,γ都相交,则这三个平面有2条或3条交线;②如果a,b是两条直线,a∥b,那么a平行于经过b的任何一个平面;③直线a不平行于平面α,则a不平行于α内任何一条直线;④如果α∥β,a∥α,那么a∥β.A.0个B.1个C.2个D.3个解析:①中,交线也可能是1条;②a也可能在过b的平面内;③中a不平行于平面α,则a可能在平面α内,平面α内有与a平行的直线;④中,a可能在β内.故四个命题都是错误的,选A.答案:A12.如图所示,G,H,M,N分别是三棱柱的顶点或所在棱的中点,则表示直线GH,MN是异面直线的图形有________(填上所有正确答案的序号).解析:图(1)中,直线GH∥MN;图(2)中,G,H,N三点共面,但M∉平面GHN,因此直线GH与MN异面;图(3)中,连接MG,HN,GM∥HN,因此GH与MN共面;图(4)中,G,M,N共面,但H∉平面GMN,因此GH与MN异面.所以图(2),(4)中GH与MN异面.答案:(2)(4)13.求证:两两相交且不过同一点的四条直线必在同一平面内.证明:(1)如图所示,设直线a、b、c相交于点O,直线d和a、b、c分别相交于A、B、C三点,直线d和点O确定平面α,由O∈平面α,A∈平面α,O∈直线a,A∈直线a,知直线a⊂平面α.同理,b⊂平面α,c⊂平面α,故直线a、b、c、d共面于α.(2)如图所示,设直线a、b、c、d两两相交,且任何三线不共点,交点分别是M、N、P、Q、R、G.由直线a∩b=M,知直线a和b确定平面α.由a∩c=N,b∩c=Q,知点N、Q都在平面α内.故cα,同理可证dα.所以直线a、b、c、d共面于α.由(1)(2)可知,两两相交且不过同一点的四条直线必在同一平面内.14.如图所示,在正方体ABCD-A1B1C1D1中,E为AB的中点,F为AA1的中点.求证:CE,D1F,DA三线交于一点.证明:连接EF,D1C,A1B,因为E 为AB 的中点,F 为AA 1的中点,所以EF 綊12A 1B .又因为A 1B 綊D 1C ,所以EF 綊12D 1C ,所以E ,F ,D 1,C 四点共面, 可设D 1F ∩CE =P .又D 1F ⊂平面A 1D 1DA ,CE ⊂平面ABCD ,所以点P 为平面A 1D 1DA 与平面ABCD 的公共点. 又因为平面A 1D 1DA ∩平面ABCD =DA ,所以据公理3可得P ∈DA ,即CE ,D 1F ,DA 三线交于一点. 课时作业5 公理4及定理|基础巩固|(25分钟,60分)一、选择题(每小题5分,共25分)1.若直线a ∥b ,b ∩c =A ,则a 与c 的位置关系是( ) A .异面 B .相交C .平行D .异面或相交解析:a 与c 不可能平行,否则由a ∥b ,得b ∥c 与b ∩c =A 矛盾.故选D. 答案:D2.若∠AOB =∠A 1O 1B 1,且OA ∥O 1A 1,OA 与O 1A 1方向相同,则下列结论正确的是( )A .OB ∥O 1B 1且方向相同 B .OB ∥O 1B 1,方向可能不同C .OB 与O 1B 1不平行D .OB 与O 1B 1不一定平行解析:在空间中两角相等,角的两边不一定平行,即定理的逆命题不一定成立.故选D.答案:D 3.(2017·安徽宿州十三校联考)在正方体ABCD -A 1B 1C 1D 1的所有面对角线中,与AB 1成异面直线且与AB 1成60°的有( )A .1条B .2条C .3条D .4条 解析:如图,△AB 1C 是等边三角形,所以每个内角都为60°,所以面对角线中,所有与B 1C 平行或与AC 平行的直线都与AB 1成60°角.所以异面的有2条.又△AB 1D 1也是等边三角形,同理满足条件的又有2条,共4条,选D. 答案:D4.如图,在四面体S -ABC 中,G 1,G 2分别是△SAB 和△SAC 的重心,则直线G 1G 2与BC 的位置关系是( )A .相交B .平行C .异面D .以上都有可能解析:连接SG 1,SG 2并延长,分别与AB ,AC 交于点M ,N ,连接MN ,则M ,N 分别为AB ,AC 的中点,由重心的性质,知SG 1SM =SG 2SN,∴G 1G 2∥MN .又M ,N 分别为AB ,AC的中点,∴MN ∥BC ,再由平行公理可得G 1G 2∥BC ,故选B.答案:B5.如图所示,在三棱柱ABC -A 1B 1C 1中,AA 1⊥底面ABC ,AB =BC =AA 1,∠ABC =90°,点E ,F 分别是棱AB ,BB 1的中点,则直线EF 和BC 1所成的角是( )A .45°B .60°C .90°D .120°解析:连接AB 1,易知AB 1∥EF ,连接B 1C ,B 1C 与BC 1交于点G ,取AC 的中点H ,连接GH ,则GH ∥AB 1∥EF .设AB =BC =AA 1=a ,连接HB ,在三角形GHB 中,易知GH=HB =GB =22a ,故所求的两直线所成的角即为∠HGB =60°.答案:B二、填空题(每小题5分,共15分)6.不共面的四点可以确定________个平面.解析:任何三点都可以确定一个平面,从而可以确定4个平面.答案:47.用一个平面去截一个正方体,截面可能是________.①三角形;②四边形;③五边形;④六边形.解析:(注:这儿画了其中的特例来说明有这几种图形)答案:①②③④8.如图,在正方体AC1中,AA1与B1D所成角的余弦值是________.解析:因为B1B∥A1A,所以∠BB1D就是异面直线AA1与B1D所成的角,连接BD.在Rt△B1BD中,设棱长为1,则B1D= 3.cos∠BB1D=BB1B1D=13=33.所以AA1与B1D所成的角的余弦值为3 3.答案:3 3三、解答题(每小题10分,共20分)9.在三棱柱ABC-A1B1C1中,M,N,P分别为A1C1,AC和AB的中点.求证:∠PNA1=∠BCM.证明:因为P,N分别为AB,AC的中点,所以PN∥BC.①又因为M,N分别为A1C1,AC的中点,所以A1M綊NC.所以四边形A1NCM为平行四边形,于是A1N∥MC.②由①②及∠PNA1与∠BCM对应边方向相同,得∠PNA1=∠BCM.10.在正方体ABCD-A1B1C1D1中,(1)求AC 与A 1D 所成角的大小;(2)若E ,F 分别为AB ,AD 的中点,求A 1C 1与EF 所成角的大小. 解析:(1)如图所示,连接B 1C ,AB 1,由ABCD -A 1B 1C 1D 1是正方体,易知A 1D ∥B 1C ,从而B 1C 与AC 所成的角就是AC 与A 1D 所成的角. ∵AB 1=AC =B 1C , ∴∠B 1CA =60°.即A 1D 与AC 所成的角为60°.(2)如图所示,连接BD ,在正方体ABCD -A 1B 1C 1D 1中, AC ⊥BD ,AC ∥A 1C 1,∵E ,F 分别为AB ,AD 的中点, ∴EF ∥BD ,∴EF ⊥AC . ∴EF ⊥A 1C 1.即A 1C 1与EF 所成的角为90°. |能力提升|(20分钟,40分)11.(2017·江西师大附中月考)已知a 和b 是成60°角的两条异面直线,则过空间一点且与a 、b 都成60°角的直线共有( )A .1条B .2条C .3条D .4条解析:把a 平移至a ′与b 相交,其夹角为60°. 60°角的补角的平分线c 与a 、b 成60°角. 过空间这一点作直线c 的平行线即满足条件. 又在60°角的“平分面”上还有两条满足条件,选C. 答案:C 12.(2017·江西新余一中月考)如图所示,在空间四边形ABCD 中,E ,H 分别为AB ,AD 的中点,F ,G 分别是BC ,CD 上的点,且CF CB =CG CD =23,若BD =6 cm ,梯形EFGH 的面积为28 cm 2,则平行线EH ,FG 间的距离为________.解析:EH =3,FG =6×23=4,设EH ,FG 间的距离为h ,则S 梯形EFGH =(EH +FG )h2=28,得h =8 (cm).答案:8 cm 13.在如图所示的正方体ABCD -A 1B 1C 1D 1中,E ,F ,E 1,F 1分别是棱AB ,AD ,B 1C 1,C 1D 1的中点,求证:(1)EF 綊E 1F 1; (2)∠EA 1F =∠E 1CF 1.证明:(1)连接BD ,B 1D 1, 在△ABD 中,因为E ,F 分别为AB ,AD 的中点,所以EF 綊12BD .同理,E 1F 1綊12B 1D 1.在正方体ABCD -A 1B 1C 1D 1中,因为A 1A 綊B 1B ,A 1A 綊D 1D ,所以B 1B 綊D 1D .所以四边形BDD 1B 1是平行四边形,所以BD 綊B 1D 1. 所以EF 綊E 1F 1.(2)取A 1B 1的中点M ,连接BM ,F 1M .因为MF 1綊B 1C 1,B 1C 1綊BC ,所以MF 1綊BC . 所以四边形BCF 1M 是平行四边形.所以MB ∥CF 1.因为A 1M 綊EB ,所以四边形EBMA 1是平行四边形. 所以A 1E ∥MB ,所以A 1E ∥CF 1.同理可证:A 1F ∥E 1C .又∠EA 1F 与∠F 1CE 1两边的方向均相反, 所以∠EA 1F =∠E 1CF 1.14.如图,P 是△ABC 所在平面外一点,D ,E 分别是△P AB 和△PBC 的重心.求证:DE ∥AC ,DE =13AC .证明:如图,连接PD ,PE 并延长分别交AB ,BC 于M ,N .因为D ,E 分别是△P AB ,△PBC 的重心,所以M ,N 分别是AB ,BC 的中点,连接。
高三数学一轮复习课时作业(36)空间几何体的结构特征及三视图和直观图 理 北师大版
[时间:45分钟 分值:100分]基础热身1.有一个几何体的三视图如图K36-1所示,这个几何体应是一个 ( )K36-1A .棱台B .棱锥C .棱柱D .都不对2.如图K36-2所示几何体各自的三视图中,有且仅有两个视图相同的是( )K36-2A .①②B .①③C .①④D .②④3.一个几何体的主视图和左视图如图K36-3所示,其中主视图的底边长为1,左视图的底边长为3、高为2,则这个空间几何体俯视图的面积是( )A .2B .3 C.72 D .4图K364.已知三棱锥的俯视图与左视图如图K36-4,俯视图是边长为2的正三角形,左视图是有一直角边为2的直角三角形,则该三棱锥的主视图可能为( )K36-K36-能力提升5.将正三棱柱截去三个角(如图K36-6(1)所示A 、B 、C 分别是△GHI 三边的中点)得到的几何体如图K36-6(2),则该几何体按图(2)所示方向的左视图(或称左视图)为( )-6图K36-6.[2011·浙江卷] 若某几何体的三视图如图K36-8所示,则这个几何体的直观图可以是( )图K36-8图K36-97.[2011·江西卷] 将长方体截去一个四棱锥,得到的几何体如图K36-10所示,则该几何体的左视图为( )图K36-10图K36-11 8.某几何体的三视图如图K36-12所示,那么这个几何体是( )-12A.三棱锥 B.四棱锥C.四棱台 D.三棱台9.某几何体的一条棱长为m,在该几何体的主视图中,这条棱的投影是长为7的线段,在该几何体的左视图与俯视图中,这条棱的投影分别是长为6和5的线段,则m的值为( )A.3 B.2 3 C.4 D.2 510.如果一个几何体的三视图如图K36-13所示,其中主视图中△ABC是边长为2的正________.-1311.[2011·潍坊二模] 一个平面四边形的斜二测画法的直观图是一个边长为a的正方形,则原平面四边形的面积等于________.12.[2011·惠州模拟] 已知一几何体的三视图如图K36-14,主视图和左视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,这些几何形体是(写出所有正确结论的编号)________.①矩形;②不是矩形的平行四边形;③有三个面为直角三角形,有一个面为等腰三角形的四面体;-1413.一个几何体的主视图和左视图如图K36-15所示,其中主视图的底边长为1,左视图的底边长为3、高为2,则这个空间几何体俯视图的面积是________.K3614.(10分)已知,如图K36-16是一个空间几何体的三视图.(1)该空间几何体是如何构成的?(2)画出该几何体的直观图;(3)求该几何体的表面积和体积.15.(13分)有一块多边形菜地,它的水平放置的平面图形的斜二测直观图是直角梯形(如图K36-17所示),∠A′B′C′=45°,D′C′⊥A′D′,A′B′=A′D′=1 m,若平均每1 m2菜地所产生的经济效益是300元,则这块菜地所产生的总经济效益是多少元?(精确到1元)难点突破16.(12分)一个几何体的三视图如图K36-18所示,其中主视图和左视图是腰长为6的两个全等的等腰直角三角形.(1)请画出该几何体的直观图,并求出它的体积;(2)用多少个这样的几何体可以拼成一个棱长为6的正方体ABCD-A1B1C1D1?如何组拼?试证明你的结论;(3)在(2)的情形下,设正方体ABCD-A1B1C1D1的棱CC1的中点为E, 求平面AB1E与平面ABC所成锐二面角的余弦值.K36-18课时作业 (三十六)【基础热身】1.A [解析] 根据三视图,这个空间几何体是棱台.2.D [解析] 正方体的三个视图都相同,而三棱台的三个视图各不相同,正确答案为D.3.B [解析] 这是一个将一个侧面水平放置的三棱柱,其俯视图如图,俯视图是一个边长分别为1,3的矩形,故其面积为3.4.C [解析] 2,主视图和俯视图“长对正”,故主视图的底面边长为2,根据左视图中的直角说明这个空间几何体最前面的面垂直于底面,这个面遮住了后面的一个侧棱,综合这些可知,这个空间几何体的主视图可能是C.【能力提升】5.A [解析] 截前的左视图是一个矩形,截后改变的只是B ,C ,F 方向上的.6.B [解析] 由主视图可排除A ,C ;由左视图可判断该几何体的直观图是B.7.D [解析] 被截去的四棱锥的三条可见侧棱中有两条为正方体的面对角线,它们在右侧面上的投影与右侧面(正方形)的两条边重合,另一条为正方体的体对角线,它在右侧面上的投影与右侧面的对角线重合,对照各图及对角线方向,只有选项D 符合.8.B [解析] 由所给三视图与直观图的关系,可以判定对应的几何体为如图所示的四棱锥,且PA ⊥面ABCD ,AB ⊥BC ,BC ∥AD.9.A [解析]a 2+c 2=7,b 2+c 2=6,a 2+b 2= 5⇒a 2+b 2+c 2=9,所以对角线的长为a 2+b 2+c 2=3.∴选A.10.32[解析] 根据三视图的信息可以知道相应的空间几何体是一个正六棱锥,结合数据可知其底面正六边形的边长为1,棱锥的高为h = 3.由于三视图中“宽相等”,那么左视图中的三角形的底边边长与俯视图中正六边形的高相等,可得其长度为3,则该几何体的左视图的面积为S =12×3×3=32. 11.22a 2[解析] 一个平面图形的面积S 与它的直观图的面积S ′之间的关系是S ′=24S ,而直观图面积S ′=a 2.所以原平面四边形的面积为a 224=22a 2. 12.①③④ [解析] 如图所示长方体为几何体的直观图.当选择的四个点为A 、B 、C 、D当选择B 、A 、B 1、C 时,可知③正确;当选择A 、B 、D 、D 1时,可知④正确.13.3 [解析] 这是一个将一个侧面水平放置的三棱柱,其俯视图如图.俯视图是一个边长分别为1,3的矩形,故其面积为3.14.[解答] (1)2,高为1的长方体,上半部分是一个底面各边长为2,高为1的正四棱锥.(2)按照斜二测画法可以得到其直观图,如图.(3)由题意可知,该几何体′B ′C ′D ′与正四棱锥P -A ′B ′C ′D ′构成的简单几何体.由图易得:AB =AD =2,AA ′=1,PO ′=1,取A ′B ′中点Q ,连接PQ ,从而PQ =PO ′2+O ′Q 2=12+12=2,所以该几何体表面积S =12(A ′B ′+B ′C ′+C ′D ′+D ′A ′)PQ +(A ′B ′+B ′C ′+C ′D ′+D ′A ′)AA ′+AB ·AD =42+12.体积V =2×2×1+13×2×2×1=163. 15.[解答] 在直观图中,过A ′点作A ′E ⊥B ′C ′,垂足为E ,则在Rt △A ′B ′E 中,A ′B ′=1 m ,∠A ′B ′E =45°,∴B ′E =22m. 而四边形A ′EC ′D ′为矩形,A ′D ′=1 m ,∴B ′C ′=B ′E +EC ′=⎝ ⎛⎭⎪⎫22+1m. 由此可还原图形,如图所示,在原图形中,AD =1 m ,AB =2 m ,BC =⎝ ⎛⎭⎪⎫22+1m ,且AD ∥BC ,AB ⊥BC ,∴这块菜地的面积为S =12(AD +BC )·AB =12×1+1+22×2=⎝⎛⎭⎪⎫2+22(m 2), 所以这块菜地所产生的总的经济效益是300S ≈300(2+0.707)=812.1≈812(元).【难点突破】16.[解答] (1)该几何体的直观图如图(1)所示,它是有一条侧棱垂直于底面的四棱锥.其中底面ABCD 是边长为6的正方形,高为CC 1=6,故所求体积是V =13×62×6=72. (2)依题意,正方体的体积是原四棱锥体积的3倍,故用3个这样的四棱锥可以拼成一个棱长为6的正方体,其拼法如图(2)所示.证明:∵面ABCD 、面ABB 1A 1、面AA 1D 1D 为全等的正方形,于是VC 1-ABCD =VC 1-ABB 1A 1=VC 1-AA 1D 1D ,故所拼图形成立.(3)设B 1E ,BC 的延长线交于点G ,连接GA ,在底面ABC 内作BH ⊥AG ,垂足为H ,连接HB 1,如图(2),则B 1H ⊥AG ,故∠B 1HB 为平面AB 1E 与平面ABC 所成锐二面角或其补角的平面角.在Rt △ABG 中,AG =180,则BH =6×12180=125,B 1H = BH 2 + BB 21 = 185, cos ∠B 1HB =HB HB 1=23. 故平面AB 1E 与平面ABC 所成锐二面角的余弦值为23.。
数学北师大版高中必修2立体几何---三视图

(A)
(B)
(C)
(D)
正(主)视图
俯(左)视图
(2)如图,已知三棱锥的底面是直角三角形,直角边长分别为3和4,过直角顶 点的侧棱长为4,且垂直于底面,该三棱锥的主视图是( ) z 3
4 4 A. 3 B.
4
4
5
4 x 3 4 y
4 O
C.
D.
(3)将正三棱柱截去三个角(如图1所示 A,B,C 分别是 △GHI 三边的中点)得到几 何体如图2,则该几何体按图2所示方向的侧视图(或称左视图)为( )
6 3 6
(单位:cm)
(6)一空间几何体的三视图如图所示,则该几何体的体积为( 2 3 2 3 A.2π+2 3 B.4π+2 3 C.2π+ D.4π+
3 3
2 2
)
2
2 正(主)视图
2 侧(左)视图
俯视图
4、直观图与三视图综合运用
(1)某高速公路收费站入口处的安全标识墩如图1所示.墩的上半部分是正四棱 锥 P EFGH ,下半部分是长方体 ABCD EFGH .图2、图3分别是该标识墩的 正(主)视图和俯视图. (Ⅰ)请画出该安全标识墩的侧(左)视图; (Ⅱ)求该安全标识墩的体积; (Ⅲ)证明:直线 BD 平面 PEG . (
1 主视图 1
左视图
2
(3)如图,网格纸的小正方形的边长是1,在其上用粗线画出了某多面体的三视 图,则这个多面体最长的一条棱的长为______. (4)图4中的三个直角三角形是一个体积为20cm 的几何体的 三视图,则 h . h cm
5 正视图 6
侧视图
1
1
俯视图
3
(单位:cm) 俯视图
高三北师大文科数学课时作业 第讲 空间几何体的结构及三视图和直观图 含解析

课时作业(三十七)[第37讲空间几何体的结构及三视图和直观图](时间:45分钟分值:100分)基础热身1.下列命题正确的是()A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥D.棱台各侧棱的延长线交于一点2.两条不平行的直线,其平行投影不可能是()A.两条平行直线B.一点和一条直线C.两条相交直线D.两个点3.[2012·广东六校联考] 沿一个正方体三个面的对角线截得的几何体如图K37-1所示,则该几何体的左视图为()图K37-1-34.[2012·宜春模拟] 一个体积为123的正三棱柱的三视图如图K37-3所示,则这个三棱柱的左视图的面积为________.能力提升5.[2012·福州模拟] 利用斜二测画法得到的:①三角形的直观图一定是三角形;②正方形的直观图一定是菱形;③等腰梯形的直观图可以是平行四边形;④菱形的直观图一定是菱形.以上结论正确的个数是()A.1个B.2个C.4个D.0个6.图K37-4()图K37-4图K377.如果四棱锥的四条侧棱都相等,就称它为“等腰四棱锥”,四条侧棱称为它的腰,以下四个命题中,假命题是()A.等腰四棱锥的腰与底面所成的角都相等B.等腰四棱锥的侧面与底面所成的二面角都相等或互补C.等腰四棱锥的底面四边形必存在外接圆D.等腰四棱锥的各顶点必在同一球面上8.棱长为1的正方体ABCD-A1B1C1D1的8个顶点都在球O的表面上,E,F分别是棱AA1,DD1的中点,则直线EF被球O截得的线段长为()A.22B.1 C.1+22 D. 29.[2012·佛山一模] 一个简单几何体的主视图、左视图如图K37-6所示,则其俯视图不可能为....:①长方形;②正方形;③圆;④椭圆.其中正确的是()-A.①②B.②③C.③④D10.如图K37-7所示,E,F分别是正方体的面ADD1A1,面BCC1B1的中心,则四边形BFD1E在该正方体的面上的正投影可能是图K37-8中的________.(要求:把可能的图的序号都填上)11.如图K37-9是由大小相同的长方体木块堆成的几何体的三视图,则此几何体共由________块木块堆成.K37-912.[2012·大连、沈阳二联] 如图K37-10所示,一个三棱锥的三视图是三个直角三角形(单位:cm),则该三棱锥的外接球的表面积为________cm2.13.棱长为a的正四面体ABCD的四个顶点均在一个球面上,则此球的半径R=________.14.(10分)[2012·太原模拟] 一个正方体内接于高为40 cm,底面半径为30 cm的圆锥中,求正方体的棱长.15.(13分)在四棱锥P-ABCD中,底面为正方形,PC与底面ABCD垂直,图K37-11为该四棱锥的主视图和左视图,它们是腰长为6 cm的全等的等腰直角三角形.(1)根据图所给的主视图、左视图,画出相应的俯视图,并求出该俯视图的面积;(2)求P A的长.难点突破16.(12分)从一个底面半径和高均为R的圆柱中挖去一个以圆柱上底面为底,下底面中心为顶点的圆锥,得到如图K37-12所示的几何体,如果用一个与圆柱下底面距离等于l课时作业(三十七)【基础热身】1.D [解析] 如果上、下两个面平行,但它们是大小不一样的多边形,即使各面是四边形,那也不能是棱柱,A 错;如图,图中平面ABC ∥平面A 1B 1C 1,但图中的几何体每相邻两个四边形的公共边并不都互相平行,故不是棱柱,B 错;棱锥有一个面是多边形,而棱台是用一个平行于底面的平面去截棱锥而得到的,故C 错,D 对.2.D [解析] 平行投影是两个点的直线一定平行,所以两条不平行的直线,其平行投影不可能是两个点,选D.3.B [解析] 外围轮廓线为正方形,其中截面的一个边的左视图为正方形的一条对角线.4.63 [解析] 左视图的宽为23,即为底面正三角形的高,得底面三角形的边长为4,可求得底面积为43,又体积为123,则可推出三棱柱的高为3,故左视图的面积为6 3.【能力提升】5.A [解析] 由斜二测画法的规则可知①正确;②错误,是一般的平行四边形;③错误,等腰梯形的直观图不可能是平行四边形;而菱形的直观图也不一定是菱形,④也错误.6.C [解析] 根据斜二测画法的规则,将直观图还原,可知选C.7.B [解析] 选项B 由于底面形状未定,仅依靠等腰不能确定B 选项.8.D [解析] 由题知球O 半径为32,球心O 到直线EF 的距离为12,所以直线EF 被球O 截得的线段长d =234-14= 2.9.B [解析] 根据三视图画法规则“长对正,高平齐、宽相等”,俯视图应与主视图同长为3,与左视图同宽为2,故一定不可能是圆和正方形.故选B.10.②③ [解析] 由正投影的定义,四边形BFD 1E 在面AA 1D 1D 与面BB 1C 1C 上的正投影是图③;其在面ABB 1A 1与面DCC 1D 1上的正投影是图②;其在面ABCD 与面A 1B 1C 1D 1上的正投影也是②,故①④错误.11.5 [解析] 根据题意可知,几何体的最底层有4块长方体,第2层有1块长方体,一共5块.12.29π [解析] 根据三视图可知三棱锥的三侧棱两两垂直,长度分别为a =2,b =3,c =4,将其补成棱长为2,3,4的长方体,则长方体的体对角线长即为所求的外接球的直径,故有2R =22+32+42=29,因此球的表面积为S =4πR 2=29π cm 2.13.64a [解析] 如图所示,设正四面体ABCD 内接于球O ,由D 点向底面ABC 作垂线,垂足为H ,连接AH ,OA ,则可求得AH =33a ,DH在Rt △AOH 中,⎝⎛⎭⎫33a 2+⎝⎛⎭⎫63a -R 2=R 2,解得R =64a .14.解:x cm ,则OC =22x ,∴22x 30=40-x 40,解得x =120(3-22),∴正方体的棱长为120(3-22) cm.15.解:(1)该四棱锥的俯视图如下(内含对角线),为边长为6 cm 的正方形,如图,其面积为36 cm 2.(2)由左视图可求得PD =PC 2+CD 262.由主视图可知AD =6,且AD ⊥PD 所以在Rt △APD 中,P A =PD 2+AD 2=(62)2+62=6 3 cm. 【难点突破】16.解:O 1C =R ,设圆锥截面半径O 1D =x , ∵OA =AB =R ,∴△OAB 为等腰直角三角形. 又CD ∥OA ,∴BC =CD =R -x , 又BC =R -l ,故x =l ,截面面积为S =πR 2-πl 2=π(R 2-l 2).。
2021年高考数学 3.3三角函数的图像与性质课时提升作业 理 北师大版

2021年高考数学 3.3三角函数的图像与性质课时提升作业理北师大版一、选择题1.(xx·福州模拟)已知函数f(x)=3cos(2x-)在[0,]上的最大值为M,最小值为m,则M+m等于( )(A)0 (B)3+(C)3- (D)2.(xx·岳阳模拟)函数y=-cos2x+的递增区间是( )(A)(kπ,kπ+)(k∈Z)(B)(kπ+,kπ+π)(k∈Z)(C)(2kπ,2kπ+π)(k∈Z)(D)(2kπ+π,2kπ+2π)(k∈Z)3.已知函数f(x)=sin(2x-),若存在a∈(0,π),使得f(x+a)=f(x-a)恒成立,则a的值是( )(A) (B) (C) (D)4.(xx·咸阳模拟)已知函数y=Asin(ωx+φ)在同一周期内,当x=时有最大值2,当x=0时有最小值-2,那么函数的解析式为( )(A)y=2sinx (B)y=2sin(3x+)(C)y=2sin(3x-) (D)y=sin3x5.(xx·景德镇模拟)下列命题正确的是( )(A)函数y=sin(2x+)在区间(-,)内单调递增(B)函数y=cos4x-sin4x的最小正周期为2π(C)函数y=cos(x+)的图像是关于点(,0)成中心对称的图形(D)函数y=tan(x+)的图像是关于直线x=成轴对称的图形6.(xx·铜川模拟)已知函数f(x)=f(π-x),且当x∈(-,)时,f(x)=x+sinx,设a=f(1),b=f(2),c=f(3),则( )(A)a<b<c (B)b<c<a (C)c<b<a (D)c<a<b7.函数y=2sin(2x+)的图像关于点P(x0,0)对称,若x0∈[-,0],则x0等于( )(A)- (B)- (C)- (D)-8.函数y=lg(sinx)+的定义域为( )(A)(2kπ,2kπ+](k∈Z) (B)(2kπ,2kπ+](k∈Z)(C)(2kπ,2kπ+](k∈Z) (D)[2kπ,2kπ+](k∈Z)9.(xx·抚州模拟)设f(x)=xsinx,x∈[-,],若f(x1)>f(x2),则( )(A)x1+x2>0 (B)> (C)x1>x2(D)x1<x210.(xx·西安模拟)已知函数y=sin(-2x),则其图像的下列结论中,正确的是( )(A)关于点(-,1)中心对称(B)关于直线x=轴对称(C)向左平移后得到奇函数(D)向左平移后得到偶函数二、填空题11.(xx·宿州模拟)若函数y=a-bsin(4x-)(b>0)的最大值是5,最小值是1,则a2-b2= .12.(能力挑战题)已知直线y=b(b<0)与曲线f(x)=sin(2x+)在y轴右侧依次的三个交点的横坐标成等比数列,则b的值是.13.给出如下五个结论:①存在α∈(0,),使sinα+cosα=;②存在区间(a,b),使y=cosx为减少的而sinx<0;③y=tanx在其定义域内为增加的;④y=cos2x+sin(-x)既有最大值和最小值,又是偶函数;⑤y=sin|2x+|的最小正周期为π.其中正确结论的序号是.14.对于函数f(x)=给出下列四个命题:①该函数是以π为最小正周期的周期函数;②当且仅当x=π+kπ(k∈Z)时,该函数取得最小值-1;③该函数的图像关于x=+2kπ(k∈Z)对称;④当且仅当2kπ<x<+2kπ(k∈Z)时,0<f(x)≤.其中正确命题的序号是.(请将所有正确命题的序号都填上)三、解答题15.(能力挑战题)已知a>0,函数f(x)=-2asin(2x+)+2a+b,当x∈[0,]时,-5≤f(x)≤1.(1)求常数a,b的值.(2)设g(x)=f(x+)且lgg(x)>0,求g(x)的单调区间.答案解析1.【解析】选C.由x∈[0,]得2x-∈[-,],故M=f()=3cos 0=3,m=f()=3cos=-,故M+m=3-.2.【解析】选A.由2kπ<2x<2kπ+π,k∈Z得,kπ<x<kπ+,k∈Z.所以函数y=-cos2x+的递增区间是(kπ,kπ+)(k∈Z).3.【解析】选D.因为函数满足f(x+a)=f(x-a),所以函数是周期函数,且周期为2a,又a∈(0,π),所以2a=,所以a=.【方法技巧】对周期函数的理解(1)周期函数定义中的等式:f(x+T)=f(x)是定义域内的恒等式,即对定义域内的每个x值都成立,若只是存在个别x满足等式的常数T不是周期.(2)每个周期函数的定义域是一个无限集,其周期有无穷多个,对于周期函数y=f(x),T是周期,则kT(k∈Z,k≠0)也是周期,但并非所有周期函数都有最小正周期.【变式备选】已知函数f(x)=Asin(ωx+φ)(A>0,ω>0)满足条件f(x+)+f(x)=0,则ω的值为( )(A)2π(B)π (C) (D)【解析】选A.由f(x+)+f(x)=0得f(x+)=-f(x),所以f(x+1)=f(x),故函数的周期是1,又由=1得ω=2π.4.【解析】选C.由条件知A=2,=,所以T=,因此ω==3,所以f(x)=2sin(3x+φ).把x=0,y=-2代入上式得-2=2sinφ,得sinφ=-1,所以φ=2kπ-(k∈Z),因此f(x)=2sin(3x+2kπ-)(k∈Z)=2sin(3x-).5.【解析】选 C.对于A,当x∈(-,)时,2x+∈(-,),故函数y=sin(2x+)不单调,故A错误;对于B,y=cos4x-sin4x=(cos2x-sin2x)(cos2x+sin2x)=cos2x-sin2x=cos2x,最小正周期为π,故错误;对于C,当x=时,cos(+)=0,所以(,0)是对称中心,故C正确;对于D,正切函数的图像不是轴对称图形,故错误.6.【思路点拨】利用函数y=f(x)的单调性比较.【解析】选D.由条件知f(x)=x+sinx在(-,)上是增加的,又b=f(2)=f(π-2),c=f(3)=f(π-3),而1,π-2,π-3∈(-,),且π-3<1<π-2,所以f(π-3)<f(1)<f(π-2),即c<a<b.7.【解析】选B.由题意可知2x0+=kπ,k∈Z,故x0=-,k∈Z,故k=0时,x0=-∈[-,0],故选B.8.【解析】选C.由得所以,2kπ<x≤2kπ+,k∈Z,故函数的定义域为(2kπ,2kπ+](k∈Z).9.【思路点拨】根据f(x)=xsinx的奇偶性和在[0,]上的单调性求解.【解析】选B.由f(-x)=-xsin(-x)=xsinx=f(x)知,函数y=f(x)为偶函数.又f'(x)=sinx+xcosx,当x∈(0,)时,f'(x)>0,故f(x)在[0,]上是增加的.因为f(x1)>f(x2),故f(|x1|)>f(|x2|),所以|x1|>|x2|,因此>.10.【解析】选C.对于A,由题意知函数图像的对称中心应在x轴上,故A不正确.对于B,由-2x=kπ+(k∈Z),得x=--(k∈Z),故B不正确.对于C,将函数向左平移后得到f(x)=sin[-2(x+)]=sin(-2x)=-sin2x,为奇函数,故C正确.从而D不正确.11.【解析】∵-1≤sin(4x-)≤1,b>0,∴-b≤-bsin(4x-)≤b,∴a-b≤a-bsin(4x-)≤a+b,由题意知解得∴a2-b2=5.答案:512.【思路点拨】化简函数式之后数形结合可解.【解析】设三个交点的横坐标依次为x1,x2,x3,由图及题意有:f(x)=sin(2x+)=cos2x.且解得x2=,所以b=f()=-.答案:-13.【解析】①中α∈(0,)时,如图,由三角函数线知OM+MP>1,得sinα+cos α>1,故①错.②由y=cosx的减区间为(2kπ,2kπ+π)(k∈Z),故sinx>0,因而②错.③正切函数的单调区间是(kπ-,kπ+),k∈Z.故y=tanx在定义域内不单调,故③错.④y=cos2x+sin(-x)=cos2x+cosx=2cos2x+cosx-1=2(cosx+)2-.y max=2,y min=-.故函数既有最大值和最小值,又是偶函数,故④正确.⑤结合图像可知y=sin|2x+|不是周期函数,故⑤错.答案:④14.【解析】画出函数f(x)的图像.由图像可得函数的最小正周期为2π,故①错误;当x=π+2kπ(k∈Z)或x=+ 2kπ(k∈Z)时,函数取得最小值-1,故②不正确;结合图像可得③④正确.答案:③④15.【解析】(1)∵x∈[0,],∴2x+∈[,].∴sin(2x+)∈[-,1],∴-2asin(2x+)∈[-2a,a].∴f(x)∈[b,3a+b].又∵-5≤f(x)≤1,∴b=-5,3a+b=1,因此a=2,b=-5.(2)由(1)得a=2,b=-5,∴f(x)=-4sin(2x+)-1,g(x)=f(x+)=-4sin(2x+)-1=4sin(2x+)-1,又由lgg(x)>0得g(x)>1,∴4sin(2x+)-1>1,∴sin(2x+)>,∴2kπ+<2x+<2kπ+,k∈Z,其中当2kπ+<2x+≤2kπ+,k∈Z时,g(x)是增加的,即kπ<x≤kπ+,k∈Z.∴g(x)的递增区间为(kπ,kπ+],k∈Z.又∵当2kπ+<2x+<2kπ+,k∈Z时,g(x)是减少的,即kπ+<x<kπ+,k∈Z.∴g(x)的递减区间为(kπ+,kπ+),k∈Z.Q21616 5470 呰 21254 5306 匆527505 6B71 歱40369 9DB1 鶱N38945 9821 頡37243 917B 酻Y29737 7429 琩`W。
2020-2021学年高中数学北师大版必修二课时分层作业:1.3三视图

温馨提示:此套题为Word版,请按住Ctrl,滑动鼠标滚轴,调节合适的观看比例,答案解析附后。
关闭Word文档返回原板块。
课时分层作业三三视图一、选择题(每小题5分,共25分)1.如图所示的一个几何体,它的俯视图是( )【解析】选C.根据三视图的画法及特点可知C正确.2.某几何体的主视图和左视图均如图所示,则该几何体的俯视图不可能是 ( )【解析】选C.A是两个圆柱的组合体,B是一个圆柱和一个四棱柱的组合体,C选项的主视图与左视图不相同,D可以是一个底面为等腰直角三角形的直三棱柱与一个四棱柱的组合体.3.已知某空间几何体的三视图如图所示,则此几何体为( )A.圆台B.四棱锥C.四棱柱D.四棱台【解析】选D.由主视图和左视图可以判断一定为棱台或圆台,又由俯视图可知其一定为棱台且为四棱台.4.如图所示,表示的是组合在一起的模块,在四个选项中,是这个模块的俯视图的是 ( )【解析】选A.两个组合的模块,上面为圆锥,下面为长方体,所以选A.5.若某几何体的三视图如图所示,则此几何体的直观图是 ( )【解析】选A.结合选项逐一排除,从主视图看选项C不正确,从左视图看B错,D错,对于A三视图均正确.【补偿训练】如图所示,五棱柱的左视图应为( )【解析】选B.从五棱柱左面看,是2个矩形,上面的小一点,故选B.二、填空题(每小题5分,共15分)6.如图所示的几何体中,主视图与左视图都是长方形的是_________.【解析】②的左视图是三角形,⑤的主视图和左视图都是等腰梯形,其余的都符合条件.答案:①③④7.如图为长方体木块堆成的几何体的三视图,则组成此几何体的长方体木块共有_________块.【解析】由主视图可知有两列,由俯视图可知有两排,再结合左视图可得,几何体共分两层,下面一层3块,上面一层1块,如图所示,其中小长方形中的数字表示此位置木块的块数.答案:48.如图所示是一个圆锥的三视图,则该圆锥的高为_________cm.【解析】由三视图知,圆锥的母线长为3 cm,底面圆的直径为3 cm,所以圆锥的轴截面也是边长为 3 cm的等边三角形,所以圆锥的高为=(cm).答案:三、解答题(每小题10分,共20分)9.画出如图所示物体的三视图.【解析】三视图如图所示.10.如图是简单组合体的三视图,想象它们表示的组合体的结构特征,并画出其示意图.【解析】简单组合体的示意图如图:一、选择题(每小题5分,共20分)1.一个几何体的三视图如图所示,则该几何体的直观图可以是( )【解析】选D.由俯视图是圆环可排除A,B,C,进一步将三视图还原为几何体,可得选项D.2.将一个长方体沿相邻三个面的对角线截去一个棱锥,得到的几何体的主视图与俯视图如图所示,则该几何体的左视图为( )【解析】选B.由几何体的主视图和俯视图可知该几何体如图所示,故其左视图为B中的图像.3.如图所示为一个简单几何体的三视图,则其对应的几何体是( )【解析】选A.根据主视图中的三条对角线均为实线,结合三个观察方向,知A项正确.4.将正方体(如图(1)所示)截去两个三棱锥,得到如图(2)所示的几何体,则该几何体的左视图为( )【解析】选B.还原正方体后,将D1,D,A三点分别向正方体右侧面作垂线.D1A的射影为C1B,且为实线,B1C被遮挡应为虚线.【补偿训练】一个正方体截去两个角后所得几何体的主视图、左视图如图所示,则其俯视图为( )【解析】选C.依题意可知该几何体的直观图如图所示,故其俯视图应为C.二、填空题(每小题5分,共15分)5.桌上摆着一个由若干个相同正方体组成的几何体,其主视图和左视图如图所示,这个几何体最多可以由_________个这样的正方体组成.【解析】由于物体对视线的遮挡,只知道两种视图是无法确定这一物体的摆放情况的,所以从下数第一层最多9个,第二层最多4个,共13个.答案:136.一个几何体的主视图为一个三角形,则这个几何体可能是下列几何体中的_________(填入所有可能的几何体前的编号).①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.【解析】三棱锥、四棱锥和圆锥的主视图都是三角形.当三棱柱的一个侧面平行于水平面,底面对着观测者时其主视图是三角形,四棱柱、圆柱无论怎样放置,其主视图都不可能是三角形.答案:①②③⑤7.已知某组合体的主视图与左视图相同(其中AB=AC,四边形BCDE为矩形),则该组合体的俯视图可以是图中的_________.(把你认为所有正确图像的序号都填上)【解析】由主视图和左视图可知几何体为锥体和柱体的组合体.①若几何体为圆柱与圆锥的组合体,则俯视图为③;②若几何体为棱柱与圆锥的组合体,则俯视图为④;③若几何体为棱柱与棱锥的组合体,则俯视图为①;④若几何体为圆柱与棱锥的组合体,则俯视图为②.答案:①②③④三、解答题(每小题10分,共20分)8.说出下面的三视图表示的几何体的结构特征.【解析】几何体为三棱台,结构特征如图:9.如图所示,某一种型号的滚筒洗衣机抽象出来的几何体,数据如图中所示(单位:cm),试画出它的三视图.【解析】这个几何体是由一个长方体和一个圆柱体构成的.三视图如图所示:关闭Word文档返回原板块莘莘学子,最重要的就是不要去看远方模糊的,而要做手边清楚的事。
北师大版高中数学必修三视图课件(33张)

北师大版高中数学 必修三视图 课件(33张)
俯视图
主视图与左视图 高平齐 俯视图与左视图 宽相等
※三视图能反映物体真实的形状和长、宽、高。
复习巩固 几个常见的简单旋转体的三视图
圆柱 圆锥
圆台
球
复习巩固
主视图 左视图
主视图 左视图
俯视图
·
俯视图
圆台
俯
左
主
主视图 左视图
俯视图
圆台
左
俯 主视图 左视图
俯视图
同一物体放置的位置或者观察的角 度不同,所画的三视图可能不同。
北师大版高中数学 必修2 第一章
§3 三 视 图
新课引入
前面 侧面 上面
建国70周年阅兵视频
探究新知
在立体几何中,一般从三个方向研究物体
1、从正前方研究物体的正投影图 —— 主视图 也称为正视图
2、从正左方研究物体的正投影图 —— 左视图 也称为侧视图
3、从正上方研究物体的正投影图 —— 俯视图
北师大版高中数学 必修三视图 课件(33张)
北师大版高中数学 必修三视图 课件(33张)
横看成岭侧成峰,远近高低各不同。 不识庐山真面目,只缘身在此山中。
——苏轼《题西林壁》
北师大版高中数学 必修三视图 课件(33张)
北师大版高中数学 必修三视图 课件(33张)
作业布置
1、家庭作业:
P18
A组 T1、T2、T3
练习4、画出下面几何体的三视图.
北师大版高中数学 必修三视图 课件(33张)
主视
北师大版高中数学 必修三视图 课件(33张)
练习4、画出下面几何体的三视图.
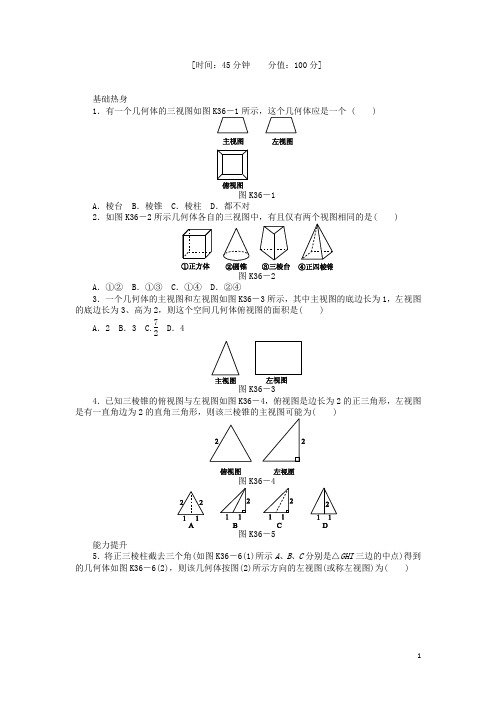
北师大版高一数学下册《三视图》同步习题解析

北师大版高一数学下册《三视图》同步习题解析数学是一个要求大伙儿严谨对待的科目,有时一不小心一个小小的小数点都会阻碍最后的结果。
下文就为三视图同步习题答案,期望大伙儿认真对待。
◆基础训练1.球的三视图是(? )A.三个圆B.三个圆且其中一个包括圆心C.两个圆和一个半圆弧D.以上都不对2.若一个几何体的三视图差不多上正方形,则那个几何体是(? )A.长方体B.正方体C.圆柱D.圆锥3.下列命题正确的是(? )A.三视图是中心投影B.小华观看牡丹花,牡丹花确实是视点C.球的三视图均是半径相等的圆D.阳光从矩形窗子里照耀到地面上,得到的光区仍是矩形4.如图是由四个相同的小立方体堆成的几何体,试指出其余三个平面图形分别是那个物体的哪个视图.5.如图,A是一组立方块,请说出B,C各是什么视图.6.如图,电视台的摄像机1,2,3,4在不同位置拍照了四幅画面,则A•图像是_____号摄像机所拍;B图像是______号摄像机所拍;C图像是_____ _号摄像机所拍;•D图像是_____号摄像机所拍.7.画出下列几何体(尺寸如图所示)的三视图.8.在一个长方体上搁一个圆柱,如图(1)所示,它的主视图,•左视图如图(2)所示,请你补画出它的俯视图.◆提高训练9.一个正六棱柱和长方体如图所示放置,你能说出下面的(a),(b),(c)三个视图分别是哪个视图吗?[来10.如图是正三棱锥,请你画出它的三视图.11.如图是一个圆台及其主视图,你能把它的俯视图和左视图补上吗?•请试一试.12.如图所示,是一个槽形块(它是长方体中间切去一个小三角形块),请你画出它的三视图.[13.已知一个几何体的主视图,俯视图如图,你能补画出它的左视图吗?动手画一画.14.小明在学完了画几何体的三视图的方法后,画出了如图所示的几何体的俯视图,你认为小明画得对吗?假如不对,请你改正;如画得正确,•请你补画它的主视图与左视图.◆拓展训练15.小强把一个由若干个小立方体叠成的几何体的俯视图画成如图所示,每个小方格上的数字表示该位置上重叠的小立方体的个数,请你想一想:•应该如何样画出它的主视图与左视图?请与同伴交流.参考答案1.A?2.B?3.C?4.俯视图,主视图,左视图5.主视图,俯视图?6.3,4,1,2?7.略?8.略9.左视图,俯视图,主视图? 10.略教师范读的是阅读教学中不可缺少的部分,我常采纳范读,让幼儿学习、仿照。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021-2022年高中数学课时作业31.3三视图北师大版
|基础巩固|(25分钟,60分)
一、选择题(每小题5分,共25分)
1.某几何体的正视图和侧视图均如图1所示,则该几何体的俯视图不可能是( )
解析:本题是组合体的三视图问题,由几何体的正视图和侧视图均如图1所示知,原图下面图为圆柱或直四棱柱,上面是圆柱或直四棱柱或下底是直角的三棱柱,A,B,C,都可能是该几何体的俯视图,D不可能是该几何体的俯视图,因为它的正视图上面应为如图的矩形.
答案:D
2.如图所示,甲、乙、丙是三个几何体的三视图,则甲、乙、丙对应的几何体分别为( )
①长方体;②圆锥;③三棱锥;④圆柱.
A.④③②B.①③②
C.①②③ D.④②③
解析:由于甲中的俯视图是圆,则甲对应的几何体是旋转体,又主视图和左视图均是
矩形,所以该几何体是圆柱;易知乙对应的几何体是三棱锥;由丙中的俯视图,可知丙对应的几何体是旋转体,又主视图和左视图均是三角形,所以该几何体是圆锥.答案:A
3.(xx·河北名师俱乐部3月模拟)某几何体的三视图如图所示,记A为此几何体所有棱的长度构成的集合,则( )
A.3∈A B.5∈A
C.26∈A D.43∈A
解析:由三视图可得,该几何体的直观图如图所示,其中底面是边长为4的正方形,AF⊥平面ABCD,AF∥DE,AF=2,DE=4,可求得BE的长为43,BF的长为25,EF的长为25,EC的长为42,故选D.
答案:D
4.如图为某组合体的三视图,则俯视图中的长和宽分别为( )
A.10,4 B.10,8
C.8,4 D.10,5
解析:根据三视图中的“主、俯视图长对正,主、左视图高平齐,俯、左视图宽相等”,可知俯视图的长和主视图的长相等,为2+6+2=10,俯视图的宽与左视图的宽相等,为1
+2+1=4,所以选A.
答案:A
5.(xx·东北四市联考(二))如图,在正方体ABCD-A1B1C1D1中,P是线段CD的中点,则三棱锥P-A1B1A的侧视图为( )
解析:如图,画出原正方体的侧视图,显然对于三棱锥P-A1B1A,B(C)点均消失了,其余各点均在,从而其侧视图为D.
答案:D
二、填空题(每小题5分,共15分)
6.桌上放着一个半球,如图所示,则在它的三视图及右面看到的图形中,有三个图相同,这个不同的图应该是________.
解析:俯视图为圆,主视图与左视图均为半圆.
答案:俯视图
7.
如图,已知正三棱柱ABC-A1B1C1的底面边长为2,高为3,则其左视图的面积为________.解析:由三视图的画法可知,该几何体的左视图是一个矩形,其底面边长为2sin60°=3,高为3,∴面积S=3 3.
答案:3 3
8.(xx·山东安丘市高二上期末)一个几何体的三视图如图所示,其中正视图是边长为2的正三角形,俯视图是正方形,那么该几何体的侧视图的面积是________.
解析:
根据三视图可知该几何体是一个四棱锥,其底面是正方形,侧棱相等,所以这是一个
正四棱锥.其侧视图与正视图是完全一样的正三角形.故其面积为
3
4
×22= 3.
答案: 3
三、解答题(每小题10分,共20分)
9.
试画出如图所示的正四棱台的三视图.
解析:如图.
10.根据图中的三视图想象物体原形,并画出物体的实物草图.
解析:由俯视图并结合其他两个视图可以看出,这个物体是由上面一个正四棱台和下面一个正方体组合而成的,它的实物草图如图所示.
|能力提升|(20分钟,40分)
11.(xx·广东省台山市华侨中学高二上期末)定义:底面是正三角形,侧棱与底面垂直的三棱柱叫做正三棱柱.将正三棱柱截去一个角(如图1所示,M,N分别是AB,BC的中点)得到几何体如图2,则该几何体按图2所示方向的侧视图为( )
解析:N的投影是C,M的投影是AC的中点.对照各图.选D.
答案:D
12.一个几何体的正视图为一个三角形,则这个几何体可能是下列几何体中的________(填入所有可能的几何体前的编号).
①三棱锥;②四棱锥;③三棱柱;④四棱柱;⑤圆锥;⑥圆柱.
解析:三棱锥、四棱锥和圆锥的正视图都是三角形,当三棱柱的一个侧面平行于水平面,底面对着观测者时其正视图是三角形,四棱柱、圆柱无论怎样放置,其正视图都不可能是三角形.
答案:①②③⑤
13.如图所示,是一个长方体截去一个角所得多面体的直观图和它的主视图和左视图(单位:cm).请在正视图下面,按照画三视图的要求画出该多面体的俯视图.
解析:依据三视图的绘图原则,可作出该几何体的俯视图如图.
14.某建筑由相同的若干房间组成,该楼房的三视图如图所示,问:
(1)该楼房有几层?从前往后最多要经过几个房间?
(2)最高一层的房间在什么位置?请画出此楼房的大致形状.
解析:(1)由主视图和左视图可以知道,该楼房有3层;由俯视图知道,从前往后最多要经过3个房间;
(2)从主视图和左视图可以知道,最高一层的房间在左侧的最后一排的房间.楼房大致形状如图所示.
U33364 8254 艔A36043 8CCB 賋\24434 5F72 彲<vf4xI36128 8D20 贠21925 55A5 喥25050 61DA 懚。
