人工智能–多层感知器基础知识解读
100. 什么是深度学习中的多层感知器?

100. 什么是深度学习中的多层感知器?关键信息项:1、深度学习的定义2、多层感知器的概念3、多层感知器的组成结构4、多层感知器的工作原理5、多层感知器的训练方法6、多层感知器的优势7、多层感知器的局限性8、多层感知器的应用领域11 深度学习的定义深度学习是一种基于人工神经网络的机器学习技术,它试图模拟人脑的学习方式,通过构建多层的神经网络模型来自动从数据中提取特征和模式,以实现对复杂数据的准确预测和分类。
111 深度学习的特点深度学习具有以下几个显著特点:1111 强大的表示能力:能够处理高维度、复杂的数据,并自动学习数据中的隐藏特征和模式。
1112 端到端的学习:无需人工进行特征工程,直接从原始数据中学习到最终的预测或分类结果。
1113 大规模数据驱动:通常需要大量的数据来训练模型,以提高模型的性能和泛化能力。
12 多层感知器的概念多层感知器(Multilayer Perceptron,MLP)是一种常见的深度学习模型,它是由多个神经元组成的多层网络结构。
121 神经元的定义神经元是多层感知器的基本组成单元,它接收多个输入信号,并通过一个激活函数对输入进行加权求和和非线性变换,产生输出信号。
122 多层感知器的层次结构多层感知器通常包括输入层、隐藏层和输出层。
输入层接收外部输入数据,隐藏层用于对数据进行特征提取和变换,输出层产生最终的预测或分类结果。
13 多层感知器的组成结构131 输入层输入层的神经元数量取决于输入数据的特征维度,每个神经元对应一个输入特征。
132 隐藏层隐藏层可以有一层或多层,每层包含多个神经元。
隐藏层的神经元数量和层数是模型设计中的关键参数,它们决定了模型的学习能力和复杂度。
133 输出层输出层的神经元数量取决于任务的类型,例如对于二分类问题,输出层通常只有一个神经元;对于多分类问题,输出层的神经元数量等于类别数。
134 连接权重神经元之间通过连接权重进行连接,这些权重在训练过程中不断调整,以优化模型的性能。
多层感知器网络

多层感知器网络
权重优化与训练方法
权重优化与训练方法
权重初始化
1.权重初始化是训练多层感知器网络的重要步骤,可以防止模型在训练初期陷入局部最优解。常见 的初始化方法有随机初始化、Xavier初始化和He初始化等。 2.随机初始化将权重随机初始化为一个小值,可以保证模型在各个方向上的更新幅度大致相同,从 而提高模型的泛化能力。 3.Xavier初始化和He初始化则是针对特定激活函数提出的初始化方法,可以使得各层的激活值在进 行前向传播时能保持相同的分布。
学习率调整
1.学习率是影响多层感知器网络训练效果的重要因素之一,它决定了模型在每次更新时的步长大小 。 2.过大的学习率可能导致模型在训练过程中无法收敛,而过小的学习率则可能导致训练时间过长或 陷入局部最优解。 3.因此,在训练多层感知器网络时,需要根据模型的表现和训练轮数来动态调整学习率,以保证模 型的训练效果和收敛速度。
▪ L1正则化
1.L1正则化是在损失函数中加入模型参数的绝对值,通过约束 参数的范数来控制模型的复杂度。 2.L1正则化可以使一些参数变为零,从而起到特征选择的作用 ,有助于提高模型的泛化能力。 3.L1正则化的优化较为困难,需要使用一些特殊的优化算法, 如坐标下降法和近端梯度下降法等。
过拟合与正则化技术
权重优化与训练方法
▪ 批次归一化
1.批次归一化是一种提高多层感知器网络训练稳定性和收敛速 度的技术,它通过对每个批次的数据进行归一化处理来消除数 据间的差异。 2.批次归一化可以减少模型对初始权重的敏感性,提高模型的 泛化能力,同时也可以减少训练过程中出现的梯度消失和梯度 爆炸等问题。 3.在训练多层感知器网络时,加入批次归一化层可以有效地提 高模型的训练效果和收敛速度。
多层感知器算法原理

多层感知器算法原理多层感知器(Multilayer Perceptron,MLP)是一种前馈结构的人工神经网络,可以对一组输入向量进行非线性映射,从而实现分类或回归等任务。
MLP由多个节点层组成,每一层都与上一层和下一层相连,每个节点都是一个带有非线性激活函数的神经元。
MLP 的学习过程主要依赖于反向传播算法,即通过计算输出误差对网络权重进行反向调整,从而达到最优化的目的。
网络结构MLP的网络结构一般包括三层或以上,分别是输入层、隐藏层和输出层。
输入层接收外部输入的数据,输出层产生网络的预测结果,隐藏层位于输入层和输出层之间,可以有多个,用于提取输入数据的特征。
每一层中的节点都与相邻层中的所有节点相连,每条连接都有一个权重,表示该连接的强度。
每个节点除了接收来自上一层的加权输入外,还有一个偏置项,表示该节点的阈值。
每个节点的输出由其输入和激活函数共同决定,激活函数的作用是引入非线性,增强网络的表达能力。
常用的激活函数有Sigmoid函数、双曲正切函数、ReLU函数等。
学习过程MLP的学习过程主要分为两个阶段,即前向传播和反向传播。
前向传播是指从输入层到输出层逐层计算节点的输出,反向传播是指从输出层到输入层逐层计算节点的误差,并根据误差对权重进行更新。
具体步骤如下:前向传播从输入层开始,将输入数据乘以相应的权重,加上偏置项,得到每个节点的输入。
对每个节点的输入应用激活函数,得到每个节点的输出。
将每个节点的输出作为下一层的输入,重复上述过程,直到达到输出层。
在输出层,根据预测结果和真实标签,计算损失函数,评估网络的性能。
反向传播从输出层开始,根据损失函数对每个节点的输出求导,得到每个节点的误差。
对每个节点的误差乘以激活函数的导数,得到每个节点的梯度。
将每个节点的梯度作为上一层的误差,重复上述过程,直到达到输入层。
在每一层,根据节点的梯度和输入,计算权重的梯度,并根据学习率对权重进行更新。
MLP的学习过程可以采用批量梯度下降、随机梯度下降或小批量梯度下降等优化方法,也可以使用动量、自适应学习率或正则化等技术来提高收敛速度和泛化能力。
36.什么是感知机

什么是多层感知机(MLP)
多层感知机(Multilayer Perceptron,简称MLP)是一种基于人工神经网络的模型结构,常用于解决各种机器学习问题,特别是在深度学习领域中广泛应用。
MLP由多个层组成,包括输入层、多个隐藏层和输出层。
每个层都由多个神经元(或称为节点)组成,神经元之间通过连接权重进行信息传递。
在MLP中,每个神经元接收来自上一层神经元的输入信号,并通过激活函数进行非线性变换后输出。
随着信号从输入层传递到输出层,神经元逐渐提取和组合输入特征,最终得出模型对输入的预测或分类结果。
MLP的训练过程使用反向传播算法(Backpropagation)来自动调整连接权重,以最小化模型预测结果与真实结果之间的误差。
通过反复迭代训练,MLP能够逐渐优化权重,并学习到输入数据的复杂模式和关系。
MLP的优势在于它能够处理非线性模式和高维数据。
通过引入非线性激活函数和多个隐藏层,MLP能够学习到更复杂的特征和模式,从而提高模型的表达能力和预测性能。
此外,MLP还可以应用于各种机器学习任务,包括分类、回归、聚类等。
然而,MLP也存在一些挑战和限制。
其中一个挑战是模型的复杂性和训练过程中的计算开销。
当网络层数较多时,训练过程可能会变得更加困难和耗时。
此外,
MLP对于数据量的需求较高,需要足够的数据样本来进行训练,以避免过拟合等问题。
总的来说,多层感知机是一种基于神经网络的模型结构,通过多个神经元和隐藏层的组合,能够学习到输入数据的复杂模式和特征。
它在深度学习中是一种基础并且有效的模型,为各种机器学习任务提供了一个强大的工具。
多层感知器网络
y(l ) j
j (v j (n))
如果神经元j是第一隐藏层,即l=1,置
y(0) j
(n)
xj
(n)
这里 xj (n)是输入向量X(n)的第j个元素。如果 神经元j在输出层,令
y(L) j
oj
(n)
计算误差信号
ej (n) d j (n) oj (n)
④、反向计算。
计算网络的局域梯度,定义为
这样做是因为设计受到感知器的学习 算法的限制,对于多层网络,当然有更 好的学习算法,比如BP网络学习算法。
1.在学习率知识点中提到的动量常数 在整个计 算中扮演什么样的角色?
2.假设隐藏层神经元个数一定,那么隐藏层的层数 取不同的值时,对于多层感知器的计算能力的影响是 怎样的?
3.动量和学习率参数随着训练迭代次数的增加而调 整(通常是减少的),为什么?
以图2所示两层感知器网络来实现, 其中隐层为随机感知器层(net1),神 经元数目设计为3,其权值和阈值是随机 的,它的输出作为输出层(分类层)的 输入;输出层为感知器层(net2),其 神经元数为1,这里仅对该层进行训练。
图4 例子中的两层感知器神经网络模型
(3)多层感知器神经网络的MATLAB程序实现
(l )
e(j L
)
(
n
)
' j
( v(j L
)
(
n
)),对输出层L的神经元j Nhomakorabean) j
' j
(
v(jl
)
(
n
))
k(l1) (n)k(jl1) (n),对隐藏层l的神经元j
k
多层感知器AI技术中的多层感知器结构与模式识别

多层感知器AI技术中的多层感知器结构与模式识别多层感知器(Multi-Layer Perceptron, MLP)技术是人工智能(Artificial Intelligence, AI)领域中非常重要的一种技术。
它是一种前向人工神经网络,通过多个神经元层次的连接来模拟人脑中的神经元网络,并用于实现模式识别。
本文将介绍多层感知器的结构以及在模式识别中的应用。
一、多层感知器的结构多层感知器是由多个神经元层次组成的人工神经网络。
典型的多层感知器包括输入层、隐藏层和输出层。
1. 输入层输入层接收来自外部的数据输入,并将其传递到隐藏层。
输入层通常是根据具体问题设定的,可以是一组数字、图像或者其他形式的数据。
2. 隐藏层隐藏层是多层感知器中的核心部分。
它由多个神经元(节点)组成,每个神经元都与前一层的所有神经元相连。
隐藏层的层数以及每层的神经元数量都是可以调整的。
隐藏层通过对输入数据的加权求和和激活函数的作用,将处理后的数据输出到下一层。
3. 输出层输出层接收隐藏层的输出,并生成最终的输出结果。
输出层通常根据具体问题需要选择不同的激活函数,比如用于二分类问题的Sigmoid 函数或者用于多分类问题的Softmax函数。
二、多层感知器在模式识别中的应用多层感知器在模式识别领域有广泛的应用。
以下列举几个常见的应用场景。
1. 图像识别多层感知器可以用于图像识别任务,比如人脸识别、车牌识别等。
通过将图像数据输入到多层感知器中,隐藏层的神经元可以学习到图像的特征,输出层可以输出对应的分类结果。
2. 文本分类多层感知器可以用于文本分类任务,比如垃圾邮件过滤、情感分析等。
将文本数据表示成向量形式,输入到多层感知器中进行分类,可以实现对文本的自动分类。
3. 语音识别多层感知器可以用于语音识别任务,比如语音指令识别、语音转文字等。
将语音信号转换为频谱图或其他形式的特征表示,并输入到多层感知器进行识别,可以实现对语音的自动识别。
多层感知器--MLP神经网络算法

多层感知器--MLP神经⽹络算法提到⼈⼯智能(Artificial Intelligence,AI),⼤家都不会陌⽣,在现今⾏业领起风潮,各⾏各业⽆不趋之若鹜,作为技术使⽤者,到底什么是AI,我们要有⾃⼰的理解.⽬前,在⼈⼯智能中,⽆可争议的是深度学习占据了统治地位,,其在图像识别,语⾳识别,⾃然语⾔处理,⽆⼈驾驶领域应⽤⼴泛.如此,我们要如何使⽤这门技术呢?下⾯我们来⼀起了解"多层感知器",即MLP算法,泛称为神经⽹络.神经⽹络顾名思义,就像我们⼈脑中的神经元⼀样,为了让机器来模拟⼈脑,我们在算法中设置⼀个个节点,在训练模型时,输⼊的特征与预测的结果⽤节点来表⽰,系数w(⼜称为"权重")⽤来连接节点,神经⽹络模型的学习就是⼀个调整权重的过程,训练模型⼀步步达到我们想要的效果.理解了原理,下⾯来上代码直观看⼀下:1.神经⽹络中的⾮线性矫正每个输⼊数据与输出数据之间都有⼀个或多个隐藏层,每个隐藏层包含多个隐藏单元.在输⼊数据和隐藏单元之间或隐藏单元和输出数据之间都有⼀个系数(权重).计算⼀系列的加权求和和计算单⼀的加权求和和普通的线性模型差不多.线性模型的⼀般公式:y = w[0]▪x[0]+w[1]▪x[1] + ▪▪▪ + w[p]▪x[p] + b为了使得模型⽐普通线性模型更强⼤,所以我们要进⾏⼀些处理,即⾮线性矫正(rectifying nonlinearity),简称为(rectified linear unit,relu).或是进⾏双曲正切处理(tangens hyperbolicus,tanh)############################# 神经⽹络中的⾮线性矫正 ########################################导⼊numpyimport numpy as np#导⼊画图⼯具import matplotlib.pyplot as plt#导⼊numpyimport numpy as py#导⼊画图⼯具import matplotlib.pyplot as plt#⽣成⼀个等差数列line = np.linspace(-5,5,200)#画出⾮线性矫正的图形表⽰plt.plot(line,np.tanh(line),label='tanh')plt.plot(line,np.maximum(line,0),label='relu')#设置图注位置plt.legend(loc='best')#设置横纵轴标题plt.xlabel('x')plt.ylabel('relu(x) and tanh(x)')#显⽰图形plt.show()tanh函数吧特征X的值压缩进-1到1的区间内,-1代表的是X中较⼩的数值,⽽1代表X中较⼤的数值.relu函数把⼩于0的X值全部去掉,⽤0来代替2.神经⽹络的参数设置#导⼊MLP神经⽹络from sklearn.neural_network import MLPClassifier#导⼊红酒数据集from sklearn.datasets import load_wine#导⼊数据集拆分⼯具from sklearn.model_selection import train_test_splitwine = load_wine()X = wine.data[:,:2]y = wine.target#下⾯我们拆分数据集X_train,X_test,y_train,y_test = train_test_split(X,y,random_state=0)#接下来定义分类器mlp = MLPClassifier(solver='lbfgs')mlp.fit(X_train,y_train)MLPClassifier(activation='relu', alpha=0.0001, batch_size='auto', beta_1=0.9,beta_2=0.999, early_stopping=False, epsilon=1e-08,hidden_layer_sizes=(100,), learning_rate='constant',learning_rate_init=0.001, max_iter=200, momentum=0.9,n_iter_no_change=10, nesterovs_momentum=True, power_t=0.5,random_state=None, shuffle=True, solver='lbfgs', tol=0.0001,validation_fraction=0.1, verbose=False, warm_start=False)identity对样本特征不做处理,返回值是f(x) = xlogistic返回的结果会是f(x)=1/[1 + exp(-x)],其和tanh类似,但是经过处理后的特征值会在0和1之间#导⼊画图⼯具import matplotlib.pyplot as pltfrom matplotlib.colors import ListedColormap#定义图像中分区的颜⾊和散点的颜⾊cmap_light = ListedColormap(['#FFAAAA','#AAFFAA','#AAAAFF'])cmap_bold = ListedColormap(['#FF0000','#00FF00','#0000FF'])#分别⽤样本的两个特征值创建图像和横轴和纵轴x_min,x_max = X_train[:, 0].min() - 1,X_train[:, 0].max() + 1y_min,y_max = X_train[:, 1].min() - 1,X_train[:, 1].max() + 1xx,yy = np.meshgrid(np.arange(x_min,x_max, .02),np.arange(y_min,y_max, .02))Z = mlp.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z = Z.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:solver=lbfgs")plt.show()(1)设置隐藏层中节点数为10#设置隐藏层中节点数为10mlp_20 = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10])mlp_20.fit(X_train,y_train)Z1 = mlp_20.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z1 = Z1.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z1, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:nodes=10")plt.show()(2)设置神经⽹络有两个节点数为10的隐藏层#设置神经⽹络2个节点数为10的隐藏层mlp_2L = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10])mlp_2L.fit(X_train,y_train)ZL = mlp_2L.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊ZL = ZL.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, ZL, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:2layers")plt.show()(3)设置激活函数为tanh#设置激活函数为tanhmlp_tanh = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10],activation='tanh')mlp_tanh.fit(X_train,y_train)Z2 = mlp_tanh.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z2 = Z2.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z2, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:2layers with tanh")plt.show()(4)修改模型的alpha参数#修改模型的alpha参数mlp_alpha = MLPClassifier(solver='lbfgs',hidden_layer_sizes=[10,10],activation='tanh',alpha=1)mlp_alpha.fit(X_train,y_train)Z3 = mlp_alpha.predict(np.c_[xx.ravel(),yy.ravel()])#给每个分类中的样本分配不同的颜⾊Z3 = Z3.reshape(xx.shape)plt.figure()plt.pcolormesh(xx, yy, Z3, cmap=cmap_light)#⽤散点图把样本表⽰出来plt.scatter(X[:, 0],X[:, 1],c=y,edgecolor='k',s=60)plt.xlim(xx.min(),xx.max())plt.ylim(yy.min(),yy.max())plt.title("MLPClassifier:alpha=1")plt.show()总结: 如此,我们有4种⽅法可以调节模型的复杂程度: 第⼀种,调整神经⽹络每⼀个隐藏层上的节点数 第⼆种,调节神经⽹络隐藏层的层数 第三种,调节activation的⽅式 第四种,通过调整alpha值来改变模型正则化的过程 对于特征类型⽐较单⼀的数据集来说,神经⽹络的表现还是不错的,但是如果数据集中的特征类型差异⽐较⼤的话,随机森林或梯度上升随机决策树等基于决策树的算法的表现会更好⼀点. 神经⽹络模型中的参数调节⾄关重要,尤其是隐藏层的数量和隐藏层中的节点数. 这⾥给出⼀个参考原则:神经⽹络中的隐藏层的节点数约等于训练数据集的特征数量,但⼀般不超过500. 如果想对庞⼤复杂⾼维的数据集做处理与分析,建议往深度学习发展,这⾥介绍两个流⾏的python深度学习库:keras,tensor-flow⽂章引⾃ : 《深⼊浅出python机器学习》。
深度学习笔记二:多层感知机(MLP)与神经网络结构

深度学习笔记二:多层感知机(MLP)与神经网络结构为了尽量能形成系统的体系,作为最基本的入门的知识,请参考一下之前的两篇博客:神经网络(一):概念神经网络(二):感知机上面的两篇博客让你形成对于神经网络最感性的理解。
有些看不懂的直接忽略就行,最基本的符号的记法应该要会。
后面会用到一这两篇博客中的一些记号和用法的约定什么的之后就不再啰嗦了。
一.基本结构看完上面给出的两个博客或者已经有基本概念的同学应该对于神经网络的基本结构有基本的认识了。
但是上面那个还只是涉及到单层结构,并没有推广到多层结构,同时,也没有在实践中使用这种结构的经验。
所以,这节的内容就是以手写体识别为例子来讲一下基本结构,和实践中的基本使用思想。
这是推广到更加复杂任务上的基础。
假设你现在已经有了神经网络的一些感性认识了,那就就看下面这幅图。
输入层(最左边),隐藏层(中间两层),和输出层(最右边),在之前列出的博客就讲过了,这里回顾一下。
感受一下大概的架构。
神经网络的流程分为前向过程和反向过程。
反向过程一般用于训练,后面讲,这里只讲前向过程。
还记得每个神经元上面都有对于一个输入的权值,以及一个偏置,还有一个激活函数。
(不知道的话看之前列出来的博客,后面不再强调了),所以一个前向过程的流程就是input输入,然后经过第一层神经元运算(乘上权值,加上偏执,激活函数运算一次),得到输出,然后第一层的输出作为第二层的输入,运算,得到第二层的输出…..直到到输出层运算,然后得到结果。
神经网络就是依靠这样一套机制来进行计算和预测的。
假如你的权值和偏置已经是被训练好了。
对于一个新的输入,进行这样的过程,就能够得到一个预测。
那么你就能够通过这个预测来解决一些问题了。
所以有机器学习思想的话,这些概念是很容易理解的。
而我们的任务就是找到权值和偏置这些参数的值,使得输出的东西让我们满意,达到我们的要求。
这里先补充一个思想:假如我们改变了某个神经元或者某几个神经元的权值或者偏置一点点,那么该神经元的输出肯定会变得不同,这些不同最终将反应在输出上面。
多层感知器原理

多层感知器原理
嘿,朋友们!今天咱来聊聊多层感知器原理。
这多层感知器啊,就像是一个超级厉害的魔法盒子。
你看啊,它里面有好多好多的小零件,这些小零件就像是一个个小精灵,它们各自有着自己的任务和作用呢。
这些小精灵们相互配合,共同努力,就能完成一些特别神奇的事情。
比如说,我们可以把它想象成一个厨艺大师。
不同的小精灵就像是不同的调料和食材,有的负责盐的分量,有的负责火候,有的负责切菜的形状。
只有它们都完美配合,才能做出一道美味佳肴。
多层感知器也是这样啊,它通过这些小精灵的协同工作,来处理各种复杂的信息。
这多厉害呀!它可以识别图像、理解语言、做出各种判断。
咱再打个比方,它就像是一个经验丰富的老船长。
在茫茫大海上,要应对各种风浪和情况。
老船长得根据风向、海浪、船只状态等等好多因素来做出决策,指挥着船只前进。
多层感知器不也是这样嘛,面对那么多的数据和情况,它得准确判断,给出最合适的结果。
而且哦,它还特别能学习。
就像咱人一样,不断地积累经验,变得越来越厉害。
它能从大量的数据中发现规律,然后把这些规律记住,下次再遇到类似的情况,就能轻松应对啦。
你说这神奇不神奇?这多层感知器可真是个宝啊!它在我们的生活中发挥着越来越重要的作用。
想想看,我们的手机、电脑,好多智能设备里都有它的身影呢。
它能帮我们更方便地生活,更高效地工作。
它就像是我们的好帮手,默默地在背后为我们服务。
所以啊,咱可得好好了解了解它,说不定哪天咱也能利用它做出点什么了不起的事情来呢!这多层感知器原理,真的是充满了奥秘和惊喜,等着我们去探索和发现呀!不是吗?。
多层感知器

s
(2) j
Eq x
(2) j
f (s )
'
(2) j
x(j2) f (s(j2) )
9
Eq x (2) j
n2 1 n3 (3) (2) 2 (2) [d qk f ( wkh xh )] x j 2 k 1 h 1 (3) (3) (3) d qk f ( sk ) f ' ( sk ) wkj k 1 n3 (3) k(3) wkj k 1 n3
n3 d q : 期望输出 1 1 T 2 Eq (d q yq ) (d q yq ) (dqj yqj ) 2 2 j 1 yq : 网络输出
由梯度法
w
(l ) ji (l )
Eq w
(l ) ji
, l 1, 2,3
: 学习率
(3) (2) s (3) W x j
xn0 xn0
3
第一隐含层:由W(1)与输入层全连接。 第二隐含层:由W(2)与第一隐含层全连接。 1 激活函数: y j f ( s j ) bs j 1 e
() 1 x (1) f ( s ) =f (W (1) x (0) ) () 2 x (2) =f ( s ) f (W (2) x (1) ) 4
3)带动量项修正的BP算法
为使学习率μ足够大,又不产生振荡,通常在标准BP算法上 再加上一个动量项。
(l ) (l ) w(jil ) k 1 w(jil ) k (l ) (j l ) xi(l 1) w ( k ) w ji ( k 1) ji
二、多层前馈网络与BP算法
多层感知器神经网络在图像识别中的应用教程

多层感知器神经网络在图像识别中的应用教程随着深度学习的发展,神经网络被广泛应用于各种领域,尤其是图像识别。
在图像识别中,多层感知器(Multilayer Perceptron, MLP)神经网络是一种常见的模型。
这篇文章将介绍多层感知器神经网络的基本原理,并提供一个实际的应用教程。
一、多层感知器神经网络的基本原理多层感知器神经网络是一种前向传播的神经网络模型,由一个输入层、一个或多个隐藏层和一个输出层组成。
每一层都由多个神经元组成,神经元之间通过权重连接。
在图像识别中,我们可以将图像看作是一个矩阵,其中每个元素表示像素的灰度值或颜色值。
我们需要将这个矩阵转换为一个向量作为输入层的输入。
多层感知器神经网络的每个神经元都具有两个主要功能:激活函数和权重。
激活函数对输入的加权和进行非线性变换,而权重表示了每个神经元与其前一层神经元的连接强度。
训练多层感知器神经网络需要使用反向传播算法。
该算法通过比较网络输出与预期输出之间的差异来更新权重,以让神经网络逐渐学习到正确的输出。
二、多层感知器神经网络的应用教程现在,让我们通过一个实际的图像识别案例来演示多层感知器神经网络的应用。
任务名称:识别手写数字图像1. 数据准备首先,我们需要准备一个手写数字图像数据集作为训练集。
这个数据集可以包含从0到9的手写数字的图像,每个图像的尺寸应保持一致。
2. 构建神经网络我们可以使用Python中的深度学习框架,如TensorFlow或Keras,来构建多层感知器神经网络。
具体的网络结构可以根据实际情况进行调整,但通常我们可以选择一个或多个隐藏层,每个隐藏层包含128到256个神经元。
输出层的神经元数量应与分类的类别数相等。
3. 数据预处理在输入图像进入神经网络之前,我们需要对其进行预处理。
这包括将图像转换为灰度图像、调整图像尺寸,并将图像像素值进行归一化处理。
4. 网络训练将预处理后的图像作为训练集输入,使用反向传播算法进行网络训练。
简述单层感知器与多层感知器的具体内容

单层感知器与多层感知器是人工智能领域中常用的两种神经网络模型。
它们分别具有不同的结构和功能,应用范围也有所不同。
下面将分别对单层感知器和多层感知器的具体内容进行简述。
一、单层感知器的具体内容1. 结构单层感知器是由输入层和输出层构成的,输入层接收外部输入信号,并将信号通过神经元进行加权求和处理,然后传递给输出层。
输出层对输入信号进行阈值判定,输出0或1的二元信号。
2. 功能单层感知器主要用于解决线性可分问题,即可以通过在二维平面上找到一条直线将两类样本完全分开的问题。
由于单层感知器只具有简单的线性分类功能,因此在处理复杂的非线性问题时表现较差。
3. 应用单层感知器常被用于简单的逻辑运算、线性分类等问题。
使用单层感知器可以实现与门、或门、非门等基本逻辑运算,也可以用于简单的模式识别和分类任务。
二、多层感知器的具体内容1. 结构多层感知器由输入层、隐藏层和输出层构成。
隐藏层可以包含多个神经元,并且隐藏层与输出层之间存在多个连接。
隐藏层可以对输入信号进行非线性变换,从而使多层感知器具有较强的非线性建模能力。
2. 功能多层感知器通过对输入信号的多次非线性变换和权值调整,可以逼近任意复杂的非线性函数。
这使得多层感知器在处理复杂的模式识别、分类和回归等问题时具有很强的表达能力和建模能力。
3. 应用多层感知器在人工智能领域中被广泛应用,包括图像识别、语音识别、自然语言处理、游戏智能等方面。
深度学习模型中的卷积神经网络(CNN)和循环神经网络(RNN)就是基于多层感知器设计和构建的。
总结:单层感知器和多层感知器分别具有不同的结构和功能,应用范围也有所不同。
单层感知器主要用于解决线性可分问题,而多层感知器则适用于解决复杂的非线性问题。
随着人工智能领域的不断发展,多层感知器将在更多领域展现出其强大的建模能力和应用价值。
多层感知器(MLP)的结构之所以能够处理复杂的非线性问题,主要得益于其隐藏层的非线性变换和权值调整能力。
多层感知器神经网络的原理与应用

多层感知器神经网络的原理与应用神经网络是一种模拟人脑工作的计算模型,它可以通过训练学习数据,从而得出模式和规律。
多层感知器(MLP)是一种最常见的神经网络结构,它由多个神经元和多个层级组成,可以用于分类、回归、图像处理等领域。
本文将介绍多层感知器神经网络的原理与应用。
一、多层感知器神经网络的原理1.1 感知器模型感知器是一个二元分类的模型,输入层的神经元接收外部输入,输出层的神经元输出一个二元结果(0或1)。
感知器可以用来解决线性可分问题,也就是能把不同类别的样本完整的分隔开。
1.2 多层感知器模型多层感知器(MLP)是一种前向神经网络,至少包含一个输入层、一个输出层和一个或多个隐藏层。
隐藏层和输出层中的每个神经元都接受前一层中所有神经元的连接和计算,从而形成多个线性和非线性变换,建立了一种非线性的从输入到输出的映射关系。
1.3 反向传播算法反向传播算法是用来训练神经网络的一种常用方法。
在训练过程中,首先随机初始化权重参数,然后通过前向传播来计算输出结果,再与样本标签进行比较计算误差,最后通过反向传播算法来调整权重参数以减小误差。
通过反复迭代训练,最终可以得到模型参数的优化参数,使得模型能够更好地实现预测。
二、多层感知器神经网络的应用2.1 分类问题多层感知器算法可以用于分类问题的解决,如判别某个人物是否是男性或女性、鸟类的种类是何种等等。
在处理分类问题的时候,我们需要对网络进行训练以便它能够识别和预测样本标签,从而对新的样本进行分类。
2.2 回归问题多层感知器算法也可以用于回归问题,如预测某个房子的价格。
在这种情况下,网络的输出层通常只有一个神经元,并且它的权重与偏置的调节也有所不同。
反向传播算法的目的在于将预测结果与样本的真实值之间的误差减小到最小。
2.3 图像处理多层感知器算法还可以用于图像处理方面。
在图像处理中,网络需要学习特征以便识别出不同的对象和图案。
在这种情况下,我们经常使用卷积神经网络(CNN)这一更为复杂的结构,它能够更好地处理图像数据和特征提取。
人工智能的多层感知机

人工智能的多层感知机在当今科技发展的时代,人工智能技术正在飞速发展和应用。
其中深度学习算法是人工智能技术中重要的一部分,而多层感知机作为深度学习算法的一种可以进行监督学习的神经网络结构,正在被广泛应用于图像识别、自然语言处理、语音识别、数据挖掘等领域。
那么什么是多层感知机,它是如何工作的呢?一、多层感知机的概念及原理多层感知机是一种基于神经网络结构的深度学习算法,它是由多个神经元组成的层层叠加的全连接神经网络,其中每一层都有多个神经元相连。
它可以通过反向传播算法来训练模型,实现分类任务、回归任务等。
具体来说,多层感知机可以通过输入层、隐藏层和输出层来实现数据向目标进行转化。
其中,输入层负责将数据输入进来,隐藏层负责处理输入数据,并提取出特征信息,输出层则负责将处理后的数据进行输出。
每层的神经元都可以通过一个激活函数来将输入的信号进行处理,并传递给下一层。
使用多层感知机时,常用的激活函数有Sigmoid函数、ReLU函数等。
多层感知机的原理是通过前向传播计算获得输出结果,然后通过反向传播算法来优化各层之间的权重和偏置,使得输出结果更加准确,从而实现学习任务。
二、多层感知机的应用由于多层感知机具有较高的准确率和较强的处理能力,在多个领域都有广泛的应用。
1. 图像识别在图像识别方面,多层感知机能够学习到图像的特征信息,通过前向传播计算,将图像转化为数值,然后训练模型,实现自动图像识别。
应用于人脸识别、手写数字识别等方面。
2. 自然语言处理在自然语言处理方面,多层感知机能够预测词汇、短语、语句和文本的意义,实现机器翻译、情感分析等应用。
3. 语音识别在语音识别领域,多层感知机可以通过前向传播计算将声波数据转化为数值表示,然后进行训练学习,实现语音识别应用。
4. 数据挖掘多层感知机也被广泛应用于数据挖掘领域,通过学习数据的特征、规律、趋势等信息,提高对数据的解释、挖掘、预测和建模的能力。
三、多层感知机的优化方法为了提高多层感知机的性能和准确率,需要进行参数优化。
多层感知机的深入理解及应用

多层感知机的深入理解及应用多层感知机(Multi-Layer Perceptron, 简称 MLP)是一种人工神经网络模型,由多层神经元组成。
它能够模拟人脑神经元之间的相互联系,具有很强的非线性建模能力,被广泛应用于图像识别、自然语言处理、语音识别、控制系统等领域。
1. MLP的基本原理在MLP中,输入层将输入数据传输到第一隐藏层。
每个神经元都收到输入并进行加权计算,然后将激活值传递到下一层。
这个过程不断重复,直到输出层输出预测结果,而这些预测结果可以与实际结果进行比较。
输出层的神经元数目取决于具体的问题。
比如,一个二分类问题只需要一个神经元,而多分类问题需要多个神经元。
每个神经元的加权计算在数学上表示为:$a_j=f(\sum_{i=1}^{n}w_{ij}a_{i} + b_j)$其中,$n$是上一层神经元总数,$w_{ij}$是连接第$i$个输入层神经元和第$j$个隐藏层神经元的权重,$a_{i}$是上一层神经元的输出,$b_j$是偏置值,$f$是激活函数。
常用的激活函数有sigmoid函数、ReLU函数、tanh函数等。
2. MLP的训练MLP的训练过程中需要优化相应的损失函数,使得预测结果与真实结果尽可能接近。
通常采用反向传播算法(Backpropagation, BP)进行训练。
反向传播算法通过梯度下降法,不断地调整网络的参数,使得损失函数最小化。
另外,为了防止过度拟合,常用的方法是dropout和正则化。
Dropout可以在训练过程中随机丢弃一些神经元,使得网络无法过度依赖某些神经元,从而提高网络的泛化能力。
正则化是通过在损失函数中加入正则化项,使得模型的复杂度适当降低,从而避免过度拟合。
3. MLP的应用随着深度学习技术的飞速发展,MLP在各个领域得到了广泛的应用。
在图像识别方面,MLP已被用于人脸识别、物体识别等领域。
比如,Google的研究人员使用了一个22层的深度神经网络,在ImageNet数据集上实现了惊人的表现。
第三章 多层感知器神经网络(1)

络来实现“异或”运算。
10
神经网络的发展历程
神经网络的发展历性的热潮,
分别是1943年的神经网络的诞生、1983年的神经网络的复兴及2006年的深度学习
的崛起。
➢ 神经网络的诞生(1943—1969年)
➢ 在1943年,心理学家Warren McCulloch和数学家Walter Pitts和最早
➢ 我们主要关注采用误差反向传播进行学习的神经网络,神经元之间的连接权重就是 需要学习的参数,可以在机器学习的框架下通过梯度下降法来进行学习。作为对人 工神经网络的初步认识,本章主要介绍感知器神经网络和反向传播网络。
2
第一节
感知器及其发展过程
3.1
感知器及其发展过程
感知器及其发展过程
➢ 1943年,McCulloch和Pitts发表了他们关于人工神经网络的第一个系统研究。 ➢ 1947年,他们又开发出了一个用于模式识别的网络模型——感知器,通常就叫作
➢ Rosenblatt [1958]最早提出可以模拟人类感知能力的神经网络模型,
并称之为感知器(Perceptron),并提出了一种接近于人类学习过程
(迭代、试错)的学习算法。
11
神经网络的发展历程
神经网络的发展历程(二)
神经网络之后经历了长达10年的冷落期,主要由于当时基本感知机无法处理异或 回路,并且计算机处理能力还非常有限。1974年,哈佛大学的Paul Webos发明反向 传播算法,但当时没有收到重视。随后几年,反向传播算法引起了新的复兴。
描述了一种理想化的人工神经网络,并构建了一种基于简单逻辑运算的
计算机制。他们提出的神经网络模型称为MP模型。
➢ 阿兰·图灵在1948年的论文中描述了一种“B型图灵机”。(赫布型学习)
多层感知器

第三章
多层感知器网络
两层感知器网络 线性阈值单元组成的多层感知器 BP网及BP算法
一、两层感知器网络
基 函 数:线性函数 激活函数:硬极限函数 输入矢量: x = ( x1 , x2 ,..., xn )T ∈ R n 权 矩 阵: W = ⎡ wij ⎤ ∈ R n×m ⎣ ⎦
wij 为输入节点
η (d ( m ) − y ( m ) ) z ( m ) = w* − w( m )
转置后乘z(m)得
η (d
若输入x属B类,则 d = 0,但 x 被错分为A类,即 y = 1。
y = f ( wT x) ,说明 wT x > 0 , 由 w和 x 成锐角。为正确分类, 要求权矢量 w应向与 x 成钝角 的方向调整,而算法中 Δw(n0 ) = η (d − y ) x = −η x Δw(n0 ) 与 x 反向,由图可见, 这时算法确实是使 w(n0 + 1) 和 x 逐步成钝角,与要求的 方向一致。
+η z
2
(m) 2
+ 2η ( d ( m ) − y ( m ) )( w( m ) − w* )T z ( m )
(d [注意: ( m ) − y ( m ) ) 2 = 1 ]
对于被错误分类的模式z(m)存在两种情况:
(1) d = 1, y = 0, w*T z ( m) > 0, w( m)T z ( m) < 0 (2) d = 0, y = 1, w z
基于多层感知器的人工智能算法研究

基于多层感知器的人工智能算法研究随着科技的快速发展,人工智能技术在各个领域都得到了广泛应用,人们对于人工智能的探索也越来越深入。
其中,多层感知器作为一种重要的人工神经网络模型,其在人工智能算法研究中具有重要的应用意义。
一、多层感知器简介多层感知器是一种前馈人工神经网络,也被称为全连接神经网络。
它由输入层、隐藏层和输出层组成。
每个神经元之间都有权重,通过学习和训练,可以调整权重的值,使得网络能够准确预测输出结果。
多层感知器被广泛应用于图像处理、语音识别、自然语言处理等领域,是目前应用最为广泛的人工神经网络之一。
二、多层感知器的学习算法多层感知器的学习算法主要包括反向传播算法和正向传播算法。
反向传播算法是最常用的学习算法,其主要思路是通过计算误差来更新权值,使得网络的输出结果更加接近实际结果。
正向传播算法是计算各个层的输出结果,根据不同的激活函数得到最终结果。
在多层感知器的学习过程中,需要大量的数据来进行训练,并且需要经过多次迭代才能够得到较为准确的结果。
同时,对于隐藏层的数量和神经元的数量,也需要进行调整和优化,以达到最优的性能。
三、多层感知器在图像识别中的应用多层感知器在图像识别领域中得到了广泛的应用。
以手写数字识别为例,多层感知器可以将图像中的像素点作为输入,然后通过学习和训练,识别出图像中的数字。
同时,多层感知器还可以对图像进行分割、特征提取等操作,从而提高识别的准确率和速度。
四、多层感知器在语音识别中的应用多层感知器在语音识别领域中也得到了广泛的应用。
通过将语音信号输入多层感知器,可以得到语音信号的频谱特征,从而进行语音识别。
同时,多层感知器还可以用于声音信号的分类、降噪等操作,提高语音识别的准确率和鲁棒性。
五、多层感知器的发展趋势随着深度学习等新技术的出现,多层感知器也在不断发展和完善。
其中,深度学习算法能够更好地处理大规模数据,同时在神经网络结构的设计上也有更多的创新与尝试。
同时,基于多层感知器的深度学习算法也得到了广泛的应用,为人工智能的发展提供了更多的可能性。
第6章 深度学习多层感知器

神经元
基础概念
连接权值
◦ 连接权值向量为一组张量 = {1 , 2 , … , }, 其
中 对应输入 的连接权值;神经元将输入进行加
权求和
=
◦ 写成向量形式
=
偏置
◦ 有时候加权求和时会加上一项常数项作为偏置;
其中张量的形状要与的形状保持一致
= +
基础概念
激活函数
◦ 激活函数f(∙)被施加到输入加权和sum上,产生神
经元的输出;这里,若sum为大于1阶的张量,则
f(∙)被施加到sum的每一个元素上
o = f(sum)
◦ 常用的激活函数有SoftMax、Sigmoid、Tanh、ReLU
号函数
−1,
<0
= () = ቊ
1,
≥0
根据感知器训练算法,在训练过程中,若实际输出
的激活状态与预期输出的激活状态不一致,则权
值按以下方式更新:
′ ← + ⋅ ( − ) ⋅
其中, ′ 为更新后的权值,为原权值,为预期输
出, 为输入; 称为学习率,学习率可以为固定值,
4 ⋅ 4 )
后向传播
在梯度下降中,为了求得Δ , 我们需要用链式规则
去求
;
例如求
1
3 2 1
=
⋅
⋅
⋅
1
3 2 1 1
通过这种方式,误差得以后向传播到并用于更新每
一个连接权值,使得神经网络在整体上逼近损失函
多层感知器
(一)导入
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
人工智能–多层感知器基础知识解读
今天我们重点探讨一下多层感知器MLP。
感知器(Perceptron)是ANN人工神经网络的一个概念,由Frank Rosenblatt于1950s第一次引入。
单层感知器(Single Layer Perceptron)是最简单的ANN人工神经网络。
它包含输入层和输出层,而输入层和输出层是直接相连的。
单层感知器仅能处理线性问题,不能处理非线性问题。
今天想要跟大家探讨的是MLP多层感知器。
MLP多层感知器是一种前向结构的ANN人工神经网络,多层感知器(MLP)能够处理非线性可分离的问题。
MLP概念:
MLP多层感知器(MulTI-layerPerceptron)是一种前向结构的人工神经网络ANN,映射一组输入向量到一组输出向量。
MLP可以被看做是一个有向图,由多个节点层组成,每一层全连接到下一层。
除了输入节点,每个节点都是一个带有非线性激活函数的神经元。
使用BP反向传播算法的监督学习方法来训练MLP。
MLP是感知器的推广,克服了感知器不能对线性不可分数据进行识别的弱点。
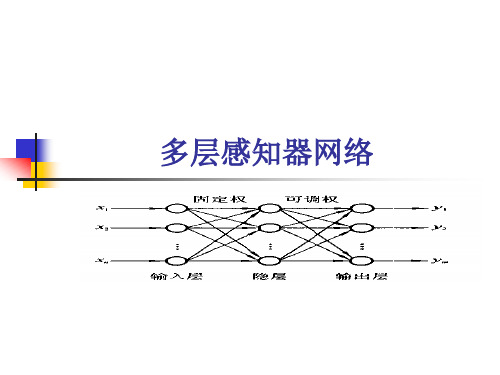
相对于单层感知器,MLP多层感知器输出端从一个变到了多个;输入端和输出端之间也不光只有一层,现在又两层:输出层和隐藏层。
基于反向传播学习的是典型的前馈网络,其信息处理方向从输入层到各隐层再到输出层,逐层进行。
隐层实现对输入空间的非线性映射,输出层实现线性分类,非线性映射方式和线性判别函数可以同时学习。
MLP激活函数
MLP可使用任何形式的激活函数,譬如阶梯函数或逻辑乙形函数(logisTIc sigmoid funcTIon),但为了使用反向传播算法进行有效学习,激活函数必须限制为可微函数。
由于具有良好可微性,很多乙形函数,尤其是双曲正切函数(Hyperbolictangent)及逻辑乙形函数,被采用为激活函数。
