广东省广州市第三中学初高中数学教材衔接导学案:第七课方程与方程组
广东省广州市第三中学七年级数学下册导学案(无答案)第七章 第4课时----7.2.2练习
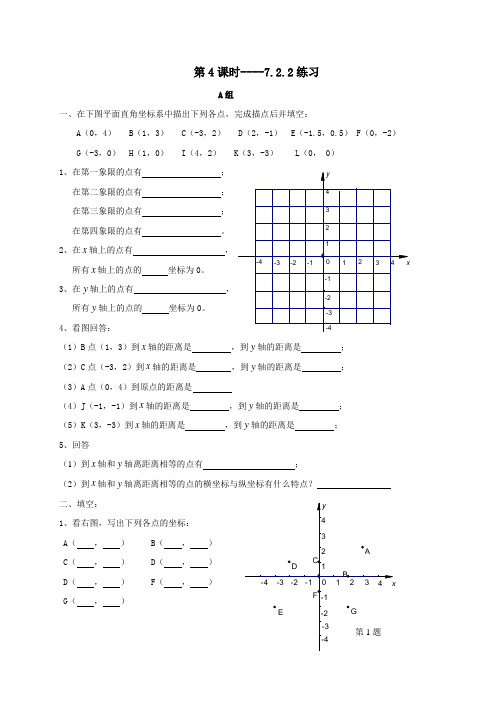
第4课时----7.2.2练习A 组一、在下图平面直角坐标系中描出下列各点,完成描点后并填空:A (0,4)B (1,3)C (-3,2)D (2,-1)E (-1.5,0.5)F (0,-2)G (-3,0)H (1,0)I (4,2) K (3,-3) L (0, 0) 1、在第一象限的点有 ; 在第二象限的点有 ; 在第三象限的点有 ; 在第四象限的点有 。
2、在x 轴上的点有 ,所有x 轴上的点的 坐标为0。
3、在y 轴上的点有 ,所有y 轴上的点的 坐标为0。
4、看图回答:(1)B 点(1,3)到x 轴的距离是 ,到(2)C 点(-3,2)到x 轴的距离是 ,到y 轴的距离是 ; (3)A 点(0,4)到原点的距离是(4)J (-1,-1)到x 轴的距离是 ,到y 轴的距离是 ; (5)K (3,-3)到x 轴的距离是 ,到y 轴的距离是 ; 5、回答(1)到x 轴和y 轴离距离相等的点有;(2)到x 轴和y 轴离距离相等的点的横坐标与纵坐标有什么特点? 二、填空:1、看右图,写出下列各点的坐标: A ( , ) B ( , ) C ( , ) D ( , ) D ( , ) F ( , ) G ( , )2、点(3,-4)在第 象限;点(-2,-3)在第 象限; 点(-3,4)在第 象限;点(2,3)在第 象限; 点(-2,0)在 上;点(0,3)在 上。
3、点P 在第二象限内,写出一个符合条件的点 。
4、已知点M (a ,b )在第三象限内,则a 0,b 0(填“>”或“<”或“=”)。
5、若点P (x ,y )在x 轴的正半轴上,则x 0,y 0; 若点P (x ,y )在y 轴的负半轴上,则x 0,y 06、点P (x ,y )在第一、三象限夹角的平分线上,则x ,y 的关系是 。
7、点P 在第四象限内,且横坐标和纵坐标的差为5,写出一个符合条件的点 。
8、点M 在第四象限,点M 到x 轴的距离为3,到y 轴的距离为2,则M 点坐标是( )。
广东省广州市高中数学初高中教材衔接第一课绝对值导学案(无答案)新人教A版(new)

第一课绝对值一、知识点1.绝对值的定义:2。
绝对值的代数意义:a3.绝对值的几何意义:4.两个数的差的绝对值的几何意义:5。
绝对值的性质:二、例题例1 解方程: (1)13x x+=-x+=(2)5665例2解方程:156++-=x x例3 解不等式:(1)5x<(2)3x>(3)|1|2x-≤(4)257x+>例4解不等式:134x x-+->三、练习1.解方程:(1)2334xx+=-(2)525x x-+=-(3)311x x x+--=+(4)352x x-+-=2.解下列不等式:(1)125-<(2)3215x-≥x(3)3233+-->-x xx x++-≥(4)134尊敬的读者:本文由我和我的同事在百忙中收集整编出来,本文档在发布之前我们对内容进行仔细校对,但是难免会有不尽如人意之处,如有疏漏之处请指正,希望本文能为您解开疑惑,引发思考。
文中部分文字受到网友的关怀和支持,在此表示感谢!在往后的日子希望与大家共同进步,成长。
This article is collected and compiled by my colleagues and I in our busy schedule. We proofread the content carefully before the release of this article, but it is inevitable that there will be some unsatisfactory points. If there are omissions, please correct them. I hope this article can solve your doubts and arouse your thinking. Part of the text by the user's care and support, thank you here! I hope to make progress and grow with you in the future.。
广东省广州市第三中学七年级数学下册导学案(无答案)第八章第12课时 8.4.6实际问题与二元一次方程组复习

第十二课时8.4.6实际问题与二元一次方程组复习
【学习目标】
1、会分析实际问题中的数量关系,能用字母表示题目中的两个未知数。
2、能够找出两个表示应用题全部含义的相等关系。
并根据这两个相等关系列出需要的代数式,从而列出方程组。
3、能用不同的方法解决开放性的问题。
【相应练习】
A组
1、某部队官兵共500人到甲、乙两处训练基地训练,已知到甲处训练的人数比到乙地训练的人数
的2倍少4人,求到甲、乙两处训练的人数分别是多少?
2、某一农户养了若干只鸡和兔子,它们一共有24个头和74只脚,求这个农户一共养了多少只鸡
和兔子?
3、运往某地的救灾物资,第一批运走460吨,共用10节火车皮和15辆汽车装完;第二批运走340
吨,共用8节火车皮和5辆汽车装完,求1节火车皮和1辆汽车分别装运物资多少吨?
4、车间有140人,每人平均每天加工15个螺栓或12个螺母,为了能使每天生产的螺栓和螺母正
好装配成套(一个螺栓配两个螺母),则应该分配多少人生产螺栓,多少人生产螺母?
B组
1、甲、乙两人相距20千米,二人同时出发,同向而行,甲5小时可追上乙;相向而行,2小时相遇,二人的平均速度分别是多少?
2、根据一家商店的账目记录,某天卖出39支牙刷和21盒牙膏,收入396元;另一天,以同样的价格卖出同样的52支牙刷和28盒牙膏,收入518元。
这个记录是否有误?如果有误,请说明理由。
广东省广州市第三中学七年级数学下册导学案(无答案)第九章第7课时 9.3一元一次不等式组(1)

(4)第7课时 9.3一元一次不等式组(1)【学习目标】1.了解一元一次不等式组及其相关概念;2.掌握一元一次不等式组的解法并会在数轴上表示解集。
【学习过程】一、预习导入:1.现有两根木条a 和b ,a 长10 cm ,b 长3 cm.如果再找一根木条c ,用这三根木条钉成一个三角形木框,那么对木条c 的长度有什么要求?①考虑三角形两边之和大于第三边,可列不等式为考虑三角形两边之差小于第三边,可列不等式为②把 一元一次不等式组。
二、探究新知:1.我们可以利用数轴确定不等式组的解集:(1)⎩⎨⎧>>24x x 其解集为(2)⎩⎨⎧><24x x 其解集为(3)⎩⎨⎧<>24x x 其解集为(4)⎩⎨⎧<<24x x 其解集为上面的表示可以用口诀来概括为2、将下列数轴上的x 的范围用不等式表示出来:(2)(3) (1)【小结】设a 、b 是已知实数且a >b ,那么不等式组表一:不等式组解集例1、解不等式组:⎩⎨⎧>-<+423532x x ⎪⎩⎪⎨⎧->-++<+x x x x 213521132例2、x 取哪些整数值时,不等式)1(325->+x x 与x x 237121-≤-都成立?三、对应练习1、解不等式组:(1)⎩⎨⎧->--<-2541662x x x x (2) 521,10.x x -≥-⎧⎨->⎩ (3)(32)41214x x x x --≤⎧⎪⎨-<-⎪⎩2.不等式组10213xx-≥⎧⎨->-⎩的整数解是()A、-1,0B、-1,1C、0,1D、无解四、总结归纳:1、由几个一元一次不等式组组合起来,组成了___________________________________2、解一元一次不等式组时,先_____________________,再___________________________。
初高数学衔接导学案第六至第九课《韦达定理》《方程》《方程组》《不等式》

第六课 根的判别式与韦达定理一、知识点1.一元二次方程ax 2+bx +c =0(a ≠0)根的判别式:2.韦达定理:如果一元二次方程ax 2+bx +c =0(a ≠0)的两个根是12,x x ,那么有: 12x x +=_________ 12x x =_________ 二、例题例1 解关于x 的方程:(1)x 2-3x +3=0 (2)x 2-2x +a =0 (3)2210mx x ++=例2 已知方程2560x kx +-=的一个根是2,求它的另一个根及k 的值.例3 已知关于x 的方程x 2+2(m -2)x +m 2+4=0有两个实数根,并且这两个实数根的平方和比两个根的积大21,求m 的值.例4 已知12,x x 是方程2520x x --=两个实数根,求下列式子的值:①1211x x +;②2212x x +;③3312x x +;④()()1211x x --;⑤12x x -例5 已知两个数的和为4,积为-12,求这两个数.例6 求作一个方程,使它的根是方程2780x x -+=的两根的平方的负倒数.例7 若关于x 的一元二次方程x 2-x +a -4=0的一根大于零、另一根小于零,求实数a 的取值范围.三、练习: 1.填空题:(1)若关于x 的方程mx 2+ (2m +1)x +m =0有两个不相等的实数根,则实数m 的取值范围是 .(2)方程kx 2+4x -1=0的两根之和为-2,则k = .(3)已知关于x 的方程x 2-ax -3a =0的一个根是-2,则它的另一个根是 .(4)如果a ,b 是方程x 2+x -1=0的两个实数根,那么代数式a 3+a 2b +ab 2+b 3的值是 . (5)已知一个直角三角形的两条直角边长恰好是方程2x 2-8x +7=0的两根,则这个直角三角形的斜边长等于 .2.已知关于x 的方程x 2-kx -2=0.(1)求证:方程有两个不相等的实数根;(2)设方程的两根为x 1和x 2,如果2(x 1+x 2)>x 1x 2,求实数k 的取值范围.3.已知一元二次方程22450x x --=的两个根分别是12,x x ,求下列式子的值:(1)12(2)(2)x x ++ (2)3312x x + (3)12x x -4.求一个一元二次方程,使它的两根分别是方程x 2-7x -1=0各根的相反数.5.若关于x 的方程x 2+x +a =0的一个根大于1,另一根小于1,求实数a 的取值范围.第七课 分式方程高次方程与无理方程一、知识点解分式方程高次方程与无理方程的常用方法: 二、例题例1 解方程:⑴、354147=--+x x⑵、06)1(5)1(2=++-+x x x x(3)222223(21)20212x x x x +--+=-+例2 解方程:(1)322530x x +-= (2)024)5(2)5(222=----x x x x(3)(2)(1)(3)(6)16x x x x -+++= (4)43226210x x x x +-++=例3 解方程:(11x =+ (23=(3)23152x x ++=三、练习: 解下列方程: (1)2315()6022x x -+=-- (2)43253222=+-+xx x x (3)22324123x x x x =---- (4)xx x x x x 3133512=-++-+(5)22)12(31222222-=+---+x x x x (6)03)76(2)76(222=----x x x x(71= (8)22415x x -+=第八课 二元二次方程组与三元一次方程组一、知识点解方程组的方法: 二、例题例 解下列方程组:(1)22210410x y x y x y --=⎧⎨---+=⎩ (2)1128x y xy +=⎧⎨=⎩(3)222255043x y x y x xy y ⎧---=⎪⎨++=⎪⎩ (4)22124x xy xy y ⎧+=⎪⎨+=⎪⎩(5)2222384x y x xy y ⎧-=⎪⎨++=⎪⎩ (6)2311322114324x y z x y z x y z ++=⎧⎪+-=⎨⎪--=⎩三、练习:解下列方程组(1)⎩⎨⎧=-=+1543222y x y x(2)⎪⎩⎪⎨⎧=+=--52322222y x y xy x(3)⎩⎨⎧-==+103xy y x(4)⎪⎩⎪⎨⎧=---=+-+3)(2)(5)(4)(22y x y x y x y x(5)⎪⎩⎪⎨⎧=-+-=-++09412902522222y xy x y xy x (6)1226310x y z x y z x y z ++=⎧⎪+-=⎨⎪-+=⎩第九课 一元二次不等式一、知识点:一元二次不等式的解集:二、例题例1 解下列不等式:⑴ 036>-x (2) 0322<-+x x (3)062<+-x x变式: (1)23520x x +-≥ (2)2210x x -++<(3)2450x x -+> (4)2440x x -+->例2 解下列不等式(1)04312>--x x (2) 012>+-x x (3)81153x x +≥+例3 解关于x 的不等式2(1)0x x a a ++->(a 为常数).例4 已知不等式)0(02≠<++a c bx ax 的解是2<x 或3>x ,求不等式02>++c ax bx 的解.三、练习:1.解下列不等式 (1)0432>--x x(2)0122≤--x x(3)0432>-+x x(4)08162≤+-x x(5)01232<+-x x(6)0432<-x(7)122-≥-x x(8)(2)(53)0x x +-≤(9)3112>--xx (10)0)1(2<++-a x a x (a 为常数).2.已知关于x 不等式022>-+c bx x 的解为1-<x 或3>x 。
广东省广州市第三中学七年级数学下册导学案(无答案)第六章 第7课时 6.3.2实数(2)

第七课时 6.3.2实数(2)
【学习目标】
1、 了解实数的运算法则及运算律,会进行实数的运算
2、 明确有理数与实数的对比
【学习环节】
一、预习导入:
1、 把下列各数填入相应的集合内:
有理数集合{ } 无理数集合{ }
整数集合{ } 分数集合{ }
实数集合{ }
2、下列各数中,是无理数的是( )
A. 1.732-
B. 1.414
C.
D. 3.14
3、若(2
2x =,则x = _________
二、探究新知:
自学课本56页内容,完成下列问题:
1、 回顾复习有理数的绝对值;
2、 小组交流课本55-56例1和例2,归纳实数的相反数和绝对值的结果;
3、 明白有理数的运算法则及运算性质在进行实数的运算中,同样适用。
4、 明白任意一个实数可以进行开立方根,而可以开平方根的只有非负数。
例题2 计算下列各式的值:
(1)2)23(-+; (2)3233+
【小结】在实数运算中,当遇到无理数并且要求出结果的近似数时,可以按所要求的精确度用相应的近似有限小数去代替无理数,再进行计算。
三、对应练习:
1、写出下列各数的相反数:
(1)-6(2)-3.14(3)一
2、||=___;若|a|=,则a=___.
3、计算下列各式的值:
(1)(+)-(2)3+2
(3)(-)-2(-)
4、课本56页练习第4题,课本57页第4、5题。
四、归纳总结:
这节课你有什么新发现?知道了哪些新知识?。
初升高衔接课数学教案及答案(总共8讲)

初升高衔接课数学教案(总共8讲)初高一衔接课:基本运算问题初高一衔接课:基本运算问题(一)绝对值一、知识梳理:⑴ 数轴上,一个数所对应的点与原点的距离叫做该数的绝对值.⑵ 数的绝对值是他本身,负数的绝对值是他的相反数,0的绝对值是0,即(0)0(0)(0)a a a a a a >⎧⎪==⎨⎪-<⎩.⑶ 个负数比较大小,绝对值大的反而小.⑷ 个绝对值不等式:||(0)x a a a x a <>⇔-<<; ||(0)x a a x a >>⇔<-或x a >. ⑸ 两个数的差的绝对值的几何意义:b a -表示在数轴上,数a 和数b 之间的距离.二、例题讲解:例1 解不等式:13x x -+->4.解法一:由01=-x ,得1=x ;由30x -=,得3x =; ①若1<x ,不等式可变为(1)(3)4x x ---->, 即24x -+>4,解得x <0, 又x <1, ∴x <0;②若12x ≤<,不等式可变为(1)(3)4x x --->, 即1>4,∴不存在满足条件的x ;③若3x ≥,不等式可变为(1)(3)4x x -+->, 即24x ->4, 解得x >4. 又x ≥3, ∴x >4.综上所述,原不等式的解为 x <0,或x >4.解法二:如图1.1-1,1-x 表示x 轴上坐标为x 的点P 到坐标为1的点A 之间的距离|PA |,即|PA |=|x -1|;|x -3|表示x 轴上点P 到坐标为2的点B 之间的距离|PB |,即|PB |=|x -3|.所以,不等式13x x -+->4的几何意义即为 |PA |+|PB |>4. 由|AB |=2,可知点P 在点C (坐标为0)的左侧、或点P 在点D (坐标为4)的右侧. x <0,或x >4.三、强化练习1.填空:(1)若5=x ,则x =_________;若4-=x ,则x =_________.(2)如果5=+b a ,且1-=a ,则b =________;若21=-c ,则c =________. 2.选择题:下列叙述正确的是 ( ) (A )若a b =,则a b = (B )若a b >,则a b > (C )若a b <,则a b < (D )若a b =,则a b =±13A B x0 4C D xP |x -1||x -3| 图1.1-1x原式=(+说明:本题若先从方程7∴-x x=⨯364∴+x x13此例可以看出,常数项为正数时,应分解为两个同号因数,它们的符号与一次项系数的符号相同.∴+x x5-=15∴-x x2此例可以看出,常数项为负数时,应分解为两个异号的因数,其中绝对值较大的因数与一次项系数的符答案:1.222(3)(39),(2)(42),(23)(469),a a a m m m x x x +-+-++-++2.2222()(),()(),nx x y y xy x x x y x xy y +-+-++ 22432(1)(4321)y x x x x x --+++ 3.(2)(1)x x --,(9)(3)x x -+, (5)()m n m n -+4.3(2)(8)ax x x -- ;(3)(2)na ab a b +- ;2(3)(1)(23)x x x x -+-+;(2)(415),x y x y -+(772)(1)a b a b +++-5.2()(3),(21)(21),(3)(52)x y a y x x x x y -++--+;(12)(12),x y x y -++-23333()(),(1)(1),()(1)ab a b a b x y x y x x y x y +----+-++.6.2837.5354(2)(1)(1)(2)n n n n n n n n -+=--++8.322322()()a a c b c abc b a ab b a b c ++-+=-+++初高一衔接课:基本运算问题初高一衔接课:基本运算问题(四)根式一、知识梳理:二次根式的性质(1)一般地,形如(0)a a ≥的代数式叫做二次根式.根号下含有字母、且不能够开得尽方的式子称为无理式. 例如 232a a b b +++,22a b +等是无理式,而22212x x ++,222x xy y ++,2a 等是有理式. (2)二次根式2a 的意义2a a ==,0,,0.a a a a ≥⎧⎨-<⎩(3)二次根式的化简与运算二次根式的乘法:ab b a =),(0≥0≥b a ;二次根式的除法:先把除法写成分式的形式,然后通过分母有理化进行运算; 二次根式的加减法:合并同类二次根式. (4)其性质如下:(五)分式一、知识梳理:当分式A B 的分子、分母中至少有一个是分式时,AB就叫做繁分式,繁分式的化简常用以下两种方法:(1) 利用除法法则;(2) 利用分式的基本性质.二、例题讲解:【例1】化简11xx x x x-+-解法一:原式=222(1)11(1)1(1)(1)11x x x x x xx x x x x x x x x x x x x x x x x x x++=====--⋅+-+-+++--+解法一:原式=22(1)1(1)(1)111()x x x x x x x x x x x x x x x x x x x x x x x++====-⋅-+--+++--⋅ 说明:解法一的运算方法是从最内部的分式入手,采取通分的方式逐步脱掉繁分式,解法二则是利用分式的基本性质A A mB B m⨯=⨯进行化简.一般根据题目特点综合使用两种方法. 【例2】化简222396162279x x x x x x x x++-+-+--=61x -.【解法二】原式=22(1)(1)(1)(1)x x x x x x +-+-++ =33(1)(1)x x +-=61x -.例2 已知4a b c ++=,4ab bc ac ++=,求222a b c ++的值. 【解】 2222()2()8a b c a b c ab bc ac ++=++-++=. 例3 解不等式:13x x -+->4.【解法一】由01=-x ,得1=x ;由30x -=,得3x =;①若1<x ,不等式可变为(1)(3)4x x ---->, 即24x -+>4,解得x <0,又x <1,∴x <0; ②若12x ≤<,不等式可变为(1)(3)4x x --->, 即1>4,∴不存在满足条件的x ;③若3x ≥,不等式可变为(1)(3)4x x -+->, 即24x ->4, 解得x >4. 又3x ≥,∴x >4.综上所述,原不等式的解为 x <0,或x >4.【解法二】如图1-1,1-x 表示x 轴上坐标为x 的点P 到坐标为1的点A 之间的距离|PA |,即|PA |=|x -1|;|x -3|表示x 轴上点P 到坐标为2的点B 之间的距离|PB |,即|PB |=|x -3|.所以,不等式13x x -+->4的几何意义即为 |PA |+|PB |>4. 由|AB |=2,可知点P 在点C (坐标为0)的左侧、或点P 在点D (坐标为4)的右侧.∴x <0,或x >4.例4 分解因式:(1)x 2-3x +2; (2)x 2+4x -12; (3)22()x a b xy aby -++; (4)1xy x y -+-.【解】(1)如图1.2-1,将二次项x 2分解成图中的两个x 的积,再将常数项2分解成-1与-2的乘积,而图中的对角线上的两个数乘积的和为-3x ,就是x 2-3x +2中的一次项,所以,有x 2-3x +2=(x -1)(x -2).今后在分解与本例类似的二次三项式时,可以直接将图1.2-1中的两个x 用1来表示(如图1.2-2所示).13A B x4C D xP |x -1||x -3|图1-1-1 -2 x x 图1.2-1 -1 -2 1 1 图1.2-2-2 6 1 1 图1.2-3 -ay -by x x 图1.2-4(2)由图1.2-3,得x 2+4x -12=(x -2)(x +6). (3)由图1.2-4,得22()x a b xy aby -++=()()x ay x by -- (4)1xy x y -+-=xy +(x -y )-1=(x -1) (y+1) (如图1.2-5所示).例5 分解因式:(1)32933x x x +++; (2)222456x xy y x y +--+-. 【解】(1)32933x x x +++=32(3)(39)x x x +++=2(3)3(3)x x x +++ =2(3)(3)x x ++.或 32933x x x +++=32(331)8x x x ++++=3(1)8x ++=33(1)2x ++提 示熟练进行分解因式运算是高中数学的基本要求.=22[(1)2][(1)(1)22]x x x +++-+⨯+ =2(3)(3)x x ++.(2)222456x xy y x y +--+-=222(4)56x y x y y +--+-=22(4)(2)(3)x y x y y +----=(22)(3)x y x y -++-. 或 222456x xy y x y +--+-=22(2)(45)6x xy y x y +----=(2)()(45)6x y x y x y -+--- =(22)(3)x y x y -++-.例6 试比较下列各组数的大小:(1)1211-和1110-; (2)264+和226-. 【解】 (1)∵1211(1211)(1211)11211112111211--+-===++,1110(1110)(1110)11110111101110--+-===++, 又12111110+>+, ∴1211-<1110-.-1 1x y图1.2-5910+⨯(1)n n ++1910+⨯(910-1(1)n n ++(4n n -是正整数,(1)n n ++513.计算:1111132435911++++⨯⨯⨯⨯.4.试证:对任意的正整数n ,有111123234(1)(2)n n n +++⨯⨯⨯⨯++<14 .答案 A 组 1.(1)2x <-或4x > (2)-4<x <3 (3)x <-3,或x >3 2.1 3.(1)23- (2)11a -≤≤ (3)61- B 组1.(1)37 (2)52,或-15 2.4.C 组1.(1)C (2)C 2.121,22x x == 3.36554.提示:1111[](1)(2)2(1)(1)(2)n n n n n n n =-+++++.一次函数和反比例函数初高一衔接课:(一)一次函数和反比例函数一、基础知识梳理1、平面直角坐标系(1)在平面内,两条互相垂直且有公共原点的数轴组成平面直角坐标系.水平的数轴叫做x 轴或横轴,铅直的数轴叫做y 轴或纵轴,x 轴与y 轴统称坐标轴,他们的公共原点O 称为直角坐标系的原点. (2)点的坐标和象限.(3)平面直角坐标系内的对称点:设11(,)M x y ,22(,)M x y '是直角坐标系内的两点.① 若M 和'M 关于y 轴对称,则有1212x x y y =-⎧⎨=⎩.② 若M 和'M 关于x 轴对称,则有1212x x y y =⎧⎨=-⎩.③ 若M 和'M 关于原点对称,则有1212x x y y =-⎧⎨=-⎩.所以,22x =-,13y =-,则()2,3A -、()2,3B --. (3)因为A 、B 关于原点对称,它们的横纵坐标都互为相反数, 所以22x =-,13y =,则()2,3A 、()2,3B --.例2已知一次函数y =kx +2的图象过第一、二、三象限且与x 、y 轴分别交于A 、B 两点,O 为原点,若ΔAOB 的面积为2,求此一次函数的表达式.【解】∵B 是直线2+=kx y 与y 轴交点,∴B (0,2),∴OB =2, 1222AOB S AO BO AO ∆=⋅=∴=又, 2y kx =+又,过第二象限,(20)A ∴-,1120212x y y kx k y x =-==+=∴=+把,代入中得,例3反比例函数xk y 1-=与一次函数)1(+=x k y 只可能是( )(A ) (B ) (C ) (D )【解】因直线)1(+=x k y 必过点()0,1-,所以选择(C )、(D )一定错误.又直线)1(+=x k y 与y 轴的交点为()k ,0,所以当1>k ,双曲线xk y 1-=必在第一、三象限. 故选(A )例4 如图,反比例函数ky x=的图象与一次函数y mx b =+的图象交于(13)A ,,(1)B n -,两点.(1)求反比例函数与一次函数的解析式;(2)根据图象回答:当x 取何值时,反比例函数的值大于一次函数的值. 【解】(1)(13)A ,在ky x=的图象上, 3k ∴=,3y x∴=又(1)B n -,在3y x =的图象上,3n ∴=-,即(31)B --,,313m bm b =+⎧⎨-=-+⎩,解得:1m =,2b =,反比例函数的解析式为3y x=,一次函数的解析式为2y x =+,(2)从图象上可知,当3x <-或01x <<时,反比例函数图象在一次函数图象的上方,所以反比例函数的值大于一次函数的值.例5 如图,正比例函数x y 3=的图象与反比例函数xky =)>,>(00x k 的图象交于点A .过A 作AB ⊥x 轴于B 点.若k 取1,2,3,…,20时,对应的Rt △AOB 的面积分别 为1S ,2S ,3S ,…,20S ,则1S +2S +3S +…+20S =_ .【解】过正比例函数与反比例函数的交点作x 轴的垂线.x 轴、正比例函数图象及垂线所围成的三角形的面积是k 的 一半.于是 1S +2S +3S +…+20S =22020121×)+(×=105.例6 已知反比例函数xky 2=和一次函数12-=x y ,其中一次函数的图象经过()b a ,、()k b a ++,1两点. (1)求反比例函数的解析式;(2)若点A 坐标是()1,1,请问,在x 轴上是否存在点P ,使AOP ∆为等腰三角形?若存在,把符合条件的点P 的坐标都求出来,若不存在,请说明理由. 【解】 (1)根据题意,得()⎩⎨⎧-+=+-=.112,12a k b a by xA OB图(12)ABOxy两式相减,得2=k .所以所求的反比例函数的解析式是xy 1=. (2)由勾股定理,得21122=+=OA ,OA 与x 轴所夹的角为︒45.①当OA 为AOP ∆的腰时,由OP OA =,得()0,21P ,()0,22-P ;由AP OA =,得()0,23P .②当OA 为AOP ∆的底时,得()0,14P . 所以,这样的点有4个,分别是()0,2、()0,2-、()0,2、()0,1.例7已知一次函数y ax b =+的图象经过点()3,32A +,()1,3B -,()2,C c -.求222a b c ab bc ca++---的值.【解】 由点点()3,32A +,()1,3B -,()2,C c -在次函数y ax b =+的图象上,于是有233+=+b a ,3=+b a ,c b a =+2,解得31,231,1a b c =-=-=,3,232,23a b b c c a ∴-=--=--=-.222a b c ab bc ca ++---=()()()2221136 3.2a b b c c a ⎡⎤-+-+-=-⎣⎦例8如图,点A 、C 在反比例函数()30y x x=<的图象上,B 、D 在x 轴上,△OAB ,△BCD 均为正三角形,则点C 的坐标是 .【解】 作AE ⊥OB 于E ,CF ⊥BD 于F ,易求OE =EB =1, 设BF =m ,则(2,3)C m m ---,代入3y x= 得2222210,2m m m -±+-==.D CB AOyx又0,12m m >∴=-+,∴点C 的坐标为 ()12,36---.四、课后巩固练习 A 组1.函数y kx m =+与(0)my m x=≠在同一坐标系内的图象可以是( )2.如图,平行四边形ABCD 中,A 在坐标原点,D 在第一象限角平分线上,又知6AB =,22AD =,求,,B C D 点的坐标.3.如图,已知直线12y x =与双曲线(0)ky k x=>交于A B ,两点,且点A 的横坐标为4.(1)求k 的值;(2)过原点O 的另一条直线l 交双曲线(0)ky k x=>于P Q ,两点(P 点在第一象限),若由点P 为顶点组成的四边形面积为24,求点P 的坐标.B 组1.选择题如图是三个反比例函数y =1k x ,y =2kx ,y =3k x在x 轴上方的图象,由此观察得到k 1、k 2、k 3∴的大小关 系为( )A .k 1>k 2>k 3B .k 3>k 2>k 1C .k 2>k 3>k 1D .k 3>k 1>k 2 2.选择题xyO A . xyO B .xyO C . xyO D .OxAyByxO第2题 第3题yxCB AO yx图 1 OA B DC P4 9图 2如图,正比例函数kx y =和()0>=a ax y 的图象 与反比例函数()0>=k xky 的图象分别相交于A 点和 C 点.若AOB Rt ∆和COD Rt ∆的面积分别为1S 和2S ,则1S 与2S 的关系是( )(A )1S >2S (B )1S =2S (C )1S <2S (D )不能确定3.如图,已知Rt △ABC 的锐角顶点A 在反比例函数y =m x的 图象上,且△AOB 的面积为3,OB =3. (1)求点A 的坐标; (2)求函数y =mx的解析式; (3)若直线AC 的函数关系式为y =27x +87, 求△ABC 的面积.4.如图1,在矩形ABCD 中,动点P 从点B 出发, 沿BC ,CD ,DA 运动至点A 停止.设点P 运动 的路程为x ,△ABP 的面积为y ,如果y 关于x 的 函数图象如图2所示,则△ABC 的面积是( )A .10B .16C .18D .20C 组1.如图,如果x x >,且0<kp ,那么,在自变量x 的取值范围内,正比例函数kx y =和反比例函数xpy =在同一直角坐标系中的图象示意图正确的是( )(A ) (B ) (C ) (D )2.已知反比例函数xmy 21-=的图象上两点()()2211,,,y x B y x A ,当210x x <<时,有21y y <,则m 的取值范围是___ __.3.已知点()a P ,1在反比例函数()0≠=k xky 的图象上,其中322++=m m a (m 为实数),则这个函数的图象在第_____象限.4.已知3=b ,且反比例函数x b y +=1的图象在每个象限内,y 随x 的增大而增大,如果点()3,a 在双曲线xby +=1上,则_____=a .5.如果不等式0<+n mx 的解集是4>x ,点()n ,1在双曲线xy 2=上,那么一次函数 ()m x n y 21+-=的图象不经过第___象限.6.已知直线b kx y +=经过反比例函数xy 8-=的图象上两点()1,2y A 与()2,2x B ,则.______=kb五、参考答案与解析A 组 1. B2. D(2,2)、C(8,2)、B(6,0).3.(1)8k =.(2)点P 的坐标是(24)P ,或(81)P ,.B 组 1.B2.B 解析:设()()2211,,,y x C y x A .则根据题意,k y x y x ==2211. 所以k y x AB OB S 212121111==×=, k y x CD OC S 212121222==×=.根据题意,把()4,2-A 、()2,4-B 两点的坐标代入直线b kx y +=中,得 ⎩⎨⎧=+--=+.24,42b k b k 解得⎩⎨⎧-=-=.2,1b k故()2121-=-=-k b .二次函数初高一衔接课:(二)二次函数一、基础知识梳理1、二次函数的图像与性质(1)二次函数y =ax 2+bx +c (a ≠0)的图象由于y =ax 2+bx +c =a (x 2+b x a )+c =a (x 2+bx a+224b a )+c -24b a224()24b b aca x a a-=++, 所以,y =ax 2+bx +c (a ≠0)的图象可以看作是将函数y =ax 2的图象作左右平移、上下平移得到的.其图像为①当a >0时,函数y =ax 2+bx +c 图象是开口向上的抛物线,顶点坐标为24(,)24b ac b a a--,对称轴为直线x =-2ba;②当a <0时,函数y =ax 2+bx +c 图象是开口向下的抛物线,顶点坐标为24(,)24b ac b a a--,对称轴为直线x =-2ba; (2)二次函数y =ax 2+bx +c (a ≠0)的性质(1); (2).【解】 由于函数和的自变量x 的取值范围是全体实数,所以只要确定它们的图象有最高点或最低点,就可以确定函数有最大值或最小值. (1)因为二次函数中的二次项系数2>0, 所以抛物线有最低点,即函数有最小值.因为=,所以当时,函数有最小值是. (2)因为二次函数中的二次项系数-1<0, 所以抛物线有最高点,即函数有最大值. 因为=, 所以当时,函数有最大值.例3 (1)当12x ≤≤时,求函数21y x x =--+的最大值和最小值. (2)当0x ≥时,求函数(2)y x x =--的取值范围. 【解】 (1)作出函数21y x x =--+的图像(如右图),当1x =时,=max y -1,当2x =时,=min y -5. (2)作出函数2(2)2y x x x x =--=-在0x ≥内的 图像(如右图),可以看出:当1x =时,min 1y =-,无最大值. 所以,当0x ≥时,函数的取值范围是1y ≥-.例4 某商场以每件30元的价格购进一种商品,试销中发现这种商品每天的销售量m (件)与每件的销售价x (元)满足一次函数1623,3054m x x =-≤≤.5322--=x x y 432+--=x x y 5322--=x x y 432+--=x x y 5322--=x x y 5322--=x x y 5322--=x x y 849)43(22--x 43=x 5322--=x x y 849-432+--=x x y 432+--=x x y 432+--=x x y 425)23(2++-x 23-=x 432+--=x x y 425A.B.C.D.于是可设二次函数为y =a (x +1)2+2,或y =a (x +1)2-2,由于函数图象过点(1,0),∴0=a (1+1)2+2,或0=a (1+1)2-=-12,或a =12. 2.∴a所以,所求的函数为y =-12(x +二次2,或y =12(x +1)21)2+-2.(3)设该二次函数为y =ax 2+bx +c (a ≠0).由函数图象过点(-1,-22),(0,-8),(2,8),可得 228842a b c c a b c -=-+⎧⎪-=⎨⎪=++⎩,解得 a =-2,b =12,c =-8.故所求的二次函数为y =-2x 2+12x -8.例6二次函数bx ax y +=2和反比例函数by x=在同一坐标系中的图象大致是( )。
广东省广州市第三中学七年级数学下册导学案(无答案)第八章第8课时 8.4.2实际问题与二元一次方程组(2)

第八课时 8.4.2实际问题与二元一次方程组(2)
【学习目标】1、进一步熟练掌握列二元一次方程组解应用题的一般过程;
2、能正确列出方程组解决实际问题,提高分析、解决实际问题的能力。
【学习环节】 一、预习导入:
若1头大牛每天用饲料x 千克,1头小牛每天用饲料y 千克, 那么:(1)30头大牛每天用饲料 千克; (2)15头小牛每天用饲料 千克;
(3)30头大牛和15头大牛每天一共用饲料 千克。
二、探究新知:阅读课文P99—100
例题:养牛场原有大牛30头和小牛15头,1天约用饲料675kg 。
一周后又购进12头大牛和5头小牛,这时1天约用饲料940kg 。
求每头大牛和每头小牛1天用饲料多少千克? 分析:利用右表完成数据整理:
解:设 。
根据题意列方程组
得⎩
⎨⎧
答: 。
思考:饲养员李大叔估计每头大牛1天约用饲料18~20kg ,每头小牛1天约用饲料7~8kg 。
你认为他的估计是否准确?
【小结】列方程(组)解应用题的步骤:①设未知数.②找相等关系.③列方程组.④检验并作答.
三、对应练习:
1、运输360吨化肥,装了6节火车皮与15辆汽车;运输440吨化肥,装了8节火车皮与10辆汽车。
每节火车皮与每辆汽车平均各装多少吨化肥?
解:设 。
根据题意列方程组
得⎩
⎨⎧
2、一种蜂王精有大、小盒两种包装,3大盒、4小盒共装108瓶,2大盒、3小盒共装76瓶。
大盒与小盒每盒各装多少瓶?
解:设 。
根据题意列方程组 得⎩
⎨⎧
四、总结归纳:
1、通过本课学习,你有何收获?
2、。
《方程》教案(精选8篇)

《方程》教案《方程》教案(精选8篇)作为一位优秀的人民教师,往往需要进行教案编写工作,教案是教学活动的总的组织纲领和行动方案。
我们该怎么去写教案呢?以下是小编帮大家整理的《方程》教案,欢迎大家分享。
《方程》教案篇1教学内容:教科书第12~13页,“回顾与”、“练习与应用”第1~4题。
教学目标:1、通过回顾与,使学生进一步加深等式与方程的意义,等式的性质的理解。
帮助学生理清知识的脉络,建立合理的认知结构。
2、通过练习与运用,使学生进一步掌握方程的方法和一般步骤,会列方程解决简单实际问题。
教学过程:一、回顾与1、谈话引入。
本单元我们学习了哪些内容?你能说说什么是等式的性质吗?什么是方程?什么是解方程呢?在小组中互相说说。
2、组织讨论。
(1)出示讨论题。
(2)小组交流,巡视指导。
(3)汇报交流。
你是怎么获得这个知识的?我们在学习这个知识时运用了什么方法?(等式与方程都是等式;等式不一定是方程,方程一定是等式。
)(含有未知数的等式是方程。
)(等式性质:)(求方程中未知数的值的过程叫做解方程。
)同学们对这一单元的知识点掌握得很好,我们不仅要理解概念和意义,还要会熟练地运用。
二、练习与应用1、完成第1题。
(1)独立完成计算。
(2)汇报与展示,说说错误的原因及改正的方法。
2、完成第2题。
(1)学生独立完成。
(2)你用怎样的方法连线的?(解方程求出未知数的值;把x的值代入方程。
)3、完成第3题。
(1)列出方程,不解答。
(2)你是怎样列的?怎么想的?大家同意吗?(3)完成计算。
4、完成第4题。
单价、数量、总价之间有怎样的数量关系?指出:抓住基本关系列方程,y也可以表示未知数。
三、课堂通过回顾与,大家共同复习了有关方程的知识,你还有什么疑问吗?《方程》教案篇2教学目标:1、通过回顾等式、不等式、用字母表示的式子等内容,进一步巩固加深学生对方程的理解和认识。
2、会用方程表示简单的等量关系,会列方程解决简单问题。
3、感受式与方程在解决问题中的价值,培养初步的代数思想。
广东省广州市第三中学七年级数学下册导学案(无答案)第八章第11课时 8.4.5实际问题与二元一次方程组(5)

第十一课时 8.4.5实际问题与二元一次方程组(5)【学习目标】1、进一步熟练掌握列二元一次方程组解应用题的一般过程; 2、通过对探究性问题的研究,提高分析、解决实际问题的能力。
【学习环节】 一、预习导入:已知一个长方形的长与宽的比为3:1 (1)若长为6cm ,则宽为 cm ;(2)若这个长方形的面积为30cm 2,则宽为 cm 。
二、探究新知:问题1 根据以往的统计资料,甲、乙两种作物的单位面积的产量比是1∶2,现在要在一块长为200m ,宽100 m 的长方形的土地上种植这两种作物,如图将这块地分为两个长方形,当BE 和CE 的长度分别是多少的时候甲、乙两种作物的总产量比为3∶4?分析:(1)“甲、乙两种作物的单位面积的产量比是1∶2”的意思是当甲作物的单位面积产量为时,乙作物的单位面积产量为 ;(2)甲、乙两种作物的单位面积的产量比是1∶2,若两部分的面积分别为S1、S2,,那么甲、乙两种作物的总产量比为3∶4用式子表示是: 。
解:设BE 的长为x m ,CE 的长为y m 。
【小结】对于出现比例的问题,通常可以运用小学所学的知识 法,把比例形式转化为整式。
问题2 一个长方形的长减少5 cm ,宽增加2cm ,就成为一个正方形,并且这两个图形的面积相等。
这个长方形的长、宽各是多少?(只要求列出方程组) 解:三、对应练习:1、一个两位数的数字之和为10,十位数字与个位数字互换后,所得新数比原数小36,求原来的两位数。
2、一支部队第一天行军4小时,第二天行军5小时,两天共行军98 km ,且第一天比第二天少走2 km ,第一天和第二天行军的平均速度各是多少? 解:四、总结归纳:1、通过本课学习,你有何收获?2、。
【数学】广东省广州市第三中学初高中数学教材衔接导学案第十一课二次函数的最值

文档来源为:从网络收集整理.word版本可编辑.欢迎下载支持.
【关键字】数学
第十一课二次函数的最值
一、知识点:
二次函数的最值
2、例题
例1求二次函数的最大值以及取得最大值时的值.
变式1:⑴⑵⑶
变题2:求函数()的最大值.
变题3:求函数()的最大值.
例2 已知()的最大值为3,最小值为2,求的取值范围.
例3 若,是二次方程的两个实数根,求的最小值.
三、练习:
1.函数的最小值是4,且当=2时,=5,则=______,=_______.
2.试求关于的函数在上的最大值.
3.已知函数当时,取最大值为2,求实数的值.
、
4.已知是方程的两实根,求的最大值和最小值.
此文档是由网络收集并进行重新排版整理.word可编辑版本!。
广东省广州市第三中学七年级数学下册导学案(无答案)第九章第5课时 9.2一元一次不等式(2)

第5课时 9.2一元一次不等式(2)【学习目标】1.理解一元一次不等式的概念2.掌握求一元一次不等式的解集的步骤。
【学习过程】一、预习导入:解下列不等式,并在数轴上表示解集:(1)2x+5<10; (2)2(1+x)<3二、探究新知:我们知道,解不等式的依据是不等式的性质,而不等式的性质与等式的性质类似,因此,解一元一次不等式的步骤与解一元一次方程的步骤基本相同。
练习:解方程21x-1=32 (2x+1) 仿做:解不等式21x-1≤32 (2x+1) 解:去分母,得 解:去分母,得_______________ _______________去括号,得 去括号,得_______________ _______________ 移项,得 移项,得_______________ _______________合并,得 合并,得_______________ _______________系数化为1,得 系数化为1,得_______________ _______________【小结】解一元一次不等式一般的步骤是:,,,,。
三、对应练习1、解下列不等式,并在数轴上表示解集:(1)5x+15>4x-1; (2)2(x+5)≤3(x-5);(4)17x-<253x+; (5)16x+≥254x-+ 1.2、当x或y满足什么条件时,下列关系成立?(1)2(x+1)大于或等于1; (2)4x与7的和不小于6;(3)y与1的差不大于2y与3的差; (4)3y与7的和的四分之一小于-2.3.根据下列条件求正整数x:(1)x+2<6; (2)32x-≥253x-; (3)22x+≥213x--2.四、归纳总结:1、解不等式的步骤有________________________________________2、_________________________________________________________。
广东省广州市第三中学七年级数学下册9.3一元一次不等式组教案

广东省广州市第三中学七年级数学下册9.3 一元一次不等式组教课设计(1)教课设计9.3 一元一次不等式组(第一课时)教材解析:本节课以前学生已经学习了一元一次不等式,并会解简单的一元一次不等式,知道了用数轴表示一元一次不等式的解集分三步进行:画数轴、定界点、走方向。
而本节主要学习一元一次不等式组及其解集,这是学好利用一元一次不等式组解决实质问题的要点,同时要修业生会用数轴确立解集。
并且本课也经过一元一次不等式,一元一次不等式的解集,解不等式的看法来类推学习一元一次不等式组的一些看法,试试对学生类比推理能力进行培育。
七年级学生的理解能力和思想特色是,他们的抽象想象能力不强,常常需要依靠直观形象来解决问题。
为使课堂高效、生动、针对性强,我特将观察、思虑、谈论贯穿于整个教课环节之中,采纳启迪式教课法和师生互动式教课模式,注意师生之间的感情交流,并教给学生“多观察、动脑想、勇敢猜、勤研究”的商议式学习方法。
在教课中,踊跃利用板书和练习中的问题,向学生供给更多的活动机遇和空间,使学生在动脑、着手、动口的过程中获取充足的体验和发展,从而培育学生灵巧的把理论与实质问题应用相联合。
学生状况解析:学生已经学习了一元一次不等式,本节我们要学习一元一次不等式组,所以由一元一次不等式猜想一元一次不等式组的看法学生易于接受,同时能更好的培育学生的类比推理能力。
本节所选例题也真切的实现了低起点小台阶,次序渐进,能使学生更好的掌握知识。
教课目标: 1、知识与能力目标:认识一元一次不等式组和、一元一次不等式组的解集的看法,掌握一元一次不等式组的解法,会用数轴确立一元一次不等式组的解集。
2、过程与方法目标:让学生经历知识的拓展过程,会应用数轴确立一元一次不等式组的解集,感觉并掌握数形联合思想。
3、感情态度与价值观目标:让学生能踊跃参加问题的谈论,感觉数形联合思想解决问题的作用,养成自主研究学习的优异习惯。
教课要点解析:1、理解有关不等式组的看法。
广东省广州市第三中学七年级数学下册导学案(无答案)第八章 第1课时 8.1二元一次方程组

第一课时 8.1二元一次方程组【学习目标】1、了解二元一次方程(组)、二元一次方程(组)的解的概念;并会检验一对数是不是某个二元一次方程组的解;2、会利用有关知识解决相关问题。
【学习环节】一、预习导入:1、已知方程52=+y x ,若2=x 时,则y 的值是 ;若3=y 时,则x 的值是 。
2、解方程:()222348x x +-=①二、探究新知:阅读课本P88—891、二元一次方程(组)的概念:23y x =-② 2248x y +=③(1)观察以上所列的方程,它们有何区别:方程①:含有 个未知数,未知数的次数都是 ,这样的方程叫做 ; 方程②③:含有 个未知数,未知数的次数都是 ,这样的方程叫做 。
(2)把两个二元一次方程组成一个方程组,即把方程②③写成以下形式:②③ 称为二元一次方程组。
2、二元一次方程的解:满足二元一次方程的一对未知数的值。
(1)以下 是二元一次方程 2x y +=的解(填编号)(a)10x y =⎧⎨=⎩ (b)24x y =-⎧⎨=⎩ (c) 2.64.6x y =-⎧⎨=⎩ (d)46x y =-⎧⎨=-⎩ (e) 1.512x y =⎧⎪⎨=⎪⎩ (f)46x y =⎧⎨=-⎩ 【小结】二元一次方程有 个解。
3、二元一次方程组的解:(1) 判断下列各对数,哪些是方程②的解,哪些是方程③的解:(a)⎩⎨⎧==33y x (b)⎩⎨⎧==75y x (c)⎩⎨⎧==175y x (d)⎩⎨⎧==159y x (e)1014x y =⎧⎨=⎩ 方程②的解有: (填编号)方程③的解有: ;其中方程②和方程③的公共解是:(2)我们把两个二元一次方程的 ,叫做二元一次方程组的解。
即:方程组⎩⎨⎧=+-=482232y x x y 的解为⎩⎨⎧==y x 【小结】二元一次方程组有 个解。
三、对应练习:1、下列各式中,是二元一次方程的是 (填编号)①37x y -= ②243x z y +=- ③310x += ④3450p q +-= ⑤468a b -=2、下列各方程组中,属于二元一次方程组的是( )A.23275x y x y +=⎧⎨=⎩B.212x y x z +=⎧⎨+=⎩C.132342x y x y ⎧-=⎪⎨⎪+=⎩D.513223y x x y ⎧-=⎪⎨⎪+=⎩ 3、填下表,使上下每对x ,y 的值是方程35x y +=的解。
广东省广州市第三中学七年级数学下册导学案(无答案)第八章 第5课时 8.3.1简单的三元一次方程组

第五课时 8.3.1简单的三元一次方程组【学习目标】1、熟练掌握二元一次方程组的解法;2、掌握三元一次方程组的解法,进一步体会消元转化的思想。
【学习环节】一、预习导入:1、解二元一次方程组的基本思路:通过 转化为 方程,具体的方法是: 和 。
2、用指定的方法解下列方程组:(1)⎩⎨⎧=+=-122553t s t s (代入法) (2)⎩⎨⎧-=+--=-34352y x y x (加减法)二、探究新知:阅读课文P103—105 解三元一次方程组:⎪⎩⎪⎨⎧=++=-+=+-)3(6)2(1232)1(43z y x z y x z y x 分析:解方程组的基本思路是: ,由“三元”→“ ”→“ ”。
解: ,得 (4)……………(用方程1、2消去z ),得 (5)……………(用方程2、3消去z )(4)和(5)组成方程组解这个方程组,得⎩⎨⎧==y x 把x= ,y= 代入 ,得∴⎪⎩⎪⎨⎧===z y x【小结】三元一次方程组有 个解。
三、对应练习:1、 解下列三元一次方程组:(1) ()()()⎪⎩⎪⎨⎧==++=++3422252112y x z y x z y x 分析一:由于这个方程组中方程(3)只含 分析二:可以考虑把方程(3)分别代入方 有x 、y 这两个未知数,因此可考虑利用方 程(1)、(2),消去未知数x , 把“三元” 程(1)、(2)消去未知数z ,从而把“三 转化为“二元”。
元”转化为“二元”。
解法二:解法一:(2)⎪⎩⎪⎨⎧=-=++-=443223572z x z y x x y (3)⎪⎩⎪⎨⎧=+=+=+392z y z x y x四、归纳总结:1、解三元一次方程组的基本思想是 。
2、这种方法的思路是把三元转化为 ,再把 转化为 。
3、。
初高中数学方程组教案模板

一、教学目标1. 知识与技能:(1)理解并掌握方程组的定义及分类;(2)熟练运用代入消元法和加减消元法解二元一次方程组;(3)初步了解三元一次方程组的解法。
2. 过程与方法:(1)通过观察、分析、比较等活动,培养学生对数学问题的抽象思维能力和逻辑推理能力;(2)通过小组合作、探究交流,提高学生合作学习和解决问题的能力。
3. 情感态度与价值观:(1)激发学生学习数学的兴趣,培养学生对数学的热爱;(2)培养学生严谨求实的科学态度和勇于探索的精神。
二、教学重难点1. 教学重点:(1)方程组的定义及分类;(2)代入消元法和加减消元法解二元一次方程组;(3)三元一次方程组的解法。
2. 教学难点:(1)代入消元法和加减消元法的运用;(2)三元一次方程组的解法。
三、教学准备1. 教师准备:(1)多媒体课件;(2)教学辅助工具(如:卡片、白板等)。
2. 学生准备:(1)预习方程组的定义及分类;(2)复习代入消元法和加减消元法。
四、教学过程1. 导入新课(1)通过生活中的实际问题引入方程组的概念;(2)引导学生回顾二元一次方程组的解法,为学习三元一次方程组做好铺垫。
2. 新授(1)讲解方程组的定义及分类,让学生举例说明;(2)通过实例讲解代入消元法和加减消元法的解题步骤,让学生理解并掌握;(3)引导学生思考三元一次方程组的解法,讲解并演示解题过程。
3. 小组合作(1)将学生分成小组,每组发放一组方程组;(2)要求学生在规定时间内,运用所学方法解决方程组问题;(3)各小组汇报解题过程,教师点评并总结。
4. 练习巩固(1)布置课后作业,要求学生独立完成;(2)教师巡视指导,解答学生疑问。
5. 总结反思(1)引导学生回顾本节课所学内容,总结方程组的解法;(2)强调解题过程中应注意的事项,提高学生解题能力。
五、作业布置1. 完成课后习题,巩固所学知识;2. 搜集生活中与方程组相关的问题,尝试用所学知识解决。
六、板书设计1. 方程组的定义及分类2. 代入消元法3. 加减消元法4. 三元一次方程组的解法七、教学反思本节课通过生活中的实际问题引入方程组的概念,引导学生掌握代入消元法和加减消元法解二元一次方程组,初步了解三元一次方程组的解法。
