修正Newton法求解函数
非线性方程组的求解(汇编)

非线性方程组的求解摘要:非线性方程组求解是数学教学中,数值分析课程的一个重要组成部分,作为一门学科,其研究对象是非线性方程组。
求解非线性方程组主要有两种方法:一种是传统的数学方法,如牛顿法、梯度法、共轭方向法、混沌法、BFGS 法、单纯形法等。
传统数值方法的优点是计算精度高,缺点是对初始迭代值具有敏感性,同时传统数值方法还会遇到计算函数的导数和矩阵求逆的问题,对于某些导数不存在或是导数难求的方程,传统数值方法具有一定局限性。
另一种方法是进化算法,如遗传算法、粒子群算法、人工鱼群算法、差分进化算法等。
进化算法的优点是对函数本身没有要求,不需求导,计算速度快,但是精度不高。
关键字:非线性方程组、牛顿法、BFGS 法、记忆梯度法、Memetic 算法1: 三种牛顿法:Newton 法、简化Newton 法、修改的Newton 法【1-3】求解非线性方程组的Newton 法是一个最基本而且十分重要的方法, 目前使用的很多有效的迭代法都是以Newton 法为基础, 或由它派生而来。
n 个变量n 个方程的非线性方程组, 其一般形式如下:⎪⎪⎩⎪⎪⎨⎧===0),...,(...0),...,(0),...,(21212211n n n n x x x f x x x f x x x f (1)式(1)中,),...,(21n i x x x f ( i=1, ⋯, n) 是定义在n 维Euclid 空间Rn 中开域 D 上 的实值函数。
若用向量记号,令:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n x x x ...X 21,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡====)(...)()(0),...,(...0),..,(0)...,()(2121212,211X f X f X f x x x f x x x f x x x f X F nn n n n则方程组(1)也可表示为:0)(=X F(2) 其中:X ∈R n ,F ∶R n →R 0, F(X) ∈R n , R n 为赋值空间。
非线性方程组的求解

非线性方程组的求解摘要:非线性方程组求解是数学教学中,数值分析课程的一个重要组成部分,作为一门学科,其研究对象是非线性方程组。
求解非线性方程组主要有两种方法:一种是传统的数学方法,如牛顿法、梯度法、共轭方向法、混沌法、BFGS 法、单纯形法等。
传统数值方法的优点是计算精度高,缺点是对初始迭代值具有敏感性,同时传统数值方法还会遇到计算函数的导数和矩阵求逆的问题,对于某些导数不存在或是导数难求的方程,传统数值方法具有一定局限性。
另一种方法是进化算法,如遗传算法、粒子群算法、人工鱼群算法、差分进化算法等。
进化算法的优点是对函数本身没有要求,不需求导,计算速度快,但是精度不高。
关键字:非线性方程组、牛顿法、BFGS 法、记忆梯度法、Memetic 算法1: 三种牛顿法:Newton 法、简化Newton 法、修改的Newton 法【1-3】 求解非线性方程组的Newton 法是一个最基本而且十分重要的方法, 目前使用的很多有效的迭代法都是以Newton 法为基础, 或由它派生而来。
n 个变量n 个方程的非线性方程组, 其一般形式如下:⎪⎪⎩⎪⎪⎨⎧===0),...,(...0),...,(0),...,(21212211n n n n x x x f x x x f x x x f (1)式(1)中,),...,(21n i x x x f ( i=1, ⋯, n) 是定义在n 维Euclid 空间Rn 中开域 D 上 的实值函数。
若用向量记号,令:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n x x x ...X 21,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡====)(...)()(0),...,(...0),..,(0)...,()(2121212,211X f X f X f x x x f x x x f x x x f X F nn n n n则方程组(1)也可表示为:0)(=X F(2) 其中:X ∈R n ,F ∶R n →R 0, F(X) ∈R n , R n 为赋值空间。
Newton法

实验名称 Newton 法及修正Newton 法一、 实验目的:Newton 法及修正Newton 法二、 实验要求:理解Newton 法及修正Newton 法算法的思想,利用计算机编写出此算法的程序。
三、 实验学时数:2学时四、 实验类别:基础实验五、 实验内容:1)、 用Newton 法求解2122212141060)(min x x x x x x x f -++--=,初始点[]01.0,0,00==εT X2)、 用Newton 法求解10)1(2)1(4)(min 212221+++-++=x x x x x f ,初始点[]01.0,0,00==εT X六、 实验报告a) 实验程序流程图b)主要模块代码#include<math.h>#include<stdio.h># define eps 0.01double f (double coe[], double x[]) //返回待求函数的函数值{returncoe[0]*pow(x[0],2)+coe[1]*pow(x[1],2)+coe[2]*x[0]*x[1]+coe[3]*x[0]+coe[4]*x[1]+coe[5] ;}void grads (double coe[], double x[],double grads_x[]) //求解函数的梯度{grads_x[0] = 2*coe[0]*x[0]+coe[2]*x[1]+coe[3];grads_x[1] = 2*coe[1]*x[1]+coe[2]*x[0]+coe[4];}void H (double coe[], double h[])//求解海赛矩阵{h[0] = 2.0*coe[0];h[1] = coe[2];h[2] = coe[2];h[3] = 2.0*coe[1];}void inverseH (double h[], double inverseh[])//求解海赛矩阵的逆矩阵{double deter;deter = h[0]*h[3]-h[1]*h[2];inverseh[0] = h[3]/deter;inverseh[1] = -h[1]/deter;inverseh[2] = -h[2]/deter;inverseh[3] = h[0]/deter;}void main()//主函数{double coe[6] = {1,1,-1,-10,-4,60},x[2] = {0 , 0},grads_x[2],h[4],inverseh[4],fx = 0;grads(coe, x, grads_x);//求梯度while(sqrt(pow(grads_x[0],2)+pow(grads_x[1],2))-eps>0){H(coe, h);//求海赛矩阵inverseH(h, inverseh);//海赛矩阵求逆x[0] = x[0]-(inverseh[0]*grads_x[0]+inverseh[1]*grads_x[1]);x[1] = x[1]-(inverseh[2]*grads_x[0]+inverseh[3]*grads_x[1]);grads(coe, x, grads_x);}fx = f(coe, x);printf("最优解为:");for(int i=0;i<2;i++){printf("\n%f\n",x[i]);}printf("\n最优值为:");printf("\nfx=%f \n",fx);}c)实例计算结果d)收获体会用Newton法求解,只经一轮迭代就得到最优解。
用Matlab编写二分法和Newton迭代法求解非线性函数
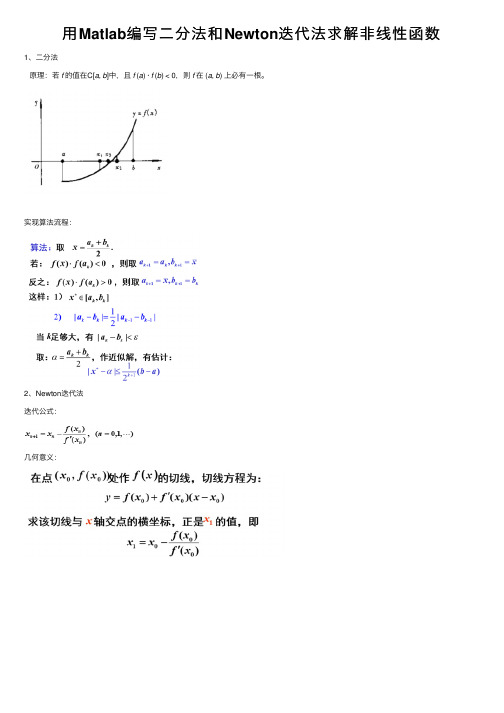
⽤Matlab编写⼆分法和Newton迭代法求解⾮线性函数1、⼆分法原理:若f的值在C[a, b]中,且f (a) · f (b) < 0,则f在 (a, b) 上必有⼀根。
实现算法流程:2、Newton迭代法迭代公式:⼏何意义:3、求解问题⽤Newton法和⼆分法求的解。
4、代码实现1 clear;close;clc2 a=0;b=1;%根区间3 e=10^(-6);%根的容许误差4 [X , N]=dichotomy(e,a,b);%⼆分法5 p0=0.5;%初始值6 N=15;%迭代次数7 [X1]=Newdon(p0,e,N);%Newton迭代法89 function [X , N]=dichotomy(deta,a,b)10 % 函数dichotomy:⼆分法11 %输⼊值:12 %fun:⽅程函数13 %deta:根的容许误差14 %有根区间:[a,b]15 %输出值16 %X:求解到的⽅程的根17 %N:总的迭代次数18 N=1+fix(log2((b-a)/deta));%由公式7.2求得,取整数|X_N-X*|<=(b-a)/2^N<deta,求N19 n=1;20 f1=myfunction(a);21 f2=myfunction(b);22if (f1*f2>0)23 disp('根不在输⼊的区间⾥,请重新输⼊区间');24else25while n <= N26 x=(a+b)/2;27if myfunction(a)*myfunction(x)>028 a=x;29else30 b=x;31 end32 n=n+1;33 end34 X=x;35 fprintf('第%d次⼆分法求出的⽅程的根:\n',N);36 fprintf('X=\n');37 disp(X);38 end39 end4041 function [P]=Newdon(p0,TOL,N)42 %求⽅程组的解43 %输⼊参数44 %初始值:p045 %误差容限:TOL46 %最⼤迭代次数:N47 %输出参数:48 %⽅程近似解:p49 %或失败信息“Method failed”50 format long;51 n=1;%初始迭代次数52 syms x;53while n<=N54if abs(subs(diff(myfunction(x)),x,p0))<TOL55 P=p0;56break;57else58if subs(diff(myfunction(x),2),x,p0)==059 disp('Method failed');60break;61else62 p=p0-myfunction(p0)/subs(diff(myfunction(x)),x,p0);63 p=eval(p);%将exp的值转为⼩数值64if(abs(p-p0)<TOL)65 P=p;66break;67else68 p0=p;69 end70 end71 end72 n=n+1;73 end74 % P=vpa(P,10);%将分数转为⼩数并保留8位⼩数75 fprintf('第%d次NeWton迭代法求出的⽅程的根:\n',N);76 fprintf('P=\n');77 disp(P);78 end7980 function f=myfunction(x)81 f=x*exp(x)-1;82 end5、求解结果。
第二节_牛顿迭代法

2 3 xk
2 f ( x) 3 x
k 0,1, 2,
4、牛顿迭代法的局部收敛性定理 设 x* 为方程 f (x) = 0的根,在包含x*的某个开区间内 f ( x) 连 B ( x *) [ x , x ], f ( x ) 0 续,且 ,则存在 x* 的邻域 使得任取初值 x0 B ( x*),由牛顿迭代法产生的序列xk 以不 低于二阶的收敛速度收敛于x*.
标即为 xk 1 。 y
( x0 , f ( x0 ))
x* x2 x x0 1
x
例2.5:写出求 a (a 0) 的牛顿迭代格式;写出求 a (a 0) 的牛顿迭代格式,要求公式中既无开方运算,又无除法运算。
2 f ( x ) x a 0 (a 0) 的正根 f ( x) 2x 解: 等价于求方程
f ( x ) f ( x0 ) f ( x0 )( x x0 ) f ( ) ( x x 0 ) 2 , 2!
在 x0 和 x 之间
* 取 x x ,可将 (x* x0)2 看成高阶小量,则有:
0 f ( x*) f ( x0 ) f ( x0 )( x * x0 )
lim x n 注意到ξn 在xn 及x*之间,及 n
x n1 x* x n x*
2
x*
,故
f" ( n ) f " ( x* ) * 2 f ' ( xn ) 2 f' ( x )
0(二阶收敛)若 f "( x* ) 0 0(大于二阶收敛)若 f "( x* ) 0
Newton迭代公式是一种特殊的不动点迭代,其 迭代函数为: f ( x) ( x) x f '( x )
牛顿力学高速运动修正式的两种推导方法

牛顿力学高速运动修正式的两种推导方法李丽萍方法一李映华在其所著《物理学的几个重大理论问题》一书中,首次从经典理论推出下述牛顿力学高速运动修正式。
(参阅李映华:《物理学的几个重大理论问题》第31-35页):e VA = (1)1 + a e V上式中:A——电场力对带粒子做的功;e——粒子电荷;V——加速电压;a为常数。
是移动电荷在移动始点势能的倒数。
势能为f r,设为Uo,则a =1/Uo,故式(1)可改变为:e VA = (1a)1+(1/Uo)e Vm e C2设电子在原子核外的最大势能f r = Uo= ,代入上式,得 2e VA =m e C21 + ( 1 / ) e V2即:e VA =1 + ( 1 / m e C2 ) 2 e V (1b)上式中:分母分子分别乘以 m e C 2 ,得:m e C 2 e VA = (1c ) m e C 2+2 e V这就是,从(1)式中考虑了电场力作用速度C 后引出的又一形式的牛顿力学高速运动表达式。
我们从(1 c )式中,代入A = m e υ2/2 ,推出电子速度υ和其它物理量的关系,得:m e υ2 m e C 2 e V =2 m e C 2 +2 e V整理后,得:(2)(2a )方法二电子在电场力作用下的运动,是一种波粒相互作用。
电磁波─作为电磁场载体,我们称它为真空物质,对电子的作用速度为c 。
随着eVc m eV e c222+=υeV c m eVc e 22222+=υ电子在电场力作用下获得速度υ后,真空物质对电子作用的相对速度随c -υ而递减。
当电子获得的速度υ→c 时,真空物质对对电子作用相对速度c →0。
故电子能达到的最大速度υ只能趋近c 。
传统计算公式忽略了这一情况。
所以在考虑电场力对电子相互作用时必须引入“功量递减系数”。
这个系数可由(c 2-υ2)/c 2表示。
因此,牛顿力学在考虑波粒作用这一特征时,描述电场力对电子做功的计算应作如下修正:A = eV (c 2-υ2)/c 2 (3)上式中,A 为电场力对电子做的功,e 为电子电荷,V 为加速电压,c 为光速,υ为电子得到的速度。
改进的Newton法解决二次优化问题

最优化理论与算法实验报告(三)实验名称 改进的Newton 法解决二次优化问题 实验时间姓名专业班级学号成绩一、实验目的和内容实验目的:通过实验, 让学生掌握改进的Newton 法解决优化问题的具体实现, 同时对于具体的问题设计, 让学生根据在实验中出现的数值计算结果,. 理解改进的Newton 法的基本思想. 实验内容:(问题同实验二) 请采用改进的Newton 法求解2221212min ()33n x f x x x x x ∈=+-终止的准则610k g -≤, 分别用如下不同的初时结点进行迭代. 1. ()0 1.5,1.5Tx =, 2. ()02,4Tx =-, 3. ()00,3Tx =二、相关背景知识介绍一、Goldstein —Price (1967) 修正方案:当k G 非正定时, 采用最速下降方向k g -替代牛顿方向. 若进一步将搜索方向与负梯度方向的角度准则结合起来, 则有if cos , elseN Nk k k k k d d g d g η⎧-≥⎪=⎨-⎪⎩其中: 1N k k k d G g -=-,二、Goldfeld (1966) 修正方案若k G 非不正定, 则用k k k G G v I =+来修正k G . 通过适当选取0k v >, 可以使k G 正定. 三、代码牛顿改进算法代码:function re=New(x,Gk,var,n) e=10^n; xk=x;gk=fgk(@f,xk,1); t=[1;0]; k=0;while(norm(gk)>e)mGk=subs(Gk,var,xk);if((t'*mGk*t)>0)[L U]=lu(mGk);dk=U\(L\-gk);xk=xk+dk;gk=fgk(@f,xk,1);k=k+1;elsee=diag(mGk);f1=min(diag(mGk));f1=0.01-f1;E=eye(length(e));mGk=mGk+f1.*E;[L U]=lu(mGk);dk=U\(L\-gk);xk=xk+dk;gk=fgk(@f,xk,1);k=k+1;endend计算梯度的函数:function gk=fgk(f,xk,h)if(h==1)t=f(xk);xk(1)=xk(1)+1;gk(1,1)=f(xk)-txk(1)=xk(1)-1;xk(2)=xk(2)+1;gk(2,1)=f(xk)-t;end初始化函数:syms x1 x2var=[x1,x2];f=3*x1^2+3*x2^2-x1^2*x2;A=jacobian(f,var);e=jacobian(A,var);Gk=e;n=-12;x=[0;0];目标函数:function r=f(x)r=3*x(1)^2+3*x(2)^2-x(1)^2*x(2)四、数值结果X=[-2;4] K=2 Xk=[-4.8087;3.0196]X=[1.5;1.5] K=12 Xk=[-0.5;-0.4583]五、计算结果的分析与New法相互比较,在X=[1.5;1.5]处的迭代次数并未下降,反倒是在鞍点X=[-2;4]处的迭代次数减少了不少,可视为将鞍面做了一个稍稍的倾斜,加快了下降速度。
最优化:最速下降法和Newton法

定理 3.1.1 设假设 2.4.1的条件成立 , 那么采用精确搜索 , 或 Armijo搜索或 Wolfe- P owell搜索的最速下降法产生 的迭 代序列{xk }满足 lim || f ( xk ) || 0
k
由前面的例子看到, 最速下降法的收敛速度至多是线性的, 具体 见下面的两个定理.
第一节
最速下降法
最古老的优化方法,十九世纪中叶由Cauchy提出
1、 思想 :每次沿负梯度方向进行搜索
●
x*
xk 1
等值线(面)
●
xk
●
f ( xk )
负梯度方向也称为最速下降方向:
事实上,对任意p R n 且 || p || , 由Cauchy - Schwarz 不等式得 f ( xk ) T P - || f ( xk ) || || P || - || f ( xk ) || - f ( xk ) - f ( xk ) 当取p 时等号成立,即 p 是下列问题 || f ( xk ) || || f ( xk ) || 的解 min f ( xk ) T P
从上面的例子看到, 对于简单的二元二次函数极小化问题, 最速下降法在有限次迭代并没有求出其精确最优解, 但能 以较慢的速度无限接近最优解.
事实上,上面的例子刻画了最速下降法的所有收 敛特征
3、 最速下降法的收敛性 全局收敛性
由于最速下降法的搜索方向与负梯度方向一致, 即 k 0, 且 || f ( xk ) || || d k || 所以, 由定理2.4.1 - 2.4.3, 我们很容易得到最速下降算法的全 局收敛性.
2
max 其中 , 且max 和min分别是 f ( x * )的最大和最小特征值 . min
用牛顿法求解

最优化理论与方法--牛顿法牛顿法一、牛顿法的介绍迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法,即一次性解决问题。
但多数方程不存在求根公式,因此求解根非常困难,甚至不可能,从而寻找方程的近似根就显得特别重要。
迭代算法是用计算机解决问题的一种基本方法。
它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值。
利用迭代算法解决问题,需要做好以下3个方面的工作:1,确定迭代变量。
在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量。
2,建立迭代关系式。
所谓迭代关系式,是指如何从变量的前一个值推出下一个值的公式(或关系)。
迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成。
3,对迭代过程进行控制。
在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题。
不能让迭代过程无休止地重复下去。
迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定。
对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件。
牛顿迭代法(Newton ’s method )又称为牛顿-拉夫逊方法(Newton-Raphson method ),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,其基本思想是利用目标函数的二次Taylor 展开,并将其极小化。
牛顿法使用函数()f x 的泰勒级数的前面几项来寻找方程()0f x =的根。
牛顿法是求方程根的重要方法之一,其最大优点是在方程()0f x =的单根附近具有平方收敛,而且该法还可以用来求方程的重根、复根,此时非线性收敛,但是可通过一些方法变成线性收敛。
非线性方程组的一个修正牛顿法公式

s to t ceeae i -re o vre c[] h dwi aclrtdt r od r n egn eJ . me h hd c
Ap l d M ah maisLetr , 0 0 1 ( ) 8 - 3 pi t e tc tes 2 0 , 3 8 : 7 9 . e
中G 3 一 (一 () z 去 ) () 且有G ) = c Fz) ~, , = :
J 一 ) ( )一 0 一 .
引理 5] 设 G( )D E z :
一 在
处 可
I I 根据 经典 牛顿 法 的收敛 性有 : l , ) , )I 口J l J ( 一F ( F l≤ I z— l l ( ) G x )I— I 一 ( ) ( ) c l s 一 ( f G f F z 一 l— I , )。F x 一F x ) ( ( l I ( _I ( ) z F ( 一 z )z一 7 ) 一 F () ()一 F ( ) ( 2 ] ,z一[ z , ]z— z )I≤ } l , ) F x -F( 一 l ( r ( ) F x) ) — ) l ( ]l + l , )IF () 一 F ( ]z — )I ≤ l ( -[ , z F , )( z l l ) l l ( )一 F x )一 F ( ( l ( l・ J I F z F ( , )z— z
,
1 )由中点迭代公式所得 的迭代序列 { ) 是≥ 0 收敛 于 S 且有 C
l i m
~ o 扣 。
一 o .
f l 一 z l l
证毕.
2 a 0V ) > , z∈D有 l , ) , )l l ( 一F ( z F l ≤ aI — l 则存在一个常数 M> 0使得 『 z l I , , I z f≤ M z 一I l. I l z 。 l l
Newton迭代法Matlab程序求函数极小值点

Newton迭代法Matlab程序求函数极小值点
clear all
clc
%Newton迭代法求解极小值点
%定义误差初始值为10
deta=10;
i=1;
%循环用求出的近似解迭代Newton方程
%求出下一个近似解,并在规定的误差范围内
while deta>=1e-10&i<10
A=x(:,i);
gi=subs(g,{x1,x2},{A(1),A(2)})';
Gi=subs(G,{x1,x2},{A(1),A(2)});
i=i+1;
x(:,i)=x(:,i-1)-inv(Gi)*gi;
A=x(:,i);
F(i)=subs(f,{x1,x2},{A(1),A(2)});
deta=F(i)-F(i-1);
end
k=(1:n+1)';
F=[f0 F]';
x=[x0,x]';
disp '===================================================='
disp '迭代的各步结果如下:'
disp ' k x(k) F{x(k)}'
[k x F]
%=====================================
%一些初始值的计算
g0=subs(g,{x1,x2},{x0(1),x0(2)})';
牛顿(Newton)插值法

Newton插值C 的求法
i
Nn(x) = c0 + c1(x – x0) + c2(x – x0) (x – x1) + …..+ cn(x – x0) (x – x1) …. (x-xn)
令x = x0得:Nn(x0) = c0 = y0 = f(x0) x = x1得:Nn(x1) = c0 + c1(x1 –x0) = y1 = f(x1) 由此可解出:c0,c1;ci 依次类推。
x y x0 y0 x1 y1 …………. …………. xn-1 yn-1 xn yn xn+1 yn+1
Nn+1(x) = c0 + c1(x – x0) + c2(x – x0)(x – x1) + …. + cn(x – x0) (x – x1) …(x –xn-1) + cn+1(x – x0) (x –x1) ….(x – xn-1) (x - xn)
求n次多项式Nn(x)使得:
Nn(xi) = f(xi) = yi, i = 0,1,… ,n Nn(x) = c0 + c1(x – x0) + c2(x – x0) (x – x1) + …..+ cn(x – x0) (x – x1) …. (x-xn)
Newton插值的承袭性
增加一个点之后
p1xp0xc1xx0其中p0xfx0其修正项的系数01011xxxfxfc???再进一步修正p1x可以进一步得到抛物线插值公式p2xp1xc2xx0xx10201011212xxxxxfxfxxxfxf??????c2差商的概念差商的定义定义1
牛顿(Newton)插值法
修正牛顿(newton)法求解无约束问题

修正牛顿(newton)法求解无约束问题------------------基于成都理工大学最优化教材#include <iostream.h>#include "Matrix.h"#include<LIMITS.H>#define MAX_M 2048#include<math.h>#define beta (sqrt(5)-1)/2#define eclipse 0.01CMatrixhesse(){CMatrixtemp(2,2);temp.A[0][0] = 8;temp.A[0][1] = 0;temp.A[1][0] = 0;temp.A[1][1] =4;return temp;}double fun(double t,CMatrix&X1,CMatrix &X2){double x1 = X1.A[0][0] + t*X2.A[0][0];double x2 = X1.A[1][0] + t*X2.A[1][0];return 4*(x1+1)*(x1+1) + 2*(x2-1)*(x2-1) + x2 + x1 +10;}doubleMax_Num(double a,double b){if(a>b){return a;}else{return b;}}doubleMin_Num(double a,double b){if(a<b){return a;}else{return b;}}voidStepAdding_Search(double &a,double&b,CMatrix&mt1,CMatrix &mt2) {double t[MAX_M]={0};double h[MAX_M]={0};double f[MAX_M]={0};double result=0;double p=2.1;t[0]=0;h[0]=1;f[0]=fun(t[0],mt1,mt2);for(int k=0;k<MAX_M-1;k++){t[k+1]=t[k]+h[k];f[k+1]=fun(t[k+1],mt1,mt2);if(f[k+1]<f[k]){h[k+1]=p*h[k];result=t[k];t[k]=t[k+1];f[k]=f[k+1];}else if(k == 0){h[k]=-h[k];result=t[k+1];}else{a=Min_Num(result,t[k+1]);b=Max_Num(result,t[k+1]);}}}double Fibonacci(double &a,double&b,CMatrix mt1,CMatrix mt2){double t2,t1,result_1,result_2;t2 = a + beta*(b-a);result_2 = fun(t2,mt1,mt1);while(true){t1 = a+b-t2;result_1 = fun(t1,mt1,mt2);if(fabs(t1-t2)<eclipse){return (t1+t2)/2;}else if(result_1 < result_2){b = t1;t1 = t2;result_1 = result_2;t2 = a+beta*(b-a);result_2 = fun(t2,mt1,mt2);}else if(result_1 == result_2){a = t1;b = t2;result_2 = fun(a,mt1,mt2);}else{a = t2;t2 = t1;result_2 = result_1;}}}double distance(CMatrix&X1,CMatrix &X2) {double x1 = X1.A[0][0] - X2.A[0][0];double x2 = X1.A[1][0] - X2.A[1][0];return x1*x1 + x2*x2;}CMatrixdiff_fun(CMatrix&mt){CMatrixtemp(2,1);temp.A[0][0] = 8*(mt.A[0][0] +1) +1;temp.A[1][0] = 4*(mt.A[1][0] -1) +1;return temp;}void main(){CMatrix X1(2,1);X1.A[0][0] = 0;X1.A[1][0] = 0;CMatrixm_temp = hesse();CMatrixn_temp = diff_fun(X1);CMatrix X2 = (m_temp.Inverse()* n_temp).Matrix_Multiply(-1);doublea,b;StepAdding_Search(a,b,X1,X2);double m = Fibonacci(a,b,X1,X2);CMatrix X3 = X1 + X2.Matrix_Multiply(m);while(distance(X1,X3) > eclipse){X1 = X3;X2 = m_temp.Inverse()* diff_fun(X1);StepAdding_Search(a,b,X1,X2);m = Fibonacci(a,b,X1,X2);X3 = X1 + X2.Matrix_Multiply(m);}cout<<"求解的结果是:"<<endl;cout<<"("<<X1.A[0][0]<<","<<X1.A[1][0]<<")"<<endl;cout<<"最优解是:"<<endl;cout<<fun(m,X1,X2)<<endl;}。
用Newton法、DFP法和BFGS法求函数极值

ᓔ ྟ 䆒㕂㊒ᑺˈ㒭ᅮ߱ྟⱘ䗁ҷ⚍
yes
ℹ䭓||S||<㊒ᑺ˛
no
䅵ㅫk䗁ҷ⚍໘ⱘ⍋Ểⶽ䰉H ẃᑺ䞣 k+1ℹ 䗮䖛㾷㒓ᗻᮍˈᕫࠄkℹⱘᮍ Sk 㒧ᴳ䗁 ҷˈᕫࠄ ᵕؐ⚍X
ЎSk=X k+1 -Xk; ᠔ҹˈᕫࠄᮄⱘ䗁ҷ⚍Xk+1=X k +S k.
图 1: Newton方法的算法简图 b)计算(xk , yk , zk )点处的海森矩阵和梯度向量时,调用函数[Hessen, grads] = HessenM atrica ndg rids(x, y, z )求 解。 → − → c)由于− x− k+1 和xk 满足方程: → − − → − → − → −1 ∗ − →) x− ∇ f (x k+1 = xk − Hf (xk ) k 所以为了避免求海森矩阵的逆矩阵,令 − → → − → sk = − x− k+1 − xk 就转化为解线性方程组: − − − − − → → → Hf (xk ) ∗ − sk = −∇f (− x k)
− → 考 察 梯 度 向 量 ∇ (f (x, y, z ))容 易 看 出 , 在(x, y, z ) ∈ [−1, 1] ∗ [−1, 1] ∗ [−1, 1]范 围 内 , 只 − → 有(0, 0, 0)点能使得 ∇ (f (0, 0, 0)) = 0,其余点梯度均不为0,所以,(0, 0, 0)点是唯一的一个 极值点,且,求得海森矩阵 2.0200 0 0 Hf = (12) 0 0.6000 0 0 0 4.0000 因为|Hf | = 4.8480 > 0,所以(0, 0, 0)点是函数的一个极小值点。相应的极小值为f (0, 0, 0) = 0. 下文分别用Newton法、DFP方法和BFGS方法三种方法求取函数极值点,并比较其特点。
牛顿法 重根问题-概述说明以及解释

牛顿法重根问题-概述说明以及解释1.引言1.1 概述牛顿法是一种经典的数值计算方法,广泛应用于解决方程和优化问题。
它基于牛顿-拉夫逊方程而得名,由数学家伊萨克·牛顿在17世纪提出。
牛顿法的基本思想是通过不断迭代逼近函数的零点或最值点。
它通过计算函数在某点的导数和函数值的比值,确定函数在该点的局部线性近似,然后以该近似替代原函数,再求出近似函数的零点或最值点,不断迭代直至满足收敛条件。
重根问题是在求解方程时遇到的一类特殊情况。
当一个多项式函数有重复根时,常规的数值方法往往会失效,因为函数的导数在重根处为零,导致求解过程中出现除零操作或梯度无法更新的情况。
因此,如何有效地解决重根问题一直是数值计算中的挑战之一。
本文将从牛顿法的基本原理出发,介绍牛顿法在解决重根问题中的应用。
首先,我们将详细讨论牛顿法的原理和算法流程,以及收敛性和速度等方面的特点。
接着,我们将引入重根问题的定义和背景,并讨论重根问题对牛顿法的影响。
最后,我们将重点探讨牛顿法在解决重根问题中的应用方法及改进策略,并通过实例验证其有效性。
通过本文的研究,我们将对牛顿法在解决重根问题中的优势和局限性有更深入的了解,为其在实际问题中的应用提供指导和参考。
此外,我们还将展望牛顿法在其他数值计算问题中的潜在应用,并总结研究结果,为今后的相关研究提供思路和方向。
综上所述,本文旨在探讨牛顿法在解决重根问题中的应用,并通过分析和研究为其在实践中的应用提供理论基础和实践指导。
希望通过本文的阐述,读者能够更好地理解牛顿法及其在解决重根问题中的价值。
1.2文章结构文章结构部分的内容可以从以下几个方面展开:1.2 文章结构:本文将分为三个主要部分来介绍牛顿法在解决重根问题中的应用。
首先,在引言部分,我们将对牛顿法和重根问题进行概述,介绍文章的主要结构和目的。
接着,在正文部分,我们将详细阐述牛顿法的基本原理,并给出重根问题的定义和背景。
然后,我们将重点讨论牛顿法在解决重根问题中的应用,探讨其优势和适用性。
牛顿迭代法.

牛顿迭代法李保洋数学科学学院信息与计算科学学号:060424067指导老师:苏孟龙摘要:牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方法,即牛顿迭代法.迭代法是一种不断用变量的旧值递推新值的过程•跟迭代法相对应的是直接法或者称为一次解法,即一次性解决问题•迭代法又分为精确迭代和近似迭代“牛顿迭代法”属于近似迭代法,本文主要讨论的是牛顿迭代法,方法本身的发现和演变和修正过程,避免二阶导数计算的Newton迭代法的一个改进,并与中国古代的算法,即盈不足术,与牛顿迭代算法的比较•关键词:Newton迭代算法;近似求解;收敛阶;数值试验;中国古代数学;九章算术;Duffing方程;非线性方程;收敛速度;渐进性0引言:迭代法也称辗转法,是一种不断用变量的旧值递推新值的过程,跟迭代法相对应的是直接法或者称为一次解法,即一次性解决问题•迭代法又分为精确迭代和近似迭代•“二分法”和“牛顿迭代法”属于近似迭代法•迭代算法是用计算机解决问题的一种基本方法•它利用计算机运算速度快、适合做重复性操作的特点,让计算机对一组指令(或一定步骤)进行重复执行,在每次执行这组指令(或这些步骤)时,都从变量的原值推出它的一个新值•具体使用迭代法求根时应注意以下两种可能发生的情况:(1)如果方程无解,算法求出的近似根序列就不会收敛,迭代过程会变成死循环,因此在使用迭代算法前应先考察方程是否有解,并在程序中对迭代的次数给予限制•(2)方程虽然有解,但迭代公式选择不当,或迭代的初始近似根选择不合理,也会导致迭代失败•所以利用迭代算法解决问题,需要做好以下三个方面的工作:1、确定迭代变量•在可以用迭代算法解决的问题中,至少存在一个直接或间接地不断由旧值递推出新值的变量,这个变量就是迭代变量2、建立迭代关系式.所谓迭代关系式,指如何从变量的前一个值推出其下一个值的公式(或关系).迭代关系式的建立是解决迭代问题的关键,通常可以使用递推或倒推的方法来完成.3、对迭代过程进行控制,在什么时候结束迭代过程?这是编写迭代程序必须考虑的问题.不能让迭代过程无休止地重复执行下去.迭代过程的控制通常可分为两种情况:一种是所需的迭代次数是个确定的值,可以计算出来;另一种是所需的迭代次数无法确定.对于前一种情况,可以构建一个固定次数的循环来实现对迭代过程的控制;对于后一种情况,需要进一步分析出用来结束迭代过程的条件.1牛顿迭代法:洛阳师范学院本科毕业论文X 0 牛顿迭代有十分明显的几何意义,如图所示:牛顿 迭代法(Newton method)又称为牛顿-拉夫逊方法(Newto n-Rapfsonmethod),它是牛顿在17世纪提出的一种在实数域和复数域上近似求解方程的方 法.多数方程不存在求根公式,因此求精确根非常困难甚至不可能,从而寻找方程的近似根就显得特别重要•方法使用函数f x 的泰勒级数的前面几项来寻找方程f x =0的根•牛顿迭代法是求方程根的重要方法之一,其最大优点是在方程f x =0的单根附近具有平方收敛性,而且该法还可以用来求方程的重根、复根. 另外该方法广泛用于计算机编程中:解非线性方程f x ]=0的牛顿(Newton)法是把非线性的方程线性化的一种近似方法•把f x 的x 点附近展开泰勒(Taylor )级' 2 f x = f x 0 f X - X 0 f x 0 ]亠 ix - X 0取其线性部分作为非线性方程f x =0的近似方程,则有:f X 。
非线性方程组的求解

非线性方程组的求解摘要:非线性方程组求解是数学教学中,数值分析课程的一个重要组成部分,作为一门学科,其研究对象是非线性方程组。
求解非线性方程组主要有两种方法:一种是传统的数学方法,如牛顿法、梯度法、共轭方向法、混沌法、BFGS 法、单纯形法等。
传统数值方法的优点是计算精度高,缺点是对初始迭代值具有敏感性,同时传统数值方法还会遇到计算函数的导数和矩阵求逆的问题,对于某些导数不存在或是导数难求的方程,传统数值方法具有一定局限性。
另一种方法是进化算法,如遗传算法、粒子群算法、人工鱼群算法、差分进化算法等。
进化算法的优点是对函数本身没有要求,不需求导,计算速度快,但是精度不高。
关键字:非线性方程组、牛顿法、BFGS 法、记忆梯度法、Memetic 算法1: 三种牛顿法:Newton 法、简化Newton 法、修改的Newton 法【1-3】 求解非线性方程组的Newton 法是一个最基本而且十分重要的方法, 目前使用的很多有效的迭代法都是以Newton 法为基础, 或由它派生而来。
n 个变量n 个方程的非线性方程组, 其一般形式如下:⎪⎪⎩⎪⎪⎨⎧===0),...,(...0),...,(0),...,(21212211n n n n x x x f x x x f x x x f (1)式(1)中,),...,(21n i x x x f ( i=1, ⋯, n) 是定义在n 维Euclid 空间Rn 中开域 D 上 的实值函数。
若用向量记号,令:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=n x x x ...X 21,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡====)(...)()(0),...,(...0),..,(0)...,()(2121212,211X f X f X f x x x f x x x f x x x f X F nn n n n则方程组(1)也可表示为:0)(=X F(2) 其中:X ∈R n ,F ∶R n →R 0, F(X) ∈R n , R n 为赋值空间。
