2021年降水计算公式
利用月温度和降水计算指数的公式

利用月温度和降水计算指数的公式
月温度和降水指数的计算公式是一种常用的方法,用于评估一个地区的气候条件。
这个指数可以帮助我们了解一个地区的气温和降水情况,从而更好地进行农业生产、水资源管理等方面的决策。
在计算月温度和降水指数时,我们需要收集一段时间内的月平均温度和降水量数据。
然后,我们可以使用以下公式来计算指数:
指数 = 月平均温度 × 降水量
其中,月平均温度是指某个月份的平均温度,单位可以是摄氏度或华氏度;降水量是指某个月份的降水量,单位可以是毫米或英寸。
通过计算指数,我们可以得到一个数值,这个数值可以反映出该地区的气候条件。
如果指数较高,说明该地区气温较高且降水量较大;如果指数较低,说明该地区气温较低且降水量较少。
通过计算月温度和降水指数,我们可以更好地了解一个地区的气候特点,为农业生产、水资源管理等提供重要的参考依据。
同时,这个指数也可以用于比较不同地区的气候条件,从而帮助我们做出更明智的决策。
月温度和降水指数是一种有效的方法,用于评估一个地区的气候条件。
通过计算指数,我们可以更好地了解一个地区的气温和降水情况,从而为农业生产、水资源管理等提供参考依据。
这个指数的计
算公式简单易懂,可以方便地应用于实际工作中。
2021年河南省一次罕见暴雨过程的降水特征及成因

精品文档供您编辑修改使用专业品质权威编制人:______________审核人:______________审批人:______________编制单位:____________编制时间:____________序言下载提示:该文档是本团队精心编制而成,希望大家下载或复制使用后,能够解决实际问题。
文档全文可编辑,以便您下载后可定制修改,请根据实际需要进行调整和使用,谢谢!同时,本团队为大家提供各种类型的经典资料,如办公资料、职场资料、生活资料、学习资料、课堂资料、阅读资料、知识资料、党建资料、教育资料、其他资料等等,想学习、参考、使用不同格式和写法的资料,敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you!And, this store provides various types of classic materials for everyone, such as office materials, workplace materials, lifestylematerials, learning materials, classroom materials, reading materials, knowledge materials, party building materials, educational materials, other materials, etc. If you want to learn about different data formats and writing methods, please pay attention!2021年河南省一次罕见暴雨过程的降水特征及成因【前言】2021年7月,河南省遭遇了一场罕见的暴雨过程,导致了严峻的洪涝灾难。
人教版地理八年级上2.2降水(共24张PPT)

•
降水空间分布不均的影响因素
海陆因素(夏季风) 地形因素(山脉阻挡)
降水东西差异 加剧东西差异
纬度因素
东部降水的南北差异
降水时间分布不均:季节不均
• 影响体育活动,在湿润的南方地区,游 泳、赛龙舟是一常见的运动,半干旱的 内蒙古草原骑马、射箭是常见的运动。
不同的干湿地区对我们的生产与生活的影响
饮食习惯
北方人:
喜食面
南方人:
吃米饭
总结
我国的降水规律
我国降水的空间分布:从东南沿海向西北 内陆递减
夏季风
我国降水的时间变化:降水集中在4-10月,南 方雨季长,北方雨季短;降水年际变化很大。
2.图中等降水量 线数值变化的方向 有何规律?
由东南向西北 逐渐减少
降水空间分布不均
知道我国降水量最多和最少的 地方都是哪里吗?
吐鲁番盆地中的托克逊是我国降 水最少的地方,年平均降水量仅 5.9毫米,年降水天数不足10天, 有些年份滴水不见。在吐鲁番, 常常见到一幢幢专门晾制葡萄干 的“荫房”。在干旱少雨的气候 下,葡萄挂在通风的室内就可以 自然风干。
台湾岛东北部的火烧寮是我国 降水最多的地方,年平均降水 量达6 558毫米。1912年更创 下年降水量8 409毫米的记录。
降水空间分布不均
探寻原因
为什么降水 从东南沿海向西 北内陆递减?
•9、要学生做的事,教职员躬亲共做;要学生学的知识,教职员躬亲共学;要学生守的规则,教职员躬亲共守。2021/8/122021/8/12Thursday, August 12, 2021 •10、阅读一切好书如同和过去最杰出的人谈话。2021/8/122021/8/122021/8/128/12/2021 3:06:35 PM •11、只有让学生不把全部时间都用在学习上,而留下许多自由支配的时间,他才能顺利地学习……(这)是教育过程的逻辑。2021/8/122021/8/122021/8/12Aug-2112-Aug-21 •12、要记住,你不仅是教课的教师,也是学生的教育者,生活的导师和道德的引路人。2021/8/122021/8/122021/8/12Thursday, August 12, 2021
概率匹配订正法在湖北襄阳地区降水预报中的应用

沙漠与绿洲气象Desert and Oasis Meteorology第18卷第2期2024年4月襄阳地处北亚热带季风气候区,居汉水中游,西高东低。
西部、中部、东部分别为山地、岗地、丘陵,地形比较复杂,由于气候和地形的原因,容易出现极端强降水。
因此,做好汛期降水预报对襄阳市经济发展和防灾减灾至关重要。
数值天气预报(NWP )为定量降水预报提供了重要的参考依据,但大气本身的混沌特性等使得预报结果具有不确定性[1-3]。
因此,要在业务中充分发挥NWP 产品的指导作用,需要采用一定的释用方法对NWP 产品进行处理,从而改进模式的预报效果。
目前常用的提高预报准确率的途径是不断对数值预报产品进行效果检验评估,从多种模式的降水预报产品中选择性能最稳定的,并在检验的基础上运用多种方法开展解释应用[4-8]。
赵声蓉等[9]、陆如华等[10]分别采用神经元网络、卡尔曼滤波等统计方法对数值预报产品进行解释应用研究。
韩焱红等[11]采用历史观测资料和集合预报资料,基于贝叶斯理论得到了集成贝叶斯降水的概率预报,其预报结果的可靠性高于采用集合预报方法得到的概率预报。
刘琳等[12]根据观测与集合预报累积概率分布函数,建立了集合预报与模式历史预报连续差异的数学模型。
李莉等[13]、包慧濛等[14]、李俊等[15]采用频率匹配法开展试验,结果表明该方法能有效减小模式预报偏差,但降水落区改进效果有限。
该方法在确定订正系数时所有的格点或站点降水预报订正系数是相同的。
中国幅员辽阔,气候背景不尽相同,模式系统性偏差分布有差异,运用同一订正系数进行降水订正,使较为干旱的地区订正后预报偏湿,增加了空报,而较为湿润的地区订正后预报偏干,使漏报增加。
周迪等[16]、陈翔翔等[17]、郭达烽等[18]为解决此问题,引入累积概率分布函数,采用点对点的方式进行概率匹配,得到了不同站点或格点降水预报的订正值。
曹萍萍等[19-20]将观测与模式预报的累积概率分布进行概率概率匹配订正法在湖北襄阳地区降水预报中的应用袁良,谭江红*,闫彩霞,张玉翠(襄阳市气象局,湖北襄阳441021)摘要:利用2016—2020年汛期ECMWF 模式预报降水与湖北襄阳区域站观测降水进行对比分析,结果表明:ECMWF 对中雨及以上降雨的预报,第1、2天预报值偏小,第3天预报值偏大;3个预报时段强降雨中心位置偏差无规律。
(2021年整理)环评中常用到的计算公式

环评中常用到的计算公式编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(环评中常用到的计算公式)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为环评中常用到的计算公式的全部内容。
环评中常用到的计算公式1。
起尘量计算方法 ................................................ 1 2。
居民区与工作区标准限值转换公式 ................................ 5 3。
锅炉燃煤烟气 .................................................. 6 4. 焊接废气 ...................................................... 7 5。
注塑废气 ...................................................... 8 6。
液体(除水以外)蒸发量的计算 .................................. 9 7. C X H Y 与COD 的转化关系 .......................................... 11 8. COD 的理论计算 ................................................ 11 9。
湿式除尘器耗水量 ............................................. 17 10。
江苏省城市用水与公共用水定额 ................................ 18 11. 等效排气筒速率以及排气筒高度计算 . (22)1. 起尘量计算方法(一)建设工地起尘量计算:()⎪⎭⎫⎝⎛⨯⎥⎦⎤⎢⎣⎡-⨯⎪⎭⎫ ⎝⎛⨯⨯⨯=43653653081.0T w V s P E式中:E —单辆车引起的工地起尘量散发因子,kg/km;P —可扬起尘粒(直径<30um)比例数;石子路面为0.62,泥土路面为0。
第三章第三节降水的变化与分布-2021年初中同步测控优化设计七年级《地理》福建专版-配套PPT课件

A
解析 答案
快乐预习感知 互动课堂理解 轻松尝试应用
1
2
3
4
5
6
6.用表中的降水量数据,补绘降水量柱状图。
月份
1 2 3 4 5 6 7 8 9 10 11 12
降水量 10 5 22 47 71 81 135 169 112 57 24 12
毫米
略。
关闭
答案
6
5.下列关于世界年降水量分布的叙述,正确的是( )
A.赤道地区降水多
B.北回归线附近地区降水量均很少
C.两极地区降水多
D.中纬度地带,内陆降水多于沿海地区
关闭
世界年降水量分布的一般规律是:赤道地区、回归线附近的大陆东岸、
中纬度沿海地区降水多,两极地区、回归线附近的大陆西岸、中纬度
内陆地区降水少。
关闭
一二
快乐预习感知 互动课堂理解 轻松尝试应用
快乐预习感知 互动课堂理解 轻松尝试应用
一二
【例1】 你学会判读降水量柱状图了吗?请说出下面四地在降水 量分配上的异同。
解析:降水较多的月份:广州为4~9月,武汉为3~8月,北京为7、8月, 哈尔滨为7、8 月;四地的雨季长短不同,越往北降水月份越集中,降 水量越少。
生活
有着重要的影响。
5.降水的季节变化:通常用各月 降水量柱状图
来表示
一个地区一年内降水的季节变化。
一二
快乐预习感知 互动课堂理解 轻松尝试应用
二、降水的分布
1.表示方法
通常用等降水量线图来表示,在同一条等降水量线上,各点的降 水量 相等 。
2.分布规律 (1)赤道附近地带降水 多 ,两极地区降水 少 。 (2)南、北回归线两侧,大陆东岸降水 多 ,西岸降水 少 。 (3)中纬度沿海地区降水 多 ,内陆地区降水 少 。
全国雷达分钟降水方法在面雨量预报上应用的检验

全国雷达分钟降水方法在面雨量预报上应用的检验作者:丁劲张国平高金兵王曙东王阔音薛冰章芳杨静来源:《安徽农业科学》2021年第17期摘要为了解基于全国雷达分钟降水方法在面雨量上的短期预报效果,利用2020年7月25日08:00—28日08:00安徽巢湖及其子流域的实况面雨量数据,依据平均绝对误差、均方根误差、TS评分、漏报率和空报率几项检验指标,对安徽巢湖及其子流域研究时段内逐小时和累计2 h面雨量预报结果进行检验评估。
结果表明,全国雷达分钟降水方法对巢湖北部平原区子流域的预报效果好于南部丘陵地区子流域;累积2 h产品的预报效果好于逐小时产品的预报效果;对小雨量的预报结果优于大雨量的预报结果。
关键词全国雷达分钟降水方法;流域;面雨量;短期预报;检验中图分类号 S165 文献标识码 A文章编号 0517-6611(2021)17-0221-05doi:10.3969/j.issn.0517-6611.2021.17.056Abstract In order to understand the short-term forecasting effect on the surface rainfall based on the minute quantitative precipitation forecast (MQPF),the actual surface rainfall data of Anhui Chaohu Lake and its sub-catchments from 08:00 July 25 to 08:00 July 28, 2020 were used to relyon the average absolute error,root mean square error,TS score,omission rate and false prediction ratio were several test indicators to test and evaluate the hourly and cumulative 2-h area rainfall forecast results during the study period of Chaohu Lake and its sub-catchments in Anhui.The results showed that the MQPF forecast had a better forecasting effect on the sub-basins in the northern plain area of Chaohu Lake than those in the southern hilly area.More accurate forecast could be seen in cumulative two-hour products than hourly products.The low rainfall level showed better results than the forecast for high rainfall level.Key words Minute quantitative precipitation forecast (MQPF);Basins;Area rainfall;Short-term forecast;Verification面雨量是水文预报中的一个重要参量,面雨量预报的精度直接关系到洪水预报精度和洪水调度决策的科学性[1]。
汉中市暴雨强度公式推算与适用性分析

吴素良,蔡新玲,张文静,等.汉中市暴雨强度公式推算与适用性分析$%陕西气象#021(2):38-43.文章编号!006-4354(2021)02-0038-06汉中市暴雨强度公式推算与适用性分析吴素良,蔡新玲,张文静,张侠(陕西省气候中心,西安710014)摘要:汉中市原暴雨强度公式为利用1980年前资料推算所得,为科学、合理地制定汉中城市总体规划、排水专业规划和排水防涝工程设计,有必要推算满足现阶段设计需求的暴雨强度公式(利用汉中1961-2013年逐年逐分钟降水资料,采用多种算法得到皮尔逊&型分布曲线拟合,应用最小二乘法求参推算的暴雨强度公式,精度满足《室外排水设计规范》要求。
暴雨强度的皮尔逊&型频率分布表明,暴雨历时越短暴雨强度越大,重现期越短暴雨强度越小,长历时降水强度的相对变幅比短历时更大,低重现期降水强度的相对变幅比高重现期更大(适用性分析表明:原公式计算的暴雨强度均显著小于新公式计算值,而且短历时偏小较多,长历时偏小相对较少;将前后两个时段暴雨强度公式的计算值进行对比发现,随着历时缩短,在一定重现期下,1981-2013年比1961-1980年暴雨强度增强,反之随着历时延长,暴雨强度减弱)014—2019年暴雨强度统计值小于新公式推算值,但大于原公式的强度。
总体上,新的暴雨强度公式具有较好的适用性和安全性(关键词:暴雨强度公式;皮尔逊&型;适用性;汉中中图分类号:TU992.02文献标识码:A设计暴雨是城市室外排水系统规划、设计和建设的重要标准,它的可靠性是城市安全的基础汉中市原暴雨强度公式是西北建筑工程学院利用20世纪60—70年代19a资料,采用数理统计方法编制的。
在过去二十多年使用中,有效地指导了城市雨水排水规划设计工作,在城市雨水灾害防治管理、预警和应急处置及城市建设等方面起到了重要作用。
由于区域暴雨频发致灾2,降水年际变化大为科学、合理地制定汉中城规划、水专规划和水防涝工设计,按照《室外排水设计规范》4和《城市暴雨强度公式编制和设计暴雨雨型确定技术导则》5推求出一个满足现阶段设计需求的暴雨强度公式,提升城市排水设施能力,减少城市内涝发生。
2020-2021初中地理天气与气候练习题(及答案)

一、天气与气候选择题1.一年中最冷月和最热月的平均气温之差为气温年较差。
下图是欧洲部分城市一月和七月气温状况示意图。
读图,回答下面小题。
(1)关于图中城市气温的描述,正确的是()A. 越往东,气温越高B. 越往东,气温越低C. 越往东,气温年较差越大D. 越往东,气温年较差越小(2)影响图中城市气温分布特点的主要因素是()A. 纬度位置B. 太阳辐射C. 海陆位置D. 地形地势【答案】(1)C(2)C【解析】【分析】气温的变化受纬度因素、海陆因素和地形因素的影响,在全球大致呈由低纬度向高纬度递减的分布规律,欧洲西部受大西洋西风的影响明显,海洋性特征显著。
(1)由图可知,图示气温数据既有最高气温也有最低气温,二者变化情况需分开来看,故AB两项错误;越往东气温的年较差越大,这是由于越往东离海洋越远,温差越大,故选C。
(2)由图可知,图中城市气温分布是越往东气温年较差越大,这是由于受海陆位置的影响而形成的,故选C。
故答案为:(1)C;(2)C。
【点评】(1)该小题考查气温的变化特征,侧面考查学生的读图提取信息的能力,难度不大,要求学生仔细读图逐项解答。
(2)该小题考查影响气温的因素,是常考的重要考点,有一定难度,需结合所给城市位置分析。
2.电视天气预报节日中出现“ ”天气符号时,表示的天气状况是()A. 睛转多云,西北风6级B. 睛转阴,东南风3级C. 多云转睛,东南风3级D. 睛转阵雨。
西北风6级【答案】 A【解析】【分析】解:风向是指风吹来的方向,用符号表示就是:风杆上的小横道叫风尾,风杆上画有风尾的一方,即指示风向,标在风杆的左侧。
风级的表示方法是:一道风尾,风力是2级,半道风尾是1级风,一个风旗表示8级风。
读题干可知,电视天气预报节目中出现“ ”天气符号时,表示的天气状况是晴转多云,西北风6级。
故答案为:A。
【点评】天气符号是代表各种天气现象、云状、天空状况等的专用符号,包括供观测记录使用的天气现象符号和供媒体传播使用的天气图形符号。
降水现象仪测量结果的不确定度评定方法

t
rumen
t me
a
su
r
emen
t and t
e
s
t
i
ng l
abo
r
a
t
o
r
he me
a
su
r
emen
t
p
p
y t
unc
e
r
t
a
i
n
t
l
ua
t
i
onme
t
hodo
fr
a
i
nd
r
opde
t
e
c
t
i
onr
e
su
l
t
so
fpr
e
c
i
i
t
a
t
i
onphenomenoni
ns
t
rumen
ti
s
yeva
23
3)扩展不确定度
依据国家计量 校 准 规 范 要 求,计 算 出 被 测 降
水现象仪雨滴粒 径、粒 速 的 合 成 不 确 定 度 和 扩 展
不确定度.由式(
3)先 计 算 出 被 测 降 水 现 象 仪 雨
滴粒径、粒 速 的 合 成 不 确 定 度 uc,计 算 结 果 如 表
uc =
2
B2
u +u +u
vi 为
n 次降水现象仪测 量 值 的 算 术 平 均 值;
uA 为 各 测
uA =
量点上测量 结 果 均 值 的 标 准 不 确 定 度;
n 为各测
量点上的测量次数(
i=1,
2,
还下!今年郑州降雨量到底有多少?

还下!今年郑州降⾬量到底有多少?2021年7⽉,郑州连遭暴⾬袭击引发⽹友关注。
近⼏天,⾬云再次覆盖河南,暴⾬⽉度返场!据统计数据显⽰:今年郑州年⾬量或超1400毫⽶,这可能打破北京1404.6毫⽶的北⽅省会年降⾬量纪录。
⼀个⼩时下17个西湖7.20郑州的暴⾬引发了全国⼈民的关注,⽹传郑州⼀个⼩时下了17个西湖,这个数据到底是如何⽽来?在国家⽓象信息中⼼的⽹站上,根据 24 ⼩时降⾬量将暴⾬分为了三个等级,即 50-99.9 毫⽶的称作“暴⾬”、 100-249.9毫⽶的称作“⼤暴⾬”、250 毫⽶以上的称作“特⼤暴⾬”。
据郑州⽓象局的测算,郑州7⽉20⽇16时到17时,⼀⼩时达到了201.9毫⽶。
在以往郑州的降⾬历史记录中,⾬量最⼤的⼀次是1986年7⽉3⽇的下午 3 点,⽽那⼀次累计6⼩时的降⽔量才201毫⽶。
这是什么概念?也就是说常年平均全年降⾬量才640.8mm的郑州,仅7⽉20⽇这⼀天,郑州就下了以往⼀年的⾬量。
究竟如何向别⼈解释这1⼩时⾬量有多恐怖?⼀个众所周知的参照物——西湖映⼊眼帘,最终,问题可以转化成:“郑州在⼀个⼩时内下了多少个西湖?”于是乎,就有了如下计算。
已知:(1)有如下单位转换:1毫⽶ = 0.1厘⽶ = 0.001⽶;1公⾥=1000⽶;1吨⽔=1000千克(公⽄)。
(2)1毫⽶的降⽔量是指单位⾯积上⽔深1毫⽶。
备注:“任何⼀个拥有固定横截⾯的开⼝容器都可以作为⾬量计”(来源《⽓象学与⽣活》(原书第12版)第122页),故拿个直筒⽔杯就可以在家量了。
(3)⽔在3.98℃时密度最⼤,即999.97kg/m³,近似计算中常取1000kg/m³。
备注:此处取近似计算值。
按照1000千克=1吨,则1吨/⽴⽅⽶。
(4)《郑州市⼈民政府关于2019年郑州市城市建成区规模的通告》中,2019年郑州市市域城市建成区⾯积合计为1181.51平⽅公⾥,中⼼城区建成区⾯积651.35平⽅公⾥。
基于QDM方法的江淮流域极端降水模拟能力评估

DOI:10.16660/ki.1674-098X.2012-5640-3391基于QDM方法的江淮流域极端降水模拟能力评估①姚壹壹1* 艾力亚尔·艾海提1 朱连华1,2(1.南京信息工程大学 数学与统计学院 江苏南京 210044;2.南京信息工程大学 气象灾害教育部重点实验室 气候与环境变化国际联合实验室 气象灾害预报预警与评估协同创新中心 江苏南京 210044)摘 要:本文利用江淮流域1961—2005年76站夏季逐日降水观测资料和BCC-CSM1.1(m)模式模拟数据,构建基于经验和理论分布函数的分位数增量映射(Quantile Delta Mapping, QDM)偏差订正模型eQDM、dQDM,并评估其对江淮流域逐日降水及极端降水的订正效果。
研究结果表明:相较于理论分布,基于经验分布的eQDM方法显著改善模式对观测降水的概率分布和空间分布特征的模拟能力;除连续干日订正效果欠佳外,其余四个极端降水指数的均方根误差明显降低,其气候态基本与观测一致,大部分站点的相对误差保持在-20%~20%。
关键词:偏差订正 分位数增量映射 极端降水 江淮流域中图分类号:P45 文献标识码:A 文章编号:1674-098X(2021)01(c)-0027-06 Performance Evaluation of Quantile Delta Mapping for Extreme Precipitation Simulation Over the Yangtze-Huaihe River BasinYAO Yiyi1* AIHAITI Ailiyaer1 ZHU Lianhua1,2(1.School of Mathematics and Statistics, Nanjing University of Information Science & Technology, Nanjing,Jiangsu Province, 210044 China; 2. Key Laboratory of Meteorological Disaster of Ministry of Education,Joint International Research Laboratory of Climate and Environment Change, Collaborative Innovation Center on Forecast and Evaluation of Meteorological Disaster, Nanjing University of Information Science &Technology, Nanjing , Jiangsu Province, 210044 China)Abstract:The observed summer daily precipitation in 76 stations over the Yangtze-Huaihe River Basin (1961-2005) and the simulation results of BCC-CSM1.1(m) model in the same period are used. Quantile delta mapping (QDM) bias correction method based on empirical and theoretical distribution functions (expressed as eQDM and dQDM) are introduced to evaluate their correction effects on daily precipitation, especially extreme precipitation over the Yangtze-Huaihe River Basin. The results showed that compared with the dQDM, the eQDM significantly improved the model's capacity to simulate the probability distribution and spatial distribution characteristics of observed precipitation. In addition to the poor performance for the continuous dry days, the root-mean-square error (RMSE) of the other four extreme precipitation indexes were significantly reduced, and the climate state were basically consistent with observation with the relative error from -20% to 20% at most of stations.Key Words: Bias correction; Quantile delta mapping; Extreme precipitation; The Yangtze-Huaihe River Basin目前,长期气候变化的规划依赖于对未来气候的合理预测。
抚仙湖流域1964-2021年气象干旱演变特征分析

由于降水量的分布一般不是正态分布%而是一 种偏态分布%所以在进行降水分析和干旱监测'评估 中%采用 &分布概率来描述降水量的变化& ?B4就 是在计算某时段内降水量的 &分布概率后%再进行 正态标准化处理%最终用标准化降水累积频率分布 来划分干旱等级%其等级划分见表 5&
表 #$标准化降水指数干旱等级划分
图 !$抚仙湖流域 #5(&!"!# 年旱情类型发生率
59:@$59I: 年%仅发生 K /以轻旱为主的间歇 性干旱%59IK$59I9 年为重旱到中旱的连续 8 /干 旱%599=$5998 年为重旱到轻旱的连续 = /干旱% 599@$=66I 年发生 8 /间歇性轻旱%=669$=658 年 为中旱#轻旱#特旱#重旱 # 轻旱的连续 > /干 旱%=659'=6=5 年分别发生了中旱和轻旱& 从这样 的干旱情势统计可湖流域水资源量不断减 少%给流域经济社会发展及 生 态 环 境 带 来 较 大 影 响(5) & 湖泊水位持续波动下降%长期低水位运行使 湖泊水生态危机日益显现& 干旱与水资源短缺两者 间具有相互关系(=) %干旱类型通常分为气象干旱' 水文干旱'农业干旱和经济社会干旱%其中气象干旱 是影响最直接的干旱%也是其他类型干旱发生的主 要原因(8) %气象干旱是导致流域水资源量减少的重 要因素& 湖泊水资源持续损失成为影响地区经济社 会发展的主要问题之一(@) %为做好抚仙湖流域水资 源科学管理研究%对流域干旱演变规律进行分析尤 为重要& 目前对流域干旱特征研究的较新成果主要 有!韩冬梅等(>) 基于海河流域气象数据和 g^4B> 的 > 种全球气候模式模拟数据%通过构建分时预估模 型预测海河流域未来"=6=6$=6>6 年# 干旱时空演 变,冯仕远等(:) 基于西北地区有关气象资料%采用 ?BC4" 标准化降雨蒸散指数# 分析计算 59:6$=65I 年干旱进程%结合其他多种方法对近 :6 /西北干旱 时空变化特征进行分析, 陈亚利等(K) 基 于 59>9$ =659 年辽河流域气象数据%应用标准化降水蒸散指
基于贝叶斯三角帽法的多源降水数据融合分析及应用

第34卷第5期2023年9月㊀㊀水科学进展ADVANCES IN WATER SCIENCE Vol.34,No.5Sep.2023DOI:10.14042/ki.32.1309.2023.05.004基于贝叶斯三角帽法的多源降水数据融合分析及应用赵㊀君1,2,刘㊀雨1,徐进超1,2,王国庆2,邵月红1,杨㊀林1(1.南京信息工程大学水文与水资源工程学院,江苏南京㊀210044;2.南京水利科学研究院水灾害防御全国重点实验室,江苏南京㊀210029)摘要:目前的降水产品依然存在较大的不确定性,采用多源降水数据融合可以更准确地估计降水量和空间分布情况㊂为实现无资料地区的数据融合,本文在不使用任何先验信息的前提下,通过整合站点插值㊁卫星遥感和再分析的降水产品,基于贝叶斯三角帽(Bayesian-Three Cornered Hat,BTCH)法,融合多源降水数据,探究不同输入数量的降水产品对于融合数据精度的影响以及每个降水产品对于融合数据精度的贡献率,并在黄河源区进行应用㊂结果表明:在月尺度上,融合数据性能优于原始降水产品;在日尺度上,融合数据性能明显高于卫星遥感和再分析降水产品,但低于基于站点的降水产品CHM_PRE;2套基于站点的降水产品CN05.1和CHM_PRE 对于融合数据有最大的贡献率㊂在黄河源区的应用表明,该数据融合方法确实能够更准确地估计降水量,可应用于无实测降水资料地区,为数据融合分析及应用提供参考㊂关键词:多源降水;数据融合;不确定性分析;贝叶斯三角帽中图分类号:P426.6㊀㊀㊀文献标志码:A㊀㊀㊀文章编号:1001-6791(2023)05-0685-12收稿日期:2023-05-08;网络出版日期:2023-09-07网络出版地址:https :ʊ /urlid /32.1309.P.20230907.0939.002基金项目:国家重点研发计划资助项目(2021YFC3201101);江苏省重点研发计划资助项目(BE2020633)作者简介:赵君(1983 ),女,山东烟台人,副教授,博士,主要从事气候变化与水循环方面研究㊂E-mail:zsmzyq@ 通信作者:刘雨,E-mail:2811306430@ 降水是陆地水文循环的主要驱动因素㊂研究表明,径流预报的误差主要由降水数据的偏差主导[1],因此量化评估和减少这种误差,可以提高对水文系统和模型模拟的理解[2]㊂目前,地面站点㊁卫星遥感和气象雷达的观测数据都存在一定的不确定性[3-5]㊂为了解决降水观测数据存在的不确定性,通常采用多源数据融合来提高对降水时空分布的估计[6]㊂现在已有大量关于数据融合的算法,如最优插值㊁卡尔曼滤波㊁概率密度函数最优插值等[7-9]㊂然而,这些方法大多需要地面实测数据,对于数据匮乏或无资料地区,基于机器学习的迁移学习[10]以及基于TC(Triple Collocation)算法[11]的多源降水数据融合都以得到应用,但关于无资料地区的数据融合研究依然相对较少㊂针对缺乏实测数据的区域,三角帽(Three Cornered Hat,TCH)法已被用于量化降水㊁GRACE㊁土壤湿度和蒸散发等[12-15]在区域或全球尺度上的不确定性㊂这为无资料地区的数据融合提供了思路,即利用三角帽法计算数据集的不确定性,并根据不确定性的大小为每个数据集分配权重,从而实现无实测数据地区的数据融合[16-17]㊂Xu 等[18]利用广义三角帽分析了13套月降水数据集和11套日降水数据集在全球尺度上的相对不确定性,并根据各降水产品的不确定性通过加权进行多源降水数据融合,结果表明基于广义三角帽法的多源数据融合要优于其他方法;He 等[19]基于一种贝叶斯三角帽(Bayesian-Three Cornered Hat,BTCH)方法,通过整合多源地表蒸散发产品来提高地表蒸散发(ET)的估计,结果表明BTCH 方法能够有效地减少ET 产品之间的差异,并提高ET 估计的精度和稳定性㊂这些研究主要集中在融合算法的发展方面,但融合数据的精度不仅被算法影响,同时也受到输入源的影响[20]㊂全球范围内降水产品种类繁多,如何选择降水产品进行数据融合是值得考虑的问题㊂因此,在融合数据之前,分析并选择不同数量和类型的降水产品对融合数据精度686㊀水科学进展第34卷㊀也是非常重要的[21]㊂如何更加合理地构建多源降水融合框架有待深入研究㊂本文基于贝叶斯三角帽方法融合多源降水数据,采用2001 2020年中国大陆地区8套基于站点㊁卫星遥感和再分析原始降水产品,以实测站点数据作为参照,定量分析不同输入数量下融合数据的精度差异以及每个降水产品对于融合数据精度的贡献率㊂1㊀研究区域与数据1.1㊀研究区概况本次研究选取中国大陆作为研究区域,选取了834个地面气象站点,站点分布如图1(a)所示㊂研究区包括热带㊁亚热带㊁温带㊁亚寒带等多种气候类型㊂为验证融合降水数据的效果,选取黄河源区作为验证区㊂黄河源区地处青藏高原东部边缘,目前区域内国家设立的气象站点仅有12个,数量严重不足且已有站点大部分分布在河谷地带,在空间分布上不具有代表性,属于典型的资料匮乏地区,数据的缺失严重制约了黄河源区的水文预报精度[22]㊂黄河源区的地理位置分布如图1(b)所示㊂图1㊀研究区示意Fig.1Diagram of study area1.2㊀研究数据本文中的实测降水资料来源于国家气象信息中心(CMA),所选用的降水产品包括CMORPH(Climate Pre-diction Center MORPHing technique)数据集[23]㊁中国科学院气候变化研究中心CN05格点化观测数据集[24]㊁PERSIANN(The Precipitation Estimation from Remotely Sensed Information using Artificial Neural Networks)数据集[25]㊁国家青藏高原科学数据中心CHM_PRE数据集[26]㊁欧洲中期天气预报中心ERA5-Land降水数据集[27]㊁日本宇宙航空研究开发机构(JAXA)GSMaP(Global Satellite Mapping of Precipitation)数据集[28]㊁IME-㊀第5期赵君,等:基于贝叶斯三角帽法的多源降水数据融合分析及应用687㊀RG(Integrated Multi-satellitE Retrievals for GPM)数据集[29]以及CHIRPS(Rainfall Estimates from Rain Gauge and Satellite Observations)数据集[30]㊂数据详细信息如表1所示㊂选取2001 2020年作为研究时段,采用双线性插值法(Bilinear)将所有降水产品的空间分辨率统一为0.25ʎ,时间分辨率统一为1d㊂表1㊀研究数据概况Table 1Overview of research data数据名称时间分辨率空间分辨率时间跨度空间范围获取网址站点数据1d 2001 2020年中国大陆https:ʊ /CMORPH1d 0.25ʎˑ0.25ʎ1998年至今60ʎS 60ʎN,180ʎW 180ʎE https:ʊ /CN05.11d 0.25ʎˑ0.25ʎ1961 2021年中国https:ʊ /resource /PERSIANN1d 0.25ʎˑ0.25ʎ2000年至今60ʎS 60ʎN,180ʎW 180ʎE https:ʊ /CHM_PRE 1d0.1ʎˑ0.1ʎ1961 2022年中国https:ʊ /ERA5-Land 1h 0.1ʎˑ0.1ʎ1950年至今全球https:ʊcds.climate.copernicus.eu /GSMaP_NRT_V60.5h 0.1ʎˑ0.1ʎ2000年至今60ʎS 60ʎN,180ʎW 180ʎE https:ʊsharaku.eorc.jaxa.jp /IMERG_Final_V60.5h 0.1ʎˑ0.1ʎ2000年至今全球https:ʊ /data /imerg CHIRPS 1d 0.05ʎˑ0.05ʎ1981年至今50ʎS 50ʎN,180ʎW 180ʎE https:ʊ /2㊀研究方法2.1㊀基于贝叶斯理论的三角帽方法降水观测序列可以表示为{X i },其中的i 代表不同观测序列,X i 的概率密度函数(PDF)表示为p (X i |X ture )=1σi 2πexp -ε2i 2σ2i ()=L (X i |X ture )㊀㊀㊀㊀εi =X i -X ture (1)式中:X ture 为X i 的真值;εi 和σi 分别为X i 的零均值白噪声和误差方差;L (X |Y )为似然函数㊂X ture 的最大似然值是其联合概率分布的最大值,即max L (X i |X ture ,X j )=p (X i |X ture )p (X j |X ture )=12πσi σj exp -ε2i 2σ2i -ε2j 2σ2j ()(2)为获得(2)式中X ture 的最大似然值,定义代价函数J 为J (X ture )=ε2i 2σ2i +ε2j 2σ2j =12(X i -X ture )2σ2i +(X j -X ture )2σ2j [](3)通过将J (X ture )的第1个变化值设为零,可以得到X ture 为X ture =σ2i σ2i +σ2j X i +σ2j σ2i +σ2j X j (4)设w i =σ2i /(σ2i +σ2j ),则(4)式可表示为X ture =w i X i +w j X j ,因此对于N 个降水数据集,X ture 可以表示为X ture =w 1X 1+ +w n X n ㊂每个降水数据集权重w i 中的σ2可通过TCH 法计算得到㊂TCH 法是由Tavella 等[31]提出的一种用于评估多个(3个或以上)数据集之间不确定性的方法㊂该方法不需要真实测量值,而是利用数据集之间的差异来推导特定变量的不确定性(随机误差)㊂该方法主要假设降水观测序列X i 是由真值X ture 和误差项εi 组成,即X i =X ture +εi ㊀㊀㊀㊀i =1,2, ,N (5)688㊀水科学进展第34卷㊀要获得误差项εi,必须首先知道真值X ture,但在实际情况中这很难获得,TCH方法通过任意选取其中1个数据集作为参考值X R,剩余2个数据集与该参考数据集作差,差值矩阵可以表示为Yi,M=X i-X R=εi-εR㊀㊀㊀㊀i=1,2, ,N-1(6)式中:Y为Mˑ(N-1)阶矩阵,M为降水序列的长度;εR为X R的零均值白噪声㊂引入未知的NˑN噪声协方差矩阵R,差值矩阵的协方差矩阵S可以表示为S=J㊃R㊃J T(7) J为(N-1)ˑN阶矩阵,即JN-1,N =10 0-101 0-1︙︙︙000 -1éëêêêêêùûúúúúú(8)矩阵R为R=σ11σ12 σ1Nσ12σ22 σ2N︙︙︙σ1Nσ2N σNNéëêêêêêùûúúúúú(9)式(7)中有N(N+1)/2个未知数,但只有Nˑ(N-1)/2个方程,因此剩余的N个自由参数需要合理的方式来获得唯一解㊂Galindo等[32]提出的约束条件,给出了更适合Kuhn-Tucher理论的约束函数:F(q1N q NN)=1K2ðN i<j q2ij(10)其约束条件为H(q1N q NN)=-|Q||S|K<0(11)式中:Q是由σ11,σ22, ,σNN组成的对角矩阵㊂这些数组可以通过初始条件迭代最小化公式(10)得到㊂R对角线元素的平方根(σ11,σ22, ,σNN)表示各降水数据的相对不确定性㊂2.2㊀评估方法与统计指标本文采用点对点的方式进行数据之间的对比,即利用观测站点坐标提取其所在降水产品格网的降水数据值,以实测站点数据为基准,对比分析降水产品的质量精度㊂采用皮尔逊相关系数(C C)㊁均方根误差(E RMS)㊁相对偏差(R B)㊁修正Kling-Gupta效率系数(E KG)㊁纳什效率系数(E NS)来定量评估降水产品的线性相关性㊁系统偏差㊁总误差水平和综合精度等指标㊂采用命中率(Probability of detection,D PO)㊁误报率(False alarm ratio,R FA)和公平技巧评分(Equitable Threat Score,S ET)3个分类统计指标评估降水产品在日尺度对不同量级降水事件的捕捉能力,并以实测降水大于0.1mm作为判断雨日和非雨日的依据㊂为了定量评估不同输入降水产品对融合数据精度的影响,通过控制变量法的方式,单独控制减少1个降水产品,以评估其对于融合数据精度的贡献率[21],计算公式如下:P=X change-X initialX initialˑ100%(12)式中:P为减少降水产品后原融合数据精度变化所引起的百分比变化;X change和X initial分别为减少降水产品后和原融合数据的E KG值㊂如果P>0,表示减少的降水产品提高了融合数据的精度;如果P<0,表示减少的降水产品降低了融合数据的精度㊂㊀第5期赵君,等:基于贝叶斯三角帽法的多源降水数据融合分析及应用689㊀3㊀结果与分析3.1㊀降水产品不确定性分析图2为2001 2020年使用TCH法计算的单个降水产品不确定性的箱线图㊂其中,CMORPH㊁ERA5-Land和GSMaP相对不确定性的中位数分别为20.6㊁18.3和26.1mm,表明它们的不确定性比其他降水产品高得多;CHIRPS和PERSIANN不确定性的中位数分别为14.3和13.3mm,表明这两者的不确定性相对较低;而CN05.1㊁CHM_PRE和IMERG不确定性的中位数分别为9.3㊁10.0和10.1mm,表明这3套降水产品拥有最小的相对不确定性㊂图2㊀基于TCH法的降水产品不确定性Fig.2Uncertainty of precipitation products based on TCH method图3显示了2001 2020年使用TCH法计算的不确定性空间分布图㊂可以看出,8套降水产品的不确定性呈现从东南沿海向西北内陆递减的趋势,这与中国的降水分布类似,因此降水多的地区通常存在较大的不确定性㊂特别地,IMERG㊁CHM_PRE和CN05.1在全国范围内具有较小的不确定性;此外,ERA5-Land㊁CHIRPS和GSMaP在南方地区和青藏高原的部分地区存在较大的不确定性㊂3.2㊀月尺度融合数据精度对比为了探究输入降水产品数量对融合数据精度的影响,按照图2中各降水产品不确定性从小到大的顺序,将不确定性最小的前3个降水产品组成融合数据BTCH3(融合了CN05.1㊁CHM_PRE㊁IMERG),以此类推,不确定性最小的前4个降水产品组成BTCH4,直至前8个产品组成BTCH8㊂基于贝叶斯三角帽方法分别计算BTCH3 BTCH8相应的融合数据,每个分组中,不同降水产品在每个格点上的平均权重如图4所示㊂可以看出,不确定性最小的CHM_PRE和CN05.1在每个分组中都拥有最大的权重,随着降水产品数量的增加,每种降水产品的权重都不同程度的下降㊂这会 稀释 精度高的降水产品在融合数据中的分量,或是随着精度不高的降水产品的增多 拉低 融合数据的整体精度㊂使用E KG㊁C C㊁E RMS和R B定量评估不同分组融合数据的精度也证实了这一点㊂图5展示了融合数据随输入数据集数量增加各评价指标中位数的变化情况㊂BTCH3在各项指标的综合表现优于其他组合,其E KG(0.859)㊁C C(0.955)最高,E RMS(21.718mm)最小㊂因此,对于多源数据融合单纯增加数据集的数量可能并不会提升融合数据的精度㊂最佳融合数据BTCH3和参与融合的原始降水产品的精度对比如图6所示,共选用全国834个实测站点的数据进行对比分析,可以看到多源融合数据相较于原始降水产品在C C㊁E RMS㊁R B方面都有所改善㊂690㊀水科学进展第34卷㊀图3㊀基于TCH法的降水产品不确定性空间分布Fig.3Spatial distribution of the uncertainty of precipitation products based on TCH method图4㊀每个降水产品在不同分组中的权重Fig.4Weight of each precipitation product in different groups为了更直观地展示评价指标的空间分布情况,图7展示了融合数据BTCH3和参与融合的原始降水产品在月尺度上的精度评价指标空间分布图㊂由图7(a)㊁7(d)㊁7(g)㊁7(j)可知,融合数据和各原始降水产品反映的中国大陆地区相关系数分布格局总体上相似,即东部季风区相关系数较高(0.91~0.99),西北地区㊀第5期赵君,等:基于贝叶斯三角帽法的多源降水数据融合分析及应用691㊀图5㊀月尺度上不同输入数量降水产品对于融合数据的影响Fig.5Influence of precipitation products with different input quantities on the monthly fusion data图6㊀融合数据与原始降水产品在月尺度上的精度对比Fig.6Precision comparison between the fusion data and the original precipitation products on the monthly scale和青藏高原地区相关系数偏低(0.43~0.72),融合数据和CHM_PRE在总体精度和空间分布类似,CN05.1表现弱于两者,IMERG在总体精度上表现最差㊂图7(b)㊁7(e)㊁7(h)㊁7(k)显示E RMS沿西北地区向东南沿海递增㊂图7(c)㊁7(f)㊁7(i)㊁7(l)表明融合数据和各降水产品在东部季风区的部分区域存在低估降水的情况,但大部分地区都不同程度地高估了降水㊂3.3㊀日尺度融合数据的精度对比采用与融合月尺度降水相同的方法,将8套不同降水产品按照不同组合融合为一个新的日降水数据㊂图8为不同分组下各评价指标的中位数,结果显示融合数据在日尺度上的表现和月尺度上相似㊂其中,最佳融合数据由不确定性最小的3套降水产品(BTCH3)组成㊂一个有趣的现象是,日尺度融合数据受降水产品数量的影响更显著㊂在日尺度上,融合数据的修正Kling-Gupta效率系数随降水产品数量的增加下降了25.6% (波动范围为0.497~0.668),而在月尺度上下降了5.1%(波动范围为0.815~0.859)㊂换句话说,在日尺度上,融合数据对于输入的降水产品数量更加敏感㊂表2为精度最高的融合数据(BTCH3)和原始降水产品在日尺度上各种评价指标的中位数㊂在参与数据融合的原始降水产品中,CHM_PRE在各项评价指标上均明显优于其他原始降水产品和融合数据㊂IMERG的精度较低,在所有降水产品和融合数据中表现最差㊂尽管融合数据的精度明显优于IMERG和CN05.1,但总体精度不及CHM_PRE㊂造成融合数据在日尺度上的融合效果不如月尺度的原因,一方面是因为CHM_PRE是基于中国境内及周边共2839个雨量站点,利用月值降水约束和地形特征矫正得到的数据集[26],其数据精度足够高;另一方面,随着时间尺度减小,降水序列中周期性的成分不断降低,随机性成分和背景噪声的增加导致融合算法难以获取真正的降水信息,这也导致在日尺度上融合数据的精度对于不同输入数量的降水产品更加敏感㊂692㊀水科学进展第34卷㊀图7㊀融合数据和原始降水产品精度评价指标空间分布Fig.7Spatial distribution of accuracy evaluation indexes of fusion data and original precipitation products㊀第5期赵君,等:基于贝叶斯三角帽法的多源降水数据融合分析及应用693㊀图8㊀日尺度上不同输入数量降水产品对于融合数据的影响Fig.8Influence of precipitation products with different input quantities on the daily fusion data表2㊀融合数据与原始降水产品在日尺度上的精度对比Table2Precision comparison of fusion data and the original precipitation products on the daily scale降水产品E KG C C E RMS/mm R B/%D PO R FA S ET BTCH30.6680.848 3.716 5.7120.9930.5230.736 CHM_PRE0.7580.871 2.774 2.8260.9980.3820.866 CN05.10.6530.791 3.849 6.8710.9760.5000.758 IMERG0.3660.3998.0017.6600.8540.5380.7723.4㊀降水产品贡献率的定量评估为了定量评估不同降水产品对于融合数据精度的影响,采用式(12)来计算从BTCH4至BTCH3和BTCH5至BTCH4等变化情况下每个降水产品的相对贡献率㊂表3总结了不同输入下各降水产品的相对贡献率㊂例如,去除BTCH4中的PERSIANN(即由BTCH4变为BTCH3)导致融合数据的精度(E KG)由0.581变为0.668,因此PERSIANN对融合数据的相对贡献率为-14.896%;同样,去除BTCH4中的CHM_PRE使得融合数据的精度由0.581变为0.478,因此CHM_PRE对于BTCH4精度的相对贡献率为17.73%,其他数据依次类推㊂通过表3可以看出,2套基于站点的降水产品(CHM_PRE和CN05.1)对于融合数据的贡献率最大,而卫星遥感和再分析降水产品对于融合数据精度的相对贡献率基本为负㊂随着降水产品数量的增加,CHM_PRE 和CN05.1的相对贡献率不断降低,这与3.2节中的增加过多的降水产品会 稀释 融合数据精度的结论相符㊂Wei等[21]关于数据融合的研究也表明基于站点的CPC(Climate Prediction Center)数据集对于融合数据精度的影响最大,在贝叶斯模型平均(BMA)中增加CPC数据集显著提高了融合数据的精度㊂因此,数据融合过程中的数据集选择至关重要㊂表3㊀不同分组中各降水产品的贡献率Table3Contribution rate of precipitation products in different groups单位:%分组CHM_PRE CN05.1IMERG PERSIANN CHIRPS ERA5-Land CMORPH GSMaP BTH4至BTCH317.73018.836-12.906-14.896BTH5至BTCH417.16215.565-6.555-13.251-6.289BTH6至BTCH514.97913.005-4.739-9.503-4.739-2.108BTH7至BTCH614.51512.157-4.169-8.889-4.588-1.195-3.327BTH8至BTCH714.02410.662-3.104-8.465-3.816-0.777-3.077-4.361694㊀水科学进展第34卷㊀3.5㊀融合数据的适用性分析为了验证基于贝叶斯三角帽法的融合数据在资料匮乏地区的适用性,选取黄河源区内的玛多㊁兴海㊁河南㊁达日和若尔盖5个典型气象站点进行验证㊂由于该地区的地面降水观测数据匮乏,严重制约了该区域的水文预报精度㊂本文使用E NS来验证融合数据BTCH3在相应站点处的模拟精度,并与精度最高的降水产品CHM_PRE进行对比㊂结果如图9所示,基于贝叶斯三角帽法的融合数据在各个站点上的E NS均优于CHM_ PRE㊂这表明基于贝叶斯三角帽法的数据融合方法确实可以更准确地估计降水量,适用于资料匮乏的地区㊂图9㊀融合数据在黄河源区的模拟精度对比Fig.9Comparison of simulation accuracy of fusion data in the source region of the Yellow River4㊀结㊀㊀论本文基于贝叶斯三角帽法,使用了8套不同的降水产品,包括CMORPH㊁CN05.1㊁PERSIANN㊁CHM_ PRE㊁ERA5-Land㊁GSMaP㊁IMERG和CHIRPS,探究了不同输入数量的降水产品对于融合数据精度的影响和各降水产品的相对贡献率,并验证了融合数据在资料匮乏的黄河源区的适用性㊂主要结论如下: (1)在8套不同的降水产品中基于站点的CN05.1和CHM_PRE以及基于卫星遥感的IMERG相较于其他降水产品拥有较小的不确定性㊂各降水产品的不确定性存在明显的空间分布差异,基本呈现出从东南沿海向西北内陆递减的趋势㊂(2)使用过多的降水产品会降低融合数据的精度,本文中融合数据的修正Kling-Gupta效率系数随着降水产品数量的增加逐渐降低,在月尺度上降低了5.1%,在日尺度上降低了25.6%㊂精度最高的融合数据是由CN05.1㊁CHM_PRE和IMERG这3套不确定性最小的降水产品组成的㊂(3)各降水产品中CHM_PRE和CN05.1对于融合数据有最大的相对贡献率㊂黄河源区的适用性分析表明,基于贝叶斯三角帽法的数据融合方法可以更准确地估计降水量㊂虽然基于贝叶斯三角帽法的数据融合方法在无资料或数据匮乏的地区得到成功应用,但本研究依然存在一些不确定因素和限制㊂例如,在本文中,贝叶斯三角帽法在日尺度上的融合效果不如月尺度融合效果好,该数据融合模型还需进一步优化㊂此外,有很多因素可能会限制三角帽法的准确性,如数据集中样本的数量㊀第5期赵君,等:基于贝叶斯三角帽法的多源降水数据融合分析及应用695㊀和异常值㊁数据集的真实偏差以及未知误差的相关性,相关问题还需要进一步研究㊂参考文献:[1]YATHEENDRADAS S,WAGENER T,GUPTA H,et al.Understanding uncertainty in distributed flash flood forecasting for semi-arid regions[J].Water Resources Research,2008,44(5):w05S19.[2]REICHERT P,MIELEITNER J.Analyzing input and structural uncertainty of nonlinear dynamic models with stochastic,time-de-pendent parameters[J].Water Resources Research,2009,45(10):w10402.[3]POLLOCK M D,OᶄDONNELL G,QUINN P,et al.Quantifying and mitigating wind-induced undercatch in rainfall measurements [J].Water Resources Research,2018,54(6):3863-3875.[4]MCMILLAN H,KRUEGER T,FREER J.Benchmarking observational uncertainties for hydrology:rainfall,river discharge and water quality[J].Hydrological Processes,2012,26(26):4078-4111.[5]TAN X H,YONG B,REN L L.Error features of the hourly GSMaP multi-satellite precipitation estimates over nine major basins of China[J].Hydrology Research,2018,49(3):761-779.[6]BECK H E,WOOD E F,PAN M,et al.MSWEP V2global3-hourly0.1ʎprecipitation:methodology and quantitative assess-ment[J].Bulletin of the American Meteorological Society,2019,100(3):473-500.[7]SAPIANO M R P,SMITH T M,ARKIN P A.A new merged analysis of precipitation utilizing satellite and reanalysis data[J]. Journal of Geophysical Research,2008,113(D22):D22103.[8]JOYCE R J,XIE P P.Kalman filter-based CMORPH[J].Journal of Hydrometeorology,2011,12(6):1547-1563.[9]SHEN Y,ZHAO P,PAN Y,et al.A high spatiotemporal gauge-satellite merged precipitation analysis over China[J].Journal of Geophysical Research:Atmospheres,2014,119(6):3063-3075.[10]LIU Z Y,YANG Q L,SHAO J M,et al.Improving daily precipitation estimation in the data scarce area by merging rain gaugeand TRMM data with a transfer learning framework[J].Journal of Hydrology,2022,613:128455.[11]CHEN C,HE M N,CHEN Q W,et al.Triple collocation-based error estimation and data fusion of global gridded precipitationproducts over the Yangtze River basin[J].Journal of Hydrology,2022,605:127307.[12]LIU Y,ZHENG Y J,LI W P,et al.Evaluating the performance of satellite-based precipitation products using gauge measure-ment and hydrological modeling:a case study in a dry basin of Northwest China[J].Journal of Hydrometeorology,2022,23(4):541-559.[13]YAN X,ZHANG B,YAO Y B,et al.GRACE and land surface models reveal severe drought in Eastern China in2019[J].Journal of Hydrology,2021,601:126640.[14]LIU J,CHAI L N,DONG J Z,et al.Uncertainty analysis of eleven multisource soil moisture products in the third pole environ-ment based on the three-corned hat method[J].Remote Sensing of Environment,2021,255:112225.[15]XU T R,GUO Z X,XIA Y L,et al.Evaluation of twelve evapotranspiration products from machine learning,remote sensingand land surface models over conterminous United States[J].Journal of Hydrology,2019,578:124105.[16]SHANGGUAN Y L,MIN X X,SHI Z.Inter-comparison and integration of different soil moisture downscaling methods over theQinghai-Tibet Plateau[J].Journal of Hydrology,2023,617:129014.[17]SHAO X M,ZHANG Y Q,LIU C M,et al.Can indirect evaluation methods and their fusion products reduce uncertainty in ac-tual evapotranspiration estimates?[J].Water Resources Research,2022,58(6):e2021WR031069.[18]XU L,CHEN N C,MORADKHANI H,et al.Improving global monthly and daily precipitation estimation by fusing gauge obser-vations,remote sensing,and reanalysis data sets[J].Water Resources Research,2020,56(3):e2019WR026444. [19]HE X L,XU T R,XIA Y L,et al.A Bayesian three-cornered hat(BTCH)method:improving the terrestrial evapotranspirationestimation[J].Remote Sensing,2020,12(5):878.[20]TANG G Q,CLARK M P,PAPALEXIOU S M,et al.Have satellite precipitation products improved over last two decades?Acomprehensive comparison of GPM IMERG with nine satellite and reanalysis datasets[J].Remote Sensing of Environment,2020, 240:111697.[21]WEI L Y,JIANG S H,DONG J Z,et al.Fusion of gauge-based,reanalysis,and satellite precipitation products using Bayesianmodel averaging approach:determination of the influence of different input sources[J].Journal of Hydrology,2023,618:129234.[22]雍斌,张建云,王国庆.黄河源区水文预报的关键科学问题[J].水科学进展,2023,34(2):159-171.(YONG B,ZHANG J Y,WANG G Q.Key scientific issues of hydrological forecast in the headwater area of Yellow River[J].Advances in696㊀水科学进展第34卷㊀Water Science,2023,34(2):159-171.(in Chinese))[23]JOYCE R J,JANOWIAK J E,ARKIN P A,et al.CMORPH:a method that produces global precipitation estimates from passivemicrowave and infrared data at high spatial and temporal resolution[J].Journal of Hydrometeorology,2004,5(3):487-503.[24]吴佳,高学杰.一套格点化的中国区域逐日观测资料及与其它资料的对比[J].地球物理学报,2013,56(4):1102-1111.(WU J,GAO X J.A gridded daily observation dataset over China region and comparison with the other datasets[J].Chi-nese Journal of Geophysics,2013,56(4):1102-1111.(in Chinese))[25]ASHOURI H,HSU K L,SOROOSHIAN S,et al.PERSIANN-CDR:daily precipitation climate data record from multisatelliteobservations for hydrological and climate studies[J].Bulletin of the American Meteorological Society,2015,96(1):69-83.[26]HAN J Y,MIAO C Y,GOU J J,et al.A new daily gridded precipitation dataset for the Chinese mainland based on gauge obser-vations[J].Earth System Science Data,2023,15(7):3147-3161.[27]MUÑOZ-SABATER J,DUTRA E,AGUSTÍ-PANAREDA A,et al.ERA5-Land:a state-of-the-art global reanalysis dataset forland applications[J].Earth System Science Data,2021,13(9):4349-4383.[28]KUBOTA T,SHIGE S,HASHIZUME H,et al.Global precipitation map using satellite-borne microwave radiometers by the GS-MaP project:production and validation[J].IEEE Transactions on Geoscience and Remote Sensing,2007,45(7):2259-2275.[29]HOU A Y,KAKAR R K,NEECK S,et al.The global precipitation measurement mission[J].Bulletin of the American Meteor-ological Society,2014,95(5):701-722.[30]FUNK C,PETERSON P,LANDSFELD M,et al.The climate hazards infrared precipitation with stations:a new environmentalrecord for monitoring extremes[J].Scientific Data,2015,2:150066.[31]TAVELLA P,PREMOLI A.Estimating the instabilities of N Clocks by measuring differences of their readings[J].Metrologia,1994,30(5):479-486.[32]GALINDO F J,PALACIO J.Estimating the instabilities of N correlated clocks[C]ʊProceedings of the31th Annual Precise Timeand Time Interval Systems and Applications Meeting.Dana Point,California:Institute of Navigation,1999:285-296.Multi-source precipitation data fusion analysis and application based onBayesian-Three Cornered Hat method∗ZHAO Jun1,2,LIU Yu1,XU Jinchao1,2,WANG Guoqing2,SHAO Yuehong1,YANG Lin1(1.School of Hydrology and Water Resources,Nanjing University of Information Science&Technology,Nanjing210044,China;2.The National Key Laboratory of Water Disaster Prevention,Nanjing Hydraulic Research Institute,Nanjing210029,China) Abstract:At present,precipitation products still have great uncertainty.Precipitation and its spatial distribution can be estimated more accurately by using multi-source precipitation data fusion.To achieve data fusion in no-gauged areas,Bayesian-Three Cornered Hat method is adopted to integrate precipitation products based on gauged data, satellite remote sensing and reanalysis data without any prior information,to explore the influence of precipitation products with different input quantities on the accuracy of fusion data,and to study the contribution rates of each precipitation product to the accuracy of fusion data.It is applied in the source region of the Yellow River.The results show that the performance of the fusion data is better than that of the original precipitation products on the monthly scale.On the daily scale,the performance of the fusion data is obviously better than that of satellite remote sensing and reanalysis precipitation products,but lower than that of the gauge-based precipitation product CHM_PRE.Two gauge-based precipitation products,CN05.1and CHM_PRE,have the largest contribution rates to the fusion data. The application in the source region of the Yellow River shows that the Bayesian-Three Cornered Hat method can estimate precipitation more accurately.It is suitable for no-gauged areas,and can provide the reference basis for data fusion analysis and its application.Key words:multi-source precipitation;data fusion;uncertainty analysis;Bayesian-Three Cornered Hat∗The study is financially supported by the National Key R&D Program of China(No.2021YFC3201101)and Key R&D Project of Jiangsu Province,China(No.BE2020633).。
秘籍08 地理计算与地理图表阅读(课件)-备战2023年中考地理抢分秘籍(全国通用)

B.1:300
C.1:400
D.1:800
1 比例尺的计算
3.下列各图中的图幅相同,其中表示图中河段最长的是( ) 4.下列四幅经纬网图的图幅大小相等,则其比例尺大小关系是( )
A.甲>乙>丙>丁 B.丙>丁>乙>甲 C.甲>乙>丁>丙 D.丁>丙>甲>乙
1 比例尺的计算
读下列两幅地图,完成下面5-6小题。
B.②
C.③
D.④3.四个国家中,人口不断减少的是( )A.①
B.②
C.③
D.④
4 人口自然增长率和人口密度的计算
读2016年“世界部分国家人口状况图”,完成下面4-5小题。
4.下列国家中人口自然增长率最高的是( )A.尼日利亚
B.中国
C.印度
D.日本5.图示年份,下列说法中正确的是( )A.人口数量多的国
气温为12.9℃,则D处(500米)的气温可能是( )A.15℃
B.10℃ቤተ መጻሕፍቲ ባይዱ
C.16℃
D.14℃
3 气温、降水的相关计算
1、关于气温的计算(1)气温日较差=当日最高气温一当日最低气温(2)气温年较差= 最热月平均气温一最冷月平均气温(3)年平均气温=各月平均气温之和/122、关于降水 的计算年降水量等于各月降水量之和。
示。人口自然增长率=人口出生率一人口死亡率
=年内出生人口数/总人口
数×100%-年内死亡人口数/总人口数× 100%
=(年内出生人口一年内死
亡人口)/总人口×100%2、人口密度:(1)人口密度是指平均每平方千米居住的人口数,
单位为:人/平方千米。(2)人口密度=该地区总面积(平方千米)/该地区人口总数(人)
长白山地区暴雨特征及重现期几种计算方法对比

第22卷第1期北华大学学报(自然科学版)Vol.22No.12021年1月JOURNAL OF BEIHUA UNIVERSITY(Natural Science)Jan.2021文章编号:1009-4822(2021)01-0021-07DOI :10.11713/j.issn.1009-4822.2021.01.004长白山地区暴雨特征及重现期几种计算方法对比张伶俐1,2,成㊀坤1,2,刘春泽3,史国强4(1.长白山气象局,吉林二道白河㊀133613;2.长白山气象与气候变化吉林省重点实验室,吉林二道白河㊀133613;3.松原市气象台,吉林松原㊀138000;4.长白山科学研究院动物研究所,吉林二道白河㊀133613)摘要:利用长白山地区59a 地面观测资料,分析暴雨发生的气候规律;基于年最大值法选样,选取指数㊁耿贝尔Ⅰ型㊁皮尔逊Ⅲ型㊁韦布尔4种分布函数对长白山地区不同海拔3个站点暴雨重现期进行拟合计算,推求4种分布函数参数,得出重现期-年最大日降水量关系曲线,并进行χ2检验.结果表明:长白山地区暴雨具有明显的时空分布特征.天池站暴雨日数7月最多,其他站8月占比最大;2000年以来,平均暴雨日数呈增多趋势;指数分布年最大日降水量较小,其他3种算法预测值比较一致;在χ2检验中,耿贝尔Ⅰ型分布法在二道站和东岗站暴雨重现期计算中表现优异,韦布尔分布法在天池暴雨年最大日降水量的预测中更胜一筹.关键词:长白山地区;暴雨;气候特征;重现期;韦布尔分布中图分类号:P466文献标志码:A收稿日期:2020-07-21基金项目:长白山气象局科研课题(201902);长白山气象与气候变化吉林省重点实验室项目.作者简介:张伶俐(1989 ),女,硕士研究生,工程师,主要从事气候预测㊁气象预报与服务研究,E-mail:2802208708@.Characteristics of Rainstorm and Comparison of Several Calculation Methods about Recurrence Period in Changbai Mountain AreaZHANG Lingli 1,2,CHENG Kun 1,2,LIU Chunze 3,SHI Guoqiang 4(1.Changbai Mountain Weather Service ,Erdaobaihe 133613,China ;2.Jilin Provincial Key Laboratory of Changbai Mountain Weather &Climate ,Erdaobaihe 133613,China ;3.Songyuan Meteorological Observatory ,Songyuan 138000,China ;4.Institute of Zoology ,Changbai Mountain Academy of Sciences ,Erdaobaihe 133613,China )Abstract :Based on the surface observation data of Changbai Mountain area in recent 59years,the climate characteristics of rainstorm were analyzed firstly.According to the annual maximum value sampling method,four functions of exponential distribution,Gumbel-Ⅰdistribution,P-III distribution and Weibull-distribution were selected to make the fitting calculation of recurrence period for three stations at different altitudes in Changbai Mountain area,the formula parameters of four distribution functions were deduced,the relationship curve between recurrence period and annual maximum daily precipitation was given.The χ2test was made.The results show that rainstorm in Changbai Mountain area has obvious time-space distribution characteristics,with the most rainstorm days in Tianchi station in July and the largest proportion in other stations in August;Since 2000s,the average rainstorm days show a significant increasing trend;The annual maximum daily precipitation of exponential distribution is small,whereas other three functions are consistent.By means of χ2test,Gumbel-Ⅰdistribution shows an outstanding performance in the calculation of rainstorm annual maximum daily precipitation at Erdao station,as well as Donggang station,while Weibull distribution method is better at Tianchi station.Key words :Changbai Mountain area;rainstorm;climate characteristics;occurrence period;Weibull-Distribution㊀㊀长白山位于吉林省东南部,呈东北-西南走向,是东北地区海拔最高的山脉,也是鸭绿江㊁松花江和图们江的发源地.长白山具有保存完好的植被带,是东北亚重要的气候调节带.近年来,随着全球气候变化,极端气候事件发生频次持续升高,强度加大.我国东北地区山环水绕,西㊁北㊁东三面环山,降水与局地地形有较大关系[1].作为 水源 地之一,需要评估长白山天池极端降水量变化规律以及地形动力作用对长白山地区暴雨的贡献.近年来,有学者对暴雨极值进行了模型构建㊁影响评估,如袭祝香等[2]利用逐日降水资料分析了东北地区1961 2000年的明显暴雨过程特征,建立了反映明显暴雨程度的3项单项指标及综合评估指数,在此基础上划分了明显暴雨过程的评估等级;郭渠等[3]使用皮尔逊Ⅲ型分布㊁耿贝尔分布和指数分布编制了暴雨强度公式,为重庆市主城区雨水排水系统规划㊁设计和管理提供了重要依据;王晓光[4]计算了呼伦贝尔市日最高气温㊁日最低气温㊁日降水量㊁日最大风速的重现期,并对计算结果进行了χ2检验;庞文保等[5]用皮尔逊Ⅲ型和极值Ⅰ型绘制了最大风速分布曲线,估算了30a 一遇风速和50a 一遇风速;黄玉贞等[6]用皮尔逊Ⅲ型曲线分析了阜新地区干旱发生时间㊁频率.还有学者[7-14]用不同方法对能见度㊁寒潮㊁大风等进行了评估.本文利用长白山地区3个气象站59a 气象观测数据,通过多种评估方法研究长白山地区暴雨特征和年最大日降水量.研究成果可为长白山景区建设㊁安全调度㊁下游水库排洪泄洪㊁有效降低灾害带来的经济损失提供依据;同时,长白山地区自然资源极为丰富,研究暴雨的空间分布特征㊁时间变化特征对境内生态保护具有重要意义.1㊀研究材料与方法1.1㊀研究材料研究材料为长白山地区二道站㊁东岗站㊁天池站3个气象站1960 2018年59a 实际降水数据.其中,天池站1960 1989年为全年站,1990年至今为季节站.1990 2011年和2018年6 9月观测,2012 2017年5 10月观测,时次为当日20时至翌日20时的24h 总降水量,时间分辨率为小时.东岗站位于长白山山脉西风带迎风坡,地形动力抬升作用明显,天气系统较稳定,也容易被激发而呈对称不稳定性;二道站为长白山北坡的典型气象站,只有在西风槽过境及气流转为偏北气流时动力抬升作用才明显;天池站位于长白山主峰,海拔2623m,处于对流层中㊁下层,以暴雨为主的极端天气时有发生.1.2㊀研究方法本次研究使用统计学方法[15-16]统计二道站㊁东岗站㊁天池站暴雨数据,分析气候变化规律及空间分布特征.基于年最大值法选样,利用气象学常用的指数分布㊁耿贝尔Ⅰ型分布㊁皮尔逊Ⅲ型分布㊁韦布尔分布4种函数进行拟合计算,借助MATLAB 软件绘制重现期与年最大日降水量分布曲线,通过χ2检验对比选出最优分布函数.1)指数分布:x =r ln A +β,其中:r 为离散程度参数;β为分布曲线下限;A 为特定再现期极值.2)耿贝尔Ⅰ型分布在特定再现期下的极值计算函数为x T =b -1aln -ln 1-1T æèöø=m x -m y σy σx -σx σyln -ln 1-1T æèöø,其中:a 为尺度参数;b 为位置参数;m x ㊁σx 分别为观测得到N 个样本的平均值和均方差;m y ㊁σy 分别为耿贝尔Ⅰ型分布中不同样本容量N 的均值和均方差;T 为特定再现期.3)皮尔逊Ⅲ型分布的3参数概率密度函数和分布函数:f (x )=1βaΓ(α)(x -a 0)a -1e -x -a 0β,㊀a 0ɤx <+ɕ,α,β>0,F (x )=1βaΓ(α)ʏx a 0(t -a )a -1e-x -a 0βd t ,㊀α,β>0,其中:a 0为随机变量可能取的最小值;α为形状参数;β为尺度参数.4)韦布尔分布3参数概率密度函数和分布函数:f (x )=c b x -a b æèöøc -1e -x -a b ()c ,x ȡa ,22北华大学学报(自然科学版)第22卷F (x )=1-e -x -a b()c .最大值再现期T (x )=11-F (x )=e x -a b ()c .年最大日降水量x T =a +b (ln T )1c .式中:a ㊁b ㊁c 分别为位置参数㊁尺度参数㊁形状参数.5)χ2适合度检验函数:χ2=ðki =1(n i -Np i )2Np i,(1)其中:n i 为第i 组实际观测频数;N 为实际观测样本的个数;p i 为概率密度与组距的乘积.χ2值很小,说明理论频数与实际频数很接近.给定信度范围α后,查χ2分布表,得出χ2α,若χ2<χ2α,则认为该样本服从χ2分布;反之,若χ2ȡχ2α,则认为该样本不服从χ2分布.式(1)将把实际观测样本值分成组距相等的i 个组.2㊀长白山地区暴雨气候特征图1暴雨年代际变化Fig.1Variation of decadal rainstorm2.1㊀暴雨日数时空变化从年际变化看,天池站㊁东岗站㊁二道站出现暴雨的频率分别是95%㊁66%㊁47%.暴雨年代际变化见图1.由图1可知:20世纪60年代,天池站年平均暴雨日数为3.7d,二道站和东岗站不足1d;20世纪70年代㊁80年代天池站暴雨日数略有减少,到90年代达到最少,仅为2.4d,二道站和东岗站平均暴雨日数较前期略有增加;自2000年以来,长白山地区平均暴雨日数显著增多,其中,21世纪10年代天池站达4.6d,二道站和东岗站均超过1d.暴雨月分布情况见表1.由表1可见:1960 2018年,长白山地区4 10月均有暴雨发生,大部分出现在69月.其中,天池站7月暴雨日数最多,占总暴雨日数的44.2%;其次是8月,天池夏季(6 8月)暴雨日数占总暴雨日数的87%.低海拔的二道站和东岗站8月暴雨日数最多.与天池站和东岗站相比,二道站暴雨出现最晚,结束最早.综上可知:近59a 长白山地区年平均暴雨日为1.8d,在空间分布上,天池站最多,为3.7d,东岗站次之(1d),二道站最少(0.7d).表1㊀1960—2018年暴雨月分布特征Tab.1㊀Monthly distribution characteristics of rainstorm from 1960to 2018/d站名暴雨日数4月5月6月7月8月9月10月二道002132130东岗211212561天池241896752022.2㊀不同量级暴雨日数分布1960 2018年,长白山地区不同量级暴雨日数分布见表2.由表2可见:二道站暴雨量级主要分布在50~80mm,东岗站暴雨分布区间较二道站大,天池站暴雨分布区间最广.天池站24h 降水量有1d 超过200mm.从各区间频数看,不同量级暴雨频数随区间增大呈下降趋势.暴雨强度表现为天池站最强,东岗站次之,可能是因为天池站海拔高,地形的动力作用㊁云物理作用在此表现最强烈,同时,天池作为 三江源头 ,具备丰富的水汽条件;东岗站处于西风带的迎风坡,地形的动力抬升作用表现比较明显.32第1期张伶俐,等:长白山地区暴雨特征及重现期几种计算方法对比表2㊀1960 2018年长白山地区不同量级暴雨日数分布Tab.2㊀Distribution of rainstorm days with different magnitude from 1960to 2018in Changbai Mountain aera /d站名暴雨日数50~59.9mm 60~69.9mm 70~79.9mm 80~89.9mm 90~99.9mm 100~109.9mm 110~119.9mm 120~129.9mm ȡ130mm ȡ140mm ȡ150mm ȡ160mm ȡ170mm ȡ200mm二道227610101000000东岗2812743200111100天池804026191057511743113㊀基于年最大日降水量的重现期曲线拟合3.1㊀长白山地区各气象站年最大日降水量对比从二道站㊁东岗站㊁天池站近59a 年最大日降水量箱线图(图2a)可以看出:3站年最大日降水量的最小值较一致,下边缘㊁下四分位数㊁中位数㊁上四分位数㊁上边缘都表现为天池站>东岗站>二道站,而二道站的异常值最多,天池站异常值上限最大,3站的异常值都集中在较大值一侧,χ2分布均表现为右偏态,为正偏;天池站中位数表现为偏向于下四分位数,偏度系数为正,右偏度表现得最明显,表明天池站在达到中位数之前的降水量离散程度最高.因此,评估长白山地区的暴雨情况可以从年最大日降水量着手.3.2㊀年最大日降水量的月分布特征根据天池站1960 1989年年最大日降水量的月分布特征(图2b)可知:年最大日降水量发生在6月的频率为17%,7月为33%,8月达50%,即发生在6 8月(夏季)的频率为100%,故天池站1990 2018年全年最大日降水量可以用6 8月的最大日降水量代替进行分析.图2年最大日降水量Fig.2Annual maximum daily precipitation3.3㊀4种分布函数参数目前,推算年最大日降水量的算法有两类:一类是水文气象法;另一类是频率计算法,也称数理统计法.由于长白山地区地形复杂,降水受地形㊁大气稳定度等影响较大,因此,本次研究采取指数㊁耿贝尔Ⅰ型㊁皮尔逊Ⅲ型㊁韦布尔4种分布函数对长白山地区年最大日降水量进行推算.各分布函数参数见表3.表3㊀1960 2018年最大日降水量4种分布函数参数Tab.3㊀Parameters of four different distribution functions of annual maximum daily precipitation from 1960to 2018分布函数参数名称参数值二道东岗天池指数离散程度8.6214.4723.92曲线下限38.7836.6761.06耿贝尔Ⅰ型尺度参数0.070.050.03位置参数43.9848.1760.1042北华大学学报(自然科学版)第22卷表3(续)分布函数参数名称参数值二道东岗天池形状参数 1.25 1.32 2.30皮尔逊Ⅲ型尺度参数15.6120.4125.18可能取的最小值32.6432.2940.37尺度参数19.1031.6653.79韦布尔形状参数 1.09 1.11 1.33位置参数33.5828.5148.673.4㊀重现期-年最大日降水量关系令T =1~1000a,间隔为1a,推算不同重现期下可能出现的曲线走势,见图3.由图3可知:在相同重现期下,二道站最大日降水量耿贝尔Ⅰ型㊁皮尔逊Ⅲ型与韦布尔曲线走向一致,指数分布法曲线相对平缓;东岗站年最大日降水量曲线为指数法最平缓,韦布尔曲线最陡峭,年最大日降水量关系为韦布尔分布>耿贝尔Ⅰ型分布ȡ皮尔逊Ⅲ型分布>指数分布;天池站年最大日降水量4种分布函数在110mm 相交后呈发散状态,耿贝尔Ⅰ型分布发散得最快,皮尔逊Ⅲ型分布和韦布尔分布次之,指数分布最慢,在相同重现期下降水量值表现为耿贝尔Ⅰ型分布>皮尔逊Ⅲ型分布ȡ韦布尔分布>指数分布.由预测降水量可知:1~1000a 年最大日降水量预测上线分别为二道站150mm,东岗站210mm,天池站310mm.图3二道站㊁东岗站㊁天池站1~1000a 重现期日最大降水量Fig.3Maximum daily precipitation for reproduction period 1~1000a at Erdao station ,Donggang station and Tianchi station3.5㊀不同重现期下的年最大日降水量从防灾减灾㊁趋利避害㊁提前部署景区建设,以及为长白山植被生长㊁动物繁殖研究提供参考等角度出发,借助上述4种分布函数推算重现期分别为10㊁20㊁50和100a 的年最大日降水量,并选取最优分布法.长白山地区不同海拔站点不同重现期年最大日降水量见表4~表7.由表4~表7可知:指数分布推算的10㊁20㊁50㊁100a 暴雨年最大日降水量都偏小,耿贝尔Ⅰ型分布㊁皮尔逊Ⅲ型分布和韦布尔分布推算的预测52第1期张伶俐,等:长白山地区暴雨特征及重现期几种计算方法对比值较一致,后3种分布函数推算的降水量误差范围为2%~10%,且年最大日降水量的误差随着重现期的增大而略增加,与实际接近,能满足极端暴雨量级预测服务的需要.表4㊀重现期为10a年的最大日降水量Tab.4㊀Annual maximum daily precipitation a with a10-year recurrence period/mm站名年最大日降水量指数耿贝尔Ⅰ型皮尔逊Ⅲ型韦布尔最优拟合二道站59777475耿贝尔Ⅰ型东岗站70939096耿贝尔Ⅰ型㊁韦布尔天池站116153149149.5韦布尔㊁皮尔逊Ⅲ型表5㊀重现期为20a年的最大日降水量Tab.5㊀Annual maximum daily precipitation with a20-year recurrence period/mm站名年最大日降水量指数耿贝尔Ⅰ型皮尔逊Ⅲ型韦布尔最优拟合二道站65888686韦布尔㊁皮尔逊Ⅲ型东岗站80107105114耿贝尔Ⅰ型㊁皮尔逊Ⅲ型天池站133176171172韦布尔表6㊀重现期为50a年的最大日降水量Tab.6㊀Annual maximum daily precipitation with a50-year recurrence period/mm站名年最大日降水量指数耿贝尔Ⅰ型皮尔逊Ⅲ型韦布尔最优拟合二道站72102101100耿贝尔Ⅰ型㊁皮尔逊Ⅲ型东岗站93125124137耿贝尔Ⅰ型㊁皮尔逊Ⅲ型天池站155206199199皮尔逊Ⅲ型㊁韦布尔表7㊀重现期为100a年的最大日降水量Tab.7㊀Annual maximum daily precipitation with a100-year recurrence period/mm站名年最大日降水量指数耿贝尔Ⅰ型皮尔逊Ⅲ型韦布尔最优拟合二道站78112112111耿贝尔Ⅰ型㊁皮尔逊Ⅲ型东岗站103139139154耿贝尔Ⅰ型㊁皮尔逊Ⅲ型天池站171229219219皮尔逊Ⅲ型㊁韦布尔4㊀极值重现期的χ2适合度检验由于相同重现期下指数分布计算的年最大日降水量与实际值拟合度不高,因此对皮尔逊Ⅲ型分布㊁耿贝尔Ⅰ型分布㊁韦布尔分布3种函数进行χ2检验.在0.05信度范围查χ2分布表,得出临界值χ2α,挑选拟合度最好的分布方法.长白山区各站点年最大日降水量的χ2适合度检验结果见表8.由表8可知:皮尔逊Ⅲ型分布和耿贝尔Ⅰ型分布在二道站年最大日降水量评估中均通过了0.05的信度检验,但耿贝尔Ⅰ型分布拟合度更高(χ2=0.813<5.250);耿贝尔Ⅰ型分布在3种分布函数中表现最优异,并通过了0.05信度检验,而韦布尔分布在天池站的χ2检验值为5.260,远超过耿贝尔Ⅰ型分布和皮尔逊Ⅲ型分布,在给定信度范围内小于χ2检验临界值.综上,耿贝尔Ⅰ型分布在二道站和东岗站年最大日降水量预测中表现最佳,而韦布尔分布在天池站表现得更完美.表8㊀长白山区各气象站年最大日降水量χ2适合度检验Tab.8㊀Chi-square test about the maximum daily precipitation in Changbai Mountain area台站皮尔逊Ⅲ分布耿贝尔Ⅰ分布韦布尔分布χ2χ2αχ2χ2αχ2χ2α最佳拟合分布二道 5.250 5.9910.813 5.991 6.040 5.991耿贝尔Ⅰ型东岗7.140 5.991 3.490 5.9918.870 5.991耿贝尔Ⅰ型天池81.3009.48825.47011.071 5.2609.488韦布尔㊀注:α=0.05.62北华大学学报(自然科学版)第22卷5 结论和讨论长白山地区暴雨具有明显的时空分布特征,平均暴雨日数呈逐年增多趋势,极端气候事件多发,这与全球变暖密不可分.本次研究显示,在暴雨日数空间分布上,天池站最多,东岗站次之;二道站暴雨量级主要分布在50~80mm,东岗站暴雨分布区间较二道站大,天池站暴雨分布区间最广,这与长白山地区的特殊地形有关,东岗站位于西风带的迎风坡,地形的强迫抬升作用表现得比二道站更明显,而天池站是高海拔气象站,无论在何种天气系统下,地形动力作用㊁云物理作用都能得到极好发挥,同时,作为水源地,天池为暴雨的发生提供了丰富的水汽条件,这些都可为以后划分长白山地区暴雨量级提供参考标准;二道站㊁东岗站㊁天池站年最大日降水量达到暴雨的频率分别为49%㊁66%㊁95%,天池站中位数表现为偏向于下四分位数,偏度系数为正,右偏度表现得最明显;天池站降水的离散程度最高,发生极端降水的概率较大.对长白山地区不同海拔3个站点暴雨重现期进行拟合计算显示:指数分布计算的10㊁20㊁50㊁100a 暴雨年最大日降水量都偏小,耿贝尔Ⅰ型分布㊁皮尔逊Ⅲ型分布和韦布尔分布预测值较一致;耿贝尔Ⅰ型分布在二道站和东岗站年最大日降水量预测中线性拟合度最好,而韦布尔分布则是在天池站暴雨预测表现得更完美.目前,已有许多专家基于年最大值选样算法,利用不同频率曲线确定重现期㊁暴雨强度和历时,构建了暴雨强度模型,取得了良好的社会效益和经济效益.在全球变暖㊁极端天气事件多发的背景下,构建长白山地区不同海拔站点的暴雨强度模型也是未来要开展的工作之一.长白山暴雨受地形影响较大,表现在不同天气系统下的增幅不同.目前还没有对长白山地区不同天气系统下地形对降水量级,尤其是暴雨的影响研究.因此,从防灾减灾㊁趋利避害角度考虑,有必要对长白山地区暴雨特征进行深入研究,完善预测模型.参考文献:[1]王凌梓,苗峻峰,韩芙蓉.近10年中国地区地形对降水影响研究进展[J].气象科技,2018,46(1):64-75.[2]袭祝香,孙力,刘实.东北地区重大暴雨过程评估方法研究[J].灾害学,2009,24(2):61-64.[3]郭渠,廖代强,孙佳,等.重庆主城区暴雨强度公式推算和应用探讨[J].气象,2015,41(3):336-345.[4]王晓光.气象要素重现期的计算方法与比较[J].内蒙古气象,2015(5):29-32.[5]庞文保,白光弼,滕跃,等.P-Ⅲ型和极值Ⅰ型分布曲线在最大风速计算中的应用[J].气象科技,2009,37(2):221-223.[6]黄玉贞,张玉龙,王芳.阜新地区干旱发生规律研究[J].气象与环境学报,2010,26(2):45-49.[7]姬兴杰,朱业玉,顾万龙,等.河南省大风日数时空分布及其对沙尘天气的影响[J].气象与环境学报,2012,28(1):31-37.[8]胥珈珈,刘娜,王鑫.白山市低温极值重现期的计算方法与比较[J].气象灾害防御,2018,25(1):21-24.[9]尹文有,郑皎,王继红,等.年最大日雨量极值分布拟合与推算[J].气象科技,2011,39(2):137-140.[10]袭祝香,孙力,刘实.吉林省单站暴雨特征分析及评估方法[J].气象科学,2009,29(2):230-234.[11]彭嘉栋,叶成志,张剑明,等.中国中部典型高山气象站风速的均一性检验及其变化特点[J].气象与环境学报,2019,35(4):139-144.[12]郑石,王冠,林中冠,等.1961 2013年中国强降水特征分析[J].气象与环境学报,2018,34(6):102-107.[13]李祥,寿绍文,白艳辉,等.1960 2013年白洋淀湿地气候变化特征分析[J].气象与环境学报,2016,32(1):75-83.[14]毛炜峄,陈颖,曹兴.单站寒潮降温过程强度评估指标及其在乌鲁木齐市的应用[J].气象与环境学报,2016,32(5):139-146.[15]马开玉,张耀存,陈星.现代应用统计学[M].北京:气象出版社,2004:177-196.[16]姬兴杰,李凤秀,朱业玉,等.河南省洛河上游暴雨山洪致灾临界面雨量的确定[J].气象与环境学报,2015,31(6):43-50.ʌ责任编辑:郭㊀伟ɔ72第1期张伶俐,等:长白山地区暴雨特征及重现期几种计算方法对比。
降水的变化与分布 -七年级地理上册课件(人教版)

降水丰富的是( B)
A.①③ B.②⑥ C.③⑤ D.④⑥
——
世 界 “ 雨 极 ”
乞 拉 朋 齐
典例剖析
(2021·山东滨州·中考真题)下图为某岛屿沿20°纬线的地形剖面图及甲、 乙两地气候资料图。读图完成下面小题。
1.对于甲、乙两地的叙述,正确的是(A)
A.地处南半球 B.全年多雨 C.1月气温最低 D.冬暖夏凉
典例剖析
(2021·山东滨州·中考真题)下图为某岛屿沿20°纬线的地形剖面图及甲、 乙两地气候资料图。读图完成下面小题。
规律三: 中纬度 沿海地区降水多 内陆地区降水少 受海陆位置影响
世界降水分布规律
4.地形因素对降水又会有什么影响呢?
受地形因素影响,山地迎风坡降水多,背风坡降水少
降水
上升冷却 暖湿气流
山地
下沉增温 空气干燥
世界降水分布规律
小
结
1.赤道地区降水__多__,两极地区降水__少__。受_纬__度__位___置__因素影响。 2.南北回归线两侧,大陆东岸降水__多__,大陆西岸降水__少__。 3.中纬度,沿海地区降水__多__ ,内陆地区降水__少__ 。受_海__陆___位__置__因素影响。 4.山地迎风坡降水__多__ ,背风坡降水__少__ 。受___地___形____因素影响。
世界降水分布规律
2.在南、北回归线附近 大陆东岸的年降水量大约是多少毫米? 1000mm以上 大陆西岸的年降水量大约是多少毫米? 200mm以下
西
东
规律二:
南北回归线两侧 大陆东岸降水多 西 东 大陆西岸降水少
2021年中国各省年降水量排行
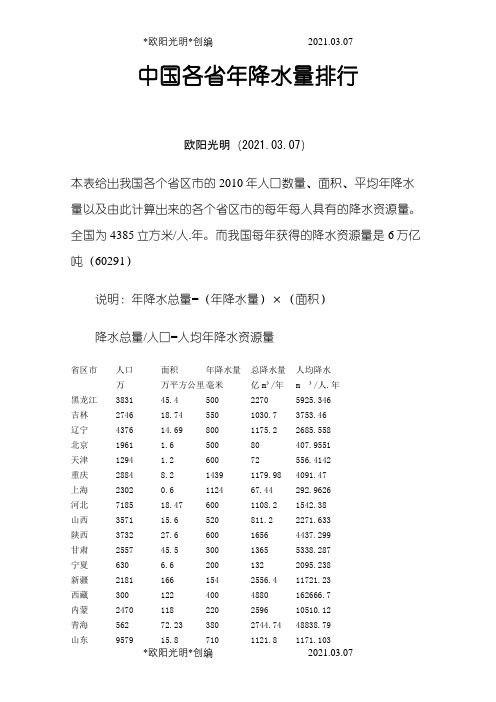
中国各省年降水量排行欧阳光明(2021.03.07)本表给出我国各个省区市的2010年人口数量、面积、平均年降水量以及由此计算出来的各个省区市的每年每人具有的降水资源量。
全国为4385立方米/人.年。
而我国每年获得的降水资源量是6万亿吨(60291)说明:年降水总量=(年降水量)×(面积)降水总量/人口=人均年降水资源量省区市人口面积年降水量总降水量人均降水万万平方公里毫米亿m³/年m ³/人.年黑龙江3831 45.4 500 2270 5925.346吉林2746 18.74 550 1030.7 3753.46辽宁4376 14.69 800 1175.2 2685.558北京1961 1.6 500 80 407.9551天津1294 1.2 600 72 556.4142重庆2884 8.2 1439 1179.98 4091.47上海2302 0.6 1124 67.44 292.9626河北7185 18.47 600 1108.2 1542.38山西3571 15.6 520 811.2 2271.633陕西3732 27.6 600 1656 4437.299甘肃2557 45.5 300 1365 5338.287宁夏630 6.6 200 132 2095.238新疆2181 166 154 2556.4 11721.23西藏300 122 400 4880 162666.7内蒙2470 118 220 2596 10510.12青海562 72.23 380 2744.74 48838.79山东9579 15.8 710 1121.8 1171.103河南10975 16.8 700 1176 1071.526 江苏7866 10.2 1000 1020 1296.72 浙江5442 10.2 1400 1428 2624.035 安徽5950 13.9 1200 1668 2803.361 湖南6568 21.2 1500 3180 4841.657 湖北5723 18.36 1200 2203.2 3849.729 江西4456 16.69 1600 2670.4 5992.819 广西4602 23.67 1600 3787.2 8229.465 广东10430 17.79 1800 3202.2 3070.182 福建3686 12.4 1600 1984 5382.528 云南4597 39 1100 4290 9332.173 贵州3474 17.6 1200 2112 6079.447 四川8041 48.5 1100 5335 6634.747 海南岛867 3.5 1639 573.65 6616.494 台湾1883 3.6 2200 792 4206.054 香港702 0.1 2214 22.14 315.3846 澳门55 0.003 2200 0.66 120合计137478 971.743 60291.11 4385.5。
2021年地质灾害气象风险预警建议

地质灾害气象风险预警建议1.地质灾害气象风险预警模型地质灾害气象风险预警是指在一定的地质环境和人为活动背景条件下,基于前期过程降水量和预报降水量,对某区域发生地质灾害的可能性及成灾大小的预测。
参考《地质灾害区域气象风险预警标准》中“基于综合预警指数的地质灾害气象风险预警模型”,地质灾害预警模型如下:P=v*R式中:P——预警综合指数;v——易发指数,对应前面的地质灾害易发性评价成果;R——有效降水量;在该预警模型中最重要的是探究**市高新区地质灾害发生的有效降水量数值。
所谓前期有效降水量,是指前期降水进入岩土体并一直滞留至研究当日的降雨量,国内外学者已做过相应的研究,并提出了计算进入岩土体雨量的经验公式:R=k r1+k2r2+…+k n rn式中:R——前期有效降水量;k——有效降水系数,一般取0.84;r n——前n日的日降水量;2.地质灾害气象预报预警原理及阈值(1)地质灾害气象预报预警原理在综合考虑地质、地貌、构造、岩性等控制因素外,还应着重分析研究降雨量与滑坡、崩塌等地质灾害之间的关系。
由于滑坡、崩塌多发生在前期降雨充沛、松散固体物质处于充分饱和或过饱和状态,再遇到短时特大暴雨就可激发滑坡、崩塌。
因此,进行滑坡、崩塌气象预报预警工作时,其临界降雨量指标的选取主要考虑前期降雨量以及未来日降雨量。
通过采用一定的数学决策模型,对降水数据进行集成,将研究区的降水集成结果及前期降雨量分布与临界雨量指标进行比较,然后进行滑坡、崩塌气象预报预警工作。
(2)滑坡预警阈值根据前人的研究,国内外采用了许多与滑坡发生的关系密切的降雨特性参数,包括降雨强度、降雨持续时间、累积雨量、当日降雨量及临界降雨量等。
其中,当日降雨量为滑坡发生的激发因素,而前期降雨量则是地质灾害形成的潜在因素。
前期降雨量的多少,不仅会影响坡体地下水位、土壤含水量,进而还会影响激发滑坡所需的当日降雨量。
根据大量学者研究成果表明:降雨诱发滑坡与前期降雨以及当日降雨关系密切。
生态系统生产总值(GEP)核算技术规范2021版

生态系统生产总值(GEP)核算技术规范1范围本文件规定了生态系统生产总值(GEP)的核算指标体系、核算步骤和核算方法。
本文件适用于生态系统生产总值(GEP)的核算。
2规范性引用文件下列文件中的内容通过文中的规范性引用而构成本文件必不可少的条款。
其中,注日期的引用文件,仅该日期对应的版本适用于本文件;不注日期的引用文件,其最新版本(包括所有的修改单)适用于本文件。
GB/T 38582 森林生态系统服务功能评估规范3术语和定义下列术语和定义适用于本文件。
3.13.1生态系统生产总值gross ecosystem product, GEP一定区域在一定时间内生态系统的产品与服务的价值总和,是生态系统为人类福祉提供的产品和服务及其经济价值总量。
3.23.2生态系统生产总值(GEP)核算gross ecosystem product (GEP) accounting分析与评价生态系统为人类生存与福祉提供的产品与服务及其经济价值,包括生态功能量和价值量核算,一般以一年为核算时间单位。
生态系统生产总值包括生态物质产品价值、生态调节服务价值和人居文化服务价值三类。
3.33.3生态功能量 ecosystem amount人类从生态系统中直接或间接得到的最终产品与服务的物质量。
3.43.4价值量核算 GEP accounting在生态功能量核算的基础上,结合各类生态产品的参考价格,通过一定数学运算得到以货币化形式呈现的生态产品价值的计算过程。
3.53.51DB3201/T 1041—2021生态物质产品ecological material products自然生态系统提供的可为人类直接利用的自然物质产品,如食物、木材、药材与其他物质产品。
3.63.6生态调节服务ecological regulation services生态系统提供改善人类生存与生活环境的惠益,如土壤保持、涵养水源、水质净化、固碳释氧、气候调节等服务功能。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、潜水计算公式欧阳光明(2021.03.07)1、公式1式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);H为潜水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m)。
r2、公式2式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);H为潜水含水层厚度(m);S为水位降深(m);b为基坑中心距岸边的距离(m);为基坑半径(m)。
r3、公式3式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);H为潜水含水层厚度(m);S为水位降深(m);为基坑中心距A河岸边的距离(m);b1为基坑中心距B河岸边的距离(m);b2b'=b1+b2;为基坑半径(m)。
r4、公式4式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);H为潜水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rb''为基坑中心至隔水鸿沟的距离。
5、公式5式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);H为潜水含水层厚度(m);R为引用影响半径(m);为基坑半径(m);rl 为过滤器有效工作长度(m);h 为基坑动水位至含水层底板深度(m);h 为潜水层厚与动水位以下的含水层厚度的平均值(m)。
6、公式6式中:Q 为基坑涌水量(m 3/d);k 为渗透系数(m/d);r 0为基坑半径(m);S 为水位降深(m);l 为过滤器有效工作长度(m);b 为基坑中心距岸边的距离(m);m 为含水层底板到过滤器有效工作部分中点的长度。
7、公式7(1)、b>l(2)、b>l式中:Q 为基坑涌水量(m 3/d);k 为渗透系数(m/d);r 0为基坑半径(m);S 为水位降深(m);l 为过滤器有效工作长度(m);b 为基坑中心距岸边的距离(m)。
8、公式8式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);H为潜水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rb''为基坑中心至隔水鸿沟的距离(m);为过滤器进水部分长度0.5处至静水位的距离(m);hsT为过滤器进水部分长度0.5处至含水层底板的距离(m); 为不完整井阻力系数。
9、公式9式中:Q为基坑涌水量(m3/d);为上层含水层的渗透系数(m3/d);k2为下层含水层的渗透系数(m3/d);k1为上层含水层厚度(m);H1为下层含水层厚度(m);M1为基坑动水位到上层含水层底板的距离(m);hR为引用影响半径(m);为基坑半径(m)。
r10、公式10式中:Q为基坑涌水量(m3/d);k 3、k2、k1为上、中、下含水层的渗透系数(m3/d);H1为上层含水层厚度(m);M1为下层含水层厚度(m);M2为中层含水层厚度(m);h为基坑动水位到上层含水层底板的距离(m);R为引用影响半径(m);r为基坑半径(m)。
二、承压水计算公式1、公式1式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);r为基坑半径(m)。
2、公式2式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);b为基坑中心距岸边的距离(m);为基坑半径(m)。
r3、公式3式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);为基坑中心距A河岸边的距离(m);b1为基坑中心距B河岸边的距离(m);b2b'=b1+b2;为基坑半径(m)。
r4、公式4式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rb''为基坑中心至隔水鸿沟的距离。
5、公式5式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);R为引用影响半径(m);为基坑半径(m);rl为过滤器有效工作长度(m);6、公式6(1)、l<0.3M,b<2l(2)、l<0.3M,b>2l式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);R为引用影响半径(m);为基坑半径(m);rl为过滤器有效工作长度(m);b为基坑中心距岸边的距离(m)。
7、公式7式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rb''为基坑中心至隔水鸿沟的距离(m);为不完整井阻力系数。
8、公式8式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rh为含水层底板到动水位距离(m)。
9、公式9式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M'为过滤器进水部分长度0.5处至含水层顶板的距离(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rl为过滤器有效工作长度(m);H'为过滤器进水部分长度0.5处至静水位的距离(m);T为过滤器进水部分长度0.5处至含水层底板的距离(m); 为不完整井阻力系数。
10、公式10式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);H为含水层水头高度(m);M为承压水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rb''为基坑中心至隔水鸿沟的距离。
11、公式11式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M'为过滤器进水部分长度0.5处至含水层顶板的距离(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rl为过滤器有效工作长度(m);H'为过滤器进水部分长度0.5处至静水位的距离(m);T为过滤器进水部分长度0.5处至含水层底板的距离(m);b''为基坑中心至隔水鸿沟的距离(m);为不完整井阻力系数。
三、条形基坑降水计算公式1、公式1式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);L为基坑长度(m);R为引用影响半径(m);2、公式2式中:q为单井出水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);d为井间距之半(m);为井点半径(单排)或排距之半(双排)(m)。
rw3、公式3式中:q为单井出水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);d为井间距之半(m);为不完整井阻力系数。
4、公式4式中:Q为基坑涌水量(m3/d);q为单井出水量(m3/d);k为渗透系数(m/d);L为基坑长度(m);H为含水层水头高度(m);M为承压水含水层厚度(m);S为水位降深(m);R为引用影响半径(m);d为井间距之半(m);为井点半径(单排)或排距之半(双排)(m)。
rw5、公式5式中:q为单井出水量(m3/d);k为渗透系数(m/d);为过滤器进水部分长度0.5处至静水位的距离(m);HsS为水位降深(m);R为引用影响半径(m);d为井间距之半(m);为井点半径(单排)或排距之半(双排)(m);rw为不完整井阻力系数。
6、公式6式中:q为单井出水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);h为含水层底板到动水位距离(m)。
H为含水层水头高度(m);R为引用影响半径(m);d为井间距之半(m);为井点半径(单排)或排距之半(双排)(m)。
rw7、公式7式中:q为单井出水量(m3/d);k为渗透系数(m/d);M'为过滤器进水部分长度0.5处至含水层顶板的距离(m);S为水位降深(m);R为引用影响半径(m);为基坑半径(m);rl为过滤器有效工作长度(m);H'为过滤器进水部分长度0.5处至静水位的距离(m);T为过滤器进水部分长度0.5处至含水层底板的距离(m);d为井间距之半(m);为井点半径(单排)或排距之半(双排)(m)。
rwζ为不完整井阻力系数。
四、单井出水量计算公式1、轻型井点/喷射井点式中:q为单井出水量(m3/d);i为水力坡度,开始抽水时i=1;k为渗透系数(m/d);D为钻孔直径(m);H为含水层厚度。
2、管井井点式中:q为单井出水量(m3/d);2/);φ为单井单位长度出水量(m dα'为经验系数;l为过滤器浸没长度(m);d为过滤器外径(mm);五、水位降深计算公式1、潜水式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);H为含水层厚度(m);S为某点水位降深(m);R为引用影响半径(m);...为某点到各井点中心的距离;x x xn12n为井数量。
2、承压水式中:Q为基坑涌水量(m3/d);k为渗透系数(m/d);M为承压水含水层厚度(m);S为某点水位降深(m);R为引用影响半径(m);...为某点到各井点中心的距离;x x x12nn为井数量。
六、井深计算公式井深式中:L为井点管埋设深度(m);H为基坑深度(m);h为降水后水面距基坑底的深度(m) ;一般取0.5;i为降水区内的水力坡度;一般取0.10.3;为基坑等效半径(m);rZ为降水期内地下水位变更幅度(m) ;Y为过滤器工作部分长度(m);T为沉砂管长度(m);一般取为0.5。
