信号与系统复习题》
《信号与系统》复习

物理意义:非周期信号可以分解为无数个频率为, 复振幅为[X(j)/2p]d 的虚指数信号ejw t的线性组合。
简述傅氏反变换公式的物理意义?
傅里叶变换性质
F 时移特性 x(t t 0 ) X( j) e jt
0
x(t)
X(j)
展缩特性
1 F x (at) X( j ) a a
(n = 1,2) (n = 1,2)
奇对称周期信号其傅里叶级数只含有正弦项。
周期信号的傅里叶级数 周期信号x(t) 如图 所示,其傅氏级数系数的特点是
偶对称周期信号其傅里叶级数只含有直流项与余弦项 周期信号f(t)如图所示,其直流分量等于_____
周期信号的频谱及特点
Cn是频率的函数,它反映了组成信号各次谐波 的幅度和相位随频率变化的规律,称频谱函数。
《信号与系统》复习
考核方式
平时成绩20% 实验成绩20% 期末成绩60%
题型: 选择题(每题3分,共30分) 填空题(每空2分,共20分) 简答题(每题4分,共20分)
计算题(每题10分,共30分)
第一章:信号与系统分析导论
周期信号平均功率计算 若电路中电阻R=1Ω,流过的电流为周期电流i(t)= 4cos(2πt)+2cos(3πt) A,其平均功率为( ) 系统的数学模型 连续时间系统:系统的输入激励与输出响应都必须为 连续时间信号,其数学模型是微分方程式。 离散时间系统: 系统的输入激励与输出响应都必须 为离散时间信号,其数学模型是差分方程式。
L[ yzs (t )] Yzs ( s) H ( s) L[ x(t )] X ( s)
写出系统函数H (s) 的定义式
简述拉氏变换求解微分方程的过程
(完整版)信号与系统复习题

信号与系统试题库一、填空题绪论:1。
离散系统的激励与响应都是____离散信号 __。
2.请写出“LTI ”的英文全称___线性非时变系统 ____。
3.单位冲激函数是__阶跃函数_____的导数. 4.题3图所示波形可用单位阶跃函数表示为()(1)(2)3(3)t t t t εεεε+-+---。
5.如果一线性时不变系统的输入为f(t ),零状态响应为y f (t )=2f (t —t 0),则该系统的单位冲激响应h (t )为____02()t t δ-_________。
6。
线性性质包含两个内容:__齐次性和叠加性___。
7。
积分⎰∞∞-ω--δ-δdt )]t t ()t ([e 0t j =___01j t e ω--_______。
8。
已知一线性时不变系统,当激励信号为f (t)时,其完全响应为(3sint-2cost )ε(t );当激励信号为2f (t )时,其完全响应为(5sint+cost )ε(t),则当激励信号为3f(t )时,其完全响应为___7sint+4cost _____。
9。
根据线性时不变系统的微分特性,若:f (t)−−→−系统y f (t)则有:f ′(t)−−→−系统_____ y ′f (t )_______。
10。
信号f (n )=ε(n )·(δ(n)+δ(n-2))可_____δ(n)+δ(n —2)_______信号。
11、图1所示信号的时域表达式()f t =()(1)(1)tu t t u t --- 。
12、图2所示信号的时域表达式()f t =()(5)[(2)(5)]u t t u t u t +----。
13、已知()()()2f t t t t εε=--⎡⎤⎣⎦,则()f t '=()(2)2(2)u t u t t δ----.14、[]2cos32t d ττδτ-∞⎛⎫+ ⎪⎝⎭⎰=8()u t 。
信号与系统复习试题(含答案)

76.某二阶LTI系统的频率响应H (j)
A.y2y3y
B。y3y2yf2
D。y3y2yf
H(s)的共轭极点在虚轴上,则它的
2,-1,H ()1,则系统函数H(s)为(
C。(s1)(s2)
(t)的傅氏变换是(
B。j(
D。j(2
A.系统在(t)作用下的全响应
C.系统单位阶跃响应的导数
6。对于一个三阶常系数线性微分方程描述的连续时间系统进行系统的时域模拟时,所需积
分器数目最少是__3个_____个。
7。一线性时不变连续因果系统是稳定系统的充分且必要条件是系统函数的极点位于S平面
的___左半平面_______。
8.如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为
其中x(0)是初始状态,
f(t)为激励,y(t)为全响应,试回答该系统是否是线性的?[答案:非线性]
2.y'(t)sinty(t)f(t)试判断该微分方程表示的系统是线性的还是非线性的,
是时变的还是非时变的?[答案:线性时变的]
3.已知有限频带信号f(t)的最高频率为100Hz,若对f(2t)*f(3t)进行时域取样,
B。f(t)f(t8)
12
C.f(t)f(t8)
D。f(t3)f(t1)
69.已知一连续系统在输入f(t)的作用下的零状态响应为yzs(t)f(4t),则该系统为()
70.已知f(t)是周期为T的函数,f(t)-f (t
T)的傅里叶级数中,只可能有(
71.一个线性时不变的连续时间系统,其在某激励信号作用下的自由响应为(e
h(t)=(1et)(t),则其系统函数
15.已知一信号f(t)的频谱F(j)的带宽为,则f(2t)的频谱的带宽为
信号与系统自考复习参考题

一、连续与离散时间信号与系统1、单项选择题1. 按照信号时间特性的分类,信号nj e n x π=)(属于( )。
A. 连续时间周期信号B. 连续时间非周期信号C. 离散时间周期信号D. 离散时间非周期信号2.题2图f(t)的表达式是( )A.[])1t ()1t ()t (t -ε+-ε-εB.-[])1t ()t (t -ε-εC.[])1t ()t ()1t (-ε-ε--D.[])2t ()t (t -ε-ε2. 下列表达式中错误的是( ) A.)t ()t (-δ=δB.)t t ()t t (00-δ=-δC.)t ()t (δ-=δD.)()(t t e tδδ=-3. 按照信号时间特性的分类,信号)]1()1()[3/cos()(--+=t t t t f εεπ属于( )。
A. 连续时间周期信号 B. 连续时间非周期信号 C. 离散时间周期信号 D. 离散时间非周期信号4. 设信号f 1(t)=t u(t)-t u(t-2),信号f 2(t)=f 1(t-1),则:f 2(1)的值为( )。
A.0 B.1 C.2 D.35.已知信号f(t)如题3(a)图所示,则f(-2t-2)为题3(b)图中的( )6.下列对线性系统稳定性的说明不正确的是()A.对于有界激励信号产生有界响应的系统是稳定系统B.系统稳定性是系统自身的性质之一C.系统是否稳定与激励信号有关D.当t趋于无穷大时,h(t)趋于有限值或0,则系统可能稳定7.信号f1(t)、f2(t)的波形如题6图所示,则f(t)=f1(t)*f2(t)的表达式为()A.)1t()1t(-ε-+ε B.)2t()2t(-ε-+εC.)1t()1t(+ε--ε D.)2t()2t(+ε--ε8. 下列关于系统的描述中,错误的是( )。
A.全部由电阻组成的系统是即时系统B .动态系统可用代数方程描述C .因果系统的零状态响应一定不会出现在激励之前D .当激励有界时,稳定系统的零状态响应一定是有界的9.两个有限长序列的非零序列值的宽度分别为10和6,则两个序列卷积所得的序列为()A.宽度为16的有限宽度序列B.宽度为17的有限宽度序列C.宽度为15的有限宽度序列D.宽度为大于17的有限宽度序列2、填空题1. 积分⎰∞∞-=-dttt)2()/(sinδπ_________。
信号与系统期末考试复习题及答案(共8套)

信号与系统考试题及答案(一)1. 系统的激励是)t (e ,响应为)t (r ,若满足dt)t (de )t (r =,则该系统为 线性、时不变、因果。
(是否线性、时不变、因果?) 2. 求积分dt )t ()t (212-+⎰∞∞-δ的值为 5 。
3. 当信号是脉冲信号f(t)时,其 低频分量 主要影响脉冲的顶部,其 高频分量 主要影响脉冲的跳变沿。
4. 若信号f(t)的最高频率是2kHz ,则t)f(2的乃奎斯特抽样频率为 8kHz 。
5. 信号在通过线性系统不产生失真,必须在信号的全部频带内,要求系统幅频特性为 一常数相频特性为_一过原点的直线(群时延)。
6. 系统阶跃响应的上升时间和系统的 截止频率 成反比。
7. 若信号的3s F(s)=(s+4)(s+2),求该信号的=)j (F ωj 3(j +4)(j +2)ωωω。
8. 为使LTI 连续系统是稳定的,其系统函数)s (H 的极点必须在S 平面的 左半平面 。
9. 已知信号的频谱函数是))00(()j (F ωωδωωδω--+=,则其时间信号f(t)为01sin()t j ωπ。
10. 若信号f(t)的211)s (s )s (F +-=,则其初始值=+)(f 0 1 。
二、判断下列说法的正误,正确请在括号里打“√”,错误请打“×”。
(每小题2分,共10分)1.单位冲激函数总是满足)()(t t -=δδ ( √ )2.满足绝对可积条件∞<⎰∞∞-dt t f )(的信号一定存在傅立叶变换,不满足这一条件的信号一定不存在傅立叶变换。
( × ) 3.非周期信号的脉冲宽度越小,其频带宽度越宽。
( √ )4.连续LTI 系统的冲激响应的形式取决于系统的特征根,于系统的零点无关。
( √ )5.所有周期信号的频谱都是离散谱,并且随频率的增高,幅度谱总是渐小的。
( × )三、计算分析题(1、3、4、5题每题10分,2题5分, 6题15分,共60分)1.信号)t (u e )t (f t-=21,信号⎩⎨⎧<<=其他,01012t )t (f ,试求)t (f *)t (f 21。
信号与系统复习题

一、选择题 1.积分(cos )(1)d t t t t t t π∞∞-∞-∞+δ-=0δ-=⎰⎰的值为 .. A. )(3t etδ-B.1C.)1(-t δD.02.积分⎰∞∞-+dtt t )()1(δ的值为A.4B.3C.2D.1 3.()()[]=*-t t e dtd tεε2 A.()t δ B.()t e tε2- C.()t δ2- D.t e 22-- 4、信号)()(2t e t f tε=的拉氏变换及收敛域为 ..B.2]Re[,21)(-<-=s s s FC. 2]Re[,21)(->+=s s s F D.2]Re[,21)(<+=s s s F 5. 信号ft=εt*δt -δt -4的单边拉氏变换Fs= .. A.s1B.4s 1s 1+-D.se -4s6.某一因果线性时不变系统;其初始状态为零;当输入信号为εt 时;其输出rt 的拉氏变换为Rs;问当输入r 1t=εt -1-εt -2时;响应r 1t 的拉氏变换R 1s= .. A.e-s-e-2sRs B.Rs-1-Rs-2 C.2-s 11-s 1-Rs D.Rs s )e -(e -2s -s 7.已知信号ft 的波形如下图所示;则ft 的表达式为 ..A.)1()()(--=t u t u t fB.)1()()(-+=t u t u t fC.)1()()(+-=t u t u t fD.)()1()(t u t u t f -+= 8.求信号)()52(t u etj +-的傅里叶变换 ..A.ωω521j e j +C.)5(21-+-ωj D.ωω251j e j +t9.)2)(1()2(2)(-++=s s s s s H ;属于其极点的是 ..A.1B.2C.0D.-210.已知信号ft 的频带宽度为Δω;则f 3t -2的频带宽度为 .. A.3Δω B.13Δω C.13Δω-2 D.13Δω-6 11. 系统的线性性质是指系统要同时具有 .. A 、叠加性和时延性B 、齐次性和时延性C 、叠加性和因果性D 、叠加性和齐次性12.已知G τt ↔Y jω=τSa 2ωτ;则ft=G 2t-1↔Fjω为 .. A.Fjω=Saωe jωB.Fj ω=Sa ωe-j ωC.Fjω=2Saωe jωD.Fjω=2Saωe -jω13.已知某一线性时不变系统;当激励信号为xt 时;对应的零状态响应为4dtt dx )2(-;则该系统函数H jw= .. A.4)(ωF B.4ωωj ej 2- C.4ωj e2-/ω D.4ωωj e X 2)(-14.下列叙述正确的是 ..A. ft 为周期奇函数;则其傅里叶级数只有正弦分量..B.ft 为周期偶函数;则其傅里叶级数只有余弦偶次谐波分量..C.ft 为周期奇函数;则其傅里叶级数只有奇次谐波..D. ft 为周期偶函数;则其傅里叶级数只有偶次谐波.. 15.若矩形脉冲信号的宽度加宽;则它的频谱带宽 .. A.不变B. 变窄C. 变宽D. 与脉冲宽度无关16.设信号ft 为包含0~10Hz 的频带有限信号;则f2t 的奈奎斯特频率..A.20HzB.40HzC.10HzD.30Hz 17.理想低通滤波器的传输函数)(ωj H 是 .. A.0t j Keω- B.)]()([0C C t j u u Keωωωωω--+- C.)]()([0C C tj u u Ke ωωωωω--+-18.离散信号f 1k 和f 2k 的如下图所示;设yk =f 1k *f 2k ;则y 2等于 .. A.1 B.2 C.3 D.5(k)f 1k-1-2-121231(k)f 1k-1-2-12123219.下图所示信号中; 是非因果信号..A. B.C. D.20.下图所示信号中; 是抽样信号..A. B.C. D.21.下列表达式错误的是 .. A.()()dt t t u ⎰+∞∞-=δB.()()t u t ,=δC.()()t g t h ,=D.()()t t δδ=-22.设:ft ↔F ω=ωωj 2e 0t j +;则ft 为 ..A.ft=e )(20t t +-ut B.ft=e)(20t t --ut+t 0C.ft=e)(20t t --ut-t 0 D.ft=e)(20t t +-ut+t 023.36.信号 f5-3t 是 .. A . f3t 右移 5B. f3t 左移 C . f-3t 左移 5D. f-3t 右移 5/324.下列说法不正确的是 ..A.H s 在左半平面的极点所对应的响应函数为衰减的..即当t →∞时;响应均趋于0..B. H s 在虚轴上的一阶极点所对应的响应函数为稳态分量..C. H s 在虚轴上的高阶极点或右半平面上的极点;其所对应的响应函数都是递增的..D.H s 的零点在左半平面所对应的响应函数为衰减的..即当t →∞时;响应均趋于0.. 25.()()[]='*-t u t u et2 .. A -2()t u et2- B ()t u C ()t u e t 2- D ()()t t u e t δ+-226.一非周期连续信号被理想冲激取样后;取样信号的频谱F s jω是 ..A.离散频谱B.连续周期频谱C. 连续频谱D.不确定;要依赖于信号而变化 27.下列叙述正确的是 ..A. ft 为周期奇函数;则其傅里叶级数只有正弦分量..B.ft 为周期偶函数;则其傅里叶级数只有余弦偶次谐波分量..C.ft 为周期奇函数;则其傅里叶级数只有奇次谐波..D. ft 为周期偶函数;则其傅里叶级数只有偶次谐波.. 28.周期奇函数的傅里叶级数中;只可能含有 ..A.正弦项B.直流项和余弦项C.直流项和正弦项D.余弦项 29.)1()1()2(2)(22+++=s s s s H ;属于其零点的是 ..A. -1B. -2C. -jD. j30.若使信号经过线性系统不产生失真;则系统函数)(ωj H 为 .. A.0t j Ke ω- B.tj Ke0ω- C.00t j Keω-D.)]()([0c c t j u u Keωωωωω--+- 为常数、、、w 00K t c ωω31. 连续时间信号ft 的最高频率ωm =104π rad/s ;若对其取样;并从取样后的信号中恢复原信号ft ;则奈奎斯特间隔和所需低通滤波器的截止频率分别为 ..A.10-4s;104HzB.10-4s;5×103HzC.5×10-3s;5×103HzD.5×10-3s; 104Hz 32.以下是一些系统函数的收敛域;则其中稳定的是 .. A .|z| > 2 B .|z| < 0.5 C .0.5 < |z| < 2D .|z| < 0.933.已知某序列Z 变换的收敛域为∞>|z |>0;则该序列为 A.有限长序列 B.右边序列 C.左边序列 D.双边序列 34.已知某序列xn 的z 变换为z +z 2;则xn -2的z 变换为A. 45z z +B. 222---z zC. z z +2D. 11+-z35. 若对ft 进行理想取样;其奈奎斯特取样频率为f s ;则对)3(t f 进行取样;其奈奎斯特取样频率为 .. A 、3f s B 、s f 31 C 、3f s -2 D 、)2(31-s f 36.函数ft 的图像如图所示;ft 为 ..A.偶函数B.奇函数C.奇谐函数D.都不是37. 欲使信号通过线性系统不产生失真;则该系统应具有 .. A.幅频特性为线性;相频特性也为线性; B. 幅频特性为常数;相频特性为线性; C. 幅频特性为线性;相频特性为常数;38. 已知某一线性时不变系统;当激励信号为xt 时;对应的零状态响应为4dtt dx )2(-;则该系统函数H jw= ..A.4)(ωFB.4ωωj e j 2-C.4ωj e 2-/ωD.4ωωj e X 2)(- 39. δn 的Z 变换是 ..A. 1B.δωC.2πδωD.2π40. 一个线性移不变系统稳定的充分必要条件是其系统函数的收敛域包含 .. A .单位圆B .原点C .实轴D .虚轴二、填空题 1、 2,2)(>-=z z zz X 的逆Z 变换=)(n x .. 2、 按信号是否可以用确定的时间函数来表示;可以分为 和 .. 3、 系统对信号进行无失真传输时应满足的条件之一是系统的幅频特性在整个频率范围内应为 ..4、 如果系统在激励信号作用之前不产生响应;称这样的系统具有 性..5、 如图系统;已知)()(),1()(21t u t h t t h =-=δ;系统的冲激响应h t =..6、 设有周期方波信号f t ;其脉冲宽度τ = 1ms;该信号的频带宽度带宽为________ ;若τ压缩为0.2ms;其带宽又为________..7、 若已知f 1t 的拉氏变换F 1s=s1 ;则ft=f 1t* f 1t 的拉氏变换Fs= _________________. 8、 冲激信号与阶跃信号之间的关系是 ..9、 如果一线性时不变系统的输入为ft;零状态响应为yt=2ft-t 0;则该系统的单位冲激响应ht 为_________________.10、 周期信号的频谱具有离散性、 和 .. 11、 将高频信号频谱搬移到低频0=ω附近;这一过程称为 .. 12、 )()(21t f t f 、波形如下图所示;则)()(21t f t f *的波形为______ __..13、如果一线性时不变系统的单位阶跃响应为st;则该系统的单位冲激响应h t 为_________. 14、函数)5)(2()6(+++s s s 的拉普拉斯反变换的初值与终值分别为_____和 ..15、如果一线性时不变系统的单位冲激响应h t= u t;则当该系统的输入信号f t=u t-2时;其零状态响应为________ _________..16、按信号是否在所有时间点上连续;可以分为_______和________..17、函数()3-t δ 的单边拉氏变换Fs 等于 .. 18、将低频信号频谱搬移到高频附近;这一过程称为 .. 19、系统函数)1)(1()2(2)(2+++=s s s s H ;其极点为 .. 20、利用信号的各种对称性;下图所示信号的傅里叶级数所包含的分量形式分别为 ..21、信号)1(2)1(5---t u e t 的拉普拉斯变换为 ..22、离散信号)6()2()(---=n u n u n f 的波形为..23、设有周期方波信号f t ;其脉冲宽度τ = 1ms;该信号的频带宽度带宽为________ ;若τ压缩为0.2ms;其带宽又为________.. 24、函数)5)(2()6(+++s s s 的拉普拉斯反变换的初值与终值分别为_____和 ..25、)(2n u n的Z 变换为 ;收敛域为 .. 三、判断题1、 非周期信号的频谱是离散谱 ..2、 单位冲激样值函数)(n δ 在n=0时;值为无穷大..3、 信号绝对可积;该信号一定存在傅氏变换..4、 周期脉冲的脉冲宽度与带宽成正比..5、 信号周期 T 0越大;w 0就越小;则谱线越密..6、 两个周期信号之和一定是周期信号..7、Xz 的表达式可以唯一确定原函数xn..8、单位冲激响应是由单位冲激信号引起的全响应..9、提高信号的传输速率以牺牲信号带宽为代价.. 10、抽样信号是数字信号.. 11、任何信号都可以分解为偶分量与奇分量之和..12、连续周期信号的频谱是离散谱.. 13、两个周期信号之和一定是周期信号.. 14、任意周期信号的傅里叶级数都存在.. 15、)(s H 极点在s 平面的左半平面;该系统稳定.. 16、信号在时域内压缩;则对应的频域压缩;时域展宽;则频域展宽.. 17、左边序列的收敛域为圆外.. 18、差分方程的特解只与自由项有关.. 19、系统函数Hs 是系统的零输入响应的拉氏变换与输入信号的拉氏变换之比.. 20、冲激偶函数是偶函数.. 四、计算题1、 知一线性时不变连续时间系统的单位冲激响应)()(0t t t h -=δ;若)(t f 的傅里叶变换为ωωj F +=32)( ;用频域分析法求当输入为)1()(-+t f t f 时系统的零状态响应)(t y ..2、 已知⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧===↑↑1,2,3)(,1,2,3,4)(0021n n n x n x ;试用不进位相乘法求)(*)()(21n x n x n y =..3、离散信号fk 如下图所示;求yk = f 2k * fk ;并绘出的yk 图形..(k)f 0.5k2113465(2k )f 0.5k21134图J3.7-1图J3.7-24、设有序列f 1 n 和f 2 n ;如下图所示;计算这两个序列的卷积..5、已知某离散系统由下面的差分方程描述)1()()2(4)1(4)(--=-+-+n x n x n y n y n y若给定)()(n u n x =及y0=1、y1=2;试求yn..6、设系统差分方程为)()2(6)1(5)(n f n y n y n y =-+-- 起始状态y -1 = 3;y -2 = 2;当f n = 2u n 时;求系统的响应y n ..7、已知一因果LTI 系统如图 a 所示;求:1描述系统的微分方程;2系统函数Hs 和单位冲激响应ht ;8、如下图所示系统;()()()ωωωj H j H F 21、、均给定;试画出()()()ωωω21Y Y Y 、、的频谱图..9、如下图所示系统;()()ωωjH F 、均给定;写出y 1t 、y 2t 的频谱函数 ()()ωω21Y Y 和;并画出它们的频谱图..10、描述某一线性时不变系统的微分方程为()()()()t f t y t y t y '=+'+''65;当()10='-y ;y 0-=2;ft =u t 时;试用拉式变换法求系统的全响应..。
信号与系统复习题

信号与系统期末复习题一、填空题1.描述线性非时变连续系统的数学模型是_微分方程______________________________。
2.离散系统的激励与响应都是___离散时间信号_____。
4.请写出“LTI ”的英文全称___线性时不变____。
5.若信号f(t)的FT 存在,则它满足条件是_____________________。
8、周期信号的频谱是离散的,频谱中各谱线的高度,随着谐波次数的增高而逐渐减小,当谐波次数无限增多时,谐波分量的振幅趋向于无穷小,该性质称为__收敛性____ 9、若某信号)(t f 的最高频率为3kHz ,则)3(t f 的奈奎斯特取样频率为 18 kHz 。
10、某系统的频率特性为23)(3)(2+++=ωωωωj j j j H ,则其冲激响应为h(t)= )()3(2t e e tt ε--- 。
11、=*)(3)(2n n n n εε )()23(11n n n ε++- 。
12、已知1)(2-=z z z F ,则f(n)= )(])1(1[21n nε-- 。
13、某LTI 连续系统的输入信号为)()(2t e t f t ε-=,其冲激响应)()(t t h ε=,则该系统的零状态响应为)(n y zs 为)(]1[212t e t ε-- 。
14.(4分)()()u t u t *= t u (t )[][]u n u n *= (n +1)u [n +1]=(n +1) u [n ]15.(4分)已知信号f (t )= Sa (100t )* Sa (200t ),其最高频率分量为f m = 50/π Hz ,奈奎斯特取样率f s = 100/π Hz 16.(4分)已知F )()]([ωj F t f =,则F 3[()]j tf t e = [(3)]F j ω-F()(2)n f t t n δ∞=-∞⎡⎤-⎢⎥⎣⎦∑= 1[()]2n F j n ωπ∞=-∞-∑17.(2分)设某因果离散系统的系统函数为az zz H +=)(,要使系统稳定,则a 应满足 | a | < 118.(2分)已知某系统的频率响应为3()4j H j e ωω-=,则该系统的单位阶跃响应为 4 u (t -3)19.(3分)已知某系统的系统函数为2()1H s s =+,激励信号为()3cos 2x t t =,则该系统的稳态响应为()2(arctan 2)y t t =- 20.(3分)已知)2)(21()(--=z z z z X ,收敛域为221<<z ,其逆变换为 21()[]2[1]32n n u n u n ⎡⎤-+--⎢⎥⎣⎦二、选择题1.连续信号)(t f 与)(0t t -δ的卷积,即=-*)()(0t t t f δ(a) )(t f (b) )(0t t f - (c) )(t δ (d) )(0t t -δ 2.连续信号)(t f 与)(0t t -δ的乘积,即=-)()(0t t t f δ(a) )()(0t t f δ (b) )(0t t f - (c) )(t δ (d) )()(00t t t f -δ 3.线性时不变系统的数学模型是(a) 线性微分方程 (b) 微分方程 (c) 线性常系数微分方程 (d) 常系数微分方程4.若收敛坐标落于原点,S 平面有半平面为收敛区,则(a) 该信号是有始有终信号 (b) 该信号是按指数规律增长的信号 (c) 该信号是按指数规律衰减的信号(d) 该信号的幅度既不增长也不衰减而等于稳定值,或随时间n t t ,成比例增长的信号 5.若对连续时间信号进行频域分析,则需对该信号进行 (a) LT (b) FT (c) Z 变换 (d) 希尔伯特变换 6.无失真传输的条件是(a) 幅频特性等于常数 (b) 相位特性是一通过原点的直线 (c) 幅频特性等于常数,相位特性是一通过原点的直线(d) 幅频特性是一通过原点的直线,相位特性等于常数 7.描述离散时间系统的数学模型是(a) 差分方程 (b) 代数方程 (c) 微分方程 (d) 状态方程 8.若Z 变换的收敛域是 1||x R z > 则该序列是(a) 左边序列 (b)右边序列 (c)双边序列 (d) 有限长序列 9.若以信号流图建立连续时间系统的状态方程,则应选(a) 微分器的输出作为状态变量 (b) 延时单元的输出作为状态变量 (c) 输出节点作为状态变量 (d)积分器的输出作为状态变量 10.若离散时间系统是稳定因果的,则它的系统函数的极点 (a) 全部落于单位圆外 (b) 全部落于单位圆上 (c) 全部落于单位圆内 (d) 上述三种情况都不对11、某LTI 系统的微分方程为)()(2)(t f t y t y =+',在f(t)作用下其零状态响应为t e -+1,则当输入为)()(2t f t f '+时,其零状态响应为: (a) t e -+2 (b) t e --2 (c) t e -+32 (d)1 12、某3阶系统的系统函数为ks s s ks s H ++++=32)(23,则k 取何值时系统稳定。
信号与系统期末考试复习资料

第一章绪论1、选择题1.1、f(5—2t)是如下运算的结果 CA、f(-2t)右移5B、f(-2t)左移5C、f(-2t)右移D、f(-2t)左移1.2、f(t0-a t)是如下运算的结果 C .A、f(—a t)右移t0;B、f(—a t)左移t0;C、f(—a t)右移;D、f(—a t)左移1。
3、已知系统的激励e(t)与响应r(t)的关系为:则该系统为 B 。
A、线性时不变系统;B、线性时变系统;C、非线性时不变系统;D、非线性时变系统1.4、已知系统的激励e(t)与响应r(t)的关系为: 则该系统为 C 。
A、线性时不变系统B、线性时变系统C、非线性时不变系统D、非线性时变系统1。
5、已知系统的激励e(t)与响应r(t)的关系为:则该系统为B 。
A、线性时不变系统B、线性时变系统C、非线性时不变系统D、非线性时变系统1。
6、已知系统的激励e(t)与响应r(t)的关系为:则该系统为 BA、线性时不变系统B、线性时变系统C、非线性时不变系统D、非线性时变系统1.7。
信号的周期为 C 。
A、B、C、D、1。
8、信号的周期为: B 。
A、B、C、D、1.9、等于 B 。
A。
0 B.-1 C.2 D。
-21。
10、若是己录制声音的磁带,则下列表述错误的是:BA. 表示将此磁带倒转播放产生的信号B。
表示将此磁带放音速度降低一半播放C. 表示将此磁带延迟时间播放D. 表示将磁带的音量放大一倍播放1.11。
AA.B。
C. D。
1。
12.信号的周期为 B . A B C D1.13.如果a〉0,b>0,则f(b—a t)是如下运算的结果 C 。
A f(-a t)右移bB f(-a t)左移bC f(—a t)右移b/aD f(-a t)左移b/a1.14.线性时不变系统的响应,下列说法错误的是 C 。
A 零状态响应是线性时不变的B 零输入响应是线性时不变的C全响应是线性时不变的 D 强迫响应是线性时不变的2、填空题与判断题2。
信号与系统 期末复习试卷1

, 22t k
第2页共4页
三、(10 分)如图所示信号 f t,其傅里叶变换
F jw F
f t,求(1)
F
0
(2)
F
jwdw
四 、( 10
分)某
LTI
系统的系统函数
H s
s2
s2 2s 1
,已知初始状态
y0 0, y 0 2, 激励 f t ut, 求该系统的完全响应。
参考答案 一、选择题(共 10 题,每题 3 分 ,共 30 分,每题给出四个答案,其中只有一 个正确的)1、D 2、A 3、C 4、B 5、D 6、D 7、D 8、A 9、B 10、A
二、填空题(共 9 小题,每空 3 分,共 30 分)
1、 0.5k uk 2、 (0.5)k1u(k)
3、
s s
2 5
5、 (t) u(t) etu(t)
8、 et cos2tut
三、(10 分)
6、 1 0.5k1 uk
9、 66 , 22k!/Sk+1 s
解:1)
F ( ) f (t)e jt dt
Atut Btut 2 Ct 2ut Dt 2ut 2
10、信号 f t te3tut 2的单边拉氏变换 Fs等于
A
2s
s
7 e 2s3 32
C
se
s
2 s 3
32
B
e 2s
s 32
D
e 2s3
ss 3
二、填空题(共 9 小题,每空 3 分,共 30 分)
1、卷积和[(0.5)k+1u(k+1)]* (1 k) =________________________
信号与系统复习题含答案完整版

信号与系统复习题含答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】(C ))(t δ+(-6e -t +8e -2t)u(t) (D )3)(t δ +(-9e -t +12e -2t)u(t)6、 连续周期信号的频谱具有(A ) 连续性、周期性 (B )连续性、收敛性 (C )离散性、周期性 (D )离散性、收敛性7、 周期序列2)455.1(0+k COS π的 周期N 等于(A) 1 (B )2 (C )3 (D ) 48、序列和()∑∞-∞=-k k 1δ等于(A )1 (B) ∞ (C) ()1-k u (D) ()1-k ku9、单边拉普拉斯变换()se s s s F 2212-+=的愿函数等于10、信号()()23-=-t u te t f t的单边拉氏变换()s F 等于二、填空题(共9小题,每空3分,共30分) 1、 卷积和[()k+1u(k+1)]*)1(k -δ=________________________2、 单边z 变换F(z)= 12-z z的原序列f(k)=______________________ 3、 已知函数f(t)的单边拉普拉斯变换F(s)=1+s s,则函数y(t)=3e -2t·f(3t)的单边拉普拉斯变换Y(s)=_________________________4、 频谱函数F(j ω)=2u(1-ω)的傅里叶逆变换f(t)=__________________5、 单边拉普拉斯变换s s s s s F +++=2213)(的原函数 f(t)=__________________________6、 已知某离散系统的差分方程为)1(2)()2()1()(2-+=----kf k f k y k y k y ,则系统的单位序列响应h(k)=_______________________7、 已知信号f(t)的单边拉氏变换是F(s),则信号⎰-=2)()(t dxx f t y 的单边拉氏变换Y(s)=______________________________ 8、描述某连续系统方程为 该系统的冲激响应h(t)=9、写出拉氏变换的结果()=t u 66 ,=k t 22三(8分)已知信号()()()⎪⎩⎪⎨⎧><==↔./1,0,/1,1s rad s rad jw F j F t f ωωω设有函数()(),dtt df t s =求⎪⎭⎫ ⎝⎛2ωs 的傅里叶逆变换。
《信号与系统引论》(第二版)郑君里 课后题答案 客观题(附答案)

《信号与系统》复习参考练习题一、单项选择题:14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为() A .400rad /s B 。
200 rad /s C 。
100 rad /s D 。
50 rad /sf如下图(a)所示,其反转右移的信号f1(t) 是()15、已知信号)(tf如下图所示,其表达式是()16、已知信号)(1tA、ε(t)+2ε(t-2)-ε(t-3)B、ε(t-1)+ε(t-2)-2ε(t-3)C、ε(t)+ε(t-2)-ε(t-3)D、ε(t-1)+ε(t-2)-ε(t-3)17、如图所示:f(t)为原始信号,f1(t)为变换信号,则f1(t)的表达式是()A、f(-t+1)B、f(t+1)C、f(-2t+1)D、f(-t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是()19。
信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为( )A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ,则该系统是()>-系统的系统函数.已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( )A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( )A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( )A )0(fB )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应D.全响应与强迫响应之差 2A 、1-eB 、3eC 、3-eD 、127.信号〔ε(t)-ε(t -2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28.已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae 2--+,则其2个特征根为() A 。
信号与系统复习题(含答案)

.试题一一. 选择题(共10题,20分) 1、n j n j een x )34()32(][ππ+=,该序列是 。
A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint),该系统是 。
A.因果时不变B.因果时变C.非因果时不变D.非因果时变 3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u e t h t ,该系统是 。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号,则其傅立叶级数系数a k 是 。
A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇 5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω,,j X ,则x(t)为 。
A. t t 22sinB. tt π2sin C. t t 44sin D.t t π4sin6、一周期信号∑∞-∞=-=n n t t x )5()(δ,其傅立叶变换)(ωj X 为 。
A. ∑∞-∞=-k k )52(52πωδπ B. ∑∞-∞=-k k )52(25πωδπC. ∑∞-∞=-k k )10(10πωδπD. ∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ,则x[n]奇部的傅立叶变换为 。
A.)}(Re{ωj e X j B. )}(Re{ωj e XC. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ,则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 。
A. 500B. 1000C. 0.05D. 0.001 9、一信号x(t)的有理拉普拉斯共有两个极点s=-3和s=-5,若)()(4t x e t g t =,其傅立叶变换)(ωj G 收敛,则x(t)是 。
A. 左边B. 右边C. 双边D. 不确定10、一系统函数1}Re{1)(->+=s s e s H s,,该系统是 。
信号与系统复习题(答案全)

1、 若系统的输入f (t )、输出y (t) 满足()3()4t y t e ft -=,则系统为 线性的 (线性的、非线性的)、 时变的 (时变的、时不变)、 稳定的 (稳定的、非稳定的).2、 非周期、连续时间信号具有 连续 、非周期频谱;周期、连续时间信号具有离散、非周期 频谱;非周期、离散时间信号具有 连续 、周期频谱;周期、离散时间信号具有离散、 周期 频谱。
3、 信号f(t)的占有频带为0-10KHz,被均匀采样后,能恢复原信号的最大采样周期为 5×10—5 s 。
4、 )100()(2t Sa t f =是 能量信号 (功率信号、能量信号、既非功率亦非能量信号)。
5、 ()2cos()f t t =+是 功率信号 (功率信号、能量信号、既非功率亦非能量信号)。
6、 连续信号f(t )=sint 的周期T 0= 2π ,若对f (t )以fs=1Hz 进行取样,所得离散序列f(k)=sin(k ) ,该离散序列是周期序列? 否 。
7、 周期信号2sin(/2)()j n tn n f t e n ππ+∞=-∞=∑,此信号的周期为 1s 、直流分量为 2/π 、频率为5Hz 的谐波分量的幅值为 2/5 。
8、 f (t) 的周期为0。
1s 、傅立叶级数系数**03355532F F F F F j --=====、其余为0。
试写出此信号的时域表达式f (t ) = 5 + 6 cos ( 60 π t ) - 4 sin (100 π t ) . 9、 f (k ) 为周期N=5的实数序列,若其傅立叶级数系数()205=F ()52511,πjeF -+=()54512πjeF -+=、 则F 5 (3 )= ()54512πjeF +=- 、F 5 (4 )= ()52511πj eF +=- 、F 5 (5 )= 2 ;f(k ) =())1.7254cos(62.052)9.3552cos(62.152525140525︒-⨯+︒-⨯+=∑=k k e n F n k jn πππ。
信号与系统复习题

。
↑
n=0
50.使序列Z变换存在的取值范围称作 51.因果系统是未加激励不会产生 52.若系统的系统函数为H(S),其零点的位置 53.若系统的系统函数为H(S),其极点的位置
。 响应的系统。
系统的稳定性。 系统的稳定性。
54.若因果系统函数H(S)的所有极点均在S左半开平面,则系统
。
55.若因果系统函数H(S)的所有极点均在S右半开平面,则系统
A.相位相同,大小相等
B.相位相同,大小不等
C.相位相反,大小相等
D.相位相反,大小不等
4.GCL 并联谐振电路发生谐振时,电容 C 和电感 L 上的电流有以下关系:
A.相位相同,大小相等
B.相位相同,大小不等
C.相位相反,大小相等
D.相位相反,大小不等
5.RLC 并联谐振电路的固有谐振频率取决于:
求该离散系统的系统函数和差分方程。
96.已知序列f1(n) { 1 ,l,2,1,},f2(n){ 1 ,0,0,2}
↑
↑
n=0
n=0
若序列以f3(n)= f1(n)∗ f2(n),请用离散卷积定理计算f3(n)序列。
97.已知序列f1(n){ 1 ,0,l,2},f2(n)={ 1 ,l}
↑
↑
n=0
n=0
试求两序列的卷积和。
98.描述某系统的差分方程为 y(n) − 1 y(n −1) − 1 y(n − 2) = f (n) + 2 f (n −1)
A.电源电压幅值 B.电源电压的初始相位
C.电源电压频率 D.电路参数
6.已知信号 f(t)如(a)所示,其反转左移的信号 f1(t)是
7.已知信号 f(t)如图所示,其表达式为:
信号与系统复习套题一答案

《信号与系统》套题一参考答案一、简答题1、dtt df t f t f x e t y t)()()()0()(+⋅=- 其中x(0)是初始状态,为激励)(t f 为全响应,,)(t y 试回答该系统是否是线性的? 解:由于无法区分零输入响应和零状态响应,因而系统为非线性的。
3、 若信号)(t f 的最高频率为20KHz ,则信号)3()2()(2t f t f t f +=的最高频率为___________KHz ;若对信号)(2t f 进行抽样,则奈奎斯特频率s f 为 ____________KHz 。
解:本题目主要考查的是取样定理的条件:)2(21)2(ωj F t f ↔)3(31)3(ωj F t f ↔ 因而:)2(t f 的最高频率为40KHz ,)3(t f 的最高频率为60KHz)3()2()(2t f t f t f +=的最高频率为两个分信号最高频率,为60KHz ,若对信号)(2t f 进行抽样,奈奎斯特频率12022=≥m s f f KHz4、 设系统的激励为()f t ,系统的零状态响应)(t y zs 与激励之间的关系为:)()(t f t y zs -=,判断该系统是否是时不变的,并说明理由。
解:设)()(01t t f t f -=,若系统为时不变的,则必有结论)(01t t y y zs zs -=。
根据题意,由)(1t f 作用于系统的零状态响应为:)()(011t t f t y zs -=,根据信号的基本运算,)()()(0011t t f t t f t y zs +-=-=,很明显,)(01t t y y zs zs -≠,因而系统为时变的。
7、 设系统的激励为()f t ,系统的零状态响应)(t y zs 与激励之间的关系为:)1(*)()(-=k f k f k y zs ,判断该系统是否是线性的,并说明理由。
解:系统为非线性的。
因为表达式中出现了)(k f 的二次方。
信号于系统复习题

复习题填空题1.2()5(0)2(),0y t y x t t =+>是否为线性系统 。
2. ()()y t tf t =是否为时变系统 。
3.2(1)(4)t t dt δ∞-∞-+=⎰。
4.线性时不变系统,无初始储能,当激励1()()f t t ε=时,响应31()()t y t e t ε-=当激励2()()f t t δ=时,其响应2()y t = 。
5. 函数sin ()2tf t t=频谱函数 。
6.设某系统输入f(t)的矩形脉冲如下图所示,其冲击响应为()(2)(h t tt δδ=++- f(t)*h(t) 为 。
7.F(s)= 2322222s s s s s +-+--的原函数为 。
1. 系统的输入为f(t),输出为y(t)=tf(t),判断系统是否是时变的 。
2.2(1)(4)t t dt δ∞-∞-+=⎰。
3. 信号()t f 的傅氏变换存在的充分条件是 。
4. 若连续线性时不变系统的输入信号为t f ,响应为t y ,则系统无失真传输的时域表示式为()t y = 。
5. 为使线性时不变系统是稳定的,其系统函数()s H 的极点必须在S 平面的 。
1.设有定义在区间上的两个函数1()f t 和2()f t ,则1()f t 和2()f t 的卷积12()()()_____________y t f t f t =*=(卷积定义)。
2. t δ( t - 1 )= ,⎰∞∞--t t t d )1(δ=3.信号()2=e cos t f t t -的单边拉氏变换为 。
4. 信号sin ()2tf t t=频谱函数 。
5. 若连续线性时不变系统的输入信号为f(t),响应为y(t),则无失真传输系统的系统函数必须满足:()H ω= 。
二.填空。
1.(5分)有一线性时不变系统,当激励1()()f t t ε=时,响应1()()at y t e t ε-=,则当激励2()()f t t δ=时,响应2()_____________y t =(假定起始时刻系统无储能)。
(完整版)信号与系统复习试题(含答案)
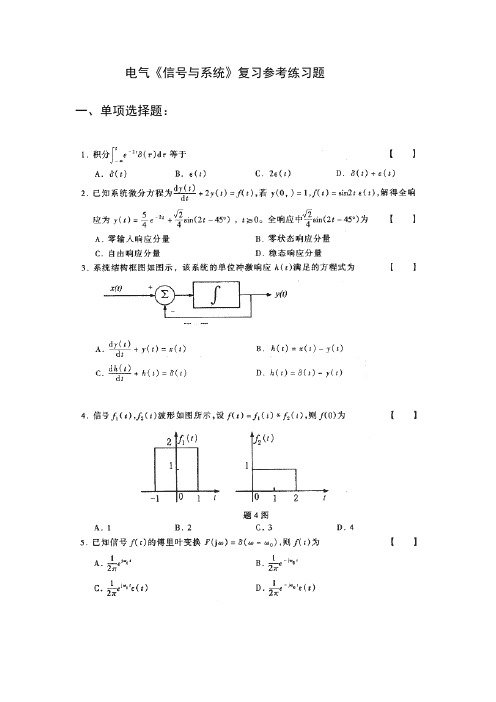
电气《信号与系统》复习参考练习题一、单项选择题:14、已知连续时间信号,)2(100)2(50sin )(--=t t t f 则信号t t f 410cos ·)(所占有的频带宽度为() A .400rad /s B 。
200 rad /s C 。
100 rad /s D 。
50 rad /sf如下图(a)所示,其反转右移的信号f1(t) 是( d )15、已知信号)(tf如下图所示,其表达式是()16、已知信号)(1tA、ε(t)+2ε(t-2)-ε(t-3)B、ε(t-1)+ε(t-2)-2ε(t-3)C、ε(t)+ε(t-2)-ε(t-3)D、ε(t-1)+ε(t-2)-ε(t-3)17、如图所示:f(t)为原始信号,f1(t)为变换信号,则f1(t)的表达式是()A、f(-t+1)B、f(t+1)C、f(-2t+1)D、f(-t/2+1)18、若系统的冲激响应为h(t),输入信号为f(t),系统的零状态响应是( c )19。
信号)2(4sin 3)2(4cos 2)(++-=t t t f ππ与冲激函数)2(-t δ之积为( )A 、2B 、2)2(-t δC 、3)2(-t δD 、5)2(-t δ,则该系统是()>-系统的系统函数.已知2]Re[,651)(LTI 202s s s s s H +++= A 、因果不稳定系统 B 、非因果稳定系统C 、因果稳定系统D 、非因果不稳定系统21、线性时不变系统的冲激响应曲线如图所示,该系统微分方程的特征根是( )A 、常数B 、 实数C 、复数D 、实数+复数22、线性时不变系统零状态响应曲线如图所示,则系统的输入应当是( )A 、阶跃信号B 、正弦信号C 、冲激信号D 、斜升信号23. 积分⎰∞∞-dt t t f )()(δ的结果为( ) A )0(f B )(t f C.)()(t t f δ D.)()0(t f δ24. 卷积)()()(t t f t δδ**的结果为( )A.)(t δB.)2(t δC. )(t fD.)2(t f25. 零输入响应是( )A.全部自由响应B.部分自由响应C.部分零状态响应 D .全响应与强迫响应之差2A 、1-eB 、3eC 、3-e D 、1 27.信号〔ε(t)-ε(t -2)〕的拉氏变换的收敛域为 ( )A.Re[s]>0B.Re[s]>2C.全S 平面D.不存在28.已知连续系统二阶微分方程的零输入响应)(t y zi 的形式为t t Be Ae 2--+,则其2个特征根为( )A 。
信号与系统复习试题

1.下列信号的分类方法不正确的是( A ):A 、数字信号和离散信号B 、确定信号和随机信号C 、周期信号和非周期信号D 、因果信号与反因果信号2。
下列说法正确的是( D ): A 、两个周期信号x (t ),y (t )的和x (t )+y(t )一定是周期信号.B 、两个周期信号x (t ),y (t )的周期分别为2和2,则其和信号x (t )+y(t ) 是周期信号。
C 、两个周期信号x (t ),y (t )的周期分别为2和π,其和信号x (t )+y (t )是周期信号。
D 、两个周期信号x (t ),y (t )的周期分别为2和3,其和信号x (t )+y (t )是周期信号。
3。
下列说法不正确的是( D )。
A 、一般周期信号为功率信号.B 、 时限信号(仅在有限时间区间不为零的非周期信号)为能量信号。
C 、ε(t )是功率信号;D 、e t 为能量信号;4。
将信号f (t )变换为( A )称为对信号f (t )的平移或移位。
A 、f (t –t 0) B 、f (k–k 0) C 、f (at ) D 、f (—t )5.将信号f (t )变换为( A )称为对信号f (t )的尺度变换。
A 、f (at ) B 、f (t –k 0) C 、f (t –t 0) D 、f (—t )6。
下列关于冲激函数性质的表达式不正确的是( B )。
A 、)()0()()(t f t t f δδ=B 、()t aat δδ1)(=C 、)(d )(t tεττδ=⎰∞- D 、)()-(t t δδ=7.下列关于冲激函数性质的表达式不正确的是( D )。
A 、⎰∞∞-='0d )(t t δ B 、)0(d )()(f t t t f =⎰+∞∞-δC 、)(d )(t tεττδ=⎰∞- D 、⎰∞∞-=')(d )(t t t δδ8.下列关于冲激函数性质的表达式不正确的是( B ).A 、)()1()()1(t f t t f δδ=+B 、)0(d )()(f t t t f '='⎰∞∞-δC 、)(d )(t tεττδ=⎰∞- D 、)0(d )()(f t t t f =⎰+∞∞-δ9。
《信号与系统复习题(有答案)》

信号与系统复习题说明: 以下给出了绝大多数题目的答案, 答案是我个人做的,不保证正确性,仅供参考.请务必把复习题弄明白并结合复习题看书.请务必转发给每个同学!!!补充要点(务必搞明白):1 教材p.185例6-12 已知离散时间LTI 系统的单位冲激响应为h(n)=…,又已知输入信号x(n)=…,则系统此时的零状态响应为h(n)和x(n)的卷积.3 已知连续时间LTI 系统在输入信号为f(t)时的零状态响应为y(t),则输入信号为f(t)的导函数时对应的零状态响应为y(t)的导函数(即输入求导,对应的零状态响应也求导)4 教材p.138倒数第3行到139页上半页,请理解并记忆,必考.一、单项选择题1.信号5sin 410cos3t t ππ+为 ( A )A.周期、功率信号B.周期、能量信号C.非周期、功率信号D.非周期、能量信号2.某连续系统的输入-输出关系为2()()y t f t =,此系统为 ( C )A.线性、时不变系统B.线性、时变系统C.非线性、时不变系统D.非线性、时变系统3.某离散系统的输入-输出关系为()()2(1)y n f n f n =+-,此系统为 ( A )A.线性、时不变、因果系统B.线性、时变、因果系统C.非线性、时不变、因果系统D.非线性、时变、非因果系统4.积分(t t dt t--⎰20)()δ等于( B )A.-2δ()tB.2()u t -C.(2)u t -D.22δ()t - 5. 积分(3)t e t dt δ∞--∞-⎰等于( C )(此类题目务必做对)A.t e -B.(3)t e t δ--C. 3e -D.06.下列各式中正确的是 ( B )A.12()(2)2t t δδ=B.1(2)()2t t δδ= C. (2)()t t δδ= D. (2)2()t t δδ= 7.信号)(),(21t f t f 波形如图所示,设12()()*()f t f t f t =,则(1)f 为( D )A .1B .2C .3D .48.已知f(t)的波形如图所示,则f(5-2t)的波形为( C )9. 描述某线性时不变连续系统的微分方程为()3()()y t y t x t '+=。
信号与系统考试题及答案

信号与系统考试题及答案第一题:问题描述:什么是信号与系统?答案:信号与系统是电子工程和通信工程中重要的基础学科。
信号是信息的传递载体,可以是电流、电压、声音、图像等形式。
系统是对信号进行处理、传输和控制的装置或网络。
信号与系统的研究内容包括信号的产生、变换、传输、处理和控制等。
第二题:问题描述:信号的分类有哪些?答案:信号可以根据多种特征进行分类。
按照时间域和频率域可以将信号分为连续时间信号和离散时间信号;按照信号的能量和功率可以分为能量信号和功率信号;按照信号的周期性可以分为周期信号和非周期信号;按照信号的波形可以分为正弦信号、方波信号、脉冲信号等。
第三题:问题描述:什么是线性时不变系统?答案:线性时不变系统是信号与系统领域中重要的概念。
线性表示系统满足叠加性原理,即输入信号的线性组合经过系统后,输出信号也是输入信号的线性组合。
时不变表示系统的性质不随时间变化而改变。
线性时不变系统具有许多重要的性质和特点,可以通过线性时不变系统对信号进行处理和分析。
第四题:问题描述:系统的冲激响应有什么作用?答案:系统的冲激响应是描述系统特性的重要参数。
当输入信号为单位冲激函数时,系统的输出即为系统的冲激响应。
通过分析冲激响应可以得到系统的频率响应、幅频特性、相频特性等,从而对系统的性能进行评估和优化。
冲激响应还可以用于系统的卷积运算和信号的滤波等应用。
第五题:问题描述:如何对信号进行采样?答案:信号采样是将连续时间信号转换为离散时间信号的过程。
常用的采样方法包括周期采样和非周期采样。
周期采样是将连续时间信号按照一定的时间间隔进行等间隔采样;非周期采样是在信号上选取一系列采样点,采样点之间的时间间隔可以不相等。
采样频率和采样定理是采样过程中需要考虑的重要因素。
第六题:问题描述:什么是离散傅里叶变换(DFT)?答案:离散傅里叶变换是对离散时间信号进行频域分析的重要工具。
通过计算离散傅里叶变换可以将离散时间信号转换为复数序列,该复数序列包含了信号的频率成分和相位信息。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
信号与系统复习题一、 单项选择题1.信号5sin 410cos3t t ππ+为 ( )A.周期、功率信号B.周期、能量信号C.非周期、功率信号D.非周期、能量信号2.某连续系统的输入-输出关系为2()()y t f t =,此系统为 ( )A.线性、时不变系统B.线性、时变系统C.非线性、时不变系统D.非线性、时变系统3.某离散系统的输入-输出关系为()()2(1)y n f n f n =+-,此系统为 ( )A.线性、时不变、因果系统B.线性、时变、因果系统C.非线性、时不变、因果系统D.非线性、时变、非因果系统4.积分(t t dt t--⎰20)()δ等于( ) A.-2δ()tB.2()u t -C.(2)u t -D.22δ()t - 5. 积分(3)t e t dt δ∞--∞-⎰等于( )A.t e -B.(3)t e t δ--C. 3e -D.06.下列各式中正确的是 ( ) A.12()(2)2t t δδ= B.1(2)()2t t δδ= C. (2)()t t δδ= D. (2)2()t t δδ=7.信号)(),(21t f t f 波形如图所示,设12()()*()f t f t f t =,则(1)f 为( )A .1B .2C .3D .48.已知f(t)的波形如图所示,则f(5-2t)的波形为( )9. 描述某线性时不变连续系统的微分方程为()3()()y t y t x t '+=。
已知3(0)2y =,()x t =3()u t , 则21e -3t ()u t 为系统的( )。
A. 零输入响应B. 零状态响应C. 自由响应D. 强迫响应10.一线性非时变连续系统,已知当激励信号为()x t 时,系统的零状态响应为()()t y t e u t -=,当激励信号为2()x t +(1)x t -时,系统的零状态响应为 ( )A.2()t e u t -B. (1)(1)t e u t ---C. 2()t e u t -+(1)(1)t e u t ---D. 3()t e u t -11. 已知某系统,当输入2()()t x t e u t -=时的零状态响应()()t y t e u t -=,则系统的冲激响应h(t)的表达式为( )。
A. δ(t)+e t ()u tB. δ(t)+e t ()u t -C. δ(t)+e -t ()u tD. δ(t)+e -t ()u t -12.离散系统的差分方程为()2(1)()y n y n u n +-=初始值(0)1y =-,则零输入响应()zi y n为( )。
A.(2)()n u n --B. 1(2)()n u n +-C. (2)()n u n -D. 2(2)()n u n -13.()f n 如图所示,则()()()y n f n f n =*为( )A.{1,1,1}B.{2,2,2}C.{1,2,2,2,1}D.{1,2,3,2,1}14.序列f 1(n)和f 2(n)的波形如图所示,设f(n)=f 1(n)*f 2(n),则f(2)等于( )A.0B.1C.3D.515. 图(b)中与图(a)所示系统等价的系统是( )16.周期矩形脉冲的谱线间隔与( )A .脉冲幅度有关B .脉冲宽度有关C .脉冲周期有关D .周期和脉冲宽度有关17.若矩形脉冲信号的宽度加宽,则它的频谱带宽( )A .不变B .变窄C .变宽D .与脉冲宽度无关18.已知信号f t ()如图所示,则其傅里叶变换为( )A .τωττωτ2422Sa Sa ()()+ B .τωττωτSa Sa ()()422+ C .τωττωτ242Sa Sa ()()+ D .)2()4(ωττωττSa Sa + 19.信号f t 1()和f t 2()分别如图所示,已知F )()]([11ωj F t f =,则f t 2()的傅里叶变换为( )A .F j e j t 10()--ωωB .F j e j t 10()ωω- C .F j e j t 10()-ωω D .F j e j t 10()ωω 20.已知 F [()](),f t F j =ω则信号f t ()25-的傅里叶变换为( ) A.1225F j e j ()ωω- B.F j e j ()ωω25- C.F j e j ()ωω252- D.12252F j e j ()ωω- 21. 已知信号f t ()的傅里叶变换00()()(),F j u u ωωωωω=+--则f t ()为( ) A.ωπω00Sa t () B.ωπω002Sa t () C.200ωωSa t () D.2200ωωSa t () 22.信号2sin()ππ⎡⎤⎢⎥⎣⎦s s B t B t 的带宽为( ) A s B π B 2s B π C 3s B π D 4s B π23.有一线性时不变因果系统,其频率响应21)(+=ωωj j H ,对于某一输入()x t 所得 输出信号的傅里叶变换为1()(2)(3)Y j j j ωωω=++,则该输入()x t 为( ) A .3()t e u t -- B .3()t e u t - C .3()t e u t - D .3()t e u t24.一个有限长连续时间信号,时间长度2分钟,频谱包含直流至100Hz 分量。
为便于计算机处理,对其取样以构成离散信号,最小的理想取样点数为( )A. 36000B. 24000C. 12000D. 600025. 已知带限信号()f t 的最高频率为1000Hz ,若对信号()()f t f t *进行采样,则允许采样的最低采样频率为( )。
A 1000 HzB 2000 HzC 3000 HzD 4000 Hz26.2()()t f t e u t =的拉氏变换及收敛域为( )A .122s s +>-,Re{} B .122s s +<-,Re{} C .122s s ->,Re{} D .122s s -<,Re{} 27.()()(1)f t u t u t =--的拉氏变换为( )A .)1(1s e s --B .)1(1s e s -C .)1(s e s --D .)1(s e s - 28.652)(2+++=s s s s F 的拉氏反变换为( ) A .32[2]()t t e e u t --+ B .32[2]()t t e e u t ---C .3()()t t e u t δ-+D .3()t e u t -29.信号0()sin (2)(2)f t t u t ω=--的拉氏变换为( )A.s s e s 2022+-ω B.s s e s 2022+ω C.ωω02022s e s + D.ωω02022s e s +- 30. 已知某系统的系统函数为H s (),唯一决定该系统单位冲激响应h t ()函数形式的是( )A.H s ()的零点B.H s ()的极点C.系统的输入信号D.系统的输入信号与H s ()的极点31、连续时间系统的自由响应取决于( )A.H s ()的零点B.H s ()的极点C.系统的输入信号D.系统的输入信号与H s ()的极点32. 若212()(),()(),t f t e u t f t u t -==则f t f t f t ()()()=*12的拉氏变换为( )A.12112〔〕s s -+ B.12121〔〕s s +- C.12112〔〕s s ++ D.14121〔〕s s +- 33.图(a )中ab 段电路是某复杂电路的一部分,其中电感L 和电容C 都含有初始状态,请在图(b )中选出该电路的复频域模型。
( )34.全通系统的H(S)对零极点分布的要求为( )A 零极点位与复平面的左半平面B 零极点位与复平面的单位圆内C 极点处与复平面的左半平面,零点与极点关与虚轴对称D 零点处与复平面的左半平面,极点与零点关与虚轴对称35.已知双边序列()f n 的单边Z 变换为()F z ,则(2)f n -的Z 变换为( )A.2()z F z -B.2()z F zC.21()(1)(2)z F z z f f --+-+-D.21()(1)(2)z F z z f f ------36.已知23()252z X z z z -=-+,对应序列()x n 为( )。
A.1()()2()2n n u n u n - B. 1()(1)2(1)2n n u n u n ---+-- C. 1()()2(1)2n n u n u n +-- D.无法确定 二、 填空题1、信号是随时间变化的某种物理量,是传送各种 的工具。
常见的信号形式为 和 。
2、同时满足 性和 性的系统称为线性系统。
线性时不变连续系统时域分析时可以用 方程来描述,线性时不变离散系统时域分析可以用 方程来描述。
按照不同的观点,系统响应可分为零输入响应和 响应、 响应和 响应、 响应和 响应。
3、 卷积式2()()t e u t u t -*=___ _____。
4、()*(2)t e u t t δ-'-= 。
5、如果一线性时不变系统的单位冲激响应为h(t),则该系统的阶跃响应g(t)为_________。
6、H(s)的零点和极点中 决定了h(t)的函数形式, 影响h(t)的幅度和相位。
7、已知线性时不变连续系统的系统函数22()25s H s s s +=++,则其冲激响应为 ()h t = ,系统稳定性判断为 。
8、已知线性时不变离散系统的系统函数2()56z H z z z =++,3z >,则其单位函数响应为()h n = ,系统稳定性判断为 。
9、信号的频谱包括两个部分,它们分别是 谱和 谱10、周期信号频谱的三个基本特点是(1)离散性,(2) ,(3) 。
11、绝对可积是非期信号频谱存在的 条件;非期信号频谱的基本特点是和收敛性。
12、已知一周期信号的幅度谱和相位谱分别如图(a)和图(b)所示,则该周期信号f(t)= 。
13、频谱函数F(j ω)=δ(ω-2)+δ(ω+2)的傅里叶逆变换f(t)=__ _____。
14、一个周期矩形脉冲信号f(t)的脉冲宽度为τ,τ=0.2秒,其周期为T 秒;T=1秒;则f(t)的傅里叶级数的幅度频谱的第一个过零点的频率将在________谐波处。
15、信号的频带宽度与信号的脉冲宽度成比;脉冲宽度为τ的矩形脉冲的频带宽度为。
16、系统无失真传输信号的条件是=H;若不满足将产生(ωj)幅度失真,若不满足将产生相位失真。
