七年级数学中的角度计算题
七年级数学动角与角度计算问题教师版

动角与角度计算问题如图,N BOC 在N AOB 的外部,/AOC 与N BOC 互为补角,OD 平分/AOC , OE 平分 Z BOC 。
(1)若N AOB = 100°,求N DOE 的度数; (3)若N BOD : N BOC =3 : 4,求N DOE 的度数。
一.£30后十二月■二行门仁=180../工O ㈢十二&C?仁十/v150"•.上 工口行=l (V0”,上.-lO/J-l-Z DOC = lOU 0 +40 fl = 14O-3-SO 平分上月c?u-.£LCOD = ^AOC = 7^-、-QR 平分3—Z<7C?£)—ZCf£'=70c --2O fl =3O &故答案为:加口(3)设 ZBCffl= ,上BfU 4.V,£ACD = £D0J=£B 口口 +2 60 c=8宕* h =T?■.'^.AOC^LBOC=^f「,7工+7 工+4E =1SO 4r=1T,/-DOE =2i l +3it=5jj= &口"-(2)-.-上月白C 十二UOO =LEy: £CJDE = W£E 口C = W5" —/ JM..AAOG=ZAOB +ZBf?G=9(rC(备用图),ZBOE=Z.CQE = \Z BOC=2X3isci n -"n 1/.zgo<7-… T*--mr —j.2五2量-Z.C'QD — ^COE- 4S* +4x0 — 4鼻"-k 1 n ”■;故答案为:::£•(2)若N AOB =废,求N DOE 的度数;..AAOB-tr i 2^BCfC= ISO °1、角度问题的常考题型:角度的基本概念、角度的转换与计算、角平分线与方位角的计算、方程思想求角度、选择压轴的角度多结论问题,分类讨论及定值问题。
求角的度量度分秒的计算及习题

七年级数学求角的度量度分秒的计算及习题第三节角(二)角的度量与画法一. 教学内容:角的度量与画法【知识点讲解】1. 角的度量:按对线、对中、度数的步骤用量角器量出角的度数2. 角的度数计算:角的单位是度分秒,都是60进制,可以比照时间中的时分秒理解,分别用“°”、“ ’”、“ ””来表示。
3 . 余角、补角的概念与性质:如果两个角的和是90度(或直角)时,叫做两个角互余;4. 如果两个角的和是180度(或平角)时,叫做两个角互补。
(补角同理)性质:同角(或等角)的余角相等;同角(或等角)的补角相等(补角同理)5. 能利用三角板画出15°、30°、45°、60°、75°、90°等11种特殊角6. 会用尺规画一个角等于已知角,角的和、差的画法。
【技能要求】1. 掌握度、分、秒的计算。
2. 逐步掌握学过的几何图形的表示方法,懂得学过的几何语句,能由这些语句准确、整洁地画出图形。
认识学过的图形,会用语句描述这些简单的几何图形。
【典型例题】例1. 将33.72°用度、分、秒表示。
解:33.72°=33°+(0.72×60′)=33°+43.2′=33°+43′+(0.2′×60″)=33°43′12″例2. 用度表示152°13′30″。
解:152°13′30″=152°+(13 )′=152°+13.5′=152°+( )°=152.225°例3. 判断下列计算的对错,对的画“√”,错的说明错在哪里,并改正。
(1)31°56′÷3=10°52′(2)138°29′+44°49′=183°18′(3) 13.5°×3=39.50(4) 21.36°-18°30′=3.14°.解:(1)错,因为用1°=100′计算的。
与角度有关的计算问题(35题提分练)(原卷版)—七年级数学上册(北师大版2024)

与角度有关的计算问题(解答题35题)(基础题&提升题&压轴题)题型一基础题1.(2023秋•同安区期末)如图,点O在直线AB上,∠BOC=20°,∠COD=90°,OE是∠BOD的角平分线,求∠COE的度数.2.(2023秋•吉安期末)如图,已知∠1:∠3:∠4=1:2:4,∠2=80°,求∠1、∠3、∠4的度数.3.(2023秋•西峡县期末)如图,∠AOB=∠COD=90°,OC平分∠AOB,∠BOD=3∠DOE.试求∠COE 的度数.4.(2023秋•天心区期末)如图,O为直线AB上一点,OC平分∠AOD,∠AOC=60°,∠BOD=3∠DOE,求∠DOE的度数.5.(2023秋•泉港区期末)如图,∠COD=45°,∠BOD=13∠COD,OC是∠AOB的平分线,求∠AOD的度数.6.(2023秋•泸县校级期末)如图,OE是∠COA的平分线,∠AOB=∠COD.(1)若∠AOE=50°,∠COD=18°,求∠BOC的度数;(2)比较∠AOC和∠BOD7.(2023秋•南沙区期末)如图,将一副三角尺叠放在一起.三角尺ABC的三个角是45°,45°,90°,三角尺ADE的三个角是30°,60°,90°.(1)若∠CAE=58°,求∠BAE的度数;(2)若∠CAE=2∠BAD,求∠CAD的度数.8.(2023秋•大荔县期末)将一副直角三角板ABC和BDE的一个顶点B重合在一起,按如图所示方式摆放,其中∠ACB=∠DBE=90°,∠ABC=30°,三角板ABC在∠DBE内可任意转动.(1)以点B为顶点的所有锐角有 个.(2)求以点B9.(2023秋•九龙坡区校级期末)如图,∠AOB:∠BOC=1:4,OM平分∠AOB,∠BON:∠NOC=3:1,若∠MON=91°.(1)∠AOB ∠NOC(填“>”或“<”或“=”)(2)求∠AOC的度数.10.(2023秋•娄底期末)如图,点O在直线AB上,∠COD=60°,∠AOE=2∠DOE.(1)若∠BOD=60°,求∠COE的度数;(2)试猜想∠BOD和∠COE的数量关系,并说明理由.11.(2023秋•瑶海区校级期末)已知点O为直线AB上一点,∠MON=90°,在∠MON内部作射线OC,且OC恰好平分∠MOB.(1)若∠CON=20°,求∠AOM的度数;(2)若∠BON=2∠NOC,求∠AOM的度数.12.(2023秋•高安市期末)如图,已知∠AOB=80°,OC是∠AOB的平分线,OD是∠BOC的平分线.(1)求∠AOD的度数;(2)若∠COE=14∠COB,求∠的度数.题型二提升题13.(2023秋•福田区校级期末)如图,点A,O,B在同一条直线上,OD,OE分别平分∠AOC和∠BOC.(1)求∠DOE的度数;(2)如果∠COD=65°,求∠AOE的度数;(3)如果∠COD:∠COE=3:2,求∠AOE的度数.14.(2023秋•慈溪市期末)如图,直角三角板DOE的直角顶点O在直线AB上,OD平分∠AOF.(1)比较∠EOF和∠EOB的大小,并说明理由;(2)若OF平分∠AOE,求∠的度数.15.(2023秋•武昌区期末)已知∠AOB=50°,∠COD=20°.(1)如图1,若∠AOD=80°,∠COD在OB的左侧,则∠BOC= ;(2)如图2,OP平分∠AOD,OQ平分∠BOC,求∠POQ.16.(2023秋•无为市期末)利用折纸可以作出角平分线,如图1折叠,则OC为∠AOB的平分线,如图2、图3,折叠长方形纸片,OC,OD均是折痕,折叠后,点A落在点A',点B落在点B',连接OA′.(1)如图2,若点B'恰好落在OA′上,且∠AOC=32°,则∠BOD= ;(2)如图3,当点B'在∠COA'的内部时,连接OB′,若∠AOC=44°,∠BOD=61°,求∠A'OB'的度数.17.(2023秋•彭水县期末)已知∠AOB内部有三条射线OD,OC,OE且在同一个平面内,∠AOC=2∠BOC,射线OD始终在射线OE的上方,∠AOB=108°,∠DOE=36°.(1)如图1,当OE平分∠BOC时,求∠AOD的度数;(2)如图2,若∠AOD=5∠COE时,求∠BOE的度数.18.(2023秋•沙坪坝区校级期末)如图1,已知∠AOC=160°,OB是∠AOC内的射线,且∠AOB=3 5∠BOC,射线OD、OE将∠AOC分割,使得∠AOD:∠BOD:∠COE=1:2:3.(1)求∠DOE.(2)如图2,作∠BOD,∠EOC的平分线OM,ON.求∠MON的值.19.(2023秋•渝北区期末)OC ,OD ,OE 在∠AOB 内,∠AOC =2∠BOC ,∠AOB =108°,∠DOE =66°.(1)如图1,当OE 为∠BOC 的角平分线时,求∠AOD 的度数;(2)如图2,当∠AOD =53∠COE ,求∠BOE 的度数.20.(2023秋•汉中期末)如图,已知∠AOB =120°,从∠AOB 的顶点O 引出一条射线OC ,射线OC 在∠AOB 的内部,将射线OC 绕点O 逆时针旋转到OD ,且∠COD =60°.(1)如图①,若∠AOD =90°,试判断∠AOC 与∠BOD 之间的大小关系并说明理由;(2)如图②,作射线OE ,射线OE 为∠AOD 的平分线,设∠AOC =α,当0°<α<60°时,若射线OC 恰好平分∠AOE ,求∠BOD 的度数.21.(2023秋•宿豫区期末)已知,将一副三角板的直角顶点O按如图所式叠放在一起.(1)若∠BOD=55°,则∠BOC= ,∠BOC ∠AOD(填>、<、=);(2)①若∠BOD=50°,则∠AOC= ;若∠AOC=120°,则∠BOD= ;②猜想∠BOD与∠AOC之间的数量关系,并说明理由.22.(2023秋•庄河市期末)如图,点O为直线上AB一点,∠COD=90°,∠BOD=18°,若OE是∠BOC 的平分线,(1)求∠BOE的度数;(2)若点F是平面内一点,连接射线OF,且∠AOF=13∠AOC,求∠COF的度数.23.(2023秋•黄陂区校级期末)将三角板COD的直角顶点O放置在直线AB上.(1)如图,且∠AOC=40°射线OE平分∠BOC,则∠BOE的大小为 ;(2)在(1)的条件下,射线OE平分∠BOC,射线OF平分∠BOD,求∠EOF的度数;(3)若将三角板COD绕点O旋转,射线OE平分∠BOC,射线OF平分∠BOD.请写出∠COD与∠EOF 度数的等量关系: .题型二压轴题24.(2023秋•斗门区期末)如图①,OC是∠AOE内部的一条射线,OB、OD分别平分∠AOC,∠EOC.(1)若∠AOE=140°,∠COD=30°,求∠BOC= ;(2)∠AOE与∠BOD的大小有什么关系,写出你的结论并说明理由.(3)如图②,如果OC是∠AOE外部的一条射线,OB、OD分别平分∠AOC,∠EOC.那么(2)中∠AOE与∠BOD的大小关系还成立吗?请说明理由.25.(2023秋•海陵区校级期末)已知∠AOB=2∠COD=140°,OE平分∠AOD.(1)如图①,若∠COE=10°,求∠AOC的度数;(2)将∠COD绕顶点O按逆时针方向旋转至如图②的位置,∠BOD和∠COE有怎样的数量关系?请说明理由;(3)将∠COD绕顶点O按逆时针方向旋转至如图③的位置,(2)中的关系是否成立?请说明理由.26.(2023秋•思明区校级期末)如图,点M,O,N在同一条直线上,将一直角三角板的60°锐角顶点放在点O处,一边OA在射线OM上,另一边OB在直线MN的上方.OC平分∠BON,OD平分∠CON.(1)求∠BOD的度数;(2)把三角板绕点O沿逆时针方向旋转,当OB转到射线OM上时停止,若在旋转过程中,∠AOM=(x﹣120)°,同时在∠BOC内部有一条射线OE,使得∠BOE=(34x―90)°,试探究在旋转过程中,射线OE始终是哪个角的平分线?27.(2023秋•宝安区期末)将一副三角板如图1放置(∠AOB=90°,∠A=45°,∠OCD=90°,∠COD =30°),在∠BOD、∠AOC(∠BOD≤180°、∠AOC≤180°)内作射线OM、ON,且∠MOB=2∠DOM,∠NOA=2∠NOC,将三角板OCD绕着点O顺时针旋转.(1)如图1,当点O、A、C在一条直线上时,∠MON= ;(2)如图2,若旋转角为α(0°<α<90°),∠MON的度数是否会发生改变?若不变,求其值;若变化,说明理由.(3)如图3,当三角板OCD旋转到∠AOB内部时,求∠MON的值.28.(2024•两江新区校级开学)将一副三角板的两个锐角顶点重合,∠AOB=45°,∠COD=30°,OM,ON分别是∠AOC,∠BOD(1)如图①所示,当OB与OC重合时,则∠MON的大小为 ;(2)当∠COD绕着点O旋转至如图②所示,当∠BOC=14°,则∠MON的大小为多少?(3)当∠COD绕着点O旋转至如图③所示,当∠BOC=α时,求∠MON的大小.29.(2023秋•于洪区期末)【提出问题】已知点O是直线AB上一点,∠COD=90°,射线OE是∠AOD的平分线.(1)如图1,若∠BOD=110°,求∠COE的度数.请补充完成下列解答过程:解:∵∠AOB=180°,∠BOD=110°,∴∠AOD= °.∵∠COD=90°,∴∠AOC=∠COD﹣∠AOD= °.∵OE是∠AOD的平分线,∴∠AOE= ∠AOD= °.∴∠COE=∠AOC+ = °.【类比分析】(2)如图2,设∠COE=α,求∠BOD的度数(用含α的代数式表示).【变式探索】(3)如图3,若3∠COE﹣2∠BOD=78°,求∠COE的度数.30.(2023秋•渑池县期末)如图.已知∠MON=140°,∠AOC与∠BOC互余,OC平分∠MOB.(1)在图①中.若∠AOC=40°,则∠BOC= °.∠NOB= °;(2)在图①中,设∠AOC=α,∠NOB=β,请探究α与β之间的数量关系(必须写出推理的主要过程,但每一步后面不必写出理由);(3)在图①中,当∠AOB绕着点O顺时针转动到如图②的位置时,(2)中α与β之间的数量关系是否还成立?若成立,请说明理由;若不成立,请直接写出此时α与β之间的数量关系.31.(2023秋•青岛期末)如图,OM是∠AOC的平分线,ON是∠BOC的平分线.(1)如图1,当∠AOB是直角,∠BOC=60°时,求∠MON的度数是多少?(2)如图2,当∠AOB=α,∠BOC=60°时,尝试发现∠MON与α的数量关系.(3)如图3,当∠AOB=α,∠BOC=β时,猜想:∠MON与α、β有数量关系吗?直接写出结论即可.32.(2024春•高青县期末)【实践活动】如图1,将一副三角板的直角顶点重合摆放.(1)∠ACE与∠BCD的大小关系是∠ACE ∠BCD.(填“>”“=”或“<”)(2)∠ACB与∠DCE之间的数量关系是 .【拓展探究】(3)如图2,若∠ACD≠∠BCE,且∠ACD+∠BCE=180°,探索∠ACB与∠DCE之间的数量关系,并说明理由.33.(2023秋•和平区校级期末)已知∠AOB=120°,从∠AOB的顶点O引出一条射线OC,射线OC在∠AOB的内部,将射线OC绕点O逆时针旋转60°形成∠COD.(1)如图1,若∠AOD=90°,比较∠AOC和∠BOD的大小,并说明理由;(2)作射线OE,射线OE为∠AOD的平分线,设∠AOC=α.①如图2,当0°<α<60°,若射线OC恰好平分∠AOE,求∠BOD的度数;②当α≠60°时,请探究∠EOC与∠BOD之间的数量关系.34.(2023秋•山西期末)综合与探究特例感知:(1)如图1.线段AB=16cm,C为线段AB上的一个动点,点D,E分别是AC,BC的中点.①若AC=4cm,则线段DE的长为 cm.②设AC=a cm,则线段DE的长为 cm.知识迁移:(2)我们发现角的很多规律和线段一样,如图2,若∠AOB=120°,OC是∠AOB内部的一条射线,射线OM平分∠AOC,射线ON平分∠BOC,求∠MON的度数.拓展探究:(3)已知∠COD在∠AOB内的位置如图3所示,∠AOB=α,∠COD=30°,且∠DOM=2∠AOM,∠CON=2∠BON,求∠MON的度数.(用含α的代数式表示)35.(2023秋•青羊区校级期末)如图所示,O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图1,若∠AOC=30°,求∠DOE的度数.(2)在图1中,若∠AOC=α,直接写出∠DOE的度数: (用含α的代数式表示).(3)将图1中的∠COD绕顶点O顺时针开始旋转.①当∠COD旋转至如图2的位置时,请探究∠AOD与∠BOE的度数之间的关系,写出你的结论,并说明理由;②过点O的一条射线OF,使得OC恰好平分∠BOF,在图1和图2中分别探究∠AOF与∠DOE的度数之间的关系,请直接写出结论.。
七年级上册数学钟表上的角度计算题

一、概述时钟是我们日常生活中常见的物品,我们常常需要根据时钟所指的时间来进行日常活动安排。
时钟上的指针可以用来计算角度,这也是数学中常见的问题。
本文将介绍七年级上册数学中关于钟表上的角度计算题,帮助读者更好地理解和掌握这一知识点。
二、时钟上的角度计算1. 时针和分针指向的角度计算在时钟上,时针和分针指向的角度可以通过简单的数学计算得出。
在整点时刻,时针和分针之间的角度是固定的,具体计算公式如下:角度 = |30 * 时针所指小时数 - (11/2) * 分针所指分钟数|当时钟指向3点时(15:00),时针和分针之间的角度为:角度 = |30 * 3 - (11/2) * 0| = |90 - 0| = 90°2. 分针指向的角度计算分针所指的角度也可以通过简单的公式计算得出:角度 = 6 * 分针所指的分钟数当时钟指向15分钟时,分针所指的角度为:角度 = 6 * 15 = 90°三、练习题示例1. 时钟指向6点,分针指向10分钟,求时针和分针之间的角度。
解:时针指向6,分针指向10,根据公式计算可得:角度 = |30 * 6 - (11/2) * 10| = |180 - 55| = 125°2. 时钟指向9点,分针指向25分钟,求时针和分针之间的角度。
解:时针指向9,分针指向25,根据公式计算可得:角度 = |30 * 9 - (11/2) * 25| = |270 - 137.5| = 132.5°3. 分针指向35分钟,求分针所指的角度。
解:分针指向35,根据公式计算可得:角度= 6 * 35 = 210°四、总结时钟上的角度计算题是中学数学中一个基础而重要的知识点,通过掌握时钟上的角度计算方法,我们可以更好地理解和应用数学知识。
本文通过介绍时钟上的角度计算方法,并给出了相应的练习题示例,希望读者能够通过本文的学习更好地掌握这一知识点。
同时也希望读者能够在日常生活中运用数学知识,更好地理解和利用周围的事物。
七年级上册+专题练习+数学角度问题(基础难度)
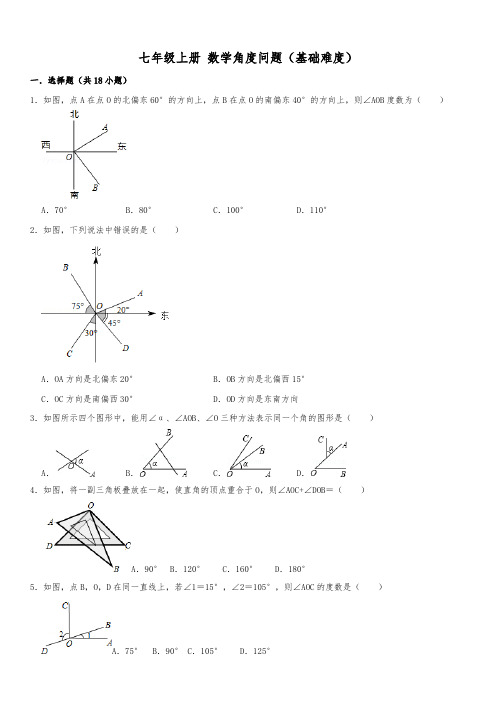
七年级上册数学角度问题(基础难度)一.选择题(共18小题)1.如图,点A在点O的北偏东60°的方向上,点B在点O的南偏东40°的方向上,则∠AOB度数为()A.70°B.80°C.100°D.110°2.如图,下列说法中错误的是()A.OA方向是北偏东20°B.OB方向是北偏西15°C.OC方向是南偏西30°D.OD方向是东南方向3.如图所示四个图形中,能用∠α、∠AOB、∠O三种方法表示同一个角的图形是()A.B.C.D.4.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=()A.90°B.120°C.160°D.180°5.如图,点B,O,D在同一直线上,若∠1=15°,∠2=105°,则∠AOC的度数是()6.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于()A.30°B.45°C.50°D.60°7.如图,∠AOC和∠DOB都是直角,如果∠AOB=150°,那么∠DOC=()A.30°B.40°C.50°D.60°8.如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON是()A.45°B.45°+∠AOC C.60°﹣∠AOC D.不能计算9.如图所示,已知∠AOC=∠BOD=70°,∠BOC=30°,则∠AOD的度数为()A.100°B.110°C.130°D.140°10.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于()A.65°B.50°C.40°D.25°11.如图,已知∠AOC=∠BOD=90°,∠AOD=150°,则∠BOC的度数为()A.30°B.45°C.50°D.60°12.下列图形中表示北偏东60°的射线是()A.B.C.D.13.如图,下列说法正确的是()A.∠1与∠BOC表示同一个角B.∠β表示的是∠AOCC.∠1+∠β=∠AOC D.∠β>∠114.如图,已知∠AOB=120°,∠COD在∠AOB内部且∠COD=60°,则∠AOD与∠COB一定满足的关系为()A.∠AOD=∠COB B.∠AOD+∠COB=180°C.∠AOD=∠COB D.∠AOD+∠COB=120°15.如图,点O在直线AB上,若∠AOD=159.5°,∠BOC=51°30′,则∠COD的度数为()A.30°B.31°C.30°30′D.31°30′16.如图,∠AOC=∠BOD=80°,如果∠AOD=140°,那么∠BOC等于()A.20°B.30°C.50°D.40°17.如图,已知∠AOC=∠BOD=80°,∠BOC=25°,则∠AOD的度数为()A.150°B.145°C.140°D.135°18.有下列说法:①射线是直线的一半;②线段AB是点A与点B的距离;③角的大小与这个角的两边所画的长短有关;④两个锐角的和一定是钝角.其中正确的个数有()A.0个B.1个C.2个D.3个二.填空题(共5小题)19.如图,直线AB、CD相交于点O,∠DOE=∠BOE,OF平分∠AOD,若∠BOE=28°,则∠EOF的度数为.20.如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=度.21.将两块直角三角尺的直角顶点重合为如图的位置,若∠AOD=110°,则∠COB=度.22.如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=度.23.如图,A,O,B是同一直线上的三点,OC,OD,OE是从O点引出的三条射线,且∠1:∠2:∠3:∠4=1:2:3:4,则∠5=度.三.解答题(共17小题)24.如图,点O在直线AC上,OD平分∠AOB,∠BOE=∠EOC,∠DOE=70°,求∠EOC.25.如图,已知∠AOB=120°,OE平分∠AOB,射线OC在∠AOE内部,∠BOC=90°,(1)求∠EOC的度数.(2)作射线OF,使射线OC是∠EOF三等分线,则∠AOF的度数为.26.(1)在∠AOB内部画1条射线OC,则图1中有个不同的角;(2)在∠AOB内部画2条射线OC,OD,则图2中有个不同的角;(3)在∠AOB内部画3条射线OC,OD,OE,则图3中有个不同的角;(4)在∠AOB内部画10条射线OC,OD,OE…,则图中有个不同的角;(5)在∠AOB内部画n条射线OC,OD,OE…,则图中有个不同的角.27.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数;(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.28.如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.29.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.30.如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,(1)求∠DOE的度数;(2)若OF⊥OE,求∠COF的度数.31.已知:O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图1.若∠AOC=30°.求∠DOE的度数;(2)在图1中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置,探究∠AOC和∠DOE的度数之间的关系.写出你的结论,并说明理由.32.如图,已知∠1=65°15′,∠2=78°30′,求∠1+∠2和∠3.33.已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.(1)如图①,当∠BOC=70°时,求∠DOE的度数;(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数;(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.34.(1)平面内将一副三角板按如图1所示摆放,∠EBC=°;(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α=°;(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.35.如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD.36.已知∠AOB是一个定角,记为α,在∠AOB的内部作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.(1)如图①,当α=120°,∠AOC=40°时,求∠DOE的度数;(2)如图①,当射线OC在∠AOB内绕点O旋转时,∠DOE的度数是否发生变化?若变化,请说明理由;若不变,猜想∠DOE与α的关系,并证明;(3)当射线OC在∠AOB外绕点O旋转到图②位置时,直接写出∠DOE的度数(用含a的代数式表示).37.如图,将两块直角三角尺的直角顶点C叠放在一起,(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=140°,求∠DCE的度数;(3)猜想∠ACB与∠DCE的大小关系,并说明理由.38.(1)如图所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数.(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数.(4)从(1)(2)(3)的结果你能看出什么规律?(5)线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法,请你模仿(1)~(4),设计一道以线段为背景的计算题,并写出其中的规律来?39.如图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.(1)若∠COD=30°,求∠BOE的度数;(2)若∠BOE=85°,求∠COD的度数.(提示:设∠COD=x°)40.如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.(1)求∠EOF的度数;(2)若将条件“∠AOB是直角,∠BOC=60°”改为:∠AOB=x°,∠EOF=y°,其它条件不变.①则请用x的代数式来表示y;②如果∠AOB+∠EOF=156°.则∠EOF是多少度?七年级上册数学角度问题(基础难度)参考答案与试题解析一.选择题(共18小题)1.如图,点A在点O的北偏东60°的方向上,点B在点O的南偏东40°的方向上,则∠AOB度数为()A.70°B.80°C.100°D.110°【分析】根据方向角的定义以及角的和差,可得∠AOB的度数.【解答】解:∵点A在点O的北偏东60°的方向上,点B在点O的南偏东40°的方向上,∴∠AOB=180°﹣60°﹣40°=80°,故选:B.【点评】本题考查了方向角的定义,用方向角描述方向时,通常以正北或正南方向为角的始边,以对象所处的射线为终边.2.如图,下列说法中错误的是()A.OA方向是北偏东20°B.OB方向是北偏西15°C.OC方向是南偏西30°D.OD方向是东南方向【分析】直接利用方向角的确定方法分别分析得出答案.【解答】解:A、OA方向是北偏东70°,符合题意;B、OB方向是北偏西15°,不符合题意;C、OC方向是南偏西30°,不符合题意;D、OD方向是东南方向,不合题意.故选:A.【点评】此题主要考查了方向角,正确把握方向角的概念是解题关键.3.如图所示四个图形中,能用∠α、∠AOB、∠O三种方法表示同一个角的图形是()A.B.C.D.【分析】根据角的表示方法进行逐一分析,即角可以用一个大写字母表示,也可以用三个大写字母表示.其中顶点字母要写在中间,唯有在顶点处只有一个角的情况,才可用顶点处的一个字母来记这个角,否则分不清这个字母究竟表示哪个角.角还可以用一个希腊字母(如∠α,∠β,∠γ、…)表示,或用阿拉伯数字(∠1,∠2…)表示.【解答】解:A、因为顶点O处有四个角,所以这四个角均不能用∠O表示,故本选项错误;B、因为顶点O处只有一个角,所以这个角能用∠O、∠α及∠AOB表示,故本选项正确;C、因为顶点O处有三个角,所以这三个角均不能用∠O表示,故本选项错误;D、因为∠O与∠α表示的不是同一个角,故本选项错误.故选:B.【点评】本题考查的是角的表示方法,熟知角的三种表示方法是解答此题的关键.4.如图,将一副三角板叠放在一起,使直角的顶点重合于O,则∠AOC+∠DOB=()A.90°B.120°C.160°D.180°【分析】因为本题中∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.【解答】解:设∠AOD=a,∠AOC=90°+a,∠BOD=90°﹣a,所以∠AOC+∠BOD=90°+a+90°﹣a=180°.故选:D.【点评】本题考查了角度的计算问题,在本题中要注意∠AOC始终在变化,因此可以采用“设而不求”的解题技巧进行求解.5.如图,点B,O,D在同一直线上,若∠1=15°,∠2=105°,则∠AOC的度数是()A.75°B.90°C.105°D.125°【分析】由图示可得,∠2与∠BOC互补,结合已知可求∠BOC,又因为∠AOC=∠COB+∠1,即可解答.【解答】解:∵∠2=105°,∴∠BOC=180°﹣∠2=75°,∴∠AOC=∠1+∠BOC=15°+75°=90°.故选:B.【点评】本题考查了角的计算,解决本题的关键是利用补角求出∠BOC.6.如图,一副三角板(直角顶点重合)摆放在桌面上,若∠AOD=150°,则∠BOC等于()A.30°B.45°C.50°D.60°【分析】从如图可以看出,∠BOC的度数正好是两直角相加减去∠AOD的度数,从而问题可解.【解答】解:∵∠AOB=∠COD=90°,∠AOD=150°∴∠BOC=∠AOB+∠COD﹣∠AOD=90°+90°﹣150°=30°.故选:A.【点评】此题主要考查学生对角的计算的理解和掌握,解答此题的关键是让学生通过观察图示,发现几个角之间的关系.7.如图,∠AOC和∠DOB都是直角,如果∠AOB=150°,那么∠DOC=()A.30°B.40°C.50°D.60°【分析】根据图象∠AOB等于两个直角的和减去∠COD计算.【解答】解:∠DOC=90°+90°﹣∠AOB=180°﹣150°=30°.故选A.【点评】本题注意,∠COD是两个直角重叠的部分.8.如图,已知∠AOB是直角,∠AOC是锐角,ON平分∠AOC,OM平分∠BOC,则∠MON是()A.45°B.45°+∠AOC C.60°﹣∠AOC D.不能计算【分析】结合图形,根据角的和差,以及角平分线的定义,找到∠MON与∠AOB的关系,即可求出∠MON的度数.【解答】解:∵OM平分∠BOC,ON平分∠AOC,∴∠MOC=∠BOC,∠NOC=∠AOC,∴∠MON=∠MOC﹣∠NOC=(∠BOC﹣∠AOC),=(∠BOA+∠AOC﹣∠AOC),=∠BOA,=45°.故选:A.【点评】本题考查了角的计算,属于基础题,此类问题,注意结合图形,运用角的和差和角平分线的定义求解.9.如图所示,已知∠AOC=∠BOD=70°,∠BOC=30°,则∠AOD的度数为()A.100°B.110°C.130°D.140°【分析】根据图形和题目中的条件,可以求得∠AOB的度数和∠COD的度数,从而可以求得∠AOD的度数.【解答】解:∵∠AOC=70°,∠BOC=30°,∴∠AOB=40°;同理可得,∠COD=40°.∴∠AOD=∠AOB+∠BOC+∠COD=40°+30°+40°=110°,故选:B.【点评】本题考查角的计算,解答本题的关键是明确角之间的关系,利用数形结合的思想解答.10.如图,∠AOB是一直角,∠AOC=40°,OD平分∠BOC,则∠AOD等于()A.65°B.50°C.40°D.25°【分析】由∠AOB是一直角,∠AOC=40°,可知∠COB=50°,又知OD平分∠BOC,故可知∠AOD的度数.【解答】解:∵∠AOB是一直角,∠AOC=40°,∴∠COB=50°,∵OD平分∠BOC,∴∠COD=25°,∵∠AOD=∠AOC+∠COD,∴∠AOD=65°.故选:A.【点评】本题考查角与角之间的运算,注意结合图形,发现角与角之间的关系,进而求解.11.如图,已知∠AOC=∠BOD=90°,∠AOD=150°,则∠BOC的度数为()A.30°B.45°C.50°D.60°【分析】由∠AOC=∠BOD=90°,∠AOD=150°,可求出∠BOC的度数,再根据角与角之间的关系求解.【解答】解:∵∠AOC=∠BOD=90°,∠AOD=150°,∴∠BOC=∠AOC+∠BOD﹣∠AOD=180°﹣150°=30°,故选:A.【点评】此题考查的知识点是角的计算,注意此题的解题技巧:两个直角相加和∠BOC相比,多加了∠BOC一次.12.下列图形中表示北偏东60°的射线是()A.B.C.D.【分析】根据方向角的定义解答即可.【解答】解:北偏东60°就是从北向东偏60°,即从上往右偏60°,故选:A.【点评】本题考查了方向角的定义,解答时注意方向和角度.13.如图,下列说法正确的是()A.∠1与∠BOC表示同一个角B.∠β表示的是∠AOCC.∠1+∠β=∠AOC D.∠β>∠1【分析】根据角的概念和表示方法可知,当角的顶点处只有一个角时这个角可以用顶点来表示,由此可得结论.【解答】解:A、∠1与∠AOB表示的是同一个角,故A说法错误;B、∠β表示的是∠BOC,故B说法错误;C、∠1+∠β=∠AOC,故C说法正确;D、∠AOC>∠1,故D说法错误.故选:C.【点评】此题考查了角的表示方法,根据图形特点将每个角用合适的方法表示出来是解题的关键.14.如图,已知∠AOB=120°,∠COD在∠AOB内部且∠COD=60°,则∠AOD与∠COB一定满足的关系为()A.∠AOD=∠COB B.∠AOD+∠COB=180°C.∠AOD=∠COB D.∠AOD+∠COB=120°【分析】根据角的和差,可得∠AOD+∠COB=∠AOC+∠COD+∠COD+∠DOB=∠AOB+∠COD,再代入计算即可求解.【解答】解:∵∠AOD=∠AOC+∠COD,∠COB=∠COD+∠DOB,∴∠AOD+∠COB=∠AOC+∠COD+∠COD+∠DOB,=∠AOC+∠COD+∠DOB+∠COD=∠AOB+∠COD∵∠AOB=120°,∠COD=60°,∴∠AOD+∠COB=120°+60°=180°.故选:B.【点评】本题考查了角的计算.解题的关键是利用了角的和差关系求解.15.如图,点O在直线AB上,若∠AOD=159.5°,∠BOC=51°30′,则∠COD的度数为()A.30°B.31°C.30°30′D.31°30′【分析】将∠AOD转化成159°30′,将其代入∠COD=∠AOD+∠BOC﹣∠AOB中,即可求出结论.【解答】解:∵∠AOD=159.5°=159°30′,∴∠COD=∠AOD+∠BOC﹣∠AOB=159°30′+51°30′﹣180°=31°.故选:B.【点评】本题考查了角的计算以及度分秒的换算,牢记“将高级单位化为低级单位时乘以60,将低级单位转化为高级单位时除以60”是解题的关键.16.如图,∠AOC=∠BOD=80°,如果∠AOD=140°,那么∠BOC等于()A.20°B.30°C.50°D.40°【分析】先求出∠COD的度数,然后根据∠BOC=∠BOD﹣∠COD,即可得出答案.【解答】解:∵∠AOC=80°,∠AOD=140°,∴∠COD=∠AOD﹣∠AOC=60°,∵∠BOD=80°,∴∠BOC=∠BOD﹣∠COD=80°﹣60°=20°.故选:A.【点评】本题主要考查了角的计算能力,熟练掌握角相互间的和差关系是基础.17.如图,已知∠AOC=∠BOD=80°,∠BOC=25°,则∠AOD的度数为()A.150°B.145°C.140°D.135°【分析】先求∠AOC与∠BOC的度数差即可得出∠AOB的度数,再求∠AOB与∠DOB的和即可.【解答】解:∵∠AOC=∠BOD=80°,∠BOC=25°,∴∠AOB=∠AOC﹣∠BOC=80°﹣25°=55°,∴∠AOD=∠BOD+∠AOB=80°+55°=135°,故选:D.【点评】本题考查了角的运算,较为简单,解题关键是不要忘了减去两个角的重合部分.18.有下列说法:①射线是直线的一半;②线段AB是点A与点B的距离;③角的大小与这个角的两边所画的长短有关;④两个锐角的和一定是钝角.其中正确的个数有()A.0个B.1个C.2个D.3个【分析】根据射线的定义和射线、直线没有长度极快判断①;根据两点间的距离的定义即可判断②,根据角的特点即可判断③,举出反例即可判断④.【解答】解:∵射线是指直线上的一点和它一旁的部分所组成的图形,没有长度,直线也没有长度,∴①的说法错误;∵点A与点B的距离是指线段AB的长度,是一个数,而线段是一个图形,∴②错误;∵角的大小与这个角的两边的长短无关,∴③错误;∵当这两个锐角的度数是10°和20°时,10°+20°=30°,30°的角是锐角,不是钝角,∴④错误;∴正确的个数是0个,故选:A.【点评】本题考查了学生对角的定义,直线、射线的定义,两点间的距离的定义的理解和运用,主要考查学生的理解能力和辨析能力,题目比较好,但是一道比较容易出错的题目.二.填空题(共5小题)19.如图,直线AB、CD相交于点O,∠DOE=∠BOE,OF平分∠AOD,若∠BOE=28°,则∠EOF的度数为90°.【分析】根据已知条件“∠DOE=∠BOE,OF平分∠AOD,若∠BOE=28°”和平角的定义可以求得∠AOF=∠DOF =∠AOD=62°,∠DOE=∠BOE=28°;然后根据图形求得∠EOF=∠DOF+∠DOE=62°+28°=90°.【解答】解:∵∠DOE=∠BOE,∠BOE=28°,∴∠DOB=2∠BOE=56°;又∵∠AOD+∠BOD=180°,∴∠AOD=124°;∵OF平分∠AOD,∴∠AOF=∠DOF=∠AOD=62°,∴∠EOF=∠DOF+∠DOE=62°+28°=90°.故答案是:90°.【点评】本题考查了角的计算.解题时,注意利用隐含在题干中的已知条件“∠AOB=180°”.20.如图,将一副直角三角板叠在一起,使直角顶点重合于点O,则∠AOB+∠DOC=180 度.【分析】先利用∠AOD+∠COD=90°,∠COD+∠BOC=90°,可得∠AOD+∠COD+∠COD+∠BOC=180°,而∠BOD=∠COD+∠BOC,∠AOD+∠BOD=∠AOB,于是有∠AOB+∠COD=180°.【解答】解:如右图所示,∵∠AOD+∠COD=90°,∠COD+∠BOC=90°,∠BOD=∠COD+∠BOC,∠AOD+∠BOD=∠AOB,∴∠AOD+∠COD+∠COD+∠BOC=180°,∴∠AOD+2∠COD+∠BOC=180°,∴∠AOB+∠COD=180°.故答案是180.【点评】本题考查了角的计算、三角板的度数,注意分清角之间的关系.21.将两块直角三角尺的直角顶点重合为如图的位置,若∠AOD=110°,则∠COB=70 度.【分析】∠COB是两个直角的公共部分,同时两个直角的和是180°,所以∠AOB+∠COD=∠AOD+∠COB.【解答】解:由题意可得∠AOB+∠COD=180°,又∠AOB+∠COD=∠AOC+2∠COB+∠BOD=∠AOD+∠COB,∵∠AOD=110°,∴∠COB=70°.故答案为:70.【点评】求解时正确地识图是求解的关键.22.如图,点A、O、B在一条直线上,且∠AOC=50°,OD平分∠AOC,则∠BOD=155 度.【分析】根据点A、O、B在一条直线上,∠AOB为平角,求出∠COB,再利用OD平分∠AOC,求出∠COD,然后用∠COB+∠COD即可求解.【解答】解:∵点A、O、B在一条直线上,∴∠COB=180°﹣∠AOC=180°﹣50°=130°,∵OD平分∠AOC,∴∠COD=×50°=25°,∴∠BOD=∠COB+∠COD=130°+25°=155°.故答案为:155.【点评】此题主要考查学生对角的计算的理解和掌握,此题的关键是点A、O、B在一条直线上,∠AOB为平角,此题难度不大,属于基础题.23.如图,A,O,B是同一直线上的三点,OC,OD,OE是从O点引出的三条射线,且∠1:∠2:∠3:∠4=1:2:3:4,则∠5=60 度.【分析】利用平角和角的比例关系即可求出.【解答】解:A,O,B是同一直线上的三点,即∠AOB=180°∠1:∠2:∠3=1:2:3,可知∠1=30°∠2=60°∠3=90°;∠1:∠2:∠3:∠4=1:2:3:4,∠4=120°,∠5=180°﹣120°=60°.故填60.【点评】此题是对角进行度的比例计算,相对比较简单,但要准确求出各角大小是本题的难点.另外此题答案不能带单位.三.解答题(共17小题)24.如图,点O在直线AC上,OD平分∠AOB,∠BOE=∠EOC,∠DOE=70°,求∠EOC.【分析】设∠AOB=x,根据角平分线的定义、补角的概念,结合题意列出方程,解方程即可.【解答】解:设∠AOB=x,则∠BOC=180°﹣x,∵OD平分∠AOB,∴∠BOD=∠AOB=x,∵∠BOE=∠EOC,∴∠BOE=∠BOC=60°﹣x,由题意得,x+60°﹣x=70°,解得,x=60°,∠EOC=(180°﹣x)=80°.【点评】本题考查的是角的计算、角平分线的定义,正确进行角的计算、掌握角平分线的定义是解题的关键.25.如图,已知∠AOB=120°,OE平分∠AOB,射线OC在∠AOE内部,∠BOC=90°,(1)求∠EOC的度数.(2)作射线OF,使射线OC是∠EOF三等分线,则∠AOF的度数为30°或15°.【分析】(1)由角平分线知,结合∠BOC=90°可得答案;(2)由射线OC是∠EOF三等分线可分∠EOC=∠EOF和∠EOC=∠EOF两种情况求解可得.【解答】解:(1)∵OE平分∠AOB,∠AOB=120°,∴,∵∠BOC=90°,∴∠EOC=∠BOC﹣∠EOB=30°;(2)若∠EOC=∠EOF,则∠EOF=3∠EOC=90°,∵∠AOE=∠AOB=60°,∴∠AOF=∠EOF﹣∠EOA=30°;若∠EOC=∠EOF,则∠EOF=∠EOC=45°,∴∠AOF=∠AOE﹣∠EOF=15°;综上,∠AOF的度数为30°或15°,故答案为:30°或15°.【点评】本题主要考查角的计算,学会计算角的和、差、倍、分.也考查了角平分线的定义.26.(1)在∠AOB内部画1条射线OC,则图1中有 3 个不同的角;(2)在∠AOB内部画2条射线OC,OD,则图2中有 6 个不同的角;(3)在∠AOB内部画3条射线OC,OD,OE,则图3中有10 个不同的角;(4)在∠AOB内部画10条射线OC,OD,OE…,则图中有66 个不同的角;(5)在∠AOB内部画n条射线OC,OD,OE…,则图中有个不同的角.【分析】(1)根据图形数出即可;(2)根据图形数出即可;(3)根据图形数出即可;(4)有1+2+3+…+9+10+11=66个角;(5)求出1+2+3+…+n+(n+1)的值即可.【解答】解:(1)在∠AOB内部画1条射线OC,则图中有3个不同的角,故答案为:3.(2)在∠AOB内部画2条射线OC,OD,则图中有6个不同的角,故答案为:6.(3)在∠AOB内部画3条射线OC,OD,OE,则图中有10个不同的角,故答案为:10.(4)在∠AOB内部画10条射线OC,OD,OE,…,则图中有1+2+3+…+10+11=66个不同的角,故答案为:66.(5)在∠AOB内部画n条射线OC,OD,OE,…,则图中有1+2+3+…+n+(n+1)=个不同的角.故答案为:.【点评】本题考查了角的有关概念的应用,关键是能根据题意得出规律.27.如图,直线AB,CD相交于点O,OA平分∠EOC.(1)若∠EOC=70°,求∠BOD的度数;(2)若∠EOC:∠EOD=2:3,求∠BOD的度数.【分析】(1)根据角平分线定义得到∠AOC=∠EOC=×70°=35°,然后根据对顶角相等得到∠BOD=∠AOC =35°;(2)先设∠EOC=2x,∠EOD=3x,根据平角的定义得2x+3x=180°,解得x=36°,则∠EOC=2x=72°,然后与(1)的计算方法一样.【解答】解:(1)∵OA平分∠EOC,∴∠AOC=∠EOC=×70°=35°,∴∠BOD=∠AOC=35°;(2)设∠EOC=2x,∠EOD=3x,根据题意得2x+3x=180°,解得x=36°,∴∠EOC=2x=72°,∴∠AOC=∠EOC=×72°=36°,∴∠BOD=∠AOC=36°.【点评】考查了角的计算:1直角=90°;1平角=180°.也考查了角平分线的定义和对顶角的性质.28.如图所示,直线AB、CD、EF交于点O,OG平分∠BOF,且CD⊥EF,∠AOE=70°,求∠DOG的度数.【分析】求出∠BOF,根据角平分线求出∠GOF,求出∠EOD,代入∠DOG=180°﹣∠GOF﹣∠EOD求出即可.【解答】解:∵∠AOE=70°,∴∠BOF=∠AOE=70°,又∵OG平分∠BOF,∴∠GOF=∠BOF=35°,又∵CD⊥EF,∴∠EOD=90°,∴∠DOG=180°﹣∠GOF﹣∠EOD=180°﹣35°﹣90°=55°.【点评】本题考查了角平分线定义,垂直,邻补角的应用,主要考查学生的计算能力.29.如图,已知∠AOC=60°,∠BOD=90°,∠AOB是∠DOC的3倍,求∠AOB的度数.【分析】设∠COD=x,则∠AOD可表示为60°﹣x,于是∠AOB=90°+60°﹣x=150°﹣x,再根据∠AOB是∠DOC 的3倍得到150°﹣x=3x,解得x=37.5°,然后计算3x即可.【解答】解:设∠COD=x,∵∠AOC=60°,∠BOD=90°,∴∠AOD=60°﹣x,∴∠AOB=90°+60°﹣x=150°﹣x,∵∠AOB是∠DOC的3倍,∴150°﹣x=3x,解得x=37.5°,∴∠AOB=3×37.5°=112.5°.【点评】本题考查了角的计算:会利用角的倍、分、差进行角度计算.30.如图,两直线AB,CD相交于点O,已知OE平分∠BOD,且∠AOC:∠AOD=3:7,(1)求∠DOE的度数;(2)若OF⊥OE,求∠COF的度数.【分析】(1)根据∠AOC:∠AOD=3:7,可求出∠AOC的度数,再根据对顶角的性质可求出∠DOB的度数,根据角平分线的性质即可解答.(2)根据垂直的定义可求出∠DOF的度数,再根据平角的定义解答即可.【解答】解:(1)∵两直线AB,CD相交于点O,∠AOC:∠AOD=3:7,∴∠AOC=180°×=54°,∴∠BOD=54°,又∵OE平分∠BOD,∴∠DOE=54°÷2=27°.(2)∵OF⊥OE,∠DOE=27°,∴∠DOF=63°,∠COF=180°﹣63°=117°.【点评】本题主要考查了角的计算,熟练掌握对顶角的性质,余角补角的定义,角平分线的性质并进行计算是解答本题的关键.31.已知:O是直线AB上的一点,∠COD是直角,OE平分∠BOC.(1)如图1.若∠AOC=30°.求∠DOE的度数;(2)在图1中,若∠AOC=a,直接写出∠DOE的度数(用含a的代数式表示);(3)将图1中的∠DOC绕顶点O顺时针旋转至图2的位置,探究∠AOC和∠DOE的度数之间的关系.写出你的结论,并说明理由.【分析】(1)求出∠BOD,求出∠BOC,根据角平分线求出∠BOE,代入∠DOE=∠BOE﹣∠BOD求出即可.(2)求出∠BOD,求出∠BOC,根据角平分线求出∠BOE,代入∠DOE=∠BOE﹣∠BOD求出即可.(3)把∠AOC当作已知数求出∠BOC,求出∠BOD,根据角平分线求出∠BOE,代入∠DOE=∠BO+∠BOD求出即可.【解答】解:(1)∵∠COD是直角,∠AOC=30°,∴∠BOD=180°﹣90°﹣30°=60°,∴∠COB=90°+60°=150°,∵OE平分∠BOC,∴∠BOE=∠BOC=75°,∴∠DOE=∠BOE﹣∠BOD=75°﹣60°=15°.(2)∵∠COD是直角,∠AOC=α,∴∠BOD=180°﹣90°﹣α=90°﹣α,∴∠COB=90°+90°﹣α=180°﹣α,∵OE平分∠BOC,∴∠BOE=∠BOC=90°﹣α,∴∠DOE=∠BOE﹣∠BOD=90°﹣α﹣(90°﹣α)=α.(3)∠AOC=2∠DOE,理由是:∵∠BOC=180°﹣∠AOC,OE平分∠BOC,∴∠BOE=∠BOC=90°﹣∠AOC,∵∠COD=90°,∴∠BOD=90°﹣∠BOC=90°﹣(180°﹣∠AOC)=∠AOC﹣90°,∴∠DOE=∠BOD+∠BOE=(∠AOC﹣90°)+(90°﹣∠AOC)=∠AOC,即∠AOC=2∠DOE.【点评】本题考查了角的有关计算和角平分线定义的应用,主要考查学生的计算能力,求解过程类似.32.附加题:如图,已知∠1=65°15′,∠2=78°30′,求∠1+∠2和∠3.【分析】根据∠+∠2+∠3=180°求解.【解答】解:∵∠1=65°15′,∠2=78°30′,∴∠1+∠2=65°15′+78°30′=143°45′.∴∠3=180°﹣(∠1+∠2)=180°﹣143°45′=36°15′.故答案为143°45′、36°15′.【点评】本题主要考查角的比较与运算,利用了平角的概念求解.33.已知:∠AOB是一个直角,作射线OC,再分别作∠AOC和∠BOC的平分线OD、OE.(1)如图①,当∠BOC=70°时,求∠DOE的度数;(2)如图②,若射线OC在∠AOB内部绕O点旋转,当∠BOC=α时,求∠DOE的度数;(3)如图③,当射线OC在∠AOB外绕O点旋转时,画出图形,直接写出∠DOE的度数.【分析】(1)由∠BOC的度数求出∠AOC的度数,利用角平分线定义求出∠COD与∠COE的度数,相加即可求出∠DOE的度数;(2)∠DOE度数不变,理由为:利用角平分线定义得到∠COD为∠AOC的一半,∠COE为∠COB的一半,而∠DOE =∠COD+∠COE,即可求出∠DOE度数为45度;(3)分两种情况考虑,同理如图3,则∠DOE为45°;如图4,则∠DOE为135°.【解答】解:(1)如图①中,∠AOC=90°﹣∠BOC=20°,∵OD、OE分别平分∠AOC和∠BOC,∴∠COD=∠AOC=10°,∠COE=∠BOC=35°,∴∠DOE=∠COD+∠COE=45°;(2)如图②中,∠DOE的大小不变,理由是:∠DOE=∠COD+∠COE=∠AOC+∠COB=(∠AOC+∠COB)=∠AOB=45°;(3)∠DOE的大小发生变化情况为,如图3,则∠DOE为45°;如图4,则∠DOE为135°,分两种情况:如图3所示,∵OD、OE分别平分∠AOC和∠BOC,∴∠COD=∠AOC,∠COE=∠BOC,∴∠DOE=∠COD﹣∠COE=(∠AOC﹣∠BOC)=45°;如图4所示,∵OD、OE分别平分∠AOC和∠BOC,∴∠COD=∠AOC,∠COE=∠BOC,∴∠DOE=∠COD+∠COE=(∠AOC+∠BOC)=×270°=135°.【点评】此题考查了角的计算,熟练掌握角平分线定义是解本题的关键.容易出错的地方是解(3)小题漏掉其中的一种情况.34.(1)平面内将一副三角板按如图1所示摆放,∠EBC=150 °;(2)平面内将一副三角板按如图2所示摆放,若∠EBC=165°,那么∠α=15 °;(3)平面内将一副三角板按如图3所示摆放,∠EBC=115°,求∠α的度数.【分析】(1)(2)根据角的和差关系可直接算出答案;(3)首先计算出∠DBC的度数,再用∠ABC的度数减去∠DBC的度数即可.【解答】解:(1)∠EBC=90°+60°=150°;(2)∠α=∠EBC﹣∠DBE﹣∠ABC=165°﹣90°﹣60°=15°;(3)因为∠EBC=115°,∠EBD=90°,所以∠DBC=∠EBC﹣∠EBD=25°.因为∠ABC=60°,所以∠α=∠ABC﹣∠DBC=35°.【点评】此题主要考查了角的计算以及一副三角板各角之间的关系,根据图象得出是解题关键.35.如图,已知∠AOC=∠BOD=75°,∠BOC=30°,求∠AOD.【分析】根据∠AOC=∠BOD=75°,∠BOC=30°,利用角的和差关系先求出∠AOB的度数,再求∠AOD.【解答】解:∵∠AOC=75°,∠BOC=30°,∴∠AOB=∠AOC﹣∠BOC=75°﹣30°=45°,又∵∠BOD=75°,∴∠AOD=∠AOB+∠BOD=45°+75°=120°.故答案为120°.【点评】此题主要考查了角相互间的和差关系,比较简单.36.已知∠AOB是一个定角,记为α,在∠AOB的内部作射线OC,再分别作∠AOC和∠BOC的平分线OD,OE.(1)如图①,当α=120°,∠AOC=40°时,求∠DOE的度数;(2)如图①,当射线OC在∠AOB内绕点O旋转时,∠DOE的度数是否发生变化?若变化,请说明理由;若不变,猜想∠DOE与α的关系,并证明;(3)当射线OC在∠AOB外绕点O旋转到图②位置时,直接写出∠DOE的度数(用含a的代数式表示).【分析】(1)根据角平分线的定义,OD、OE分别平分∠AOC和∠BOC,则可求得∠COE、∠COD的值,∠DOE=∠COE+∠COD;(2)结合角的特点∠DOE=∠DOC+∠COE,求得结果进行判断和计算;(3)根据周角的定义,结合角的特点∠DOE=∠DOC+∠COE,求得结果进行判断和计算.【解答】解:(1)∵α=120°,∠AOC=40°,∴∠BOC=80°,∵OD、OE分别平分∠AOC和∠BOC,∴∠COE=∠BOC=40°,∠COD=∠AOC=20°,∴∠DOE=60°;(2)∵∠BOC=α﹣∠AOC,OD、OE分别平分∠AOC和∠BOC,∴∠COE=∠BOC=α﹣∠AOC,∠COD=∠AOC,∴∠DOE=∠COE+∠COD=α;(3)∠DOE=(360°﹣α)=180°﹣α.【点评】考查了角的计算,熟记角的特点与角平分线的定义是解决此题的关键.37.如图,将两块直角三角尺的直角顶点C叠放在一起,(1)若∠DCE=35°,求∠ACB的度数;(2)若∠ACB=140°,求∠DCE的度数;(3)猜想∠ACB与∠DCE的大小关系,并说明理由.【分析】本题已知两块直角三角尺实际就是已知三角板的各个角的度数,根据角的和差就可以求出∠ACB,∠DCE 的度数;根据前两个小问题的结论猜想∠ACB与∠DCE的大小关系,结合前两问的解决思路得出证明.【解答】解:(1)∵∠ECB=90°,∠DCE=35°∴∠DCB=90°﹣35°=55°∵∠ACD=90°∴∠ACB=∠ACD+∠DCB=145°.(2)∵∠ACB=140°,∠ACD=90°∴∠DCB=140°﹣90°=50°∵∠ECB=90°∴∠DCE=90°﹣50°=40°.(3)猜想得∠ACB+∠DCE=180°(或∠ACB与∠DCE互补)理由:∵∠ECB=90°,∠ACD=90°∴∠ACB=∠ACD+∠DCB=90°+∠DCB∠DCE=∠ECB﹣∠DCB=90°﹣∠DCB∴∠ACB+∠DCE=180°.【点评】记忆三角板各角的度数,把所求的角转化为已知角的和与差.38.(1)如图所示,∠AOB=90°,∠BOC=30°,OM平分∠AOC,ON平分∠BOC,求∠MON的度数.(2)如果(1)中∠AOB=α,其他条件不变,求∠MON的度数.(3)如果(1)中∠BOC=β(β为锐角),其他条件不变,求∠MON的度数.(4)从(1)(2)(3)的结果你能看出什么规律?(5)线段的计算与角的计算存在着紧密的联系,它们之间可以互相借鉴解法,请你模仿(1)~(4),设计一道以线段为背景的计算题,并写出其中的规律来?【分析】(1)首先根据题中已知的两个角度数,求出角AOC的度数,然后根据角平分线的定义可知角平分线分成的两个角都等于其大角的一半,分别求出角MOC和角NOC,两者之差即为角MON的度数;(2)(3)的计算方法与(1)一样.(4)通过前三问求出的角MON的度数可发现其都等于角AOB度数的一半.(5)模仿线段的计算与角的计算存在着紧密的联系,也在已知条件中设计两条线段的长,设计两个中点,求中点间的线段长.【解答】解:(1)∵∠AOB=90°,∠BOC=30°,∴∠AOC=90°+30°=120°,又OM平分∠AOC,∴∠MOC=∠AOC=60°,又∵ON平分∠BOC,∴∠NOC=∠BOC=15°∴∠MON=∠MOC﹣∠NOC=45°;(2)∵∠AOB=α,∠BOC=30°,∴∠AOC=α+30°,又OM平分∠AOC,∴∠MOC=∠AOC=+15°,又∵ON平分∠BOC,∴∠NOC=∠BOC=15°∴∠MON=∠MOC﹣∠NOC=;(3)∵∠AOB=90°,∠BOC=β,∴∠AOC=90°+β,又OM平分∠AOC,∴∠MOC=∠AOC=+45°,又∵ON平分∠BOC,∴∠NOC=∠BOC=∴∠MON=∠MOC﹣∠NOC=45°;(4)从(1)(2)(3)的结果可知∠MON=∠AOB;(5)①已知线段AB的长为20,线段BC的长为10,点M是线段AC的中点,点N是线段BC的中点,求线段MN的长;②若把线段AB的长改为a,其余条件不变,求线段MN的长;③若把线段BC的长改为b,其余条件不变,求线段MN的长;④从①②③你能发现什么规律.规律为:MN=AB.【点评】本题考查了学会对角平分线概念的理解,会求角的度数,同时考查了学会归纳总结规律的能力,以及会根据角和线段的紧密联系设计实验的能力.39.如图,已知OA⊥OD,∠FOD=2∠COD,OB平分∠AOC,OE平分∠COF.(1)若∠COD=30°,求∠BOE的度数;(2)若∠BOE=85°,求∠COD的度数.(提示:设∠COD=x°)【分析】(1)根据∠COD=30°,OA⊥OD,可求出∠AOC,根据OB平分∠AOC和∠FOD=2∠COD,可求出∠FOD,再根据OE平分∠COF,求出∠COE,即可求出∠BOE;(2)设∠COD=x°,根据已知条件可得∠BOC=,∠COE=,然后列方程,解方程即可求出答案.【解答】解:(1)∵∠COD=30°,OA⊥OD,∴∠AOC=60°,∵OB平分∠AOC,∴∠BOC=30°,∵∠FOD=2∠COD,∴∠FOD=60°,∵OE平分∠COF,∴∠COE=45°,∴∠BOE=30+45=75°;(2)设∠COD=x°,由已知可得:∠BOC=,∠COE=,∴+=85,解之x=40答:∠COD=40°.【点评】此题主要考查学生对角的计算的理解和掌握,此题涉及到方程思想,有一定拔高难度,属于中档题.40.如图,已知∠AOB是直角,∠BOC=60°,OE平分∠AOC,OF平分∠BOC.(1)求∠EOF的度数;(2)若将条件“∠AOB是直角,∠BOC=60°”改为:∠AOB=x°,∠EOF=y°,其它条件不变.①则请用x的代数式来表示y;②如果∠AOB+∠EOF=156°.则∠EOF是多少度?【分析】(1)根据角平分线的性质和角的和差倍分关系求∠EOF的度数;(2)①用字母代替数字理由同(1);。
七年级数学人教版(上册)小专题(十五)角度的计算

(2)当转动至图 3 位置时,CM 平分∠ACE,CN 平分∠BCD,求
∠MCN 的度数.
解:(2)因为 CM 平分∠ACE,CN 平分∠BCD,
1
1
所以∠MCE=∠ACM=2∠ACE,∠NCD=∠BCN=2∠BCD.
所以∠MCN=∠MCE+∠ECB+∠BCN
1
1
=2∠ACE+∠ECB+2∠BCD
即∠AOM-∠NOC=30°.
(3)将图 1 中的三角板绕点 O 以每秒 10°的速度沿逆时针方向旋 转一周,在旋转的过程中,若直线 ON 恰好平分∠AOC,则此时三 角板绕点 O 旋转的时间是 6或24 秒.
1
1
∠AOC)=2∠AOB=2θ.
【拓展】 若∠EOF=γ,求∠AOB 的度数.
解:因为 OE 平分∠BOC,OF 平分∠AOC,
1
1
所以∠EOC=2∠BOC,∠COF=2∠AOC.
1
1
1
所以∠EOF=∠EOC+∠COF=2∠BOC+2∠AOC=2(∠BOC
1 +∠AOC)=2∠AOB.
因为∠EOF=γ,所以∠AOB=2γ.
1 所以∠AOC=2∠AOB. 因为∠AOB=60°, 所以∠AOC=30°.
(2)在(1)的条件下,若∠EOC=90°,请在图中补全图形,并求 ∠AOE 的度数.
解:(2)如图 1,∠AOE=∠EOC+∠AOC=90°+30°=120°; 如图 2,∠AOE=∠EOC-∠AOC=90°-30°=60°. 所以∠AOE 的度数为 120°或 60°.
因为∠NOM=90°,
1
1
所以∠NOM=2∠DOB+∠COD+2∠AOC=90°,
1
1
即2×4x+3x+2×2x=90.
人教版七年级数学知识点试题精选-度分秒的换算

人教版七年级数学知识点试题精选-度分秒的换算七年级上册度分秒的换算1.选择题(共20小题)1.如果∠1=45°24′,∠2=45.3°,∠3=45°18′,那么()A.∠1≠∠2 B.∠2≠∠3 C.∠1≠∠3 D.以上都不对2.0.25°=()′=()″.A.15′,900″ B.15′,900″ C.()′,()″ D.15′,0.5″3.把18°15′36″化为度表示,正确的是()A.18.15° B.18.16° C.18.26° D.18.36°4.将8.35°用度、分、秒表示正确的是()A.8°20′ B.8°21′ C.8°3′5″ D.8°30′5″5.40°15′的是()A.20°7′30″ B.20°7′ C.20°8′ D.20°6.4°32′35″×6的结果是()A.27°15′30″ B.28°27′30″ C.24°200′ D.24°32′35″7.38.33°可化为()A.38°19′48″ B.38°19′8″ C.38°20′3″ D.38°30′3″8.若∠1=25°12′,∠2=25.12°,∠3=25.2°,则下面说法正确的是()A.∠1=∠2 B.∠2=∠3 C.∠1=∠3 D.∠1,∠2,∠3互不相等9.把一个周角7等分,每一份是(精确到分)()A.51°28′ B.51°27′ C.51°26′ D.51°25′10.若∠A=20°18′,∠B=20°15′30″,∠C=20.25°,则()A.∠A>∠B>∠C B.∠B>∠A>∠C C.∠A>∠C >∠B D.∠C>∠A>∠B11.下列计算错误的是()A.0.25°=900″ B.1.5°=90′ C.1000″=16.67°D.125.45°=1254.5′12.把15°48′36″化成以度为单位是()A.15.8° B.15.4836° C.15.81° D.15.36°13.如图∠1=35°19′,则∠2的度数为()A.144°81′ B.54°81′ C.54°41′ D.144°41′14.已知:∠A=25°12′,∠B=25.12°,∠C=25.2°,下列结论正确的是()A.∠A=∠B B.∠B=∠C C.∠A=∠C D.三个角互不相等15.如图所示:若∠DEC=50°17′,则∠AED=()A.129°43′ B.129°83′ C.130°43′ D.128°43′2.答案解析1.题目中∠2=45.3°,应该改为∠2=45°18′,因此答案为C。
角的计算题20道初一

角的计算题20道初一1.已知一个角的补角是它的余角的3倍,求这个角的度数。
2.已知一个角的余角比它的补角的31还小10°,求这个角。
3.一个角的补角比它的余角的2倍大90°,求这个角。
4.已知一个角的余角等于45∘,求这个角。
5.已知一个角的补角是130∘,求这个角。
6.一个角的补角与它的余角的和等于180∘,求这个角。
7.已知两个角的和是180∘,其中一个角比另一个角的3倍还多10∘,求这两个角的度数。
8.一个角的补角与它的余角的2倍的和等于270∘,求这个角的余角。
9.一个角的补角比它的余角的4倍少15∘,求这个角的度数。
10.一个角的余角比它的补角的61大10∘,求这个角的余角及补角。
11.一个角的补角与它的余角的3倍的和等于90∘,求这个角的度数。
12.两个角的和是90∘,其中一个角是另一个角的4倍,求这两个角的度数。
13.一个角的补角是它的3倍,求这个角的余角。
14.已知一个角的补角比它的余角的2倍多45∘,求这个角的度数。
15.一个角的余角比它的补角小54∘,求这个角的度数。
16.两个角的和是180∘,且它们的差是30∘,求这两个角的度数。
17.一个角的补角比它的余角的5倍还多20∘,求这个角的度数。
18.已知两个角的和是90∘,且其中一个角是另一个角的2倍多15∘,求这两个角的度数。
19.一个角的补角比它的余角的6倍小30∘,求这个角的度数。
20.一个角的补角是它的余角的7倍,求这个角的度数。
【新】七年级上册 数学 人教版 几何图形的初步 角度及其计算【例题+练习题】

角度1. 知识要点回顾1、角:由公共端点的两条射线所组成的图形叫做角。
2、角的表示法(四种):(1)用三个大写英文字母表示任意一个角(角的顶点必须写在中间,其它两个字母可以调换位置);(2)用一个大写英文字母表示一个独立..的角(在一顶点处只有一个....角); (3)加弧线、标数字表示一个角 (在一个顶点处有两个以上角时,建议使用此法); (4)加弧线、标小写希腊字母表示一个角。
3、角的度量单位及换算●1个周角=2个平角=4个直角=360° ●1°=60′=3600″●用一副三角尺能画的角都是15°的整数倍 4、角的分类∠β 锐角 直角 钝角平角 周角 范围0<∠β<90°∠β=90°90°<∠β<180°∠β=180°∠β=360°5、角的平分线定义:从一个角的顶点出发,把这个角分成相等的两个角的射线叫做角的平分线。
·如图,射线OB 是∠AOC 的平分线,则有∠AOB=∠BOC=21∠AOC 或 2∠AOB=2∠COB=∠AOC用几何语言表示就是:∵OB 平分∴∠AOB=∠BOC=21∠AOC(或 2∠AOB=2∠COB=∠AOC )类似的,从一个角的顶点出发,把这个角分成相等的n 个角的射线,叫做这个角n 等分线。
6、互余、互补(1)若∠1+∠2=90°,则∠1与∠2互为余角。
其中∠1是∠2的余角,∠2是∠1的余角。
(2)若∠1+∠2=180°,则∠1与∠2互为补角。
其中∠1是∠2的补角,∠2是∠1的补角。
(3)余(补)角的性质:等角的补(余)角相等。
7、方向角 (1)正方向(2)北(南)偏东(西)方向 (3)东(西)北(南)方向用角度表示方向:一般以正北、正南为基准,用向东或向西旋转的角度表示方向,如图所示,OA 方向可表示为北偏西60º 。
几何语言2.例题剖析例11、计算:56695376)1('︒+'︒757123(2)180'''︒-︒(3)'"562512︒=_________° (4)36.52°=_____°______′______″2、2点30分时,时钟与分钟所成的角为度.3、60°=____平角;32直角=______度;65周角=______度。
()七年级数学中角度计算题

七年级数学--角有关的计算问题1、如下列图,AB为一条直线,OC是∠AOD的平分线,OE在∠BOD内,∠DOE=1∠,∠°,求∠35、,如图∠BOC为∠AOC内的一个锐角,射线OM、ON分别平分∠AOC、∠BOC。
的度数。
〔1〕假设∠AOB=90°,∠BOC=30°,求∠MON的度数;BOD COE=72E OB〔2〕假设∠AOB=,∠BOC=30°,求∠MON的度数;〔3〕假设∠AOB=90°,∠BOC=,还能否求出∠MON的度数?假设能,求出其值,假设不能,说明理由。
〔4〕从前三问的结果你发现了什么规律?2、如图,∠AOB是∠AOC的余角,∠AOD是∠AOC的补角,且BOC 1B OD2求∠BOD、∠AOC的度数DCO A6〔2021?漳州〕如图是一副学生用的三角形板摆放的位置,A、O、C三点在同一直线上,那么∠3、一条射线OA,假设从点O再引两条射线 OB、OC,使∠AOB=60°,∠BOC=20°,求∠AOC的度数。
数是度.BA O C 〔第13题〕4、∠AOB=100°,∠BOC=20°,假设OM平分∠AOB,ON平分∠BOC,求∠MON的度数。
19、如图,∠BOC=2∠AOC,OD平分∠AOB,且∠COD=29°,求∠AOB的度数。
7、点O是直线AB上一点,∠COD是直角,OE平分∠BOC。
〔1〕如图1,假设∠AOC=40°,求∠DOE的度数;〔2〕在如1中,假设∠AOC=,直接写出∠DOE的度数〔用含的代数式表示〕D CB AO10、如图,OB平分∠AOC,且∠2:∠3:∠4=1:3:4 ,求∠1、∠2、∠3、∠4。
CB31DO48如图,AB=40,点C是线段AB的中点,点D为线段CB上的一E为线段DB的中11(如图,将一幅三角尺叠放在一起,使直角顶O,绕点O任意转动其中一个点,点点,点重合于点角尺,那么与∠AOD始终相等的角是.EB=6,求线段CD的长。
角的计算方法总结归纳

七年级上学期第四章:角的计算方法总结归纳1、七年级上学期数学第四章:几何图形中角的计算基本理解问题一:图中有几个角?答:三个,∠BAC,∠CAD,∠BAD问题二:这三个角之间有什么联系?答:∠BAC+∠CAD=∠BAD,∠BAD−∠BAC=∠CAD∠BAD−∠CAD=∠BAC∠BAD 问题三:如果射线AC是∠BAD的角平分线,那么∠BAC=∠CAD =12问题四:如果∠BAC:∠CAD=2:3,∠BAD=500,求其他的角解:设∠BAC的度数为2x,则∠CAD的度数为3x2x+3x=50解得x=10则∠BAC=2x=200, ∠CAD=3x=3002、角的计算①直接计算典型例题1、如图,已知∠AOB=90°,∠EOF=60°,OE平分∠AOB,OF平分∠BOC,求∠COB和∠AOC的度数.解:因为∠AOB=90°,OE平分∠AOB所以∠BOE=12∠AOB=450因为∠EOF=60°所以∠BOF=∠EOF−∠BOE=150因为OE平分∠AOB所以∠COB=2∠BOF=300所以∠AOC=∠AOB+∠COB=1200分析:正推:将题目所给的条件联系起来,通过一个条件(已知)或者两个条件(已知)联合可以推出哪些(未知),最后联系已知和推出来的未知联合在一起,看能否得出结论。
反推:又或者倒推题目,要求出所求的问题,求出知道哪些,进而求出这些所需要的条件是什么,再看看题目已经知道的条件是什么,还需要什么变式训练:1、如下图所示,已知∠AOC=∠BOD=800,∠BOC=350,求∠AOD的度数O DCBA2、O是直线上一点,OC是任一条射线,OD、OF分别是∠AOC和∠BOC的平分线。
(1)请你直接写出图中∠BOD的补角,∠BOE的余角。
(2)当∠BOF=25°时,试求∠DFE和∠AOD的度数分别是多少。
3、如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°(1)请你数一数, 图中有_______个小于平角的角;(2)求出∠BOD的度数;(3)请通过计算说明OE是否平分∠BOC.②方程的思想典型例题1、如图,O是直线AB上一点,∠AOC=∠BOD,射线OE 平分∠BOC,∠EOD=42°,求∠EOC的大小.解:设∠AOC的度数为x度,则∠BOD的度数也是x度因为∠EOD=42°所以∠BOE=x+420因为射线OE平分∠BOC∠EOC=∠BOE=x+420则x+x+42+x+42=180解得:x=320∠EOC=x+420=740分析:一般用方程思想的题目,给出的角的度数比较少,角与角之间的关系比较多。
苏科版七年级上数学期末复习压轴题---角的旋转(难题)训练
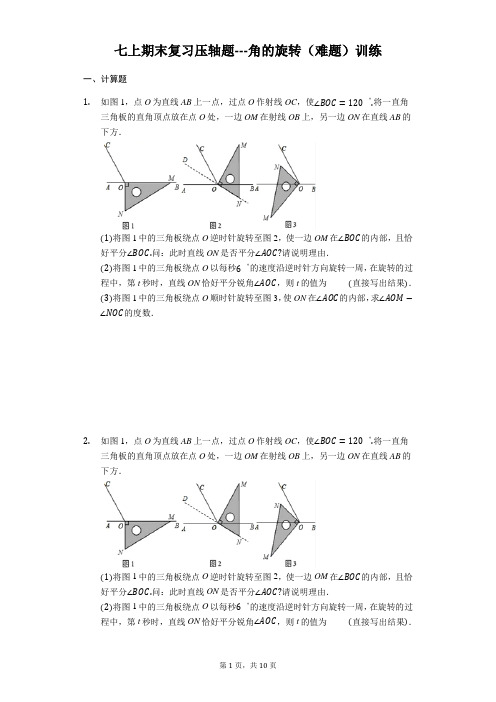
七上期末复习压轴题---角的旋转(难题)训练一、计算题1.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120∘.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.(2)将图1中的三角板绕点O以每秒6∘的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM−∠NOC的度数.2.如图1,点O为直线AB上一点,过点O作射线OC,使∠BOC=120∘.将一直角三角板的直角顶点放在点O处,一边OM在射线OB上,另一边ON在直线AB的下方.(1)将图1中的三角板绕点O逆时针旋转至图2,使一边OM在∠BOC的内部,且恰好平分∠BOC.问:此时直线ON是否平分∠AOC?请说明理由.(2)将图1中的三角板绕点O以每秒6∘的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为_____(直接写出结果).(3)将图1中的三角板绕点O顺时针旋转至图3,使ON在∠AOC的内部,求∠AOM−∠NOC的度数.3.如图1,点O是直线AB上的一点.(1)如图1,当∠AOD是直角,3∠AOC=∠BOD,求∠COD的度数;(2)在(1)中∠COD绕着点O顺时针旋转(OD与OB重合即停止),如图2,OE、OF分别平分∠AOC、∠BOD,则在旋转过程中∠EOF的大小是否变化?若不变,求出∠EOF的大小;若改变,说明理由;(3)在图1中,∠AOD=90°,∠AOC=30°,线段OC、OD绕着点O顺时针旋转,速度分别为每秒20°和每秒10°(当.OD..重合时旋转都停止........),OM、ON分别平..与.OB分∠BOC、∠BOD,多少秒时∠COM=∠BON(直接写出答案,不必写出过程).二、解答题4.如图1,已知∠AOC=2∠BOC,∠AOC的余角比∠BOC小30°(1)求∠COB的度数(2)经过点O作射线OD,使得∠AOC=4∠AOD,求∠BOD的度数(3)如图2,在∠AOB的内部作∠EOF,OM、ON分别为∠AOE和∠BOF的平分线,当∠EOF绕点O在∠AOB的内部转动时,请写出∠AOB、∠EOF、∠MON之间的数量关系,并说明理由。
人教版七年级数学《角度换算》计算题专项练习(含答案)

人教版七年级数学《角度换算》计算题专项练习学校:班级:姓名:得分:1.计算:13°58ʹ+28°37ʹ×2.2.计算(结果用度、分、秒表示):22°18ʹ20ʺ×5﹣28°52ʹ46ʺ.3.计算:(1)90°﹣36°12'15ʺ(2)32°17'53“+42°42'7ʺ(3)25°12'35“×5;(4)53°÷6.5.计算:(1)27°26ʹ+53°48ʹ(2)90°﹣79°18ʹ6ʺ.6.计算(1)25°34ʹ48ʺ﹣15°26ʹ37ʺ(2)105°18ʹ48ʺ+35.285°.7.计算:(1)40°26ʹ+30°30ʹ30ʺ÷6;(2)13°53ʹ×3﹣32°5ʹ31ʺ.8.计算:180°﹣48°39ʹ40ʺ.9.计算:26°21ʹ30ʺ+42°38ʹ30ʺ.10.(1)180°﹣(34°55ʹ+21°33ʹ);(2)(180°﹣91°31ʹ24ʺ)÷2.11.计算:72°35ʹ÷2+18°33ʹ×4.48°39ʹ39ʹ+67°41ʹ.12.计算:48°13.计算:18°20ʹ32ʺ+30°15ʹ22ʺ.14.计算:180°﹣22°18ʹ×5.15.计算:56°31ʹ+29°43ʹ×6.16.计算:49°28ʹ52ʺ÷4.人教版七年级数学《角度换算》计算题专项练习参考答案参考答案1.计算:13°58ʹ+28°37ʹ×2.【解答】解:13°58ʹ+28°37ʹ×2,=13°58ʹ+57°14ʹ,=71°12ʹ.2.计算(结果用度、分、秒表示)22°18ʹ20ʺ×5﹣28°52ʹ46ʺ.【解答】解:22°22°18'20''18'20''×5﹣28°28°52'46''52'46'' =110°=110°90'100''90'100''﹣28°28°52'46''=82°52'46''=82°52'46''=82°38'54''38'54''.3.计算:(1)90°﹣36°12'15ʺ(2)32°17'53“+42°42'7ʺ(3)25°12'35“×5; (4)53°÷6.【解答】解:(1)90°﹣36°12'15ʺ=53°ʹ45ʺ;(2)32°17'53“+42°42'7ʺ=74°59ʹ60ʺ=75°(3)25°12'35“×5=125°60ʹ175ʺ=126°2ʹ55ʺ; (4)53°÷6=8°50ʹ.4.计算:(1)27°26ʹ+53°48ʹ(2)90°﹣79°18ʹ6ʺ.【解答】解:(1)原式=80°74ʹ=81°14ʹ;(2)原式=89°59ʹ60ʺ﹣79°18ʹ6ʺ=10°41ʹ54ʺ.5.计算(1)25°34ʹ48ʺ﹣15°26ʹ37ʺ(2)105°18ʹ48ʺ+35.285°.【解答】解:(1)25°34ʹ48ʺ﹣15°26ʹ37ʺ=10°8ʹ11ʺ; (2)105°18ʹ48ʺ+35.285°=105°18ʹ48ʺ+35°17ʹ6ʺ=140°35ʹ54ʺ.6.计算:(1)4040°26ʹ°26ʹ+30°30ʹ30ʺ÷6; (2)13°53ʹ×3﹣32°5ʹ31ʺ.【解答】解:解:(1)40°26ʹ+30°30ʹ30ʺ÷6=40°26ʹ+5°5ʹ5ʺ=45°31ʹ5ʺ;(2)13°53ʹ×3﹣32°5ʹ31ʺ=41°39ʹ﹣32°5ʹ31ʺ=9°33ʹ29ʺ.7.计算:180°﹣48°39ʹ40ʺ.【解答】解:180°﹣48°39ʹ40ʺ=179°59ʹ60ʺ﹣48°39ʹ40ʺ=131°20ʹ20ʺ8.计算:26°21ʹ30ʺ+42°38ʹ30ʺ.【解答】解:26°21ʹ30ʺ+42°38ʹ30ʺ=68°59ʹ60ʺ=69°.9.(1)180°﹣(34°55ʹ+21°33ʹ);(2)(180°﹣91°31ʹ24ʺ)÷2.【解答】解:(1)原式=180°﹣55°88ʹ=179°60ʹ﹣56°28ʹ=123°32ʹ;(2)原式=(179°59ʹ60ʺ﹣91°31ʹ24ʺ)÷2=88°28ʹ36ʺ÷2=44°14ʹ18ʺ.10.计算:72°35ʹ÷2+18°33ʹ×4.【解答】解:原式=36° 17ʹ30ʺ+74° 12ʹ=110° 29ʹ30ʺ.°39ʹ+67°41ʹ.11.计算:4848°39ʹ【解答】解:48°39ʹ+67°41ʹ=115°80ʹ=116°20ʹ.12.计算:18°20ʹ32ʺ+30°15ʹ22ʺ.【解答】解:原式=48°35'54ʺ.(4分)13.计算:180°﹣22°18ʹ×5.【解答】解:原式=180°﹣110°90ʹ=179°60ʹ﹣111°30ʹ=68°30ʹ.14.计算:56°31ʹ+29°43ʹ×6.【解答】解;原式=56°31ʹ+174°258ʹ=230°289ʹ=234°49ʹ.15.计算:49°28ʹ52ʺ÷4.【解答】解:49°28ʹ52ʺ÷4=12°22ʹ13ʺ.。
七年级数学中的角度计算题

角的问题 【1 】BOD BOC ∠=∠21 1.如图,已知∠AOB 是∠AOC 的余角,∠AOD 是∠AOC 的补角,且求∠BOD.∠AOC 的度数2.一条射线OA,若从点O 再引两条射线OB.OC,使∠AOB=60°,∠BOC=20°,求∠AOC 的度数.3.已知,如图∠BOC 为∠AOC 内的一个锐角,射线OM.ON 分离等分∠AOC.∠BOC.(1)若∠AOB=90°,∠BOC=30°,求∠MON的度数; (2)若∠AOB=α,∠BOC=30°,求∠MON 的度数;(3)若∠AOB=90°,∠BOC=β,还可否求出∠MON 的度数?若能,求出其值,若不克不及,解释来由. (4)从前三问的成果你发明了什么纪律?AO BC NM5.点O 是直线AB 上一点,∠COD 是直角,OE 等分∠BOC.(1)如图1,若∠AOC=40°,求∠DOE 的度数;(2)在如1中,若∠AOC=α,直接写出∠DOE 的度数(用含α的代数式暗示)(3)将图1中的∠COD 按顺时针偏向扭转至图2所示的地位.①探讨∠AOC 与∠DOE 的度数之间的关系,写出你的结论,并解释来由;②在∠AOC 的内部有一条射线OF,知足:)(212AOF AOC BOE AOF ∠-∠=∠+∠,试肯定∠AOF 与∠DOE 的度数之间的关系.6.如图,∠1=∠2,∠3=∠4,∠5=130度,那么∠A =()度.7.如图5,点0为直线AB 上的一点,∠BOC 是直角,∠BOD :∠COD=4:1.则∠AOD 是()度. D O CB A8.如图,∠AOB 的极点0在直线l 上,已知图中所有小于平角的角之和是400度,则∠AOB =________度.9.三个正方形叠放在一路,如图所示.求:∠1的度数.10.一个角的补角比它的余角的二倍还多18度,这个角有若干度?11.如图,直线AB.CD 订交于点O,OE 等分∠AOC,∠BOC —∠BOD =20°,求∠BOE 的度数.12.如图,已知∠BOC =2∠AOC,OD 等分∠AOB,且∠COD =29°,求∠AOB 的度数. 13.如图,OB 等分∠AOC,且∠2 : ∠3 : ∠4 = 1:3:4,求∠1.∠2.∠3.∠4. 14.如图,已知∠AOB=120°,OC 是∠AOB 的一等分线,OD 是∠BOC 的等分线,求∠AOD 的度数. 15.如图,已知O 是直线AB 上的点,OD 是∠AOC 的等分线,OE 是∠COB 的等分线, 求∠DOE 的度数. 16.如图,已知∠AOC=∠BOD=78°,∠BOC=35°,求∠AOD.17.如图,已知∠AOB =150°,∠AOC =∠BOD =90°,求∠COD 的度数.18.如图,已知直线AB 和CD 订交于O 点,∠COE 是直角,OF 等分∠AOE,∠COF=34°,求∠BOD 的度数.20.(1)如图,已知∠AOB=90°,∠BOC=30°,OM 等分∠AOC,ON 等分∠BOC,求∠MON 的度数.(2)假如(1)中的∠AOB=α,其他前提不变,求∠MON 的度数.(3)假如(1)中∠BOC= β(β为锐角),其他前提不变,求∠MON 的度数.C EB A D OC B AD O 3 D CB A 214 O。
七年级数学下册 专题 与平行线有关的角度计算(四大题型)(解析版 )

(人教版)七年级下册数学《第五章相交线与平行线》专题与平行线有关的角度计算1.(2023秋•惠安县期末)如图,直线l1和l2被l3所截,若l1∥l2,∠1+∠2=232°,则∠3的度数为()A.64°B.66°C.84°D.86°【分析】根据对顶角相等结合已知可求出∠1的度数,再根据两直线平行,同旁内角互补即可求出∠4的度数,再根据对顶角相等即可得出∠3的度数.【解答】解:如图,∵∠1+∠2=232°,又∵∠1=∠2,∴∠1=116°,∵l1∥l2,∴∠1+∠4=180°,∴∠4=64°,∵∠3=∠4,∴∠3=64°,故选:A.【点评】本题考查了平行线的性质,对顶角的性质,熟练掌握平行线的性质及对顶角的性质是解题的关键.2.如图,DA⊥AB,CD⊥DA,∠B=56°,则∠C的度数是()A.154°B.144°C.134°D.124°【分析】根据平行线的判定和性质定理即可得到结论.【解答】解:∵DA⊥AB,CD⊥DA,∴∠A=∠D=90°,∴∠A+∠D=180°,∴AB∥CD,∴∠B+∠C=180°,∵∠B=56°,∴∠C=180°﹣∠B=124°,故选:D.【点评】本题考查了平行线的判定和性质,熟练掌握平行线的判定和性质定理是解题的关键.3.(2023秋•遂平县期末)如图.直线a∥b,直线L与a、b分别交于点A、B,过点A作AC⊥b于点C.若∠1=50°,则∠2的度数为()A.130°B.50°C.40°D.25°【分析】直接利用垂直的定义得出∠ACB=90°,再利用平行线的性质得出答案.【解答】解:∵AC⊥b,∴∠ACB=90°,∵∠1=50°,∴∠ABC=40°,∵a∥b,∴∠ABC=∠2=40°.故选:C.【点评】此题主要考查了垂线以及平行线的性质,正确得出∠ABC的度数是解题关键.4.如图,直线l1∥l2,CD⊥AB于点D,∠1=44°,则∠2的度数为()A.30°B.44°C.46°D.56°【分析】根据直角三角形的两个锐角互余,可以得到∠CBD的度数,再根据直线l1∥l2,可以得到∠CBD =∠2,从而可以得到∠2的度数,本题得以解决.【解答】解:∵CD⊥AB于点D,∠1=44°,∴∠CBD=46°,∵直线l1∥l2,∴∠CBD=∠2,∴∠2=46°,故选:C.【点评】本题考查平行线的性质、垂线,解答本题的关键是明确题意,利用数形结合的思想解答.5.如图,一个由4条线段a,b,c,d组成的“鱼”形图案,若∠1=45°,∠2=45°,∠3=140°,则∠4的度数为()A.35°B.40°C.45°D.50°【分析】先由∠1、∠2的关系得到b与c的关系,再利用平行线的性质求出∠4.【解答】解:∵∠1=45°,∠2=45°,∴∠1=∠2.∴b∥c.∴∠3+∠4=180°.∵∠3=140°,∴∠4=180°﹣140°=40°.故选:B.【点评】本题考查了平行线的判定与性质,解决本题的关键是注意平行线的性质和判定定理的综合运用.6.(2023秋•泰兴市期末)如图,AB∥CD,直线EF和AB、CD分别交于点G、H,若∠EGB=(2x+30)°,∠CHF=(80﹣3x)°,则x的值为()A.10B.20C.100D.110【分析】根据平行线的性质和对顶角的性质,可以得到∠EGB和∠CHF的关系,然后即可求得x的值.【解答】解:∵AB∥CD,∴∠EGB=∠EHD,∵∠EHD=∠CHF,∴∠EGB=∠CHF,∵∠EGB=(2x+30)°,∠CHF=(80﹣3x)°,∴2x+30=80﹣3x,解得x=10,故选:A.【点评】本题考查平行线的性质、对顶角的性质,解答本题的关键是明确题意,利用数形结合的思想解答.7.如图,DE∥BC,点A在直线DE上,∠DAB=78°,∠ACF=135°,∠BAC=度.【分析】由DE∥BC可知∠DAC=∠ACF=135°,再利用角的差求∠BAC即可.【解答】解:∵DE∥BC,∴∠DAC=∠ACF=135°,∵∠DAB=78°,∴∠BAC=∠DAC﹣∠DAB=57°.故答案为:57.【点评】本题考查平行线的性质,解题关键是结合图形利用平行线的性质进行角的转化和计算.8.(2023秋•东坡区期末)如图,AB∥CD,∠ACD=155°,∠AFE=26°,则∠CEF的度数为.【分析】先利用平行线的性质可得∠A=25°,然后利用三角形的外角性质进行计算,即可解答.【解答】解:∵AB∥CD,∠ACD=155°,∴∠A=180°﹣∠ACD=25°,∵∠CEF是△AEF的一个外角,∠AFE=26°,∴∠CEF=∠A+∠AFE=51°,故答案为:51°.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.9.如图,直线AB∥EF,直线AG,BD分别交直线EF于点C,D.若∠A=2∠B,∠ECG=108°,则∠BDF的度数为°.【分析】由∠ECG=108°,AB∥EF,可得∠A=72°,而∠A=2∠B,知∠B=12∠A=36°;故∠BDF=∠B=36°.【解答】解:∵∠ECG=108°,∴∠ACD=108°,∵AB∥EF,∴∠A=180°﹣∠ACD=72°,∵∠A=2∠B,∴∠B=12∠A=36°;∵AB∥EF,∴∠BDF=∠B=36°;故答案为:36.【点评】本题考查平行线的性质,掌握两直线平行,内错角相等,同旁内角互补是解题的关键.10.(2022春•五莲县期末)如图,已知AB∥DE∥CF,若∠ABC=70°,∠CDE=130°,则∠BCD的度数为.【分析】由AB∥CF,∠ABC=70°,易求∠BCF,又DE∥CF,∠CDE=130°,那么易求∠DCF,于是∠BCD=∠BCF﹣∠DCF可求.【解答】解:∵AB∥CF,∠ABC=70°,∴∠BCF=∠ABC=70°,又∵DE∥CF,∴∠DCF+∠CDE=180°,∴∠DCF=50°,∴∠BCD=∠BCF﹣∠DCF=70°﹣50°=20°.故答案为:20°.【点评】本题主要考查了平行线的性质,两直线平行,内错角相等;两直线平行,同旁内角互补.11.(2023秋•商水县期末)如图,已知DE∥CB,∠B=∠D.(1)判断AB、CD是否平行,并说明理由.(2)若∠B+∠F=102°,求∠DEF的度数.【分析】(1)由平行线的性质可得∠D=∠BCF,从而可求得∠BCF=∠B,即可判定AB∥CD;(2)由平行线的性质可得∠B+∠BED=180°,∠F=∠BEF,结合条件即可求解.【解答】解:(1)AB∥CD,理由如下:∵DE∥CB,∴∠D=∠BCF,∵∠B=∠D,∴∠BCF=∠B,∴AB∥CD;(2)∵DE∥CB,∴∠B+∠BED=180°,∴∠B+∠BEF+∠DEF=180°,∵AB∥CD,∴∠F=∠BEF,∴∠B+∠F+∠DEF=180°,∵∠B+∠F=102°,∴∠DEF=78°.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的判定定理与性质并灵活运用.12.(2023秋•长沙期末)如图,直线EF与CD交于点O,OA平分∠COE交直线l于点A,OB平分∠DOE交直线l于点B,且∠1+∠2=90°.(1)求∠AOB的度数;(2)求证:AB∥CD;(3)若∠2:∠3=2:5,求∠AOF的度数.【分析】(1)利用角平分线的定义可得∠A=12∠A,∠A=12∠A,然后利用平角定义,以及角的和差关系进行计算,即可解答;(2)利用(1)的结论可得:∠AOB=90°,从而利用平角定义可得:∠AOC+∠2=90°,然后利用同角的余角相等可得∠AOC=∠1,从而利用内错角相等,两直线平行可得AB∥CD,即可解答;(3)利用角平分线的定义可得∠2=12∠DOE,从而可得∠DOE:∠3=4:5,然后利用平角定义可得∠DOE+∠3=180°,从而可得∠3=100°,进而可得∠COE=∠3=100°,最后利用角平分线的定义可得∠AOE =50°,从而利用平角定义进行计算,即可解答.【解答】(1)解:∵OA,OB分别平分∠COE和∠DOE,∴∠A=12∠A,∠A=12∠A,∴∠AOE+∠BOE=12∠COE+12∠DOE=12(∠COE+∠DOE)=12×180°=90°,∴∠AOB=90°,∴∠AOB的度数为90°;(2)证明:由(1)得:∠AOB=90°,∴∠AOC+∠2=180°﹣∠AOB=180°﹣90°=90°,∵∠1+∠2=90°,∴∠AOC=∠1,∴AB∥CD;(3)解:∵OB平分∠DOE,∴∠2=12∠DOE,∵∠2:∠3=2:5,∴∠DOE:∠3=4:5,∵∠DOE+∠3=180°,∴∠3=180°×59=100°,∴∠COE=∠3=100°,∵OA平分∠COE,∠A=12∠A=50°,∴∠AOF=180°﹣∠AOE=130°,∴∠AOF的度数为130°.【点评】本题考查了平行线的性质,三角形的外角性质,根据题目的已知条件并结合图形进行分析是解题的关键.1.(2023秋•南关区校级期末)如图,一把长方形直尺沿直线断开并错位摆放,点E、D、B、F在同一条直线上,若∠ADE=131°,则∠DBC的度数为.【分析】由平行线是的性质推出∠GED=∠ADE=131°,∠DBC+∠GED=180°,即可求出∠DBC的度数.【解答】解:∵AD∥EG,∴∠GED=∠ADE=131°,∵EG∥BC,∴∠DBC+∠GED=180°,∴∠DBC=49°.故答案为:49°.【点评】本题考查平行线的性质,关键是由平行线的性质得到∠GED=∠ADE,∠DBC+∠GED=180°.2.(2023秋•威宁县期末)一把直尺按如图所示摆放,AB∥CD,且∠1=70°,则∠2的度数是()A.70°B.60°C.30°D.80°【分析】根据题意可得:EF∥HG,从而利用平行线的性质可得∠1=∠3=70°,然后再利用平行线的性质可得∠3=∠2=70°,即可解答.【解答】解:如图:由题意得:EF∥HG,∴∠1=∠3=70°,∵AB∥CD,∴∠3=∠2=70°,故选:A.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.3.(2023秋•海安市期末)将一直尺和一块含30°角的三角尺按如图放置,若∠CDE=40°,则∠BF A 的度数为()A.40°B.50°C.130°D.140°【分析】先求∠CFA的度数,再求∠BFA的度数.【解答】解:∵DE∥AF,∴∠CDE=∠CFA,∵∠CDE=40°,∴∠CFA=40°,∴∠BFA=180°﹣∠CFA=140°.故选:D.【点评】本题主要考查平行线的性质,解决本题的关键是熟练运用平行线的性质.4.(2023秋•铜官区期末)如图,将一块含有45°角的三角板的两个顶点放在直尺的一组对边上.如果∠2=65°,那么∠1的度数为()A.15°B.20°C.25°D.30°【分析】根据题意∠2=65°即可算出∠3度数,再利用平行性质即可算出本题答案.【解答】解:如下图所示:∵∠2=65°,一块含有45°角的三角板,∴∠3=90°﹣65°=25°,∵两个顶点放在直尺的一组对边上,∴∠3=∠4=25°,∴∠1=45°﹣25°=20°,故选:B.【点评】本题考查平行线性质,关键是余角定义,角度计算.5.(2023秋•锦江区校级期末)一块含30°角的直角三角板,按如图所示方式放置,顶点A,C分别落在直线a,b上,若直线a∥b,∠1=35°,则∠2的度数是()A.45°B.35°C.30°D.25°【分析】先根据题意得出∠1+∠BAC的度数,再由平行线的性质即可得出结论.【解答】解:∵∠1=35°,∴∠1+∠BAC=35°+30°=65°,∵a∥b,∴∠2+∠ACB+∠1+∠BAC=180°,即∠2+90°+35°+30°=180°,∴∠2=25°.故选:D.【点评】本题考查的是平行线的性质,熟知两直线平行,同旁内角互补是解题的关键.6.如图,将一副三角尺按如图所示的位置在同一平面内摆放,其中∠ACB=∠CED=90°,∠B=30°,∠ECD=45°.若AB∥CE,CB与DE相交于点F,则∠BCD的度数为()A.15°B.20°C.25°D.30°【分析】根据平行线的性质得出∠ECA=120°,进而利用角的关系解答即可.【解答】解:∵AB∥CE,∴∠ECA=180°﹣∠A=180°﹣60°=120°,∵∠ECD=45°,∴∠DCA=120°﹣45°=75°,∵∠BCA=90°,∴∠BCD=90°﹣75°=15°,故选:A.【点评】此题考查平行线的性质,关键是根据两直线平行,同旁内角互补解答.7.(2023秋•新都区期末)如图,将含有30°的直角三角尺CAB(∠C=60°)直角顶点A放到矩形DEFH 的边DE上,若∠EAB=15°,则∠FQG的度数是()A.25°B.30°C.35°D.45°【分析】先根据∠EAB=15°,∠CAB=90°得出∠CAE的度数,再由HF∥DE得出∠CMF的度数,由三角形内角和定理得出∠CQM的度数,进而可得出结论.【解答】解:∵∠EAB=15°,∠CAB=90°,∴∠CAE=90°﹣15°=75°,∵HF∥DE,∴∠CMF=∠CAE=75°,∵∠C=60°,∴∠CQM=180°﹣60°﹣75°=45°,∴∠FQG=∠CQM=45°.故选:D.【点评】本题考查的是平行线的性质,熟知两直线平行,同位角相等是解题的关键.8.将一副三角尺如图放置,其中∠D=∠BAC=90°,∠F=30°,∠B=45°,则∠BCF的度数为()A.105°B.120°C.150°D.165°【分析】由∠D=∠BAC,利用“同位角相等,两直线平行”,可得出AC∥DF,利用“两直线平行,同位角相等”,可求出∠ACE的度数,结合∠BCE=∠ACB﹣∠ACE,可求出∠BCE的度数,再利用邻补角互补,即可求出∠BCF的度数.【解答】解:∵∠D=∠BAC=90°,∴AC∥DF,∴∠ACE=∠F=30°,∴∠BCE=∠ACB﹣∠ACE=45°﹣30°=15°.又∵∠BCE+∠BCF=180°,∴∠BCF﹣180°﹣∠BCE=180°﹣15°=165°.故选:D.【点评】本题考查了平行线的判定与性质以及邻补角,根据各角之间的关系,求出∠BCE的度数是解题的关键.9.一副三角形板如图放置,DE∥BC,∠C=∠DBE=90°,∠E=45°,∠A=30°,则∠ABD的度数为()A.5°B.15°C.20°D.25°【分析】根据三角形内角和定理以及平行线的性质,即可得到∠DC=45°,∠AB=60据此可得∠ABD的度数.【解答】解:Rt△ABC中,∠A=30°,∴∠ABC=60,∵BC∥DE,∠EDB=∠E=45°,∴∠DBC=45°,∴∠ABD=60°﹣45°=15°,故选:B.【点评】本题主要考查了平行线的性质的运用,解题时注意:两直线平行,内错角相等.10.如图,将一副三角尺按图中所示位置摆放,点F在AC上,∠ACB=90°,∠ABC=60°,∠EFD=90°,∠DEF=45°,AB∥DE.则∠AFD的度数是()A.25°B.20°C.15°D.10°【分析】利用三角板的度数可得∠A=30°,∠D=45°,由平行线的性质定理可得∠1=∠D=45°,利用三角形外角的性质可得结果.【解答】解:如图,∵∠ACB=90°,∠ABC=60°,∴∠A=180°﹣∠ACB﹣∠ABC=180°﹣90°﹣60°=30°,∵∠EFD=90°,∠DEF=45°,∴∠D=180°﹣∠EFD﹣∠DEF=180°﹣90°﹣45°=45°,∵AB∥DE,∴∠1=∠D=45°,∴∠AFD=∠1﹣∠A=45°﹣30°=15°,故选:C.【点评】本题主要考查了平行线的性质定理和外角的性质,求出∠A,∠D的度数是解本题的关键.11.(2023秋•莲湖区期末)如图,把一块三角板的60°角的顶点放在直尺的一边上,若∠2=55°,求∠1的度数.【分析】先根据两直线平行的性质,得到∠3=∠2,再根据平角的定义,即可得出∠1的度数.【解答】解:∵AB∥CD,∴∠2=∠3.∵∠2=55°,∴∠3=55°.∵∠1+60°+∠3=180°,∴∠1=65°.【点评】本题主要考查了平行的性质,解题的关键是掌握:两直线平行,同位角相等.12.将一副直角三角板如图1摆放在直线MN上(直角三角板ABC和直角三角板EDC,∠EDC=90°,∠DEC=60°,∠ABC=90°,∠BAC=45°),保持三角板EDC不动,将三角板ABC绕点C以每秒5°的速度顺时针旋转,旋转时间为t秒,当AC与射线CN重合时停止旋转.(1)如图2,当AC为∠DCE的角平分线时,t=.(2)当t=18时,求∠BCD的度数?(3)在旋转过程中,当三角板ABC的AB边平行于三角板EDC的某一边时(不包含重合的情形),求此时t的值为.(直接写出答案即可)【分析】(1)当AC为∠DCE的角平分线时,可以求出旋转角,再根据旋转的速度即可求解.(2)当t=18时,旋转角为90°,可求出∠ACD,即可求出∠BCD.(3)数形结合,分情况进行讨论即可.【解答】解:(1)当AC为∠DCE的角平分线时,旋转角为15°,∴t=155=3,故答案为3.(2)当t=18时,旋转角为90°,如图:∵∠DCE=30°,∠ACB=45°,∴∠ACD=60°,∠BCD=60°﹣45°=15°.(3)当三角板ABC的AB边平行于三角板EDC的某一边时,有3种情况:①当AB∥DE时,如图:此时,BC与CD重合,t=(30+40)÷5=15,②当AB∥CE时,如图:∵AB∥CE,∴∠BCE=∠B=90°,∴∠ACE=90°+45°=135°,∴t=135÷5=27,③当AB∥CD时,如图:∵AB∥CD,∴∠BCD=∠D=90°,∴∠ACE=30°+90°+45°=165°,∴t=165÷3=33.综上所述,t=15或27或33.【点评】本题考查旋转的性质,角平分线的性质,平行线的性质,关键在于数形结合,分类讨论.1.如图,在弯形管道ABCD中,若AB∥CD,拐角∠ABC=122°,则∠BCD的大小为()A.58°B.68°C.78°D.122°【分析】根据平行线的性质得出∠ABC+∠BCD=180°,代入求出即可.【解答】解:∵AB∥CD,∴∠ABC+∠BCD=180°,∵∠ABC=122°,∴∠BCD=180°﹣122°=58°,故选:A.【点评】本题考查了平行线的性质,能熟练地运用平行线的性质定理进行推理是解此题的关键,注意:两直线平行,同旁内角互补.2.如图,万岁山大宋武侠城的两条小路AB∥CD,则∠BAE+∠AEC+∠ECD=()A.180°B.270°C.360°D.540°【分析】作辅助线EF∥AB,然后根据平行线的性质,可以得到∠BAE+∠AEC+∠ECD的度数.【解答】解:过点E作EF∥AB,如图:∵AB∥CD,∴AB∥CD∥EF,∴∠BAE+∠AEF=180°,∠FEC+∠ECD=180°,∵∠AEF+∠FEC=∠AEC,∴∠BAE+∠AEC+∠ECD=360°,故选:C.【点评】本题考查平行线的性质,解答本题的关键是熟练掌握平行线的性质,明确题意,利用数形结合的思想解答.3.(2023秋•海门区期末)如图,两面镜子AB,BC的夹角为∠α,入射光线OM经过镜子两次反射后的出射光线NO平行于AB,图中∠1=∠2,∠3=∠4.当OM∥BC时,∠α的度数是()A.30°B.45°C.60°D.75°【分析】由平行线的性质推出∠4=∠α,∠1=∠α,又∠3=∠4,∠2=∠1,得到∠1=∠2=∠α,判定△MNB是等边三角形,得到∠α=60°.【解答】解:∵ON∥AB,∴∠4=∠α,∵∠3=∠4,∴∠3=∠α,∵OM∥BN,∴∠1=∠α,∵∠2=∠1,∴∠2=∠α,∴∠3=∠2=∠α,∴△MNB是等边三角形,∴∠α=60°.故选:C.【点评】本题考查平行线的性质,关键是由平行线的性质推出∠3=∠2=∠α.4.(2023秋•即墨区期末)生活中的椅子一般依据人体工学原理设计,如图为生活中一把椅子的侧面图,从人体脊柱的形势而言,当靠背角度∠DEF=115°时,能产生较为接近自然腰部的形状,此时最舒适.已知DE与地面平行,支撑杆BD与地面夹角∠ABD=50°,则制作时用螺丝固定时支撑杆BD和AF需构成夹角∠ACB为()A.70°B.65°C.60°D.50°【分析】先求出∠DEC的度数,再求出∠CAB的度数,最后求出∠ACB的度数.【解答】解:∵∠DEF=115°,∴∠DEC=180°﹣∠DEF=65°,∵DE∥AB,∴∠CAB=∠DEC=65°,∵∠ABD=50°,∴∠ACB=180°﹣∠ABD﹣∠CAB=65°.故选:B.【点评】本题主要考查了平行线的性质,解题的关键是熟练运用平行线的性质.5.当光从一种介质射向另一种介质时,光线会发生折射,不同介质的折射率不同.如图,水平放置的水槽中装有适量水,空气中两条平行光线射入水中,两条折射光线也互相平行.若∠1=110°,则∠2的度数为()A.70°B.60°C.50°D.40°【分析】根据题意可得:AB∥CE,然后利用平行线的性质可得∠ACE=70°,再利用两直线平行,内错角相等可得∠2=∠ACE=70°,即可解答.【解答】解:如图:由题意得:AB∥CE,∴∠1+∠ACE=180°,∴∠ACE=180°﹣∠1=70°,∵AC∥BE,∴∠2=∠ACE=70°,故选:A.【点评】本题考查了平行线的性质,熟练掌握平行线的性质是解题的关键.6.(2023秋•鹿寨县期末)如图1是某景区电动升降门,将其抽象为几何图形,如图2所示,BA垂直于地面AE于A,当CD平行于地面AE时,则∠ABC+∠BCD=.【分析】过点B作BF∥AE,如图,由于CD∥AE,则BF∥CD,根据两直线平行,同旁内角互补得∠BCD+∠CBF=180°,由AB⊥AE得AB⊥BF,所以∠ABF=90°,于是有∠ABC+∠BCD=∠ABF+∠CBF+∠BCD =270°.【解答】解:过点B作BF∥AE,如图:∵CD∥AE,∴BF∥CD,∴∠BCD+∠CBF=180°,∵AB⊥AE,∴AB⊥BF,∴∠ABF=90°,∴∠ABC+∠BCD=∠ABF+∠CBF+∠BCD=90°+180°=270°.故答案为:270°.【点评】本题主要考查了平行线的性质,正确作出辅助线,并熟记两直线平行,同旁内角互补是解决问题的关键.7.(2023秋•鼓楼区校级期末)如图是路灯维护工程车的工作示意图,工作篮底部与支撑平台平行.若∠1=30°,则∠2+∠3的度数为.【分析】过∠2顶点做直线l∥支撑平台,直线l将∠2分成两个角,根据平行的性质即可求解.【解答】解:过∠2顶点做直线l∥支撑平台,∴l∥支撑平台∥工作篮底部,∴∠1=∠4=30°、∠5+∠3=180°,∴∠4+∠5+∠3=30°+180°=210°,∵∠4+∠5=∠2,∴∠2+∠3=210°.故答案为:210°.【点评】本题考查平行线的性质,熟练掌握平行线的性质是解题的关键.8.某兴趣小组利用几何图形画出螳螂的简笔画,如图,已知∠BAC=130°,AB∥DE,∠D=70°,则∠ACD=.【分析】过点C作CF∥AB,先证明CF∥DE,然后根据平行线的性质求出∠ACF=130°,∠DCF=110°,最后利用角的和差关系求解即可.【解答】解:过点C作CF∥AB,∵AB∥DE,∴CF∥DE,∴∠ACF=∠BAC,∠D+∠DCF=180°,又∠BAC=130°,∠D=70°,∴∠ACF=130°,∠DCF=110°,∴∠ACD=∠ACF﹣∠DCF=20°.故答案为:20°.【点评】本题考查了平行线的判定与性质,添加合适的辅助线是解题的关键.9.乐乐观察“抖空竹”时发现,可以将某一时刻的情形抽象成数学问题:如图,已知AB∥CD,∠BAE=92°,∠DCE=121°,则∠AEC的度数是()A.30°B.29°C.28°D.27°【分析】延长DC交AE于F,依据AB∥CD,∠BAE=92°,可得∠CFE=92°,再根据三角形外角性质,即可得到∠AEC=∠DCE﹣∠CFE.【解答】解:如图,延长DC交AE于F,∵AB∥CD,∠BAE=92°,∴∠CFE=92°,又∵∠DCE=121°,∴∠AEC=∠DCE﹣∠CFE=121°﹣92°=29°.故选:B.【点评】本题主要考查了平行线的性质,解决问题的关键是掌握:两直线平行,同位角相等.10.(2023秋•鹰潭期末)生活现象如图1,杆秤是中国最古老也是现今人们仍然在使用的衡量工具,是利用杠杆原理来称质量的简易衡器,由木制的带有秤星的秤杆、金属秤砣、提绳等组成.数学模型如图2,是杆秤的示意图,AC∥BD,经测量发现∠A=104°,∠BOE=76°,请判断OE与BD的位置关系,并说明理由.【分析】由AC∥BD可得∠A+∠ABD=180°,进而得出∠ABD=76°,再根据内错角相等,两直线平行可得答案.【解答】解:OE∥BD,理由如下:∵AC∥BD,∴∠A+∠ABD=180°,∴∠ABD=180°﹣104°=76°,∴∠ABD=∠BOE,∴OE∥BD.【点评】本题考查了平行线的判定和性质,熟练掌握这些判定和性质解题的关键.11.如图所示①是一种网红弹弓的示意图,在两头系上皮筋,拉动皮筋可形成如图②所示的平面示意图,弹弓的两边可看成平行的,即AB∥CD.活动小组在探索∠APD与∠A,∠D的数量关系时,有如下发现:当拉起皮筋使∠A=∠D时,瞄准最准确.现测得∠A=160°,∠APD=40°,判断此时瞄准是否最准确,请说明理由.【分析】如图所示,过点P作PQ∥AB,利用平行线的性质得到∠APQ=180°﹣∠A=20°,∠D=180°﹣∠DPQ,在求出∠DPQ的度数即可得到答案.【解答】解:此时瞄准最准确.如图所示,过点P作PQ∥AB,∵AB∥CD,∴AB∥PQ∥CD,∴∠APQ=180°﹣∠A=20°,∠D=180°﹣∠DPQ,∵∠APD=40°,∴∠DPQ=∠APD﹣∠APQ=20°∴∠D=160°,此时瞄准最准确.【点评】本题主要考查了平行线的性质,正确作出辅助线是解题的关键.1.(2023秋•天元区期末)如图,把一张长方形纸片ABCD沿EF折叠后,D、C分别在M、N的位置上,EM与BC的交点为G,若∠EFC=125°,则∠1=()A.35°B.55°C.70°D.65°【分析】根据两直线平行,同旁内角互补可得∠DEF+∠EFC=180°,再根据翻折的性质和平角的定义列式计算,即可求出∠1.【解答】解:∵长方形对边AD∥BC,∴∠DEF+∠EFC=180°,∴∠DEF=180°﹣∠EFC=180°﹣125°=55°,由翻折的性质得:∠DEF=∠MEF=55°,∴∠1=180°﹣55°×2=70°,故选:C.【点评】本题主要考查平行线的性质,折叠的性质,熟练掌握平行线的性质和折叠的性质是解题的关键.2.如图,将长方形纸片ABCD折叠,使点D与点B重合,点C落在点C′处,折痕为EF,若∠ABE=30°,则∠EFC′的度数为()A.120°B.100°C.150°D.90°【分析】根据折叠的性质知∠BEF=∠DEF,而∠AEB的度数可在Rt△ABE中求得,根据平角定义可求出∠BED的度数,即得∠BEF的度数,再根据平行线的性质即可得解.【解答】解:Rt△ABE中,∠ABE=30°,∴∠AEB=60°,由折叠的性质知:∠BEF=∠DEF=12∠BED,∵∠BED=180°﹣∠AEB=120°,∴∠BEF=60°,∵BE∥C′F,∴∠BEF+∠EFC′=180°,∴∠EFC′=180°﹣∠BEF=120°.故选:A.【点评】本题考查平行线的性质,熟记折叠的性质及“两直线平行,同旁内角互补”是解题的关键.2.如图,把一张长方形纸片ABCD沿EF折叠后,点A落在CD边上的点A'处,点B落在点B'处,若∠1=115°,则图中∠2的度数为()A.40°B.45°C.50°D.60°【分析】由邻补角概念和翻折变换性质得出∠EFB′=∠1=115°,∠EFC=65°,据此知∠CFB′=50°,结合∠B=∠B′=90°知∠2=90°﹣∠CFB′,从而得出答案.【解答】解:∵∠1=115°,∴∠EFB′=∠1=115°,∠EFC=65°,∴∠CFB′=50°,又∵∠B=∠B′=90°,∴∠2=90°﹣∠CFB′=40°,故选:A.【点评】本题主要考查翻折变换的性质,解题的关键是掌握翻折变换的对应边、对应角相等的性质及直角三角形两锐角互余、对顶角相等的性质.3.(2022•南京模拟)如图,将一块长方形纸条折成如图的形状,若已知∠1=α,则∠2的度数为()A.90°﹣αB.45°+αC.45°+2D.90°−2【分析】根据平行线的性质即可求解.【解答】解:如图,作过点B的射线AF',∵AB∥CD,∴∠1+∠FBC+∠2=180°,∠F'BC=∠2∵纸条是对折,∴∠FBC=∠F'BC=∠2,∴2∠2+∠1=180°,∵∠1=α,∴∠2=12×(180°﹣α),∴∠2=90°−12α,故选:D.【点评】本题考查了平行线的性质,本题的解题关键找出是纸条对折后的角度关系.4.(2022秋•宛城区校级期末)如图,把一个长方形纸片沿OG折叠后,C,D两点分别落在C',D'两点处,若∠AOD':∠D'OG=4:3,则∠BGO=度.【分析】设∠AOD'=4x,则∠D'OG=3x,由翻折可知∠DOG=∠D'OG=3x,根据平角的定义解出x,由矩形的性质进而可以得出∠BGO的度数.【解答】解:∵∠AOD':∠D'OG=4:3,设∠AOD'=4x,则∠D'OG=3x,由翻折可知∠DOG=∠D'OG=3x∵∠AOD'+∠D'OG+∠DOG=180°,即10x=180°,解得x=18°,∵AD∥BC,∴∠BGO=∠DOG=3x=54°,故答案为:54.【点评】本题考查了折叠的性质和平角的等于180°,解题关键是发现图中折叠前后重合的角相等.5.(2023秋•北林区校级期末)将长方形ABCD纸片沿AE折叠得到如图所示的图形,已知∠CED′=68°,则∠EAB的度数是.【分析】由折叠可得∠DEA=∠D'EA,再由已知的条件可求得∠DEA的度数,从长方形可得AB∥CD,从而可求∠EAB的度数.【解答】解:由折叠得:∠DEA=∠D'EA,∵∠CED′=68°,∴∠DED'=180°﹣∠CED'=112°,∴∠DEA=12∠DED'=56°,∵四边形ABCD是长方形,∴AB∥CD,∴∠EAB=∠DEA=56°.故答案为:56°.【点评】本题主要考查平行线的性质,解答的关键是熟记平行线的性质:两直线平行,内错角相等.6.(2023秋•萍乡期末)如图,△ABC中,∠B=40°,点D为边BC上一点,将△ADC沿直线AD折叠后,点C落到点E处,若DE∥AB,则∠ADE的度数为°.【分析】根据平行线的性质得到∠BDE=∠B=40°,根据折叠的性质得到∠ADE=∠ADC,根据平角的定义可得∠ADB+∠ADC=180°,由此可以求出∠ADC的度数即可得到答案.【解答】解:∵DE∥AB,∠B=40°,∴∠BDE=40°,由折叠的性质得∠ADE=∠ADC,∵∠ADB+∠ADC=180°,∠ADB=∠ADE﹣∠BDE=∠ADC﹣40°,∴∠ADC﹣40°+∠ADC=180°,∴∠ADC=110°,∴∠ADE=∠ADC=110°.故答案为:110.【点评】本题考查了折叠的性质,平行线的性质,熟练掌握平行线的性质、折叠的性质是解题的关键.7.(2023秋•淮南期末)如图,在Rt△ABC中,∠C=90°,∠1=76°,D、E分别在AB、AC上,将△ADE沿DE折叠得△FDE,且满足EF∥AB,则∠B的度数为.【分析】由折叠的性质得∠FED=∠1,∠A=∠F,根据平角的定义求出∠FEC的度数,再根据平行线的性质求出∠F的度数,即可得出∠A的度数,从而求出∠B的度数.【解答】解:由折叠的性质得∠FED=∠1,∠A=∠F,∵∠1=76°,∴∠FED=76°,∴∠FEC=180°﹣∠FED﹣∠1=180°﹣76°﹣76°=28°,∵EF∥AB,∴∠F=∠FEC=28°,∴∠A=28°,∵∠C=90°,∴∠B=90°﹣∠A=90°﹣28°=62°,故答案为:62°.【点评】本题考查了平行线的性质,折叠的性质,平角的定义,三角形内角和定理,熟练掌握这些知识点是解题的关键.8.(2023秋•丹徒区期末)如图,长方形ABCD沿AE折叠,使D点落在BC边上的F点处,如果∠EFC =30°,则∠DAE等于.【分析】由长方形的性质得出∠D=90°,AD∥BC,再由折叠的性质得出∠DAE=∠FAE,∠AFE=∠D =90°,结合已知∠EFC=30°即可求出∠AFB的度数,从而求出∠DAE的度数.【解答】解:∵四边形ABCD为长方形,∴∠D=90°,AD∥BC,由折叠得,∠DAE=∠FAE,∠AFE=∠D=90°,∵∠EFC=30°,∴∠AFB=180°﹣∠AFE﹣∠EFC=180°﹣90°﹣30°=60°,∵AD∥BC,∴∠AFB=∠DAF,即60°=2∠DAE,∴∠DAE=30°,故答案为:30°.【点评】本题考查了平行线的性质,长方形的性质,折叠的性质,熟练掌握这些图形的性质是解题的关键.9.(2022•郑州模拟)如图,将一张长方形纸带沿EF折叠,点C、D的对应点分别为C'、D'.若∠DEF =α,用含α的式子可以将∠C'FG表示为()A.2αB.90°+αC.180°﹣αD.180°﹣2α【分析】由折叠的性质可得:∠DEG=2α,C'F∥D'E,由AD∥BC可得∠D'GF=∠DEG=2α,从而有∠C'FG=180°﹣∠D'GF,即可得出结果.【解答】解:由长方形纸带ABCD及折叠性质可得:∠D'EF=∠DEF=α,C'F∥D'E,∴∠DEG=2∠DEF=2α,∠C'FG=180°﹣∠D'GF,∵AD∥BC,∴∠D'GF=∠DEG=2α,∴∠C'FG=180°﹣2α.故选:D.【点评】本题主要考查平行线的性质,折叠的性质,解答的关键是熟记折叠的性质.10.(2023秋•泉州期末)如图,四边形ABCD是一条两边互相平行的纸带,将其沿着EG折叠,使得点B,C分别落在点H,I处,EH与DG相交于点F,若∠EGF=56°,求∠EFD的度数.【分析】利用平行线的性质可得∠BEG=∠EGD=56°,再利用折叠的性质可得:∠BEF=2∠BEG=112°,然后利用平行线的性质可得∠BEF=∠EFD=112°,即可解答.【解答】解:∵AB∥CD,∴∠BEG=∠EGD=56°,由折叠得:∠BEF=2∠BEG=112°,∵AB∥CD,∴∠BEF=∠EFD=112°,∴∠EFD的度数为112°.【点评】本题考查了平行线的性质,根据题目的已知条件并结合图形进行分析是解题的关键.11.在图中,图1是长方形纸带,将纸带沿EF折叠成图2,再沿BF折叠成图3.(1)若在图1中,∠DEF=20°,则图3中∠C2FE的度数是多少?(2)若∠DEF=α,请用α表示图3中的∠C2FE的度数.【分析】(1)根据两直线平行,同旁内角互补可得∠CFE=160°,根据两直线平行,内错角相等可得∠BFE=∠DEF,然后求出∠BFC1,再根据翻折的性质可得∠CFE=∠EFC1,∠C2FB+∠BFC1,即可得解;(2)同(1)的方法求解即可.【解答】解:(1)∵矩形对边AD∥BC,∴CF∥DE,∴∠CFE=180°﹣∠DEF=180°﹣20°=160°,∵AD∥BC,∴∠BFE=∠DEF=20°,由翻折的性质得,∠CFE=∠EFC1,∴∠BFC1=160°﹣20°=140°,由翻折的性质得,∠C2FB+∠BFC1,所以,∠C2FE=140°﹣20°=120°;(2)∵矩形对边AD∥BC,∴CF∥DE,∴∠CFE=180°﹣∠DEF=180°﹣α,∵AD∥BC,∴∠BFE=∠DEF=α,由翻折的性质得,∠CFE=∠EFC1,∴∠BFC1=180°﹣α﹣α=180°﹣2α,由翻折的性质得,∠C2FB+∠BFC1,所以,∠C2FE=180°﹣2α﹣α=180°﹣3α.【点评】本题考查了平行线的性质,翻折变换的性质,熟记各性质并准确识图,理清翻折前后重叠的角是解题的关键.12.(2022秋•东阳市期末)如图,长方形纸片ABCD中,G、H分别是AB、CD边上的动点,连GH,将长方形纸片ABCD沿着GH翻折,使得点B,C分别落在点E,F位置.(1)若∠BGH=110°,求∠AGE的度数.(2)若∠FHD=20°,求∠CHG的度数.(3)已知∠BGH和∠CHG始终互补,若∠BGH=α,请直接写出∠FHC的度数(含α的代数式).【分析】(1)根据折叠得到∠BGH=∠EGH=110°,再根据平角的定义,利用∠AGE=∠BGH+∠EGH ﹣180°计算可得;(2)根据折叠得到∠CHG=∠FHG,再根据平角的定义计算即可;(3)根据互补得到∠BGH+∠CHG=180°,从而求出∠CHG=∠FHG=180°﹣α,分情况继而可得结果.【解答】解:(1)由折叠可得:∠BGH=∠EGH=110°,∵∠BGH+∠AGH=180°,∴∠AGE=∠BGH+∠EGH﹣180°=40°;(2)由折叠可得:∠CHG=∠FHG,∴∠C=12(180°−∠Cp=80°;(3)情况一:∵∠BGH和∠CHG始终互补,∴∠BGH+∠CHG=180°,∵∠BGH=α,∴∠CHG=180°﹣α,∴∠FHG=180°﹣α,∴∠FHC=∠FHG+∠CHG=360°﹣2α.情况二:由第一种情况可知:∠1=360°﹣2α,∴∠FHC=360°﹣(360°﹣2α)=2α.【点评】本题考查了折叠的性质,平角的定义,解题的关键是掌握折叠前后对应角相等.。
七年级数学上册压轴题专题10 角度的计算

专题10 角度的计算(压轴题专项讲练)【典例1】如图,点O为直线AB上一点,∠BOC=40°,OD平分∠AOC.(1)求∠AOD的度数;∠COE,求∠COE的度数;(2)作射线OE,使∠BOE=23(3)在(2)的条件下,作∠FOH=90°,使射线OH在∠BOE的内部,若∠DOF=3∠BOH,求∠AOH的度数.【思路点拨】(1)根据平角定义和角平分线定义即可得结果;(2)根据题意分两种情况画图:∠如图1,当射线OE在AB上方时,∠如图2,当射线OE在AB下方时,∠COE,利用角的和差进行计算即可;∠BOE=23(3)根据题意分四种情况画图:∠如图3,当射线OE在AB上方,OF在AB上方时,作∠FOH=90°,使射线OH在∠BOE的内部,∠DOF=3∠BOH,∠如图4,当射线OE在AB上方,OF在AB下方时,∠如图5,当射线OE在AB下方,OF在AB上方时,∠如图6,当射线OE在AB下方,OF在AB下方时,利用角的和差进行计算即可.【解答过程】解:(1)∠∠BOC=40°,∠∠AOC=180°﹣∠BOC=140°,∠OD平分∠AOC,∠AOC=70°;∠∠AOD=12∠COE,(2)∠如图1,当射线OE在AB上方时,∠BOE=23∠∠BOE+∠COE=∠BOC,∠COE+∠COE=40°,∠23∠∠COE=24°;∠COE,∠如图2,当射线OE在AB下方时,∠BOE=23∠∠COE﹣∠BOE=∠BOC,∠∠COE−2∠COE=40°,3∠∠COE=120°;综上所述:∠COE的度数为24°或120°;(3)∠如图3,当射线OE在AB上方,OF在AB上方时,作∠FOH=90°,使射线OH在∠BOE的内部,∠DOF=3∠BOH,设∠BOH=x°,则∠DOF=3x°,∠FOC=∠COD﹣∠DOF=70°﹣3x°,∠∠AOH=∠AOD+∠DOF+∠FOH=70°+3x°+90°=160°+3x°,∠EOH=∠BOC﹣∠COE﹣∠BOH=40°﹣24°﹣x°=16°﹣x°,∠∠FOH=∠FOC+∠COE+∠EOH=70°﹣3x°+24°+16°﹣x°=90°,∠x°=5°,∠∠AOH=160°+3x°=175°;∠如图4,当射线OE在AB上方,OF在AB下方时,∠∠AOF=∠DOF﹣∠AOD=3x°﹣70°,∠BOF=∠FOH﹣∠BOH=90°﹣x°,∠AOF+∠BOF=180°,∠3x°﹣70°+90°﹣x°=180°,解得x°=80°,∠∠COB=40°,∠80°>40°,∠x°=80°不符合题意舍去;∠如图5,当射线OE在AB下方,OF在AB上方时,∠∠AOF=∠DOF+∠AOD=3x°+70°,∠BOF=∠FOH﹣∠BOH=90°﹣x°,∠AOF+∠BOF=180°,∠3x°+70°+90°﹣x°=180°,解得x°=10°,∠∠AOH=180°﹣∠BOH=180°﹣x°=170°;∠如图6,当射线OE在AB下方,OF在AB下方时,∠∠AOF=∠DOF﹣∠AOD=3x°﹣70°,∠BOF=∠FOH+∠BOH=90°+x°,∠AOF+∠BOF=180°,∠3x°﹣70°+90°+x°=180°,解得x°=40°,∠∠AOH=∠AOF+∠FOH=50°+90°=140°.综上所述:∠AOH的度数为175°或170°或140°.1.如图所示,能用∠α,∠AOB,∠O表示同一个角的是()A.B.C.D.2.如图所示,AOB是直线,图中小于180°的角共有()A.7个B.9个C.8个D.10个3.(2020秋•锦江区校级期末)杨老师到几何王国去散步,刚走到“角”的家门,就听到∠A、∠B、∠C在吵架,∠A说:“我是48°15′,我应该最大!”∠B说:“我是48.3°,我应该最大!”.∠C也不甘示弱:“我是48.15°,我应该和∠A一样大!”听到这里,杨老师对它们说:“别吵了,你们谁大谁小,由我来作评判!”,杨老师评判的结果是()A.∠A最大B.∠B最大C.∠C最大D.∠A=∠C4.(2020秋•含山县期末)如图,已知点A在点O的北偏东42°40′方向上,点B在点O的正南方向,OE平分∠AOB,则E点相对于点O的方位可表示为()A.南偏东68°40′方向B.南偏东69°40′方向C.南偏东68°20′方向D.南偏东69°10′方向5.(2020秋•宁波期末)如图,点O在直线AB上,∠COB=∠EOD=90°,那么下列说法错误的是()A.∠1与∠2相等B.∠AOE与∠2互余C.∠AOD与∠1互补D.∠AOE与∠COD互余6.(2020秋•成华区期末)亲爱的同学,现在是北京时间下午2:47,按正常做题速度,你应该做到此题了,此时钟表上的时针和分针的夹角度数是.7.(2020秋•皇姑区期末)看下面小明和小丽的对话:小明:“我今天12点10分到达图书馆时,你已经开始看书了,你是什么时间到的呢?小丽:“我11点30分从家出发,到达图书馆时,钟表的时针与分针的夹角恰好是11°.”回答问题:小丽从家到图书馆共用了分钟.8.(2020秋•桥东区校级期中)观察下图,回答下列问题:(1)在图∠中有几个角?(2)在图∠中有几个角?(3)在图∠中有几个角?(4)以此类推,如图∠所示,若一个角内有n条射线,此时共有多少个角?9.(2020秋•兴业县期末)如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.(1)若∠BOC=70°,求∠COD和∠EOC的度数;(2)写出∠COD与∠EOC具有的数量关系并说明理由.10.(2020秋•江北区期末)将一副三角板叠放在一起,使直角顶点重合于点O.(1)如图1,若∠AOD=35°,求∠BOC的度数.(2)若三角板AOB保持不动,将三角板COD的边OD与边OA重合,然后将其绕点O旋转.试猜想在旋转过程中,∠AOC与∠BOD有何数量关系?请说明理由.11.(2020秋•铁西区期末)(1)如图1所示,已知∠AOC=90°,∠AOB=38°,OD平分∠BOC,请判断∠AOD 和∠BOD之间的数量关系,并说明理由;(2)已知:如图2,点O在直线AD上,射线OC平分∠BOD.求证:∠AOC与∠BOC互补;(3)已知∠EPQ和∠FPQ互余,射线PM平分∠EPQ,射线PN平分∠FPQ.若∠EPQ=β(0°<β<90°),直接写出锐角∠MPN的度数是.12.(2021春•乳山市期末)【问题回顾】我们曾解决过这样的问题:如图1,点O在直线AB上,OC,OD分别平分∠AOE,∠BOE,可求得∠COD=90°.(不用求解)【问题改编】点O在直线AB上,∠COD=90°,OE平分∠BOC.(1)如图2,若∠AOC=50°,求∠DOE的度数;(2)将图2中的∠COD按图3所示的位置进行放置,写出∠AOC与∠DOE度数间的等量关系,并写明理由.13.(2020秋•温江区校级期末)已知∠AOB=60°,求:(1)如图1,OC为∠AOB内部任意一条射线,OM平分∠AOC,ON平分∠BOC,求∠MON=;(2)如图2,当OC旋转到∠AOB的外部时,∠MON的度数会发生变化吗?请说明原因;(3)如图3,当OC旋转到∠AOB(∠BOC<120°)的外部且射线OC在OB的下方时,OM平分∠AOC,射线ON在∠BOC内部,∠NOC=14∠BOC,求∠COM−23∠BON的值?14.(2020秋•南宁期末)如图,已知∠AOB=120°,OC是∠AOB内的一条射线,且∠AOC:∠BOC=1:2.(1)求∠AOC,∠BOC的度数;(2)作射线OM平分∠AOC,在∠BOC内作射线ON,使得∠CON:∠BON=1:3,求∠MON的度数;(3)过点O作射线OD,若2∠AOD=3∠BOD,求∠COD的度数.15.(2020秋•城厢区期末)已知∠AOB和∠COD是直角.(1)如图1,当射线OB在∠COD的内部时,请探究∠AOD和∠BOC之间的关系,并说明理由.∠BOC,∠DOF=(2)如图2,当射线OA,OB都在∠COD的外部时,过点O作射线OE,OF,满足∠BOE=143∠AOD,求∠EOF的度数.4(3)在(2)的条件下,在平面内是否存在射线OG,使得∠GOF:∠GOE=3:7?若存在,求出∠GOF的度数;若不存在,请说明理由.16.(2020秋•镇海区期末)新定义问题如图∠,已知∠AOB,在∠AOB内部画射线OC,得到三个角,分别为∠AOC、∠BOC、∠AOB.若这三个角中有一个角是另外一个角的2倍,则称射线OC为∠AOB的“幸运线”.(本题中所研究的角都是大于0°而小于180°的角.)【阅读理解】(1)角的平分线这个角的“幸运线”;(填“是”或“不是”)【初步应用】(2)如图∠,∠AOB=45°,射线OC为∠AOB的“幸运线”,则∠AOC的度数为;【解决问题】(3)如图∠,已知∠AOB=60°,射线OM从OA出发,以每秒20°的速度绕O点逆时针旋转,同时,射线ON从OB出发,以每秒15°的速度绕O点逆时针旋转,设运动的时间为t秒(0<t<9).若OM、ON、OA 三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的t值.17.(2020秋•和平区期末)如图,点O是直线AB上的一点,∠COD=80°,OE平分∠BOC.(1)如图1,若∠AOC=40°,求∠DOE的度数.(2)在图1中若∠AOC=α(其中20°<α<100°),请直接用含α的代数式表示∠DOE的度数,不用说明理由.(3)如图2,∠请直接写出∠AOC和∠DOE的度数之间的关系,不用说明理由.∠在∠AOC的内部有一条射线OF,满足∠AOC﹣4∠AOF=2∠BOE+∠AOF.试确定∠AOF与∠DOE的度数之间的关系,直接写出关系式即可,不用说明理由.18.(2020秋•越秀区校级月考)如图1,已知∠AOB =120°,∠COD =60°,OM 在∠AOC 内,ON 在∠BOD 内,∠AOM =13∠AOC ,∠BON =13∠BOD .(本题中所有角均大于0°且小于等于180°) (1)∠COD 从图1中的位置绕点O 逆时针旋转到OC 与OB 重合时,如图2,则∠MON = °;(2)∠COD 从图2中的位置绕点O 逆时针旋转n°(0<n <120且n≠60),求∠MON 的度数;(3)∠COD 从图2中的位置绕点O 顺时针旋转n°(0<n <180且n≠60a ,其中a 为正整数),直接写出所有使∠MON =2∠BOC 的n 值.19.(2020秋•渝中区校级期末)如图1,∠AOB=40°,∠COD=60°,OM、ON分别为∠AOB和∠BOD的角平分线.(1)若∠MON=70°,则∠BOC=°;(2)如图2,∠COD从第(1)问中的位置出发,绕点O逆时针以每秒4°的速度旋转;当OC与OA重合时,∠COD立即反向绕点O顺时针以每秒6°的速度旋转,直到OC与OA互为反向延长线时停止运动.整个运动过程中,∠COD的大小不变,OC旋转后的对应射线记为OC′,OD旋转后的对应射线记为OD′,∠BOD′的角平分线记为ON′,∠AOD′的角平分线记为OP.设运动时间为t秒.∠当OC′平分∠BON′时,求出对应的t的值;∠请问在整个运动过程中,是否存在某个时间段使得|∠BOP﹣∠MON′|的值不变?若存在,请直接写出这个定值及其对应的t的取值范围(包含运动的起止时间);若不存在,请说明理由.20.(2020秋•江岸区期末)已知如图1,线段∠AOB=40°.∠BOC,则∠BOC=;(1)若∠AOC=13(2)如图2,∠AOC=20°,OM为∠AOB内部的一条直线,ON是∠MOC四等分线,且3∠CON=∠NOM,求4∠AON+∠COM的值;(3)如图3,∠AOC=20°,射线OM绕着O点从OB开始以5度/秒的速度逆时针旋转一周至OB结束,在旋转过程中,设运动的时间为t,ON是∠MOC四等分线,且3∠CON=∠NOM,当t在某个范围内4∠AON+∠BOM会为定值,请直接写出定值,并指出对应t的范围(本题中的角均为大于0°且小于180°的角).专题10 角度的计算(压轴题专项讲练)【典例1】如图,点O为直线AB上一点,∠BOC=40°,OD平分∠AOC.(1)求∠AOD的度数;∠COE,求∠COE的度数;(2)作射线OE,使∠BOE=23(3)在(2)的条件下,作∠FOH=90°,使射线OH在∠BOE的内部,若∠DOF=3∠BOH,求∠AOH的度数.【思路点拨】(1)根据平角定义和角平分线定义即可得结果;(2)根据题意分两种情况画图:∠如图1,当射线OE在AB上方时,∠如图2,当射线OE在AB下方时,∠COE,利用角的和差进行计算即可;∠BOE=23(3)根据题意分四种情况画图:∠如图3,当射线OE在AB上方,OF在AB上方时,作∠FOH=90°,使射线OH在∠BOE的内部,∠DOF=3∠BOH,∠如图4,当射线OE在AB上方,OF在AB下方时,∠如图5,当射线OE在AB下方,OF在AB上方时,∠如图6,当射线OE在AB下方,OF在AB下方时,利用角的和差进行计算即可.【解答过程】解:(1)∠∠BOC=40°,∠∠AOC=180°﹣∠BOC=140°,∠OD平分∠AOC,∠AOC=70°;∠∠AOD=12∠COE,(2)∠如图1,当射线OE在AB上方时,∠BOE=23∠∠BOE+∠COE=∠BOC,∠COE+∠COE=40°,∠23∠∠COE=24°;∠COE,∠如图2,当射线OE在AB下方时,∠BOE=23∠∠COE﹣∠BOE=∠BOC,∠∠COE−2∠COE=40°,3∠∠COE=120°;综上所述:∠COE的度数为24°或120°;(3)∠如图3,当射线OE在AB上方,OF在AB上方时,作∠FOH=90°,使射线OH在∠BOE的内部,∠DOF=3∠BOH,设∠BOH=x°,则∠DOF=3x°,∠FOC=∠COD﹣∠DOF=70°﹣3x°,∠∠AOH=∠AOD+∠DOF+∠FOH=70°+3x°+90°=160°+3x°,∠EOH=∠BOC﹣∠COE﹣∠BOH=40°﹣24°﹣x°=16°﹣x°,∠∠FOH=∠FOC+∠COE+∠EOH=70°﹣3x°+24°+16°﹣x°=90°,∠x°=5°,∠∠AOH=160°+3x°=175°;∠如图4,当射线OE在AB上方,OF在AB下方时,∠∠AOF=∠DOF﹣∠AOD=3x°﹣70°,∠BOF=∠FOH﹣∠BOH=90°﹣x°,∠AOF+∠BOF=180°,∠3x°﹣70°+90°﹣x°=180°,解得x°=80°,∠∠COB=40°,∠80°>40°,∠x°=80°不符合题意舍去;∠如图5,当射线OE在AB下方,OF在AB上方时,∠∠AOF=∠DOF+∠AOD=3x°+70°,∠BOF=∠FOH﹣∠BOH=90°﹣x°,∠AOF+∠BOF=180°,∠3x°+70°+90°﹣x°=180°,解得x°=10°,∠∠AOH=180°﹣∠BOH=180°﹣x°=170°;∠如图6,当射线OE在AB下方,OF在AB下方时,∠∠AOF=∠DOF﹣∠AOD=3x°﹣70°,∠BOF=∠FOH+∠BOH=90°+x°,∠AOF+∠BOF=180°,∠3x°﹣70°+90°+x°=180°,解得x°=40°,∠∠AOH=∠AOF+∠FOH=50°+90°=140°.综上所述:∠AOH的度数为175°或170°或140°.1.如图所示,能用∠α,∠AOB,∠O表示同一个角的是()A.B.C.D.【思路点拨】角可以用一个大写字母表示,也可以用三个大写字母表示.角还可以用一个希腊字母表示,或用阿拉伯数字表示.【解答过程】解:能用∠α,∠AOB,∠O三种方法表示同一个角的图形是选项D中的图,选项B,C,D中的图都不能用∠α,∠AOB,∠O三种方法表示同一个角的图形,故选:D.2.如图所示,AOB是直线,图中小于180°的角共有()A.7个B.9个C.8个D.10个【思路点拨】按一定的规律数即可.【解答过程】解:有两种方法:(1)先数出以OA为一边的角,再数出以OB、OC、OD、OE为一边的角,把他们加起来.(2)可根据公式:n(n−1)来计算,其中,n指从点O发出的射线的条数.2图中角共有4+3+2+1=10个,根据题意要去掉平角,所以图中小于180°的角共有10﹣1=9个.故选:B.3.(2020秋•锦江区校级期末)杨老师到几何王国去散步,刚走到“角”的家门,就听到∠A、∠B、∠C在吵架,∠A说:“我是48°15′,我应该最大!”∠B说:“我是48.3°,我应该最大!”.∠C也不甘示弱:“我是48.15°,我应该和∠A一样大!”听到这里,杨老师对它们说:“别吵了,你们谁大谁小,由我来作评判!”,杨老师评判的结果是()A.∠A最大B.∠B最大C.∠C最大D.∠A=∠C【思路点拨】根据度、分、秒的换算1度=60分,即1°=60′,1分=60秒,即1′=60″.将48°15′,48.3°,48.15°的单位统一,再进行大小的比较.【解答过程】)°=48.25°,∠B=48.3°,∠C=48.15°,解:∠∠A=48°15′=48°+(1560∠∠B>∠A>∠C,即∠B最大,故选:B.4.(2020秋•含山县期末)如图,已知点A在点O的北偏东42°40′方向上,点B在点O的正南方向,OE平分∠AOB,则E点相对于点O的方位可表示为()A.南偏东68°40′方向B.南偏东69°40′方向C.南偏东68°20′方向D.南偏东69°10′方向【思路点拨】根据方向角的定义以及角的和差,可得∠BOE的度数.【解答过程】解:∠点A在点O的北偏东42°40′方向上,点B在点O的正南方向,∠∠AOB=90°+(90°﹣42°40′)=137°20′,∠OE平分∠AOB,∠∠BOE=12∠AOB=12×137°20′=68°40′,∠E点相对于点O的方位为:南偏东68°40′方向,故选:A.5.(2020秋•宁波期末)如图,点O在直线AB上,∠COB=∠EOD=90°,那么下列说法错误的是()A.∠1与∠2相等B.∠AOE与∠2互余C.∠AOD与∠1互补D.∠AOE与∠COD互余【思路点拨】根据余角和补角的定义逐一判断即可得.【解答过程】解:∠∠COB=∠EOD=90°,∠∠1+∠COD=∠2+∠COD=90°,∠∠1=∠2,故A选项正确;∠∠AOE+∠1=90°,∠∠AOE+∠2=90°,即∠AOE与∠2互余,故B选项正确;∠∠COB=90°,∠∠AOD+∠2=180°,∠∠1=∠2,∠∠AOD+∠1=180°,即∠AOD与∠1互补,故C选项正确;无法判断∠AOE与∠COD是否互余,D选项错误;故选:D.6.(2020秋•成华区期末)亲爱的同学,现在是北京时间下午2:47,按正常做题速度,你应该做到此题了,此时钟表上的时针和分针的夹角度数是.【思路点拨】根据时针每分钟转0.5度,分针每分钟转6度计算即可.【解答过程】解:下午2:47钟表上的时针和分针的夹角度数是360°﹣[47×6°﹣(60°+47×0.5°)]=161.5°,故答案为161.5°.7.(2020秋•皇姑区期末)看下面小明和小丽的对话:小明:“我今天12点10分到达图书馆时,你已经开始看书了,你是什么时间到的呢?小丽:“我11点30分从家出发,到达图书馆时,钟表的时针与分针的夹角恰好是11°.”回答问题:小丽从家到图书馆共用了分钟.【思路点拨】11点30分时,时针与分针的夹角为165°,分针每分钟转过6°,而时针每分钟转过0.5°,此问题可以转化为追及问题,当分针从与时针的夹角为165°减少到还有11°时所用的时间,以及超过时针11°时所用的时间,设未知数,列方程解答即可,同时注意分钟在时针前11°和在时针后11°两种情况.【解答过程】解:11点30分时,时针与分针的夹角为165°,由钟表时针、分针的旋转规律得,分针每分钟转过6°,而时针每分钟转过0.5°,设小丽从家出发用x分钟到达图书馆,由题意得:(6°﹣0.5°)x=165°﹣11°或(6°﹣0.5°)x=165°+11°,解得:x=28或x=32,经检验,28分,32分钟均符合题意,故答案为:28或32.8.(2020秋•桥东区校级期中)观察下图,回答下列问题:(1)在图∠中有几个角?(2)在图∠中有几个角?(3)在图∠中有几个角?(4)以此类推,如图∠所示,若一个角内有n条射线,此时共有多少个角?【思路点拨】解答此题首先要弄清楚题目的规律:当角内有n条射线时,每条射线都与(n﹣1)条射线构成了(n﹣1)个角,则共有n(n﹣1)个角,由于两条射线构成一个角,因此角的总数为:n(n−1),可根据这个规律,直接求2出(1)(2)(3)的结论;在解答(4)题时,首先要弄清图中共有多少条射线,已知角内共n条射线,那么图中共有(n+2)条射线,代入上面的规律,即可得到所求的结论.【解答过程】解:由分析知:=1(个);(1)∠图中有2条射线,则角的个数为:2×(2−1)2=3(个);(2)∠图中有3条射线,则角的个数为:3×(3−1)2=6(个);(3)∠图中有4条射线,则角的个数为:4×(4−1)2(4)由前三问类推,角内有n条射线时,图中共有(n+2)条射线,则角的个数为(n+1)(n+2)个.29.(2020秋•兴业县期末)如图,O是直线AB上一点,OC为任一条射线,OD平分∠BOC,OE平分∠AOC.(1)若∠BOC=70°,求∠COD和∠EOC的度数;(2)写出∠COD 与∠EOC 具有的数量关系并说明理由.【思路点拨】(1)根据角平分线的定义求出∠COD 的度数即可,先求出∠AOC 的度数,再根据角平分线的定义解答; (3)根据角平分线的定义表示出∠COD 与∠EOC ,然后整理即可得解. 【解答过程】解:(1)∠OD 平分∠BOC ,∠BOC =70°, ∠∠COD =12∠BOC =12×70°=35°, ∠∠BOC =70°,∠∠AOC =180°﹣∠BOC =180°﹣70°=110°, ∠OE 平分∠AOC ,∠∠EOC =12∠AOC =12×110°=55°; (2)∠COD 与∠EOC 互余,理由如下:∠OD 平分∠BOC ,OE 平分∠AOC , ∠∠COD =12∠BOC ,∠EOC =12∠AOC ,∠∠COD+∠EOC =12(∠BOC+∠AOC )=12×180°=90°, ∠∠COD 与∠EOC 互余.10.(2020秋•江北区期末)将一副三角板叠放在一起,使直角顶点重合于点O . (1)如图1,若∠AOD =35°,求∠BOC 的度数.(2)若三角板AOB 保持不动,将三角板COD 的边OD 与边OA 重合,然后将其绕点O 旋转.试猜想在旋转过程中,∠AOC 与∠BOD 有何数量关系?请说明理由.【思路点拨】(1)由于是两直角三角形板重叠,根据∠AOD的度数可得∠BOD,再根据∠DOC=90°可得∠BOC;(2)当分两种情况:∠AOB与∠DOC有重叠部分时和当∠AOB与∠DOC没有重叠部分时.【解答过程】解:(1)若∠AOD=35°,∠∠AOB=∠COD=90°,∠∠BOD=90°﹣35°=55°,∠∠BOC=90°﹣∠BOD=90°﹣55°=35°;(2)∠AOC与∠BOD互补.当∠AOB与∠DOC有重叠部分时,∠∠AOB=∠COD=90°,∠∠AOD+∠BOD+∠BOD+∠BOC=180°.∠∠AOD+∠BOD+∠BOC=∠AOC,∠∠AOC+∠BOD=180°,当∠AOB与∠DOC没有重叠部分时,∠AOB+∠COD+∠AOC+∠BOD=360°,又∠∠AOC=∠BOD=90°,∠∠AOB+∠DOC=180°.11.(2020秋•铁西区期末)(1)如图1所示,已知∠AOC=90°,∠AOB=38°,OD平分∠BOC,请判断∠AOD 和∠BOD之间的数量关系,并说明理由;(2)已知:如图2,点O在直线AD上,射线OC平分∠BOD.求证:∠AOC与∠BOC互补;(3)已知∠EPQ和∠FPQ互余,射线PM平分∠EPQ,射线PN平分∠FPQ.若∠EPQ=β(0°<β<90°),直接写出锐角∠MPN的度数是.【思路点拨】(1)根据角的计算,可求解∠BOC的度数,结合角平分线的定义求解∠BOD的度数,进而可求解∠AOD的度数,利用∠AOD+∠BOC的度数;(2)由角平分线的定义可得∠BOC=∠COD,利用补角的定义可证明结论;∠EPF,利用∠EPQ和∠FPQ互余可求解∠EPF (3)先根据题意画出图形,由考角平分线的定义可得∠MON=12=90°,进而可求解.【解答过程】解:(1)∠AOD+∠BOD=90°,理由如下:∠∠AOC=90°,∠AOB=38°,∠∠BOC=∠AOC﹣∠AOB=90°﹣38°=52°,∠OD平分∠BOC,∠BOC=26°,∠∠BOD=12∠∠AOD=∠AOB+∠BOD=38°+26°=64°,∠∠AOD+∠BOC=64°+26°=90°.(2)∠OC平分∠BOD,∠∠BOC=∠COD,∠∠AOC+∠COD=180°,∠∠AOC+∠BOC=180°,即∠AOC与∠BOC互补;(3)如图,∠PM平分∠EPQ,PN平分∠FPQ,∠∠MPQ=12∠EPQ,∠NPQ=12∠FPQ,∠∠MON=∠MPQ+∠NPQ=12∠EPQ+12∠FPQ=12∠EPF,∠∠EPQ和∠FPQ互余,∠∠EPQ+∠FPQ=90°,即∠EPF=90°,∠∠MON=45°,故答案为45°.12.(2021春•乳山市期末)【问题回顾】我们曾解决过这样的问题:如图1,点O在直线AB上,OC,OD分别平分∠AOE,∠BOE,可求得∠COD=90°.(不用求解)【问题改编】点O在直线AB上,∠COD=90°,OE平分∠BOC.(1)如图2,若∠AOC=50°,求∠DOE的度数;(2)将图2中的∠COD按图3所示的位置进行放置,写出∠AOC与∠DOE度数间的等量关系,并写明理由.【思路点拨】(1)先求∠COB,利用角平分线定义再求∠COE,最终求∠DOE的度数;(2)设∠AOC=α,再根据(1)的求解过程,用含α的式子表示两个角的数量关系.【解答过程】解:(1)∠∠COD=90°,∠∠AOC+∠BOD=90°.∠∠AOC=50°,∠∠BOD=40°.∠∠COB=∠COD+∠BOD=90°+40°=130°.∠OE平分∠BOC,∠∠COE=12∠BOC=12×130°=65°.∠∠DOE=∠COD﹣∠COE=90°﹣65°=25°.(2)设∠AOC=α.则∠BOC=180°﹣α.∠OE平分∠BOC,∠∠BOE=12∠BOC=12(180−α)=90°−12α.∠∠BOD=∠COD﹣∠BOC=90°﹣(180°﹣α)=α﹣90°,∠∠DOE=∠DOB+∠BOE=α−90°+90°−12α=12α..∠按图3所示的位置放置时,∠AOC与∠DOE度数间的等量关系为:∠DOE=12∠AOC.13.(2020秋•温江区校级期末)已知∠AOB=60°,求:(1)如图1,OC 为∠AOB 内部任意一条射线,OM 平分∠AOC ,ON 平分∠BOC ,求∠MON = ; (2)如图2,当OC 旋转到∠AOB 的外部时,∠MON 的度数会发生变化吗?请说明原因;(3)如图3,当OC 旋转到∠AOB (∠BOC <120°)的外部且射线OC 在OB 的下方时,OM 平分∠AOC ,射线ON 在∠BOC 内部,∠NOC =14∠BOC ,求∠COM −23∠BON 的值? 【思路点拨】(1)先利用角平分线的性质得到∠MOC =12∠AOC ,∠NOC =12∠BOC ,再利用∠MON =∠COM+∠CON 计算; (2)根据角平分线的性质并结合∠MON =∠COM ﹣∠CON 解答即可;(3)根据题意得到∠COM =12∠AOC ,∠BON =34∠BOC ,再利用∠COM −23∠BON 计算,即可解答. 【解答过程】解:(1)∠OM 平分∠AOC ,ON 平分∠BOC ,∠AOB =60°, ∠∠MOC =12∠AOC , ∠∠NOC =12∠BOC ,∠∠MON =∠MOC+∠NOC =12∠BOC +12∠AOC =12∠AOB =12×60°=30°. 故答案为:30°; (2)不变,当OC 旋转到∠AOB 的外部时,∠OM 平分∠AOC ,ON 平分∠BOC ,∠AOB =60°, ∠∠MOC =12∠AOC ,∠∠NOC =12∠BOC ,∠∠MON =∠MOC ﹣∠NOC =12∠BOC −12∠AOC =12∠AOB =12×60°=30°. ∠∠MON 的度数不会发生变化;(3)当OC 旋转到∠AOB (∠BOC <120°)的外部且射线OC 在OB 的下方时, ∠OM 平分∠AOC ,∠NOC =14∠BOC , ∠∠COM =12∠AOC ,∠BON =34∠BOC ,∠∠COM −23∠BON =12∠AOC −23×34∠BOC =12∠BOC −12∠AOC =12∠AOB =30°.14.(2020秋•南宁期末)如图,已知∠AOB =120°,OC 是∠AOB 内的一条射线,且∠AOC :∠BOC =1:2.(1)求∠AOC ,∠BOC 的度数;(2)作射线OM 平分∠AOC ,在∠BOC 内作射线ON ,使得∠CON :∠BON =1:3,求∠MON 的度数;(3)过点O 作射线OD ,若2∠AOD =3∠BOD ,求∠COD 的度数.【思路点拨】(1)根据∠AOC :∠BOC =1:2,即可求解;(2)先求出∠COM ,再求出∠CON ,相加即可求解;(3)分OD 在∠AOB 内部和外部两种情况分类讨论即可求解.【解答过程】解:(1)∠∠AOC :∠BOC =1:2,∠AOB =120°,∠∠AOC =13∠AOB =13×120°=40°,∠BOC =23∠AOB =23×120°=80°; (2)∠OM 平分∠AOC ,∠∠COM =12∠AOC =12×40°=20°,∠∠CON :∠BON =1:3,∠∠CON =14∠BOC =14×80°=20°,∠∠MON =∠COM+∠CON =20°+20°=40°;(3)如图,当OD 在∠AOB 内部时,设∠BOD=x°,∠2∠AOD=3∠BOD,x°,∠∠AOD=32∠∠AOB=120°,x=120,∠x+32解得:x=48,∠∠BOD=48°,∠∠COD=∠BOC﹣∠BOD=80°﹣48°=32°,如图,当OD在∠AOB外部时,设∠BOD=y°,∠2∠AOD=3∠BOD,y°,∠∠AOD=32∠∠AOB=120°,y﹣y=120,∠32解得:y=240,∠∠BOD=240°,此时∠COD=320°,综上所述,∠COD的度数为32°或320°.15.(2020秋•城厢区期末)已知∠AOB和∠COD是直角.(1)如图1,当射线OB在∠COD的内部时,请探究∠AOD和∠BOC之间的关系,并说明理由.∠BOC,∠DOF=(2)如图2,当射线OA,OB都在∠COD的外部时,过点O作射线OE,OF,满足∠BOE=143∠AOD,求∠EOF的度数.4(3)在(2)的条件下,在平面内是否存在射线OG,使得∠GOF:∠GOE=3:7?若存在,求出∠GOF的度数;若不存在,请说明理由.【思路点拨】(1)根据已知条件,∠AOB和∠COD是直角,可得出∠BOD和∠AOC与∠BOC的关系式,再根据∠AOC 与∠AOB和∠BOD列出等量关系,即可得出答案;∠BOC,可设∠BOE=a,则∠BOC=4a,再根据周角的关系可得到∠AOD的等(2)根据已知条件∠BOE=14∠AOD,可得到∠AOF的等量关系式,由∠BOE、∠AOB和∠AOF可列出等量关量关系,再根据∠DOF=34系,即可得到答案;(3)分两种情况,∠当射线OG在∠EOF内部时,由∠GOF:∠GOE=3:7,可得出结果,当射线OG在∠EOF外部时,由∠GOF:∠GOE=3:7,可得出结果.【解答过程】(1)∠AOD+∠BOC=180°.证明:∠∠AOB和∠COD是直角,∠∠AOB=∠COD=90°,∠∠BOD+∠BOC=∠COD,∠∠BOD=90°﹣∠BOC,同理:∠AOC=90°﹣∠BOC,∠∠AOD=∠AOB+∠BOD=90°+90°﹣∠BOC=180°﹣∠BOC,∠∠AOD+∠BOC=180°;(2)解:设∠BOE=a,则∠BOC=4a,∠∠BOE+∠EOC=∠BOC,∠∠EOC=∠BOC﹣∠BOE=3a,∠∠AOD+∠COD+∠BOC+∠AOB =360°,∠∠AOD =360°﹣∠COD ﹣∠BOC ﹣∠AOB=360°﹣90°﹣4a ﹣90°=180°﹣4a ,∠∠DOF =34∠AOD , ∠∠DOF =34(180°﹣4a )=135°﹣3a ,∠∠AOF =14∠AOD =14(180°﹣4a )=45°﹣a , ∠∠EOF =∠BOE+∠AOB+∠AOF =a+90°+45°﹣a =135°,∠EOF 的度数为135°;(3)∠当射线OG 在∠EOF 内部时,∠∠GOF :∠GOE =3:7,∠∠GOF =33+7(∠GOF+∠GOE )=310∠EOF =310×135°=40.5°;∠当射线OG 在∠EOF 外部时,∠∠GOF :∠GOE =3:7,∠∠GOF =33+7(∠GOE ﹣∠GOF ) =310∠EOF =310(∠DOF+∠COD+∠EOC ) =310 (135°﹣3a+90°+3a )=67.5°.综上所述,∠GOF 的度数是40.5°或67.5°.16.(2020秋•镇海区期末)新定义问题如图∠,已知∠AOB ,在∠AOB 内部画射线OC ,得到三个角,分别为∠AOC 、∠BOC 、∠AOB .若这三个角中有一个角是另外一个角的2倍,则称射线OC 为∠AOB 的“幸运线”.(本题中所研究的角都是大于0°而小于180°的角.)【阅读理解】(1)角的平分线这个角的“幸运线”;(填“是”或“不是”)【初步应用】(2)如图∠,∠AOB=45°,射线OC为∠AOB的“幸运线”,则∠AOC的度数为;【解决问题】(3)如图∠,已知∠AOB=60°,射线OM从OA出发,以每秒20°的速度绕O点逆时针旋转,同时,射线ON从OB出发,以每秒15°的速度绕O点逆时针旋转,设运动的时间为t秒(0<t<9).若OM、ON、OA 三条射线中,一条射线恰好是以另外两条射线为边的角的“幸运线”,求出所有可能的t值.【思路点拨】(1)根据幸运线定义即可求解;(2)分3种情况,根据幸运线定义得到方程求解即可;(3)分3种情况,根据幸运线定义得到方程求解即可.【解答过程】解:(1)一个角的平分线是这个角的“幸运线”;故答案为:是;(2)∠设∠AOC=x,则∠BOC=2x,由题意得,x+2x=45°,解得x=15°,∠设∠AOC=x,则∠BOC=x,由题意得,x+x=45°,解得x=22.5°,x,∠设∠AOC=x,则∠BOC=12x=45°,解得x=30°,由题意得,x+12故答案为:15°或22.5°或30°;(3)当0<t≤6时,∠MON=60+5t,∠AON=60﹣15t,若OA是射线OM与ON的幸运线,则∠AON =12∠MON ,即60﹣15t =12(60+5t ),解得t =127;∠AON =13∠MON ,即60﹣15t =13(60+5t ),解得t =125; ∠AON =23∠MON ,即60﹣15t =23(60+5t ),解得t =1211;当6<t <9时,∠MOA =20t ,∠AON =15t ﹣60,若ON 是射线OM 与OA 的幸运线,则∠AON =12∠MOA 即15t ﹣60=12×20t ,解得t =12(舍);∠AON =13∠MOA ,即15t ﹣60=13×20t ,解得t =365; ∠AON =23∠MOA ,即15t ﹣60=23×20t ,解得t =36(舍);故t 的值是127或125或1211或365. 17.(2020秋•和平区期末)如图,点O 是直线AB 上的一点,∠COD =80°,OE 平分∠BOC .(1)如图1,若∠AOC =40°,求∠DOE 的度数.(2)在图1中若∠AOC =α(其中20°<α<100°),请直接用含α的代数式表示∠DOE 的度数,不用说明理由.(3)如图2,∠请直接写出∠AOC 和∠DOE 的度数之间的关系,不用说明理由.∠在∠AOC 的内部有一条射线OF ,满足∠AOC ﹣4∠AOF =2∠BOE+∠AOF .试确定∠AOF 与∠DOE 的度数之间的关系,直接写出关系式即可,不用说明理由.【思路点拨】(1)由∠AOC 的度数可以求得∠BOC 的度数,由OE 平分∠BOC ,可以求得∠COE 的度数,又由∠DOC =80°可以求得∠DOE 的度数;(2)由第(1)问的求法,可以直接写出∠DOE 的度数;(3)∠首先写出∠AOC 和∠DOE 的度数之间的关系,由∠COD =80°,OE 平分∠BOC ,∠BOC+∠AOC =180°,可以建立各个角之间的关系,从而可以得到∠AOC和∠DOE的度数之间的关系;∠首先得到∠AOF与∠DOE的度数之间的关系,由∠AOC﹣4∠AOF=2∠BOE+∠AOF,∠COD=80°,OE平分∠BOC,∠AOC和∠DOE的关系,可以建立各个角之间的关系,从而可以得到∠AOF与∠DOE的度数之间的关系.【解答过程】解:(1)∠∠AOC=40°,∠∠BOC=180°﹣∠AOC=140°.∠OE平分∠BOC,∠∠COE=12∠BOC.∠∠COE=70°.∠∠DOE=∠COD﹣∠COE=80°﹣70°=10°.(2)∠DOE=α2−10°.∠∠AOC=α,∠∠BOC=180°﹣α.∠OE平分∠BOC,∠∠COE=12∠BOC.∠∠COE=90°−12α.∠∠DOE=∠COD﹣∠COE=80°﹣90°+α2=α2−10°.(3)∠∠AOC=2∠DOE+20°.理由:∠OE平分∠BOC,∠∠BOC=2∠COE.∠∠COD=80°,∠AOC+∠BOC=180°,∠∠DOE+∠COE=80°,∠∠COE=80°﹣∠DOE.∠∠AOC+2∠COE=180°.∠∠AOC+2(80°﹣∠DOE)=180°.化简,得:∠AOC=2∠DOE+20°;∠4∠DOE ﹣5∠AOF =140°.理由:∠∠AOC ﹣4∠AOF =2∠BOE+∠AOF ,∠∠AOC ﹣2∠BOE =5∠AOF .∠OE 平分∠BOC ,∠∠EOC =∠BOE ,∠∠AOC ﹣2∠EOC =5∠AOF .由(3)∠知:∠AOC =2∠DOE+20°,∠2∠DOE+20°﹣2∠EOC =5∠AOF .∠∠EOC =∠COD ﹣∠DOE =80°﹣∠DOE ,∠2∠DOE+20°﹣2(80°﹣∠DOE )=5∠AOF .∠4∠DOE ﹣140°=5∠AOF .即4∠DOE ﹣5∠AOF =140°.18.(2020秋•越秀区校级月考)如图1,已知∠AOB =120°,∠COD =60°,OM 在∠AOC 内,ON 在∠BOD 内,∠AOM =13∠AOC ,∠BON =13∠BOD .(本题中所有角均大于0°且小于等于180°)(1)∠COD 从图1中的位置绕点O 逆时针旋转到OC 与OB 重合时,如图2,则∠MON = 100 °;(2)∠COD 从图2中的位置绕点O 逆时针旋转n°(0<n <120且n≠60),求∠MON 的度数;(3)∠COD 从图2中的位置绕点O 顺时针旋转n°(0<n <180且n≠60a ,其中a 为正整数),直接写出所有使∠MON =2∠BOC 的n 值.【思路点拨】(1)当∠COD 从图1中的位置绕点O 逆时针旋转到OC 与OB 重合时,如图2,可得∠MON =∠MOB+∠BON ,再根据已知条件进行计算即可;(2)根据∠COD 从图2中的位置绕点O 逆时针旋转n°(0<n <120且n≠60),分两种情况画图:∠当0<n <60时,如(图1),∠当60<n <120时,如(图2),结合(1)进行角的和差计算即可;(3)根据∠COD 从图2中的位置绕点O 顺时针旋转n°(0<n <180且n≠60a ,其中a 为正整数),∠MON =2∠BOC ,分两种情况画图:∠当0<n <60时,如图3,∠当60<n <180时,如图4,结合(2)进行角的和差计算即可.【解答过程】解:(1)∠∠AOM =13∠AOC ,∠BON =13∠BOD ,∠∠MOC =23∠AOC ,∠DON =23∠BOD ,当∠COD 从图1中的位置绕点O 逆时针旋转到OC 与OB 重合时,如图2,∠∠MON =∠MOB+∠BON=23∠AOC +13∠BOD=23×120°+13×60°=80°+20°=100°;故答案为:100°;(2)∠COD 从图2中的位置绕点O 逆时针旋转n°(0<n <120且n≠60),∠当0<n <60时,如(图1),∠∠BOC =n°,∠∠AOC =∠AOB ﹣∠BOC =120°﹣n°,∠BOD =∠COD ﹣∠BOC =60°﹣n°,∠∠MON =∠MOC+∠BOC+∠BON=23(120°﹣n°)+n°+13(60°﹣n°)=100°;∠当60<n<120时,如(图2),∠∠BOC=n°,∠∠AOC=∠AOB﹣∠BOC=120°﹣n°,∠BOD=∠BOC﹣∠DOC=n°﹣60°,∠∠MON=∠MOC+∠DOC+∠DON=23(120°﹣n°)+60°+23(n°﹣60°)=100°;综上所述:∠MON的度数为100°;(3)∠COD从图2中的位置绕点O顺时针旋转n°(0<n<180且n≠60a,其中a为正整数),∠MON=2∠BOC,∠当0<n<60时,如图3,∠∠BOC=n°,∠∠MON=2∠BOC=2n°,∠∠AOC=∠AOB+∠BOC=120°+n°,∠BOD=∠BOC+∠DOC=n°+60°,∠∠MON=∠MOC+∠DOC﹣∠DON=23(120°+n°)+60°−23(n°+60°)=100°,∠2n°=100°∠n =50;∠当60<n <180时,如图4,∠∠BOC =n°,∠∠MON =2∠BOC =2n°,∠∠AOC =360°﹣(∠AOB+∠BOC )=360°﹣(120°+n°)=240°﹣n°,∠BOD =∠BOC+∠DOC =n°+60°,∠∠MON =360°﹣∠AOM ﹣∠AOB ﹣∠BON=360°−13(240°﹣n°)﹣120°−13(60°+n°) =140°,∠2n°=140°,∠n =70;综上所述:n 的值为50或70.19.(2020秋•渝中区校级期末)如图1,∠AOB =40°,∠COD =60°,OM 、ON 分别为∠AOB 和∠BOD 的角平分线.(1)若∠MON =70°,则∠BOC = °;(2)如图2,∠COD 从第(1)问中的位置出发,绕点O 逆时针以每秒4°的速度旋转;当OC 与OA 重合时,∠COD 立即反向绕点O 顺时针以每秒6°的速度旋转,直到OC 与OA 互为反向延长线时停止运动.整个运动过程中,∠COD 的大小不变,OC 旋转后的对应射线记为OC′,OD 旋转后的对应射线记为OD′,∠BOD′的角平分线记为ON′,∠AOD′的角平分线记为OP .设运动时间为t 秒.∠当OC′平分∠BON′时,求出对应的t 的值;∠请问在整个运动过程中,是否存在某个时间段使得|∠BOP ﹣∠MON′|的值不变?若存在,请直接写出这个定值及其对应的t的取值范围(包含运动的起止时间);若不存在,请说明理由.【思路点拨】(1)根据角平分线的定义结合图形根据已知条件求角的大小;(2)∠分类讨论顺时针、逆时针转两种情况,根据角平分线的定义用t表示出角的度数,列出等量关系式求出t;∠分类讨论顺时针、逆时针转两种情况,当C′在B下方时,当C′在B上方时,根据角平分线的定义用t表示出角的度数,求在某个时间段使得|∠BOP﹣∠MON′|的值不变,求出这个定值及其对应的t的取值范围.【解答过程】解:(1)∠OM为∠AOB的角平分线、∠AOB=40°,∠∠MOB=20°.∠∠MON=70°,∠∠BON=∠MON﹣∠MOB=50°.∠ON为∠BOD的角平分线,∠∠BON=∠DON=50°.∠∠CON=∠COD﹣∠DON=10°∠∠BOC=∠DON﹣∠CON=40°.故答案为:40°.(2)如图∠:∠逆时针旋转时:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
七年级数学中的角度计
算题
Standardization of sany group #QS8QHH-HHGX8Q8-GNHHJ8-HHMHGN#
七年级数学--角有关的计算问题
1、如图所示,AB 为一条直线,OC 是∠AOD 的平分线,OE 在∠BOD 内,∠DOE=3
1
∠BOD ,∠
COE=72°,求∠EOB 的度数。
2、如图,已知∠AOB 是∠AOC 的余角,∠AOD 是∠AOC 的补角,且BOD BOC ∠=∠2
1
求∠BOD 、∠AOC 的度数
3、一条射线OA ,若从点O 再引两条射线OB 、OC ,使∠AOB=60°,∠BOC=20°,求∠AOC 的度数。
4、已知∠AOB=100°,∠BOC=20°,若OM 平分∠AOB ,ON 平分∠BOC ,求∠MON 的度数。
5、已知,如图∠BOC 为∠AOC 内的一个锐角,射线OM 、ON 分别平分∠AOC 、∠BOC 。
(1)若∠AOB=90°,∠BOC=30°,求∠MON 的度数; (2)若∠AOB=α,∠BOC=30°,求∠MON 的度数;
(3)若∠AOB=90°,∠BOC=β,还能否求出∠MON 的度数若能,求出其值,若不能,说明
理由。
(4)从前三问的结果你发现了什么规律
6(2014?漳州)如图是一副学生用的三角形板摆放的位置,A 、O 、C 三点在同一直线上,则∠AOB 的度数是 度.
B (第 13 题)
A
C
O
D
O C
B A
7、点O 是直线AB 上一点,∠COD 是直角,OE 平分∠BOC 。
(1)如图1,若∠AOC=40°,求∠DOE 的度数;
(2)在如1中,若∠AOC=α,直接写出∠DOE 的度数(用含α的代数式表示)
8如图,已知AB= 40,点C 是线段AB 的中点,点D 为线段CB 上的一点,点E 为线段DB 的中点,EB=6,求线段CD 的长。
A
B
C
D
E
9、如图,已知∠BOC =2∠AOC ,OD 平分∠AOB ,且∠COD =29°,求∠AOB 的度数。
10、如图,OB 平分∠AOC ,且∠2 : ∠3 : ∠4 = 1:3:4,求∠1、∠2、∠3、∠4。
11(如图,将一幅三角尺叠放在一起,使直角顶点重合于点O ,绕点O 任意转动其中一个三角尺,则与∠AOD 始终相等的角是 .
C
B
A
D
O
3
D
C
B A
2
1
4 O。
