大学物理下册第三版课后答案16电磁感应

合集下载

大学物理_电磁感应和电磁波及习题解答

线圈在此位置瞬时电动势
d
-
a
-
17-4(感生） B=0I/2r
I(t)
ds=Ldr a b a b I t L I t 1 t L dr dr 2r a 2 a r

L d a
d t dt
对r，I(t)是常数
L a b ln wI 0 cos wt 2 a
b
补充题在半径为R的圆筒内，有方向与轴线平行的均匀磁场B，它以dB/ dt=1.0×10-2T/s 的变化率减小。P点离轴线的距离r=5.0cm，如图所示，试问电子在各点处可获的加速度的大小和方向如何？解:轴对称
E dl E 2r d dB dB r 2 S dt dt dt
自感电动势：
自感系数：
L
d m 0 dt
判别自感电动势和自感电流的方向与一般情况相同。
反映线圈自身特性
d d LI dI L L dt dt dt
例1.N 匝的螺线管长l，截面积为 S，绕在铁心上，求自感系数。解：螺线管内部的磁感应强度：
B nI
1 K 2
L R
*解释：K接通1时，电池和线圈充当灯泡的电源(电池对L充电)； K接通2时，线圈充当灯泡的电源 (L向灯泡放电)。
电感器储能
WL dq d Idt dt LIdI
dq I dt
d dt
LI d LdI
1 2 LI 2
二、磁场的能量电感器所储能量只能分布在磁场中长直螺线管
以O为圆心,OP为半径作圆
P
Ek
o
r dB E 2 dt
r dB 2 E dl 2 dl cos 2 dt 0 0

大学物理第三版下册答案(供参考)

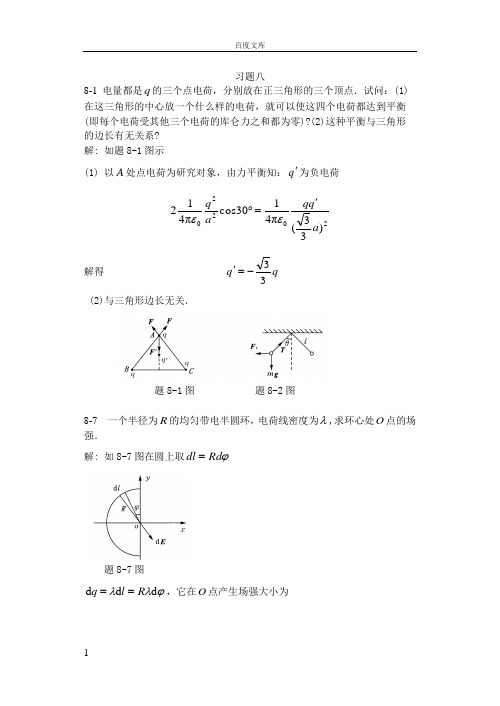
习题八8-1 电量都是q的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A处点电荷为研究对象，由力平衡知：q'为负电荷2220)33(π4130cosπ412aq qaq'=︒εε解得qq33-='(2)与三角形边长无关．题8-1图题8-2图8-7 一个半径为R的均匀带电半圆环，电荷线密度为λ,求环心处O点的场强．解: 如8-7图在圆上取ϕRddl=题8-7图ϕλλddd Rlq==，它在O点产生场强大小为20π4d d RR E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x ==ϕϕελϕπd cos π4)cos(d d 0RE E y -=-=积分RR E x 000π2d sin π4ελϕϕελπ==⎰0d cos π400=-=⎰ϕϕελπRE y∴ RE E x 0π2ελ==，方向沿x 轴正向．8-11 半径为1R 和2R (2R ＞1R )的两无限长同轴圆柱面，单位长度上分别带有电量λ和-λ,试求:(1)r ＜1R ；(2) 1R ＜r ＜2R ；(3) r ＞2R 处各点的场强．解: 高斯定理0d ε∑⎰=⋅q S E s取同轴圆柱形高斯面，侧面积rl S π2= 则 rl E S E Sπ2d =⋅⎰对(1) 1R r <0,0==∑E q(2) 21R r R << λl q =∑∴ rE 0π2ελ=沿径向向外(3) 2R r >=∑q∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．解: 如题8-12图示，两带电平面均匀带电，电荷面密度分别为1σ与2σ，两面间， n E)(21210σσε-= 1σ面外， n E )(21210σσε+-= 2σ面外， n E)(21210σσε+= n：垂直于两平面由1σ面指为2σ面．题8-16图8-16 如题8-16图所示，在A ，B 两点处放有电量分别为+q ,-q 的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求移动过程中电场力作的功．解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-=8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强和电势．解: (1)由于电荷均匀分布与对称性，AB 和CD 段电荷在O 点产生的场强互相抵消，取θd d R l =则θλd d R q =产生O 点Ed 如图，由于对称性，O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=［)2sin(π-2sin π-］R0π2ελ-=(2) AB 电荷在O 点产生电势，以0=∞U⎰⎰===AB200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O 8-22 三个平行金属板A ，B 和C 的面积都是200cm 2，A 和B 相距4.0mm ，A与C 相距2.0 mm ．B ，C 都接地，如题8-22图所示．如果使A 板带正电3.0×10-7C ，略去边缘效应，问B 板和C 板上的感应电荷各是多少?以地的电势为零，则A 板的电势是多少?解: 如题8-22图示，令A 板左侧面电荷面密度为1σ，右侧面电荷面密度为2σ题8-22图(1)∵ AB AC U U =，即 ∴ AB AB AC AC E E d d = ∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A=得 ,32S q A =σ Sq A 321=σ而 7110232-⨯-=-=-=A C q S q σC C10172-⨯-=-=S q B σ(2) 301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R （1R ＜2R )的同心薄金属球壳，现给内球壳带电+q ，试计算：(1)外球壳上的电荷分布及电势大小；(2)先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及电势；*(3)再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变量．解: (1)内球带电q +；球壳内表面带电则为q -,外表面带电为q +，且均匀分布，其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εε (2)外壳接地时，外表面电荷q +入地，外表面不带电，内表面电荷仍为q -．所以球壳电势由内球q +与内表面q -产生：0π4π42020=-=R q R q U εε8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳，介质相对介电常数为r ε，金属球带电Q ．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势；(3)金属球的电势．解: 利用有介质时的高斯定理∑⎰=⋅q S D Sd(1)介质内)(21R r R <<场强303π4,π4rrQ E r r Q D r εε ==内; 介质外)(2R r <场强303π4,π4r r Q E r Qr D ε ==外(2)介质外)(2R r >电势rQE U 0rπ4r d ε=⋅=⎰∞外介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε(3)金属球的电势r d r d 221⋅+⋅=⎰⎰∞R R R E E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdrr Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示，在平行板电容器的一半容积内充入相对介电常数为rd r d ⋅+⋅=⎰⎰∞∞rrE E U 外内r ε的电介质．试求：在有电介质部分和无电介质部分极板上自由电荷面密度的比值．解: 如题8-28图所示，充满电介质部分场强为2E ，真空部分场强为1E，自由电荷面密度分别为2σ与1σ 由∑⎰=⋅0d q S D得11σ=D ，22σ=D而 101E D ε=,202E D r εε=d21U E E == ∴r D D εσσ==1212题8-28图题8-29图8-29 两个同轴的圆柱面，长度均为l ，半径分别为1R 和2R (2R ＞1R )，且l >>2R -1R ，两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时，求：(1)在半径r 处(1R ＜r ＜2R ＝，厚度为dr ，长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量；(2)电介质中的总电场能量； (3)圆柱形电容器的电容．解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰当)(21R r R <<时，Q q =∑∴ rlQD π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222=== (2)电介质中总电场能量⎰⎰===211222ln π4π4d d R R VR R l Q rl r Q W W εε (3)电容：∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== 习题九9-8 在真空中，有两根互相平行的无限长直导线1L 和2L ，相距0.1m ，通有方向相反的电流，1I =20A,2I =10A ，如题9-8图所示．A ，B 两点与导线在同一平面内．这两点与导线2L 的距离均为5.0cm ．试求A ，B 两点处的磁感应强度，以及磁感应强度为零的点的位置．题9-8图解：如题9-8图所示,A B方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r mT9-11 氢原子处在基态时，它的电子可看作是在半径a =0.52×10-8cm 的轨道上作匀速圆周运动，速率v =2.2×108cm ·s -1．求电子在轨道中心所产生的磁感应强度和电子磁矩的值．解：电子在轨道中心产生的磁感应强度3004aav e B πμ ⨯= 如题9-11图，方向垂直向里，大小为134200==a evB πμ T 电子磁矩m P在图中也是垂直向里，大小为242102.92-⨯===eva a T e P m π 2m A ⋅ 题9-11图题9-12图9-12 两平行长直导线相距d =40cm ，每根导线载有电流1I =2I =20A ，如题9-12图所示．求：(1)两导线所在平面内与该两导线等距的一点A 处的磁感应强度；(2)通过图中斜线所示面积的磁通量．(1r=3r =10cm,l=25cm)．解：(1) 5210104)2(2)2(2-⨯=+=dIdIBAπμπμT方向⊥纸面向外(2)取面元rlS dd=6121110102.23ln31ln23ln2])(22[1211-+⨯=πμ=πμ-πμ=-πμ+πμ=⎰l Il Il IldrrdIrIrrrΦWb9-13 一根很长的铜导线载有电流10A，设电流均匀分布.在导线内部作一平面S，如题9-13图所示．试计算通过S平面的磁通量(沿导线长度方向取长为1m的一段作计算)．铜的磁导率μμ=.解：由安培环路定律求距圆导线轴为r处的磁感应强度⎰∑μ=⋅lIlBd222RIrrBμπ=∴22RIrBπμ=题 9-13 图磁通量602)(1042-===⋅=Φ⎰⎰πμπμIdrRIrS dB RsmWb题9-15图9-15 题9-15图中所示是一根很长的长直圆管形导体的横截面，内、外半径分别为a ,b ，导体内载有沿轴线方向的电流I ，且I 均匀地分布在管的横截面上．设导体的磁导率0μμ≈，试证明导体内部各点)(b r a << 的磁感应强度的大小由下式给出：r a r a b IB 22220)(2--=πμ解：取闭合回路r l π2= )(b r a <<则 ⎰π=⋅lr B l B 2d2222)(a b Ia r I ππππ--=∑∴ )(2)(22220a b r a r I B --=πμ 9-16 一根很长的同轴电缆，由一导体圆柱(半径为a )和一同轴的导体圆管(内、外半径分别为b ,c )构成，如题9-16图所示．使用时，电流I 从一导体流去，从另一导体流回．设电流都是均匀地分布在导体的横截面上，求：(1)导体圆柱内(r ＜a ),(2)两导体之间(a ＜r ＜b )，（3）导体圆筒内(b ＜r ＜c )以及(4)电缆外(r ＞c )各点处磁感应强度的大小解： ⎰∑μ=⋅LI l B 0d(1)a r < 2202RIr r B μπ=202R IrB πμ=(2) b r a << I r B 02μπ=rIB πμ20=(3)c r b << I bc b r I r B 0222202μμπ+---= )(2)(22220b c r r c I B --=πμ (4)c r > 02=r B π0=B题9-16图题9-17图题9-21图9-21 边长为l =0.1m 的正三角形线圈放在磁感应强度B =1T 的均匀磁场中，线圈平面与磁场方向平行.如题9-21图所示，使线圈通以电流I =10A ，求： (1)线圈每边所受的安培力； (2)对O O '轴的磁力矩大小；(3)从所在位置转到线圈平面与磁场垂直时磁力所作的功．解： (1) 0=⨯=B l I F bcB l I F ab⨯= 方向⊥纸面向外，大小为866.0120sin ==︒IlB F ab NB l I F ca⨯=方向⊥纸面向里，大小866.0120sin ==︒IlB F ca N(2)IS P m =B P M m⨯= 沿O O '方向，大小为221033.443-⨯===B l I ISB M m N ⋅(3)磁力功 )(12ΦΦ-=I A∵ 01=Φ B l 2243=Φ ∴221033.443-⨯==B l IA J9习题十10-1 一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中．回路平面与B垂直．当回路半径以恒定速率tr d d =80cm ·s -1收缩时，求回路中感应电动势的大小．解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V 10-2 一对互相垂直的相等的半圆形导线构成回路，半径R =5cm ，如题10-2图所示．均匀磁场B =80×10-3T ，B 的方向与两半圆的公共直径(在Oz 轴上)垂直，且与两个半圆构成相等的角α 当磁场在5ms 内均匀降为零时，求回路中的感应电动势的大小及方向．解: 取半圆形cba 法向为i，题10-2图则 αΦcos 2π21B R m =同理，半圆形adc 法向为j，则αΦcos 2π22B R m=∵ B 与i 夹角和B 与j夹角相等，∴ ︒=45α则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV方向与cbadc 相反，即顺时针方向．题10-4图10-4 如题10-4图所示，载有电流I 的长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度v 平行导线平移．求半圆环内感应电动势的大小和方向及MN 两端的电压 N M U U -．解: 作辅助线MN ，则在MeNM 回路中，沿v方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵ 0cos d ln 02a bMN a bIv a bvB l a bμεππ+--==<+⎰所以MeN ε沿NeM 方向，大小为ba ba Iv -+ln20πμ M 点电势高于N 点电势，即ba ba Iv U U N M -+=-ln20πμ 题10-5图10-5如题10-5所示，在两平行载流的无限长直导线的平面内有一矩形线圈．两导线中的电流方向相反、大小相等，且电流以tId d 的变化率增大，求： (1)任一时刻线圈内所通过的磁通量；(2)线圈中的感应电动势．解: 以向外磁通为正则 (1)]ln [lnπ2d π2d π2000dad b a b Ilr l r Ir l r Iab b ad d m +-+=-=⎰⎰++μμμΦ(2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε10-6 如题10-6图所示，用一根硬导线弯成半径为r 的一个半圆．令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转．整个电路的电阻为R ．求：感应电流的最大值．题10-6图解: )cos(2π02ϕωΦ+=⋅=t r B S B m∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε ∴ RBfr R I m22π==ε 10-7 如题10-7图所示，长直导线通以电流I =5A ，在其右方放一长方形线圈，两者共面．线圈长b =0.06m ，宽a =0.04m ，线圈以速度v =0.03m ·s -1垂直于直线平移远离．求：d =0.05m 时线圈中感应电动势的大小和方向．题10-7图解: AB 、CD 运动速度v方向与磁力线平行，不产生感应电动势． DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰με∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεε V 方向沿顺时针．10-8 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动．已知导轨处于均匀磁场B 中，B 的方向与回路的法线成60°角(如题10-8图所示)，B的大小为B =kt (k 为正常)．设t =0时杆位于cd 处，求：任一时刻t 导线回路中感应电动势的大小和方向．解: ⎰==︒=⋅=22212160cos d klvt lvkt Blvt S B mΦ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向．题10-8图10-9 一矩形导线框以恒定的加速度向右穿过一均匀磁场区，B的方向如题10-9图所示．取逆时针方向为电流正方向，画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0)．解: 如图逆时针为矩形导线框正向，则进入时0d d <Φt,0>ε；题10-9图(a)题10-9图(b) 在磁场中时0d d =tΦ,0=ε；出场时0d d >tΦ，0<ε，故t I -曲线如题10-9图(b)所示. 题10-10图10-10 导线ab 长为l ，绕过O 点的垂直轴以匀角速ω转动，aO =3l磁感应强度B 平行于转轴，如图10-10所示．试求：（1）ab 两端的电势差；（2）b a ,两端哪一点电势高?解: (1)在Ob 上取dr r r +→一小段则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高．题10-11图10-11 如题10-11图所示，长度为b 2的金属杆位于两无限长直导线所在平面的正中间，并以速度v平行于两直导线运动．两直导线通以大小相等、方向相反的电流I ，两导线相距2a ．试求：金属杆两端的电势差及其方向．解：在金属杆上取r d 距左边直导线为r ，则ba b a Iv r r a r Iv l B v ba ba BAAB -+-=-+-=⋅⨯=⎰⎰+-ln d )211(2d )(00πμπμε∵ 0<AB ε ∴实际上感应电动势方向从A B →，即从图中从右向左， ∴ ba ba Iv U AB -+=ln0πμ 题10-12图10-12 磁感应强度为B的均匀磁场充满一半径为R 的圆柱形空间，一金属杆放在题10-12图中位置，杆长为2R ，其中一半位于磁场内、另一半在磁场外．当tBd d ＞0时，求：杆两端的感应电动势的大小和方向．解： ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε=-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=-- ∴ tB R R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →10-13 半径为R 的直螺线管中，有dtdB＞0的磁场，一任意闭合导线abca ，一部分在螺线管内绷直成ab 弦，a ,b 两点与螺线管绝缘，如题10-13图所示．设ab =R ，试求：闭合导线中的感应电动势．解：如图，闭合导线abca 内磁通量)436π(22R R B S B m -=⋅= Φ∴ tB R R i d d )436π(22--=ε ∵0d d >tB∴0<i ε，即感应电动势沿acba ，逆时针方向．题10-13图题10-14图∴ 题10-15图 10-15 一无限长的直导线和一正方形的线圈如题10-15图所示放置(导线与线圈接触处绝缘)．求：线圈与导线间的互感系数．解：设长直电流为I ，其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2aaIa r r Ia μμΦ∴ 2ln π2012aI M μΦ==10-16 一矩形线圈长为a =20cm ，宽为b =10cm ，由100匝表面绝缘的导线绕成，放在一无限长导线的旁边且与线圈共面．求：题10-16图中(a)和(b)两种情况下，线圈与长直导线间的互感．解：(a)见题10-16图(a)，设长直电流为I ，它产生的磁场通过矩形线圈的磁通为2ln π2d 2πd 020)(12Ia r r Ia S B bb S μμΦ⎰⎰==⋅= ∴ 6012108.22ln π2-⨯===a N I N M μΦ H (b)∵长直电流磁场通过矩形线圈的磁通012=Φ，见题10-16图(b) ∴ 0=M题10-16图题10-17图10-20 一无限长圆柱形直导线，其截面各处的电流密度相等，总电流为I ．求：导线内部单位长度上所储存的磁能．解：在R r <时 20π2R I B r μ=∴ 4222002π82Rr I B w m μμ== 取 r r V d π2d =(∵导线长1=l )则 ⎰⎰===R R m I R r r I r r w W 00204320π16π4d d 2μμπ。

大学物理学第三版修订版下册第章标准答案(赵近芳)

大学物理学第三版修订版下册第章答案(赵近芳)————————————————————————————————作者：————————————————————————————————日期：习题1111.1选择题(1）一圆形线圈在磁场中作下列运动时，那些情况会产生感应电流（）（A ）沿垂直磁场方向平移；（B ）以直径为轴转动，轴跟磁场垂直；（C ）沿平行磁场方向平移；（D ）以直径为轴转动，轴跟磁场平行。

[答案：B](2)下列哪些矢量场为保守力场（）（A ）静电场；（B ）稳恒磁场；（C ）感生电场；（D ）变化的磁场。

[答案：A](3) 用线圈的自感系数 L 来表示载流线圈磁场能量的公式221LI W m=（）( A )只适用于无限长密绕线管； ( B ) 只适用于一个匝数很多，且密绕的螺线环； ( C ) 只适用于单匝圆线圈； ( D )适用于自感系数L 一定的任意线圈。

[答案：D](4)对于涡旋电场，下列说法不正确的是（）：（A ）涡旋电场对电荷有作用力；（B ）涡旋电场由变化的磁场产生；（C ）涡旋场由电荷激发；（D ）涡旋电场的电力线闭合的。

[答案：C]11.2 填空题(1)将金属圆环从磁极间沿与磁感应强度垂直的方向抽出时，圆环将受到。

[答案：磁力](2)产生动生电动势的非静电场力是，产生感生电动势的非静电场力是，激发感生电场的场源是。

[答案：洛伦兹力，涡旋电场力，变化的磁场](3)长为l 的金属直导线在垂直于均匀的平面内以角速度ω转动，如果转轴的位置在，这个导线上的电动势最大，数值为；如果转轴的位置在，整个导线上的电动势最小，数值为。

[答案：端点，221l B ω；中点，0]11.3一半径r =10cm 的圆形回路放在B =0.8T 的均匀磁场中．回路平面与B ϖ垂直．当回路半径以恒定速率tr d d =80cm ·s -1收缩时，求回路中感应电动势的大小．解: 回路磁通 2πr B BS m ==Φ感应电动势大小40.0d d π2)π(d d d d 2====trr B r B t t m Φε V11.4 一对互相垂直的相等的半圆形导线构成回路，半径R =5cm ，如题11.4图所示．均匀磁场B =80×10-3T ，B 的方向与两半圆的公共直径(在Oz 轴上)垂直，且与两个半圆构成相等的角α当磁场在5ms 内均匀降为零时，求回路中的感应电动势的大小及方向．解: 取半圆形cba 法向为i ϖ，题11.4图则 αΦcos 2π21B R m =同理，半圆形adc 法向为j ϖ，则αΦcos 2π22B R m=∵ B ϖ与i ϖ夹角和B ϖ与j ϖ夹角相等，∴ ︒=45α 则 αΦcos π2R B m =221089.8d d cos πd d -⨯-=-=Φ-=tBR t m αεV方向与cbadc 相反，即顺时针方向．题11.5图11.5 如题11.5图所示，载有电流I 的长直导线附近，放一导体半圆环MeN 与长直导线共面，且端点MN 的连线与长直导线垂直．半圆环的半径为b ，环心O 与导线相距a ．设半圆环以速度v 平行导线平移．求半圆环内感应电动势的大小和方向及MN 两端的电压N M U U -．解: 作辅助线MN ，则在MeNM 回路中，沿v ϖ方向运动时0d =m Φ ∴ 0=MeNM ε 即 MN MeN εε= 又∵ ⎰+-<+-==ba ba MN ba ba Iv l vB 0ln 2d cos 0πμπε 所以MeN ε沿NeM 方向，大小为ba ba Iv -+ln 20πμ M 点电势高于N 点电势，即ba ba Iv U U N M -+=-ln 20πμ题11.6图11.6如题11.6所示，在两平行载流的无限长直导线的平面内有一矩形线圈．两导线中的电流方向相反、大小相等，且电流以tId d 的变化率增大，求： (1)任一时刻线圈内所通过的磁通量； (2)线圈中的感应电动势．解: 以向外磁通为正则 (1) ]ln [lnπ2d π2d π2000dad b a b Ilr l rIr l rIab bad dm +-+=-=⎰⎰++μμμΦ (2) tIb a b d a d l t d d ]ln [ln π2d d 0+-+=-=μΦε11.7 如题11.7图所示，用一根硬导线弯成半径为r 的一个半圆．令这半圆形导线在磁场中以频率f 绕图中半圆的直径旋转．整个电路的电阻为R ．求：感应电流的最大值．题11.7图解: )cos(2π02ϕωΦ+=⋅=t r B S B m ϖϖ ∴ Bfr f r B r B t r B t m m i 222202ππ22π2π)sin(2πd d ===+=-=ωεϕωωΦε ∴ RBfr R I m22π==ε11.8 如题11.8图所示，长直导线通以电流I =5A ，在其右方放一长方形线圈，两者共面．线圈长b =0.06m ，宽a =0.04m ，线圈以速度v =0.03m ·s -1垂直于直线平移远离．求：d =0.05m 时线圈中感应电动势的大小和方向．题11.8图解: AB 、CD 运动速度v ϖ方向与磁力线平行，不产生感应电动势． DA 产生电动势⎰==⋅⨯=AD I vb vBb l B v d2d )(01πμεϖϖϖBC 产生电动势)(π2d )(02d a Ivbl B v CB+-=⋅⨯=⎰μεϖϖϖ∴回路中总感应电动势8021106.1)11(π2-⨯=+-=+=ad d Ibv μεεεV方向沿顺时针．11.9 长度为l 的金属杆ab 以速率v 在导电轨道abcd 上平行移动．已知导轨处于均匀磁场Bϖ中，B ϖ的方向与回路的法线成60°角(如题11.9图所示)，B ϖ的大小为B =kt (k 为正常)．设t =0时杆位于cd 处，求：任一时刻t 导线回路中感应电动势的大小和方向．解: ⎰==︒=⋅=22212160cos d klvt lv kt Blvt S B m ϖϖΦ∴ klvt tm-=-=d d Φε 即沿abcd 方向顺时针方向．题11.9图11.10 一矩形导线框以恒定的加速度向右穿过一均匀磁场区，B ϖ的方向如题11.10图所示．取逆时针方向为电流正方向，画出线框中电流与时间的关系(设导线框刚进入磁场区时t =0)．解: 如图逆时针为矩形导线框正向，则进入时0d d <Φt,0>ε；题11.10图(a)题11.10图(b)在磁场中时0d d =tΦ,0=ε；出场时0d d >tΦ，0<ε，故t I -曲线如题10-9图(b)所示. 题11.11图11.11 导线ab 长为l ，绕过O 点的垂直轴以匀角速ω转动，aO =3l磁感应强度B 平行于转轴，如图11.11所示．试求：（1）ab 两端的电势差；（2）b a ,两端哪一点电势高? 解: (1)在Ob 上取dr r r +→一小段则 ⎰==320292d l Ob l B r rB ωωε 同理 ⎰==302181d l Oa l B r rB ωωε ∴ 2261)92181(l B l B Ob aO ab ωωεεε=+-=+= (2)∵ 0>ab ε 即0<-b a U U ∴b 点电势高．题11.12图11.12 如题11.12图所示，长度为b 2的金属杆位于两无限长直导线所在平面的正中间，并以速度v ϖ平行于两直导线运动．两直导线通以大小相等、方向相反的电流I ，两导线相距2a ．试求：金属杆两端的电势差及其方向．解：在金属杆上取r d 距左边直导线为r ，则 ba b a Iv r r a r Iv l B v b a b a BA AB-+-=-+-=⋅⨯=⎰⎰+-ln d )211(2d )(00πμπμεϖϖϖ ∵ 0<AB ε ∴实际上感应电动势方向从A B →，即从图中从右向左， ∴ ba ba Iv U AB -+=ln 0πμ题11.13图11.13 磁感应强度为B ϖ的均匀磁场充满一半径为R 的圆柱形空间，一金属杆放在题11.13图中位置，杆长为2R ，其中一半位于磁场内、另一半在磁场外．当tBd d ＞0时，求：杆两端的感应电动势的大小和方向．解： ∵ bc ab ac εεε+=tBR B R t t ab d d 43]43[d d d d 21=--=-=Φε =-=tabd d 2Φεt BR B R t d d 12π]12π[d d 22=-- ∴ tBR R acd d ]12π43[22+=ε∵0d d >tB∴ 0>ac ε即ε从c a →11.14 半径为R 的直螺线管中，有dtdB＞0的磁场，一任意闭合导线abca ，一部分在螺线管内绷直成ab 弦，a ,b 两点与螺线管绝缘，如题10-13图所示．设ab =R ，试求：闭合导线中的感应电动势．解：如图，闭合导线abca 内磁通量)436π(22R R B S B m -=⋅=ϖϖΦ∴ tBR R i d d )436π(22--=ε ∵0d d >tB∴0<i ε，即感应电动势沿acba ，逆时针方向．题11.14图题11.15图11.15 如题11.15图所示，在垂直于直螺线管管轴的平面上放置导体ab 于直径位置，另一导体cd 在一弦上，导体均与螺线管绝缘．当螺线管接通电源的一瞬间管内磁场如题11.15图示方向．试求：（1）ab 两端的电势差；（2）cd 两点电势高低的情况．解：由⎰⎰⋅-=⋅l S t B l E ϖϖϖϖd d d d 旋知，此时旋E ϖ以O 为中心沿逆时针方向． (1)∵ab 是直径，在ab 上处处旋E ϖ与ab 垂直∴ ⎰=⋅ll 0d ϖ旋∴0=ab ε,有b a U U =(2)同理， 0d >⋅=⎰l E cddc ϖϖ旋ε∴ 0<-c d U U 即d c U U >题11.16图11.16 一无限长的直导线和一正方形的线圈如题11.16图所示放置(导线与线圈接触处绝缘)．求：线圈与导线间的互感系数．解：设长直电流为I ，其磁场通过正方形线圈的互感磁通为⎰==32300122ln π2d π2a a Iar rIaμμΦ∴ 2ln π2012aIM μΦ==11.17两线圈顺串联后总自感为1.0H ，在它们的形状和位置都不变的情况下，反串联后总自感为0.4H ．试求：它们之间的互感．解： ∵顺串时 M L L L 221++= 反串联时M L L L 221-+='∴ M L L 4='-15.04='-=L L M H11题11.18图11.18 一矩形截面的螺绕环如题11.18图所示，共有N 匝．试求：(1)此螺线环的自感系数；(2)若导线内通有电流I ，环内磁能为多少? 解：如题11.18图示(1)通过横截面的磁通为⎰==b a ab NIh r h r NIln π2d π200μμΦ 磁链 ab IhN N ln π220μΦψ== ∴ ab hN I L ln π220μψ== (2)∵ 221LI W m = ∴ a b h I N W m ln π4220μ=11.19 一无限长圆柱形直导线，其截面各处的电流密度相等，总电流为I ．求：导线内部单位长度上所储存的磁能．解：在R r <时 20π2R I B rμ=∴ 4222002π82Rr I B w m μμ== 取 r r V d π2d =(∵导线长1=l )则 ⎰⎰===RR m I R rr I r r w W 00204320π16π4d d 2μμπ。

10.电磁感应大学物理习题答案

0I ldr 2r
B 2l 2 cos 2 t mR
) ， v max
Hale Waihona Puke mgR sin 。 B 2 l 2 cos 2
感生电动势 10-7 一长直导线中通有交变电流 I＝5.0sin100πt A，在与其相距 d＝5.0cm 处放有一矩形线圈，共 100 匝，线圈长 l＝4.0cm，宽 a＝2.0cm，如图 10-7 所示。求 t 时刻：（1）线圈中的磁通链数是多少？（2）线圈中的感生电动势是多少？解：（1）取矩形线圈的回路方向为顺时针方向，在距长直电流为 x 处取宽为 dx 的小面元
大学物理练习册—电磁感应
法拉第电磁感应定律 10-1 如图 10-1 所示，一半径 a＝0.10m，电阻 R＝1.0×10 3Ω 的圆形导体回路置于均匀磁场中，磁场方向与回路面积的法向之间的夹角为π/3，若磁场变化的规律为
B(t ) (3t 2 8t 5) 10 4 T
求：（1）t＝2s 时回路的感应电动势和感应电流；（2）最初 2s 内通过回路截面的电量。解：（1） B S BS cos
若 C 线圈匝数增加 N 倍，则 M N
52
大学物理练习册—电磁感应
10-12 一长直导线旁，共面放置一长 20cm、宽 10cm、共 100 匝的密绕矩形线圈，长直导线与矩形线圈的长边平行且与近边相距 10cm，如图 10-12 所示。求两电路的互感系数。解：在距长直导线 r 处，取一面元 dS ldr ，则 d BdS
0 R2 I 2( R 2 l 2 ) 3 2
A
R r C l 图 10-11
M
0R2 I 0R 2 r 2 BS r 2 I I 2( R 2 l 2 ) 3 2 I 2( R 2 l 2 ) 3 2 NR 2 r 2 BS 02 2 32 I 2( R l )

大学物理学第三版答案16电磁感应.docx

习题1616・1・如图所示，金属圆环半径为/?,位于磁感应强度为P的均匀磁场中，圆环平面与磁场方向垂直。

当圆环以恒定速度▽在环所在平面内运动时，求环中的感应电动势及环上位于与运动方向垂直的直径两端〃间的电势差。

解：(1)由法拉第电磁感应定律考虑到圆环内的磁通量不变，所以，环中的感dtr u ——(2)利用：8ah= £ (vxB)-dl ,有：£ah = Bv・2R = 2BvR。

【注：相同电动势的两个电源并联，并联后等效电源电动势不变】16-2.如图所示，长直导线屮通有电流/ = 5.0/1,在与其相距d = 0.5cm 处放有一矩形线圈，共1000匝，设线圈长/ = 4.0cm ,宽a = 2.0cm。

不计线圈口感，若线圈以速度v = 3.0cm/s沿垂直于长导线的方向向右运动，线圈中的感生电动势多大？解法一：利用法拉第电磁感应定律解决。

首先用［fp•〃二工/求出电场分布，易得:则矩形线圈内的磁通量为:rh s = -N有:dxdt八=1.92x107 V。

2 兀（d + a）解法二：利用动生电动势公式解决。

由击j〃二“0工/求出电场分布，易得:“（）/ 17tr考虑线圈框架的两个平行长直导线部分产生动生电动势,近端部分：®=NBJv,远端部分：E2=NB2I V,吗丄—丄”心2兀 ' d d + a 27ld（d 十= l・92xlOP。

16・3・如图所示，长直导线屮通有电流强度为/的电流，长为/的金属棒必与长直导线共面且垂直于导线放置，其。

端离导线为d,并以速度E平行于长直导线作匀速运动，求金属棒中的感应电动势£并比较4、5的电势大小。

解法一：利用动生电动势公式解决：d£ = (yxBydl如力,171 r"o" dr“0以［〃 + /------ ——= -------- In -----17C r 2兀 d由右手定则判定：u（l>u ho解法二：利用法拉第电磁感应定律解决。

电磁学部分题解-大学物理第三版

εi = εL +εbcao = 0
∴ εbcao 1 5 2 = ε L = BωL = BωR2 2 2
O点电势高
《精选》P137页第22题精选》P137页第题页第22
如图，两导线电流方向相反，求直导线如图，两导线电流方向相反， CD中的动生电动势 εi CD中的动生电动势建立坐标如图
+ + + +
d
《精选》P114页第10题精选》P114页第题页第10 （1）B板不接地时，VAB = ? ）板不接地时板不接地时，（2）B板接地时， VAB = ? 板接地时， ′ 板接地时解：（1）B板不接地时）板不接地时 σ 而 EAB = 2 V = E ⋅d
AB AB
A
µ0ih B= 2πR
4、关于电荷作机械运动形成电流产生磁场或磁矩的计算《精选》P126页第30题精选》P126页第30题页第30 表面均匀带电的圆筒绕中心轴线旋转，旋转，求圆筒内部的 B 该带电圆筒绕轴线旋转，等效一个长直螺线管该带电圆筒绕轴线旋转，圆筒表面（轴线方向）圆筒表面（轴线方向）单位长度带电量圆筒以旋转，单位长度的等效电流（电流密度） ω 旋转，单位长度的等效电流（电流密度） ω j= q′ = ωRσ 2π
《精选》P134页第10题精选》P134页第10题页第10 半径为L的圆盘在均匀磁场中匀速转动，半径为L的圆盘在均匀磁场中匀速转动，则
a
ω
c o d a
b
1 Va −Vo = − BωL2 即 o 端电势高 2 Va −Vb = 0 因不切割磁力线
Va −Vc =Vao +Voc
1 1 1 2 2 = − BωL + Bω(d − L) = − Bωd(2L − d) 2 2 2

大学物理第9章电磁感应和电磁场课后习题及答案

第9章电稳感应和电磁场习题及答案1. 通过某回路的磁场与线圈平面垂直指向纸面内，磁通量按以下关系变化：23(65)10t t Wb -Φ=++⨯。

求2t s =时，回路中感应电动势的大小和方向。

解：310)62(-⨯+-=Φ-=t dtd ε当s t 2=时，V 01.0-=ε由楞次定律知，感应电动势方向为逆时针方向2. 长度为l 的金属杆ab 以速率υ在导电轨道abcd 上平行移动。

已知导轨处于均匀磁场B中，B 的方向与回路的法线成60°角，如图所示，B 的大小为B =kt (k 为正常数)。

设0=t 时杆位于cd 处，求：任一时刻t 导线回路中感应电动势的大小和方向。

解：任意时刻通过通过回路面积的磁通量为202160cos t kl t Bl S d B m υυ==⋅=Φ导线回路中感应电动势为 t kl tmυε-=Φ-=d d 方向沿abcda 方向。

3. 如图所示，一边长为a ，总电阻为R 的正方形导体框固定于一空间非均匀磁场中，磁场方向垂直于纸面向外，其大小沿x 方向变化，且)1(x k B +=，0>k 。

求：（1）穿过正方形线框的磁通量；（2）当k 随时间t 按t k t k 0)(=(0k 为正值常量)变化时，线框中感生电流的大小和方向。

解：（1）通过正方形线框的磁通量为⎰⎰=⋅=Φa S Badx S d B 0 ⎰+=a dx x ak 0)1()211(2a k a +=（2）当t k k 0=时，通过正方形线框的磁通量为)211(02a t k a +=Φ 正方形线框中感应电动势的大小为dt d Φ=ε)211(02a k a += 正方形线框线框中电流大小为)211(02a R k a R I +==ε，方向：顺时针方向4.如图所示，一矩形线圈与载有电流t I I ωcos 0=长直导线共面。

设线圈的长为b ，宽为a ；0=t 时，线圈的AD 边与长直导线重合；线圈以匀速度υ垂直离开导线。

大学物理第14章思考题解

大学物理第14章思考题解《大学物理学》（下册）思考题解第14章电磁感应14-1 在电磁感应定律i d dtΦ=-?中，负号的含义是什么? 如何根据负号来判断感应电动势的方向？答：电磁感应定律i d dtΦ=-中的负号来自于楞次定律。

由于磁通量Φ变化而引起感应电动势i ?变化、从而产生感应电流，这个电流的磁场将阻碍原磁通量Φ的变化。

例如原磁通量Φ正在增加，所激发的感应电动势的感应电流的感应磁场将阻碍这个Φ增加。

14-2 如题图所示的几种形状的导线回路，假设均匀磁场垂直于纸面向里，且随时渐减小。

试判断这几种形状的导线回路中，感应电流的流向答：14-3 将一磁铁插入一个由导线组成的闭合电路线圈中，一次迅速插入，另一次缓慢插入。

问：(1)两次插入时在线圈中的感生电荷量是否相同？ (2)两次手推磁铁的力所做的功是否相同？(3)若将磁铁插入一个不闭合的金属环中，在环中间发生什么变化？答：始末两态的磁通1Φ、2Φ不变，所以 (1) 感生电荷量12 q RΦ-Φ=，与时间、速度无关，仅与始末两态的磁通有关，所以两次插入线圈的感生电荷量相同。

(2)从感应电流作功考虑，W I t =??，定性地判断：两种情况下I t q ?=不变，12d dttΦ-ΦΦ=?=-?分子不变分母有区别，所以两次手推磁铁的力，慢慢插入的作功少，快速插入的作功多。

(3) 若将磁铁插入一个不闭合的金属环中，在环的两端将产生感应电动势。

14-4 让一块很小的磁铁在一根很长的竖直钢管内下落，若不计空气阻力，试定性说明磁铁进入钢管上部、中部和下部的运动情况，并说明理由。

答：把小磁铁看作磁矩为m的磁偶极子，下落至钢管口附近时，由于钢管口所围面积的磁通量发生了变化，管壁将产生感生电动势和感生电流，感生电流将激发感生磁场'1B ，由于磁矩m 自己产生的磁感B 在管口产生的磁通正在增加，根据楞次定律，它所激发的感生磁场'1B 将阻碍这个增加，因此，' 1B 与B 反方向。

张三慧《大学物理学：力学、电磁学》(第3版)(B版)(课后习题电磁感应)【圣才出品】

第15章　电磁感应15.1 在通有电流I ＝5 A 的长直导线近旁有一导线段ab ，长l ＝20 Cm ，离长直导线距离d ＝10 cm （图15-1）。

当它沿平行于长直导线的方向以速度v ＝10 m ／s 平移时，导线段中的感生电动势多大？a，b哪端的电势高？图15-1解：（如图15-1所示）由于所以a 端电势高。

15.2 平均半径为12 cm 的4×103匝线圈，在强度为0.5G 的地磁场中每秒钟旋转30周，线圈中可产生最大感生电动势为多大？如何旋转和转到何时，才有这样大的电动势？解：线圈绕垂直于磁场的直径旋转，当线圈平面法线与磁场垂直时感生电动势出现此最大值。

15.3 如图15-2所示，长直导线中通有电流l＝5.0 A，另一矩形线圈共1×103匝，宽a＝10 cm，长L＝20 cm，以v＝2 m／s的速度向右平动，求当d＝10 cm时线圈中的感生电动势。

图15-2解：如图15-2所示，线圈向右平移时，上下两边不产生动生电动势。

因此，整个线圈内的感生电动势为15.4 习题15.3中若线圈不动，而长导线中通有交变电流，线圈内的感生电动势将为多大？解：通过线圈的磁链为15.5 在半径为R的圆柱形体积内，充满磁感应强度为B的均匀磁场。

有一长为L的金属棒放在磁场中，如图15-3所示。

设磁场在增强，并且已知，求棒中的感生电动势，并指出哪端电势高。

图15-3解：方法一如图15-3所示，考虑△Oba。

以S表示其面积，则通过S的磁通量。

当磁通变化时，感应电场的电场线为圆心在O的同心圆。

由法拉第电磁感应定律可得由此得由于，所以，因而b端电势高方法二直接对感应电场积分。

在棒上dl处的感应电场的大小为，方向如图15-3所示由于，所以b 端电势高。

15.6 在50周年国庆盛典上我FBC-1“飞豹”新型超音速歼击轰炸机在天安门上空沿水平方向自东向西呼啸而过。

该机翼展12.705m 。

设北京地磁场的竖直分量为0.42×10－4T ，该机又以最大M 数1.70（M 数即“马赫数”，表示飞机航速相当于声速的倍数）飞行，求该机两翼尖间的电势差。

《大学物理》电磁感应练习题及答案

《大学物理》电磁感应练习题及答案一、简答题1、简述电磁感应定律答：当穿过闭合回路所围面积的磁通量发生变化时，不论这种变化是什么原因引起的，回路中都会建立起感应电动势，且此感应电动势等于磁通量对时间变化率的负值，即dtd i φε-=。

2、简述动生电动势和感生电动势答：由于回路所围面积的变化或面积取向变化而引起的感应电动势称为动生电动势。

由于磁感强度变化而引起的感应电动势称为感生电动势。

3、简述自感和互感答：某回路的自感在数值上等于回路中的电流为一个单位时，穿过此回路所围成面积的磁通量，即LI LI =Φ=Φ。

两个线圈的互感M M 值在数值上等于其中一个线圈中的电流为一单位时，穿过另一个线圈所围成面积的磁通量，即212121MI MI ==φφ或。

4、简述位移电流与传导电流有什么异同答：共同点：都能产生磁场。

不同点：位移电流是变化电场产生的（不表示有电荷定向运动，只表示电场变化），不产生焦耳热；传导电流是电荷的宏观定向运动产生的，产生焦耳热。

5 简述感应电场与静电场的区别？答：感生电场和静电场的区别6、写出麦克斯韦电磁场方程的积分形式。

答：⎰⎰==⋅s v q dv ds D ρ dS tB l E s L ⋅∂∂-=⋅⎰⎰d 0d =⋅⎰S S B dS t D j l H s l ⋅⎪⎭⎫ ⎝⎛∂∂+=⋅⎰⎰d 7、简述产生动生电动势物理本质答：在磁场中导体作切割磁力线运动时，其自由电子受洛仑滋力的作用，从而在导体两端产生电势差8、简述磁能密度, 并写出其表达式答：单位体积中的磁场能量,221H μ。

9、简述何谓楞次定律答：闭合的导线回路中所出现的感应电流，总是使它自己所激发的磁场反抗任何引发电磁感应的原因（反抗相对运动、磁场变化或线圈变形等）.这个规律就叫做楞次定律。

10、全电流安培环路定理答：磁场强度沿任意闭合回路的积分等于穿过闭合回路围成的曲面的全电流 s d t D j l d H s e •⎪⎪⎭⎫ ⎝⎛∂∂+=•⎰⎰二、选择题1、有一圆形线圈在均匀磁场中做下列几种运动，那种情况在线圈中会产生感应电流( D )A 、线圈平面法线沿磁场方向平移B 、线圈平面法线沿垂直于磁场方向平移C 、线圈以自身的直径为轴转动，轴与磁场方向平行D 、线圈以自身的直径为轴转动，轴与磁场方向垂直2、有两个线圈，线圈1对线圈2的互感系数为21M ，而线圈2对线圈1的互感系数为12M .若它们分别流过1i 和2i 的变化电流且dt di dt di 21<，并设由2i 变化在线圈1中产生的互感电动势为12ε，由1i 变化在线圈1中产生的互感电动势为21ε，下述论断正确的是( D )A 、 12212112,εε==M MB 、 12212112,εε≠≠M MC 、 12212112,εε>=M MD 、 12212112,εε<=M M3、对于位移电流，下列四种说法中哪一种说法是正确的 ( A )A 、位移电流的实质是变化的电场B 、位移电流和传导电流一样是定向运动的电荷C 、位移电流服从传导电流遵循的所有规律D 、位移电流的磁效应不服从安培环路定理4、下列概念正确的是 ( B )。

电磁感应习题(有答案)

大学物理6丫头5《大学物理AI 》作业 No.11 电磁感应班级 ________________ 学号 ______________ 姓名 ____________ 成绩 ___________一、选择题：（注意：题目中可能有一个或几个正确答案） 1．一块铜板放在磁感应强度正在增大的磁场中时，铜板中出现涡流（感应电流），则涡流将： (A)加速铜板中磁场的增加 (B)减缓铜板中磁场的增加(C)对磁场不起作用 (D)使铜板中磁场反向[ B ] 解：根据愣次定律，感应电流的磁场总是力图阻碍原磁场的变化。

故选B2．一无限长直导体薄板宽度为l ，板面与Z 轴垂直，板的长度方向沿Y 轴，板的两侧与一个伏特计相接，如图。

整个系统放在磁感应强度为B的均匀磁场中，B的方向沿Z 轴正方向，如果伏特计与导体平板均以速度v向Y 轴正方向移动，则伏特计指示的电压值为(A) 0 (B)vBl 21(C) vBl (D) vBl 2[ A ]解：在伏特计与导体平板运动过程中，dc ab εε=，整个回路0=∑ε，0=i ，所以伏特计指示0=V 。

故选A3．两根无限长平行直导线载有大小相等方向相反的电流I ，I 以tId d 的变化率增长，一矩形线圈位于导线平面内（如图），则： (A)线圈中无感应电流。

(B)线圈中感应电流为顺时针方向。

(C)线圈中感应电流为逆时针方向。

(D)线圈中感应电流方向不确定。

[ B ]解：0d d >t I ，在回路产生的垂直于纸面向外的磁场⊗增强，根据愣次定律，回路中产生的电流为顺时针，用以反抗原来磁通量的变化。

故选B4．在一通有电流I 的无限长直导线所在平面内，有一半经为r ，电阻为R 的导线环，环中心距直导线为a ，如图所示，且r a >>。

当aIroabcVdYBZlI直导线的电流被切断后，沿着导线环流过的电量约为：(A))11(220ra a R Ir +-πμ(B)a ra R Ir +ln20πμ (C)aRIr 220μ (D)rRIa 220μ[ C ]解：直导线切断电流的过程中，在导线环中有感应电动势大小：td d Φ=ε 感应电流为：tR Ri d d 1Φ==ε则沿导线环流过的电量为 ∆Φ=⋅Φ==⎰⎰Rt t R t i q 1d d d 1daRIr R r a I R S B 212120200μππμ=⋅⋅=⋅∆≈故选C5．如图所示，直角三角形金属框架abc 放在均匀磁场中，磁场B平行于ab 边，bc 的边长为l 。

大学物理电磁感应小结与习题

例.空气中有一无限长金属薄壁圆筒，在表面上沿圆周方向均匀地空气中有一无限长金属薄壁圆筒，流着一层随时间变化的面电流，流着一层随时间变化的面电流， ∫sB⋅ ds = 0, ∫sEi ⋅ ds = 0 则筒内例. 一导线构成正方形线圈然后对折，并使其平面垂直置于均匀一导线构成正方形线圈然后对折，当线圈的一半不动，磁场 B 中，当线圈的一半不动，另一半以角速度 ω张开时（线圈边长为 2l 、此时张角为 θ ），张开时（线圈中感应电动势的大小 ε = ___________ 2 B 2 sinθ ωl
2 1
讨论: 讨论:
dφ dω 2 µ 0σ ( R2 − R1 ) εi = − = −πr ⋅ dt 2 dt 1 dω ε µσ i = i = − πr 2 ⋅ 0 ( R2 − R1 ) R′ 2 dt R′
dω >0 dt dω <0 dt
i < 0 顺时针 i > 0 逆时针
7
例. 一矩形金属线框，边长为 a、b (b足够长），线框质一矩形金属线框，足够长），、足够长），线框质电阻忽略，量为 m自感系数为 L ，电阻忽略，线框以初速度 v0 沿 x 自感系数为轴方向从磁场外进入磁感应强度为B 的均匀磁场中，轴方向从磁场外进入磁感应强度为 0 的均匀磁场中，求矩形线圈在磁场内的速度与时间的关系式 v = v(t) 和沿 x 轴方向移动的距离与时间的关系式 x=x(t) × × × B 0
4b
思考与练习题金属圆环，电阻R=1Ω 例. 桌子上水平放置一个半径 r =10 cm 金属圆环，电阻 Ω，若
3⋅14×10 C q = ___________ .
−6
地球磁场磁感应强度的竖直分量为 5×10-5 T，那么，将环面翻转一 × ，那么，沿环流过任一截面的电量。次，沿环流过任一截面的电量。

大学物理第三版下册课后习题答案

习题八8-1 电量都是q 的三个点电荷，分别放在正三角形的三个顶点．试问：(1)在这三角形的中心放一个什么样的电荷，就可以使这四个电荷都达到平衡(即每个电荷受其他三个电荷的库仑力之和都为零)?(2)这种平衡与三角形的边长有无关系?解: 如题8-1图示(1) 以A 处点电荷为研究对象，由力平衡知：q '为负电荷2220)33(π4130cos π412a q q a q '=︒εε解得 q q 33-=' (2)与三角形边长无关．题8-1图题8-2图8-2 两小球的质量都是m ，都用长为l 的细绳挂在同一点，它们带有相同电量，静止时两线夹角为2θ ,如题8-2图所示．设小球的半径和线的质量都可以忽略不计，求每个小球所带的电量．解: 如题8-2图示⎪⎩⎪⎨⎧===220)sin 2(π41sin cos θεθθl q F T mg T e解得 θπεθtan 4sin 20mg l q = 8-3 根据点电荷场强公式204r q E πε=，当被考察的场点距源点电荷很近(r →0)时，则场强→∞，这是没有物理意义的，对此应如何理解?解: 020π4r r q E ϖϖε=仅对点电荷成立，当0→r 时，带电体不能再视为点电荷，再用上式求场强是错误的，实际带电体有一定形状大小，考虑电荷在带电体上的分布求出的场强不会是无限大．8-4 在真空中有A ，B 两平行板，相对距离为d ，板面积为S ，其带电量分别为+q 和-q ．则这两板之间有相互作用力f ，有人说f =2024dq πε,又有人说，因为f =qE ,SqE 0ε=，所以f =Sq 02ε．试问这两种说法对吗?为什么? f 到底应等于多少?解: 题中的两种说法均不对．第一种说法中把两带电板视为点电荷是不对的，第二种说法把合场强Sq E 0ε=看成是一个带电板在另一带电板处的场强也是不对的．正确解答应为一个板的电场为S q E 02ε=，另一板受它的作用力Sq S qq f 02022εε==，这是两板间相互作用的电场力．8-5一电偶极子的电矩为l q p ϖϖ=，场点到偶极子中心O 点的距离为r ,矢量r ϖ与l ϖ的夹角为θ,(见题8-5图)，且l r >>．试证P 点的场强E 在r 方向上的分量r E 和垂直于r 的分量θE 分别为r E =302cos r p πεθ, θE =304sin r p πεθ证: 如题8-5所示，将p ϖ分解为与r ϖ平行的分量θsin p 和垂直于r ϖ的分量θsin p ．∵ l r >> ∴ 场点P 在r 方向场强分量30π2cos r p E r εθ=垂直于r 方向，即θ方向场强分量300π4sin r p E εθ=题8-5图题8-6图 8-6 长l =15.0cm的直导线AB 上均匀地分布着线密度λ=5.0x10-9C ·m-1的正电荷．试求：(1)在导线的延长线上与导线B 端相距1a =5.0cm 处P 点的场强；(2)在导线的垂直平分线上与导线中点相距2d =5.0cm 处Q 点的场强．解：如题8-6图所示(1)在带电直线上取线元x d ，其上电量q d 在P 点产生场强为20)(d π41d x a x E P -=λε222)(d π4d x a x E E l l P P -==⎰⎰-ελ]2121[π40l a l a +--=ελ)4(π220l a l-=ελ用15=l cm ，9100.5-⨯=λ1m C -⋅, 5.12=a cm 代入得21074.6⨯=P E 1C N -⋅方向水平向右(2)同理2220d d π41d +=x xE Qλε 方向如题8-6图所示由于对称性⎰=l QxE 0d ，即Q E ϖ只有y 分量，∵22222220dd d d π41d ++=x x x E Qyλε22π4d d ελ⎰==l QyQy E E ⎰-+2223222)d (d l l x x2220d4π2+=l lελ以9100.5-⨯=λ1cm C -⋅, 15=l cm ,5d 2=cm 代入得21096.14⨯==Qy Q E E 1C N -⋅，方向沿y 轴正向8-7 一个半径为R 的均匀带电半圆环，电荷线密度为λ,求环心处O 点的场强．解: 如8-7图在圆上取ϕRd dl =题8-7图ϕλλd d d R l q ==，它在O 点产生场强大小为 20π4d d R R E εϕλ=方向沿半径向外则 ϕϕελϕd sin π4sin d d 0RE E x==ϕϕελϕπd cos π4)cos(d d 0RE E y-=-= 积分RR E x 000π2d sin π4ελϕϕελπ==⎰ 0d cos π400=-=⎰ϕϕελπRE y ∴ RE E x0π2ελ==，方向沿x 轴正向． 8-8 均匀带电的细线弯成正方形，边长为l ，总电量为q ．(1)求这正方形轴线上离中心为r 处的场强E ；(2)证明：在l r >>处，它相当于点电荷q 产生的场强E ．解: 如8-8图示，正方形一条边上电荷4q在P 点产生物强P E ϖd 方向如图，大小为()4π4cos cos d 22021l r E P +-=εθθλ∵ 22cos 221l r l +=θ12cos cos θθ-=∴24π4d2222lrllrEP++=ελPEϖd在垂直于平面上的分量βcosddPEE=⊥∴424π4d222222lrrlrlrlE+++=⊥ελ题8-8图由于对称性，P点场强沿OP方向，大小为2)4(π44d42222lrlrlrEEP++=⨯=⊥ελ∵lq4=λ∴2)4(π42222lrlrqrEP++=ε方向沿OP8-9 (1)点电荷q位于一边长为a的立方体中心，试求在该点电荷电场中穿过立方体的一个面的电通量；(2)如果该场源点电荷移动到该立方体的一个顶点上，这时穿过立方体各面的电通量是多少?*(3)如题8-9(3)图所示，在点电荷q的电场中取半径为R的圆平面．q在该平面轴线上的A点处，求：通过圆平面的电通量．(xRarctan=α)解: (1)由高斯定理dεqSEs⎰=⋅ϖϖ立方体六个面，当q在立方体中心时，每个面上电通量相等∴各面电通量6εqe=Φ．(2)电荷在顶点时，将立方体延伸为边长a2的立方体，使q处于边长a2的立方体中心，则边长a2的正方形上电通量6εqe=Φ对于边长a的正方形，如果它不包含q所在的顶点，则24εqe=Φ，如果它包含q所在顶点则0=Φe．如题8-9(a)图所示．题8-9(3)图题8-9(a)图题8-9(b)图题8-9(c)图 (3)∵通过半径为R 的圆平面的电通量等于通过半径为22x R +的球冠面的电通量，球冠面积*]1)[(π22222xR x x R S +-+=∴ )(π42200x R Sq +=Φε02εq =[221xR x +-]*关于球冠面积的计算：见题8-9(c)图ααα⎰⋅=0d sin π2r r Sααα⎰⋅=02d sin π2r)cos 1(π22α-=r8-10 均匀带电球壳内半径6cm ，外半径10cm ，电荷体密度为2×510-C ·m -3求距球心5cm ，8cm ,12cm 各点的场强．解: 高斯定理0d ε∑⎰=⋅qS E s ϖϖ,02π4ε∑=qr E当5=r cm 时，0=∑q ,0=E ϖ8=r cm 时，∑q 3π4p=3(r )3内r - ∴ ()2023π43π4rr r E ερ内-=41048.3⨯≈1C N -⋅，方向沿半径向外． 12=r cm时,3π4∑=ρq -3(外r ）内3r ∴ ()420331010.4π43π4⨯≈-=r r r E ερ内外 1C N -⋅ 沿半径向外.8-11 半径为1R 和2R (2R ＞1R )的两无限长同轴圆柱面，单位长度上分别带有电量λ和-λ,试求:(1)r ＜1R ；(2) 1R ＜r ＜2R ；(3) r ＞2R 处各点的场强．解: 高斯定理0d ε∑⎰=⋅qS E sϖϖ取同轴圆柱形高斯面，侧面积rl S π2=则 rl E S E Sπ2d =⋅⎰ϖϖ对(1) 1R r < 0,0==∑E q (2) 21R r R << λl q =∑ ∴ rE 0π2ελ=沿径向向外(3) 2R r > 0=∑q ∴ 0=E题8-12图8-12 两个无限大的平行平面都均匀带电，电荷的面密度分别为1σ和2σ，试求空间各处场强．解: 如题8-12图示，两带电平面均匀带电，电荷面密度分别为1σ与2σ，两面间， n E ϖϖ)(21210σσε-= 1σ面外， n E ϖϖ)(21210σσε+-= 2σ面外， n E ϖϖ)(21210σσε+= n ϖ：垂直于两平面由1σ面指为2σ面．8-13 半径为R 的均匀带电球体内的电荷体密度为ρ,若在球内挖去一块半径为r ＜R 的小球体，如题8-13图所示．试求：两球心O 与O '点的场强，并证明小球空腔内的电场是均匀的．解: 将此带电体看作带正电ρ的均匀球与带电ρ-的均匀小球的组合，见题8-13图(a)． (1) ρ+球在O 点产生电场010=E ϖ，ρ-球在O 点产生电场'dπ4π3430320OO r E ερ=ϖ∴ O 点电场'd 33030OO r E ερ=ϖ；(2) ρ+在O '产生电场'dπ4d 3430301OO E ερπ='ϖρ-球在O '产生电场002='E ϖ∴ O ' 点电场 003ερ='E ϖ'OO题8-13图(a) 题8-13图(b)(3)设空腔任一点P 相对O '的位矢为rϖ'，相对O 点位矢为r ϖ (如题8-13(b)图) 则 03ερrE PO ϖϖ=，3ερr E O P '-='ϖϖ,∴ 0003'3)(3ερερερd OO r r E E E O P PO P ϖϖϖϖϖϖ=='-=+=' ∴腔内场强是均匀的．8-14 一电偶极子由q =1.0×10-6C 的两个异号点电荷组成，两电荷距离d=0.2cm ，把这电偶极子放在1.0×105N ·C-1的外电场中，求外电场作用于电偶极子上的最大力矩．解: ∵ 电偶极子p ϖ在外场E ϖ中受力矩E p Mϖϖϖ⨯=∴ qlE pE M ==max 代入数字4536max 100.2100.1102100.1---⨯=⨯⨯⨯⨯⨯=M m N ⋅8-15 两点电荷1q =1.5×10-8C ，2q =3.0×10-8C ，相距1r =42cm ，要把它们之间的距离变为2r =25cm ，需作多少功?解: ⎰⎰==⋅=22210212021π4π4d d r r r rq q r r q q r F A εεϖϖ)11(21r r - 61055.6-⨯-=J外力需作的功 61055.6-⨯-=-='A A J题8-16图8-16 如题8-16图所示，在A ，B 两点处放有电量分别为+q ,-q 的点电荷，AB 间距离为2R ，现将另一正试验点电荷0q 从O 点经过半圆弧移到C 点，求移动过程中电场力作的功．解: 如题8-16图示0π41ε=O U 0)(=-RqR q 0π41ε=O U )3(R qR q -Rq 0π6ε-= ∴ Rqq U U q A o C O 00π6)(ε=-= 8-17 如题8-17图所示的绝缘细线上均匀分布着线密度为λ的正电荷,两直导线的长度和半圆环的半径都等于R ．试求环中心O 点处的场强和电势．解: (1)由于电荷均匀分布与对称性，AB 和CD 段电荷在O 点产生的场强互相抵消，取θd d R l =则θλd d R q =产生O 点E ϖd 如图，由于对称性，O 点场强沿y 轴负方向题8-17图θεθλππcos π4d d 2220⎰⎰-==R R E E yR 0π4ελ=［)2sin(π-2sin π-］ R0π2ελ-=(2) AB 电荷在O 点产生电势，以0=∞U⎰⎰===A B200012ln π4π4d π4d R R x x x x U ελελελ同理CD 产生 2ln π402ελ=U 半圆环产生 0034π4πελελ==R R U∴ 0032142ln π2ελελ+=++=U U U U O8-18 一电子绕一带均匀电荷的长直导线以2×104m ·s -1的匀速率作圆周运动．求带电直线上的线电荷密度．(电子质量0m =9.1×10-31kg ，电子电量e =1.60×10-19C) 解: 设均匀带电直线电荷密度为λ，在电子轨道处场强rE 0π2ελ=电子受力大小 re eE F e0π2ελ== ∴ rv mr e 20π2=ελ得 1320105.12π2-⨯==emv ελ1m C -⋅ 8-19 空气可以承受的场强的最大值为E =30kV ·cm -1，超过这个数值时空气要发生火花放电．今有一高压平行板电容器，极板间距离为d =0.5cm ，求此电容器可承受的最高电压．解: 平行板电容器内部近似为均匀电场 ∴ 4105.1d ⨯==E U V8-20 根据场强E ϖ与电势U 的关系U E -∇=ϖ，求下列电场的场强：(1)点电荷q 的电场；(2)总电量为q ，半径为R 的均匀带电圆环轴上一点；*(3)偶极子ql p =的l r >>处(见题8-20图)．解: (1)点电荷 rqU 0π4ε=题 8-20 图∴ 0200π4r r q r r U E ϖϖϖε=∂∂-= 0r ϖ为r 方向单位矢量．(2)总电量q ，半径为R 的均匀带电圆环轴上一点电势220π4xR q U +=ε∴ ()i x R qxi x U E ϖϖϖ2/3220π4+=∂∂-=ε(3)偶极子l q p ϖϖ=在l r >>处的一点电势200π4cos ])cos 21(1)cos 2(1[π4r ql llr q U εθθθε=+--=∴ 30π2cos r p r U E rεθ=∂∂-= 30π4sin 1r p U r E εθθθ=∂∂-=8-21 证明：对于两个无限大的平行平面带电导体板(题8-21图)来说，(1)相向的两面上，电荷的面密度总是大小相等而符号相反；(2)相背的两面上，电荷的面密度总是大小相等而符号相同．证: 如题8-21图所示，设两导体A 、B 的四个平面均匀带电的电荷面密度依次为1σ，2σ，3σ，4σ题8-21图(1)则取与平面垂直且底面分别在A 、B 内部的闭合柱面为高斯面时，有 0)(d 32=∆+=⋅⎰S S E s σσϖϖ ∴ +2σ03=σ 说明相向两面上电荷面密度大小相等、符号相反；(2)在A 内部任取一点P ，则其场强为零，并且它是由四个均匀带电平面产生的场强叠加而成的，即0222204030201=---εσεσεσεσ 又∵ +2σ03=σ ∴ 1σ4σ=说明相背两面上电荷面密度总是大小相等，符号相同．8-22 三个平行金属板A ，B 和C 的面积都是200cm 2，A 和B 相距4.0mm ，A 与C 相距2.0 mm ．B ，C 都接地，如题8-22图所示．如果使A 板带正电3.0×10-7C ，略去边缘效应，问B 板和C 板上的感应电荷各是多少?以地的电势为零，则A 板的电势是多少?解: 如题8-22图示，令A 板左侧面电荷面密度为1σ，右侧面电荷面密度为2σ题8-22图(1)∵ AB ACU U =，即 ∴ AB AB AC AC E E d d =∴2d d 21===ACABAB AC E E σσ 且 1σ+2σSq A =得 ,32Sq A =σ Sq A 321=σ而 7110232-⨯-=-=-=A Cq S q σCC10172-⨯-=-=S q B σ (2)301103.2d d ⨯===AC AC AC A E U εσV 8-23 两个半径分别为1R 和2R （1R ＜2R )的同心薄金属球壳，现给内球壳带电+q ，试计算：(1)外球壳上的电荷分布及电势大小；(2)先把外球壳接地，然后断开接地线重新绝缘，此时外球壳的电荷分布及电势；*(3)再使内球壳接地，此时内球壳上的电荷以及外球壳上的电势的改变量．解: (1)内球带电q +；球壳内表面带电则为q -,外表面带电为q +，且均匀分布，其电势题8-23图⎰⎰∞∞==⋅=22020π4π4d d R R R qrr q r E U εεϖϖ (2)外壳接地时，外表面电荷q +入地，外表面不带电，内表面电荷仍为q -．所以球壳电势由内球q +与内表面q -产生：0π4π42020=-=R q R q U εε(3)设此时内球壳带电量为q '；则外壳内表面带电量为q '-，外壳外表面带电量为+-q q ' (电荷守恒)，此时内球壳电势为零，且0π4'π4'π4'202010=+-+-=R q q R q R q U A εεε 得 q R R q 21=' 外球壳上电势()22021202020π4π4'π4'π4'R qR R R q q R q R q U B εεεε-=+-+-=8-24 半径为R 的金属球离地面很远，并用导线与地相联，在与球心相距为R d 3=处有一点电荷+q ，试求：金属球上的感应电荷的电量．解: 如题8-24图所示，设金属球感应电荷为q '，则球接地时电势0=O U8-24图由电势叠加原理有：=O U 03π4π4'00=+RqR q εε 得 -='q 3q8-25 有三个大小相同的金属小球，小球1，2带有等量同号电荷，相距甚远，其间的库仑力为0F ．试求：(1)用带绝缘柄的不带电小球3先后分别接触1，2后移去，小球1，2之间的库仑力； (2)小球3依次交替接触小球1，2很多次后移去，小球1，2之间的库仑力．解: 由题意知 2020π4r q F ε=(1)小球3接触小球1后，小球3和小球1均带电 2q q =', 小球3再与小球2接触后，小球2与小球3均带电 q q 43=''∴ 此时小球1与小球2间相互作用力 00220183π483π4"'2F r qr q q F =-=εε (2)小球3依次交替接触小球1、2很多次后，每个小球带电量均为 32q .∴ 小球1、2间的作用力 00294π432322F r q q F ==ε *8-26 如题8-26图所示，一平行板电容器两极板面积都是S ，相距为d ，分别维持电势A U =U ，B U =0不变．现把一块带有电量q 的导体薄片平行地放在两极板正中间，片的面积也是S ，片的厚度略去不计．求导体薄片的电势．解: 依次设A ,C ,B 从上到下的6个表面的面电荷密度分别为1σ，2σ，3σ，4σ,5σ,6σ如图所示．由静电平衡条件，电荷守恒定律及维持U U AB =可得以下6个方程题8-26图⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧++++==+=+-==+=+===+6543215432065430021001σσσσσσσσσσεσσσσεσσd US q S qdU U C S S q B A解得 Sq 261==σσSq dU2032-=-=εσσ Sq dU2054+=-=εσσ所以CB 间电场 S qd U E 00422εεσ+==)2d(212d 02Sq U E U U CB C ε+=== 注意：因为C 片带电，所以2U U C≠，若C 片不带电，显然2U U C =8-27 在半径为1R 的金属球之外包有一层外半径为2R 的均匀电介质球壳，介质相对介电常数为r ε，金属球带电Q ．试求： (1)电介质内、外的场强； (2)电介质层内、外的电势； (3)金属球的电势．解: 利用有介质时的高斯定理∑⎰=⋅q S D S ϖϖd(1)介质内)(21R r R <<场强 303π4,π4r r Q E r r Q D r εεϖϖϖϖ==内;介质外)(2R r <场强 303π4,π4r rQ E r Qr D εϖϖϖ==外(2)介质外)(2R r >电势 rQE U 0r π4r d ε=⋅=⎰∞ϖϖ外介质内)(21R r R <<电势2020π4)11(π4R Q R r qr εεε+-=)11(π420R r Qr r -+=εεε (3)金属球的电势 r d r d 221ϖϖϖϖ⋅+⋅=⎰⎰∞R R RE E U 外内⎰⎰∞+=22220π44πdr R R Rr r Qdr r Q εεε)11(π4210R R Qr r-+=εεε 8-28 如题8-28图所示，在平行板电容器的一半容积内充入相对介电常数为r ε的电介质．试求：在r d r d ϖϖϖϖ⋅+⋅=⎰⎰∞∞rrE E U 外内有电介质部分和无电介质部分极板上自由电荷面密度的比值．解: 如题8-28图所示，充满电介质部分场强为2E ϖ，真空部分场强为1E ϖ，自由电荷面密度分别为2σ与1σ由∑⎰=⋅0d q S D ϖϖ得 11σ=D ，22σ=D 而 101E D ε=,202E D r εε=d21U E E ==∴r D D εσσ==1212题8-28图题8-29图8-29 两个同轴的圆柱面，长度均为l ，半径分别为1R 和2R (2R ＞1R )，且l >>2R -1R ，两柱面之间充有介电常数ε的均匀电介质.当两圆柱面分别带等量异号电荷Q 和-Q 时，求：(1)在半径r 处(1R ＜r ＜2R ＝，厚度为dr ，长为l 的圆柱薄壳中任一点的电场能量密度和整个薄壳中的电场能量；(2)电介质中的总电场能量； (3)圆柱形电容器的电容．解: 取半径为r 的同轴圆柱面)(S则 rlD S D S π2d )(=⋅⎰ϖϖ当)(21R r R <<时，Q q =∑ ∴ rlQ D π2=(1)电场能量密度 22222π82l r Q D w εε== 薄壳中 rlrQ rl r l r Q w W εευπ4d d π2π8d d 22222===(2)电介质中总电场能量 ⎰⎰===211222ln π4π4d d R RV R R l Q rl r Q W W εε(3)电容：∵ CQ W 22=∴ )/ln(π22122R R lW Q C ε== *8-30 金属球壳A 和B 的中心相距为r ，A 和B 原来都不带电．现在A 的中心放一点电荷1q ，在B 的中心放一点电荷2q ，如题8-30图所示．试求： (1) 1q 对2q 作用的库仑力，2q 有无加速度；(2)去掉金属壳B ，求1q 作用在2q 上的库仑力，此时2q 有无加速度．解: (1)1q 作用在2q 的库仑力仍满足库仑定律，即2210π41r q q F ε=但2q 处于金属球壳中心，它受合力．．为零，没有加速度． (2)去掉金属壳B ，1q 作用在2q 上的库仑力仍是2210π41r q q F ε=，但此时2q 受合力不为零，有加速度．题8-30图题8-31图8-31 如题8-31图所示，1C =0.25μF ，2C =0.15μF ，3C =0.20μF ．1C 上电压为50V ．求：AB U ．解: 电容1C 上电量111U C Q =电容2C 与3C 并联3223C C C += 其上电荷123Q Q =∴ 355025231123232⨯===C U C C Q U 86)35251(5021=+=+=U U U AB V 8-32 1C 和2C 两电容器分别标明“200 pF 、500 V ”和“300 pF 、900 V ”，把它们串联起来后等值电容是多少?如果两端加上1000 V 的电压，是否会击穿?解: (1) 1C 与2C 串联后电容1203002003002002121=+⨯=+='C C C C C pF (2)串联后电压比231221==C C U U ，而100021=+U U∴ 6001=U V ,4002=U V即电容1C 电压超过耐压值会击穿，然后2C 也击穿．8-33 将两个电容器1C 和2C 充电到相等的电压U 以后切断电源，再将每一电容器的正极板与另一电容器的负极板相联．试求： (1)每个电容器的最终电荷； (2)电场能量的损失．解: 如题8-33图所示，设联接后两电容器带电分别为1q ,2q题8-33图则⎪⎪⎩⎪⎪⎨⎧==-=-=+2122112121201021U U U C U Cq q U C U C q q q q解得 (1) =1q UC C C C C q U C C C C C 21212221211)(,)(+-=+-(2)电场能量损失W W W -=∆0)22()2121(2221212221C q C q U C U C +-+= 221212U C C C C +=8-34 半径为1R =2.0cm 的导体球，外套有一同心的导体球壳，壳的内、外半径分别为2R =4.0cm 和3R =5.0cm ，当内球带电荷Q =3.0×10-8C 时，求：(1)整个电场储存的能量；(2)如果将导体壳接地，计算储存的能量； (3)此电容器的电容值．解: 如图，内球带电Q ，外球壳内表面带电Q -，外表面带电Q题8-34图(1)在1R r <和32R r R <<区域0=E ϖ在21R r R <<时 301π4r r Q E εϖϖ=3R r >时 302π4r r Q E εϖϖ=∴在21R r R <<区域⎰=21d π4)π4(21222001R R r r rQ W εε ⎰-==21)11(π8π8d 2102202R R R R Q rr Q εε 在3R r >区域⎰∞==32302220021π8d π4)π4(21R R Q r r rQ W εεε∴ 总能量 )111(π83210221R R R Q W W W +-=+=ε41082.1-⨯=J(2)导体壳接地时，只有21R r R <<时30π4r r Q E εϖϖ=,02=W∴ 4210211001.1)11(π8-⨯=-==R R Q W W ε J(3)电容器电容 )11/(π422102R R QW C -==ε 121049.4-⨯=F习题九9-1 在同一磁感应线上，各点B ϖ的数值是否都相等?为何不把作用于运动电荷的磁力方向定义为磁感应强度B ϖ的方向?解: 在同一磁感应线上，各点B ϖ的数值一般不相等．因为磁场作用于运动电荷的磁力方向不仅与磁感应强度B ϖ的方向有关，而且与电荷速度方向有关，即磁力方向并不是唯一由磁场决定的，所以不把磁力方向定义为B ϖ的方向．9-2 (1)在没有电流的空间区域里，如果磁感应线是平行直线，磁感应强度B ϖ的大小在沿磁感应线和垂直它的方向上是否可能变化(即磁场是否一定是均匀的)?(2)若存在电流，上述结论是否还对?解: (1)不可能变化，即磁场一定是均匀的．如图作闭合回路abcd 可证明21B B ρϖ=∑⎰==-=⋅0d 021I bc B da B l B abcdμϖϖ∴ 21B B ρϖ=(2)若存在电流，上述结论不对．如无限大均匀带电平面两侧之磁力线是平行直线，但B ϖ方向相反，即21B B ρϖ≠.9-3 用安培环路定理能否求有限长一段载流直导线周围的磁场?答: 不能，因为有限长载流直导线周围磁场虽然有轴对称性，但不是稳恒电流，安培环路定理并不适用．9-4 在载流长螺线管的情况下，我们导出其内部nI B 0μ=，外面B =0，所以在载流螺线管外面环绕一周(见题9-4图)的环路积分⎰外B L ϖ·d l ϖ=0 但从安培环路定理来看，环路L 中有电流I 穿过，环路积分应为⎰外B L ϖ·d l ϖ=I 0μ这是为什么?解: 我们导出nl B 0μ=内,0=外B 有一个假设的前提，即每匝电流均垂直于螺线管轴线．这时图中环路L 上就一定没有电流通过，即也是⎰∑==⋅LI l B 0d 0μϖϖ外，与⎰⎰=⋅=⋅Ll l B 0d 0d ϖϖϖ外是不矛盾的．但这是导线横截面积为零，螺距为零的理想模型．实际上以上假设并不真实存在，所以使得穿过L 的电流为I ，因此实际螺线管若是无限长时，只是外B ϖ的轴向分量为零，而垂直于轴的圆周方向分量rI B πμ20=⊥,r 为管外一点到螺线管轴的距离．题 9 - 4 图9-5 如果一个电子在通过空间某一区域时不偏转，能否肯定这个区域中没有磁场?如果它发生偏转能否肯定那个区域中存在着磁场?解：如果一个电子在通过空间某一区域时不偏转，不能肯定这个区域中没有磁场，也可能存在互相垂直的电场和磁场，电子受的电场力与磁场力抵消所致．如果它发生偏转也不能肯定那个区域存在着磁场，因为仅有电场也可以使电子偏转． 9-6 已知磁感应强度0.2=B Wb ·m-2的均匀磁场，方向沿x 轴正方向，如题9-6图所示．试求：(1)通过图中abcd 面的磁通量；(2)通过图中befc 面的磁通量；(3)通过图中aefd 面的磁通量．解：如题9-6图所示题9-6图(1)通过abcd 面积1S 的磁通是24.04.03.00.211=⨯⨯=⋅=S B ϖϖΦWb(2)通过befc 面积2S 的磁通量022=⋅=S B ϖϖΦ(3)通过aefd 面积3S 的磁通量24.0545.03.02cos 5.03.0233=⨯⨯⨯=θ⨯⨯⨯=⋅=S B ϖϖΦWb (或曰24.0-Wb )题9-7图9-7如题9-7图所示，AB 、CD 为长直导线，C B )为圆心在O 点的一段圆弧形导线，其半径为R ．若通以电流I ，求O 点的磁感应强度．解：如题9-7图所示，O 点磁场由AB 、C B )、CD 三部分电流产生．其中AB产生 01=B ϖCD产生RIB 1202μ=，方向垂直向里CD段产生 )231(2)60sin 90(sin 24003-πμ=-πμ=︒︒R I R I B ，方向⊥向里 ∴)6231(203210ππμ+-=++=R I B B B B ，方向⊥向里． 9-8 在真空中，有两根互相平行的无限长直导线1L 和2L ，相距0.1m ，通有方向相反的电流，1I =20A,2I =10A ，如题9-8图所示．A ，B 两点与导线在同一平面内．这两点与导线2L 的距离均为5.0cm ．试求A ，B 两点处的磁感应强度，以及磁感应强度为零的点的位置．题9-8图解：如题9-8图所示,A B ϖ方向垂直纸面向里42010102.105.02)05.01.0(2-⨯=⨯+-=πμπμI I B A T(2)设0=B ϖ在2L 外侧距离2L 为r 处则02)1.0(220=-+rI r Iπμπμ 解得 1.0=r m题9-9图9-9 如题9-9图所示，两根导线沿半径方向引向铁环上的A ，B 两点，并在很远处与电源相连．已知圆环的粗细均匀，求环中心O 的磁感应强度．解：如题9-9图所示，圆心O 点磁场由直电流∞A 和∞B 及两段圆弧上电流1I 与2I 所产生，但∞A 和∞B 在O 点产生的磁场为零。

四川大学大学物理练习册答案16电磁感应一解答

L 0 ln d a a
证:
B
BL
BR
0I 2r
0I
2 d r
r I
d 2a
O
I r
d
d a
BdS
a
0I 2
d a 1 a r
1 ldr d r
0Il ln
d a a
L F 0 ln d a
Il Il
a
旧版电磁感应二计算题 3
(D) 变大，但与电流不成反比关系．
旧版电磁感应二选择题 4
电磁感应（一）
第八章
7．将一块铜板垂直于磁场方向放在磁感应强度正在增大的磁场中时，铜板中出现的涡流（感应电流）将
(A) 加速铜板中磁场的增加．
(B) 减缓铜板中磁场的增加．
(C) 对磁场不起作用．
(D) 使铜板中磁场反向．
B
i
电磁感应（一）
b
(D) 线圈中感应电流方向不确定． x
c
直导线产生的磁场 B 0I 2x
B
0I
2 x
l
l ab
B ds
0I
l a b
1
1 cdx 0cI ln a b ln l a b
la
2 la x l x
2 a
la
向外增加
电磁感应（一）
第八章
3．一导体圆线圈在均匀磁场中运动，能使其产生感应电流的一种情况是
u×B
ei
(v
B)
dl
L
e AB
d l
uBdx
d
d l
u
d
0I 2x
dx
0 Iu 2
ln
d l d

《大学物理》电磁感应练习题及答案解析

《大学物理》电磁感应练习题及答案解析一、选择题1. 圆铜盘水平放置在均匀磁场中，B 的方向垂直盘面向上，当铜盘绕通过中心垂直于盘面的轴沿图示方向转动时.（ D ）(A) 铜盘上有感应电流产生，沿着铜盘转动的相反方向流动。

(B) 铜盘上有感应电流产生，沿着铜盘转动的方向流动。

(D) 铜盘上没有感应电流产生，铜盘边缘处电势最高。

2．在尺寸相同的铁环和铜环所包围的面积中穿过相同变化率的磁通量，则两环中（ C ）A．感应电动势相同，感应电流相同；B．感应电动势不同，感应电流不同；C．感应电动势相同，感应电流不同；D．感应电动势不同，感应电流相同。

3．两根无限长的平行直导线有相等的电流但电流的流向相反如右图，而电流的变化率均大于零，有一矩形线圈与两导线共面，则（ B ）A．线圈中无感应电流；B．线圈中感应电流为逆时针方向；C．线圈中感应电流为顺时针方向；D．线圈中感应电流不确定。

4．如图所示，在长直载流导线下方有导体细棒，棒与直导线垂直且共面。

（a）、（b）、（c）处有三个光滑细金属框。

今使以速度向右滑动。

设（a）、（b）、（c）、（d）四种情况下在细棒中的感应电动势分别为ℇa、ℇb、ℇc、ℇd，则( C )A．ℇa =ℇb =ℇc <ℇd B．ℇa =ℇb =ℇc >ℇdC．ℇa =ℇb =ℇc =ℇd D．ℇa >ℇb <ℇc <ℇd5．一矩形线圈，它的一半置于稳定均匀磁场中，另一半位于磁场外，如右图所示，磁感应强度B的方向与纸面垂直向里。

欲使线圈中感应电流为顺时针方向则（A ） A ．线圈应沿x 轴正向平动； B ．线圈应沿y 轴正向平动；C ．线圈应沿x 轴负向平动D ．线圈应沿y 轴负向平动6．在圆柱形空间内有一磁感强度为B 的均匀磁场，如图所示，B 的大小以速率dtdB变化，在磁场中有A 、B 两点，其间可以放置一直导线和一弯曲的导线，则有下列哪种情［ D ］ (A) 电动势只在直导线中产生(B) 电动势只在弯曲的导线产生 (C) 电动势在直导线和弯曲的导线中都产生，且两者大小相等(D)直导线中的电动势小于弯曲导线中的电动势知识点：电动势类型：A7、关于感生电场和静电场下列哪一种说法正确．( B )(A) 感生电场是由变化电场产生的．(B) 感生电场是由变化磁场产生的，它是非保守场． (C) 感生电场是由静电场产生的(D) 感生电场是由静电场和变化磁场共同产生的1D 2C 3B 4C 5A6D7B二、填空题1.如图所示，AB 、CD 、为两均匀金属棒，长均为0.2m ，放在磁感应强度 B=2T 的均匀磁场中，磁场的方向垂直于屏面向里，AB 和CD 可以在导轨上自由滑动，当 CD 和AB 在导轨上分别以s m v /41=、s m v /22=速率向右作匀速运动时，在CD 尚未追上AB 的时间段内ABDCA 闭合回路上动生电动势的大小______________ 方向 _____________________.1电动势的大小 0.8V 方向顺时针方向2.一匝数的线圈，通过每匝线圈的磁通量，则任意时刻线圈感应电动势的大小 ______________ . 感应电动势的大小 t ππ10cos 1057⨯ 3．感生电场产生的原因_ 变化的磁场产生感生电场4.动生电动势的产生的原因是：___电荷在磁场中运动受到洛伦兹力___ 5 。

大学所有课程答案(整理完整版)

新视野大学英语2第二版听说教程听力原文+答案(在原文后面) /a/webbase/X/2015/0302/617.html高等数学同济第六版上册课后答案/a/webbase/G/2015/0301/529.html材料力学第四版_编者干光瑜课后习题/a/webbase/javascript-ajax/2015/0301/527.html 研究生英语阅读教程（第二版提高级）教参(答案+课文翻译）/a/webbase/Y/2015/0302/637.html《大学物理教程下册第三版》(贾瑞皋著)课后习题答案科学出版16 /a/webbase/dreamweaver/2015/0305/795.html 江西财经大学08年大一期末考试微积分试题带答案/a/webbase/J/2015/0305/748.html大学基础物理学答案(习岗)第4章/a/webbase/dreamweaver/2015/0305/804.html 城市公共交通运营管理(840)/a/webbase/javascript-ajax/2015/0305/777.html 大学物理实验教程_第二版_思考题答案_(李学金_著)----示波/a/shiyanbaogao/2015/0302/659.html《大学数学概率论及试验统计》第五章_课后答案(余家林主编) /a/webbase/dreamweaver/2015/0305/785.html 新世纪研究生公共英语教材阅读A答案+课文翻译/a/webbase/X/2015/0302/613.html《大学英语精读》第三版预备级Unit_3/a/webbase/dreamweaver/2015/0305/798.html 新视角研究生英语读说写2_答案/a/webbase/X/2015/0302/615.html《大学物理简明教程》答案_赵近芳/a/webbase/dreamweaver/2015/0301/526.html 新动力_大学英语听力教程1Unit_7原文及答案/a/webbase/X/2015/0302/560.html邓小平理论和三个代表重要思想概论教学PPT/a/downloads/2015/0305/779.html《大学生心理健康教育》题目及答案/a/webbase/dreamweaver/2015/0305/782.html 近十份大学微积分下期末试题汇总(含答案)/a/webbase/J/2015/0305/749.html《大学物理教程》下册第三版(贾瑞皋著)课后习题答案科学出版14 /a/webbase/dreamweaver/2015/0305/794.html 新编剑桥商务英语(初级)学生用书答案Module12.1-12.3/a/webbase/X/2015/0301/518.html城市公共交通运营管理/a/webbase/javascript-ajax/2015/0305/778.html 大学微积分(下)第11章补充题答案上海交通/a/webbase/dreamweaver/2015/0305/831.html英语导游教程课后答案/a/webbase/Y/2015/0302/643.html《大学物理教程》下册第三版(贾瑞皋著)课后习题答案科学出版11 /a/webbase/dreamweaver/2015/0305/791.html单变量微积分11-12年/a/webbase/dreamweaver/2015/0305/828.html希望英语(第二版)综合教程1、2、3课后的翻译题/a/webbase/X/2015/0301/478.html新视野大学英语读写教程第二版第三册课后答案全书答案/a/webbase/X/2015/0302/620.html《大学物理教程》下册第三版(贾瑞皋著)课后习题答案科学出版17 /a/webbase/dreamweaver/2015/0305/796.html现代西班牙语第一册答案/a/webbase/X/2015/0301/498.html《大学数学概率论及试验统计》第一章课后答案(余家林主编) /a/webbase/dreamweaver/2015/0305/783.html城市公共交通练习题(答案)/a/webbase/javascript-ajax/2015/0305/776.html 《大学物理教程》下册第三版(贾瑞皋著)课后习题答案科学出版18 /a/webbase/dreamweaver/2015/0305/797.html研究生英语精读教程(第三版上)--课文翻译及课后题解答/a/webbase/Y/2015/0302/633.html《测度论讲义》习题答案/a/webbase/javascript-ajax/2015/0305/775.html标准日语初级上册练习题与答案/a/webbase/div-css/2015/0305/774.html《大学物理教程》下册第三版(贾瑞皋著)课后习题答案科学出版社13 /a/webbase/dreamweaver/2015/0305/793.html新视野大学英语读写教程第二版第2册课后练习答案/a/webbase/X/2015/0301/533.html大学英语精读第三版预备级unit3/a/webbase/dreamweaver/2015/0305/837.html大学基础物理学答案/a/webbase/dreamweaver/2015/0305/801.html大学英语基础教程课件ppt课后答案U11/a/webbase/dreamweaver/2015/0305/835.html新世纪英语答案/a/webbase/X/2015/0302/614.html标准日本语下册答案/a/webbase/div-css/2015/0305/773.html新世纪大学英语综合教程1课后答案(全)/a/webbase/X/2015/0302/605.html现代大学英语精读5翻译及课后习题答案(5个单元)/a/webbase/X/2015/0301/487.html希望英语综合教程(第二版)task_8_翻译答案/a/webbase/X/2015/0301/481.html综合教程德语第四册答案/a/webbase/Z/2015/0302/654.html整理版外国新闻传播史课后题全/a/webbase/Z/2015/0302/653.html英语听力教程答案unit1-unit7/a/webbase/Y/2015/0302/645.html语言学概论课后答案/a/webbase/Y/2015/0302/652.html语言学导论课后习题答案/a/webbase/Y/2015/0302/651.html现代大学英语精读1课后练习答案/a/webbase/X/2015/0301/483.html应用写作答案/a/webbase/Y/2015/0302/649.html新世纪大学英语综合教程3课后答案Unit1-Unit8/a/webbase/X/2015/0302/607.html应用文写作教材_第2版_习题答案/a/webbase/Y/2015/0302/648.html21世纪大学实用英语综合教程(第二册)课文翻译及课后习题答/a/webbase/2/2015/0305/780.html新动力大学英语听力教程1Unit10原文及答案/a/webbase/X/2015/0302/569.html应用文书写作重点习题附答案/a/webbase/Y/2015/0302/647.html英国文学选读课后答案/a/webbase/Y/2015/0302/642.html大学体验英语综合教程4答案/a/webbase/dreamweaver/2015/0305/825.html 21世纪大学实用英语综合教程1练习及课文翻译答案/a/webbase/2/2015/0305/768.html艺术美学题型和答案/a/webbase/Y/2015/0302/641.html新时代交互英语视听说1级答案五单元/a/webbase/X/2015/0302/598.html大学基础物理学答案(习岗)第12章波动/a/webbase/dreamweaver/2015/0305/808.html 医学拉丁语课后词汇及习题答案/a/webbase/Y/2015/0302/640.html《大学数学概率论及试验统计》第六章_课后答案(余家林主编) /a/webbase/dreamweaver/2015/0305/786.html 经济数学-微积分答案2008年-2009年第一学_武汉理工大学考/a/webbase/J/2015/0305/750.html《应用文写作教程》课后答案/a/webbase/Y/2015/0302/629.html学前教育学答案/a/webbase/X/2015/0302/627.html大学基础物理学答案(习岗)第8章/a/webbase/dreamweaver/2015/0305/806.html新编剑桥商务英语(初级)学生用书答案Module11.1-11.3/a/webbase/X/2015/0301/517.html《大学数学概率论及试验统计》第四章_课后答案(余家林主编) /a/webbase/dreamweaver/2015/0305/784.html大学基础物理学答案(习岗)振动与波动/a/webbase/dreamweaver/2015/0305/810.html学前教育史答案/a/webbase/X/2015/0302/626.html新动力大学英语听力教程1Unit14原文及答案/a/webbase/X/2015/0302/570.html学前教育评价答案/a/webbase/X/2015/0302/625.html大学基础物理学答案(习岗)第2章/a/webbase/dreamweaver/2015/0305/802.html新闻评论答案及记忆重点/a/webbase/X/2015/0302/624.html《大学物理教程》下册第三版(贾瑞皋著)课后习题答案科学出版社12 /a/webbase/dreamweaver/2015/0305/792.html新东方大学俄语第二册课本答案和课文翻译/a/webbase/X/2015/0302/559.html新东方大学俄语2课本答案/a/webbase/X/2015/0302/558.html新大学日语简明教程至15课后练习答案/a/webbase/X/2015/0302/557.html大学基础物理学答案(习岗)第10章电磁感应与电磁场/a/webbase/dreamweaver/2015/0305/807.html研究生英语阅读教程-基础级-第三版-教师用书/a/webbase/Y/2015/0302/635.html新大学日语标准教程(基础篇1)译文/a/webbase/X/2015/0302/555.html新动力大学英语听力教程第2册unit13/a/webbase/X/2015/0302/574.html新大学法语12册课后翻译练习答案（全）[整理]/a/webbase/X/2015/0302/554.html《大学基础物理学》(第二版)上_清华大学出版社-课后答案/a/webbase/dreamweaver/2015/0305/781.html新编商务英语精读4答案/a/webbase/X/2015/0302/544.html新大学法语1课后答案/a/webbase/X/2015/0302/553.html《大学数学概率论及试验统计》第一章课后答案(余家林主编) /a/webbase/dreamweaver/2015/0305/787.html 新编日语教程4答案/a/webbase/X/2015/0302/541.html新编日语教程3答案/a/webbase/X/2015/0302/540.html大学基础物理学答案(习岗)第7章/a/webbase/dreamweaver/2015/0305/805.html 新编日语第一册练习答案/a/webbase/X/2015/0302/539.html《大学物理教程》下册_第三版_(贾瑞皋_著)课后习题答案_科/a/webbase/dreamweaver/2015/0305/789.html 新编日语4课后习题答案/a/webbase/X/2015/0302/538.html新动力大学英语听力教程Book_1_Unit_1-6/a/webbase/X/2015/0302/571.html新编日语2_课后答案/a/webbase/X/2015/0302/537.html理论力学答案/a/webbase/L/2015/0301/531.html新编教育学作业二参考答案及评分标准/a/webbase/X/2015/0301/523.html新编教育学重点对应提纲答案/a/webbase/X/2015/0301/522.html新编基础日语语法整理/a/webbase/X/2015/0301/514.html新编大学德语答案/a/webbase/X/2015/0301/511.html概率论与数理统计教程(第四版)_课后习题答案_沈恒范著/a/webbase/G/2015/0301/528.html线性代数_课后答案(戴天时_陈殿友_著)_吉林大学数学学院/a/webbase/X/2015/0301/532.html新编大学德语2 课后答案及课文翻译教师手册/a/webbase/X/2015/0301/510.html新编大学德语1习题答案/a/webbase/X/2015/0301/509.html新编标准日语第一、第二册课后答案/a/webbase/X/2015/0301/508.html高等数学同济第六版下册课后答案/a/webbase/G/2015/0301/530.html新编阿拉伯语12课作业参考答案/a/webbase/X/2015/0301/507.html新版中日交流标准日本语初级上下册测试题/a/webbase/X/2015/0301/506.html写作答案/a/webbase/X/2015/0301/504.html小学科学教学评价概述作业答案/a/webbase/X/2015/0301/503.html小学教育学答案/a/webbase/X/2015/0301/502.html现代远程学习概论作业参考答案/a/webbase/X/2015/0301/501.html现代西班牙语第四册答案/a/webbase/X/2015/0301/500.html现代西班牙语答案第三册/a/webbase/X/2015/0301/497.html现代日本语文法/a/webbase/X/2015/0301/496.html现代教育学答案/a/webbase/X/2015/0301/495.html现代教育理论各章练习题及参考答案/a/webbase/X/2015/0301/494.html现代教育技术学答案大全/a/webbase/X/2015/0301/493.html现代汉语增订四版课后答案/a/webbase/X/2015/0301/492.html《大学物理教程》下册第三版(贾瑞皋著)课后习题答案科学出版社10/a/webbase/list_1_5.html现代汉语下册答案/a/webbase/X/2015/0301/491.html现代汉语课后习题答案(全)/a/webbase/X/2015/0301/490.html大学体验英语课本答案/a/webbase/dreamweaver/2015/0305/815.html《大学物理基础》的课后习题答案————吴百诗(4)/a/webbase/dreamweaver/2015/0305/788.html现代汉语II答案/a/webbase/X/2015/0301/489.html现代汉语1(上)课后答案/a/webbase/X/2015/0301/488.html大学体验英语上机答案U14/a/webbase/dreamweaver/2015/0305/818.html研究生英语精读教程答案(下)分章节/a/webbase/Y/2015/0302/634.html【因为太多了，没办法再粘贴到这里了，更多答案，直接进入以下网址搜索下载就好】西方文化概论课后题部分答案/a/webbase/X/2015/0301/477.html21世纪大学英语读写教程第二册课文翻译及课后答案1-7单元/a/webbase/2/2015/0305/769.html大学体验英语答案/a/webbase/dreamweaver/2015/0305/814.html 西方文化导论课件1-6课后题答案/a/webbase/X/2015/0301/476.html综合教程德语第四册答案/a/webbase/Z/2015/0302/654.html《大学英语精读》第三版预备级Unit5/a/webbase/dreamweaver/2015/0305/799.html 整理版外国新闻传播史课后题全/a/webbase/Z/2015/0302/653.html语言学概论课后答案/a/webbase/Y/2015/0302/652.html语言学导论课后习题答案/a/webbase/Y/2015/0302/651.html应用型大学英语综合教程课后翻译练习答案/a/webbase/Y/2015/0302/650.html新世纪研究生公共英语教材-听说(上)参考答案/a/webbase/X/2015/0302/609.html应用写作答案/a/webbase/Y/2015/0302/649.html大学基础物理学答案(习岗)第3章/a/webbase/dreamweaver/2015/0305/803.html 应用文写作教材_第2版_习题答案/a/webbase/Y/2015/0302/648.html英语听说教程第三册答案/a/webbase/Y/2015/0302/646.html研究生英语读写译教程习题答案/a/webbase/Y/2015/0302/631.html新发展大学英语听力教程(3)参考答案/a/webbase/X/2015/0302/576.html应用文书写作重点习题附答案/a/webbase/Y/2015/0302/647.html英语听说教程第三册答案/a/webbase/Y/2015/0302/646.html英语听力教程答案1-7/a/webbase/Y/2015/0302/645.html新编实用英语综合教程1第二版答案/a/webbase/X/2015/0302/545.html英语听力教程4答案(前6单元)/a/webbase/Y/2015/0302/644.html英语导游教程课后答案/a/webbase/Y/2015/0302/643.html英国文学选读课后答案/a/webbase/Y/2015/0302/642.html艺术美学题型和答案/a/webbase/Y/2015/0302/641.html医学拉丁语课后词汇及习题答案/a/webbase/Y/2015/0302/640.html研究生英语综合教程上课后练习答案/a/webbase/Y/2015/0302/639.html新版研究生英语精读教程翻译练习参考答案(1-5单元)/a/webbase/X/2015/0301/505.html研究生英语阅读教程答案-重庆大学出版社Unit8Medicine/a/webbase/Y/2015/0302/638.html新公共法语汉译法参考答案(中级教程)/a/webbase/X/2015/0302/583.html研究生英语阅读教程（第二版提高级）教参(答案+课文翻译）/a/webbase/Y/2015/0302/637.html新编进出口英语函电课后习题翻译/a/webbase/X/2015/0302/536.html研究生英语阅读教程-提高级-第三版-教师用书/a/webbase/Y/2015/0302/636.html现代大学英语精读4课后答案(外语教学出版社)/a/webbase/X/2015/0301/486.html研究生英语阅读教程-基础级-第三版-教师用书/a/webbase/Y/2015/0302/635.html自考学前比较教育试题及答案详解/a/shijuanjidaan/Z/2015/0228/267.html新动力_大学英语听力教程Unit_3原文及答案/a/webbase/X/2015/0302/563.html大学物理实验教程_第二版_思考题答案_(李学金_著)----测量/a/shiyanbaogao/2015/0302/656.html自考学前比较教育试题及答案详解(113)/a/shijuanjidaan/Z/2015/0228/266.html影视动画视听语言期末考试试题-A卷答案/a/shijuanjidaan/Y/2015/0228/265.html音乐学院曲式与作品分析考试题(b卷)参考答案/a/shijuanjidaan/Y/2015/0228/264.html大学英语快速阅读4答案/a/webbase/dreamweaver/2015/0305/832.html江西财经大学08年大一期末考试微积分试题带答案/a/shijuanjidaan/J/2015/0305/713.html希望英语综合教程2课文翻译/a/webbase/X/2015/0301/482.html中央电大邓小平理论与三个代表重要思想概论试题与答案3 /a/shijuanjidaan/Z/2015/0305/764.html《大学英语自学教程》课文译文注释习题答案/a/webbase/dreamweaver/2015/0305/800.html 新发展大学英语听力教程(4)参考答案/a/webbase/X/2015/0302/577.html中山大学微积分期中考试答案/a/shijuanjidaan/Z/2015/0305/762.html大学体验英语上机听说答案五级(完整版)/a/webbase/dreamweaver/2015/0305/822.html 郑州大学2013级微积分(上)试题(A卷)及其参考答案/a/shijuanjidaan/Z/2015/0305/761.html21世纪大学英语读写教程第三册答案/a/webbase/2/2015/0305/770.html浙江大学历年微积分(1)试卷解答(4)-级数/a/shijuanjidaan/Z/2015/0305/759.html新编国际商务英语函电课后习题句子翻译/a/webbase/X/2015/0301/513.html厦门大学一元微积分(翔安理工A)期中试卷-2013-11-23解答/a/shijuanjidaan/X/2015/0305/757.html21世纪大学英语读写教程第一册答案[1]/a/webbase/2/2015/0305/772.html大学英语听力4答案/a/webbase/dreamweaver/2015/0305/834.html 武汉大学数学与统计学院2003-2004年第一学期《微积分》期/a/shijuanjidaan/W/2015/0305/756.html大学体验英语6级答案/a/webbase/dreamweaver/2015/0305/813.html 大学文科数学课后习题答案详解!考试专用/a/shijuanjidaan/list_39_4.html21世纪大学英语读写教程第四册答案及课文翻译/a/webbase/2/2015/0305/771.html大学体育理论试题及答案(全部)/a/shijuanjidaan/D/2015/0305/731.html大学数学组合数学试题与答案(修正版)5(1)/a/shijuanjidaan/D/2015/0305/729.html大学生党课考试题及答案/a/shijuanjidaan/D/2015/0305/724.html大学高等数学下考试题库(附答案)/a/shijuanjidaan/D/2015/0305/721.html《大学生职业生涯发展与规划》期末考试题副本/a/shijuanjidaan/D/2015/0305/715.html 新起点大学基础英语教程修订版课件/a/downloads/2015/0305/699.html大学生党课学习结业报告/a/downloads/2015/0305/691.html《大学数学(三)》试题(2)与参考答案/a/shijuanjidaan/D/2015/0305/716.html 应用型大学英语综合教程课后翻译练习答案/a/webbase/Y/2015/0302/650.html新编剑桥商务英语(初级)学生用书_答案_Module_9.1-9.3 /a/webbase/X/2015/0301/516.htm 2013上半年大学生职业生涯规划试题答案/a/shijuanjidaan/2/2015/0305/712.html 英语听力教程4答案(前6单元)/a/webbase/Y/2015/0302/644.html (大学计算机基础实验指导)模拟试题(四)参考答案/a/shijuanjidaan/D/2015/0305/701.html 英汉汉英实用翻译教程/a/webbase/X/2015/0302/628.html学前卫生学题目及答案/a/shijuanjidaan/X/2015/0228/260.html 新动力_大学英语听力教程1Unit_15原文及答案/a/webbase/X/2015/0302/562.html研究生学术英语写作答案2/a/webbase/Y/2015/0302/630.html新编基础日语试题1答案/a/shijuanjidaan/X/2015/0228/245.html 新视野大学英语读写教程第二版第一册答案/a/webbase/X/2015/0301/534.html希望英语第二版综合教程2课后翻译(考试复习)/a/webbase/X/2015/0301/480.html西方文化概论试卷及答案(一)/a/shijuanjidaan/X/2015/0228/228.html 现代大学英语精读2课后答案/a/webbase/X/2015/0301/484.html文书学配套复习题及答案二/a/shijuanjidaan/W/2015/0228/220.html 水文学试题及答案/a/shijuanjidaan/S/2015/0228/208.html 希望英语_综合教程3_课后练习答案/a/webbase/X/2015/0301/479.html新世纪研究生公共英语教材听力(下)答案/a/webbase/X/2015/0302/611.html世界近代史综合测试题/a/shijuanjidaan/S/2015/0228/204.html 研究生英语阅读教程-提高级-第三版-教师用书/a/webbase/Y/2015/0302/636.html世界近代史试卷及答案（二）/a/shijuanjidaan/S/2015/0228/202.html 全国2011年01月高等教育自学考试外国法制史试题答案/a/shijuanjidaan/Q/2015/0228/193.html 新时代交互英语视听说1级答案二单元/a/webbase/X/2015/0302/593.html新编大学英语视听说教程3(浙江大学版)听力标准答案/a/webbase/X/2015/0301/512.html全国2008年10月高等教育自学考试外国法制史试题答案/a/shijuanjidaan/Q/2015/0228/190.html 现代大学英语精读3课后答案/a/webbase/X/2015/0301/485.html研究生英语核心教材综合教程下1——10章课后题答案/a/webbase/Y/2015/0302/632.html美国文学史及选读期末复习题/a/shijuanjidaan/list_39_16.html新起点_大学基础英语教程_读写教程2_课后翻译题答案/a/webbase/X/2015/0302/585.html全国2008年01月高等教育自学考试外国法制史试题答案/a/shijuanjidaan/Q/2015/0228/189.html 新公共法语_初级教程_参考答案/a/webbase/X/2015/0302/582.html普通教育学第1套试题及答案/a/shijuanjidaan/P/2015/0228/183.html 新动力_大学英语听力教程Unit_18原文及答案/a/webbase/X/2015/0302/566.html新风尚大学实用英语综合教程4课后答案/a/webbase/X/2015/0302/580.html模拟导游练习题答案(六)/a/shijuanjidaan/M/2015/0228/181.html 新时代交互英语视听说1级答案六单元/a/webbase/X/2015/0302/595.html科技英语语法试题/a/shijuanjidaan/K/2015/0228/176.html 新风尚大学实用英语综合教程3全册答案/a/webbase/X/2015/0302/579.html新编英语教程答案/a/webbase/X/2015/0302/551.html健康教育与健康促进复习题与答案/a/shijuanjidaan/J/2015/0228/169.html公文写作考试试题及答案/a/shijuanjidaan/G/2015/0228/161.html当代教育学必备试卷及答案/a/shijuanjidaan/D/2015/0228/149.html大学普通物理实验报告答案/a/shiyanbaogao/2015/0305/836.html大学物理演示实验讲义/a/shiyanbaogao/2015/0305/698.html新世纪大学英语综合教程2答案/a/webbase/X/2015/0302/606.html大学物理演示实验报告2/a/shiyanbaogao/2015/0305/697.html大学计算机基础实验指导书/a/shiyanbaogao/2015/0305/688.html标准实验报告模版/a/shiyanbaogao/2015/0218/113.html物化实验思考题答案全集/a/shiyanbaogao/2015/0218/116.html物理化学实验总结/a/shiyanbaogao/2015/0218/117.html大学物理实验教程_第二版_思考题答案/a/shiyanbaogao/2015/0302/661.html十个物化实验思考题参考答案及数据记录格式/a/shiyanbaogao/2015/0218/115.html大学物理实验教程_第二版_思考题答案_(李学金_著)----等厚/a/shiyanbaogao/2015/0302/660.html【因为太多了，没办法再粘贴到这里了，更多答案，直接进入以下网址搜索下载就好】。

大学物理课后习题答案电磁感应电磁场 (电磁场)

的方向由 B 到 A 即 x 轴负方向。 10、根据电容的定义传导电流
C
q U
q CU
dq du C 由于全电流连续得： dt dt du Id Ic C 20 10 6 1.5 10 5 3 A dt d0 dD s dDR 2 d 0 ER 2 dE 0R 2 11、 I d dt dt dt dt dt Ic
E
q 4 0 R 2
r
q 4 0 R 2
cost i sin t j

dD d q d q jd 0E cos t i sin t j sin t i cos t j 2 2 dt dt 4R dt 4R

12、充电过程中上极板带正电故 p 处电场强度的方向向下，且电场强度增大，位移电流密度的方向向下即位移电流向下，圆柱状向下的位移电流在 p 处产生的 H 根据右手法则是垂直纸 B 向里。
i

P
H E
i d D 13、 j d 因为 E 增大故 dD 0 ， jd 的方向和 E 相同。即垂直纸面向里。 dt
n D ds q0 即q自说明电荷总伴随有电场。
s i 1
9、当 A 板带正电， B 板带负电，当将开关 K 合上时， AB 极间的电场方向由正电荷指向负
dD 电荷即沿 x 的正方向。位移电流密度 jd 的方向即的方向，因电容器放电， D 减少 dt
dD 0 dD 的方向和 D 的方向相反，故沿 x 轴负方向或根据全电流连续的性质，位移电流
第十三章 1、[D]
电磁感应电磁场（电磁场）

大学物理D-05稳恒磁场、电磁感应定律-参考答案

0i ，选回路的绕行方向为顺时针方向， 2r
dr r
Bds
0 I ldr 2 r
当矩形线圈距离长直导线为 R 时，通过矩形线圈的磁通量为
d
Ra
R
0 I I Ra ldr 0 l ln R 2 r 2
d I
l
4
a
Ra d ln 1 dR 0 R 1 d lI n n 0 l I 则： n dt 2 2 dt R R a dt
2 B2 lv
0 Ilv 得 2 ( d a )
n( 1 2)
0 Ilvn 1 1 ( ) d d a 2
1
2
5
a点电势高于O点．∴ U a U b 2 1
1 16 15 3 BL2 BL2 BL2 BL2 50 50 50 10
如果金属细杆绕杆中央旋转，则ab两端电势差为0. 5.2.5 如图所示，一无限长直导线通有电流 I=5.0A，一矩形单匝线圈与此长直导线共面。设矩形线圈以 v=2.0m/s 的速度垂直于长直导线向右运动。已知：l=0.40m, a=0.20m, d=0.20m,求矩形线圈中的感应电动势。（不计线圈的自感）解：方法（一）如图，距离长直导线为 r 处的磁感应强度为： B 则通过窄条面积 ds 的磁通量为： d
B dS 0 说明了下面的哪些叙述是正确的？

（
A ）
穿入闭合曲面的磁感应线条数必然等于穿出的磁感应线条数；穿入闭合曲面的磁感应线条数不等于穿出的磁感应线条数；一根磁感应线可以终止在闭合曲面内；一根磁感应线可以完全处于闭合曲面内。
（A）ad；（B）ac；（C）cd；（D）ab。 5.2.3. 如图，无限长直载流导线与正三角形载流线圈在同一平面内，若长直导线固定不动，则载流三角形线圈将 (A) 向着长直导线平移; (B) 离开长直导线平移; (C) 转动; (D) 不动。

大学物理课后习题答案电磁感应电磁场

第十三章电磁感应电磁场 1、[D]分析：应用楞次定律为分析的根据，若要产生乙线圈中的，则乙线圈中电流产生的电感应强度是由右向左，说明甲线圈中电流产生的由右向左的电感应强度在减小，即产生该磁场的电流在减小，由此可见，将抽出甲中铁心，nI B r 0μμ=，在I 不变时，B 减小。

2、[D]依据法拉第电磁感应规律，td d φε-=在上述条件下，ε应相同。

依据欧姆定律，RI ε=因为是不同的导体电阻率不同，所以R 不同，I 也不同。

3、[B]应用楞次定律分析，在I 增长时，垂直通过线圈平面内向外的磁通量是增大，因此感应电流产生的磁感强度垂直平面向里，为顺时针方向。

4、[C]分析：当a >>r 时，有以r 为半径的圆周内各点的B可视为常矢量。

断电前通过导体环的磁通量：2012r aIBS S B ππμφ==⋅=。

断电后通过导体环的磁通量：02=φ。

对纯电阻电路有：aRIr RRq 2)(120112μφφφ==--=5、[D]θαεcos d sin d )(d l vB l B v =⋅⨯=)(B v ⨯和l d 之间夹角2πθ=，∴0d =ε 0d ==⎰εε6、[D]在t ωθθ+=，θαεcos d sin d l vB =其中θ是)(B v⨯和l d 之间夹角r r l vB d cos d sin d ωθαε-== 2OP 21d BL r r B ωωε-=-=⎰O 处为高电势 221BL ωε=7、[D]两自感线圈顺接和反接的自感系数：M L L L 221++=顺21L L KM =10≤≤KM L L L 221-+=反图（1）为反接：1111ab 2L L K L L L -+=，由于1<K ，∴0ab >L 图（2）为反接：1111ab 2L L KL L L -+=，由于1=K ，∴0ab =L8、[C]V 0.8161225.0d d 11=-⨯-=∆∆-=-=tI LtI Lε9、[C]a Ia IaIB πμπμπμ000P 22=+=10、tS B td d d d ）（ ⋅-=-=φεt mIa nI a nI BS BS S B mωπμπμθcos cos 2020====⋅t mIa nI mωωπμεcos 20-=11、解：Wb 1057.1)1.0(1416.310562521--⨯=⨯⨯⨯===⋅=rB BS S B πφWb 1057.1612-⨯-=-=φφC 1014.3)(1612-⨯=--=φφRq12、（1）向右移动时，垂直纸面向内的φ减小。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

习题16GG 上传16-1．如图所示，金属圆环半径为R ，位于磁感应强度为B的均匀磁场中，圆环平面与磁场方向垂直。

当圆环以恒定速度v在环所在平面内运动时，求环中的感应电动势及环上位于与运动方向垂直的直径两端a 、b 间的电势差。

解：（1）由法拉第电磁感应定律i d dtεΦ=-，考虑到圆环内的磁通量不变，所以，环中的感应电动势0i ε=；（2）利用：()aab bv B dl ε=⨯⋅⎰，有：22ab Bv R Bv R ε=⋅=。

【注：相同电动势的两个电源并联，并联后等效电源电动势不变】16-2．如图所示，长直导线中通有电流A I 0.5=，在与其相距cm 5.0=d 处放有一矩形线圈，共1000匝，设线圈长cm 0.4=l ，宽cm 0.2=a 。

不计线圈自感，若线圈以速度cm/s 0.3=v 沿垂直于长导线的方向向右运动，线圈中的感生电动势多大？解法一：利用法拉第电磁感应定律解决。

首先用0lB dl I μ⋅=∑⎰ 求出电场分布，易得：02I B rμπ=，则矩形线圈内的磁通量为：00ln22x axI I l x al dr r xμμππ++Φ=⋅=⎰，由i d Nd t εΦ=-，有：011()2i N I l d xx a x dtμεπ=--⋅+ ∴当x d =时，有：041.92102()i N I l a v V d a μεπ-==⨯+。

解法二：利用动生电动势公式解决。

由0lB dl I μ⋅=∑⎰ 求出电场分布，易得：02I B rμπ=，考虑线圈框架的两个平行长直导线部分产生动生电动势，近端部分：11NB l v ε=，远端部分：22NB lv ε=，则：12εεε=-=00411() 1.921022()N I N I al v l v V d d a d d a μμππ--==⨯++。

16-3．如图所示，长直导线中通有电流强度为I 的电流，长为l 的金属棒ab 与长直导线共面且垂直于导线放置，其a 端离导线为d ，并以速度v平行于长直导线作匀速运动，求金属棒中的感应电动势ε并比较U a 、U b 的电势大小。

解法一：利用动生电动势公式解决：()d v B dl ε=⨯⋅02I v d r rμπ=⋅，∴02d ldv Idr rμεπ+=-⎰0ln 2v I d l d μπ+=-，由右手定则判定：U a >U b 。

解法二：利用法拉第电磁感应定律解决。

作辅助线，形成闭合回路''abb a ，如图，S B d S Φ=⋅⎰ 02d l d I y dr rμπ+=⎰0ln 2I y d l d μπ+=， ∴d dt εΦ=-00ln ln22I Iv d l d y d l d dt dμμππ++=-⋅=-。

由右手定则判定：U a >U b 。

16-4．电流为I 的无限长直导线旁有一弧形导线，圆心角为120，几何尺寸及位置如图所示。

求当圆弧形导线以速度v平行于长直导线方向运动时，弧形导线中的动生电动势。

解法一：（用等效法）连接AO 、OB ，圆弧形导线与AO 、OB 形成闭合回路，闭合回路的电动势为0，所以圆弧形导线电动势与 AOB 直导线的电动势相等。

200()ln 222R AOR Iv I v v B dl d x x μμεππ=⨯⋅=-=-⎰⎰，500225()ln 224R OBR Iv Iv v B dl d x x μμεππ=⨯⋅=-=-⎰⎰，∴05ln 22AB AO OBIv μεεεπ=+=-。

解法二：（直接讨论圆弧切割磁感应线）从圆心处引一条半径线，与水平负向夹角为θ，那么，00022(2cos )2(2cos )I I I B x R R R μμμππθπθ===--，再由()v B dl ε=⨯⋅⎰有：AOBAOBθsin d B Rd v εθθ=⋅⋅，∴2030sin 2(2cos )IRv d R πμεθθπθ=-⋅-⎰05ln 22Iv μπ=-。

16-5．电阻为R 的闭合线圈折成半径分别为a 和a 2的两个圆，如图所示，将其置于与两圆平面垂直的匀强磁场内，磁感应强度按0sin B B t ω=的规律变化。

已知cm 10=a ，T 10220-⨯=B ，rad/s 50=ω，Ω=10R ，求线圈中感应电流的最大值。

解：由于是一条导线折成的两个圆，所以，两圆的绕向相反。

2220(4)3cos i d d Ba a a B t dt dtεπππωωΦ=-=--⋅+=， ∴203cos ia B t I R Rεπωω== A πR ωB a πI 32202max1042.910501021.035--⨯=⨯⨯⨯⨯==。

16-6．直导线中通以交流电，如图所示，置于磁导率为μ 的介质中，已知：0sin I I t ω=，其中ω、0I 是大于零的常量，求：与其共面的 N 匝矩形回路中的感应电动势。

解：首先用0lB dl I μ⋅=∑⎰ 求出电场分布，易得：02I B xμπ=，则矩形线圈内的磁通量为：0000ln sin ln222d adI I l I l d a d al dr t r d dμμμωπππ+++Φ=⋅==⎰， ∴00cos ln 2N I l d d aN t dt dμεωωπΦ+=-=-。

16-7．如图所示，半径为a 的长直螺线管中，有0d d >tB的磁场，一直导线弯成等腰梯形的闭合回路ABCDA ，总电阻为R ，上底为a ，下底为a 2，求：（1）AD 段、BC 段和闭合回路中的感应电动势；（2）B 、C 两点间的电势差C B U U -。

解：（1）首先考虑OAD ∆，212OAD S a ∆==，∴24OAD d dB dBS a d t d t d tε∆Φ=-=-⋅=-⋅感1，而DA lAOODADDAE d l E d l E d l E d l E d l εε=⋅=⋅+⋅+⋅=⋅=⎰⎰⎰⎰⎰涡涡涡涡涡感1∴2AD d Bd tε=⋅；再考虑OBC ∆，有效面积为2123OAD S a π=⋅扇，∴26dBa d tπε=-⋅感2，同理可得：26BC dBa d tπε=⋅；那么，梯形闭合回路的感应电动势为：2(64BC AD dBa d tπεεε=-=-⋅，逆时针方向。

（2）由图可知，AB CD a ==，所以，梯形各边每段a 上有电阻5Rr =，回路中的电流：2(64a d BI R R d tεπ==-⋅，逆时针方向；那么，2225B C BC BC dBU U I r I R a dtεε-=⋅-=⋅-=-⋅。

16-8．圆柱形匀强磁场中同轴放置一金属圆柱体，半径为R ，高为h ，电阻率为ρ，如图所示。

若匀强磁场以d Bk dt=（0k k >，为恒量）的规律变化，求圆柱体内涡电流的热功率。

解：在圆柱体内任取一个半径为r ，厚度为dr ，高为h 的小圆柱通壁，有：2l d B E dl r dtπ⋅=⋅⎰ 涡，即：22d B r k r dt εππ=⋅=涡，由电阻公式lR S ρ=，考虑涡流通过一个d r 环带，如图，有电阻：2rR hdrπρ=，而热功率：22223()22k r k h d P i R r d r r hd rπππρρ===，∴2243028R k h k h R P r dr ππρρ==⎰。

16-9．一螺绕环，每厘米绕40匝，铁心截面积2cm 0.3，磁导率0200μμ=，绕组中通有电流mA 0.5，环上绕有二匝次级线圈，求：（1）两绕组间的互感系数；（2）若初级绕组中的电流在s 10.0内由A 0.5降低到0，次级绕组中的互感电动势。

解：已知4040000.01n ==初匝，2N =次，50200810μμπ-==⨯，42310S m -=⨯。

（1）由题意知螺绕环内：B nI μ=，则通过次级线圈的磁链： N BS N nI S ψμ==次次次，∴54428104000310 6.0310M N nS H I ψμπ---===⨯⨯⨯⨯⨯=⨯次初；（2）42506.0310 3.02100.1I MV t ε--∆-==⨯⨯=⨯∆初次。

16-10．磁感应强度为B 的均匀磁场充满一半径为R 的圆形空间B ，一金属杆放在如图14-47所示中位置，杆长为2R ，其中一半位于磁场内，另一半位于磁场外。

当0d Bdt>时，求：杆两端感应电动势的大小和方向。

解：∵ac ab bc εεε=+，而：Oababd dtεΦ=-扇形， ∴abε=2[]d R B dt -=， Obcbc d dtε∆Φ=-=22[]1212d R R d B B dt dt ππ--=，∴ac ε=2]12R d Bdtπ； ∵0d Bdt>，∴0ac ε>，即ac ε从a c →。

16-11．一截面为长方形的螺绕环，其尺寸如图所示，共有N 匝，求此螺绕环的自感。

解：如果给螺绕环通电流，有环内磁感应强度：012()2N I B R r R rμπ=<<则SB d S Φ=⋅⎰⎰，有：210201ln22R R N I h R N Ih dr r R μμππΦ=⋅⋅=⎰利用自感定义式：L I ψ=，有：L =2021ln 2N h R R μπ。

16-12．一圆形线圈A 由50匝细导线绕成，其面积为4cm 2，放在另一个匝数等于100匝、半径为20cm 的圆形线圈B 的中心，两线圈同轴。

设线圈B 中的电流在线圈A 所在处激发的磁场可看作匀强磁场。

求：（1）两线圈的互感；（2）当线圈B 中的电流以50A/s 的变化率减小时，线圈A 中的感生电动势的大小。

解：设B 中通有电流I ，则在A 处产生的磁感应强度为：002242B B B B BN I N I B R R R μμππ=⋅=（1）A 中的磁通链为：02A B A A A A BN N IN BS S R μψ==⋅。

则：02A B AABBN N S M I R μψ==，∴7476410501004102010 6.281020.2M H ππ----⨯⋅⋅⋅⨯==⨯=⨯⋅。

（2）∵0646.281050 3.14102A B A A B N N S d d IV d t R dtμψ--=⋅=⨯⋅=⨯,∴43.1410A V ε-=⨯。

16-13．如图，半径分别为b 和a 的两圆形线圈（b >>a ），在0=t 时共面放置，大圆形线圈通有稳恒电流I ，小圆形线圈以角速度ω绕竖直轴转动，若小圆形线圈的电阻为R ，求：（1）当小线圈转过90时，小线圈所受的磁力矩的大小；（2）从初始时刻转到该位置的过程中，磁力矩所做功的大小。